YÜKSEKLİKLERİN ÖLÇÜLMESİ - NİVELMAN GENEL
|
|
|
- Batur Akbaba
- 10 yıl önce
- İzleme sayısı:
Transkript
1 YÜKSEKLİKLERİN ÖLÇÜLMESİ - NİVELMAN GENEL Yeryüzü noktalarının, karaların altında da devam ettiği varsayılan durgun durumdaki denizlerin ortalama yüzeyinden (karşılaştırma yüzeyi) olan düşey uzaklığına bu noktaların yükseltisi, herhangi bir noktadan geçtiği düşünülen bir yüzey veya yatay bir düzlemden olan düşey uzaklığına ise.yüksekliği. veya kotu denilmektedir
2 Noktalar arasındaki düşey uzaklık farkına yükseklik farkı, bu yükseklik farklarının ölçülmesine ise nivelman ismi verilmektedir. Konum plânı çıkarılan bir arazi parçasının gerçek biçimi ile gösterilmesi isteniyorsa, yer yüzündeki noktaların düşey konumlarının da belirlenmesi gerekmektedir. Bu amaçla noktalardan geçen düşey doğrultulardaki uzaklıklar veya,yükseklik farkları nivelman işlemi ile saptanır. Nivelman ölçmelerini değerlendirmek için bir karşılaştırma (kıyas) yüzeyine gerek vardır. A h B H A H B H A ve H B, A ve B noktalarının kotlarını, h iki nokta arasındaki yükseklik farkını göstermektedir. Çalışma alanı büyük olmayan bölgelerde, karşılaştırma yüzeyi olarak herhangi bir noktadan geçen yatay düzlem alınabilir. Bu bölümde geniş olmayan bölgelerde yapılan nivelman ölçmeleri ve hesapları söz konusu edilecektir.
3 Mutlak Yükselti 1879 senesinden evvel, Avrupa'da bütün milletler değişik karşılaştırma yüzeyleri almakta iken, o sene toplanan Uluslararası bir komisyonca, Amsterdam şehrindeki maregrafın (ortalama deniz yüzeyini saptayan donanım) sıfırı, karşılaştırma yüzeyinin sıfırı olarak alınmıştır. Bu nedenle bu yüzeye normal sıfır (NN) ismi verilmiştir. NN
4 Bir ülkeyi kapsayan yükseltisi saptanmış noktaların oluşturduğu ağa ülke nivelman ağı denir. Bu amaçla çapları km arasında değişin geniş nivelman devrelerinin oluşturduğu I. dereceden nivelman ağı kurulur ve ölçmeler yüksek presizyonda yapılır. I. dereceden nivelman devreleri II. dereceden nivelman noktaları ile km çaplı nivelman devrelerine ayrılır. I. ve II. dereceden nivelman ağları ülke nivelman ağının temelini oluşturur. II. dereceden nivelman devresinin içi bölgesel koşullara ve amaca uygun olarak daha küçük bölgeyi çeviren III. dereceden nivelman noktalarının oluşturduğu nivelman devreleri ile örülür. Harita yapımı ile uğraşan tüm özel ve resmi kuruluşlar bu noktalardan yararlanır
5 Yükseklik farklarının ölçülmesinde başlıca üç yöntem kullanılmaktadır : 1- Geometrik nivelman ( ± 1 mm ile ± 1 cm presizyonda) 2- Trigonometrik nivelman ( ± 1 cm ile ± 1 dm presizyonda) 3- Barometrik nivelman ( ± 1 m ile ± 2 m presizyonda)
6 GEOMETRİK NİVELMAN Geometrik nivelmanda genel olarak yatay gözlemeler yapabilen nivo adı verilen dürbünlü aletler ve yükseklik farkları bulunacak noktalar üzerine düşey olarak tutulan ve mira adı verilen 3 veya 4 m uzunluğunda üzerinde m, dm ve cm bölümleri olan latalar kullanılır. Geometrik nivelman, nivo dürbünündeki yatay gözleme çizgisinin, mira bölümlerini kestiği nokta okunup bu okuma farklarından iki nokta arasındaki yükseklik farklarının bulunmasına esasına dayanmaktadır. Okumalar metre cinsinden yapılır ve milimetreler tahmin edilir (Şekil 7.5) deki mira okuması m Ters görüntü veren miralarda büyüme yönünün yukardan aşağı doğru olduğuna dikkat edilmelidir. Büyüme Yönü
7 Yeni tip nivolar düz görüntülü olduğundan düz miralarla kullanılmalıdır (Şekil 7.6a) da ki ters mira okuması m ve b deki düz görüntülü nivolarda mira okuması m dir Üst Çizgi Orta Çizgi Alt Çizgi Mirada orta çizgi okuması ile beraber, bazı durumlarda üst ve alt çizgi okumaları da yapılır. Bunun nedeni, orta çizgi okumasının doğruluğunun kontrolü ve mira ile nivo arasındaki uzaklığın bulunması içindir. Orta çizgi okuması: Alt çizgi okuması : m Üst çizgi okuması : m m Mira ile nivo arasındaki yatay uzaklık : ( ) x 100 = 0.146x 100 = 14.6 m
8 Nivolar Nivo bir düzeç yardımı ile dürbünü yatay konuma getirilerek gözlemeler yapılabilen bir alettir. Aletin ana kısmı bir dürbün, küresel, silindir düzeç ve tesviye vidalarından oluşur. Bazı nivolarda yatay açıyı ölçmek için basit bir yatay daire bulunur. Nivo, teodolit gibi sehpa üzerinde kullanılır. Dürbün düşey hareket etmediği için, sadece yatay hareket bağlama ve yatay az hareket vidası vardır. Gözleme eksenlerinin yatay konuma getirilmesi için. kullanılan düzenlere göre değişik nivo tipleri vardır,bunlar: 1- Düzeci ve dürbünü sabit nivolar a- Fenkalaj vidasız nivolar b- Fenkalaj vidalı nivolar 2- Kompansatörlü (otomatik) nivolar 3- Elektronik nivolar
9 1- Düzeci ve dürbünü sabit nivolar Bu tip nivolarda düzeç dürbüne ve dürbün de alete tespit edilmiştir (Şekil 7.7). Nivo dürbünü, teodolitte kullanılan dürbününle aynı özelliktedir. Dürbün düşey (asal) bir eksen etrafında yatay düzlemde hareket eder. Nivonun kaba tesviyesi yani küresel düzeç kabarcığı ortalanma işlemi, tesviye vidalarının her üçünün de kullanılması ile yapılır. İnce tesviye yani silindir düzeç kabarcığı ortalanma işlemi ise kaba tesviyeden sonra düzeç doğrultusundaki tek tesviye vidası kullanılarak yapılır. Dürbün Silindir düzeç Tesviye Vidası Bu tip nivolarda düzeç dürbüne ve dürbün de alete tespit edilmiştir (Şekil 7.7). Nivo dürbünü, teodolitte kullanılan dürbününle aynı özelliktedir. Dürbün düşey (asal) bir eksen etrafında yatay düzlemde hareket eder. Nivonun kaba tesviyesi yani küresel düzeç kabarcığı ortalanma işlemi, tesviye vidalarının her üçünün de kullanılması ile yapılır. İnce tesviye yani silindir düzeç kabarcığı ortalanma işlemi ise kaba tesviyeden sonra düzeç doğrultusundaki tek tesviye vidası kullanılarak yapılır.
10 b- Fenkalaj vidalı nivolar Bu tip nivoların, fenkalaj vidasız nivolardan farkı, dürbünün bir mafsalla alete tespit edilmiş olmasıdır Mafsal Fenkalaj Vidası Fenkalaj (ince yataylık) vidası ile dürbün bir miktar düşey hareket edebilmektedir. Böylece silindir düzeç, tesviye vidaları ve küresel düzeçten bağımsız olarak fenkalaj vidası ile ortalanır. Silindir düzecin ortalanması, tesviye vidaları ile yapılan kaba tesviyeden sonra, ya doğrudan düzece bakılarak, ya da yandaki şekil de görüldüğü gibi optik bir donanımla çakıştırmalı biçimde yapılır ve silindir düzeç kabarcığının daha hassas ortalanması sağlanır Bazı tip fenkalajlı nivolarda (Kern firması vb) tesviye vidası ve yatay hareket bağlama vidası yoktur. Küresel başlık kullanılarak kaba tesviye yapılır. Yatay hareket sürtünmelidir ve küçük çarpmalardan etkilenmez.
11 2- Kompansatörlü (otomatik) nivolar Bu nivolarda kaba tesviyeden sonra optik eksen kompansatör adı verilen bir düzen ile otomatik olarak presizyonlu bir biçimde yatay duruma gelmektedir (şekil 7.10). Kompansatör, nivelman ölçmelerine büyük bir hız kazandırmıştır. Silindir düzeç kabarcığının ortalanmasının unutulmasından kaynaklanan kişisel hata da ortadan kalkmıştır. Kompansatör Sönümleme tertibatı Kompansatör kolaylıkla salınım yapabilen bir sarkaç ve üzerinde ışınların yansıtılmasında kullanılan prizmalardan oluşur. Sarkacın salınımları durduğu anda çekül gibi hareketle tam düşey doğrultuda durur ve üzerindeki prizmalar optik eksenden gelen ışınları tam yatay konumda yansıtarak gözümüze gelmesini sağlarlar. Bu işlem belli sınır içinde gerçekleşir ve buna kompansatörün çalışma aralığı denir. Kompansatörün çalışması için kaba tesviye yani küresel düzeç kabarcığının ortalanması yeterlidir. Kompansatörün çalışma aralığı optik eksenin yatay düzlemle yaptığı eğim açısı türünde ifade edilir ve bu açı ne kadar küçükse nivo o kadar presizyonludur.
12 3- Elektronik nivolar Elektronik nivolar kompansatörlüdür ve özel miralar ile kullanılırlar. Mira üzerindeki rakamlar bar kod okuma düzeni ile okunur ve kaydedebilir. Dürbünleri, otomatik netleştirme tertibatlı olanları da vardır.
13 Nivoların Kullanılması a- Düzeci dürbünü sabit fenkalajsız nivonun kullanılması Nivo yükseklik farkı ölçülecek iki noktaya yaklaşık eşit uzaklıkta bir yere getirilir ve sehpa başlığı yatay olacak biçimde kurulur. Sehpa başlığının yatay konumdan çok farklı olması durumunda, tesviye vidaları ile küresel düzeç kabarcığının ortalanması oldukça güç olur. Daha sonra aşağıdaki gibi hareket edilir. 1- Tesviye vidaları kullanılarak, küresel düzeç kabarcığı ortalanır. 2- Dürbünün üzerindeki nişan alma tertibatı ile miraya kaba yöneltme yapılır. 3- Dürbün göze uydurulur. 4- Yatay hareket bağlama vidası sıkılır ve az hareket vidası ile düşey gözleme çizgisi miranın bir kenarına çakıştırılır. Böylece miranın nivoya göre, sağa ve sola doğru düşey konumdan farklı durumu da kontrol edilebilir. 5- Silindir düzeç kabarcığı dürbün doğrultusuna en yakın tesviye vidası döndürülerek ortalanır. 6- Dürbünden bakılarak yatay gözleme çizgisinin mira bölümlerini kestiği yer okunur. Okumalarda m, dm, cm, ler doğrudan, mm ler ise gözle kestirilerek yapılır ve metre cinsinden yazılır.
14 b- Fenkalajlı, Kompansatörlü ve Elektronik nivoların kullanılması 1- Fenkalajsız nivolarda olduğu gibi 4. maddeye kadar olan işlemler aynen uygulanır. 2- Fenkalajlı nivolarda mira okumasından önce fenkalaj vidası ile silindir düzeç kabarcığı ortalanarak mira okuması yapılır. 3- Kompansatörlü ve elektronik nivolarda doğrudan mira okuması yapılır.
15 İki nokta arasında yükseklik farkının bulunması Arazide, A ve B gibi iki nokta arasındaki yükseklik farkı bulunmak isteniyorsa, nivonun kullanılmasında söz konusu edilen işlemler sıra ile uygulanarak A noktasında düşey tutulan mirada g A (geri mira okuması) ve B noktasında düşey tutulan mirada i B (ileri mira okuması) yapılır (Şekil 7.11). Bu durumda A ve B noktaları arasındaki yükseklik farkı şekil 7.11 de görüldüğü gibi, geri mira okuması ile ileri mira okumasının farkına eşittir. g A Gözleme uzaklığı Gözleme uzaklığı i B h AB g A i B h 0 ise arazi çıkış h B h 0 ise arazi iniş H B A noktasının kotu H A ise, B noktasının kotu: H A A H B = H A + h AB Karşılaştırma yüzeyi
16 Ölçmeler sırasında gözleme uzaklığı ortalama, 60 m yi geçmemeli her iki miraya eşit gözleme uzaklığı sağlanmalı ve mira, okuması da 0.60 m den aşağı olmamalıdır. Eşit gözleme uzaklığı seçilirken, nivonun iki noktanın doğrultusu üzerinde bir noktaya kurulması gerekmez. Doğrultu dışında ve bir sonraki mira okuması yapılacak nokta da göz önüne alınarak en uygun yer seçilmelidir. Yukarıdaki koşulları sağlamak üzere A ve B noktalarında düşey olarak tutulan miraya nivonun bir konumunda ölçme yapılamıyor ise A ve B noktaları arasında 1, 2, 3 gibi yardımcı noktalar alınır (Şekil 7.12 ). Bu yardımcı noktalara değişme noktaları denir. B noktasının kotu, A noktasının kotundan yararlanarak bulunabilir. Şekil 7.12 den A ve B noktaları arasındaki yükseklik farkı : = h 1 h 2 h 3 h 4 = h g 1 i 2 g 3 i B g A A i 1 g A g 2 i 3 h h 4 B 2 h h 3 H B H A Karşılaştırma yüzeyi
17 g A A g 1 i 2 g 3 i B i 1 g 2 i 3 h 4 B h h h 3 H B H A Karşılaştırma yüzeyi = h 1 h 2 h 3 h 4 = h ( h 1, h 2, h 3, h 4, ( + ) veya ( - ) işarette olabilir) B noktasının Kotu : H B = H A + h 1 g A i h 2 g 1 i 2 h 3 g 2 i 3 h 4 g 3 i B g a g 1 g 2 g 3 i i 2 i 3 i b g i
18 Nivonun bir kuruluşunda yerini değiştirmeden, ikiden fazla noktada mira okuması yapılmış ise, ilk yapılan okumaya geri okuma, son okumaya ileri okuma ve bu okumaların arasında yapılan bütün mira okumalarına orta (O 0 ) okuma denir. Şekil 7.12 de 2 ve 3 numaralı noktalarda orta okuma yapılmıştır. Orta okumalar, nivelman güzergahında kotları mutlak belirlenmesi gereken noktalar isteniyor ve noktalar orta okumaya elverişli ise yapılır. Şekil.7.13 deki nivelman güzergahında, 2 ve 3 numaralı noktaların, proje gereği kotlarının belirlenmesi istenmiştir. 1 ve 4 numaralı noktalarsa, A ve B noktaları arasındaki yükseklik farklarını belirlemek için kullanılan geçiş noktalarıdır. Orta okumalar genellikle, boyuna, enine kesitlerin çıkarılması ve yüzey nivelmanı yöntemi ile nokta kotlarının belirlenmesinde kullanılır. Orta okumaların, nivonun yeniden kurulmasına gerek olmadan yapılması, nivelman ölçmelerinin hızlı bir biçimde yapılmasına olanak sağlar. g A i 1 O 3 g 4 A g 1 1 O i 4 B i B Orta okumalar, yükseklik farkının bulunması için yapılan hesaplamada, bir önceki mira okuması için ileri okuma bir sonraki mira okuması için geri okuma kabul edilirler. Şekil de h yükseklik farkları hesaplanır, ve taraf, tarafa toplanırsa (g A i 1 ) + (g 1 o 2 ) + (o 2 o 3 ) + (o 3 i 4 ) + (g 4 i B ) = ( g i ) h 1 + h 2 + h 1 + h 1 + h 1 = h
19 Nivoların Kontrol ve Düzenlenmesi Nivelman ölçmelerine başlamadan önce kullanılacak nivonun düzgün çalışıp çalışmadığı mutlaka kontrol edilmelidir. Kontrol ve düzenlemesi yapılmadan kullanılan nivo ile istenilen ölçme sonucunu elde etmek mümkün değildir. Kontrol için nivonun eksen koşullarının yerinde olup olmadığına bakılması gerekir. Kısa bir süre içinde yapılabilen bu kontroller ile yapılacak yanlış ölçmeler önlenir ve arazide zaman kaybedilmemiş olur A S O S O K K A Nivoda dört eksen vardır. Bu eksenler : a Asal eksen (AA) b Optik eksen (OO) c Silindir düzeç ekseni (SS) d Küresel Düzeç ekseni (KK)
20 Düzeci dürbünü sabit fenkalajsız ve fenkalajlı nivolarda bu eksenler arasında şu koşullar vardır 1 Asal eksen küresel düzeç eksenine dik olmalıdır. 2 Silindir düzeç ekseni asal eksene dik olmalıdır. 3 Dürbün yatay gözleme çizgisi asal eksene dik olmalıdır. 4 Optik eksen silindir düzeç eksenine paralel olmalıdır (ana eksen koşulu) A S O S O K K
21 Asal eksen küresel düzeç eksenine dik olmalıdır koşulunun kontrol ve düzenlenmesi Küresel düzeç tesviye vidaları kullanılarak ortalanır. Küresel düzeç kabarcığı nivonun her konumunda ortada bulunmalıdır. Nivo asal ekseni etrafında 90 0 lik bölümler halinde döndürülerek düzeç kabarcığının ortada olup olmadığı kontrol edilir. Düzeç kabarcığı herhangi bir konumda ortada değilse, düzenlenmesi gerekir d Düzenleme : Hata düzeçle merkezini birleştiren doğrultudadır. Kaçma doğrultusundaki tesviye vidası ile hatanın yarısı (d/2), diğer yarısı da uygun düzeç düzenleme vidası döndürülerek giderilir ve kabarcık ortalanır
22 Silindir düzeç ekseni asal eksene dik olmalıdır koşulunun kontrol ve düzenlenmesi Söz konusu kontrol ve düzenleme fenkalaj vidasız nivolarda yapılır. Alet bir kaç kez tesviye edilmesine rağmen düzeç kabarcığı her konumda ortada kalmıyorsa alette bu şart sağlanmıyor ve düzeç düzensiz demektir. Düzenleme : Teodolitlerdeki ana eksen koşulu düzenlemesi gibi yapılır. Silindir düzeç ekseni tesviye vidalarından ikisine paralel konuma getirilir. Silindir düzeç kabarcığı bu konumda itina ile ortalanır. Sonra, alet yarım devir (~200 grad) döndürülür. Bu durumda kabarcığın ortadan ayrılma miktarı bu hatanın iki katına eşittir. Ayrılma miktarının yarısı, iki tesviye vidasından birisi ile diğer yarısı da silindir düzeç düzenleme vidası ile, uygun şekilde döndürülerek giderilir. Bu düzenleme doğru sonuç elde edilinceye kadar birkaç kez tekrarlanılır.
23 Dürbün yatay gözleme çizgisinin asal eksene dik olması koşulunun kontrolü ve düzenlenmesi Bu koşulun kontrolü için şu işlemler yapılır: 1- Nivo tesviye edilir ve dürbün göze uydurulur. 2- Yatay gözleme çizgisinin bir ucu keskin ve net görülen bir noktaya ince olarak yöneltilir 3- Az hareket vidası yardımı ile yatay çizginin öteki ucu nokta üzerine gelinceye kadar dürbün hareket ettirilir. Çizgi noktadan ayrılmamışsa hata yoktur. Eğer ayrılma var ise düzenlenmesi gerekir. Düzenleme: Ayrılma miktarı hatanın iki katıdır. Düzenleme için okülerin önündeki gözleme çizgilerini koruyan kapak açılır. Gözleme çizgilerini aşağı ve yukarı doğru hareket ettiren vidalar dikkatlice gevşetilir ve hata miktarı kadar gözleme çizgileri plakası döndürülerek vidalar sıkıştırılır.
24 Optik eksen Silindir düzeç eksenine paralel olmalıdır koşulunun kontrolü ve düzenlemesi Kontrol : Buşartın kontrol edilmesi için ortadan ve yandan gözleme yöntemi uygulanır. Buamaçla birbirlerinden m uzakta A ve B gibi iki nokta seçilir. Nivo bu iki noktadan eşit uzaklıkta bir noktaya kurulur, tesviye edilir ve her iki noktada mira okuması yapılır. Ortadan gözleme : Eğer optik eksen silindir düzeç eksenine paralel ise; a 1 N b 1 h 1 h B A h 2 h = h 1 h 2 değilse; h 1 = a 1 b 1 ve N h 1 a 1 ile Nh 2 b 1 üçgenleri eşit olduğundan N b 1 h A h 2 h = h 1 h 2 = a 1 b 1 Yandan gözleme: A h m m. B h 2 = h A h B h 1 = h 2 bulunursa koşul yerindedir. Değilse B noktasındaki mira okuması: h B = h A h
25 Düzenleme: B noktasındaki mirada, hesaplanan h B mira okuması elde edilinceye kadar, gözleme çizgilerini taşıyan halka, yukarı ve aşağı hareket vidaları uygun yöne döndürülerek orta çizgi hareket ettirilir
26 Nivelmanda Dikkat Edilecek Hususlar 1- Hava sıcaklığı ve güneş radyasyonunun etkisi sonucu, yer yüzüne yakın hava tabakalarının titreşimi nedeniyle 0.60 m den daha aşağı mira okuması yapılmamalıdır. 2- Bulutlu havalar tercih edilmeli, veya sabahları erken ve akşam üstü saatlerinde nivelman yapılmalıdır. 3- Rüzgarlı havalarda miranın düşey konumda tutulması çok zorlaşır. Bu nedenle Kısa gözleme aralıkları seçilmelidir. Geometrik nivelmanda 60 m den daha uzak gözleme yapılmamalıdır. 4- Miraların üzerinde düşey konumda tutulması için küresel düzeç bulunmuyorsa, portatif mira düzeci kullanılmalıdır (Şekil 7.20a). 5- İleri okumalardan sonra mira nivoya döndürülürken, toprak zeminde çukur açmamasına ve miranın kaydırılıp yer değiştirmemesine özen gösterilmelidir. Gerekirse mira altlığı kullanılmalıdır (Şekil).
27 NİVELMAN ÇİZELGELERİNİ HESAPLAMA YÖNTEMLERİ Yükseklik Farkı Yöntemi h yükseklik farkları hesaplandıktan sonra işaretine göre bir evvelki nokta kotu ile toplanarak nokta kotu bulunur. Nivelman kotu bilinen bir noktadan geri okuması ile başlar ve ileri okuması ile son bulur. Yükseklik farklarının hesabı: = = = = = = = Kotların hesabı: H 1 = = m H 2 = = m H 3 = = m H 4 = = m H 5 = = m H 6 = = m H B = = m Nokta No A B Mira Okumaları (m) Geri Orta İleri Yükseklik Farkı (m) Kotlar (m) KONTROL g - i = h = H B H A = =
28 Gözleme düzlemi kotu yöntemi Bir nivelman çizelgesinin gözleme düzlemi kotu (G.D.K.) yöntemine göre hesabı Çizelge 2 de verilmiştir. Bu yöntemde her nivo kuruluşu için dürbünün optik ekseninden geçen yatay düzlemden yararlanılır. Bu yatay düzleme gözleme düzlemi ismi verilir Gözleme düzlemi kotu (G.D.K), mirada yapılan geri okuma ile, kotu verilen o noktanın kotu toplanarak elde edilir. Yani G.D.K = H A + g A Bulunan gözleme düzlemi kotundan, o nivo kuruluşunda yapılmış olan orta ve ileri okumalar çıkarılarak, miranın konulduğu noktaların kotları bulunur. Aletin yeri değiştiği zaman gözleme düzleminin kotu da değişir. Nivonun bir evvelki konumunda yapılmış olan son (ileri) okuma noktasına bir geri okuma yapılır ve yeni gözleme düzlemi kotu bulunur.
29 Nokta No Mira Okumaları Geri Orta İleri Gözleme Düzlemi Kotu (m) + G.D.K Kotlar (m) A B KONTROL G.D.K + H A = Kotlar + O + i =
30 Nivelman Poligonlarına Ait Ölçme Hataları Nivelman poligonlarında, ölçmelerin kontrolü için poligon biçimine göre bir takım koşullar vardır. Açık, kapalı ve bağlı poligonlarda bu koşullar şöyledir: 1- Açık Nivelman Poligonunda Açık poligonlarda gidiş nivelmanının kontrolü için ters doğrultuda bir dönüş nivelmanı yapılır. Bu durumda gidiş nivelmanındaki yükseklik farkları toplamı h g, dönüş nivelmanındaki h d ise h g h d = 0 f h h g h d 2- Kapalı Nivelman poligonunda Nivelmana kotu bilinen noktadan başlanıp tekrar aynı noktaya ge lindiğinden h = 0 f h h Bağlı Nivelman poligonunda Kotu bilinen A noktasından kotu bilinen B noktasına gidildiğinden h = H B H A f h h ( H B H A )
31 Nivelman Ölçmelerine Ait Hata Sınırı İfadeleri Bu kapanma hatalarının bir hata sınırı içinde kalması gerekir. Hata sınırı ifadeleri yönetmeliklerce saptanır. d 0.02 mm L km veya d 0.18 mm L km Büyük Ölçekli Haritaların Yapım Yönetmeliğine (1998) göre, gidiş ve dönüş nivelmanları arasındaki fark Ana ve dizi nivelmanda d 0.02 L h (7.17) Ara nivelmanda d 0.02 L h (7.18) formülleri ile bulunan değerleri aşamaz. Burada; L : Km cinsinden nivelman güzergah uzunluğu h : Geri ve ileri okuma farklarının mutlak değerlerinin metre cinsinden toplamıdır. L, kilometre biriminde h, metre biriminden alındığından hata sınır metre biriminde elde edilir.
32 Ölçme Hatalarının Dağıtılması f h kapanma hatası, hata sınırının verdiği d miktarından büyük ise ölçmeler tekrarlanır, aksi durumda, yani f h d ise ölçmeler kabul edilir ve v h = f h ile düzeltme miktarı bulunur. Bu v h düzeltme miktarı 1 - Gözleme uzaklıkları 2- Yükseklik farkları 3- Alet kurma sayısı ile orantılı olmak üzere iki biçimde dağıtılır :
33 1 - Gözleme uzaklıkları ile orantılı olarak dağıtma Çizelge yükseklik, farkları yöntemi ile hesaplanmış ise h; yükseklik farkına uygulanacak düzeltme miktarı v hi f h i ifadesi ile hesaplanır. Çizelge gözleme düzlemi kotu yöntemine göre hesaplanmış ise geçici olarak bulunmuş olan kotlara uygulanacak düzeltme miktarı v hi f h l L i ifadesi ile hesaplanır.
34 2- Yükseklik farkları ile orantılı olarak dağıtma Karne yükseklik farkı yöntemi ile hesaplanmış ise h, yükseklik farkına uygulanacak düzeltme miktarı v hi f h h h ifadesi ile hesaplanır. Çizelge gözleme düzlemi kotu yöntemine göre hesaplanmışsa geçici olarak bulunmuş kotlara uygulanacak düzeltme miktarı v i f h h H i ifadesi ile hesaplanır.
35 3 Alet kurma sayısı ile orantılı dağıtma Yükseklik farkı veya gözleme düzlemi kotu yöntemi ile bulunmuş olan geçici kotlara uygulanacak düzeltme miktarı, v h i f h n n i ifadesi ile hesaplanır.
36 Z
TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri
 TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri
 TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Yüksekliklerin Ölçülmesi Nivelman Yöntemleri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
ÖLÇME BİLGİSİ DÜŞEY MESAFELERİN (YÜKSEKLİKLERİN) ÖLÇÜLMESİ NİVELMAN ALETLERİ. Doç. Dr. Alper Serdar ANLI. 8. Hafta
 ÖLÇME BİLGİSİ DÜŞEY MESAFELERİN (YÜKSEKLİKLERİN) ÖLÇÜLMESİ NİVELMAN ALETLERİ Doç. Dr. Alper Serdar ANLI 8. Hafta DÜŞEY MESAFELERİN (YÜKSEKLİKLERİN) ÖLÇÜLMESİ Noktaların yükseklikleri düşey ölçmelerle belirlenir.
ÖLÇME BİLGİSİ DÜŞEY MESAFELERİN (YÜKSEKLİKLERİN) ÖLÇÜLMESİ NİVELMAN ALETLERİ Doç. Dr. Alper Serdar ANLI 8. Hafta DÜŞEY MESAFELERİN (YÜKSEKLİKLERİN) ÖLÇÜLMESİ Noktaların yükseklikleri düşey ölçmelerle belirlenir.
02.04.2012. Düşey mesafelerin (Yüksekliklerin) Ölçülmesi. Düşey Mesafelerin (Yüksekliklerin) Ölçülmesi. Düşey Mesafelerin (Yüksekliklerin) Ölçülmesi
 Düşey mesafelerin (Yüksekliklerin) Ölçülmesi Noktalar arasındaki düşey mesafelerin ölçülmesine yükseklik ölçmesi ya da nivelman denir. Yükseklik: Ölçülmek istenen nokta ile sıfır yüzeyi olarak kabul edilen
Düşey mesafelerin (Yüksekliklerin) Ölçülmesi Noktalar arasındaki düşey mesafelerin ölçülmesine yükseklik ölçmesi ya da nivelman denir. Yükseklik: Ölçülmek istenen nokta ile sıfır yüzeyi olarak kabul edilen
Ölçme Bilgisi Jeofizik Mühendisliği Bölümü
 Ölçme Bilgisi Jeofizik Mühendisliği Bölümü Yrd. Doç. Dr. H. Ebru ÇOLAK [email protected] Karadeniz Teknik Üniversitesi, GISLab Trabzon www.gislab.ktu.edu.tr/kadro/ecolak DÜŞEY MESAFELERİN YÜKSEKLİKLERİN
Ölçme Bilgisi Jeofizik Mühendisliği Bölümü Yrd. Doç. Dr. H. Ebru ÇOLAK [email protected] Karadeniz Teknik Üniversitesi, GISLab Trabzon www.gislab.ktu.edu.tr/kadro/ecolak DÜŞEY MESAFELERİN YÜKSEKLİKLERİN
YÜKSEKLİK ÖLÇÜMÜ. Ölçme Bilgisi Ders Notları
 YÜKSEKLİK ÖLÇÜMÜ Yeryüzündeki herhangi bir noktanın sakin deniz yüzeyi üzerinde (geoitten itibaren) çekül doğrultusundaki en kısa mesafesine yükseklik denir. Yükseklik ölçümü; belirli noktalar arasındaki
YÜKSEKLİK ÖLÇÜMÜ Yeryüzündeki herhangi bir noktanın sakin deniz yüzeyi üzerinde (geoitten itibaren) çekül doğrultusundaki en kısa mesafesine yükseklik denir. Yükseklik ölçümü; belirli noktalar arasındaki
ORMANCILIKTA ÖLÇME, HARİTA VE KADASTRO DERSİ UYGULAMA FÖYÜ. HAZIRLAYANLAR Yrd. Doç. Dr. Saliha ÜNVER OKAN Arş. Gör.
 ORMANCILIKTA ÖLÇME, HARİTA VE KADASTRO DERSİ UYGULAMA FÖYÜ HAZIRLAYANLAR Yrd. Doç. Dr. Saliha ÜNVER OKAN Arş. Gör. Taha Yasin HATAY Trabzon, 2015 UYGULAMA II. NİVO İLE YÜKSEKLİK FARKI ÖLÇÜMÜ UYGULAMANIN
ORMANCILIKTA ÖLÇME, HARİTA VE KADASTRO DERSİ UYGULAMA FÖYÜ HAZIRLAYANLAR Yrd. Doç. Dr. Saliha ÜNVER OKAN Arş. Gör. Taha Yasin HATAY Trabzon, 2015 UYGULAMA II. NİVO İLE YÜKSEKLİK FARKI ÖLÇÜMÜ UYGULAMANIN
TOPOĞRAFYA Topoğrafya Aletleri ve Parçaları (Teodolit)
 TOPOĞRAFYA Topoğrafya Aletleri ve Parçaları (Teodolit) Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Topoğrafya Aletleri ve Parçaları (Teodolit) Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
Yükseklik Ölçme (Nivelman) Prof.Dr.Mustafa KARAŞAHİN
 Yükseklik Ölçme (Nivelman) Prof.Dr.Mustafa KARAŞAHİN Yükseklik Ölçümü Arazide, yerleri belli olan noktaların deviz seviyesine göre yüksekliklerinin belirlenmesi işlemidir. Noktalar arasındaki yükseklik
Yükseklik Ölçme (Nivelman) Prof.Dr.Mustafa KARAŞAHİN Yükseklik Ölçümü Arazide, yerleri belli olan noktaların deviz seviyesine göre yüksekliklerinin belirlenmesi işlemidir. Noktalar arasındaki yükseklik
PDF created with FinePrint pdffactory trial version Düşey mesafelerin (Yüksekliklerin) Ölçülmesi
 Düşey mesafelerin (Yüksekliklerin) Noktalar arasındaki düşey mesafelerin ölçülmesine yükseklik ölçmesi ya da nivelman denir. Yükseklik: Ölçülmek istenen nokta ile sıfır yüzeyi olarak kabul edilen deniz
Düşey mesafelerin (Yüksekliklerin) Noktalar arasındaki düşey mesafelerin ölçülmesine yükseklik ölçmesi ya da nivelman denir. Yükseklik: Ölçülmek istenen nokta ile sıfır yüzeyi olarak kabul edilen deniz
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü TOPOGRAFYA (HRT3351) Yrd. Doç. Dr. Ercenk ATA
 Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü 4. HAFTA KOORDİNAT SİSTEMLERİ VE HARİTA PROJEKSİYONLARI Coğrafi Koordinat Sistemi Yeryüzü üzerindeki bir noktanın konumunun enlem
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü 4. HAFTA KOORDİNAT SİSTEMLERİ VE HARİTA PROJEKSİYONLARI Coğrafi Koordinat Sistemi Yeryüzü üzerindeki bir noktanın konumunun enlem
KESİTLERİN ÇIKARILMASI
 KESİTLERİN ÇIKARILMASI Karayolu, demiryolu, kanal, yüksek gerilim hattı gibi inşaat işlerinde projelerin hazırlanması, toprak hacminin bulunması amacı ile boyuna ve enine kesitlere ihtiyaç vardır. Boyuna
KESİTLERİN ÇIKARILMASI Karayolu, demiryolu, kanal, yüksek gerilim hattı gibi inşaat işlerinde projelerin hazırlanması, toprak hacminin bulunması amacı ile boyuna ve enine kesitlere ihtiyaç vardır. Boyuna
Açı Ölçümü. Prof.Dr.Mustafa KARAŞAHİN
 Açı Ölçümü Prof.Dr.Mustafa KARAŞAHİN Açı Nedir? İki doğru arasındaki, doğrultu farkına açı adı verilir. Açılar, teodolit veya takeometre ile yapılır. Teodolit sadece açı ölçmede kullanılır iken, takeometreler
Açı Ölçümü Prof.Dr.Mustafa KARAŞAHİN Açı Nedir? İki doğru arasındaki, doğrultu farkına açı adı verilir. Açılar, teodolit veya takeometre ile yapılır. Teodolit sadece açı ölçmede kullanılır iken, takeometreler
YÜKSEKLİKLERİN ÖLÇÜLMESİ NİVELMAN
 YÜKSEKLİKLERİN ÖLÇÜLMESİ NİVELMAN Yeryüzü noktalarının karaların altında da devam ettiği varsayılan ortalama deniz yüzeyinden ( karşılaştırma yüzeyi) olan düşey uzaklığına yükseltisi, herhangi bir noktadan
YÜKSEKLİKLERİN ÖLÇÜLMESİ NİVELMAN Yeryüzü noktalarının karaların altında da devam ettiği varsayılan ortalama deniz yüzeyinden ( karşılaştırma yüzeyi) olan düşey uzaklığına yükseltisi, herhangi bir noktadan
BAĞLI POLİGON BAĞLI POLİGON
 BAĞLI POLİGON BAĞLI POLİGON 1 BAĞLI POLİGON BAĞLI POLİGON 2 BAĞLI POLİGON BAĞLI POLİGON 6 3 TRİGONOMETRİK NİVELMAN 7 H B - H A = Δh AB = S AB * cotz AB + a t H B = H A + S AB * cotz AB + a - t TRİGONOMETRİK
BAĞLI POLİGON BAĞLI POLİGON 1 BAĞLI POLİGON BAĞLI POLİGON 2 BAĞLI POLİGON BAĞLI POLİGON 6 3 TRİGONOMETRİK NİVELMAN 7 H B - H A = Δh AB = S AB * cotz AB + a t H B = H A + S AB * cotz AB + a - t TRİGONOMETRİK
Ölçme Bilgisi DERS 7-8. Yatay Kontrol Noktaları Ve Yükseklik ölçmeleri. Kaynak: İ.ASRİ (Gümüşhane Ü) T. FİKRET HORZUM( AÜ )
 Ölçme Bilgisi DERS 7-8 Yatay Kontrol Noktaları Ve Yükseklik ölçmeleri Kaynak: İ.ASRİ (Gümüşhane Ü) T. FİKRET HORZUM( AÜ ) Bir alanın üzerindeki detaylarla birlikte harita veya planının yapılabilmesi için
Ölçme Bilgisi DERS 7-8 Yatay Kontrol Noktaları Ve Yükseklik ölçmeleri Kaynak: İ.ASRİ (Gümüşhane Ü) T. FİKRET HORZUM( AÜ ) Bir alanın üzerindeki detaylarla birlikte harita veya planının yapılabilmesi için
TEODOLIT. Açiklanan yatay ve düsey açilari ölçmek için kullanilan optik mekanik topografya aleti, teodolit olarak adlandirilir.
 TEODOLIT Açiklanan yatay ve düsey açilari ölçmek için kullanilan optik mekanik topografya aleti, teodolit olarak adlandirilir. Teodolit genel olarak dürbün, açi ölçme ve okuma donanimi, düzeçler, yatay
TEODOLIT Açiklanan yatay ve düsey açilari ölçmek için kullanilan optik mekanik topografya aleti, teodolit olarak adlandirilir. Teodolit genel olarak dürbün, açi ölçme ve okuma donanimi, düzeçler, yatay
TOPOĞRAFYA Kesitlerin Çıkarılması, Alan Hesapları, Hacim Hesapları
 TOPOĞRAFYA Kesitlerin Çıkarılması, Alan Hesapları, Hacim Hesapları Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Kesitlerin Çıkarılması, Alan Hesapları, Hacim Hesapları Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
YÜKSEKLİK ÖLÇMELERİ DERSİ GEOMETRİK NİVELMAN
 YÜKSEKLİK ÖLÇMELERİ DERSİ GEOMETRİK NİVELMAN Yrd. Doç. Dr. Ayhan CEYLAN Yrd. Doç. Dr. İsmail ŞANLIOĞLU 9.3. Nivelman Ağları ve Nivelman Röper Noktası Haritası yapılacak olan arazi üzerinde veya projenin
YÜKSEKLİK ÖLÇMELERİ DERSİ GEOMETRİK NİVELMAN Yrd. Doç. Dr. Ayhan CEYLAN Yrd. Doç. Dr. İsmail ŞANLIOĞLU 9.3. Nivelman Ağları ve Nivelman Röper Noktası Haritası yapılacak olan arazi üzerinde veya projenin
Yatay Eksen: Dürbünün etrafında döndüğü eksendir. Asal Eksen: Çekül doğrultusundaki eksen Düzeç Ekseni: Düzecin üzerinde bulunduğueksen Yöneltme
 Teodolit Yatay Eksen: Dürbünün etrafında döndüğü eksendir. Asal Eksen: Çekül doğrultusundaki eksen Düzeç Ekseni: Düzecin üzerinde bulunduğueksen Yöneltme Ekseni: Kıllar şebekesinin kesim noktası ile objektifin
Teodolit Yatay Eksen: Dürbünün etrafında döndüğü eksendir. Asal Eksen: Çekül doğrultusundaki eksen Düzeç Ekseni: Düzecin üzerinde bulunduğueksen Yöneltme Ekseni: Kıllar şebekesinin kesim noktası ile objektifin
TOPOĞRAFYA Takeometri
 TOPOĞRAFYA Takeometri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Takeometri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
GENEL TANIMLAR. 1-Düşey doğrultu : Yeryüzünün herhangi bir O noktasındaki yerçekimi doğrultusudur (ZN doğrultusu).
 GENEL TANIMLAR Ölçme bilgisinde kullanılan bazı tanımları şekil 5.1 üzerinde inceleyelim. 1-Düşey doğrultu : Yeryüzünün herhangi bir O noktasındaki yerçekimi doğrultusudur (ZN doğrultusu). 2-Yatay doğrultu
GENEL TANIMLAR Ölçme bilgisinde kullanılan bazı tanımları şekil 5.1 üzerinde inceleyelim. 1-Düşey doğrultu : Yeryüzünün herhangi bir O noktasındaki yerçekimi doğrultusudur (ZN doğrultusu). 2-Yatay doğrultu
TAKEOMETRİ GENEL BİLGİLER
 TAKEOMETRİ GENEL BİLGİLER Optik olarak yatay uzunlukların ve yükseklik farklarının klasik teodolit ve mira kullanılarak bulunması yöntemine takeometri adı verilmektedir. Takeometrik yöntemde amaç, bir
TAKEOMETRİ GENEL BİLGİLER Optik olarak yatay uzunlukların ve yükseklik farklarının klasik teodolit ve mira kullanılarak bulunması yöntemine takeometri adı verilmektedir. Takeometrik yöntemde amaç, bir
 Geometrik nivelmanda önemli hata kaynakları Nivelmanda oluşabilecek model hataları iki bölümde incelenebilir. Bunlar: Aletsel (Nivo ve Mira) Hatalar Çevresel Koşullardan Kaynaklanan Hatalar 1. Aletsel
Geometrik nivelmanda önemli hata kaynakları Nivelmanda oluşabilecek model hataları iki bölümde incelenebilir. Bunlar: Aletsel (Nivo ve Mira) Hatalar Çevresel Koşullardan Kaynaklanan Hatalar 1. Aletsel
ARAZİ ÇALIŞMASI -1 DERSİ ELEKTRONİK ALETLERİN KONTROL VE KALİBRASYONU UYGULAMALARI
 ARAZİ ÇALIŞMASI -1 DERSİ ELEKTRONİK ALETLERİN KONTROL VE KALİBRASYONU UYGULAMALARI HARİTA MÜHENDİSLİĞİ BÖLÜMÜ ÖLÇME TEKNİĞİ ANABİLİM DALI JEODEZİK METROLOJİ LABORATUVARI İstanbul, 2018 1.ELEKTRONİK TAKEOMETRELERİN
ARAZİ ÇALIŞMASI -1 DERSİ ELEKTRONİK ALETLERİN KONTROL VE KALİBRASYONU UYGULAMALARI HARİTA MÜHENDİSLİĞİ BÖLÜMÜ ÖLÇME TEKNİĞİ ANABİLİM DALI JEODEZİK METROLOJİ LABORATUVARI İstanbul, 2018 1.ELEKTRONİK TAKEOMETRELERİN
ARAZİ ÇALIŞMASI -1 DERSİ ELEKTRONİK ALETLERİN KONTROL VE KALİBRASYONU UYGULAMALARI
 ARAZİ ÇALIŞMASI -1 DERSİ ELEKTRONİK ALETLERİN KONTROL VE KALİBRASYONU UYGULAMALARI HARİTA MÜHENDİSLİĞİ BÖLÜMÜ ÖLÇME TEKNİĞİ ANABİLİM DALI JEODEZİK METROLOJİ LABORATUVARI İstanbul, 016 1.ELEKTRONİK TAKEOMETRELERİN
ARAZİ ÇALIŞMASI -1 DERSİ ELEKTRONİK ALETLERİN KONTROL VE KALİBRASYONU UYGULAMALARI HARİTA MÜHENDİSLİĞİ BÖLÜMÜ ÖLÇME TEKNİĞİ ANABİLİM DALI JEODEZİK METROLOJİ LABORATUVARI İstanbul, 016 1.ELEKTRONİK TAKEOMETRELERİN
YÜKSEKLİK ÖLÇMELERİ 2017-KTU
 YÜKSEKLİK ÖLÇMELERİ 2017-KTU 2.Trigonometrik Nivelman: GEOMETRİK NİVELMAN Nivelman aletleri incelik yönünden 4 grupta ele alınabilir. 3- Yüksek İncelikli Nivolar Bu tür nivolar, III. Derece nivelman
YÜKSEKLİK ÖLÇMELERİ 2017-KTU 2.Trigonometrik Nivelman: GEOMETRİK NİVELMAN Nivelman aletleri incelik yönünden 4 grupta ele alınabilir. 3- Yüksek İncelikli Nivolar Bu tür nivolar, III. Derece nivelman
Uzunluk Ölçümü (Şenaj) Prof.Dr.Mustafa KARAŞAHİN
 Uzunluk Ölçümü (Şenaj) Prof.Dr.Mustafa KARAŞAHİN Uzunlukların Ölçülmesi (Şenaj) Arazide uzunlukların doğru ve hassas bir şekilde ölçülmesi, projelerin doğru hazırlanmasında ve projelerin araziye uygulaması
Uzunluk Ölçümü (Şenaj) Prof.Dr.Mustafa KARAŞAHİN Uzunlukların Ölçülmesi (Şenaj) Arazide uzunlukların doğru ve hassas bir şekilde ölçülmesi, projelerin doğru hazırlanmasında ve projelerin araziye uygulaması
1. Nivelman Ölçü Aletlerinin Kısımları Düzeçler Dürbünler Sehpalar 2. Yükseklik Farkı Ölçme Aletleri Nivolar Hortum Teraziler
 NİVELMAN ALETLERİ 1. Nivelman Ölçü Aletlerinin Kısımları Düzeçler Dürbünler Sehpalar. Yükseklik Farkı Ölçme Aletleri Nivolar Hortum Teraziler Düzeçler üzeçler: Jeodezik ölçü aletlerinin eksenlerini çekü
NİVELMAN ALETLERİ 1. Nivelman Ölçü Aletlerinin Kısımları Düzeçler Dürbünler Sehpalar. Yükseklik Farkı Ölçme Aletleri Nivolar Hortum Teraziler Düzeçler üzeçler: Jeodezik ölçü aletlerinin eksenlerini çekü
ULAŞIM YOLLARINA AİT TANIMLAR
 ULAŞIM YOLLARINA AİT TANIMLAR Geçki: Karayolu, demiryolu gibi ulaştıma yapılarının, yuvarlanma yüzeylerinin ortasından geçtiği varsayılan eksen çizgisinin harita ya da arazideki izdüşümüdür. Topografik
ULAŞIM YOLLARINA AİT TANIMLAR Geçki: Karayolu, demiryolu gibi ulaştıma yapılarının, yuvarlanma yüzeylerinin ortasından geçtiği varsayılan eksen çizgisinin harita ya da arazideki izdüşümüdür. Topografik
ÖLÇME BİLGİSİ TANIM KAPSAM ÖLÇME ÇEŞİTLERİ BASİT ÖLÇME ALETLERİ
 ÖLÇME BİLGİSİ TANIM KAPSAM ÖLÇME ÇEŞİTLERİ BASİT ÖLÇME ALETLERİ Doç. Dr. Alper Serdar ANLI 1.Hafta Ölçme Bilgisi Dersi 2013 Bahar Dönemi Ders Programı HAFTA KONU 1.Hafta 2.Hafta 3.Hafta 4.Hafta 5.Hafta
ÖLÇME BİLGİSİ TANIM KAPSAM ÖLÇME ÇEŞİTLERİ BASİT ÖLÇME ALETLERİ Doç. Dr. Alper Serdar ANLI 1.Hafta Ölçme Bilgisi Dersi 2013 Bahar Dönemi Ders Programı HAFTA KONU 1.Hafta 2.Hafta 3.Hafta 4.Hafta 5.Hafta
ULAŞIM YOLLARINA İLİŞKİN TANIMLAR 1. GEÇKİ( GÜZERGAH) Karayolu, demiryolu gibi ulaşım yollarının yuvarlanma yüzeylerinin ortasından geçtiği
 ULAŞIM YOLLARINA İLİŞKİN TANIMLAR 1. GEÇKİ( GÜZERGAH) Karayolu, demiryolu gibi ulaşım yollarının yuvarlanma yüzeylerinin ortasından geçtiği varsayılan eksen çizgilerinin topoğrafik harita ya da arazi üzerindeki
ULAŞIM YOLLARINA İLİŞKİN TANIMLAR 1. GEÇKİ( GÜZERGAH) Karayolu, demiryolu gibi ulaşım yollarının yuvarlanma yüzeylerinin ortasından geçtiği varsayılan eksen çizgilerinin topoğrafik harita ya da arazi üzerindeki
3. Alım için sıklaştırma noktaları (tamamlayıcı nokta, ara ve dizi nirengi),
 ÖLÇME BİLGİSİ 2 DERS NOTLARI YER KONTROL NOKTALARI Genel Bilgi Bir alanın ve üzerindeki örtülerin harita veya planının yapılabilmesi için yeryüzünde konumu sabit ve koordinat değerleri belli bir takım
ÖLÇME BİLGİSİ 2 DERS NOTLARI YER KONTROL NOKTALARI Genel Bilgi Bir alanın ve üzerindeki örtülerin harita veya planının yapılabilmesi için yeryüzünde konumu sabit ve koordinat değerleri belli bir takım
DİK KOORDİNAT SİSTEMİ VE
 Ölçme Bilgisi DERS 6 DİK KOORDİNAT SİSTEMİ VE TEMEL ÖDEVLER Kaynak: İ.ASRİ (Gümüşhane Ü) M. Zeki COŞKUN ( İTÜ ) TEODOLİT Teodolitler, yatay ve düşey açıları yeteri incelikte ölçmeye yarayan optik aletlerdir.
Ölçme Bilgisi DERS 6 DİK KOORDİNAT SİSTEMİ VE TEMEL ÖDEVLER Kaynak: İ.ASRİ (Gümüşhane Ü) M. Zeki COŞKUN ( İTÜ ) TEODOLİT Teodolitler, yatay ve düşey açıları yeteri incelikte ölçmeye yarayan optik aletlerdir.
Kabarcıklı Düzeç ÖLÇME ALETLERİNİN ORTAK PARÇALARI. Küresel Düzeç. Küresel Düzeç 3/8/2010
 Sunu, Doç. Dr. Hande Demirel in ders notları ve Gündoğdu Özgen` e ait Ölçme Bilgisi kitabından düzenlenmiştir. Kabarcıklı Düzeç Doğru ve düzlemlerin yatay ve düşey tutulmalarını sağlayan yardımcı parçadır.
Sunu, Doç. Dr. Hande Demirel in ders notları ve Gündoğdu Özgen` e ait Ölçme Bilgisi kitabından düzenlenmiştir. Kabarcıklı Düzeç Doğru ve düzlemlerin yatay ve düşey tutulmalarını sağlayan yardımcı parçadır.
DERS 3 ÖLÇÜ HATALARI Kaynak: İ.ASRİ
 Ölçme Bilgisi DERS 3 ÖLÇÜ HATALARI Kaynak: İ.ASRİ Çizim Hassasiyeti Haritaların çiziminde veya haritadan bilgi almada ne kadar itina gösterilirse gösterilsin kaçınılmayacak bir hata vardır. Buna çizim
Ölçme Bilgisi DERS 3 ÖLÇÜ HATALARI Kaynak: İ.ASRİ Çizim Hassasiyeti Haritaların çiziminde veya haritadan bilgi almada ne kadar itina gösterilirse gösterilsin kaçınılmayacak bir hata vardır. Buna çizim
YÜKSEKLİK ÖLÇMELERİ 2016-KTU
 YÜKSEKLİK ÖLÇMELERİ 2016-KTU GPS ölçüleri ile jeosantrik bir koordinat sisteminde seçilen bir referans elipsoidine göre elde edilen elipsoidal yükseklik, fiziksel yeryüzündeki bir P noktasının elipsoid
YÜKSEKLİK ÖLÇMELERİ 2016-KTU GPS ölçüleri ile jeosantrik bir koordinat sisteminde seçilen bir referans elipsoidine göre elde edilen elipsoidal yükseklik, fiziksel yeryüzündeki bir P noktasının elipsoid
ARAZİ ÖLÇMELERİ. Koordinat sistemleri. Kartezyen koordinat sistemi
 Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
1D 14.50 110 ----- 2D 14.20 140 290 3D 15.10 320
 ORMAN YOLLARININ ARAZİYE APLİKASYONU Planı yapılan yolların kullanılabilmesi için araziye aplike edilmesi gerekmektedir. Araziye gidildiği zaman, plan üzerinde gösterilen yolun başlangıç ve bitiş noktaları
ORMAN YOLLARININ ARAZİYE APLİKASYONU Planı yapılan yolların kullanılabilmesi için araziye aplike edilmesi gerekmektedir. Araziye gidildiği zaman, plan üzerinde gösterilen yolun başlangıç ve bitiş noktaları
ÖLÇME BİLGİSİ ALANLARIN ÖLÇÜLMESİ
 ÖLÇME BİLGİSİ ALANLARIN ÖLÇÜLMESİ Doç. Dr. Alper Serdar ANLI 5.Hafta ALANLARIN ÖLÇÜLMESİ Genel bir deyişle herhangi bir arazi parçasının şeklini ve büyüklüğünü belirtecek planın çıkarılabilmesi için gereken
ÖLÇME BİLGİSİ ALANLARIN ÖLÇÜLMESİ Doç. Dr. Alper Serdar ANLI 5.Hafta ALANLARIN ÖLÇÜLMESİ Genel bir deyişle herhangi bir arazi parçasının şeklini ve büyüklüğünü belirtecek planın çıkarılabilmesi için gereken
1.Geometrik Nivelman
 .Geometrik Nivelman Ülke nivelman ağlara larının n oluşturulmas turulmasında, Yüksek doğruluk gerektiren her türlt rlü mühendislik hizmetlerinde, Baraj, köprk prü vb. büyük b k yapılar ların deformasyon
.Geometrik Nivelman Ülke nivelman ağlara larının n oluşturulmas turulmasında, Yüksek doğruluk gerektiren her türlt rlü mühendislik hizmetlerinde, Baraj, köprk prü vb. büyük b k yapılar ların deformasyon
Alan Hesapları. Şekil 14. Üç kenarı belli üçgen alanı
 lan Hesapları lan hesabının doğruluğu alım şekline ve istenile hassasiyet derecesine göre değişir. lan hesapları üç kısma ayrılmıştır. Ölçü değerlerine göre alan hesabı Ölçü ve plan değerlerine göre alan
lan Hesapları lan hesabının doğruluğu alım şekline ve istenile hassasiyet derecesine göre değişir. lan hesapları üç kısma ayrılmıştır. Ölçü değerlerine göre alan hesabı Ölçü ve plan değerlerine göre alan
ARAZİ ÖLÇMELERİ Z P. O α X P. α = yatay açı. ω = düşey açı. µ =eğim açısı. ω + µ = 100 g
 Trigonometrik Fonksiyonlar Z Z P P ω µ P O α α = yatay açı P P ω = düşey açı µ =eğim açısı ω + µ = 100 g Şekil 9 üç Boyutlu koordinat sisteminde açı tiplerinin tasviri. Trigonometrik kavramlara geçmeden
Trigonometrik Fonksiyonlar Z Z P P ω µ P O α α = yatay açı P P ω = düşey açı µ =eğim açısı ω + µ = 100 g Şekil 9 üç Boyutlu koordinat sisteminde açı tiplerinin tasviri. Trigonometrik kavramlara geçmeden
MÜHENDİSLİK ÖLÇMELERİ UYGULAMASI (HRT4362) 8. Yarıyıl
 İnşaat Fakültesi Harita Mühendisliği Bölümü Ölçme Tekniği Anabilim Dalı MÜHENDİSLİK ÖLÇMELERİ UYGULAMASI (HRT4362) 8. Yarıyıl D U L K Kredi 2 0 2 3 ECTS 2 0 2 3 UYGULAMA-1 ELEKTRONİK ALETLERİN KALİBRASYONU
İnşaat Fakültesi Harita Mühendisliği Bölümü Ölçme Tekniği Anabilim Dalı MÜHENDİSLİK ÖLÇMELERİ UYGULAMASI (HRT4362) 8. Yarıyıl D U L K Kredi 2 0 2 3 ECTS 2 0 2 3 UYGULAMA-1 ELEKTRONİK ALETLERİN KALİBRASYONU
TABAKA KAVRAMI ve V-KURALI
 Eğim Hesaplama - İki nokta arasındaki yükseklik farkının bu iki nokta arasındaki yatay uzaklığa oranına eğim denir. Yüzde veya binde olarak hesaplanır. Eğim (E)= Yükseklik farkı (h) Yatay uzaklık (L) x100
Eğim Hesaplama - İki nokta arasındaki yükseklik farkının bu iki nokta arasındaki yatay uzaklığa oranına eğim denir. Yüzde veya binde olarak hesaplanır. Eğim (E)= Yükseklik farkı (h) Yatay uzaklık (L) x100
T.C AHİ EVRAN ÜNİVERSİTESİ KAMAN MESLEK YÜKSEK OKULU ÖĞRENCİ NO: 116723072,116723072 ADI SOYADI: CELAL TUĞRUL, KADİR TUNCEL
 T.C AHİ EVRAN ÜNİVERSİTESİ KAMAN MESLEK YÜKSEK OKULU ÖĞRENCİ NO: 116723072,116723072 ADI SOYADI: CELAL TUĞRUL, KADİR TUNCEL HRT-213 ARAŞTIRMA TEKNİKLERİ VE SEMİNERİ KONU ADI: YOL APLİKASYONU KASIM, 2012
T.C AHİ EVRAN ÜNİVERSİTESİ KAMAN MESLEK YÜKSEK OKULU ÖĞRENCİ NO: 116723072,116723072 ADI SOYADI: CELAL TUĞRUL, KADİR TUNCEL HRT-213 ARAŞTIRMA TEKNİKLERİ VE SEMİNERİ KONU ADI: YOL APLİKASYONU KASIM, 2012
ÖLÇME BİLGİSİ UZUNLUKLARIN ÖLÇÜLMESİ DİK İNME VE ÇIKMA İŞLEMLERİ VE ARAÇLARI
 ÖLÇME BİLGİSİ UZUNLUKLARIN ÖLÇÜLMESİ DİK İNME VE ÇIKMA İŞLEMLERİ VE ARAÇLARI Doç. Dr. Alper Serdar ANLI 3.Hafta UZUNLUK ÖLÇME ARAÇLARI VE UZUNLUKLARIN ÖLÇÜLMESİ Ölçme Mesafe Açı Yatay (Uzunluk) Düşey (Yükseklik)
ÖLÇME BİLGİSİ UZUNLUKLARIN ÖLÇÜLMESİ DİK İNME VE ÇIKMA İŞLEMLERİ VE ARAÇLARI Doç. Dr. Alper Serdar ANLI 3.Hafta UZUNLUK ÖLÇME ARAÇLARI VE UZUNLUKLARIN ÖLÇÜLMESİ Ölçme Mesafe Açı Yatay (Uzunluk) Düşey (Yükseklik)
İnşaat Mühendisliğine Giriş İNŞ-101. Yrd.Doç.Dr. Özgür Lütfi Ertuğrul
 İnşaat Mühendisliğine Giriş İNŞ-101 Yrd.Doç.Dr. Özgür Lütfi Ertuğrul Ölçme Bilgisine Giriş Haritaların ve Ölçme Bilgisinin Kullanım Alanları Ölçmeler sonucunda üretilen haritalar ve planlar pek çok mühendislik
İnşaat Mühendisliğine Giriş İNŞ-101 Yrd.Doç.Dr. Özgür Lütfi Ertuğrul Ölçme Bilgisine Giriş Haritaların ve Ölçme Bilgisinin Kullanım Alanları Ölçmeler sonucunda üretilen haritalar ve planlar pek çok mühendislik
Şekil 3.1 Yatay doğrultu ve düşey açı
 BÖLÜM 3 DOĞRULTU ÖLÇÜMÜ Kavramsal Kazanımlar: Yatay doğrultu ve düşey açı kavramları ile açı ölçme yöntemleri ve donanımları Uygulamalar: Silsile yöntemi ile yatay doğrultu ölçümü Düşey açı ölçümü 3.1
BÖLÜM 3 DOĞRULTU ÖLÇÜMÜ Kavramsal Kazanımlar: Yatay doğrultu ve düşey açı kavramları ile açı ölçme yöntemleri ve donanımları Uygulamalar: Silsile yöntemi ile yatay doğrultu ölçümü Düşey açı ölçümü 3.1
ÖLÇME BİLGİSİ. PDF created with FinePrint pdffactory trial version http://www.fineprint.com. Tanım
 ÖLÇME BİLGİSİ Dersin Amacı Öğretim Üyeleri Ders Programı Sınav Sistemi Ders Devam YRD. DOÇ. DR. HAKAN BÜYÜKCANGAZ ÖĞR.GÖR.DR. ERKAN YASLIOĞLU Ders Programı 1. Ölçme Bilgisi tanım, kapsamı, tarihçesi. 2.
ÖLÇME BİLGİSİ Dersin Amacı Öğretim Üyeleri Ders Programı Sınav Sistemi Ders Devam YRD. DOÇ. DR. HAKAN BÜYÜKCANGAZ ÖĞR.GÖR.DR. ERKAN YASLIOĞLU Ders Programı 1. Ölçme Bilgisi tanım, kapsamı, tarihçesi. 2.
TOPOĞRAFYA Temel Ödevler / Poligonasyon
 TOPOĞRAFYA Temel Ödevler / Poligonasyon Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Temel Ödevler / Poligonasyon Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
YÜKSEKLİK ÖLÇMELERİ(NİVELMAN) Öğr. Grv. Çağrı URFALI
 YÜKSEKLİK ÖLÇMELERİ(NİVELMAN) Öğr. Grv. Çağrı URFALI Geometrik nivelmanda noktalar arasındaki yükseklik farkları, bu noktaların yatay bir düzleme olan düşey uzaklıkları ölçülerek, bunların farkı alınmak
YÜKSEKLİK ÖLÇMELERİ(NİVELMAN) Öğr. Grv. Çağrı URFALI Geometrik nivelmanda noktalar arasındaki yükseklik farkları, bu noktaların yatay bir düzleme olan düşey uzaklıkları ölçülerek, bunların farkı alınmak
Şekil. Yatay doğrultu ve düşey açı
 1. Doğrultu ve Açı Kavramları Noktaların konumları (x,y,z) çoğunlukla doğrultu ve uzunluk ölçmesiyle belirlenir. Deniz yüzeyinden farklı yükseklikte olan A, B, C gibi üç nokta arasında üç çeşit açı vardır.
1. Doğrultu ve Açı Kavramları Noktaların konumları (x,y,z) çoğunlukla doğrultu ve uzunluk ölçmesiyle belirlenir. Deniz yüzeyinden farklı yükseklikte olan A, B, C gibi üç nokta arasında üç çeşit açı vardır.
YÜKSEKLİKLERİN ÖLÇÜLMESİ NİVELMAN
 YÜKSEKLİKLERİN ÖLÇÜLMESİ NİVELMAN Yeryüzü noktalarının karaların altında da devam ettiği varsayılan ortalama deniz yüzeyinden ( karşılaştırma yüzeyi) olan düşey uzaklığına yükseltisi, herhangi bir noktadan
YÜKSEKLİKLERİN ÖLÇÜLMESİ NİVELMAN Yeryüzü noktalarının karaların altında da devam ettiği varsayılan ortalama deniz yüzeyinden ( karşılaştırma yüzeyi) olan düşey uzaklığına yükseltisi, herhangi bir noktadan
Şekil-1: Teodolit ve Kutusu
 Bir istasyon Noktasında Teodoliti ölçmelere hazır hale getirmenin PÜFF noktaları Giriş Prof.Dr.Cengizhan İpbüker Teodolitin sehpa üzerinde bir istasyon noktası üzerine kurulup ölçmelere hazır hale getirilmesi
Bir istasyon Noktasında Teodoliti ölçmelere hazır hale getirmenin PÜFF noktaları Giriş Prof.Dr.Cengizhan İpbüker Teodolitin sehpa üzerinde bir istasyon noktası üzerine kurulup ölçmelere hazır hale getirilmesi
ORMANCILIKTA ÖLÇME, HARİTA VE KADASTRO DERSİ UYGULAMA FÖYÜ. HAZIRLAYANLAR Yrd. Doç. Dr. Saliha ÜNVER OKAN Arş. Gör.
 ORMANCILIKTA ÖLÇME, HARİTA VE KADASTRO DERSİ UYGULAMA FÖYÜ HAZIRLAYANLAR Yrd. Doç. Dr. Saliha ÜNVER OKAN Arş. Gör. Taha Yasin HATAY Trabzon, 2015 UYGULAMA-1: BASİT EL ALETLERİ KULLANILARAK TEMEL ÖLÇÜMLER
ORMANCILIKTA ÖLÇME, HARİTA VE KADASTRO DERSİ UYGULAMA FÖYÜ HAZIRLAYANLAR Yrd. Doç. Dr. Saliha ÜNVER OKAN Arş. Gör. Taha Yasin HATAY Trabzon, 2015 UYGULAMA-1: BASİT EL ALETLERİ KULLANILARAK TEMEL ÖLÇÜMLER
ARAZİ ÖLÇMELERİ. Koordinat sistemleri. Kartezyen koordinat sistemi
 Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
KALINLIK VE DERİNLİK HESAPLAMALARI
 KALINLIK VE DERİNLİK HESAPLAMALARI Herhangi bir düzlem üzerinde doğrultuya dik olmayan düşey bir düzlem üzerinde ölçülen açıdır Görünür eğim açısı her zaman gerçek eğim açısından küçüktür Görünür eğim
KALINLIK VE DERİNLİK HESAPLAMALARI Herhangi bir düzlem üzerinde doğrultuya dik olmayan düşey bir düzlem üzerinde ölçülen açıdır Görünür eğim açısı her zaman gerçek eğim açısından küçüktür Görünür eğim
Tanımlar, Geometrik ve Matemetiksel Temeller. Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ. JDF329 Fotogrametri I Ders Notu
 FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İzdüşüm merkezi(o):
FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İzdüşüm merkezi(o):
MÜHENDİSLİK ÖLÇMELERİ UYGULAMASI (HRT4362) 8. Yarıyıl
 İnşaat Fakültesi Harita Mühendisliği Bölümü Ölçme Tekniği Anabilim alı MÜHENİSLİK ÖLÇMELERİ UYGULAMASI (HRT436) 8. Yarıyıl U L K Kredi 3 ECTS 3 UYGULAMA-5 ELEKTRONİK ALETLERİN KALİBRASYONU Prof.r.Engin
İnşaat Fakültesi Harita Mühendisliği Bölümü Ölçme Tekniği Anabilim alı MÜHENİSLİK ÖLÇMELERİ UYGULAMASI (HRT436) 8. Yarıyıl U L K Kredi 3 ECTS 3 UYGULAMA-5 ELEKTRONİK ALETLERİN KALİBRASYONU Prof.r.Engin
Fotogrametrinin Optik ve Matematik Temelleri
 Fotogrametrinin Optik ve Matematik Temelleri Resim düzlemi O : İzdüşüm (projeksiyon ) merkezi P : Arazi noktası H : Asal nokta N : Nadir noktası c : Asal uzaklık H OH : Asal eksen (Alım ekseni) P OP :
Fotogrametrinin Optik ve Matematik Temelleri Resim düzlemi O : İzdüşüm (projeksiyon ) merkezi P : Arazi noktası H : Asal nokta N : Nadir noktası c : Asal uzaklık H OH : Asal eksen (Alım ekseni) P OP :
JDF/GEO 120 ÖLÇME BİLGİSİ II POLİGONASYON
 JDF/GEO 120 ÖLÇME BİLGİSİ II POLİGONASYON Dr. Öğr. Üyesi HÜSEYİN KEMALDERE Sınıflandırma (BÖHHBÜY (26.06.2018)-Md:8) Bu yönetmelik kapsamındaki kontrol noktalarının hiyerarşik sınıflandırılması aşağıda
JDF/GEO 120 ÖLÇME BİLGİSİ II POLİGONASYON Dr. Öğr. Üyesi HÜSEYİN KEMALDERE Sınıflandırma (BÖHHBÜY (26.06.2018)-Md:8) Bu yönetmelik kapsamındaki kontrol noktalarının hiyerarşik sınıflandırılması aşağıda
Ölçme Bilgisi DERS 9-10. Hacim Hesapları. Kaynak: İ.ASRİ (Gümüşhane Ü) T. FİKRET HORZUM( AÜ )
 Ölçme Bilgisi DERS 9-10 Hacim Hesapları Kaynak: İ.ASRİ (Gümüşhane Ü) T. FİKRET HORZUM( AÜ ) Büyük inşaatlarda, yol ve kanal çalışmalarında kazılacak toprak miktarının hesaplanması, maden işletmelerinde
Ölçme Bilgisi DERS 9-10 Hacim Hesapları Kaynak: İ.ASRİ (Gümüşhane Ü) T. FİKRET HORZUM( AÜ ) Büyük inşaatlarda, yol ve kanal çalışmalarında kazılacak toprak miktarının hesaplanması, maden işletmelerinde
YÜKSEKLİKLERİN ÖLÇÜLMESİ NİVELMAN
 YÜKSEKLİKLERİN ÖLÇÜLMESİ NİVELMAN Yeryüzü noktalarının karaların altında da devam ettiği varsayılan ortalama deniz yüzeyinden ( karşılaştırma yüzeyi) olan düşey uzaklığına yükseltisi, herhangi bir noktadan
YÜKSEKLİKLERİN ÖLÇÜLMESİ NİVELMAN Yeryüzü noktalarının karaların altında da devam ettiği varsayılan ortalama deniz yüzeyinden ( karşılaştırma yüzeyi) olan düşey uzaklığına yükseltisi, herhangi bir noktadan
TOPOGRAFYA DERS NOTLARI 1. ÖLÇÜ BİRİMLERİ- ÖLÇEK KAVRAMI
 TOPOGRAFYA DERS NOTLARI 1. ÖLÇÜ BİRİMLERİ- ÖLÇEK KAVRAMI Yeryüzünde bulunan veya yeryüzüne yakın dogal ve yapay noktalar ile bunların oluşturduğu cisimlerin belirli bir karşılaştırma düzlem veya yüzeyine
TOPOGRAFYA DERS NOTLARI 1. ÖLÇÜ BİRİMLERİ- ÖLÇEK KAVRAMI Yeryüzünde bulunan veya yeryüzüne yakın dogal ve yapay noktalar ile bunların oluşturduğu cisimlerin belirli bir karşılaştırma düzlem veya yüzeyine
ÖLÇME UYGULAMASI YÖNERGESİ YILDIZ TEKNİK ÜNİVERSİTESİ HARİTA MÜHENDİSLİĞİ BÖLÜMÜ ÖLÇME TEKNİĞİ ANABİLİM DALI. Ders Koordinatörü: Prof.Dr.
 YILDIZ TEKNİK ÜNİVERSİTESİ HARİTA MÜHENDİSLİĞİ BÖLÜMÜ ÖLÇME TEKNİĞİ ANABİLİM DALI ÖLÇME UYGULAMASI YÖNERGESİ Ders Koordinatörü: Prof.Dr. Engin GÜLAL 2015-2016 Güz Yarıyılı GRUP BİLGİLERİ Grup No Kapasite
YILDIZ TEKNİK ÜNİVERSİTESİ HARİTA MÜHENDİSLİĞİ BÖLÜMÜ ÖLÇME TEKNİĞİ ANABİLİM DALI ÖLÇME UYGULAMASI YÖNERGESİ Ders Koordinatörü: Prof.Dr. Engin GÜLAL 2015-2016 Güz Yarıyılı GRUP BİLGİLERİ Grup No Kapasite
TOPOĞRAFYA. Ölçme Bilgisinin Konusu
 TOPOĞRAFYA Topoğrafya, bir arazi yüzeyinin tabii veya suni ayrıntılarının meydana getirdiği şekil. Bu şeklin kâğıt üzerinde harita ve tablo şeklinde gösterilmesiyle ilgili ölçme, hesap ve çizim işlerinin
TOPOĞRAFYA Topoğrafya, bir arazi yüzeyinin tabii veya suni ayrıntılarının meydana getirdiği şekil. Bu şeklin kâğıt üzerinde harita ve tablo şeklinde gösterilmesiyle ilgili ölçme, hesap ve çizim işlerinin
İÇİNDEKİLER BÖLÜM 1 ÖLÇME TEKNİĞİ VE HARİTA ALMA YÖNTEMLERİ
 İÇİNDEKİLER II Sayfa No: ÖNSÖZ...I İÇİNDEKİLER...III ŞEKİLLER LİSTESİ...VIII ÇİZELGELER LİSTESİ...XII EKLER LİSTESİ...XIII BÖLÜM 1 ÖLÇME TEKNİĞİ VE HARİTA ALMA YÖNTEMLERİ 1. ÖLÇME TEKNİĞİ VE HARİTA ALMA
İÇİNDEKİLER II Sayfa No: ÖNSÖZ...I İÇİNDEKİLER...III ŞEKİLLER LİSTESİ...VIII ÇİZELGELER LİSTESİ...XII EKLER LİSTESİ...XIII BÖLÜM 1 ÖLÇME TEKNİĞİ VE HARİTA ALMA YÖNTEMLERİ 1. ÖLÇME TEKNİĞİ VE HARİTA ALMA
TOPOĞRAFİK HARİTALAR VE KESİTLER
 TOPOĞRAFİK HARİTALAR VE KESİTLER Prof.Dr. Murat UTKUCU Yrd.Doç.Dr. ŞefikRAMAZANOĞLU TOPOĞRAFİK HARİTALAR VE Haritalar KESİTLER Yeryüzü şekillerini belirli bir yöntem ve ölçek dahilinde plan konumunda gösteren
TOPOĞRAFİK HARİTALAR VE KESİTLER Prof.Dr. Murat UTKUCU Yrd.Doç.Dr. ŞefikRAMAZANOĞLU TOPOĞRAFİK HARİTALAR VE Haritalar KESİTLER Yeryüzü şekillerini belirli bir yöntem ve ölçek dahilinde plan konumunda gösteren
TOPOĞRAFYA Ölçü Birimleri, Ölçek Kavramı, Ölçme Kavramı, Hata kaynakları ve Türleri, Arazi Ölçmelerine Giriş
 TOPOĞRAFYA Ölçü Birimleri, Ölçek Kavramı, Ölçme Kavramı, Hata kaynakları ve Türleri, Arazi Ölçmelerine Giriş Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI
TOPOĞRAFYA Ölçü Birimleri, Ölçek Kavramı, Ölçme Kavramı, Hata kaynakları ve Türleri, Arazi Ölçmelerine Giriş Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI
Yrd. Doç. Dr. Aycan M. MARANGOZ. BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF329 FOTOGRAMETRİ I DERSi NOTLARI
 FOTOGRAMETRİ I GEOMETRİK ve MATEMATİK TEMELLER Yrd. Doç. Dr. Aycan M. MARANGOZ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF329 FOTOGRAMETRİ I DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
FOTOGRAMETRİ I GEOMETRİK ve MATEMATİK TEMELLER Yrd. Doç. Dr. Aycan M. MARANGOZ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF329 FOTOGRAMETRİ I DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
14/05/2004 31/05/2004
 ARAZİ ÇALIŞMASI 1 EKİP - 11 14/05/2004 31/05/2004 2 İçindekiler Ekip Çalışması Ekip Elemanları Donanım Yapılan İşlemler Maliyet Sonuç 3 Ekip Çalışması Bir işin gerçekleştirilebilmesi için değişik beceri
ARAZİ ÇALIŞMASI 1 EKİP - 11 14/05/2004 31/05/2004 2 İçindekiler Ekip Çalışması Ekip Elemanları Donanım Yapılan İşlemler Maliyet Sonuç 3 Ekip Çalışması Bir işin gerçekleştirilebilmesi için değişik beceri
ELEKTRİK-ELEKTRONİK ÖLÇME TESİSAT GRUBU TEMRİN-1-Mikrometre ve Kumpas Kullanarak Kesit ve Çap Ölçmek
 ELEKTRİK-ELEKTRONİK ÖLÇME TESİSAT GRUBU TEMRİN-1-Mikrometre ve Kumpas Kullanarak Kesit ve Çap Ölçmek Amaç: Mikrometre ve kumpas kullanarak kesit ve çap ölçümünü yapabilir. Kullanılacak Malzemeler: 1. Yankeski
ELEKTRİK-ELEKTRONİK ÖLÇME TESİSAT GRUBU TEMRİN-1-Mikrometre ve Kumpas Kullanarak Kesit ve Çap Ölçmek Amaç: Mikrometre ve kumpas kullanarak kesit ve çap ölçümünü yapabilir. Kullanılacak Malzemeler: 1. Yankeski
PROJE AŞAMALARI : Karayolu Geçkisi (Güzergahı Araştırması, Plan ve Boykesit):
 Bartın Üniversitesi Ad Soyad : Mühendislik Fakültesi Numara : İnşaat Mühendisliği Bölümü Pafta No : KONU : INS36 ULAŞTIRMA II (PROJE) DERSİ P R O J E V E R İ L E R İ /2000 ölçekli tesviye (eşyükselti)
Bartın Üniversitesi Ad Soyad : Mühendislik Fakültesi Numara : İnşaat Mühendisliği Bölümü Pafta No : KONU : INS36 ULAŞTIRMA II (PROJE) DERSİ P R O J E V E R İ L E R İ /2000 ölçekli tesviye (eşyükselti)
Ölçü Hataları Hatasız ölçü olmaz
 Ölçü Hataları Yeryüzünde ister bir kenar, ister bir açı birkaç kez ölçüldüğünde her ölçü değeri arasında az çok farkların olduğu görülür. Aynı büyüklüğe ait yapılan her geometrik veya fiziksel ölçünün
Ölçü Hataları Yeryüzünde ister bir kenar, ister bir açı birkaç kez ölçüldüğünde her ölçü değeri arasında az çok farkların olduğu görülür. Aynı büyüklüğe ait yapılan her geometrik veya fiziksel ölçünün
Yatay Kontrol Noktaları
 Yatay Kontrol Noktaları Bir alanın üzerindeki detaylarla birlikte harita veya planının yapılabilmesi için yeryüzünde konumu sabit ve koordinat değeri belli olan noktalara ihtiyaç vardır. Bu noktalara yatay
Yatay Kontrol Noktaları Bir alanın üzerindeki detaylarla birlikte harita veya planının yapılabilmesi için yeryüzünde konumu sabit ve koordinat değeri belli olan noktalara ihtiyaç vardır. Bu noktalara yatay
ARAZIDE NOKTALARIN ISARETLENMESI- ARAZI ISLERI
 ARAZIDE NOKTALARIN ISARETLENMESI- ARAZI ISLERI Arazide açi ve uzunluk ölçmelerinin yapilabilmesi için noktalara ve bu noktalarla belirlenen dogrulara gereksinim vardir. Noktalar görünebilir olmali ve arandiklarinda
ARAZIDE NOKTALARIN ISARETLENMESI- ARAZI ISLERI Arazide açi ve uzunluk ölçmelerinin yapilabilmesi için noktalara ve bu noktalarla belirlenen dogrulara gereksinim vardir. Noktalar görünebilir olmali ve arandiklarinda
Topografya (Ölçme Bilgisi) Prof.Dr.Mustafa KARAŞAHİN
 Topografya (Ölçme Bilgisi) Prof.Dr.Mustafa KARAŞAHİN Topografya (Surveying) Nedir? Topografya geleneksel olarak, Dünya yüzeyinin üzerindeki, üstündeki veya altındaki noktalarının rölatif konumlarını belirleyen
Topografya (Ölçme Bilgisi) Prof.Dr.Mustafa KARAŞAHİN Topografya (Surveying) Nedir? Topografya geleneksel olarak, Dünya yüzeyinin üzerindeki, üstündeki veya altındaki noktalarının rölatif konumlarını belirleyen
ARAZİ ÖLÇMELERİ. Coğrafik Objenin Alan Bilgisinin Bulunması
 Coğrafik Objenin Alan Bilgisinin Bulunması Bina, kadastro / İmar parseli, göl gibi kapalı alan obje tipinde ki coğrafik objelere ait en önemli bilgi alandır. Coğrafik objelerin alan bilgileri farklı yollarla
Coğrafik Objenin Alan Bilgisinin Bulunması Bina, kadastro / İmar parseli, göl gibi kapalı alan obje tipinde ki coğrafik objelere ait en önemli bilgi alandır. Coğrafik objelerin alan bilgileri farklı yollarla
ÖLÇME UYGULAMASI YÖNERGESİ YILDIZ TEKNİK ÜNİVERSİTESİ HARİTA MÜHENDİSLİĞİ BÖLÜMÜ ÖLÇME TEKNİĞİ ANABİLİM DALI
 YILDIZ TEKNİK ÜNİVERSİTESİ HARİTA MÜHENDİSLİĞİ BÖLÜMÜ ÖLÇME TEKNİĞİ ANABİLİM DALI ÖLÇME UYGULAMASI YÖNERGESİ Ders Koordinatörler: Doç.Dr.Engin GÜLAL Doç.Dr.Atınç PIRTI 2014-2015 Güz Yarıyılı GRUP BİLGİLERİ
YILDIZ TEKNİK ÜNİVERSİTESİ HARİTA MÜHENDİSLİĞİ BÖLÜMÜ ÖLÇME TEKNİĞİ ANABİLİM DALI ÖLÇME UYGULAMASI YÖNERGESİ Ders Koordinatörler: Doç.Dr.Engin GÜLAL Doç.Dr.Atınç PIRTI 2014-2015 Güz Yarıyılı GRUP BİLGİLERİ
Jeodezi
 1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
APLİKASYON VE İP İSKELESİ
 APLİKASYON VE İP İSKELESİ Celal Bayar Üniversitesi Turgutlu Meslek Yüksekokulu İnşaat Bölümü Öğretim Görevlisi Tekin TEZCAN İnşaat Yüksek Mühendisi APLİKASYON Yapılan imar planlarını, yapı projelerini,
APLİKASYON VE İP İSKELESİ Celal Bayar Üniversitesi Turgutlu Meslek Yüksekokulu İnşaat Bölümü Öğretim Görevlisi Tekin TEZCAN İnşaat Yüksek Mühendisi APLİKASYON Yapılan imar planlarını, yapı projelerini,
HARİTA BİLGİSİ ve TOPOĞRAFİK HARİTALAR
 HARİTA BİLGİSİ ve TOPOĞRAFİK HARİTALAR Harita nedir? Yeryüzünün veya bir parçasının belli bir orana göre küçültülerek ve belirli işaretler kullanılarak yatay düzlem üzerinde gösterilmesine harita adı verilir.
HARİTA BİLGİSİ ve TOPOĞRAFİK HARİTALAR Harita nedir? Yeryüzünün veya bir parçasının belli bir orana göre küçültülerek ve belirli işaretler kullanılarak yatay düzlem üzerinde gösterilmesine harita adı verilir.
HARİTA BİLGİSİ. Produced by M. EKER 1
 HARİTA BİLGİSİ Produced by M. EKER 1 ÖLÇÜ BİRİMLERİ Uzunluk, Alan ve AçıA Ölçü Birimleri Herhangi bir objenin ölçülmesinden, aynı nitelikteki objeden birim olarak belirlenen bir büyüklükle kle kıyaslanmask
HARİTA BİLGİSİ Produced by M. EKER 1 ÖLÇÜ BİRİMLERİ Uzunluk, Alan ve AçıA Ölçü Birimleri Herhangi bir objenin ölçülmesinden, aynı nitelikteki objeden birim olarak belirlenen bir büyüklükle kle kıyaslanmask
3. TABAKA KAVRAMI ve V-KURALI
 1 3. T VRMI ve V-URLI Tabaka nedir? lt ve üst sınırlarıyla bir diğerinden ayrılan, kendine has özellikleri olan, sabit hidrodinamik koşullar altında çökelmiş, 1 cm den daha kalın, en küçük litostratigrafi
1 3. T VRMI ve V-URLI Tabaka nedir? lt ve üst sınırlarıyla bir diğerinden ayrılan, kendine has özellikleri olan, sabit hidrodinamik koşullar altında çökelmiş, 1 cm den daha kalın, en küçük litostratigrafi
Sayısal Nivolar. Turgut UZEL* - Engin GÜLAL**
 Sayısal Nivolar Turgut UZEL* - Engin GÜLAL** ÖZET Bu çalışmada, Leicha firmasının ürünü olan Wild NA 2000 ve NA 3000 sayısal nivolarının çalışma ilkesi, klasik cm bölümlü miraların yerine kullanılmaya
Sayısal Nivolar Turgut UZEL* - Engin GÜLAL** ÖZET Bu çalışmada, Leicha firmasının ürünü olan Wild NA 2000 ve NA 3000 sayısal nivolarının çalışma ilkesi, klasik cm bölümlü miraların yerine kullanılmaya
2 Hata Hesabı. Hata Nedir? Mutlak Hata. Bağıl Hata
 Hata Hesabı Hata Nedir? Herhangi bir fiziksel büyüklüğün ölçülen değeri ile gerçek değeri arasındaki farka hata denir. Ölçülen bir fiziksel büyüklüğün sayısal değeri, yapılan deneysel hatalardan dolayı
Hata Hesabı Hata Nedir? Herhangi bir fiziksel büyüklüğün ölçülen değeri ile gerçek değeri arasındaki farka hata denir. Ölçülen bir fiziksel büyüklüğün sayısal değeri, yapılan deneysel hatalardan dolayı
ÇATI MAKASINA GELEN YÜKLER
 ÇATI MAKASINA GELEN YÜKLER Bir yapıyı dış etkilere karşı koruyan taşıyıcı sisteme çatı denir. Belirli aralıklarla yerleştirilen çatı makaslarının, yatay taşıyıcı eleman olan aşıklarla birleştirilmesi ile
ÇATI MAKASINA GELEN YÜKLER Bir yapıyı dış etkilere karşı koruyan taşıyıcı sisteme çatı denir. Belirli aralıklarla yerleştirilen çatı makaslarının, yatay taşıyıcı eleman olan aşıklarla birleştirilmesi ile
Yaşar EREN-2003. Altınekin-Konya. Altınekin-Konya. Meydanköy-Konya
 Altınekin-Konya Altınekin-Konya Meydanköy-Konya Yaşar EREN-2003 Tabakalı kayaçlar homojen olmayan gerilmelerle kıvrımlanırlar. Kıvrımlar kayaç deformasyonunun en göze çarpan yapılarındandır. Meydanköy-Konya
Altınekin-Konya Altınekin-Konya Meydanköy-Konya Yaşar EREN-2003 Tabakalı kayaçlar homojen olmayan gerilmelerle kıvrımlanırlar. Kıvrımlar kayaç deformasyonunun en göze çarpan yapılarındandır. Meydanköy-Konya
YOL PROJELERİNDE YATAY KURPTA YAPILACAK KÜBAJ HESABININ YENİDEN DÜZENLENMESİ
 YOL PROJELERİNDE YATAY KURPTA YAPILACAK KÜBAJ HESABININ YENİDEN DÜZENLENMESİ Yrd.Doc.Dr. Hüseyin İNCE ÖZET Yol projelerinde yatay kurpta enkesitler arasında yapılacak kübaj hesabında, kurbun eğrilik durumu
YOL PROJELERİNDE YATAY KURPTA YAPILACAK KÜBAJ HESABININ YENİDEN DÜZENLENMESİ Yrd.Doc.Dr. Hüseyin İNCE ÖZET Yol projelerinde yatay kurpta enkesitler arasında yapılacak kübaj hesabında, kurbun eğrilik durumu
Fotogrametride işlem adımları
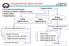 Fotogrametride işlem adımları Uçuş planının hazırlanması Arazide yer kontrol noktalarının tesisi Resim çekimi Değerlendirme Analitik değerlendirme Dijital değerlendirme Değerlendirme Analog değerlendirme
Fotogrametride işlem adımları Uçuş planının hazırlanması Arazide yer kontrol noktalarının tesisi Resim çekimi Değerlendirme Analitik değerlendirme Dijital değerlendirme Değerlendirme Analog değerlendirme
5. ÜNİTE İZDÜŞÜMÜ VE GÖRÜNÜŞ ÇIKARMA
 5. ÜNİTE İZDÜŞÜMÜ VE GÖRÜNÜŞ ÇIKARMA KONULAR 1. İzdüşüm Metodları 2. Temel İzdüşüm Düzlemleri 3. Cisimlerin İzdüşümleri 4. Görünüş Çıkarma BU ÜNİTEYE NEDEN ÇALIŞMALIYIZ? İz düşümü yöntemlerini, Görünüş
5. ÜNİTE İZDÜŞÜMÜ VE GÖRÜNÜŞ ÇIKARMA KONULAR 1. İzdüşüm Metodları 2. Temel İzdüşüm Düzlemleri 3. Cisimlerin İzdüşümleri 4. Görünüş Çıkarma BU ÜNİTEYE NEDEN ÇALIŞMALIYIZ? İz düşümü yöntemlerini, Görünüş
1- AYNALI STEREOSKOP UYGULAMASI. X (Uçuş Doğrultusu) H1 H1. 1. resim (sol) 2. resim (sağ) KARTON ÜZERİNDEKİ İŞLEMLER D 1 D 2
 - YNLI STEREOSKO UYGULMSI KRTON ÜZERİNDEKİ İŞLEMLER D D 70 cm 6 cm X (Uçuş Doğrultusu) 00 cm Yukardaki bilgiler karton üzerine çizilir. Kartonun sağ alt köşesine çalışan kişilerin no-adı soadı, resim numaraları,
- YNLI STEREOSKO UYGULMSI KRTON ÜZERİNDEKİ İŞLEMLER D D 70 cm 6 cm X (Uçuş Doğrultusu) 00 cm Yukardaki bilgiler karton üzerine çizilir. Kartonun sağ alt köşesine çalışan kişilerin no-adı soadı, resim numaraları,
İNŞAAT TEKNOLOJİSİ ÖNLİSANS EĞİTİMİNDE HARİTACILIĞIN YERİ. Orhan KURT 1
 İNŞAAT TEKNOLOJİSİ ÖNLİSANS EĞİTİMİNDE HARİTACILIĞIN YERİ Orhan KURT 1 1 Kocaeli Üniversitesi, Mühendislik Fakültesi, Harita Mühendisliği Bölümü, Kocaeli, [email protected] Özet Bir inşaat teknikeri haritacılık
İNŞAAT TEKNOLOJİSİ ÖNLİSANS EĞİTİMİNDE HARİTACILIĞIN YERİ Orhan KURT 1 1 Kocaeli Üniversitesi, Mühendislik Fakültesi, Harita Mühendisliği Bölümü, Kocaeli, [email protected] Özet Bir inşaat teknikeri haritacılık
ÖLÇME BİLGİSİ. Sunu 1- Yatay Ölçme. Yrd. Doç. Dr. Muhittin İNAN & Arş. Gör. Hüseyin YURTSEVEN
 ÖÇME BİGİİ unu - atay Ölçme rd. Doç. Dr. Muhittin İNAN & Arş. Gör. Hüseyin URTEVEN COĞRAFİ BİGİ İTEMİNİ OUŞTURABİMEK İÇİN BİGİ TOPAMA ÖNTEMERİ ATA ÖÇMEER (,) ATA AÇIAR VE MEAFEERİN ÖÇÜMEİ ERE ÖÇMEER DÜŞE
ÖÇME BİGİİ unu - atay Ölçme rd. Doç. Dr. Muhittin İNAN & Arş. Gör. Hüseyin URTEVEN COĞRAFİ BİGİ İTEMİNİ OUŞTURABİMEK İÇİN BİGİ TOPAMA ÖNTEMERİ ATA ÖÇMEER (,) ATA AÇIAR VE MEAFEERİN ÖÇÜMEİ ERE ÖÇMEER DÜŞE
FOTOYORUMLAMA UZAKTAN ALGILAMA
 FOTOYORUMLAMA VE UZAKTAN ALGILAMA (Photointerpretation and Remote Sensing) 1 Ders İçeriği Hava fotoğrafının tanımı Fotogrametrinin geometrik ilkeleri Fotogrametride fotoğrafik temel ilkeler Stereoskopik
FOTOYORUMLAMA VE UZAKTAN ALGILAMA (Photointerpretation and Remote Sensing) 1 Ders İçeriği Hava fotoğrafının tanımı Fotogrametrinin geometrik ilkeleri Fotogrametride fotoğrafik temel ilkeler Stereoskopik
ARAZİ ÖLÇMELERİ. Temel Ödev I: Koordinatları belirli iki nokta arasında ki yatay mesafenin
 Temel ödevler Temel ödevler, konum değerlerinin bulunması ve aplikasyon işlemlerine dair matematiksel ve geometrik hesaplamaları içeren yöntemlerdir. öntemlerin isimleri genelde temel ödev olarak isimlendirilir.
Temel ödevler Temel ödevler, konum değerlerinin bulunması ve aplikasyon işlemlerine dair matematiksel ve geometrik hesaplamaları içeren yöntemlerdir. öntemlerin isimleri genelde temel ödev olarak isimlendirilir.
Yapılma Yöntemleri: » Arazi ölçmeleri (Takeometri)» Hava fotoğrafları (Fotoğrametri) TOPOĞRAFİK KONTURLAR
 TOPOĞRAFİK HARİTALAR EŞ YÜKSELTİ EĞRİLERİ TOPOĞRAFİK HARİTALAR Yapılma Yöntemleri:» Arazi ölçmeleri (Takeometri)» Hava fotoğrafları (Fotoğrametri) HARİTALAR ve ENİNE KESİT HARİTALAR Yeryüzü şekillerini
TOPOĞRAFİK HARİTALAR EŞ YÜKSELTİ EĞRİLERİ TOPOĞRAFİK HARİTALAR Yapılma Yöntemleri:» Arazi ölçmeleri (Takeometri)» Hava fotoğrafları (Fotoğrametri) HARİTALAR ve ENİNE KESİT HARİTALAR Yeryüzü şekillerini
