A; e A; A kümelerini tan mlay n z. (x) = fb 2 B : x 2 Bg
|
|
|
- Osman Atay
- 8 yıl önce
- İzleme sayısı:
Transkript
1 Genel Topolojiye Giriş I Ara S nav Sorular 30 Kas m (X; T ) bir topolojik uzay ve A X olsun. 2 (a) Ikinci say labilir topolojik uzay ne demektir? Tan mlay n z. A; e A; A kümelerini tan mlay n z. (b) Ikinci say labilir her topolojik uzay n ayr labilir oldu¼gunu ispatlay n z. 3 (a) Komşuluklar taban ne demektir? Tan mlay n z. (b) (X; T ) bir topolojik uzay ve B T olsun. B ailesinin T topolojisinin bir taban olmas için gerekli ve yeterli koşul, her x 2 X için (x) = fb 2 B : x 2 Bg ailesinin x noktas n n bir komşuluklar taban olmas d r. Ispatlay n z. 4 (a) Birinci say labilir topolojik uzay ne demektir? Tan mlay n z. (b) Her metrik uzay birinci say labilir bir topolojik uzayd r. Ispatlay n z. Her soru 25 puan ve süre 80 dakikad r.
2 Genel Topolojiye Giriş I Final S nav Sorular 14 Ocak X = fa; b; cg kümesi üzerinde ayr k topoloji ve ayr k olmayan topoloji d ş nda T 0 = T koşulunu sa¼glayan bir T topolojisi tan mlay n z. 2 Bir (X; T ) topolojik uzay nda her A X için A c (A c ) 3 Birinci say labilir her topolojik uzay ikinci say labilir midir? Nedenleriyle aç klay n z. 4 R üzerindeki üst limit topolojisinin standart topolojiden daha ince 5 (X; T X ) bir topolojik uzay ve Y boş olmayan bir küme olsun. Y üzerinde, her f : (X; T X )! (Y; T Y ) fonksiyonunu sürekli yapan bir T Y 6 Zay f topolojiyi tan mlay n z. topolojisi bulunuz. 7 Ayr labilir bir topolojik uzay n her alt uzay ayr labilirdir. Ispatlay n z. (???????) 8 (X; T X ) ve (Y; T Y ) birer topolojik uzay olsunlar. (X Y; P) çarp m uzay n n bir taban n yaz n z. 9 (X; T X ) ve (Y; T Y ) birer topolojik uzay olsunlar. (X Y; P) çarp m uzay nda her A X ve her B Y (A eşitli¼gi sa¼glan r m? Nedenleriyle aç klay n z. 10 (X; T X ) ve (Y; T Y ) birer topolojik uzay, x 2 X; y 2 Y ve z = (x; y) olsun. (x) x noktas n n bir komşuluklar taban ve (y) y noktas n n bir komşuluklar taban ise (z) := fu W : U 2 (x) ; W 2 (y)g ailesi (X Y; P) çarp m uzay nda z noktas n n bir komşuluklar taban olur. Ispatlay n z. Her soru 10 puan ve süre 60 dakikad r.
3 Genel Topolojiye Giriş I Final S nav Sorular (2. Ö¼gretim) 14 Ocak X = fa; b; cg ve A = fa; cg olsun. X kümesi üzerinde A 2 T ve A 2 T 0 olacak şekilde bir T topolojisi tan mlay n z. 2 Bir (X; T ) topolojik uzay nda her A X için A c (A c ) 3 Ayr labilir her topolojik uzay ikinci say labilir midir? Nedenleriyle aç klay n z. 4 R üzerindeki alt limit topolojisinin standart topolojiden daha ince 5 (Y; T Y ) bir topolojik uzay ve X boş olmayan bir küme olsun. X üzerinde, her f : (X; T X )! (Y; T Y ) fonksiyonunu sürekli yapan bir T X topolojisi bulunuz. 6 Alt uzay topolojisini tan mlay n z. 7 Ikinci say labilir bir topolojik uzay n her alt uzay ikinci say labilirdir. Ispatlay n z. 8 (X; T X ) ve (Y; T Y ) birer topolojik uzay olsunlar. (X Y; P) çarp m uzay n n bir alt taban n yaz n z. 9 (X; T X ) ve (Y; T Y ) birer topolojik uzay olsunlar. (X Y; P) çarp m uzay nda her A X ve her B Y için (A B) = e A e B eşitli¼gi sa¼glan r m? Nedenleriyle aç klay n z. 10 (X; T X ) ve (Y; T Y ) birer topolojik uzay, x 2 X; y 2 Y ve z = (x; y) olsun. V 2 N (x) ve W 2 N (y) ise (X Y; P) çarp m uzay nda V W 2 N (z) olur. Ispatlay n z. Her soru 10 puan ve süre 60 dakikad r.
4 Genel Topolojiye Giriş I Bütünleme S nav Sorular 2 Şubat X = fa; b; cg ve A = fb; cg olsun. X kümesi üzerinde A 2 T ve A 2 T 0 olacak şekilde bir T topolojisi tan mlay n z. 2 Bir (X; T ) topolojik uzay nda her A X için A c (A c ) 3 Ayr labilir her topolojik uzay ikinci say labilir midir? Nedenleriyle aç klay n z. 4 Birinci say labilir her topolojik uzay ikinci say labilir midir? Nedenleriyle aç klay n z. 5 (Y; T Y ) bir topolojik uzay ve X boş olmayan bir küme olsun. X üzerinde, her f : (X; T X )! (Y; T Y ) fonksiyonunu sürekli yapan bir T X topolojisi bulunuz. 6 Alt uzay topolojisini tan mlay n z. 7 Ikinci say labilir bir topolojik uzay n her alt uzay ikinci say labilirdir. Ispatlay n z. 8 (X; T X ) ve (Y; T Y ) birer topolojik uzay olsunlar. (X Y; P) çarp m uzay n n bir taban n yaz n z. 9 (X; T X ) ve (Y; T Y ) birer topolojik uzay olsunlar. Bu uzaylar ayr labilir ise (X Y; P) çarp m uzay da ayr labilirdir. Ispatlay n z. 10 (X; T X ) ve (Y; T Y ) birer topolojik uzay, x 2 X; y 2 Y ve z = (x; y) olsun. V 2 N (x) ve W 2 N (y) ise (X Y; P) çarp m uzay nda V W 2 N (z) olur. Ispatlay n z. Her soru 10 puan ve süre 60 dakikad r.
5 Genel Topolojiye Giriş II Ara S nav Sorular 8 Nisan (X; T ) bir topolojik uzay, (x n ) bu uzayda bir dizi ve x 2 X olsun. (x n ) dizisinin x noktas na yak nsamas ne demektir? Tan mlay n z. 2 Bir topolojik uzayda yak nsak her dizinin limiti tek olur mu? Nedenleriyle aç klay n z. 3 Topolojik uzaylarda dizilerin yetersiz kald ¼g durumlardan bir tanesini yaz n z. 4 (X; T ) bir topolojik uzay, A X ve x 2 X olsun. x 2 A ise x! x olacak şekilde bir (x ) A a¼g vard r. Ispatlay n z. 5 (X; T ) bir topolojik uzay, x 2 X ve (x) x noktas n n bir komşuluklar taban olsun. F (x) ; (x) süzgeç taban n n üretti¼gi süzgeç olmak üzere oldu¼gunu ispatlay n z. F (x) = N (x) 6 (X; T ) bir topolojik uzay, x 2 X ve F X üzerinde bir süzgeç olsun. F! x olmas ne demektir? Tan mlay n z. 7 (X; T X ) ve (Y; T Y ) birer topolojik uzay, f : X! Y bir fonksiyon ve x 2 X olsun. biçimindeki her F süzgeci için F T X! x f (F) T Y! f (x) oluyorsa f fonksiyonu x noktas nda süreklidir. Ispatlay n z. 8 T 1 uzay ve T 2 uzay kavramlar n tan mlay n z. 9 Her T 1 uzay bir T 2 uzay m d r? Nedenleriyle aç klay n z. 10 (X; T X ) ve (Y; T Y ) birer topolojik uzay olsunlar. (X Y; P) çarp m uzay bir T 2 uzay ise (X; T X ) ve (Y; T Y ) uzaylar da birer T 2 uzay olurlar. Ispatlay n z. Her soru 10 puan ve süre 60 dakikad r.
6 Genel Topolojiye Giriş II Final S nav Sorular 14 Haziran Düzenli topolojik uzay ne demektir? Tan mlay n z ve bir örnek veriniz. 2 T 3 uzay ne demektir? Tan mlay n z ve bir örnek veriniz. 3 Metrik uzay olmayan T 3 uzaylar na örnek veriniz. 4 Hangi topolojik uzaylar n kapal alt kümeleri kompaktt r? 5 Kompakt metrik uzaylarda geçerli oldu¼gu halde kompakt topolojik uzaylarda geçerli olmayan özelliklerden bir tanesini yaz n z. 6 Say labilir kompakt olan hangi topolojik uzaylar ayn zamanda dizisel kompakt olurlar? 7 (X; T X ) yerel kompakt bir topolojik uzay ve (Y; T Y ) bir topolojik uzay olsun. E¼ger, sürekli, aç k ve örten bir f : X! Y fonksiyonu varsa (Y; T Y ) uzay da yerel kompakt olur. Ispatlay n z. 8 (R; R ) topolojik uzay n n bir kompaktlaşt rmas n n [ 1; 1] ; R [ 1;1] 7: ve 8: sorular 20 şer puan, di¼ger sorular 10 ar puand r. Süre 60 dakikad r.
7 Genel Topolojiye Giriş II Final S nav Sorular ( Ikinci Ö¼gretim) 14 Haziran Normal topolojik uzay ne demektir? Tan mlay n z ve bir örnek veriniz. 2 T 4 uzay ne demektir? Tan mlay n z ve bir örnek veriniz. 3 Metrik uzay olmayan T 4 uzaylar na örnek veriniz. 4 Hangi topolojik uzaylarda kompakt alt kümeler kapal d r? 5 Kompakt metrik uzaylarda geçerli oldu¼gu halde kompakt topolojik uzaylarda geçerli olmayan özelliklerden bir tanesini yaz n z. 6 Dizisel kompakt olan hangi topolojik uzaylar ayn zamanda say labilir kompakt olurlar? 7 (X; T X ) ve (Y; T Y ) topolojik uzaylar yerel kompakt ise (X Y; P) uzay da yerel kompakt olur. Ispatlay n z. 8 (R; R ) topolojik uzay n n bir kompaktlaşt rmas n n C = f(x; y) 2 R 2 : x 2 + y 2 = 1g çemberi 7: ve 8: sorular 20 şer puan, di¼ger sorular 10 ar puand r. Süre 60 dakikad r.
8 Genel Topolojiye Giriş II Bütünleme S nav Sorular 28 Haziran T 2 uzay ne demektir? Tan mlay n z ve bir örnek veriniz. 2 Metrik uzay olmayan T 2 uzaylar na iki örnek veriniz. 3 (a) Hangi topolojik uzaylarda kompakt alt kümeler kapal d r? (b) Hangi topolojik uzaylarda kapal alt kümeler kompaktt r? 4 Kompakt metrik uzaylarda geçerli oldu¼gu halde kompakt topolojik uzaylarda geçerli olmayan özelliklerden iki tanesini yaz n z. 5 Kompaktlaşt rma ne demektir? Tan mlay n z ve bir örnek veriniz. Her soru 20 puan ve süre 60 dakikad r.
Analiz III Ara S nav Sorular 24 Kas m 2010
 Analiz III Ara S nav Sorular 24 Kas m 2010 1 Aşa¼g daki ifadelerin do¼gru olup olmad klar n nedenlerini aç klayarak yaz n z. (a) R n uzay n n aç k olmayan her alt kümesi kapal d r. (b) A = fx 2 [0; 1]
Analiz III Ara S nav Sorular 24 Kas m 2010 1 Aşa¼g daki ifadelerin do¼gru olup olmad klar n nedenlerini aç klayarak yaz n z. (a) R n uzay n n aç k olmayan her alt kümesi kapal d r. (b) A = fx 2 [0; 1]
Fonksiyonel Analize Giriş I Ara S nav Sorular 29 Kas m Bir metrik uzayda her kapal yuvar kapal bir kümedir. Ispatlay n z.
 Fonksiyonel Analize Giriş I Ara S nav Sorular 29 Kas m 2010 1 Bir metrik uzayda her kapal yuvar kapal bir kümedir. Ispatlay n z. 2 (a) d (x; y) = Z 1 0 jx (t) y (t)j 1 + jx (t) y (t)j dt fonksiyonunun
Fonksiyonel Analize Giriş I Ara S nav Sorular 29 Kas m 2010 1 Bir metrik uzayda her kapal yuvar kapal bir kümedir. Ispatlay n z. 2 (a) d (x; y) = Z 1 0 jx (t) y (t)j 1 + jx (t) y (t)j dt fonksiyonunun
Ad ve Soyad : Numaras : Analiz III Aras nav Sorular
 Analiz III Aras nav Sorular 30. 11. 2006 1. (a) A = fx 2 R : x 2 4x 5 < 0g ise sup A =? (b) A R boş olmayan ve üstten s n rl bir küme olsun. > 0 ise sup(a) = sup A oldu¼gunu gösteriniz. 2. A = f(x; y)
Analiz III Aras nav Sorular 30. 11. 2006 1. (a) A = fx 2 R : x 2 4x 5 < 0g ise sup A =? (b) A R boş olmayan ve üstten s n rl bir küme olsun. > 0 ise sup(a) = sup A oldu¼gunu gösteriniz. 2. A = f(x; y)
FONKS IYONEL ANAL IZE G IR IŞ I Aras nav Sorular
 Ad ve Soyad : Numaras : FONKS IYONEL ANAL IZE G IR IŞ I Aras nav Sorular 30.11.2007 1. Aşa¼g daki ifadelerin do¼gru olup olmad klar n nedenlerini aç klayarak yaz n z. (a) (X; kk) bir normlu uzay ve M bunun
Ad ve Soyad : Numaras : FONKS IYONEL ANAL IZE G IR IŞ I Aras nav Sorular 30.11.2007 1. Aşa¼g daki ifadelerin do¼gru olup olmad klar n nedenlerini aç klayarak yaz n z. (a) (X; kk) bir normlu uzay ve M bunun
1.3. Normal Uzaylar. Bu bölümde; regülerlikten daha kuvvetli bir ay rma aksiyomu tan mlanarak. baz temel özellikleri incelenecektir.
 1.3. Normal Uzaylar Bu bölümde; regülerlikten daha kuvvetli bir ay rma aksiyomu tan mlanarak baz temel özellikleri incelenecektir. Tan m 1.3.1. (X; ) bir Hausdor uzay olsun. E¼ger, 8F; K 2 F; F \ K = ;
1.3. Normal Uzaylar Bu bölümde; regülerlikten daha kuvvetli bir ay rma aksiyomu tan mlanarak baz temel özellikleri incelenecektir. Tan m 1.3.1. (X; ) bir Hausdor uzay olsun. E¼ger, 8F; K 2 F; F \ K = ;
ANAL IZ III Aras nav Sorular
 Ad ve Soyad : Numaras : ANAL IZ III Aras nav Sorular 26.11.27 1. x 1 = p 3 ve x n+1 = p 3 + x n ; n = 1; 2; ::: biçiminde tan mlanan (x n ) dizisinin yak nsak oldu¼gunu gösteriniz ve limitini bulunuz.(2)
Ad ve Soyad : Numaras : ANAL IZ III Aras nav Sorular 26.11.27 1. x 1 = p 3 ve x n+1 = p 3 + x n ; n = 1; 2; ::: biçiminde tan mlanan (x n ) dizisinin yak nsak oldu¼gunu gösteriniz ve limitini bulunuz.(2)
2. Topolojik Uzaylarda Ba¼glant l l k Ba¼glant l Topolojik Uzaylar. Tan m (X; ) topolojik uzay n n her biri boş kümeden farkl olan ayr k
 2. Topolojik Uzaylarda Ba¼glant l l k 2.1. Ba¼glant l Topolojik Uzaylar Tan m 2.1.1. (X; ) topolojik uzay n n her biri boş kümeden farkl olan ayr k iki aç ktan oluşan bir örtüsü yok ise, (X; ) topolojik
2. Topolojik Uzaylarda Ba¼glant l l k 2.1. Ba¼glant l Topolojik Uzaylar Tan m 2.1.1. (X; ) topolojik uzay n n her biri boş kümeden farkl olan ayr k iki aç ktan oluşan bir örtüsü yok ise, (X; ) topolojik
Soru Toplam Puanlama Alınan Puan
 18.11.2013 No: Ad-Soyad: İmza: Soru 1. 2. 3. 4. 5. 6. 7. 8. Toplam Puanlama 20 20 20 20 20 20 20 20 100 Alınan Puan 405024142006.1 CEBİRSEL TOPOLOJİ ARASINAVI CEVAP ANAHTARI (ÖRGÜN ÖĞRETİM) Not: Süre 90
18.11.2013 No: Ad-Soyad: İmza: Soru 1. 2. 3. 4. 5. 6. 7. 8. Toplam Puanlama 20 20 20 20 20 20 20 20 100 Alınan Puan 405024142006.1 CEBİRSEL TOPOLOJİ ARASINAVI CEVAP ANAHTARI (ÖRGÜN ÖĞRETİM) Not: Süre 90
TOPOLOGY TEST A³a dakilerden hangisi bir süzgeç de ildir? 3. A³a dakilerden hangisi a³kn bir süzgeç de ildir?
 1 TOPOLOGY TEST 02 1. S ailesi X kümesi üzerinde bir süzgeç ise, a³a dakilerden hangisi sa lanmaz? (a) / S (b) * S (c) X S (d) A, B S A B S (e) (V S ) (V W ) W S 2. A³a dakilerden hangisi bir süzgeç de
1 TOPOLOGY TEST 02 1. S ailesi X kümesi üzerinde bir süzgeç ise, a³a dakilerden hangisi sa lanmaz? (a) / S (b) * S (c) X S (d) A, B S A B S (e) (V S ) (V W ) W S 2. A³a dakilerden hangisi bir süzgeç de
' : (X; kk)! (R; jj) ; ' (x) = kxk fonksiyonunun
 Fonksiyonel Analize Giriş I Aras nav Sorular 24. 11. 2006 1. (a) Normun tan m n yaz n z. (b) (X; kk) bir normlu uzay olsun. sürekli oldu¼gunu gösteriniz. ' : (X; kk)! (R; jj) ; ' (x) = kxk fonksiyonunun
Fonksiyonel Analize Giriş I Aras nav Sorular 24. 11. 2006 1. (a) Normun tan m n yaz n z. (b) (X; kk) bir normlu uzay olsun. sürekli oldu¼gunu gösteriniz. ' : (X; kk)! (R; jj) ; ' (x) = kxk fonksiyonunun
Önsav 1. Her fley yukardaki gibi olsun. {ƒ 1 (V) g 1 (W) : V X, W Y, V ve W aç k}
 Kapak Konusu: Topoloji Çarp m Topolojisi Bu yaz da topolojik uzaylar n kartezyen çarp m n do al bir topolojik uzay yap s yla donataca z. E er ve topolojik uzaylarsa, üzerine en do al topolojik yap, herhalde,
Kapak Konusu: Topoloji Çarp m Topolojisi Bu yaz da topolojik uzaylar n kartezyen çarp m n do al bir topolojik uzay yap s yla donataca z. E er ve topolojik uzaylarsa, üzerine en do al topolojik yap, herhalde,
14.Konu Reel sayılarının topolojisi. 1.Tanım:, verilsin. açık aralığına noktasının -komşuluğu denir. { } kümesine nın delinmiş -komşuluğu denir.
 14.Konu Reel sayılarının topolojisi 1.Teorem: cismi tamdır. 1.Tanım:, verilsin. açık aralığına noktasının -komşuluğu denir. { } kümesine nın delinmiş -komşuluğu denir. 2.Tanım: ve verilsin. nın her komşuluğunda
14.Konu Reel sayılarının topolojisi 1.Teorem: cismi tamdır. 1.Tanım:, verilsin. açık aralığına noktasının -komşuluğu denir. { } kümesine nın delinmiş -komşuluğu denir. 2.Tanım: ve verilsin. nın her komşuluğunda
1.4 Tam Metrik Uzay ve Tamlaması
 1.4. Tam Metrik Uzay ve Tamlaması 15 1.4 Tam Metrik Uzay ve Tamlaması Öncelikle şunu not edelim: (X, d) bir metrik uzay, (x n ), X de bir dizi ve x X ise lim n d(x n, x) = 0 = lim n,m d(x n, x m ) = 0
1.4. Tam Metrik Uzay ve Tamlaması 15 1.4 Tam Metrik Uzay ve Tamlaması Öncelikle şunu not edelim: (X, d) bir metrik uzay, (x n ), X de bir dizi ve x X ise lim n d(x n, x) = 0 = lim n,m d(x n, x m ) = 0
TOPOLOJ TEST B. (d) Dizinin limiti yoktur; y lma noktas yoktur. 4. Dizisel süreklilik hangi uzaylarda süreklili e denktir?
 1 TOPOLOJ TEST B 1. {( 1) n 1 n : n > 0} dizisi için a³a dakilerden hangisi do rudur? (a) Dizinin limiti 1 ve +1 dir; y lma noktas 1 ve +1 dir. (b) Dizinin limiti 1 ve +1 dir; y lma noktas yoktur. (c)
1 TOPOLOJ TEST B 1. {( 1) n 1 n : n > 0} dizisi için a³a dakilerden hangisi do rudur? (a) Dizinin limiti 1 ve +1 dir; y lma noktas 1 ve +1 dir. (b) Dizinin limiti 1 ve +1 dir; y lma noktas yoktur. (c)
TOPOLOJ TEST A. 1. A³a dakilerden hangisi topoloji tanmlama yöntemi de ildir?
 1 TOPOLOJ TEST A 1. A³a dakilerden hangisi topoloji tanmlama yöntemi de ildir? (a) Açk kümeleri belirleme (b) Kapal kümeleri belirleme (c) Alt-kümeleri belirleme (d) Kaplamlar belirleme (e) çlemleri belirleme
1 TOPOLOJ TEST A 1. A³a dakilerden hangisi topoloji tanmlama yöntemi de ildir? (a) Açk kümeleri belirleme (b) Kapal kümeleri belirleme (c) Alt-kümeleri belirleme (d) Kaplamlar belirleme (e) çlemleri belirleme
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ GENELLEŞTİRİLMİŞ TOPOLOJİLERDE BAZI YENİ SONUÇLAR. Sevda SAĞIROĞLU PEKER
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ GENELLEŞTİRİLMİŞ TOPOLOJİLERDE BAZI YENİ SONUÇLAR Sevda SAĞIROĞLU PEKER MATEMATİK ANABİLİM DALI ANKARA 2009 Her hakkı saklıdır ÖZET Doktora Tezi
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ GENELLEŞTİRİLMİŞ TOPOLOJİLERDE BAZI YENİ SONUÇLAR Sevda SAĞIROĞLU PEKER MATEMATİK ANABİLİM DALI ANKARA 2009 Her hakkı saklıdır ÖZET Doktora Tezi
Topolojik Uzaylarda Süreklilik Çeşitleri Üzerine
 S Ü Fen Ed Fak Fen Derg Sayı 26 (2005) 43-50, KONYA Topolojik Uzaylarda Süreklilik Çeşitleri Üzerine Kemal USLU 1, Şaziye YÜKSEL Selçuk Üniversitesi Fen Edebiyat Fakültesi Matematik Bölümü Kampüs-Konya
S Ü Fen Ed Fak Fen Derg Sayı 26 (2005) 43-50, KONYA Topolojik Uzaylarda Süreklilik Çeşitleri Üzerine Kemal USLU 1, Şaziye YÜKSEL Selçuk Üniversitesi Fen Edebiyat Fakültesi Matematik Bölümü Kampüs-Konya
Soru Toplam Puanlama Alnan Puan
 ..04 No: Ad-Soyad: mza: Soru.. 3. 4. 5. 6. 7. 8. Toplam Puanlama 0 0 0 5 0 0 0 0 00 Alnan Puan 04043006. CEB RSEL TOPOLOJ ARASINAVI CEVAP ANAHTARI ( K NC Ö RET M) Not: Süre 90 Dakika. stedi iniz 7 soruyu
..04 No: Ad-Soyad: mza: Soru.. 3. 4. 5. 6. 7. 8. Toplam Puanlama 0 0 0 5 0 0 0 0 00 Alnan Puan 04043006. CEB RSEL TOPOLOJ ARASINAVI CEVAP ANAHTARI ( K NC Ö RET M) Not: Süre 90 Dakika. stedi iniz 7 soruyu
1. Metrik Uzaylar ve Topolojisi
 1. Metrik Uzaylar ve Topolojisi Euclidean R uzayının tabanının B = {(a, b) : a, b R} olduğunu biliyoruz. Demek ki bu uzayda belirleyiçi unsur açık aralıklar. Her açık aralık (a, b) için, olmak üzere, d
1. Metrik Uzaylar ve Topolojisi Euclidean R uzayının tabanının B = {(a, b) : a, b R} olduğunu biliyoruz. Demek ki bu uzayda belirleyiçi unsur açık aralıklar. Her açık aralık (a, b) için, olmak üzere, d
f( F) f(f) K = K F f 1 f( F) f 1 (K) = F F f 1 (S ) = [f 1 (S)] f(x) S V
![f( F) f(f) K = K F f 1 f( F) f 1 (K) = F F f 1 (S ) = [f 1 (S)] f(x) S V f( F) f(f) K = K F f 1 f( F) f 1 (K) = F F f 1 (S ) = [f 1 (S)] f(x) S V](/thumbs/59/43279328.jpg) Bölüm 6 SÜREKL FONKS YONLAR 6.1 YEREL SÜREKL L K Tanm 6.1.1. (X, T ) ve (Y, S) topolojik uzaylar ile f : X Y fonksiyonu verilsin. E er f(x 0 ) ö esinin her V kom³ulu una kar³lk f(u) V olacak ³ekilde x
Bölüm 6 SÜREKL FONKS YONLAR 6.1 YEREL SÜREKL L K Tanm 6.1.1. (X, T ) ve (Y, S) topolojik uzaylar ile f : X Y fonksiyonu verilsin. E er f(x 0 ) ö esinin her V kom³ulu una kar³lk f(u) V olacak ³ekilde x
1998 ULUSAL ANTALYA MATEMAT IK OL IMP IYATI B IR INC I AŞAMA SORULARI
 1998 ULUSL NTLY MTEMT IK OL IMP IYTI IR INC I ŞM SORULRI Lise 1- S nav Sorular 1. T = 1! +! + 3! + ::: + 1997! + 1998! toplam n n son iki basama¼g ndaki rakamlar n toplam kaçt r? ) 13 ) 9 C) 6 D) E) Hiçbiri.
1998 ULUSL NTLY MTEMT IK OL IMP IYTI IR INC I ŞM SORULRI Lise 1- S nav Sorular 1. T = 1! +! + 3! + ::: + 1997! + 1998! toplam n n son iki basama¼g ndaki rakamlar n toplam kaçt r? ) 13 ) 9 C) 6 D) E) Hiçbiri.
NÜMER IK ANAL IZ. Nuri ÖZALP. Sabit Nokta ve Fonksiyonel Yineleme. Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP Sabit Nokta ve Fonksiyonel Yineleme Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 3 7! Sabit Nokta ve Fonksiyonel Yineleme 1 / 23 Sabit Nokta
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP Sabit Nokta ve Fonksiyonel Yineleme Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 3 7! Sabit Nokta ve Fonksiyonel Yineleme 1 / 23 Sabit Nokta
7 TAYLOR SER I GÖSTER IMLER I
 7 TAYLOR SER I GÖSTER IMLER I Bir f fonksiyonu analitiklik bölgesi içinde f () X a n ( 0 ) n şeklinde bir kuvvet serisi gösterimine sahiptir. E¼ger a n f (n) ( 0 ) seçilirse bu kuvvet serisi Taylor serisi
7 TAYLOR SER I GÖSTER IMLER I Bir f fonksiyonu analitiklik bölgesi içinde f () X a n ( 0 ) n şeklinde bir kuvvet serisi gösterimine sahiptir. E¼ger a n f (n) ( 0 ) seçilirse bu kuvvet serisi Taylor serisi
MAT216 TOPOLOJ IYE G IR IŞ DERS NOTLARI by Mehmet K rdar
 MAT216 TOPOLOJ IYE G IR IŞ DERS NOTLARI by Mehmet K rdar Içindekiler 1. Topolojinin Tan m, Ilk Örnekler, Aç k ve Kapal Kümeler 2. Topolojilerin Karş laşt r lmas ve Alt Uzay 3. Baz ve Alt Baz 4. Metrik
MAT216 TOPOLOJ IYE G IR IŞ DERS NOTLARI by Mehmet K rdar Içindekiler 1. Topolojinin Tan m, Ilk Örnekler, Aç k ve Kapal Kümeler 2. Topolojilerin Karş laşt r lmas ve Alt Uzay 3. Baz ve Alt Baz 4. Metrik
1) 6 kişilik bir aile yuvarlak bir masa etraf nda, anne ile baban n yan yana oturmamas koşulu ile kaç farkl biçimde oturabilir?
 ) 6 kişilik bir aile yuvarlak bir masa etraf nda, anne ile baban n yan yana oturmamas koşulu ile kaç farkl biçimde oturabilir? Çözüm: Önce, anne ile baban n yan yana oturma durumunu düşünelim. Anne ile
) 6 kişilik bir aile yuvarlak bir masa etraf nda, anne ile baban n yan yana oturmamas koşulu ile kaç farkl biçimde oturabilir? Çözüm: Önce, anne ile baban n yan yana oturma durumunu düşünelim. Anne ile
1999 ULUSAL ANTALYA MATEMAT IK OL IMP IYATI B IR INC I AŞAMA SORULARI
 1999 ULUSL NTLY MTMT IK L IMP IYTI IR IN I ŞM SRULRI Lise 1- S nav Sorular 1. f1; ; 3; :::; 1999g kümesinin, eleman say s tek say olan kaç tane alt kümesi vard r? ) 1999 ) 1998 ) 1998-1 ) 999 ) hiçbiri.
1999 ULUSL NTLY MTMT IK L IMP IYTI IR IN I ŞM SRULRI Lise 1- S nav Sorular 1. f1; ; 3; :::; 1999g kümesinin, eleman say s tek say olan kaç tane alt kümesi vard r? ) 1999 ) 1998 ) 1998-1 ) 999 ) hiçbiri.
GENELLEŞTİRİLMİŞ FUZZY KOMŞULUK SİSTEMİ ÜZERİNE
 ÖZEL EGE LİSESİ GENELLEŞTİRİLMİŞ FUZZY KOMŞULUK SİSTEMİ ÜZERİNE HAZIRLAYAN ÖĞRENCİ: Berk KORKUT DANIŞMAN ÖĞRETMEN: Gizem GÜNEL İZMİR 2013 İÇİNDEKİLER 1. PROJENİN AMACI 3.33 2. GİRİŞ... 3 3. YÖNTEM 3 4.
ÖZEL EGE LİSESİ GENELLEŞTİRİLMİŞ FUZZY KOMŞULUK SİSTEMİ ÜZERİNE HAZIRLAYAN ÖĞRENCİ: Berk KORKUT DANIŞMAN ÖĞRETMEN: Gizem GÜNEL İZMİR 2013 İÇİNDEKİLER 1. PROJENİN AMACI 3.33 2. GİRİŞ... 3 3. YÖNTEM 3 4.
fonksiyonu, her x 6= 1 reel say s için tan ml d r. (x 1)(x+1) = = x + 1 yaz labilir. Bu da; f (x) = L
 Limit Bu bölümde, matematik analizde temel bir görevi olan it kavram incelenecektir. Analizdeki bir çok problemin çözümünde it kavram na gereksinim duyulmaktad r. Bunlardan baz lar ; bir noktada bir e¼griye
Limit Bu bölümde, matematik analizde temel bir görevi olan it kavram incelenecektir. Analizdeki bir çok problemin çözümünde it kavram na gereksinim duyulmaktad r. Bunlardan baz lar ; bir noktada bir e¼griye
BMT 206 Ayrık Matematik. Yük. Müh. Köksal GÜNDOĞDU 1
 BMT 206 Ayrık Matematik Yük. Müh. Köksal GÜNDOĞDU 1 Fonksiyonlar Yük. Müh. Köksal GÜNDOĞDU 2 Fonksiyonlar Tanım: A ve B boş olmayan kümeler. A dan B ye bir f fonksiyonu f: A B ile gösterilir ve A nın her
BMT 206 Ayrık Matematik Yük. Müh. Köksal GÜNDOĞDU 1 Fonksiyonlar Yük. Müh. Köksal GÜNDOĞDU 2 Fonksiyonlar Tanım: A ve B boş olmayan kümeler. A dan B ye bir f fonksiyonu f: A B ile gösterilir ve A nın her
f fonksiyonuna bir üç değişkenli fonksiyon adı verilir. Daha çok değişkenli fonksiyonlar benzer şekilde tanımlanır.
 Çok Değişkenli Fonksiyonlar Tanım 1. D düzlemin bir bölgesi, f de D nin her bir (x, y) noktasına bir f(x, y) reel sayısı karşılık getiren bir fonksiyon ise f fonksiyonuna bir iki değişkenli fonksiyon adı
Çok Değişkenli Fonksiyonlar Tanım 1. D düzlemin bir bölgesi, f de D nin her bir (x, y) noktasına bir f(x, y) reel sayısı karşılık getiren bir fonksiyon ise f fonksiyonuna bir iki değişkenli fonksiyon adı
Çarpm ve Bölüm Uzaylar
 1 Ksm I Çarpm ve Bölüm Uzaylar ÇARPIM UZAYLARI 1 ÇARPIM TOPOLOJ S 2 KARMA P R O B E M L E R 1. A ile B, srasyla, (X, T )X ile (Y, S ) topolojik uzaylarnn birer alt-kümesi olsunlar. (a) (A B) = A B (b)
1 Ksm I Çarpm ve Bölüm Uzaylar ÇARPIM UZAYLARI 1 ÇARPIM TOPOLOJ S 2 KARMA P R O B E M L E R 1. A ile B, srasyla, (X, T )X ile (Y, S ) topolojik uzaylarnn birer alt-kümesi olsunlar. (a) (A B) = A B (b)
MAT355 Kompleks Fonksiyonlar Teorisi I Hafta 3
 1.3. Kompleks Düzlemin Topolojisi Tanım 1. D ε (z 0 ) = {z C : z z 0 < ε} kümesine z 0 ın bir ε komşuluğu denir. Tanım 2. Bir A C kümesi verilsin. z 0 ın sadece A nın elemanlarından oluşan bir komşuluğu
1.3. Kompleks Düzlemin Topolojisi Tanım 1. D ε (z 0 ) = {z C : z z 0 < ε} kümesine z 0 ın bir ε komşuluğu denir. Tanım 2. Bir A C kümesi verilsin. z 0 ın sadece A nın elemanlarından oluşan bir komşuluğu
AKDEN IZ ÜN IVERS ITES I 21. ULUSAL ANTALYA MATEMAT IK OL IMP IYATI SORULARI
 KDEN IZ ÜN IVERS ITES I 21. ULUSL NTLY MTEMT IK OL IMP IYTI SORULRI DI SOYDI :...CEP TEL :... OKUL...ŞEH IR :... SINIF :...Ö ¼GRETMEN :... eposta :... IMZ :... SINV TR IH I VE ST I : 14 May s 2016 - Cumartesi
KDEN IZ ÜN IVERS ITES I 21. ULUSL NTLY MTEMT IK OL IMP IYTI SORULRI DI SOYDI :...CEP TEL :... OKUL...ŞEH IR :... SINIF :...Ö ¼GRETMEN :... eposta :... IMZ :... SINV TR IH I VE ST I : 14 May s 2016 - Cumartesi
ab H bulunur. Şu halde önceki önermenin i) koşulu da sağlanır ve H G bulunur.
 3.ALT GRUPLAR HG, Tanım 3.. (G, ) bir grup ve nin boş olmayan bir alt kümesi olsun. Eğer (H, ) bir grup ise H ye G nin bir alt grubu denir ve H G ile gösterilir. Not 3.. a)(h, ), (G, ) grubunun alt grubu
3.ALT GRUPLAR HG, Tanım 3.. (G, ) bir grup ve nin boş olmayan bir alt kümesi olsun. Eğer (H, ) bir grup ise H ye G nin bir alt grubu denir ve H G ile gösterilir. Not 3.. a)(h, ), (G, ) grubunun alt grubu
1956 da... Ali Nesin
 1956 da... Ali Nesin Nesin Yayıncılık Ltd. Şti. künye... Ali Nesin Analiz IV İçindekiler Üçüncü Basıma Önsöz.......................... 1 İkinci Basıma Önsöz........................... 1 Önsöz...................................
1956 da... Ali Nesin Nesin Yayıncılık Ltd. Şti. künye... Ali Nesin Analiz IV İçindekiler Üçüncü Basıma Önsöz.......................... 1 İkinci Basıma Önsöz........................... 1 Önsöz...................................
Bu tanım aralığı pozitif tam sayılar olan f(n) fonksiyonunun değişim aralığı n= 1, 2, 3,, n,
 DİZİLER Tamamen belirli bir kurala göre sıralanmış sayılar topluluğuna veya kümeye Dizi denir. Belirli bir kurala göre birbiri ardınca gelen bu sayıların her birine dizinin terimi ve hepsine birden dizinin
DİZİLER Tamamen belirli bir kurala göre sıralanmış sayılar topluluğuna veya kümeye Dizi denir. Belirli bir kurala göre birbiri ardınca gelen bu sayıların her birine dizinin terimi ve hepsine birden dizinin
f 1 (H ) T f 1 (H ) = T
 Bölüm 15 TIKIZLIK 15.1 TIKIZ UZAYLAR 15.1.1 Problemler 1. Her sonlu topolojik uzay tkzdr. 2. Ayrk bir topolojik uzayn tkz olmas için gerekli ve yeterli ko³ul sonlu olmasdr. 3. Ayn bir küme üzerinde S T
Bölüm 15 TIKIZLIK 15.1 TIKIZ UZAYLAR 15.1.1 Problemler 1. Her sonlu topolojik uzay tkzdr. 2. Ayrk bir topolojik uzayn tkz olmas için gerekli ve yeterli ko³ul sonlu olmasdr. 3. Ayn bir küme üzerinde S T
Topolojik Uzay. Kapak Konusu: Topoloji
 Kapak Konusu: Topoloji Topolojik Uzay Geçen yaz da nin, ad na aç k dedi imiz baz altkümelerini tan mlad k ve bir fonksiyonun süreklili ini tamamen aç k kümeler yard m yla (hiç ve kullanmadan) ifade ettik.
Kapak Konusu: Topoloji Topolojik Uzay Geçen yaz da nin, ad na aç k dedi imiz baz altkümelerini tan mlad k ve bir fonksiyonun süreklili ini tamamen aç k kümeler yard m yla (hiç ve kullanmadan) ifade ettik.
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ TOPLANABİLME METOTLARI VE İTERASYON. Rüya YEĞİN MATEMATİK ANABİLİM DALI ANKARA 2011
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ TOPLANABİLME METOTLARI VE İTERASYON Rüya YEĞİN MATEMATİK ANABİLİM DALI ANKARA 2011 Her hakkı saklıdır ÖZET Yüksek Lisans Tezi TOPLANAB ILME
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ TOPLANABİLME METOTLARI VE İTERASYON Rüya YEĞİN MATEMATİK ANABİLİM DALI ANKARA 2011 Her hakkı saklıdır ÖZET Yüksek Lisans Tezi TOPLANAB ILME
Ders 2: RP 1 ve RP 2 - Reel izdüşümsel doğru ve
 Ders 2: RP 1 ve RP 2 - Reel izdüşümsel doğru ve düzlem Geçen ders doğrusal cebir aracılığıyla izdüşümsel geometri için bir model kurduk. Şimdi bu modeli daha somut bir şekle sokalım, F = R durumunda kurduğumuz
Ders 2: RP 1 ve RP 2 - Reel izdüşümsel doğru ve düzlem Geçen ders doğrusal cebir aracılığıyla izdüşümsel geometri için bir model kurduk. Şimdi bu modeli daha somut bir şekle sokalım, F = R durumunda kurduğumuz
Doğrusal Olmayan Devreler, Sistemler ve Kaos
 Elektronik ve Haberleşme Mühendisliği İstanbul Teknik Üniversitesi 25 Nisan 2013 Outline 1 2 3 Sabit noktaları: x 1 = 0 ve x 2 = 1 1 r x 0 (, 0) (0, ) = x n x(k + 1) = f (x(k)) f r (x) = rx(1 x) r = 4.2
Elektronik ve Haberleşme Mühendisliği İstanbul Teknik Üniversitesi 25 Nisan 2013 Outline 1 2 3 Sabit noktaları: x 1 = 0 ve x 2 = 1 1 r x 0 (, 0) (0, ) = x n x(k + 1) = f (x(k)) f r (x) = rx(1 x) r = 4.2
ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
 ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ Nuray GÜL İKİ TOPOLOJİLİ UZAYLARDA BAZI AYIRMA AKSİYOMLARI MATEMATİK ANABİLİM DALI ADANA, 2011 ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ Nuray GÜL İKİ TOPOLOJİLİ UZAYLARDA BAZI AYIRMA AKSİYOMLARI MATEMATİK ANABİLİM DALI ADANA, 2011 ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
Çözümlü Yüksek Matematik Problemleri. Yrd. Doç. Dr. Erhan Pişkin
 Çözümlü Yüksek Matematik Problemleri Yrd. Doç. Dr. Erhan Pişkin 1 Yrd. Doç. Dr. Erhan PİŞKİN ÇÖZÜMLÜ YÜKSEK MATEMATİK PROBLEMLERİ 1 ISBN 978-605-318-249-8 Kitap içeriğinin tüm sorumluluğu yazarına aittir.
Çözümlü Yüksek Matematik Problemleri Yrd. Doç. Dr. Erhan Pişkin 1 Yrd. Doç. Dr. Erhan PİŞKİN ÇÖZÜMLÜ YÜKSEK MATEMATİK PROBLEMLERİ 1 ISBN 978-605-318-249-8 Kitap içeriğinin tüm sorumluluğu yazarına aittir.
6 Devirli Kodlar. 6.1 Temel Tan mlar
 6 Devirli Kodlar 6.1 Temel Tan mlar Tan m S F n q için e¼ger (a 0 ; a 1 ; : : : ; a n 1 ) 2 S iken (a n 1 ; a 1 ; : : : ; a n 2 ) 2 S oluyorsa S kümesine devirli denir. E¼ger bir C do¼grusal kodu devirli
6 Devirli Kodlar 6.1 Temel Tan mlar Tan m S F n q için e¼ger (a 0 ; a 1 ; : : : ; a n 1 ) 2 S iken (a n 1 ; a 1 ; : : : ; a n 2 ) 2 S oluyorsa S kümesine devirli denir. E¼ger bir C do¼grusal kodu devirli
S = {T Y, X S T T, S S} (9.1)
 Bölüm 9 ÇARPIM UZAYLARI 9.1 ÇARPIM TOPOLOJ S Bo³ olmayan kümelerden olu³an bo³ olmayan bir ailenin kartezyen çarpmnn da bo³ olmad n, Seçme Aksiyomu [13],[20], [8] ile kabul ediyoruz. imdi verilen aileye
Bölüm 9 ÇARPIM UZAYLARI 9.1 ÇARPIM TOPOLOJ S Bo³ olmayan kümelerden olu³an bo³ olmayan bir ailenin kartezyen çarpmnn da bo³ olmad n, Seçme Aksiyomu [13],[20], [8] ile kabul ediyoruz. imdi verilen aileye
MIT Açık Ders Malzemeleri Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için
 MIT Açık Ders Malzemeleri http://ocw.mit.edu Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için http://ocw.mit.edu/terms veya http://www.acikders.org.tr adresini ziyaret
MIT Açık Ders Malzemeleri http://ocw.mit.edu Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için http://ocw.mit.edu/terms veya http://www.acikders.org.tr adresini ziyaret
M IKRO IKT ISAT 2. V IZE SINAVI 19 ARALIK 2009
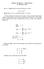 M IKRO IKT ISAT 2. V IZE SINAVI 19 ARALIK 2009 Soru 1: Aşa¼g daki gibi bir üretim fonksiyonu verilsin: = L 1=3 K 2=3 Eme¼gin yat w = ve sermayenin yat r = 1 olsun. a- Firma kadar ç kt üretmek istemektedir.
M IKRO IKT ISAT 2. V IZE SINAVI 19 ARALIK 2009 Soru 1: Aşa¼g daki gibi bir üretim fonksiyonu verilsin: = L 1=3 K 2=3 Eme¼gin yat w = ve sermayenin yat r = 1 olsun. a- Firma kadar ç kt üretmek istemektedir.
Ders 10: Düzlemde cebirsel eğriler
 Ders 10: Düzlemde cebirsel eğriler İzdüşümsel geometride bir doğruyu derecesi 1 olan homojen bir polinomun sıfırları kümesi olarak tarif ettik. Bir kuadrik, derecesi 2 olan homojen bir polinomla anlatılıyordu
Ders 10: Düzlemde cebirsel eğriler İzdüşümsel geometride bir doğruyu derecesi 1 olan homojen bir polinomun sıfırları kümesi olarak tarif ettik. Bir kuadrik, derecesi 2 olan homojen bir polinomla anlatılıyordu
SDÜ Matematik Bölümü Analiz-IV Final S nav
 Dersin Kodu: MAT0 Dönemi: 00-0 Bahar Tarihi: 0.0.0 Saat:. 00 Yer: Am III-IV Süre: 90 Dakika Dersin Sorumlusu Gözetmenler SDÜ Matematik Bölümü Analiz-IV Final S nav : Prof. Dr. Seril PEHL IVAN : Araş. Gör.
Dersin Kodu: MAT0 Dönemi: 00-0 Bahar Tarihi: 0.0.0 Saat:. 00 Yer: Am III-IV Süre: 90 Dakika Dersin Sorumlusu Gözetmenler SDÜ Matematik Bölümü Analiz-IV Final S nav : Prof. Dr. Seril PEHL IVAN : Araş. Gör.
17. ULUSAL ANTALYA MATEMAT IK OL IMP IYATLARI B IR INC I AŞAMA SORULARI A A A A A A A
 AKDEN IZ ÜN IVERS ITES I 17. ULUSAL ANTALYA MATEMAT IK OL IMP IYATLARI B IR INC I AŞAMA SORULARI A A A A A A A SINAV TAR IH I VE SAAT I : 24 MART 2012 - Cumartesi 10.00-12.30 Bu s nav 25 sorudan oluşmaktad
AKDEN IZ ÜN IVERS ITES I 17. ULUSAL ANTALYA MATEMAT IK OL IMP IYATLARI B IR INC I AŞAMA SORULARI A A A A A A A SINAV TAR IH I VE SAAT I : 24 MART 2012 - Cumartesi 10.00-12.30 Bu s nav 25 sorudan oluşmaktad
MIT Açık Ders Malzemeleri Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için
 MIT Açık Ders Malzemeleri http://ocw.mit.edu Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için http://ocw.mit.edu/terms veya http://www.acikders.org.tr adresini ziyaret
MIT Açık Ders Malzemeleri http://ocw.mit.edu Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için http://ocw.mit.edu/terms veya http://www.acikders.org.tr adresini ziyaret
SORULAR. 1. Aşa¼g daki limitleri bulunuz. Cevab n z n aşamalar n belirtiniz. lim. 1 n sin. lim. q 1 x 1+x
 SOULA. Aşa¼g daki limitleri bulunuz. Cevab n z n aşamalar n belirtiniz. lim! lim sin(t )dt sin 4 np n! i= n sin i n. q + arcsin belirli integralini hesalay n z. Cevab n z n aşamalar n belirtiniz. 3. 4
SOULA. Aşa¼g daki limitleri bulunuz. Cevab n z n aşamalar n belirtiniz. lim! lim sin(t )dt sin 4 np n! i= n sin i n. q + arcsin belirli integralini hesalay n z. Cevab n z n aşamalar n belirtiniz. 3. 4
2. SİMETRİK GRUPLAR. Tanım 2.1. X boş olmayan bir küme olmak üzere X den X e birebir örten fonksiyona permütasyon denir.
 2. SİMETRİK GRUPLAR Tanım 2.1. X boş olmayan bir küme olmak üzere X den X e birebir örten fonksiyona permütasyon denir. Tanım 2.2. X boş olmayan bir küme olsun. S X ile X den X e tüm birebir örten fonksiyonlar
2. SİMETRİK GRUPLAR Tanım 2.1. X boş olmayan bir küme olmak üzere X den X e birebir örten fonksiyona permütasyon denir. Tanım 2.2. X boş olmayan bir küme olsun. S X ile X den X e tüm birebir örten fonksiyonlar
13.Konu Reel sayılar
 13.Konu Reel sayılar 1. Temel dizi 2. Temel dizilerde toplama ve çarpma 3. Reel sayılar kümesi 4. Reel sayılar kümesinde toplama ve çarpma 5. Reel sayılar kümesinde sıralama 6. Reel sayılar kümesinin tamlık
13.Konu Reel sayılar 1. Temel dizi 2. Temel dizilerde toplama ve çarpma 3. Reel sayılar kümesi 4. Reel sayılar kümesinde toplama ve çarpma 5. Reel sayılar kümesinde sıralama 6. Reel sayılar kümesinin tamlık
Lys x 2 + y 2 = (6k) 2. (x 2k) 2 + y 2 = (2k 5) 2 olduğuna göre x 2 y 2 =? Cevap: 14k 2
 1. 1 =? Lys 1 7. x + y = (6k) (x k) + y = (k 5) olduğuna göre x y =?. 6 a.b = ise a + 1 b. b 1 a =? 1k 8. x ve y birbirinden farklı pozitif gerçel sayılar olmak üzere, x y y x. x.y = (x y) ise x y =?.
1. 1 =? Lys 1 7. x + y = (6k) (x k) + y = (k 5) olduğuna göre x y =?. 6 a.b = ise a + 1 b. b 1 a =? 1k 8. x ve y birbirinden farklı pozitif gerçel sayılar olmak üzere, x y y x. x.y = (x y) ise x y =?.
MIT Açık Ders Malzemeleri Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için
 MIT Açık Ders Malzemeleri http://ocw.mit.edu Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için http://ocw.mit.edu/terms veya http://www.acikders.org.tr adresini ziyaret
MIT Açık Ders Malzemeleri http://ocw.mit.edu Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için http://ocw.mit.edu/terms veya http://www.acikders.org.tr adresini ziyaret
Fen Edebiyat Fakültesi Matematik
 Fen Edebiyat Fakültesi Matematik MATH 402 - Topoloji II DERS TANITIM BÝLGÝLERÝ Dersin Adý Kodu Yarýyýl Teori (saat/hafta) Uygulama/Laboratuar (saat/hafta) Yerel Kredi AKTS Topoloji II MATH 402 Bahar 3
Fen Edebiyat Fakültesi Matematik MATH 402 - Topoloji II DERS TANITIM BÝLGÝLERÝ Dersin Adý Kodu Yarýyýl Teori (saat/hafta) Uygulama/Laboratuar (saat/hafta) Yerel Kredi AKTS Topoloji II MATH 402 Bahar 3
(z z 0 ) n. n=1. Z f (z) dz = 2ib 1
 0 RE IDÜ TEOR IS I Tan m. f fonksiyonu z 0 noktas nda ayr k singülerli¼ge sahip olsun. Bu durumda f fonksiyonu 0 < jz z 0 j < " bölgesinde X X f(z) = a n (z z 0 ) n b n + (z z 0 ) n Laurent seri aç l m
0 RE IDÜ TEOR IS I Tan m. f fonksiyonu z 0 noktas nda ayr k singülerli¼ge sahip olsun. Bu durumda f fonksiyonu 0 < jz z 0 j < " bölgesinde X X f(z) = a n (z z 0 ) n b n + (z z 0 ) n Laurent seri aç l m
MATEMAT IK-I (SORULAR)
 Part I MATEMAT IK-I (SORULAR) SAYILAR. irrasyonel midir?. 7 say s n n irrasyonel oldu¼gunu gösteriniz. (Gauss Teoremini kullan n z.) 3. + 3 say s n n irrasyonel oldu¼gunu gösteriniz. (Gauss Teoremini kullan
Part I MATEMAT IK-I (SORULAR) SAYILAR. irrasyonel midir?. 7 say s n n irrasyonel oldu¼gunu gösteriniz. (Gauss Teoremini kullan n z.) 3. + 3 say s n n irrasyonel oldu¼gunu gösteriniz. (Gauss Teoremini kullan
Soru 1. Soru 5. Soru 2. Soru 6. Soru 3. Soru 7.
 İstanbul Kültür Üniversitesi Matematik -Bilgisayar Bölümü MB1001 Analiz I 6 Aralık 013. Yıliçi Sınavı Öğrenci Numarası: Adı Soyadı: - Talimatlar: Sınav süresi 90 dakikadır. İlk 30 dakika sınav salonunu
İstanbul Kültür Üniversitesi Matematik -Bilgisayar Bölümü MB1001 Analiz I 6 Aralık 013. Yıliçi Sınavı Öğrenci Numarası: Adı Soyadı: - Talimatlar: Sınav süresi 90 dakikadır. İlk 30 dakika sınav salonunu
T.C. SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
 T.C. SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ SOFT TOPOLOJİK UZAYLAR ÜZERİNE Uğur ÇOŞKUN YÜKSEK LİSANS Matematik Anabilim Dalı HAZİRAN-2014 KONYA Her Hakkı Saklıdır TEZ BİLDİRİMİ Bu tezdeki bütün bilgilerin
T.C. SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ SOFT TOPOLOJİK UZAYLAR ÜZERİNE Uğur ÇOŞKUN YÜKSEK LİSANS Matematik Anabilim Dalı HAZİRAN-2014 KONYA Her Hakkı Saklıdır TEZ BİLDİRİMİ Bu tezdeki bütün bilgilerin
MIT Açık Ders Malzemeleri Kompleks Değişkenli Fonksiyonlar 2008 Güz
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 18.112 Kompleks Değişkenli Fonksiyonlar 2008 Güz Bu materyallerden alıntı yapmak ya Kullanım Şartları hakkında bilgi almak için http://ocw.mit.edu/terms http://tuba.acikders.org.tr
MIT Açık Ders Malzemeleri http://ocw.mit.edu 18.112 Kompleks Değişkenli Fonksiyonlar 2008 Güz Bu materyallerden alıntı yapmak ya Kullanım Şartları hakkında bilgi almak için http://ocw.mit.edu/terms http://tuba.acikders.org.tr
Yan t Bilinmeyen Bir Soru
 Yan t Bilinmeyen Bir Soru Ö nce yan t n dünyada kimsenin bilmedi i bir soru soraca- m, sonra yan t n dünyada kimsenin bilmedi i bu soru üzerine birkaç kolay soru yan tlayaca m. Herhangi bir pozitif do
Yan t Bilinmeyen Bir Soru Ö nce yan t n dünyada kimsenin bilmedi i bir soru soraca- m, sonra yan t n dünyada kimsenin bilmedi i bu soru üzerine birkaç kolay soru yan tlayaca m. Herhangi bir pozitif do
8 LAURENT SER I GÖSTER IMLER I
 8 LAURENT SER I GÖSTER IMLER I Tan m. C n ; n 0; ; ; : : : kompleks sabitler olmak üere serisine Laurent serisi denir. Burada n X C n ( X X X C n ( 0 ) n a n ( 0 ) n b n + ( 0 ) n 0 ) n dir. Teore8.. (Laurent
8 LAURENT SER I GÖSTER IMLER I Tan m. C n ; n 0; ; ; : : : kompleks sabitler olmak üere serisine Laurent serisi denir. Burada n X C n ( X X X C n ( 0 ) n a n ( 0 ) n b n + ( 0 ) n 0 ) n dir. Teore8.. (Laurent
Soru 1. Soru 5. Soru 2. Soru 6. Soru 3. Soru 7.
 İstanbul Kültür Üniversitesi Matematik -Bilgisayar Bölümü MB00 Analiz I 3 Aralık 03 Final Sınavı Öğrenci Numarası: Adı Soyadı: - Taatlar: Sınav süresi 0 dakikadır. İlk 30 dakika sınav salonunu terk etmeyiniz.
İstanbul Kültür Üniversitesi Matematik -Bilgisayar Bölümü MB00 Analiz I 3 Aralık 03 Final Sınavı Öğrenci Numarası: Adı Soyadı: - Taatlar: Sınav süresi 0 dakikadır. İlk 30 dakika sınav salonunu terk etmeyiniz.
 Ğ Ğ Ğ ç ç Ü Ü Ü Ç Ş ğ ç Ş ğ ğ ç ğ ğ ğ ŞÇ Ş ç Ö ğ Ş ç ç ğ ğ ğ ğ Ş Ş ç Ş ŞÇ ç ç Ü Ö Ş ğ ğ ğ ğ ç ŞÇ Ü Ö ç ğ ç Ü Ö ç Ş ç Ç Ü Ü ğ ğ ç ğ ğ ç ç ç Ö Ş ğ ŞÇ ğ ğ ç ğ Ü ğ ç Ü ç ç ç ç Ş Ç Ö Ç Ş ğ Ş ğ ğ ç ğ ğ Ş ğ ç
Ğ Ğ Ğ ç ç Ü Ü Ü Ç Ş ğ ç Ş ğ ğ ç ğ ğ ğ ŞÇ Ş ç Ö ğ Ş ç ç ğ ğ ğ ğ Ş Ş ç Ş ŞÇ ç ç Ü Ö Ş ğ ğ ğ ğ ç ŞÇ Ü Ö ç ğ ç Ü Ö ç Ş ç Ç Ü Ü ğ ğ ç ğ ğ ç ç ç Ö Ş ğ ŞÇ ğ ğ ç ğ Ü ğ ç Ü ç ç ç ç Ş Ç Ö Ç Ş ğ Ş ğ ğ ç ğ ğ Ş ğ ç
2013 YGS MATEMATİK. a a olduğuna göre, a kaçtır? olduğuna göre, m kaçtır? A) 1 2 C) 1 4 E) 4 9 B) 3 2 D) 1 9 A) 3 B) 4 C) 5 D) 6 E) 7
 0 YGS MATEMATİK. m olduğuna göre, m kaçtır?. a a a a olduğuna göre, a kaçtır? A) B) ) D) 6 E) 7 A) B) ) D) 9 E) 9.. (0,) (0,) işleminin sonucu kaçtır? A) 0,06 B) 0,08 ) 0, D) 0, E) 0, A B B D B A BD 9?
0 YGS MATEMATİK. m olduğuna göre, m kaçtır?. a a a a olduğuna göre, a kaçtır? A) B) ) D) 6 E) 7 A) B) ) D) 9 E) 9.. (0,) (0,) işleminin sonucu kaçtır? A) 0,06 B) 0,08 ) 0, D) 0, E) 0, A B B D B A BD 9?
TEMEL MATEMAT K TEST
 TEMEL MATEMAT K TEST KKAT! + Bu bölümde cevaplayaca n z soru say s 40 t r + Bu bölümdeki cevaplar n z cevap ka d ndaki "TEMEL MATEMAT K TEST " bölümüne iflaretleyiniz. 2 4. 4. 0,5 2. iflleminin sonucu
TEMEL MATEMAT K TEST KKAT! + Bu bölümde cevaplayaca n z soru say s 40 t r + Bu bölümdeki cevaplar n z cevap ka d ndaki "TEMEL MATEMAT K TEST " bölümüne iflaretleyiniz. 2 4. 4. 0,5 2. iflleminin sonucu
FONKSİYONUN TANIMI ve FONKSİYON ÇEŞİTLERİ
 KONU: Fonksionlar FONKSİYONUN TANIMI ve FONKSİYON ÇEŞİTLERİ. A,, kümesinden B a, b, c, d kümesine tanımlanan aşağıdaki bağıntılardan hangisi bir fonksiondur?,a,,b,,c,,d,a,,d,,a,a,,b,,c,,d,b,, c,,d,a,,b,,c,,a.
KONU: Fonksionlar FONKSİYONUN TANIMI ve FONKSİYON ÇEŞİTLERİ. A,, kümesinden B a, b, c, d kümesine tanımlanan aşağıdaki bağıntılardan hangisi bir fonksiondur?,a,,b,,c,,d,a,,d,,a,a,,b,,c,,d,b,, c,,d,a,,b,,c,,a.
ASYMMETRIC TOPOLOGICAL SPACES ESRA KARATAŞ
 ASİMETRİK TOPOLOJİK UZAYLAR ASYMMETRIC TOPOLOGICAL SPACES ESRA KARATAŞ HACETTEPE ÜNİVERSİTESİ Lisansüstü Eğitim-Öğretim ve Sınav Yönetmeliğinin Matematik Anabilim Dalı için YÜKSEK LİSANS TEZİ olarak hazırlanmıştır.
ASİMETRİK TOPOLOJİK UZAYLAR ASYMMETRIC TOPOLOGICAL SPACES ESRA KARATAŞ HACETTEPE ÜNİVERSİTESİ Lisansüstü Eğitim-Öğretim ve Sınav Yönetmeliğinin Matematik Anabilim Dalı için YÜKSEK LİSANS TEZİ olarak hazırlanmıştır.
LYS MATEMATİK DENEME - 1
 LYS MATEMATİK DENEME - BU SORULAR FİNAL EĞİTİM KURUMLARI TARAFINDAN SAĞLANMIŞTIR. İZİNSİZ KOPYALANMASI VE ÇOĞALTILMASI YASAKTIR, YAPILDIĞI TAKDİRDE CEZAİ İŞLEM UYGULANACAKTIR. LYS MATEMATİK TESTİ. Bu testte
LYS MATEMATİK DENEME - BU SORULAR FİNAL EĞİTİM KURUMLARI TARAFINDAN SAĞLANMIŞTIR. İZİNSİZ KOPYALANMASI VE ÇOĞALTILMASI YASAKTIR, YAPILDIĞI TAKDİRDE CEZAİ İŞLEM UYGULANACAKTIR. LYS MATEMATİK TESTİ. Bu testte
MAT 321SOYUT CEBİR I KONU TEKRAR SORULARI. ise < A > nedir?
 MAT 321SOYUT CEBİR I KONU TEKRAR SORULARI 1. Pozitif rasyonel sayılar kümesi Q + üzerinde x y = xy 2 işlemi tanımlansın. (Q+, ) bir grup mudur? Gösteriniz. 2. (G, ) bir grup olsun. a G olmak üzere her
MAT 321SOYUT CEBİR I KONU TEKRAR SORULARI 1. Pozitif rasyonel sayılar kümesi Q + üzerinde x y = xy 2 işlemi tanımlansın. (Q+, ) bir grup mudur? Gösteriniz. 2. (G, ) bir grup olsun. a G olmak üzere her
Bir değişkenin bir sabite mümkün olduğu kadar çok yaklaşması durumu ancak onun limitiyle ifade edilebilir.
 LİMİT VE SÜREKLİLİK A- LİMİTLER Bir top 10 metre yükseklikten bırakılmaktadır. Top yere vurduktan sonra ilk yüksekliğin 2/5 i kadar sıçramakta ve bunu her yükseliş için devam ettirmektedir. Topun sıçrayacağı
LİMİT VE SÜREKLİLİK A- LİMİTLER Bir top 10 metre yükseklikten bırakılmaktadır. Top yere vurduktan sonra ilk yüksekliğin 2/5 i kadar sıçramakta ve bunu her yükseliş için devam ettirmektedir. Topun sıçrayacağı
Dersin Kodu 1206.1105
 Genel Matematik I Dersin Adı Genel Matematik I Dersin Kodu 1206.1105 Dersin Türü Zorunlu Dersin Seviyesi Dersin AKTS Kredisi 5,00 Haftalık Ders Saati (Kuramsal) 4 Haftalık Uygulama Saati 0 Haftalık Laboratuar
Genel Matematik I Dersin Adı Genel Matematik I Dersin Kodu 1206.1105 Dersin Türü Zorunlu Dersin Seviyesi Dersin AKTS Kredisi 5,00 Haftalık Ders Saati (Kuramsal) 4 Haftalık Uygulama Saati 0 Haftalık Laboratuar
Topoloji (MATH372) Ders Detayları
 Topoloji (MATH372) Ders Detayları Ders AdıDers Kodu Dönemi Ders Uygulama Saati Saati Laboratuar Saati Kredi AKTS Topoloji MATH372 Bahar 3 0 0 3 6 Ön Koşul Ders(ler)i MATH 251 Dersin Dili Dersin Türü Dersin
Topoloji (MATH372) Ders Detayları Ders AdıDers Kodu Dönemi Ders Uygulama Saati Saati Laboratuar Saati Kredi AKTS Topoloji MATH372 Bahar 3 0 0 3 6 Ön Koşul Ders(ler)i MATH 251 Dersin Dili Dersin Türü Dersin
ARA SINAV II. (1) (x k ) k N, R n içinde yaknsak ve limiti x olan bir dizi olsun. {x} = oldu unu gösteriniz.
 MC 411/ANAL Z IV ARA SINAV II ÇÖZÜMLER 1 x k k N, R n içinde yaknsak iti x olan bir dizi olsun. {x} = {x m m k} k=1 Çözüm. Her k N için A k := {x m m k} olsun. x k k N dizisinin iti x oldu undan, A k =
MC 411/ANAL Z IV ARA SINAV II ÇÖZÜMLER 1 x k k N, R n içinde yaknsak iti x olan bir dizi olsun. {x} = {x m m k} k=1 Çözüm. Her k N için A k := {x m m k} olsun. x k k N dizisinin iti x oldu undan, A k =
 Ğ Ğ ğ ğ ğ ç ç ç ğ ğ ğ ğ ğ ğ ç ğ ğ ğ ç ğ ç ç ç ğ ç ç ç ç ğ ç ğ ğ ç ğ ç ç ç ç ç ğ ğ ç ğ ç ç ç ç ç ğ ğ ç ğ ç ç ğ ç ğ ç ğ ç ğ ğ ç ç ğ ç ç ç çğ ç ç ç ç ğ ç ç ğ ğ ç ç ğ ğ ç ğ ç ç ç ç ğ ğ ç ğ ç ğ ğ ç ğ ç ğ ğ
Ğ Ğ ğ ğ ğ ç ç ç ğ ğ ğ ğ ğ ğ ç ğ ğ ğ ç ğ ç ç ç ğ ç ç ç ç ğ ç ğ ğ ç ğ ç ç ç ç ç ğ ğ ç ğ ç ç ç ç ç ğ ğ ç ğ ç ç ğ ç ğ ç ğ ç ğ ğ ç ç ğ ç ç ç çğ ç ç ç ç ğ ç ç ğ ğ ç ç ğ ğ ç ğ ç ç ç ç ğ ğ ç ğ ç ğ ğ ç ğ ç ğ ğ
DOĞU AKDENİZ ÜNİVERSİTESİ MATEMATİK BÖLÜMÜ 23. LİSELERARASI MATEMATİK YARIŞMASI
 DOĞU AKDENİZ ÜNİVERSİTESİ MATEMATİK BÖLÜMÜ 23. LİSELERARASI MATEMATİK YARIŞMASI BİREYSEL YARIŞMA SORULARI CEVAPLARI CEVAP KAĞIDI ÜZERİNE YAZINIZ. SORU KİTAPÇIĞINI KARALAMA MAKSATLI KULLANABİLİRSİNİZ 1
DOĞU AKDENİZ ÜNİVERSİTESİ MATEMATİK BÖLÜMÜ 23. LİSELERARASI MATEMATİK YARIŞMASI BİREYSEL YARIŞMA SORULARI CEVAPLARI CEVAP KAĞIDI ÜZERİNE YAZINIZ. SORU KİTAPÇIĞINI KARALAMA MAKSATLI KULLANABİLİRSİNİZ 1
28/04/2014 tarihli LYS-1 Matematik-Geometri Testi konu analizi SORU NO LYS 1 MATEMATİK TESTİ KAZANIM NO KAZANIMLAR 1 / 31
 SORU NO LYS 1 MATEMATİK TESTİ A B KAZANIM NO KAZANIMLAR 1 1 / 31 11 32159 Rasyonel sayı kavramını açıklar. 2 12 32151 İki ya da daha çok doğal sayının en büyük ortak bölenini ve en küçük ortak katını bulur.
SORU NO LYS 1 MATEMATİK TESTİ A B KAZANIM NO KAZANIMLAR 1 1 / 31 11 32159 Rasyonel sayı kavramını açıklar. 2 12 32151 İki ya da daha çok doğal sayının en büyük ortak bölenini ve en küçük ortak katını bulur.
A = i IA i = i I A = A = i IA i = {x α((α I) (x A α ))} (7.7) A = (α,β I) (α β) A α A β = (7.8) A A
 Bölüm 7 KÜME A LELER 7.1 DAMGALANMI KÜMELER E er inceledi imiz kümelerin says, alfabenin harerinden daha çok de ilse, onlara,b,...,w gibi harerle temsil edebiliriz. E er elimizde albenin harerinden daha
Bölüm 7 KÜME A LELER 7.1 DAMGALANMI KÜMELER E er inceledi imiz kümelerin says, alfabenin harerinden daha çok de ilse, onlara,b,...,w gibi harerle temsil edebiliriz. E er elimizde albenin harerinden daha
FONKSİYONLAR. Örnek: (2x-2,y-3)=(10,-3) olduğuna göre x ve y sayılarını bulunuz.
 1 FONKSİYONLAR Sıralı İkili: A ve B boş olmayan iki küme olmak üzere, aa ve bb iken (a, b) ifadesine bir sıralı ikili denir. Burada a ya, sıralı ikilinin birinci bileşeni, b ye de ikinci bileşeni denir.
1 FONKSİYONLAR Sıralı İkili: A ve B boş olmayan iki küme olmak üzere, aa ve bb iken (a, b) ifadesine bir sıralı ikili denir. Burada a ya, sıralı ikilinin birinci bileşeni, b ye de ikinci bileşeni denir.
(a,b) şeklindeki ifadelere sıralı ikili denir. Burada a'ya 1. bileşen b'ye 2. bileşen denir.
 BĞANTI - FONKSİYON 1. Sıralı İkili : (a,b) şeklindeki ifadelere sıralı ikili denir. Burada a'ya 1. bileşen b'ye 2. bileşen denir.! (x 1,x 2, x 3,x 4,...x n ) : sıralı n li denir. Örnek, (a,b,c) : sıralı
BĞANTI - FONKSİYON 1. Sıralı İkili : (a,b) şeklindeki ifadelere sıralı ikili denir. Burada a'ya 1. bileşen b'ye 2. bileşen denir.! (x 1,x 2, x 3,x 4,...x n ) : sıralı n li denir. Örnek, (a,b,c) : sıralı
T k z Topolojik Uzaylar
 Kapak Konusu: Metrik Uzaylar ve Topoloji T k z Topolojik Uzaylar Yaz n n uzunlu undan da anlafl laca üzere, bir topolojik uzay n t k z altkümeleri çok önemlidir. (Bu girifl yaz s daha ilginç bir cümleyle
Kapak Konusu: Metrik Uzaylar ve Topoloji T k z Topolojik Uzaylar Yaz n n uzunlu undan da anlafl laca üzere, bir topolojik uzay n t k z altkümeleri çok önemlidir. (Bu girifl yaz s daha ilginç bir cümleyle
Reel Analiz I (MATH 244) Ders Detayları
 Reel Analiz I (MATH 244) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Reel Analiz I MATH 244 Bahar 4 0 0 4 7 Ön Koşul Ders(ler)i Dersin Dili Dersin Türü
Reel Analiz I (MATH 244) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Reel Analiz I MATH 244 Bahar 4 0 0 4 7 Ön Koşul Ders(ler)i Dersin Dili Dersin Türü
İÇİNDEKİLER ÖNSÖZ Bölüm 1 SAYILAR 11 Bölüm 2 KÜMELER 31 Bölüm 3 FONKSİYONLAR
 İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 11 1.1. Sayı Kümeleri 12 1.1.1.Doğal Sayılar Kümesi 12 1.1.2.Tam Sayılar Kümesi 13 1.1.3.Rasyonel Sayılar Kümesi 14 1.1.4. İrrasyonel Sayılar Kümesi 16 1.1.5. Gerçel
İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 11 1.1. Sayı Kümeleri 12 1.1.1.Doğal Sayılar Kümesi 12 1.1.2.Tam Sayılar Kümesi 13 1.1.3.Rasyonel Sayılar Kümesi 14 1.1.4. İrrasyonel Sayılar Kümesi 16 1.1.5. Gerçel
MATEMATİK ÖĞRETMENLİK ALAN BİLGİSİ - DENEME SINAVI DENEME. Diğer sayfaya geçiniz.
 MATEMATİK. DENEME ÖĞRETMENLİK ALAN BİLGİSİ - DENEME SINAVI. f : X tanımlı y = f() fonksiyonu için lim f ( ) = L ise aşağıdaki önermelerden kaç tanesi kesinlikle doğrudur? 0 I. X dir. 0 II. f() fonksiyonu
MATEMATİK. DENEME ÖĞRETMENLİK ALAN BİLGİSİ - DENEME SINAVI. f : X tanımlı y = f() fonksiyonu için lim f ( ) = L ise aşağıdaki önermelerden kaç tanesi kesinlikle doğrudur? 0 I. X dir. 0 II. f() fonksiyonu
12.SINIF A VE B GRUBU MATEMATİK-GEOMETRİ DERSİ KURS KONULARI VE TESTLERİ
 .SINIF A VE B GRUBU MATEMATİK-GEOMETRİ DERSİ KURS KONULARI VE TESTLERİ A-TEST SAYILAR- TEMEL KAVRAMLAR A-TEST SAYILAR- POLİNOMLAR B-TEST POLİNOMLAR- PARALEL DOĞRULARDA VE ÜÇGENDE AÇILAR A- B TEST PARALEL
.SINIF A VE B GRUBU MATEMATİK-GEOMETRİ DERSİ KURS KONULARI VE TESTLERİ A-TEST SAYILAR- TEMEL KAVRAMLAR A-TEST SAYILAR- POLİNOMLAR B-TEST POLİNOMLAR- PARALEL DOĞRULARDA VE ÜÇGENDE AÇILAR A- B TEST PARALEL
EĞİTİM ÖĞRETİM YILI. ANADOLU LİSESİ 11.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI 11.SINIF KAZANIM VE SÜRE TABLOSU
 08-09 EĞİTİM ÖĞRETİM YILI. ANADOLU LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. TRİGONOMETRİ 7 6 6.. Yönlü
08-09 EĞİTİM ÖĞRETİM YILI. ANADOLU LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. TRİGONOMETRİ 7 6 6.. Yönlü
;] u Y hb* p(a/ > V aaa!a!a!a!!!!!a! BASIN KİTAPÇIĞI
![;] u Y hb* p(a/ > V aaa!a!a!a!!!!!a! BASIN KİTAPÇIĞI ;] u Y hb* p(a/ > V aaa!a!a!a!!!!!a! BASIN KİTAPÇIĞI](/thumbs/49/25879173.jpg) BASIN KİTAPÇIĞI 00000000 AÇIKLAMA 1. Bu kitapç kta Lisans Yerle tirme S nav -1 Matematik Testi bulunmaktad r. 2. Bu test için verilen toplam cevaplama süresi 75 dakikadır. 3. Bu kitapç ktaki testlerde
BASIN KİTAPÇIĞI 00000000 AÇIKLAMA 1. Bu kitapç kta Lisans Yerle tirme S nav -1 Matematik Testi bulunmaktad r. 2. Bu test için verilen toplam cevaplama süresi 75 dakikadır. 3. Bu kitapç ktaki testlerde
1. GRUPLAR. c (Birleşme özelliği) sağlanır. 2) a G için a e e a a olacak şekilde e G (e ye birim eleman denir) vardır.
 1. GRUPLAR Tanım 1.1. G boş olmayan bir küme ve, G de bir ikili işlem olsun. (G yapısına aşağıdaki aksiyomları sağlıyorsa bir grup denir., ) cebirsel 1) a b cg,, için a( bc) ( ab) c (Birleşme özelliği)
1. GRUPLAR Tanım 1.1. G boş olmayan bir küme ve, G de bir ikili işlem olsun. (G yapısına aşağıdaki aksiyomları sağlıyorsa bir grup denir., ) cebirsel 1) a b cg,, için a( bc) ( ab) c (Birleşme özelliği)
EĞİTİM ÖĞRETİM YILI. FEN LİSESİ 11.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI 11.SINIF KAZANIM VE SÜRE TABLOSU
 08-09 EĞİTİM ÖĞRETİM YILI. FEN LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. TRİGONOMETRİ 8 6 6.. Yönlü Açılar
08-09 EĞİTİM ÖĞRETİM YILI. FEN LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. TRİGONOMETRİ 8 6 6.. Yönlü Açılar
x 2i + A)( 1 yj 2 + B) u (v + B), y 1
 Ders 11: Örnekler 11.1 Kulplarla inşalar Bu bölümde kulpları birbirine yapıştırıp tanıdık manifoldlar elde edeceğiz. Artık bu son ders. Özellikle dersin ikinci bölümünde son meyveleri toplamak adına koşarak
Ders 11: Örnekler 11.1 Kulplarla inşalar Bu bölümde kulpları birbirine yapıştırıp tanıdık manifoldlar elde edeceğiz. Artık bu son ders. Özellikle dersin ikinci bölümünde son meyveleri toplamak adına koşarak
Alıştırmalar 1. 1) Aşağıdaki diferansiyel denklemlerin mertebesini ve derecesini bulunuz. Bağımlı ve bağımsız değişkenleri belirtiniz.
 Alıştırmalar 1 1) Aşağıdaki diferansiyel denklemlerin mertebesini ve derecesini bulunuz. Bağımlı ve bağımsız değişkenleri belirtiniz. Denklem Mertebe Derece a) 2 1 ( ) 4 6 c) 2 1 d) 2 2 e) 3 1 f) 2 4 g)
Alıştırmalar 1 1) Aşağıdaki diferansiyel denklemlerin mertebesini ve derecesini bulunuz. Bağımlı ve bağımsız değişkenleri belirtiniz. Denklem Mertebe Derece a) 2 1 ( ) 4 6 c) 2 1 d) 2 2 e) 3 1 f) 2 4 g)
BASIN KİTAPÇIĞI ÖSYM
 BASIN KİTAPÇIĞI 00000000 AÇIKLAMA 1. Bu kitapç kta Lisans Yerle tirme S nav -1 Matematik Testi bulunmaktad r. 2. Bu test için verilen toplam cevaplama süresi 75 dakikadır. 3. Bu kitapç ktaki testlerde
BASIN KİTAPÇIĞI 00000000 AÇIKLAMA 1. Bu kitapç kta Lisans Yerle tirme S nav -1 Matematik Testi bulunmaktad r. 2. Bu test için verilen toplam cevaplama süresi 75 dakikadır. 3. Bu kitapç ktaki testlerde
TÜREV VE UYGULAMALARI
 TÜREV VE UYGULAMALARI A R, a A ve f de A da tanımlı bir fonksiyon olsun. Eğer f(x) f(a) lim x a x a limiti veya x=a+h koymakla elde edilen f(a+h) f(a) lim h 0 h Bu türev f (a), df dx limiti varsa f fonksiyonu
TÜREV VE UYGULAMALARI A R, a A ve f de A da tanımlı bir fonksiyon olsun. Eğer f(x) f(a) lim x a x a limiti veya x=a+h koymakla elde edilen f(a+h) f(a) lim h 0 h Bu türev f (a), df dx limiti varsa f fonksiyonu
Temel Bilgisayar Programlama
 BÖLÜM 9: Fonksiyonlara dizi aktarma Fonksiyonlara dizi aktarmak değişken aktarmaya benzer. Örnek olarak verilen öğrenci notlarını ekrana yazan bir program kodlayalım. Fonksiyon prototipi yazılırken, dizinin
BÖLÜM 9: Fonksiyonlara dizi aktarma Fonksiyonlara dizi aktarmak değişken aktarmaya benzer. Örnek olarak verilen öğrenci notlarını ekrana yazan bir program kodlayalım. Fonksiyon prototipi yazılırken, dizinin
