BÖLÜM I GİRİŞ (1.1) y(t) veya y(x) T veya λ. a t veya x. Şekil 1.1 Dalga. a genlik, T peryod (veya λ dalga boyu)
|
|
|
- Irmak Karakoç
- 8 yıl önce
- İzleme sayısı:
Transkript
1 BÖLÜM I GİRİŞ 1.1 Sinyal Bir sistemin durum ve davranış bilgilerini taşıyan, bir veya daha fazla değişken ile tanımlanan bir fonksiyon olup veri işlemde dalga olarak adlandırılır. Bir dalga, genliği, dalga boyu (veya peryodu) ve fazı ile tanımlanır (Şekil 1.1). y(t) veya y(x) veya λ 2a a t veya x a Şekil 1.1 Dalga. a genlik, peryod (veya λ dalga boyu) Örnek:Merkezi etrafında sabit bir hızla dönen r yarıçaplı bir diskin kenarındaki itme koluna bağlanmış bir kalem, bir mesnet içerisinde aşağı yukarı hareket edebilsin. Kalem, bu mesnetin altında sabit hızla hareket eden kağıt üzerine bir sinüs dalgası çizer (Şekil 1.2a). Bu sinüs dalgasının; genliği (a) diskin yarıçapına eşittir ve peryodu ise diskin dönme hızının bir fonksiyonudur. Bu sinüs dalgasına, yukarıda anlatılan mekanik sistemin davranış bilgisini veren bir sinyal gözü ile bakılabilir. Böyle bir sinyalin herhangi bir pozisyondaki genlik değeri y = a sinφ (1.1)
2 ya eşittir. Bu düzenekte, tam bir dalga şeklinin çizilmesi için disk 360 (veya radyan) lık tam bir devir yapmalıdır. Kalem, kağıt üzerinde herhangi bir konuma getirilerek sistem harekete geçirilsin. Sinüs dalgasının bu andaki faz açısı; kalemin başlangıç anındaki konumunu disk merkezine birleştiren doğrunun yatayla yaptığı açıya eşdeğerdir.(şekil 1.2b de φ açısı). Faz açısının değişimine, diğer bir deyişle kalemin konumuna, göre sinyalin şekli (Şekil 1.3) de görülmektedir. Mekanik sisteme bağlı kalemin kağıt üzerindeki herhangi bir x uzaklığından itibaren kayıda başlandığı ve daha sonra hareketin durdurulduğu kabul edilsin. O andaki genlik t a = asin + α a = a sin + α (1.2) -a- Şekil 1.2 Doğrusal dönme hareketini bir sinüs dalgasına dönüştüren mekanik sistem, a) Diskin yarıçapı ve her hangi bir konumunun yatay ile yaptığı açısının, sinüs dalgasının genlik ve faz açısı arasındaki ilişki, b) Disk tam bir devir yaptığında açının 0 dan radyana kadar değiştiği görülmektedir (Davis, 1973). olacaktır. (1.1) bağıntısı göz önüne alınacak olursa, faz açısı -b- t φ = + α φ = + α (1.3) olarak hesaplanır. Burada dikkat edilmesi gereken en önemli konu başlangıç noktasında bir sabit olan φ = α faz açısının daha sonraki bütün genlik ve faz hesaplamalarında sabit olarak görülmesidir.α sabiti; faz, faz açısı (başlangıç fazı) veya faz sabiti olarak bilinir. 5
3 Ayrıca bir sinüs dalgasının faz açısının yatay merkez çizgisinden ölçüldüğüne dikkat edilmelidir. Şekil 1.3 Başlangıç değeri α dan faz açısının değişimi. Herhangi bir x i uzaklıktaki genlik değeri = a sin π x / λ + α φ = 2 π / λ + α a ( 2 ) ve ( ). i x i Faz ve faz farkı kavramının daha iyi anlaşılması için eşit peryodlu iki dalga kaynağının aynı anda dalga üretmeye başladığını varsayalım. Oluşan dalgalar aynı anda maksimum değere ulaşıyor ise bu iki kaynağın maksimum fazda olduğu söylenir. Eğer kaynaklardan birisi t süre gecikme ile dalga üretiyor ise bu kaynağın oluşturduğu dalgalar, maksimuma diğer kaynağın dalgalarına göre, t süre gecikme ile ulaşırlar. Bu gecikme peryodunun kesri olarak ifade edilirse p = t x p = λ 6
4 Şekil 1.4 Disk dönmesine bağlı olarak sinüs ve kosinüs dalgaları arasındaki ilişki. Sinüs ve kosinüs dalgalarının faz açıları sırası ile α ve β, Kayıt; φ = 0 başlayıp den daha büyük değerlere doğru devam edildiğini göstermektedir. olur ve p ye faz farkı denir. Bu p değeri 0 p 1bağıntısını sağlar. p=0 veya p=1 ise iki kaynak aynı fazda çalışıyor p=1/2 ise iki kaynak zıt fazda çalışıyor denir. Sinüs dalga şeklinin tanımına benzer şekilde, bir kosinüs dalgası diskin orijinindeki düşey çizgiden itibaren ölçülen β faz açısına sahip bir dalga olarak tanımlanabilir. Bu, yani kosinüs dalgası, sinüs dalgasının 90 0 (veya β radyan) ötesinde bir faza sahiptir. Yani aralarında 90 0 lik bir faz farkı vardır. Şekil 1.2 deki sinyal üretecine bir başka kalem bağlanırsa (Şekil 1.4) hem sinüs hemde kosinüs dalgası aynı anda üretilebilir. Bu iki dalganın genlik ve dalga boyları aynı olacağına göre birbirlerinden ancak faz açısı ile ayrılabilirler. 1.2 Sinyal Parametreleri Bir sinyalde; genlik, peryod (veya dalga boyu) ve faz açısı parametrelerinin üçü tam bir dalga şekli tanımlar (Şekil 1.1). Burada peryod (veya λ dalga boyu) olup; birbirini izleyen eşdeğer genlikli iki nokta arasındaki zaman farkı veya bir sinyalde ard arda gelen iki tepe noktası arasındaki uzaklık olarak tanımlanır. Peryodun tersi frekans veya zamansal frekans(f t ) ve dalga boyunun tersi ise uzaysal frekans (f x ) f t = 1/ f x = 1/ λ (1.4) olup birim zaman veya uzaklıktaki tam dalga şekillerinin sayısıdır. Zaman birimi saniye olarak alınırsa f t =f in birimi s -1 (yani Hertz) uzaklığın birimi metre alınırsa f x in birimi m - 1 dir. Sinyalin kendi kendisini düzenli olarak tam bir tekrarlaması için gereksindiği zamana 7
5 sinyalin peryodu denir. Periyod terimi dalga boyuna eşdeğerdir. Fakat dalga boyunun uzaklık (metre gibi) birimiyle ölçülmesine karşılık, periyod zaman birimiyle (saniye gibi) ölçülür. Düzenli aralıklarla tekrarlanan sinyallere periyodik sinyaller denir. Dalganın ilerleme doğrultusundaki hızı (çizgisel hız) v ise yapılabilir. v f t =, λ = v dönüşümleri t Bir dalga şeklinin en çukurundan en tepesine kadar olan yüksekliğin yarısına genlik (amplitüd) denir. Birbirinden farklı dalga şekilleri oluşturmak için genlik ve dalga boyu veya faz açısı değiştirilmelidir. (1.4) bağıntısı (1.2) de yerine konularak yazılırsa herhangibir x uzaklığındaki genlik; ( π + φ ) a = a sin 2 kx (1.5) olur. Olay zamana bağlı olarak değişiyor ise (1.4) ile verilen k=1/ λ denkleminde dalga boyu λ yerine peryodu gelecek ve frekans f=1/ olacak ve (1.2) bağıntısında x yerine t gelecektir. Buna göre yukarıdaki denklem zamana bağlı olarak; ( f t + φ ) a = a sin (1.6) olacaktır. Fazdaki gecikme zamanda kaymaya neden olacaktır. Bu da t = φ / f bağıntısı ile verilip φ negatif ise t=0 a göre sağda, pozitif ise solda olur. Şekil 1.5 de genlik ve dalga boyları aynı olan ve biri diğerine göre biraz kaymış özdeş iki sinüs dalgası görülmektedir. y(t) y 1 y 2 t C t Şekil 1.5 Genlik ve dalga boyları aynı olan özdeş iki sinüs dalgası. Iki dalga arasında sadece faz farkı vardır. 8
6 Genlik ve dalga boylarının aynı olmasına rağmen t zamanındaki iki sinyalin y 1 ve y 2 genlikleri birbirinden farklıdır. Bu fark tamamen iki dalga şekli arasındaki açıklığa karşılık gelir. Bu açıklık ise, her iki sinyalin faz açıları arasındaki farka eşdeğer olup iki sinyal arasındaki faz farkı olarak adlandırılırlar. Dönen cisimler için olay ele alınacak olursa frekans açısının fonksiyonu olarak da tanımlanabilir. Buna göre, ω = f = olarak tanımlanır ve birim zamanda taranan açıdır. Benzer durum uzaklık boyutu için de geçerlidir. ω ya açısal (veya dairesel) frekans denir. = f k x = λ Burada da birim uzaklıkta taranan açı ifade edilmektedir. Burada k dalga sayısı olarak adlandırılır. k ve ω arasında ω = kv ilişkisi vardır. Nicelik Birimi Hız Uzaklık/Zaman ω λ v = = fλ = k Peryod Zaman 1 λ = = = ω f v Açısal frekans Zaman -1 ω = = f = kv Frekans (çizgisel) Zaman -1 1 f = = = λ Dalga boyu Uzaklık 2 ω λ = π = k v f v = v ω π k = = = 2 λ v Dalga sayısı Uzaklık -1 vf 9
7 1.3 Problemler 1. Peryodları 1 = 2 =200 ms olan iki sinyal arasında t=16.6 ms lik bir zaman farkı ölçülmüştür. Bu iki sinyal arasındaki faz farkını bulunuz. t (Çözüm için p = eşitliğinden yararlanınız) 2. Frekansı 10 Hz olan bir sinyalin t=0.08 sn. deki faz açısını bulunuz. t (Çözüm için φ = + α eşitliğinden yararlanınız. Burada başlangıç fazının verilmediğine dikkat ediniz) 3. Peryodu 1 =50 ms ve 2 =20 ms olan iki sinyal arasında t=122 ms deki faz farkını bulunuz. 4. Dalga boyu 30 m olan bir sinyalin x=65 m deki fazını hesaplayınız. (Çözüm için φ = + α eşitliğinden yararlanınız. Burada başlangıç fazının verilmediğine dikkat ediniz) 5. Dalga boyu 30 m olan bir sinyalin x=65 m deki fazını hesaplayınız. (Çözüm için φ = + α eşitliğinden yararlanınız. Burada başlangıç fazının verilmediğine dikkat ediniz) Dalga boyları λ 1 =λ 2 =200 m olan iki sinyal arasında x=34 m lik bir uzaklık farkı ölçülmüştür. Bu iki sinyal arasındaki faz farkını bulunuz. x (Çözüm için p = eşitliğinden yararlanınız) λ 6. Başlangıç fazı 0 o, 30 o, 40 o, 60 o genikleri 2 cm ve frekansları 0.1 Hz olan sinüs dalgaları çiziniz. 10
Alternatif Akım Devre Analizi
 Alternatif Akım Devre Analizi Öğr.Gör. Emre ÖZER Alternatif Akımın Tanımı Zamaniçerisindeyönüveşiddeti belli bir düzen içerisinde (periyodik) değişen akıma alternatif akımdenir. En bilinen alternatif akım
Alternatif Akım Devre Analizi Öğr.Gör. Emre ÖZER Alternatif Akımın Tanımı Zamaniçerisindeyönüveşiddeti belli bir düzen içerisinde (periyodik) değişen akıma alternatif akımdenir. En bilinen alternatif akım
TİTREŞİM VE DALGALAR BÖLÜM PERİYODİK HAREKET
 TİTREŞİM VE DALGALAR Periyodik Hareketler: Belirli aralıklarla tekrarlanan harekete periyodik hareket denir. Sabit bir nokta etrafında periyodik hareket yapan cismin hareketine titreşim hareketi denir.
TİTREŞİM VE DALGALAR Periyodik Hareketler: Belirli aralıklarla tekrarlanan harekete periyodik hareket denir. Sabit bir nokta etrafında periyodik hareket yapan cismin hareketine titreşim hareketi denir.
ALTERNATİF AKIMIN TEMEL ESASLARI
 ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİNE GİRİŞ DERSİ ALTERNATİF AKIMIN TEMEL ESASLARI Dr. Öğr. Üyesi Ahmet ÇİFCİ Elektrik enerjisi, alternatif akım ve doğru akım olarak
ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİNE GİRİŞ DERSİ ALTERNATİF AKIMIN TEMEL ESASLARI Dr. Öğr. Üyesi Ahmet ÇİFCİ Elektrik enerjisi, alternatif akım ve doğru akım olarak
ALTERNATİF AKIMIN DENKLEMİ
 1 ALTERNATİF AKIMIN DENKLEMİ Ani ve Maksimum Değerler Alternatif akımın elde edilişi incelendiğinde iletkenin 90 ve 270 lik dönme hareketinin sonunda maksimum emk nın indüklendiği görülür. Alternatif akımın
1 ALTERNATİF AKIMIN DENKLEMİ Ani ve Maksimum Değerler Alternatif akımın elde edilişi incelendiğinde iletkenin 90 ve 270 lik dönme hareketinin sonunda maksimum emk nın indüklendiği görülür. Alternatif akımın
Alternatif Akım; Zaman içerisinde yönü ve şiddeti belli bir düzen içerisinde değişen akıma alternatif akım denir.
 ALTERNATiF AKIM Alternatif Akım; Zaman içerisinde yönü ve şiddeti belli bir düzen içerisinde değişen akıma alternatif akım denir. Doğru akım ve alternatif akım devrelerinde akım yönleri şekilde görüldüğü
ALTERNATiF AKIM Alternatif Akım; Zaman içerisinde yönü ve şiddeti belli bir düzen içerisinde değişen akıma alternatif akım denir. Doğru akım ve alternatif akım devrelerinde akım yönleri şekilde görüldüğü
DENEY-2 ANİ DEĞER, ORTALAMA DEĞER VE ETKİN DEĞER
 DENEY-2 ANİ DEĞER, ORTALAMA DEĞER VE ETKİN DEĞER TEORİK BİLGİ Alternatıf akımın elde edilmesi Zaman içerisinde yönü ve şiddeti belli bir düzen içerisinde değişen akıma alternatif akım denir. Alternatif
DENEY-2 ANİ DEĞER, ORTALAMA DEĞER VE ETKİN DEĞER TEORİK BİLGİ Alternatıf akımın elde edilmesi Zaman içerisinde yönü ve şiddeti belli bir düzen içerisinde değişen akıma alternatif akım denir. Alternatif
Leyla Yıldırım Bölüm BÖLÜM 2
 BÖLÜM 2 PERİYODİK HAREKETLERİN ÜSTÜSTE GELMESİ Birçok fiziksel durum, aynı sistemde iki veya daha fazla harmonik titreşimin aynı anda uygulanmasını gerektirir. Burada aşağıdaki temel kabule bağlı olarak
BÖLÜM 2 PERİYODİK HAREKETLERİN ÜSTÜSTE GELMESİ Birçok fiziksel durum, aynı sistemde iki veya daha fazla harmonik titreşimin aynı anda uygulanmasını gerektirir. Burada aşağıdaki temel kabule bağlı olarak
Şekil-1. Doğru ve Alternatif Akım dalga şekilleri
 2. Alternatif Akım =AC (Alternating Current) Değeri ve yönü zamana göre belirli bir düzen içerisinde değişen akıma AC denir. En çok bilinen AC dalga biçimi Sinüs dalgasıdır. Bununla birlikte farklı uygulamalarda
2. Alternatif Akım =AC (Alternating Current) Değeri ve yönü zamana göre belirli bir düzen içerisinde değişen akıma AC denir. En çok bilinen AC dalga biçimi Sinüs dalgasıdır. Bununla birlikte farklı uygulamalarda
ALTERNATİF AKIMIN DENKLEMİ
 1 ALTERNATİF AKIMIN DENKLEMİ ALTERNATİF AKIM Lineer ve Açısal Hız Lineer ve Açısal Hız Lineer hız v, lineer(doğrusal) yer değişiminin(s) bu sürede geçen zamana oranı olarak tanımlanır. Lineer hızın birimi
1 ALTERNATİF AKIMIN DENKLEMİ ALTERNATİF AKIM Lineer ve Açısal Hız Lineer ve Açısal Hız Lineer hız v, lineer(doğrusal) yer değişiminin(s) bu sürede geçen zamana oranı olarak tanımlanır. Lineer hızın birimi
DENEY 7 DALGALI GERİLİM ÖLÇÜMLERİ - OSİLOSKOP
 DENEY 7 DALGALI GERİLİM ÖLÇÜMLERİ - OSİLOSKOP Amaç: Bu deneyin amacı, öğrencilerin alternatif akım ve gerilim hakkında bilgi edinmesini sağlamaktır. Deney sonunda öğrencilerin, periyot, frekans, genlik,
DENEY 7 DALGALI GERİLİM ÖLÇÜMLERİ - OSİLOSKOP Amaç: Bu deneyin amacı, öğrencilerin alternatif akım ve gerilim hakkında bilgi edinmesini sağlamaktır. Deney sonunda öğrencilerin, periyot, frekans, genlik,
Mekanik Titreşimler ve Kontrolü. Makine Mühendisliği Bölümü
 Mekanik Titreşimler ve Kontrolü Makine Mühendisliği Bölümü s.selim@gtu.edu.tr 10.10.018 Titreşim sinyalinin özellikleri Daimi sinyal Daimi olmayan sinyal Herhangi bir sistemden elde edilen titreşim sinyalinin
Mekanik Titreşimler ve Kontrolü Makine Mühendisliği Bölümü s.selim@gtu.edu.tr 10.10.018 Titreşim sinyalinin özellikleri Daimi sinyal Daimi olmayan sinyal Herhangi bir sistemden elde edilen titreşim sinyalinin
KATI CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 KATI CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ Bu bölümde, düzlemsel kinematik, veya bir rijit cismin düzlemsel hareketinin geometrisi incelenecektir. Bu inceleme, dişli, kam ve makinelerin yaptığı birçok işlemde
KATI CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ Bu bölümde, düzlemsel kinematik, veya bir rijit cismin düzlemsel hareketinin geometrisi incelenecektir. Bu inceleme, dişli, kam ve makinelerin yaptığı birçok işlemde
BÖLÜM-2. Sabit katsayılı çizgisel homojen diferansiyel denklem örneği olarak
 BÖLÜM-2 2.1 PERİYODİK TİTREŞİMLERİN ÜST ÜSTE GELMESİ (Süperpozisyon) Kütle-yay problemlerini geri çağırıcı kuvvetin sadece x ile orantılı olduğu durumlar için inceleyeceğiz, yani Hook yasasının ( ) geçerli
BÖLÜM-2 2.1 PERİYODİK TİTREŞİMLERİN ÜST ÜSTE GELMESİ (Süperpozisyon) Kütle-yay problemlerini geri çağırıcı kuvvetin sadece x ile orantılı olduğu durumlar için inceleyeceğiz, yani Hook yasasının ( ) geçerli
HAREKET HAREKET KUVVET İLİŞKİSİ
 HAREKET HAREKET KUVVET İLİŞKİSİ Sabit kabul edilen bir noktaya göre bir cismin konumundaki değişikliğe hareket denir. Bu sabit noktaya referans noktası denir. Fizikte hareket üçe ayrılır Ötelenme Hareketi:
HAREKET HAREKET KUVVET İLİŞKİSİ Sabit kabul edilen bir noktaya göre bir cismin konumundaki değişikliğe hareket denir. Bu sabit noktaya referans noktası denir. Fizikte hareket üçe ayrılır Ötelenme Hareketi:
ELASTİK DALGA YAYINIMI
 18.0.016 ELASTİK DALGA YAYINIMI Prof.Dr. Eşref YALÇINKAYA (016-1. DERS 1 Zaman ve Yer Ders saati : 10:0 13:00 Ara : 11:15 11:30 Ders yeri : D-331 1 18.0.016 Sizden beklenen Derse devamın sağlanması çok
18.0.016 ELASTİK DALGA YAYINIMI Prof.Dr. Eşref YALÇINKAYA (016-1. DERS 1 Zaman ve Yer Ders saati : 10:0 13:00 Ara : 11:15 11:30 Ders yeri : D-331 1 18.0.016 Sizden beklenen Derse devamın sağlanması çok
V = g. t Y = ½ gt 2 V = 2gh. Serbest Düşme NOT:
 Havada serbest bırakılan cisimlerin aşağı doğru düşmesi etrafımızda her zaman gördüğümüz bir olaydır. Bu düşme hareketleri, cisimleri yerin merkezine doğru çeken bir kuvvetin varlığını gösterir. Daha önceki
Havada serbest bırakılan cisimlerin aşağı doğru düşmesi etrafımızda her zaman gördüğümüz bir olaydır. Bu düşme hareketleri, cisimleri yerin merkezine doğru çeken bir kuvvetin varlığını gösterir. Daha önceki
T.C. SAKARYA ÜNİVERSİTESİ FİZİK-1 LABORATUVARI DENEY RAPORU
 Adı-Soyadı : ÖĞRENCİNİN Numarası : İmza :. Bölümü : Deney No Deney Adı Bir Boyutta Hareket: Konum, Hız ve İvme Deneyin Amacı Deneyin Teorisi (Kendi cümleleriniz ile yazınız) (0 P) T.C. SAKARYA ÜNİVERSİTESİ
Adı-Soyadı : ÖĞRENCİNİN Numarası : İmza :. Bölümü : Deney No Deney Adı Bir Boyutta Hareket: Konum, Hız ve İvme Deneyin Amacı Deneyin Teorisi (Kendi cümleleriniz ile yazınız) (0 P) T.C. SAKARYA ÜNİVERSİTESİ
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
5.DENEY. d F. ma m m dt. d y. d y. -kx. Araç. Basit. denge (1) (2) (3) denklemi yazılabilir. (4)
 YAYLI ve BASİ SARKAÇ 5.DENEY. Amaç: i) Bir spiral yayın yay sabitinin belirlenmesi vee basit harmonik hareket yapan bir cisminn periyodununn incelenmesi. ii) Basit sarkaç kullanılarak yerçekimi ivmesininn
YAYLI ve BASİ SARKAÇ 5.DENEY. Amaç: i) Bir spiral yayın yay sabitinin belirlenmesi vee basit harmonik hareket yapan bir cisminn periyodununn incelenmesi. ii) Basit sarkaç kullanılarak yerçekimi ivmesininn
ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ
 ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ DENEY FÖYÜ DENEY ADI AC AKIM, GERİLİM VE GÜÇ DENEYİ DERSİN ÖĞRETİM ÜYESİ DENEY SORUMLUSU DENEY GRUBU: DENEY TARİHİ : TESLİM
ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ DENEY FÖYÜ DENEY ADI AC AKIM, GERİLİM VE GÜÇ DENEYİ DERSİN ÖĞRETİM ÜYESİ DENEY SORUMLUSU DENEY GRUBU: DENEY TARİHİ : TESLİM
FIZ Uygulama Vektörler
 Vektörler Problem 1 - Serway 61/75 Bir dikdörtgenler prizmasının boyutları şekildeki gibi a=10,0 cm, b=20,0 cm ve c=15,0 cm dir. a) Yüz köşegen vektörü R 1 nedir? b) Cisim köşegen vektörü R 2 nedir? c)
Vektörler Problem 1 - Serway 61/75 Bir dikdörtgenler prizmasının boyutları şekildeki gibi a=10,0 cm, b=20,0 cm ve c=15,0 cm dir. a) Yüz köşegen vektörü R 1 nedir? b) Cisim köşegen vektörü R 2 nedir? c)
Trigonometrik Fonksiyonlar
 Trigonometrik Fonksiyonlar Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 6 Amaçlar Bu üniteyi çalıştıktan sonra; açı kavramını hatırlayacak, açıların derece ölçümünü radyan ölçümüne ve tersine çevirebilecek, trigonometrik
Trigonometrik Fonksiyonlar Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 6 Amaçlar Bu üniteyi çalıştıktan sonra; açı kavramını hatırlayacak, açıların derece ölçümünü radyan ölçümüne ve tersine çevirebilecek, trigonometrik
DENEY FÖYÜ 4: Alternatif Akım ve Osiloskop
 Deneyin Amacı: DENEY FÖYÜ 4: Alternatif Akım ve Osiloskop Osiloskop kullanarak alternatif gerilimlerin incelenmesi Deney Malzemeleri: 5 Adet 1kΩ, 5 adet 10kΩ, 5 Adet 2k2Ω, 1 Adet potansiyometre(1kω), 4
Deneyin Amacı: DENEY FÖYÜ 4: Alternatif Akım ve Osiloskop Osiloskop kullanarak alternatif gerilimlerin incelenmesi Deney Malzemeleri: 5 Adet 1kΩ, 5 adet 10kΩ, 5 Adet 2k2Ω, 1 Adet potansiyometre(1kω), 4
ALTERNATĐF AKIM (AC) I AC NĐN ELDE EDĐLMESĐ; KARE VE ÜÇGEN DALGALAR
 ALTERNATĐF AKIM (AC) I AC NĐN ELDE EDĐLMESĐ; KARE VE ÜÇGEN DALGALAR 1.1 Amaçlar AC nin Elde Edilmesi: Farklı ve değişken DC gerilimlerin anahtar ve potansiyometreler kullanılarak elde edilmesi. Kare dalga
ALTERNATĐF AKIM (AC) I AC NĐN ELDE EDĐLMESĐ; KARE VE ÜÇGEN DALGALAR 1.1 Amaçlar AC nin Elde Edilmesi: Farklı ve değişken DC gerilimlerin anahtar ve potansiyometreler kullanılarak elde edilmesi. Kare dalga
İŞ : Şekilde yörüngesinde hareket eden bir parçacık üzerine kuvveti görülmektedir. Parçacık A noktasından
 İŞ : Şekilde yörüngesinde hareket eden bir parçacık üzerine etkiyen F kuvveti görülmektedir. Parçacık A noktasından r geçerken konum vektörü uygun bir O orijininden ölçülmektedir ve A dan A ne diferansiyel
İŞ : Şekilde yörüngesinde hareket eden bir parçacık üzerine etkiyen F kuvveti görülmektedir. Parçacık A noktasından r geçerken konum vektörü uygun bir O orijininden ölçülmektedir ve A dan A ne diferansiyel
İşaret ve Sistemler. Ders 2: Spektral Analize Giriş
 İşaret ve Sistemler Ders 2: Spektral Analize Giriş Spektral Analiz A 1.Cos (2 f 1 t+ 1 ) ile belirtilen işaret: f 1 Hz frekansında, A 1 genliğinde ve fazı da Cos(2 f 1 t) ye göre 1 olan parametrelere sahiptir.
İşaret ve Sistemler Ders 2: Spektral Analize Giriş Spektral Analiz A 1.Cos (2 f 1 t+ 1 ) ile belirtilen işaret: f 1 Hz frekansında, A 1 genliğinde ve fazı da Cos(2 f 1 t) ye göre 1 olan parametrelere sahiptir.
6. DENEY Alternatif Akım Kaynağı ve Osiloskop Cihazlarının Kullanımı
 6. DENEY Alternatif Akım Kaynağı ve Osiloskop Cihazlarının Kullanımı Deneyin Amacı: Osiloskop kullanarak alternatif gerilimlerin incelenmesi Deney Malzemeleri: Osiloskop Alternatif Akım Kaynağı Uyarı:
6. DENEY Alternatif Akım Kaynağı ve Osiloskop Cihazlarının Kullanımı Deneyin Amacı: Osiloskop kullanarak alternatif gerilimlerin incelenmesi Deney Malzemeleri: Osiloskop Alternatif Akım Kaynağı Uyarı:
Bölüm 2. Bir boyutta hareket
 Bölüm 2 Bir boyutta hareket Kinematik Dış etkenlere maruz kalması durumunda bir cismin hareketindeki değişimleri tanımlar Bir boyutta hareketten kasıt, cismin bir doğru boyunca hareket ettiği durumların
Bölüm 2 Bir boyutta hareket Kinematik Dış etkenlere maruz kalması durumunda bir cismin hareketindeki değişimleri tanımlar Bir boyutta hareketten kasıt, cismin bir doğru boyunca hareket ettiği durumların
Bölüm 3 AC Devreler. 1. AC devrede, seri RC ağının karakteristiklerini anlamak. 2. Kapasitif reaktans, empedans ve faz açısı kavramlarını anlamak.
 Bölüm 3 AC Devreler DENEY 3-1 AC RC Devresi DENEYİN AMACI 1. AC devrede, seri RC ağının karakteristiklerini anlamak. 2. Kapasitif reaktans, empedans ve faz açısı kavramlarını anlamak. GENEL BİLGİLER Saf
Bölüm 3 AC Devreler DENEY 3-1 AC RC Devresi DENEYİN AMACI 1. AC devrede, seri RC ağının karakteristiklerini anlamak. 2. Kapasitif reaktans, empedans ve faz açısı kavramlarını anlamak. GENEL BİLGİLER Saf
18.034 İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
DALGALAR. Dalgalar titreşim doğrultusuna ve Taşıdığı enerjiye göre aşağıdaki şekilde sınıflandırılır.
 DALGALAR Dalga hareketi Nedir? Durgun bir su birikintisine bir tas attığımızda, tasın suya düştüğü noktadan dışarıya doğru daireler seklinde bir hareketin yayıldığını görürüz. Bu hareket bir dalga hareketidir.
DALGALAR Dalga hareketi Nedir? Durgun bir su birikintisine bir tas attığımızda, tasın suya düştüğü noktadan dışarıya doğru daireler seklinde bir hareketin yayıldığını görürüz. Bu hareket bir dalga hareketidir.
BASİT HARMONİK HAREKET
 BASİT HARMONİK HAREKET Bir doğru üzerinde bulunan iki nokta arasında periyodik olarak yer değiştirme ve ivmesi değişen hareketlere basit harmonik hareket denir. Sarmal yayın ucuna bağlanmış bir cismin
BASİT HARMONİK HAREKET Bir doğru üzerinde bulunan iki nokta arasında periyodik olarak yer değiştirme ve ivmesi değişen hareketlere basit harmonik hareket denir. Sarmal yayın ucuna bağlanmış bir cismin
DİNAMİK (2.hafta) Yatay Hareket Formülleri: a x =0 olduğundan ilk hız ile yatay bileşende hareketine devam eder.
 EĞİK ATIŞ Bir merminin serbest uçuş hareketi iki dik bileşen şeklinde, yatay ve dikey hareket olarak incelenir. Bu harekette hava direnci ihmal edilerek çözüm yapılır. Hava direnci ihmal edilince yatay
EĞİK ATIŞ Bir merminin serbest uçuş hareketi iki dik bileşen şeklinde, yatay ve dikey hareket olarak incelenir. Bu harekette hava direnci ihmal edilerek çözüm yapılır. Hava direnci ihmal edilince yatay
Su Dalgaları Testlerinin Çözümleri. Test 1 in Çözümleri
 Test 1 in Çözümleri 1. 5 dalga tepesi arası 4λ eder.. Su Dalgaları Testlerinin Çözümleri 4λ = 0 cm 1 3 4 5 λ = 5 cm bulunur. Stroboskop saniyede 8 devir yaptığına göre frekansı 4 s 1 dir. Dalgaların frekansı;
Test 1 in Çözümleri 1. 5 dalga tepesi arası 4λ eder.. Su Dalgaları Testlerinin Çözümleri 4λ = 0 cm 1 3 4 5 λ = 5 cm bulunur. Stroboskop saniyede 8 devir yaptığına göre frekansı 4 s 1 dir. Dalgaların frekansı;
r r r F İŞ : Şekil yörüngesinde hareket eden bir parçacık üzerine kuvvetini göstermektedir. Parçacık A noktasından
 İŞ : Şekil yörüngesinde hareket eden bir parçacık üzerine etkiyenf r kuvvetini göstermektedir. Parçacık A noktasından r r geçerken konum vektörü uygun bir O orijininden ölçülmektedir ve d r A dan A ne
İŞ : Şekil yörüngesinde hareket eden bir parçacık üzerine etkiyenf r kuvvetini göstermektedir. Parçacık A noktasından r r geçerken konum vektörü uygun bir O orijininden ölçülmektedir ve d r A dan A ne
ALTERNATİF AKIMIN DENKLEMİ
 1 ALTERNATİF AKIMIN DENKLEMİ ALTERNATİF AKIM Lineer ve Açısal Hız Lineer ve Açısal Hız Linneer Hız Lineer hız v, lineer(doğrusal) yer değişiminin( s ) bu sürede geçen zamana oranı olarak tanımlanır. Lineer
1 ALTERNATİF AKIMIN DENKLEMİ ALTERNATİF AKIM Lineer ve Açısal Hız Lineer ve Açısal Hız Linneer Hız Lineer hız v, lineer(doğrusal) yer değişiminin( s ) bu sürede geçen zamana oranı olarak tanımlanır. Lineer
ELK-301 ELEKTRİK MAKİNALARI-1
 ELK-301 ELEKTRİK MAKİNALARI-1 KAYNAKLAR 1. Prof. Dr. Güngör BAL, Elektrik Makinaları I, Seçkin Yayınevi, Ankara 2016 2. Stephen J. Chapman, Elektrik Makinalarının Temelleri, Çağlayan Kitabevi, 2007, Çeviren:
ELK-301 ELEKTRİK MAKİNALARI-1 KAYNAKLAR 1. Prof. Dr. Güngör BAL, Elektrik Makinaları I, Seçkin Yayınevi, Ankara 2016 2. Stephen J. Chapman, Elektrik Makinalarının Temelleri, Çağlayan Kitabevi, 2007, Çeviren:
5. Elektriksel Büyüklüklerin Ölçülebilen Değerleri
 Elektrik devrelerinde ölçülebilen büyüklükler olan; 5. Elektriksel Büyüklüklerin Ölçülebilen Değerleri Akım Gerilim Devrede bulunan kaynakların tiplerine göre değişik şekillerde olabilir. Zamana bağlı
Elektrik devrelerinde ölçülebilen büyüklükler olan; 5. Elektriksel Büyüklüklerin Ölçülebilen Değerleri Akım Gerilim Devrede bulunan kaynakların tiplerine göre değişik şekillerde olabilir. Zamana bağlı
T.C. SAKARYA ÜNİVERSİTESİ FİZİK-1 LABORATUARI DENEY RAPORU. Deneyin yapılış amacının ne olabileceğini kendi cümlelerinizle yazınız.
 T.C. SAKARYA ÜNİVERSİTESİ FİZİK- LABORATUARI DENEY RAPORU Ad Soyad Numara Bölüm Grup Deney No Deneyin Adı Deneyin Amacı Teorik Bilgi Deneyin yapılış amacının ne olabileceğini kendi cümlelerinizle yazınız.
T.C. SAKARYA ÜNİVERSİTESİ FİZİK- LABORATUARI DENEY RAPORU Ad Soyad Numara Bölüm Grup Deney No Deneyin Adı Deneyin Amacı Teorik Bilgi Deneyin yapılış amacının ne olabileceğini kendi cümlelerinizle yazınız.
KATI CİSİMLERİN BAĞIL İVME ANALİZİ:
 KATI CİSİMLERİN BAĞIL İVME ANALİZİ: Genel düzlemsel hareket yapmakta olan katı cisim üzerinde bulunan iki noktanın ivmeleri aralarındaki ilişki, bağıl hız v A = v B + v B A ifadesinin zamana göre türevi
KATI CİSİMLERİN BAĞIL İVME ANALİZİ: Genel düzlemsel hareket yapmakta olan katı cisim üzerinde bulunan iki noktanın ivmeleri aralarındaki ilişki, bağıl hız v A = v B + v B A ifadesinin zamana göre türevi
4. Sunum: AC Kalıcı Durum Analizi. Kaynak: Temel Mühendislik Devre Analizi, J. David IRWIN-R. Mark NELMS, Nobel Akademik Yayıncılık
 4. Sunum: AC Kalıcı Durum Analizi Kaynak: Temel Mühendislik Devre Analizi, J. David IRWIN-R. Mark NELMS, Nobel Akademik Yayıncılık 1 Giriş Aşağıdaki şekillere ve ifadelere bakalım ve daha önceki derslerimizden
4. Sunum: AC Kalıcı Durum Analizi Kaynak: Temel Mühendislik Devre Analizi, J. David IRWIN-R. Mark NELMS, Nobel Akademik Yayıncılık 1 Giriş Aşağıdaki şekillere ve ifadelere bakalım ve daha önceki derslerimizden
Bölüm-4. İki Boyutta Hareket
 Bölüm-4 İki Boyutta Hareket Bölüm 4: İki Boyutta Hareket Konu İçeriği 4-1 Yer değiştirme, Hız ve İvme Vektörleri 4-2 Sabit İvmeli İki Boyutlu Hareket 4-3 Eğik Atış Hareketi 4-4 Bağıl Hız ve Bağıl İvme
Bölüm-4 İki Boyutta Hareket Bölüm 4: İki Boyutta Hareket Konu İçeriği 4-1 Yer değiştirme, Hız ve İvme Vektörleri 4-2 Sabit İvmeli İki Boyutlu Hareket 4-3 Eğik Atış Hareketi 4-4 Bağıl Hız ve Bağıl İvme
TRIGONOMETRI AÇI, YÖNLÜ AÇI, YÖNLÜ YAY
 TRIGONOMETRI AÇI, YÖNLÜ AÇI, YÖNLÜ YAY A. AÇI Başlangıç noktaları aynı olan iki ışının birleşim kümesine açı denir. Bu ışınlara açının kenarları, başlangıç noktasına ise açının köşesi denir. B. YÖNLÜ AÇI
TRIGONOMETRI AÇI, YÖNLÜ AÇI, YÖNLÜ YAY A. AÇI Başlangıç noktaları aynı olan iki ışının birleşim kümesine açı denir. Bu ışınlara açının kenarları, başlangıç noktasına ise açının köşesi denir. B. YÖNLÜ AÇI
DİNAMİK. Ders_9. Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü. Ders notları için: GÜZ
 DİNAMİK Ders_9 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2018-2019 GÜZ RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ: ÖTELENME&DÖNME Bugünün
DİNAMİK Ders_9 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2018-2019 GÜZ RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ: ÖTELENME&DÖNME Bugünün
ELEKTRİKSEL POTANSİYEL
 ELEKTRİKSEL POTANSİYEL Elektriksel Potansiyel Enerji Elektriksel potansiyel enerji kavramına geçmeden önce Fizik-1 dersinizde görmüş olduğunuz iş, potansiyel enerji ve enerjinin korunumu kavramları ile
ELEKTRİKSEL POTANSİYEL Elektriksel Potansiyel Enerji Elektriksel potansiyel enerji kavramına geçmeden önce Fizik-1 dersinizde görmüş olduğunuz iş, potansiyel enerji ve enerjinin korunumu kavramları ile
MEKANİZMA TEKNİĞİ (3. Hafta)
 MEKANİZMALARIN KİNEMATİK ANALİZİ Temel Kavramlar MEKANİZMA TEKNİĞİ (3. Hafta) Bir mekanizmanın Kinematik Analizinden bahsettiğimizde, onun üzerindeki tüm uzuvların yada istenilen herhangi bir noktanın
MEKANİZMALARIN KİNEMATİK ANALİZİ Temel Kavramlar MEKANİZMA TEKNİĞİ (3. Hafta) Bir mekanizmanın Kinematik Analizinden bahsettiğimizde, onun üzerindeki tüm uzuvların yada istenilen herhangi bir noktanın
8. ALTERNATİF AKIM VE SERİ RLC DEVRESİ
 8. ATENATİF AKIM E SEİ DEESİ AMAÇA 1. Alternatif akım ve gerilim ölçmeyi öğrenmek. Direnç, kondansatör ve indüktans oluşan seri bir alternatif akım devresini analiz etmek AAÇA oltmetre, ampermetre, kondansatör
8. ATENATİF AKIM E SEİ DEESİ AMAÇA 1. Alternatif akım ve gerilim ölçmeyi öğrenmek. Direnç, kondansatör ve indüktans oluşan seri bir alternatif akım devresini analiz etmek AAÇA oltmetre, ampermetre, kondansatör
T.C. SAKARYA ÜNİVERSİTESİ FİZİK-1 LABORATUVARI DENEY RAPORU
 Adı-Soyadı : ÖĞRENCİNİN Numarası : İmza :. Bölümü : Deney No Deney Adı Bir Boyutta Hareket: Konum, Hız ve İvme Deneyin Amacı Deneyin Teorisi (Kendi cümleleriniz ile yazınız) (0 P) T.C. SAKARYA ÜNİVERSİTESİ
Adı-Soyadı : ÖĞRENCİNİN Numarası : İmza :. Bölümü : Deney No Deney Adı Bir Boyutta Hareket: Konum, Hız ve İvme Deneyin Amacı Deneyin Teorisi (Kendi cümleleriniz ile yazınız) (0 P) T.C. SAKARYA ÜNİVERSİTESİ
Fiz Ders 10 Katı Cismin Sabit Bir Eksen Etrafında Dönmesi
 Fiz 1011 - Ders 10 Katı Cismin Sabit Bir Eksen Etrafında Dönmesi Açısal Yerdeğiştirme, Hız ve İvme Dönme Kinematiği: Sabit Açısal İvmeli Dönme Hareketi Açısal ve Doğrusal Nicelikler Dönme Enerjisi Eylemsizlik
Fiz 1011 - Ders 10 Katı Cismin Sabit Bir Eksen Etrafında Dönmesi Açısal Yerdeğiştirme, Hız ve İvme Dönme Kinematiği: Sabit Açısal İvmeli Dönme Hareketi Açısal ve Doğrusal Nicelikler Dönme Enerjisi Eylemsizlik
1) Bir sarkacın hareketini deneysel olarak incelemek ve teori ile karşılaştırmak. 2) Basit sarkaç yardımıyla yerçekimi ivmesini belirlemek.
 DENEY 4. BASİT SARKAÇ Amaç: 1) Bir sarkacın hareketini deneysel olarak incelemek ve teori ile karşılaştırmak. ) Basit sarkaç yardımıyla yerçekimi ivmesini belirlemek. Kuramsal Bili: Kendini belirli zaman
DENEY 4. BASİT SARKAÇ Amaç: 1) Bir sarkacın hareketini deneysel olarak incelemek ve teori ile karşılaştırmak. ) Basit sarkaç yardımıyla yerçekimi ivmesini belirlemek. Kuramsal Bili: Kendini belirli zaman
Mühendislik Mekaniği Dinamik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 16 Rijit Cismin Düzlemsel Kinematiği Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 16 Rijit
Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 16 Rijit Cismin Düzlemsel Kinematiği Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 16 Rijit
YILDIZLARIN HAREKETLERİ
 Öz Hareket Gezegenlerden ayırdetmek için sabit olarak isimlendirdiğimiz yıldızlar da gerçekte hareketlidirler. Bu, çeşitli yollarla anlaşılır. Bir yıldızın ve sı iki veya üç farklı tarihte çok dikkatle
Öz Hareket Gezegenlerden ayırdetmek için sabit olarak isimlendirdiğimiz yıldızlar da gerçekte hareketlidirler. Bu, çeşitli yollarla anlaşılır. Bir yıldızın ve sı iki veya üç farklı tarihte çok dikkatle
DENEY 3 ATWOOD MAKİNASI
 DENEY 3 ATWOOD MAKİNASI AMAÇ Bu deney bir cismin hareketi ve hareketi doğuran sebepler arasındaki ilişkiyi inceler. Bu deneyde eğik hava masası üzerine kurulmuş Atwood makinesini kullanarak Newton un ikinci
DENEY 3 ATWOOD MAKİNASI AMAÇ Bu deney bir cismin hareketi ve hareketi doğuran sebepler arasındaki ilişkiyi inceler. Bu deneyde eğik hava masası üzerine kurulmuş Atwood makinesini kullanarak Newton un ikinci
ALTERNATİF AKIMIN TANIMI
 ALTERNATİF AKIM ALTERNATİF AKIMIN TANIMI Belirli üreteçler sürekli kutup değiştiren elektrik enerjisi üretirler. (Örnek: Döner elektromekanik jeneratörler) Voltajın zamana bağlı olarak sürekli yön değiştirmesi
ALTERNATİF AKIM ALTERNATİF AKIMIN TANIMI Belirli üreteçler sürekli kutup değiştiren elektrik enerjisi üretirler. (Örnek: Döner elektromekanik jeneratörler) Voltajın zamana bağlı olarak sürekli yön değiştirmesi
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ
 BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
Newton un II. yasası. Bir cismin ivmesi, onun üzerine etki eden bileşke kuvvetle doğru orantılı ve kütlesi ile ters orantılıdır.
 Newton un II. yasası Bir cismin ivmesi, onun üzerine etki eden bileşke kuvvetle doğru orantılı ve kütlesi ile ters orantılıdır. Bir cisme F A, F B ve F C gibi çok sayıda kuvvet etkiyorsa, net kuvvet bunların
Newton un II. yasası Bir cismin ivmesi, onun üzerine etki eden bileşke kuvvetle doğru orantılı ve kütlesi ile ters orantılıdır. Bir cisme F A, F B ve F C gibi çok sayıda kuvvet etkiyorsa, net kuvvet bunların
BAŞKENT ÜNİVERSİTESİ
 BAŞKENT ÜNİVERSİTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ EEM-201 DEVRE TEORİSİ-1 LAB. DENEY-1 SİNYAL ÜRETECİ ve OSİLOSKOP AMAÇ Bu deneyde iki yeni cihazla tanışacaksınız: Sinyal (işaret) üreteci ve
BAŞKENT ÜNİVERSİTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ EEM-201 DEVRE TEORİSİ-1 LAB. DENEY-1 SİNYAL ÜRETECİ ve OSİLOSKOP AMAÇ Bu deneyde iki yeni cihazla tanışacaksınız: Sinyal (işaret) üreteci ve
Fizik 101-Fizik I 2013-2014. Dönme Hareketinin Dinamiği
 -Fizik I 2013-2014 Dönme Hareketinin Dinamiği Nurdan Demirci Sankır Ofis: 364, Tel: 2924332 İçerik Vektörel Çarpım ve Tork Katı Cismin Yuvarlanma Hareketi Bir Parçacığın Açısal Momentumu Dönen Katı Cismin
-Fizik I 2013-2014 Dönme Hareketinin Dinamiği Nurdan Demirci Sankır Ofis: 364, Tel: 2924332 İçerik Vektörel Çarpım ve Tork Katı Cismin Yuvarlanma Hareketi Bir Parçacığın Açısal Momentumu Dönen Katı Cismin
Massachusetts Teknoloji Enstitüsü-Fizik Bölümü
 Massachusetts Teknoloji Enstitüsü-Fizik Bölümü Fizik 8.01 Ödev # 8 Güz, 1999 ÇÖZÜMLER Dru Renner dru@mit.edu 14 Kasım 1999 Saat: 18.20 Problem 8.1 Bir sonraki hareket bir odağının merkezinde gezegenin
Massachusetts Teknoloji Enstitüsü-Fizik Bölümü Fizik 8.01 Ödev # 8 Güz, 1999 ÇÖZÜMLER Dru Renner dru@mit.edu 14 Kasım 1999 Saat: 18.20 Problem 8.1 Bir sonraki hareket bir odağının merkezinde gezegenin
DENEY 5 DÖNME HAREKETİ
 DENEY 5 DÖNME HAREKETİ AMAÇ Deneyin amacı merkezinden geçen eksen etrafında dönen bir diskin dinamiğini araştırmak, açısal ivme, açısal hız ve eylemsizlik momentini hesaplamak ve mekanik enerjinin korunumu
DENEY 5 DÖNME HAREKETİ AMAÇ Deneyin amacı merkezinden geçen eksen etrafında dönen bir diskin dinamiğini araştırmak, açısal ivme, açısal hız ve eylemsizlik momentini hesaplamak ve mekanik enerjinin korunumu
BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM
 BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM 4.1. Giriş Bir önceki bölümde, hareket denklemi F = ma nın, maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini
BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM 4.1. Giriş Bir önceki bölümde, hareket denklemi F = ma nın, maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini
Elektromanyetik Dalga Teorisi
 Elektromanyetik Dalga Teorisi Ders-2 Dalga Denkleminin Çözümü Düzlem Elektromanyetik Dalgalar Enine Elektromanyetik Dalgalar Kayıplı Ortamda Düzlem Dalgalar Düzlem Dalgaların Polarizasyonu Dalga Denkleminin
Elektromanyetik Dalga Teorisi Ders-2 Dalga Denkleminin Çözümü Düzlem Elektromanyetik Dalgalar Enine Elektromanyetik Dalgalar Kayıplı Ortamda Düzlem Dalgalar Düzlem Dalgaların Polarizasyonu Dalga Denkleminin
KUVVET, MOMENT ve DENGE
 2.1. Kuvvet 2.1.1. Kuvvet ve cisimlere etkileri Kuvvetler vektörel büyüklüklerdir. Kuvvet vektörünün; uygulama noktası, kuvvetin cisme etkidiği nokta; doğrultu ve yönü, kuvvetin doğrultu ve yönü; modülüyse
2.1. Kuvvet 2.1.1. Kuvvet ve cisimlere etkileri Kuvvetler vektörel büyüklüklerdir. Kuvvet vektörünün; uygulama noktası, kuvvetin cisme etkidiği nokta; doğrultu ve yönü, kuvvetin doğrultu ve yönü; modülüyse
SU DALGALARINDA GİRİŞİM
 SU DALGALARINDA GİRİŞİM Yukarıda iki kaynağın oluşturduğu dairesel su dalgalarının meydana getirdiği girişim deseni gösterilmiştir Burada kesikli çizgiler dalga çukurlarını, düz çizgiler dalga tepelerini
SU DALGALARINDA GİRİŞİM Yukarıda iki kaynağın oluşturduğu dairesel su dalgalarının meydana getirdiği girişim deseni gösterilmiştir Burada kesikli çizgiler dalga çukurlarını, düz çizgiler dalga tepelerini
MIT 8.02, Bahar 2002 Ödev # 8 Çözümler
 Adam S. Bolton bolton@mit.edu MIT 8.02, Bahar 2002 Ödev # 8 Çözümler 24 Nisan 2002 Problem 8.1 RLC devresi. (a) Derste (ve Giancoli Kesim 31-6,s. 780 de) tartışıldığı gibi, bir akımın bir maksimuma (rezonans)
Adam S. Bolton bolton@mit.edu MIT 8.02, Bahar 2002 Ödev # 8 Çözümler 24 Nisan 2002 Problem 8.1 RLC devresi. (a) Derste (ve Giancoli Kesim 31-6,s. 780 de) tartışıldığı gibi, bir akımın bir maksimuma (rezonans)
Metrik sistemde uzaklık ve yol ölçü birimi olarak metre (m) kullanılır.
 LİNEAR (DÜZGÜN DOĞRUSAL) BİOKİNEMATİK ÖZELLİKLER Düzgün doğrusal hareket bir cismin düz bir doğrultuda ilerlemesi, yer değiştirmesidir. Uzunluk, hız, ivmelenme bu bölümde incelenir. Yol-Uzaklık kavramları:
LİNEAR (DÜZGÜN DOĞRUSAL) BİOKİNEMATİK ÖZELLİKLER Düzgün doğrusal hareket bir cismin düz bir doğrultuda ilerlemesi, yer değiştirmesidir. Uzunluk, hız, ivmelenme bu bölümde incelenir. Yol-Uzaklık kavramları:
MADDESEL NOKTANIN EĞRİSEL HAREKETİ
 Silindirik Koordinatlar: Bazı mühendislik problemlerinde, parçacığın hareketinin yörüngesi silindirik koordinatlarda r, θ ve z tanımlanması uygun olacaktır. Eğer parçacığın hareketi iki eksende oluşmaktaysa
Silindirik Koordinatlar: Bazı mühendislik problemlerinde, parçacığın hareketinin yörüngesi silindirik koordinatlarda r, θ ve z tanımlanması uygun olacaktır. Eğer parçacığın hareketi iki eksende oluşmaktaysa
BÖLÜM 9 ÇÖZÜLMESİ ÖNERİLEN ÖRNEK VE PROBLEMLER
 BÖLÜM 9 ÇÖZÜLMESİ ÖNERİLEN ÖRNEK VE PROBLEMLER b) İkinci süreç eğik atış hareketine karşılık geliyor. Orada örendiğin problem çözüm adımlarını kullanarak topun sopadan ayrıldığı andaki hızını bağıntı olarak
BÖLÜM 9 ÇÖZÜLMESİ ÖNERİLEN ÖRNEK VE PROBLEMLER b) İkinci süreç eğik atış hareketine karşılık geliyor. Orada örendiğin problem çözüm adımlarını kullanarak topun sopadan ayrıldığı andaki hızını bağıntı olarak
T.C. SÜLEYMAN DEMĐREL ÜNĐVERSĐTESĐ MÜHENDĐSLĐK FAKÜLTESĐ MAKĐNE MÜHENDĐSLĐĞĐ BÖLÜMÜ
 T.C. SÜLEYMAN DEMĐREL ÜNĐVERSĐTESĐ MÜHENDĐSLĐK FAKÜLTESĐ MAKĐNE MÜHENDĐSLĐĞĐ BÖLÜMÜ MAKĐNE TEORĐSĐ VE DĐNAMĐĞĐ LABORATUARI DENEY FÖYÜ DENEY ADI MEKANĐK TĐTREŞĐM DENEYĐ DERSĐN ÖĞRETĐM ÜYESĐ Dr. Öğretim
T.C. SÜLEYMAN DEMĐREL ÜNĐVERSĐTESĐ MÜHENDĐSLĐK FAKÜLTESĐ MAKĐNE MÜHENDĐSLĐĞĐ BÖLÜMÜ MAKĐNE TEORĐSĐ VE DĐNAMĐĞĐ LABORATUARI DENEY FÖYÜ DENEY ADI MEKANĐK TĐTREŞĐM DENEYĐ DERSĐN ÖĞRETĐM ÜYESĐ Dr. Öğretim
6. Osiloskop. Periyodik ve periyodik olmayan elektriksel işaretlerin gözlenmesi ve ölçülmesini sağlayan elektronik bir cihazdır.
 6. Osiloskop Periyodik ve periyodik olmayan elektriksel işaretlerin gözlenmesi ve ölçülmesini sağlayan elektronik bir cihazdır. Osiloskoplar üç gruba ayrılabilir; 1. Analog osiloskoplar 2. Dijital osiloskoplar
6. Osiloskop Periyodik ve periyodik olmayan elektriksel işaretlerin gözlenmesi ve ölçülmesini sağlayan elektronik bir cihazdır. Osiloskoplar üç gruba ayrılabilir; 1. Analog osiloskoplar 2. Dijital osiloskoplar
DENEY 2 SABİT İVME İLE DÜZGÜN DOĞRUSAL HAREKET VE DÜZLEMDE HAREKET
 DENEY 2 SABİT İVME İLE DÜZGÜN DOĞRUSAL HAREKET VE DÜZLEMDE HAREKET AMAÇ: Sabit ivme ile düzgün doğrusal hareket çalışılıp analiz edilecek ve eğik durumda bulunan hava masasındaki diskin hareketi incelenecek
DENEY 2 SABİT İVME İLE DÜZGÜN DOĞRUSAL HAREKET VE DÜZLEMDE HAREKET AMAÇ: Sabit ivme ile düzgün doğrusal hareket çalışılıp analiz edilecek ve eğik durumda bulunan hava masasındaki diskin hareketi incelenecek
elde ederiz. Bu son ifade yeniden düzenlenirse,
 Deney No : M2 Deneyin Adı : İKİ BOYUTTA ESNEK ÇARPIŞMA Deneyin Amacı : İki boyutta esnek çarpışmada, enerji ve momentum korunum bağıntılarını incelemek, momentumun vektörel, enerjini skaler bir büyüklük
Deney No : M2 Deneyin Adı : İKİ BOYUTTA ESNEK ÇARPIŞMA Deneyin Amacı : İki boyutta esnek çarpışmada, enerji ve momentum korunum bağıntılarını incelemek, momentumun vektörel, enerjini skaler bir büyüklük
A A A A A A A A A A A
 S 2 FİZİ TESTİ. Bu testte 0 soru vardır. 2. Cevaplarınızı, cevap kâğıdının Fizik Testi için ayrılan kısmına işaretleyiniz.. Aşağıdakilerden hangisi momentum birimidir? joule joule A) B) newton saniye weber
S 2 FİZİ TESTİ. Bu testte 0 soru vardır. 2. Cevaplarınızı, cevap kâğıdının Fizik Testi için ayrılan kısmına işaretleyiniz.. Aşağıdakilerden hangisi momentum birimidir? joule joule A) B) newton saniye weber
Fizik Dr. Murat Aydemir
 Fizik-1 2017-2018 Dr. Murat Aydemir Ankara University, Physics Engineering, Bsc Durham University, Physics, PhD University of Oxford, Researcher, Post-Doc Ofis No: 35 Merkezi Derslikler Binasi murat.aydemir@erzurum.edu.tr
Fizik-1 2017-2018 Dr. Murat Aydemir Ankara University, Physics Engineering, Bsc Durham University, Physics, PhD University of Oxford, Researcher, Post-Doc Ofis No: 35 Merkezi Derslikler Binasi murat.aydemir@erzurum.edu.tr
EĞİTİM ÖĞRETİM YILI. ANADOLU LİSESİ 11.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI 11.SINIF KAZANIM VE SÜRE TABLOSU
 08-09 EĞİTİM ÖĞRETİM YILI. ANADOLU LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. TRİGONOMETRİ 7 6 6.. Yönlü
08-09 EĞİTİM ÖĞRETİM YILI. ANADOLU LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. TRİGONOMETRİ 7 6 6.. Yönlü
VERİLER. Yer çekimi ivmesi : g=10 m/s 2
 VERİLER Yer çekimi ivmesi : g=10 m/s 2 Metrik Ön Takılar sin 45 = cos 45 = 0,7 Numara Ön Takı Simge sin 37 = cos 53 = 0,6 sin 53 = cos 37 = 0,8 10 9 giga G tan 37 = 0,75 10 6 mega M tan 53 = 1,33 10 3
VERİLER Yer çekimi ivmesi : g=10 m/s 2 Metrik Ön Takılar sin 45 = cos 45 = 0,7 Numara Ön Takı Simge sin 37 = cos 53 = 0,6 sin 53 = cos 37 = 0,8 10 9 giga G tan 37 = 0,75 10 6 mega M tan 53 = 1,33 10 3
Bir cismin iki konumu arasındaki vektörel uzaklıktır. Başka bir ifadeyle son konum (x 2 ) ile ilk konum
 DOĞRUSAL ve BAĞIL HAREKET Hareket Maddelerin zamanla yer değiştirmesine hareket denir. Fakat cisimlerin nereye göre yer değiştirdiği ve nereye göre hareket ettiği belirtilmelidir. Örneğin at üstünde giden
DOĞRUSAL ve BAĞIL HAREKET Hareket Maddelerin zamanla yer değiştirmesine hareket denir. Fakat cisimlerin nereye göre yer değiştirdiği ve nereye göre hareket ettiği belirtilmelidir. Örneğin at üstünde giden
TEMEL DC ÖLÇÜMLERİ: AKIM ÖLÇMEK: Ampermetre ile ölçülür. Ampermetre devreye seri bağlanır.
 TEMEL DC ÖLÇÜMLERİ: AKIM ÖLÇMEK: Ampermetre ile ölçülür. Ampermetre devreye seri bağlanır. AMPERMETRENİN ÖLÇME ALANININ GENİŞLETİLMESİ: Bir ampermetre ile ölçebileceği değerden daha yüksek bir akım ölçmek
TEMEL DC ÖLÇÜMLERİ: AKIM ÖLÇMEK: Ampermetre ile ölçülür. Ampermetre devreye seri bağlanır. AMPERMETRENİN ÖLÇME ALANININ GENİŞLETİLMESİ: Bir ampermetre ile ölçebileceği değerden daha yüksek bir akım ölçmek
Radyo Antenler
 AST406 Radyo Antenler Dipol Antenler: Hertz Dipolü Alıcı Dipolün Yön Diyagramı c 2 S E sabit sin 2 4 R Şekil 1 Dipolün anlık yön diyagramı Şekil 2 Yön diyagramı Anten Türleri Çok Yönlü antenler
AST406 Radyo Antenler Dipol Antenler: Hertz Dipolü Alıcı Dipolün Yön Diyagramı c 2 S E sabit sin 2 4 R Şekil 1 Dipolün anlık yön diyagramı Şekil 2 Yön diyagramı Anten Türleri Çok Yönlü antenler
11. SINIF. No Konular Kazanım Sayısı GEOMETRİ TRİGONOMETRİ Yönlü Açılar Trigonometrik Fonksiyonlar
 11. SINIF No Konular Kazanım Sayısı GEOMETRİ Ders Saati Ağırlık (%) 11.1. TRİGONOMETRİ 7 56 26 11.1.1. Yönlü Açılar 2 10 5 11.1.2. Trigonometrik Fonksiyonlar 5 46 21 11.2. ANALİTİK GEOMETRİ 4 24 11 11.2.1.
11. SINIF No Konular Kazanım Sayısı GEOMETRİ Ders Saati Ağırlık (%) 11.1. TRİGONOMETRİ 7 56 26 11.1.1. Yönlü Açılar 2 10 5 11.1.2. Trigonometrik Fonksiyonlar 5 46 21 11.2. ANALİTİK GEOMETRİ 4 24 11 11.2.1.
EĞİTİM ÖĞRETİM YILI. FEN LİSESİ 11.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI 11.SINIF KAZANIM VE SÜRE TABLOSU
 08-09 EĞİTİM ÖĞRETİM YILI. FEN LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. TRİGONOMETRİ 8 6 6.. Yönlü Açılar
08-09 EĞİTİM ÖĞRETİM YILI. FEN LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. TRİGONOMETRİ 8 6 6.. Yönlü Açılar
FİZİK II - Final UYGULAMA
 FİZİK II - Final UYGULAMA Problem 1 /Ders 1 (Elektrik Alan ve Kuvvet) Şekildeki gibi 1.00 g lık yüklü bir mantar top ince bir iplikle düzgün bir elektrik alanının bulunduğu bölgede asılıyor. İpin yatayla
FİZİK II - Final UYGULAMA Problem 1 /Ders 1 (Elektrik Alan ve Kuvvet) Şekildeki gibi 1.00 g lık yüklü bir mantar top ince bir iplikle düzgün bir elektrik alanının bulunduğu bölgede asılıyor. İpin yatayla
ELEKTRİK VE ELEKTRİK DEVRELERİ 2
 1 ELEKTİK VE ELEKTİK DEVELEİ ALTENATİF AKIM Enstrümantal Analiz, Doğru Akım Analitik sinyal transduserlerinden çıkan elektrik periyodik bir salınım gösterir. Bu salınımlar akım veya potansiyelin zamana
1 ELEKTİK VE ELEKTİK DEVELEİ ALTENATİF AKIM Enstrümantal Analiz, Doğru Akım Analitik sinyal transduserlerinden çıkan elektrik periyodik bir salınım gösterir. Bu salınımlar akım veya potansiyelin zamana
DERS: MATEMATİK I MAT101(04)
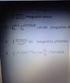 DERS: MATEMATİK I MAT0(0) ÜNİTE: FONKSİYONLAR KONU:. TRİGONOMETRİK FONKSİYONLAR Öncelikle açı ölçü birimlerine göz atalım: Bilindiği gibi bir tam açının ölçüsü 0 derecedir. Diğer bir açı ölçü birimi de
DERS: MATEMATİK I MAT0(0) ÜNİTE: FONKSİYONLAR KONU:. TRİGONOMETRİK FONKSİYONLAR Öncelikle açı ölçü birimlerine göz atalım: Bilindiği gibi bir tam açının ölçüsü 0 derecedir. Diğer bir açı ölçü birimi de
ANALOG HABERLEŞME (GM)
 ANALOG HABERLEŞME (GM) Taşıyıcı sinyalin sinüsoidal olduğu haberleşme sistemidir. Sinüs işareti formül olarak; V. sin(2 F ) ya da i I. sin(2 F ) dır. Formülde; - Zamana bağlı değişen ani gerilim (Volt)
ANALOG HABERLEŞME (GM) Taşıyıcı sinyalin sinüsoidal olduğu haberleşme sistemidir. Sinüs işareti formül olarak; V. sin(2 F ) ya da i I. sin(2 F ) dır. Formülde; - Zamana bağlı değişen ani gerilim (Volt)
SES DALGALARı Dalgalar genel olarak, mekanik ve elektromanyetik dalgalar olmak üzere iki ana gruba ayrılır. Elektromanyetik dalgalar, yayılmak için bi
 SES FĠZĠĞĠ SES DALGALARı Dalgalar genel olarak, mekanik ve elektromanyetik dalgalar olmak üzere iki ana gruba ayrılır. Elektromanyetik dalgalar, yayılmak için bir ortama ihtiyaç duymazlar ve boşlukta da
SES FĠZĠĞĠ SES DALGALARı Dalgalar genel olarak, mekanik ve elektromanyetik dalgalar olmak üzere iki ana gruba ayrılır. Elektromanyetik dalgalar, yayılmak için bir ortama ihtiyaç duymazlar ve boşlukta da
DENEY FÖYÜ 7: Seri ve Paralel Rezonans Devreleri
 DENEY FÖYÜ 7: Seri ve Paralel Rezonans Devreleri Deneyin Amacı: Seri ve paralel rezonans devrelerini incelemek, devrelerin karakteristik parametrelerini hesaplamak ve ölçmek, rezonans eğrilerini çizmek.
DENEY FÖYÜ 7: Seri ve Paralel Rezonans Devreleri Deneyin Amacı: Seri ve paralel rezonans devrelerini incelemek, devrelerin karakteristik parametrelerini hesaplamak ve ölçmek, rezonans eğrilerini çizmek.
Işıma Şiddeti (Radiation Intensity)
 Işıma Şiddeti (Radiation Intensity) Bir antenin birim katı açıdan yaydığı güçtür U=Işıma şiddeti [W/sr] P or =Işıma yoğunluğu [ W/m 2 ] Örnek-4 Bir antenin güç yoğunluğu Olarak verildiğine göre, ışıyan
Işıma Şiddeti (Radiation Intensity) Bir antenin birim katı açıdan yaydığı güçtür U=Işıma şiddeti [W/sr] P or =Işıma yoğunluğu [ W/m 2 ] Örnek-4 Bir antenin güç yoğunluğu Olarak verildiğine göre, ışıyan
BMT104 ELEKTRONİK DEVRELER DERSİ LABORATUVAR UYGULAMALARI
 T.C. DÜZCE ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ BİLGİSAYAR MÜHENDİSLİĞİ BÖLÜMÜ BMT104 ELEKTRONİK DEVRELER DERSİ LABORATUVAR UYGULAMALARI CİHAZLARIN TANITIMI ve SİNYALLER Doç. Dr. İbrahim YÜCEDAĞ Arş. Gör.
T.C. DÜZCE ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ BİLGİSAYAR MÜHENDİSLİĞİ BÖLÜMÜ BMT104 ELEKTRONİK DEVRELER DERSİ LABORATUVAR UYGULAMALARI CİHAZLARIN TANITIMI ve SİNYALLER Doç. Dr. İbrahim YÜCEDAĞ Arş. Gör.
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
EKİM MAKİNALARINA İLİŞKİN ÇÖZÜMLÜ PROBLEMLER
 EKİM MAKİNALARINA İLİŞKİN ÇÖZÜMLÜ PROBLEMLER Problem 1: Çift diskli bir gömücü ayağın çapı (D) 330 mm, diskler arasındaki açısı (β) 1 o ve çizi genişliği (S) 15 mm dir. a. Değme noktası yükseklik açısını
EKİM MAKİNALARINA İLİŞKİN ÇÖZÜMLÜ PROBLEMLER Problem 1: Çift diskli bir gömücü ayağın çapı (D) 330 mm, diskler arasındaki açısı (β) 1 o ve çizi genişliği (S) 15 mm dir. a. Değme noktası yükseklik açısını
Yay Dalgaları. Test 1 Çözümleri cm m = 80 cm
 Yay Dalgaları YY DGRI 1 Test 1 Çözüleri 3. 0 c = 80 c 1. = 8 biri 0 c rdaşık iki tepe arasındaki uzaklık dalga boyudur. Bu duruda dalga boyu şekildeki gibi 80 c olarak bulunur. v = f bağıntısına göre hız;
Yay Dalgaları YY DGRI 1 Test 1 Çözüleri 3. 0 c = 80 c 1. = 8 biri 0 c rdaşık iki tepe arasındaki uzaklık dalga boyudur. Bu duruda dalga boyu şekildeki gibi 80 c olarak bulunur. v = f bağıntısına göre hız;
ARAZİ ÖLÇMELERİ. Temel Ödev I: Koordinatları belirli iki nokta arasında ki yatay mesafenin
 Temel ödevler Temel ödevler, konum değerlerinin bulunması ve aplikasyon işlemlerine dair matematiksel ve geometrik hesaplamaları içeren yöntemlerdir. öntemlerin isimleri genelde temel ödev olarak isimlendirilir.
Temel ödevler Temel ödevler, konum değerlerinin bulunması ve aplikasyon işlemlerine dair matematiksel ve geometrik hesaplamaları içeren yöntemlerdir. öntemlerin isimleri genelde temel ödev olarak isimlendirilir.
HİDROLİK. Yrd. Doç. Dr. Fatih TOSUNOĞLU
 HİDROLİK Yrd. Doç. Dr. Fatih TOSUNOĞLU Ders Hakkında Genel Bilgiler Görüşme Saatleri:---------- Tavsiye edilen kitaplar: 1-Hidrolik (Prof. Dr. B. Mutlu SÜMER, Prof. Dr. İstemi ÜNSAL. ) 2-Akışkanlar Mekaniği
HİDROLİK Yrd. Doç. Dr. Fatih TOSUNOĞLU Ders Hakkında Genel Bilgiler Görüşme Saatleri:---------- Tavsiye edilen kitaplar: 1-Hidrolik (Prof. Dr. B. Mutlu SÜMER, Prof. Dr. İstemi ÜNSAL. ) 2-Akışkanlar Mekaniği
Uçlarındaki gerilim U volt ve içinden t saniye süresince Q coulomb luk elektrik yükü geçen bir alıcıda görülen iş:
 Etrafımızda oluşan değişmeleri iş, bu işi oluşturan yetenekleri de enerji olarak tanımlarız. Örneğin bir elektrik motorunun dönmesi ile bir iş yapılır ve bu işi yaparken de motor bir enerji kullanır. Mekanikte
Etrafımızda oluşan değişmeleri iş, bu işi oluşturan yetenekleri de enerji olarak tanımlarız. Örneğin bir elektrik motorunun dönmesi ile bir iş yapılır ve bu işi yaparken de motor bir enerji kullanır. Mekanikte
Manyetizma. Manyetik alan çizgileri, çizim. Manyetik malzeme türleri. Manyetik alanlar. BÖLÜM 29 Manyetik alanlar
 ÖLÜM 29 Manyetik alanlar Manyetik alan Akım taşıyan bir iletkene etkiyen manyetik kuvvet Düzgün bir manyetik alan içerisindeki akım ilmeğine etkiyen tork Yüklü bir parçacığın düzgün bir manyetik alan içerisindeki
ÖLÜM 29 Manyetik alanlar Manyetik alan Akım taşıyan bir iletkene etkiyen manyetik kuvvet Düzgün bir manyetik alan içerisindeki akım ilmeğine etkiyen tork Yüklü bir parçacığın düzgün bir manyetik alan içerisindeki
STATİĞİN TEMEL PRENSİPLERİ
 1.1. Temel Kavramlar ve Tanımlar Mühendislik mekaniği: Kuvvet etkisi altındaki cisimlerin denge veya hareket koşullarını inceleyen bilim dalı Genel olarak mühendislik mekaniği Sert (rijit) katı cisimlerin
1.1. Temel Kavramlar ve Tanımlar Mühendislik mekaniği: Kuvvet etkisi altındaki cisimlerin denge veya hareket koşullarını inceleyen bilim dalı Genel olarak mühendislik mekaniği Sert (rijit) katı cisimlerin
Fizik 101: Ders 23 Gündem
 Fizik 101: Ders 3 Gündem Basit Harmonik Hereket Yatay yay ve kütle Sinus ve cosinus lerin anlamı Düşey yay ve kütle Enerji yaklaşımı Basit sarkaç Çubuk sarkaç Basit Harmonik Hareket (BHH) Ucunda bir kütle
Fizik 101: Ders 3 Gündem Basit Harmonik Hereket Yatay yay ve kütle Sinus ve cosinus lerin anlamı Düşey yay ve kütle Enerji yaklaşımı Basit sarkaç Çubuk sarkaç Basit Harmonik Hareket (BHH) Ucunda bir kütle
KOÜ. Mühendislik Fakültesi Makine Mühendisliği ( 1. ve 2. Öğretim ) Bölümü Dinamik Dersi (Türkçe Dilinde) 2. Çalişma Soruları / 21 Ekim 2018
 SORU-1) Şekilde gösterilen uzamasız halat makara sisteminde A'daki ipin ucu aşağı doğru 1 m/s lik bir hızla çekilirken, E yükünün hızının sayısal değerini ve hareket yönünü sistematik bir şekilde hesaplayarak
SORU-1) Şekilde gösterilen uzamasız halat makara sisteminde A'daki ipin ucu aşağı doğru 1 m/s lik bir hızla çekilirken, E yükünün hızının sayısal değerini ve hareket yönünü sistematik bir şekilde hesaplayarak
Bölüm 1. Elektriksel Büyüklükler ve Elektrik Devre Elemanları
 Bölüm Elektriksel Büyüklükler ve Elektrik Devre Elemanları. Temel Elektriksel Büyüklükler: Akım, Gerilim, Güç, Enerji. Güç Polaritesi.3 Akım ve Gerilim Kaynakları F.Ü. Teknoloji Fak. EEM M.G. .. Temel
Bölüm Elektriksel Büyüklükler ve Elektrik Devre Elemanları. Temel Elektriksel Büyüklükler: Akım, Gerilim, Güç, Enerji. Güç Polaritesi.3 Akım ve Gerilim Kaynakları F.Ü. Teknoloji Fak. EEM M.G. .. Temel
