1. Giriş 2. Kristal Yapılar 3. Kristal Kafes Noktaları 4. Kristal Kafes Doğrultuları ve Düzlemler MALZEME BILGISI B3
|
|
|
- İbrahi̇m Sançar
- 9 yıl önce
- İzleme sayısı:
Transkript
1 1. Giriş 2. Kristal Yapılar 3. Kristal Kafes Noktaları 4. Kristal Kafes Doğrultuları ve Düzlemler
2
3 Katı malzemeler, atomların veya iyonların oluşturdukları düzene göre sınıflandırılabilir. Bir kristal malzemede uzun aralıkta düzen mevcuttur. Atomlar, atomsal ölçekte uzun mesafelerde tekrar eden düzenli bir yapı oluştururlar. Yani katılaşma sırasında atomlar, en yakın komşu atomlara bağlanırken üç boyutta tekrar eden bir düzenin içinde yerlerini alırlar. Normal katılaşma koşullarında, bütün metallerde, seramik malzemelerin çoğunda ve polimerlerin bir kısmında kristal yapı oluşur. Kristalleşmeyen malzemelerde, uzun aralıkta atomsal düzen bulunmaz.
4 Kristal katıların bazı özellikleri, malzemelerin kristal yapılarına, yani atomların, iyonların ya da moleküllerin üç boyutlu olarak meydana getirdikleri düzene bağlıdır. Metaller de bulunan nispeten basit olanlardan, bazı seramik ve polimerlerde bulunan son derecede karmaşık olanlara kadar, uzun aralıkta düzene sahip çok sayıda farklı kristal yapı söz konusudur. Bu bölümde, metallerde yaygın olarak bulunan bazı kristal yapılar ele alınacaktır. Kristal yapılar anlatılırken atomların (veya iyonların), belirli çaplara sahip katı küreler şeklinde olduğu düşünülür. Katı küre atom modeli olarak adlandırılan bu modelde, en yakın komşuluğa sahip olan atomları temsil eden küreler birbirleri ile temas halinde bulunur.
5 Kristal yapılarda bulunan atomsal düzen, yapının bir grup atomdan oluşan küçük bir birimin tekrar etmesi ile oluştuğuna işaret eder. Bu açıdan kristal yapıları tanımlamak ve birim hücre anlatmak için, birim hücre olarak adlandırılan, kristalin tekrar eden bu en küçük öğesinin kullanılması kolaylık sağlar. Çoğu kristal yapıda, birim hücreler birbirine paralel üç çift yüzeyi olan prizmalardan oluşur. Şekil 3.1c de bir grup atomun oluşturduğu hacim içinde gösterilen birim hücre kübik bir şekle sahiptir. Kristalin simetrisini temsil edecek şekilde seçilen birim hücrenin, atom konumlarından, kenar uzunluğu kadar yapılacak ötelemelerle kristalin içindeki bütün atom noktaları elde edilebilir. Dolayısıyla, birim hücre kristal yapıyı oluşturan temel yapı taşıdır, geometrisi ve içerdiği atomların konumları kristal yapıyı tanımlar ve temsil eder. Kolaylık açısından, her kristal yapının birim hücresi, genellikle birim hücrelerin köşeleri, atomların merkezlerine denk gelecek şekilde seçilir. Bununla birlikte, belirli bir kristal yapıda birden fazla birim hücre seçeneği olsa da genellikle en yüksek geometrik simetriye sahip birim hücre tercih edilir.
6 Bu malzemelerde bulunan metalsel bağlar yöne bağımlı olmadığı için, bir atomun en yakın komşuluğunda bulunan atomların sayısı ve konumu üzerindeki kısıtlar minimumdur. Bu nedenle, metalik kristal yapılarda en yakın komşu atom sayısı ve atomsal istiflenme nispeten yüksektir. Metallerin kristal yapıları için katı küre modelinin kullanılması durumunda, her bir küre serbest elektronları hariç olmak üzere bir atomu (ya da metal iyonu) temsil eder. Tablo 3.1 de bazı metaller için atom yarıçapları verilmiştir. Yaygın olarak bilinen metallerin çoğu, yüzeymerkezli kübik, hacim merkezli kübik ve sıkı paket hekzagonal olmak üzere, nispeten basit olan üç farklı kristal yapıda bulunur.
7 Birçok metalde bulunan bir kristal yapı, bütün köşelerinde ve yüzey merkezlerinde birer atomun bulunduğu, kübik geometride bir birim hücreye sahiptir. Uygun bir şekilde yüzey merkezli kübik (YMK) kristal yapı olarak adlandırılmıştır. Bakır, alüminyum, gümüş ve altın gibi iyi bilinen bazı metaller YMK yapıya sahiptir (Tablo 3.1). Şekil 3. 1a da YMK birim hücre katı küre modeliyle gösterilmiş, Şekil 3.1b de ise tüm atomların görünürlüğü açısından atom merkezleri küçük dairelerle işaretlenmiştir. Şekil 3. 1 c de ise çok sayıda YMK birim hücrenin oluşturduğu bir kristal hacim gösterilmiştir. Bu yapıda, küreler veya iyonlar yüzey köşegeninde birbirleri ile temas halinde bulundukları için, küpün kenar uzunluğu, a ve atom yarıçapı, R arasında aşağıdaki ilişki geçerlidir.
8 YMK kristal yapıda, köşelerde bulunan her bir atom sekiz, yüzey merkezlerindeki her bir atom ise sadece iki birim hücre tarafından paylaşılır. Dolayısıyla, bir birim hücre içinde, sekiz köşe atomunun sekizde biri, altı yüzey atomunun yarısı olmak üzere, toplam dört atom vardır. Bu durum, kürelerin sadece birim hücre içinde kalan kısımlarının resmedildiği Şekil 3.1a da gösterilmiştir. Hücre, küp köşeleri, şekilde gösterilen köşe atomlarının merkezlerine denk gelecek şekilde oluşturulmuştur. Aslında, köşe ve yüzey atom konumları arasında bir fark yoktur yani eşdeğerdir. Küp köşesinin, bir köşe atomu merkezinden bir yüzey atomu merkezine ötelenmesi durumunda, hücre yapısında hiç bir değişiklik meydana gelmez.
9 Koordinasyon sayısı ve atomsal dolgu faktörü (ADF) kristal yapılar için önemli diğer sayısı iki özelliktir. Metallerde her atomun koordinasyon sayısı aynıdır. Bir başka ifadeyle, her atom atomsal dolgu için en yakın komşuluğunda bulunan veya kendisiyle temas halinde bulunan atomların sayısı aynıdır. Yüzey merkezli kübik yapılar için koordinasyon sayısı 12 dir. Şekil 3.1a yardımıyla bu sayı teyit edilebilir. Ön yüzeydeki atomun en yakın komşuluğunda (yani onunla temas halinde bulunan) dört köşe atomu, arka tarafında dört yüzey atomu ve şekilde gösterilmeyen ön tarafındanki bitişik hücrede ise arka taraftakilere özdeş dört tane daha yüzey atomu vardır. ADF, birim hücredeki bütün atomların, katı küre modeline göre, birim hücre içinde kalan toplam küresel hacimlerinin, birim hücre hacmine oranıdır.
10 Metallerde yaygın olarak bulunan bir diğer kristal yapı; hacim merkezinde bir ve köşelerinde sekiz atomun bulunduğu, kübik bir birim hücreye sahip olan hacimmerkezli kübik (HMK) yapıdır. Şekil 3.2c de bu kristal yapıya sahip bir grup küreden oluşan, bir hacim gösterilmiştir. Şekil 3.2a ve 3.2b de ise HMK birim hücre, sırasıyla katı küre ve küçük küre modeliyle gösterilmiştir. Bu yapıda, merkez ve köşe atomları hacim köşegeni üzerinde temas halinde bulundukları için, birim hücre kenarı, a ve atom yarıçapı, R arasında aşağıdaki eşitlik geçerlidir:
11 HMK yapı içinde toplam iki atom bulunur. Hacim merkezindeki atomun tamamı birim hücre içinde kalırken köşe atomları sekiz birim hücre tarafindan paylaşılır. Bunun yanında, köşe ve merkez atom konumları eşdeğerdir. HMK yapıda koordinasyon sayısı 8 dir. Her merkez atomunun en yakın komşuluğunda sekiz köşe atomu vardır. Koordinasyon sayısı gibi, HMK yapının atomsal dolgu faktörü de YMK yapınınkine göre daha düşüktür. ADF, YMK yapı için 0,74 iken HMK için bu değer O,68 dir.
12 Bazı metallerin birim hücrelerinde kübik simetri bulunmaz. Ele alınacak son kristal yapı hekzagonal bir birim hücreye sahiptir. Şekil 3.3a da sıkı paket hekzagonal (SPH) yapı olarak adlandırılan bu yapının birim hücresi küçük küreler ile gösterilmiştir. Şekil 3.3b de ise SPH birim hücrelerinden oluşmuş bir hacim gösterilmiştir.1 Birim hücrenin alt ve üst yüzeyleri, merkezlerinde bulunan bir atomun etrafında düzgün altıgen oluşturan altı atomdan (yani merkezdeki atomla birlikte toplam yedi atomdan) meydana gelir. Birim hücrenin içinde, alt ve üst yüzeyler arasında, 3 atomun bulunduğu başka bir düzlem vardır. Bu ara düzlemdeki atomlar, en yakın komşuluğunda bulunan alt ve üst düzlemlerdeki atomlar ile temas halindedir.
13 SPH kristal yapıda, bir birim hücrede, alt ve üst yüzeylerin köşelerinde bulunan 12 atomun altıda biri, alt ve üst yüzeylerin merkezinde bulunan iki atomun yarısı ve ara düzlemdeki 3 atom olmak üzere toplam 6 atom bulunur. Şekil 3.3a da gösterilen a ve c kenarları, birim hücrede kısa ve uzun kenarlara karşılık gelmeleri durumunda, c/a oranı 1,633 olmalıdır. Ancak, bazı SPH metallerde bu ideal değerden sapma söz konusudur. YMK yapıda olduğu gibi, SPH yapının koordinasyon sayısı ve atomsal dolgu faktörü, sırasıyla 12 ve O,74 tür. Kadmiyum, magnezyum, titanyum ve çinko gibi bazı metaller SPH yapıda bulunurlar. Bu yapıya sahip bazı metaller Tablo 3.1 de verilmiştir.
14 YMK birim hücre hacmini atom yarıçapı, R cinsinden hesaplayınız: atomlar 4R uzunluğundaki yüzey köşegeninde birbirlerine temas etmektedir. Kenar uzunluğu a olan kübik bir geometriye sahip olduğuna göre, birim hücrenin hacmi a3 e eşittir. Birim hücrenin ön yüzeyinde gösterilen, iki küp kenarı ve yüzey köşege ninin oluşturduğu dik üçgene göre aşağıdaki eşitlik yazılabilir: YMK birim hücre hacmi, VBH aşağıdaki gibi hesaplanahilir:
15 YMK yapı için atomsal dolgu faktörünün 0,74 olduğunu gösteriniz. Atomsal dolgu faktörü, birim hücrede atomların kapladığı toplam hacmin, birim hücre hacmine bölünmesiyle bulunur: Birim hücrenin ve atomların toplam hacmi atom yarıçapı, R ye göre hesaplanabilir. YMK birim hücrede, her birinin hacmi 4/3πR 3 olan toplam dört atom bulunduğuna göre, YMK birim hücredeki toplam atom (ya da küre) hacmi aşağıda gösterilen şekilde hesaplanır: birim hücrenin hacmi atom yarıçapı, R cinsinden aşağıdaki gibi bulunmuştu:
16 Kristal yapı bilgisi sayesinde metallerin teorik yoğunlukları aşağıdaki gibi hesaplanabilir: Burada; n = birim hücredeki toplam atom sayısı A = atom ağırlığı VBH = birim hücre hacmi NA = Avagadro sayısıdır (6,023x10 23 atom/mol)
17 Bakırın atom yarıçapı 0,128 nm, kristal yapısı YMK ve atom ağırlığı 63,5 gr/mol olduğuna göre, bakırın teorik yoğunluğunu hesaplayınız ve deneysel olarak bulunan yoğunluğu ile kıyaslayınız. Çözüm Bu problemin çözümu için Denklem 3.5 kullanılacaktır. Bakırın kristal yapısı YMK olduğu için birim hücredeki atom sayısı 4 tür. YMK birim hücresinin hacmi Örnek Problem 3.1 de olarak hesaplanmıştı. Bakırın atom yarıçapı, R = 0,128 nm ve ağırlığı Acu= 63,5 gr/mol olarak verildiğine göre: n = birim hücredeki toplam atom sayısı A = atom ağırlığı V BH = birim hücre hacmi N A = Avagadro sayısıdır Bu değer, bakırın literatürde belirtilen gerçek yoğunluğu olan 8,94 gr/cm3 e çok yakındır.
18 Bazı metaller ve metal dışı malzemeler birden fazla kristal yapıda bulunabilirler. Bu özelliğe polimorfizm denir. Element halindeki katılar için, allotropi olarak adlandırılan bu allotropi özelliğe sahip malzemelerin hangi kristal yapıda bulunduğu, sıcaklığa ve dış basınca bağlıdır. Örneğin, normal koşullarda karbon kararlı grafit halinde bulunurken, aşırı yüksek basınçlar altında elmas oluşur. Oda sıcaklığında HMK kristal yapıda bulunan saf demir ise 912 C de YMK yapılı demire dönüşür. Genellikle, polimorfik dönüşümler sırasındamalzemelerinyoğunlukları ve diğer fizikselözelliklerideğişir.
19 Çok sayıda farklı kristal yapı bulunduğu için, kristal yapıları birim hücre biçimlerine ve/veya atom dizilişlerine göre sınıflandırmak kolaylık sağlamaktadır. Sınıflandırma, birim hücredeki atom konumlarına bakılmaksızın, sadece birim hücre geometrisine veya uygun prizmatik birim hücre biçimine göre yapılabilir. Bu çerçevede, Şekil 3.4 te gösterildiği gibix, yvez eksenleri birim hücre kenarları üzerinde olacak şekilde, orijini birim hücrenin bir köşesine yerleştirilen, bir xyz koordinat sistemi oluşturulur. Birim hücre geometrisi, kenar uzunlukları a,b,cveiçaçıları α,β,γ oluşan altı parametre yardımıyla tam olarak tanımlanır.
20 a, b, c ve α,β,γ nın, her biri ayrı bir kristal sistemi temsil eden, yedi farklı kombinasyonu vardır. Kübik, hekzagonal, tetragonal, rombohedral, ortorombik, monoklinik ve triklinik olmak üzere bu yedi kristal sistemin kafes parametreleri arasındaki ilişki ve birim hücreleri Tablo 3.2 de gösterilmiştir a = b = c ve α=β=γ =90 olan kübik sistem en yüksek simetriye sahipken, a b c ve α β γ olan triklinik sistem, simetrisi en az olan sistemdir. Bu bölu mde ele alınan metallere özgu kristal yapılarından, YMK ve HMK yapıların kübik, SPH in ise hekzoganal sisteme ait olduğu açıktır.
21
22 Kristal malzemelerle ilgi yapılan çalışmalarda, birim hücre içinde belirli bir noktanın, bir kafes doğrultusunun ya da kafes düzleminin belirtilmesi gerekebilir. Kafes noktalarını, doğrultularını ve düzlemlerini adlandırmak için ü. rakamdan veya indisten oluşan bir sistem benimsenmiştir. İndis değerlerinin belirlenmesi için Şekil 3.4 te gösterildiği gibi, birim hücre ve x, y ve z eksenleri sağ el kuralına göre birim hücrenin kenarlarına denk gelecek şekilde, birim hücrenin bir köşesine yerleştirilen bir koordinat sistemi kullanılır. Hekzagonal, rombohedral, monoklinik ve triklinik sistemlerde, kartezyen koordinat sisteminden farklı olarak, bu eksenlerin hepsi birbirlerine dik değildir.
23 Birim hücre içinde her hangi noktanın yeri, birim hücre kenarları (a, b ve c) ile orantılı koordinatlarına göre belirtilir. Koordinatların nasıl bulunduğunu göstermek için, Şekil 3.5 teki, içinde bir P noktasının bulunduğu birim hücreyi ele alalım. P nin konumu genelleştirilmiş q, r ve s koordinatları ile belirlenir. q, x ekseni üzerinde a ile orantılı bir uzunluğu belirtir. Benzer şekilde r, y ekseni üzerinde h ile ve s ise z ekseni üzerinde c ile orantılı bir uzunluktur. Dolayısıyla, P nin konumu, değerleri bire eşit ya da birden daha küçük olabilen qr s koordinatları ile gösterilir. Ayrıca, genel uygulamaya uygun olarak, bu kitapta bu koordinatları ayırmak için virgül veya başka noktalarna işaretlerinin kullanıl ması tercih edilmemiştir.
24
25 Bir kristal kafes doğrultusu iki nokta arasında çizilen bir doğru ya da vektör ile tamamlanır. Bir doğrultuya ait üç indisinin belirlenmesi için aşağıdaki adımlar uygulanır: 1. Uygun uzunlukta bir vektör, koordinat sisteminin orijininden geçecek şekilde yerleştirilir. Paralellik korunduğu sürece, bir vektör kristal kafes içinde istenilen noktaya taşınabilir. Bu şekilde yapılan bir taşıma, doğrultunun miller indislerini değiştirmez. 2. Vektörün ü. eksen üzerindeki iz düşüm uzunlukları belirlenir. Bu uzunluklar birim hücre boyutları a, b ve c ye bölünür. 3. Gerektiğinde, bulunan sayıları en küçük tam sayılara dönüştürmek için, ortak bir sayı ile bölme ya da çarpma işlemi yapılır. 4. Sayılar köşeli parantezin içine virgül koymaksızın alınır [uvw]. u, v ve w tam sayıları vektörün x, y ve z eksenleri üzerindeki indirgenmiş (kafes parametreleri ile orantılı) iz düşümlerdir.
26 Her ü. eksende pozitif ve negatif koordinatlar söz konusu olduğundan, indisler önlerine negatif işaret de alabilirler. Böyle negatif işaretli indisler, üzerlerine çizilen bir eksi işareti ya da çizgi yardımıyla gösterilir. Örneğin, [111] doğrultusunun y yönu nde bir bile şeni vardır. Ayrıca, bir doğrultunun bütün indislerinin negatifterinin alınmasıyla bulunan yeni indisler, doğrultunun kendisine paralel, ancak zıt yönde bir doğrultuyu gösterir. [ 11 1] doğrultusu, [1 11] doğrultusuna göre tam ters yönde uzanır. Belirli bir kristal yapıda birden fazla doğrultu (ya da düzlem) belirlenecek ise pozitif ve negatifyönlerin bir defa belirlen mesinin ardından değiştirilmemeleri gerekir. Şekil 3.6 daki birim hücrede [100], [110] ve [111] doğrultuları gösterilmiştir.
27
28
29 Hekzagonal Kristaller Hekzagonal (altıgen) simetriye sahip kristallerde eşdeğer doğrultuların aynı indislere sahip olmamaları nedeniyle ortaya çıkan bir problem söz konusudur. Bu durum Şekil 3.7 degösterilen, dört eksenli veya Miller Bravais koordinat sisteminin kullanılmasıyla giderilebilir. Taban (bazal) düzlemi olarak adlandırılan, tek bir düzlem üzerinde bulunan a1, a > ve (13 eksenleri arasındaki açılar 120 C dir. z ekseni taban düzlemine dik olarak uzanır. Daha önce bahsedildiği gibi, elde edilen doğrultu indisleri, [uvtw] şeklinde dört indis ile belirtilir. Bu indislerden ilk üçü taban düzlemindeki a1, a2 ve a3 eksenleri üzerindeki iz düşümleri gösterir.
30 Bu denklemlerde u, v, w üç indis sistemine ve u, v, t, w ise Bravais Miller dört indis sistemine ait indislerdir. Örneğin, [0101 doğrultusu [İ2TOj haline gelir. Ayrıca, daha önce belirtildiği gibi indislerin en küçük tam sayılı hale dönüştürülmeleri gerekir. Şekil 3.8a da hekzagonal birim hücrede birkaç farklı doğrultu gösterilmiştir.
31 Hekzagonal sistemlerde kristal kafes doğrultularını göstermek diğer altı sistemde bulunan kristallere göre daha karmaşıktır. Hekzagonal kristaller için Şekil 3.9 da gösterilen dört eksenli koordinat sisteminin kullanılması daha kullanışlıdır. Şekilde görüleceği üzere, taban düzlemi üzerinde a1, a2 ve a3 eksenlerine paralel çizgiler bulunmaktadır. Sadece eksenlerden birine paralel olarak çizilen bu çizgiler, paralel olmadıkları diğer iki eksen üzerinde kafes parametreleri mesafelerini üç eşit parçaya bölecek şekilde, eşit aralıklarla yerleştirilmiştir. Ayrıca, Şekil 3.9 daki z ekseni üzerindeki kafes parametresi uzunluğu damvennoktaları ile üç eşit parçaya bölünmüştür. Bu şekilde gösterilen koordinat sistemi indirgenmiş koordinat sistemi olarak anılacaktır Dört indis ile belirtilmiş bir doğrultunun çizilmesi daha önce anlatılan, ilgili eksenler üzerindeki vektör iz düşümlerini içeren işlemlere benzer bir şekilde gerçekleştirilir. Bu durumda, a (a1, a2 ve a3 ü temsilen) ve z den oluşan kafes parametreleri üzerindeki iz düşümler yerine, Şekil 3.9 daki indirgenmiş ölçek uygulanarak, a13 ve c13 kullanılır. Bu işlem aşağıdaki örnek problemde gösterilmiştir
32
33
34
35 KRİSTAL KAFES DÜZLEMLERİ Kristal yapılarda düzlemler benzer bir şekilde gösterilir. Şekil 3.4 te gösterildiği gibi, yine birim hücre ve üç eksenli koordinat sistemi temel alınır. Hekzagonal kristal sistemi dışın da bütün düzlemler (hkl) şeklinde üç Miller indisi ile belirtilir. Birbirlerine paralel olan herhangi iki kristal kafes düzlemi, birbirine eşdeğerdir ve aynı indislerle gösterilir. h, k ve l indislerinin belirlenmesi için uygulanan işlemler aşağıda sıralanmıştır: 1. Düzlem orijinden geçiyorsa düzlem uygun bir şekilde paralel olarak taşınır veya orijin başka bir birim hücrenin köşesine taşınır. 2. Bu noktada kristal kafes düzlemi tüm eksenleri ya da en azından bir ekseni keser. Kesmediği eksenler varsa bu eksenlere paralel olarak uzanıyor demektir. Düzlemin eksenleri kestiği noktaların orijine uzaklıkları a, b ve c kafes parametreleri cinsinden belirlenir. 3. Bu sayıların çarpmaya göre tersleri alınır. Düzlemin herhangi bir eksene paralel olarak uzanması durumunda, 0 ekseni sonsuzda kestiği düşünülür ve çarpmaya göre tersi olarak 0 sayısı alınır. 4. Gerektiğinde bu üç sayı, en küçük tamsayıları verecek bir sayı ile çarpılır ya da bölünür. 5. Son olarak indisler virgül ile ayrılmaksızın (hkl) şeklinde parantez içine alınarak yazılır.
36 Düzlem herhangi bir ekseni orijinin negatif tarafinda kesiyorsa, ilgili indis üzerine çizilen eksi ya da çizgi işareti ile gösterilir. Ayrıca, bütün indislerin negatifterinin alınması ile bulunan yeni indisler, orijinin diğer tarafında, eksenleri eşit mesafelerde kesen, diğer bir paralel düzlemi belirtir. Şekil 3.10 da bazı düzlemler gösterilmiştir. Ayrıca, kübik kristallerde aynı indisli düzlem ve doğrultular birbirlerine diktir. Ancak, diğer kristal sistemlerde aynı indisli düzlemler ve doğrultular arasında basit geometrik ilişkiler bulunmaz.
37
38
39
KATILARDA KRİSTAL YAPI. Hekzagonal a b c 90 o, 120. Tetragonal a b c 90 o. Rombohedral (Trigonal) Ortorombik a b c 90 o. Monoklinik a b c 90 o
 KATILARDA KRİSTAL YAPI Kristal yapı atomun bir üst seviyesinde incelenen ve atomların katı halde oluşturduğu düzeni ifade eden birim hücre (kafes) geometrik parametreleri ve atom dizilimi ile tarif edilen
KATILARDA KRİSTAL YAPI Kristal yapı atomun bir üst seviyesinde incelenen ve atomların katı halde oluşturduğu düzeni ifade eden birim hücre (kafes) geometrik parametreleri ve atom dizilimi ile tarif edilen
MALZEME BİLGİSİ DERS 6 DR. FATİH AY.
 MALZEME BİLGİSİ DERS 6 DR. FATİH AY www.fatihay.net fatihay@fatihay.net GEÇEN HAFTA TEMEL KAVRAMLAR BİRİM HÜCRE METALLERDE KRİSTAL YAPILAR YOĞUNLUK HESAPLAMA BÖLÜM III KATILARDA KRİSTAL YAPILAR KRİSTAL
MALZEME BİLGİSİ DERS 6 DR. FATİH AY www.fatihay.net fatihay@fatihay.net GEÇEN HAFTA TEMEL KAVRAMLAR BİRİM HÜCRE METALLERDE KRİSTAL YAPILAR YOĞUNLUK HESAPLAMA BÖLÜM III KATILARDA KRİSTAL YAPILAR KRİSTAL
MALZEME BİLGİSİ DERS 5 DR. FATİH AY. www.fatihay.net fatihay@fatihay.net
 MALZEME BİLGİSİ DERS 5 DR. FATİH AY www.fatihay.net fatihay@fatihay.net GEÇEN HAFTA BAĞ KUVVETLERİ VE ENERJİLERİ ATOMLARARASI BİRİNCİL BAĞLAR İKİNCİL VEYA VAN DER WAALS BAĞLARI MOLEKÜLLER BÖLÜM III KATILARDA
MALZEME BİLGİSİ DERS 5 DR. FATİH AY www.fatihay.net fatihay@fatihay.net GEÇEN HAFTA BAĞ KUVVETLERİ VE ENERJİLERİ ATOMLARARASI BİRİNCİL BAĞLAR İKİNCİL VEYA VAN DER WAALS BAĞLARI MOLEKÜLLER BÖLÜM III KATILARDA
Bir kristal malzemede uzun-aralıkta düzen mevcu4ur.
 Bir kristal malzemede uzun-aralıkta düzen mevcu4ur. Kristal ka8ların bazı özellikleri, malzemelerin kristal yapılarına, yani atomların, iyonların ya da moleküllerin üç boyutlu olarak meydana ge@rdikleri
Bir kristal malzemede uzun-aralıkta düzen mevcu4ur. Kristal ka8ların bazı özellikleri, malzemelerin kristal yapılarına, yani atomların, iyonların ya da moleküllerin üç boyutlu olarak meydana ge@rdikleri
MALZEME BİLGİSİ. Kristal Yapılar ve Kristal Geometrisi
 MALZEME BİLGİSİ Dr.- Ing. Rahmi ÜNAL Konu: Kristal Yapılar ve Kristal Geometrisi 1 KRİSTAL YAPILAR Malzemelerin iç yapısı atomların diziliş biçimine bağlıdır. Kristal yapı Kristal yapılarda atomlar düzenli
MALZEME BİLGİSİ Dr.- Ing. Rahmi ÜNAL Konu: Kristal Yapılar ve Kristal Geometrisi 1 KRİSTAL YAPILAR Malzemelerin iç yapısı atomların diziliş biçimine bağlıdır. Kristal yapı Kristal yapılarda atomlar düzenli
Bölüm 3 - Kristal Yapılar
 Bölüm 3 - Kristal Yapılar Katı malzemeler, atomların veya iyonların oluşturdukları düzene göre sınıflandırılır. Kristal malzemede uzun-aralıkta atomsal ölçekte tekrarlayan bir düzen mevcuttur. Katılaşma
Bölüm 3 - Kristal Yapılar Katı malzemeler, atomların veya iyonların oluşturdukları düzene göre sınıflandırılır. Kristal malzemede uzun-aralıkta atomsal ölçekte tekrarlayan bir düzen mevcuttur. Katılaşma
KATILARIN ATOMİK DÜZENİ KRİSTAL YAPILAR
 KATILARIN ATOMİK DÜZENİ KRİSTAL YAPILAR KRİSTAL YAPILAR Mühendislik açısından önemli olan katı malzemelerin fiziksel özelikleri; katı malzemeleri meydana getiren atom, iyon veya moleküllerin dizilişine
KATILARIN ATOMİK DÜZENİ KRİSTAL YAPILAR KRİSTAL YAPILAR Mühendislik açısından önemli olan katı malzemelerin fiziksel özelikleri; katı malzemeleri meydana getiren atom, iyon veya moleküllerin dizilişine
Malzeme Bilimi I Metalurji ve Malzeme Mühendisliği
 I Metalurji ve Malzeme Mühendisliği Doç. Dr. Rıdvan YAMANOĞLU 2017-2018 Metaller katılaşırken kendilerine has, elektron düzenlerinin neden olduğu belli bir kafes sisteminde kristalleşirler. Aluminyum,
I Metalurji ve Malzeme Mühendisliği Doç. Dr. Rıdvan YAMANOĞLU 2017-2018 Metaller katılaşırken kendilerine has, elektron düzenlerinin neden olduğu belli bir kafes sisteminde kristalleşirler. Aluminyum,
MBM 304 Kristal Kimyası 4. Hafta Dr. Sedat ALKOY 1
 MBM 304 Kristal Kimyası 4. Hafta Dr. Sedat ALKOY 1 Kristal Sistemleri 7 temel kristal sistem ve bunlara ait 14 adet Bravais örgüsü vardır. z c β α y x b γ a Kafes - Birim Hücre x,y,z = koordinat eksenleri
MBM 304 Kristal Kimyası 4. Hafta Dr. Sedat ALKOY 1 Kristal Sistemleri 7 temel kristal sistem ve bunlara ait 14 adet Bravais örgüsü vardır. z c β α y x b γ a Kafes - Birim Hücre x,y,z = koordinat eksenleri
KRİSTAL YAPISI VE KRİSTAL SİSTEMLERİ
 KRİSTAL YAPISI VE KRİSTAL SİSTEMLERİ Kristal Yapı: Atomların, üç boyutlu uzayda düzenli (kendini tekrar eden) bir şekilde dizilmesiyle oluşan yapıya kristal yapı denir. Bir kristal yapı birim hücresiyle
KRİSTAL YAPISI VE KRİSTAL SİSTEMLERİ Kristal Yapı: Atomların, üç boyutlu uzayda düzenli (kendini tekrar eden) bir şekilde dizilmesiyle oluşan yapıya kristal yapı denir. Bir kristal yapı birim hücresiyle
KATILARIN ATOMIK DÜZENI Kristal Düzlemleri, Dogrulari ve Yönleri
 Kristal Düzlemleri, Dogrulari ve Yönleri Bölüm İçeriği Kristal malzemelerin Özeliklerinin Belirlenmesi. Kristal Geometri! Kristal Yapı Doğruları! Doğrusal atom Yoğunluğu! Kristal Düzlemler! Kristal Düzlemlerin
Kristal Düzlemleri, Dogrulari ve Yönleri Bölüm İçeriği Kristal malzemelerin Özeliklerinin Belirlenmesi. Kristal Geometri! Kristal Yapı Doğruları! Doğrusal atom Yoğunluğu! Kristal Düzlemler! Kristal Düzlemlerin
Kristallerdeki yüzeyler, simetri ve simetri elemanları 2 boyutta nasıl gösterilir?
 13/17 EKİM 2014 Kristallerdeki yüzeyler, simetri ve simetri elemanları 2 boyutta nasıl gösterilir? Küresel projeksiyon ile stereografik projeksiyonun farkı? Stereo-net (Wullf-net) Nokta grubu ne demek?
13/17 EKİM 2014 Kristallerdeki yüzeyler, simetri ve simetri elemanları 2 boyutta nasıl gösterilir? Küresel projeksiyon ile stereografik projeksiyonun farkı? Stereo-net (Wullf-net) Nokta grubu ne demek?
BÖLÜM 3. Katı malzemeler yapılarındaki atom ve iyonların birbirlerine göre düzenlerine bağlı olarak sınıflandırılırlar.
 KRİSTAL YAPISI ve KRİSTAL KUSURLARI Katı malzemeler yapılarındaki atom ve iyonların birbirlerine göre düzenlerine bağlı olarak sınıflandırılırlar. Kristal yapı içinde atomlar büyük atomik mesafeler boyunca
KRİSTAL YAPISI ve KRİSTAL KUSURLARI Katı malzemeler yapılarındaki atom ve iyonların birbirlerine göre düzenlerine bağlı olarak sınıflandırılırlar. Kristal yapı içinde atomlar büyük atomik mesafeler boyunca
BÖLÜM 2. Kristal Yapılar ve Kusurlar
 BÖLÜM 2 Kristal Yapılar ve Kusurlar 1- ATOMİK VE İYONİK DÜZENLER Kısa Mesafeli Düzenler-Uzun Mesafeli Düzenler Kısa Mesafeli Düzenler (SRO): Kısa mesafede atomların tahmin edilebilir düzenlilikleridir.
BÖLÜM 2 Kristal Yapılar ve Kusurlar 1- ATOMİK VE İYONİK DÜZENLER Kısa Mesafeli Düzenler-Uzun Mesafeli Düzenler Kısa Mesafeli Düzenler (SRO): Kısa mesafede atomların tahmin edilebilir düzenlilikleridir.
KRİSTAL KAFES SİSTEMLERİ
 KRİSTAL KAFES SİSTEMLERİ Doç. Dr. Ramazan YILMAZ Sakarya Üniversitesi, Teknoloji Fakültesi, Metalurji ve Malzeme Mühendisliği Bölümü Esentepe Kampüsü, 54187, SAKARYA 1 Giriş 2 Kristal Yapısı ve Birim Hücreler
KRİSTAL KAFES SİSTEMLERİ Doç. Dr. Ramazan YILMAZ Sakarya Üniversitesi, Teknoloji Fakültesi, Metalurji ve Malzeme Mühendisliği Bölümü Esentepe Kampüsü, 54187, SAKARYA 1 Giriş 2 Kristal Yapısı ve Birim Hücreler
Malzeme I Katılarda Kristal Yapılar
 Malzeme I Katılarda Kristal Yapılar 1 2 Atomik Yapılarda Düzen a) Düzensiz yapı: Atomların dağılımında herhangi bir düzen yoktur. Asal gazlarda görülür. b-c) Kısa aralıklı düzen: Atomların dağılımında
Malzeme I Katılarda Kristal Yapılar 1 2 Atomik Yapılarda Düzen a) Düzensiz yapı: Atomların dağılımında herhangi bir düzen yoktur. Asal gazlarda görülür. b-c) Kısa aralıklı düzen: Atomların dağılımında
FZM 220. Malzeme Bilimine Giriş
 FZM 220 Yapı Karakterizasyon Özellikler İşleme Performans Prof. Dr. İlker DİNÇER Fakültesi, Fizik Mühendisliği Bölümü 1 Ders Hakkında FZM 220 Dersinin Amacı Bu dersin amacı, fizik mühendisliği öğrencilerine,
FZM 220 Yapı Karakterizasyon Özellikler İşleme Performans Prof. Dr. İlker DİNÇER Fakültesi, Fizik Mühendisliği Bölümü 1 Ders Hakkında FZM 220 Dersinin Amacı Bu dersin amacı, fizik mühendisliği öğrencilerine,
bir atomun/iyonun bulunduğu kafes içindeki en yakın komşu atomlarının/iyonlarının sayısıdır.
 Koordinasyon sayısı; bir atomun/iyonun bulunduğu kafes içindeki en yakın komşu atomlarının/iyonlarının sayısıdır. Arayer boşlukları Kristal yapılarda kafes noktalarında bulunan atomlar arasındaki boşluklara
Koordinasyon sayısı; bir atomun/iyonun bulunduğu kafes içindeki en yakın komşu atomlarının/iyonlarının sayısıdır. Arayer boşlukları Kristal yapılarda kafes noktalarında bulunan atomlar arasındaki boşluklara
Kristal Yapılar KONU BAŞLIKLARI... Katılarda atomlar nasıl dizilirler? (mühendislik malzemelerindeki dizilişler)
 Kristal Yapılar KONU BAŞLIKLARI... Katılarda atomlar nasıl dizilirler? (mühendislik malzemelerindeki dizilişler) Malzemenin yoğunluğu ile yapısı arasında nasıl bir ilişki vardır? Atom dizilişi malzeme
Kristal Yapılar KONU BAŞLIKLARI... Katılarda atomlar nasıl dizilirler? (mühendislik malzemelerindeki dizilişler) Malzemenin yoğunluğu ile yapısı arasında nasıl bir ilişki vardır? Atom dizilişi malzeme
1. Düzensiz yapı : Atom veya moleküllerin rastgele dizilmesi. Argon gibi asal gazlarda görülür.
 Malzemeler atomların bir araya gelmesi ile oluşur. Bu yapı içerisinde atomları bir arada tutan kuvvete atomlar arası bağ denir. Yapı içerisinde bir arada bulunan atomlar farklı düzenlerde bulunabilir.
Malzemeler atomların bir araya gelmesi ile oluşur. Bu yapı içerisinde atomları bir arada tutan kuvvete atomlar arası bağ denir. Yapı içerisinde bir arada bulunan atomlar farklı düzenlerde bulunabilir.
Kristallografik düzlemler;
 Kristallografik düzlemler; Atomların dizildikleri tabaka veya düzlemlerdir Miller indisleri ile gösterilirler (hkl) Birim hücrenin bir köşesi koordinat sisteminin orijin ya da başlangıç noktası olarak
Kristallografik düzlemler; Atomların dizildikleri tabaka veya düzlemlerdir Miller indisleri ile gösterilirler (hkl) Birim hücrenin bir köşesi koordinat sisteminin orijin ya da başlangıç noktası olarak
1. Amaç Kristallerin üç boyutlu yapısı incelenecektir. Ön bilgi için İnorganik Kimya, Miessler ve Tarr, Bölüm 7 okunmalıdır.
 14 DENEY KATI HAL 1. Amaç Kristallerin üç boyutlu yapısı incelenecektir. Ön bilgi için İnorganik Kimya, Miessler ve Tarr, Bölüm 7 okunmalıdır. 2. Giriş Atomlar arası (veya moleküller arası) çekim kuvvetleri
14 DENEY KATI HAL 1. Amaç Kristallerin üç boyutlu yapısı incelenecektir. Ön bilgi için İnorganik Kimya, Miessler ve Tarr, Bölüm 7 okunmalıdır. 2. Giriş Atomlar arası (veya moleküller arası) çekim kuvvetleri
Metalurji Mühendisliğine Giriş
 Metalurji Mühendisliğine Giriş Temel Malzeme Grupları Yrd. Doç. Dr. Rıdvan YAMANOĞLU Demir esaslı metaller Günümüzde kullanılan metal ve alaşımların % 85 i demir esaslıdır. Bunun nedenleri: Yerkabuğunda
Metalurji Mühendisliğine Giriş Temel Malzeme Grupları Yrd. Doç. Dr. Rıdvan YAMANOĞLU Demir esaslı metaller Günümüzde kullanılan metal ve alaşımların % 85 i demir esaslıdır. Bunun nedenleri: Yerkabuğunda
ATOMLAR ARASI BAĞLAR
 MALZEME 2. HAFTA 1 ATOMSAL BAĞ ATOMLAR ARASI BAĞLAR Atomlar, atomlar arası bağ kuvvetleri ile bir araya gelirler. Malzemenin en küçük yapı taşı olan atomları bağ kuvvetleri bir arada tutar. Atomsal bağların
MALZEME 2. HAFTA 1 ATOMSAL BAĞ ATOMLAR ARASI BAĞLAR Atomlar, atomlar arası bağ kuvvetleri ile bir araya gelirler. Malzemenin en küçük yapı taşı olan atomları bağ kuvvetleri bir arada tutar. Atomsal bağların
Katılar & Kristal Yapı
 Katılar & Kristal Yapı Katılar Kristal katılar Amorf katılar Belli bir geometrik şekle sahip olan katılardır, tanecikleri belli bir düzene göre istiflenir. Belli bir geometrik şekli olmayan katılardır,
Katılar & Kristal Yapı Katılar Kristal katılar Amorf katılar Belli bir geometrik şekle sahip olan katılardır, tanecikleri belli bir düzene göre istiflenir. Belli bir geometrik şekli olmayan katılardır,
MALZEME BİLİMİ MAL213 Kristal Yapı-Doğrultu ve Düzlemlere ait Miller İndisleri Metal ve Seramik Yapılar, Polimer Yapıları, X Işını Difraksiyonu
 MALZEME BİLİMİ MAL213 Kristal Yapı-Doğrultu ve Düzlemlere ait Miller İndisleri Metal ve Seramik Yapılar, Polimer Yapıları, X Işını Difraksiyonu EYLÜL 2018 KRİSTAL YAPILAR Malzemeler atomların biraraya
MALZEME BİLİMİ MAL213 Kristal Yapı-Doğrultu ve Düzlemlere ait Miller İndisleri Metal ve Seramik Yapılar, Polimer Yapıları, X Işını Difraksiyonu EYLÜL 2018 KRİSTAL YAPILAR Malzemeler atomların biraraya
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 9 Ağırlık Merkezi ve Geometrik Merkez Kaynak: Mühendislik Mekaniği: Statik, R. C. Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 9. Ağırlık
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 9 Ağırlık Merkezi ve Geometrik Merkez Kaynak: Mühendislik Mekaniği: Statik, R. C. Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 9. Ağırlık
BMM 205 Malzeme Biliminin Temelleri
 BMM 205 Malzeme Biliminin Temelleri Katıların Kristal Yapıları Dr. Ersin Emre Ören Biyomedikal Mühendisliği Bölümü Malzeme Bilimi ve Nanoteknoloji Mühendisliği Bölümü TOBB Ekonomi ve Teknoloji Üniversitesi
BMM 205 Malzeme Biliminin Temelleri Katıların Kristal Yapıları Dr. Ersin Emre Ören Biyomedikal Mühendisliği Bölümü Malzeme Bilimi ve Nanoteknoloji Mühendisliği Bölümü TOBB Ekonomi ve Teknoloji Üniversitesi
Malzeme Bilimi Dersi
 Malzeme Bilimi Dersi Kristal Yapıları ve Kristal Geometrisi Kaynaklar 1) Malzeme Bilimi ve Mühendisliği William F. Smith Çeviren: Nihat G. Kınıkoğlu 2) Malzeme Biliminin Temelleri Hüseyin Uzun, Fehim Fındık,
Malzeme Bilimi Dersi Kristal Yapıları ve Kristal Geometrisi Kaynaklar 1) Malzeme Bilimi ve Mühendisliği William F. Smith Çeviren: Nihat G. Kınıkoğlu 2) Malzeme Biliminin Temelleri Hüseyin Uzun, Fehim Fındık,
Dik koordinat sisteminde yatay eksen x ekseni (apsis ekseni), düşey eksen ise y ekseni (ordinat ekseni) dir.
 ANALĐTĐK GEOMETRĐ 1. Analitik Düzlem Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da
ANALĐTĐK GEOMETRĐ 1. Analitik Düzlem Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da
Paslanmaz Çelik Gövde. Yalıtım Sargısı. Katalizör Yüzey Tabakası. Egzoz Emisyonları: Su Karbondioksit Azot
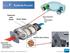 Paslanmaz Çelik Gövde Yalıtım Sargısı Egzoz Emisyonları: Su Karbondioksit Azot Katalizör Yüzey Tabakası Egzoz Gazları: Hidrokarbonlar Karbon Monoksit Azot Oksitleri Bu bölüme kadar, açıkça ifade edilmese
Paslanmaz Çelik Gövde Yalıtım Sargısı Egzoz Emisyonları: Su Karbondioksit Azot Katalizör Yüzey Tabakası Egzoz Gazları: Hidrokarbonlar Karbon Monoksit Azot Oksitleri Bu bölüme kadar, açıkça ifade edilmese
Kristal Yapılar / Temel Kavramlar
 Kristal Yapılar / Temel Kavramlar Bir kristal malzemede uzun-aralıkta düzen mevcuttur. Atomlar, atomsal ölçekte uzun mesafelerde tekrar eden düzenli bir yapı oluştururlar. Yani, katılaşma sırasında atomlar,
Kristal Yapılar / Temel Kavramlar Bir kristal malzemede uzun-aralıkta düzen mevcuttur. Atomlar, atomsal ölçekte uzun mesafelerde tekrar eden düzenli bir yapı oluştururlar. Yani, katılaşma sırasında atomlar,
Dislokasyon hareketi sonucu oluşan plastik deformasyon süreci kayma olarak adlandırılır.
 Dislokasyon hareketi sonucu oluşan plastik deformasyon süreci kayma olarak adlandırılır. Bütün metal ve alaşımlarda bulunan dislokasyonlar, katılaşma veya plastik deformasyon sırasında veya hızlı soğutmadan
Dislokasyon hareketi sonucu oluşan plastik deformasyon süreci kayma olarak adlandırılır. Bütün metal ve alaşımlarda bulunan dislokasyonlar, katılaşma veya plastik deformasyon sırasında veya hızlı soğutmadan
KATIHAL FİZİĞİ DERS 2. Tipik Kristal Yapılar Kuasi-kristaller Doluluk Oranı
 KATIHAL FİZİĞİ DERS 2 Tipik Kristal Yapılar Kuasi-kristaller Doluluk Oranı Tipik Kristal Yapılar Yüzey Merkezli Kübik Kristal Yapı (Face centered Cubic (fcc)) Yüzey merkezleri ve köşelerde atomlar vardır.
KATIHAL FİZİĞİ DERS 2 Tipik Kristal Yapılar Kuasi-kristaller Doluluk Oranı Tipik Kristal Yapılar Yüzey Merkezli Kübik Kristal Yapı (Face centered Cubic (fcc)) Yüzey merkezleri ve köşelerde atomlar vardır.
UZAYDA VEKTÖRLER ve DOĞRU DÜZLEM
 UD VEKTÖRLER ve DĞRU DÜLEM. ir küpün ayrıtlarını taşıyan doğrular kaç farklı doğrultu oluşturur? ) ) ) D) 7 E) 8. ir düzgün altıgenin en uzun köşegeni ile aynı doğrultuda kaç farklı kenar vardır?. şağıdaki
UD VEKTÖRLER ve DĞRU DÜLEM. ir küpün ayrıtlarını taşıyan doğrular kaç farklı doğrultu oluşturur? ) ) ) D) 7 E) 8. ir düzgün altıgenin en uzun köşegeni ile aynı doğrultuda kaç farklı kenar vardır?. şağıdaki
Eğer piramidin tabanı düzgün çokgense bu tip piramitlere düzgün piramit denir.
 PİRAMİTLER Bir düzlemde kapalı bir bölge ile bu düzlemin dışında bir T noktası alalım. Kapalı bölgenin tüm noktalarının T noktası ile birleştirilmesi sonucunda oluşan cisme piramit denir. T noktası piramidin
PİRAMİTLER Bir düzlemde kapalı bir bölge ile bu düzlemin dışında bir T noktası alalım. Kapalı bölgenin tüm noktalarının T noktası ile birleştirilmesi sonucunda oluşan cisme piramit denir. T noktası piramidin
şeklinde, katı ( ) fazın ağırlık oranı ise; şeklinde hesaplanır.
 FAZ DİYAGRAMLARI Malzeme özellikleri görmüş oldukları termomekanik işlemlerin sonucunda oluşan içyapılarına bağlıdır. Faz diyagramları mühendislerin içyapı değişikliği için uygulayacakları ısıl işlemin
FAZ DİYAGRAMLARI Malzeme özellikleri görmüş oldukları termomekanik işlemlerin sonucunda oluşan içyapılarına bağlıdır. Faz diyagramları mühendislerin içyapı değişikliği için uygulayacakları ısıl işlemin
4. Çok büyük ve çok küçük pozitif sayıları bilimsel gösterimle ifade eder.
 LENDİRME ŞEMASI ÜNİTE Üslü 1. Bir tam sayının negatif kuvvetini belirler ve rasyonel sayı olarak ifade eder.. Ondalık kesirlerin veya rasyonel sayıların kendileriyle tekrarlı çarpımını üslü sayı olarak
LENDİRME ŞEMASI ÜNİTE Üslü 1. Bir tam sayının negatif kuvvetini belirler ve rasyonel sayı olarak ifade eder.. Ondalık kesirlerin veya rasyonel sayıların kendileriyle tekrarlı çarpımını üslü sayı olarak
T.C. Ölçme, Seçme ve Yerleştirme Merkezi
 T.C. Ölçme, Seçme ve Yerleştirme Merkezi LİSANS YERLEŞTİRME SINAVI-1 GEOMETRİ TESTİ 19 HAZİRAN 2016 PAZAR Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının veya bir kısmının
T.C. Ölçme, Seçme ve Yerleştirme Merkezi LİSANS YERLEŞTİRME SINAVI-1 GEOMETRİ TESTİ 19 HAZİRAN 2016 PAZAR Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının veya bir kısmının
Bu bölümde Coulomb yasasının bir sonucu olarak ortaya çıkan Gauss yasasının kullanılmasıyla simetrili yük dağılımlarının elektrik alanlarının çok
 Gauss Yasası Bu bölümde Coulomb yasasının bir sonucu olarak ortaya çıkan Gauss yasasının kullanılmasıyla simetrili yük dağılımlarının elektrik alanlarının çok daha kullanışlı bir şekilde nasıl hesaplanabileceği
Gauss Yasası Bu bölümde Coulomb yasasının bir sonucu olarak ortaya çıkan Gauss yasasının kullanılmasıyla simetrili yük dağılımlarının elektrik alanlarının çok daha kullanışlı bir şekilde nasıl hesaplanabileceği
2013 2014 EĞİTİM ÖĞRETİM YILI 8. SINIF MATEMATİK DERSİ KONULARININ ÇALIŞMA TAKVİMİNE GÖRE DAĞILIM ÇİZELGESİ ALT ÖĞRENME. Örüntü ve Süslemeler
 2013 2014 EĞİTİM ÖĞRETİM YILI 8. SINIF MATEMATİK DERSİ KONULARININ ÇALIŞMA TAKVİMİNE GÖRE DAĞILIM ÇİZELGESİ SÜRE ÖĞRENME Ay Hafta D.Saati ALANI EYLÜL 2 Geometri 2 3 Geometri 2 Geometri 2 Olasılıkve ALT
2013 2014 EĞİTİM ÖĞRETİM YILI 8. SINIF MATEMATİK DERSİ KONULARININ ÇALIŞMA TAKVİMİNE GÖRE DAĞILIM ÇİZELGESİ SÜRE ÖĞRENME Ay Hafta D.Saati ALANI EYLÜL 2 Geometri 2 3 Geometri 2 Geometri 2 Olasılıkve ALT
9. SINIF Geometri TEMEL GEOMETRİK KAVRAMLAR
 TEMEL GEOMETRİK KAVRAMLAR 9. SINIF Geometri Amaç-1: Nokta, Doğru, Düzlem, Işın ve Uzayı Kavrayabilme. 1. Nokta, doğru, düzlem ve uzay kavramlarım açıklama. 2. Farklı iki noktadan geçen doğru sayışım söyleme
TEMEL GEOMETRİK KAVRAMLAR 9. SINIF Geometri Amaç-1: Nokta, Doğru, Düzlem, Işın ve Uzayı Kavrayabilme. 1. Nokta, doğru, düzlem ve uzay kavramlarım açıklama. 2. Farklı iki noktadan geçen doğru sayışım söyleme
HACETTEPE ÜNİVERSİTESİ HACETTEPE ASO 1.OSB MESLEK YÜKSEKOKULU HMK 211 CNC TORNA TEKNOLOJİSİ
 HACETTEPE ÜNİVERSİTESİ HACETTEPE ASO 1.OSB MESLEK YÜKSEKOKULU HMK 211 CNC TORNA TEKNOLOJİSİ Öğr. Gör. RECEP KÖKÇAN Tel: +90 312 267 30 20 http://yunus.hacettepe.edu.tr/~rkokcan/ E-mail_1: rkokcan@hacettepe.edu.tr
HACETTEPE ÜNİVERSİTESİ HACETTEPE ASO 1.OSB MESLEK YÜKSEKOKULU HMK 211 CNC TORNA TEKNOLOJİSİ Öğr. Gör. RECEP KÖKÇAN Tel: +90 312 267 30 20 http://yunus.hacettepe.edu.tr/~rkokcan/ E-mail_1: rkokcan@hacettepe.edu.tr
METALİK MALZEMELERİN GENEL KARAKTERİSTİKLERİ BAHAR 2010
 METALİK MALZEMELERİN GENEL KARAKTERİSTİKLERİ BAHAR 2010 WEBSİTE www2.aku.edu.tr/~hitit Dersler İÇERİK Metalik Malzemelerin Genel Karakteristiklerİ Denge diyagramları Ergitme ve döküm Dökme demir ve çelikler
METALİK MALZEMELERİN GENEL KARAKTERİSTİKLERİ BAHAR 2010 WEBSİTE www2.aku.edu.tr/~hitit Dersler İÇERİK Metalik Malzemelerin Genel Karakteristiklerİ Denge diyagramları Ergitme ve döküm Dökme demir ve çelikler
FZM 220. Malzeme Bilimine Giriş
 FZM 220 Yapı Karakterizasyon Özellikler İşleme Performans Prof. Dr. İlker DİNÇER Fakültesi, Fizik Mühendisliği Bölümü 1 Atomsal Yapı ve Atomlararası Bağ1 Ders Hakkında FZM 220 Dersinin Amacı Bu dersin
FZM 220 Yapı Karakterizasyon Özellikler İşleme Performans Prof. Dr. İlker DİNÇER Fakültesi, Fizik Mühendisliği Bölümü 1 Atomsal Yapı ve Atomlararası Bağ1 Ders Hakkında FZM 220 Dersinin Amacı Bu dersin
UZAY KAVRAMI VE UZAYDA DOĞRULAR
 UZAY KAVRAMI VE UZAYDA DOĞRULAR Cisimlerin kapladığı yer ve içinde bulundukları mekan uzaydır. Doğruda sadece uzunluk, düzlemde uzunluk ve genişlik söz konusudur. Uzayda ise uzunluk ve genişliğin yanında
UZAY KAVRAMI VE UZAYDA DOĞRULAR Cisimlerin kapladığı yer ve içinde bulundukları mekan uzaydır. Doğruda sadece uzunluk, düzlemde uzunluk ve genişlik söz konusudur. Uzayda ise uzunluk ve genişliğin yanında
KRİSTALLERİN PLASTİK DEFORMASYONU
 KRİSTALLERİN PLASTİK DEFORMASYONU Turgut Gülmez METALLERDE PLASTİK ŞEKİL DEĞİŞİMİ MEKANİZMALARI :Kayma, ikizlenme, tane sınırı kayması ve yayınma sürünmesi METALLERDE PLASTİK ŞEKİL DEĞİŞİMİ MEKANİZMALARI
KRİSTALLERİN PLASTİK DEFORMASYONU Turgut Gülmez METALLERDE PLASTİK ŞEKİL DEĞİŞİMİ MEKANİZMALARI :Kayma, ikizlenme, tane sınırı kayması ve yayınma sürünmesi METALLERDE PLASTİK ŞEKİL DEĞİŞİMİ MEKANİZMALARI
DÜZLEMDE GERİLME DÖNÜŞÜMLERİ
 3 DÜZLEMDE GERİLME DÖNÜŞÜMLERİ Gerilme Kavramı Dış kuvvetlerin etkisi altında dengedeki elastik bir cismi matematiksel bir yüzeyle rasgele bir noktadan hayali bir yüzeyle ikiye ayıracak olursak, F 3 F
3 DÜZLEMDE GERİLME DÖNÜŞÜMLERİ Gerilme Kavramı Dış kuvvetlerin etkisi altında dengedeki elastik bir cismi matematiksel bir yüzeyle rasgele bir noktadan hayali bir yüzeyle ikiye ayıracak olursak, F 3 F
ATOMİK YAPI. Elektron Yükü=-1,60x10-19 C Proton Yükü=+1,60x10-19 C Nötron Yükü=0
 ATOMİK YAPI Atom, birkaç türü birleştiğinde çeşitli molekülleri, bir tek türü ise bir kimyasal öğeyi oluşturan parçacıktır. Atom, elementlerin özelliklerini taşıyan en küçük yapı birimi olup çekirdekteki
ATOMİK YAPI Atom, birkaç türü birleştiğinde çeşitli molekülleri, bir tek türü ise bir kimyasal öğeyi oluşturan parçacıktır. Atom, elementlerin özelliklerini taşıyan en küçük yapı birimi olup çekirdekteki
ELEKTRİKSEL POTANSİYEL
 ELEKTRİKSEL POTANSİYEL Elektriksel Potansiyel Enerji Elektriksel potansiyel enerji kavramına geçmeden önce Fizik-1 dersinizde görmüş olduğunuz iş, potansiyel enerji ve enerjinin korunumu kavramları ile
ELEKTRİKSEL POTANSİYEL Elektriksel Potansiyel Enerji Elektriksel potansiyel enerji kavramına geçmeden önce Fizik-1 dersinizde görmüş olduğunuz iş, potansiyel enerji ve enerjinin korunumu kavramları ile
FZM 220. Malzeme Bilimine Giriş
 FZM 220 Yapı Karakterizasyon Özellikler İşleme Performans Prof. Dr. İlker DİNÇER Fakültesi, Fizik Mühendisliği Bölümü 1 Ders Hakkında FZM 220 Dersinin Amacı Bu dersin amacı, fizik mühendisliği öğrencilerine,
FZM 220 Yapı Karakterizasyon Özellikler İşleme Performans Prof. Dr. İlker DİNÇER Fakültesi, Fizik Mühendisliği Bölümü 1 Ders Hakkında FZM 220 Dersinin Amacı Bu dersin amacı, fizik mühendisliği öğrencilerine,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
1.GİRİŞ. 1.1. Metal Şekillendirme İşlemlerindeki Değişkenler, Sınıflandırmalar ve Tanımlamalar
 1.GİRİŞ Genel olarak metal şekillendirme işlemlerini imalat işlemlerinin bir parçası olarak değerlendirmek mümkündür. İmalat işlemleri genel olarak şu şekilde sınıflandırılabilir: 1) Temel şekillendirme,
1.GİRİŞ Genel olarak metal şekillendirme işlemlerini imalat işlemlerinin bir parçası olarak değerlendirmek mümkündür. İmalat işlemleri genel olarak şu şekilde sınıflandırılabilir: 1) Temel şekillendirme,
a) Çıkarma işleminin; eksilen ile çıkanın ters işaretlisinin toplamı anlamına geldiğini kavrar.
 7. SINIF KAZANIM VE AÇIKLAMALARI M.7.1. SAYILAR VE İŞLEMLER M.7.1.1. Tam Sayılarla Toplama, Çıkarma, Çarpma ve Bölme İşlemleri M.7.1.1.1. Tam sayılarla toplama ve çıkarma işlemlerini yapar; ilgili problemleri
7. SINIF KAZANIM VE AÇIKLAMALARI M.7.1. SAYILAR VE İŞLEMLER M.7.1.1. Tam Sayılarla Toplama, Çıkarma, Çarpma ve Bölme İşlemleri M.7.1.1.1. Tam sayılarla toplama ve çıkarma işlemlerini yapar; ilgili problemleri
Gelin bugün bu yazıda ilkokul sıralarından beri bize öğretilen bilgilerden yeni bir şey keşfedelim, ya da ne demek istediğini daha iyi anlayalım.
 Kristal Yapılar Gelin bugün bu yazıda ilkokul sıralarından beri bize öğretilen bilgilerden yeni bir şey keşfedelim, ya da ne demek istediğini daha iyi anlayalım. Evrende, kimyasal özellik barındıran maddelerin
Kristal Yapılar Gelin bugün bu yazıda ilkokul sıralarından beri bize öğretilen bilgilerden yeni bir şey keşfedelim, ya da ne demek istediğini daha iyi anlayalım. Evrende, kimyasal özellik barındıran maddelerin
1. Giriş 2. Yayınma Mekanizmaları 3. Kararlı Karasız Yayınma 4. Yayınmayı etkileyen faktörler 5. Yarı iletkenlerde yayınma 6. Diğer yayınma yolları
 1. Giriş 2. Yayınma Mekanizmaları 3. Kararlı Karasız Yayınma 4. Yayınmayı etkileyen faktörler 5. Yarı iletkenlerde yayınma 6. Diğer yayınma yolları Sol üstte yüzey seftleştirme işlemi uygulanmış bir çelik
1. Giriş 2. Yayınma Mekanizmaları 3. Kararlı Karasız Yayınma 4. Yayınmayı etkileyen faktörler 5. Yarı iletkenlerde yayınma 6. Diğer yayınma yolları Sol üstte yüzey seftleştirme işlemi uygulanmış bir çelik
MALZEME BILIMI DERS NOTU
 MALZEME BILIMI DERS NOTU Bölüm 2. Malzemelerin Yapısı ve Atomik ve İyonik Düzenler Doç. Dr. Özkan ÖZDEMİR HEDEFLER: Yapının bağlı olduğu fiziksel kavramları tanımlamak, Atomların yapısı- bağlar-mühendislik
MALZEME BILIMI DERS NOTU Bölüm 2. Malzemelerin Yapısı ve Atomik ve İyonik Düzenler Doç. Dr. Özkan ÖZDEMİR HEDEFLER: Yapının bağlı olduğu fiziksel kavramları tanımlamak, Atomların yapısı- bağlar-mühendislik
Manyetik Alanlar. Benzer bir durum hareketli yükler içinde geçerli olup bu yüklerin etrafını elektrik alana ek olarak bir manyetik alan sarmaktadır.
 Manyetik Alanlar Manyetik Alanlar Duran ya da hareket eden yüklü parçacığın etrafını bir elektrik alanın sardığı biliyoruz. Hatta elektrik alan konusunda şu sonuç oraya konulmuştur. Durgun bir deneme yükü
Manyetik Alanlar Manyetik Alanlar Duran ya da hareket eden yüklü parçacığın etrafını bir elektrik alanın sardığı biliyoruz. Hatta elektrik alan konusunda şu sonuç oraya konulmuştur. Durgun bir deneme yükü
MALZEME BİLGİSİ. Katı Eriyikler
 MALZEME BİLGİSİ Dr.- Ing. Rahmi ÜNAL Konu: Katı Eriyikler 1 Giriş Endüstriyel metaller çoğunlukla birden fazla tür eleman içerirler, çok azı arı halde kullanılır. Arı metallerin yüksek iletkenlik, korozyona
MALZEME BİLGİSİ Dr.- Ing. Rahmi ÜNAL Konu: Katı Eriyikler 1 Giriş Endüstriyel metaller çoğunlukla birden fazla tür eleman içerirler, çok azı arı halde kullanılır. Arı metallerin yüksek iletkenlik, korozyona
V =, (V = hacim, m = kütle, d = özkütle) Bu bağıntı V = olarak da yazılabilir G: ağırlık (yerçekimi kuvveti) G = mg p = özgül ağırlık p = dg dir.
 Geometrik Cisimlerin Hacimleri Uzayda yer kaplayan (üç boyutlu) nesnelere cisim denir. Düzgün geometrik cisimlerin hacimleri bağıntılar yardımıyla bulunur. Eğer cisim düzgün değilse cismin hacmi cismin
Geometrik Cisimlerin Hacimleri Uzayda yer kaplayan (üç boyutlu) nesnelere cisim denir. Düzgün geometrik cisimlerin hacimleri bağıntılar yardımıyla bulunur. Eğer cisim düzgün değilse cismin hacmi cismin
ATOMSAL YAPILAR. Düzensiz yapı(amorph-orderless): Atom veya moleküllerin rastgele dizilmesi.
 MARMARA ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MALZEME BİLİMİ Kristal Yapısı Yrd. Doç. Dr. Abdullah DEMİR ATOMSAL YAPILAR Malzemeler atomların bir araya gelmesi ile oluşur. Atomları
MARMARA ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MALZEME BİLİMİ Kristal Yapısı Yrd. Doç. Dr. Abdullah DEMİR ATOMSAL YAPILAR Malzemeler atomların bir araya gelmesi ile oluşur. Atomları
ATOM HAREKETLERİ ve ATOMSAL YAYINIM
 ATOM HAREKETLERİ ve ATOMSAL YAYINIM 1. Giriş Malzemelerde üretim ve uygulama sırasında görülen katılaşma, çökelme, yeniden kristalleşme, tane büyümesi gibi olaylar ile kaynak, lehim, sementasyon gibi işlemler
ATOM HAREKETLERİ ve ATOMSAL YAYINIM 1. Giriş Malzemelerde üretim ve uygulama sırasında görülen katılaşma, çökelme, yeniden kristalleşme, tane büyümesi gibi olaylar ile kaynak, lehim, sementasyon gibi işlemler
Viyana İmam Hatip Lisesi Öğrenci Seçme Sınavı - Matematik
 Viyana İmam Hatip Lisesi Öğrenci Seçme Sınavı - Matematik 1. Ünite: Geometriden Olasılığa 1. Bölüm: Yansıyan ve Dönen Şekiller, Fraktallar Yansıma, Öteleme, Dönme Fraktallar 2. Bölüm: Üslü Sayılar Tam
Viyana İmam Hatip Lisesi Öğrenci Seçme Sınavı - Matematik 1. Ünite: Geometriden Olasılığa 1. Bölüm: Yansıyan ve Dönen Şekiller, Fraktallar Yansıma, Öteleme, Dönme Fraktallar 2. Bölüm: Üslü Sayılar Tam
ATOMİK YAPI. Elektron Yükü=-1,60x10-19 C Proton Yükü=+1,60x10-19 C Nötron Yükü=0
 ATOMİK YAPI Elektron Yükü=-1,60x10-19 C Proton Yükü=+1,60x10-19 C Nötron Yükü=0 Elektron Kütlesi 9,11x10-31 kg Proton Kütlesi Nötron Kütlesi 1,67x10-27 kg Bir kimyasal elementin atom numarası (Z) çekirdeğindeki
ATOMİK YAPI Elektron Yükü=-1,60x10-19 C Proton Yükü=+1,60x10-19 C Nötron Yükü=0 Elektron Kütlesi 9,11x10-31 kg Proton Kütlesi Nötron Kütlesi 1,67x10-27 kg Bir kimyasal elementin atom numarası (Z) çekirdeğindeki
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
MALZEME BİLİMİ VE MÜHENDİSLİĞİ
 MALZEME BİLİMİ VE MÜHENDİSLİĞİ Bölüm 3 Atomik ve İyonik Düzenler Hazırlayanlar Prof. Dr. Gültekin Göller Doç. Dr. Özgül Keleş Araş. Gör. İpek Akın 1 Bölüm 3. Hedefler Atomik/iyonik düzenlemelerine bağlı
MALZEME BİLİMİ VE MÜHENDİSLİĞİ Bölüm 3 Atomik ve İyonik Düzenler Hazırlayanlar Prof. Dr. Gültekin Göller Doç. Dr. Özgül Keleş Araş. Gör. İpek Akın 1 Bölüm 3. Hedefler Atomik/iyonik düzenlemelerine bağlı
MMT407 Plastik Şekillendirme Yöntemleri
 K O C A E L İ ÜNİVERSİTESİ Metalurji ve Malzeme Mühendisliği Bölümü MMT407 Plastik Şekillendirme Yöntemleri 3 Şekillendirmenin Metalurjik Esasları Yrd. Doç. Dr. Ersoy Erişir 2012-2013 Güz Yarıyılı 3. Şekillendirmenin
K O C A E L İ ÜNİVERSİTESİ Metalurji ve Malzeme Mühendisliği Bölümü MMT407 Plastik Şekillendirme Yöntemleri 3 Şekillendirmenin Metalurjik Esasları Yrd. Doç. Dr. Ersoy Erişir 2012-2013 Güz Yarıyılı 3. Şekillendirmenin
ARAZİ ÖLÇMELERİ. Koordinat sistemleri. Kartezyen koordinat sistemi
 Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
ELEMETLER VE BİLEŞİKLER ELEMENTLER VE SEMBOLLERİ
 ELEMENTLER VE SEMBOLLERİ Elementler Aynı cins atomlardan oluşan, fiziksel ya da kimyasal yollarla kendinden daha basit ve farklı maddelere ayrılamayan saf maddelere element denir. Elementler çok sayıda
ELEMENTLER VE SEMBOLLERİ Elementler Aynı cins atomlardan oluşan, fiziksel ya da kimyasal yollarla kendinden daha basit ve farklı maddelere ayrılamayan saf maddelere element denir. Elementler çok sayıda
İNS1101 MÜHENDİSLİK ÇİZİMİ. Bingöl Üniversitesi İnşaat Mühendisliği Bölümü 2018
 İNS1101 MÜHENDİSLİK ÇİZİMİ Bingöl Üniversitesi İnşaat Mühendisliği Bölümü 2018 TEKNİK RESİM Teknik resim, teknik elemanların üretim yapabilmeleri için anlatmak istedikleri teknik özelliklerin biçim ve
İNS1101 MÜHENDİSLİK ÇİZİMİ Bingöl Üniversitesi İnşaat Mühendisliği Bölümü 2018 TEKNİK RESİM Teknik resim, teknik elemanların üretim yapabilmeleri için anlatmak istedikleri teknik özelliklerin biçim ve
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 2 Laminanın Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 2 Laminanın Makromekanik
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 2 Laminanın Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 2 Laminanın Makromekanik
Üç Boyutlu Uzayda Koordinat sistemi
 Üç Boyutlu Uzayda Koordinat sistemi Uzayda bir noktayı ifade edebilmek için ilk önce O noktasını (başlangıç noktası) ve bu noktadan geçen ve birbirine dik olan üç yönlü doğruyu seçerek sabitlememiz gerekir.
Üç Boyutlu Uzayda Koordinat sistemi Uzayda bir noktayı ifade edebilmek için ilk önce O noktasını (başlangıç noktası) ve bu noktadan geçen ve birbirine dik olan üç yönlü doğruyu seçerek sabitlememiz gerekir.
Malzemelerin Deformasyonu
 Malzemelerin Deformasyonu Malzemelerin deformasyonu Kristal, etkiyen kuvvete deformasyon ile cevap verir. Bir malzemeye yük uygulandığında malzeme üzerinde çeşitli yönlerde ve çeşitli şekillerde yükler
Malzemelerin Deformasyonu Malzemelerin deformasyonu Kristal, etkiyen kuvvete deformasyon ile cevap verir. Bir malzemeye yük uygulandığında malzeme üzerinde çeşitli yönlerde ve çeşitli şekillerde yükler
Parametrik doğru denklemleri 1
 Parametrik doğru denklemleri 1 A noktasından geçen, doğrultman (doğrultu) vektörü w olan d doğrusunun, k parametresine göre parametrik denklemi: AP k w P A k w P A k w P A k W (P değişken nokta) A w P
Parametrik doğru denklemleri 1 A noktasından geçen, doğrultman (doğrultu) vektörü w olan d doğrusunun, k parametresine göre parametrik denklemi: AP k w P A k w P A k w P A k W (P değişken nokta) A w P
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Katılar. MÜHENDİSLİK KİMYASI DERS NOTLARI Yrd. Doç. Dr. Atilla EVCİN. Yrd. Doç. Dr. Atilla EVCİN Afyonkarahisar Kocatepe Üniversitesi 2006
 Katılar Tüm maddeler, yeteri kadar soğutulduğunda katıları oluştururlar. MÜHENDİSLİK KİMYASI DERS NOTLARI Yrd. Doç. Dr. Atilla EVCİN Oluşan katıların doğası atom, iyon veya molekülleri birarada tutan kuvvetlere
Katılar Tüm maddeler, yeteri kadar soğutulduğunda katıları oluştururlar. MÜHENDİSLİK KİMYASI DERS NOTLARI Yrd. Doç. Dr. Atilla EVCİN Oluşan katıların doğası atom, iyon veya molekülleri birarada tutan kuvvetlere
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
3. KUVVET SİSTEMLERİ
 3. KUVVET SİSTEMLERİ F F W P P 3.1 KUVVET KAVRAMI VE ETKİLERİ Kuvvet, bir cisme etki eden yapısal yüklerdir. Kuvvet Şiddeti, yönü ve uygulama noktası olan vektörel bir büyüklüktür. Bir cismin üzerine uygulanan
3. KUVVET SİSTEMLERİ F F W P P 3.1 KUVVET KAVRAMI VE ETKİLERİ Kuvvet, bir cisme etki eden yapısal yüklerdir. Kuvvet Şiddeti, yönü ve uygulama noktası olan vektörel bir büyüklüktür. Bir cismin üzerine uygulanan
elektrikle yüklenmiş
 ELEKTRİK ALANLARI Birkaç basit deneyle elektrik yüklerinin ve kuvvetlerinin varlığı kanıtlanabilmektedir. Örneğin; Saçınızı kuru bir günde taradıktan sonra, tarağı küçük kağıt parçalarına dokundurursanız
ELEKTRİK ALANLARI Birkaç basit deneyle elektrik yüklerinin ve kuvvetlerinin varlığı kanıtlanabilmektedir. Örneğin; Saçınızı kuru bir günde taradıktan sonra, tarağı küçük kağıt parçalarına dokundurursanız
KÜTLE VE AĞIRLIK MERKEZİ
 VEKTÖRLER KUVVET KAVRAMI MOMENT KÜTLE VE AĞIRLIK MERKEZİ BASİT MAKİNELER -1- VEKTÖRLER -2- Fizik te büyüklükleri ifade ederken sadece sayı ile ifade etmek yetmeye bilir örneğin aşağıdaki büyüklükleri ifade
VEKTÖRLER KUVVET KAVRAMI MOMENT KÜTLE VE AĞIRLIK MERKEZİ BASİT MAKİNELER -1- VEKTÖRLER -2- Fizik te büyüklükleri ifade ederken sadece sayı ile ifade etmek yetmeye bilir örneğin aşağıdaki büyüklükleri ifade
Bazı atomlarda proton sayısı aynı olduğu halde nötron sayısı değişiktir. Bunlara izotop denir. Şekil II.1. Bir atomun parçaları
 8 II. MİNERALLER II.1. Element ve Atom Elementlerin en ufak parçasına atom denir. Atomlar, proton, nötron ve elektron gibi taneciklerden oluşur (Şekil II.1). Elektron negatif, proton pozitif elektrik yüküne
8 II. MİNERALLER II.1. Element ve Atom Elementlerin en ufak parçasına atom denir. Atomlar, proton, nötron ve elektron gibi taneciklerden oluşur (Şekil II.1). Elektron negatif, proton pozitif elektrik yüküne
Nötr (yüksüz) bir için, çekirdekte kaç proton varsa çekirdeğin etrafındaki yörüngelerde de o kadar elektron dolaşır.
 ATOM ve YAPISI Elementin özelliğini taşıyan en küçük parçasına denir. Atom Numarası Bir elementin unda bulunan proton sayısıdır. Protonlar (+) yüklü olduklarından pozitif yük sayısı ya da çekirdek yükü
ATOM ve YAPISI Elementin özelliğini taşıyan en küçük parçasına denir. Atom Numarası Bir elementin unda bulunan proton sayısıdır. Protonlar (+) yüklü olduklarından pozitif yük sayısı ya da çekirdek yükü
Karabük Üniversitesi, Mühendislik Fakültesi...www.IbrahimCayiroglu.com. STATİK (2. Hafta)
 AĞIRLIK MERKEZİ STATİK (2. Hafta) Ağırlık merkezi: Bir cismi oluşturan herbir parçaya etki eden yerçeki kuvvetlerinin bileşkesinin cismin üzerinden geçtiği noktaya Ağırlık Merkezi denir. Şekil. Ağırlık
AĞIRLIK MERKEZİ STATİK (2. Hafta) Ağırlık merkezi: Bir cismi oluşturan herbir parçaya etki eden yerçeki kuvvetlerinin bileşkesinin cismin üzerinden geçtiği noktaya Ağırlık Merkezi denir. Şekil. Ağırlık
2013 2014 EĞİTİM ÖĞRETİM YILI 8. SINIF MATEMATİK DERSİ KAZANIMLARININ ÇALIŞMA TAKVİMİNE GÖRE DAĞILIM ÇİZELGESİ KAZANIMLAR
 KASIM EKİM EYLÜL Ay Hafta D.Saat i 0 04 EĞİTİM ÖĞRETİM YILI 8. SINIF MATEMATİK DERSİ KAZANIMLARININ ÇALIŞMA TAKVİMİNE GÖRE SÜRE ÖĞRENME ALANI ALT ÖĞRENME ALANI Örüntü Süslemeler si KAZANIMLAR.Doğru, çokgen
KASIM EKİM EYLÜL Ay Hafta D.Saat i 0 04 EĞİTİM ÖĞRETİM YILI 8. SINIF MATEMATİK DERSİ KAZANIMLARININ ÇALIŞMA TAKVİMİNE GÖRE SÜRE ÖĞRENME ALANI ALT ÖĞRENME ALANI Örüntü Süslemeler si KAZANIMLAR.Doğru, çokgen
2014 LYS GEOMETRİ 3. A. parabolü ile. x 1 y a 9 çemberinin üç noktada kesişmesi için a kaç olmalıdır?
 014 LYS GOMTRİ 1. y 1 1 y a 9 çemberinin üç noktada kesişmesi için a kaç olmalıdır? parabolü ile. O merkezli çeyrek çemberde O deltoid olduğuna göre, taralı alan kaç birim karedir? O. d:y a b doğrusu -ekseni
014 LYS GOMTRİ 1. y 1 1 y a 9 çemberinin üç noktada kesişmesi için a kaç olmalıdır? parabolü ile. O merkezli çeyrek çemberde O deltoid olduğuna göre, taralı alan kaç birim karedir? O. d:y a b doğrusu -ekseni
Tanımlar, Geometrik ve Matemetiksel Temeller. Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ. JDF329 Fotogrametri I Ders Notu
 FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İzdüşüm merkezi(o):
FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İzdüşüm merkezi(o):
Bölüm 4: Kusurlar. Kusurlar
 Bölüm 4: Kusurlar Malzemelerin bazı özellikleri kusurların varlığıyla önemli derecede etkilenir. Kusurların türleri ve malzeme davranışı üzerindeki etkileri hakkında bilgi sahibi olmak önemlidir. Saf metallerin
Bölüm 4: Kusurlar Malzemelerin bazı özellikleri kusurların varlığıyla önemli derecede etkilenir. Kusurların türleri ve malzeme davranışı üzerindeki etkileri hakkında bilgi sahibi olmak önemlidir. Saf metallerin
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ
 BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
2012 YGS MATEMATİK Soruları
 01 YGS MATEMATİK Soruları 1. 10, 1, 0, 0, işleminin sonucu kaçtır? A) B), C) 6 D) 6, E) 7. + ABC 4 x 864 Yukarıda verilenlere göre, çarpma işleminin sonucu kaçtır? A) 8974 B) 907 C) 9164 D) 94 E) 98. 6
01 YGS MATEMATİK Soruları 1. 10, 1, 0, 0, işleminin sonucu kaçtır? A) B), C) 6 D) 6, E) 7. + ABC 4 x 864 Yukarıda verilenlere göre, çarpma işleminin sonucu kaçtır? A) 8974 B) 907 C) 9164 D) 94 E) 98. 6
Matematikte karşılaştığınız güçlükler için endişe etmeyin. Emin olun benim karşılaştıklarım sizinkilerden daha büyüktür.
 - 1 - ÖĞRENME ALANI CEBİR BÖLÜM KARMAŞIK SAYILAR ALT ÖĞRENME ALANLARI 1) Karmaşık Sayılar Karmaşık Sayıların Kutupsal Biçimi KARMAŞIK SAYILAR Kazanım 1 : Gerçek sayılar kümesini genişletme gereğini örneklerle
- 1 - ÖĞRENME ALANI CEBİR BÖLÜM KARMAŞIK SAYILAR ALT ÖĞRENME ALANLARI 1) Karmaşık Sayılar Karmaşık Sayıların Kutupsal Biçimi KARMAŞIK SAYILAR Kazanım 1 : Gerçek sayılar kümesini genişletme gereğini örneklerle
T.C. Ölçme, Seçme ve Yerleştirme Merkezi
 T.C. Ölçme, Seçme ve Yerleştirme Merkezi LİSANS YERLEŞTİRME SINAVI-1 MATEMATİK TESTİ 11 HAZİRAN 2017 PAZAR Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının veya bir kısmının
T.C. Ölçme, Seçme ve Yerleştirme Merkezi LİSANS YERLEŞTİRME SINAVI-1 MATEMATİK TESTİ 11 HAZİRAN 2017 PAZAR Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının veya bir kısmının
MAT 103 ANALİTİK GEOMETRİ I FİNAL ÇALIŞMA SORULARI
 MAT 103 ANALİTİK GEOMETRİ I FİNAL ÇALIŞMA SORULARI SORU 1. Köşeleri (1,4) (3,0) (7,2) noktaları olan ABC üçgeninin bir ikizkenar dik üçgen (İpucu:, ve vektörlerinden yararlanın) SORU 2. Bir ABC üçgeninin
MAT 103 ANALİTİK GEOMETRİ I FİNAL ÇALIŞMA SORULARI SORU 1. Köşeleri (1,4) (3,0) (7,2) noktaları olan ABC üçgeninin bir ikizkenar dik üçgen (İpucu:, ve vektörlerinden yararlanın) SORU 2. Bir ABC üçgeninin
JFM 301 SİSMOLOJİ ELASTİSİTE TEORİSİ Elastisite teorisi yer içinde dalga yayılımını incelerken çok yararlı olmuştur.
 JFM 301 SİSMOLOJİ ELASTİSİTE TEORİSİ Elastisite teorisi yer içinde dalga yayılımını incelerken çok yararlı olmuştur. Prof. Dr. Gündüz Horasan Deprem dalgalarını incelerken, yeryuvarının esnek, homojen
JFM 301 SİSMOLOJİ ELASTİSİTE TEORİSİ Elastisite teorisi yer içinde dalga yayılımını incelerken çok yararlı olmuştur. Prof. Dr. Gündüz Horasan Deprem dalgalarını incelerken, yeryuvarının esnek, homojen
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 4 Kuvvet Sistemi Bileşkeleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 4. Kuvvet Sitemi Bileşkeleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 4 Kuvvet Sistemi Bileşkeleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 4. Kuvvet Sitemi Bileşkeleri
T.C. Ölçme, Seçme ve Yerleştirme Merkezi
 T.C. Ölçme, Seçme ve Yerleştirme Merkezi LİSANS YERLEŞTİRME SINAVI-1 MATEMATİK TESTİ 11 HAZİRAN 2017 PAZAR Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının veya bir kısmının
T.C. Ölçme, Seçme ve Yerleştirme Merkezi LİSANS YERLEŞTİRME SINAVI-1 MATEMATİK TESTİ 11 HAZİRAN 2017 PAZAR Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının veya bir kısmının
BMM 205 Malzeme Biliminin Temelleri
 BMM 205 Malzeme Biliminin Temelleri Atom Yapısı ve Atomlar Arası Bağlar Dr. Ersin Emre Ören Biyomedikal Mühendisliği Bölümü Malzeme Bilimi ve Nanoteknoloji Mühendisliği Bölümü TOBB Ekonomi ve Teknoloji
BMM 205 Malzeme Biliminin Temelleri Atom Yapısı ve Atomlar Arası Bağlar Dr. Ersin Emre Ören Biyomedikal Mühendisliği Bölümü Malzeme Bilimi ve Nanoteknoloji Mühendisliği Bölümü TOBB Ekonomi ve Teknoloji
KRİSTAL KUSURLARI BÖLÜM 3. Bağlar + Kristal yapısı + Kusurlar. Özellikler. Kusurlar malzeme özelliğini önemli ölçüde etkiler.
 KRİSTAL KUSURLARI Bağlar + Kristal yapısı + Kusurlar Özellikler Kusurlar malzeme özelliğini önemli ölçüde etkiler. 2 1 Yarıiletken alttaş üretiminde kullanılan silikon kristalleri neden belli ölçüde fosfor
KRİSTAL KUSURLARI Bağlar + Kristal yapısı + Kusurlar Özellikler Kusurlar malzeme özelliğini önemli ölçüde etkiler. 2 1 Yarıiletken alttaş üretiminde kullanılan silikon kristalleri neden belli ölçüde fosfor
Teknik Resim TEKNİK BİLİMLER MESLEK YÜKSEKOKULU. 3. Geometrik Çizimler. Yrd. Doç. Dr. Garip GENÇ
 TEKNİK BİLİMLER MESLEK YÜKSEKOKULU Teknik Resim Genel Bilgi Teknik resimde bir şekli çizmek için çizim takımlarından faydalanılır. Çizilecek şekil üzerinde eşit bölüntüler, paralel doğrular, teğet birleşmeler,
TEKNİK BİLİMLER MESLEK YÜKSEKOKULU Teknik Resim Genel Bilgi Teknik resimde bir şekli çizmek için çizim takımlarından faydalanılır. Çizilecek şekil üzerinde eşit bölüntüler, paralel doğrular, teğet birleşmeler,
Bölüm 24 Gauss Yasası
 Bölüm 24 Gauss Yasası Elektrik Akısı Gauss Yasası Gauss Yasasının Yüklü Yalıtkanlara Uygulanması Elektrostatik Dengedeki İletkenler Öğr. Gör. Dr. Mehmet Tarakçı http://kisi.deu.edu.tr/mehmet.tarakci/ Elektrik
Bölüm 24 Gauss Yasası Elektrik Akısı Gauss Yasası Gauss Yasasının Yüklü Yalıtkanlara Uygulanması Elektrostatik Dengedeki İletkenler Öğr. Gör. Dr. Mehmet Tarakçı http://kisi.deu.edu.tr/mehmet.tarakci/ Elektrik
