İÇİNDEKİLER. Sayfa No:
|
|
|
- Batur Karatay
- 9 yıl önce
- İzleme sayısı:
Transkript
1 İÇİNDEKİLER Sayfa No: Giriş... 1 Mekanizmanın çeşitli açılardaki konumu... 2 Boyutlar ve denge denklemleri... 4 Serbest cisim diyagramları... 5 Denge denklemlerinin çıkartılması... 5 Uzuvlara gelen kuvvet bileşenleri hesaplamaları... 7 Kriko koluna uygulanması gereken kuvvetin hesabı İtme milinin etkidiği pernonun kontrolü Yan saçlardaki delik ezilmesi kontrolü Delik yırtılması kontrolü Kaldırma kolunun eğilmeye göre kontrolü Ana gövdenin eğilme kontrolü Yük traversinin eğilme kontrolü Muyluların kesilme kontrolü Delik ezilmesi kontrolü Kesit hesabı Krikoya ait teknik resimler... 24
2 GİRİŞ KRİKOLAR: Kaldırma araçlarını görevleri sırasında etkilendikleri önemli zorlanma çeşidine göre ikiye ayrılır. 1. Basınca zorlanarak yük kaldıran araçlar 2. Çekmeye zorlanarak yük kaldıran araçlar Krikolar basınca zorlanarak çalışan kaldırma araçlarıdır. Krikolar kısa kaldırma yükseklikleri içinde oldukça büyük yükleri rahatlıkla kaldıra bilirler. Genellikle kaldırma yükseklikleri mm kadardır. Kaldırma güçleri 25Mp kadar olabilir. Bazı özel hallerde krikoların kaldırma yükseklikleri yukarıda verilen sınırların üzerine çıkartmak ve kaldırma güçlerini 25Mp ın çok üzerine çıkartmak mümkündür. Krikolar genellikle montaj,bakım ve tamir işlerinde kullanılmaktadır. KRİKO ÇEŞİTLERİ: Krikolar başlıca üç sınıfa ayırmak mümkündür. 1. Vidalı Krikolar 2. Kramiyerli Krikolar 3. Hidrolik Krikolar -1-
3 MEKANİZMANIN KONUMU ϕ 2 = 0 o için N, F D A B K,E ϕ 2 =30 o için D E C N F ϕ A L B K -2-
4 D E ϕ 2 =60 o için C N F ϕ L B A K D E ϕ 2 =75 o için C F ϕ N L B A K E -3-
5 BOYUTLAR F= N AC=850 mm. BC=205 mm. CD=420 mm. DE=130 mm. CF=130 mm. EF=420 mm. CK=220 mm. AK=825 mm. ACK=75 DENGE DENKLEMLERİ 1. BL=BC.Sinϕ 2 2. BN=BC.Cosϕ 2 3. BE =CK-BN 4. AE =AK+BL 5. R 12x + R 32x + R 52x = 0 6. R 12y + R 32y + R 52y = 0 7. R 32y.CD.Cosϕ 2 -R 32x.CD. Sinϕ 2 + R 52y.BL + R 52x.BN = 0 8. R 34x + R 23x = 0 9. R 43y + R 23y + F = R 34x + R 14x = R 34y + R 14y = R 34y.FE. Cosϕ 2 - R 34x.FE. Sinϕ 2 = R 15x + R 25x = R 15y + R 25y = R 25y.AE -R 25x.BE = 0-4-
6 DENGE DENKLEMLERİNİN ÇIKARTILMASI 2 NOLU UZUV R 32y R 12y D R 32x + C ϕ 2 52y 2 R 12x B R 52x 4 NOLU UZUV 34y E R 14y 4 R 34x ϕ 2 + F R 14x -5-
7 5 NOLU UZUV 52y R 15y 5 25x B + A R 15x 3 NOLU UZUV R 15y F R 43y 23x D 3 E R 43x -6-
8 ϕ 2 =0 için BL=BCxSinϕ 2 BL=205xSin(0) = 0 mm. BN=BCxCosϕ 2 BN=205xCos(0) = 205 mm. BE =CK-BN BE = = 15 mm. AE =AK+BL AE =825+0 = 825 mm. R 14x =0 ve R 43x + R 14x = 0 => R 43x =0 R 14y =0 ve R 43y + R 14y = 0 => R 43y =0 R 14 = 0 R 43 = 0 R 34x + R 23x = 0 ve R 34x = 0 => R 23x =0 R 34y + R 23y + F = 0 R 23y = 0 R 23y = N R 32y = N R 32y xcdxcosϕ 2 R 32x xcdxsinϕ 2 +R 52y xbl+r 52x xbn = x420xCos(0) 0x420x0+R 52y x0+r 52x x205 = 0 R 52x = = ,976 N R 52x = ,976 N 25x = ,976 N R 25y xae -R 25x xbe = 0 R 25y x ,976x15 = 0 R 25y = 1.192,018 N R 52y = ,018 N R 15y + R 25y = 0 => R 15y = ,018 N R 15x + R 25x = 0 => R 15x = ,976 N R 12x +R 32x +R 52x = 0 => R 12x ,976 = 0 => R 12x = ,976 N R 12y +R 32y +R 52y = 0 => R 12y ,018 = 0 => R 12y = ,98 N -7-
9 ϕ 2 =10 için BL=BCxSinϕ 2 =205xSin(10) => BL=35,599 mm. BN=BCxCosϕ 2 =205xCos(10) => BN=201,886 mm. BE =CK-BN = ,886 => BE =18,114 mm. AE =AK+BL =825+35,599 => AE =860,599 mm. R 14x =0 ve R 34x + R 14x = 0 => R 34x = 0 R 14y =0 ve R 34y + R 14y = 0 => R 34y = 0 R 43x + R 23x = 0 ve R 43x = 0 => R 23x = 0 R 43y +R 23y +F=0 0+R 23y = 0 => R 23y = N R 32y = N R 32y xcdxcosϕ 2 R 32x xcdxsinϕ 2 +R 52y xbl+r 52x xbn = 0 (1) x420xCos(10) 0x420xSin(10)+R 52y x35,599+r 52x x201,886 = 0 (1) 35,599xR 52y +201,886xR 52x = ,2 (1) -R 52y x860,599 + R 52x x18,114 = 0 (2) (1) ve (2) denklemlerinin çözümü; 24,1748x(35,599xR 52y + 201,886xR 52x = ,2) 860,599xR 52y ,127xR 52x = ,5-860,599xR 52y + 18,114xR 52x = ,241xR 52x = ,5 R 52x = ,684 N R 25x = ,684 N R 52x (2) denkleminde yerine konulursa; -R 52y x860, ,684x18,114 R 52y = ,364 N ve R 25y = 1.316,364 N R 15y + R 25y = 0 => R 15y = ,364 N R 15x + R 25x = 0 => R 15x = ,684 N R 12x + R 32x + R 52x = 0 R 12x ,684 = 0 R 12x = ,684 R 12y + R 32y + R 52y = 0 R 12y ,364 = 0 => R 12y = ,836 N -8-
10 ϕ 2 =20 için BL=BCxSinϕ 2 =205xSin(20) => BL=70,114 mm. BN=BCxCosϕ 2 =205xCos(20) => BN=192,637 mm. BE =CK-BN = ,637 => BE =27,363 mm. AE =AK+BL =825+70,114 => AE =895,114 mm. R 14x =0 ve R 34x + R 14x = 0 => R 34x = 0 R 14y =0 ve R 34y + R 14y = 0 => R 34y = 0 R 43x + R 23x = 0 => 23x = 0 R 43y +R 23y +F=0 0+R 23y = 0 => R 23y = N R 32y = N R 32y xcdxcosϕ 2 R 32x xcdxsinϕ 2 +R 52y xbl+r 52x xbn = 0 (1) x420xCos(20) 0x420xSin(20)+R 52y x70,114+r 52x x192,637 = 0 (1) 70,114xR 52y +192,637xR 52x = ,82 (1) R 25y xae - R 25x xbe = 0-895,114xR 52y + R 52x x27,363 = 0 (2) (1) ve (2) denklemlerinin çözümü; 12,76656x(70,114xR 52y + 192,637xR 52x = ,82) 895,114xR 52y ,312xR 52x = ,4-895,114xR 52y + 27,363xR 52x = ,675xR 52x = ,4 R 52x = ,543 N R 25x = ,543 N R 52x (2) denkleminde yerine konulursa; -895,114xR 52y ,543x27,363 = 0 R 52y = ,098 N ve R 25y = 1.982,098 N R 15y + R 25y = 0 => R 15y = ,098 N R 15x + R 25x = 0 => R 15x = ,543 N R 12x + R 32x + R 52x = 0 => R 12x ,543 = 0 R 12x = ,543 N R 12y + R 32y + R 52y = 0 R 12y ,098 = 0 => R 12y = ,902 N -9-
11 ϕ 2 =30 için BL=BCxSinϕ 2 =205xSin(30) => BL=102,5 mm. BN=BCxCosϕ 2 =205xCos(30) => BN=177,535 mm. BE =CK-BN = ,535 => BE =42,465 mm. AE =AK+BL = ,5 => AE =927,5 mm. R 14x =0 ve R 34x + R 14x = 0 => R 34x = 0 R 14y =0 ve R 34y + R 14y = 0 => R 34y = 0 R 43x + R 23x = 0 => 23x = 0 R 43y +R 23y +F=0 0+R 23y = 0 => R 23y = N R 32y = N R 32y xcdxcosϕ 2 R 32x xcdxsinϕ 2 +R 52y xbl+r 52x xbn = 0 (1) x420xCos(30) 0x420xSin(30)+R 52y x102,5+r 52x x177,535 = 0 102,5xR 52y +177,535xR 52x = ,43 (1) R 25y xae - R 25x xbe = 0 927,5xR 25y - R 25x x42,465 = 0-927,5xR 52y + R 52x x42,465 = 0 (2) (1) ve (2) denklemlerinin çözümü; 9,0488x(102,5xR 52y + 177,535xR 52x = ,43) -927,5xR 52y + 42,465xR 52x = 0 927,5xR 52y ,479xR 52x = , ,944xR 52x = ,7 R 52x = ,657 N R 25x = ,657 N R 52x (2) denkleminde yerine konulursa; -927,5xR 52y + 42,465x( ,657) = 0 R 52y = ,369 N ve R 25y = 2.924,369 N R 15y + R 25y = 0 => R 15y = ,369 N R 15x + R 25x = 0 => R 15x = ,657 N R 12x + R 32x + R 52x = 0 => R 12x ,657 = 0 R 12x = ,657 N R 12y + R 32y + R 52y = 0 R 12y ,369 = 0 => R 12y = ,631 N -10-
12 ϕ 2 =40 için BL=BCxSinϕ 2 =205xSin(40) => BL=131,77 mm. BN=BCxCosϕ 2 =205xCos(40) => BN=157,04 mm. BE =CK-BN = ,04 => BE =62,96 mm. AE =AK+BL = ,77 => AE =956,77 mm. R 14x =0 ve R 34x + R 14x = 0 => R 34x = 0 R 14y =0 ve R 34y + R 14y = 0 => R 34y = 0 R 43x + R 23x = 0 => 23x = 0 R 43y +R 23y +F=0 0+R 23y = 0 => R 23y = N R 32y = N R 32y xcdxcosϕ 2 R 32x xcdxsinϕ 2 +R 52y xbl+r 52x xbn = 0 (1) x420xCos(40) 0x420xSin(40)+R 52y x131,77+r 52x x157,04 = 0 131,77xR 52y +157,04xR 52x = ,32 (1) R 25y xae - R 25x xbe = 0 956,77xR 25y - R 25x x62,96 = 0-956,77xR 52y + R 52x x62,96 = 0 (2) (1) ve (2) denklemlerinin çözümü; 7,26091x(131,77xR 52y + 157,04xR 52x = ,32) -956,77xR 52y + 62,96xR 52x = 0 956,77xR 52y ,25xR 52x = , ,21xR 52x = ,97 R 52x = ,215 N R 25x = ,215 N R 52x (2) denkleminde yerine konulursa; -956,77xR 52y + 62,96x( ,215) = 0 R 52y = ,463 N ve R 25y = 4.088,463 N R 15y + R 25y = 0 => R 15y = ,463 N R 15x + R 25x = 0 => R 15x = ,215 N R 12x + R 32x + R 52x = 0 => R 12x ,215 = 0 R 12x = ,215 N R 12y + R 32y + R 52y = 0 R 12y ,463 = 0 => R 12y = ,537 N -11-
13 ϕ 2 =50 için BL=BCxSinϕ 2 =205xSin(50) => BL=157,039 mm. BN=BCxCosϕ 2 =205xCos(50) => BN=131,77 mm. BE =CK-BN = ,77 => BE =88,23 mm. AE =AK+BL = ,039 => AE =982,039 mm. R 14x =0 ve R 34x + R 14x = 0 => R 34x = 0 R 14y =0 ve R 34y + R 14y = 0 => R 34y = 0 R 43x + R 23x = 0 => 23x = 0 R 43y +R 23y +F=0 0+R 23y = 0 => R 23y = N R 32y = N R 32y xcdxcosϕ 2 R 32x xcdxsinϕ 2 +R 52y xbl+r 52x xbn = 0 (1) x420xCos(50) 0x420xSin(50)+R 52y x157,039+r 52x x131,77 = 0 157,039xR 52y +131,77xR 52x = ,475 (1) R 25y xae - R 25x xbe = 0 982,039xR 25y - R 25x x88,23 = 0-982,039xR 52y + R 52x x88,23 = 0 (2) (1) ve (2) denklemlerinin çözümü; 6,25347x(157,039xR 52y + 131,77xR 52x = ,475) -982,039xR 52y + 88,23xR 52x = 0 982,039xR 52y + 824,02xR 52x = , ,25x52x = ,78 R 52x = ,758 N R 25x = ,758 N R 52x (2) denkleminde yerine konulursa; -982,039xR 52y + 88,23x( ,758) = 0 R 52y = ,611 N ve R 25y = 5.320,611 N R 15y + R 25y = 0 => R 15y = ,611 N R 15x + R 25x = 0 => R 15x = ,758 N R 12x + R 32x + R 52x = 0 => R 12x ,758 = 0 R 12x = ,758 N R 12y + R 32y + R 52y = 0 R 12y ,611 = 0 => R 12y = ,389 N -12-
14 ϕ 2 =60 için BL=BCxSinϕ 2 =205xSin(60) => BL=177,535 mm. BN=BCxCosϕ 2 =205xCos(60) => BN=102,5 mm. BE =CK-BN = ,5 => BE =117,5 mm. AE =AK+BL = ,535 => AE =1.002,535 mm. R 14x =0 ve R 34x + R 14x = 0 => R 34x = 0 R 14y =0 ve R 34y + R 14y = 0 => R 34y = 0 R 43x + R 23x = 0 => 23x = 0 R 43y +R 23y +F=0 0+R 23y = 0 => R 23y = N R 32y = N R 32y xcdxcosϕ 2 R 32x xcdxsinϕ 2 +R 52y xbl+r 52x xbn = x420xCos(60) 0x420xSin(60)+R 52y x177,535+r 52x x102,5 = 0 177,535xR 52y +102,5xR 52x = (1) R 25y xae - R 25x xbe = ,535xR 25y - R 25x x117,5 = ,535xR 52y + R 52x x117,5 = 0 (2) (1) ve (2) denklemlerinin çözümü; 5,64697x(177,535xR 52y + 102,5xR 52x = ) ,535xR 52y + 117,5xR 52x = ,535xR 52y + 578,814xR 52x = , ,314xR 52x = ,4 R 52x = ,882 N R 25x = ,882 N R 52x (2) denkleminde yerine konulursa; ,535xR 52y + 117,5x( ,882) = 0 R 52y = ,309 N ve R 25y = 6.387,309 N R 15y + R 25y = 0 => R 15y = ,309 N R 15x + R 25x = 0 => R 15x = ,882 N R 12x + R 32x + R 52x = 0 => R 12x ,882 = 0 R 12x = ,882 N R 12y + R 32y + R 52y = 0 R 12y ,309 = 0 => R 12y = ,691 N -13-
15 ϕ 2 =70 için BL=BCxSinϕ 2 =205xSin(70) => BL=192,637 mm. BN=BCxCosϕ 2 =205xCos(70) => BN=70,114 mm. BE =CK-BN =220-70,114 => BE =149,886 mm. AE =AK+BL = ,637 => AE =1.017,637 mm. R 14x =0 ve R 34x + R 14x = 0 => R 34x = 0 R 14y =0 ve R 34y + R 14y = 0 => R 34y = 0 R 43x + R 23x = 0 => 23x = 0 R 43y +R 23y +F=0 0+R 23y = 0 => R 23y = N R 32y = N R 32y xcdxcosϕ 2 R 32x xcdxsinϕ 2 +R 52y xbl+r 52x xbn = x420xCos(70) 0x420xSin(70)+R 52y x192,637+r 52x x70,114 = 0 192,637xR 52y +70,114xR 52x = ,726 N (1) R 25y xae - R 25x xbe = ,637xR 25y - R 25x x149,886 = ,637xR 52y + R 52x x149,886 = 0 (2) (1) ve (2) denklemlerinin çözümü; 5,28267x(192,637xR 52y + 70,114xR 52x = ,726) ,637xR 52y + 149,886xR 52x = ,637xR 52y + 370,389xR 52x = , ,275xR 52x = ,16 R 52x = ,619 N R 25x = ,619 N R 52x (2) denkleminde yerine konulursa; ,637xR 52y + 149,886x( ,619) = 0 R 52y = ,477 N ve R 25y = 6.874,477 N R 15y + R 25y = 0 => R 15y = ,477 N R 15x + R 25x = 0 => R 15x = ,619 N R 12x + R 32x + R 52x = 0 => R 12x ,619 = 0 R 12x = ,619 N R 12y + R 32y + R 52y = 0 R 12y ,477 = 0 => R 12y = ,523 N -14-
16 ϕ 2 =80 için BL=BCxSinϕ 2 =205xSin(80) => BL=201,886 mm. BN=BCxCosϕ 2 =205xCos(80) => BN=35,598 mm. BE =CK-BN =220-35,598 => BE =184,402 mm. AE =AK+BL = ,886 => AE =1.026,886 mm. R 14x =0 ve R 34x + R 14x = 0 => R 34x = 0 R 14y =0 ve R 34y + R 14y = 0 => R 34y = 0 R 43x + R 23x = 0 => 23x = 0 R 43y +R 23y +F=0 0+R 23y = 0 => R 23y = N R 32y = N R 32y xcdxcosϕ 2 R 32x xcdxsinϕ 2 +R 52y xbl+r 52x xbn = x420xCos(80) 0x420xSin(80)+R 52y x201,886+r 52x x35,598 = 0 201,886xR 52y +35,598xR 52x = ,508 N (1) R 25y xae - R 25x xbe = ,886xR 25y - R 25x x184,402 = ,886xR 52y + R 52x x184,402 = 0 (2) (1) ve (2) denklemlerinin çözümü; 5,08646x(201,886xR 52y + 35,598xR 52x = ,508) ,886xR 52y + 184,402xR 52x = ,886xR 52y + 181,068xR 52x = , ,470xR 52x = ,61 R 52x = ,299 N R 25x = ,299 N R 52x (2) denkleminde yerine konulursa; ,886xR 52y + 184,402x( ,299) = 0 R 52y = ,796 N ve R 25y = 5.832,796 N R 15y + R 25y = 0 => R 15y = ,796 N R 15x + R 25x = 0 => R 15x = ,299 N R 12x + R 32x + R 52x = 0 => R 12x ,299 = 0 R 12x = ,299 N R 12y + R 32y + R 52y = 0 R 12y ,796 = 0 => R 12y = ,204 N -15-
17 ϕ 2 =90 için BL=BCxSinϕ 2 =205xSin(90) => BL=205 mm. BN=BCxCosϕ 2 =205xCos(90) => BN=0 mm. BE =CK-BN =220-0 => BE =220 mm. AE =AK+BL = => AE =1.030 mm. R 14x =0 ve R 34x + R 14x = 0 => R 34x = 0 R 14y =0 ve R 34y + R 14y = 0 => R 34y = 0 R 43x + R 23x = 0 => 23x = 0 R 43y +R 23y +F=0 0+R 23y = 0 => R 23y = N R 32y = N R 32y xcdxcosϕ 2 R 32x xcdxsinϕ 2 +R 52y xbl+r 52x xbn = x420xCos(90) 0x420xSin(90)+R 52y x205+r 52x x0 = 0 205xR 52y +0xR 52x = 0 => R 52y =0 R 25y =0 R 25y xae - R 25x xbe = x0 - R 25x x220 = 0 => R 25x =0 R 52x =0 R 15y + R 25y = 0 => R 15y = 0 R 15x + R 25x = 0 => R 15x = 0 R 12x + R 32x + R 52x = 0 => R 12x = 0 R 12x = 0 R 12y + R 32y + R 52y = 0 R 12y = 0 => R 12y = N -16-
18 ϕ AE , , ,5 956,77 BE 15 18,114 27,363 42,465 62,96 BL 0 35, , ,5 131,77 BN ,886 70, , ,04 F x 65560, , , , ,215 12y , , , , ,54 14x y x , , , , ,21 15y -1192, , , , ,463 23x y x 65560, , , , ,215 25y 1192, , , , ,463 34x y ϕ AE 982, , , , BE 88,23 117,5 149, , BL 157, , , , BN 131,77 102,5 70,114 35,598 0 F x 59220, , , , y , , , , x y x , , , , y -5320, , , , x y x 59220, , , , y 6320, , , , x y
19 ϕ , , , , , , , , , , , , , , , , , , , , , , , , , , , KRİKO KLUNA UYGULANMASI GEREKEN KUVVET HESABI R 25max =65571,81 N d 1 : Kaldırma silindiri çapı = 70 mm d 2 : Etki silindiri çapı = 25 mm η mk : Etki kolundaki mekanik verimi η mk =800/40 = 20 R 25max ı oluşturacak hidrolik basınç ; P= R 25max /( πd 2 1 /4 ) P=65571,81/( π 70 2 /4 ) P=17,038 N/mm 2 Bu basıncı oluşturacak etki silindirine gerekli itme kuvveti ; F=Pxπd 2 2 /4 => F=17,038xπ(25) 2 /4 => F=8363,51 N Manivela kolunun ucunda gerekli kuvvet ; F mani = F/ η mk => F mani =418,18 N I II φ
20 İtme milinin etkidiği pernonun kontrolü ; St60 için σ=600 N/mm 2 τ =300 n/mm 2 S=2,5 σ em = σ/s => σ em =600/2,5=240 N/mm 2 τ em = τ/s => τ em =300/2,5 =120 N/mm 2 I ve II kesitlerindeki kayma gerilmesi τ= R 25max /(2πd 2 /4) => τ = 65571,81/(2πx20 2 /4) => τ =104,36 N/mm 2 perno kesme gerilmesine karşı emniyetlidir (104,36<140) 30 R R25max Yan sac malzemesi St37 için σ em =148 N/mm 2 τ em =75 N/mm 2 Yan saclardaki delik ezilmesi kontrolü ; σ= R 25max /(2πd(a+b)) => σ = 65571,81/(2πx20(7+7)) => σ =117,09 N/mm 2 (117,09<148) olduğundan ezilmeye emniyetlidir. Delik yırtılması kontrolü ; τ= R 25max /(4lb) => τ = 65571,81/(4x35x7) => τ =66,91N/mm 2 (66,91<75) olduğundan yırtılmaya karşı emniyetlidir. 12y C N D 1192,02 N B
21 Malzeme St37 σ em =370/2,5=148 N/mm 2 M max = M B = x ,98x30 M max = M B = ,6 Nm Y G =Σ A i X i Y i / ΣA i Y G = (2x150x7x80+151,5x3x99) / (2x150x7+3x99) Y G = 88,86 mm I X = 2x((7x150 3 x/12)+7x150x(80-61,14) 2 )+(99x3 3 /12)+99x3x(61,14-3) 2 I X = ,011 mm 4 e =150-y G =150-88,86 => e = 61,14 mm σ max =M max x e /I X = ,6x61,14=/ ,011 σ max = 120,759 N/mm 2 σ max < σ em olduğundan emniyetlidir ,14 x x 150 yg
22 Ana gövde eğilme kontrolü ; Malzeme St37 σ em = 148 N/mm 2 R 21y A O C O / R 51y Y Y 1 A O C O / M max ΣMo ı = 0 -y 1 x ,02x ,98x350=0 => y 1 =10.142,89 N ΣFo = , , ,98+y 2 =0 => y 2 =19.473,07 N Mo = 1.192,02x250 = N mm Mc = ,07x350 = ,5 N mm M max =Mc= ,5 N mm O noktasındaki gövdenin kesiti ; I X =2x5x170 3 /12= ,67 mm 4 e = 85 mm σ max = M max e/i X = ( ,5/ ,67)x85 = 141,5 N/mm 2 σ max < σ em olduğundan emniyetlidir. -21-
23 90 x x x x φ15 φ35 Yük traversinin kontrolü ; σ em =240 N/mm 2 τ em =120 N/mm 2 M max =16.000x(50+5/2) = N mm I X = 35 4 /12-15x35 3 /12 = 71458,3333 mm 4 e=17,5 mm σ max =M max x e / I X x17,5/71458,3333 = 205,71 N/mm 2 σ max < σ em olduğundan eğilmeye karşı emniyetlidir. -22-
24 F = A φ 35 φ 22 A 5 5 M max Muyluların kesilme kontrolü ; τ =(F/2)/(πxd 2 /4) τ = (32.000/2)/(πx22 2 /4) = 42,074 N/mm 2 < τ em emniyetli. Delik ezilmesi kontrolü ; σ = (F/2)/(axd) σ = (32.000/2)/(5x22) = 145,45 N/mm 2 1. Yük traversi için ; Muylularda KESİT HESABI τ em = (F/2)/(πxd 2 /4) 120 = (32.000/2)/(πxd 2 /4) => d = 13,029 mm σ em = (F/2)/(axd) 148 = (32.000/2)/(5xd) => d = 21,623 mm 2. O noktasındaki perno için ; 1 ve 2 kesitleri için ; τ em = R 25max /(2xπxd 2 /4) 120 = (65571,81)/(2xπxd 2 /4) => d = 18,65 mm yan saclardaki delik için ; σ em = R 25max /(2d(a+b)) 148 = (65571,81)/(2xd(7+7)) => d = 15,82 mm -23-
MAKİNE ELEMANLARI 1 GENEL ÇALIŞMA SORULARI 1) Verilen kuvvet değerlerini yükleme türlerini yazınız.
MAKİNE ELEMANLARI 1 GENEL ÇALIŞMA SORULARI 1) Verilen kuvvet değerlerini yükleme türlerini yazınız. F = 2000 ± 1900 N F = ± 160 N F = 150 ± 150 N F = 100 ± 90 N F = ± 50 N F = 16,16 N F = 333,33 N F =
BURSA TECHNICAL UNIVERSITY (BTU) Department of Mechanical Engineering
Uygulama Sorusu-1 Şekildeki 40 mm çaplı şaft 0 kn eksenel çekme kuvveti ve 450 Nm burulma momentine maruzdur. Ayrıca milin her iki ucunda 360 Nm lik eğilme momenti etki etmektedir. Mil malzemesi için σ
ÖRNEK SAYISAL UYGULAMALAR
ÖRNEK SAYISAL UYGULAMALAR 1-Vidalı kriko: Şekil deki kriko için; Verilenler Vidalı Mil Malzemesi: Ck 45 Vidalı mil konumu: Düşey Somun Malzemesi: Bronz Kaldırılacak en büyük (maksimum) yük: 50.000 N Vida
Perçinli ve Bulonlu Birleşimler ve Perçin Hesapları Amaçlar
Perçinli ve Bulonlu Birleşimler ve Perçin Hesapları Amaçlar Perçinli/bulonlu birleşimlerin ne olduğunu inceleyeceğiz, Perçinli/bulonlu birleşimleri oluştururken yapılan kontrolleri öğreneceğiz. Perçinli
Perçinli ve Bulonlu Birleşimler ve Hesapları Amaçlar
Amaçlar Perçinli/bulonlu birleşimlerin ne olduğunu inceleyeceğiz, Perçinli/bulonlu birleşimleri oluştururken yapılan kontrolleri öğreneceğiz. Kayma Gerilmesinin Önemli Olduğu Yükleme Durumları En kesitte
MAK 305 MAKİNE ELEMANLARI-1
MAK 305 MAKİNE ELEMANLARI-1 BÖLÜM 1- MAKİNE ELEMANLARINDA MUKAVEMET HESABI Doç. Dr. Ali Rıza YILDIZ 1 BU DERS SUNUMDAN EDİNİLMESİ BEKLENEN BİLGİLER Makine Elemanlarında mukavemet hesabına neden ihtiyaç
MENGENE HESAPLARI A-VĐDALI MENGENE MĐLĐ. www.muhendisiz.net
www.muhendisiz.net MENGENE HESAPLARI A-VĐDALI MENGENE MĐLĐ Hareket civatasında bir güç iletimi söz konusu olduğundan verimin yüksek olması istenir.bu nedenle Trapez profilli vida kullanılır. Yük ; F =
Sıkma sırasında oluşan gerilmeden öngerilme kuvvetini hesaplarız. Boru içindeki basınç işletme basıncıdır. Buradan işletme kuvvetini buluruz.
Ø50 Şekilde gösterilen boru bağlantısında flanşlar birbirine 6 adet M0 luk öngerilme cıvatası ile bağlanmıştır. Cıvatalar 0.9 kalitesinde olup, gövde çapı 7,mm dir. Cıvatalar gövdelerindeki akma mukavemetinin
T.C. KOCAELĠ ÜNĠVERSĠTESĠ MÜHENDĠSLĠK FAKÜLTESĠ MEKATRONĠK MÜHENDĠSLĠĞĠ BÖLÜMÜ MEKATRONĠK YAPI ELEMANLARI UYGULAMASI
T.C. KOCAELĠ ÜNĠVERSĠTESĠ MÜHENDĠSLĠK FAKÜLTESĠ MEKATRONĠK MÜHENDĠSLĠĞĠ BÖLÜMÜ MEKATRONĠK YAPI ELEMANLARI UYGULAMASI 1.) Düz kayış kasnağı bir mil üzerine radyal yönde feder kaması ile eksenel yönde ise
KOÜ. Mühendislik Fakültesi Makine Mühendisliği Bölümü (1. ve 2.Öğretim / B Şubesi) MMK208 Mukavemet II Dersi - 1. Çalışma Soruları 23 Şubat 2019
SORU-1) Aynı anda hem basit eğilme hem de burulma etkisi altında bulunan yarıçapı R veya çapı D = 2R olan dairesel kesitli millerde, oluşan (meydana gelen) en büyük normal gerilmenin ( ), eğilme momenti
Cetvel-13 Güvenirlik Faktörü k g. Güvenirlik (%) ,9 99,99 99,999
Cetvel-12 Büyüklük Faktörü k b d,mm 10 20 30 50 100 200 250 300 k b 1 0,9 0,8 0,7 0,6 0,57 0,56 0,56 Cetvel-13 Sıcaklık Faktörü k d Cetvel-13 Güvenirlik Faktörü k g T( o C) k d T 350 1 350
BÖLÜM-2 ÇELİK YAPILARDA BİRLEŞİM ARAÇLARI
BÖLÜM-2 ÇELİK YPILRD BİRLEŞİM RÇLRI Çelik yapılarda kullanılan hadde ürünleri için, aşağıdaki sebeplerle birleşimler yapılması gerekmektedir. Bu aşamada bulon (cıvata), kaynak ve perçin olarak isimlendirilen
GERİLMELER Çekme-Basma-Kesme
MK 08: MUKVEMET Öğr.Gör.r. met Taşkesen GERİLMELER Çekme-asma-Kesme φd Çelik 1500N a cm lüm 70cm r. met TŞKESEN lüm ve çelikteki tellerin kesitlerini tablasının sapma çısını bulunuz? σem çelik 10000 N/cm
ÇELİK YAPILARDA BİRLEŞİMLER
ÇELİK YAPILARDA BİRLEŞİMLER Çelik yapılarda birleşimlerin kullanılma sebepleri; 1. Farklı tasıyıcı elemanların (kolon-kolon, kolon-kiris,diyagonalkolon, kiris-kiris, alt baslık-üst baslık, dikme-alt baslık
STATIK MUKAVEMET. Doç. Dr. NURHAYAT DEĞİRMENCİ
STATIK MUKAVEMET Doç. Dr. NURHAYAT DEĞİRMENCİ STATİK DENGE KOŞULLARI Yapı elemanlarının tasarımında bu elemanlarda oluşan iç kuvvetlerin dağılımının bilinmesi gerekir. Dış ve iç kuvvetlerin belirlenmesinde
Perçin malzemesinin mekanik özellikleri daha zayıf olduğundan hesaplamalarda St34 malzemesinin değerleri esas alınacaktır.
Kalınlığı s 12 mm, genişliği b 400 mm, malzemesi st37 olan levhalar, iki kapaklı perçin bağlantısı ile bağlanmıştır. Perçin malzemesi st34 olarak verilmektedir. Perçin bağlantısı 420*10 3 N luk bir kuvvet
MAKĠNE ELEMANLARI II REDÜKTÖR PROJESĠ
T.C PAMUKKALE ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAKĠNE ELEMANLARI II REDÜKTÖR PROJESĠ Öğrencinin; Adı: Cengiz Görkem Soyadı: DENGĠZ No: 07223019 DanıĢman: Doç. Dr. TEZCAN ġekercġoğlu
= ε s = 0,003*( ,3979)/185,3979 = 6,2234*10-3
1) Şekilde verilen kirişte sehim denetimi gerektirmeyen donatı sınırı kadar donatı altında moment taşıma kapasitesi M r = 274,18 knm ise b w kiriş genişliğini hesaplayınız. d=57 cm Malzeme: C25/S420 b
Birleşim Araçları Prof. Dr. Ayşe Daloğlu Karadeniz Teknik Üniversitesi İnşaat Mühendisliği Bölümü
Birleşim Araçları Birleşim Araçları Çelik yapılar çeşitli boyut ve biçimlerdeki hadde ürünlerinin kesilip birleştirilmesi ile elde edilirler. Birleşim araçları; Çözülebilen birleşim araçları (Cıvata (bulon))
GERİLME Cismin kesilmiş alanı üzerinde O
GERİLME Cismin kesilmiş alanı üzerinde O ile tanımlı noktasına etki eden kuvvet ve momentin kesit alana etki eden gerçek yayılı yüklerin bileşke etkisini temsil ettiği ifade edilmişti. Cisimlerin mukavemeti
29- Eylül KOÜ. Mühendislik Fakültesi Makine Mühendisliği Bölümü ( 1. ve 2. Öğretim 2. Sınıf / B Şubesi) Mukavemet Dersi - 1.
SORU-1) Şekildeki dikdörtgen kesitli kolonun genişliği b=200 mm. ve kalınlığı t=100 mm. dir. Kolon, kolon kesitinin geometrik merkezinden geçen ve tarafsız ekseni üzerinden etki eden P=400 kn değerindeki
δ / = P L A E = [+35 kn](0.75 m)(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir.
(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir.](/thumbs/68/59308868.jpg "δ / = P L A E = [+35 kn](0.75 m)(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir.")
A-36 malzemeden çelik çubuk, şekil a gösterildiği iki kademeli olarak üretilmiştir. AB ve BC kesitleri sırasıyla A = 600 mm ve A = 1200 mm dir. A serbest ucunun ve B nin C ye göre yer değiştirmesini belirleyiniz.
ÇELİK YAPILARIN TASARIM, HESAP ve YAPIM ESASLARI. ÖRNEKLER ve TS648 le KARŞILAŞTIRILMASI
ÇELİK YAPILARIN TASARIM, HESAP ve YAPIM ESASLARI ÖRNEKLER ve TS648 le KARŞILAŞTIRILMASI Eksenel Çekme Etkisi KARAKTERİSTİK EKSENEL ÇEKME KUVVETİ DAYANIMI (P n ) Eksenel çekme etkisindeki elemanların tasarımında
Ara Sınav. Verilen Zaman: 2 saat (15:00-17:00) Kitap ve Notlar Kapalı. Maksimum Puan
MAK 303 MAKİNA ELEMANLARI I Ara ınav 9 Kasım 2008 Ad, oyad Dr. M. Ali Güler Öğrenci No. Verilen Zaman: 2 saat (15:00-17:00) Kitap ve Notlar Kapalı Her soruyu dikkatle okuyunuz. Yaptığınız işlemleri gösteriniz.
MAK 305 MAKİNE ELEMANLARI-1
MAK 305 MAKİNE ELEMANLARI-1 8.BÖLÜM Mil-Göbek Bağlantıları Paralel Kama, Kamalı Mil, Konik Geçme, Sıkı ve Sıkma Geçme Doç.Dr. Ali Rıza Yıldız 1 BU SLAYTTAN EDİNİLMESİ BEKLENEN BİLGİLER Şekil Bağlı Mil-Göbek
Çözüm: Borunun et kalınlığı (s) çubuğun eksenel kuvvetle çekmeye zorlanması şartından;
Soru 1) Şekilde gösterilen ve dış çapı D 10 mm olan iki borudan oluşan çelik konstrüksiyon II. Kaliteli alın kaynağı ile birleştirilmektedir. Malzemesi St olan boru F 180*10 3 N luk değişken bir çekme
2005/2006 ÖĞRETİM YILI GÜZ YARIYILI MUKAVEMET 1 DERSİ 1. VİZE SORU VE CEVAPLARI
00/00 ÖĞRTİ YILI GÜZ YRIYILI UKT 1 RSİ 1. İZ SORU PLRI SORU 1: 0 0 kn 0, m 8 kn/m 0, m 0, m t t Şekildeki sistde, a) Y 0 Pa ve niet katsaısı n olduğuna göre çubuğunun kesit alanını, b) Y 00 Pa ve n için
MAK 305 MAKİNE ELEMANLARI-1
MAK 305 MAKİNE ELEMANLARI-1 7.BÖLÜM Bağlama Elemanları Cıvata Bağlantıları Doç.Dr. Ali Rıza Yıldız MAK 305 Makine Elemanları-Doç. Dr. Ali Rıza YILDIZ 1 BU SLAYTTAN EDİNİLMESİ BEKLENEN BİLGİLER Cıvata Hakkında
MUKAVEMET-I DERSİ BAUN MAKİNA MÜHENDİSLİĞİ FİNAL ÖNCESİ UYGULAMA SORULARI ARALIK-2018
MUKAVEMET-I DERSİ BAUN MAKİNA MÜHENDİSLİĞİ FİNAL ÖNCESİ UYGULAMA SORULARI ARALIK-2018 UYGULAMA-1 AB ve CD çelik çubuklar rijit BD platformunu taşımaktadır. F noktasından uygulanan 10 Kip yük etkisinde
PERÇİN BAĞLANTILARI. Bu sunu farklı kaynaklardan derlemedir.
PERÇİN BAĞLANTILARI Perçin çözülemeyen bağlantı elemanıdır. Kaynak teknolojisindeki hızlı gelişme sonucunda yerini çoğunlukla kaynaklı bağlantılara bırakmıştır. Sınırlı olarak çelik kazan ve kap konstrüksiyonlarında
FL 3 DENEY 4 MALZEMELERDE ELASTĐSĐTE VE KAYMA ELASTĐSĐTE MODÜLLERĐNĐN EĞME VE BURULMA TESTLERĐ ĐLE BELĐRLENMESĐ 1. AMAÇ
Malzemelerde Elastisite ve Kayma Elastisite Modüllerinin Eğme ve Burulma Testleri ile Belirlenmesi 1/5 DENEY 4 MAZEMEERDE EASTĐSĐTE VE KAYMA EASTĐSĐTE MODÜERĐNĐN EĞME VE BURUMA TESTERĐ ĐE BEĐRENMESĐ 1.
Burulma (Torsion) Amaçlar
(Torsion) Amaçlar Bu bölümde şaftlara etkiyen burulma kuvvetlerinin etkisi incelenecek. Analiz dairesel kesitli şaftlar için yapılacak. Eleman en kesitinde oluşan gerilme dağılımı ve elemanda oluşan burulma
ÇALIŞMA SORULARI 1) Yukarıdaki şekilde AB ve BC silindirik çubukları B noktasında birbirleriyle birleştirilmişlerdir, AB çubuğunun çapı 30 mm ve BC çubuğunun çapı ise 50 mm dir. Sisteme A ucunda 60 kn
MAK 305 MAKİNE ELEMANLARI-1
MAK 305 MAKİNE ELEMANLARI-1 5.BÖLÜM Bağlama Elemanları Kaynak Bağlantıları Doç.Dr. Ali Rıza Yıldız 1 BU SLAYTTAN EDİNİLMESİ BEKLENEN BİLGİLER Bağlama Elemanlarının Tanımı ve Sınıflandırılması Kaynak Bağlantılarının
TEKNOLOJİNİN BİLİMSEL İLKELERİ. Bölüm-4 MALZEMELERDE ÇEKME-BASMA - KESME GERİLMELERİ VE YOUNG MODÜLÜ. 4.1. Malzemelerde Zorlanma ve Gerilme Şekilleri
Bölüm-4 MALZEMELERDE ÇEKME-BASMA - KESME GERİLMELERİ VE YOUNG MODÜLÜ 4.1. Malzemelerde Zorlanma ve Gerilme Şekilleri Malzemeler genel olarak 3 çeşit zorlanmaya maruzdurlar. Bunlar çekme, basma ve kesme
Burulma (Torsion): Dairesel Kesitli Millerde Gerilme ve Şekil Değiştirmeler
Burulma (orsion): Dairesel Kesitli Millerde Gerilme ve Şekil Değiştirmeler Endüstiryel uygulamalarda en çok rastlanan yükleme tiplerinden birisi dairsel kesitli millere gelen burulma momentleridir. Burulma
Gerilme Dönüşümleri (Stress Transformation)
Gerilme Dönüşümleri (Stress Transformation) Bubölümdebirnoktayaetkiyen vebelli bir koordinat ekseni/düzlemi ile ilişkili gerilme bileşenlerini, başka bir koordinat sistemi/başka bir düzlem ile ilişkili
MUKAVEMET. BURULMA L uzunluğunda R yarıçapında burulma çubuğu, merkezden r kadar uzaklı ktaki, diferansiyel eleman kesit alanı A,
1 MUKAVEMET BURULMA L uzunluğunda R yarıçapında burulma çubuğu, merkezden r kadar uzaklı ktaki, diferansiyel eleman kesit alanı A, Kayma gerilmesi: = (r/r). 2 3 Diferansiyel Kuvvet. Diferansiyel burulma
3. 2 Bulonlu Birleşimler
3. 2 Bulonlu Birleşimler Birleşimin gerçekleştirilmesi az kalifiye işçi Bulonların Kullanılma Alanları: Geçici birleşimler ve yapılar Şantiye birleşim ve ekleri Dinamik karakterli yüklerin aktarılması
MUKAVEMET FATİH ALİBEYOĞLU
MUKAVEMET FATİH ALİBEYOĞLU Rijit Cisimler Mekaniği Statik Dinamik Şekil Değiştiren Cisimler Mekaniği (MUKAVEMET) Akışkanlar Mekaniği STATİK: Dış kuvvetlere maruz kalmasına rağmen durağan halde, yani dengede
Makine Elemanları I Prof. Dr. Akgün ALSARAN. Temel bilgiler-flipped Classroom Akslar ve Miller
Makine Elemanları I Prof. Dr. Akgün ALSARAN Temel bilgiler-flipped Classroom Akslar ve Miller İçerik Giriş Temel kavramlar Sınıflandırma Aks ve mil mukavemet hesabı Millerde titreşim kontrolü Konstrüksiyon
MAKİNE ELEMANLARI DERS SLAYTLARI
MAKİNE ELEMANLARI DERS SLAYTLARI PERÇİN VE YAPIŞTIRICI BAĞLANTILARI P r o f. D r. İ r f a n K A Y M A Z P r o f. D r. A k g ü n A L S A R A N A r ş. G ör. İ l y a s H A C I S A L İ HOĞ LU Perçin; iki veya
Makine Elemanları I. Yorulma Analizi. Prof. Dr. İrfan KAYMAZ. Erzurum Teknik Üniversitesi. Mühendislik Fakültesi Makine Mühendisliği Bölümü
Makine Elemanları I Prof. Dr. İrfan KAYMAZ Mühendislik Fakültesi Makine Mühendisliği Bölümü Yorulma hasarı Aloha Havayolları Uçuş 243: Hilo dan Honolulu (Havai) Uçuşu Tarih: 28 Nisan 1988 Makine elemanlarının
Pnömatik Silindir Tasarımı Ve Analizi
Pnömatik Silindir Tasarımı Ve Analizi Burak Gökberk ÖZÇİÇEK İzmir Katip Çelebi Üniversitesi [email protected] Özet Bu çalışmada, bir pnömatik silindirin analitik yöntemler ile tasarımı yapılmıştır.
Gerilme. Bölüm Hedefleri. Normal ve Kayma gerilmesi kavramının anlaşılması Kesme ve eksenel yük etkisindeki elemanların analiz ve tasarımı
Gerilme Bölüm Hedefleri Normal ve Kayma gerilmesi kavramının anlaşılması Kesme ve eksenel yük etkisindeki elemanların analiz ve tasarımı Copyright 2011 Pearson Education South sia Pte Ltd GERİLME Kesim
Uygulanan dış yüklemelere karşı katı cisimlerin birim alanlarında sergiledikleri tepkiye «Gerilme» denir.
Gerilme ve şekil değiştirme kavramları: Uygulanan dış yüklemelere karşı katı cisimlerin birim alanlarında sergiledikleri tepkiye «Gerilme» denir. Bir mühendislik sistemine çok farklı karakterlerde dış
Temel bilgiler-flipped Classroom Akslar ve Miller
Makine Elemanları I Prof. Dr. İrfan KAYMAZ Temel bilgiler-flipped Classroom Akslar ve Miller İçerik Aks ve milin tanımı Akslar ve millerin mukavemet hesabı Millerde titreşim hesabı Mil tasarımı için tavsiyeler
Hesapların yapılması;modül,mil çapı,rulman,feder ve yağ miktarı gibi değerlerin seçilmesi isteniyor.
PROJE KONUSU : İKİ KADEMELİ REDÜKTÖR. VERİLEN BİLGİLER VE İSTENENLER : Giriş gücü = P giriş =,5 kw Kademe sayısı = Giriş mil devri = n g = 750 devir/dakika.kademe dişli tipi = Düz dişli çark Çıkış mil
Örnek: Şekilde bir dişli kutusunun ara mili ve mile etki eden kuvvetler görülmektedir. Mildeki döndürme momenti : M d2 = Nmm dur.
il ve kama hesaplamaları ile ilgili uygulama: Örnek: Şekilde bir dişli kutusunun ara mili ve mile etki eden kuvvetler görülmektedir. ildeki döndürme momenti : d =140375 Nmm dur. r : Radyal, a : Eksenel,
Gerilme Dönüşümleri (Stress Transformation)
Gerilme Dönüşümleri (Stress Transformation) Bu bölümde, bir noktaya etkiyen ve bir koordinat ekseni ile ilişkili gerilme bileşenlerini, başka bir koordinat sistemi ile ilişkili gerilme bileşenlerine dönüştürmek
MAKİNE ELEMANLARI - (9.Hafta) VİDALAR -2
VİDA HESAPLARI MAKİNE ELEMANLARI - (9.Hafta) VİDALAR -2 A. Ön Yükleme Kuvveti (FÖ) ile Sıkma/Çözme Kuvvetleri (FH) arasındaki İlişki İki malzemeyi birleştirmek için civata ve somun kullanılırsa, somunun
olup uygu kaması A formuna sahiptir. Müsaade edilen yüzey basıncı p em kasnak malzemesi GG ve mil malzemesi St 50 dir.
ÖRNEK 1: Düz kayış kasnağı bir mil üzerine radyal yönde uygu kaması ile eksenel yönde İse bir pul ve cıvata ile sabitleştirilmiştir. İletilecek güç 1 kw ve devir sayısı n=500 D/d olup uygu kaması A formuna
İSTİNAT DUVARLARI DOÇ.DR. MEHMET BERİLGEN
İSTİNAT DUVARLARI DOÇ.DR. MEHMET BERİLGEN İstinat Duvarı Zemin kütlelerini desteklemek için kullanılır. Şevlerin stabilitesini artırmak için Köprü kenar ayağı olarak Deniz yapılarında Rıhtım duvarı Doklar
ZM-I FİNAL SORU ve CEVAPLARI SORU-1 [10]: Sıvılık indisi (I L ) ne demektir? Sıvılık indisinin 2.1, 0 ve -0.6 olması ne ifade eder?
![ZM-I FİNAL SORU ve CEVAPLARI SORU-1 [10]: Sıvılık indisi (I L ) ne demektir? Sıvılık indisinin 2.1, 0 ve -0.6 olması ne ifade eder?](/thumbs/73/68841849.jpg "ZM-I FİNAL SORU ve CEVAPLARI SORU-1 [10]: Sıvılık indisi (I L ) ne demektir? Sıvılık indisinin 2.1, 0 ve -0.6 olması ne ifade eder?")
28-29 ZM-I FİNAL SORU ve CEVAPLARI SORU-1 [1]: Sıvılık indisi (I L ) ne demektir? Sıvılık indisinin 2.1, ve -.6 olması ne ifade eder? SORU 2 [2]: Aşağıdaki kesit için a) Siltin doygun birim hacim ağırlığını
Mukavemet. Betonarme Yapılar. Giriş, Malzeme Mekanik Özellikleri. Dr. Haluk Sesigür İ.T.Ü. Mimarlık Fakültesi Yapı ve Deprem Mühendisliği
Mukavemet Giriş, Malzeme Mekanik Özellikleri Betonarme Yapılar Dr. Haluk Sesigür İ.T.Ü. Mimarlık Fakültesi Yapı ve Deprem Mühendisliği GİRİŞ Referans kitaplar: Mechanics of Materials, SI Edition, 9/E Russell
Hidrolik Devre Elemanları. Hidrolik Silindirler
Hidrolik Devre Elemanları Hidrolik Silindirler Hidrolik Silindirlerin Tanımı Hidrolik enerjiyi mekanik enerjiye dönüştüren ve doğrusal hareket elde etmek amacıyla kullanılan devre elemanlarına silindir
MUKAVEMET HESAPLARI : ÇİFT KİRİŞLİ GEZER KÖPRÜLÜ VİNÇ
MUKAVEMET HESAPLARI ÜRÜN KODU MAKİNA ADI : 20+5 TON : ÇİFT KİRİŞLİ GEZER KÖPRÜLÜ VİNÇ İÇİNDEKİLER ÇELİK YAPI ANALİZİ (VİNÇ KÖPRÜSÜ) TEKER HESAPLARI HALAT HESAPLARI KANCA BLOĞU HESABI TAMBUR HESAPLARI SAYFA
MAKİNE ELEMANLARI - (5.Hafta) BAĞLAMA ELEMANLARI. Bağlama elemanları, bağlantı şekillerine göre 3 grupta toplanırlar. Bunlar;
MAKİNE ELEMANLARI - (5.Hafta) BAĞLAMA ELEMANLARI Bağlama elemanları; makinayı oluşturan elmanları, özelliklerini bozmadan, fonksiyonlarını ortadan kaldırmadan birbirine bağlayan elemanlardır. Çoğunlukla
MUKAVEMET Ders Notları (Son güncelleme )
Püf Noktalarıyla MUKAVEMET Ders Notları (Son güncelleme 21.12.2018) Prof. Dr. Mehmet Zor KONU 1 a-giriş, b-gerilme Kavramı ve Eksenel Yükleme, c-bağlantı Elemanları (Pimler, Perçinler, Civatalar vb.) 21.12.2018
MAKİNE ELEMANLARI - (2.Hafta)
MAKİNE ELEMANLARI - (2.Hafta) SÜREKLİ MUKAVEMET DİYAĞRAMLARI PROBLEMLERİ ÖRNEK 1 Şekildeki gibi Fe50 malzemeden yapılmış faturalı mil ince talaş alınarak işlenmiştir. Aşağıdaki zorlanma durumuna göre sürekli
İNŞAAT MÜHENDİSLİĞİNE GİRİŞ
İNŞAAT MÜHENDİSLİĞİNE GİRİŞ MEKANİK ve MUKAVEMET BİLGİSİ Prof.Dr. Zekai Celep MEKANİK VE MUKAVEMET BİLGİSİ 1. Gerilme 2. Şekil değiştirme 3. Gerilme-şekil değiştirme bağıntısı 4. Basit mukavemet halleri
Nlαlüminyum 5. αlüminyum
Soru 1. Bileşik bir çubuk iki rijit mesnet arasına erleştirilmiştir. Çubuğun sol kısmı bakır olup kesit alanı 60 cm, sağ kısmı da alüminum olup kesit alanı 40 cm dir. Sistem 7 C de gerilmesidir. Alüminum
Aşağıdaki Web sitesinden dersle ilgili bilgi alınabilir. Ders, uygulama ve ödevlerle ilgili bilgiler yeri geldiğinde yayınlanacaktır.
MK 04: MUKVEMET Öğr.Gör.Dr. hmet Taşkesen MUKVEMET GİRİŞ DERS STLERİ Öğr.Gör.Dr. hmet Taşkesen, Makina Bölümü, Tel: 1680/1844, e-posta: [email protected] Teorik Ders (3 saat) + Ödevler + Quizler Uygulama
2009 Kasım. www.guven-kutay.ch MUKAVEMET DEĞERLERİ ÖRNEKLER. 05-5a. M. Güven KUTAY. 05-5a-ornekler.doc
2009 Kasım MUKAVEMET DEĞERLERİ ÖRNEKLER 05-5a M. Güven KUTAY 05-5a-ornekler.doc İ Ç İ N D E K İ L E R 5. MUKAVEMET HESAPLARI İÇİN ÖRNEKLER...5.3 5.1. 1. Grup örnekler...5.3 5.1.1. Örnek 1, aturalı mil
11/6/2014 İNŞAAT MÜHENDİSLİĞİNE GİRİŞ. MEKANİK ve MUKAVEMET BİLGİSİ MEKANİK VE MUKAVEMET BİLGİSİ
MEKANİK VE MUKAVEMET BİLGİSİ İNŞAAT MÜHENDİSLİĞİNE GİRİŞ MEKANİK ve MUKAVEMET BİLGİSİ Prof.Dr. Zekai Celep 1. Gerilme 2. Şekil değiştirme 3. Gerilme-şekil değiştirme bağıntısı 4. Basit mukavemet halleri
GERİLME ANALİZİ VE MOHR ÇEMBERİ MUKAVEMET
GERİLME ANALİZİ VE MOHR ÇEMBERİ MUKAVEMET Yrd. Doç. Dr. Emine AYDIN Yrd. Doç. Dr. Elif BORU 1 GENEL YÜKLEME DURUMUNDA GERİLME ANALİZİ Daha önce incelenen gerilme örnekleri eksenel yüklü yapı elemanları
ASİSTAN ARŞ. GÖR. GÜL DAYAN
ASİSTAN ARŞ. GÖR. GÜL DAYAN VİSKOZİTE ÖLÇÜMÜ Viskozite, bir sıvının iç sürtünmesi olarak tanımlanır. Viskoziteyi etkileyen en önemli faktör sıcaklıktır. Sıcaklık arttıkça sıvıların viskoziteleri azalır.
MAK341 MAKİNA ELEMANLARI I 2. Yarıyıl içi imtihanı 24/04/2012 Müddet: 90 dakika Ögretim Üyesi: Prof.Dr. Hikmet Kocabas, Doç.Dr.
MAK3 MAKİNA EEMANARI I. Yarıyıl içi imtihanı /0/0 Müddet: 90 daia Ögretim Üyesi: Prof.Dr. Himet Kocabas, Doç.Dr. Cemal Bayara. (0 puan) Sıı geçmelerde sürtünme orozyonu nasıl ve neden meydana gelir? Geçmeye
3. BİRLEŞİMLER VE BİRLEŞİM ARAÇLARI
3. BİRLEŞİMLER VE BİRLEŞİM ARAÇLARI Birleşim yapma gereği: elemanların boyunu uzatma, elemanların en kesitini arttırma (birleşik en kesitler), düğüm noktalarının ve mesnetlerin teşkili,... Birleşimlerin
2009 Kasım. BANTLI FRENLER. 40-4d. M. Güven KUTAY. 40-4d-bantli-frenler.doc
009 Kasım BANTI RENER 40-4d M. Güven KUTAY 40-4d-bantli-frenler.doc İ Ç İ N D E K İ E R 4 renler... 4.3 4. ntlı frenlerler... 4.3 4..1 ntlı basit frenler... 4.3 4.. Çıkarmalı frenler... 4.6 4..3 Toplamalı
Makine Elemanları I. Perçin bağlantıları. Prof. Dr. İrfan KAYMAZ. Erzurum Teknik Üniversitesi. Mühendislik Fakültesi Makine Mühendisliği Bölümü
Makine Elemanları I Prof. Dr. İrfan KAYMAZ Mühendislik Fakültesi Makine Mühendisliği Bölümü İÇERİK Giriş Perçin Çeşitleri Perçinleme işlemi Perçin bağlantı şekilleri Mukavemet hesapları Örnekler Giriş
SÜRTÜNME ETKİLİ (KAYMA KONTROLLÜ) BİRLEŞİMLER:
SÜRTÜME ETKİLİ (KYM KOTROLLÜ) BİRLEŞİMLER: Birleşen parçaların temas yüzeyleri arasında kaymayı önlemek amacıyla bulonlara sıkma işlemi (öngerme) uygulanarak sürtünme kuvveti ile de yük aktarımı sağlanır.
MUKAVEMET I ÇÖZÜMLÜ ÖRNEKLER
MUKAEMET I ÇÖZÜMÜ ÖRNEKER ders notu Yard. Doç. Dr. Erdem DAMCI Şubat 15 Mukavemet I - Çözümlü Örnekler / 7 Örnek 1. Üzerinde yalnızca yayılı yük bulunan ve açıklığı olan bir basit kirişe ait eğilme momenti
YTÜ İnşaat Fakültesi Geoteknik Anabilim Dalı. Ders 5: İÇTEN DESTEKLİ KAZILAR. Prof.Dr. Mehmet BERİLGEN
YTÜ İnşaat Fakültesi Geoteknik Anabilim Dalı Ders 5: İÇTEN DESTEKLİ KAZILAR Prof.Dr. Mehmet BERİLGEN İçten Destekli Kazılar İçerik: Giriş Uygulamalar Tipler Basınç diagramları Tasarım Toprak Basıncı Diagramı
MEKANİK LABORATUARI-1
MEKANİK LABORATUARI-1 Deney Sorumlusu ve Uyg. Öğr. El. Doç. Dr. Mete Onur KAMAN Yrd. Doç. Dr. Mustafa GÜR Yrd. Doç. Dr. Murat Yavuz SOLMAZ Arş. Gör. Serkan ERDEM Arş. Gör. Yunus Onur YILDIZ 1 Laboratuar-I
MUKAVEMET-2 DERSİ BAUN MAKİNA MÜHENDİSLİĞİ VİZE ÖNCESİ UYGULAMA SORULARI MART Burulma 2.Kırılma ve Akma Kriterleri
MUKAVEMET-2 DERSİ BAUN MAKİNA MÜHENDİSLİĞİ VİZE ÖNCESİ UYGULAMA SORULARI MART-2019 1.Burulma 2.Kırılma ve Akma Kriterleri UYGULAMA-1 Şekildeki şaft C noktasında ankastre olarak sabitlenmiş ve üzerine tork
BURULMA (TORSİON) Dairesel Kesitli Çubukların (Millerin) Burulması MUKAVEMET - Ders Notları - Prof.Dr. Mehmet Zor
3 BURULMA (TORSİON) Dairesel Kesitli Çubukların (Millerin) Burulması 1.1.018 MUKAVEMET - Ders Notları - Prof.Dr. Mehmet Zor 1 3. Burulma Genel Bilgiler Burulma (Torsion): Dairesel Kesitli Millerde Gerilme
METİN SORULARI. Hareket Cıvataları. Pim ve Perno Bağlantıları
Hareket Cıvataları METİN SORULARI. Hareket cıvatalarını bağlama cıvataları ile karşılaştırınız ve özelliklerini anlatınız. 2. Hareket vidalarının verimi hangi esaslara göre belirlenir? Açıklayınız ve gereken
GEMİ VE AÇIKDENİZ YAPILARI ELEMANLARI Hafta 3
GEMİ VE AÇIKDENİZ YAPILARI ELEMANLARI Hafta 3 Doç. Dr. Barbaros Okan Temel kavramlar Sefer tipleri Sınırsız sefer (Bütün dünya) Yakın sefer (Kıta Avrupası) Kıyı Seferleri (Karadeniz) K50 (kıyıdan 50 milden
Problemler çeşitli kaynaklardaki çözümlü ve çözümsüz problemlerden derlenmiştir ve adapte edilerek çözülmüştür.
PERÇİN BAĞLANTILARI Ekseel Yüklü Perçiler Perçi kesilmesi z( d Delik ezilmesi p zsd p Levha mukaveti c ( b id) s Levha yırtılması z( e d / ) s Eksatrik Yüklü Perçiler Kesme kuvveti K z Eğilme mometide
B-B AKSI KİRİŞLERİ BETONARME HESAPLARI
B-B AKSI KİRİŞLERİ BETONARE HESAPLARI B-B AKSI KİRİŞLERİ ELVERİŞSİZ OENT DİYAGRALARI 1.. ve 3.Grup yüklemeler için hesap momentleri olarak kolon yüzündeki (x=0) düzeltilmiş moment değerleri esas alınacaktır.
Makine Elemanları I. Bağlama Elemanları. Prof. Dr. İrfan KAYMAZ. Erzurum Teknik Üniversitesi. Mühendislik Fakültesi Makine Mühendisliği Bölümü
Bağlama Elemanları Makine Elemanları I Prof. Dr. İrfan KAYMAZ Mühendislik Fakültesi Makine Mühendisliği Bölümü İçerik Bağlama Elemanlarının Sınıflandırılması Şekil Bağlı bağlama elemanlarının hesabı Kuvvet
Makina Elemanları I (G3) Ödev 1:
Makina Elemanları I (G3) Ödev 1: 1. Şekilde verilen dönen aks aynı düzlemde bulunan F 1 ve F 2 kuvvetleri ile yüklenmiştir. Değişken eğilme zorlanması etkisindeki aks Fe50 malzemeden yapılmıştır. Yatakların
METALİK MALZEMELERİN ÇEKME DENEYİ
METALİK MALZEMELERİN ÇEKME DENEYİ Çekme deneyi, malzemelerin statik yük altında elastik ve plastik davranışını belirlemek amacıyla uygulanır. Çekme deneyi, asıl malzemeyi temsil etmesi için hazırlanan
Mukavemet 1. Fatih ALİBEYOĞLU. -Çalışma Soruları-
1 Mukavemet 1 Fatih ALİBEYOĞLU -Çalışma Soruları- Soru 1 AB ve BC silindirik çubukları şekilde gösterildiği gibi, B de kaynak edilmiş ve yüklenmiştir. P kuvvetinin büyüklüğünü, AB çubuğundaki çekme gerilmesiyle
Cıvata-somun bağlantıları
Cıvata-somun bağlantıları 11/30/2014 İçerik Vida geometrik büyüklükleri Standart vidalar Vida boyutları Cıvata-somun bağlantı şekilleri Cıvata-somun imalatı Cıvata-somun hesabı Cıvataların mukavemet hesabı
MAKİNE ELEMANLARI DERS SLAYTLARI
MAKİNE ELEMANLARI DERS SLAYTLARI AKSLAR VE MİLLER P r o f. D r. İ r f a n K A Y M A Z P r o f. D r. A k g ü n A L S A R A N A r ş. G ör. İ l y a s H A C I S A L İ HOĞ LU Dönen parça veya elemanlar taşıyan
Çelik Yapılar - INS /2016
Çelik Yapılar - INS4033 2015/2016 DERS IV Dayanım Limit Durumu Enkesitlerin Dayanımı Fatih SÖYLEMEZ Yük. İnş. Müh. İçerik Dayanım Limit Durumu Enkesitlerin Dayanımı Çekme Basınç Eğilme Momenti Kesme Burulma
MİLLER ve AKSLAR SAKARYA ÜNİVERSİTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAKİNE ELEMANLARI-I DERS NOTU
MİLLER ve AKSLAR MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAKİNE ELEMANLARI-I DERS NOTU Miller ve Akslar 2 / 40 AKS: Şekil olarak mile benzeyen, ancak döndürme momenti iletmediği için burulmaya zorlanmayan, sadece eğilme
Mukavemet Hesabı . 4. d 4. C) Vidanın zorlanması. A) Öngerilmesiz cıvatalar. B) Öngerilme ile bağlanan cıvatalar. d 4
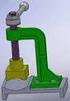ç A) Öngerilmeiz cıvatalar iş. d ç.d ön Boyutlandırma için ç Statik zorlanmada To. d i) Sıkma ıraında ; M 3.d ; B 6 c b ön : ç. d Mukavemet Heabı B) Öngerilme ile bağlanan cıvatalar a) Dış kuvvet ekenel
Vidalı Bağlantılarğ (Cıvatalar) Vedat Temiz
Vidalı Bağlantılarğ (Cıvatalar) Vedat Temiz Genel Bilgiler En yaygın kullanılan çözülebilen bağlama elemanıdır. Prensip olarak bir silindir üzerine bir profilin eşit hatveli olarak khli helisel l şekilde
MUKAVEMET(8. Hafta) MALZEMENİN MEKANİK ÖZELLİKLERİ ÇEKME DENEYİ
MALZEMENİN MEKANİK ÖZELLİKLERİ ÇEKME DENEYİ MUKAVEMET(8. Hafta) Malzemenin mekanik özelliklerini ortaya çıkarmak için en yaygın kullanılan deney Çekme Deneyidir. Bu deneyden elde edilen sonuçlar mühendislik
ÇELİK YAPILAR 2. Hafta. Onur ONAT Munzur Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü, Tunceli
ÇELİK YAPILAR 2. Hafta Onur ONAT Munzur Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü, Tunceli 1 Haddelenmiş Çelik Ürünleri Nelerdir? Haddelemeyi tekrar hatırlayacak olursak; Haddeleme
ÖNSÖZ. Kitabın kapak tasarımında katkılarından dolayı A-Ztech Ltd. den Sn Ali ÖGE ye teşekkür ederim.
ÖNSÖZ Katıların mekaniği kendi içinde Katı Cisimlerin Mekaniği (veya kısaca Mekanik) ve Şekil Değiştiren Cisimlerin Mekaniği (veya kısaca Mukavemet) olmak üzere iki alt gruba ayrılmıştır. Bunlardan mekaniğin
KİRİŞLERDE VE İNCE CİDARLI ELEMANLARDA KAYMA GERİLMELERİ
KİRİŞLERDE VE İNCE CİDARLI ELEMANLARDA KAYMA GERİLMELERİ x Göz önüne alınan bir kesitteki Normal ve Kayma gerilmelerinin dağılımı statik denge denklemlerini sağlamalıdır: F F F x y z = = = σ da = 0 x τ
YAPI MALZEMELERİ DERS NOTLARI
YAPI MALZEMELERİ DERS NOTLARI YAPI MALZEMELERİ Herhangi bir yapının projelendirmesi ve inşaatı aşamasında amaç aşağıda belirtilen üç koşulu bir arada gerçekleştirmektir: a) Yapı istenilen işlevi yapabilmelidir,
Çelik yapılarda birleşim araçları şu sebeplerle kullanılır:
BÖLÜ II. Çelik Birleşim Gereçleri Çelik yapılar, profillerin ve levhaların birleştirme elanları ile birleştirilmesi sonucunda elde edilir. Birleştirilen elanların zarar vermeden sökülüp, söküle durumuna
PLASTİK ŞEKİL VERMEDE METALURJİK ESASLAR
PLASTİK ŞEKİL VERMEDE METALURJİK ESASLAR METALLERİN KRİSTAL YAPISI Metallerde en sık rastlanan üç çeşit kristal kafes yapısı : Kayma Düzlemleri Metaller, ya kocaman tek kristalden ya da çok taneli çok
MAKİNE ELEMANLARI DERS SLAYTLARI
MAKİNE ELEMANLARI DERS SLAYTLARI YORULMA P r o f. D r. İ r f a n K A Y M A Z P r o f. D r. A k g ü n A L S A R A N A r ş. G ör. İ l y a s H A C I S A L İ HOĞ LU Aloha Havayolları Uçuş 243: Hilo dan Honolulu
DİŞLİ ÇARKLAR II: HESAPLAMA
DİŞLİ ÇARLAR II: HESAPLAMA Prof. Dr. İrfan AYMAZ Atatürk Üniversitesi Mühendislik Fakültesi Makine Mühendisliği Bölümü Giriş Bu bölüm sonunda öğreneceğiniz konular: Dişli Çark uvvetleri Diş Dibi Gerilmeleri