ACİL SAĞLIK HİZMETLERİ
|
|
|
- Serhat Taşkıran
- 8 yıl önce
- İzleme sayısı:
Transkript
1 T.C. MİLLÎ EĞİTİM BAKANLIĞI ACİL SAĞLIK HİZMETLERİ İSTATİSTİKSEL İŞLEMLER II 462I00008 Ankara, 2011
2 Bu modül, mesleki ve teknik eğitim okul/kurumlarında uygulanan Çerçeve Öğretim Programlarında yer alan yeterlikleri kazandırmaya yönelik olarak öğrencilere rehberlik etmek amacıyla hazırlanmış bireysel öğrenme materyalidir. Millî Eğitim Bakanlığınca ücretsiz olarak verilmiştir. PARA İLE SATILMAZ.
3 İÇİNDEKİLER AÇIKLAMALAR... iii GİRİŞ... 1 ÖĞRENME FAALİYETİ MERKEZî EĞİLİM ÖLÇÜLERİ (ORTALAMALAR) Aritmetik Ortalama (Mean) Sınıflandırılmamış Verilerde Aritmetik Ortalamanın Hesaplanması Sınıflandırılmış Verilerde Aritmetik Ortalamanın Hesaplanması Aritmetik Ortalamanın Özellikleri Ortanca (Medyan) Sınıflandırılmamış Verilerde Ortancanın Hesaplanması Sınıflandırılmış Verilerde Ortancanın Hesaplanması Ortancanın Özellikleri Tepe Değer (Mod) Sınıflandırılmamış Verilerde Tepe Değerinin Hesaplanması Sınıflandırılmış Verilerde Tepe Değerinin Hesaplanması Tepe Değerinin Özellikleri Aritmetik Ortalama, Ortanca ve Tepe Değeri İlişkileri UYGULAMA FAALİYETİ ÖLÇME VE DEĞERLENDİRME ÖĞRENME FAALİYETİ DAĞILIM (Yayılma) ÖLÇÜLERİ Yayılma (Dağılım) Genişliği Standart Sapma Sınıflandırılmamış Verilerde Standart Sapma Sınıflandırılmış Verilerde Standart Sapma Varyasyon Katsayısı (Değişim Katsayısı) Çeyrek Sapma Sınıflandırılmamış Verilerde Çeyrek Sapma Sınıflandırılmış Verilerde Çeyrek Sapma Standart Hata UYGULAMA FAALİYETİ ÖLÇME VE DEĞERLENDİRME ÖĞRENME FAALİYETİ TOPLUMUN NÜFUS YAPISI VE ÖZELLİKLERİ Nüfusun Büyüklüğünü ve Yapısını Etkileyen Faktörler Doğumlar Ölümler Göçler Nüfus Veri Kaynakları Nüfus Sayımları Nüfus Araştırmaları Nüfusa İlişkin Kayıtlar Nüfusun Değerlendirilmesi Nüfusla İlgili Hız ve Oranlar Nüfus Piramitleri i
4 Nüfus Piramidinin Çizimi Nüfus Piramitlerinin Yorumlanması UYGULAMA FAALİYETİ ÖLÇME VE DEĞERLENDİRME ÖĞRENME FAALİYETİ SAĞLIK HİZMETLERİNDE KULLANILAN HIZ VE ORANLAR Hız ve Oran Doğumlarla (Fertilite) İlgili Hızlar Ölümlerle (Mortalite) İlgili Hızlar Hastalıklarla (Morbidite) İlgili Hızlar UYGULAMA FAALİYETİ ÖLÇME VE DEĞERLENDİRME MODÜL DEĞERLENDİRME CEVAP ANAHTARLARI KAYNAKÇA ii
5 AÇIKLAMALAR KOD ALAN DAL/MESLEK AÇIKLAMALAR 462I00008 Acil Sağlık Hizmetleri Acil Tıp Teknisyenliği MODÜLÜN ADI MODÜLÜN TANIMI SÜRE 40/16 ÖNKOŞUL İstatistiksel İşlemler II Verilerin merkezî eğilim ve dağılım ölçülerinin hesaplanması, nüfusun yapı ve özelliklerinin ayırt edilmesi ve sağlık hizmetlerinde kullanılan hız ve oranların hesaplanması ile ilgili bilgi ve becerilerin kazandırıldığı öğrenme materyalidir. YETERLİK MODÜLÜN AMACI EĞİTİM ÖĞRETİM ORTAMLARI VE DONANIMLARI ÖLÇME VE DEĞERLENDİRME İstatistiksel işlemleri yapmak Genel Amaç Verilerin merkezî eğilim ölçülerini, dağılım ölçülerini sağlık hizmetlerinde kullanılan hız ve oranları hesaplayabilecek ve toplumun nüfus yapısı ve özelliklerini ayırt edebileceksiniz. Amaçlar 1. Verilerin merkezî eğilim ölçülerini tam ve doğru olarak hesaplayabileceksiniz. 2. Verilerin dağılım ölçülerini tam ve doğru olarak hesaplayabileceksiniz. 3. Toplumun nüfus yapısı ve özelliklerini ayırt edebileceksiniz. 4. Sağlık hizmetlerinde kullanılan hız ve oranları doğru olarak hesaplayabileceksiniz. Donanım: Tahta, kalem, silgi, formlar, bilgisayar, tepegöz, projeksiyon, DVD, VCD vb. Ortam: Sınıf ve bilgisayar laboratuvarı Modül içinde yer alan her öğrenme faaliyetinden sonra verilen ölçme araçları ile kendinizi değerlendireceksiniz. Öğretmen modül sonunda ölçme aracı (çoktan seçmeli test, doğru-yanlış testi, boşluk doldurma, eşleştirme vb.) kullanarak modül uygulamaları ile kazandığınız bilgi ve becerileri ölçerek sizi değerlendirecektir. iii
6 iv
7 GİRİŞ GİRİŞ Sevgili Öğrenci, İstatistik amaçlı toplanan verilerin sıraya konulması, frekans tablosunun düzenlenmesi gibi işlemler veriler hakkında çok genel bilgiler vermektedir. Lord Kelvin Gözlemlerinizi ölçemiyor ve sayılarla anlatamıyorsanız bilginiz değersizdir. demiştir. Gözlenen verinin düzenlenerek tablolarla, grafiklerle sunulması çoğu kez yeterli olmayabilir. Verilerin bütününe ait bilgilere ulaşmak için yer gösteren, merkezî eğilim/ortalamalar ve dağılım (yaygınlık) ölçütleri kullanılır. Demografi bilimi sayesinde toplumun nüfus yapısı ve özellikleri hakkında detaylı bilgilere ulaşırız. Nüfusun yapısı ve özellikleri hakkında elde edilen bilgiler, sağlık hizmetlerinin planlanması ve uygulanması aşamalarında en çok başvurulan kaynaklardır. Toplumun sağlık düzeyini objektif olarak ve sayısal değerler hâlinde belirlemek için geliştirilen sağlık durum göstergeleri kullanılır. Bu göstergelerle ülke veya bölgesel toplumlardaki doğum, ölüm ve hastalıklar hakkında bilgiler elde edilir. Bu modül ile kazanacağınız bilgi ve becerileri öğrenim hayatınızda ve çalışma hayatınızda her zaman kullanabileceksiniz. 1
8 2
9 ÖĞRENME FAALİYETİ 1 ÖĞRENME FAALİYETİ 1 AMAÇ Verilerin merkezî eğilim ölçülerini tam ve doğru olarak hesaplayabileceksiniz. ARAŞTIRMA Merkezî eğilim ölçülerinin niçin hesaplandığını araştırınız. Elde ettiğiniz bilgileri sınıf ortamında arkadaşlarınızla paylaşınız. Sınıflandırılmamış ve sınıflandırılmış verilerde ortalamaların nasıl hesaplandığını araştırınız. 1. MERKEZÎ EĞİLİM ÖLÇÜLERİ (ORTALAMALAR) Düzenlenmiş verilerin yorumlanması ve daha ileri düzeydeki işlemler için verilerin bütününe ait tanımlayıcı ve özetleyici ölçülere ihtiyaç vardır. Bu ölçüler, verileri yalnızca özlü bir biçimde belirtmekle kalmaz karşılaştırmalara, genellemelere, yorumlamalara olanak sağlar. Ölçüler incelenirken her ölçünün anlamı, hangi koşullarda kullanılabileceği ve hesaplama işlemleri açıklanmalıdır. Araştırmalarda denekler değişik değerler alır. Deneklerin kimi küçük, kimi orta kimi ise yüksek değerler (birimler) alacaktır. Bu değerlerin teker teker incelenmesi ya da en büyük ve en küçük değerleri belirtmek bir anlam taşımaz. Örneğin, öğrencilerin istatistik dersi sınavında aldıkları puanların arasında değiştiğini söylemek anlamlı değildir. Öğrencilerin çoğu 95 civarında puan almış bir veya iki tanesi 45 puan almış olabilir ya da çoğunluğu 45 civarında iken bir veya iki tanesi 95 puan almış olabilir. Dağılımın tümünü temsil edecek bir ölçüye gereksinim vardır. Verilerin bütününe ait özellikleri ortaya koymada merkezî eğilim (ortalamalar) ölçülerinden yararlanılmaktadır. Bu amaçla kullanılan en uygun ölçü ortalamadır. Ortalama; dağılım orta noktasını gösteren ve incelenen bireylerin değerlerinin tek değerle temsil edilmesini sağlayan ölçüdür. Sağlık bilimlerinde en çok kullanılan merkezî eğilim ölçüleri şunlardır: Aritmetik ortalama (Mean) Ortanca (Medyan) Tepe değer (Mod) 3
10 1.1. Aritmetik Ortalama (Mean) Şema 1.1: Merkezî eğilim ölçüleri Aritmetik ortalama; incelenen deneklerin aldığı değerler toplamının birim sayısına bölünmesiyle elde edilen matematiksel gerçek bir değerdir. Aritmetik ortalama; örnek için hesaplandığında, evren (yığın) için hesaplandığında µ (mü) simgeleri kullanılır. Aritmetik ortalama sınıflandırılmamış ve sınıflandırılmış verilerde farklı yollarla hesaplanır Sınıflandırılmamış Verilerde Aritmetik Ortalamanın Hesaplanması Sınıflandırılmamış verilerde aritmetik ortalama, bütün deneklerin değerlerinin toplanıp denek sayısına bölünmesiyle elde edilir. Formülde: : Aritmetik ortalama formülü ile hesaplanır. : Her bir deneğin aldığı değer n: Denek sayısı 4
11 Örnek: A okulundaki 10 öğrencinin diploma notları; dır. Bu puanların aritmetik ortalaması kaçtır? Sınıflandırılmış Verilerde Aritmetik Ortalamanın Hesaplanması Veri sayısı çok olan araştırmalarda veya çalışmalarda aritmetik ortalamayı sınıflandırmadan hesaplamak, zor ve yorucudur. Ayrıca zaman alıcı ve hata yapma olasılığı fazladır. Sınıflandırılmış verilerde aritmetik ortalama şu şekilde hesaplanır: Sınıflar yazılır. Sınıf değeri (SD) bulunur ve sınıfın karşısına yazılır. SD, sınıfın ortalamasıdır. Her sınıfın alt ve üst sınırları toplanarak ikiye bölünür. Çıkan sonuç SD yi oluşturur. Aşağıda verilen örnek problemde ilk sınıfın sınıf değeri (SD) = (25+29)/2 = 27 dir. Her sınıfın frekansı karşısına yazılır. Frekans toplamı alınarak alt bölüme yazılır. Çalışma birimi olarak adlandırılan b kolonu oluşturulur. Herhangi bir sınıfın (genellikle frekansı en büyük sınıfın karşısına) 0 değeri yazılır. Üste doğru eksi (-) olarak 1 den başlanarak ve birer artırılarak alta doğru artı (+) olarak 1 den başlanarak ve birer artırılarak çalışma birimleri yazılır (Örnek problemde olduğu gibi). Frekansla çalışma biriminin çarpımları alınarak ve sınıfların karşısına yazılarak fb kolonu oluşturulur. Rakamların önündeki eksi ve artı işaretlerine dikkat ederek toplanır. Toplam fb (Σfb) bulunur, eksi veya artı olarak yazılır. Değerler, formüle yerleştirilir ve aritmetik ortalama bulunur. 5
12 Sınıflandırılmış verilerde aritmetik ortalama; Formülde: : Aritmetik ortalama formülü ile hesaplanır. A: b kolonunda karşısına sıfır konulan sınıfın sınıf değeri (Genellikle frekansı yüksek olan sınıfın karşısına yazılır.) C: Sınıf aralığı Σfb: Frekansla çalışma biriminin çarpımlarının toplamı n: Denek sayısı Örnek: Sağlık meslek lisesindeki öğretmenlerin yaş dağılımı verilmiştir. Aşağıdaki dağılımın aritmetik ortalaması nedir? A = 42 C = 5 n = 56 Σfb = -42 Değerler formülde yerine yerleştirilir. Tablo 1.1: Öğretmenlerin yaş dağılımı 6
13 Aritmetik Ortalamanın Özellikleri En kolay hesaplanan ve en çok kullanılan ortalamadır. Ne tür olduğu belirtilmeden bir ortalamadan bahsediliyorsa muhtemelen kastedilen aritmetik ortalamadır. Ancak bazı dağılımlara aritmetik ortalama uygun olmayabilir. Aritmetik ortalamanın özellikleri: Hesaplaması basit ve anlaşılması kolaydır. Her dağılımda bir tane aritmetik ortalama vardır. Aritmetik işlemler için elverişlidir. Verilerin bütünü işleme katılır. Hassas bir ortalamadır, değerlerdeki küçük bir değişim ortalamayı önemli ölçüde etkiler. Aritmetik ortalama ile birim değerleri arasındaki farkları toplamı sıfırdır. Diğer ortalamalara göre daha güvenilirdir. Standart sapma, korelasyon katsayısı gibi istatistiksel hesaplamalar aritmetik ortalamaya bağlıdır ve beraber yorumlanır. Dağılımdaki aşırı değerlerden etkilenir. Dağılımdaki aşırı değerler aritmetik ortalamayı kendilerine doğru kaydırır. Bu etkileme aşırı değerlerin aşırılık ölçüsüyle doğru dağılımdaki veri sayısı ile ters orantılıdır. Ters yöndeki aşırı değerler birbirlerinin etkisini azaltır. Dağılımda aşırı değerler varsa; Aşırı değerler değerlendirmeden çıkarılabilir. Aşırı değerler yerine yakın değer atanabilir. Bunlar yapılamıyorsa aritmetik ortalama yerine başka bir ortalama ölçüsü kullanılabilir. Bu durumda sıklıkla ortanca tercih edilir. Aşırı değerler katılarak aritmetik ortalama hesaplanırsa sonuç gerçeği yansıtmayabilir ve yanlış yorumlamaya neden olabilir. Aşağıdaki örnekte bu durum gösterilmiştir. 7
14 A serisindeki aritmetik ortalama 28, B serisindeki ortalama 39 dur. A serisindeki değerler incelendiğinde değerlerin ortalamaya yakın olduğu görülür. B serisinde ise aşırı değer (87) ortalamayı olumsuz etkileyerek gerçek değer bulunamamış ve yanlış sonuca ulaşılmıştır Ortanca (Medyan) Büyüklük sırasına konulmuş bir veri grubunda ortadaki değere ortanca (medyan) denir. Araştırmalarda yığındaki verilerin sayısı çok olduğu durumlarda verilerin özetlenmesi için merkezî eğilim ölçüsü olarak medyan kullanılabilir. Ortanca, bütün birimlere değil sadece tam ortaya düşen birim ya da birim değerlerine bağlıdır. Dağılımı iki eşit parçaya böler. Dağılımdaki değerlerin % 50 si ortancadan küçük, % 50 si ise ortancadan büyüktür. Ortanca sınıflandırılmış ve sınıflandırılmamış verilerde farklı şekillerde hesaplanır Sınıflandırılmamış Verilerde Ortancanın Hesaplanması Basit dağılımdaki değerlerin medyanını bulabilmek için değerler ya büyükten küçüğe ya da küçükten büyüğe doğru sıralanır ve tam ortaya düşen değer bulunur. Bulunan değer ilgili dağılımın (serinin) medyanıdır. Medyan, denek sayısının tek veya çift olmasına göre hesaplanır. Denek sayısı tek ise: formülü ile hesaplanır. Formülde: n: denek sayısını ifade etmektedir. Örnek: Ana sınıfındaki 9 çocuğun boy uzunlukları ölçülerek aşağıdaki sonuçlar elde edilmiştir: 1,23-1,16-1,25-1,18-1,20-1,14-1,20-1,19; 1,15 serisinin medyan boy uzunluğunu bulunuz. Serideki boy uzunlukları küçükten büyüğe doğru sıralanır tan ca n Or sıradaki değer. Yani; Ortanca = X5 = 1,19 dur. 8
15 Denek sayısı çift ise: Dağılımdaki denek sayısı, çift olduğu zaman medyan arada kalır. Arasında kaldığı değerlerin aritmetik ortalaması medyanı verir. X ( n / 2) X ( n 2) / 2 Or tan ca formülü ile hesaplanır. 2 Örnek: 12 öğrencinin matematik I dersi sınavından aldıkları puanlar aşağıda verilmiştir: , serisinin medyanını bulunuz. Serideki puanlar büyükten küçüğe doğru sıralanır. X6 = Altıncı sıradaki değer X7 = Yedinci sıradaki değer Sınıflandırılmış Verilerde Ortancanın Hesaplanması Sınıflandırılmış verilerde ortanca birikimli frekanslar yardımıyla hesaplanır. Ancak bu tür serilerde tam ortadaki terim bir sınıf içinde yer alır. Ortanca değerini içinde bulunduran sınıfa ortanca sınıfı denir. Sınıflandırılmış verilerde ortanca hesaplamasında sırasıyla şu işlemler yapılır. Sınıflar yazılır. Her sınıfın frekansı yazılır. Yığılımlı (birikimli) frekans bulunur. Yığılımlı frekans, her frekansın önceki frekanslarla toplamıdır. Bu toplam her sınıfın karşısına yazılır. 9
16 Sınıflandırılmış verilerde ortanca formülü: Formülde: L: Ortancanın içinde bulunduğu sınıfın ara değeri (SAD) dir. Sınıf ara değeri, bir üst sınıfın üst sınırı ile bir alttaki sınıfın (ortanca sınıfının) alt sınırının ortalamasıdır. Örnek: serisinde SAD i bulunuz. Birinci sınıfın üst sınırı (19) ile ikinci sınıfın alt sınırı (20) toplanır ve ikiye bölünür. Yfi: Ortancanın içinde bulunduğu sınıfın bir üstündeki sınıfın yığımlı (birikimli) frekansı. f: Ortancanın içinde bulunduğu sınıfın frekansı C: Sınıf aralığı n: Denek sayısı Örnek: 100 hastanın açlık kan şekeri ölçümüne ait dağılım aşağıda verilmiştir. Dağılımın ortancasını hesaplayınız. Tablo 1.2: 100 hastanın açlık kan şeker oranı 10
17 Önce ortancanın hangi sınıfın içinde olduğu bulunur. Ortancanın içinde bulunduğu sınıfı belirlemek için: n/2=100/2=50 50 yığılımlı frekans kolonunda 63 ün içinde olduğundan ortancanın içinde bulunduğu sınıf sınıfıdır. Buna göre; L= /2=119.5(SAD) n/2=50 Yfi=40 C = 20 f = 23 Değerler formülde yerine yerleştirilir Ortancanın Özellikleri Çok küçük ve çok büyük değerlerden etkilenmez. Açık uçlu dağılımlar içinde hesaplanabilir Tepe Değer (Mod) Bir veri dağılımında en çok tekrarlanan değere tepe değer (mod) denir Sınıflandırılmamış Verilerde Tepe Değerinin Hesaplanması Sınıflandırılmamış verilerde tepe değeri dağılımda en çok görülen (en çok tekrarlayan) değerdir. 11
18 Örnek: 20 hastanın hastanede yatış süreleri aşağıda verilmiştir. Dağılımın tepe değerini bulunuz Tepe değeri kolayca saptamak için veriler küçüklük/büyüklük durumuna göre sıralanır Yukarıdaki dağılımın tepe değeri en çok görülen değer olan 8 dir. Tepe değer (Mod)= 8 dir. Bir seride tek bir mod varsa tek modlu seriler, birden fazla aynı sayıda tekrarlanan değer varsa bu serilere çok modlu seriler denir. Örnek: Yukarıdaki seride 3 değer (4, 8 ve 12) tepe değeri olabilecek durumdadır. Birbirinden farklı bu 3 değeri tepe değeri olarak kullanmak anlamlı olmaz. Bu nedenle tepe değeri böyle serilerde kullanılmaz Sınıflandırılmış Verilerde Tepe Değerinin Hesaplanması Sınıflandırılmış verilerde tepe değeri en fazla frekansa sahip olan sınıfın sınıf değeridir. Sınıflandırılmış verilerde tepe değeri hesaplanırken sırasıyla şu işlemler yapılır. Sınıflar yazılır. Her sınıfın frekansı yazılır. Mod sınıfı belirlenir. Sınıflandırılmış verilerde tepe değer formülü; Formülde: TD: Tepe Değeri L: Frekansı en fazla olan sınıfın alt sınır değeri d 1 : Tepe sınıfı ile bir önceki sınıfın frekansları farkları d 2 : Tepe sınıfı ile bir sonraki sınıfın frekansları farkları C: Sınıf aralığı 12
19 Örnek: 60 hastanın kanında bulunan kolesterol düzeylerine göre dağılımı aşağıda verilmiştir. Dağılımın tepe değerini hesaplayınız. Tablo 1.3: 60 hastanın kan kolesterol düzeyi Önce frekansı en fazla sınıf bulunur. En fazla frekansa sahip olan sınıf 3 numaralı sınıf tepe değer (mod) sınıfıdır. L = 190 d1 = = 2 d2 = 15-9 = 6 C = = 19 Değerler formülde yerine yerleştirilir Tepe Değerinin Özellikleri Tepe değer uç noktalardan etkilenmez. Bu özelliği bakımında ortancaya benzer. Hesaplanması ve anlaşılması kolaydır. Bazı dağılışlarda tepe değeri bulunmayabilir, bazılarında da birden fazla tepe değeri bulunabilir. İki tepe değeri bulunan dağılışlara bimodal dağılış adı verilir. Tepe değeri aritmetik işlemler için elverişli değildir. 13
20 1.4. Aritmetik Ortalama, Ortanca ve Tepe Değeri İlişkileri Eşit (simetrik) dağılımlarda aritmetik ortalama, ortanca ve tepe değeri birbirine eşittir. Aritmetik Ortalama=Ortanca=Tepe Değeri Örnek: 40 kız öğrencinin boy uzunlukları aşağıda verilmiştir. Tablo 1.4: Kız öğrencilerin boy uzunluğu Bu dağılımın aritmetik ortalama, ortanca ve tepe değerini hesapladığımızda üçünün de sonucu 157 dir. Dağılımın değerleri grafik üzerine işaretlenirse dağılımın ortalamaya göre simetrik olduğu görülür. Grafik 1.1: Simetrik dağılım 14
21 Aritmetik ortalama, ortanca ve tepe değeri arasında tepe değeri< ortanca< aritmetik ortalama ilişkisi varsa dağılım sağa çarpıktır. Sağa çarpık dağılımlarda küçük değerlerde yığılma vardır. Grafik 1.2: Sağa çarpık dağılım Aritmetik ortalama, ortanca ve tepe değeri arasında aritmetik ortalama<ortanca<tepe değeri ilişkisi varsa dağılım sola çarpıktır. Sola çarpık dağılımlarda büyük değerlerde yığılma vardır. Grafik 1.3: Sola çarpık dağılım 15
22 UYGULAMA FAALİYETİ UYGULAMA FAALİYETİ Verilerin merkezî eğilim ölçülerini tam ve doğru olarak hesaplayınız. İşlem Basamakları sersinin aritmetik ortalamasını hesaplayınız. Sınıfınızdaki öğrencilerin boy uzunluklarını sınıflandırarak aritmetik ortalamasını hesaplayınız serisinin ortancasını hesaplayınız. Sınıfınızdaki arkadaşlarınızın Temel Sağlık Uygulamaları dersinden aldığı notları sınıflandırarak ortancasını hesaplayınız. Sınıfınızda 10 arkadaşınızın ağırlıklarının tepe değerini hesaplayınız. Öneriler Sınıflandırılmamış verilerde aritmetik ortalama, deneklerin aldığı değerler toplanıp denek sayısına bölünmesi ile elde edildiğini unutmayınız. Verileri sınıflandırırken sınıflandırma kurallarına uyunuz. Sınıflandırılmış verilerde aritmetik ortalamayı hesaplarken tablonuzu formülde yerine koyacağınız değerlere göre geliştirmeyi unutmayınız. Ortancanın veri sayısının tek veya çift olmasında nasıl hesaplandığını hatırlayınız. Sınıflanmış verilerde ortancayı hesaplarken yığılımlı frekans almayı unutmayınız. Ortancanın açık uçlu dağılımlarda da hesaplanabileceğini unutmayınız. Veri dağılımında birden çok tepe değeri bulunabileceğini unutmayınız. Sınıflandırılmış verilerde tepe değeri en fazla frekansa sahip olan sınıfın sınıf değeri olduğunu hatırlayınız. 16
23 ÖLÇME VE DEĞERLENDİRME ÖLÇME VE DEĞERLENDİRME Aşağıdaki soruları dikkatlice okuyarak doğru seçeneği işaretleyiniz. 1. Aşağıdakilerden hangisi aritmetik ortalamayı tanımlar? A) Dağılımın tam orta noktasını gösteren ölçüttür. B) Değerler büyüklük sırasına göre sıralanır, tam ortadaki değer ortalamadır. C) Dağılımın birim değerlerinin toplamının denek sayısına bölümü ortalamayı verir. D) Dağılımda en çok tekrarlayan değer aritmetik ortalamadır. E) Dağılımın frekans toplamı aritmetik ortalamayı verir. 2. Aşağıdakilerden hangisi, aritmetik ortalama için söylenemez? A) En çok kullanılan ölçüdür. B) Aşırı uçlardan etkilenir. C) Hesaplaması basit ve kolay anlaşılır. D) Açık uçlu dağılımlarda da hesaplanır. E) Aritmetik ortalama ile birim değerleri arasındaki farkların toplamı sıfırdır serinin aritmetik ortalaması kaçtır? A) 8,66 B) 8,45 C) 8,7 D) 8,93 E) 8, hastanın hastanede kalış süreleri aşağıda verilmiştir. Bu dağılımın ortancası kaçtır? A) 7 B) 6 C) 8 D) 5 E) 9 5. Aşağıda verilen dağılımın tepe değeri kaçtır? A) 8,82 B) 8,14 C) 8,24 D) 8,33 E) 8,42 DEĞERLENDİRME Cevaplarınızı cevap anahtarıyla karşılaştırınız. Yanlış cevap verdiğiniz ya da cevap verirken tereddüt ettiğiniz sorularla ilgili konuları faaliyete geri dönerek tekrarlayınız. Cevaplarınızın tümü doğru ise bir sonraki öğrenme faaliyetine geçiniz. 17
24 ÖĞRENME FAALİYETİ 2 AMAÇ ÖĞRENME FAALİYETİ 2 Verilerin dağılım ölçülerini doğru ve tam olarak hesaplayabileceksiniz. ARAŞTIRMA Dağılım ölçülerinin hangi durumlarda kullanıldığını araştırınız. Standart sapmanın niçin hesaplandığını araştırınız. Elde ettiğiniz bilgileri sınıfta arkadaşlarınızla paylaşınız. Aritmetik ortalama ile standart sapma ilişkisini araştırınız. Değişim katsayısı hangi durumlarda kullanılır? Araştırınız. 2. DAĞILIM (YAYILMA) ÖLÇÜLERİ Dağılımdaki her bir verinin ilgili değişken bakımından ne ölçüde farklı olduğunu gösteren ya da dağılımdaki her bir verinin ortalama değer etrafındaki dağılım derecesini gösteren ölçülerdir. Bazı dağılımlarda değişkenler bir ortalama değer etrafında diğer dağılımlara göre daha fazla yığılma gösterir. Örnek: Ortalamaları eşit iki serinin dağılımı aşağıda verildiği gibidir: Yukarıda birinci serideki birimler ortalamaya daha yakın konumda yer alırken ikinci serideki birimler ortalamaya daha uzak konumda yer almaktadır. 18
25 Örnekte olduğu gibi sadece bir ortak değer, bir dağılımı temsil etmede yeterli değildir. Bu nedenle dağılımın özelliklerini ortaya koymada ortak değerlerle birlikte değişkenlerin ortalama etrafındaki dağılış oranının belirleyen ölçülere ihtiyaç vardır. Dağılımda yayılma (veriler arasındaki büyüklük farkı) arttıkça ortalamanın temsil yeteneği azalır. Ortalama ile dağılım ölçüleri arasında ters orantı vardır. Örnek: 5 öğrencinin matematik, fizik ve kimya derslerinden aldıkları notlar aşağıdaki gibidir. Örnekte olduğu gibi matematik, fizik ve kimya derslerinden 5 öğrencinin aldığı notların ortalaması 56 olmasına rağmen derslerdeki başarısız öğrenci sayısı farklıdır. Matematik dersinden 1 öğrenci (20), kimya dersinden 2 öğrenci (20, 30) başarısız olurken fizik dersinden başarısız olan öğrenci yoktur. Aritmetik ortalama tek başına bu serileri temsil etmemektedir. Dağılım ölçüleri: Yayılma (dağılım) genişliği Standart sapma Varyasyon katsayısı (Değişim katsayısı) Çeyrek sapma Standart hatadır. Şema 2.1: Dağılım ölçüleri 19
26 2.1. Yayılma (Dağılım) Genişliği Dağılımdaki en büyük değer ile en küçük değer arasındaki farka yayılma genişliği (Range/Açıklık) denir. Dağılım ölçüleri içinde hesaplanması kolay olmakla beraber veri hakkında en kaba bilgi veren ölçüdür ve güvenirliği azdır. Yayılma genişliği R ile gösterilir ve aşağıdaki formülle hesaplanır. R = XMaks XMin XMaks = Veri grubundaki en büyük değer XMin = Veri grubundaki en küçük değer Örnek: 6-12 ay arası 10 bebeğin vücut ağırlıkları aşağıda verilmiştir. Xi (kg) : Verilen serinin yayılma genişliğinin hesaplanması: XMaks = XMin = R = XMaks XMin R = R = dur. Yayılma genişliğinin dağılımın diğer değerleri dikkate alınmadan sadece en büyük ve en küçük değerler arasındaki farka dayanması bilinen önemli sakıncalarındandır. Merkeze yığılma ölçüsü olarak sadece modun kullanılabildiği verilerde dağılım ölçüsü olarak da ranj kullanılır Standart Sapma Standart sapma; dağılımdaki her bir gözlem değerinin aritmetik ortalamaya göre ne kadar uzakta olduğunu gösteren ölçüdür. Dağılımın yaygınlığını gösteren ölçüler içinde en sık kullanılan ve güvenilen ölçüdür. Standart sapma büyüdükçe dağılımın yaygınlığı artar, standart sapma küçüldükçe dağılımın yaygınlığı küçülür. Standart sapma, S, S S, S D, gibi sembollerle gösterilir Sınıflandırılmamış Verilerde Standart Sapma Sırası ile şu işlemler yapılır. Deneklerin (verilerin) aldığı değerler toplanır. Deneklerin aldığı değerlerin tek tek kareleri alınır ve toplanır. Yukarıda elde edilen değerler formülde yerine konularak standart sapma hesaplanır. 20
27 Sınıflandırılmamış verilerde standart sapma formülü: S: Standart sapma : Deneklerin aldıkları değerlerin karelerinin toplamı (2. işlemden elde edilen değer) : Deneklerin aldıkları değerlerin toplamı (1. İşlemden elde edilen değer) n: Denek sayısı Örnek: 10 öğrencinin okula devamsızlık ettikleri gün sayısı aşağıda verilmiştir. Tablo 2.1: Öğrencilerin devamsızlık süreleri Bu serinin standart sapmasının hesaplanması: 21
28 Sınıflandırılmış Verilerde Standart Sapma Sırası ile şu işlemler yapılır. Sınıflar yazılır. Her sınıfın frekansı karşısına yazılır. Çalışma birimi (b) kolonu oluşturulur. fb kolonu oluşturularak toplamı alınır (İlk 3 işlem aritmetik ortalamayı hesaplamak için yapılan işlemlerle aynıdır.). b kolonundaki değerlerin karesi alınır ve her sınıfın karşısına yazılır (b² kolonu oluşur). Her sınıfın frekansı, kendi b² değeri ile çarpılır fb² kolonu olarak yazılır. Bulunan değerler formülde yerine konulur. Sınıflandırılmış verilerde standart sapma formülü: S: Standart sapma C: Sınıf aralığı : fb² kolonundaki değerlerinin toplamı : fb kolonundaki değerlerin toplamının karesi n: Denek (birim) sayısı Örnek: 60 kadın hastanın hemotokrit değerleri aşağıda verildiği gibidir. Tablo 2.2: 60 kadın hastanın hemotokrit değeri 22
29 C=3 ΣFb = -32 ΣFb² =152 n = 60 Değerleri formülde yerine konulur Varyasyon Katsayısı (Değişim Katsayısı) Varyasyon katsayısı (değişim katsayısı) standart sapmanın ortalamaya göre yüzde kaçlık bir değişim gösterdiğini belirtir. Varyans ve standart sapma büyüdükçe dağılım yaygınlaşır, küçüldükçe dağılım daralır. Standart sapma için bulunan değerin büyüklüğü ya da küçüklüğü hakkında karar verebilmek için varyasyon katsayısının hesaplanması gerekir. Varyasyon katsayısı dağılım ölçüleri içinde kullanılması oldukça yaygın olup verilerin homojenlik yapısı hakkında karşılaştırmalı olarak bilgi verir. Varyasyan katsayısı (V K ) aşağıdaki formülle hesaplanır. 23
30 Örnek: Aritmetik ortalaması ve standart sapması 6.23 olan dağılımın varyasyon katsayısı: Bu dağılımdaki değerler ortalamaya göre % 3,23 lük bir değişim göstermektedir Çeyrek Sapma Merkezî eğilim ölçüsü olarak ortalama yerine ortancanın kullanıldığı dağılımlarda dağılım ölçüsü olarak çeyrek sapma kullanılır. Çeyrek sapma standart sapma gibi aşırı uçlardan etkilenmez. Aşırı uç değerlerin çok olduğu çarpık dağılımlarda çeyrek sapma tercih edilen bir dağılım ölçüsüdür. Çeyrek sapma Q sembolü ile gösterilir. Çeyrek sapma üçüncü yüzdelik (Q3) ile birinci yüzdelik (Q1 ) arasındaki farkın yarısına eşittir. Q1 birinci çeyrek dağılımın ilk % 25 ni; Q2 ikinci çeyrek, serinin % 50 sini yani medyanı; Q3 üçüncü çeyrek, dağılımın % 75 ini ifade eder. Çeyrek sapma aşağıdaki formüle hesaplanır. Öncellikle Q1 ve Q3 istatistikleri (çeyrek yüzdelikleri) hesaplamak gerekir Sınıflandırılmamış Verilerde Çeyrek Sapma Öncelikle veriler sıralanır. Serinin ortancası bulunur. Medyandan büyük değerlerin ortancası bulunur (Q3, bu değerlerin % 75 oranına karşılık gelir). Serinin ortancasından küçük değerlerin ortancası bulunur (Q1, bu değerlerin % 25 oranına karşılık gelir). 24
31 Örnek: 10 öğrencinin fizik dersi not ortalamaları aşağıda verildiği gibidir. Xi = 75, 48, 69, 37, 83, 73, 68, 52, 55, 71 serisinin çeyrek ayrılışını hesaplayınız. Veriler küçükten büyüğe sıralanır. Xi = 37, 48, 52, 55, 68, 69, 71, 73, 75, 83 Serinin ortancası bulunur. Denek sayısı çift olduğu için; n = 10 Birinci çeyrek bulunur. Serinin ortancasından (68,5) küçük değerlerin ortancası ile bulunur. Bulunan ortanca birinci çeyrektir. 25
32 Üçüncü çeyrek bulunur. Serinin ortancasından (68,5) büyük değerlerin ortancası ile bulunur. Bulunan ortanca üçüncü çeyrektir. Bu serinin çeyrek sapması: Sınıflandırılmış Verilerde Çeyrek Sapma Sınıflandırılmış verilerde aynı formül kullanılır. Burada değişen birinci ve üçüncü çeyreğin hesaplama durumudur. Önce Q1 ve Q3 değerleri belirlenir. formülleri ile hesaplanır. 26
33 Bu formüllerde; L1: Birinci dörttebirlik sınıfının başlangıç değeri F1: Birinci dörttebirlik sınıfından önceki sınıfın yığılımlı frekansı fa: Birinci dörttebirlik sınıfının frekansı L3: Üçüncü dörttebirlik sınıfının başlangıç değeri F3: Üçüncü dörttebirlik sınıfından önceki sınıfın yığılımlı frekansı fc: Üçüncü dörttebirlik sınıfının frekansı C: Sınıf aralığı n: Denek sayısını ifade eder. Örnek: Aşağıda frekansları ve yığımlı frekansları verilen 50 hastanın sistolik kan basınç dağılımının çeyrek sapmasını hesaplayınız. Önce Q1 hesaplanır. Tablo 2.3: 50 hastanın sistolik kan basıncı değeri Q1 = X (n/4) Q1 = X (50/4) Q1= X 12.5 (12,5 değeri; Yf si 20, f sı 9 olan 120< X >130 sınıfında yer almaktadır.) L1 = 120 F1 = 11 fa = 9 C = 10 n = 50 Hastaların % 25 inin sistolik kan basınç değerleri 121,66 dan küçüktür. 27
34 Sonra Q3 hesaplanır. Q3 = X (3n/4) Q3 = X (3x50/4) Q3 = X ( 37,5) (37,5 değeri; Tabloda Yf si 40, f sı 7 olan 140< X >150 sınıfında yer almaktadır.) L3 = 140 F3 = 33 fc = 7 C = 10 n = 50 Hastaların % 75 inin sistolik kan basınç değerleri 146,42 den küçüktür. Buna göre çeyrek sapma; 2.5. Standart Hata Standart hata, farklı genişlikteki örneklem ortalamalarının standart sapmasıdır. Bir başka deyişle örneklem ortalamalarının yaygınlığını gösterir. Aritmetik ortalamanın anlamlı olabilmesi için standart hata ile birlikte gösterilmesi gerekir. Ortalama standart hata ile birlikte; ± şeklinde ifade edilir. Bu durumda ortalamanın hangi aralıkta olacağı konusunda bir fikir edinilebilir. Standart hata aşağıdaki formül ile hesaplanır. S S X n 28
35 Formülde; : Standart hata S: Standart sapma N: Denek sayısı Örnek: Aşağıda verilen serinin standart hata değerini hesaplayınız. Xi: 8, 11, 6, 9, 13, 14, 17, 15, 7, 10 Öncelikle serinin örnek ortalaması ve standart sapması hesaplanır. = 11 S= 3,65 Buradan standart hata hesaplanırsa; Aritmetik ortalama, standart hata ile birlikte gösterilir. = 3,65± 1,15 olarak yazılır. 29
36 UYGULAMA FAALİYETİ UYGULAMA FAALİYETİ Verilerin dağılım ölçülerini doğru ve tam olarak hesaplayınız. İşlem Basamakları Öneriler A sınıfındaki 15 erkek öğrencinin ağırlıkları aşağıda verildiği gibidir. Xi = 63, 59, 72, 61, 58, 56, 65, 62, 70, 58, 67, 60, 63, 74, 57 Yukarıdaki verilerin yayılma genişliğini hesaplayınız. Sınıflandırılmamış verilerin standart sapmasını hesaplayınız. Sınıflandırılmış verilerin standart sapmasını hesaplayınız. Verilerin varyasyon katsayını hesaplayınız. Sınıflandırılmamış verilerin çeyrek sapmasını hesaplayınız. Sınıflandırılmış verilerin çeyrek sapmasını hesaplayınız. Verilerin standart hatasını hesaplayınız. Yayılma genişliğinin özelliklerini hatırlayınız. Aritmetik ortalamaları aynı olan iki veri grubunun yaygınlığının da aynı olup olmadığını karşılaştırınız. Sınıflandırılmamış verilerin standart sapmasını hesaplarken değerlerin karelerini alıp toplamayı unutmayınız. Sınıflandırılmış verilerin standart sapmasını hesaplamak için gerekli işlem basamaklarını tablo üzerinde oluşturabilirsiniz. Varyasyon katsayısı, standart sapmanın ortalamaya göre yüzde kaçlık bir değişim gösterdiğini belirttiğini unutmayınız. Merkezi eğilim ölçüsü olarak ortalama yerine ortancanın kullanıldığı bir durumda dağılımın ölçüsü olarak ortancadan olan sapmaya ilişkin bilgi veren çeyrek sapma kullanıldığını unutmayınız. Çeyrek sapmanın, standart sapmanın tersine aşırı değerlerden etkilenmediğini unutmayınız. Sınıflandırılmış verilerin çeyrek sapmasını hesaplarken tablo oluşturmayı unutmayınız. Standart hatanın aritmetik ortalama ile birlikte gösterilmesi gerektiğini unutmayınız. 30
37 ÖLÇME VE DEĞERLENDİRME ÖLÇME VE DEĞERLENDİRME Aşağıdaki soruları dikkatlice okuyarak doğru seçeneği işaretleyiniz. 1. Sınıflandırılmış verilerde standart sapma hesaplanırken hangi işlem yapılmaz? A) Seri sınıflandırılır. B) Her sınıfın frekansı bulunur. C) b kolonu oluşturulur. D) Yf kolonu oluşturulur. E) Fb kolonu oluşturulur. 2. Xi: 8, 4, 5, 3, 9 serisinin varyasyon katsayısı aşağıdakilerden hangisidir? A) 44,48 B) 44,00 C) 4,448 D) 44,50 E) 44,42 3. Aşağıdakilerden hangisi, dağılım ölçüleri içinde hesaplanması kolay olmakla beraber veri hakkında en kaba bilgi veren ölçüdür? A) Standart sapma B) Yayılma genişliği C) Çeyrek sapma D) Varyasyon katsayısı E) Standart hata 4. Aşağıdakilerden hangisi, aşırı uç değerlerin çok olduğu çarpık dağılımlarda tercih edilen bir dağılım ölçüsüdür? A) Standart hata B) Standart sapma C) Çeyrek sapma D) Varyans E) Aritmetik ortalama 5. Aşağıdakilerden hangisi, ortalamanın hangi aralıkta olacağını gösteren dağılım ölçüsüdür? A) Aritmetik ortalama B) Çeyrek sapma C) Standart sapma D) Varyasyon katsayısı E) Standart hata DEĞERLENDİRME Cevaplarınızı cevap anahtarıyla karşılaştırınız. Yanlış cevap verdiğiniz ya da cevap verirken tereddüt ettiğiniz sorularla ilgili konuları faaliyete geri dönerek tekrarlayınız. Cevaplarınızın tümü doğru ise bir sonraki öğrenme faaliyetine geçiniz. 31
38 ÖĞRENME FAALİYETİ 3 ÖĞRENME FAALİYETİ 3 AMAÇ Toplumun nüfus yapısı ve özelliklerini ayırt edebileceksiniz. ARAŞTIRMA TÜİK in nüfus ile ilgili istatistik yayınlarını araştırınız. Yaşadığınız ilin veya bölgenin nüfusunun yapısal özellikleri (nüfus miktarı, yaş grupları, nüfusun cinsiyeti, eğitim durumu ve ekonomik faaliyet kollarına dağılımı) araştırınız. Yaşadığınız ilin nüfus verilerinden yararlanarak kadın ve erkek nüfus oranlarını karşılaştırınız. Elde ettiğiniz bilgileri sınıf ortamında arkadaşlarınızla tartışınız. Yaşadığınız yerde nüfusun artma ve azalma nedenleri nelerdir? Araştırınız. 3. TOPLUMUN NÜFUS YAPISI VE ÖZELLİKLERİ 3.1. Nüfusun Büyüklüğünü ve Yapısını Etkileyen Faktörler Bir ülkenin veya bölgenin nüfus yapısı ve özellikleri sağlık hizmetlerinin sunumu açısından önemlidir. Sağlık hizmetlerini planlama, örgütleme, uygulama ve yeniden düzenleme aşamalarında en çok başvurulan veri, bölgenin nüfusu ve nüfus yapısı özellikleridir. Resim 3.1: Nüfus Nüfus yapısı, cinsiyet, yaş, eğitim, meslek ve çeşitli yaş grupları yönünden dağılım konularını kapsar. Doğum, ölüm, iç ve dış göçler, evlenme ve boşanma gibi olaylar ise nüfus büyüklüğünü (nüfusta artış veya azalış) etkiler. 32
39 Nüfus olaylarını inceleyen bilim dalına demografi denir. Demografi bilimi dışında coğrafya, sosyoloji, ekonomi, tarih, biyoloji, tıp ve istatistik gibi bilim dalları nüfus konusu ile yakından ilgilenmektedir. Toplumların kalıcı olabilmeleri ve varlıklarını devam ettirebilmeleri, her şeyden önce o toplum nüfus miktarına ve daha önemlisi nüfusun kalitesine, yani nüfus yapısına bağlıdır. Bu nedenle ülkelerin veya bölgelerin nüfus hareketleri, kır ve kent nüfus yoğunluğu ve eğitim durumu gibi özellikleri incelemek büyük önem taşır. Nüfusla ilgili kavramlar şunlardır: Nüfus; sınırları belirli bir alanda yaşayan insan sayısına denir. Dünya nüfusu, ülke nüfusu, kent nüfusu, ilçe nüfusu vb. (milyon kişi) Tablo 3.1: yılları arasında kıtalara göre nüfus dağılış miktarları (Dünya Bankası) Genç nüfus; 15 yaş altı çocuk nüfusunun toplam nüfus içinde % 40 tan fazla olduğu toplumların nüfus yapısına denir. Bu nüfus yapısında ortalama yaş düşük ve gelişmemiş ülke nüfus yapısını temsil eder. Yaşlı nüfus; 65 yaş ve üzeri nüfusun toplam nüfus içinde % 10 dan fazla olduğu toplumların nüfus yapısına denir. Gelişmiş ülke nüfus yapısı bu özelliktedir. Orta yaşlı nüfus; yaş grubundaki nüfusun toplam nüfus içinde % oranlarında olduğu toplumların nüfus yapısına denir. Gelişmekte olan ülkelerin nüfus özelliğini taşır. Yıl ortası nüfus; Bir bölgede meydana gelen doğum ve iç göçlerin eklenip ölüm ve dış göçlerin çıkarıldığı 30 haziran veya 1 temmuzdaki nüfustur. Bağımlı nüfus; genellikle 0-14 ve 65 yaş üstü yaş grubu, bağımlı nüfus olarak tanımlanır. Çalışan nüfusun bakım ve sorumluluğuna ihtiyaç duyan çocuk, öğrenci, yaşlı, hasta vb. gruplardan oluşan nüfustur. Çalışan nüfus; bağımlı nüfus dışında kalan yaşları arasındaki nüfustur. Nüfus politikaları; nüfus değişimlerini (nüfus artışını yavaşlatıcı veya hızlandırıcı) etkileyen önlemlerin tümüne denir. 33
40 Nüfus hareketleri; bir bölgede olagelen doğum, ölüm, göç, evlenme ve boşanma olaylarının tümüdür. Nüfus sayımları; belli bir zamanda, bir ülke sınırları içinde kişilere yönelik yapılan demografik, ekonomik, sosyal verilerin toplanması ve bu verilerin değerlendirilmesi işlemidir. Nüfus sayımları iki ayrı yöntemle yapılır. Bunlar: De facto sayım yöntemi; sayım anında bölge sınırları içinde bulunan bireylerin sayılmasıdır yılına kadar Türkiye de nüfus sayımı bu yöntemle yapılmıştır. De juro sayım yöntemi; sayım anında nerede bulunursa bulunsunlar bireylerin sürekli olarak oturdukları yerde sayılmasıdır. Hane halkı; aynı evde yaşayan, aynı tencereden yemek yiyen kişilerin oluşturduğu topluluktur. Aile; Aralarında kan bağlılığı olan, evlilik ya da yasal yollardan ilişkisi bulunan iki ya da daha çok kişinin oluşturduğu topluluktur. Çekirdek aile; anne, baba ve evlenmemiş çocuklardan oluşan topluluktur. Geniş aile; birkaç kuşağın yatay, dikey veya her iki yönde genişlediği ve birden fazla evli çiftin bulunduğu topluluktur. Parçalanmış aile; ölüm, boşanma ve ayrı yaşama gibi nedenlerle eşlerden birinin veya her ikisinin bulunmadığı aile tipidir. Doğumlar, ölümler, iç ve dış göçler, evlenmeler ve boşanmalar nüfusun büyüklüğünü ve yapısını etkileyen faktörlerdir. Doğumlar ve ölümler; nüfus sayısını, iç ve dış göçler; hem nüfus yapısını hem de nüfus sayısını, evlilik ve boşanmalarsa nüfusun medeni durumu ile doğumların azalması ya da artması olaylarını etkiler Doğumlar Doğumlar, nüfusun büyüklüğünü, genç veya yaşlı olmasını etkileyen faktörlerdendir. Toplumlardaki doğum oranında artış, nüfusun gençleşmesine; doğum oranında azalma nüfusun yaşlanmasına neden olur. Demografik durum, (yaş, evlilik oranı, aile planlaması vb.) ekonomik durum, din, gelenek, kültürel özellikler ve yerleşim yeri gibi faktörler, doğurganlık olayını etkiler. Grafik 3.1: Türkiye de dönemlere göre toplam doğurganlık hızı 34
41 Grafik 3.2: Türkiye de yaşa özel doğurganlık hızı Türkiye de yılları arasında doğurganlık hızında artış olmuş, kadın başına (15-49 yaş aralığındaki kadın nüfusuna) düşen çocuk sayısı 5,5 den 7,0 a yükselmiştir li yıllarda kadın başına ortalama 5 çocuk düşerken bu sayı 1990 lı yılların sonunda 2,6 çocuğa düşmüştür Türkiye İstatistik Kurumu (TÜİK) verilerine göre doğurganlık hızı 2,2 olarak hesaplanmıştır. Kaba doğum hızı da 2000 li yılların 2. yarısında %0 18 olarak tahmin edilmiştir Ölümler Nüfusun yapısı ve büyüklüğünü etkileyen diğer faktör ölümlerdir. Nüfusun azalması ölüm ve dış göçler sonucu oluşur. Ölüm oranları, toplumun kalkınma ve sağlık hizmetlerinin derecesinin önemli bir göstergesidir. Ölüm oranları içinde en önemlisi bebek ölüm hızı (BÖH) dır. Gelişmiş ülkelerde BÖH %0 14, Avrupa Topluluğu ülkelerinde %0 10 civarındadır. Ülkemizde BÖH, 1940 lı yıllarda %0 274, 1970 li yıllarda %0 130 ve 2006 yılında %0 97 olarak tespit edilmiştir. 35
42 Grafik 3.3: Türkiye de yılları arasında doğum ve ölüm oranları (TÜİK, 2004) Türkiye de kaba ölüm hızı, 1940 lı yıllarda %0 30 iken, 2000 li yılların ikinci yarısında %0 6 ya düşmüştür. Türkiye İstatistik Kurumu, 2006 verilerine göre beklenen yaşam süresinin erkekler için 71 yıl, kadınlar için 75 yıl olacağını tahmin etmektedir Göçler Nüfusun devamlı yaşadığı sahayı, kişi, aile veya gruplar hâlinde terk edip geçici veya sürekli yaşamak amacıyla bir başka yere gitmesine "göç" denir. Önemli nüfus parametrelerinden biri olan göç hareketi, değişik sosyal, siyasi ve ekonomik nedenlerden kaynaklanmakta ve tarih öncesi dönemlere kadar dayanmaktadır. Göç hareketleri, iç göçler ve dış göçler olarak sınıflandırılır. İç göç; ülke içinde nüfusun yer değiştirmesine denir. İç göçlerle bir ülkenin toplum nüfusunda değişme olmaz. Sadece bölgelerin ve illerin nüfusunda artma ya da azalma meydana gelir. Türkiye de cumhuriyetin başlangıcından günümüze kadar özellikle kırsal alanlardan kentlere doğru hızlı göç olayı gerçekleşmiştir. İç göçün nedenleri arasında; Kırsal nüfus artışı, Miras yoluyla tarım alanlarının daralması, Tarımda makineleşmenin artması, Kırsal alanda iş imkânlarının sınırlı olması, Ekonomik istikrarsızlık, Eğitim ve sağlık hizmetlerinin yetersizliği, İklim ve yer şekillerinin olumsuz etkilenmesidir. 36
43 Resim 3.2: İç göç nedenleri Dış göçler; çalışmak veya uzun süre kalmak amacıyla bir ülkeden diğer ülkelere yapılan nüfus hareketidir. Göç alan ülkede nüfus artar, göç veren ülkede nüfus azalır. Dış göçün nedenleri arasında; Ekonomik nedenler, Savaşlar, Etnik nedenler, Sınırların değişmesi, Uluslararası anlaşmalarla sağlanan nüfus değişimidir. Türkiye de 1927 yılında nüfusun % 83,62 si kırsal alanda yaşarken % 16,38 i kentlerde yaşamaktaydı den sonra kırsal alanlardan kentlere göç sonucu, hızlı bir kentleşme sürecine girilmiştir yılında kentlerde yaşayan nüfusun payı % 25 iken 2007 yılında % 70 e yükselmiştir döneminde kent nüfus oranı % 32 olarak gerçekleşmiştir. Grafik 3.4: Türkiye kentsel ve kırsal nüfusu (TÜİK, 2004) 37
44 Ülkemiz, 1960 lı ve 1970 li yıllarda başta Almanya olmak üzere batı Avrupa ya göç veren ülke olmuştur li yıllarda bu göç olayı Ortadoğu petrol üreticisi ülkelere yönelmiştir. Son 20 yıl boyunca bölgedeki politik dalgalanma ve Avrupa Birliği iş gücü politika uygulamalarında meydana gelen değişiklikler göç örüntüsünü etkilemeye devam etmektedir. Sovyetler Birliği nin dağılmasından sonra Bağımsız Devletler Topluluğu ve Ortadoğu ülkeleri Türk iş adamları ve işçileri için yeni göç bölgeleri olmuştur. Türkiye, son yıllarda Balkan, Ortadoğu, Asya ve Afrika ülkelerinden gelen sığınmacı dalgalarına maruz kalmaktadır Nüfus Veri Kaynakları Şekil 3.1: Türkiye de nüfus hareketleri Nüfusla ilgili istatistikler demografik çalışmalarda, siyasal, sosyal ve ekonomik alanlarda en çok başvurulan kaynaklardır. 38
45 Nüfus Sayımları Tarih boyunca çeşitli amaçlarla birçok nüfus sayımı yapılmıştır. Bu nüfus sayımlarının temel amaçları, askere alınacak ve vergi verecek kişi sayısını belirlemektir. Ancak dünyada nüfus sayımları tüm ülkelerde düzenli olarak yapılmadığından dünya nüfusu hakkında doğru bilgilere ulaşılamamıştır. Tablo 3.2: Yıllara göre dünya nüfusu Grafik 3.5: Yıllara göre dünya nüfusu (Dünya Bankası) Modern nüfus sayımları, ilk defa İskandinav ülkelerinde yapılmıştır. Osmanlı Devleti'nde ilk kapsamlı nüfus sayımı II. Mahmut döneminde 1831 yılında yapılmış olup asker ve vergi yükümlülerini belirlemeye yöneliktir. 39
46 Bir ülkenin kalkınmasında alınan kararların amaçlanan hedeflere ulaşması için mevcut kaynakların bilinmesi gerekir. Bu kaynaklardan biri de insandır. Bir ülkedeki nüfusun miktarı, niteliği, ekonomik faaliyetlere göre dağılımı, yaş grubu ve cinsiyet yapısı gibi özelliklerin bilinmesi gerekir ki gerçekçi bir kalkınma planı yapılabilsin. Modern nüfus sayımlarının yapılmasının nedeni nüfusun niteliklerini tespit etmektir. Çünkü ülke kaynaklarının doğru kullanılmasında ve kalkınma önceliklerinin belirlenmesinde nüfusun niteliklerinin bilinmesi önemlidir. Grafik 3.6: yılları arasında dünya nüfus artış oranları (Dünya Bankası) Nüfus sayımlarının yapılmasında hedeflenen amaçlar şunlardır: Ülkenin nüfus miktarı Yaş grupları Kent ve kır nüfusu Nüfusun eğitim durumu Nüfusun mesleklere göre dağılımı Nüfusun cinsiyet durumu Nüfus hareketleri Resim 3.3: Atatürk ün Nüfus Hüviyet Cüzdanı 40
47 Cumhuriyet döneminde ilk kapsamlı nüfus sayımı 1927 yılında yapılmıştır. Türkiye nüfusu 13,6 milyon olarak saptanmıştır yılındaki ikinci nüfus sayımından sonra 1990 yılına kadar her beş yılda bir nüfus sayımı yapılmıştır yılından sonra 10 yılda bir sayım yapılması kanunla belirlenmiştir. 22 Ekim 2000 tarihinde gerçekleştirilen 14. genel nüfus sayımında Türkiye nüfusu 64,7 milyon sayılmıştır (TÜİK, 2003) dönemi içinde Türkiye nüfusu sürekli olarak artmıştır. Yıllık nüfus artış hızı döneminde %0 29 olarak gerçekleşmiştir dönemi için hesaplanan sayımlar arası nüfus artış hızı %0 18 dir. Grafik 3.7: Türkiye nüfusunun yıllara göre artışı (TÜİK, 2004) 2006 yılında çıkarılan 5490 Sayılı Nüfus Hizmetleri Kanunu ile ülkemizdeki nüfus sayımlarında veri kaynağını oluşturacak yeni bir sistem kurulmuştur. Sistemin kurulmasına yönelik tüm çalışmalar TÜİK koordinasyonunda yürütülmektedir. İl ve ilçelerde, vali ve kaymakamların başkanlığında oluşturulan yürütme tarafından gerçekleştirilmektedir. Bu çalışmada öncelikle bütün adres bilgileri kaydedilerek Ulusal Adres Veri Tabanı oluşturulmuştur. Bu adreslerde ikamet eden vatandaşlar T.C. kimlik numaralarıyla yabancılar ise pasaport numaraları aracılığıyla adresle ilişkilendirilerek kayıt altına alınmış ve Adrese Dayalı Nüfus Kayıt Sistemi (ADNKS) oluşturulmuştur. Merkezi Nüfus İdaresi Sistemi (MERNİS): Adrese Dayalı Nüfus Kayıt Sistemi Nedir? Kişilerin yerleşim yerlerine göre nüfus bilgilerinin güncel olarak tutulduğu, nüfus hareketlerinin her an izlenebildiği, MERNİS kayıtlarındaki TC Kimlik Numarasına göre kişiler ile ikamet adreslerinin eşleştirildiği bir kayıt sistemidir. Bu Sistemin Eski Nüfus Sayımlarından Farkı Nedir? Adrese Dayalı Nüfus Kayıt Sistemi nüfus sayımı değil, devamlı yapılacak güncellemeler ile yaşatılan modern bir veritabanıdır. Daha önce 10 yılda bir sokağa çıkma yasağı ile uygulanan nüfus sayımları artık yapılmayacaktır. Ayrıca bu sistemde TC Kimlik Numaralarına göre kayıt yapılacağından mükerrer kayıt ya da kayıt olamama gibi riskler yoktur. Tablo 3.3: Merkezi Nüfus İdaresi Sistemi 41
48 Nüfus sayımlarında yaşanan mükerrer kayıt ve kayıt olmama gibi sorunlar bu sistemle ortadan kalkmıştır. TÜİK tarafından kurulan ADNKS, 5490 sayılı kanun gereği İçişleri Bakanlığına devredilmiştir. Söz konusu kanun uyarınca kamu kurum ve kuruluşları adrese dayalı tüm idari işlemlerinde bu sistemden yararlanacak ve güncel bilgiler elde edilecektir. Ülkemizde nüfus bilgileri 2007 yılından itibaren de juro yöntemi olarak bilinen ikamet adresine dayalı nüfus sayımları ile elde edilmektedir. Elde edilen bilgiler TÜİK tarafından kamuoyuna duyurulmaktadır. 31 Aralık 2007 tarihi itibariyle Türkiye nüfusu kişidir. Nüfusun ünü erkek nüfusu, ünü ise kadın nüfusu oluşturmaktadır. Nüfusun % 70,5 kentlerde, % 29,5 kırsal alanda yaşamaktadır. 31 Aralık 2009 tarihi itibarıyla Türkiye nüfusu kişidir yılında Türkiye nin yıllık nüfus artış hızı binde 14,5 olarak gerçekleşmiştir. Grafik 3.8: Türkiye de nüfusun yıllara göre sayısal artma durumu Grafik 3.9: Türkiye nüfusunun cinsiyetlere göre okuryazarlık oranları (TÜİK, 2000) 42
49 Türkiye nüfusunun yarısı, 28,3 yaşından küçük, % 66,5 i yaşları arasında, % 26,4 ü 0-14 yaş grubunda ve % 7,1 i ise 65 ve daha yukarı yaş grubundadır. 1 km² ye düşen kişi sayısı 92 dir (nüfus yoğunluğu) Nüfus Araştırmaları Nüfus sayımlarından elde edilen bilgiler bazen yeterli veya istenilen düzeyde olmayabilir. Ayrıca ülkemizde nüfus hareketleri ve sorunlarını sürekli olarak izleme ve inceleme olayını nüfus sayımlarıyla gerçekleştiremeyiz. Geçmişte ve günümüzde nüfus hareketleri ve sorunlarıyla ilgili araştırmalar yapılmış ve yapılmaktadır. Örnek: , yıllarında hıfzıssıhha okulunun yaptığı Türkiye Nüfus Araştırmaları 1975 yılında Devlet İstatistik Enstitüsünün yaptığı Türkiye Nüfus Araştırmaları 1993, 1998, 2003 ve 2008 yıllarında Hacettepe Üniversitesi Nüfus Etütleri Enstitüsünün yaptığı Nüfus ve Sağlık Araştırmaları gibi. Hacettepe Üniversitesi Nüfus Etütleri Enstitüsünün çalışmaları eğitim, araştırma, demografik veri/bilgi üretilmesi ve yayılması olmak üzere üç ana başlık altında yer almaktadır. Türkiye Nüfus ve Sağlık araştırmaları 1968 den bu yana sayımlar arası yıllara denk gelecek şekilde her beş yılda bir yapılmaktadır. Bu araştırmalarla Türkiye başka hiç bir ülkede olmadığı şekilde 35 yılı kapsayan bir dizi araştırma verisine ve uluslararası düzeyde karşılaştırılabilir nüfus ve sağlık veri tabanına sahip olmuştur Nüfusa İlişkin Kayıtlar Ülkemizde sağlık hizmetlerinin sosyalleştirildiği bölgelerde nüfusun her yıl haziran ayının ortasında, o bölgede çalışan sağlık personeli tarafından ev ev dolaşılarak her hane için bir tane olacak şekilde düzenlenen Evhalkı Tespit Fişleri (EFT) kullanılarak periyodik nüfus tespitleri yapılır. Periyodik nüfus kayıtları ilgili bölge halkı hakkında (nüfus yapısı, hane sayısı, bölgesel göçler, doğumlar, ölümler, oturulan ev ve çevre özellikleri, hastalıklar vb.) önemli bilgi/veri toplanmasını sağlar. Her yıl bilgilerin güncellenmesi, sağlık hizmetlerinin daha sağlıklı planlanmasını ve uygulanmasını sağlar. Ülkemizde bireylere ait önemli hayati olaylar (ölüm ve doğum kayıtları gibi) kayıt altına alınmaktadır. Kayıtlar; Vatandaşlıkla ilgili tüm işlemlerin doğru ve kesin bir yasal dayanağa göre yapılmasını sağlamak, Sağlık düzeyini, bu düzeydeki değişimleri belirlemek ve planlar yapmak, Toplumun genel yapısına, doğurganlık, ölüm düzeyleri ve ortalama yaşam süresi hakkında bilgi elde etmek amacıyla tutulmalıdır. 43
50 Kayıtların yararlı olabilmesi için toplumdaki tüm hayati olayların aralıksız biçimde kaydedilmesi gerekir. Kayıt formundaki tüm sorular yanıtlanmalı ve bilgiler kaydedilmelidir. Kaydedilen bilgiler yasa ve yönetmeliklerde belirtilen süre içinde ilgili birimlere bildirilmelidir. Kayıt formundaki bilgiler, yanıtlar gizli tutulmalı, ölümle ilgili formlarda ölüm nedeninin doğru saptanabilmesi için her türlü çaba harcanmalıdır Nüfusun Değerlendirilmesi Nüfus sayımları ile elde edilen veriler, toplumun ve kurumların bilgi ihtiyacını karşılayacak şekilde gruplandırılır ve kullanıma sunulur. Bu bilgilerin derlenmesi ve değerlendirilmesi sonucu toplumun nüfus yapısı hakkında detaylı bilgilere ulaşılır. Tablo 3.4: Nüfusu değerlendirme kriterleri 44
51 3.4. Nüfusla İlgili Hız ve Oranlar Nüfusla ilgili bazı hız ve oran hesaplamaları aşağıda verilmiştir. Nüfus yoğunluğu: Bir bölgede 1 km² ye kaç kişinin düştüğünü gösteren ölçüdür. formülüyle hesaplanır. Yıl ortası nüfus (YON): Genellikle sağlıkla ilgili istatistiksel çalışmalarda 30 Haziran/ 1 Temmuz tarihindeki nüfus kullanılır. İki şekilde hesaplanır. Yılbaşı ve yılsonu nüfus biliniyorsa; O bölgede o yıl içinde olan doğumlar ve iç göçler toplanır. Bu toplamdan o yıl içinde olan ölümler ve dış göçler toplamı çıkarılır, ikiye bölünür ve yılbaşı nüfusuna eklenir. formülüyle hesaplanır. Yıllık doğal artış hızı: Bir bölgedeki nüfusun bir yıl içinde yalnız doğumlar ve ölümlere bağlı azalması ya da çoğalmasına doğal artış hızı denir. hesaplanır. formülü ile 45
52 Yıllık toplam artış hızı: Ölümler ve doğumlara ek olarak iç ve dış göçlerin eklenmesiyle hesaplanan ve nüfusun azalmasını ya da çoğalmasını gösteren ölçüttür. formülü ile hesaplanır. Genel cinsiyet oranı: Ülke veya bölge nüfusu içinde her 100 kadına kaç erkeğin düştüğünü belirleyen ölçüdür Nüfus Piramitleri formülü ile hesaplanır. Nüfus piramidi, nüfusun yaşa ve cinsiyet yapısının incelenmesi ve gösterilmesini sağlayan grafiklerdir. Beşer yıllık yaş grupları yatay bir dikdörtgen çubukla gösterilir. Küçük yaş grubu alttan başlayarak tepeye doğru yaş grupları büyüyerek artar ve dikdörtgen çubuklar üst üste gelecek şekilde dizilir. Bu şekliyle grafik bir piramide benzer Nüfus Piramidinin Çizimi Cinsiyetlere göre yaş gruplaması yapılır. En çok kullanılan beşerli yaş gruplarıdır. İleri yaştakiler toplanabilir (Örn: 75+ / 80+ vb.). Her yaş grubundan kadın ve erkek nüfusu yazılır. Her cinsiyetin yaş grubu toplam kadın veya erkek nüfusuna göre yüzdeye çevrilir. Bazen de nüfus toplamı üzerinden eşit aralıklı rakamlarla ifade edilebilir. Bu verilerle nüfusun yaşa ve cinsiyete göre dağılımını gösteren tablo oluşturulur. X ekseni çizilir, tam ortadan bir doğru ile ikiye ayrılır. X ekseninin soluna bakan kolon erkek nüfus, sağında kalan kolon ise kadın nüfus için kullanılır. En küçük yaş grubu altta kalacak şekilde bütün yaş grupları büyüklük sırasına göre tam ortaya yerleştirilir. X ekseninde yüzde ya da sayı (nüfus milyon) olarak belirli yaş ve cinsiyet gruplarında var olan nüfusu gösteren ölçü kullanılır. Yüzde ifade kullanıldığında her yaş grubundaki kadın ve erkek yüzdeleri toplam nüfusa göre ya da kadın ve erkek nüfusuna göre ayrı ayrı olarak alınır. Her yaş grubundaki nüfus, erkek ve kadın bölümlerinde kullanılan ölçeğe göre X eksenine paralel olarak dikdörtgen çubuklar çizilir. 46
53 Grafik 3.10: Nüfus piramidi Örnek: Türkiye nin 2000 yılına ait nüfus verileri ve bu veriler doğrultusunda düzenlenmiş örnek nüfus piramidi aşağıda verilmiştir. Bu piramitte nüfuslar, X ekseninde yüzde ölçeğine göre düzenlenmiştir. 0-4 yaş kadın nüfusunun yüzdelik hesabını toplam kadın nüfusuna göre hesaplanırsa; 47
54 Tablo 3.5: Türkiye erkek ve kadın nüfus oranları (2000) Grafik 3.11: Türkiye nüfus piramidi (2000) Piramidin tabanı, yeni doğan ve 5 yaşına kadar olan nüfusu gösterirken piramit yükseldikçe yaş grubu artar. Piramidin en üst kısmı en yaşlı olan nüfusu gösterir. Piramitler amaca göre farklı yaş grupları ile sınıflandırılabilir. 48
55 Nüfus Piramitlerinin Yorumlanması Nüfus piramitleri, bölgelerin veya ülkelerin demografik özellikleri hakkında (nüfusun yaşa, cinsiyete göre dağılımı, iç ve dış göçlerin ve savaşların nüfusa etkisi gibi) bilgi verir. Grafik 3.12: Dünya nüfus piramidi (2050 yılı için) Tabanı geniş piramidin yaş grupları ilerledikçe daralmaya uğraması, ileriki yaşlarda nüfusun, ölüm veya göçlerle kaybedildiği anlamına gelir. Piramidin sadece erkek bloğunda görülen bir girinti o yıllarda gerçekleşen göçleri veya savaşta ölen erkek nüfusun kaybedildiğini düşündürebilir. Toplumda doğumlarda önemli dalgalanmalar yoksa bebek ve genç yaş ölümleri az ise piramit, yanlara ve yukarı doğru genişleme gösterir. Geri kalmış ülkelerin ortak özellikleri Geri kalmış ülkeler; sanayileşememiş, nüfusunun büyük bölümü tarımda çalışan yoksul ülkelerdir. Ülke nüfusun büyük bölümü köylerde yaşar. Kentleşme oranı düşüktür. Kişi başına yıllık milli gelir, çoğunlukla 2000 doların altındadır. Eğitim, sağlık, barınma hizmetleri ve beslenme imkânları yetersizdir. İç göç ve dışarıya göç fazladır. Geri kalmış ülke piramitlerinin özellikleri Nüfus piramidi üçgene benzer. Ülke nüfusu kırda yoğunlaştığı için doğum oranları fazladır. Sağlık hizmetleri yetersiz olduğundan bebek ve çocuk ölümleri fazladır. Olumsuz sağlık koşulları nedeniyle ortalama yaşam süresi kısadır. Yaşlı nüfus oranı düşüktür. Sağlık hizmetlerinin yanı sıra, eğitim hizmetleri ve beslenme şartları yetersizdir. 49
56 Çocuk ve genç nüfus, ülke nüfusunun önemli bir bölümünü oluşturur. Grafik 3.13: Afganistan nüfus piramidi (2000) Gelişmekte olan ülkelerin ortak özellikleri Ülke sanayileşmektedir. Tarımda makineleşmenin artması, kentte sanayileşme ve dolayısıyla iş imkânları köyden kente göçü artırmaktadır. Tarımsal nüfus ve dolayısıyla kır nüfusu her geçen gün azalmakta ve nüfusun büyük bölümü bir veya daha fazla kentte yoğunlaşmıştır. Ülkenin gelişmesine bağlı olarak kentlerde hastane, okul, konut imkânı fazlalaşmış sağlık, eğitim, barınma şartlarında, düzelme görülmektedir. Ülke nüfusu, doğal artış ile bir süre daha artar. Kentleşme hızlandıkça doğum oranı da zamanla azalır. Ayrıca bebek ölümlerinde azalma ve ortalama yaşam süresinde artış söz konusudur. Bunlarda ülke nüfusunu artıran diğer nedenlerdir. Gelişmekte olan ülke piramitlerinin özellikleri Gelişmekte olan ülkelerin nüfus piramidi üçgen şeklinden çok çan eğrisine benzemeye başlamıştır. Gelişmekte olan ülkelerde doğum oranlarında azalma dikkati çeker. Ortalama yaşam süresi artmıştır. Ülkenin nüfus piramidinde 60 yaş sonrası önemli bir orana sahiptir. Orta yaş ve yaşlı nüfus, genç nüfusa göre oransal olarak artmaya başlar. 50
57 Ülke geliştikçe nüfus piramidi de gelişmiş ülkelere özgü olan çan eğrisi şekline dönüşür. Grafik 3.14: Brezilya nüfus piramidi (2000) Gelişmiş ülkelerin ortak özellikleri Gelişmiş ülkelerde nüfusun büyük bölümü sanayi sektöründe ve hizmet sektöründe çalışır. Tarımda çalışan nüfus ortalama olarak % 2 - % 5 oranındadır. Eğitim, sağlık, altyapı, barınma hizmetleri oldukça gelişmiştir. Kent nüfus oranı % 95 civarındayken kır nüfusu % 5 civarındadır. Ülke içi nüfus hareketleri, yani iç göç çok düşük oranlardadır. Dış göç alımı, ülke dışına göç verme oranından çok daha fazladır. Doğum oranları düşük, bebek ve çocuk ölümü çok azdır. Ortalama yaşam süresi fazladır. Doğal nüfus artış hızı düşüktür. Zengin ülkelerdir. Nüfusun yaşlanması söz konusudur. Toplam nüfusunun önemli bir bölümünü orta yaş ve yaşlı nüfus grubu oluşturur. Gelişmiş ülkelerin nüfus piramidinde 80 li, 90 lı yaş grupları önemli bir yer tutar. Gelişmiş ülke piramitlerinin özellikleri Gelişmiş bir ülkede piramidin tabanı ile önceki dönemler arasında pek bir değişim yoktur. Ülkenin özel şartlarına göre doğumlarda önemsiz miktarlarda artış ya da azalış görülebilir. Doğum oranları düşük, bebek ve çocuk ölümü çok azdır. Ortalama yaşam süresi fazladır. Nüfusun doğal artış hızı düşüktür. Toplam nüfusunun önemli bir bölümünü orta yaş ve yaşlı nüfus grubu oluşturur. Gelişmiş bir ülkede piramidin yaşlı nüfusu gösteren üst kısımları geniş sayılabilecek bir biçimdedir. 51
58 Gelişmiş ülkelerin nüfus piramidi çan eğrisine benzer. Grafik 3.15: Belçika nüfus piramidi (2000) Ülkemizdeki durum Türkiye gelişmekte olan bir ülkedir. Sanayide ve hizmet sektöründe çalışan nüfusun oranı zaman geçtikçe artarken, tarımsal nüfus oranı azalmaktadır. İç göç ve dış göç hareketleri çok yoğundur. Günümüzde ülkemiz nüfusunun % 35 i köylerde yaşarken % 65 i kentlerde yaşar. Grafik 3.16: Türkiye nüfus piramidi (2008) 52
Prof.Dr.İhsan HALİFEOĞLU
 Prof.Dr.İhsan HALİFEOĞLU FREKANS DAĞILIMLARINI TANIMLAYICI ÖLÇÜLER Düzenlenmiş verilerin yorumlanması ve daha ileri düzeydeki işlemler için verilerin bütününe ait tanımlayıcı ve özetleyici ölçülere ihtiyaç
Prof.Dr.İhsan HALİFEOĞLU FREKANS DAĞILIMLARINI TANIMLAYICI ÖLÇÜLER Düzenlenmiş verilerin yorumlanması ve daha ileri düzeydeki işlemler için verilerin bütününe ait tanımlayıcı ve özetleyici ölçülere ihtiyaç
Örnek 4.1: Tablo 2 de verilen ham verilerin aritmetik ortalamasını hesaplayınız.
 .4. Merkezi Eğilim ve Dağılım Ölçüleri Merkezi eğilim ölçüleri kitleye ilişkin bir değişkenin bütün farklı değerlerinin çevresinde toplandığı merkezi bir değeri gösterirler. Dağılım ölçüleri ise değişkenin
.4. Merkezi Eğilim ve Dağılım Ölçüleri Merkezi eğilim ölçüleri kitleye ilişkin bir değişkenin bütün farklı değerlerinin çevresinde toplandığı merkezi bir değeri gösterirler. Dağılım ölçüleri ise değişkenin
Prof.Dr.İhsan HALİFEOĞLU
 Prof.Dr.İhsan HALİFEOĞLU Örnek: Aşağıda 100 yetişkine ilişkin kolesterol değerlerini sınıflandırılarak aritmetik ortalamasını bulunuz (sınıf aralığını 20 alınız). 2 x A fb C 229.5 n 40 20 100 221.5 3 Örnek:.
Prof.Dr.İhsan HALİFEOĞLU Örnek: Aşağıda 100 yetişkine ilişkin kolesterol değerlerini sınıflandırılarak aritmetik ortalamasını bulunuz (sınıf aralığını 20 alınız). 2 x A fb C 229.5 n 40 20 100 221.5 3 Örnek:.
Merkezi Yığılma ve Dağılım Ölçüleri
 1.11.013 Merkezi Yığılma ve Dağılım Ölçüleri 4.-5. hafta Merkezi eğilim ölçüleri, belli bir özelliğe ya da değişkene ilişkin ölçme sonuçlarının, hangi değer etrafında toplandığını gösteren ve veri grubunu
1.11.013 Merkezi Yığılma ve Dağılım Ölçüleri 4.-5. hafta Merkezi eğilim ölçüleri, belli bir özelliğe ya da değişkene ilişkin ölçme sonuçlarının, hangi değer etrafında toplandığını gösteren ve veri grubunu
Temel İstatistik. Y.Doç.Dr. İbrahim Turan Mart Tanımlayıcı İstatistik. Dağılımları Tanımlayıcı Ölçüler Dağılış Ölçüleri
 Temel İstatistik Tanımlayıcı İstatistik Dağılımları Tanımlayıcı Ölçüler Dağılış Ölçüleri Y.Doç.Dr. İbrahim Turan Mart 2011 DAĞILIM / YAYGINLIK ÖLÇÜLERİ Verilerin değişkenlik durumu ve dağılışın şeklini
Temel İstatistik Tanımlayıcı İstatistik Dağılımları Tanımlayıcı Ölçüler Dağılış Ölçüleri Y.Doç.Dr. İbrahim Turan Mart 2011 DAĞILIM / YAYGINLIK ÖLÇÜLERİ Verilerin değişkenlik durumu ve dağılışın şeklini
Temel Ġstatistik. Tanımlayıcı Ġstatistik. Dağılımları Tanımlayıcı Ölçüler Yer Ölçüleri. Y.Doç.Dr. Ġbrahim Turan Mart 2011
 Temel Ġstatistik Tanımlayıcı Ġstatistik Dağılımları Tanımlayıcı Ölçüler Yer Ölçüleri Y.Doç.Dr. Ġbrahim Turan Mart 2011 Yer / Konum Ölçüleri 1- Aritmetik Ortalama (Mean): Deneklerin aldıkları değerlerin
Temel Ġstatistik Tanımlayıcı Ġstatistik Dağılımları Tanımlayıcı Ölçüler Yer Ölçüleri Y.Doç.Dr. Ġbrahim Turan Mart 2011 Yer / Konum Ölçüleri 1- Aritmetik Ortalama (Mean): Deneklerin aldıkları değerlerin
JEODEZİK VERİLERİN İSTATİSTİK ANALİZİ. Prof. Dr. Mualla YALÇINKAYA
 JEODEZİK VERİLERİN İSTATİSTİK ANALİZİ Prof. Dr. Mualla YALÇINKAYA Karadeniz Teknik Üniversitesi, Harita Mühendisliği Bölümü Trabzon, 2018 VERİLERİN İRDELENMESİ Örnek: İki nokta arasındaki uzunluk 80 kere
JEODEZİK VERİLERİN İSTATİSTİK ANALİZİ Prof. Dr. Mualla YALÇINKAYA Karadeniz Teknik Üniversitesi, Harita Mühendisliği Bölümü Trabzon, 2018 VERİLERİN İRDELENMESİ Örnek: İki nokta arasındaki uzunluk 80 kere
BÖLÜM 5 MERKEZİ EĞİLİM ÖLÇÜLERİ
 1 BÖLÜM 5 MERKEZİ EĞİLİM ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel sayma
1 BÖLÜM 5 MERKEZİ EĞİLİM ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel sayma
Genel olarak test istatistikleri. Merkezi Eğilim (Yığılma) Ölçüleri Dağılım (Yayılma) Ölçüleri. olmak üzere 2 grupta incelenebilir.
 4.SUNUM Genel olarak test istatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Dağılım (Yayılma) Ölçüleri olmak üzere 2 grupta incelenebilir. 2 Ranj Çeyrek Kayma Çeyrekler Arası Açıklık Standart Sapma Varyans
4.SUNUM Genel olarak test istatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Dağılım (Yayılma) Ölçüleri olmak üzere 2 grupta incelenebilir. 2 Ranj Çeyrek Kayma Çeyrekler Arası Açıklık Standart Sapma Varyans
Merkezi Eğilim ve Dağılım Ölçüleri
 Merkezi Eğilim ve Dağılım Ölçüleri Soru Öğrencilerin derse katılım düzeylerini ölçmek amacıyla geliştirilen 16 soruluk bir test için öğrencilerin ilk 8 ve son 8 soruluk yarılardan aldıkları puanlar arasındaki
Merkezi Eğilim ve Dağılım Ölçüleri Soru Öğrencilerin derse katılım düzeylerini ölçmek amacıyla geliştirilen 16 soruluk bir test için öğrencilerin ilk 8 ve son 8 soruluk yarılardan aldıkları puanlar arasındaki
Tanımlayıcı İstatistikler. Yrd. Doç. Dr. Emre ATILGAN
 Tanımlayıcı İstatistikler Yrd. Doç. Dr. Emre ATILGAN 1 Tanımlayıcı İstatistikler Yer Gösteren Ölçüler Yaygınlık Ölçüleri Merkezi Eğilim Ölçüleri Konum Ölçüleri 2 3 Aritmetik Ortalama Aritmetik ortalama,
Tanımlayıcı İstatistikler Yrd. Doç. Dr. Emre ATILGAN 1 Tanımlayıcı İstatistikler Yer Gösteren Ölçüler Yaygınlık Ölçüleri Merkezi Eğilim Ölçüleri Konum Ölçüleri 2 3 Aritmetik Ortalama Aritmetik ortalama,
Genel olarak test istatistikleri. Merkezi Eğilim (Yığılma) Ölçüleri Merkezi Dağılım (Yayılma) Ölçüleri. olmak üzere 2 grupta incelenebilir.
 3.SUNUM Genel olarak test istatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Merkezi Dağılım (Yayılma) Ölçüleri olmak üzere 2 grupta incelenebilir. 2 Merkezi Eğilim Ölçüleri, belli bir özelliğe ya da değişkene
3.SUNUM Genel olarak test istatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Merkezi Dağılım (Yayılma) Ölçüleri olmak üzere 2 grupta incelenebilir. 2 Merkezi Eğilim Ölçüleri, belli bir özelliğe ya da değişkene
BİYOİSTATİSTİK Merkezi Eğilim ve Değişim Ölçüleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH
 BİYOİSTATİSTİK Merkezi Eğilim ve Değişim Ölçüleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 İstatistik
BİYOİSTATİSTİK Merkezi Eğilim ve Değişim Ölçüleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 İstatistik
Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü
 Mühendislikte İstatistiksel Yöntemler Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü 1 Araştırma sonuçlarının açıklanmasında frekans tablosu
Mühendislikte İstatistiksel Yöntemler Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü 1 Araştırma sonuçlarının açıklanmasında frekans tablosu
Mühendislikte İstatistik Yöntemler
 .0.0 Mühendislikte İstatistik Yöntemler İstatistik Parametreler Tarih Qma.3.98 4..98 0.3.983 45 7..984 37.3.985 48 0.4.986 67.4.987 5 0.3.988 45.5.989 34.3.990 59.4.99 3 4 34 5 37 6 45 7 45 8 48 9 5 0
.0.0 Mühendislikte İstatistik Yöntemler İstatistik Parametreler Tarih Qma.3.98 4..98 0.3.983 45 7..984 37.3.985 48 0.4.986 67.4.987 5 0.3.988 45.5.989 34.3.990 59.4.99 3 4 34 5 37 6 45 7 45 8 48 9 5 0
TEMEL İSTATİSTİK BİLGİSİ. İstatistiksel verileri tasnif etme Verilerin grafiklerle ifade edilmesi Vasat ölçüleri Standart puanlar
 TEMEL İSTATİSTİK BİLGİSİ İstatistiksel verileri tasnif etme Verilerin grafiklerle ifade edilmesi Vasat ölçüleri Standart puanlar İstatistiksel Verileri Tasnif Etme Verileri daha anlamlı hale getirmek amacıyla
TEMEL İSTATİSTİK BİLGİSİ İstatistiksel verileri tasnif etme Verilerin grafiklerle ifade edilmesi Vasat ölçüleri Standart puanlar İstatistiksel Verileri Tasnif Etme Verileri daha anlamlı hale getirmek amacıyla
TANIMLAYICI İSTATİSTİKLER
 TANIMLAYICI İSTATİSTİKLER Tanımlayıcı İstatistikler ve Grafikle Gösterim Grafik ve bir ölçüde tablolar değişkenlerin görsel bir özetini verirler. İdeal olarak burada değişkenlerin merkezi (ortalama) değerlerinin
TANIMLAYICI İSTATİSTİKLER Tanımlayıcı İstatistikler ve Grafikle Gösterim Grafik ve bir ölçüde tablolar değişkenlerin görsel bir özetini verirler. İdeal olarak burada değişkenlerin merkezi (ortalama) değerlerinin
 A t a b e y M e s l e k Y ü k s e k O k u l u İstatistik Sunum 4 Öğr.Gör. Şükrü L/O/G/O KAYA www.sukrukaya.org www.themegallery.com 1 Yer Ölçüleri Yer ölçüleri, verilerin merkezini veya yığılma noktasını
A t a b e y M e s l e k Y ü k s e k O k u l u İstatistik Sunum 4 Öğr.Gör. Şükrü L/O/G/O KAYA www.sukrukaya.org www.themegallery.com 1 Yer Ölçüleri Yer ölçüleri, verilerin merkezini veya yığılma noktasını
EĞĠTĠMDE ÖLÇME VE DEĞERLENDĠRME BÖLÜM IV Ölçme Sonuçları Üzerinde Ġstatistiksel ĠĢlemler VERİLERİN DÜZENLENMESİ VERİLERİN DÜZENLENMESİ
 09.0.0 Temel Kavramlar EĞĠTĠMDE ÖLÇME VE DEĞERLENDĠRME BÖLÜM IV Ölçme Sonuçları Üzerinde Ġstatistiksel ĠĢlemler Dr. Aylin ALBAYRAK SARI Hacettepe Üniversitesi Eğitim Fakültesi Evren: Üzerinde çalışılacak
09.0.0 Temel Kavramlar EĞĠTĠMDE ÖLÇME VE DEĞERLENDĠRME BÖLÜM IV Ölçme Sonuçları Üzerinde Ġstatistiksel ĠĢlemler Dr. Aylin ALBAYRAK SARI Hacettepe Üniversitesi Eğitim Fakültesi Evren: Üzerinde çalışılacak
ORTALAMA ÖLÇÜLERİ. Ünite 6. Öğr. Gör. Ali Onur CERRAH
 ORTALAMA ÖLÇÜLERİ Ünite 6 Öğr. Gör. Ali Onur CERRAH Araştırma sonucunda elde edilen nitelik değişkenler hakkında tablo ve grafikle bilgi sahibi olunurken, sayısal değişkenler hakkında bilgi sahibi olmanın
ORTALAMA ÖLÇÜLERİ Ünite 6 Öğr. Gör. Ali Onur CERRAH Araştırma sonucunda elde edilen nitelik değişkenler hakkında tablo ve grafikle bilgi sahibi olunurken, sayısal değişkenler hakkında bilgi sahibi olmanın
BÖLÜM 6 MERKEZDEN DAĞILMA ÖLÇÜLERİ
 1 BÖLÜM 6 MERKEZDEN DAĞILMA ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel
1 BÖLÜM 6 MERKEZDEN DAĞILMA ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel
VERİ SETİNE GENEL BAKIŞ
 VERİ SETİNE GENEL BAKIŞ Outlier : Veri setinde normal olmayan değerler olarak tanımlanır. Ders: Kantitatif Yöntemler 1 VERİ SETİNE GENEL BAKIŞ Veri setinden değerlendirme başlamadan çıkarılabilir. Yazım
VERİ SETİNE GENEL BAKIŞ Outlier : Veri setinde normal olmayan değerler olarak tanımlanır. Ders: Kantitatif Yöntemler 1 VERİ SETİNE GENEL BAKIŞ Veri setinden değerlendirme başlamadan çıkarılabilir. Yazım
TEMEL İSTATİSTİKİ KAVRAMLAR YRD. DOÇ. DR. İBRAHİM ÇÜTCÜ
 TEMEL İSTATİSTİKİ KAVRAMLAR YRD. DOÇ. DR. İBRAHİM ÇÜTCÜ 1 İstatistik İstatistik, belirsizliğin veya eksik bilginin söz konusu olduğu durumlarda çıkarımlar yapmak ve karar vermek için sayısal verilerin
TEMEL İSTATİSTİKİ KAVRAMLAR YRD. DOÇ. DR. İBRAHİM ÇÜTCÜ 1 İstatistik İstatistik, belirsizliğin veya eksik bilginin söz konusu olduğu durumlarda çıkarımlar yapmak ve karar vermek için sayısal verilerin
TRB2 BÖLGESİ MEVCUT DURUM ANALİZİ. NÜFUS ve KENTLEŞME
 TRB2 BÖLGESİ MEVCUT DURUM ANALİZİ NÜFUS ve KENTLEŞME 211 İÇİNDEKİLER 1.NÜFUS... 1 1.1. Nüfus Büyüklüğü, Nüfus Yoğunluğu ve Nüfus Artış Hızı... 3 1.2. Yaş ve Cinsiyet Dağılım Özellikleri... 8 1.2.1. Nüfusun
TRB2 BÖLGESİ MEVCUT DURUM ANALİZİ NÜFUS ve KENTLEŞME 211 İÇİNDEKİLER 1.NÜFUS... 1 1.1. Nüfus Büyüklüğü, Nüfus Yoğunluğu ve Nüfus Artış Hızı... 3 1.2. Yaş ve Cinsiyet Dağılım Özellikleri... 8 1.2.1. Nüfusun
Bölüm 3 Merkezi Konum (Eğilim) Ölçüleri. Giriş Veri kümesi. Ortalamalar iki grupta incelenir. A. Duyarlı olan ortalama. B. Duyarlı olmayan ortalama
 GM-220 MÜH. ÇALIŞ. İSTATİSTİKSEL YÖNTEMLER Bölüm 3 Merkezi Konum (Eğilim) Ölçüleri Yrd. Doç. Dr. Safa KARAMAN 1 2 Giriş Veri kümesi Verileri betimlemenin ve özetlemenin bir diğer yolu da verilerin bir
GM-220 MÜH. ÇALIŞ. İSTATİSTİKSEL YÖNTEMLER Bölüm 3 Merkezi Konum (Eğilim) Ölçüleri Yrd. Doç. Dr. Safa KARAMAN 1 2 Giriş Veri kümesi Verileri betimlemenin ve özetlemenin bir diğer yolu da verilerin bir
Nicel / Nitel Verilerde Konum ve Değişim Ölçüleri. BBY606 Araştırma Yöntemleri 2013-2014 Bahar Dönemi 13 Mart 2014
 Nicel / Nitel Verilerde Konum ve Değişim Ölçüleri BBY606 Araştırma Yöntemleri 2013-2014 Bahar Dönemi 13 Mart 2014 1 Konum ölçüleri Merkezi eğilim ölçüleri Verilerin ortalamaya göre olan gruplanması nasıl?
Nicel / Nitel Verilerde Konum ve Değişim Ölçüleri BBY606 Araştırma Yöntemleri 2013-2014 Bahar Dönemi 13 Mart 2014 1 Konum ölçüleri Merkezi eğilim ölçüleri Verilerin ortalamaya göre olan gruplanması nasıl?
Test İstatistikleri AHMET SALİH ŞİMŞEK
 Test İstatistikleri AHMET SALİH ŞİMŞEK İçindekiler Test İstatistikleri Merkezi Eğilim Tepe Değer (Mod) Ortanca (Medyan) Aritmetik Ortalama Merkezi Dağılım Dizi Genişliği (Ranj) Standart Sapma Varyans Çarpıklık
Test İstatistikleri AHMET SALİH ŞİMŞEK İçindekiler Test İstatistikleri Merkezi Eğilim Tepe Değer (Mod) Ortanca (Medyan) Aritmetik Ortalama Merkezi Dağılım Dizi Genişliği (Ranj) Standart Sapma Varyans Çarpıklık
EĞİTİMDE ÖLÇME VE DEĞERLENDİRME UĞUR YILMAZER 1
 EĞİTİMDE ÖLÇME VE DEĞERLENDİRME UĞUR YILMAZER 1 5. BÖLÜM (9. KONU) TEST PUANLARI ÜZERİDE İSTATİSTİKİ İŞLEMLER MERKEZİ EĞİLİM/YIĞILIM ÖLÇÜLERİ ÇARPIKLIK VE YORUMU UĞUR YILMAZER 2 TEST İSTATİSTİKLERİ 1-
EĞİTİMDE ÖLÇME VE DEĞERLENDİRME UĞUR YILMAZER 1 5. BÖLÜM (9. KONU) TEST PUANLARI ÜZERİDE İSTATİSTİKİ İŞLEMLER MERKEZİ EĞİLİM/YIĞILIM ÖLÇÜLERİ ÇARPIKLIK VE YORUMU UĞUR YILMAZER 2 TEST İSTATİSTİKLERİ 1-
Bölüm 3. Tanımlayıcı İstatistikler
 Bölüm 3 Tanımlayıcı İstatistikler 1 Tanımlayıcı İstatistikler Bir veri setini tanımak veya birden fazla veri setini karşılaştırmak için kullanılan ve ayrıca örnek verilerinden hareket ile frekans dağılışlarını
Bölüm 3 Tanımlayıcı İstatistikler 1 Tanımlayıcı İstatistikler Bir veri setini tanımak veya birden fazla veri setini karşılaştırmak için kullanılan ve ayrıca örnek verilerinden hareket ile frekans dağılışlarını
Örnek...4 : İlk iki sınavında 75 ve 82 alan bir öğrencinin bu dersin ortalamasını 5 yapabilmek için son sınavdan kaç alması gerekmektedir?
 İSTATİSTİK Bir sonuç çıkarmak ya da çözüme ulaşabilmek için gözlem, deney, araştırma gibi yöntemlerle toplanan bilgiye veri adı verilir. Örnek...4 : İlk iki sınavında 75 ve 82 alan bir öğrencinin bu dersin
İSTATİSTİK Bir sonuç çıkarmak ya da çözüme ulaşabilmek için gözlem, deney, araştırma gibi yöntemlerle toplanan bilgiye veri adı verilir. Örnek...4 : İlk iki sınavında 75 ve 82 alan bir öğrencinin bu dersin
YANLILIK. Yanlılık örneklem istatistiği değerlerinin evren parametre değerinden herhangi bir sistematik sapması olarak tanımlanır.
 AED 310 İSTATİSTİK YANLILIK Yanlılık örneklem istatistiği değerlerinin evren parametre değerinden herhangi bir sistematik sapması olarak tanımlanır. YANLILIK Yanlı bir araştırma tasarımı uygulandığında,
AED 310 İSTATİSTİK YANLILIK Yanlılık örneklem istatistiği değerlerinin evren parametre değerinden herhangi bir sistematik sapması olarak tanımlanır. YANLILIK Yanlı bir araştırma tasarımı uygulandığında,
İSTATİSTİK STATISTICS (2+0) Yrd.Doç.Dr. Nil TOPLAN SAÜ.MÜH. FAK. METALURJİ VE MALZEME MÜH. BÖLÜMÜ ÖĞRETİM ÜYESİ ÖĞRETİM YILI
 İSTATİSTİK STATISTICS (+) Yrd.Doç.Dr. Nil TOPLAN SAÜ.MÜH. FAK. METALURJİ VE MALZEME MÜH. BÖLÜMÜ ÖĞRETİM ÜYESİ ÖĞRETİM YILI KONU BAŞLIKLARI :. İSTATİSTİĞE GİRİŞ. VERİLERİN DÜZENLENMESİ. MERKEZİ EĞİLİM ÖLÇÜLERİ.
İSTATİSTİK STATISTICS (+) Yrd.Doç.Dr. Nil TOPLAN SAÜ.MÜH. FAK. METALURJİ VE MALZEME MÜH. BÖLÜMÜ ÖĞRETİM ÜYESİ ÖĞRETİM YILI KONU BAŞLIKLARI :. İSTATİSTİĞE GİRİŞ. VERİLERİN DÜZENLENMESİ. MERKEZİ EĞİLİM ÖLÇÜLERİ.
Konum ve Dağılım Ölçüleri. BBY606 Araştırma Yöntemleri Güleda Doğan
 Konum ve Dağılım Ölçüleri BBY606 Araştırma Yöntemleri Güleda Doğan Konum ölçüleri Merkezi eğilim ölçüleri Verilerin ortalamaya göre olan gruplanması nasıl? Yakın, uzak? Sıklık dağılımlarının karşılaştırılması
Konum ve Dağılım Ölçüleri BBY606 Araştırma Yöntemleri Güleda Doğan Konum ölçüleri Merkezi eğilim ölçüleri Verilerin ortalamaya göre olan gruplanması nasıl? Yakın, uzak? Sıklık dağılımlarının karşılaştırılması
MATE211 BİYOİSTATİSTİK
 MATE211 BİYOİSTATİSTİK ÇALIŞMA SORULARININ ÇÖZÜM VE CEVAPLARI Yapılan bir araştırmada, 136 erişkin kişinin kanlarındaki kolesterol düzeyleri gr/dl cinsinden aşağıda verilmiştir: 180 230 190 186 220 191
MATE211 BİYOİSTATİSTİK ÇALIŞMA SORULARININ ÇÖZÜM VE CEVAPLARI Yapılan bir araştırmada, 136 erişkin kişinin kanlarındaki kolesterol düzeyleri gr/dl cinsinden aşağıda verilmiştir: 180 230 190 186 220 191
IİSTATIİSTIİK. Mustafa Sezer PEHLI VAN
 IİSTATIİSTIİK Mustafa Sezer PEHLI VAN İstatistik nedir? İstatistik, veri anlamına gelir, İstatistik, sayılarla uğraşan bir bilim dalıdır, İstatistik, eksik bilgiler kullanarak doğru sonuçlara ulaştıran
IİSTATIİSTIİK Mustafa Sezer PEHLI VAN İstatistik nedir? İstatistik, veri anlamına gelir, İstatistik, sayılarla uğraşan bir bilim dalıdır, İstatistik, eksik bilgiler kullanarak doğru sonuçlara ulaştıran
Biyoistatistiğe Giriş: Temel Tanımlar ve Kavramlar DERS I VE II
 Biyoistatistiğe Giriş: Temel Tanımlar ve Kavramlar DERS I VE II İstatistik Nedir? İstatistik kelimesi farklı anlamlar taşımaktadır. Bunlar; Genel anlamda; üretim, tüketim, nüfus, sağlık, eğitim, tarım,
Biyoistatistiğe Giriş: Temel Tanımlar ve Kavramlar DERS I VE II İstatistik Nedir? İstatistik kelimesi farklı anlamlar taşımaktadır. Bunlar; Genel anlamda; üretim, tüketim, nüfus, sağlık, eğitim, tarım,
Gruplanmış serilerde standart sapma hesabı
 Gruplanmış serilerde standart sapma hesabı Örnek: Verilen gruplanmış serinin standart sapmasını bulunuz? Sınıflar f i X X X m i f i. m i m i - (m i - ) f i.(m i - ) 0 den az 3 4 den az 7 4 6 dan az 4 6
Gruplanmış serilerde standart sapma hesabı Örnek: Verilen gruplanmış serinin standart sapmasını bulunuz? Sınıflar f i X X X m i f i. m i m i - (m i - ) f i.(m i - ) 0 den az 3 4 den az 7 4 6 dan az 4 6
Verilerin Düzenlenmesi
 Verilerin Düzenlenmesi İstatistiksel verileri anlamlı hale getirmenin 5 ayrı yolu: 1. Sözel ifadelerle açıklama 2. Tablolar halinde düzenleme 3. Seriler halinde düzenleme 4. Grafiklerle gösterme 5. Bu
Verilerin Düzenlenmesi İstatistiksel verileri anlamlı hale getirmenin 5 ayrı yolu: 1. Sözel ifadelerle açıklama 2. Tablolar halinde düzenleme 3. Seriler halinde düzenleme 4. Grafiklerle gösterme 5. Bu
Ölçme Sonuçları Üzerinde İstatistiksel İşlemler
 Ölçme Sonuçları Üzerinde İstatistiksel İşlemler Bir grup birey veya nesnenin belli bir özelliğe sahip olup olmadığı ya da belli bir özelliğe ne derece sahip olduğunu belirlemek amacı ile ölçme işlemi yapılır.
Ölçme Sonuçları Üzerinde İstatistiksel İşlemler Bir grup birey veya nesnenin belli bir özelliğe sahip olup olmadığı ya da belli bir özelliğe ne derece sahip olduğunu belirlemek amacı ile ölçme işlemi yapılır.
Veri Analizi. Isınma Hareketleri. Test İstatistikleri. b) En çok tekrar eden: 7 (mod) c) Açıklık = En büyük En küçük = 10 1 = 9. d)
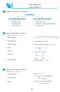 Isınma Hareketleri 1 Aşağıda verilenleri inceleyiniz. Test İstatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Aritmetik ortalama Tepe değer (mod) Ortanca (medyan) Merkezi Dağılım (Yayılma) Ölçüleri Açıklık
Isınma Hareketleri 1 Aşağıda verilenleri inceleyiniz. Test İstatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Aritmetik ortalama Tepe değer (mod) Ortanca (medyan) Merkezi Dağılım (Yayılma) Ölçüleri Açıklık
ENM 5210 İSTATİSTİK VE YAZILIMLA UYGULAMALARI. Ders 2 Merkezi Eğilim Ölçüleri
 ENM 5210 İSTATİSTİK VE YAZILIMLA UYGULAMALARI Ders 2 Merkezi Eğilim Ölçüleri Basit Seriler Elde edilecek ham verilerin küçükten büyüğe doğru sıralanması ile elde edilen serilere basit seri denir ÖRNEK:
ENM 5210 İSTATİSTİK VE YAZILIMLA UYGULAMALARI Ders 2 Merkezi Eğilim Ölçüleri Basit Seriler Elde edilecek ham verilerin küçükten büyüğe doğru sıralanması ile elde edilen serilere basit seri denir ÖRNEK:
ÖLÇME VE DEĞERLENDİRME. Antrenörlük Eğitimi 4. Sınıf. Ölçme ve Değerlendirme - Yrd. Doç. Dr. Yetkin Utku KAMUK
 ÖLÇME VE DEĞERLENDİRME Antrenörlük Eğitimi 4. Sınıf ÖLÇME VE DEĞERLENDİRME Merkezi Eğilim Ölçütleri Mod En çok görülen puandır ve hesaplanma yöntemi yoktur. İnceleme yolu ile bulunur. Terminal istatistiktir.
ÖLÇME VE DEĞERLENDİRME Antrenörlük Eğitimi 4. Sınıf ÖLÇME VE DEĞERLENDİRME Merkezi Eğilim Ölçütleri Mod En çok görülen puandır ve hesaplanma yöntemi yoktur. İnceleme yolu ile bulunur. Terminal istatistiktir.
VERİ KÜMELERİNİ BETİMLEME
 BETİMLEYİCİ İSTATİSTİK VERİ KÜMELERİNİ BETİMLEME Bir amaç için derlenen verilerin tamamının olduğu, veri kümesindeki birimlerin sayısal değerlerinden faydalanarak açık ve net bir şekilde ilgilenilen özellik
BETİMLEYİCİ İSTATİSTİK VERİ KÜMELERİNİ BETİMLEME Bir amaç için derlenen verilerin tamamının olduğu, veri kümesindeki birimlerin sayısal değerlerinden faydalanarak açık ve net bir şekilde ilgilenilen özellik
Kitle: Belirli bir özelliğe sahip bireylerin veya birimlerin tümünün oluşturduğu topluluğa kitle denir.
 BÖLÜM 1: FREKANS DAĞILIMLARI 1.1. Giriş İstatistik, rasgelelik içeren olaylar, süreçler, sistemler hakkında modeller kurmada, gözlemlere dayanarak bu modellerin geçerliliğini sınamada ve bu modellerden
BÖLÜM 1: FREKANS DAĞILIMLARI 1.1. Giriş İstatistik, rasgelelik içeren olaylar, süreçler, sistemler hakkında modeller kurmada, gözlemlere dayanarak bu modellerin geçerliliğini sınamada ve bu modellerden
Merkezi eğilim ölçüleri ile bir frekans dağılımının merkezi belirlenirken; yayılma ölçüleri ile değişkenliği veya yayılma düzeyini tespit eder.
 Yayılma Ölçütleri Merkezi eğilim ölçüleri ile bir frekans dağılımının merkezi belirlenirken; yayılma ölçüleri ile değişkenliği veya yayılma düzeyini tespit eder. Bir başka ifade ile, bir veri setinin,
Yayılma Ölçütleri Merkezi eğilim ölçüleri ile bir frekans dağılımının merkezi belirlenirken; yayılma ölçüleri ile değişkenliği veya yayılma düzeyini tespit eder. Bir başka ifade ile, bir veri setinin,
Copyright 2004 Pearson Education, Inc. Slide 1
 Slide 1 Bölüm 2 Verileri Betimleme, Keşfetme, ve Karşılaştırma 2-1 Genel Bakış 2-2 Sıklık Dağılımları 2-3 Verilerin Görselleştirilmesi 2-4 Merkezi Eğilim Ölçüleri 2-5 Değişimin Ölçülmesi 2-6 Nispi Sabitlerin
Slide 1 Bölüm 2 Verileri Betimleme, Keşfetme, ve Karşılaştırma 2-1 Genel Bakış 2-2 Sıklık Dağılımları 2-3 Verilerin Görselleştirilmesi 2-4 Merkezi Eğilim Ölçüleri 2-5 Değişimin Ölçülmesi 2-6 Nispi Sabitlerin
TR63 BÖLGESİ MEVCUT DURUM ANALİZİ DEMOGRAFİK GÖSTERGELER
 g TR63 BÖLGESİ MEVCUT DURUM ANALİZİ DEMOGRAFİK GÖSTERGELER TABLOLAR Tablo 1. TR63 Bölgesi Doğum Sayısının Yaş Gruplarına Göre Dağılımı (2011)... 1 Tablo 2. Ölümlerin Yaş Gruplarına Göre Dağılımı (2011)...
g TR63 BÖLGESİ MEVCUT DURUM ANALİZİ DEMOGRAFİK GÖSTERGELER TABLOLAR Tablo 1. TR63 Bölgesi Doğum Sayısının Yaş Gruplarına Göre Dağılımı (2011)... 1 Tablo 2. Ölümlerin Yaş Gruplarına Göre Dağılımı (2011)...
8.Hafta. Değişkenlik Ölçüleri. Öğr.Gör.Muhsin ÇELİK. Uygun değişkenlik ölçüsünü hesaplayıp yorumlayabilecek,
 İSTATİSTİK 8.Hafta Değişkenlik Ölçüleri Hedefler Bu üniteyi çalıştıktan sonra; Uygun değişkenlik ölçüsünü hesaplayıp yorumlayabilecek, Serilerin birbirlerine değişkenliklerini yorumlayabileceksiniz. 2
İSTATİSTİK 8.Hafta Değişkenlik Ölçüleri Hedefler Bu üniteyi çalıştıktan sonra; Uygun değişkenlik ölçüsünü hesaplayıp yorumlayabilecek, Serilerin birbirlerine değişkenliklerini yorumlayabileceksiniz. 2
KARŞILAŞTIRMA İSTATİSTİĞİ, ANALİTİK YÖNTEMLERİN KARŞILAŞTIRILMASI, BİYOLOJİK DEĞİŞKENLİK. Doç.Dr. Mustafa ALTINIŞIK ADÜTF Biyokimya AD 2005
 KARŞILAŞTIRMA İSTATİSTİĞİ, ANALİTİK YÖNTEMLERİN KARŞILAŞTIRILMASI, BİYOLOJİK DEĞİŞKENLİK Doç.Dr. Mustafa ALTINIŞIK ADÜTF Biyokimya AD 2005 1 Karşılaştırma istatistiği Temel kavramlar: Örneklem ve evren:
KARŞILAŞTIRMA İSTATİSTİĞİ, ANALİTİK YÖNTEMLERİN KARŞILAŞTIRILMASI, BİYOLOJİK DEĞİŞKENLİK Doç.Dr. Mustafa ALTINIŞIK ADÜTF Biyokimya AD 2005 1 Karşılaştırma istatistiği Temel kavramlar: Örneklem ve evren:
17/01/2015. PowerPoint Template. Dr. S.Nihat ŞAD LOGO. İnönü University. Company Logo
 PowerPoint Template LOGO Dr. S.Nihat ŞAD İnönü University www.thmemgallery.com Company Logo 1 Contents www.thmemgallery.com geliştirme süreci Birey hakkında bilgi toplama yolları lerin sınıflandırılması
PowerPoint Template LOGO Dr. S.Nihat ŞAD İnönü University www.thmemgallery.com Company Logo 1 Contents www.thmemgallery.com geliştirme süreci Birey hakkında bilgi toplama yolları lerin sınıflandırılması
rasgele değişkeninin olasılık yoğunluk fonksiyonu,
 3.6. Bazı Sürekli Dağılımlar 3.6.1 Normal Dağılım Normal dağılım hem uygulamalı hem de teorik istatistikte kullanılan oldukça önemli bir dağılımdır. Normal dağılımın istatistikte önemli bir yerinin olmasının
3.6. Bazı Sürekli Dağılımlar 3.6.1 Normal Dağılım Normal dağılım hem uygulamalı hem de teorik istatistikte kullanılan oldukça önemli bir dağılımdır. Normal dağılımın istatistikte önemli bir yerinin olmasının
ÖLÇME VE DEĞERLENDĠRME (3)
 ÖLÇME VE DEĞERLENDĠRME (3) ÖLÇME SONUÇLARI ÜZERĠNDE ĠSTATĠSTĠKSEL ĠġLEMLER VERĠLERĠN DÜZENLENMESĠ -Herhangi bir test uygulamasından önce verilerin düzenlenmesi için önce bütün puanların büyüklüklerine
ÖLÇME VE DEĞERLENDĠRME (3) ÖLÇME SONUÇLARI ÜZERĠNDE ĠSTATĠSTĠKSEL ĠġLEMLER VERĠLERĠN DÜZENLENMESĠ -Herhangi bir test uygulamasından önce verilerin düzenlenmesi için önce bütün puanların büyüklüklerine
İstatistik ve Olasılık
 İstatistik ve Olasılık Ders 8: Prof. Dr. İrfan KAYMAZ Tanım Tahmin (kestirim veya öngörü): Mevcut bilgi ve deneylere dayanarak olayın bütünü hakkında bir yargıya varmaktır. Bu anlamda, anakütleden çekilen
İstatistik ve Olasılık Ders 8: Prof. Dr. İrfan KAYMAZ Tanım Tahmin (kestirim veya öngörü): Mevcut bilgi ve deneylere dayanarak olayın bütünü hakkında bir yargıya varmaktır. Bu anlamda, anakütleden çekilen
Projenin Adı: İstatistik yardımıyla YGS ye hazırlık için soru çözme planlaması
 Projenin Adı: İstatistik yardımıyla YGS ye hazırlık için soru çözme planlaması Projenin Amacı : YGS de başarılı olmak isteyen bir öğrencinin, istatistiksel yöntemler çerçevesinde, sınavda çıkan soru sayısını,
Projenin Adı: İstatistik yardımıyla YGS ye hazırlık için soru çözme planlaması Projenin Amacı : YGS de başarılı olmak isteyen bir öğrencinin, istatistiksel yöntemler çerçevesinde, sınavda çıkan soru sayısını,
Ders 8: Verilerin Düzenlenmesi ve Analizi
 Ders 8: Verilerin Düzenlenmesi ve Analizi Betimsel İstatistik Merkezsel Eğilim Ölçüleri Dağılım Ölçüleri Grafiksel Gösterimler Bir kitlenin tamamını, ya da kitleden alınan bir örneklemi özetlemekle (betimlemekle)
Ders 8: Verilerin Düzenlenmesi ve Analizi Betimsel İstatistik Merkezsel Eğilim Ölçüleri Dağılım Ölçüleri Grafiksel Gösterimler Bir kitlenin tamamını, ya da kitleden alınan bir örneklemi özetlemekle (betimlemekle)
İÇİNDEKİLER ÖN SÖZ...
 İÇİNDEKİLER ÖN SÖZ... v GİRİŞ... 1 1. İSTATİSTİK İN TARİHÇESİ... 1 2. İSTATİSTİK NEDİR?... 3 3. SAYISAL BİLGİDEN ANLAM ÇIKARILMASI... 4 4. BELİRSİZLİĞİN ELE ALINMASI... 4 5. ÖRNEKLEME... 5 6. İLİŞKİLERİN
İÇİNDEKİLER ÖN SÖZ... v GİRİŞ... 1 1. İSTATİSTİK İN TARİHÇESİ... 1 2. İSTATİSTİK NEDİR?... 3 3. SAYISAL BİLGİDEN ANLAM ÇIKARILMASI... 4 4. BELİRSİZLİĞİN ELE ALINMASI... 4 5. ÖRNEKLEME... 5 6. İLİŞKİLERİN
Verilerin Özetlenmesinde Kullanılan Sayısal Yöntemler
 Verilerin Özetlenmesinde Kullanılan Sayısal Yöntemler Merkezi Eğilim Ölçüleri Merkezi eğilim ölçüsü, bir veri setindeki merkezi, yada tipik, tek bir değeri ifade eder. Nicel veriler için, reel sayı çizgisindeki
Verilerin Özetlenmesinde Kullanılan Sayısal Yöntemler Merkezi Eğilim Ölçüleri Merkezi eğilim ölçüsü, bir veri setindeki merkezi, yada tipik, tek bir değeri ifade eder. Nicel veriler için, reel sayı çizgisindeki
SÜREKLĠ OLASILIK DAĞILIMLARI
 SÜREKLĠ OLASILIK DAĞILIMLARI Sayı ekseni üzerindeki tüm noktalarda değer alabilen değişkenler, sürekli değişkenler olarak tanımlanmaktadır. Bu bölümde, sürekli değişkenlere uygun olasılık dağılımları üzerinde
SÜREKLĠ OLASILIK DAĞILIMLARI Sayı ekseni üzerindeki tüm noktalarda değer alabilen değişkenler, sürekli değişkenler olarak tanımlanmaktadır. Bu bölümde, sürekli değişkenlere uygun olasılık dağılımları üzerinde
7. HAFTA. Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar. Yrd. Doç. Dr.
 7. HAFTA Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar Yrd. Doç. Dr. Sedat ŞEN 14.04.2016 1 Veri nedir? Bir öğrenci kümesine uygulanan
7. HAFTA Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar Yrd. Doç. Dr. Sedat ŞEN 14.04.2016 1 Veri nedir? Bir öğrenci kümesine uygulanan
Türkiye Nüfusunun Yapısal Özellikleri Nüfus; 1- Nüfusun Yaş Gruplarına Göre Dağılımı Genç (Çocuk) Nüfus ( 0-14 yaş )
 Türkiye Nüfusunun Yapısal Özellikleri Nüfus; ülkelerin kalkınmasında, ülkenin dünyadaki etki alanını genişletmesinde potansiyel bir güç olarak önemli bir faktördür. Nüfusun potansiyel gücü, nüfus miktarı
Türkiye Nüfusunun Yapısal Özellikleri Nüfus; ülkelerin kalkınmasında, ülkenin dünyadaki etki alanını genişletmesinde potansiyel bir güç olarak önemli bir faktördür. Nüfusun potansiyel gücü, nüfus miktarı
7. HAFTA. Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar. Yrd. Doç. Dr.
 7. HAFTA Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar Yrd. Doç. Dr. Sedat ŞEN 23.02.2016 1 Veri nedir? Bir öğrenci kümesine uygulanan
7. HAFTA Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar Yrd. Doç. Dr. Sedat ŞEN 23.02.2016 1 Veri nedir? Bir öğrenci kümesine uygulanan
TEST VE MADDE ANALİZLERİ
 TEST VE MADDE ANALİZLERİ Madde güçlüğü Madde ayırt ediciliği Madde varyansı ve madde standart sapması Madde güvenirliği Çeldiricilerin işlerliği Test Analizleri Merkezi Eğilim(Yığılma Ölçüleri) Merkezi
TEST VE MADDE ANALİZLERİ Madde güçlüğü Madde ayırt ediciliği Madde varyansı ve madde standart sapması Madde güvenirliği Çeldiricilerin işlerliği Test Analizleri Merkezi Eğilim(Yığılma Ölçüleri) Merkezi
İÇİNDEKİLER. BÖLÜM 1 Değişkenler ve Grafikler 1. BÖLÜM 2 Frekans Dağılımları 37
 İÇİNDEKİLER BÖLÜM 1 Değişkenler ve Grafikler 1 İstatistik 1 Yığın ve Örnek; Tümevarımcı ve Betimleyici İstatistik 1 Değişkenler: Kesikli ve Sürekli 1 Verilerin Yuvarlanması Bilimsel Gösterim Anlamlı Rakamlar
İÇİNDEKİLER BÖLÜM 1 Değişkenler ve Grafikler 1 İstatistik 1 Yığın ve Örnek; Tümevarımcı ve Betimleyici İstatistik 1 Değişkenler: Kesikli ve Sürekli 1 Verilerin Yuvarlanması Bilimsel Gösterim Anlamlı Rakamlar
5. SUNUM. Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar. Yrd. Doç. Dr.
 5. SUNUM Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar Yrd. Doç. Dr. Sedat ŞEN 08.09.2016 1 Veri nedir? Bir öğrenci kümesine uygulanan
5. SUNUM Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar Yrd. Doç. Dr. Sedat ŞEN 08.09.2016 1 Veri nedir? Bir öğrenci kümesine uygulanan
 009 BS 400- İstatistik sonılannın cevaplanmasında gerekli olabilecek tablolar ve formüller bu kitapçığın sonunda verilmiştir. 1. şağıdakilerden hangisi doğal birimdir? l TV alıcısı Bl Trafik kazası CL
009 BS 400- İstatistik sonılannın cevaplanmasında gerekli olabilecek tablolar ve formüller bu kitapçığın sonunda verilmiştir. 1. şağıdakilerden hangisi doğal birimdir? l TV alıcısı Bl Trafik kazası CL
EĞĠTĠMDE ÖLÇME ve DEĞERLENDĠRME
 EĞĠTĠMDE ÖLÇME ve DEĞERLENDĠRME Öğrenci başarısının veya başarısızlığının kaynağında; öğrenci, öğretmen, çevre ve program vardır. Eğitimde değerlendirme yapılırken bu kaynaklar dikkate alınmaz. Eğitimciler,
EĞĠTĠMDE ÖLÇME ve DEĞERLENDĠRME Öğrenci başarısının veya başarısızlığının kaynağında; öğrenci, öğretmen, çevre ve program vardır. Eğitimde değerlendirme yapılırken bu kaynaklar dikkate alınmaz. Eğitimciler,
1844 te kimlik belgesi vermek amacıyla sayım yapılmıştır. Bu dönemde Anadolu da nüfus yaklaşık 10 milyondur.
 Türkiye de Nüfusun Tarihsel Gelişimi Türkiye de Nüfus Sayımları Dünya nüfusu gibi Türkiye nüfusu da sürekli bir değişim içindedir. Nüfustaki değişim belirli aralıklarla yapılan genel nüfus sayımlarıyla
Türkiye de Nüfusun Tarihsel Gelişimi Türkiye de Nüfus Sayımları Dünya nüfusu gibi Türkiye nüfusu da sürekli bir değişim içindedir. Nüfustaki değişim belirli aralıklarla yapılan genel nüfus sayımlarıyla
ANADOLU ÜNİVERSİTESİ İST 213 OLASILIK DERSİ TANIMLAR VE VERİ SINIFLAMASI
 ANADOLU ÜNİVERSİTESİ İST 213 OLASILIK DERSİ TANIMLAR VE VERİ SINIFLAMASI DOÇ. DR. NİHAL ERGİNEL TANIMLAR VE VERİ SINIFLAMASI Olasılık, ilgilenilen olay/olayların meydana gelme olabilirliğinin ölçülmesidir.
ANADOLU ÜNİVERSİTESİ İST 213 OLASILIK DERSİ TANIMLAR VE VERİ SINIFLAMASI DOÇ. DR. NİHAL ERGİNEL TANIMLAR VE VERİ SINIFLAMASI Olasılık, ilgilenilen olay/olayların meydana gelme olabilirliğinin ölçülmesidir.
objektif değerlendirilmesini sağlayan bilim - veri arasındaki farkın olup olmadığını tespit
 İSTATİST STİK A. G E N E L B İ L G İ A. G E N E L B İ L G İ İstatistik, belli amacla tespit edilen verilerin objektif değerlendirilmesini sağlayan bilim dalıdır. Hedef - verilere anlam kazandırmak - veri
İSTATİST STİK A. G E N E L B İ L G İ A. G E N E L B İ L G İ İstatistik, belli amacla tespit edilen verilerin objektif değerlendirilmesini sağlayan bilim dalıdır. Hedef - verilere anlam kazandırmak - veri
TEMEL EĞİTİMDEN ORTAÖĞRETİME GEÇİŞ ORTAK SINAV BAŞARISININ ÇEŞİTLİ DEĞİŞKENLER AÇISINDAN İNCELENMESİ
 T.C. MİLLÎ EĞİTİM BAKANLIĞI ÖLÇME, DEĞERLENDİRME VE SINAV HİZMETLERİ GENEL MÜDÜRLÜĞÜ VERİ ANALİZİ, İZLEME VE DEĞERLENDİRME DAİRE BAŞKANLIĞI TEMEL EĞİTİMDEN ORTAÖĞRETİME GEÇİŞ ORTAK SINAV BAŞARISININ ÇEŞİTLİ
T.C. MİLLÎ EĞİTİM BAKANLIĞI ÖLÇME, DEĞERLENDİRME VE SINAV HİZMETLERİ GENEL MÜDÜRLÜĞÜ VERİ ANALİZİ, İZLEME VE DEĞERLENDİRME DAİRE BAŞKANLIĞI TEMEL EĞİTİMDEN ORTAÖĞRETİME GEÇİŞ ORTAK SINAV BAŞARISININ ÇEŞİTLİ
BKİ farkı Standart Sapması (kg/m 2 ) A B BKİ farkı Ortalaması (kg/m 2 )
 4. SUNUM 1 Gözlem ya da deneme sonucu elde edilmiş sonuçların, rastlantıya bağlı olup olmadığının incelenmesinde kullanılan istatistiksel yöntemlere HİPOTEZ TESTLERİ denir. Sonuçların rastlantıya bağlı
4. SUNUM 1 Gözlem ya da deneme sonucu elde edilmiş sonuçların, rastlantıya bağlı olup olmadığının incelenmesinde kullanılan istatistiksel yöntemlere HİPOTEZ TESTLERİ denir. Sonuçların rastlantıya bağlı
ÖRNEKLEME DAĞILIŞLARI VE TAHMİNLEYİCİLERİN ÖZELLİKLERİ
 ÖRNEKLEME DAĞILIŞLARI VE TAHMİNLEYİCİLERİN ÖZELLİKLERİ TEMEL KAVRAMLAR PARAMETRE: Populasyonun sayısal açıklayıcı bir ölçüsüdür ve anakütledeki tüm elemanlar dikkate alınarak hesaplanabilir. Ana kütledeki
ÖRNEKLEME DAĞILIŞLARI VE TAHMİNLEYİCİLERİN ÖZELLİKLERİ TEMEL KAVRAMLAR PARAMETRE: Populasyonun sayısal açıklayıcı bir ölçüsüdür ve anakütledeki tüm elemanlar dikkate alınarak hesaplanabilir. Ana kütledeki
İstatistik ve Olasılık
 İstatistik ve Olasılık KORELASYON ve REGRESYON ANALİZİ Doç. Dr. İrfan KAYMAZ Tanım Bir değişkenin değerinin diğer değişkendeki veya değişkenlerdeki değişimlere bağlı olarak nasıl etkilendiğinin istatistiksel
İstatistik ve Olasılık KORELASYON ve REGRESYON ANALİZİ Doç. Dr. İrfan KAYMAZ Tanım Bir değişkenin değerinin diğer değişkendeki veya değişkenlerdeki değişimlere bağlı olarak nasıl etkilendiğinin istatistiksel
GİRİŞ. Bilimsel Araştırma: Bilimsel bilgi elde etme süreci olarak tanımlanabilir.
 VERİ ANALİZİ GİRİŞ Bilimsel Araştırma: Bilimsel bilgi elde etme süreci olarak tanımlanabilir. Bilimsel Bilgi: Kaynağı ve elde edilme süreçleri belli olan bilgidir. Sosyal İlişkiler Görgül Bulgular İşlevsel
VERİ ANALİZİ GİRİŞ Bilimsel Araştırma: Bilimsel bilgi elde etme süreci olarak tanımlanabilir. Bilimsel Bilgi: Kaynağı ve elde edilme süreçleri belli olan bilgidir. Sosyal İlişkiler Görgül Bulgular İşlevsel
ÖĞRENCİNİN ADI SOYADI:. NO:
 ÖĞRENCİNİN ADI SOYADI:. NO: İMZA: 2011-2012 ÖĞRETİM YILI TIP 1. SINIF TEMEL BİYOİSTATİSTİK DERSİ ARA SINAVI (04.11.2011) Biyoistatistik ve Tıp Bilişimi Anabilim Dalı Başarılar Temel Biyoistatistik dersi
ÖĞRENCİNİN ADI SOYADI:. NO: İMZA: 2011-2012 ÖĞRETİM YILI TIP 1. SINIF TEMEL BİYOİSTATİSTİK DERSİ ARA SINAVI (04.11.2011) Biyoistatistik ve Tıp Bilişimi Anabilim Dalı Başarılar Temel Biyoistatistik dersi
Zaman Serileri. IENG 481 Tahmin Yöntemleri Dr. Hacer Güner Gören
 Zaman Serileri IENG 481 Tahmin Yöntemleri Dr. Hacer Güner Gören Zaman Serisi nedir? Kronolojik sırayla elde edilen verilere sahip değișkenlere zaman serisi adı verilmektedir. Genel olarak zaman serisi,
Zaman Serileri IENG 481 Tahmin Yöntemleri Dr. Hacer Güner Gören Zaman Serisi nedir? Kronolojik sırayla elde edilen verilere sahip değișkenlere zaman serisi adı verilmektedir. Genel olarak zaman serisi,
Halk Sağlığı-Ders 8 Sağlık Düzeyinin Ölçülmesi ve Epidemiyoloji
 Halk Sağlığı-Ders 8 Sağlık Düzeyinin Ölçülmesi ve Epidemiyoloji Öğr. Gör. Hüseyin ARI 1 İstanbul Arel Üniversitesi M.Y.O Sağlık Kurumları İşletmeciliği Epidemiyoloji; hastalık ve sağlıkla ilgili olayların
Halk Sağlığı-Ders 8 Sağlık Düzeyinin Ölçülmesi ve Epidemiyoloji Öğr. Gör. Hüseyin ARI 1 İstanbul Arel Üniversitesi M.Y.O Sağlık Kurumları İşletmeciliği Epidemiyoloji; hastalık ve sağlıkla ilgili olayların
ALKÜ EKONOMİ ve FİNANS BÖLÜMÜ ISL 207 İSTATİSTİK I ALIŞTIRMALAR
 ALKÜ EKONOMİ ve FİNANS BÖLÜMÜ ISL 207 İSTATİSTİK I ALIŞTIRMALAR 1- İlaçla tedavi edilen 7 hastanın ortalama iyileşme süresi 22.6 gün ve standart sapması.360 gündür. Ameliyatla tedavi edilen 9 hasta için
ALKÜ EKONOMİ ve FİNANS BÖLÜMÜ ISL 207 İSTATİSTİK I ALIŞTIRMALAR 1- İlaçla tedavi edilen 7 hastanın ortalama iyileşme süresi 22.6 gün ve standart sapması.360 gündür. Ameliyatla tedavi edilen 9 hasta için
İstatistik ve Olasılığa Giriş. İstatistik ve Olasılığa Giriş. Ders 3 Verileri Sayısal Ölçütlerle İfade Etme. Verileri Sayısal Ölçütlerle İfade Etme
 İstatistik ve Olasılığa Giriş Robert J. Beaver Barbara M. Beaver William Mendenhall Presentation designed and written by: Barbara M. Beaver İstatistik ve Olasılığa Giriş Ders 3 Verileri Sayısal Ölçütlerle
İstatistik ve Olasılığa Giriş Robert J. Beaver Barbara M. Beaver William Mendenhall Presentation designed and written by: Barbara M. Beaver İstatistik ve Olasılığa Giriş Ders 3 Verileri Sayısal Ölçütlerle
Veri nedir? Bir öğrenci kümesine uygulanan bir sınavdan elde edilen puanların herhangi bir işlem yapılmamış haline ham veri denir (ham puanlar) denir.
 Dr. Sedat Şen 1 Veri nedir? Bir öğrenci kümesine uygulanan bir sınavdan elde edilen puanların herhangi bir işlem yapılmamış haline ham veri denir (ham puanlar) denir. Değer nedir? Bir veriyi (puanlar dizisini)
Dr. Sedat Şen 1 Veri nedir? Bir öğrenci kümesine uygulanan bir sınavdan elde edilen puanların herhangi bir işlem yapılmamış haline ham veri denir (ham puanlar) denir. Değer nedir? Bir veriyi (puanlar dizisini)
KONU2 MERKEZİ EĞİLİM ÖLÇÜLERİ EĞİLİM ÖLÇÜLERİ ANALİTİK ORTALAMALAR ANALİTİK OLMAYAN MERKEZİ. Aritmetik ortalama **Medyan(median)
 KONU2 MERKEZİ EĞİLİM ÖLÇÜLERİ 1 MERKEZİ EĞİLİM ÖLÇÜLERİ ANALİTİK ORTALAMALAR Bir örneklemde mevcut olan tüm veriler hesaba katılır. ANALİTİK OLMAYAN MERKEZİ EĞİLİM ÖLÇÜLERİ Bir örneklemdeki verilerin bir
KONU2 MERKEZİ EĞİLİM ÖLÇÜLERİ 1 MERKEZİ EĞİLİM ÖLÇÜLERİ ANALİTİK ORTALAMALAR Bir örneklemde mevcut olan tüm veriler hesaba katılır. ANALİTİK OLMAYAN MERKEZİ EĞİLİM ÖLÇÜLERİ Bir örneklemdeki verilerin bir
ÖLÇME DEĞERLENDİRME ÜNİTE BAŞLIKLARI
 ÖLÇME DEĞERLENDİRME ÜNİTE BAŞLIKLARI 1. TEMEL KAVRAMLAR 2. ÖLÇMEDE HATA (GÜVENİRLİK GEÇERLİK) 3. İSTATİSTİK 1. TEMEL KAVRAMLAR Ölçme, Ölçüm, Ölçme Kuralı, Ölçüt, Değerlendirme. Ölçme Türleri: Doğrudan,
ÖLÇME DEĞERLENDİRME ÜNİTE BAŞLIKLARI 1. TEMEL KAVRAMLAR 2. ÖLÇMEDE HATA (GÜVENİRLİK GEÇERLİK) 3. İSTATİSTİK 1. TEMEL KAVRAMLAR Ölçme, Ölçüm, Ölçme Kuralı, Ölçüt, Değerlendirme. Ölçme Türleri: Doğrudan,
RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI. Yrd. Doç. Dr. Emre ATILGAN
 RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI Yrd. Doç. Dr. Emre ATILGAN 1 RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI Olasılığa ilişkin olayların çoğunluğunda, deneme sonuçlarının bir veya birkaç yönden incelenmesi
RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI Yrd. Doç. Dr. Emre ATILGAN 1 RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI Olasılığa ilişkin olayların çoğunluğunda, deneme sonuçlarının bir veya birkaç yönden incelenmesi
Türkiye nin Nüfus Özellikleri ve Dağılışı
 Türkiye nin Nüfus Özellikleri ve Dağılışı 1 Nüfusun Yaş Gruplarına Göre Dağılımı Nüfus miktarı kadar önem taşıyan bir başka kriter de nüfusun yaş yapısıdır. Çünkü, yaş grupları nüfusun genel yapısı ve
Türkiye nin Nüfus Özellikleri ve Dağılışı 1 Nüfusun Yaş Gruplarına Göre Dağılımı Nüfus miktarı kadar önem taşıyan bir başka kriter de nüfusun yaş yapısıdır. Çünkü, yaş grupları nüfusun genel yapısı ve
Doğu ATEŞ ADRESE DAYALI NÜFUS KAYIT SİSTEMİ 2007 NÜFUS SAYIMI SONUÇLARI HAKKINDA İLK YORUMLAR
 ADRESE DAYALI NÜFUS KAYIT SİSTEMİ 2007 NÜFUS SAYIMI SONUÇLARI HAKKINDA İLK YORUMLAR 2007 yılında çalışmaları sürdürülmekte olan nüfus sayımının ilk sonuçları açıklanmış bulunmaktadır. Bu sonuçlara göre
ADRESE DAYALI NÜFUS KAYIT SİSTEMİ 2007 NÜFUS SAYIMI SONUÇLARI HAKKINDA İLK YORUMLAR 2007 yılında çalışmaları sürdürülmekte olan nüfus sayımının ilk sonuçları açıklanmış bulunmaktadır. Bu sonuçlara göre
İSTATİSTİK HAFTA. ÖRNEKLEME METOTLARI ve ÖRNEKLEM BÜYÜKLÜĞÜNÜN TESPİTİ
 ÖRNEKLEME METOTLARI ve ÖRNEKLEM BÜYÜKLÜĞÜNÜN TESPİTİ HEDEFLER Bu üniteyi çalıştıktan sonra; Örneklemenin niçin ve nasıl yapılacağını öğreneceksiniz. Temel Örnekleme metotlarını öğreneceksiniz. Örneklem
ÖRNEKLEME METOTLARI ve ÖRNEKLEM BÜYÜKLÜĞÜNÜN TESPİTİ HEDEFLER Bu üniteyi çalıştıktan sonra; Örneklemenin niçin ve nasıl yapılacağını öğreneceksiniz. Temel Örnekleme metotlarını öğreneceksiniz. Örneklem
NORMAL DAĞILIM VE ÖNEMLİLİK TESTLERİ İLE İLGİLİ PROBLEMLER
 NORMAL DAĞILIM VE ÖNEMLİLİK TESTLERİ İLE İLGİLİ PROBLEMLER A) Normal Dağılım ile İlgili Sorular Sayfa /4 Hamileler ile ilgili bir araştırmada, bu grubun hemoglobin değerlerinin normal dağılım gösterdiği
NORMAL DAĞILIM VE ÖNEMLİLİK TESTLERİ İLE İLGİLİ PROBLEMLER A) Normal Dağılım ile İlgili Sorular Sayfa /4 Hamileler ile ilgili bir araştırmada, bu grubun hemoglobin değerlerinin normal dağılım gösterdiği
GELİR VE YAŞAM KOŞULLARI ARAŞTIRMASI. Son Güncelleme
 TÜRKİYE ŞEKER SANAYİİ İŞÇİLERİ SENDİKASI GENEL MERKEZİ GELİR VE YAŞAM KOŞULLARI ARAŞTIRMASI 2008 Son Güncelleme 29/07/2010 Şeker-İş Sendikası Genel Merkezi AR-GE(Araştırma Geliştirme) Birimi Karanfil Sokak,
TÜRKİYE ŞEKER SANAYİİ İŞÇİLERİ SENDİKASI GENEL MERKEZİ GELİR VE YAŞAM KOŞULLARI ARAŞTIRMASI 2008 Son Güncelleme 29/07/2010 Şeker-İş Sendikası Genel Merkezi AR-GE(Araştırma Geliştirme) Birimi Karanfil Sokak,
BÖLÜM 1 GİRİŞ: İSTATİSTİĞİN MÜHENDİSLİKTEKİ ÖNEMİ
 BÖLÜM..AMAÇ GİRİŞ: İSTATİSTİĞİ MÜHEDİSLİKTEKİ ÖEMİ Doğa bilimlerinde karşılaştığımız problemlerin birçoğunda olaydaki değişkenlerin değerleri bilindiğinde probleme kesin ve tek bir çözüm bulunabilir. Örneğin
BÖLÜM..AMAÇ GİRİŞ: İSTATİSTİĞİ MÜHEDİSLİKTEKİ ÖEMİ Doğa bilimlerinde karşılaştığımız problemlerin birçoğunda olaydaki değişkenlerin değerleri bilindiğinde probleme kesin ve tek bir çözüm bulunabilir. Örneğin
Biyoistatistiğin Tanımı Biyoistatistikte Kullanılan Terimler Değişken Tipleri Parametre ve İstatistik Tanımlayıcı İstatistikler
 Biyoistatistiğin Tanımı Biyoistatistikte Kullanılan Terimler Değişken Tipleri Parametre ve İstatistik Tanımlayıcı İstatistikler Doç. Dr. Ertuğrul ÇOLAK Eskişehir Osmangazi Üniversitesi Tıp Fakültesi Biyoistatistik
Biyoistatistiğin Tanımı Biyoistatistikte Kullanılan Terimler Değişken Tipleri Parametre ve İstatistik Tanımlayıcı İstatistikler Doç. Dr. Ertuğrul ÇOLAK Eskişehir Osmangazi Üniversitesi Tıp Fakültesi Biyoistatistik
LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I BAHAR DÖNEMĐ BÜTÜNLEME SINAVI SORULARI
 LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I 2015-2016 BAHAR DÖNEMĐ BÜTÜNLEME SINAVI SORULARI Tarih/Saat/Yer: 24.06.16/11:00-12:30/AS010 Instructor: Prof. Dr. Hüseyin Oğuz
LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I 2015-2016 BAHAR DÖNEMĐ BÜTÜNLEME SINAVI SORULARI Tarih/Saat/Yer: 24.06.16/11:00-12:30/AS010 Instructor: Prof. Dr. Hüseyin Oğuz
LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I BAHAR DÖNEMĐ TELAFĐ SINAVI SORULARI
 LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I 2015-2016 BAHAR DÖNEMĐ TELAFĐ SINAVI SORULARI Tarih/Saat/Yer: 20.06.16/15:00-16:30/AS010 Instructor: Prof. Dr. Hüseyin Oğuz Öğrenci
LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I 2015-2016 BAHAR DÖNEMĐ TELAFĐ SINAVI SORULARI Tarih/Saat/Yer: 20.06.16/15:00-16:30/AS010 Instructor: Prof. Dr. Hüseyin Oğuz Öğrenci
Yrd. Doç. Dr. Sedat Şen 9/27/2018 2
 2.SUNUM Belirli bir amaç için toplanmış verileri anlamlı haline getirmenin farklı yolları vardır. Verileri sözel ifadelerle açıklama Verileri tablolar halinde düzenleme Verileri grafiklerle gösterme Veriler
2.SUNUM Belirli bir amaç için toplanmış verileri anlamlı haline getirmenin farklı yolları vardır. Verileri sözel ifadelerle açıklama Verileri tablolar halinde düzenleme Verileri grafiklerle gösterme Veriler
Sıklık Tabloları, BASİT ve TEK değişkenli Grafikler Ders 3 ve 4 ve 5
 Sıklık Tabloları, BASİT ve TEK değişkenli Grafikler Ders 3 ve 4 ve 5 Sıklık Tabloları Veri dizisinde yer alan değerlerin tekrarlama sayılarını içeren tabloya sıklık tablosu denir. Tek değişken için çizilen
Sıklık Tabloları, BASİT ve TEK değişkenli Grafikler Ders 3 ve 4 ve 5 Sıklık Tabloları Veri dizisinde yer alan değerlerin tekrarlama sayılarını içeren tabloya sıklık tablosu denir. Tek değişken için çizilen
İSTATİSTİK I KISA ÖZET KOLAYAOF
 DİKKATİNİZE: BURADA SADECE ÖZETİN İLK ÜNİTESİ SİZE ÖRNEK OLARAK GÖSTERİLMİŞTİR. ÖZETİN TAMAMININ KAÇ SAYFA OLDUĞUNU ÜNİTELERİ İÇİNDEKİLER BÖLÜMÜNDEN GÖREBİLİRSİNİZ. İSTATİSTİK I KISA ÖZET KOLAYAOF 2 Kolayaof.com
DİKKATİNİZE: BURADA SADECE ÖZETİN İLK ÜNİTESİ SİZE ÖRNEK OLARAK GÖSTERİLMİŞTİR. ÖZETİN TAMAMININ KAÇ SAYFA OLDUĞUNU ÜNİTELERİ İÇİNDEKİLER BÖLÜMÜNDEN GÖREBİLİRSİNİZ. İSTATİSTİK I KISA ÖZET KOLAYAOF 2 Kolayaof.com
DOĞURGANLIĞI BELİRLEYEN DİĞER ARA DEĞİŞKENLER 7
 DOĞURGANLIĞI BELİRLEYEN DİĞER ARA DEĞİŞKENLER 7 Banu Akadlı Ergöçmen ve Mehmet Ali Eryurt Bu bölümde gebeliği önleyici yöntem kullanımı dışında kadının gebe kalma riskini etkileyen temel faktörler incelenmektedir.
DOĞURGANLIĞI BELİRLEYEN DİĞER ARA DEĞİŞKENLER 7 Banu Akadlı Ergöçmen ve Mehmet Ali Eryurt Bu bölümde gebeliği önleyici yöntem kullanımı dışında kadının gebe kalma riskini etkileyen temel faktörler incelenmektedir.
İstatistik ve Olasılık
 İstatistik ve Olasılık Ders 2: Prof. Dr. İrfan KAYMAZ Tanım İnceleme sonucu elde edilen ham verilerin istatistiksel yöntemler kullanılarak özetlenmesi açıklayıcı istatistiği konusudur. Açıklayıcı istatistikte
İstatistik ve Olasılık Ders 2: Prof. Dr. İrfan KAYMAZ Tanım İnceleme sonucu elde edilen ham verilerin istatistiksel yöntemler kullanılarak özetlenmesi açıklayıcı istatistiği konusudur. Açıklayıcı istatistikte
Oluşturulan evren listesinden örnekleme birimlerinin seçkisiz olarak çekilmesidir
 Bilimsel Araştırma Yöntemleri Prof. Dr. Şener Büyüköztürk Doç. Dr. Ebru Kılıç Çakmak Yrd. Doç. Dr. Özcan Erkan Akgün Doç. Dr. Şirin Karadeniz Dr. Funda Demirel Örnekleme Yöntemleri Evren Evren, araştırma
Bilimsel Araştırma Yöntemleri Prof. Dr. Şener Büyüköztürk Doç. Dr. Ebru Kılıç Çakmak Yrd. Doç. Dr. Özcan Erkan Akgün Doç. Dr. Şirin Karadeniz Dr. Funda Demirel Örnekleme Yöntemleri Evren Evren, araştırma
BÖLÜM 3 KURAMSAL ÇATI VE HİPOTEZ GELİŞ
 BÖLÜM 3 KURAMSAL ÇATI VE HİPOTEZ GELİŞ İŞTİRME Araştırma rma SüreciS 1.Gözlem Genel araştırma alanı 3.Sorunun Belirlenmesi Sorun taslağının hazırlanması 4.Kuramsal Çatı Değişkenlerin açıkça saptanması
BÖLÜM 3 KURAMSAL ÇATI VE HİPOTEZ GELİŞ İŞTİRME Araştırma rma SüreciS 1.Gözlem Genel araştırma alanı 3.Sorunun Belirlenmesi Sorun taslağının hazırlanması 4.Kuramsal Çatı Değişkenlerin açıkça saptanması
Mühendislikte İstatistiksel Yöntemler
 Mühendislikte İstatistiksel Yöntemler BÖLÜM 7 TAHMİNLER Yrd. Doç. Dr. Fatih TOSUNOĞLU 1 Tahmin (kestirim veya öngörü): Mevcut bilgi ve deneylere dayanarak olayın bütünü hakkında bir yargıya varmaktır.
Mühendislikte İstatistiksel Yöntemler BÖLÜM 7 TAHMİNLER Yrd. Doç. Dr. Fatih TOSUNOĞLU 1 Tahmin (kestirim veya öngörü): Mevcut bilgi ve deneylere dayanarak olayın bütünü hakkında bir yargıya varmaktır.
