7. HAFTA. Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar. Yrd. Doç. Dr.
|
|
|
- Nesrin Suvari
- 7 yıl önce
- İzleme sayısı:
Transkript
1 7. HAFTA Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar Yrd. Doç. Dr. Sedat ŞEN
2 Veri nedir? Bir öğrenci kümesine uygulanan bir sınavdan elde edilen puanların herhangi bir işlem yapılmamış haline ham veri denir (ham puanlar) denir. Değer nedir? Bir veriyi (puanlar dizisini) oluşturan ölçümlerin her birine değer (puan) denir. Frekans nedir? Frekans bir değere (puana) ait tekrar sayısıdır. Bir puanın kaç öğrenci tarafından alındığını belirten tekrar sayısına frekans denir. 2
3 Bir durumdan diğerine farklılık gösteren özelliklere değişken denilir. Değişkenler gözlemden gözleme farklı değerler alabilir. Bir özellik her gözlemde aynı değeri alıyorsa, yani gözlemden gözleme değişmiyorsa bu duruma SABİT denir. Boy uzunluğu, cinsiyet, yaş, kilo vb. değişkenlere örnek olarak verilebilir. Değişkenler sayılarla ifade edilmesi yönünden, nitel ve nicel, aldıkları değere göre; sürekli ve süreksiz, başka bir değişkene bağlılık derecesine göre; bağımlı ve bağımsız, olarak gruplara ayrılırlar. 3
4 Verilerin Sıraya Dizilmesi Frekans Tablosu Bağıl Frekans Tablosu Grafikler Çubuk Grafiği (Bar Grafik) Histogram Grafiği Çizgi Grafiği 4
5 Hiçbir şekilde işlenmemiş üzerinde herhangi bir işlem yapılmamış (sıraya konmamış) puanlardan oluşan veriye ham veri denir. ÖĞRENCİ PUAN ÖĞRENCİ PUAN ÖĞRENCİ PUAN AHMET 42 FATMA 97 NURCAN 98 AHMET 81 GÜLLÜ 86 ÖMER 88 AYBERK 61 HACER 98 RAHİME 93 AYŞE 93 HASAN 75 SAİT 36 AYŞEGÜL 84 HAZARE 79 SALİH 69 BEDİA 80 İMRAN 88 SEDAT 71 BETÜL 84 KEMAL 79 SONGÜL 86 BÜŞRA 93 KÜBRA 93 TUBA 93 CUMA 81 MEDİNE 79 TUBA 95 ELİF 87 MEHMET 52 ÜMRAN 87 ESMA 86 MEHMET 69 YASEMİN 73 FATMA 91 MEHMET 84 ZEYNEP 77 FATMA 93 MERVE 85 ZEYNEP 86 5
6 ÖĞRENCİ PUAN ÖĞRENCİ PUAN ÖĞRENCİ PUAN Verilerin düzenlenmesi, puanların büyükten küçüğe ya da küçükten büyüğe doğru sıralanması yoluyla yapılır. Puanlar sıralandıktan sonra puan dizisinin üst ve alt sınırları rahatça belirlenir. Puanlar 36 ile 98 arasında değişiklik göstermekte ve bazı puanlar birden fazla gözlenmektedir. SAİT 36 BEDİA 80 ÖMER 88 AHMET 42 AHMET 81 İMRAN 88 MEHMET 52 CUMA 81 FATMA 91 AYBERK 61 MEHMET 84 KÜBRA 93 MEHMET 69 BETÜL 84 TUBA 93 SALİH 69 AYŞEGÜL 84 AYŞE 93 SEDAT 71 MERVE 85 RAHİME 93 YASEMİN 73 ESMA 86 FATMA 93 HASAN 75 GÜLLÜ 86 BÜŞRA 93 ZEYNEP 77 ZEYNEP 86 TUBA 95 KEMAL 79 SONGÜL 86 FATMA 97 HAZARE 79 ELİF 87 HACER 98 MEDİNE 79 ÜMRAN 87 NURCAN 98 Yrd. Doç. Dr. Sedat ŞEN
7 Toplamlı frekansın en altındaki değer sınıf mevcudunu verir. Bu veriye göre sınıf mevcudu 39 dur. Puanla Frekan Toplamlı r s Frekans Yüzde Toplamlı Yüzdeler Yrd. Doç. Dr. Sedat ŞEN
8 Frekans tablosunda hem puanlar sıralanır, hem de puandan kaç tane olduğu sayılarak frekanslar bulunur. Ancak hem puan dağılımının hem genel durumu daha iyi görebilmek hem de hesaplamaları kolaylaştırmak için verilerin gruplandırılması gerekmektedir. Verileri gruplandırırken öncelikle grup sayısı saptanır. Grup sayısının puan dağılımının gerçek özelliklerinin kaybolmaması için küçük seçilmemesine ve hesaplama işlemlerinin kolaylığı için büyük seçilmemesine dikkat edilmelidir. Ayrıca grup sayısının tek olması, puan dağılımında simetri sağladığı için, puanların 7,9,11 ve 13 gibi tek sayıda gruba ayrılması tavsiye edilir. 8
9 Puan Aralığı Çetele Frekans Toplamlı Frekans // 2 2 Puan Dağılımını 7 gruba ayırmak istiyoruz / / /// /////// ////////////// //////////// (98-36)/7=8.9 aralık genişliği olarak hesaplanır. Yrd. Doç. Dr. Sedat ŞEN
10 Frekans Puan 39 öğrencinin ölçme ara sınavından aldığı puanların gruplandırılmış halini gösteren bar grafiği Yrd. Doç. Dr. Sedat ŞEN
11 Frekans öğrencinin ölçme ara sınavından aldığı puanların gruplandırılmış halini gösteren çizgi grafiği Puan Yrd. Doç. Dr. Sedat ŞEN
12 Bu da aynı verinin histogram grafiği ile gösterilmesi. Frekans Puan 12
13 Bar (çubuk) grafiği ile histogram arasındaki fark nedir? 13
14 Genel olarak test istatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Merkezi Dağılım (Yayılma) Ölçüleri olmak üzere 2 grupta incelenebilir. 14
15 Merkezi Eğilim Ölçüleri, belli bir özelliğe ya da değişkene ilişkin ölçme sonuçlarının, hangi değer etrafında toplandığını gösteren ve veri grubunu özetleyen ölçülerdir. Merkezi eğilim ölçüleri: Mod (Tepe Değeri) Aritmetik Ortalama Medyan (Ortanca) Ağırlıklı Ortalama 15
16 Bir veri grubunda en çok tekrar eden ölçme sonucuna (puana) mod denir. Yani en fazla frekansa sahip değer olarak tanımlanır. Mod, verilerin en çok tekrar eden değer etrafında toplandığını ifade eden bir ölçüdür. Veri grubunu betimlemede, tüm verilerden ziyade en çok tekrar eden verinin kullanılmasından dolayı mod, diğer merkezi eğilim ölçülerine kıyasla veri hakkında en az bilgi veren ölçüdür. Hiçbir aritmetik işlem gerektirmez. Örnek: 1, 2, 7, 5, 6, 4, 4, 4, 3, 2,1, 7, 8,10, 9, 2, 2, 4, 4 Bu verideki sayılar arasında 4 sayısı en çok tekrarlanan (5 defa) sayıdır. Dolayısıyla bu verinin modu=4 tür. 16
17 Bazı durumlarda, en yüksek frekansa sahip değer iki veya daha fazla sayıda olabilir. Bu durumda dağılımın tek tepe değeri olmaz. Dağılım iki veya daha fazla tepe değere sahiptir (eğer en çok gözlenen değerler art arda gelmiyorsa). Öğrencilerin matematik sınavından aldığı puanlar: 45, 55, 50, 60, 60, 60, 45, 35, 45, 75 ve 50 olsun. 45 ve 60 puanlarının her ikisi de aynı ve en yüksek frekansa sahiptir. Bu durumda dağılım tek değil çift tepe değerlidir çünkü 45 ve 60 ın arasında 50 ve 55 var. Bir puan dağılımında frekansı en yüksek olan birden çok değer varsa ve bunlar art arda geliyorsa en çok tekrar eden bu puanlar toplanıp ortalaması alınır ve modu bu ortalamaya eşittir denilir! Ör: 45, 60, 60, 60, 62, 62, 35, 62, 75, 55 en çok tekrar eden (3 defa ile) 60 ve 62 sayılarıdır ve bu iki sayının arasında başka bir sayı bulunmamaktadır. Bu durumda mod=(60+62)/2 = 61 dir. 17
18 Bir dağılımın birden fazla tepe değere sahip olması verilerin hangi değer etrafında yığıldığı hakkında sağlıklı bilgi vermez. Grubun homojen değil heterojen bir yapıya sahip olduğunu gösterir. Bazı durumlarda da verideki değerlerin hepsi aynı sayıda gözlenir. Bu durumda tepe değer yoktur denilir. 50, 60,70, 80 verisinde tepe değer yoktur. Önceki slaytlarda vermiş olduğumuz verinin modu 93 tür 18
19 Tepe değer bulunurken sadece en çok tekrarlayan ölçme sonucu alındığından tepe değer kaba ve kullanışsızdır. Hesaplaması çok kolaydır. Nitel veriler ve sınıflama düzeyindeki ölçme sonuçları üzerinde uygulanabilecek tek merkezi eğilim ölçüsüdür. Veri grubundaki en ufak değişiklik tepe değerin beklenmedik şekilde değişmesine yol açtığı için tepe değer küçük değişikliklere duyarlıdır ve bu yüzden kullanışsızdır. 19
20 Puanlar Frekans Tepedeğer =? Tepedeğer =? Puanlar Frekans
21 Örnek 1 Puan Frekans Aritmetik ortalama=? Medyan=? Mod=? Normal Dağılım 21
22 Örnek 2 Puan Frekans Aritmetik ortalama=? Medyan=? Mod=? Sola Çarpık 22
23 Örnek 3 Puan Frekans Aritmetik ortalama=? Medyan=? Mod=? Sağa Çarpık 23
24 Örnek 4 Puan Frekans Çift modlu Örnek 5 Puan Frekans çünkü Tepe (değer) yok Mod hesaplanamaz
25 Sıralanmış bir veri grubunu tam ortadan ikiye ayıran noktaya rastlayan ölçme sonucuna ortanca denir. Ortancanın sırası (yeri) gruplandırılmış ve sıralanmış verilerde (N+1)/2 formülüyle hesaplanır. Bulunan sayı ortancanın en düşük sayıdan uzaklığını verir. Veri sayısının tek olması durumunda: 1, 4, 5, 6, 7, 8, 11 şeklinde sıralı halde verilmiş olan puan dağılımının ortancası, (7+1)/2=4 yani 4. sıradaki sayıdır. Bu puanların tam orta noktasına rastlayan ölçme sonucu olan 6'dır. Veri sayısının çift olması durumunda: 11, 12, 13, 13, 16, 17, 18, 19, 21, 22, 23, 24 şeklinde sıralı halde verilmiş olan puan dağılımının ortancası en ortadaki iki sayının ortalamasıdır (17+18)/2 = 17.5' tir. Önceki slaytlarda vermiş olduğumuz verinin ortancası 85 tir. 25
26 1, 4, 5, 6, 7, 8, 11 11, 12, 13, 13, 16, 17, 18, 19, 21, 22, 23, 24 17,5 Ortanca sıralanmış veriyi tam ortadan ikiye bölen sayı(lar) ile bulunur. 26
27 En çok kullanılan merkezi yığılma ölçüsüdür. Aritmetik ortalama, verideki puanların toplamının verideki eleman sayısına bölünmesiyle bulunur. 27
28 10, 20, 30, 30, 40 dağılımına sahip olan bir veri için aritmetik ortalama hesaplaması aşağıdaki gibidir. Önceki slaytlarda vermiş olduğumuz 39 kişilik verinin ortalaması tür. 28
29 X f fx Toplam Yrd. Doç. Dr. Sedat ŞEN
30 X f Xo f *Xo Toplam
31 Birden çok veri kümesinin bulunduğu durumlarda, bunların farklı katsayılarla ağırlıklandırılması gerekir. Örneğin, bir yarıyılda herhangi bir dersten yapılan ölçme işlemlerinin farklı katsayılarla çarpıldıktan sonra ortalamalarının hesaplanması gerekir. Bu şekilde hesaplanan ortalamaya ağırlıklı ortalama denir. Yrd. Doç. Dr. Sedat ŞEN
32 Örneğin, ikinci yarıyılda aldığı fizik dersindeki yazılı, sözlü ve ödev notları sırasıyla 7, 9, 8 olan bir öğrencinin fizik dersi ağırlıklı not ortalaması, yazılı, sözlü ve ödev notlarına verilmek istenen ağırlığa bağlıdır. Sırasıyla bu notlara verilmek istenen ağırlık %50, %30 ve %20 şeklinde belirlenmişse, o derse ilişkin öğrencinin ağırlıklı not ortalaması şu şekilde hesaplanır: 32
33 Ders Kredi Not Puan*Kredi Fizik Kimya Biyoloji Matematik Resim Müzik Beden Eğitimi Türkçe Toplam Ağrılıklı ortalama=77/18=
34 Ar. Ortalama=Medyan=Mod Ar. Ortalama>Medyan>Mod Ar. Ortalama <Medyan<Mod 34
35 Ranj Çeyrek Kayma Çeyrekler Arası Açıklık Standart Sapma Varyans 35
36 Bir veri grubunda bulunan en büyük veri ile en küçük veri arasındaki farktır. Ranj = maksimum puan minimum puan Eğer bir sınavda en yüksek puan 90 ve en düşük puan 50 ise ranj değeri 40 a eşittir. Buna göre bu sınavın puanları 40 puanlık bir aralığa dağılmaktadır. Ranjın büyük olması sınavın ayırt ediciliğinin yüksek olduğu anlamına gelir. Ayırt edici, dolayısıyla geçerliği ve güvenirliği yüksek bir sınavda hesaplanan ranj, o sınavdan elde edilmesi mümkün en yüksek puanın yarısına yakın olmalıdır. 36
37 Ranj sadece maksimum ve minimum değerlerden etkilenir aradaki diğer ölçümlerin ranj üzerinde hiç bir etkisi yoktur. Aşağıdaki 2 veri çok farklı olmasına rağmen aynı ranj değerine sahiptir. Ranj1: 10, 20, 20, 20, 20, 20, 30 Ranj2: 10, 21, 22, 23, 24, 25, 30 Ranj1=Ranj2=30-10=20 Ranj da mod (merkezi eğilim ölçüsü) gibi kaba ve az bilgi verir. 37
38 Ölçme sonuçlarına ilişkin dağılımın normal olmadığı durumlarda ve merkezi eğilim ölçüsü olarak ortanca kullanıldığı durumlarda, yayılma ölçüsü olarak çeyrek sapma kullanılır. Çeyrek sapma, birinci ve üçüncü çeyreğin farkının yarısı, diğer bir ifadeyle, 75. yüzdelikler 25. yüzdeliğin farkının yarısıdır ve Q sembolü ile gösterilir. 38
39 Çeyrek sapma, birinci ve üçüncü çeyreğin farkıdır. Üçüncü çeyrek (%75) ile birinci çeyrek (%25) arasında kalan yüzde 50 lik kısma tekabül eder. Örnek: 1, 2, 7, 8, 10, 5, 4, 3, 9, 8, 6 verisi için çeyrekler arası açıklığı bulalım. Önce veriyi sıraya koyalım: 1, 2, 3, 4, 5, 6, 7, 8, 8, 9, 10 Ortanca=6 Alt çeyrek 1,2,3,4,5 verisinin orta noktası olan 3 tür Üst çeyrek 7,8,8,9,10 verisinin orta noktası olan 8 dir. Çeyrekler arası açıklık: 8-3=5 tir. 39
40 Dağılım (yayılım) ölçüleri arasında en çok kullanılan standart sapma, bir veri grubundaki verilerin aritmetik ortalamadan ne derece uzaklara yayıldıklarını puan biriminde gösteren bir ortalamadır. 40
41 Öğrenci Puan Metin 10 Ali 20 Feyyaz adım: Standard sapmayı hesaplamak için önce aritmetik ortalamayı hesaplamamız gereklidir. Bu tablodaki verilerin aritmetik ortalaması ( )/3=20 41
42 2. Adım her bir değerden aritmetik ortalamayı çıkarmak. Öğrenci Puan Farklar Metin Ali Feyyaz Hesaplanmış hali: Öğrenci Puan Farklar Metin Ali 20 0 Feyyaz
43 3. Adım her bir değer için hesaplanan farkların karesini almak. Yani farkı kendisiyle çarparsak karesini elde etmiş oluruz. Öğrenci Puan Farklar Metin 10 (-10)*-(10) Ali 20 0*0 Feyyaz 30 10*10 4. adım: Karelerin toplamını hesaplamak. Öğrenci Puan Farklar Metin Ali 20 0 Feyyaz Toplam=200 Bu değer standart sapma formülünde pay kısmına yazılacak. 43
44 Buraya bir önceki slaytta bulunan değer yazılır. Cevap: Buraya veri sayısının 1 eksiği yazılır 44
45 Puanlar f farklar Farkların karesi f*farkların karesi Toplam Aritmetik ortalama=65 45
46 Öğrenci Puan Farklar Farklar Farkların Karesi Tolga Veli Gökhan Olcay Oğuzhan Toplam=512 Aritmetik ortalama=78 46
47 Öğrenci Puan Serkan 20 Ebru 20 Deniz 40 Ahmet 40 Tuba 80 Tablodaki verilerin aritmetik ortalaması ve standart sapmasını hesaplayınız. 47
48 Standart sapma, ölçme sonuçlarının yayılımıyla ilgili bir istatistiktir. Puanların yayılımının genişliğiyle doğru orantılı olarak büyür. St. Sapma ne kadar büyük olursa puanların yayılımı da o kadar geniş olur. Bu durum ölçülen özellik açısından grubun heterojen (farklı) yapıya sahip olduğunu gösterir. Eğer iki grubun aritmetik ortalaması eşit ise, standart sapması küçük olan grup daha başarılıdır. 48
49 Bir veri grubunda ölçme sonuçlarının aritmetik ortalamadan farklarının karelerinin aritmetik ortalamasına varyans denir. Yani kısaca standart sapmanın karesine varyans denir:) Varyans = (standart sapma)^2 Mesela standart sapması 10 olan bir verinin varyansı 10x10 dan 100 olarak bulunur. Açık formülü: 49
50 Varyans, dağılımdaki tüm ölçme sonuçlarına ilişkin bir yayılım ölçüsü olduğundan ranjdan, aritmetik ve cebirsel işlemlere olanak verdiğinden dolayı da ortalama kaymadan daha iyi bir değişkenlik ölçüsüdür. Daha önce bahsettiğimiz gibi varyans standart sapmanın karesi olarak da tanımlanabilir. Standart sapma hesaplanırken ölçme sonuçlarının orijinal birimi cinsinden ifade edildiği için standart sapma, varyanstan daha kullanışlıdır. Yani varyans kullanıldığı zaman cm ile ölçülen uzunluklarda varyans cmxcm kullanıldığı için cm^2 çıkacaktır. Bu sebeple birimi değişir. 50
51 Aritmetik ortalama ve standart sapma değeri kullanılarak hesaplanır. Bağıl değişkenlik katsayısı (V) puan dağılımının farklılığını daha doğru yorumlamamızı sağlayan başka dağılım ölçüsüdür. Bağıl değişkenlik katsayısı aritmetik ortalamanın (A.O.) 100 olduğu bir durumda standart sapmanın (St. Sp.) aldığı değerdir. V= (St.Sp./A.O.)x arası değer dağılımın normal olduğunu, 20 den küçük değer dağılımın homojen olduğunu, 25ten büyük değerler dağılımın heterojen olduğunu gösterir. 51
52 Eğitimde ve psikolojide üzerinde çalışılan değişkenlerin çoğu, evrende normal dağılıma sahiptir. Normal olasılık dağılımı sürekli bir dağılımdır. Sürekli değişkenlerin hemen hemen tamamı normal bir dağılım gösterir. Hatta kesikli değişkenlerin dağılımı da örneklemdeki eleman sayısı arttıkça normale yaklaşır. 52
53 53
54 Çan biçiminde sağ ve sol alanları birbirine eşit simetrik bir eğridir. Normal dağılımda tepe değer (mod), medyan ve aritmetik ortalama değerleri birbirine eşit ve dağılımın tam orta noktasındadır. Orta kısımdan sağa ve sola, her iki yöne doğru gidildikçe, yığılmalar önce yavaş yavaş, sonra da hızlıca düşerek iki uçta uzun bir kuyruk oluşturur. Normal dağılım eğrisinin temel çizgisi, standart sapma birimleriyle bölünmüştür. Bu çizgi üzerinde aritmetik ortalamanın bulunduğu noktaya sıfır değeri verilir ve çizgi bu noktanın sağına +1SS, +2SS, +3SS, soluna ise -1SS, -2SS,-3SS olmak üzere standart sapma birimi kullanarak alanlara ayrılır. SS: STANDART SAPMA 54
55 Normal dağılımda ölçümlerin yaklaşık, %68,26 sı X±1SS %95,44 ü X± 2SS %99,74 ü X± 3SS alanı içine düşer. 55
56 İki veya daha fazla dağılımı birbiriyle karşılaştırabilmek için, dağılımlara ait merkezi eğilim ve dağılım ölçüsünün bilinmesi gereklidir. Farklı dağılımlara sahip iki bireye ilişkin ölçme sonucunu, sadece ölçme sonuçlarına bakarak birbiriyle karşılaştırmak için, dağılımların merkezi eğilim ve dağılım ölçüsünün aynı olması gerekir. Fakat çoğu zaman farklı dağılımlarda bu iki ölçünün aynı olması mümkün olmaz. Eğer iki dağılımın ortalaması ve standart sapması farklıysa, bu dağılımların aynı standart sapma ve ortalamaya sahip bir dağılıma, yani birim normal dağılıma (standart normal dağılıma) dönüştürülmesi gerekir. Böylece farklı dağılımlardaki ölçme sonuçları aynı ölçek üzerinde görülebilir. Bu sayede farklı dağılımlardaki ölçme sonuçlarını karşılaştırmak mümkün olabilir. Bu işleme puanların standartlaştırılması da diyebiliriz. 56
57 Bir öğrencinin grup içindeki başarısı hakkında yorum yapmak istendiğinde kullanılır. Puanlara göre karşılaştırma yapmak istendiğinde kullanılır. Öğrencinin farklı derslerden aldığı puanlara göre hangi dersten daha başarılı olduğunu söylemek için kullanılır. Farklı sınıflarda uygulanan testlerden öğrencilerin aldıkları puanları karşılaştırmak amacıyla kullanılır. 57
58 Ölçme sonuçları Z puanına dönüştürülerek, aritmetik ortalaması 0 ve standart sapması 1 olacak biçimde normal dağılımlı hale getirilir. Z puanı ile elde edilen aritmetik ortalaması 0 ve standart sapması 1 olan bu dağılıma standart normal dağılım ya da birim normal dağılım denir. 58
59 50 öğrencinin 100 soruluk bir testten aldıkları puanların aritmetik ortalaması 50, standart sapması ise 15tir. Bu durumda 80 puan alan öğrencinin Z puanını hesaplayalım. Bulduğumuz bu Z puanına dayalı olarak, öğrencinin grup içerisindeki başarısı hakkında yorum yapılabilir: Z puanı 2 olarak bulunan bu öğrenci, tüm grubun yaklaşık olarak %98 inden daha yüksek başarıya sahiptir ve grubun %2sinden daha düşük başarıya sahiptir. 59
60 Z puanı simetrik bir dağılımdır. Bu nedenle ortalama olan 0 ın sağındaki ve solundaki alan eşittir ve her ikisi de %50 yi gösterir. Bu nedenle Z puanı 0 olan bir öğrenci; sınıfın %50 sinden daha başarılı diğer %50 sinden daha düşük başarılıdır. Z puanı -2 olan bir öğrenci; grubun yaklaşık olarak %2 sinden başarılı, %98 inden daha düşük başarıya sahiptir. Z puanı +2 olan öğrenci ise, grubun %98 inden daha başarılı ve %2 sinden daha düşük başarıya sahiptir. Z puanı -1 olan bir öğrenci; grubun yaklaşık olarak %16sından başarılı, %84 ünden daha az başarılıdır. Z puanı +1 olan bir öğrenci ise; grubun yaklaşık olarak %84 ünden başarılı, %16 sından daha az başarılıdır. 60
61 Bir sınıfta 4 ayrı test kullanılmıştır. Her bir testten elde edilen puanların sınıf ortalaması, standart sapması ve bir öğrencinin bu testlerden aldıkları puanlar şöyledir. Test1 Test2 Test3 Test4 Öğrenci Puanı Aritmetik Ortalama Standart Sapma Bu durumda öğrenci hangi testte daha başarılıdır? İpucu: Z puanlar hesaplanır. En yüksek Z puanı bir öğrencinin en başarılı olduğu dersi en düşük Z puanı da bir öğrencinin en başarısız olduğu dersi gösterir. 61
62 T puanı Z puanının Özel bir halidir. Z puan dağılımı; aritmetik ortalaması 50 ve standart sapması 10 olacak şekilde T puanına dönüştürülür. Yani T puanı aritmetik ortalaması 50 ve standart sapması 10 olan bir standart puan dağılımıdır. T puanı da Z puanı gibi yorumlanır. Z puanı T puanı
63 Formülümüz: T puanı = X Z Matematik Fizik Öğrenci Puanı Ortalama Standart Sapma Z puanları: (50-50)/10=0 ve (60-50)/10=1 bulunur. T puanları: 50+(10*0)=50 ve 50+(10*1)=60 bulunur. 63
64 Z puanının ortalaması 0 standart sapması 1 dir. T puanının ortalaması 50 standart sapması 10 dur. 64
7. HAFTA. Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar. Yrd. Doç. Dr.
 7. HAFTA Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar Yrd. Doç. Dr. Sedat ŞEN 14.04.2016 1 Veri nedir? Bir öğrenci kümesine uygulanan
7. HAFTA Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar Yrd. Doç. Dr. Sedat ŞEN 14.04.2016 1 Veri nedir? Bir öğrenci kümesine uygulanan
5. SUNUM. Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar. Yrd. Doç. Dr.
 5. SUNUM Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar Yrd. Doç. Dr. Sedat ŞEN 08.09.2016 1 Veri nedir? Bir öğrenci kümesine uygulanan
5. SUNUM Verilerin düzenlenmesi Verilerin gruplandırılması Merkezi eğilim ölçüleri Merkezi dağılım ölçüleri Standart puanlar Yrd. Doç. Dr. Sedat ŞEN 08.09.2016 1 Veri nedir? Bir öğrenci kümesine uygulanan
Genel olarak test istatistikleri. Merkezi Eğilim (Yığılma) Ölçüleri Dağılım (Yayılma) Ölçüleri. olmak üzere 2 grupta incelenebilir.
 4.SUNUM Genel olarak test istatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Dağılım (Yayılma) Ölçüleri olmak üzere 2 grupta incelenebilir. 2 Ranj Çeyrek Kayma Çeyrekler Arası Açıklık Standart Sapma Varyans
4.SUNUM Genel olarak test istatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Dağılım (Yayılma) Ölçüleri olmak üzere 2 grupta incelenebilir. 2 Ranj Çeyrek Kayma Çeyrekler Arası Açıklık Standart Sapma Varyans
Veri nedir? Bir öğrenci kümesine uygulanan bir sınavdan elde edilen puanların herhangi bir işlem yapılmamış haline ham veri denir (ham puanlar) denir.
 Dr. Sedat Şen 1 Veri nedir? Bir öğrenci kümesine uygulanan bir sınavdan elde edilen puanların herhangi bir işlem yapılmamış haline ham veri denir (ham puanlar) denir. Değer nedir? Bir veriyi (puanlar dizisini)
Dr. Sedat Şen 1 Veri nedir? Bir öğrenci kümesine uygulanan bir sınavdan elde edilen puanların herhangi bir işlem yapılmamış haline ham veri denir (ham puanlar) denir. Değer nedir? Bir veriyi (puanlar dizisini)
Genel olarak test istatistikleri. Merkezi Eğilim (Yığılma) Ölçüleri Merkezi Dağılım (Yayılma) Ölçüleri. olmak üzere 2 grupta incelenebilir.
 3.SUNUM Genel olarak test istatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Merkezi Dağılım (Yayılma) Ölçüleri olmak üzere 2 grupta incelenebilir. 2 Merkezi Eğilim Ölçüleri, belli bir özelliğe ya da değişkene
3.SUNUM Genel olarak test istatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Merkezi Dağılım (Yayılma) Ölçüleri olmak üzere 2 grupta incelenebilir. 2 Merkezi Eğilim Ölçüleri, belli bir özelliğe ya da değişkene
Yrd. Doç. Dr. Sedat Şen 9/27/2018 2
 2.SUNUM Belirli bir amaç için toplanmış verileri anlamlı haline getirmenin farklı yolları vardır. Verileri sözel ifadelerle açıklama Verileri tablolar halinde düzenleme Verileri grafiklerle gösterme Veriler
2.SUNUM Belirli bir amaç için toplanmış verileri anlamlı haline getirmenin farklı yolları vardır. Verileri sözel ifadelerle açıklama Verileri tablolar halinde düzenleme Verileri grafiklerle gösterme Veriler
Merkezi Yığılma ve Dağılım Ölçüleri
 1.11.013 Merkezi Yığılma ve Dağılım Ölçüleri 4.-5. hafta Merkezi eğilim ölçüleri, belli bir özelliğe ya da değişkene ilişkin ölçme sonuçlarının, hangi değer etrafında toplandığını gösteren ve veri grubunu
1.11.013 Merkezi Yığılma ve Dağılım Ölçüleri 4.-5. hafta Merkezi eğilim ölçüleri, belli bir özelliğe ya da değişkene ilişkin ölçme sonuçlarının, hangi değer etrafında toplandığını gösteren ve veri grubunu
Örnek 4.1: Tablo 2 de verilen ham verilerin aritmetik ortalamasını hesaplayınız.
 .4. Merkezi Eğilim ve Dağılım Ölçüleri Merkezi eğilim ölçüleri kitleye ilişkin bir değişkenin bütün farklı değerlerinin çevresinde toplandığı merkezi bir değeri gösterirler. Dağılım ölçüleri ise değişkenin
.4. Merkezi Eğilim ve Dağılım Ölçüleri Merkezi eğilim ölçüleri kitleye ilişkin bir değişkenin bütün farklı değerlerinin çevresinde toplandığı merkezi bir değeri gösterirler. Dağılım ölçüleri ise değişkenin
EĞĠTĠMDE ÖLÇME VE DEĞERLENDĠRME BÖLÜM IV Ölçme Sonuçları Üzerinde Ġstatistiksel ĠĢlemler VERİLERİN DÜZENLENMESİ VERİLERİN DÜZENLENMESİ
 09.0.0 Temel Kavramlar EĞĠTĠMDE ÖLÇME VE DEĞERLENDĠRME BÖLÜM IV Ölçme Sonuçları Üzerinde Ġstatistiksel ĠĢlemler Dr. Aylin ALBAYRAK SARI Hacettepe Üniversitesi Eğitim Fakültesi Evren: Üzerinde çalışılacak
09.0.0 Temel Kavramlar EĞĠTĠMDE ÖLÇME VE DEĞERLENDĠRME BÖLÜM IV Ölçme Sonuçları Üzerinde Ġstatistiksel ĠĢlemler Dr. Aylin ALBAYRAK SARI Hacettepe Üniversitesi Eğitim Fakültesi Evren: Üzerinde çalışılacak
JEODEZİK VERİLERİN İSTATİSTİK ANALİZİ. Prof. Dr. Mualla YALÇINKAYA
 JEODEZİK VERİLERİN İSTATİSTİK ANALİZİ Prof. Dr. Mualla YALÇINKAYA Karadeniz Teknik Üniversitesi, Harita Mühendisliği Bölümü Trabzon, 2018 VERİLERİN İRDELENMESİ Örnek: İki nokta arasındaki uzunluk 80 kere
JEODEZİK VERİLERİN İSTATİSTİK ANALİZİ Prof. Dr. Mualla YALÇINKAYA Karadeniz Teknik Üniversitesi, Harita Mühendisliği Bölümü Trabzon, 2018 VERİLERİN İRDELENMESİ Örnek: İki nokta arasındaki uzunluk 80 kere
TEMEL İSTATİSTİK BİLGİSİ. İstatistiksel verileri tasnif etme Verilerin grafiklerle ifade edilmesi Vasat ölçüleri Standart puanlar
 TEMEL İSTATİSTİK BİLGİSİ İstatistiksel verileri tasnif etme Verilerin grafiklerle ifade edilmesi Vasat ölçüleri Standart puanlar İstatistiksel Verileri Tasnif Etme Verileri daha anlamlı hale getirmek amacıyla
TEMEL İSTATİSTİK BİLGİSİ İstatistiksel verileri tasnif etme Verilerin grafiklerle ifade edilmesi Vasat ölçüleri Standart puanlar İstatistiksel Verileri Tasnif Etme Verileri daha anlamlı hale getirmek amacıyla
Merkezi Eğilim ve Dağılım Ölçüleri
 Merkezi Eğilim ve Dağılım Ölçüleri Soru Öğrencilerin derse katılım düzeylerini ölçmek amacıyla geliştirilen 16 soruluk bir test için öğrencilerin ilk 8 ve son 8 soruluk yarılardan aldıkları puanlar arasındaki
Merkezi Eğilim ve Dağılım Ölçüleri Soru Öğrencilerin derse katılım düzeylerini ölçmek amacıyla geliştirilen 16 soruluk bir test için öğrencilerin ilk 8 ve son 8 soruluk yarılardan aldıkları puanlar arasındaki
Tanımlayıcı İstatistikler. Yrd. Doç. Dr. Emre ATILGAN
 Tanımlayıcı İstatistikler Yrd. Doç. Dr. Emre ATILGAN 1 Tanımlayıcı İstatistikler Yer Gösteren Ölçüler Yaygınlık Ölçüleri Merkezi Eğilim Ölçüleri Konum Ölçüleri 2 3 Aritmetik Ortalama Aritmetik ortalama,
Tanımlayıcı İstatistikler Yrd. Doç. Dr. Emre ATILGAN 1 Tanımlayıcı İstatistikler Yer Gösteren Ölçüler Yaygınlık Ölçüleri Merkezi Eğilim Ölçüleri Konum Ölçüleri 2 3 Aritmetik Ortalama Aritmetik ortalama,
Temel İstatistik. Y.Doç.Dr. İbrahim Turan Mart Tanımlayıcı İstatistik. Dağılımları Tanımlayıcı Ölçüler Dağılış Ölçüleri
 Temel İstatistik Tanımlayıcı İstatistik Dağılımları Tanımlayıcı Ölçüler Dağılış Ölçüleri Y.Doç.Dr. İbrahim Turan Mart 2011 DAĞILIM / YAYGINLIK ÖLÇÜLERİ Verilerin değişkenlik durumu ve dağılışın şeklini
Temel İstatistik Tanımlayıcı İstatistik Dağılımları Tanımlayıcı Ölçüler Dağılış Ölçüleri Y.Doç.Dr. İbrahim Turan Mart 2011 DAĞILIM / YAYGINLIK ÖLÇÜLERİ Verilerin değişkenlik durumu ve dağılışın şeklini
BÖLÜM 5 MERKEZİ EĞİLİM ÖLÇÜLERİ
 1 BÖLÜM 5 MERKEZİ EĞİLİM ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel sayma
1 BÖLÜM 5 MERKEZİ EĞİLİM ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel sayma
TEMEL İSTATİSTİKİ KAVRAMLAR YRD. DOÇ. DR. İBRAHİM ÇÜTCÜ
 TEMEL İSTATİSTİKİ KAVRAMLAR YRD. DOÇ. DR. İBRAHİM ÇÜTCÜ 1 İstatistik İstatistik, belirsizliğin veya eksik bilginin söz konusu olduğu durumlarda çıkarımlar yapmak ve karar vermek için sayısal verilerin
TEMEL İSTATİSTİKİ KAVRAMLAR YRD. DOÇ. DR. İBRAHİM ÇÜTCÜ 1 İstatistik İstatistik, belirsizliğin veya eksik bilginin söz konusu olduğu durumlarda çıkarımlar yapmak ve karar vermek için sayısal verilerin
Ölçme Sonuçları Üzerinde İstatistiksel İşlemler
 Ölçme Sonuçları Üzerinde İstatistiksel İşlemler Bir grup birey veya nesnenin belli bir özelliğe sahip olup olmadığı ya da belli bir özelliğe ne derece sahip olduğunu belirlemek amacı ile ölçme işlemi yapılır.
Ölçme Sonuçları Üzerinde İstatistiksel İşlemler Bir grup birey veya nesnenin belli bir özelliğe sahip olup olmadığı ya da belli bir özelliğe ne derece sahip olduğunu belirlemek amacı ile ölçme işlemi yapılır.
TANIMLAYICI İSTATİSTİKLER
 TANIMLAYICI İSTATİSTİKLER Tanımlayıcı İstatistikler ve Grafikle Gösterim Grafik ve bir ölçüde tablolar değişkenlerin görsel bir özetini verirler. İdeal olarak burada değişkenlerin merkezi (ortalama) değerlerinin
TANIMLAYICI İSTATİSTİKLER Tanımlayıcı İstatistikler ve Grafikle Gösterim Grafik ve bir ölçüde tablolar değişkenlerin görsel bir özetini verirler. İdeal olarak burada değişkenlerin merkezi (ortalama) değerlerinin
Test İstatistikleri AHMET SALİH ŞİMŞEK
 Test İstatistikleri AHMET SALİH ŞİMŞEK İçindekiler Test İstatistikleri Merkezi Eğilim Tepe Değer (Mod) Ortanca (Medyan) Aritmetik Ortalama Merkezi Dağılım Dizi Genişliği (Ranj) Standart Sapma Varyans Çarpıklık
Test İstatistikleri AHMET SALİH ŞİMŞEK İçindekiler Test İstatistikleri Merkezi Eğilim Tepe Değer (Mod) Ortanca (Medyan) Aritmetik Ortalama Merkezi Dağılım Dizi Genişliği (Ranj) Standart Sapma Varyans Çarpıklık
BÖLÜM 6 MERKEZDEN DAĞILMA ÖLÇÜLERİ
 1 BÖLÜM 6 MERKEZDEN DAĞILMA ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel
1 BÖLÜM 6 MERKEZDEN DAĞILMA ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel
Prof.Dr.İhsan HALİFEOĞLU
 Prof.Dr.İhsan HALİFEOĞLU Örnek: Aşağıda 100 yetişkine ilişkin kolesterol değerlerini sınıflandırılarak aritmetik ortalamasını bulunuz (sınıf aralığını 20 alınız). 2 x A fb C 229.5 n 40 20 100 221.5 3 Örnek:.
Prof.Dr.İhsan HALİFEOĞLU Örnek: Aşağıda 100 yetişkine ilişkin kolesterol değerlerini sınıflandırılarak aritmetik ortalamasını bulunuz (sınıf aralığını 20 alınız). 2 x A fb C 229.5 n 40 20 100 221.5 3 Örnek:.
Verilerin Özetlenmesinde Kullanılan Sayısal Yöntemler
 Verilerin Özetlenmesinde Kullanılan Sayısal Yöntemler Merkezi Eğilim Ölçüleri Merkezi eğilim ölçüsü, bir veri setindeki merkezi, yada tipik, tek bir değeri ifade eder. Nicel veriler için, reel sayı çizgisindeki
Verilerin Özetlenmesinde Kullanılan Sayısal Yöntemler Merkezi Eğilim Ölçüleri Merkezi eğilim ölçüsü, bir veri setindeki merkezi, yada tipik, tek bir değeri ifade eder. Nicel veriler için, reel sayı çizgisindeki
EĞİTİMDE ÖLÇME VE DEĞERLENDİRME UĞUR YILMAZER 1
 EĞİTİMDE ÖLÇME VE DEĞERLENDİRME UĞUR YILMAZER 1 5. BÖLÜM (9. KONU) TEST PUANLARI ÜZERİDE İSTATİSTİKİ İŞLEMLER MERKEZİ EĞİLİM/YIĞILIM ÖLÇÜLERİ ÇARPIKLIK VE YORUMU UĞUR YILMAZER 2 TEST İSTATİSTİKLERİ 1-
EĞİTİMDE ÖLÇME VE DEĞERLENDİRME UĞUR YILMAZER 1 5. BÖLÜM (9. KONU) TEST PUANLARI ÜZERİDE İSTATİSTİKİ İŞLEMLER MERKEZİ EĞİLİM/YIĞILIM ÖLÇÜLERİ ÇARPIKLIK VE YORUMU UĞUR YILMAZER 2 TEST İSTATİSTİKLERİ 1-
Prof.Dr.İhsan HALİFEOĞLU
 Prof.Dr.İhsan HALİFEOĞLU FREKANS DAĞILIMLARINI TANIMLAYICI ÖLÇÜLER Düzenlenmiş verilerin yorumlanması ve daha ileri düzeydeki işlemler için verilerin bütününe ait tanımlayıcı ve özetleyici ölçülere ihtiyaç
Prof.Dr.İhsan HALİFEOĞLU FREKANS DAĞILIMLARINI TANIMLAYICI ÖLÇÜLER Düzenlenmiş verilerin yorumlanması ve daha ileri düzeydeki işlemler için verilerin bütününe ait tanımlayıcı ve özetleyici ölçülere ihtiyaç
VERİ SETİNE GENEL BAKIŞ
 VERİ SETİNE GENEL BAKIŞ Outlier : Veri setinde normal olmayan değerler olarak tanımlanır. Ders: Kantitatif Yöntemler 1 VERİ SETİNE GENEL BAKIŞ Veri setinden değerlendirme başlamadan çıkarılabilir. Yazım
VERİ SETİNE GENEL BAKIŞ Outlier : Veri setinde normal olmayan değerler olarak tanımlanır. Ders: Kantitatif Yöntemler 1 VERİ SETİNE GENEL BAKIŞ Veri setinden değerlendirme başlamadan çıkarılabilir. Yazım
Nicel / Nitel Verilerde Konum ve Değişim Ölçüleri. BBY606 Araştırma Yöntemleri 2013-2014 Bahar Dönemi 13 Mart 2014
 Nicel / Nitel Verilerde Konum ve Değişim Ölçüleri BBY606 Araştırma Yöntemleri 2013-2014 Bahar Dönemi 13 Mart 2014 1 Konum ölçüleri Merkezi eğilim ölçüleri Verilerin ortalamaya göre olan gruplanması nasıl?
Nicel / Nitel Verilerde Konum ve Değişim Ölçüleri BBY606 Araştırma Yöntemleri 2013-2014 Bahar Dönemi 13 Mart 2014 1 Konum ölçüleri Merkezi eğilim ölçüleri Verilerin ortalamaya göre olan gruplanması nasıl?
Konum ve Dağılım Ölçüleri. BBY606 Araştırma Yöntemleri Güleda Doğan
 Konum ve Dağılım Ölçüleri BBY606 Araştırma Yöntemleri Güleda Doğan Konum ölçüleri Merkezi eğilim ölçüleri Verilerin ortalamaya göre olan gruplanması nasıl? Yakın, uzak? Sıklık dağılımlarının karşılaştırılması
Konum ve Dağılım Ölçüleri BBY606 Araştırma Yöntemleri Güleda Doğan Konum ölçüleri Merkezi eğilim ölçüleri Verilerin ortalamaya göre olan gruplanması nasıl? Yakın, uzak? Sıklık dağılımlarının karşılaştırılması
ÖLÇME DEĞERLENDİRME ÜNİTE BAŞLIKLARI
 ÖLÇME DEĞERLENDİRME ÜNİTE BAŞLIKLARI 1. TEMEL KAVRAMLAR 2. ÖLÇMEDE HATA (GÜVENİRLİK GEÇERLİK) 3. İSTATİSTİK 1. TEMEL KAVRAMLAR Ölçme, Ölçüm, Ölçme Kuralı, Ölçüt, Değerlendirme. Ölçme Türleri: Doğrudan,
ÖLÇME DEĞERLENDİRME ÜNİTE BAŞLIKLARI 1. TEMEL KAVRAMLAR 2. ÖLÇMEDE HATA (GÜVENİRLİK GEÇERLİK) 3. İSTATİSTİK 1. TEMEL KAVRAMLAR Ölçme, Ölçüm, Ölçme Kuralı, Ölçüt, Değerlendirme. Ölçme Türleri: Doğrudan,
 A t a b e y M e s l e k Y ü k s e k O k u l u İstatistik Sunum 4 Öğr.Gör. Şükrü L/O/G/O KAYA www.sukrukaya.org www.themegallery.com 1 Yer Ölçüleri Yer ölçüleri, verilerin merkezini veya yığılma noktasını
A t a b e y M e s l e k Y ü k s e k O k u l u İstatistik Sunum 4 Öğr.Gör. Şükrü L/O/G/O KAYA www.sukrukaya.org www.themegallery.com 1 Yer Ölçüleri Yer ölçüleri, verilerin merkezini veya yığılma noktasını
Örnek...4 : İlk iki sınavında 75 ve 82 alan bir öğrencinin bu dersin ortalamasını 5 yapabilmek için son sınavdan kaç alması gerekmektedir?
 İSTATİSTİK Bir sonuç çıkarmak ya da çözüme ulaşabilmek için gözlem, deney, araştırma gibi yöntemlerle toplanan bilgiye veri adı verilir. Örnek...4 : İlk iki sınavında 75 ve 82 alan bir öğrencinin bu dersin
İSTATİSTİK Bir sonuç çıkarmak ya da çözüme ulaşabilmek için gözlem, deney, araştırma gibi yöntemlerle toplanan bilgiye veri adı verilir. Örnek...4 : İlk iki sınavında 75 ve 82 alan bir öğrencinin bu dersin
Bölüm 3 Merkezi Konum (Eğilim) Ölçüleri. Giriş Veri kümesi. Ortalamalar iki grupta incelenir. A. Duyarlı olan ortalama. B. Duyarlı olmayan ortalama
 GM-220 MÜH. ÇALIŞ. İSTATİSTİKSEL YÖNTEMLER Bölüm 3 Merkezi Konum (Eğilim) Ölçüleri Yrd. Doç. Dr. Safa KARAMAN 1 2 Giriş Veri kümesi Verileri betimlemenin ve özetlemenin bir diğer yolu da verilerin bir
GM-220 MÜH. ÇALIŞ. İSTATİSTİKSEL YÖNTEMLER Bölüm 3 Merkezi Konum (Eğilim) Ölçüleri Yrd. Doç. Dr. Safa KARAMAN 1 2 Giriş Veri kümesi Verileri betimlemenin ve özetlemenin bir diğer yolu da verilerin bir
BİYOİSTATİSTİK Merkezi Eğilim ve Değişim Ölçüleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH
 BİYOİSTATİSTİK Merkezi Eğilim ve Değişim Ölçüleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 İstatistik
BİYOİSTATİSTİK Merkezi Eğilim ve Değişim Ölçüleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 İstatistik
Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü
 Mühendislikte İstatistiksel Yöntemler Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü 1 Araştırma sonuçlarının açıklanmasında frekans tablosu
Mühendislikte İstatistiksel Yöntemler Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü 1 Araştırma sonuçlarının açıklanmasında frekans tablosu
Veri Analizi. Isınma Hareketleri. Test İstatistikleri. b) En çok tekrar eden: 7 (mod) c) Açıklık = En büyük En küçük = 10 1 = 9. d)
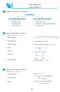 Isınma Hareketleri 1 Aşağıda verilenleri inceleyiniz. Test İstatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Aritmetik ortalama Tepe değer (mod) Ortanca (medyan) Merkezi Dağılım (Yayılma) Ölçüleri Açıklık
Isınma Hareketleri 1 Aşağıda verilenleri inceleyiniz. Test İstatistikleri Merkezi Eğilim (Yığılma) Ölçüleri Aritmetik ortalama Tepe değer (mod) Ortanca (medyan) Merkezi Dağılım (Yayılma) Ölçüleri Açıklık
Mühendislikte İstatistik Yöntemler
 .0.0 Mühendislikte İstatistik Yöntemler İstatistik Parametreler Tarih Qma.3.98 4..98 0.3.983 45 7..984 37.3.985 48 0.4.986 67.4.987 5 0.3.988 45.5.989 34.3.990 59.4.99 3 4 34 5 37 6 45 7 45 8 48 9 5 0
.0.0 Mühendislikte İstatistik Yöntemler İstatistik Parametreler Tarih Qma.3.98 4..98 0.3.983 45 7..984 37.3.985 48 0.4.986 67.4.987 5 0.3.988 45.5.989 34.3.990 59.4.99 3 4 34 5 37 6 45 7 45 8 48 9 5 0
ÖLÇME VE DEĞERLENDİRME. Antrenörlük Eğitimi 4. Sınıf. Ölçme ve Değerlendirme - Yrd. Doç. Dr. Yetkin Utku KAMUK
 ÖLÇME VE DEĞERLENDİRME Antrenörlük Eğitimi 4. Sınıf ÖLÇME VE DEĞERLENDİRME Merkezi Eğilim Ölçütleri Mod En çok görülen puandır ve hesaplanma yöntemi yoktur. İnceleme yolu ile bulunur. Terminal istatistiktir.
ÖLÇME VE DEĞERLENDİRME Antrenörlük Eğitimi 4. Sınıf ÖLÇME VE DEĞERLENDİRME Merkezi Eğilim Ölçütleri Mod En çok görülen puandır ve hesaplanma yöntemi yoktur. İnceleme yolu ile bulunur. Terminal istatistiktir.
Ders 8: Verilerin Düzenlenmesi ve Analizi
 Ders 8: Verilerin Düzenlenmesi ve Analizi Betimsel İstatistik Merkezsel Eğilim Ölçüleri Dağılım Ölçüleri Grafiksel Gösterimler Bir kitlenin tamamını, ya da kitleden alınan bir örneklemi özetlemekle (betimlemekle)
Ders 8: Verilerin Düzenlenmesi ve Analizi Betimsel İstatistik Merkezsel Eğilim Ölçüleri Dağılım Ölçüleri Grafiksel Gösterimler Bir kitlenin tamamını, ya da kitleden alınan bir örneklemi özetlemekle (betimlemekle)
Ölçme ve Değerlendirme
 Ölçme ve Değerlendirme Z Puanı T Puanı Yrd. Doç. Dr. Yetkin Utku KAMUK Standart Puan Herhangi bir ölçüm sonucunda elde edilen ve farklı birimlere sahip ham puanların, standart bir dağılım haline dönüştürülmesi
Ölçme ve Değerlendirme Z Puanı T Puanı Yrd. Doç. Dr. Yetkin Utku KAMUK Standart Puan Herhangi bir ölçüm sonucunda elde edilen ve farklı birimlere sahip ham puanların, standart bir dağılım haline dönüştürülmesi
17/01/2015. PowerPoint Template. Dr. S.Nihat ŞAD LOGO. İnönü University. Company Logo
 PowerPoint Template LOGO Dr. S.Nihat ŞAD İnönü University www.thmemgallery.com Company Logo 1 Contents www.thmemgallery.com geliştirme süreci Birey hakkında bilgi toplama yolları lerin sınıflandırılması
PowerPoint Template LOGO Dr. S.Nihat ŞAD İnönü University www.thmemgallery.com Company Logo 1 Contents www.thmemgallery.com geliştirme süreci Birey hakkında bilgi toplama yolları lerin sınıflandırılması
Yrd. Doç. Dr. Sedat ŞEN
 6. SUNUM Test Geliştirme Aşamaları Madde Analizleri Madde Güçlüğü Madde Ayırıcılığı Madde varyansı ve standart sapması Madde güvenirlik katsayısı Test ortalaması, standart sapması ve ortalama güçlüğü Yrd.
6. SUNUM Test Geliştirme Aşamaları Madde Analizleri Madde Güçlüğü Madde Ayırıcılığı Madde varyansı ve standart sapması Madde güvenirlik katsayısı Test ortalaması, standart sapması ve ortalama güçlüğü Yrd.
YANLILIK. Yanlılık örneklem istatistiği değerlerinin evren parametre değerinden herhangi bir sistematik sapması olarak tanımlanır.
 AED 310 İSTATİSTİK YANLILIK Yanlılık örneklem istatistiği değerlerinin evren parametre değerinden herhangi bir sistematik sapması olarak tanımlanır. YANLILIK Yanlı bir araştırma tasarımı uygulandığında,
AED 310 İSTATİSTİK YANLILIK Yanlılık örneklem istatistiği değerlerinin evren parametre değerinden herhangi bir sistematik sapması olarak tanımlanır. YANLILIK Yanlı bir araştırma tasarımı uygulandığında,
ÖLÇME VE DEĞERLENDĠRME (3)
 ÖLÇME VE DEĞERLENDĠRME (3) ÖLÇME SONUÇLARI ÜZERĠNDE ĠSTATĠSTĠKSEL ĠġLEMLER VERĠLERĠN DÜZENLENMESĠ -Herhangi bir test uygulamasından önce verilerin düzenlenmesi için önce bütün puanların büyüklüklerine
ÖLÇME VE DEĞERLENDĠRME (3) ÖLÇME SONUÇLARI ÜZERĠNDE ĠSTATĠSTĠKSEL ĠġLEMLER VERĠLERĠN DÜZENLENMESĠ -Herhangi bir test uygulamasından önce verilerin düzenlenmesi için önce bütün puanların büyüklüklerine
Yrd. Doç. Dr. Sedat ŞEN
 8. HAFTA Test Geliştirme Aşamaları Madde Analizleri Madde Güçlüğü Madde Ayırıcılığı Madde varyansı ve standart sapması Madde güvenirlik katsayısı Test ortalaması, standart sapması ve ortalama güçlüğü Yrd.
8. HAFTA Test Geliştirme Aşamaları Madde Analizleri Madde Güçlüğü Madde Ayırıcılığı Madde varyansı ve standart sapması Madde güvenirlik katsayısı Test ortalaması, standart sapması ve ortalama güçlüğü Yrd.
IİSTATIİSTIİK. Mustafa Sezer PEHLI VAN
 IİSTATIİSTIİK Mustafa Sezer PEHLI VAN İstatistik nedir? İstatistik, veri anlamına gelir, İstatistik, sayılarla uğraşan bir bilim dalıdır, İstatistik, eksik bilgiler kullanarak doğru sonuçlara ulaştıran
IİSTATIİSTIİK Mustafa Sezer PEHLI VAN İstatistik nedir? İstatistik, veri anlamına gelir, İstatistik, sayılarla uğraşan bir bilim dalıdır, İstatistik, eksik bilgiler kullanarak doğru sonuçlara ulaştıran
8.Hafta. Değişkenlik Ölçüleri. Öğr.Gör.Muhsin ÇELİK. Uygun değişkenlik ölçüsünü hesaplayıp yorumlayabilecek,
 İSTATİSTİK 8.Hafta Değişkenlik Ölçüleri Hedefler Bu üniteyi çalıştıktan sonra; Uygun değişkenlik ölçüsünü hesaplayıp yorumlayabilecek, Serilerin birbirlerine değişkenliklerini yorumlayabileceksiniz. 2
İSTATİSTİK 8.Hafta Değişkenlik Ölçüleri Hedefler Bu üniteyi çalıştıktan sonra; Uygun değişkenlik ölçüsünü hesaplayıp yorumlayabilecek, Serilerin birbirlerine değişkenliklerini yorumlayabileceksiniz. 2
ORTALAMA ÖLÇÜLERİ. Ünite 6. Öğr. Gör. Ali Onur CERRAH
 ORTALAMA ÖLÇÜLERİ Ünite 6 Öğr. Gör. Ali Onur CERRAH Araştırma sonucunda elde edilen nitelik değişkenler hakkında tablo ve grafikle bilgi sahibi olunurken, sayısal değişkenler hakkında bilgi sahibi olmanın
ORTALAMA ÖLÇÜLERİ Ünite 6 Öğr. Gör. Ali Onur CERRAH Araştırma sonucunda elde edilen nitelik değişkenler hakkında tablo ve grafikle bilgi sahibi olunurken, sayısal değişkenler hakkında bilgi sahibi olmanın
ENM 5210 İSTATİSTİK VE YAZILIMLA UYGULAMALARI. Ders 2 Merkezi Eğilim Ölçüleri
 ENM 5210 İSTATİSTİK VE YAZILIMLA UYGULAMALARI Ders 2 Merkezi Eğilim Ölçüleri Basit Seriler Elde edilecek ham verilerin küçükten büyüğe doğru sıralanması ile elde edilen serilere basit seri denir ÖRNEK:
ENM 5210 İSTATİSTİK VE YAZILIMLA UYGULAMALARI Ders 2 Merkezi Eğilim Ölçüleri Basit Seriler Elde edilecek ham verilerin küçükten büyüğe doğru sıralanması ile elde edilen serilere basit seri denir ÖRNEK:
Bölüm 3. Tanımlayıcı İstatistikler
 Bölüm 3 Tanımlayıcı İstatistikler 1 Tanımlayıcı İstatistikler Bir veri setini tanımak veya birden fazla veri setini karşılaştırmak için kullanılan ve ayrıca örnek verilerinden hareket ile frekans dağılışlarını
Bölüm 3 Tanımlayıcı İstatistikler 1 Tanımlayıcı İstatistikler Bir veri setini tanımak veya birden fazla veri setini karşılaştırmak için kullanılan ve ayrıca örnek verilerinden hareket ile frekans dağılışlarını
İstatistik: Sayısal verilerin toplanmasını, analiz edilmesini ve yorumlanmasını içeren bir matematik koludur.
 1.SUNUM İstatistik: Sayısal verilerin toplanmasını, analiz edilmesini ve yorumlanmasını içeren bir matematik koludur. İstatistikçi: Veri toplama, analiz ve yorumlama işini yapa(bile)n kişidir. Dr. Sedat
1.SUNUM İstatistik: Sayısal verilerin toplanmasını, analiz edilmesini ve yorumlanmasını içeren bir matematik koludur. İstatistikçi: Veri toplama, analiz ve yorumlama işini yapa(bile)n kişidir. Dr. Sedat
rasgele değişkeninin olasılık yoğunluk fonksiyonu,
 3.6. Bazı Sürekli Dağılımlar 3.6.1 Normal Dağılım Normal dağılım hem uygulamalı hem de teorik istatistikte kullanılan oldukça önemli bir dağılımdır. Normal dağılımın istatistikte önemli bir yerinin olmasının
3.6. Bazı Sürekli Dağılımlar 3.6.1 Normal Dağılım Normal dağılım hem uygulamalı hem de teorik istatistikte kullanılan oldukça önemli bir dağılımdır. Normal dağılımın istatistikte önemli bir yerinin olmasının
SÜREKLİ OLASILIK DAĞILIMI
 SÜREKLİ OLASILIK DAĞILIMI Normal Olasılık Dağılımı Akülerin dayanma süresi, araçların belli bir zamanda aldığı yol, bir koşuya katılanların bitirme süresi gibi sayılamayacak kadar çok değer alabilen sürekli
SÜREKLİ OLASILIK DAĞILIMI Normal Olasılık Dağılımı Akülerin dayanma süresi, araçların belli bir zamanda aldığı yol, bir koşuya katılanların bitirme süresi gibi sayılamayacak kadar çok değer alabilen sürekli
1.SUNUM. Yrd. Doç. Dr. Sedat Şen
 1.SUNUM Yrd. Doç. Dr. Sedat Şen 1 İstatistik: Sayısal verilerin toplanmasını, analiz edilmesini ve yorumlanmasını içeren bir matematik koludur. İstatistikçi: Veri toplama, analiz ve yorumlama işini yapa(bile)n
1.SUNUM Yrd. Doç. Dr. Sedat Şen 1 İstatistik: Sayısal verilerin toplanmasını, analiz edilmesini ve yorumlanmasını içeren bir matematik koludur. İstatistikçi: Veri toplama, analiz ve yorumlama işini yapa(bile)n
Copyright 2004 Pearson Education, Inc. Slide 1
 Slide 1 Bölüm 2 Verileri Betimleme, Keşfetme, ve Karşılaştırma 2-1 Genel Bakış 2-2 Sıklık Dağılımları 2-3 Verilerin Görselleştirilmesi 2-4 Merkezi Eğilim Ölçüleri 2-5 Değişimin Ölçülmesi 2-6 Nispi Sabitlerin
Slide 1 Bölüm 2 Verileri Betimleme, Keşfetme, ve Karşılaştırma 2-1 Genel Bakış 2-2 Sıklık Dağılımları 2-3 Verilerin Görselleştirilmesi 2-4 Merkezi Eğilim Ölçüleri 2-5 Değişimin Ölçülmesi 2-6 Nispi Sabitlerin
TEST VE MADDE ANALİZLERİ
 TEST VE MADDE ANALİZLERİ Madde güçlüğü Madde ayırt ediciliği Madde varyansı ve madde standart sapması Madde güvenirliği Çeldiricilerin işlerliği Test Analizleri Merkezi Eğilim(Yığılma Ölçüleri) Merkezi
TEST VE MADDE ANALİZLERİ Madde güçlüğü Madde ayırt ediciliği Madde varyansı ve madde standart sapması Madde güvenirliği Çeldiricilerin işlerliği Test Analizleri Merkezi Eğilim(Yığılma Ölçüleri) Merkezi
Merkezi eğilim ölçüleri ile bir frekans dağılımının merkezi belirlenirken; yayılma ölçüleri ile değişkenliği veya yayılma düzeyini tespit eder.
 Yayılma Ölçütleri Merkezi eğilim ölçüleri ile bir frekans dağılımının merkezi belirlenirken; yayılma ölçüleri ile değişkenliği veya yayılma düzeyini tespit eder. Bir başka ifade ile, bir veri setinin,
Yayılma Ölçütleri Merkezi eğilim ölçüleri ile bir frekans dağılımının merkezi belirlenirken; yayılma ölçüleri ile değişkenliği veya yayılma düzeyini tespit eder. Bir başka ifade ile, bir veri setinin,
İstatistik ve Olasılığa Giriş. İstatistik ve Olasılığa Giriş. Ders 3 Verileri Sayısal Ölçütlerle İfade Etme. Verileri Sayısal Ölçütlerle İfade Etme
 İstatistik ve Olasılığa Giriş Robert J. Beaver Barbara M. Beaver William Mendenhall Presentation designed and written by: Barbara M. Beaver İstatistik ve Olasılığa Giriş Ders 3 Verileri Sayısal Ölçütlerle
İstatistik ve Olasılığa Giriş Robert J. Beaver Barbara M. Beaver William Mendenhall Presentation designed and written by: Barbara M. Beaver İstatistik ve Olasılığa Giriş Ders 3 Verileri Sayısal Ölçütlerle
VERİ KÜMELERİNİ BETİMLEME
 BETİMLEYİCİ İSTATİSTİK VERİ KÜMELERİNİ BETİMLEME Bir amaç için derlenen verilerin tamamının olduğu, veri kümesindeki birimlerin sayısal değerlerinden faydalanarak açık ve net bir şekilde ilgilenilen özellik
BETİMLEYİCİ İSTATİSTİK VERİ KÜMELERİNİ BETİMLEME Bir amaç için derlenen verilerin tamamının olduğu, veri kümesindeki birimlerin sayısal değerlerinden faydalanarak açık ve net bir şekilde ilgilenilen özellik
OLASILIK ve KURAMSAL DAĞILIMLAR
 OLASILIK ve KURAMSAL DAĞILIMLAR Kuramsal Dağılımlar İstatistiksel çözümlemelerde; değişkenlerimizin dağılma özellikleri, çözümleme yönteminin seçimi ve sonuçlarının yorumlanmasında önemlidir. Dağılma özelliklerine
OLASILIK ve KURAMSAL DAĞILIMLAR Kuramsal Dağılımlar İstatistiksel çözümlemelerde; değişkenlerimizin dağılma özellikleri, çözümleme yönteminin seçimi ve sonuçlarının yorumlanmasında önemlidir. Dağılma özelliklerine
LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I BAHAR DÖNEMĐ TELAFĐ SINAVI SORULARI
 LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I 2015-2016 BAHAR DÖNEMĐ TELAFĐ SINAVI SORULARI Tarih/Saat/Yer: 20.06.16/15:00-16:30/AS010 Instructor: Prof. Dr. Hüseyin Oğuz Öğrenci
LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I 2015-2016 BAHAR DÖNEMĐ TELAFĐ SINAVI SORULARI Tarih/Saat/Yer: 20.06.16/15:00-16:30/AS010 Instructor: Prof. Dr. Hüseyin Oğuz Öğrenci
BÖLÜM 4 FREKANS DAĞILIMLARININ GRAFİKLE GÖSTERİLMESİ
 BÖLÜM 4 FREKANS DAĞILIMLARININ GRAFİKLE GÖSTERİLMESİ Frekans dağılımlarının betimlenmesinde frekans tablolarının kullanılmasının yanı sıra grafik gösterimleri de sıklıkla kullanılmaktadır. Grafikler, görselliği
BÖLÜM 4 FREKANS DAĞILIMLARININ GRAFİKLE GÖSTERİLMESİ Frekans dağılımlarının betimlenmesinde frekans tablolarının kullanılmasının yanı sıra grafik gösterimleri de sıklıkla kullanılmaktadır. Grafikler, görselliği
Sıklık Tabloları, BASİT ve TEK değişkenli Grafikler Ders 3 ve 4 ve 5
 Sıklık Tabloları, BASİT ve TEK değişkenli Grafikler Ders 3 ve 4 ve 5 Sıklık Tabloları Veri dizisinde yer alan değerlerin tekrarlama sayılarını içeren tabloya sıklık tablosu denir. Tek değişken için çizilen
Sıklık Tabloları, BASİT ve TEK değişkenli Grafikler Ders 3 ve 4 ve 5 Sıklık Tabloları Veri dizisinde yer alan değerlerin tekrarlama sayılarını içeren tabloya sıklık tablosu denir. Tek değişken için çizilen
LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I BAHAR DÖNEMĐ BÜTÜNLEME SINAVI SORULARI
 LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I 2015-2016 BAHAR DÖNEMĐ BÜTÜNLEME SINAVI SORULARI Tarih/Saat/Yer: 24.06.16/11:00-12:30/AS010 Instructor: Prof. Dr. Hüseyin Oğuz
LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I 2015-2016 BAHAR DÖNEMĐ BÜTÜNLEME SINAVI SORULARI Tarih/Saat/Yer: 24.06.16/11:00-12:30/AS010 Instructor: Prof. Dr. Hüseyin Oğuz
Yrd.Doç.Dr. Ali SICAK BEÜ. EREĞLİ EĞİTİM FAKÜLTESİ EĞİTİM BİLİMLERİ BÖLÜMÜ
 Yrd.Doç.Dr. Ali SICAK BEÜ. EREĞLİ EĞİTİM FAKÜLTESİ EĞİTİM BİLİMLERİ BÖLÜMÜ YARARLANILACAK ANA KAYNAK: SOSYAL BİLİMLER İÇİN İSTATİSTİK/ ŞENER BÜYÜKÖZTÜRK, ÖMAY ÇOKLUK, NİLGÜN KÖKLÜ/PEGEM YAY. YARDIMCI KAYNAKLAR:
Yrd.Doç.Dr. Ali SICAK BEÜ. EREĞLİ EĞİTİM FAKÜLTESİ EĞİTİM BİLİMLERİ BÖLÜMÜ YARARLANILACAK ANA KAYNAK: SOSYAL BİLİMLER İÇİN İSTATİSTİK/ ŞENER BÜYÜKÖZTÜRK, ÖMAY ÇOKLUK, NİLGÜN KÖKLÜ/PEGEM YAY. YARDIMCI KAYNAKLAR:
KONU2 MERKEZİ EĞİLİM ÖLÇÜLERİ EĞİLİM ÖLÇÜLERİ ANALİTİK ORTALAMALAR ANALİTİK OLMAYAN MERKEZİ. Aritmetik ortalama **Medyan(median)
 KONU2 MERKEZİ EĞİLİM ÖLÇÜLERİ 1 MERKEZİ EĞİLİM ÖLÇÜLERİ ANALİTİK ORTALAMALAR Bir örneklemde mevcut olan tüm veriler hesaba katılır. ANALİTİK OLMAYAN MERKEZİ EĞİLİM ÖLÇÜLERİ Bir örneklemdeki verilerin bir
KONU2 MERKEZİ EĞİLİM ÖLÇÜLERİ 1 MERKEZİ EĞİLİM ÖLÇÜLERİ ANALİTİK ORTALAMALAR Bir örneklemde mevcut olan tüm veriler hesaba katılır. ANALİTİK OLMAYAN MERKEZİ EĞİLİM ÖLÇÜLERİ Bir örneklemdeki verilerin bir
İstatistik, genel olarak, rassal bir olayı (ya da deneyi) matematiksel olarak modellemek ve bu model yardımıyla, anakütlenin bilinmeyen karakteristik
 6.SUNUM İstatistik, genel olarak, rassal bir olayı (ya da deneyi) matematiksel olarak modellemek ve bu model yardımıyla, anakütlenin bilinmeyen karakteristik özellikleri (ortalama, varyans v.b. gibi) hakkında
6.SUNUM İstatistik, genel olarak, rassal bir olayı (ya da deneyi) matematiksel olarak modellemek ve bu model yardımıyla, anakütlenin bilinmeyen karakteristik özellikleri (ortalama, varyans v.b. gibi) hakkında
Oluşturulan evren listesinden örnekleme birimlerinin seçkisiz olarak çekilmesidir
 Bilimsel Araştırma Yöntemleri Prof. Dr. Şener Büyüköztürk Doç. Dr. Ebru Kılıç Çakmak Yrd. Doç. Dr. Özcan Erkan Akgün Doç. Dr. Şirin Karadeniz Dr. Funda Demirel Örnekleme Yöntemleri Evren Evren, araştırma
Bilimsel Araştırma Yöntemleri Prof. Dr. Şener Büyüköztürk Doç. Dr. Ebru Kılıç Çakmak Yrd. Doç. Dr. Özcan Erkan Akgün Doç. Dr. Şirin Karadeniz Dr. Funda Demirel Örnekleme Yöntemleri Evren Evren, araştırma
GİRİŞ. Bilimsel Araştırma: Bilimsel bilgi elde etme süreci olarak tanımlanabilir.
 VERİ ANALİZİ GİRİŞ Bilimsel Araştırma: Bilimsel bilgi elde etme süreci olarak tanımlanabilir. Bilimsel Bilgi: Kaynağı ve elde edilme süreçleri belli olan bilgidir. Sosyal İlişkiler Görgül Bulgular İşlevsel
VERİ ANALİZİ GİRİŞ Bilimsel Araştırma: Bilimsel bilgi elde etme süreci olarak tanımlanabilir. Bilimsel Bilgi: Kaynağı ve elde edilme süreçleri belli olan bilgidir. Sosyal İlişkiler Görgül Bulgular İşlevsel
İSTATİSTİK. İstatistik Nedir? İstatistiksel Araştırmanın Amacı
 İSTATİSTİK İstatistik, belirli amaçlar için veri toplama, toplanan verileri tasnif etme, çözümleme ve yorumlama bilimidir Yrd. Doç. Dr. Hamit AYDIN İstatistik Nedir? Latince de durum anlamına gelen status
İSTATİSTİK İstatistik, belirli amaçlar için veri toplama, toplanan verileri tasnif etme, çözümleme ve yorumlama bilimidir Yrd. Doç. Dr. Hamit AYDIN İstatistik Nedir? Latince de durum anlamına gelen status
BİYOİSTATİSTİK. Ödev Çözümleri. Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH
 BİYOİSTATİSTİK Ödev Çözümleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr Ödev 1 Çözümleri 2 1. Bir sonucun
BİYOİSTATİSTİK Ödev Çözümleri Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr Ödev 1 Çözümleri 2 1. Bir sonucun
Grafik üzerindeki bilgiler özetlenmiştir. Veriler arasındaki ilişkiler görünür haldedir.
 GRAFİK VE İSTATİSTİK Grafikler,verileri görsel hale getirerek,veriler üzerinde daha kolay işlem yapılmasına ve elde edilen sonuçları değerlendirerek üzerinde tahmin yapılmasına olanak sağlar. Grafik üzerindeki
GRAFİK VE İSTATİSTİK Grafikler,verileri görsel hale getirerek,veriler üzerinde daha kolay işlem yapılmasına ve elde edilen sonuçları değerlendirerek üzerinde tahmin yapılmasına olanak sağlar. Grafik üzerindeki
Biyoistatistiğin Tanımı Biyoistatistikte Kullanılan Terimler Değişken Tipleri Parametre ve İstatistik Tanımlayıcı İstatistikler
 Biyoistatistiğin Tanımı Biyoistatistikte Kullanılan Terimler Değişken Tipleri Parametre ve İstatistik Tanımlayıcı İstatistikler Doç. Dr. Ertuğrul ÇOLAK Eskişehir Osmangazi Üniversitesi Tıp Fakültesi Biyoistatistik
Biyoistatistiğin Tanımı Biyoistatistikte Kullanılan Terimler Değişken Tipleri Parametre ve İstatistik Tanımlayıcı İstatistikler Doç. Dr. Ertuğrul ÇOLAK Eskişehir Osmangazi Üniversitesi Tıp Fakültesi Biyoistatistik
KARŞILAŞTIRMA İSTATİSTİĞİ, ANALİTİK YÖNTEMLERİN KARŞILAŞTIRILMASI, BİYOLOJİK DEĞİŞKENLİK. Doç.Dr. Mustafa ALTINIŞIK ADÜTF Biyokimya AD 2005
 KARŞILAŞTIRMA İSTATİSTİĞİ, ANALİTİK YÖNTEMLERİN KARŞILAŞTIRILMASI, BİYOLOJİK DEĞİŞKENLİK Doç.Dr. Mustafa ALTINIŞIK ADÜTF Biyokimya AD 2005 1 Karşılaştırma istatistiği Temel kavramlar: Örneklem ve evren:
KARŞILAŞTIRMA İSTATİSTİĞİ, ANALİTİK YÖNTEMLERİN KARŞILAŞTIRILMASI, BİYOLOJİK DEĞİŞKENLİK Doç.Dr. Mustafa ALTINIŞIK ADÜTF Biyokimya AD 2005 1 Karşılaştırma istatistiği Temel kavramlar: Örneklem ve evren:
İÇİNDEKİLER. BÖLÜM 1 Değişkenler ve Grafikler 1. BÖLÜM 2 Frekans Dağılımları 37
 İÇİNDEKİLER BÖLÜM 1 Değişkenler ve Grafikler 1 İstatistik 1 Yığın ve Örnek; Tümevarımcı ve Betimleyici İstatistik 1 Değişkenler: Kesikli ve Sürekli 1 Verilerin Yuvarlanması Bilimsel Gösterim Anlamlı Rakamlar
İÇİNDEKİLER BÖLÜM 1 Değişkenler ve Grafikler 1 İstatistik 1 Yığın ve Örnek; Tümevarımcı ve Betimleyici İstatistik 1 Değişkenler: Kesikli ve Sürekli 1 Verilerin Yuvarlanması Bilimsel Gösterim Anlamlı Rakamlar
Temel Ġstatistik. Tanımlayıcı Ġstatistik. Dağılımları Tanımlayıcı Ölçüler Yer Ölçüleri. Y.Doç.Dr. Ġbrahim Turan Mart 2011
 Temel Ġstatistik Tanımlayıcı Ġstatistik Dağılımları Tanımlayıcı Ölçüler Yer Ölçüleri Y.Doç.Dr. Ġbrahim Turan Mart 2011 Yer / Konum Ölçüleri 1- Aritmetik Ortalama (Mean): Deneklerin aldıkları değerlerin
Temel Ġstatistik Tanımlayıcı Ġstatistik Dağılımları Tanımlayıcı Ölçüler Yer Ölçüleri Y.Doç.Dr. Ġbrahim Turan Mart 2011 Yer / Konum Ölçüleri 1- Aritmetik Ortalama (Mean): Deneklerin aldıkları değerlerin
Ortalamaların karşılaştırılması
 Parametrik ve Parametrik Olmayan Testler Ortalamaların karşılaştırılması t testleri, ANOVA Mann-Whitney U Testi Wilcoxon İşaretli Sıra Testi Kruskal Wallis Testi BBY606 Araştırma Yöntemleri Güleda Doğan
Parametrik ve Parametrik Olmayan Testler Ortalamaların karşılaştırılması t testleri, ANOVA Mann-Whitney U Testi Wilcoxon İşaretli Sıra Testi Kruskal Wallis Testi BBY606 Araştırma Yöntemleri Güleda Doğan
BİYOİSTATİSTİK. Genel Uygulama 1. Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH
 BİYOİSTATİSTİK Genel Uygulama 1 Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr Soru 1 Ege Üniversitesi Diş
BİYOİSTATİSTİK Genel Uygulama 1 Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr Soru 1 Ege Üniversitesi Diş
İÇİNDEKİLER ÖN SÖZ...
 İÇİNDEKİLER ÖN SÖZ... v GİRİŞ... 1 1. İSTATİSTİK İN TARİHÇESİ... 1 2. İSTATİSTİK NEDİR?... 3 3. SAYISAL BİLGİDEN ANLAM ÇIKARILMASI... 4 4. BELİRSİZLİĞİN ELE ALINMASI... 4 5. ÖRNEKLEME... 5 6. İLİŞKİLERİN
İÇİNDEKİLER ÖN SÖZ... v GİRİŞ... 1 1. İSTATİSTİK İN TARİHÇESİ... 1 2. İSTATİSTİK NEDİR?... 3 3. SAYISAL BİLGİDEN ANLAM ÇIKARILMASI... 4 4. BELİRSİZLİĞİN ELE ALINMASI... 4 5. ÖRNEKLEME... 5 6. İLİŞKİLERİN
LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I BAHAR DÖNEMĐ DÖNEM SONU SINAV SORULARI
 LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I 2015-2016 BAHAR DÖNEMĐ DÖNEM SONU SINAV SORULARI Tarih/Saat/Yer: 15.06.16/09:00-10:30/AS115-116-117 Instructor: Prof. Dr. Hüseyin
LAÜ FEN EDEBĐYAT FAKÜLTESĐ PSĐKOLOJĐ BÖLÜMÜ PSK 106 ĐSTATĐSTĐK YÖNTEMLER I 2015-2016 BAHAR DÖNEMĐ DÖNEM SONU SINAV SORULARI Tarih/Saat/Yer: 15.06.16/09:00-10:30/AS115-116-117 Instructor: Prof. Dr. Hüseyin
SÜREKLĠ OLASILIK DAĞILIMLARI
 SÜREKLĠ OLASILIK DAĞILIMLARI Sayı ekseni üzerindeki tüm noktalarda değer alabilen değişkenler, sürekli değişkenler olarak tanımlanmaktadır. Bu bölümde, sürekli değişkenlere uygun olasılık dağılımları üzerinde
SÜREKLĠ OLASILIK DAĞILIMLARI Sayı ekseni üzerindeki tüm noktalarda değer alabilen değişkenler, sürekli değişkenler olarak tanımlanmaktadır. Bu bölümde, sürekli değişkenlere uygun olasılık dağılımları üzerinde
BÖLÜM I:TEMEL KAVRAMLAR
 İÇİNDEKİLER Önsöz. III BÖLÜM I:TEMEL KAVRAMLAR 13 Eğitim.. 13 Eğitim Türleri ve Sınıflandırılması. 17 Formal (Resmi, Biçimsel) Eğitim.... 18 İnformal (Resmi Olmayan, Biçimsel Olamayan).. 20 Davranış..
İÇİNDEKİLER Önsöz. III BÖLÜM I:TEMEL KAVRAMLAR 13 Eğitim.. 13 Eğitim Türleri ve Sınıflandırılması. 17 Formal (Resmi, Biçimsel) Eğitim.... 18 İnformal (Resmi Olmayan, Biçimsel Olamayan).. 20 Davranış..
DAĞILMA YADA DEĞİ KENLİK ÖLÇÜLERİ (MEASURE OF DISPERSION) Prof.Dr.A.KARACABEY Doç.Dr.F.GÖKGÖZ
 DAĞILMA YADA DEĞİ KENLİK ÖLÇÜLERİ (MEASURE OF DISPERSION) 1 AMAÇ... Mevcut veri seti için bulunan merkezi eğilim ölçüsünün yorumlamak Birden fazla veri seti için dağılımlar arası kıyaslama yapabilmek amaçlarıyla
DAĞILMA YADA DEĞİ KENLİK ÖLÇÜLERİ (MEASURE OF DISPERSION) 1 AMAÇ... Mevcut veri seti için bulunan merkezi eğilim ölçüsünün yorumlamak Birden fazla veri seti için dağılımlar arası kıyaslama yapabilmek amaçlarıyla
ALKÜ EKONOMİ ve FİNANS BÖLÜMÜ ISL 207 İSTATİSTİK I ALIŞTIRMALAR
 ALKÜ EKONOMİ ve FİNANS BÖLÜMÜ ISL 207 İSTATİSTİK I ALIŞTIRMALAR 1- İlaçla tedavi edilen 7 hastanın ortalama iyileşme süresi 22.6 gün ve standart sapması.360 gündür. Ameliyatla tedavi edilen 9 hasta için
ALKÜ EKONOMİ ve FİNANS BÖLÜMÜ ISL 207 İSTATİSTİK I ALIŞTIRMALAR 1- İlaçla tedavi edilen 7 hastanın ortalama iyileşme süresi 22.6 gün ve standart sapması.360 gündür. Ameliyatla tedavi edilen 9 hasta için
İSTATİSTİKSEL MERKEZİ EĞİLİM ÖLÇÜLERİ (DUYARSIZ ORTALAMALAR)
 SAÜ 5. BÖLÜM İSTATİSTİKSEL MERKEZİ EĞİLİM ÖLÇÜLERİ (DUYARSIZ ORTALAMALAR) PROF. DR. MUSTAFA AKAL İÇİNDEKİLER 1. HASSAS OLMAYAN ORTALAMALAR 1.1. Mod (Tepe Noktası) 1.1.1.1. Basit Serilerde Mod 1.1.1.2.
SAÜ 5. BÖLÜM İSTATİSTİKSEL MERKEZİ EĞİLİM ÖLÇÜLERİ (DUYARSIZ ORTALAMALAR) PROF. DR. MUSTAFA AKAL İÇİNDEKİLER 1. HASSAS OLMAYAN ORTALAMALAR 1.1. Mod (Tepe Noktası) 1.1.1.1. Basit Serilerde Mod 1.1.1.2.
İSTATİSTİK MHN3120 Malzeme Mühendisliği
 İSTATİSTİK MHN3120 Malzeme Mühendisliği CBÜ - Malzeme Mühendisliği Bölümü Ofis: Mühendislik Fakültesi A Blok Ofis no:311 Tel: 0 236 2012404 E-posta :emre.yalamac@cbu.edu.tr YARDIMCI KAYNAKLAR Mühendiler
İSTATİSTİK MHN3120 Malzeme Mühendisliği CBÜ - Malzeme Mühendisliği Bölümü Ofis: Mühendislik Fakültesi A Blok Ofis no:311 Tel: 0 236 2012404 E-posta :emre.yalamac@cbu.edu.tr YARDIMCI KAYNAKLAR Mühendiler
RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI. Yrd. Doç. Dr. Emre ATILGAN
 RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI Yrd. Doç. Dr. Emre ATILGAN 1 RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI Olasılığa ilişkin olayların çoğunluğunda, deneme sonuçlarının bir veya birkaç yönden incelenmesi
RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI Yrd. Doç. Dr. Emre ATILGAN 1 RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI Olasılığa ilişkin olayların çoğunluğunda, deneme sonuçlarının bir veya birkaç yönden incelenmesi
EĞĠTĠMDE ÖLÇME ve DEĞERLENDĠRME
 EĞĠTĠMDE ÖLÇME ve DEĞERLENDĠRME Öğrenci başarısının veya başarısızlığının kaynağında; öğrenci, öğretmen, çevre ve program vardır. Eğitimde değerlendirme yapılırken bu kaynaklar dikkate alınmaz. Eğitimciler,
EĞĠTĠMDE ÖLÇME ve DEĞERLENDĠRME Öğrenci başarısının veya başarısızlığının kaynağında; öğrenci, öğretmen, çevre ve program vardır. Eğitimde değerlendirme yapılırken bu kaynaklar dikkate alınmaz. Eğitimciler,
BÖLÜM 1 ÖLÇME VE DEĞERLENDİRMEDE TEMEL KAVRAMLAR
 İÇİNDEKİLER BÖLÜM 1 ÖLÇME VE DEĞERLENDİRMEDE TEMEL KAVRAMLAR I. Öğretimde Ölçme ve Değerlendirmenin Gerekliliği... 2 II. Ölçme Kavramı... 3 1. Tanımı ve Unsurları... 3 2. Aşamaları... 3 2.1. Ölçülecek
İÇİNDEKİLER BÖLÜM 1 ÖLÇME VE DEĞERLENDİRMEDE TEMEL KAVRAMLAR I. Öğretimde Ölçme ve Değerlendirmenin Gerekliliği... 2 II. Ölçme Kavramı... 3 1. Tanımı ve Unsurları... 3 2. Aşamaları... 3 2.1. Ölçülecek
Sürekli Rastsal Değişkenler
 Sürekli Rastsal Değişkenler Normal Dağılım: Giriş Normal Dağılım: Tamamen ortalaması ve standart sapması ile tanımlanan bir rastsal değişken, X, için oluşturulan sürekli olasılık dağılımına normal dağılım
Sürekli Rastsal Değişkenler Normal Dağılım: Giriş Normal Dağılım: Tamamen ortalaması ve standart sapması ile tanımlanan bir rastsal değişken, X, için oluşturulan sürekli olasılık dağılımına normal dağılım
MADDE VE TEST ANALİZİ. instagram: sevimasiroglu
 MADDE VE TEST ANALİZİ Sunu Sırası Madde Analizi Madde Güçlüğü Madde Ayırıcılık Gücü Test Analizi Dizi Genişliği Ortanca Ortalama Standart Sapma Testin Ortalama Güçlüğü Testin Çarpıklık Düzeyi Test Güvenirliği
MADDE VE TEST ANALİZİ Sunu Sırası Madde Analizi Madde Güçlüğü Madde Ayırıcılık Gücü Test Analizi Dizi Genişliği Ortanca Ortalama Standart Sapma Testin Ortalama Güçlüğü Testin Çarpıklık Düzeyi Test Güvenirliği
İstatistik Dersi Çalışma Soruları Arasınav(Matematik Müh. Bölümü-2014)
 İstatistik Dersi Çalışma Soruları Arasınav(Matematik Müh. Bölümü-2014) S-1) Bir otoyol üzerinde radarla hız kontrolü yapan, polis ekipler tarafından tespit edilen tane aracın hızları aşağıdaki tabloda
İstatistik Dersi Çalışma Soruları Arasınav(Matematik Müh. Bölümü-2014) S-1) Bir otoyol üzerinde radarla hız kontrolü yapan, polis ekipler tarafından tespit edilen tane aracın hızları aşağıdaki tabloda
İstatistik Temel Kavramlar- Devam
 İstatistik Temel Kavramlar- Devam 26.12.2016 Dr. Seher Yalçın 1 Değişken türleri Değişken; gözlemden gözleme farklı değerler alabilen objelere, niteliklere ya da durumlara denir (Arıcı, 2006). Bir özellik
İstatistik Temel Kavramlar- Devam 26.12.2016 Dr. Seher Yalçın 1 Değişken türleri Değişken; gözlemden gözleme farklı değerler alabilen objelere, niteliklere ya da durumlara denir (Arıcı, 2006). Bir özellik
BKİ farkı Standart Sapması (kg/m 2 ) A B BKİ farkı Ortalaması (kg/m 2 )
 4. SUNUM 1 Gözlem ya da deneme sonucu elde edilmiş sonuçların, rastlantıya bağlı olup olmadığının incelenmesinde kullanılan istatistiksel yöntemlere HİPOTEZ TESTLERİ denir. Sonuçların rastlantıya bağlı
4. SUNUM 1 Gözlem ya da deneme sonucu elde edilmiş sonuçların, rastlantıya bağlı olup olmadığının incelenmesinde kullanılan istatistiksel yöntemlere HİPOTEZ TESTLERİ denir. Sonuçların rastlantıya bağlı
ÖĞRENCİNİN ADI SOYADI:. NO:
 ÖĞRENCİNİN ADI SOYADI:. NO: İMZA: 2011-2012 ÖĞRETİM YILI TIP 1. SINIF TEMEL BİYOİSTATİSTİK DERSİ ARA SINAVI (04.11.2011) Biyoistatistik ve Tıp Bilişimi Anabilim Dalı Başarılar Temel Biyoistatistik dersi
ÖĞRENCİNİN ADI SOYADI:. NO: İMZA: 2011-2012 ÖĞRETİM YILI TIP 1. SINIF TEMEL BİYOİSTATİSTİK DERSİ ARA SINAVI (04.11.2011) Biyoistatistik ve Tıp Bilişimi Anabilim Dalı Başarılar Temel Biyoistatistik dersi
BÖLÜM 13 HİPOTEZ TESTİ
 1 BÖLÜM 13 HİPOTEZ TESTİ Bilimsel yöntem aşamalarıyla tanımlanmış sistematik bir bilgi üretme biçimidir. Bilimsel yöntemin aşamaları aşağıdaki gibi sıralanabilmektedir (Karasar, 2012): 1. Bir problemin
1 BÖLÜM 13 HİPOTEZ TESTİ Bilimsel yöntem aşamalarıyla tanımlanmış sistematik bir bilgi üretme biçimidir. Bilimsel yöntemin aşamaları aşağıdaki gibi sıralanabilmektedir (Karasar, 2012): 1. Bir problemin
MATE211 BİYOİSTATİSTİK
 MATE211 BİYOİSTATİSTİK ÇALIŞMA SORULARININ ÇÖZÜM VE CEVAPLARI Yapılan bir araştırmada, 136 erişkin kişinin kanlarındaki kolesterol düzeyleri gr/dl cinsinden aşağıda verilmiştir: 180 230 190 186 220 191
MATE211 BİYOİSTATİSTİK ÇALIŞMA SORULARININ ÇÖZÜM VE CEVAPLARI Yapılan bir araştırmada, 136 erişkin kişinin kanlarındaki kolesterol düzeyleri gr/dl cinsinden aşağıda verilmiştir: 180 230 190 186 220 191
Projenin Adı: İstatistik yardımıyla YGS ye hazırlık için soru çözme planlaması
 Projenin Adı: İstatistik yardımıyla YGS ye hazırlık için soru çözme planlaması Projenin Amacı : YGS de başarılı olmak isteyen bir öğrencinin, istatistiksel yöntemler çerçevesinde, sınavda çıkan soru sayısını,
Projenin Adı: İstatistik yardımıyla YGS ye hazırlık için soru çözme planlaması Projenin Amacı : YGS de başarılı olmak isteyen bir öğrencinin, istatistiksel yöntemler çerçevesinde, sınavda çıkan soru sayısını,
1.58 arasındaki her bir değeri alabileceği için sürekli bir
 7.SUNUM Hatırlanacağı gibi, kesikli rassal değişkenler sonlu (örneğin; 0, 1, 2,...,10) veya sayılabilir sonsuzlukta (örneğin; 0, 1, 2,...) değerler alabilmektedir. Fakat birçok uygulamada, rassal değişkenin
7.SUNUM Hatırlanacağı gibi, kesikli rassal değişkenler sonlu (örneğin; 0, 1, 2,...,10) veya sayılabilir sonsuzlukta (örneğin; 0, 1, 2,...) değerler alabilmektedir. Fakat birçok uygulamada, rassal değişkenin
Hatalar Bilgisi ve İstatistik Ders Kodu: Kredi: 3 / ECTS: 5
 Ders Kodu: 0010070021 Kredi: 3 / ECTS: 5 Yrd. Doç. Dr. Serkan DOĞANALP Necmettin Erbakan Üniversitesi Harita Mühendisliği Bölümü Konya 07.01.2015 1 Giriş 2 Giriş Matematiksel istatistiğin konusu yığın
Ders Kodu: 0010070021 Kredi: 3 / ECTS: 5 Yrd. Doç. Dr. Serkan DOĞANALP Necmettin Erbakan Üniversitesi Harita Mühendisliği Bölümü Konya 07.01.2015 1 Giriş 2 Giriş Matematiksel istatistiğin konusu yığın
ÖRNEKLEME DAĞILIŞLARI VE TAHMİNLEYİCİLERİN ÖZELLİKLERİ
 ÖRNEKLEME DAĞILIŞLARI VE TAHMİNLEYİCİLERİN ÖZELLİKLERİ TEMEL KAVRAMLAR PARAMETRE: Populasyonun sayısal açıklayıcı bir ölçüsüdür ve anakütledeki tüm elemanlar dikkate alınarak hesaplanabilir. Ana kütledeki
ÖRNEKLEME DAĞILIŞLARI VE TAHMİNLEYİCİLERİN ÖZELLİKLERİ TEMEL KAVRAMLAR PARAMETRE: Populasyonun sayısal açıklayıcı bir ölçüsüdür ve anakütledeki tüm elemanlar dikkate alınarak hesaplanabilir. Ana kütledeki
ANADOLU ÜNİVERSİTESİ İST 213 OLASILIK DERSİ TANIMLAR VE VERİ SINIFLAMASI
 ANADOLU ÜNİVERSİTESİ İST 213 OLASILIK DERSİ TANIMLAR VE VERİ SINIFLAMASI DOÇ. DR. NİHAL ERGİNEL TANIMLAR VE VERİ SINIFLAMASI Olasılık, ilgilenilen olay/olayların meydana gelme olabilirliğinin ölçülmesidir.
ANADOLU ÜNİVERSİTESİ İST 213 OLASILIK DERSİ TANIMLAR VE VERİ SINIFLAMASI DOÇ. DR. NİHAL ERGİNEL TANIMLAR VE VERİ SINIFLAMASI Olasılık, ilgilenilen olay/olayların meydana gelme olabilirliğinin ölçülmesidir.
