DİK ÜÇGEN. şekilde, m(a) = 90. [BC] kenarı hipotenüs. [AB] ve [AC] kenarları. dik kenarlardır. P İSAGOR BAĞINTISI
|
|
|
- Nilüfer Günaydın
- 7 yıl önce
- İzleme sayısı:
Transkript
1 DİK ÜÇGEN Bir açısının ölçüsü 90 olan üçgene dik üçgen denir. Dik üçgende 90 nin karşısındaki kenara hipotenüs, diğer kenarlara dik kenar adı verilir. Hipotenüs üçgenin daima en uzun kenarıdır. şekilde, m(a) = 90 [BC] kenarı hipotenüs [AB] ve [AC] kenarları dik kenarlardır. P İSAGOR BAĞINTISI Dik üçgende dik kenarların uzunluklarının kareleri toplamı hipotenüsün uzunluğunun karesine eşittir. ABC üçgeninde m(a) = 90 a 2 =b 2 +c 2 ÖZEL DİK ÜÇGENLER 1. (3 4 5) Üçgeni Kenar uzunlukları (3 4 5) sayıları veya bunların katı olan bütün üçgenler dik üçgendir. (6 8 10), ( ), gibi 2. ( ) Üçgeni
2 Kenar uzunlukları ( ) sayıları ve bunların katı olan bütün üçgenler dik üçgenlerdir. ( ), ( ), gibi. Kenar uzunlukları 8, 15, 17 sayıları ile orantılı olan üçgenler dik üçgenlerdir. Kenar uzunlukları 7, 24, 25 sayıları ile orantılı olan üçgenler dik üçgenlerdir. 3. İkizkenar dik üçgen ABC dik üçgen AB = BC = a AC = a 2 m(a) = m(c) = 45 İkizkenar dik üçgende hipotenüs dik kenarların 2 katıdır. 4. ( ) Üçgeni
3 ABC eşkenar üçgeni yükseklikle ikiye bölündüğünde ABH ve ACH ( ) üçgenleri elde edilir. AB = AC = a BH = HC = pisagordan ( ) dik üçgeninde; 30 'nin karşısındaki kenar hipotenüsün yarısına eşittir. 60 nin karşısındaki kenar, 30 nin karşısındaki kenarın 3 katıdır. 5. ( ) Üçgeni ( ) üçgeninde 30 lik açıların karşılarındaki kenarlara a dersek 120 lik açının karşısındaki kenar a 3 olur. 6. ( ) Üçgeni ( ) üçgeninde hipotenüse ait yükseklik AH = h dersek, hipotenüs BC = 4h olur. Hipotenüs kendisine ait yüksekliğin dört katıdır. ÖKLİT BAĞINTILARI
4 Dik üçgenlerde hipotenüse ait yüksekliğin verildiği durumlarda benzerlikten kaynaklanan öklit bağıntıları kullanılır. 1. Yüksekliğin hipotenüste ayırdığı parçaların çarpımı yüksekliğin karesine eşittir. h 2 = p.k 2. b 2 = k.a c 2 = p.a 3. ABC üçgeninin alanını iki farklı şekilde yazıp eşitlediğimizde a.h =b.c Yukarıda anlatılan öklit bağıntıları kullanılarak elde edilir. Genellikle bu öklit bağıntısını kullanmak yerine, yukarıdaki öklit bağıntıları ve pisagor bağıntısını kullanarak çözüme gideriz. İKİZKENAR ÜÇGEN İkizkenar üçgenin tepe açısından tabanına çizilen yükseklik, hem açıortay, hem de kenarortaydır.
5 1. Bir üçgende, açıortay aynı zamanda yükseklik ise bu üçgen ikizkenar üçgendir. AB = AC BH = HC m(b) = m(c) 2. Bir üçgende, açıortay aynı zamanda kenarortay ise bu üçgen ikizkenar üçgendir. AB = AC, [AH] [BC] m(b) = m(c) 3. Bir üçgende, yükseklik aynı zamanda kenarortay ise bu üçgen ikizkenar üçgendir. AB = AC m(bah) = m(hac) m(b) = m(c) İkizkenar üçgende açıortay, kenarortay ve yüksekliğin aynı olması birçok yerde karşımıza çıktığından çok iyi bilinmesi gereken bir özelliktir. 4. İkizkenar üçgende ikizkenara ait yükseklikler eşittir. Bu durumda yüksekliklerin kesim noktasının ayırdığı parçalarda eşit olur. 5. İkizkenar üçgende ikizkenara ait kenarortaylar ve kenarortayların kesim noktasının ayırdığı parçalar da birbirine eşittir.
6 6. İkizkenar üçgende eşit açılara ait açıortaylar da eşittir. Açıortaylar birbirini aynı oranda bölerler. 7. İkizkenar üçgende ikiz olmayan kenar üzerindeki herhangi bir noktadan ikiz kenarlara çizilen dikmelerin toplamı, ikizkenarlara ait yüksekliği verir. AB = AC LC = HP + KP 8. İkizkenar üçgende tabandan ikiz kenarlara çizilen paralellerin toplamı, ikiz kenarların uzunluğuna eşittir. EŞKENAR ÜÇGEN 1. Eşkenar üçgende bütün açıortay, kenarortay yükseklikler çakışık ve hepsinin uzunlukları eşittir. n A = n B = n C = V a = V b = V c = h a = h b = h c
7 2. Eşkenar üçgenin bir kenarına a dersek yük seklik Bu durumda eşkenar üçgenin alanı yükseklik cinsinden alan değeri Alan(ABC) = 3. Eşkenar üçgenin içindeki herhangi bir noktadan kenarlara çizilen dik uzunlukların toplamı, eşkenar üçgene ait yüksekliği verir. Bir kenarı a olan eşkenar üçgende; 4. Eşkenar üçgenin içindeki herhangi bir noktadan kenarlara çizilen paralellerin toplamı bir kenar uzunluğuna eşittir. Bir kenarı a olan ABC eşkenar üçgeninde
EVVET ARKADAŞLAR HOŞGELDİNİZ BU DERSİMİZDE ÜÇGENLER VE ÖZELLİKLERİNE GÖZ ATACAĞIZ.
 DERS : GEOMETRİ KONU : ÜÇGEN EVVET ARKADAŞLAR HOŞGELDİNİZ BU DERSİMİZDE ÜÇGENLER VE ÖZELLİKLERİNE GÖZ ATACAĞIZ. AMAN SIKILMAYIN NOT BİRAZ UZUN DA :-) Doğrusal olmayan üç noktayı birleştiren üç doğru parçasının
DERS : GEOMETRİ KONU : ÜÇGEN EVVET ARKADAŞLAR HOŞGELDİNİZ BU DERSİMİZDE ÜÇGENLER VE ÖZELLİKLERİNE GÖZ ATACAĞIZ. AMAN SIKILMAYIN NOT BİRAZ UZUN DA :-) Doğrusal olmayan üç noktayı birleştiren üç doğru parçasının
ÜÇGENDE AÇILAR. Doğrusal olmayan üç noktayı birleştiren üç doğru parçasının birleşimine üçgen denir. AB] [AC] [BC] = ABC dir.
![ÜÇGENDE AÇILAR. Doğrusal olmayan üç noktayı birleştiren üç doğru parçasının birleşimine üçgen denir. AB] [AC] [BC] = ABC dir. ÜÇGENDE AÇILAR. Doğrusal olmayan üç noktayı birleştiren üç doğru parçasının birleşimine üçgen denir. AB] [AC] [BC] = ABC dir.](/thumbs/51/27890487.jpg) ÜÇGENDE AÇILAR Doğrusal olmayan üç noktayı birleştiren üç doğru parçasının birleşimine üçgen denir. AB] [AC] [BC] = ABC dir. Burada; A, B, C noktaları üçgenin köşeleri, [AB], [AC], [BC] doğru parçaları
ÜÇGENDE AÇILAR Doğrusal olmayan üç noktayı birleştiren üç doğru parçasının birleşimine üçgen denir. AB] [AC] [BC] = ABC dir. Burada; A, B, C noktaları üçgenin köşeleri, [AB], [AC], [BC] doğru parçaları
7. ÜNİTE DOĞRUDA VE ÜÇGENDE AÇILAR
 7. ÜNİTE DOĞRUDA VE ÜÇGENDE AÇILAR KONULAR 1. DOĞRUDA AÇILAR 2. Açı 3. Açının Düzlemde Ayırdığı Bölgeler 4. Açı Ölçü Birimleri 5. Ölçülerine Göre Açılar 6. Açıortay 7. Tümler Açı 8. Bütünler Açı 9. Ters
7. ÜNİTE DOĞRUDA VE ÜÇGENDE AÇILAR KONULAR 1. DOĞRUDA AÇILAR 2. Açı 3. Açının Düzlemde Ayırdığı Bölgeler 4. Açı Ölçü Birimleri 5. Ölçülerine Göre Açılar 6. Açıortay 7. Tümler Açı 8. Bütünler Açı 9. Ters
qwertyuiopasdfghjklzxcvbnmq wertyuiopasdfghjklzxcvbnmqw ertyuiopasdfghjklzxcvbnmqwer tyuiopasdfghjklzxcvbnmqwerty uiopasdfghjklzxcvbnmqwertyui
 qwertyuiopasdfghjklzxcvbnmq wertyuiopasdfghjklzxcvbnmqw ertyuiopasdfghjklzxcvbnmqwer FİZİK İÇİN MATEMATİK tyuiopasdfghjklzxcvbnmqwerty --------------------------------------- uiopasdfghjklzxcvbnmqwertyui
qwertyuiopasdfghjklzxcvbnmq wertyuiopasdfghjklzxcvbnmqw ertyuiopasdfghjklzxcvbnmqwer FİZİK İÇİN MATEMATİK tyuiopasdfghjklzxcvbnmqwerty --------------------------------------- uiopasdfghjklzxcvbnmqwertyui
ÜÇGEN VE KENARLARI ARASINDA BAĞINTILAR
 ÜÇGEN VE KENARLARI ARASINDA BAĞINTILAR 1. Bir üçgende ölçüsü büyük olan açının karşısındaki kenar uzunluğu, ölçüsü küçük olan açının karşısındaki kenar uzunluğundan daha büyüktür. ABC üçgeninde m(a) >
ÜÇGEN VE KENARLARI ARASINDA BAĞINTILAR 1. Bir üçgende ölçüsü büyük olan açının karşısındaki kenar uzunluğu, ölçüsü küçük olan açının karşısındaki kenar uzunluğundan daha büyüktür. ABC üçgeninde m(a) >
ÜÇGENLER ÜNİTE 4. ÜNİTE 4. ÜNİTE 4. ÜNİTE 4. ÜNİT
 ÜÇGNLR ÜNİT. ÜNİT. ÜNİT. ÜNİT. ÜNİT ÜÇGNLRİN ŞLİĞİ Üçgende çılar. azanım : ir üçgenin iç açılarının ölçüleri toplamının 80, dış açılarının ölçüleri toplamının 0 olduğunu gösterir. İki Üçgenin şliği. azanım
ÜÇGNLR ÜNİT. ÜNİT. ÜNİT. ÜNİT. ÜNİT ÜÇGNLRİN ŞLİĞİ Üçgende çılar. azanım : ir üçgenin iç açılarının ölçüleri toplamının 80, dış açılarının ölçüleri toplamının 0 olduğunu gösterir. İki Üçgenin şliği. azanım
çemberi ile O Çemberlerin birbirine göre durumlarını inceleyelim. İlk durumda alalım. olduğu takdirde O2K1
 . merkezli R yarıçaplı Ç çemberi ile merkezli R yarıçaplı ve noktasından geçen Ç çemberi veriliyor. Ç üzerinde, T Ç K T Ç, ve K K T K olacak şekilde bir T noktası alınıyor. Buna göre, uzunluklarından birinin
. merkezli R yarıçaplı Ç çemberi ile merkezli R yarıçaplı ve noktasından geçen Ç çemberi veriliyor. Ç üzerinde, T Ç K T Ç, ve K K T K olacak şekilde bir T noktası alınıyor. Buna göre, uzunluklarından birinin
CEVAP ANAHTARI 1-B 2-C 3-C 4-C 5-B 6-E 7-D 8-E 9-C 10-E 11-E 12-A 13-A 1-A 2-D 3-C 4-D 5-D 6-B 7-D 8-B 9-D 10-E 11-D 12-C
 1. BÖLÜM: AÇISAL KAVRAMLAR VE DOĞRUDA AÇILAR 1-B 2-C 3-C 4-C 5-B 6-E 7-D 8-E 9-C 10-E 11-E 12-A 13-A 1-E 2-A 3-E 4-C 5-C 6-C 7-D 8-D 9-D 10-E 11-B 12-C 2. BÖLÜM: ÜÇGENDE AÇILAR 1-A 2-D 3-C 4-D 5-D 6-B
1. BÖLÜM: AÇISAL KAVRAMLAR VE DOĞRUDA AÇILAR 1-B 2-C 3-C 4-C 5-B 6-E 7-D 8-E 9-C 10-E 11-E 12-A 13-A 1-E 2-A 3-E 4-C 5-C 6-C 7-D 8-D 9-D 10-E 11-B 12-C 2. BÖLÜM: ÜÇGENDE AÇILAR 1-A 2-D 3-C 4-D 5-D 6-B
8. SINIF PİSAGOR BAĞINTISI
 06. SINIF PİSGOR ĞINTISI a c (hipotenüs) 5 b 6 a 2 +b 2 =c 2 Pisagor bağıntısını kullanabilmek için dik üçgen olması gerekir. ÖR: şağıda verilmeyen kenarları bulunuz. 6 2 Pisagor bağıntısı kullanırken
06. SINIF PİSGOR ĞINTISI a c (hipotenüs) 5 b 6 a 2 +b 2 =c 2 Pisagor bağıntısını kullanabilmek için dik üçgen olması gerekir. ÖR: şağıda verilmeyen kenarları bulunuz. 6 2 Pisagor bağıntısı kullanırken
Bu e-kitabın her hakkı saklıdır. Tüm hakları Ali Selim YAMAN a aittir. Kısmen de olsa alıntı yapılamaz.metin, biçim ve sorular elektronik, mekanik,
 Bu e-kitabın her hakkı saklıdır. Tüm hakları Ali Selim YAMAN a aittir. Kısmen de olsa alıntı yapılamaz.metin, biçim ve sorular elektronik, mekanik, fotokopi ya da herhangi bir kayıt sistemiyle çoğaltılamaz,
Bu e-kitabın her hakkı saklıdır. Tüm hakları Ali Selim YAMAN a aittir. Kısmen de olsa alıntı yapılamaz.metin, biçim ve sorular elektronik, mekanik, fotokopi ya da herhangi bir kayıt sistemiyle çoğaltılamaz,
9. ÜNİTE ÜÇGENLER, ÇOKGENLER VE MESLEKÎ UYGULAMALARI
 9. ÜNİTE ÜÇGENLER, ÇOKGENLER VE MESLEKÎ UYGULAMALARI KONULAR DİK ÜÇGENLERDE METRİK BAĞINTILAR 1. Pythagoras (Pisagor) Bağıntısı. Euclides (öklit) Bağıntısı 3. Pisagor ve öklit Bağıntıları ile İlgili Problemler
9. ÜNİTE ÜÇGENLER, ÇOKGENLER VE MESLEKÎ UYGULAMALARI KONULAR DİK ÜÇGENLERDE METRİK BAĞINTILAR 1. Pythagoras (Pisagor) Bağıntısı. Euclides (öklit) Bağıntısı 3. Pisagor ve öklit Bağıntıları ile İlgili Problemler
9. SINIF Geometri TEMEL GEOMETRİK KAVRAMLAR
 TEMEL GEOMETRİK KAVRAMLAR 9. SINIF Geometri Amaç-1: Nokta, Doğru, Düzlem, Işın ve Uzayı Kavrayabilme. 1. Nokta, doğru, düzlem ve uzay kavramlarım açıklama. 2. Farklı iki noktadan geçen doğru sayışım söyleme
TEMEL GEOMETRİK KAVRAMLAR 9. SINIF Geometri Amaç-1: Nokta, Doğru, Düzlem, Işın ve Uzayı Kavrayabilme. 1. Nokta, doğru, düzlem ve uzay kavramlarım açıklama. 2. Farklı iki noktadan geçen doğru sayışım söyleme
5. ÜNİTE AÇILAR, ÜÇGENLER VE MESLEKİ UYGULAMALARI
 5. ÜNİTE ÇILR, ÜÇGENLER VE MESLEKİ UYGULMLRI açılar KONULR 1. çı, çı Türleri ve Mesleki Uygulamaları 2. Tümler ve ütünler çılar ÜÇGENLER 1. Üçgene it Temel ilgiler 2. Üçgen Türleri 3. Üçgenin Yardımcı
5. ÜNİTE ÇILR, ÜÇGENLER VE MESLEKİ UYGULMLRI açılar KONULR 1. çı, çı Türleri ve Mesleki Uygulamaları 2. Tümler ve ütünler çılar ÜÇGENLER 1. Üçgene it Temel ilgiler 2. Üçgen Türleri 3. Üçgenin Yardımcı
LYS 2016 GEOMETRİ ÇÖZÜMLERİ
 LYS 016 GEOMETRİ ÇÖZÜMLERİ Dikdörtgenin içinde köşegeni çizerek alanı iki eşit parçaya ayırabiliriz. 7 / 36 BED üçgeni ile DEC üçgeninin alanlarının oranı, tabanları arasındaki orana eşittir. Buna göre;
LYS 016 GEOMETRİ ÇÖZÜMLERİ Dikdörtgenin içinde köşegeni çizerek alanı iki eşit parçaya ayırabiliriz. 7 / 36 BED üçgeni ile DEC üçgeninin alanlarının oranı, tabanları arasındaki orana eşittir. Buna göre;
AÇILAR / TEST-1. B, C, E doğrusal = 50 E C. A, B, L doğrusal = 100 = 30 = 40 C 60 D
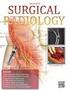 ÇIR / TST-1 P = [P] m( P ) = //,, doğrusal m( ) = 30 // m( ) m( ) = = 30 d3 // d3 // d4 m( ) = Verilenlere göre, + + ) 250 ) 260 ) 270 ) 280 ) 300 Verilenlere göre, m( ) ) 25 ) 30 ) 35 ) 40 ) 50 10 Verilenlere
ÇIR / TST-1 P = [P] m( P ) = //,, doğrusal m( ) = 30 // m( ) m( ) = = 30 d3 // d3 // d4 m( ) = Verilenlere göre, + + ) 250 ) 260 ) 270 ) 280 ) 300 Verilenlere göre, m( ) ) 25 ) 30 ) 35 ) 40 ) 50 10 Verilenlere
Eğer piramidin tabanı düzgün çokgense bu tip piramitlere düzgün piramit denir.
 PİRAMİTLER Bir düzlemde kapalı bir bölge ile bu düzlemin dışında bir T noktası alalım. Kapalı bölgenin tüm noktalarının T noktası ile birleştirilmesi sonucunda oluşan cisme piramit denir. T noktası piramidin
PİRAMİTLER Bir düzlemde kapalı bir bölge ile bu düzlemin dışında bir T noktası alalım. Kapalı bölgenin tüm noktalarının T noktası ile birleştirilmesi sonucunda oluşan cisme piramit denir. T noktası piramidin
Öğrenci Seçme Sınavı (Öss) / 18 Nisan Matematik Soruları ve Çözümleri
 Öğrenci Seçme Sınavı (Öss) / 8 Nisan 99 Matematik Soruları ve Çözümleri. Bir sayının inin fazlası, aynı sayıya eşittir. Bu sayı kaçtır? A) B) 0 C) D) 0 E) Çözüm Sayı olsun.. + +. Bir sınıftaki toplam öğrenci
Öğrenci Seçme Sınavı (Öss) / 8 Nisan 99 Matematik Soruları ve Çözümleri. Bir sayının inin fazlası, aynı sayıya eşittir. Bu sayı kaçtır? A) B) 0 C) D) 0 E) Çözüm Sayı olsun.. + +. Bir sınıftaki toplam öğrenci
TEST 1. ABCD bir dörtgen AF = FB DE = EC AD = BC D E C. ABC bir üçgen. m(abc) = 20. m(bcd) = 10. m(acd) = 50. m(afe) = 80.
 11 ÖLÜM SİZİN İÇİN SÇTİLR LRİMİZ 1 80 0 bir dörtgen = = = m() = 80 m() = 0 Verilenlere göre, açısının ölçüsü kaç derecedir? 0 10 0 bir üçgen m() = 0 m() = 10 m() = 0 Yukarıda verilenlere göre, oranı kaçtır?
11 ÖLÜM SİZİN İÇİN SÇTİLR LRİMİZ 1 80 0 bir dörtgen = = = m() = 80 m() = 0 Verilenlere göre, açısının ölçüsü kaç derecedir? 0 10 0 bir üçgen m() = 0 m() = 10 m() = 0 Yukarıda verilenlere göre, oranı kaçtır?
Öğrenci Seçme Sınavı (Öss) / 17 Nisan 1994. Matematik Soruları ve Çözümleri = 43. olduğuna göre a kaçtır?
 Öğrenci Seçme Sınavı (Öss) / 17 Nisan 1994 Matematik Soruları ve Çözümleri 4.10 +.10 1. 4 10 4 işleminin sonucu kaçtır? A) 0,4 B) 4, C) 4 D) 40 E) 400 Çözüm 1 4.10 +.10 4 10 4 4.10 +.10 10 1+ 1 = 4 4 (40+
Öğrenci Seçme Sınavı (Öss) / 17 Nisan 1994 Matematik Soruları ve Çözümleri 4.10 +.10 1. 4 10 4 işleminin sonucu kaçtır? A) 0,4 B) 4, C) 4 D) 40 E) 400 Çözüm 1 4.10 +.10 4 10 4 4.10 +.10 10 1+ 1 = 4 4 (40+
6. ABCD dikdörtgeninde
 Çokgenler ve örtgenler Test uharrem Şahin. enar sayısı ile köşegen sayısı toplamı olan düzgün çokgenin bir dış açısı kaç derecedir? ) ) 0 ) ) 0 ). Şekilde dikdörtgeninin içindeki P noktasının üç köşeye
Çokgenler ve örtgenler Test uharrem Şahin. enar sayısı ile köşegen sayısı toplamı olan düzgün çokgenin bir dış açısı kaç derecedir? ) ) 0 ) ) 0 ). Şekilde dikdörtgeninin içindeki P noktasının üç köşeye
ÜÇGEN LE LG L TEMEL KAVRAMLAR
 III. ÖLÜM ÜÇGN L LG L TML KVRMLR Tan m (Çokgen) : n > olmak üzere, bir düzlemde 1,, 3,..., n gibi birbirinden farkl, herhangi üçü do rusal olmayan n nokta verilsin. Uç noktalar d fl nda kesiflmeyen [ 1
III. ÖLÜM ÜÇGN L LG L TML KVRMLR Tan m (Çokgen) : n > olmak üzere, bir düzlemde 1,, 3,..., n gibi birbirinden farkl, herhangi üçü do rusal olmayan n nokta verilsin. Uç noktalar d fl nda kesiflmeyen [ 1
PH AB, PH =x kaç cm.dir?
 ABCD bir kare. ABCD bir kare. AB =10 cm. m(pcb)=x kaç derecedir? PH AB, PH =x kaç cm.dir? PA ve PB ait oldukları çemberlerin yarıçaplarıdır. PA = AB =PB olduğundan PAB eşkenar üçgendir. m(pab)=60 o AB
ABCD bir kare. ABCD bir kare. AB =10 cm. m(pcb)=x kaç derecedir? PH AB, PH =x kaç cm.dir? PA ve PB ait oldukları çemberlerin yarıçaplarıdır. PA = AB =PB olduğundan PAB eşkenar üçgendir. m(pab)=60 o AB
pisagor bağıntısı örnek: örnek: örnek: örnek: Kazanım : Pisagor bağıntısını oluşturur; ilgili problemleri çözer. dik kenar c b dik kenar
 pisagor bağıntısı Kazanım : Pisagor bağıntısını oluşturur; ilgili problemleri çözer. 4 Hi dik kenar ir dik üçgende dik kenar uzunluklarının kareleri toplamı, hipotenüs uzunluğunun karesine eşittir. Dik
pisagor bağıntısı Kazanım : Pisagor bağıntısını oluşturur; ilgili problemleri çözer. 4 Hi dik kenar ir dik üçgende dik kenar uzunluklarının kareleri toplamı, hipotenüs uzunluğunun karesine eşittir. Dik
GEOMETRİ SORU BANKASI KİTABI
 LİSE ÖĞRENCİLERİNİN ÜNİVERSİTE SINAVLARINA HAZIRLANMALARI İÇİN GEOMETRİ SORU BANKASI KİTABI HAZIRLAYAN Erol GEDİKLİ Matematik Öğretmeni SUNUŞ Sevgili öğrenciler! Bu kitap; hazırlandığınız üniversite sınavlarında,
LİSE ÖĞRENCİLERİNİN ÜNİVERSİTE SINAVLARINA HAZIRLANMALARI İÇİN GEOMETRİ SORU BANKASI KİTABI HAZIRLAYAN Erol GEDİKLİ Matematik Öğretmeni SUNUŞ Sevgili öğrenciler! Bu kitap; hazırlandığınız üniversite sınavlarında,
Geometrik Cisimlerin Hacimleri
 1 Ülkemizin kongre ve fuar merkezlerinden biri, Antalya daki Cam Piramit Kongre ve Fuar Merkezi dir. Renkli ısıcamlı uzay çatı ile örülerek piramit şeklinde inşa edilmiştir. 2 Şekildeki piramidin tabanı
1 Ülkemizin kongre ve fuar merkezlerinden biri, Antalya daki Cam Piramit Kongre ve Fuar Merkezi dir. Renkli ısıcamlı uzay çatı ile örülerek piramit şeklinde inşa edilmiştir. 2 Şekildeki piramidin tabanı
Lisans Yerleştirme Sınavı 1 (Lys 1) / 18 Haziran Geometri Soruları ve Çözümleri
 Lisans Yerleştirme Sınavı (Lys ) / 8 Haziran 0 Geometri Soruları ve Çözümleri. Bir ikizkenar üçgenin eş kenarlarının her birinin uzunluğu 0 cm ve üçüncü kenarının uzunluğu 4 cm olduğuna göre, alanı kaç
Lisans Yerleştirme Sınavı (Lys ) / 8 Haziran 0 Geometri Soruları ve Çözümleri. Bir ikizkenar üçgenin eş kenarlarının her birinin uzunluğu 0 cm ve üçüncü kenarının uzunluğu 4 cm olduğuna göre, alanı kaç
Ö.S.S. 1994. MATEMATĐK SORULARI ve ÇÖZÜMLERĐ = 43. olduğuna göre a kaçtır?
 Ö.S.S. 1994 MATEMATĐK SORULARI ve ÇÖZÜMLERĐ 4.10 1. 4 10 +.10 4 işleminin sonucu kaçtır? A) 0,4 B) 4, C) 4 D) 40 E) 400 Çözüm 1 4.10 +.10 4 10 4 4.10 +.10 10 1+ 1 4 4 (40+ ).10 10 4 4 4 (98² 98²) 00.9.
Ö.S.S. 1994 MATEMATĐK SORULARI ve ÇÖZÜMLERĐ 4.10 1. 4 10 +.10 4 işleminin sonucu kaçtır? A) 0,4 B) 4, C) 4 D) 40 E) 400 Çözüm 1 4.10 +.10 4 10 4 4.10 +.10 10 1+ 1 4 4 (40+ ).10 10 4 4 4 (98² 98²) 00.9.
İç bükey Dış bükey çokgen
 Çokgen Çokgensel bölge İç bükey Dış bükey çokgen Köşeleri: Kenarları: İç açıları: Dış açıları: Köşegenleri: Çokgenin temel elemanları Kenar Köşegen ilişkisi Bir köşe belirleyiniz ve belirlediğiniz köşeden
Çokgen Çokgensel bölge İç bükey Dış bükey çokgen Köşeleri: Kenarları: İç açıları: Dış açıları: Köşegenleri: Çokgenin temel elemanları Kenar Köşegen ilişkisi Bir köşe belirleyiniz ve belirlediğiniz köşeden
[ AN ] doğrusu açıortay olduğundan;
![[ AN ] doğrusu açıortay olduğundan; [ AN ] doğrusu açıortay olduğundan;](/thumbs/69/60247548.jpg) . Bir havuzu bir musluk 6 saatte, başka bir musluk 8 saatte dolduruyor. Bu iki musluk kapalı iken, havuzun altında bulunan üçüncü bir musluk, dolu havuzu saatte boşaltabiliyor. Üç musluk birden açılırsa,boş
. Bir havuzu bir musluk 6 saatte, başka bir musluk 8 saatte dolduruyor. Bu iki musluk kapalı iken, havuzun altında bulunan üçüncü bir musluk, dolu havuzu saatte boşaltabiliyor. Üç musluk birden açılırsa,boş
Öğrenci Seçme Sınavı (Öss) / 19 Nisan Matematik Soruları ve Çözümleri
 Öğrenci Seçme Sınavı (Öss) / 9 Nisan 99 Matematik Soruları ve Çözümleri. Üç basamaklı bir sayının iki basamaklı bir sayıyla çarpımı en az kaç basamaklı bir sayı olur? A) B) C) D) 6 E) 7 Çözüm I. Yol basamaklı
Öğrenci Seçme Sınavı (Öss) / 9 Nisan 99 Matematik Soruları ve Çözümleri. Üç basamaklı bir sayının iki basamaklı bir sayıyla çarpımı en az kaç basamaklı bir sayı olur? A) B) C) D) 6 E) 7 Çözüm I. Yol basamaklı
Ö.Y.S MATEMATĐK SORULARI ve ÇÖZÜMLERĐ
 Ö.Y.S. 996 MATEMATĐK SORULARI ve ÇÖZÜMLERĐ. Bir sınıftaki örencilerin nin fazlası kız örencidir. Sınıfta erkek öğrenci olduğuna göre, kız öğrencilerin sayısı kaçtır? A) B) 8 C) 6 D) E) Çözüm Toplam öğrenci
Ö.Y.S. 996 MATEMATĐK SORULARI ve ÇÖZÜMLERĐ. Bir sınıftaki örencilerin nin fazlası kız örencidir. Sınıfta erkek öğrenci olduğuna göre, kız öğrencilerin sayısı kaçtır? A) B) 8 C) 6 D) E) Çözüm Toplam öğrenci
TEST. Dik Üçgen ve Pisagor Bağıntısı. 4. Dik Kenarlar Hipotenüs. 5. Aşağıdaki dik üçgenlerden hangisinin çevre uzunluğu en fazladır?
 ik Üçgen ve Pisagor ağıntısı. Sınıf atematik Soru ankası TEST 1.. ik enarlar Hipotenüs m m cm 1 cm cm 60 cm y cm 100 cm z cm 1, cm 1,3 cm ir el fenerinden çıkan ışık m yol alarak yukarıdaki m uzunluğundaki
ik Üçgen ve Pisagor ağıntısı. Sınıf atematik Soru ankası TEST 1.. ik enarlar Hipotenüs m m cm 1 cm cm 60 cm y cm 100 cm z cm 1, cm 1,3 cm ir el fenerinden çıkan ışık m yol alarak yukarıdaki m uzunluğundaki
1. Analitik düzlemde P(-4,3) noktasının eksenlerden ve O başlangıç noktasından uzaklığı kaç birimdir?
 HAZİNE- HAZİNE-2 O başlangıç noktasında dik kesişen iki sayı ekseninin oluşturduğu sisteme koordinat sistemi denir. Bir noktanın x-eksenindeki dik izdüşümüne karşılık gelen x sayısına noktanın apsis i
HAZİNE- HAZİNE-2 O başlangıç noktasında dik kesişen iki sayı ekseninin oluşturduğu sisteme koordinat sistemi denir. Bir noktanın x-eksenindeki dik izdüşümüne karşılık gelen x sayısına noktanın apsis i
π a) = cosa Öğrenci Seçme Sınavı (Öss) / 17 Haziran 2007 Matematik II Soruları ve Çözümleri
 Öğrenci Seçme Sınavı (Öss) 7 Haziran 7 Matematik II Soruları ve Çözümleri. Karmaşık sayılar kümesi üzerinde * işlemi, Z * Z Z + Z + Z Z biçiminde tanımlanıyor. Buna göre, ( i) * ( + i) işleminin sonucu
Öğrenci Seçme Sınavı (Öss) 7 Haziran 7 Matematik II Soruları ve Çözümleri. Karmaşık sayılar kümesi üzerinde * işlemi, Z * Z Z + Z + Z Z biçiminde tanımlanıyor. Buna göre, ( i) * ( + i) işleminin sonucu
PİRAMİTLER ENFORMATİK BİLGİSAYAR DERSİ
 2011 PİRAMİTLER ENFORMATİK BİLGİSAYAR DERSİ 15.12.2011 ĠÇĠNDEKĠLER ÜNİTE HAKKINDA GENEL BİLGİ... 3 KONULAR... 4 PİRAMİTLER... 4 KARE PİRAMİT... 5 EŞKENAR ÜÇGEN PİRAMİT... 6 DÜZGÜN DÖRTYÜZLÜ... 6 DÜZGÜN
2011 PİRAMİTLER ENFORMATİK BİLGİSAYAR DERSİ 15.12.2011 ĠÇĠNDEKĠLER ÜNİTE HAKKINDA GENEL BİLGİ... 3 KONULAR... 4 PİRAMİTLER... 4 KARE PİRAMİT... 5 EŞKENAR ÜÇGEN PİRAMİT... 6 DÜZGÜN DÖRTYÜZLÜ... 6 DÜZGÜN
EKSTREMUM PROBLEMLERİ. Örnek: Çözüm: Örnek: Çözüm:
 EKSTREMUM PROBLEMLERİ Ekstremum Problemleri Bu tür problemlerde bir büyüklüğün (çokluğun alabileceği en büyük (maksimum değer ya da en küçük (minimum değer bulunmak istenir. İstenen çokluk bir değişkenin
EKSTREMUM PROBLEMLERİ Ekstremum Problemleri Bu tür problemlerde bir büyüklüğün (çokluğun alabileceği en büyük (maksimum değer ya da en küçük (minimum değer bulunmak istenir. İstenen çokluk bir değişkenin
Lisans Yerleştirme Sınavı 1 (Lys 1) / 19 Haziran 2010. Geometri Soruları ve Çözümleri. ABC bir üçgen CA = CD. m(acd) = m(dcb) m(bac) = 80.
 Lisans Yerleştirme Sınavı (Lys ) / 9 Haziran 00 Geometri Soruları ve Çözümleri. ABC bir üçgen CA = CD m(acd) = m(dcb) m(bac) = 80 m(abc) = x Yukarıdaki verilere göre x kaç derecedir? A) 40 B) 45 C) 50
Lisans Yerleştirme Sınavı (Lys ) / 9 Haziran 00 Geometri Soruları ve Çözümleri. ABC bir üçgen CA = CD m(acd) = m(dcb) m(bac) = 80 m(abc) = x Yukarıdaki verilere göre x kaç derecedir? A) 40 B) 45 C) 50
YGS MATEMATİK DENEMESİ-1
 YGS MATEMATİK DENEMESİ- Mustafa SEVİMLİ Fatih KAYGISIZ İbrahim KUŞÇUOĞLU Aydın DANIŞMAN ÇAKABEY ANADOLU LİSESİ Serkan TÜRKER Nejdet KİRPİ Şenay TAĞ GÜRLER Taner KAHYA Çakabey Anadolu Lisesi 0-0 . x olduğuna
YGS MATEMATİK DENEMESİ- Mustafa SEVİMLİ Fatih KAYGISIZ İbrahim KUŞÇUOĞLU Aydın DANIŞMAN ÇAKABEY ANADOLU LİSESİ Serkan TÜRKER Nejdet KİRPİ Şenay TAĞ GÜRLER Taner KAHYA Çakabey Anadolu Lisesi 0-0 . x olduğuna
Öğrenci Seçme Sınavı (Öss) / 15 Nisan Matematik Soruları ve Çözümleri
 Öğrenci Seçme Sınavı (Öss) / 5 Nisan 990 Matematik Soruları ve Çözümleri. 0,0703.(0,3 0,) işleminin sonucu kaçtır? A) 0,00703 B) 0,0703 C) 0,703 D) 0,0703 E) 0,00703 Çözüm 0,0703.(0,3 0,) 0,0703.0, 0,00703.
Öğrenci Seçme Sınavı (Öss) / 5 Nisan 990 Matematik Soruları ve Çözümleri. 0,0703.(0,3 0,) işleminin sonucu kaçtır? A) 0,00703 B) 0,0703 C) 0,703 D) 0,0703 E) 0,00703 Çözüm 0,0703.(0,3 0,) 0,0703.0, 0,00703.
ÜÇGENLER ÜNİTE 4. ÜNİTE 4. ÜNİTE 4. ÜNİTE 4. ÜNİT
 ÜÇGNLR ÜNİT. ÜNİT. ÜNİT. ÜNİT. ÜNİT ÜÇGNLRİN ŞLİĞİ Üçgende çılar 1. Kazanım : ir üçgenin iç açılarının ölçüleri toplamının 180, dış açılarının ölçüleri toplamının 0 olduğunu gösterir. İki Üçgenin şliği.
ÜÇGNLR ÜNİT. ÜNİT. ÜNİT. ÜNİT. ÜNİT ÜÇGNLRİN ŞLİĞİ Üçgende çılar 1. Kazanım : ir üçgenin iç açılarının ölçüleri toplamının 180, dış açılarının ölçüleri toplamının 0 olduğunu gösterir. İki Üçgenin şliği.
8. SINIF MATEMATiK ÜÇGEN
 05 8. SINIF MTMTiK ÜÇGN Kenarortay: ir kenarın orta noktası ile karşısındaki köşe arasına çekilen doğru parçasına kenarortay denir. çıortay: ir köşeden, karşısındaki kenara kadar giden ve bu köşedeki açıyı
05 8. SINIF MTMTiK ÜÇGN Kenarortay: ir kenarın orta noktası ile karşısındaki köşe arasına çekilen doğru parçasına kenarortay denir. çıortay: ir köşeden, karşısındaki kenara kadar giden ve bu köşedeki açıyı
4. 8. A. D 2. ABC üçgeninin alanı kaç birim karedir? ABC üçgeninin alanı kaç birim karedir? A) 16 B) 18 C) 20 D) 24 E) 32 120º 135º
 ğlence başlıyor yor 1 º 0º üçgeninin alanı kaç birim karedir? ) ) 9 LN SI 1 LN SI 1 )1 ) üçgeninin alanı kaç birim karedir? üçgeninin alanı kaç birim karedir? ) ) ) ) ) ) üçgen, = birim, = birim, m() =
ğlence başlıyor yor 1 º 0º üçgeninin alanı kaç birim karedir? ) ) 9 LN SI 1 LN SI 1 )1 ) üçgeninin alanı kaç birim karedir? üçgeninin alanı kaç birim karedir? ) ) ) ) ) ) üçgen, = birim, = birim, m() =
Olimpiyat Eğitimi TUĞBA DENEME SINAVI
 TUSİ Ortaöğretim Öğretmenleri için Olimpiyat Eğitimi TUĞBA DENEME SINAVI 10.01.2014-17.01.2014 2 1. Tuğba üç test yapar. İlkinde, 25 sorudan %60 ını, ikinci de 30 sorudan ve %70 ini ve son olarak 45 sorudan
TUSİ Ortaöğretim Öğretmenleri için Olimpiyat Eğitimi TUĞBA DENEME SINAVI 10.01.2014-17.01.2014 2 1. Tuğba üç test yapar. İlkinde, 25 sorudan %60 ını, ikinci de 30 sorudan ve %70 ini ve son olarak 45 sorudan
LİSE ÖĞRENCİLERİNE OKULDA YARDIMCI VE ÜNİVERSİTE SINAVLARINA (YGS ve LYS NA) HAZIRLIK İÇİN
 LİSE ÖĞRENCİLERİNE OKULDA YARDIMCI VE ÜNİVERSİTE SINAVLARINA (YGS ve LYS NA) HAZIRLIK İÇİN Konu Anlatımlı Örnek Çözümlü Test Çözümlü Test Sorulu Karma Testli GEOMETRİ 1 Hazırlayan Erol GEDİKLİ Matematik
LİSE ÖĞRENCİLERİNE OKULDA YARDIMCI VE ÜNİVERSİTE SINAVLARINA (YGS ve LYS NA) HAZIRLIK İÇİN Konu Anlatımlı Örnek Çözümlü Test Çözümlü Test Sorulu Karma Testli GEOMETRİ 1 Hazırlayan Erol GEDİKLİ Matematik
6. loga log3a log5a log4a. 7. x,y R olmak üzere;
 log. 5 5 0 olduğuna göre, değeri kaçtır? A) 5 B) 0 C) 6 8 E) 6. loga loga log5a loga eşitliğini sağlaan a değeri kaçtır? 5 A) 5 5 B) 5 5 C) 5 E) 5. loga logb logc ifadesinin eşiti aşağıdakilerden a c A)
log. 5 5 0 olduğuna göre, değeri kaçtır? A) 5 B) 0 C) 6 8 E) 6. loga loga log5a loga eşitliğini sağlaan a değeri kaçtır? 5 A) 5 5 B) 5 5 C) 5 E) 5. loga logb logc ifadesinin eşiti aşağıdakilerden a c A)
EĞİTİM ÖĞRETİM YILI. ANADOLU LİSESİ 9.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLIK PLANI 9.SINIF KAZANIM VE SÜRE TABLOSU
 08 09 EĞİTİM ÖĞRETİM YILI. ANADOLU LİSESİ 9.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLIK PLANI 9.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%) SAYILAR VE CEBİR 9. MANTIK
08 09 EĞİTİM ÖĞRETİM YILI. ANADOLU LİSESİ 9.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLIK PLANI 9.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%) SAYILAR VE CEBİR 9. MANTIK
ÜN TE II ÇOKGENSEL BÖLGELER N ALANLARI
 ÜN TE II ÇOKGENSEL BÖLGELER N ALANLARI 1. ÇOKGENSEL BÖLGELER N ALANLARI 2. D KDÖRTGEN N ALANI 3. ÜÇGENSEL BÖLGELER N ALANI 4. ÜÇGENSEL ALAN PROBLEMLER ÇÖZÜLÜRKEN KULLANILACAK FORMÜLLER 5. PARALELKENARIN
ÜN TE II ÇOKGENSEL BÖLGELER N ALANLARI 1. ÇOKGENSEL BÖLGELER N ALANLARI 2. D KDÖRTGEN N ALANI 3. ÜÇGENSEL BÖLGELER N ALANI 4. ÜÇGENSEL ALAN PROBLEMLER ÇÖZÜLÜRKEN KULLANILACAK FORMÜLLER 5. PARALELKENARIN
EĞİTİM ÖĞRETİM YILI. FEN LİSESİ 9.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLIK PLANI 9.SINIF KAZANIM VE SÜRE TABLOSU
 08 09 EĞİTİM ÖĞRETİM YILI. FEN LİSESİ 9.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLIK PLANI 9.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%) SAYILAR VE CEBİR 9. MANTIK 8
08 09 EĞİTİM ÖĞRETİM YILI. FEN LİSESİ 9.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLIK PLANI 9.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%) SAYILAR VE CEBİR 9. MANTIK 8
DOĞRUNUN ANALİTİK İNCELEMESİ
 Koordinatlar DOĞRUNUN ANALİTİK İNCELEMESİ Bilindiği gibi, düzlemdeki her bir noktaya bir (a,b) sıralı ikilisi, her bir (a,b) sıralı ikilisine bir nokta karşılık gelir. Eğer bir A noktasına karşılık gelen
Koordinatlar DOĞRUNUN ANALİTİK İNCELEMESİ Bilindiği gibi, düzlemdeki her bir noktaya bir (a,b) sıralı ikilisi, her bir (a,b) sıralı ikilisine bir nokta karşılık gelir. Eğer bir A noktasına karşılık gelen
UZAY KAVRAMI VE UZAYDA DOĞRULAR
 UZAY KAVRAMI VE UZAYDA DOĞRULAR Cisimlerin kapladığı yer ve içinde bulundukları mekan uzaydır. Doğruda sadece uzunluk, düzlemde uzunluk ve genişlik söz konusudur. Uzayda ise uzunluk ve genişliğin yanında
UZAY KAVRAMI VE UZAYDA DOĞRULAR Cisimlerin kapladığı yer ve içinde bulundukları mekan uzaydır. Doğruda sadece uzunluk, düzlemde uzunluk ve genişlik söz konusudur. Uzayda ise uzunluk ve genişliğin yanında
OKUL ADI : ÖMER ÇAM ANADOLU İMAM HATİP LİSESİ EĞİTİM VE ÖĞRETİM YILI : 2015 2016 DERSİN ADI : MATEMATİK SINIFLAR : 9
 OKUL ADI : ÖMER ÇAM ANADOLU İMAM HATİP LİSESİ EĞİTİM VE ÖĞRETİM YILI : 015 01 1 Eylül 18 Eylül Kümelerde Temel Kavramlar 1. Küme kavramını örneklerle açıklar ve kümeleri ifade etmek için farklı gösterimler.
OKUL ADI : ÖMER ÇAM ANADOLU İMAM HATİP LİSESİ EĞİTİM VE ÖĞRETİM YILI : 015 01 1 Eylül 18 Eylül Kümelerde Temel Kavramlar 1. Küme kavramını örneklerle açıklar ve kümeleri ifade etmek için farklı gösterimler.
EĞİTİM-ÖĞRETİM YILI 8. SINIF MATEMATİK DERSİ KAZANIMLARININ ÇALIŞMA TAKVİMİNE GÖRE DAĞILIM ÇİZELGESİ SÜRE
 Ay 2016 2017 EĞİTİM-ÖĞRETİM YILI 8. SINIF MATEMATİK DERSİ KAZANIMLARININ ÇALIŞMA TAKVİMİNE GÖRE DAĞILIM ÇİZELGESİ SÜRE Hafta ÖĞRENME ALANI ALT ÖĞRENME ALANI KAZANIMLAR EYLÜL 3 4 Sayılar ve İşlemler Çarpanlar
Ay 2016 2017 EĞİTİM-ÖĞRETİM YILI 8. SINIF MATEMATİK DERSİ KAZANIMLARININ ÇALIŞMA TAKVİMİNE GÖRE DAĞILIM ÇİZELGESİ SÜRE Hafta ÖĞRENME ALANI ALT ÖĞRENME ALANI KAZANIMLAR EYLÜL 3 4 Sayılar ve İşlemler Çarpanlar
Dik koordinat sisteminde yatay eksen x ekseni (apsis ekseni), düşey eksen ise y ekseni (ordinat ekseni) dir.
 ANALĐTĐK GEOMETRĐ 1. Analitik Düzlem Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da
ANALĐTĐK GEOMETRĐ 1. Analitik Düzlem Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da
Öklid alıştırmaları. Mat 113, MSGSÜ. İçindekiler. 36. önermeden sonra önermeden sonra 8. Çarpma 11
 Öklid alıştırmaları Mat 113, MSSÜ 30 kim 2013 İçindekiler 1. önermeden sonra 2 5. önermeden sonra 2 6. önermeden sonra 2 7. önermeden sonra 3 8. önermeden sonra 3 9. önermeden sonra 3 10. önermeden sonra
Öklid alıştırmaları Mat 113, MSSÜ 30 kim 2013 İçindekiler 1. önermeden sonra 2 5. önermeden sonra 2 6. önermeden sonra 2 7. önermeden sonra 3 8. önermeden sonra 3 9. önermeden sonra 3 10. önermeden sonra
Öğrenci Yerleştirme Sınavı (Öys) / 24 Haziran Matematik Soruları Ve Çözümleri
 Öğrenci Yerleştirme Sınavı (Öys) / Haziran 99 Matematik Soruları Ve Çözümleri. 7 si olan sayının 7 si kaçtır? A) 9 B) 8 C) 7 D) 6 E) 5 Çözüm Sayı a olsun. a. 7 a 9 9. 7 5 elde edilir.. Ağırlıkça % si şeker
Öğrenci Yerleştirme Sınavı (Öys) / Haziran 99 Matematik Soruları Ve Çözümleri. 7 si olan sayının 7 si kaçtır? A) 9 B) 8 C) 7 D) 6 E) 5 Çözüm Sayı a olsun. a. 7 a 9 9. 7 5 elde edilir.. Ağırlıkça % si şeker
SİDRE 2000 ORTAOKULU EĞİTİM-ÖĞRETİM YILI 8. SINIFLAR MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLIK PLAN
 E Y L Ü L ÜNİTE SİDRE 000 ORTAOKULU 06-07 EĞİTİM-ÖĞRETİM YILI 8. SINIFLAR MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLIK PLAN 9.09.06/.09.06 6.09.06/0.09.06 Çarpanlar ve Katlar Çarpanlar ve Katlar 8... Verilen
E Y L Ü L ÜNİTE SİDRE 000 ORTAOKULU 06-07 EĞİTİM-ÖĞRETİM YILI 8. SINIFLAR MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLIK PLAN 9.09.06/.09.06 6.09.06/0.09.06 Çarpanlar ve Katlar Çarpanlar ve Katlar 8... Verilen
BİRLİKTE ÇÖZELİM. ayırdığı parçalardan birinin uzunluğuna. Şekildeki ABC dik üçgeninde [AB] ^ [BC], G noktası ağırlık merkezi,
![BİRLİKTE ÇÖZELİM. ayırdığı parçalardan birinin uzunluğuna. Şekildeki ABC dik üçgeninde [AB] ^ [BC], G noktası ağırlık merkezi, BİRLİKTE ÇÖZELİM. ayırdığı parçalardan birinin uzunluğuna. Şekildeki ABC dik üçgeninde [AB] ^ [BC], G noktası ağırlık merkezi,](/thumbs/88/116416355.jpg) . SINI TTİ İRİT ÇÖZİ 1. P Yandaki, PRS ve üçgenlerinin sırasıyla [], [RS] ve [] ye ait kenarortaylarını çiziniz. R S 2. r O O merkezli, r yarıçaplı çemberde çapı gören açısının ölçüsü 90 dir. [O], hem
. SINI TTİ İRİT ÇÖZİ 1. P Yandaki, PRS ve üçgenlerinin sırasıyla [], [RS] ve [] ye ait kenarortaylarını çiziniz. R S 2. r O O merkezli, r yarıçaplı çemberde çapı gören açısının ölçüsü 90 dir. [O], hem
a) BP = P H olmalıdır. b) BP = 2 P H olmalıdır. c) P H = 2 BP olmalıdır. d) Böyle bir P noktası yoktur. e) Hiçbiri
 TÜBİTAK TÜRKİYE BİLİMSEL VE TEKNOLOJİK ARAŞTIRMA KURUMU BİLİM İNSANI DESTEKLEME DAİRE BAŞKANLIĞI 7. ULUSAL İLKÖĞRETİM MATEMATİK OLİMPİYATI SINAVI - 00 Birinci Bölüm Soru kitapçığı türü A 1. Bir ikizkenar
TÜBİTAK TÜRKİYE BİLİMSEL VE TEKNOLOJİK ARAŞTIRMA KURUMU BİLİM İNSANI DESTEKLEME DAİRE BAŞKANLIĞI 7. ULUSAL İLKÖĞRETİM MATEMATİK OLİMPİYATI SINAVI - 00 Birinci Bölüm Soru kitapçığı türü A 1. Bir ikizkenar
NİSAN 2010 DENEMESİ A)75 B)80 C)85 D)90 E)95 A)0 B)1 C)2 D)3 E)4
 NİSAN 21 DENEMESİ 1) ABCD dikdörtgeninin AB kenarı üzerindeki M noktasından geçen ve CM doğrusuna dik olan doğru AD kenarını E noktasında kesiyor. M noktasından CE doğrusuna indirilen dikmenin ayağı P
NİSAN 21 DENEMESİ 1) ABCD dikdörtgeninin AB kenarı üzerindeki M noktasından geçen ve CM doğrusuna dik olan doğru AD kenarını E noktasında kesiyor. M noktasından CE doğrusuna indirilen dikmenin ayağı P
TRİGONMETRİK FONKSİYONLAR: DİK ÜÇGEN YAKLAŞIMI
 TRİGONMETRİK FONKSİYONLAR: DİK ÜÇGEN YAKLAŞIMI Diyelim ki yeryüzünden güneşe olan mesafeyi bulmak istiyoruz. Şerit metre kullanmak açıkçası pratik değildir. Bu nedenle bu sorunun üstesinden gelmek için
TRİGONMETRİK FONKSİYONLAR: DİK ÜÇGEN YAKLAŞIMI Diyelim ki yeryüzünden güneşe olan mesafeyi bulmak istiyoruz. Şerit metre kullanmak açıkçası pratik değildir. Bu nedenle bu sorunun üstesinden gelmek için
E.Ö.Y TEKİRDAĞ S.B LİSESİ 9. SINIF MATEMATİK DERSİ YILLIK PLANI Alt Öğrenme Alanı
 A ELÜL 9 Eylül Eylül Eylül 0 Eylül 0-07 E.Ö. TEKİRDAĞ S.B LİSESİ 9. SINIF MATEMATİK İ ILLIK PLANI Temel Kavramlar Temel Kavramlar Temel Kavramlar Temel Kavramlar. Küme kavramını örneklerle açıklar ve kümeleri
A ELÜL 9 Eylül Eylül Eylül 0 Eylül 0-07 E.Ö. TEKİRDAĞ S.B LİSESİ 9. SINIF MATEMATİK İ ILLIK PLANI Temel Kavramlar Temel Kavramlar Temel Kavramlar Temel Kavramlar. Küme kavramını örneklerle açıklar ve kümeleri
2.3. KAZANIM SAYISI VE SÜRE TABLOSU
 3. Öğretim materyalleri hazırlanırken zümre öğretmenleri ve diğer disiplinlerin öğretmenleriyle iş birliği yapılmalıdır. 4. Matematiğin konu ve kavramlarının tarihsel gelişimi ile beraber öne çıkan bilim
3. Öğretim materyalleri hazırlanırken zümre öğretmenleri ve diğer disiplinlerin öğretmenleriyle iş birliği yapılmalıdır. 4. Matematiğin konu ve kavramlarının tarihsel gelişimi ile beraber öne çıkan bilim
3. Ünsal Tülbentçi Matematik Yarışması Mayıs 2014 8.Sınıf Sayfa 1
 . Alanı 36 5 olan bir ABC ikizkenar üçgeninde ==2 ise bu üçgende B den AC ye inilen dikmenin ayağının C noktasına olan uzaklığı nedir? ) 2,8) 3) 3,2 ) 3,7 ) 4, 2. Ayrıt uzunlukları 4, 0 ve 4 5 olan dikdörtgenler
. Alanı 36 5 olan bir ABC ikizkenar üçgeninde ==2 ise bu üçgende B den AC ye inilen dikmenin ayağının C noktasına olan uzaklığı nedir? ) 2,8) 3) 3,2 ) 3,7 ) 4, 2. Ayrıt uzunlukları 4, 0 ve 4 5 olan dikdörtgenler
DEVREK ANADOLU LİSESİ 9. SINIF MATEMATİK DERSİ YILLIK PLANI Alt Öğrenme Alanı
 ELÜL TRİH/SÜRE HFT Eylül 0Eylül Eylül 7 Eylül STİ LNI 0-0 DEVREK NDOLU LİSESİ 9. SINIF MTEMTİK İ ILLIK PLNI lt de Temel Kavramlar de Temel Kavramlar de Temel Kavramlar de Temel Kavramlar de de de de. Küme
ELÜL TRİH/SÜRE HFT Eylül 0Eylül Eylül 7 Eylül STİ LNI 0-0 DEVREK NDOLU LİSESİ 9. SINIF MTEMTİK İ ILLIK PLNI lt de Temel Kavramlar de Temel Kavramlar de Temel Kavramlar de Temel Kavramlar de de de de. Küme
Çarpanlar ve Katlar
 8.1.1. Çarpanlar ve Katlar 8.1.2. Üslü İfadeler 8.1.3. Kareköklü İfadeler 8.2.1. Cebirsel İfadeler ve Özdeşlikler 8.1.1.1 Verilen pozitif tam sayıların çarpanlarını bulur; pozitif tam sayıları üslü ifade
8.1.1. Çarpanlar ve Katlar 8.1.2. Üslü İfadeler 8.1.3. Kareköklü İfadeler 8.2.1. Cebirsel İfadeler ve Özdeşlikler 8.1.1.1 Verilen pozitif tam sayıların çarpanlarını bulur; pozitif tam sayıları üslü ifade
12-B. Polinomlar - 1 TEST. olduğuna göre P(x - 2, y + 4) polinomunun katsayılar toplamı kaçtır? olduğuna göre A B kaçtır? A) 78 B) 73 C) 62 D 58 E) 33
 -B TEST Polinomlar -. Py _, i= y- y + 5y- olduğuna göre P( -, y + ) polinomunun katsayılar toplamı. - 6 = A - 5 + - + B - olduğuna göre A B 78 B) 7 6 D 58 E) B) D) - E) -. -a- b = _ + -5i_ -ci eşitliğine
-B TEST Polinomlar -. Py _, i= y- y + 5y- olduğuna göre P( -, y + ) polinomunun katsayılar toplamı. - 6 = A - 5 + - + B - olduğuna göre A B 78 B) 7 6 D 58 E) B) D) - E) -. -a- b = _ + -5i_ -ci eşitliğine
GEOMETR 7 ÜN TE IV KON
 ÜN TE IV KON 1. KON K YÜZEY VE TANIMLAR 2. KON a. Tan m b. Dik Dairesel Koni I. Tan mlar II. Dik Dairesel Koninin Özelikleri III. Dönel Koni c. E ik Dairesel Koni 3. D K DA RESEL KON N N ALANI 4. DA RESEL
ÜN TE IV KON 1. KON K YÜZEY VE TANIMLAR 2. KON a. Tan m b. Dik Dairesel Koni I. Tan mlar II. Dik Dairesel Koninin Özelikleri III. Dönel Koni c. E ik Dairesel Koni 3. D K DA RESEL KON N N ALANI 4. DA RESEL
1. BÖLÜM Polinomlar BÖLÜM II. Dereceden Denklemler BÖLÜM II. Dereceden Eşitsizlikler BÖLÜM Parabol
 ORGANİZASYON ŞEMASI . BÖLÜM Polinomlar... 7. BÖLÜM II. Dereceden Denklemler.... BÖLÜM II. Dereceden Eşitsizlikler... 9. BÖLÜM Parabol... 5 5. BÖLÜM Trigonometri... 69 6. BÖLÜM Karmaşık Sayılar... 09 7.
ORGANİZASYON ŞEMASI . BÖLÜM Polinomlar... 7. BÖLÜM II. Dereceden Denklemler.... BÖLÜM II. Dereceden Eşitsizlikler... 9. BÖLÜM Parabol... 5 5. BÖLÜM Trigonometri... 69 6. BÖLÜM Karmaşık Sayılar... 09 7.
SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLIK PLAN... YAYINLARI HAZIRLAYANLAR
 06-07 8.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLIK PLAN... YAYINLARI HAZIRLAYANLAR Sıra No Adı ve Soyadı İmza Sıra No 8 9 0 6 Adı ve Soyadı İmza 7 Ömer Askerden 06 07 EĞİTİM VE ÖĞRETİM YILI FATİH SULTAN
06-07 8.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLIK PLAN... YAYINLARI HAZIRLAYANLAR Sıra No Adı ve Soyadı İmza Sıra No 8 9 0 6 Adı ve Soyadı İmza 7 Ömer Askerden 06 07 EĞİTİM VE ÖĞRETİM YILI FATİH SULTAN
ÖZEL EGE LİSESİ SİMEDYAN ÜÇGENİ VE NOKTADAŞLIK
 ÖZEL EGE LİSESİ SİMEDYAN ÜÇGENİ VE NOKTADAŞLIK HAZIRLAYAN ÖĞRENCİLER: Barış BALKAN Meryem Nilsu ÇETİN DANIŞMAN ÖĞRETMEN: Gizem GÜNEL AÇIKSÖZ İZMİR 2016 İçindekiler Sayfa 1. Giriş... 2 1.1 Projenin Amacı....
ÖZEL EGE LİSESİ SİMEDYAN ÜÇGENİ VE NOKTADAŞLIK HAZIRLAYAN ÖĞRENCİLER: Barış BALKAN Meryem Nilsu ÇETİN DANIŞMAN ÖĞRETMEN: Gizem GÜNEL AÇIKSÖZ İZMİR 2016 İçindekiler Sayfa 1. Giriş... 2 1.1 Projenin Amacı....
SINIF CEVAP ANAHTARI
 8. SINIF CEVAP ANAHTARI 1. ÜNİTE: ÇARPANLAR, KATLAR, ÜSLÜ SAYILAR, KAREKÖKLÜ İFADELER ÇARPANLAR VE KATLAR (ASAL ÇARPANLAR) 1-B 2-D 3-A 4-D 5-D 6-C 7-C 8-A 9-B 10-A 11-A 12-D ÇARPANLAR VE KATLAR (EBOB -
8. SINIF CEVAP ANAHTARI 1. ÜNİTE: ÇARPANLAR, KATLAR, ÜSLÜ SAYILAR, KAREKÖKLÜ İFADELER ÇARPANLAR VE KATLAR (ASAL ÇARPANLAR) 1-B 2-D 3-A 4-D 5-D 6-C 7-C 8-A 9-B 10-A 11-A 12-D ÇARPANLAR VE KATLAR (EBOB -
12.SINIF A VE B GRUBU MATEMATİK-GEOMETRİ DERSİ KURS KONULARI VE TESTLERİ
 .SINIF A VE B GRUBU MATEMATİK-GEOMETRİ DERSİ KURS KONULARI VE TESTLERİ A-TEST SAYILAR- TEMEL KAVRAMLAR A-TEST SAYILAR- POLİNOMLAR B-TEST POLİNOMLAR- PARALEL DOĞRULARDA VE ÜÇGENDE AÇILAR A- B TEST PARALEL
.SINIF A VE B GRUBU MATEMATİK-GEOMETRİ DERSİ KURS KONULARI VE TESTLERİ A-TEST SAYILAR- TEMEL KAVRAMLAR A-TEST SAYILAR- POLİNOMLAR B-TEST POLİNOMLAR- PARALEL DOĞRULARDA VE ÜÇGENDE AÇILAR A- B TEST PARALEL
Öğrenci Yerleştirme Sınavı (Öys) / 22 Haziran Matematik Soruları Ve Çözümleri. olduğuna göre, k kaçtır? 5 k 3
 Öğrenci Yerleştirme Sınavı (Öys) / Haziran 997 Matematik Soruları Ve Çözümleri.,,, k olduğuna göre, k kaçtır? A) B) C) D) E) Çözüm,,, k k k k 7. [( ) ( )] [ (9 ) ( )] işleminin sonucu kaçtır? A) B) C)
Öğrenci Yerleştirme Sınavı (Öys) / Haziran 997 Matematik Soruları Ve Çözümleri.,,, k olduğuna göre, k kaçtır? A) B) C) D) E) Çözüm,,, k k k k 7. [( ) ( )] [ (9 ) ( )] işleminin sonucu kaçtır? A) B) C)
ÖZEL EGE LİSESİ OKULLAR ARASI 14.MATEMATİK YARIŞMASI 8. SINIFLAR FİNAL SORULARI
 8 SINIFLAR FİNAL SORULARI 1 3+ 1 denkleminin çözüm kümesini bulunuz ( R ) Aritmetik bir dizinin ilk 0 teriminin toplamı 400 ve dördüncü terimi olduğuna göre, birinci terimini bulunuz 3 4 öğrencinin katıldığı
8 SINIFLAR FİNAL SORULARI 1 3+ 1 denkleminin çözüm kümesini bulunuz ( R ) Aritmetik bir dizinin ilk 0 teriminin toplamı 400 ve dördüncü terimi olduğuna göre, birinci terimini bulunuz 3 4 öğrencinin katıldığı
Kamu Personel Seçme Sınavı. KPSS / Genel Yetenek Testi / Lisans / 30 Haziran Matematik Soruları ve Çözümleri = = 10
 Kamu Personel Seçme Sınavı KPSS / Genel Yetenek Testi / Lisans / 0 Haziran 007 Matematik Soruları ve Çözümleri. 5 9 işleminin sonucu kaçtır? 0, 0,5 A) 9 B) 0 C) D) 5 E) 6 Çözüm 5 9 5 0 9 000.( ).( ) 0,
Kamu Personel Seçme Sınavı KPSS / Genel Yetenek Testi / Lisans / 0 Haziran 007 Matematik Soruları ve Çözümleri. 5 9 işleminin sonucu kaçtır? 0, 0,5 A) 9 B) 0 C) D) 5 E) 6 Çözüm 5 9 5 0 9 000.( ).( ) 0,
Öğrenci Seçme Sınavı (Öss) / 6 Nisan Matematik Soruları ve Çözümleri E) 6 = 4
 Öğrenci Seçme Sınavı (Öss) / 6 Nisan 997 Matematik Soruları ve Çözümleri. 4 ( ) + ( ) 4.( ) işleminin sonucu kaçtır? A) B) 8 C) D) 6 4 E) 6 Çözüm 4 ( ) + ( ) 4.( ) 4+ 4.( ) 4. 40. 80 8 işleminin sonucu
Öğrenci Seçme Sınavı (Öss) / 6 Nisan 997 Matematik Soruları ve Çözümleri. 4 ( ) + ( ) 4.( ) işleminin sonucu kaçtır? A) B) 8 C) D) 6 4 E) 6 Çözüm 4 ( ) + ( ) 4.( ) 4+ 4.( ) 4. 40. 80 8 işleminin sonucu
dir. Bu avcı en çok 3 atışta bu hedefi vurabilme
 1. 3 mavi, 3 kırmızı, 3 siyah kalemin bulunduğu bir torbada rasgele alınan iki kalemin farklı renkte olma olasılığı kaçtır? A) 1 3 B) 2 3 C) 3 4 D) 3 5 E) 4 5 2. 43 kişilik bir sınıfta Almanca İngilizce
1. 3 mavi, 3 kırmızı, 3 siyah kalemin bulunduğu bir torbada rasgele alınan iki kalemin farklı renkte olma olasılığı kaçtır? A) 1 3 B) 2 3 C) 3 4 D) 3 5 E) 4 5 2. 43 kişilik bir sınıfta Almanca İngilizce
Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı. ALES / Sonbahar / Sayısal II / 16 Kasım Matematik Soruları ve Çözümleri
 Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı ALES / Sonbahar / Sayısal II / 6 Kasım 008 Matematik Soruları ve Çözümleri. a 3 < 5 7 eşitsizliğini sağlayan en küçük a doğal sayısı kaçtır? A) 4 B)
Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı ALES / Sonbahar / Sayısal II / 6 Kasım 008 Matematik Soruları ve Çözümleri. a 3 < 5 7 eşitsizliğini sağlayan en küçük a doğal sayısı kaçtır? A) 4 B)
4. Çok büyük ve çok küçük pozitif sayıları bilimsel gösterimle ifade eder.
 LENDİRME ŞEMASI ÜNİTE Üslü 1. Bir tam sayının negatif kuvvetini belirler ve rasyonel sayı olarak ifade eder.. Ondalık kesirlerin veya rasyonel sayıların kendileriyle tekrarlı çarpımını üslü sayı olarak
LENDİRME ŞEMASI ÜNİTE Üslü 1. Bir tam sayının negatif kuvvetini belirler ve rasyonel sayı olarak ifade eder.. Ondalık kesirlerin veya rasyonel sayıların kendileriyle tekrarlı çarpımını üslü sayı olarak
TEKNİK RESİM. Ders Notları: Mehmet Çevik Dokuz Eylül Üniversitesi. Geometrik Çizimler-1
 TEKNİK RESİM 2010 Ders Notları: Mehmet Çevik Dokuz Eylül Üniversitesi Geometrik Çizimler-1 2/32 Geometrik Çizimler - 1 Geometrik Çizimler-1 T-cetveli ve Gönye kullanımı Bir doğrunun orta noktasını bulma
TEKNİK RESİM 2010 Ders Notları: Mehmet Çevik Dokuz Eylül Üniversitesi Geometrik Çizimler-1 2/32 Geometrik Çizimler - 1 Geometrik Çizimler-1 T-cetveli ve Gönye kullanımı Bir doğrunun orta noktasını bulma
8. SINIF ESLiK ve BENZERLiK
 0 8. SINI SLiK ve NZRLiK şlik: Karşılıklı açılar ve kenar uzunlukları eşit olmalı. Sembolleri enzerlik: Karşılıklı açılar eşit, karşılıklı kenarlar orantılı olmalı. Sembolleri ~ veya olduğuna göre verilmeyen
0 8. SINI SLiK ve NZRLiK şlik: Karşılıklı açılar ve kenar uzunlukları eşit olmalı. Sembolleri enzerlik: Karşılıklı açılar eşit, karşılıklı kenarlar orantılı olmalı. Sembolleri ~ veya olduğuna göre verilmeyen
Öğrenci Seçme Sınavı (Öss) / 18 Haziran Matematik II Soruları ve Çözümleri. ise fonksiyonu için, = b olduğuna göre, a b kaçtır? = 1 olur.
 Öğrenci Seçme Sınavı (Öss) 8 Haziran 6 Matematik II Soruları ve Çözümleri. f (x) + x lim f ( x) a x x ve, x ise fonksiyonu için,, x lim f ( x) b olduğuna göre, a b kaçtır? x A) B) C) D) E) Çözüm x x için,
Öğrenci Seçme Sınavı (Öss) 8 Haziran 6 Matematik II Soruları ve Çözümleri. f (x) + x lim f ( x) a x x ve, x ise fonksiyonu için,, x lim f ( x) b olduğuna göre, a b kaçtır? x A) B) C) D) E) Çözüm x x için,
Öğrenci Seçme Sınavı (Öss) / 7 Nisan Matematik Soruları ve Çözümleri
 Öğrenci Seçme Sınavı (Öss) / 7 Nisan 996 Matematik Soruları ve Çözümleri. 0,09 ın karekökü kaçtır? A) 0,008 B) 0,08 C) 0,8 D) 0, E) 0,0 Çözüm 0,09 9 00 ² 0² ( )² 0, 0 0 0. Rakamları faklı, üç basamaklı
Öğrenci Seçme Sınavı (Öss) / 7 Nisan 996 Matematik Soruları ve Çözümleri. 0,09 ın karekökü kaçtır? A) 0,008 B) 0,08 C) 0,8 D) 0, E) 0,0 Çözüm 0,09 9 00 ² 0² ( )² 0, 0 0 0. Rakamları faklı, üç basamaklı
ÖZEL EGE LİSESİ EGE BÖLGESİ 14. OKULLAR ARASI MATEMATİK YARIŞMASI 8. SINIF ELEME SINAVI TEST SORULARI
 EGE ÖLGESİ 4. OKULLR RSI MTEMTİK YRIŞMSI 8. SINIF ELEME SINVI TEST SORULRI. n bir tamsayı olmak üzere, n n 0 ( 4.( ) +.( ) + 7 + 8 ) işleminin sonucu kaçtır? ) 0 ) 5 ) 6 ). ir kitapçıda rastgele seçilen
EGE ÖLGESİ 4. OKULLR RSI MTEMTİK YRIŞMSI 8. SINIF ELEME SINVI TEST SORULRI. n bir tamsayı olmak üzere, n n 0 ( 4.( ) +.( ) + 7 + 8 ) işleminin sonucu kaçtır? ) 0 ) 5 ) 6 ). ir kitapçıda rastgele seçilen
Matematik Örnek Soruları
 Matematik Örnek Soruları. a ve b birer doğal sayı olmak üzere a b = a 2 b dir. Kerem oyuncak arabasının boyunu 0 santimetrelik bir cetvel ile aşağıdaki gibi ölçüyor. Buna göre oyuncak arabanın boyu santimetre
Matematik Örnek Soruları. a ve b birer doğal sayı olmak üzere a b = a 2 b dir. Kerem oyuncak arabasının boyunu 0 santimetrelik bir cetvel ile aşağıdaki gibi ölçüyor. Buna göre oyuncak arabanın boyu santimetre
Matematik Örnek Soruları
 Matematik Örnek Soruları. a ve b birer doğal sayı olmak üzere a b = a b dir. Kerem oyuncak arabasının boyunu 0 santimetrelik bir cetvel ile aşağıdaki gibi ölçüyor. Buna göre oyuncak arabanın boyu santimetre
Matematik Örnek Soruları. a ve b birer doğal sayı olmak üzere a b = a b dir. Kerem oyuncak arabasının boyunu 0 santimetrelik bir cetvel ile aşağıdaki gibi ölçüyor. Buna göre oyuncak arabanın boyu santimetre
1. Bir ayrıtının uzunluğu 1 olan küpler üst üste konularak tüm alanı A olan bir kare dik prizma yapılırsa, A sayısı aşağıdakilerden hangisi olabilir?
 1. Bir ayrıtının uzunluğu 1 olan küpler üst üste konularak tüm alanı A olan bir kare dik prizma yapılırsa, A sayısı aşağıdakilerden hangisi olabilir? a) 12 b) 16 c) 26 d) 36 e) 44 2. Aşağıdakilerden hangisi
1. Bir ayrıtının uzunluğu 1 olan küpler üst üste konularak tüm alanı A olan bir kare dik prizma yapılırsa, A sayısı aşağıdakilerden hangisi olabilir? a) 12 b) 16 c) 26 d) 36 e) 44 2. Aşağıdakilerden hangisi
Yükseköğretime Geçiş Sınavı (Ygs) / 11 Nisan 2010. Matematik Soruları ve Çözümleri 12 E) 25
 Yükseköğretime Geçiş Sınavı (Ygs) / Nisan 00 Matematik Soruları ve Çözümleri. 0, 0,0 0, işleminin sonucu kaçtır? A) B) 4 7 C) 0 8 D) E) Çözüm 0, 0,0 0, = 0,00 0,0 0, = 0,7 0, 000 7 7. = = 000 00 0... işleminin
Yükseköğretime Geçiş Sınavı (Ygs) / Nisan 00 Matematik Soruları ve Çözümleri. 0, 0,0 0, işleminin sonucu kaçtır? A) B) 4 7 C) 0 8 D) E) Çözüm 0, 0,0 0, = 0,00 0,0 0, = 0,7 0, 000 7 7. = = 000 00 0... işleminin
V =, (V = hacim, m = kütle, d = özkütle) Bu bağıntı V = olarak da yazılabilir G: ağırlık (yerçekimi kuvveti) G = mg p = özgül ağırlık p = dg dir.
 Geometrik Cisimlerin Hacimleri Uzayda yer kaplayan (üç boyutlu) nesnelere cisim denir. Düzgün geometrik cisimlerin hacimleri bağıntılar yardımıyla bulunur. Eğer cisim düzgün değilse cismin hacmi cismin
Geometrik Cisimlerin Hacimleri Uzayda yer kaplayan (üç boyutlu) nesnelere cisim denir. Düzgün geometrik cisimlerin hacimleri bağıntılar yardımıyla bulunur. Eğer cisim düzgün değilse cismin hacmi cismin
ÖRNEK 3712 nin esas ölçüsünü bulunuz. ÇÖZÜM esas ölçüsü 112 olur. ÖRNEK ÇÖZÜM cos 1, 1 sin 1
 MTEMTİK TRİGONOMETRİ - I irim Çember II III sin I IV 0 nin esas ölçüsünü bulunuz 0 00 0 00 + olduğundan, esas ölçüsü olur I ölge (0 < < II ölge ( ) < < ) III ölge ( < < IV ölge ( ) < < ) sin tan cot +
MTEMTİK TRİGONOMETRİ - I irim Çember II III sin I IV 0 nin esas ölçüsünü bulunuz 0 00 0 00 + olduğundan, esas ölçüsü olur I ölge (0 < < II ölge ( ) < < ) III ölge ( < < IV ölge ( ) < < ) sin tan cot +
1983 ÖSS. 6. x.y çarpımında her çarpana 2 eklenirse çarpım ne kadar büyür? işleminin sonucu nedir? A) x+y+2 B) 2(x+y+2) C) x+y D) 2 E) 4
 198 ÖSS 1. 0,1 0,01 0,04 0,0 0, işleminin sonucu nedir? A) 4 B) 7 C) 15 D) E) 41 6..y çarpımında er çarpana eklenirse çarpım ne kadar üyür? A) +y+ B) (+y+) C) +y D) E) 4. 0,5 11 1, 44 işleminin sonucu
198 ÖSS 1. 0,1 0,01 0,04 0,0 0, işleminin sonucu nedir? A) 4 B) 7 C) 15 D) E) 41 6..y çarpımında er çarpana eklenirse çarpım ne kadar üyür? A) +y+ B) (+y+) C) +y D) E) 4. 0,5 11 1, 44 işleminin sonucu
MATEMATİK FORMÜLLERİ
 MATEMATİK FORMÜLLERİ ÜSLÜ SAYILAR x. a n + y. a n z. a n = (x + y z). a n a m. a n = a m + n a m. b m = (a. b) m a m : a n = a m - n KARE'NİN ALANI: A=a.a (a karenin bir kenarı) DİKDÖRTGEN'İN ALANI: A
MATEMATİK FORMÜLLERİ ÜSLÜ SAYILAR x. a n + y. a n z. a n = (x + y z). a n a m. a n = a m + n a m. b m = (a. b) m a m : a n = a m - n KARE'NİN ALANI: A=a.a (a karenin bir kenarı) DİKDÖRTGEN'İN ALANI: A
Öğrenci Seçme Sınavı (Öss) / 6 Haziran Matematik Soruları ve Çözümleri
 Öğrenci Seçme Sınavı (Öss) / 6 Haziran 999 Matematik Soruları ve Çözümleri. 0, 0, 0, + 0, 0,4 0,44 işleminin sonucu kaçtır? A) B), C) D) E) Çözüm 0, 0, 0, + 0, 0,4 0,44 0 0 + 40 44 0 0 0 +, 0 0. a, b,
Öğrenci Seçme Sınavı (Öss) / 6 Haziran 999 Matematik Soruları ve Çözümleri. 0, 0, 0, + 0, 0,4 0,44 işleminin sonucu kaçtır? A) B), C) D) E) Çözüm 0, 0, 0, + 0, 0,4 0,44 0 0 + 40 44 0 0 0 +, 0 0. a, b,
2. Matematiksel kavramları organize bir şekilde sunarak, bu kavramları içselleştirmenizi sağlayacak pedagojik bir alt yapı ile yazılmıştır.
 Sevgili Öğrenciler, Matematik ilköğretimden üniversiteye kadar çoğu öğrencinin korkulu rüyası olmuştur. Buna karşılık, istediğiniz üniversitede okuyabilmeniz büyük ölçüde YGS ve LYS sınavlarında matematik
Sevgili Öğrenciler, Matematik ilköğretimden üniversiteye kadar çoğu öğrencinin korkulu rüyası olmuştur. Buna karşılık, istediğiniz üniversitede okuyabilmeniz büyük ölçüde YGS ve LYS sınavlarında matematik
2000 ÖSS. 7. Üç basamaklı 9KM sayısı iki basamaklı KM sayısının 31 katıdır. Buna göre, K+M toplamı. İşleminin sonucu kaçtır? kaçtır?
 000 ÖSS., 0,, 0, İşleminin sonucu A) B) C) D) E) 7. Üç basamaklı 9KM sayısı iki basamaklı KM sayısının katıdır. Buna göre, K+M toplamı A) B) C) 5 D) 6 E) 9. : İşleminin sonucu 8. Toplamları 6 olan a ve
000 ÖSS., 0,, 0, İşleminin sonucu A) B) C) D) E) 7. Üç basamaklı 9KM sayısı iki basamaklı KM sayısının katıdır. Buna göre, K+M toplamı A) B) C) 5 D) 6 E) 9. : İşleminin sonucu 8. Toplamları 6 olan a ve
IX. Ulusal İlköğretim Matematik Olimpiyatı
 IX. Ulusal İlköğretim Matematik Olimpiyatı B 1. Bir su tankerinin tam doluyken toplam ağırlığı x ton; yarı yarıya doluyken toplam ağırlığı y ton ise, boş tankerin ağırlığı kaç tondur? a) 2x 2y b) 2y x
IX. Ulusal İlköğretim Matematik Olimpiyatı B 1. Bir su tankerinin tam doluyken toplam ağırlığı x ton; yarı yarıya doluyken toplam ağırlığı y ton ise, boş tankerin ağırlığı kaç tondur? a) 2x 2y b) 2y x
AÖĞRENCİLERİN DİKKATİNE!
 A KİTAPÇIK TÜRÜ T.C. MİLLÎ EĞİTİM BAKANLIĞI 8. SINIF MATEMATİK 2015 8. SINIF 2. DÖNEM MATEMATİK DERSİ MERKEZİ ORTAK SINAVI (GÖRME ENGELLİ) 29 NİSAN 2015 Saat: 10.10 Adı ve Soyadı :... Sınıfı :... Öğrenci
A KİTAPÇIK TÜRÜ T.C. MİLLÎ EĞİTİM BAKANLIĞI 8. SINIF MATEMATİK 2015 8. SINIF 2. DÖNEM MATEMATİK DERSİ MERKEZİ ORTAK SINAVI (GÖRME ENGELLİ) 29 NİSAN 2015 Saat: 10.10 Adı ve Soyadı :... Sınıfı :... Öğrenci
 LYS Y ĞRU MTMTİK TSTİ. u testte Matematik ile ilgili 0 soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için ayrılan kısmına işaretleyiniz.. u testteki süreniz 7 dakikadır.., y reel sayılar
LYS Y ĞRU MTMTİK TSTİ. u testte Matematik ile ilgili 0 soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için ayrılan kısmına işaretleyiniz.. u testteki süreniz 7 dakikadır.., y reel sayılar
1983 ÖSS. A) x+y+2 B) 2(x+y+2) C) x+y D) 2 E) 4. işleminin sonucu nedir?
 98 ÖSS. 0, 0,0 0,0 0,0 0, işleminin sonucu nedir? 7. 0,, işleminin sonucu nedir?,7-0, -9, -9, -9,. +y+ (+y+) +y 7. n ir doğal sayı olmak üzere den n ye kadar olan sayıların toplamı, ten n ye kadar olan
98 ÖSS. 0, 0,0 0,0 0,0 0, işleminin sonucu nedir? 7. 0,, işleminin sonucu nedir?,7-0, -9, -9, -9,. +y+ (+y+) +y 7. n ir doğal sayı olmak üzere den n ye kadar olan sayıların toplamı, ten n ye kadar olan
Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı. ALES / Sonbahar / Sayısal II / 16 Kasım Matematik Soruları ve Çözümleri
 Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı ALES / Sonbahar / Sayısal II / 6 Kasım 008 Matematik Soruları ve Çözümleri. a 3 < 5 7 eşitsizliğini sağlayan en küçük a doğal sayısı kaçtır? A) 4 B)
Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı ALES / Sonbahar / Sayısal II / 6 Kasım 008 Matematik Soruları ve Çözümleri. a 3 < 5 7 eşitsizliğini sağlayan en küçük a doğal sayısı kaçtır? A) 4 B)
