Doğrusal ve karesel optimizasyon problemleri için dinamik çözümleyiciler
|
|
|
- Bilge Okur
- 5 yıl önce
- İzleme sayısı:
Transkript
1 tüdegs/d mühedslk Clt:4, Syı:1, Şubt 2005 Doğusl ve kesel optmzsyo poblemle ç dmk çözümleycle Yüksel ÇAKIR, Cüeyt GÜZELİŞ İÜ Elektk-Elektok Fkültes, Elektok ve Hbeleşme Mühedslğ Bölümü, 34469, Ayzğ, İstbul Özet Bu çlışmd, eyleme (optmzto) kumıdk geleeksel gdy zdüşüme (pojeksyo) yötem temel lık doğusl kısıtlı (lely costed), doğusl (le) ve dödü (quc) eyleme poblemle ç gdy zdüşümel ğ (gdet pojectg etwok) olk dldııl ye b çözümleyc tıtılmktdı. Bu dmk system, gdy zdüşüme yötem (gdet pojecto method) süekl hl geçeklemesd. Gdy zdüşüme şlemde dolyı öele çözümleyc sğ tfı, gdy y d gdy-gb (qus-gde sstemlede fklı olk, süeksz ypıddı. Bu ğme öele ğ, gdy ve gdy-gb sstemle ykısm özellklee shpt. ıtıl sstem ykısy olduğu, y, he b çözümü dege oktsıd soldığı L Slle' değşmez küme teoem, sğ tfı süeksz sstemle ç geşletlmes le göstelmşt. Aht Kelmele: Kısıtlı eyleme, gdy zdüşüme, dmk çözümleyc Dymc solves fo le d quc optmzto Abstct I ths study, dymc solve fo lely costed le d quc optmzto poblems, clled gdet pojecto etwok, s toduced. he system s gdet bsed. Gdet dymcl systems e descbed by set of dffeetl equtos stte equto fom whose vecto feld s poduced by the gdet of scl fucto, clled eegy. hese systems do ot hve complex dymcs lke oscllto so tht y bouded soluto of them coveges to oe of the equlbum pots whch e deed exteme of the ssocted eegy fucto. As cosequece of the dymcl popetes, gdet systems hve bee wdely used s tul models fo solvg ucosted mmzto poblems by cosdeg the cost fucto s the eegy. Costed mmzto poblems c lso be solved the sme wy, by ddg to the cost some pelty fucto tems epesetg costt voltos. I the poposed dymcs, fesblty of solutos s stsfed by utlzg the cocept of pojecto to fesble ego. Becuse of pojecto opeto the poposed dymcs s dscotuous, so t s ot gdet but hs the popetes sml to tht of gdet systems. o show ths, L Slle's Ivce heoem hs bee exteded to system wth dscotuous ght-hd sde, d bsed o ths exteso t s show tht the toduced dymcl solve s covege.e., y tjectoy of t eds t oe of the equlb. Keywods: Costed optmzto, gdet pojecto, dymc solve Yzışmlı ypılcğı yz: Yüksel ÇAKIR. yuksel@ehb.tu.edu.t; el: (212) Bu mkle, bc yz tfıd İÜ Elektk-Elektok Fkültes'de tmmlmış "Dymc solves fo le d quc optmzto" dlı dokto tezde hzılmıştı. Mkle met thde degye ulşmış, thde bsım kı lımıştı. Mkle le lgl ttışml the kd degye gödelmeld.
2 Y. Çkı, C. Güzelş Gş So yılld, Hopfeld le bşlmk üzee, eyleme poblemle ç bçok dmk çözümleyc öelmşt (Zk vd., 1995; Bozedoum ve Pttso 1993; Pekeg vd., 1999; Smth, 1999). Eyleme poblemle çözümü ç bu tü b yol zlemes ede bu ypıdk çözümleycle deve olk geçekleeblmes, dolyısıyl çözümü geçek zmd elde edleblmesd. Adışıl ypıd çlış geleeksel çözümleyclele kıysldığıd dmk çözümleycle plel ypıd geçekleeblmelede dolyı dh kıs süede çözüm üetmektele. B dğe fklı d, geleeksel tekklele hesplmld elde edle değele yıkke dmk çözümleyclele elde edle çözümle süekl ypıd olmsıdı. Geel olk dmk çözümleyclede eejs zl dmk ypı kullılmktdı. Bu ypıld sstem dmğ, eej foksyou olk kbul edle eyleme poblemdek mç ölçütüü (cost fucto) zml zltck bçmde tslı, öyle k, değe foksyou ez (mmum) değee ulşıp sstem degeye otuduğud dege oktsı optmzsyo poblem çözümüe kşılık gels. Dege duumud eej foksyouu gdyı sıfı olmkt k bu d yı zmd bu duumu optmzsyo poblem ekstemum oktsı olmsı ç geek şttı. Gdy sstem olk dldııl bu tüdek sstemle tsımıd, Rus mtemtkç ve müheds A. M. Lpuov u dmk sstemle klılık lz ç öedğ ve ked dıyl ıl yötemdek fk temel lımktdı (Hsch ve Smle 1974). Yötem, dmk sstem eejs temsl ede poztf değel, sıılı, zml zl ve soud mmum değede sbt kl b Lpuov foksyouu oluştuulblmese dymktdı. Böyle b foksyou vlığı duumud sstem klı olduğu, y çözümü klı b dege oktsıd soldığı blmekted. Gdy sstemle otk özellğ, çözümle sıılı olmsı duumud bu çözümle he zm b dege oktsıd solıyo olmsıdı, y sstem ykısy ypıddı. Gdy sstemle b dğe özellğ lmt çevm vey kotk ypılı çözümle olmmsıdı. Gdy sstemlede, vele b lk koşul göe eej foksyouu e z yp e ykı dege oktsı buluu. Bu ypılıd dolyı bu tüdek sstemle eyleme poblemle ç üettğ çözümle yeeld (lokl). Bçok eyleme poblemde, özellkle kombtoyl ypıdklede, globl e y çözümü elde etmek ç geeke süe poblem boyutuyl üstel bçmde t (Vvss 1991, Cchock ve Ubehube 1993). Bu tüdek poblemle ç yklşık çözümle de lmlıdı. Gdy temell yötemlele bu tüdek optmzsyo poblemle ç ttm edc yklşık çözümle elde edleblmekted (Pekeg vd., 1999). Kısıtlı optmzsyo poblemle de, uygu eej foksyou oluştuulk gdy temell dmk ypıll çözüleblle. Eej fosyouu oluştuulmsıd zlee yold b, değe foksyou ek olk, kısıt ştlıd oluş bleşele de eej foksyou ht tem olk eklemesd, öyle k, kısıt ştlı sğlmdığı süece bu ht temle poztf değel bleşele olk eej foksyoud ye lmktl, kısıt ştlı sğldığıd se değele sıfı olmktdı. Bu yötem peltı yötem olk dldıılmkt ve çözüme kısıtlı sğlmdığı geçesz (ufesble) bölgede yklşıldığıd dış yötemlede syılmktdı. Bu yötem le geçesz çözümle elde edleblmekted. Buu sebeb, ptkte peltı pmetele uygu değelede seçlememesd. Kısıtlı optmzsyo poblemle kısıtsız hle getlmesde zlee dğe b yol egell foksyo yötemd. Bu yötemde eej foksyou, geçel bölge sıılıd sosuz değelee ulş temle ekle. Bu yötem, çözüme he zm geçel bölgede yklşıldığıd, ç yötemlede syılmktdı. Sııdk oktl ulşılmdığıd bu yklşım, çözümle kısıt bölges sıılıd ol poblemle ç uygu değld. Kısıtlı poblemle çözümüdek b dğe yklşım d gdy zdüşümel yötem kullılmsıdı. Bu yötemde kısıt ştlı sğldığı süece değe foksyou gdyıı tes
3 Doğusl ve kesel optmzsyo poblemle doğultusud gdleek e z ı. Hehg b kısıt hll duumud, bşk b deyşle geçel bölge sıııdyke egtf gdy bleşe geçesz bölgede elde edlyos, egtf gdy, kısıt ştıı belledğ yüzeye zdüşüüleek e z değe msı zdüşüülmüş bu gdy bleşe doğultusud südüülü (Luebege, 1973). Eyleme poblem ez değee, zdüşüülmüş gdy değe sıfı olduğud ulşılı. Bu duumd y gdy değe sıfıdı (k bu d eyleme poblemde ez ç bc deece ştlı sğlmsı lmıı tşı) y d egtf gdy kısıt yüzeye dk ve geçesz bölge doğultusuddı demekt. İkc duum heket edleblecek b yö olmmsı lmıı tşı, dolyısıyl ulşıl okt eyleme poblem ezıdı. Bu çlışmd öele dmk çözümleyc, gdy zdüşüme yötem temel lık tslmıştı. Öele sstem gdy y d gdy-gb (qus-gde olmmsı ğme gdy dmk sstemle ykısm özellklee shpt. Öele dmk çözümleyc ykısy ypıd olduğu L Slle değşmez küme teoem (L Slle, 1960) sğ tfı süeksz sstemle ç geşletlmesyle sptlmıştı. Gdy dmk system Gdy sstemle x = V ( ; x R (1) bçmde tımlı dmk sstemled. Bu sstemle ykısy ypıd olduğuu sptı L Slle değşmez küme teoem le göstel. 1 eoem 1 (L Slle, 1960) x = f ( ; f ( ) C fdes le tımlı sstem gözöüe lısı. V ( ) : R R de tımlı, tüetlebl ve şğıdk özellkle sğly b Lpuov foksyouu olduğu vsyılsı: ) Ω = { x R V ( } kümes > 0 değele ç sıılı b küme olsu, ) V () foksyou Ω kümesdek değele ç ltt sıılı olsu, ) V 0 x Ω olsu. Bu duumd = 0) Ω değede bşly he x ( çözümü, S: = { x Ω V() = 0} Ω de bulu b e geş değşmez kümede (lgest vt se solı. Değşmez kümede dege oktlıı yısı lmt çevmle de bulubl. Aşğıd vele teoem sğlmsı hlde e geş değşmez küme dege oktlıd meyd geldğ göülü (Chu ve Wg, 1978). eoem 2 (Chu ve Wg, 1978): 1 x = f ( ; f ( ) C le tımlı otoom sstem çözümle sıılı se ve ssteme lşk, tüm çözüm eğle boyuc V 0 x R ol ve ck dege oktsı ç V = 0 ol b V () Lpuov foksyou vs sstem ykısydı, bşk b deyşle çözümle ulştığı e geş değşmez küme dege oktlıd meyd gelmekted. Gdy sstemle öeml b özellğ de smptotk klı dege oktlıı eej foksyouu kes (stc yeel ezlı kşılık gelmesd. Bu özellk gdy dmk sstemle eyleme poblemlee çözümleyc olk kullılbl kılmktdı. Gdy zdüşümlü dmk sstem Bu çlışmd (2) bçmde tıml doğusl kısıtlı, dödü optmzsyo poblemle ç gdy temell b dmk çözümleyc öelmekted. mφ( = x Qx c x ; g( = Ax - b Bu fdede; m A R, b R ve g ( = ( Ax b) M : {1,2,..., m}. = 0. (2)
4 Y. Çkı, C. Güzelş Öele çözümleyc dmk ypısı (3) deklemyle velmekted. x = P (. E( (3) Bu deklemde göüle E (, eyleme poblemdek Φ ( mç ölçütüe kşılık gelmekted PI se I y bğlı zdüşüme mts olup deklem (4) de veldğ gb elde edlmekted. P 1 [ I G ( G G ) G ] =. (4) Bu fdede göüe I ds kümes olup I = { M g g ( = 0 ve (. Φ( 0} (5) bçmde tımlmktdı. Bu kümede, ktf ol, bşk b deyşle, eştlk duumu gele ve y zmd d gdylı geçesz bölgey şet ede kısıtlı umlı tutulmktdı. Doğusl kısıt duumud: g ı ( ( Ax b) = ( A) = (6) bu göe de I y lşk fde I = { M ( Ax b) = 0 ve ( A). Φ( 0} (7) bçm lmktdı. GI mts, dsle I d tutul ktf kısıtld oluşmuş kısıt mtsd. Bu mts boyutu I olup he b ( ( GI ) j( ) = ( A) bçmde oluştuulmktdı, j ) {1,2,..., I } stıı. dse bğlı olk bşk b fdeyle GI mts ktf olup yı zmd gdyı geçesz bölgey şet ede kısıtld oluşmktdı. Dmk fdes (3) de vele çözümleyc, P I mts x e göe değşm göstedğde, sğ tfı süeksz b ypıddı. Buul blkte hehg b 0) K : = { x Ax b} bşlgıç koşulu ç çözüm ye de vdı, tekt ve süekld fkt tüetlebl değld. Ayı zmd bu çözüm K polhedl bölgesde klmktdı. Çözümü vlığı ve teklğ şu şeklde göstelebl. He b 0) K bşlgıç koşulu ç l { 0,1,..., m} te kısıtı ktf olduğu ve gdylıı geçesz bölgey göstedğ vsyılsı. Bu kısıtlı belledğ hpeyüzeyde (2) sstem lee duum deklemleyle fde edle sstem ypısıddı. Bu edele, bu bölgede bşly ve bölge çde kl çözüm eğle tek süekld ve tüetleblle. Bölge dışı çık çözüm eğle ye b ktf kısıt kümes oluştuduğu hpeyüzeydek bşlgıç koşuluu oluştumktdıl, bu edele bu ye bölgede de çözüm vdı tekt ve süekld. oplm çözüm eğs bu tüdek bölgesel çözümle bleşmde oluşu, tek süekld fkt hpeyüzey sıılıd tüetlebl değld. Buul blkte hehg b bşlgıç duumu ç çözüm v ve tek olduğud çözüm eğs sğ tft tüetlebl ypıddı. Öele dmk çözümleyc ykısy ypıd olduğuu sptı ç eej foksyouu gdy sstemledek gb zml zl y V ( = [ V ( ] f ( 0 olduğuu göstelmes geek. Öele gdy temell çözümleyc sğ tfı süekl olmdığıd, bu sp gdy sstemlede olduğu gb ypılmz. Bu edele, bu ypıdk sstemle lzde L Slle ı yptığı beze olk (L Slle, 1968), çözümü sğd tüetlebl olm özellğ kullılk sstem ykısy olduğu sptlcktı. Bu mçl öcelkle tüev tımı tek velecekt. ım 1: ): R R foksyouu sğd d t ) tüev = lm bçmde 0 tımlmktdı. Bud 0 sıfı poztf syıld yklşıldığıı beltmekted. Şegö ve dğele, (1999) dk spt beze olk bud d:
5 Doğusl ve kesel optmzsyo poblemle E o ( ) = [ E( ] olduğu göstelebl. Bu fde ışığıd eej foksyouu zml zldığı göstelecekt. Vsyım 1: Dmk ypısı (3) le vele ssteme lşk eej foksyou E( = x Qx c x bçmde olsu. Bu duumd, he x K: = { x Ax b} E o ( ç 0 ve ck dege oktsı E o ( ol x değele ç = 0 dı. İspt: Kesel eej foksyou E( süekl ve x e göe tüetlebl ypıddı. Cözüm eğs x () de süekl ve zm göe sğd tüetlebl ypıddı. Bu göe: de ( ) E o ) = = ) [ E( ] = [ E( ] PI ( E( olu. İzdüşüme mts smetk ve dempotet özellkted, y P = I P ve I P I. P I = P I. Bu özellk kullılk yukıdk fde E o ) 2 = [ E( ] PI ( hl lı. Bu souç eej foksyouu, çözüm eğle boyuc zml tmy ypıd olduğuu, ve ck ve ck PI ( E( = 0 ke E o ) = 0 olduğuu göstemekted. Dh öcede Şegö ve dğele, (1999) d bm hpeküp kısıt bölges ç (3) le vele çözümleyc ykısy ypıd olduğu göstelmşt. Bud, beze yoll hehg b K : = { x Ax b} polhedl kısıt bölges ç de çözümleyc ykısy ypıd olduğu sptlmktdı. eoem 3: (3) fdesyle vele otoom sstem ve bu lşk E( = x Qx c x skle foksyou göz öüe lısı. Bu sstem K : = { x Ax b} bölgesde bşly he çözümü b dege oktsıd solı. İspt: He = 0) K bşlgıç duumu ç elde edle x ( çözümü zdüşüme şlem geeğ sıılıdı ve K polhedl bölgede klmktdı. E( foksyou süekl b foksyodu ve o d K polyhedl bölgede sıılı klmktdı. Vsyım 1 geeğ de( ) 0 x K, bu d E ( x ) 0 çözüm eğle boyuc tmy ypıd olduğuu göstemekted. E ( foksyouu ltt sıılı olduğu d göz öüe lıdığıd, E ( ) zml E gb b lmt değee ykısdığıı, y lmt E( ) = E olduğuu göstemekted. Süekl olmsıd dolyı, E( ) zml E lmt değee ykıske x ( de { x E( x ) = E } kümese ykısmktdı. Bu küme x ( çözüm eğse lşk L poztf lmt kümed. üm çözüm eğle ç E ( ) E lmt kümese ykısdığıd, x L ç E ( = E d. L poztf lmt küme değşmez küme olmsı edeyle (Vdysg, 1978) he x L ç x ( x L, bu d L lmt kümesdek he bşlgıç koşulu ç elde edle çözüm eğs boyuc E ( foksyo değe sbt kldığıı göstemekted. Bşk de( b deyşle = 0 x L. Vsyım 1 geeğ çözüm eğle pöztf lmt kümes L dege oktlıd oluşmktdı. Çözümle teklğde dolyı, he b bşlgıç koşulu ç çözüm b dege oktsıd solmktdı. Elde edle bu souç, (3) le tımlı dmk çözümleyc de gdy sstemle gb ykısy özellkte olduğuu göstemekted.
6 Y. Çkı, C. Güzelş Souç ve ttışm Bu çlışmd doğusl kısıtlı kesel mç ölçütlü eyleme poblemle ç gdy temell b çözümleyc öeld. L Slle değşmez küme teoem, sğ tfı süeksz sstemle ç geşletleek öele çözümleyc de gdy sstemle gb ykısy olduğu gösteld. Öele çözümleyc doğusl kısıtlı tüetlebl hehg b mç ölçütlü eyleme poblem ç de çözümleyc olduğu göstelebl. Öele çözümleyc doım olk geçekleeblmes hlde çözümle geçek zmd elde edleblecekt. Kykl Bouzedoum, A. ve Pttso,.R., (1993). Neul etwok fo quc optmzto wth boud costts, IEEE sctos o Neul Netwoks, 4, 2, , July. Chu, L.O. ve Wg, N.N., (1978). Complete stblty of utoomus ecpocl ole etwoks, It. Joul of Ccut heoy d Applctos, 6, Cchock, A, ve Ubehube, R., (1993). Neul etwoks fo optmzto d sgl pocessg, Joh Wley d Sos d B.G.eube, Stuttgt. Hsch, M.W. ve Smle, S., (1974). Dffeetl equtos, dymcl systems, d le lgeb, Akdemc Pess. L Slle J.P., (1960). Some extesos of Lpuov's secod method, IRE s. Ccut heoy, C- 7, 4, L Slle J.P., (1968). Stblty theoy fo ody dffetl equtos, Joul of Dffeetl Equtos, 4, Luebege, D.G., (1973). Itoducto to le d ole pogmmg, Addso-Wesley Publshg Com. Pekeg, F., Mogül, Ö. ve Güzelş, C. (1999). A stuted le dymcl etwok fo ppoxmtg mxmum clque, IEEE sctos o CAS Pt-I, 46, 6, , Jue Smth, K.A., (1999). Neul etwoks fo combtol optmzto: A evew of moe th decde of esech, INFORMS Joul o Computg, 11, 1, 15-34, Wte. Şegö, N.S., Çkı, Y., Güzelş, C., Pekeg, F ve Mogül, (1999). A lyss of mxmum clque fomultos d stuted le dymcl etwok, ARI, 51, , Spge-Velg. Vvss, S.A., (1991). Nole optmzto, Oxfod Uvesty Pess, New Yok. Vdysg, M., (1978). ole systems lyss, Petce Hll. Zk, S.H., Uptsg, V. d Hu, S., (1995). Solvg le pogmmg poblems wth eul etwoks: A comptve study, IEEE sctos o Neul Netwoks, 6, 1, , Juy.
TÜMEVARIM DİZİ - SERİ
 99 A = {, N } ve P() öemes vels. Eğe :. P() doğu,. A ç P() doğu e P(+) öemes de doğu se; P() öemes A ç doğudu. TOPLAM SEMBOLÜ R ve N olm üzee;... dı. c c. c c b b < m < ç m m p p p 0 F F F F F F F F A
99 A = {, N } ve P() öemes vels. Eğe :. P() doğu,. A ç P() doğu e P(+) öemes de doğu se; P() öemes A ç doğudu. TOPLAM SEMBOLÜ R ve N olm üzee;... dı. c c. c c b b < m < ç m m p p p 0 F F F F F F F F A
Başlangıç değerleri. olduğundan iterasyona devam!
 ESKİŞEHİR OSMANGAZİ ÜNİVERSİESİ Mühedl Mmlı Fülte İşt Mühedlğ Bölümü E-Pot: ogu.hmet.topcu@gml.com Web: http://mmf.ogu.edu.t/topcu Blgy Detel Nüme Alz De otlı Ahmet OPÇU m X X X.5.5.5.5.75 -.5.5.875.75
ESKİŞEHİR OSMANGAZİ ÜNİVERSİESİ Mühedl Mmlı Fülte İşt Mühedlğ Bölümü E-Pot: ogu.hmet.topcu@gml.com Web: http://mmf.ogu.edu.t/topcu Blgy Detel Nüme Alz De otlı Ahmet OPÇU m X X X.5.5.5.5.75 -.5.5.875.75
İKİNCİ BÖLÜM REEL SAYI DİZİLERİ
 Prof.Dr.Hüseyi ÇAKALLI İKİNCİ BÖLÜM REEL SAYI DİZİLERİ Bu ölümde dizileri, yi tım kümesi doğl syılr kümesi, değer kümesi, reel syılr kümesii ir lt kümesi ol foksiyolrı iceleyeceğiz... Ykısk Diziler. Öce
Prof.Dr.Hüseyi ÇAKALLI İKİNCİ BÖLÜM REEL SAYI DİZİLERİ Bu ölümde dizileri, yi tım kümesi doğl syılr kümesi, değer kümesi, reel syılr kümesii ir lt kümesi ol foksiyolrı iceleyeceğiz... Ykısk Diziler. Öce
ÖĞRENME ETKİLİ ÇİZELGELEME PROBLEMİNDE MAKSİMUM GECİKMENİN ENKÜÇÜKLENMESİ İÇİN ÇÖZÜM YAKLAŞIMLARI
 V. Ulusl Üetim Aştımlı Sempozyumu, İstbul Ticet Üivesitesi, 25-27 Ksım 2005 ÖĞRENME ETKİLİ ÇİZELGELEME PROBLEMİNDE MAKSİMUM GECİKMENİN ENKÜÇÜKLENMESİ İÇİN ÇÖZÜM YAKLAŞIMLARI Tme EREN Kııkkle Üivesitesi
V. Ulusl Üetim Aştımlı Sempozyumu, İstbul Ticet Üivesitesi, 25-27 Ksım 2005 ÖĞRENME ETKİLİ ÇİZELGELEME PROBLEMİNDE MAKSİMUM GECİKMENİN ENKÜÇÜKLENMESİ İÇİN ÇÖZÜM YAKLAŞIMLARI Tme EREN Kııkkle Üivesitesi
4. DEVİRLİ ALT GRUPLAR
 4. DEVİRLİ ALT GRUPLAR Tım 4.1. M, bi G gubuu bi lt kümei olu. M yi kpy, G i bütü lt guplıı keitie M i üettiği (doğuduğu) lt gup dei ve M ile göteili. M i elemlı d M gubuu üeteçlei (doğuylı) dei. Öeme
4. DEVİRLİ ALT GRUPLAR Tım 4.1. M, bi G gubuu bi lt kümei olu. M yi kpy, G i bütü lt guplıı keitie M i üettiği (doğuduğu) lt gup dei ve M ile göteili. M i elemlı d M gubuu üeteçlei (doğuylı) dei. Öeme
Optoelektronik Ara Sınav-Çözümler
 Optelektk Aa Sıav-Çöümle s (.57 ) Su : Dğusal laak kutuplamış ışık ç elektk ala 5 π + t + ( + ) 5 velmekted. uada ala gelğ ˆ ˆ se bu ışık dalgasıı, a) aetk alaı (vektöel) ç b fade tüet ( pua) b) Otamı
Optelektk Aa Sıav-Çöümle s (.57 ) Su : Dğusal laak kutuplamış ışık ç elektk ala 5 π + t + ( + ) 5 velmekted. uada ala gelğ ˆ ˆ se bu ışık dalgasıı, a) aetk alaı (vektöel) ç b fade tüet ( pua) b) Otamı
Hidrojen Atomunda Enerji Seviyelerindeki Kaymaların Pertürbasyon Teorisi ile Hesaplanması
 S.Ü. Fe-debyt Fkültes Fe Degs Syı () 89-98, KONYA doje Atomud ej Sevyeledek Kymlı Petübsyo Teos le esplmsı Memet RDOĞAN, Rız OĞUL Özet: Bu çlışmd, doje tomuu eej düzeyle, Scödge deklem kullılk bellemşt.
S.Ü. Fe-debyt Fkültes Fe Degs Syı () 89-98, KONYA doje Atomud ej Sevyeledek Kymlı Petübsyo Teos le esplmsı Memet RDOĞAN, Rız OĞUL Özet: Bu çlışmd, doje tomuu eej düzeyle, Scödge deklem kullılk bellemşt.
tanımlanabilir. Bu nedenle olasılık konusu küme teorisini bir araç olarak kullanmaktadır.
 . OLASILIK TEORİSİ İsttstsel ştımlı temel oulıd b souu öede es ol blmeye bzı şs bğlı olylı (deemele) olsı tüm mümü souçlıı hg sılıl oty çıtığıı belleyeblmet. Bu sou sttstte olsılı poblem ol dldıılı ve
. OLASILIK TEORİSİ İsttstsel ştımlı temel oulıd b souu öede es ol blmeye bzı şs bğlı olylı (deemele) olsı tüm mümü souçlıı hg sılıl oty çıtığıı belleyeblmet. Bu sou sttstte olsılı poblem ol dldıılı ve
Fresnel Denklemleri. 2008 HSarı 1
 Feel Deklemle 8 HSaı 1 De İçeğ Aa Yüzeyde Mawell Deklemle Feel şlkle Yaıma Kıılma 8 HSaı Kayak(la Oc ugee Hech, Alfed Zajac Addo-Weley,199 Kuaum leko-diamğ (KDİ, Rchad Feyma, (Çev. Ömü Akyuz, NAR Yayılaı,
Feel Deklemle 8 HSaı 1 De İçeğ Aa Yüzeyde Mawell Deklemle Feel şlkle Yaıma Kıılma 8 HSaı Kayak(la Oc ugee Hech, Alfed Zajac Addo-Weley,199 Kuaum leko-diamğ (KDİ, Rchad Feyma, (Çev. Ömü Akyuz, NAR Yayılaı,
21. İlk 5 dakikanın sonunda Burak ve Onur un bulundukları. Cevap B. Burak 100. = 45 olup farkları = 22 bulunur. Cevap C
 Deneme - / Mt MEMİK DENEMESİ Çözümle.. c + m. d ı. 4 4 6 4 4 6 ( 6) ( 4) ( ) ( ) y 5 7. y c + m. y d ı. 4 8 6 ( ) ( ) ( ) olduğun göe, 6 6y 8y bulunu.. y - + + y - y - y y - y 6 6. ^009, h. ^0, 07h > c
Deneme - / Mt MEMİK DENEMESİ Çözümle.. c + m. d ı. 4 4 6 4 4 6 ( 6) ( 4) ( ) ( ) y 5 7. y c + m. y d ı. 4 8 6 ( ) ( ) ( ) olduğun göe, 6 6y 8y bulunu.. y - + + y - y - y y - y 6 6. ^009, h. ^0, 07h > c
DUAL KUATERNİYONLAR ÜZERİNDE SİMPLEKTİK GEOMETRİ E. ATA
 DÜ Fe Blmle Esttüsü Degs Dual Kuateyola 6. Sayı (Em l004) Üzede Smlet Geomet DUAL KUATERNİYONLAR ÜZERİNDE SİMLEKTİK GEOMETRİ E. ATA Özet Bu maalede dual uateyola üzede smlet gu, smlet etö uzayı e smlet
DÜ Fe Blmle Esttüsü Degs Dual Kuateyola 6. Sayı (Em l004) Üzede Smlet Geomet DUAL KUATERNİYONLAR ÜZERİNDE SİMLEKTİK GEOMETRİ E. ATA Özet Bu maalede dual uateyola üzede smlet gu, smlet etö uzayı e smlet
5. ( 8! ) 2 ( 6! ) 2 = ( 8! 6! ). ( 8! + 6! ) Cevap E. 6. Büyük boy kutu = 8 tane. Cevap A dakika = 3 saat 15 dakika olup Göksu, ilk 3 saatte
 Deneme - / Mt MTEMTİK DENEMESİ Çözümle. 7 7 7, 0, 7, + + = + + 03, 00,, 3 0 0 7 0 0 7 =. +. +. 3 = + + = 0 ulunu.. P ve pd eklenecek sı olsun. - + =- + + & - + =-- - & + = ^--h + & =- ulunu. + 3. Veilen
Deneme - / Mt MTEMTİK DENEMESİ Çözümle. 7 7 7, 0, 7, + + = + + 03, 00,, 3 0 0 7 0 0 7 =. +. +. 3 = + + = 0 ulunu.. P ve pd eklenecek sı olsun. - + =- + + & - + =-- - & + = ^--h + & =- ulunu. + 3. Veilen
Genelleştirilmiş Ortalama Fonksiyonu ve Bazı Önemli Eşitsizliklerin Öğretimi Üzerine
 Geelleşrlmş Oralama Foksyou ve Bazı Öeml Eşszlkler Öğrem Üzere Gabl ADİLOV, Gülek TINAZTEPE & Serap KEALİ * Öze Armek oralama, Geomerk oralama, Harmok oralama, Kuvadrak oralama ve bular arasıdak lşk vere
Geelleşrlmş Oralama Foksyou ve Bazı Öeml Eşszlkler Öğrem Üzere Gabl ADİLOV, Gülek TINAZTEPE & Serap KEALİ * Öze Armek oralama, Geomerk oralama, Harmok oralama, Kuvadrak oralama ve bular arasıdak lşk vere
Belirsizliği Belirsizliği Belirsizliği Belirsizliği Bir Dizinin Limiti...
 LİMİT VE SÜREKLİLİK Limit ve Süeklilik...8 Bi Foksiou Limiti... 9 Özel Tımlı Foksiolı Limiti... Pçlı Foksiolı Limiti... Mutlk Değe Foksiouu Limiti... 7 Limit Özelliklei... Geişletilmiş Geçel Sıl Kümeside
LİMİT VE SÜREKLİLİK Limit ve Süeklilik...8 Bi Foksiou Limiti... 9 Özel Tımlı Foksiolı Limiti... Pçlı Foksiolı Limiti... Mutlk Değe Foksiouu Limiti... 7 Limit Özelliklei... Geişletilmiş Geçel Sıl Kümeside
AMORTİSMAN MALİYETİ SAPTAMA YÖNTEMLERİ
 AMORTİSMAN MALİYETİ SAPTAMA YÖNTEMLERİ Geel olrk 4 tp yötem kullılır.. Düz çzg yötem: Mlı değer zml doğrusl olrk zldığı vrsyılır. Mlı hzmet ömrü boyuc her yıl ç yı mktr mortsm olrk yrılır. V V d = S d:
AMORTİSMAN MALİYETİ SAPTAMA YÖNTEMLERİ Geel olrk 4 tp yötem kullılır.. Düz çzg yötem: Mlı değer zml doğrusl olrk zldığı vrsyılır. Mlı hzmet ömrü boyuc her yıl ç yı mktr mortsm olrk yrılır. V V d = S d:
FZM450 Elektro-Optik. 7.Hafta. Fresnel Eşitlikleri
 FZM45 leko-ok 7.Hafa Feel şlkle 28 HSaı 1 7. Hafa De İçeğ Feel şlkle Yaıma Kıılma lekomayek dalgaı dalga özellkle kullaaak ışığı faklı kıılma de ah yüzeydek davaışı celeecek 28 HSaı 2 Feel şlkle-1 Şekldek
FZM45 leko-ok 7.Hafa Feel şlkle 28 HSaı 1 7. Hafa De İçeğ Feel şlkle Yaıma Kıılma lekomayek dalgaı dalga özellkle kullaaak ışığı faklı kıılma de ah yüzeydek davaışı celeecek 28 HSaı 2 Feel şlkle-1 Şekldek
Cüneyt F. BAZLAMAÇCI 1 2. e-posta: e-posta:
 Cüneyt F. BAZLAMAÇCI lektk- alle, Ankaa e-posta: cuneytb@metu.edu.t e-posta: BKaadenz@hc.aselsan.com.t ABTRACT The fequency assgnment poblem ases when a lage numbe of tansmtte ae opeatng n a egon and the
Cüneyt F. BAZLAMAÇCI lektk- alle, Ankaa e-posta: cuneytb@metu.edu.t e-posta: BKaadenz@hc.aselsan.com.t ABTRACT The fequency assgnment poblem ases when a lage numbe of tansmtte ae opeatng n a egon and the
3. BEKLENEN DEĞER VE MOMENTLER
 3. BKLNN DĞR V ONTLR emksel bekle kvmı şs oulıd doğmuşu. lı bçmle, b oucuu kzbleceğ mk le kzm olsılığıı çpımıdı. Sözgelm büük ödülü 48TL olduğu b çeklşek. blee b bzmse memksel beklemz 48*/. =,48 olu. 3.
3. BKLNN DĞR V ONTLR emksel bekle kvmı şs oulıd doğmuşu. lı bçmle, b oucuu kzbleceğ mk le kzm olsılığıı çpımıdı. Sözgelm büük ödülü 48TL olduğu b çeklşek. blee b bzmse memksel beklemz 48*/. =,48 olu. 3.
denklemini sağlayan tüm x kompleks sayılarını bulunuz. denklemini x = 64 = 2 i şeklinde yazabiliriz. Bu son kompleks sayıları için x = 2iy
 Ders Sorumlusu: Doç. Dr. Necp ŞİMŞEK Problem. deklem sağlaya tüm kompleks sayılarıı buluu. Çöüm deklem şeklde yaablr. Bu so y kompleks sayıları ç y yaalım. Bu taktrde deklemde, baı y ( ) y elde edlr. Burada
Ders Sorumlusu: Doç. Dr. Necp ŞİMŞEK Problem. deklem sağlaya tüm kompleks sayılarıı buluu. Çöüm deklem şeklde yaablr. Bu so y kompleks sayıları ç y yaalım. Bu taktrde deklemde, baı y ( ) y elde edlr. Burada
REEL ANALĐZ UYGULAMALARI
 www.uukcevik.com REE NĐZ UYGUMRI Sou : (, Α, µ ) ölçü uzayı olsu. = N, Α= ( N ) ve µ ( E) olduğuu östeiiz. N üzeide alması içi eek ve yete koşul < di. Gösteiiz. µ oksiyouu veile taımıı uyulayalım; µ (
www.uukcevik.com REE NĐZ UYGUMRI Sou : (, Α, µ ) ölçü uzayı olsu. = N, Α= ( N ) ve µ ( E) olduğuu östeiiz. N üzeide alması içi eek ve yete koşul < di. Gösteiiz. µ oksiyouu veile taımıı uyulayalım; µ (
Trace ve Kellogg Yöntemleri Kullanılarak İntegral Operatörlerinin Özdeğerlerinin Nümerik Hesabı
 Trce ve Kellogg Yöemleri Kullılrk İegrl Operörlerii Özdeğerlerii Nümerik Hesı Erk Tşdemir () ; Yüksel Soyk () ; Melih Göce (3) (¹)Kırklreli Üiversiesi, Kırklreli, Türkiye, erksdemir@homil.com (²)Büle Ecevi
Trce ve Kellogg Yöemleri Kullılrk İegrl Operörlerii Özdeğerlerii Nümerik Hesı Erk Tşdemir () ; Yüksel Soyk () ; Melih Göce (3) (¹)Kırklreli Üiversiesi, Kırklreli, Türkiye, erksdemir@homil.com (²)Büle Ecevi
ÇSD SİSTEMLERİN ZORLANMIŞ TİTREŞİMİ
 ÇSD SİSELERİN ZORLANIŞ İREŞİİ u u u u bşlgıç koşullrı eksdek br N serbeslk derecel ssem hreke deklem mrs formd; u C u u şeklde yzılblr. Bu mrs formdk hreke deklem, u ve ürevler çere brbre bğlı N de deklem
ÇSD SİSELERİN ZORLANIŞ İREŞİİ u u u u bşlgıç koşullrı eksdek br N serbeslk derecel ssem hreke deklem mrs formd; u C u u şeklde yzılblr. Bu mrs formdk hreke deklem, u ve ürevler çere brbre bğlı N de deklem
7. BÖLÜM DOĞRUSAL DÖNÜŞÜMLER
 7. BÖLÜM DOĞRUSAL DÖNÜŞÜMLER DOĞRUSAL DÖNÜŞÜMLER Bir V ektör uzyıı bir bşk W ektör uzyı döüştüre foksiyolr şu şekilde gösterilir: : V W Burd kullıl termioloji foksiyolrl yıdır. Öreği, V ektör uzyı foksiyouu
7. BÖLÜM DOĞRUSAL DÖNÜŞÜMLER DOĞRUSAL DÖNÜŞÜMLER Bir V ektör uzyıı bir bşk W ektör uzyı döüştüre foksiyolr şu şekilde gösterilir: : V W Burd kullıl termioloji foksiyolrl yıdır. Öreği, V ektör uzyı foksiyouu
0,1,..., n p polinomu bulma işlemine interpolasyon ve px ( )
 Ç.Ü Fe Blmler Esttüsü Yl:29 Clt:2-1 İNTERPOLASYON VE KALAN TEORİSİ Iterpolto d Remder Theory Fge GÜLTÜRK Mtemt Ablm Dl Yusuf KARAKUŞ Mtemt Ablm Dl ÖZET Bu çlşmd İterpolsyo tmlmş, Lgrge İterpolsyo Formülü
Ç.Ü Fe Blmler Esttüsü Yl:29 Clt:2-1 İNTERPOLASYON VE KALAN TEORİSİ Iterpolto d Remder Theory Fge GÜLTÜRK Mtemt Ablm Dl Yusuf KARAKUŞ Mtemt Ablm Dl ÖZET Bu çlşmd İterpolsyo tmlmş, Lgrge İterpolsyo Formülü
Akademik Araştırma Projelerinin AHP ve TOPSIS Yöntemleri Kullanılarak Değerlendirilmesi
 Poltekk Degs, 2016; 19 (2) : 163-173 Joul of Polytechc, 2016; 19 (2) : 163-173 Akdemk Aştım Pojele AHP ve TOPI Yötemle Kullılk Değeledlmes Mut ARIBAŞ 1, Uğu ÖZCAN 2 1 Eejs, Kızılımk Mhlles Ufuk Üvestes
Poltekk Degs, 2016; 19 (2) : 163-173 Joul of Polytechc, 2016; 19 (2) : 163-173 Akdemk Aştım Pojele AHP ve TOPI Yötemle Kullılk Değeledlmes Mut ARIBAŞ 1, Uğu ÖZCAN 2 1 Eejs, Kızılımk Mhlles Ufuk Üvestes
TYT / MATEMATİK Deneme - 3
 TYT / MTEMTİK Deneme -. (0,) 0 (0,) = 0 00 00 0 80 00 = = = bulunu. 00 00 00 6. 7! 8! = 7 6! 8! =! ( 8) = 0! = 0 0 = = b c budn b c = = 8 bulunu.. Syı = olsun = & = 8 & = 0 u syının ü ise 0 = bulunu. 7.
TYT / MTEMTİK Deneme -. (0,) 0 (0,) = 0 00 00 0 80 00 = = = bulunu. 00 00 00 6. 7! 8! = 7 6! 8! =! ( 8) = 0! = 0 0 = = b c budn b c = = 8 bulunu.. Syı = olsun = & = 8 & = 0 u syının ü ise 0 = bulunu. 7.
Küme Teorisi Ve Olasılık Hesapları. Yrd. Doç. Dr. Tijen ÖVER ÖZÇELİK
 Küme Teoisi Ve Olsılık Hesplı Yd. Doç. D. Tije ÖVER ÖZÇELİK tove@sky.edu.t IV. Küme Teoisi Ve Olsılık Hesplı Küme Kvmı; Küme, tek bi isim ltıd toplbile ve beze özellik göstee biimlei meyd getidiği topluluk
Küme Teoisi Ve Olsılık Hesplı Yd. Doç. D. Tije ÖVER ÖZÇELİK tove@sky.edu.t IV. Küme Teoisi Ve Olsılık Hesplı Küme Kvmı; Küme, tek bi isim ltıd toplbile ve beze özellik göstee biimlei meyd getidiği topluluk
AB YE ÜYE ÜLKELERİN VE TÜRKİYE NİN EKONOMİK PERFORMANSLARINA GÖRE VIKOR YÖNTEMİ İLE SIRALANMASI
 İstabul Tcaet Üvestes Sosyal Blmle Degs Yıl: Sayı: Baha 0 / s.455-468 AB YE ÜYE ÜLKELERİN VE TÜRKİYE NİN EKONOMİK PERFORMANSLARINA GÖRE VIKOR YÖNTEMİ İLE SIRALANMASI Üal H. ÖZDEN 6 ÖZET Çalışmada, AB ye
İstabul Tcaet Üvestes Sosyal Blmle Degs Yıl: Sayı: Baha 0 / s.455-468 AB YE ÜYE ÜLKELERİN VE TÜRKİYE NİN EKONOMİK PERFORMANSLARINA GÖRE VIKOR YÖNTEMİ İLE SIRALANMASI Üal H. ÖZDEN 6 ÖZET Çalışmada, AB ye
Pr[ ] 1 Pr[ ] 1 ( ) 1 ( ) What if not known?
![Pr[ ] 1 Pr[ ] 1 ( ) 1 ( ) What if not known? Pr[ ] 1 Pr[ ] 1 ( ) 1 ( ) What if not known?](/thumbs/86/94489430.jpg) 1 Mrkov ve Chebychev Eşitsizlikleri Pr [ ] = 1 Pr [ < ] = 1 f ( ) dx = 1 () x dx F Pr[ ] 1 Pr[ ] 1 ( ) 1 ( ) Wht if ot kow? bilimiyor olbilir r.d. i sdece ortlmsıı ve vrysıı bildiğimizi vrsylım. Ortlm
1 Mrkov ve Chebychev Eşitsizlikleri Pr [ ] = 1 Pr [ < ] = 1 f ( ) dx = 1 () x dx F Pr[ ] 1 Pr[ ] 1 ( ) 1 ( ) Wht if ot kow? bilimiyor olbilir r.d. i sdece ortlmsıı ve vrysıı bildiğimizi vrsylım. Ortlm
ELEKTROSTATİK (II) Giriş
 Elektomnyetik Teoi Bh 5-6 önemi ELEKTROTATİK (II) Giiş Bundn önceki bölümde yük dğılımı bilindiğinde elektik lnın Coulomb yssı kullnılk nsıl hesp edileceği üeine konuştuk. Htılycğını gibi Coulomb yssını
Elektomnyetik Teoi Bh 5-6 önemi ELEKTROTATİK (II) Giiş Bundn önceki bölümde yük dğılımı bilindiğinde elektik lnın Coulomb yssı kullnılk nsıl hesp edileceği üeine konuştuk. Htılycğını gibi Coulomb yssını
MEKANİK TİTREŞİMLER. (Dynamics of Machinery, Farazdak Haideri, 2007)
 MEKANİK TİTREŞİMLER TİTREŞİM ÖLÇÜMÜ: Titeşim ölçümü oldukça kapsamlı bi koudu ve mekaik, elektik ve elektoik bilgisi içeiklidi. Titeşim ölçümleide titeşim geliği (ye değiştime-displacemet, hız-velocity
MEKANİK TİTREŞİMLER TİTREŞİM ÖLÇÜMÜ: Titeşim ölçümü oldukça kapsamlı bi koudu ve mekaik, elektik ve elektoik bilgisi içeiklidi. Titeşim ölçümleide titeşim geliği (ye değiştime-displacemet, hız-velocity
H 2 :O 2 :Ar KARIŞIMININ 1 BOYUTLU, EKSENEL SİMETRİK (SİLİNDİRİK) VE KÜRESEL SİMETRİK PATLAMASININ MODELLENMESİ
 H :O :A KARIŞIMII BOYTL KL İMTRİK İLİDİRİK V KÜRL İMTRİK ATLAMAII MODLLMİ Bşe RDM D M Al AK d Aoc of D İml Hkkı TCR TÜBİTAK-AG K 6 Mmk/AKARA 66 B çlışmd emel olk plm poblemlede Boyl ekeel mek ldk ve küeel
H :O :A KARIŞIMII BOYTL KL İMTRİK İLİDİRİK V KÜRL İMTRİK ATLAMAII MODLLMİ Bşe RDM D M Al AK d Aoc of D İml Hkkı TCR TÜBİTAK-AG K 6 Mmk/AKARA 66 B çlışmd emel olk plm poblemlede Boyl ekeel mek ldk ve küeel
1. GAZLARIN DAVRANI I
 . GZLRIN DRNI I İdeal Gazlar ç: lm 0 RT İdeal gazlar ç: RT Hacm() basıçla() değşk sıcaklıklarda değşm ekl.. de gösterlmştr. T >T 8 T T T 3 asıç T 4 T T 5 T 7 T 8 Molar Hacm ekl.. Gerçek br gazı değşk sıcaklıklardak
. GZLRIN DRNI I İdeal Gazlar ç: lm 0 RT İdeal gazlar ç: RT Hacm() basıçla() değşk sıcaklıklarda değşm ekl.. de gösterlmştr. T >T 8 T T T 3 asıç T 4 T T 5 T 7 T 8 Molar Hacm ekl.. Gerçek br gazı değşk sıcaklıklardak
DERS 4. Determinantlar, Leontief Girdi - Çıktı Analizi
 DERS Determitlr eotief Girdi - Çıktı lizi.. ir Kre Mtrisi Determitı. Determit kvrmıı tümevrıml tımlycğız. mtrisleri determitıı tımlyrk şlylım. Tım. tımlır. mtrisiidetermitı olrk Örek. mtrisii determitı
DERS Determitlr eotief Girdi - Çıktı lizi.. ir Kre Mtrisi Determitı. Determit kvrmıı tümevrıml tımlycğız. mtrisleri determitıı tımlyrk şlylım. Tım. tımlır. mtrisiidetermitı olrk Örek. mtrisii determitı
Bölüm 7: Fresnel Eşitlikleri Alıştırmalar
 Bölüm 7: Feel şlkle Alışımala 7. Kıılma dle faklı la k aı aa yüzeye gele ve kııla ışığı dalga veköle fakıı kk -k aa yüzey mal veköüe aalel lduğuu göez. k ( ˆ ( c ˆ k k j k ( ˆ ( c ˆ k k j ˆ / k ( ( ( ˆ
Bölüm 7: Feel şlkle Alışımala 7. Kıılma dle faklı la k aı aa yüzeye gele ve kııla ışığı dalga veköle fakıı kk -k aa yüzey mal veköüe aalel lduğuu göez. k ( ˆ ( c ˆ k k j k ( ˆ ( c ˆ k k j ˆ / k ( ( ( ˆ
Nesrin ALPTEKĐN 1, Emel ŞIKLAR 2
 Tük Hsse Seed Emekllk Yatıım Folaıı Çok Ktel Pefomas Değeledmes: Topsıs Metodu N.Alptek, E.Şıkla Tük Hsse Seed Emekllk Yatıım Folaıı Çok Ktel Pefomas Değeledmes: Topsıs Metodu Nes ALPTEKĐN 1, Emel ŞIKLAR
Tük Hsse Seed Emekllk Yatıım Folaıı Çok Ktel Pefomas Değeledmes: Topsıs Metodu N.Alptek, E.Şıkla Tük Hsse Seed Emekllk Yatıım Folaıı Çok Ktel Pefomas Değeledmes: Topsıs Metodu Nes ALPTEKĐN 1, Emel ŞIKLAR
Tahmin Edicilerin ve Test Đstatistiklerinin Simülasyon ile Karşılaştırılması
 . Ders ĐSTATĐSTĐKTE SĐMÜLASYON Tahm Edcler ve Test Đstatstkler Smülasyo le Karşılaştırılması Đstatstk rasgelelk olgusu çere olay süreç ve sstemler modellemesde özellkle bu modellerde souç çıkarmada ve
. Ders ĐSTATĐSTĐKTE SĐMÜLASYON Tahm Edcler ve Test Đstatstkler Smülasyo le Karşılaştırılması Đstatstk rasgelelk olgusu çere olay süreç ve sstemler modellemesde özellkle bu modellerde souç çıkarmada ve
FIRÇASIZ DOĞRU AKIM MOTOR SİSTEMİNİNİN DENEYSEL OLARAK GERÇEKLEŞTİRİLMESİ VE SİMÜLASYONU
 FRÇASZ DOĞRU AKM MOOR SİSEMİNİNİN DENEYSE OARAK GERÇEKEŞİRİMESİ VE SİMÜASYONU Es KANDEMİR 1 H.ık DURU 2 Si ÇAMUR 3 Biol ARİFOĞU 4 Esoy BEŞER 5 Elektik Mühendisliği Bölümü Mühendislik Fkültesi Koceli Ünivesitesi,
FRÇASZ DOĞRU AKM MOOR SİSEMİNİNİN DENEYSE OARAK GERÇEKEŞİRİMESİ VE SİMÜASYONU Es KANDEMİR 1 H.ık DURU 2 Si ÇAMUR 3 Biol ARİFOĞU 4 Esoy BEŞER 5 Elektik Mühendisliği Bölümü Mühendislik Fkültesi Koceli Ünivesitesi,
Katı cisimlerin hareketlerinin tanımlanması ve analizi iki yönden önem taşır.
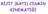 RİJİT (KTI) CİSMİN KİNEMTİĞİ Ktı cisimlein heketleinin tnımlnmsı e nlizi iki yönden önem tşı. iincisi sıkç kşılşıln bi duum olup mç, değişik tipte km, dişli, çubuk e bu gibi mkin elemnlını kullnk belili
RİJİT (KTI) CİSMİN KİNEMTİĞİ Ktı cisimlein heketleinin tnımlnmsı e nlizi iki yönden önem tşı. iincisi sıkç kşılşıln bi duum olup mç, değişik tipte km, dişli, çubuk e bu gibi mkin elemnlını kullnk belili
θ A **pozitif dönüş yönü
 ENT B Kuvvetn B Noktaa Göe oment o o d θ θ d.snθ o..snθ d. **poztf dönüş önü noktasına etk eden hehang b kuvvetnn noktasında medana geteceğ moment o ; ı tanımlaan e vektöü le kuvvet vektöünün vektöel çapımıdı.
ENT B Kuvvetn B Noktaa Göe oment o o d θ θ d.snθ o..snθ d. **poztf dönüş önü noktasına etk eden hehang b kuvvetnn noktasında medana geteceğ moment o ; ı tanımlaan e vektöü le kuvvet vektöünün vektöel çapımıdı.
Yaklaşık Temsil Polinomları
 Yklşık Tesl ololrı Teke for eğrler tesl ede ofset oktlrıd htlı oktlr bulusı duruud terpolso pololrı sıırlı kullı lı bulblektedr. Arıc terpolso pololrı le verle oktlrd geçe eğrler elde edldğde teke for
Yklşık Tesl ololrı Teke for eğrler tesl ede ofset oktlrıd htlı oktlr bulusı duruud terpolso pololrı sıırlı kullı lı bulblektedr. Arıc terpolso pololrı le verle oktlrd geçe eğrler elde edldğde teke for
Elektromanyetik Teori Bahar Dönemi. KOORDİNAT SİSTEMLERİ ve DÖNÜŞÜMLER
 KOORDİNT SİSTEMLERİ ve DÖNÜŞÜMLER i önceki bölümde Kteen koodint sisteminde işlemleimii ptık. Kteen koodint sisteminden bşk biçok koodint sistemlei vdı. u bölümde kteen koodint sistemine ek olk silindiik
KOORDİNT SİSTEMLERİ ve DÖNÜŞÜMLER i önceki bölümde Kteen koodint sisteminde işlemleimii ptık. Kteen koodint sisteminden bşk biçok koodint sistemlei vdı. u bölümde kteen koodint sistemine ek olk silindiik
Estimation of Weibull Renewal Function for Censored Data. Bilinmeyen Veri için Weibull Yenileme Fonksiyonun Tahminlenmesi
 Iteatoal Joual of Scetfc ad Techologcal Reseach ISSN 4-870 (Ole) www.ste.og Estmato of Webull Reewal ucto fo Cesoed Data Cgdem Cegz (Coespodg autho) aculty of Ats ad Sceces, Btls Ee Uvesty Besmae M. Rahva
Iteatoal Joual of Scetfc ad Techologcal Reseach ISSN 4-870 (Ole) www.ste.og Estmato of Webull Reewal ucto fo Cesoed Data Cgdem Cegz (Coespodg autho) aculty of Ats ad Sceces, Btls Ee Uvesty Besmae M. Rahva
HARRAN ÜNİVERSİTESİ ZİRAAT FAKÜLTESİ BAHAR YARIYILI VİZE PROGRAMI
 GÜ C C C3 C4 C5 C6 C7 C8 C C C3 EK EK ) HYV YEE K4) EYVE VE Ğ Z. ) HYV YE. EKĞ ) HYV YE. EKĞ 5 PZ E 6 - : 3:- 4:3 4:3-6: - : 3:- 4:3 4:3-6: 4) K EYVEE -... YUEVE. Y. C. C K3) ÖCEK EKOOJ 3) K GE. KY. VE
GÜ C C C3 C4 C5 C6 C7 C8 C C C3 EK EK ) HYV YEE K4) EYVE VE Ğ Z. ) HYV YE. EKĞ ) HYV YE. EKĞ 5 PZ E 6 - : 3:- 4:3 4:3-6: - : 3:- 4:3 4:3-6: 4) K EYVEE -... YUEVE. Y. C. C K3) ÖCEK EKOOJ 3) K GE. KY. VE
Dış Etki Olarak Sıcaklık Değişmesi ve/veya Mesnet Çökmelerinin Göz Önüne Alınması Durumu
 Dış Etk Olrk Sıcklık Değşmes ve/vey eset Çökmeler Göz Öüe Alımsı Durumu Dış etk olrk göz öüe lı sıcklık eğşm ve meset çökmeler hpersttk sstemlere şekl eğştrme le brlkte kest zoru mey getrr. Sıcklık eğşm:
Dış Etk Olrk Sıcklık Değşmes ve/vey eset Çökmeler Göz Öüe Alımsı Durumu Dış etk olrk göz öüe lı sıcklık eğşm ve meset çökmeler hpersttk sstemlere şekl eğştrme le brlkte kest zoru mey getrr. Sıcklık eğşm:
a bir reel (gerçel) sayı ve n bir pozitif tam sayı olsun. 1 dir. n a ye üslü ifade
 ÜSLÜ İFADELER A. Tı bir reel (gerçel syı ve bir pozitif t syı olsu.... te olck şekilde, te ı çrpıı ol deir. ye üslü ifde Kurl. sıfırd frklı bir reel syı olk üzere,. 0 0 0 ifdesi tısızdır.. ( R... 0 7..
ÜSLÜ İFADELER A. Tı bir reel (gerçel syı ve bir pozitif t syı olsu.... te olck şekilde, te ı çrpıı ol deir. ye üslü ifde Kurl. sıfırd frklı bir reel syı olk üzere,. 0 0 0 ifdesi tısızdır.. ( R... 0 7..
B T A n a l o g T r a n s m i t t e r. T e k n i k K ı l a v u z u. R e v 1. 2
 B T - 111 A n a l o g T r a n s m i t t e r T e k n i k K ı l a v u z u R e v 1. 2 1. Ö N G Ö R Ü N Ü M, Ü S T Ü N L Ü K L E R İ VE Ö Z E L L İ K L E R İ M i k r o k o n t r o l ö r t a b a n l ı BT- 111
B T - 111 A n a l o g T r a n s m i t t e r T e k n i k K ı l a v u z u R e v 1. 2 1. Ö N G Ö R Ü N Ü M, Ü S T Ü N L Ü K L E R İ VE Ö Z E L L İ K L E R İ M i k r o k o n t r o l ö r t a b a n l ı BT- 111
SİSTEM DİNAMİĞİ VE KONTROL
 SİSTEM DİNAMİĞİ VE KONTROL ) KONTROL SİSTEMLERİNE GİRİŞ: Kotrol: Br sste çıkışlrıı stee değerlere yöeltek y d öcede belrleş br dvrışı zleeler sğlk ç sste grşler üzerde ypıl şlelere kotrol der. Ototk Kotrol:
SİSTEM DİNAMİĞİ VE KONTROL ) KONTROL SİSTEMLERİNE GİRİŞ: Kotrol: Br sste çıkışlrıı stee değerlere yöeltek y d öcede belrleş br dvrışı zleeler sğlk ç sste grşler üzerde ypıl şlelere kotrol der. Ototk Kotrol:
HAVA FOTOĞRAFLARININ SENSÖR VE GELENEKSEL YÖNELTME MODELLERİ İLE YÖNELTİLMESİ
 HAVA FOTOĞRAFLARININ SENSÖR VE GELENEKSEL ÖNELTME MODELLERİ İLE ÖNELTİLMESİ A Öztük, *, F Kslı, M Dhk KTU, Tzo Meslek üksek Okulu, Ht ve Kdsto Pogmı, 6 Akçt/Tzo - (oztuk_l66@hotmlom) KTU, Mühedslk Fkültes,
HAVA FOTOĞRAFLARININ SENSÖR VE GELENEKSEL ÖNELTME MODELLERİ İLE ÖNELTİLMESİ A Öztük, *, F Kslı, M Dhk KTU, Tzo Meslek üksek Okulu, Ht ve Kdsto Pogmı, 6 Akçt/Tzo - (oztuk_l66@hotmlom) KTU, Mühedslk Fkültes,
HARRAN ÜNİVERSİTESİ ZİRAAT FAKÜLTESİ BAHAR YARIYILI VİZE PROGRAMI
 GÜ C C C3 C4 C5 C6 C7 C8 C C C3 EK EK ) HYV YEE K4) EYVE VE Ğ Z. ) HYV YE. EKĞ ) HYV YE. EKĞ 5 PZ E 6 7 - : 3:3-5: 5:- 6:3 - : 3:3-5: 5:- 6:3 - : 3:3-5: 5:- 6:3 4) K EYVEE -... YUEVE. Y. C. C K3) ÖCEK
GÜ C C C3 C4 C5 C6 C7 C8 C C C3 EK EK ) HYV YEE K4) EYVE VE Ğ Z. ) HYV YE. EKĞ ) HYV YE. EKĞ 5 PZ E 6 7 - : 3:3-5: 5:- 6:3 - : 3:3-5: 5:- 6:3 - : 3:3-5: 5:- 6:3 4) K EYVEE -... YUEVE. Y. C. C K3) ÖCEK
Çok Yanıtlı Taguchi Eniyilemesine Yönelik Bir Bilgisayar Uygulamasının Geliştirilmesi
 Poltekk Degs, 2016; 19 (3) : 311- Joul of Polytechc, 2016; 19 (3) : 311- Çok Yıtlı Tguch Eylemese Yöelk B Blgsy Uygulmsıı Gelştlmes Yusuf Tsel İÇ, Hkmet DURAN, Bış KEÇECİ, Emec İLİK, Bek BİLGİÇ Bşket Üvestes,
Poltekk Degs, 2016; 19 (3) : 311- Joul of Polytechc, 2016; 19 (3) : 311- Çok Yıtlı Tguch Eylemese Yöelk B Blgsy Uygulmsıı Gelştlmes Yusuf Tsel İÇ, Hkmet DURAN, Bış KEÇECİ, Emec İLİK, Bek BİLGİÇ Bşket Üvestes,
SAYISAL ANALİZ. Doç.Dr. Cüneyt BAYILMIŞ. Sayısal Analiz. Doç.Dr. Cüneyt BAYILMIŞ
 SAYISAL ANALİZ Doç.Dr. Cüet BAYILMIŞ Doç.Dr. Cüet BAYILMIŞ Sısl Alz SAYISAL ANALİZ EĞRİ UYDURMA (Curve Fttg) Doç.Dr. Cüet BAYILMIŞ Sısl Alz İÇİNDEKİLER Eğr Udurm (Curve Fttg) E Küçük Kreler Yötem Doç.Dr.
SAYISAL ANALİZ Doç.Dr. Cüet BAYILMIŞ Doç.Dr. Cüet BAYILMIŞ Sısl Alz SAYISAL ANALİZ EĞRİ UYDURMA (Curve Fttg) Doç.Dr. Cüet BAYILMIŞ Sısl Alz İÇİNDEKİLER Eğr Udurm (Curve Fttg) E Küçük Kreler Yötem Doç.Dr.
TG 10 ÖABT İLKÖĞRETİM MATEMATİK
 KAMU PERSONEL SEÇME SINAVI ÖĞRETMENLİK ALAN BİLGİSİ TESTİ İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ TG ÖABT İLKÖĞRETİM MATEMATİK Bu testlei he hkkı sklıdı. Hgi mçl olus olsu, testlei tmmıı vey i kısmıı İhtiyç
KAMU PERSONEL SEÇME SINAVI ÖĞRETMENLİK ALAN BİLGİSİ TESTİ İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ TG ÖABT İLKÖĞRETİM MATEMATİK Bu testlei he hkkı sklıdı. Hgi mçl olus olsu, testlei tmmıı vey i kısmıı İhtiyç
TG 6 ÖABT ORTAÖĞRETİM MATEMATİK
 KAMU PERSONEL SEÇME SINAVI ÖĞRETMENLİK ALAN BİLGİSİ TESTİ ORTAÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ TG 6 ÖABT ORTAÖĞRETİM MATEMATİK Bu testle he hkkı sklıı. Hg mçl olus olsu, testle tmmıı ve kısmıı İhtç Yıcılık
KAMU PERSONEL SEÇME SINAVI ÖĞRETMENLİK ALAN BİLGİSİ TESTİ ORTAÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ TG 6 ÖABT ORTAÖĞRETİM MATEMATİK Bu testle he hkkı sklıı. Hg mçl olus olsu, testle tmmıı ve kısmıı İhtç Yıcılık
LYS1 / 4.DENEME MATEMATİK TESTİ ÇÖZÜMLERİ
 . İki bsmklı toplm sı vdı. ile lınd sl olmsı için ve e tm bölünmemeli e bölünen sıl 8 det e bölünen sıl det LYS /.NM MTMTİK TSTİ ÇÖZÜMLİ 8. - ` j - 8 k - 8 8-8 8 nck ʼin ktı oln sıl ( tne) kee lındı. -
. İki bsmklı toplm sı vdı. ile lınd sl olmsı için ve e tm bölünmemeli e bölünen sıl 8 det e bölünen sıl det LYS /.NM MTMTİK TSTİ ÇÖZÜMLİ 8. - ` j - 8 k - 8 8-8 8 nck ʼin ktı oln sıl ( tne) kee lındı. -
1. SAYI CİSİMLERİ SÜREKLİ KESRİN UYGULAMALARI ELİPTİK EĞRİLER...88
 ANKARA ÜNİVERSİTESİ FEN BİİMERİ ENSTİTÜSÜ YÜKSEK İSANS TEZİ CEBİRSE SAYIAR TEORİSİNDEN BAZI AGORİTMAAR Züleyh MUTU MATEMATİK ANABİİM DAI ANKARA 5 He hı slıdı İÇİNDEKİER ÖZET i ABSTRACT ii TEŞEKKÜR iii
ANKARA ÜNİVERSİTESİ FEN BİİMERİ ENSTİTÜSÜ YÜKSEK İSANS TEZİ CEBİRSE SAYIAR TEORİSİNDEN BAZI AGORİTMAAR Züleyh MUTU MATEMATİK ANABİİM DAI ANKARA 5 He hı slıdı İÇİNDEKİER ÖZET i ABSTRACT ii TEŞEKKÜR iii
2 Diğer sayfaya geçiniz
 TYT / MTEMTİK Deneme - 5. + c m $ ^+ & & + & Cevp : 5. ^ ise 'dn son gelen tm ke oln syı ^ + di. Yni ^ + + + ulunu. Cevp : E 6. 5! + 6! + 7! 5! + 6$ 5! + 7$ 6$ 5! 8! 7! 8$ 7! 7!. ise ^ + ^ + > H ^ + +
TYT / MTEMTİK Deneme - 5. + c m $ ^+ & & + & Cevp : 5. ^ ise 'dn son gelen tm ke oln syı ^ + di. Yni ^ + + + ulunu. Cevp : E 6. 5! + 6! + 7! 5! + 6$ 5! + 7$ 6$ 5! 8! 7! 8$ 7! 7!. ise ^ + ^ + > H ^ + +
DEÜ MÜHENDİSLİK FAKÜLTESİ FEN BİLİMLERİ DERGİSİ
 DEÜ MÜHENDİSLİK FAKÜLTESİ FEN BİLİMLERİ DERGİSİ Clt: 2 Sayı: 3 sh 87-02 Ekm 200 VOLTERRA SERİLERİ METODU İLE DOĞRUSAL OLMAYAN SİSTEMLERİN FREKANS BOYUTUNDA ANALİZİ İÇİN NET TABANLI ARAYÜZ TASARIMI (DESIGN
DEÜ MÜHENDİSLİK FAKÜLTESİ FEN BİLİMLERİ DERGİSİ Clt: 2 Sayı: 3 sh 87-02 Ekm 200 VOLTERRA SERİLERİ METODU İLE DOĞRUSAL OLMAYAN SİSTEMLERİN FREKANS BOYUTUNDA ANALİZİ İÇİN NET TABANLI ARAYÜZ TASARIMI (DESIGN
TANIMLAYICI İSTATİSTİKLER
 4 TANIMLAYICI İSTATİSTİKLER 4.. Mekez Eğlm Ölçüle 4... Atmetk Otalama 4... Ağılıklı Atmetk Otalama 4... Geometk Otalama 4..4. Hamok Otalama 4..5 Kuadatk Otalama 4..6. Medya 4..7. Katlle 4..8. Decle ve
4 TANIMLAYICI İSTATİSTİKLER 4.. Mekez Eğlm Ölçüle 4... Atmetk Otalama 4... Ağılıklı Atmetk Otalama 4... Geometk Otalama 4..4. Hamok Otalama 4..5 Kuadatk Otalama 4..6. Medya 4..7. Katlle 4..8. Decle ve
ÖĞRENME ETKİLİ AKIŞ TİPİ ÇİZELGELEMEDE ORTALAMA AKIŞ ZAMANININ ENKÜÇÜKLENMESİ
 Gzi Üiv. Müh. Mim. Fk. De. J. Fc. Eg. Ach. Gzi Uiv. Cilt 9, No 2, 9-24, 2004 Vol 9, No 2, 9-24, 2004 ÖĞRENME ETKİLİ AKIŞ TİPİ ÇİZELGELEMEDE ORTALAMA AKIŞ ZAMANININ ENKÜÇÜKLENMESİ Tme EREN ve Et GÜNER *
Gzi Üiv. Müh. Mim. Fk. De. J. Fc. Eg. Ach. Gzi Uiv. Cilt 9, No 2, 9-24, 2004 Vol 9, No 2, 9-24, 2004 ÖĞRENME ETKİLİ AKIŞ TİPİ ÇİZELGELEMEDE ORTALAMA AKIŞ ZAMANININ ENKÜÇÜKLENMESİ Tme EREN ve Et GÜNER *
Alamouti Uzay-Zaman Kodlu ve Kuvvetlendir-Aktar Röleli Çeşitlemelerin OFDM İşaretleri için Başarım Karşılaştırması
 Kelms Fen ve Müendslk Degs / Kelms Scence nd Engneeng Jounl (), 47-54, Kelms Scence nd Engneeng Jounl Jounl ome pge: www.fbd.kelms.edu.t Aştım Mkles Almout Uzy-Zmn Kodlu ve Kuvvetlend-Akt Rölel Çeştlemelen
Kelms Fen ve Müendslk Degs / Kelms Scence nd Engneeng Jounl (), 47-54, Kelms Scence nd Engneeng Jounl Jounl ome pge: www.fbd.kelms.edu.t Aştım Mkles Almout Uzy-Zmn Kodlu ve Kuvvetlend-Akt Rölel Çeştlemelen
BASİT MAKİNELER BÖLÜM 4
 BASİ AİNEER BÖÜ 4 ODE SORU DE SORUARIN ÇÖZÜER fi ip fiekil-i fi fiekil-i ip N fiekil-ii fiekil-ii Çuuklın he iinin ğılığın diyelim Şekil-I de: Desteğe göe moment lısk, Şekil-I de: Şekil-II de: 4 ESEN AINARI
BASİ AİNEER BÖÜ 4 ODE SORU DE SORUARIN ÇÖZÜER fi ip fiekil-i fi fiekil-i ip N fiekil-ii fiekil-ii Çuuklın he iinin ğılığın diyelim Şekil-I de: Desteğe göe moment lısk, Şekil-I de: Şekil-II de: 4 ESEN AINARI
DOĞRUSAL OLMAYAN PROGRAMLAMA TEK DEĞİŞKENLİ KISITSIZ OPTİMİZASYON:
 DOĞRUSA OMAYAN PROGRAMAMA TEK DEĞİŞKENİ KISITSIZ OPTİMİZASYON: Kısıtsız optmzsyo herhg r kısıtlm olmksızı r oksyou mksmum vey mmum değerler rştırılmsı prolem le uğrşır. Y kısıtlrıı d sğlmsı gerekl ol r
DOĞRUSA OMAYAN PROGRAMAMA TEK DEĞİŞKENİ KISITSIZ OPTİMİZASYON: Kısıtsız optmzsyo herhg r kısıtlm olmksızı r oksyou mksmum vey mmum değerler rştırılmsı prolem le uğrşır. Y kısıtlrıı d sğlmsı gerekl ol r
Evolvent Dişli Üretimi Esnasında Meydana Gelen Kesme Kuvvetlerinin Teorik ve Deneysel Olarak Belirlenmesi
 UluslrrsıKtılımlı 7. MkTeorsSempozyumu, İzmr, 4-7 Hzr 5 Evolvet Dşl Üretm Essıd Meyd Gele Kesme Kuvvetler Teork ve Deeysel Olrk Belrlemes İ. EŞİLUT * H. GÜSO Uşk Üverstes Uşk Üverstes Uşk Uşk Özet Bu bldrde
UluslrrsıKtılımlı 7. MkTeorsSempozyumu, İzmr, 4-7 Hzr 5 Evolvet Dşl Üretm Essıd Meyd Gele Kesme Kuvvetler Teork ve Deeysel Olrk Belrlemes İ. EŞİLUT * H. GÜSO Uşk Üverstes Uşk Üverstes Uşk Uşk Özet Bu bldrde
ELEKTRIKSEL POTANSIYEL
 FİZK 14-22 Des 7 ELEKTRIKSEL POTANSIYEL D. Ali ÖVGÜN DAÜ Fizik Bölümü Kynkl: -Fizik 2. Cilt (SERWAY) -Fiziğin Temellei 2.Kitp (HALLIDAY & RESNIK) -Ünivesite Fiziği (Cilt 2) (SEARS ve ZEMANSKY) www.ovgun.com
FİZK 14-22 Des 7 ELEKTRIKSEL POTANSIYEL D. Ali ÖVGÜN DAÜ Fizik Bölümü Kynkl: -Fizik 2. Cilt (SERWAY) -Fiziğin Temellei 2.Kitp (HALLIDAY & RESNIK) -Ünivesite Fiziği (Cilt 2) (SEARS ve ZEMANSKY) www.ovgun.com
YILLAR ÖSS-YGS ) a 0 ve b 0 olmak üzere; 8) Üslü Denklemler: a -1, a 0, a 1
 YILLAR 00 00 00 00 00 00 008 009 00 0 ÖSS-YGS Böle: i,( 0 ÜSLÜ İFADELER R ve Z olk üzere te ı çrpıı deir. ii, (b 0 b b... te Not:.... dır. te... 0 ve... 0. 0 te 0 te ÜSLÜ ÇOKLUKLARLA İLGİLİ ÖZELLİKLER
YILLAR 00 00 00 00 00 00 008 009 00 0 ÖSS-YGS Böle: i,( 0 ÜSLÜ İFADELER R ve Z olk üzere te ı çrpıı deir. ii, (b 0 b b... te Not:.... dır. te... 0 ve... 0. 0 te 0 te ÜSLÜ ÇOKLUKLARLA İLGİLİ ÖZELLİKLER
BÖLÜM 3 3. ÇOK DEĞİŞKENLİ REGRESYON İÇİN VEKTÖR VE MATRİS CEBRİ
 BÖLÜM. ÇOK DEĞİŞKENLİ REGRESYON İÇİN VEKÖR VE MRİS CEBRİ Bölüm de, doğrusl regresyo tek değşkel bst model olrk ele lırk çıklmıştı. Bölüm de se çok değşkel (k değşkel) model ç grş ypılcktır. Çok değşkel
BÖLÜM. ÇOK DEĞİŞKENLİ REGRESYON İÇİN VEKÖR VE MRİS CEBRİ Bölüm de, doğrusl regresyo tek değşkel bst model olrk ele lırk çıklmıştı. Bölüm de se çok değşkel (k değşkel) model ç grş ypılcktır. Çok değşkel
7. Ders Fresnel Eşitlikleri
 7. De Feel şlkle k k θ θ z 1 Bu bölümü bdğzde, Gelş düzlem, - ve -kuulu ışık, Feel kaayılaı, Kuulama (Bewe) açıı, Yaıma ve geçme kaayılaı koulaıda blg ahb olacakıız. 2 Bu bölümü öem, Geomek ok aa yüzeye
7. De Feel şlkle k k θ θ z 1 Bu bölümü bdğzde, Gelş düzlem, - ve -kuulu ışık, Feel kaayılaı, Kuulama (Bewe) açıı, Yaıma ve geçme kaayılaı koulaıda blg ahb olacakıız. 2 Bu bölümü öem, Geomek ok aa yüzeye
Ankara Üniversitesi Fen Fakültesi Kimya Bölümü 2014-2015 Bahar Yarıyılı Bölüm-4 30.03.2015 Ankara Aysuhan OZANSOY
 FİZ2 FİZİK-II Ank Ünivesitesi Fen Fkültesi Kimy Bölümü 24-25 Bh Yıyılı Bölüm-4 Ank Aysuhn OZANSOY Bölüm 4. Elektiksel Potnsiyel. Elektiksel Potnsiyel Eneji 2. Elektiksel Potnsiyel ve Potnsiyel Fk 3. Noktsl
FİZ2 FİZİK-II Ank Ünivesitesi Fen Fkültesi Kimy Bölümü 24-25 Bh Yıyılı Bölüm-4 Ank Aysuhn OZANSOY Bölüm 4. Elektiksel Potnsiyel. Elektiksel Potnsiyel Eneji 2. Elektiksel Potnsiyel ve Potnsiyel Fk 3. Noktsl
KISMİ DEVAMLI FONKSİYONLAR KULLANARAK SOĞUTUCU AKIŞKANLARIN DOYMA BASINÇ EĞRİLERİNİN HASSAS OLARAK OLUŞTURULMASI
 KISMİ DEVAMLI FONKSİYONLAR KULLANARAK SOĞUTUCU AKIŞKANLARIN DOYMA BASINÇ EĞRİLERİNİN HASSAS OLARAK OLUŞTURULMASI M. Turh ÇOBAN Ege Üverstes, Mühedslk Fkultes, Mke Mühedslğ Bölüü, Borov, İZMİR Turh.cob@ege.edu.tr
KISMİ DEVAMLI FONKSİYONLAR KULLANARAK SOĞUTUCU AKIŞKANLARIN DOYMA BASINÇ EĞRİLERİNİN HASSAS OLARAK OLUŞTURULMASI M. Turh ÇOBAN Ege Üverstes, Mühedslk Fkultes, Mke Mühedslğ Bölüü, Borov, İZMİR Turh.cob@ege.edu.tr
Faiz oranının rastlantı değişkeni olması durumunda tam hayat ve dönem sigortaları
 wwwsascleog İsasçle Degs 009-8 İsasçle Degs Fa oaıı aslaı değşe olması duumuda am haya ve döem sgoalaı sa Saıcı Haceee Üveses Fe Faüles İsas Bölümü eelago@haceeeedu Cea dem Haceee Üveses Fe Faüles üeya
wwwsascleog İsasçle Degs 009-8 İsasçle Degs Fa oaıı aslaı değşe olması duumuda am haya ve döem sgoalaı sa Saıcı Haceee Üveses Fe Faüles İsas Bölümü eelago@haceeeedu Cea dem Haceee Üveses Fe Faüles üeya
LYS1 / 3.DENEME MATEMATİK TESTİ ÇÖZÜMLERİ
 . `n 5j- `n- j - n - n vey n- n n 8. 8 8 LYS /.NM MTMTİK TSTİ ÇÖZÜMLRİ evp: evp:. - f p$ f - p f p 9 - - 5! 5 -! 5 5 5. 8... 5 5. 5.. y 8 8 5 5... z < y < z _. ` j. $ ` j ` ise y. ` j y $ ` j ` j yk. `
. `n 5j- `n- j - n - n vey n- n n 8. 8 8 LYS /.NM MTMTİK TSTİ ÇÖZÜMLRİ evp: evp:. - f p$ f - p f p 9 - - 5! 5 -! 5 5 5. 8... 5 5. 5.. y 8 8 5 5... z < y < z _. ` j. $ ` j ` ise y. ` j y $ ` j ` j yk. `
TEST 12-1 KONU. çembersel hareket. Çözümlerİ ÇÖZÜMLERİ s ise. 1. H z ve ivme vektörel olduğundan her ikisinin yönü değişkendir. 7.
 KOU çebesel heket Çözüle S - ÇÖÜMLR. H z ve ive vektöel olduğundn he ikisinin yönü değişkendi. 6. 30 s ise 3 4 sniye f Hz 4. F, ıçp vektöü ile hız vektöü sındki çı 90 di. k 7. 000 7. 7 h 3600s 0 /s X t
KOU çebesel heket Çözüle S - ÇÖÜMLR. H z ve ive vektöel olduğundn he ikisinin yönü değişkendi. 6. 30 s ise 3 4 sniye f Hz 4. F, ıçp vektöü ile hız vektöü sındki çı 90 di. k 7. 000 7. 7 h 3600s 0 /s X t
DENKLEM KURMA PROBLEMLERİ
 DENKLEM KURM İ SYI KESİR İ Örnek... : H a n g i s a yın ın d ö r t t e b i r i n i n 4 e k s i ğ i n i n 2 k a t ı 5 6 d ır? i r p r o b l e m i ç ö ze r k e n, s o r u d a ye r a l a n v e r i l e r i,
DENKLEM KURM İ SYI KESİR İ Örnek... : H a n g i s a yın ın d ö r t t e b i r i n i n 4 e k s i ğ i n i n 2 k a t ı 5 6 d ır? i r p r o b l e m i ç ö ze r k e n, s o r u d a ye r a l a n v e r i l e r i,
ELİPSOİDAL YÜKSEKLİKLERİN ORTOMETRİK YÜKSEKLİĞE DÖNÜŞÜMÜNDE ENTERPOLASYON YÖNTEMLERİNİN KULLANILABİLİRLİĞİ
 SÜ ü-m Fk Derg, c9, s, 4 J FcEgArc Selcuk Uv, v9,, 4 EİPSOİDA YÜSEİERİN ORTOETRİ YÜSEİĞE DÖNÜŞÜÜNDE ENTERPOASYON YÖNTEERİNİN UANIABİİRİĞİ Cevt İNA ve Ceml Özer YİĞİT SÜü-mFkültes, Jeod ve Fot ü Bölümü,
SÜ ü-m Fk Derg, c9, s, 4 J FcEgArc Selcuk Uv, v9,, 4 EİPSOİDA YÜSEİERİN ORTOETRİ YÜSEİĞE DÖNÜŞÜÜNDE ENTERPOASYON YÖNTEERİNİN UANIABİİRİĞİ Cevt İNA ve Ceml Özer YİĞİT SÜü-mFkültes, Jeod ve Fot ü Bölümü,
KATILARDA DAYANIKLILIK
 BÖÜM 3 ATIARDA DAANIII MODE SORU - DEİ SORUARIN ÇÖZÜMERİ 4.. Cnlılın dynıklılığı, biim ğılığ düşen kesitlnı olk ifde edili., kkteistik uzunlukolmk üzee, kesitlnı kesitlnı Dynıklılık ğılık cim 3 di. Bu
BÖÜM 3 ATIARDA DAANIII MODE SORU - DEİ SORUARIN ÇÖZÜMERİ 4.. Cnlılın dynıklılığı, biim ğılığ düşen kesitlnı olk ifde edili., kkteistik uzunlukolmk üzee, kesitlnı kesitlnı Dynıklılık ğılık cim 3 di. Bu
... SERİLER Tanım: 2 3 toplamı kaçtır? Çözüm: serisinde 10. kısmi terimler. Ör: bir reel sayı dizisi olmak üzere
 SERİLER Tım: bir reel syı dizisi olm üzere...... 3 toplmı SERİ deir. gerçel syısı serii geel terimi deir. S 3... toplmı SERİNİN N. KISMİ (PARÇA) TOPLAMI deir. S dizisie SERİNİN N. KISMİ TOPLAMLAR DİZİSİ
SERİLER Tım: bir reel syı dizisi olm üzere...... 3 toplmı SERİ deir. gerçel syısı serii geel terimi deir. S 3... toplmı SERİNİN N. KISMİ (PARÇA) TOPLAMI deir. S dizisie SERİNİN N. KISMİ TOPLAMLAR DİZİSİ
RANKI 2 OLAN SERBEST LIE CEBİRLERİNİN OTOMORFİZM GRUPLARININ SUNUMLARI 1 Reports Of Free Groups Otomorfizm Rank 2 Lie Algebras
 RANKI OLAN SERBEST LIE CEBİRLERİNİN OTOMORFİZM GRUPLARININ SUNUMLARI Reports Of Free Groups Otomorfzm Rak Le Algebras Özge ÖZTEKİN Matematk Aa Blm Dalı Name EKİCİ Matematk Aa Blm Dalı ÖZET Bu çalışmada,
RANKI OLAN SERBEST LIE CEBİRLERİNİN OTOMORFİZM GRUPLARININ SUNUMLARI Reports Of Free Groups Otomorfzm Rak Le Algebras Özge ÖZTEKİN Matematk Aa Blm Dalı Name EKİCİ Matematk Aa Blm Dalı ÖZET Bu çalışmada,
TG 2 ÖABT İLKÖĞRETİM MATEMATİK
 KAMU PERSONEL SEÇME SINAVI ÖĞRETMENLİK ALAN BİLGİSİ TESTİ İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ TG ÖABT İLKÖĞRETİM MATEMATİK Bu testlei he hkkı sklıdı. Hgi mçl olus olsu, testlei tmmıı ve bi kısmıı İhtiç Yıcılık
KAMU PERSONEL SEÇME SINAVI ÖĞRETMENLİK ALAN BİLGİSİ TESTİ İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ TG ÖABT İLKÖĞRETİM MATEMATİK Bu testlei he hkkı sklıdı. Hgi mçl olus olsu, testlei tmmıı ve bi kısmıı İhtiç Yıcılık
ESKİŞEHİR OSMANGAZİ ÜNİVERSİTESİ
 ESKİŞEHİR OSMNGZİ ÜNİVERSİTESİ Mühedslk Mmrlık Fkültes İşt Mühedslğ Bölümü EPost: oguhmettopcu@gmlcom Web: http://mmfoguedutr/topcu Blgsyr Destekl Nümerk lz Ders otlrı hmet TOPÇU Ktsyılr mtrs Özdeğer Özvektör
ESKİŞEHİR OSMNGZİ ÜNİVERSİTESİ Mühedslk Mmrlık Fkültes İşt Mühedslğ Bölümü EPost: oguhmettopcu@gmlcom Web: http://mmfoguedutr/topcu Blgsyr Destekl Nümerk lz Ders otlrı hmet TOPÇU Ktsyılr mtrs Özdeğer Özvektör
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ İÇ-İÇE TASARIMLARDA DAYANIKLI ANALİZ VE UYGULAMALARI. İklim GEDİK
 NKR ÜNİVERSİTESİ EN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSNS TEZİ İÇ-İÇE TSRIMLRD DYNIKLI NLİZ VE UYGULMLRI İklm GEDİK İSTTİSTİK NBİLİM DLI NKR 00 er hkkı sklıdır ÖZET Yüksek Lss Tez İÇ-İÇE TSRIMLRD DYNIKLI NLİZ
NKR ÜNİVERSİTESİ EN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSNS TEZİ İÇ-İÇE TSRIMLRD DYNIKLI NLİZ VE UYGULMLRI İklm GEDİK İSTTİSTİK NBİLİM DLI NKR 00 er hkkı sklıdır ÖZET Yüksek Lss Tez İÇ-İÇE TSRIMLRD DYNIKLI NLİZ
değerine bu matrisin bir girdisi(elemanı,bileşeni) denir. Bir sütundan (satırdan) oluşan bir matrise bir sütun (satır) matrisi denir.
 Bölüm 2 Matrsler aım 2.1 F br csm, m, brer doğal sayı olsu. a F ( 1,.., m; j 1,..., ) olmak üzere, a11... a1 fadese m satır sütuda oluşa (veya m tpde) br F matrs der. am 1... a m Böyle br matrs daha sade
Bölüm 2 Matrsler aım 2.1 F br csm, m, brer doğal sayı olsu. a F ( 1,.., m; j 1,..., ) olmak üzere, a11... a1 fadese m satır sütuda oluşa (veya m tpde) br F matrs der. am 1... a m Böyle br matrs daha sade
ş ş şğ ş ş ş ö Ö ş ö ğ ş ö ö ğ ş ö ö ö ğ ğ ş ş ö ğ ö ş Ü ö ğ ş ş ö ş ğ ş ğ ğ ğ ö ğ ş
 Ü ğ ğ ş ş ş ş ğ Ğ Ç Ş» ş ö ş ş ğ ş ğ ş Ç ş ğ ş ş ğ ş ş ÜÜ ş ş ö ş Ö Ş Ö ğ ş ö ğ ğ Ü Ş ş ş şğ ş ş ş ö Ö ş ö ğ ş ö ö ğ ş ö ö ö ğ ğ ş ş ö ğ ö ş Ü ö ğ ş ş ö ş ğ ş ğ ğ ğ ö ğ ş ş Ö» Ö Ç ö ğ ş ş ş ö ş ö ö ğ ğ
Ü ğ ğ ş ş ş ş ğ Ğ Ç Ş» ş ö ş ş ğ ş ğ ş Ç ş ğ ş ş ğ ş ş ÜÜ ş ş ö ş Ö Ş Ö ğ ş ö ğ ğ Ü Ş ş ş şğ ş ş ş ö Ö ş ö ğ ş ö ö ğ ş ö ö ö ğ ğ ş ş ö ğ ö ş Ü ö ğ ş ş ö ş ğ ş ğ ğ ğ ö ğ ş ş Ö» Ö Ç ö ğ ş ş ş ö ş ö ö ğ ğ
KIRIKKALE ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MATEMATİK ANABİLİM DALI YÜKSEK LİSANS TEZİ KOMPLEKS FONKSİYONLARDA REZİDÜ VE BAZI UYGULAMALARI
 KIRIKKALE ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MATEMATİK ANABİLİM DALI YÜKSEK LİSANS TEZİ KOMPLEKS FONKSİYONLARDA REZİDÜ VE BAZI UYGULAMALARI SEVGİ İŞLER EYLÜL 5 ÖZET KOMPLEKS FONKSİYONLARDA REZİDÜ VE
KIRIKKALE ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MATEMATİK ANABİLİM DALI YÜKSEK LİSANS TEZİ KOMPLEKS FONKSİYONLARDA REZİDÜ VE BAZI UYGULAMALARI SEVGİ İŞLER EYLÜL 5 ÖZET KOMPLEKS FONKSİYONLARDA REZİDÜ VE
ğ ğ ğ ş ğ ş ğ ğ ği ğ ş ğ İ ş ğ ş ş ş ğ ş İ ğ ğ ş ş
 ş Ğ İ ş ş ş ğ ğ ğ ğ ş İ ğ ğ ğ ş ğ ş ğ ğ ği ğ ş ğ İ ş ğ ş ş ş ğ ş İ ğ ğ ş ş İ ş ş ş ş ş ş ş ş ğ ğ ş ğ ş ğğ ş ş ş ş ğ ş ş ğ ş ş ş ğ ş ş ş ğ ğğ ş ğ ş ş ğ İ ş ş ğ ş ş ğ ğ ğ ş ş ğ ğ ş İ ş ğ şğ ş ş ş ş ş ş ğ
ş Ğ İ ş ş ş ğ ğ ğ ğ ş İ ğ ğ ğ ş ğ ş ğ ğ ği ğ ş ğ İ ş ğ ş ş ş ğ ş İ ğ ğ ş ş İ ş ş ş ş ş ş ş ş ğ ğ ş ğ ş ğğ ş ş ş ş ğ ş ş ğ ş ş ş ğ ş ş ş ğ ğğ ş ğ ş ş ğ İ ş ş ğ ş ş ğ ğ ğ ş ş ğ ğ ş İ ş ğ şğ ş ş ş ş ş ş ğ
Quality Planning and Control
 Qualty Plag ad Cotrol END 3618 KALİTE PLANLAMA VE KONTROL Prof. Dr. Mehmet ÇAKMAKÇI Dokuz Eylül Üverstes Edüstr Mühedslğ Aablm Dalı 1 Qualty Maagemet İstatstksel Proses Kotrol Kotrol Kartları 2 END 3618
Qualty Plag ad Cotrol END 3618 KALİTE PLANLAMA VE KONTROL Prof. Dr. Mehmet ÇAKMAKÇI Dokuz Eylül Üverstes Edüstr Mühedslğ Aablm Dalı 1 Qualty Maagemet İstatstksel Proses Kotrol Kotrol Kartları 2 END 3618
Đst201 Đstatistik Teorisi I
 Đst20 Đstatstk Teors I DERSĐN TÜRÜ Zorulu DERSĐN DÖNEMĐ Yaz DERSĐN KREDĐSĐ Ulusal Kred: (4, 0, 0 ) 4 KTS: 7 DERSĐN VERĐLDĐĞĐ Bölüm: Đstatstk 200/20 Öğretm Yılı DERSĐN MCI Đstatstğ matematksel temeller
Đst20 Đstatstk Teors I DERSĐN TÜRÜ Zorulu DERSĐN DÖNEMĐ Yaz DERSĐN KREDĐSĐ Ulusal Kred: (4, 0, 0 ) 4 KTS: 7 DERSĐN VERĐLDĐĞĐ Bölüm: Đstatstk 200/20 Öğretm Yılı DERSĐN MCI Đstatstğ matematksel temeller
ÖĞRETMENLİK ALAN BİLGİSİ MATEMATİK
 ÖABT ÖĞRETMENLİK ALAN BİLGİSİ MATEMATİK DENEME SINAVI ÇÖZÜMLERİ ÖĞRETMENLİK ALAN BİLGİSİ DENEME SINAVI / çözümlei. DENEME. Veile öemelede yalız III kesi olaak doğudu. Bu edele doğu cevap seçeeği B di..
ÖABT ÖĞRETMENLİK ALAN BİLGİSİ MATEMATİK DENEME SINAVI ÇÖZÜMLERİ ÖĞRETMENLİK ALAN BİLGİSİ DENEME SINAVI / çözümlei. DENEME. Veile öemelede yalız III kesi olaak doğudu. Bu edele doğu cevap seçeeği B di..
Faure Dizili Genetik Algoritmalar İle Toprak Özdirencinin Mevsimsel Değişiminde Transformatör Merkezi Topraklama Sisteminin Optimum Tasarım Stratejisi
 Süleym Demrel Üverstes, Fe Blmler Esttüsü Dergs, 6- ), 6-76 Fure Dzl Geetk Algortmlr İle Toprk Özdrec Mevsmsel Değşmde Trsformtör Merkez Toprklm Sstem Optmum Tsrım Strtejs Brış GÜRSU *, Melh Cevdet İNCE
Süleym Demrel Üverstes, Fe Blmler Esttüsü Dergs, 6- ), 6-76 Fure Dzl Geetk Algortmlr İle Toprk Özdrec Mevsmsel Değşmde Trsformtör Merkez Toprklm Sstem Optmum Tsrım Strtejs Brış GÜRSU *, Melh Cevdet İNCE
BÖLÜM 3 SAYISAL TÜREV VE İNTEGRAL
 BÖLÜM SAYISAL TÜREV VE İNTEGRAL. Blgsyrl türe.. Bölümüş rk tblolrıyl türe.. Eşt rlıklı er oktlrı ç türe.. Eşt rlıklı er oktlrı ç er oktlrıd türe.. Yüksek mertebede türeler. Syısl tegrl.. Trpez krlı.. Romberg
BÖLÜM SAYISAL TÜREV VE İNTEGRAL. Blgsyrl türe.. Bölümüş rk tblolrıyl türe.. Eşt rlıklı er oktlrı ç türe.. Eşt rlıklı er oktlrı ç er oktlrıd türe.. Yüksek mertebede türeler. Syısl tegrl.. Trpez krlı.. Romberg
GENELLEŞTİRİLMİŞ FRACTİONAL İNTEGRALLER İÇİN FENG Qİ TİPLİ İNTEGRAL EŞİTSİZLİKLERİ ÜZERİNE. Abdullah AKKURT 1, Hüseyin YILDIRIM 1
 IAAOJ, Scietific Sciece, 23,(2), 22-25 GENELLEŞTİRİLMİŞ FRACTİONAL İNTEGRALLER İÇİN FENG Qİ TİPLİ İNTEGRAL EŞİTSİZLİKLERİ ÜZERİNE Adullh AKKURT, Hüseyi YILDIRIM Khrmmrş Sütçü İmm Üirsitesi, Fe-Edeiyt Fkültesi
IAAOJ, Scietific Sciece, 23,(2), 22-25 GENELLEŞTİRİLMİŞ FRACTİONAL İNTEGRALLER İÇİN FENG Qİ TİPLİ İNTEGRAL EŞİTSİZLİKLERİ ÜZERİNE Adullh AKKURT, Hüseyi YILDIRIM Khrmmrş Sütçü İmm Üirsitesi, Fe-Edeiyt Fkültesi
Başlangıç değerleri. 1 4 olduğundan iterasyona devam!
 ESKİŞEHİR OSMANGAZİ ÜNİVERSİESİ Mühedl Mmlı Fülte İşt Mühedlğ Bölümü E-Pot: ogu.hmet.topcu@gml.com Web: http://mmf.ogu.edu.t/topcu Blgy Detel Nüme Alz De otlı Ahmet OPÇU m X X X.5.5.5.5.75 -.5.5.875.75
ESKİŞEHİR OSMANGAZİ ÜNİVERSİESİ Mühedl Mmlı Fülte İşt Mühedlğ Bölümü E-Pot: ogu.hmet.topcu@gml.com Web: http://mmf.ogu.edu.t/topcu Blgy Detel Nüme Alz De otlı Ahmet OPÇU m X X X.5.5.5.5.75 -.5.5.875.75
Ankara Üniversitesi Fen Fakültesi Kimya Bölümü B-Grubu 2014-2015 Bahar Yarıyılı Bölüm-II 25.02.2015 Ankara. Aysuhan OZANSOY
 FİZ10 FİZİK-II Ankaa Ünvestes Fen Fakültes Kmya Bölümü B-Gubu 014-015 Baha Yaıyılı Bölüm-II 5.0.015 Ankaa Aysuhan OZANSOY Bölüm : Elektk Alan 1. Elektk Alan. Elektk Alan Çzgle 3. Süekl Yük Dağılımlaı 4.
FİZ10 FİZİK-II Ankaa Ünvestes Fen Fakültes Kmya Bölümü B-Gubu 014-015 Baha Yaıyılı Bölüm-II 5.0.015 Ankaa Aysuhan OZANSOY Bölüm : Elektk Alan 1. Elektk Alan. Elektk Alan Çzgle 3. Süekl Yük Dağılımlaı 4.
Cebir Notları. Geometrik Dizi ( ) ( ) Mustafa YAĞCI,
 www.mustfygci.com, 006 Cebi Notlı Mustf YAĞCI, ygcimustf@yhoo.com Geometik Dizi Aitmetik diziyi bi htılylım bklım. Tüm dışık teimlei sıdki fkl sbitti. Yi stgele bi ilk teim vdı, o ilk teime bi d eel syısı
www.mustfygci.com, 006 Cebi Notlı Mustf YAĞCI, ygcimustf@yhoo.com Geometik Dizi Aitmetik diziyi bi htılylım bklım. Tüm dışık teimlei sıdki fkl sbitti. Yi stgele bi ilk teim vdı, o ilk teime bi d eel syısı
Bir kuvvet tarafından yapılan iş ve enerji arasındaki ilişki
 Elektk Ptansyel kuvvet taaından yapılan ş ve enej aasındak lşk csm üzene kuvvet uygulayıp csm vmelend dlayısıyla hızlandıısanız, csmn knetk enejsn attımış lusunuz KE dek bu değşmle enej tanse sebebyled:
Elektk Ptansyel kuvvet taaından yapılan ş ve enej aasındak lşk csm üzene kuvvet uygulayıp csm vmelend dlayısıyla hızlandıısanız, csmn knetk enejsn attımış lusunuz KE dek bu değşmle enej tanse sebebyled:
TOPLAM FARK FORMÜLLERİ İKİ KAT AÇI FORMÜLLERİ TRİGONOMETRİK DENKLEMLER ANALİZ TESTLERİ
 ÖÜ OP OÜİ inüs oplm - k omülü... osinüs oplm - k omülü...9 njnt ve otnjnt oplm - k omüllei... oplm - k omülleinin Geometik Şekillee ygulnmsı... G İ...9 ÖÜ İİ Ç OÜİ inüs İki t çı omülü... osinüs İki t çı
ÖÜ OP OÜİ inüs oplm - k omülü... osinüs oplm - k omülü...9 njnt ve otnjnt oplm - k omüllei... oplm - k omülleinin Geometik Şekillee ygulnmsı... G İ...9 ÖÜ İİ Ç OÜİ inüs İki t çı omülü... osinüs İki t çı
4. 89 / 5 ( mod p ) 84 / 0 ( mod p ) 60 / 4 ( mod p ) 56 / 0 ( mod p ) Cevap E. Cevap C. 6. x 0 f ( 0 ) = 1, f ( 1 ) = 2,...
 eneme - / YT / MT MTMTİK NMSİ Çözümle. O ( b, c ) d ise b dm, c dk O ( a, b ) d ise b dm, a dn I. d tek saı iken a çift ise m ve n nin otak böleni olu. O ( a, b ) d olmaz. d tek ise a tek saıdı. ( oğu
eneme - / YT / MT MTMTİK NMSİ Çözümle. O ( b, c ) d ise b dm, c dk O ( a, b ) d ise b dm, a dn I. d tek saı iken a çift ise m ve n nin otak böleni olu. O ( a, b ) d olmaz. d tek ise a tek saıdı. ( oğu
b göz önünde tutularak, a,
 3.ALT GRUPLAR Tnım 3.. bir grup ve G, nin boş olmyn bir lt kümesi olsun. Eğer ( ise ye G nin bir lt grubu denir ve G ile gösterilir. ) bir grup Not 3.. ) grubunun lt grubu olsun. nin birimi ve nin birimi
3.ALT GRUPLAR Tnım 3.. bir grup ve G, nin boş olmyn bir lt kümesi olsun. Eğer ( ise ye G nin bir lt grubu denir ve G ile gösterilir. ) bir grup Not 3.. ) grubunun lt grubu olsun. nin birimi ve nin birimi


