Geçici Elektromanyetik Alan Difüzyonunun Du Fort-Frankel Sonlu Farklar Yaklaşımı ile İki Boyutlu Modellenmesi

Transkript

1 Yerbilimleri, 33 (3), 69-8 Hacettepe Üniversitesi Yerbilimleri Uygulama ve Araştırma Merkezi Bülteni Bulletin of the Earth Sciences Application and Research Centre of Hacettepe University Geçici Elektromanyetik Alan Difüzyonunun Du Fort-Frankel Sonlu Farklar Yaklaşımı ile İki Boyutlu Modellenmesi Two Dimensional Modeling of Diffusion of Transient Electromagnetic Fields by Du Fort-Frankel Finite Difference Approximation GÜNGÖR DİDEM BEŞKARDEŞ 1, GÜLÇİN ÖZÜRLAN AĞAÇGÖZGÜ 1 İstanbul Teknik Üniversitesi, Maden Fakültesi Jeofizik Mühendisliği Bölümü C-117, Ayazağa Kampüsü, 369 Sarıyer, İstanbul İstanbul Teknik Üniversitesi, Maden Fakültesi Jeofizik Mühendisliği Bölümü D-107, Ayazağa Kampüsü, 369 Sarıyer, İstanbul Geliş (received) : 1 Şubat (February) 01 Kabul (accepted) : 01 Kasım (November) 01 ÖZ Bu çalışmada, iki boyutlu (B) yerelektrik yapıların yarı sonsuz uzayda oluşturduğu elektromanyetik tepki yanıtı Du Fort-Frankel sonlu farklar yaklaşımı kullanılarak zaman ortamında modellenmiştir. İki boyutlu yapı doğrultusundaki (TE modu) zaman ortamı elektromanyetik difüzyon denklemleri, bu yaklaşım ile belirlenen zaman adımlarında yinelemeli olarak çözülerek birincil ve ikincil elektrik alanların difüzyonu hesaplanmıştır. Bu amaçla, iki çizgisel akım kaynağı için Dirichlet ve Neuma sınır koşullarıyla iki boyutlu iletkenlik yapılarının geçici elektromanyetik tepki yanıtlarını hesaplayan bir algoritma MATLAB programlama dili kullanılarak geliştirilmiştir. Yarı-sonsuz tekdüze ortam için sınanan algoritma ile çeşitli modeller hesaplanmış ve iki boyutlu yer modellerinde difüzyon sürecini etkileyen faktörler incelenmiştir. Ülkemizin önemli çevre sorunlarından biri olan kıyılardaki tuzlu su girişiminin simülasyonu amacıyla hesaplanan kontur kesitlerinde, geçici elektromanyetik alanların difüzyonunun net olarak izlenebildiği ve yöntemin bu sorunun çözümünde üstün yanlarının bulunduğu gözlemlenmiştir. Anahtar Kelimeler: Jeofizik Yöntem, geçici elektromanyetik, iki boyutlu modelleme, Du Fort-Frankel, sonlu farklar. ABSTRACT In this study, the electromagnetic response of a two dimensional (D) body in a half-space is modeled in time domain by using Du Fort-Frankel finite difference approximation. Time domain electromagnetic diffusion equations for two-dimensional Transverse Electric (TE) mode are solved for specified time steps iteratively by this approximation and diffusion of primary and secondary electric fields are obtained. Using Dirichlet and Neuma boundary conditions, the transient electromagnetic responses of two-dimensional bodies under the excitation of a double line source are modeled by using the MATLAB. Numerical models were generated in order to simulate saltwater intrusion that is one of the most important environmental problems in Turkey. In the cross-sections of saltwater model, the diffusion of the transient electromagnetic fields can be seen very clearly and this verifies that transient electromagnetic method has high potential to solve the saltwater intrusion problem. Keywords: Geophysical method, transient electromagnetic, two dimensional modeling, Du Fort-Frankel, finite differences. * G.Beşkardeş E-posta: beskardes@itu.edu.tr

2 70 Yerbilimleri GİRİŞ YÖNTEM Geçici elektromanyetik YÖNTEM yöntem (Transient ElectroMagnetic, TEM) uzun yıllardan beri sığ jeolojik Du Fort-Frankel Sonlu Farklar Yaklaşımı YÖNTEM Du Fort-Frankel Sonlu Farklar Yaklaşımı ve hidrojeolojik problemlerin çözümü için standart bir yöntem olarak kabul edilmektedir. Bu Kaynak YÖNTEM Du Fort-Frankel bulunmayan Sonlu bir ortam Farklar için yapı YÖNTEM Yaklaşımı doğrul- YÖNTEM Kaynak bulunmayan bir ortam için YÖNTEM YÖNTEM yapı doğrultusundaki (TE modu) elektrik alan ( = ) ve nedenle, YÖNTEMgeçici elektromanyetik (EM) alanların buna Du Kaynak Fort-Frankel dik manyetik bulunmayan Sonlu alan, bir Farklar yer ortam değiştirme Yaklaşımı için Du yapı akımlarının YÖNTEM ihmal edildiği quasi-statik durum için; Fort-Frankel doğrultusundak Sonlu F yayılım süreçlerinin buna dik manyetik modellenmesi alan, yer ve değiştirme yüzeyde akımlarının Du Fort-Frankel Sonlu Farklar Yaklaşımı Du Fort-Frankel Sonlu Farklar Yaklaşımı Du Fort-Frankel ihmal Sonlu edildiği Farklar quasi-statik Yaklaşımı durum için; ölçülebilecek Du Fort-Frankel EM Sonlu tepki yanıtlarının Farklar Yaklaşımı hesaplanabilmesi Kaynak çok (xx, boyutlu bulunmayan zz, tt) = ortamların Kaynak buna dik bulunmayan manyetik bir alan, ortam yer için değiştirme yapı Kaynak doğrultusundaki akımlarının bulunmayan (TE ihm bir m o Kaynak bulunmayan bir ortam için yapı doğrultusundaki (TE modu) bir ortam yorumlanabilmesi için yapı Kaynak doğrultusundaki bulunmayan Du Fort-Frankel (xx, zz, (TE bir tt) ortam = modu) için elektrik Sonlu yapı Farklar doğrultusundaki alan ( Yaklaşımı = buna dik manyetik alan, yer değiştirme buna ) ve akımlarının dik (TE manyetik modu) elektrik ihmal alan, edildi y Kaynak için oldukça bulunmayan önemlidir. bir ortam için yapı doğrultusundaki (TE modu) elektrik alan ( = buna dik manyetik alan, yer değiştirme ) ve buna dik manyetik alan, yer değiştirme akımlarının ihmal edildiği quasi-statik akımlarının durum için; ihmal edildiği qu Bu buna çalışmada, dik manyetik HH(xx, zz, tt) TEM alan, = HH buna dik manyetik (xx, Kaynak alan, zz, tt) bulunmayan yer = değiştirme bir ortam akımlarının için yapı ihmal doğrultusundaki edildiği quasi-stati (TE m xx yönteminde yer xx + değiştirme HH zz zz B modelleme akımlarının ihmal HH(xx, edildiği zz, tt) quasi-statik = HH xx xx + durum HH zz zz için; (xx, zz, tt) = (xx, zz, tt) = yapan bir algoritma geliştirilmiştir. Algoritmada, (xx, çizgisel zz, tt) olmak (xx, zz, buna tt) = dik (xx, zz, tt) = manyetik alan, yer değiştirme akımlarının ihmal edild (xx, zz, tt) = olmak HH(xx, zz, üzere, tt) = iki HHboyutlu xx xx + HH zz difüzyon zz eşitliği = bir akım üzere, iki boyutlu difüzyon eşitliği kaynağı uyartımı ile oluşan HH(xx, zz, tt) = HH xx xx + HH zz zz HH(xx, zz, tt) = HH xx xx + HH zz zz elektromanyetik HH(xx, zz, tt) = alanların HH xx xx + HHiki zz zz boyutlu difüzyonu- HH(xx, zz, (xx, tt) = HH xx xx + HH zz zz xx xx zz, tt) nu tanımlayan parabolik denklem çözümünde Du Fort-Frankel sonlu farklar yaklaşımı kullanılmıştır. olmak üzere, Parabolik iki boyutlu denklemlerin difüzyon eşitliği çözümünde, xx + zz zz = HH(xx, zz, tt) = HH xx xx + HH zz zz HH(xx, zz, tt) = HH xx xx + HH zz zz olmak üzere, iki boyutlu olmak üzere, zziki boyutlu = difüzyon 0 difüzyon eşitliği eşitliği olmak üzere, (1) iki boyutlu d xx olmak üzere, + zz = 0 (1) olmak HH(xx, üzere, zz, iki tt) = boyutlu HH xx xx + difüzyon HH zz zz eşitliği iki boyutlu difüzyon eşitliği olmak üzere, iki boyutlu difüzyon eşitliği koşulsuz kararlı ve açık yapısı ile üstünlük sağlayan yaklaşım, kurbağa adımı şeklindeki etkili uzaysal xx + şeklinde ifade edilmektedir; burada, xx ve zz zz değişkenler, = tt 0 ise zaman değişkenidir. zaman xx adımlaması + zz ve düzensiz = 0 xx + zz = 0 xx + zz = 0 (1) xx + zz = 0 grid kullanılan xx + xx + şeklinde ifade edilmektedir; burada, xx ve zz uzaysal olmak değişkenler, üzere, zz iki μμμμ boyutlu tt ise zaman = difüzyon 0 değişkenidir. eşitliği Şekil 1'de verilen sonlu farklar ağı üzerindeki zz = 0 Şekil (1) 1'de verilen sonlu farklar ağı üzerindeki tüm modellere uygulanabilirliği sebebiyle de EM di- şeklinde tüm ifade ifade edilmektedir; burada, burada, xx şeklinde ve zzxx uzaysal ve ifade zz uzaysal değişkenler edilmekted şeklinde hücreler xxifade için edilmektedir; manyetik burada, geçirgenliğin xx ve zz serbest uzaysal havadaki 1'de değeri sabittir sonlu değişkenler, tt ise füzyon şeklinde denklemleri ifade edilmektedir; çözümü için burada, sıklıkla xxşeklinde kullanılmaktadır. Oristaglio ve Hohma (198), Du Şekil ; iletkenlik 1'de verilen değerleri sonlu (σσ farklar = σσ(xx, ağı zz)) üzerindeki ve zz uzaysal ifade edilmektedir; + hücreler için manyetik geçirgenliğin serbest havadaki değeri sabittir (μμ = μμ zz = 0 0 = ππππ10 7 HH/mm); iletkenlik değerleri (σσ = σσ(xx, zz)) değişkenler, ttburada, ise zaman xx ve değişkenidir. zzzz uzaysal değişkenler, (μμ = farklar μμ 0 = ππππ10 ağı üzerindeki 7 tttt ise zaman şeklinde ifade ise hücreden edilmektedir; hücreye burada, değişebilmektedir. xx ve zz uzaysal değişkenler, tt ise zaman değişkenidir. Şekil HH/mm); 1'de verilen tüm hücrele sonlu Şekil 1'de verilen sonlu farklar ağı üzerindeki tüm Şekil 1'de verilen sonlu farklar ağı üzerindeki ise hücreden tüm hücreler için Şekil 1'de verilen şeklinde Fort-Frankel sonlu farklar yaklaşımını çift çizgisel kaynak serbest havadaki uyartımı için değeri toplam sabittir elektrik (μμ μμalan 0 = ππππ10 hücreye tüm hücreler sonlu ifade farklar edilmektedir; için değişebilmektedir. değeri manyetik ağı üzerindeki burada, sabittir geçirgenliğin xxtüm (μμ serbest ve zzhücreler uzaysal 0 ππππ10 havadaki 7 için değişkenle HH/mm); değeri manye ilet sa Şekil 1'de Kısmi verilen türevlerin sonlu farklar sonlu fark ağı karşılıkları, üzerindeki serbest eşit tüm grid hücreler serbest Kısmi ise 7 havadaki aralıkları havadaki için değeri için manyetik ( = sabittir değeri xx geçirgenliğin (μμ = sabittir = zz), μμ HH/mm); iletkenlik değerleri (σσ 0 (1) = (μμ ππππ10 = σσ(xx, zz)) 7 HH/mm); iletkenli serbest havadaki serbest havadaki değeri sabittir (μμ = μμ 0 = ππππ10 7 değeri sabittir (μμ = μμ hücreden türevlerin hücreye sonlu değişebilmektedir. 0 ππππ10 7 eşitliğinde = μμ 0 = ππππ10 7 HH/ ise hücreden hücreye yerine yazılırsa, Şekil 1'de verilen sonlu farklar ağı HH/mm); üzerindeki iletkenlik tüm hücrel değer fark karşılıkları, eşit grid eldesi ise için hücreden kullanmış, hücreye Adhidjaja değişebilmektedir. ve Hohma ise HH/mm); hücreden ise hücreden iletkenlik hücreye hücreye değerleri değişebilmektedir. değişebilmektedir. (σσ = σσ(xx, zz)) ise hücreden hücreye aralıkları serbest değişebilmektedir. havadaki için ( = değeri xx = sabittir zz),, (1) (μμ eşitliğinde = yerine yazılırsa, (1985; ise hücreden 1988) hücreye ise aynı değişebilmektedir. yaklaşımı ikincil elektrik Kısmi türevlerin sonlu fark karşılıkları, Kısmi μμ 0 = ππππ10 eşit türevlerin 7 HH/mm); grid aralıkları sonlu için fa ile Kısmi alanın Kısmi çözümü türevlerin için kullanmıştır. sonlu fark karşılıkları, eşit grid yerine türevlerin aralıkları yazılırsa, sonlu fark karşılıkları, eşit yerine grid aralıkları yazılırsa, için ( = Kısmi türevlerin Kısmi ise sonlu hücreden türevlerin için fark hücreye ( = karşılıkları, xx sonlu değişebilmektedir. = zz), eşit fark (1) grid karşılıkları, eşitliğinde aralıkları için eşit ( = grid xx aralık tt = ii+1,jj + ii 1,jj = Kısmi yerine yazılırsa, yerine türevlerin yazılırsa, sonlu fark karşılıkları, μμσσ eşit () yerine grid yazılırsa, aralıkları yerine için yazılırsa, ( = xx = zz), (1) eşitliğinde Oristaglio yerine yazılırsa, ve Hohma (198) dan yola çıkılarak Kısmi türevlerin geliştirilen iki boyutlu modelleme algoritmasının tt ii 1,jj μμσσ doğruluğunun sınanması amacıyla, tekdüze () tt = sonlu fark karşılıkları, eşit grid ii+1,jj + ii 1,jj μμσσ tt = ii+1,jj + ii 1,jj tt = ii+1,jj ii 1,jj +1 1 tt = aralıkları ii+1,jj + içi ii 1,jj + ortam sonuçları analitik çözümlerle μμσσ μμσσ () tt = μμ ii+1,jj + ii 1,jj tt tt = yerine yazılırsa, Şekil 'de, herhangi bir noktası en yakın ii+1,jj + komşuları ii 1,jj tt = olan ii+1,jj + ii+1,jj, ii 1,jj + ii 1,jj, , 1 1 noktaları ile çevrelenmiştir. karşılaştırılmış, duyarlılığına güvenilen sonuçlar ilerleyen noktası en yakın komşuları olan ii+ Şekil Burada, ii ve jj indisleri μμσσ μμσσ μμσσ () Şekil 'de, herhangi bir tt 'de, = xx = jj. ii+1,jj + xx, zz = ii 1,jj + ii. zz ve +1 + zamanı 1 temsil herhangi bir Şekil noktası en 'de, yakın komşuları herhangi bir ola eden ise tt =. tt olarak Şekil bölümlerde Şekil sunulmuştur. 'de, herhangi Modelleme bir noktası çalışmala- verilmektedir. en yakın komşuları noktaları 'de, herhangi ile olan çevrelenmiştir. bir Burada, ii ve jj indisleri xx = jj. xx, zz noktaları ile çevrelenmiştir. ii+1,jj, noktası μμσσ en yakın komşuları olan Şekil 'de, herhangi tt = olmak ii 1,jj, Burada, +1, ii+ üzere, zaman terimi bir noktası en yakın komşuları noktaları ii 1 nok- olan ve jj indisleri ile çevrelenmi ii+1,jj,, xx = jj. ii rında, Şekil birincil 'de, herhangi ve ikincil bir elektrik alan noktası değerlerinin en yakın komşuları Şekil olan 'de, noktaları ile çevrelenmiştir. ii+1,jj herhangi, ii 1,jj, bir Burada, +1, ii 1 noktası en yakın komşu ve jj indisleri eden ise tt =. tt olarak verilmektedir. yanısıra; elektrik alan değerlerinin sayısal türevlerinden yatay ve düşey elektromotor kuvvet eden ayrıklaştırılması Euler yönteminden farklı olarak merkezi farklar tt xx = = jj. noktaları ayrıklaştırılması ile çevrelenmiştir. Euler yönteminden Burada, ii ve jj indisleri xx = jj. xx, zz = ii. zz iive zamanı temsil zz xx, zz noktaları farklı olarak ile Şekil çevrelenmiştir. merkezi 'de, farklar herhangi Burada, yardımıyla bir ii ve yapılmaktadır: jjnoktası indisleri en xx yakın = jj. xx, komşuları zz = ii. olma noktaları ile çevrelenmiştir. Burada, ii ve jj indisleri eden xx = jj. xx, ise zz = tt ii. = zz. tt ve zamanı olarak temsil verilmektedir. eden ise ise tt tt = zz o noktaları ile çevrelenmiştir. Burada, ii ve jj yar eden ise tt =. tt olarak verilmektedir. tt ise = tt =. tt olarak verilmektedir. olmak üzere, zaman terimi tt = indisleri =. tt tt olma (emk) eden profil ise eğrileri tt =. hesaplanmıştır. tt olarak verilmektedir. ayrıklaştırılması Euler yönteminden farklı olarak merkezi farkla ayrıklaştırılması tt = olmak üzere, zaman terimi ayrıklaştırılması tt eden ise noktaları tt =. tt ile olarak çevrelenmiştir. verilmektedir. Burada, tt ii ve = jj indisleri olmak xx Euler üzer = jj. yö tt OO( tt) olmak eden üzere, ayrıklaştırılması Euler yönteminden farklı olarak merkezi farklar Bu çalışma kapsamında, yeraltındaki iletken tt +1 Euler ise zaman tt yönteminden =. tt terimi olarak 1 farklı ayrıklaştırılması olarak verilmektedir. (3) tt merkezi farklar tt yar ayrıklaştırılması eden Euler yönteminden ise tt yardımıyla =. tt farklı olarak yapılmaktadır: olarak verilmektedir. merkezi farklar yardımıyla ayrıklaştırılması Euler yönteminden farklı olarak merkezi Euler farklar yönteminden + OO( tt) yapılara oldukça duyarlı olan TEM yönteminin tt tt yardımıyla farklı +1 yapılmaktadır: olarak merkezi farklar tt = 1 + OO( tt) ülkemizin önemli sorunlarından biri olan tuzlu tt Buradan hareketle tt OO( tt) tt +1 1 tt OO( tt) tt su girişimi problemi için çözüm üretme yeteneği, tuzlu su girişim yer modelleri için hesaplanan Buradan hareketle,, (3) tt tt +1 1 tt yardımıyla ayrıklaştırılması yapılmaktadır: Euler yönteminden farklı olarak merke Buradan hareketle, tt tt ayrıklaştırılması Euler yönteminden farklı olarak merkezi fark OO( tt) + OO( tt) tt (3) tt Buradan hareketle OO( tt) (3) tt, +1 1 anomaliler Buradan ile değerlendirilmiştir. hareketle Buradan hareketle + OO( tt),, Buradan hareketle Buradan hareketle tt tt,, Buradan hareketle,,

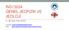
3 Beşkardeşler vd 71 Şekil 1. Sonlu farklar ağına bir örnek (Oristaglio ve Hohma, 198). Figure 1. A finite difference mesh (Oristaglio and Hohma, 198). Şekil. Sonlu farklar ağında tipik bir E i,j noktası (Oristaglio ve Hohma, 198). Figure. A typical grid point E i,j in the finite difference grid (Oristaglio ve Hohma, 198).

4 7 Yerbilimleri +1 1 ) OO( tt ) () OO( tt ) Biçiminde ve ortalama yerel ağ oranı ise; () + OO( tt OO( tt ) () ) () rr şeklinde +1 = rr xx + rr zz rr rr xx zz rr rr rr xx zz rr rr = rr xx zz + rr 1 basit ortalama + OO( tt olarak ) () ifade edilebilir. (3) ve rr () = ifadeleri rr xx + zz rr (1) rr = rr xx zz + rr rr = rr xx zz + rr olarak verilmektedir. (1) olarak () eşitliğinde yerine yazılır, (1) eklinde basit ortalama şeklinde şeklinde olarak basit basit olarak verilmektedir. olarak olarak verilmektedir. verilmektedir. olarak verilmektedir. ortalama ortalama ifade edilebilir. olarak olarak ifade ifade (3) ve edilebilir. edilebilir. () ifadeleri (3) ve () () eşitliğinde ifadeleri () yerine eşitliğinde yazılır, yerine yazılır, (3) şeklinde +1 ve () ifadeleri () eşitliğinde yerine yazılır, +1 1 ) = basit 1 ortalama +1 ii+1,jj + 1 ii 1,jj ( +1 1 = olarak ) = ii+1,jj + ii 1,jj ifade + edilebilir (3) 1 ve () ifadeleri ( +1 () eşitliğinde 1 ) yerine yazılır, +1 olarak 1 verilmiştir. verilmektedir. + OO( tt ii+1,jj + ) İkincil ii 1,jj Elektrik ( +1 Alan OO( tt tt ) () 1 () μμσσ ) (5) İkincil +1 1 = ii+1,jj + ii 1,jj ( tt μμσσ (5) tt +1 1 ) μμσσ (5) (5) +1 1Elektrik tt = Alan İkincil İkincil İkincil Elektrik ii+1,jj + ii 1,jj ( +1 Elektrik Elektrik Alan 1 Alan Alan Alan İkincil Elektrik Alan şeklinde basit ortalama olarak ifade edilebilir. (3) ve () ifadeleri () eşitliğinde yerine yazılır, ) şeklinde μμσσ tt basit ortalama olarak ifade edilebilir. e ve +1 ve +1 μμσσ (3) +1 terimi eşitliğinden çekilirse; ve Kaynak () ifadeleri İkincil () Elektrik eşitliğinde Alan (5) Kaynak bulunan bir ortam yerine için yazılır, TE modunda elektrik alan ( Kaynak bulunan bir ortam bir ortam için TE için modunda TE elektrik elektrik alan ala ( Kaynak +1 1 Kaynak bulunan bir ortam için TE modunda elektrik Kaynak terimi ve eşitliğinden alan bulunan ( = bir ortam ), için TE modunda akımlarının elektrik ala bulunan = ii+1,jj + ii 1,jj + bir ortam +1 + için 1 ( TE +1 modunda 1 ) elektrik çekilirse; terimi terimi eşitliğinden eşitliğinden çekilirse; çekilirse; +1 1 ihmal yerdeğiştirme akımlarının edildiği alan ( +1 + OO( tt ) () ve +1 1 (6) +1 ) = 1 rr +1 = 1 terimi = ii+1,jj + rr eşitliğinden ii 1,jj + çekilirse; ( +1 Kaynak ihmal 1 quasi-statik = ), yerdeğiştirme bulunan ) durum bir ortam için, akımlarının tt μμσσ (5) ihmal için TE modunda elektrik ala ihmal edildiği quasi-statik rr rr rr + rr durum için, ihmal ihmal edildiği edildiği edildiği quasi-statik quasi-statik durum durum durum için, için, için, ihmal ve edildiği quasi-statik durum için, tt 1 rr 1 ii+1,jj ii 1,jj ) (6) rr rr μμσσ (5) +1 terimi eşitliğinden çekilirse; ( 1 + rr ii+1,jj + ihmal ii 1,jj + edildiği +1 + quasi-statik 1 ) durum için, şeklinde basit ortalama olarak ifade edilebilir. (3) ve () ifadeleri () eşitliğinde yerine yazılır, (6) ( 1 rr ii+1,jj + ii 1,jj ) (6) = 1 rr 1 = ii+1,jj rr + + rr ve +1 terimi σσσσ eşitliğinden çekilirse; ( ii 1,jj ( +1 1 ) 1 + rr ii+1,jj + ii 1,jj ) (6) = μμ jj ρρ tt μμσσ edilir. Bu denklem, eşit (5) gridli sonlu farklar ağı σσσσ σσσσ μμ jj ρρ (13) σσσσ μμ jj ρρ σσσσ = μμ jj ρρ için Du Fort-Frankel sonlu farklar lde e edilir. Bu elde denklem, edilir. Bu Bu eşit denklem, denklem, gridli eşit sonlu gridli eşit farklar sonlu gridli farklar sonlu ağı için farklar Du Fort-Frankel ağı için Du sonlu Fort-Frankel farklar sonlu farklar ve çözümüdür. elde +1 için +1 = edilir. 1 rr terimi Du Fort-Frankel eşitliğinden Bu Burada denklem, 1 çekilirse; rrsonlu yerel eşit farklar gridli ağ çözümüdür. oranı sonlu ve farklar σσ ise için noktasını Du Fort-Frankel çevreleyen sonlu iletkenliklerin farklar 1 + rr + rr = μμ jj (13) σσσσ = μμ jj ρρ σσσσ = μμ jj +1 = 1 rr 1 ρρ 1 + rr + rr ( 1 + rr ii+1,jj + ii 1,jj ) (6) (13) ρρ elde edilir. Bu denklem, eşit gridli sonlu farklar ağı için Du Fort-Frankel sonlu farklar şeklinde ifade ifade edilmektedir. Burada, jj ρρ kaynağın akım çözümüdür. Burada yerel ağ oranı ve σσ ise noktasını çevreleyen iletkenliklerin şeklinde kay- alan şeklinde ifade edilmektedir. ( 1 + rr ii+1,jj Burada, + ii 1,jj + jj ρρ+1 şeklinde ifade kaynağın + 1 ) ifade ifade edilmektedir. akım edilmektedir. Burada, yoğunluğunu (6) Burada, Burada, jj ρρ kaynağın göstermektedir. Çalış- jj jj ρρ akım şeklinde ifade edilmektedir. Burada, jj ρρ Çalışmada, kaynağın akım alan özümüdür. Burada rr rr yerel ağ oranı rr yerel ve σσ σσ ağ ise oranı ve noktasını nok- σσ ise çevreleyen kaynak yoğunluğunu çözümüdür. noktasını iletkenliklerin çevreleyen iletkenliklerin alan alan tasını ağırlıklı çevreleyen ortalamasıdır iletkenliklerin ve aşağıdaki alan ağırlıklı şekilde ortalamasıdır 1 + rr + rr rr yerel ağ oranı ve σσ ise noktasını şeklinde çevreleyen ifade terimi ifade edilirler: ğırlıklı ortalamasıdır +1 = 1 rr Burada ve aşağıdaki 1 şekilde ifade edilirler: edilmektedir. tanımlamasına göstermektedir. ρρ kaynağın ağırlıklı ortalamasıdır ve aşağıdaki şekilde ifade edilirler: Çalışmada, gerek iletkenliklerin alan Burada, jj ρρ kaynağın duyulm terimi tanımlamasına gerek du- Çalışmada, kaynak terimi tanımlamasına Çalışmada, kaynak gerek duyulmaması kaynak kaynak terimi terimi terimi tanımlamasına ve iletken tanımlamasına gerek yapılardan gerek gerek duyul d Çalışmada, rr = tt kaynak terimi tanımlamasına ( 1 + rr ii+1,jj + ii 1,jj kaynaklanan gerek yulmaması ) (6) elde ağırlıklı edilir. ortalamasıdır Bu denklem, ve aşağıdaki ve ve şekilde aşağıdaki eşit gridli ifade şekilde sonlu edilirler: şekilde ifade farklar ifade edilirler: ağı duyulmaması ikincil ve iletken edilirler: için Du Fort-Frankel elektrik ve yapılardan alanın iletken sonlu farklar daha kaynaklanan yapılardan doğru şekilde elde e μμσσ (7) kaynaklanan kaynaklanan ikincil elektrik alanın daha doğru ikincil kaynaklanan Çalışmada, ikincil şekilde elektrik elde ikincil kaynak ikincil elektrik alanın edilmesi daha elektrik elektrik terimi alanın amacıyla doğru alanın alanın tanımlamasına daha şekilde toplam daha daha doğru elde doğru doğru şekilde elektrik şekilde gerek şekilde elde de kaynaklanan = tt elde edilir. Bu rr tt ikincil elektrik alanın daha doğru alan, şekilde birincil çözümüdür. Burada rr denklem, eşit yerel ağ oranı ve σσ gridli sonlu farklar ağı ise için Du noktasını elde ve edilmesi ikincil çevreleyen iletkenliklerin elektrik amacıyla alan toplam bileşenlerine elektrik edilmesi amacıyla toplam alan, birincil ayrılmıştır: σσ = σσ + σσ ii+1,jj + σσ +1 + σσ ii+1,jj+1 alan, Fort-Frankel alan, sonlu farklar μμσσ μμσσ tt (7) çözümüdür. rr Burada rr yerel ağ oranı ve σσ ise noktasını çevreleyen iletkenliklerin alan = tt kaynaklanan birincil (8) birincil ve ikincil ve ikincil ikincil elektrik elektrik alan alanın bileşenlerine daha doğru ayrılmıştır: şekilde alan, birincil ve ikincil elektrik alan bileşenlerine alan, ayrılmıştır: birincil ve ikincil elektrik bileşenlerine ayrılme alan, birincil ve ikincil elektrik alan bileşenlerine ayrılmıştır: ve ikincil elektrik alan bileşenlerine ayrılmıştır: ağırlıklı ortalamasıdır ve aşağıdaki şekilde ifade edilirler: (6) ifadesi düzensiz μμσσ (7) μμσσ (7) (7) ağırlıklı ortalamasıdır grid aralıkları için düzenlenirse, alan, (7) ve aşağıdaki şekilde ifade edilirler: pp birincil ss. ve ikincil elektrik alan bileşenlerine ayrılm = σσ σσ σσ = σσ + σσσσ ii+1,jj σσ = rr tt pp + ss pp + pp ss. ss (1) = pp + σσ +1 + σσ ii+1,jj+1 σσ σσ ss. = pp + ss.. (1) (1) +1 = 1 rr zz σσ ii+1,jj + σσ +1 σσ ii+1,jj+1 rr = tt + σσ ii+1,jj + σσ +1 + σσ (8) μμσσ ii+1,jj+1 (8) (7) σσ = σσ 1 rr 1 + rr + zz ii μμσσ + σσ ii+1,jj + σσ +1 + σσ ii+1,jj+1 = pp + ss 1 + rr zz ii+1,jj + zz ii+1 zz ii 1,jj Toplam Toplam (7) elektrik elektrik alandan. çekilerek ikincil (8) elektrik Toplam alan, Toplam elektrik elektrik alandan alandan çekilerek ikincil (8) ikincil elektrik elektrik alan, alan, rr Toplam (8) elektrik alandan çekilerek ikincil elektrik alan, Toplam elektrik xx Toplam alan, elektrik alandan çekilerek ikincil elektrik alan, + xx jj σσ + σσ ii+1,jj + σσ +1 + σσ ii+1,jj+1 σσ (8) (6) = σσ 1 + alandan çekilerek ikincil elektrik alan, rr xx +1 + xx jj+1 jj xx 1 (9) jj + σσ ii+1,jj + σσ +1 + σσ ii+1,jj+1 Toplam elektrik alandan çekilerek ikincil elektrik alan, ifadesi düzensiz grid aralıkları için için düzenlenirse, düzenle- (8) 6) ) ifadesi düzensiz nirse, (6) ifadesi grid aralıkları düzensiz için grid düzenlenirse, aralıkları için düzenlenirse, (6) ifadesi düzensiz ss σσgrid μμ ss aralıkları için düzenlenirse, zz ii +1 ii ii = 1 rr zz 1 rr ii 1 + rr zz ii 1 + rr zz ii+1,jj + zz ii+1 +1 = rr zz rr zz 1 rr +1 rr + 1 rr zz ii ii 1,jj 1 + rr + zz ii 1 + rr zz ii+1,jj + zz ii rr zz ii+1,jj + zz ii+1 zz ii 1,jj +1 = 1 = 1 rr zz (6) ifadesi düzensiz grid rr 1 aralıkları rr için zz 1 rr 1 + rr rr + zz zz düzenlenirse, ii ii ii 1 + rr zz ii+1,jj + zz ii rr zz ii+1,jj + zz ii+1 ss ii zz ii ii 1,jj zz ii 1,jj σσ μμ ss = μμ(σσ σσ) pp = μμ(σσ σσ) pp ss σσ μμ ss μμ(σσ σσ) pp ss σσ μμ ss μμ(σσ σσ) pp ss σσ μμ ss (15) = μμ(σσ σσ) pp şeklinde edilmektedir. Burada ortalama grid aralıkları, izleyen biçimde ss (15) σσ μμ ss = μμ(σσ σσ) pp ss σσ μμ ss = μμ(σσ σσ) pp zz (15) ii = zzii+1 + zz ii vvvv xx jj = xx jj+1 + xx jj, (10) difüzyon için x ve z yönündeki yerel ağ oranları şeklinde şeklinde ii elde edilmektedir. Burada, σσ ortamın ve σσ ise şeklinde elde elde şeklinde ii iiii iiii zz ii 1,jj +1 = 1 rr elde edilmektedir. zz xx ii rr rr + xx xx rr jj jj + xx rr xx xx 1 rr 1 + rr xx jj xx jj rr 1 + rr xx +1 + xx jj xx jj jj 1 (9) 1 + rr xx +1 + xx jj+1 rr xx +1 + xx 1 jj+1 rr xx +1 + xx jj+1 jj xx + xx + zz Burada, σσ jj 1 (9) (9) 1 + rr xx +1 + xx ii 1 + rr zz ii+1,jj + zz Frankel ortamın ve σσ elde edilmektedir. Burada, Burada, σσ ortamın şeklinde σσ ortamın ve σσ ve ise σσ şeklinde elde edilmektedir. Burada, σσ ortamın ise yapının iletkenliğidir. Du Fort- ii+1 ve jj+1 ii zz ii 1,jj σσsonlu elde edilmektedir. Burada, σσ ortamın ve σσ farklar yaklaşımıyla (15) Du eşitliği xx tt = vvvv zz tt ise yapının iletkenliğidir. Du Fort-Frankel μμσσ xx jj xx =, (11) jj+1 μμσσ zz ii zz ii+1 Frankel ayrıklaştırılara Frankel sonlu farklar yaklaşımıyla jj jj xx 1 (15) eşitliği ii sonlu Frankel şeklinde Frankel sonlu farklar ayrıklaştırılarak sonlu sonlu elde farklar yaklaşımıyla farklar farklar edilmektedir. yaklaşımıyla ikincil yaklaşımıyla (15) eşitliği elektrik Burada, (15) σσ ortamın ve σσ (9) alan (15) (15) ayrıklaştırılarak hesaplanmıştır. (9) eşitliği yinelemeli eşitliği eşitliği ayrıklaştırılar ayrıklaştı Frankel Biçiminde ve sonlu ortalama farklar yerel ağ oranı yaklaşımıyla ise; (15) eşitliği jj olarak ayrıklaştırılarak jj xx 1 olarak xx olarak hesaplanmıştır. rr jj ifade edilmektedir. Burada ortalama grid aralıkları, jjjj xx izleyen 1 biçimde (9) şeklinde + ifade edilmektedir. xx jj Burada, ortalama şeklinde ifade 1 + edilmektedir. Burada ortalama jj grid aralıkları, izleyen biçimde grid zz şeklinde aralıkları, ifade edilmektedir. Burada ortalama grid aralıkları, izleyen biçimde eklinde ifade edilmektedir. ii = zz ii+1 + zz ii izleyen rr xx +1 + xx Frankel olarak hesaplanmıştır. ikincil elektrik ikincil elektrik alan yinelemeli alan yinelemeli olarak hesaplanmıştır. olarak hesaplanmıştır. sonlu farklar yaklaşımıyla (15) eşitliği ayrıklaşt olarak hesaplanmıştır. jj+1 biçimde jj xx 1 Du Fort-Frankel (9) jj Du olarak hesaplanmıştır. sonlu farklar yaklaşımı, seçilen her zaman sonlu farklar seçilen her z Du Fort-Frankel vvvv xx ifade Burada jj = xx jj+1 sonlu + xx jj farklar, yaklaşımı, seçilen Du Fort-Frankel sonlu sonlu her (10) zaman adımı sonlu farklar için farklar yaklaşımı, kararlıdır. yaklaşımı, seçilen Fakat seçilen her zaman EM her za Du Fort-Frankel sonlu farklar yaklaşımı, seçilen ortalama şeklinde Burada grid aralıkları, ortalama grid izleyen aralıkları, biçimde izleyen biçimde zz ii difüzyon zz ii = zz ifade için ii jj jj ii ii, ii = zz ii+1 + zz ii ii = zz ii+1 + edilmektedir. zz ii x vvvv xx jj = xx jj+1 + xx jj ii zz ii+1 ve z + yönündeki zz vvvv ii yerel xx Burada jj ağ = xx modelleme her oranları ii+1 + zz vvvv xx ii jj = xx jj+1 ortalama + xx zaman çalışmalarında, adımı için için kararlıdır. EM Fakat alanlarda Fakat EM EM mo- sönümlü dalg jj grid aralıkları, modelleme Du izleyen Fort-Frankel çalışmalarında, biçimde modelleme çalışmalarında, EM sonlu farklar EM EM yaklaşımı, alanlarda seçilen sönümlü her da z vvvv, (10) xx jj = xx jj+1 + xx, (10) alanlarda modelleme sönümlü çalışmalarında, dalga çalışmalarında, özelliğinden EM alanlarda (10) EM çok sönümlü alanlarda difüzyon sönümlü modelleme çalışmalarında, EM alanlarda jj davranışının sönümlü jj+1 + xx jj, (10) rr zz xx tt = vvvv rr zz tt difüzyon ii = davranışının zz ii+1 + zz ii vvvv baskın, (10) μμσσ xx jj için xx = xx, (11) jj+1 x ve z yönündeki jj = xx davranışının dalga baskın özelliğinden olması istenmektedir. çok difüzyon Bu nedenle, za dalga olması jj+1 + xx istenmektedir. jj özelliğinden modelleme baskın çalışmalarında, baskın olması çok olması difüzyon istenmektedir. davranışının EM alanlarda Bu nedenle, Bu sönümlü z davranışının baskın olması istenmektedir., Bu Bu davranışının nedenle, baskın zaman olması adımının istenmektedir. (10) bu kritere göre Bu nedenl μμσσ zz ii zz ii+1 yerel ağ oranları seçilmesi nedenle, baskın seçilmesi gerekmektedir. olması zaman istenmektedir. adımının Çalışmada, bu Bu kritere nedenle, Du Fort-Frankel göre za- yaklaş seçilmesi gerekmektedir. Çalışmada, Du Fort-Frankel davranışının gerekmektedir. yaklaşımı baskın Çalışmada, için olması Oristaglio istenmektedir. Du Fort-Frankel Du ve Hohma Bu neden yakla man seçilmesi adımının gerekmektedir. bu kritere göre Çalışmada, seçilmesi Du gerekmektedir. tarafından yaklaşımı önerilen için Oristaglio zaman adımı ve Hohma kullanılmıştır: (198) tarafından önerilen yerel ağ oranları seçilmesi (198) tarafından Çalışmada, Fort-Frankel y seçilmesi difüzyon için gerekmektedir. için ve x ve yönündeki z Çalışmada, yerel yerel ağ oranları Du ağ oranları Fort-Frankel (198) Biçiminde ve ortalama yerel ağ oranı ise; ifüzyon için difüzyon x difüzyon rr ve xx z yönündeki için tt x ve z yönündeki için x ve yerel z yönündeki ağ oranları = vvvv rr zz yerel ağ ttoranları (198) gerekmektedir. önerilen Du zaman Fort-Frankel Çalışmada, zaman adımı adımı yaklaşımı kullanılmıştır: Du Fort-Frankel y (198) μμσσ tarafından xx xx tt xx tt jj xx önerilen zaman = zaman adımı, kullanılmıştır: (11) jj+1 μμσσ zz adımı ii zz kullanılmıştır: için (198) Oristaglio tarafından ve Hohma önerilen zaman (198) adımı tarafından kullanılmıştır: rr zz = vvvv rr zz tt rr jj, μμσσ xx jj xx xx tt vvvv rr zz tt ii+1 rr xx tt = vvvv rr = =, (11) jj+1 μμσσ xx jj xx μμσσ jj+1 vvvv zz rr iiii zz ii zz tt xx jj xx zz tt önerilen =, (198) tarafından önerilen zaman adımı (11) kullanılmıştır: Biçiminde μμσσ xx ve jj xx =, (11) (11) ortalama jj+1 jj+1 yerel ağ μμσσ = oranı μμσσ zz zz ise; zz ii+1 zz ii+1, (11) tt μμmin (σσ ) tt μμmin (σσ ) tt μμmin (σσ ) tt μμmin (σσ zaman ) adımı kullanılmıştır: ii+1 μμσσ zz ii zz ii+1 Biçiminde ve ve ortalama yerel yerel ağ oranı ağ oranı ise; ise; tt μμmin (σσ tt μμmin (σσ ) tt μμmin (σσ ) (16) ) (16) (16) içiminde ve ortalama Biçiminde yerel ve ortalama ağ oranı ise; yerel ağ oranı ise;

5 Beşkardeşler vd 73 EM alan difüzyonunun erken zamanlarda ani, geç zamanlarda ise daha yavaş değişimler göstermesi sebebiyle, EM alan modellemelerinde daha doğru sonuçlar elde etmek için erken zamanlarda daha küçük, geç zamanlarda ise daha büyük zaman adımları kullanılmıştır. Birincil ve ikincil elektrik alanların belirlenmiş zaman adımlarında yinelemeli olarak modellenebilmesi için öncelikle başlangıç durumunun verilmesi gerekmektedir. Kaynak tanımı yapılmadığından, elektrik alanların tt = 0 anında kaynağın kapatılması sonucu yerin iletkenlik dağılımlarına bağlı olarak oluştuğu durumun verilmesi gerekmektedir. Yinelemeli ifadeler gereği, çift çizgisel kaynak uyartımı altında birincil elektrik alanın önceki iki zamana ait (tt 0 ve tt 1 ) ve değerleri analitik ifadeler yardımıyla hesaplanmıştır (Wait, 1971). Uygulamalarda, tt 0 = 0 olarak kullanılmak yerine, birincil elektrik alanın en az 1.5 grid aralığı kadar yeriçine nüfuz ettiği bir zaman başlangıç zamanı olarak seçilmektedir. tt 1 zamanı ise, tt 0 zamanı üzerine seçilen zaman adımının eklenmesiyle elde edilmektedir. İkincil elektrik alanın indüklenebilme ölçütü, iletkenlik kontrastı olduğundan başlangıç durumunda sıfır olarak kabul edilmektedir. Sınır koşulları olarak sağ, sol ve alt sınırlarda homojen Dirichlet sınır koşulları kullanılmıştır. Bu sınır koşullarını sağlamak amacıyla, dereceli ağ aralıkları kullanılarak sınırlar kaynak noktalarından olabildiğince uzağa taşınmıştır. Yer-hava arayüzeyinde, sonlu farklar ağında hava tabakasının gerekliliğini ortadan kaldırmak amacıyla yukarı uzanım sınır koşulu kullanılmıştır (Oristaglio ve Hohma, 198). Aksi halde, yüksek özdirenç ile tanımlanan hava tabakası nedeniyle başlangıç zaman adımı da küçük olacaktır. Yukarı uzanım sınır koşulu gereği, elektrik alan, havada Laplace denklemini sağlamalıdır. Düşey ve Yatay emk TEM ölçümlerinde, doğrudan manyetik alan ölçümlerinin yapılamaması nedeniyle yer iletkenlik yapısı ile ilgili bilgiler manyetik alan bileşenlerinin zamana göre türevleri yardımıyla elde edilmektedir. Bu nedenle, geçici EM yönteminde, manyetik alan bileşenlerinin zamana göre türevleri oldukça önemlidir. Elektrik alanın sadece y yönünde değiştiği durum için, Faraday yasası diferansiyel olarak, BB zz = BB xx = (17) şeklinde yazılmaktadır. Bu sayede, elektrik alanın yatay ve düşey sayısal türevleri alınarak manyetik alanın zamana göre türevi elde edilebilmektedir. Çalışmada, düşey ve yatay emk anomalileri uzaklığa bağlı olarak farklı zaman adımları için grafikler şeklinde sunulmuştur. MODELLEME Tekdüze Ortam Bu çalışmada geliştirilen algoritmanın sınanması amacıyla, elektromanyetik tepkisi bilinen tekdüze ortam modeli için belirlenmiş zaman aralıklarında elektrik alan difüzyonu hesaplanmıştır. Modellemede kullanılan sonlu farklar ağı düşey ve yatayda olmak üzere, 79x199 düğüm noktası içermektedir. Düzensiz grid aralıkları kullanılan hesaplama ağında sağ ve sol sınırlar sırasıyla 3910 ve metrede, alt sınır ise -855 metrededir. Şekil 3 de verilen 300 Ωm özdirençli tekdüze ortam modeli için elektrik alan değerleri sonlu farklar ağındaki her bir düğüm noktasında belli zaman adımları için hesaplanmıştır (Şekil ). Bu ve diğer difüzyon kesitlerinde sıfır konturunun solunda kalan bölümde elektrik alan değerleri negatif değerlidir. Programın test edilmesi için Du Fort-Frankel sonlu farklar yöntemiyle elde edilen elektrik alan değerleri analitik karşılıklarıyla kıyaslanmıştır. Şekil 5 de görüldüğü üzere, elektrik alan değerleri yeterli hassasiyette hesaplanabilmektedir. Literatür Örneği: Dipol modeli İki boyutlu elektromanyetik alanların modellenmesinde literatürde yeralan önemli modellerden biri düşey dipol modelidir. Oristaglio ve Hohma (198) ın gerek ikincil ve toplam elektrik alanın iletken yapılara bağlı olarak nasıl oluştuğu hakkında fikir vermesi; gerekse elektrik alandan yararlanılarak sayısal türevler aracılığıyla hesaplanan ve manyetik alanlarla doğrudan

6 7 Yerbilimleri Şekil Ωm özdirençli tekdüze ortam modeli; 0 ile simgelenmiş negatif kaynak (-50 m, 0 m) de, x ile verilen pozitif kaynak ise (50, 0) noktasındadır. Figure 3. A 300 Ωm homogeneous half-space model; negative source is denoted by 0 at (-50 m, 0 m), positive source is denoted by x at (50, 0). Şekil. 300 Ωm özdirençli tekdüze ortamda, 0.1 ms, 1ms ve 10 ms için elektrik alan kontur haritaları. Bu şekilde ve diğer şekillerde sıfır konturu beyaz düz çizgi ile gösterilmiştir. Figure. Electric field cross-sections of a 300 Ωm homogeneous half-space at 0.1 ms, 1ms and 10 ms. The white colored line shows the zero contour line in this figure and the following figures.

7 Beşkardeşler vd 75 Şekil Ωm özdirençli tekdüze ortamda pozitif kaynaktan 100 m uzaklıktaki bir noktadaki elektrik alan için sonlu farklar çözümü ve analitik çözüm kıyaslaması. Figure 5. Comparison of analytical and finite difference solution for a 300 Ωm homogeneous half-space at a point which is located at 100 m far from positive source. Şekil 6. Oristaglio ve Hohma (198) ın dipol modeli. Figure 6. Dipol model (Oristaglio ve Hohma, 198). ilişkili olan düşey ve yatay emk anomalilerinin iletken yapılardan nasıl etkilendiği hakkında bilgi vermesi açısından oldukça önemlidir. Bu çalışma kapsamında geliştirilen algoritma ile hesaplanan Oristaglio ve Hohma (198) ın dipol modeli Şekil 6 da, elektrik alanların zamana bağlı difüzyonu Şekil 7 de gösterilmiştir. Şekil 7 deki toplam elektrik alan kontur haritaları incelendiğinde, değişen elektrik alanın etkisiyle dipol içerisinde indüklenen emk ve buna bağlı olarak dipolün yeni bir kaynak gibi oluşturduğu kendi ikincil elektrik alanı farklı zaman adımlarında görülmektedir. Dipol modeli için yatay emk bileşeninin farklı zaman adımlarında çizdirilen

8 76 Yerbilimleri Şekil 7. Dipol modeli için toplam elektrik alanın (0.1 ms, 1 ms, 3 ms, 8 ms ve 10 ms) zamana bağlı difüzyonu. Figure 7. Total electric field diffusion at 0.1 ms, 1 ms, 3 ms, 8 ms and 10 ms.

9 Beşkardeşler vd 77 Şekil 8. Dipol modeli için (1 ms, 3 ms, 5 ms, 8 ms, 10 ms ve 1 ms zaman adımlarında) yatay emk profilleri. Figure 8. Profiles of the horizontal emk for the dipol model (at 1 ms, 3 ms, 5 ms, 8 ms, 10 ms and 1 ms). Şekil 9. Dipol modeli için (1 ms, 3 ms, 5 ms, 8 ms, 10 ms ve 1 ms zaman adımlarında) düşey emk profilleri. Figure 9. Profiles of the vertical emk for the dipol model (at 1 ms, 3 ms, 5 ms, 8 ms, 10 ms and 1 ms).

10 78 Yerbilimleri Şekil 10. Dipol modeli için birincil elektrik alanın yüzeydeki [(-70 m, 0 m), (0 m, 0 m) ve (100 m, 0 m) noktalarındaki mesafe ve zamana bağlı sönüm eğrileri Figure 10. Decay curves of Primary electric field respect to time and distance for the dipol model (points at (-70 m, 0 m), (0 m, 0 m) ve (100 m, 0 m)).

11 Beşkardeşler vd 79 anomalilerinde (Şekil 8), iletken yapı üzerinde maksimum genliğe yükselme ve zamana bağlı olarak sönümlenme izlenmektedir. Aynı modelin düşey emk bileşeninin farklı zaman adımlarındaki anomalilerinde ise (Şekil 9) dipol üzerinde sıfır geçişleri görülmektedir. Düşey emk bileşeninin genliği difüzyon etkisiyle yatay emk bileşenine benzer olarak zamanla sönümlenmektedir. Bu grafikte, özellikle düşey bileşen anomalilerinin iletken yapının konumuna ait önemli bilgiler verdiği net olarak izlenmektedir. Şekil 10 da toplam elektrik alanın yüzeydeki farklı noktalardaki zamana bağlı sönüm eğrileri verilmiştir. Bu eğriler, dipolün kaynaktan olan uzaklığına bağlı olarak oluşan ikincil elektrik alandaki değişimleri açıkça göstermektedir. Kaynağa en yakın noktadaki (100 m, 0 m) sönüm eğrisinde, zaman içerisinde değişen birincil elektrik alana bağlı olarak, iletken dipolde indüklenen ikincil elektrik alanın eğride oluşturduğu dönel yapısı oldukça belirgin olarak görülmektedir. Kaynaktan uzak olan noktalarda birincil elektrik alan değeri daha düşük ve dipolün etkileri ise geç zamanlarda düşük genlikli olarak kendini göstermektedir. Tuzlu Su Girişim Modeli Literatür örneğinden sonra bu çalışmada, ülkemizde kıyı bölgelerinde karşılaşılan tuzlu su girişimi probleminin simülasyonu gerçekleştirilmiştir. Bunun için olayı basit bir biçimde gösterebilecek çok iletken bir yatay dipol modeli seçilmiştir. Yeryüzünde farklı iki noktada, yatay ve düşey emk genlikleri için olası anomaliler elde edilmiştir. Modelde tekdüze ortam 150 Ωm ve tuzlu su içeren birim 0.3 Ωm özdirenç ile temsil edilmiştir (Şekil 11). Tuzlu su girişiminin derinliği genel olarak ülkemizde karşılaşılan durumlar gözönünde bulundurularak 100 m olarak seçilmiştir. Şekil 1 deki toplam elektrik alan kontur haritaları incelendiğinde, yatay yönde ortama giriş yapan tuzlu suyun etkisi çok net bir biçimde izlenmektedir. Tuzlu su girişim modeli için çizdirilen yatay emk bileşeninin farklı zaman adımlarındaki davranışları Şekil 13 de verilmiştir. Düşey dipol modelinde olduğu gibi, iletken yapı üzerinde maksimum genliğine ulaşacak şekilde karşımıza çıkmaktadır. Zaman içerisinde anomalinin genliğinin azaldığı açıkça görülmektedir. Bu model için, düşey emk bileşeninin farklı zaman adımlarındaki davranışı incelendiğinde, yatay emk lardan farklı olarak düşey bileşenlerde tuzlu su girişimini temsil eden yatay dipolün başladığı yerden itibaren eğrilerde büyük bir değişim gözlenmektedir. Yatay dipol için öncelikle emk bileşenleri kaynağa yakın bölgelerde oluşmakta, daha sonra da yatay yönde ilerlemektedir. Buna bağlı olarak, düşey emk bileşeninin sıfır geçişi tam da iletken yapının kaynağa en yakın köşesinin yeryüzündeki izdüşüm noktasında görülmektedir. Zaman içerisinde, düşey emk bileşenine ait sıfır geçişleri yanal yönde hareket etmektedir. Tuzlu su girişim modeli için hesaplanan difüzyon zamana bağlı kesitler ile yeryüzünde oluşturacağı düşey ve yatay emk davranışları gözönüne alındığında, TEM yönteminin çok iletken tuzlu Şekil 11. Tuzlu su girişim modelinin şematik gösterimi. 150 Ωm özdirençli tekdüze bir ortamda 0.3 Ωm özdirençli tuzlu su içeren iletken birim 0 m kalınlığında, 100 m derinde ve kaynaktan 300 m uzaktadır. Figure 11. Schematic view of the salt-water intrusion model. The 0.3 Ωm conductor with saltwater in a 150 Ωm host rock is at 100 m depth with 0 m thickness and 300 m away from the source.

12 80 Yerbilimleri Şekil 1. Tuzlu su girişim modelleri için hesaplanan toplam elektrik alanın (0.01 ms, 0.1 ms, 0.5 ms, 1 ms, 3 ms ve 15 ms) zamana bağlı difüzyon süreci Figure 1. Total electric diffusion at 0.01 ms, 0.1 ms, 0.5 ms, 1 ms, 3 ms and 15 ms) for salt intrusion model. Şekil 13. Tuzlu su girişim modeli için (3 ms, 5 ms, 8 ms, 10 ms ve 1.5 ms zaman adımlarında) hesaplanan yatay emk profilleri. Figure 13. Profiles of the horizontal emk for the salt-water intrusion (3 ms, 5 ms, 8 ms, 10 ms ve 1.5 ms).

13 Beşkardeşler vd 81 su girişim problemine oldukça duyarlı olduğu görülmektedir. Dolayısıyla, TEM yönteminin tuzlu su içeren birim sınırlarının belirlenmesi ve bu tür sorunların çözümünde gerçekçi bilgiler vereceği ortadadır. Ayrıca, zamana bağlı olarak tuzlu suyun gözenekli birimler içerisine ilerleme oranı (monitoring) belirli zaman aralıklarıyla ölçülen TEM verilerinin değerlendirilmesiyle elde edilebileceği görülmektedir. SONUÇ VE ÖNERİLER Jeolojik ve hidrojeolojik problemlerin çözümünde yaygın olarak kullanılan geçici elektromanyetik yöntemle ilgili yeraltında oluşan elektromanyetik alanların yayılım süreçlerinin modellenmesi fiziksel sürecin anlaşılabilmesi açısından oldukça önemlidir. Farklı zaman dilimlerinde yeraltındaki elektromanyetik difüzyonun kesitler halinde sunumu kadar, yer yüzeyinde ölçülebilecek olası anomalilerin hesaplanarak görüntülenmesi de yeraltında iletken cisimlerin etkilerini açık olarak ortaya koymakta ve çok boyutlu ortamların yorumlanabilmesi yolunda olanaklar sağlamaktadır. Bu çalışmada, zaman ortamı elektromanyetik alanların difüzyon süreci iki boyutlu olarak modellenmiştir. Bunun için, Maxwell denklemleri Du Fort-Frankel sonlu farklar yaklaşımı ile çözülmüştür. Oristaglio ve Hohma (198) dan yola çıkılarak geliştirilen iki boyutlu modelleme algoritmasının doğruluğunun sınanması amacıyla, tekdüze ortam sonuçları analitik çözümlerle karşılaştırılmış, duyarlılığına güvenilebilir sonuçlar bulunmuştur. Modelleme çalışmalarında, birincil ve ikincil elektrik alan değerlerinin yanısıra; elektrik alan değerlerinin sayısal türevlerinden yatay ve düşey elektromotor kuvvet (emk) profil eğrileri hesaplanmıştır. Sayısal türevlerden hesaplanan yatay ve düşey emk profil eğrileri, uygulamada özellikle çok kanallı ölçümlerde elde edilen sonuçlarla doğrudan karşılaştırma olanağı sağlaması açısından önem kazanmaktadır. Literatür örnekleri dışında, ülkemizin önemli çevre sorunlarından biri olan kıyılarda tuzlu su girişiminin simülasyonu amacıyla yatay dipol modeli oluşturulmuş, elde edilen kontur haritalarında, geçici elektromanyetik alanların difüzyonu açık olarak izlenebilmiş ve geçici elektromanyetik yöntemin (TEM) kıyılardaki tuzlu su Şekil 1. Tuzlu su girişim modeli için (3 ms, 5 ms, 8 ms, 10 ms ve 1.5 ms zaman adımlarında) hesaplanan düşey emk profilleri. Figure 1. Profiles of the vertical emk for the salt-water intrusion (3 ms, 5 ms, 8 ms, 10 ms and 1.5 ms).

14 8 Yerbilimleri girişimi problemini çözme potansiyeli bir kez daha vurgulanmıştır. KATKI BELİRLEME Yazarlar makaledeki öneri ve düzeltmelerinden dolayı, M. Emin Candansayar a teşekkür ederler. KAYNAKLAR Adhidjaja, J.I. ve Hohma, G.W, Twodimensional transient electromagnetic responses. Geophysics, 50, Adhidjaja, J.I. ve Hohma, G.W, Step responses for two-dimensional electromagnetic models. Geoexploration, 5, Oristaglio, M. L ve Hohma, G. W., 198. Diffusion of electromagnetic fields into a two-dimensional earth: A finite-difference approach. Geophysics, 9, Wait, J.R., Transient Excitation of the Earth by a Line Source of Current. Proc. IE Lett., 59,