YAPISAL EŞİTLİK MODELLEMESİ: İNTERNET SERVİS SAĞLAYICILARI SEKTÖRÜNDE MÜŞTERİ SADAKATİ ÜZERİNE BİR UYGULAMA
|
|
|
- Mehmet Çiçek
- 5 yıl önce
- İzleme sayısı:
Transkript
1 T.C. İSTANBUL ÜNİVERSİTESİ SOSYAL BİLİMLER ENSTİTÜSÜ EKONOMETRİ ANABİLİM DALI DOKTORA TEZİ YAPISAL EŞİTLİK MODELLEMESİ: İNTERNET SERVİS SAĞLAYICILARI SEKTÖRÜNDE MÜŞTERİ SADAKATİ ÜZERİNE BİR UYGULAMA SEDA KARAKAŞ GEYİK TEZ DANIŞMANI: PROF. DR. AHMET GÖKÇEN İSTANBUL 2014
2
3 YAPISAL EŞİTLİK MODELLEMESİ: İNTERNET SERVİS SAĞLAYICILARI SEKTÖRÜNDE MÜŞTERİ SADAKATİ ÜZERİNE BİR UYGULAMA SEDA KARAKAŞ ÖZ Yapısal eģitlik modellemesi gizil değiģkenler arasındaki nedensel iliģkilerin sınanmasında kullanılan kapsamlı bir istatistiksel analiz tekniğidir. Yapısal eģitlik modellemesi Doğrulayıcı Faktör Analizi, Yol Analizi ve Regresyon Analizi yaklaģımlarının sentezlenmesiyle ortaya çıkan bir yöntem olup bu çalıģmada bütün teorik ayrıntıları ile incelenmiģtir. ÇalıĢmanın uygulama kısmında Türkiye de Ġnternet Servis Sağlayıcıları sektöründe müģteri sadakati ve bileģenleri arasındaki iliģkilerin modellenmesi amaçlanmaktadır. Söz konusu pazarda müģteri sadakati olgusunun bileģenleri olan kurumsal imaj, güven, firmaya yönelik beklentiler, müģteri Ģikâyetleri yönetimi, hizmet kalitesi, değiģtirme maliyeti ve fiyat algısı değiģkenleri arasındaki iliģkilerin teorik altyapıları ile incelenmesi ardından kuramsal model ve araģtırma kapsamında belirlenen hipotezler yapısal eģitlik modellemesi kullanılarak istatistiksel olarak analiz edilmiģtir. AraĢtırma sonucunda önerilen teorik modelin istatistiksel olarak geçerliliği belirlenmiģ ve ileri sürülen ondört hipotezden yalnızca biri reddedilmiģtir. Anahtar Kelimler: Yapısal Eşitlik Modellemesi, Yol Analizi, Doğrulayıcı Faktör Analizi, Gizil Değişken, Müşteri Sadakati, İnternet Servis Sağlayıcıları Sektörü. iii
4 STRUCTURAL EQUATION MODELING: AN APPLICATION ON CUSTOMER LOYALTY IN TURKISH INTERNET SERVICE PROVIDER SECTOR SEDA KARAKAŞ ABSTRACT Structural equation modeling is a comprehensive statistical analysis method which is used to test causal relationships between latent variables. Structural Equation Modeling is a statistical method that emerged as a result of assembling and synthesizing the Confirmatory Factor Analysis, Path Analysis and Regression Analysis in a model and has been analyzed in this thesis study with all its theoretical details. In the empirical partof the study, it is aimed to determine a theoretical model that would explain relationships between customer loyalty and its components in the Turkish Internet Service Provider Sector. In accordance with this purpose,as being the components of customer loyalty, corporate reputation, trust, expectations from company, handling customercomplaints, service quality, switching cost and price perception have beenexamined together with their theoretical infrastructures and the hypotheses that were determined within the scope of theoretical model and research were analyzed statistically by using the structural equation modeling. As a result of the study, statistical validity of the theoretical model was determined at the end of the research and only one in fourteen suggested research hypotheses was rejected. Keywords: Structural Equation Modeling, Path Analysis, Confirmatory Factor Analysis, Latent Variables, Customer Loyalty, Internet Service Providers Market. iv
5 ÖNSÖZ Akademik hayatın önemli bir aģaması olan bu zorlu doktora tezi çalıģması sürecimde çalıģmalarımı tamamlamamda pek çok değerli hocamın katkısı oldu. En baģta bu süreçte benden ilgi ve alakasını hiç esirgemeyen, görüģ ve eleģtirileri ile çalıģmama yön veren, her konuda sonsuz anlayıģ gösteren büyük sevgi ve saygı duyduğum değerli hocam ve danıģmanım Prof. Dr. Ahmet GÖKÇEN e sonsuz teģekkürlerimi sunarım. Ayrıca bu tez çalıģması süresince bana değerli vakitlerini ayıran, çalıģmamın geliģimi süresinde katkılarını esirgemeyen tez komitesi üyeleri, değerli hocalarım Prof. Dr. Selahattin GÜRĠġ ve Doç. Dr. Mustafa TEKĠN e teģekkürlerimi sunarım. Sayın Prof. Dr. Selahattin GÜRĠġ bu süreçte bana sonsuz anlayıģ ve destek gösterdi, çalıģmam ile ilgili kararsızlıklarımı aģmamda her zaman yol gösterici oldu, doktora tezi çalıģmam sayesinde tanıģma fırsatı bulduğum değerli hocama tekrar tekrar teģekkür ediyorum. Tezimin her aģamasında desteğini esirgemeyen, çalıģmamı okuyup eleģtirilerini sunan, her zaman daha iyisini yapmam konusunda teģvik eden değerli hocalarım Doç. Dr. Aylin AKTÜKÜN ve Doç. Dr. Hakan SATMAN a çok teģekkür ederim. Özellikle çalıģmamın uygulama kısmında sık sık danıģtığım, bilgi ve deneyimlerini benle paylaģan sevgili arkadaģım değerli hocam Yard. Doç. Dr. Oylum KORKUT a çok teģekkür ediyorum. Ayrıca baģta Prof. Dr. Enis SINIKSARAN olmak üzere bugüne dek üzerimde emeği olan bütün değerli hocalarıma da teģekkürü bir borç biliyorum. Bu çalıģma süresince bana sonsuz anlayıģ gösteren, ilgisi, sevgisi ve yardımları ile en zor anlarımda bile sabırla destek olan sevgili eģim Gökhan GEYĠK e ne kadar teģekkür etsem azdır. Sevgili Gökhan, sen bir insanın sahip olabileceği en mükemmel eģsin her Ģey için defalarca teģekkür ederim. Son olarak baģta annem ve kardeģim olmak üzere bütün aileme ve ailemden ayırmadığım canım dostlarıma çok teģekkür ediyorum. Bu zorlu çalıģma sürecinde sizleri çok ihmal etmeme rağmen desteğinizi hiç esirgemediniz, sonsuz anlayıģ gösterdiniz, iyi ki varsınız. v
6 İÇİNDEKİLER Sayfa ÖZ ABSTRACT ÖNSÖZ ĠÇĠNDEKĠLER ġekġller LĠSTESĠ.. TABLOLAR LĠSTESĠ. KISALTMALAR LĠSTESĠ. iii iv v vi ix x xi GĠRĠġ YAPISAL EġĠTLĠK MODELLEMESĠNE GENEL BĠR BAKIġ Temel Kavramlar ve DeğiĢkenler Yapısal EĢitlik Modellemesinin Kuramsal Temelleri Yapısal EĢitlik Modellemesinin GeliĢimi ve Uygulama Alanları YAPISAL EġĠTLĠK MODELLEMESĠNĠN TEMELLERĠ 2.1. Yol Analizi Temel Kavram ve Gösterimler Model Yapısal Model Ölçme Modeli Kovaryans ve Korelasyon Yapısı Toplam, Doğrudan ve Dolaylı Etkiler Doğrulayıcı Faktör Analizi Açıklayıcı Faktör Analizi ve Temel Kavramlar Doğrulayıcı Faktör Analizi Modeli Modelin Teorik Yapısı Modelin Tanımlanması t Kuralı vi
7 Üç Gösterge Kuralı Ġki Gösterge Kuralı Modelin Tahmini Modelin Değerlendirilmesi Ölçme Modellerinde Geçerlilik ve Güvenilirlik Geçerlilik Güvenilirlik YAPISAL EġĠTLĠK MODELLEMESĠ 3.1. Gözlenen DeğiĢkenlerle Yapısal EĢitlik Modellemesi Yapısal EĢitlik Modelinin Spesifikasyonu Yapısal EĢitlik Modelinin Kovaryans Yapısı Yapısal EĢitlik Modelinin Tanımlanması t Kuralı Ġki Adım Kuralı Çoklu Gösterge Çoklu Nedensellik Kuralı Yapısal EĢitlik Modelinin Tahmini Ençok Olabilirlik Yöntemi AğırlıklandırılmamıĢ En Küçük Kareler Yöntemi GenelleĢtirilmiĢ En Küçük Kareler Yöntemi Dağılımsal Varsayımlar ve Çok DeğiĢkenli Normallik AğırlıklandırılmıĢ En Küçük Kareler Yöntemi DayanıklıYöntemler Satorra-Bentler ÖlçeklendirilmiĢ ve Dayanıklı Standart Hatalar Yöntemi DayanıklıAğırlıklandırılmıĢ En Küçük Kareler Yöntemi Uyum Fonksiyonlarının En Küçüklenmesinde Kullanılan Nümerik Yöntemler 3.6. StandartlaĢtırılmıĢ ve StandartlaĢtırılmamıĢ Katsayılar EĢitlik Sabitleri ve Ortalamalar vii
8 3.8. Toplam, Doğrudan ve Dolaylı Etkiler Yapısal EĢitlik Modellemesinde Sıralı DeğiĢkenlerin Kullanımı Yapısal EĢitlik Modelinin Değerlendirilmesi ve Uyum Ölçütleri Genel Modelin Değerlendirilmesi Kesin Uyum Ölçütleri Artımsal Uyum Ölçütleri Yalınlık Uyum Ölçütleri Merkezi Olmayan Uyum Ölçütleri Model BileĢenlerinin Değerlendirilmesi ĠNTERNET SERVĠS SAĞLAYICILARI SEKTÖRÜNDE MÜġTERĠ SADAKATĠ VE BĠLEġENLERĠNĠN YAPISAL EġĠTLĠK MODELLEMESĠ ĠLE ĠNCELENMESĠ MüĢteri Sadakati Kavramı 4.2. MüĢteri Sadakatinin BileĢenleri 4.3. MüĢteri Sadakati Modelleri Uygulama AraĢtırmanın Amaç ve Kapsamı AraĢtırma Tasarımı ve Örnekleme Planı AraĢtırma Yöntemi Ölçme Modellerinin OluĢturulması Ölçme Modelinin Geçerliliği ve Güvenilirliği Yapısal EĢitlik Modelinin OluĢturulması SONUÇ KAYNAKÇA EK 1 Anket Formu EK 2 AraĢtırma DeğiĢkenleri için Mann-Whitney U Testi Sonuçları. 197 EK 3Ölçme Aracı Nihai Formu: Gizil Kavramlar, Göstergeler, Geçerlilik ve 199 Güvenilirlikleri ÖZGEÇMĠġ. 201 viii
9 ŞEKİLLER LİSTESİ Sayfa ġekil 2.1. Bir yol diyagramı örneği 15 ġekil 2.2. Üç gizil değiģkenli yapısal model için yol diyagramı 17 ġekil 2.3. Bir gizil dört gösterge değiģkenli yol diyagramı 23 ġekil 2.4. Yapısal model ve ölçme modeli birlikte gösterimi 25 ġekil 2.5. Açıklayıcı faktör analizi modeli (Üç faktörlü model) 27 ġekil 2.6. Doğrulayıcı faktör analizi modeli (Üç faktörlü model) 30 ġekil 2.7. DıĢsal gizil değiģkenli DFA modeli ve temel gösterimler 34 ġekil 2.8. Ġçsel gizil değiģkenli DFA modeli ve temel gösterimler 35 ġekil 3.1. Yinelemeli modeller için örnekler 48 ġekil 3.2. Yinelemeli modellerin matrissel gösterimi için bir örnek 49 ġekil 3.3. Yinelemesiz model için varsayımsal bir örnek 50 ġekil 3.1. Ġki gizil değiģkenli varsayımsal model 58 ġekil 4.1. Önerilen geniģletilmiģ müģteri sadakati modeli 127 ġekil 4.2. Ölçme Modeli 4 için yol diyagramı 151 ġekil 4.3. AraĢtırma Modeli için YEM in yol diyagramı 157 ġekil 4.4. AraĢtırma hipotezlerine iliģkin diyagram 163 ix
10 TABLOLAR LİSTESİ Sayfa Tablo 2.1. Yol Analizinde Kullanılan Semboller 14 Tablo 2.2. Yapısal Model için Temel Gösterimler 19 Tablo 2.3. Ölçme Modeli için Temel Gösterimler 22 Tablo 3.1. EÇO ve GEKK Tahmincilerinin Özellikleri 74 Tablo 3.2. Çok DeğiĢkenli Çarpıklık ve Basıklık için Test Ġstatistikleri 77 Tablo 3.3. YEM de BaĢlangıç Değerlerinin Seçimi 84 Tablo 3.4. Doğrudan, Dolaylı ve Toplam Etkilerin AyrıĢtırılması 90 Tablo 3.5. Korelasyon Katsayısı Türleri 91 Tablo 4.1. Katılımcıların Demografik Özelliklerinin Dağılımı 131 Tablo 4.2. Katılımcıların ĠSSFirma Tercihlerinin Dağılımı 132 Tablo 4.3. AraĢtırma Modelinde Yer Alan Gizil ve Gösterge DeğiĢkenler 134 Tablo 4.4. Gösterge DeğiĢkenler için Tek DeğiĢkenli Normallik Testi 137 Tablo 4.5. DeğiĢkenler için Mardia nın Çarpıklık ve Basıklık Katsayıları ve Çok DeğiĢkenli Normallik Testi Tablo 4.6. Ölçme Modeli 1 için Doğrulayıcı Faktör Analizi Sonuçları 140 Tablo 4.7. Ölçme Modeli 1 için Uyum Ölçütleri 143 Tablo 4.8. Model 2 için Doğrulayıcı Faktör Analizi Sonuçları 144 Tablo 4.9. Ölçme Modeli 2 için Uyum Ölçütleri 145 Tablo Model 3 için Doğrulayıcı Faktör Analizi Sonuçları 147 Tablo Ölçme Modeli 3 için Uyum Ölçütleri 148 Tablo Model 4 için Doğrulayıcı Faktör Analizi Sonuçları 149 Tablo Ölçme Modeli 4 için Uyum Ölçütleri 150 Tablo 4.14 Ölçme Modeli için Güvenilirlik Katsayıları 152 Tablo 4.15 Ölçme Modelinde Yer Alan DeğiĢkenlerin Ayırsama Geçerliliği Tablo Yapısal EĢitlik Modeli için Uyum Ölçütleri 158 Tablo AraĢtırma Modeli için Yapısal EĢitlik Modellemesi Sonuçları 161 Tablo 4.18 AraĢtırma Modeli için Hipotezler x
11 KISALTMALARLİSTESİ ACOV :Asimptotik Kovaryans AEKK :AğırlıklandırılmıĢ En Küçük Kareler AEKK-O: Ortalamaya Göre ÖlçeklendirilmiĢ AğırlıklandırılmıĢ En Küçük Kareler AEKK-OV : Ortalama ve VaryansaGöre ÖlçeklendirilmiĢ AğırlıklandırılmıĢ En Küçük Kareler AFA : Açıklayıcı Faktör Analizi AGFI : AdjustedGoodness-of-fit Index (DüzeltilmiĢ Uyum Ġyiliği Ölçütü) AIC : Akaike s Information Criteria (Akaike Bilgi Kriteri) ASCI :AmericanCustomerSatisfaction Index (Amerikan MüĢteri Memnuniyeti Ġndeksi) BEK : Beklentiler BTK :BiliĢim Teknolojileri ve ĠletiĢim Kurumu CAIC :ConsistentAkaike s Information Criteria (Tutarlı Akaike Bilgi Kriteri) CFI : Comparative Fit Index ( KarĢılaĢtırmalı Uyum Ölçütü) CN : Critical n (Kritik n) COV : Kovaryans CVI : Cross-Validation Index (Çapraz Geçerlilik Indeksi) ÇGÇS : Çok Gösterge Çok Sebep DAEKK : Diyagonel Olarak AğırlıklandırılmıĢ En Küçük Kareler DFA : Doğrulayıcı Faktör Analizi Diag : KöĢegen EÇO : En Çok Olabilirlik ECVI :Expected Cross-Validation Index (Beklenen Çapraz Geçerlilik Ölçütü) EKK : En Küçük Kareler FA : Faktör Analizi FYT : Fiyat Algısı GDYEM : Gözlenen DeğiĢkenlerle Yapısal EĢitlik Modeli GEKK : GenelleĢtirilmiĢ En Küçük Kareler GFI : Goodness-of-fit Index ( Uyum Ġyiliği Ölçütü) GUV : Güven HKAL : Hizmet Kalitesi I : Information Matrix (Bilgi Matrisi) IFI : IncrementalFıt Index ( Artımsal Uyum Ölçütü) İSS : Ġnternet Servis Sağlayıcı KUR : Kurumsal Ġmaj LISREL : LinearStructuralRelationships MAL : DeğiĢtirme Maliyeti MEM : MüĢteri Memnuniyeti MIMIC :Çok Gösterge- Çok Sebep (MultipleIndicator- MultipleCause) NFI : Normed Fit Index (NormlaĢtırılmıĢ Uyum Ölçütü) NNFI : Non-Normed Fit Index veya-tuckerlewis Index (NormlaĢtırılmamıĢUyum Ölçütü veya Tucker-LewisÖlçütü) PGFI : ParsimonyGoodness-of-fit Index (Yalınlık Uyumun Ġyiliği Ölçütü) xi
12 PNFI : ParsimoniousNormed Fit Index ( Yalınlık NormlaĢtırılmıĢ Uyumun ĠyiliğiÖlçütü) RFI : RelativeFıt Index ( Bağıl Uyum Ölçütü) RMR : RootMeanSquareError (Hata Kareleri Ortalamasının Karekökü) RMSEA :RootMeanSquareError of Approximation (YaklaĢım Hatasının KareliOrtalamasının Karekökü) SAD : Marka veya MüĢteri Sadakati SKY :ġikayet Yönetimi SRMR : StandardizedRootMeanSquareError(StandartlaĢtırılmıĢ Hata Kareleri Ortalamasının Karekökü) Tr : Trace (iz) TUİK :Türkiye Ġstatistik Kurumu VAR : Varyans YA : Yol Analizi YEM : Yapısal EĢitlik Modellemesi xii
13 GĠRĠġ Son birkaç on yılda ekonomi, psikoloji, sosyoloji, pazarlama, eğitim bilimleri gibi sosyal bilim ve davranış bilimleri alanlarında yapılan uygulama çalışmalarının pek çoğunda ölçülebilen ve gizil (latent) değişkenler arasındaki nedensel ilişkileri ortaya koymaya olanak sağlayan birçok değişkenli istatistiksel yöntem olan Yapısal EĢitlik Modellemesi (Structural Equation Modeling) analizlerinin sıklıkla kullanıldığı görülmektedir. Ekonometri ve istatistik literatüründe modelleme çalışmalarında, teorik olarak var oldukları düşünülen ancak birtakım göstergeler (indicator) aracılığı ile ölçülebildikleri varsayılan ve bu nedenle farazi veya varsayımsal değişkenler olarak da adlandırılan gizil değişkenlerin yer aldığı analizlerin incelenmesi bu çalışmanın temel amacını oluşturmaktadır. Çalışma, bu amaç çerçevesinde aşağıdaki şekilde düzenlenecektir. Bilimsel çalışmalarda gerçek yaşamdaki ilişkileri açıklamak, öngörmek ve kontrol etmek amacı ile modellerden faydalanılır. Söz konusu modeller nicel ve nitel değişkenler yardımı ile tanımlanır. Nicel değişkenler ölçülebilen, kolayca sayısallaştırılabilen değişkenler olarak karşımıza çıkarken; nitel değişkenler ölçülebilir olmaktan çok algılanabilen soyut kavramlardır. Gizil değişkenler olarak adlandırdığımız söz konusu değişkenler; ekonomi, işletme, pazarlama gibi sosyal bilimler alanlarında müşteri memnuniyeti, marka algısı, tüketici davranışları, kalite algısı gibi kavramlar ve psikoloji, sosyoloji gibi davranış bilimleri alanlarında ise motivasyon, kaygı, depresyon, mutluluk, çaresizlik, benlik bilinci, özsaygı gibi kavramlar olarak örneklendirilebilir. Ölçülemeyen ancak gerçek yaşamın içinde var olmaları nedeniyle dolaylı olarak gözlemlenebilen kavramlardır. Gizil değişkenlerin kendi aralarındaki ve gözlenen değişkenler ile aralarındaki ilişkilerin incelendiği modellere Yapısal Eşitlik Modelleri adı verilmekte olup, söz konusu modeller ölçme modeli ve yapısal model olarak iki bölümde incelenmektedir. Gizil değişkenlerin kullanımının, gözlenen değişkenlere en büyük üstünlüğü, gözlenen değişkenlerin 1
14 ölçme işleminden kaynaklanan sistematik olan ya da olmayan bir hata içermesidir. Buna karşılık gizil değişkenlerde benzer bir hata söz konusu olmamaktadır. Çalışmanın birinci bölümünde, genel olarak daha sonraki bölümlere temel oluşturması açısından yapısal eşitlik modellemesine temel oluşturan kavramlar ve değişkenler tanıtılacaktır. Gizil değişkenlerin tanımı, ölçülebilen değişkenlerden farkları, kullanım alanları ve sosyal bilimlerde modelleme çalışmalarında neden daha çok tercih edildikleri ile ilgili temel bilgilerin yanı sıra söz konusu değişkenlerin kullanıldığı modellerin tarihçesine ilişkin de geniş bir literatür taramasına yer verilecektir. Aynı zamanda yapısal eşitlik modellemesinin kuramsal temellerine de değinilecektir. İkinci bölümde, gizil değişken modellerinin temeli olan iki istatistiksel yöntem: Yol Analizi (Path Analysis) ve Doğrulayıcı Faktör Analizi (Confirmatory Factor Analysis) incelenecektir. Yol analizi, çoklu regresyon analizinin bir uzantısı olarak eşanlı bir denklemler sisteminin şekil olarak ifade edilmesi neredeyse bir resminin çizilmesi olarak düşünülebilir. Bu nedenle yol analizi için öncelikli ve en önemli adım yol diyagramı (path diagram) olarak adlandırılan çizimlerin doğru oluşturulmasıdır. Yol diyagramları, her ne kadar sayısal hesaplamaların gerçekleştirilmesi için gerekli olmasa da, değişkenler arası dolaylı ve doğrudan ilişkileri açıkça ortaya koyması açısından çok kullanışlıdır. Bu nedenle bu kısımda öncelikle, yol analizinde kullanılan başlıca sembol ve şekiller tanıtılacak ve yol modelinin teorik yapısı ortaya konulacaktır. Çalışmanın bu kısmında yol modelleri gizil değişkenlerin kendi aralarındaki ilişkileri yansıtan yapısal model ve gizil değişkenler ile ilgili gösterge değişkenler arasındaki ilişkileri yansıtan ölçme modeli olmak üzere iki başlık altında incelenecek ve ilerleyen kısımlarda incelenecek yapısal eşitlik modellerine temel oluşturması ve çalışmanın bütününde bir notasyon birliği sağlanması amacı ile kullanılacak temel model değişkenler ve gösterimlere ayrıntıları ile yer verilecektir. Daha sonra ölçme modellerinin tahmini ve veriye uyumunun saptanması amacı ile geliştirilmiş çok değişkenli istatistiksel yöntemlerden biri olan doğrulayıcı faktör analizi incelenecektir. Ayrıca ölçme modellerinin mantığına değinilerek, geçerlilik güvenilirlik analizleri anlatılacaktır. 2
15 Üçüncü bölümde, gizil değişken modelleri ailesinin en geniş kapsamlı üyesi olan bir anlamda da ölçme modelleri, doğrulayıcı faktör analizi, yol analizi gibi modellerin tek bir modelde toplanıp sentezlenmesi ile ortaya çıkmış çok değişkenli bir analizi türü olan yapısal eşitlik modelleri incelenecektir. Yapısal eşitlik modelleri özellikle son birkaç on yılda sosyal bilimler alanında yapılan çalışmaların olmazsa olmazı haline gelmiştir. Araştırmacılara çok geniş avantajlar sağlaması nedeniyle neredeyse başlı başına bir araştırma yöntemi olarak adlandırılmaya başlamıştır. Söz konusu avantajlar, gözlenen ve gizil değişkenler arasındaki neden-sonuç ilişkisinin ortaya konulabilmesi, ölçme hatalarının açıkça modellenmesi, bağımlı değişkenler arasındaki kovaryans yapısını ve hatalar arasındaki kovaryans yapısını açıkça ortaya koyması olarak özetlenebilir. Bu kısımda, yapısal eşitlik modeli ortaya konularak teorik yapısı ve tanımlanabilirliği incelenecektir. Daha sonra modelin tahmininde kullanılan yöntemler ve modelin testi için önerilen uyum kriterleri ayrıntıları ile incelenerek modelin kullanımına ilişkin yorumlarda bulunulacaktır. Aynı zamanda sıralı ölçekte ölçülmüş veriler için YEM çalışmalarının teorisine de yer verilerek uygulama çalışmasına zemin oluşturulacaktır. Dördüncü ve son bölümde ise Türkiye de İnternet Servis Sağlayıcıları (İSS) sektöründe tüketicilerin müşteri sadakati davranışlarını gizil değişkenli yapısal eşitlik modellemesi çerçevesinde inceleyen bir uygulama çalışmasına yer verilecektir. Yapısal eşitlik modellemesi çalışmalarının en önemli özelliğinin tamamen teoriye dayalı olması nedeniyle, iktisat ve işletme teorisinde müşteri sadakati tutumları ve müşteri sadakatini etkileyen faktörler arasındaki ilişkilerin teorik ayrıntılarına yer verilecektir. Teorik çerçeve ortaya konulduktan sonra söz konusu davranışları ölçmek için amprik bir çalışma gerçekleştirilerek söz konusu pazarda ilgilenilen kavramlar arası ilişkiler incelenecek ve sonuçlar raporlanarak yorumlanacaktır. 3
16 BÖLÜM 1 YAPISAL EġĠTLĠK MODELLEMESĠNE GENEL BĠR BAKIġ Sosyal bilimleri pozitif bilimlerden ayıran en temel unsur çalışma alanının madde yerine insan ve toplum olmasıdır. İnsan ve topluma ait kavramlar, pozitif bilimlere konu olan olgulardan farklı olarak daha soyut ve teorik yapıları içermektedirler. Bu nedenle söz konusu yapıların ve kavramların ölçülmesi için gözlem ve deneye dayanan deterministik süreçler yerine soyutlaştırma ve kavramsallaştırmaya dayanan birtakım farklı süreçler geliştirilmiştir. Söz konusu soyut ve teorik yapıların ve bu yapıların kendi aralarındaki ilişkilerin incelenmesi ile gerçekleştirilen analizler geleneksel yöntemlere göre farklılık göstermektedir. Çalışmanın bu bölümünde; bahsedilen soyut kavramların açıklanması ve modellemesi çalışmalarında kullanılan Yapısal Eşitlik Modellemesi (YEM) ne temel oluşturacak kavramlar, modellerde kullanılan değişkenler, yapısal eşitlik modellerinin kuramsal temelleri kavramsal olarak incelenecek ve ilerleyen bölümlerde teorik ayrıntılarına yer verilecek yöntemlere temel oluşturacak bilgilere değinilecektir TEMEL KAVRAMLAR VE DEĞĠġKENLER Yapısal eşitlik modellemesi çalışmalarının geleneksel yöntemlerden farkı analize konu olan değişkenlerin yapısıdır. Bu nedenle modellerde kullanılan değişken tiplerinin tanımlanmasında fayda vardır. Sosyal bilimlerde araştırmacılar genellikle doğrudan gözlemlenemeyen teorik yapılar ile ilgilenmektedirler. Örneğin psikolojide; benlik kavramı, motivasyon, sosyolojide; güçsüzlük ve anomi kavramı, eğitim biliminde; sözel/ sayısal yetenek, öğretmen beklentisi, derse duyulan kaygı düzeyi, ekonomide; sosyal sınıf 4
17 farklılıkları, kapitalizm gibi olgular söz konusu teorik yapılara verilebilecek örneklerden birkaçıdır (Byrne; 2001: 4). Teorik yapılar doğrudan gözlenip ölçülemeyen varsayımsal yapılar olduğundan araştırmacılar modellerinde yer alan değişkenlerle ilgili bir takım ayrımlar yapmaktadırlar. Bu ayrımlardan en temeli değişkenlerin gözlenen (observed) ve gizil (latent) değişkenler olarak ikiye ayrılmasıdır. Söz konusu varsayımsal yapılar gizil değişken olarak adlandırılırken, bu değişkenlerin ölçülebilmesi için kullanılan gözleme dayalı yöntemlerle ölçülebilen değişkenler ise gözlenen değişken olarak tanımlanmaktadır. Yapılar, boyutlar, faktörler gibi isimler de alan gizil değişkenler, direkt olarak gözlenebilen değişkenler aracılığı ile dolaylı olarak ölçülebilirler. Örneğin; zekâ kavramı (gizil değişken) psikolojik bir yapı iken kullanılan IQ testleri doğrudan gözlemlenip ölçülemeyen zekâ olgusunu açıklamak için kullanılan gözlenen ve skorlar (gözlenen değişken) ile ölçülebilen bir göstergedir. Gösterge değişken ya da bir gizil değişkenin indikatörü olarak adlandırılan bu değişkenler için bir diğer örnek; kurumsal ekonomik yapı olgusunu açıklamak için borsa endeksinin kullanılması ya da insan sağlığı gibi genel bir kavramı açıklamak için fiziksel kondüsyon ölçümü, boy, kilo veya vücut kitle endeksi gibi skorlar ya da basit kan sayımı ölçümü gibi bir değişkenin kullanılması olarak gösterilebilir. Bu örnekler gizil değişkenler ile gözlenen değişkenler arasındaki ilişkiyi ortaya koymaktadır (Schumacker ve Lomak; 2004: 2). Gizil rastlantı değişkenleri en basit tanımıyla tek boyutlu bir kavramı ifade etmektedirler. Gizil değişkenlere ait gösterge değişkenler veya indikatörler rastlantısal ya da rastlantısal olmayan hatalar içermesine rağmen gizil değişkenler hata içermeyen kavramlar, yapılar veya olgulardır. Bütün gizil değişkenler bir kavram ya da olguya karşılık geldiğinden bu değişkenler birtakım varsayımsal ve soyut yapılar olarak karşımıza çıkmaktadır. Söz konusu gizil değişkenlerin soyutluk derecesi farklılık gösterebilir. Örneğin; Emile Durkheim in sosyal dayanışma ve intihar arasındaki ters ilişki hipotezinde her iki türden de gizil değişkene rastlamak mümkündür. Sosyal dayanışma oldukça soyut bir kavram olarak karşımıza çıkarken, intihar buna oranla doğrudan gözlemlenebilir bir olgu olup soyut olmayan bir 5
18 kavramdır. Ancak bir şekilde yanlış ölçülmüş olması mümkündür. Bu nedenle ölçülebilen bir değişkenin de gizil değişken olması mümkündür. Başka bir örnek olarak; zekâ, sosyal sınıf, güç ve beklenti gibi soyut kavramlar gizil değişkenler iken, bunlara oranla daha az soyut yapılar olan yaş, gelir, eğitim, nüfus gibi kavramlar da gizil değişken başlığı altında incelenebilmektedir (Bollen; 1989: 11). Gizil değişkenler ve gözlenen değişkenler arasındaki ayrım yukarıda anlatıldığı gibi ifade edilmesine rağmen literatürde bu iki kavram arasındaki ayrımın bilişsel temelleri de tartışılmaktadır. Borsboom (2008) e göre; değişkenler arası gözlenebilir olan ve olmayan gibi kaba bir ayrım yapmak yeterli değildir. Temel ayrım bilişsel karakterde olup, bir değişken araştırmacılar tarafından bilişsel olarak algılanabilir ve erişilebilir özellikte ise gözlenen değişken, bilişsel olarak erişilebilir olmaktan uzak ise gizil değişken olarak adlandırılmalıdır. Örneğin yaş ve cinsiyet gibi kavramlar doğada ağaçlar, kayalar gibi somut nesneler gibi gözlemlenmese de ölçülebilir yapılar oldukları ve bilişsel olarak algılanabildikleri için gözlenen değişkenler olarak kabul edilebilirler. Yeryüzünde atom, quark, element gibi fiziksel soyutluk taşıyan kavramlar hiçbir insan tarafından gözle görülmüş olmamasına rağmen çok hassas bir şekilde ölçülebilir durumdadır. Bu nedenle bir değişkenin gizil olarak adlandırılıp adlandırmamasını gözlemlenmesi durumuna bağlı olarak açıklamak oldukça yüzeysel kalacaktır. Aynı yazara göre bir diğer ayrım ise gözlenen değişkenlerin de en az gizil değişkenler kadar teorik yapılar olabileceği yönündedir (Borsboom, 2008: 27-28). 1.2.YAPISAL EġĠTLĠK MODELLEMESĠNĠN KURAMSAL TEMELLERĠ Yapısal eşitlik modelleri, gözlenen ve gizil değişkenler arasındaki nedensel ve karşılıklı ilişkilerin birlikte yer aldığı modellerin test edilmesinde kullanılan kapsamlı istatistiksel tekniklerin bir bütünüdür. Sosyal, eğitim ve davranış bilimlerinden, pazarlama, biyoloji, tıpa kadar pek çok bilim alanında araştırmacılar 6
19 tarafından kullanılan yapısal eşitlik modelleri, bilimsel yöntemin bir unsuru olan teorilerin test edilmesi ve ölçme amacı için kapsamlı bir yöntem sağlar. Yapısal eşitlik modelleri, içerisinde yol analizi ve faktör analizi gibi istatistiksel teknikleri barındıran söz konusu çok değişkenli istatistik tekniklerini bir araya getiren modellerdir. YEM çalışmalarının en temel özelliği tamamen teoriye dayalı olmalarıdır. Yani, araştırmacı analize başlamadan önce elindeki değişkenler arasındaki ilişkiler hakkında teorik bir bilgiye sahip olmak zorundadır. YEM in amacı önceden belirlenen bu ilişki örüntülerinin veri tarafından doğrulanıp doğrulanmadığını ortaya koymaktır (Şimşek, 2007: 1). YEM in istatistiksel yapısının incelenmesinden önce bilimsel yöntemin unsurları hipotez, varsayım, teori, nedensellik gibi kavramlar açısından YEM in bilimsel felsefesindeki yerine kısaca değinilmesi yöntemin anlaşılması için faydalı olacaktır. Bilim felsefesinin en önemli tartışmalarından biri, bilimsel yöntem denilince akla gelen iki süreç: tümevarım ve tümdengelim süreçleri arasındaki öncelik sorunudur. Tümevarım, tek tek yapılan gözlem ve deneylerin sistemli bir biçimde incelenmesiyle elde edilen genellemeler bütünüdür. Bacon a göre bilim, açıklamanın özelden genele yapılmasını gerektiren tümevarımcı bir süreçtir (Susser, 1986). Tümevarım yönteminde bilgi edinme süreci öncelikle gözlem ile başlamaktadır. Burada temel eleştiri gözlem sayısı hakkındadır, çünkü teorik olarak hiçbir gözlem söz konusu önerme ya da hipotezleri doğrulamaya yetmeyecektir. Burada bilimsel yöntemin temelinin önerme ya da hipotezleri doğrulamak yerine yanlışlamak olduğunu ileri süren tümdengelimci yaklaşım devreye girmektedir. Karl Popper (1959) a göre bilim genelden özele açıklanması gereken bir süreçtir. Tümdengelimci yaklaşım için bilgi edinme süreci birtakım genellemeler ile başlar. Yani gözlem yapmaya başlamadan önce araştırmacının elinde birtakım önermeler olması gerekmektedir. Bütün araştırma yöntemleri bir genelleme etkinliği ile başlamakta ve genellemeler daha üst düzeydeki genellemelere doğru ilerlemekte 7
20 ve sonunda teori ya da kuram adını verdiğimiz üst düzeydeki yapılar ortaya çıkmaktadır. Bu bakış açısı ile bakıldığında YEM çalışmaları özü itibariyle doğrulayıcı bir karaktere sahiptir. Araştırmacı modelini veri ile test etmeden önce teorik olarak modelini kesin bir şekilde oluşturmuş olmak zorundadır (Şimşek, 2007:2). Bahsedildiği üzere YEM, değişkenlerin sebep-sonuç ilişkisini açıklayabilen ve kuramsal modellerin bir bütün olarak test edilmesine olanak veren etkili bir model test etme ve geliştirme yöntemidir. YEM in bazı temel karakteristik özellikleri aşağıdaki şekilde özetlenebilir. 1. Modeller genellikle doğrudan ölçülemeyen ve tam olarak iyi tanımlanmamış kuramsal ya da hipotetik yapıları içermektedir. Kaygı, tutum, hedef, zeka, motivasyon, kişilik, okuma yazma yeteneği, saldırganlık, sosyo-ekonomik statü gibi kavramlar bu tür yapılara örnek olabilir. 2. Modeller genellikle gözlenen değişkenlerdeki ölçme hatalarını hesaba katmaktadır. Hatalı her bir ölçüm için bir hata terimi modele dâhil edilmektedir. Hata terimine ilişkin varyanslar model ile uyumlu olduğunda bir model parametresi olarak değerlendirilir. 3. Modeller, karşılıklı ilişkili gösterge matrislerine (gözlenen değişkenler arası kovaryans ve korelasyon matrisleri) uygundur. Söz konusu karakteristik özellikler, YEM i klasik doğrusal modelleme yaklaşımlarından ayırmaktadır. Klasik yaklaşımların temelinde, YEM e benzer olarak kovaryans, varyans ve regresyon analizi yatsa da YEM den farklı olarak bağımsız değişkenlerin hatasız olarak ölçüldüğü varsayılmaktadır. YEM in ölçme hatalarının modele dâhil edilmesine izin vermesi, yöntemi klasik yaklaşımlardan farklı kılmaktadır (Raykov ve Marcoulides, 2006: 2-3). 8
21 1.3. YAPISAL EġĠTLĠK MODELLEMESĠNĠN GELĠġĠMĠ VE UYGULAMA ALANLARI Bilimin temel amacı olan ölçme faaliyetinin gerçekleştirilebilmesi için gözlenen değişkenlerce ölçülen olguların, sosyal bilimlerde gerçekte ilgilenilen olguları bütünüyle açıklamadığı sorunu, gizil değişken modellerinin literatüre kazandırılmasına neden olan en temel unsur olmuştur. Nedensel modeller olarak adlandırdığımız bu modellerin analizi için kullanılan yöntemler tarihsel süreç içersinde; regresyon analizi, yol analizi, doğrulayıcı faktör analizi ve yapısal eşitlik modellemesi olarak karışımıza çıkmaktadır (Schumacker ve Lomax, 2004: 4). Gizil değişkenlerin istatistikî ve ekonometrik modellere konu olmalarının temelleri regresyon analizine dayanmaktadır. Regresyon analizi, gözlenen bağımsız değişkenlerle, bağımlı değişken arasında nedensel ilişki kurmayı amaçlayan bir teknik olarak ortaya atılmıştır. Regresyon teriminin ilk kullanımı Galton (1886) tarafından belli boylardaki ebeveynlerin çocuklarının ortalama boyunun nüfusun boy ortalamasına yaklaşması eğiliminde olduğunu bulması ile gerçekleşmiştir. Daha sonra Galton un bu teorisini doğrulamak amacı ile Pearson (1903) aile boylarına ilişkin veri toplayarak boyların ortalamaya doğru çekilme eğiliminde olduğunu sayısal olarak ispatlamıştır. Ayrıca Karl Pearson (1896) tarafından iki değişken arasında standart bir ölçü ortaya koymak amacı ile hesaplanan korelasyon katsayısına ait formülün ortaya konması ile birlikte korelasyon katsayısını temel alarak ölçümlerini yapan regresyon analizinin temelleri atılmış olmaktadır. Pearson (1896) tarafından formüle edilen korelasyon katsayısına ilaveten Spearman (1904, 1927) tarafından sıralı (ordinal) ölçekler için formüle edilen korelasyon katsayısının ortaya konulması ile değişkenler arası ilişkilerin incelenmesinde yeni bir boyut kazanılmıştır. Spearman ilk kez faktör modelinin oluşturulmasında korelasyon katsayısını kullanmıştır. Zekânın teorisi için iki faktörlü bir yapıyı açıklamada ilk kez faktör analizi kullanılmıştır. Bu temel çalışmanın ardından Lawley ve Thurstone 9
22 1940 ta faktör analizi uygulamalarını geliştiren çalışmalar yapmışlardır. Günümüzdeki kullanımı ile doğrulayıcı faktör analizini konu alan ilk çalışmalar ise; Howe (1955), Anderson ve Rubin (1956), Lawley (1958) tarafından gerçekleştirilmiştir. Değişkenlerin belirli faktör yapıları ile açıklanıp açıklanamayacağını analiz etmede kullanılan doğrulayıcı faktör analizi daha kapsamlı olarak Karl Jöreskog (1960) tarafından incelenmiş olup, doğrulayıcı faktör analizi uygulamaları için ilk yazılım da aynı yazar tarafından geliştirilmiştir (Schumacker ve Lomax, 2004: 5). Gözlenen değişkenler arasındaki karmaşık ilişkilerin analizi ile regresyon analizine bağlı olarak ortaya çıkan yol analizi, ilk kez bir biyometrisyen olan Wright (1918, 1921, 1934, 1960) tarafından ortaya konulmuştur. İlk kez hayvan davranışlarını modellemek amacı ile yapılan bir çalışmada kullanılan yol analizinin üç temel bileşeni vardır. Bunlar sırası ile yol diyagramı, kovaryanslar ve korelasyonlar, etkilerin ayrıştırılmasıdır. Yol diyagramları aynı zamanda ekonometrideki eş anlı denklem sistemlerinin grafiksel bir gösterimi olarak da adlandırılmaktadır (Bollen, 1989: 4). Yapısal eşitlik modellemesi ise; ilerleyen tarihsel süreç içersinde başlıca üç bileşenin ortaya çıkmasının doğal bir sonucu olarak geliştirilen bir istatistiksel yöntem olarak karşımıza çıkmaktadır. Bu bileşenler: yol analizi, yapısal model ve ölçme modelleri ve genel tahmin süreçleridir (Bollen, 1989: 4). Yol analizine ilaveten gizil değişken ve ölçme modellerinin kavramsal sentezi YEM modellerinin temelini oluşturmaktadır. Gözlenen değişkenler arasındaki ilişkilerden yola çıkarak gizil değişken yapılarını açıklamaya çalışan analizler olarak da adlandırılabilen YEM modelleri ile ilgili ilk çalışmalar Keesling (1972), Jöreskog (1973), Wiley (1973) tarafından gerçekleştirilmiştir. Ortaya çıktığı ilk yıllarda JKW modeli olarak da adlandırılan YEM analizinin, ilk yazılımı olan LISREL (LInear Structural RELation) programının geliştirilmesi ardından modeller doğrusal yapısal eşitlik modelleri olarak adlandırılmaya başlamıştır. Ancak son yıllarda doğrusal olmayan YEM analizleri ile ilgili yapılmaya başlanan çalışmalar nedeni ile sadece YEM kavramının kullanılması daha uygun olmaktadır (Bollen, 1989: 6-8). 10
23 1976 yılında LISREL programının piyasaya sürülmesinin ardından, YEM analizinin uygulanması için pek çok yazılım geliştirilmiştir. Bunlardan en çok kullanılanları AMOS (Arbuckle, 1994, 1997), EQS (Bentler, 1989, 1995), LISCOMP (Muthén, 1988), MPLUS (Muthén ve Muthén, 1998) olarak karşımıza çıkmaktadır. Sosyal bilimlerde ilgilenilen olguların neredeyse tamamı gizil özellikler taşıyan, teorik kavramsal olgulardır. Söz konusu yapıların istatistikî ve ekonometrik modellere konu olmaları ölçme modellerinin ortaya atılması ile gerçekleşmiştir. Gizil değişkenlerin kullanıldığı; gizil değişkenlerle yol analizi, yapısal eşitlik modellemesi gibi araçlar ile bilimsel araştırmanın temeli olan ölçme eylemi daha hassas gerçekleştirilebilmektedir. Bu avantajları nedeni ile gizil değişkenlerin konu olduğu modellerin kullanımı pek çok alanda tercih edilir hale gelmiştir. Yapısal eşitlik modelleri hem iktisat, işletme, sosyoloji, psikoloji, pazarlama gibi sosyal bilimlerde hem de davranış ve eğitim bilimlerinde sıklıkla kullanılmaktadır. Bunun yanı sıra biyoloji ve tıp gibi alanlarda da pek çok çalışmaya konu olarak karşımıza çıkmaktadırlar. Temel olarak psikolojik araştırmalarda kullanılan bu modellerin son yıllarda özellikle işletme ve iktisat alanında yaygın bir biçimde kullanılmaya başlandığı gözlemlenmektedir. Özellikle, tüketici tercihleri, tüketici teorisi, pazarlama araştırmaları, marka araştırmaları, müşteri sadakati gibi iktisat teorisinin, tüketici ve müşteri davranışları dikkate alınarak incelendiği çalışmaların sayısı gün geçtikçe artmaktadır. 11
24 BÖLÜM 2 YAPISAL EġĠTLĠK MODELLEMESĠNĠN TEMELLERĠ incelenecektir. Bu kısımda yapısal eşitlik modellemesinin temellerini oluşturan analizler 2.1. YOL ANALĠZĠ Yol Analizi (YA), değişkenler arasındaki doğrudan ve doğrudan olmayan nedensel ilişkilerin gösteriminde kullanılan grafiksel bir yöntem olarak tanımlanmaktadır. YA eşanlı denklemler sisteminin grafiksel bir gösterimi olup aynı zamanda çoklu regresyon analizinin doğal bir uzantısıdır. Bu bölümde YEM analizine temel oluşturması açısından YA modellerinin teorik yapısı incelenecektir TEMEL KAVRAM VE GÖSTERĠMLER Karmaşık nedensel ilişkileri kapsayan sistemleri açıklamak ve görsel bir şekilde yorumlayabilmek amacı ile kullanılan YA modelleri daha önceki kısımlarda bahsedildiği gibi ilk kez Sewall Wright (1918, 1921) tarafından geliştirilmiştir. Sonrasında Simon (1954) tarafından ekonometri de nedensellik analizi çalışmalarında, Ballock (1961) tarafından sosyoloji alanında kullanılmıştır (Duncan, 1975: 33). YA modelleri üç temel kısımdan oluşmaktadır. Bunlar sırası ile 1. Yol diyagramı 2. Kovaryans ve Korelasyonların Ayrıştırılması 3. Doğrudan, Dolaylı ve Toplam Etkilerin Ayrıştırılması 12
25 şeklinde ifade edilmektedir (Bollen, 1989: 32). YA, incelenen değişkenler arası nedensel ve nedensel olmayan ilişkilerin gösterildiği diyagramlar ve bu değişkenler arası ilişkilerin kovaryans ve korelasyonların hesaplandığı yapısal denklemler setinin tahminini kapsamaktadır. YA modeli çoklu regresyon analizi ile benzerlikler taşısa da pek çok açıdan çoklu regresyon analizine üstünlük sağlamıştır. Regresyon analizinde yalnızca nedensel ilişkiler ele alınırken, YA da nedensel ve nedensel olmayan ilişkiler ortaya konulabilmektedir. Ayrıca YA modelleri ilişkilerin ortaya konmasından çok, var olan ilişkilerin teorik yapıların test edilmesi fikrine dayanmaktadır (Schumacker ve Lomax, 2004:7). YA modellerinde çoklu regresyon analizindeki bağımlı bağımsız değişken ayrımı yerine içsel ve dışsal değişken kavramları kullanılmaktadır. YA da model belirlenirken dışsal değişkenlerin içsel değişkenler üzerindeki etkilerinin yönünün belirlenmesi temel alınarak analizler gerçekleştirilir. Yol katsayıları dışsal değişkende meydana gelen bir birimlik artışın içsel değişkenlerin ortalamasında ne kadar değişim meydana getirdiği şeklinde yorumlanmaktadır. Ayrıca YA da yol katsayıları standartlaştırılmış çoklu regresyon katsayıları olarak ifade edilmektedirler (Loehlin, 1992: 80). YA çalışmalarının temel ve en önemli aşaması yol diyagramının oluşturulmasıdır. Bu diyagram istatistikî analiz için gerekli olmamasına rağmen değişkenler arası ilişkilerin yönünü ve yapısını ortaya koyması açısından son derece önemli ve faydalı bir araçtır. Burada önemli olan araştırmacının ilgilenilen konuya ilişkin teorik bilgisinin tam olması ve konuya çok hâkim olması gerekmektedir. Değişkenler arası ilişkilerin yanlış yansıtılması analizin sonucunda toplam etkilerin hesaplanmasında sapmalara neden olacaktır (Pedhazur, 1997: ). YA da kullanılan semboller ve gösterimler aşağıdaki tabloda verilmiştir. 13
26 Tablo 2.1 Yol Analizinde Kullanılan Semboller Kare veya dikdörtgen kutu gözlenen değişkenleri simgelemektedir. Çember veya elips şekilleri gizil değişkenleri simgelemektedir. Zarflanmamış değişkenler hata terimini simgelemektedir. Tek yönlü oklar iki değişken arasındaki tek yönlü nedensel ilişkiyi simgelemektedir. Okun başlangıcındaki değişkenin okun sonundaki değişkenin nedeni olduğu varsayılır. Çift yönlü eğri oklar, değişkenler arasındaki korelasyonları simgelemektedir. İki değişkeni bağlayan tek yönlü iki ok geri beslemeli bir ilişkiyi veya karşılıklı nedenselliği simgelemektedir. YA da yol diyagramı kullanılarak bir modele ilişkin bütün eşitliklerin yazılması mümkündür. Şekil 2.1 de verilen yol diyagramı incelendiğinde, ilgili diyagramın aşağıdaki eşanlı denklem sistemlerine denk geldiği görülmektedir. 14
27 ġekil 2.1 Bir yol diyagramı örneği (Bollen, 1989: 34) Şekil 2.1 iki gizil ve toplam dört gösterge değişkenden oluşan bir yol diyagramı örneğidir. YA da hem değişkenler hem de hata terimleri ile ilgili varsayımlar yol diyagramından açıkça okunabilmektedir. Hata terimlerine ilişkin varsayımlar, ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 15
28 şeklinde topluca ifade edilebilir. Son olarak, YA nın temel varsayımları çoklu regresyon analizindeki varsayımlara benzer olarak aşağıdaki şekilde özetlenebilir: 1. Model değişkenleri itibari ile doğrusaldır. 2. Etkileşim etkisi yoktur. 3. Hata terimleri içsel değişkenlerle ilişkisizdir. 4. Dışsal değişkenler arasında şiddetli çoklu doğrusal bağlantı olmamalıdır. 5. Model aşarı tanımlanmış olmamalıdır. 6. Model ardışık olmalıdır, yani tek yönlü bir nedensellik akışı olmalıdır. 7. Yol katsayılarının yorumlanabilmesi için modelin doğru belirlenmesi gerekmektedir. 8. Girdi olarak kullanılacak olan korelasyonlar verilerin ölçekleri ile uyumlu olmalıdır. 9. Bağımsız değişkenlerde ölçme hatası yoktur MODEL Gizil değişken modellerinde kullanılan değişken tipleri birinci kısımda ayrıntıları ile incelenmiştir. YA modelleri, söz konusu değişkenlerin kendi aralarında ve birbirleri ile olan ilişkilerini kapsayan grafiksel bir yöntem olmakla beraber YA modellerinde temel model, yapısal model ve ölçme modeli olarak adlandırılan iki modelin birleşiminden oluşmaktadır. 16
29 YAPISAL MODEL Gizil değişkenler arası yapısal ilişkileri tanımlayan modeller gizil değişken modelleri veya yapısal model olarak adlandırılmaktadır. Değişkenler arasındaki bağlantılar yapısal parametrelerle ifade edilmekte ve iki değişken arasındaki nedensel ilişkileri göstermektedir. Yapısal model ayrıntıları ile incelenmeden önce bu modellerde değişkenler için kullanılan diğer sınıflandırmaları da tanımlamak gerekmektedir. Gizil değişkenler kendi aralarında içsel gizil değişkenler ve dışsal gizil değişkenler olarak ayrılırlar. İçsel değişken; değeri model içerisinde açıklanan, dışsal değişken ise değeri model dışında belirlenen ancak içsel değişkenleri etkileyen değişken olarak tanımlanmaktadır. İki dışsal gizil değişken ve bir içsel gizil değişkenden oluşan bir yapısal model için yol diyagramı Şekil 2.2 de verilsin. ġekil 2.2 Üç gizil değiģkenli yapısal model için yol diyagramı Söz konusu yapısal model için ilgili yapısal eşitlikler, (2.1) (2.2) 17
30 şeklinde olacaktır. Modelde yer alan dışsal gizil değişkenleri ve içsel gizil değişkenleri göstermektedir. Dışsal değişkene ait gösterge değişkenler, içsel değişkene ait gösterge değişkenler ile ifade edilmektedir. Modelde açıklanamayan bileşenler başka bir deyişle eşitliklerde yer alan rassal hatalar ile gösterilmektedir. Gizil değişken modellerinde hiçbir gizil değişkenin tam olarak ölçülemeyeceği kabul edildiğinden gizil değişkenlere ait hataların varyansları da modele dâhil edilir. Bu durumda, ilgili içsel gizil değişkendeki, dışsal gizil değişkenler tarafından açıklanamayan hata varyansını göstermektedir. ve hatalarının dışsal değişkenler ile ilişkisiz ve beklenen değerinin sıfır olduğu varsayılır., deki değişim sabitken deki bir birimlik değişimden sonra nin beklenen değerindeki değişimi ifade eder. ve katsayıları için de benzer bir yorum söz konusudur. içsel gizil değişken ile ilgiliyken, ve katsayıları dışsal gizil değişken ile ilgilidirler. Eşitlik 2.1 ve 2.2 ile verilen yapısal modelin matrissel notasyon ile gösterimi, 0 1 [ ] , - [ ] (2.3) şeklinde olacaktır. Söz konusu tanımlamalar ışığında yapısal model için genel matris gösterimi (2.4) şeklinde verilebilir., m değişken sayısını göstermek üzere ( ) boyutlu içsel gizil değişken vektörü ve, n değişken sayısını göstermek üzere ( ) boyutlu dışsal gizil değişken vektörünü ifade eder.,( ) boyutlu hata vektörünü içsel gizil değişkende dışsal değişkenler tarafından açıklanmayan hata varyansını göstermektedir. Hataların dışsal değişkenlerle ilişkisiz ve ortalamalarının sıfır olduğu gizil değişken modelinin temel varsayımlarından biridir. Bu varsayımın ihlal edilmesi durumunda parametre tahmincileri tutarlı olma özelliklerini yitirirler. Ayrıca hata terimlerinin otokorelasyonsuz ve sabit varyanslı oldukları varsayılır. Bir diğer önemli varsayım modelin hem parametreleri hem de değişkenleri açısından doğrusal olmasıdır., ( ) boyutlu içsel değişkenler için yapısal parametreleri 18
31 gösteren matristir. Matrisin köşegen elemanları daima sıfırdır. Bu durum gizil bir içsel değişken üzerinde başka bir gizil içsel değişkenin etkisi olmadığını göstermektedir yani bir değişken kendisinin nedeni olarak görülmemektedir. ise ( ) boyutlu dışsal değişkenler için yapısal parametreleri gösteren matristir. Elemanları ile gösterilmektedir (Bollen, 1989: 12-15). Tablo 2.2 de yapısal modelde yer alan değişkenlerin boyutları, tanımları, modelin genel gösterimi ve varsayımları topluca özetlenmiştir. Tablo 2.2 Yapısal Model için Temel Gösterimler Yapısal Model Genel Gösterimi Varsayımlar ( ) ( ) ( ) ( ) ( ) tekil olmayan bir matris Sembol Ġsim Boyut DeğiĢkenler eta ( ) İçsel gizil değişken ksi ( ) Dışsal gizil değişken zeta ( ) Eşitliklerdeki gizil hatalar Sembol Ġsim Boyut Katsayılar beta ( ) İçsel gizil değişkenler için katsayılar matrisi gamma ( ) Dışsal gizil değişkenler için katsayılar matrisi Sembol Ġsim Boyut Kovaryans Matrisleri phi ( ) ( ) ( ların kovaryans matrisi) psi ( ) ( ) ( ların kovaryans matrisi) 19
32 Yapısal modelin bir parçası da ve kovaryans matrisleridir., ( ) boyutlu denklemdeki hataların kovaryans matrisi olmak üzere tipik elemanı ile gösterilmektedir. nin asal köşegen elemanlarının her biri i. eşitlikte nin açıklayıcı değişkenlerce açıklanamayan kısmına karşılık gelen varyans değeridir. Köşegen dışı elemanlar ise ve arasındaki kovaryansları ifade etmektedirler. ise ( ) boyutlu dışsal değişkenlere ait kovaryans matrisini göstermekte olup tipik elemanı şeklinde gösterilmektedir (Bollen,1989: 16) ÖLÇME MODELĠ Gizil değişkenler ile gözlenen değişkenler arasındaki ilişkileri gösteren yapısal denklemlerin bir bütünü olarak ifade edilen modeller ölçme modeli olarak adlandırılmaktadır. Şekil 2.2 de verilen üç gizil değişkenli yapısal model için, dışsal gizil değişkeninin üç ve ve içsel gizil değişkenlerinin dörder gösterge değişkenle ölçüldüğü varsayılsın. Söz konusu ölçme modeli için ilgili yapısal eşitlikler, gizil değişkeni için (2.5) şeklinde olacaktır. Gizil değişkenleri açıklayan elemanların birbirleri ile ilişkisiz olması varsayımı altında modelin matrissel notasyon ile gösterimi de [ ] [ ], - [ ] (2.6) 20
33 şeklindedir. ve gizil değişkenleri için ise söz konusu eşitlikler ve modelin matrissel notasyon ile gösterimi (2.7) 0 1 (2.8) [ ] [ ] [ ] şeklinde olacaktır. Sonuç olarak ölçme modelinin genel biçimi (2.9) (2.10) eşitlikleri ile verilebilir. Eşitlik 2.9 ve 2.10 sırasıyla, dışsal gizil değişkenler ile gözlenen değişkenler arasındaki ve içsel gizil değişkenlerle gözlenen değişkenler arasındaki yapısal bağlantıları ortaya koyan eşitliklerdir., (i = 1,2,3) in üç göstergesidir. den e kadar olan değişkenler in, ten e kadar olan değişkenler ise nin göstergeleridir. matrislerinin elemanları katsayıları gizil değişkenlerdeki bir birimlik değişimin gözlenen değişkenlerin ortalamasında meydana getirdiği değişimin oranını göstermektedir. ve, sırasıyla dışsal ve içsel değişkenlere ait ölçme hatalarıdır. Ölçme hatalarının beklenen değerinin sıfır olduğu 21
34 ve tüm gizil değişkenler ve gizil değişkenlere ilişkin hatalar ile ilişkisiz oldukları varsayılmaktadır. Ölçme hatalarının söz konusu değişkenlerle ilişkili olması durumunda parametre tahmincileri tutarlı olma özelliklerini yitireceklerdir. Ayrıca ölçme hatalarının gözlemler itibari ile otokorelasyonsuz ve sabit varyanslı olduğu varsayılmaktadır (Bollen, 1989: 18). Tablo 2.3 ile ölçme modelinde yer alan değişkenlerin boyutları, tanımları, modelin genel gösterimi ve varsayımları topluca özetlenmiştir. Tablo 2.3 Ölçme Modeli için Temel Gösterimler Ölçme Modeli Genel Gösterimler Varsayımlar lar lar ( ) ( ) ( ) ( ) ile korelasyonsuz ile korelasyonsuz Sembol Ġsim Boyut DeğiĢkenler - ( ) için gözlenen göstergeler - ( ) için gözlenen göstergeler epsilon ( ) y deki ölçme hataları delta ( ) x deki ölçme hataları Sembol Ġsim Boyut Katsayılar lamda y ( ) y yi ile ilişkililendiren katsayılar lamda x ( ) i ile ilişkilendiren katsayılar Sembol Ġsim Boyut Kovaryans Matrisleri theta-epsilon ( ) ( ) ( ların kovaryans matrisi) theta-delta ( ) ( ) ( ların kovaryans matrisi) 22
35 ve ise ölçme hatalarının kovaryans matrisleri olup, asal köşegen elemanları gözlenen değişkenlere ait hata varyanslarını içerir. Asal köşegen haricindeki elemanlar ise farklı gösterge değişkenler için ölçme hatalarının kovaryanslarıdır. Gözlenen değişkenlere ilişkin hatalar birbirleri ile korelasyonlu olabilirler (Bollen,1989: 19) KOVARYANS VE KORELASYON YAPISI YA modelleri ile iki değişken arasındaki kovaryans ya da korelasyonun model parametrelerinin bir fonksiyonu olarak yazılması mümkün olmaktadır. Bir ilüstüratif model ve kovaryans cebri yardımı ile açıklanmaya çalışılırsa, Şekil 2.3 bir gizil, dört gösterge değişkenli basit bir modeli ifade etsin. ġekil 2.3 Bir gizil dört gösterge değiģkenli yol diyagramı (Bollen, 1989: 35) Burada, dört gösterge değişkene sahip bir gizil değişkeni ifade etmekte olup, modelde ikinci ve üçüncü değişkene ait ölçme hataları haricinde bütün ler korelasyonsuzdur. Bütün ölçme hataları aynı zamanda gizil değişken ile de korelasyonsuz olup, ( ) kabul edilmektedir. 23
36 YA da kovaryans ya da korelasyonların model parametrelerinin bir fonksiyonu olarak nasıl ayrıştırıldığını ifade etmek için bir örnek ele alınırsa; ve değişkenlerine ait kovaryans, 2.5 te verilen eşitliklere benzer şekilde yazılması ve kovaryansının elde edilmesi ile, ( ) ( ) şeklinde elde edilir. Burada ( ) ün gizil değişken nın varyansının bir fonksiyonu olduğu görülmektedir. Değişken sayısı arttıkça cebirsel gösterimler zorlaşacağından matris cebri kullanılarak genel bir model oluşturulursa, söz konusu kovaryans matrisi aşağıdaki şekilde oluşturulabilir. modeli için matrisinin beklenen değeri in kovaryansını oluşturur ve söz konusu matris sembolü ile ifade edilir. ( )( ) ( )( ) ( ) ( ) ( ) ( ) ( ) (2.11) Eşitlik 2.11 den de görülebileceği üzere in kovaryans matrisi,, ve açısından ayrıştırılmıştır (Bollen, 1989: 35) TOPLAM, DOĞRUDAN VE DOLAYLI ETKĠLER YA modelleri etkileri, doğrudan etkiler, dolaylı etkiler ve toplam etkiler olmak üzere üç gruba ayırır. Doğrudan etkiler, bir değişkenin diğer bir değişkene başka bir değişkenin aracılığı olmadan doğrudan etkisi olarak tanımlanırken dolaylı etkiler ise bir değişkenin diğer bir değişkeni başka bir değişken aracılığı ile 24
37 etkilemesinden oluşmaktadır. Toplam etkiler ise, doğrudan ve dolaylı etkilerin toplamı olarak hesaplanmaktadır (Bollen, 1989: 36). Toplam Etkiler = Doğrudan Etkiler + Dolaylı Etkiler Toplam etkiler aynı zamanda iki değişken arasındaki korelasyonun nedensellikten kaynaklanan kısmı, nedensel etkiler, olarak da kabul edilir. Bunun yanı sıra iki değişken arasındaki korelasyonu etkileyen nedensel olmayan etkiler de vardır. Nedensel olmayan etkiler bir değişkenin nedeni olan değişkenlerin korelasyonlu olmasından kaynaklanan analiz edilemeyen etki ve ortak neden değişkenlerinden kaynaklanan sahte etkilerdir (Maruyama,1998: 37). Çalışmanın temelini oluşturan YEM de daha çok nedensel etkiler ile ilgilenileceğinden bu kısımda sadece nedensel etkilerin ayrıntılarına yer verilecektir. YA modellerinde etkilerin ayrıştırılmasını daha iyi açıklamak için yapısal model ve ölçme modelinin bir arada yer aldığı genel model için Şekil 2.4 ile verilen yol diyagramı incelenecektir. ġekil 2.4 Yapısal model ve ölçme modeli birlikte gösterimi (Bollen, 1989: 37) 25
38 Şekil 2.4 e göre, in üzerindeki doğrudan etkisi ile gösterilmektedir. de bir birimlik değişme nin birim kadar değişmesine neden olacaktır. ve arasında aracılık eden başka bir değişken yoktur. in, üzerinde doğrudan etkisi iken, nin üzerindeki etkisi dir. Dolaylı etkiler ise, örneğin in, üzerinde etkisi göz önünde bulundurulduğunda değişkeni aracılığı ile gerçekleşmektedir. deki bir birimlik değişme de birim beklenen değişmeye neden olur. de bu birimlik beklenen değişim ise de kadar doğrudan bir değişime neden olur. Böylece in üzerindeki dolaylı etkisi olmaktadır. Benzer şekilde in üzerindeki dolaylı etkisi şeklindedir (Bollen,1989: 36-37) DOĞRULAYICI FAKTÖR ANALĠZĠ Çalışmanın bu kısmında öncelikle doğrulayıcı faktör analizine temel olan açıklayıcı faktör analizi ve ardından teorik ayrıntıları ile doğrulayıcı faktör analizi incelenecektir AÇIKLAYICI FAKTÖR ANALĠZĠ Açıklayıcı Faktör Analizi (AFA), çok sayıda gözlenen değişken arasındaki ilişkiyi nispeten daha az sayıda gizil değişken ile açıklamak için kullanılan bir veri indirgeme yöntemi olarak da tanımlanan önemli bir, çok değişkenli istatistiksel tekniktir. Aksi belirtilmediği sürece faktör analizi, AFA olarak kabul edilir. AFA, bir dizi gözlenen değişken ile az sayıda bilinmeyen gizil rassal değişken arasındaki korelasyonu açıklamaya çalışan nedensel bir modeldir. İlk olarak 1900 lü yılların başlangıcında Spearman tarafından insan zekâsını modellemek amacı ile ortaya atılan AFA nın temeli olarak gösterilebilecek bu çalışmada, birkaç disipline ait test skorları ile gizil bir değişken olan insan zekâsı arasındaki nedensel ilişkinin ortaya konması amaçlanmıştır. Spearman a göre kişilerin birbirleri ile ilişkili olduğu varsayılan test skorları arasındaki ilişkiyi insan zekâsı adı 26
39 verebileceğimiz tek bir ortak gizil faktör ile açıklamak mümkündür. Spearman (1904) ın tek faktörlü modeli daha sonra Thurstone (1931, 1947) tarafından çok faktörlü olarak geliştirilmiştir (Timm, 2002: 496). Birbirleri ile ilgili gözlenen çok sayıda değişkenin sayısını azaltmak, başka bir deyişle boyut indirgemek ve söz konusu değişkenler arasındaki ilişkilerden yararlanarak yeni yapılar, yeni gizil değişkenler tanımlamak için kullanılan bir teknik olarak özetleyebileceğimiz AFA analizinin temel modeli Şekil 2.5 teki gibi gösterilebilir. ġekil 2.5 Açıklayıcı faktör analizi modeli (Üç faktörlü model) Burada YA da olduğu gibi, çemberler ile ifade edilen değişkenler gizil değişkenleri, kare simgesi ile ifade edilen değişkenler ise gözlenen değişkenleri göstermektedir. Gizil değişkenlerden gözlenen değişkenlere doğru tek yönlü çizilen oklar ise, gizil değişkenin gözlenen değişken üzerindeki nedensel etkisini ifade 27
40 etmektedir. Gizil değişkenler arasındaki çift yönlü eğrisel oklar ise gizil değişkenler arasındaki nedensel ilişkiyi ifade etmektedir. Şekilde ifade edilen model 7 gözlenen, 3 gizil değişkenden oluşan bir AFA modelidir. ile ifade edilen faktörlerin etkileri ler ile ifade edilen gözlenen değişkenlerin hepsinin üzerinde ayrı ayrı görülmektedir. Bir gizil değişkenin etkisi birden çok gözlenen değişken üzerinde ortak olarak görülmesi nedeniyle bu değişkenlere başka bir deyişle faktörlere ortak faktör adı verilmektedir. ile ifade edilen faktörler ise her bir gözlenen değişkene ait hataları göstermekte olup sadece ilgili olduğu gözlenen değişkeni etkilediğinden bu faktörlere tekil faktörler adı verilmektedir. AFA modelinde faktörler ve değişkenler arasındaki nedensel yapıyı araştırmacı belirleyememektedir, araştırma öncesinde herhangi bir önsel bilgiye dayanılmamaktadır. Araştırmacı kısmen de olsa gözlenen değişken sayısı ve ortak faktör sayısı haricinde analize müdahale edememektedir (Long, 1983: 11-12). AFA nın uygulanabilmesi için bazı temel varsayımların gerçekleşmesi gerekmektedir. Söz konusu varsayımlar istatistiksel olmaktan çok kavramsal varsayımlardır. Çok değişkenli normal dağılıma uygunluk ve doğrusallık gibi istatistiksel varsayımlardan sapmalar durumunda hesaplanan korelasyon katsayıları küçülecektir. Normallik varsayımı ise yalnızca faktörlerin anlamlılığı test edilecekse gereklidir. AFA da değişkenler arasındaki iç ilişkiler araştırıldığından, burada en önemli varsayım değişkenler arasında belirli bir oranda çoklu doğrusal bağlantının var olmasıdır (Hair v.d., 1998: ). Söz konusu istatistiksel varsayımların yanı sıra kavramsal varsayımlar ise aşağıdaki şekilde özetlenebilir: 1. Tüm ortak faktörler korelasyonsuz ya da hepsi birbirleriyle korelasyonludur. 2. Gözlenen değişkenler, tüm ortak faktörler tarafından doğrudan etkilenir. 3. Tekil faktörler arasında korelasyon yoktur. 4. Ortak faktörler ile tekil faktörler arasında korelasyon yoktur (Long, 1983: 11-12). 28
41 AFA nın temel amacı gözlenebilen ve ölçülebilen çok sayıda değişkenin arkasında yatan, gözlenemeyen başka bir deyişle ölçülemeyen gizil yapıları ortaya çıkarmak olup aynı zamanda elde edilen bu yapılar ile daha sonra regresyon, korelasyon ya da diskriminant analizi gibi analizlerde orijinal değişkenlerin yerine kullanılacak faktörleri elde etmeye de yardımcı olmaktadır. Değişkenler arasındaki ilişkilere dayanarak uygulanan faktör analizine R-tipi Faktör Analizi adı verilmektedir. Birimler arasındaki ilişkilere dayanarak gerçekleştirilen faktör analizi ise Q-tipi Faktör Analizi olarak adlandırılmaktadır (Hair v.d., 1998: 95-97). Uzun yıllardır pek çok disiplinde kullanılan ve ilgi gören faktör analizi ile ilgili literatür oldukça kapsamlı ve geniştir. Bu alanda temel çalışmalar arasında en kapsamlı olanları Harmon (1976), Mulaik (1972) ye aittir. Bunun yanı sıra ilerleyen yıllarda konu ile ilgili gelişmeler Jöreskog ve Sörbom (1979), McDonald (1985), Bollen (1989), Basilevsky (1994) gibi yazarlardan takip edilebilmektedir (Timm, 2002: 497) DOĞRULAYICI FAKTÖR ANALĠZĠ MODELĠ İlk olarak 1970 lerde Jöreskog tarafından geliştirilen Doğrulayıcı Faktör Analizi (DFA), önsel olarak hiçbir teorik bilgi içermeyen AFA dan farklı olarak faktör yapısı ile ilgili kesin teorik bir önsel bilginin var olduğu durumlarda verinin söz konusu faktör yapısını doğrulayıp doğrulamadığını test etmek için kullanılan bir yöntemdir (Timm, 2002: 497). DFA modelleri, gizil değişken modellerinin daha geniş bir sınıfını kapsayan ve ilerleyen bölümlerde ayrıntıları ile incelenecek olan YEM in temel bir bileşenidir. Gözlenen değişkenlerle gizil yapılar arasındaki ilişkiyi ölçme modelleri ile tasvir eden bir YEM türü olarak kabul edilen analiz, ölçme modellerinin doğruluğunu sınamak için de kullanılmaktadır. Ayrıca hem AFA modelleri hem de 29
42 DFA modelleri genel lineer modeller çerçevesinde incelenmektedirler (Thompson, 2004: ). DFA modeli ile örneklem verilenin başlangıçtaki teorik modeli doğrulayıp doğrulamadığının araştırılması amaçlanır. Bu durumu sağlayan bir faktör yapısının varlığı ve söz konusu yapının istatistiksel olarak anlamlılığı test edilmektedir. Bunun sonrasında modele uygun olan ek örneklem verisiyle, hipotezlenen modelin geçerliliği doğrulanır (Schumacker ve Lomak; 2004: 168). Kısıtlı Faktör Analizi olarak da bilinen DFA, teorik modeli gerçekten ifade edebilen mantıklı kısıtların modele dahil edilebilmesini sağlar (Jöreskog, 1969: 184). DFA nın uygulanabilmesi için araştırmacı üç temel unsur hakkında bilgi sahibi olmalıdır. Bunlar; (1) Kullanılacak faktör sayısı, (2) Hangi değişkenlerin hangi faktörleri belirlediği, (3) Faktörlerin korelasyonlu olup olmadığı şeklindedir. AFA ile DFA arasındaki ilişkiyi ve temel farklılıkları ortaya koymak için Şekil 2.6 incelenebilir. ġekil 2.6 Doğrulayıcı faktör analizi modeli (Üç faktörlü model) 30
43 Şekil 2.6 da 3 ortak faktör ve 7 gözlenen değişkenden oluşan DFA modeli yer almaktadır. AFA nın temel varsayımı ortak faktörlerinin tümünün korelasyonlu olması ya da hepsinin ilişkisiz olması idi, DFA modelinde ise ortak faktörlerin korelasyonlu olduğu varsayılmaktadır. Aynı zaman AFA da gözlemlenen değişkenler bütün ortak faktörlerden etkilenirken DFA da gözlemlenen değişkenler bazı ortak faktörlerden etkilenmektedirler. Şekildeki eğri oklardan anlaşılacağı üzere ortak faktörler kendi aralarında ve tekil faktörlerden bazıları kendi aralarında korelasyonlu olmasına olanak tanınmaktadır. AFA daki gözlenen değişkenlerin her birine ait tekil faktörler olması gerektiği varsayımı DFA da ortadan kalkmaktadır. DFA modeli ile AFA da kısıtlamaların pek çoğu ortadan kalkmaktadır. Bunlar aşağıdaki şekilde, 1. Hangi ortak faktör çiftlerinin ilişkili olabileceği, 2. Hangi gözlenen değişkenlerin, hangi ortak faktörler tarafından etkileneceği, 3. Hangi gözlenen değişkenlerin tekil faktörler tarafından etkileneceği, 4. Hangi tekil faktör çiftlerinin ilişkili olacağı, 5. Analizden önce faktörlerin sayısı belirlenebilinmesi (Long, 1983: 16) olarak özetlenebilir. Varsayımsal bir faktör modelinin verilere uyumunu test eden DFA modeli diğer modellere en büyük üstünlüğü ortak faktörler arasındaki yapısal ilişkilere izin vermesidir. Gizil değişkenlerin ölçme hatalarını gidererek tahmin edilmesini sağlayan ölçme modellerinde, birden çok gösterge değişkene sahip modellerde ve ortak faktörler arasındaki korelasyonların belirlenmesinde, her bir özelliğin ölçme yöntemlerinin bozucu etkilerini gidermek amacıyla birden çok yöntemle ölçüldüğü çoklu özellik-çoklu grup (Multitrait-Multimethod Model) modellerinde, gözlenen değişkenlere doğrudan etkisi olmadığı halde bu değişkenleri etkileyen gizil değişkenleri etkileyen gizil değişkenler olması durumunda yani yüksek mertebe faktör modellerinde kullanılması oldukça faydalı olmaktadır (Rindskopf ve Rose, 1988: 52). Ayrıca DFA bir ölçüm aracının gizil yapısını 31
44 belirlemek için ölçek geliştirme sürecinde ve uygulamalı araştırmalarda çok maddeli ölçme araçlarının psikometrik değerlendirilmesi için de kullanılmaktadır (Floyd ve Widaman, 1995) MODELĠN TEORĠK YAPISI DFA modeli ile ilgili analizlerin gerçekleştirilebilmesi için bazı önsel bilgilere ihtiyaç vardır. Bunlar daha önceki kısımlarda da belirtildiği gibi ortak faktör sayısı, değişken sayısı, hangi değişkenlerin hangi ortak faktörlerle ilişkili olduğu ve hem tekil faktörler hem ortak faktörlerin kendi aralarındaki ilişkilerdir. Bu önsel bilgilere sahip olunduğunda DFA modeli, gözlenen değişkenlere ait eşitlikler Eşitlik 2.9 ve 2.10 ile verilen ölçme modellerine eşit olacak şekilde, ve şeklinde ifade edilir. Burada x ve y gözlemlenen değişkenler, dışsal gizil değişken içsel gizil değişken, dışsal gizil değişkenli modelde tekil faktörlerin varyansı ve içsel gizil değişkenli modelde tekil faktörlerin varyansını göstermektedir. Gizil değişkenlerin gösterge değişkenler üzerindeki etkileri ve katsayılar matrislerinin elemanları ile belirlenmektedir. Örneğin Eşitlik 2.9 için ( ) ve ( ) varsayılmaktadır. ile belirtilen tekil faktörler ya da hatalar olarak tanımladığımız değişken ise iki bileşenden oluşmaktadır. (2.12) Burada s her değişkenin kendine özgü varyansı ve e ise te geriye kalan rassal hata bileşenini göstermektedir. Bu iki bileşen birlikte in tekil faktörünü oluştururlar. Her iki bileşende ölçülürken teki hatayı temsil etmelerinin yanı sıra birbirileri ile 32
45 ve ile korelasyonsuz olduklarından rassal ölçme hatası olarak adlandırılmaktadırlar (Bollen, 1989: 233). DFA modelinin kovaryans yapısının incelenmesi için ise 2.9 eşitliği kullanılırsa, in kovaryans matrisi in beklenen değerine eşit olacaktır. Kovaryans matrisi nın bir fonksiyonu olmak üzere, ( ) ( ),( ) ( )- = E ( ) + ( ) (2.13) şeklinde ifade edilir ile verilen kovaryans denkleminde gizil değişkenlerin kovaryans matrisini ve da ölçme hataları için kovaryans matrisini ifade etmektedir (Bollen, 1989: 236). Şekil 2.7 ve 2.8 ile sırasıyla dışsal gizil ve içsel gizil değişkenler için örnek DFA modellerinin yol diyagramları, temel gösterimler, terimler ve anlamlarına yer verilmiştir. 33
46 Adı Parametre Matris Türü Tanımlama Lamda-x Regresyon Faktör yükleri Theta delta Varyans-kovaryans Hata varyans ve kovaryansları Phi Varyans-kovaryans Faktör varyans ve kovaryansları Tau-x Ortalama vektör Gösterge kesişimleri Kappa κ Ortalama vektör Gizil ortalamalar Ksi Vektör Dışsal değişkenlerin isimleri ġekil 2.7 DıĢsal gizil değiģkenli DFA modeli ve temel gösterimler*(brown, 2006: 55) Şekil 2.7 bir hata kovaryansı ile iki faktörlü bir DFA modeli için dışsal gizil değişken gösterimi iken Şekil 2.8 bir hata kovaryansı ile iki faktörlü bir DFA modeli için içsel gizil değişken gösterimini ifade etmektedir. DFA modellerinde dışsal değişkenler in eşiti olarak gösterilebilir, bağımsız değişken ya da açıklayıcı değişkenler olarak adlandırılırlar. İçsel değişkenler ise ye eşit olmakta ve bağımlı değişken olarak adlandırılmaktadır (Brown, 2006: 54). 34
47 Adı Parametre Matris Türü Tanımlama Lamda-y Regresyon Faktör yükleri Theta epsilon Varyans-kovaryans Hata varyans ve kovaryansları Psi Ψ Varyans-kovaryans Faktör varyans ve kovaryansları Tau-y Ortalama vektör Gösterge kesişimleri Alfa Ortalama vektör Gizil ortalamalar Eta Vektör Dışsal değişkenlerin isimleri ġekil 2.8 Ġçsel gizil değiģkenli DFA modeli ve temel gösterimler*(brown, 2006: 56) Şekil 2.7 ve 2.8 ile verilen şekillerde, gizil değişkenlerden ( ve ) gözlenen değişkenlere ( ve ) doğru tek yönlü oklar gizil değişkenlerin başka bir deyişle ortak faktörlerin gözlenen değişkenler üzerinde doğrudan etkisini göstermektedir. λ ile gösterilen katsayılar ise regresyon katsayılarını ifade etmektedir. 35
48 ve gözlenen değişkenlere ait hata varyans ve kovaryanslarının simetrik matrisini ifade etmektedirler. gizil içsel değişkenin kullanıldığı modeller için ise dışsal gizil değişkenin kullanıldığı modeller için kullanılmaktadır. ve değerleri, tek yönlü ok ile gösterge değişkenlere bağlanmış olsalar da bir regresyon ilişkisini ifade etmezler. Ortak faktörler başka bir deyişle içsel ya da dışsal gizil değişkenler arasındaki korelasyonlar çift yönlü eğri oklarla belirtilmiştir. Ψ ve ϕ sembolleri ile gösterilen katsayılar λ lardan farklı olarak regresyon katsayılarını değil faktör varyansları ve kovaryanslarını ifade eder. Söz konusu modelleri matrissel notasyonla ifade edersek matrisi aşağıdaki şekilde ifade edilir: [ ] Burada örneğin; katsayısı in dışsal gizil değişken üzerindeki etkisidir. Benzer şekilde faktörler arasındaki ilişkileri ifade eden matris, [ ] şeklinde olup, burada ve ile gösterilen matrisin köşegen elemanları ortak faktörlerin varyanslarını ise faktör kovaryansını ifade etmektedir. Şekil 2.7 de yer alan matrisi ise köşegen elemanları hatalardan oluşan ( ) boyutlu simetrik bir matristir. 36
49 [ ] Burada örneğin;, ve değişkenlerinin ölçme hatalarının kovaryansını ifade etmektedir (Brown, 2006: 58) MODELĠN TANIMLANMASI DFA modellerinde parametre tahminlerinin hesaplanabilmesi için ölçme modellerinin tanımlanmış olması gerekmektedir. Bir DFA modelinin tanımlanabilir olması için modelde yer alan ve değerleri bilinmeyen her bir parametre için parametre tahminlerinin bir tek setinin elde edilmesi gerekmektedir ancak bu durumda modelin tanımlanmış olduğundan bahsedebilinir (Brown, 2006: 62). Orta derecede karmaşık modeller ile ilgilenildiğinde cebirsel yöntemler ile modelin tanımlanabilirliğini araştırılması oldukça zor bir süreçtir. Söz konusu durumlar için DFA modellerinin tanımlanabilirliğinin araştırılması amacıyla geliştirilen yöntemler mevcuttur. Bunlardan başlıcaları t-kuralı, iki gösterge kuralı ve üç gösterge kuralıdır (Bollen, 1989: 242). Tanımlama ölçütlerinin kullanılabilmesi için her biri ölçülemeyen, gözlenemeyen teorik yapılar olarak adlandırdığımız her bir gizil değişkenin tanımlanmış bir ölçeğe sahip olması gerekmektedir. Bu durumda DFA analizinde gizil değişkenlerin bir ölçekle tanımlanması için iki yaklaşım kullanılmaktadır. Bunlardan ilki gizil değişkenin ilgili gösterge değişkenlerinden birinin ölçü birimini, gizil değişkenin ölçü birimi olarak kabul etmektir. Söz konusu gösterge işaretleyici veya referans göstergesi olarak adlandırılmakta ve bu yaklaşım araştırmacılar 37
50 tarafından en çok tercih edilen en popüler yaklaşım olmaktadır. İkinci yaklaşım ise, gizil değişkenlerin varyansının belli bir değere sabitlenmesidir. Genellikle bir olarak kabul edilen bu değer sayesine modeldeki değişkenlerin standartlaştırılması sağlanır (Brown, 2006: 62-63) t KURALI t kuralından bahsetmek için öncelikle Eşitlik 2.13 ile verilen DFA modelinin kovaryans yapısını incelemek gerekmektedir. ( ) matrisi, q gözlenen değişken sayısı ve n gizil değişken sayısını göstermek üzere qn tane elemana sahiptir. matrisinde ( ) tane artıksız parametre ve hata varyansları matrisinde ( ) tane tekil parametre bulunmaktadır., ( ) ( ) tane parametrede bileşenlerine ayrılır. teki tane değişken ile, ( ) tane tanımlanabilen parametreye sahiptir. Eğer, ve daki parametrelerin hiçbiri bilinmez ise, in kovaryans matrisindeki bilinen ( ) tane parametre ile daki ( ) ( ) tane eleman için çözüm bulmak mümkün olmamaktadır. Bu nedenle yapılması gereken kısıtlama t, daki serbest değişkenlerin sayısını göstermek üzere, ( ) (2.14) şeklindedir. Söz konusu eşitlik DFA modelinin tanımlanmasında t kuralı olarak bilinir ve serbest parametre sayısı, in kovaryans matrisindeki tekil elemanların sayısına eşit veya fazla olması durumunda DFA modeli tanımlanabilir olarak yorumlanmaktadır. t kuralı tanımlama için gerekli ancak yeterli olmayan bir koşuldur (Bollen, 1989: ). 38
51 ÜÇ GÖSTERGE KURALI Üç gösterge kuralı tanımlanabilirlik için yeterli ancak gerekli olmayan bir koşuldur. Tek gizil değişkenli bir DFA modeli için yeter şart, yükleri sıfırdan farklı en az üç göstergenin bulunmasıdır. Çoklu faktör modellerinde ise, üç gösterge kuralının geçerli olması için, 1. Her gizil değişken için üç veya daha fazla gösterge değişken bulunması, 2. her bir satırında yalnızca bir tane sıfırdan farklı eleman bulunması, 3. in köşegen bir matris olması gerekmektedir. Üç gösterge kuralına göre söz konusu şartların sağlanması durumunda DFA modeli tanımlanabilmektedir (Bollen, 1989: 244) ĠKĠ GÖSTERGE KURALI Birden çok içeren modellerin tanımlanabilirliği için alternatif bir yöntem olan iki gösterge kuralı yeterli bir koşuldur. Tıpkı üç gösterge kuralında olduğu gibi burada da nin köşegen bir matris olduğu ve her bir gizil değişkenin ölçeklendirilmiş olduğu varsayılmaktadır. Bu koşullar altında her gizil değişken için iki gösterge değişkene sahip ölçme modeli, her için matrisinde sıfır elemanı bulunmadığı sürece tanımlıdır. Daha sonra çok faktörlü modellerin tanımlanabilirliğinin araştırılmasında bu model genelleştirilmiş ve aşağıdaki dört koşulun sağlanması durumunda modelin tanımlanabilir olduğu ifade edilmiştir. 1. her bir satırında yalnızca bir tane sıfırdan farklı eleman bulunması, 2. Her gizil değişken için en az iki gösterge değişken bulunması, 3. nın her bir satırında en az bir köşegen dışı sıfırdan farklı eleman bulunması, 4. in köşegen bir matris olması gerekmektedir. 39
52 Söz konusu koşulların başlangıçtaki iki gösterge koşulundan temel farkı nın bazı köşegen dışı elemanlarının sıfır olmasına imkân tanımasıdır (Bollen, 1989: ). Buraya kadar verilen kurallar çerçevesinde DFA modelleri eksik tanımlanmış, tam tanımlanmış ve aşırı tanımlanmış olarak üç farklı durumda karşımıza çıkmaktadır. Burada dikkat edilecek husus modelde serbest tahmin edilen parametre sayısı ile girdi matrisinin eleman sayısının karşılaştırılmasıdır. Serbest tahmin edilen parametre sayısının girdi matrisinin eleman sayısına eşit olması durumunda model tam tanımlanmış, serbest tahmin edilen parametre sayısının girdi matrisinin eleman sayısından büyük olması durumunda model eksik tanımlanmış, serbest tahmin edilen parametre sayısının girdi matrisinin eleman sayısından küçük olması durumunda model aşırı tanımlanmış olur MODELĠN TAHMĠNĠ DFA modelinin tanımlanabilirliği araştırıldıktan sonra model parametreleri tahmin edilebilir. DFA modellerinin tahmini için kullanılan yöntemlerden başlıcaları: En Çok Olabilirlik Yöntemi (EÇO), Genelleştirilmiş En Küçük Kareler Yöntemi (GEKK), Ağırlıklandırılmamış En Küçük Kareler Yöntemi (EKK) olarak sayılabilir. DFA modelinde bütün tahmin yöntemleri için amaç fonksiyonu modelden elde edilen kovaryans matrisi ile örneklemden elde edilen kovaryans matrisi arasındaki farkın en az olmasını sağlayan parametre tahminlerini elde etmektir. Sırası ile EÇO, GEKK ve EKK yöntemlerine ait amaç fonksiyonları aşağıda verilmiştir. ( ). ( )/ (2.15). /.{[( ( )) ] } / (2.16) 40
53 . /,( ( )) - (2.17) Söz konusu yöntemler çalışmanın Kısım 3 te ayrıntıları ile inceleneceğinden bu kısımda yalnızca amaç fonksiyonlarının verilmesi ile yetinilmiştir DOĞRULAYICI FAKTÖR ANALĠZĠ MODELĠNĠN DEĞERLENDĠRĠLMESĠ Modelin tahmininden sonra değerlendirilmesi aşamasına geçilmektedir. Bir modelin kabul edilebilir olması için, modelin veriye ne derece uyumlu olduğunun ölçülmesi gerekmektedir. Bu nedenle gerek DFA gerek YA gerekse YEM için kullanılabilecek pek çok istatistiksel ölçüt geliştirilmiştir. Uyum ölçütleri olarak adlandırılan bu ölçütler ayrıntıları ile Kısım 3 te incelenecektir ÖLÇME MODELLERĠNDE GEÇERLĠLĠK VE GÜVENĠLĠRLĠK Ölçme bir nesne, olgu ya da tutuma ait bir özelliği sayılabilir simgelerle göstermektir. Bilimsel ölçümler belirli bir olguyla ilgili olarak değer oluşturmaya ya da önceden belirlenmiş bir değerle karşılaştırma yapmaya yöneliktir (Çakmur, 2012: 339). Gizil değişken modellerinde ise ölçme, bir kavramın bir veya daha çok gizil değişkene, gizil değişkenlerin de gözlenen değişkenlere bağlandığı bir süreçtir (Carmines ve Zelner, 1979: 9). Gizil değişkenler ölçme modellerinde kavramları temsil etmektedirler. Gözlenen değişkenler ise anket sorularına verilen cevaplar, uzunluk ölçümleri, sayım ölçümleri gibi gözlem yolu ile elde edilebilen verilerdir. Gizil değişkenler için ölçüm süreci dört aşamadan oluşmaktadır. 1. Kavrama anlam verilmesi 41
54 2. Kavramı temsil eden boyutların ve gizil değişkenlerin belirlenmesi 3. Ölçeklerin oluşturulması 4. Ölçekler ile gizil değişkenler arasındaki ilişkilerin tanımlanması Kavrama anlam verilmesi başka bir deyişle kavramın tanımlanması, kavrama ait boyutların da ortaya konmasını sağlar. Boyutlar her biri bir gizil değişken ile ifade edilirken, söz konusu tanım bağlamında boyutlar iki veya daha fazla gösterge ile ölçülmektedir (Bagozzi, 1994: 2-3). Ölçümlerde, yapılan ölçümün genellenebilirliğini gösteren önceden saptanmış bir norm yok ise güvenilirlik ve geçerlilik sorunu ortaya çıkar. Klasik ölçüm kuramında güvenilirlik; test veya ölçek sonuçlarının kavramsal yapıya ilişkin olguyu doğru bir şekilde ortaya çıkarması, ölçüm sonuçları farklı yerlerde uygulandığında benzer sonucu vermesidir. Modern ölçüm kuramında ise güvenilirlik örneklemden bağımsız olarak maddeye verilen yanıtın fonksiyonudur. Bir ölçümün güçlü olmasını sağlayan ikinci unsur geçerliliktir. Geçerlilik ölçümün amacına uygunluk ve ölçüm yapılan kitleye genelleme yapabilme anlamına gelir. Ölçüm aracının ölçmeyi amaçladığını ölçebilirliği, geçerlilik kavramıyla değerlendirilir. Geçerlilik, test sonucuyla ne yapılabileceğini belirler (Çakmur, 2012: 339) GEÇERLĠLĠK Geçerlilik ölçülmek istenilen özelliğin amaca uygun olarak ölçülme derecesi olarak tanımlanmaktadır. Geçerlilik, kapsam geçerliliği, ölçüt geçerliliği, yapı geçerliliği ve yakınsama geçerliliği olarak dört başlık altında incelenmektedir. Kapsam geçerliliği, ölçme aracı içindeki maddeler veya soruların ölçme aracının ölçmeyi amaçladığı konuları dengeli bir şekilde temsil etme derecesidir (Cronbach, 1990: 171). 42
55 Ölçüt geçerliliği, bir ölçü ve bir ölçüt değişkeni arasında korelasyon kullanılarak elde edilen uyumun derecesidir. Bu geçerlilik türünde elde edilen ölçümlerin karşılaştırılması için standart bir değişkene ihtiyaç duyulur ve bu değişken ölçüt değişkeni olarak adlandırılır (Çelik, 2009: 85). Yapı geçerliliği, bir ölçünün kuramsal tanımı ile tutarlı olacak şekilde diğer gözlenen değişkenler ile ilişkili olup olmama durumunun değerlendirilmesidir. Yapılar arasında aynı yönlü ya da ters yönlü bir ilişki hipotezi olabileceği gibi, yapılar arasında birliktelik olmadığı yönünde bir tanımlama da yapılabilmektedir. Tek başına test edilen tek bir test ya da yaklaşım olmamakla birlikte yapı geçerliliği, yapılar arasındaki kuramsal ilişkiler hakkında hipotezlerin kurulması, değişkenler arası korelasyonların tahmin edilmesi ve tahmin edilen korelasyonlar ile yapılar ve önerilen diğer ilişkilerin yeniden incelenmesi aşamalarından oluşmaktadır (Şimşek, 2007: 114). Yakınsama geçerliliği, genellikle çoklu özellik-çoklu grup (Multitrait-Multimethod Model) analizlerinde uygulanmakta ve aynı özelliğin farklı ölçüleri arasındaki korelasyonların istatistiki olarak anlamlı ve yeteri derecede yüksek olmasını gerektirmektedir (Laroche v.d., 2001: 32). Geçerlilik kavramının klasik tanımlarından çok YEM çalışmalarında ölçme modellerinin geçerliliği çalışmanın konusunu oluşturmaktadır. Ölçme modellerinde geçerlilik, gözlenen değişken ile bir gizil değişken arasında nedensel bir ilişkinin varlığı olarak tanımlanabilir. Örneğin, nin ölçüsünün geçerliliği ve arasındaki yapısal ilişkinin büyüklüğünü göstermektedir. Literatürde bu temel mantık ile oluşturulan pek çok geçerlilik ölçütü mevcuttur. Sıklıkla kullanılan ölçütler aşağıda incelenecektir. StandartlaĢtırılmamıĢ Geçerlilik Katsayısı: Bu katsayı ve arasındaki yapısal ilişkinin doğrudan ölçüsü olan katsayısıdır. Bu katsayılar çoklu regresyondaki 43
56 katsayıları gibi yorumlanmaktadırlar. standartlaştırılmamış geçerlilik katsayıları farklı kitlelerden gelen örneklemlerin karşılaştırılmasında da kullanılmaktadır. StandartlaĢtırılmıĢ Geçerlilik Katsayısı: Bu ölçü farklı gizil değişkenlerin aynı ölçü üzerindeki etkilerinin ve gizil değişkendeki ölçülerin etkilerinin birbiri ile karşılaştırılmasında kullanılır. Standartlaştırılmış geçerlilik katsayısı, ( ( ) * şeklinde tanımlanır ve standartlaştırılmış regresyon katsayıları gibi yorumlanır. Bu ölçünün dezavantajı farklı kitlelerin karşılaştırılması için uygun olmamasıdır. Özgün Geçerlilik Varyansı: Bu ölçü ( ) şeklinde formüle edilmiş olup nin açıklanan varyansının tarafından açıklanan kısmını ifade eder. Özgün geçerlilik katsayısı, 0 ile 1 arasında değer alabilmektedir. nin varyansının yalnızca bir tarafından açıklanması durumunda değerini almaktadır. nin varyansının yalnızca bir tarafından açıklanmaması durumunda 0 olmaktadır. Doğrusal Bağlantı Derecesi: Bir ölçüyü etkileyen birden çok gizil değişkenin yer aldığı modellerde, gizil değişkenler arasında yüksek korelasyon olması durumunda özgün geçerlilik varyansı düşük çıkmaktadır. Bu durumda nin de doğrudan etkisi olan diğer gizil değişkenlerle regresyonundan elde edilen çoklu belirginlik katsayısı YEM de doğrusal bağlantı derecesi olarak 44
57 ( ) ( ) ( ) şeklinde tanımlanan geçerlilik ölçüsüdür (Şimşek, 2007: 119) GÜVENĠLĠRLĠK Güvenilirlik ölçümün tutarlılığının bir ölçüsü olarak tanımlanabilir. Gözlenen bir değişken olan ölçü değişkeni ve bu ölçünün gizil değişkeni arasındaki belirginlik katsayısı olarak güvenirliliğin bir ölçüsüdür. Güvenilirlik için ölçme aracının tekrarlanabilir ve aktarılabilir özellikte olması gerekmektedir. Güvenilirlik bir ölçme aracında bütün soruların birbiriyle tutarlılığını ortaya koyan bir kavramdır. Güvenilirlik ve geçerlilik bir ölçme arasında bulunması gereken iki farklı kavram olup, güvenilir olan bir ölçme aracı geçerli olmayabilmektedir. temel eşitlik, Klasik ölçme teorisinde güvenilirliğin açıklanması amacı ile oluşturulan şeklinde olup burada, i. gözlenen değişkeni (test skoru) ve şeklinde ifade edilen hata terimini ve ise nin temel oluşturduğu gerçek puanı göstermektedir. ( ) ve ( ) varsayılmaktadır. İki ölçümün korelasyonu onların gerçek puanlarının ilişkisinden meydana gelmektedir. Gerçek puanlar gözlenen değişkenlerin ilişkilerinin neden olduğu sistematik bileşenlerdir. Paralel, tau-eşdeğer (tau-equivalent) ve konjenerik (türdeş) ölçümler test teorisindeki gözlenen değişkenlerin üç ana türüdür (Bollen, 1989: ). ve ölçümleri, 45
58 şeklindedir. ve ilişkisiz ve gerçek puanlar ve birbirine eşit olduğu varsayılır. Eğer ve bire eşit ve de ( ) ( ) ise ve ölçümleri paralel ölçümlerdir. Bu iki maddenin ortalamaları, kovaransları ve faktör yükleri birbirine eşittir. Eğer ve bire eşit ancak ( ) ( ) ise ve ölçümleri paralel ölçüm tau-eşdeğerdir. Son olarak ve birbine eşit değil ve ( ) ( ) ise ölçümler konjeneriktir. Konjenerik ölçümler bu üç tür içinde en genel olanıdır. güvenilirlik ölçüsü, ( ) ( ) şeklinde tanımlanmaktadır. ( ), ( ) ( ) ye eşit ve ( ) negatif olmadığı için güvenilirlik hiçbir zaman birden büyük olamaz. Tau-eşdeğer ve paralel ölçümler için güvenilirlik, ( ) ( ) şeklinde gözlenen değişkenlerin varyanslarının, gerçek puanlara ilişkin varyanslara oranıdır (Bollen,1989: 208). Klasik ölçme teorisinde, ölçülerin güvenilirliklerini tahmininde genel olarak; test-tekrar test, alternatif form yaklaşımı, yarıya bölme ve Cronbach s yöntemleri kullanılmaktadır (Carmines ve Zeller, 1979:37). 46
59 3. BÖLÜM YAPISAL EġĠTLĠK MODELLEMESĠ Bu bölümde, ikinci kısımda incelenen DFA ve YA modellerini birlikte ele alan gizil değişken modelleri başka bir deyişle Yapısal Eşitlik Modelleri (YEM) incelenecektir. YEM modelleri, hem gözlenen değişkenlerle gizil değişkenler arasında ilişki kuran ölçme modellerini hem de gizil değişkenlerin kendi aralarındaki ilişkiyi analiz eden yapısal modelleri birlikte ele alma avantajına sahip modellerdir. Çalışmanın bu bölümünde öncelikle YEM in özel bir hali olan gözlenen değişkenlerle yapısal eşitlik modellemesi (GDYEM) kısaca incelenecek ve daha sonra gizil değişkenler için yapısal eşitlik modellemesi bütün teorik ayrıntıları ile incelecektir GÖZLENEN DEĞĠġKENLERLE YAPISAL EġĠTLĠK MODELLEMESĠ Gözlenen değişkenlerle yapısal eşitlik modelleri, regresyon temelli modeller olup bir içsel değişkeni açıklamaya yönelik tek denklemli ya da birden çok denklem içeren eşanlı bir sistemden oluşabilen modellerdir. GDYEM için temel varsayım, içsel ve dışsal değişkenlerin ölçme hatası olmadan doğru gözlenmiş olduklarıdır. Eğer bir ölçme hatası mevcut olsa da bu hatanın herhangi bir denklemde dışsal değişken olarak görev yapmayan içsel değişkenden kaynaklanmasına izin verilmektedir. GDYEM için genel gösterim, (3.1) şeklinde verilebilir. Burada (m m) boyutlu katsayılar matrisi, (m n) boyutlu katsayılar matrisi,, (p 1) boyutlu içsel değişkenler vektörü,, (q 1) boyutlu dışsal değişkenler vektörü ve, (p 1) boyutlu hatalar vektörüdür., modelde ve arasındaki rassal hataları ifade ettiğinden bazen denklemdeki hatalar olarak da 47
60 adlandırılmaktadır. Söz konusu model için standart varsayım denklemdeki hataların, lerle korelasyonsuz olmasıdır. GDYEM de ölçme modeli ise aşağıdaki şekilde tanımlanır: Burada (p 1) boyutlu ve (q 1) boyutlu gözlenen değişkenler vektörüdür. ve gözlenen değişkenleri, ve gizil değişkenlerini tam olarak temsil ettiği varsayılan gösterge değişkenlerdir. Ayrıca modelde her bir gizil değişkeni yalnızca bir gösterge değişkenin temsil ettiği varsayılmaktadır. Bu durumda değişkenlerinin sayısı değişkenlerine (p = m) ve değişkenlerinin sayısı değişkenlerine (q = n) eşit olmaktadır. GDYEM nin yinelemeli (recursive) ve yinelemesiz (non-recursive) modeller olmak üzere iki temel türü mevcuttur. Yinelemeli modeller nedenselliğin tek yönlü olduğu ve geri beslemeli bir döngü içermeyen denklem sistemlerinden oluşan modellerdir. Bu durumda katsayılar matrisi bir alt üçgen matris olarak yazılabilmekte ve denklemdeki hataların kovaryans matrisi, köşegen matris olmaktadır. Bu bir denklemdeki hata teriminin diğer denklemdeki hata terimi ile korelasyonsuz olduğu anlamına gelmektedir. Özetle yinelemeli modeller, karşılıklı nedensellik içermeyen ve hata terimlerinin korelasyonsuz olduğu varsayılan modellerdir. Şekil 3.1 de ise söz konusu modeller için örnekler verilmiştir. ġekil 3.1 Yinelemeli modeller için örnekler 48
61 Şekil 3.1 in (a) şıkkı incelendiğinde örneğin nin nedeni ise doğrudan veya diğer değişkenler aracılığı ile dolaylı olarak i etkileyemez. Aynı zamanda denklemdeki ile ise denklemdeki ile korelasyonsuz olmalıdır. Bu durumda alt üçgen matris ve köşegen matris olmalıdır. Yinelemeli modellerde söz konusu matrislerin gösterimi için aşağıdaki model incelenebilir. ġekil 3.2 Yinelemeli modellerin matrissel gösterimi için bir örnek Şekil 3.2 incelendiğinde, iki dışsal üç içsel gizil değişkene ait gösterge değişkenler ve bu değişkenler arasındaki ilişkileri ortaya koyan bir yol diyagramı görülmektedir. Söz konusu ilişkiler matrissel notasyonla [ ] [ ] [ ] [ ] 0 1 [ ] şeklinde gösterilebilir. yalnız ü, ve yi etkilemektedir. İçsel değişkenler ise kendi aralarında ve ü etkileyecek şekilde ilişkilidir. Bu durumda alt üçgen matris ve köşegen matris olduğundan Şekil 3.2 ile verilen modelin yinelemeli bir model olduğu söylenebilir (Bollen,1989: 80-83). GDYEM nin bir diğer türü de yinelemesiz modellerdir. Yinelemesiz modeller yinelemeli modellerin aksine, karşılıklı neden sonuç ilişkilerine, geri beslemeli 49
62 döngülere veya hata terimlerinin korelasyonlu olmasına izin veren modellerdir. Bu durumda yinelemesiz modellerde alt üçgen matris ve köşegen matris olmamaktadır. Yinelemesiz modeller için aşağıdaki varsayımsal model örnek gösterilebilir. ġekil 3.3 Yinelemesiz modeller için varsayımsal bir örnek (Bollen, 1989: 83) Model incelendiğinde ve içsel değişkenleri arasında karşılıklı nedensellik ve hata terimleri arasında korelasyonlu bir yapı gözlemlenmektedir. Ayrıca model matrissel notasyon ile ifade edilirse, [ ] [ ] < = [ ] 50
63 nın alt üçgen matris ve nın köşegen matris olmadıkları görülmektedir. Bu durumda Şekil 3.3 ile verilen modelin yinelemesiz bir model olduğu söylenebilir (Bollen, 1989: 84). Gerek çalışmanın uygulama konusu gizil değişkenlerin açıklanması yönünde olması nedeniyle gerekse literatürde YEM in daha çok gizil değişkenler için kullanımının yaygın olması nedeni ile GDYEM nin ayrıntısına girilmeyecek olup çalışmanın devam eden kısmında YEM kısaltması sadece gizil değişkenli yapısal eşitlik modelleri için kullanılacak ve buradan sonra bütün analiz ve açıklamalar Gizil Değişkenli Yapısal Eşitlik Modelleri için yapılacaktır YAPISAL EġĠTLĠK MODELĠNĠN SPESĠFĠKASYONU Yapısal eşitlik modelinin ilk bileşeni gizil değişkenlerin kendi arasındaki ilişkiyi ifade eden yapısal modeldir. (3.2) Burada, ( ) boyutlu içsel rassal gizil değişkenler vektörü, ( ) boyutlu dışsal rassal gizil değişkenler vektörü,, ( ) boyutlu içsel gizil değişkenler arasındaki ilişkileri gösteren katsayılar matrisi, ise ( ) boyutlu dışsal gizil değişkenlerin içsel gizil değişkenler üzerindeki etkilerini gösteren katsayılar matrisini ifade etmektedir. Modelin temel varsayımları; ( ) nin tekil olmayan bir matris olduğu ve hata vektörü nin beklenen değerinin sıfır olduğudur., - olmasının yanı sıra hataların dışsal gizil değişkenlerle de korelasyonsuz olduğu ( ) varsayılmaktadır. Modelin ikinci bileşeni ise, gözlenen değişkenlerle gizil değişkenler arasındaki ilişkiyi ifade eden ölçme modelleridir. (3.3) 51
64 (3.4) Burada, ( ) boyutlu ve, ( ) boyutlu gözlenen değişkenler vektörleri, ( ) boyutlu ile arasındaki ilişkileri gösteren katsayılar matrisi ve ( ) boyutlu ile arasındaki ilişkileri gösteren katsayılar matrisidir. ( ) boyutlu ve ( ) boyutlu sırasıyla ve e ilişkin ölçme hatalarını gösteren vektörlerdir. Ölçme modelinin temel varsayımı ise, ölçme hataları ile nın hem ve ile hem de kendi aralarında korelasyonsuz olmasıdır. Aynı zamanda, - ve, - olması gerekmektedir. Modeli basite indirgemek ve gösterim kolaylığı sağlamak için gizil ve gözlenen değişkenlerin tamamı (,,, ) kendi ortalamalarından farkları şeklinde ifade edilmektedir (Bollen, 1989: 320). Ölçme modelleri incelendiğinde Eşitlik 3.3 ve 3.4 ün ikinci bölümde yer alan DFA modelleri ile aynı olduğu görülmektedir. Gizil değişkenler ile yapısal eşitlik modelleri daha öncede bahsedildiği gibi ölçme modelleri yani DFA modelleri ile yapısal modelin bir arada ele alınması ile ortaya çıkan genel modellerdir. Genel modelin üzerinde birtakım varsayımlarla diğer gizil değişken modellerinin söz konusu genel modelin birer özel hali olduğu ortaya konulabilir., ve, olması durumunda gizil değişkenler ile yapısal eşitlik modelinin daha önce Eşitlik 3.1 ile verilen gözlenen değişkenlerle yapısal eşitlik modeline dönüştüğü gözlemlenebilir. ve olması durumunda genel model, şeklinde bilinen Çoklu Gösterge-Çoklu Sebep (Multiple Indicator- Multiple Cause, MIMIC) Modellerine dönüşmektedir. 52
65 Ölçme modellerinde değişkeninin olmaması durumunda ise genel YEM modelleri, şeklinde ikinci derece FA modellerine dönüşmektedir. Genel YEM modelinin kullanılabilmesi için şeklinde gösterilen sekiz matrisin ayrı ayrı tanımlanması gerekmektedir YAPISAL EġĠTLĠK MODELĠNĠN KOVARYANS YAPISI YEM modelleri ile yapılacak analizin ilk adımı kovaryans matrisinin tanımlanmasıdır. YEM modellerinde temel hipotez, ( ) (3.5) olup, burada, ve için kitle kovaryans matrisidir. ( ) ise, modelin serbest parametrelerinin bir fonksiyonu olarak yazılan modele ilişkin kovaryans matrisini göstermektedir. Bu eşitlik kovaryans matrisinin her bir bileşeninin modelin bir ya da daha fazla parametresinin fonksiyonu olduğunu ifade etmektedir. ( ) nın üç temel bileşeni vardır: 1. nin kovaryans matrisi ( ), 2. ve nin kovaryans matrisi ( ), 3. in kovaryans matrisi ( ). Her üç kovaryans matrisi de aşağıdaki şekilde hesaplanmaktadır: ( ) = ( ) 53
66 ( )= ( ) ( )= ( ) Sırası ile incelendiğinde, nin kovaryans matrisi: ( ) = ( ) (3.6) [( ) ( )] = E ( ) + ( ) hesaplanması için Eşitlik 3.2 de nın indirgenmiş formu ( ) ( ) elde edilir ve Eşitlik 3.6 da yerine konulursa, ( ) = ( ) ( ),( ) - (3.7) eşitliği elde edilir. ile nin kovaryans matrisi ise ( ) = ( ) [( )( )] (3.8) = ( ) olup nın indirgenmiş formu kullanılarak ( ) = ( ) (3.9) eşitliği yazılabilir. in kovaryans matrisi ise ( ) = (3.10) şeklinde olup, model parametrelerinin fonksiyonu olan gözlenen ve değişkenlerinin kovaryans matrisi aşağıdaki şekilde yazılabilir (Bollen, 1989: 325). 54
67 ( ) 6 ( ) ( ) ( ) ( ) 7 (3.11) ( ) [ ( ) ( )[( ) ] ( ) [( ) ] ] (3.12) 3.4. YAPISAL EġĠTLĠK MODELĠNĠN TANIMLANMASI Tanımlanma problemi modelin tahmininden önce aşılması gereken ve bütün YEM leri ilgilendiren önemli bir sorundur. Matematiksel olarak bir modelin tanımlanması, daki bilinmeyen her parametrenin nın bir veya daha çok elemanının bir fonksiyonu olarak yazılabilmesi anlamına gelir. eşitliği sağlanmadıkça, ( ) ( ) eşitliğini sağlayacak bir vektörleri olmaması durumunda nın her parametresi tanımlanmış olur. daki bütün parametrelerin tanımlı olması durumunda model tanımlanmış olur (Bollen, 1989: 326). Modelin tanımlanabilirliği araştırmalarının başında parametrelerin bilinen ve bilinmeyen parametreler olarak belirlenmesi gerekmektedir. Bir parametrenin bilinen olması değerinin bilinmesi değil tanımlı olup olmadığının bilinmesi anlamına gelir. Bilinen parametreler, genellikle tutarlı tahmincileri bulunan ve tanımlanma sorunu olmayan varyans, kovaryans gibi gözlenen değişkenlerin dağılımının kitle karakteristikleridir. Tanımlanma, ancak bilinmeyen parametrelerin sadece tanımlanmış parametrelerin bir fonksiyonu olarak yazılması ve bu fonksiyonlardan da sadece tek bir çözüm elde edilebileceğinin gösterilmesi ile ortaya konulmaktadır. Bilinmeyen parametreler ancak bu şekilde gösterilebildiklerinde tanımlı olmaktadırlar. Bu durumda amaç bilinmeyen parametrelerin tanımlı oldukları bilinen parametreler cinsinden çözülmesi sağlamaktır. Örneğin; ( ) tanımlı bir parametre, ve bilinmeyen parametreler ve aralarındaki ilişkiyi gösteren eşitliğin ( ) olduğu varsayılırsa burada tanımlanma için ve nin tekil 55
68 değerlerinin elde edilip edilemediğine bakılmalıdır. Bilinmeyen parametre sayısı iki ancak denklem sayısı bir olduğundan, ( ) eşitliğini sağlayacak sonsuz sayıda değeri bulmak mümkündür. Bu nedenlerle ve nin tanımlı olmadığı açıktır. Eğer gibi bir eşitlik daha olduğu varsayılırsa bu sefer, verilen her bir ( ) için ve nin sırasıyla ( ) ve ( ) şeklinde birer tek çözümü olacağından parametreler tanımlı olacaktır. Tanımlanmanın araştırılmasında bilinen ve bilinmeyen parametre ayrımının yanı sıra serbest parametre (free parameter), sabit parametre (fixed parameter) ve kısıtlı parametre (constrained parameter) ayrımlarını da yapmakta fayda vardır. Serbest parametre, bilinmeyen ve tahmin edilmesi gereken parametredir. Sabit parametre ise, serbest olmayan fakat başka bir değere eşitlenmiş parametredir. Bu değer genellikle 0 veya 1 dir. Kısıtlı parametre ise bilinmeyen bir parametre olup diğer parametre veya parametrelere eşitlenerek kısıtlanmıştır (Schumacker ve Lomax, 2004: 63-64). YEM de tanımlanmanın araştırılması için benzer bir yol izlenebilir. YEM de tanımlı olduğu bilinen parametreler gözlenen değişkenlerin kitle kovaryans matrisi nın elemanlarıdır. Tanımlanma durumu bilinmeyen parametreler ise da yer almaktadır., nın kısıtlı parametreleri ve t tane serbest parametreyi kapsamaktadır. ile yı ilişkilendiren YEM in temel hipotezi ( ) kovaryans yapısı eşitliği kullanılarak parametrelerin tanımlılıkları ispat edilebilir. daki bilinmeyen bir parametre nın bir veya birden fazla elemanının fonksiyonu olarak yazılabiliyorsa parametre tanımlıdır. Eğer daki bilinmeyen parametrelerin tümü tanımlanmış ise model de tanımlı olacaktır (Bollen, 1989: 89). Tanımlanmanın üç seviyesi vardır. Örneklem kovaryans matrisinden model parametrelerinin tekil olarak tahmin edilip edilmemesine göre modelin tanımlanma seviyesi belirlenir. Örneklem kovaryans matrisinde bilgi yetersizliği sebebiyle kitle parametrelerinden bir veya daha çoğu tahmin edilemiyorsa model eksik tanımlanmış olarak adlandırılır. Örneklem kovaryans matrisinde bilginin yeterli olması durumunda model parametrelerinin her biri tekil olarak tahmin edilebiliyorsa model 56
69 tam tanımlanmış ve örneklem kovaryans matrisindeki bilgi fazlalığı nedeni ile model parametrelerine ait birden çok tahmin değeri elde ediliyorsa model aşırı tanımlanmış olarak adlandırılır. Bir modelin tanımlanmış olması için, tam tanımlı veya aşırı tanımlı olması gerekmektedir. Eksik tanımlanma durumunda parametre tahminleri güvenilir olmamakta ve modelin serbestlik derecesi sıfır veya negatif bir değer almaktadır. Bu nedenle model parametreleri üzerine bir takım kısıtlamalar getirilerek serbestlik derecesinin 1 veya daha büyük olması garantilenmektedir (Schumacker ve Lomax, 2004: 64). YEM de tanımlanabilirliğin sağlanması için ise model parametreleri üzerine belirli kısıtlamalar konulmalıdır. Bütün parametrelerin serbest ve değişkenler arası ilişkilerin yalnızca veriden elde edilmesi istenen durumlarda model eksik tanımlanmış olacak ve parametre tahminleri gerçekleştirilemeyecektir. Bu nedenle YEM de parametrelerin kısıtlanması, güvenilir ve yorumlanabilir parametre tahminleri elde etmek için gereklidir. Bu amaçla, matrislerinin elemanlarından bazıları sıfır veya bir sabit sayıya eşitlenebileceği gibi parametreler için eşitlik ya da eşitsizlik kısıtları da konulabilir veya bütün bu kısıtlar birlikte kullanabilir. Eşitlik 3.2 de verilen yapısal model denkleminde açıkça görülmediği halde iki kısıt kullanılmıştır. Bunlardan ilki içsel değişkenler arasındaki ilişkileri gösteren katsayılar matrisinin köşegen elemanları 0 a sabitlenmiştir. Bu durum her içsel değişkenin kendisi üzerinde doğrudan etkisi olmadığını göstermektedir. Normalleştirme işlemi olarak da adlandırılan bu durum YEM in eksik tanımlanmış olmamasını sağlamaktadır. Diğer kısıt ise hata vektöründeki değişkenleri doğrudan gözlemlenebilen değişkenler olmadığından yorumlanabilirliğini sağlamak için ölçeklendirilmesi gerektiğidir. Bunun için iki yöntem benimsenebilir: Bunlardan ilki gizil değişkenlerin varyansını bir sabite (örneğin 1 e) eşitlemektir. İkinci ve daha sık tercih edilen yöntem ise nın gözlenen bir değişken olduğunu varsayarak katsayısının 1 e eşitlenmesidir (Bollen, 1989: 91). Model parametrelerinin tanımlanabilirliğinin gösterilmesi için ( ) kovaryans eşitliğinden faydalanılabileceğinden daha önce bahsedilmişti. ( ) 57
70 kovaryans yapısı, nın ij. elemanı ve ( ) ise ( ) nın ij. elemanını göstermek üzere ( )( ) tane ( ) ( ) eşitliğini gösterir. Eğer nın her bir elemanı bir veya daha çok nin fonksiyonu olarak yazılabilirse modelin tanımlı olacaktır. Şimdi varsayımsal bir örnek üzerinde parametrelerin bu kovaryans eşitliğinden yararlanılarak tanımlanabilir olma durumlarının nasıl gösterileceği incelenecektir. Bir içsel bir dışsal gizil değişken ve dört gösterge değişkenden oluşan varsayımsal bir YEM için verilen yol diyagramı Şekil 3.4 de yer almaktadır. ġekil 3.4 Ġki gizil değiģkenli varsayımsal model Modelin matrissel notasyonla ifadesi ise, -, -, -, - 0 1=[ ], -+0 1, diag (3.13) 0 1=[ ], -+[ ], diag 58
71 şeklindedir. Gözlenen değişkenlerin kovaryans matrisi, [ ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )] (3.14) şeklinde olup, Eşitlik 3.12 ile ifade edilen, modele ait tahmini kovaryans matrisinde, Eşitlik 3.13 ile verilen modele ait matrisler yerlerine konulursa, modele ilişkin kovaryans matrisi aşağıdaki şekilde açık olarak ifade edilebilir. [ ( ) ( ) ( ) ( ) ( ) ( )] (3.15) ve ise = [ ( ) ( ) ( ) ( ) ] olacaktır. Bu örnek için, ( ) kovaryans yapısı bilinmeyen 9 tane parametreyi içeren 10 tane [ ( )( )] eşitliğe sahiptir. Modelin tanımlanmış olması için her bir bilinmeyen parametrenin bu eşitlikler tarafından çözülmesinin sağlanması gerekmektedir. Söz konusu eşitlikler yardımı ile daki parametrelerin nasıl tahmin edildiği bir örnek ile gösterilmek istenirse aşağıdaki işlemler yapılabilir. ( ) ( ) ( ) ( ) 59
72 Bu durumda tanımlanmıştır. Benzer cebirsel işlemler gerçekleştirerek daki bütün parametrelerin tanımlı olduğu göstermek mümkündür. Bu şekilde ( ) kovaryans yapısı kullanılarak modelin tanımlanmış olduğu gösterilebilir. Bu örnekte ve benzer basit modellerde cebirsel işlemler yoluyla modelin tanımlanabilirliğinin gösterilmesinin faydaları olsa da daha karışık modeller için bu cebirsel yaklaşım yöntemi aşırı derecede zor ve yanlış sonuçlar vermeye eğilimli bir hal alacaktır. Bu nedenle tanımlanmanın tespiti için geliştirilmiş kurallar vardır. Burada YEM için kullanılan tanımlama kurallarından başlıcaları, t Kuralı, İki Adım Kuralı, Çoklu Gösterge Çoklu Nedensellik Kuralı ve diğer yöntemler incelenecektir t KURALI Tanımlanma için gerekli ancak yeterli olmayan bir koşuldur. DFA ve YA modellerinde de kullanılan bu koşul aynı zamanda YEM de de geçerlidir. t Kuralı, gözlenen değişkenlerin kovaryans matrisi daki gereksiz olmayan elemanların sayısının, daki serbest ve sınırlandırılmamış parametrelerin sayısından büyük veya eşit olmasıdır. ( )( ) (3.16) t, daki serbest ve sınırlandırılmamış parametre sayısını ve ( ) gözlenen değişken sayısını ifade ederken eşitsizliğin sağ tarafı ( ) nın gereksiz olmayan elemanlarının ( )( ) tane eşitlik içerdiği anlamına gelmektedir. Modelin tanımlanmış olduğundan bahsedilebilmesi için söz konusun eşitsizliğin sağlanması gereklidir ancak bu tek başına tanımlanmayı garanti etmeyeceğinden diğer kurallar geliştirilmiştir ĠKĠ ADIM KURALI İki Adım Kuralı tanımlanma için yeterli bir şarttır. İki kısımdan oluşan bu kuralın ilk kısmında model DFA modeli gibi ele alınır. Öncelikle ve 60
73 değişkenleri, değişkeni gibi ve değişkenleri ise değişkeni gibi yazılır. Bu aşamada gizil değişkenler arasındaki ilişkilerle ilgilenilir. Bu ilişkiler gizil değişkenlerin varyans ve kovaryanslarıdır ( ). matrislerinin elemanları göz ardı edilir. Bu şekilde ele alınan YEM bir DFA modelidir ve DFA modelinin tanımlanabilirliği ile ilgili önceki kısımlarda bahsedilen kurallar kullanılarak modelin tanımlanabilirliği araştırılır. Eğer model tanımlanmış ise ikinci aşamaya geçilir. YEM in tanımlı olabilmesi için her iki aşamada da modelin tanımlı olması gerekmektedir. İkinci aşamada yapısal model incelenir. Her bir gizil değişken hatasız ölçülmüş bir gözlenen değişken gibi ele alınır ve matrislerinin elemanlarının tanımlılığı araştırılır. Birinci aşamada ölçme modeli parametrelerinin ikinci aşamada ise yapısal model parametrelerinin tanımlı olduğu belirlenirse sonuç olarak YEM tanımlıdır denir. matrislerinin elemanlarının tanımlılığı araştırılması için Sıfır B Kuralı kullanılır. Bir içsel değişkenin diğer bir içsel değişkeni etkilemediği çok denklemli bir modelde matrisi sıfır olmaktadır. olması durumunda matrislerindeki bilinmeyen parametrelerin her biri, gözlenen değişkenlerin kovaryans matrisindeki tanımlı parametrelerin fonksiyonları olarak gösterilebilir. Sıfır B Kuralı, tanımlılık için gerekli olmayan ama yeterli bir koşuldur (Bollen, 1989: 94-95) ÇOKLU GÖSTERGE-ÇOKLU NEDENSELLĠK KURALI YEM in en çok uygulama alanı bulan özel durumlarından biri Çoklu Gösterge Çoklu Nedensellik (MIMIC) Modelleridir. MIMIC modeller tek bir gizil değişkenin çoklu göstergesi ve çoklu nedenselliği olan gösterge değişkenleri içermekte olup daha önce bahsedildiği gibi 61
74 şeklinde gösterilir. MIMIC modellerde tanımlanma koşulu p, y değişkenlerinin sayısını göstermek üzere ve q, x değişkenlerinin sayısını göstermek üzere eşitsizliklerinin sağlanmasıdır. Bu durum tanımlama için gerekli olmayan ancak yeterli bir koşuldur. Bollen ve Davis (2009) MIMIC modellerin tanımlanabilirliğinin testi için daha genel bir yeterli kural geliştirmeyi ve ispat etmeyi amaçlamışlardır. Dışsal X kuralı adı verilen bir kural önermişlerdir. Bu kuralın uygulanabilmesi için aşağıdaki koşulların sağlanması gerekmektedir: 1. Her bir gizil değişken yalnızca kendisini etkileyen en az bir gösterge değişkene sahip olmalıdır ve her bir gizil değişken ölçme hatalarından bağımsız olmalıdır. 2. Her bir gizil değişken toplamda en az iki gösterge değişkene sahip olmalıdır. 3. matrisi tam ranka sahip olmalıdır. 4. Yapısal model tanımlanabilir yapıda olmalıdır. Tanımlama yapısal eşitlik modellerinin temel problemlerinden biridir. Eksik tanımlanmış parametreler nedeniyle çoğu zaman tahminler de güvenilir olmayan beklenmedik sonuçlar elde edilir. Farklı tip YEM ler için geliştirilmiş pek çok tanımlama yöntemi mevcut olsa da ne yazık ki bütün YEM ler için genel geçer hem gereklilik hem de yeterlilik koşulunu bir arada sağlayan bir tanımlama yöntemi yoktur. Ampirik yöntemler model parametrelerinden elde edilen bilgi matrisinin tekilliğine bağlı olup aynı zamanda da dörtdörtlük bir kontrol sağlamazlar (Bollen ve Davis, 2009: 523). Bekker, Merckens ve Wansbeek (1994) yerel olarak tanımlanmanın testi için jakobi matrisine dayalı bir yazılım geliştirmiştir (Rigdon, 1997). Ancak bütün bu yöntemler her ne kadar yardımcı olsa da bütün YEM leri 62
75 kapsamamaktadır. Bu eleştirilerin doğal bir sonucu olarak son yıllarda daha özel durumları da içeren daha genel tanımlama testleri geliştirilmiştir. Bentler ve Chou (1988: 175) tek bir gizil değişkenin tek bir gösterge değişken ile açıklandığı modellerin asla geçerli olmayacağını iddia etmişlerdir. Keny ise bazı özel durumlarda özellikle yapısal modelin aşırı tanımlanmış olma durumunda bir gizil yapı için tek bir gösterge değişkenin gerekli olduğunu göstermişlerdir (Keny, 1979: ). Bollen ve Davis (2009) ise tanımlanabilirlik için gösterge değişken sayısından çok her bir gizil değişkenden çıkan yol sayısını baz alan 2 + Yol Kuralı olarak adlandırılan bir kural önermişlerdir YAPISAL EġĠTLĠK MODELĠNĠN TAHMĠNĠ YEM sürecinde tanımlanmadan sonra gelen aşama modelin tahminidir. Modelden elde edilecek sonuçların güvenilirliği açısından, bu aşamada seçilecek yöntemin doğruluğu ve başarısı son derece önemlidir. Tahminin başarısı için ilk şart parametrelerin tanımlanmış olmasıdır. Model parametreleri tanımlanmış ve gözlenen kovaryans matrisi verilmişse, model parametreleri uygun tahmin yöntemi seçilerek tahmin edilebilir. YEM de test edilmesi gereken temel hipotez modelin veriye uyumlu olduğunu gösteren; gözlenen kovaryans matrisinin tahmini kovaryans matrisine eşitliğinin sınanmasıdır. ( ) ( ) (3.17) Eşitlik 3.17 de verilen sıfır hipotezinde, (q 1) boyutlu model parametre vektörü olmak üzere, YEM de model doğru ve parametreler biliniyor ise, ( ) ya eşit olacaktır. Ancak pratikte kitle parametreleri genellikle bilinmez bu nedenle parametreler vektörü, örneklem kovaryans matrisi kullanılarak tahmin edilir. Burada, (p p) boyutlu ve kitle kovaryans matrisinin yansız bir tahmincisidir. 63
76 Modele ilişkin parametreler bilinmeyip tahmin edilmeleri gerektiğinden denklemde yerine ikame edileceğinden öne sürülen kovaryans matrisi ( ) yerine kullanılmaktadır ( = ( )). Parametre tahminleri için, örneklem kovaryans matrisi ile modele ilişkin tahmini kovaryans matrisi arasındaki farkın en küçüklenmesini sağlayacak bir fonksiyon gereklidir. Söz konusu fonksiyon, ( )- uyum fonksiyonudur. F fonksiyonunun en küçük olmasını sağlayan değer için uyum fonksiyonu, - şeklindedir. Uyum fonksiyonunun taşıması gereken özellikler aşağıdaki şekilde özetlenebilir: 1., ( )- bir skalerdir. 2., ( )- olmalıdır. 3. Sadece ( ) eşitliği sağlandığında, ( )- olur. 4., ( )-, ve ( ) da süreklidir. Browne (1984: 66) e göre ancak bu koşulları sağlayan uyum fonksiyonunun en küçüklenmesi ile nın tutarlı tahmincileri elde edilebilir (Bollen, 1989: 106). YEM de ile arasındaki farkın en küçüklenmesinde kullanılan uyum fonksiyonları için dört temel tip mevcuttur: Ağırlıklandırılmamış En Küçük Kareler Yöntemi Unweighted Least Squares (ULS), En Çok Olabilirlik Yöntemi (EÇO) Maximum Likelihood (MLE), Genelleştirilmiş En Küçük Kareler Yöntemi (GEKK) Generalized Least Squares (GLS), Ağırlıklandırılmış En Küçük Kareler (AEKK) Weighted Least Squares (WLS). Tahmin yöntemlerinden ilki EKK tahmin yöntemi, ile arasındaki farkın karelerinin toplamının en küçüklenmesine dayanan bir yöntem olup, istatistiksel testler için dağılım varsayımı gerektirmez ancak ölçekten bağımsız olmadığı için benzer ya da aynı ölçekle ölçülmüş veriler için kullanılması önerilir. EÇO ve GEKK yöntemleri için gözlenen verinin normal dağılıma uygunluğu aranmaktadır. Ölçekten bağımsız olup, asimptotik yöntemlerdir. Bu nedenle büyük örneklemde kullanılmaları gerekir. Normallik varsayımından sapmanın büyük olduğu durumlarda, asimptotik olarak dağılımdan bağımsız bir yöntem olan AEKK yöntemi kullanılır. Söz konusu dört yöntem için de parametre 64
77 tahmincileri tutarlılık özelliğine sahiptir. Benzer şekilde normallik varsayımı gerektirmeyen bir diğer yöntem Satorra-Bentler Dayanıklı EÇO (Robust ML) yöntemidir (Raykov ve Marcoulides, 2006: 27-32). Bu yöntem gibi pek çok başka dayanıklı tahminci ve varsayımlardan sapmalar durumunda kullanılan pek çok başka tahmin yöntemi mevcuttur. Bu yöntemler ise dayanıklı yöntemler başlığı altında incelenecek ve bölümün sonunda YEM de parametre tahminleri gerçekleştirmek için kullanılan nümerik çözümlere de yer verilecektir EN ÇOK OLABĠLĠRLĠK YÖNTEMĠ YEM de kullanılan en yaygın tahmin tekniği En Çok Olabilirlik (EÇO) yöntemidir. Bu yöntemde en küçüklenmesi istenilen uyum fonksiyonu, ( ). ( )/ ( ) (3.18) şeklinde olup ve ( ) matrislerinin pozitif tanımlı (tekil olmayan) matrislerdir. uyum fonksiyonu iki farklı yaklaşımla türetilebilir. Bu yaklaşımlardan ilki, ve in çok değişkenli normal dağılıma uygunluk göstermesi varsayımına diğeri ise örneklem kovaryans matrisi nin Wishart dağılımına uygunluk göstermesi varsayımına bağlıdır. EÇO tahmininde, çok değişkenli normal dağılıma uygunluk gösteren x ve y rastlantı değişkenlerinden türetilen bağımsız gözlem için bu değişkenlerin birleştirilmesi ile elde edilecek ( ) boyutlu vektörü için olasılık yoğunluk fonksiyonu ( ) ( ) ( ) 0 1 (3.19) şeklindedir. fonksiyonu ise bağımsız gözlemli rassal bir örneğin birleşik olasılık yoğunluk 65
78 ( ) ( ) ( ) ( ) (3.20) şeklinde gösterilebilir. birimlik örneklemin olabilirlik fonksiyonu ise ( ) kovaryans yapısı hipotezi dikkate alınarak çekilen ( ) ( ) ( ) ( ) 0 ( ) 1 (3.21) şeklindedir. Eşitlik 3.21 in logaritması alınırsa ( ) ( ) ( ). / ( ). / ( ) (3.22) elde edilir ve bu fonksiyonun son terimi yeniden yazılırsa. / ( ). /, ( ) -. /, ( )-. /, ( )- (3.23) şeklinde ifade edilebilir. Burada kovaryans matrisinin EÇO tahmincisidir. Eşitlik 3.23 ile elde edilen sonuç Eşitlik 3.22 de yerine yazılırsa ( ) fonksiyonu aşağıdaki gibi yeniden yazılabilir: ( ). / ( ). /, ( )- ( ). / * ( ), ( )-+ (3.24) Eşitlik 3.24 ile Eşitlik 3.18 karşılaştırıldığında, bazı farklılıklar görülse de bu farklılıklar nın tahminini etkilemeyecektir. Eşitlik 3.24 teki sabit terimin nın elde edilmesinde bir etkisi olmayacağından Eşitlik 3.18 de bulunmasının bir 66
79 sakıncası yoktur. Ayrıca verilen bir örneklem için ve ( ) sabit olduklarından ( ) nun Eşitlik 3.18 de yer alması da nın elde edilmesinde bir değişiklik yaratmayacaktır. Bunların haricinde Eşitlik 3.24 te yer alıp 3.18 de yer almayan. / teriminin nın elde edilmesinde etkisi olacaktır. Bu nedenle Eşitlik 3.24 ün en büyüklenmesi yerine Eşitlik 3.18 in en küçüklenmesi bu değişikliği ortadan kaldıracaktır. İki eşitlik arasındaki son fark ise Eşitlik 3.18 de kullanılan yansız örneklem kovaryans matrisi yerine Eşitlik 3.24 te örneklem kovaryans matrisinin EÇO tahmini olan matrisinin kullanılmış olmasıdır.,( ) - olduğundan söz konusu matrisler büyük örneklem için eşit olacaktır. Bu nedenle olması beklenir (Bollen, 1989: ). ve EÇO gösterimleri ile elde edilen tahmincilerinin eşit nun türetilmesinde ikinci yaklaşım örneklem kovaryans matrisi nin Wishart dağılımına uygunluğu varsayımı ile ilgilidir. x ve y değişkenlerinin çok değişkenli normal dağılıma uygunluğu varsayımı altında yansız örneklem kovaryans matrisi, wishart dağılımına uygunluk göstermektedir (Anderson, 1958: ). Verilen bir örneklemdeki için ( ) [ ( ) 2. /, ( )-3. / ( ) ( )(( ) ) ( ),( )( )- ] ( ) şeklindedir. Burada ve,( )( )- gamma fonksiyonu ( ) değişken ve örneklem hacmi için sabittir. Eşitlik 3.25 te logaritmalar alınıp ifade sadeleştirildiğinde ( ). / * ( ), ( )-+ (3.26) 67
80 fonksiyonu elde edilir. Eşitlik 3.18 ile Eşitlik 3.26 karşılaştırıldığında her ikisinin de matrisini içerdiği ve ( ) yı en büyükleyen değerinin yu en küçükleyeceği görülmektedir. nın EÇO tahmincisinin asimptotik kovaryans matrisi ( ) 8 6 ( ) 79 ( ) şeklindedir. Eşitlik 3.26 ile verilen ( ) nın ya göre kısmi türevi alındığında sabit terimin ve Eşitlik 3.18 deki ifade için söz konusu türev alındığında son iki ifadenin değeri sıfır olacaktır. Bu iki fonksiyonun ikinci mertebeden kısmi türevleri arasındaki ilişki ise ( ) ( * ( ) şeklinde gösterilebilir. Eşitlik 3.27 ve 3.28 birleştirilirse ( ) ( * ( ) şeklinde asimptotik kovaryans matrisi elde edilmiş olur (Bollen, 1989: 135). EÇO yönteminde, parametresinin tahmininde ( ) olabilirlik fonksiyonunun en büyüklenmesi ya da uyum fonksiyonunun en küçüklenmesi durumudur. Bu yöntem ile elde edilen parametre tahmincileri, modele ilişkin tahmini kovaryans matrisi ( ) nın geçerliliği için gözlenen kovaryans matrisi nin olabilirliğini en büyükleyen tahmin değerleridir. Modelde yapısal parametrelerin tahmini için kesin sonuçlar nun en küçüklenmesi ile elde edilir. Burada uyum fonksiyonunun yapısal parametrelere göre birinci mertebeden kısmi türevinin 68
81 alınarak sıfıra eşitlenmesi ile elde edilen değerler parametre tahminlerini verecektir. Uyum fonksiyonunun söz konusu parametrelere göre ikinci mertebeden türevler matrisinde tahmin değerleri yerine konulduğunda elde edilecek matrisin pozitif tanımlı olması da uyum fonksiyonunun en küçüklenmesi koşulunu garantileyecektir., yapısal parametrelerin doğrusal olmayan karmaşık bir fonksiyonu olduğundan genellikle yu minimum yapan matrislerindeki serbest ve kısıtlı parametreleri bulmak için iteratif nümerik yöntemler kullanılmaktadır. Tahmin yöntemlerinin sonunda söz konusu nümerik yöntemlerden bazılarına yer verilecektir. EÇO yönteminin temel varsayımlarından biri ( ) ve matrislerinin pozitif tanımlı olmasıdır. Aksi halde uyum fonksiyonu söz konusu fonksiyonların logaritmasını içerdiğinden tanımsız olacaktır. nun sıfır olması ise yani durumunda, uyum fonksiyonu ( ) yerine koyulduğunda ( ) ( ) (3.30) halini alacak ve ( ) ( ) eşit olacağından sıfır değerini alacaktır. Bu durum mükemmel uyumu, örneklem kovaryans matrisinin bütün elemanlarının tahmin edilebildiği durumu işaret etmektedir. EÇO yöntemin bir diğer önemli varsayımı da modeldeki değişkenlerin çok değişkenli normal dağılıma uygunluk göstermesi gerekliliğidir. Modelin doğru tanımlanmış ve yöntemin bütün varsayımlarının sağlandığı durumda EÇO tahmincileri, küçük örneklemde yanlı olsalar dahi asimptotik olarak yansız, tutarlı ve etkindirler. Örneklem büyüklüğü arttıkça EÇO tahmincilerinin dağılımının normal dağılıma yaklaşmaktadırlar. Bu özellik sayesinde EÇO tahmincilerinin standart hatalarının bilinmesi durumunda ilgili parametreler için büyük örneklemde istatistiksel çıkarsama sürecinin araçları kullanılabilmekte anlamlılık testi yapılabilmektedir. Büyük örnekler için ilgili standart hatalar Eşitlik 3.29 ile verilen asimptotik kovaryans matrisinden elde edilmektedir. Aynı zamanda EÇO tahmincileri ölçekte sabitlik ve bağımsızlık özellikleri taşımaktadırlar. 69
82 EÇO tahmincilerinin bir diğer önemli avantajı ise aşırı tanımlanmış modeller için bütün modelin değerlendirilmesine yönelik kapsamlı bir uyum testine olanak sağlamasıdır. Değeri asimptotik olarak ( ) gözlenen değişken sayısı ve t bilinmeyen parametre sayısını göstermek üzere ( )( ) serbestlik dereceli dağılımına uygunluk göstermektedir AĞIRLIKLANDIRILMAMIġ EN KÜÇÜK KARELER YÖNTEMĠ YEM de kullanılan bir diğer parametre tahmin yöntemi Ağırlıklandırılmamış En Küçük Kareler Yöntemidir. Bu yöntem de EÇO yönteminden farklı olarak gözlenen değişkenlere i çin herhangi bir dağılım varsayımı bulunmamaktadır. Ancak burada da diğer tüm tahmin tekniklerinde olduğu gibi nın tanımlı olması varsayımı mevcuttur. Bu yöntemde en küçüklenmesi istenilen uyum fonksiyonu,. /,( ( )) - (3.31) şeklinde olup, tr matrisin izi, gözlenen kovaryans matrisi, ( ) modele ilişkin tahmini kovaryans matrisi ve parametre vektörüdür. Bu yöntemde ( ( ))kalıntı matrisi örneklem kovaryans matrisi ile modele ilişkin tahmin matrisi arasındaki farktan oluşmaktadır. Ağırlıklandırılmamış EKK yöntemi tahmin edilen ve gözlenen kovaryanslar arasındaki fark dikkate alınmaktadır. Bu fonksiyonun çözümleme sürecinde nın birinci mertebe kısmi türevleri alınıp sıfıra eşitlenerek parametre tahminleri elde edilir ve daha sonra uyum fonksiyonunun ikinci mertebe kısmi türevlerinde tahmin değerleri yerlerine konulduğunda elde edilen matrisin pozitif tanımlı olması ile fonksiyon en küçüklenmiş olur. Karmaşık modellerde söz konusu işlemleri basit türev çözümleri ile yapmak zor olacağından bu 70
83 yöntemde de EÇO yönteminde olduğu gibi iteratif nümerik yöntemler kullanılmaktadır. Ağırlıklandırılmamış EKK yöntemi ile nın tutarlı tahmincileri elde edilmektedir. Bu nedenle elde edilen tahmin değerleri için istatistiksel çıkarsama sürecinin araçları kullanılabilir ancak Ağırlıklandırılmamış EKK tahmincileri asimptotik olarak EÇO tahmincilerinin aksine etkin olma özelliğine sahip değildirler. Ağırlıklandırılmamış EKK tahmincilerinin bir diğer dezavantajı ise ölçek değişmezlik ve ölçek bağımsızlık özelliklerine sahip olmamasıdır. Çalışmanın genelinde, ağırlıklandırılmamış EKK tahmincisine ait uyum fonksiyonu olarak kullanılacak ve EKK kısaltması bundan sonraki kısımlarda ağırlıklandırılmamış en küçük kareler yöntemi için kullanılacaktır GENELLEġTĠRĠLMĠġ EN KÜÇÜK KARELER YÖNTEMĠ Genelleştirilmiş En Küçük Kareler (GEKK) tahmincisi ilk olarak Aitken (1934,1935) tarafından geliştirilmiş ve daha sonra Jöreskog ve Goldberger (1972) tarafından YEM için uyarlanmıştır (Kaplan, 2000: 28). GEKK, EKK yönteminin kullanılabilmesi için gerekli bazı varsayımların sağlanmadığı durumlarda tercih edilen bir yöntemdir. Ağırlıklandırılmamış EKK yönteminde kalıntılara ilişkin ortalamanın sıfır ve kalıntıların her değişken için sabit varyanslı olduğu varsayılır. Aynı zamanda kalıntıların birbirinden bağımsız olması gerekmektedir. Bu varsayımların YEM de her zaman sağlanması mümkün olmamaktadır. Söz konusu varsayımların sağlanmaması durumunda EKK tahmincisinin kullanılması sonuçların güvenilirliği açısından hatalı olacağından bu durumda kalıntılara ilişkin varsayımlar gerektirmeyen GEKK tahmincisini kullanmak uygun olacaktır. GEKK tahmincisinde uyum fonksiyonu,. /.{[( ( )) ] } / (3.32) 71
84 şeklinde olup, kalıntılar için bir ağırlık matrisidir. EKK yönteminde ( ( )) nın her bir elemanına aynı varyans ve kovaryansa sahipmiş gibi işlem yapılmasına rağmen GEKK yönteminde ( ( )) nin her bir elemanı diğer elemanların varyans ve kovaryansları ile ağırlıklandırılmaktadır. matrisi kalıntılar için ağırlık matrisi olup, n sonsuza yaklaşırken pozitif tanımlı matrise yakınsayan bir rassal matris ya da sabitlerin pozitif tanımlı bir matrisidir. olması durumunda olacaktır. Bu durumda EKK tahmincisinin GEKK nın özel hali olduğu söylenebilir. dan elde edilen, ve tahmincilerinde olduğu gibi nın tutarlı tahmincisidir. Aynı zamanda nın asimptotik dağılımı, bilinen bir asimptotik kovaryans matrisi ile çok değişkenli normaldir. dan elde edilen tahmincilerinin aranılan özelliklere sahip olması ve ağırlık matrisinin seçiminin doğru olması gözlenen kovaryans matrisi üzerine yapılan iki varsayıma bağlıdır. Bunlardan ilki, ( )., nin yansız bir tahmincisidir. İkincisi nin elemanlarının asimptotik dağılımı, ortalamaları ve asimptotik kovaryansları ( ) ( ) eşit olan ve ile çok değişkenli normal dağılıma uygunluk göstermesidir. İkinci varsayımın gerçekleşmesi için gözlemlerin bağımsız ve aynı dağılımlı olması ve ile nin dördüncü momentlerinin olması yeterlidir. ve nin çok değişkenli normal dağılıma uyması durumunda ikinci varsayım sağlanmaktadır. Aynı zamanda basıklık değeri çok yüksek olmayan dağılımlar için de bu varsayım sağlanmaktadır (Browne,1974:7). Söz konusu varsayımların sağlanması durumunda, eşitliği sağlanacak şekilde seçilmelidir. Burada c sabiti genellikle 1 kabul edilmektedir. Bu durumda GEKK tahmincileri asimptotik olarak normal dağılımlı ve etkin olma özelliğine sahiptirler. dan elde edilen asimptotik kovaryans matrisi, bilgi matrisinin beklenen değerinin tersinin ( ( )) ile çarpımı olup, ( ) ( * ( ) 72
85 şeklinde ifade edilmektedir (Jöreskog, 1981). Burada yerine konularak asimptotik kovaryanslar ve standart hatalar tahmin edilebilir. Her ne kadar pek çok, in tutarlı tahmincisi olsa da için en yaygın olarak kullanılan ağırlık matrisi seçimi şeklindedir. Bu durumda amaç fonksiyonu,. /.{[( ( )) ] } / (3.34). / 20 ( ) 13 (3.35) şeklinde ifade edilir., tıpkı gibi ölçekte değişmezlik ve ölçekte bağımsızlık özelliklerine sahiptir. Bir diğer özelliği ise model doğru olduğunda dan elde edilen tahmin değerleri ( ) değeri, ( )( ) serbestlik dereceli dağılımına uygunluk göstermektedir. ( ) ya benzer olarak ( ) de büyük örneklerde sağlanması durumunda asimptotik olarak dağılımına yakınsamaktadır. Model geçerli ise ( ) ve ( ) asimptotik olarak eşit ve tahmin edilen değerleri büyük örneklemde birbirine çok yakın olacaktır. her ne kadar aranılan özelliklere sahip olsa da bazı sınırlılıkları mevcuttur. Bunlardan en önemlisi gözlenen değişkenlerin dağılımının çok kalın veya çok ince kuyruklu olması durumunda ve nin asimptotik kovaryansı ( ) den farklı olacağından anlamlılık testinin yapılmasında testine ve asimptotik standart hatalara güvenilemeyecek olmasıdır. matrisine ilişkin yapılan varsayımlar sağlansa bile bütün özellikler asimptotiktir (Bollen, 1989: 115) DAĞILIMSAL VARSAYIMLAR ve ÇOK DEĞĠġKENLĠ NORMALLĠK YEM modellerinde değişkenlerin dağılımlarına ilişkin temel varsayımlar bulunmaktadır. Gerek uygun tahmin yönteminin seçilmesi gerekse elde edilen 73
86 tahmincilerin istenilen istatistiksel özelliklere sahip olmaları ve sonuçların güvenilirliği açısından dağılımsal varsayımlar son derece önemlidir. tahmincisinin uyum fonksiyonu Kısım de incelendiği üzere gözlenen değişkenlerin normal dağılımından üretilmektedir. ve fonksiyonları gözlenen değişkenlerin dağılımının aşırı basıklığa sahip olmaması durumunda doğrulanmaktadır. Söz konusu koşulların sağlanması ve modelin geçerli olması durumunda ve dan elde edilen tutarlı ve asimptotik olarak etkin bir tahminci olacaktır. nın ve uyum fonksiyonlarında yerine konularak ( ) ile çarpılmasından elde edilecek ( ) ve ( ) değerleri asimptotik olarak dağılımına uygunluk göstermekte ve genel model uyumunun testinde bu değer kullanılabilmektedir. Aynı zamanda bu varsayımların sağlanması ile ve dan elde edilen için asimptotik kovaryans matrisleri de elde edilebilmek ve bu durum parametreler için ayrı ayrı ve topluca anlamlılık testlerinin yapılabilmesine olanak sağlamaktadır (Bollen, 1989: 416). Gözlenen değişkenlerin dağılımlarının EÇO ve GEKK tahmincileri üzerindeki etkileri Tablo 3.1 aracılığı ile incelenebilir. Tablo 3.1 EÇO ve GEKK Tahmincilerinin Özellikleri Dağılım Tutarlılık Asimptotik Etkinlik ( ) Tahmincisi Çok değişkenli Normal Evet Evet Doğru Doğru Basık Olmayan Evet Evet Doğru Doğru Eliptik Evet Evet Yanlış Yanlış Keyfi Evet Hayır Yanlış Yanlış 74
87 Tablo 3.1 in birinci sütununda gözlenen değişkenlerin dağılımı yer almaktadır. Çok değişkenli normalliğin sağlandığı durumlarda tahminciler istenen özellikleri taşımaktadır. Normallikten sapmanın boyutuna göre tahmincilerin özelliklerinde meydana gelen değişiklikler Tablo 3.1 aracılığı ile görülmektedir. Çok değişkenli normalliğe göre çok daha az kısıtlamaların olduğu durumlarda ( ) ( ) eşitliği sağlanmaktadır. Bu durumda gözlenen değişiklikler aşırı basıklığa sahip değildirler. Bu durum Tablo 3.1 de ikinci satırda yer almaktadır. Eliptik dağılımlar ise çarpıklığı olmayan ve her bir gözlenen değişken için aynı basıklık derecesine sahiptirler. YEM modellerinde EÇO ve GEKK tahmincilerinin kullanılabilmesi için önemli bir yere sahip olan çok değişkenli normallik konusunun incelenmesi gerekmektedir. Burada önce tek değişkenli normallikten bahsetmek gerekmektedir. Tek değişkenli normallik çok değişkenli normallik için gerekli ama yeterli olmayan bir koşuldur. veri matrisi çok değişkenli normal dağılıma sahipse, veri matrisindeki herhangi değişkeni tek değişkenli normal dağılım gösterirken, değişken çiftlerinin oluşturduğu birleşik dağılımlar ise iki değişkenli normal dağılım gösterir. Daha genel bir ifade ile p boyutlu çok değişkenli normal dağılımdaki değişkenli alt kümeler ( ), q boyutlu çok değişkenli normal dağılım gösterirler. Ayrıca normal dağılıma uygunluk gösteren değişkenlerin bir doğrusal kombinasyonu da tek değişkenli normal dağılım gösterir. Ancak bunun tersi doğru olmayabilir. Yani, tüm değişkenlerin tek tek normal dağılım göstermesi ya da tüm olası çiftlerin iki değişkenli normal dağılım göstermesi çok değişkenli normalliği garanti etmemektedir. Tek değişkenli normal dağılıma uygunluğun araştırılmasında histogram, kutu çizgi grafikleri, Q-Q grafiği, PP grafiği gibi görsel yöntemler ve bunun yanı sıra Shapiro-Wilks, Kolmogorov-Smirnov testleri gibi istatistiksel yöntemler kullanılmaktadır (Alpar, 2003: 75). Bir dağılımın ortalama etrafındaki momentleri normallikten sapmayı ortaya koyan temel ölçüttür. Kitle ortalaması olan rassal değişkeninin inci momenti 75
88 ( ) (3.36) şeklinde tanımlanmaktadır. Normal dağılımın ortalaması ve varyansı ise ile tanımlanmaktadır. Normal dağılımın yüksek mertebe momentleri sıfırdır veya ortalama ve varyansın fonksiyonu olarak yazılabilirler. Normal dağılımdan sapmalar bu şekilde yüksek mertebe momentlerin incelenmesi ile saptanabilmektedir. Sırasıyla çarpıklık (skewness) ve basıklık (curtosis) katsayısı olarak adlandırılan üçüncü ve dördüncü momentler ( ) şeklindedir. Normal dağılım için standartlaştırılmış çarpıklık katsayısı 0 ve standartlaştırılmış basıklık katsayısı 3 olmalıdır (Bollen,1989: ). Çok değişkenli normal dağılıma uygunluk için ise tek değişkenli normal dağılıma uygunluğun araştırılmasında kullanılan yöntemlere benzer bir yaklaşım kullanılarak çok değişkenli çarpıklık ve basıklık katsayılarına dayanan normallik testleri geliştirilmiştir. Mardia (1970, 1974, 1985) ve Mardia ve Foster (1983) tarafından çok değişkenli normalliğin sınanması için pek çok alternatif test önerilmiştir. Mardia nın çok değişkenli çarpıklık ( ) ve basıklık katsayısı ( ) formülleri ( ) 2( ) ( )3 (3.37) 2( ) ( )3 (3.38) şeklinde ifade edilmektedir. Burada bütün değişkenlerin i. gözlem için değerlerini içeren sütun vektörü, bütün değişkenlerin j. gözlem için değerlerini içeren sütun vektörü ve ise örneklem ortalamalarına karşılık gelen sütun vektörünü 76
89 göstermektedir. Çok değişkenli çarpıklık ve basıklık katsayılarının çok değişkenli normal dağılımın çarpıklık ve basıklık katsayılarının eşitliği birleşik hipotezinin testi için kullanılacak test istatistiği ( ) ( ) (3.39) şeklinde olup, Tablo 3.2 de ve ye dayanan ve asimptotik olarak normal dağılıma uygunluk gösteren ( ) ve ( ) nin elde edilme adımları verilmiştir. Omnibus test istatistiği olarak adlandırılan dağılımına uygunluk göstermektedir., iki serbestlik derecesi ile Tablo 3.2 Çok DeğiĢkenli Çarpıklık ve Basıklık için Test Ġstatistikleri Çarpıklık Basıklık ( ) Hesaplama: (1) (2) ( ), ( )( )- Hesaplama: (1) (2) ( ) ( ) ( ) {, ( ) ( ) - ( )( ) + (3) ( ) ( ) (4) ( ) ( ) [ ( )] (5), ( )( ) ( ) - {,( ) ( )- ( ), ( )( ) - } (6) ( ). / [ ( * 4 ( ), ( )- 5 ] 77
90 AĞIRLIKLANDIRILMIġ EN KÜÇÜK KARELER YÖNTEMĠ YEM çalışmalarında kullanılan tahmin yöntemlerinden bir diğeri Ağırlıklandırılmış En Küçük Kareler (AEKK) yöntemidir. Bu yöntem modelde bulunan değişkenlerin sürekli bir dağılımdan gelmesi ancak normallikten büyük ölçüde sapmış olması veya modelde yer alan değişkenlerin bir kısmının sıralı ölçekte bir kısmının sürekli olması nedeniyle EÇO tahmincisinin kullanılamadığı durumlarda tercih edilen başlıca yöntemdir. ve için dağılımsal varsayımların sağlanmaması durumunda ağırlıklı en küçük kareler uyum fonksiyonundan elde edilecek tahmincilerin asimptotik olarak etkin olmasını sağlayacak ağırlık matrisinin kullanılması ile uyum fonksiyonu,, ( )-, ( )- (3.40) şeklinde elde edilir., gözlenen kovaryans matrisindeki artıksız elemanların ( )( ) boyutlu vektörü ve ( ) tahmini kovaryans matrisinin artıksız elemanlarının bir vektörü,, ( ) parametre vektörü ve gözlenen değişkenlerin sayısı ( ) ve ( ) olacak şekilde ( ) boyutlu pozitif tanımlı ağırlık matrisidir (Bollen, 1989: 425). matrisi asimptotik kovaryans matrisinin tutarlı bir tahmincisi olup, in elemanları genellikle matrisinin tersinden elde edilir. matrisinin tipik bir elemanı ( ) ( ) ( ) 78
91 şeklinde ifade edilebilir., ağırlıklı dördüncü moment (çok değişkenli basıklık ölçüsü), örneklem kovaryansları ve kitle kovaryanslarıdır (Çelik, 2009: 59). Bu yöntem, Browne (1984) tarafından asimptotik olarak dağılımdan bağımsız GEKK tahmincisi olarak adlandırılmıştır. Browne a göre değişkenlerin basıklık değerinin sıfırdan farklı olması haricinde hiçbir varsayım gerekmeksizin bu yöntem ile parametre tahminlerinin ve standart hataların hesaplanmasında normallik varsayımının incelenmesine gerek yoktur. Daha sonra Bentler (1995) tarafından bu yöntem Keyfi Dağılım Fonksiyonu (Arbitrary Distribution Function- ADF) ya da Keyfi Olarak Genelleştirilmiş EKK olarak adlandırılmıştır. AEKK yönteminde örneklem yeterince büyükse elde edilen tahminciler tutarlı ve yeterlidir. Literatürde AEKK nın dağılım varsayımlarından etkilenmediğini gösteren pek çok simülasyon çalışması mevcuttur (Hoogland ve Boosma,1998, West, v.d., 1995, Schermelleh-Engel v.d., 2003, 2003 incelenebilir.) AEKK nin bir diğer avantajı ise tahmin sürecinde korelasyon matrisinin kullanılmasına olanak sağlamasıdır. Eğer örneklem büyüklüğü yeterince genişse AEKK yöntemi uygun bir test istatistiği ve doğru standart hatalar meydana getirmektedir (Schermelleh- Engel v.d., 2003). AEKK yöntemi dağılım varsayımından bağımsız olması nedeniyle çeşitli avantajlara sahip olsa da bununla birlikte birtakım dezavantajları da mevcuttur. Yöntemin en büyük dezavantajı ağırlık matrisi nin hızlı bir şekilde değişken sayısına bağlı olarak artıyor olmasıdır. Asimptotik kovaryans matrisinin boyutu gözlenen değişken sayısının fonksiyonu olduğundan örneğin ( ) için ( ) olacaktır. olacak ve asimptotik kovaryans matrisinin mertebesi ( ) AEKK yöntemi EÇO ve GEKK yöntemi ile karşılaştırıldığında, EÇO ve GEKK yöntemi yeterli ve tutarlı tahminciler elde etmek için büyük örneklem ve 79
92 normal dağılım varsayımına ihtiyaç duyar. Örneklem büyüklüğünün fazla ve değişkenlerin dağılımın normallikten büyük ölçüde sapma göstermediği durumlarda EÇO ve GEKK tahmincisi AEKK tahmincisine oranla daha güvenilir sonuçlar vermektedir. Ancak normallikten sapma büyük ölçüde olduğu durumlarda AEKK tahmincisi tercih edilmelidir (Chou ve Bentler, 1995) DAYANIKLI YÖNTEMLER Çalışmanın bu kısmında klasik yöntemlerden farklı olarak normallik varsayımından sapmaların bulunması ya da veri tipinin klasik yöntemlerle tahmini mümkün kılmaması durumlarında kullanılabilecek yöntemler incelenecektir SATORRA-BENTLER ÖLÇEKLENDĠRĠLMĠġ ve DAYANIKLI STANDART HATALAR YÖNTEMĠ AEKK yöntemi dışında normallik varsayımından sapmaların olduğu durumlarda son birkaç on yılda popüler olan yöntemlerden biri Satoora-Bentler tarafından geliştirilen ve Dayanıklı EÇO yöntemi olarak da bilinen, verideki normallikten sapmanın ölçüsüne göre test istatistiğini, standart hataları, uyum indekslerini yeniden düzenleyen bir yöntemdir (Finney ve Distefano, 2006: 289). Bu yöntem bilinen test istatistiğinin normallik varsayımından uzaklaştığı durumlarda, söz konusu istatistiğin beklenen dağılımına uygun olmasa da referans edilen dağılımına yakınsayacak şekilde düzeltilmesi veya ölçeklendirilmesini temel almaktadır (West v.d., 1995: 65-66). Veriler normal dağıldığında, modelin doğru belirlenmiş olması varsayımı altında nin beklenen değeri modelin serbestlik derecesine eşit olacaktır. Ancak veriler orta derecede normallikten sapma gösterdiğinde model doğru belirlenmiş olsa dahi EÇO tahmincisinden elde edilen test istatistiği yanlı olacaktır. Bu durumda 80
93 Satorra-Bentler ( ) düzeltmesi olarak adlandırılan süreçle, EÇO istatistiğini gözlenen verilerin dağılımsal özelliklerinden yararlanılarak (3.42) şeklinde bir ilişki kurulmaktadır. Burada sabiti, ölçekleme için kullanılan ve modelin çok değişkenli basıklık ölçüsünün bir fonksiyonu olan bir değerdir. Çok değişkenli basıklık söz konusu olmadığı durumlarda her iki değeri eşit olacaktır. Satorra-Bentler yöntemi EÇO tahmincisine uygulanmasının nedeni AEKK tahmincisinden kaynaklı hesaplama zorlukları olmasıdır. Hatırlanacağı gibi AEKK tahmincisinde ağırlık matrisi çok büyük boyutlu bir matris haline gelebilmektedir. Satorra-Bentler yöntemi ağırlık matrisi yerinde, ölçekleme faktörünü hesaplamak için daha küçük boyutlu matrisler kullanmaktadır. Benzer düzeltme ve ölçekleme süreci EÇO tahmincisinden elde edilen standart hatalar için de uygulanmaktadır (Finney ve Distefano, 2006: 289). Normallikten sapma olması halinde bu yöntem ile hesaplanan standart hataların kullanılması genellikle Dayanıklı EÇO yöntemi olarak adlandırılmaktadır DAYANIKLI AĞIRLIKLANDIRILMIġ EN KÜÇÜK KARELER YÖNTEMĠ YEM çalışmalarında kategorik verilerle çalışılması durumunda Muthén (1993) tarafından geliştirilen iki dayanıklı tahminci olan AEKK-O ve AEKK-OV tahmincileri kullanılmaktadır. AEKK-O ve AEKK-OV tahmincileri sırasıyla AEKK tahmincisinin ortalama ve hem ortalama hem varyansa göre yeniden ölçeklendirilmesi ile edilen iki dayanıklı tahmin yöntemidir. Aynı zamanda bu iki tahminci Diyagonal Olarak Ağırlıklandırılmış En Küçük Kareler (DAEKK) yöntemi olarak da adlandırılmaktadır. 81
94 Bu yöntemlerin AEKK den farkı, AEKK nin asimptotik kovaryans matrisinin tamamına gerek duyarken, AEKK-O ve AEKK-OV nin asimptotik kovaryans matrisinin sadece diyagonal elemanlarına gereksinim duymasıdır. AEKK-O ve AEKK-OV tahmincileri arasındaki tek fark uyumun iyiliği kriterlerinin seçiminde olup, AEKK-OV tahmincisi diyagonal ağırlık matrisi W, dayanıklı standart hatalar ve ortalama ve varyans ile ölçeklendirilmiş test istatistiklerinin kullanılarak EKK parametrelerinin tahminini sağlar. AEKK-OV tahmincileri parametreleri dayanıklı ve doğru tahmin etmek için polychoric korelasyonları kullanırlar (Finney ve Distefano,2006: ). Muthén (1978) e göre ( ) kitle polychoric korelasyon matrisini göstermek üzere EKK fonksiyonu ( ( )) ( ( )) (3.43) şeklinde ifade edilmektedir. Burada en küçüklenmiş olup,, tahmin edilen polychoric korelasyonların asimptotik kovaryans matrisinin bir tahmini olmak üzere, olduğunda AEKK yöntemidir. ( ) olması durumunda ise ağırlıklar sadece tahmin edilen polychoric korelasyonların tahmin edilen varyansları olacak ve yöntem DAEKK olacaktır UYUM FONKSĠYONLARININ EN KÜÇÜKLENMESĠNDE KULLANILAN NÜMERĠK YÖNTEMLER YEM modellerinde tahmin sürecinin uyum fonksiyonlarının en küçüklenmesine dayalı olduğu önceki kısımlarda tartışılmıştır. Bu kısımda ise YEM de tahmin sürecinde uyum fonksiyonlarının en küçüklenmesinde kullanılacak sayısal yöntemler için genel bir bakış ortaya konulacaktır. Herhangi bir ( ) fonksiyonunun en küçüklenmesinde gerek koşul fonksiyonun ye göre kısmi türevinin alınıp sıfıra eşitlenerek her bir için 82
95 çözülmesidir. Elde edilen bu değerlerin ( ) yı en küçüklemesinin yeterli koşulu ise fonksiyonun ikinci mertebeden kısmi türevlerinin ( ( ) ) bu değerler için pozitif tanımlı olmasıdır. ( ) fonksiyonunun birinci dereceden kısmi türevleri,, ( ) boyutlu bir vektör olması durumunda ( ) ( ) olacaktır. Burada ( ) boyutlu vektörünün eleman sayısı kadar denklem elde edilir. YEM modellerinde söz konusu ( ) fonksiyonunun,, gibi uyum fonksiyonlarına eşit olduğu düşünüldüğünde, ilgili uyum fonksiyonlarının birinci türevlerinin sıfıra eşitlenmesi ile elde edilen t tane denklemin, parametreleri itibariyle doğrusal olmaması nedeniyle en küçükleme sorununun çözümünde nümerik iteratif yöntemlere başvurulmaktadır. En küçükleme süreci üç temel aşamadan oluşmaktadır: 1. Başlangıç değeri in seçilmesi, 2. Bir sonraki adıma göre serideki bir adımdan hareket kurallarının belirlenmesi ( den e geçiş), 3. İterasyonun durdurulması. Başlangıç değeri in seçilmesi en küçükleme süreci için önemlidir. Amaç fonksiyonu başlangıç değerinden etkilenmekte ve seçilen başlangıç değeri nihai çözüme ulaşmak için gerçekleştirilecek iterasyon sayısını belirlemektedir. Başlangıç değeri sonuç değerine yakın bir değer olarak seçilmelidir. Başlangıç değerinin nihai çözümden çok uzak bir değer seçilmesi durumunda global minimuma ulaşmayı zorlaştırmakta, bir yerel minimum bulunmakta veya yakınsama sağlanamamaktadır. Başlangıç değerinin seçilmesi için çeşitli stratejiler mevcuttur. Bunlardan ilki araç değişken yöntemi gibi iteratif olmayan bir yöntem ile elde edilen parametre tahminlerinin başlangıç değeri olarak kullanılmasıdır (Jöreskog ve Sörbom, 1986: 83
96 56-58). Alternatif bir yöntem ise, önceden belirlenmiş bazı kriterlere göre başlangıç değerinin seçilmesidir. Söz konusu kriterler Tablo 3.3 te verilmiştir. Tablo 3.3 YEM de BaĢlangıç Değerlerinin Seçimi Parametreler BaĢlangıç Değeri α Değeri ( ) 4 5 ( ) 4 5 ( ) ( ) =0.9 güçlü ilişki =0.4 orta ilişki =0.2 zayıf ilişki =0.9 güçlü ilişki =0.4 orta ilişki =0.2 zayıf ilişki = 0.9 güçlü uyum = 0.4 orta uyum = 0.2 zayıf uyum ( ) =0.9 güçlü korelasyon =0.4 orta korelasyon in örneklem kovaryans matrisi =0.2 zayıf korelasyon Tablo 3.3 ün birinci sütununda tahmin edilecek parametreler, ikinci sütununda başlangıç değerleri ve son sütunda araştırmacının değişkenler arasındaki uyumun ve korelasyonun gücünün tahminine bağlı olan α değerleri yer almaktadır. değerleri araştırmacının en iyi nesnel tahminlerine bağlıdır. ve parametreleri için standartlaştırılmış değişkenler ile çalışılması durumunda α değeri başlangıç değerine eşit olmaktadır. için hata varyansının negatif olmasını veya ( ) den büyük olmasını ve için de ve arasındaki korelasyonun ± 1 arasında olmasını garantilemek amacıyla ve için başlangıç değerlerine kısıtlar konulmaktadır (Bollen, 1989: 138). 84
97 Başlangıç değerinin belirlenmesinden sonra ikinci aşamada iterasyon sürecinin her bir adımı için den e geçişte ( ) nin ( ) den daha küçük olması gerekmektedir. Uyum fonksiyonunun gradyeni olan ( ), tanjant doğrularının eğimini verdiğinden fonksiyonunun en büyük değişme hızının doğrultusunda bir vektördür. Eğimin ( ) deki işaretinin negatif olması nin arttırılması gerektiğini, pozitif olması nin azaltılması gerektiğini göstermektedir. Eğimin sıfır olması ise minimum değere ulaşıldığını ifade eder. Bu şekilde gradyen vektörünün yönünün tersinden hareketle uyum fonksiyonunu en küçükleyen tahmin değerleri bulunabilmektedir (Şimşek, 2007: 96). ( ), gradyen vektörünün ( ) deki değeri ve ( ) de pozitif tanımlı bir matrisi göstermek üzere, den e geçişte ( ) ( ) ( ) ( ) (3.45) formülünden yararlanılmaktadır. Uyum fonksiyonlarının en küçüklenmesinde ( ) kullanılan yöntemler matrisinin seçimine bağlı olarak farklılaşmaktadır. Burada ( en basit yöntem ) nin birim matris olarak seçilmesidir. Dik düşüş yöntemi olarak da adlandırılan bu yöntem de yakınsama oldukça yavaş ve uyum fonksiyonunun ( ) şeklinden bağımsızdır. matrisinin seçimi için bir diğer alternatif uyum fonksiyonunun ya göre ikinci türevinden oluşan Hessian matrisinin tersinde ( ) ( deki değerlerin yerine konulmasından elde edilen matrisin seçilmesidir. ) nin bu yöntem ile seçilmesi nın uyum fonksiyonunun ( ) civarında Taylor serisi açılımına dayanmakta olup Eşitlik 3.45 deki Newton-Raphson algoritması yardımı ile çözümlenebilmektedir. ( ) ( ) 6 ( ) 7 ( ) ( ) 85
98 YEM modelleri için tahmin sürecinde, Newton-Raphson algoritmasına alternatif olarak Fletcher-Powell ve Gauss-Newton algoritmalarına dayanan en küçükleme yöntemleri de mevcuttur. LISREL yazılımının da kullandığı Fletcher- Powell algoritmasının Newton-Raphson algoritmasından farkı her bir adımda ikinci mertebe kısmi türevlerin tersine ihtiyaç duyulmamasıdır (Bollen,1989: ). Uyum fonksiyonlarının en küçüklenmesinde sürecinde üçüncü ve son aşama iterasyonun durdurulmasıdır. Burada izlenecek kural, iterasyonun durdurulması için uyum fonksiyonları arasındaki farklılıkların daha önceden belirlenen çok küçük bir farktan daha küçük olmasıdır. Eğer birbirini izleyen adımlar sırasında fonksiyon bir noktaya yakınsamıyorsa iterasyon belli bir sayısal değerde sonlandırılabilir. LISREL yazılımı için bu değer 250 iterasyondur. YEM modellerinin tahmininde nümerik yöntemlerin kullanılması çoklu parametreler içeren modeller için oldukça karmaşıktır. Bu nedenle basitleştirici varsayımlar ile Bollen (1989) tarafından tek parametreleri bir model için bu süreç incelenmiştir. Daha sonra Ferron ve Hess (2007) EÇO tahmincisi için söz konusu nümerik yöntemle iki parametreli bir model için aynı yöntemin uygulanışını göstermişlerdir STANDARTLAġTIRILMIġ VE STANDARTLAġTIRIL- MAMIġ KATSAYILAR Gözlenen değişkenlerin kovaryans matrisinin analizi ile değişkenlerin ölçeklerine bağlı olarak standartlaştırılmamış katsayılar elde edilmektedir. Özellikle aynı bağımlı değişkeni açıklamada kullanılan iki veya daha fazla değişkenin farklı ölçekle ölçülmüş olması durumunda, söz konusu değişkenlerin aynı bağımlı değişkendeki etkilerinin birbirinden ayrılması oldukça karmaşıktır. Bu nedenle farklı bağımsız değişkenlerin göreli etkilerinin araştırılmasında standartlaştırılmış katsayıların kullanılması gereklidir. Burada değişkenler, kendi ortalamalarından farkları alınıp, standart sapmalarına bölünerek standartlaştırılmaktadır. Başka bir deyişle değişkenler ölçekten bağımsız hale getirilip, varyansları bire eşitlenmektedir. 86
99 YEM modellerinde, standartlaştırılmış katsayılar doğrudan standartlaştırılmamış katsayılar kullanılarak, 4 5 ( ) 4 5 ( ) 4 5 ( ) şeklinde elde edilebilir. Burada s üst simgesi standartlaştırılmış katsayıyı, i indisi bağımlı değişkeni, j indisi bağımsız veya açıklayıcı değişkeni ve ile sırasıyla i. ve j. değişken için model tarafından tahmin edilen varyanslarını göstermektedir. Standartlaştırılmış katsayılar, diğer değişkenler sabit tutulduğunda bağımsız değişkendeki bir standart sapma kadar değişime karşılık bağımlı değişkenin standart sapmasında beklenen değişimi ifade etmektedirler. Standartlaştırılmış katsayıların matris gösterimi için ise, nın kovaryans matrisinin tersini göstermek üzere aşağıdaki eşitler yazılabilir (Bollen, 1989: ). [ ( )] [ ( )] (3.50) [ ( )], ( )- (3.51) [ ( )] [ ( )] (3.52) ( ) ( ) ( )( ) (3.53) 87
100 3.7. EġĠTLĠK SABĠTLERĠ VE ORTALAMALAR YEM modellerinde ölçme ve yapısal modellere sabit terimlerin ilave edilmesi ile değişken ortalamalarının tahmini mümkün olmaktadır. YEM genel modeline eşitlik sabitlerinin eklenmesi ile model (3.54) şeklinde ifade edilir. Burada,, ( ) boyutlu, ise ( ) boyutlu ölçme modelleri için sabit terim vektörleridir. Yapısal modelde ise, ( ) boyutlu sabit terim vektörüdür. Dışsal değişkenlerin ortalama değeri, -, ( ) boyutlu vektöründe yer almaktadır. Gizil içsel değişkenlerin ortalaması ise, -,( ) ( )- ( ) ( ) (3.55) şeklindedir. Gizil içsel değişkenlerin ortalaması yalnızca ya bağlı olmayıp, ve daki yapısal parametrelere de bağlıdır. Ölçme modeli için ise ortalama vektörleri,, - ( ) ( ) (3.56), - (3.57) şeklindedir. Ölçme modellerine ait ortalamalar da yapısal parametre matrislerine ilaveten,,, ve daki parametreler bağlı olmaktadır. Bu nedenle sabit terimlerin yer aldığı YEM modellerinin tanımlanması diğer YEM modellerine oranla daha karmaşık olacaktır. Parametrelerin tanımlanması için kullanılacak yöntemlerden ilki her bir gizil değişkene ait ortalama değerinin sıfıra eşitlenmesidir. Diğer bir 88
101 yöntem ise bir gizil değişkenin ölçeğinin gözlenen değişkenlerden birine denk gelecek şekilde düzenlemesidir (Bollen, 1989: ) TOPLAM, DOĞRUDAN VE DOLAYLI ETKĠLER YEM modellerinde değişkenler arası ilişkiler incelenirken sadece doğrudan etkilerin dikkate alınması bilgi kaybına neden olmaktadır. Bir değişkenin başka bir değişken üzerinde doğrudan etkisinin yanı sıra başka bir değişken vasıtasıyla söz konusu değişkene dolaylı olarak etkisi ve toplam etkisi de söz konusudur. Doğrudan etkiler YEM modellerinde,,, matrislerinde yer almaktadır. Dolaylı etkiler ise, toplam etkiler ile doğrudan etkiler arasındaki fark olarak hesaplanır. Dolaylı etkiler aynı zamanda aracılık etkisi olarak da adlandırılmaktadır. Toplam etkiler ise iki yolla hesaplanabilmektedir. Bunlardan ilki, toplam etkilerin katsayı matrislerinin güçlerinin toplamına eşit olması ikincisi ise, indirgenmiş katsayıların kullanılmasıyla hesaplanmasıdır., -,( ) ( )- (3.58) içsel değişken sayısını göstermek üzere ve nin mutlak değerce en büyük özdeğerinin birden küçük olması şartının sağlanarak, ( ) serisinin yakınsak bir seri ve genel toplamının da ( ) olması durumunda YEM de etkilerin ayrıştırılması için Tablo 3.4 te verilen formüller kullanılmaktadır (Bentler ve Freeman, 1983: 145). 89
102 Tablo 3.4 Doğrudan, Dolaylı ve Toplam Etkilerin AyrıĢtırılması üzerinde üzerinde üzerinde nin Etkileri Doğrudan Etkiler Dolaylı Etkiler Toplam Etkiler ( ) ( ) 0 ( ) 0 ( ) nın Etkileri Doğrudan Etkiler Dolaylı Etkiler Toplam Etkiler ( ) ( ) ( ) ( ) YAPISAL EġĠTLĠK MODELLEMESĠNDE SIRALI DEĞĠġKENLERĠN KULLANIMI Çalışmanın daha önceki kısımlarında YEM e ilişkin açıklamalarda gizil ve gözlenen değişkenlerin sürekli değişkenler olduğu varsayılmaktadır. Ancak bu varsayımın özellikle gözlenen değişkenler için her zaman mümkün olmamaktadır. Sıralı ölçek veya likert tipi ölçekler sosyal bilimler alanında sıklıkla kullanılan ölçme araçları olduğundan YEM de sıralı ölçekle ölçülmüş değişkenler ile çalışılması ayrı bir literatür olarak incelenmiştir. YEM de bu tür sıralı veya dikatom değişkenlerin ardında bir gizil sürekli değişken olduğu varsayılarak doğrusal olmayan bir eşik değer fonksiyonu tanımlanmakta ve gizil sürekli değişkenlere uygun korelasyonlarla çalışılmaktadır (Muthén,1982: 66). Ölçümlerde kullanılan ölçek (nominal, sıralı, aralıklı ve oranlı ölçekler) hesaplanacak korelasyon katsayısının da farklılaşmasına neden olmaktadır. Ölçek türüne göre kullanılacak korelasyon katsayılarının türleri Tablo 3.5 ile verilmiştir. 90
103 Tablo 3.5 Korelasyon Katsayısı Türleri*(Çelik, 2009: 160) Korelasyon Katsayısı Ölçme Düzeyi DeğiĢken I DeğiĢken II Pearson (product-moment korelasyon) Aralıklı Aralıklı Spearman ın Sıra, Kendall ın tau su Sıralı Sıralı Dörtlü korelasyon katsayısı (Phi) Nominal Nominal Nokta çift serili (point biserial) Aralıklı İki düzeyli Gamma, Sıra çift serili Sıralı Nominal Olumsallık Nominal Nominal İki serili Aralıklı Yapay değişken* Polyserial Aralıklı Temel bir sürekli değişken ile ordinal Tetrachoric (dört düzeyli) İki düzeyli İki düzeyli (nominalyapay) (nominalyapay) Polychoric Temel sürekli bir değişken ile sıralı *İki düzeyli bir değişken olarak değerleri kaydedilir. Sıralı ölçek ile ölçülen değişkenlerin sürekli ölçekmiş gibi değerlendirilmeleri durumunda YEM de bazı varsayımlardan sapmalar meydana gelmektedir., gizil değişkenine ait sürekli gösterge değişkenlerin ( ) boyutlu bir vektörü olduğunda ölçüm modeli (3.59) şeklindedir. Burada ( ), ( ) ve ( ) varsayımları mevcuttur. ın doğrudan gözlemlenmediği ancak ın kategorik ölçekteki karşılığı olan y değişkeninin gözlemlendiği durumda olacağından için sağlanan ölçme modeli y için sağlanmayacaktır. Örneğin normal dağılan bir değişken iken normal dağılıma uygunluk göstermeyecektir. sürekli değişkenler iken bu değişkenler için Eşitlik 3.59 geçerli iken, bunlara 91
104 karşılık gelen sıralı ölçekteki y değerleri için söz konusu eşitlik geçerli değildir. Benzer durum ve için de geçerlidir. Sıralı ölçekli değişkenlerin sürekli kabul edilmesinin yaratacağı bir diğer sorun sıralı ölçekteki değişkenlerin dağılımı ile sürekli gizil göstergelerin dağılımı aynı olmaması durumudur. Bu durumda ve in kovaryans matrisi elemanları ve, ve ın kovaryans matrisi elemanları ve olmak üzere ( ) ve ( ) eşit olmamaktadır. ve normal dağılsa dahi y ve normal dağılmayacaktır. Bu durumda y ve değişkenlerinin asimptotik özelliklere sahip olmaları için Asimptotik Olarak Dağılımdan Bağımsız (ADF) teori kullanılmaktadır. Bu durumda AEKK tahmin yöntemi kullanılarak model tahmin edilebilmektedir. Ancak bu yöntemde asimptotik özelliklere ulaşmak için oldukça geniş bir örneklem büyüklüğüne ihtiyaç duyulmaktadır. Aksi halde AEKK yöntemi değişen varyansın olmadığını hata terimi varsayımı gerektirdiğinden sıralı ölçekteki değişkenler kalıntıların değişen varyanslı olmasına neden olacaktır. ( ) Sıralı ölçekteki değişkenlerin sürekli olarak değerlendirilmesinin ortaya çıkaracağı en ciddi problem ise sürekli göstergelere ait ve karşılık gelen sıralı ölçekteki göstergelere ait kovaryans matrislerinin eşit olmaması nedeniyle, ( ) kovaryans yapısı eşitliği sağlanamayacağından ( ) olacaktır. Aynı zamanda, nin tutarlı bir tahmincisi ve ın da ın tutarlı bir tahmincisi olduğu varsayılır ise den elde edilen parametre tahmincisi gerçek parametre vektörü nın tutarlı olmayan bir tahmincisi olacaktır (Bollen, 1989: ). Sıralı değişkenler ile YEM in tahmini iki aşamadan oluşmaktadır. Birinci aşama; genellikle çok değişkenli normal dağılıma uygunluk gösterdiği varsayılan, gizil sürekli değişkenleri arasındaki korelasyonun tahmin edilmesini içermektedir. ve gizil sürekli değişkenlerinin göstergelerinin tahmin edilen korelasyonlarına verilen isimler ve y değişkenlerinin ölçeklerine göre farklılık göstermektedir. Tablo 3.5 te farklı ölçekler için hangi korelasyonların kullanılacağı incelenmiştir. Her iki değişken de sıralı ölçekte ise polychoric korelasyon, her iki değişken de dikatom ise 92
105 tetrachoric (dört düzeyli), değişkenlerden biri sıralı diğeri ise sürekli olduğunda polyserial korelasyonlar kullanılmaktadır. İkinci aşamada ise tahmin edilen korelasyonların asimptotik kovaryans matrisinin tutarlı tahmini olan bir ağırlık matrisi kullanılarak modelin AEKK yöntemi ile tahmini söz konusudur. Öncelikle polychoric korelasyon kavramı açıklanacaktır. ve sıralı değişkenleri sırasıyla ve kategoriye sahip olduğunda bu değişkenlerin marjinal dağılımları ( ) şeklinde bir kontenjans tablosu ile gösterilmektedir., birinci değişken için i ve ikinci değişken için j kategorisindeki olayların sayısıdır. ve değişkenleri sıfır ortalama ve birim varyanslı normal dağılıma sahip olduklarından ve, korelasyonlu iki değişkenli normal dağılıma sahip olacaklardır. Polychoric korelasyon ise ve değişkenlerinin iki değişkenli normal dağılımdaki korelasyonudur. Burada eşitliği olduğunda söz konusu korelasyon tetrachoric (dört düzeyli) korelasyon olarak adlandırılır (Jöreskog, 2005: 11). Polychoric korelasyon sadece sıralı ölçekte değişkenlerin verildiği iki tane gözlenemeyen sürekli değişken arasındaki doğrusal ilişkinin tahminini veren katsayıdır (Flora ve Curran, 2004: ) y ile arasında ilişki kuran ve korelasyonların tahmin edilmesinde kullanılan doğrusal olmayan eşik değer fonksiyonu (3.60) şeklindedir. Burada, 93
106 (3.61) eşik değer olarak adlandırılan parametrelerdir. Daha açık bir ifade ile örneğin göstergesi için { eşitliği söz konusudur. Burada, için kategori sayısı, ( ) kategori eşikleri (threshold) ve sürekli gizil göstergelerdir. m kategoriye sahip y değişkeni için tane eşik parametresi mevcuttur. Sadece ordinal bir bilgiye sahip olması nedeniyle ın dağılımı monotonik bir dönüşüme bağlı olarak tanımlanır. için herhangi bir sürekli değişken seçilebilmektedir. Bunun nedeni bir dağılım fonksiyonuna sahip herhangi bir sürekli değişkenin monotonik dönüşüm aracılığıyla normal dağılıma dönüştürülebilmesidir. Sıralı ölçekteki y değişkeni için, ın dağılım fonksiyonu ( ) ve ( ) yoğunluk fonksiyonu ile standart normal dağılımın seçilmesi uygundur. i kategorisindeki bir yanıtın gerçekleşme olasılığı, -, - ( ) ( ) ( ) (3.62) ( ) (3.63) şeklinde gösterilmektedir. Burada standart normal dağılım fonksiyonunun tersi olup ( ) niceliği i kategorisindeki bir yanıtın olasılığı ve olasılıkları bilinmeyen kitle nicelikleridir. olasılık değerleri, i kategorisindeki yanıtların yüzdeleri olan ler aracılığı ile 94
107 ( ) şeklinde tahmin edilmektedir (Jöreskog,2005: 10). ( ) ( ) ( ), değişkeninin ve ( ) ( ) ( ), değişkeninin eşik değerleridir. Polychoric korelasyon, multinominal dağılımın en büyüklenen logolabilirliği ile tahmin edilebilir. Log-olabilirlik fonksiyonu, ( ) şeklinde olup, ( ), - ( ) (3.64) ve ( ) ( ) ( ) ( ) korelasyonu ile iki değişkenli standart normal dağılımın olasılık yoğunluk fonksiyonudur. Eşitlik 3.64 ile verilen model ( ) nin ve olasılıkları ile gösterilmektedir. ( ( ) ( ) ( ) ( ) ( ) ( ) (3.65) Eşitlik 3.65 ile gösterilen parametre vektörü polychoric korelasyon ve iki değişkene ait eşiklerden meydana gelmektedir. Buradan en büyüklenen LnL ve en küçüklenmiş uyum fonksiyonundan edilecek değerler eşittir. ( ) [ ( )] [ ( )] (3.67) 95
108 Burada olmak üzere örneklem oranlarıdır (Jöreskog, 2005: 12). Daha sonra modelin önceki kısımlarda anlatılan Dayanıklı EÇO ya da AEKK yöntemlerden biri ile tahmini gerçekleştirilebilir YAPISAL EġĠTLĠK MODELĠNĠN DEĞERLENDĠRĠLMESĠ VE UYUM ÖLÇÜTLERĠ YEM de model tahmininden sonraki aşama modelin değerlendirilmesidir. Model değerlendirilmesi için uyumun iyiliği ölçütleri olarak adlandırılan pek çok farklı ölçüt geliştirilmiştir. YEM de modelin değerlendirilmesi konusunda diğer çok değişkenli istatistiksel tekniklerden farklı olarak kesin kabul görmüş bir test ve ya ölçüt bulunmamaktadır. Gerek modelin değerlendirilmesinde gerekse alternatif modeller arasında seçim yapma konusunda en iyi sonucu veren kesin bir ölçüt olmamasına rağmen belirli stratejilerde kullanılmak üzere geliştirilmiş ve test edilmiş pek çok uyumun iyiliği ölçütü bulunmaktadır. Çalışmanın bu kısmında söz konusu ölçütler sınıflandırılarak incelenecektir. YEM de modelin değerlendirilmesi konusunda yapılacak en temel sınıflandırma: genel modelin uyumu test ve ölçütleri ve modelin ölçme bileşenindeki güvenilirliklerini ile yapısal bileşenindeki parametrelerin anlamlılıklarını tek tek ve ayrıntılı olarak inceleyen model bileşenlerinin uyum ölçütleri olacaktır (Şimşek, 2007: ) GENEL MODELĠN DEĞERLENDĠRĠLMESĠ Genel modelin uyum ölçütleri ile değerlendirilmesinde test edilecek olan hipotez kovaryans yapısı eşitliği olarak bahsedilen ( ) eşitliğidir. Bu başlık altında incelenen bütün uyum ölçütleri bu hipotezin geçerli olup olmadığını test etmektedir. Hipotezin geçerli olmadığı durumda nın ( ) dan farkının ölçülmesini sağlar. Uyum ölçütlerinin hesaplanmasında kitle parametreleri ve ( ) yerine sırasıyla örneklemden elde edilen ve ( ) değerleri kullanılır. Uyum ölçütleri, 96
109 nin ( ) ya yakınlığının bir ölçüsü olup bu yakınlık pek çok farklı yolla ölçülebilmektedir. Genel model uyum ölçütleri temel avantajı tüm modelin değerlendirilmesi ile birlikte eşitlikler ve parametre tahminleri gibi model bileşenlerinin uyumu tarafından açıklanamayan yetersizlikleri belirtebilmesidir. Uyum ölçütlerine ait bazı sınırlılıklar mevcuttur. Bunlardan ilki uyum ölçütlerinin tam tanımlanmış modellere uygulanamamasıdır. Tam tanımlanmış modellerde daima olacağından, genel modelin uyumunun değerlendirilmesinin konusu olmaktan çıkacaktır. Özetle ifade etmek gerekirse bu ölçütler aşırı tanımlanmış modeller için söz konusudur. İkinci sınırlılık durumu ise, genel modelin uyum ölçütlerinin model bileşenlerinin uyumuna ilişkin farklılık gösterebilmesidir. Örneğin; modelin genel uyumu iyi olmasına rağmen, parametre tahminleri istatistiksel olarak anlamlı olmayabilir ya da beklenenden farklı işarete sahip olabilirler. Ayrıca nın ile tam olarak eşleşmesi bağımsız değişkenlerin uyumunun ne kadar iyi olduğunu göstermemektedir. Uyum ölçütlerinin tamamı modeldeki bütün eşitliklerin değerlerini özetlememektedir (Bollen,1989: ). Genel modelin uyum kriterleri başlığı altında incelenen uyum ölçütlerinin sayısı oldukça fazla olup birbirini ikame etmeyen pek çok test ve ölçüt geliştirilmiştir. Neredeyse otuzdan fazla farklı ölçüt arasından hangisinin en iyi olduğuna dair bir uzlaşma sağlanmamıştır (Tanguma, 2001: 759). Aynı zamanda söz konusu ölçütlerin sınıflandırılması açısından da literatürde bir görüş birliği bulunmamaktadır. Widaman (2003) e göre YEM deki uyum ölçütlerini iki grupta incelemek mümkündür. Mutlak Uyum Ölçütleri (Absolute Fit Index) ve Artımsal Uyum Ölçütleri (Incremental Fit Index). Hoyle ve Panter (1995) ise Mutlak Uyum Ölçütleri, Örnek Çapına Bağlı Ölçütler ve Merkezi Olmayan Ölçütler şeklinde üçlü bir sınıflandırma yapmıştır. Bu çalışmada Tanaka (1993) ün üçlü sınıflandırması benimsenmiş olup uyum ölçütleri: Mutlak Uyum Ölçütleri, Artımsal Uyum Ölçütleri ve Yalınlık Uyum Ölçütleri (Parsimony Fit Index) şeklinde incelenecektir. Merkezi olmayan dağılımlarla ilgili ölçütler ise ayrı bir başlık altında incelenecektir. 97
110 YEM de ortaya çıkan temel sorun, bu kadar farklı ve her zaman tutarlı sonuçlar vermeyen pek çok uyum ölçütü olması durumunda uyumun kabul edilebilir düzeyinin ne olduğudur? Bu sorunun cevabını Bollen (1989), artan uyum ölçütleri için tam bir eşik değerinin seçimi çoklu regresyondaki en büyük nin seçimi gibidir. Yani belirlenecek herhangi bir değer tartışmalı olacaktır. şeklinde verirken, Jaccard ve Wan (1996) model tahmini içeren YEM çalışmalarında ölçütler arasındaki tutarsızlıktan etkilenilmemesi için en az üç ölçütün, Kline (1998) ise en az dört ölçütün raporlanması gerektiğini savunmuşlardır KESĠN UYUM ÖLÇÜTLERĠ Kesin uyum ölçütleri genel modelin gözlenen kovaryans ve korelasyon matrislerinin tahminin derecesi hakkında bilgi verir. Başka bir deyişle gözlenen ve tahmin edilen kovaryans matrisleri arasındaki ilişkiyi test etmek üzere kullanılır. Bu başlık altında incelenecek olan ölçütler: Testi, Uyumun İyiliği Ölçütü (Goodness of Fit Index-GFI), Düzeltilmiş Uyumun İyiliği Ölçütü (Adjusted Goodness of Fit Index-AGFI), Hata Kareler Ortalamasının Karekökü (Root Mean Square Residual- RMR), Standartlaştırılmış Hata Kareler Ortalamasının Karekökü (Standardized Root Mean Square Residual-SRMR), Hoelter in Kritik N Ölçütü (Hoelter s Critical N- CN) şeklidedir. Bu grupta yer alan ölçütlerin tamamı merkezi dağılımına sahip olup bütün formüller dağılımının farklı varyasyonlarından türetilmektedir. Bu nedenle öncelikle istatistiği ayrıntıları ile incelenecektir. 1) Uyumun Ġyiliği Ölçütü Genel modelin değerlendirilmesinde kullanılan ölçütlerin en temel olanı test istatistiğidir. Bu ölçüt modelin verilere uygunluğunun belirlemek için, örneklem kovaryans matrisi ile modelden elde edilen kovaryans matrisi arasındaki farkın ölçümünü içermektedir. testi, küçük değerinin iyi uyumun, büyük 98
111 değerinin ise kötü uyumun karşılığı olduğu bir kötülük uyum ölçütü olarak da düşünülebilir (Akıncı, 2007: 28). uyumun iyiliği ölçütü ile eğer dağılımsal varsayımlar sağlanıyorsa, kitle kovaryans matrisi ile modele ilişkin tahmini kovaryans matrisi ( ) eşit olup olmadığı hipotezi sınanmaktadır. Burada sıfır hipotezi daima; ( ) şeklinde olacaktır. Burada söz konusu matrisler kitle parametreleri olduğundan yerlerine sırasıyla örneklemden elde edilen ve ( ) değerleri kullanılır. Burada tahmin edilen parametrelerin ( ) boyutlu vektörü olup hipotezi altında tahminleri ( ), ( )- (3.68) şeklinde olacaktır. Burada s, deki artıksız elemanların sayısı, t tahmin edilen parametre sayısı, N, örneklem büyüklüğü ve ve ( ) sırasıyla gözlenen kovaryans matrisi ve modele ilişkin tahmini kovaryans matrisleridir. değerinin elde edilmesi tahmin metoduna bağlıdır. EÇO, AEKK, GEKK tahmincilerinin her biri için farklı bir değeri hesaplanacaktır. Genellikle yüksek değeri kitle kovaryans matrisi ile modele ilişkin tahmini kovaryans matrisi ( ) nın anlamlı olarak birbirlerinden farklı olduklarını gösterir. ( ) elemanlarının sıfıra eşitliği mükemmel uyumun göstergesi olacaktır. Eğer istatistiği için elde edilen -değeri 0,05 ten büyük ise sıfır hipotezi kabul edilir ve modelin kitle kovaryans matrisi ile uyumlu olduğu sonucuna varılır (Schermelleh-Engel v.d., 2003: 32). Modelin değerlendirilmesinde ölçütünün kullanılması belirli varsayımların sağlanmasına bağlıdır. Söz konusu varsayımlar: 1. değişkeninin dağılımı basık olmamalıdır. Basıklık özelliği olmayan dağılımlar arasında en çok kullanılan çok değişkenli normal dağılım olup, YEM çalışmalarında kullanılan veriler genelde çok değişkenli normal dağılımdan aşırı sapma eğilimdedirler. 99
112 2. Kovaryans matrisi analiz edilmelidir. Jöreskog ve Sörbom (1986) korelasyon matrisi analiz edildiğinde, tahminlerinin hatalı sonuçlar verebileceğini iddia etmektedirler. 3. Örneklem yeterince büyük olmalıdır. Boomsma (1983) örneklem büyüklüğü ile ilgili simülasyon çalışmasında 50 den küçük örnek büyüklüğü için testinin güvenilir olmayacağını, örneklem büyüklüğünün en az 100 olması gerektiğini savunmuştur. değeri örneklem büyüklüğüne bağlı olarak artacağından, ile büyük örneklem ile çalışılması durumunda aslında uyumlu olan bir modeli uyumlu bulmama (1. tip hata) ve küçük örneklem ile çalışılması durumunda aslında uyumlu olmayan bir modeli uyumlu bulma durumu (2. tip hata) söz konusu olabilmektedir. Bu gibi sakıncalardan kaçınmak için örneklemin çok geniş olduğu durumlarda alternatif ölçütler kullanılarak sonuç doğrulanmalıdır. 4. ( ) hipotezi tam olarak sağlanması gerekmektedir. şeklindedir (Bollen, 1989: ). Bu ölçütün bir diğer dezavantajı ise modele eklenen her parametrenin değerini düşürmesidir. Bu durumda oldukça fazla parametreli modellere ilişkin değerleri serbestlik derecesinin azalmasından dolayı daha basit modellere göre küçük bir değer çıkma eğilimde olacak ve bu durum yanıltıcı sonuçlar meydana getirecektir. Bahsedilen sakıncalar nedeniyle Jöreskog ve Sörbom (1993) test istatistiğinin kullanımının yerine örnekleme dağılımının beklenen değeri ile nin gücünün karşılaştırılmasını farklı bir ölçüt olarak önermişlerdir. İyi bir model için oranı küçük olmalı ve bu oran 2 ile 3 arasında olması durumunda verinin model ile uyumlu olduğu düşünülmektedir (Bollen, 1989: 278). 100
113 Kovaryans yapısı analizlerinde sıklıkla karşılaşılan bir sorun da alternatif modeller arasında seçim yapma sorunudur. Burada kullanılacak ölçüt modellerin yuvalanmış olup olmamasına göre değişiklik göstermektedir. Yuvalanmış modeller için test istatistiği temel alan fark testi yaklaşımı kullanılmaktadır. Bu yaklaşımda herhangi bir model (Model A) kendisine göre daha az kısıtlanmış bir modelden (Model B), en az bir serbest parametrenin kısıtlanması ile türetilebiliyorsa Model A nın kendisine göre daha çok parametre ve daha az serbestlik derecesine sahip olan Model B nin içine yuvalandığı söylenebilir. Yuvalanmış modellerin her biri için uyumun ölçütü olarak test istatistiği ve dağılımı kullanılır. Yuvalanmış iki modelden elde edilen değerleri arasındaki fark da dağılımına uygunluk göstermektedir (Steiger v.d., 1985). Söz konusu fark için serbestlik derecesi yuvalanmış modellerin her birine ait değerlerinin serbestlik dereceleri arasındaki farka eşit olacaktır. Bu varsayımlar altında fark testi için test istatistiği, ( ) ( ) ( ) şeklinde olup, istatistiğinin anlamlı olması durumunda iki modelin gösterdiği uyumun aynı olduğunu iddia eden hipotezi reddedilecek ve Model B seçilecektir. Aksi durumda yuvalanmış modellere ilişkin uyumun aynı olduğunu iddia eden hipotezi reddilemez ve Model A seçilir (Schermelleh-Engel v.d., 2003: 34). 2) Uyumun Ġyiliği Ölçütü (GFI) Genel modelin değerlendirilmesi için Jöreskog ve Sörbom (1989) ve Tanaka ve Huba (1984) tarafından geliştirilen uyum ölçütü olan GFI ölçütü, gözlenen kovaryans matrisi de tarafından açıklanan göreli varyans ve kovaryans miktarı olarak tanımlanır. Jöreskog ve Sörbom (1993) e göre bu ölçüt; sıfır modeli olarak tanımlanan, bütün parametrelerin sıfır olduğu yani modelin olmadığı, durum ile mevcut modelin karşılaştırılmasında modelin ne ölçüde iyi olduğunu test eder. Bu nedenle regresyondaki belirginlik katsayısına benzemektedir. GFI ölçütü, 101
114 [ ( )], ( )- ( ) şeklinde olup, burada değeri sıfır modeli olarak ifade edilen modelin değeri ve ise uyumu test edilen mevcut modelin değeri, fonksiyonları ise ilgili tahmin metodu için en küçüklenecek uyum fonksiyonunun değeridir. GFI ölçütü, bazı durumlarda negatif değerler alsa da genellikle 0 ile 1 arasında olması gerekmektedir. Büyük değerler iyi uyuma işaret eder. Bu ölçütün 0,95 değerini alması iyi bir uyumu gösterirken, 0,90 dan büyük değerlerde kabul edilebilir bir uyumun göstergesi olarak değerlendirilir (Schermelleh-Engel v.d., 2003: 42-43). GFI ölçütü aynı örnek büyüklüğüne ait iki modelin karşılaştırılmasının yanı sıra farklı örnek büyüklüğüne sahip modellerin karşılaştırılmasında da kullanılmaktadır (Çerezci, 2010: 52). 3) DüzeltilmiĢ Uyumun Ġyiliği Ölçütü (AGFI) GFI ölçütünün değişken sayısı fazla karmaşık modellerde her zaman iyi sonuç vermemesi nedeniyle model karmaşıklığından kaynaklanan yanlılığın giderilmesi amacı ile Düzeltilmiş Uyumun İyiliği Ölçütü AGFI geliştirilmiştir. Jöreskog ve Sörbom (1989) tarafından önerilen AGFI, ( ) ( ) şeklinde formüle edilebilir. Burada ( ) şeklinde sıfır modelinin serbestlik derecesi ve olacak şekilde mevcut modelin serbestlik derecesini ifade etmektedir. AGFI nın yüksek değerleri iyi bir uyumu göstermektedir. Genellikle 0 ile 1 arasında değer almasına rağmen, örneğin küçük serbestlik derecesine rağmen örneklem büyüklüğünün fazla olduğu durumlar gibi bazı durumlarda negatif değerler alabilmektedir. Modelin serbestlik derecesi sıfır 102
115 modelinin serbestlik derecesine yaklaşırsa, AGFI değeri GFI değerine yakınsayacaktır. AGFI için 0,90 iyi bir uyum ölçüsü iken 0,85 ten büyük değerler de kabul edilebilir bir uyumun göstergesi olarak değerlendirilir (Schermelleh-Engel v.d., 2003: 43). 4) Hata Kareler Ortalamasının Karekökü (RMR) ve StandartlaĢtırılmıĢ Hata Kareler Ortalamasının Karekökü (SRMR) RMR ölçütü, ( ) olarak tanımlanan hataların temel alan bir ölçüttür. Hataların kareli ortalamasının karekökü olarak tanımlanan bu ölçüt ( ) ( ) ( ) şeklinde formüle edilmektedir. Burada, gözlenen kovaryans matrisinin, ise modele ait tahmini kovaryans matrisi ( ) nın bir elemanını ve ise gözlenen değişken sayısını göstermektedir. RMR değeri 0 ile 1 arasında değer almaktadır. Ölçütün değerinin küçük olması verinin modele iyi uyum gösterdiğini ifade etmektedir. 0,05 ten küçük RMR değerleri iyi uyumun göstergesidir. Değerin 0,05 ile 0,10 arasında olması ise kabul edilir bir uyumun göstergesidir (Schermelleh-Engel v.d., 2003: 37). RMR ölçütünün dezavantajı ise ölçekten bağımsız olmamasıdır. Değişkenlere ait ölçeğin bilinmediği durumlarda elde edilen RMR değerini yorumlamak mümkün olmayacaktır. Aynı zamanda bu ölçüt, değişkenler varyans ve kovaryansının büyüklüğüne göre de değişkenlik göstermektedir. Bu problemi aşmak için Standartlaştırılmış Hata Ortalamasının Karekökü-SRMR ölçütü geliştirilmiştir (Bentler, 1995: 271). hataları öncelikle ve standart sapma değerlerine bölünür ise söz konusu hatalar ( ) ( ) ( ) şeklinde 103
116 standartlaştırılmış elemanlara sahip bir matris haline gelecektir. Burada değişkenler arasındaki korelasyonu göstermektedir. SRMR değerinin 0 a eşitliği mükemmel uyumu, 0,05 ten küçük değerleri için iyi bir uyumu ve 0,05 ile 0,10 arasındaki değerler için kabul edilebilir bir uyumu işaret etmektedir. Hem RMR hem de SRMR ölçütleri kareli hataları temel alan ölçütler olması nedeniyle ve ( ) arasındaki uyumsuzluğun yönü hakkında bir bilgi vermemektedirler. Fakat modelin uyumsuzluğu araştırılırken hataların işaretinin bilinmesi son derece önemlidir. Pozitif bir hata modelin eksik tahmin edildiğini negatif bir hata ise modelin aşırı tahmin edildiğinin göstergesi olabilmektedir (Schermelleh-Engel v.d., 2003: 38-39). 5) Hoelter in Kritik N Ölçütü (CN) Hoelter (1993) tarafından geliştirilen bu ölçüt bir modelin uyumun iyiliği ölçütü ile kabul edilebilir olması için gereken örneklem büyüklüğünün saptanmasını sağlamaktadır. Kritik N Sayısı CN ölçütü, ( ) şeklinde ifade edilir. Kritik değeri, test edilen modelin değeri ve tahminde kullanılan uyum fonksiyonunun değeri olmak üzere CN daima pozitif değer alacaktır. Belirli bir sınırı olmayan CN değeri için 200 den büyük değerlerin iyi bir uyuma işaret edeceği söylenilebilir (Bollen ve Liang,1988: 492) ARTIMSAL UYUM ÖLÇÜTLERĠ Artımsal uyum ölçütleri, mutlak uyum ölçütlerinden farklı olarak modelin tahmin edilen kovaryans matrisi ile örneklemden elde edilen kovaryans matrisi arasındaki fark yerine önerilen modelin sıfır model olarak adlandırılan bağımsız bir 104
117 modelle karşılaştırılmasını temel almaktadır. Bağımsız model ya da sıfır modeli, gözlenen değişkenlerin mükemmel ölçüldüğü tek bir gizil değişkeni olan bir modeldir. Bu başlık altında incelenecek ölçütler Normlandırılmış Uyum Ölçütü (Normed Fit Index-NFI), Normlandırılmamış Uyum Ölçütü (Non-Normed Fit Index- NNFI) veya Tucker-Lewis Uyum Ölçütü, Bollen in Artımsal Uyum Ölçütü (Incremental Fit Index-IFI) ve Bağıl Uyum Ölçütü (Relative Fit Index-RFI) şeklindedir. 1) NormalandırılmıĢ Uyum Ölçütü (NFI) Bentler ve Bonnet (1980) tarafından önerilen NFI literatürde Bentler ve Bonnet Ölçütü olarak da bilinmektedir. ( ) şeklinde formüle edilen NFI değeri 0 ile 1 arasında değer almaktadır. i indisi bağımsız modele ait değerleri, t indisi ise mevcut önerilen modele ait değerleri göstermektedir. Ölçütün yüksek değerleri iyi uyumun göstergesi olup, 0,95 iyi uyum ve 0,90 ise kabul edilebilir uyum için eşik değerlerdir. Parametre sayısından önemli ölçüde etkilenen bu ölçüt ile çalışırken araştırmacıların dikkat etmesi gereken nokta modele parametre eklendiğinde NFI da meydana gelecek artışın değerinin düşmesine bağlı olarak oluşan yapay bir değişme olup olmadığıdır. 2) NormalandırılmamıĢ Uyum Ölçütü (NNFI) Tucker ve Lewis (1973 ) tarafından önerilen FA modelleri için önerilen daha sonra Bentler ve Bonnet (1980) tarafından YEM için geliştirilen NNFI ölçütü, NFI ölçütünün parametre sayısı ve örneklem büyüklüğünden etkilenmesi gibi dezavantajları ortadan kaldırmak için ileri sürülen bir diğer artımsal uyum ölçütüdür. 105
118 ( )( ) ( ) ( ) ( ) ( ) ( ) ( ) şeklinde formüle edilen bu ölçüt genellikle 0 ile 1 arasında değer almaktadır. NNFI normlandırılmamış bir ölçüt olması nedeniyle zaman zaman [0,1] aralığının dışında da değerler alabilmektedir. Yüksek NNFI değerleri iyi bir uyumun göstergesi olmakla beraber 0,97 iyi uyum ve 0,95 değeri ise kabul edilebilir uyum için eşik değerlerdir (Schermelleh-Engel v.d., 2003: 41). 3) Bollen in Artımsal Uyum Ölçütü (IFI) NFI ölçütünün hesaplanmasında her ne kadar örneklem büyüklüğü kullanılmasa da yapılan benzetim çalışmaları ile NFI değerlerinin örnekleme dağılımının n örneklem büyüklüğüne bağlı olduğu gösterilmiştir. Bu nedenle modelin değerlendirilmesinde serbestlik derecesini de hesaba katan IFI ( ) ( ) ( ), ( )- ( ) şeklinde geliştirilmiştir. 0,90 dan büyük IFI değerleri modelin kabul edilebilir uyuma sahip olduğunu göstermekte olup 1 e yakın değerler iyi uyuma işaret etmektedir (Bollen, 1990: 256). 4-) Bağıl Uyum Ölçütü (RFI) Bollen (1986) tarafından NFI ölçütüne alternatif olarak önerilen ve NFI ölçütünde yer alan uyum fonksiyonu değerleri olan lerin kendi serbestlik derecelerine bölünmesi ile elde edilen RFI ölçütü ( ) ( ) ( ) ( ) 106
119 şeklinde formüle edilir. 0,90 dan büyük RFI değerleri modelin kabul edilebilir uyuma sahip olduğunu göstermekte olup 1 e yakın değerler iyi uyuma işaret etmektedir (Bollen, 1986: 375) YALINLIK UYUM ÖLÇÜTLERĠ YEM çalışmalarında genellikle karmaşık ve birçok varsayımı bir arada gerektiren modeller ile çalışılması nedeniyle modelin değerlendirilmesinde model uyumu ve sadeliğini sağlamak amacıyla birtakım ölçütler yeniden düzenlenmiştir. Yalınlık Uyum Ölçütleri olarak anılan bu ölçütlerin temelinde, karşılaştırılan modeller arasında daha az serbest parametreye ya da daha çok serbestlik derecesine sahip olan modelin seçilmesi yatar. Bu ölçütlerin temelinde yatan yalınlık kavramı (parsimonious), parametre tahminlerinin doğruluğunu etkiler ve alternatif modellerin seçimi için bir ölçüt olarak değerlendirilir. Söz konusu ölçüt uyumun belirli bir seviyeye ulaşması için tahmin edilmesi gereken parametre sayısını kapsamakta ve çoklu regresyondaki benzerlik göstermektedir. Yalınlık uyum ölçütlerinin temelinde aşırı tanımlı bir model ile kısıtlı bir modelin karşılaştırılması yatar ve bu kriterler için istatistiksel testler uygun değildir (Williams ve Holahan, 1994: ). Yalınlık uyum ölçütleri öncelikle uyum ve serbestlik derecesi arasında yapılan bir fayda-maliyet tercihidir (Kelloway,1998: 32). Bu ölçütlerin hemen hepsi, artımsal uyum ölçütlerine yapılan birtakım düzenlemelerle meydana gelmektedir. Bu ölçütlerin başlıcaları: Yalınlık Uyumun İyiliği Ölçütü (Parsimonious Goodness of Fit Index-PGFI), Yalınlık Normlaştırılmış Uyum Kriteri (Parsimonious Normed Fit Index-PNFI), Akaike Bilgi Kriteri (Akaike s Information Criteria-AIC), Tutarlı Akaike Bilgi Kriteri (Consistent Akaike s Information Criteria-CAIC), Beklenen Çapraz Geçerlilik Ölçütü (Expected Cross-Validation Index-ECVI). 107
120 1) Akaike Bilgi Kriteri (AIC) Akaike (1985) tarafından bir bilgi kriteri olarak geliştirilen orijinal Akaike ölçütü (AIC) model uygunluğunun değerlendirilmesinde en çok kullanılan ölçütlerden biridir. AIC, (3.77) şeklinde ifade edilir. Burada, model için log-olabilirlik fonksiyonunu en büyükleyen değerdir. YEM modelleri için ise literatürdeki çalışmalarda farklı tanımlamalara sahip olsa da en yaygın olarak kullanılan hali (3.78) şeklindedir. Burada AIC olabilirlik fonksiyonunun logaritmasının iki katının dağılımına uygunluk gösterdiği varsayımı ile hesaplanmaktadır. Uyumun kötülüğü ölçütü olarak da adlandırılan AIC ölçütünün uygulama biçimi diğer ölçütlerden farklıdır. AIC de temel amaç elde edilen veriler ile mümkün modeller arasında gerçeğe en yakın modelin seçimini sağlamaktır. En küçük AIC değerini veren modelin en iyi model olduğu kabul edilir. Ancak burada unutulmaması gereken AIC nin bir anlamlılık testi değil betimsel bir ölçüt olduğudur. 2) Tutarlı Akaike Bilgi Kriteri (CAIC) Bozdoğan (1987), Akaike nin prensiplerini bozmadan matematiksel istatistik araçlarını kullanarak AIC i analitik olarak genişletmiş ve geliştirmiştir. Çalışmaları sonucunda AIC ölçütü asimptotik olarak tutarlı duruma gelmiş ve doğru modellerin en basitini seçmek için daha sıkı olarak fazla-parametreleşme cezalandırılmıştır (Akıncı, 2007: 36). CAIC ölçütü ceza fonksiyonunda örneklem büyüklüğünün de dikkate alınması ile 108
121 ( ) (3.79) şeklinde ifade edilir. AIC e benzer şekilde rakip modellerin karşılaştırılmasında en küçük CAIC değerine sahip model seçilmektedir (Bozdoğan, 1987:345). 3) Beklenen Çapraz Geçerlilik Ölçütü (ECVI) AIC ölçütünden türeyen bir diğer yalınlık uyum kriteri de Browne ve Cudeck (1989, 1993) tarafından geliştirilen ECVI ölçütüdür. Bu ölçüt tahmin edilen model için en iyi uyumu sağlayacak örneklem büyüklüğünün saptanmasında kullanılmaktadır. ECVI ölçütü, analiz edilen örneklemdeki modele ilişkin beklenen kovaryans matrisi ile aynı büyüklükteki diğer örnekleme ilişkin beklenen kovaryans matrisi arasındaki farkın bir ölçüsü olarak değerlendirilmektedir. ECVI,. ( )/ ( ) t tahmin edilen parametre sayısı, F uyum fonksiyonunun en küçüklenen değerini göstermektedir. ECVI değeri daima 0 dan farklı çıkmakta ve rakip modellerin kıyaslanmasında değeri en küçük model seçilmektedir (Schermelleh-Engel v.d., 2003: 48). 4) Yalınlık Uyumun Ġyiliği Ölçütü (PGFI) PGFI ölçütü, AGFI ölçütüne benzer bir yaklaşım ile alternatif modeller arasında seçim yapmak için kullanılan ve Mulaik v.d. (1989) tarafından geliştirilen bir yalınlık uyum ölçütüdür. GFI ölçütünün tahmin edilecek parametre sayısı arttıkça cezalandırılması temeline dayanan PGFI, ( ( ) * ( ) 109
122 şeklinde ifade edilir. Burada gözlenen değişken sayısını göstermekte olup ölçüt 0 ile 1 arasında değer almaktadır (Mulaik v.d., 1989: 180). PGFI için genel kabul görmüş bir eşik değeri olmamakla birlikte yüksek değerlerin daha iyi bir uyumun göstergesi olduğu ifade edilmektedir. 5) Yalınlık NormlaĢtırılmıĢ Uyum Ölçütü (PNFI) James v.d. (1982) tarafından NFI ölçütünün serbestlik dereceleri de hesaba katılarak yeniden düzenlenmesi ile elde edilen PNFI ölçütü, ( * ( ) şeklindedir. Genellikle 0 ile 1 arasında değer almakta ve yüksek değerleri daha iyi bir uyuma işaret etmektedir. Ancak alternatif modeller arasında seçim yapmak için kullanılırken bütün yalınlık ölçütlerinde olduğu gibi burada da, PNFI değeri kabul edilebilir iki model arasında, daha az parametreye sahip olan model seçilmelidir MERKEZĠ OLMAYAN UYUM ÖLÇÜTLERĠ Merkezi olmayan hipotezlerde değeri, yerine hipotezi üzerine kuruludur. ( ) olmadığı durumlarda ( ) istatistiği serbestlik derecesi ve merkezi olmama parametreleri ile merkezi olmayan dağılımına uygunluk gösterecektir. Burada merkezi olmama parametresi, ile ( ) arasındaki farklılığın bir ölçüsü kabul edilir. Söz konusu fark büyüdükçe alternatif hipotez sıfır hipotezinden uzaklaşacaktır. değerinin 0 olması durumunda merkezi olmayan dağılımı, merkezi dağılımına eşit olacaktır. Bu kısımda merkezi olmayan ölçütlerinden RMSEA ve CFI ölçütleri incelenecektir. dağılımına uygunluk gösteren uyum 110
123 1) YaklaĢım Hatasının Kareli Ortalamasının Karekökü (RMSEA) YEM de en yaygın kullanılan uyum ölçütlerinin başında RMSEA ölçütü gelmektedir. Kitledeki yaklaşık uyumun bir ölçütü olarak kabul edilen bu ölçüt, {( * } ( ) şeklinde hesaplanır. RMSEA değeri merkezi olmayan bir dağılımına uygunluk gösterir. Merkezi olmayan dağılımının kümülatif dağılım fonksiyonu ( ) olmak üzere. / şeklinde tanımlanır. Bu ölçüt için oluşturulacak güven aralığının alt ve üst sınırları: ( ) ve ( ) olmak üzere RMSEA için güven aralığı ( ) : ( ) ( ) ; ( ) şeklinde oluşturulmaktadır. RMSEA ölçütünün alabileceği en küçük değer 0 dır. Güven aralığının en küçük sınırı tam uyum için 0 değerini içermelidir. Yakın uyum için ise 0,05 ten küçük olmalıdır. Browne ve Cuddeck (1993) e göre 0,05 e eşit veya daha küçük bir RMSEA değeri iyi bir uyumu, 0,05 ile 0,08 arasındaki değerleri yeterli uyumu ve 0,08 ile 0,10 arasındaki değerleri ise vasat uyumu işaret etmektedir. 0,10 dan büyük değerler ise kabul edilemez olarak yorumlanmalıdır. Her ne kadar YEM literatüründe iyi bir model için RMSEA nın 0,05 ten küçük olması gerektiği genel olarak kabul görmüş olsa da Hu ve Bentler (1999) çalışmalarında 0,06 dan küçük RMSEA değerini kesim noktası olarak önermişlerdir. Modelin değerlendirilmesinde kurulacak hipotezler de seçilecek RMSEA eşik değerine göre değişecektir. Modelin veriye tam uyumlu olduğu düşünülüyor ise, 111
124 şeklinde eğer modelin veriye yeterli uyum gösterdiği düşünülüyor ise, şeklinde ve modelin veriye uyumlu olmadığı düşünülüyor ise hipotezler şeklinde kurulmaktadır. RMSEA ölçütünün en büyük avantajı, diğer pek çok uyum ölçütünden farklı olarak model değerlendirilmesinde modelin karmaşıklığından etkilenmemesidir. Serbestlik derecesinin bir fonksiyonu olarak hesaplanması nedeniyle modelin yapısından bağımsızdır. Aynı zamanda güven aralığı oluşturulmasına elverişli olması araştırmacıların daha sağlıklı karar vermesine neden olmaktadır. Örneklem büyüklüğü küçük ve tahmin edilen parametre sayısı fazla ise güven aralığı genişleyecektir. Bu nedenle karmaşık bir modelde daha dar bir güven aralığı elde edebilmek için örneklem büyüklüğünün arttırılması gerekmektedir. Bununla birlikte daha küçük bir örneklemde tahmin edilecek parametre sayısının az olması yeterli ölçüde dar bir güven aralığı sağlamaktadır. RMSEA ölçütünün doğru anlaşılabilmesi için yaklaşım hatası ve tahmin hatası kavramları arasındaki farkın bilinmesi gerekmektedir. Yaklaşım hatası, kitle kovaryans matrisine göre modelin uyumsuzluğunu, tahmin hatası ise kitle kovaryans matrisine uyumlu model ile örneklem kovaryans matrisine uyumlu model arasındaki farkı yansıtmaktadır (Schermelleh-Engel v.d., 2003: 36-37). 112
125 2) KarĢılaĢtırmalı Uyum Ölçütü (CFI) CFI ölçütü, Mc Donald ve Marsh (1990) tarafından geliştirilen Göreli Merkezi Olmayan Ölçüt (Relative Noncentrality Index-RNI) RNI nın geliştirilmesi ile elde edilen bir diğer merkezi olmayan uyum ölçütüdür.,( ) -,( ) ( ) - ( ) şeklinde formüle edilir., uyumu değerlendirilen modelin ise bağımsız modele ait değerlerdir. CFI ölçütü 0 ile 1 arasında değerler almakta ve yüksek değerler iyi bir uyuma işaret etmektedir. CFI ölçütü, 0,97 olduğunda söz konusu uyumun bağımsız modele göre göreceli olarak daha iyi olduğu söylenmektedir. 0,95 ten büyük değerler kabul edilebilir uyumun göstergesidir. NFI ölçeği ile karşılaştırıldığında örneklem büyüklüğünden daha az etkilenen bir ölçüt olarak karşımıza çıkmaktadır. Başka bir deyişle CFI ölçütü, NFI ölçütünün örneklem büyüklüğüne duyarsız hale getirilmiş şeklidir (Schermelleh-Engel v.d., 2003: 42) MODEL BĠLEġENLERĠNĠN DEĞERLENDĠRĠLMESĠ YEM de modelinin değerlendirilmesinin bir aşaması da genel modelin uyumunun değerlendirilmesi ile birlikte parametre tahminlerinin de tek tek incelenmesidir. Hem ölçme modellerinde gizil değişkene ait göstergeler hem de yapısal model de gizil değişkenlerin kendi aralarındaki ilişkilerde parametre tahminlerinin istatistiksel olarak anlamlı ve teorik olarak beklenen işaretlere uygun olması gerekmektedir., ( ) boyutlu tahmin edilen parametreler vektörü ve nın asimptotik kovaryans matrisi 113
126 ( ) olsun. Burada 0 1 ( ) Fisher in bilgi matrisi olarak tanımlanır. Buradan elde edilecek asimptotik standart hatalar olmak üzere parametrelerin anlamlılığının sınanmasında kullanılacak test istatistiği, ( ) şeklinde olacaktır. Gizil değişkenlerin standartlaştırılması durumunda ise ölçme modelindeki parametrelerin anlamlı olması geçerlilik için bir göstergedir. Yapısal modeldeki parametrelerin anlamlı olması ise gizil değişkenler arasındaki teorik olarak varlığı kabul edilen ilişkilerin istatistiksel olarak kanıtıdır. Model bileşenlerinin uyumunun incelenmesinde, modelin geçerliliğinin yanı sıra güvenilirliğinin incelenmesi gerekmektedir. ve gözlenen değişkeni için güvenilirlik ölçüsü, ( ) şeklinde belirginlik katsayısıdır. Burada herhangi bir ve gözlenen değişkenini,, nin model tarafından tahmin edilen varyansını, ise ve matrislerinin i. köşegen elemanını (değişkene ait hata varyansı) göstermektedir. nin yüksek olması nin ilgili gizil değişkenin iyi bir göstergesi olduğunu ifade etmektedir. Benzer şekilde sırasıyla gizil değişkenler ve için de belirginlik katsayısı aşağıdaki şekilde hesaplanabilir (Şimşek, 2007: ). ( ) 114
127 ( ) Model bileşenlerinin değerlendirilmesinde ise yapı güvenilirliği (bir gizil değişkenin güvenilirliği), gizil değişkenden göstergelerine yönelik yol katsayılarından hareketle, ( ) bir gizil değişkenin her bir gösterge değişkenine ait hata terimini göstermek üzere, ( ( ) ) ( ( ) ) ( ) ( ) şeklinde hesaplanır ve 0,70 değerinden büyük olması istenir. Aynı zamanda raporlanması gereken bir diğer ölçüt açıklanan varyans olup ( ) ( ) ( ) ( ) şeklinde hesaplanır ve 0,50 den büyük olması istenmektedir (Hair v.d., 1998: 612). 115
128 4.BÖLÜM ĠNTERNET SERVĠS SAĞLAYICILARI SEKTÖRÜNDE MÜġTERĠ SADAKATĠ ve BĠLEġENLERĠNĠN YAPISAL EġĠTLĠK MODELLEMESĠ ĠLE ĠNCELENMESĠ Çalışmanın bu kısmında önceki kısımlarda teorik ayrıntıları verilen YEM analizine ilişkin bir uygulama çalışması gerçekleştirilecektir. Türkiye de İnternet Servis Sağlayıcı (İSS) firmalar sektöründe tüketici davranışlarının ve müşteri sadakati oluşturma sürecinin incelenmesi amacıyla YEM analizi ile bir modelleme çalışması gerçekleştirilecektir. Öncelikle müşteri sadakati kavramı, bileşenleri ve müşteri sadakati modelleri incelenecek olup daha sonra ampirik çalışmaya yer verilecektir MÜġTERĠ SADAKATĠ KAVRAMI Dar anlamda müşteri sadakati, müşterilerin belli bir kategoride sürekli aynı firma ya da markadan satın almaları şeklinde tanımlanmaktadır (Keiningham v.d., 2006). Geniş anlamda ise müşteri sadakati, müşterilerin seçim hakkı olduğunda, aynı markayı satın alma ya da benzer ihtiyaçlarına çözüm bulmak için aynı mağazayı tercih etme eğilimi, arzusu ve eylemi olarak tanımlanabilir (Odabaşı, 2006: 17). Benzer şekilde Gremler ve Brown (1996) müşteri sadakatini, müşterinin sergilediği tekrarlı satın alma davranışının derecesi, firmaya karşı olumlu tutum içinde olma eğilimi ve ihtiyaç duyduğu mal ve hizmetler için yalnızca söz konusu firmayı tercih etmesi olarak tanımlamaktadırlar. Literatürde müşteri sadakati kavramını tanımlamak için üç farklı yol vardır. Stokastik yaklaşıma göre müşteri sadakati bütünüyle davranışsal, deterministik yaklaşıma göre bir tutum ve karma yaklaşıma göre tutum ve davranışın birleşimini olarak tanımlanır (Boora ve Singh, 2011: 153). Davranışsal müşteri sadakati yaklaşımı, müşteri hareketlerini yansıtmakta olup müşterinin aynı markadan geçmişte yaptığı satın alımların ölçüsünü veya geçmişteki satın alımlarına bakılarak gelecekteki satın alma olasılığını içeren bir kavramdır (Bandyopadhy ve 116
129 Martell, 2007). Davranışsal yaklaşımı benimseyen bir diğer yazar Zeithaml v.d. (1996) ya göre müşteri sadakati, bir ürün ya da hizmete müşteri olma sıklığı, sürekli olarak aynı mal ve hizmeti ya da firmayı tercih etmek olarak tanımlanmıştır. Tutumsal müşteri sadakati yaklaşımında, Kim v.d. (2007) ye göre müşteri sadakati bir müşterinin hizmete, ürüne, markaya ya da işletmeye olan tutumu olarak tanımlanır. Özetle müşteri sadakatinin davranışsal yönü müşterilerin satın alma davranışını sürekli olarak tekrar etmesi üzerinedir. Tutumsal yaklaşım da ise müşterilerin söz konusu mal, hizmet veya firmadan tekrarlı bir satın alma faaliyeti içerisinde olmasalar bile söz konusu mal, hizmet ya da firma hakkında olumlu konuşmaları, tavsiye etmeleri ve başkalarının firmadan alışveriş yapmalarını sağlamaları şeklinde firmaya olumlu bir katkılarının olmasıdır. Karma müşteri sadakati yaklaşımı ise, bu iki yaklaşım bir bileşimi olarak literatürde geniş bir yer bulmuştur. Dick ve Basu (1994) karma müşteri sadakati kavramını, müşterinin ürüne karşı göreceli tutumu ve tekrar eden satın alma davranışı şeklinde her iki kavramın bir bileşeni olarak tanımışlardır. Aynı yazarlar müşteri sadakatinin bilişsel, duygusal ve davranışsal bileşenleri olduğunu vurgulayarak kavramı sınıflandırmaktadırlar. Bu yaklaşımda müşteri sadakatinden bahsedilmesi için altı koşulun yerilene getirilmesi gerekmektedir. Bu koşullar: 1. Satın alma işleminin bilinçli olarak tesadüfî olmayan bir şekilde yapılması, 2. Satın alma davranışının gerçekleşmesi, 3. Söz konusu davranışın belirli bir süreç içinde gerçekleşmesi, 4. Aynı karar verici grubu tarafından yapılması, 5. Bir veya daha fazla alternatifi bulunan bir marka grubu arasından seçilmesi, 6. Satın almanın belli bir psikolojik değerlendirme sürecinin fonksiyonu olması gerekmektedir (Jacoby ve Kyner, 1973: 2). Literatürde müşteri sadakatini etkileyen temel faktörler arasında kurumsal imaj, güven, müşteri beklentileri, müşteri memnuniyeti, değiştirme maliyeti, müşteri şikâyetleri yönetimi, fiyat algısı ve hizmet kalitesi gibi pek çok unsur incelenmiştir. Bu çalışmada öncelikle söz konusu değişkenlerin müşteri sadakati olgusunu 117
130 açıklamada etkisi ve birbirleri arasında ilişkilerin incelendiği bir literatür taramasına yer verilecektir MÜġTERĠ SADAKATĠNĠN BĠLEġENLERĠ Çalışmanın bu kısmında müşteri sadakati kavramını doğrudan ve/veya dolaylı olarak etkileyen değişkenlerle ilgili açıklamalar ve ilgili değişkenler arasındaki ilişkilerin daha önce incelendiği çalışmalar ile ilgili bir literatür taramasına yer verilecektir. KURUMSAL ĠMAJ Kurumsal imaj; hem imajın kaynağı olan kurum, hem de imajın algılayıcısı durumundaki hedef kitleler için son derece önemlidir. Kurumsal imaj kurumun tüketiciler ile kurduğu iletişimin başlangıcıdır. Kurumsal imaj bir süreç olarak, kurumun sunmaya veya göstermeye çalıştığı imajı ile tüketicilerin bundan almış olduğu mesajların ilişkilendirilmesidir şeklinde tanımlanabilir (Aksoy ve Bayramoğlu, 2008:86). Barich ve Kotler (1991), kurumsal imajı halkın bir firma hakkında aklında kalan genel izlenimler olarak tanımlamaktadırlar. Kurumsal imaj, bir firmanın fiziksel ve davranışsal özellikleri ile ilgili olup, firmanın ismine, mimarisine, ürün veya hizmetlerinin çeşitliliğine ve firmanın müşterileri ile ilişkili olan herkesin ilettiği izlenimin niteliğine bağlıdır (Nguyen ve Leblanc, 2001: 228). Kurum imajı, bir isletmenin ürünlerinin kalitesi ve çalışanların ilişkilerinin doğasından, onun binalarının ve yerinin görünümü ve onun yazışmalarındaki kâğıtlarda kullandığı başlıkların yazılış şekline kadar bir işletmenin bütün eylemlerinden etkilenmektedir (Cerit, 2006: 344). Fishbein ve Ajzen (1975) tutumların, davranışları belirlemeye yönelik niyetlerle fonksiyonel olarak ilişkili olduğunu tartışmışlardır. Bu durumda bir tutum 118
131 olarak kurum imajı davranışsal niyetleri yani müşteri sadakatini etkilemelidir. Nguyen ve Leblanc (2001) üç farklı sektörde (telekomünikasyon, perakende bankacılık ve eğitim) yaptıkları çalışmalarda, kurumsal imajın müşteri sadakatini olumlu yönde etkileyeceği sonucuna varmışlardır. Aynı zamanda Kristensen v.d. (2000) ve Juhn v.d. (2002) posta hizmetleri ve bankacılık sektörleri üzerine yaptıkları çalışmalarda aynı ilişkiyi doğrulayan sonuçlar elde etmişlerdir. BEKLENTĠ Firmaların temel amacı müşteri talep ve beklentilerini karşılamaktır. Beklenti, kişilerin satın aldıkları ürün ya da hizmet ile ilgili ilk deneyimlerinin sonucu olup, kişiden kişiye değişen sübjektif bir kavramdır. Müşteri beklentilerinin doğru tahmin edilmesi ve karşılanması başta müşteri memnuniyetinin arttırılması olmak üzere pek çok kavramla yakından ilişkilidir. Müşteri memnuniyeti açısından bakıldığında beklenti kavramı, ürün ya da hizmetin kullanımı sonrası beklenen performansı olarak tanımlanabilir. Yapılan çalışmalarda tüketicilerin satın alma ya da hizmet kullanımı sırasında beklentilerini karşılamanın, tüketicilerin aynı iş yerinden tekrar satın alma olasılığını arttırdığı bilinmektedir (Wong ve Sohol, 2003). Aynı zamanda müşterinin üründen öncelikli beklentileri ve kullanımı sonrası algıladığı performans arasındaki fark müşterinin üründen memnuniyetini ya da memnuniyetsizliğini ortaya koymaktadır (Tse ve Wilton, 1988). Bu nedenle müşterilerin ürün veya hizmete yönelik beklentilerinin müşteri memnuniyetini açıklamada etkisinin büyük olduğu düşünülmektedir. Müşteri beklentileri kavramı aynı zamanda hizmet kalitesi ile de yakından ilişkilidir. Hizmet kalitesi literatüründe müşteri beklentileri, müşterilerin geleceğe yönelik isteklerinin normatif bir standardı olarak tanımlanmaktadır (Çalkaya, 2009: 51). 119
132 DEĞĠġTĠRME MALĠYETĠ Değiştirme maliyeti, bir tüketicinin bir hizmet sağlayıcıyı başka bir hizmet sağlayıcı ile değiştirdiğinde maruz kalacağı maliyet olarak tanımlanır (Porter, 1998: 10). Bu maliyet, parasal değer olarak ölçülen bir maliyet özelliği taşımasının yanı sıra yeni bir firmanın müşterisi olmanın getirdiği belirsizlikten kaynaklanan psikolojik etki, yeni ürün veya hizmet satın alma çabası ve zaman boyutunu kapsamaktadır (Klemperer, 1995; Kim v.d., 2003). Jackson (1985) e göre ise değiştirme maliyeti, bir tüketicinin kullandığı markayı değiştirdiğinde katlanacağı ekonomik, fiziksel ve psikolojik maliyetlerin bütünüdür. Değiştirme maliyeti tüketicinin rakip firmalara yönelmesini pahalı ve zor kılmaktadır. Bu nedenle tüketici hizmet sağlayıcısını değiştirmek istediğinde kazanacağı karı ve katlanacağı maliyetleri değerlendirmek zorundadır. Eğer elde edeceği getiri değiştirme maliyetinden yüksek ise hizmet sağlayıcısını değiştirmeye karar verecektir. Değiştirme maliyetleri arttıkça tüketicinin memnuniyete olan duyarlılığı azalacaktır. Bu nedenle pek çok çalışmada gösterildiği üzere, algılanan değiştirme maliyeti müşteri sadakati oluşturmada önemli bir maliyettir. Değiştirme maliyeti ile ilgili bir diğer önemli konu ise değiştirme maliyetine neden olan unsurların sektörlere göre farklılık göstermesidir. Aynı zamanda bazı sektörler için müşterilerin tercih etmiş oldukları firmayı değiştirerek rakiplerine kaymalarını engellemek için çok ciddi parasal ve parasal olmayan engeller bulunmaktadır. Özellikle araştırmaya konu olan İSS sektöründe ciddi firma değiştirme maliyetleri söz konusudur. HĠZMET KALĠTESĠ Hizmet kalitesi, müşterinin bir hizmete ilişkin beklentileri ve yararlandığı gerçek hizmet deneyimindeki algısı arasındaki farktan oluşan bir tutum olarak tanımlanmaktadır (Parasuraman v.d., 1988). Bu durum Hizmet kalitesi = Algılanan 120
133 Hizmet Kalitesi Beklenen Hizmet Kalitesi şeklinde formüle edilebilir. Bu formüle göre hizmet kalitesi, sıfıra eşit veya büyükse, tüketicinin hizmet kalitesi değerlendirmesi olumlu, negatif ise olumsuzdur (Parasuraman, v.d., 1994: 122). Hizmet kalitesinin ölçümü için kullanılan pek çok ölçek vardır. Ancak bunlardan en yaygın olarak kullanılanı Parasuraman v.d. (1985) tarafından geliştirilen hizmet kalitesi ölçeğidir. Yazarlar, öncelikle müşteri beklentilerini temel alarak hizmet kalitesi olgusunu açıklamak için öncelikle on boyut elde etmişlerdir (Parasuraman v.d., 1985: 43-47). Daha sonra yaptıkları çalışmalarda söz konusu on boyutu beşe indirgeyerek günümüzde hala yaygın olarak kullanılan SERVQUAL adlı hizmet kalitesi ölçeğini geliştirmişlerdir. 22 sorudan oluşan ve likert tipi ölçekle ölçümledikleri beş boyut: Somut özellikler, güvenilirlik, yeterlilik, güven ve empatidir (Parasuraman v.d., 1988: ). Hizmet kalitesi ile müşteri sadakati arasındaki ilişki literatürde pek çok çalışmada incelenmiştir. Cronin ve Taylor (1992) yeniden satın alma niyeti ile hizmet kalitesi arasındaki ilişkiyi incelemiştir. Hizmet kalitesinin yeniden satın alma niyeti üzerinde anlamlı pozitif bir etkisi olmadığı sonucuna ulaşmışlardır. Boulding v.d. (1993) ise hizmet kalitesi ile hem yeniden satın alma niyeti hem de hizmeti tavsiye etmeye gönüllü olma açısından müşteri sadakati üzerindeki etkisini incelemişlerdir. Bu çalışmada ise hizmet kalitesinin müşteri sadakati üzerinde anlamlı pozitif bir etkisi olduğu sonucuna varılmıştır. Aynı zamanda pek çok araştırmada hizmet kalitesinin müşteri sadakati üzerindeki etkisi müşteri memnuniyeti üzerinden dolaylı olarak da incelenmiştir (Magin v.d., 2010). GÜVEN Müşteri sadakati sağlamada firmaların özellikle üzerinde durduğu konulardan biri de güvendir. Güven, bir bireyin riskle karşılaşma olasılığına rağmen başka bir gruba inanç duyma isteği olarak tanımlanabilir (Lau ve Lee, 1999). Pazarlama literatüründe ise tüketici pazarı açısından bakıldığında Doney ve Canon (1997) ye 121
134 göre güven, karşı tarafın ya da markanın kendisinden beklentileri yerine getirmesine dayalı sürekli bir süreçtir. Güvenin var olabilmesi için bir tarafın diğer tarafın kendisi için pozitif çıktılarla sonuçlanacak faaliyetlerde bulunacağına (Anderson ve Narus, 1990), müşterinin firmadan bugün sağladığı faydayı ileride de sağlayacağına (Doney ve Canon, 1997) inanması gerekmektedir. Eğer bir taraf diğerine güvenirse ona karşı pozitif davranışsal niyet gerçekleştirecektir. Bir müşteri bir firmaya güvenirse, bu müşteri bu firmaya karşı pozitif bir satın alma niyeti de gerçekleştirecektir. Aynı zamanda satıcısına karşı güven duymayan müşteri firmaya karşı bağlılık hissetmeme eğiliminde de olacaktır. Bu bağlamda güven ile müşteri sadakati arasında pozitif yönlü kuvvetli bir ilişki olduğu hipotezi, Garbarino ve Johnson (1999), Chaudhuri ve Holbrook (2001) ve Sirdeshmukh v.d. (2002) gibi yazarlarca incelenmiştir. Aynı zamanda güven sadece müşteri sadakati ile değil müşteri memnuniyeti ile de ilişkilidir. Müşterilerin sonuçtaki değerlendirmelerinde güven önemli bir faktör olduğundan, müşterilerin algıladığı güven genel memnuniyetlerini de etkilemektedir (Chiou, 2004). MÜġTERĠ MEMNUNĠYETĠ Bir tüketicinin belirli bir ürün ile olan tüketim deneyimini değerlendirmesi sonucunda geliştirdiği tutum tüketici memnuniyeti ve memnuniyetsizliği olarak bilinmektedir. En genel tanımı ile müşteri memnuniyeti, müşterinin ürün veya hizmetin arzu, beklenti ve ihtiyaçlarını karşılama yetisinden kaynaklanan genel memnuniyet derecesi, yapılan ürün veya hizmet tercihinin rakiplerine göre yaratabildiği iç huzur ve rahatlık hissidir (Hellier v.d., 2003: 1765). Müşteri sadakati ile müşteri memnuniyeti arasındaki ilişki literatürde pek çok araştırmacı tarafından incelenmiştir. Bu çalışmalar arasında en popüler olanlardan biri Fornell v.d. (1996) tarafından gerçekleştirilen Amerikan Müşteri Memnuniyeti İndeksi (ASCI) modelidir ve çalışmada söz konusu modelin değişkenleri temel alınacaktır. ASCI modeline göre müşteri beklentileri ve algılanılan kalite kavramları müşteri memnuniyetini algılanılan değer üzerinden etkilemekte olup aynı zamanda 122
135 müşteri memnuniyeti müşteri sadakatini olumlu yönde etkilemektedir. Aynı model müşteri sadakatinin temel unsurlarından birinin de müşteri şikâyetleri yönetimi olduğunu ortaya koymaktadır. ġġkâyet YÖNETĠMĠ Firmaların müşteri sadakati ve müşteri memnuniyeti sağlamada etkin olarak kullandıkları yöntemlerden biri de müşteri şikâyetleri uygulamalarıdır. Bu uygulamalar ile işletmeler müşteri ile olan ilişkisini güçlendirme, müşteri memnuniyetsizliklerini giderme, yasal yollara başvurmadan müşterileri sorunlarının çözülmesi, tekrar satın alma niyetinin olumlu desteklenmesi gibi çok önemli rekabet üstünlükleri yakalamaktadırlar. Ancak tüm bu fırsatların yakalanabilmesi için işletmenin müşterilerinin şikâyet etme veya etmeme davranışlarını incelemesi, müşterilerini şikâyet etmeye teşvik etmesi ve cesaretlendirmesi, şikâyetlerin müşteriyi memnun edecek şekilde ve ücretsiz bir şekilde çözmesi gerekmektedir (Burucuoğlu, 2011: 94). FĠYAT ALGISI Fiyat, tüketiciler için ürünün kalitesi ya da faydasının bir ölçütü olarak algılanır. Zeithaml (1988) e göre fiyat, müşterilerin bilişsel kavramalarında belli ürün çeşitlerini ve hizmetlerini alabilmek için feda edilmesi gereken bir şeydir. Fiyatı bütün öteki işaretler ortadan kalktığında en iyi kalite ölçüsü olarak tanımlar. Başka bir bilgi olmadığında, müşteriler fiyatı kalite kullanmak, yerleştirmek, ölçmek için kullanır. Müşteri sadakati yüksek olan tüketiciler genellikle fiyattan bağımsız hareket ederler ve tercih ettiği firmaların ürün ya da hizmetleri için istenilen fiyatı ödemeye isteklidirler. Başka bir deyişle sadık müşterilerin diğerlerine oranla fiyat duyarlılığı daha düşüktür. Bu nedenle fiyat düzeyindeki değişimlerin doğrudan müşteri sadakati üzerinde etkili olmadığı düşünülür. Bu nedenle pazarlama literatüründe genellikle fiyatın müşteri memnuniyeti ve kalite kavramları ile ilişkisi araştırılmıştır. Zeithaml, 123
136 (1998), Fornell (1992) Anderson ve Sullivan (1993), Anderson v.d. (1994), Cronin v.d. (2000) gibi yazarlar fiyatın müşteri memnuniyeti ile ilişkisini ve Zeithaml ve Bitner (1996) memnuniyetin hizmet kalitesi, ürün kalitesi, fiyat, durum, ve kişisel etkenler faktörleri ile olan teorik ilişkisini araştırmışlardır. Ancak, fiyat önceki ampirik çalışmalarda tam olarak araştırılmamıştır (Çalkaya, 2009: 45) MÜġTERĠ SADAKATĠ MODELLERĠ Araştırmada İSS sektöründe kurumsal imaj, güven, müşteri beklentileri, müşteri şikâyetleri yönetimi, değiştirme maliyeti, fiyat algısı ve hizmet kalitesi değişkenlerinin müşteri sadakatini nasıl ve ne ölçüde etkilediğinin analiz edilmesi amaçlanmıştır. İSS sektörü için müşteri sadakati modeli oluşturulurken söz konusu değişkenler arasındaki ilişkilerin incelendiği daha önceki çalışmalar göz önünde bulundurulmuştur. Müşteri sadakati ile ilgili yapılan çalışmalar söz konusu soyut kavramlar arasındaki ilişkilerden çok bahsedilen kavramların nasıl ölçülmesi gerektiği ile ilgili çalışmalardır. Son birkaç on yılda gizil değişken modelleri ile ilgili analizlerin kullanımının artması ile müşteri sadakati modellerinde gizil değişkenler arasındaki eş anlı ilişkiler literatürde incelenmeye başlanmıştır. Ancak geçmiş çalışmalar daha çok söz konusu yapıların birbirleri ya da birkaçının bir arada incelenmesi şeklinde olmakta genellikle pazarlama literatürde müşteri sadakati ile ilgili bütün kavramlar arası ilişkilerin bir arada ölçüldüğü modeller ile ilgili ampirik çalışmaların sınırlı olduğu görülmektedir. Özellikle Türkiye de İSS sektöründe müşteri sadakatinin ölçümü ile ampirik çalışmaya rastlanmamıştır. Hem söz konusu değişkenlerin birlikte analizi açısından hem de ampirik çalışmanın uygulanacağı sektör açısından özgün bir araştırma olması nedeniyle araştırma modelinin kurulmasında geçmişte benzer sektörler için yapılmış çalışmalar temel alınmıştır. Söz konusu araştırmalarda kabul edilen hipotezler incelenerek değişkenler arası ilişkilerin öngörülmesi amaçlanmıştır. 124
137 Müşteri memnuniyetini etkileyen faktörler için Fornell v.d. (1996) ile verilen ASCI modeli temel alınarak araştırma modeli için hizmet kalitesi ve beklentiler ile müşteri memnuniyeti arasında pozitif yönlü ilişki ve müşteri memnuniyeti ile müşteri sadakati arasında yine pozitif yönlü bir ilişki öngörülmüştür. Aynı zamanda söz konusu çalışmada müşteri şikâyetleri ile müşteri sadakati arasında ilişki analiz edilmiştir. Müşteri memnuniyeti ile müşteri şikâyetleri arasındaki ilişkinin ise negatif yönlü olduğu aynı çalışmada ortaya konulmuştur. Bu çalışmada müşteri şikâyetleri, şikâyet yönetimi olarak modele dahil edileceğinden ilişkinin beklenen yönü pozitif olacaktır. Benzer şekilde müşteri memnuniyeti ile müşteri sadakati arasında pozitif yönlü ilişki olduğuna dair hipotez Andreassen ve Lindestad (1998), Liljander ve Strandvik (1995), Söderlund (1998), Stauss ve Neuhaus (1997), Şimşek (2007), Caruana (2002) tarafından farklı sektörler için doğrulanmıştır. Müşteri sadakatini etkileyen bir diğer unsur fiyat değişkenin müşteri sadakati ile pozitif yönlü bir ilişkiye sahip olduğu hipotezi Johnson v.d. (2001) tarafından doğrulanmıştır. Aynı zamanda fiyat ile müşteri memnuniyeti arasındaki ilişki Zeithaml (1998), Fornell (1992), Anderson ve Sullivan (1993), Anderson v.d. (1994) Cronin v.d. (2000) yazarları tarafından incelenmiştir. Aydın ve Özer (2005) çalışmaları ile GSM sektöründe müşteri sadakatinin modellenmesi amacı ile hizmet kalitesinin içsel gizil değişken olduğu kurumsal imaj, güven ve değiştirme maliyeti değişkenlerini etkilediğini ve bu üç değişkenin de müşteri sadakatini etkilediği varsayılan bir model incelemişlerdir. Ampirik çalışmalarının bulguları neticesinde güven ve değiştirme maliyeti değişkenleri ile müşteri sadakati arasındaki ilişki istatistiksel olarak anlamlı bulunurken, firma imajı ile müşteri sadakati arasındaki ilişki istatistiksel olarak anlamlı bulunmamıştır. Ancak literatürde Kristensen v.d. (2000), Nguyen ve Leblanc (2001) ve Juhl v.d. (2002) tarafından yapılan çalışmalarda kurumsal imajın müşteri sadakatini pozitif yönde etkilediği hipotezi doğrulanmıştır. Aynı zamanda Aydın ve Özer (2005) in çalışmasına ilaveten değiştirme maliyeti ve müşteri sadakati arasında pozitif yönlü 125
138 ilişki olduğu hipotezi Bloemer v.d. (1998), Lee v.d. (2001), Jones v.d. (2002), Burnham v.d. (2003) tarafından da doğrulanmıştır. Güven ile müşteri sadakati arasındaki ilişkiyi doğrulayan diğer araştırmacılar ise Morgan ve Hunt (1994), Lau ve Lee (1999), Chaudhuri ve Holbrook (2001) şeklindedir. İSS sektöründe ise, Magin v.d. (2010) çalışmasında müşteri memnuniyeti, rakip malların çekiciliği, psikolojik ve sosyal değiştirme engelleri, ekonomik değiştirme engelleri ile müşteri sadakati arasındaki ilişkiler incelenmiş ve memnuniyet ve sadakat arasında pozitif yönlü ilişki, rakip malların çekiciliği ve sadakat arasında negatif yönlü ilişki olduğu hipotezleri kabul edilirken, sosyo psikolojik değiştirme engelleri ile müşteri sadakati arasında öngörülen pozitif yönlü ve ekonomik değiştirme engelleri ile sadakat arasında öngörülen negatif yönlü ilişki hipotezleri reddedilmiştir. Aynı zamanda söz konusu değişkenlerin müşteri memnuniyeti ile arasındaki ilişki doğrulanmıştır. Chiou (2004) ise yine İSS sektöründe müşteri memnuniyeti, algılanılan değer, algılanılan güven, gelecek beklentisi gibi kavramların müşteri sadakati ile olan ilişkisini incelemiş gelecek beklentisi hariç bütün değişkenlerin kendi aralarında ve müşteri sadakati ile arasındaki ilişkileri anlamlı bulacak sonuçlar elde etmiştir. Gerek diğer sektörlerde gerekse İSS sektöründe müşteri sadakati ve bileşenleri ile ilgili değişkenler için bahsedilen teorik ilişkiler göz önünde bulundurularak Şekil 4.1 ile verilen araştırma modeli önerilmiştir. Önerilen model ASCI ve İSS sektörü için önerilmiş olan Magin (2010) un modellerinin temel alınarak daha önceki çalışmalarda incelenen ilişkilerin de modele dahil edilmesi ile genişletilmiş bir müşteri sadakati modeli olup söz konusu modelin İSS sektörü için incelenmesi amacıyla ampirik bir çalışma gerçekleştirilmiştir. 126
139 ġekil 4.1 Önerilen GeniĢletilmiĢ MüĢteri Sadakati Modeli 4.4. UYGULAMA Çalışmanın bu kısmında uygulanacak analizin bütün adımları ayrıntıları ile ele alınmıştır. Araştırmanın amacı ve kapsamı, yöntemi ve hipotezleri verilmiş daha sonra araştırma modelinin kurulması ve tahmin aşamaları ayrıntıları ile incelenmiştir ARAġTIRMANIN AMAÇ VE KAPSAMI Son yıllarda hızlanan küreselleşme süreci ile firmalar arası rekabet artmakta, müşteri istek ve ihtiyaçlarında köklü değişimler meydana gelmektedir. Bu sürecin doğal bir sonucu olarak müşteri sadakati sağlanması firmaların devamlılıklarını sağlamak ve rekabet avantajı yakalamak gibi konularda son derece önemlidir. Gerek yapılan bilimsel çalışmalarda gerekse piyasada pek çok pazarlama uzmanı tarafından yaygın olarak kabul edilen görüş pazarlamada güç dengesinin 127
140 üretici, dağıtıcı ya da perakendeciden çok müşterilere kaydığı yönündedir. Müşterilerin bir işletmeye bağlılığının artması diğer işletmelere rağmen o işletmeyi tercih etmeleri işletme için önemli bir avantajdır. Çünkü yeni müşteri elde etmenin maliyeti mevcut müşterileri elde tutmanın maliyetinden daha yüksektir (Lin ve Wang, 2006: 272). Ayrıca müşteri sadakatindeki küçük bir artış bile çok daha büyük bir kar artışına neden olmaktadır. Müşteri sadakatindeki %5 lik bir artış karda %25-80 oranında bir artış yaratabilir. Memnuniyeti yüksek bir müşteri, ortalama memnun bir müşteriden altı kat daha sadıktır. Memnuniyetsiz müşterilerin sadece %4 ü şikâyetlerini işletmeye iletir ve memnuniyetsiz müşteri 9 kişiyi etkilerken memnun müşteri 5 kişiyi etkilemektedir (Şimşek, 2007: 186). Müşteri davranışları ile ilgili bu istatistiklerden de açıkça anlaşılacağı üzere müşteri sadakatinin sağlanması firmalar için son derece önemlidir. Çalışmanın amacı internet servis sağlayıcıları pazarında müşteri sadakati olgusunun bileşenleri arasındaki ilişkileri açıklamak olup özellikle kurumsal imaj, hizmet kalitesi, değiştirme maliyeti, firmaya duyulan güven, müşteri memnuniyeti, şikâyet yönetimi, fiyat algısı, firmaya yönelik beklentiler değişkenlerinin müşteri sadakati oluşturma sürecindeki etkilerinin incelenmesidir. Söz konusu kavramların tamamı soyut, ölçülemeyen, gizil (latent) olarak adlandırdığımız değişkenlerdir ve bu değişkenler arasındaki ilişkilerin incelenmesi için kullanılacak istatistiksel yöntem YEM olacaktır ARAġTIRMA TASARIMI VE ÖRNEKLEME PLANI Araştırma süreci keşifsel ve tanımsal süreç olmak üzere iki aşamadan oluşmaktadır. Keşifsel araştırma sürecinde öncelikle ikincil kaynaklardan yararlanılarak literatür taraması gerçekleştirilmiştir. Literatür taraması sonucunda, geçmiş yıllarda yapılan çalışmalardan müşteri sadakati olgusunu etkileyen bileşenler ve Kısım 4.2 de yer verilen söz konusu bileşenler arası teorik ilişkiler tespit edilmiştir. 128
141 Literatür taraması sonrasında, elde edilen unsurların dışında kalan unsurlara ulaşmak ve sektörel farklılıklardan kaynaklanabilecek etkileri ortadan kaldırabilmek adına internet kullanımının yoğun olduğu yaş grubunu temsil ettiği düşünülen 150 sayıda üniversite öğrencisi ile açık uçlu sorulardan oluşan bir anket ile bir pilot çalışma gerçekleştirilmiştir. Daha sonra bu kısımdan elde edilen sorular araştırma değişkenlerine ilave edilmiştir. İSS sektöründe faaliyet gösteren ve ilgili sektörün pazar payı açısından önde gelen üç firması olan TT Net, Superonline ve Doğan Tv Digital (Smile ADSL) den konusunda uzman üç yönetici ile görüşülerek alınan uzman görüşlerinin de ışığında anket sorularının nihai haline ulaşılmıştır. 67 değişkenden oluşan ilk anketin pilot çalışma kapsamında 150 katılımcıya uygulanması sonucunda yapılan AFA ve ardından uygulanan DFA sonuçları ile birlikte 14 değişkenin dışlanarak analize 5 i demografik sorular, 1 i İSS firma tercihi ve 53 ü müşteri sadakati ve bileşenlerine ilişkin tutumların incelendiği tutum soruları olmak üzere toplam 59 soru ve 3 sayfadan oluşan Ek 1 ile verilen anket formu ile devam edilmiştir. TUİK in 2013 yılı Bilişim Teknolojileri Hane Halkı kullanım araştırmasına göre yaş arası nüfusun internet kullanım oranları % 48.9 dur. Aynı rapora göre internet kullanım oranının en yüksek olduğu yaş grubu tür yaş grubunda internet kullanım oranı %69 iken, yaş grubunda %59 ve yaş grubunda ise %45 olarak verilmiştir. Söz konusu oran, yaş yükseldikçe azalmakta olup yaş grubu için %24, yaş grubu için %11 ve yaş grubu için %4 dür. Çalışmada TUİK in internet kullanım oranlarının hesaplanmasında yaş grupları için tasnifi benimsenmiştir. Bu çerçevede araştırma için kota örneklemesi yöntemi temel alınarak örneklem, yaş gruplarına göre azalan oranlarda kotalandırılarak seçilmiştir. Bu çerçevede 750 katılımcı ile yüz yüze görüşülerek anket gerçekleştirilmiştir. Katılımcıları 300 tanesi İstanbul Üniversitesi nin ön lisans, lisans ve lisansüstü programlarında eğitim gören öğrencilerden oluşmaktadır. Araştırmada katılımcıların bir kısmının üniversite öğrencilerinden oluşmasının analiz sonuçlarının genellenebilirliği açısından bir sapma yaratıp yaratmadığının kontrol 129
142 edilmesi için üniversite öğrencilerinde elde edilen örneklem ile diğer katılımcılardan elde edilen örneklemin, her bir araştırma değişkeni açısından ortalamalar arasında fark yaratıp yaratmadığının sınanmasında kullanılan ve parametrik olmayan bir sınama yöntemi olan Mann-Whitney U Testi geçekleştirilmiştir. Ek 2 de ayrıntısı ile yer verilen sonuçlara göre 0,05 anlamlılık düzeyinde iki grup arasında istatistiksel olarak bir fark olmadığı sonucuna ulaşılmıştır. Katılımcılara ait demografik değişkenlere verilen cevapların dağılımı ise Tablo 4.1 de yer almaktadır. Anketlerden 18 tanesi kayıp veri bulunması ve sorulara verilen cevapların çelişkili olması nedeniyle analiz dışında tutulmuştur. Bu nedenle nihai olarak araştırma örneklemi 732 birim ile sınırlandırılmıştır. Örneklem büyüklüğünün belirlenmesi için daha önce bahsedilen hane halkı internet kullanım oranı göz önünde bulundurulmuştur. Söz konusu oran = 0,49 ve duyarlılık (örneklem hatası) 0,05 ve güven düzeyi 0,95 için örneklem büyüklüğü yaklaşık 309 olarak hesaplanmıştır. Ancak uygulanacak analizlerin istatistiksel geçerlilikleri için ölçme aracında bulunan soruların da sayısı göz önünde bulundurularak örneklem büyüklüğü daha yüksek tutulmuştur. 130
143 Tablo 4.1. Katılımcıların Demografik Özelliklerinin Dağılımı DeğiĢken DeğiĢken Düzeyleri % Cinsiyet YaĢ Eğitim Durumu Gelir Meslek Erkek ,70 Kadın , , , , , ,78 İlköğretim 22 3,00 Lise ,10 Ön Lisans 43 5,90 Lisans ,30 Yüksek Lisans- Doktora 64 8, TL.' den az , TL. arası , TL. arası , TL. arası 55 7, TL. arası 22 3, TL.' den çok 7 1,00 Kamu Sektöründe Memur 27 3,69 Özel Sektör Çalışanı ,45 Orta- Üst Düzey Yönetici 24 3,28 Mühendis 14 1,91 Doktor ve Sağlık Sektörü 10 1,37 Avukat 8 1,09 Bankacı Borsacı- Muhasebeci 25 3,42 Basın - Gazete Radyo Tv. 7 0,96 Turizm Sektörü 21 2,87 Öğretmen 18 2,46 Akademisyen 20 2,73 Serbest Meslek 28 3,83 Ev Hanımı 14 1,91 Emekli 11 1,50 İşsiz 11 1,50 Öğrenci ,31 Mimar 7 0,96 Diğer 13 1,78 131
144 Örneklem çerçevesi belirleyen bir diğer unsur da İSS sektöründe faaliyet gösteren firma sayısıdır. Türkiye de İSS sektöründe aktif faaliyet gösteren üçü mobil işletmeci (Turkcell Mobil İnternet, Vodafone Mobil İnternet, Avea Mobil İnternet) olmak üzere 10 dan fazla büyük ölçekli firma mevcuttur. Söz konusu firmalar için Bilişim Teknolojileri Kurumu (BTK) nun 2013 yılı ikinci çeyreğine ait Türkiye Elektronik Haberleşme Sektörü pazar verileri raporunda yer alan pazar paylarına göre sektör lideri Türk Telekom Net (TTNet) %80,50, ardından Superonline %10,50 pazar payına sahiptirler. Söz konusu iki firma % 90 ın üzerinde bir pazar payını ellerinde bulundurmaktadırlar. Kalan % 10 luk kısım için pazarda faaliyet gösteren sırasıyla Doğan Tv Digital (Smile ADSL), Millenicom (Doping Net), Vodafone Net (Biri ADSL), Türk Net başta olmak üzere 220 adet İSS firma arasında paylaşılmaktadır. Araştırmada söz konusu firmalar arasından TT Net ve Superonline ın ardından pazar payları %1 in üzerinde firmalar analize dâhil edilmiştir. Katılımcıların tercih etmekte olduğu İSS firmaya ilişkin oranlar ise Tablo 4.2 de yer almaktadır. Tablo 4.2 Katılımcıların ĠSS Firma Tercihlerinin Dağılımı ISS Firma Frekans Yüzde TT Net 460 % 74,92 Smile 36 % 5,86 Superonline 51 % 8,31 Turk Net 7 % 1,14 Biri ADSL 8 % 1,30 Doping Net 12 % 1,95 Uydu Net 40 % 6,51 Toplam 614 % 83,88 Mobil ĠĢletme Turkcell Mobil 46 % 38,98 Vodafone Mobil 29 % 24,58 Avea Mobil 43 % 36,44 Toplam 118 % 16,12 Genel Toplam 732 % 100,0 132
145 Tablo 4.2 incelendiğinde örnekleme tasarımının gerçek pazar payları ile yaklaşık olarak uyumlu olduğunu görülmektedir. Ankete katılan 732 kişilik örneklemin %83,8 i internet hizmetini İSS firmalardan ve %16,12 mobil işletmelerden sağlamaktadır. İSS firmalar arasında ise ankete katılanların %75 i TTNet, %8,3 ü Superonline, %6,51 i Uydu Net, %5,86 sı Smile ADSL (Doğan Tv Digital) ve geri kalan %4 lük kısmı ise sırası ile Doping Net, Biri ADSL ve TurkNet oluşturmaktadır. Mobil işletmeciler de ise; ankete katılanların ve internet servisi hizmetini mobil işletmelerden alan katılımcıların firma tercihleri %38,9 Turkcell Mobil, %24,58 Vodafone Mobil ve %36,44 Avea Mobil şeklindedir ARAġTIRMA YÖNTEMĠ Araştırma modelinde 9 gizil ve 53 gösterge değişken bulunmaktadır. Söz konusu değişkenlerin ölçümü beşli likert tipi ölçek ile gerçekleştirilmiştir. Araştırmada katılımcılara müşteri sadakati ve bileşenleri ile ilgili tutum sorularındaki ifadelere, 1 = Kesinlikle Katılmıyorum, 2 = Katılmıyorum, 3 = Ne Katılıyorum, Ne Katılmıyorum, 4 = Katılıyorum ve 5 = Kesinlikle Katılıyorum olmak üzere katılım düzeylerini işaretlemeleri istenmiştir. Araştırma modelinde yer alacak gizil değişkenler ve her bir gizil değişkene ait gösterge değişkenler ve değişkenlere ait kısaltmalar Tablo 4.3 aracılığı ile verilmiştir. Ölçekte yer alan sorular, Kısım 4.2 ile bahsedilen teorik açıklamalarda yer alan kaynaklar ile çalışmanın keşifsel sürecinde uygulanan açık uçlu anket sonuçları ve ilgili sektörün özelliklerini yansıtması amacı ile uzman görüşü alınarak eklenen soruların derlenmesi ile hazırlanmıştır. Ankette yer alan soruların uyarlandığı kaynaklardan Türkçe ye çevrilmesi iki dil bilimci tarafından back-translation yöntemi ile gerçekleştirilmiştir. Soruların yazımında yalın ve doğrudan anlaşılır bir dil kullanılmasına özen gösterilmiştir. Araştırma modelinde değişkenlerin ölçülmesi için öncelikle DFA gerçekleştirilecek ve daha sonra gizil değişkenler için yapısal modelin tahmini 133
146 gerçekleştirilerek son aşamadan YEM ile ölçme modeli ve yapısal modelin bir arada analizi gerçekleştirilecektir. Tablo 4.3 AraĢtırma Modelinde Yer Alan Gizil ve Gösterge DeğiĢkenler Gizil Kavramlar KUR KUR1 KUR2 KUR3 KUR4 KUR5 GUV GUV1 GUV2 GUV3 GUV4 GUV5 SAD SAD1 SAD2 SAD3 SAD4 SAD5 BEK BEK1 BEK2 BEK3 BEK4 MEM MEM1 MEM2 MEM3 KURUMSAL ĠMAJ Bu firma istikrarlı ve sağlamdır. Gösterge DeğiĢkenler Bu firma yenilikçi ve ileri görüşlüdür. Bu firma sosyal sorumluluk çalışmalarına önem vermektedir. Bu firma Internet Servis Sağlayıcıları sektöründe lider konumundadır. Bu firma pozitif bir imaja sahiptir. GÜVEN Bu firmaya güvenirim. Bu firmadan iyi hizmet alacağıma inanırım. Bu firmanın faturalama sistemine güvenirim. Bu firmanın beni kazıklamaya çalışmayacağına inanırım. Bu firmanın güvenilir olduğuna inanırım çünkü çoğunlukla müşteri çıkarlarını ön planda tutmaktadırlar. SADAKAT Bu firmanın müşterisi olmaya devam etmeyi düşünüyorum Yeni bir internet servis sağlayıcı kullanmak zorunda kalırsam yine bu firmayı tercih ederim. Bu firmayı herkese tavsiye ederim. Arkadaşlarımı bu firmayı kullanmaları konusunda teşvik ederim. Diğer firmaların daha ucuz fiyat alternatifleri olsa dahi bu firmayı tercih ederim. BEKLENTĠ Bu firmayı tercih ettiğimde tüm beklentilerimi karşılayacağını umuyordum. Bu firmayı kullanmaya başladığımda aldığım hizmetler ile ilgili beklentilerim yüksektir. Bu firmayı kullanmaya başladığımda tarife/ aylık ödeyeceğim ücretten memnun olacağımı bekliyordum. Bu firmayı tercih ettiğimde kişisel ihtiyaçlarıma uygun hizmet almayı bekliyorum. MEMNUNĠYET Diğer internet servis sağlayıcı firmalar ile karşılaştırdığımda bu firmadan memnunum. Genel olarak kullandığım internet servis sağlayıcı firmadan memnunum. Bir internet servis sağlayıcıdan beklentilerimi düşündüğümde bu firmadan memnunum. 134
147 Gizil Kavramlar MEM4 MEM5 FYT FYT1 FYT2 FYT3 MAL MAL1 MAL2 MAL3 MAL4 MAL5 MAL6 MAL7 MAL8 MAL9 SKY SKY1 SKY2 SKY3 SKY4 HKAL HKAL1 HKAL2 HKAL3 HKAL4 Gösterge DeğiĢkenler Sunulan hizmetin kalitesini göz önünde bulundurduğumda bu firmadan memnunum. Bu firmayı seçerek doğru tercihi yaptığıma inanıyorum. FĠYAT Sunulan hizmet kalitesine göre makul bir fiyat ödediğime inanıyorum. Diğer firmalara göre ödediğim fiyatın uygun olduğunu düşünüyorum. Beklentime göre ödediğim fiyatın uygun olduğunu düşünüyorum. DEĞĠġTĠRME MALĠYETĠ Kullandığım internet servis sağlayıcıyı değiştirmek parasal bir maliyete neden olur. Yeni bir internet servis sağlayıcıya geçersem beklediğim kadar iyi hizmet alamayabilirim. Yeni bir internet servis sağlayıcının faturalama sisteminin benim için daha iyi olacağından emin değilim. Yeni bir internet servis sağlayıcıya geçersem sektördeki bütün firmaları karşılaştırmam gerekir. Yeteri kadar bilgiye sahip olsam da bütün internet servis sağlayıcı firmaları karşılaştırmak çok fazla zaman ve enerji gerektirecektir. İnternet servis sağlayıcımı değiştirmek istediğimde ödeyeceğim cayma bedeli yüksektir. Eğer başka bir internet servis sağlayıcıya geçersem bütün hizmetlerini öğrenmem uzun zaman alacaktır. İnternet servis sağlayıcımı değiştirdiğimde kurulum ve üyelik işlemleri çok zaman alır. Taahhüdüm nedeniyle geriye dönük ödeme yapmak yerine aynı internet servis sağlayıcıyı kullanmayı tercih ederim. ġġkâyet YÖNETĠMĠ Bu firma müşteri şikâyetlerini dikkate almaktadır. Bu firma müşteri önerilerini dikkate almaktadır. Bu firma müşteri problem ve şikâyetlerini en kısa sürede çözer. Bu firmada, müşterilerin şikâyet ve önerilerini iletebileceği seçenekler çoktur. HĠZMET KALĠTESĠ Internet servis sağlayıcınızın bağlantı kalitesini değerlendiriniz. Internet servis sağlayıcınızın müģteri hizmetleri kalitesini (çağrı merkezi kalitesi, arıza kayıtlarına dönüş hızı vb.) değerlendiriniz. İnternet servis sağlayıcınızın abone merkezi ve bölge ofislerinde (ofislerin fiziki görünümü, donanımı) verilen hizmetin kalitesini değerlendiriniz. İnternet servis sağlayıcınızın çalıģanlarının yaklaşım, problem çözme kabiliyeti ve istekliliğini değerlendiriniz. 135
148 Gizil Kavramlar HKAL5 HKAL6 HKAL7 HKAL8 HKAL9 HKAL10 HKAL11 HKAL12 HKAL13 Gösterge DeğiĢkenler Internet servis sağlayıcınızın ek hizmetlerinin (yeni nesil TV platformları, uydu alıcı hizmeti, servisi, web alanı sağlama hizmeti, vb.) kalitesini değerlendiriniz. Internet servis sağlayıcınızın reklamlarının kalitesini değerlendiriniz. Internet servis sağlayıcınızın kampanyalarının kalitesini değerlendiriniz. Internet servis sağlayıcınızın üyelik esnasında verdiğiniz doğum günü, yıl dönümü vb. tarihlerin hatırlanması ve kutlanması gibi bireysel ilgi gerektiren hizmetlerinin kalitesini değerlendiriniz. İnternet servis sağlayıcınızın online hizmetlerinin kalitesini değerlendiriniz. Internet servis sağlayıcınızın teknik destek hizmetlerinin kalitesini değerlendiriniz. İnternet servis sağlayıcınızın gizlilik politikasını değerlendiriniz. İnternet servis sağlayıcınızın ihtiyaçlarınıza cevap vermedeki yetkinlik düzeyini değerlendiriniz. İnternet servis sağlayıcınız ile problem yaşadığınızda çalışanların ve firma politikalarının güvenilirlik düzeyini değerlendiriniz. YEM de kullanılan çeşitli tahmin yöntemleri çalışmanın Kısım 3 te incelenmiştir. Değişkenlerin sıralı ölçek ile ölçülmüş olması nedeni ile çok değişkenli normallik varsayımı altında kullanılan EÇO, GEKK vb. yöntemler kullanılamamaktadır. Verinin sıralı ölçekle ölçülmesi durumda kullanılacak yöntemler AEKK, Dayanıklı EÇO, DAEKK yöntemleridir. AEKK yönteminin uygulanmasında gerekli örneklem büyüklüğü için kesin bir birim sayısı olmamasına rağmen, 10 gösterge değişken için bile en az 1000 birimlik örneklem ile çalışılması gerekmektedir (Muthén, 1989: 25). Araştırmada yer alan 53 değişken için söz konusu örneklem büyüklüğü sağlanamayacağından tahmin yöntemi olarak AEKK nın seçilmesi uygun olmamaktadır. Aynı zaman AEKK yöntemi gösterge değişkenlerin ardında yatan sürekli değişkenlerin normal dağıldığı varsayımı yapmaktadır. Bu durumdan da anlaşılacağı gibi analiz aşamasında kullanılacak verinin dağılımının biçiminin belirlenmesi kullanılacak tahmin yönteminin seçimi için son derece büyük bir önem teşkil etmektedir. Bu nedenle değişkenlerin tek değişkenli ve çok değişkenli normalliğinin sınanması amacı ile Mardia nın çarpıklık ve basıklık katsayıları kullanılarak tek değişkenli ve çok değişkenli normallik testleri yapılmıştır. 136
149 Elde edilen sonuçlar Tablo 4.4 ve Tablo 4.5 te verilmiştir. Tablo 4.4 incelendiğinde değişkenlerin pek çoğu tek değişkenli normallik varsayımına uymamaktadır. KUR3, GUV5, BEK1, BEK2, BEK3, BEK4 ve MAL3 değişkenleri haricindeki bütün değişkenler için tek değişkenli normallik sağlanmamaktadır ( < 0,05). Tek değişkenli normallik sağlanmadığından çok değişkenli normalliğin sınanmasına gerek kalmadan verinin çok değişkenli normal dağılıma uyum sağlamadığı sonucuna varılmaktadır. Ancak verinin çok değişkenli normallikten ne ölçüde saptığının bir göstergesi olan Mardia nın çok değişkenli çarpıklık ve basıklık katsayılarının incelenmesinde fayda vardır. Tablo 4.4 ile verilen sonuçlar incelendiğinde çok değişkenli normallik için de çarpıklık ve basıklık katsayılarına ilişkin -değerlerinin 0.05 den küçük olması nedeniyle veride çok değişkenli normallik varsayımının sağlanmadığı açıkça söylenebilir. Tablo 4.4. Gösterge DeğiĢkenler için Tek DeğiĢkenli Normallik Testi Çarpıklık Basıklık Çarpıklık ve Basıklık DeğiĢken değeri - değeri değeri -değeri -değeri KUR1-1,687 0,092-2,449 0,014 8,845 0,012 KUR2-1,073 0,283-2,037 0,042 5,302 0,071 KUR3-0,034 0,973-1,568 0,117 2,461 0,292 KUR4-1,788 0,074-6,042 0,000 39,706 0,000 KUR5-1,725 0,084-2,688 0,007 10,201 0,006 GUV1-1,421 0,155-3,143 0,002 11,896 0,003 GUV2-1,259 0,208-2,510 0,012 7,883 0,019 GUV3-0,781 0,435-3,615 0,000 13,680 0,001 GUV4-0,102 0,919-4,597 0,000 21,146 0,000 GUV5 0,172 0,864-2,383 0,017 5,709 0,058 SAD1 1,437 0,151-3,931 0,000 17,517 0,000 SAD2-0,242 0,809-4,732 0,000 22,452 0,000 SAD3-0,282 0,778-4,389 0,000 19,345 0,000 SAD4 0,009 0,993-3,596 0,000 12,931 0,002 SAD5 1,272 0,203-6,095 0,000 38,761 0,000 BEK1-2,125 0,034-0,771 0,441 5,113 0,078 BEK2-2,148 0,032-1,018 0,309 5,650 0,059 BEK3-2,215 0,027-0,640 0,522 5,316 0,070 BEK4-2,181 0,029-0,453 0,651 4,961 0,084 MEM -1,230 0,219-3,401 0,001 13,082 0,001 MEM2-1,256 0,209-2,819 0,005 9,520 0,009 MEM3-1,124 0,261-2,224 0,026 6,211 0,045 MEM4-0,987 0,324-2,900 0,004 9,386 0,009 MEM5-0,883 0,377-3,657 0,000 14,151 0,001 FYT1 0,199 0,843-5,113 0,000 26,178 0,
150 Çarpıklık Basıklık Çarpıklık ve Basıklık DeğiĢken değeri - değeri değeri -değeri -değeri FYT2 0,152 0,879-3,931 0,000 15,477 0,000 FYT3 0,120 0,904-4,246 0,000 18,039 0,000 MAL1-1,549 0,121-4,780 0,000 25,244 0,000 MAL2-0,762 0,446-2,687 0,007 7,802 0,020 MAL3-0,885 0,376-1,722 0,085 3,749 0,153 MAL4-2,796 0,005-4,120 0,000 24,797 0,000 MAL5-1,598 0,110-4,638 0,000 24,067 0,000 MAL6-0,814 0,416-4,039 0,000 16,979 0,000 MAL7-1,360 0,174-5,118 0,000 28,046 0,000 MAL8-0,811 0,417-4,705 0,000 22,795 0,000 MAL9-1,629 0,103-4,053 0,000 19,079 0,000 SKY1-0,509 0,611-4,522 0,000 20,706 0,000 SKY2 0,017 0,987-3,257 0,001 10,610 0,005 SKY3-0,065 0,948-3,695 0,000 13,658 0,001 SKY4-0,078 0,938-3,694 0,000 13,655 0,001 HKAL1-1,163 0,245-4,427 0,000 20,949 0,000 HKAL2-0,526 0,599-3,595 0,000 13,204 0,001 HKAL3-0,572 0,567-2,528 0,011 6,716 0,035 HKAL4-0,838 0,402-3,856 0,000 15,574 0,000 HKAL5-0,589 0,556-3,169 0,002 10,391 0,006 HKAL6-1,634 0,102-4,493 0,000 22,856 0,000 HKAL7-0,709 0,478-2,934 0,003 9,109 0,011 HKAL8-0,038 0,970-6,666 0,000 44,437 0,000 HKAL9-0,697 0,486-3,679 0,000 14,020 0,001 HKAL10-0,644 0,519-3,681 0,000 13,967 0,001 HKAL11-1,437 0,151-3,578 0,000 14,865 0,001 HKAL12-0,698 0,485-3,194 0,001 10,688 0,005 HKAL13-1,045 0,296-2,757 0,006 8,690 0,013 Tablo 4.5 DeğiĢkenler için Mardia nın Çarpıklık ve Basıklık Katsayıları ve Çok DeğiĢkenli Normallik Testi Çarpıklık Basıklık Çarpıklık ve Basıklık Katsayı değeri - değeri Katsayı değeri - değeri -değeri 402,168 74,047 0, ,544 39,313 0, ,396 0,000 Bu durumda veride çok değişkenli normalliğin sağlanamaması ve örneklem büyüklüğünün AEKK yöntemini destekleyecek kadar geniş tutulamaması yönünde 138
151 kısıtlılıkların olması nedeniyle DFA ve YEM tahminlerinde çok değişkenli normallik dağılımından bağımsız olarak güvenilir tahminler sağlayan Dayanıklı EÇO yönteminin kullanılması tercih edilmiştir. Dayanıklı EÇO yöntemi EÇO tahmininde uyum fonksiyonunda asimptotik kovaryans matrisinin kullanılması ve modelin genel uyumunun değerlendirilmesinde Satorra-Bentler ölçeklendirilmiş değerinin kullanılmasını önermektedir. Araştırma boyunca yapılacak analizlerin tümü için LISREL 8.80 yazılımı kullanılacaktır ÖLÇME MODELLERĠNĠN OLUġTURULMASI Daha önceki kısımlarda belirtildiği gibi YEM çalışmalarında biri ölçme modeli biri yapısal model olmak üzere iki modelin eşanlı olarak tahmin edilmesi ile modelin veriye uygunluğunun test edilmesi amaçlanmaktadır. Yapısal modelin geçerliliği doğrudan ölçme modelinin geçerliliğine bağlı olduğundan hem yapısal modelin hem de ölçme modelinin ayrı ayrı değerlendirilerek istatistikî açıdan uygunluğunun ortaya konulması daha sık tercih edilen bir yaklaşımdır. Çalışmada, Tablo 4.3 ile verilen gizil değişkenlerin ilgili göstergeler ile ölçülüp ölçülmediğinin sınanması amacı ile ölçme modelleri kurulmakta ve ölçme modelinin kabul edilebilir uyum değerleri üretecek şekilde düzeltme ölçütleri de kullanılarak geliştirilmesi amaçlanmaktadır. Ölçme modellerinin tahmini ve değerlendirilmesi aşamalarında DFA yaklaşımı kullanılmış olup, değişkenlerin varyansları 1 e sabitlenerek ölçek belirsizliği ortadan kaldırılmıştır. Ölçme modelinin oluşturulması için 9 gizil 53 gösterge değişkenden oluşan tam model ile başlanarak, genel model ve model bileşenleri için uyum ölçütleri ve düzeltme ölçütleri göz önünde bulundurularak model aşamalı olarak geliştirilmiştir. Modelleme sürecinde çok sayıda model denenmiş olup aşağıda teorik açıdan Kısım 4.1 deki açıklamalar uygunluk ve uyum ölçütleri açısından en başarılı olan modellere yer verilmiştir. 139
152 ÖLÇME MODELĠ 1: Ölçme modeli 1 olarak tanımlanan modelde Tablo 4.3 te yer alan KUR, GUV, SAD, BEK, MEM, FYT, MAL, SKY, HKAL gizil değişkenler ve ilgili gösterge değişkenlerinin tamamı modele dâhil edilerek DFA gerçekleştirilmiştir. Elde edilen sonuçlar; yol katsayıları, hata varyansları ve belirginlik katsayıları Tablo 4.6 ile özetlenmiştir. Modelin güvenilirliği belirlemek amacıyla öncelikle Cronbach s katsayısı hesaplanmıştır. Modeli açıkladığı varsayılan 9 gizil ve 53 gösterge değişken için güvenilirlik katsayısı olarak elde edilmiş olup ve bu değer ölçme aracının yüksek düzeyde güvenilir olduğunu ortaya koymaktadır. Ölçme modeli 1 için hesaplanan uyum ölçütlerine ise Tablo 4.7 ile yer verilmiştir. Söz konusu uyum ölçütleri incelendiğinde bazı ölçütler kabul edilir uyum ya da iyi uyumu işaret etse de diğer pek çok ölçütün modelin veriye uyumunun yeterli olmadığı göstermesi nedeni ile modelin düzeltme ölçütleri ve Tablo 4.6 da yer alan sonuçlar değerlendirilerek geliştirilmesine karar verilmiştir. Ayrıca Tablo 4.7 de yer alan uyum ölçütlerinden Kritik N değeri ölçütü (CN) yeterli modelin uygunluğu için gerekli örneklem sayısı konusunda fikir vermektedir. Model 1 için hesaplanan bu değer 278,39 olup çalışma kullanılan 732 birimlik örneklemin yeterli olduğunu göstermektedir. Tablo 4.6. Ölçme Modeli 1 için Doğrulayıcı Faktör Analizi Sonuçları Gösterge Hata Gizil DeğiĢken Katsayı Standart hata t-değeri Hata varyansı Hata varyansının standart hatası t-değeri KUR1 0,85 0,034 25,07 0,41 0,027 15,40 0,64 KUR2 0,79 0,033 24,19 0,41 0,026 15,88 0,60 KUR3 0,59 0,035 16,89 0,65 0,036 18,00 0,35 KUR4 0,58 0,044 13,06 1,13 0,061 18,52 0,23 KUR5 0,85 0,034 24,77 0,43 0,028 15,57 0,62 GUV1 0,92 0,033 27,79 0,34 0,022 14,93 0,72 GUV2 0,91 0,032 28,05 0,31 0,021 14,73 0,72 140
153 Gösterge Hata Gizil DeğiĢken Katsayı Standart hata t-değeri Hata varyansı Hata varyansının standart hatası t-değeri GUV3 0,72 0,038 18,62 0,76 0,042 18,05 0,40 GUV4 0,58 0,042 13,97 1,02 0,055 18,60 0,25 GUV5 0,72 0,035 20,73 0,57 0,032 17,68 0,48 SAD1 0,88 0,036 24,72 0,51 0,029 17,31 0,61 SAD2 0,99 0,036 27,54 0,42 0,026 16,37 0,70 SAD3 1,05 0,033 31,53 0,24 0,018 13,47 0,82 SAD4 0,96 0,033 29,11 0,31 0,020 15,55 0,75 SAD5 0,78 0,041 18,89 0,87 0,048 18,32 0,41 BEK1 0,65 0,034 19,12 0,49 0,032 15,32 0,47 BEK2 0,67 0,032 21,24 0,37 0,027 13,77 0,55 BEK3 0,67 0,034 19,53 0,48 0,032 15,06 0,48 BEK4 0,66 0,032 20,37 0,40 0,028 14,47 0,52 MEM1 0,92 0,033 27,74 0,36 0,021 16,81 0,70 MEM2 0,95 0,033 29,30 0,30 0,019 16,14 0,75 MEM3 0,92 0,031 29,50 0,27 0,017 16,04 0,76 MEM4 0,96 0,032 29,78 0,28 0,018 15,89 0,77 MEM5 0,99 0,033 29,85 0,29 0,019 15,85 0,77 FYT1 1,07 0,036 30,03 0,28 0,027 10,38 0,81 FYT2 0,93 0,035 26,39 0,41 0,028 14,62 0,68 FYT3 0,98 0,036 27,60 0,37 0,027 13,50 0,72 MAL1 0,59 0,044 13,33 0,99 0,056 17,62 0,26 MAL2 0,48 0,041 11,74 0,89 0,049 18,00 0,21 MAL3 0,46 0,038 12,34 0,74 0,042 17,87 0,23 MAL4 0,59 0,041 14,54 0,83 0,048 17,28 0,30 MAL5 0,77 0,041 18,75 0,71 0,046 15,53 0,45 MAL6 0,73 0,041 17,76 0,76 0,047 16,04 0,42 MAL7 0,62 0,044 14,11 0,97 0,056 17,41 0,28 MAL8 0,67 0,044 15,28 0,93 0,055 17,04 0,33 MAL9 0,61 0,043 14,26 0,92 0,053 17,36 0,29 SKY1 0,95 0,036 26,62 0,42 0,028 14,84 0,68 SKY2 0,91 0,034 26,87 0,37 0,025 14,66 0,69 SKY3 0,91 0,035 25,95 0,42 0,028 15,27 0,66 SKY4 0,84 0,036 23,19 0,54 0,033 16,56 0,57 HKAL1 0,76 0,038 20,11 0,70 0,039 18,11 0,45 HKAL2 0,84 0,036 23,55 0,53 0,031 17,49 0,57 HKAL3 0,74 0,034 21,69 0,54 0,030 17,86 0,50 HKAL4 0,84 0,036 23,55 0,54 0,031 17,49 0,57 HKAL5 0,74 0,036 20,40 0,64 0,035 18,06 0,46 HKAL6 0,56 0,040 14,13 0,93 0,050 18,70 0,25 HKAL7 0,71 0,036 19,88 0,63 0,035 18,14 0,44 HAKL8 0,74 0,043 17,39 0,99 0,054 18,43 0,36 HKAL9 0,82 0,036 22,70 0,57 0,032 17,67 0,54 HKAL10 0,88 0,035 25,39 0,46 0,027 17,01 0,63 HKAL11 0,61 0,036 17,00 0,72 0,039 18,47 0,34 HKAL12 0,86 0,034 25,67 0,42 0,025 16,92 0,64 HKAL13 0,78 0,033 23,42 0,47 0,027 17,52 0,56 141
154 Tablo 4.6 incelendiğinde, bütün gösterge değişkenler için yol katsayılarının istatistiksel olarak anlamlı oldukları görülmektedir ( ). Söz konusu değişkenlerin anlamlılığına rağmen KUR gizil değişkeninden KUR3 ve KUR4 e, GUV gizil değişkeninden GUV4 e, SAD gizil değişkeninden SAD5 e, MAL gizil değişkeninden MAL2, MAL3 ve MAL9 a, SKY gizil değişkeninden SKY4 e ve HKAL gizil değişkeninden HKAL6, HKAL8 ve HKAL11 e giden yollara ilişkin yol katsayılarının, ilgili değerlerinin ve belirginlik katsayılarının diğer yol katsayılarına oranla oldukça düşük olduğu dikkat çekmektedir. Aynı zamanda söz konusu değişkenlere ait hata varyanslarının da ilgili faktördeki diğer değişkenlerden yüksek olduğu gözlemlenmektedir. Bu durum ve LISREL 8.80 tarafından Ölçme Modeli 1 için hesaplanan düzeltme ölçütleri incelenerek Ölçme Modeli 2 ye geçilecektir. Düzeltme ölçütleri ile gözlenen değişkenlere ilişkin hata terimleri arasındaki ilişkiler önerilmektedir. Ancak YEM in temel varsayımlarından biri modelde değişkenlere ilişkin hataların birbirinden bağımsız olmasıdır. Bu nedenle hataları birbiri ile ilişkili olan değişkenler her bir gizil değişkenin kuramsal yapısını bozmakta ve ölçme modelini oluşturan gizil değişkenlerin birbirinden bağımsız olduğu varsayımı etkilemektedir. Bu nedenle modelin tek boyutluluk yapısını korumak ve hataların bağımsız olması varsayımını sağlamak nedeniyle hataları birbiriyle ilişki değişkenlerden modelin genel uyum istatistiği olan değerinde önemli ölçüde düşüşe neden olan değişkenler modelden dışlanmalıdır. Ölçme modeli 1 için verilen düzeltme indeksleri incelendiğinde, BEK3 değişkenine ait hata teriminin KUR1, KUR3, KUR4, SAD5 ve BEK2 değişkenlerinin hatalarıyla ilişkili olduğu ve daha önce Tablo 4.6 incelenerek yol katsayılarının düşük olması gerekçesi ile seçilen değişkenlerden MAL2 nin hata teriminin, KUR4, SAD5, MEM1 ile, MAL3 ün hata teriminin MAL2 ile MAL9 un hata teriminin SAD1, MAL5, MAL6 ve MAL7 ile, HKAL6 nın hata teriminin KUR4, GUV3, HKAL2, HKAL4 ve HKAL5 ile, HKAL8 in hata teriminin HKAL2 ve HKAL7 ile, HKAL11 in hata teriminin GUV5 ve HKAL2 ile ilişkili olması nedeniyle modelden çıkartılmıştır. 142
155 Tablo 4.7 Ölçme Modeli 1 için Uyum Ölçütleri Uyum Ölçütü Referans Değeri Değer Uyum Model sd χ2 Minimum 4000,81 χ2/sd. < 2 2,88 Ret RMSEA < 0,05 0,054 Kabul edilebilir RMSEA için %90 Kabul Minimum (0,052 ; 0,056) Güven Aralığı edilebilir P (RMSEA<0.05) > ,00075 Ret RMR Minimum 0,077 Ret SRMR < 0,05 0,063 Ret GFI > 0, Ret AGFI > 0,90 0,81 Ret PGFI Minimum 0,75 Ret ECVI Minimum 5,86 - Doymuş model için ECVI > ECVI 3,92 Ret AIC Minimum 4284,81 - Doymuş model için AIC > AIC 2862 Ret CAIC Minimum Doymuş model için CAIC > CAIC 10869,56 Ret NFI > 0,90 0,97 Kabul NNFI > 0,90 0,98 Kabul PNFI Minimum 0,91 Ret CFI > 0,90 0,98 Kabul IFI > 0,90 0,98 Kabul RFI > 0,90 0,97 Kabul CN > ,39 Kabul Özetle ölçme modeli 1 de yol katsayılarının ilgili faktördeki diğer yol katsayılarına oranla oldukça düşük olması nedeniyle KUR3, KUR4, GUV4, SAD5, SKY4 değişkenleri ve modelde yer alan diğer pek çok değişkenin hatası ile yüksek derecede ilişkili olmaları nedeniyle BEK3, MAL2, MAL3, MAL9, HKAL6, 143
156 HKAL8, HKAL11 değişkenleri modelden dışlanarak ölçme modeli 2 nin tahminine geçilmiştir. ÖLÇME MODELĠ 2: Ölçme modeli 2 de ölçme modeli 1 için gerçekleştirilen bütün analiz aşamaları tekrar edilmiştir. Elde edilen sonuçlar Tablo 4.8 ve Tablo 4.9 aracılığı ile özetlenmiştir: Tablo 4.8 Model 2 için Doğrulayıcı Faktör Analizi Sonuçları Gizil DeğiĢken Katsayı Gösterge Standart hata t-değeri Hata varyansı Hata Hata varyansının standart hatası t-değeri KUR1 0, 84 0,034 24,72 0,42 0,028 15,26 0,63 KUR2 0,78 0,033 23,63 0,42 0,027 15,89 0,59 KUR5 0,84 0,034 24,46 0,44 0,028 15,43 0,62 GUV1 0,93 0,033 28,30 0,32 0,022 14,57 0,73 GUV2 0,92 0,032 28,38 0,30 0,021 14,50 0,74 GUV3 0,70 0,039 18,03 0,78 0,043 18,16 0,38 GUV5 0,70 0,035 20,01 0,60 0,034 17,84 0,45 SAD1 0,89 0,036 24,78 0,50 0,029 17,20 0,61 SAD2 0,99 0,036 27,36 0,43 0,026 16,30 0,69 SAD3 1,06 0,033 31,60 0,23 0,018 13,03 0,83 SAD4 0,96 0,033 28,98 0,31 0,020 15,44 0,75 BEK1 0,67 0,035 18,87 0,47 0,034 13,76 0,49 BEK2 0,71 0,033 21,38 0,32 0,030 10,55 0,61 BEK4 0,60 0,034 17,63 0,47 0,032 14,92 0,43 MEM1 0,92 0,033 27,65 0,36 0,021 16,84 0,70 MEM2 0,95 0,033 29,33 0,30 0,018 16,13 0,75 MEM3 0,92 0,031 29,57 0,27 0,017 16,00 0,76 MEM4 0,96 0,032 29,80 0,28 0,018 15,87 0,77 MEM5 0,99 0,033 29,82 0,30 0,019 15,86 0,77 FYT1 1,07 0,036 29,98 0,28 0,027 10,36 0,80 FYT2 0,93 0,035 26,35 0,41 0,028 14,61 0,68 FYT3 0,98 0,036 27,65 0,37 0,027 13,38 0,72 MAL1 0,53 0,045 11,60 1,06 0,059 17,85 0,21 MAL4 0,55 0,042 13,04 0,88 0,050 17,45 0,55 MAL5 0,83 0,041 20,31 0,60 0,045 13,38 0,53 MAL6 0,83 0,041 20,32 0,60 0,045 13,36 0,53 MAL7 0,62 0,045 13,87 0,97 0,056 17,19 0,28 144
157 Gizil DeğiĢken Katsayı Gösterge Standart hata t-değeri Hata varyansı Hata Hata varyansının standart hatası t-değeri MAL8 0,69 0,044 15,54 0,91 0,055 16,54 0,34 SKY1 0,98 0,036 27,70 0,36 0,028 13,09 0,73 SKY2 0,93 0,034 27,57 0,33 0,025 13,22 0,72 SKY3 0,88 0,036 24,50 0,48 0,031 15,55 0,62 HKAL1 0,76 0,038 20,29 0,69 0,038 17,97 0,46 HKAL2 0,86 0,035 24,24 0,50 0,029 17,13 0,59 HKAL3 0,75 0,034 21,79 0,54 0,030 17,70 0,51 HKAL4 0,85 0,036 23,82 0,53 0,030 17,24 0,58 HKAL5 0,73 0,036 20,02 0,65 0,036 18,01 0,45 HKAL7 0,68 0,036 18,96 0,66 0,037 18,16 0,41 HKAL9 0,80 0,036 21,91 0,60 0,034 17,68 0,51 HKAL10 0,89 0,035 25,64 0,45 0,027 16,69 0,64 HKAL12 0,87 0,034 25,83 0,41 0,025 16,62 0,65 HKAL13 0,77 0,034 22,89 0,49 0,028 17,47 0,55 Tablo 4.9. Ölçme Modeli 2 için Uyum Ölçütleri Uyum Ölçütü Referans Değeri Değer Uyum Model sd χ2 Minimum 2007,05 χ2/sd. < 2 2,7 Ret RMSEA < 0,05 0,048 Kabul RMSEA için %90 Güven Aralığı Minimum (0.046 ; 0,051) Kabul P(RMSEA<0.05) > 0,05 0,87 Kabul RMR Minimum 0,054 Ret SRMR < 0,05 0,044 Kabul GFI > 0,90 0,88 Ret AGFI > 0,90 0,86 Ret PGFI Minimum 0,76 Ret ECVI Minimum 3,07 - Doymuş model için ECVI > ECVI 2,36 Ret AIC Minimum 2243,05 - Doymuş model için AIC > AIC 1722 Ret CAIC Minimum 2903,35-145
158 Uyum Ölçütü Referans Değeri Değer Uyum Doymuş model için CAIC > CAIC 6539,97 Ret NFI > 0,90 0,98 Kabul NNFI > 0,90 0,99 Kabul PNFI Minimum 0,89 Ret CFI > 0,90 0,99 Kabul IFI > 0,90 0,99 Kabul RFI > 0,90 0,98 Kabul CN > ,74 Kabul Tablo 4.8 incelendiğinde modelde yer alan bütün göstergelere ait katsayıların istatistiksel olarak anlamlı olduğu gözlemlenmektedir ( ). Tablo 4.9 incelendiğinde ise genel olarak modelin veriye uyumunun istatistiksel olarak uygun olduğu görülmektedir. Ölçme modeli 1 e oranla uyum ölçütleri daha kabul edilir bir uyumu gösteriyor olsa da bazı ölçütlere göre modelin uyumu kabul edilebilir ölçüde olamamaktadır. Bu nedenle modelin kuramsal yapısı ve düzeltme ölçütleri de göz önünde bulundurularak hem görece olarak yol katsayıları düşük hem de diğer değişkenlerin hata terimleri ile yüksek düzeyde ilişkili olan GUV3, GUV5, SAD1, BEK4, MEM1, FYT1, MAL1, MAL4, MAL7, MAL8, HKAL1, HKAL5, HKAL7 değişkenleri modelden dışlanarak ölçme modeli 3 e geçilmiştir. ÖLÇME MODELĠ 3: Ölçme modeli 3 de ölçme modeli 2 için gerçekleştirilen bütün analiz aşamaları tekrar edilmiştir. Elde edilen sonuçlar Tablo 4.10 ve Tablo 4.11 aracılığı ile özetlenmiştir. Tablo 4.10 incelendiğinde gösterge değişkenlere ait yol katsayılarının model 3 için de istatistiksel olarak anlamlı olduğu gözlemlenmektedir ( ). Modele ait uyum ölçütleri incelendiğinde ise neredeyse tamamının iyi uyuma işaret ettiği görülmektedir. Yalnızca AIC ve ECVI ölçütlerinin modelin veriye uyumunu reddettiği görülmektedir. Bu nedenle ölçme modelinin geliştirilmesi amacı ile son 146
159 olarak yol katsayıları düşük ve hata terimlerinin diğer değişkenlerle yüksek korelasyonlu olduğu görülen MEM5, HKAL9 ve HKAL13 değişkenleri Kısım 4.1 ve 4.2 de yapılan kuramsal açıklamalara da bağlı kalınarak modelin teorik çerçevesine uyum sağlayacak şekilde modelden dışlanarak ölçme modeli 4 kurulmuştur. Tablo 4.10 Model 3 için Doğrulayıcı Faktör Analizi Sonuçları Gizil DeğiĢken Katsayı Gösterge Standart hata t-değeri Hata varyansı Hata Hata varyansının standart hatası t-değeri KUR1 0,84 0,034 24,65 0,42 0,028 15,28 0,62 KUR2 0, ,52 0,43 0,027 15,92 0,58 KUR5 0,84 0,034 24,58 0,43 0,028 15,32 0,62 GUV1 0,95 0,033 29,14 0,27 0,022 12,58 0,77 GUV2 0,93 0,032 28,97 0,27 0,021 12,82 0,76 SAD2 0,97 0,036 26,59 0,46 0,028 16,36 0,67 SAD3 1,08 0,033 32,76 0,18 0,018 10,12 0,87 SAD4 0,97 0,033 29,40 0,29 0,020 14,62 0,76 BEK1 0,69 0,042 16,65 0,43 0,046 9,52 0,53 BEK2 0,69 0,040 17,30 0,34 0,043 7,85 0,59 MEM2 0,94 0,033 28,32 0,31 0,020 15,88 0,74 MEM3 0,92 0,031 29,49 0,27 0,017 15,48 0,76 MEM4 0,97 0,032 29,93 0,27 0,018 15,18 0,77 MEM5 0,99 0,033 29,88 0,29 0,019 15,22 0,77 FYT2 0,92 0,039 23,56 0,42 0,042 10,05 0,67 FYT3 1,01 0,040 25,57 0,31 0,046 6,63 0,77 MAL5 0,97 0,069 14,13 0,35 0,12 3,02 0,73 MAL6 0,81 0,062 13,08 0,64 0,087 7,40 0,50 SKY1 0,98 0,036 27,66 0,36 0,028 13,15 0,73 SKY2 0,93 0,034 27,52 0,33 0,025 13,29 0,72 SKY3 0,88 0,036 24,59 0,48 0,031 15,50 0,62 HKAL2 0,87 0,035 24,83 0,47 0,029 16,50 0,62 HKAL3 0,75 0,034 21,68 0,54 0,031 17,43 0,51 HKAL4 0,87 0,035 24,55 0,49 0,029 16,60 0,61 HKAL9 0,78 0,037 21,13 0,63 0,036 17,56 0,49 HKAL10 0,90 0,035 25,71 0,44 0,027 16,14 0,65 HKAL12 0,88 0,034 26,00 0,40 0,025 16,01 0,66 HKAL13 0,76 0,034 22,60 0,49 0,029 17,20 0,54 147
160 Tablo 4.11 Ölçme Modeli 3 için Uyum Ölçütleri Uyum Ölçütü Referans Değeri Değer Uyum Model sd χ2 Minimum 705,78 χ2/sd. < 2 2,24 Kabul Edilebilir RMSEA < 0,05 0,041 Kabul RMSEA için %90 Güven Aralığı Minimum (0,037; 0,045) Kabul P(RMSEA<0.05) > Kabul RMR Minimum 0,031 Kabul SRMR < 0,05 0,026 Kabul GFI > 0,90 0,94 Kabul AGFI > 0,90 0,92 Kabul PGFI Minimum 0,72 Kabul ECVI Minimum 1,22 - Doymuş model için ECVI > ECVI 1,11 Ret AIC Minimum 889,78 - Doymuş model için AIC > AIC 812 Ret CAIC Minimum 1404,59 - Doymuş model için CAIC > CAIC 3083,89 Kabul NFI > 0,90 0,99 Kabul NNFI > 0,90 0,99 Kabul PNFI Minimum 0,82 Kabul CFI > 0,90 0,99 Kabul IFI > 0,90 0,99 Kabul RFI > 0,90 0,98 Kabul CN > ,40 Kabul ÖLÇME MODELĠ 4: Ölçme modeli 3 ile anılan değişkenlerin modelden çıkartılması ile ölçme modeli 4 tahmin edilmiştir. Tablo 4.12 de modele ilişkin DFA sonuçları, Tablo 4.13 de modelin uyum ölçütleri ve Şekil 4.2 ile ise ölçüm modeli 4 için yol diyagramı verilmiştir. Tablo 4.12 incelendiğinde modelde yer alan her gösterge 148
161 değişkenin yol katsayılarının istatistiksel olarak anlamlı ( beklenen işaretlere sahip oldukları görülmektedir. ) ve teorik açıdan Tablo 4.12 Model 4 için Doğrulayıcı Faktör Analizi Sonuçları Gizil DeğiĢken Katsayı Gösterge Standart hata t-değeri Hata varyansı Hata Hata varyansının standart hatası t-değeri KUR1 0,84 0,034 24,64 0,43 0,028 15,30 0,62 KUR2 0,77 0,033 23,51 0,43 0,027 15,94 0,58 KUR5 0,84 0,034 24,61 0,43 0,028 15,32 0,62 GUV1 0,95 0,033 29,15 0,27 0,022 12,52 0,77 GUV2 0,93 0,032 28,93 0,27 0,021 12,82 0,76 SAD2 0,97 0,036 26,50 0,46 0,028 16,35 0,67 SAD3 1,08 0,033 32,80 0,17 0,018 9,88 0,87 SAD4 0,97 0,033 29,38 0,29 0,020 14,54 0,76 BEK1 0,69 0,042 16,55 0,44 0,045 9,72 0,52 BEK2 0,70 0,040 17,37 0,33 0,044 7,61 0,59 MEM2 0,96 0,033 29,53 0,28 0,020 14,29 0,77 MEM3 0,93 0,031 29,95 0,24 0,017 13,89 0,78 MEM4 0,95 0,033 29,10 0,30 0,020 14,65 0,75 FYT2 0,92 0,039 23,29 0,43 0,043 10,05 0,66 FYT3 1,02 0,040 25,50 0,30 0,047 6,26 0,78 MAL5 0,97 0,069 14,14 0,35 0,12 3,02 0,73 MAL6 0,81 0,062 13,09 0,64 0,087 7,40 0,50 SKY1 0,98 0,036 27,51 0,37 0,028 13,27 0,72 SKY2 0,93 0,034 27,56 0,33 0,025 13,22 0,72 SKY3 0,88 0,036 24,66 0,47 0,031 15,44 0,62 HKAL2 0,90 0,035 25,71 0,43 0,028 15,36 0,65 HKAL3 0,75 0,035 21,60 0,53 0,031 17,04 0,51 HKAL4 0,88 0,036 24,86 0,47 0,030 15,81 0,63 HKAL10 0,89 0,035 25,19 0,45 0,029 15,64 0,64 HKAL12 0,86 0,034 25,22 0,42 0,027 15,63 0,64 Bunun yanı sıra Tablo 4.13 incelendiğinde modelin genel uyum ölçütlerinin tamamının iyi uyuma işaret ettiği görülmektedir. Model 1, Model 2 ve Model 3 karşılaştırıldığında model 4 e ilişkin değeri 463,01 diğer bütün modellerinkinden küçüktür. Kesin uyum ölçütlerinden, GFI, AGFI sırasıyla 0,95 ve 0,93 olarak elde edilmiş olup kabul edilebilir uyum için verilen eşik değeri 0,90 ın üzerinde ve diğer modellere oranla daha yüksektir. RMR ve SRMR ölçütleri 0,028 ve 0,023 olup diğer modellere göre daha düşüktür. Artımsal uyum ölçütlerinden NFI, NNFI, IFI, RFI değerleri 0,99 olarak hesaplanmış olup diğer modellere oranla daha yüksek olup aynı 149
162 zamanda mükemmel uyumu işaret etmektedirler. Merkezi olmayan ölçütler olarak anılan RMSEA değeri ve CFI ölçütü ise sırasıyla ve 0.99 olarak tespit edilmiştir. Söz konusu değerler oldukça iyi bir uyuma işaret etmektedir. Son olarak yalınlık uyum kriterleri incelendiğinde AIC, CAIC ve ECVI değerlerinin doymuş modellere oranla ölçme modeli 4 için daha düşük değerler verdiği görülmektedir. Son olarak CN ölçütü ise gerekli örneklem büyüklüğünü 381,40 olarak hesaplamış olup çalışmanın örneklem büyüklüğü olan 732 birimin analiz için yeterli olduğu sonucuna ulaşılmıştır. Tablo 4.13 Ölçme Modeli 4 için Uyum Ölçütleri Uyum Ölçütü Referans Değeri Değer Uyum Model sd χ2 Minimum 463,01 χ2/sd. < 2 1,93 Kabul RMSEA < 0,05 0,036 Kabul RMSEA için %90 Güven Aralığı Minimum (0,031;0,041) Kabul P(RMSEA<0.05) > Kabul RMR Minimum 0,028 Kabul SRMR < 0,05 0,023 Kabul GFI > 0,90 0,95 Kabul AGFI > 0,90 0,93 Kabul PGFI Minimum 0,70 Kabul ECVI Minimum 0,87 - Doymuş model için ECVI > ECVI 0,89 Kabul AIC Minimum 635,01 - Doymuş model için AIC > AIC 650 Kabul CAIC Minimum 1116,25 - Doymuş model için CAIC > CAIC 2468,63 Kabul NFI > 0,90 0,99 Kabul NNFI > 0,90 0,99 Kabul PNFI Minimum 0,79 Kabul CFI > 0,90 0,99 Kabul IFI > 0,90 0,99 Kabul RFI > 0,90 0,99 Kabul CN > ,40 Kabul 150
163 Şekil 4.2 ile standartlaştırılmış yol katsayıları ile ölçme modeli 4 için yol diyagramı verilmiştir. ġekil 4.2 Ölçme Modeli 4 için yol diyagramı 151
164 Gizil değişkenlerin her birinin gösterge değişkenleri ile arasındaki ilişkinin derecesini gösteren yol katsayılarının tamamının 0,70 den büyük olduğu görülmektedir. Son olarak ölçme modeli 4 ile elde edilen ölçek için ayırt edici geçerlilik ve güvenilirlik analizi yapıldıktan sonra yapısal modele geçilecektir. Bu kısımdan sonra ölçme modeli 4 nihai ölçme modeli olarak kabul edildiğinden sadece ölçme modeli olarak anılacaktır ÖLÇME MODELĠNĠN GEÇERLĠLĠĞĠ ve GÜVENĠLĠRLĠĞĠ YEM analizine başlamadan önce DFA ile elde edilen nihai ölçme modelinin geçerlilik ve güvenilirliğinin incelenmesi gerekmektedir. Her bir gizil değişkenin oluşturduğu yapının güvenilirliği incelemek için Kısım de bahsedilen ve Eşitlik 3.90 ve Eşitlik 3.91 ile formülleri verilen yapı güvenilirliği, açıklanan varyans oranı ve klasik ölçme teorisinde sıklıkla kullanılan Cronbach s güvenilirlik ölçütü hesaplanacaktır. Nunnally (1978) sosyal bilimlerde ölçme aracının güvenilirliği için her bir yapıya ait Cronbach s değerinin 0,70 den büyük olması gerektiğini savunmaktadır. Hair v.d. (1998) e göre yapı güvenilirliği katsayısının 0,70 ve açıklanan varyans oranının 0,50 den büyük olması gizil değişken güvenilirlikleri için yeterli kabul edilmektedir. Analizde kullanılacak ölçme modeli için yapı güvenilirliği katsayısı, açıklanan varyans oranı ve Cronbach s verilmiştir. Tablo Ölçme Modeli için Güvenilirlik Katsayıları Gizil Yapı Cronbach's Yapı Güvenilirliği Açıklanan Varyans KUR 0,827 0,822 0,600 GUV 0,871 0,867 0,765 SAD 0,905 0,907 0,766 BEK 0,721 0,714 0,555 MEM 0,908 0,908 0,767 FYT 0,842 0,836 0,718 MAL 0,763 0,759 0,614 SKY 0,866 0,863 0,678 HKAL 0,888 0,888 0,614 değerleri Tablo 4.14 ile 152
165 Tablo 4.14 incelendiğinde bütün gizil değişkenler için Cronbach s değerleri ve yapı güvenilirliği katsayılarının 0,70 ten büyük olduğu görülmektedir. Açıklanan varyans oranlarının ise tamamı 0,50 den büyüktür. Gizil yapılar arasında en yüksek güvenilirliğe sahip olan SAD ve MEM değişkenleridir. Yalnızca BEK ve MAL değişkenleri için hesaplanan güvenilirlik katsayıları görece olarak daha düşük olsa her ikisi de kabul edilebilir düzeyin üzerindedir. Sonuç olarak 9 gizil değişken ve bunlara ait toplam 25 gösterge değişken için crobach s katsayısı ise 0,94 olup bu değer güvenilirlik analizi sonucunda ölçme aracının bütün olarak güvenilirliğinin de oldukça yüksek olduğunu ortaya koymaktadır. Ölçme modelinin geçerliliğinin analizi için ise ayırsama geçerliliği araştırılacaktır. Ayırsama geçerliliği, ölçme modelinde yer alan gizil değişkenlerin aynı yapıları ölçüp ölçmediğinin belirlenmesini başka bir deyişle ölçülecek kavramın diğer kavramlarla karışmadan ölçülüp ölçülemediğinin analiz edilmesi anlamına gelmektedir. Ayırsama geçerliliği farklı yapılardaki ölçümlerin diğer yapılardan yeterince ayırt edilme derecesini göstermektedir. Ayırsama geçerliliğinin sınanması için iki model tanımlanmaktadır. Bunlardan biri gizil değişkenlerin arasındaki korelasyonun 1 e sabitlendiği sınırlanmış model (Model A) diğeri ise gizil değişkenler arasındaki korelasyonların serbest bırakıldığı sınırlandırılmamış model (Model B) olmaktadır. Her iki rakip model için de DFA gerçekleştirilmekte ve söz konusu iki modelin değerleri arasındaki farkın anlamlılığı için Fark Testi uygulanmaktadır. Her iki model arasındaki tek fark gizil değişkenlerin korelasyonları olmaktadır ve bu nedenle kurulan hipotez, : şeklindedir. hipotezi aynı zamanda modelin tek boyutlu bir yapıya sahip olduğu anlamına da gelmektedir. Gizil değişkenler arasında ayırsama geçerliliğinin olduğunun kabul edilmesi için sınırlandırılmış ve sınırlandırılmamış model arasındaki uyumun iyileşmesinin anlamlı olması yani hipotezinin reddedilmesi gerekmektedir (Şimşek, 2007: ). Karar kriteri ise rakip iki modelden elde edilen değerleri ve serbestlik dereceleri arasındaki farktan elde edilen ve değerleri için hesaplanan p değeridir. p değerinin 0,05 den küçük olması hipotezinin reddedilmesi yönünde 153
166 önemli istatistiksel kanıt sunmakta olacaktır. Araştırma modeli için Kısım de incelenen fark testi uygulandığında, tüm mümkün gizil değişken ikilileri incelenmiş olup 36 ayrı karşılaştırma gerçekleştirilmiştir. Karşılaştırmalarda Model B için hesaplanan değerleri ve serbestlik dereceleri Model A için hesaplanan değerlerden küçük olarak belirlenmiştir. fark testleri sonucunda iki model arasındaki farkın anlamlığını ifade eden p değeri 0,05 den küçük tespit edilmiş ve her bir gizil değişken için hipotezi reddedilmiştir. Söz konusu karşılaştırmalar için elde edilen sonuçlar Tablo 4.15 de yer almaktadır. Tablo Ölçme Modelinde Yer Alan DeğiĢkenlerin Ayırsama Geçerliliği Gizil değiģken çiftleri Model A Model B Fark p-değeri KUR-GUV 46, , ,00 1 0,0000 KUR-SAD 72, , ,17 1 0,0000 KUR-BEK 112,81 5 4, ,91 1 0,0000 KUR-MEM 79, , ,61 1 0,0000 KUR-FYT 131,48 5 3, ,55 1 0,0000 KUR-MAL 178, , ,21 1 0,0000 KUR-SKY 95, , ,46 1 0,0000 KUR-HKAL 159, , ,89 1 0,0000 GUV-SAD 49, , ,63 1 0,0000 GUV-BEK 116,63 2 4, ,26 1 0,0000 GUV-MEM 52, , ,07 1 0,0000 GUV-FYT 101,48 2 0, ,91 1 0,0000 GUV-MAL 144,59 2 0, ,06 1 0,0000 GUV-SKY 94, , ,90 1 0,0000 GUV-HKAL 116, , ,92 1 0,0000 SAD-BEK 92,20 5 1, ,75 1 0,0000 SAD-MEM 115, , ,52 1 0,0000 SAD-FYT 45, , ,24 1 0,0000 SAD-MAL 182,29 5 7, ,80 1 0,0000 SAD-SKY 87, , ,68 1 0,0000 SAD-HKAL 120, , ,59 1 0,0000 BEK-MEM 158,82 5 7, ,28 1 0,0000 BEK-FYT 188,14 2 4, ,78 1 0,0000 BEK-MAL 175,56 2 0, ,38 1 0,
167 Gizil değiģken çiftleri Model A Model B Fark p-değeri BEK-SKY 172,82 5 6, ,65 1 0,0000 BEK-HKAL 227, , ,08 1 0,0000 MEM-FYT 78,01 5 6, ,88 1 0,0000 MEM-MAL 158,98 5 7, ,68 1 0,0000 MEM-SKY 95, , ,26 1 0,0000 MEM-HKAL 137, , ,25 1 0,0000 FYT-MAL 153,49 2 0, ,38 1 0,0000 FYT-SKY 86, , ,33 1 0,0000 FYT-HKAL 158, , ,77 1 0,0000 MAL-SKY 160,04 5 5, ,77 1 0,0000 MAL-HKAL 223, , ,50 1 0,0000 SKY-HKAL 130, , ,98 1 0, YAPISAL EġĠTLĠK MODELĠNĠN OLUġTURULMASI Araştırma modelinde kullanılacak olan ölçme modelinin nihai olarak seçilmesi ve geçerlilik güvenilirliğinin araştırılması sonrasında ölçme modelinde yer alan gizil yapılar arasındaki eşanlı ilişkilerin YEM analizi ile incelenmesi amaçlanmıştır. Araştırma hipotezleri, Kısım 4.1 ve 4.2 de verilen teorik açıklamalara ve Kısım 4.3 de yer alan daha önceki çalışmalarda araştırılan ilişkilere dayanılarak aşağıdaki şekilde oluşturulmuştur. AraĢtırma hipotezleri Kurumsal imajın firmaya duyulan güven üzerinde pozitif bir etkisi vardır. (KUR GUV) Şikâyet yönetiminin firmaya duyulan güven üzerinde pozitif bir etkisi vardır. (SKY GUV) Kurumsal imajın müşteri sadakati üzerinde pozitif bir etkisi vardır. (KUR SAD) 155
168 Fiyat algısının müşteri sadakati üzerinde pozitif bir etkisi vardır. (FYT SAD) Değiştirme maliyetinin müşteri sadakati üzerinde negatif bir etkisi vardır. (MAL SAD) Şikâyet yönetiminin müşteri sadakati üzerinde pozitif bir etkisi vardır. (SKY SAD) Müşteri memnuniyetinin müşteri sadakati üzerinde pozitif bir etkisi vardır. (MEM SAD) Beklentilerin müşteri memnuniyeti üzerinde pozitif bir etkisi vardır. (BEK MEM) Fiyat algısının müşteri memnuniyeti üzerinde pozitif bir etkisi vardır. (FYT MEM) Şikâyet yönetiminin müşteri memnuniyeti üzerinde pozitif bir etkisi vardır. (SKY MEM) Hizmet kalitesinin müşteri memnuniyeti üzerinde pozitif bir etkisi vardır. (HKAL MEM) Güvenin müşteri memnuniyeti üzerinde pozitif bir etkisi vardır. (GUV MEM) Beklentilerin hizmet kalitesi üzerinde pozitif bir etkisi vardır. (BEK HKAL) Şikâyet yönetiminin hizmet kalitesi üzerinde pozitif bir etkisi vardır. (SKY HKAL) YEM analizinde daha önceki kısımlarda belirtildiği üzere çok değişkenli normallik varsayımının sağlanamaması nedeniyle tahmin yöntemi olarak Dayanıklı EÇO yöntemi kullanılmıştır. Tahmin edilen yapısal eşitlik modeline ait standartlaştırılmış katsayılı yol diyagramı Şekil 4.3 ile verilmiştir. 156
169 ġekil 4.3 AraĢtırma Modeli için YEM in yol diyagramı Öncelikle önerilen modelin istatistiksel uygunluğu analiz edilecektir. YEM analizi sonucunda önerilen modelin değerine ilişkin p- değeri 0,05 ten küçük bulunmuş ve modele ilişkin elde edilen varyans- kovaryans matrisinin kitle varyanskovaryans matrisi ile uyumlu olduğu sonucuna ulaşılmıştır. değerinin serbestlik derecesine oranı ise verinin model ile uyumunun bir başka göstergesi olmaktadır. Ancak daha önceki kısımlarda belirtildiği üzere değerinin genel model uyumu için biçimsel bir test olarak kullanılması yönünde yapılan eleştiriler nedeniyle modele ait diğer bütün alternatif uyum ölçütleri Tablo 4.16 ile incelenmiştir. 157
170 Tablo Yapısal EĢitlik Modeli için Uyum Ölçütleri Uyum Ölçütü Referans Değeri Değer Uyum Model sd χ2 Minimum 506,51 χ2/sd. < 2 2 Kabul Edilebilir RMSEA < 0,05 0,037 Kabul RMSEA için %90 Güven Aralığı Minimum (0,033;0,042) Kabul P(RMSEA<0.05) > Kabul RMR Minimum 0,031 Kabul SRMR < 0,05 0,026 Kabul GFI > 0,90 0,95 Kabul AGFI > 0,90 0,93 Kabul PGFI Minimum 0,73 Kabul ECVI Minimum Doymuş model için ECVI > ECVI 0.9 Kabul AIC Minimum 650,51 - Doymuş model için AIC > AIC 654 Kabul CAIC Minimum 1068,60 - Doymuş model için CAIC > CAIC 2468,63 Kabul NFI > 0,90 0,99 Kabul NNFI > 0,90 0,99 Kabul PNFI Minimum 0,83 Kabul CFI > 0,90 0,99 Kabul IFI > 0,90 0,99 Kabul RFI > 0,90 0,99 Kabul CN > ,14 Kabul Kesin uyum ölçütlerinden, GFI, AGFI sırasıyla 0,95 ve 0,93 olarak elde edilmiş olup kabul edilebilir uyum için verilen eşik değeri 0,90 ın üzerindedir. RMR ve SRMR ölçütleri 0,031 ve 0,026 olup oldukça düşük değerlerdir. Artımsal uyum ölçütlerinden NFI, NNFI, IFI, RFI değerleri 0,99 olarak hesaplanmış olup mükemmel uyumu işaret etmektedirler. Merkezi olmayan ölçütler olarak anılan RMSEA değeri ve CFI ölçütü ise sırasıyla 0,037 ve 0,99 olarak tespit edilmiştir. Söz 158
171 konusu değerler oldukça iyi bir uyuma işaret etmektedir. Yalınlık uyum kriterleri incelendiğinde AIC, CAIC ve ECVI değerlerinin doymuş modellere oranla araştırma modeli için daha düşük değerler verdiği görülmektedir. Son olarak CN ölçütü ise gerekli örneklem büyüklüğünü 441,14 olarak hesaplamış olup çalışmanın örneklem büyüklüğü olan 732 birimin analiz için yeterli olduğu sonucuna ulaşılmıştır. Modelin istatistiksel olarak anlamlılığı ve tutarlılığının incelenmesinden sonra gizil değişkenler ile gözlenen değişkenler arasındaki ilişkiler ve gizil değişkenlerin kendi aralarındaki ilişkilerini ortaya koyan yapısal eşitlikler incelenecektir. Modelde gizil değişkenler ile gösterge değişkenler arasındaki ilişkilerin her biri istatistiksel olarak anlamlı bulunmuştur (p < 0,05). Modelde SKY, FYT, BEK, KUR, MAL değişkenleri dışsal gizil değişken olarak yer alırken GUV, SAD, HKAL ve MEM değişkenleri içsel gizil değişken olarak yer almaktadırlar. İçsel değişkenlere ait yapısal eşitlikler aşağıda verilmiştir. GUV = 0,84*KUR + 0,15*SKY R² = 0,90 (0,049) (0,04) 17,02 3,75 SAD = 0,59*MEM + 0,21*KUR + 0,05*FYT - 0,070*MAL + 0,13*SKY (0,056) (0,046) (0,037) (0,027) (0,042) 10,45 4,48 1,34-2,58 3,05 R² = 0,77 159
172 MEM = 0,48*GUV + 0,12*HKAL + 0,10*BEK + 0,22*FYT + 0,14*SKY (0,046) (0,054) (0,032) (0,033) (0,066) 10,34 2,22 3,04 6,49 2,11 R² = 0,76 HKAL = 0,15*BEK + 0,76*SKY R² = 0,67 (0,036) (0,040) 4,10 18,65 Söz konusu eşitlikler incelendiğinde ikinci denklemde yer alan FYT değişkeni hariç bütün değişkenlerin ilgili gizil değişkeni açıklamada istatistiksel olarak anlamlı (p < 0,05) ve katsayıların işaretlerinin teorik beklentilere uygun oldukları görülmektedir. Aynı zamanda belirginlik katsayılarının da kabul edilebilir düzeyde olduğu görülmektedir. Son olarak gizil değişkenler arasındaki yapısal ilişkiler incelendiğinde her bir değişken çifti için elde edilen standartlaştırılmış yol katsayıları ve ilgili t değerleri Tablo 4.17 ile verilmiştir. Tablo 4.17 ve yapısal eşitlikler incelendiğinde, KUR dışsal değişkeninin GUV içsel değişkeni ile arasında pozitif yönde anlamlı bir ilişki bulunmuş olup hesaplanan yol katsayısı 0,84 tür. Bu değer diğer değişkenlerin etkisi sabitken, KUR değişkenindeki bir birimlik artışın GUV değişkeninin ortalama değerinde 0,84 birimlik artışa neden olacağı şeklinde yorumlanır. SKY dışsal değişkeni ve GUV içsel değişkeni arasındaki yol katsayısı ise 0,15 olup, söz konusu değişkenler arasındaki ilişki istatistiksel olarak anlamlıdır. Bu katsayı diğer değişkenler sabitken, SKY deki bir birimlik artışın GUV değişkeninin ortalamasında 0,15 birimlik bir artışa neden olacağını ifade etmektedir. GUV değişkenini açıkladığı varsayılan KUR ve SKY değişkenlerinin katsayıları kullanılarak elde edilen yapısal eşitlik sonucunda çoklu belirginlik katsayısı 0,90 olarak hesaplanmıştır. KUR içsel değişkenindeki 160
173 değişimin yaklaşık 0,90 ının GUV ve SKY dışsal değişkenleri tarafından açıklandığı belirlenmiştir. Tablo AraĢtırma Modeli için Yapısal EĢitlik Modellemesi Sonuçları Yapısal EĢitlikler Katsayı t değeri KUR GUV 0,84 17,02 SKY GUV 0,15 3,75 KUR SAD 0,21 4,48 FYT SAD 0,05 1,34 MAL SAD -0,07-2,58 SKY SAD 0,13 3,05 MEM SAD 0,59 10,45 BEK MEM 0,10 3,04 FYT MEM 0,22 6,49 SKY MEM 0,14 2,11 HKAL MEM 0,12 2,22 GUV MEM 0,48 10,34 BEK HKAL 0,15 4,10 SKY HKAL 0,76 18,65 SAD içsel gizil değişkenini etkileyen KUR, MAL, SKY, MEM değişkenleri ile arasındaki ilişki istatistiksel olarak anlamlı bulunmuştur. KUR, SKY ve MEM değişkenleri için SAD değişkeni ile aralarında öngörülen pozitif yönlü ilişkinin yol katsayıları sırasıyla, 0,21, 0,13, 0,59 şeklindedir. Bu katsayılar sırasıyla, diğer değişkenlerdeki değişim sabitken, KUR değişkenindeki bir birimlik artışın SAD değişkeninin ortalama değerinde 0,21 birimlik bir artışa, SKY değişkenindeki bir birimlik artışın SAD değişkeninin ortalama değerinde 0,13 birimlik bir artışa ve MEM değişkenindeki bir birimlik artışın SAD değişkeninin ortalama değerinde 0,59 161
174 birimlik bir artışa neden olacağı şeklinde yorumlanır. MAL değişkeni ile SAD değişkeni arasında negatif yönlü bir ilişki öngörülmüş olup elde edilen yol katsayısı - 0,07 dir. Söz konusu katsayı MAL değişkeninde bir birimlik artışın SAD değişkeninin ortalama değerinde 0,07 birimlik bir azalışa neden olacağını göstermektedir. FYT değişkeni ile SAD değişkeni arasında öngörülen pozitif yönlü ilişki istatistiksel olarak anlamsızdır (p > 0,05). KUR, MAL, SKY, MEM, FYT değişkenlerinin katsayıları kullanılarak elde edilen yapısal eşitlik sonucunda çoklu belirginlik katsayısı 0,77 olarak hesaplanmıştır. SAD içsel değişkenindeki değişimin yaklaşık 0,77 sinin KUR, MAL, SKY, MEM, FYT değişkenleri tarafından açıklandığı belirlenmiştir. BEK dışsal gizil değişkeni ile MEM içsel gizil değişkeni arasında pozitif yönde istatistiksel olarak anlamlı bir ilişki bulunmuş olup hesaplanan yol katsayısı 0,10 dur. Bu değer diğer değişkenler sabitken BEK teki bir birimlik artışın MEM değişkeninin ortalama değerinde 0,10 birimlik bir artışa neden olacağını ifade etmektedir. SKY dışsal değişkeni ile MEM içsel gizil değişkeni arasında pozitif yönde istatistiksel olarak anlamlı bir ilişki bulunmuş olup hesaplanan yol katsayısı 0,14 dür. Bu değer diğer değişkenler sabitken SKY deki bir birimlik artışın MEM değişkeninin ortalama değerinde 0,14 birimlik bir artışa neden olacağını ifade etmektedir. FYT ile MEM arasında pozitif yönde istatistiksel olarak anlamlı bir ilişki olup yol katsayısı 0,22 dir. Bu katsayı diğer değişkenler sabitken FYT deki bir birimlik artışın MEM değişkeninin ortalama değerinde 0,22 birimlik bir artışa neden olacağını ifade etmektedir. HKAL dışsal değişkeni ile MEM içsel değişkeni arasında pozitif yönde istatistiksel olarak anlamlı bir ilişki bulunmuş olup yol katsayısı 0,12 dir. Diğer değişkenler sabitken HKAL deki bir birimlik artışın MEM değişkeninin ortalama değerinde 0,12 birimlik bir artışa neden olacağını ifade etmektedir. GUV değişkeni ile MEM değişkeni arasında pozitif yönlü istatistiksel olarak anlamlı bir ilişki bulunmuş olup yol katsayısı 0,48 dir. Diğer değişkenler sabitken GUV deki bir birimlik artışın MEM değişkeninin ortalama değerinde 0,48 birimlik bir artışa neden olacağını ifade etmektedir. GUV değişkeni MEM içsel değişkeni üzerinde en büyük etkiye sahip olan değişkendir. BEK, SKY, FYT, HKAL, GUV değişkenlerinin katsayıları kullanılarak elde edilen yapısal eşitlik 162
175 sonucunda çoklu belirginlik katsayısı 0,76 olarak hesaplanmıştır. MEM içsel değişkenindeki değişimin yaklaşık 0,76 sının GUV, HKAL, BEK, FYT, SKY değişkenleri tarafından açıklandığı belirlenmiştir. BEK dışsal gizil değişkeni ile HKAL içsel gizil değişkeni arasında pozitif yönde istatistiksel olarak anlamlı bir ilişki bulunmuş olup yol katsayısı 0,15 dir. Bu değer diğer değişkenler sabitken BEK teki bir birimlik artışın HKAL değişkeninin ortalama değerinde 0,15 birimlik bir artışa neden olacağını ifade etmektedir. SKY dışsal gizil değişkeni ile HKAL içsel gizil değişkeni arasında pozitif yönde istatistiksel olarak anlamlı bir ilişki bulunmuş olup yol katsayısı 0,76 dır. Bu değer diğer değişkenler sabitken SKY deki bir birimlik artışın HKAL değişkeninin ortalama değerinde 0,76 birimlik bir artışa neden olacağını ifade etmektedir. BEK, SKY değişkenlerinin katsayıları kullanılarak elde edilen yapısal eşitlik sonucunda çoklu belirginlik katsayısı 0,67 olarak hesaplanmıştır. HKAL içsel değişkenindeki değişimin yaklaşık 0,67 sinin BEK ve SKY değişkenleri tarafından açıklandığı belirlenmiştir. Sonuç olarak Şekil 4.4 ile topluca verilen hipotezlerin yukarıda istatistiksel olarak geçerliliği ortaya konulmuş yapısal eşitlik modeli ile değerlendirilmesi sonucunda elde edilen sonuçlar Tablo 4.18 yardımıyla özetlenmiştir. ġekil 4.4 AraĢtırma hipotezlerine iliģkin diyagram 163
3. TAHMİN En Küçük Kareler (EKK) Yöntemi 1
 3. TAHMİN 3.1. En Küçük Kareler (EKK) Yöntemi 1 En Küçük Kareler (EKK) yöntemi, regresyon çözümlemesinde en yaygın olarak kullanılan, daha sonra ele alınacak bazı varsayımlar altında çok aranan istatistiki
3. TAHMİN 3.1. En Küçük Kareler (EKK) Yöntemi 1 En Küçük Kareler (EKK) yöntemi, regresyon çözümlemesinde en yaygın olarak kullanılan, daha sonra ele alınacak bazı varsayımlar altında çok aranan istatistiki
T.C. SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
 T.C. SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ BAYESCİ DOĞRUSAL OLMAYAN YAPISAL EŞİTLİK MODELİ İlkay ALTINDAĞ DOKTORA TEZİ İstatistik Anabilim Dalını Ağustos-05 KONYA Her Hakkı Saklıdır TEZ KABUL VE
T.C. SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ BAYESCİ DOĞRUSAL OLMAYAN YAPISAL EŞİTLİK MODELİ İlkay ALTINDAĞ DOKTORA TEZİ İstatistik Anabilim Dalını Ağustos-05 KONYA Her Hakkı Saklıdır TEZ KABUL VE
İÇİNDEKİLER. BÖLÜM 1 Değişkenler ve Grafikler 1. BÖLÜM 2 Frekans Dağılımları 37
 İÇİNDEKİLER BÖLÜM 1 Değişkenler ve Grafikler 1 İstatistik 1 Yığın ve Örnek; Tümevarımcı ve Betimleyici İstatistik 1 Değişkenler: Kesikli ve Sürekli 1 Verilerin Yuvarlanması Bilimsel Gösterim Anlamlı Rakamlar
İÇİNDEKİLER BÖLÜM 1 Değişkenler ve Grafikler 1 İstatistik 1 Yığın ve Örnek; Tümevarımcı ve Betimleyici İstatistik 1 Değişkenler: Kesikli ve Sürekli 1 Verilerin Yuvarlanması Bilimsel Gösterim Anlamlı Rakamlar
Korelasyon, Korelasyon Türleri ve Regresyon
 Korelasyon, Korelasyon Türleri ve Regresyon İçerik Korelasyon Korelasyon Türleri Korelasyon Katsayısı Regresyon KORELASYON Korelasyon iki ya da daha fazla değişken arasındaki doğrusal ilişkiyi gösterir.
Korelasyon, Korelasyon Türleri ve Regresyon İçerik Korelasyon Korelasyon Türleri Korelasyon Katsayısı Regresyon KORELASYON Korelasyon iki ya da daha fazla değişken arasındaki doğrusal ilişkiyi gösterir.
İÇİNDEKİLER ÖN SÖZ...
 İÇİNDEKİLER ÖN SÖZ... v GİRİŞ... 1 1. İSTATİSTİK İN TARİHÇESİ... 1 2. İSTATİSTİK NEDİR?... 3 3. SAYISAL BİLGİDEN ANLAM ÇIKARILMASI... 4 4. BELİRSİZLİĞİN ELE ALINMASI... 4 5. ÖRNEKLEME... 5 6. İLİŞKİLERİN
İÇİNDEKİLER ÖN SÖZ... v GİRİŞ... 1 1. İSTATİSTİK İN TARİHÇESİ... 1 2. İSTATİSTİK NEDİR?... 3 3. SAYISAL BİLGİDEN ANLAM ÇIKARILMASI... 4 4. BELİRSİZLİĞİN ELE ALINMASI... 4 5. ÖRNEKLEME... 5 6. İLİŞKİLERİN
İstatistik ve Olasılık
 İstatistik ve Olasılık KORELASYON ve REGRESYON ANALİZİ Doç. Dr. İrfan KAYMAZ Tanım Bir değişkenin değerinin diğer değişkendeki veya değişkenlerdeki değişimlere bağlı olarak nasıl etkilendiğinin istatistiksel
İstatistik ve Olasılık KORELASYON ve REGRESYON ANALİZİ Doç. Dr. İrfan KAYMAZ Tanım Bir değişkenin değerinin diğer değişkendeki veya değişkenlerdeki değişimlere bağlı olarak nasıl etkilendiğinin istatistiksel
AMOS (Analysis of Moment Structures) ve Yapısal Eşitlik Modeli
 AMOS (Analysis of Moment Structures) ve Yapısal Eşitlik Modeli Veri seti bulunur Değişkenler sürüklenerek kutucuklara yerleştirilir Hata terimi eklenir Mouse sağ tıklanır ve hata terimi tanımlanır.
AMOS (Analysis of Moment Structures) ve Yapısal Eşitlik Modeli Veri seti bulunur Değişkenler sürüklenerek kutucuklara yerleştirilir Hata terimi eklenir Mouse sağ tıklanır ve hata terimi tanımlanır.
Örnek. Aşağıdaki veri setlerindeki X ve Y veri çiftlerini kullanarak herbir durumda X=1,5 için Y nin hangi değerleri alacağını hesaplayınız.
 Örnek Aşağıdaki veri setlerindeki X ve Y veri çiftlerini kullanarak herbir durumda X=1,5 için Y nin hangi değerleri alacağını hesaplayınız. i. ii. X 1 2 3 4 1 2 3 4 Y 2 3 4 5 4 3 2 1 Örnek Aşağıdaki veri
Örnek Aşağıdaki veri setlerindeki X ve Y veri çiftlerini kullanarak herbir durumda X=1,5 için Y nin hangi değerleri alacağını hesaplayınız. i. ii. X 1 2 3 4 1 2 3 4 Y 2 3 4 5 4 3 2 1 Örnek Aşağıdaki veri
İçindekiler vii Yazarların Ön Sözü xiii Çevirenin Ön Sözü xiv Teşekkürler xvi Semboller Listesi xvii. Ölçme, İstatistik ve Araştırma...
 İçindekiler İçindekiler vii Yazarların Ön Sözü xiii Çevirenin Ön Sözü xiv Teşekkürler xvi Semboller Listesi xvii BÖLÜM 1 Ölçme, İstatistik ve Araştırma...1 Ölçme Nedir?... 3 Ölçme Süreci... 3 Değişkenler
İçindekiler İçindekiler vii Yazarların Ön Sözü xiii Çevirenin Ön Sözü xiv Teşekkürler xvi Semboller Listesi xvii BÖLÜM 1 Ölçme, İstatistik ve Araştırma...1 Ölçme Nedir?... 3 Ölçme Süreci... 3 Değişkenler
Matris Cebiriyle Çoklu Regresyon Modeli
 Matris Cebiriyle Çoklu Regresyon Modeli Hüseyin Taştan Mart 00 Klasik Regresyon Modeli k açıklayıcı değişkenden oluşan regresyon modelini her gözlem i için aşağıdaki gibi yazabiliriz: y i β + β x i + β
Matris Cebiriyle Çoklu Regresyon Modeli Hüseyin Taştan Mart 00 Klasik Regresyon Modeli k açıklayıcı değişkenden oluşan regresyon modelini her gözlem i için aşağıdaki gibi yazabiliriz: y i β + β x i + β
Doç. Dr. Dilek ALTAŞ İSTATİSTİKSEL ANALİZ
 I Doç. Dr. Dilek ALTAŞ İSTATİSTİKSEL ANALİZ II Yayın No : 2845 Teknik Dizisi : 158 1. Baskı Şubat 2013 İSTANBUL ISBN 978-605 - 377 868-4 Copyright Bu kitabın bu basısı için Türkiye deki yayın hakları BETA
I Doç. Dr. Dilek ALTAŞ İSTATİSTİKSEL ANALİZ II Yayın No : 2845 Teknik Dizisi : 158 1. Baskı Şubat 2013 İSTANBUL ISBN 978-605 - 377 868-4 Copyright Bu kitabın bu basısı için Türkiye deki yayın hakları BETA
Akdeniz Üniversitesi
 F. Ders Tanıtım Formu Dersin Adı Öğretim Dili EKONOMETRİ I Türkçe Dersin Verildiği Düzey Ön Lisans ( ) Lisans (x ) Yüksek Lisans( ) Doktora( ) Eğitim Öğretim Sistemi Örgün Öğretim (x ) İkinci Örgün Öğretim
F. Ders Tanıtım Formu Dersin Adı Öğretim Dili EKONOMETRİ I Türkçe Dersin Verildiği Düzey Ön Lisans ( ) Lisans (x ) Yüksek Lisans( ) Doktora( ) Eğitim Öğretim Sistemi Örgün Öğretim (x ) İkinci Örgün Öğretim
İÇİNDEKİLER BİRİNCİ KISIM: TASARIM PAZARLAMA ARAŞTIRMASINA GİRİŞ
 İÇİNDEKİLER ÖNSÖZ... v TEŞEKKÜR... vi İKİNCİ BASKIYA ÖNSÖZ VE TEŞEKKÜR... vii İÇİNDEKİLER... ix ŞEKİLLER LİSTESİ... xviii TABLOLAR LİSTESİ... xx BİRİNCİ KISIM: TASARIM BİRİNCI BÖLÜM PAZARLAMA ARAŞTIRMASINA
İÇİNDEKİLER ÖNSÖZ... v TEŞEKKÜR... vi İKİNCİ BASKIYA ÖNSÖZ VE TEŞEKKÜR... vii İÇİNDEKİLER... ix ŞEKİLLER LİSTESİ... xviii TABLOLAR LİSTESİ... xx BİRİNCİ KISIM: TASARIM BİRİNCI BÖLÜM PAZARLAMA ARAŞTIRMASINA
HEKĠMLERDE ÖRGÜTSEL SESSĠZLĠĞĠN YAPISAL EġĠTLĠK MODELĠ ĠLE ĠNCELENMESĠ
 T.C. TRAKYA ÜNİVERSİTESİ SOSYAL BİLİMLER ENSTİTÜSÜ İŞLETME ANABİLİM DALI DOKTORA TEZİ HEKĠMLERDE ÖRGÜTSEL SESSĠZLĠĞĠN YAPISAL EġĠTLĠK MODELĠ ĠLE ĠNCELENMESĠ TÜLAY DEMİRALAY 1098225203 DANIŞMAN DOÇ.DR.
T.C. TRAKYA ÜNİVERSİTESİ SOSYAL BİLİMLER ENSTİTÜSÜ İŞLETME ANABİLİM DALI DOKTORA TEZİ HEKĠMLERDE ÖRGÜTSEL SESSĠZLĠĞĠN YAPISAL EġĠTLĠK MODELĠ ĠLE ĠNCELENMESĠ TÜLAY DEMİRALAY 1098225203 DANIŞMAN DOÇ.DR.
FARKLI VERİ YAPISI VE ÖRNEKLEM BÜYÜKLÜKLERİNDE YAPISAL EŞİTLİK MODELLERİNİN GEÇERLİĞİ VE GÜVENİRLİĞİNİN DEĞERLENDİRİLMESİ
 T.C. ESKİŞEHİR OSMANGAZİ ÜNİVERSİTESİ SAĞLIK BİLİMLERİ ENSTİTÜSÜ BİYOİSTATİSTİK ANABİLİM DALI FARKLI VERİ YAPISI VE ÖRNEKLEM BÜYÜKLÜKLERİNDE YAPISAL EŞİTLİK MODELLERİNİN GEÇERLİĞİ VE GÜVENİRLİĞİNİN DEĞERLENDİRİLMESİ
T.C. ESKİŞEHİR OSMANGAZİ ÜNİVERSİTESİ SAĞLIK BİLİMLERİ ENSTİTÜSÜ BİYOİSTATİSTİK ANABİLİM DALI FARKLI VERİ YAPISI VE ÖRNEKLEM BÜYÜKLÜKLERİNDE YAPISAL EŞİTLİK MODELLERİNİN GEÇERLİĞİ VE GÜVENİRLİĞİNİN DEĞERLENDİRİLMESİ
Ekonometri I VARSAYIMLARI
 Ekonometri I ÇOK DEĞİŞKENLİ REGRESYON MODELİNİN VARSAYIMLARI Hüseyin Taştan Temmuz 23, 2006 İçindekiler 1 Varsayım MLR.1: Parametrelerde Doğrusallık 1 2 Varsayım MLR.2: Rassal Örnekleme 1 3 Varsayım MLR.3:
Ekonometri I ÇOK DEĞİŞKENLİ REGRESYON MODELİNİN VARSAYIMLARI Hüseyin Taştan Temmuz 23, 2006 İçindekiler 1 Varsayım MLR.1: Parametrelerde Doğrusallık 1 2 Varsayım MLR.2: Rassal Örnekleme 1 3 Varsayım MLR.3:
2. REGRESYON ANALİZİNİN TEMEL KAVRAMLARI Tanım
 2. REGRESYON ANALİZİNİN TEMEL KAVRAMLARI 2.1. Tanım Regresyon analizi, bir değişkenin başka bir veya daha fazla değişkene olan bağımlılığını inceler. Amaç, bağımlı değişkenin kitle ortalamasını, açıklayıcı
2. REGRESYON ANALİZİNİN TEMEL KAVRAMLARI 2.1. Tanım Regresyon analizi, bir değişkenin başka bir veya daha fazla değişkene olan bağımlılığını inceler. Amaç, bağımlı değişkenin kitle ortalamasını, açıklayıcı
DAVRANIŞ BİLİMLERİNE GİRİŞ
 DAVRANIŞ BİLİMLERİNE GİRİŞ DAVRANIŞIN TANIMI Davranış Kavramı, öncelikle insan veya hayvanın tek tek veya toplu olarak gösterdiği faaliyetler olarak tanımlanabilir. En genel anlamda davranış, insanların
DAVRANIŞ BİLİMLERİNE GİRİŞ DAVRANIŞIN TANIMI Davranış Kavramı, öncelikle insan veya hayvanın tek tek veya toplu olarak gösterdiği faaliyetler olarak tanımlanabilir. En genel anlamda davranış, insanların
DİNAMİK PANEL VERİ MODELLERİ. FYT Panel Veri Ekonometrisi 1
 DİNAMİK PANEL VERİ MODELLERİ FYT Panel Veri Ekonometrisi 1 Dinamik panel veri modeli (tek gecikme için) aşağıdaki gibi gösterilebilir; y it y it 1 x v it ' it i Gecikmeli bağımlı değişkenden başka açıklayıcı
DİNAMİK PANEL VERİ MODELLERİ FYT Panel Veri Ekonometrisi 1 Dinamik panel veri modeli (tek gecikme için) aşağıdaki gibi gösterilebilir; y it y it 1 x v it ' it i Gecikmeli bağımlı değişkenden başka açıklayıcı
Akademisyenlerin İnternet Bankacılığı Kullanımını Etkileyen Faktörlerin Yapısal Eşitlik Modeli İle İncelenmesi
 Akademisyenlerin İnternet Bankacılığı Kullanımını Etkileyen Faktörlerin Yapısal Eşitlik Modeli İle İncelenmesi Çiğdem TATAR *, Özlem EGE ORUÇ Dokuz Eylül Üniversitesi, Fen Fakültesi İstatistik Bölümü,
Akademisyenlerin İnternet Bankacılığı Kullanımını Etkileyen Faktörlerin Yapısal Eşitlik Modeli İle İncelenmesi Çiğdem TATAR *, Özlem EGE ORUÇ Dokuz Eylül Üniversitesi, Fen Fakültesi İstatistik Bölümü,
1 PAZARLAMA ARAŞTIRMASI
 İÇİNDEKİLER ÖNSÖZ III Bölüm 1 PAZARLAMA ARAŞTIRMASI 11 1.1. Pazarlama Araştırması Kavramı ve Kapsamı 12 1.2. Pazarlama Araştırmasının Tarihçesi 14 1.3. Pazarlama Araştırması Pazarlama Bilgi Sistemi ve
İÇİNDEKİLER ÖNSÖZ III Bölüm 1 PAZARLAMA ARAŞTIRMASI 11 1.1. Pazarlama Araştırması Kavramı ve Kapsamı 12 1.2. Pazarlama Araştırmasının Tarihçesi 14 1.3. Pazarlama Araştırması Pazarlama Bilgi Sistemi ve
YAPISAL EġĠTLĠK MODELLERĠ VE KULLANILAN UYUM ĠYĠLĠĞĠ ĠNDEKSLERĠNĠN KARġILAġTIRILMASI. Esra Tuğçe ÇEREZCĠ DOKTORA TEZĠ ĠSTATĠSTĠK
 YAPISAL EġĠTLĠK MODELLERĠ VE KULLANILAN UYUM ĠYĠLĠĞĠ ĠNDEKSLERĠNĠN KARġILAġTIRILMASI Esra Tuğçe ÇEREZCĠ DOKTORA TEZĠ ĠSTATĠSTĠK GAZĠ ÜNĠVERSĠTESĠ FEN BĠLĠMLERĠ ENSTĠTÜSÜ TEMMUZ 00 ANKARA ii iii YAPISAL
YAPISAL EġĠTLĠK MODELLERĠ VE KULLANILAN UYUM ĠYĠLĠĞĠ ĠNDEKSLERĠNĠN KARġILAġTIRILMASI Esra Tuğçe ÇEREZCĠ DOKTORA TEZĠ ĠSTATĠSTĠK GAZĠ ÜNĠVERSĠTESĠ FEN BĠLĠMLERĠ ENSTĠTÜSÜ TEMMUZ 00 ANKARA ii iii YAPISAL
TEZSİZ YÜKSEK LİSANS PROJE ONAY FORMU. Eğitim Bilimleri Anabilim Dalı Eğitim Yönetimi, Denetimi, Planlaması ve Ekonomisi
 TEZSİZ YÜKSEK LİSANS PROJE ONAY FORMU Eğitim Bilimleri Anabilim Dalı Eğitim Yönetimi, Denetimi, Planlaması ve Ekonomisi Bilim Dalı öğrencisi Feyzi ÖZMEN tarafından hazırlanan Aday Öğretmenlerin Öz Yeterlilikleri
TEZSİZ YÜKSEK LİSANS PROJE ONAY FORMU Eğitim Bilimleri Anabilim Dalı Eğitim Yönetimi, Denetimi, Planlaması ve Ekonomisi Bilim Dalı öğrencisi Feyzi ÖZMEN tarafından hazırlanan Aday Öğretmenlerin Öz Yeterlilikleri
İçindekiler. Pazarlama Araştırmalarının Önemi
 İçindekiler Birinci Bölüm Pazarlama Araştırmalarının Önemi 1.1. PAZARLAMA ARAŞTIRMALARININ TANIMI VE ÖNEMİ... 1 1.2. PAZARLAMA ARAŞTIRMASI İŞLEVİNİN İŞLETME ORGANİZASYONU İÇİNDEKİ YERİ... 5 1.3. PAZARLAMA
İçindekiler Birinci Bölüm Pazarlama Araştırmalarının Önemi 1.1. PAZARLAMA ARAŞTIRMALARININ TANIMI VE ÖNEMİ... 1 1.2. PAZARLAMA ARAŞTIRMASI İŞLEVİNİN İŞLETME ORGANİZASYONU İÇİNDEKİ YERİ... 5 1.3. PAZARLAMA
BÖLÜM 1 ÖLÇME VE DEĞERLENDİRMEDE TEMEL KAVRAMLAR
 İÇİNDEKİLER BÖLÜM 1 ÖLÇME VE DEĞERLENDİRMEDE TEMEL KAVRAMLAR I. Öğretimde Ölçme ve Değerlendirmenin Gerekliliği... 2 II. Ölçme Kavramı... 3 1. Tanımı ve Unsurları... 3 2. Aşamaları... 3 2.1. Ölçülecek
İÇİNDEKİLER BÖLÜM 1 ÖLÇME VE DEĞERLENDİRMEDE TEMEL KAVRAMLAR I. Öğretimde Ölçme ve Değerlendirmenin Gerekliliği... 2 II. Ölçme Kavramı... 3 1. Tanımı ve Unsurları... 3 2. Aşamaları... 3 2.1. Ölçülecek
Doğrulayıcı Faktör Analizinde Örneklem Hacmi, Tahmin Yöntemleri ve Normalliğin Uyum Ölçütlerine Etkisi. Murat Doğan YÜKSEK LİSANS TEZİ
 Doğrulayıcı Faktör Analizinde Örneklem Hacmi, Tahmin Yöntemleri ve Normalliğin Uyum Ölçütlerine Etkisi Murat Doğan YÜKSEK LİSANS TEZİ İstatistik Anabilim Dalı Haziran 2013 Influence of Sample Size, Estimation
Doğrulayıcı Faktör Analizinde Örneklem Hacmi, Tahmin Yöntemleri ve Normalliğin Uyum Ölçütlerine Etkisi Murat Doğan YÜKSEK LİSANS TEZİ İstatistik Anabilim Dalı Haziran 2013 Influence of Sample Size, Estimation
GİRİŞ. Bilimsel Araştırma: Bilimsel bilgi elde etme süreci olarak tanımlanabilir.
 VERİ ANALİZİ GİRİŞ Bilimsel Araştırma: Bilimsel bilgi elde etme süreci olarak tanımlanabilir. Bilimsel Bilgi: Kaynağı ve elde edilme süreçleri belli olan bilgidir. Sosyal İlişkiler Görgül Bulgular İşlevsel
VERİ ANALİZİ GİRİŞ Bilimsel Araştırma: Bilimsel bilgi elde etme süreci olarak tanımlanabilir. Bilimsel Bilgi: Kaynağı ve elde edilme süreçleri belli olan bilgidir. Sosyal İlişkiler Görgül Bulgular İşlevsel
YAPISAL EġĠTLĠK MODELLEMESĠNDE ÇOK DEĞĠġKENLĠ NORMALLĠK VARSAYIMI ALTINDA BĠR UYGULAMA
 ISSN:306-3 e-journal of New World Sciences Academy 0, Volume: 6, Number: 4, Article Number: 3A004 H. Eray Çelik Sinan Saraçlı PHYSICAL SCIENCES Veysel Yılmaz 3 Received: March 0 Yuzuncu Yıl University
ISSN:306-3 e-journal of New World Sciences Academy 0, Volume: 6, Number: 4, Article Number: 3A004 H. Eray Çelik Sinan Saraçlı PHYSICAL SCIENCES Veysel Yılmaz 3 Received: March 0 Yuzuncu Yıl University
Yatırım Analizi ve Portföy Yönetimi 5. Hafta
 Yatırım Analizi ve Portföy Yönetimi 5. Hafta Dr. Mevlüt CAMGÖZ 1 Dr. Mevlüt Camgöz İçerik Tek Endeks / Pazar Modeli Sistematik Risk Sistematik Olmayan Risk Sermaye Varlıklarını Fiyatlandırma Modeli (SVFM)
Yatırım Analizi ve Portföy Yönetimi 5. Hafta Dr. Mevlüt CAMGÖZ 1 Dr. Mevlüt Camgöz İçerik Tek Endeks / Pazar Modeli Sistematik Risk Sistematik Olmayan Risk Sermaye Varlıklarını Fiyatlandırma Modeli (SVFM)
Örneklemden elde edilen parametreler üzerinden kitle parametreleri tahmin edilmek istenmektedir.
 ÇIKARSAMALI İSTATİSTİKLER Çıkarsamalı istatistikler, örneklemden elde edilen değerler üzerinde kitleyi tanımlamak için uygulanan istatistiksel yöntemlerdir. Çıkarsamalı istatistikler; Tahmin Hipotez Testleri
ÇIKARSAMALI İSTATİSTİKLER Çıkarsamalı istatistikler, örneklemden elde edilen değerler üzerinde kitleyi tanımlamak için uygulanan istatistiksel yöntemlerdir. Çıkarsamalı istatistikler; Tahmin Hipotez Testleri
DOĞRUSAL ZAMAN SERİSİ MODELLERİ. Durağan ARIMA Modelleri: Otoregresiv Modeller AR(p) Süreci
 DOĞRUSAL ZAMAN SERİSİ MODELLERİ Durağan ARIMA Modelleri: Otoregresiv Modeller AR(p) Süreci Tek Değişkenli Zaman Serisi Modelleri Ekonomik verilerin analizi ile ekonomik değişkenlerin gelecekte alabilecekleri
DOĞRUSAL ZAMAN SERİSİ MODELLERİ Durağan ARIMA Modelleri: Otoregresiv Modeller AR(p) Süreci Tek Değişkenli Zaman Serisi Modelleri Ekonomik verilerin analizi ile ekonomik değişkenlerin gelecekte alabilecekleri
Çocuklara Yabancı Dil Öğretiminin Duyuşsal Hedefleri Ölçeği
 Çocuklara Yabancı Dil Öğretiminin Duyuşsal Hedefleri Ölçeği Şad, S. N., & Gürbüztürk, O. (2015). The affective objectives in early foreign language teaching: A scale development study. International Journal
Çocuklara Yabancı Dil Öğretiminin Duyuşsal Hedefleri Ölçeği Şad, S. N., & Gürbüztürk, O. (2015). The affective objectives in early foreign language teaching: A scale development study. International Journal
Yrd. Doç. Dr. Mehmet Güçlü
 Dersin Adı DERS ÖĞRETİM PLANI Ekonometri I Dersin Kodu ECO 301 Dersin Türü (Zorunlu, Seçmeli) Dersin Seviyesi (Ön Lisans, Lisans, Yüksek Lisans, Doktora) Dersin AKTS Kredisi 6 Haftalık Ders Saati 4 Haftalık
Dersin Adı DERS ÖĞRETİM PLANI Ekonometri I Dersin Kodu ECO 301 Dersin Türü (Zorunlu, Seçmeli) Dersin Seviyesi (Ön Lisans, Lisans, Yüksek Lisans, Doktora) Dersin AKTS Kredisi 6 Haftalık Ders Saati 4 Haftalık
İLERİ BİYOİSTATİSTİK KURSU
 1.GÜN (14 Eylül 2017) 08:30-09:00 Kurs Kayıt Açılış Konuşması 09:00-10:00 Tanışma -Katılımcıların Temel İstatistik Bilgisinin Değerlendirilmesio Çok Değişkenli İstatistiksel Yöntemlere Giriş o Basit Doğrusal
1.GÜN (14 Eylül 2017) 08:30-09:00 Kurs Kayıt Açılış Konuşması 09:00-10:00 Tanışma -Katılımcıların Temel İstatistik Bilgisinin Değerlendirilmesio Çok Değişkenli İstatistiksel Yöntemlere Giriş o Basit Doğrusal
Yatırım Analizi ve Portföy Yönetimi 6. Hafta
 Yatırım Analizi ve Portföy Yönetimi 6. Hafta Dr. Mevlüt CAMGÖZ 1 Dr. Mevlüt CAMGÖZ İçerik Karakteristik Doğru ve Beta Katsayısı Karakteristik Doğrunun Tahmini Beta Katsayısının Hesaplanması Agresif ve
Yatırım Analizi ve Portföy Yönetimi 6. Hafta Dr. Mevlüt CAMGÖZ 1 Dr. Mevlüt CAMGÖZ İçerik Karakteristik Doğru ve Beta Katsayısı Karakteristik Doğrunun Tahmini Beta Katsayısının Hesaplanması Agresif ve
BANKACILIK SEKTÖRÜNDE MÜŞTERİ MEMNUNİYETİ ve BANKAYA BAĞLILIK ARASINDANKİ İLİŞKİNİN YAPISAL EŞİTLİK MODELLERİYLE ARAŞTIRILMASI
 BANKACILIK SEKTÖRÜNDE MÜŞTERİ MEMNUNİYETİ ve BANKAYA BAĞLILIK ARASINDANKİ İLİŞKİNİN YAPISAL EŞİTLİK MODELLERİYLE ARAŞTIRILMASI Veysel Yılmaz H.Eray Çelik Osmangazi Üniversitesi, Fen-Edebiyat Fakültesi,
BANKACILIK SEKTÖRÜNDE MÜŞTERİ MEMNUNİYETİ ve BANKAYA BAĞLILIK ARASINDANKİ İLİŞKİNİN YAPISAL EŞİTLİK MODELLERİYLE ARAŞTIRILMASI Veysel Yılmaz H.Eray Çelik Osmangazi Üniversitesi, Fen-Edebiyat Fakültesi,
BÖLÜM 13 HİPOTEZ TESTİ
 1 BÖLÜM 13 HİPOTEZ TESTİ Bilimsel yöntem aşamalarıyla tanımlanmış sistematik bir bilgi üretme biçimidir. Bilimsel yöntemin aşamaları aşağıdaki gibi sıralanabilmektedir (Karasar, 2012): 1. Bir problemin
1 BÖLÜM 13 HİPOTEZ TESTİ Bilimsel yöntem aşamalarıyla tanımlanmış sistematik bir bilgi üretme biçimidir. Bilimsel yöntemin aşamaları aşağıdaki gibi sıralanabilmektedir (Karasar, 2012): 1. Bir problemin
QUANTILE REGRESYON * Quantile Regression
 QUANTILE REGRESYON * Quantile Regression Fikriye KURTOĞLU İstatistik Anabilim Dalı Olcay ARSLAN İstatistik Anabilim Dalı ÖZET Bu çalışmada, Lineer Regresyon analizinde kullanılan en küçük kareler yöntemine
QUANTILE REGRESYON * Quantile Regression Fikriye KURTOĞLU İstatistik Anabilim Dalı Olcay ARSLAN İstatistik Anabilim Dalı ÖZET Bu çalışmada, Lineer Regresyon analizinde kullanılan en küçük kareler yöntemine
3 KESİKLİ RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI
 ÖNSÖZ İÇİNDEKİLER III Bölüm 1 İSTATİSTİK ve SAYISAL BİLGİ 11 1.1 İstatistik ve Önemi 12 1.2 İstatistikte Temel Kavramlar 14 1.3 İstatistiğin Amacı 15 1.4 Veri Türleri 15 1.5 Veri Ölçüm Düzeyleri 16 1.6
ÖNSÖZ İÇİNDEKİLER III Bölüm 1 İSTATİSTİK ve SAYISAL BİLGİ 11 1.1 İstatistik ve Önemi 12 1.2 İstatistikte Temel Kavramlar 14 1.3 İstatistiğin Amacı 15 1.4 Veri Türleri 15 1.5 Veri Ölçüm Düzeyleri 16 1.6
Akademisyenlerin İnternet Bankacılığı Kullanımını Etkileyen Faktörlerin Yapısal Eşitlik Modeli İle İncelenmesi
 Akademisyenlerin İnternet Bankacılığı Kullanımını Etkileyen Faktörlerin Yapısal Eşitlik Modeli İle İncelenmesi Çiğdem TATAR1*, Özlem EGE ORUÇ1 Dokuz Eylül Üniversitesi, Fen Fakültesi İstatistik Bölümü,
Akademisyenlerin İnternet Bankacılığı Kullanımını Etkileyen Faktörlerin Yapısal Eşitlik Modeli İle İncelenmesi Çiğdem TATAR1*, Özlem EGE ORUÇ1 Dokuz Eylül Üniversitesi, Fen Fakültesi İstatistik Bölümü,
MEÜ. SAĞLIK BĠLĠMLERĠ ENSTĠTÜSÜ DERS TANIMI FORMU
 MEÜ. SAĞLIK BĠLĠMLERĠ ENSTĠTÜSÜ DERS TANIMI FORMU Dersin Adı-Kodu: BİS 601 Örnek Genişliği ve Güç Programın Adı: Biyoistatistik Dersin düzeyi Doktora Ders saatleri ve Teori Uyg. Lab. Proje/Alan Çalışması
MEÜ. SAĞLIK BĠLĠMLERĠ ENSTĠTÜSÜ DERS TANIMI FORMU Dersin Adı-Kodu: BİS 601 Örnek Genişliği ve Güç Programın Adı: Biyoistatistik Dersin düzeyi Doktora Ders saatleri ve Teori Uyg. Lab. Proje/Alan Çalışması
HANGİ TÜR ARAŞTIRMALARDA PATH ANALİZİ KULLANILMALIDIR? IX Ulusal Biyoistatistik Kongresi 5-9 Eylül 2006 Zonguldak
 HANGİ TÜR ARAŞTIRMALARDA PATH ANALİZİ KULLANILMALIDIR? * M.Mutlu DAŞDAĞ * M.Yusuf ÇELİK *Ömer SATICI *Zeki AKKUŞ *H. Coşkun ÇELİK IX Ulusal Biyoistatistik Kongresi 5-9 Eylül 2006 Zonguldak Zonguldak Karaelmas
HANGİ TÜR ARAŞTIRMALARDA PATH ANALİZİ KULLANILMALIDIR? * M.Mutlu DAŞDAĞ * M.Yusuf ÇELİK *Ömer SATICI *Zeki AKKUŞ *H. Coşkun ÇELİK IX Ulusal Biyoistatistik Kongresi 5-9 Eylül 2006 Zonguldak Zonguldak Karaelmas
İÇİNDEKİLER 1. GİRİŞ...
 İÇİNDEKİLER 1. GİRİŞ... 1 1.1. Regresyon Analizi... 1 1.2. Uygulama Alanları ve Veri Setleri... 2 1.3. Regresyon Analizinde Adımlar... 3 1.3.1. Problemin İfadesi... 3 1.3.2. Konu ile İlgili Potansiyel
İÇİNDEKİLER 1. GİRİŞ... 1 1.1. Regresyon Analizi... 1 1.2. Uygulama Alanları ve Veri Setleri... 2 1.3. Regresyon Analizinde Adımlar... 3 1.3.1. Problemin İfadesi... 3 1.3.2. Konu ile İlgili Potansiyel
KORELASYON VE REGRESYON ANALİZİ. Ankara Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı
 KORELASYON VE REGRESYON ANALİZİ Ankara Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı İki ya da daha çok değişken arasında ilişki olup olmadığını, ilişki varsa yönünü ve gücünü inceleyen korelasyon
KORELASYON VE REGRESYON ANALİZİ Ankara Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı İki ya da daha çok değişken arasında ilişki olup olmadığını, ilişki varsa yönünü ve gücünü inceleyen korelasyon
Maliye Anabilim Dalı- Tezli Yüksek Lisans (Sak.Üni.Ort) Programı Ders İçerikleri
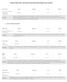 Maliye Anabilim Dalı- Tezli Yüksek Lisans (Sak.Üni.Ort) Programı Ders İçerikleri Sosyal Bilimlerde Araştırma Yöntemleri MLY733 1 3 + 0 6 Araştırma yöntemlerindeki farklı anlayışları, yaygın olarak kullanılan
Maliye Anabilim Dalı- Tezli Yüksek Lisans (Sak.Üni.Ort) Programı Ders İçerikleri Sosyal Bilimlerde Araştırma Yöntemleri MLY733 1 3 + 0 6 Araştırma yöntemlerindeki farklı anlayışları, yaygın olarak kullanılan
Hipotez Kurma. Prof. Dr. Cemal YÜKSELEN Ġstanbul Arel Üniversitesi. 4. Pazarlama Araştırmaları Eğitim Semineri 26-29 Ekim 2010
 Hipotez Kurma Prof. Dr. Cemal YÜKSELEN Ġstanbul Arel Üniversitesi 4. Pazarlama Araştırmaları Eğitim Semineri 26-29 Ekim 2010 Hipotez Nedir? Araştırmacının ilgilendiği bir konuda ispatlanmamış bir önerme
Hipotez Kurma Prof. Dr. Cemal YÜKSELEN Ġstanbul Arel Üniversitesi 4. Pazarlama Araştırmaları Eğitim Semineri 26-29 Ekim 2010 Hipotez Nedir? Araştırmacının ilgilendiği bir konuda ispatlanmamış bir önerme
Yapısal Eşitlik Modellemesinin (YEM) Ormancılıkta Sosyo-ekonomik Sorunların Çözümlenmesinde Kullanımı
 Yapısal Eşitlik Modellemesinin (YEM) Ormancılıkta Sosyo-ekonomik Sorunların Çözümlenmesinde Kullanımı Bekir Kayacan 1, Yaşar Selman Gültekin 2 1 Bekir Kayacan, Düzce Üniversitesi Orman Fakültesi Orman
Yapısal Eşitlik Modellemesinin (YEM) Ormancılıkta Sosyo-ekonomik Sorunların Çözümlenmesinde Kullanımı Bekir Kayacan 1, Yaşar Selman Gültekin 2 1 Bekir Kayacan, Düzce Üniversitesi Orman Fakültesi Orman
BKİ farkı Standart Sapması (kg/m 2 ) A B BKİ farkı Ortalaması (kg/m 2 )
 4. SUNUM 1 Gözlem ya da deneme sonucu elde edilmiş sonuçların, rastlantıya bağlı olup olmadığının incelenmesinde kullanılan istatistiksel yöntemlere HİPOTEZ TESTLERİ denir. Sonuçların rastlantıya bağlı
4. SUNUM 1 Gözlem ya da deneme sonucu elde edilmiş sonuçların, rastlantıya bağlı olup olmadığının incelenmesinde kullanılan istatistiksel yöntemlere HİPOTEZ TESTLERİ denir. Sonuçların rastlantıya bağlı
REGRESYON ANALĐZĐ. www.fikretgultekin.com 1
 REGRESYON ANALĐZĐ Regresyon analizi, aralarında sebep-sonuç ilişkisi bulunan iki veya daha fazla değişken arasındaki ilişkiyi belirlemek ve bu ilişkiyi kullanarak o konu ile ilgili tahminler (estimation)
REGRESYON ANALĐZĐ Regresyon analizi, aralarında sebep-sonuç ilişkisi bulunan iki veya daha fazla değişken arasındaki ilişkiyi belirlemek ve bu ilişkiyi kullanarak o konu ile ilgili tahminler (estimation)
Meslek lisesi ve devlet lisesine giden N tane öğrenci olduğu ve bunların yıllık okul harcamalarına ait verilerin olduğu varsayılsın.
 KUKLA DEĞİŞKENLİ MODELLER Bir kukla değişkenli modeller (Varyans Analiz Modelleri) Kukla değişkenlerin diğer kantitatif değişkenlerle alındığı modeller (Kovaryans Analizi Modeller) Kukla değişkenlerin
KUKLA DEĞİŞKENLİ MODELLER Bir kukla değişkenli modeller (Varyans Analiz Modelleri) Kukla değişkenlerin diğer kantitatif değişkenlerle alındığı modeller (Kovaryans Analizi Modeller) Kukla değişkenlerin
PARAMETRİK TESTLER. Tek Örneklem t-testi. 200 öğrencinin matematik dersinden aldıkları notların ortalamasının 70 e eşit olup olmadığını test ediniz.
 PARAMETRİK TESTLER Tek Örneklem t-testi 200 öğrencinin matematik dersinden aldıkları notların ortalamasının 70 e eşit olup olmadığını test ediniz. H0 (boş hipotez): 200 öğrencinin matematik dersinden aldıkları
PARAMETRİK TESTLER Tek Örneklem t-testi 200 öğrencinin matematik dersinden aldıkları notların ortalamasının 70 e eşit olup olmadığını test ediniz. H0 (boş hipotez): 200 öğrencinin matematik dersinden aldıkları
2- VERİLERİN TOPLANMASI
 2- VERİLERİN TOPLANMASI Bu bölümde yararlanılan kaynaklar: İşletme İstatistiğine Giriş (Prof. Dr. İsmail Hakkı Armutlulu) ve İşletme İstatistiğinin Temelleri (Bowerman, O Connell, Murphree, Orris Editör:
2- VERİLERİN TOPLANMASI Bu bölümde yararlanılan kaynaklar: İşletme İstatistiğine Giriş (Prof. Dr. İsmail Hakkı Armutlulu) ve İşletme İstatistiğinin Temelleri (Bowerman, O Connell, Murphree, Orris Editör:
Örnek 4.1: Tablo 2 de verilen ham verilerin aritmetik ortalamasını hesaplayınız.
 .4. Merkezi Eğilim ve Dağılım Ölçüleri Merkezi eğilim ölçüleri kitleye ilişkin bir değişkenin bütün farklı değerlerinin çevresinde toplandığı merkezi bir değeri gösterirler. Dağılım ölçüleri ise değişkenin
.4. Merkezi Eğilim ve Dağılım Ölçüleri Merkezi eğilim ölçüleri kitleye ilişkin bir değişkenin bütün farklı değerlerinin çevresinde toplandığı merkezi bir değeri gösterirler. Dağılım ölçüleri ise değişkenin
BÖLÜM-1.BİLİM NEDİR? Tanımı...1 Bilimselliğin Ölçütleri...2 Bilimin İşlevleri...3
 KİTABIN İÇİNDEKİLER BÖLÜM-1.BİLİM NEDİR? Tanımı...1 Bilimselliğin Ölçütleri...2 Bilimin İşlevleri...3 BÖLÜM-2.BİLİMSEL ARAŞTIRMA Belgesel Araştırmalar...7 Görgül Araştırmalar Tarama Tipi Araştırma...8
KİTABIN İÇİNDEKİLER BÖLÜM-1.BİLİM NEDİR? Tanımı...1 Bilimselliğin Ölçütleri...2 Bilimin İşlevleri...3 BÖLÜM-2.BİLİMSEL ARAŞTIRMA Belgesel Araştırmalar...7 Görgül Araştırmalar Tarama Tipi Araştırma...8
Bilimsel Araştırmanın Temelleri
 Temel kavramlar Bilimsel Araştırmanın Temelleri İstatistik nedir? Sayısal değerleri ifade etmek için kullanılan bir dil Evren (population) Belirli bir özellik yönünden, birbirine benzeyen elemanların oluşturduğu
Temel kavramlar Bilimsel Araştırmanın Temelleri İstatistik nedir? Sayısal değerleri ifade etmek için kullanılan bir dil Evren (population) Belirli bir özellik yönünden, birbirine benzeyen elemanların oluşturduğu
Temel Kavramlar. Bağlanım Çözümlemesi. Temel Kavramlar. Ekonometri 1 Konu 6 Sürüm 2,0 (Ekim 2011)
 Bağlanım Çözümlemesi Temel Kavramlar Ekonometri 1 Konu 6 Sürüm 2,0 (Ekim 2011) UADMK Açık Lisans Bilgisi İşbu belge, Creative Commons Attribution-Non-Commercial ShareAlike 3.0 Unported (CC BY-NC-SA 3.0)
Bağlanım Çözümlemesi Temel Kavramlar Ekonometri 1 Konu 6 Sürüm 2,0 (Ekim 2011) UADMK Açık Lisans Bilgisi İşbu belge, Creative Commons Attribution-Non-Commercial ShareAlike 3.0 Unported (CC BY-NC-SA 3.0)
DERS BİLGİLERİ Ders Kodu Yarıyıl T+U Saat Kredi AKTS Çok Değişkenli İstatistik EKO428 Bahar Ön Koşul Dersin Dili
 DERS BİLGİLERİ Ders Kodu Yarıyıl T+U Saat Kredi AKTS Çok Değişkenli İstatistik EKO428 Bahar 3+0 3 3 Ön Koşul Yok Dersin Dili Türkçe Dersin Seviyesi Lisans Dersin Türü Seçmeli Dersi Veren Öğretim Elemanı
DERS BİLGİLERİ Ders Kodu Yarıyıl T+U Saat Kredi AKTS Çok Değişkenli İstatistik EKO428 Bahar 3+0 3 3 Ön Koşul Yok Dersin Dili Türkçe Dersin Seviyesi Lisans Dersin Türü Seçmeli Dersi Veren Öğretim Elemanı
BÖLÜM 2 VERİ SETİNİN HAZIRLANMASI VE DÜZENLENMESİ
 1 BÖLÜM 2 VERİ SETİNİN HAZIRLANMASI VE DÜZENLENMESİ Veri seti; satırlarında gözlem birimleri, sütunlarında ise değişkenler bulunan iki boyutlu bir matristir. Satır ve sütunların kesişim bölgelerine 'hücre
1 BÖLÜM 2 VERİ SETİNİN HAZIRLANMASI VE DÜZENLENMESİ Veri seti; satırlarında gözlem birimleri, sütunlarında ise değişkenler bulunan iki boyutlu bir matristir. Satır ve sütunların kesişim bölgelerine 'hücre
Nimet ERYİĞİT İNSAN KAYNAKLARI YÖNETİMİ YENİLİK
 Nimet ERYİĞİT İNSAN KAYNAKLARI YÖNETİMİ VE YENİLİK Yay n No : 3084 İşletme-Ekonomi : 652 1. Baskı Mart 2014 İSTANBUL ISBN 978-605 - 333-111 - 7 Copyright Bu kitab n bu bas s n n Türkiye deki yay n haklar
Nimet ERYİĞİT İNSAN KAYNAKLARI YÖNETİMİ VE YENİLİK Yay n No : 3084 İşletme-Ekonomi : 652 1. Baskı Mart 2014 İSTANBUL ISBN 978-605 - 333-111 - 7 Copyright Bu kitab n bu bas s n n Türkiye deki yay n haklar
Koşullu Öngörümleme. Bu nedenle koşullu öngörümleme gerçekleştirilmelidir.
 Koşullu Öngörümleme Ex - ante (tasarlanan - umulan) öngörümleme söz konusu iken açıklayıcı değişkenlerin hatasız bir şekilde bilindiği varsayımı gerçekçi olmayan bir varsayımdır. Çünkü bazı açıklayıcı
Koşullu Öngörümleme Ex - ante (tasarlanan - umulan) öngörümleme söz konusu iken açıklayıcı değişkenlerin hatasız bir şekilde bilindiği varsayımı gerçekçi olmayan bir varsayımdır. Çünkü bazı açıklayıcı
BÖLÜM I ARAŞTIRMANIN DOĞASI
 İÇİNDEKİLER ÖNSÖZ...... V BÖLÜM I ARAŞTIRMANIN DOĞASI... 1 1.1. GERÇEĞİ ARAMA YOLLARI..... 1 1.1.1.Deneyim..... 2 1.1.2. Mantık... 2 1.1.3. Bilimsel Araştırma... 3 1.1.4. Yansıtma... 4 1.2. BİLGİ EDİNME
İÇİNDEKİLER ÖNSÖZ...... V BÖLÜM I ARAŞTIRMANIN DOĞASI... 1 1.1. GERÇEĞİ ARAMA YOLLARI..... 1 1.1.1.Deneyim..... 2 1.1.2. Mantık... 2 1.1.3. Bilimsel Araştırma... 3 1.1.4. Yansıtma... 4 1.2. BİLGİ EDİNME
D 3 KURAM VE ARAŞTIRMA. Neumann, 2000 Chapter 3, 4
 D 3 KURAM VE ARAŞTIRMA Neumann, 2000 Chapter 3, 4 KURAM (TEORİ) Her kuram NEDEN ve NASIL sorularına yanıt vermeye çalışır! Bir kuram ortaya koyan kişinin bilime ve topluma katkısı nedir? İleri sürülen
D 3 KURAM VE ARAŞTIRMA Neumann, 2000 Chapter 3, 4 KURAM (TEORİ) Her kuram NEDEN ve NASIL sorularına yanıt vermeye çalışır! Bir kuram ortaya koyan kişinin bilime ve topluma katkısı nedir? İleri sürülen
SIRADAN EN KÜÇÜK KARELER (OLS)
 SIRADAN EN KÜÇÜK KARELER (OLS) YÖNTEMİNİN ASİMPTOTİK ÖZELLİKLERİ Hüseyin Taştan 1 1 Yıldız Teknik Üniversitesi İktisat Bölümü Ders Kitabı: Introductory Econometrics: A Modern Approach (2nd ed.) J. Wooldridge
SIRADAN EN KÜÇÜK KARELER (OLS) YÖNTEMİNİN ASİMPTOTİK ÖZELLİKLERİ Hüseyin Taştan 1 1 Yıldız Teknik Üniversitesi İktisat Bölümü Ders Kitabı: Introductory Econometrics: A Modern Approach (2nd ed.) J. Wooldridge
AVRASYA ÜNİVERSİTESİ
 Ders Tanıtım Formu Dersin Adı Öğretim Dili ARAŞTIRMA YÖNTEMLERİ-II Türkçe Dersin Verildiği Düzey Ön Lisans () Lisans (X) Yüksek Lisans() Doktora ( ) Eğitim Öğretim Sistemi Örgün Öğretim (X) Uzaktan Öğretim(
Ders Tanıtım Formu Dersin Adı Öğretim Dili ARAŞTIRMA YÖNTEMLERİ-II Türkçe Dersin Verildiği Düzey Ön Lisans () Lisans (X) Yüksek Lisans() Doktora ( ) Eğitim Öğretim Sistemi Örgün Öğretim (X) Uzaktan Öğretim(
Araştırma Problemleri: Problem İfadeleri, Araştırma Soruları ve Hipotezler
 Araştırma Problemleri: Problem İfadeleri, Araştırma Soruları ve Hipotezler Araştırma Problemleri Problem Belirleme Kaynakları Genel problem Yapısı Problem Oluşturmanın Önemi Nicel Problem Oluşturma 1-
Araştırma Problemleri: Problem İfadeleri, Araştırma Soruları ve Hipotezler Araştırma Problemleri Problem Belirleme Kaynakları Genel problem Yapısı Problem Oluşturmanın Önemi Nicel Problem Oluşturma 1-
BÖLÜM 6 MERKEZDEN DAĞILMA ÖLÇÜLERİ
 1 BÖLÜM 6 MERKEZDEN DAĞILMA ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel
1 BÖLÜM 6 MERKEZDEN DAĞILMA ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel
İÇİNDEKİLER. Birinci Bölüm UYGULAMA VERİLERİ
 İÇİNDEKİLER Birinci Bölüm UYGULAMA VERİLERİ VERİ GRUBU 1. Yüzücü ve Atlet Verileri... 1 VERİ GRUBU 2. Sutopu, Basketbol ve Voleybol Oyuncuları Verileri... 4 VERİ 3. Solunum Yolları Verisi... 7 VERİ 4.
İÇİNDEKİLER Birinci Bölüm UYGULAMA VERİLERİ VERİ GRUBU 1. Yüzücü ve Atlet Verileri... 1 VERİ GRUBU 2. Sutopu, Basketbol ve Voleybol Oyuncuları Verileri... 4 VERİ 3. Solunum Yolları Verisi... 7 VERİ 4.
Sosyal Ağ Servislerinde Kullanıcı Güveni: Facebook ve Linkedin Karşılaştırması. A.Kübra Özkoç Bilgisayar Ortamında Sanat ve Tasarım Seminer
 Sosyal Ağ Servislerinde Kullanıcı Güveni: Facebook ve Linkedin Karşılaştırması A.Kübra Özkoç Bilgisayar Ortamında Sanat ve Tasarım Seminer Sosyal Ağ Servisleri, kişilerin fiziksel dünyada oluşturdukları
Sosyal Ağ Servislerinde Kullanıcı Güveni: Facebook ve Linkedin Karşılaştırması A.Kübra Özkoç Bilgisayar Ortamında Sanat ve Tasarım Seminer Sosyal Ağ Servisleri, kişilerin fiziksel dünyada oluşturdukları
SPSS Uygulamalı Çok Değişkenli İstatistik Teknikleri
 Elementary Education Online, 12(1), k: 1 6, 2013. İlköğretim Online, 12(1), b:1 6, 2013. [Online]: http://ilkogretim online.org.tr KİTAP İNCELEMESİ SPSS Uygulamalı Çok Değişkenli İstatistik Teknikleri
Elementary Education Online, 12(1), k: 1 6, 2013. İlköğretim Online, 12(1), b:1 6, 2013. [Online]: http://ilkogretim online.org.tr KİTAP İNCELEMESİ SPSS Uygulamalı Çok Değişkenli İstatistik Teknikleri
Kullanılacak İstatistikleri Belirleme Ölçütleri. Değişkenin Ölçek Türü ya da Yapısı
 ARAŞTIRMA MODELLİLERİNDE KULLANILACAK İSTATİSTİKLERİ BELİRLEME ÖLÇÜTLERİ Parametrik mi Parametrik Olmayan mı? Kullanılacak İstatistikleri Belirleme Ölçütleri Değişken Sayısı Tek değişkenli (X) İki değişkenli
ARAŞTIRMA MODELLİLERİNDE KULLANILACAK İSTATİSTİKLERİ BELİRLEME ÖLÇÜTLERİ Parametrik mi Parametrik Olmayan mı? Kullanılacak İstatistikleri Belirleme Ölçütleri Değişken Sayısı Tek değişkenli (X) İki değişkenli
İÇİNDEKİLER ÇİZELGELER LİSTESİ GİRİŞ 1
 iv İÇİNDEKİLER ÖZET ABSTRACT ÖNSÖZ İÇİNDEKİLER i ii iii iv ÇİZELGELER LİSTESİ GİRİŞ 1 vii BİRİNCİ BÖLÜM MARKA KAVRAMI 1.1 GENEL OLARAK MARKA KAVRAMI 3 1.1.1. Marka Kavramının Tarihçesi 3 1.1.2. Marka Kavramının
iv İÇİNDEKİLER ÖZET ABSTRACT ÖNSÖZ İÇİNDEKİLER i ii iii iv ÇİZELGELER LİSTESİ GİRİŞ 1 vii BİRİNCİ BÖLÜM MARKA KAVRAMI 1.1 GENEL OLARAK MARKA KAVRAMI 3 1.1.1. Marka Kavramının Tarihçesi 3 1.1.2. Marka Kavramının
2 Tarihsel, Kültürel ve Yasal/Etik Konular 35
 İçİndekİler Önsöz xiii K I S I M I Genel Bir Bakış 1 Psikolojik Test ve Değerleme 1 Test ve Değerleme 1 Psikolojik Test ve Değerleme 1 Psikolojik Değerleme Araçları 5 Testler 5 Görüşme 7 Portfolyo 9 Vaka
İçİndekİler Önsöz xiii K I S I M I Genel Bir Bakış 1 Psikolojik Test ve Değerleme 1 Test ve Değerleme 1 Psikolojik Test ve Değerleme 1 Psikolojik Değerleme Araçları 5 Testler 5 Görüşme 7 Portfolyo 9 Vaka
TÜRKİYE DE İNTERNET SERVİS SAĞLAYICILARI SEKTÖRÜNDE MÜŞTERİ SADAKATİ VE BİLEŞENLERİNİN YAPISAL EŞİTLİK MODELLEMESİ İLE İNCELENMESİ
 Marmara Üniversitesi İ.İ.B. Dergisi YIL 2014, CİLT XXXVI, SAYI II, S. 159-184 Doi No: 10.14780/iibd.00100 TÜRKİYE DE İNTERNET SERVİS SAĞLAYICILARI SEKTÖRÜNDE MÜŞTERİ SADAKATİ VE BİLEŞENLERİNİN YAPISAL
Marmara Üniversitesi İ.İ.B. Dergisi YIL 2014, CİLT XXXVI, SAYI II, S. 159-184 Doi No: 10.14780/iibd.00100 TÜRKİYE DE İNTERNET SERVİS SAĞLAYICILARI SEKTÖRÜNDE MÜŞTERİ SADAKATİ VE BİLEŞENLERİNİN YAPISAL
İçindekiler. Ön Söz... xiii
 İçindekiler Ön Söz.................................................... xiii Bölüm 1 İstatistiğe Giriş....................................... 1 1.1 Giriş......................................................1
İçindekiler Ön Söz.................................................... xiii Bölüm 1 İstatistiğe Giriş....................................... 1 1.1 Giriş......................................................1
İSTATİSTİK STATISTICS (2+0) Yrd.Doç.Dr. Nil TOPLAN SAÜ.MÜH. FAK. METALURJİ VE MALZEME MÜH. BÖLÜMÜ ÖĞRETİM ÜYESİ ÖĞRETİM YILI
 İSTATİSTİK STATISTICS (+) Yrd.Doç.Dr. Nil TOPLAN SAÜ.MÜH. FAK. METALURJİ VE MALZEME MÜH. BÖLÜMÜ ÖĞRETİM ÜYESİ ÖĞRETİM YILI KONU BAŞLIKLARI :. İSTATİSTİĞE GİRİŞ. VERİLERİN DÜZENLENMESİ. MERKEZİ EĞİLİM ÖLÇÜLERİ.
İSTATİSTİK STATISTICS (+) Yrd.Doç.Dr. Nil TOPLAN SAÜ.MÜH. FAK. METALURJİ VE MALZEME MÜH. BÖLÜMÜ ÖĞRETİM ÜYESİ ÖĞRETİM YILI KONU BAŞLIKLARI :. İSTATİSTİĞE GİRİŞ. VERİLERİN DÜZENLENMESİ. MERKEZİ EĞİLİM ÖLÇÜLERİ.
YABANCI DİL EĞİTİMİ VEREN ÖZEL BİR EĞİTİM KURUMUNDAKİ ÖĞRENCİLERİN BEKLENTİLERİNİN ARAŞTIRILMASI. Sibel SELİM 1 Efe SARIBAY 2
 Dokuz Eylül Üniversitesi Sosyal Bilimler Enstitüsü Dergisi Cilt 5, Sayı:2, 2003 YABANCI DİL EĞİTİMİ VEREN ÖZEL BİR EĞİTİM KURUMUNDAKİ ÖĞRENCİLERİN BEKLENTİLERİNİN ARAŞTIRILMASI Sibel SELİM 1 Efe SARIBAY
Dokuz Eylül Üniversitesi Sosyal Bilimler Enstitüsü Dergisi Cilt 5, Sayı:2, 2003 YABANCI DİL EĞİTİMİ VEREN ÖZEL BİR EĞİTİM KURUMUNDAKİ ÖĞRENCİLERİN BEKLENTİLERİNİN ARAŞTIRILMASI Sibel SELİM 1 Efe SARIBAY
İstatistik ve Olasılık
 İstatistik ve Olasılık Ders 8: Prof. Dr. İrfan KAYMAZ Tanım Tahmin (kestirim veya öngörü): Mevcut bilgi ve deneylere dayanarak olayın bütünü hakkında bir yargıya varmaktır. Bu anlamda, anakütleden çekilen
İstatistik ve Olasılık Ders 8: Prof. Dr. İrfan KAYMAZ Tanım Tahmin (kestirim veya öngörü): Mevcut bilgi ve deneylere dayanarak olayın bütünü hakkında bir yargıya varmaktır. Bu anlamda, anakütleden çekilen
Bilimsel Araştırma Yöntemleri I
 İnsan Kaynakları Yönetimi Bilim Dalı Tezli Yüksek Lisans Programları Bilimsel Araştırma Yöntemleri I Dr. M. Volkan TÜRKER 7 Bilimsel Araştırma Süreci* 1. Gözlem Araştırma alanının belirlenmesi 2. Ön Bilgi
İnsan Kaynakları Yönetimi Bilim Dalı Tezli Yüksek Lisans Programları Bilimsel Araştırma Yöntemleri I Dr. M. Volkan TÜRKER 7 Bilimsel Araştırma Süreci* 1. Gözlem Araştırma alanının belirlenmesi 2. Ön Bilgi
İŞSİZ BİREYLERİN KREDİ KARTLARINA İLİŞKİN TUTUM VE DAVRANIŞLARININ YAPISAL EŞİTLİK MODELİYLE İNCELENMESİ: ESKİŞEHİR ÖRNEĞİ
 Makalenin Yayınlandığı Dergi: İktisat İşletme ve Finans Yayınlanma Tarihi: 2014-08-01 00:00:00 Cilt: 29, Sayı: 341, Yıl: 2014 Sayfa(lar): 57-86 ISSN: 1300-610X Digital Object Identifier (DOI): 10.3848/iif.2014.341.4074
Makalenin Yayınlandığı Dergi: İktisat İşletme ve Finans Yayınlanma Tarihi: 2014-08-01 00:00:00 Cilt: 29, Sayı: 341, Yıl: 2014 Sayfa(lar): 57-86 ISSN: 1300-610X Digital Object Identifier (DOI): 10.3848/iif.2014.341.4074
İSTATİSTİKTE TEMEL KAVRAMLAR
 İSTATİSTİKTE TEMEL KAVRAMLAR 1. ve 2. Hafta İstatistik Nedir? Bir tanım olarak istatistik; belirsizlik altında bir konuda karar verebilmek amacıyla, ilgilenilen konuya ilişkin verilerin toplanması, düzenlenmesi,
İSTATİSTİKTE TEMEL KAVRAMLAR 1. ve 2. Hafta İstatistik Nedir? Bir tanım olarak istatistik; belirsizlik altında bir konuda karar verebilmek amacıyla, ilgilenilen konuya ilişkin verilerin toplanması, düzenlenmesi,
Ch. 12: Zaman Serisi Regresyonlarında Ardışık Bağıntı (Serial Correlation) ve Değişen Varyans
 Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri II Ders Notları Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. ed., 2002, Thomson Learning. Ch. 12: Zaman Serisi Regresyonlarında
Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri II Ders Notları Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. ed., 2002, Thomson Learning. Ch. 12: Zaman Serisi Regresyonlarında
Maliye Anabilim Dalı- Tezli Yüksek Lisans Programı Ders İçerikleri
 Maliye Anabilim Dalı- Tezli Yüksek Lisans Programı Ders İçerikleri Sosyal Bilimlerde Araştırma Yöntemleri MLY733 1 3 + 0 6 Araştırma yöntemlerindeki farklı anlayışları, yaygın olarak kullanılan araştırma
Maliye Anabilim Dalı- Tezli Yüksek Lisans Programı Ders İçerikleri Sosyal Bilimlerde Araştırma Yöntemleri MLY733 1 3 + 0 6 Araştırma yöntemlerindeki farklı anlayışları, yaygın olarak kullanılan araştırma
EK -13: NİCEL ANALİZLERDE KULLANILAN YÖNTEMLER NACE REV Lİ KODDA İMALAT SANAYİ FAALİYETLERİNİN TEKNOLOJİ SINIFLAMASI,EUROSTAT
 EK -13: NİCEL ANALİZLERDE KULLANILAN YÖNTEMLER NACE REV.2.00 2 Lİ KODDA İMALAT SANAYİ FAALİYETLERİNİN TEKNOLOJİ SINIFLAMASI,EUROSTAT EKLER 3 YILDIZ ANALİZİ TEMEL BİLEŞENLER ANALİZİ Temel bileşenler analizi
EK -13: NİCEL ANALİZLERDE KULLANILAN YÖNTEMLER NACE REV.2.00 2 Lİ KODDA İMALAT SANAYİ FAALİYETLERİNİN TEKNOLOJİ SINIFLAMASI,EUROSTAT EKLER 3 YILDIZ ANALİZİ TEMEL BİLEŞENLER ANALİZİ Temel bileşenler analizi
EŞANLI DENKLEM MODELLERİ
 EŞANLI DENKLEM MODELLERİ Eşanlı denklem modelleri, tek denklemli modeller ile açıklanamayan iktisadi olayları açıklamak için kullanılan model türlerinden birisidir. Çift yönlü neden-sonuç ilişkisi söz
EŞANLI DENKLEM MODELLERİ Eşanlı denklem modelleri, tek denklemli modeller ile açıklanamayan iktisadi olayları açıklamak için kullanılan model türlerinden birisidir. Çift yönlü neden-sonuç ilişkisi söz
TEMEL İSTATİSTİKİ KAVRAMLAR YRD. DOÇ. DR. İBRAHİM ÇÜTCÜ
 TEMEL İSTATİSTİKİ KAVRAMLAR YRD. DOÇ. DR. İBRAHİM ÇÜTCÜ 1 İstatistik İstatistik, belirsizliğin veya eksik bilginin söz konusu olduğu durumlarda çıkarımlar yapmak ve karar vermek için sayısal verilerin
TEMEL İSTATİSTİKİ KAVRAMLAR YRD. DOÇ. DR. İBRAHİM ÇÜTCÜ 1 İstatistik İstatistik, belirsizliğin veya eksik bilginin söz konusu olduğu durumlarda çıkarımlar yapmak ve karar vermek için sayısal verilerin
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DÖNEM PROJESİ TAŞINMAZ DEĞERLEMEDE HEDONİK REGRESYON ÇÖZÜMLEMESİ. Duygu ÖZÇALIK
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DÖNEM PROJESİ TAŞINMAZ DEĞERLEMEDE HEDONİK REGRESYON ÇÖZÜMLEMESİ Duygu ÖZÇALIK GAYRİMENKUL GELİŞTİRME VE YÖNETİMİ ANABİLİM DALI ANKARA 2018 Her hakkı saklıdır
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DÖNEM PROJESİ TAŞINMAZ DEĞERLEMEDE HEDONİK REGRESYON ÇÖZÜMLEMESİ Duygu ÖZÇALIK GAYRİMENKUL GELİŞTİRME VE YÖNETİMİ ANABİLİM DALI ANKARA 2018 Her hakkı saklıdır
Ekonometrinin Konusu ve Yöntembilimi. Ekonometri Nedir? Ekonometrinin Konusu ve Yöntembilimi. Ekonometri 1 Konu 4 Sürüm 2,0 (Ekim 2011)
 Ekonometri Nedir? ve Yöntembilimi Ekonometri 1 Konu 4 Sürüm 2,0 (Ekim 2011) Ders Planı ve Yöntembilimi 1 ve Yöntembilimi Sözcük Anlamı ile Ekonometri Ekonometri Sözcük anlamı ile ekonometri, ekonomik ölçüm
Ekonometri Nedir? ve Yöntembilimi Ekonometri 1 Konu 4 Sürüm 2,0 (Ekim 2011) Ders Planı ve Yöntembilimi 1 ve Yöntembilimi Sözcük Anlamı ile Ekonometri Ekonometri Sözcük anlamı ile ekonometri, ekonomik ölçüm
İLKÖĞRETİMDE SINIF YÖNETİMİNİN ETKİLİLİĞİNİ BELİRLEMEYE YÖNELİK ÖLÇEK GELİŞTİRME ÇALIŞMASI *
 The Journal of Academic Social Science Studies International Journal of Social Science Doi number:http://dx.doi.org/10.9761/jasss2544 Number: 29, p. 367-385, Autumn III 2014 İLKÖĞRETİMDE SINIF YÖNETİMİNİN
The Journal of Academic Social Science Studies International Journal of Social Science Doi number:http://dx.doi.org/10.9761/jasss2544 Number: 29, p. 367-385, Autumn III 2014 İLKÖĞRETİMDE SINIF YÖNETİMİNİN
Araştırma Teknikleri
 Prof.Dr. Filiz Karaosmanoğlu Yrd.Doç.Dr. Bayram Kılıç Ekim 11, 2010 Yalova Bilimsel Yöntem Modeli Bilimsel Yöntem Bilimsel yöntem, tümevarım ile tümdengelim yaklaşımlarının ayrı ayrı yeterli olamayışları
Prof.Dr. Filiz Karaosmanoğlu Yrd.Doç.Dr. Bayram Kılıç Ekim 11, 2010 Yalova Bilimsel Yöntem Modeli Bilimsel Yöntem Bilimsel yöntem, tümevarım ile tümdengelim yaklaşımlarının ayrı ayrı yeterli olamayışları
İçindekiler. 1 Giriş 2. 3 Psikoloji Araştırmalarında Etik Meseleler Bilimsel Yöntem 27. KISIM I Genel Meseleler 1
 Ön Söz xiii KISIM I Genel Meseleler 1 1 Giriş 2 PSİKOLOJİ BİLİMİ 3 BİLİMİN BAĞLAMI 6 Tarihsel Bağlam 6 Sosyal ve Kültürel Bağlam 9 Ahlakî Bağlam 13 BİR ARAŞTIRMACI GİBİ DÜŞÜNMEK 14 Medyada Yayımlanan Araştırma
Ön Söz xiii KISIM I Genel Meseleler 1 1 Giriş 2 PSİKOLOJİ BİLİMİ 3 BİLİMİN BAĞLAMI 6 Tarihsel Bağlam 6 Sosyal ve Kültürel Bağlam 9 Ahlakî Bağlam 13 BİR ARAŞTIRMACI GİBİ DÜŞÜNMEK 14 Medyada Yayımlanan Araştırma
Appendix B: Olasılık ve Dağılım Teorisi
 Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri I Ders Notları Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. edition, Thomson Learning Appendix B: Olasılık ve Dağılım
Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri I Ders Notları Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. edition, Thomson Learning Appendix B: Olasılık ve Dağılım
1: DENEYLERİN TASARIMI VE ANALİZİ...
 İÇİNDEKİLER Bölüm 1: DENEYLERİN TASARIMI VE ANALİZİ... 1 1.1. Deneyin Stratejisi... 1 1.2. Deneysel Tasarımın Bazı Tipik Örnekleri... 11 1.3. Temel Kurallar... 16 1.4. Deneyleri Tasarlama Prensipleri...
İÇİNDEKİLER Bölüm 1: DENEYLERİN TASARIMI VE ANALİZİ... 1 1.1. Deneyin Stratejisi... 1 1.2. Deneysel Tasarımın Bazı Tipik Örnekleri... 11 1.3. Temel Kurallar... 16 1.4. Deneyleri Tasarlama Prensipleri...
YTÜ İktisat Bölümü EKONOMETRİ I Ders Notları
 Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri I Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. edition, Thomson Learning Appendix B: Olasılık ve Dağılım Teorisi
Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri I Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. edition, Thomson Learning Appendix B: Olasılık ve Dağılım Teorisi
YTÜ İktisat Bölümü EKONOMETRİ I Ders Notları
 Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri I Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. edition, Thomson Learning Appendix B: Olasılık ve Dağılım Teorisi
Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri I Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. edition, Thomson Learning Appendix B: Olasılık ve Dağılım Teorisi
H.Ü. Bilgi ve Belge Yönetimi Bölümü BBY 208 Sosyal Bilimlerde Araştırma Yöntemleri II (Bahar 2012) SPSS Ders Notları II (19 Nisan 2012)
 H.Ü. Bilgi ve Belge Yönetimi Bölümü BBY 208 Sosyal Bilimlerde Araştırma Yöntemleri II (Bahar 2012) SPSS Ders Notları II (19 Nisan 2012) Aşağıdaki analizlerde lise öğrencileri veri dosyası kullanılmıştır.
H.Ü. Bilgi ve Belge Yönetimi Bölümü BBY 208 Sosyal Bilimlerde Araştırma Yöntemleri II (Bahar 2012) SPSS Ders Notları II (19 Nisan 2012) Aşağıdaki analizlerde lise öğrencileri veri dosyası kullanılmıştır.
ÇOK DEĞĐŞKENLĐ ĐSTATĐSTĐKLERĐN ARAŞTIRMALARDA KULLANIMI
 ÇOK DEĞĐŞKENLĐ ĐSTATĐSTĐKLERĐN ARAŞTIRMALARDA KULLANIMI Araştırmalarda incelenen olaylar göstermektedir ki tek değişkenli istatistiklerin kullanılması problemi açıklamakta yetersiz ve eksik kalmaktadır.
ÇOK DEĞĐŞKENLĐ ĐSTATĐSTĐKLERĐN ARAŞTIRMALARDA KULLANIMI Araştırmalarda incelenen olaylar göstermektedir ki tek değişkenli istatistiklerin kullanılması problemi açıklamakta yetersiz ve eksik kalmaktadır.
2. Klasik Kümeler-Bulanık Kümeler
 2. Klasik Kümeler-Bulanık Kümeler Klasik Küme Teorisi Klasik kümelerde bir nesnenin bir kümeye üye olması ve üye olmaması söz konusudur. Bu yaklaşıma göre istediğimiz özelliğe sahip olan bir birey, eleman
2. Klasik Kümeler-Bulanık Kümeler Klasik Küme Teorisi Klasik kümelerde bir nesnenin bir kümeye üye olması ve üye olmaması söz konusudur. Bu yaklaşıma göre istediğimiz özelliğe sahip olan bir birey, eleman
Bilişim Sistemleri. Modelleme, Analiz ve Tasarım. Yrd. Doç. Dr. Alper GÖKSU
 Bilişim Sistemleri Modelleme, Analiz ve Tasarım Yrd. Doç. Dr. Alper GÖKSU Ders Akışı Hafta 10-11. Nesneye Yönelik Sistem Analizi Haftanın Amacı Bilişim sistemleri geliştirmede nesneye yönelik sistem analizi
Bilişim Sistemleri Modelleme, Analiz ve Tasarım Yrd. Doç. Dr. Alper GÖKSU Ders Akışı Hafta 10-11. Nesneye Yönelik Sistem Analizi Haftanın Amacı Bilişim sistemleri geliştirmede nesneye yönelik sistem analizi
BİYOİSTATİSTİK DERSLERİ AMAÇ VE HEDEFLERİ
 BİYOİSTATİSTİK DERSLERİ AMAÇ VE HEDEFLERİ DÖNEM I-I. DERS KURULU Konu: Bilimsel yöntem ve istatistik Amaç: Biyoistatistiğin tıptaki önemini kavrar ve sonraki dersler için gerekli terminolojiye hakim olur.
BİYOİSTATİSTİK DERSLERİ AMAÇ VE HEDEFLERİ DÖNEM I-I. DERS KURULU Konu: Bilimsel yöntem ve istatistik Amaç: Biyoistatistiğin tıptaki önemini kavrar ve sonraki dersler için gerekli terminolojiye hakim olur.
