T.C. KİLİS 7 ARALIK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ BİR İKİ VE ÜÇ BOYUTTA KUANTUM PSEUDODOT YAPILARI
|
|
|
- Özge Dağdelen
- 8 yıl önce
- İzleme sayısı:
Transkript
1 T.C. KİLİS 7 ARALIK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ BİR İKİ VE ÜÇ BOYUTTA KUANTUM PSEUDODOT YAPILARI Yunus SAKAR FİZİK ANABİLİM DALI Danışman: Doç. Dr. Abdurahman ÇETİN KİLİS 2012 Her Hakkı Saklıdır
2
3 ÖZET Yüksek Lisans Tezi Bir İki ve Üç boyutta Kuantum Pseudodot Yapıları Yunus SAKAR Kilis 7 Aralık Üniversitesi Fen Bilimleri Enstitüsü Fizik Anabilim Dalı Danışman: Doç. Dr. Abdurahman ÇETİN Yıl: 2012 Sayfa:45 Bu çalışmada, Pseudo Harmonik potansiyel altında bir parçacığın enerji özdeğerlerinin nasıl bir değişim sergilediği enerjinin bağımlı olduğu parametrelere göre araştırılmıştır. Bu anlamda teorik bir çalışma yürütülmüştür. Bundan dolayı bir, iki ve üç boyutlu sistemlerde Pseudodot çözümlerinin belirlenmesi için Schrödinger denkleminin çözümü ele alınmıştır. Elde edilen sonuçlardan; bir boyutta enerji seviyeleri sadece n kuantum sayısına, iki boyutta n ve m kuantum sayısına bağlı bir değişim sergilerken üç boyutlu uygulamalarda bu değişim hem n kuantum sayısına ve l kuantum sayısına bağlı olarak karşımıza çıkmaktadır. Bir ve iki boyutlu uygulamalarda dejenerelik olmazken, üç boyutlu Pseudodot çözümlerinde enerjinin manyetik kuantum sayısına bağlı olmamasından dolayı dejenerelik söz konusudur. Pseudodot yapıları için enerji ve parçacığın belirli bir konumda bulunma ihtimali Mathematica programı yardımıyla nümerik olarak değerlendirilmiştir. Anahtar Kelimeler: Pseudodot, Pseudo Harmonik Potansiyel i
4 ABSTRACT MSc. Thesis Quantum Pseudodot Structures in One Two and Three Dimensions Yunus SAKAR Kilis 7 Aralık University Institute of Scienceandtechnology Department of Physics Supervisor: Assoc. Prof. Dr. Abdurahman ÇETİN Year: 2012 Page:45 In this study, energy eigenvalue of a particle under the pseudo harmonic potential have been investigated according to the related parameters. In this sense, a theoretical study was carried out. Therefore, Schrödinger equations solutions are discussed for the consequences of the solution in one, two and three dimensional Pseudo-harmonic potential. The results obtained, energy levels in one dimension depend on quantum number and energy levels in two dimensions depend on quantum number ad while three dimensional energy levels depend on quantum number and angular momentum quantum number. While there is not a degeneracy in one and twodimensional applications, there is degeneracy in three-dimensional applications due to energy do not depend on magnetic quantum number at Pseudodot solutions. Energy and probability of the particle according to the position was evaluated numerically by using Mathematica program for the Pseudodot structures. Key Words: Pseudodot, Pseudo Harmonic Potential ii
5 TEŞEKKÜR Bu tez çalışmasında bana her türlü konuda destek olan ve yardımlarını esirgemeyen değerli hocam, sayın Doç. Dr. Abdurahman ÇETİN e, Her konuda yardıma hazır olan Fizik Anabilim Dalına bağlı diğer bölüm hocalarıma, Ev arkadaşlarım Bahadır PALTA ve Ferhat POLAT a, Ayrıca maddi ve manevi anlamda her zaman yanımda olan değerli aileme, ağabeyime, kuzenlerim Yasin SAKAR a ve Cihan CAN a en içten teşekkürlerimi sunuyorum. Yunus SAKAR Kilis, Haziran, 2012 iii
6 İÇİNDEKİLER TABLOSU ÖZET... i ABSTRACT... ii TEŞEKKÜR... i İÇİNDEKİLER TABLOSU... iv SİMGELER VE KISALTMALAR DİZİNİ... v ŞEKİLLER DİZİNİ... vii ÖZGEÇMİŞ... viii 1. GİRİŞ PSEUDO POTANSİYELİNİN TARİHÇESİ: PSEUDOHARMONİK POTANSİYELİ NERELERDE VE NEDEN KULLANILIR BİR BOYUTLU HARMONİK OSİLATÖR Diferansiyel Denklemin Çözümü ÜÇ BOYUTLU HARMONİK SALINICI PROBLEMİ HİDROJEN ATOMU PROBLEMİNİN RADYAL KISMININ ÇÖZÜMÜ PSEUDO HARMONİK POTANSİYEL KULLANILARAK YAPILAN ÇALIŞMALAR PSEUDODOT ÇÖZÜMLERİ BİR BOYUTLU PSEUDODOT ÇÖZÜMÜ VE ENERJİ SEVİYELERİ İKİ BOYUTLU PSEUDODOT ÇÖZÜMÜ VE ENERJİ SEVİYELERİ ÜÇ BOYUTLU PSEUDODOT ÇÖZÜMÜ VE ENERJİ SEVİYELERİ BULGULAR VE TARTIŞMA KAYNAKLAR iv
7 SİMGELER VE KISALTMALAR DİZİNİ v
8 vi
9 ŞEKİLLER DİZİNİ Şekil 1:Sert ve Yumuşak Potansiyeller... 1 Şekil 2: Kartezyen Koordinatlarda Pseudo Harmonik Potansiyel... 3 Şekil 3: Bir Boyutta, Taban Durumunda Pseudo harmonik Potansiyelde Bulunan Bir Parçacığın Bulunma Olasılığı Şekil 4: Dalga Fonksiyonunun Temel Kuantum Sayısının Arttırılmasıyla Değişimi Şekil 5:n=0, 1, 2 ve Gama=6 Değerleriyle Pseudo harmonik Potansiyelde Bir Parçacığın Dalga Fonksiyonunun Gösterdiği Değişim Şekil 6:Birinci Uyarılmış Durumda Gama=1, 2, 3 Değerleri Pseudo harmonik Potansiyelde bulunan Parçacığın Bulunma Olasılıklarının Değişimi Şekil 7:Artan Uyarılma Sayısıyla(Sol Taraf) ve Artan Gama Sayısıyla(Sağ Taraf) Bulunma Olasılıklarının Potansiyel Eksenli Değişimi Şekil 8:Bir Boyutlu Pseudodot Yapısında Hapis Boyutunun (r 0 ) Artmasıyla Enerji Değişimi Şekil 9:Artan Uyarılma Sayısı, Hapis Boyutu(Solda) ve Artan Yörünge Açısal Momentum Katsayısı, Hapis Boyutu(Sağda) ile Enerji Değerlerinde Meydana Gelen Değişim Şekil 10:Potansiyel değişim aralığının artmasıyla artan uyarılma sayısına bağlı olarak enerji değişimi(solda) ve artan uyarılma sayısıyla potansiyel değişim aralığının azalmasıyla enerjinin değişimi(sağda) Şekil 11:Potansiyel Değişiminin Enerji Üzerindeki Etkisi vii
10 ÖZGEÇMİŞ Temmuz 1988 de Batman da doğmuş, ilk ve orta öğrenimini Batman da tamamlamıştır. Haziran 2010 tarihinde Gaziantep Üniversitesi Kilis Fen Edebiyat Fakültesi Fizik bölümünü başarıyla tamamlamıştır. Mezun olduğu yıl Kilis 7 Aralık Üniversitesi Fen Bilimleri Enstitüsü Fizik Anabilim Dalı nda Yüksek Lisansına başlamıştır. viii
11 1. GİRİŞ 1.1. PSEUDO POTANSİYELİNİN TARİHÇESİ: Pseudo potansiyeli fikri, çekirdek potansiyeli için problemlerde kullanılan güçlü Coulomb potansiyelinin yerine çok daha yumuşak bir potansiyel tanımlamak amacıyla ortaya atılmıştır. Bu kavramın uzun bir geçmişi vardır ve Fermi nin 1930 larda yayımladığı makalelerine kadar uzanır. Deneysel Pseudo potansiyeli, yılları arasında bant yapısı hesaplamalarında çoğu analitik ve nümerik olmak üzere başarıyla kullanılmıştır. Baştan sona geçişli (ab-inito) ve tam Pseudo potansiyeli yılları arasında yoğunluk fonksiyonu teorisiyle (DFT) yapılabilen hesaplamalarda geliştirilmiştir. Günümüzde ise kullanılan pek çok farklı Pseudo potansiyeli çeşitleri vardır. Aşağıda şekil1 de sert ve yumuşak potansiyellerin karşılaştırılması verilmiştir (Krasheninnikov, Helsinki University of Technology, 2008). Sert Yumuşak Çekirdekten Uzaklık Çekirdekten Uzaklık Şekil 1:Sert ve Yumuşak Potansiyeller 1
12 1.2. PSEUDOHARMONİK POTANSİYELİ NERELERDE VE NEDEN KULLANILIR Pseudo potansiyeli yoğun madde fiziği ve malzeme biliminde deneysel ve teorik çalışmalarda kullanılan bir potansiyeldir. Yapılan bu tez çalışması teorik ağırlıklı bir çalışma olduğundan dolayı bu potansiyelin deneysel çalışmalarda kullanılma nedenlerine de değinmek daha doğru olur. Deneysel olarak yapılan çalışmalarda maddenin elektronik özellikleri, teorik olarak yapılan çalışmalarda ise Schrödinger denkleminin çözümüne yönelik araştırmalar göze çarpmaktadır. Pseudo potansiyeli elektronik yapıda genellikle atom yapısında bulunan elektronların varlığından nasıl kurtulabileceğinin bir yoludur. Çünkü farklı atomlarda çekirdek etrafındaki elektronları örtüşmez. Çekirdek etrafında bulunan elektronların oluşturduğu karmaşa; fizik, kimya, biyoloji gibi alanlarda önemini korur. Bu sebeple Pseudo Potansiyeli bu tür karmaşıklıkları gidermede önemlidir. Donmuş-çekirdek yaklaşımıyla atom yapısında var olan elektronların yapısal enerji değişimindeki rolü lere kadar minimize edilmektedir. Ki buda çok küçük bir orandır. Bu yaklaşımla atom çekirdeği etrafında bulunan elektronların bağ yapısına katılması söz konusu değildir. Pseudo potansiyeli tüm elektron potansiyellerinden daha yumuşaktır. Pseudo Potansiyelinde çekirdek öz durumları yoktur. Pseudo potansiyelinin öngördüğü düzlem dalga metodu yoğunluk fonksiyonu teorisiyle (DFT) uyumludur. Elektronik yapıda Pseudo potansiyelinin kullanılması, daha öncede değinilmiş olarak çekirdek yapısındaki elektronlarından kurtulmak amaçlıdır. Bizim beklentimiz, Pseudo potansiyelinin çözülmesi kolay ve Pauli Prensibine uyan fonksiyonlar üretmesidir. Bir potansiyel katkılı (additive) ve geçişli (transferable) olmalıdır. Pseudo potansiyeli eldeki malzemenin yapısının anlaşılması adına teorik çalışmalarda uygulanacak yöntemleri basitleştirir. Etkili bir hesaplama yapabilmek için baz setinin boyutunu indirger. Sistemdeki elektron sayılarının etkisini azaltarak serbestlik derecelerinin sayılarını indirger. Rölativistik etkileri, etkili potansiyel içerisine kısmen dâhil eder. Pseudo harmonik potansiyeli Hamiltonyendeki 2
13 serbestlik dereceleri yerine geçer (Krasheninnikov, Helsinki University of Technology, 2008). Bütün bu nedenlerden dolayı çalışılan problemin çözümüne yönelik kullanılacak potansiyel seçimi çok önemlidir. Potansiyel seçimi, uğraşılan problemin güçlük indeksini doğrudan etkiler. Pseudo potansiyeli, elektronun doğru davranışını ifade etmek açısından önemlidir fakat mükemmel değildir. Sadece hesaplama tekniklerinde verimliliği artırır. Çekirdek bölgeleri dışında Pseudo potansiyeli ve toplam potansiyel benzer davranışlar sergiler: Değerlik elektronları için saçılma özellikleri aynıdır. Buraya kadar anlatılan kısımda Pseudo potansiyelinin deneysel ve teorik uygulamalarda neden kullanıldığına değindik. Şekil 2: Kartezyen Koordinatlarda Pseudo Harmonik Potansiyel Şekil 2 de Kartezyen koordinatlarda temsil edilen Pseudo harmonik potansiyeli verilmiştir. Yaptığımız Pseudodot çalışması böyle bir potansiyelin varlığındadır. Bundan sonra bu potansiyel altında Schrödinger denkleminin çözümünü yaparak kuantumlu enerji özdeğerlerinin nasıl değiştiği inceleyebilir. Konuya başlamadan önce basit harmonikosilatörün çözümüne değinmek doğru olacaktır. Basit harmonikosilatörün çözümü de bir Schrödinger dalga denkleminin çözümüdür. Sadece bu denkleme değişik potansiyeller uygulayarak kuantumlu farklı enerji değerleri elde edilir. Bu sistemlerin doğruluk dereceleri kullanılan potansiyel seçimi ve sistemi tanımlayacak dalga fonksiyonlarıyla doğru orantılıdır. Sisteminize uyguladığınız potansiyel ve dalga fonksiyonları ne kadar uygun ve kullanışlı ise elde edeceğiniz sonuçlardaki doğruluk derecesi de o derece hassas olur. 3
14 1.2. BİR BOYUTLU HARMONİK OSİLATÖR Bir denge konumu etrafında salınımlar yapan bir parçacığın hareketi, fiziğin en temel problemlerinden birini oluşturur. Değişik birçok fiziksel sistemin (diatomik moleküllerin titreşimi, kristal örgülerde atomların veya çekirdek içinde nükleonların salınımları, vs.) temel yapısı bir harmoniksalınıcı problemidir. Burada vereceğimiz harmoniksalınıcının kuantal incelenmesi, tüm bu sistemlerin fiziksel davranışlarını doğru olarak tanımlayabilmektedir. Ayrıca, elektromanyetik alanların kuantum teorisi yapılmak istendiğinde, harmoniksalınıcının temsilleri anahtar rol oynamaktadır (Kuantum Alanlar Teorisi). Salınıcı problemine iki farklı şekilde yaklaşılabilir: Bir yöntem Schrödinger diferansiyel denklemini doğrudan çözmek, diğer bir yöntemde ise salınıcıhamiltonyeni bir takım operatörler cinsinden yazmak ve operatör cebiri yardımıyla sonuca varmaktır. Burada biz diferansiyel denklem çözümü üzerinde duracağız. Kütlesi m olan ve bir denge konumundan uzaklığına bağlı olarak gibi bir kuvvetin etkisinde hareket eden bir parçacık ele alalım. Bu sistemin toplam enerjisi olarak yazılabilir. Burada açısal frekanstır. Kuantal çözümü bulmak için Schrödinger denklemi yazılırsa Matematiksel işlemlerde kolaylık sağlamak adına bu denklem boyutsuz hale getirilir. Önce bağımsız x değişkenini boyutsuz yapan bir sabiti olduğunu varsayalım. Buna göre yeni bağımsız değişken olur. olduğu göz önüne alınırsa Schrödinger denklemi 4
15 [ ] şeklinde yazılabilir. Şimdi nin katsayısını yapan değeri seçilir. Bu yaptığımız işlem denklemimizi boyutsuzlaştırmaya dönüktür. olur. Daha sonra E enerji terimini boyutsuz yapan bir sabiti seçilir. Şimdi boyutsuz Schrödinger denklemimizi yazabiliriz. Daha sonra bu diferansiyel denklem için bir çözüm önereceğiz. Schrödinger denklemini Pseudo potansiyeli altında çözdüğümüzde benzer metodu uygulayacağımız için bu kısımda anlatılanlara tekrardan değinilmeyecektir. İndirgenmiş diferansiyel denklemimiz aşağıdaki gibidir: Diferansiyel Denklemin Çözümü Diferansiyel denklemin çözümüne yönelik bir fikir edinmek üzere dalga fonksiyonumuzu uzun ve kısa limitte incelemeye tabi tutacağız. Bu limit değerlerinde inceleme yaparken lı terim küçük kalacağından ihmal edilebilir. Yaklaşık olarak elde edilen denklem; olur. Bu diferansiyel denklemin çözümünü sağlayan dalga fonksiyonu; şeklindedir. Şimdide acaba sonlu değerleri için de bu asimptotik davranışı gösteren çözümler yakalanabilir mi diye bakılır. 5
16 şeklinde çözümler aransın. Burada dikkat edilmesi gereken bir hususta; sonsuzda sınırlı kalabilmek için negatif üslü çözümün alınmasıdır. Schrödinger denkleminde kullanılmak üzere, [ ] İfadeleri yerine yazılırsa, yeni fonksiyonunun sağlayacağı denklem, olur. Bu denklem kuvvet serisine açılarak veya Frobenius yöntemi kullanılarak çözülebilir. Bunun için fonksiyonu bir kuvvet serisi şeklinde açılarak bir üstteki denklemde yerine yazılır. Burada katsayıları bulunursa fonksiyonları bulunmuş olur. Bu seri cinsinden ve ifadeleri hesaplanarak denkleminde yerine yazılırsa; şeklinde bir denklem elde edilir. Bu denklemde gerekli ara işlemler yapıldığında aşağıdaki şekle indirgenir. Buradan hareketle katsayıları arasında bir tekrarlama (rekürans) bağıntısı elde edilir: 6
17 Kuvvet serisinin ilk iki katsayıları olan ve biliniyorsa, serinin diğer katsayıları da bu bağıntı sayesinde türetilebilir. Bu katsayıların oluşturduğu sonsuz terimli seri, aradığımız fonksiyonu olacaktır. Ancak burada karşımıza yeni bir sorun çıkmaktadır. Acaba bu sonsuz terimli seri çözümü yakınsak mıdır? Aksi takdirde dalga fonksiyonu olarak kabul edilemez. Bu sorunun yanıtını vermek üzere dolaylı bir yol izleyerek ardışık katsayılar oranı olan ifadesinin m indisinin büyümesiyle nasıl değiştiğine bakalırsa: Bu serinin davranışının fonksiyonunun davranışı şeklinde olduğu açıktır. Yani yine fonksiyonunun davranışı gibidir. ( ) olduğu göz önüne alınırsa bu serinin katsayılarının asimptotik davranışı, ( ) ( ) Buradan da anlaşılacağı üzere serinin başlangıç terimleri farklı olabilir fakat kuvvetleri yükseldikçe iki seride aynı davranışı sergiler. Bu durumda fonksiyonu dalga gibi davranacak, yani sonsuzda ıraksak olacaktır. O halde sonsuz terimli bir seri çözümü kabul edilemez. Bu güçlüğü aşmanın bir yolu vardır: katsayılarını veren ifadeye tekrar bakılacak olursa indisinin bir değerinde geldiğimizde payın sıfır olması gerekir. Burada şeklinde ilerlemektedir. Seri bu değerinde biter, çünkü bu değerinden itibaren olacak demektir. Böylece çözümleri birer polinom olurlar. Bu durumda; 7
18 olmalıdır. Burada daha önce tanımladığımız katsayısının ne olduğu hatırlanırsa; olur. Böylece seri çözümlerinin dalga fonksiyonu olabilme koşulunu sağlamasını isteyerek kuantumlu enerji öz değerlerini nin değişen değerleriyle bulmuş oluruz. Şimdi dalga fonksiyonlarını bulmaya çalışalım. Bu katsayıları hesaplarken ve katsayıları keyfi seçilebilir. Özel olarak ve değerleri seçilirse çift çözümler, ve değerleri seçilirse tek çözümler olmak üzere, matematikte bilinen özel polinomlar ailesinden Hermite polinomları elde edilir. Başlangıçta dalga fonksiyonunu seçtiğimiz hatırlanırsa, harmonik salınıcı fonksiyonları da kuantum sayısına bağlı olarak ( ) bulunur. sabitini bulmak için dalga fonksiyonunun normlanması gerekmektedir. 8
19 Bu son integralin Hermite polinomları için diklik bağıntısı olduğu açıkça görülmektedir( ). Bunun değeri yazılırsa, bulunur. Özetle harmoniksalınıcı dalga fonksiyonlarının değişimi aşağıdaki gibi değişim sergilemektedir. Sonuçları değerlendirecek olursak; E n özdeğerlerinin kuantize olduğunu ve eşit aralıklarla değiştiğini görebilirsiniz. Gerçektende diatomik moleküllerin titreşim yoluyla uyarılması sonucu elde edilen spektrumlarda her bir radyasyonun frekansı, doğal frekans denilen bir değerinin tam katları şeklinde değişim sergilemektedir. Taban durumu enerjisinin sıfırdan farklı oluşu tamamen bir kuantal etkidir. Eğer olsaydı parçacık hem durgun ve hem de denge konumunda olurdu. Buda momentum ve konumun birlikte kesin olarak bilinmesi anlamına gelir ki bu durumda belirsizlik ilkesine aykırı olurdu. Taban durumu enerjisine sıfır-noktası enerjisi denir. Her bir dalga fonksiyonunun tam tane reel kökü veya düğüm noktası vardır. Bu özellik çok geneldir: Enerji arttıkça dalga fonksiyonunun düğüm noktalarının sayısı da artar. Yine aynı yöntemle üç boyutta harmonikosilatörün enerji özdeğerleri için bir çözüm bulmak üzere işlemlerimize devam edeceğiz. Bir boyutlu çözümde gerekli ayrıntılara değindiğimizden dolayı üç boyutta ara işlemler üzerinde durulmayacaktır(karaoğlu, 2008). 9
20 1.3. ÜÇ BOYUTLU HARMONİK SALINICI PROBLEMİ Burada iki boyutlu harmoniksalınıcı probleminin çözümüne, üç boyutlu uygulamanın çözümünden ulaşılabileceğinden dolayı değinilmemiştir. Daha önce yaptığımız gibi 3- boyutlu harmoniksalınıcı hamiltonyenini tanımlayarak işe başlayalım. Burada her eksen boyunca denir. Bu potansiyelde kürsel simetriktir, çünkü elastik sabiti aynı alındığından, buna izotropik salınıcı da olur ve potansiyel açıdan bağımsızdır. O halde, radyal Schrödinger denklemimiz, [ ] olmaktadır. Bu denklemin her için çözümü karmaşık olduğundan dolayı burada sadece durumları yani durumu için çözümler arayacağız. Önce yerine bir fonksiyonu tanımlayalım: Bu fonksiyonu cinsinden radyal denklem için yazılırsa olur. Bu denklemin çözümü bildiğimiz tek boyutlu harmoniksalınıcı denklemidir. Ancak bu kez sınır koşulları farklıdır. Radyal denklemin genel özellikleri incelerken [ ] olması gerektiğini daha önce görmüştük. O halde, ancak tek indisli Hermite polinomları da sıfır olacağından, çözümler 10
21 [ ] şeklinde bulunur. Burada normlama sabitidir ve daha önce tanımlanmıştır. Görüldüğü gibi enerji özdeğerleri sıfır durumu enerjisiyle başlamakta ve iki birim artmaktadır. Şimdide hidrojen atomunun radyal kısmının çözümüne kısaca değindikten sonra Pseudo potansiyeli altında radyal Schrödinger denklemimizin bir, iki ve üç boyutta çözümlerini ele alacağız. Bu problemlerin çözümünü vermemizin amacı, ilerleyen aşamalarda karşımıza çıkacak zorlukların çözülmesi adına fikir edinmektir. Bir harmonik salınıcı probleminin bir, iki ve üç boyuttaki çözümleri ve Hidrojen atomu probleminin çözümü bilinmeden Pseudo potansiyeli altındaki çözümleri kavramak güçtür. Bu problemlerden yola çıkarak Pseudo potansiyeli altında radyal Schrödinger denklemini çözerek enerji özdeğerlerini bulmamız daha da kolaylaşır. Çünkü bu problemler ileriki aşamalarda çıkmamız gereken merdivenin alt basamaklarını oluşturmaktadırlar. 11
22 1.4. HİDROJEN ATOMU PROBLEMİNİN RADYAL KISMININ ÇÖZÜMÜ İndirgenmiş kütleli bir parçacığın 3-boyutlu uzayda potansiyeli altındaki hareketi için radyal Schrödinger denklemi, [ ] şeklindedir. Burada potansiyeli çekici olduğu için, bağlı durumların varlığı ancak olduğunda mümkündür. Burada sadece bağlı durumlar incelenecektir. Radyal denklemi boyutsuz hale getirmek amacıyla, boyutsuz bir değişkeni ve enerji parametresi tanımlanırsa: ( ) Boyutsuz radyal denklemimiz; [ ] şekline dönüşür. Önce bu diferansiyel denklemin asimptotik davranışına bakılırsa; Küçük değerleri için şeklinde davranır. Buna fonksiyonun kısa limitte davranışı da denir. 12
23 Daha sonra büyük değerleri için, denklemdeki terimi diğerlerini bastıracağı için, yaklaşık olarak, alınabilir. Bu genel çözümü, olmaktadır. Dikkat edilecek olursa bu çözümün sonsuzda ıraksak olmaması için olması gerekir. Bu fonksiyonun asimptotik davranışını inceledikten sonra, dalga fonksiyonu için şeklinde bir çözüm aranması gerekmektedir. Bu asimptotik davranışı ele almaktaki amaç, kalan fonksiyonu için polinom şeklinde bir çözüm yakalamaktır. Eğer ara işlemler yapılırsa bir Laguerre polinomu şeklinde bir denklem elde edileceği görülecektir. Bu ifade radyal denklemde kullanılırsa, nun sağladığı yeni denklem halini alır. Bu denklem için daha öncede belirtilmiş olarak kuvvet serisi yöntemiyle çözüme gidilir. fonksiyonu bir kuvvet serisine açılarak yukarıdaki denkleme uyarlanacak şekilde türevler alındığında varacağımız yer; [ ] 13
24 Bu eşitliğin her değerinde sağlanabilmesi için köşeli parantez içerisindeki terimlerin sıfır olması gerekir. Buradan katsayıları için bir tekrarlama bağıntısı elde edilir: Daha sonra bu seri çözümü, yakınsak mı yoksa ıraksak mı şeklinde daha öncede bahsedilmiş olarak bir denemeye tabi tutulur. Bu sorunun çözülmesi içinde seri çözümünün sonlu bir değerde bitmesi gerektiği kanaatine varılacaktır. Bunun için de tekrarlama bağıntısında belli bir değerinden sonra payın sıfır olması gerektiği anlaşılacaktır. Eşitliğin sol tarafındaki indisler birer tamsayı olduğundan, sağ taraftaki enerji parametreside tamsayı olmak durumundadır. Bu tamsayı değeri ile gösterilir ve temel kuantum sayısı adını alır. Burada gibi her değeri alabileceği için yörünge kuantum sayısı da ancak ( ) değerlerini alabilir veya olur. parametresini enerjiye bağlayan ifade kullanılırsa Hidrojen atomu için enerji düzeyleri elde edilmiş olur: 14
25 2. PSEUDO HARMONİK POTANSİYEL KULLANILARAK YAPILAN ÇALIŞMALAR Pseudo harmonik potansiyeli hem dot hemde antidot potansiyelini içermektedir. Daha öncede belirtildiği gibi Coulomb potansiyelinden daha yumuşak bir potansiyeldir. Bizim yapmış olduğumuz çalışmada Pseudo harmonik potansiyelinde antidot ifadesi sıfır yapan değerlerin limiti alındığında sistemin basit harmonikosilatöre indirgenmesini bekleyebiliriz. Pseudo harmonik potansiyel kullanılarak hem deneysel hem de teorik çalışmalar yapılmıştır. Şimdi bu çalışmalardan kısaca bahsedelim. Kaliforniya üniversitesinden James R. Chelikowsky ve Marvin L. Cohen yerel olmayan deneysel bir Pseudo potansiyeli şeması altında Si, Ge, α-sn, GaP, GaAs, GaSb, InP, InAs, InSb, ZnSe, ve CdTe gibi on bir yarı iletkenin elektronik yapısı için hesaplamalar yapmışlardır. Bant yapısı, yansıma spektrumları, elektronik yoğunluk durumları ve değerlik yük yoğunlukları belirlenmiş ve deneysel verilerle karşılaştırılmıştır. Optik boşluklar, optik kritik nokta topolojileri, valans bant genişlikleri ve değerlik yük dağılımları geliştirilerek daha önceki yerel Pseudo potansiyeliyle elde edilen sonuçlarla karşılaştırılmıştır (Chelikowsky & Cohen, 1976). A. Çetin Aharanov-Bohm etkisiyle birlikte bir manyetik alan varlığında hem dot hem de antidot içeren Pseudo harmonik potansiyelde, hapsedilmiş bir elektrona karşılık gelen dalga fonksiyonlarını ve enerji seviyelerini araştırmıştır. Enerji seviyeleri ve dalga fonksiyonlarını böyle tam çözülebilir sistemler için bulmuştur. Bunların hepsi çeşitli koşullar altında test edilmiş ve literatürdeki verilerle kıyaslanmıştır (Cetin, 2008). Kaliforniya üniversitesi kimya bölümünden, Jiangtao Hu, Lin-wangWang, LiangshiLiWeidongyang ve A.Paul AlivisatosCdSe kuantum çubuklarının uzunluğu ve çapının elektronik durumlara bağımlılığını, yarı deneysel Pseudo potansiyeli hesaplamalarını kullanarak araştırmışlardır. Boy oranı karşısında çapraz enerji seviyeleri farklı uzunluklarına bağlı olarak artmıştır. Bu hesaplamalar sıfır boyutlu kuantum noktalarından bir boyutlu kuantum tellerine elektronik geçişi göstermektedir (Hu, Wang, Li, Yang, & Alivisatos, 2002). 15
26 G. Simons, H 2 O ve HF ninvalans elektron özelliklerini bir Pseudo potansiyeli modelini kullanarak hesaplamıştır. Hesaplanan geometriler, kuvvet sabitleri ve iyonizasyon potansiyelleri tüm elektronlara karşılık gelen hesaplama sonuçlarıyla mükemmel bir uyum içerisinde olduğunu tespit etmiştir (Simons, 1973). G. Rezaei ve arkadaşları yakın zamanda düzgün bir manyetik alan etkisi altında bantlar arası geçişlerle ilgili kırılma indeksi değişiklikleri ve optik soğurma katsayısı değişiklikleri üzerine teorik bir çalışma yapmışlardır. Pseudodot sisteminin elektronik yapısı tek bant etkin kütle yaklaşımı kullanılarak incelemelerinin yanı sırayoğunluk matrisi yaklaşımı kullanılarak doğrusal ve doğrusal olmayan optikselabsorbsiyon katsayısı değişiklikleriyle kırılma indisi değişikliklerini hesaplamışlardır. Optikselabsorbsiyon katsayısı ve kırılma indisi değişimlerini, Pseudodot sisteminin boyutları ve manyetik alanın etkisinde incelemişlerdir. Absorbsiyon katsayısı ve kırılma indisi değişimlerini sadece güçlü bir dış manyetik alanın değil aynı zamanda Pseudot sisteminin geometrik boyutlarının da etkilediği bulunmuştur (Rezaei G., Vaseghi, Taghizadeh, Vahdani, & Karimi, 2010). R. Khordad dış bir manyetik alan etkisi altında, kuantum Pseudodot sisteminde doğrudan bant geçişleri üzerinde çalışmıştır. Kuantum Pseudodot sisteminin geometrik boyutu ve uygulanan manyetik alanın bir fonksiyonu olarak soğurma eşik frekansı ve soğurma katsayısı için ifadeler elde etmiştir. Yapılan çalışmada soğurma eşik frekansı üzerinde uygulanan manyetik alanın ve Pseudodot sisteminin boyutlarının önemli bir rolü olduğu belirlenmiştir (Khordad, 2010). Wenfang Xie yakın zamanda bir kuantum Pseudodot sisteminin Raman saçılma özellikleri üzerinde inceleme yapmıştır. İki boyutlu Pseudodot sisteminde Raman elektron saçılmanı ele almıştır. Kesit farklılığının sistemin boyutundan ve uygulanan manyetik alandan etkilendiği belirlenmiştir. Daha büyük saçılma yoğunluklarının farklı potansiyeller altında elde edilebileceği belirtmiştir (Xie, Electron Raman scattering of a two-dimensional pseudodot system, 2012). G. Rezaei düzgün bir manyetik alan etkisi altında iki boyutlu kuantum Pseudot sistemlerinde bantlar arası geçişle ilgili optikselrektifikasyon katsayısını teorik olarak incelemiştir. Bu bağlamda Pseudodot sisteminin optikselrektifikasyon katsayısını 16
27 yoğunluk matrisi yaklaşımı ve iteratif metodunu kullanarak bulmuştur. Dış bir manyetik alan, geometrik boyutlar ve kimyasal potansiyelin etkisi altında Pseudodot sistemlerinde bu katsayı incelenmiştir. Optikselrektifikasyon katsayısının Pseudodot sisteminin kimyasal potansiyeli, geometrik boyutları ve dış bir manyetik alanın etkisiyle değiştiği bulunmuştur (Rezaei G., Vaseghi, Khordad, & Azadi Kenary, 2011). R. Schuster ve arkadaşları süper iletken bir filmde bir antidot örgüyle Shapiro basamaklarını incelemişlerdir. Sınırlı sayıda periyotlarda antidot örgüleri üretmişlerdir. Öyle ki toplam sistemin boyutu düşük sıcaklıklarda elektronların faz uyumu uzunluğundan çok küçüktür. Manyetik direnç klasik özdeş titreşimlerin yanı sıra tekrarlanabilir kuantum dalgalanmalarından baskındır. Aharanov Bohm titreşiminin varlığı belirlenmiş ve klasik olarak yörüngeye tutturulmuş elektron varlığıyla ilişkilendirilmiştir (Schuster, Ensslin, Wharam, Kühn, & Kotthaus, 1994). M. Kataoka, C. J. B. Ford ve arkadaşları Kuantum Hall Rejiminde bir antidot etrafında Coulomb elektriklenmesi üzerinde çalışmışlardır. Büyük bir B manyetik alanın fonksiyonu olarak iki boyutlu bir elektron gazında potansiyel tepesi (antidot) etrafındaki yüklerin titreşimleri belirlenmiştir. Kapalı yörüngelerde antidot etrafında alanla sınırlandırılan elektronlar söz konusu bölgede, Aharonov - Bohm etkisiyle kuantumlanmıştır. Artan manyetik alan her durumun alanını azaltır, elektronları merkeze yakın bölgelere iter, tünel dışına çıkan bir elektron için yeterli yük kurar. Bu elektrostatiksel sınırlı dotlarda görülen yeni bir Coulomb ablukası şeklidir. DC geriliminde toplama ve uyarılma spektrumları Coulombblockade tünelini desteklemiştir (Kataoka, et al., 1999). J. Reijniers ve F. M. Peeters manyetik bir antidotta kuantum durumları üzerinde çalışmıştır. İki boyutta homojen olmayan bir manyetik alanla sınırlandırılan elektronlardan oluşan bir sistem üzerinde çalışmışlardır. Sistem bir heteroyapıyla bunun üzerindeki bir süper iletken diskten oluşmaktadır. Sistemde yer alan elektronların dot bölgelerinde sınırlandırılabileceği görülmüştür. Bu manyetik antidot ilginç özelliklere sahiptir, öyle ki dolu dotlar manyetik alanın kesikli bir fonksiyonudur. Bağlı durumların bazıları için dot içinde ve dışında elektron akışı ters yönde olabilir. Böyle durumlar manyetik alanın artmasıyla paramanyetik geçişe bir diyamantizma sergilemektedir (Reijniers, Peeters, & Matilus, 1999). 17
28 3. PSEUDODOT ÇÖZÜMLERİ Bir boyutta Pseudo harmonik potansiyelinde hapsolmuş bir elektronun enerji özdeğerlerinin değişimini belirlemek için öncelikle Schrödinger denkleminin çözülmesi gerekir. Bütün küresel simetrik potansiyellerde açısal kısmın çözümü değişmediğinden ve kullandığımız Pseudo harmonik potansiyelinin açıya bağlı olmamasından dolayı yapacağımız hesaplamalar Schrödinger denkleminin radyal kısmı üzerinde yoğunlaşacaktır. Fakat açısal kısım da radyal kısmın yanı sıra ele alınacaktır. Bu potansiyelde hapsolan elektronun maksimum bulunabileceği yer r 0 noktalarının eksenleri kestiği yerdir. Çünkü burada potansiyel minimumdur ve dolayısıyla elektronumuzun burada bulunma ihtimali diğer potansiyel değerlerinden daha fazladır. Bu bilgiler ışığında bir boyutta Pseudo harmonik potansiyelinde hapsolan elektronun davranışını incelemeye başlayabiliriz BİR BOYUTLU PSEUDODOT ÇÖZÜMÜ VE ENERJİ SEVİYELERİ Pseudo harmonik potansiyelde hapsolmuş m kütleli E enerjili bir parçacık için bir boyutlu Schrödinger denklemi yazılırsa; Pseudo potansiyeli altındaki radyal denklem olmak üzere, 18
29 Yukarıdaki denklemi düzenlemek adına eşitliğin her tarafını ile çarpalım: [ ] Bu denklemin çözülebilmesi için denklemde yer alan ifadelerinin bir basamak indirgenmesi gerekmektedir. Bu durumda işlemlerimize yeni değişkenler tanımlayarak devam edeceğiz. Burada tanımlamış olduğumuz değişken değişiminin Denklem ( değeri denklemimizi bir basamak indirgeyecektir. Bu ) yerine yazılmasıyla; ( ) [ ] Elde etmiş olduğumuz bu denklemde gerekli düzenlemeler yapıp, denklemin her tarafını önce ile ve daha sonra e bölersek; [ ( )] Şimdide bulduğumuz denklemi boyutsuz hale getirmek için bazı sabitler tanımlayarak işlemlerimize devam edeceğiz. 19
30 O halde boyutsuz indirgenmiş denklem, [ ] halini alır. Bundan sonra elde edilmiş olan indirgenmiş denklemin asimptotik davranışını, daha öncede bir boyutlu harmoniksalınıcı probleminin çözümünde de değinildiği gibi uzun limit ve kısa limitlerde ele almak faydalı olacaktır. Uzun limitte davranış için ; [ ] halini alır. Bu denklemin çözümü, dir. Kısa limitte davranış için ; [ ] Şekline gelir ki, bu denkleme gibi bir çözüm önerilirse ve bu ifadenin türevleri alınıp üst denklemde yazılırsa denklem sistemimizi sağlayan değeri tespit edilmiş olur. Burada bilmemiz gereken başka bir hususta bulunacak olan değerinin pozitif bir sayı olması gerektiğidir. [ ] Bu denklemin kökleri ikinci dereceden denklemlerin çözümünden kolayca hesaplanabilir. Bu sonucu veren denklem kökü de; ( ) değeridir. nün değerini de tayin edildikten sonra indirgenmiş denklemi sağlayan fonksiyonu şu şekilde tanımlarız: 20
FİZİK 4. Ders 10: Bir Boyutlu Schrödinger Denklemi
 FİZİK 4 Ders 10: Bir Boyutlu Schrödinger Denklemi Bir Boyutlu Schrödinger Denklemi Beklenen Değer Kuyu İçindeki Parçacık Zamandan Bağımsız Schrödinger Denklemi Kare Kuyu Tünel Olayı Basit Harmonik Salınıcı
FİZİK 4 Ders 10: Bir Boyutlu Schrödinger Denklemi Bir Boyutlu Schrödinger Denklemi Beklenen Değer Kuyu İçindeki Parçacık Zamandan Bağımsız Schrödinger Denklemi Kare Kuyu Tünel Olayı Basit Harmonik Salınıcı
TİTREŞİM VE DALGALAR BÖLÜM PERİYODİK HAREKET
 TİTREŞİM VE DALGALAR Periyodik Hareketler: Belirli aralıklarla tekrarlanan harekete periyodik hareket denir. Sabit bir nokta etrafında periyodik hareket yapan cismin hareketine titreşim hareketi denir.
TİTREŞİM VE DALGALAR Periyodik Hareketler: Belirli aralıklarla tekrarlanan harekete periyodik hareket denir. Sabit bir nokta etrafında periyodik hareket yapan cismin hareketine titreşim hareketi denir.
Bölüm 1: Lagrange Kuramı... 1
 İÇİNDEKİLER Bölüm 1: Lagrange Kuramı... 1 1.1. Giriş... 1 1.2. Genelleştirilmiş Koordinatlar... 2 1.3. Koordinat Dönüşüm Denklemleri... 3 1.4. Mekanik Dizgelerin Bağ Koşulları... 4 1.5. Mekanik Dizgelerin
İÇİNDEKİLER Bölüm 1: Lagrange Kuramı... 1 1.1. Giriş... 1 1.2. Genelleştirilmiş Koordinatlar... 2 1.3. Koordinat Dönüşüm Denklemleri... 3 1.4. Mekanik Dizgelerin Bağ Koşulları... 4 1.5. Mekanik Dizgelerin
BÖLÜM 12-15 HARMONİK OSİLATÖR
 BÖLÜM 12-15 HARMONİK OSİLATÖR Hemen hemen her sistem, dengeye yaklaşırken bir harmonik osilatör gibi davranabilir. Kuantum mekaniğinde sadece sayılı bir kaç problem kesin olarak çözülebilmektedir. Örnekler
BÖLÜM 12-15 HARMONİK OSİLATÖR Hemen hemen her sistem, dengeye yaklaşırken bir harmonik osilatör gibi davranabilir. Kuantum mekaniğinde sadece sayılı bir kaç problem kesin olarak çözülebilmektedir. Örnekler
BÖLÜM 17 RİJİT ROTOR
 BÖLÜM 17 RİJİT ROTOR Birbirinden R sabit mesafede bulunan iki parçacığın dönmesini düşünelim. Bu iki parçacık, bir elektron ve proton (bu durumda bir hidrojen atomunu ele alıyoruz) veya iki çekirdek (bu
BÖLÜM 17 RİJİT ROTOR Birbirinden R sabit mesafede bulunan iki parçacığın dönmesini düşünelim. Bu iki parçacık, bir elektron ve proton (bu durumda bir hidrojen atomunu ele alıyoruz) veya iki çekirdek (bu
BÖLÜM 24 PAULI SPİN MATRİSLERİ
 BÖLÜM 24 PAULI SPİN MATRİSLERİ Elektron spini için dalga fonksiyonlarını tanımlamak biraz kullanışsız görünüyor. Çünkü elektron, 3B uzayda dönmek yerine sadece kendi berlirlediği bir rotada dönüyor. Elektron
BÖLÜM 24 PAULI SPİN MATRİSLERİ Elektron spini için dalga fonksiyonlarını tanımlamak biraz kullanışsız görünüyor. Çünkü elektron, 3B uzayda dönmek yerine sadece kendi berlirlediği bir rotada dönüyor. Elektron
Elektromanyetik Dalga Teorisi
 Elektromanyetik Dalga Teorisi Ders-2 Dalga Denkleminin Çözümü Düzlem Elektromanyetik Dalgalar Enine Elektromanyetik Dalgalar Kayıplı Ortamda Düzlem Dalgalar Düzlem Dalgaların Polarizasyonu Dalga Denkleminin
Elektromanyetik Dalga Teorisi Ders-2 Dalga Denkleminin Çözümü Düzlem Elektromanyetik Dalgalar Enine Elektromanyetik Dalgalar Kayıplı Ortamda Düzlem Dalgalar Düzlem Dalgaların Polarizasyonu Dalga Denkleminin
Potansiyel Engeli: Tünelleme
 Potansiyel Engeli: Tünelleme Şekil I: Bir potansiyel engelinde tünelleme E
Potansiyel Engeli: Tünelleme Şekil I: Bir potansiyel engelinde tünelleme E
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ
 BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
8.04 Kuantum Fiziği Ders XII
 Enerji ölçümünden sonra Sonucu E i olan enerji ölçümünden sonra parçacık enerji özdurumu u i de olacak ve daha sonraki ardışık tüm enerji ölçümleri E i enerjisini verecektir. Ölçüm yapılmadan önce enerji
Enerji ölçümünden sonra Sonucu E i olan enerji ölçümünden sonra parçacık enerji özdurumu u i de olacak ve daha sonraki ardışık tüm enerji ölçümleri E i enerjisini verecektir. Ölçüm yapılmadan önce enerji
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 5- SONLU FARKLAR VE İNTERPOLASYON TEKNİKLERİ Doç. Dr. Ali Rıza YILDIZ MAK 210 - Sayısal Analiz 1 İNTERPOLASYON Tablo halinde verilen hassas sayısal değerler veya ayrık noktalardan
MAK 210 SAYISAL ANALİZ BÖLÜM 5- SONLU FARKLAR VE İNTERPOLASYON TEKNİKLERİ Doç. Dr. Ali Rıza YILDIZ MAK 210 - Sayısal Analiz 1 İNTERPOLASYON Tablo halinde verilen hassas sayısal değerler veya ayrık noktalardan
1. BÖLÜM Polinomlar BÖLÜM II. Dereceden Denklemler BÖLÜM II. Dereceden Eşitsizlikler BÖLÜM Parabol
 ORGANİZASYON ŞEMASI . BÖLÜM Polinomlar... 7. BÖLÜM II. Dereceden Denklemler.... BÖLÜM II. Dereceden Eşitsizlikler... 9. BÖLÜM Parabol... 5 5. BÖLÜM Trigonometri... 69 6. BÖLÜM Karmaşık Sayılar... 09 7.
ORGANİZASYON ŞEMASI . BÖLÜM Polinomlar... 7. BÖLÜM II. Dereceden Denklemler.... BÖLÜM II. Dereceden Eşitsizlikler... 9. BÖLÜM Parabol... 5 5. BÖLÜM Trigonometri... 69 6. BÖLÜM Karmaşık Sayılar... 09 7.
İşaret ve Sistemler. Ders 3: Periyodik İşaretlerin Frekans Spektrumu
 İşaret ve Sistemler Ders 3: Periyodik İşaretlerin Frekans Spektrumu Fourier Serileri Periyodik işaretlerin spektral analizini yapabilmek için periyodik işaretler sinüzoidal işaretlerin toplamına dönüştürülür
İşaret ve Sistemler Ders 3: Periyodik İşaretlerin Frekans Spektrumu Fourier Serileri Periyodik işaretlerin spektral analizini yapabilmek için periyodik işaretler sinüzoidal işaretlerin toplamına dönüştürülür
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM
 BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM 4.1. Giriş Bir önceki bölümde, hareket denklemi F = ma nın, maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini
BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM 4.1. Giriş Bir önceki bölümde, hareket denklemi F = ma nın, maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini
VEKTÖR UZAYLARI 1.GİRİŞ
 1.GİRİŞ Bu bölüm lineer cebirin temelindeki cebirsel yapıya, sonlu boyutlu vektör uzayına giriş yapmaktadır. Bir vektör uzayının tanımı, elemanları skalar olarak adlandırılan herhangi bir cisim içerir.
1.GİRİŞ Bu bölüm lineer cebirin temelindeki cebirsel yapıya, sonlu boyutlu vektör uzayına giriş yapmaktadır. Bir vektör uzayının tanımı, elemanları skalar olarak adlandırılan herhangi bir cisim içerir.
18.034 İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
BÖLÜM 1: TEMEL KAVRAMLAR
 BÖLÜM 1: TEMEL KAVRAMLAR Hal Değişkenleri Arasındaki Denklemler Aralarında sıfıra eşitlenebilen en az bir veya daha fazla denklem kurulabilen değişkenler birbirine bağımlıdır. Bu denklemlerden bilinen
BÖLÜM 1: TEMEL KAVRAMLAR Hal Değişkenleri Arasındaki Denklemler Aralarında sıfıra eşitlenebilen en az bir veya daha fazla denklem kurulabilen değişkenler birbirine bağımlıdır. Bu denklemlerden bilinen
İÇİNDEKİLER KISIM 1: BİRİNCİ MERTEBE ADİ DİFERENSİYEL DENKLEMLER
 İÇİNDEKİLER KISIM 1: BİRİNCİ MERTEBE ADİ DİFERENSİYEL DENKLEMLER 1.1. Fiziksel Kanunlar ve Diferensiyel Denklemler Arasındaki İlişki... 1 1.2. Diferensiyel Denklemlerin Sınıflandırılması ve Terminoloji...
İÇİNDEKİLER KISIM 1: BİRİNCİ MERTEBE ADİ DİFERENSİYEL DENKLEMLER 1.1. Fiziksel Kanunlar ve Diferensiyel Denklemler Arasındaki İlişki... 1 1.2. Diferensiyel Denklemlerin Sınıflandırılması ve Terminoloji...
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
İNSTAGRAM:kimyaci_glcn_hoca
 MODERN ATOM TEORİSİ ATOMUN KUANTUM MODELİ Bohr atom modeli 1 H, 2 He +, 3Li 2+ vb. gibi tek elektronlu atom ve iyonların çizgi spektrumlarını başarıyla açıklamıştır.ancak çok elektronlu atomların çizgi
MODERN ATOM TEORİSİ ATOMUN KUANTUM MODELİ Bohr atom modeli 1 H, 2 He +, 3Li 2+ vb. gibi tek elektronlu atom ve iyonların çizgi spektrumlarını başarıyla açıklamıştır.ancak çok elektronlu atomların çizgi
Elektromanyetik Dalga Teorisi Ders-3
 Elektromanyetik Dalga Teorisi Ders-3 Faz ve Grup Hızı Güç ve Enerji Düzlem Dalgaların Düzlem Sınırlara Dik Gelişi Düzlem Dalgaların Düzlem Sınırlara Eğik Gelişi Dik Kutuplama Paralel Kutuplama Faz ve Grup
Elektromanyetik Dalga Teorisi Ders-3 Faz ve Grup Hızı Güç ve Enerji Düzlem Dalgaların Düzlem Sınırlara Dik Gelişi Düzlem Dalgaların Düzlem Sınırlara Eğik Gelişi Dik Kutuplama Paralel Kutuplama Faz ve Grup
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Geçen Derste. ρ için sınır şartları serinin bir yerde sona ermesini gerektirir. 8.04 Kuantum Fiziği Ders XXIII
 Geçen Derste Verilen l kuantum sayılı açısal momentum Y lm (θ,φ) özdurumunun radyal denklemi 1B lu SD şeklinde etkin potansiyeli olacak şekilde yazılabilir, u(r) = rr(r) olarak tanımlayarak elde edilir.
Geçen Derste Verilen l kuantum sayılı açısal momentum Y lm (θ,φ) özdurumunun radyal denklemi 1B lu SD şeklinde etkin potansiyeli olacak şekilde yazılabilir, u(r) = rr(r) olarak tanımlayarak elde edilir.
18.034 İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak ya Kullanım Şartları hakkında bilgi almak için
MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak ya Kullanım Şartları hakkında bilgi almak için
ÜNİTE. MATEMATİK-1 Doç.Dr.Erdal KARADUMAN İÇİNDEKİLER HEDEFLER ÖZDEŞLİKLER, DENKLEMLER VE EŞİTSİZLİKLER
 HEDEFLER İÇİNDEKİLER ÖZDEŞLİKLER, DENKLEMLER VE EŞİTSİZLİKLER Özdeşlikler Birinci Dereceden Bir Bilinmeyenli Denklemler İkinci Dereceden Bir Bilinmeyenli Denklemler Yüksek Dereceden Denklemler Eşitsizlikler
HEDEFLER İÇİNDEKİLER ÖZDEŞLİKLER, DENKLEMLER VE EŞİTSİZLİKLER Özdeşlikler Birinci Dereceden Bir Bilinmeyenli Denklemler İkinci Dereceden Bir Bilinmeyenli Denklemler Yüksek Dereceden Denklemler Eşitsizlikler
İstatistik ve Olasılık
 İstatistik ve Olasılık KORELASYON ve REGRESYON ANALİZİ Doç. Dr. İrfan KAYMAZ Tanım Bir değişkenin değerinin diğer değişkendeki veya değişkenlerdeki değişimlere bağlı olarak nasıl etkilendiğinin istatistiksel
İstatistik ve Olasılık KORELASYON ve REGRESYON ANALİZİ Doç. Dr. İrfan KAYMAZ Tanım Bir değişkenin değerinin diğer değişkendeki veya değişkenlerdeki değişimlere bağlı olarak nasıl etkilendiğinin istatistiksel
SCHRÖDİNGER: Elektronun yeri (yörüngesi ve orbitali) birer dalga fonksiyonu olan n, l, m l olarak ifade edilen kuantum sayıları ile belirlenir.
 . ATOMUN KUANTUM MODELİ SCHRÖDİNGER: Elektronun yeri (yörüngesi ve orbitali) birer dalga fonksiyonu olan n, l, m l olarak ifade edilen kuantum sayıları ile belirlenir. Orbital: Elektronların çekirdek etrafında
. ATOMUN KUANTUM MODELİ SCHRÖDİNGER: Elektronun yeri (yörüngesi ve orbitali) birer dalga fonksiyonu olan n, l, m l olarak ifade edilen kuantum sayıları ile belirlenir. Orbital: Elektronların çekirdek etrafında
8.04 Kuantum Fiziği Ders X. Schrödinger denk. bir V(x) potansiyeli içinde bir boyutta bir parçacığın hareketini inceler.
 Schrödinger denklemi Schrödinger denk. bir V(x) potansiyeli içinde bir boyutta bir parçacığın hareketini inceler. Köşeli parantez içindeki terim, dalga fonksiyonuna etki eden bir işlemci olup, Hamilton
Schrödinger denklemi Schrödinger denk. bir V(x) potansiyeli içinde bir boyutta bir parçacığın hareketini inceler. Köşeli parantez içindeki terim, dalga fonksiyonuna etki eden bir işlemci olup, Hamilton
İnce Antenler. Hertz Dipolü
 İnce Antenler Çapları boylarına göre küçük olan antenlere ince antenler denir. Alanların hesabında antenlerin sonsuz ince kabul edilmesi kolaylık sağlar. Ancak anten empedansı bulunmak istendiğinde kalınlığın
İnce Antenler Çapları boylarına göre küçük olan antenlere ince antenler denir. Alanların hesabında antenlerin sonsuz ince kabul edilmesi kolaylık sağlar. Ancak anten empedansı bulunmak istendiğinde kalınlığın
8.04 Kuantum Fiziği DersXIX
 Bu takdirde yani, 1 = a ˆ 0 de bir enerji özdurumudur, ancak 0 için enerjisi 1hω yerine 3 hω dir. 2 2 Benzer şekilde, 2 = a ˆ 1 inde bir enerji özdurumu olduğunu fakat enerjisinin 5 hω, vs. 2 söyleyebiliriz.
Bu takdirde yani, 1 = a ˆ 0 de bir enerji özdurumudur, ancak 0 için enerjisi 1hω yerine 3 hω dir. 2 2 Benzer şekilde, 2 = a ˆ 1 inde bir enerji özdurumu olduğunu fakat enerjisinin 5 hω, vs. 2 söyleyebiliriz.
Nötr (yüksüz) bir için, çekirdekte kaç proton varsa çekirdeğin etrafındaki yörüngelerde de o kadar elektron dolaşır.
 ATOM ve YAPISI Elementin özelliğini taşıyan en küçük parçasına denir. Atom Numarası Bir elementin unda bulunan proton sayısıdır. Protonlar (+) yüklü olduklarından pozitif yük sayısı ya da çekirdek yükü
ATOM ve YAPISI Elementin özelliğini taşıyan en küçük parçasına denir. Atom Numarası Bir elementin unda bulunan proton sayısıdır. Protonlar (+) yüklü olduklarından pozitif yük sayısı ya da çekirdek yükü
A B = A. = P q c A( X(t))
 Ders 19 Metindeki ilgili bölümler 2.6 Elektromanyetik bir alanda yüklü parçacık Şimdi, kuantum mekaniğinin son derece önemli başka bir örneğine geçiyoruz. Verilen bir elektromanyetik alanda hareket eden
Ders 19 Metindeki ilgili bölümler 2.6 Elektromanyetik bir alanda yüklü parçacık Şimdi, kuantum mekaniğinin son derece önemli başka bir örneğine geçiyoruz. Verilen bir elektromanyetik alanda hareket eden
8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
FİZ217 TİTREŞİMLER VE DALGALAR DERSİNİN 2. ARA SINAV SORU CEVAPLARI
 1) Gerilmiş bir ipte enine titreşimler denklemi ile tanımlıdır. Değişkenlerine ayırma yöntemiyle çözüm yapıldığında için [ ] [ ] ifadesi verilmiştir. 1.a) İpin enine titreşimlerinin n.ci modunu tanımlayan
1) Gerilmiş bir ipte enine titreşimler denklemi ile tanımlıdır. Değişkenlerine ayırma yöntemiyle çözüm yapıldığında için [ ] [ ] ifadesi verilmiştir. 1.a) İpin enine titreşimlerinin n.ci modunu tanımlayan
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
TERMODİNAMİĞİN BİRİNCİ YASASI
 İç Enerji Fonksiyonu ve C v Isınma Isısı Kimyasal tepkimelerin olmadığı kapalı sistemlerde kütle yanında molar miktar da sabit kalmaktadır. Madde miktarı n mol olan kapalı bir ideal gaz sistemi düşünelim.
İç Enerji Fonksiyonu ve C v Isınma Isısı Kimyasal tepkimelerin olmadığı kapalı sistemlerde kütle yanında molar miktar da sabit kalmaktadır. Madde miktarı n mol olan kapalı bir ideal gaz sistemi düşünelim.
1.ÜNİTE MODERN ATOM TEORİSİ -2.BÖLÜM- ATOMUN KUANTUM MODELİ
 1.ÜNİTE MODERN ATOM TEORİSİ -2.BÖLÜM- ATOMUN KUANTUM MODELİ Bohr Modelinin Yetersizlikleri Dalga-Tanecik İkiliği Dalga Mekaniği Kuantum Mekaniği -Orbital Kavramı Kuantum Sayıları Yörünge - Orbital Kavramları
1.ÜNİTE MODERN ATOM TEORİSİ -2.BÖLÜM- ATOMUN KUANTUM MODELİ Bohr Modelinin Yetersizlikleri Dalga-Tanecik İkiliği Dalga Mekaniği Kuantum Mekaniği -Orbital Kavramı Kuantum Sayıları Yörünge - Orbital Kavramları
MIT Açık Ders Malzemeleri http://ocw.mit.edu. 5.62 Fizikokimya II 2008 Bahar
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 5.62 Fizikokimya II 2008 Bahar Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak in http://ocw.mit.edu/terms ve http://tuba.acikders.org.tr
MIT Açık Ders Malzemeleri http://ocw.mit.edu 5.62 Fizikokimya II 2008 Bahar Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak in http://ocw.mit.edu/terms ve http://tuba.acikders.org.tr
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 6- İSTATİSTİK VE REGRESYON ANALİZİ Doç. Dr. Ali Rıza YILDIZ 1 İSTATİSTİK VE REGRESYON ANALİZİ Bütün noktalardan geçen bir denklem bulmak yerine noktaları temsil eden, yani
MAK 210 SAYISAL ANALİZ BÖLÜM 6- İSTATİSTİK VE REGRESYON ANALİZİ Doç. Dr. Ali Rıza YILDIZ 1 İSTATİSTİK VE REGRESYON ANALİZİ Bütün noktalardan geçen bir denklem bulmak yerine noktaları temsil eden, yani
5. Salih Zeki Matematik Araştırma Projeleri Yarışması PROJENİN ADI DİZİ DİZİ ÜRETEÇ PROJEYİ HAZIRLAYAN ESRA DAĞ ELİF BETÜL ACAR
 5. Salih Zeki Matematik Araştırma Projeleri Yarışması PROJENİN ADI DİZİ DİZİ ÜRETEÇ PROJEYİ HAZIRLAYAN ESRA DAĞ ELİF BETÜL ACAR ÖZEL BÜYÜKÇEKMECE ÇINAR KOLEJİ 19 Mayıs Mah. Bülent Ecevit Cad. Tüyap Yokuşu
5. Salih Zeki Matematik Araştırma Projeleri Yarışması PROJENİN ADI DİZİ DİZİ ÜRETEÇ PROJEYİ HAZIRLAYAN ESRA DAĞ ELİF BETÜL ACAR ÖZEL BÜYÜKÇEKMECE ÇINAR KOLEJİ 19 Mayıs Mah. Bülent Ecevit Cad. Tüyap Yokuşu
A. Seçilmiş bağıntılar Zamana bağlı Schrödinger denklemi: Zamandan bağımsız Schrödinger denklemi: Hamilton işlemcisinin konum temsili
 A. Seçilmiş bağıntılar Zamana bağlı Schrödinger denklemi: Zamandan bağımsız Schrödinger denklemi: Hamilton işlemcisinin konum temsili Momentum işlemcisinin konum temsili Konum işlemcisinin momentum temsili
A. Seçilmiş bağıntılar Zamana bağlı Schrödinger denklemi: Zamandan bağımsız Schrödinger denklemi: Hamilton işlemcisinin konum temsili Momentum işlemcisinin konum temsili Konum işlemcisinin momentum temsili
18.034 İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Cebirsel Fonksiyonlar
 Cebirsel Fonksiyonlar Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 4 Amaçlar Bu üniteyi çalıştıktan sonra; polinom, rasyonel ve cebirsel fonksiyonları tanıyacak ve bu türden bazı fonksiyonların grafiklerini öğrenmiş
Cebirsel Fonksiyonlar Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 4 Amaçlar Bu üniteyi çalıştıktan sonra; polinom, rasyonel ve cebirsel fonksiyonları tanıyacak ve bu türden bazı fonksiyonların grafiklerini öğrenmiş
8.04 Kuantum Fiziği Ders IV. Kırınım olayı olarak Heisenberg belirsizlik ilkesi. ise, parçacığın dalga fonksiyonu,
 Geçen Derste Kırınım olayı olarak Heisenberg belirsizlik ilkesi ΔxΔp x 2 Fourier ayrışımı Bugün φ(k) yı nasıl hesaplarız ψ(x) ve φ(k) ın yorumu: olasılık genliği ve olasılık yoğunluğu ölçüm φ ( k)veyahut
Geçen Derste Kırınım olayı olarak Heisenberg belirsizlik ilkesi ΔxΔp x 2 Fourier ayrışımı Bugün φ(k) yı nasıl hesaplarız ψ(x) ve φ(k) ın yorumu: olasılık genliği ve olasılık yoğunluğu ölçüm φ ( k)veyahut
EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER
 EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER LAGRANGE YÖNTEMİ Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde değişkenler ve kısıtlar genel olarak şeklinde gösterilir. fonksiyonlarının
EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER LAGRANGE YÖNTEMİ Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde değişkenler ve kısıtlar genel olarak şeklinde gösterilir. fonksiyonlarının
BÖLÜM 16 KUANTUM : AYRILABİLEN SİSTEMLER
 BÖLÜM 16 KUANTUM : AYRILABİLEN SİSTEMLER Farklı eksenlere karşılık gelen operatörler, komut verilerek birbiriyle komute olabilir. Ayrıca, bir değişken için olan operatör, başka bir operatörün fonksiyonu
BÖLÜM 16 KUANTUM : AYRILABİLEN SİSTEMLER Farklı eksenlere karşılık gelen operatörler, komut verilerek birbiriyle komute olabilir. Ayrıca, bir değişken için olan operatör, başka bir operatörün fonksiyonu
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 9 Ağırlık Merkezi ve Geometrik Merkez Kaynak: Mühendislik Mekaniği: Statik, R. C. Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 9. Ağırlık
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 9 Ağırlık Merkezi ve Geometrik Merkez Kaynak: Mühendislik Mekaniği: Statik, R. C. Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 9. Ağırlık
Şekil 6.1 Basit sarkaç
 Deney No : M5 Deney Adı : BASİT SARKAÇ Deneyin Amacı yer çekimi ivmesinin belirlenmesi Teorik Bilgi : Sabit bir noktadan iple sarkıtılan bir cisim basit sarkaç olarak isimlendirilir. : Basit sarkaçta uzunluk
Deney No : M5 Deney Adı : BASİT SARKAÇ Deneyin Amacı yer çekimi ivmesinin belirlenmesi Teorik Bilgi : Sabit bir noktadan iple sarkıtılan bir cisim basit sarkaç olarak isimlendirilir. : Basit sarkaçta uzunluk
Elastisite Teorisi Düzlem Problemleri için Sonuç 1
 Elastisite Teorisi Düzlem Problemleri için Sonuç 1 Düzlem Gerilme durumu için: Bilinmeyenler: Düzlem Şekil değiştirme durumu için: Bilinmeyenler: 3 gerilme bileşeni : 3 gerilme bileşeni : 3 şekil değiştirme
Elastisite Teorisi Düzlem Problemleri için Sonuç 1 Düzlem Gerilme durumu için: Bilinmeyenler: Düzlem Şekil değiştirme durumu için: Bilinmeyenler: 3 gerilme bileşeni : 3 gerilme bileşeni : 3 şekil değiştirme
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
FİZ4001 KATIHAL FİZİĞİ-I
 FİZ4001 KATIHAL FİZİĞİ-I Bölüm 3. Örgü Titreşimleri: Termal, Akustik ve Optik Özellikler Dr. Aytaç Gürhan GÖKÇE Katıhal Fiziği - I Dr. Aytaç Gürhan GÖKÇE 1 Bir Boyutlu İki Atomlu Örgü Titreşimleri M 2
FİZ4001 KATIHAL FİZİĞİ-I Bölüm 3. Örgü Titreşimleri: Termal, Akustik ve Optik Özellikler Dr. Aytaç Gürhan GÖKÇE Katıhal Fiziği - I Dr. Aytaç Gürhan GÖKÇE 1 Bir Boyutlu İki Atomlu Örgü Titreşimleri M 2
Doğrusal Demet Işıksallığı 2. Fatma Çağla Öztürk
 Doğrusal Demet Işıksallığı Fatma Çağla Öztürk İçerik Demet Yönlendirici Mıknatıslar Geleneksel Demir Baskın Mıknatıslar 3.07.01 HPFBU Toplantı, OZTURK F. C. Demet Yönlendirici Mıknatıslar Durgun mıknatıssal
Doğrusal Demet Işıksallığı Fatma Çağla Öztürk İçerik Demet Yönlendirici Mıknatıslar Geleneksel Demir Baskın Mıknatıslar 3.07.01 HPFBU Toplantı, OZTURK F. C. Demet Yönlendirici Mıknatıslar Durgun mıknatıssal
Toplam İkinci harmonik. Temel Üçüncü harmonik. Şekil 1. Temel, ikinci ve üçüncü harmoniğin toplamı
 FOURIER SERİLERİ Bu bölümde Fourier serilerinden bahsedeceğim. Önce harmoniklerle (katsıklıklarla) ilişkili sinüsoidin tanımından başlıyacağım ve serilerin trigonometrik açılımlarını kullanarak katsayıları
FOURIER SERİLERİ Bu bölümde Fourier serilerinden bahsedeceğim. Önce harmoniklerle (katsıklıklarla) ilişkili sinüsoidin tanımından başlıyacağım ve serilerin trigonometrik açılımlarını kullanarak katsayıları
Bölüm 3. Tek Serbestlik Dereceli Sistemlerin Zorlanmamış Titreşimi
 Bölüm 3 Tek Serbestlik Dereceli Sistemlerin Zorlanmamış Titreşimi Sönümsüz Titreşim: Tek serbestlik dereceli örnek sistem: Kütle-Yay (Yatay konum) Bir önceki bölümde anlatılan yöntemlerden herhangi biri
Bölüm 3 Tek Serbestlik Dereceli Sistemlerin Zorlanmamış Titreşimi Sönümsüz Titreşim: Tek serbestlik dereceli örnek sistem: Kütle-Yay (Yatay konum) Bir önceki bölümde anlatılan yöntemlerden herhangi biri
Magnetic Materials. 7. Ders: Ferromanyetizma. Numan Akdoğan.
 Magnetic Materials 7. Ders: Ferromanyetizma Numan Akdoğan akdogan@gyte.edu.tr Gebze Institute of Technology Department of Physics Nanomagnetism and Spintronic Research Center (NASAM) Moleküler Alan Teorisinin
Magnetic Materials 7. Ders: Ferromanyetizma Numan Akdoğan akdogan@gyte.edu.tr Gebze Institute of Technology Department of Physics Nanomagnetism and Spintronic Research Center (NASAM) Moleküler Alan Teorisinin
1.1 Yapı Dinamiğine Giriş
 1.1 Yapı Dinamiğine Giriş Yapı Dinamiği, dinamik yükler etkisindeki yapı sistemlerinin dinamik analizini konu almaktadır. Dinamik yük, genliği, doğrultusu ve etkime noktası zamana bağlı olarak değişen
1.1 Yapı Dinamiğine Giriş Yapı Dinamiği, dinamik yükler etkisindeki yapı sistemlerinin dinamik analizini konu almaktadır. Dinamik yük, genliği, doğrultusu ve etkime noktası zamana bağlı olarak değişen
İÇİNDEKİLER ÖNSÖZ Bölüm 1 KÜMELER Bölüm 2 SAYILAR
 İÇİNDEKİLER ÖNSÖZ III Bölüm 1 KÜMELER 11 1.1. Küme 12 1.2. Kümelerin Gösterimi 13 1.3. Boş Küme 13 1.4. Denk Küme 13 1.5. Eşit Kümeler 13 1.6. Alt Küme 13 1.7. Alt Küme Sayısı 14 1.8. Öz Alt Küme 16 1.9.
İÇİNDEKİLER ÖNSÖZ III Bölüm 1 KÜMELER 11 1.1. Küme 12 1.2. Kümelerin Gösterimi 13 1.3. Boş Küme 13 1.4. Denk Küme 13 1.5. Eşit Kümeler 13 1.6. Alt Küme 13 1.7. Alt Küme Sayısı 14 1.8. Öz Alt Küme 16 1.9.
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
6. HAFTA DERS NOTLARI İKTİSADİ MATEMATİK MİKRO EKONOMİK YAKLAŞIM. Yazan SAYIN SAN
 6. HAFTA DERS NOTLARI İKTİSADİ MATEMATİK MİKRO EKONOMİK YAKLAŞIM Yazan SAYIN SAN SAN / İKTİSADİ MATEMATİK / 2 A.5. Doğrusal olmayan fonksiyonların eğimi Doğrusal fonksiyonlarda eğim her noktada sabittir
6. HAFTA DERS NOTLARI İKTİSADİ MATEMATİK MİKRO EKONOMİK YAKLAŞIM Yazan SAYIN SAN SAN / İKTİSADİ MATEMATİK / 2 A.5. Doğrusal olmayan fonksiyonların eğimi Doğrusal fonksiyonlarda eğim her noktada sabittir
MIT Açık Ders Malzemeleri Fizikokimya II 2008 Bahar
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 5.62 Fizikokimya II 2008 Bahar Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için http://ocw.mit.edu/terms ve http://tuba.acikders.org.tr
MIT Açık Ders Malzemeleri http://ocw.mit.edu 5.62 Fizikokimya II 2008 Bahar Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için http://ocw.mit.edu/terms ve http://tuba.acikders.org.tr
Fen ve Mühendislik Bilimleri için Fizik
 Fen ve Mühendislik Bilimleri için Fizik Giriş Fizik Temel Bilimlerin Amacı Doğanın işleyişinde görev alan temel kanunları anlamak. Diğer fen ve mühendislik bilimleri için temel hazırlamaktır. Temelde gerekli
Fen ve Mühendislik Bilimleri için Fizik Giriş Fizik Temel Bilimlerin Amacı Doğanın işleyişinde görev alan temel kanunları anlamak. Diğer fen ve mühendislik bilimleri için temel hazırlamaktır. Temelde gerekli
Kuantum Mekaniğinin Varsayımları
 Kuantum Mekaniğinin Varsayımları Kuantum mekaniği 6 temel varsayım üzerine kurulmuştur. Kuantum mekaniksel problemler bu varsayımlar kullanılarak (teorik/kuramsal olarak) çözülmekte ve elde edilen sonuçlar
Kuantum Mekaniğinin Varsayımları Kuantum mekaniği 6 temel varsayım üzerine kurulmuştur. Kuantum mekaniksel problemler bu varsayımlar kullanılarak (teorik/kuramsal olarak) çözülmekte ve elde edilen sonuçlar
ELEKTRİKSEL POTANSİYEL
 ELEKTRİKSEL POTANSİYEL Elektriksel Potansiyel Enerji Elektriksel potansiyel enerji kavramına geçmeden önce Fizik-1 dersinizde görmüş olduğunuz iş, potansiyel enerji ve enerjinin korunumu kavramları ile
ELEKTRİKSEL POTANSİYEL Elektriksel Potansiyel Enerji Elektriksel potansiyel enerji kavramına geçmeden önce Fizik-1 dersinizde görmüş olduğunuz iş, potansiyel enerji ve enerjinin korunumu kavramları ile
Projenin Adı: Metalik Oranlar ve Karmaşık Sayı Uygulamaları
 Projenin Adı: Metalik Oranlar ve Karmaşık Sayı Uygulamaları Projenin Amacı: Metalik Oranların elde edildiği ikinci dereceden denklemin diskriminantını ele alarak karmaşık sayılarla uygulama yapmak ve elde
Projenin Adı: Metalik Oranlar ve Karmaşık Sayı Uygulamaları Projenin Amacı: Metalik Oranların elde edildiği ikinci dereceden denklemin diskriminantını ele alarak karmaşık sayılarla uygulama yapmak ve elde
Kuantum Fiziği (PHYS 201) Ders Detayları
 Kuantum Fiziği (PHYS 201) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Kuantum Fiziği PHYS 201 Her İkisi 3 0 0 3 5 Ön Koşul Ders(ler)i PHYS 102, MATH 158
Kuantum Fiziği (PHYS 201) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Kuantum Fiziği PHYS 201 Her İkisi 3 0 0 3 5 Ön Koşul Ders(ler)i PHYS 102, MATH 158
Tek Boyutlu Potansiyeller: Potansiyel eşiği
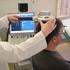 Tek Boyutlu Potansiyeller: Potansiyel eşiği Şekil I: V 0 yüksekliğindeki potansiyel eşiği. Parçacık soldan gelmekte olup, enerjisi E dir. Zamandan bağımsız bir durumu analiz ediyoruz ki burada iyi belirlenmiş
Tek Boyutlu Potansiyeller: Potansiyel eşiği Şekil I: V 0 yüksekliğindeki potansiyel eşiği. Parçacık soldan gelmekte olup, enerjisi E dir. Zamandan bağımsız bir durumu analiz ediyoruz ki burada iyi belirlenmiş
ATOMİK YAPI. Elektron Yükü=-1,60x10-19 C Proton Yükü=+1,60x10-19 C Nötron Yükü=0
 ATOMİK YAPI Atom, birkaç türü birleştiğinde çeşitli molekülleri, bir tek türü ise bir kimyasal öğeyi oluşturan parçacıktır. Atom, elementlerin özelliklerini taşıyan en küçük yapı birimi olup çekirdekteki
ATOMİK YAPI Atom, birkaç türü birleştiğinde çeşitli molekülleri, bir tek türü ise bir kimyasal öğeyi oluşturan parçacıktır. Atom, elementlerin özelliklerini taşıyan en küçük yapı birimi olup çekirdekteki
Enerji Sistemleri Mühendisliği Bölümü
 YALOVA ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ Enerji Sistemleri Mühendisliği Bölümü ESM 413 Enerji Sistemleri Laboratuvarı-II RL, RC ve RLC DEVRELERİNİN AC ANALİZİ Puanlandırma Sistemi: Hazırlık Soruları:
YALOVA ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ Enerji Sistemleri Mühendisliği Bölümü ESM 413 Enerji Sistemleri Laboratuvarı-II RL, RC ve RLC DEVRELERİNİN AC ANALİZİ Puanlandırma Sistemi: Hazırlık Soruları:
Özet: Açısal momentumun türetimi. Açısal momentum değiştirme bağıntıları. Artırıcı ve Eksiltici İşlemciler Kuantum Fiziği Ders XXI
 Özet: Açısal momentumun türetimi Açısal momentum değiştirme bağıntıları Levi- Civita simgesi Genel olarak, L x, L y, L z, nin eşzamanlı özdurumları yoktur L 2 ve bir bileşeni (L z ) nin eşzamanlı özdurumlarıdır.
Özet: Açısal momentumun türetimi Açısal momentum değiştirme bağıntıları Levi- Civita simgesi Genel olarak, L x, L y, L z, nin eşzamanlı özdurumları yoktur L 2 ve bir bileşeni (L z ) nin eşzamanlı özdurumlarıdır.
İÇİNDEKİLER. BÖLÜM 1 Değişkenler ve Grafikler 1. BÖLÜM 2 Frekans Dağılımları 37
 İÇİNDEKİLER BÖLÜM 1 Değişkenler ve Grafikler 1 İstatistik 1 Yığın ve Örnek; Tümevarımcı ve Betimleyici İstatistik 1 Değişkenler: Kesikli ve Sürekli 1 Verilerin Yuvarlanması Bilimsel Gösterim Anlamlı Rakamlar
İÇİNDEKİLER BÖLÜM 1 Değişkenler ve Grafikler 1 İstatistik 1 Yığın ve Örnek; Tümevarımcı ve Betimleyici İstatistik 1 Değişkenler: Kesikli ve Sürekli 1 Verilerin Yuvarlanması Bilimsel Gösterim Anlamlı Rakamlar
Örnek...3 : Aşağıdaki ifadelerden hangileri bir dizinin genel terim i olabilir?
 DİZİLER Tanım kümesi pozitif tam sayılar kümesi olan her fonksiyona dizi denir. Örneğin f : Z + R, f (n )=n 2 ifadesi bir dizi belirtir. Diziler, değer kümelerine göre adlandırı - lırlar. Dizinin değer
DİZİLER Tanım kümesi pozitif tam sayılar kümesi olan her fonksiyona dizi denir. Örneğin f : Z + R, f (n )=n 2 ifadesi bir dizi belirtir. Diziler, değer kümelerine göre adlandırı - lırlar. Dizinin değer
ATOMİK YAPI. Elektron Yükü=-1,60x10-19 C Proton Yükü=+1,60x10-19 C Nötron Yükü=0
 ATOMİK YAPI Elektron Yükü=-1,60x10-19 C Proton Yükü=+1,60x10-19 C Nötron Yükü=0 Elektron Kütlesi 9,11x10-31 kg Proton Kütlesi Nötron Kütlesi 1,67x10-27 kg Bir kimyasal elementin atom numarası (Z) çekirdeğindeki
ATOMİK YAPI Elektron Yükü=-1,60x10-19 C Proton Yükü=+1,60x10-19 C Nötron Yükü=0 Elektron Kütlesi 9,11x10-31 kg Proton Kütlesi Nötron Kütlesi 1,67x10-27 kg Bir kimyasal elementin atom numarası (Z) çekirdeğindeki
Sistem Dinamiği. Bölüm 2- Dinamik Cevap ve Laplace Dönüşümü. Doç.Dr. Erhan AKDOĞAN
 Sistem Dinamiği - Dinamik Cevap ve Laplace Dönüşümü Doç. Sunumlarda kullanılan semboller: El notlarına bkz. Yorum Soru MATLAB Bolum No.Alt Başlık No.Denklem Sıra No Denklem numarası Şekil No Şekil numarası
Sistem Dinamiği - Dinamik Cevap ve Laplace Dönüşümü Doç. Sunumlarda kullanılan semboller: El notlarına bkz. Yorum Soru MATLAB Bolum No.Alt Başlık No.Denklem Sıra No Denklem numarası Şekil No Şekil numarası
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 8- SAYISAL İNTEGRASYON 1 GİRİŞ Mühendislikte sık karşılaşılan matematiksel işlemlerden biri integral işlemidir. Bilindiği gibi integral bir büyüklüğün toplam değerinin bulunması
MAK 210 SAYISAL ANALİZ BÖLÜM 8- SAYISAL İNTEGRASYON 1 GİRİŞ Mühendislikte sık karşılaşılan matematiksel işlemlerden biri integral işlemidir. Bilindiği gibi integral bir büyüklüğün toplam değerinin bulunması
KİNETİK GAZ KURAMI. Doç. Dr. Faruk GÖKMEŞE Kimya Bölümü Hitit Üniversitesi Fen Edebiyat Fakültesi 1
 Kinetik Gaz Kuramından Gazların Isınma Isılarının Bulunması Sabit hacimdeki ısınma ısısı (C v ): Sabit hacimde bulunan bir mol gazın sıcaklığını 1K değiştirmek için gerekli ısı alışverişi. Sabit basınçtaki
Kinetik Gaz Kuramından Gazların Isınma Isılarının Bulunması Sabit hacimdeki ısınma ısısı (C v ): Sabit hacimde bulunan bir mol gazın sıcaklığını 1K değiştirmek için gerekli ısı alışverişi. Sabit basınçtaki
2. REGRESYON ANALİZİNİN TEMEL KAVRAMLARI Tanım
 2. REGRESYON ANALİZİNİN TEMEL KAVRAMLARI 2.1. Tanım Regresyon analizi, bir değişkenin başka bir veya daha fazla değişkene olan bağımlılığını inceler. Amaç, bağımlı değişkenin kitle ortalamasını, açıklayıcı
2. REGRESYON ANALİZİNİN TEMEL KAVRAMLARI 2.1. Tanım Regresyon analizi, bir değişkenin başka bir veya daha fazla değişkene olan bağımlılığını inceler. Amaç, bağımlı değişkenin kitle ortalamasını, açıklayıcı
İÇİNDEKİLER ÖNSÖZ Bölüm 1 SAYILAR 11 Bölüm 2 KÜMELER 31 Bölüm 3 FONKSİYONLAR
 İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 11 1.1. Sayı Kümeleri 12 1.1.1.Doğal Sayılar Kümesi 12 1.1.2.Tam Sayılar Kümesi 13 1.1.3.Rasyonel Sayılar Kümesi 14 1.1.4. İrrasyonel Sayılar Kümesi 16 1.1.5. Gerçel
İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 11 1.1. Sayı Kümeleri 12 1.1.1.Doğal Sayılar Kümesi 12 1.1.2.Tam Sayılar Kümesi 13 1.1.3.Rasyonel Sayılar Kümesi 14 1.1.4. İrrasyonel Sayılar Kümesi 16 1.1.5. Gerçel
Modern Fizik (Fiz 206)
 Modern Fizik (Fiz 206) 3. Bölüm KUANTUM Mekaniği Bohr modelinin sınırları Düz bir dairenin çevresinde hareket eden elektronu tanımlar Saçılma deneyleri elektronların çekirdek etrafında, çekirdekten uzaklaştıkça
Modern Fizik (Fiz 206) 3. Bölüm KUANTUM Mekaniği Bohr modelinin sınırları Düz bir dairenin çevresinde hareket eden elektronu tanımlar Saçılma deneyleri elektronların çekirdek etrafında, çekirdekten uzaklaştıkça
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
İTKİLİ MOTORLU UÇAĞIN YATAY UÇUŞ HIZI
 İTKİLİ MOTORLU UÇAĞIN YATAY UÇUŞ HIZI Mustafa Cavcar Anadolu Üniversitesi Havacılık ve Uzay Bilimleri Fakültesi 26470 Eskişehir Yatay uçuş sabit uçuş irtifaında yeryüzüne paralel olarak yapılan uçuştur.
İTKİLİ MOTORLU UÇAĞIN YATAY UÇUŞ HIZI Mustafa Cavcar Anadolu Üniversitesi Havacılık ve Uzay Bilimleri Fakültesi 26470 Eskişehir Yatay uçuş sabit uçuş irtifaında yeryüzüne paralel olarak yapılan uçuştur.
Gamma Bozunumu
 Gamma Bozunumu Genelde beta ( ) ve alfa ( ) bozunumu sonunda çekirdek uyarılmış haldedir. Uyarılmış çekirdek gamma ( ) salarak temel seviyeye döner. Gamma görünür ışın ve x ışını gibi elektromanyetik radyasyon
Gamma Bozunumu Genelde beta ( ) ve alfa ( ) bozunumu sonunda çekirdek uyarılmış haldedir. Uyarılmış çekirdek gamma ( ) salarak temel seviyeye döner. Gamma görünür ışın ve x ışını gibi elektromanyetik radyasyon
Fen ve Mühendislik Bilimleri için Fizik
 Fen ve Mühendislik Bilimleri için Fizik Giriş Fizik Temel Bilimlerin Amacı Doğanın işleyişinde görev alan temel kanunları anlamak. Diğer fen ve mühendislik bilimleri için temel hazırlamaktır. Temelde gerekli
Fen ve Mühendislik Bilimleri için Fizik Giriş Fizik Temel Bilimlerin Amacı Doğanın işleyişinde görev alan temel kanunları anlamak. Diğer fen ve mühendislik bilimleri için temel hazırlamaktır. Temelde gerekli
İstatistiksel Mekanik I
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
8.Konu Vektör uzayları, Alt Uzaylar
 8.Konu Vektör uzayları, Alt Uzaylar 8.1. Düzlemde vektörler Düzlemdeki her noktası ile reel sayılardan oluşan ikilisini eşleştirebiliriz. Buna P noktanın koordinatları denir. y-ekseni P x y O dan P ye
8.Konu Vektör uzayları, Alt Uzaylar 8.1. Düzlemde vektörler Düzlemdeki her noktası ile reel sayılardan oluşan ikilisini eşleştirebiliriz. Buna P noktanın koordinatları denir. y-ekseni P x y O dan P ye
18.034 İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
ATOM BİLGİSİ Atom Modelleri
 1. Atom Modelleri BÖLÜM2 Maddenin atom adı verilen bir takım taneciklerden oluştuğu fikri çok eskiye dayanmaktadır. Ancak, bilimsel bir (deneye dayalı) atom modeli ilk defa Dalton tarafından ileri sürülmüştür.
1. Atom Modelleri BÖLÜM2 Maddenin atom adı verilen bir takım taneciklerden oluştuğu fikri çok eskiye dayanmaktadır. Ancak, bilimsel bir (deneye dayalı) atom modeli ilk defa Dalton tarafından ileri sürülmüştür.
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 7- SAYISAL TÜREV Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ İntegral işlemi gibi türev işlemi de mühendislikte çok fazla kullanılan bir işlemdir. Basit olarak bir fonksiyonun bir noktadaki
MAK 210 SAYISAL ANALİZ BÖLÜM 7- SAYISAL TÜREV Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ İntegral işlemi gibi türev işlemi de mühendislikte çok fazla kullanılan bir işlemdir. Basit olarak bir fonksiyonun bir noktadaki
BÖLÜM 25 HELYUM ATOMU
 BÖLÜM 25 HELYUM ATOMU Şimdi, Hidrojene benzer atomları daha detaylı inceleyelim. Bir sonraki en basit sistemi tartışmaya başlayalım: Helyum atomu. Bu durumda, R noktasında konumlanmış Z = 2 yükü bulunan
BÖLÜM 25 HELYUM ATOMU Şimdi, Hidrojene benzer atomları daha detaylı inceleyelim. Bir sonraki en basit sistemi tartışmaya başlayalım: Helyum atomu. Bu durumda, R noktasında konumlanmış Z = 2 yükü bulunan
3.5. Devre Parametreleri
 3..3 3.5. Devre Parametreleri 3.5. Devre Parametreleri Mikrodalga mühendisliğinde doğrusal mikrodalga devrelerini karakterize etmek için dört tip devre parametreleri kullanılır: açılma parametreleri (parametreleri)
3..3 3.5. Devre Parametreleri 3.5. Devre Parametreleri Mikrodalga mühendisliğinde doğrusal mikrodalga devrelerini karakterize etmek için dört tip devre parametreleri kullanılır: açılma parametreleri (parametreleri)
GENEL KİMYA. Yrd.Doç.Dr. Tuba YETİM
 GENEL KİMYA ATOMUN ELEKTRON YAPISI Bohr atom modelinde elektronun bulunduğu yer için yörünge tanımlaması kullanılırken, kuantum mekaniğinde bunun yerine orbital tanımlaması kullanılır. Orbital, elektronun
GENEL KİMYA ATOMUN ELEKTRON YAPISI Bohr atom modelinde elektronun bulunduğu yer için yörünge tanımlaması kullanılırken, kuantum mekaniğinde bunun yerine orbital tanımlaması kullanılır. Orbital, elektronun
= 2 6 Türevsel denkleminin 1) denge değerlerinin bulunuz. 2) Bulmuş olduğunuz dengenin istikrarlı olup olmadığını tespit ediniz.
 Siyasal Bilgiler Fakültesi İktisat Bölümü Matematiksel İktisat Ders Notu Prof. Dr. Hasan Şahin Faz Diyagramı Çizimi Açıklamarı = 2 6 Türevsel denkleminin 1) denge değerlerinin bulunuz. 2) Bulmuş olduğunuz
Siyasal Bilgiler Fakültesi İktisat Bölümü Matematiksel İktisat Ders Notu Prof. Dr. Hasan Şahin Faz Diyagramı Çizimi Açıklamarı = 2 6 Türevsel denkleminin 1) denge değerlerinin bulunuz. 2) Bulmuş olduğunuz
SAYISAL KARARLILIK. Zaman Uzayı Sonlu Farklar Yöntemi
 Dr. Serkan Aksoy SAYISAL KARARLILIK Sayısal çözümlerin kararlı olması zorunludur. Buna göre ZUSF çözümleri de uzay ve zamanda ayrıklaştırma kapsamında kararlı olması için kararlılık koşullarını sağlaması
Dr. Serkan Aksoy SAYISAL KARARLILIK Sayısal çözümlerin kararlı olması zorunludur. Buna göre ZUSF çözümleri de uzay ve zamanda ayrıklaştırma kapsamında kararlı olması için kararlılık koşullarını sağlaması
Türev Uygulamaları ÜNİTE. Amaçlar. İçindekiler. Yazar Prof.Dr. Vakıf CAFEROV
 Türev Uygulamaları Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 10 Amaçlar Bu üniteyi çalıştıktan sonra; türev kavramı yardımı ile fonksiyonun monotonluğunu, ekstremum noktalarını, konvekslik ve konkavlığını, büküm
Türev Uygulamaları Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 10 Amaçlar Bu üniteyi çalıştıktan sonra; türev kavramı yardımı ile fonksiyonun monotonluğunu, ekstremum noktalarını, konvekslik ve konkavlığını, büküm
FEM ile, Hapsolmuş Kuantum Mekaniksel Sistemlerin Çözümü
 FEM ile, Hapsolmuş Kuantum Mekaniksel Sistemlerin Çözümü Yöntem Bir boyutlu bir problem için etkin kütle yaklaşımı ve zarf fonksiyonu (envelope function) yaklaşımı çerçevesinde Hamiltoniyen ve Schrodinger
FEM ile, Hapsolmuş Kuantum Mekaniksel Sistemlerin Çözümü Yöntem Bir boyutlu bir problem için etkin kütle yaklaşımı ve zarf fonksiyonu (envelope function) yaklaşımı çerçevesinde Hamiltoniyen ve Schrodinger
BÖLÜM 1: Matematiğe Genel Bakış 1. BÖLÜM:2 Fizik ve Ölçme 13. BÖLÜM 3: Bir Boyutta Hareket 20. BÖLÜM 4: Düzlemde Hareket 35
 BÖLÜM 1: Matematiğe Genel Bakış 1 1.1. Semboller, Bilimsel Gösterimler ve Anlamlı Rakamlar 1.2. Cebir 1.3. Geometri ve Trigometri 1.4. Vektörler 1.5. Seriler ve Yaklaşıklıklar 1.6. Matematik BÖLÜM:2 Fizik
BÖLÜM 1: Matematiğe Genel Bakış 1 1.1. Semboller, Bilimsel Gösterimler ve Anlamlı Rakamlar 1.2. Cebir 1.3. Geometri ve Trigometri 1.4. Vektörler 1.5. Seriler ve Yaklaşıklıklar 1.6. Matematik BÖLÜM:2 Fizik
tayf kara cisim ışınımına
 13. ÇİZGİ OLUŞUMU Yıldızın iç kısımlarından atmosfere doğru akan ışınım, dalga boyunun yaklaşık olarak sürekli bir fonksiyonudur. Çünkü iç bölgede sıcaklık gradyenti (eğimi) küçüktür ve madde ile ışınım
13. ÇİZGİ OLUŞUMU Yıldızın iç kısımlarından atmosfere doğru akan ışınım, dalga boyunun yaklaşık olarak sürekli bir fonksiyonudur. Çünkü iç bölgede sıcaklık gradyenti (eğimi) küçüktür ve madde ile ışınım
