elde edilir. Akışkan dinamiğinde değişik akım tipleri vardır. Bunlar aşağıdaki gibi tanımlanabilir (Ayyıldız 1983).
|
|
|
- Duygu Karatay
- 6 yıl önce
- İzleme sayısı:
Transkript
1 3. AKIŞKAN DİNAMİĞİ 3.. Newton un İkinci Kanunu Bir akışkan taneciği bir noktadan başka bir noktaya giderken pozitif ya da negatif ivmeyle hareket etmekte ve bu süreçte, üzerine F m. a kuvveti etkimektedir. Bu eşitliğe Newton un ikinci kanunu (yasası) denmektedir. Akışkan taneciğine bu kanunu uygularken akışkan viskozitesiz kabul edilir. Yani akışkanda ısı iletimi sıfırdır ve viskoz kuvvetler yoktur. Akışkana yalnızca basınç kuvveti(f=p.a) ve yerçekimi kuvvetlerinin(w=m.g) etkidiğini kabul ederek Newton un ikinci kanununu bir akışkan taneciğine uyguladığımızda; W+F= m.a elde edilir. Akışkan dinamiğinde değişik akım tipleri vardır. Bunlar aşağıdaki gibi tanımlanabilir (Ayyıldız 983). Homojen(üniform) akım: Bu tip akışta akış hızının doğrultusu ve değeri akışkanın her noktasında değişmez, aynıdır. Homojen olmayan akım(non-üniform): Herhangi bir anda akış hızı her noktada aynı değildir, değişir. Pratikte viskoz alt tabakadaki akışkan her zaman homojen olmayan akımdır. Ancak, akışkan demetinin boyutu ve kesit alanı değişmiyorsa akım homojen kabul edilebilir. Kararlı (düzenli) akım: Bu rejimde akım alanı içerisinde herhangi bir noktadaki akış hızının büyüklük ve yönü zamanla değişmez. Akım alanı içerisindeki farklı noktalarda yani farklı yerlerde hızlar farklı olabilir. Ancak hızın her noktasındaki büyüklüğü ve yönü zamana göre sabittir. Özetle bu akım biçiminde ölçüt olarak zaman göz önüne alınmaktadır. Kararsız (düzensiz) akım: Bu akımda akışkan içerisinde her hangi bir noktadaki koşulların zamanla değiştiği akımlardır. Uygulamada her zaman hız ve basınçta küçük de olsa değişimler vardır. Ancak ortalama değerler sabit ise o akım kararlı kabul edilebilir. Kararlı homojen akım: Akım içerisinde koşulların zamanla ve konumla değişmediği akım tipidir. Örneğin sabit çaplı boruda sabit hızla akan suyun akışı bu tip akıma örnek verilebilir. Kararlı homojen olmayan akım: Koşulların bir noktadan diğer noktaya değiştiği ancak zamanla sabit kaldığı akışlardır. Örneğin gittikçe daralan boruda sabit hızla boruya giren akışkanın, çıkışa doğru hızının değişmesi. 8
2 Kararsız homojen akım: Belirli bir andaki koşulların noktadan noktaya değil zamanla değiştiği akımlardır. Örnek olarak sabit çaplı boruyla sabit debili pompaya bağlı borudaki akışın aniden kesilmesiyle ortaya çıkan durum verilebilir. Kararsız homojen olmayan akımda akış koşulları hem zamanla ve hem de noktadan noktaya değişir. Kanallardaki dalga akımları buna örnektir. 3.. Akım Çizgisi Kararlı (düzenli) akım rejiminde herhangi bir (t) anında ardı ardına sıralanmış noktalardaki hız vektörlerine çizilen teğetlere akım çizgisi denir. Hızlar akım çizgilerine her yerde teğettir. Hızın akım çizgisine dik yönde bir bileşeni yoktur (Ayyıldız 983,White 0). Akım çizgisi üzerinde taneciğin hareketi s= s(t) uzaklığıyla ve akım çizgisinin yerel eğrilik yarıçapıyla R= R(s) tanımlanır. Akım çizgisi boyunca meydana gelen uzaklık, tanecik hızıyla ( V ds / dt) ve eğrilik yarıçapı da akım çizgisinin biçimiyle ilgilidir (Şekil 3.). Akım çizgisi boyunca oluşan (s) koordinatına ilaveten akım çizgisine dik (n) koordinatı da kullanılmaktadır. Şekil 3.. Akım çizgisi ve tanecik hareketi (Munson vd. 994) Akım çizgisi boyunca hareket eden bir akışkan taneciğine birisi akım çizgisi boyunca (as) ve diğeri akım çizgisine dik (n) doğrultusunda (an) ivmesi etkimektedir. Bu ivmeler aşağıdaki gibi yazılabilir (Edis 97a, Munson vd. 994). a s a s a dv V ds. dt s dt V.V s n V R as dv dt : Akım çizgisi boyunca yani (s) koordinatı üzerindeki tanecik ivmesi (m/s ), : Hızın zamana göre türevi (m/s ), 8
3 V s : Hızın (s) koordinatı üzerindeki yola göre kısmi türevi (s - ), ds : (s) koordinatı üzerindeki yolun zamana göre türevi (m/s), dt a : (n) koordinatı üzerindeki akışkan taneciği ivmesi (m/s ), n V R : Tanecik hızı (m/s), : Akışkan taneciğinin eğrilik yarıçapı (m) dir Akım Çizgisi Boyunca Bernoulli Eşitliği Bir akışkan taneciğine F ma eşitliğini uygularken akım çizgisine dik ( n) ve akım çizgisi boyunca olan ( s ) birim vektörleri ve koordinatları göz önüne alındığında akışkan taneciğine akım çizgisi boyunca yalnızca basınç ve ağırlık kuvvetlerinin etkili olduğu kabul edilir. Viskoz kuvvetler ihmal edildiğinde akım çizgisi boyunca etkili olan kuvvetler F ma eşitliği yardımıyla aşağıdaki gibi yazılabilir. P. Sin s V V s a s Burada;.Sin : Akışkan tanecik ağırlığının akım çizgisi boyunca oluşan bileşeni (N/m 3 ). Akım çizgisi yataysa = 0 alınır. P : Akışkan taneciğine (s) koordinat doğrultusunda etkili olan s basınç gradyenti (N/m 3 ), : Akışkanın özgül kütlesi (kg/m 3 ), V V : (s) koordinat doğrultusundaki tanecik ivmesi (m/s ) dir. s Yukarıdaki bağıntıda akışkan taneciğinin hızında meydana gelen değişikliği, basınç gradyenti ve tanecik ağırlığının meydana getirdiği görülmektedir. Sabit (statik) akışkanlarda basınç ve ağırlık kuvvetleri birbirini dengelemekte ve hareket olmamaktadır. Hâlbuki hareketli akışkanlarda burada olduğu gibi basınç ve ağırlık kuvvetleri birbirini dengeleyememekte ve ivme meydana gelmektedir. Yukarıdaki eşitlik bir takım kabullenmelerden sonra aşağıdaki biçime dönüştürülebilir (Buffer 009, McDonough 009): P..V.z sabit 83
4 Bu eşitliğe Bernoulli eşitliği denir ve akım çizgisi boyunca kullanılır ve aşağıdaki koşullarda geçerlidir (Sleigh 00). a) Viskoz kuvvetler ihmal edilmeli, b) Akış kararlı akım alınmalı, c) Akışkan sıkıştırılamaz kabul edilmelidir. Bernoulli eşitliğinin her terimini özgül ağırlığa () böldüğümüzde bir başka kullanımı elde edilmektedir. Bu da; P V g z sabit şeklinde ifade edilir (Sığıner ve Sümer 995, Hewakandamby 0). Bu eşitlik Bernoulli eşitliğinin hareketli ideal akışkanlarda enerji toplamının sabit olduğunu gösterir. Sıkıştırılamaz akışkanların, yükseklik ve basınç enerjisi ile kinetik enerji gibi 3 çeşit enerjisi vardır. Eşitlikteki terimler akışkanın birim ağırlığına düşen enerjiler olduğundan her terim uzunluk boyutundadır. Yukarıdaki bağıntılarda; gz: Potansiyel yük tür (enerji) (m). P : Ele alınan noktanın basıncı olup birimi Pa dır, : Akışkanın özgül kütlesi (kg/m 3 ), V : Akışkanın hızı (m/s), : Akışkanın özgül ağırlığı (N/m 3 ), z : Ele alınan noktanın referans eksenine uzaklığı (m) ya da seviye yükü olup potansiyel enerjiyi gösterir (m). P : Basınç yükü (enerjisi) olup P basıncının üretilebilmesi için gerekli akışkan yüksekliğini verir (m). V : Hız yükü (kinetik enerji) olup akışkanın V hızına ulaşabilmesi için g sürtünmeli ortamda serbest düşme yüksekliğini verir (m) Akım Çizgisine Dik Yönde Bernoulli Eşitliği Pratikte akışlar çoğunlukla akım çizgisi boyuncadır ve bir boyutludur. Ancak bazı durumlarda iki boyutlu akış da önemli olmakta ve kullanılmaktadır. Akım çizgisine dik hareket eden bir akışkan taneciğine etkili olan basınç ve ağırlık kuvvetleri ile Newton un ikinci kanunu arasındaki ilişki aşağıdaki gibi yazılabilir (Munson vd. 994) dz P.V dn n R 84
5 Burada; : Akışkanın özgül ağırlığı (N/m 3 ), dz Cos : Akışkan taneciğinin göz önüne alınan noktadaki akım dn çizgisine dik doğrultuyla yaptığı açının kosünüsü (-), P : Akım çizgisine dik yöndeki basınç gradyenti (N/m 3 ), n : Akışkanın özgül kütlesi (kg/m 3 ), V : Akışkan taneciğinin hızı (m/s), R : Eğrilik yarıçapı (m) dir. Yukarıdaki eşitlik bize, bir akışkan taneciğinin akışa dik doğrultudaki değişiminin basınç gradyenti ve akım çizgisine dik ağırlık kuvvetleri tarafından gerçekleştirildiğini göstermektedir. Ağırlık kuvvetleri ihmal edilirse ya da akış yatay bir düzlemde yani dz/dn=cosθ= 0 ise formül aşağıdaki biçime dönüşür. P n V R Bu da eğriliğin merkezinden uzaklaştıkça basıncın arttığını göstermektedir. Akım çizgisine dik yönde Bernoulli eşitliğini yukarıdaki eşitliklerden bazı kabullenmeler yaparak aşağıdaki biçimde yazabiliriz. V P dn z sabit R Akım çizgisine dik yöndeki Bernoulli eşitliği de akım çizgisi boyunca oluşan Bernoulli eşitliği gibi kararlı akım, viskozitesiz akım ve sıkıştırılamaz akım koşullarında geçerlidir (Munson vd. 994) 3.5. Statik, Dinamik, Ölü Nokta ve Toplam Basınç Bernoulli eşitliğiyle ilgili önemli bir kuram da ölü nokta (kabarma basıncı, durma noktasındaki basınç) ve dinamik basınçtır. Bu basınçlar hareketli akışkanın durdurulması sırasında kinetik enerjinin basınç yüksekliğine dönüşmesiyle meydana gelir. Bernoulli eşitliğindeki P, hareketli akışkanın gerçek termodinamik basıncıdır ve akıma dik yönde boru çevresinde ölçüldüğü için statik basınç adını alır (Şekil 3.). Bernoulli eşitliğindeki.v ye dinamik basınç denir. 85
6 Şekil 3.. Basıncın ölçümü (Edis 97b) Bu basınç Şekil 3. deki gibi akışkanın ortasına yerleştirilmiş pitot tüpü ile ölçülebilmektedir. Şekildeki boruda akan akışkan tüp içerisinde H yüksekliğine kadar çıkmaktadır. Pitot tüpü içerisindeki akışkan statiktir ve V= 0 dır. İşte bu () noktasındaki basınca ölü nokta basıncı denir. Ölü nokta basıncı borunun çevresine açılan bir delik yardımıyla ölçülen statik basınç (P) ve dinamik basıncın ( Pd V ) toplamından oluşmaktadır. () noktasındaki ölü nokta basıncı ( P ), () ve () noktalarına Bernoulli denklemini uygulayarak bulunmaktadır. P P. V Görüldüğü gibi ölü noktadaki basınç(p), statik basınçtan (P), dinamik basınç ( P d.. V ) kadar daha büyüktür. Dinamik basınç bu bağıntıdan; P h P H P d.. V P P.( H h) ile elde edilmektedir. Yani bir boruya bir piyezometre borusu ve bir de pitot tüpü yerleştirildiğinde bu borularda yükselen sıvı seviyeleri arasındaki fark sıvının özgül ağırlığıyla çarpılarak dinamik basınç bulunabilir. Borudaki akışkanın hızı (V) ise, dinamik basınçtan yararlanılarak belirlenir (Edis 97b, Sleigh 00, Hewakandamby 0). V V g( H h) Bernoulli denklemindeki.z terimi hidrostatik basınçtır. Bu terim gerçekte bir basınç değildir. Yükseklik değişiminin neden olduğu akışkanın potansiyel enerjisini göstermektedir. 86
7 denir. Statik, dinamik ve hidrostatik basınçların toplamına toplam basınç (PT) P T P..V.z sabit Bir akışkanda statik ve ölü nokta basınçlarının bilinmesiyle akışkanın hızı saptanabilir. Ancak bunun için bir piyezometre ve bir pitot tüpüne ihtiyacın olması ve iki farklı yerde okumanın yapılması gerekir. Bunun yerine aşağıdaki şekilde(şekil 3.3) görülen statik pitot tüpü kullanılarak tek bir okumayla basınç bulunabilmekte ve hız kolayca hesaplanabilmektedir. Statik pitot tüpünün her iki tarafındaki delikler manometrenin bir ucuna bağlı olup statik basıncı, ortasındaki delik ise manometrenin diğer ucuna bağlı olup ölü nokta basıncını göstermektedir. Şekil 3.3. Statik pitot tüpü (Edis 97b, Sleigh 00, Hewakandamby 0) Statik pitot tüpünün merkez çizgisini göz önüne alarak A ve B noktalarındaki basınçları eşitleyelim. P B P gx P A p g( x h) man gh 87
8 PA P B P gx p g( x h) man gh P V P. olduğu yukarıda bulunmuştu. Buna göre borudaki akışkanın hızı statik pitot tüpü yardımıyla aşağıdaki gibi bulunur. P hg( V man ) P gh( ) man V yukarıdaki formüllerde man,manometredeki akışkanın özgül kütlesini ve,borudaki akışkanın özgül kütlesini göstermektedir (Edis 97b) Süreklilik Denklemi Sıkıştırılamaz akışkanlarda sisteme giren ve sistemden çıkan akım miktarı (verdi) sabit kabul edilmektedir. Buna kütlenin korunumu denir ve süreklilik denklemiyle ifade edilir (Sığıner ve Sümer 995). Q Q A Bu bağıntıda;.v A. V Q ve Q : Sırasıyla sisteme giren ve sistemden çıkan verdiler (m 3 /s), A : Birinci durumdaki kesit alanı (m ), V : Birinci kesitteki akışkan hızı (m/s), A : İkinci durumdaki kesit alanı (m ), V : İkinci kesitteki akışkanın hızı (m/s) dir Bernoulli Eşitliğinin Uygulama Alanları Bernoulli eşitliği sürtünmesiz, sıkıştırılamaz ve düzenli akım koşullarında, pratikte, değişik ortamlarda kullanılabilir. Bu kullanım alanlarından bazıları aşağıdaki gibidir. 88
9 3.7.. Orifis (sukbe) Bir deponun yüzeyine açılan ve sıvının dışarı çıkmasını sağlayan çevresi kapalı olan açıklıklara orifis denir. Şekil 3.4 de verilen bir deponun tabanına açılan orifisin () ve (5) noktalarındaki teorik akışkan hızı (Vt) Bernoulli eşitliğini kullanarak aşağıdaki gibi yazılabilir (Hewakandamby 0). V t / (. g. h) V t Bu bağıntılarda; 5 ( g( h H)) / Vt : Orifis çıkışındaki teorik akışkan hızı (m/s), h : Orifisin orta noktasının depodaki serbest sıvı yüzeyine olan uzaklığı (m), V5t : Orifis dışında (5) noktasındaki teorik akışkan hızı (m/s), H : Orifis dışındaki (5) noktasının orifis orta noktasına () olan uzaklığı (m) dir. Şekil 3.4. Tank tabanına açılmış orifisten sıvı akışı (Munson vd. 994, Hewakandamby 0) Orifis düz değilse, iyi taşlanmamışsa Şekil 3.5 de görüldüğü gibi orifisten çıkan sıvıda bir daralma meydana gelir. Yani orifisin çapı (dh), orifisten çıkan sıvının çapından (dj) daha büyüktür (dh > dj). Bu farklılığa büzülme etkisi (vena contracta) denir ve orifis kesit alanı (Ah) ile sıvı kesit alanı (Aj) arasındaki ilişkiyi göstermektedir. C c Bu eşitlikte; A A j h d d j h Aj : Orifisten çıkan sıvı jetinin kesit alanı (m ), Ah: Orifis kesit alanı (m ), Cc: Büzülme katsayısı olup Şekil 3.6 da bazı orifisler için verilmiştir, 89
10 dj : Sıvı jetinin çapı (m), dh : Orifisin çapı (m) dir. Şekil 3.5. Keskin kenarlı orifiste büzülme etkisi (Munson vd. 994, Hewakandamby 0) Şekil 3.5 de () noktasındaki hız, () noktasındaki hızdan büyük, (3) noktasındaki hızdan küçüktür. Orifisten çıkan sıvının hızını, () noktasındaki ortalama hız olarak kabul etmezsek bir hız katsayısını tanımlamamız gerekir. Şekil 3.6. Değişik orifis düzenlemeleri ve büzülme katsayıları (Cc) (Hewakandamby 0) 90
11 Bu hız katsayısını (Cv) kullanarak orifisten çıkan sıvının gerçek hızı bulunabilir (Douglas 986a, Hewakandamby 0). Burada; V g C.(. g. h) v / V g : Orifisten çıkan sıvının pratikteki (gerçek) hızı (m/s), C v : Orifisin değişik noktalarındaki hızların farklılığından kaynaklanan hız katsayısı olup gerçek hız C v teorik hız ile bulunur. Yukarıdaki verilenlere göre bir orifisten akan sıvının verdisi aşağıdaki gibi bulunur. Q AV Q A. j V g Q C.A. V c Q C.A h g / c h.cv.(.g.h ) Eğer hız katsayısı v ( v C bilinmiyorsa, hız katsayısı ) katsayısının ( Cc ) çarpımından oluşan verdi katsayısı ( Cd ) gerçek debi katsayısı Cd = C. C c v 0, 6 teorik debi Hewakandamby 0) Sifon C ile büzülme kullanılabilir ve verdi kabul edilebilir (Douglas 986a, Depoları, yan yüzeylerinde bir delik açmadan yukarıdan daldırılan bir boru yardımıyla boşaltmak da olanaklıdır. Sıvıya daldırılan borunun bir kısmının, sıvı seviyesinin üstünde kalmasıyla oluşan düzeneğe sifon denir (Şekil 3.7). Şekil 3.7. Sifon (Edis 97b) 9
12 Şekil 3.7 deki sifon borusunun (3) noktasındaki sıvı çıkış hızı; (), () ve (3) noktalarına Bernoulli eşitliğini, () ile (3) noktasına da süreklilik denklemini uygulayarak aşağıdaki gibi yazılabilir (Edis 97b, McDonough 009). Burada; V / 3 (.g.(z z3)) V3 : Sifonun çıkışındaki sıvı hızı (m/s), g : 9,8 m/s z-z3 : Depodaki su düzeyi ile (3) noktası arasındaki düşey uzaklık (m). Bu uzaklıkları belirlerken deponun tabanı referans ekseni olarak kabul edilecektir. Bu durumda z pozitif, z3 ise negatif ve z-(-z3)= z+z3 olacaktır. Sifonlarda da, daha önceki sıvı akışının sürtünmesiz, düzenli ve sıkıştırılamaz kabullenmeleri geçerlidir. Sifon içerisinde en düşük basınç () noktasında elde edilecektir. () noktasındaki basınç negatif olup atmosfer basıncından daha küçüktür. Bu noktadaki basınç (P), () ve () noktalarındaki Bernoulli eşitliğinden; P.(z z).. V bağıntısıyla bulunabilir. Burada; P : Sifonun () noktasındaki basınç (Pa), : Sıvının özgül ağırlığı (N/m 3 ), z : Depodaki serbest sıvı yüzeyinin depo tabanına uzaklığı (m), z : () noktasının depo tabanına olan uzaklığı (m), : Sıvının özgül kütlesi (kg/m 3 ), V : Sifonun () noktasındaki sıvı hızı (m/s) dir Verdi ölçümü Bernoulli eşitliğinden yararlanılarak akışkanların verdilerini ölçmede kullanılan pek çok cihaz vardır. Bunlardan bazıları pitot tüpü, orifis ve sifondur. Verdinin borularda ölçülmesinde en etkin ve en basit yöntem boruya bir engel takarak düşük hızlı-yüksek basınçlı () bölge ile yüksek hızlı-düşük basınçlı () bölge arasındaki basınç farkını belirlemektir (şekil 3.8). Şekilde bu esasa dayalı üç değişik verdi ölçüm cihazı (orifis, lüle ve venturimetre) görülmektedir. 9
13 Şekil 3.8. Borulardaki verdinin ölçülmesinde kullanılan ölçüm cihazları (a: orifis, b: lüle, c: venturimetre) (Munson vd. 994, Hewakandamby 0) Bu cihazların ortak yanı hızın artmasıyla basıncın azalmasıdır. Akışı sürtünmesiz, düzenli, sıkıştırılmaz ve yatay (z=z) kabul ederek () ve () noktalarına Bernoulli eşitliği ve süreklilik denklemini uyguladığımızda, yine () ve () noktalarındaki hız dağılımını homojen aldığımızda borudan geçen akışkan verdisini veren formül aşağıdaki gibi bulunur (Munson vd. 994). Q A. V.( P P ) A.. A A Q : Borudan geçen akışkan verdisi (m 3 /s), A : () kesitinin alanı (m ), A : () kesitinin alanı (m ), P : () noktasındaki basınç (Pa), P : () noktasındaki basınç (Pa) : Akışkanın özgül kütlesi (kg/m 3 ). D :Boru çapı (m) d :Kesitin daraldığı noktasındaki çap(m) 93
14 Bu formüle göre A ve A kesitlerindeki basınç farkı (P-P) ölçüldüğünde akışkan verdisi kolaylıkla bulunabilmekedir. Burada ölçülen verdi teorik verdidir. Gerçek verdi bundan % ila % 40 daha küçüktür. Açık kanallara Bernoulli eşitliğini uygulayarak verdinin ölçülmesinde kullanılan en önemli iki verdi ölçer; savaklar ve açılır-kapanır kapılardır. Şekil 3.9 de görülen açılır kapanır kapıda () ve () noktalarına Bernoulli ve süreklilik denklemlerini uyguladığımızda kapıdan geçen akışkan verdisi (Q); Şekil 3.9. Açılır-kapanır kapı (Munson vd. 994). Bu formülde; 94 /.g.(z z) Q z.b. bulunur (Munson vd. 994). (z / z) Q : Kapıdan geçen akışkan verdisi (m 3 /s), z : Kapıdan geçen akışkanın referans eksenine olan uzaklığı (m), z : Depodaki akışkanın serbest sıvı yüzeyinin depo tabanı olan referans eksenine olan uzaklığı (m), b : Kapı genişliği (m) dir. Eğer z, z e göre çok küçükse verdi denklemi aşağıdaki biçimde sadeleşir. Q z /. b.(. g. z) Bu son eşitlikten z/z oranının çok büyük olduğu, depodaki sıvının kinetik enerjisinin ihmal edildiği, sıvı hızının z-z= z den dolayı V= (.g.z) / değerine düştüğü sonucu çıkarılabilir. Verdi hesabında dikkat edilirse kapı açıklığı (a) yerine, çıkan sıvının akış derinliği (z) kullanılmıştır. Açılır kapanır kapılarda da verdi hesabı yapılırken büzülme katsayısının tanımlanması gerekir. Buna göre büzülme katsayısı (Cc)
15 z Cc a olup, daima birden küçüktür. Eğer 0 0, z a ise büzülme katsayısı Cc= 0,6 a alınabilir. in z 0, den büyük değerleri için büzülme katsayısı çok büyümektedir. Açık kanallarda verdi ölçülmesinde kullanılan diğer bir verdi ölçer ise savaklardır. Şekil 3.0 da dikdörtgen bir savak gösterilmiştir. Savaklarda Şekil 3.0. Savaklarda verdi ölçümü (Munson vd. 994). akan akışkanın verdisi savak yüksekliğine (Pv), savak genişliğine (b) ve savak üzerinde akan akışkan yüksekliğine (H) bağlıdır. Şekildeki savak için verdi (Q) / Q C.H.b.(.g.H ) 3 / /.(.g) Q C.b.H bulunur (Munson vd. 994). Burada; Q : Savaktan geçen akışkan verdisi (m 3 /s), C : Sabit olup denemelerle bulunur, H : Savaktan geçen akışkan yüksekliği (m), b : Savak genişliği (m) dir. Bulunan bu verdi teorik verdidir. Her savak tipi için deneysel yöntemlerle elde edilen verdiler gerçek verdilerin bulunmasında kullanılabilir Enerji Çizgisi ve Hidrolik Eğim Çizgisi Bilindiği gibi Bernoulli eşitliği bir akışkandaki toplam enerjiyi göstermekte ve sürtünmesiz, sıkıştırılamaz, düzenli akım koşullarında sabit kalmaktadır. Bernoulli eşitliği yardımıyla hidrolik eğim çizgisi (HEÇ), enerji 95
16 çizgisi (EÇ) tanımlanmakta ve pek çok problemin çözümüne yardımcı olmaktadır (şekil 3.). 96 Şekil 3.. Enerji (EÇ) ve hidrolik eğim (HEÇ) çizgisi (Ayyıldız 983) Bernoulli eşitliğinin her terimi yükü ifade etmektedir. Bu yükler pitot tüpü ve piyezometre borusu ile şekil düzleminde tanımlanmaktadır. Akış boyunca farklı noktalarda bulunan pitot tüplerindeki ölçülen basınç noktalarından geçen çizgiye enerji çizgisi (EÇ) denir ve ideal akışkanlarda kıyas düzlemine paralel kalır. Enerji çizgisi Bernoulli eşitliğindeki her bir yükün toplanmasıyla elde edilir. Burada; P V H z sabit.g H : Toplam yük (m), z : Potansiyel yük (m), P : Basınç yükü (m), V : Hız yükü (m) dür. g Hidrolik eğim çizgisi (z+p/) terimine karşılık gelen statik yük, piyezometrik yük ya da hidrolik yükü içermektedir. Borunun dış kenarına yerleştirilen piyezometre borusunda yükselen akışkan seviyesinden geçen çizgiye hidrolik eğim çizgisi (HEÇ) denir. HEÇ; akışkanın hızına bağlı olduğundan sabit kalmamakta akış boyunca değişebilmektedir. Enerji çizgisini oluşturan pitot tüpündeki yükselen akışkan seviyesi ile piyezometre borusunda
17 yükselen akışkan seviyesi arasındaki fark, hız yükü kadardır. Eğer akım pratikte olduğu gibi sürtünmeli kabul edilirse enerji çizgisi sabit kalmaz, akış boyunca değişebilir. 97
Akışkanların Dinamiği
 Akışkanların Dinamiği Akışkanların Dinamiğinde Kullanılan Temel Prensipler Gaz ve sıvı akımıyla ilgili bütün problemlerin çözümü kütlenin korunumu, enerjinin korunumu ve momentumun korunumu prensibe dayanır.
Akışkanların Dinamiği Akışkanların Dinamiğinde Kullanılan Temel Prensipler Gaz ve sıvı akımıyla ilgili bütün problemlerin çözümü kütlenin korunumu, enerjinin korunumu ve momentumun korunumu prensibe dayanır.
Akışkanların Dinamiği
 Akışkanların Dinamiği Akışkanların Dinamiğinde Kullanılan Temel Prensipler Gaz ve sıvı akımıyla ilgili bütün problemlerin çözümü kütlenin korunumu, enerjinin korunumu ve momentumun korunumu prensibe dayanır.
Akışkanların Dinamiği Akışkanların Dinamiğinde Kullanılan Temel Prensipler Gaz ve sıvı akımıyla ilgili bütün problemlerin çözümü kütlenin korunumu, enerjinin korunumu ve momentumun korunumu prensibe dayanır.
Selçuk Üniversitesi. Mühendislik-Mimarlık Fakültesi. Kimya Mühendisliği Bölümü. Kimya Mühendisliği Laboratuvarı. Venturimetre Deney Föyü
 Selçuk Üniversitesi Mühendislik-Mimarlık Fakültesi Kimya Mühendisliği Bölümü Kimya Mühendisliği Laboratuvarı Venturimetre Deney Föyü Hazırlayan Arş.Gör. Orhan BAYTAR 1.GİRİŞ Genellikle herhangi bir akış
Selçuk Üniversitesi Mühendislik-Mimarlık Fakültesi Kimya Mühendisliği Bölümü Kimya Mühendisliği Laboratuvarı Venturimetre Deney Föyü Hazırlayan Arş.Gör. Orhan BAYTAR 1.GİRİŞ Genellikle herhangi bir akış
2. Basınç ve Akışkanların Statiği
 2. Basınç ve Akışkanların Statiği 1 Basınç, bir akışkan tarafından birim alana uygulanan normal kuvvet olarak tanımlanır. Basıncın birimi pascal (Pa) adı verilen metrekare başına newton (N/m 2 ) birimine
2. Basınç ve Akışkanların Statiği 1 Basınç, bir akışkan tarafından birim alana uygulanan normal kuvvet olarak tanımlanır. Basıncın birimi pascal (Pa) adı verilen metrekare başına newton (N/m 2 ) birimine
Bernoulli Denklemi, Basınç ve Hız Yükleri Borularda Piezometre ve Enerji Yükleri Venturi Deney Sistemi
 Bernoulli Denklemi, Basınç ve Hız Yükleri Borularda Piezometre ve Enerji Yükleri Venturi Deney Sistemi Akışkanlar dinamiğinde, sürtünmesiz akışkanlar için Bernoulli prensibi akımın hız arttıkça aynı anda
Bernoulli Denklemi, Basınç ve Hız Yükleri Borularda Piezometre ve Enerji Yükleri Venturi Deney Sistemi Akışkanlar dinamiğinde, sürtünmesiz akışkanlar için Bernoulli prensibi akımın hız arttıkça aynı anda
VENTURİMETRE DENEYİ 1. GİRİŞ
 VENTURİMETRE DENEYİ 1. GİRİŞ Genellikle herhangi bir akış esnasında akışkanın tabakaları farklı hızlarda hareket ederler ve akışkanın viskozitesi, uygulanan kuvvete karşı direnç gösteren tabakalar arasındaki
VENTURİMETRE DENEYİ 1. GİRİŞ Genellikle herhangi bir akış esnasında akışkanın tabakaları farklı hızlarda hareket ederler ve akışkanın viskozitesi, uygulanan kuvvete karşı direnç gösteren tabakalar arasındaki
KBM0308 Kimya Mühendisliği Laboratuvarı I BERNOLLİ DENEYİ. Bursa Teknik Üniversitesi DBMMF Kimya Mühendisliği Bölümü 1
 BERNOLLİ DENEYİ Bursa Teknik Üniversitesi DBMMF Kimya Mühendisliği Bölümü 1 1. Amaç Yapılacak olan Bernoulli deneyinin temel amacı, akışkanlar mekaniğinin en önemli denklemlerinden olan, Bernoulli (enerjinin
BERNOLLİ DENEYİ Bursa Teknik Üniversitesi DBMMF Kimya Mühendisliği Bölümü 1 1. Amaç Yapılacak olan Bernoulli deneyinin temel amacı, akışkanlar mekaniğinin en önemli denklemlerinden olan, Bernoulli (enerjinin
HİDROLİK. Yrd. Doç. Dr. Fatih TOSUNOĞLU
 HİDROLİK Yrd. Doç. Dr. Fatih TOSUNOĞLU Ders Hakkında Genel Bilgiler Görüşme Saatleri:---------- Tavsiye edilen kitaplar: 1-Hidrolik (Prof. Dr. B. Mutlu SÜMER, Prof. Dr. İstemi ÜNSAL. ) 2-Akışkanlar Mekaniği
HİDROLİK Yrd. Doç. Dr. Fatih TOSUNOĞLU Ders Hakkında Genel Bilgiler Görüşme Saatleri:---------- Tavsiye edilen kitaplar: 1-Hidrolik (Prof. Dr. B. Mutlu SÜMER, Prof. Dr. İstemi ÜNSAL. ) 2-Akışkanlar Mekaniği
Akışkan Kinematiği 1
 Akışkan Kinematiği 1 Akışkan Kinematiği Kinematik, akışkan hareketini matematiksel olarak tanımlarken harekete sebep olan kuvvetleri ve momentleri gözönüne almadan; Yerdeğiştirmeler Hızlar ve İvmeler cinsinden
Akışkan Kinematiği 1 Akışkan Kinematiği Kinematik, akışkan hareketini matematiksel olarak tanımlarken harekete sebep olan kuvvetleri ve momentleri gözönüne almadan; Yerdeğiştirmeler Hızlar ve İvmeler cinsinden
ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1. Y. Doç. Dr. Güray Doğan
 ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1 Y. Doç. Dr. Güray Doğan 1 Kinematik Kinematik: akışkanların hareketlerini tanımlar Kinematik harekete sebep olan kuvvetler ile ilgilenmez. Akışkanlar mekaniğinde
ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1 Y. Doç. Dr. Güray Doğan 1 Kinematik Kinematik: akışkanların hareketlerini tanımlar Kinematik harekete sebep olan kuvvetler ile ilgilenmez. Akışkanlar mekaniğinde
BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ
 BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ MÜHENDİSLİKTE DENEYSEL METODLAR -I BERNOULLİ DENEYİ FÖYÜ 2014 1. GENEL BİLGİLER Bernoulli denklemi basınç, hız
BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ MÜHENDİSLİKTE DENEYSEL METODLAR -I BERNOULLİ DENEYİ FÖYÜ 2014 1. GENEL BİLGİLER Bernoulli denklemi basınç, hız
T.C. GAZİ ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ
 T.C. GAZİ ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ LABORATUVARI BERNOULLİ DENEYİ FÖYÜ 1. GENEL BİLGİLER Bernoulli denklemi basınç, hız ve yükseklik arasındaki
T.C. GAZİ ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ LABORATUVARI BERNOULLİ DENEYİ FÖYÜ 1. GENEL BİLGİLER Bernoulli denklemi basınç, hız ve yükseklik arasındaki
İ çindekiler. xvii GİRİŞ 1 TEMEL AKIŞKANLAR DİNAMİĞİ BERNOULLİ DENKLEMİ 68 AKIŞKANLAR STATİĞİ 32. xvii
 Last A Head xvii İ çindekiler 1 GİRİŞ 1 1.1 Akışkanların Bazı Karakteristikleri 3 1.2 Boyutlar, Boyutsal Homojenlik ve Birimler 3 1.2.1 Birim Sistemleri 6 1.3 Akışkan Davranışı Analizi 9 1.4 Akışkan Kütle
Last A Head xvii İ çindekiler 1 GİRİŞ 1 1.1 Akışkanların Bazı Karakteristikleri 3 1.2 Boyutlar, Boyutsal Homojenlik ve Birimler 3 1.2.1 Birim Sistemleri 6 1.3 Akışkan Davranışı Analizi 9 1.4 Akışkan Kütle
İnşaat Mühendisliği Bölümü Uygulama VIII ÇÖZÜMLER
 Soru 1 : Şekildeki hazne boru sisteminde sıkışmaz ve ideal akışkanın (su) permanan bir akımı mevcuttur. Su yatay eksenli ABC borusu ile atmosfere boşalmaktadır. Mutlak atmosfer basıncını 9.81 N/cm 2 ve
Soru 1 : Şekildeki hazne boru sisteminde sıkışmaz ve ideal akışkanın (su) permanan bir akımı mevcuttur. Su yatay eksenli ABC borusu ile atmosfere boşalmaktadır. Mutlak atmosfer basıncını 9.81 N/cm 2 ve
ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1. Y. Doç. Dr. Güray Doğan
 ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1 Y. Doç. Dr. Güray Doğan 1 Kinematik Kinematik: akışkanların hareketlerini tanımlar Kinematik harekete sebep olan kuvvetler ile ilgilenmez. Akışkanlar mekaniğinde
ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1 Y. Doç. Dr. Güray Doğan 1 Kinematik Kinematik: akışkanların hareketlerini tanımlar Kinematik harekete sebep olan kuvvetler ile ilgilenmez. Akışkanlar mekaniğinde
DÜZENLİ AKIMLARDA ENERJİ DENKLEMİ VE UYGULAMALARI
 DÜZENLİ AKIMLARDA ENERJİ DENKLEMİ VE UYGULAMALARI, iş yapabilme yeteneği olarak tanımlanır(kg.m yada Kwh). Bir sıvının enerjisi, sıvı birim ağırlığının sahip olduğu iş yapabilme yeteneğidir. 1. Potansiyel
DÜZENLİ AKIMLARDA ENERJİ DENKLEMİ VE UYGULAMALARI, iş yapabilme yeteneği olarak tanımlanır(kg.m yada Kwh). Bir sıvının enerjisi, sıvı birim ağırlığının sahip olduğu iş yapabilme yeteneğidir. 1. Potansiyel
ÇÖZÜMLER ( ) ( ) ( ) ( ) ( ) ( ) ( ) İnşaat Mühendisliği Bölümü Uygulama VII
 Soru 1 : Şekildeki hazne boru sisteminde; a- 1, 2, 3 noktalarındaki akışkanın basınçlarını bulunuz. b- Rölatif enerji ve piyezometre çizgilerini çiziniz. Sonuç: p 1=28.94 kn/m 2 ; p 2=29.23 kn/m 2 ; p
Soru 1 : Şekildeki hazne boru sisteminde; a- 1, 2, 3 noktalarındaki akışkanın basınçlarını bulunuz. b- Rölatif enerji ve piyezometre çizgilerini çiziniz. Sonuç: p 1=28.94 kn/m 2 ; p 2=29.23 kn/m 2 ; p
AKM 205 BÖLÜM 3 - UYGULAMA SORU VE ÇÖZÜMLERİ. Doç.Dr. Ali Can Takinacı Ar.Gör. Yük. Müh. Murat Özbulut
 AKM 205 BÖLÜM 3 - UYGULAMA SORU VE ÇÖZÜMLERİ Doç.Dr. Ali Can Takinacı Ar.Gör. Yük. Müh. Murat Özbulut 1. 70 kg gelen bir bayanın 400 cm 2 toplam ayak tabanına sahip olduğunu göz önüne alınız. Bu bayan
AKM 205 BÖLÜM 3 - UYGULAMA SORU VE ÇÖZÜMLERİ Doç.Dr. Ali Can Takinacı Ar.Gör. Yük. Müh. Murat Özbulut 1. 70 kg gelen bir bayanın 400 cm 2 toplam ayak tabanına sahip olduğunu göz önüne alınız. Bu bayan
ÇÖZÜMLER. γ # γ + z A = 2 + P A. γ + z # # γ # = 2 + γ # γ + 2.
 Soru : Şekildeki hazne boru sisteminde; a-, 2, 3 noktalarındaki akışkanın basınçlarını bulunuz. b- Rölatif enerji ve piyezometre çizgilerini çiziniz. Sonuç: p =28.9 kn/m 2 ; p 2=29.23 kn/m 2 ; p 3=26.98
Soru : Şekildeki hazne boru sisteminde; a-, 2, 3 noktalarındaki akışkanın basınçlarını bulunuz. b- Rölatif enerji ve piyezometre çizgilerini çiziniz. Sonuç: p =28.9 kn/m 2 ; p 2=29.23 kn/m 2 ; p 3=26.98
YILDIZ TEKNİK ÜNİVERSİTESİ
 YILDIZ TEKNİK ÜNİVERSİTESİ Makine Fakültesi Makine Mühendisliği Bölümü Termodinamik ve Isı Tekniği Anabilim Dalı Akışkanlar Mekaniği Genel Laboratuvar Föyü Güz Dönemi Öğrencinin Adı Soyadı : No : Grup
YILDIZ TEKNİK ÜNİVERSİTESİ Makine Fakültesi Makine Mühendisliği Bölümü Termodinamik ve Isı Tekniği Anabilim Dalı Akışkanlar Mekaniği Genel Laboratuvar Föyü Güz Dönemi Öğrencinin Adı Soyadı : No : Grup
Akışkanlar Mekaniği Yoğunluk ve Basınç: Bir maddenin yoğunluğu, birim hacminin kütlesi olarak tanımlanır.
 Akışkanlar Mekaniği Yoğunluk ve Basınç: Bir maddenin yoğunluğu, birim hacminin kütlesi olarak tanımlanır. Basıncın derinlikle değişimi Aynı derinlikteki bütün noktalar aynı basınçta y yönünde toplam kuvvet
Akışkanlar Mekaniği Yoğunluk ve Basınç: Bir maddenin yoğunluğu, birim hacminin kütlesi olarak tanımlanır. Basıncın derinlikle değişimi Aynı derinlikteki bütün noktalar aynı basınçta y yönünde toplam kuvvet
Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü
 Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü 1 kışkan Statiğine Giriş kışkan statiği (hidrostatik, aerostatik), durgun haldeki akışkanlarla
Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü 1 kışkan Statiğine Giriş kışkan statiği (hidrostatik, aerostatik), durgun haldeki akışkanlarla
AKM 205 BÖLÜM 8 - UYGULAMA SORU VE ÇÖZÜMLERİ
 AKM 205 BÖLÜM 8 - UYGULAMA SORU VE ÇÖZÜMLERİ Doç.Dr. Ali Can Takinacı Ar.Gör. Yük. Müh. Murat Özbulut 1. Yoğunluğu 850 kg/m 3 ve kinematik viskozitesi 0.00062 m 2 /s olan yağ, çapı 5 mm ve uzunluğu 40
AKM 205 BÖLÜM 8 - UYGULAMA SORU VE ÇÖZÜMLERİ Doç.Dr. Ali Can Takinacı Ar.Gör. Yük. Müh. Murat Özbulut 1. Yoğunluğu 850 kg/m 3 ve kinematik viskozitesi 0.00062 m 2 /s olan yağ, çapı 5 mm ve uzunluğu 40
MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ II FİNAL SINAVI 22.05.2015 Numara: Adı Soyadı: SORULAR-CEVAPLAR
 MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ II FİNAL SINAVI 22.05.2015 Numara: Adı Soyadı: 1- (24 Puan) Şekildeki 5.08 cm çaplı 38.1 m uzunluğunda, 15.24 cm çaplı 22.86 m uzunluğunda ve 7.62 cm çaplı
MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ II FİNAL SINAVI 22.05.2015 Numara: Adı Soyadı: 1- (24 Puan) Şekildeki 5.08 cm çaplı 38.1 m uzunluğunda, 15.24 cm çaplı 22.86 m uzunluğunda ve 7.62 cm çaplı
İdeal Akışkanların 2 ve 3 Boyutlu Akımları
 AKM 204 / Kısa Ders Notu H11-S1 İdeal Akışkanların 2 ve 3 Boyutlu Akımları Kütlenin Korunumu Prensibi : Süreklilik Denklemi Gözönüne alınan ortam ve akışkan özellikleri; Permanan olmayan akım ortamında
AKM 204 / Kısa Ders Notu H11-S1 İdeal Akışkanların 2 ve 3 Boyutlu Akımları Kütlenin Korunumu Prensibi : Süreklilik Denklemi Gözönüne alınan ortam ve akışkan özellikleri; Permanan olmayan akım ortamında
T.C. GAZİ ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ LABORATUVARI
 T.C. GAZİ ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ LABORATUVARI BORULARDA VE HİDROLİK ELEMANLARDA SÜRTÜNME KAYIPLARI DENEY FÖYÜ 1. DENEYİN AMACI Borularda
T.C. GAZİ ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ LABORATUVARI BORULARDA VE HİDROLİK ELEMANLARDA SÜRTÜNME KAYIPLARI DENEY FÖYÜ 1. DENEYİN AMACI Borularda
HİDROLİK MAKİNALAR YENİLENEBİLİR ENERJİ KAYNAKLARI
 HİDROLİK MAKİNALAR YENİLENEBİLİR ENERJİ KAYNAKLARI HİDROLİK TÜRBİN ANALİZ VE DİZAYN ESASLARI Hidrolik türbinler, su kaynaklarının yerçekimi potansiyelinden, akan suyun kinetik enerjisinden ya da her ikisinin
HİDROLİK MAKİNALAR YENİLENEBİLİR ENERJİ KAYNAKLARI HİDROLİK TÜRBİN ANALİZ VE DİZAYN ESASLARI Hidrolik türbinler, su kaynaklarının yerçekimi potansiyelinden, akan suyun kinetik enerjisinden ya da her ikisinin
1. Aşağıda verilen fiziksel büyüklüklerin dönüşümünde? işareti yerine gelecek sayıyı bulunuz.
 Şube Adı- Soyadı: Fakülte No: NÖ-A NÖ-B Kimya Mühendisliği Bölümü, 2016/2017 Öğretim Yılı, 00323-Akışkanlar Mekaniği Dersi, 2. Ara Sınavı Soruları 10.12.2016 Soru (puan) 1 (20) 2 (20) 3 (20) 4 (20) 5 (20)
Şube Adı- Soyadı: Fakülte No: NÖ-A NÖ-B Kimya Mühendisliği Bölümü, 2016/2017 Öğretim Yılı, 00323-Akışkanlar Mekaniği Dersi, 2. Ara Sınavı Soruları 10.12.2016 Soru (puan) 1 (20) 2 (20) 3 (20) 4 (20) 5 (20)
2. SUYUN BORULARDAKİ AKIŞI
 . SUYUN BORULARDAKİ AKIŞI.. Birim Sistemleri Diğer bilim dallarında olduğu gibi suyun borulardaki akış formüllerinde de çeşitli birim sistemleri kullanılabilir. Bunlar: a) MKS (Meter-Kilogram-Second),
. SUYUN BORULARDAKİ AKIŞI.. Birim Sistemleri Diğer bilim dallarında olduğu gibi suyun borulardaki akış formüllerinde de çeşitli birim sistemleri kullanılabilir. Bunlar: a) MKS (Meter-Kilogram-Second),
2.6. Düzlemsel Yüzeylere Etkiyen Hidrostatik Kuvvet. Yatay bir düzleme bir akışkanın uyguladığı kuvvet FR= P.A bağıntısıyla bulunur.
 . KIŞKN STTİĞİ.6. Düzlemsel Yüzeylere Etkiyen Hidrostatik Kuvvet Yatay bir düzleme bir akışkanın uyguladığı kuvvet F= P. bağıntısıyla bulunur. Burada; F : Yatay düzleme uygulanan idrostatik kuvvet (N),
. KIŞKN STTİĞİ.6. Düzlemsel Yüzeylere Etkiyen Hidrostatik Kuvvet Yatay bir düzleme bir akışkanın uyguladığı kuvvet F= P. bağıntısıyla bulunur. Burada; F : Yatay düzleme uygulanan idrostatik kuvvet (N),
AKIŞKANLAR MEKANİĞİ UYGULAMA SORULARI
 1 AKIŞKANLAR MEKANİĞİ UYGULAMA SORULARI AKIŞKANLARIN ÖZELLİKLERİ SORU 1: Şekilde görülen dairesel kesitli düşey bir tüpte 0 C deki suyun kapiler yüksekliğinin 1 mm den az olması için gerekli olan minimum
1 AKIŞKANLAR MEKANİĞİ UYGULAMA SORULARI AKIŞKANLARIN ÖZELLİKLERİ SORU 1: Şekilde görülen dairesel kesitli düşey bir tüpte 0 C deki suyun kapiler yüksekliğinin 1 mm den az olması için gerekli olan minimum
Manyetik Alanlar. Benzer bir durum hareketli yükler içinde geçerli olup bu yüklerin etrafını elektrik alana ek olarak bir manyetik alan sarmaktadır.
 Manyetik Alanlar Manyetik Alanlar Duran ya da hareket eden yüklü parçacığın etrafını bir elektrik alanın sardığı biliyoruz. Hatta elektrik alan konusunda şu sonuç oraya konulmuştur. Durgun bir deneme yükü
Manyetik Alanlar Manyetik Alanlar Duran ya da hareket eden yüklü parçacığın etrafını bir elektrik alanın sardığı biliyoruz. Hatta elektrik alan konusunda şu sonuç oraya konulmuştur. Durgun bir deneme yükü
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ
 BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
Alınan Puan NOT: Yalnızca 5 soru çözünüz, çözmediğiniz soruyu X ile işaretleyiniz. Sınav süresi 90 dakikadır. SORULAR ve ÇÖZÜMLER
 Gıda Mühendisliği Bölümü, 2016/2017 Öğretim Yılı, Bahar yarıyılı 0216-Akışkanlar Mekaniği Dersi, Dönem Sonu Sınavı Soru Çözümleri 30.05.2017 Adı- Soyadı: Soru (puan) 1 (20) 2 (20) 3 (20) 4 (20) 5 (20)
Gıda Mühendisliği Bölümü, 2016/2017 Öğretim Yılı, Bahar yarıyılı 0216-Akışkanlar Mekaniği Dersi, Dönem Sonu Sınavı Soru Çözümleri 30.05.2017 Adı- Soyadı: Soru (puan) 1 (20) 2 (20) 3 (20) 4 (20) 5 (20)
4.Sıkıştırılamayan Akışkanlarda Sürtünme Kayıpları
 4.Sıkıştırılamayan Akışkanlarda Sürtünme Kayıpları Bursa Teknik Üniversitesi DBMMF Kimya Mühendisliği Bölümü 1 1. Amaç Sıkıştırılamayan bir akışkan olan suyun silindirik düz bir boru içerisinde akarken
4.Sıkıştırılamayan Akışkanlarda Sürtünme Kayıpları Bursa Teknik Üniversitesi DBMMF Kimya Mühendisliği Bölümü 1 1. Amaç Sıkıştırılamayan bir akışkan olan suyun silindirik düz bir boru içerisinde akarken
AÇIK KANAL AKIMI. Hopa Yukarı Sundura Deresi-ARTVİN
 AÇIK KANAL AKIMI Hopa Yukarı Sundura Deresi-ARTVİN AÇIK KANAL AKIMI (AKA) Açık kanal akımı serbest yüzeyli akımın olduğu bir akımdır. serbest yüzey hava ve su arasındaki ara yüzey @ serbest yüzeyli akımda
AÇIK KANAL AKIMI Hopa Yukarı Sundura Deresi-ARTVİN AÇIK KANAL AKIMI (AKA) Açık kanal akımı serbest yüzeyli akımın olduğu bir akımdır. serbest yüzey hava ve su arasındaki ara yüzey @ serbest yüzeyli akımda
AKIŞ ÖLÇÜMLERİ. Kütlenin korunumu prensibine göre içerisinde üretim olmayan bir sistem için;
 ÖLÇME TEKNİĞİ DERS NOTLARI 2 AKIŞ ÖLÇÜMLERİ Akışkanın hareketi sırasındaki hızı ve debisi, bilim ve sanayinin pek çok yerinde ihtiyaç duyulan bilgilerdir. Bu verilerin ölçülmesi için pek çok cihaz geliştirilmiştir.
ÖLÇME TEKNİĞİ DERS NOTLARI 2 AKIŞ ÖLÇÜMLERİ Akışkanın hareketi sırasındaki hızı ve debisi, bilim ve sanayinin pek çok yerinde ihtiyaç duyulan bilgilerdir. Bu verilerin ölçülmesi için pek çok cihaz geliştirilmiştir.
İÇİNDEKİLER ÖNSÖZ Bölüm 1 DAİRESEL HAREKET Bölüm 2 İŞ, GÜÇ, ENERJİ ve MOMENTUM
 ÖNSÖZ İÇİNDEKİLER III Bölüm 1 DAİRESEL HAREKET 11 1.1. Dairesel Hareket 12 1.2. Açısal Yol 12 1.3. Açısal Hız 14 1.4. Açısal Hız ile Çizgisel Hız Arasındaki Bağıntı 15 1.5. Açısal İvme 16 1.6. Düzgün Dairesel
ÖNSÖZ İÇİNDEKİLER III Bölüm 1 DAİRESEL HAREKET 11 1.1. Dairesel Hareket 12 1.2. Açısal Yol 12 1.3. Açısal Hız 14 1.4. Açısal Hız ile Çizgisel Hız Arasındaki Bağıntı 15 1.5. Açısal İvme 16 1.6. Düzgün Dairesel
1 AKIŞKANLARIN ÖZELLİKLERİ
 1 AKIŞKANLARIN ÖZELLİKLERİ SORU 1: Şekilde görülen dairesel kesitli düşey bir tüpte 20 C deki suyun kapiler yüksekliğinin 1 mm den az olması için gerekli olan minimum yarıçap değeri nedir? (20 C de su
1 AKIŞKANLARIN ÖZELLİKLERİ SORU 1: Şekilde görülen dairesel kesitli düşey bir tüpte 20 C deki suyun kapiler yüksekliğinin 1 mm den az olması için gerekli olan minimum yarıçap değeri nedir? (20 C de su
Hareket Kanunları Uygulamaları
 Fiz 1011 Ders 6 Hareket Kanunları Uygulamaları Sürtünme Kuvveti Dirençli Ortamda Hareket Düzgün Dairesel Hareket http://kisi.deu.edu.tr/mehmet.tarakci/ Sürtünme Kuvveti Çevre faktörlerinden dolayı (hava,
Fiz 1011 Ders 6 Hareket Kanunları Uygulamaları Sürtünme Kuvveti Dirençli Ortamda Hareket Düzgün Dairesel Hareket http://kisi.deu.edu.tr/mehmet.tarakci/ Sürtünme Kuvveti Çevre faktörlerinden dolayı (hava,
5. Boyut Analizi. 3) Bir deneysel tasarımda değişken sayısının azaltılması 4) Model tasarım prensiplerini belirlemek
 Boyut analizi, göz önüne alınan bir fiziksel olayı etkileyen deneysel değişkenlerin sayısını ve karmaşıklığını azaltmak için kullanılan bir yöntemdir. Akışkanlar mekaniğinin gelişimi ağırlıklı bir şekilde
Boyut analizi, göz önüne alınan bir fiziksel olayı etkileyen deneysel değişkenlerin sayısını ve karmaşıklığını azaltmak için kullanılan bir yöntemdir. Akışkanlar mekaniğinin gelişimi ağırlıklı bir şekilde
NÖ-A NÖ-B. Şube. Alınan Puan. Adı- Soyadı: Fakülte No: 1. Aşağıda verilen fiziksel büyüklüklerin eşit olduğunu gösteriniz. 1/6
 Şube NÖ-A NÖ-B Adı- Soyadı: Fakülte No: Kimya Mühendisliği Bölümü, 2015/2016 Öğretim Yılı, 00323-Akışkanlar Mekaniği Dersi, Bütünleme Sınavı Soru ve Çözümleri 20.01.2016 Soru (puan) 1 (20) 2 (20) 3 (20)
Şube NÖ-A NÖ-B Adı- Soyadı: Fakülte No: Kimya Mühendisliği Bölümü, 2015/2016 Öğretim Yılı, 00323-Akışkanlar Mekaniği Dersi, Bütünleme Sınavı Soru ve Çözümleri 20.01.2016 Soru (puan) 1 (20) 2 (20) 3 (20)
SORULAR - ÇÖZÜMLER. NOT: Toplam 5 (beş) soru çözünüz. Sınav süresi 90 dakikadır. 1. Aşağıdaki çizelgede boş bırakılan yerleri doldurunuz. Çözüm.1.
 SORULAR - ÇÖZÜMLER 1. Aşağıdaki çizelgede boş bırakılan yerleri doldurunuz. Çözüm.1. Gıda Mühendisliği Bölümü, 2014/2015 Öğretim Yılı, Bahar Yarıyılı 0216-Akışkanlar Mekaniği Dersi, Dönem Sonu Sınavı Soru
SORULAR - ÇÖZÜMLER 1. Aşağıdaki çizelgede boş bırakılan yerleri doldurunuz. Çözüm.1. Gıda Mühendisliği Bölümü, 2014/2015 Öğretim Yılı, Bahar Yarıyılı 0216-Akışkanlar Mekaniği Dersi, Dönem Sonu Sınavı Soru
Orifis, Nozul ve Venturi Tip Akışölçerler
 Orifis, Nozul ve Venturi Tip Akışölçerler Bu tür akışölçerlerde, akışta kısıtlama yapılarak yaratılan basınç farkı (fark basınç), Bernoulli denkleminde işlenerek akış miktarı hesaplanır. Bernoulli denkleminin
Orifis, Nozul ve Venturi Tip Akışölçerler Bu tür akışölçerlerde, akışta kısıtlama yapılarak yaratılan basınç farkı (fark basınç), Bernoulli denkleminde işlenerek akış miktarı hesaplanır. Bernoulli denkleminin
AKIŞKANLAR MEKANİĞİ 1. YILİÇİ SINAVI ( )
 1 3 4 5 6 T AKIŞKANLAR MEKANİĞİ 1. YILİÇİ SINAVI (13.11.008) Ad-Soad: No: Grup: 1) a) İdeal ve gerçek akışkan nedir? Hız dağılımlarını çiziniz. Pratikte ideal akışkan var mıdır? Açıklaınız. İdeal Akışkan;
1 3 4 5 6 T AKIŞKANLAR MEKANİĞİ 1. YILİÇİ SINAVI (13.11.008) Ad-Soad: No: Grup: 1) a) İdeal ve gerçek akışkan nedir? Hız dağılımlarını çiziniz. Pratikte ideal akışkan var mıdır? Açıklaınız. İdeal Akışkan;
ONDOKUZ MAYIS ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ KİMYA MÜHENDİSLİĞİ BÖLÜMÜ KMB 305 KİMYA MÜHENDİSLİĞİ LABORATUVARI - 1
 ONDOKUZ MAYIS ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ KİMYA MÜHENDİSLİĞİ BÖLÜMÜ KMB 305 KİMYA MÜHENDİSLİĞİ LABORATUVARI - 1 AKIŞKANLAR MEKANİĞİ DENEY FÖYÜ (BORULARDA SÜRTÜNME KAYIPLARI) Hazırlayan: Araş. Gör.
ONDOKUZ MAYIS ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ KİMYA MÜHENDİSLİĞİ BÖLÜMÜ KMB 305 KİMYA MÜHENDİSLİĞİ LABORATUVARI - 1 AKIŞKANLAR MEKANİĞİ DENEY FÖYÜ (BORULARDA SÜRTÜNME KAYIPLARI) Hazırlayan: Araş. Gör.
BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER
 BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER Yrd. Doç. Dr. Beytullah EREN Çevre Mühendisliği Bölümü BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER Atatürk Barajı (Şanlıurfa) BATMIŞ YÜZEYLERE ETKİYEN KUVVETLER
BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER Yrd. Doç. Dr. Beytullah EREN Çevre Mühendisliği Bölümü BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER Atatürk Barajı (Şanlıurfa) BATMIŞ YÜZEYLERE ETKİYEN KUVVETLER
Ercan Kahya. Hidrolik. B.M. Sümer, İ.Ünsal, M. Bayazıt, Birsen Yayınevi, 2007, İstanbul
 Ercan Kahya 1 Hidrolik. B.M. Sümer, İ.Ünsal, M. Bayazıt, Birsen Yayınevi, 2007, İstanbul BÖLÜM 10 BORULAR İÇERİSİNDE AKIM 10.5. u; Bir önceki bölümde (10.3 'to / p ile 2 f V ENERJI KAYBI 10.5. HIDROLIK
Ercan Kahya 1 Hidrolik. B.M. Sümer, İ.Ünsal, M. Bayazıt, Birsen Yayınevi, 2007, İstanbul BÖLÜM 10 BORULAR İÇERİSİNDE AKIM 10.5. u; Bir önceki bölümde (10.3 'to / p ile 2 f V ENERJI KAYBI 10.5. HIDROLIK
Ders Notları 3 Geçirimlilik Permeabilite
 Ders Notları 3 Geçirimlilik Permeabilite Zemindeki mühendislik problemleri, zeminin kendisinden değil, boşluklarında bulunan boşluk suyundan kaynaklanır. Su olmayan bir gezegende yaşıyor olsaydık, zemin
Ders Notları 3 Geçirimlilik Permeabilite Zemindeki mühendislik problemleri, zeminin kendisinden değil, boşluklarında bulunan boşluk suyundan kaynaklanır. Su olmayan bir gezegende yaşıyor olsaydık, zemin
Kütlesel kuvvetlerin sadece g den kaynaklanması hali;
 KDN03-1 AKIŞKANLARIN STATİĞİ: HİDROSTATİK Basınç kavramı z σ a dz ds σx α x dx y σz Hidrostatikte ise olduğundan i = 0; Hidrostatik problemlerde sadece 1, 2, 3 olabilir. İnceleme kolaylığı için 2-boyutlu
KDN03-1 AKIŞKANLARIN STATİĞİ: HİDROSTATİK Basınç kavramı z σ a dz ds σx α x dx y σz Hidrostatikte ise olduğundan i = 0; Hidrostatik problemlerde sadece 1, 2, 3 olabilir. İnceleme kolaylığı için 2-boyutlu
Su seviyesi = ha Qin Kum dolu sütun Su seviyesi = h Qout
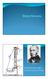 Su seviyesi = h a in Kum dolu sütun out Su seviyesi = h b 1803-1858 Modern hidrojeolojinin doğumu Henry Darcy nin deney seti (1856) 1 Darcy Kanunu Enerjinin yüksek olduğu yerlerden alçak olan yerlere doğru
Su seviyesi = h a in Kum dolu sütun out Su seviyesi = h b 1803-1858 Modern hidrojeolojinin doğumu Henry Darcy nin deney seti (1856) 1 Darcy Kanunu Enerjinin yüksek olduğu yerlerden alçak olan yerlere doğru
AKIŞ ÖLÇÜMLERİ. Harran Üniversitesi Makina Mühendisliği Bölümü. Dr.M.Azmi AKTACİR-2010-ŞANLIURFA 1
 AKIŞ ÖLÇÜMLERİ Dr.M.Azmi AKTACİR-2010-ŞANLIURFA 1 Akış ölçümleri neden gereklidir? Akış hız ve debisinin ölçülmesi bir çok biyolojik, meteorolojik olayların incelenmesi, endüstrinin çeşitli işlemlerinde
AKIŞ ÖLÇÜMLERİ Dr.M.Azmi AKTACİR-2010-ŞANLIURFA 1 Akış ölçümleri neden gereklidir? Akış hız ve debisinin ölçülmesi bir çok biyolojik, meteorolojik olayların incelenmesi, endüstrinin çeşitli işlemlerinde
NÖ-A NÖ-B. Adı- Soyadı: Fakülte No:
 Şube Adı- Soyadı: Fakülte No: NÖ-A NÖ-B Kimya Mühendisliği Bölümü, 2016/2017 Öğretim Yılı, 00323-Akışkanlar Mekaniği Dersi, Dönem Sonu Sınavı Soru ve Çözümleri 05.01.2017 Soru (puan) 1 (20) 2 (20) 3 (20)
Şube Adı- Soyadı: Fakülte No: NÖ-A NÖ-B Kimya Mühendisliği Bölümü, 2016/2017 Öğretim Yılı, 00323-Akışkanlar Mekaniği Dersi, Dönem Sonu Sınavı Soru ve Çözümleri 05.01.2017 Soru (puan) 1 (20) 2 (20) 3 (20)
Bölüm 5: Sonlu Kontrol Hacmi Analizi
 Bölüm 5: Sonlu Kontrol Hacmi Analizi Reynolds Transport Teoremi (RTT) Temel korunma kanunları (kütle,enerji ve momentumun korunumu) doğrudan sistem yaklaşımı ile türetilmiştir. Ancak, birçok akışkanlar
Bölüm 5: Sonlu Kontrol Hacmi Analizi Reynolds Transport Teoremi (RTT) Temel korunma kanunları (kütle,enerji ve momentumun korunumu) doğrudan sistem yaklaşımı ile türetilmiştir. Ancak, birçok akışkanlar
LİNEER DALGA TEORİSİ. Page 1
 LİNEER DALGA TEORİSİ Giriş Dalgalar, gerçekte viskoz akışkan içinde, irregüler ve değişken geçirgenliğe sahip bir taban üzerinde ilerlerler. Ancak, çoğu zaman akışkan hareketi neredeyse irrotasyoneldir.
LİNEER DALGA TEORİSİ Giriş Dalgalar, gerçekte viskoz akışkan içinde, irregüler ve değişken geçirgenliğe sahip bir taban üzerinde ilerlerler. Ancak, çoğu zaman akışkan hareketi neredeyse irrotasyoneldir.
TEKNOLOJİNİN BİLİMSEL İLKELERİ. Bölüm-8 SIVI AKIŞKANLARDA BASINÇ. Akışkanlar sıvı ve gaz olarak ikiye ayrılırlar.
 Bölüm-8 SIVI AKIŞKANLARDA BASINÇ 8.1. Sıvı Akışkanlarda Basınç Akışkanlar sıvı ve gaz olarak ikiye ayrılırlar. Sıvı akışkanlar sıkıştırılamayan, gaz akışkanlar ise sıkıştırılabilen akışkanlar olarak isimlendirilirler.
Bölüm-8 SIVI AKIŞKANLARDA BASINÇ 8.1. Sıvı Akışkanlarda Basınç Akışkanlar sıvı ve gaz olarak ikiye ayrılırlar. Sıvı akışkanlar sıkıştırılamayan, gaz akışkanlar ise sıkıştırılabilen akışkanlar olarak isimlendirilirler.
11.1 11.2. Tanım Akışkanların Statiği (Hidrostatik) Örnekler Kaldırma Kuvveti. 11.3 Örnek Eylemsizlik Momenti. 11.4 Eylemsizlik Yarıçapı
 11.1 11. Tanım Akışkanların Statiği (Hidrostatik) Örnekler Kaldırma Kuvveti 11.3 Örnek Eylemsizlik Momenti 11.4 Eylemsizlik Yarıçapı 11.5 Eksen Takımının Değiştirilmesi 11.6 Asal Eylemsizlik Momentleri
11.1 11. Tanım Akışkanların Statiği (Hidrostatik) Örnekler Kaldırma Kuvveti 11.3 Örnek Eylemsizlik Momenti 11.4 Eylemsizlik Yarıçapı 11.5 Eksen Takımının Değiştirilmesi 11.6 Asal Eylemsizlik Momentleri
Açık Kanallarda Debi Ölçümü. Hazırlayan: Onur Dündar
 Açık Kanallarda Debi Ölçümü Hazırlayan: Onur Dündar Doğal nehirlerde debi ölçümü ğ ç Orta nokta yöntemi ile debi hesabı Debi ölçümünde doğru kesitin belirlenmesi Dbiöl Debi ölçümü ü yapılacak kkesit nehrin
Açık Kanallarda Debi Ölçümü Hazırlayan: Onur Dündar Doğal nehirlerde debi ölçümü ğ ç Orta nokta yöntemi ile debi hesabı Debi ölçümünde doğru kesitin belirlenmesi Dbiöl Debi ölçümü ü yapılacak kkesit nehrin
FLOWING FLUIDS and PRESSURE VARIATION
 4. FLOWING FLUIDS and PRESSURE VARIATION Akışkan Kinematiği Akışkan kinematiği, harekete neden olan kuvvet ve momentleri dikkate almaksızın, akışkan hareketinin tanımlanmasını konu alır. Yapı üzerindeki
4. FLOWING FLUIDS and PRESSURE VARIATION Akışkan Kinematiği Akışkan kinematiği, harekete neden olan kuvvet ve momentleri dikkate almaksızın, akışkan hareketinin tanımlanmasını konu alır. Yapı üzerindeki
Proses Tekniği 3.HAFTA YRD.DOÇ.DR. NEZAKET PARLAK
 Proses Tekniği 3.HAFTA 3.HAFTA YRD.DOÇ.DR. NEZAKET PARLAK Sürekli Akışlı Açık Sistemlerde Enerji Korunumu de = d dt Sistem dt eρdv + eρ V b n A Bu denklemde e = u + m + gz Q net,g + W net,g = d dt eρdv
Proses Tekniği 3.HAFTA 3.HAFTA YRD.DOÇ.DR. NEZAKET PARLAK Sürekli Akışlı Açık Sistemlerde Enerji Korunumu de = d dt Sistem dt eρdv + eρ V b n A Bu denklemde e = u + m + gz Q net,g + W net,g = d dt eρdv
HİDROLİK-PNÖMATİK. Prof. Dr. İrfan AY. Makina. Prof.Dr.İrfan AY. Arş.Gör.T.Kerem DEMİRCİOĞLU. Balıkesir - 2008
 Makina * Prof. Dr. İrfan AY Arş.Gör.T.Kerem DEMİRCİOĞLU * Balıkesir - 008 1 HİDROLİK VE PNÖMATİK 1.BÖLÜM HİDROLİK VE PNÖMATİĞE GİRİŞ TARİHÇESİ: Modern hidroliğin temelleri 1650 yılında Pascal ın kendi
Makina * Prof. Dr. İrfan AY Arş.Gör.T.Kerem DEMİRCİOĞLU * Balıkesir - 008 1 HİDROLİK VE PNÖMATİK 1.BÖLÜM HİDROLİK VE PNÖMATİĞE GİRİŞ TARİHÇESİ: Modern hidroliğin temelleri 1650 yılında Pascal ın kendi
MANOMETRELER 3.1 PİEZOMETRE
 18 3 MANOMETRELER Düşük sıvı basınçlarını hassas olarak ölçmek için yaygın bir metot, bir veya birden fazla denge kolonu kullanan piezometre ve manometrelerin kullanılmasıdır. Burada çeşitli tipleri tartışılacaktır,
18 3 MANOMETRELER Düşük sıvı basınçlarını hassas olarak ölçmek için yaygın bir metot, bir veya birden fazla denge kolonu kullanan piezometre ve manometrelerin kullanılmasıdır. Burada çeşitli tipleri tartışılacaktır,
Newton un ikinci yasası: Bir cisim ivmesi cisim üzerine etki eden toplam kuvvet ile doğru orantılı cismin kütlesi ile ters orantılıdır.
 Bölüm 5: Hareket Yasaları(Özet) Önceki bölümde hareketin temel kavramları olan yerdeğiştirme, hız ve ivme tanımlanmıştır. Bu bölümde ise hareketli cisimlerin farklı hareketlerine sebep olan etkilerin hareketi
Bölüm 5: Hareket Yasaları(Özet) Önceki bölümde hareketin temel kavramları olan yerdeğiştirme, hız ve ivme tanımlanmıştır. Bu bölümde ise hareketli cisimlerin farklı hareketlerine sebep olan etkilerin hareketi
5. Boyut Analizi. 3) Bir deneysel tasarımda değişken sayısının azaltılması 4) Model tasarım prensiplerini belirlemek
 Boyut analizi, göz önüne alınan bir fiziksel olayı etkileyen deneysel değişkenlerin sayısını ve karmaşıklığını azaltmak için kullanılan bir yöntemdir. kışkanlar mekaniğinin gelişimi ağırlıklı bir şekilde
Boyut analizi, göz önüne alınan bir fiziksel olayı etkileyen deneysel değişkenlerin sayısını ve karmaşıklığını azaltmak için kullanılan bir yöntemdir. kışkanlar mekaniğinin gelişimi ağırlıklı bir şekilde
Bölüm 5: Sonlu Kontrol Hacmi Analizi
 Bölüm 5: Sonlu Kontrol Hacmi Analizi Reynolds Transport Teoremi (RTT) Temel korunma kanunları (kütle,enerji ve momentumun korunumu) doğrudan sistem yaklaşımı ile türetilmiştir. Ancak, birçok akışkanlar
Bölüm 5: Sonlu Kontrol Hacmi Analizi Reynolds Transport Teoremi (RTT) Temel korunma kanunları (kütle,enerji ve momentumun korunumu) doğrudan sistem yaklaşımı ile türetilmiştir. Ancak, birçok akışkanlar
VENTURİ, ORİFİS VE ROTAMETRE İLE DEBİ ÖLÇÜMÜ
 VENTURİ, ORİFİS VE ROTMETRE İLE DEİ ÖLÇÜMÜ Ölçüm Cihazı Deney cihazı debi ölçümünü sağlayan bir cihazdır metre gittikçe daralan ve bunu takiben bir boğaz ve gittikçe genişleyen uzun bir bölümden meydana
VENTURİ, ORİFİS VE ROTMETRE İLE DEİ ÖLÇÜMÜ Ölçüm Cihazı Deney cihazı debi ölçümünü sağlayan bir cihazdır metre gittikçe daralan ve bunu takiben bir boğaz ve gittikçe genişleyen uzun bir bölümden meydana
HİDROSTATİK. PDF created with FinePrint pdffactory trial version http://www.fineprint.com
 HİDRSTTİK Hidrostatik, hareketsiz yada durgun durumda bulunan sıvıların ve diğer ivmelerden doğan basınç ve kuvvetleri ile uğraşan bilim dalıdır. Hidrostatik, denge durumunda bulunan sıvıların denge koşullarını
HİDRSTTİK Hidrostatik, hareketsiz yada durgun durumda bulunan sıvıların ve diğer ivmelerden doğan basınç ve kuvvetleri ile uğraşan bilim dalıdır. Hidrostatik, denge durumunda bulunan sıvıların denge koşullarını
Bölüm 8: Borularda sürtünmeli Akış
 Bölüm 8: Borularda sürtünmeli Akış Laminer ve Türbülanslı Akış Laminer Akış: Çalkantısız akışkan tabakaları ile karakterize edilen çok düzenli akışkan hareketi laminer akış olarak adlandırılır. Türbülanslı
Bölüm 8: Borularda sürtünmeli Akış Laminer ve Türbülanslı Akış Laminer Akış: Çalkantısız akışkan tabakaları ile karakterize edilen çok düzenli akışkan hareketi laminer akış olarak adlandırılır. Türbülanslı
ATIK SULARIN TERFİSİ VE TERFİ MERKEZİ
 ATIK SULARIN TERFİSİ VE TERFİ MERKEZİ Pompa; suya basınç sağlayan veya suyu aşağıdan yukarıya terfi ettiren (yükselten) makinedir. Terfi merkezi; atık suların, çamurun ve arıtılmış suların bir bölgeden
ATIK SULARIN TERFİSİ VE TERFİ MERKEZİ Pompa; suya basınç sağlayan veya suyu aşağıdan yukarıya terfi ettiren (yükselten) makinedir. Terfi merkezi; atık suların, çamurun ve arıtılmış suların bir bölgeden
KOÜ. Mühendislik Fakültesi Makine Mühendisliği ( 1. ve 2. Öğretim ) Bölümü Dinamik Dersi (Türkçe Dilinde) 2. Çalişma Soruları / 21 Ekim 2018
 SORU-1) Şekilde gösterilen uzamasız halat makara sisteminde A'daki ipin ucu aşağı doğru 1 m/s lik bir hızla çekilirken, E yükünün hızının sayısal değerini ve hareket yönünü sistematik bir şekilde hesaplayarak
SORU-1) Şekilde gösterilen uzamasız halat makara sisteminde A'daki ipin ucu aşağı doğru 1 m/s lik bir hızla çekilirken, E yükünün hızının sayısal değerini ve hareket yönünü sistematik bir şekilde hesaplayarak
AKIŞ ÖLÇÜMLERİ. Harran Üniversitesi Makina Mühendisliği Bölümü. Dr.M.Azmi AKTACİR-2010-ŞANLIURFA 1
 AKIŞ ÖLÇÜMLERİ Dr.M.Azmi AKTACİR-2010-ŞANLIURFA 1 Akış ölçümleri neden gereklidir? Akış hız ve debisinin ölçülmesi bir çok biyolojik, meteorolojik olayların incelenmesi, endüstrinin çeşitli işlemlerinde
AKIŞ ÖLÇÜMLERİ Dr.M.Azmi AKTACİR-2010-ŞANLIURFA 1 Akış ölçümleri neden gereklidir? Akış hız ve debisinin ölçülmesi bir çok biyolojik, meteorolojik olayların incelenmesi, endüstrinin çeşitli işlemlerinde
KBM0308 Kimya Mühendisliği Laboratuvarı I HAVA AKIŞ DENEYİ. Bursa Teknik Üniversitesi DBMMF Kimya Mühendisliği Bölümü 1
 HAVA AKIŞ DENEYİ Bursa Teknik Üniversitesi DBMMF Kimya Mühendisliği Bölümü 1 1. Amaç Hava akış deneyinin amacı sıkıştırılabilen bir akışkan olan havanın, akış debisinin ölçülmesi ve orifismetre için K
HAVA AKIŞ DENEYİ Bursa Teknik Üniversitesi DBMMF Kimya Mühendisliği Bölümü 1 1. Amaç Hava akış deneyinin amacı sıkıştırılabilen bir akışkan olan havanın, akış debisinin ölçülmesi ve orifismetre için K
r r r F İŞ : Şekil yörüngesinde hareket eden bir parçacık üzerine kuvvetini göstermektedir. Parçacık A noktasından
 İŞ : Şekil yörüngesinde hareket eden bir parçacık üzerine etkiyenf r kuvvetini göstermektedir. Parçacık A noktasından r r geçerken konum vektörü uygun bir O orijininden ölçülmektedir ve d r A dan A ne
İŞ : Şekil yörüngesinde hareket eden bir parçacık üzerine etkiyenf r kuvvetini göstermektedir. Parçacık A noktasından r r geçerken konum vektörü uygun bir O orijininden ölçülmektedir ve d r A dan A ne
Maddeye hareket veren kuvveti, Isaac Newton (1642-1727) aşağıdaki matematiksel ifadeyle tanımlamıştır.
 1 1. TEMEL TARİF VE KAVRAMLAR (Ref. e_makaleleri) Kuvvet Maddeye hareket veren kuvveti, Isaac Newton (1642-1727) aşağıdaki matematiksel ifadeyle tanımlamıştır. F=ma Burada F bir madde parçacığına uygulanan
1 1. TEMEL TARİF VE KAVRAMLAR (Ref. e_makaleleri) Kuvvet Maddeye hareket veren kuvveti, Isaac Newton (1642-1727) aşağıdaki matematiksel ifadeyle tanımlamıştır. F=ma Burada F bir madde parçacığına uygulanan
O )molekül ağırlığı 18 g/mol ve 1g suyun kapladığı hacimde
 1) Suyun ( H 2 O )molekül ağırlığı 18 g/mol ve 1g suyun kapladığı hacimde 10 6 m 3 olduğuna göre, birbirine komşu su moleküllerinin arasındaki uzaklığı Avagadro sayısını kullanarak hesap ediniz. Moleküllerin
1) Suyun ( H 2 O )molekül ağırlığı 18 g/mol ve 1g suyun kapladığı hacimde 10 6 m 3 olduğuna göre, birbirine komşu su moleküllerinin arasındaki uzaklığı Avagadro sayısını kullanarak hesap ediniz. Moleküllerin
Şekil 4.1. Döner, santrifüj ve alternatif hareketli pompaların basınç ve verdilerinin değişimi (Karassik vd. 1985)
 4. POMPALAR 4.1. Giriş Pompalar imalat şekilleri ve çalışma prensiplerine göre genel olarak pozitif (hacimsel-volumetrik-yer değiştirmeli) pompalar ve roto dinamik (santrifüj) pompalar olarak ayrılırlar.
4. POMPALAR 4.1. Giriş Pompalar imalat şekilleri ve çalışma prensiplerine göre genel olarak pozitif (hacimsel-volumetrik-yer değiştirmeli) pompalar ve roto dinamik (santrifüj) pompalar olarak ayrılırlar.
AKM 205 BÖLÜM 6 - UYGULAMA SORU VE ÇÖZÜMLERİ Doç.Dr. Ali Can Takinacı Ar.Gör. Yük. Müh. Murat Özbulut
 AKM 205 BÖLÜM 6 - UYGULAMA SORU VE ÇÖZÜMLERİ Doç.Dr. Ali Can Takinacı Ar.Gör. Yük. Müh. Murat Özbulut 1. Bir püskürtücü dirsek, 30 kg/s debisindeki suyu yatay bir borudan θ=45 açıyla yukarı doğru hızlandırarak
AKM 205 BÖLÜM 6 - UYGULAMA SORU VE ÇÖZÜMLERİ Doç.Dr. Ali Can Takinacı Ar.Gör. Yük. Müh. Murat Özbulut 1. Bir püskürtücü dirsek, 30 kg/s debisindeki suyu yatay bir borudan θ=45 açıyla yukarı doğru hızlandırarak
AÇIK KANAL HİDROLİĞİ
 AÇIK KANAL HİDROLİĞİ Tanım : Serbest su yüzeyinin hava ile temas ettiği akımlardır. SERBEST YÜZEYLİ AKIMLAR Su yüzeyi atmosferle temas halindedir. Sıvı sadece atmosfer basıncı etkisindedir. Akımı sağlayan
AÇIK KANAL HİDROLİĞİ Tanım : Serbest su yüzeyinin hava ile temas ettiği akımlardır. SERBEST YÜZEYLİ AKIMLAR Su yüzeyi atmosferle temas halindedir. Sıvı sadece atmosfer basıncı etkisindedir. Akımı sağlayan
ONDOKUZ MAYIS ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ KİMYA MÜHENDİSLİĞİ BÖLÜMÜ KMB-305 KİMYA MÜHENDİSLİĞİ LABORATUVARI I
 ONDOKUZ MAYIS ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ KİMYA MÜHENDİSLİĞİ BÖLÜMÜ KMB-305 KİMYA MÜHENDİSLİĞİ LABORATUVARI I DENEY 2 : BORULARDA BASINÇ KAYBI VE SÜRTÜNME DENEYİ (AKIŞKANLAR MEKANİĞİ) DENEYİN AMACI:
ONDOKUZ MAYIS ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ KİMYA MÜHENDİSLİĞİ BÖLÜMÜ KMB-305 KİMYA MÜHENDİSLİĞİ LABORATUVARI I DENEY 2 : BORULARDA BASINÇ KAYBI VE SÜRTÜNME DENEYİ (AKIŞKANLAR MEKANİĞİ) DENEYİN AMACI:
BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM
 BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM 4.1. Giriş Bir önceki bölümde, hareket denklemi F = ma nın, maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini
BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM 4.1. Giriş Bir önceki bölümde, hareket denklemi F = ma nın, maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini
HAVALANDIRMA DAĞITICI VE TOPLAYICI KANALLARIN HESAPLANMASI
 1.1.1. Temel Bilgiler a) Statik Basınç: Statik basınç, sıkıştırılmış havanın 1 m³ ünün serbest kalması halinde meydana çıkacak potansiyel enerjiyi gösterir. Ayrıca vantilatörlerde güç tecrübeleri kaidelerine
1.1.1. Temel Bilgiler a) Statik Basınç: Statik basınç, sıkıştırılmış havanın 1 m³ ünün serbest kalması halinde meydana çıkacak potansiyel enerjiyi gösterir. Ayrıca vantilatörlerde güç tecrübeleri kaidelerine
BORULARDA BASINÇ KAYBI VE SÜRTÜNME DENEYİ
 ONDOKUZ MAYIS ÜNİERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ MM30 MAKİNA MÜHENDİSLİĞİ LABORATUARI DERSİ BORULARDA BASINÇ KAYBI E SÜRTÜNME DENEYİ Hazırlayan Yrd.Doç.Dr. Mustafa ÖZBEY SAMSUN
ONDOKUZ MAYIS ÜNİERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ MM30 MAKİNA MÜHENDİSLİĞİ LABORATUARI DERSİ BORULARDA BASINÇ KAYBI E SÜRTÜNME DENEYİ Hazırlayan Yrd.Doç.Dr. Mustafa ÖZBEY SAMSUN
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
Newton un II. yasası. Bir cismin ivmesi, onun üzerine etki eden bileşke kuvvetle doğru orantılı ve kütlesi ile ters orantılıdır.
 Newton un II. yasası Bir cismin ivmesi, onun üzerine etki eden bileşke kuvvetle doğru orantılı ve kütlesi ile ters orantılıdır. Bir cisme F A, F B ve F C gibi çok sayıda kuvvet etkiyorsa, net kuvvet bunların
Newton un II. yasası Bir cismin ivmesi, onun üzerine etki eden bileşke kuvvetle doğru orantılı ve kütlesi ile ters orantılıdır. Bir cisme F A, F B ve F C gibi çok sayıda kuvvet etkiyorsa, net kuvvet bunların
DİNAMİK - 7. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi. Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 DİNAMİK - 7 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü 7. HAFTA Kapsam: Parçacık Kinetiği, Kuvvet İvme Yöntemi Newton hareket
DİNAMİK - 7 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü 7. HAFTA Kapsam: Parçacık Kinetiği, Kuvvet İvme Yöntemi Newton hareket
3.1. Basınç 3. BASINÇ VE AKIŞKAN STATİĞİ
 3. BASINÇ VE AKIŞKAN STATİĞİ Doç.Dr. Serdar GÖNCÜ (Ağustos 2011) 3.1. Basınç Bir akışkan tarafından birim alana uygulanan normal kuvvete basınç denir Basınç birimi N/m 2 olup buna pascal (Pa) denir. 1
3. BASINÇ VE AKIŞKAN STATİĞİ Doç.Dr. Serdar GÖNCÜ (Ağustos 2011) 3.1. Basınç Bir akışkan tarafından birim alana uygulanan normal kuvvete basınç denir Basınç birimi N/m 2 olup buna pascal (Pa) denir. 1
Enerji var veya yok edilemez sadece biçim değiştirebilir (1.yasa)
 Termodinamik: Enerjinin bilimi. Enerji: Değişikliklere sebep olma yeteneği. Termodinamik sözcüğü, Latince therme (ısı) ile dynamis (güç) sözcüklerinden türemiştir. Enerjinin korunumu prensibi: Bir etkileşim
Termodinamik: Enerjinin bilimi. Enerji: Değişikliklere sebep olma yeteneği. Termodinamik sözcüğü, Latince therme (ısı) ile dynamis (güç) sözcüklerinden türemiştir. Enerjinin korunumu prensibi: Bir etkileşim
YAVAŞ DEĞİŞEN ÜNİFORM OLMAYAN AKIM
 YAVAŞ DEĞİŞEN ÜNİFORM OLMAYAN AKIM Yavaş değişen akımların analizinde kullanılacak genel denklem bir kanal kesitindeki toplam enerji yüksekliği: H = V g + h + z x e göre türevi alınırsa: dh d V = dx dx
YAVAŞ DEĞİŞEN ÜNİFORM OLMAYAN AKIM Yavaş değişen akımların analizinde kullanılacak genel denklem bir kanal kesitindeki toplam enerji yüksekliği: H = V g + h + z x e göre türevi alınırsa: dh d V = dx dx
KATI CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 KATI CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ Bu bölümde, düzlemsel kinematik, veya bir rijit cismin düzlemsel hareketinin geometrisi incelenecektir. Bu inceleme, dişli, kam ve makinelerin yaptığı birçok işlemde
KATI CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ Bu bölümde, düzlemsel kinematik, veya bir rijit cismin düzlemsel hareketinin geometrisi incelenecektir. Bu inceleme, dişli, kam ve makinelerin yaptığı birçok işlemde
SAKARYA ÜNİVERSİTESİ SAKARYA MESLEK YÜKSEKOKULU
 TERMODİNAMİK Öğr. Gör. SAKARYA ÜNİVERSİTESİ SAKARYA MESLEK YÜKSEKOKULU ISI Maddenin kütlesine, cinsine ve sıcaklık farkına bağımlı olarak sıcaklığını birim oranda değiştirmek için gerekli olan veri miktarına
TERMODİNAMİK Öğr. Gör. SAKARYA ÜNİVERSİTESİ SAKARYA MESLEK YÜKSEKOKULU ISI Maddenin kütlesine, cinsine ve sıcaklık farkına bağımlı olarak sıcaklığını birim oranda değiştirmek için gerekli olan veri miktarına
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve Çözümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLE 1. GİİŞ - Skalerler ve ektörler - Newton Kanunları 2. KUET SİSTEMLEİ - İki Boyutlu
Statik Ders Notları Sınav Soru ve Çözümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLE 1. GİİŞ - Skalerler ve ektörler - Newton Kanunları 2. KUET SİSTEMLEİ - İki Boyutlu
SU ÜRÜNLERİNDE MEKANİZASYON
 SU ÜRÜNLERİNDE MEKANİZASYON 8 Yrd.Doç.Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları & Teknolojileri Mühendisliği Bölümü Su Ürünleri Teknolojileri Su temini Boru parçaları
SU ÜRÜNLERİNDE MEKANİZASYON 8 Yrd.Doç.Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları & Teknolojileri Mühendisliği Bölümü Su Ürünleri Teknolojileri Su temini Boru parçaları
1. HAFTA Giriş ve Temel Kavramlar
 1. HAFTA Giriş ve Temel Kavramlar TERMODİNAMİK VE ISI TRANSFERİ Isı: Sıcaklık farkının bir sonucu olarak bir sistemden diğerine transfer edilebilen bir enerji türüdür. Termodinamik: Bir sistem bir denge
1. HAFTA Giriş ve Temel Kavramlar TERMODİNAMİK VE ISI TRANSFERİ Isı: Sıcaklık farkının bir sonucu olarak bir sistemden diğerine transfer edilebilen bir enerji türüdür. Termodinamik: Bir sistem bir denge
Bölüm 6 AKIŞ SİSTEMLERİNİN MOMENTUM ANALİZİ
 Akışkanlar Mekaniği Bölüm 6 AKIŞ SİSTEMLERİNİN MOMENTUM ANALİZİ Doç. Dr. İ. Gökhan AKSOY Denizanasının (Aurelia aurita) düzenli yüzme hareketi. Denizanası gövdesini kasıp akışkanı ittikten sonra süzülerek
Akışkanlar Mekaniği Bölüm 6 AKIŞ SİSTEMLERİNİN MOMENTUM ANALİZİ Doç. Dr. İ. Gökhan AKSOY Denizanasının (Aurelia aurita) düzenli yüzme hareketi. Denizanası gövdesini kasıp akışkanı ittikten sonra süzülerek
ZEMİN SUYU Zeminde Su Akımı ve Akım Ağları. Y.Doç.Dr. Saadet A. Berilgen
 ZEMİN SUYU Zeminde Su Akımı ve Akım Ağları Y.Doç.Dr. Saadet A. Berilgen 1 Zeminde Su Akımının Matematiksel İfadesi Laplace Denklemi ve iki boyutlu akım (2D- Seepage) Yer altı suyu akım bölgesi içinde bir
ZEMİN SUYU Zeminde Su Akımı ve Akım Ağları Y.Doç.Dr. Saadet A. Berilgen 1 Zeminde Su Akımının Matematiksel İfadesi Laplace Denklemi ve iki boyutlu akım (2D- Seepage) Yer altı suyu akım bölgesi içinde bir
İnstagram:kimyaci_glcn_hoca GAZLAR-1.
 GAZLAR-1 Gazların Genel Özellikleri Maddenin en düzensiz hâlidir. Maddedeki molekül ve atomlar birbirinden uzaktır ve çok hızlı hareket eder. Tanecikleri arasında çekim kuvvetleri, katı ve sıvılarınkine
GAZLAR-1 Gazların Genel Özellikleri Maddenin en düzensiz hâlidir. Maddedeki molekül ve atomlar birbirinden uzaktır ve çok hızlı hareket eder. Tanecikleri arasında çekim kuvvetleri, katı ve sıvılarınkine
VANTİLATÖR DENEYİ. Pitot tüpü ile hız ve debi ölçümü; Vantilatör karakteristiklerinin devir sayısına göre değişimlerinin belirlenmesi
 VANTİLATÖR DENEYİ Deneyin amacı Pitot tüpü ile hız ve debi ölçümü; Vantilatör karakteristiklerinin devir sayısına göre değişimlerinin belirlenmesi Deneyde vantilatör çalışma prensibi, vantilatör karakteristiklerinin
VANTİLATÖR DENEYİ Deneyin amacı Pitot tüpü ile hız ve debi ölçümü; Vantilatör karakteristiklerinin devir sayısına göre değişimlerinin belirlenmesi Deneyde vantilatör çalışma prensibi, vantilatör karakteristiklerinin
İnşaat Mühendisliği Bölümü UYGULAMA 1- BOYUT ANALİZİ
 UYGULAMA - BOYUT ANALİZİ INS 36 HİDROLİK 03-GÜZ (Buckingham) teoremini tanımlayınız. Temel (esas) büyüklük ve temel (esas) boyut ne emektir? Açıklayınız. Bir akışkanlar mekaniği problemine teoremi uygulanığına
UYGULAMA - BOYUT ANALİZİ INS 36 HİDROLİK 03-GÜZ (Buckingham) teoremini tanımlayınız. Temel (esas) büyüklük ve temel (esas) boyut ne emektir? Açıklayınız. Bir akışkanlar mekaniği problemine teoremi uygulanığına
İŞ : Şekilde yörüngesinde hareket eden bir parçacık üzerine kuvveti görülmektedir. Parçacık A noktasından
 İŞ : Şekilde yörüngesinde hareket eden bir parçacık üzerine etkiyen F kuvveti görülmektedir. Parçacık A noktasından r geçerken konum vektörü uygun bir O orijininden ölçülmektedir ve A dan A ne diferansiyel
İŞ : Şekilde yörüngesinde hareket eden bir parçacık üzerine etkiyen F kuvveti görülmektedir. Parçacık A noktasından r geçerken konum vektörü uygun bir O orijininden ölçülmektedir ve A dan A ne diferansiyel
Bölüm 5 KÜTLE, BERNOULLi VE ENERJİ DENKLEMLERİ
 Akışkanlar Mekaniği: Temelleri ve Uygulamaları 3 üncü Baskıdan Çeviri Yunus A. Cengel, John M. Cimbala McGraw-Hill, 2014 Bölüm 5 KÜTLE, BERNOULLi VE ENERJİ DENKLEMLERİ http://personel.klu.edu.tr/utkuyilmaz
Akışkanlar Mekaniği: Temelleri ve Uygulamaları 3 üncü Baskıdan Çeviri Yunus A. Cengel, John M. Cimbala McGraw-Hill, 2014 Bölüm 5 KÜTLE, BERNOULLi VE ENERJİ DENKLEMLERİ http://personel.klu.edu.tr/utkuyilmaz
