İNM Ders 5. Zeminlerde Su Akımı - 3
|
|
|
- Ilker Gülpınar
- 9 yıl önce
- İzleme sayısı:
Transkript
1 İNM Ders 5. Zeminlerde Su Akımı - 3 Doç. Dr. Havvanur KILIÇ İnşaat Mühendisliği Bölümü Geoteknik Anabilim Dalı
2 ZEMİNDE SU AKIMININ MATEMATİKSEL İFADESİ (La Place Denklemi) Yeraltı suyu problemleri iki boyutlu akım koşuluna yakın olup, bu tür problemlerin iki boyutlu olarak analiz edilmesi gereklidir. İki boyutlu akımda i ve A akış rejiminin tamamında değişken olduğundan, Darcy Yasası iki boyutlu analizde doğrudan kullanılamamaktadır. Genel olarak bu analizler karmaşık olup, LaPlace denklemi olarak bilinen matematiksel fonksiyonun kullanılması gerekir. Yapılan Kabuller Darcy yasası geçerlidir. Zemin tamamen suya doygundur Zemin elemanının boyutu sabit kalır Zemin homojendir
3 İki boyutlu olarak incelenebilecek akım problemleri Zemin mekaniği problemleri gerçekte üç boyutlu problemler olmakla beraber, uygulamada bunların birçoğu çözümü basitleştirmek için iki boyutlu problem haline indirgenerek incelenmektedir. Problemi üç boyutlu halden iki boyutlu hale indirgemek çoğu problemde çözümün doğruluk derecesini çok az etkilemektedir.
4 İki boyutlu olarak incelenebilecek akım problemleri
5 Zeminlerde Su Akımı Yeraltı suyu akım bölgesi içindeki bir zemin elemanını göz önüne alalım. Şekil de dx, dy, dz boyutlarında ve içinden x, y, z doğrultularında yeraltı suyu akımı gerçekleşen bir zemin elemanı gösterilmiştir. Herhangi bir doğrultudaki su akımının Darcy Kanunu na uygun hareket ettiği kabul edilebilir. ædh ö q = kia= k ç A è L ø 3 boyutlu akım durumu Kararlı akım durumunda (elemanın boşluk oranı sabit, suya doygunluğu sabit) elemana giren su örneğin: x ekseninde q x =(v x A x ) burada v x x yönündeki hız bileşeni ve A x = (dz dy) akım yönüne dik kesit alanıdır.
6 Örneğin, z- doğrultusundaki akım gözönüne alındığında, zemin elemanına birim zamanda giren ve çıkan su miktarları, sırasıyla, k z zeminin z doğrultusundaki permeabilite katsayısı olmaktadır. Zemin elemanı için z doğrultusundaki net su akımı miktarı, giren ve çıkan su miktarlarının farkı olacağı için, Aynı şekilde, x- ve y- doğrultuları için yazmak mümkündür.
7 Zeminlerde Su Akımı Su akımı sırasında zemin elemanının hacminin sabit kaldığı göz önüne alınarak, birim zamandaki toplam net su akımının sıfıra eşit olacağını (elemana giren toplam suyun çıkan su miktarına eşit olacağını) söyleyebiliriz. Şeklinde yazarak zeminlerde su akımını tanımlayan genel diferansiyel denklemi elde edebiliriz. Bu denklem hidrolik yükün akım bölgesi içinde değişimini matematiksel olarak ifade etmektedir. Denklemin çözümü ile, akım bölgesi içindeki bütün noktalarda toplam hidrolik yükün değeri elde edilmiş olmaktadır. Toplam hidrolik yük değerleri bulunduktan sonra, hidrolik eğimler, akım hızları, akım miktarı, sızma kuvvetleri ve su basınçları kolaylıkla elde edilebilmektedir.
8 Zeminlerde Su Akımı Zeminin her doğrultusundaki permeabilitenin aynı olduğu izotropik koşullarda k x =k y =k z olacağı durumlarda diferansiyel denklem h h h x y z = şeklini alacaktır. (La Place denklemi) Bu ikinci derece kısmi diferansiyel denklem matematikte La Place denklemi olarak bilinir. La Place denkleminin çözümünü elde etmek nisbeten daha kolay olduğu için akım problemlerinde genellikle zeminin izotropik özelliklere (k x = k y = k z ) sahip olduğu varsayılmaktadır. İki boyutlu problemlerde, zemin içinde su akımını tanımlayan La Place denklemi 2 2 x Denklemde h(x,z) potansiyel fonksiyonu, akım bölgesindeki herhangi bir noktada toplam hidrolik yükün değerini temsil etmektedir. Buna göre x ve z doğrultusundaki hidrolik eğim edilebilir. 2 2 h h + = 0 z i x = æ ç è h x ö ø i z = æ ç è hö z ø şeklinde ifade
9 Akım Çizgileri ve Eş Potansiyel Çizgileri Darcy Kanunu na göre akım hızının hidrolik eğim ile doğru orantılı olarak artacağını biliyoruz. h(x,z) potansiyel fonksiyonu, akım bölgesindeki herhangi bir noktada toplam hidrolik yükün değerini temsil etmektedir. Y(x,z) hız potansiyel fonksiyonu, akım bölgesindeki herhangi bir noktada akım hızının değerini temsil etmektedir. x ve z doğrultularındaki akım hızlarını, Y(x,z) hız potansiyel fonksiyonundan yararlanarak (v=ki) Y h = -k z x Y h = k x z şeklinde ifade edebiliriz. Yukarıdaki ifadelerin x ve z ye göre türevlerini alıp birbiri ile toplayarak 2 x Y z Y 2 = k 2 h x z 2 h z x Y(x,z) hız potansiyel fonksiyonunun da La Place denklemini sağladığını kanıtlayabiliriz. - k = 0
10 Akım Çizgileri ve Eş Potansiyel Çizgileri Akım bölgesi içinde Y hız potansiyel fonksiyonunun değerinin sabit kaldığı (Y=sabit) bir eğri üzerinde, türevin sıfıra eşit olacağı gözönüne alınarak dy = Y x dx + Y z dz = 0 Böyle bir eğrinin eğimi edilebilir. dz Y/ x h/ z v =- = = dx Y/ z h/ x v z x şeklinde ifade Bu durumda, Y=sabit eğrilerine çizilecek teğetler, o noktadaki hız vektörünü göstermekte Y=sabit eğrileri ise zemin içinde akan bir su damlasının takip edeceği izler olmaktadır. Bu eğrilere, zemin mekaniğinde akım eğrileri adı verilir.
11 Akım Çizgileri ve Eş Potansiyel Çizgileri Akım bölgesi içinde hidrolik yük dağılımını gösteren h(x, z) potansiyel fonksiyonunun sabit değerler aldığı (h=sabit) ve eğrilerin eğimi ise dh = h x dx + h z dz = 0 şeklinde elde edilebilir. dz h / x v eğim = =- =- dx h / z v x z Görüldüğü gibi h=sabit eğrilerinin (eş potansiyel çizgileri) eğimi, akım çizgilerinin eğiminin tersine ve ters işaretlisine eşit olmaktadır. Bu da bize akım çizgileri ile eşpotansiyel çizgilerinin birbirini dik açılar ile kestiğini, başka bir ifade ile, h (x,z) ve Y(x,z) potansiyel fonksiyonlarının birbirine dik (ortogonal) iki fonksiyon olduğunu göstermektedir. Bir akım bölgesi içindeki akım çizgilerini gösteren Y=sabit ile eşpotansiyel çizgilerini gösteren h=sabit eğri takımlarını bir arada çizerek, o akım bölgesi için akım ağını elde edebiliriz.
12 Akım Ağları Şekil de bu şekilde elde edilmiş bir akım ağının bir parçası,
13 Akım Ağları ve Sızmanın Hesaplanması Zemin kütlesinin birim uzunluğu için, iki akım çizgisi arasında kalan bölgeden (akım kanalı) geçen su miktarı Darcy yasasından yararlanılarak, ( h1 - h2 ) a D q = kia = k ( ax1) = k( ) Dh b b Burada, a ve b sırası ile ardışık akım çizgileri ve eşpotansiyel çizgileri arasındaki uzaklıklar olmaktadır. Görüldüğü gibi, akım hızı vektörü eşpotansiyel çizgilerine dik olmakta, şiddeti ise hidrolik eğim ( h h i ) 1 2 = - b ile zeminin permeabilite katsayısı çarpılarak elde edilmektedir v=ki
14 Sınır koşulları Zemin ile su arasındaki sınır eşpotansiyel çizgidir. Zemin ile geçirimsiz malzemeler arasındaki herhangi bir sınır akım çizgisidir. Geçirimsiz malzeme, geçirimsiz bir tabaka da olabilir, bir temelin tabanı da olabilir, bir palplanş perde de olabilir. Akım problemleri sınır koşulları açısından 2 gruba ayrılır. A) basınçlı akım B) serbest yüzeyli akım
15 Akım bölgesi sınırlarının fiziksel olarak kısıtlandığı durumlar (basınçlı akım). Bu tür akım problemlerinde su akımı belirlenmiş sınırlar içinde kalmak zorundadır. Beton bağlama altından sızan su akımı bağlamanın tabanı ile geçirimsiz tabaka arasından geçecek şekilde kısıtlanmıştır. Ayrıca su geçirimsizlik perdesinin de altından dolaşmak zorundadır. Geçirimsiz sınırlara dik doğrultuda akım olmayacağı için, böyle bir sınıra ulaşan su damlaları geçirimsiz yüzeye parallel akmak zorundadır. Dolayısıyla geçirimsiz yüzeyler akım çizgilerini oluşturmaktadır. A B, B C, CD, DE ve FG akım bölgesini sınırlayan akım çizgilerini oluşturur. AA, BB ve EE sınırları ise hidrolik yükün sabit olduğu eşpotansiyel çizgileridir.
16 Akım bölgesinin tam olarak kısıtlanmadığı durumlar (serbest yüzeyli akım). Bu tür problemlerde, akım bölgesi sınırlarından en az bir tanesi fiziksel olarak belirlenmemiştir. Bu sınırın saptanması araştırılan çözümün bir parçasını oluşturur. Toprak dolgu barajda su sızması problemini inceleyelim. Geçirimsiz tabaka sızma bölgesinin alt sınırını oluşturmaktadır. Sızma bölgesinin üst sınırı ise fiziksel olarak belirlenmemiştir. A D ile gösterilen üst akım çizgisinin saptanması problemin bir parçasını oluşturmaktadır. Dren geçirimli olduğu için bir serbest yüzey oluşturmakta, buraya erişen su çok az hidrolik yük kaybı ile yatay yönde kolaylıkla akabilmektedir. A B eşpotansiyel çizgi (su basıncı ve hidrolik yüklerin toplamı sabit kaldığı için), B C akım çizgisi, CDE eşpotansiyel çizgisi, A D üst akım çizgisidir (başlangıçta bilinmemektedir). Su akımı eşpotansiyel çizgilere dik doğrultudadır.
17 LA PLACE DENKLEMİ NİN ÇÖZÜMÜ 1. Grafik çözümler (Akım Ağları) 2. Sayısal çözümler (sonlu farklar, sonlu elemanlar, sınır elemanlar) 3. Elektrik analojisi (benzeşimi) 17
18 Akım Ağlarının Özellikleri ve Çizilmesi 1. Akım çizgileri ve eşpotansiyel çizgiler birbirlerini dik açılarla kesmelidir (sınırlar dahil) 2. Birbiri ile kesişen akım ve eşpotansiyel çizgilerin oluşturduğu eğri kenarlı dikdörtgenler birbirine benzer olmalıdır (genişlik/uzunluk=sabit) 3. Birbirini takip eden eşpotansiyel çizgileri arasındaki hidrolik yük farkı sabit olmalıdır (h 1 -h 2 =h 2 -h 3 =h 3 -h 4 =.). 4. Akım kanalları arasından eşit miktarda su geçmelidir (2. ve 3. koşullar ile bu otomatikman sağlanır). 5. Serbest akım problemlerinde eşpotansiyel çizgileri, üst akım çizgisini eşit düşey aralıklarla kesmelidir. 6. Sınırları oluşturan yüzeylerde, akım çizgisi veya eşpotansiyel çizgi olmalarına göre sınır koşulları ile uyum sağlamalıdır.
19 Akım Ağı Çizilmesi 1. Çizgisiz bir kağıt üzerine ölçekli olarak akım bölgesinin sınırları mürekkepli kalemle çizilir. 2. Akım bölgesi için çizilecek akım kanalı sayısı seçilir (genellikle 4-5 yeterli) ve kurşun kalemle çizilir. İlk denemede akım çizgileri aralıkları yaklaşık eşit çizilebilir. Akım çizgilerinin eşpotansiyel çizgi olan sınırlara dik doğrultuda olmasına dikkat edilir. 3. İkinci adımda çizilen akım çizgilerini dik açıyla kesecek ve bunlarla genişlik/uzunluk oranı sabit dikdörtgenler oluşturacak şekilde eşpotansiyel çizgileri çizilir. Genellikle akım ağları dikdörtgenlerin genişlik/uzunluk oranı bire eşit çizilmekle beraber bu oranın sabit olması yeterlidir. Eşpotansiyel çizgilerin akım çizgisini oluşturan geçirimsiz sınır yüzeylerine dik olmasına dikkate edilmelidir. 4. Çizilen akım ağının, bir akım ağının sahip olması gereken koşullar ile uyumlu olup olmadığı kontrol edilir, uyumsuzluklar giderilir. 19
20 Akım ağlarının bazı geometrik özellikleri Eşit akım taşıyan akım kanalları, eşpotansiyel çizgileri uzunluk/genişlik oranı aynı olan dikdörtgenler oluşacak şekilde keserler. Akım ağlarını elle çizmek için, her bir akım kanalının aynı debiyi (akımı) taşıdığını ve komşu iki eşpotansiyel çizgi arasında meydana gelen enerji kaybının (yük kaybının) hep eşit olduğunu varsaymak gerekir. Bu durumda tüm elemanlar dikdörtgenimsi olup birbirine benzer geometrilere sahip olacaktır. Akım ağlarını bu dikdörtgenleri kare olacak şekilde çizmek son derece uygundur (Şekil de gösterildiği gibi) akım kanalı içine 4 noktada değecek şekilde daire çizerek kareler oluşturabiliriz).
21 Akım ağı çizmek için yöntem
22 1 Boyutlu Akım Problemlerinde Akım Ağı Piezometreler değişik noktalardaki toplam hidrolik yükü göstermektedir. Yatay bir çizgi üzerindeki noktaların yerçekimi yükleri aynı olduğu halde toplam hidrolik yüklerdeki farklılıklar basınç farklılıklarından kaynaklanmaktadır. H Akım çizgileri Eş potansiyel çizgileri (kesikli çizgiler) L Birbirini takip eden eşpotansiyel çizgileri arasındaki toplam hidrolik yük kaybı Δh=H/4=sabit Zemin içinde her noktada hidrolik eğim i=h/l, akım hızı v=ki=k (H/L) Akım miktarı q=kia=k (H/L) A A ve B de toplam hidrolik yük h A ve h B C noktası h C = h A i x (zemin boyu) h C = h A H/L x (3/4L) h C = h A (3/4H) h C = h B + i x (zemin boyu) h C = h B + H/L x L/4 h C = h B + H/4
23 1 Boyutlu Akım Problemlerinde Akım Ağı Akım çizgileri 3H/4 2H/4 H/4 0. A Birbirini takip eden eşpotansiyel çizgileri arasındaki toplam hidrolik yük kaybı H/4=sabit Akım boyu = L=H Hidrolik eğim i= H/H=1.0 birim boydaki yük kaybı V=ki=k Bütün tabaka derinliği boyunca su basınçları sıfır (u=0). Eş potansiyel çizgileri Üst yüzeyi ince bir su tabakası ile kaplı, alt yüzeyi ise permeabilitesi çok yüksek bir çakıl dren (serbest akım yüzeyi) ile temas halinde bir zemin tabakasından suyun sızması gösterilmiştir. Burada akım düşey yöndedir ve akım çizgileri düşey doğrular ile gösterilmiştir. Eş potansiyel çizgileri (kesikli çizgiler) ise bunlara dik yatay doğrulardan oluşmaktadır. Alt ve üst yüzeylerde su basıncı sıfır (atmosferik basınç) olduğu için toplam hidrolik yük yerçekimi yükünden oluşmaktadır. A noktası h A = H i x (L) = H 1 x H = 0
24 2 Boyutlu Akım: Beton Bağlama
25 2 Boyutlu Akım: Beton Bağlama Eş Potansiyel çizgileri aralık sayısı N d Akım kanalı sayısı N f Birbirini takip eden eşpotansiyel çizgileri arasındaki toplam hidrolik yük kaybı Δh/N d = Δh/10= sabit Akım çizgileri ve eşpotansiyel çizgileri eşit aralıklı değil (genişlik/uzunluk sabit)! A da hidrolik eğim i A =0.10 (Δh/b) Eşpotansiyel çizgilerin birbirine yaklaştığı bölgeler hidrolik eğimin ve akım hızının arttığı bölgeler! Ara noktalardaki hidrolik yük interpolasyonla bulunabilir (h A =0.35Δh) A noktasında su basıncı u A =[h A -(z A )]g w = (h A +z A )g w Bağlamanın altından birim zamanda sızan su miktarları: Bağlamanın birim uzunluğu için, bir akım kanalından geçen su miktarı Bağlamanın birim uzunluğu için, akım kanalı sayısı N f iken geçen su miktarı Dq æ q = k. ç è æ Dh = k. a. ç è Nd a b öæ ç øè N N f d ö 1 ø b ö D h ø
26 Simetrik problemler Bazı problemlerde simetriden yararlanarak akım ağının sadece yarısını çizebiliriz. Şekil de kenarları palplanşlar ile tutulmuş bir hendeğe sızan su problemi için akım ağı gösterilmiştir. Akım ağının değerlendirilmesinden, hidrolik eğimler (kazı tabanının stabilitesi açısından önemli), kazıya sızan su miktarları ve palplanş perdesine etkiyen hidrolik basınçlar hesaplanabilir.
27 Serbest akım yüzeyi Toprak dolgu bir barajda akım probleminin özelliği, üst akım çizgisinin saptanması oluşturmaktadır. Ayrıca permeabilitesi çok yüksek bir topuk dreninin varlığıda akım özelliklerini etkilemektedir.
28
29 Su yapılarında problemler
30 Granüler zeminlerde borulanma Çıkışta hidrolik eğim i çıkış Dh = D l ΔH Beton bağlama R.D. Dl Dh = hidrolik yük farkı Geçirimsiz tabaka zemin
31 Granüler zeminlerde borulanma i çıkış > (i cr ) Zemin daneleri yıkanır Bu olay sonucunda menbaya doğru ilerleyen oyulma (borulanma) meydana gelir. ΔH F borulanma ic = ñ5-6 i çıkış Beton bağlama R.D. Zemin yok; su dolu zemin Geçirimsiz tabaka
32 Drenler ve Filtreler Toprak barajlar veya sızmanın olduğu problemlerde zemin suyunda basınç artışlarını kontrol etmek için geçirgenliği(permeabilitesi) yüksek drenaj tabakaları kullanılmaktadır. Drenlerin esas amacı suyun rahat hareketini sağlamak ve böylece zemin veya kaya içerisinde hidrostatik basınçların artmasına engel olmaktır.
33 Drenler ve Filtreler Drenaj tabakası iki ana koşulu sağlamalıdır: 1. Drenaj malzemesinin granülometrisi ve boşlukların boyutları yakınındaki ince danelerin dren içine sızmasına ve tıkanmaya yol açmasına engel olacak şekilde seçilmeli 2. Zeminin granülometrisi ve boşlukların boyutları dren tabakasının yüksek permeabiliteye sahip olmasına imkan verecek şekilde seçilmeli
34 Drenler ve Filtreler
35 Drenler ve Filtreler Her iki koşulu birlikte sağlamak için
36 Birçok problemde, iri daneli zeminlerden oluşan drenler permeabilitesi çok düşük ince daneli zeminler ile yanyana yerleştirilmek durumunda olmaktadır. Böyle durumlarda yukarıdaki koşulları doğrudan sağlamak mümkün olamayacağı için, dren ile ince daneli tabii zemin arasına geçiş tabakası olarak filitreler yerleştirilmektedir. Filitre tabakalarının granülometrisi ince daneli zemin ve dren malzemesinin her ikisi ile de yukarıdaki koşulları sağlayacak zeminlerden seçilmelidir. Bu şekilde teşkil edilmiş bir filitre tabakası dreni koruyacak şekilde işlev görecektir. Drenle birlikte filtre kullanılması durumunda 36
37 Filtre Uygulamaları
38 38
39 h=h-n d Dh h A =6-5.6x0.429=3.64 h B =6-6x0.429=3.43 h C =6-7x0.429=
40 40
41 Örnek
42 ÇÖZÜM
43 KAYNAKLAR Özaydın, K. (2011), Zemin Mekaniği, Birsen Yayınevi, Güncelleştirilmiş Baskı, İstanbul. Uzuner, B. (2007), Temel Zemin Mekaniği, Derya Kitabevi, Trabzon. Casagrande, A. (1937) Seepage Through Dams, Journal of the New England Water Works Association, Vol. 51, Reprinted in Contributions to Soil Mechanics, , Boston Society of Civil Engineers, Cedergren, H. R. (1977) Seepage, Drainage and Flow Nets, 2nd Ed., John Wiley and Sons, Inc., New York. Dunn, I. S., Anderson, L. R. and Kiefer, F. W. (1980) Fundamentals of Geotechnical Analyis, John Wiley and Sons, Inc., New York. Ernst, L. F. (1950) Een nieuwe formule voor de berekening van de doorlaatfactor met de boorgatenmethode, Rap. Landbouwproefsta en Bodemkunding Inst. T. N. O., Groningen, Netherlands. Hazen A. (1911) Discussion of Dams on Sand Foundations, by A. C:Koenig, Transactions, American Society of Civil Engineers, Vol. 73, Hooghoudt, S. B. (1936) Bijdragen tot de kennis van eenige natuur kundige grootheden van den grond, 4 Versl. Lamdb., Ond. 42 (13) B : , Algemeene Landsdrukkerji, The Hague. Lambe, T. W. And Whitman, R. V. (1969) Soil Mechanics, John Wiley and Sons, Inc., New York. Perloff, W. H. and Baron, W. (1976) Soil Mechanics-Principles and Applications, The Ronald Pres Company, New York. 43
ZEMİNDE SU AKIMININ MATEMATİKSEL İFADESİ (LAPLACE DENKLEMİ)
 ZEMİNDE SU AKIMININ MATEMATİKSEL İFADESİ (LAPLACE DENKLEMİ) 1 3 Boyutlu Yeraltısuyu Akımı q zo Yeraltı suyu akım bölgesi Darcy yasası geçerli dz Su akımı sırasında zemin elemanının hacmi sabit Z Y X dx
ZEMİNDE SU AKIMININ MATEMATİKSEL İFADESİ (LAPLACE DENKLEMİ) 1 3 Boyutlu Yeraltısuyu Akımı q zo Yeraltı suyu akım bölgesi Darcy yasası geçerli dz Su akımı sırasında zemin elemanının hacmi sabit Z Y X dx
ZEMİN SUYU Zeminde Su Akımı ve Akım Ağları. Y.Doç.Dr. Saadet A. Berilgen
 ZEMİN SUYU Zeminde Su Akımı ve Akım Ağları Y.Doç.Dr. Saadet A. Berilgen 1 Zeminde Su Akımının Matematiksel İfadesi Laplace Denklemi ve iki boyutlu akım (2D- Seepage) Yer altı suyu akım bölgesi içinde bir
ZEMİN SUYU Zeminde Su Akımı ve Akım Ağları Y.Doç.Dr. Saadet A. Berilgen 1 Zeminde Su Akımının Matematiksel İfadesi Laplace Denklemi ve iki boyutlu akım (2D- Seepage) Yer altı suyu akım bölgesi içinde bir
Ders: 5 Zemin Suyu - I. Doç. Dr. Havvanur KILIÇ İnşaat Mühendisliği Bölümü Geoteknik Anabilim Dalı
 0423111 Ders: 5 Zemin Suyu - I Doç. Dr. Havvanur KILIÇ İnşaat Mühendisliği Bölümü Geoteknik Anabilim Dalı Giriş - Zemin içinde bulunan su miktarı (su muhtevası), - Zemin suyundaki basınç (boşluk suyu basıncı),
0423111 Ders: 5 Zemin Suyu - I Doç. Dr. Havvanur KILIÇ İnşaat Mühendisliği Bölümü Geoteknik Anabilim Dalı Giriş - Zemin içinde bulunan su miktarı (su muhtevası), - Zemin suyundaki basınç (boşluk suyu basıncı),
ZEMİNLERİN GEÇİRİMLİLİĞİ
 ZEMİNLERİN GEÇİRİMLİLİĞİ 21 GİRİŞ İnşaat Mühendisliğinde, zemin içindeki su akımları ile birçok durumda karşılaşılır. Toprak yapılar [toprak baraj, toprak set (sedde) vb.] içinden suların sızması, yapıların
ZEMİNLERİN GEÇİRİMLİLİĞİ 21 GİRİŞ İnşaat Mühendisliğinde, zemin içindeki su akımları ile birçok durumda karşılaşılır. Toprak yapılar [toprak baraj, toprak set (sedde) vb.] içinden suların sızması, yapıların
Ders Notları 3 Geçirimlilik Permeabilite
 Ders Notları 3 Geçirimlilik Permeabilite Zemindeki mühendislik problemleri, zeminin kendisinden değil, boşluklarında bulunan boşluk suyundan kaynaklanır. Su olmayan bir gezegende yaşıyor olsaydık, zemin
Ders Notları 3 Geçirimlilik Permeabilite Zemindeki mühendislik problemleri, zeminin kendisinden değil, boşluklarında bulunan boşluk suyundan kaynaklanır. Su olmayan bir gezegende yaşıyor olsaydık, zemin
5. YERALTISUYU & SIZMA BASINCI (SEEPAGE PRESSURE)
 5. YERALTISUYU & SIZMA BASINCI (SEEPAGE PRESSURE) Toprak içindeki su: Toprağa giren su, yerçekimi etkisi ile aşağı doğru harekete başlar ve bir geçirimsiz tabakayla karşılaştığında, birikerek su tablasını
5. YERALTISUYU & SIZMA BASINCI (SEEPAGE PRESSURE) Toprak içindeki su: Toprağa giren su, yerçekimi etkisi ile aşağı doğru harekete başlar ve bir geçirimsiz tabakayla karşılaştığında, birikerek su tablasını
Prof. Dr. Osman SİVRİKAYA Zemin Mekaniği I Ders Notu
 C - Zeminde Su Akımları Giriş 1-2 Boyutlu Akımın Denklemleri Akım Ağları * Sızan su miktarının bulunması * Akış durumunda b.s.basıncının belirlenmesi * Hidrolik eğimin bulunması Akım kuvveti ve Kaynama
C - Zeminde Su Akımları Giriş 1-2 Boyutlu Akımın Denklemleri Akım Ağları * Sızan su miktarının bulunması * Akış durumunda b.s.basıncının belirlenmesi * Hidrolik eğimin bulunması Akım kuvveti ve Kaynama
BÖLÜM : 9 SIZMA KUVVETİ VE FİLTRELER
 ZEMİN MEKANİĞİ 1 BÖLÜM : 9 FİLTRELER SIZMA KUVVETİ VE Akan suların bir kuvvete sahip olduğu, taşıdığı katı maddelerden bilinmektedir. Bu sular ile taşınan katı maddelerin kütlesi, hidrolik eğime göre değişen
ZEMİN MEKANİĞİ 1 BÖLÜM : 9 FİLTRELER SIZMA KUVVETİ VE Akan suların bir kuvvete sahip olduğu, taşıdığı katı maddelerden bilinmektedir. Bu sular ile taşınan katı maddelerin kütlesi, hidrolik eğime göre değişen
5. YERALTISUYU & SIZMA BASINCI (SEEPAGE PRESSURE)
 5. YERALTISUYU & SIZMA BASINCI (SEEPAGE PRESSURE) Toprak içindeki su: Toprağa giren su, yerçekimi etkisi ile aşağı doğru harekete başlar ve bir geçirimsiz tabakayla karşılaştığında, birikerek su tablasını
5. YERALTISUYU & SIZMA BASINCI (SEEPAGE PRESSURE) Toprak içindeki su: Toprağa giren su, yerçekimi etkisi ile aşağı doğru harekete başlar ve bir geçirimsiz tabakayla karşılaştığında, birikerek su tablasını
Yüzeyaltı Drenaj (Subsurface Drainage) Prof.Dr.Mustafa KARAŞAHİN
 Yüzeyaltı Drenaj (Subsurface Drainage) Prof.Dr.Mustafa KARAŞAHİN Neden gerekli? Hat üstyapısının drenajı için Yer altı suyunu kontrol etmek için Şevlerin drene edilmesi için gereklidir. Yüzeyaltı drenaj,
Yüzeyaltı Drenaj (Subsurface Drainage) Prof.Dr.Mustafa KARAŞAHİN Neden gerekli? Hat üstyapısının drenajı için Yer altı suyunu kontrol etmek için Şevlerin drene edilmesi için gereklidir. Yüzeyaltı drenaj,
ELASTİSİTE TEORİSİ I. Yrd. Doç Dr. Eray Arslan
 ELASTİSİTE TEORİSİ I Yrd. Doç Dr. Eray Arslan Mühendislik Tasarımı Genel Senaryo Analitik çözüm Fiziksel Problem Matematiksel model Diferansiyel Denklem Problem ile ilgili sorular:... Deformasyon ne kadar
ELASTİSİTE TEORİSİ I Yrd. Doç Dr. Eray Arslan Mühendislik Tasarımı Genel Senaryo Analitik çözüm Fiziksel Problem Matematiksel model Diferansiyel Denklem Problem ile ilgili sorular:... Deformasyon ne kadar
Prof. Dr. Osman SİVRİKAYA Zemin Mekaniği I Ders Notu
 B - Zeminlerin Geçirimliliği Giriş Darcy Kanunu Geçirimliği Etkileyen Etkenler Geçirimlilik (Permeabilite) Katsayısnın (k) Belirlenmesi * Ampirik Yaklaşımlar ile * Laboratuvar deneyleri ile * Arazi deneyleri
B - Zeminlerin Geçirimliliği Giriş Darcy Kanunu Geçirimliği Etkileyen Etkenler Geçirimlilik (Permeabilite) Katsayısnın (k) Belirlenmesi * Ampirik Yaklaşımlar ile * Laboratuvar deneyleri ile * Arazi deneyleri
INM 305 Zemin Mekaniği
 Hafta_8 INM 305 Zemin Mekaniği Zeminlerde Gerilme ve Dağılışı Yrd.Doç.Dr. İnan KESKİN [email protected], [email protected] Haftalık Konular Hafta 1: Zeminlerin Oluşumu Hafta 2: Hafta 3: Hafta
Hafta_8 INM 305 Zemin Mekaniği Zeminlerde Gerilme ve Dağılışı Yrd.Doç.Dr. İnan KESKİN [email protected], [email protected] Haftalık Konular Hafta 1: Zeminlerin Oluşumu Hafta 2: Hafta 3: Hafta
ZEMİNLERİN GEÇİRİMLİLİĞİ YRD. DOÇ. DR. TAYLAN SANÇAR
 ZEMİNLERİN GEÇİRİMLİLİĞİ YRD. DOÇ. DR. TAYLAN SANÇAR Suyun Toprak ve Kayalar içerisindeki hareketi Suyun Toprak ve Kayalar içerisindeki hareketi Hatırlanması gereken iki kural vardır 1. Darcy Kanunu 2.
ZEMİNLERİN GEÇİRİMLİLİĞİ YRD. DOÇ. DR. TAYLAN SANÇAR Suyun Toprak ve Kayalar içerisindeki hareketi Suyun Toprak ve Kayalar içerisindeki hareketi Hatırlanması gereken iki kural vardır 1. Darcy Kanunu 2.
Zeminlerin Sıkışması ve Konsolidasyon
 Zeminlerin Sıkışması ve Konsolidasyon 2 Yüklenen bir zeminin sıkışmasının aşağıdaki nedenlerden dolayı meydana geleceği düşünülür: Zemin danelerinin sıkışması Zemin boşluklarındaki hava ve /veya suyun
Zeminlerin Sıkışması ve Konsolidasyon 2 Yüklenen bir zeminin sıkışmasının aşağıdaki nedenlerden dolayı meydana geleceği düşünülür: Zemin danelerinin sıkışması Zemin boşluklarındaki hava ve /veya suyun
14. ZEMİNLERDE SUYUN HAREKETİ
 14. ZEMİNLERDE SUYUN HAREKETİ Geçirimlilik (Permeabilite) Zemin taneleri arasındaki boşluklar irtibatlı olup, suyun akışına izin verir. Suyun hareketi enel hidrolik kanunlarına uyun olarak sürer. Genel
14. ZEMİNLERDE SUYUN HAREKETİ Geçirimlilik (Permeabilite) Zemin taneleri arasındaki boşluklar irtibatlı olup, suyun akışına izin verir. Suyun hareketi enel hidrolik kanunlarına uyun olarak sürer. Genel
Yrd. Doç.. Dr. Selim ALTUN
 İN371 ZEMİN N MEKANİĞİ I Yrd. Doç.. Dr. Selim ALTUN Dersin Amacı ve Hedefi Zemin mekaniği, inşaat mühendisliği öğrencileri için diğer mühendislik derslerinde gereksinim duyacakları araçların öğretildiği
İN371 ZEMİN N MEKANİĞİ I Yrd. Doç.. Dr. Selim ALTUN Dersin Amacı ve Hedefi Zemin mekaniği, inşaat mühendisliği öğrencileri için diğer mühendislik derslerinde gereksinim duyacakları araçların öğretildiği
Zemin Suyu. Yrd.Doç.Dr. Saadet BERİLGEN
 Zemin Suyu Yrd.Doç.Dr. Saadet BERİLGEN Giriş Zemin içinde bulunan su miktarı (su muhtevası), zemin suyundaki basınç (boşluk suyu basıncı) ve suyun zemin içindeki hareketi zeminlerin mühendislik özelliklerini
Zemin Suyu Yrd.Doç.Dr. Saadet BERİLGEN Giriş Zemin içinde bulunan su miktarı (su muhtevası), zemin suyundaki basınç (boşluk suyu basıncı) ve suyun zemin içindeki hareketi zeminlerin mühendislik özelliklerini
Kx, Ky, Kz ; Birim kütleye etki eden kütlesel kuvvet bileşenleri
 KM 204 / Ders Notu H05-S1 kışkanların Statiği - GENELLEŞTİRME STTİĞİN TEMEL DENKLEMLERİ/ þ = þ (, y, ) idi ve ilk olarak þ = þ (); þ þ (, y) hali ele alınmıştı. þ = þ (, y, ) genel hali ele alınacak. Kütlesel
KM 204 / Ders Notu H05-S1 kışkanların Statiği - GENELLEŞTİRME STTİĞİN TEMEL DENKLEMLERİ/ þ = þ (, y, ) idi ve ilk olarak þ = þ (); þ þ (, y) hali ele alınmıştı. þ = þ (, y, ) genel hali ele alınacak. Kütlesel
HİDROLİK. Yrd. Doç. Dr. Fatih TOSUNOĞLU
 HİDROLİK Yrd. Doç. Dr. Fatih TOSUNOĞLU Ders Hakkında Genel Bilgiler Görüşme Saatleri:---------- Tavsiye edilen kitaplar: 1-Hidrolik (Prof. Dr. B. Mutlu SÜMER, Prof. Dr. İstemi ÜNSAL. ) 2-Akışkanlar Mekaniği
HİDROLİK Yrd. Doç. Dr. Fatih TOSUNOĞLU Ders Hakkında Genel Bilgiler Görüşme Saatleri:---------- Tavsiye edilen kitaplar: 1-Hidrolik (Prof. Dr. B. Mutlu SÜMER, Prof. Dr. İstemi ÜNSAL. ) 2-Akışkanlar Mekaniği
Gevşek Zemin - Geçirgenlik kolay - Yüksek Permeabilite. Sıkı Zemin - Geçirgenlik zor - Düşük Permeabilite
 DARCY YASASI Gözenekli bir ortamda suyun akış hızı, yük kaybı ile doğru, suyun aktığı yolun uzunluğuyla ters orantılıdır. Laminar akış için geçerlidir. Ortalama akış kızı hidrolik eğim ( h/ L) ile doğru
DARCY YASASI Gözenekli bir ortamda suyun akış hızı, yük kaybı ile doğru, suyun aktığı yolun uzunluğuyla ters orantılıdır. Laminar akış için geçerlidir. Ortalama akış kızı hidrolik eğim ( h/ L) ile doğru
1. Temel zemini olarak. 2. İnşaat malzemesi olarak. Zeminlerin İnşaat Mühendisliğinde Kullanımı
 Zeminlerin İnşaat Mühendisliğinde Kullanımı 1. Temel zemini olarak Üst yapıdan aktarılan yükleri güvenle taşıması Deformasyonların belirli sınır değerleri aşmaması 2. İnşaat malzemesi olarak 39 Temellerin
Zeminlerin İnşaat Mühendisliğinde Kullanımı 1. Temel zemini olarak Üst yapıdan aktarılan yükleri güvenle taşıması Deformasyonların belirli sınır değerleri aşmaması 2. İnşaat malzemesi olarak 39 Temellerin
ZEMİNLERİN SIKIŞMASI, KONSOLİDASYONU VE OTURMASI. Yrd. Doç. Dr. Taylan SANÇAR
 ZEMİNLERİN SIKIŞMASI, KONSOLİDASYONU VE OTURMASI Yrd. Doç. Dr. Taylan SANÇAR Zeminlerin herhangi bir yük altında sıkışması ve konsolidasyonu sonucu yapıda meydana gelen oturmalar, yapının mimari ve/veya
ZEMİNLERİN SIKIŞMASI, KONSOLİDASYONU VE OTURMASI Yrd. Doç. Dr. Taylan SANÇAR Zeminlerin herhangi bir yük altında sıkışması ve konsolidasyonu sonucu yapıda meydana gelen oturmalar, yapının mimari ve/veya
İNM 305 ZEMİN MEKANİĞİ
 İNM 305 ZEMİN MEKANİĞİ 2015-2016 GÜZ YARIYILI Prof. Dr. Zeki GÜNDÜZ 1 2 Zeminde gerilmeler 3 ana başlık altında toplanabilir : 1. Doğal Gerilmeler : Özağırlık, suyun etkisi, oluşum sırası ve sonrasında
İNM 305 ZEMİN MEKANİĞİ 2015-2016 GÜZ YARIYILI Prof. Dr. Zeki GÜNDÜZ 1 2 Zeminde gerilmeler 3 ana başlık altında toplanabilir : 1. Doğal Gerilmeler : Özağırlık, suyun etkisi, oluşum sırası ve sonrasında
Ders: 6 ZEMİN GERİLMELERİ. Doç. Dr. Havvanur KILIÇ İnşaat Mühendisliği Bölümü Geoteknik Anabilim Dalı
 0423111 Ders: 6 ZEMİN GERİLMELERİ Doç. Dr. Havvanur KILIÇ İnşaat Mühendisliği Bölümü Geoteknik Anabilim Dalı Gerilme kavramı Zemin tabakalarının kendi ağırlıkları ve uygulanan dış yükler, zemin içindeki
0423111 Ders: 6 ZEMİN GERİLMELERİ Doç. Dr. Havvanur KILIÇ İnşaat Mühendisliği Bölümü Geoteknik Anabilim Dalı Gerilme kavramı Zemin tabakalarının kendi ağırlıkları ve uygulanan dış yükler, zemin içindeki
Prof. Dr. Osman SİVRİKAYA Zemin Mekaniği I Ders Notu
 HAFTALIK DERS PLANI Hafta Konular Kaynaklar 1 Zeminle İlgili Problemler ve Zeminlerin Oluşumu [1], s. 1-13 2 Zeminlerin Fiziksel Özellikleri [1], s. 14-79; [23]; [24]; [25] 3 Zeminlerin Sınıflandırılması
HAFTALIK DERS PLANI Hafta Konular Kaynaklar 1 Zeminle İlgili Problemler ve Zeminlerin Oluşumu [1], s. 1-13 2 Zeminlerin Fiziksel Özellikleri [1], s. 14-79; [23]; [24]; [25] 3 Zeminlerin Sınıflandırılması
ZEMİNLERDE SU ZEMİN SUYU
 ZEMİNLERDE SU ZEMİN SUYU Bir zemin kütlesini oluşturan taneler arasındaki boşluklar kısmen ya da tamamen su ile dolu olabilir. Zeminlerin taşıma gücü, yük altında sıkışması, şevler ve toprak barajlar gibi
ZEMİNLERDE SU ZEMİN SUYU Bir zemin kütlesini oluşturan taneler arasındaki boşluklar kısmen ya da tamamen su ile dolu olabilir. Zeminlerin taşıma gücü, yük altında sıkışması, şevler ve toprak barajlar gibi
 Geometrik nivelmanda önemli hata kaynakları Nivelmanda oluşabilecek model hataları iki bölümde incelenebilir. Bunlar: Aletsel (Nivo ve Mira) Hatalar Çevresel Koşullardan Kaynaklanan Hatalar 1. Aletsel
Geometrik nivelmanda önemli hata kaynakları Nivelmanda oluşabilecek model hataları iki bölümde incelenebilir. Bunlar: Aletsel (Nivo ve Mira) Hatalar Çevresel Koşullardan Kaynaklanan Hatalar 1. Aletsel
12.163/12.463 Yeryüzü Süreçleri ve Yüzey Şekillerinin Evrimi K. Whipple Eylül, 2004
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 12.163./12.463 Yeryüzü Süreçleri ve Yüzey Şekillerinin Evrimi 2004 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için http://ocw.mit.edu/terms
MIT Açık Ders Malzemeleri http://ocw.mit.edu 12.163./12.463 Yeryüzü Süreçleri ve Yüzey Şekillerinin Evrimi 2004 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için http://ocw.mit.edu/terms
YTÜ İnşaat Fakültesi Geoteknik Anabilim Dalı. Ders 5: İÇTEN DESTEKLİ KAZILAR. Prof.Dr. Mehmet BERİLGEN
 YTÜ İnşaat Fakültesi Geoteknik Anabilim Dalı Ders 5: İÇTEN DESTEKLİ KAZILAR Prof.Dr. Mehmet BERİLGEN İçten Destekli Kazılar İçerik: Giriş Uygulamalar Tipler Basınç diagramları Tasarım Toprak Basıncı Diagramı
YTÜ İnşaat Fakültesi Geoteknik Anabilim Dalı Ders 5: İÇTEN DESTEKLİ KAZILAR Prof.Dr. Mehmet BERİLGEN İçten Destekli Kazılar İçerik: Giriş Uygulamalar Tipler Basınç diagramları Tasarım Toprak Basıncı Diagramı
11.1 11.2. Tanım Akışkanların Statiği (Hidrostatik) Örnekler Kaldırma Kuvveti. 11.3 Örnek Eylemsizlik Momenti. 11.4 Eylemsizlik Yarıçapı
 11.1 11. Tanım Akışkanların Statiği (Hidrostatik) Örnekler Kaldırma Kuvveti 11.3 Örnek Eylemsizlik Momenti 11.4 Eylemsizlik Yarıçapı 11.5 Eksen Takımının Değiştirilmesi 11.6 Asal Eylemsizlik Momentleri
11.1 11. Tanım Akışkanların Statiği (Hidrostatik) Örnekler Kaldırma Kuvveti 11.3 Örnek Eylemsizlik Momenti 11.4 Eylemsizlik Yarıçapı 11.5 Eksen Takımının Değiştirilmesi 11.6 Asal Eylemsizlik Momentleri
Gerilme kavramı Zemin tabakalarının kendi ağırlıkları ve uygulanan dış yükler, zemin içindeki herhangi bir elemanda gerilmeler oluştururlar. Mekanikte
 Gerilme kavramı Zemin tabakalarının kendi ağırlıkları ve uygulanan dış yükler, zemin içindeki herhangi bir elemanda gerilmeler oluştururlar. Mekanikte gerilme, birim alana uygulanan yükün şiddeti olarak
Gerilme kavramı Zemin tabakalarının kendi ağırlıkları ve uygulanan dış yükler, zemin içindeki herhangi bir elemanda gerilmeler oluştururlar. Mekanikte gerilme, birim alana uygulanan yükün şiddeti olarak
İNM 305 ZEMİN MEKANİĞİ
 İNM 305 ZEMİN MEKANİĞİ 015-016 GÜZ YARIYILI Prof. Dr. Zeki GÜNDÜZ 1 ZEMİNDE SU (ZEMİN HİDROLİĞİ) HİDROLOJİK DÖNGÜ 3 ZEMİNDEKİ SU TÜRLERİ Zemin ortamının boşluklarında bulunan suya, zemin suyu denilir.
İNM 305 ZEMİN MEKANİĞİ 015-016 GÜZ YARIYILI Prof. Dr. Zeki GÜNDÜZ 1 ZEMİNDE SU (ZEMİN HİDROLİĞİ) HİDROLOJİK DÖNGÜ 3 ZEMİNDEKİ SU TÜRLERİ Zemin ortamının boşluklarında bulunan suya, zemin suyu denilir.
YAVAŞ DEĞİŞEN ÜNİFORM OLMAYAN AKIM
 YAVAŞ DEĞİŞEN ÜNİFORM OLMAYAN AKIM Yavaş değişen akımların analizinde kullanılacak genel denklem bir kanal kesitindeki toplam enerji yüksekliği: H = V g + h + z x e göre türevi alınırsa: dh d V = dx dx
YAVAŞ DEĞİŞEN ÜNİFORM OLMAYAN AKIM Yavaş değişen akımların analizinde kullanılacak genel denklem bir kanal kesitindeki toplam enerji yüksekliği: H = V g + h + z x e göre türevi alınırsa: dh d V = dx dx
Türev Uygulamaları ÜNİTE. Amaçlar. İçindekiler. Yazar Prof.Dr. Vakıf CAFEROV
 Türev Uygulamaları Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 10 Amaçlar Bu üniteyi çalıştıktan sonra; türev kavramı yardımı ile fonksiyonun monotonluğunu, ekstremum noktalarını, konvekslik ve konkavlığını, büküm
Türev Uygulamaları Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 10 Amaçlar Bu üniteyi çalıştıktan sonra; türev kavramı yardımı ile fonksiyonun monotonluğunu, ekstremum noktalarını, konvekslik ve konkavlığını, büküm
AÇIK KANAL HİDROLİĞİ
 AÇIK KANAL HİDROLİĞİ Tanım : Serbest su yüzeyinin hava ile temas ettiği akımlardır. SERBEST YÜZEYLİ AKIMLAR Su yüzeyi atmosferle temas halindedir. Sıvı sadece atmosfer basıncı etkisindedir. Akımı sağlayan
AÇIK KANAL HİDROLİĞİ Tanım : Serbest su yüzeyinin hava ile temas ettiği akımlardır. SERBEST YÜZEYLİ AKIMLAR Su yüzeyi atmosferle temas halindedir. Sıvı sadece atmosfer basıncı etkisindedir. Akımı sağlayan
25. f: R { 4} R 28. ( ) 3 2 ( ) 26. a ve b reel sayılar olmak üzere, 27. ( ) eğrisinin dönüm noktasının ordinatı 10 olduğuna göre, m kaçtır?
 . f: R { 4} R, > ise ( ) 4 f =, ise 6 8. ( ) f = 6 + m + 4 eğrisinin dönüm noktasının ordinatı olduğuna göre, m kaçtır? ) 7 ) 8 ) 9 ) E) fonksiyonu aşağıdaki değerlerinin hangisinde süreksizdir? ) ) )
. f: R { 4} R, > ise ( ) 4 f =, ise 6 8. ( ) f = 6 + m + 4 eğrisinin dönüm noktasının ordinatı olduğuna göre, m kaçtır? ) 7 ) 8 ) 9 ) E) fonksiyonu aşağıdaki değerlerinin hangisinde süreksizdir? ) ) )
BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER
 BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER Yrd. Doç. Dr. Beytullah EREN Çevre Mühendisliği Bölümü BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER Atatürk Barajı (Şanlıurfa) BATMIŞ YÜZEYLERE ETKİYEN KUVVETLER
BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER Yrd. Doç. Dr. Beytullah EREN Çevre Mühendisliği Bölümü BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER Atatürk Barajı (Şanlıurfa) BATMIŞ YÜZEYLERE ETKİYEN KUVVETLER
Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü
 Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü 1 kışkan Statiğine Giriş kışkan statiği (hidrostatik, aerostatik), durgun haldeki akışkanlarla
Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü 1 kışkan Statiğine Giriş kışkan statiği (hidrostatik, aerostatik), durgun haldeki akışkanlarla
Kütlesel kuvvetlerin sadece g den kaynaklanması hali;
 KDN03-1 AKIŞKANLARIN STATİĞİ: HİDROSTATİK Basınç kavramı z σ a dz ds σx α x dx y σz Hidrostatikte ise olduğundan i = 0; Hidrostatik problemlerde sadece 1, 2, 3 olabilir. İnceleme kolaylığı için 2-boyutlu
KDN03-1 AKIŞKANLARIN STATİĞİ: HİDROSTATİK Basınç kavramı z σ a dz ds σx α x dx y σz Hidrostatikte ise olduğundan i = 0; Hidrostatik problemlerde sadece 1, 2, 3 olabilir. İnceleme kolaylığı için 2-boyutlu
Su seviyesi = ha Qin Kum dolu sütun Su seviyesi = h Qout
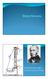 Su seviyesi = h a in Kum dolu sütun out Su seviyesi = h b 1803-1858 Modern hidrojeolojinin doğumu Henry Darcy nin deney seti (1856) 1 Darcy Kanunu Enerjinin yüksek olduğu yerlerden alçak olan yerlere doğru
Su seviyesi = h a in Kum dolu sütun out Su seviyesi = h b 1803-1858 Modern hidrojeolojinin doğumu Henry Darcy nin deney seti (1856) 1 Darcy Kanunu Enerjinin yüksek olduğu yerlerden alçak olan yerlere doğru
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
BÖLÜM 1: TEMEL KAVRAMLAR
 BÖLÜM 1: TEMEL KAVRAMLAR Hal Değişkenleri Arasındaki Denklemler Aralarında sıfıra eşitlenebilen en az bir veya daha fazla denklem kurulabilen değişkenler birbirine bağımlıdır. Bu denklemlerden bilinen
BÖLÜM 1: TEMEL KAVRAMLAR Hal Değişkenleri Arasındaki Denklemler Aralarında sıfıra eşitlenebilen en az bir veya daha fazla denklem kurulabilen değişkenler birbirine bağımlıdır. Bu denklemlerden bilinen
İNM 305 ZEMİN MEKANİĞİ
 İNM 305 ZEMİN MEKANİĞİ 2015-2016 GÜZ YARIYILI Prof. Dr. Zeki GÜNDÜZ 1 ZEMİNLERİN SIKIŞMASI, KONSOLİDASYON ve OTURMALAR 2 3 4 ZEMİNLERİN SIKIŞMASI ve KONSOLİDASYON 1. Giriş 2. Kohezyonsuz ve Kohezyonlu
İNM 305 ZEMİN MEKANİĞİ 2015-2016 GÜZ YARIYILI Prof. Dr. Zeki GÜNDÜZ 1 ZEMİNLERİN SIKIŞMASI, KONSOLİDASYON ve OTURMALAR 2 3 4 ZEMİNLERİN SIKIŞMASI ve KONSOLİDASYON 1. Giriş 2. Kohezyonsuz ve Kohezyonlu
YAPI ELEMANLARI DERS SUNUMLARI 4. HAFTA
 YAPI ELEMANLARI DERS SUNUMLARI 4. HAFTA 1 IV.1.1. Basit Kanallarda İksa Şekilleri aşağıda verilen bu iksa türü genellikle derinliği ve akıcılığı az olan ve düşey olarak 1.00-2.00 m. aralıklarla kalasların
YAPI ELEMANLARI DERS SUNUMLARI 4. HAFTA 1 IV.1.1. Basit Kanallarda İksa Şekilleri aşağıda verilen bu iksa türü genellikle derinliği ve akıcılığı az olan ve düşey olarak 1.00-2.00 m. aralıklarla kalasların
508 HİDROLOJİ ÖDEV #1
 508 HİDROLOJİ ÖDEV #1 Teslim tarihi: 30 Mart 2009 16:30 1. Yüzey alanı 40 km 2 olan bir gölde Haziran ayında göle giren akarsuyun ortalama debisi 0.56 m 3 /s, gölden çıkan suyun ortalama debisi 0.48 m
508 HİDROLOJİ ÖDEV #1 Teslim tarihi: 30 Mart 2009 16:30 1. Yüzey alanı 40 km 2 olan bir gölde Haziran ayında göle giren akarsuyun ortalama debisi 0.56 m 3 /s, gölden çıkan suyun ortalama debisi 0.48 m
INM 308 Zemin Mekaniği
 Hafta_7 INM 308 Zemin Mekaniği Yanal Zemin Basınçları Yrd.Doç.Dr. İnan KESKİN [email protected], [email protected] www.inankeskin.com ZEMİN MEKANİĞİ Haftalık Konular Hafta 1: Hafta 2: Hafta
Hafta_7 INM 308 Zemin Mekaniği Yanal Zemin Basınçları Yrd.Doç.Dr. İnan KESKİN [email protected], [email protected] www.inankeskin.com ZEMİN MEKANİĞİ Haftalık Konular Hafta 1: Hafta 2: Hafta
Zemin Gerilmeleri. Zemindeki gerilmelerin: 1- Zeminin kendi ağırlığından (geostatik gerilme),
 Zemin Gerilmeleri Zemindeki gerilmelerin: 1- Zeminin kendi ağırlığından (geostatik gerilme), 2- Zemin üzerine eklenmiş yüklerden (Binalar, Barağlar vb.) kaynaklanmaktadır. 1 YERYÜZÜ Y.S.S Bina yükünden
Zemin Gerilmeleri Zemindeki gerilmelerin: 1- Zeminin kendi ağırlığından (geostatik gerilme), 2- Zemin üzerine eklenmiş yüklerden (Binalar, Barağlar vb.) kaynaklanmaktadır. 1 YERYÜZÜ Y.S.S Bina yükünden
KARAYOLLARINDA YÜZEY DRENAJI. Prof. Dr. Mustafa KARAŞAHİN
 KARAYOLLARINDA YÜZEY DRENAJI Prof. Dr. Mustafa KARAŞAHİN Drenajın Amacı Yağmur veya kar suyunun yolun taşkına neden olmasına engel olmak ve yol yüzeyinde suyun birikmesine engel olmak, Karayolu üstyapısı
KARAYOLLARINDA YÜZEY DRENAJI Prof. Dr. Mustafa KARAŞAHİN Drenajın Amacı Yağmur veya kar suyunun yolun taşkına neden olmasına engel olmak ve yol yüzeyinde suyun birikmesine engel olmak, Karayolu üstyapısı
Kirişlerde Kesme (Transverse Shear)
 Kirişlerde Kesme (Transverse Shear) Bu bölümde, doğrusal, prizmatik, homojen ve lineer elastik davranan bir elemanın eksenine dik doğrultuda yüklerin etkimesi durumunda en kesitinde oluşan kesme gerilmeleri
Kirişlerde Kesme (Transverse Shear) Bu bölümde, doğrusal, prizmatik, homojen ve lineer elastik davranan bir elemanın eksenine dik doğrultuda yüklerin etkimesi durumunda en kesitinde oluşan kesme gerilmeleri
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 1- GİRİŞ Doç. Dr. Ali Rıza YILDIZ 1 Mühendislikte, herhangi bir fiziksel sistemin matematiksel modellenmesi sonucu elde edilen karmaşık veya analitik çözülemeyen denklemlerin
MAK 210 SAYISAL ANALİZ BÖLÜM 1- GİRİŞ Doç. Dr. Ali Rıza YILDIZ 1 Mühendislikte, herhangi bir fiziksel sistemin matematiksel modellenmesi sonucu elde edilen karmaşık veya analitik çözülemeyen denklemlerin
ELEKTRİKSEL POTANSİYEL
 ELEKTRİKSEL POTANSİYEL Elektriksel Potansiyel Enerji Elektriksel potansiyel enerji kavramına geçmeden önce Fizik-1 dersinizde görmüş olduğunuz iş, potansiyel enerji ve enerjinin korunumu kavramları ile
ELEKTRİKSEL POTANSİYEL Elektriksel Potansiyel Enerji Elektriksel potansiyel enerji kavramına geçmeden önce Fizik-1 dersinizde görmüş olduğunuz iş, potansiyel enerji ve enerjinin korunumu kavramları ile
İLERİ ZEMİN MEKANİĞİ. Ders 1. Genel Giriş. Doç. Dr. Havvanur KILIÇ İnşaat Mühendisliği Bölümü Geoteknik Anabilim Dalı
 0426102 İLERİ ZEMİN MEKANİĞİ Ders 1. Genel Giriş Doç. Dr. Havvanur KILIÇ İnşaat Mühendisliği Bölümü Geoteknik Anabilim Dalı HAFTALIK KONULAR VE İLGİLİ ÖN HAZIRLIK ÇALIŞMALARI Hafta / Week Konular / Subjects
0426102 İLERİ ZEMİN MEKANİĞİ Ders 1. Genel Giriş Doç. Dr. Havvanur KILIÇ İnşaat Mühendisliği Bölümü Geoteknik Anabilim Dalı HAFTALIK KONULAR VE İLGİLİ ÖN HAZIRLIK ÇALIŞMALARI Hafta / Week Konular / Subjects
Bölüm 8: Borularda sürtünmeli Akış
 Bölüm 8: Borularda sürtünmeli Akış Laminer ve Türbülanslı Akış Laminer Akış: Çalkantısız akışkan tabakaları ile karakterize edilen çok düzenli akışkan hareketi laminer akış olarak adlandırılır. Türbülanslı
Bölüm 8: Borularda sürtünmeli Akış Laminer ve Türbülanslı Akış Laminer Akış: Çalkantısız akışkan tabakaları ile karakterize edilen çok düzenli akışkan hareketi laminer akış olarak adlandırılır. Türbülanslı
İSTİNAT YAPILARI TASARIMI. İstinat Yapıları-Giriş
 İNM 0424122 İSTİNAT YAPILARI TASARIMI İstinat Yapıları-Giriş Doç. Dr. Mehmet BERİLGEN İnşaat Mühendisliği Bölümü Geoteknik Anabilim Dalı İstinat (Dayanma) Yapıları Geoteknik mühendisliğinde yanal zemin
İNM 0424122 İSTİNAT YAPILARI TASARIMI İstinat Yapıları-Giriş Doç. Dr. Mehmet BERİLGEN İnşaat Mühendisliği Bölümü Geoteknik Anabilim Dalı İstinat (Dayanma) Yapıları Geoteknik mühendisliğinde yanal zemin
eğim Örnek: Koordinat sisteminde bulunan AB doğru parçasının
 eğim Doğrunun eğimi Eğim konusunu koordinat sistemine ve doğrunun eğimine taşımadan önce kareli zemindeki doğru parçalarının eğimini bulmaya çalışalım. Koordinat sisteminde bulunan AB doğru parçasının
eğim Doğrunun eğimi Eğim konusunu koordinat sistemine ve doğrunun eğimine taşımadan önce kareli zemindeki doğru parçalarının eğimini bulmaya çalışalım. Koordinat sisteminde bulunan AB doğru parçasının
STATİK AĞIRLIK MERKEZİ. 3.1 İki Boyutlu Cisimler 3.2 Düzlem Eğriler 3.3 Bileşik Cisimler. 3.4 Integrasyon ile ağırlık merkezi hesabı
 1 STATİK AĞIRLIK MERKEZİ 3.1 İki Boyutlu Cisimler 3.2 Düzlem Eğriler 3.3 Bileşik Cisimler 3.4 Integrasyon ile ağırlık merkezi hesabı 3.5 Pappus-Guldinus Teoremi 3.6 Yayılı Yüke Eşdeğer Tekil Yük 3.7 Sıvı
1 STATİK AĞIRLIK MERKEZİ 3.1 İki Boyutlu Cisimler 3.2 Düzlem Eğriler 3.3 Bileşik Cisimler 3.4 Integrasyon ile ağırlık merkezi hesabı 3.5 Pappus-Guldinus Teoremi 3.6 Yayılı Yüke Eşdeğer Tekil Yük 3.7 Sıvı
STATİK. Ders_9. Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü. Ders notları için: GÜZ
 STATİK Ders_9 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2017-2018 GÜZ ALANLAR İÇİN ATALET MOMENTİNİN TANIMI, ALAN ATALET YARIÇAPI
STATİK Ders_9 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2017-2018 GÜZ ALANLAR İÇİN ATALET MOMENTİNİN TANIMI, ALAN ATALET YARIÇAPI
HİDROJEOLOJİ. Hidrolojik Çevrim Bileşenleri Akış ve süzülme. 3.Hafta. Prof.Dr.N.Nur ÖZYURT
 HİDROJEOLOJİ 3.Hafta Hidrolojik Çevrim Bileşenleri Akış ve süzülme Prof.Dr.N.Nur ÖZYURT [email protected] Hidrolojik Çevrim Bileşenleri Buharlaşma-terleme Yağış Yüzeysel akış Yeraltına süzülme ve
HİDROJEOLOJİ 3.Hafta Hidrolojik Çevrim Bileşenleri Akış ve süzülme Prof.Dr.N.Nur ÖZYURT [email protected] Hidrolojik Çevrim Bileşenleri Buharlaşma-terleme Yağış Yüzeysel akış Yeraltına süzülme ve
AÇIK KANAL AKIMI. Hopa Yukarı Sundura Deresi-ARTVİN
 AÇIK KANAL AKIMI Hopa Yukarı Sundura Deresi-ARTVİN AÇIK KANAL AKIMI (AKA) Açık kanal akımı serbest yüzeyli akımın olduğu bir akımdır. serbest yüzey hava ve su arasındaki ara yüzey @ serbest yüzeyli akımda
AÇIK KANAL AKIMI Hopa Yukarı Sundura Deresi-ARTVİN AÇIK KANAL AKIMI (AKA) Açık kanal akımı serbest yüzeyli akımın olduğu bir akımdır. serbest yüzey hava ve su arasındaki ara yüzey @ serbest yüzeyli akımda
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ
 BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Bernoulli Denklemi, Basınç ve Hız Yükleri Borularda Piezometre ve Enerji Yükleri Venturi Deney Sistemi
 Bernoulli Denklemi, Basınç ve Hız Yükleri Borularda Piezometre ve Enerji Yükleri Venturi Deney Sistemi Akışkanlar dinamiğinde, sürtünmesiz akışkanlar için Bernoulli prensibi akımın hız arttıkça aynı anda
Bernoulli Denklemi, Basınç ve Hız Yükleri Borularda Piezometre ve Enerji Yükleri Venturi Deney Sistemi Akışkanlar dinamiğinde, sürtünmesiz akışkanlar için Bernoulli prensibi akımın hız arttıkça aynı anda
Doğrusal Demet Işıksallığı 2. Fatma Çağla Öztürk
 Doğrusal Demet Işıksallığı Fatma Çağla Öztürk İçerik Demet Yönlendirici Mıknatıslar Geleneksel Demir Baskın Mıknatıslar 3.07.01 HPFBU Toplantı, OZTURK F. C. Demet Yönlendirici Mıknatıslar Durgun mıknatıssal
Doğrusal Demet Işıksallığı Fatma Çağla Öztürk İçerik Demet Yönlendirici Mıknatıslar Geleneksel Demir Baskın Mıknatıslar 3.07.01 HPFBU Toplantı, OZTURK F. C. Demet Yönlendirici Mıknatıslar Durgun mıknatıssal
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 7 İç Kuvvetler Kaynak: Mühendislik Mekaniği: Statik, R. C. Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 7. İç Kuvvetler Bu bölümde, bir
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 7 İç Kuvvetler Kaynak: Mühendislik Mekaniği: Statik, R. C. Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 7. İç Kuvvetler Bu bölümde, bir
8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için
10. KONSOLİDASYON. Konsolidasyon. σ gerilmedeki artış zeminin boşluk oranında e azalma ve deformasyon yaratır (gözeneklerden su dışarı çıkar).
 . KONSOLİDASYON Konsolidasyon σ gerilmedeki artış zeminin boşluk oranında e azalma ve deformasyon yaratır (gözeneklerden su dışarı çıkar). σ nasıl artar?. Yeraltısuyu seviyesi düşer 2. Zemine yük uygulanır
. KONSOLİDASYON Konsolidasyon σ gerilmedeki artış zeminin boşluk oranında e azalma ve deformasyon yaratır (gözeneklerden su dışarı çıkar). σ nasıl artar?. Yeraltısuyu seviyesi düşer 2. Zemine yük uygulanır
Akışkan Kinematiği 1
 Akışkan Kinematiği 1 Akışkan Kinematiği Kinematik, akışkan hareketini matematiksel olarak tanımlarken harekete sebep olan kuvvetleri ve momentleri gözönüne almadan; Yerdeğiştirmeler Hızlar ve İvmeler cinsinden
Akışkan Kinematiği 1 Akışkan Kinematiği Kinematik, akışkan hareketini matematiksel olarak tanımlarken harekete sebep olan kuvvetleri ve momentleri gözönüne almadan; Yerdeğiştirmeler Hızlar ve İvmeler cinsinden
Ölçme Bilgisi DERS 9-10. Hacim Hesapları. Kaynak: İ.ASRİ (Gümüşhane Ü) T. FİKRET HORZUM( AÜ )
 Ölçme Bilgisi DERS 9-10 Hacim Hesapları Kaynak: İ.ASRİ (Gümüşhane Ü) T. FİKRET HORZUM( AÜ ) Büyük inşaatlarda, yol ve kanal çalışmalarında kazılacak toprak miktarının hesaplanması, maden işletmelerinde
Ölçme Bilgisi DERS 9-10 Hacim Hesapları Kaynak: İ.ASRİ (Gümüşhane Ü) T. FİKRET HORZUM( AÜ ) Büyük inşaatlarda, yol ve kanal çalışmalarında kazılacak toprak miktarının hesaplanması, maden işletmelerinde
BÖLÜM 6 GERÇEK AKIŞKANLARIN HAREKETİ
 BÖLÜM 6 GERÇEK AKIŞKANLARIN HAREKETİ Gerçek akışkanın davranışı viskoziteden dolayı meydana gelen ilave etkiler nedeniyle ideal akışkan akımlarına göre daha karmaşık yapıdadır. Gerçek akışkanlar hareket
BÖLÜM 6 GERÇEK AKIŞKANLARIN HAREKETİ Gerçek akışkanın davranışı viskoziteden dolayı meydana gelen ilave etkiler nedeniyle ideal akışkan akımlarına göre daha karmaşık yapıdadır. Gerçek akışkanlar hareket
Elastisite Teorisi Hooke Yasası Normal Gerilme-Şekil değiştirme
 Elastisite Teorisi Hooke Yasası Normal Gerilme-Şekil değiştirme Gerilme ve Şekil değiştirme bileşenlerinin lineer ilişkileri Hooke Yasası olarak bilinir. Elastisite Modülü (Young Modülü) Tek boyutlu Hooke
Elastisite Teorisi Hooke Yasası Normal Gerilme-Şekil değiştirme Gerilme ve Şekil değiştirme bileşenlerinin lineer ilişkileri Hooke Yasası olarak bilinir. Elastisite Modülü (Young Modülü) Tek boyutlu Hooke
fonksiyonunun [-1,1] arasındaki grafiği hesaba katılırsa bulunan sonucun
![fonksiyonunun [-1,1] arasındaki grafiği hesaba katılırsa bulunan sonucun fonksiyonunun [-1,1] arasındaki grafiği hesaba katılırsa bulunan sonucun](/thumbs/31/15329792.jpg) . UŞAK FEN EDEBİYAT FAKÜLTESİ MATEMATİK BÖLÜMÜ ANALİZ II FİNAL SORULARI ÇÖZÜMLERİ d belirli integralinin aşağıdaki çözümünün doğru olup olmadığını belirtiniz. Eğer çözüm yanlış ise sebebini açıklayınız.
. UŞAK FEN EDEBİYAT FAKÜLTESİ MATEMATİK BÖLÜMÜ ANALİZ II FİNAL SORULARI ÇÖZÜMLERİ d belirli integralinin aşağıdaki çözümünün doğru olup olmadığını belirtiniz. Eğer çözüm yanlış ise sebebini açıklayınız.
Yapı veya dolgu yüklerinin neden olduğu gerilme artışı, zemin tabakalarını sıkıştırır.
 18. KONSOLİDASYON Bir mühendislik yapısının veya dolgunun altında bulunan zeminin sıkışmasına konsolidasyon denir. Sıkışma 3 boyutlu olmasına karşılık fark ihmal edilebilir nitelikte olduğundan 2 boyutlu
18. KONSOLİDASYON Bir mühendislik yapısının veya dolgunun altında bulunan zeminin sıkışmasına konsolidasyon denir. Sıkışma 3 boyutlu olmasına karşılık fark ihmal edilebilir nitelikte olduğundan 2 boyutlu
Hidrolik Yapılarda (Kanallar, Kıyı Koruma Yapıları, Göletler) Erozyon Koruması
 HİDROLİK YAPILAR»» Taşkın Kanalları Yeterli mesafenin olmadığı durumlarda hücre içleri beton veya kırmataş ile doldurularak Flexi HDS istinat duvarı uygulaması yapılabilir.»» Dere ve Akarsular»» Hendek
HİDROLİK YAPILAR»» Taşkın Kanalları Yeterli mesafenin olmadığı durumlarda hücre içleri beton veya kırmataş ile doldurularak Flexi HDS istinat duvarı uygulaması yapılabilir.»» Dere ve Akarsular»» Hendek
AERODİNAMİK KUVVETLER
 AERODİNAMİK KUVVETLER Prof.Dr. Mustafa Cavcar Anadolu Üniversitesi, Sivil Havacılık Yüksekokulu, 26470 Eskişehir Bir uçak üzerinde meydana gelen aerodinamik kuvvetlerin bileşkesi ( ); uçağın etrafından
AERODİNAMİK KUVVETLER Prof.Dr. Mustafa Cavcar Anadolu Üniversitesi, Sivil Havacılık Yüksekokulu, 26470 Eskişehir Bir uçak üzerinde meydana gelen aerodinamik kuvvetlerin bileşkesi ( ); uçağın etrafından
ÇEVRE GEOTEKNİĞİ DERSİ
 ÇEVRE GEOTEKNİĞİ DERSİ ATIK VE ZEMİNLERİN OTURMASI DERSİN SORUMLUSU YRD. DOÇ DR. AHMET ŞENOL HAZIRLAYANLAR 2013138017 ALİHAN UTKU YILMAZ 2013138020 MUSTAFA ÖZBAY OTURMA Yapının(dolayısıyla temelin ) düşey
ÇEVRE GEOTEKNİĞİ DERSİ ATIK VE ZEMİNLERİN OTURMASI DERSİN SORUMLUSU YRD. DOÇ DR. AHMET ŞENOL HAZIRLAYANLAR 2013138017 ALİHAN UTKU YILMAZ 2013138020 MUSTAFA ÖZBAY OTURMA Yapının(dolayısıyla temelin ) düşey
2. Dereceden Denklem ve Eşitsizlikler x 2 2x + 2m + 1 = 0 denkleminin kökleri x 1 ve x 2 dir. 4x 1 + 5x 2 = 7 ise m aşağıdakilerden hangisidir?
 MC www.matematikclub.com, 006 Cebir Notları Gökhan DEMĐR, [email protected]. Dereceden Denklem ve Eşitsizlikler- TEST I A) 1 B) C) 3 D) 4 E) 5 1. 1/ = 0 denkleminin köklerinin toplamı aşağıdakilerden
MC www.matematikclub.com, 006 Cebir Notları Gökhan DEMĐR, [email protected]. Dereceden Denklem ve Eşitsizlikler- TEST I A) 1 B) C) 3 D) 4 E) 5 1. 1/ = 0 denkleminin köklerinin toplamı aşağıdakilerden
AKIŞKANLAR MEKANİĞİ-II
 AKIŞKANLAR MEKANİĞİ-II Şekil 1. Akışa bırakılan parçacıkların parçacık izlemeli hızölçer ile belirlenmiş cisim arkasındaki (iz bölgesi) yörüngeleri ve hızlarının zamana göre değişimi (renk skalası). Akış
AKIŞKANLAR MEKANİĞİ-II Şekil 1. Akışa bırakılan parçacıkların parçacık izlemeli hızölçer ile belirlenmiş cisim arkasındaki (iz bölgesi) yörüngeleri ve hızlarının zamana göre değişimi (renk skalası). Akış
Selçuk Üniversitesi. Mühendislik-Mimarlık Fakültesi. Kimya Mühendisliği Bölümü. Kimya Mühendisliği Laboratuvarı. Venturimetre Deney Föyü
 Selçuk Üniversitesi Mühendislik-Mimarlık Fakültesi Kimya Mühendisliği Bölümü Kimya Mühendisliği Laboratuvarı Venturimetre Deney Föyü Hazırlayan Arş.Gör. Orhan BAYTAR 1.GİRİŞ Genellikle herhangi bir akış
Selçuk Üniversitesi Mühendislik-Mimarlık Fakültesi Kimya Mühendisliği Bölümü Kimya Mühendisliği Laboratuvarı Venturimetre Deney Föyü Hazırlayan Arş.Gör. Orhan BAYTAR 1.GİRİŞ Genellikle herhangi bir akış
BÖLÜM-1 HİDROLOJİNİN TANIMI VE ÖNEMİ
 BÖLÜM-1 HİDROLOJİNİN TANIMI VE ÖNEMİ 1.1 GİRİŞ Hidrolojinin kelime anlamı su bilimi olup böyle bir bilime ihtiyaç duyulması suyun doğadaki bütün canlıların yaşamını devam ettirebilmesi için gereken çok
BÖLÜM-1 HİDROLOJİNİN TANIMI VE ÖNEMİ 1.1 GİRİŞ Hidrolojinin kelime anlamı su bilimi olup böyle bir bilime ihtiyaç duyulması suyun doğadaki bütün canlıların yaşamını devam ettirebilmesi için gereken çok
2. Sonsuz uzunluk kabul edilebilmesi için çubuklar ne kadar uzunlukta olmalıdır? Resim 1
 Örnek 3-9*: 5 mm çapında çok uzun bir çubuğun bir ucu T b =100 C sabit sıcaklıkta tutulmaktadır. Çubuğun yüzeyi T =25 C de ve ısı transfer katsayısı (h) 100 W/m 2 K olan çevresindeki hava (air) ile temastadır.
Örnek 3-9*: 5 mm çapında çok uzun bir çubuğun bir ucu T b =100 C sabit sıcaklıkta tutulmaktadır. Çubuğun yüzeyi T =25 C de ve ısı transfer katsayısı (h) 100 W/m 2 K olan çevresindeki hava (air) ile temastadır.
ZEMİNLERİN KAYMA DİRENCİ
 ZEMİNLERİN KYM İRENİ Problem 1: 38.m çapında, 76.m yüksekliğindeki suya doygun kil zemin üzerinde serbest basınç deneyi yapılmış ve kırılma anında, düşey yük 129.6 N ve düşey eksenel kısalma 3.85 mm olarak
ZEMİNLERİN KYM İRENİ Problem 1: 38.m çapında, 76.m yüksekliğindeki suya doygun kil zemin üzerinde serbest basınç deneyi yapılmış ve kırılma anında, düşey yük 129.6 N ve düşey eksenel kısalma 3.85 mm olarak
FİZ217 TİTREŞİMLER VE DALGALAR DERSİNİN 2. ARA SINAV SORU CEVAPLARI
 1) Gerilmiş bir ipte enine titreşimler denklemi ile tanımlıdır. Değişkenlerine ayırma yöntemiyle çözüm yapıldığında için [ ] [ ] ifadesi verilmiştir. 1.a) İpin enine titreşimlerinin n.ci modunu tanımlayan
1) Gerilmiş bir ipte enine titreşimler denklemi ile tanımlıdır. Değişkenlerine ayırma yöntemiyle çözüm yapıldığında için [ ] [ ] ifadesi verilmiştir. 1.a) İpin enine titreşimlerinin n.ci modunu tanımlayan
DRENAJ YAPILARI. Yrd. Doç. Dr. Sercan SERİN
 DRENAJ YAPILARI Yrd. Doç. Dr. Sercan SERİN DRENAJ Yapımı tamamlanıp trafiğe açılan bir yolun gerek yüzey suyu ve gerekse yer altı suyuna karşı sürekli olarak korunması, suyun yola olan zararlarının önlenmesi
DRENAJ YAPILARI Yrd. Doç. Dr. Sercan SERİN DRENAJ Yapımı tamamlanıp trafiğe açılan bir yolun gerek yüzey suyu ve gerekse yer altı suyuna karşı sürekli olarak korunması, suyun yola olan zararlarının önlenmesi
2004 Üniversitesi Y. Lisans İnşaat Mühendisliği İzmir Yüksek 2008 Teknoloji Enstitüsü Doktora İnşaat Mühendisliği Ege Üniversitesi 2015
 ÖZGEÇMİŞ 1. Adı Soyadı: Eyyüb KARAKAN 2. Doğum Tarihi: 23.06.1980 3. Ünvanı: Yrd. Doç. Dr. 4. Öğrenim Durumu: Doktora Derece Alan Üniversite Yıl Lisans Çukurova 2004 Üniversitesi Y. Lisans İzmir Yüksek
ÖZGEÇMİŞ 1. Adı Soyadı: Eyyüb KARAKAN 2. Doğum Tarihi: 23.06.1980 3. Ünvanı: Yrd. Doç. Dr. 4. Öğrenim Durumu: Doktora Derece Alan Üniversite Yıl Lisans Çukurova 2004 Üniversitesi Y. Lisans İzmir Yüksek
Akifer Özellikleri
 Akifer Özellikleri Doygun olmayan bölge Doygun bölge Bütün boşluklar su+hava ile dolu Yer altı su seviyesi Bütün boşluklar su ile dolu Doygun olmayan (doymamış bölgede) zemin daneleri arasında su ve hava
Akifer Özellikleri Doygun olmayan bölge Doygun bölge Bütün boşluklar su+hava ile dolu Yer altı su seviyesi Bütün boşluklar su ile dolu Doygun olmayan (doymamış bölgede) zemin daneleri arasında su ve hava
Dik koordinat sisteminde yatay eksen x ekseni (apsis ekseni), düşey eksen ise y ekseni (ordinat ekseni) dir.
 ANALĐTĐK GEOMETRĐ 1. Analitik Düzlem Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da
ANALĐTĐK GEOMETRĐ 1. Analitik Düzlem Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 7- SAYISAL TÜREV Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ İntegral işlemi gibi türev işlemi de mühendislikte çok fazla kullanılan bir işlemdir. Basit olarak bir fonksiyonun bir noktadaki
MAK 210 SAYISAL ANALİZ BÖLÜM 7- SAYISAL TÜREV Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ İntegral işlemi gibi türev işlemi de mühendislikte çok fazla kullanılan bir işlemdir. Basit olarak bir fonksiyonun bir noktadaki
ZEMİNDE SU Geoteknik: yeraltına giren suyun etkileri ve hareketi ile ilgilenir Yer altı suyu hidroliği, zemin hidroliği
 ZEMİNDE SU Geoteknik: yeraltına giren suyun etkileri ve hareketi ile ilgilenir Yer altı suyu hidroliği, zemin hidroliği Hidrolik Döngü Yer altı suyu atmosfer basıncıyla statik dengeye gelmişse bunun üst
ZEMİNDE SU Geoteknik: yeraltına giren suyun etkileri ve hareketi ile ilgilenir Yer altı suyu hidroliği, zemin hidroliği Hidrolik Döngü Yer altı suyu atmosfer basıncıyla statik dengeye gelmişse bunun üst
ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1. Y. Doç. Dr. Güray Doğan
 ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1 Y. Doç. Dr. Güray Doğan 1 Kinematik Kinematik: akışkanların hareketlerini tanımlar Kinematik harekete sebep olan kuvvetler ile ilgilenmez. Akışkanlar mekaniğinde
ÇEV207 AKIŞKANLAR MEKANİĞİ KİNEMATİK-1 Y. Doç. Dr. Güray Doğan 1 Kinematik Kinematik: akışkanların hareketlerini tanımlar Kinematik harekete sebep olan kuvvetler ile ilgilenmez. Akışkanlar mekaniğinde
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
INM 305 Zemin Mekaniği
 Hafta_12 INM 305 Zemin Mekaniği Sıkışma ve Konsolidasyon Teorisi Yrd.Doç.Dr. İnan KESKİN [email protected], [email protected] Haftalık Konular Hafta 1: Zeminlerin Oluşumu Hafta 2: Hafta 3: Hafta
Hafta_12 INM 305 Zemin Mekaniği Sıkışma ve Konsolidasyon Teorisi Yrd.Doç.Dr. İnan KESKİN [email protected], [email protected] Haftalık Konular Hafta 1: Zeminlerin Oluşumu Hafta 2: Hafta 3: Hafta
EMAT ÇALIŞMA SORULARI
 EMAT ÇALIŞMA SORULARI 1) A = 4. ı x 2. ı y ı z ve B = ı x + 4. ı y 4. ı z vektörlerinin dik olduğunu gösteriniz. İki vektörün skaler çarpımlarının sıfır olması gerekir. A. B = 4.1 + ( 2). 4 + ( 1). ( 4)
EMAT ÇALIŞMA SORULARI 1) A = 4. ı x 2. ı y ı z ve B = ı x + 4. ı y 4. ı z vektörlerinin dik olduğunu gösteriniz. İki vektörün skaler çarpımlarının sıfır olması gerekir. A. B = 4.1 + ( 2). 4 + ( 1). ( 4)
çemberi ile O Çemberlerin birbirine göre durumlarını inceleyelim. İlk durumda alalım. olduğu takdirde O2K1
 . merkezli R yarıçaplı Ç çemberi ile merkezli R yarıçaplı ve noktasından geçen Ç çemberi veriliyor. Ç üzerinde, T Ç K T Ç, ve K K T K olacak şekilde bir T noktası alınıyor. Buna göre, uzunluklarından birinin
. merkezli R yarıçaplı Ç çemberi ile merkezli R yarıçaplı ve noktasından geçen Ç çemberi veriliyor. Ç üzerinde, T Ç K T Ç, ve K K T K olacak şekilde bir T noktası alınıyor. Buna göre, uzunluklarından birinin
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 8- SAYISAL İNTEGRASYON 1 GİRİŞ Mühendislikte sık karşılaşılan matematiksel işlemlerden biri integral işlemidir. Bilindiği gibi integral bir büyüklüğün toplam değerinin bulunması
MAK 210 SAYISAL ANALİZ BÖLÜM 8- SAYISAL İNTEGRASYON 1 GİRİŞ Mühendislikte sık karşılaşılan matematiksel işlemlerden biri integral işlemidir. Bilindiği gibi integral bir büyüklüğün toplam değerinin bulunması
Sıvılaşma hangi ortamlarda gerçekleşir? Sıvılaşmaya etki eden faktörler nelerdir? Arazide tahkik; SPT, CPT, Vs çalışmaları
 SIVILAŞMA Sıvılaşma Nedir? Sıvılaşma hangi ortamlarda gerçekleşir? Sıvılaşmaya etki eden faktörler nelerdir? Sıvılaşmanın Etkileri Geçmiş Depremlerden Örnekler Arazide tahkik; SPT, CPT, Vs çalışmaları
SIVILAŞMA Sıvılaşma Nedir? Sıvılaşma hangi ortamlarda gerçekleşir? Sıvılaşmaya etki eden faktörler nelerdir? Sıvılaşmanın Etkileri Geçmiş Depremlerden Örnekler Arazide tahkik; SPT, CPT, Vs çalışmaları
1. KEYNESÇİ PARA TALEBİ TEORİSİ
 DERS NOTU 06 IS/LM EĞRİLERİ VE BAZI ESNEKLİKLER PARA VE MALİYE POLİTİKALARININ ETKİNLİKLERİ TOPLAM TALEP (AD) Bugünki dersin içeriği: 1. KEYNESÇİ PARA TALEBİ TEORİSİ... 1 2. LM EĞRİSİ VE PARA TALEBİNİN
DERS NOTU 06 IS/LM EĞRİLERİ VE BAZI ESNEKLİKLER PARA VE MALİYE POLİTİKALARININ ETKİNLİKLERİ TOPLAM TALEP (AD) Bugünki dersin içeriği: 1. KEYNESÇİ PARA TALEBİ TEORİSİ... 1 2. LM EĞRİSİ VE PARA TALEBİNİN
DÜZLEMDE GERİLME DÖNÜŞÜMLERİ
 3 DÜZLEMDE GERİLME DÖNÜŞÜMLERİ Gerilme Kavramı Dış kuvvetlerin etkisi altında dengedeki elastik bir cismi matematiksel bir yüzeyle rasgele bir noktadan hayali bir yüzeyle ikiye ayıracak olursak, F 3 F
3 DÜZLEMDE GERİLME DÖNÜŞÜMLERİ Gerilme Kavramı Dış kuvvetlerin etkisi altında dengedeki elastik bir cismi matematiksel bir yüzeyle rasgele bir noktadan hayali bir yüzeyle ikiye ayıracak olursak, F 3 F
ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ LABORATUARI
 ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ LABORATUARI DENEY FÖYÜ DENEY ADI SINIR TABAKA DENEYİ DERSİN ÖĞRETİM ÜYESİ DENEYİ YAPTIRAN ÖĞRETİM ELEMAN
ERCİYES ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ENERJİ SİSTEMLERİ MÜHENDİSLİĞİ BÖLÜMÜ AKIŞKANLAR MEKANİĞİ LABORATUARI DENEY FÖYÜ DENEY ADI SINIR TABAKA DENEYİ DERSİN ÖĞRETİM ÜYESİ DENEYİ YAPTIRAN ÖĞRETİM ELEMAN
