VECTOR MECHANICS FOR ENGINEERS: STATICS
|
|
|
- Berna Altıntop
- 8 yıl önce
- İzleme sayısı:
Transkript
1 Seventh Edition VECTOR MECHANICS OR ENGINEERS: STATICS erdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi Tel: / acarh@itu.edu.tr Web: 6. Taşıyıcı Sistemlerin Analizi 2002 The McGraw-Hill Companies, Inc. All rights reserved.
2 Giriş Kafes Sistemlerin Tanımı Basit Kafes Sistemler Kafes Sistemlerin Düğüm Noktaları Metodu ile Analizi Özel Yükleme Durumlarındaki Düğüm Noktaları Uzay Kafes Sistemleri Kafes Sistemlerin Kesit Alma Metodu ile Analizi Bileşik Kafes Sistemler Çerçevelerin Analizi Mesnetlerinden Ayrıldığında Rijit Olmayan Çerçeveler Makinalar
3 Giriş Bir kaç elemandan oluşan yapıların dengesi için, dış kuvvetler gibi iç kuvvetlerin de düşünülmesi gerekir. Birleştirilmiş parçalar arasındaki etkileşim, Newton un 3. yasası ile bulunur: birbirine temas eden cisimlerde etki ve tepki kuvvetleri eş şiddet ve tesir çizgili fakat zıt yönlüdür. Mühendislik yapıları üç kategoride sınıflandırılır: a) Çerçeveler: En azından bir tane çok-kuvvet (3 veya daha fazla) içeren elemana sahip yapılar. b) Kafes Sistemler: İki kuvvet elemanlarından oluşturulmuş yapılar c) Makinalar: kuvvet aktarımı ve kuvvet değişimi için tasarlanmış, hareketli elemanlara sahip yapılar.
4 Kafes Sistemlerin Tanımı Kafes sistemi dik elmanların birleştirilmesinden oluşur. Çubuklardan hiç biri düğüm noktasından ileri geçmez. Düğüm noktası Civatalanmış veya kaynaklanmış bağlantılar pim ile bağlanmış gibi düşünülür. Elemana etkiyen kuvvetler tek bir kuvvete indirgenebilir ve kuvvet çifti oluşturmaz. Bunun için iki kuvvetli elemanlar olarak düşünülebilir.
5 Aynı doğrultuda iki çubuğun birleştiği düğüm noktası göz önüne alınsın AD AB İki kuvvet etkisi altındaki eleman, ancak kuvvetler aynı şiddete ve tesir çizgisine sahip zıt yönlü olduğu durumda dengededir. Kuvvetler çubuktan dışarı doğru ise çubuk çekme etkisindedir. Kuvvetler çubuğa doğru ise çubuk basma etkisindedir.
6 Boylama kirişleri Enleme kirişleri Kafes sistemlerin elemanları narindir ve fazla yanal kuvvet taşıyamazlar. Bu nedenle, yükler bağlantı noktalarına uygulanmalıdır.
7 Kafes sistemler birçok mühendislik probleminde pratik ve ekenomik çözüm sağlar: Köprülerde, çatı sistemlerinde sıkça kullanılır.
8 Çelik kafes sistemler Yüksek gerilim hatları
9
10 Kafes kiriş türleri Tipik çatı kafes kirişleri Tipik köprü kafes kirişleri K kafes kirişi Bir kafes kirişin konsol kısmı Baskül Stadyum kafes kirişi Diğer kafes kirişler
11 Basit Kafes Sistemler Rijit Kafes Sistem yük uygulaması sonucunda göçmeyen sistemdir. Şekil değişimi çok azdır. Basit kafes sistem temel üçgen kafes sisteme, iki eleman ve bir düğüm noktası ilave ederek oluşturulur. Yalnız üçgenlerden olması şart değildir.
12 Üçgen kafes sistem Düğüm noktası Eleman m 3 n 3 eleman sayısı m 2n - 3 Basit kafes sistem düğüm noktası sayısı m 5 n 4
13 Kafes Sistemlerin Düğüm Noktaları Metodu ile Analizi Kafes elemanları çözülerek her bir eleman ve pim için serbest cisim diyagramı çizilir. Her elemana etki eden iki kuvvetin eşit şiddetli ve tesir çizgili ve zıt yönlü olması gerekir. Mafsala eleman tarafından uygalanan kuvvet eş şiddet ve tesir çizgili ve zıt yönlüdür.
14 Her düğüm noktası için iki denge denklemi vardır. Denklem sayısı: 2n 2n kadar bilinmeyen çözülebilir. Basit kafes sistem için: m 2n 3 idi. 2n m + 3 tür. m + 3 kadar bilinmeyen çözülebilir. Mafsal denge denklemlerine ilave olarak, tüm sistemin denge şartlarından elde edilen 3 denklem daha vardır. akat bu denklemler düğüm noktasından bağımsız değilleridir. Mesnetlerdeki tepki kuvvetlerinin kısa yoldan çözümü için kullanılabilir.
15 Özel Yükleme Durumlarındaki Düğüm Noktaları Mafsal SCD İkişer ikişer aynı doğrultuda bulunan dört çubuğu birleştiren düğüm noktası göz önüne alınsın Mafsal iki çift zıt yönlü kuvvet etkisindedir Aynı doğrultudaki karşıt çubuklarda kuvvetler eşittir.
16 İkisi aynı doğrultuda olan üç çubuğu birleştiren ve bir P yükünü taşıyan düğüm noktası göz önüne alınsın İkisi aynı doğrultuda olan üç çubuğu birleştiren düğüm noktası göz önüne alınsın Mafsal SCD AC Sıfır kuvvet çubuğu AB AD AC 0 P Aynı doğrultudaki iki karşıt çubukta kuvvetler birbirine eşit ve diğer elemandaki kuvvet P ye eşittir. Aynı doğrultudaki iki karşıt çubukta kuvvetler birbirine eşit ve diğer elemandaki kuvvet sıfıra eşittir.
17 arklı doğrultuda iki çubuğun birleştiği düğüm noktası göz önüne alınsın Sıfır kuvvet çubukları İki kuvvet etkisi altındaki eleman, ancak kuvvetler sıfır olduğu durumda dengededir. Sıfır kuvvet çubukları
18 Örnek N 1000 N 12 m 12 m 12 m 6 m 6 m 8 m Çözüm: Tüm kafes sisteminin SCD ile E ve C bağlantılarındaki tepki kuvvetleri bulunur. Şekil incelendiğinde A düğüm noktasında sadece 2 bilinmeyen kuvvet olduğu görülür. Çözüme bu düğüm noktasından başlanabilir. Daha sonra sırasıyla D, B veedüğüm noktaları kullanılarak çözüm tamamlanır. Verilen kafes sistemde düğüm noktaları metodunu kullanarak her bir çubuktaki kuvvetleri bulunuz. Yapılan hesaplamanın doğru olup olmadığı C düğüm noktasındaki çözüm ile karşılaştırılabilir.
19 SCD 2000 N 1000 N 12 m 12 m 8 m Çözüm: Tüm kafes sisteminin SCD ile E ve C bağlantılarındaki tepki kuvvetleri bulunur. 12 m 6 m 6 m M C 0 E ( 2000 N)( 24 m) + ( 1000 N)( 12 m) ( 6 m) E N x 0 C C 0 x x y N N + 10,000 N + C C 7000 N y y
20 2000 N 1000 N 12 m 12 m 8 m Şekil incelendiğinde A düğüm noktasında sadece 2 bilinmeyen kuvvet olduğu görülür. Çözüme bu düğün noktasından başlanabilir. 12 m 6 m 6 m 2000 N 2000 N 2000 N AB AD AB AD 1500 N 2500 N Çekme Basma
21 2000 N 1000 N 12 m 12 m 12 m 6 m 6 m 8 m A düğüm noktasından sonra komşu düğüm noktalarına geçilecektir. Şekil incelenirse B düğüm noktasına geçilirse 3 bilinmeyen kuvvet, D düğüm noktasına geçilirse 2 bilinmeyen kuvvet olduğu görülür. Bunun için D düğüm noktası seçilir. DA 2500 N D DB DE DB DE 2 DA () 3 5 DA 2500 N Çekme 3000 N Basma
22 2000 N 1000 N 12 m 12 m 12 m 6 m 6 m BA 1500 N BD 2500 N 1000 N 8 m D düğüm noktasından sonra komşu düğüm noktalarına geçilecektir. Şekil incelenirse E düğüm noktasına geçilirse 3 bilinmeyen kuvvet, B düğüm noktasına geçilirse 2 bilinmeyen kuvvet olduğu görülür. Bunun için B düğüm noktası seçilir. y BE x BC 3750 N ( 2500) N BE 3750 N BE Basma 3 ( 2500) ( 3750) 0 BC BC 5250 N Çekme
23 2000 N 1000 N 12 m 12 m 12 m 6 m 6 m 8 m B düğüm noktasından sonra komşu düğüm noktalarına geçilecektir. Şekil incelenirse E düğüm noktasına geçilirse 2 bilinmeyen kuvvet olduğu görülür. B düğüm noktasına geçilebilir. C düğüm noktasında 1 bilinmeyen kuvvet vardır. Bu düğüm noktası da seçilebilir. EB 3750 N x EC EC N ( 3750) ED 3000 N EC 8750 N Basma E N
24 2000 N 1000 N 12 m 12 m 8 m Kafes sistemdeki tüm bilinmeyen kuvvetler bulundu. Çözüm yapılmayan C düğüm noktası var. Bu düğüm noktasındaki çözümü yaparak yaptığımız hesaplamanın doğru olup olmadığını belirleyebiliriz. 12 m 6 m 6 m C y 7000 N CB 5250 N CE 8750 N x ( 8750) 0 ( dogru) y ( 8750) 0 ( dogru)
25 Uzay Kafes Sistemleri Doğrusal elemanlar 3 boyutlu şekil oluşturacak şekilde birleştirilirse uzay kafes sistemi oluştururlar. En küçük uzay kafes sistemi 6 elemana ve 4 düğüm noktasına sahiptir. (tetrahedron yapı) Basit uzay kafes sistemi bu yapıya yeni 3 eleman ve 1 düğüm noktası ilavesiyle yapılır. Basit kafes sistemde: m 3n -6 m: eleman sayısı, n :düğüm noktası sayısı Her düğüm noktası için 3 denklem vardır. Denklem sayısı: 3n. 3n m + 6 Bu denklemler m eleman ve 6 bağlantı kuvveti için kullanılır. Tüm sistemin serbest cisim diyagramı ile 6 denklem daha kullanılabilir fakat bu denklemler düğüm noktasından elde edilenlerle ilişkilidir.
26 Kafes Sistemleri Kesit Alma Yöntemi ile Analizi Kafes sistemde tüm elemanlardaki kuvvetlerin hesaplanması gerekmiyorsa ve bir veya daha fazla elemandaki kuvvet araştırılıyorsa Kesit alma yöntemi kullanılır. BD elemanındaki kuvvet araştırılıyorsa, bu elemanı kapsayacak ve en az çubuk kesecek şekilde kesme işlemi yapılarak SCD çizilmelidir. Bu örnekte 3 eleman kesilmiştir. Kuvvet ve moment denge denklemleri kullanılarak BD elemanındak kuvet dahil olmak üzere bilinmeyen eleman kuvvetleri hesaplanır.
27 Basit Kafes Sistemlerden Oluşan Kafesler ABC kafesi ABD kafesi DE kafesi AB kafesi Bileşik kafes sistem statikçe belirli ve rijit ise: m 2n 3 eleman sayısı düğüm sayısı Basit kafes değil çünkü İki eleman eklemesi ile oluşturulamazlar Kafes sistem gereksiz bir elemana sahipse, statikçe belirsizdir: m > 2n 3 BD, BE, CD veya CE elemanlarından biri fazladır
28 Örnek 6.3 6x5m 30m Çözüm Tüm kafes yapı için SCD oluşturulur. A ve L noktalarındaki tepki kuvvetleri denge denklemleri ile bulunur. H, GH ve GI elemanlarını kapsayacak şekilde kesme işlemi yapılır ve daha az kuvvet içerdiği için sağ taraftaki grup için SCD çizilir. Denge denklemleri kullanılarak elemanlardaki kuvvetler bulunur. Şekildeki kafes sistemde H, GH ve GI elemanlarındaki kuvvetleri bulunuz.
29 Çözüm Tüm kafes yapı için SCD oluşturulue. A ve L noktalarındaki tepki kuvvetleri denge denklemleri ile bulunur. A x 0 A L M A 0 6x5m 30m ( 5 m)( 6 kn) ( 10 m)( 6 kn) ( 15 m)( 6 kn) ( 20 m)( 1kN) ( 25 m)( 1kN) + ( 25 m) L L 7.5 kn y 0 20 kn + L + A A 12.5 kn
30 H, GH ve GI elemanlarını kapsayacak şekilde kesme işlemi yapılır ve daha az kuvvet içerdiği için sağ taraftaki grup için SCD çizilir. Denge denklemleri kullanılarak elemanlardaki kuvvetler bulunur. M H 0 ( 7.50 kn)( 10 m) ( 1kN)( 5 m) ( 5.33 m) GI GI kn kn Çekme GI 0
31 tanα M G 8 m 15 m ( 7.5 kn)( 15 m) ( 1kN)( 10 m) ( 1kN)( 5 m) + ( cosα )( 8 m) 0 G GL 0 H H kn H kn C α tan β m ( 8 m) M L 0 ( 1kN)( 10 m) + ( 1kN)( 5 m) + ( cos β )( 10 m) GH GI HI kn GH 1.371kN C GH β
32 Yapıların Analizi Çerçeveler ve makinalar en azından bir tane çok kuvvetli eleman içeren yapılardır. Çerçeveler genellikle yüklemeleri desteklemek için kullanılır ve sabittirler. Makinalar hareketli parçalar içerirler ve kuvvet aktarımı veya dönüşümü için kullanılırlar. (Mesnetlerin yardımı olmadan da biçimini korumaktadır) Tüm çerçevenin SCD çizilerek çerçeveye gelen dış kuvvetler bulunur. Çerçevenin her elemanı için ayrı ayrı SCD çizilir ve elemanlara gelen iç kuvvetler bulunur. İki kuvvet içeren elemanlarda kuvvetin tesir çizgisi biliniyor fakat şiddeti ve yönü bilinmiyor. Çok kuvvet içeren elemanlarda ise kuvvetlerin tesir çizgisi, yönü ve şiddeti bilinmiyor. Bu nedenle iki bileşenli kuvvet (eksen takımına göre yatay ve düşey) olarak gösterilirler. Birbirine bağlı olan elemanlarda temas noktalarındaki kuvvetler eş şiddetli fakat ters yönlüdürler.
33 Mesnetlerinden Ayrıldığında Rijit Olmayan Yapılar Bazı yapılar mesnetlerinden ayrıldığında çökebilirler. Bu yapılar rijit olarak tanımlanamazlar. Tüm yapının SCD oluşturulduğunda 4 tane bilinmeyen tepki kuvvetine sahiptir ve 3 denge denklemi ile belirlenemezler. Bu nedenle yapı iki farklı fakat rijit cisim olarak düşünülebilir. Eş şiddetli fakat zıt yönlü olan tepki kuvvetleriyle birlikte 6 bilinmeyen kuvvet olacaktır. Bunun yanında denge denklemi sayısı da 6 olacaktır (her eleman için 3 denklem vardır). Böylece bilinmeyen kuvvetler bulunabilir.
34 Örnek 6.4 Şekildeki çerçevede ACE ile BCD elemanları C noktasından bir pimle, ayrıca DE çubuğuyala bağlıdır. Verilen yüklemeye göre, DE çubuğundaki kuvveti ve C noktasında BCD elemanına gelen kuvvetin bileşenlerini hesaplayınız. Çözüm: Tüm yapı için SCD çizilir ve bilinmeyen tepki kuvvetleri hesaplanır. BCD elemanı için SCD çizilir. DE çubuğundan gelen kuvvetin tesir çizgisi bellidir ama şiddet ve yönü belli değildir. Bunun için C noktasına göre moment denge denklemi kullanılabilir. DE çubuğundan gelen kuvvet bilinirse C noktasından BCD elemanına gelen kuvvet hesaplabilir. ACE elemanı için SCD çizilirse yukarıda hesaplanan kuvvetlerin doğruluğu kontrol edilebilir.
35 Çözüm: Tüm yapı için SCD çizilir ve bilinmeyen tepki kuvvetleri hesaplanır. y 0 A 480 N y A y 480 N ( 480 N)( 100 mm) ( 160 mm) M A 0 + B B 300 N x 0 B + A x A x 300 N α tan
36 BCD elemanı için SCD çizilir. DE çubuğundan gelen kuvvetin tesir çizgisi bellidir ama şiddet ve yönü belli değildir. Bunun için C noktasına göre moment denge denklemi kullanılabilir. M C DE N ( sinα )( 250 mm) + ( 300 N)( 60 mm) + ( 480 N)( 100 mm) DE DE 561 N C x 0 0 C C x x DE cosα N ( 561 N) cosα N C x 795 N y 0 0 C C y y DE sinα 480 N ( 561 N) sinα 480 N C y 216 N
37 ACE elemanı için SCD çizilirse yukarıda hesaplanan kuvvetlerin doğruluğu kontrol edilebilir. M A ( DE cosα )( 300 mm) + ( DE sinα )( 100 mm) Cx ( 220 mm) ( 561cosα )( 300 mm) + ( 561sinα )( 100 mm) ( 795)( 220 mm) 0 (kontrol edilecek)
38 Makinalar Makinalar kuvvet aktarımı ve değiştirilmesi için kullanılan yapılardır. Giriş kuvvetlerini çıkış kuvvetlerine çevirirler. Bir teli kesmek için kullanılan keski aletine P kuvveti uygulanmakta. P kuvvetinin şiddeti biliniyorsa, Q kuvvetinin şiddetini bulunuz. Tüm makinanın SCD si çizilir. Telden gelen tepki kuvveti de ilave edilir. Makina rijit olmayan bir yapıdır. Elemanlardan biri serbest cisim olarak seçilir. A noktasına göre moment alınırsa: M A 0 ap bq Q a b P
39 Örnek P C 2.4 kn şiddetinde bir P kuvveti, şekilde gösterilen motor sisteminin pistonuna etkimektedir. Sistemi dengede tutacak olan M momentini bulunuz. B M 250 mm 100 mm A 75 mm
40 B C P N BC BCx BCy P P BC BCy BC BCx BCy BC BC BCy Piston SCD P P BCy BCy y Σ 0 0
41 AB Karankı SCD m BCx M 0.1 m A x BCy A y + ΣM BCx A (0.1) 0 + BCy (0.075) M 0 M 0.3P(0.1) + P(0.075) M 0.105P P 2.4 kn için M 0.105(2.4) M 252 Nm (saat ibreleri yönünde)
Basit Kafes Sistemler
 YAPISAL ANALİZ 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla kullanılan ahşap gergi elemanları
YAPISAL ANALİZ 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla kullanılan ahşap gergi elemanları
YAPISAL ANALİZ YRD.DOÇ.DR. KAMİLE TOSUN FELEKOĞLU
 YAPISAL ANALİZ YRD.DOÇ.DR. KAMİLE TOSUN FELEKOĞLU 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla
YAPISAL ANALİZ YRD.DOÇ.DR. KAMİLE TOSUN FELEKOĞLU 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla
VECTOR MECHANICS FOR ENGINEERS: STATICS
 Seventh Edition VECTOR MECHANICS FOR ENGINEERS: STATICS Fedinand P. Bee E. Russell Johnston, J. Des Notu: Hayi ACAR İstanbul Teknik Üniveistesi Tel: 285 31 46 / 116 E-mail: acah@itu.edu.t Web: http://atlas.cc.itu.edu.t/~acah
Seventh Edition VECTOR MECHANICS FOR ENGINEERS: STATICS Fedinand P. Bee E. Russell Johnston, J. Des Notu: Hayi ACAR İstanbul Teknik Üniveistesi Tel: 285 31 46 / 116 E-mail: acah@itu.edu.t Web: http://atlas.cc.itu.edu.t/~acah
BĐSĐKLET FREN SĐSTEMĐNDE KABLO BAĞLANTI AÇISININ MEKANĐK VERĐME ETKĐSĐNĐN ĐNCELENMESĐ
 tasarım BĐSĐKLET FREN SĐSTEMĐNDE KABLO BAĞLANTI AÇISININ MEKANĐK VERĐME ETKĐSĐNĐN ĐNCELENMESĐ Nihat GEMALMAYAN Y. Doç. Dr., Gazi Üniversitesi, Makina Mühendisliği Bölümü Hüseyin ĐNCEÇAM Gazi Üniversitesi,
tasarım BĐSĐKLET FREN SĐSTEMĐNDE KABLO BAĞLANTI AÇISININ MEKANĐK VERĐME ETKĐSĐNĐN ĐNCELENMESĐ Nihat GEMALMAYAN Y. Doç. Dr., Gazi Üniversitesi, Makina Mühendisliği Bölümü Hüseyin ĐNCEÇAM Gazi Üniversitesi,
VECTOR MECHANICS FOR ENGINEERS: STATICS
 Seventh Edition VECTOR ECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi Tel: 85 31 46 / 116 E-mail: acarh@itu.edu.tr Web: http://atlas.cc.itu.edu.tr/~acarh
Seventh Edition VECTOR ECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi Tel: 85 31 46 / 116 E-mail: acarh@itu.edu.tr Web: http://atlas.cc.itu.edu.tr/~acarh
İ.T.Ü. Makina Fakültesi Mekanik Ana Bilim Dalı Bölüm 4 BÖLÜM IV. Düzlem Kafesler. En çok kullanılan köprü kafesleri. En çok kullanılan çatı kafesleri
 İ.T.Ü. Makina akültesi ÖLÜM IV üzlem Kafesler En çok kullanılan köprü kafesleri En çok kullanılan çatı kafesleri İ.T.Ü. Makina akültesi Mühendislik olalarında genel olarak birden çok katı cisim birbirine
İ.T.Ü. Makina akültesi ÖLÜM IV üzlem Kafesler En çok kullanılan köprü kafesleri En çok kullanılan çatı kafesleri İ.T.Ü. Makina akültesi Mühendislik olalarında genel olarak birden çok katı cisim birbirine
VECTOR MECHANICS FOR ENGINEERS: STATICS
 Seventh E 4 Equilibrium CHAPTER VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. of Rigid Bodies Lecture Notes: J. Walt Oler Texas Tech University Seventh E CHAPTER VECTOR
Seventh E 4 Equilibrium CHAPTER VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. of Rigid Bodies Lecture Notes: J. Walt Oler Texas Tech University Seventh E CHAPTER VECTOR
KAFES SİSTEMLER. Mühendislik Yapıları. birleştirilen doğrusal elemanlar) oluşurlar.
 KAFES SİSTEMLER Mühendislik Yapıları a) Kafesler: İki-kuvvet elemanlarından (uçlarından birleştirilen doğrusal elemanlar) oluşurlar. b) Çerçeveler: En az bir birçok kuvvetin etkisindeki eleman içerenler
KAFES SİSTEMLER Mühendislik Yapıları a) Kafesler: İki-kuvvet elemanlarından (uçlarından birleştirilen doğrusal elemanlar) oluşurlar. b) Çerçeveler: En az bir birçok kuvvetin etkisindeki eleman içerenler
Taşıyıcı Sistem Elemanları
 BETONARME BİNALARDA OLUŞAN YAPI HASAR BİÇİMLERİ Bu çalışmanın amacı betonarme binaların taşıyıcı sistemlerinde meydana gelen hasarlar ve bu hasarların nedenleri tanıtılacaktır. Yapılarda hasarın belirtisi
BETONARME BİNALARDA OLUŞAN YAPI HASAR BİÇİMLERİ Bu çalışmanın amacı betonarme binaların taşıyıcı sistemlerinde meydana gelen hasarlar ve bu hasarların nedenleri tanıtılacaktır. Yapılarda hasarın belirtisi
 ÖLÜM 3 DENGE, İR KUVVETİN MOMENTİ 3.1 ir Kuvvetin Momenti elirli bir doğrultu ve şiddete sahip bir kuvvetin, bir cisim üzerine etkisi, kuvvetin etki çizgisine bağlıdır. Şekil.3.1 de F 1 kuvveti cismi sağa
ÖLÜM 3 DENGE, İR KUVVETİN MOMENTİ 3.1 ir Kuvvetin Momenti elirli bir doğrultu ve şiddete sahip bir kuvvetin, bir cisim üzerine etkisi, kuvvetin etki çizgisine bağlıdır. Şekil.3.1 de F 1 kuvveti cismi sağa
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve leri DĞHN MÜHENDİSLİK MEKNİĞİ STTİK MÜHENDİSLİK MEKNİĞİ STTİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki Boyutlu Kuvvet
Statik Ders Notları Sınav Soru ve leri DĞHN MÜHENDİSLİK MEKNİĞİ STTİK MÜHENDİSLİK MEKNİĞİ STTİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki Boyutlu Kuvvet
T.C. TURGUT ÖZAL ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ
 T.C. TURGUT ÖZAL ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ 3 NOKTA EĞME DENEY FÖYÜ (TEK EKSENLİ EĞİLME DENEYİ) ÖĞRETİM ÜYESİ YRD.DOÇ.DR. AHMET TEMÜGAN DERS ASİSTANI ARŞ.GÖR. FATİH KAYA
T.C. TURGUT ÖZAL ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ 3 NOKTA EĞME DENEY FÖYÜ (TEK EKSENLİ EĞİLME DENEYİ) ÖĞRETİM ÜYESİ YRD.DOÇ.DR. AHMET TEMÜGAN DERS ASİSTANI ARŞ.GÖR. FATİH KAYA
Makine Elemanları II Prof. Dr. Akgün ALSARAN. Helisel Dişli Çarklar-Flipped Classroom DİŞLİ ÇARKLAR
 Makine Elemanları II Prof. Dr. Akgün ALSARAN Helisel Dişli Çarklar-Flipped Classroom DİŞLİ ÇARKLAR İçerik Giriş Helisel dişli geometrisi Kavrama oranı Helisel dişli boyutları Helisel dişlilerin mukavemet
Makine Elemanları II Prof. Dr. Akgün ALSARAN Helisel Dişli Çarklar-Flipped Classroom DİŞLİ ÇARKLAR İçerik Giriş Helisel dişli geometrisi Kavrama oranı Helisel dişli boyutları Helisel dişlilerin mukavemet
DENEY 2: PROTOBOARD TANITIMI VE DEVRE KURMA
 A. DENEYİN AMACI : Protoboard kullanımını öğrenmek ve protoboard üzerinde basit direnç devreleri kurmak. B. KULLANILACAK ARAÇ VE MALZEMELER : 1. DC güç kaynağı, 2. Multimetre, 3. Protoboard, 4. Değişik
A. DENEYİN AMACI : Protoboard kullanımını öğrenmek ve protoboard üzerinde basit direnç devreleri kurmak. B. KULLANILACAK ARAÇ VE MALZEMELER : 1. DC güç kaynağı, 2. Multimetre, 3. Protoboard, 4. Değişik
TEMEL MEKANİK 14. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 TEMEL MEKANİK 14 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
TEMEL MEKANİK 14 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
TEMEL MEKANİK 12. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 TEMEL MEKANİK 12 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
TEMEL MEKANİK 12 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
SU YAPILARI. Su Alma Yapıları. 5.Hafta. Doç.Dr.N.Nur ÖZYURT nozyurt@hacettepe.edu.tr
 SU YAPILARI 5.Hafta Su Alma Yapıları Doç.Dr.N.Nur ÖZYURT nozyurt@hacettepe.edu.tr Su alma yapısı nedir? Akarsu ya da baraj gölünden suyu alıp iletim sistemlerine veren yapılara su alma yapısı denir. Su
SU YAPILARI 5.Hafta Su Alma Yapıları Doç.Dr.N.Nur ÖZYURT nozyurt@hacettepe.edu.tr Su alma yapısı nedir? Akarsu ya da baraj gölünden suyu alıp iletim sistemlerine veren yapılara su alma yapısı denir. Su
Kafes Sistemler. Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir.
 Kafes Sistemler Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir. Kafes Sistemler Birçok uygulama alanları vardır. Çatı sistemlerinde, Köprülerde, Kulelerde, Ve benzeri
Kafes Sistemler Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir. Kafes Sistemler Birçok uygulama alanları vardır. Çatı sistemlerinde, Köprülerde, Kulelerde, Ve benzeri
TEKNİK RESİM. Ders Notları: Mehmet Çevik Dokuz Eylül Üniversitesi. Görünüşler - 1
 TEKNİK RESİM 2010 Ders Notları: Mehmet Çevik Dokuz Eylül Üniversitesi 2/25 Görünüşler Birinci İzdüşüm Metodu Üçüncüİzdüşüm Metodu İzdüşüm Sembolü Görünüşlerin Çizilmesi Görünüş Çıkarma Kuralları Tek Görünüşle
TEKNİK RESİM 2010 Ders Notları: Mehmet Çevik Dokuz Eylül Üniversitesi 2/25 Görünüşler Birinci İzdüşüm Metodu Üçüncüİzdüşüm Metodu İzdüşüm Sembolü Görünüşlerin Çizilmesi Görünüş Çıkarma Kuralları Tek Görünüşle
Girdi kuvvetleri ile makinaya değişik biçimlerde uygulanan dış kuvvetler kastedilmektedir (input forces). Çıktı kuvvetleri ise elde edilen kuvvetleri
 ÇERÇEVELER Çerçeveler kafesler gibi genellikle sabit duran taşıyıcı sistemlerdir. Bir çerçeveyi kafesten ayıran en belirgin özellik, en az bir elemanının çok kuvvet elemanı (multi force member) oluşudur.
ÇERÇEVELER Çerçeveler kafesler gibi genellikle sabit duran taşıyıcı sistemlerdir. Bir çerçeveyi kafesten ayıran en belirgin özellik, en az bir elemanının çok kuvvet elemanı (multi force member) oluşudur.
 ÇALIŞMA SORULARI 1) Yukarıdaki şekilde AB ve BC silindirik çubukları B noktasında birbirleriyle birleştirilmişlerdir, AB çubuğunun çapı 30 mm ve BC çubuğunun çapı ise 50 mm dir. Sisteme A ucunda 60 kn
ÇALIŞMA SORULARI 1) Yukarıdaki şekilde AB ve BC silindirik çubukları B noktasında birbirleriyle birleştirilmişlerdir, AB çubuğunun çapı 30 mm ve BC çubuğunun çapı ise 50 mm dir. Sisteme A ucunda 60 kn
ÇELİK YAPI BİRLEŞİM ELEMANLARI
 ÇELİK YAPI BİRLEŞİM ELEMANLARI Çelik yapılarda, kullanılan üç farklı birleşim elemanı vardır. Bunlar; 1. Perçinli birleşimler, 2. Cıvatalı (Bulonlu) birleşimleri. 3. Kaynaklı birleşimler 2 1 1. PERÇİNLİ
ÇELİK YAPI BİRLEŞİM ELEMANLARI Çelik yapılarda, kullanılan üç farklı birleşim elemanı vardır. Bunlar; 1. Perçinli birleşimler, 2. Cıvatalı (Bulonlu) birleşimleri. 3. Kaynaklı birleşimler 2 1 1. PERÇİNLİ
2. KUVVETLERİN VEKTÖREL TOPLANMASI. Hazırlayan Arş. Grv. A. E. IRMAK
 2. KUVVETLERİN VEKTÖREL TOPLANMASI AMAÇ Hazırlaan Arş. Grv. A. E. IRMAK Eş zamanlı kuvvetler etkisinde dengede bulunan bir cismin incelenmesi, analitik ve vektörel metotları kullanarak denge problemlerinin
2. KUVVETLERİN VEKTÖREL TOPLANMASI AMAÇ Hazırlaan Arş. Grv. A. E. IRMAK Eş zamanlı kuvvetler etkisinde dengede bulunan bir cismin incelenmesi, analitik ve vektörel metotları kullanarak denge problemlerinin
FOTOGRAMETRİK DEĞERLENDİRME - ÇİFT FOT. DEĞ. Analog ve Analitik Stereodeğerlendirme. Yrd. Doç. Dr. Aycan M. MARANGOZ
 FOTOGRAMETRİ II FOTOGRAMETRİK DEĞERLENDİRME - ÇİFT FOT. DEĞ. Analog ve Analitik Stereodeğerlendirme BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
FOTOGRAMETRİ II FOTOGRAMETRİK DEĞERLENDİRME - ÇİFT FOT. DEĞ. Analog ve Analitik Stereodeğerlendirme BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
Çerçeveler ve Basit Makinalar
 Çerçeveler ve Basit Makinalar Çeşitli elemanların birbirlerine bağlanması ile oluşan sistemlerdir. Kafes sistemlerden farklı olarak, elemanlar birbirlerine 2 den fazla noktadan bağlanabilir ve dış kuvvetler
Çerçeveler ve Basit Makinalar Çeşitli elemanların birbirlerine bağlanması ile oluşan sistemlerdir. Kafes sistemlerden farklı olarak, elemanlar birbirlerine 2 den fazla noktadan bağlanabilir ve dış kuvvetler
Elektrik Makinaları I. Senkron Makinalar Stator Sargılarının oluşturduğu Alternatif Alan ve Döner Alan, Sargıda Endüklenen Hareket Gerilimi
 Elektrik Makinaları I Senkron Makinalar Stator Sargılarının oluşturduğu Alternatif Alan ve Döner Alan, Sargıda Endüklenen Hareket Gerilimi Bir fazlı, iki kutuplu bir stator sargısının hava aralığında oluşturduğu
Elektrik Makinaları I Senkron Makinalar Stator Sargılarının oluşturduğu Alternatif Alan ve Döner Alan, Sargıda Endüklenen Hareket Gerilimi Bir fazlı, iki kutuplu bir stator sargısının hava aralığında oluşturduğu
Şaft: Şaft ve Mafsallar:
 Şaft ve Mafsallar: Motor ve tahrik aksı farklı yerde olan araçlarda, vites kutusu ile diferansiyel arasında hareket iletimi için şaft ve açısal sapmalar için gerekli olan mafsallar karşımıza çıkmaktadır.
Şaft ve Mafsallar: Motor ve tahrik aksı farklı yerde olan araçlarda, vites kutusu ile diferansiyel arasında hareket iletimi için şaft ve açısal sapmalar için gerekli olan mafsallar karşımıza çıkmaktadır.
MALZEMELERİN FİZİKSEL ÖZELLİKLERİ
 MALZEMELERİN FİZİKSEL ÖZELLİKLERİ (Ders Notu) Manyetik Özellikler Doç.Dr. Özkan ÖZDEMİR MANYETİK ÖZELLİK Giriş Bazı malzemelerde mevcut manyetik kutup çiftleri, elektriksel kutuplara benzer şekilde, çevredeki
MALZEMELERİN FİZİKSEL ÖZELLİKLERİ (Ders Notu) Manyetik Özellikler Doç.Dr. Özkan ÖZDEMİR MANYETİK ÖZELLİK Giriş Bazı malzemelerde mevcut manyetik kutup çiftleri, elektriksel kutuplara benzer şekilde, çevredeki
Çerçeve ve Makineler
 Çerçeve ve Makineler Hedefler Mafsal (pim) ile tutturulmuş çerçeve ve makine elemanlarına etki eden kuvvetlerin analizi. Çerçeve ve Makineler Çok kuvvet elemanı içeren mafsal ile tutturulmuş yapılardır.
Çerçeve ve Makineler Hedefler Mafsal (pim) ile tutturulmuş çerçeve ve makine elemanlarına etki eden kuvvetlerin analizi. Çerçeve ve Makineler Çok kuvvet elemanı içeren mafsal ile tutturulmuş yapılardır.
Fizik ve Ölçme. Fizik deneysel gözlemler ve nicel ölçümlere dayanır
 Fizik ve Ölçme Fizik deneysel gözlemler ve nicel ölçümlere dayanır Fizik kanunları temel büyüklükler(nicelikler) cinsinden ifade edilir. Mekanikte üç temel büyüklük vardır; bunlar uzunluk(l), zaman(t)
Fizik ve Ölçme Fizik deneysel gözlemler ve nicel ölçümlere dayanır Fizik kanunları temel büyüklükler(nicelikler) cinsinden ifade edilir. Mekanikte üç temel büyüklük vardır; bunlar uzunluk(l), zaman(t)
STATİK-BETONARME PROJE KONTROL FORMU Evet Hayır
 STATİK-BETONARME PROJE KONTROL FORMU Evet Hayır 1. TAŞIYICI SİSTEM SEÇİMİ Mimari ve statik proje kolon sistemi uyumluymuş Mimari projedeki kat planları ile statik projedeki kalıp planları uyumluymuş. Mimari
STATİK-BETONARME PROJE KONTROL FORMU Evet Hayır 1. TAŞIYICI SİSTEM SEÇİMİ Mimari ve statik proje kolon sistemi uyumluymuş Mimari projedeki kat planları ile statik projedeki kalıp planları uyumluymuş. Mimari
4 ab sayısı 26 ile tam bölünebildiğine göre, kalanı 0 dır.
 BÖLME, BÖLÜNEBİLME A. Bölme İşlemi A, B, C, K doğal sayılar ve B 0 olmak üzere, Bölünen A 75, bölen B 9, bölüm C 8 ve kalan K tür. Yukarıdaki bölme işlemine göre, 1. 9 yani, K B dir. işlemine bölme denir.
BÖLME, BÖLÜNEBİLME A. Bölme İşlemi A, B, C, K doğal sayılar ve B 0 olmak üzere, Bölünen A 75, bölen B 9, bölüm C 8 ve kalan K tür. Yukarıdaki bölme işlemine göre, 1. 9 yani, K B dir. işlemine bölme denir.
TEMEL MEKANİK 10. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 TEMEL MEKANİK 10 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
TEMEL MEKANİK 10 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
08.11.2014-10:30 Adı-Soyadı:... No:... NOT:...
 OREN435 TESİS PLNLM 014-015 GÜZ YRIYILI RSINVI CEVP NHTRI 1 08.11.014-10:30 dı-soyadı:... No:... NOT:... Sorular eşit puanlıdır. Yardımcı bellek kullanılabilir. Süre 70 fakikadır. 1. Endüstriyel üretim
OREN435 TESİS PLNLM 014-015 GÜZ YRIYILI RSINVI CEVP NHTRI 1 08.11.014-10:30 dı-soyadı:... No:... NOT:... Sorular eşit puanlıdır. Yardımcı bellek kullanılabilir. Süre 70 fakikadır. 1. Endüstriyel üretim
Deney 4: Güç Ölçümü. Şekil 4.1 : Alternatif akımda alıcıların akım ve gerilim vektörleri ile faz farkı
 Deneyin Amacı: Deney 4: Güç Ölçümü Elektrik devrelerinde gücün tanımının yapılması ve güç bileşenlerinin öğrenilmesi. Elektrik panolarının kullanımının uygulamalı olarak öğrenilmesi. A.ÖNBİLGİ Güç, iş
Deneyin Amacı: Deney 4: Güç Ölçümü Elektrik devrelerinde gücün tanımının yapılması ve güç bileşenlerinin öğrenilmesi. Elektrik panolarının kullanımının uygulamalı olarak öğrenilmesi. A.ÖNBİLGİ Güç, iş
STATİK. Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -8-
 1 STATİK Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -8- Giriş 2 Denge denklemlerini, mafsala bağlı elemanlarda oluşan yapıları analiz etmek için kullanacağız. Bu analiz, dengede olan bir yapının
1 STATİK Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -8- Giriş 2 Denge denklemlerini, mafsala bağlı elemanlarda oluşan yapıları analiz etmek için kullanacağız. Bu analiz, dengede olan bir yapının
δ / = P L A E = [+35 kn](0.75 m)(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir.
(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir. δ / = P L A E = [+35 kn](0.75 m)(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir.](/thumbs/68/59308868.jpg) A-36 malzemeden çelik çubuk, şekil a gösterildiği iki kademeli olarak üretilmiştir. AB ve BC kesitleri sırasıyla A = 600 mm ve A = 1200 mm dir. A serbest ucunun ve B nin C ye göre yer değiştirmesini belirleyiniz.
A-36 malzemeden çelik çubuk, şekil a gösterildiği iki kademeli olarak üretilmiştir. AB ve BC kesitleri sırasıyla A = 600 mm ve A = 1200 mm dir. A serbest ucunun ve B nin C ye göre yer değiştirmesini belirleyiniz.
DENEY 2. Şekil 1. Çalışma bölümünün şematik olarak görünümü
 Deney-2 /5 DENEY 2 SĐLĐNDĐR ÜZERĐNE ETKĐ EDEN SÜRÜKLEME KUVVETĐNĐN BELĐRLENMESĐ AMAÇ Bu deneyin amacı, silindir üzerindeki statik basınç dağılımını, akışkan tarafından silindir üzerine uygulanan kuvveti
Deney-2 /5 DENEY 2 SĐLĐNDĐR ÜZERĐNE ETKĐ EDEN SÜRÜKLEME KUVVETĐNĐN BELĐRLENMESĐ AMAÇ Bu deneyin amacı, silindir üzerindeki statik basınç dağılımını, akışkan tarafından silindir üzerine uygulanan kuvveti
Araştırma Notu 15/177
 Araştırma Notu 15/177 02 Mart 2015 YOKSUL İLE ZENGİN ARASINDAKİ ENFLASYON FARKI REKOR SEVİYEDE Seyfettin Gürsel *, Ayşenur Acar ** Yönetici özeti Türkiye İstatistik Kurumu (TÜİK) tarafından yapılan enflasyon
Araştırma Notu 15/177 02 Mart 2015 YOKSUL İLE ZENGİN ARASINDAKİ ENFLASYON FARKI REKOR SEVİYEDE Seyfettin Gürsel *, Ayşenur Acar ** Yönetici özeti Türkiye İstatistik Kurumu (TÜİK) tarafından yapılan enflasyon
TEMEL MEKANİK 4. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 TEMEL MEKANİK 4 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
TEMEL MEKANİK 4 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
ANALOG LABORATUARI İÇİN BAZI GEREKLİ BİLGİLER
 ANALOG LABORATUARI İÇİN BAZI GEREKLİ BİLGİLER Şekil-1: BREADBOARD Yukarıda, deneylerde kullandığımız breadboard un şekli görünmektedir. Bu board üzerinde harflerle isimlendirilen satırlar ve numaralarla
ANALOG LABORATUARI İÇİN BAZI GEREKLİ BİLGİLER Şekil-1: BREADBOARD Yukarıda, deneylerde kullandığımız breadboard un şekli görünmektedir. Bu board üzerinde harflerle isimlendirilen satırlar ve numaralarla
01 OCAK 2015 ELEKTRİK AKIMI VE LAMBA PARLAKLIĞI SALİH MERT İLİ DENİZLİ ANADOLU LİSESİ 10/A 436
 01 OCAK 2015 ELEKTRİK AKIMI VE LAMBA PARLAKLIĞI SALİH MERT İLİ DENİZLİ ANADOLU LİSESİ 10/A 436 ELEKTRİK AKIMI VE LAMBALAR ELEKTRİK AKIMI Potansiyelleri farklı olan iki iletken cisim birbirlerine dokundurulduğunda
01 OCAK 2015 ELEKTRİK AKIMI VE LAMBA PARLAKLIĞI SALİH MERT İLİ DENİZLİ ANADOLU LİSESİ 10/A 436 ELEKTRİK AKIMI VE LAMBALAR ELEKTRİK AKIMI Potansiyelleri farklı olan iki iletken cisim birbirlerine dokundurulduğunda
II. Bölüm HİDROLİK SİSTEMLERİN TANITIMI
 II. Bölüm HİDROLİK SİSTEMLERİN TANITIMI 1 Güç Kaynağı AC Motor DC Motor Diesel Motor Otto Motor GÜÇ AKIŞI M i, ω i Güç transmisyon sistemi M 0, ω 0 F 0, v 0 Makina (doğrusal veya dairesel hareket) Mekanik
II. Bölüm HİDROLİK SİSTEMLERİN TANITIMI 1 Güç Kaynağı AC Motor DC Motor Diesel Motor Otto Motor GÜÇ AKIŞI M i, ω i Güç transmisyon sistemi M 0, ω 0 F 0, v 0 Makina (doğrusal veya dairesel hareket) Mekanik
İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz Sıfır-Kuvvet Elemanları Kesme Metodu ile Analiz
 Yapıların Analizi Konu Çıktıları İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz Sıfır-Kuvvet Elemanları Kesme Metodu ile Analiz Kafesleri oluşturan elemenlara etki eden
Yapıların Analizi Konu Çıktıları İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz Sıfır-Kuvvet Elemanları Kesme Metodu ile Analiz Kafesleri oluşturan elemenlara etki eden
İçindekiler Şekiller Listesi
 1 İçindekiler 1.GĠRĠġ 3 2. Mekânsal Sentez ve Analiz ÇalıĢmaları... 4 3. Konsept....5 4. Stratejiler.....6 5.1/1000 Koruma Amaçlı Ġmar Planı.....7 6.1/500 Vaziyet Planı Sokak Tasarımı....7 7.1/200 Özel
1 İçindekiler 1.GĠRĠġ 3 2. Mekânsal Sentez ve Analiz ÇalıĢmaları... 4 3. Konsept....5 4. Stratejiler.....6 5.1/1000 Koruma Amaçlı Ġmar Planı.....7 6.1/500 Vaziyet Planı Sokak Tasarımı....7 7.1/200 Özel
Olasılık ve İstatistik Dersinin Öğretiminde Deney ve Simülasyon
 Olasılık ve İstatistik Dersinin Öğretiminde Deney ve Simülasyon Levent ÖZBEK Fikri ÖZTÜRK Ankara Üniversitesi Fen Fakültesi İstatistik Bölümü Sistem Modelleme ve Simülasyon Laboratuvarı 61 Tandoğan/Ankara
Olasılık ve İstatistik Dersinin Öğretiminde Deney ve Simülasyon Levent ÖZBEK Fikri ÖZTÜRK Ankara Üniversitesi Fen Fakültesi İstatistik Bölümü Sistem Modelleme ve Simülasyon Laboratuvarı 61 Tandoğan/Ankara
TEMEL MEKANİK 9. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 TEMEL MEKANİK 9 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
TEMEL MEKANİK 9 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi
 FOTOGRAMETRİ I Fotogrametrik Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi Tanımlar Metrik Kameralar Mercek Kusurları
FOTOGRAMETRİ I Fotogrametrik Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi Tanımlar Metrik Kameralar Mercek Kusurları
KONU 3. STATİK DENGE
 KONU 3. STATİK DENGE 3.1 Giriş Bir cisme etki eden dış kuvvet ve momentlerin toplamı 0 ise cisim statik dengededir denir. Kuvvet ve moment toplamlarının 0 olması sırasıyla; ötelenme ve dönme denge şartlarıdır.
KONU 3. STATİK DENGE 3.1 Giriş Bir cisme etki eden dış kuvvet ve momentlerin toplamı 0 ise cisim statik dengededir denir. Kuvvet ve moment toplamlarının 0 olması sırasıyla; ötelenme ve dönme denge şartlarıdır.
Rijit Cisimlerin Dengesi
 Rijit Cisimlerin Dengesi 1 Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Rijit Cisimlerin Dengesi 1 Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
YAPI ve DEPREM MÜHENDİSLİĞİNDE MATRİS YÖNTEMLER. Prof. Dr. Hikmet Hüseyin ÇATAL. Prof. Dr. Hikmet Hüseyin ÇATAL. (III. Baskı)
 DOKUZ EYLÜL ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ YAYINLARI NO:294 YAPI ve DEPREM MÜHENDİSLİĞİNDE MATRİS YÖNTEMLER YAPI ve DEPREM MÜHENDİSLİĞİNDE MATRİS YÖNTEMLER (III. Baskı) Prof. Dr. Hikmet Hüseyin ÇATAL
DOKUZ EYLÜL ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ YAYINLARI NO:294 YAPI ve DEPREM MÜHENDİSLİĞİNDE MATRİS YÖNTEMLER YAPI ve DEPREM MÜHENDİSLİĞİNDE MATRİS YÖNTEMLER (III. Baskı) Prof. Dr. Hikmet Hüseyin ÇATAL
Mahya Aşığı. Kenar Aşık
 . AŞIK HESABI.1 Yük Analizi lar makas üzerine basit mesnetli olarak teşkil edildikleri için, çatı örtüsü vasıtasıla her iki taraftan gelen alan ükünün arısına maruz kalacakları kabul edilebilir. Bu durumda;
. AŞIK HESABI.1 Yük Analizi lar makas üzerine basit mesnetli olarak teşkil edildikleri için, çatı örtüsü vasıtasıla her iki taraftan gelen alan ükünün arısına maruz kalacakları kabul edilebilir. Bu durumda;
Öğrenci Seçme Sınavı (Öss) / 14 Haziran 2009. Matematik I Soruları ve Çözümleri E) 6 ). 6 5 = 25 6 =
 Öğrenci Seçme Sınavı (Öss) / 4 Haziran 009 Matematik I Soruları ve Çözümleri. ( ).( + ) işleminin sonucu kaçtır? A) 6 B) 6 C) D) 6 E) 6 Çözüm ( ).( + ) 0 ( ).( ) + ( 4 9 ). 6 36 6 36. 6 6. 0, 0,0 0,0 işleminin
Öğrenci Seçme Sınavı (Öss) / 4 Haziran 009 Matematik I Soruları ve Çözümleri. ( ).( + ) işleminin sonucu kaçtır? A) 6 B) 6 C) D) 6 E) 6 Çözüm ( ).( + ) 0 ( ).( ) + ( 4 9 ). 6 36 6 36. 6 6. 0, 0,0 0,0 işleminin
OPERATÖRLER BÖLÜM 4. 4.1 Giriş. 4.2. Aritmetik Operatörler
 BÖLÜM 4. OPERATÖRLER 4.1 Giriş Turbo Pascal programlama dilinde de diğer programlama dillerinde olduğu gibi operatörler, yapılan işlem türüne göre aritmetik, mantıksal ve karşılaştırma operatörleri olmak
BÖLÜM 4. OPERATÖRLER 4.1 Giriş Turbo Pascal programlama dilinde de diğer programlama dillerinde olduğu gibi operatörler, yapılan işlem türüne göre aritmetik, mantıksal ve karşılaştırma operatörleri olmak
Makine Elemanları I Prof. Dr. İrfan KAYMAZ. Temel bilgiler-flipped Classroom Bağlama Elemanları
 Makine Elemanları I Prof. Dr. İrfan KAYMAZ Temel bilgiler-flipped Classroom Bağlama Elemanları 11/22/2014 İçerik Bağlama Elemanlarının Sınıflandırılması Şekil Bağlı bağlama elemanlarının hesabı Kuvvet
Makine Elemanları I Prof. Dr. İrfan KAYMAZ Temel bilgiler-flipped Classroom Bağlama Elemanları 11/22/2014 İçerik Bağlama Elemanlarının Sınıflandırılması Şekil Bağlı bağlama elemanlarının hesabı Kuvvet
 İÇİNDEKİLER SAYFA Önsöz 4 Stratejik Planlama ve Bütçe Yol Haritası 5 Örnek İşletme Hakkında 6 Gider Yükleme Sistemi 8 Satış Bütçesi Oluşturma 9 Faaliyet Gider Bütçesi Oluşturma 12 Bütçe Sistem Otomasyonu
İÇİNDEKİLER SAYFA Önsöz 4 Stratejik Planlama ve Bütçe Yol Haritası 5 Örnek İşletme Hakkında 6 Gider Yükleme Sistemi 8 Satış Bütçesi Oluşturma 9 Faaliyet Gider Bütçesi Oluşturma 12 Bütçe Sistem Otomasyonu
Hedefler. Kafeslerde oluşan kuvvetlerin hesaplanması: düğüm noktaları metodu kesme metodu
 Yapıların Analizi Hedefler Kafeslerde oluşan kuvvetlerin hesaplanması: düğüm noktaları metodu kesme metodu Konu Çıktıları İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz
Yapıların Analizi Hedefler Kafeslerde oluşan kuvvetlerin hesaplanması: düğüm noktaları metodu kesme metodu Konu Çıktıları İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz
YAPISAL ANALİZ DOÇ.DR. KAMİLE TOSUN FELEKOĞLU
 YAPISAL ANALİZ DOÇ.DR. KAMİLE TOSUN FELEKOĞLU 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla
YAPISAL ANALİZ DOÇ.DR. KAMİLE TOSUN FELEKOĞLU 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla
SÜREÇ YÖNETİMİ VE SÜREÇ İYİLEŞTİRME H.Ömer Gülseren > ogulseren@gmail.com
 SÜREÇ YÖNETİMİ VE SÜREÇ İYİLEŞTİRME H.Ömer Gülseren > ogulseren@gmail.com Giriş Yönetim alanında yaşanan değişim, süreç yönetimi anlayışını ön plana çıkarmıştır. Süreç yönetimi; insan ve madde kaynaklarını
SÜREÇ YÖNETİMİ VE SÜREÇ İYİLEŞTİRME H.Ömer Gülseren > ogulseren@gmail.com Giriş Yönetim alanında yaşanan değişim, süreç yönetimi anlayışını ön plana çıkarmıştır. Süreç yönetimi; insan ve madde kaynaklarını
2.4. ELASTĠK DEPREM YÜKLERĠNĠN TANIMLANMASI : SPEKTRAL ĠVME KATSAYISI
 2.4. ELASTĠK DEPREM YÜKLERĠNĠN TANIMLANMASI : SPEKTRAL ĠVME KATSAYISI Deprem yüklerinin belirlenmesi için esas alınacak olan Spektral İvme Katsayısı, A(T), Denk.(2.1) ile verilmiştir. %5 sönüm oranı için
2.4. ELASTĠK DEPREM YÜKLERĠNĠN TANIMLANMASI : SPEKTRAL ĠVME KATSAYISI Deprem yüklerinin belirlenmesi için esas alınacak olan Spektral İvme Katsayısı, A(T), Denk.(2.1) ile verilmiştir. %5 sönüm oranı için
ÜÇGEN,TESTERE işaret ÜRETEÇLERi VE veo
 Karadeniz Teknik Üniversitesi Elektrik-Elektronik Mühendisliği Bölümü Elektronik Lab. 2 ÜÇGEN,TESTERE işaret ÜRETEÇLERi VE veo. Ön Bilgiler. Üçgen Dalga işaret Üreteci Üçgen dalga işareti kare dalga işaretinin
Karadeniz Teknik Üniversitesi Elektrik-Elektronik Mühendisliği Bölümü Elektronik Lab. 2 ÜÇGEN,TESTERE işaret ÜRETEÇLERi VE veo. Ön Bilgiler. Üçgen Dalga işaret Üreteci Üçgen dalga işareti kare dalga işaretinin
EEM 334. Elektrik Makinaları Laboratuvarı
 EEM 334 Elektrik Makinaları Laboratuvarı Öğrencinin Adı-Soyadı: Öğrenci Numarası: Grup Numarası: Amasya Üniversitesi Teknoloji Fakültesi Elektrik-Elektronik Mühendisliği Bölümü Deney No:2 Deneyin Adı:
EEM 334 Elektrik Makinaları Laboratuvarı Öğrencinin Adı-Soyadı: Öğrenci Numarası: Grup Numarası: Amasya Üniversitesi Teknoloji Fakültesi Elektrik-Elektronik Mühendisliği Bölümü Deney No:2 Deneyin Adı:
EGZERSİZ TEST SONUÇLARININ YORUMLANMASI. Doç.Dr.Mitat KOZ
 EGZERSİZ TEST SONUÇLARININ YORUMLANMASI Doç.Dr.Mitat KOZ Fiziksel Uygunluk Test Sonuçları Klinik Egzersiz Test Sonuçları Fiziksel Uygunluk Test Sonuçlarının Yorumlanması Bireyler arası karşılaştırmalar
EGZERSİZ TEST SONUÇLARININ YORUMLANMASI Doç.Dr.Mitat KOZ Fiziksel Uygunluk Test Sonuçları Klinik Egzersiz Test Sonuçları Fiziksel Uygunluk Test Sonuçlarının Yorumlanması Bireyler arası karşılaştırmalar
VECTOR MECHANICS FOR ENGINEERS: STATICS
 Seventh Edition VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi 8. Sürtünme Tel: 85 31 46 / 116 E-mail: acarh@itu.edu.tr
Seventh Edition VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi 8. Sürtünme Tel: 85 31 46 / 116 E-mail: acarh@itu.edu.tr
KUVVETLER VEKTÖRDÜR BU YÜZDEN CEBİRSEL VEKTÖR TEKNİKLERİ KULLANMALIYIZ
 Rijit Cisim Dengesi KUVVETLER VEKTÖRDÜR BU YÜZDEN CEBİRSEL VEKTÖR TEKNİKLERİ KULLANMALIYIZ KUVVET SİSTEMİ 2 B KUVVET SİSTEMLERİ Detaylar 1- KO-LİNEER 2- BİR NOKTADA BULUŞAN (KONKÜRENT) 3- PARALEL 4- GENEL
Rijit Cisim Dengesi KUVVETLER VEKTÖRDÜR BU YÜZDEN CEBİRSEL VEKTÖR TEKNİKLERİ KULLANMALIYIZ KUVVET SİSTEMİ 2 B KUVVET SİSTEMLERİ Detaylar 1- KO-LİNEER 2- BİR NOKTADA BULUŞAN (KONKÜRENT) 3- PARALEL 4- GENEL
olup uygu kaması A formuna sahiptir. Müsaade edilen yüzey basıncı p em kasnak malzemesi GG ve mil malzemesi St 50 dir.
 ÖRNEK 1: Düz kayış kasnağı bir mil üzerine radyal yönde uygu kaması ile eksenel yönde İse bir pul ve cıvata ile sabitleştirilmiştir. İletilecek güç 1 kw ve devir sayısı n=500 D/d olup uygu kaması A formuna
ÖRNEK 1: Düz kayış kasnağı bir mil üzerine radyal yönde uygu kaması ile eksenel yönde İse bir pul ve cıvata ile sabitleştirilmiştir. İletilecek güç 1 kw ve devir sayısı n=500 D/d olup uygu kaması A formuna
Makina Dinamiği MEKANİZMALARDA HIZ VE İVMELERİN BELİRLENMESİ
 MEKANİZMALARDA HIZ VE İVMELERİN BELİRLENMESİ Mekanizmalar daha çok düzlemsel mekanizmalardan meydana gelir. Hacimsel mekanizmalara çok az rastlanır. Düzlemsel mekanizma denilince derinliği olmayan veya
MEKANİZMALARDA HIZ VE İVMELERİN BELİRLENMESİ Mekanizmalar daha çok düzlemsel mekanizmalardan meydana gelir. Hacimsel mekanizmalara çok az rastlanır. Düzlemsel mekanizma denilince derinliği olmayan veya
GERİLME Cismin kesilmiş alanı üzerinde O
 GERİLME Cismin kesilmiş alanı üzerinde O ile tanımlı noktasına etki eden kuvvet ve momentin kesit alana etki eden gerçek yayılı yüklerin bileşke etkisini temsil ettiği ifade edilmişti. Cisimlerin mukavemeti
GERİLME Cismin kesilmiş alanı üzerinde O ile tanımlı noktasına etki eden kuvvet ve momentin kesit alana etki eden gerçek yayılı yüklerin bileşke etkisini temsil ettiği ifade edilmişti. Cisimlerin mukavemeti
SORU 6: Su yapılarının tasarımında katı madde hareketinin (aşınma, oyulma, yığılma vb. olayları) incelenmesi neden önemlidir, açıklayınız (4 puan).
 KIRIKKALE ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ 014-015 GÜZ YARIYILI SU KAYNAKLARI MÜHENDİSLİĞİ I ARASINAV SORULARI Tarih: 16 Kasım 014 SORULAR VE CEVAPLAR Adı Soyadı: No: İmza:
KIRIKKALE ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ 014-015 GÜZ YARIYILI SU KAYNAKLARI MÜHENDİSLİĞİ I ARASINAV SORULARI Tarih: 16 Kasım 014 SORULAR VE CEVAPLAR Adı Soyadı: No: İmza:
Rijit Cisimlerin Dengesi
 Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
DEVRELER VE ELEKTRONİK LABORATUVARI
 DENEY NO: 1 DENEY GRUBU: C DİRENÇ ELEMANLARI, 1-KAPILI DİRENÇ DEVRELERİ VE KIRCHHOFF UN GERİLİMLER YASASI Malzeme ve Cihaz Listesi: 1. 10 Ω direnç 1 adet 2. 100 Ω direnç 3 adet 3. 180 Ω direnç 1 adet 4.
DENEY NO: 1 DENEY GRUBU: C DİRENÇ ELEMANLARI, 1-KAPILI DİRENÇ DEVRELERİ VE KIRCHHOFF UN GERİLİMLER YASASI Malzeme ve Cihaz Listesi: 1. 10 Ω direnç 1 adet 2. 100 Ω direnç 3 adet 3. 180 Ω direnç 1 adet 4.
STATİK. Ders_6. Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü. Ders notları için: GÜZ
 STATİK Ders_6 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2017-2018 GÜZ BASİT KAFESLER, DÜĞÜM NOKTALARI METODU VE SIFIR KUVVET ELEMANLARI
STATİK Ders_6 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2017-2018 GÜZ BASİT KAFESLER, DÜĞÜM NOKTALARI METODU VE SIFIR KUVVET ELEMANLARI
V. KAFES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir.
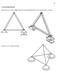 78 V. KES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir. Uzayda ise en az 6 çubuk gereklidir. 79 İhtiyaçlara göre yeni çubukların ilavesiyle
78 V. KES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir. Uzayda ise en az 6 çubuk gereklidir. 79 İhtiyaçlara göre yeni çubukların ilavesiyle
Elemanlardaki İç Kuvvetler
 Elemanlardaki İç Kuvvetler Bölüm Öğrenme Çıktıları Yapı elemanlarında oluşan iç kuvvetler. Eksenel kuvvet, Kesme kuvvet ve Eğilme Momenti Denklemleri ve Diyagramları. Bölüm Öğrenme Çıktıları Elemanlarda
Elemanlardaki İç Kuvvetler Bölüm Öğrenme Çıktıları Yapı elemanlarında oluşan iç kuvvetler. Eksenel kuvvet, Kesme kuvvet ve Eğilme Momenti Denklemleri ve Diyagramları. Bölüm Öğrenme Çıktıları Elemanlarda
BELĐRLĐ BĐR SIKMA KUVVETĐ ETKĐSĐNDE BĐSĐKLET FREN KOLU KUVVET ANALĐZĐNĐN YAPILMASI
 tasarım BELĐRLĐ BĐR SIKMA KUVVETĐ ETKĐSĐNDE BĐSĐKLET FREN KOLU KUVVET ANALĐZĐNĐN YAPILMASI Nihat GEMALMAYAN, Hüseyin ĐNCEÇAM Gazi Üniversitesi, Makina Mühendisliği Bölümü GĐRĐŞ Đlk bisikletlerde fren sistemi
tasarım BELĐRLĐ BĐR SIKMA KUVVETĐ ETKĐSĐNDE BĐSĐKLET FREN KOLU KUVVET ANALĐZĐNĐN YAPILMASI Nihat GEMALMAYAN, Hüseyin ĐNCEÇAM Gazi Üniversitesi, Makina Mühendisliği Bölümü GĐRĐŞ Đlk bisikletlerde fren sistemi
İSTANBUL TİCARET ÜNİVERSİTESİ BİLGİSAYAR MÜHENDİSLİĞİ BÖLÜMÜ BİLGİSAYAR SİSTEMLERİ LABORATUARI YÜZEY DOLDURMA TEKNİKLERİ
 İSTANBUL TİCARET ÜNİVERSİTESİ BİLGİSAYAR MÜHENDİSLİĞİ BÖLÜMÜ BİLGİSAYAR SİSTEMLERİ LABORATUARI YÜZEY DOLDURMA TEKNİKLERİ Deneyde dolu alan tarama dönüşümünün nasıl yapıldığı anlatılacaktır. Dolu alan tarama
İSTANBUL TİCARET ÜNİVERSİTESİ BİLGİSAYAR MÜHENDİSLİĞİ BÖLÜMÜ BİLGİSAYAR SİSTEMLERİ LABORATUARI YÜZEY DOLDURMA TEKNİKLERİ Deneyde dolu alan tarama dönüşümünün nasıl yapıldığı anlatılacaktır. Dolu alan tarama
Ek 1. Fen Maddelerini Anlama Testi (FEMAT) Sevgili öğrenciler,
 Ek 1. Fen Maddelerini Anlama Testi (FEMAT) Sevgili öğrenciler, Bu araştırmada Fen Bilgisi sorularını anlama düzeyinizi belirlemek amaçlanmıştır. Bunun için hazırlanmış bu testte SBS de sorulmuş bazı sorular
Ek 1. Fen Maddelerini Anlama Testi (FEMAT) Sevgili öğrenciler, Bu araştırmada Fen Bilgisi sorularını anlama düzeyinizi belirlemek amaçlanmıştır. Bunun için hazırlanmış bu testte SBS de sorulmuş bazı sorular
TG 12 ÖABT İLKÖĞRETİM MATEMATİK
 KAMU PERSONEL SEÇME SINAVI ÖĞRETMENLİK ALAN BİLGİSİ TESTİ İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ TG ÖABT İLKÖĞRETİM MATEMATİK Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının
KAMU PERSONEL SEÇME SINAVI ÖĞRETMENLİK ALAN BİLGİSİ TESTİ İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ TG ÖABT İLKÖĞRETİM MATEMATİK Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının
ÖĞRENME FAALİYETİ 1 ÖĞRENME FAALİYETİ 1 1. KARE VİDA AÇMA
 ÖĞRENME FAALİYETİ 1 ÖĞRENME FAALİYETİ 1 AMAÇ Kare vida çekme işlemlerini yapabileceksiniz. ARAŞTIRMA Kare vidaların kullanım alanları hakkında bilgi toplayınız. 1. KARE VİDA AÇMA Diş dolusu ve diş boşluğu
ÖĞRENME FAALİYETİ 1 ÖĞRENME FAALİYETİ 1 AMAÇ Kare vida çekme işlemlerini yapabileceksiniz. ARAŞTIRMA Kare vidaların kullanım alanları hakkında bilgi toplayınız. 1. KARE VİDA AÇMA Diş dolusu ve diş boşluğu
Taş, Yaman ve Kayran. Altan KAYRAN. akayran@metu.edu.tr ÖZET
 HAVA TAŞITLARINA UYGULANAN GÜÇLENDİRİLMİŞ, SİLİNDİRİK BİR DIŞ DEPONUN YAPISAL ANALİZİ Caner TAŞ ASELSAN, MST Mekanik Tasarım Müdürlüğü, Macunköy 06370, ANKARA, tas@aselsan.com.tr Yavuz YAMAN Orta Doğu
HAVA TAŞITLARINA UYGULANAN GÜÇLENDİRİLMİŞ, SİLİNDİRİK BİR DIŞ DEPONUN YAPISAL ANALİZİ Caner TAŞ ASELSAN, MST Mekanik Tasarım Müdürlüğü, Macunköy 06370, ANKARA, tas@aselsan.com.tr Yavuz YAMAN Orta Doğu
BÖLÜM 4 YAPISAL ANALİZ (KAFESLER-ÇERÇEVELER-MAKİNALAR)
 BÖLÜM 4 YAPISAL ANALİZ (KAESLER-ÇERÇEVELER-MAKİNALAR) 4.1 Kafesler: Basit Kafes: İnce çubukların uçlarından birleştirilerek luşturulan apıdır. Bileştirme genelde 1. Barak levhalarına pimler ve kanak vasıtası
BÖLÜM 4 YAPISAL ANALİZ (KAESLER-ÇERÇEVELER-MAKİNALAR) 4.1 Kafesler: Basit Kafes: İnce çubukların uçlarından birleştirilerek luşturulan apıdır. Bileştirme genelde 1. Barak levhalarına pimler ve kanak vasıtası
Şekil 6.24. İki girişli kod çözücünün blok şeması. Tablo 6.10. İki girişli kod çözücünün doğruluk tablosu. Şekil 6.25. İki girişli kod çözücü devre
 6.C. KOD ÇÖZÜCÜLER (DECODER) İkilik sayı sisteminde kodlanmış bilgileri, anlaşılması ve değerlendirilmesi daha kolay bilgilere dönüştüren devrelere Kod Çözücü denir. Kod Çözücüler (Decoder), Kodlayıcıların
6.C. KOD ÇÖZÜCÜLER (DECODER) İkilik sayı sisteminde kodlanmış bilgileri, anlaşılması ve değerlendirilmesi daha kolay bilgilere dönüştüren devrelere Kod Çözücü denir. Kod Çözücüler (Decoder), Kodlayıcıların
En İyi Uygulamalar ve Kullanım Kılavuzu
 En İyi Uygulamalar ve Kullanım Kılavuzu Bu kılavuz, GBT En İyi Uygulamaları ve Kullanım Kılavuzu na bir tamamlayıcı kılavuz oluşturmak için tasarlanmıştır. Green Break Patlamasız Güvenlik Güç Kartuşlarının
En İyi Uygulamalar ve Kullanım Kılavuzu Bu kılavuz, GBT En İyi Uygulamaları ve Kullanım Kılavuzu na bir tamamlayıcı kılavuz oluşturmak için tasarlanmıştır. Green Break Patlamasız Güvenlik Güç Kartuşlarının
JET MOTORLARININ YARI-DĐNAMĐK BENZETĐŞĐMĐ ve UÇUŞ ŞARTLARINA UYGULANMASI
 makale JET MOTORLARININ YARI-DĐNAMĐK BENZETĐŞĐMĐ ve UÇUŞ ŞARTLARINA UYGULANMASI Bekir NARĐN *, Yalçın A. GÖĞÜŞ ** * Y.Müh., TÜBĐTAK-SAGE ** Prof. Dr., Orta Doğu Teknik Üniversitesi, Havacılık ve Uzay Mühendisliği
makale JET MOTORLARININ YARI-DĐNAMĐK BENZETĐŞĐMĐ ve UÇUŞ ŞARTLARINA UYGULANMASI Bekir NARĐN *, Yalçın A. GÖĞÜŞ ** * Y.Müh., TÜBĐTAK-SAGE ** Prof. Dr., Orta Doğu Teknik Üniversitesi, Havacılık ve Uzay Mühendisliği
EEM 202 DENEY 5 SERİ RL DEVRESİ
 SERİ RL DEVRESİ 5.1 Amaçlar i, v, v R ve v L için RMS değerlerini hesaplama Seri RL devresinde voltaj ve empedans üçgenlerini tanımlama Seri RL devresinin empdansının kazanç ve faz karakteristiklerini
SERİ RL DEVRESİ 5.1 Amaçlar i, v, v R ve v L için RMS değerlerini hesaplama Seri RL devresinde voltaj ve empedans üçgenlerini tanımlama Seri RL devresinin empdansının kazanç ve faz karakteristiklerini
ELITE A.G. KS100/HEFM SICAK-SOĞUK ETĐKET BOY KESME VE ĐŞARETLEME MAKĐNASI KULLANIM KILAVUZU
 ELITE A.G. KS100/HEFM SICAK-SOĞUK ETĐKET BOY KESME VE ĐŞARETLEME MAKĐNASI KULLANIM KILAVUZU ANA EKRAN Makinenin şalteri açıldığında 5 sn boyunca açılış ekranı gelir. Daha sonra ana ekrana geçilir. Bu ekranda
ELITE A.G. KS100/HEFM SICAK-SOĞUK ETĐKET BOY KESME VE ĐŞARETLEME MAKĐNASI KULLANIM KILAVUZU ANA EKRAN Makinenin şalteri açıldığında 5 sn boyunca açılış ekranı gelir. Daha sonra ana ekrana geçilir. Bu ekranda
BİR SAYININ ÖZÜ VE DÖRT İŞLEM
 ÖZEL EGE LİSESİ BİR SAYININ ÖZÜ VE DÖRT İŞLEM HAZIRLAYAN ÖĞRENCİ: Sıla Avar DANIŞMAN ÖĞRETMEN: Gizem Günel İZMİR 2012 İÇİNDEKİLER 1. PROJENİN AMACI.. 3 2. GİRİŞ... 3 3. YÖNTEM. 3 4. ÖN BİLGİLER... 3 5.
ÖZEL EGE LİSESİ BİR SAYININ ÖZÜ VE DÖRT İŞLEM HAZIRLAYAN ÖĞRENCİ: Sıla Avar DANIŞMAN ÖĞRETMEN: Gizem Günel İZMİR 2012 İÇİNDEKİLER 1. PROJENİN AMACI.. 3 2. GİRİŞ... 3 3. YÖNTEM. 3 4. ÖN BİLGİLER... 3 5.
Şekil 5.12 Eski beton yüzeydeki kırıntıların su jetiyle uzaklaştırılması
 Şekil 5.12 Eski beton yüzeydeki kırıntıların su jetiyle uzaklaştırılması 5.6.4 Yapıştırılmamış Aşınma Tabakası (Yüzen Şap) Döşeme ile aşınma tabakası arasında aderans yoktur, aksine aderansı önlemek için
Şekil 5.12 Eski beton yüzeydeki kırıntıların su jetiyle uzaklaştırılması 5.6.4 Yapıştırılmamış Aşınma Tabakası (Yüzen Şap) Döşeme ile aşınma tabakası arasında aderans yoktur, aksine aderansı önlemek için
MÜHENDİSLİK YAPILARI ÇERÇEVELER VE MAKİNALAR
 MÜHENDİSLİK YAPILARI ÇERÇEVELER VE MAKİNALAR ÇERÇEVELER Çerçeveler kafesler gibi genellikle sabit duran taşıyıcı sistemlerdir. Bir çerçeveyi kafesten ayıran en belirgin özellik, en az bir elemanının çok
MÜHENDİSLİK YAPILARI ÇERÇEVELER VE MAKİNALAR ÇERÇEVELER Çerçeveler kafesler gibi genellikle sabit duran taşıyıcı sistemlerdir. Bir çerçeveyi kafesten ayıran en belirgin özellik, en az bir elemanının çok
DENEY DC Gerilim Ölçümü
 DENEY DC Gerilim Ölçümü DENEY N AMACI 1. DC gerilimin nas l ölçüldü ünü ö renmek. 2. KL-22001 Deney Düzene ini tan mak. 3. Voltmetrenin nas l kullan ld n ö renmek. GENEL B LG LER Devre eleman üzerinden
DENEY DC Gerilim Ölçümü DENEY N AMACI 1. DC gerilimin nas l ölçüldü ünü ö renmek. 2. KL-22001 Deney Düzene ini tan mak. 3. Voltmetrenin nas l kullan ld n ö renmek. GENEL B LG LER Devre eleman üzerinden
BAŞLICA ÇATI ŞEKİLLERİ
 ÇATILAR Yapıları dış atmosferden gelen yağmur, rüzgar, kar ve dolu gibi etkenlerden koruyan elemanlara "ÇATI" denilmektedir. Genellikle ahşap, çelik ve betonarmeden yapılan çatılar konut, işyeri, atelye,
ÇATILAR Yapıları dış atmosferden gelen yağmur, rüzgar, kar ve dolu gibi etkenlerden koruyan elemanlara "ÇATI" denilmektedir. Genellikle ahşap, çelik ve betonarmeden yapılan çatılar konut, işyeri, atelye,
ENERJĠ DAĞITIMI-I. Dersin Kredisi 4 + 0 + 0
 ENERJĠ DAĞITIMI-I Dersin Kredisi 4 + 0 + 0 Açma-Kapama Cihazları Elektrik enerjisinin açılması, ayrılması, kesilmesi veya kapatılması işlevlerini yapan cihazlardır. Alçak Gerilim Ayırıcı Nitelikli Orta
ENERJĠ DAĞITIMI-I Dersin Kredisi 4 + 0 + 0 Açma-Kapama Cihazları Elektrik enerjisinin açılması, ayrılması, kesilmesi veya kapatılması işlevlerini yapan cihazlardır. Alçak Gerilim Ayırıcı Nitelikli Orta
Noktasal Cismin Dengesi
 Noktasal Cismin Dengesi Bu bölümde; Kuvvetleri bieşenlerine ayırma ve kartezyen vektör şeklinde ifade etme yöntemleri noktasal cismin dengesini içeren problemleri çözmede kullanılacaktır. Bölüm 3 DOÇ.DR.
Noktasal Cismin Dengesi Bu bölümde; Kuvvetleri bieşenlerine ayırma ve kartezyen vektör şeklinde ifade etme yöntemleri noktasal cismin dengesini içeren problemleri çözmede kullanılacaktır. Bölüm 3 DOÇ.DR.
Üç-fazlı 480 volt AC güç, normalde-açık "L1", "L2" ve "L3" olarak etiketlenmiş vida bağlantı uçları yoluyla kontaktörün tepesinde kontak hale gelir
 Kontaktörler Röle kontakları üzerinden büyük bir miktar elektrik gücü anahtarlamak için kullanıldığında kontaktör terimi ile adlandırılır.. Kontaktörler tipik olarak çoklu kontaklara sahiptir ve kontakları
Kontaktörler Röle kontakları üzerinden büyük bir miktar elektrik gücü anahtarlamak için kullanıldığında kontaktör terimi ile adlandırılır.. Kontaktörler tipik olarak çoklu kontaklara sahiptir ve kontakları
ZEMİN MUKAVEMETİ: LABORATUVAR DENEY YÖNTEMLERİ
 ZEMİN MUKAVEMETİ: LABORATUVAR DENEY YÖNTEMLERİ Arazide bir yapı temeli veya toprak dolgu altında kalacak, veya herhangi bir başka yüklemeye maruz kalacak zemin tabakalarının gerilme-şekil değiştirme davranışlarını
ZEMİN MUKAVEMETİ: LABORATUVAR DENEY YÖNTEMLERİ Arazide bir yapı temeli veya toprak dolgu altında kalacak, veya herhangi bir başka yüklemeye maruz kalacak zemin tabakalarının gerilme-şekil değiştirme davranışlarını
Temel Bilgisayar Programlama
 BÖLÜM 9: Fonksiyonlara dizi aktarma Fonksiyonlara dizi aktarmak değişken aktarmaya benzer. Örnek olarak verilen öğrenci notlarını ekrana yazan bir program kodlayalım. Fonksiyon prototipi yazılırken, dizinin
BÖLÜM 9: Fonksiyonlara dizi aktarma Fonksiyonlara dizi aktarmak değişken aktarmaya benzer. Örnek olarak verilen öğrenci notlarını ekrana yazan bir program kodlayalım. Fonksiyon prototipi yazılırken, dizinin
Mak-204. Üretim Yöntemleri II. Vida ve Genel Özellikleri Kılavuz Çekme Pafta Çekme Rayba Çekme
 Mak-204 Üretim Yöntemleri II Vida ve Genel Özellikleri Kılavuz Çekme Pafta Çekme Rayba Çekme Kubilay ASLANTAŞ Afyon Kocatepe Üniversitesi Teknik Eğitim Fakültesi Makine Eğt. Bölümü Üretim Yöntemleri 1
Mak-204 Üretim Yöntemleri II Vida ve Genel Özellikleri Kılavuz Çekme Pafta Çekme Rayba Çekme Kubilay ASLANTAŞ Afyon Kocatepe Üniversitesi Teknik Eğitim Fakültesi Makine Eğt. Bölümü Üretim Yöntemleri 1
TEMEL MEKANİK 5. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 TEMEL MEKANİK 5 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
TEMEL MEKANİK 5 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
KLASİK MANTIK (ARİSTO MANTIĞI)
 KLASİK MANTIK (ARİSTO MANTIĞI) A. KAVRAM Varlıkların zihindeki tasarımı kavram olarak ifade edilir. Ağaç, kuş, çiçek, insan tek tek varlıkların tasarımıyla ortaya çıkmış kavramlardır. Kavramlar genel olduklarından
KLASİK MANTIK (ARİSTO MANTIĞI) A. KAVRAM Varlıkların zihindeki tasarımı kavram olarak ifade edilir. Ağaç, kuş, çiçek, insan tek tek varlıkların tasarımıyla ortaya çıkmış kavramlardır. Kavramlar genel olduklarından
Gerilme. Bölüm Hedefleri. Normal ve Kayma gerilmesi kavramının anlaşılması Kesme ve eksenel yük etkisindeki elemanların analiz ve tasarımı
 Gerilme Bölüm Hedefleri Normal ve Kayma gerilmesi kavramının anlaşılması Kesme ve eksenel yük etkisindeki elemanların analiz ve tasarımı Copyright 2011 Pearson Education South sia Pte Ltd GERİLME Kesim
Gerilme Bölüm Hedefleri Normal ve Kayma gerilmesi kavramının anlaşılması Kesme ve eksenel yük etkisindeki elemanların analiz ve tasarımı Copyright 2011 Pearson Education South sia Pte Ltd GERİLME Kesim
