Rijit Cisimlerin Dengesi
|
|
|
- Mehmed Yerlikaya
- 6 yıl önce
- İzleme sayısı:
Transkript
1 Rijit Cisimlerin Dengesi 1
2 Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest cisim diyagramı çizilmesi Denge denklemlerini kullanarak, rijit cisimlerin denge problemlerinin çözülmesi 2
3 Rijit cisim denge koşulları Şekilde cisme, kuvvet ve moment (kuvvet çifti) vektörleri etkimektedir. Bu kuvvetler, yerçekimi, elektriksel, manyetik veya temas kuvvetlerinden dolayı olabilir. İç kuvvetlerin toplamı sıfırdır, çünkü cisim içindeki parçacıklar arasındaki iç kuvvetler, Newtonun üçüncü kanununa göre eşit, fakat zıt yönlü doğrusal çiftler şeklindedir, yani dengededir. 3
4 4 Bir önceki bölümde anlatılan yöntemle, bir cisme etki eden kuvvet ve moment çifti sistemi, cismin herhangi bir O noktasına eşdeğer bir bileşke kuvvet ve bileşke moment çiftine indirgenebilir. Bu bileşke kuvvet ve moment çiftinin ikisi de sıfıra eşitse, cismin dengede olduğu söylenebilir. 0 ) ( 0 O O R R M M F F
5 İki Boyutta Denge Bu bölümde aynı düzlemdeki kuvvetlerden ve bu düzleme dik momentlerin dengesi incelenecek. Bu tür sistemlere iki boyutlu kuvvet sistemleri denir. Şekildeki uçak, merkezden geçen eksene göre simetrik olduğu için, tekerleklerde oluşan kuvvetler T ve T, 2T olarak gösterilmiştir. 5
6 Serbest Cisim Diyagramları Denge denklemlerinin başarıyla uygulanması için, cisim üzerine etkiyen bilinen ve bilinmeyen bütün dış kuvvetlerin cisim üzerinde gösterilmesi gerekir. Bunun için serbest cisim diyagramı çizilmelidir. Bu diyagram cismi, çevresinden izole edilmiş veya serbest kalmış bir şekilde ana hatlarını, yani bir serbest cismi gösteren bir taslaktır. Serbest cisim diyagramını çizmek için: 1) Cisim üzerine etkiyen dış kuvvetler, bilinen ve bilinmeyen tüm kuvvetler cisim üzerinde gösterilir. Bu kuvvetler: cisme etkiyen dış kuvvetler, reaksiyon/mesnet kuvvetleri ve cismin ağırlığıdır. 2) Bilinen kuvvetler/momentler bilinen şiddet ve yönleriyle gösterilmelidir. Bilinmeyen kuvvetler/momentlerin yön ve şiddetleri harflerle gösterilmelidir 3) Bir x-y koordinat eksenleri oluşturulmalı ve bilinmeyen kuvvetler, bu eksenlerdeki bileşenlerine ayrılarak gösterilmelidir. 4) Cismin boyutları belirtilmelidir, bu boyutlar momentler bulunurken kullanılacaktır. 6
7 Mesnet Reaksiyonları Genel kural: bir mesnet cismin verilen bir doğrultuda ötelenmesini engelliyorsa, cisim üzerinde sözkonusu doğrultuda bir kuvvet ortaya çıkar. Aynı şekilde, cismin dönmesi engelleniyorsa, cisim üzerinde bir kuvvet çifti momenti uygulanır. Örneğin, bir kirişte görülen üç mesnet türüne bakalım: Kayar mesnet: sadece kirişin düşey doğrultuda ötelenmesini önler, tekerlek kiriş üzerinde sadece bu doğrultuda bir kuvvet uygular. Kuvvet mesnetten kirişe etkiyor şeklinde gösterildi (yani cisim üzerinde) Mesnet serbestçe döndüğü için ve yatay yönde hareket edebildiği için o yönlerde mesnet kuvvetleri oluşmaz. 7
8 Basit mesnet (pimli mesnet): kiriş şekildeki gibi, bir pim kullanılarak daha kısıtlayıcı bir şekilde mesnetlenebilir. Pim yere tutturulmuş iki elemandan ve kirişteki bir delikten geçer. Pim kirişin herhangi bir doğrultusunda, ötelenmesini önler ve bu yüzden pim kiriş üzerinde bu doğrultuda bir F kuvveti uygulamalıdır. Bu etkiyi F x ve F y bileşenleri ile ifade etmek daha kolaydır. Hem düşey hem yatay yönde hareket engellenmiştir, dolayısıyla reaksiyon kuvvetleri bu iki yönde oluşur. Kiriş sadece serbestçe dönebilir. 8
9 Ankastre mesnet: Kirişi mesnetlemenin en kısıtlayıcı yolu, şekildeki gibi bir sabit mesnet (ankastre mesnet) kullanmaktır. Bu mesnet kirişin hem ötelenmesine, hem de dönmesine engel olur. Bu durumda, mesnette x ve y yönlerinde kuvvetler ve z ekseni doğrultusunda (moment ekseni) moment oluşacaktır. Kuvvet mafsallı mesnette olduğu gibi F x ve F y bileşenleri ile ifade edilir, ve bu kuvvetler bilinirse açısı da kolaylıkla bulunur. Kirişin bir noktadan her yöndeki hareketi sınırlanmıştır. 9
10 Diğer Rijit Cisim Mesnet Türleri Tabloda, sıklıkla kullanılan diğer mesnet türleri verilmiştir. Tüm durumlarda açısının bilindiği kabul edilmiştir. Kablo: 1 bilinmeyen, tepki kablo doğrultusunda elemandan uzaklaşan yönde etkiyen bir çekme kuvveti Ağırlıksız çubuk; 1 bilinmeyen, tepki bağlantı çubuğu ekseni boyunca iki yönlü kuvvet Kayar mesnet: 1 bilinmeyen, tepki temas noktasında yüzeye dik etkiyen bir kuvvettir. 10
11 Sürtünmesiz yuva içinde kayar mesnet: 1 bilinmeyen, tepki yuvaya dik etkiyen bir kuvvettir. Sallanan mesnet: 1 bilinmeyen, tepki temas noktasında yüzeye dik etkiyen bir kuvvettir. Sürtünmesiz yüzey: 1 bilinmeyen, tepki temas noktasında yüzeye dik etkiyen bir kuvvettir. Mafsallı kayar eleman: 1 bilinmeyen, tepki elemana dik etkiyen bir kuvvettir. 11
12 Mafsallı sabit mesnet: İki bilinmeyen, kuvvetin iki bileşeni veya bileşke kuvvetin büyüklüğü ve doğrultusu. Ankastre kayar mesnet: iki bilinmeyen. Kuvvet çifti momenti ve çubuğa dik etkiyen bir kuvvet Ankastre mesnet: üç bilinmeyen. Kuvvet çifti momenti ve iki kuvvet bileşeni veya kuvvet çifti momenti ve bileşke kuvvetin büyüklüğü ve doğrultusu. 12
13 kablo Kayar mesnet Sürtünmesiz yüzey Sabit mesnet ankastre 13
14 Dış ve İç kuvvetler Bir rijit cisim parçacıkların birleşimi olduğundan, üzerine hem dış hem de iç yükler etki eder. Ancak cismin serbest cisim diyagramında iç kuvvetler gösterilmez. İç ve dış kuvvetler daima eşit, fakat zıt yönlü doğrusal çiftler şeklinde ortaya çıkar ve bu nedenle cisim üzerindeki net etkileri sıfırdır. Motora etkiyen tüm iç kuvvetler ( bulon, vida vb. kuvvetleri) birbirlerini dengeler. Sadece zincir kuvvetleri ve motor ağırlığı serbest cisim diyagramında gösterilir. 14
15 Ağırlık ve Ağırlık Merkezi Cismin ağırlığı önemli mertebedeyse bu sorularda belirtilir. Ayrıca cisim üniformsa (aynı malzemeden yapıldıysa) ağırlık merkezi cismin geometrik merkeziyle çakışır. Cisim üniform değilse, veya karmaşık bir geometriye sahipse bu durumda ağırlık merkezi verilecektir. 15
16 İdealize edilmiş modeller Herhangi bir sistemin kuvvet analizi yapılacağı zaman, gerçek duruma en yakın analitik veya idealize modeli düşünülmelidir. Bunun için mesnet tipleri, malzeme davranışı ve cismin boyutları uygun bir şekilde seçilmelidir. Kompleks durumlarda birden fazla modelin analiz edilmesi gerekebilir. 16
17 Örnek 21 Şekildeki üniform kirişin serbest cisim diyagramını çiziniz. Kirişin kütlesi 100 kg dır. 17
18 Örnek er kg kütleli iki sürtünmesiz boru şekildeki görüldüğü gibi traktörle taşınmaktadır. Serbest cisim diyagramını her boru için ve birlikte çiziniz. 18
19 19
20 Örnek 23 Şekilde gösterilen sistemin matematiksel modelini kurun ve serbest cisim diyagramını çiziniz. 20
21 Denge denklemleri Rijit bir cismin dengesi için gerekli ve yeterli olan iki koşul: 0 F 0 ve M 0 Cisim x-y düzleminde yer alan bir kuvvetler sistemine maruzsa, kuvvetler x ve y bileşenlerine ayrılabilir. F F x y M 0 0 O 0 Cisim üzerine etkiyen tüm kuvvetlerin x ve y bileşenlerinin toplamı Kuvvet çifti momentleri ile tüm kuvvet bileşenlerinin x-y düzlemine dik olan ve cismin üzerinde veya dışındaki keyfi bir O noktasından geçen bir eksene göre momentlerinin toplamı 21
22 22 Alternatif Denge Denklemi Setleri O y x M F F denklemleri düzlemsel denge problemlerinin çözümünde sıklıkla kullanılmakla birlikte üç bağımsız denklemden oluşan iki alternatif denklem seti de kullanılabilir: B A x M M F Bu denklemlerin kullanılabilmesi için, A ve B moment noktalarının, x eksenine dik bir doğru üzerinde yer almamaları gerekir. Aksi durumda denklemler birbirinden bağımsız olmaz C B A M M M 2 Bu denklemlerin kullanılabilmesi için, A, B ve C'nin üçü birden aynı doğru üzerinde olmamalıdır.
23 Analizde İzlenecek yol: Serbest Cisim Diyagramının çizilmesi: Cisim üzerine etkiyen tüm dış kuvvetler ve kuvvet çifti momentlerinin gösterilmesi gereklidir. Bu vektörlerin büyüklükleri ve oluşturulan bir x-y eksen takımına göre belirlenen doğrultuları belirtilmelidir. Kuvvetlerin momentlerinin hesaplanması için gerekli olan cismin boyutları da serbest cisim diyagramına dahil edilir. Bilinmeyenler belirlenir. Etki çizgisi bilinen ancak büyüklüğü bilinmeyen bir kuvvet veya kuvvet çifti momentinin yönü varsayım ile belirlenebilir. Denge denklemlerinin uygulanması: Bütün denklemleri aynı anda çözmek zorunda kalmamak için iki bilinmeyen kuvvetin etki çizgilerinin kesişme noktasında yer alan bir O noktasına göre M 0 =0 moment denklemi uygulanır (ki bu bilinmeyen kuvvetlerin O noktasına göre momentleri sıfır olsun). Oluşturulan x-y eksenleri kullanılarak F x =0 ve F y =0 denge denklemleri uygulanır. Denge denkleminin çözümü sonucunda negatif bir skaler çıkarsa, sözkonusu kuvvet veya momentinin yönünün, serbest cisim diyagramında varsayılanın tersine olduğu anlaşılır. 23
24 Örnek 24 Şekildeki yüklemeye maruz kalan kirişteki mesnet kuvvetlerini bulunuz. A: kayar mesnet B: basit mesnet 24
25 1- Serbest cisim diyagramı * Bilinmeyen reaksiyon kuvvetleri mesnet noktalarına, yön kabuluyle etki ettirildi. 25
26 2- Denge Denklemleri kontrol 26
27 Örnek 25 3 m 750 N 3 m A ve B noktasında oluşan reaksiyon kuvvetlerini bulunuz. 2 m A: basit mesnet B: kayar mesnet 750 N 3 m 3 m 2 m 27
28 Denge Denklemleri NB reaksiyonunu bulmak için A noktasına göre moment alınır: N N B B M A 0 cos30.(6m) 536.2N Ax 268N Ay 286N N B sin 30.(2m) 750N.(3m) 0 Fx 0 Ax (536.2N)sin 30 0 Fy 0 Ay (536.2N)cos30 750N 750 N 3 m 0 3 m 2 m 28
29 Örnek 26 Şekildeki sistemin mesnet reaksiyonlarını bulunuz. Not: A noktası düşey yönde hareket edebiliyor A: mafsallı kayar eleman B: kayar mesnet 29
30 SERBEST CİSİM DİYAGRAMI 30
31 DENGE DENKLEMLERİ A x ve N B kuvvet denklemlerinin dengesinden bulunabilir: daha sonra A noktasına göre moment alınır: veya 31
32 Örnek 27 A noktasından mafsallı eleman B noktasında sürtünmesiz bir mesnetle desteklenmiştir. A mafsalındaki mesnet kuvvetlerini bulunuz. A: sabit mesnet B: sürtünmesiz mesnet 32
33 33
34 Örnek 28 A mesnedinde oluşan reaksiyon kuvvetlerini bulunuz. A: ankastre mesnet F F M x y A A A y M x A M 400.cos 30 0 A 3.90 knm A x 346N sin (2.5) 200(3.5) 200(4.5) 400.sin 30(4.5) 400.cos 30(3sin 60) 0 A y 800N 34
35 Ödev 12 Mesnet tepkilerini ve C noktasında oluşan kuvveti bulunuz kn 35
36 Çalışma sorusu-1 Şekilde görülen 200 kg ağırlığındaki kasa AB ve AC halatları ile taşınmaktadır. Her halat kopmadan en fazla 10 kn luk yük taşıyabilmektedir. AB halatının yatay pozisyonda olması koşuluyla, halatlardan biri kopmadan kasanın dengede kalması için gerekli en küçük açısını hesaplayınız. 36
37 Çözüm 37
38 Çalışma sorusu-2 AB, AC ve AD kablolarında oluşan kuvvetleri bulunuz. 300 N 38
39 Çözüm 300 N 39
40 40 Hatırlatma: Bir vektörün kartezyen bileşenleri Bir A vektörünün x, y, z koordinat eksenlerinde bileşenleri olabilir. Paralelkenar kuralını iki kez ard arda uygulayarak; z y x y x z A A A A A A A A A A
41 Kartezyen birim vektörler Üç boyutlu uzayda, i, j, k kartezyen birim vektörleri sırasıyla x, y, z eksenlerinin doğrultusunu göstermek için kullanılır. Şekilde verilen vektörler, pozitif birim vektörlerdir. 41
42 Kartezyen vektör gösterimi Vektörleri kartezyen bileşenler cinsinden yazmak önemli bir avantaj sağlar. Her bir bileşen vektörün şiddeti ve yönünü belirtir. A A iˆ x A y ˆj A kˆ z 42
43 Kartezyen vektörün yönleri A vektörünün doğrultusu, A nın başlangıç noktası ve bu noktada yer alan pozitif x, y, z eksenleri arasında ölçülen (alfa), (beta), (gama) doğrultu açıları ile tanımlanır. Bu açılar 0 ile 180 arasındadır., ve yı belirlemek için A nın x, y, z eksenleri üzerindeki izdüşümleri kullanılır. 43
44 Yön kosinüsleri 44
45 A vektörünün doğrultu kosinüslerini elde etmenin kolay bir yolu, A doğrultusunda bir birim vektör oluşturmaktır. ** Eğer bir vektörün şiddeti ve yön kosinüsleri biliniyorsa, A vektörü kartezyen koordinatlarda ifade edilebilir. 45
Rijit Cisimlerin Dengesi
 Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Rijit Cisimlerin Dengesi
 Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
STATIK VE MUKAVEMET 3. Rijit cisimlerin dengesi, Denge denklemleri, Serbest cisim diyagramı. Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ
 STATIK VE MUKAVEMET 3. Rijit cisimlerin dengesi, Denge denklemleri, Serbest cisim diyagramı Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları
STATIK VE MUKAVEMET 3. Rijit cisimlerin dengesi, Denge denklemleri, Serbest cisim diyagramı Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 5 Rijit Cisim Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 5. Rijit Cisim Dengesi Denge,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 5 Rijit Cisim Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 5. Rijit Cisim Dengesi Denge,
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 5 Rijit Cisim Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 5. Rijit Cisim Dengesi Denge,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 5 Rijit Cisim Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 5. Rijit Cisim Dengesi Denge,
YAPI STATİĞİ MESNETLER
 YAPI STATİĞİ MESNETLER Öğr.Gör. Gültekin BÜYÜKŞENGÜR STATİK Kirişler Yük Ve Mesnet Çeşitleri Mesnetler Ve Mesnet Reaksiyonları 1. Kayıcı Mesnetler 2. Sabit Mesnetler 3. Ankastre (Konsol) Mesnetler 4. Üç
YAPI STATİĞİ MESNETLER Öğr.Gör. Gültekin BÜYÜKŞENGÜR STATİK Kirişler Yük Ve Mesnet Çeşitleri Mesnetler Ve Mesnet Reaksiyonları 1. Kayıcı Mesnetler 2. Sabit Mesnetler 3. Ankastre (Konsol) Mesnetler 4. Üç
Ödev 1. Ödev1: 600N luk kuvveti u ve v eksenlerinde bileşenlerine ayırınız. 600 N
 Ödev 1 Ödev1: 600N luk kuvveti u ve v eksenlerinde bileşenlerine ayırınız. 600 N 1 600 N 600 N 600 N u sin120 600 N sin 30 u 1039N v sin 30 600 N sin 30 v 600N 2 Ödev 2 Ödev2: 2 kuvvetinin şiddetini, yönünü
Ödev 1 Ödev1: 600N luk kuvveti u ve v eksenlerinde bileşenlerine ayırınız. 600 N 1 600 N 600 N 600 N u sin120 600 N sin 30 u 1039N v sin 30 600 N sin 30 v 600N 2 Ödev 2 Ödev2: 2 kuvvetinin şiddetini, yönünü
3B Kuvvet Momenti. Üç Boyutlu Kuvvet Sistemi
 3B Kuvvet Momenti Üç Boyutlu Kuvvet Sistemi M = r (vektör) X F (vektör) Her F kuvvetinin uzunluk r vektörünü bul Eğer verilmemişse, F kuvvetini de vektörel ifade et. Uzunluk vektörünü r bulmak için: Uzunlık
3B Kuvvet Momenti Üç Boyutlu Kuvvet Sistemi M = r (vektör) X F (vektör) Her F kuvvetinin uzunluk r vektörünü bul Eğer verilmemişse, F kuvvetini de vektörel ifade et. Uzunluk vektörünü r bulmak için: Uzunlık
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 4 Kuvvet Sistemi Bileşkeleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 4. Kuvvet Sitemi Bileşkeleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 4 Kuvvet Sistemi Bileşkeleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 4. Kuvvet Sitemi Bileşkeleri
Noktasal Cismin Dengesi
 Noktasal Cismin Dengesi Bu bölümde; Kuvvetleri bieşenlerine ayırma ve kartezyen vektör şeklinde ifade etme yöntemleri noktasal cismin dengesini içeren problemleri çözmede kullanılacaktır. Bölüm 3 DOÇ.DR.
Noktasal Cismin Dengesi Bu bölümde; Kuvvetleri bieşenlerine ayırma ve kartezyen vektör şeklinde ifade etme yöntemleri noktasal cismin dengesini içeren problemleri çözmede kullanılacaktır. Bölüm 3 DOÇ.DR.
Mühendislik Mekaniği Dinamik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 17 Rijit Cismin Düzlemsel Kinetiği; Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok.
Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 17 Rijit Cismin Düzlemsel Kinetiği; Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok.
Doç. Dr. Muhammet Cerit Öğretim Üyesi Makine Mühendisliği Bölümü (Mekanik Ana Bilim Dalı) Elektronik posta ( ):
 Tanışma ve İletişim... Doç. Dr. Muhammet Cerit Öğretim Üyesi Makine Mühendisliği Bölümü (Mekanik Ana Bilim Dalı) Elektronik posta (e-mail): mcerit@sakarya.edu.tr Öğrenci Başarısı Değerlendirme... Öğrencinin
Tanışma ve İletişim... Doç. Dr. Muhammet Cerit Öğretim Üyesi Makine Mühendisliği Bölümü (Mekanik Ana Bilim Dalı) Elektronik posta (e-mail): mcerit@sakarya.edu.tr Öğrenci Başarısı Değerlendirme... Öğrencinin
2. KUVVET SİSTEMLERİ 2.1 Giriş
 2. KUVVET SİSTEMLERİ 2.1 Giriş Kuvvet: Şiddet (P), doğrultu (θ) ve uygulama noktası (A) ile karakterize edilen ve bir cismin diğerine uyguladığı itme veya çekme olarak tanımlanabilir. Bu parametrelerden
2. KUVVET SİSTEMLERİ 2.1 Giriş Kuvvet: Şiddet (P), doğrultu (θ) ve uygulama noktası (A) ile karakterize edilen ve bir cismin diğerine uyguladığı itme veya çekme olarak tanımlanabilir. Bu parametrelerden
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 3 Parçacık Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 3 Parçacık Dengesi Bu bölümde,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 3 Parçacık Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 3 Parçacık Dengesi Bu bölümde,
TEKNOLOJİNİN BİLİMSEL İLKELERİ
 TEKNOLOJİNİN BİLİMSEL İLKELERİ Öğr. Gör. Fatih KURTULUŞ 4.BÖLÜM: STATİK MOMENT - MOMENT (TORK) Moment (Tork): Kuvvetin döndürücü etkisidir. F 3 M ile gösterilir. Vektörel büyüklüktür. F 4 F 3. O. O F 4
TEKNOLOJİNİN BİLİMSEL İLKELERİ Öğr. Gör. Fatih KURTULUŞ 4.BÖLÜM: STATİK MOMENT - MOMENT (TORK) Moment (Tork): Kuvvetin döndürücü etkisidir. F 3 M ile gösterilir. Vektörel büyüklüktür. F 4 F 3. O. O F 4
STATİK. Ders_5. Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü. Ders notları için: GÜZ
 STATİK Ders_5 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2017-2018 GÜZ RİJİT CİSMİN DENGESİ VE SERBEST CİSİM DİYAGRAMI Bugünün Hedefleri:
STATİK Ders_5 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2017-2018 GÜZ RİJİT CİSMİN DENGESİ VE SERBEST CİSİM DİYAGRAMI Bugünün Hedefleri:
KUVVET, MOMENT ve DENGE
 2.1. Kuvvet 2.1.1. Kuvvet ve cisimlere etkileri Kuvvetler vektörel büyüklüklerdir. Kuvvet vektörünün; uygulama noktası, kuvvetin cisme etkidiği nokta; doğrultu ve yönü, kuvvetin doğrultu ve yönü; modülüyse
2.1. Kuvvet 2.1.1. Kuvvet ve cisimlere etkileri Kuvvetler vektörel büyüklüklerdir. Kuvvet vektörünün; uygulama noktası, kuvvetin cisme etkidiği nokta; doğrultu ve yönü, kuvvetin doğrultu ve yönü; modülüyse
KONU 3. STATİK DENGE
 KONU 3. STATİK DENGE 3.1 Giriş Bir cisme etki eden dış kuvvet ve momentlerin toplamı 0 ise cisim statik dengededir denir. Kuvvet ve moment toplamlarının 0 olması sırasıyla; ötelenme ve dönme denge şartlarıdır.
KONU 3. STATİK DENGE 3.1 Giriş Bir cisme etki eden dış kuvvet ve momentlerin toplamı 0 ise cisim statik dengededir denir. Kuvvet ve moment toplamlarının 0 olması sırasıyla; ötelenme ve dönme denge şartlarıdır.
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
VECTOR MECHANICS FOR ENGINEERS: STATICS
 Seventh E 4 Equilibrium CHAPTER VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. of Rigid Bodies Lecture Notes: J. Walt Oler Texas Tech University Seventh E CHAPTER VECTOR
Seventh E 4 Equilibrium CHAPTER VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. of Rigid Bodies Lecture Notes: J. Walt Oler Texas Tech University Seventh E CHAPTER VECTOR
 5. 5. 5.3 5.4 5.5 5.6 5.7 5.8 Rijit Cisimde Denge Düzlem Kuvvetlerde Denge Hali Düzlemde Serbestlik Derecesi Bağ Çeşitleri Pandül Ayak Düzlem Taşıyıcı Sistemler Düzlem Taşıyıcı Sistemlerde Yükleme Durumları
5. 5. 5.3 5.4 5.5 5.6 5.7 5.8 Rijit Cisimde Denge Düzlem Kuvvetlerde Denge Hali Düzlemde Serbestlik Derecesi Bağ Çeşitleri Pandül Ayak Düzlem Taşıyıcı Sistemler Düzlem Taşıyıcı Sistemlerde Yükleme Durumları
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 7 İç Kuvvetler Kaynak: Mühendislik Mekaniği: Statik, R. C. Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 7. İç Kuvvetler Bu bölümde, bir
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 7 İç Kuvvetler Kaynak: Mühendislik Mekaniği: Statik, R. C. Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 7. İç Kuvvetler Bu bölümde, bir
ÇALIŞMA SORULARI. Şekilde gösterildiği gibi yüklenmiş ankastre mesnetli kirişteki mesnet tepkilerini bulunuz.
 ÇALIŞMA SORULARI Üniform yoğunluğa sahip plaka 270 N ağırlığındadır ve A noktasından küresel mafsal ile duvara bağlanmıştır. Ayrıca duvara C ve D noktasından bağlanmış halatlarla desteklenmektedir. Serbest
ÇALIŞMA SORULARI Üniform yoğunluğa sahip plaka 270 N ağırlığındadır ve A noktasından küresel mafsal ile duvara bağlanmıştır. Ayrıca duvara C ve D noktasından bağlanmış halatlarla desteklenmektedir. Serbest
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
Mukavemet-II PROF. DR. MURAT DEMİR AYDIN
 Mukavemet-II PROF. DR. MURAT DEMİR AYDIN KAYNAK KİTAPLAR Cisimlerin Mukavemeti F.P. BEER, E.R. JOHNSTON Mukavemet-2 Prof.Dr. Onur SAYMAN, Prof.Dr. Ramazan Karakuzu Mukavemet Mehmet H. OMURTAG 1 SİMETRİK
Mukavemet-II PROF. DR. MURAT DEMİR AYDIN KAYNAK KİTAPLAR Cisimlerin Mukavemeti F.P. BEER, E.R. JOHNSTON Mukavemet-2 Prof.Dr. Onur SAYMAN, Prof.Dr. Ramazan Karakuzu Mukavemet Mehmet H. OMURTAG 1 SİMETRİK
YARIYIL İÇİ ÇALIŞMALARI SIRA KATKI YÜZDESİ Ara Sınav 1 60 Kısa Sınav 2 30 Ödev 1 10 Toplam 100 Finalin Başarıya Oranı 50 Yıliçinin Başarıya Oranı 50
 YARIYIL İÇİ ÇALIŞMALARI SIRA KATKI YÜZDESİ Ara Sınav 1 60 Kısa Sınav 2 30 Ödev 1 10 Toplam 100 Finalin Başarıya Oranı 50 Yıliçinin Başarıya Oranı 50 Toplam 100 1 Mukavemet ve Statiğin Önemi 2 Statiğin
YARIYIL İÇİ ÇALIŞMALARI SIRA KATKI YÜZDESİ Ara Sınav 1 60 Kısa Sınav 2 30 Ödev 1 10 Toplam 100 Finalin Başarıya Oranı 50 Yıliçinin Başarıya Oranı 50 Toplam 100 1 Mukavemet ve Statiğin Önemi 2 Statiğin
Karabük Üniversitesi, Mühendislik Fakültesi...www.IbrahimCayiroglu.com. STATİK (3. Hafta)
 TAŞIYICI SİSTEMLER VE MESNET TEPKİLERİ STATİK (3. Hafta) Taşıyıcı Sistemler Bir yapıya etki eden çeşitli kuvvetleri güvenlik sınırları içinde taşıyan ve bu kuvvetleri zemine aktaran sistemlere taşıyıcı
TAŞIYICI SİSTEMLER VE MESNET TEPKİLERİ STATİK (3. Hafta) Taşıyıcı Sistemler Bir yapıya etki eden çeşitli kuvvetleri güvenlik sınırları içinde taşıyan ve bu kuvvetleri zemine aktaran sistemlere taşıyıcı
TEMEL MEKANİK 10. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 TEMEL MEKANİK 10 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
TEMEL MEKANİK 10 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
Rijit cisim mekaniği, diyagramdan da görüldüğü üzere statik ve dinamik olarak ikiye ayrılır. Statik dengede bulunan cisimlerle, dinamik hareketteki
 Rijit cisim mekaniği, diyagramdan da görüldüğü üzere statik ve dinamik olarak ikiye ayrılır. Statik dengede bulunan cisimlerle, dinamik hareketteki cisimlerle uğraşır. Statik, kuvvet etkisi altında cisimlerin
Rijit cisim mekaniği, diyagramdan da görüldüğü üzere statik ve dinamik olarak ikiye ayrılır. Statik dengede bulunan cisimlerle, dinamik hareketteki cisimlerle uğraşır. Statik, kuvvet etkisi altında cisimlerin
3. KUVVET SİSTEMLERİ
 3. KUVVET SİSTEMLERİ F F W P P 3.1 KUVVET KAVRAMI VE ETKİLERİ Kuvvet, bir cisme etki eden yapısal yüklerdir. Kuvvet Şiddeti, yönü ve uygulama noktası olan vektörel bir büyüklüktür. Bir cismin üzerine uygulanan
3. KUVVET SİSTEMLERİ F F W P P 3.1 KUVVET KAVRAMI VE ETKİLERİ Kuvvet, bir cisme etki eden yapısal yüklerdir. Kuvvet Şiddeti, yönü ve uygulama noktası olan vektörel bir büyüklüktür. Bir cismin üzerine uygulanan
KİNETİK ENERJİ, İŞ-İŞ ve ENERJİ PRENSİBİ
 KİNETİK ENERJİ, İŞ-İŞ ve ENERJİ PRENSİBİ Amaçlar 1. Kuvvet ve kuvvet çiftlerinin yaptığı işlerin tanımlanması, 2. Rijit cisme iş ve enerji prensiplerinin uygulanması. UYGULAMALAR Beton mikserinin iki motoru
KİNETİK ENERJİ, İŞ-İŞ ve ENERJİ PRENSİBİ Amaçlar 1. Kuvvet ve kuvvet çiftlerinin yaptığı işlerin tanımlanması, 2. Rijit cisme iş ve enerji prensiplerinin uygulanması. UYGULAMALAR Beton mikserinin iki motoru
TEMEL MEKANİK 4. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 TEMEL MEKANİK 4 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
TEMEL MEKANİK 4 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
STATİK KUVVET ANALİZİ (2.HAFTA)
 STATİK KUVVET ANALİZİ (2.HAFTA) Mekanik sistemler üzerindeki kuvvetler denge halindeyse sistem hareket etmeyecektir. Sistemin denge hali için gerekli kuvvetlerin hesaplanması statik hesaplamalarla yapılır.
STATİK KUVVET ANALİZİ (2.HAFTA) Mekanik sistemler üzerindeki kuvvetler denge halindeyse sistem hareket etmeyecektir. Sistemin denge hali için gerekli kuvvetlerin hesaplanması statik hesaplamalarla yapılır.
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve leri DĞHN MÜHENDİSLİK MEKNİĞİ STTİK MÜHENDİSLİK MEKNİĞİ STTİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki Boyutlu Kuvvet
Statik Ders Notları Sınav Soru ve leri DĞHN MÜHENDİSLİK MEKNİĞİ STTİK MÜHENDİSLİK MEKNİĞİ STTİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki Boyutlu Kuvvet
TEMEL MEKANİK 9. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 TEMEL MEKANİK 9 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
TEMEL MEKANİK 9 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
STATIK VE MUKAVEMET 4. Ağırlık Merkezi. Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ
 STATIK VE MUKAVEMET 4. Ağırlık Merkezi Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ AĞIRLIK MERKEZİ Gerçekte yükler yayılı olup, tekil yük problemlerin çözümünü kolaylaştıran bir idealleştirmedir. Statikte çok küçük
STATIK VE MUKAVEMET 4. Ağırlık Merkezi Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ AĞIRLIK MERKEZİ Gerçekte yükler yayılı olup, tekil yük problemlerin çözümünü kolaylaştıran bir idealleştirmedir. Statikte çok küçük
BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM
 BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM 4.1. Giriş Bir önceki bölümde, hareket denklemi F = ma nın, maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini
BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM 4.1. Giriş Bir önceki bölümde, hareket denklemi F = ma nın, maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini
Gerçekte yükler yayılı olup, tekil yük problemlerin çözümünü kolaylaştıran bir idealleştirmedir.
 STATIK VE MUKAVEMET 4. Ağırlık Merkezi AĞIRLIK MERKEZİ Gerçekte yükler yayılı olup, tekil yük problemlerin çözümünü kolaylaştıran bir idealleştirmedir. Statikte çok küçük bir alana etki eden birbirlerine
STATIK VE MUKAVEMET 4. Ağırlık Merkezi AĞIRLIK MERKEZİ Gerçekte yükler yayılı olup, tekil yük problemlerin çözümünü kolaylaştıran bir idealleştirmedir. Statikte çok küçük bir alana etki eden birbirlerine
TEKNOLOJİNİN BİLİMSEL İLKELERİ. Öğr. Gör. Adem ÇALIŞKAN
 TEKNOLOJİNİN BİLİMSEL İLKELERİ 4 Skaler: Fiziki büyüklükler SKALER BÜYÜKLÜK SEMBOLÜ BİRİMİ Kütle m Kilogram Hacim V m 3 Zaman t Saniye Sıcaklık T Kelvin Sadece sayısal değer ve birim verilerek ifade edilen
TEKNOLOJİNİN BİLİMSEL İLKELERİ 4 Skaler: Fiziki büyüklükler SKALER BÜYÜKLÜK SEMBOLÜ BİRİMİ Kütle m Kilogram Hacim V m 3 Zaman t Saniye Sıcaklık T Kelvin Sadece sayısal değer ve birim verilerek ifade edilen
MÜHENDİSLİK MEKANİĞİ (STATİK)
 MÜHENDİSLİK MEKANİĞİ (STATİK) Prof. Dr. Metin OLGUN Ankara Üniversitesi Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü HAFTA KONU 1 Giriş, temel kavramlar, statiğin temel ilkeleri 2-3 Düzlem kuvvetler
MÜHENDİSLİK MEKANİĞİ (STATİK) Prof. Dr. Metin OLGUN Ankara Üniversitesi Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü HAFTA KONU 1 Giriş, temel kavramlar, statiğin temel ilkeleri 2-3 Düzlem kuvvetler
MAK 308 MAKİNA DİNAMİĞİ Bahar Dr. Nurdan Bilgin
 MAK 308 MAKİNA DİNAMİĞİ 2017-2018 Bahar Dr. Nurdan Bilgin MAKİNALARDA KUVVET ANALİZİ Mekanizmalar, sadece kinematik özellikleri karşılamak üzere tasarlandıklarında, bir makinenin parçası olarak kullanıldığında
MAK 308 MAKİNA DİNAMİĞİ 2017-2018 Bahar Dr. Nurdan Bilgin MAKİNALARDA KUVVET ANALİZİ Mekanizmalar, sadece kinematik özellikleri karşılamak üzere tasarlandıklarında, bir makinenin parçası olarak kullanıldığında
KUVVETLER VEKTÖRDÜR BU YÜZDEN CEBİRSEL VEKTÖR TEKNİKLERİ KULLANMALIYIZ
 Rijit Cisim Dengesi KUVVETLER VEKTÖRDÜR BU YÜZDEN CEBİRSEL VEKTÖR TEKNİKLERİ KULLANMALIYIZ KUVVET SİSTEMİ 2 B KUVVET SİSTEMLERİ Detaylar 1- KO-LİNEER 2- BİR NOKTADA BULUŞAN (KONKÜRENT) 3- PARALEL 4- GENEL
Rijit Cisim Dengesi KUVVETLER VEKTÖRDÜR BU YÜZDEN CEBİRSEL VEKTÖR TEKNİKLERİ KULLANMALIYIZ KUVVET SİSTEMİ 2 B KUVVET SİSTEMLERİ Detaylar 1- KO-LİNEER 2- BİR NOKTADA BULUŞAN (KONKÜRENT) 3- PARALEL 4- GENEL
Dinamik. Fatih ALİBEYOĞLU -10-
 1 Dinamik Fatih ALİBEYOĞLU -10- Giriş & Hareketler 2 Rijit cismi oluşturan çeşitli parçacıkların zaman, konum, hız ve ivmeleri arasında olan ilişkiler incelenecektir. Rijit Cisimlerin hareketleri Ötelenme(Doğrusal,
1 Dinamik Fatih ALİBEYOĞLU -10- Giriş & Hareketler 2 Rijit cismi oluşturan çeşitli parçacıkların zaman, konum, hız ve ivmeleri arasında olan ilişkiler incelenecektir. Rijit Cisimlerin hareketleri Ötelenme(Doğrusal,
TEKNOLOJİNİN BİLİMSEL İLKELERİ. Öğr. Gör. Adem ÇALIŞKAN
 TEKNOLOJİNİN BİLİMSEL İLKELERİ 5 Ağırlık merkezi STATİK Bir cisim moleküllerden meydana gelir. Bu moleküllerin her birine yer çekimi kuvveti etki eder. Bu yer çekimi kuvvetlerinin cismi meydana getiren
TEKNOLOJİNİN BİLİMSEL İLKELERİ 5 Ağırlık merkezi STATİK Bir cisim moleküllerden meydana gelir. Bu moleküllerin her birine yer çekimi kuvveti etki eder. Bu yer çekimi kuvvetlerinin cismi meydana getiren
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 6 Yapısal Analiz Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 6. Yapısal Analiz Şekilde görüldüğü
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 6 Yapısal Analiz Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 6. Yapısal Analiz Şekilde görüldüğü
DİNAMİK - 7. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi. Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 DİNAMİK - 7 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü 7. HAFTA Kapsam: Parçacık Kinetiği, Kuvvet İvme Yöntemi Newton hareket
DİNAMİK - 7 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü 7. HAFTA Kapsam: Parçacık Kinetiği, Kuvvet İvme Yöntemi Newton hareket
KATI CİSMİN DÜZLEMSEL KİNETİĞİ (Kinetik Enerji)
 KATI CİSMİN DÜZLEMSEL KİNETİĞİ (Kinetik Enerji) Partikülün kinetiği bahsinde, hız ve yer değiştirme içeren problemlerin iş ve enerji prensibini kullanarak kolayca çözülebildiği söylenmişti. Ayrıca, kuvvet
KATI CİSMİN DÜZLEMSEL KİNETİĞİ (Kinetik Enerji) Partikülün kinetiği bahsinde, hız ve yer değiştirme içeren problemlerin iş ve enerji prensibini kullanarak kolayca çözülebildiği söylenmişti. Ayrıca, kuvvet
Elemanlardaki İç Kuvvetler
 Elemanlardaki İç Kuvvetler Bölüm Öğrenme Çıktıları Yapı elemanlarında oluşan iç kuvvetler. Eksenel kuvvet, Kesme kuvvet ve Eğilme Momenti Denklemleri ve Diyagramları. Bölüm Öğrenme Çıktıları Elemanlarda
Elemanlardaki İç Kuvvetler Bölüm Öğrenme Çıktıları Yapı elemanlarında oluşan iç kuvvetler. Eksenel kuvvet, Kesme kuvvet ve Eğilme Momenti Denklemleri ve Diyagramları. Bölüm Öğrenme Çıktıları Elemanlarda
STATIK MUKAVEMET. Doç. Dr. NURHAYAT DEĞİRMENCİ
 STATIK MUKAVEMET Doç. Dr. NURHAYAT DEĞİRMENCİ STATİK DENGE KOŞULLARI Yapı elemanlarının tasarımında bu elemanlarda oluşan iç kuvvetlerin dağılımının bilinmesi gerekir. Dış ve iç kuvvetlerin belirlenmesinde
STATIK MUKAVEMET Doç. Dr. NURHAYAT DEĞİRMENCİ STATİK DENGE KOŞULLARI Yapı elemanlarının tasarımında bu elemanlarda oluşan iç kuvvetlerin dağılımının bilinmesi gerekir. Dış ve iç kuvvetlerin belirlenmesinde
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve Çöümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki Boutlu
Statik Ders Notları Sınav Soru ve Çöümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki Boutlu
STATİK. Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -8-
 1 STATİK Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -8- Giriş 2 Denge denklemlerini, mafsala bağlı elemanlarda oluşan yapıları analiz etmek için kullanacağız. Bu analiz, dengede olan bir yapının
1 STATİK Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -8- Giriş 2 Denge denklemlerini, mafsala bağlı elemanlarda oluşan yapıları analiz etmek için kullanacağız. Bu analiz, dengede olan bir yapının
KATI CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 KATI CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ Bu bölümde, düzlemsel kinematik, veya bir rijit cismin düzlemsel hareketinin geometrisi incelenecektir. Bu inceleme, dişli, kam ve makinelerin yaptığı birçok işlemde
KATI CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ Bu bölümde, düzlemsel kinematik, veya bir rijit cismin düzlemsel hareketinin geometrisi incelenecektir. Bu inceleme, dişli, kam ve makinelerin yaptığı birçok işlemde
Bölüm 3 - Parçacık Dengesi. Spring 2002 Equilibrium of a Particle 1
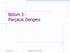 Bölüm 3 - Parçacık Dengesi Spring 2002 Equilibrium of a Particle 1 3 Boyutta denge 0 Burada parçacık üzerineetkiyen tüm kuvvetlerin toplamıdır. Spring 2002 Equilibrium of a Particle 2 Spring 2002 Equilibrium
Bölüm 3 - Parçacık Dengesi Spring 2002 Equilibrium of a Particle 1 3 Boyutta denge 0 Burada parçacık üzerineetkiyen tüm kuvvetlerin toplamıdır. Spring 2002 Equilibrium of a Particle 2 Spring 2002 Equilibrium
İÇ KUVVETLER. Amaçlar: Bir elemanda kesit yöntemiyle iç kuvvetlerin bulunması Kesme kuvveti ve moment diyagramlarının çizilmesi
 İÇ KUVVETLER maçlar: ir elemanda kesit yöntemiyle iç kuvvetlerin bulunması Kesme kuvveti ve moment diyagramlarının çizilmesi Yapısal elemanlarda oluşan iç kuvvetler ir yapısal veya mekanik elemanın tasarımı,
İÇ KUVVETLER maçlar: ir elemanda kesit yöntemiyle iç kuvvetlerin bulunması Kesme kuvveti ve moment diyagramlarının çizilmesi Yapısal elemanlarda oluşan iç kuvvetler ir yapısal veya mekanik elemanın tasarımı,
MEKANİZMA TEKNİĞİ (3. HAFTA)
 MEKANİZMA TEKNİĞİ (3. HAFTA) STATİĞİN TEMEL İLKELERİ VE VEKTÖR MATEMATİĞİ Mekanik sistemler üzerindeki kuvvetler denge halindeyse sistem hareket etmeyecektir. Sistemin denge hali için gerekli kuvvetlerin
MEKANİZMA TEKNİĞİ (3. HAFTA) STATİĞİN TEMEL İLKELERİ VE VEKTÖR MATEMATİĞİ Mekanik sistemler üzerindeki kuvvetler denge halindeyse sistem hareket etmeyecektir. Sistemin denge hali için gerekli kuvvetlerin
DİNAMİK. Ders_10. Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü. Ders notları için: GÜZ
 DİNAMİK Ders_10 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2016-2017 GÜZ KÜTLE ATALET MOMENTİ Bugünün Hedefleri: 1. Rijit bir cismin
DİNAMİK Ders_10 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2016-2017 GÜZ KÜTLE ATALET MOMENTİ Bugünün Hedefleri: 1. Rijit bir cismin
MUKAVEMET Öğr. Gör. Fatih KURTULUŞ
 www.sakarya.edu.tr MUKAVEMET Öğr. Gör. Fatih KURTULUŞ www.sakarya.edu.tr 1. DÜŞEY YÜKLÜ KİRİŞLER Cisimlerin mukavemeti konusunun esas problemi, herhangi bir yapıya uygulanan bir kuvvetin oluşturacağı gerilme
www.sakarya.edu.tr MUKAVEMET Öğr. Gör. Fatih KURTULUŞ www.sakarya.edu.tr 1. DÜŞEY YÜKLÜ KİRİŞLER Cisimlerin mukavemeti konusunun esas problemi, herhangi bir yapıya uygulanan bir kuvvetin oluşturacağı gerilme
KATI CİSİMLERİN BAĞIL İVME ANALİZİ:
 KATI CİSİMLERİN BAĞIL İVME ANALİZİ: Genel düzlemsel hareket yapmakta olan katı cisim üzerinde bulunan iki noktanın ivmeleri aralarındaki ilişki, bağıl hız v A = v B + v B A ifadesinin zamana göre türevi
KATI CİSİMLERİN BAĞIL İVME ANALİZİ: Genel düzlemsel hareket yapmakta olan katı cisim üzerinde bulunan iki noktanın ivmeleri aralarındaki ilişki, bağıl hız v A = v B + v B A ifadesinin zamana göre türevi
İÇ KUVVETLER. Amaçlar: Bir elemanda kesit yöntemiyle iç kuvvetlerin bulunması Kesme kuvveti ve moment diyagramlarının çizilmesi
 İÇ KUVVELER maçlar: ir elemanda kesit yöntemiyle iç kuvvetlerin bulunması Kesme kuvveti ve moment diyagramlarının çizilmesi Yapısal elemanlarda oluşan iç kuvvetler ir yapısal veya mekanik elemanın tasarımı,
İÇ KUVVELER maçlar: ir elemanda kesit yöntemiyle iç kuvvetlerin bulunması Kesme kuvveti ve moment diyagramlarının çizilmesi Yapısal elemanlarda oluşan iç kuvvetler ir yapısal veya mekanik elemanın tasarımı,
STATİĞİN TEMEL PRENSİPLERİ
 1.1. Temel Kavramlar ve Tanımlar Mühendislik mekaniği: Kuvvet etkisi altındaki cisimlerin denge veya hareket koşullarını inceleyen bilim dalı Genel olarak mühendislik mekaniği Sert (rijit) katı cisimlerin
1.1. Temel Kavramlar ve Tanımlar Mühendislik mekaniği: Kuvvet etkisi altındaki cisimlerin denge veya hareket koşullarını inceleyen bilim dalı Genel olarak mühendislik mekaniği Sert (rijit) katı cisimlerin
Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü
 Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü 1 kışkan Statiğine Giriş kışkan statiği (hidrostatik, aerostatik), durgun haldeki akışkanlarla
Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü 1 kışkan Statiğine Giriş kışkan statiği (hidrostatik, aerostatik), durgun haldeki akışkanlarla
OREN3002 STATİK VE MUKAVEMET
 Karadeniz Teknik Üniversitesi Orman Endüstri Mühendisliği Bölümü OREN3002 STATİK VE MUKAVEMET Yrd.Doç.Dr. Kemal ÜÇÜNCÜ Trabzon - 2017 1 1. Bölüm STATİK ders notları 2 1. TEMEL KAVRAMLAR 3 1.1. Mekanik
Karadeniz Teknik Üniversitesi Orman Endüstri Mühendisliği Bölümü OREN3002 STATİK VE MUKAVEMET Yrd.Doç.Dr. Kemal ÜÇÜNCÜ Trabzon - 2017 1 1. Bölüm STATİK ders notları 2 1. TEMEL KAVRAMLAR 3 1.1. Mekanik
DÜZLEMDE GERİLME DÖNÜŞÜMLERİ
 3 DÜZLEMDE GERİLME DÖNÜŞÜMLERİ Gerilme Kavramı Dış kuvvetlerin etkisi altında dengedeki elastik bir cismi matematiksel bir yüzeyle rasgele bir noktadan hayali bir yüzeyle ikiye ayıracak olursak, F 3 F
3 DÜZLEMDE GERİLME DÖNÜŞÜMLERİ Gerilme Kavramı Dış kuvvetlerin etkisi altında dengedeki elastik bir cismi matematiksel bir yüzeyle rasgele bir noktadan hayali bir yüzeyle ikiye ayıracak olursak, F 3 F
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ
 İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
Mekanik, Statik Denge
 Mekanik, Statik Denge Mardin Artuklu Üniversitesi 2. Hafta-01.03.2012 İdris Bedirhanoğlu url : www.dicle.edu.tr/a/idrisb e-mail : idrisbed@gmail.com 0532 657 14 31 Statik **Statik; uzayda kuvvetler etkisi
Mekanik, Statik Denge Mardin Artuklu Üniversitesi 2. Hafta-01.03.2012 İdris Bedirhanoğlu url : www.dicle.edu.tr/a/idrisb e-mail : idrisbed@gmail.com 0532 657 14 31 Statik **Statik; uzayda kuvvetler etkisi
BELĐRLĐ BĐR SIKMA KUVVETĐ ETKĐSĐNDE BĐSĐKLET FREN KOLU KUVVET ANALĐZĐNĐN YAPILMASI
 tasarım BELĐRLĐ BĐR SIKMA KUVVETĐ ETKĐSĐNDE BĐSĐKLET FREN KOLU KUVVET ANALĐZĐNĐN YAPILMASI Nihat GEMALMAYAN, Hüseyin ĐNCEÇAM Gazi Üniversitesi, Makina Mühendisliği Bölümü GĐRĐŞ Đlk bisikletlerde fren sistemi
tasarım BELĐRLĐ BĐR SIKMA KUVVETĐ ETKĐSĐNDE BĐSĐKLET FREN KOLU KUVVET ANALĐZĐNĐN YAPILMASI Nihat GEMALMAYAN, Hüseyin ĐNCEÇAM Gazi Üniversitesi, Makina Mühendisliği Bölümü GĐRĐŞ Đlk bisikletlerde fren sistemi
DİNAMİK Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi. Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 DİNAMİK - 11 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü 11. HAFTA Kapsam: İmpuls Momentum yöntemi İmpuls ve momentum ilkesi
DİNAMİK - 11 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü 11. HAFTA Kapsam: İmpuls Momentum yöntemi İmpuls ve momentum ilkesi
DİNAMİK. Ders_9. Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü. Ders notları için: GÜZ
 DİNAMİK Ders_9 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2018-2019 GÜZ RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ: ÖTELENME&DÖNME Bugünün
DİNAMİK Ders_9 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2018-2019 GÜZ RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ: ÖTELENME&DÖNME Bugünün
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve Çözümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLE 1. GİİŞ - Skalerler ve ektörler - Newton Kanunları 2. KUET SİSTEMLEİ - İki Boyutlu
Statik Ders Notları Sınav Soru ve Çözümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLE 1. GİİŞ - Skalerler ve ektörler - Newton Kanunları 2. KUET SİSTEMLEİ - İki Boyutlu
3.1 Vektör Tipleri 3.2 Vektörlerin Toplanması. 3.4 Poligon Kuralı 3.5 Bir Vektörün Skaler ile Çarpımı RİJİT CİSİMLER MEKANİĞİ
 1-STATİĞİN TEMEL İLKELERİ 1- BİRİMLER 2-TRİGONOMETRİ 3-VEKTÖRLER 3.1 Vektör Tipleri 3.2 Vektörlerin Toplanması 3.3 Vektörlerin uç-uca eklenerek toplanması 3.4 Poligon Kuralı 3.5 Bir Vektörün Skaler ile
1-STATİĞİN TEMEL İLKELERİ 1- BİRİMLER 2-TRİGONOMETRİ 3-VEKTÖRLER 3.1 Vektör Tipleri 3.2 Vektörlerin Toplanması 3.3 Vektörlerin uç-uca eklenerek toplanması 3.4 Poligon Kuralı 3.5 Bir Vektörün Skaler ile
TEMEL MEKANİK 6. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 TEMEL MEKANİK 6 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
TEMEL MEKANİK 6 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
TEMEL MEKANİK 5. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 TEMEL MEKANİK 5 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
TEMEL MEKANİK 5 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
Newton un ikinci yasası: Bir cisim ivmesi cisim üzerine etki eden toplam kuvvet ile doğru orantılı cismin kütlesi ile ters orantılıdır.
 Bölüm 5: Hareket Yasaları(Özet) Önceki bölümde hareketin temel kavramları olan yerdeğiştirme, hız ve ivme tanımlanmıştır. Bu bölümde ise hareketli cisimlerin farklı hareketlerine sebep olan etkilerin hareketi
Bölüm 5: Hareket Yasaları(Özet) Önceki bölümde hareketin temel kavramları olan yerdeğiştirme, hız ve ivme tanımlanmıştır. Bu bölümde ise hareketli cisimlerin farklı hareketlerine sebep olan etkilerin hareketi
MKM 308 Makina Dinamiği. Eşdeğer Noktasal Kütleler Teorisi
 MKM 308 Eşdeğer Noktasal Kütleler Teorisi Eşdeğer Noktasal Kütleler Teorisi Maddesel Nokta (Noktasal Kütleler) : Mekanikte her cisim zihnen maddesel noktalara ayrılabilir yani noktasal kütlelerden meydana
MKM 308 Eşdeğer Noktasal Kütleler Teorisi Eşdeğer Noktasal Kütleler Teorisi Maddesel Nokta (Noktasal Kütleler) : Mekanikte her cisim zihnen maddesel noktalara ayrılabilir yani noktasal kütlelerden meydana
Q27.1 Yüklü bir parçacık manyetik alanfda hareket ediyorsa, parçacığa etki eden manyetik kuvvetin yönü?
 Q27.1 Yüklü bir parçacık manyetik alanfda hareket ediyorsa, parçacığa etki eden manyetik kuvvetin yönü? A. Manyetik Alan doğrultusunda. B. Manyetik Alan doğrultusuna zıt. C. Manyetik Alan doğrultusuna
Q27.1 Yüklü bir parçacık manyetik alanfda hareket ediyorsa, parçacığa etki eden manyetik kuvvetin yönü? A. Manyetik Alan doğrultusunda. B. Manyetik Alan doğrultusuna zıt. C. Manyetik Alan doğrultusuna
DİNAMİK. Ders_10. Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü. Ders notları için: GÜZ
 DİNAMİK Ders_10 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2018-2019 GÜZ RÖLATİF DÖNME ANALİZİ:HIZ Bugünün Hedefleri: 1. Ötelenme
DİNAMİK Ders_10 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2018-2019 GÜZ RÖLATİF DÖNME ANALİZİ:HIZ Bugünün Hedefleri: 1. Ötelenme
BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER
 BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER Yrd. Doç. Dr. Beytullah EREN Çevre Mühendisliği Bölümü BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER Atatürk Barajı (Şanlıurfa) BATMIŞ YÜZEYLERE ETKİYEN KUVVETLER
BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER Yrd. Doç. Dr. Beytullah EREN Çevre Mühendisliği Bölümü BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER Atatürk Barajı (Şanlıurfa) BATMIŞ YÜZEYLERE ETKİYEN KUVVETLER
PROF.DR. MURAT DEMİR AYDIN. ***Bu ders notları bir sonraki slaytta verilen kaynak kitaplardan alıntılar yapılarak hazırlanmıştır.
 PO.D. MUAT DEMİ AYDIN ***Bu ders notları bir sonraki slatta verilen kanak kitaplardan alıntılar apılarak hazırlanmıştır. Mühendisler için Vektör Mekaniği: STATİK.P. Beer, E.. Johnston Çeviri Editörü: Ömer
PO.D. MUAT DEMİ AYDIN ***Bu ders notları bir sonraki slatta verilen kanak kitaplardan alıntılar apılarak hazırlanmıştır. Mühendisler için Vektör Mekaniği: STATİK.P. Beer, E.. Johnston Çeviri Editörü: Ömer
ELASTİSİTE TEORİSİ I. Yrd. Doç Dr. Eray Arslan
 ELASTİSİTE TEORİSİ I Yrd. Doç Dr. Eray Arslan Mühendislik Tasarımı Genel Senaryo Analitik çözüm Fiziksel Problem Matematiksel model Diferansiyel Denklem Problem ile ilgili sorular:... Deformasyon ne kadar
ELASTİSİTE TEORİSİ I Yrd. Doç Dr. Eray Arslan Mühendislik Tasarımı Genel Senaryo Analitik çözüm Fiziksel Problem Matematiksel model Diferansiyel Denklem Problem ile ilgili sorular:... Deformasyon ne kadar
VEKTÖRLER KT YRD.DOÇ.DR. KAMİLE TOSUN FELEKOĞLU
 VEKTÖRLER KT YRD.DOÇ.DR. KMİLE TOSUN ELEKOĞLU 1 Mekanik olaları ölçmekte a da değerlendirmekte kullanılan matematiksel büüklükler: Skaler büüklük: sadece bir saısal değeri tanımlamakta kullanılır, pozitif
VEKTÖRLER KT YRD.DOÇ.DR. KMİLE TOSUN ELEKOĞLU 1 Mekanik olaları ölçmekte a da değerlendirmekte kullanılan matematiksel büüklükler: Skaler büüklük: sadece bir saısal değeri tanımlamakta kullanılır, pozitif
Gerilme. Bölüm Hedefleri. Normal ve Kayma gerilmesi kavramının anlaşılması Kesme ve eksenel yük etkisindeki elemanların analiz ve tasarımı
 Gerilme Bölüm Hedefleri Normal ve Kayma gerilmesi kavramının anlaşılması Kesme ve eksenel yük etkisindeki elemanların analiz ve tasarımı Copyright 2011 Pearson Education South sia Pte Ltd GERİLME Kesim
Gerilme Bölüm Hedefleri Normal ve Kayma gerilmesi kavramının anlaşılması Kesme ve eksenel yük etkisindeki elemanların analiz ve tasarımı Copyright 2011 Pearson Education South sia Pte Ltd GERİLME Kesim
Kesit Tesirleri Tekil Kuvvetler
 Statik ve Mukavemet Kesit Tesirleri Tekil Kuvvetler B ÖĞR.GÖR.GÜLTEKİN BÜYÜKŞENGÜR Çevre Mühendisliği Mukavemet Şekil Değiştirebilen Cisimler Mekaniği Kesit Tesiri ve İşaret Kabulleri Kesit Tesiri Diyagramları
Statik ve Mukavemet Kesit Tesirleri Tekil Kuvvetler B ÖĞR.GÖR.GÜLTEKİN BÜYÜKŞENGÜR Çevre Mühendisliği Mukavemet Şekil Değiştirebilen Cisimler Mekaniği Kesit Tesiri ve İşaret Kabulleri Kesit Tesiri Diyagramları
Mühendislik Mekaniği Dinamik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 16 Rijit Cismin Düzlemsel Kinematiği Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 16 Rijit
Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 16 Rijit Cismin Düzlemsel Kinematiği Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 16 Rijit
Fizik 101-Fizik I Hareket Kanunları. Nurdan Demirci Sankır Ofis: 325, Tel:4331 Enerji Araştırmalrı Laboratuarı (YDB- Bodrum Kat) İçerik
 Fizik 101-Fizik I 2013-2014 Hareket Kanunları Nurdan Demirci Sankır Ofis: 325, Tel:4331 Enerji Araştırmalrı Laboratuarı (YDB- Bodrum Kat) İçerik Kuvvet Kavramı Newton nun Birinci Yasası ve Eylemsizlik
Fizik 101-Fizik I 2013-2014 Hareket Kanunları Nurdan Demirci Sankır Ofis: 325, Tel:4331 Enerji Araştırmalrı Laboratuarı (YDB- Bodrum Kat) İçerik Kuvvet Kavramı Newton nun Birinci Yasası ve Eylemsizlik
TORK VE DENGE 01 Torkun Tanımı ve Yönü
 TORK VE DENGE 01 Torkun Tanımı ve Yönü Kuvvetin döndürme etkisine tork ya da moment denir. Bir kuvvetin bir noktaya göre torku; kuvvet ile dönme noktasının kuvvete dik uzaklığının çarpımına eşittir. Moment
TORK VE DENGE 01 Torkun Tanımı ve Yönü Kuvvetin döndürme etkisine tork ya da moment denir. Bir kuvvetin bir noktaya göre torku; kuvvet ile dönme noktasının kuvvete dik uzaklığının çarpımına eşittir. Moment
YAPISAL ANALİZ DOÇ.DR. KAMİLE TOSUN FELEKOĞLU
 YAPISAL ANALİZ DOÇ.DR. KAMİLE TOSUN FELEKOĞLU 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla
YAPISAL ANALİZ DOÇ.DR. KAMİLE TOSUN FELEKOĞLU 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla
δ / = P L A E = [+35 kn](0.75 m)(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir.
(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir. δ / = P L A E = [+35 kn](0.75 m)(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir.](/thumbs/68/59308868.jpg) A-36 malzemeden çelik çubuk, şekil a gösterildiği iki kademeli olarak üretilmiştir. AB ve BC kesitleri sırasıyla A = 600 mm ve A = 1200 mm dir. A serbest ucunun ve B nin C ye göre yer değiştirmesini belirleyiniz.
A-36 malzemeden çelik çubuk, şekil a gösterildiği iki kademeli olarak üretilmiştir. AB ve BC kesitleri sırasıyla A = 600 mm ve A = 1200 mm dir. A serbest ucunun ve B nin C ye göre yer değiştirmesini belirleyiniz.
Bölüm 3: Vektörler. Kavrama Soruları. Konu İçeriği. Sunuş. 3-1 Koordinat Sistemleri
 ölüm 3: Vektörler Kavrama Soruları 1- Neden vektörlere ihtiyaç duyarız? - Vektör ve skaler arasındaki fark nedir? 3- Neden vektörel bölme işlemi yapılamaz? 4- π sayısı vektörel mi yoksa skaler bir nicelik
ölüm 3: Vektörler Kavrama Soruları 1- Neden vektörlere ihtiyaç duyarız? - Vektör ve skaler arasındaki fark nedir? 3- Neden vektörel bölme işlemi yapılamaz? 4- π sayısı vektörel mi yoksa skaler bir nicelik
MEKANİK NEDİR? Bu Ders Gerçek Hayatta Ne İşe Yarayacak?
 MEKANİK NEDİR? Mekaniğin bir dalı olan statiği daha iyi anlayabilmek için öncelikle mekaniği ve ona bağlı konuları hızlı bir şekilde gözden geçirmekte yarar vardır. Mekanik; kuvvetlerin etkisi altında
MEKANİK NEDİR? Mekaniğin bir dalı olan statiği daha iyi anlayabilmek için öncelikle mekaniği ve ona bağlı konuları hızlı bir şekilde gözden geçirmekte yarar vardır. Mekanik; kuvvetlerin etkisi altında
VECTOR MECHANICS FOR ENGINEERS: STATICS
 Seventh Edition VECTOR ECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi Tel: 85 31 46 / 116 E-mail: acarh@itu.edu.tr Web: http://atlas.cc.itu.edu.tr/~acarh
Seventh Edition VECTOR ECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi Tel: 85 31 46 / 116 E-mail: acarh@itu.edu.tr Web: http://atlas.cc.itu.edu.tr/~acarh
Gerilme Dönüşümleri (Stress Transformation)
 Gerilme Dönüşümleri (Stress Transformation) Bubölümdebirnoktayaetkiyen vebelli bir koordinat ekseni/düzlemi ile ilişkili gerilme bileşenlerini, başka bir koordinat sistemi/başka bir düzlem ile ilişkili
Gerilme Dönüşümleri (Stress Transformation) Bubölümdebirnoktayaetkiyen vebelli bir koordinat ekseni/düzlemi ile ilişkili gerilme bileşenlerini, başka bir koordinat sistemi/başka bir düzlem ile ilişkili
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
 9.1 9.2 9.3 9.4 9.5 9.6 Uzayda Serbestlik Derecesi Rijit Cismin Uzayda Dengesi Bir Uzay Kuvvetin Bileşenleri Bir Noktada Kesişen Uzay Kuvvetlerde Bileşke Bir Eksene Göre Statik Moment Kuvvetler Sistemini
9.1 9.2 9.3 9.4 9.5 9.6 Uzayda Serbestlik Derecesi Rijit Cismin Uzayda Dengesi Bir Uzay Kuvvetin Bileşenleri Bir Noktada Kesişen Uzay Kuvvetlerde Bileşke Bir Eksene Göre Statik Moment Kuvvetler Sistemini
1. STATİĞE GİRİŞ 1.1 TANIMLAR MEKANİK RİJİT CİSİMLER MEKANİĞİ ŞEKİL DEĞİŞTİREN CİSİMLER AKIŞKANLAR MEKANİĞİ DİNAMİK STATİK
 STATİK Ders Notları Kaynaklar: 1.Engineering Mechanics: Statics, 9e, Hibbeler, Prentice Hall 2.Engineering Mechanics: Statics, SI Version, 6th Edition, J. L. Meriam, L. G. Kraige 1. STATİĞE GİRİŞ 1.1 TANIMLAR
STATİK Ders Notları Kaynaklar: 1.Engineering Mechanics: Statics, 9e, Hibbeler, Prentice Hall 2.Engineering Mechanics: Statics, SI Version, 6th Edition, J. L. Meriam, L. G. Kraige 1. STATİĞE GİRİŞ 1.1 TANIMLAR
Newton un II. yasası. Bir cismin ivmesi, onun üzerine etki eden bileşke kuvvetle doğru orantılı ve kütlesi ile ters orantılıdır.
 Newton un II. yasası Bir cismin ivmesi, onun üzerine etki eden bileşke kuvvetle doğru orantılı ve kütlesi ile ters orantılıdır. Bir cisme F A, F B ve F C gibi çok sayıda kuvvet etkiyorsa, net kuvvet bunların
Newton un II. yasası Bir cismin ivmesi, onun üzerine etki eden bileşke kuvvetle doğru orantılı ve kütlesi ile ters orantılıdır. Bir cisme F A, F B ve F C gibi çok sayıda kuvvet etkiyorsa, net kuvvet bunların
GERİLME Cismin kesilmiş alanı üzerinde O
 GERİLME Cismin kesilmiş alanı üzerinde O ile tanımlı noktasına etki eden kuvvet ve momentin kesit alana etki eden gerçek yayılı yüklerin bileşke etkisini temsil ettiği ifade edilmişti. Cisimlerin mukavemeti
GERİLME Cismin kesilmiş alanı üzerinde O ile tanımlı noktasına etki eden kuvvet ve momentin kesit alana etki eden gerçek yayılı yüklerin bileşke etkisini temsil ettiği ifade edilmişti. Cisimlerin mukavemeti
MÜHENDİSLİK MEKANİĞİ (STATİK)
 MÜHENDİSLİK MEKANİĞİ (STATİK) Prof. Dr. Metin OLGUN Ankara Üniversitesi Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü HAFTA KONU 1 Giriş, temel kavramlar, statiğin temel ilkeleri 2-3 Düzlem kuvvetler
MÜHENDİSLİK MEKANİĞİ (STATİK) Prof. Dr. Metin OLGUN Ankara Üniversitesi Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü HAFTA KONU 1 Giriş, temel kavramlar, statiğin temel ilkeleri 2-3 Düzlem kuvvetler
Kirişlerde Kesme (Transverse Shear)
 Kirişlerde Kesme (Transverse Shear) Bu bölümde, doğrusal, prizmatik, homojen ve lineer elastik davranan bir elemanın eksenine dik doğrultuda yüklerin etkimesi durumunda en kesitinde oluşan kesme gerilmeleri
Kirişlerde Kesme (Transverse Shear) Bu bölümde, doğrusal, prizmatik, homojen ve lineer elastik davranan bir elemanın eksenine dik doğrultuda yüklerin etkimesi durumunda en kesitinde oluşan kesme gerilmeleri
Fizik 101-Fizik I 2013-2014. Dönme Hareketinin Dinamiği
 -Fizik I 2013-2014 Dönme Hareketinin Dinamiği Nurdan Demirci Sankır Ofis: 364, Tel: 2924332 İçerik Vektörel Çarpım ve Tork Katı Cismin Yuvarlanma Hareketi Bir Parçacığın Açısal Momentumu Dönen Katı Cismin
-Fizik I 2013-2014 Dönme Hareketinin Dinamiği Nurdan Demirci Sankır Ofis: 364, Tel: 2924332 İçerik Vektörel Çarpım ve Tork Katı Cismin Yuvarlanma Hareketi Bir Parçacığın Açısal Momentumu Dönen Katı Cismin
