BÖLÜM 4 YAPISAL ANALİZ (KAFESLER-ÇERÇEVELER-MAKİNALAR)
|
|
|
- Derya Yildiz Çatlı
- 8 yıl önce
- İzleme sayısı:
Transkript
1 BÖLÜM 4 YAPISAL ANALİZ (KAESLER-ÇERÇEVELER-MAKİNALAR) 4.1 Kafesler: Basit Kafes: İnce çubukların uçlarından birleştirilerek luşturulan apıdır. Bileştirme genelde 1. Barak levhalarına pimler ve kanak vasıtası ile, 2. Büük çaplı birleştirme parçalarına tutturarak gerçekleşir. Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
2 Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
3 4.1.1 Düzlem Kafesler: Kafesin tüm elemanları anı düzlem içindedir. Kabuller: 1. Tüm ükler bağlantı nkatalarından etkitilir. 2. Bağlantılar sürtünmesiz pimlerle apılmışlardır. 3. Tüm elemanlar çift kuvvet elemanıdır. 4. Elemanlar sadece çeki vea basıa zrlanırlar. Kafesler arıca rijit larak kabul edilir. Yani ükleme altında ve destek nktalarından arıldıklarında şeklillerinin değişmediği kabul edilir. En basit kafes apısı: Kafes apısının luşturulması: ABC kafes apısına B ve C birleşim nktalarından BD ve DC çubukları eklendiğinde kafes sistemi genişletilmiş lunacaktır. Yeni sistem ine rijittir. Çubuk ekleme işine devam edilerek basit kafes apısı genişetilebilir. Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
4 Hesap: m = ( j - 3 ) m=çubuk saısı j=bağlantı nktası saısı r=reaksin kuvveti saısı İzstatiklik şartı: m< 2j r m= 2j r m> 2j r Stabil değil Statikle çözülebilir Statik larak tanımsız Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
5 Kafeslerin Analizi 1. Dış denge Reaksin kuvvetleri bulunur. 2. İç denge Herbir çubuktaki kuvvetler bulunur. -Düğüm Yöntemi -Kesme Yöntemi Düğüm Yöntemi Düğüm dengesi göz önüne alınır. Düğümün SCD ı çizilir Kiriş elemanları çift kuvvet elemanlarıdır. Düğümün SCD ı eş nktasal kuvvetlerdir. İki denge denklemi mevcuttur.( ) Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
6 Örnek Prblem 4.1. Her bir çubuktaki kuvvetleri bulunuz. ÇÖZÜM: A ( ) ( ) 500 A C A A = 500 N A = C M C 2 A = C = 500 N BC BC BA sin 45 BC BC = N ( ) = N C cs 45 ( ) = 500 N T BA cs 45 CA ( ) = 500 N T C C CA 707.1sin 45 = 500 N A A = 500 N A A = 500 N Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
7 Yüksüz çubuklar (sıfır kuvvet elemanları) Kafes apılarında bazı çubuklar ük taşımazlar. Bu üksüz çubukların bulunma kuralları: 1. İki eleman birbirine bağlı ise ve bu bağlantı nktası ükün ugulandığı nkta vea mesnet nktası değilse, bu iki eleman ük taşımır demektir. 2. İkisi rtak çizgide lacak şekilde üç çubuğun bağlandığı düğüme dışarıdan ükleme k ise rtak çizgide lmaan çubuk üksüzdür. Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
8 Örnek Prblem 4.2 Yandaki çatı kafesteki bş çubukları bulalım. Düğüm öntemi ile çözümlemede bazen bazı çubukların çekie mi ksa basıa mı çalıştığı ilk anda belirlenemeebilir. Bu üzden düğüm öntemini ugulamada genel bir prsedürün rtaa knulması önem arz etmektedir. Düğüm öntemi aşağıdaki sırada ugulanmalıdır. 1. Tüm kafesin Serbest Cisim Diagramı çizilir ve mesnet tepkileri bulunur. 2. En az bir, en fazla iki bilinmeecek lacak şekilde düğümlerin Serbest Cisim Diagramları çizilir. 3. Düğümlerin SCD nda bilinen kuvvetler kendi önlerinde, bilinmeen tüm kuvvetler düğümden dışarı lacak şekilde (çeki) erleştirilir. Bilinmeen kuvvette snuç pzitifse çubuk çekidir ve negatifse çubuk basıdır madde ugulanmaacaksa gözlem snucu bilinmeen kuvvetin önü belirtilir. Bilinmeen kuvvette snuç pzitifse alınan ön dğrudur ve negatifse alınan ön terstir. Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
9 Örnek Prblem 4.3. Yandaki kafeste her bir çubuktaki kuvvetlerin şiddetini ve çubukların basıa vea çekie zrlandıklarını bulunuz. ÇÖZÜM: 4 1 AD + AB 17 2 P AD + AB ( ) ( ).687 P T AD.943 P C AB Simetriden : ( ) ( ).943 P T CD.943 P C CB A A A + C P= 0 M Pa+ C (2a) C P P = A = DB ( P) ( P) = 1.33 P T DB ( ) Çubuklardaki kuvvetlerin önleri CD (T) AD (T) CB (C) AB (C) DB (T) Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
10 Kesme Yöntemi Eğer bir apı dengede ise içerisinden çıkarılan bir parçası da dengededir. Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
11 Örnek Prblem 4.4 GE, GC ve BC çubuklarındaki kuvvetleri bulunuz. ÇÖZÜM: 400 A A = 400 N A A + D 1200 M 1200(8) 400(3) + D (12) D A = 900 N = 300 N BC M G 300(4) 400(3) + (3) = 800 N (T) BC GE GE M C 300(8) (3) GE = 800 N = 800 N (C) GC GC = 0 5 = 500 N (T) CEVAP: Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
12 Örnek Prblem 4.5 C çubuğundaki kuvvetleri bulunuz. ÇÖZÜM: Menet tepkileri: O ( ) ( )( ) ( )( ) ( ) C sin 45 12m 3kN 8 m 4.75kN 4m 0 C M + =.589kN C Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
13 Örnek Prblem 4.6 EB çubuğundaki kuvveti bulunuz. ÇÖZÜM: Bu prblemi tek kesme ile apamaız. Şekilde gösterildiği gibi iki kesme apılması gerekir. ED ED M ED B 1000(4) (2) 4000(4) sin 30 (4) = 3000 N = 3000 N (C) E E EB E E cs cs 30 = 3000 N = 3000 N (C) sin sin = 2000 N (T) EB Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
14 Kafes Çeşitleri -Çatı Kafesler: -Köprü Kafesler: Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
15 Örnek Prblem 4.7. DE, EH ve HG çubuklarındaki kuvvetleri bulunuz. M A A 20(4) 20(8) 40(12) + G (16) A G = 45 kn A + G A = 65 kn H 45(4) + (4) DE = 45 kn = 45 kn ( C) DE = 5 kn ( T) EH DE EH 45 HG = 45 kn ( T) HG M Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
16 4.1.2 Uza Kafesler: Uza kafeste temel eleman tetrahedrndur. Tetrahedrnlarda 6 eleman ve 4 düğüm mevcuttur. Kafesi genişletebilmek için üç eleman ve bir düğüm eklemek gerekir. Düğüm öntemi ile çözüm apılabilir. z Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
17 Örnek Prblem 4.8: ÇÖZÜM: P= 4 j AB AC = AB = AC r 2i+ 2j 2k AE = = = 0.577i j 0.577k AE AE AE AE r AE AE j k ( ) AC AB = P+ + + z.577 AE AC AE = = = 4kN AB AC AE AB ( T ) AE AE = BE BD = R cs B BE = 4+ RBsin45 = z BD BE = R = 5.66kN B = 2kN Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
18 4.2. Çerçeveler ve Makinalar: Çk önlü kuvvetlerin geldiği elemanların luşturduğu apılardır. Hareketsiz lup ükü desteklemek için kullanılan apılara çerçeve denir. İçerisinde hareketli parçaların lduğu ükü aktarmak ve değiştirmek gibi görevleri lan apılara makine denir. Her iki apıda da çözüm rtaktır: 1. Sistem parçalara arılarak Serbest Cisim Diagramları çizilir. Bazen bunu aparken dış çizgi sınırları alınır. Tüm kuvvetler gösterilir. 2. Çift kuvvet elemanları belirlenir. 3. Temas halindeki elemanlara ait rtak kuvvetler eşit şiddetli ve zıt önlüdür. 4. Eğer iki vea daha fazla eleman sistem larak ele alınırsa, bunların arılmasına gerek ktur. Serbest cisim diagramlarında birleşim erlerindeki kuvvetler gösterilmez. Arılan nktalarda kuvvetlerin gösterilmesi gerekir. Yu kar ıda ki örn ekt e de görüldüğü gibi çerçevei B nktasından aırmaa gerek ktur. Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
19 Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
20 Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
21 Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
22 Örnek Prblem 4.9: Yandaki çerçeve elemanlarında mesnet tepkilerini i bulunuz. ÇÖZÜM: B 2000(2) + C (4) C AB AB C AB M = 1000 N sin 60 + C 2000 = N cs 60 C = N Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
23 Örnek Prblem 4.10: Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
24 Örnek SCD ları: Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
25 Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
26 Makinalara örnekler: Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
27 Örnek Prblem 4.11 CD M E CD CD ( ) 5(4) sin (1) = lb ( ) E cs E = lb A ( )( ) ( )( ) ( ) sin cs E 1.75 A A A M = 36.0 lb Ugulanan kuvvetin 7 katı etki mevcut!!!!! Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
28 Örnek Prblem E ve AD pistnlarına gelen kuvvetleri bulunuz. Kepçenin içinde 1500 kg ük mevcuttur. E pistnu gösterilen knumda HG elemanına diktir. H 1250(9.81)(0.5) + (1.5sin 30 ) E = 8175 N = 8.18 kn ( T) E M AD M C 1250(9.81)(2 cs ) (cs 40 )(0.25) = N = 158 kn (C) AD Bu sunumun hazırlanılmasında ararlanılan kanak: Hibbeler, Engineering Mechanics: Statics,9e, Prentice Hall
Kafes Sistemler. Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir.
 Kafes Sistemler Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir. Kafes Sistemler Birçok uygulama alanları vardır. Çatı sistemlerinde, Köprülerde, Kulelerde, Ve benzeri
Kafes Sistemler Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir. Kafes Sistemler Birçok uygulama alanları vardır. Çatı sistemlerinde, Köprülerde, Kulelerde, Ve benzeri
STATİK. Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -8-
 1 STATİK Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -8- Giriş 2 Denge denklemlerini, mafsala bağlı elemanlarda oluşan yapıları analiz etmek için kullanacağız. Bu analiz, dengede olan bir yapının
1 STATİK Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -8- Giriş 2 Denge denklemlerini, mafsala bağlı elemanlarda oluşan yapıları analiz etmek için kullanacağız. Bu analiz, dengede olan bir yapının
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik ers Notları Sınav Soru ve Çözümleri ĞHN MÜHENİSİK MEKNİĞİ STTİK MÜHENİSİK MEKNİĞİ STTİK İÇİNEKİER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMERİ - İki Boutlu Kuvvet Sistemleri
Statik ers Notları Sınav Soru ve Çözümleri ĞHN MÜHENİSİK MEKNİĞİ STTİK MÜHENİSİK MEKNİĞİ STTİK İÇİNEKİER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMERİ - İki Boutlu Kuvvet Sistemleri
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve leri DĞHN MÜHENDİSLİK MEKNİĞİ STTİK MÜHENDİSLİK MEKNİĞİ STTİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki Boyutlu Kuvvet
Statik Ders Notları Sınav Soru ve leri DĞHN MÜHENDİSLİK MEKNİĞİ STTİK MÜHENDİSLİK MEKNİĞİ STTİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki Boyutlu Kuvvet
Hedefler. Kafeslerde oluşan kuvvetlerin hesaplanması: düğüm noktaları metodu kesme metodu
 Yapıların Analizi Hedefler Kafeslerde oluşan kuvvetlerin hesaplanması: düğüm noktaları metodu kesme metodu Konu Çıktıları İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz
Yapıların Analizi Hedefler Kafeslerde oluşan kuvvetlerin hesaplanması: düğüm noktaları metodu kesme metodu Konu Çıktıları İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz
Çerçeveler ve Basit Makinalar
 Çerçeveler ve Basit Makinalar Çeşitli elemanların birbirlerine bağlanması ile oluşan sistemlerdir. Kafes sistemlerden farklı olarak, elemanlar birbirlerine 2 den fazla noktadan bağlanabilir ve dış kuvvetler
Çerçeveler ve Basit Makinalar Çeşitli elemanların birbirlerine bağlanması ile oluşan sistemlerdir. Kafes sistemlerden farklı olarak, elemanlar birbirlerine 2 den fazla noktadan bağlanabilir ve dış kuvvetler
6.12 Örnekler PROBLEMLER
 6.1 6. 6.3 6.4 6.5 6.6 6.7 Çok Parçalı Taşıyıcı Sistemler Kafes Sistemler Kafes Köprüler Kafes Çatılar Tam, Eksik ve Fazla Bağlı Kafes Sistemler Kafes Sistemler İçin Çözüm Yöntemleri Kafes Sistemlerde
6.1 6. 6.3 6.4 6.5 6.6 6.7 Çok Parçalı Taşıyıcı Sistemler Kafes Sistemler Kafes Köprüler Kafes Çatılar Tam, Eksik ve Fazla Bağlı Kafes Sistemler Kafes Sistemler İçin Çözüm Yöntemleri Kafes Sistemlerde
TEMEL MEKANİK 14. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 TEMEL MEKANİK 14 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
TEMEL MEKANİK 14 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
STATİK. Ders_6. Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü. Ders notları için: GÜZ
 STATİK Ders_6 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2017-2018 GÜZ BASİT KAFESLER, DÜĞÜM NOKTALARI METODU VE SIFIR KUVVET ELEMANLARI
STATİK Ders_6 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2017-2018 GÜZ BASİT KAFESLER, DÜĞÜM NOKTALARI METODU VE SIFIR KUVVET ELEMANLARI
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 5 Rijit Cisim Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 5. Rijit Cisim Dengesi Denge,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 5 Rijit Cisim Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 5. Rijit Cisim Dengesi Denge,
VECTOR MECHANICS FOR ENGINEERS: STATICS
 Seventh Edition VECTOR MECHANICS OR ENGINEERS: STATICS erdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi Tel: 285 31 46 / 116 E-mail: acarh@itu.edu.tr Web: http://atlas.cc.itu.edu.tr/~acarh
Seventh Edition VECTOR MECHANICS OR ENGINEERS: STATICS erdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi Tel: 285 31 46 / 116 E-mail: acarh@itu.edu.tr Web: http://atlas.cc.itu.edu.tr/~acarh
TEMEL MEKANİK 12. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 TEMEL MEKANİK 12 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
TEMEL MEKANİK 12 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
Ödev 1. Ödev1: 600N luk kuvveti u ve v eksenlerinde bileşenlerine ayırınız. 600 N
 Ödev 1 Ödev1: 600N luk kuvveti u ve v eksenlerinde bileşenlerine ayırınız. 600 N 1 600 N 600 N 600 N u sin120 600 N sin 30 u 1039N v sin 30 600 N sin 30 v 600N 2 Ödev 2 Ödev2: 2 kuvvetinin şiddetini, yönünü
Ödev 1 Ödev1: 600N luk kuvveti u ve v eksenlerinde bileşenlerine ayırınız. 600 N 1 600 N 600 N 600 N u sin120 600 N sin 30 u 1039N v sin 30 600 N sin 30 v 600N 2 Ödev 2 Ödev2: 2 kuvvetinin şiddetini, yönünü
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve Çöümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki Boutlu
Statik Ders Notları Sınav Soru ve Çöümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki Boutlu
KONU 3. STATİK DENGE
 KONU 3. STATİK DENGE 3.1 Giriş Bir cisme etki eden dış kuvvet ve momentlerin toplamı 0 ise cisim statik dengededir denir. Kuvvet ve moment toplamlarının 0 olması sırasıyla; ötelenme ve dönme denge şartlarıdır.
KONU 3. STATİK DENGE 3.1 Giriş Bir cisme etki eden dış kuvvet ve momentlerin toplamı 0 ise cisim statik dengededir denir. Kuvvet ve moment toplamlarının 0 olması sırasıyla; ötelenme ve dönme denge şartlarıdır.
7. STABİLİTE HESAPLARI
 7. STABİLİTE HESAPLARI Çatı sistemlerinde; Kafes kirişlerin (makasların) montaj aşamasında ve kafes düzlemine dik rüzgar ve deprem etkileri altında, mesnetlerini birleştiren eksen etrafında dönerek devrilmelerini
7. STABİLİTE HESAPLARI Çatı sistemlerinde; Kafes kirişlerin (makasların) montaj aşamasında ve kafes düzlemine dik rüzgar ve deprem etkileri altında, mesnetlerini birleştiren eksen etrafında dönerek devrilmelerini
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 5 Rijit Cisim Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 5. Rijit Cisim Dengesi Denge,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 5 Rijit Cisim Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 5. Rijit Cisim Dengesi Denge,
YAPISAL ANALİZ DOÇ.DR. KAMİLE TOSUN FELEKOĞLU
 YAPISAL ANALİZ DOÇ.DR. KAMİLE TOSUN FELEKOĞLU 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla
YAPISAL ANALİZ DOÇ.DR. KAMİLE TOSUN FELEKOĞLU 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla
İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz Sıfır-Kuvvet Elemanları Kesme Metodu ile Analiz
 Yapıların Analizi Konu Çıktıları İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz Sıfır-Kuvvet Elemanları Kesme Metodu ile Analiz Kafesleri oluşturan elemenlara etki eden
Yapıların Analizi Konu Çıktıları İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz Sıfır-Kuvvet Elemanları Kesme Metodu ile Analiz Kafesleri oluşturan elemenlara etki eden
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 6 Yapısal Analiz Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 6. Yapısal Analiz Şekilde görüldüğü
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 6 Yapısal Analiz Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 6. Yapısal Analiz Şekilde görüldüğü
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve Çözümleri DĞHN MÜHENDİSLİK MEKNİĞİ STTİK MÜHENDİSLİK MEKNİĞİ STTİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki outlu Kuvvet
Statik Ders Notları Sınav Soru ve Çözümleri DĞHN MÜHENDİSLİK MEKNİĞİ STTİK MÜHENDİSLİK MEKNİĞİ STTİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki outlu Kuvvet
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 7 İç Kuvvetler Kaynak: Mühendislik Mekaniği: Statik, R. C. Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 7. İç Kuvvetler Bu bölümde, bir
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 7 İç Kuvvetler Kaynak: Mühendislik Mekaniği: Statik, R. C. Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 7. İç Kuvvetler Bu bölümde, bir
Çerçeve ve Makineler
 Çerçeve ve Makineler Hedefler Mafsal (pim) ile tutturulmuş çerçeve ve makine elemanlarına etki eden kuvvetlerin analizi. Çerçeve ve Makineler Çok kuvvet elemanı içeren mafsal ile tutturulmuş yapılardır.
Çerçeve ve Makineler Hedefler Mafsal (pim) ile tutturulmuş çerçeve ve makine elemanlarına etki eden kuvvetlerin analizi. Çerçeve ve Makineler Çok kuvvet elemanı içeren mafsal ile tutturulmuş yapılardır.
Karabük Üniversitesi, Mühendislik Fakültesi...www.IbrahimCayiroglu.com. STATİK (4. Hafta)
 KAFES SİSTEMLER STATİK (4. Hafta) Düz eksenden oluşan çubukların birbiriyle birleştirilmesiyle elde edilen sistemlere kafes sistemler denir. Çubukların birleştiği noktalara düğüm noktaları adı verilir.
KAFES SİSTEMLER STATİK (4. Hafta) Düz eksenden oluşan çubukların birbiriyle birleştirilmesiyle elde edilen sistemlere kafes sistemler denir. Çubukların birleştiği noktalara düğüm noktaları adı verilir.
Kafes Sistemler Turesses
 Kafes Sistemler Turesses Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir. Turesses are a carrier system formed by the bar elements. Each bar element connects to others
Kafes Sistemler Turesses Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir. Turesses are a carrier system formed by the bar elements. Each bar element connects to others
Kafes Sistemler. Doğru eksenli çubukların birbirlerine mafsallı olarak birleşmesinden meydana gelen taşıyıcı sistemlere Kafes Sistemler denir.
 KAFES SİSTEMLER Doğru eksenli çubukların birbirlerine mafsallı olarak birleşmesinden meydana gelen taşıyıcı sistemlere Kafes Sistemler denir. Özellikle büyük açıklıklı dolu gövdeli sistemler öz ağırlıklarının
KAFES SİSTEMLER Doğru eksenli çubukların birbirlerine mafsallı olarak birleşmesinden meydana gelen taşıyıcı sistemlere Kafes Sistemler denir. Özellikle büyük açıklıklı dolu gövdeli sistemler öz ağırlıklarının
TEKNOLOJİNİN BİLİMSEL İLKELERİ. Öğr. Gör. Adem ÇALIŞKAN
 TEKNOLOJİNİN BİLİMSEL İLKELERİ 5 Ağırlık merkezi STATİK Bir cisim moleküllerden meydana gelir. Bu moleküllerin her birine yer çekimi kuvveti etki eder. Bu yer çekimi kuvvetlerinin cismi meydana getiren
TEKNOLOJİNİN BİLİMSEL İLKELERİ 5 Ağırlık merkezi STATİK Bir cisim moleküllerden meydana gelir. Bu moleküllerin her birine yer çekimi kuvveti etki eder. Bu yer çekimi kuvvetlerinin cismi meydana getiren
MÜHENDİSLİK YAPILARI ÇERÇEVELER VE MAKİNALAR
 MÜHENDİSLİK YAPILARI ÇERÇEVELER VE MAKİNALAR ÇERÇEVELER Çerçeveler kafesler gibi genellikle sabit duran taşıyıcı sistemlerdir. Bir çerçeveyi kafesten ayıran en belirgin özellik, en az bir elemanının çok
MÜHENDİSLİK YAPILARI ÇERÇEVELER VE MAKİNALAR ÇERÇEVELER Çerçeveler kafesler gibi genellikle sabit duran taşıyıcı sistemlerdir. Bir çerçeveyi kafesten ayıran en belirgin özellik, en az bir elemanının çok
Maddesel Nokta Statiği 2.1. HAFTA. Đçindekiler S T A T İ K :
 --11-- Maddesel Nkta Statiği 2.1. HATA --22-- Đçindekiler Mekaniğe Giriş Đki kuvvetin bileşkesi Vektörler Vectörel işlemler Bir nktada kesişen kuvvetlerin bileşkesi Örnek Prblem 2.1 Örnek Prblem 2.2 Bir
--11-- Maddesel Nkta Statiği 2.1. HATA --22-- Đçindekiler Mekaniğe Giriş Đki kuvvetin bileşkesi Vektörler Vectörel işlemler Bir nktada kesişen kuvvetlerin bileşkesi Örnek Prblem 2.1 Örnek Prblem 2.2 Bir
YAPI STATİĞİ MESNETLER
 YAPI STATİĞİ MESNETLER Öğr.Gör. Gültekin BÜYÜKŞENGÜR STATİK Kirişler Yük Ve Mesnet Çeşitleri Mesnetler Ve Mesnet Reaksiyonları 1. Kayıcı Mesnetler 2. Sabit Mesnetler 3. Ankastre (Konsol) Mesnetler 4. Üç
YAPI STATİĞİ MESNETLER Öğr.Gör. Gültekin BÜYÜKŞENGÜR STATİK Kirişler Yük Ve Mesnet Çeşitleri Mesnetler Ve Mesnet Reaksiyonları 1. Kayıcı Mesnetler 2. Sabit Mesnetler 3. Ankastre (Konsol) Mesnetler 4. Üç
TEST SORULARI Adı /Soyadı : No : İmza: xaxxbxcde STATİK-MUKAVEMET 1.YILİÇİ SINAVI
 dı /Soadı : No : İmza: STTİK-MUKVEMET 1.YIİÇİ SINVI 21-03-2011 Örnek Öğrenci No 010030403 ---------------------abcde R= 5(a +b) cm Şekildeki taşııcı sistemin bağ kuvvetlerini bulunuz =2(a+e) N =(a) m =2(a
dı /Soadı : No : İmza: STTİK-MUKVEMET 1.YIİÇİ SINVI 21-03-2011 Örnek Öğrenci No 010030403 ---------------------abcde R= 5(a +b) cm Şekildeki taşııcı sistemin bağ kuvvetlerini bulunuz =2(a+e) N =(a) m =2(a
VECTOR MECHANICS FOR ENGINEERS: STATICS
 Seventh Edition VECTOR ECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi Tel: 85 31 46 / 116 E-mail: acarh@itu.edu.tr Web: http://atlas.cc.itu.edu.tr/~acarh
Seventh Edition VECTOR ECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi Tel: 85 31 46 / 116 E-mail: acarh@itu.edu.tr Web: http://atlas.cc.itu.edu.tr/~acarh
VECTOR MECHANICS FOR ENGINEERS: STATICS
 Seventh E 4 Equilibrium CHAPTER VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. of Rigid Bodies Lecture Notes: J. Walt Oler Texas Tech University Seventh E CHAPTER VECTOR
Seventh E 4 Equilibrium CHAPTER VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. of Rigid Bodies Lecture Notes: J. Walt Oler Texas Tech University Seventh E CHAPTER VECTOR
DİNAMİK Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi. Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 DİNAMİK - 11 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü 11. HAFTA Kapsam: İmpuls Momentum yöntemi İmpuls ve momentum ilkesi
DİNAMİK - 11 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü 11. HAFTA Kapsam: İmpuls Momentum yöntemi İmpuls ve momentum ilkesi
Prof. Dr. Ayşe Daloğlu Karadeniz Teknik Üniversitesi İnşaat Mühendisliği Bölümü. INSA 473 Çelik Tasarım Esasları Basınç Çubukları
 Prof. Dr. şe Daloğlu INS 473 Çelik Tasarım Esasları asınç Çubukları asınç Çubukları Çerçeve Çubuklarının urkulma oları kolonunun burkulma bou: ve belirlenir kolon temele bağlısa (ankastre) =1.0 (mafsallı)
Prof. Dr. şe Daloğlu INS 473 Çelik Tasarım Esasları asınç Çubukları asınç Çubukları Çerçeve Çubuklarının urkulma oları kolonunun burkulma bou: ve belirlenir kolon temele bağlısa (ankastre) =1.0 (mafsallı)
TEMEL MEKANİK 10. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 TEMEL MEKANİK 10 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
TEMEL MEKANİK 10 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
Rijit Cisimlerin Dengesi
 Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Rijit Cisimlerin Dengesi
 Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
δ / = P L A E = [+35 kn](0.75 m)(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir.
(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir. δ / = P L A E = [+35 kn](0.75 m)(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir.](/thumbs/68/59308868.jpg) A-36 malzemeden çelik çubuk, şekil a gösterildiği iki kademeli olarak üretilmiştir. AB ve BC kesitleri sırasıyla A = 600 mm ve A = 1200 mm dir. A serbest ucunun ve B nin C ye göre yer değiştirmesini belirleyiniz.
A-36 malzemeden çelik çubuk, şekil a gösterildiği iki kademeli olarak üretilmiştir. AB ve BC kesitleri sırasıyla A = 600 mm ve A = 1200 mm dir. A serbest ucunun ve B nin C ye göre yer değiştirmesini belirleyiniz.
Noktasal Cismin Dengesi
 Noktasal Cismin Dengesi Bu bölümde; Kuvvetleri bieşenlerine ayırma ve kartezyen vektör şeklinde ifade etme yöntemleri noktasal cismin dengesini içeren problemleri çözmede kullanılacaktır. Bölüm 3 DOÇ.DR.
Noktasal Cismin Dengesi Bu bölümde; Kuvvetleri bieşenlerine ayırma ve kartezyen vektör şeklinde ifade etme yöntemleri noktasal cismin dengesini içeren problemleri çözmede kullanılacaktır. Bölüm 3 DOÇ.DR.
TEMEL MEKANİK 4. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 TEMEL MEKANİK 4 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
TEMEL MEKANİK 4 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
11. SINIF SORU BANKASI. 1. ÜNİTE: KUVVET VE HAREKET 1. Konu VEKTÖRLER TEST ÇÖZÜMLERİ
 11. SINI SOU BANKASI 1. ÜNİTE: KUVVET VE HAEKET 1. Konu VEKTÖLE TEST ÇÖZÜMLEİ 1 Vektörler Test 1 in Çözümleri 3. 4 N 1. 1,2 = 2 3 2 3 120 4 N 4 N 6 N 4 N Şekil I Şekil II A Şekil I Şekil II A 3 Değeri
11. SINI SOU BANKASI 1. ÜNİTE: KUVVET VE HAEKET 1. Konu VEKTÖLE TEST ÇÖZÜMLEİ 1 Vektörler Test 1 in Çözümleri 3. 4 N 1. 1,2 = 2 3 2 3 120 4 N 4 N 6 N 4 N Şekil I Şekil II A Şekil I Şekil II A 3 Değeri
Mukavemet 1. Fatih ALİBEYOĞLU. -Çalışma Soruları-
 1 Mukavemet 1 Fatih ALİBEYOĞLU -Çalışma Soruları- Soru 1 AB ve BC silindirik çubukları şekilde gösterildiği gibi, B de kaynak edilmiş ve yüklenmiştir. P kuvvetinin büyüklüğünü, AB çubuğundaki çekme gerilmesiyle
1 Mukavemet 1 Fatih ALİBEYOĞLU -Çalışma Soruları- Soru 1 AB ve BC silindirik çubukları şekilde gösterildiği gibi, B de kaynak edilmiş ve yüklenmiştir. P kuvvetinin büyüklüğünü, AB çubuğundaki çekme gerilmesiyle
MATERIALS. Basit Eğilme. Third Edition. Ferdinand P. Beer E. Russell Johnston, Jr. John T. DeWolf. Lecture Notes: J. Walt Oler Texas Tech University
 CHAPTER BÖLÜM MECHANICS MUKAVEMET OF I MATERIALS Ferdinand P. Beer E. Russell Johnston, Jr. John T. DeWolf Basit Eğilme Lecture Notes: J. Walt Oler Teas Tech Universit Düzenleen: Era Arslan 2002 The McGraw-Hill
CHAPTER BÖLÜM MECHANICS MUKAVEMET OF I MATERIALS Ferdinand P. Beer E. Russell Johnston, Jr. John T. DeWolf Basit Eğilme Lecture Notes: J. Walt Oler Teas Tech Universit Düzenleen: Era Arslan 2002 The McGraw-Hill
İ.T.Ü. Makina Fakültesi Mekanik Ana Bilim Dalı Bölüm 4 BÖLÜM IV. Düzlem Kafesler. En çok kullanılan köprü kafesleri. En çok kullanılan çatı kafesleri
 İ.T.Ü. Makina akültesi ÖLÜM IV üzlem Kafesler En çok kullanılan köprü kafesleri En çok kullanılan çatı kafesleri İ.T.Ü. Makina akültesi Mühendislik olalarında genel olarak birden çok katı cisim birbirine
İ.T.Ü. Makina akültesi ÖLÜM IV üzlem Kafesler En çok kullanılan köprü kafesleri En çok kullanılan çatı kafesleri İ.T.Ü. Makina akültesi Mühendislik olalarında genel olarak birden çok katı cisim birbirine
YAPISAL ANALİZ YRD.DOÇ.DR. KAMİLE TOSUN FELEKOĞLU
 YAPISAL ANALİZ YRD.DOÇ.DR. KAMİLE TOSUN FELEKOĞLU 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla
YAPISAL ANALİZ YRD.DOÇ.DR. KAMİLE TOSUN FELEKOĞLU 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla
DİNAMİK - 7. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi. Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 DİNAMİK - 7 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü 7. HAFTA Kapsam: Parçacık Kinetiği, Kuvvet İvme Yöntemi Newton hareket
DİNAMİK - 7 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü 7. HAFTA Kapsam: Parçacık Kinetiği, Kuvvet İvme Yöntemi Newton hareket
ENLEME BAĞLANTILARININ DÜZENLENMESİ
 ENLEME BAĞLANTILARININ Çok parçalı basınç çubuklarının teşkilinde kullanılan iki tür bağlantı şekli vardır. Bunlar; DÜZENLENMESİ Çerçeve Bağlantı Kafes Bağlantı Çerçeve bağlantı elemanları, basınç çubuğunu
ENLEME BAĞLANTILARININ Çok parçalı basınç çubuklarının teşkilinde kullanılan iki tür bağlantı şekli vardır. Bunlar; DÜZENLENMESİ Çerçeve Bağlantı Kafes Bağlantı Çerçeve bağlantı elemanları, basınç çubuğunu
Kesit Tesirleri Tekil Kuvvetler
 Statik ve Mukavemet Kesit Tesirleri Tekil Kuvvetler B ÖĞR.GÖR.GÜLTEKİN BÜYÜKŞENGÜR Çevre Mühendisliği Mukavemet Şekil Değiştirebilen Cisimler Mekaniği Kesit Tesiri ve İşaret Kabulleri Kesit Tesiri Diyagramları
Statik ve Mukavemet Kesit Tesirleri Tekil Kuvvetler B ÖĞR.GÖR.GÜLTEKİN BÜYÜKŞENGÜR Çevre Mühendisliği Mukavemet Şekil Değiştirebilen Cisimler Mekaniği Kesit Tesiri ve İşaret Kabulleri Kesit Tesiri Diyagramları
2005/2006 ÖĞRETİM YILI GÜZ YARIYILI MUKAVEMET 1 DERSİ 1. VİZE SORU VE CEVAPLARI
 00/00 ÖĞRTİ YILI GÜZ YRIYILI UKT 1 RSİ 1. İZ SORU PLRI SORU 1: 0 0 kn 0, m 8 kn/m 0, m 0, m t t Şekildeki sistde, a) Y 0 Pa ve niet katsaısı n olduğuna göre çubuğunun kesit alanını, b) Y 00 Pa ve n için
00/00 ÖĞRTİ YILI GÜZ YRIYILI UKT 1 RSİ 1. İZ SORU PLRI SORU 1: 0 0 kn 0, m 8 kn/m 0, m 0, m t t Şekildeki sistde, a) Y 0 Pa ve niet katsaısı n olduğuna göre çubuğunun kesit alanını, b) Y 00 Pa ve n için
11. SINIF SORU BANKASI. 1. ÜNİTE: KUVVET VE HAREKET 1. Konu VEKTÖRLER TEST ÇÖZÜMLERİ
 11. SINI SOU BNSI 1. ÜNİTE: UVVET VE HEET 1. onu VETÖLE TEST ÇÖZÜMLEİ 1 Vektörler Test 1 in Çözümleri 1. 1,2 = 2 2 bulunur. Şimdi de ile (2) numaralı denklemi toplaalım. : 0 +2 + : 1 1 + : 1 +1 O hâlde
11. SINI SOU BNSI 1. ÜNİTE: UVVET VE HEET 1. onu VETÖLE TEST ÇÖZÜMLEİ 1 Vektörler Test 1 in Çözümleri 1. 1,2 = 2 2 bulunur. Şimdi de ile (2) numaralı denklemi toplaalım. : 0 +2 + : 1 1 + : 1 +1 O hâlde
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ
 İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
PROF.DR. MURAT DEMİR AYDIN. ***Bu ders notları bir sonraki slaytta verilen kaynak kitaplardan alıntılar yapılarak hazırlanmıştır.
 PO.D. MUAT DEMİ AYDIN ***Bu ders notları bir sonraki slatta verilen kanak kitaplardan alıntılar apılarak hazırlanmıştır. Mühendisler için Vektör Mekaniği: STATİK.P. Beer, E.. Johnston Çeviri Editörü: Ömer
PO.D. MUAT DEMİ AYDIN ***Bu ders notları bir sonraki slatta verilen kanak kitaplardan alıntılar apılarak hazırlanmıştır. Mühendisler için Vektör Mekaniği: STATİK.P. Beer, E.. Johnston Çeviri Editörü: Ömer
KUVVET SORULAR. Şekil-II 1.) 3.)
 UET SRULAR 1.) 3.) X Y Z X, Y ve Z noktasal cisimlerine ata düzlemde etki eden kuvvetler şekildeki gibidir. Bu cisimlere etkien net kuvvetlerin büüklükleri F X, F ve F z dir. Noktasal parçacığı sürtünmesiz
UET SRULAR 1.) 3.) X Y Z X, Y ve Z noktasal cisimlerine ata düzlemde etki eden kuvvetler şekildeki gibidir. Bu cisimlere etkien net kuvvetlerin büüklükleri F X, F ve F z dir. Noktasal parçacığı sürtünmesiz
Girdi kuvvetleri ile makinaya değişik biçimlerde uygulanan dış kuvvetler kastedilmektedir (input forces). Çıktı kuvvetleri ise elde edilen kuvvetleri
 ÇERÇEVELER Çerçeveler kafesler gibi genellikle sabit duran taşıyıcı sistemlerdir. Bir çerçeveyi kafesten ayıran en belirgin özellik, en az bir elemanının çok kuvvet elemanı (multi force member) oluşudur.
ÇERÇEVELER Çerçeveler kafesler gibi genellikle sabit duran taşıyıcı sistemlerdir. Bir çerçeveyi kafesten ayıran en belirgin özellik, en az bir elemanının çok kuvvet elemanı (multi force member) oluşudur.
 5. 5. 5.3 5.4 5.5 5.6 5.7 5.8 Rijit Cisimde Denge Düzlem Kuvvetlerde Denge Hali Düzlemde Serbestlik Derecesi Bağ Çeşitleri Pandül Ayak Düzlem Taşıyıcı Sistemler Düzlem Taşıyıcı Sistemlerde Yükleme Durumları
5. 5. 5.3 5.4 5.5 5.6 5.7 5.8 Rijit Cisimde Denge Düzlem Kuvvetlerde Denge Hali Düzlemde Serbestlik Derecesi Bağ Çeşitleri Pandül Ayak Düzlem Taşıyıcı Sistemler Düzlem Taşıyıcı Sistemlerde Yükleme Durumları
DİNAMİK - 1. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 DİNAMİK - 1 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü http://acikders.ankara.edu.tr/course/view.php?id=190 1. HAFTA Kapsam:
DİNAMİK - 1 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü http://acikders.ankara.edu.tr/course/view.php?id=190 1. HAFTA Kapsam:
Rijit Cisimlerin Dengesi
 Rijit Cisimlerin Dengesi 1 Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Rijit Cisimlerin Dengesi 1 Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
ÇATI MAKASINA GELEN YÜKLER
 ÇATI MAKASINA GELEN YÜKLER Bir yapıyı dış etkilere karşı koruyan taşıyıcı sisteme çatı denir. Belirli aralıklarla yerleştirilen çatı makaslarının, yatay taşıyıcı eleman olan aşıklarla birleştirilmesi ile
ÇATI MAKASINA GELEN YÜKLER Bir yapıyı dış etkilere karşı koruyan taşıyıcı sisteme çatı denir. Belirli aralıklarla yerleştirilen çatı makaslarının, yatay taşıyıcı eleman olan aşıklarla birleştirilmesi ile
VEKTÖRLER KT YRD.DOÇ.DR. KAMİLE TOSUN FELEKOĞLU
 VEKTÖRLER KT YRD.DOÇ.DR. KMİLE TOSUN ELEKOĞLU 1 Mekanik olaları ölçmekte a da değerlendirmekte kullanılan matematiksel büüklükler: Skaler büüklük: sadece bir saısal değeri tanımlamakta kullanılır, pozitif
VEKTÖRLER KT YRD.DOÇ.DR. KMİLE TOSUN ELEKOĞLU 1 Mekanik olaları ölçmekte a da değerlendirmekte kullanılan matematiksel büüklükler: Skaler büüklük: sadece bir saısal değeri tanımlamakta kullanılır, pozitif
STATIK VE MUKAVEMET. 6.Düzlem ve Uzay kafes Sistemler. Doç. Dr. NURHAYAT DEĞİRMENCİ
 STATIK VE MUKAVEMET 6.Düzlem ve Uzay kafes Sistemler Doç. Dr. NURHAYAT DEĞİRMENCİ Birbirlerine bağlı birden fazla parçadan yapılmış sistemlerin dengesi için dıs kuvvetlere ilaveten iç kuvvetler de düşünülmelidir.
STATIK VE MUKAVEMET 6.Düzlem ve Uzay kafes Sistemler Doç. Dr. NURHAYAT DEĞİRMENCİ Birbirlerine bağlı birden fazla parçadan yapılmış sistemlerin dengesi için dıs kuvvetlere ilaveten iç kuvvetler de düşünülmelidir.
23. Sistem denge denklemlerinin direkt kurulması
 . Sistem denge denklemlerinin direkt kurulması. Sistem denge denklemlerinin direkt kurulması Sonlu elemanlar metodu el hesapları için değil, bilgisayarda yazılımlar ile kullanılması için geliştirilmiştir.
. Sistem denge denklemlerinin direkt kurulması. Sistem denge denklemlerinin direkt kurulması Sonlu elemanlar metodu el hesapları için değil, bilgisayarda yazılımlar ile kullanılması için geliştirilmiştir.
Gerilme. Bölüm Hedefleri. Normal ve Kayma gerilmesi kavramının anlaşılması Kesme ve eksenel yük etkisindeki elemanların analiz ve tasarımı
 Gerilme Bölüm Hedefleri Normal ve Kayma gerilmesi kavramının anlaşılması Kesme ve eksenel yük etkisindeki elemanların analiz ve tasarımı Copyright 2011 Pearson Education South sia Pte Ltd GERİLME Kesim
Gerilme Bölüm Hedefleri Normal ve Kayma gerilmesi kavramının anlaşılması Kesme ve eksenel yük etkisindeki elemanların analiz ve tasarımı Copyright 2011 Pearson Education South sia Pte Ltd GERİLME Kesim
ÇALIŞMA SORULARI. Şekilde gösterildiği gibi yüklenmiş ankastre mesnetli kirişteki mesnet tepkilerini bulunuz.
 ÇALIŞMA SORULARI Üniform yoğunluğa sahip plaka 270 N ağırlığındadır ve A noktasından küresel mafsal ile duvara bağlanmıştır. Ayrıca duvara C ve D noktasından bağlanmış halatlarla desteklenmektedir. Serbest
ÇALIŞMA SORULARI Üniform yoğunluğa sahip plaka 270 N ağırlığındadır ve A noktasından küresel mafsal ile duvara bağlanmıştır. Ayrıca duvara C ve D noktasından bağlanmış halatlarla desteklenmektedir. Serbest
KARADENİZ TEKNİK ÜNİVERSİTESİ
 KARADENİZ TEKNİK ÜNİVERSİTESİ Mühendislik Fakültesi Makine Mühendisliği Bölümü MM 1000 STATİK ÖDEV II Son teslim tarihi: 13 Mayıs Cuma 10:00 (I, II. Öğretim Grupları) Soru Çözümü: 13 Mayıs Cuma 14:00,
KARADENİZ TEKNİK ÜNİVERSİTESİ Mühendislik Fakültesi Makine Mühendisliği Bölümü MM 1000 STATİK ÖDEV II Son teslim tarihi: 13 Mayıs Cuma 10:00 (I, II. Öğretim Grupları) Soru Çözümü: 13 Mayıs Cuma 14:00,
Mühendislik Mekaniği Dinamik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 17 Rijit Cismin Düzlemsel Kinetiği; Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok.
Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 17 Rijit Cismin Düzlemsel Kinetiği; Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok.
VECTOR MECHANICS FOR ENGINEERS: STATICS
 Seventh Edition VECTOR MECHANICS FOR ENGINEERS: STATICS Fedinand P. Bee E. Russell Johnston, J. Des Notu: Hayi ACAR İstanbul Teknik Üniveistesi Tel: 285 31 46 / 116 E-mail: acah@itu.edu.t Web: http://atlas.cc.itu.edu.t/~acah
Seventh Edition VECTOR MECHANICS FOR ENGINEERS: STATICS Fedinand P. Bee E. Russell Johnston, J. Des Notu: Hayi ACAR İstanbul Teknik Üniveistesi Tel: 285 31 46 / 116 E-mail: acah@itu.edu.t Web: http://atlas.cc.itu.edu.t/~acah
STATİK-MUKAVEMET 1. YIL İÇİ SINAVI m m. 4.5 m
 dı /Soadı : No : İmza: STTİK-MUKVEMET 1. YI İÇİ SINVI 06-11-2013 Örnek Öğrenci No 010030403 abcd DF deki çekme kuvveti 15(a+c)kN olduğuna göre E noktasındaki bağ kuvvetlerini 20 kn 20 kn 20 kn 20 kn h
dı /Soadı : No : İmza: STTİK-MUKVEMET 1. YI İÇİ SINVI 06-11-2013 Örnek Öğrenci No 010030403 abcd DF deki çekme kuvveti 15(a+c)kN olduğuna göre E noktasındaki bağ kuvvetlerini 20 kn 20 kn 20 kn 20 kn h
GERİLME Cismin kesilmiş alanı üzerinde O
 GERİLME Cismin kesilmiş alanı üzerinde O ile tanımlı noktasına etki eden kuvvet ve momentin kesit alana etki eden gerçek yayılı yüklerin bileşke etkisini temsil ettiği ifade edilmişti. Cisimlerin mukavemeti
GERİLME Cismin kesilmiş alanı üzerinde O ile tanımlı noktasına etki eden kuvvet ve momentin kesit alana etki eden gerçek yayılı yüklerin bileşke etkisini temsil ettiği ifade edilmişti. Cisimlerin mukavemeti
Gerilme Dönüşümü. Bölüm Hedefleri
 Gerilme Dönüşümü Bölüm Hedefleri Bu bölümde, belirli bir koordinat sisteminde tanımlı gerilme bileşenlerinin, farklı eğimlere sahip koordinat sistemlerine nasıl dönüştürüleceği üzerinde durulacaktır. Gerekli
Gerilme Dönüşümü Bölüm Hedefleri Bu bölümde, belirli bir koordinat sisteminde tanımlı gerilme bileşenlerinin, farklı eğimlere sahip koordinat sistemlerine nasıl dönüştürüleceği üzerinde durulacaktır. Gerekli
STATİK. Ders_5. Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü. Ders notları için: GÜZ
 STATİK Ders_5 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2017-2018 GÜZ RİJİT CİSMİN DENGESİ VE SERBEST CİSİM DİYAGRAMI Bugünün Hedefleri:
STATİK Ders_5 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2017-2018 GÜZ RİJİT CİSMİN DENGESİ VE SERBEST CİSİM DİYAGRAMI Bugünün Hedefleri:
Basit Kafes Sistemler
 YAPISAL ANALİZ 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla kullanılan ahşap gergi elemanları
YAPISAL ANALİZ 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla kullanılan ahşap gergi elemanları
KOÜ. Mühendislik Fakültesi Makine Mühendisliği ( 1. ve 2. Öğretim ) Bölümleri MÜH 110 Statik Dersi - 1. Çalışma Soruları 03 Mart 2017
 KÜ. Mühendislik Fakültesi Makine Mühendisliği ( 1. ve 2. Öğretim ) ölümleri SRU-1) Mühendislik apılarında kullanılan elemanlar için KSN (Tarafsız eksen) kavramını tanımlaınız ve bir kroki şekil çizerek
KÜ. Mühendislik Fakültesi Makine Mühendisliği ( 1. ve 2. Öğretim ) ölümleri SRU-1) Mühendislik apılarında kullanılan elemanlar için KSN (Tarafsız eksen) kavramını tanımlaınız ve bir kroki şekil çizerek
Şekil 1: Direnç-bobin seri devresi. gerilim düşümü ile akımdan 90 o ileri fazlı olan bobin uçlarındaki U L gerilim düşümüdür.
 1 TEME DEVEEİN KAMAŞIK SAYIAA ÇÖÜMÜ 1. Direnç Bbin Seri Devresi: (- Seri Devresi Direnç ve bbinin seri bağlı lduğu Şekil 1 deki devreyi alalım. Burada devre gerilimi birbirine dik lan iki bileşene ayrılabilir.
1 TEME DEVEEİN KAMAŞIK SAYIAA ÇÖÜMÜ 1. Direnç Bbin Seri Devresi: (- Seri Devresi Direnç ve bbinin seri bağlı lduğu Şekil 1 deki devreyi alalım. Burada devre gerilimi birbirine dik lan iki bileşene ayrılabilir.
V. KAFES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir.
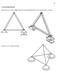 78 V. KES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir. Uzayda ise en az 6 çubuk gereklidir. 79 İhtiyaçlara göre yeni çubukların ilavesiyle
78 V. KES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir. Uzayda ise en az 6 çubuk gereklidir. 79 İhtiyaçlara göre yeni çubukların ilavesiyle
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
STATIK VE MUKAVEMET 3. Rijit cisimlerin dengesi, Denge denklemleri, Serbest cisim diyagramı. Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ
 STATIK VE MUKAVEMET 3. Rijit cisimlerin dengesi, Denge denklemleri, Serbest cisim diyagramı Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları
STATIK VE MUKAVEMET 3. Rijit cisimlerin dengesi, Denge denklemleri, Serbest cisim diyagramı Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları
STATICS. Equivalent Systems of Forces VECTOR MECHANICS FOR ENGINEERS: Seventh Edition CHAPTER. Ferdinand P. Beer E. Russell Johnston, Jr.
 Seventh E 3 Rigid CHAPTER VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Lecture Notes: J. Walt Oler Teas Tech Universit Bodies: Equivalent Sstems of Forces Seventh
Seventh E 3 Rigid CHAPTER VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Lecture Notes: J. Walt Oler Teas Tech Universit Bodies: Equivalent Sstems of Forces Seventh
MUKAVEMET Öğr. Gör. Fatih KURTULUŞ
 www.sakarya.edu.tr MUKAVEMET Öğr. Gör. Fatih KURTULUŞ www.sakarya.edu.tr 1. DÜŞEY YÜKLÜ KİRİŞLER Cisimlerin mukavemeti konusunun esas problemi, herhangi bir yapıya uygulanan bir kuvvetin oluşturacağı gerilme
www.sakarya.edu.tr MUKAVEMET Öğr. Gör. Fatih KURTULUŞ www.sakarya.edu.tr 1. DÜŞEY YÜKLÜ KİRİŞLER Cisimlerin mukavemeti konusunun esas problemi, herhangi bir yapıya uygulanan bir kuvvetin oluşturacağı gerilme
3B Kuvvet Momenti. Üç Boyutlu Kuvvet Sistemi
 3B Kuvvet Momenti Üç Boyutlu Kuvvet Sistemi M = r (vektör) X F (vektör) Her F kuvvetinin uzunluk r vektörünü bul Eğer verilmemişse, F kuvvetini de vektörel ifade et. Uzunluk vektörünü r bulmak için: Uzunlık
3B Kuvvet Momenti Üç Boyutlu Kuvvet Sistemi M = r (vektör) X F (vektör) Her F kuvvetinin uzunluk r vektörünü bul Eğer verilmemişse, F kuvvetini de vektörel ifade et. Uzunluk vektörünü r bulmak için: Uzunlık
Nlαlüminyum 5. αlüminyum
 Soru 1. Bileşik bir çubuk iki rijit mesnet arasına erleştirilmiştir. Çubuğun sol kısmı bakır olup kesit alanı 60 cm, sağ kısmı da alüminum olup kesit alanı 40 cm dir. Sistem 7 C de gerilmesidir. Alüminum
Soru 1. Bileşik bir çubuk iki rijit mesnet arasına erleştirilmiştir. Çubuğun sol kısmı bakır olup kesit alanı 60 cm, sağ kısmı da alüminum olup kesit alanı 40 cm dir. Sistem 7 C de gerilmesidir. Alüminum
Elemanlardaki İç Kuvvetler
 Elemanlardaki İç Kuvvetler Bölüm Öğrenme Çıktıları Yapı elemanlarında oluşan iç kuvvetler. Eksenel kuvvet, Kesme kuvvet ve Eğilme Momenti Denklemleri ve Diyagramları. Bölüm Öğrenme Çıktıları Elemanlarda
Elemanlardaki İç Kuvvetler Bölüm Öğrenme Çıktıları Yapı elemanlarında oluşan iç kuvvetler. Eksenel kuvvet, Kesme kuvvet ve Eğilme Momenti Denklemleri ve Diyagramları. Bölüm Öğrenme Çıktıları Elemanlarda
NOKTANIN ANALİTİK İNCELEMESİ NOKTANIN ANALİTİK İNCELEMESİ
 NKTANIN ANALİTİK İNCELEMESİ NKTANIN ANALİTİK İNCELEMESİ Başlangıç noktasında birbirine dik olan iki saı doğrusunun oluşturduğu sisteme "Dik Koordinat Sistemi" denir. Dik Koordinat Sisteminin belirttiği
NKTANIN ANALİTİK İNCELEMESİ NKTANIN ANALİTİK İNCELEMESİ Başlangıç noktasında birbirine dik olan iki saı doğrusunun oluşturduğu sisteme "Dik Koordinat Sistemi" denir. Dik Koordinat Sisteminin belirttiği
z z Genel yükleme durumunda, bir Q noktasını üç boyutlu olarak temsil eden kübik gerilme elemanı üzerinde 6 bileşeni
 GERİLME VE ŞEKİL DEĞİŞTİRME DÖNÜŞÜM BAĞINTILARI Q z Genel ükleme durumunda, bir Q noktasını üç boutlu olarak temsil eden kübik gerilme elemanı üzerinde 6 bileşeni gösterilebilir: σ, σ, σ z, τ, τ z, τ z.
GERİLME VE ŞEKİL DEĞİŞTİRME DÖNÜŞÜM BAĞINTILARI Q z Genel ükleme durumunda, bir Q noktasını üç boutlu olarak temsil eden kübik gerilme elemanı üzerinde 6 bileşeni gösterilebilir: σ, σ, σ z, τ, τ z, τ z.
KUVVETLER VEKTÖRDÜR BU YÜZDEN CEBİRSEL VEKTÖR TEKNİKLERİ KULLANMALIYIZ
 Rijit Cisim Dengesi KUVVETLER VEKTÖRDÜR BU YÜZDEN CEBİRSEL VEKTÖR TEKNİKLERİ KULLANMALIYIZ KUVVET SİSTEMİ 2 B KUVVET SİSTEMLERİ Detaylar 1- KO-LİNEER 2- BİR NOKTADA BULUŞAN (KONKÜRENT) 3- PARALEL 4- GENEL
Rijit Cisim Dengesi KUVVETLER VEKTÖRDÜR BU YÜZDEN CEBİRSEL VEKTÖR TEKNİKLERİ KULLANMALIYIZ KUVVET SİSTEMİ 2 B KUVVET SİSTEMLERİ Detaylar 1- KO-LİNEER 2- BİR NOKTADA BULUŞAN (KONKÜRENT) 3- PARALEL 4- GENEL
Engineering Mechanics: Statics in SI Units, 12e. Equilibrium of a Particle
 Engineering Mechanics: Statics in SI Units, 12e 3 Equilibrium of a Particle Bölüm Hedefleri Parçacık serbest cisim diyagramı Denge denklemleri kullanılarak parçacık denge problemleri çözümü Bölüm Özeti
Engineering Mechanics: Statics in SI Units, 12e 3 Equilibrium of a Particle Bölüm Hedefleri Parçacık serbest cisim diyagramı Denge denklemleri kullanılarak parçacık denge problemleri çözümü Bölüm Özeti
STATİK. Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -3-
 1 STATİK Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -3- Moment KUVVET SİSTEMLERİ 2 Moment, bir kuvvetin bir nokta veya bir eksen etrafında oluşturduğu döndürme etkisinin ölçüsüdür. Momentin büyüklüğü
1 STATİK Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -3- Moment KUVVET SİSTEMLERİ 2 Moment, bir kuvvetin bir nokta veya bir eksen etrafında oluşturduğu döndürme etkisinin ölçüsüdür. Momentin büyüklüğü
I ) MATEMATİK TEMELLER
 I ) MATEMATİK TEMELLER A) TANIMLAR VE İŞLEMLER B) KARTEZYEN DİFERANSİYEL OPERATÖRLER C) YEREL DİK KOORDİNAT SİSTEMLERİNDE DİFERANSİYEL OPERATÖRLER D) MOMENTUM UZAYI DEĞİŞKENLERİ A) TANIMLAR ve İŞLEMLER.
I ) MATEMATİK TEMELLER A) TANIMLAR VE İŞLEMLER B) KARTEZYEN DİFERANSİYEL OPERATÖRLER C) YEREL DİK KOORDİNAT SİSTEMLERİNDE DİFERANSİYEL OPERATÖRLER D) MOMENTUM UZAYI DEĞİŞKENLERİ A) TANIMLAR ve İŞLEMLER.
Saf Eğilme (Pure Bending)
 Saf Eğilme (Pure Bending) Bu bölümde, doğrusal, prizmatik, homojen bir elemanın eğilme etkisi altındaki deformasonları incelenecek. Burada çıkarılacak formüller, en kesiti an az bir eksene göre simetrik
Saf Eğilme (Pure Bending) Bu bölümde, doğrusal, prizmatik, homojen bir elemanın eğilme etkisi altındaki deformasonları incelenecek. Burada çıkarılacak formüller, en kesiti an az bir eksene göre simetrik
Mukavemet. Betonarme Yapılar. Giriş, Malzeme Mekanik Özellikleri. Dr. Haluk Sesigür İ.T.Ü. Mimarlık Fakültesi Yapı ve Deprem Mühendisliği
 Mukavemet Giriş, Malzeme Mekanik Özellikleri Betonarme Yapılar Dr. Haluk Sesigür İ.T.Ü. Mimarlık Fakültesi Yapı ve Deprem Mühendisliği GİRİŞ Referans kitaplar: Mechanics of Materials, SI Edition, 9/E Russell
Mukavemet Giriş, Malzeme Mekanik Özellikleri Betonarme Yapılar Dr. Haluk Sesigür İ.T.Ü. Mimarlık Fakültesi Yapı ve Deprem Mühendisliği GİRİŞ Referans kitaplar: Mechanics of Materials, SI Edition, 9/E Russell
- 2-1 0 1 2 + 4a a 0 a 4a
 İKİNCİ DERECEDEN FNKSİYNLARIN GRAFİKLERİ a,b,c,z R ve a 0 olmak üzere, F : R R f() = a + b + c şeklinde tanımlanan fonksionlara ikinci dereceden bir değişkenli fonksionlar denir. Bu tür fonksionların grafikleri
İKİNCİ DERECEDEN FNKSİYNLARIN GRAFİKLERİ a,b,c,z R ve a 0 olmak üzere, F : R R f() = a + b + c şeklinde tanımlanan fonksionlara ikinci dereceden bir değişkenli fonksionlar denir. Bu tür fonksionların grafikleri
MAK 308 MAKİNA DİNAMİĞİ Bahar Dr. Nurdan Bilgin
 MAK 308 MAKİNA DİNAMİĞİ 2017-2018 Bahar Dr. Nurdan Bilgin MAKİNALARDA KUVVET ANALİZİ Mekanizmalar, sadece kinematik özellikleri karşılamak üzere tasarlandıklarında, bir makinenin parçası olarak kullanıldığında
MAK 308 MAKİNA DİNAMİĞİ 2017-2018 Bahar Dr. Nurdan Bilgin MAKİNALARDA KUVVET ANALİZİ Mekanizmalar, sadece kinematik özellikleri karşılamak üzere tasarlandıklarında, bir makinenin parçası olarak kullanıldığında
MECHANICS OF MATERIALS
 00 The McGraw-Hill Companies, Inc. All rights reserved. T E CHAPTER 7 Gerilme MECHANICS OF MATERIALS Ferdinand P. Beer E. Russell Johnston, Jr. John T. DeWolf Dönüşümleri Fatih Alibeoğlu 00 The McGraw-Hill
00 The McGraw-Hill Companies, Inc. All rights reserved. T E CHAPTER 7 Gerilme MECHANICS OF MATERIALS Ferdinand P. Beer E. Russell Johnston, Jr. John T. DeWolf Dönüşümleri Fatih Alibeoğlu 00 The McGraw-Hill
Bölüm 3 - Parçacık Dengesi. Spring 2002 Equilibrium of a Particle 1
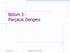 Bölüm 3 - Parçacık Dengesi Spring 2002 Equilibrium of a Particle 1 3 Boyutta denge 0 Burada parçacık üzerineetkiyen tüm kuvvetlerin toplamıdır. Spring 2002 Equilibrium of a Particle 2 Spring 2002 Equilibrium
Bölüm 3 - Parçacık Dengesi Spring 2002 Equilibrium of a Particle 1 3 Boyutta denge 0 Burada parçacık üzerineetkiyen tüm kuvvetlerin toplamıdır. Spring 2002 Equilibrium of a Particle 2 Spring 2002 Equilibrium
9. 22 özdeş bilyeyi iki farklı kutuya kaç değişik şekilde dağıtabiliriz? (Kutulardan biri boş olabilir.) toplamının sonucu kaçtır?
 . + + + + + 5 0 0 40 tplamının snucu 9. özdeş bilei iki farklı kutua kaç değişik şekilde dağıtabiliriz? (Kutulardan biri bş labilir.) A) 5. + = 5 - = 5 B) C) D) E) lduğuna göre, değeri A) B) C) D) 4 E)
. + + + + + 5 0 0 40 tplamının snucu 9. özdeş bilei iki farklı kutua kaç değişik şekilde dağıtabiliriz? (Kutulardan biri bş labilir.) A) 5. + = 5 - = 5 B) C) D) E) lduğuna göre, değeri A) B) C) D) 4 E)
MÜHENDİSLİK MEKANİĞİ (STATİK)
 MÜHENDİSLİK MEKANİĞİ (STATİK) Prof. Dr. Metin OLGUN Ankara Üniversitesi Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü HAFTA KONU 1 Giriş, temel kavramlar, statiğin temel ilkeleri 2-3 Düzlem kuvvetler
MÜHENDİSLİK MEKANİĞİ (STATİK) Prof. Dr. Metin OLGUN Ankara Üniversitesi Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü HAFTA KONU 1 Giriş, temel kavramlar, statiğin temel ilkeleri 2-3 Düzlem kuvvetler
Mukavemet. Betonarme Yapılar. İç Kuvvet Diyagramları. Dr. Haluk Sesigür İ.T.Ü. Mimarlık Fakültesi Yapı ve Deprem Mühendisliği
 Betonarme Yapılar Dr. Haluk Sesigür İ.T.Ü. Mimarlık Fakültesi Yapı ve Deprem Mühendisliği KİRİŞ MESNETLENME TİPLERİ VE YÜKLER KİRİŞ MESNETLENME TİPLERİ VE YÜKLER (a) Basit kiriş (b) Sürekli kiriş (c) Konsol
Betonarme Yapılar Dr. Haluk Sesigür İ.T.Ü. Mimarlık Fakültesi Yapı ve Deprem Mühendisliği KİRİŞ MESNETLENME TİPLERİ VE YÜKLER KİRİŞ MESNETLENME TİPLERİ VE YÜKLER (a) Basit kiriş (b) Sürekli kiriş (c) Konsol
TRİGONMETRİK FONKSİYONLAR: DİK ÜÇGEN YAKLAŞIMI
 TRİGONMETRİK FONKSİYONLAR: DİK ÜÇGEN YAKLAŞIMI Diyelim ki yeryüzünden güneşe lan mesafeyi bulmak istiyruz. Şerit metre kullanmak açıkçası pratik değildir. Bu nedenle bu srunun üstesinden gelmek için basit
TRİGONMETRİK FONKSİYONLAR: DİK ÜÇGEN YAKLAŞIMI Diyelim ki yeryüzünden güneşe lan mesafeyi bulmak istiyruz. Şerit metre kullanmak açıkçası pratik değildir. Bu nedenle bu srunun üstesinden gelmek için basit
Rijit cisim mekaniği, diyagramdan da görüldüğü üzere statik ve dinamik olarak ikiye ayrılır. Statik dengede bulunan cisimlerle, dinamik hareketteki
 Rijit cisim mekaniği, diyagramdan da görüldüğü üzere statik ve dinamik olarak ikiye ayrılır. Statik dengede bulunan cisimlerle, dinamik hareketteki cisimlerle uğraşır. Statik, kuvvet etkisi altında cisimlerin
Rijit cisim mekaniği, diyagramdan da görüldüğü üzere statik ve dinamik olarak ikiye ayrılır. Statik dengede bulunan cisimlerle, dinamik hareketteki cisimlerle uğraşır. Statik, kuvvet etkisi altında cisimlerin
SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering
 SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering İNM 212 YAPI STATİĞİ I STABİLİTE STATİKÇE BELİRSİZLİK KİNEMATİK BELİRSİZLİK Y.DOÇ.DR. MUSTAFA KUTANİS kutanis@sakarya.edu.tr
SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering İNM 212 YAPI STATİĞİ I STABİLİTE STATİKÇE BELİRSİZLİK KİNEMATİK BELİRSİZLİK Y.DOÇ.DR. MUSTAFA KUTANİS kutanis@sakarya.edu.tr
