SAYISAL ÜRETİLMİŞ, YA DA SAYISALLAŞTIRILMIŞ PAFTALAR ÎLE UYGULAMALAR
|
|
|
- Erdem Kızılkaya
- 9 yıl önce
- İzleme sayısı:
Transkript
1 20 SAYISAL ÜRETİLMİŞ, YA DA SAYISALLAŞTIRILMIŞ PAFTALAR ÎLE UYGULAMALAR Ahmet YAŞAYAN. GİRİŞ Büyük ölçekli haritaların alışılmış yöntemlerle üretiminde, arazide uygulama amacı ile de kullanılabilecek poligon vb. sabit noktalar bulunur. Uygulamada karşılaşılacak sorunlar bu noktalar yardımı ile çözümlenir. Bu noktalar kaybolmuş olsa da röperleri yardımı ile yeniden tesis edilebilir. Sayısal yöntemlerle üretilmiş paftalarda bu tür noktalar yeteri sıklıkta bulunmayabilir. Fotogrametrik yöntemle üretilmiş büyük ölçekli haritalarda, örneğin, uygulama amacı ile kullanılabilecek koordinatı bilinen poligon benzeri nokta sayısı yetersizdir. Buna karşılık tüm ayrıntı noktalarının koordinatları vardır. Güncelleştirme, yenileme, iyileştirme ya da bilgi sistemleri için geometrik bir altlık oluşturma amacı ile, eski paftaların sayısallaştırilması durumunda da yine ölçme ve uygulama çalışmalarında kullanılabilecek yeteri sıklıkta sabit nokta bulunmayabilir. Yakın çevrede çok sayıda koordinatları bilinen noktaların bulunması, teorik olarak, koordinatları bilinen yeni noktaların üretilmesine olanak verir. Bu yeni üretilen noktalar sayısal haritaya eklenecek noktalar olabilir. Ya da koordinatları bilinen proje noktalarının araziye uygulanmasını sağlayacak noktalardır. Bu yazı çerçevesinde, klasik ölçme bilgisi uygulamalarından farklı olarak, yakın çevrede koordinatları bilinen noktalardan yeni noktalar nasıl üretilebilir konusu irdelenecektir. Bu tür ölçme problemlerinde elbette pratik sorunlar ve güçlükler de söz konusudur. Örneğin, koordinatları bilinen noktalar nirengi ve poligon noktaları gibi belirgin hedef noktaları değildir. Fotogrametrik" üretilmiş paftalardaki çatı olayı diğer bir pratik güçlük örneğidir. Konu, teorik bir temel üzerinde ele alınacağı için pratik sorunlar bu incelemenin dışında tutulmuştur. PROBLEMİN TANIMI Poligon noktalarına dayalı konum saptama yöntemleri, Şekil 1, Şekil 2 ve Şekil 3'te gösterilmiştir. Çok iyi bilinen alışılmış bu yöntemler şu biçimde sınıflandırılır: 1. Kutupsal Yöntem : Her tür takeometre ile uygulanan ölçme yöntemidir. Koordinatı bilinen sabit noktaya takeometre kurulur. Koordinatı bilinen diğer bir noktaya göre doğrultu saptandıktan sonra tüm ayrıntı noktalarına olan doğrultular ve eğik uzaklıklar ölçülür. Düşey açı ölçüleri yardımı ile eğik uzaklıklar ölçülür. Düşey açı ölçüleri yardımı île eğik uzaklıklar yatay uzaklığa dönüştürülür. Alet kurulan noktadan doğrultu alman sabit noktaya olan kuzey açısı bulunduktan sonra problem jeodezik temel probleme dönüşür. Kuzey açısı ve yatay uzaklığı bilinen bir noktanın koordinat farkları, dolayısıyle koordinatları bulunur.
2 Aynnü noktalarından bu ölçü doğrularına, prizma ile, dikler düşülür. Dik ayaklan ve dik boylan ölçülür. Ayrıntı noktalarının koordinatları "Yan Nokta Hesabı" yöntemine göre bulunur. Bu hesap, temelde, üç parametreli bir ortogonal dönüşümdür. Son noktanın ölçü değerleri de kullanılırsa bu hesap dört parametreli bir benzerlik dönüşümüdür. Dönüşüm parametreleri bulunduktan sonra, tüm ayrıntı noktalannın koordinattan dönüşüm formülleri uygulanarak bulunur. 3. Kesiştirme Yöntemleri: Koordinatı bilinen iki noktadan doğrultular Ölçmek ve bunları kesiştirmek suretiyle de konum saptanabilir. (Şekil 3a). İlerden kestirme yöntemi olarak pratikte uzun süre uygulanmıştır. Diğer bir kesiştirme yöntemi de, koordinattan bilinen iki noktadan yatay uzaklıktan ölçerek uygulanır. (Şekil 3b). Bağlama Yöntemi adı verilen bu yöntem ile de aynnü noktalannın koordinatları bulunabilir. Elektronik takeometrelerdeki son gelişmeler ayrıntı ölçmelerinde sonucun kolayca elde edilmesi ve duyarlılığın arttınlması doğrultusunda olmaktadır. Bu eğilim, kutupsal yöntemin yakın gelecekte diğer yöntemlerin yerini alacağını göstermektedir. Bununla birlikte, burada böyle bir aynım yapılmaksızın sayılan yöntemler uygulanan yöntemler olarak varsayılmıştır. Doğrultularla kesiştirme yöntemi dışında, bu aynntı ölçme ve konum belirleme yöntemleri, noktalann araziye uygulanmasında da söz konusudur. 21
3 22 Sayısal haritalar ile çalışırken problem, klasik ölçme bilgisindeki ayrıntı alımından ya da uygulamasından farklıdır. Ayrıntı noktalarının koordinatları bilinmekte, buna karşılık üzerine alet kurulan noktanın, ya da oluşturulan ölçü doğrularının konumları bilinmemektedir. Kesiştirme yöntemindeki iki noktanın oluşturduğu doğru parçası da ölçü doğrusu olarak düşünülebilir. Kısaca, bilinen ve bilinmeyen noktalar yer. değiştirmiştir. Alışılmış ölçme bilgisi problemlerinin tersine bir durum ortaya çıkmaktadır. Bu nedenle, bu tür ölçme problemlerine invers (ters) ölçme problemleri olarak bakılabilir. Şekil 4, Şekil 5 ve Şekil 6 ; Şekil 1, Şekil 2 ve Şekil 3 ile bağlantılı olarak invers problemleri göstermektedir. Şekil 5'in dışında, diğerleri, ölçme bilgisinde çok iyi bilinen kestirme problemleridir. Bu problemler çeşitli yollarla kolayca çözülür. Gereğinden fazla ölçünün bulunması da problemin çözümüne bir güçlük getirmez. Tersine, ölçmelerde gereğinden bir fazla ölçünün bulunması kaçınılmaz bir zorunluluktur. Ölçü artı düzeltilmesi eşittir bilinmeyen koordinatların fonksiyonu olarak düşünülür. Düzeltmelerin karelerinin toplamı minimum olacak bir çözüm yapılır. En Küçük Kareler Dengelemesi adı ile bilinen bu yaklaşım ile, teorik olarak, aranılan büyüklüklere daha iyi ulaşılır. Daha da ötesi, standart bir çözüm oluşturulur. Aynı ölçü verileri ile değişik hesaplayıcılar, ya da değişik hesaplama programlan aynı sonuçlan verir. Ölçüler için bir stokastik model söz konusu ise çözüm sırasında dikkate alınabilir. Örneğin, doğrultu ve kenar ölçmelerinin farklı duyarlıkları hesaplama sırasında gözönünde tutulabilir. Çıkış alman noktaların (dayanak noktalannm) stokastik özellikleri biliniyorsa, söz gelişi, bu noktaların koordinat ortalama hatalan verilmişse dengeleme hesabında dikkate alınabilir. Kısaca, Şekil 5'in dışındaki invers problemler, teorik olarak çok iyi bilinen kestirme problemlerine benzemektedir. Ne var ki kestirme problemleri kontrol noktalan ölçümleri için düşünülmüş ve geliştirilmiş problemlerdir. Burada ele alınan invers ölçme problemleri ise, klasik kestirme problemlerinden oldukça farklıdır. En azından, soruna teorik olarak farklı bakılmasını zorunlu kılan şu farklann altı çizilebilir:. Noktalar kümesinin bulunduğu alan bakımından farklılık vardır. Kestirmelerde bir kaç yüz metre, ya da bir kaç km'lik uzaklıklar söz konusu iken ele alınan invers problemlerde üç-beş on metrelik uzaklıklar söz konusudur. Bu nedenle açı ölçü duyarlıklarının sonuca etkisi oldukça farklıdır.. Dayanak noktalannm duyarlıklıklan farklıdır. Kestirmelerde bu noktaların duyarlılıklan hakkında bilgiler sağlanabilir. Ya da bunlara ilişkin geçerli varsayımlar ileri sürülebilir. Söz gelişi bu noktalann hatasız olduğu varşayılabilir. Oysa invers problemlerde dayanak noktalannm duyarlıklan konusunda hesaplarda dikkate alınabilecek düzeyde sağlam bir bilgi bulunmaz; benzeri bir varsayım da geçerli olamaz.
4 23 Şekil 6- Kesiştirme Yöntemleri (İnvers problem) a) Doğrultularla, b) Uzunluklarla. Dayanak noktalarının duyarlıkları ile ölçülerin duyarlıkları arasındaki göreceli durum farklıdır. Kestirmelerde, dayanak noktalan ölçülere göre daha duyarlı, ya da aynı duyarlık düzeyindedir. İnvers problemde ise ölçüler her durumda dayanak noktalarından daha duyarlıdır. Durumun daha iyi açıklanabilmesi için şu örnek verilebilir: Koordinat ortalama hataları 1 m düzeyinde olan noktalardan çıkış alınarak bir kestirme probleminin çözümü düşünülsün. Dengeleme hesabından bu noktaların hatalı olduğu varsayılırsa, bu noktaların koordinatları ile ilgili ağırlık katsayıları küçük olacaklarından gerçek ölçülere getirilecek düzeltmelere fazla bir etkisi olmayacaktır. Buna karşılık bu noktalara getirilecek düzeltmeler büyük olacaktır. Ancak, dayanak noktalarının elde edilen koordinatları geliştirilmiş ve kuşkusuz gerçeğe daha yakın olacaktır. Dayanak noktalarının konumu bir tartışma konusu olmayacaksa, yani yeni koordinatlar kullanılmayacaksa, bu noktalara getirilecek düzeltmelerin de pratik bir anlamı olmayacaktır. Dayanak noktalarının koordinatları ölçü duyarlığı düzeyinin çok üstünde olmasına karşılık kestirme hesabında hatasız olarak varsayılır ve dengeleme hesabı da bu varsayıma dayandınlırsa, bu kez de ölçülere büyük ve anlamsız düzeltmelerin getirilmesi kaçınılmazdır. Bu örnekteki sorun, üç-beş cm duyarlığmdaki ölçmelere karşılık 1 m dolayındaki dayanak noktalan arasındaki duyarlık farklılığından ileri gelmiştir. învers problemlerde de durum bu örneğe benzemektedir. Bir-iki dm duyarlığındaki dayanak noktalarına karşılık bir-iki cm duyarlığında ölçüler söz konusu olmaktadır. Bu irdelemeler, Şekil 4 ve Şekil 6'daki problemlere ölçme bilgisindeki klasik kestirme problemleri olarak ele alınmasının uygun olmayacağını göstermektedir. PROBLEMİN ÇÖZÜMÜ Şekil 4, Şekil 5 ve Şekil 6'daki ölçme problemlerine, duyarlık düzeyleri farklı iki ölçü kümesi olarak bakılabilir. Dayanak noktalan kümesi ile buna göre duyarlıktan çok yüksek olan yeni ölçmelerden elde edilen noktalar kümesi. Öyleyse problem, duyarlık düzeyleri farklı iki sistemin birbirine uyuşturulması sorunudur. Çok daha duyarlı ölçme sisteminin bütünlüğünü bozmadan, dayanak noktalanndan oluşan çerçeve ile en iyi uyuşum sağlanmalıdır. Böyle bir uyuşum için iki öteleme ve bir dönüklük olmak üzere üç hareket serbestliği yeterlidir. Bu da ortogonal dönüşüm ile gerçekleştirilebilir. En iyi uyuşum, dönüşümden sonra dayanak noktalanndaki artık hatalann, ya da aykırılıklara!, karelerinin toplamının mi-
5 24 nünüm yapılması ile sağlanabilir. Üç parametreli ortogonal dönüşüm yerine parametreli benzerlik dönüşümü de uygulanabilir. Dördüncü parametre ölçektir. Ölçek düzeltmesi, ölçme sisteminin bütünlüğünü bir ölçüde zedeleyebilir ise de ortogonal dönüşüm yerine benzerlik dönüşümünün alınmasında şu pratik yararlar olabilir:. Ortogonal dönüşüm formüllerinde dönüklüğün sinüsü ve cosinüsü geçmektedir. Bu nedenle çözüme elverişli değildir. Buna karşılık benzerlik dönüşümü çok iyi bilinen ve her zaman uygulanan bir dönüşümdür.. Her iki ölçü sistemi arasında bir ölçek farklılaşmasının varsayımı gerçeğe aykırı değildir.. Dayanak noktalarının bulunduğu alanda kısmi bir sistematik hata söz konusu olabilir. Bu sistematik hatanın bir bölümü de ölçek parametresi ile giderilebilir. Tüm dayanak noktalarının bir miktar ötelenmiş olması durumunda bu kısmi sistematik hatanın dönüşüm sırasında öteleme parametreleri yardımı ile giderilcbildiği gibi, ölçek parametresi de böyle bir kısmi düzenli ölçek hatasını etkisizleştirebilir. Bilindiği gibi, benzerlik dönüşümü formülleri X=ax-by+c Y=bx+ay+d (1) biçimindedir. Dönüşüm parametreleri a,b,c,d; sırası ile, k cos 9, k sin 0, X o ve Y o büyüklükleridir. Ölçek katsayısı k, k = (a 2 + b 2 ) ^ ve 0 dönüklük açısı da 0 = arc tan (b/a) dır. x,y koordinat sisteminin başlangıç noktasının X,Y sistemindeki koordinatları X o, Y o dır Dönüşüm parametreleri her iki sistemde de koordinatları bilinen noktalar (ortak noktalar, özdeş noktalar) yardımı ile hesaplanır. İkiden fazla ortak nokta ile bu parametreler En Küçük Kareler Yöntemi ilkesine göre bulunur. Düzeltme (hata) denklemleri ve normal denklemler oluşturularak dört bilinmeyen parametreyi bu dört normal denklemden hesaplamak yerine, ilk kez Helmert tarafından uygulanan ve bu yüzden kendi adı ile anılan bir hesaplama biçimi uygulanır. Bunun için önce ortak noktalar kümesinin her iki koordinat sisteminde de ağırlık merkezleri (x g y g ) (X g Y g ) bulunur. Daha sonra ortak noktalar, yine her iki sistemde de başlangıçları bu ağırlık merkezleri olacak biçimde ötelenir. Böylece üstü çizgilerle gösterilen ötelenmiş koordinatlar bulunur: 5q = xi-xg ) yt=yi-y g, Xj= Xj - X gı Yj = Yİ - Yg. Bu önlem dört bilinmeyenli normal denklem çözümünü ortadan kaldırır. Parametreler, ötelenmiş koordinatlarla aşağıdaki formülleri uygulayarak kolayca bulunur.
6 25 (1) dönüşüm formüllerindeki X, Y koordinatları dönüştürülecek sistemdeki koordinatlardır. Bu koordinatlar sayısal üretilmiş, ya da sayısallaştırılînış pafta koordinattandır. Bu sistem ülke koordinat sistemi olabileceği gibi yerel koordinat sistemi de olabilir. Her iki durumda da X ekseni kuzeye, Y eksenidc doğuya yönelmiştir. Bu bir sol sistemdir. X ekseninden başlayarak saat yönünde 90 lik bir açısal hareketle, yani kısa yoklan Y eksenine ulaşılır. x, y koordinatları ise, yeni ölçü sisteminde noktaların tanımlanacağı koordinat sistemidir. Bu sistem serbestçe seçilebilecektir. Ne var ki bu eksen sisteminin, (1) dönüşüm formülleri gereği, X, Y koordinat sistemi ile çakışabilir olması gerekir. Başka bir deyişle bu eksen sisteminin de bir sol sistem olması zorunludur. x, y koordinat sisteminin başlangıç noktasının özel bir konumda seçilmesinin pratik yararı vardır. Örneğin, Şekil 4'lcki A noktasının x,y koordinat sisteminin başlangıç olarak alınması, diğer noktaların (1,2,3,4) x,y koordinatlarının hesaplanmasını kolaylaştırır. Diğer yandan, bu noktanın dönüştürülmüş koordinatları, (1) dönüşüm formüllerinden de hemen görüleceği gibi, c ve d öteleme elemanlarına eşit olur. x ekseni herhangi bir doğrultu ile çakıştırılabilir. Bu eksen seçildikten sonra da, y ekseninin pozitif yönü, X,Y koordinat sisteminde olduğu gibi, saat yönünde ve kısa yoldan bu eksene ulaşacak biçimde alınmalıdır. Söz gelimi, Şekil 5'teki x ekseninin yönü A noktasından B noktasına pozitif olacak şekilde alınırsa, y ekseninin pozitif yönü de sağa doğru artacaktır. Ölçü doğrusu y ekseni olarak alınır ve pozitif yönü de yine A noktasından B noktasına doğru alınırsa, x ekseninin pozitif yönü sola doğru alınacaktır. Sonuç olarak, Şekil 4, Şekil 5 ve Şekil 6'daki yöntemlerle yapılan ölçmeler ve verilen dayanak noktaları koordinatları yardımı ile yeni noktalann koordinatları aşağıdaki işlem adımlan ile ve tek anlamlı olarak elde edilecektir: - Ölçülen noktaların bir koordinat sisteminde tanımlanabilmesi için, X,Y koordinat siste mi ile çakışabilir bir x,y koordinat sisteminin seçilmesi, - Ölçülen büyüklükler yardımı ile dayanak noktalarının ve varsa diğer noktaların x,y koor dinatlarının hesaplanması, - (2) formülleri ile dönüşüm parametrelerinin bulunması ve (1) dönüşüm formülleri ile noktaların koordinatlarının dönüşümü. SAYISAL ÖRNEKLER Önerilen çözüm yönteminin daha kolay anlaşılmasını sağlamak amacı ile Şekil 4, Şekil 5, Şekil 6a ve Şekil 6b'de gösterilen ölçme yöntemlerine uygun sayısal örnekler düzenlenmiştir. Bu sayısal örneklerde aynı noktalar kümesi kullanılmıştır. Bu noktaların nominal koordinatlarına göre ölçü büyüklükleri oluşturulmuş; 1,2,3 ve 4 numaralı dayanak noktalarının koordinatlarına, standart sapması 9 ve maksimum halası 15 cm olan koordinat hata-
7 26 lan eklenmiştir. Böylece yaklaşık 1 dm doğruluğunda sayısal harita verileri oluşturulmuştur. Sayısal Örnek 1 -^Kutupsal Yöntem Şekil 7'de gösterilen noktalara ilişkin ölçüler ve veriler Çizelge 1'dedir. x,y koordinat sisteminin başlangıcı A noktası alınmıştır. Hesaplama kolaylığı için, x ekseni, yatay doğrultuların başlangıç doğrusu ile çakıştınlmıştır. x,y koordinat sistemi Şekil 7'de gösterilen biçimde alındığı için 1,2,3,4 ve B noktasının x,y koordinatları, sıra ile, (s cos«0 ve (s sin c) dır. Bu koordinatlar: x=s cos <= y=s sin g B
8 1,2,3 ve 4 dayanak (ortak) noktalan ile benzerlik dönüşümü parametreleri hesaplanırsa aşağıdaki değerler bulunur: 27 a = b = c = d = A noktasının koordinatları, x,y eksen sisteminin başlangıcı bu nokta alındığı için, c ve d'ye eşittir. B noktasının koordinatlan da bu parametrelerle dönüşüm yapılarak elde edilir. Aşağıda A ve B noktalannın hesaplanan koordinatlan verilmiştir. Dayanak noktalannın dönüştürülmüş koordinatları ile verilen koordinatlar arasındaki farklar (aykırılıklar) da hesaplanarak şu değerler bulunur: V X V Y m o = Sayısal Örnek 2- Ortogonal Yöntem Şekil 8'de ortogonal ölçü krokisi verilmiştir. x,y koordinat sistemi Şekil 8'de gösterildiği gibi seçilirse, dik ayaklan ve dik boylan doğrudan doğruya x,y koordinaüandır. Bu koordinatlar ve dayanak noktalannın verilen koordinatlan Çizelge 2'de gösterilmiştir.
9 28 Çizelge 2- Ortogonal yöntem, ölçüler ve veriler 1,2,3 ve 4 dayanak (ortak) noktaları ile benzerlik dönüşümü parametreleri hesaplanırsa aşağıdaki değerler bulunur: a = b = e = d = Bu parametrelerle ve B noktasının x,y koordinatları ile dönüşüm yapılırsa B noktasının X,Y koordinatları elde edilir. A noktasının X,Y koordinatları ise, x,y koordinat sisteminin başlangıcı olması nedeni ile c ve d'ye eşittir. X Y A B Dayanak noktalarındaki aykırılıklar hesaplanırsa şu değerler bulunur: V X V Y m o =
10 29 Sayısal Örnek 3- Doğrultularla Kesiştirme Yöntemi Şekil 9'da ölçülerin durumu gösterilmiştir. x,y koordinat sis teminin başlangıç noktası A nol tası alınmıştır. AB doğru parças bu kez y ekseni olarak seçilmiştir. x ekseni de buna uygun olacak biçimde alınmıştır. Ölçü değerleri ve veriler Çizelge 3'te gösterilmiştir. Şekil 9 Çizelge 3 - Doğrultularla kesiştirme, ölçüler ve veriler Ölçülen doğrultular yardımı ile i (i = 1,2,3,4) dayanak noktalarının A,B, noktalan ile oluşturdukları üçgenlerin A ve B noktalarındaki İAB İBA açılan kolayca bulunabilir. A noktasındaki bu açılar, sıra ile, 44.96, 25.24, 18.89, grattır. B noktasındaki açılar da, yine sıra ile 25.10,20.48,65.01, dır. Bu üçgenlerin AB tabanı m ölçülen büyüklük olarak verildiğine göre ve A,B taban açılan bilindiğine göre, sinüs teoreminden Ai kenarları hesaplanabilir. Bu kenarlar da, sıra ile, 14.09,15.71,28.80, olarak bulunur. i dayanak noktalanna ait Ai doğrultularının x ekseni ile yaptığı açılan ise, y ekseni AB doğrusu ile çakışık olarak alındığından, A noktasındaki taban açüannı 100 grattan çıkararak, ya da bu açılara 100 grat ekleyerek bulunabilir, bu açılar sıra ile, 55.04, , 81.11, grattır. Hesaplanan bu ara büyüklükler ile x,y koordinattan aşağıdaki gibi kolayca bulunabilir.
11 30 Nokta Doğrultu Kenar s cos = s sin «= (<*) (s) x y B ,23 ve 4 dayanak noktalan ile benzerlik dönüşümü parametreleri hesaplanırsa şu değerler bulunur: a = b = c = d = B noktasının koordinatları da bu parametrelerle dönüştürülerek elde edilir. A noktasının koordinatları, c ve d'ye eşittir. Aşağıda bu koordinatlar ve dayanak noktalarındaki aykırılıklar verilmiştir. X Y_ A B Sayısal Örnek 4- Bağlama Yöntemi V X V Y m o = Şekil 10'da Bağlama Yöntemine göre ölçülen kenarlar gösterilmiştir. x,y koordinat sistemi, bu örnekte de bir öncekinde olduğu gibi seçilmiştir. Çizelge 4'te ölçülen uzunluk değerleri ile dayanak noktalarının koordinatları verilmiştir.
12 Bu problemde de, x,y koordinatlarının bulunabilmesi için, önce iab üçgenlerinin A noktasındaki açılarının bulunması gerekir. Bu açılar, üç kenarı bilinen bir üçgende, cosinüs teoremi uygulayarak bulunabilir. A ve B noktalarından ölçülen uzaklıklar ile AB uzunluğu verildiğine göre, bu açılar için şu değerler bulunur : 44.95, 25.28, 18.91, grat. Dayanak noktalarına giden doğrultuların x ekseni ile yaptığı alfa açılan da, bir önceki örnekte olduğu gibi, hesaplanan A noktasındaki açılan 100 grattan çıkararak, ya da 100 grat ekleyerek elde edilir. Bulunan alfa açıları ve ölçülen uzunluklar yardımı ile de, dayanak noktalanmn ve B noktasının x,y koordinatları kolayca hesaplanabilir. 31 Nokta Doğrultu Kenar s cos = s sin = W; 00 x y B ,2,3 ve 4 dayanak noktaları ile benzerlik dönüşümü parametreleri hesaplanırsa şu değerler bulunur: a = b= c= d= Koordinat sisteminin başlangıcı olarak alındığından A noktasının koordinatlan c ve d'ye eşittir. B noktasının koordinatlan ise dönüşüm yapılarak bulunur. Bu koordinatlar ve dönüşümden sonra dayanak noktalarındaki ayknılıklar aşağıda gösterilmiştir. X Y V X A B m o = Sayısal örneklerden de görüldüğü gibi, ölçme bilgisi ve jeodezik hesap bilgileri kullanılarak yeni ölçü değerleri ile tüm noktalar uygun bir koordinat sisteminde tanımlanmaktadır. Dayanak noktalarının yeni sistemdeki koordinatlan ile verilen koordinatlan yardımı ile bir benzerlik dönüşümü uygulanmaktadır. Örneklerde benzerlik dönüşümü parametrelerinin bulunması ayrıntılı olarak gösterilmiştir. Bilindiği, ya da bir hesaplama programının bulunduğu varsayılmıştır. Parametreler bulunduktan sonra, (1) dönüşüm formülleri uygulanarak noktalann dönüştürülmüş koordinatlan elde edilmektedir. Dayanak noktalanmn dönüştürülmüş koordi- V Y
13 32 nadan ile verilen koordinatları arasındaki farklar-aykırüıklar-bu noktaların duyarlılığı ve niteliği konusunuda bilgi vermektedir. İRDELEME-DEĞERLENPtRME Invers ölçme problemlerinin çözümü için burada önerilen yöntem şu ilkeye dayanmaktadır: Yeni ölçme sistemi kendi içinde değişmez bir bütündür. Bu bütün çevresi ile eniyi biçimde uzlaştınlacaktır. İnvers problem deyimi, alışılmışın tersine alet kurulan noktanın, ya da oluşturulan ölçü doğrusunun iki ucunun koordinatlarının bilinmemesi, buna karşılık ayrıntı noktalarının koordinatlarının bilinmesi durumunu ifade etmektedir. Eniyi uzlaşma, aykırılıkların karelerinin toplamının minimum yapılması anlamına gelir. Bu ilke şu şekilde gerçekleştirilmektedir: yeni ölçü değerleri yardımı ile tüm noktalar uygun bir koordinat sisteminde tanımlamakta, koordinatları bilinen ayrıntı noktalan-dayanak noktaları-yardımı ile bir benzerlik dönüşümü yapılarak noktaların pafta koordinatları elde edilmektedir. Bu ilke, tüm ayrıntı ölçme yöntemlerine uygulanabilir. Tek anlamlı çözüme ulaşılmaktadır. Öyleyse, ilkeli bu yaklaşım standart bir çözüm yöntemi olarak kabul edilebilir ve uygulanabilir. Yeni ölçü sonuçlarının değişmez bir bütün olarak alınması, pratik olarak yeni ölçülerin hatasız olması anlamına gelir. Ayrıntı noktalarının koordinatlarının duyarlığı 1-2 cm düzeyindeki yeni ölçmelerin duyarlığı oldukça yüksektir. Bu nedenle, yeni ölçülerin hatasız olarak alınması isabetsiz bir varsayım değildir. İster sayısal üretilmiş ve ister sayısallaştınlmış paftalar olsun, ayrıntı noktalarının duyarlılığı, en çok 1 dm düzeyindedir. Aynca, bu noktaların arazide tanınması en iyimser kestirîmle 3-5 cm düzeyindedir. Bu belirsizliğin de noktaların güvenilirlilik sınırlarını genişleteceği kuşkusuzdur. Bu incelemede problem basitleffirilerek, bir ölçü noktası, ya da bir ölçü doğrusu ile dört dayanak noktasından oluşan küçük ölçü birimleri ele alınmıştır. Daha çok sayıda ölçü noktası ve ölçü doğrusu olması durumunda da, önerilen ilke hiç bir güçlükle karşılaşmaksızm uygulanabilir. Geniş ölçü alanlarının söz konusu olması durumunda, problem birbirinden bağımsız parcçalara ayrılarak çözülebileceği gibi, daha büyük bir bütün oluş turularak da çözülebilir. Söz gelimi, A,B,C,D, noktalarından oluşan bir poligon di zisinden ölçüler yapılmış olabilir. B,C,D... noktalarındaki kırılma açılan da ölçül düğü için bu diziyi tüm dayanak noktaları ile birlikte bir bütün olarak almak kaçınılmazdır. Çok sayıda dayanak noktası ile dönüşüm yapmak problem oluyorsa, ya bu noktalardan bir kısmını çıkararak, ya da bütünü bindirmeli parçalara ayırarar çözüm yapmak düşünülebilir. Dayanak noktalarındaki aykırılıklar, bu noktaların koordinatlarının bağıl doğruluğu ve bunların tanınmasındaki belirsizlikle doğrudan ilgilidir. Öyleyse, belirgin ayrıntı noktalan kullanılarak, sayısal üretilmiş, ya da sayısallaşünlmış paftalara! geometrik nitelikleri bu yöntemle denetlenebilir; duyarlık düzeyleri saptanabilir. Dayanak noktalarından birinin koordinatları hatalı ise, dönüşüm sonucunda, bu noktada beklenenden büyük bir aykırılık ortaya çıkar. Doğal olarak bu hatalı koordinatın A,B,
KADASTRO HARİTALARININ SAYISALLAŞTIRILMASINDA KALİTE KONTROL ANALİZİ
 KADASTRO HARİTALARININ SAYISALLAŞTIRILMASINDA KALİTE KONTROL ANALİZİ Yasemin ŞİŞMAN, Ülkü KIRICI Sunum Akış Şeması 1. GİRİŞ 2. MATERYAL VE METHOD 3. AFİN KOORDİNAT DÖNÜŞÜMÜ 4. KALİTE KONTROL 5. İRDELEME
KADASTRO HARİTALARININ SAYISALLAŞTIRILMASINDA KALİTE KONTROL ANALİZİ Yasemin ŞİŞMAN, Ülkü KIRICI Sunum Akış Şeması 1. GİRİŞ 2. MATERYAL VE METHOD 3. AFİN KOORDİNAT DÖNÜŞÜMÜ 4. KALİTE KONTROL 5. İRDELEME
KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ
 KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ Doç. Dr. İsmail Hakkı GÜNEŞ İstanbul Teknik Üniversitesi ÖZET Küresel ve Elipsoidal koordinatların.karşılaştırılması amacı ile bir noktasında astronomik
KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ Doç. Dr. İsmail Hakkı GÜNEŞ İstanbul Teknik Üniversitesi ÖZET Küresel ve Elipsoidal koordinatların.karşılaştırılması amacı ile bir noktasında astronomik
ARAZİ ÖLÇMELERİ. Temel Ödev I: Koordinatları belirli iki nokta arasında ki yatay mesafenin
 Temel ödevler Temel ödevler, konum değerlerinin bulunması ve aplikasyon işlemlerine dair matematiksel ve geometrik hesaplamaları içeren yöntemlerdir. öntemlerin isimleri genelde temel ödev olarak isimlendirilir.
Temel ödevler Temel ödevler, konum değerlerinin bulunması ve aplikasyon işlemlerine dair matematiksel ve geometrik hesaplamaları içeren yöntemlerdir. öntemlerin isimleri genelde temel ödev olarak isimlendirilir.
Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi
 JEODEZİ 6 1 Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi Jeodezik gözlemler, hesaplamalarda kullanılmadan önce, referans elipsoidin yüzeyine indirgenir. Bu işlem, arazide yapılan gözlemler l jeoidin
JEODEZİ 6 1 Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi Jeodezik gözlemler, hesaplamalarda kullanılmadan önce, referans elipsoidin yüzeyine indirgenir. Bu işlem, arazide yapılan gözlemler l jeoidin
TOPOĞRAFYA Temel Ödevler / Poligonasyon
 TOPOĞRAFYA Temel Ödevler / Poligonasyon Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Temel Ödevler / Poligonasyon Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
Tanımlar, Geometrik ve Matemetiksel Temeller. Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ. JDF329 Fotogrametri I Ders Notu
 FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İzdüşüm merkezi(o):
FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İzdüşüm merkezi(o):
deniyle - birden çok aletin aynı anda bir tek derleme bilgisayarmca denetlenmesi bazı aksakıklara neden olmaktadır.
 deniyle - birden çok aletin aynı anda bir tek derleme bilgisayarmca denetlenmesi bazı aksakıklara neden olmaktadır. 7) Fotogrametrik modellerden harita üretim amacına yönelik olarak derlenen veriler, mikrobilgisayarların
deniyle - birden çok aletin aynı anda bir tek derleme bilgisayarmca denetlenmesi bazı aksakıklara neden olmaktadır. 7) Fotogrametrik modellerden harita üretim amacına yönelik olarak derlenen veriler, mikrobilgisayarların
Fotogrametride işlem adımları
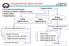 Fotogrametride işlem adımları Uçuş planının hazırlanması Arazide yer kontrol noktalarının tesisi Resim çekimi Değerlendirme Analitik değerlendirme Dijital değerlendirme Değerlendirme Analog değerlendirme
Fotogrametride işlem adımları Uçuş planının hazırlanması Arazide yer kontrol noktalarının tesisi Resim çekimi Değerlendirme Analitik değerlendirme Dijital değerlendirme Değerlendirme Analog değerlendirme
ÖLÇME BİLGİSİ. Sunu 1- Yatay Ölçme. Yrd. Doç. Dr. Muhittin İNAN & Arş. Gör. Hüseyin YURTSEVEN
 ÖÇME BİGİİ unu - atay Ölçme rd. Doç. Dr. Muhittin İNAN & Arş. Gör. Hüseyin URTEVEN COĞRAFİ BİGİ İTEMİNİ OUŞTURABİMEK İÇİN BİGİ TOPAMA ÖNTEMERİ ATA ÖÇMEER (,) ATA AÇIAR VE MEAFEERİN ÖÇÜMEİ ERE ÖÇMEER DÜŞE
ÖÇME BİGİİ unu - atay Ölçme rd. Doç. Dr. Muhittin İNAN & Arş. Gör. Hüseyin URTEVEN COĞRAFİ BİGİ İTEMİNİ OUŞTURABİMEK İÇİN BİGİ TOPAMA ÖNTEMERİ ATA ÖÇMEER (,) ATA AÇIAR VE MEAFEERİN ÖÇÜMEİ ERE ÖÇMEER DÜŞE
Yrd. Doç. Dr. Aycan M. MARANGOZ. BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI
 FOTOGRAMETRİ II FOTOGRAMETRİK DEĞERLENDİRME - TEK RESİM DEĞERLENDİRMESİ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
FOTOGRAMETRİ II FOTOGRAMETRİK DEĞERLENDİRME - TEK RESİM DEĞERLENDİRMESİ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
ARAZİ ÖLÇMELERİ. Koordinat sistemleri. Kartezyen koordinat sistemi
 Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
TAKEOMETRİ GENEL BİLGİLER
 TAKEOMETRİ GENEL BİLGİLER Optik olarak yatay uzunlukların ve yükseklik farklarının klasik teodolit ve mira kullanılarak bulunması yöntemine takeometri adı verilmektedir. Takeometrik yöntemde amaç, bir
TAKEOMETRİ GENEL BİLGİLER Optik olarak yatay uzunlukların ve yükseklik farklarının klasik teodolit ve mira kullanılarak bulunması yöntemine takeometri adı verilmektedir. Takeometrik yöntemde amaç, bir
Uygulamada Gauss-Kruger Projeksiyonu
 JEODEZİ12 1 Uygulamada Gauss-Kruger Projeksiyonu Gauss-Kruger Projeksiyonunda uzunluk deformasyonu, noktanın X ekseni olarak alınan ve uzunluğu unluğu koruyan koordinat başlangıç meridyenine uzaklığının
JEODEZİ12 1 Uygulamada Gauss-Kruger Projeksiyonu Gauss-Kruger Projeksiyonunda uzunluk deformasyonu, noktanın X ekseni olarak alınan ve uzunluğu unluğu koruyan koordinat başlangıç meridyenine uzaklığının
ARAZİ ÖLÇMELERİ. Doğrultuya dik inme veya dik çıkma (Yan Nokta Hesabı) Dik İnmek. A Dik Çıkmak
 Doğrultuya dik inme veya dik çıkma (Yan Nokta Hesabı) P1 P2 Dik İnmek P3 P4 Dik Çıkmak Şekil 76 Şekil 76 da dik inme ve çıkmaya birer örnek gösterilmiştir. Dik çıkmadan anlaşılması gereken belirlenen bir
Doğrultuya dik inme veya dik çıkma (Yan Nokta Hesabı) P1 P2 Dik İnmek P3 P4 Dik Çıkmak Şekil 76 Şekil 76 da dik inme ve çıkmaya birer örnek gösterilmiştir. Dik çıkmadan anlaşılması gereken belirlenen bir
ARAZİ ÇALIŞMASI -1 DERSİ ELEKTRONİK ALETLERİN KONTROL VE KALİBRASYONU UYGULAMALARI
 ARAZİ ÇALIŞMASI -1 DERSİ ELEKTRONİK ALETLERİN KONTROL VE KALİBRASYONU UYGULAMALARI HARİTA MÜHENDİSLİĞİ BÖLÜMÜ ÖLÇME TEKNİĞİ ANABİLİM DALI JEODEZİK METROLOJİ LABORATUVARI İstanbul, 2018 1.ELEKTRONİK TAKEOMETRELERİN
ARAZİ ÇALIŞMASI -1 DERSİ ELEKTRONİK ALETLERİN KONTROL VE KALİBRASYONU UYGULAMALARI HARİTA MÜHENDİSLİĞİ BÖLÜMÜ ÖLÇME TEKNİĞİ ANABİLİM DALI JEODEZİK METROLOJİ LABORATUVARI İstanbul, 2018 1.ELEKTRONİK TAKEOMETRELERİN
ARAZİ ÖLÇMELERİ. Koordinat sistemleri. Kartezyen koordinat sistemi
 Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
DERS 3 ÖLÇÜ HATALARI Kaynak: İ.ASRİ
 Ölçme Bilgisi DERS 3 ÖLÇÜ HATALARI Kaynak: İ.ASRİ Çizim Hassasiyeti Haritaların çiziminde veya haritadan bilgi almada ne kadar itina gösterilirse gösterilsin kaçınılmayacak bir hata vardır. Buna çizim
Ölçme Bilgisi DERS 3 ÖLÇÜ HATALARI Kaynak: İ.ASRİ Çizim Hassasiyeti Haritaların çiziminde veya haritadan bilgi almada ne kadar itina gösterilirse gösterilsin kaçınılmayacak bir hata vardır. Buna çizim
NÎRENÇİ NOKTALARININ ARANMASI
 NÎRENÇİ NOKTALARININ ARANMASI Yazan ; -.. İsmail Hakkı GÜNEŞ 1, '. ' ' (Ankara) Haritaları yapılmış meskun ve meskun olmayan alanlarda bulunamıyan ve taşları kaybolan nirengilerin yeraltındaki sigorta
NÎRENÇİ NOKTALARININ ARANMASI Yazan ; -.. İsmail Hakkı GÜNEŞ 1, '. ' ' (Ankara) Haritaları yapılmış meskun ve meskun olmayan alanlarda bulunamıyan ve taşları kaybolan nirengilerin yeraltındaki sigorta
Fotogrametrinin Optik ve Matematik Temelleri
 Fotogrametrinin Optik ve Matematik Temelleri Resim düzlemi O : İzdüşüm (projeksiyon ) merkezi P : Arazi noktası H : Asal nokta N : Nadir noktası c : Asal uzaklık H OH : Asal eksen (Alım ekseni) P OP :
Fotogrametrinin Optik ve Matematik Temelleri Resim düzlemi O : İzdüşüm (projeksiyon ) merkezi P : Arazi noktası H : Asal nokta N : Nadir noktası c : Asal uzaklık H OH : Asal eksen (Alım ekseni) P OP :
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü TOPOGRAFYA (HRT3351) Yrd. Doç. Dr. Ercenk ATA
 Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü Ölçme Hataları Ölçme Hatası Herhangi bir ölçme aleti ile yapılan ölçüm sonucu bulunan değer yaklaşık değerdir. Bir büyüklük aynı ölçme
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü Ölçme Hataları Ölçme Hatası Herhangi bir ölçme aleti ile yapılan ölçüm sonucu bulunan değer yaklaşık değerdir. Bir büyüklük aynı ölçme
YOL PROJELERİNDE YATAY KURPTA YAPILACAK KÜBAJ HESABININ YENİDEN DÜZENLENMESİ
 YOL PROJELERİNDE YATAY KURPTA YAPILACAK KÜBAJ HESABININ YENİDEN DÜZENLENMESİ Yrd.Doc.Dr. Hüseyin İNCE ÖZET Yol projelerinde yatay kurpta enkesitler arasında yapılacak kübaj hesabında, kurbun eğrilik durumu
YOL PROJELERİNDE YATAY KURPTA YAPILACAK KÜBAJ HESABININ YENİDEN DÜZENLENMESİ Yrd.Doc.Dr. Hüseyin İNCE ÖZET Yol projelerinde yatay kurpta enkesitler arasında yapılacak kübaj hesabında, kurbun eğrilik durumu
Harita Projeksiyonları
 Harita Projeksiyonları Bölüm Prof.Dr. İ. Öztuğ BİLDİRİCİ Amaç ve Kapsam Harita projeksiyonlarının amacı, yeryüzü için tanımlanmış bir referans yüzeyi üzerinde belli bir koordinat sistemine göre tanımlı
Harita Projeksiyonları Bölüm Prof.Dr. İ. Öztuğ BİLDİRİCİ Amaç ve Kapsam Harita projeksiyonlarının amacı, yeryüzü için tanımlanmış bir referans yüzeyi üzerinde belli bir koordinat sistemine göre tanımlı
olmak üzere 4 ayrı kütükte toplanan günlük GPS ölçüleri, baz vektörlerinin hesabı için bilgisayara aktarılmıştır (Ersoy.97).
 1-) GPS Ölçülerinin Yapılması Ölçülerin yapılacağı tarihlerde kısa bir süre gözlem yapılarak uydu efemerisi güncelleştirilmiştir. Bunun sonunda ölçü yapılacak bölgenin yaklaşık koordinatlarına göre, bir
1-) GPS Ölçülerinin Yapılması Ölçülerin yapılacağı tarihlerde kısa bir süre gözlem yapılarak uydu efemerisi güncelleştirilmiştir. Bunun sonunda ölçü yapılacak bölgenin yaklaşık koordinatlarına göre, bir
ARAZİ ÇALIŞMASI -1 DERSİ ELEKTRONİK ALETLERİN KONTROL VE KALİBRASYONU UYGULAMALARI
 ARAZİ ÇALIŞMASI -1 DERSİ ELEKTRONİK ALETLERİN KONTROL VE KALİBRASYONU UYGULAMALARI HARİTA MÜHENDİSLİĞİ BÖLÜMÜ ÖLÇME TEKNİĞİ ANABİLİM DALI JEODEZİK METROLOJİ LABORATUVARI İstanbul, 016 1.ELEKTRONİK TAKEOMETRELERİN
ARAZİ ÇALIŞMASI -1 DERSİ ELEKTRONİK ALETLERİN KONTROL VE KALİBRASYONU UYGULAMALARI HARİTA MÜHENDİSLİĞİ BÖLÜMÜ ÖLÇME TEKNİĞİ ANABİLİM DALI JEODEZİK METROLOJİ LABORATUVARI İstanbul, 016 1.ELEKTRONİK TAKEOMETRELERİN
ARAZİ ÖLÇMELERİ. İki Boyutlu Koordinat sistemleri Arası Dönüşüm
 İki Boyutlu Koordinat sistemleri Arası Dönüşüm Amaç, bir koordinat sistemine göre elde edilmiş olan koordinatların, diğer bir koordinat sistemindeki koordinat değerlerini elde etmektir. İki haritanın koordinat
İki Boyutlu Koordinat sistemleri Arası Dönüşüm Amaç, bir koordinat sistemine göre elde edilmiş olan koordinatların, diğer bir koordinat sistemindeki koordinat değerlerini elde etmektir. İki haritanın koordinat
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü TOPOGRAFYA (HRT3350)
 Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü Ders Adı Kodu Yerel Kredi ECTS Ders (saat/hafta) Uygulama (saat/hafta) Laboratuvar (saat/hafta) Topografya HRT3350 3 4 3 0 0 DERSİN
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü Ders Adı Kodu Yerel Kredi ECTS Ders (saat/hafta) Uygulama (saat/hafta) Laboratuvar (saat/hafta) Topografya HRT3350 3 4 3 0 0 DERSİN
KALINLIK VE DERİNLİK HESAPLAMALARI
 KALINLIK VE DERİNLİK HESAPLAMALARI Herhangi bir düzlem üzerinde doğrultuya dik olmayan düşey bir düzlem üzerinde ölçülen açıdır Görünür eğim açısı her zaman gerçek eğim açısından küçüktür Görünür eğim
KALINLIK VE DERİNLİK HESAPLAMALARI Herhangi bir düzlem üzerinde doğrultuya dik olmayan düşey bir düzlem üzerinde ölçülen açıdır Görünür eğim açısı her zaman gerçek eğim açısından küçüktür Görünür eğim
ÖLÇME BİLGİSİ ALANLARIN ÖLÇÜLMESİ
 ÖLÇME BİLGİSİ ALANLARIN ÖLÇÜLMESİ Doç. Dr. Alper Serdar ANLI 5.Hafta ALANLARIN ÖLÇÜLMESİ Genel bir deyişle herhangi bir arazi parçasının şeklini ve büyüklüğünü belirtecek planın çıkarılabilmesi için gereken
ÖLÇME BİLGİSİ ALANLARIN ÖLÇÜLMESİ Doç. Dr. Alper Serdar ANLI 5.Hafta ALANLARIN ÖLÇÜLMESİ Genel bir deyişle herhangi bir arazi parçasının şeklini ve büyüklüğünü belirtecek planın çıkarılabilmesi için gereken
Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre
 Jeodezi 7 1 Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre Elipsoid yüzeyinin küçük parçalarında oluşan küçük üçgenlerin (kenarları 50-60 km den küçük) hesaplanmasında klasik jeodezide
Jeodezi 7 1 Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre Elipsoid yüzeyinin küçük parçalarında oluşan küçük üçgenlerin (kenarları 50-60 km den küçük) hesaplanmasında klasik jeodezide
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
Yrd. Doç. Dr. Aycan M. MARANGOZ. BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI
 FOTOGRAMETRİ II FOTOGRAMETRİK NİRENGİ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/ İÇERİK Giriş Yer Kontrol Noktaları
FOTOGRAMETRİ II FOTOGRAMETRİK NİRENGİ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/ İÇERİK Giriş Yer Kontrol Noktaları
Âna nirengi doğrultuları için p = 1 m 2 o Ara nirengi doğrultuları için p a =------------ m\
 4. ÖLÇÜLERİN AĞIRLIKLARININ SAPTANMASI Ana, ara ve tamamlayıcı nirengi doğrultularının herbiri gruplar halinde ele alınarak bunların ortalama hatalarının öncül (a priori) değerleri, üçgen kapanmalarından
4. ÖLÇÜLERİN AĞIRLIKLARININ SAPTANMASI Ana, ara ve tamamlayıcı nirengi doğrultularının herbiri gruplar halinde ele alınarak bunların ortalama hatalarının öncül (a priori) değerleri, üçgen kapanmalarından
ARAZİ ÖLÇMELERİ Z P. O α X P. α = yatay açı. ω = düşey açı. µ =eğim açısı. ω + µ = 100 g
 Trigonometrik Fonksiyonlar Z Z P P ω µ P O α α = yatay açı P P ω = düşey açı µ =eğim açısı ω + µ = 100 g Şekil 9 üç Boyutlu koordinat sisteminde açı tiplerinin tasviri. Trigonometrik kavramlara geçmeden
Trigonometrik Fonksiyonlar Z Z P P ω µ P O α α = yatay açı P P ω = düşey açı µ =eğim açısı ω + µ = 100 g Şekil 9 üç Boyutlu koordinat sisteminde açı tiplerinin tasviri. Trigonometrik kavramlara geçmeden
Haritası yapılan bölge (dilim) Orta meridyen λ. Kuzey Kutbu. Güney Kutbu. Transversal silindir (projeksiyon yüzeyi) Yerin dönme ekseni
 1205321/1206321 Türkiye de Topografik Harita Yapımı Ölçek Büyük Ölçekli Haritalar 1:1000,1:5000 2005 tarihli BÖHHBYY ne göre değişik kamu kurumlarınca üretilirler. Datum: GRS80 Projeksiyon: Transverse
1205321/1206321 Türkiye de Topografik Harita Yapımı Ölçek Büyük Ölçekli Haritalar 1:1000,1:5000 2005 tarihli BÖHHBYY ne göre değişik kamu kurumlarınca üretilirler. Datum: GRS80 Projeksiyon: Transverse
Alan Hesapları. Şekil 14. Üç kenarı belli üçgen alanı
 lan Hesapları lan hesabının doğruluğu alım şekline ve istenile hassasiyet derecesine göre değişir. lan hesapları üç kısma ayrılmıştır. Ölçü değerlerine göre alan hesabı Ölçü ve plan değerlerine göre alan
lan Hesapları lan hesabının doğruluğu alım şekline ve istenile hassasiyet derecesine göre değişir. lan hesapları üç kısma ayrılmıştır. Ölçü değerlerine göre alan hesabı Ölçü ve plan değerlerine göre alan
3. Alım için sıklaştırma noktaları (tamamlayıcı nokta, ara ve dizi nirengi),
 ÖLÇME BİLGİSİ 2 DERS NOTLARI YER KONTROL NOKTALARI Genel Bilgi Bir alanın ve üzerindeki örtülerin harita veya planının yapılabilmesi için yeryüzünde konumu sabit ve koordinat değerleri belli bir takım
ÖLÇME BİLGİSİ 2 DERS NOTLARI YER KONTROL NOKTALARI Genel Bilgi Bir alanın ve üzerindeki örtülerin harita veya planının yapılabilmesi için yeryüzünde konumu sabit ve koordinat değerleri belli bir takım
Kuzey Kutbu. Yerin dönme ekseni
 1205321/1206321 Türkiye de Topoğrafik Harita Yapımı Ölçek Büyük Ölçekli Haritalar 1:1000,1:5000 2005 tarihli BÖHHBYY ne göre değişik kamu kurumlarınca üretilirler. Datum: GRS80 Projeksiyon: Transverse
1205321/1206321 Türkiye de Topoğrafik Harita Yapımı Ölçek Büyük Ölçekli Haritalar 1:1000,1:5000 2005 tarihli BÖHHBYY ne göre değişik kamu kurumlarınca üretilirler. Datum: GRS80 Projeksiyon: Transverse
Deprem Etkisi Altında Tasarım İç Kuvvetleri
 Prof. Dr. Günay Özmen gunayozmen@hotmail.com Deprem Etkisi Altında Tasarım İç Kuvvetleri 1. Giriş Deprem etkisi altında bulunan çok katlı yapılarda her eleman için kendine özgü ayrı bir elverişsiz deprem
Prof. Dr. Günay Özmen gunayozmen@hotmail.com Deprem Etkisi Altında Tasarım İç Kuvvetleri 1. Giriş Deprem etkisi altında bulunan çok katlı yapılarda her eleman için kendine özgü ayrı bir elverişsiz deprem
İKİ BOYUTLU AĞLARDA AĞIRLIK SEÇİMİNİN DENGELEME SONUÇLARINA ETKİSİ VE GPS KOORDİNATLARI İLE KARŞILAŞTIRILMASI
 SELÇUK TEKNİK ONLİNE DERGİSİ / ISSN 1302 6178 Volume 1, Number: 3 2001 İKİ BOYUTLU AĞLARDA AĞIRLIK SEÇİMİNİN DENGELEME SONUÇLARINA ETKİSİ VE GPS KOORDİNATLARI İLE KARŞILAŞTIRILMASI Doç Dr. Cevat İNAL S.Ü.
SELÇUK TEKNİK ONLİNE DERGİSİ / ISSN 1302 6178 Volume 1, Number: 3 2001 İKİ BOYUTLU AĞLARDA AĞIRLIK SEÇİMİNİN DENGELEME SONUÇLARINA ETKİSİ VE GPS KOORDİNATLARI İLE KARŞILAŞTIRILMASI Doç Dr. Cevat İNAL S.Ü.
JDF/GEO 120 ÖLÇME BİLGİSİ II POLİGONASYON
 JDF/GEO 120 ÖLÇME BİLGİSİ II POLİGONASYON Dr. Öğr. Üyesi HÜSEYİN KEMALDERE Sınıflandırma (BÖHHBÜY (26.06.2018)-Md:8) Bu yönetmelik kapsamındaki kontrol noktalarının hiyerarşik sınıflandırılması aşağıda
JDF/GEO 120 ÖLÇME BİLGİSİ II POLİGONASYON Dr. Öğr. Üyesi HÜSEYİN KEMALDERE Sınıflandırma (BÖHHBÜY (26.06.2018)-Md:8) Bu yönetmelik kapsamındaki kontrol noktalarının hiyerarşik sınıflandırılması aşağıda
DİK KOORDİNAT SİSTEMİ VE
 Ölçme Bilgisi DERS 6 DİK KOORDİNAT SİSTEMİ VE TEMEL ÖDEVLER Kaynak: İ.ASRİ (Gümüşhane Ü) M. Zeki COŞKUN ( İTÜ ) TEODOLİT Teodolitler, yatay ve düşey açıları yeteri incelikte ölçmeye yarayan optik aletlerdir.
Ölçme Bilgisi DERS 6 DİK KOORDİNAT SİSTEMİ VE TEMEL ÖDEVLER Kaynak: İ.ASRİ (Gümüşhane Ü) M. Zeki COŞKUN ( İTÜ ) TEODOLİT Teodolitler, yatay ve düşey açıları yeteri incelikte ölçmeye yarayan optik aletlerdir.
Koordinat Dönüşümleri (V )
 KOORDİNAT DÖNÜŞÜMLERİ ve FARKLI KOORDİNAT SİSTEMLERİ İLE ÇALIŞMA FieldGenius ile birden fazla koordinat sistemi arasında geçiş yaparak çalışmak mümkündür. Yaygın olarak kullanılan masaüstü harita ve CAD
KOORDİNAT DÖNÜŞÜMLERİ ve FARKLI KOORDİNAT SİSTEMLERİ İLE ÇALIŞMA FieldGenius ile birden fazla koordinat sistemi arasında geçiş yaparak çalışmak mümkündür. Yaygın olarak kullanılan masaüstü harita ve CAD
DENGELEME HESABI-I DERS NOTLARI
 DENGELEME HESABI-I DERS NOTLARI Ağırlık ve Ters Ağırlık (Kofaktör) Prof. Dr. Mualla YALÇINKAYA Yrd. Doç. Dr. Emine TANIR KAYIKÇI Karadeniz Teknik Üniversitesi, Harita Mühendisliği Bölümü Trabzon, 016 AĞIRLIK
DENGELEME HESABI-I DERS NOTLARI Ağırlık ve Ters Ağırlık (Kofaktör) Prof. Dr. Mualla YALÇINKAYA Yrd. Doç. Dr. Emine TANIR KAYIKÇI Karadeniz Teknik Üniversitesi, Harita Mühendisliği Bölümü Trabzon, 016 AĞIRLIK
JEODEZİK AĞLARIN OPTİMİZASYONU
 JEODEZİK AĞLARIN OPTİMİZASYONU Jeodezik Ağların Tasarımı 10.HAFTA Dr.Emine Tanır Kayıkçı,2017 OPTİMİZASYON Herhangi bir yatırımın gerçekleştirilmesi sırasında elde bulunan, araç, hammadde, para, işgücü
JEODEZİK AĞLARIN OPTİMİZASYONU Jeodezik Ağların Tasarımı 10.HAFTA Dr.Emine Tanır Kayıkçı,2017 OPTİMİZASYON Herhangi bir yatırımın gerçekleştirilmesi sırasında elde bulunan, araç, hammadde, para, işgücü
DOĞRUNUN ANALİTİK İNCELEMESİ
 Koordinatlar DOĞRUNUN ANALİTİK İNCELEMESİ Bilindiği gibi, düzlemdeki her bir noktaya bir (a,b) sıralı ikilisi, her bir (a,b) sıralı ikilisine bir nokta karşılık gelir. Eğer bir A noktasına karşılık gelen
Koordinatlar DOĞRUNUN ANALİTİK İNCELEMESİ Bilindiği gibi, düzlemdeki her bir noktaya bir (a,b) sıralı ikilisi, her bir (a,b) sıralı ikilisine bir nokta karşılık gelir. Eğer bir A noktasına karşılık gelen
JEODEZİK ÖLÇME UYGULAMASI I UYGULAMA YÖNERGESİ
 ÇANAKKALE ONSEKİZ MART ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JEODEZİK ÖLÇME UYGULAMASI I UYGULAMA YÖNERGESİ HAZIRLAYANLAR Yrd. Doç. Dr. R. Cüneyt ERENOĞLU Yrd. Doç. Dr. Özgün
ÇANAKKALE ONSEKİZ MART ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JEODEZİK ÖLÇME UYGULAMASI I UYGULAMA YÖNERGESİ HAZIRLAYANLAR Yrd. Doç. Dr. R. Cüneyt ERENOĞLU Yrd. Doç. Dr. Özgün
Parametrik doğru denklemleri 1
 Parametrik doğru denklemleri 1 A noktasından geçen, doğrultman (doğrultu) vektörü w olan d doğrusunun, k parametresine göre parametrik denklemi: AP k w P A k w P A k w P A k W (P değişken nokta) A w P
Parametrik doğru denklemleri 1 A noktasından geçen, doğrultman (doğrultu) vektörü w olan d doğrusunun, k parametresine göre parametrik denklemi: AP k w P A k w P A k w P A k W (P değişken nokta) A w P
Matematikte karşılaştığınız güçlükler için endişe etmeyin. Emin olun benim karşılaştıklarım sizinkilerden daha büyüktür.
 - 1 - ÖĞRENME ALANI CEBİR BÖLÜM KARMAŞIK SAYILAR ALT ÖĞRENME ALANLARI 1) Karmaşık Sayılar Karmaşık Sayıların Kutupsal Biçimi KARMAŞIK SAYILAR Kazanım 1 : Gerçek sayılar kümesini genişletme gereğini örneklerle
- 1 - ÖĞRENME ALANI CEBİR BÖLÜM KARMAŞIK SAYILAR ALT ÖĞRENME ALANLARI 1) Karmaşık Sayılar Karmaşık Sayıların Kutupsal Biçimi KARMAŞIK SAYILAR Kazanım 1 : Gerçek sayılar kümesini genişletme gereğini örneklerle
DENGELEME HESABI-I DERS NOTLARI
 DENGELEME HESABI-I DERS NOTLARI Dengeleme Hesabı Adımları, En Küçük Kareler İlkesine Giriş, Korelasyon Prof. Dr. Mualla YALÇINKAYA Yrd. Doç. Dr. Emine TANIR KAYIKÇI Karadeniz Teknik Üniversitesi, Harita
DENGELEME HESABI-I DERS NOTLARI Dengeleme Hesabı Adımları, En Küçük Kareler İlkesine Giriş, Korelasyon Prof. Dr. Mualla YALÇINKAYA Yrd. Doç. Dr. Emine TANIR KAYIKÇI Karadeniz Teknik Üniversitesi, Harita
Tanımlar, Geometrik ve Matemetiksel Temeller. Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ. JDF329 Fotogrametri I Ders Notu
 FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İçerik Tanımlar
FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İçerik Tanımlar
Yrd. Doç. Dr. Aycan M. MARANGOZ. BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF329 FOTOGRAMETRİ I DERSi NOTLARI
 FOTOGRAMETRİ I GEOMETRİK ve MATEMATİK TEMELLER Yrd. Doç. Dr. Aycan M. MARANGOZ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF329 FOTOGRAMETRİ I DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
FOTOGRAMETRİ I GEOMETRİK ve MATEMATİK TEMELLER Yrd. Doç. Dr. Aycan M. MARANGOZ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF329 FOTOGRAMETRİ I DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
Elipsoid Yüzünde Jeodezik Dik Koordinatlar (Soldner Koordinatları) ve Temel Ödev Hesapları
 JEODEZİ8 1 Elipsoid Yüzünde Jeodezik Dik Koordinatlar (Soldner Koordinatları) ve Temel Ödev Hesapları Jeodezik dik koordinatları tanımlamak için önce bir meridyen x ekseni olarak alınır. Bunun üzerinde
JEODEZİ8 1 Elipsoid Yüzünde Jeodezik Dik Koordinatlar (Soldner Koordinatları) ve Temel Ödev Hesapları Jeodezik dik koordinatları tanımlamak için önce bir meridyen x ekseni olarak alınır. Bunun üzerinde
2 Hata Hesabı. Hata Nedir? Mutlak Hata. Bağıl Hata
 Hata Hesabı Hata Nedir? Herhangi bir fiziksel büyüklüğün ölçülen değeri ile gerçek değeri arasındaki farka hata denir. Ölçülen bir fiziksel büyüklüğün sayısal değeri, yapılan deneysel hatalardan dolayı
Hata Hesabı Hata Nedir? Herhangi bir fiziksel büyüklüğün ölçülen değeri ile gerçek değeri arasındaki farka hata denir. Ölçülen bir fiziksel büyüklüğün sayısal değeri, yapılan deneysel hatalardan dolayı
İÇİNDEKİLER BÖLÜM 1 ÖLÇME TEKNİĞİ VE HARİTA ALMA YÖNTEMLERİ
 İÇİNDEKİLER II Sayfa No: ÖNSÖZ...I İÇİNDEKİLER...III ŞEKİLLER LİSTESİ...VIII ÇİZELGELER LİSTESİ...XII EKLER LİSTESİ...XIII BÖLÜM 1 ÖLÇME TEKNİĞİ VE HARİTA ALMA YÖNTEMLERİ 1. ÖLÇME TEKNİĞİ VE HARİTA ALMA
İÇİNDEKİLER II Sayfa No: ÖNSÖZ...I İÇİNDEKİLER...III ŞEKİLLER LİSTESİ...VIII ÇİZELGELER LİSTESİ...XII EKLER LİSTESİ...XIII BÖLÜM 1 ÖLÇME TEKNİĞİ VE HARİTA ALMA YÖNTEMLERİ 1. ÖLÇME TEKNİĞİ VE HARİTA ALMA
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 6- İSTATİSTİK VE REGRESYON ANALİZİ Doç. Dr. Ali Rıza YILDIZ 1 İSTATİSTİK VE REGRESYON ANALİZİ Bütün noktalardan geçen bir denklem bulmak yerine noktaları temsil eden, yani
MAK 210 SAYISAL ANALİZ BÖLÜM 6- İSTATİSTİK VE REGRESYON ANALİZİ Doç. Dr. Ali Rıza YILDIZ 1 İSTATİSTİK VE REGRESYON ANALİZİ Bütün noktalardan geçen bir denklem bulmak yerine noktaları temsil eden, yani
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü TOPOGRAFYA (HRT3351) Yrd. Doç. Dr. Ercenk ATA
 Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü 4. HAFTA KOORDİNAT SİSTEMLERİ VE HARİTA PROJEKSİYONLARI Coğrafi Koordinat Sistemi Yeryüzü üzerindeki bir noktanın konumunun enlem
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü 4. HAFTA KOORDİNAT SİSTEMLERİ VE HARİTA PROJEKSİYONLARI Coğrafi Koordinat Sistemi Yeryüzü üzerindeki bir noktanın konumunun enlem
TOPOĞRAFİK HARİTALAR VE KESİTLER
 TOPOĞRAFİK HARİTALAR VE KESİTLER Prof.Dr. Murat UTKUCU Yrd.Doç.Dr. ŞefikRAMAZANOĞLU TOPOĞRAFİK HARİTALAR VE Haritalar KESİTLER Yeryüzü şekillerini belirli bir yöntem ve ölçek dahilinde plan konumunda gösteren
TOPOĞRAFİK HARİTALAR VE KESİTLER Prof.Dr. Murat UTKUCU Yrd.Doç.Dr. ŞefikRAMAZANOĞLU TOPOĞRAFİK HARİTALAR VE Haritalar KESİTLER Yeryüzü şekillerini belirli bir yöntem ve ölçek dahilinde plan konumunda gösteren
TOPOĞRAFYA Takeometri
 TOPOĞRAFYA Takeometri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Takeometri Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
NİRENGİ ÂĞLARININ DEĞERLENDİRİLMESİ. Ergün ÖZTÜRK ÖZET
 NİRENGİ ÂĞLARININ DEĞERLENDİRİLMESİ ÖZET Ergün ÖZTÜRK Büyük ölçekli jeodezik çalışmaların tek bir birim sistemde hesaplanan nirengi ağlarına dayandırılmasında sayısız yararlar bulunmaktadır* Bu amaçla
NİRENGİ ÂĞLARININ DEĞERLENDİRİLMESİ ÖZET Ergün ÖZTÜRK Büyük ölçekli jeodezik çalışmaların tek bir birim sistemde hesaplanan nirengi ağlarına dayandırılmasında sayısız yararlar bulunmaktadır* Bu amaçla
ARAZİ ÇALIŞMASI YÖNERGESİ
 YILDIZ TEKNİK ÜNİVERSİTESİ İNŞAAT FAKÜLTESİ HARİTA MÜHENDİSLİĞİ BÖLÜMÜ ARAZİ ÇALIŞMASI YÖNERGESİ HAZIRLAYANLAR Prof. Dr. METİN SOYCAN Prof. Dr. UĞUR DOĞAN Doç. Dr. TÜRKAY GÖKGÖZ Doç. Dr. ATINÇ PIRTI Y.
YILDIZ TEKNİK ÜNİVERSİTESİ İNŞAAT FAKÜLTESİ HARİTA MÜHENDİSLİĞİ BÖLÜMÜ ARAZİ ÇALIŞMASI YÖNERGESİ HAZIRLAYANLAR Prof. Dr. METİN SOYCAN Prof. Dr. UĞUR DOĞAN Doç. Dr. TÜRKAY GÖKGÖZ Doç. Dr. ATINÇ PIRTI Y.
Mühendislik Mekaniği Dinamik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 17 Rijit Cismin Düzlemsel Kinetiği; Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok.
Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 17 Rijit Cismin Düzlemsel Kinetiği; Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok.
Bölüm 2: Kuvvet Vektörleri. Mühendislik Mekaniği: Statik
 Bölüm 2: Kuvvet Vektörleri Mühendislik Mekaniği: Statik Hedefler Kuvvetleri toplama, bileşenlerini ve bileşke kuvvetlerini Paralelogram Kuralı kullanarak belirleme. Diktörtgen (Cartesian) koordinat sistemi
Bölüm 2: Kuvvet Vektörleri Mühendislik Mekaniği: Statik Hedefler Kuvvetleri toplama, bileşenlerini ve bileşke kuvvetlerini Paralelogram Kuralı kullanarak belirleme. Diktörtgen (Cartesian) koordinat sistemi
T.C. Ölçme, Seçme ve Yerleştirme Merkezi
 T.C. Ölçme, Seçme ve Yerleştirme Merkezi LİSANS YERLEŞTİRME SINAVI-1 MATEMATİK TESTİ 11 HAZİRAN 2017 PAZAR Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının veya bir kısmının
T.C. Ölçme, Seçme ve Yerleştirme Merkezi LİSANS YERLEŞTİRME SINAVI-1 MATEMATİK TESTİ 11 HAZİRAN 2017 PAZAR Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının veya bir kısmının
Gerilme Dönüşümleri (Stress Transformation)
 Gerilme Dönüşümleri (Stress Transformation) Bubölümdebirnoktayaetkiyen vebelli bir koordinat ekseni/düzlemi ile ilişkili gerilme bileşenlerini, başka bir koordinat sistemi/başka bir düzlem ile ilişkili
Gerilme Dönüşümleri (Stress Transformation) Bubölümdebirnoktayaetkiyen vebelli bir koordinat ekseni/düzlemi ile ilişkili gerilme bileşenlerini, başka bir koordinat sistemi/başka bir düzlem ile ilişkili
T.C. Ölçme, Seçme ve Yerleştirme Merkezi
 T.C. Ölçme, Seçme ve Yerleştirme Merkezi LİSANS YERLEŞTİRME SINAVI-1 MATEMATİK TESTİ 11 HAZİRAN 2017 PAZAR Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının veya bir kısmının
T.C. Ölçme, Seçme ve Yerleştirme Merkezi LİSANS YERLEŞTİRME SINAVI-1 MATEMATİK TESTİ 11 HAZİRAN 2017 PAZAR Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının veya bir kısmının
2. REGRESYON ANALİZİNİN TEMEL KAVRAMLARI Tanım
 2. REGRESYON ANALİZİNİN TEMEL KAVRAMLARI 2.1. Tanım Regresyon analizi, bir değişkenin başka bir veya daha fazla değişkene olan bağımlılığını inceler. Amaç, bağımlı değişkenin kitle ortalamasını, açıklayıcı
2. REGRESYON ANALİZİNİN TEMEL KAVRAMLARI 2.1. Tanım Regresyon analizi, bir değişkenin başka bir veya daha fazla değişkene olan bağımlılığını inceler. Amaç, bağımlı değişkenin kitle ortalamasını, açıklayıcı
PAFTA BÖLÜMLENDİRİLMESİ
 PAFTA BÖLÜMLENDİRİLMESİ Türkiye kadastrosunda yukarıda değinilen ada sistemi pafta bölümleme ve adlandırma sistemi dışında çeşitli pafta bölümleme ve adlandırma sistemleri kullanılmıştır ve Yapım Yönetmeliği
PAFTA BÖLÜMLENDİRİLMESİ Türkiye kadastrosunda yukarıda değinilen ada sistemi pafta bölümleme ve adlandırma sistemi dışında çeşitli pafta bölümleme ve adlandırma sistemleri kullanılmıştır ve Yapım Yönetmeliği
BÜYÜK ÖLÇEKLİ HARİTA YAPIMINDA STEREOGRAFİK ÇİFT PROJEKSİYONUN UYGULANIŞI
 36 İNCELEME - ARAŞTIRMA BÜYÜK ÖLÇEKLİ HARİTA YAPIMINDA STEREOGRAFİK ÇİFT PROJEKSİYONUN UYGULANIŞI Erdal KOÇAIC*^ ÖZET Büyük ölçekli harita yapımında G İ R İŞ uygulanabilen "Stereografik çift Stereografik
36 İNCELEME - ARAŞTIRMA BÜYÜK ÖLÇEKLİ HARİTA YAPIMINDA STEREOGRAFİK ÇİFT PROJEKSİYONUN UYGULANIŞI Erdal KOÇAIC*^ ÖZET Büyük ölçekli harita yapımında G İ R İŞ uygulanabilen "Stereografik çift Stereografik
11. SINIF. No Konular Kazanım Sayısı GEOMETRİ TRİGONOMETRİ Yönlü Açılar Trigonometrik Fonksiyonlar
 11. SINIF No Konular Kazanım Sayısı GEOMETRİ Ders Saati Ağırlık (%) 11.1. TRİGONOMETRİ 7 56 26 11.1.1. Yönlü Açılar 2 10 5 11.1.2. Trigonometrik Fonksiyonlar 5 46 21 11.2. ANALİTİK GEOMETRİ 4 24 11 11.2.1.
11. SINIF No Konular Kazanım Sayısı GEOMETRİ Ders Saati Ağırlık (%) 11.1. TRİGONOMETRİ 7 56 26 11.1.1. Yönlü Açılar 2 10 5 11.1.2. Trigonometrik Fonksiyonlar 5 46 21 11.2. ANALİTİK GEOMETRİ 4 24 11 11.2.1.
BİLİNMEYENLİ ŞART DENKLEMLERİ VE EKSİK ÖLÇÜLÜ NİRENÇİ AÖLARI
 BİLİNMEYENLİ ŞART DENKLEMLERİ VE EKSİK ÖLÇÜLÜ NİRENÇİ AÖLARI Prof. Ekrem ULSOY».----İçlerinde bilinmeyenlerin bulunduğu şart denklemleri, dengeleme li- ^: terâtüründe dengelemenin.en genel şeklî olarak
BİLİNMEYENLİ ŞART DENKLEMLERİ VE EKSİK ÖLÇÜLÜ NİRENÇİ AÖLARI Prof. Ekrem ULSOY».----İçlerinde bilinmeyenlerin bulunduğu şart denklemleri, dengeleme li- ^: terâtüründe dengelemenin.en genel şeklî olarak
JEOİD ve JEOİD BELİRLEME
 JEOİD ve JEOİD BELİRLEME İÇİNDEKİLER GİRİŞ JEODEZİDE YÜKSEKLİK SİSTEMLERİ Jeopotansiyel Yükseklikler (C) Dinamik Yükseklikler (H D ) Normal Yükseklik (H N ) Elipsoidal Yükseklik Ortometrik Yükseklik Atmosferik
JEOİD ve JEOİD BELİRLEME İÇİNDEKİLER GİRİŞ JEODEZİDE YÜKSEKLİK SİSTEMLERİ Jeopotansiyel Yükseklikler (C) Dinamik Yükseklikler (H D ) Normal Yükseklik (H N ) Elipsoidal Yükseklik Ortometrik Yükseklik Atmosferik
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ
 İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
TEMEL HARİTACILIK BİLGİLERİ. Erkan GÜLER Haziran 2018
 TEMEL HARİTACILIK BİLGİLERİ Erkan GÜLER Haziran 2018 1 HARİTA Yeryüzündeki bir noktanın ya da tamamının çeşitli özelliklere göre bir ölçeğe ve amaca göre çizilerek, düzlem üzerine aktarılmasına harita
TEMEL HARİTACILIK BİLGİLERİ Erkan GÜLER Haziran 2018 1 HARİTA Yeryüzündeki bir noktanın ya da tamamının çeşitli özelliklere göre bir ölçeğe ve amaca göre çizilerek, düzlem üzerine aktarılmasına harita
12-B. Polinomlar - 1 TEST. olduğuna göre P(x - 2, y + 4) polinomunun katsayılar toplamı kaçtır? olduğuna göre A B kaçtır? A) 78 B) 73 C) 62 D 58 E) 33
 -B TEST Polinomlar -. Py _, i= y- y + 5y- olduğuna göre P( -, y + ) polinomunun katsayılar toplamı. - 6 = A - 5 + - + B - olduğuna göre A B 78 B) 7 6 D 58 E) B) D) - E) -. -a- b = _ + -5i_ -ci eşitliğine
-B TEST Polinomlar -. Py _, i= y- y + 5y- olduğuna göre P( -, y + ) polinomunun katsayılar toplamı. - 6 = A - 5 + - + B - olduğuna göre A B 78 B) 7 6 D 58 E) B) D) - E) -. -a- b = _ + -5i_ -ci eşitliğine
JDF 116 / 120 ÖLÇME TEKNİĞİ / BİLGİSİ II POLİGONASYON
 JDF 116 / 120 ÖLÇME TEKNİĞİ / BİLGİSİ II POLİGONASYON Yrd. Doç. Dr. HÜSEYİN KEMALDERE Jeodezik Noktaların Sınıflandırması (BÖHHBÜY-Md:8) Noktaların sınıflandırılması aşağıdaki şekildedir: a) Uzay ve uydu
JDF 116 / 120 ÖLÇME TEKNİĞİ / BİLGİSİ II POLİGONASYON Yrd. Doç. Dr. HÜSEYİN KEMALDERE Jeodezik Noktaların Sınıflandırması (BÖHHBÜY-Md:8) Noktaların sınıflandırılması aşağıdaki şekildedir: a) Uzay ve uydu
2 1 fonksiyonu veriliyor. olacak şekilde ortalama değer teoremini sağlayacak bir c sayısının var olup olmadığını araştırınız. Eğer var ise bulunuz.
 ANALİZ 1.) a) sgn. sgn( 1) = 1 denkleminin çözüm kümesini b) f ( ) 3 1 fonksiyonu veriliyor. olacak şekilde ortalama değer teoremini sağlayacak bir c sayısının var olup olmadığını araştırınız. Eğer var
ANALİZ 1.) a) sgn. sgn( 1) = 1 denkleminin çözüm kümesini b) f ( ) 3 1 fonksiyonu veriliyor. olacak şekilde ortalama değer teoremini sağlayacak bir c sayısının var olup olmadığını araştırınız. Eğer var
 Geometrik nivelmanda önemli hata kaynakları Nivelmanda oluşabilecek model hataları iki bölümde incelenebilir. Bunlar: Aletsel (Nivo ve Mira) Hatalar Çevresel Koşullardan Kaynaklanan Hatalar 1. Aletsel
Geometrik nivelmanda önemli hata kaynakları Nivelmanda oluşabilecek model hataları iki bölümde incelenebilir. Bunlar: Aletsel (Nivo ve Mira) Hatalar Çevresel Koşullardan Kaynaklanan Hatalar 1. Aletsel
Küre Küre Üzerinde Hesap. Ders Sorumlusu Prof. Dr. Mualla YALÇINKAYA 2018
 Küre Küre Üzerinde Hesap Ders Sorumlusu Prof. Dr. Mualla YALÇINKAYA 2018 Küre ve Küre ile İlgili Tanımlar Küre: «Merkez» adı verilen bir noktaya eşit uzaklıktaki noktaların bir araya getirilmesiyle, ya
Küre Küre Üzerinde Hesap Ders Sorumlusu Prof. Dr. Mualla YALÇINKAYA 2018 Küre ve Küre ile İlgili Tanımlar Küre: «Merkez» adı verilen bir noktaya eşit uzaklıktaki noktaların bir araya getirilmesiyle, ya
MADDESEL NOKTANIN EĞRİSEL HAREKETİ
 Silindirik Koordinatlar: Bazı mühendislik problemlerinde, parçacığın hareketinin yörüngesi silindirik koordinatlarda r, θ ve z tanımlanması uygun olacaktır. Eğer parçacığın hareketi iki eksende oluşmaktaysa
Silindirik Koordinatlar: Bazı mühendislik problemlerinde, parçacığın hareketinin yörüngesi silindirik koordinatlarda r, θ ve z tanımlanması uygun olacaktır. Eğer parçacığın hareketi iki eksende oluşmaktaysa
Yatay Kontrol Noktaları
 Yatay Kontrol Noktaları Bir alanın üzerindeki detaylarla birlikte harita veya planının yapılabilmesi için yeryüzünde konumu sabit ve koordinat değeri belli olan noktalara ihtiyaç vardır. Bu noktalara yatay
Yatay Kontrol Noktaları Bir alanın üzerindeki detaylarla birlikte harita veya planının yapılabilmesi için yeryüzünde konumu sabit ve koordinat değeri belli olan noktalara ihtiyaç vardır. Bu noktalara yatay
"BU NOKTA HANGİ PAFTA İÇİNDEDİR?" PROBLEMİNİN ÇÖZÜMÜ İÇİN BİR ALGORİTMA Ahmet YAŞAYAN
 "BU NOKTA HANGİ PAFTA İÇİNDEDİR?" PROBLEMİNİN ÇÖZÜMÜ İÇİN BİR ALGORİTMA Ahmet YAŞAYAN 49 GİRİŞ Bir harita proje alanındaki nirengi, poligon vb sabit noktaların ve diğer ayrıntı noktalarının hangi pafta
"BU NOKTA HANGİ PAFTA İÇİNDEDİR?" PROBLEMİNİN ÇÖZÜMÜ İÇİN BİR ALGORİTMA Ahmet YAŞAYAN 49 GİRİŞ Bir harita proje alanındaki nirengi, poligon vb sabit noktaların ve diğer ayrıntı noktalarının hangi pafta
Hakan AKÇIN* SUNU Ali ihsan ŞEKERTEKİN
 AÇIK İŞLETME MADENCİLİĞİ UYGULAMALARINDA GNSS ÖLÇÜLERİNDEN YÜKSEKLİK FARKLARININ GEOMETRİK NİVELMAN ÖLÇMELERİNDEN YÜKSEKLİK FARKLARI YERİNE KULLANIMI ÜZERİNE DENEYSEL BİR ARAŞTIRMA Hakan AKÇIN* SUNU Ali
AÇIK İŞLETME MADENCİLİĞİ UYGULAMALARINDA GNSS ÖLÇÜLERİNDEN YÜKSEKLİK FARKLARININ GEOMETRİK NİVELMAN ÖLÇMELERİNDEN YÜKSEKLİK FARKLARI YERİNE KULLANIMI ÜZERİNE DENEYSEL BİR ARAŞTIRMA Hakan AKÇIN* SUNU Ali
Dünya nın şekli. Küre?
 Dünya nın şekli Küre? Dünya nın şekli Elipsoid? Aslında dünyanın şekli tam olarak bunlardan hiçbiri değildir. Biz ilkokulda ve lisede ilk önce yuvarlak olduğunu sonra ortadan basık olduğunu sonrada elipsoid
Dünya nın şekli Küre? Dünya nın şekli Elipsoid? Aslında dünyanın şekli tam olarak bunlardan hiçbiri değildir. Biz ilkokulda ve lisede ilk önce yuvarlak olduğunu sonra ortadan basık olduğunu sonrada elipsoid
EĞİTİM ÖĞRETİM YILI. ANADOLU LİSESİ 11.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI 11.SINIF KAZANIM VE SÜRE TABLOSU
 08-09 EĞİTİM ÖĞRETİM YILI. ANADOLU LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. TRİGONOMETRİ 7 6 6.. Yönlü
08-09 EĞİTİM ÖĞRETİM YILI. ANADOLU LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. TRİGONOMETRİ 7 6 6.. Yönlü
Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu
 JEODEZİ9 1 Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu u ve v Gauss parametrelerine bağlı olarak r r ( u, v) yer vektörü ile verilmiş bir Ω yüzeyinin, u*, v* Gauss parametreleri ile verilmiş
JEODEZİ9 1 Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu u ve v Gauss parametrelerine bağlı olarak r r ( u, v) yer vektörü ile verilmiş bir Ω yüzeyinin, u*, v* Gauss parametreleri ile verilmiş
Dik koordinat sisteminde yatay eksen x ekseni (apsis ekseni), düşey eksen ise y ekseni (ordinat ekseni) dir.
 ANALĐTĐK GEOMETRĐ 1. Analitik Düzlem Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da
ANALĐTĐK GEOMETRĐ 1. Analitik Düzlem Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da
Gerilme Dönüşümleri (Stress Transformation)
 Gerilme Dönüşümleri (Stress Transformation) Bu bölümde, bir noktaya etkiyen ve bir koordinat ekseni ile ilişkili gerilme bileşenlerini, başka bir koordinat sistemi ile ilişkili gerilme bileşenlerine dönüştürmek
Gerilme Dönüşümleri (Stress Transformation) Bu bölümde, bir noktaya etkiyen ve bir koordinat ekseni ile ilişkili gerilme bileşenlerini, başka bir koordinat sistemi ile ilişkili gerilme bileşenlerine dönüştürmek
MÜHENDİSLİK ÖLÇMELERİ UYGULAMASI (HRT4362) 8. Yarıyıl
 İnşaat Fakültesi Harita Mühendisliği Bölümü Ölçme Tekniği Anabilim alı MÜHENİSLİK ÖLÇMELERİ UYGULAMASI (HRT436) 8. Yarıyıl U L K Kredi 3 ECTS 3 UYGULAMA-5 ELEKTRONİK ALETLERİN KALİBRASYONU Prof.r.Engin
İnşaat Fakültesi Harita Mühendisliği Bölümü Ölçme Tekniği Anabilim alı MÜHENİSLİK ÖLÇMELERİ UYGULAMASI (HRT436) 8. Yarıyıl U L K Kredi 3 ECTS 3 UYGULAMA-5 ELEKTRONİK ALETLERİN KALİBRASYONU Prof.r.Engin
Doç. Dr. Bilge DORAN
 Doç. Dr. Bilge DORAN Bilgisayar teknolojisinin ilerlemesi doğal olarak Yapı Mühendisliğinin bir bölümü olarak tanımlanabilecek sistem analizi (hesabı) kısmına yansımıştır. Mühendislik biliminde bilindiği
Doç. Dr. Bilge DORAN Bilgisayar teknolojisinin ilerlemesi doğal olarak Yapı Mühendisliğinin bir bölümü olarak tanımlanabilecek sistem analizi (hesabı) kısmına yansımıştır. Mühendislik biliminde bilindiği
Ölçü Hataları Hatasız ölçü olmaz
 Ölçü Hataları Yeryüzünde ister bir kenar, ister bir açı birkaç kez ölçüldüğünde her ölçü değeri arasında az çok farkların olduğu görülür. Aynı büyüklüğe ait yapılan her geometrik veya fiziksel ölçünün
Ölçü Hataları Yeryüzünde ister bir kenar, ister bir açı birkaç kez ölçüldüğünde her ölçü değeri arasında az çok farkların olduğu görülür. Aynı büyüklüğe ait yapılan her geometrik veya fiziksel ölçünün
( m %n' m q >m q J > şekilde şematik olarak gösterilmiştir.
 Diğer Araştırmalar : Bir önceki bölümde açıklanan ilk araştırmaların teorik ve deneysel sonuçlarını sınamak amacı ile, seri halinde yeni teorik ve deneysel araştırmalar yapılmıştır. (Çizelge : IV) de belirtilen
Diğer Araştırmalar : Bir önceki bölümde açıklanan ilk araştırmaların teorik ve deneysel sonuçlarını sınamak amacı ile, seri halinde yeni teorik ve deneysel araştırmalar yapılmıştır. (Çizelge : IV) de belirtilen
Karabük Üniversitesi, Mühendislik Fakültesi...www.IbrahimCayiroglu.com. STATİK (4. Hafta)
 KAFES SİSTEMLER STATİK (4. Hafta) Düz eksenden oluşan çubukların birbiriyle birleştirilmesiyle elde edilen sistemlere kafes sistemler denir. Çubukların birleştiği noktalara düğüm noktaları adı verilir.
KAFES SİSTEMLER STATİK (4. Hafta) Düz eksenden oluşan çubukların birbiriyle birleştirilmesiyle elde edilen sistemlere kafes sistemler denir. Çubukların birleştiği noktalara düğüm noktaları adı verilir.
TOPOĞRAFYA Kesitlerin Çıkarılması, Alan Hesapları, Hacim Hesapları
 TOPOĞRAFYA Kesitlerin Çıkarılması, Alan Hesapları, Hacim Hesapları Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Kesitlerin Çıkarılması, Alan Hesapları, Hacim Hesapları Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
GPS/INS Destekli Havai Nirengi
 GPS/INS Destekli Havai Nirengi GPS/INS (IMU) destekli hava nirengide izdüşüm merkezi koordinatları (WGS84) ve dönüklükler direk ölçülür. İzdüşüm merkezi koordinatları kinematik GPS ile ölçülür. GPS ile
GPS/INS Destekli Havai Nirengi GPS/INS (IMU) destekli hava nirengide izdüşüm merkezi koordinatları (WGS84) ve dönüklükler direk ölçülür. İzdüşüm merkezi koordinatları kinematik GPS ile ölçülür. GPS ile
Ölçme Bilgisi DERS 7-8. Yatay Kontrol Noktaları Ve Yükseklik ölçmeleri. Kaynak: İ.ASRİ (Gümüşhane Ü) T. FİKRET HORZUM( AÜ )
 Ölçme Bilgisi DERS 7-8 Yatay Kontrol Noktaları Ve Yükseklik ölçmeleri Kaynak: İ.ASRİ (Gümüşhane Ü) T. FİKRET HORZUM( AÜ ) Bir alanın üzerindeki detaylarla birlikte harita veya planının yapılabilmesi için
Ölçme Bilgisi DERS 7-8 Yatay Kontrol Noktaları Ve Yükseklik ölçmeleri Kaynak: İ.ASRİ (Gümüşhane Ü) T. FİKRET HORZUM( AÜ ) Bir alanın üzerindeki detaylarla birlikte harita veya planının yapılabilmesi için
DENEY 0. Bölüm 1 - Ölçme ve Hata Hesabı
 DENEY 0 Bölüm 1 - Ölçme ve Hata Hesabı Amaç: Ölçüm metodu ve cihazına bağlı hata ve belirsizlikleri anlamak, fiziksel bir niceliği ölçüp hata ve belirsizlikleri tespit etmek, nedenlerini açıklamak. Genel
DENEY 0 Bölüm 1 - Ölçme ve Hata Hesabı Amaç: Ölçüm metodu ve cihazına bağlı hata ve belirsizlikleri anlamak, fiziksel bir niceliği ölçüp hata ve belirsizlikleri tespit etmek, nedenlerini açıklamak. Genel
TRIGONOMETRI AÇI, YÖNLÜ AÇI, YÖNLÜ YAY
 TRIGONOMETRI AÇI, YÖNLÜ AÇI, YÖNLÜ YAY A. AÇI Başlangıç noktaları aynı olan iki ışının birleşim kümesine açı denir. Bu ışınlara açının kenarları, başlangıç noktasına ise açının köşesi denir. B. YÖNLÜ AÇI
TRIGONOMETRI AÇI, YÖNLÜ AÇI, YÖNLÜ YAY A. AÇI Başlangıç noktaları aynı olan iki ışının birleşim kümesine açı denir. Bu ışınlara açının kenarları, başlangıç noktasına ise açının köşesi denir. B. YÖNLÜ AÇI
3 VEKTÖRLER. Pilot uçağın kokpit inden havaalanını nasıl bulur?
 3.1 Koordinat sistemleri 3.2 Kartezyen koordinatlar 3.3 Vektörler 3.4 Vektörlerin bileşenleri 3.5 Vektörlerin toplanması 3.6 Vektörlerin çıkarılması 37Bii 3.7 Birim vektör 3 VEKTÖRLER Pilot uçağın kokpit
3.1 Koordinat sistemleri 3.2 Kartezyen koordinatlar 3.3 Vektörler 3.4 Vektörlerin bileşenleri 3.5 Vektörlerin toplanması 3.6 Vektörlerin çıkarılması 37Bii 3.7 Birim vektör 3 VEKTÖRLER Pilot uçağın kokpit
PERGEL YAYINLARI LYS 1 DENEME-6 KONU ANALİZİ SORU NO LYS 1 MATEMATİK TESTİ KAZANIM NO KAZANIMLAR
 2013-2014 PERGEL YAYINLARI LYS 1 DENEME-6 KONU ANALİZİ SORU NO LYS 1 MATEMATİK TESTİ A B KAZANIM NO KAZANIMLAR 1 1 / 31 12 32173 Üslü İfadeler 2 13 42016 Rasyonel ifade kavramını örneklerle açıklar ve
2013-2014 PERGEL YAYINLARI LYS 1 DENEME-6 KONU ANALİZİ SORU NO LYS 1 MATEMATİK TESTİ A B KAZANIM NO KAZANIMLAR 1 1 / 31 12 32173 Üslü İfadeler 2 13 42016 Rasyonel ifade kavramını örneklerle açıklar ve
