Anadolu Üniversitesi Mühendislik Mimarlık Fakültesi Endüstri Mühendisliği Bölümü. Doç. Dr. Nil ARAS ENM411 Tesis Planlaması Güz Dönemi
|
|
|
- Ayla Yalaz
- 8 yıl önce
- İzleme sayısı:
Transkript
1 Anadolu Üniversitesi Mühendislik Mimarlık Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması Güz Dönemi
2 2 TP ye özel paketleri / modülleri kullanmak CAD/CAM ortamından yararlanmak Genel amaçlı bir veri tabanındaki verileri kullanmak MatemaFk Programlama, yapay zeka, benzefm gibi başka bir amaç için gelişfrilmiş yazılımlardan faydalanmak Yeni programlar yazmak
3 3 Tek tesis yer seçimi problemi Blok diyagramları
4 4 Verim ve kaliteyi armrır. Kısa zamanda çok sayısal işlem yapar. Çok seçenek türefr. Öyle değil de böyle olsa tarzı soruları cevaplandırır. Yine de insan yargı ve deneyiminin yerini alamaz!
5 5
6 6 Değer ölçüsü (benimsenen amaç) Tesis planlamacısının değer ölçüleri ve tercihlerine dayanan AMAÇLAR Bilgisayarın algılayabileceği SAYISAL DEĞERLERE dönüştürülmelidir 6
7 7 Bütün bölümler dikdörtgendir. (Ya da farklı büyüklükteki dikdörtgen parçalardan oluşmuştur) Malzeme akışı, bölüm merkezinden, bölüm merkezine olmaktadır. Malzeme aktarma maliyetleri, uzaklıkla doğru oranvlıdır. Malzeme akışı ile ilgili tüm veriler belirlidir ve eldedir. Fire söz konusu değildir. Akışlar iki boyuwa olmaktadır.
8 8
9 9 1. KULLANDIKLARI VERİLERE GÖRE ALGORİTMALAR q Nitel q Nicel q Melez (faaliyet ilişki çizelgesi) (gezi diyagramı) (ikisinin karışımı)
10 10 2. BENİMSENEN AMACA GÖRE ALGORİTMALAR 2 temel amaç 1. Toplam maliyefn enküçüklenmesi 2. Fayda / Yakınlık puanının enbüyüklenmesi
11 11 : bölüm/ faaliyet ilişkileri sayısı : iki bölüm arasında bir dönemde yapılan taşımaların sayısı : i. bölüm ile j. bölüm arasındaki uzaklık : aynı mesafedeki birim taşıma maliyef ENK z = m i=1 m j=1 f c d ij ij ij
12 12 Gezi diyagramı gibi nicel veri kullanıldığında uygun. c ij değerlerinin aktarma donanımı kullanım oranından bağımsız olduğu, taşıma mesafesiyle doğrusal ilişkili olduğu varsayımı. Bazen her i, j için c ij =1 olarak alınır. Bu durumda tesis içerisindeki toplam birim yük taşımasına odaklanılmış olur. Bazı durumlarda c ij ler, genellikle birim yükün büyüklük, ağırlık gibi özelliklerine dayanan nisbi ağırlık değerleri olarak kullanılabilir.
13 13 : bölüm/ faaliyet ilişkileri sayısı : iki bölüm arasında bir dönemde yapılan taşımaların sayısı : Yerleşim planında i. bölüm ile j. bölüm bifşikse 1, değilse 0 ENB z = m i=1 m j=1 f ij x ij Faaliyet ilişki şeması gibi nitel veriler kullanıldığında uygundur.
14 14 Normalleştirilmiş yakınlık puanı Verimlilik oranı / Etkinlik oranı (efficiency rafng) 0-1 arasında bir değer 1 olması, aralarında poziff akış olan tüm bölümlerin yanyana yerleşfğini gösterir. z = m i=1 m m j=1 m i=1 j=1 f ij f ij x ij
15 Normalleştirilmiş yakınlık puanı (negatif akış olması durumu) Bazen yanyana gelmesinin istenmediği iki bölüm için negaff akış değeri verilebilir. A: PoziFf akış olan bölümler kümesi Ā: NegaFf akış olan bölümler kümesi 15 z = f. x f. (1-x ) ij ij ij ij (i, j) A (i, j) A f ij (i, j) A (i, j) A f ij
16 16 3. YERLEŞİM PLANININ GÖSTERİMİNE GÖRE ALGORİTMALAR
17 17 Kesikli gösterimde, eldeki yerleşimin bilgisayara aktarılabilmesi için, önce hücrelerden (BİRİM KARELER) oluşan bir yapıya dönüştürülmesi gerekir D D D D B B D D D D B B D D D E E E C C D E E F A A A A A F A A A F F F
18 18 4. KULLANIM AMACINA GÖRE ALGORİTMALAR q Kurma esaslı (construcfon) q GelişErme esaslı (improvement)
19 19 Kurma Esaslı Yordamlar BAŞLANGIÇ ÇÖZÜMÜ Bulur Kurma esaslı algoritmalar, bir ön çözüme gerek duymaksızın sonuca ulaşabilmektedirler. İki temel işlem SEÇME ve SIRALAMA dır. Teknikler arasındaki farklılaşma, bu iki temel işlemin değişik şekillerde yapılabilmesinden kaynaklanmaktadır. Bütün kurma esaslı algoritmalarda seçim işlemi, bölümlerin hangi sırayla ele alınıp yerleşfrileceğini belirlemekfr.
20 20 KURMA ESASLI ALGORİTMALAR İÇİN ORTAK ADIMLAR 1. Henüz seçilmemiş bir faaliyef seç. 2. Bu faaliyef boş olan ve sırası gelen bir yere yerleşfr. 3. Faaliyetlerin hepsi bir yere atanmadıysa Adım 1'e dön, aksi halde DUR.
21 21 Geliştirme Esaslı Yordamlar MEVCUT YERLEŞİM PLANININ İYİLEŞTİRİLMESİ amaçlanır. Başlangıçta bir yerleşim planı verilmelidir. Kurma esaslı algoritmaların çıkvları, gelişfrme algoritmalarının girdisi olarak kullanılırsa, daha da iyi sonuçlar elde edilebilmektedir.
22
23 23 (Pairwise Exchange Method)
24 24 İyileşFrme esaslı bir yöntemdir. MaliyeFn enküçüklenmesi veya faydanın enbüyüklenmesi amaçlarından biri benimsenebilir. Her adımda sadece iki bölümün yeri karşılıklı olarak değişfrilebilir. Birbiri ile yerleri değişecek bölümleri bulmak için, tüm ikili kombinasyonlar denenir ve eniyi amaç fonksiyonu değerine sahip olan değişim seçilir. Bu değişim adımları, bir iyileşme elde edilemediğinde sona erer.
25 25 ÖRNEK: Eşit büyüklükte yanyana dört bölüm, maliyet esaslı, birim taşıma maliyetleri aynı (c ij =1 alınabilir) Yerleşim Planı Gezi diyagramı
26 26 Mevcut planın toplam maliyet değerinin hesaplanması Uzaklık matrisi
27 27 Mevcut planın toplam maliyet değerinin hesaplanması Akış matrisi Uzaklık matrisi z = 4 4 i=1 j=1 i j f ij c ij d ij TC 1234 =10(1)+15(2)+ 20(3)+10(1)+ 5(2)+ 5(1) =125
28 Ardıştırma 1: Mevcut planda yapılabilir ikili değişimler
29 29 Ardıştırma 1 TC 2134 (1 2) =10(1)+15(1)+ 20(2)+10(2)+ 5(3)+ 5(1) =105 TC 3214 (1 3) =10(1)+15(2)+ 20(1)+10(1)+ 5(2)+ 5(3) = 95 TC 4231 (1 4) =10(2)+15(1)+ 20(3)+10(1)+ 5(1)+ 5(2) =120 TC 1324 (2 3) =10(2)+15(1)+ 20(3)+10(1)+ 5(1)+ 5(2) =120 TC 1432 (2 4) =10(3)+15(2)+ 20(1)+10(1)+ 5(2)+ 5(1) =105 TC 1243 (3 4) =10(1)+15(3)+ 20(2)+10(2)+ 5(1)+ 5(1) =125
30 30 Ardıştırma 1 En düşük taşıma maliyef değerine sahip olan (1-3) değişimi seçilir. Mevcut ve yeni yerleşim planları Mevcut plan Toplam maliyet = Yeni plan Toplam maliyet = 95
31 31 Ardıştırma 2: Yeni planda yapılabilir ikili değişimler
32 32 Ardıştırma 2 TC 3124 (1 2) =10(1)+15(1)+ 20(2)+10(2)+ 5(1)+ 5(3) =105 TC 1234 (1 3) =10(1)+15(2)+ 20(3)+10(1)+ 5(2)+ 5(1) =125 TC 3241 (1 4) =10(2)+15(3)+ 20(1)+10(1)+ 5(1)+ 5(2) =110 TC 2314 (2 3) =10(2)+15(1)+ 20(1)+10(1)+ 5(3)+ 5(2) = 90 TC 3412 (2 4) =10(1)+15(2)+ 20(1)+10(3)+ 5(2)+ 5(1) =105 TC 4213 (3 4) =10(1)+15(1)+ 20(2)+10(2)+ 5(1)+ 5(3) =105
33 33 Ardıştırma 2 En düşük taşıma maliyef değerine sahip olan (2-3) değişimi seçilir. 1. ve 2. ardışvrmada elde edilen yerleşim planları ardıştırma Toplam maliyet = ardıştırma Toplam maliyet = 90
34 Ardıştırma 3: Yeni planda yapılabilir ikili değişimler
35 35 Ardıştırma 3 TC 1324 (1 2) =10(2)+15(1)+ 20(3)+10(1)+ 5(3)+ 5(1) =120 TC 2134 (1 3) =10(1)+15(1)+ 20(2)+10(2)+ 5(3)+ 5(1) =105 TC 2341 (1 4) =10(3)+15(2)+ 20(1)+10(1)+ 5(2)+ 5(1) =105 TC 3214 (2 3) =10(1)+15(2)+ 20(1)+10(1)+ 5(2)+ 5(3) = 95 TC 4312 (2 4) =10(1)+15(1)+ 20(2)+10(2)+ 5(3)+ 5(1) =105 TC 2413 (3 4) =10(2)+15(1)+ 20(1)+10(3)+ 5(1)+ 5(2) =100
36 36 Sonuç Daha düşük maliyetli bir plan olmadığından algoritma sonlanır Mevcut plan Toplam maliyet = ardıştırma Toplam maliyet = ardıştırma Toplam maliyet = 90
37 37 (Graph-based method)
38 38 Kurma esaslı bir algoritmadır. Faaliyetler ya da bölümler düğüm olarak gösterilir. Faaliyetler (bölümler) arası ilişkiler ikili bir ayırım yapılmasını sağlar: sağlanması gerekenler ve gerekmeyenler Sağlanması gereken komşuluklar ayrıtlarla gösterilir (BiFşik bölümler ayrıtlarla bağlanır) Serim düzlemsel olarak yayılmamışsa (ayrıtlar kesişiyorsa) çözümü yoktur. Serim düzlemsel ise, blok diyagramına geçilir.
39 39
40 40 Ayrıtlarla çevrilmiş bölgeye YÜZ denir.
41 41 Serimde Kabuller Uzaklık ve komşuluktan başka ilişki göz önüne alınmaz. Bölüm şekilleri ve sınır uzunlukları dikkate alınmaz. Ayrıtlar kesişemez (düzlem) Yerleşimin değeri, ağırlıklara duyarlıdır.
42 42 İyi yönler Faaliyet ilişki çizelgesinden, doğrudan alan- ilişki diyagramına geçilebilir. Zayıf yönler BiFşik tesislerin arasındaki ilişkiyi kuvvetli sayar. Birden fazla çözümü vardır. Bilgisayar uygulaması zordur. Serim tekniği sadece bir ARAÇ Br. Kullanabileceğimiz yerlerde bütün üstünlükleriyle kullanmalıyız.
43 43 ÖRNEK:
44 44 Adım 1: En ağır çifti seç 3 ve
45 Adım 2: Bunlara toplam ağırlığı enbüyük olanı, bir yüz oluşturacak şekilde ekle. Son düğüme kadar bu adımı tekrarla. düğümler 3 4 Toplam
46 46 Bu yüze eklendiğinde, en büyük ağırlığı veren dördüncü düğümü bir yüz oluşturacak şekilde ekle düğümler Toplam
47 47 Alternatif yerleşim Toplam
48 Son düğümü ekle. Beşinci bölüm (5), hangi yüze? 48 2 Yüzler Ağırlıklar Toplam yüz 3. yüz 3 4
49 Adım 3: Son düğümü ekle. Beşinci bölüm (5), hangi yüze?
50 50 2 blok diyagramına geçiş
51 51
52 52 Computerized Relative Allocation of Facilities Technique
53 53 CRAFT için gerekli girdiler Başlangıç yerleşim düzenlemesi planı Gezi diyagramı (Bölümler arasında birim zamandaki taşıma sayıları) Birim yükün birim mesafeye taşınma maliyetleri Düzenlemede yerleri değişmeyecek sabit bölümlerin yerleri ve sayısı
54 54 CRAFT çıktıları Yalnız ikili değişim Yalnız üçlü değişim İkili değişimi izleyen üçlü değişim Üçlü değişimi izleyen ikili değişim Eniyi ikili ve üçlü değişim
55 55 CRAFT ın Özellikleri GelişFrme esaslı bir algoritmadır. Düzenleme alanı br 2 lerden oluşur. Tesisin dış yapısı kare ya da dikdörtgen olmalıdır. Değilse, kalan alanlar sabit alan olur. Maliyet bilgisi, birim yük için birim uzaklık başına hesaplandığından, bu uzaklık biriminin yerleşim düzeni planındaki 1 br 2 nin bir kenarının uzunluk birimiyle aynı olması uygulamada büyük önem taşır. (Örn: Bir karenin kenarı 2 m. ise, maliyet matrisi elemanlarının birimi 2 m. başına (TL/adet) ya da (TL/ton) olmalıdır) Bölümler arası akış verilirken br 2 ye göre verilmelidir.
56 56 CRAFT- ALGORİTMA 1. Bölümlerin ağırlık merkezlerini bul. 2. Uzaklıkları hesapla. 3. Toplam taşıma maliyefni hesapla değişiklikleri dene. En iyisini yap. 5. Gerçek ağırlık merkezlerini hesapla. 6. Tekrarla (daha iyisi bulunmayıncaya kadar yeni seçenekler)
57 57 Adım adım İYİLEŞTİRME (2 li, 3 lü değişim) Bölümler arasında ikili ve/ veya üçlü yer değişimleri yapılır. Değişecek bölümler ya KOMŞU olmalı ya da alanları EŞİT bölümler olmalıdır. Bölümlerin alanları eşitse problem yok. Komşu ise ve alanlar da farklı ise: Ağırlık merkezleri değişebilir Bölünme olabilir
58 58 İkili değişim (5-4)
59 59 Üçlü değişim (A- B- D)
60 60 Avantajları Sabit yerlerin tanımlanabilmesi Kısa bilgisayar zamanı gerekfrmesi Karışık matemafksel hesaplamalar gerekfrmemesi Maliyet ve tasarrufları göstermesi Şekillerin değişfrilebilmesi
61 61 Dezavantajları Olası değişikliklerin hepsi sınanmaz bu yüzden yerel eniyi çözüm sağlanır. Başlangıç yerleşim düzenini kendisi oluşturmaz. İstenmeyen yakınlıkları gözönüne almaz. Bölüm sayısı sınırlıdır. Bir faaliyete ayrılan alanda bölünmeler olabilir. Bölümler birbiriyle yer değişfrirken, aynı büyüklükte olmak, veya birbiriyle komşu olmak veya ortak başka bir bölümle sınırdaş olmak zorundadır.
62 62 İstenmeyen bir duruma örnek: 2-4 değişiminde bölünme
63 63 ÖRNEK : Mevcut ve önerilen planları CRAFT algoritmasının amacına göre karşılaşvrınız. A A A C B B B B B A A A C B B B B B A A A C B B B B B Mevcut yerleşim A A A B B B B B C A A A B B B B B C A A A B B B B B C A B C A B 2-7 C Akış matrisi Önerilen yerleşim
64 64 Uzaklık matrisi (mevcut durum) Bölümlerin ağırlık merkezleri arasındaki uzaklıklar A A A C B B B B B A A A C B B B B B A A A C B B B B B A B C A B 5-3 C birim
65 65 Uzaklık matrisi (önerilen durum) Bölümlerin ağırlık merkezleri arasındaki uzaklıklar A A A B B B B B C A A A B B B B B C A A A B B B B B C 4 birim A B C A B 4-3 C 7 3 -
66 66 Toplam taşıma maliyetleri (uzaklık x akış x birim maliyet) TM (mevcut) = 10(5) + 6(2) + 2(5) + 7(3) = 93 TM (önerilen) = 10(4) + 6(7) + 2(4) + 7(3) = = 18 birimlik bir arvş olacağından, değişiklik uygun değildir.
67 67 ÖRNEK : Başlangıç yerleşim planı
68 68 Birim kare büyüklüğü = 20 x 20 R
69 69 Başlangıç yerleşim planı A A A A A A A A A A G G G G G G G G A A G G A A A A A A A A A A G G G G B B B B B C C C C C E E G G G G G G B B C C E E E E E E E E B B C C C C C E E E E E E E E B B B B B D D D D F F F F F F F E E D D D D D D D F F F F D D D F F F F F F D D D D D D D D H H H H H F F F F F
70 70 Başlangıç yerleşim planı ve ağırlık merkezleri TM = 2974 x 20 = birim
71 71 E ve F bölümlerinin yer değişimi sonucunda elde edilen plan TM = 2953 x 20 = birim
72 72 Elde edilen eniyi yerleşim TM = birim Ufak düzeltmelerden sonra elde edilen son plan
73 73 WINQSB ile çözüm
74 74
75 75
76 76
77 77
78 78
79 79
80 80 BAŞLANGIÇ YERLEŞİM CRAFT İLE ELDE EDİLEN ENİYİ YERLEŞİM A A A A A A A A A A G G G G G G G G A A G G A A A A A A A A A A G G G B B B B B B B B B B F F G G G G G G B B B B B B B B B B F F F F F F F F C C C C C C C C C C F F F F F F C C C C C D D D D E E E E E E F D D D D D D D E E F F D D D E E E E E E F F D D D D D D D D H H H H H E E F F F G F F
81 81 MicroCraft
82 â Kesikli + gelişfrme esaslı Yerleşim alanı eşit genişlikte bantlara bölünür. Bant sayısı, tesis eni ve boyu, başlangıç yerleşim vektörü (örnek : )verilir. İkili değişim için kısıt YOKTUR Bölmez, hepsini kaydırır. İlk yerleşfrme? Sabit bölüm?
83 83 (Başlangıç yerleşim vektörü: )
84 84
85 85
86 86 Kurma- veya gelişfrme esaslı 2-3 bant (kendi seçer) Bant genişlikleri değişebilir. A E Sürekli gösterim C B Akış veya yakınlık diyagramı Bölümü bir banda ata D F Eni- boyu belirle (bölme yap) Bölümleri sıraya göre diz Faaliyet ilişki şemasını kullanır. Gezi diyagramı verilse bile onu faaliyet ilişki şemasına dönüştürür. Değerlendirmede CRAFT gibi ve cij=1 Veya A=10, E=5, I=2, O=1, U=0, X= - 10 Hesapla
87 87
88 88
89 89 (Layout Optimization with Guillotine Induced Cuts)
90 90 Kurma esaslı bir algoritmadır. Akış verileri, uzaklık esaslı d/d, sürekli, kurma Böle- böle kurar (düşey- yatay kesmeler) Rassal atamalar (alan belli en- boy bul) Ağaçta değişim iyileşfrme B b B, C 4.. D A, B, C, D, E, F,G B C A b 1. D d E G D F. B, C, E, G A, D, F k Y g k Y g... E,G A D, F d b D d b D d. C. E G D F
91 91
92
93
94 94
95 95
96 96 (MULTIfloor PLant EvaluaFon)
97 97 Kurma esaslı bir algoritmadır. CRAFT a benzer İkili değişimler daha esnekfr. Boşluk dolduran eğri (Hilbert) Sabit bölümleri atlar (köşegen geçişlerâ kopukluk) (değişim ve yerleşim farklı) Eğriler çok değişik değilse â Sonuç seçilen eğriye duyarsız
98 98
99 99
100 100
101 101 A, B, C, D ve E tesislerinin alanları, sırasıyla 8, 8, 8, 4 ve 4 birim kare, BECDA sırasıyla yerleşim D D A A D D A A C C A A C C A A C C E E C C E E B B B B B B B B B C D E A B C 5 2 Maliyet: 10(6) (3)+2(3)+12(6) = 164 D 12
102 102 A-B arası d/d uzaklık = 6 br. D D A A D D A A C C A A C C A A C C E E C C E E B B B B B B B B
103 103 B D değişimi DECBA sırasıyla yerleşim D D A A D D A A C C A A C C A A C C E E C C E E B B B B B B B B B B A A B B A A B B A A B B A A C C C C C C C C D D E E D D E E B C D E A B C 5 2 D 12 BECDA DECBA Maliyetler: 10(6) (3)+2(3)+12(6) = (2) (3)+2(3)+12(2) = 78
104 104 (COmputerized RElationship LAyout Planning)
105 105 CORELAP ve ALDEP 2 önemli kurma esaslı algoritma Hücreler, savr ve sütun sayısı (dıştan dışa ölçüleri) belli olan bir matrise (oturma alanı) yerleşfrilir. YerleşFrmede iki disiplin 1. Serbest yerleşim (corelap) 2. Sınırlı yerleşim (aldep)
106 106 Seçim süreci toplam yakınlık değeri (TYD) (total closeness rafng or TCR) kavramına dayanmaktadır. Yakınlık ilişkilerine şu puanlar verilir: A=6, E=5, I=4, O=3, U=2, X=1 TYD her bölüm için ayrı ayrı hesaplanır. Bu hesaplamada, bölümün diğer bölümlerle sağlamak istediği ilişkilerin puanları toplanır. Toplam puanı en yüksek çıkan bölüm, seçilen ilk bölümdür.
107 107 Sonraki sıraya, ona en yakın olması gereken bölüm alınır. En yakın olması gereken bölüm, en yüksek ilişki puanı olan bölümdür. Birden fazla bölümün puanlarının aynı olması halinde, bunlardan TYD si en yüksek olan tercih edilir. TYD ler de aynı ise, en büyük alana sahip olan, alanlar da aynı ise en küçük bölüm numarasına sahip olan seçilir.
108 108 Amaç uzaklık puanını enküçüklemek Yerleşim puanının hesaplanması: CR: bölümler arası sayısal yakınlık oranı d : bölümler arasındaki en kısa D/D uzaklık CR i j> i ij d ij
109 109
110 110 Birim alanlar için yaklaşık değerler de alınabilir. Bu örnek için her bir birim kare alanı 2000 olarak gösterilse de, bölümlerin kaplayacağı birim kareler sırasıyla, 2, 1, 1, 2, 1, 2, 2 olarak alınmışvr.
111 111 A=6, E=5, I=4, O=3, U=2, X=1
112 112
113 113
114 114 Bölüm 5 6 TYD 1 O U 5 2 I I 8 3 U O 5 4 I U 7 7 I E 9
115 115 Bölüm TYD 1 O U U 7 2 I I U 10 3 U O U 7 4 I U U 8
116 116
117 117
118 118 A=6 E=5 I=4 O=3 U=2 X=1
119 : 2 br., : 3 br. uzaklık
120 120 (Automated Layout DEsign Program)
121 121 Sınırlı yerleşim
122 122 Seçme işlemleri, bir kesme sınırı nın belirlenmesiyle başlar. Kesme sınırı: Hangi ilişkilerin dikkate alınacağını hangilerinin ihmal edileceğini göstermektedir. (Yalnız A veya sadece A veya E gibi) İlk faaliyefn seçimi rasgele yapılır. Daha sonra onunla A ilişkisi olan bir başka faaliyet aranır; bulunamazsa, daha alt düzeylerde ilişki bekleyen faaliyetlere razı olunmaktadır. Kesme sınırı üzerinde yakınlık isteyen bir faaliyet bulunmadığı takdirde ise, yeni bir seçim yapılarak aynı işlemler tekrarlanmakta; bu iş tüm faaliyetler seçilinceye kadar sürmektedir.
123 123 Seçme işlemleri, bir kesme sınırı nın belirlenmesiyle başlar. Kesme sınırı: Hangi ilişkilerin dikkate alınacağını hangilerinin ihmal edileceğini göstermektedir. (Yalnız A veya sadece A veya E gibi) İlk faaliyefn seçimi rasgele yapılır. Daha sonra onunla A ilişkisi olan bir başka faaliyet aranır; bulunamazsa, daha alt düzeylerde ilişki bekleyen faaliyetlere razı olunmaktadır. Kesme sınırı üzerinde yakınlık isteyen bir faaliyet bulunmadığı takdirde ise, yeni bir seçim yapılarak aynı işlemler tekrarlanmakta; bu iş tüm faaliyetler seçilinceye kadar sürmektedir.
124 124
125 125
126
127 127
128 Düzgün bölümâ Düzgün yol (ä maliyet ve ã güvenlik)
129 129 İstenmeyen hücre yerleşim şekilleri Kopuk yerleşim Ortada kalan boşluk Çok köşeli şekil Ortak kenarı olmayan hücreler Basık yerleşim
130 130 DÜZGÜNLÜK ÖLÇÜLERİ Kapsayan enküçük dikdörtgen (KED) Smallest Enclosing Rectangle (SER) 1. KED alanı / Bölüm alanı 2. KED uzun kenar/ked kısa kenar
131 İzoperimetre Şekil faktörü : S = P / A (çevre/alan) İdeal şekil kare ise â S*= P/A = 4 A/A =4/( A) Başka bir şeklin, normalleşfrilmiş şekil faktörü F=S/S* =(P/A)/(4/ A) = P/(4 A) 1.0 Eğer bölüm kare â F=1.0 Kare değilse â F>1.0 Genellikle kabul edilebilir çözümlerde 1.0=< F <1.4 olmaktadır. A A
132 132
133 133 ÖRNEK (Tompkins, sayfa 350) (b) şekli için: 1. KED alanı/ Bölüm alanı = 25/16=1, KED uzun kenar/ KED kısa kenar= 5/5 =1 3. F=20/(4 16)=1,25
Mühendislik Fakültesi Endüstri Mühendisliği Bölümü. Yerleşim Tasarımı. Algoritmaları. Doç. Dr. Nil ARAS ENM411 Tesis Planlaması Güz Dönemi
 Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Yerleşim Tasarımı Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2016-2017 Güz Dönemi Algoritmaları 2 TP ye özel paketleri / modülleri kullanmak Genel amaçlı
Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Yerleşim Tasarımı Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2016-2017 Güz Dönemi Algoritmaları 2 TP ye özel paketleri / modülleri kullanmak Genel amaçlı
Yerleşim Tasarımı Algoritmaları
 Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2018-2019 Güz Dönemi Yerleşim Tasarımı Algoritmaları 2 TP ye özel paketleri /
Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2018-2019 Güz Dönemi Yerleşim Tasarımı Algoritmaları 2 TP ye özel paketleri /
Kaynak: A. İŞLİER, TESİS PLANLAMASI, 1997
 Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2016-2017 Güz Dönemi Kaynak: A. İŞLİER, TESİS PLANLAMASI, 1997 2 Tesis Yer Seçimi Problemi (TYSP) TEK AMAÇLI
Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2016-2017 Güz Dönemi Kaynak: A. İŞLİER, TESİS PLANLAMASI, 1997 2 Tesis Yer Seçimi Problemi (TYSP) TEK AMAÇLI
Anadolu Üniversitesi Endüstri Mühendisliği Bölümü İST328 Yöneylem Araştırması 2 Dersi Bahar Dönemi. Hazırlayan: Doç. Dr.
 Anadolu Üniversitesi Endüstri Mühendisliği Bölümü İST8 Yöneylem Araştırması Dersi 00-0 Bahar Dönemi Hazırlayan: Doç. Dr. Nil ARAS AÇIKLAMA Bu sunu izleyen kaynaklardaki örnek ve bilgilerden faydalanarak
Anadolu Üniversitesi Endüstri Mühendisliği Bölümü İST8 Yöneylem Araştırması Dersi 00-0 Bahar Dönemi Hazırlayan: Doç. Dr. Nil ARAS AÇIKLAMA Bu sunu izleyen kaynaklardaki örnek ve bilgilerden faydalanarak
Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü. Doç. Dr. Nil ARAS ENM411 Tesis Planlaması Güz Dönemi
 Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2018-2019 Güz Dönemi 2 Tesis ihtiyaçlarının belirlenmesinde 3 önemli faktör Akış
Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2018-2019 Güz Dönemi 2 Tesis ihtiyaçlarının belirlenmesinde 3 önemli faktör Akış
Algoritma Geliştirme ve Veri Yapıları 10 Graf Veri Modeli. Mustafa Kemal Üniversitesi
 Algoritma Geliştirme ve Veri Yapıları 10 Graf Veri Modeli Graf, matematiksel anlamda, düğümler ve bu düğümler arasındaki ilişkiyi gösteren kenarlardan oluşan bir kümedir; mantıksal ilişki düğüm ile düğüm
Algoritma Geliştirme ve Veri Yapıları 10 Graf Veri Modeli Graf, matematiksel anlamda, düğümler ve bu düğümler arasındaki ilişkiyi gösteren kenarlardan oluşan bir kümedir; mantıksal ilişki düğüm ile düğüm
Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü. Doç. Dr. Nil ARAS ENM411 Tesis Planlaması Güz Dönemi
 Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2018-2019 Güz Dönemi Tesis Planlama Süreci (imalat ve montaj tesisleri için) 2
Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2018-2019 Güz Dönemi Tesis Planlama Süreci (imalat ve montaj tesisleri için) 2
Temel yerleşim tipleri. Sistematik tesis planlaması. Mühendislik Fakültesi Endüstri Mühendisliği Bölümü
 Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Temel yerleşim tipleri Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2016-2017 Güz Dönemi Sistematik tesis planlaması 2 YER SEÇİMİ X YERLEŞİM DÜZENLEMESİ
Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Temel yerleşim tipleri Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2016-2017 Güz Dönemi Sistematik tesis planlaması 2 YER SEÇİMİ X YERLEŞİM DÜZENLEMESİ
AKIŞ SİSTEMLERİ, FAALİYET İLİŞKİLERİ ve ALAN GEREKSİNİMLERİ
 Anadolu Üniversitesi Mühendislik Mimarlık Fakültesi Endüstri Mühendisliği Bölümü AKIŞ SİSTEMLERİ, FAALİYET İLİŞKİLERİ ve ALAN GEREKSİNİMLERİ Hazırlayan: Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2010-2011
Anadolu Üniversitesi Mühendislik Mimarlık Fakültesi Endüstri Mühendisliği Bölümü AKIŞ SİSTEMLERİ, FAALİYET İLİŞKİLERİ ve ALAN GEREKSİNİMLERİ Hazırlayan: Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2010-2011
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ
 ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTIRMA MODELİNİN TANIMI Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTIRMA MODELİNİN TANIMI Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
Toplam maliyete/gelire göre yer seçimi Faktör ağırlıklandırma Başabaş noktası analizi Oyun kuramı
 Anadolu Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2013-2014 Güz Dönemi Toplam maliyete/gelire göre yer seçimi Faktör ağırlıklandırma Başabaş
Anadolu Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2013-2014 Güz Dönemi Toplam maliyete/gelire göre yer seçimi Faktör ağırlıklandırma Başabaş
Genel Graf Üzerinde Mutlak 1-merkez
 Genel Graf Üzerinde Mutlak 1-merkez Çözüm yöntemine geçmeden önce bazı tanımlara ihtiyaç vardır. Dikkate alınan G grafındaki düğümleri 1 den n e kadar numaralandırın. Uzunluğu a(i, j)>0 olarak verilen
Genel Graf Üzerinde Mutlak 1-merkez Çözüm yöntemine geçmeden önce bazı tanımlara ihtiyaç vardır. Dikkate alınan G grafındaki düğümleri 1 den n e kadar numaralandırın. Uzunluğu a(i, j)>0 olarak verilen
SİMPLEKS ALGORİTMASI! ESASLARI!
 Fen ilimleri Enstitüsü Endüstri Mühendisliği Anabilim Dalı ENM53 Doğrusal Programlamada İleri Teknikler SİMPLEKS ALGORİTMASI ESASLARI Hazırlayan: Doç. Dr. Nil ARAS AÇIKLAMA n n u sununun hazırlanmasında,
Fen ilimleri Enstitüsü Endüstri Mühendisliği Anabilim Dalı ENM53 Doğrusal Programlamada İleri Teknikler SİMPLEKS ALGORİTMASI ESASLARI Hazırlayan: Doç. Dr. Nil ARAS AÇIKLAMA n n u sununun hazırlanmasında,
Graf Veri Modeli. Düğümler kümesi. Kenarlar kümesi
 Graf Veri Modeli Graf, bir olay veya ifadenin düğüm ve çizgiler kullanılarak gösterilme şeklidir. Fizik, Kimya gibi temel bilimlerde ve mühendislik uygulamalarında ve tıp biliminde pek çok problemin çözümü
Graf Veri Modeli Graf, bir olay veya ifadenin düğüm ve çizgiler kullanılarak gösterilme şeklidir. Fizik, Kimya gibi temel bilimlerde ve mühendislik uygulamalarında ve tıp biliminde pek çok problemin çözümü
DOĞRUSAL OLMAYAN PROGRAMLAMA -I-
 DOĞRUSAL OLMAYAN PROGRAMLAMA -I- Dışbükeylik / İçbükeylik Hazırlayan Doç. Dr. Nil ARAS Anadolu Üniversitesi, Endüstri Mühendisliği Bölümü İST38 Yöneylem Araştırması Dersi 0-0 Öğretim Yılı Doğrusal olmayan
DOĞRUSAL OLMAYAN PROGRAMLAMA -I- Dışbükeylik / İçbükeylik Hazırlayan Doç. Dr. Nil ARAS Anadolu Üniversitesi, Endüstri Mühendisliği Bölümü İST38 Yöneylem Araştırması Dersi 0-0 Öğretim Yılı Doğrusal olmayan
DOĞRUSAL OLMAYAN PROGRAMLAMA -II- Tek değişkenli doğrusal olmayan karar modelinin çözümü
 DOĞRUSAL OLMAYAN PROGRAMLAMA -II- Tek değişkenli doğrusal olmayan karar modelinin çözümü Hazırlayan Doç. Dr. Nil ARAS Anadolu Üniversitesi, Endüstri Mühendisliği Bölümü İST8 Yöneylem Araştırması Dersi
DOĞRUSAL OLMAYAN PROGRAMLAMA -II- Tek değişkenli doğrusal olmayan karar modelinin çözümü Hazırlayan Doç. Dr. Nil ARAS Anadolu Üniversitesi, Endüstri Mühendisliği Bölümü İST8 Yöneylem Araştırması Dersi
SİMPLEKS ALGORİTMASI Yapay değişken kullanımı
 Fen Bilimleri Enstitüsü Endüstri Mühendisliği Anabilim Dalı ENM53 Doğrusal Programlamada İleri Teknikler SİMPLEKS ALGORİTMASI Yapay değişken kullanımı Hazırlayan: Doç. Dr. Nil ARAS, 6 AÇIKLAMA Bu sununun
Fen Bilimleri Enstitüsü Endüstri Mühendisliği Anabilim Dalı ENM53 Doğrusal Programlamada İleri Teknikler SİMPLEKS ALGORİTMASI Yapay değişken kullanımı Hazırlayan: Doç. Dr. Nil ARAS, 6 AÇIKLAMA Bu sununun
Algoritma ve Akış Diyagramları
 Algoritma ve Akış Diyagramları Bir problemin çözümüne ulaşabilmek için izlenecek ardışık mantık ve işlem dizisine ALGORİTMA, algoritmanın çizimsel gösterimine ise AKIŞ DİYAGRAMI adı verilir 1 Akış diyagramları
Algoritma ve Akış Diyagramları Bir problemin çözümüne ulaşabilmek için izlenecek ardışık mantık ve işlem dizisine ALGORİTMA, algoritmanın çizimsel gösterimine ise AKIŞ DİYAGRAMI adı verilir 1 Akış diyagramları
Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü. Doç. Dr. Nil ARAS ENM411 Tesis Planlaması Güz Dönemi
 Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2018-2019 Güz Dönemi 2 F : Vardiya başına gereken makina sayısı S : Standart süre
Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2018-2019 Güz Dönemi 2 F : Vardiya başına gereken makina sayısı S : Standart süre
Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü. Doç. Dr. Nil ARAS ENM411 Tesis Planlaması Güz Dönemi
 Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2018-2019 Güz Dönemi 2 1. Tek noktada yoğunlaşmış tesisler 2. Alana düzgün dağılmış
Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2018-2019 Güz Dönemi 2 1. Tek noktada yoğunlaşmış tesisler 2. Alana düzgün dağılmış
Graflar bilgi parçaları arasındaki ilişkileri gösterirler.
 Graflar (Graphs) Graf gösterimi Uygulama alanları Graf terminolojisi Depth first dolaşma Breadth first dolaşma Topolojik sıralama Yrd.Doç.Dr. M. Ali Akcayol Graflar Graflar bilgi parçaları arasındaki ilişkileri
Graflar (Graphs) Graf gösterimi Uygulama alanları Graf terminolojisi Depth first dolaşma Breadth first dolaşma Topolojik sıralama Yrd.Doç.Dr. M. Ali Akcayol Graflar Graflar bilgi parçaları arasındaki ilişkileri
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ
 ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTıRMA MODELININ TANıMı Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTıRMA MODELININ TANıMı Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
Bu bölümde; Çok ölçütlü karar verme yöntemlerinden biri olan TOPSİS yöntemi anlatılacaktır.
 ÇOK ÖLÇÜTLÜ KARAR VERME TOPSIS (Technique For Order Preference By Similarity To Ideal Solution) PROF. DR. İBRAHİM ÇİL 1 Bu bölümde; Çok ölçütlü karar verme yöntemlerinden biri olan TOPSİS yöntemi anlatılacaktır.
ÇOK ÖLÇÜTLÜ KARAR VERME TOPSIS (Technique For Order Preference By Similarity To Ideal Solution) PROF. DR. İBRAHİM ÇİL 1 Bu bölümde; Çok ölçütlü karar verme yöntemlerinden biri olan TOPSİS yöntemi anlatılacaktır.
BÖLÜM III: Şebeke Modelleri. Şebeke Kavramları. Şebeke Kavramları. Şebeke Kavramları. Yönlü Şebeke (Directed Network) Dal / ok
 8.0.0 Şebeke Kavramları BÖLÜM III: Şebeke Modelleri Şebeke (Network) Sonlu sayıdaki düğümler kümesiyle, bunlarla bağlantılı oklar (veya dallar) kümesinin oluşturduğu yapı şeklinde tanımlanabilir ve (N,A)
8.0.0 Şebeke Kavramları BÖLÜM III: Şebeke Modelleri Şebeke (Network) Sonlu sayıdaki düğümler kümesiyle, bunlarla bağlantılı oklar (veya dallar) kümesinin oluşturduğu yapı şeklinde tanımlanabilir ve (N,A)
EM302 Yöneylem Araştırması 2. Dr. Özgür Kabak
 EM302 Yöneylem Araştırması 2 Dr. Özgür Kabak TP Çözümü TP problemlerinin çözümü için başlıca iki yaklaşım vardır kesme düzlemleri (cutting planes) dal sınır (branch and bound) tüm yaklaşımlar tekrarlı
EM302 Yöneylem Araştırması 2 Dr. Özgür Kabak TP Çözümü TP problemlerinin çözümü için başlıca iki yaklaşım vardır kesme düzlemleri (cutting planes) dal sınır (branch and bound) tüm yaklaşımlar tekrarlı
Web Madenciliği (Web Mining)
 Web Madenciliği (Web Mining) Hazırlayan: M. Ali Akcayol Gazi Üniversitesi Bilgisayar Mühendisliği Bölümü Konular Denetimli Öğrenmenin Temelleri Karar Ağaçları Entropi ID3 Algoritması C4.5 Algoritması Twoing
Web Madenciliği (Web Mining) Hazırlayan: M. Ali Akcayol Gazi Üniversitesi Bilgisayar Mühendisliği Bölümü Konular Denetimli Öğrenmenin Temelleri Karar Ağaçları Entropi ID3 Algoritması C4.5 Algoritması Twoing
Kümeler arası. Küme içi. uzaklıklar. maksimize edilir. minimize edilir
 Kümeleme Analizi: Temel Kavramlar ve Algoritmalar Kümeleme Analizi Nedir? Her biri bir dizi öznitelik ile, veri noktalarının bir kümesi ve noktalar arasındaki benzerliği ölçen bir benzerlik ölçümü verilmiş
Kümeleme Analizi: Temel Kavramlar ve Algoritmalar Kümeleme Analizi Nedir? Her biri bir dizi öznitelik ile, veri noktalarının bir kümesi ve noktalar arasındaki benzerliği ölçen bir benzerlik ölçümü verilmiş
YZM ALGORİTMA ANALİZİ VE TASARIM DERS#9: AÇGÖZLÜ ALGORİTMALAR
 YZM 3207- ALGORİTMA ANALİZİ VE TASARIM DERS#9: AÇGÖZLÜ ALGORİTMALAR Aç Gözlü (Hırslı) Algoritmalar (Greedy ) Bozuk para verme problemi Bir kasiyer 48 kuruş para üstünü nasıl verir? 25 kuruş, 10 kuruş,
YZM 3207- ALGORİTMA ANALİZİ VE TASARIM DERS#9: AÇGÖZLÜ ALGORİTMALAR Aç Gözlü (Hırslı) Algoritmalar (Greedy ) Bozuk para verme problemi Bir kasiyer 48 kuruş para üstünü nasıl verir? 25 kuruş, 10 kuruş,
Kitle: Belirli bir özelliğe sahip bireylerin veya birimlerin tümünün oluşturduğu topluluğa kitle denir.
 BÖLÜM 1: FREKANS DAĞILIMLARI 1.1. Giriş İstatistik, rasgelelik içeren olaylar, süreçler, sistemler hakkında modeller kurmada, gözlemlere dayanarak bu modellerin geçerliliğini sınamada ve bu modellerden
BÖLÜM 1: FREKANS DAĞILIMLARI 1.1. Giriş İstatistik, rasgelelik içeren olaylar, süreçler, sistemler hakkında modeller kurmada, gözlemlere dayanarak bu modellerin geçerliliğini sınamada ve bu modellerden
Okut. Yüksel YURTAY. İletişim : (264) Sayısal Analiz. Giriş.
 Okut. Yüksel YURTAY İletişim : Sayısal Analiz yyurtay@sakarya.edu.tr www.cs.sakarya.edu.tr/yyurtay (264) 295 58 99 Giriş 1 Amaç : Mühendislik problemlerinin bilgisayar ortamında çözümünü mümkün kılacak
Okut. Yüksel YURTAY İletişim : Sayısal Analiz yyurtay@sakarya.edu.tr www.cs.sakarya.edu.tr/yyurtay (264) 295 58 99 Giriş 1 Amaç : Mühendislik problemlerinin bilgisayar ortamında çözümünü mümkün kılacak
Algoritmalar. Arama Problemi ve Analizi. Bahar 2016 Doç. Dr. Suat Özdemir 1
 Algoritmalar Arama Problemi ve Analizi Bahar 2016 Doç. Dr. Suat Özdemir 1 Arama Problemi Sıralama algoritmaları gibi arama algoritmaları da gerçek hayat bilgisayar mühendisliği problemlerinin çözümünde
Algoritmalar Arama Problemi ve Analizi Bahar 2016 Doç. Dr. Suat Özdemir 1 Arama Problemi Sıralama algoritmaları gibi arama algoritmaları da gerçek hayat bilgisayar mühendisliği problemlerinin çözümünde
YZM VERİ YAPILARI DERS#9: HASH FONKSİYONLARI
 YZM 2116- VERİ YAPILARI DERS#9: HASH FONKSİYONLARI İÇERİK Bu bölümde, Giriş Hash Tabloları Hash Fonksiyonu Çakışma (Collision) Ayrık Zincirleme Çözümü Linear Probing Çözümü Quadratic Probing Çözümü konusuna
YZM 2116- VERİ YAPILARI DERS#9: HASH FONKSİYONLARI İÇERİK Bu bölümde, Giriş Hash Tabloları Hash Fonksiyonu Çakışma (Collision) Ayrık Zincirleme Çözümü Linear Probing Çözümü Quadratic Probing Çözümü konusuna
ÜRÜN, SÜREÇ ve ÇİZELGE TASARIMI
 Anadolu Üniversitesi Mühendislik Mimarlık Fakültesi Endüstri Mühendisliği Bölümü ÜRÜN, SÜREÇ ve ÇİZELGE TASARIMI Hazırlayan: Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2010-2011 Öğretim Yılı, Güz Dönemi
Anadolu Üniversitesi Mühendislik Mimarlık Fakültesi Endüstri Mühendisliği Bölümü ÜRÜN, SÜREÇ ve ÇİZELGE TASARIMI Hazırlayan: Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2010-2011 Öğretim Yılı, Güz Dönemi
Elektrik Devre Temelleri
 Elektrik Devre Temelleri 2. TEMEL KANUNLAR Doç. Dr. M. Kemal GÜLLÜ Elektronik ve Haberleşme Mühendisliği Kocaeli Üniversitesi Bu bölümde Ohm Kanunu Düğüm, dal, çevre 2.1. Giriş Kirchhoff Kanunları Paralel
Elektrik Devre Temelleri 2. TEMEL KANUNLAR Doç. Dr. M. Kemal GÜLLÜ Elektronik ve Haberleşme Mühendisliği Kocaeli Üniversitesi Bu bölümde Ohm Kanunu Düğüm, dal, çevre 2.1. Giriş Kirchhoff Kanunları Paralel
VERİ MADENCİLİĞİ (Kümeleme) Yrd.Doç.Dr. Kadriye ERGÜN
 VERİ MADENCİLİĞİ (Kümeleme) Yrd.Doç.Dr. Kadriye ERGÜN kergun@balikesir.edu.tr İçerik Kümeleme İşlemleri Kümeleme Tanımı Kümeleme Uygulamaları Kümeleme Yöntemleri Kümeleme (Clustering) Kümeleme birbirine
VERİ MADENCİLİĞİ (Kümeleme) Yrd.Doç.Dr. Kadriye ERGÜN kergun@balikesir.edu.tr İçerik Kümeleme İşlemleri Kümeleme Tanımı Kümeleme Uygulamaları Kümeleme Yöntemleri Kümeleme (Clustering) Kümeleme birbirine
ORTALAMA ÖLÇÜLERİ. Ünite 6. Öğr. Gör. Ali Onur CERRAH
 ORTALAMA ÖLÇÜLERİ Ünite 6 Öğr. Gör. Ali Onur CERRAH Araştırma sonucunda elde edilen nitelik değişkenler hakkında tablo ve grafikle bilgi sahibi olunurken, sayısal değişkenler hakkında bilgi sahibi olmanın
ORTALAMA ÖLÇÜLERİ Ünite 6 Öğr. Gör. Ali Onur CERRAH Araştırma sonucunda elde edilen nitelik değişkenler hakkında tablo ve grafikle bilgi sahibi olunurken, sayısal değişkenler hakkında bilgi sahibi olmanın
KONU 4: DOĞRUSAL PROGRAMLAMA MODELİ İÇİN ÇÖZÜM YÖNTEMLERİ I
 KONU 4: DOĞRUSAL PROGRAMLAMA MODELİ İÇİN ÇÖZÜM YÖNTEMLERİ I 4.1. Dışbükeylik ve Uç Nokta Bir d.p.p. de model kısıtlarını aynı anda sağlayan X X X karar değişkenleri... n vektörüne çözüm denir. Eğer bu
KONU 4: DOĞRUSAL PROGRAMLAMA MODELİ İÇİN ÇÖZÜM YÖNTEMLERİ I 4.1. Dışbükeylik ve Uç Nokta Bir d.p.p. de model kısıtlarını aynı anda sağlayan X X X karar değişkenleri... n vektörüne çözüm denir. Eğer bu
ISK116 - Bölüm 1. Grup Teknolojisi
 ISK - Bölüm Grup Teknolojisi Grup Teknolojisi (GT) Grup teknolojisi benzerliklerden faydalanarak büyük ve karmaşık bir üretim sisteminin, küçük ve kolay kontrol edilebilir sistemlere dönüştürülmesi hedeflenmektedir.
ISK - Bölüm Grup Teknolojisi Grup Teknolojisi (GT) Grup teknolojisi benzerliklerden faydalanarak büyük ve karmaşık bir üretim sisteminin, küçük ve kolay kontrol edilebilir sistemlere dönüştürülmesi hedeflenmektedir.
STATİK. Ders_9. Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü. Ders notları için: GÜZ
 STATİK Ders_9 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2017-2018 GÜZ ALANLAR İÇİN ATALET MOMENTİNİN TANIMI, ALAN ATALET YARIÇAPI
STATİK Ders_9 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2017-2018 GÜZ ALANLAR İÇİN ATALET MOMENTİNİN TANIMI, ALAN ATALET YARIÇAPI
Ders Notlarının Creative Commons lisansı Feza BUZLUCA ya aittir. Lisans: http://creativecommons.org/licenses/by-nc-nd/3.0/
 Eşzamanlı (Senkron) Ardışıl Devrelerin Tasarlanması (Design) Bir ardışıl devrenin tasarlanması, çözülecek olan problemin sözle anlatımıyla (senaryo) başlar. Bundan sonra aşağıda açıklanan aşamalardan geçilerek
Eşzamanlı (Senkron) Ardışıl Devrelerin Tasarlanması (Design) Bir ardışıl devrenin tasarlanması, çözülecek olan problemin sözle anlatımıyla (senaryo) başlar. Bundan sonra aşağıda açıklanan aşamalardan geçilerek
Algoritma Geliştirme ve Veri Yapıları 2 Veri Modelleri. Mustafa Kemal Üniversitesi
 Algoritma Geliştirme ve Veri Yapıları 2 Veri Modelleri Veri modelleri, veriler arasında ilişkisel ve sırasal düzeni gösteren kavramsal tanımlardır. Her program en azından bir veri modeline dayanır. Uygun
Algoritma Geliştirme ve Veri Yapıları 2 Veri Modelleri Veri modelleri, veriler arasında ilişkisel ve sırasal düzeni gösteren kavramsal tanımlardır. Her program en azından bir veri modeline dayanır. Uygun
Microsoft Excel Uygulaması 2
 Microsoft Excel Uygulaması 2 Dört Temel İşlem: MS Excel hücrelerinde doğrudan değerlere ya da hücre başvurularına bağlı olarak hesaplamalar yapmak mümkündür. Temel aritmetik işlemlerin gerçekleştirilmesi
Microsoft Excel Uygulaması 2 Dört Temel İşlem: MS Excel hücrelerinde doğrudan değerlere ya da hücre başvurularına bağlı olarak hesaplamalar yapmak mümkündür. Temel aritmetik işlemlerin gerçekleştirilmesi
VERİ MADENCİLİĞİ (Karar Ağaçları ile Sınıflandırma) Yrd.Doç.Dr. Kadriye ERGÜN
 VERİ MADENCİLİĞİ (Karar Ağaçları ile Sınıflandırma) Yrd.Doç.Dr. Kadriye ERGÜN kergun@balikesir.edu.tr İçerik Sınıflandırma yöntemleri Karar ağaçları ile sınıflandırma Entropi Kavramı ID3 Algoritması C4.5
VERİ MADENCİLİĞİ (Karar Ağaçları ile Sınıflandırma) Yrd.Doç.Dr. Kadriye ERGÜN kergun@balikesir.edu.tr İçerik Sınıflandırma yöntemleri Karar ağaçları ile sınıflandırma Entropi Kavramı ID3 Algoritması C4.5
Görünüş çıkarmak için, cisimlerin özelliğine göre belirli kurallar uygulanır.
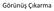 Görünüş Çıkarma Görünüş çıkarma? Parçanın bitmiş halini gösteren eşlenik dik iz düşüm kurallarına göre belirli yerlerde, konumlarda ve yeterli sayıda çizilmiş iz düşümlere GÖRÜNÜŞ denir. Görünüş çıkarmak
Görünüş Çıkarma Görünüş çıkarma? Parçanın bitmiş halini gösteren eşlenik dik iz düşüm kurallarına göre belirli yerlerde, konumlarda ve yeterli sayıda çizilmiş iz düşümlere GÖRÜNÜŞ denir. Görünüş çıkarmak
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
TOPSIS yönteminin adımları 5 Adım 1. Normalize karar matrisinin oluşturulması 6 Karar matrisinin normalizasyonu aşağıdaki formül kullanılarak yapılır:
 Giriş 2 TOPSIS Bölüm 5 TOPSIS (Technique for Order Preference by Similarity to Ideal Solution) 1981 yılında Hwang ve Yoon tarafından geliştirilmiştir. Uygulanması basit, ulaşılan sonuçlar çok gerçekçidir.
Giriş 2 TOPSIS Bölüm 5 TOPSIS (Technique for Order Preference by Similarity to Ideal Solution) 1981 yılında Hwang ve Yoon tarafından geliştirilmiştir. Uygulanması basit, ulaşılan sonuçlar çok gerçekçidir.
a) Çıkarma işleminin; eksilen ile çıkanın ters işaretlisinin toplamı anlamına geldiğini kavrar.
 7. SINIF KAZANIM VE AÇIKLAMALARI M.7.1. SAYILAR VE İŞLEMLER M.7.1.1. Tam Sayılarla Toplama, Çıkarma, Çarpma ve Bölme İşlemleri M.7.1.1.1. Tam sayılarla toplama ve çıkarma işlemlerini yapar; ilgili problemleri
7. SINIF KAZANIM VE AÇIKLAMALARI M.7.1. SAYILAR VE İŞLEMLER M.7.1.1. Tam Sayılarla Toplama, Çıkarma, Çarpma ve Bölme İşlemleri M.7.1.1.1. Tam sayılarla toplama ve çıkarma işlemlerini yapar; ilgili problemleri
VERİ YAPILARI. GRAPH LAR Düzce Üniversitesi Teknoloji Fakültesi ÖĞR.GÖR.GÜNAY TEMÜR 1
 VERİ YAPILARI GRAPH LAR Düzce Üniversitesi Teknoloji Fakültesi ÖĞR.GÖR.GÜNAY TEMÜR 1 GRAPH (ÇİZGE - GRAF) Terminoloji Çizge Kullanım Alanları Çizge Gösterimi Komşuluk Matrisi Komşuluk Listesi Çizge Üzerinde
VERİ YAPILARI GRAPH LAR Düzce Üniversitesi Teknoloji Fakültesi ÖĞR.GÖR.GÜNAY TEMÜR 1 GRAPH (ÇİZGE - GRAF) Terminoloji Çizge Kullanım Alanları Çizge Gösterimi Komşuluk Matrisi Komşuluk Listesi Çizge Üzerinde
1 ÜRETİM VE ÜRETİM YÖNETİMİ
 İÇİNDEKİLER ÖNSÖZ III Bölüm 1 ÜRETİM VE ÜRETİM YÖNETİMİ 13 1.1. Üretim, Üretim Yönetimi Kavramları ve Önemi 14 1.2. Üretim Yönetiminin Tarihisel Gelişimi 18 1.3. Üretim Yönetiminin Amaçları ve Fonksiyonları
İÇİNDEKİLER ÖNSÖZ III Bölüm 1 ÜRETİM VE ÜRETİM YÖNETİMİ 13 1.1. Üretim, Üretim Yönetimi Kavramları ve Önemi 14 1.2. Üretim Yönetiminin Tarihisel Gelişimi 18 1.3. Üretim Yönetiminin Amaçları ve Fonksiyonları
Yrd. Doç. Dr. Caner ÖZCAN
 Yrd. Doç. Dr. Caner ÖZCAN BAĞLI LİSTELER Bağlı listeler konusuna çalışmanın bazı faydaları var. Bağlı listeler gerçek programlarda kullanılabilecek bir veri yapısıdır. Bağlı listelerin güçlü ve zayıf yönlerini
Yrd. Doç. Dr. Caner ÖZCAN BAĞLI LİSTELER Bağlı listeler konusuna çalışmanın bazı faydaları var. Bağlı listeler gerçek programlarda kullanılabilecek bir veri yapısıdır. Bağlı listelerin güçlü ve zayıf yönlerini
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
Merkezi Yığılma ve Dağılım Ölçüleri
 1.11.013 Merkezi Yığılma ve Dağılım Ölçüleri 4.-5. hafta Merkezi eğilim ölçüleri, belli bir özelliğe ya da değişkene ilişkin ölçme sonuçlarının, hangi değer etrafında toplandığını gösteren ve veri grubunu
1.11.013 Merkezi Yığılma ve Dağılım Ölçüleri 4.-5. hafta Merkezi eğilim ölçüleri, belli bir özelliğe ya da değişkene ilişkin ölçme sonuçlarının, hangi değer etrafında toplandığını gösteren ve veri grubunu
İSTATİSTİK I KISA ÖZET KOLAYAOF
 DİKKATİNİZE: BURADA SADECE ÖZETİN İLK ÜNİTESİ SİZE ÖRNEK OLARAK GÖSTERİLMİŞTİR. ÖZETİN TAMAMININ KAÇ SAYFA OLDUĞUNU ÜNİTELERİ İÇİNDEKİLER BÖLÜMÜNDEN GÖREBİLİRSİNİZ. İSTATİSTİK I KISA ÖZET KOLAYAOF 2 Kolayaof.com
DİKKATİNİZE: BURADA SADECE ÖZETİN İLK ÜNİTESİ SİZE ÖRNEK OLARAK GÖSTERİLMİŞTİR. ÖZETİN TAMAMININ KAÇ SAYFA OLDUĞUNU ÜNİTELERİ İÇİNDEKİLER BÖLÜMÜNDEN GÖREBİLİRSİNİZ. İSTATİSTİK I KISA ÖZET KOLAYAOF 2 Kolayaof.com
JEODEZİK VERİLERİN İSTATİSTİK ANALİZİ. Prof. Dr. Mualla YALÇINKAYA
 JEODEZİK VERİLERİN İSTATİSTİK ANALİZİ Prof. Dr. Mualla YALÇINKAYA Karadeniz Teknik Üniversitesi, Harita Mühendisliği Bölümü Trabzon, 2018 VERİLERİN İRDELENMESİ Örnek: İki nokta arasındaki uzunluk 80 kere
JEODEZİK VERİLERİN İSTATİSTİK ANALİZİ Prof. Dr. Mualla YALÇINKAYA Karadeniz Teknik Üniversitesi, Harita Mühendisliği Bölümü Trabzon, 2018 VERİLERİN İRDELENMESİ Örnek: İki nokta arasındaki uzunluk 80 kere
Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre
 Jeodezi 7 1 Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre Elipsoid yüzeyinin küçük parçalarında oluşan küçük üçgenlerin (kenarları 50-60 km den küçük) hesaplanmasında klasik jeodezide
Jeodezi 7 1 Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre Elipsoid yüzeyinin küçük parçalarında oluşan küçük üçgenlerin (kenarları 50-60 km den küçük) hesaplanmasında klasik jeodezide
... ROBOTİK VE KODLAMA EĞİTİMİ ÇERÇEVESİNDE ÖĞRETİM YILI BİLİŞİM TEKNOLOJİLERİ DERSİ ÜNİTELENDİRİLMİŞ YILLIK DERS PLANI
 ... ROBOTİK VE KODLAMA EĞİTİMİ ÇERÇEVESİNDE 2018 2019 ÖĞRETİM YILI BİLİŞİM TEKNOLOJİLERİ DERSİ ÜNİTELENDİRİLMİŞ YILLIK DERS PLANI Hazırlayan : Özel Öğretim Kurumları Birliği (ÖZKURBİR) Dersin Adı : Bilişim
... ROBOTİK VE KODLAMA EĞİTİMİ ÇERÇEVESİNDE 2018 2019 ÖĞRETİM YILI BİLİŞİM TEKNOLOJİLERİ DERSİ ÜNİTELENDİRİLMİŞ YILLIK DERS PLANI Hazırlayan : Özel Öğretim Kurumları Birliği (ÖZKURBİR) Dersin Adı : Bilişim
Rasgele Sayı Üretme. Rasgele Sayıların Özellikleri. İki önemli istaiksel özelliği var :
 Rasgele Sayı Üretme Rasgele Sayıların Özellikleri İki önemli istaiksel özelliği var : Düzgünlük (Uniformity) Bağımsızlık R i, rasgele sayısı olasılık yoğunluk fonksiyonu aşağıdaki gibi olan uniform bir
Rasgele Sayı Üretme Rasgele Sayıların Özellikleri İki önemli istaiksel özelliği var : Düzgünlük (Uniformity) Bağımsızlık R i, rasgele sayısı olasılık yoğunluk fonksiyonu aşağıdaki gibi olan uniform bir
Ayrık Fourier Dönüşümü
 Ayrık Fourier Dönüşümü Tanım: 0 n N 1 aralığında tanımlı N uzunluklu bir dizi x[n] nin AYRIK FOURIER DÖNÜŞÜMÜ (DFT), ayrık zaman Fourier dönüşümü (DTFT) X(e jω ) nın0 ω < 2π aralığında ω k = 2πk/N, k =
Ayrık Fourier Dönüşümü Tanım: 0 n N 1 aralığında tanımlı N uzunluklu bir dizi x[n] nin AYRIK FOURIER DÖNÜŞÜMÜ (DFT), ayrık zaman Fourier dönüşümü (DTFT) X(e jω ) nın0 ω < 2π aralığında ω k = 2πk/N, k =
DEPREME DAYANIKLI YAPI TASARIMI
 DEPREME DAYANIKLI YAPI TASARIMI Düşey Doğrultuda Düzensizlik Durumları 7. Hafta Yrd. Doç. Dr. Alper CUMHUR Kaynak: Sakarya Üniversitesi / İnşaat Mühendisliği Bölümü / Depreme Dayanıklı Betonarme Yapı Tasarımı
DEPREME DAYANIKLI YAPI TASARIMI Düşey Doğrultuda Düzensizlik Durumları 7. Hafta Yrd. Doç. Dr. Alper CUMHUR Kaynak: Sakarya Üniversitesi / İnşaat Mühendisliği Bölümü / Depreme Dayanıklı Betonarme Yapı Tasarımı
SORU 1. Eleman nedir, temel özellikleri nelerdir? İşlere ilişkin elemanları örnek de vererek yazınız.
 Öğrenci Numarası Adı ve Soyadı İmzası: SORU. Eleman nedir, temel özellikleri nelerdir? İşlere ilişkin elemanları örnek de vererek yazınız. SORU. İş ölçümünde ölçülen bileşenleri (insan/makine) yazınız
Öğrenci Numarası Adı ve Soyadı İmzası: SORU. Eleman nedir, temel özellikleri nelerdir? İşlere ilişkin elemanları örnek de vererek yazınız. SORU. İş ölçümünde ölçülen bileşenleri (insan/makine) yazınız
TÜRKİYE CUMHURİYETİ DEVLETİNİN temellerinin atıldığı Çanakkale zaferinin 100. yılı kutlu olsun.
 Doç.Dr.Mehmet MISIR-2013 TÜRKİYE CUMHURİYETİ DEVLETİNİN temellerinin atıldığı Çanakkale zaferinin 100. yılı kutlu olsun. Son yıllarda teknolojinin gelişmesi ile birlikte; geniş alanlarda, kısa zaman aralıklarında
Doç.Dr.Mehmet MISIR-2013 TÜRKİYE CUMHURİYETİ DEVLETİNİN temellerinin atıldığı Çanakkale zaferinin 100. yılı kutlu olsun. Son yıllarda teknolojinin gelişmesi ile birlikte; geniş alanlarda, kısa zaman aralıklarında
YZM 2116 Veri Yapıları
 YZM 2116 Veri Yapıları Yrd. Doç. Dr. Deniz KILINÇ Celal Bayar Üniversitesi Hasan Ferdi Turgutlu Teknoloji Fakültesi Yazılım Mühendisliği BÖLÜM - 11 Bu bölümde, Graph (Çizge - Graf) Terminoloji Çizge Kullanım
YZM 2116 Veri Yapıları Yrd. Doç. Dr. Deniz KILINÇ Celal Bayar Üniversitesi Hasan Ferdi Turgutlu Teknoloji Fakültesi Yazılım Mühendisliği BÖLÜM - 11 Bu bölümde, Graph (Çizge - Graf) Terminoloji Çizge Kullanım
PROGRAMLAMAYA GİRİŞ. Öğr. Gör. Ayhan KOÇ. Kaynak: Algoritma Geliştirme ve Programlamaya Giriş, Dr. Fahri VATANSEVER, Seçkin Yay.
 PROGRAMLAMAYA GİRİŞ Öğr. Gör. Ayhan KOÇ Kaynak: Algoritma Geliştirme ve Programlamaya Giriş, Dr. Fahri VATANSEVER, Seçkin Yay., 2007 Algoritma ve Programlamaya Giriş, Ebubekir YAŞAR, Murathan Yay., 2011
PROGRAMLAMAYA GİRİŞ Öğr. Gör. Ayhan KOÇ Kaynak: Algoritma Geliştirme ve Programlamaya Giriş, Dr. Fahri VATANSEVER, Seçkin Yay., 2007 Algoritma ve Programlamaya Giriş, Ebubekir YAŞAR, Murathan Yay., 2011
C PROGRAMLAMA YRD.DOÇ.DR. BUKET DOĞAN PROGRAM - ALGORİTMA AKIŞ ŞEMASI
 C PROGRAMLAMA DİLİ YRD.DOÇ.DR. BUKET DOĞAN 1 PROGRAM - ALGORİTMA AKIŞ ŞEMASI Program : Belirli bir problemi çözmek için bir bilgisayar dili kullanılarak yazılmış deyimler dizisi. Algoritma bir sorunun
C PROGRAMLAMA DİLİ YRD.DOÇ.DR. BUKET DOĞAN 1 PROGRAM - ALGORİTMA AKIŞ ŞEMASI Program : Belirli bir problemi çözmek için bir bilgisayar dili kullanılarak yazılmış deyimler dizisi. Algoritma bir sorunun
BLM-431 YAPAY ZEKA. Ders-4 Bilgisiz Arama Yöntemleri. Yrd. Doç. Dr. Ümit ATİLA
 BLM-431 YAPAY ZEKA Ders-4 Bilgisiz Arama Yöntemleri Yrd. Doç. Dr. Ümit ATİLA umitatila@karabuk.edu.tr http://web.karabuk.edu.tr/umitatilla/ Dersin Hedefleri Aşağıda verilen arama stratejilerini anlamak
BLM-431 YAPAY ZEKA Ders-4 Bilgisiz Arama Yöntemleri Yrd. Doç. Dr. Ümit ATİLA umitatila@karabuk.edu.tr http://web.karabuk.edu.tr/umitatilla/ Dersin Hedefleri Aşağıda verilen arama stratejilerini anlamak
AHP ye Giriş Karar verici, her alternatifin her kriterde ne kadar başarılı olduğunu değerlendirir. Her kriterin amaca ulaşmadaki görece önemini değerl
 AHP ye Giriş 2 Analitik Hiyerarşi Süreci Bölüm 3 AHP, birebir değerlendirerek alternatifleri sıralamaya dayanan çok nitelikli karar verme yöntemidir. Amaçlar ve alt amaçlar iç içe katmanlar halinde ve
AHP ye Giriş 2 Analitik Hiyerarşi Süreci Bölüm 3 AHP, birebir değerlendirerek alternatifleri sıralamaya dayanan çok nitelikli karar verme yöntemidir. Amaçlar ve alt amaçlar iç içe katmanlar halinde ve
YAPAY SİNİR AĞLARI. Araş. Gör. Nesibe YALÇIN BİLECİK ÜNİVERSİTESİ
 YAPAY SİNİR AĞLARI Araş. Gör. Nesibe YALÇIN BİLECİK ÜNİVERSİTESİ İÇERİK Sinir Hücreleri Yapay Sinir Ağları Yapısı Elemanları Çalışması Modelleri Yapılarına Göre Öğrenme Algoritmalarına Göre Avantaj ve
YAPAY SİNİR AĞLARI Araş. Gör. Nesibe YALÇIN BİLECİK ÜNİVERSİTESİ İÇERİK Sinir Hücreleri Yapay Sinir Ağları Yapısı Elemanları Çalışması Modelleri Yapılarına Göre Öğrenme Algoritmalarına Göre Avantaj ve
Analitik Hiyerarşi Prosesi (AHP) Yrd.Doç.Dr. Sabahattin Kerem AYTULUN
 Analitik Hiyerarşi Prosesi (AHP) Yrd.Doç.Dr. Sabahattin Kerem AYTULUN Giriş AHP Thomas L.Saaty tarafından 1970'lerde ortaya atılmıştır. Amaç alternatifler arasından en iyisinin seçilmesidir. Subjektif
Analitik Hiyerarşi Prosesi (AHP) Yrd.Doç.Dr. Sabahattin Kerem AYTULUN Giriş AHP Thomas L.Saaty tarafından 1970'lerde ortaya atılmıştır. Amaç alternatifler arasından en iyisinin seçilmesidir. Subjektif
FORMÜL ADI (FONKSİYON) FORMÜLÜN YAZILIŞI YAPTIĞI İŞLEMİN AÇIKLAMASI
 1 SIKÇA KULLANILAN EXCEL FORMÜLLERİ 1 AŞAĞI YUVARLAMA =aşağıyuvarla(c7;2) 2 YUKARI YUVARLAMA =yukarıyuvarla(c7;2) 3 YUVARLAMA =yuvarla(c7;2) 4 TAVANA YUVARLAMA =tavanayuvarla(c7;5) 5 TABANA YUVARLAMA =TABANAYUVARLA(E2;5)
1 SIKÇA KULLANILAN EXCEL FORMÜLLERİ 1 AŞAĞI YUVARLAMA =aşağıyuvarla(c7;2) 2 YUKARI YUVARLAMA =yukarıyuvarla(c7;2) 3 YUVARLAMA =yuvarla(c7;2) 4 TAVANA YUVARLAMA =tavanayuvarla(c7;5) 5 TABANA YUVARLAMA =TABANAYUVARLA(E2;5)
YZM YAPAY ZEKA DERS#4: BİLGİSİZ ARAMA YÖNTEMLERİ
 YZM 327 - YAPAY ZEKA DERS#4: BİLGİSİZ ARAMA YÖNTEMLERİ Bilgisiz Arama Stratejisi Sadece problem formülasyonundaki mevcut bilgiyi kullanır Durum bilgisinden yararlanmazlar Çözüme ulaşmak için hiçbir bilgi
YZM 327 - YAPAY ZEKA DERS#4: BİLGİSİZ ARAMA YÖNTEMLERİ Bilgisiz Arama Stratejisi Sadece problem formülasyonundaki mevcut bilgiyi kullanır Durum bilgisinden yararlanmazlar Çözüme ulaşmak için hiçbir bilgi
MONTE CARLO BENZETİMİ
 MONTE CARLO BENZETİMİ U(0,1) rassal değişkenler kullanılarak (zamanın önemli bir rolü olmadığı) stokastik ya da deterministik problemlerin çözümünde kullanılan bir tekniktir. Monte Carlo simülasyonu, genellikle
MONTE CARLO BENZETİMİ U(0,1) rassal değişkenler kullanılarak (zamanın önemli bir rolü olmadığı) stokastik ya da deterministik problemlerin çözümünde kullanılan bir tekniktir. Monte Carlo simülasyonu, genellikle
KUVVET, MOMENT ve DENGE
 2.1. Kuvvet 2.1.1. Kuvvet ve cisimlere etkileri Kuvvetler vektörel büyüklüklerdir. Kuvvet vektörünün; uygulama noktası, kuvvetin cisme etkidiği nokta; doğrultu ve yönü, kuvvetin doğrultu ve yönü; modülüyse
2.1. Kuvvet 2.1.1. Kuvvet ve cisimlere etkileri Kuvvetler vektörel büyüklüklerdir. Kuvvet vektörünün; uygulama noktası, kuvvetin cisme etkidiği nokta; doğrultu ve yönü, kuvvetin doğrultu ve yönü; modülüyse
UYDU GÖRÜNTÜLERİ VE SAYISAL UZAKTAN ALGILAMA
 UYDU GÖRÜNTÜLERİ VE SAYISAL UZAKTAN ALGILAMA Son yıllarda teknolojinin gelişmesi ile birlikte; geniş alanlarda, kısa zaman aralıklarında ucuz ve hızlı sonuç alınabilen uzaktan algılama tekniğinin, yenilenebilir
UYDU GÖRÜNTÜLERİ VE SAYISAL UZAKTAN ALGILAMA Son yıllarda teknolojinin gelişmesi ile birlikte; geniş alanlarda, kısa zaman aralıklarında ucuz ve hızlı sonuç alınabilen uzaktan algılama tekniğinin, yenilenebilir
BMT 206 Ayrık Matematik. Yük. Müh. Köksal GÜNDOĞDU 1
 BMT 206 Ayrık Matematik Yük. Müh. Köksal GÜNDOĞDU 1 Graph (Çizge) Yük. Müh. Köksal GÜNDOĞDU 2 Graph (Çizge) Köşe (vertex) adı verilen düğümlerden ve kenar (edge) adı verilip köşeleri birbirine bağlayan
BMT 206 Ayrık Matematik Yük. Müh. Köksal GÜNDOĞDU 1 Graph (Çizge) Yük. Müh. Köksal GÜNDOĞDU 2 Graph (Çizge) Köşe (vertex) adı verilen düğümlerden ve kenar (edge) adı verilip köşeleri birbirine bağlayan
( ) (, ) Kombinasyon. Tanım: r n olmak üzere n elemanlı bir kümenin r elemanlı her alt kümesine bu n elemanın r li kombinasyonu denir.
 Kombinasyon Tanım: r n olmak üzere n elemanlı bir kümenin r elemanlı her alt kümesine bu n elemanın r li kombinasyonu denir. n elemanın tüm r li kombinasyonlarının sayısı; (, ) C n r ( ) r n P n, r n!
Kombinasyon Tanım: r n olmak üzere n elemanlı bir kümenin r elemanlı her alt kümesine bu n elemanın r li kombinasyonu denir. n elemanın tüm r li kombinasyonlarının sayısı; (, ) C n r ( ) r n P n, r n!
İÇİNDEKİLER. 1. Analitik Hiyerarşi Prosesi(AHP) Yöntemi 2. TOPSİS Yöntemi 3. ENTROPİ Yöntemi 4. MAUT Yöntemi
 İÇİNDEKİLER 1. Analitik Hiyerarşi Prosesi(AHP) Yöntemi 2. TOPSİS Yöntemi 3. ENTROPİ Yöntemi 4. MAUT Yöntemi 1. Analitik Hiyerarşi Prosesi (AHP) Analitik Hiyerarşi Süreci tekniği karmaşık karar problemlerinde
İÇİNDEKİLER 1. Analitik Hiyerarşi Prosesi(AHP) Yöntemi 2. TOPSİS Yöntemi 3. ENTROPİ Yöntemi 4. MAUT Yöntemi 1. Analitik Hiyerarşi Prosesi (AHP) Analitik Hiyerarşi Süreci tekniği karmaşık karar problemlerinde
YEDİ YENİ KALİTE ARACI Yedi yeni kalite aracı, süreçten toplanan verilerin analizlerini öngören basit problem çözme tekniklerinden farklı olarak,
 YEDİ YENİ KALİTE ARACI Yedi yeni kalite aracı, süreçten toplanan verilerin analizlerini öngören basit problem çözme tekniklerinden farklı olarak, problem hakkında uzman ve problem ile ilişki içinde bulunan
YEDİ YENİ KALİTE ARACI Yedi yeni kalite aracı, süreçten toplanan verilerin analizlerini öngören basit problem çözme tekniklerinden farklı olarak, problem hakkında uzman ve problem ile ilişki içinde bulunan
Bölüm 7: Kilitlenme (Deadlocks)
 Bölüm 7: Kilitlenme (Deadlocks) Mehmet Demirci tarafından çevrilmiştir. Silberschatz, Galvin and Gagne 2013 Bölüm 7: Kilitlenme (Deadlocks) Sistem modeli Kilitlenme Belirleme Kilitlenme Yönetim Yöntemleri
Bölüm 7: Kilitlenme (Deadlocks) Mehmet Demirci tarafından çevrilmiştir. Silberschatz, Galvin and Gagne 2013 Bölüm 7: Kilitlenme (Deadlocks) Sistem modeli Kilitlenme Belirleme Kilitlenme Yönetim Yöntemleri
Algoritmalar. Sıralama Problemi ve Analizi. Bahar 2017 Doç. Dr. Suat Özdemir 1
 Algoritmalar Sıralama Problemi ve Analizi Bahar 2017 Doç. Dr. Suat Özdemir 1 Sıralama Problemi ve Analizi Bu bölümde öncelikle bir diğer böl-ve-yönet yöntemine dayalı algoritma olan Quick Sort algoritması
Algoritmalar Sıralama Problemi ve Analizi Bahar 2017 Doç. Dr. Suat Özdemir 1 Sıralama Problemi ve Analizi Bu bölümde öncelikle bir diğer böl-ve-yönet yöntemine dayalı algoritma olan Quick Sort algoritması
SOBA BORUSU AÇINIM LEVHALARININ KESİLMESİNDE MALİYETLERİN ENKÜÇÜKLENMESİ
 SOBA BORUSU AÇINIM LEVHALARININ KESİLMESİNDE MALİYETLERİN ENKÜÇÜKLENMESİ Doğan EROL Anadolu Üniversitesi Endüstri Mühendisliği Bölümü 1. PROBLEMİN TANIMLANMASI Şekil - 1'de 5 değişik soba borusu için açınım
SOBA BORUSU AÇINIM LEVHALARININ KESİLMESİNDE MALİYETLERİN ENKÜÇÜKLENMESİ Doğan EROL Anadolu Üniversitesi Endüstri Mühendisliği Bölümü 1. PROBLEMİN TANIMLANMASI Şekil - 1'de 5 değişik soba borusu için açınım
Montaj Hatti Tasarımı ve Analizi - 8
 Balıkesir Üniversitesi, Endüstri Mühendisliği Bölümü 2017-2018 Bahar Yarıyılı Montaj Hatti Tasarımı ve Analizi - 8 Yrd. Doc. Dr. Ibrahim Kucukkoc http://ikucukkoc.baun.edu.tr Tek Modelli Düz MHD Problemlerinin
Balıkesir Üniversitesi, Endüstri Mühendisliği Bölümü 2017-2018 Bahar Yarıyılı Montaj Hatti Tasarımı ve Analizi - 8 Yrd. Doc. Dr. Ibrahim Kucukkoc http://ikucukkoc.baun.edu.tr Tek Modelli Düz MHD Problemlerinin
YZM ALGORİTMA ANALİZİ VE TASARIM DERS#6: AZALT VE FETHET YÖNTEMİ
 YZM 3207- ALGORİTMA ANALİZİ VE TASARIM DERS#6: AZALT VE FETHET YÖNTEMİ Azalt ve Fethet Algoritmaları Problemi daha küçük bir örneğine çevir: Küçük örneği çöz Çözümü asıl probleme genişlet 3 tipi vardır:
YZM 3207- ALGORİTMA ANALİZİ VE TASARIM DERS#6: AZALT VE FETHET YÖNTEMİ Azalt ve Fethet Algoritmaları Problemi daha küçük bir örneğine çevir: Küçük örneği çöz Çözümü asıl probleme genişlet 3 tipi vardır:
EXCEL 2007 ELEKTRONİK ÇİZELGE
 EXCEL 2007 ELEKTRONİK ÇİZELGE Excel, Microsoft Office paketinde yer alan ve iş hayatında en sık kullanılan programlardandır. Bir hesap tablosu programıdır. Excel, her türlü veriyi (özellikle sayısal verileri)
EXCEL 2007 ELEKTRONİK ÇİZELGE Excel, Microsoft Office paketinde yer alan ve iş hayatında en sık kullanılan programlardandır. Bir hesap tablosu programıdır. Excel, her türlü veriyi (özellikle sayısal verileri)
PROJE HAZIRLAMA. Kritik Yol Metodu CPM
 15. hafta PROJE HAZIRLAMA Kritik Yol Metodu CPM Kritik Yol Metodu CPM CPM (Critical Path Method Kritik Yol Yöntemi) ve PERT (Program Evaluation and Review Technique Program Değerlendirme ve Gözden Geçirme
15. hafta PROJE HAZIRLAMA Kritik Yol Metodu CPM Kritik Yol Metodu CPM CPM (Critical Path Method Kritik Yol Yöntemi) ve PERT (Program Evaluation and Review Technique Program Değerlendirme ve Gözden Geçirme
2- PROJE YÖNETİMİ BİLGİ ALANLARI Y R D. D O Ç. D R. K E N A N G E N Ç O L
 2- PROJE YÖNETİMİ BİLGİ ALANLARI Y R D. D O Ç. D R. K E N A N G E N Ç O L 10 TEMEL BILGI ALANı (PMI YAKLAŞıMı) Proje Entegrasyon Yönetimi Proje Kapsam Yönetimi Proje Zaman Yönetimi Proje Maliyet Yönetimi
2- PROJE YÖNETİMİ BİLGİ ALANLARI Y R D. D O Ç. D R. K E N A N G E N Ç O L 10 TEMEL BILGI ALANı (PMI YAKLAŞıMı) Proje Entegrasyon Yönetimi Proje Kapsam Yönetimi Proje Zaman Yönetimi Proje Maliyet Yönetimi
İŞ YERİ DÜZENLEME YERLEŞME DÜZENİNİN ÖNEMİ:
 İŞ YERİ DÜZENLEME YERLEŞME DÜZENİNİN ÖNEMİ: İş yeri düzenlemenin ana amacı işletme içinde üretime yönelik faaliyetlerde yer alan canlı ve cansız varlıkların tümünün hareket miktarlarının minimize edilmesidir.
İŞ YERİ DÜZENLEME YERLEŞME DÜZENİNİN ÖNEMİ: İş yeri düzenlemenin ana amacı işletme içinde üretime yönelik faaliyetlerde yer alan canlı ve cansız varlıkların tümünün hareket miktarlarının minimize edilmesidir.
GANTT ÇİZELGESİ PERT DİYAGRAMI
 GANTT ÇİZELGESİ PERT DİYAGRAMI SİSTEM ANALİZİ VE TASARIMI DERSİ YILDIZ TEKNIK ÜNIVERSITESI BİLGİSAYAR MÜHENDİSLİĞİ 1 Gantt Çizelgesi... 2 Giriş... 2 Faaliyetler Arası Öncelik İlişkisi... 3 Kritik Yol...
GANTT ÇİZELGESİ PERT DİYAGRAMI SİSTEM ANALİZİ VE TASARIMI DERSİ YILDIZ TEKNIK ÜNIVERSITESI BİLGİSAYAR MÜHENDİSLİĞİ 1 Gantt Çizelgesi... 2 Giriş... 2 Faaliyetler Arası Öncelik İlişkisi... 3 Kritik Yol...
Zeki Optimizasyon Teknikleri
 Zeki Optimizasyon Teknikleri Ara sınav - 25% Ödev (Haftalık) - 10% Ödev Sunumu (Haftalık) - 5% Final (Proje Sunumu) - 60% - Dönem sonuna kadar bir optimizasyon tekniğiyle uygulama geliştirilecek (Örn:
Zeki Optimizasyon Teknikleri Ara sınav - 25% Ödev (Haftalık) - 10% Ödev Sunumu (Haftalık) - 5% Final (Proje Sunumu) - 60% - Dönem sonuna kadar bir optimizasyon tekniğiyle uygulama geliştirilecek (Örn:
SÜREKLİ OLASILIK DAĞILIMI
 SÜREKLİ OLASILIK DAĞILIMI Normal Olasılık Dağılımı Akülerin dayanma süresi, araçların belli bir zamanda aldığı yol, bir koşuya katılanların bitirme süresi gibi sayılamayacak kadar çok değer alabilen sürekli
SÜREKLİ OLASILIK DAĞILIMI Normal Olasılık Dağılımı Akülerin dayanma süresi, araçların belli bir zamanda aldığı yol, bir koşuya katılanların bitirme süresi gibi sayılamayacak kadar çok değer alabilen sürekli
JEODEZİK AĞLARIN OPTİMİZASYONU
 JEODEZİK AĞLARIN OPTİMİZASYONU Jeodezik Ağların Tasarımı 10.HAFTA Dr.Emine Tanır Kayıkçı,2017 OPTİMİZASYON Herhangi bir yatırımın gerçekleştirilmesi sırasında elde bulunan, araç, hammadde, para, işgücü
JEODEZİK AĞLARIN OPTİMİZASYONU Jeodezik Ağların Tasarımı 10.HAFTA Dr.Emine Tanır Kayıkçı,2017 OPTİMİZASYON Herhangi bir yatırımın gerçekleştirilmesi sırasında elde bulunan, araç, hammadde, para, işgücü
11.Hafta En kısa yollar I-II-III Devam. Negatif Ağırlıklı En Kısa Yollar Doğruluk Çözümleme
 11.Hafta En kısa yollar I-II-III Devam Negatif Ağırlıklı En Kısa Yollar Doğruluk Çözümleme 1 En Kısa Yollar II Bellman-Ford algoritması 2 3 Negatif Maliyetli Çember Eğer graf negatif maliyetli çember içeriyorsa,
11.Hafta En kısa yollar I-II-III Devam Negatif Ağırlıklı En Kısa Yollar Doğruluk Çözümleme 1 En Kısa Yollar II Bellman-Ford algoritması 2 3 Negatif Maliyetli Çember Eğer graf negatif maliyetli çember içeriyorsa,
Algoritma ve Akış Diyagramları
 Algoritma ve Akış Diyagramları Bir problemin çözümüne ulaşabilmek için izlenecek ardışık mantık ve işlem dizisine ALGORİTMA, algoritmanın çizimsel gösterimine ise AKIŞ DİYAGRAMI adı verilir. 1 Akış diyagramları
Algoritma ve Akış Diyagramları Bir problemin çözümüne ulaşabilmek için izlenecek ardışık mantık ve işlem dizisine ALGORİTMA, algoritmanın çizimsel gösterimine ise AKIŞ DİYAGRAMI adı verilir. 1 Akış diyagramları
FORMÜLLER VE FONKSİYONLAR
 C FORMÜLLER VE FONKSİYONLAR Konuya Hazırlık 1. Excel de formül kullanmanın faydalarını açıklayınız. Formüller, bir sayfadaki verileri kullanarak işlem yapan denklemlerdir. Bir formülde, aynı sayfadaki
C FORMÜLLER VE FONKSİYONLAR Konuya Hazırlık 1. Excel de formül kullanmanın faydalarını açıklayınız. Formüller, bir sayfadaki verileri kullanarak işlem yapan denklemlerdir. Bir formülde, aynı sayfadaki
Yatak Katsayısı Yaklaşımı
 Yatak Katsayısı Yaklaşımı Yatak katsayısı yaklaşımı, sürekli bir ortam olan zemin için kurulmuş matematik bir modeldir. Zemin bu modelde yaylar ile temsil edilir. Yaylar, temel taban basıncı ve zemin deformasyonu
Yatak Katsayısı Yaklaşımı Yatak katsayısı yaklaşımı, sürekli bir ortam olan zemin için kurulmuş matematik bir modeldir. Zemin bu modelde yaylar ile temsil edilir. Yaylar, temel taban basıncı ve zemin deformasyonu
Elektrik Devre Temelleri 3
 Elektrik Devre Temelleri 3 TEMEL KANUNLAR-2 Doç. Dr. M. Kemal GÜLLÜ Elektronik ve Haberleşme Mühendisliği Kocaeli Üniversitesi ÖRNEK 2.5 v 1 ve v 2 gerilimlerini bulun. (KGK) PROBLEM 2.5 v 1 ve v 2 gerilimlerini
Elektrik Devre Temelleri 3 TEMEL KANUNLAR-2 Doç. Dr. M. Kemal GÜLLÜ Elektronik ve Haberleşme Mühendisliği Kocaeli Üniversitesi ÖRNEK 2.5 v 1 ve v 2 gerilimlerini bulun. (KGK) PROBLEM 2.5 v 1 ve v 2 gerilimlerini
DOĞRUSAL PROGRAMLAMANIN ÖZEL TÜRLERİ
 DOĞRUSAL PROGRAMLAMANIN ÖZEL TÜRLERİ TRANSPORTASYON (TAŞIMA, ULAŞTIRMA) TRANSİT TAŞIMA (TRANSSHIPMENT) ATAMA (TAHSİS) TRANSPORTASYON (TAŞIMA) (ULAŞTIRMA) TRANSPORTASYON Malların birden fazla üretim (kaynak,
DOĞRUSAL PROGRAMLAMANIN ÖZEL TÜRLERİ TRANSPORTASYON (TAŞIMA, ULAŞTIRMA) TRANSİT TAŞIMA (TRANSSHIPMENT) ATAMA (TAHSİS) TRANSPORTASYON (TAŞIMA) (ULAŞTIRMA) TRANSPORTASYON Malların birden fazla üretim (kaynak,
MUKAVEMET Öğr. Gör. Fatih KURTULUŞ
 www.sakarya.edu.tr MUKAVEMET Öğr. Gör. Fatih KURTULUŞ www.sakarya.edu.tr 1. DÜŞEY YÜKLÜ KİRİŞLER Cisimlerin mukavemeti konusunun esas problemi, herhangi bir yapıya uygulanan bir kuvvetin oluşturacağı gerilme
www.sakarya.edu.tr MUKAVEMET Öğr. Gör. Fatih KURTULUŞ www.sakarya.edu.tr 1. DÜŞEY YÜKLÜ KİRİŞLER Cisimlerin mukavemeti konusunun esas problemi, herhangi bir yapıya uygulanan bir kuvvetin oluşturacağı gerilme
3.2. DP Modellerinin Simpleks Yöntem ile Çözümü Primal Simpleks Yöntem
 3.2. DP Modellerinin Simpleks Yöntem ile Çözümü 3.2.1. Primal Simpleks Yöntem Grafik çözüm yönteminde gördüğümüz gibi optimal çözüm noktası, her zaman uygun çözüm alanının bir köşe noktası ya da uç noktası
3.2. DP Modellerinin Simpleks Yöntem ile Çözümü 3.2.1. Primal Simpleks Yöntem Grafik çözüm yönteminde gördüğümüz gibi optimal çözüm noktası, her zaman uygun çözüm alanının bir köşe noktası ya da uç noktası
Örnek...4 : İlk iki sınavında 75 ve 82 alan bir öğrencinin bu dersin ortalamasını 5 yapabilmek için son sınavdan kaç alması gerekmektedir?
 İSTATİSTİK Bir sonuç çıkarmak ya da çözüme ulaşabilmek için gözlem, deney, araştırma gibi yöntemlerle toplanan bilgiye veri adı verilir. Örnek...4 : İlk iki sınavında 75 ve 82 alan bir öğrencinin bu dersin
İSTATİSTİK Bir sonuç çıkarmak ya da çözüme ulaşabilmek için gözlem, deney, araştırma gibi yöntemlerle toplanan bilgiye veri adı verilir. Örnek...4 : İlk iki sınavında 75 ve 82 alan bir öğrencinin bu dersin
