BULANIK MANTIK VE SİSTEMLERİ BAHAR DÖNEMİ ÖDEV 1. Müslüm ÖZTÜRK Bilişim Teknolojileri Mühendisliği ABD Doktora Programı
|
|
|
- Umut Karadag
- 8 yıl önce
- İzleme sayısı:
Transkript
1 BULANIK MANTIK VE SİSTEMLERİ BAHAR DÖNEMİ ÖDEV 1 Müslüm ÖZTÜRK Bilişim Teknolojileri Mühendisliği ABD Doktora Programı Mart
2 SORU 1) Bulanık Küme nedir? Bulanık Kümenin (fuzzy set) kesin (crisp set) kümeye göre avantajları nelerdir? Ders notlarında olmayan bir parametreyi hem kesin hem de bulanık küme ile gösterimini yapınız. CEVAP 1) Bulanık kümeyi tanımlamadan önce biraz klasik küme kavramından bahsedelim. Klasik bir küme, kesin sınırlamalarla verilen bir kümedir. Örneğin, klasik bir küme aşağıdaki gibi belirtilebilir: A= { x x > 16 }, Kapalı sınır noktası burada 16 dır. Burada olduğu gibi eğer x bu sayıdan büyükse öyleyse x, A kümesine aittir aksi takdirde x bu kümeye ait değildir. Oysa Bulanık küme (veya belirtisiz küme) kavramı, küme kavramının eleman olmanın derecelendirilmesine dayanan bir genelleştirilmesidir. Bulanık kümeler belirtisiz mantığın doğal bir genişlemesi olarak 1965 yılında A. Zadeh tarafından tanımlanmıştır. Bir nesne bir kümenin ya elemanı ya da elemanı değilken, bir bulanık kümenin belirli bir oranda kısmen elemanı olabilir. Yani Klasik kümelere göre bulanık kümeler, adından da anlaşılacağı gibi kesin limitleri olmayan bir kümedir. Burada " kümeye ait olan" dan "kümeye ait olmayana" geçiş aşamalı olur ve bulanık kümelere "su sıcak " veya "sıcaklık çok yüksek" gibi tanımlarda olduğu gibi modellemede çoğunlukla dilsel açıklamalara esneklik kazandıran bu düzgün geçiş üyelik fonksiyonları olarak tanımlanmaktadır. Örneğin X boştan farklı bir evrensel küme olarak seçilsin. Bir A:X [0,1] fonksiyonuna X üzerinde bir bulanık küme adı verilir. Bulanık küme farklı şekillerde de tanımlanabilir ancak kümenin her nokta için [0,1] kapalı aralığında bulunan bir üyelik değerine sahip olmasını anlatması bakımından bu tanımların hepsi birbirine denktir. Bir x X elemanı için A(x) değerine x'in A'daki elemanlık derecesi denir. Bu değer kimi zaman μ Α(x) ile de gösterilir. A(x)=1 olması klasik küme anlamında x'in A'nın elemanı olması, A(x)=0 olması ise klasik kümelerdeki 'in A'nın elemanı olmaması durumuna denk gelir. Eğer bir x için A(x)= α ise x α A yazılır ve x'in A bulanık kümesinin α derecesinde elemanı olduğu söylenir. Örneğin A(x)= 0,5 yani x 0,5 A olması x'in A'nın yarı yarıya elemanı olması şeklinde yorumlanır. 1 klasik, 0 klasik sembolüne karşılık gelir. Klasik küme ve bulanık kümeye başka bir örnek vermek gerekirse; X bir nesneler uzayı, x de bu uzaya ait bir eleman olsun. A kümesi de bu X in alt kümesi olan bir klasik küme olsun. Bu durumda her bir x için bu A kümesine aittir ya da ait değildir. Her bir x elemanı için bir karakteristik fonksiyon tanımlayarak, klasik A kümesini (x,0) veya (x,1) sıralı ikililerle temsil edebiliriz. {(x,0) ın anlamı x A, (x,1) in anlamı x A dır.} Bu gösterim x elemanının A kümesine ait olup olmadığını gösteren bir gösterimdir. Bulanık kümelerin 1
3 karakteristik fonksiyonları ise bir elemanın ilgili bulanık kümeye üyeliğinin derecesini gösteren [0-1] aralığındaki değerlere sahip olmayı sağlar. Örneğin; X ayrık bulanık kümesi, X = { 1, 2, 3, 4, 5, 6, 7, 8 } olarak öğrencinin bir dönemde alabileceği kursların kümesi olsun. O halde bulanık küme olan A = "alınabilecek kursların sayısı " şeklinde olup bu bulanık A kümesi şu şekilde tanımlanabilir: A = { ( 1, 0.1 ), ( 2, 0.3 ), ( 3, 0.8 ), ( 4, 1 ), ( 5, 0.9 ), ( 6, 0.5 ), ( 7, 0.2 ), (8, 0.1 ) }. Bunun anlamı şudur: 1 sayısı 0.1 üyelik derecesiyle; 2 sayısı 0.3 üyelik derecesiyle; 3 sayısı 0.8 üyelik derecesiyle vs. A bulanık kümesine üyedirler. Burada şu hususa dikkat etmekte yarar vardır. Üyelik derecesi 0 dan 1 e doğru giderken üye olma derecesi de bir o kadar kuvvetli olur. Yukarıda verdiğimiz örnekte 3 sayısı 1 sayısına göre daha kuvvetli bir şekilde A bulanık kümesinin bir üyedir. Bulanık Kümenin (Fuzzy Set) Klasik Kümeye (Crisp Set) Göre Avantajları 1- İnsan düşünce sistemine ve tarzına yakındır. 2- Günlük hayatta olduğu gibi belirsiz, zamanla değişen, karmaşık, iyi tanımlanmamış sistemlerin denetimine basit çözümler getirir. 3- Uygulanmasında mutlaka matematiksel bir modele gereksinim duymaz. 4- Sistem basit bir matematiksel modelle tanımlanabilen bir sistem ise o zaman geleneksel bir denetim yeterli olacaktır. Ama karmaşık bir sisteme geleneksel bir mantık uygulamak hem çok zor hem de yüksek maliyetlidir. Buna karşılık bulanık mantık denetimi geleneksel mantığa göre sistemi daha iyi analiz edebileceği gibi aynı zamanda da ekonomiktir. 5- Yazılımın basit olması nedeniyle, sistem daha ekonomik olarak kurulabilir. 6- Bulanık mantıkta işaretlerin bir ön işleme tabi tutulmaları ve oldukça geniş bir alana yayılan değerlerin az sayıda üyelik fonksiyonlarına indirgenmeleri nedeni ile bulanık denetim genellikle daha küçük bir yazılımla daha hızlı bir şekilde sonuçlanır 7- Bulanık Mantık kavramını anlamak kolaydır. 8- Söz edilen az sayıda değerler üzerinde uygulanacak kural sayısı da az olduğundan sonuca ulaşmak daha da çabuklaşacaktır. Bu durum geleneksel bilgisayar ortamında böyledir. Özel geliştirilmiş bir donanımla sonuca daha da hızlı ulaşmak olasıdır. Örneğin Sanyo-Fisher firması mühendisleri, video kayıt cihazında kullanmayı düşündükleri mikro bilgisayarın yetersiz kalmasından dolayı, bulanık denetim kullanmaya karar vermişlerdir. Bulanık denetim yazılım boyutlarının daha küçük olmasını sağladığından, dış bellek kullanımına gerek kalmamıştır. 9- Üyelik değerlerinin kullanımı sayesinde, diğer kontrol tekniklerine göre daha esnektir. 10- Kesin arz etmeyen bilgiler kullanılabilir. 11- Doğrusal olmayan fonksiyonların modellenmesine izin verir. 2
4 12- Bulanık mantık denetiminin sağladığı bir diğer avantaj ise doğrudan kullanıcı girişlerine ve kullanıcının deneyimlerinden yararlanabilmesine olanak sağlamasıdır. 13- Sadece uzman kişilerin tecrübeleri ile kolaylıkla bulanık mantığa dayalı bir model yada sistem tasarlanabilir. 14- Geleneksel kontrol teknikleriyle uyum halindedir. Olarak sıralanabilir. Klasik Mantık ile Bulanık Mantık Arasındaki Farklar Klasik küme mantığı ile bulanık küme mantığı arasındaki farkları aşağıdaki tabloda görüldüğü gibi sıralayabiliriz. Klasik Mantık A veya A Değil Kesin Hepsi veya Hiçbiri Bulanık Mantık A ve A Değil Kısmi Belirli Derecelerde 0 veya 1 0 ve 1 Arasında Süreklilik İkili Birimler Bulanık Birimler Şimdi yaşlı parametresini klasik küme ve bulanık küme olarak gösterimini yapacak olursak; Şekil 1. Yaş genel uzayında tanımlı yaşlı kesin kümesi 3
5 Şekil 2. Yaş genel uzayında tanımlı yaşlı bulanık kümesi Şekil 1. Görüldüğü gibi yaşlı kesin kümesine göre, yaşı 60 ve daha büyük olanlar yaşlı, yaşı 60 dan daha küçük olanlar ise yaşlı değildirler. Yani 59 yaşındaki biri yaşlı sayılmazken 60 yaşındaki biri yaşlı sayılmaktadır. Bu da şu anlama gelmektedir. Yaşlı kesin kümesine göre 59 yaşındaki bir insan kesinlikle yaşlı değilken 60 yaşındaki bir insan kesinlikle yaşlıdır. Yaşlı insanlar bulanık bir küme ile temsil edilirse bu yeni küme şekil 2 de verildiği gibi 20 ile 75 yaşları arasındakileri de kapsar. Ancak bu kapsama klasik kümede olduğu gibi tam bir kapsama değildir. Yani yaşı 20 ile 75 arasında olanlar belirli derecelerle bu kümenin elemanlarıdırlar. Örneğin yaşı 20 nin altında olanların yaşlı bulanık kümesindeki üyelik dereceleri sıfır iken, yaşı 20 nin hemen üzerinde olanların üyelik derecesi sıfırın biraz üzerinde, yaşı 75 e gelmek üzere olanların üyelik derecesi de 1 e yakındır. Örneğin, 25 yaşındaki birisinin YAŞLI kümesindeki üyelik derecesi oldukça az iken, 65 yaşındaki birinin üyelik derecesi oldukça fazladır. SORU 2) Vücut Kitle indeksi (VKİ) en az beş bulanık kümesini oluşturunuz. Bulduğunuz bulanık kümelerin üyelik fonksiyon grafiklerini tek bir şekil üzerinde gösteriniz. (Vücut kitle indeksi ile kesin sınır değerlerini ve ayrıntılı açıklamayı adresinde bulabilirsiniz.) CEVAP 2) Vücut kitle endeksi yetişkin bir insanın kilosunun boyuna göre normal olup olmadığını gösteren bir parametredir. Vücut kitle indeksi aşağıda gösterilen aralıklarda değerlendirilir : Zayıf : Normal : Şişman : Çok Şişman (Obez) 35.0 ve üstü: Aşırı Şişman (Obez) 4
6 Aşağıda Vücut kitle İndeksine (VKİ) göre beş tane bulanık küme tanımlanmıştır. Zayıf={(1/0), (1/2), (1/5), (1/10), (1/18.4), (0.75/20), (0.45/22), (0/25)} Normal={(0/18), (0.15/18.5), (0.24/20), (0.39/21), (0.69/23), (1/25), (0.8/26), (0.4/28), (0/30)} Şişman={(0/24.9), (0.2/26), (0.4/27), (0.6/28), (1/30), (0.6/32), (0.4/33), (0/35)} Çok Şişman (Obez) ={(0/29.9), (0.2/31), (0.4/32), (0.6/33), (0.74/33.7), (0.8/34), (0.9/34.5), (1/35)} Aşırı Şişman (Obez)= {(0/34.9), (1/35), (1/37), (1/40), (1/45), (1/47), (1/52)} Aşağıdaki şekil, yukarıda tanımlanan beş farklı bulanık kümelerinin üyelik fonksiyon grafiklerini göstermektedir. SORU 3) Soru 2 deki parametrenin bulanık küme değerlerini matematiksel fonksiyon olarak gösteriniz. CEVAP 3) 1, X<=18.4 ise Zayıf = 25- X < X<25 ise 0, X >=25 ise 5
7 0, X<18.4 veya X>30 Normal = X < =X<=25 ise 30-X < X<=30 ise 0, X<25 veya X>35 Şişman = X X <= X<=30 ise 30<X<=35 ise 0, X<30 veya X>35 Çok Şişman = X <= X<=35 ise 6
8 0, X<35 Aşırı Şişman = 1, X>=35 SORU 4) Soru 2 de elde ettiğiniz bulanık kümeler üzerinde aşağıdaki bulanık işlemleri yapınız ve sonuçta bulduğunuz bulanık kümelerin üyelik fonksiyon grafiklerini tek bir şekil üzerinde gösteriniz. (a) Herhangi bir bulanık kümenin bulanık değilini alınız; (b) Herhangi iki bulanık kümenin bulanık kesişimini bulunuz; (c) Herhangi iki bulanık kümenin bulanık birleşimini bulunuz; (d) Herhangi bir bulanık kümenin yığılmasını belirleyiniz; (e) Herhangi bir bulanık kümenin genişlemesini belirleyiniz; CEVAP 4) (a) Herhangi bir bulanık kümenin bulanık değilini alınız; Zayıf={(1/0), (1/2), (1/5), (1/10), (1/18.4), (0.75/20), (0.45/22), (0/25)} bulanık kümesinin değilini alalım. Zayıf Değil= {[1-1]/0 + [1-1]/2 + [1-1]/5 + [1-1]/10 + [1-1]/ [1-0.75]/20 + [1-0.45]/22 + [1-0]/25} ise Zayıf Değil= {0/0 + 0/2 + 0/5 + 0/10 + 0/ / /22 + 1/25} bulanık kümesi bulunur. Şimdi bunu grafik üzerinde gösterelim. 7
9 b) Herhangi iki bulanık kümenin bulanık kesişimini bulunuz; İki bulanık kümede kesişim işlemi VE leme olarak adlandırılır ve bu işlem üyelik derecelerinin minimumu alınmak şartıyla gerçekleştirilir. Aşağıdaki yer alan Şişman ve Çok Şişman (Obez) bulanık kümelerinin kesişimini ele alalım. Şişman={(0/24.9), (0.2/26), (0.4/27), (0.6/28), (1/30), (0.6/32), (0.4/33), (0/35)} Çok Şişman (Obez) ={(0/29.9), (0.2/31), (0.4/32), (0.6/33), (0.74/33.7), (0.8/34), (0.9/34.5), (1/35)} Şişman VE Çok Şişman (Obez)=min(0,0/24.9) + min(0,0.2/26) + min(0,0.4/27) + min(0,0.6/28) + min(0,1/30) + min(0.6,0.4/32) + min(0.4,0.6/33) + min(0,1/35) + min(0,0/29.9) + min(0,0.2/31) + min(0,0.74/33.7) + min(0,0.8/34) + min(0,0.9/34.5) = 0/ /26 + 0/27 + 0/28 + 0/ / /33 + 0/35 + 0/29,9 + 0/31 + 0/33,7 + 0/34 + 0/34.5 bulanık kümesi bulunur. Şimdi bunu grafik üzerinde gösterelim. 8
10 (c) Herhangi iki bulanık kümenin bulanık birleşimini bulunuz; İki bulanık kümede birleşim işlemi VEYA lama olarak adlandırılır ve bu işlem üyelik derecelerinin maksimumu alınmak şartıyla gerçekleştirilir. Aşağıdaki yer alan Şişman ve Çok Şişman (Obez) bulanık kümelerinin birleşimini ele alalım. Şişman={(0/24.9), (0.2/26), (0.4/27), (0.6/28), (1/30), (0.6/32), (0.4/33), (0/35)} Çok Şişman (Obez) ={(0/29.9), (0.2/31), (0.4/32), (0.6/33), (0.74/33.7), (0.8/34), (0.9/34.5), (1/35)} Şişman VEYA Çok Şişman (Obez)=max(0,0/24.9) + max(0,0.2/26) + max(0,0.4/27) + max (0,0.6/28) + max (0,1/30) + max (0.6,0.4/32) + max (0.4,0.6/33) + max (0,1/35) + max (0,0/29.9) + max (0,0.2/31) + max (0,0.74/33.7) + max (0,0.8/34) + max (0,0.9/34.5) = 0/ / / /28 + 1/ / /33 + 1/35 + 0/ / / / /34.5 bulanık kümesi bulunur. Şimdi bunu grafik üzerinde gösterelim. 9
11 (d) Herhangi bir bulanık kümenin yığılmasını belirleyiniz; Bir bulanık kümenin yığılması demek, bir bulanık kümenin küçük değerli üyelik derecelerinin daha da küçültülmesi anlamına gelir. Örneğin burada Şişman={(0/24.9), (0.2/26), (0.4/27), (0.6/28), (1/30), (0.6/32), (0.4/33), (0/35)} bulanık kümesini ele alalım. Şişman bulanık kümesinin yığılması demek Şişman bulanık kümesini bir defa çok lamak demektir. Yani; Şişman bulanık kümesinin yığılması= Çok Şişman= (Şişman) 2 örneğimize uygularsak; dir. Şimdi bu kuralı (Şişman) 2 ={(0/24.9), (0.04/26), (0.16/27), (0.36/28), (1/30), (0.36/32), (0.16/33), (0/35)} bulanık kümesi elde edilir. Şimdi bunu grafik üzerinde gösterelim. 10
12 (e) Herhangi bir bulanık kümenin genişlemesini belirleyiniz; Bir bulanık kümenin genişlemesi demek, bir bulanık kümenin küçük değerli üyelik derecelerinin daha büyük derecelere göre daha çok büyümesi (genişlemesi)anlamına gelir. Örneğin burada Şişman={(0/24.9), (0.2/26), (0.4/27), (0.6/28), (1/30), (0.6/32), (0.4/33), (0/35)} bulanık kümesini ele alalım. Şişman bulanık kümesinin genişlemesi demek Şişman bulanık kümesini bir defa az ve az çok lamak demektir. Yani; Şişman bulanık kümesinin genişlemesi= Az/Az Çok Şişman= (Şişman) 0.5 dir. Şimdi bu kuralı örneğimize uygularsak; (Şişman) 0.5 ={(0/24.9), (0.447/26), (0.632/27), (0.774/28), (1/30), (0.774/32), (0.632/33), (0/35)}bulanık kümesi bulunur. Şimdi bunu grafik üzerinde gösterelim. 11
13 12
14 KAYNAKLAR 1. Gülcan, B (2012). Bulanık doğrusal Programlama ve Bisküvi İşletmesinde Optimum Ürün Formülü Oluşturma. Yüksek Lisans Tezi, Karamanoğlu Mehmetbey Üniversitesi, Sosyal Bilimler Enstitüsü. Türkiye S. A. Juneed (2011). Bulanık Mantık yöntemleri Kullanılarak Gazlı İçeceklerde Karbondioksit Kontrolü. Yüksek Lisans Tezi, Ankara Üniversitesi, Fen Bilimleri Enstitüsü. Türkiye. 13
DERS 2 : BULANIK KÜMELER
 DERS 2 : BULNIK KÜMELER 2.1 Gİriş Klasik bir küme, kesin sınırlamalarla verilen bir kümedir. Örneğin, klasik bir küme aşağıdaki gibi belirtilebilir: = { x x > 6 }, Kapalı sınır noktası burada 6 dır.burada
DERS 2 : BULNIK KÜMELER 2.1 Gİriş Klasik bir küme, kesin sınırlamalarla verilen bir kümedir. Örneğin, klasik bir küme aşağıdaki gibi belirtilebilir: = { x x > 6 }, Kapalı sınır noktası burada 6 dır.burada
2. Klasik Kümeler-Bulanık Kümeler
 2. Klasik Kümeler-Bulanık Kümeler Klasik Küme Teorisi Klasik kümelerde bir nesnenin bir kümeye üye olması ve üye olmaması söz konusudur. Bu yaklaşıma göre istediğimiz özelliğe sahip olan bir birey, eleman
2. Klasik Kümeler-Bulanık Kümeler Klasik Küme Teorisi Klasik kümelerde bir nesnenin bir kümeye üye olması ve üye olmaması söz konusudur. Bu yaklaşıma göre istediğimiz özelliğe sahip olan bir birey, eleman
GENELLEŞTİRİLMİŞ FUZZY KOMŞULUK SİSTEMİ ÜZERİNE
 ÖZEL EGE LİSESİ GENELLEŞTİRİLMİŞ FUZZY KOMŞULUK SİSTEMİ ÜZERİNE HAZIRLAYAN ÖĞRENCİ: Berk KORKUT DANIŞMAN ÖĞRETMEN: Gizem GÜNEL İZMİR 2013 İÇİNDEKİLER 1. PROJENİN AMACI 3.33 2. GİRİŞ... 3 3. YÖNTEM 3 4.
ÖZEL EGE LİSESİ GENELLEŞTİRİLMİŞ FUZZY KOMŞULUK SİSTEMİ ÜZERİNE HAZIRLAYAN ÖĞRENCİ: Berk KORKUT DANIŞMAN ÖĞRETMEN: Gizem GÜNEL İZMİR 2013 İÇİNDEKİLER 1. PROJENİN AMACI 3.33 2. GİRİŞ... 3 3. YÖNTEM 3 4.
Esnek Hesaplamaya Giriş
 Esnek Hesaplamaya Giriş J E O L O J İ M Ü H E N D İ S L İ Ğ İ A. B. D. E S N E K H E S A P L A M A Y Ö N T E M L E R İ - I DOÇ. DR. ERSAN KABALCI Esnek Hesaplama Nedir? Esnek hesaplamanın temelinde yatan
Esnek Hesaplamaya Giriş J E O L O J İ M Ü H E N D İ S L İ Ğ İ A. B. D. E S N E K H E S A P L A M A Y Ö N T E M L E R İ - I DOÇ. DR. ERSAN KABALCI Esnek Hesaplama Nedir? Esnek hesaplamanın temelinde yatan
KÜMELER. Kümeler YILLAR 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 MATEMATĐK ĐM /LYS. UYARI: {φ} ifadesi boş kümeyi göstermez.
 MTEMTĐK ĐM YILLR 00 00 004 005 006 007 008 009 010 011 ÖSS-YGS - 1 - - - - - 1 1 1/1 /LYS KÜMELER TNIM: in tam bir tanımı yoksa da matematikçiler kümeyi; iyi tanımlanmış nesneler topluluğu olarak kabul
MTEMTĐK ĐM YILLR 00 00 004 005 006 007 008 009 010 011 ÖSS-YGS - 1 - - - - - 1 1 1/1 /LYS KÜMELER TNIM: in tam bir tanımı yoksa da matematikçiler kümeyi; iyi tanımlanmış nesneler topluluğu olarak kabul
Bulanık Küme Kavramı BULANIK KÜME. Sonlu ve Sonsuz Bulanık Kümeler. Sonlu ve Sonsuz Bulanık Kümeler
 ULNIK KÜME ulanık Küme Kavramı Elemanları x olan bir X evrensel (universal küme düșünelim. u elemanların ÌX alt kümesine aitliği, yani bu altkümelerin elemanı olup olmadığı X in {0,1} de olan karakteristik
ULNIK KÜME ulanık Küme Kavramı Elemanları x olan bir X evrensel (universal küme düșünelim. u elemanların ÌX alt kümesine aitliği, yani bu altkümelerin elemanı olup olmadığı X in {0,1} de olan karakteristik
AYRIK YAPILAR ARŞ. GÖR. SONGÜL KARAKUŞ- FIRAT ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ YAZILIM MÜHENDİSLİĞİ BÖLÜMÜ, ELAZIĞ
 AYRIK YAPILAR P r o f. D r. Ö m e r A k ı n v e Y r d. D o ç. D r. M u r a t Ö z b a y o ğ l u n u n Ç e v i r i E d i t ö r l ü ğ ü n ü ü s t l e n d i ğ i «A y r ı k M a t e m a t i k v e U y g u l a
AYRIK YAPILAR P r o f. D r. Ö m e r A k ı n v e Y r d. D o ç. D r. M u r a t Ö z b a y o ğ l u n u n Ç e v i r i E d i t ö r l ü ğ ü n ü ü s t l e n d i ğ i «A y r ı k M a t e m a t i k v e U y g u l a
Olasılık Kuramı ve İstatistik. Konular Olasılık teorisi ile ilgili temel kavramlar Küme işlemleri Olasılık Aksiyomları
 Olasılık Kuramı ve İstatistik Konular Olasılık teorisi ile ilgili temel kavramlar Küme işlemleri Olasılık Aksiyomları OLASILIK Olasılık teorisi, raslantı ya da kesin olmayan olaylarla ilgilenir. Raslantı
Olasılık Kuramı ve İstatistik Konular Olasılık teorisi ile ilgili temel kavramlar Küme işlemleri Olasılık Aksiyomları OLASILIK Olasılık teorisi, raslantı ya da kesin olmayan olaylarla ilgilenir. Raslantı
BULANIK MANTIK DENETLEYİCİLERİ. Bölüm-4 Bulanık Çıkarım
 BULANIK MANTIK DENETLEYİCİLERİ Bölüm-4 Bulanık Çıkarım 1 Bulanık Çıkarım Bölüm 4 : Hedefleri Bulanık kuralların ve bulanık bilgi tabanlarının nasıl oluşturulacağını anlamak. Gerçekte bulanık muhakeme olan
BULANIK MANTIK DENETLEYİCİLERİ Bölüm-4 Bulanık Çıkarım 1 Bulanık Çıkarım Bölüm 4 : Hedefleri Bulanık kuralların ve bulanık bilgi tabanlarının nasıl oluşturulacağını anlamak. Gerçekte bulanık muhakeme olan
MATEMATiKSEL iktisat
 DİKKAT!... BU ÖZET 8 ÜNİTEDİR BU- RADA İLK ÜNİTE GÖSTERİLMEKTEDİR. MATEMATiKSEL iktisat KISA ÖZET KOLAY AOF Kolayaöf.com 0362 233 8723 Sayfa 2 içindekiler 1.ünite-Türev ve Kuralları..3 2.üniteTek Değişkenli
DİKKAT!... BU ÖZET 8 ÜNİTEDİR BU- RADA İLK ÜNİTE GÖSTERİLMEKTEDİR. MATEMATiKSEL iktisat KISA ÖZET KOLAY AOF Kolayaöf.com 0362 233 8723 Sayfa 2 içindekiler 1.ünite-Türev ve Kuralları..3 2.üniteTek Değişkenli
Bulanık Mantık Denetleyicileri
 Bulanık Mantık Denetleyicileri Bulanık Çıkarım BULANIK ÇIKARIM İki-değerli mantık Çok-değerli mantık Bulanık mantık Bulanık kurallar Bulanık çıkarım Bulanık anlamlandırma Bulanık Çıkarım İki-değerli mantık
Bulanık Mantık Denetleyicileri Bulanık Çıkarım BULANIK ÇIKARIM İki-değerli mantık Çok-değerli mantık Bulanık mantık Bulanık kurallar Bulanık çıkarım Bulanık anlamlandırma Bulanık Çıkarım İki-değerli mantık
8. HOMOMORFİZMALAR VE İZOMORFİZMALAR
 8. HOMOMORFİZMALAR VE İZOMORFİZMALAR Şimdiye kadar bir gruptan diğer bir gruba tanımlı olan fonksiyonlarla ilgilenmedik. Bu bölüme aşağıdaki tanımla başlayalım. Tanım 8.1: G, ve H, iki grup ve f : G H
8. HOMOMORFİZMALAR VE İZOMORFİZMALAR Şimdiye kadar bir gruptan diğer bir gruba tanımlı olan fonksiyonlarla ilgilenmedik. Bu bölüme aşağıdaki tanımla başlayalım. Tanım 8.1: G, ve H, iki grup ve f : G H
OPTİMİZASYON TEKNİKLERİ-2. Hafta
 GİRİŞ OPTİMİZASYON TEKNİKLERİ-2. Hafta Mühendislik açısından bir işin tasarlanıp, gerçekleştirilmesi yeterli değildir. İşin en iyi çözüm yöntemiyle en verimli bir şekilde yapılması bir anlam ifade eder.
GİRİŞ OPTİMİZASYON TEKNİKLERİ-2. Hafta Mühendislik açısından bir işin tasarlanıp, gerçekleştirilmesi yeterli değildir. İşin en iyi çözüm yöntemiyle en verimli bir şekilde yapılması bir anlam ifade eder.
KONU 4: DOĞRUSAL PROGRAMLAMA MODELİ İÇİN ÇÖZÜM YÖNTEMLERİ I
 KONU 4: DOĞRUSAL PROGRAMLAMA MODELİ İÇİN ÇÖZÜM YÖNTEMLERİ I 4.1. Dışbükeylik ve Uç Nokta Bir d.p.p. de model kısıtlarını aynı anda sağlayan X X X karar değişkenleri... n vektörüne çözüm denir. Eğer bu
KONU 4: DOĞRUSAL PROGRAMLAMA MODELİ İÇİN ÇÖZÜM YÖNTEMLERİ I 4.1. Dışbükeylik ve Uç Nokta Bir d.p.p. de model kısıtlarını aynı anda sağlayan X X X karar değişkenleri... n vektörüne çözüm denir. Eğer bu
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Bu bölümde eşitsizlik kısıtlarına bağlı bir doğrusal olmayan kısıta sahip problemin belirlenen stasyoner noktaları
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Bu bölümde eşitsizlik kısıtlarına bağlı bir doğrusal olmayan kısıta sahip problemin belirlenen stasyoner noktaları
18.034 İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Genetik Algoritmalar. Bölüm 1. Optimizasyon. Yrd. Doç. Dr. Adem Tuncer E-posta:
 Genetik Algoritmalar Bölüm 1 Optimizasyon Yrd. Doç. Dr. Adem Tuncer E-posta: adem.tuncer@yalova.edu.tr Optimizasyon? Optimizasyon Nedir? Eldeki kısıtlı kaynakları en iyi biçimde kullanmak olarak tanımlanabilir.
Genetik Algoritmalar Bölüm 1 Optimizasyon Yrd. Doç. Dr. Adem Tuncer E-posta: adem.tuncer@yalova.edu.tr Optimizasyon? Optimizasyon Nedir? Eldeki kısıtlı kaynakları en iyi biçimde kullanmak olarak tanımlanabilir.
Starboard dosya aç dosyayı seçerek Andropi teach menu içe aktar dosyayı seçiyoruz nesne olarak seç
 Not: Starboard programında dosya aç kısmından dosyayı seçerek açabilirsiniz. Yazı karakterlerinde bozulma oluyorsa program kapatılıp tekrar açıldığında yazı düzelecektir. Ben yaptığımda düzelmişti. Andropi
Not: Starboard programında dosya aç kısmından dosyayı seçerek açabilirsiniz. Yazı karakterlerinde bozulma oluyorsa program kapatılıp tekrar açıldığında yazı düzelecektir. Ben yaptığımda düzelmişti. Andropi
VEKTÖR UZAYLARI 1.GİRİŞ
 1.GİRİŞ Bu bölüm lineer cebirin temelindeki cebirsel yapıya, sonlu boyutlu vektör uzayına giriş yapmaktadır. Bir vektör uzayının tanımı, elemanları skalar olarak adlandırılan herhangi bir cisim içerir.
1.GİRİŞ Bu bölüm lineer cebirin temelindeki cebirsel yapıya, sonlu boyutlu vektör uzayına giriş yapmaktadır. Bir vektör uzayının tanımı, elemanları skalar olarak adlandırılan herhangi bir cisim içerir.
(a,b) şeklindeki ifadelere sıralı ikili denir. Burada a'ya 1. bileşen b'ye 2. bileşen denir.
 BĞANTI - FONKSİYON 1. Sıralı İkili : (a,b) şeklindeki ifadelere sıralı ikili denir. Burada a'ya 1. bileşen b'ye 2. bileşen denir.! (x 1,x 2, x 3,x 4,...x n ) : sıralı n li denir. Örnek, (a,b,c) : sıralı
BĞANTI - FONKSİYON 1. Sıralı İkili : (a,b) şeklindeki ifadelere sıralı ikili denir. Burada a'ya 1. bileşen b'ye 2. bileşen denir.! (x 1,x 2, x 3,x 4,...x n ) : sıralı n li denir. Örnek, (a,b,c) : sıralı
4. Bulanık Sayılar- Üyelik Fonksiyonları
 4. Bulanık Sayılar- Üyelik Fonksiyonları Bulanık Sayı Normal ve dışbükey bir bulanık kümenin alfa kesimi kapalı bir küme ise bulanık sayı olarak adlandırılmaktadır. Her bulanık sayı dış bükey bir bulanık
4. Bulanık Sayılar- Üyelik Fonksiyonları Bulanık Sayı Normal ve dışbükey bir bulanık kümenin alfa kesimi kapalı bir küme ise bulanık sayı olarak adlandırılmaktadır. Her bulanık sayı dış bükey bir bulanık
18.034 İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Veri Yapıları Laboratuvarı
 2013 2014 Veri Yapıları Laboratuvarı Ders Sorumlusu: Yrd. Doç. Dr. Hakan KUTUCU Lab. Sorumlusu: Arş. Gör. Caner ÖZCAN İÇİNDEKİLER Uygulama 1: Diziler ve İşaretçiler, Dinamik Bellek Ayırma... 4 1.1. Amaç
2013 2014 Veri Yapıları Laboratuvarı Ders Sorumlusu: Yrd. Doç. Dr. Hakan KUTUCU Lab. Sorumlusu: Arş. Gör. Caner ÖZCAN İÇİNDEKİLER Uygulama 1: Diziler ve İşaretçiler, Dinamik Bellek Ayırma... 4 1.1. Amaç
İstatistik ve Olasılık
 İstatistik ve Olasılık Rastgele Değişkenlerin Dağılımları I Prof. Dr. İrfan KAYMAZ Ders konusu Bu derste; Rastgele değişkenlerin tanımı ve sınıflandırılması Olasılık kütle fonksiyonu Olasılık yoğunluk
İstatistik ve Olasılık Rastgele Değişkenlerin Dağılımları I Prof. Dr. İrfan KAYMAZ Ders konusu Bu derste; Rastgele değişkenlerin tanımı ve sınıflandırılması Olasılık kütle fonksiyonu Olasılık yoğunluk
İSTATİSTİK 2. Hipotez Testi 21/03/2012 AYŞE S. ÇAĞLI. aysecagli@beykent.edu.tr
 İSTATİSTİK 2 Hipotez Testi 21/03/2012 AYŞE S. ÇAĞLI aysecagli@beykent.edu.tr 1 Güven aralığı ve Hipotez testi Güven aralığı µ? µ? Veriler, bir değer aralığında hangi değeri gösteriyor? (Parametrenin gerçek
İSTATİSTİK 2 Hipotez Testi 21/03/2012 AYŞE S. ÇAĞLI aysecagli@beykent.edu.tr 1 Güven aralığı ve Hipotez testi Güven aralığı µ? µ? Veriler, bir değer aralığında hangi değeri gösteriyor? (Parametrenin gerçek
8.Konu Vektör uzayları, Alt Uzaylar
 8.Konu Vektör uzayları, Alt Uzaylar 8.1. Düzlemde vektörler Düzlemdeki her noktası ile reel sayılardan oluşan ikilisini eşleştirebiliriz. Buna P noktanın koordinatları denir. y-ekseni P x y O dan P ye
8.Konu Vektör uzayları, Alt Uzaylar 8.1. Düzlemde vektörler Düzlemdeki her noktası ile reel sayılardan oluşan ikilisini eşleştirebiliriz. Buna P noktanın koordinatları denir. y-ekseni P x y O dan P ye
YÖNEYLEM ARAŞTIRMASI - I
 YÖNEYLEM ARAŞTIRMASI - I /0 İçerik Matematiksel Modelin Kurulması Grafik Çözüm DP Terminolojisi DP Modelinin Standart Formu DP Varsayımları 2/0 Grafik Çözüm İki değişkenli (X, X2) modellerde kullanılabilir,
YÖNEYLEM ARAŞTIRMASI - I /0 İçerik Matematiksel Modelin Kurulması Grafik Çözüm DP Terminolojisi DP Modelinin Standart Formu DP Varsayımları 2/0 Grafik Çözüm İki değişkenli (X, X2) modellerde kullanılabilir,
Çalışma Soruları 1. a) x > 5 b) y < -3 c) xy > 0 d) x 3 < y e) (x-2) 2 + y 2 > 1. ( ) 2x
 Çalışma Soruları. Aşağıdaki denklemleri çözünüz: a) 7x = 4x + b) x 7x = x 4 c) x 4 x + = 0. Aşağıdaki eşitsizliklerin çözüm kümelerini belirleyiniz ve aralıklar cinsinden ifade ediniz: a) 4x > 9 b) x 4
Çalışma Soruları. Aşağıdaki denklemleri çözünüz: a) 7x = 4x + b) x 7x = x 4 c) x 4 x + = 0. Aşağıdaki eşitsizliklerin çözüm kümelerini belirleyiniz ve aralıklar cinsinden ifade ediniz: a) 4x > 9 b) x 4
EM302 Yöneylem Araştırması 2 Doğrusal Olmayan Programlamaya Giriş. Dr. Özgür Kabak
 EM302 Yöneylem Araştırması 2 Doğrusal Olmayan Programlamaya Giriş Dr. Özgür Kabak Doğrusal Olmayan Programlama Eğer bir Matematiksel Programlama modelinin amaç fonksiyonu ve/veya kısıtları doğrusal değil
EM302 Yöneylem Araştırması 2 Doğrusal Olmayan Programlamaya Giriş Dr. Özgür Kabak Doğrusal Olmayan Programlama Eğer bir Matematiksel Programlama modelinin amaç fonksiyonu ve/veya kısıtları doğrusal değil
MATM 133 MATEMATİK LOJİK. Dr. Doç. Çarıyar Aşıralıyev
 MATM 133 MATEMATİK LOJİK Dr. Doç. Çarıyar Aşıralıyev 3.KONU Kümeler Teorisi; Küme işlemleri, İkili işlemler 1. Altküme 2. Evrensel Küme 3. Kümelerin Birleşimi 4. Kümelerin Kesişimi 5. Bir Kümenin Tümleyeni
MATM 133 MATEMATİK LOJİK Dr. Doç. Çarıyar Aşıralıyev 3.KONU Kümeler Teorisi; Küme işlemleri, İkili işlemler 1. Altküme 2. Evrensel Küme 3. Kümelerin Birleşimi 4. Kümelerin Kesişimi 5. Bir Kümenin Tümleyeni
Özyineleme (Recursion)
 C PROGRAMLAMA Özyineleme (Recursion) Bir fonksiyonun kendisini çağırarak çözüme gitmesine özyineleme (recursion), böyle çalışan fonksiyonlara da özyinelemeli (recursive) fonksiyonlar denilir. Özyineleme,
C PROGRAMLAMA Özyineleme (Recursion) Bir fonksiyonun kendisini çağırarak çözüme gitmesine özyineleme (recursion), böyle çalışan fonksiyonlara da özyinelemeli (recursive) fonksiyonlar denilir. Özyineleme,
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 5- SONLU FARKLAR VE İNTERPOLASYON TEKNİKLERİ Doç. Dr. Ali Rıza YILDIZ MAK 210 - Sayısal Analiz 1 İNTERPOLASYON Tablo halinde verilen hassas sayısal değerler veya ayrık noktalardan
MAK 210 SAYISAL ANALİZ BÖLÜM 5- SONLU FARKLAR VE İNTERPOLASYON TEKNİKLERİ Doç. Dr. Ali Rıza YILDIZ MAK 210 - Sayısal Analiz 1 İNTERPOLASYON Tablo halinde verilen hassas sayısal değerler veya ayrık noktalardan
Ders 4: Diziler (Arrays( Arrays) barisgokce.com
 Ders 4: Diziler (Arrays( Arrays) Hazırlayan : Öğr. Grv.. Barış GÖKÇE Đletişim im : www.barisgokce barisgokce.com Diziler Aynı tipteki bir veri gurubunun bir değişken içinde saklanmasıdır. Veriler Hafızada
Ders 4: Diziler (Arrays( Arrays) Hazırlayan : Öğr. Grv.. Barış GÖKÇE Đletişim im : www.barisgokce barisgokce.com Diziler Aynı tipteki bir veri gurubunun bir değişken içinde saklanmasıdır. Veriler Hafızada
15.433 YATIRIM. Ders 3: Portföy Teorisi. Bölüm 1: Problemi Oluşturmak
 15.433 YATIRIM Ders 3: Portföy Teorisi Bölüm 1: Problemi Oluşturmak Bahar 2003 Biraz Tarih Mart 1952 de, Şikago Üniversitesi nde yüksek lisans öğrencisi olan 25 yaşındaki Harry Markowitz, Journal of Finance
15.433 YATIRIM Ders 3: Portföy Teorisi Bölüm 1: Problemi Oluşturmak Bahar 2003 Biraz Tarih Mart 1952 de, Şikago Üniversitesi nde yüksek lisans öğrencisi olan 25 yaşındaki Harry Markowitz, Journal of Finance
yöneylem araştırması Nedensellik üzerine diyaloglar I
 yöneylem araştırması Nedensellik üzerine diyaloglar I i Yayın No : 3197 Eğitim Dizisi : 149 1. Baskı Ocak 2015 İSTANBUL ISBN 978-605 - 333-225 1 Copyright Bu kitabın bu basısı için Türkiye deki yayın hakları
yöneylem araştırması Nedensellik üzerine diyaloglar I i Yayın No : 3197 Eğitim Dizisi : 149 1. Baskı Ocak 2015 İSTANBUL ISBN 978-605 - 333-225 1 Copyright Bu kitabın bu basısı için Türkiye deki yayın hakları
KÜMELER. İyi tanımlanmış nesneler topluluğuna küme denir. Bir küme, birbirinden farklı nesnelerden oluşur. Bu nesneler somut veya soyut olabilir.
 1 KÜMELER İyi tanımlanmış nesneler topluluğuna küme denir. ir küme, birbirinden farklı nesnelerden oluşur. u nesneler somut veya soyut olabilir. Kümeyi oluşturan nesnelerin her birine eleman(öğe) denir.
1 KÜMELER İyi tanımlanmış nesneler topluluğuna küme denir. ir küme, birbirinden farklı nesnelerden oluşur. u nesneler somut veya soyut olabilir. Kümeyi oluşturan nesnelerin her birine eleman(öğe) denir.
DERS BİLGİ FORMU. IV Türkçe Zorunlu Ders. Haftalık. Ders. Okul Eğitimi Süresi. Saati
 DERS BİLGİ FORMU DERSİN ADI SİSTEM ANALİZİ VE TASARIMI I BÖLÜM PROGRAM DÖNEMİ DERSİN DİLİ DERS KATEGORİSİ ÖN ŞARTLAR SÜRE VE DAĞILIMI KREDİ DERSİN AMACI ÖĞRENME ÇIKTILARI VE YETERLİKLER DERSİN İÇERİĞİ
DERS BİLGİ FORMU DERSİN ADI SİSTEM ANALİZİ VE TASARIMI I BÖLÜM PROGRAM DÖNEMİ DERSİN DİLİ DERS KATEGORİSİ ÖN ŞARTLAR SÜRE VE DAĞILIMI KREDİ DERSİN AMACI ÖĞRENME ÇIKTILARI VE YETERLİKLER DERSİN İÇERİĞİ
Çalışma Soruları 1. a) x > 5 b) y < -3 c) xy > 0 d) x 3 < y e) (x-2) 2 + y 2 > 1. ( ) 2x
 Çalışma Soruları. Aşağıdaki denklemleri çözünüz: 7x = 4x + b) x 7x = x 4 c) x 4 x + = 0. Aşağıdaki eşitsizliklerin çözüm kümelerini belirleyiniz ve aralıklar cinsinden ifade ediniz: 4x > 9 b) x 4 < - c)
Çalışma Soruları. Aşağıdaki denklemleri çözünüz: 7x = 4x + b) x 7x = x 4 c) x 4 x + = 0. Aşağıdaki eşitsizliklerin çözüm kümelerini belirleyiniz ve aralıklar cinsinden ifade ediniz: 4x > 9 b) x 4 < - c)
Şimdi de [ ] vektörünün ile gösterilen boyu veya büyüklüğü Pisagor. teoreminini iki kere kullanarak
![Şimdi de [ ] vektörünün ile gösterilen boyu veya büyüklüğü Pisagor. teoreminini iki kere kullanarak Şimdi de [ ] vektörünün ile gösterilen boyu veya büyüklüğü Pisagor. teoreminini iki kere kullanarak](/thumbs/17/146647.jpg) 10.Konu İç çarpım uzayları ve özellikleri 10.1. ve üzerinde uzunluk de [ ] vektörünün ile gösterilen boyu veya büyüklüğü Pisagor teoreminden dir. 1.Ö.: [ ] ise ( ) ( ) ve ( ) noktaları gözönüne alalım.
10.Konu İç çarpım uzayları ve özellikleri 10.1. ve üzerinde uzunluk de [ ] vektörünün ile gösterilen boyu veya büyüklüğü Pisagor teoreminden dir. 1.Ö.: [ ] ise ( ) ( ) ve ( ) noktaları gözönüne alalım.
Temelleri. Doç.Dr.Ali Argun Karacabey
 Doğrusal Programlamanın Temelleri Doç.Dr.Ali Argun Karacabey Doğrusal Programlama Nedir? Bir Doğrusal Programlama Modeli doğrusal kısıtlar altında bir doğrusal ğ fonksiyonun değerini ğ maksimize yada minimize
Doğrusal Programlamanın Temelleri Doç.Dr.Ali Argun Karacabey Doğrusal Programlama Nedir? Bir Doğrusal Programlama Modeli doğrusal kısıtlar altında bir doğrusal ğ fonksiyonun değerini ğ maksimize yada minimize
sayıların kümesi N 1 = { 2i-1: i N } ve tüm çift doğal sayıların kümesi N 2 = { 2i: i N } şeklinde gösterilebilecektir. Hiç elemanı olmayan kümeye
 KÜME AİLELERİ GİRİŞ Bu bölümde, bir çoğu daha önceden bilinen incelememiz için gerekli olan bilgileri vereceğiz. İlerde konular işlenirken karşımıza çıkacak kavram ve bilgileri bize yetecek kadarı ile
KÜME AİLELERİ GİRİŞ Bu bölümde, bir çoğu daha önceden bilinen incelememiz için gerekli olan bilgileri vereceğiz. İlerde konular işlenirken karşımıza çıkacak kavram ve bilgileri bize yetecek kadarı ile
Küme temel olarak belli nesnelerin ya da elamanların bir araya gelmesi ile oluşur
 Kümeler Kümeler ve küme işlemleri olasılığın temellerini oluşturmak için çok önemlidir Küme temel olarak belli nesnelerin ya da elamanların bir araya gelmesi ile oluşur Sonlu sayıda, sonsuz sayıda, kesikli
Kümeler Kümeler ve küme işlemleri olasılığın temellerini oluşturmak için çok önemlidir Küme temel olarak belli nesnelerin ya da elamanların bir araya gelmesi ile oluşur Sonlu sayıda, sonsuz sayıda, kesikli
MIT Açık Ders Malzemeleri Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için
 MIT Açık Ders Malzemeleri http://ocw.mit.edu Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için http://ocw.mit.edu/terms veya http://www.acikders.org.tr adresini ziyaret
MIT Açık Ders Malzemeleri http://ocw.mit.edu Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için http://ocw.mit.edu/terms veya http://www.acikders.org.tr adresini ziyaret
Bulanık Mantık. Bulanık Mantık (Fuzzy Logic)
 Bulanık Mantık (Fuzzy Logic) Bulanık mantık, insan düşünmesini ve mantık yürütmesini modellemeye ve karşılaşılan problemlerde ihtiyaç doğrultusunda kullanmayı amaçlar. Bilgisayarlara, insanların özel verileri
Bulanık Mantık (Fuzzy Logic) Bulanık mantık, insan düşünmesini ve mantık yürütmesini modellemeye ve karşılaşılan problemlerde ihtiyaç doğrultusunda kullanmayı amaçlar. Bilgisayarlara, insanların özel verileri
MIT OpenCourseWare http://ocw.mit.edu. 14.30 Ekonomide İstatistiksel Yöntemlere Giriş Bahar 2009
 MIT OpenCourseWare http://ocw.mit.edu 14.30 Ekonomide İstatistiksel Yöntemlere Giriş Bahar 2009 Bu materyale atıfta bulunmak ve kullanım koşulları için http://ocw.mit.edu/terms sayfasını ziyaret ediniz.
MIT OpenCourseWare http://ocw.mit.edu 14.30 Ekonomide İstatistiksel Yöntemlere Giriş Bahar 2009 Bu materyale atıfta bulunmak ve kullanım koşulları için http://ocw.mit.edu/terms sayfasını ziyaret ediniz.
Bu bölümde cebirsel yapıların temelini oluşturan Grup ve özelliklerini inceleyeceğiz.
 1 BİR İŞLEMLİ SİSTEMLER Bu bölümde cebirsel yapıların temelini oluşturan Grup ve özelliklerini inceleyeceğiz. 1.1 İŞLEMLER Bir kümeden kendisine tanımlı olan her fonksiyona birli işlem denir. Örneğin Z
1 BİR İŞLEMLİ SİSTEMLER Bu bölümde cebirsel yapıların temelini oluşturan Grup ve özelliklerini inceleyeceğiz. 1.1 İŞLEMLER Bir kümeden kendisine tanımlı olan her fonksiyona birli işlem denir. Örneğin Z
Fonksiyon Blokları Açıklamaları
 Fonksiyon lokları Açıklamaları A İsim PWM Fonksiyonu Açıklama Sayısal girişi On/Off kontrole çevirir. Kullanım alanı aha çok PI kontrol sonrası çıkışın On/Off olarak yapıldığı proseslerde kullanılır. Kullanımı
Fonksiyon lokları Açıklamaları A İsim PWM Fonksiyonu Açıklama Sayısal girişi On/Off kontrole çevirir. Kullanım alanı aha çok PI kontrol sonrası çıkışın On/Off olarak yapıldığı proseslerde kullanılır. Kullanımı
KONU 3: DOĞRUSAL PROGRAMLAMA PROBLEMLERİ İLE İLGİLİ ÖRNEKLER
 KONU 3: DOĞRUSAL PROGRAMLAMA PROBLEMLERİ İLE İLGİLİ ÖRNEKLER Örnek 1: Bir boya fabrikası hem iç hem dış boya üretiyor. Boya üretiminde A ve B olmak üzere iki tip hammadde kullanılıyor. Bir günde A hammaddesinden
KONU 3: DOĞRUSAL PROGRAMLAMA PROBLEMLERİ İLE İLGİLİ ÖRNEKLER Örnek 1: Bir boya fabrikası hem iç hem dış boya üretiyor. Boya üretiminde A ve B olmak üzere iki tip hammadde kullanılıyor. Bir günde A hammaddesinden
Bilgi ve İletişim Teknolojileri (JFM 102) Ders 10. LINUX OS (Programlama) BİLGİ & İLETİŞİM TEKNOLOJİLERİ GENEL BAKIŞ
 Ders 10 LINUX OS (Programlama) BİLGİ & İLETİŞİM TEKNOLOJİLERİ GENEL BAKIŞ LINUX de Programlama LINUX işletim sistemi zengin bir programlama ortamı sağlar. Kullanıcılara sistemi geliştirme olanağı sağlar.
Ders 10 LINUX OS (Programlama) BİLGİ & İLETİŞİM TEKNOLOJİLERİ GENEL BAKIŞ LINUX de Programlama LINUX işletim sistemi zengin bir programlama ortamı sağlar. Kullanıcılara sistemi geliştirme olanağı sağlar.
Simpleks Yönteminde Kullanılan İlave Değişkenler (Eşitliğin yönüne göre):
 DP SİMPLEKS ÇÖZÜM Simpleks Yöntemi, amaç fonksiyonunu en büyük (maksimum) veya en küçük (minimum) yapacak en iyi çözüme adım adım yaklaşan bir algoritma (hesaplama yöntemi) dir. Bu nedenle, probleme bir
DP SİMPLEKS ÇÖZÜM Simpleks Yöntemi, amaç fonksiyonunu en büyük (maksimum) veya en küçük (minimum) yapacak en iyi çözüme adım adım yaklaşan bir algoritma (hesaplama yöntemi) dir. Bu nedenle, probleme bir
MANTIK. Araş. Gör. Nesibe YALÇIN BİLECİK ÜNİVERSİTESİ BULANIK MANTIK
 MANTIK Araş. Gör. Nesibe YALÇIN BİLECİK ÜNİVERSİTESİ BULANIK MANTIK İÇERİK Temel Kavramlar Bulanık Mantık Bulanık Mantık & Klasik Mantık Bulanık Küme & Klasik Küme Bulanık Sistem Yapısı Öğeleri Uygulama
MANTIK Araş. Gör. Nesibe YALÇIN BİLECİK ÜNİVERSİTESİ BULANIK MANTIK İÇERİK Temel Kavramlar Bulanık Mantık Bulanık Mantık & Klasik Mantık Bulanık Küme & Klasik Küme Bulanık Sistem Yapısı Öğeleri Uygulama
Olasılık Kavramı. Recep YURTAL. Mühendislikte İstatistik Metotlar. Çukurova Üniversitesi İnşaat Mühendisliği Bölümü
 Olasılık Kavramı Mühendislikte İstatistik Metotlar Çukurova Üniversitesi İnşaat Mühendisliği ölümü OLSILIK KVRMI KÜME KVRMI irlikte ele alınan belirli nesneler topluluğuna küme, Kümede içerilen nesnelere
Olasılık Kavramı Mühendislikte İstatistik Metotlar Çukurova Üniversitesi İnşaat Mühendisliği ölümü OLSILIK KVRMI KÜME KVRMI irlikte ele alınan belirli nesneler topluluğuna küme, Kümede içerilen nesnelere
ELN1001 BİLGİSAYAR PROGRAMLAMA I
 ELN1001 BİLGİSAYAR PROGRAMLAMA I DEPOLAMA SINIFLARI DEĞİŞKEN MENZİLLERİ YİNELEMELİ FONKSİYONLAR Depolama Sınıfları Tanıtıcılar için şu ana kadar görülmüş olan özellikler: Ad Tip Boyut Değer Bunlara ilave
ELN1001 BİLGİSAYAR PROGRAMLAMA I DEPOLAMA SINIFLARI DEĞİŞKEN MENZİLLERİ YİNELEMELİ FONKSİYONLAR Depolama Sınıfları Tanıtıcılar için şu ana kadar görülmüş olan özellikler: Ad Tip Boyut Değer Bunlara ilave
Bölüm 2 Varlık-İlişki Veri Modeli: Araçlar ve Teknikler. Fundamentals, Design, and Implementation, 9/e
 Bölüm 2 Varlık-İlişki Veri Modeli: Araçlar ve Teknikler Fundamentals, Design, and Implementation, 9/e Üç Şema Modeli Üç şema modeli 1975 de ANSI/SPARC tarafından geliştirildi Veri modellemeninç ve rolünü
Bölüm 2 Varlık-İlişki Veri Modeli: Araçlar ve Teknikler Fundamentals, Design, and Implementation, 9/e Üç Şema Modeli Üç şema modeli 1975 de ANSI/SPARC tarafından geliştirildi Veri modellemeninç ve rolünü
Zeki Optimizasyon Teknikleri
 Zeki Optimizasyon Teknikleri Ara sınav - 25% Ödev (Haftalık) - 10% Ödev Sunumu (Haftalık) - 5% Final (Proje Sunumu) - 60% - Dönem sonuna kadar bir optimizasyon tekniğiyle uygulama geliştirilecek (Örn:
Zeki Optimizasyon Teknikleri Ara sınav - 25% Ödev (Haftalık) - 10% Ödev Sunumu (Haftalık) - 5% Final (Proje Sunumu) - 60% - Dönem sonuna kadar bir optimizasyon tekniğiyle uygulama geliştirilecek (Örn:
MIT OpenCourseWare http://ocw.mit.edu. 14.30 Ekonomide İstatistiksel Yöntemlere Giriş Bahar 2009
 MIT OpenCourseWare http://ocw.mit.edu 14.30 Ekonomide İstatistiksel Yöntemlere Giriş Bahar 2009 Bu materyale atıfta bulunmak ve kullanım koşulları için http://ocw.mit.edu/terms sayfasını ziyaret ediniz.
MIT OpenCourseWare http://ocw.mit.edu 14.30 Ekonomide İstatistiksel Yöntemlere Giriş Bahar 2009 Bu materyale atıfta bulunmak ve kullanım koşulları için http://ocw.mit.edu/terms sayfasını ziyaret ediniz.
OTOMATİK KONTROL SİSTEMLERİ İŞARET AKIŞ DİYAGRAMLARI SIGNAL FLOW GRAPH
 OTOMATİK KONTROL SİSTEMLERİ İŞARET AKIŞ DİYAGRAMLARI SIGNAL FLOW GRAPH İŞARET AKIŞ DİYAGRAMLARI İşaret akış diyagramları blok diyagramlara bir alternatiftir. Fonksiyonel bloklar, işaretler, toplama noktaları
OTOMATİK KONTROL SİSTEMLERİ İŞARET AKIŞ DİYAGRAMLARI SIGNAL FLOW GRAPH İŞARET AKIŞ DİYAGRAMLARI İşaret akış diyagramları blok diyagramlara bir alternatiftir. Fonksiyonel bloklar, işaretler, toplama noktaları
Tek Değişkenli Optimizasyon OPTİMİZASYON. Gradient Tabanlı Yöntemler. Bisection (İkiye Bölme) Yöntemi
 OPTİMİZASYON Gerçek hayatta, çok değişkenli optimizasyon problemleri karmaşıktır ve nadir olarak problem tek değişkenli olur. Bununla birlikte, tek değişkenli optimizasyon algoritmaları çok değişkenli
OPTİMİZASYON Gerçek hayatta, çok değişkenli optimizasyon problemleri karmaşıktır ve nadir olarak problem tek değişkenli olur. Bununla birlikte, tek değişkenli optimizasyon algoritmaları çok değişkenli
Küme Temel Kavramları
 Kümeler Kümeler Küme, matematiksel anlamda tanımsız bir kavramdır. Bu kavram "nesneler topluluğu veya yığını" olarak yorumlanabilir. Bu tanımdaki "nesne" soyut ya da somut bir şeydir; fakat her ne olursa
Kümeler Kümeler Küme, matematiksel anlamda tanımsız bir kavramdır. Bu kavram "nesneler topluluğu veya yığını" olarak yorumlanabilir. Bu tanımdaki "nesne" soyut ya da somut bir şeydir; fakat her ne olursa
18.034 İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
KÜMELER. A = {x : (x in özelliği)} Burada x : ifadesi öyle x lerden oluşur ki diye okunur. Küme oluşturur. Çünkü Kilis in üç tane ilçesi.
 KÜMELER Canlı yada cansız varlıkların oluşturduğu iyi A = {a, b, {a, b, c}} ise, s(a) = 3 tür. tanımlanmış nesneler topluluğuna küme denir. 2. Ortak Özellik Yöntemi Kümenin elemanlarını, daha somut ya
KÜMELER Canlı yada cansız varlıkların oluşturduğu iyi A = {a, b, {a, b, c}} ise, s(a) = 3 tür. tanımlanmış nesneler topluluğuna küme denir. 2. Ortak Özellik Yöntemi Kümenin elemanlarını, daha somut ya
Bulanık Mantık Bilgisayar Mühendisliği Bölümü Arasınav - 11 Nisan 2014 Süre: 1 Saat 30 Dakika
 SORU 1 (20P). Bir tartı aletinin kalibrasyonunu yapmak üzere kurulan düzenekte, kalibrasyon katası ±10 gram arasında bakılmaktadır. Öyleki -10 ve altı kesinlikle NEGATİF BÜYÜK hata, +10 ve üstü kesinlikle
SORU 1 (20P). Bir tartı aletinin kalibrasyonunu yapmak üzere kurulan düzenekte, kalibrasyon katası ±10 gram arasında bakılmaktadır. Öyleki -10 ve altı kesinlikle NEGATİF BÜYÜK hata, +10 ve üstü kesinlikle
BULANIK MANTIK (FUZZY LOGIC)
 BULANIK MANTIK (FUZZY LOGIC) Bulanık mantık ilk olarak 1965 yılında Lütfü Aliasker Zade nin yayınladığı bir makalenin sonucu oluşmuş bir mantık yapısıdır ve yayınladığı Fuzzy Sets makalesinde bulanık kümelerin
BULANIK MANTIK (FUZZY LOGIC) Bulanık mantık ilk olarak 1965 yılında Lütfü Aliasker Zade nin yayınladığı bir makalenin sonucu oluşmuş bir mantık yapısıdır ve yayınladığı Fuzzy Sets makalesinde bulanık kümelerin
BM312 Ders Notları 2014
 Kümeler ve Bağıntılar Bir küme nesnelerden oluşur L = {a, b, c, d} a, b, c, d kümenin elemanları veya üyeleridir c L, k L şeklinde ifade edilir. Elemanların sırası ve tekrarı önemli değildir {üzüm, kiraz,
Kümeler ve Bağıntılar Bir küme nesnelerden oluşur L = {a, b, c, d} a, b, c, d kümenin elemanları veya üyeleridir c L, k L şeklinde ifade edilir. Elemanların sırası ve tekrarı önemli değildir {üzüm, kiraz,
Cebir Notları. Gökhan DEMĐR, ÖRNEK : A ve A x A nın bir alt kümesinden A ya her fonksiyona
 , 2006 MC Cebir Notları Gökhan DEMĐR, gdemir23@yahoo.com.tr Đşlem ĐŞLEM A ve A x A nın bir alt kümesinden A ya her fonksiyona ikili işlem denir. Örneğin toplama, çıkarma, çarpma birer işlemdir. Đşlemler
, 2006 MC Cebir Notları Gökhan DEMĐR, gdemir23@yahoo.com.tr Đşlem ĐŞLEM A ve A x A nın bir alt kümesinden A ya her fonksiyona ikili işlem denir. Örneğin toplama, çıkarma, çarpma birer işlemdir. Đşlemler
X ve Y boş olmayan iki küme olsun. İki küme arasında tanımlanmış olan bir bulanık ilişki R, X x Y nin bir bulanık alt kümesidir.
 Bulanık İlişkiler X ve Y boş olmayan iki küme olsun. İki küme arasında tanımlanmış olan bir bulanık ilişki R, X x Y nin bir bulanık alt kümesidir. R F(X x Y) Eğer X = Y ise R bir ikilik (binary) bulanık
Bulanık İlişkiler X ve Y boş olmayan iki küme olsun. İki küme arasında tanımlanmış olan bir bulanık ilişki R, X x Y nin bir bulanık alt kümesidir. R F(X x Y) Eğer X = Y ise R bir ikilik (binary) bulanık
ANADOLU ÜNİVERSİTESİ AÇIKÖĞRETİM FAKÜLTESİ İLKÖĞRETİM ÖĞRETMENLİĞİ LİSANS TAMAMLAMA PROGRAMI. Analiz. Cilt 2. Ünite 8-14
 ANADOLU ÜNİVERSİTESİ AÇIKÖĞRETİM FAKÜLTESİ İLKÖĞRETİM ÖĞRETMENLİĞİ LİSANS TAMAMLAMA PROGRAMI Analiz Cilt 2 Ünite 8-14 T.C. ANADOLU ÜNİVERSİTESİ YAYINLARI NO: 1082 AÇIKÖĞRETİM FAKÜLTESİ YAYINLARI NO: 600
ANADOLU ÜNİVERSİTESİ AÇIKÖĞRETİM FAKÜLTESİ İLKÖĞRETİM ÖĞRETMENLİĞİ LİSANS TAMAMLAMA PROGRAMI Analiz Cilt 2 Ünite 8-14 T.C. ANADOLU ÜNİVERSİTESİ YAYINLARI NO: 1082 AÇIKÖĞRETİM FAKÜLTESİ YAYINLARI NO: 600
Temel Kavramlar. (r) Sıfırdan farklı kompleks sayılar kümesi: C. (i) Rasyonel sayılar kümesi: Q = { a b
 Bölüm 1 Temel Kavramlar Bu bölümde bağıntı ve fonksiyon gibi bazı temel kavramlar üzerinde durulacak, tamsayıların bazı özellikleri ele alınacaktır. Bu çalışma boyunca kullanılacak bazı kümelerin gösterimleri
Bölüm 1 Temel Kavramlar Bu bölümde bağıntı ve fonksiyon gibi bazı temel kavramlar üzerinde durulacak, tamsayıların bazı özellikleri ele alınacaktır. Bu çalışma boyunca kullanılacak bazı kümelerin gösterimleri
Türev Uygulamaları ÜNİTE. Amaçlar. İçindekiler. Yazar Prof.Dr. Vakıf CAFEROV
 Türev Uygulamaları Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 10 Amaçlar Bu üniteyi çalıştıktan sonra; türev kavramı yardımı ile fonksiyonun monotonluğunu, ekstremum noktalarını, konvekslik ve konkavlığını, büküm
Türev Uygulamaları Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 10 Amaçlar Bu üniteyi çalıştıktan sonra; türev kavramı yardımı ile fonksiyonun monotonluğunu, ekstremum noktalarını, konvekslik ve konkavlığını, büküm
Lineer Programlama. Doğrusal terimi, hem amaç hem de kısıtları temsil eden matematiksel fonksiyonların doğrusal olduğunu gösterir.
 LİNEER PROGRAMLAMA Giriş Uygulamada karşılaşılan birçok optimizasyon problemi kısıtlar içerir. Yani optimizasyon probleminde amaç fonksiyonuna ilave olarak çözümü kısıtlayıcı ek denklemler mevcuttur. Bu
LİNEER PROGRAMLAMA Giriş Uygulamada karşılaşılan birçok optimizasyon problemi kısıtlar içerir. Yani optimizasyon probleminde amaç fonksiyonuna ilave olarak çözümü kısıtlayıcı ek denklemler mevcuttur. Bu
BİYOİSTATİSTİK Olasılıkta Temel Kavramlar Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH
 BİYOİSTTİSTİK Olasılıkta Temel Kavramlar Yrd. Doç. Dr. slı SUNER KRKÜLH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim D. Web: www.biyoistatistik.med.ege.edu.tr 1 OLSILIK Olasılık; Tablo
BİYOİSTTİSTİK Olasılıkta Temel Kavramlar Yrd. Doç. Dr. slı SUNER KRKÜLH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim D. Web: www.biyoistatistik.med.ege.edu.tr 1 OLSILIK Olasılık; Tablo
OTOMATİK KONTROL SİSTEMLERİ İŞARET AKIŞ DİYAGRAMLARI SIGNAL FLOW GRAPH
 OTOMATİK KONTROL SİSTEMLERİ İŞARET AKIŞ DİYAGRAMLARI SIGNAL FLOW GRAPH İŞARET AKIŞ DİYAGRAMLARI İşaret akış diyagramları blok diyagramlara bir alternatiftir. Fonksiyonel bloklar, işaretler, toplama noktaları
OTOMATİK KONTROL SİSTEMLERİ İŞARET AKIŞ DİYAGRAMLARI SIGNAL FLOW GRAPH İŞARET AKIŞ DİYAGRAMLARI İşaret akış diyagramları blok diyagramlara bir alternatiftir. Fonksiyonel bloklar, işaretler, toplama noktaları
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Hessien Matris-Quadratik Form Mutlak ve Bölgesel Maksimum-Minimum Noktalar Giriş Kısıtlı ve kısıtsız fonksiyonlar için
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Hessien Matris-Quadratik Form Mutlak ve Bölgesel Maksimum-Minimum Noktalar Giriş Kısıtlı ve kısıtsız fonksiyonlar için
8.Konu Sonlu ve sonsuz kümeler, Doğal sayılar
 8.Konu Sonlu ve sonsuz kümeler, Doğal sayılar 1. Eşit güçlü kümeler 2. Sonlu ve sonsuz kümeler 3. Doğal sayılar kümesi 4. Sayılabilir kümeler 5. Doğal sayılar kümesinde toplama 6. Doğal sayılar kümesinde
8.Konu Sonlu ve sonsuz kümeler, Doğal sayılar 1. Eşit güçlü kümeler 2. Sonlu ve sonsuz kümeler 3. Doğal sayılar kümesi 4. Sayılabilir kümeler 5. Doğal sayılar kümesinde toplama 6. Doğal sayılar kümesinde
DEĞİŞMELİ BANACH CEBİRLERİNİN GELFAND SPEKTRUMLARI ÜZERİNE
 Ekim 25 Cilt:3 No:2 Kastamonu Eğitim Dergisi 547-554 DEĞİŞMELİ BANACH CEBİRLERİNİN GELFAND SPEKRUMLARI ÜZERİNE Hayri AKAY, Ziya ARGÜN Gazi Üniversitesi, Gazi Eğitim Fakültesi, Matematik Eğitimi Bölümü,
Ekim 25 Cilt:3 No:2 Kastamonu Eğitim Dergisi 547-554 DEĞİŞMELİ BANACH CEBİRLERİNİN GELFAND SPEKRUMLARI ÜZERİNE Hayri AKAY, Ziya ARGÜN Gazi Üniversitesi, Gazi Eğitim Fakültesi, Matematik Eğitimi Bölümü,
B. Sermaye stoğunun durağan durum değerini bulunuz. C. Bu ekonomi için altın kural sermaye stoğu ne kadardır?
 A.Ü. SBE 2015-2016 Bahar Dönemi Makro İktisat - II Çalışma Soruları - 2 1. Nüfus artışı veya teknolojik ilerlemenin olmadığı Solow Modeli nde bazı parametreler şu şekilde olsun: s = 0.2(tasarruf oranı)
A.Ü. SBE 2015-2016 Bahar Dönemi Makro İktisat - II Çalışma Soruları - 2 1. Nüfus artışı veya teknolojik ilerlemenin olmadığı Solow Modeli nde bazı parametreler şu şekilde olsun: s = 0.2(tasarruf oranı)
MIT Açık Ders Malzemeleri Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için
 MIT Açık Ders Malzemeleri http://ocw.mit.edu Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için http://ocw.mit.edu/terms veya http://www.acikders.org.tr adresini ziyaret
MIT Açık Ders Malzemeleri http://ocw.mit.edu Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için http://ocw.mit.edu/terms veya http://www.acikders.org.tr adresini ziyaret
Algoritmalar ve Karmaşıklık
 Algoritmalar ve Karmaşıklık Ders 11 Algoritma Ayrık matematikte karşılaşılan bir çok problem sınıfı mevcuttur. Örneğin, verilen tamsayı grubu içindeki en büyük olanının bulunması, verilen bir kümenin bütün
Algoritmalar ve Karmaşıklık Ders 11 Algoritma Ayrık matematikte karşılaşılan bir çok problem sınıfı mevcuttur. Örneğin, verilen tamsayı grubu içindeki en büyük olanının bulunması, verilen bir kümenin bütün
OTOMATİK KONTROL SİSTEMLERİ BLOK DİYAGRAM İNDİRGEME KURALLARI
 OTOMATİK KONTROL SİSTEMLERİ BLOK DİYAGRAM İNDİRGEME KURALLARI BLOK DİYAGRAM İNDİRGEME KURALLARI Örnek 9: Aşağıdaki açık çevrim blok diyagramının transfer fonksiyonunu bulunuz? 2 BLOK DİYAGRAM İNDİRGEME
OTOMATİK KONTROL SİSTEMLERİ BLOK DİYAGRAM İNDİRGEME KURALLARI BLOK DİYAGRAM İNDİRGEME KURALLARI Örnek 9: Aşağıdaki açık çevrim blok diyagramının transfer fonksiyonunu bulunuz? 2 BLOK DİYAGRAM İNDİRGEME
KÜMELER ÜNİTE 1. ÜNİTE 1. ÜNİTE 2. ÜNİTE 1. ÜNİT
 KÜMELER ÜNİTE 1. ÜNİTE 1. ÜNİTE 2. ÜNİTE 1. ÜNİT Kümelerde Temel Kavramlar 1. Kazanım : Küme kavramını açıklar; liste, Venn şeması ve ortak özellik yöntemleri ile gösterir. 2. Kazanım : Evrensel küme,
KÜMELER ÜNİTE 1. ÜNİTE 1. ÜNİTE 2. ÜNİTE 1. ÜNİT Kümelerde Temel Kavramlar 1. Kazanım : Küme kavramını açıklar; liste, Venn şeması ve ortak özellik yöntemleri ile gösterir. 2. Kazanım : Evrensel küme,
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
BMT 206 Ayrık Matematik. Yük. Müh. Köksal GÜNDOĞDU 1
 BMT 206 Ayrık Matematik Yük. Müh. Köksal GÜNDOĞDU 1 Kümeler Yük. Müh. Köksal GÜNDOĞDU 2 Kümeler Kümeler Ayrık Matematiğin en temel konularından biridir Sayma problemleri için önemli Programlama dillerinin
BMT 206 Ayrık Matematik Yük. Müh. Köksal GÜNDOĞDU 1 Kümeler Yük. Müh. Köksal GÜNDOĞDU 2 Kümeler Kümeler Ayrık Matematiğin en temel konularından biridir Sayma problemleri için önemli Programlama dillerinin
Excel Nedir? Microsoft Excell. Excel de Çalışma sayfası-tablo
 Microsoft Excell Excel Nedir? Excel programı; veriler üzerinde hesap yapabilme, verileri tabloya dönüştürebilme, verileri karşılaştırıp sonuç üretebilme, grafik oluşturma, veri yönetimi yapabilir. http://mf.dpu.edu.tr/~eyup
Microsoft Excell Excel Nedir? Excel programı; veriler üzerinde hesap yapabilme, verileri tabloya dönüştürebilme, verileri karşılaştırıp sonuç üretebilme, grafik oluşturma, veri yönetimi yapabilir. http://mf.dpu.edu.tr/~eyup
1. ÜNİTE 2. ÜNİTE 3. ÜNİTE. Bölüm 1 : Üslü Sayılar... 8. Bölüm 2 : Doğal Sayılar... 18. Bölüm 3 : Doğal Sayı Problemleri... 30
 İçindekiler 1. ÜNİTE Bölüm 1 : Üslü Sayılar... 8 Bölüm 2 : Doğal Sayılar... 18 Bölüm 3 : Doğal Sayı Problemleri... 30 Bölüm 4 :- Çarpanlar ve Katlar, Bölünebilme... 40 Bölüm 5 : Asal Sayılar, Ortak Bölenler,
İçindekiler 1. ÜNİTE Bölüm 1 : Üslü Sayılar... 8 Bölüm 2 : Doğal Sayılar... 18 Bölüm 3 : Doğal Sayı Problemleri... 30 Bölüm 4 :- Çarpanlar ve Katlar, Bölünebilme... 40 Bölüm 5 : Asal Sayılar, Ortak Bölenler,
OPTIMIZASYON Bir Değişkenli Fonksiyonların Maksimizasyonu...2
 OPTIMIZASYON.... Bir Değişkenli Fonksiyonların Maksimizasyonu.... Türev...3.. Bir noktadaki türevin değeri...4.. Maksimum için Birinci Derece Koşulu...4.3. İkinci Derece Koşulu...5.4. Türev Kuralları...5
OPTIMIZASYON.... Bir Değişkenli Fonksiyonların Maksimizasyonu.... Türev...3.. Bir noktadaki türevin değeri...4.. Maksimum için Birinci Derece Koşulu...4.3. İkinci Derece Koşulu...5.4. Türev Kuralları...5
0.1 Küme Cebri. Teorem 1 A ve B iki küme olmak üzere i) (A B) c = A c B c ii) (A B) c = A c B c
 0. Küme Cebri Bu bölümde verilen keyfikümeler üzerinde birleşim, kesişim, fark, tümleyen,...gibi özellikleri sağlayan eşitliklerle ilgilenceğiz. İlk olarak De Morgan kurallarıdiye bilinen bir Teoremi ifade
0. Küme Cebri Bu bölümde verilen keyfikümeler üzerinde birleşim, kesişim, fark, tümleyen,...gibi özellikleri sağlayan eşitliklerle ilgilenceğiz. İlk olarak De Morgan kurallarıdiye bilinen bir Teoremi ifade
Bu durumu, konum bazında bileşenlerini, yani dalga fonksiyonunu, vererek tanımlıyoruz : ) 1. (ikx x2. (d)
 Ders 10 Metindeki ilgili bölümler 1.7 Gaussiyen durum Burada, 1-d de hareket eden bir parçacığın önemli Gaussiyen durumu örneğini düşünüyoruz. Ele alış biçimimiz kitaptaki ile neredeyse aynı ama bu örnek
Ders 10 Metindeki ilgili bölümler 1.7 Gaussiyen durum Burada, 1-d de hareket eden bir parçacığın önemli Gaussiyen durumu örneğini düşünüyoruz. Ele alış biçimimiz kitaptaki ile neredeyse aynı ama bu örnek
ÖZHENDEKCİ BASINÇ ÇUBUKLARI
 BASINÇ ÇUBUKLARI Kesit zoru olarak yalnızca eksenel doğrultuda basınca maruz kalan elemanlara basınç çubukları denir. Bu tip çubuklara örnek olarak pandül kolonları, kafes sistemlerin basınca çalışan dikme
BASINÇ ÇUBUKLARI Kesit zoru olarak yalnızca eksenel doğrultuda basınca maruz kalan elemanlara basınç çubukları denir. Bu tip çubuklara örnek olarak pandül kolonları, kafes sistemlerin basınca çalışan dikme
Algoritma ve Akış Diyagramları
 Algoritma ve Akış Diyagramları Bir problemin çözümüne ulaşabilmek için izlenecek ardışık mantık ve işlem dizisine ALGORİTMA, algoritmanın çizimsel gösterimine ise AKIŞ DİYAGRAMI adı verilir 1 Akış diyagramları
Algoritma ve Akış Diyagramları Bir problemin çözümüne ulaşabilmek için izlenecek ardışık mantık ve işlem dizisine ALGORİTMA, algoritmanın çizimsel gösterimine ise AKIŞ DİYAGRAMI adı verilir 1 Akış diyagramları
Kuantum Grupları. Orta Doğu Teknik Üniversitesi, Ankara. Münevver Çelik. Feza Gürsey Enstitüsü, İstanbul 10 Şubat, 2010
 Orta Doğu Teknik Üniversitesi, Ankara Feza Gürsey Enstitüsü, İstanbul 10 Şubat, 2010 Kuantum grubu örgülü bir Hopf cebridir. Cebir Tanım Bir k-vektör uzayı A için, µ : A A A ve η : k A birer k-doğrusal
Orta Doğu Teknik Üniversitesi, Ankara Feza Gürsey Enstitüsü, İstanbul 10 Şubat, 2010 Kuantum grubu örgülü bir Hopf cebridir. Cebir Tanım Bir k-vektör uzayı A için, µ : A A A ve η : k A birer k-doğrusal
1. GRUPLAR. c (Birleşme özelliği) sağlanır. 2) a G için a e e a a olacak şekilde e G (e ye birim eleman denir) vardır.
 1. GRUPLAR Tanım 1.1. G boş olmayan bir küme ve, G de bir ikili işlem olsun. (G yapısına aşağıdaki aksiyomları sağlıyorsa bir grup denir., ) cebirsel 1) a b cg,, için a( bc) ( ab) c (Birleşme özelliği)
1. GRUPLAR Tanım 1.1. G boş olmayan bir küme ve, G de bir ikili işlem olsun. (G yapısına aşağıdaki aksiyomları sağlıyorsa bir grup denir., ) cebirsel 1) a b cg,, için a( bc) ( ab) c (Birleşme özelliği)
Microsoft Excel. Çalışma Alanı. Hızlı Erişim Çubuğu Sekmeler Başlık Formül Çubuğu. Ad Kutusu. Sütunlar. Satırlar. Hücre. Kaydırma Çubukları
 Microsoft Excel Microsoft Excel yazılımı bir hesap tablosu programıdır. Excel, her türlü veriyi (özellikle sayısal verileri) tablolar ya da listeler halinde tutma ve bu verilerle ilgili ihtiyaç duyacağınız
Microsoft Excel Microsoft Excel yazılımı bir hesap tablosu programıdır. Excel, her türlü veriyi (özellikle sayısal verileri) tablolar ya da listeler halinde tutma ve bu verilerle ilgili ihtiyaç duyacağınız
EM302 Yöneylem Araştırması 2. Dr. Özgür Kabak
 EM302 Yöneylem Araştırması 2 Dr. Özgür Kabak GAMS Giriş GAMS (The General Algebraic Modeling System) matematiksel proglamlama ve optimizasyon için tasarlanan yüksek seviyeli bir dildir. Giriş dosyası:
EM302 Yöneylem Araştırması 2 Dr. Özgür Kabak GAMS Giriş GAMS (The General Algebraic Modeling System) matematiksel proglamlama ve optimizasyon için tasarlanan yüksek seviyeli bir dildir. Giriş dosyası:
ÜÇ ÇUBUK MEKANİZMASI
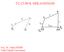 ÜÇ ÇUBUK MEKNİZMSI o l min l, lmaks B l,, B o Doç. Dr. Cihan DEMİR Yıldız Teknik Üniversitesi Dört çubuk mekanizmalarının uygulama alanı çok geniş olmasına rağmen bu uygulamalar üç değişik gurupta toplanabilir.
ÜÇ ÇUBUK MEKNİZMSI o l min l, lmaks B l,, B o Doç. Dr. Cihan DEMİR Yıldız Teknik Üniversitesi Dört çubuk mekanizmalarının uygulama alanı çok geniş olmasına rağmen bu uygulamalar üç değişik gurupta toplanabilir.
GÖRÜNTÜ İŞLEME HAFTA 2 SAYISAL GÖRÜNTÜ TEMELLERİ
 GÖRÜNTÜ İŞLEME HAFTA 2 SAYISAL GÖRÜNTÜ TEMELLERİ GÖRÜNTÜ ALGILAMA Üç temel zar ile kaplıdır. 1- Dış Zar(kornea ve Sklera) 2- Koroid 3- Retina GÖRÜNTÜ ALGILAMA ---Dış Zar İki kısımdan oluşur. Kornea ve
GÖRÜNTÜ İŞLEME HAFTA 2 SAYISAL GÖRÜNTÜ TEMELLERİ GÖRÜNTÜ ALGILAMA Üç temel zar ile kaplıdır. 1- Dış Zar(kornea ve Sklera) 2- Koroid 3- Retina GÖRÜNTÜ ALGILAMA ---Dış Zar İki kısımdan oluşur. Kornea ve
AYRIK YAPILAR ARŞ. GÖR. SONGÜL KARAKUŞ- FIRAT ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ YAZILIM MÜHENDİSLİĞİ BÖLÜMÜ, ELAZIĞ
 AYRIK YAPILAR P r o f. D r. Ö m e r A k ı n v e Y r d. D o ç. D r. M u r a t Ö z b a y o ğ l u n u n Ç e v i r i E d i t ö r l ü ğ ü n ü ü s t l e n d i ğ i «A y r ı k M a t e m a t i k v e U y g u l a
AYRIK YAPILAR P r o f. D r. Ö m e r A k ı n v e Y r d. D o ç. D r. M u r a t Ö z b a y o ğ l u n u n Ç e v i r i E d i t ö r l ü ğ ü n ü ü s t l e n d i ğ i «A y r ı k M a t e m a t i k v e U y g u l a
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Yaklaşık Düşünme Teorisi
 Yaklaşık Düşünme Teorisi Zadeh tarafından 1979 yılında öne sürülmüştür. Kesin bilinmeyen veya belirsiz bilgiye dayalı işlemlerde etkili sonuçlar vermektedir. Genellikle bir f fonksiyonu ile x ve y değişkeni
Yaklaşık Düşünme Teorisi Zadeh tarafından 1979 yılında öne sürülmüştür. Kesin bilinmeyen veya belirsiz bilgiye dayalı işlemlerde etkili sonuçlar vermektedir. Genellikle bir f fonksiyonu ile x ve y değişkeni
1-2 - * Bu Ders Notları tam olarak emin olmamakla birlikte 2012-2013 yıllarına aiitir.tekrardan Sn.Hakan Paçal'a çoook tsk ederiz...
 1-2 - * Bu Ders Notları tam olarak emin olmamakla birlikte 2012-2013 yıllarına aiitir.tekrardan Sn.Hakan Paçal'a çoook tsk ederiz... CABİR VURAL BAHAR 2006 Açıklamalar
1-2 - * Bu Ders Notları tam olarak emin olmamakla birlikte 2012-2013 yıllarına aiitir.tekrardan Sn.Hakan Paçal'a çoook tsk ederiz... CABİR VURAL BAHAR 2006 Açıklamalar
