ÜNİTE TAŞIMACILIK SİSTEMLERİ. Prof. Dr. Bülent SEZEN İÇİNDEKİLER HEDEFLER ROTA PLANLAMA
|
|
|
- Temel Ilker Yıldızoğlu
- 8 yıl önce
- İzleme sayısı:
Transkript
1 HEDEFLER İÇİNDEKİLER ROTA PLANLAMA Giriş Rota Planlama Taşıma Problemi Atama Problemi Gezgin Satıcı Problemi En Kısa Yol Problemi Rota Planlama Yazılımları TAŞIMACILIK SİSTEMLERİ Prof. Dr. Bülent SEZEN Bu üniteyi çalıştıktan sonra; Rota planlamanın tanımı ve kapsamını öğrenecek, Matematiksel anlamda tipik bir taşıma probleminin çözüm yaklaşımını anlayacak, Atama problemi, gezgin satıcı problemi ve en kısa yol problemi gibi farklı taşımacılık problemleri için matematiksel çözüm yollarını görecek, Rota planlama yazılımlarına değinilerek gerçek hayatta taşımacılıkta rota planlamasının yazılımlarla nasıl çözüldüğünü öğreneceksiniz. ÜNİTE 13
2 GİRİŞ Taşımacılıkta rota planlama bir noktadan bir başka noktaya (ya da noktalara) yapılan sevkiyatlarda güncel problemlerin çözülmesi ve taşıma maliyetlerinin minimumda tutulabilmesi için birçok lojistik firmanın önemle üzerinde durması gereken konulardan biridir. Rota planlama konusu disiplinler arası bir konu olup, Rota planlama, bir başlangıç noktası, bir varış noktası ve duruş noktaları bulunabilen bir taşıma probleminde en düşük maliyetli ya da en kısa sürede kat edilebilen rotanın belirlenmesi işlemidir. yöneylem araştırması, tedarik zinciri yönetimi, şebeke problemleri ve genel anlamda yönetim konularını kapsayan ve bu konuların bir bileşkesi konumunda olan geniş alanlı bir konudur. Rota planlama deyince ilk aklımıza gelen en kısa yol problemidir. En kısa yol problemi bir noktadan bir başka noktaya en kısa sürede ya da en düşük maliyetle gidebileceğimiz en uygun yolun bulunması problemidir. Aslında en kısa yol probleminin arka planında daha birçok farklı problem çeşidi mevcuttur. Örneğin gideceğiniz yol üzerinde uğramanız gereken noktalar varsa problem başka bir boyut kazanmaktadır. Ya da bazı durumlarda başladığınız noktaya geri dönüp seyahatinizi başlangıç noktasında bitirmeniz gerekebilir. Örneğin gezgin satıcı probleminde durum böyledir. Tahmin edilebileceği gibi bu durumda da problemin değişkenleri ve yapılandırılması farklılık arz edecektir. Bu bölümde rota planlama konusunda çeşitli problem türlerini ele alacağız. Her bir farklı problem türünün çözümünde kullanılabilecek farklı yaklaşımlara ve çözüm yöntemlerine yer vereceğiz. Tabi bu konularda kullanılabilecek formülasyonlardan, algoritmalardan ve rota planlama yazılımlarından da bahsedeceğiz. Teknolojiler geliştikçe her alanda olduğu gibi rota planlama problemlerinin çözümünde de bilgisayar teknolojilerinden ve yazılımlardan faydalanılmaktadır. Her ne kadar bu yazılımlar bize en uygun rotayı bulmamızda yardımcı olsalar da, bu yazılımların arka planında nasıl bir mantık ve algoritma işlemektedir sorusunun yanıtlanmasında bu bölümde anlatılanlar faydalı olacaktır. ROTA PLANLAMA Rota planlama, bir başlangıç noktası, bir varış noktası ve gerekli durumlarda başlangıç ve varış noktaları arasında bir veya birden çok duruş noktası (ya da uğrama noktası) bulunabilen bir taşıma probleminde en düşük maliyetli ya da en kısa sürede kat edilebilen rotanın belirlenmesi ya da hesaplanması işlemini Atatürk Üniversitesi Açıköğretim Fakültesi 2
3 kapsamaktadır. Rota planlama problemlerinin çözümünde matematiksel çözüm [(örneğin optimizasyon (eniyileme)] yöntemlerinden faydalanılır. Rota planlama problemleri aslında daha geniş kapsamlı olan şebeke (network) modellerinin bir alt dalı olarak görülebilir. Şebeke problemlerinde birbirlerine (oklarla) bağlı ve ilişkilendirilmiş noktalar ve bu noktalar arasında tanımlı fonksiyonlar (örneğin maliyet, uzaklık vb.) mevcuttur. Şebeke modellerinin tipik amaçları toplam maliyeti ya da kat edilen mesafeyi minimize etmektir. Aşağıdaki şekilde tipik bir şebeke modelinden bir kesit görünmektedir. i ij X j Şekil 13.1 Şebeke Modelinden Bir Kesit Örneği Şekilde tanımlanan Xij iki nokta (i ve j) arasındaki akış kapasitesi, i noktasından j noktasına bir birim yük taşımanın maliyeti ya da daha farklı bir fonksiyon olabilir. Taşıma probleminde amaç m tane kaynaktan n tane hedefe yapılacak sevkiyatları minimum taşıma maliyetiyle gerçekleştirecek şekilde her bir i ve j noktası arasında taşınacak miktarları belirlemektir. Şebeke problemine uygun olabilecek uygulamalara örnek olarak kara yolu, deniz ve hava taşımacılığında rota planlama, süpermarket mağaza zincirleri ve depoları arasında dağıtım planlama, bir bilgisayar içinde kablolarla birbirine bağlı yongalar (çipler) arasında veri akışının optimize edilmesi, uydu iletişimi ile televizyon istasyonları arasında sinyallerin verimli bir şekilde iletilmesi, şehir içi ve şehirlerarası otobüs (ya da tren) terminallerinin birbirleri arasındaki yolcu taşımacılığının planlanması, vb. sayılabilir. Görüldüğü gibi şebeke problemlerinin gerçek hayatta çok fazla kullanım alanı mevcuttur. Şebeke problemleri doğası itibarıyla tam sayılı programlama modelleri olmasına karşın, genellikle tam sayı kısıtı yok sayılarak nispeten daha kolay çözüm yolları türetilmiştir. Bu nedenle, rota planlama problemi gibi şebeke problemleri genellikle sezgisel (heuristic) adı verilen basit algoritmalar kullanılarak çözülebilir. TAŞIMA PROBLEMİ Taşıma problemi tipik bir şebeke problemidir. Taşıma modelinde m tane kaynak (çıkış) noktası ve n tane de hedef (varış) noktası vardır. Kaynakların indisi i harfi ile gösterilirken, hedeflerin indisi j harfi ile gösterilir. i inci kaynaktan j inci hedefe gönderilecek olan miktar Xij ile ifade edilmektedir. i inci kaynaktan Atatürk Üniversitesi Açıköğretim Fakültesi 3
4 gönderilebilecek toplam (arz) miktarı Si ile gösterilirken. j inci hedefin alabileceği toplam talep miktarı Dj ile gösterilmektedir. Son olarak, i ve j noktaları arasında bir birim yükün taşınmasının maliyeti Cij olarak tanımlanmaktadır. Taşıma probleminde amaç m tane kaynaktan n tane hedefe yapılacak olan sevkiyatları minimum taşıma maliyetiyle gerçekleştirecek şekilde her bir i ve j noktası arasında taşınacak miktarları (yani Xij leri) belirlemektir. Örnek Taşıma Problemi ABC lojistik firmasının bir müşterisinin Çanakkale, İstanbul ve Giresun da bulunan üç ayrı deposundan Balıkesir, Kastamonu, Ankara ve Samsun da bulunan bayilerine yapılacak olan sevkiyatları için minimum taşıma maliyetine sahip taşıma planını belirlemesi gerekmektedir. Ürünler her bir depodan her bir bayi adresine gönderilebilmektedir. Yani her ürün her depoda bulunmakta ve yine her bayiden de talep edilebilmektedir. Burada çözülmesi gereken, hangi depodan hangi bayi adresine ve ne kadar miktarda sevkiyat yapılması gerektiğidir. Yukarıda belirtildiği gibi depoları i indisi ile ve bayileri de j indisi ile gösterirsek, i nci depodan j inci bayi adresine gönderilen miktar Xij ile tanımlanır ve problemin karar değişkenleri (yani çözülmesi gereken değişkenler) bu Xij değerleridir. Bazı Xij değerleri sıfır olabilecektir. Bunun anlamı bazı depolardan bazı bayilere sevkiyat yapılmayacak olmasıdır. Problemin çözülebilmesi için bir karar verme kıstasına (kriterine) ihtiyaç vardır. Taşıma probleminde tipik karar verme kıstası birim taşıma maliyetidir. Şöyle ki, her bir i deposundan her bir j bayisine bir birim ürün taşıma maliyeti Cij ile tanımlanır. Cij değerleri sabit olup, bizim tarafımızdan belirlenmiş (ya da belirlenecek) olan değerlerdir. Örneğimizi basit tutmak için tek bir ürünün sevkiyatı için arz ve talep miktarlarını sayısal olarak belirleyelim. Bu hafta Çanakkale deposundan 800 birim, İstanbul deposundan 500 birim ve Giresun deposundan da 400 birim ürün arz edilebilmektedir. Yani toplamda 1700 birim ürün arzı mevcuttur. Bu haftanın dağıtım planına göre bu 1700 birimlik ürün arzı, Balıkesir bayisine 500 birim, Kastamonu bayisine 200 birim, Ankara bayisine 700 birim ve Samsun bayisine 300 birim olacak şekilde gönderilecektir. Her bir depodan her bir bayi adresine bir birim ürün göndermenin maliyeti (Cij) aşağıdaki şekilde (Şekil 13.2 de üstteki Atatürk Üniversitesi Açıköğretim Fakültesi 4
5 tablonun içindeki değerler) verilmektedir. Örneğin Çanakkale den Kastamonu ya bir birim taşıma maliyeti 50 kuruştur. Bu veriler doğrultusunda taşıma problemi için gerekli girdiler sağlanmış bulunmaktadır. Şimdi taşıma probleminin matematiksel olarak formüle edilmesi ve sonra da bu matematik modelin çözülmesi gerekmektedir. Sayısal örneğimizden devam edersek, yukarıda betimlenen taşıma (dağıtım) planlama probleminin matematiksel modeli aşağıdaki gibi olacaktır: Min (20X X X X 14 ) + (26X X X X 24 ) + (62X X X X 34 ) (X 11 + X 12 + X 13 + X 14 ) = 800 (Çanakkale arz miktarı = 800) (X 21 + X 22 + X 23 + X 24 ) = 500 (İstanbul arz miktarı = 500) (X 31 + X 32 + X 33 + X 34 ) = 400 (Giresun arz miktarı = 400) (X 11 + X 21 + X 31 ) = 500 (Balıkesir talep miktarı = 500) (X 12 + X 22 + X 32 ) = 200 (Kastamonu talep miktarı = 200) (X 13 + X 23 + X 33 ) = 700 (Balıkesir talep miktarı = 700) (X 14 + X 24 + X 34 ) = 300 (Kastamonu talep miktarı = 300) X ij 0 (Tüm Xij ler sıfırdan büyük ya da eşittirler, negatif olamazlar) Problemi yukarıdaki modelde görüldüğü gibi matematiksel olarak formüle edebiliriz. Modelin ilk kısmı amaç fonksiyonudur. Min ifadesi minimize etmek anlamında olup, toplam taşıma maliyetinin minimize edilmesi amacını göstermektedir. Diğer kısımlar ise kısıtlar olarak adlandırılır. Bu probleme özel olarak tanımlanan kısıt denklemlerinde, her bir deponun arz miktarı belirtildiği kadar olmalı ve her bir bayinin talep ettiği miktarlar da yine belirtilen haftalık talep miktarları kadar olmalıdır. Problemin Microsoft Excel Solver (Çözücü) eklentisi kullanılarak bulunan çözümü aşağıdaki şekilde verilmektedir. Atatürk Üniversitesi Açıköğretim Fakültesi 5
6 Cij: Birim Taşıma Maliyetleri (Kuruş) Balıkesir Kastamonu Ankara Samsun Çanakkale İstanbul Giresun Xij: Depolardan bayilere taşınan miktarlar (birim) Balıkesir Kastamonu Ankara Samsun Çanakkale İstanbul Giresun Şekil Örnek Taşıma Probleminin Excel İle Çözümü Matematiksel modellerin çözümünde çeşitli yazılımlar ya da programlar kullanılabilir. Biz bu örnekte MS Excel Çözücü eklentisini kullanarak optimum (en iyi) çözümü bulduk. Çözüme ulaşmak için kullanılabilecek diğer yazılımlara örnek olarak WinQSB programı ya da Matlab programlama aracı verilebilir. Şekil 2 deki çözümde görüldüğü gibi problemin en düşük maliyetli çözümünde Çanakkale deposundan Balıkesir bayisine 500 birim, Giresun deposundan Samsun bayisine 300 birim, İstanbul ve Giresun depolarından Kastamonu bayisine 100 er birim, Çanakkale deposundan Ankara bayisine 300 birim ve son olarak da İstanbul deposundan Ankara deposuna 400 birim ürün gönderilmesi öngörülmektedir. Bu çözümün taşıma maliyeti minimum maliyet olup kuruş yani 410 TL olarak bulunmuştur. ATAMA PROBLEMİ Birçok işte yöneticiler birtakım atama problemleriyle karşı karşıyadırlar. Örneğin işleri çalışanlara, makineleri işlere, projeleri araştırmacılara, bölgeleri satış elemanlarına atamak gerektiğinde söz konusu problem bir atama problemi olup minimum maliyetle atama işleminin gerçekleştirilmesi amaçlanır. Taşımacılıkta atama problemi sıklıkla karşımıza çıkmaktadır. Örneğin gemi taşımacılığında eldeki gemilerin hedef limanlara atanması, farklı kapasitelerdeki Atatürk Üniversitesi Açıköğretim Fakültesi 6
7 Örnek Rota Planlama yük taşıyıcıların farklı taşıma görevlerine atanması, depolardan mağazalara yapılacak sevkiyatlarda hangi deponun hangi mağaza(lar)a sevkiyat yapacağı ile ilgili atamanın yapılması gibi daha birçok örnek sayılabilir. Atama probleminde minimize edilmek istenen amaç değeri toplam taşıma maliyeti olabileceği gibi, harcanan toplam süre ya da kat edilen toplam mesafe de olabilir. Gemi taşımacılığında elimizde bulunan n tane gemiyi n farklı taşıma işine atama problemini ele alalım. Burada amaç, gemilerin taşıma maliyetleri, liman maliyetleri, gemilerin hızları ve siparişlerin temin süreleri ile gemilerin yük taşıma kapasiteleri de göz önünde bulundurularak en düşük toplam maliyetle bu taşıma işleminin gerçekleştirilmesidir. Kuşkusuz bu tür bir problemde eğer sipariş, liman ve gemi sayıları çok fazla olup karmaşık bir problem ile karşı karşıya kalınırsa bilgisayar destekli karar destek sistemlerinden faydalanılmalıdır. Karar destek sistemleri sayesinde her bir i gemisini her bir j taşıma işine atamanın maliyetini (Cij) belirlediğimizi varsayalım. Bu durumda tipik bir atama problemi ile karşı karşıyayız demektir. Atama problemi aslında bir önceki konuda anlatılan taşıma probleminin özel bir hâlidir. Şöyle ki, aradaki farklar: 1. Taşıma probleminde m adet başlangıç noktası ve n adet varış noktası varken atama probleminde n adet iş n adet iş görene (ya da bizim örneğimizdeki gibi gemilere) atanacaktır. 2. Karar değişkenleri olan Xij lerin tanımı atama probleminde aşağıdaki gibi olacaktır: Xij = 1 Xij = 0 atanmamışsa Eğer i gemisi j taşıma işine atanmışsa Eğer i gemisi j taşıma işine Görüldüğü gibi bu iki farklılık dışında atama problemi aslında taşıma probleminin özel bir hâlidir ve taşıma probleminin çözülme yönteminin aynısı kullanılarak bu problem de benzer şekilde çözülebilir. Atatürk Üniversitesi Açıköğretim Fakültesi 7
8 Örnek Atama Problemi RT deniz taşımacılık şirketinin mevcut 5 adet gemisi (1, 2, 3, 4 ve 5 nolu) bu ay için gelen siparişler doğrultusunda 5 farklı taşıma işine (A, B, C, D ve E limanlarına) atanacaktır. Geçmiş verilerden ve güncel maliyet bilgilerinden yola çıkarak her bir geminin her bir taşıma işine atanmasının toplam maliyeti aşağıdaki şekilde (Şekil 13.3 de üstteki tablonun içindeki değerler) verilmektedir. Bu maliyet verileri doğrultusunda karşımızda tipik bir atama problemi var demektir. Problemin çözümünde yine MS Excel Çözücü eklentisi kullanılmıştır. Bulunan optimum çözüm aşağıdaki şekilde gösterilmektedir. Gemiler Hedef Limanlara Taşıma Maliyetleri (Bin TL) A B C D E Hedef Limanlara Yapılan Atamalar (1 = Atanmış) A B C D E Gemiler Şekil 3. Örnek Atama Probleminin Excel İle Çözümü Görüldüğü gibi en uygun çözümde (Şekil 3 ün alt kısmında) 1 no lu gemi A limanına, 2 no lu gemi B limanına, 3 no lu gemi E limanına, 4 no lu gemi C limanına ve 5 no lu gemi D limanına gitmek üzere atanmıştır. Bu atamaların toplam maliyeti 43 Bin TL olmuştur. Burada belirtilmesi gereken önemli bir nokta, Atatürk Üniversitesi Açıköğretim Fakültesi 8
9 5 no lu geminin yönetim tarafından A limanına atanmasının kesinlikle uygun olmayacağının bildirilmiş olmasıdır. Bu nedenle, Şekil 3 ün üst tarafında maliyet bilgileri girilirken 5 nolu geminin A limanına gitme maliyeti için bilerek 99 gibi çok büyük bir değer girilmiştir (renkli olarak gösterilen bölge). Bu sayede 5 nolu gemi maliyeti çok yüksek olduğu için zaten A limanına atanmamıştır. Tıpkı taşıma probleminde olduğu gibi burada anlatılan örnek atama probleminde de problemin matematiksel formülasyonu üzerinden en uygun çözüm bulunmuştur. Aşağıda gösterilen atama problemi modeline dikkatlice bakılırsa, atama probleminin taşıma probleminin özel bir hâli olduğu çok daha iyi anlaşılabilecektir. Min (9X X X X X 15 ) + (13X X X X X 25 ) + (15X X X X X 35 ) + (13X X X X X 45 ) + (99X X X X X 55 ) (X 11 + X 12 + X 13 + X 14 + X 15 ) = 1 (1 no lu gemi sadece 1 işe atanır) (X 21 + X 22 + X 23 + X 24 + X 25 ) = 1 (2 no lu gemi sadece 1 işe atanır) (X 31 + X 32 + X 33 + X 34 + X 35 ) = 1 (3 no lu gemi sadece 1 işe atanır) (X 41 + X 42 + X 43 + X 44 + X 45 ) = 1 (4 no lu gemi sadece 1 işe atanır) (X 51 + X 52 + X 53 + X 54 + X 55 ) = 1 (5 no lu gemi sadece 1 işe atanır) (X 11 + X 21 + X 31 + X 41 + X 51 ) = 1 (A limanına sadece 1 gemi atanır) (X 12 + X 22 + X 32 + X 42 + X 52 ) = 1 (B limanına sadece 1 gemi atanır) (X 13 + X 23 + X 33 + X 43 + X 53 ) = 1 (C limanına sadece 1 gemi atanır) (X 14 + X 24 + X 34 + X 44 + X 54 ) = 1 (D limanına sadece 1 gemi atanır) (X 15 + X 25 + X 35 + X 45 + X 55 ) = 1 (E limanına sadece 1 gemi atanır) Xij = 1 Xij = 0 atanmamışsa Eğer i gemisi j taşıma işine atanmışsa Eğer i gemisi j taşıma işine Atatürk Üniversitesi Açıköğretim Fakültesi 9
10 (Bu son kısıt ile eğer i gemisi j limanına atanmamışsa Xij değeri sıfır olacağından maliyet hesabında bu atamanın maliyeti sıfır olacaktır.) GEZGİN SATICI PROBLEMİ Gezgin satıcı problemi adından da anlaşılabileceği gibi bir satıcının (ya da Gezgin satıcı problemi bir satıcının bir başlangıç noktasından çıkıp m tane farklı uğrama noktasını ziyaret edip başladığı yere tekrar geri dönmesi gerektiği özel bir taşıma problemidir. taşıma aracının) bir başlangıç noktasından çıkıp m tane farklı uğrama noktasını ziyaret edip başladığı yere tekrar geri dönmesi gereken özel bir taşıma problemidir. Burada gidilecek yerler zaten bellidir. Belli olmayan ise gidilecek olan yerlere hangi sırada gidileceğidir. Bu sıralamadaki farklılık seyahatin rotasını da etkileyeceğinden, problemin özünde yine toplam taşıma maliyetini (ya da süresini veya mesafesini) minimize edecek en uygun rotayı belirleme amacı vardır. Günümüzdeki yalın tedarik zinciri uygulamaları ve tam zamanında (just in time) üretim sistemlerini uygulayan firmalar (örneğin Toyota gibi otomobil firmaları), bir yandan montaj hattının sürekliliğini sağlamak ve diğer yandan da az miktarda (gerektiği kadar) stok bulundurmak için süt dağıtımı (milk run distribution) adı verilen yöntemi kullanılmaktadır. Süt dağıtımı aslında tam bir gezgin satıcı problemidir. Bu yöntemle tıpkı süt dağıtıcısının evleri dolaşıp sütlerini bıraktığı gibi, tedarikçi firmalardan gelen parça siparişleri belli bir program dâhilinde ve belli bir sırada (en uygun) toplanarak son montajları yapılmak üzere ana firmaya günlük olarak (ya da saatlik olarak) sevk edilmektedir. Böylece her bir alt parçadan gerekli olduğu miktarda, gerekli olduğu yerde ve gerekli olduğu zamanda temin edilmektedir ki bu tam zamanında sevkiyat (Just in Time, JIT) anlamına gelmektedir. Gezgin satıcı probleminde yol üzerindeki her bir nokta sadece bir defa ziyaret edilir. Ziyaret edilen her bir i ve j noktası arasındaki mesafe ya da taşıma maliyeti Cij ile gösterilir. Problemin karar değişkeni olan Xij ler aşağıdaki gibi tanımlanır: Xij = 1 Xij = 0 Eğer belirlenen rota üzerinde i bölgesinden j bölgesine gidiş varsa Eğer belirlenen rota üzerinde i bölgesinden j bölgesine gidiş yoksa Atatürk Üniversitesi Açıköğretim Fakültesi 10
11 Gezgin satıcı probleminin amaç fonksiyonu tıpkı taşıma ve atama problemlerinde olduğu gibi toplam taşıma maliyetinin (Cij ler ile Xij lerin çarpımlarının toplamı) minimize edilmesi şeklinde formüle edilmektedir. Gezgin satıcı problemi aslında atama problemine benzer. Çünkü her bir i ve j bölgesi birbirlerine tahsis edilmiş (atanmış) ve her bir bölge için sadece bir atama mevcuttur. Diğer bir deyişle, her bir bölgeye sadece bir giriş ve bir çıkış olacaktır. Atama problemine benzemesine rağmen gezgin satıcı probleminin çözümü nispeten daha zordur. Özellikle uğranacak olan bölge sayısı m arttıkça, problemin çözümü daha da zorlaşmaktadır. Örneğin 50 uğrama noktasını (şehir ya da firma olabilir) içeren bir problem için 500 trilyon kısıt denklemi yazılması gerekmektedir. Tabi bugünkü bilgisayar teknolojisi ile bu tür problemler de kısa sürelerde çözülebilmektedir. Örnek Gezgin Satıcı Problemi Tam zamanında (Just in time) sevkiyat planına uyabilmek için süt dağıtımı (milk run distribution) uygulayan bir tedarikçi firmadan çıkan bir tır 4 farklı firmaya uğradıktan sonra geri dönmektedir. Aşağıdaki tabloda her iki uğrama noktası arasındaki seyahat süreleri dakika cinsinden verilmektedir. Tablo 13.1 Örnekteki Uğrama Noktaları Arasındaki Taşıma Sürelerini (Dakika Cinsinden) Gösteren Tablo Firma 1 Firma 2 Firma 3 Firma 4 Ana Firma Firma Firma Firma Firma Problemin amacı tüm firmalara (ana firma dâhil olmak üzere m= 5) birer defa uğrayıp ana firmaya en kısa sürede geri dönmektir. Bizim burada bulmamız gereken hangi sırada ziyaretlerin gerçekleştirileceğidir. Bu problem simetrik bir Atatürk Üniversitesi Açıköğretim Fakültesi 11
12 seyahat problemidir. Çünkü her bir uğrama noktası çifti arasındaki seyahat zamanı iki yönde de aynıdır. Fakat bunun böyle olmadığı problemler de olabilir. Örneğin trafiğin tek yönde sıkışık olduğu durumlarda gidiş süresi ile dönüş süresi aynı olmayabilir. Böyle bir problemi basit bir şekilde çözmenin bir yolu bütün muhtemel rotaları alt alta yazarak bunların toplam sürelerini hesaplayıp en kısa süreli olanı bulmaktır. Aşağıda bu tarz bir çözüm yöntemi uygulanmaktadır (aşağıda firma kelimesi F olarak kısaltılmıştır, örneğin Firma 1 yerine F1 yazılmıştır): Döngü Toplam Süre Ana Firma-F1-F2-F3-F4-Ana Firma = 90 dakika 2. Ana Firma-F1-F2-F4-F3-Ana Firma = 103 dakika 3. Ana Firma-F1-F3-F2-F4-Ana Firma = 83 dakika 4. Ana Firma-F1-F3-F4-F2-Ana Firma = 85 dakika 5. Ana Firma-F1-F4-F2-F3-Ana Firma = 106 dakika 6. Ana Firma-F1-F4-F3-F2-Ana Firma = 95 dakika 7. Ana Firma-F2-F3-F1-F4-Ana Firma = 88 dakika 8. Ana Firma-F2-F1-F3-F4-Ana Firma = 85 dakika 9. Ana Firma-F2-F4-F1-F3-Ana Firma = 101 dakika 10. Ana Firma-F2-F1-F4-F3-Ana Firma = 108 dakika 11. Ana Firma-F3-F1-F2-F4-Ana Firma = 96 dakika 12. Ana Firma-F3-F2-F1-F4-Ana Firma = 106 dakika Yukarıdaki hesaplamalarda görüldüğü gibi problemin en kısa süreli çözümü 3. seçenekteki Ana Firma-F1-F3-F2-F4-Ana Firma rotasıdır. Bu rotanın toplam süresi 83 dakikadır. Bu problemde uğrama noktaları sayısı (m= 5) olduğundan ve bu problem simetrik bir problem olduğundan problemin [(m 1)!] / 2 adet muhtemel çözümü vardır. Yani m= 5 ise [(m 1)!] / 2 = [(5 1)!] / 2 = 4! / 2 = 12 Atatürk Üniversitesi Açıköğretim Fakültesi 12
13 Yukarıda görüldüğü gibi problemin 12 muhtemel çözümü vardır ki biz de zaten 12 farklı çözüm bulduk. Burada problem simetrik olmasa idi bu değeri ikiye bölmeyecektik ki bu sefer 24 farklı çözüm olacaktı. Uğranılan bölge sayısı arttıkça problemin muhtemel çözüm sayısı da artacak ve böylece artık problem elle çözülemeyecek kadar zorlaşacaktır. Gezgin satıcı problemi atama problemi şeklinde çözüldüğünde, birbirinden ayrı alt döngülerle sonuçlanacaktır. Bu alt döngüleri engellemek için normal atama problemi şeklinde tanımlanan modele ek kısıtlar ilave edilmelidir. Örneğin (Ana Firma-F2-F1-Ana Firma) şeklinde eksik uğrama noktaları şeklinde yani tamamlanmamış bir alt döngüsünün gerçekleşememesi için (Ana Firma-F2); (F2- F1) ve (F1-Ana Firma) bağlantılarının çözüme aynı anda girmesini engelleyecek bir kısıt eklemek gerekir. Ana firma için indis numarası olarak 5 i verirsek aşağıdaki kısıt denklemi (Ana Firma-F2-F1-Ana Firma) alt döngüsünün geçersiz olmasını sağlar: X52 + X21 + X15 2 Bu alt döngü sadece X52, X21, ve X15 değerlerinin hepsinin 1 e eşit olduğunda geçerli olabileceğinden yukarıdaki kısıt bunu imkânsız yapar, çünkü üçü birden 1 e eşit olduğunda 2 den büyük olacaktır ki yukarıdaki kısıt denklemi bunu engeller. Bir başka örnek olarak (F1-F2-F3-F4-F1) alt döngünün geçersiz olduğunu söylemek için aşağıdaki kısıt denklemini eklemeliyiz: X12 + X23 + X34 + X41 3 Bu gezgin satıcı problemini bir atama problemi modeli şeklinde çözebilmek için, yukarıdaki gibi muhtemel tüm alt döngülerin ek kısıtlar getirilerek engellenmesi gerekir. Bu doğrultuda örnek problemimiz için aşağıdaki kısıtlar eklenmelidir: Tek düğümlü alt döngüler için: X11 0, X22 0, X33 0, X44 0, X55 0. Atatürk Üniversitesi Açıköğretim Fakültesi 13
14 İki düğümlü alt döngüler için: X12 + X21 1 X13 + X31 1 X14 + X41 1 X15 + X51 1 X23 + X32 1 X24 + X42 1 X25 + X52 1 X34 + X43 1 X35 + X53 1 X45 + X54 1 Üç düğümlü alt döngüler için: X12 + X23 + X31 2 X12 + X24 + X41 2 X12 + X25 + X51 2 X13 + X34 + X41 2 X13 + X35 + X51 2 X14 + X45 + X51 2 X23 + X34 + X42 2 X23 + X35 + X52 2 X24 + X45 + X52 2 X34 + X45 + X53 2 Dört düğümlü alt döngüler için: X12 + X23 + X34 + X41 3 X12 + X23 + X35 + X51 3 X12 + X24 + X45 + X51 3 X13 + X34 + X45 + X51 3 X23 + X34 + X45 + X51 3 MS Excel ya da WinQSB gibi yazılım araçları ile 10 veya daha az uğrama noktası olan problemlerin gezgin satıcı problemleri çözülebilir. Daha büyük çaplı gezgin satıcı problemleri için daha kapsamlı çözüm araçları (örneğin Matlab gibi) kullanılabilir. Atatürk Üniversitesi Açıköğretim Fakültesi 14
15 EN KISA YOL PROBLEMİ Çoğumuz bir yere gideceğimiz zaman kara yolları haritasına bakarak gideceğiniz yere giden en kısa yolu bulmaya çalışırız. Genellikle en kısa yoldan gideceğimiz yere varmak isteriz ki, yolculuk maliyetimiz (benzin sarfiyatı ve yol masrafları) en az olsun. En kısa yol probleminde amacımız, başlangıç noktasından gidilecek hedef noktaya kadar giden en kısa yolu bulmaktır. En kısa yol probleminde bir giriş noktasıyla başlayan ve n inci bitiş (terminal) noktası ile biten n adet nokta vardır. En kısa yol probleminin gezgin satıcı probleminden iki farkı vardır. Şöyle ki, en kısa yol probleminde, 1. Her bir noktanın seçilen yol üzerinde yer alması gerekmemektedir. Ziyaret edilmeyen noktalar da olabilir. 2. Gezgin satıcı probleminden farklı olarak başlangıç düğümüne (noktasına) dönülmez. Örnek En Kısa Yol Problemi TLMN şirketi uluslararası bölgelerde faaliyet gösteren bir taşımacılık şirketidir. Bu şirketin bu ayki işlerinden birisi bir müşterisi için A ve B şehirleri arasında mal taşımaktır. İki şehri birleştiren muhtemel yollar üzerindeki uğranabilecek şehirler (10 adet şehir) ve bu şehirler arasındaki mesafeler (kilometre cinsinden) aşağıdaki gibidir. Şehir Şehir Mesafe (kilometre) Atatürk Üniversitesi Açıköğretim Fakültesi 15
16 Bu problemde 1 numaralı şehir A şehri olup başlangıç noktasıdır ve 10 numaralı şehir B şehri olup varış noktasıdır. Problemin şebeke gösterimi aşağıdaki şekilde görüldüğü gibidir. Başlan gıç ş Varı Şekil 13.4 Örnek En Kısa Yol Probleminin Şebeke Gösterimi Atatürk Üniversitesi Açıköğretim Fakültesi 16
17 Bu problem önceki modellere benzer bir şekilde formüle edilip çözülebilir. Xij, i ve j şehirleri arasında otoyolun kullanımını temsil etsin. Bu durumda Xij karar değişkeni aşağıdaki gibi tanımlanabilir: Xij = 1 Xij = 0 Eğer belirlenen rota üzerinde i ve j şehirleri arasındaki otoyoldan geçilecek ise Eğer belirlenen rota üzerinde i ve j şehirleri arasındaki otoyoldan geçilmeyecek ise Burada amaç kat edilen toplam uzaklığı minimize etmektir. Bu da bütün seyahat edilen yolların uzaklıklarının (dij ile gösterilebilir) karar değişkeni olan Xij ile çarpımlarının toplamıdır: Minimize dij Xij Bu şekilde eğer Xij=1 ise söz konusu i ve j şehirleri arası mesafe kat edilmiş olacak ve toplam mesafeye ilave edilecektir. En kısa yol modelinin kısıtları her bir şehir için (başlangıç ve bitiş şehirleri hariç) aşağıdaki gibi ifade edilebilir: (Şehrin içine gitmek için kullanılan otoyolların sayısı) = (şehirden ayrılırken gidilen yolların sayısı) Yani diğer bir deyişle bir şehre kaç defa giriş yapıldıysa aynı sayıda çıkış olmalıdır. Tabi bu kural başlangıç ve bitiş şehirleri için geçerli olmayacaktır. Çünkü başlangıç şehrine giriş olmayacak sadece çıkış olacaktır. Benzer şekilde bitiş şehrinden de çıkış olmayacak sadece giriş olacaktır. Yukarıdaki kısıt denklemine örnek olarak 7. şehir için aşağıdaki kısıt yazılmalıdır: X47 + X57 = X78 + X7,10 Yani, eğer 7. şehir seçilen yol üzerinde ise, 7. şehire gelirken ziyaret edilen otoyolların sayısı toplamda 1 olacaktır ve 7. şehirden çıkarken geçilen yolların sayısı da toplamda 1 olacaktır. Bunun için yukarıdaki formülde ya X47 ya da X57 değerlerinden biri 1 e eşit diğeri sıfıra eşit olacaktır. Benzer şekilde yukarıdaki formülde ya X78 ya da X710 değerlerinden biri 1 e eşit diğeri sıfıra eşit olacaktır. Atatürk Üniversitesi Açıköğretim Fakültesi 17
18 Fakat eğer 7. şehir seçilen rota üzerinde değilse, bu şehre giriş ve çıkış sayıları toplamı sıfır olacaktır. Yani X47, X57, X78 ve X7,10 değerlerinin hepsi sıfıra eşit olacaktır. Ayrıca, yukarıda belirtildiği gibi, başlangıç şehri olan 1. şehirden çıkışların sayısı tam olarak 1 olmalı, ve son durak olan 10 numaralı şehre girişlerin sayısı da 1 olmalıdır. Bu kural da, modele aşağıdaki kısıtlar eklenerek elde edilir. X12 + X13 + X14 = 1 (başlangıç şehri için) ve X7,10 + X8,10 = 1 (bitiş şehri için) Bu gibi kısıt denklemleri ilave edildiğinde problem bir doğrusal programlama problemi hâline gelir ve bilindik çözüm araçları ile çözülebilir. Karar değişkenleri (Xij ler) 0-1 li ikili değişkenler olduğundan bu problem bir İkili Tam Sayılı (Binary Integer) Doğrusal Programlama Modelidir. Yukarıdaki örnek en kısa yol probleminin çözümü aşağıdaki gibi bulunmaktadır: Önce başlangıç şehri olan 1 numaralı şehirden 3 numaralı şehre gidilir. Kat edilen mesafe 139 km Sonra 3 numaralı şehirden 6 numaralı şehre gidilir. Kat edilen mesafe 241 km Sonra 6 numaralı şehirden 8 numaralı şehre gidilir. Kat edilen mesafe 182 km Sonra 8 numaralı şehirden 9 numaralı şehre gidilir. Kat edilen mesafe 215 km Sonra 9 numaralı şehirden 10 numaralı şehre gidilir. Kat edilen mesafe 113 km Bu sonuca göre en kısa yol rotası numaralı şehirlerden geçen rota olup kat edilen toplam mesafe 890 kilometredir. Atatürk Üniversitesi Açıköğretim Fakültesi 18
19 ROTA PLANLAMA YAZILIMLARI Rota planlama yazılımları coğrafi açıdan iki nokta arasındaki optimal (en iyi) rotayı planlamak için tasarlanmış bilgisayar programlarıdır. Bu yazılımlar genellikle kara yolları şebekeleri için tasarlanmış olup, kara yolunda seyreden araçlar için en iyi rotayı belirlemede kullanılırlar. Genellikle geçilecek yerlerin listesini, kavşak noktalarını, yol numaralarını ve takip edilmesi gereken yönleri ve uzaklıkları sürücüye bildirir ve aynı zamanda bir harita ile de görsel olarak bu bilgileri gösterebilirler. Online olarak rota planlama hizmeti sunabilen web sitelerine örnek olarak Google Maps, Mapquest, Tom Tom Route Planner, ViaMichelin ve Intermodal Journey Planner vb. gibi siteler verilebilir. Bu uygulamalar tahmini seyahat süresini, ücretli geçişler varsa bunların toplam maliyetini ve bazı durumlarda yol üstündeki önemli ihtiyaç yerlerini de (örneğin, hastane, restoran vb.) kullanıcıya gösterebilirler. Rota planlama yazılımları yüzde yüz hatasız değildir. Belli bir süre kullanıldıktan sonra kullanıcı bazı durumlarda kendi inisiyatifini de kullanabilir. Büyük ya da küçük sayılarda araç filoları bulunan taşıma ve dağıtım şirketleri rota planlama yazılımlarını filo yönetim sistemleriyle bütünleştirerek araçları için optimum rotaları belirleyebilir ve daha düşük maliyetlerle taşımacılık yapabilirler. Taşıma ve dağıtım işletmeleri için en uygun rota planlama çözümleri genellikle GPS (Global Positioning System, Küresel Konumlandırma Sistemi) üzerinden izleme yeteneğine ve gelişmiş raporlama özelliklerine de sahiptirler. GPS, uydu üzerinden konum bilgisi sağlayan ve bu bilgiyi ilgili noktaya gönderen bir sistemdir. Bu sistemler sayesinde kat edilen mesafe en aza indirilebilir, plan dışı duruşlar engellenebilir ve en düşük yakıt maliyetiyle taşıma işi gerçekleştirilebilir. Günlük hayatımızda kullandığımız araç navigasyon sistemleri rota planlama yazılımlarında birtakım algoritmalardan faydalanmaktadır. Bu yazılımlar önce çeşitli algoritmalar yardımıyla gidilecek yolu bölgelere ayırmakta, sonra da bu bölümlendirmeden yola çıkarak optimum rotayı belirlemektedir (Flinsenberg, 2009). Aynı zamanda yoldaki trafik sıkışmalarını da göz önünde bulundurabilen bu sistemler aracın muhtemel varış süresini de hesaplayabilmektedir. Her firmanın geliştirdiği navigasyon sistemleri farklı algoritmalardan yararlandığı için farklı firmaların navigasyon cihazlarının bulacağı en uygun rotalar da birbirlerinden farklı olabilecektir. Atatürk Üniversitesi Açıköğretim Fakültesi 19
20 Özet Rota Planlama Bu bölümde rota planlamanın genel anlamda ne olduğu, kimler için gerekli olduğu ve rota planlamada ne tür matematiksel araçların kullanıldığı üzerinde durulmuştur. Taşımacılık sistemlerinde en temel problemlerden biri olan taşıma probleminin matematiksel anlamda tanımlaması yapılmış ve bu problemin nasıl çözülebileceği örneklerle gösterilmiştir. Taşıma probleminde amaç m tane kaynaktan n tane hedefe yapılacak olan sevkiyatları minimum taşıma maliyetiyle gerçekleştirecek şekilde her bir i ve j noktası arasında taşınacak miktarları (yani Xij leri) belirlemektir. Taşıma probleminin özel bir hâli olan atama probleminde ise işleri çalışanlara, makineleri işlere, projeleri araştırmacılara, bölgeleri satış elemanlarına atamak gerektiğinde minimum maliyetle atama işleminin gerçekleştirilmesi amaçlanır. Gezgin satıcı problemi ve en kısa yol problemleri de taşımacılık sistemlerinde sıklıkla karşılaşılan diğer problem türleridir. Her iki problem türünün önemli ayırt edici özellikleri ayrıntılı olarak açıklanmış ve ardından da örnekler verilerek bu örnek problemlerin nasıl çözülebileceği anlatılmıştır. Atatürk Üniversitesi Açıköğretim Fakültesi 20
TAŞIMACILIK SİSTEMLERİ Prof. Dr. Bülent SEZEN
 ROTA PLANLAMA İÇİNDEKİLER Giriş Rota Planlama Taşıma Problemi Atama Problemi Gezgin Satıcı Problemi En Kısa Yol Problemi Rota Planlama Yazılımları TAŞIMACILIK SİSTEMLERİ Prof. Dr. Bülent SEZEN HEDEFLER
ROTA PLANLAMA İÇİNDEKİLER Giriş Rota Planlama Taşıma Problemi Atama Problemi Gezgin Satıcı Problemi En Kısa Yol Problemi Rota Planlama Yazılımları TAŞIMACILIK SİSTEMLERİ Prof. Dr. Bülent SEZEN HEDEFLER
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ
 ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTıRMA MODELININ TANıMı Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTıRMA MODELININ TANıMı Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ
 ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTIRMA MODELİNİN TANIMI Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTIRMA MODELİNİN TANIMI Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
1 )Aşağıdakilerden hangisi intermodal yüklere hizmet veren terminallerden biridir?
 LOJİSTİK 2016 VIZE SORULARI 1 )Aşağıdakilerden hangisi intermodal yüklere hizmet veren terminallerden biridir? Genel Parça Yük Terminalleri Kuru Dökme Yük Terminalleri Özel Yük Terminalleri Sıvı Dökme
LOJİSTİK 2016 VIZE SORULARI 1 )Aşağıdakilerden hangisi intermodal yüklere hizmet veren terminallerden biridir? Genel Parça Yük Terminalleri Kuru Dökme Yük Terminalleri Özel Yük Terminalleri Sıvı Dökme
EM302 Yöneylem Araştırması 2. Dr. Özgür Kabak
 EM302 Yöneylem Araştırması 2 Dr. Özgür Kabak TP Çözümü TP problemlerinin çözümü için başlıca iki yaklaşım vardır kesme düzlemleri (cutting planes) dal sınır (branch and bound) tüm yaklaşımlar tekrarlı
EM302 Yöneylem Araştırması 2 Dr. Özgür Kabak TP Çözümü TP problemlerinin çözümü için başlıca iki yaklaşım vardır kesme düzlemleri (cutting planes) dal sınır (branch and bound) tüm yaklaşımlar tekrarlı
BÖLÜM III: Şebeke Modelleri. Şebeke Kavramları. Şebeke Kavramları. Şebeke Kavramları. Yönlü Şebeke (Directed Network) Dal / ok
 8.0.0 Şebeke Kavramları BÖLÜM III: Şebeke Modelleri Şebeke (Network) Sonlu sayıdaki düğümler kümesiyle, bunlarla bağlantılı oklar (veya dallar) kümesinin oluşturduğu yapı şeklinde tanımlanabilir ve (N,A)
8.0.0 Şebeke Kavramları BÖLÜM III: Şebeke Modelleri Şebeke (Network) Sonlu sayıdaki düğümler kümesiyle, bunlarla bağlantılı oklar (veya dallar) kümesinin oluşturduğu yapı şeklinde tanımlanabilir ve (N,A)
ATAMA (TAHSİS) MODELİ
 ATAMA (TAHSİS) MODELİ ATAMA (TAHSİS) MODELİ Doğrusal programlamada kullanılan bir başka hesaplama yöntemidir. Atama problemleri, doğrusal programlama (simpleks yöntem) veya transport probleminin çözüm
ATAMA (TAHSİS) MODELİ ATAMA (TAHSİS) MODELİ Doğrusal programlamada kullanılan bir başka hesaplama yöntemidir. Atama problemleri, doğrusal programlama (simpleks yöntem) veya transport probleminin çözüm
EM302 Yöneylem Araştırması 2. Dr. Özgür Kabak
 EM302 Yöneylem Araştırması 2 Dr. Özgür Kabak GAMS Giriş GAMS (The General Algebraic Modeling System) matematiksel proglamlama ve optimizasyon için tasarlanan yüksek seviyeli bir dildir. Giriş dosyası:
EM302 Yöneylem Araştırması 2 Dr. Özgür Kabak GAMS Giriş GAMS (The General Algebraic Modeling System) matematiksel proglamlama ve optimizasyon için tasarlanan yüksek seviyeli bir dildir. Giriş dosyası:
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Quadratic Programming Bir karesel programlama modeli aşağıdaki gibi tanımlanır. Amaç fonksiyonu: Maks.(veya Min.) z
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Quadratic Programming Bir karesel programlama modeli aşağıdaki gibi tanımlanır. Amaç fonksiyonu: Maks.(veya Min.) z
Genel Graf Üzerinde Mutlak 1-merkez
 Genel Graf Üzerinde Mutlak 1-merkez Çözüm yöntemine geçmeden önce bazı tanımlara ihtiyaç vardır. Dikkate alınan G grafındaki düğümleri 1 den n e kadar numaralandırın. Uzunluğu a(i, j)>0 olarak verilen
Genel Graf Üzerinde Mutlak 1-merkez Çözüm yöntemine geçmeden önce bazı tanımlara ihtiyaç vardır. Dikkate alınan G grafındaki düğümleri 1 den n e kadar numaralandırın. Uzunluğu a(i, j)>0 olarak verilen
Yrd.Doç.Dr. Safiye Turgay Doç.Dr. İsmail Erol Fulya Türkmen Abant Izzet Baysal Universitesi
 Lojistik Yönetim Sürecinin Analitik Modeli Ve Sektörel Uygulaması Yrd.Doç.Dr. Safiye Turgay Doç.Dr. İsmail Erol Fulya Türkmen Abant Izzet Baysal Universitesi Giriş İş dünyasında uluslar arası düzeyde rekabetin
Lojistik Yönetim Sürecinin Analitik Modeli Ve Sektörel Uygulaması Yrd.Doç.Dr. Safiye Turgay Doç.Dr. İsmail Erol Fulya Türkmen Abant Izzet Baysal Universitesi Giriş İş dünyasında uluslar arası düzeyde rekabetin
ULUSLARARASI INTERMODAL TAŞIMA AĞINDA OPTIMAL ROTA SEÇİMİ
 III. Ulusal Liman Kongresi doi: 10.18872/DEU.df.ULK.2017.005 ULUSLARARASI INTERMODAL TAŞIMA AĞINDA OPTIMAL ROTA SEÇİMİ ÖZET Melis Özdemir, Berker İnkaya, Bilge Bilgen 1 Globalleşen dünyada taşımacılık
III. Ulusal Liman Kongresi doi: 10.18872/DEU.df.ULK.2017.005 ULUSLARARASI INTERMODAL TAŞIMA AĞINDA OPTIMAL ROTA SEÇİMİ ÖZET Melis Özdemir, Berker İnkaya, Bilge Bilgen 1 Globalleşen dünyada taşımacılık
İleri Yöneylem Araştırması Uygulamaları Tam Sayılı Programlama
 İleri Yöneylem Araştırması Uygulamaları Tam Sayılı Programlama Dr. Özgür Kabak 2016-2017 Güz } Gerçek hayattaki bir çok problem } tam sayılı değişkenlerin ve } doğrusal kısıt ve amaç fonksiyonları ile
İleri Yöneylem Araştırması Uygulamaları Tam Sayılı Programlama Dr. Özgür Kabak 2016-2017 Güz } Gerçek hayattaki bir çok problem } tam sayılı değişkenlerin ve } doğrusal kısıt ve amaç fonksiyonları ile
EBEKE MODELLERİ. ebeke Yapısına Giriş. Konu 3
 EBEKE MODELLERİ Konu ebeke Yapısına Giriş Elektriksel yapıların bulunduğu şebekeler Ulaşım sistemi Ulaştırma modeli İstasyonlardan oluşan sistem - Televizy zyon şebekesi ebeke Problemi Bir şebeke problemi
EBEKE MODELLERİ Konu ebeke Yapısına Giriş Elektriksel yapıların bulunduğu şebekeler Ulaşım sistemi Ulaştırma modeli İstasyonlardan oluşan sistem - Televizy zyon şebekesi ebeke Problemi Bir şebeke problemi
ÜNİTE. MATEMATİK-1 Prof.Dr.Ahmet KÜÇÜK İÇİNDEKİLER HEDEFLER TÜREV VE TÜREV ALMA KURALLARI. Türev Türev Alma Kuralları
 HEDEFLER İÇİNDEKİLER TÜREV VE TÜREV ALMA KURALLARI Türev Türev Alma Kuralları MATEMATİK-1 Prof.Dr.Ahmet KÜÇÜK Bu üniteyi çalıştıktan sonra Burada türevin tanımı verilecek, Geometride bir eğrinin bir noktadaki
HEDEFLER İÇİNDEKİLER TÜREV VE TÜREV ALMA KURALLARI Türev Türev Alma Kuralları MATEMATİK-1 Prof.Dr.Ahmet KÜÇÜK Bu üniteyi çalıştıktan sonra Burada türevin tanımı verilecek, Geometride bir eğrinin bir noktadaki
4. UZUN MESAFE MAL NAKLİYE PLANLAMASI VE YÖNETİMİ
 4. UZUN MESAFE MAL NAKLİYE PLANLAMASI VE YÖNETİMİ Mal nakliyesi Mal nakliyesi, modern tedarik zincirlerinde önemli bir rol oynar. Hammaddelerin kaynaklardan tesislere, yarı mamullerin fabrikalar arasında
4. UZUN MESAFE MAL NAKLİYE PLANLAMASI VE YÖNETİMİ Mal nakliyesi Mal nakliyesi, modern tedarik zincirlerinde önemli bir rol oynar. Hammaddelerin kaynaklardan tesislere, yarı mamullerin fabrikalar arasında
YÖNEYLEM ARAŞTIRMASI - II
 YÖNEYLEM ARAŞTIRMASI - II Araş. Gör. Murat SARI 1/35 I Giriş Biri diğerini izleyen ve karşılıklı etkileri olan bir dizi kararın bütünüyle ele alındığı problemler için geliştirilen karar modelleri ve bunların
YÖNEYLEM ARAŞTIRMASI - II Araş. Gör. Murat SARI 1/35 I Giriş Biri diğerini izleyen ve karşılıklı etkileri olan bir dizi kararın bütünüyle ele alındığı problemler için geliştirilen karar modelleri ve bunların
Adana Toplu Taşıma Eğilimleri
 Adana Toplu Taşıma Eğilimleri Doç. Dr. Mustafa Gök Elektrik Elektronik Mühendisliği Bilgisayar Bilimleri Ana Bilim Dalı Başkanı 13.06.2014 Doç. Dr. Mustafa Gök (Ç. Ü.) Adana Toplu Taşıma Eğilimleri 13.06.2014
Adana Toplu Taşıma Eğilimleri Doç. Dr. Mustafa Gök Elektrik Elektronik Mühendisliği Bilgisayar Bilimleri Ana Bilim Dalı Başkanı 13.06.2014 Doç. Dr. Mustafa Gök (Ç. Ü.) Adana Toplu Taşıma Eğilimleri 13.06.2014
Stok Kontrol. Önceki Derslerin Hatırlatması. Örnek (Ekonomik Sipariş Miktarı Modeli)(2) Örnek (Ekonomik Sipariş Miktarı Modeli)(1)
 Stok Kontrol Önceki Derslerin Hatırlatması Ders 7 Farklı Bir Stok Yönetimi Durumu Uzun Dönemli Stok Problemi Talep hızı sabit, biliniyor Birim ürün maliyeti sabit Sipariş maliyeti sabit Tedarik Süresi
Stok Kontrol Önceki Derslerin Hatırlatması Ders 7 Farklı Bir Stok Yönetimi Durumu Uzun Dönemli Stok Problemi Talep hızı sabit, biliniyor Birim ürün maliyeti sabit Sipariş maliyeti sabit Tedarik Süresi
Tedarik Zincirlerinde Yer Seçimi Kararları (Location Decisions)
 Tedarik Zincirlerinde Yer Seçimi Kararları (Location Decisions) Öğr. Üyesi: Öznur Özdemir Kaynak: Waters, D. (2009). Supply Chain Management: An Introduction to Logistics, Palgrave Macmillan, New York
Tedarik Zincirlerinde Yer Seçimi Kararları (Location Decisions) Öğr. Üyesi: Öznur Özdemir Kaynak: Waters, D. (2009). Supply Chain Management: An Introduction to Logistics, Palgrave Macmillan, New York
Ulaştırma Problemleri
 Ulaştırma Problemleri Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir. Bu modelde, malların kaynaklardan (fabrika gibi )hedeflere (depo gibi) taşınmasıyla ilgilenir. Buradaki amaç
Ulaştırma Problemleri Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir. Bu modelde, malların kaynaklardan (fabrika gibi )hedeflere (depo gibi) taşınmasıyla ilgilenir. Buradaki amaç
Lojistik Bilgi Sistemleri ÖĞR. GÖR. MUSTAFA ÇETİNKAYA
 Lojistik Bilgi Sistemleri ÖĞR. GÖR. MUSTAFA ÇETİNKAYA LBS u Lojistik Bilgi Sistemleri tedarik zinciri üzerinde yer alan şirketlerin her birinin kendi planlama veya operasyonel ihtiyaçlarını karşılayan,
Lojistik Bilgi Sistemleri ÖĞR. GÖR. MUSTAFA ÇETİNKAYA LBS u Lojistik Bilgi Sistemleri tedarik zinciri üzerinde yer alan şirketlerin her birinin kendi planlama veya operasyonel ihtiyaçlarını karşılayan,
YÖNEYLEM ARAŞTIRMASI - I
 YÖNEYLEM ARAŞTIRMASI - I 1/19 İçerik Yöneylem Araştırmasının Dalları Kullanım Alanları Yöneylem Araştırmasında Bazı Yöntemler Doğrusal (Lineer) Programlama, Oyun Teorisi, Dinamik Programlama, Tam Sayılı
YÖNEYLEM ARAŞTIRMASI - I 1/19 İçerik Yöneylem Araştırmasının Dalları Kullanım Alanları Yöneylem Araştırmasında Bazı Yöntemler Doğrusal (Lineer) Programlama, Oyun Teorisi, Dinamik Programlama, Tam Sayılı
GEZGİN SATICI PROBLEMİ. Feasible Çözümler? Optimal Çözüm?
 7..07 ÖRNEK : Bir ilaç satış temsilcisi no lu şehirde yaşamaktadır ve mevcut programında ziyaret etmesi gereken farklı şehirde yaşayan müşterileri mevcuttur. Şehirler arasındaki mesafeler tabloda verilmiştir.
7..07 ÖRNEK : Bir ilaç satış temsilcisi no lu şehirde yaşamaktadır ve mevcut programında ziyaret etmesi gereken farklı şehirde yaşayan müşterileri mevcuttur. Şehirler arasındaki mesafeler tabloda verilmiştir.
ÜNİTE. MATEMATİK-1 Yrd.Doç.Dr.Ömer TARAKÇI İÇİNDEKİLER HEDEFLER DOĞRULAR VE PARABOLLER
 HEDEFLER İÇİNDEKİLER DOĞRULAR VE PARABOLLER Birinci Dereceden Polinom Fonksiyonlar ve Doğru Doğru Denklemlerinin Bulunması İkinci Dereceden Polinom Fonksiyonlar ve Parabol MATEMATİK-1 Yrd.Doç.Dr.Ömer TARAKÇI
HEDEFLER İÇİNDEKİLER DOĞRULAR VE PARABOLLER Birinci Dereceden Polinom Fonksiyonlar ve Doğru Doğru Denklemlerinin Bulunması İkinci Dereceden Polinom Fonksiyonlar ve Parabol MATEMATİK-1 Yrd.Doç.Dr.Ömer TARAKÇI
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Hessien Matris-Quadratik Form Mutlak ve Bölgesel Maksimum-Minimum Noktalar Giriş Kısıtlı ve kısıtsız fonksiyonlar için
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Hessien Matris-Quadratik Form Mutlak ve Bölgesel Maksimum-Minimum Noktalar Giriş Kısıtlı ve kısıtsız fonksiyonlar için
Stok Kontrol. Önceki Derslerin Hatırlatması. Örnek (Ekonomik Sipariş Miktarı Modeli)(1) Örnek (Ekonomik Sipariş Miktarı Modeli)(2)
 Stok Kontrol Önceki Derslerin Hatırlatması Ders 5 Farklı Bir Stok Yönetimi Durumu Uzun Dönemli Stok Problemi Talep hızı sabit oranlı, biliniyor Birim ürün maliyeti sabit Sipariş maliyeti sabit Tedarik
Stok Kontrol Önceki Derslerin Hatırlatması Ders 5 Farklı Bir Stok Yönetimi Durumu Uzun Dönemli Stok Problemi Talep hızı sabit oranlı, biliniyor Birim ürün maliyeti sabit Sipariş maliyeti sabit Tedarik
Stok Kontrol. Ders 6. Farklı Bir Stok Yönetimi Durumu. Önceki Derslerin Hatırlatması
 Stok Kontrol Ders 6 Farklı Bir Stok Yönetimi Durumu Önceki Derslerin Hatırlatması Uzun Dönemli Stok Problemi Talep hızı sabit, biliniyor Birim ürün maliyeti sabit Sipariş maliyeti sabit Tedarik Süresi
Stok Kontrol Ders 6 Farklı Bir Stok Yönetimi Durumu Önceki Derslerin Hatırlatması Uzun Dönemli Stok Problemi Talep hızı sabit, biliniyor Birim ürün maliyeti sabit Sipariş maliyeti sabit Tedarik Süresi
EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER
 EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER LAGRANGE YÖNTEMİ Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde değişkenler ve kısıtlar genel olarak şeklinde gösterilir. fonksiyonlarının
EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER LAGRANGE YÖNTEMİ Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde değişkenler ve kısıtlar genel olarak şeklinde gösterilir. fonksiyonlarının
Geçmiş ve Gelecek. Türkiye Lojistiği Geleceğe Nasıl Ulaşacak. Geleceğin Tedarik Zincirini Oluşturmak 13 Mayıs 2015
 Geçmiş ve Gelecek Türkiye Lojistiği Geleceğe Nasıl Ulaşacak Geleceğin Tedarik Zincirini Oluşturmak 13 Mayıs 2015 ATİLLA YILDIZTEKİN Lojistik YönetimDanışmanı atilla@yildiztekin.com Nasıl Bir Değişim Yaşıyoruz?
Geçmiş ve Gelecek Türkiye Lojistiği Geleceğe Nasıl Ulaşacak Geleceğin Tedarik Zincirini Oluşturmak 13 Mayıs 2015 ATİLLA YILDIZTEKİN Lojistik YönetimDanışmanı atilla@yildiztekin.com Nasıl Bir Değişim Yaşıyoruz?
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Bu bölümde eşitsizlik kısıtlarına bağlı bir doğrusal olmayan kısıta sahip problemin belirlenen stasyoner noktaları
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Bu bölümde eşitsizlik kısıtlarına bağlı bir doğrusal olmayan kısıta sahip problemin belirlenen stasyoner noktaları
MAT223 AYRIK MATEMATİK
 MAT223 AYRIK MATEMATİK Gezgin Satıcı Problemi 9. Bölüm Emrah Akyar Anadolu Üniversitesi Fen Fakültesi Matematik Bölümü, ESKİŞEHİR 2014 2015 Öğretim Yılı Gezgin Satıcı Problemi Soru n tane şehri olan bir
MAT223 AYRIK MATEMATİK Gezgin Satıcı Problemi 9. Bölüm Emrah Akyar Anadolu Üniversitesi Fen Fakültesi Matematik Bölümü, ESKİŞEHİR 2014 2015 Öğretim Yılı Gezgin Satıcı Problemi Soru n tane şehri olan bir
HESSİEN MATRİS QUADRATİK FORM MUTLAK ve BÖLGESEL MAKS-MİN NOKTALAR
 HESSİEN MATRİS QUADRATİK FORM MUTLAK ve BÖLGESEL MAKS-MİN NOKTALAR Kısıtlı ve kısıtsız fonksiyonlar için maksimum veya minimum (ekstremum) noktalarının belirlenmesinde diferansiyel hesabı kullanarak çeşitli
HESSİEN MATRİS QUADRATİK FORM MUTLAK ve BÖLGESEL MAKS-MİN NOKTALAR Kısıtlı ve kısıtsız fonksiyonlar için maksimum veya minimum (ekstremum) noktalarının belirlenmesinde diferansiyel hesabı kullanarak çeşitli
MATEMATiKSEL iktisat
 DİKKAT!... BU ÖZET 8 ÜNİTEDİR BU- RADA İLK ÜNİTE GÖSTERİLMEKTEDİR. MATEMATiKSEL iktisat KISA ÖZET KOLAY AOF Kolayaöf.com 0362 233 8723 Sayfa 2 içindekiler 1.ünite-Türev ve Kuralları..3 2.üniteTek Değişkenli
DİKKAT!... BU ÖZET 8 ÜNİTEDİR BU- RADA İLK ÜNİTE GÖSTERİLMEKTEDİR. MATEMATiKSEL iktisat KISA ÖZET KOLAY AOF Kolayaöf.com 0362 233 8723 Sayfa 2 içindekiler 1.ünite-Türev ve Kuralları..3 2.üniteTek Değişkenli
DERS BİLGİLERİ. Ders Kodu Yarıyıl T+U Saat Kredi AKTS LOJİSTİK SİSTEMLERİ PLANLAMA VE TASARIMI ESYE549 3+0 3 7
 DERS BİLGİLERİ Ders Kodu Yarıyıl T+U Saat Kredi AKTS LOJİSTİK SİSTEMLERİ PLANLAMA VE TASARIMI ESYE549 3+0 3 7 Ön Koşul Dersleri ISE veya eşdeğer bir optimizasyona giriş dersi Dili Seviye si Türü İngilizce
DERS BİLGİLERİ Ders Kodu Yarıyıl T+U Saat Kredi AKTS LOJİSTİK SİSTEMLERİ PLANLAMA VE TASARIMI ESYE549 3+0 3 7 Ön Koşul Dersleri ISE veya eşdeğer bir optimizasyona giriş dersi Dili Seviye si Türü İngilizce
ÜNİTE LOJİSTİK YÖNETİMİ. Yrd. Doç. Dr. Ufuk KULA İÇİNDEKİLER HEDEFLER ULAŞIM FAALİYETLERİNİN OPTİMİZASYONU
 HEDEFLER İÇİDEKİLER ULAŞIM FAALİYETLERİİ OPTİMİZASYOU Giriş Matematiksel Modelleme Örneği Ulaşım Optimizasyonu Modelleri En Kısa Yol Problemi Gezgin Satıcı Problemi Araç Rotalama Problemi LOJİSTİK YÖETİMİ
HEDEFLER İÇİDEKİLER ULAŞIM FAALİYETLERİİ OPTİMİZASYOU Giriş Matematiksel Modelleme Örneği Ulaşım Optimizasyonu Modelleri En Kısa Yol Problemi Gezgin Satıcı Problemi Araç Rotalama Problemi LOJİSTİK YÖETİMİ
ENM 316 BENZETİM ÖDEV SETİ
 ENM 16 BENZETİM ÖDEV SETİ Ödev 1. Bir depo ve N adet müşteriden oluşan bir taşımacılık sisteminde araç depodan başlayıp bütün müşterileri teker teker ziyaret ederek depoya geri dönmektedir. Sistemdeki
ENM 16 BENZETİM ÖDEV SETİ Ödev 1. Bir depo ve N adet müşteriden oluşan bir taşımacılık sisteminde araç depodan başlayıp bütün müşterileri teker teker ziyaret ederek depoya geri dönmektedir. Sistemdeki
DOĞRUSAL PROGRAMLAMANIN ÖZEL TÜRLERİ
 DOĞRUSAL PROGRAMLAMANIN ÖZEL TÜRLERİ TRANSPORTASYON (TAŞIMA, ULAŞTIRMA) TRANSİT TAŞIMA (TRANSSHIPMENT) ATAMA (TAHSİS) TRANSPORTASYON (TAŞIMA) (ULAŞTIRMA) TRANSPORTASYON Malların birden fazla üretim (kaynak,
DOĞRUSAL PROGRAMLAMANIN ÖZEL TÜRLERİ TRANSPORTASYON (TAŞIMA, ULAŞTIRMA) TRANSİT TAŞIMA (TRANSSHIPMENT) ATAMA (TAHSİS) TRANSPORTASYON (TAŞIMA) (ULAŞTIRMA) TRANSPORTASYON Malların birden fazla üretim (kaynak,
LOS Energy. Akaryakıt / Gaz Dağıtım Çözümü
 LOS Energy Akaryakıt / Gaz Dağıtım Çözümü Exepto Bilgi Teknolojileri A.Ş. 2003 Yılında kuruldu. Alışan Group Şirketi ISO 9001 Certified Microsoft Çözüm Ortağı Custom Solutions Competency Data Management
LOS Energy Akaryakıt / Gaz Dağıtım Çözümü Exepto Bilgi Teknolojileri A.Ş. 2003 Yılında kuruldu. Alışan Group Şirketi ISO 9001 Certified Microsoft Çözüm Ortağı Custom Solutions Competency Data Management
Tedarik Zinciri Yönetimi
 Tedarik Zinciri Yönetimi -Dağıtım Planlaması- Yrd. Doç. Dr. Mert TOPOYAN Dağıtım Tedarik zinciri içerisindeki ürün akıșları incelendiğinde üç temel akıș görülmektedir: Tedarik edilen girdilerin akıșı İmalat
Tedarik Zinciri Yönetimi -Dağıtım Planlaması- Yrd. Doç. Dr. Mert TOPOYAN Dağıtım Tedarik zinciri içerisindeki ürün akıșları incelendiğinde üç temel akıș görülmektedir: Tedarik edilen girdilerin akıșı İmalat
ARAÇ ROTALAMA SİSTEMLERİ VE TASARRUF ALGORİTMASI UYGULAMASI
 İstanbul Ticaret Üniversitesi..Fen Bilimleri Dergisi Yıl: 11 Sayı: 21 Bahar 2012 s.41-51 ARAÇ ROTALAMA SİSTEMLERİ VE TASARRUF ALGORİTMASI UYGULAMASI Burak KOSİF*, İsmail EKMEKÇİ** Geliş: 18.06.2012 Kabul:
İstanbul Ticaret Üniversitesi..Fen Bilimleri Dergisi Yıl: 11 Sayı: 21 Bahar 2012 s.41-51 ARAÇ ROTALAMA SİSTEMLERİ VE TASARRUF ALGORİTMASI UYGULAMASI Burak KOSİF*, İsmail EKMEKÇİ** Geliş: 18.06.2012 Kabul:
Hasan C. BEYHAN Başarso' - İş Geliş/rme ve Sa3ş Sorumlusu
 Hasan C. BEYHAN Başarso' - İş Geliş/rme ve Sa3ş Sorumlusu Servis Güzergah Op/mizasyonu 1/20 Rotaban - Servis Güzergah Op/mizasyonu Nedir? Hangi Sorunları Çözer? Nasıl Çalışır? Faydaları? Rotaban Kullanıcıları
Hasan C. BEYHAN Başarso' - İş Geliş/rme ve Sa3ş Sorumlusu Servis Güzergah Op/mizasyonu 1/20 Rotaban - Servis Güzergah Op/mizasyonu Nedir? Hangi Sorunları Çözer? Nasıl Çalışır? Faydaları? Rotaban Kullanıcıları
Montaj Hatti Tasarımı ve Analizi - 8
 Balıkesir Üniversitesi, Endüstri Mühendisliği Bölümü 2017-2018 Bahar Yarıyılı Montaj Hatti Tasarımı ve Analizi - 8 Yrd. Doc. Dr. Ibrahim Kucukkoc http://ikucukkoc.baun.edu.tr Tek Modelli Düz MHD Problemlerinin
Balıkesir Üniversitesi, Endüstri Mühendisliği Bölümü 2017-2018 Bahar Yarıyılı Montaj Hatti Tasarımı ve Analizi - 8 Yrd. Doc. Dr. Ibrahim Kucukkoc http://ikucukkoc.baun.edu.tr Tek Modelli Düz MHD Problemlerinin
OYUN TEORİSİ. Özlem AYDIN. Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü
 OYUN TEORİSİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü TANIM ''Oyun Teorisi'', iki yada daha fazla rakibi belirli kurallar altında birleştirerek karşılıklı olarak çelişen olasılıklar
OYUN TEORİSİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü TANIM ''Oyun Teorisi'', iki yada daha fazla rakibi belirli kurallar altında birleştirerek karşılıklı olarak çelişen olasılıklar
Üretim Sistemleri (IE 509) Ders Detayları
 Üretim Sistemleri (IE 509) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Üretim Sistemleri IE 509 Seçmeli 3 0 0 3 7.5 Ön Koşul Ders(ler)i Dersin Dili Dersin
Üretim Sistemleri (IE 509) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Üretim Sistemleri IE 509 Seçmeli 3 0 0 3 7.5 Ön Koşul Ders(ler)i Dersin Dili Dersin
Lojistik (AVM206) Ders Detayları
 Lojistik (AVM206) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Lojistik AVM206 Güz 3 0 0 3 4 Ön Koşul Ders(ler)i Dersin Dili Dersin Türü Dersin Seviyesi
Lojistik (AVM206) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Lojistik AVM206 Güz 3 0 0 3 4 Ön Koşul Ders(ler)i Dersin Dili Dersin Türü Dersin Seviyesi
Akıllı Bilet Online İşlem Merkezi Uygulaması
 Akıllı Bilet Online İşlem Merkezi Uygulaması www.akillibiletim.com Akıllı Bilet Online İşlem Merkezi uygulamasının tasarım ve geliştirme sürecinde göz önünde bulundurulan en önemli husus, uygulamanın herkes
Akıllı Bilet Online İşlem Merkezi Uygulaması www.akillibiletim.com Akıllı Bilet Online İşlem Merkezi uygulamasının tasarım ve geliştirme sürecinde göz önünde bulundurulan en önemli husus, uygulamanın herkes
YÖNEYLEM ARAŞTIRMALARI 1
 YÖNEYLEM ARAŞTIRMALARI 1 1.HAFTA Amacı:Karar vericiler işletmelerde sahip oldukları kaynakları; insan gücü makine ve techizat sermaye kullanarak belirli kararlar almak ister. Örneğin; en iyi üretim miktarı
YÖNEYLEM ARAŞTIRMALARI 1 1.HAFTA Amacı:Karar vericiler işletmelerde sahip oldukları kaynakları; insan gücü makine ve techizat sermaye kullanarak belirli kararlar almak ister. Örneğin; en iyi üretim miktarı
BİRİNCİ BÖLÜM: TEDARİK ZİNCİRİ YÖNETİMİNE GİRİŞ
 İÇİNDEKİLER Önsöz... v İçindekiler... vii BİRİNCİ BÖLÜM: TEDARİK ZİNCİRİ YÖNETİMİNE GİRİŞ 1.1 Tedarik Zincirinin Temel Fonksiyonları... 8 1.1.1 Üretim... 8 1.1.2 Envanter Yönetimi... 16 1.1.3 Taşıma ve
İÇİNDEKİLER Önsöz... v İçindekiler... vii BİRİNCİ BÖLÜM: TEDARİK ZİNCİRİ YÖNETİMİNE GİRİŞ 1.1 Tedarik Zincirinin Temel Fonksiyonları... 8 1.1.1 Üretim... 8 1.1.2 Envanter Yönetimi... 16 1.1.3 Taşıma ve
BİR MONTAJ HATTI ÜRETİM SİSTEMİNDE OPTİMAL İŞGÜCÜ DAĞILIMININ ARENA PROCESS ANALYZER (PAN) VE OPTQUEST KULLANILARAK BELİRLENMESİ
 BİR MONTAJ HATTI ÜRETİM SİSTEMİNDE OPTİMAL İŞGÜCÜ DAĞILIMININ ARENA PROCESS ANALYZER (PAN) VE OPTQUEST KULLANILARAK BELİRLENMESİ Özgür ARMANERİ Dokuz Eylül Üniversitesi Özet Bu çalışmada, bir montaj hattı
BİR MONTAJ HATTI ÜRETİM SİSTEMİNDE OPTİMAL İŞGÜCÜ DAĞILIMININ ARENA PROCESS ANALYZER (PAN) VE OPTQUEST KULLANILARAK BELİRLENMESİ Özgür ARMANERİ Dokuz Eylül Üniversitesi Özet Bu çalışmada, bir montaj hattı
OPERASYONEL ÜSTÜNLÜK VE TÜKETİCİ YAKINLAŞMASINI SAĞLAMAK ve KURUMSAL UYGULAMALAR
 OPERASYONEL ÜSTÜNLÜK VE TÜKETİCİ YAKINLAŞMASINI SAĞLAMAK ve KURUMSAL UYGULAMALAR Dünya üzerinde işletmeler giderek artan şekilde daha fazla hem içerideki şirketlere hem de diğer şirketlerle bağlanmaktadır.
OPERASYONEL ÜSTÜNLÜK VE TÜKETİCİ YAKINLAŞMASINI SAĞLAMAK ve KURUMSAL UYGULAMALAR Dünya üzerinde işletmeler giderek artan şekilde daha fazla hem içerideki şirketlere hem de diğer şirketlerle bağlanmaktadır.
BÖLÜMLER. Birinci Bölüm TEDARİK ZİNCİRİ YÖNETİMİNE GİRİŞ. İkinci Bölüm DIŞ KAYNAK KULLANIMI. Üçüncü Bölüm ENVANTER YÖNETİMİ
 TEDARİK ZİNCİRİ YÖNETİMİ ARKA PLANI, GELİŞİMİ, GÜNCEL UYGULAMALARI BÖLÜMLER Birinci Bölüm TEDARİK ZİNCİRİ YÖNETİMİNE GİRİŞ İkinci Bölüm DIŞ KAYNAK KULLANIMI Üçüncü Bölüm ENVANTER YÖNETİMİ Dördüncü Bölüm
TEDARİK ZİNCİRİ YÖNETİMİ ARKA PLANI, GELİŞİMİ, GÜNCEL UYGULAMALARI BÖLÜMLER Birinci Bölüm TEDARİK ZİNCİRİ YÖNETİMİNE GİRİŞ İkinci Bölüm DIŞ KAYNAK KULLANIMI Üçüncü Bölüm ENVANTER YÖNETİMİ Dördüncü Bölüm
EM302 Yöneylem Araştırması 2 Doğrusal Olmayan Programlamaya Giriş. Dr. Özgür Kabak
 EM302 Yöneylem Araştırması 2 Doğrusal Olmayan Programlamaya Giriş Dr. Özgür Kabak Doğrusal Olmayan Programlama Eğer bir Matematiksel Programlama modelinin amaç fonksiyonu ve/veya kısıtları doğrusal değil
EM302 Yöneylem Araştırması 2 Doğrusal Olmayan Programlamaya Giriş Dr. Özgür Kabak Doğrusal Olmayan Programlama Eğer bir Matematiksel Programlama modelinin amaç fonksiyonu ve/veya kısıtları doğrusal değil
Bekleme Hattı Teorisi
 Bekleme Hattı Teorisi Sürekli Parametreli Markov Zincirleri Tanım 1. * +, durum uzayı * +olan sürekli parametreli bir süreç olsun. Aşağıdaki özellik geçerli olduğunda bu sürece sürekli parametreli Markov
Bekleme Hattı Teorisi Sürekli Parametreli Markov Zincirleri Tanım 1. * +, durum uzayı * +olan sürekli parametreli bir süreç olsun. Aşağıdaki özellik geçerli olduğunda bu sürece sürekli parametreli Markov
ÜNİTE. MATEMATİK-1 Doç.Dr.Murat SUBAŞI İÇİNDEKİLER HEDEFLER TÜREV UYGULAMALARI-I
 HEDEFLER İÇİNDEKİLER TÜREV UYGULAMALARI-I Artan ve Azalan Fonksiyonlar Fonksiyonların Maksimum ve Minimumu Birinci Türev Testi İkinci Türev Testi Türevin Geometrik Yorumu Türevin Fiziksel Yorumu MATEMATİK-1
HEDEFLER İÇİNDEKİLER TÜREV UYGULAMALARI-I Artan ve Azalan Fonksiyonlar Fonksiyonların Maksimum ve Minimumu Birinci Türev Testi İkinci Türev Testi Türevin Geometrik Yorumu Türevin Fiziksel Yorumu MATEMATİK-1
GPS NAVIGATION SYSTEM QUICK START USER MANUAL
 GPS NAVIGATION SYSTEM QUICK START USER MANUAL TURKISH Başlarken Araç navigasyon yazılımını ilk kez kullanırken, bir başlangıç ayarı süreci otomatik olarak başlar. Aşağıdaki adımları takip edin: Program
GPS NAVIGATION SYSTEM QUICK START USER MANUAL TURKISH Başlarken Araç navigasyon yazılımını ilk kez kullanırken, bir başlangıç ayarı süreci otomatik olarak başlar. Aşağıdaki adımları takip edin: Program
Anadolu Üniversitesi Endüstri Mühendisliği Bölümü İST328 Yöneylem Araştırması 2 Dersi Bahar Dönemi. Hazırlayan: Doç. Dr.
 Anadolu Üniversitesi Endüstri Mühendisliği Bölümü İST8 Yöneylem Araştırması Dersi 00-0 Bahar Dönemi Hazırlayan: Doç. Dr. Nil ARAS AÇIKLAMA Bu sunu izleyen kaynaklardaki örnek ve bilgilerden faydalanarak
Anadolu Üniversitesi Endüstri Mühendisliği Bölümü İST8 Yöneylem Araştırması Dersi 00-0 Bahar Dönemi Hazırlayan: Doç. Dr. Nil ARAS AÇIKLAMA Bu sunu izleyen kaynaklardaki örnek ve bilgilerden faydalanarak
ÜNİTE. MATEMATİK-1 Doç.Dr.Murat SUBAŞI İÇİNDEKİLER HEDEFLER TÜREV UYGULAMALARI-II
 HEDEFLER İÇİNDEKİLER TÜREV UYGULAMALARI-II Fonksiyonların Bükeyliği Maksimum - Minimum Problemleri Belirsiz Haller MATEMATİK-1 Doç.Dr.Murat SUBAŞI Bu üniteyi çalıştıktan sonra; Fonksiyonların grafiklerinin
HEDEFLER İÇİNDEKİLER TÜREV UYGULAMALARI-II Fonksiyonların Bükeyliği Maksimum - Minimum Problemleri Belirsiz Haller MATEMATİK-1 Doç.Dr.Murat SUBAŞI Bu üniteyi çalıştıktan sonra; Fonksiyonların grafiklerinin
Afet Yardım Operasyonlarında CBS Tabanlı Acil Müdahale Sistemi
 Afet Yardım Operasyonlarında CBS Tabanlı Acil Müdahale Sistemi Erdinç Bakır 1, Dr. Onur Demir 1 & Dr. Linet Ozdamar 2 1 Bilg. Müh. Bölümü 2 Sistem ve End. Müh. Bölümü Yeditepe University, Istanbul, Turkey
Afet Yardım Operasyonlarında CBS Tabanlı Acil Müdahale Sistemi Erdinç Bakır 1, Dr. Onur Demir 1 & Dr. Linet Ozdamar 2 1 Bilg. Müh. Bölümü 2 Sistem ve End. Müh. Bölümü Yeditepe University, Istanbul, Turkey
EM302 Yöneylem Araştırması 2 Çok değişkenli DOP ların çözümü. Dr. Özgür Kabak
 EM302 Yöneylem Araştırması 2 Çok değişkenli DOP ların çözümü Dr. Özgür Kabak Doğrusal olmayan programlama Tek değişkenli DOP ların çözümü Uç noktaların analizi Altın kesit Araması Çok değişkenli DOP ların
EM302 Yöneylem Araştırması 2 Çok değişkenli DOP ların çözümü Dr. Özgür Kabak Doğrusal olmayan programlama Tek değişkenli DOP ların çözümü Uç noktaların analizi Altın kesit Araması Çok değişkenli DOP ların
Türk-Alman Üniversitesi. Ders Bilgi Formu
 Türk-Alman Üniversitesi Ders Bilgi Formu Dersin Adı Dersin Kodu Dersin Yarıyılı Yöneylem Araştırması WNG301 5 ECTS Ders Uygulama Laboratuar Kredisi (saat/hafta) (saat/hafta) (saat/hafta) 6 2 2 0 Ön Koşullar
Türk-Alman Üniversitesi Ders Bilgi Formu Dersin Adı Dersin Kodu Dersin Yarıyılı Yöneylem Araştırması WNG301 5 ECTS Ders Uygulama Laboratuar Kredisi (saat/hafta) (saat/hafta) (saat/hafta) 6 2 2 0 Ön Koşullar
SkyWay Güzergahı Kentsel Konsepti. Erzurum Şehri
 «Raylı Teknolojiler» A.Ş Belarus Cumhuriyeti, Minsk,. Dzerzhinskogo,104 B, www.sw-tech.by, info@sw-tech.by, Tel:. +375-17-3882020 SkyWay Güzergahı Kentsel Konsepti Erzurum Şehri Ön Teklif Minsk 2016 Teknik
«Raylı Teknolojiler» A.Ş Belarus Cumhuriyeti, Minsk,. Dzerzhinskogo,104 B, www.sw-tech.by, info@sw-tech.by, Tel:. +375-17-3882020 SkyWay Güzergahı Kentsel Konsepti Erzurum Şehri Ön Teklif Minsk 2016 Teknik
BÖLÜM 1 TEDARİK ZİNCİRİ
 İÇİNDEKİLER BÖLÜM 1 TEDARİK ZİNCİRİ 1.1. Niçin Tedarik Zinciri?... 1 1.2. Tedarik Zinciri ve Tedarik Zinciri Yönetimi... 3 1.3. Tedarik Zinciri Yapısı... 5 1.4. İş Modelleri... 6 Kaynaklar... 7 BÖLÜM 2
İÇİNDEKİLER BÖLÜM 1 TEDARİK ZİNCİRİ 1.1. Niçin Tedarik Zinciri?... 1 1.2. Tedarik Zinciri ve Tedarik Zinciri Yönetimi... 3 1.3. Tedarik Zinciri Yapısı... 5 1.4. İş Modelleri... 6 Kaynaklar... 7 BÖLÜM 2
ENDÜSTRİ MÜHENDİSLİĞİ BÖLÜM BAŞKANLIĞI DERS TANITIM BİLGİLERİ
 ENDÜSTRİ MÜHENDİSLİĞİ BÖLÜM BAŞKANLIĞI DERS TANITIM BİLGİLERİ Dersin Adı Kodu Sınıf/Y.Y. Ders Saati Kredi AKTS (T+U+L) YÖNEYLEM ARAŞTIRMA İÇİN ALGORİTMALAR EN-312 3/I 3+0+0 3 5 Dersin Dili : Türkçe Dersin
ENDÜSTRİ MÜHENDİSLİĞİ BÖLÜM BAŞKANLIĞI DERS TANITIM BİLGİLERİ Dersin Adı Kodu Sınıf/Y.Y. Ders Saati Kredi AKTS (T+U+L) YÖNEYLEM ARAŞTIRMA İÇİN ALGORİTMALAR EN-312 3/I 3+0+0 3 5 Dersin Dili : Türkçe Dersin
Tedarik Zinciri Yönetiminde Yapay Zeka Teknikler
 Tedarik Zinciri Yönetiminde Yapay Zeka Teknikler Doç.Dr.Mehmet Hakan Satman mhsatman@istanbul.edu.tr İstanbul Üniversitesi 2014.10.22 Doç.Dr.Mehmet Hakan Satmanmhsatman@istanbul.edu.tr Tedarik Zinciri
Tedarik Zinciri Yönetiminde Yapay Zeka Teknikler Doç.Dr.Mehmet Hakan Satman mhsatman@istanbul.edu.tr İstanbul Üniversitesi 2014.10.22 Doç.Dr.Mehmet Hakan Satmanmhsatman@istanbul.edu.tr Tedarik Zinciri
EM302 Yöneylem Araştırması 2 TP Modelleme. Dr. Özgür Kabak
 EM302 Yöneylem Araştırması 2 TP Modelleme Dr. Özgür Kabak Çek Tahsilatı Ofisi Örneği Bir Amerikan şirketinin Birleşik Devletlerdeki müşterilerinin ödemelerini gönderdikleri çekler ile topladığını varsayalım.
EM302 Yöneylem Araştırması 2 TP Modelleme Dr. Özgür Kabak Çek Tahsilatı Ofisi Örneği Bir Amerikan şirketinin Birleşik Devletlerdeki müşterilerinin ödemelerini gönderdikleri çekler ile topladığını varsayalım.
doğrusal programlama DOĞRUSAL PROGRAMLAMA (GENEL)
 DOĞRUSAL PROGRAMLAMA (GENEL) Belirli bir amacın gerçekleşmesini etkileyen bazı kısıtlayıcı koşulların ve bu kısıtlayıcı koşulların doğrusal eşitlik ya da eşitsizlik biçiminde verilmesi durumunda amaca
DOĞRUSAL PROGRAMLAMA (GENEL) Belirli bir amacın gerçekleşmesini etkileyen bazı kısıtlayıcı koşulların ve bu kısıtlayıcı koşulların doğrusal eşitlik ya da eşitsizlik biçiminde verilmesi durumunda amaca
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Altın Oran (Golden Section Search) Arama Metodu Tek değişkenli bir f(x) fonksiyonunu ele alalım. [Bazı x ler için f
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Altın Oran (Golden Section Search) Arama Metodu Tek değişkenli bir f(x) fonksiyonunu ele alalım. [Bazı x ler için f
Çok değişkenli fonksiyonlar. Maksimum- Minimum
 66 Bölüm 6 Ders 06 Çok değişkenli fonksiyonlar. Maksimum- Minimum 6.1 Çözümler:Alıştırmalar 06 Prof.Dr.Haydar Eş Prof.Dr.Timur Karaçay Ön Bilgi: z = f (x, y) fonksiyonu 3-boyutlu uzayda bir yüzeyin denklemidir.
66 Bölüm 6 Ders 06 Çok değişkenli fonksiyonlar. Maksimum- Minimum 6.1 Çözümler:Alıştırmalar 06 Prof.Dr.Haydar Eş Prof.Dr.Timur Karaçay Ön Bilgi: z = f (x, y) fonksiyonu 3-boyutlu uzayda bir yüzeyin denklemidir.
BULANIK MANTIK VE SİSTEMLERİ 2014 2015 BAHAR DÖNEMİ ÖDEV 1. Müslüm ÖZTÜRK 148164001004 Bilişim Teknolojileri Mühendisliği ABD Doktora Programı
 BULANIK MANTIK VE SİSTEMLERİ 2014 2015 BAHAR DÖNEMİ ÖDEV 1 Müslüm ÖZTÜRK 148164001004 Bilişim Teknolojileri Mühendisliği ABD Doktora Programı Mart 2015 0 SORU 1) Bulanık Küme nedir? Bulanık Kümenin (fuzzy
BULANIK MANTIK VE SİSTEMLERİ 2014 2015 BAHAR DÖNEMİ ÖDEV 1 Müslüm ÖZTÜRK 148164001004 Bilişim Teknolojileri Mühendisliği ABD Doktora Programı Mart 2015 0 SORU 1) Bulanık Küme nedir? Bulanık Kümenin (fuzzy
Yöneylem Araştırması III
 Yöneylem Araştırması III Doç. Dr. Hakan ÇERÇİOĞLU cercioglu@gazi.edu.tr Yöneylem Araştırması III 1 BÖLÜM I: Hedef Programlama HEDEF PROGRAMLAMAYA GİRİŞ ÖNCELİKSİZ HEDEF PROGRAMLAMA ÖNCELİKLİ HEDEF PROGRAMLAMA
Yöneylem Araştırması III Doç. Dr. Hakan ÇERÇİOĞLU cercioglu@gazi.edu.tr Yöneylem Araştırması III 1 BÖLÜM I: Hedef Programlama HEDEF PROGRAMLAMAYA GİRİŞ ÖNCELİKSİZ HEDEF PROGRAMLAMA ÖNCELİKLİ HEDEF PROGRAMLAMA
Lojistik ve Bilgi Sistemleri ÖĞR. GÖR. MUSTAFA ÇETİNKAYA
 Lojistik ve Bilgi Sistemleri ÖĞR. GÖR. MUSTAFA ÇETİNKAYA Fiziksel Dağıtımdan Tedarik Zincirine u Mallar, Hizmetler ve Bilgilerin Akışı u Tedarik Zincirinde Bilgi: Bilinirlik ve Görünürlük u Satış Noktası
Lojistik ve Bilgi Sistemleri ÖĞR. GÖR. MUSTAFA ÇETİNKAYA Fiziksel Dağıtımdan Tedarik Zincirine u Mallar, Hizmetler ve Bilgilerin Akışı u Tedarik Zincirinde Bilgi: Bilinirlik ve Görünürlük u Satış Noktası
BÖLÜM I: Hedef Programlama. Prof.Dr. Bilal TOKLU. HEDEF PROGRAMLAMAYA GİRİŞ HEDEF PROGRAMLAMA MODELLERİNİN ÇÖZÜMÜ
 Yöneylem Araştırması III Prof.Dr. Bilal TOKLU btoklu@gazi.edu.tr Yöneylem Araştırması III BÖLÜM I: Hedef Programlama HEDEF PROGRAMLAMAYA GİRİŞ ÖNCELİKSİZ HEDEF PROGRAMLAMA ÖNCELİKLİ HEDEF PROGRAMLAMA HEDEF
Yöneylem Araştırması III Prof.Dr. Bilal TOKLU btoklu@gazi.edu.tr Yöneylem Araştırması III BÖLÜM I: Hedef Programlama HEDEF PROGRAMLAMAYA GİRİŞ ÖNCELİKSİZ HEDEF PROGRAMLAMA ÖNCELİKLİ HEDEF PROGRAMLAMA HEDEF
MAT223 AYRIK MATEMATİK
 MAT223 AYRIK MATEMATİK Gezgin Satıcı Problemi 9. Bölüm Emrah Akyar Anadolu Üniversitesi Fen Fakültesi Matematik Bölümü, ESKİŞEHİR 2014 2015 Öğretim Yılı Gezgin Satıcı Problemi Soru n tane şehri olan bir
MAT223 AYRIK MATEMATİK Gezgin Satıcı Problemi 9. Bölüm Emrah Akyar Anadolu Üniversitesi Fen Fakültesi Matematik Bölümü, ESKİŞEHİR 2014 2015 Öğretim Yılı Gezgin Satıcı Problemi Soru n tane şehri olan bir
Okut. Yüksel YURTAY. İletişim : (264) Sayısal Analiz. Giriş.
 Okut. Yüksel YURTAY İletişim : Sayısal Analiz yyurtay@sakarya.edu.tr www.cs.sakarya.edu.tr/yyurtay (264) 295 58 99 Giriş 1 Amaç : Mühendislik problemlerinin bilgisayar ortamında çözümünü mümkün kılacak
Okut. Yüksel YURTAY İletişim : Sayısal Analiz yyurtay@sakarya.edu.tr www.cs.sakarya.edu.tr/yyurtay (264) 295 58 99 Giriş 1 Amaç : Mühendislik problemlerinin bilgisayar ortamında çözümünü mümkün kılacak
a2 b3 cij: birim başına ulaşım maliyeti xij: taşıma miktarı
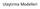 Ulaştırma Modelleri Ulaştırma modeli Ulaştırma modeli doğrusal programlama modellerinin özel bir türüdür. Modelin amacı bir işletmenin belirli kapasitedeki üretim merkezlerinden, belirli talebi olan tüketim
Ulaştırma Modelleri Ulaştırma modeli Ulaştırma modeli doğrusal programlama modellerinin özel bir türüdür. Modelin amacı bir işletmenin belirli kapasitedeki üretim merkezlerinden, belirli talebi olan tüketim
İç Servis. Dış Servis. Serbest İç Servis Mağazaya Sipariş Ver Teslimat Montaj Bilgisayar Toplama Kalite Kontrolü Teslim Et
 İç Servis Dış Servis Serbest İç Servis Mağazaya Sipariş Ver Teslimat Montaj Bilgisayar Toplama Kalite Kontrolü Teslim Et Hazırla Gönder Takip Et Teslim Al Montajını Yap Servis Girişi Müşterilerin getirdiği
İç Servis Dış Servis Serbest İç Servis Mağazaya Sipariş Ver Teslimat Montaj Bilgisayar Toplama Kalite Kontrolü Teslim Et Hazırla Gönder Takip Et Teslim Al Montajını Yap Servis Girişi Müşterilerin getirdiği
ÜNİTE. MATEMATİK-1 Prof.Dr.Abdullah MADEN İÇİNDEKİLER HEDEFLER DENKLEMLER VE EŞİTSİZLİK UYGULAMALARI
 HEDEFLER İÇİNDEKİLER DENKLEMLER VE EŞİTSİZLİK UYGULAMALARI Denklem Uygulamaları Sayı Problemleri Kar-Zarar ve Yüzde Hesapları Eşitsizlik Uygulamaları Mutlak Değerli Eşitsizlikler MATEMATİK-1 Prof.Dr.Abdullah
HEDEFLER İÇİNDEKİLER DENKLEMLER VE EŞİTSİZLİK UYGULAMALARI Denklem Uygulamaları Sayı Problemleri Kar-Zarar ve Yüzde Hesapları Eşitsizlik Uygulamaları Mutlak Değerli Eşitsizlikler MATEMATİK-1 Prof.Dr.Abdullah
*İlk aşamada, bahsedilen problemin matematiksel modelinin kurulması gerekmektedir. İlgili modelin açık ve kapalı formunu birlikte veriniz.
 Yöneylem Araştırması Proje Ödevi Teslim Tarihi: 04.12.2017 *İlk aşamada, bahsedilen problemin matematiksel modelinin kurulması gerekmektedir. İlgili modelin açık ve kapalı formunu birlikte veriniz. Filo
Yöneylem Araştırması Proje Ödevi Teslim Tarihi: 04.12.2017 *İlk aşamada, bahsedilen problemin matematiksel modelinin kurulması gerekmektedir. İlgili modelin açık ve kapalı formunu birlikte veriniz. Filo
Temelleri. Doç.Dr.Ali Argun Karacabey
 Doğrusal Programlamanın Temelleri Doç.Dr.Ali Argun Karacabey Doğrusal Programlama Nedir? Bir Doğrusal Programlama Modeli doğrusal kısıtlar altında bir doğrusal ğ fonksiyonun değerini ğ maksimize yada minimize
Doğrusal Programlamanın Temelleri Doç.Dr.Ali Argun Karacabey Doğrusal Programlama Nedir? Bir Doğrusal Programlama Modeli doğrusal kısıtlar altında bir doğrusal ğ fonksiyonun değerini ğ maksimize yada minimize
NAVİGASYON KULLANIM KILAVUZU.
 NAVİGASYON KULLANIM KILAVUZU www.fiatnavigation.com www.daiichi.com.tr Başlarken Araç navigasyon yazılımını ilk kez kullanırken, bir başlangıç ayarı süreci otomatik olarak başlar. Aşağıdaki adımları takip
NAVİGASYON KULLANIM KILAVUZU www.fiatnavigation.com www.daiichi.com.tr Başlarken Araç navigasyon yazılımını ilk kez kullanırken, bir başlangıç ayarı süreci otomatik olarak başlar. Aşağıdaki adımları takip
ÜRETİM SİSTEMLERİ ve ÖZELLİKLERİ
 ÜRETİM SİSTEMLERİ ve ÖZELLİKLERİ Üretim sistemleri hammaddelerin bitmiş ürüne dönüştürüldükleri sistemlerdir. Bu sistemler için oluşturulacak simülasyon modelleri tamamen üretim sisteminin tipine ve verilecek
ÜRETİM SİSTEMLERİ ve ÖZELLİKLERİ Üretim sistemleri hammaddelerin bitmiş ürüne dönüştürüldükleri sistemlerdir. Bu sistemler için oluşturulacak simülasyon modelleri tamamen üretim sisteminin tipine ve verilecek
Çevrimiçi Yardım Kılavuzu - SSS V1.2
 Çevrimiçi Yardım Kılavuzu - SSS V1.2 S: Haritayı kullanarak nasıl uçuş bulabilirim? Bir arama başlatmak için harita üzerinde bir noktaya Ardından uçuş bilgilerini görüntülemek için ekrandaki menüden tercih
Çevrimiçi Yardım Kılavuzu - SSS V1.2 S: Haritayı kullanarak nasıl uçuş bulabilirim? Bir arama başlatmak için harita üzerinde bir noktaya Ardından uçuş bilgilerini görüntülemek için ekrandaki menüden tercih
3.2. DP Modellerinin Simpleks Yöntem ile Çözümü Primal Simpleks Yöntem
 3.2. DP Modellerinin Simpleks Yöntem ile Çözümü 3.2.1. Primal Simpleks Yöntem Grafik çözüm yönteminde gördüğümüz gibi optimal çözüm noktası, her zaman uygun çözüm alanının bir köşe noktası ya da uç noktası
3.2. DP Modellerinin Simpleks Yöntem ile Çözümü 3.2.1. Primal Simpleks Yöntem Grafik çözüm yönteminde gördüğümüz gibi optimal çözüm noktası, her zaman uygun çözüm alanının bir köşe noktası ya da uç noktası
1. Akıllı Ulaşım Menüsü
 1. Akıllı Ulaşım Menüsü 1.1. Operasyon Takip Araç sefer durumlarıyla ilgili bilgilere ulaşmak ve haritada görüntülemek için kullanılan bölümdür. İstenilen aracın sefer bilgilerine ulaşmak ve incelemek
1. Akıllı Ulaşım Menüsü 1.1. Operasyon Takip Araç sefer durumlarıyla ilgili bilgilere ulaşmak ve haritada görüntülemek için kullanılan bölümdür. İstenilen aracın sefer bilgilerine ulaşmak ve incelemek
Her bir polis devriyesi ancak bir çağrıyı cevaplayabilir. Bir çağrıya en fazla bir devriye atanabilir.
 7. Atama Modelleri: Atama modelleri belli işlerin veya görevlerin belli kişi veya kurumlara atanması ile alakalıdır. Doğrusal programlama modellerinin bir türüdür ve yapı itibariyle ulaştırma modellerine
7. Atama Modelleri: Atama modelleri belli işlerin veya görevlerin belli kişi veya kurumlara atanması ile alakalıdır. Doğrusal programlama modellerinin bir türüdür ve yapı itibariyle ulaştırma modellerine
SÜREKLİ RASSAL DEĞİŞKENLER
 SÜREKLİ RASSAL DEĞİŞKENLER Sürekli Rassal Değişkenler Sürekli Rassal Değişken: Değerleriölçümyadatartımla elde edilen, bir başka anlatımla sayımla elde edilemeyen, değişkene sürekli rassal değişken denir.
SÜREKLİ RASSAL DEĞİŞKENLER Sürekli Rassal Değişkenler Sürekli Rassal Değişken: Değerleriölçümyadatartımla elde edilen, bir başka anlatımla sayımla elde edilemeyen, değişkene sürekli rassal değişken denir.
Araç Takip Sistemi. Araç Takip Sistemi kullandığınızda;
 1 Araç Takip Sistemi kullandığınızda; Araç ve sürücü analizi yaparak yakıt tüketimini kontrol altına alabilir ve ideal tüketim seviyesine çekebilirsiniz. Araç Takip Sistemi Araçlarınızın konumunu harita
1 Araç Takip Sistemi kullandığınızda; Araç ve sürücü analizi yaparak yakıt tüketimini kontrol altına alabilir ve ideal tüketim seviyesine çekebilirsiniz. Araç Takip Sistemi Araçlarınızın konumunu harita
ÜNİTE. MATEMATİK-1 Prof.Dr.Abdullah KOPUZLU İÇİNDEKİLER HEDEFLER LOGARİTMİK VE ÜSTEL FONKSİYONLARIN İKTİSADİ UYGULAMALARI
 HEDEFLER İÇİNDEKİLER LOGARİTMİK VE ÜSTEL FONKSİYONLARIN İKTİSADİ UYGULAMALARI Logaritmik ve Üstel Fonksiyonların İktisadi Uygulamaları Bileşik Faiz Problemleri Nüfus Problemleri MATEMATİK-1 ProfDrAbdullah
HEDEFLER İÇİNDEKİLER LOGARİTMİK VE ÜSTEL FONKSİYONLARIN İKTİSADİ UYGULAMALARI Logaritmik ve Üstel Fonksiyonların İktisadi Uygulamaları Bileşik Faiz Problemleri Nüfus Problemleri MATEMATİK-1 ProfDrAbdullah
TEDARİK ZİNCİRİ YÖNETİMİ
 Ömer Faruk GÖRÇÜN Kadir Has Üniversitesi Örnek Olay ve Uygulamalarla TEDARİK ZİNCİRİ YÖNETİMİ II Yayın No : 2874 İşletme-Ekonomi Dizisi : 573 1. Baskı - Ekim 2010 - İSTANBUL 2. Baskı - Mart 2013 - İSTANBUL
Ömer Faruk GÖRÇÜN Kadir Has Üniversitesi Örnek Olay ve Uygulamalarla TEDARİK ZİNCİRİ YÖNETİMİ II Yayın No : 2874 İşletme-Ekonomi Dizisi : 573 1. Baskı - Ekim 2010 - İSTANBUL 2. Baskı - Mart 2013 - İSTANBUL
Eme Sistem simülasyonu. Giriş. Simulasyonun Kullanım Alanları (Devam) Simulasyonun Kullanım Alanları. Sistem Simülasyonuna Giriş
 Eme 3105 Giriş Sistem simülasyonu Gerçek Dünya Sureci Sistemin davranışıyla ilişkili varsayımlar seti Modelleme & Analiz Sistem Simülasyonuna Giriş Ders 1 Simülasyon, gerçek bir dünya sureci yada sistemindeki
Eme 3105 Giriş Sistem simülasyonu Gerçek Dünya Sureci Sistemin davranışıyla ilişkili varsayımlar seti Modelleme & Analiz Sistem Simülasyonuna Giriş Ders 1 Simülasyon, gerçek bir dünya sureci yada sistemindeki
Yöneylem Araştırması II (IE 323) Ders Detayları
 Yöneylem Araştırması II (IE 323) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Yöneylem Araştırması II IE 323 Güz 3 2 0 4 5.5 Ön Koşul Ders(ler)i IE 222
Yöneylem Araştırması II (IE 323) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Yöneylem Araştırması II IE 323 Güz 3 2 0 4 5.5 Ön Koşul Ders(ler)i IE 222
Faaliyet Faaliyet zamanı dağılımı A U(5, 8) B U(6, 15) U(10,20) U(4,20) U(12,25) U(15,30)
 ENM 316 BENZETİM ÖDEV SETİ Ödev 1. Bir projede A, B, C, D, E ve F olmak üzere 6 faaliyet vardır. Projenin tamamlanması için bu faaliyetlerin sırası ile yapılması gerekmektedir. Her faaliyetin tamamlanması
ENM 316 BENZETİM ÖDEV SETİ Ödev 1. Bir projede A, B, C, D, E ve F olmak üzere 6 faaliyet vardır. Projenin tamamlanması için bu faaliyetlerin sırası ile yapılması gerekmektedir. Her faaliyetin tamamlanması
KONU 4: DOĞRUSAL PROGRAMLAMA MODELİ İÇİN ÇÖZÜM YÖNTEMLERİ I
 KONU 4: DOĞRUSAL PROGRAMLAMA MODELİ İÇİN ÇÖZÜM YÖNTEMLERİ I 4.1. Dışbükeylik ve Uç Nokta Bir d.p.p. de model kısıtlarını aynı anda sağlayan X X X karar değişkenleri... n vektörüne çözüm denir. Eğer bu
KONU 4: DOĞRUSAL PROGRAMLAMA MODELİ İÇİN ÇÖZÜM YÖNTEMLERİ I 4.1. Dışbükeylik ve Uç Nokta Bir d.p.p. de model kısıtlarını aynı anda sağlayan X X X karar değişkenleri... n vektörüne çözüm denir. Eğer bu
Gezgin Satıcı Probleminin İkili Kodlanmış Genetik Algoritmalarla Çözümünde Yeni Bir Yaklaşım. Mehmet Ali Aytekin Tahir Emre Kalaycı
 Gezgin Satıcı Probleminin İkili Kodlanmış Genetik Algoritmalarla Çözümünde Yeni Bir Yaklaşım Mehmet Ali Aytekin Tahir Emre Kalaycı Gündem Gezgin Satıcı Problemi GSP'yi Çözen Algoritmalar Genetik Algoritmalar
Gezgin Satıcı Probleminin İkili Kodlanmış Genetik Algoritmalarla Çözümünde Yeni Bir Yaklaşım Mehmet Ali Aytekin Tahir Emre Kalaycı Gündem Gezgin Satıcı Problemi GSP'yi Çözen Algoritmalar Genetik Algoritmalar
Tablo (2): Atıştırma Sayısı ve Günlük Sınav Sayısı Atıştırma Sınav Sayısı (X) 0 0.07 0.09 0.06 0.01
 Ortak Varyans ve İstatistiksel Bağımsızlık Bir rassal değişken çifti istatistiksel olarak bağımsız ise aralarındaki ortak varyansın değeri 0 dır. Ancak ortak varyans değerinin 0 olması, iki rassal değişkenin
Ortak Varyans ve İstatistiksel Bağımsızlık Bir rassal değişken çifti istatistiksel olarak bağımsız ise aralarındaki ortak varyansın değeri 0 dır. Ancak ortak varyans değerinin 0 olması, iki rassal değişkenin
EME 3105 Giriş SISTEM SIMÜLASYONU Sistem Simülasyonuna Giriş Simülasyon Ders 1 Simülasyon, Yrd.Doç.Dr.Beyazıt Ocaktan
 EME 3105 Giriş SISTEM SIMÜLASYONU Sistem Simülasyonuna Giriş Gerçek Dünya Sureci Sistemin davranışıyla ilişkili varsayımlar seti Modelleme & Analiz Ders 1 Yrd.Doç.Dr.Beyazıt Ocaktan Simülasyon, gerçek
EME 3105 Giriş SISTEM SIMÜLASYONU Sistem Simülasyonuna Giriş Gerçek Dünya Sureci Sistemin davranışıyla ilişkili varsayımlar seti Modelleme & Analiz Ders 1 Yrd.Doç.Dr.Beyazıt Ocaktan Simülasyon, gerçek
Simpleks Yönteminde Kullanılan İlave Değişkenler (Eşitliğin yönüne göre):
 DP SİMPLEKS ÇÖZÜM Simpleks Yöntemi, amaç fonksiyonunu en büyük (maksimum) veya en küçük (minimum) yapacak en iyi çözüme adım adım yaklaşan bir algoritma (hesaplama yöntemi) dir. Bu nedenle, probleme bir
DP SİMPLEKS ÇÖZÜM Simpleks Yöntemi, amaç fonksiyonunu en büyük (maksimum) veya en küçük (minimum) yapacak en iyi çözüme adım adım yaklaşan bir algoritma (hesaplama yöntemi) dir. Bu nedenle, probleme bir
Saha İş Gücü Yönetim Sistemi ve Güzergah Optimizasyonu
 Saha İş Gücü Yönetim Sistemi ve Güzergah Optimizasyonu Sahayı Bilerek Yönetin Başarsoft, hayatınıza harita tabanlı çözümler sunar. Saha İş Gücü Yönetim Sistemi Nedir? Kurum ve firmaların, saha işlerini
Saha İş Gücü Yönetim Sistemi ve Güzergah Optimizasyonu Sahayı Bilerek Yönetin Başarsoft, hayatınıza harita tabanlı çözümler sunar. Saha İş Gücü Yönetim Sistemi Nedir? Kurum ve firmaların, saha işlerini
