ÇOKLU DOĞRUSAL BAĞLANTI HALİNDE ENKÜÇÜK KARELER TEKNİĞİNİN ALTERNATİFİ YANLI TAHMİN TEKNİKLERİ VE BİR UYGULAMA
|
|
|
- Özgür Zeybek
- 8 yıl önce
- İzleme sayısı:
Transkript
1 ÇOKLU DOĞRUSAL BAĞLANTI HALİNDE ENKÜÇÜK KARELER TEKNİĞİNİN ALTERNATİFİ YANLI TAHMİN TEKNİKLERİ VE BİR UYGULAMA Yrd. Doç. Dr. Ali Sait ALBAYRAK Zonguldak Karaelmas Üniversitesi Çaycuma İktisadi ve İdari Bilimler Fakültesi Sayısal Yöntemler Anabilim Dalı Öğretim Üyesi ÖZET Bu çalışmanın amacı, beden ağırlığının tahmin edilmesinde yanlı tahmin tekniklerinin [Ridge Regression (RR) ve Principal Component (PC)] enküçük kareler [Least Squares (LS)] tekniğine karşı etkinliğini araştırmaktır. Bu amaçla beden ağırlığı ile açıklayıcı değişkenler arasındaki doğrusal ilişkinin tahmininde LS ve yanlı tahmin tekniklerinin (RR ve PC) göreceli tahmin geçerlilikleri karşılaştırılmaktadır. Araştırmada, bağımsız değişkenler arasındaki yüksek çoklu doğrusal bağlantı problemine dayanarak RR ve PC tekniklerinin LS tekniğine göre daha düşük standart hatalı, durağan ve kuramsal beklentilere uygun tahminler sağlayacağı beklenmiştir. Anahtar Kelimeler: Enküçük Kareler Tekniği, Ridge Regresyon Analizi, Temel Bileşenler Regresyonu ve Çoklu Doğrusal Bağlantı. ABSTRACT The purpose of this paper is to examine the effectiveness of applying biased estimation techniques (RR and PC) over Least Squares (LS) technique. For this purpose, the relative predictive validity of three regression techniques was compared using the weight data to study the linear relation of dependent variable to predictor variables. It was hypothesized that, given the high degree of multicolinearity of the predictor variables, biased estimation techniques would provide more stabilized coefficient and less standard errors than would the LS technique. Keywords: Least Squares Technique, Ridge Regression, Principal Components Regression and Multicolinearity.
2 Ali Sait ALBAYRAK GİRİŞ Yanlı tahmin teknikleri (RR ve PC), doğrusal regresyon modelinde bağımsız değişkenler arasında güçlü ilişkiler olduğunda enküçük kareler (LS) tekniğine alternatif olarak geliştirilmişlerdir (Shin, 1996: ). Çoklu doğrusal bağlantı halinde LS tahminleri yansız olmakta, ancak varyanslar büyüdüğünden tahminler gerçek değerlerinden uzaklaşabilmektedir. RR analizinde, LS tahminlerine küçük bir yanlılık sabiti eklenerek varyanslar küçültülerek daha durağan sonuçlar elde edilebilmektedir. RR tekniğine alternatif kullanılabilecek diğer yanlı tahmin tekniği temel bileşenler (PC) regresyon tekniğidir (Orhunbilge, 000: 40-51). Yanlı tahmin tekniklerinin varsayımları LS varsayımlarıyla aynıdır: Doğrusallık, eşvaryans ve bağımsızlık. Ancak yanlı tahmin tekniklerinde güven aralıkları hesaplanmadığından normallik varsayımı yapılmamaktadır (Rawlings, 1998:63-69). Beden ağırlığının tahmininde kullanılacak açıklayıcı değişkenler arasında yüksek derecede bir örtüşme olacağından, LS yerine yanlı tahmin tekniklerinin kullanılması daha güvenilir bir yaklaşım olarak kabul edilmektedir. Diğer taraftan çoklu doğrusal bağlantılı verilerde örnekten örneğe veya yıldan yıla tahmin edilecek doğruların birbirinden anlamlı bir şekilde farklılaşacağından, durağan ve güvenilir tahmin doğruları elde etmek güçleşmektedir. Bu yüzden, bu tür regresyon doğrularının geçerliliğinin sınanmasında çok büyük örneklere gereksinim duyulmaktadır (Maxwell, 000: ). Bu durumda LS yerine yanlı tahmin tekniklerinin kullanılmasının en uygun yaklaşım olduğu kanıtlanmıştır (Vinod, 1995:87-30). Kısaca, yanlı tahmin teknikleri çoklu doğrusal bağlantılı verilerde daha durağan tahmin doğrularının elde edilmesi ve LS tekniğinin uygun bir şekilde uygulanabilmesi için gerekli örnek büyüklüğünden daha küçük örnekler kullanılması durumunda daha etkili, geçerli ve durağan sonuçlar sağlamaktadır (Vinod, 1995:87-30). Tracey, Sedlacek ve Miars (1983), SAT puanları ile lise not ortalamalarına göre öğrencilerin üniversite birinci sınıf birikimli not ortalamalarını tahmininde ridge regresyon ve enküçük kareler tekniğinin sonuçlarını karşılaştırdılar. Çalışmalarında çapraz geçerlilik korelasyonlarına göre yanlı regresyon sonuçları ile enküçük kareler tekniğinin sonuçlarının benzer olduğunu gördüler. Yanlı regresyon analizinin LS tekniğine önemli üstünlük sağlayamamasını, değişken sayısı (p) ile örnek hacmi (n) arasındaki düşük orana (p/n) bağlı olduğunu
3 ZKÜ Sosyal Bilimler Dergisi Cilt 1, Sayı 1, ileri sürmüşlerdir. Faden (1978) RR nin LS tekniğine üstünlüğünün p/n oranının yüksekliğine bağlı olduğunu göstermiştir. Bu amaçla, yirmi kişi üzerinde toplanan verilerden yaralanarak beden ağırlığı ile açıklayıcı değişkenler arasındaki doğrusal ilişkinin tahmininde LS ve yanlı tahmin tekniklerinin göreceli geçerlilikleri karşılaştırılmaktadır. Ayrıca araştırmada, bağımsız değişkenler arasındaki güçlü çoklu doğrusal bağlantı problemine dayanarak yanlı tahmin tekniklerinin LS tekniğine göre daha düşük standart hatalı, durağan ve kuramsal (veya ampirik) beklentilere uygun tahminler sağlayacağı beklenmiştir.. ENKÜÇÜK KARELER TEKNİĞİ VE ÇOKLU DOĞRUSAL BAĞLANTI.1. Enküçük Kareler Tekniğinin Varsayımları Regresyon katsayılarının tahmininde genelde Enküçük Kareler (LS) tekniği kullanılmaktadır. 1 LS tekniğinin varsayımlarının sağlanamaması durumunda yapılan tahminler yanlı olmakta ve böylece ilgili anlamlılık testleri geçerliliğini yitirmektedir. Bu varsayımlarla ilgili ayrıntılı tartışmalar Gujarati (1995: ) ve Orhunbilge (000:15-56) kaynaklarında bulunabilir. LS ile ilgili varsayımlar aşağıdaki gibi özetlenebilir: Hataların beklenen değeri (ortalaması) sıfırdır: E(e) = 0. Hatalar birbirinden bağımsızdır. Yani, birim değerleri arasında sıra korelasyonu yoktur (absence of serial correlation): Cov(e i, e j ) = 0. = σ. Hataların varyansı sabittir (farklı varyanslılığın olmaması): Var(e i ) Hatalar (e i ) ile bağımlı değişken (Y) arasında korelasyon yoktur (absence of simultaneous equation bias): Cov(e i, Y i ) = 0. Hatalar ve bağımsız değişkenler birbirinden bağımsızdır: Cov(e i, X i ) = 0. Bağımsız değişkenler arasında anlamlı ilişki yoktur (absence of multicolinearity): Cov(X i, X j ) = 0. 1 Minimum varyans (MV) ve maksimum olabilirlik (ML) diğer kullanılan tekniklerdir (Bkz: Kleinbaum, Kupper ve Muller, 1995:49-53 ve ). Cov, kovaryans kısaltmasını ifade etmektedir.
4 Ali Sait ALBAYRAK 108 Doğrusal regresyon analizinde bağımsız değişkenler sabit (fixed, deterministic) olmasına rağmen, bağımlı değişken tesadüfidir (random). Değişkenler hatasız ölçülmüştür (absence of measurement errors). Bağımlı ve bağımsız değişkenler arasındaki ilişki doğrusaldır. Fakat bu doğrusallık koşulu kuşkusuz modelin parametreleri için gereklidir (değişkenler doğrusal olmayabilir). n>p. Birim değerleri sayısı (n), değişken sayısından (p) büyük olmalıdır: Bağımsız değişkenlerin (X i ) varyansı sıfırdan büyük olmalıdır. Değişkenin tüm gözlem değerleri (birimleri) birbirine eşitse, X i = X olacağından, regresyon doğrusunun eğimi tanımsız olmaktadır. Model doğru tanımlanmış olmalıdır. İlişkiye uygun fonksiyonun ve dahil edilmesi gereken tüm değişkenlerin dikkate alınması gerekmektedir. Yukarıdaki varsayımlardan birisinin sağlanamaması durumunda LS tahmincileri yanlı (biased), tutarsız (inconsistent) veya etkisiz (inefficient) olmaktadır. Söz konusu tahminciler aşağıdaki ilk üç koşulu sağlaması durumunda en iyi doğrusal tahminciler (BLUE = Best Linear Unbiased Estimators) olarak kabul edilmektedir. ŷ, tahmin edilen değeri gösterirse; Tahmin edilen istatistiğin beklenen değeri bilinmeyen anakütle parametresine eşitse, buna yansız (unbiased) tahmin denilmektedir: E (ŷ) = y Diğer tekniklerle elde edilen sonuçlarla kıyaslandığında minimum varyansa sahip tahmine etkili tahmin denilmektedir: Var(ŷ1 ) < Var(ŷ ) < Var(ŷ3)... Tahmin, örnek terimlerinin doğrusal bir fonksiyonu ise bu tahmine doğrusal tahmin denilmektedir: Y = Y / N = (1/ N)(Y + Y +...) = Y1 / N + Y / N 1 + Tahmin, örnek büyüklüğü artarken gerçek değerine yaklaşıyorsa tutarlıdır denir.... (1) () (3)
5 ZKÜ Sosyal Bilimler Dergisi Cilt 1, Sayı 1, Çoklu Doğrusal Bağlantı Problemi..1. Çoklu Doğrusal Bağlantı Probleminin Sonuçları Bağımsız değişkenler arasında güçlü ilişkilerin olmasına bağlantı (collinearity) veya çoklu doğrusal bağlantı (multicolinearity) adı verilmekte ve regresyon analizinde istenmeyen durumu göstermektedir (Orhunbilge, 000: 40-51). Regresyon analizinde çoklu doğrusal bağlantı aşağıdaki problemlere yol açmaktadır (Gujarati, 1995: ; Orhunbilge, 000:40-51): Tam çoklu doğrusal bağlantı durumunda regresyon katsayıları belirsiz ve bu katsayıların standart hataları sonsuz olmaktadır. Çoklu doğrusal bağlantı halinde regresyon katsayılarının varyans ve kovaryansları artmaktadır. Modelin R değeri yüksek, ancak bağımsız değişkenlerden hiçbiri veya çok azı kısmi t testine göre anlamlıdır. İlgili bağımsız değişkenlerin bağımlı değişkenle olan ilişkilerinin yönü kuramsal ve ampirik beklentilerle çelişebilmektedir. Bağımsız değişkenler birbiriyle bağıntılı ise, bunlardan bazılarının modelden çıkartılması gerekebilir. Fakat hangi değişkenler çıkartılacaktır? Modelden yanlış bir değişkenin çıkartılması, modelin hatalı tanımlanmasına (specification error) yol açacaktır. Diğer taraftan, bağımsız değişkenleri modele dahil edip çıkartmakta kullanabileceğimiz basit kurallar bulunmamaktadır (Myers, 1990; Gujarati, 1995).... Çoklu Doğrusal Bağlantının Saptanması Çoklu doğrusal bağlantının saptanmasında kullanılan birkaç yaklaşım bulunmaktadır (Neter, vd. 1996; Gujarati, 1995). Bunlar aşağıda kısaca açıklanmaktadır. 1. Bu yaklaşımlardan birincisi, basit korelasyon matrisinin incelenmesidir. Yüzeysel olarak, iki bağımsız değişken arasındaki basit korelasyon katsayısı oldukça anlamlı (r>%75) ise, bu durum çoklu doğrusal bağlantı problemine yol açabilir. Buna rağmen, istatistik açıdan anlamlı korelasyonlar her zaman çoklu doğrusal bağlantı problemine yol açmamaktadır. Lawrence Klein e göre basit korelasyon katsayısı (r), çoklu korelasyon katsayısından (R) küçükse, çoklu bağlantı problemi ortaya çıkmayabilir.. Çoklu doğrusal bağlantının saptanmasında kullanılan ikinci yaklaşım, modele yeni bağımsız değişkenler ilave edildiğinde, R deki
6 Ali Sait ALBAYRAK 110 değişimlerin incelenmesidir. R ' de önemli bir gelişme sağlanamazsa, çoklu doğrusal bağlantı problemi ortaya çıkmış olabilir. 3. Çoklu doğrusal bağlantının saptanmasında kullanılan üçüncü yaklaşım, kısmi korelasyon katsayılarının incelenmesidir. İki değişken arasındaki basit korelasyon katsayısı anlamlı, fakat kısmi korelasyon katsayısı anlamsız ise bu durum çoklu doğrusal bağlantı problemi için bir işaret olabilir. Kısmi korelasyon yaklaşımı her zaman etkili olmamaktadır. Diğer bir anlatımla, kısmi korelasyon katsayıları yüksek olması durumunda bile çoklu doğrusal bağlantı problemi olabilmektedir. 4. Çoklu doğrusal bağlantının saptanmasında kullanılan dördüncü yaklaşım, varyans arttırıcı faktör (VIF=Variance Inflation Factor) kullanılmasıdır. VIF lerin hesaplanmasını göstermek için aşağıdaki gibi üç bağımsız değişkenli bir regresyon modelini inceleyelim. y = b + b x + b x + b x + e (4) i Üç bağımsız değişkenli bir modelin VIF değerleri aşağıdaki adımlarla hesaplanmaktadır. Birinci adımda X 1 bağımlı, X ile X 3 bağımsız değişken olarak alınıp modelin R 1 ' si hesaplanır. Böylece X 1 için varyans artırıcı faktör VIF(X1 ) = 1/(1 R1 ) olarak hesaplanır. İkinci adımda X bağımlı, X 1 ile X 3 bağımsız değişken olarak alınıp modelin R ' si hesaplanır. Böylece X için varyans artırıcı faktör VIF(X ) = 1/(1 R ) olarak hesaplanır. Üçüncü adımda benzer şekilde X 3 bağımlı, X 1 ile X bağımsız değişken olarak alınıp modelin R 3 ' si hesaplanır. X 3 için varyans artırıcı faktör VIF(X ) = 1/(1 R ) olarak elde edilir. 3 3 Bağımlı değişken ile bağımsız değişkenler arasında ilişki yoksa (R = 0 olacağından) VIF 1 e [VIF = 1/(1 R ) = 1/(1 0) = 1] eşittir. Bağımlı ve bağımsız değişkenler arasında tam bir ilişki varsa (R = 1 olacağından) VIF [VIF = 1/(1 R ) = 1/(1 1) = ] sonsuz olacaktır. R %90 ise, VIF 10 [ VIF = 1/(1 0,9) = 10] olarak elde edilir. Webster (199: ) yorum için şu genel kuralı önermektedir: VIF 10 a eşit veya daha büyük ( VIF 10) ise, anlamlı çoklu doğrusal bağlantı problemi söz konusudur. i
7 ZKÜ Sosyal Bilimler Dergisi Cilt 1, Sayı 1, Çoklu doğrusal bağlantının saptanmasında kullanılan beşinci yaklaşım, bağımsız değişkenler için tolerans değerinin (TV=Tolerance Value) hesaplanmasıdır. Tolerans değeri, 1 den belirlilik katsayısının çıkartılmasıyla (TV = 1 R ) hesaplanmaktadır. Böylece daha küçük tolerans, daha büyük VIF değeri demektir. 6. Çoklu doğrusal bağlantının saptanmasında kullanılan altıncı yaklaşım yardımcı regresyon eşitliklerinden (auxiliary regression equations) yararlanarak F değerlerinin hesaplanmasıdır. Bunun için üç bağımsız değişkenli aşağıdaki regresyon modelini inceleyelim. y = b + b x + b x + b x + e (5) i Her bir bağımsız değişken ile geriye kalan diğer bağımsız değişkenler arasındaki ilişki araştırılarak R 1.3, R.13 ve R 3.1 çoklu korelasyon katsayıları hesaplanır. Daha sonra bu katsayılardan yararlanarak her bir bağımsız değişken için F değeri hesaplanmaktadır. Örneğin F değeri X 1 değişkeni için aşağıdaki gibi hesaplanmaktadır: ( k ) 1.3 ( 1 R )/( n k + 1) i R / = (6) F Formülde n birim sayısını; k ise bağımsız değişken sayısını göstermektedir. Hesaplanan F değeri ( df 1 = k ve df = n k + 1), kritik F değeriyle karşılaştırılmaktadır. F 1.3, kritik F değerinden büyükse X 1 değişkeni ile X ve X 3 değişkenleri arasındaki ilişkinin anlamlı olduğuna karar verilmektedir. 7. Çoklu doğrusal bağlantının saptanmasında kullanılan yedinci yaklaşım, koşul sayısı (CN = Condition Number) veya koşul endeksi (CI = Condition Index)) değerlerinin hesaplanmasıdır. CN ve CI aşağıdaki gibi hesaplanmaktadır: CN = [Maksimum Özdeğer / Minimum Özdeğer] CI=[Maksimum Özdeğer / Minimum Özdeğer] 1/ CI değeri 10 ile 30 (CN değeri 100 ile 1000) arasında ise orta, 30 dan (veya 1000 den) büyükse çok güçlü çoklu doğrusal bağlantı problemini gösterir (Gujarati, 1995:338). Çoklu doğrusal bağlantı probleminin saptanmasında kullanılan ve yukarıda açıklanan yaklaşımlardan her biri belirli dezavantajlara sahiptir.
8 Ali Sait ALBAYRAK 11 Ayrıca, hangi durumda hangi yaklaşımın kullanılabileceği konusunda da bir öneride bulunulamamaktadır (Gujarati, 1995:339) Çoklu Doğrusal Bağlantı Probleminin Çözümü Çoklu doğrusal bağlantı probleminin çözüm yolları aşağıda verilmektedir (Gujarati, 1995: ; Netter-Wasserman-Kunter, 1990:411-41; Orhunbilge, 000:40-51). 1. Bir veya daha çok bağımsız değişken modelden çıkartılabilir. Fakat hangi değişkenler çıkartılacaktır? Böyle bir yaklaşım, modeli yanlış tanımlamaya götürebilir.. Farklar alınarak değişkenler dönüştürülebilir. Fakat böyle bir dönüşüm hatalar arasında otokorelasyon problemine yol açabilir. Ayrıca, böyle bir dönüşüm sadece zaman serilerine uygulanabilirken, kesit verilerine uygulanamamaktadır. 3. Bazen yeni gözlem değerlerinin elde edilmesiyle çoklu doğrusal bağlantı problemi ortadan kaldırılabilir. Fakat, her zaman örneği büyütmek mümkün olmamaktadır. 4. Birbiriyle ilişkili olan iki değişken yerine bu iki değişkenin toplamı (tek bir değişken olarak) alınabilir. 5. Birbirinden bağımsız bileşenler türeten Temel Bileşenler Regresyon Analizi veya LS tekniğinin düzeltilmiş şekli olan ve yanlı standartlaştırılmış regresyon katsayılarını tahmin eden Ridge Regresyon teknikleri kullanılabilmektedir Ridge Regresyon (RR) Analizi Burada RR tekniği ana hatlarıyla özetlenmektedir. Tekniğin teorik açıklaması Orhunbilge (000:40-41) tarafından yapılmaktadır. LS 3 Bilindiği gibi çoklu doğrusal bağlantının saptanmasında en yaygın kullanılan yaklaşım bağımsız değişkenler için VIF değerlerinin hesaplanmasıdır. Fakat bu yaklaşımla da çoklu doğrusal bağlantı kesin olarak saptanabildiği iddia edilememektedir. Çünkü, bilindiği gibi herhangi bir kısmi regresyon katsayısının varyansı üç faktöre bağlıdır: σ, x i ve VIF i. Yani, Var (bˆ ) ( σ / x ) (1/(1 R ) = ( σ / x ) VIF dir. Bu eşitlikten i = i i i i görüldüğü gibi yüksek bir VIF değeri düşük bir σ veya yüksek bir xi değerleriyle de elde edilmiş olabilir. Diğer bir anlatımla yüksek bir VIF değeri, her zaman yüksek varyansların veya standart hataların elde edilmesi için gerekli ve yeterli bir neden değildir (Bkz: Gujarati: ). 4 SPSS 11.5 istatistik programında Ridge Regression için bir makro dosyası bulunmaktadır.
9 ZKÜ Sosyal Bilimler Dergisi Cilt 1, Sayı 1, tekniği ile yapılan tahminler bu tekniğin varsayımlarını sağlanması durumunda yansız olmaktadır. Çoklu doğrusal bağlantı halinde ise, regresyon katsayılarının varyans ve kovaryansları artmaktadır. Diğer bir anlatımla, önemli değişkenlere ait regresyon katsayılarının standart hataları büyür ve bu değişkenlerin regresyon katsayılarının kısmi t testleri anlamsız sonuç verir. Çoklu doğrusal bağlantı halinde herhangi bir bağımsız değişken veya birime ait veriler modelden çıkartıldığında veya modele sokulduğunda kısmi regresyon katsayılarında çok önemli değişiklikler olmaktadır. Ayrıca çoklu doğrusal bağlantı halinde kısmi regresyon katsayılarının işaretleri teoriden veya beklenenden farklı olabilmektedir. Kısaca, çoklu doğrusal bağlantılı verilerle hesaplanan standartlaştırılmış regresyon katsayıları durağanlığını veya kararlılığını kaybetmektedir (Darlington, 1978; Faden, 1978). 5 RR tekniği, bu tahminlere küçük bir yanlılık sabiti ekleyerek varyansı azaltmaya yardım etmektedir (Darlington, 1978; Dempster, Schatzoff & Wermuth, 1997; Hoerl & Kennard, 1970; Price, 1977). Genelde, varyans-kovaryans matrisinin köşegen değerlerine küçük bir yanlılık sabiti (k) ilave etmenin dışında, RR ile LS tekniklerinin işleyişi aynıdır. Diğer bir anlatımla RR ile bir taraftan tahminlerin varyansı azaltılmakta, diğer taraftan ise bu katsayı (k) oranında yanlı tahminler elde edilmektedir. Böylece iki alternatif söz konusu olmaktadır: Yansız tahminlerle yüksek varyans veya yanlı tahminlerle düşük varyans. Tahmin edilecek LS regresyon modelinin aşağıdaki gibi matris notasyonuyla gösterildiğini varsayalım (NCSS Inc, 001): Y = XB + e (7) Burada Y, bağımlı değişkeni; X, bağımsız değişkenleri; B, tahmin edilecek regresyon katsayılarını ve e, hata terimini göstermektedir. Ridge regresyon analizinde ilk olarak bağımlı ve bağımsız değişkenler ortalamalarından farkları alınıp standart sapmalarına 5 Regresyon analizi standartlaştırılmış veriler üzerine uygulanması durumunda hesaplanan katsayılara standartlaştırılmış regresyon katsayıları denilmektedir (Bkz: Norusis and SPSS Inc., 1993:314). Standartlaştırılmamış katsayılara dayanarak değişkenlerin göreceli önemlerini karşılaştırmak uygun olmadığından, analizde kullanılan değişkenler kendi ortalamalarından farkları alınıp standart sapmalarına bölünerek standartlaştırılmaktadır. Diğer bir anlatımla değişkenler ölçü birimlerinden arındırılarak varyansları bire eşitlenmektedir. Ancak standartlaştırılmış katsayılar, doğrudan standartlaştırılmamış katsayılardan yararlanarak aşağıdaki eşitlik yardımıyla da hesaplanabilmektedir: Beta = b (s / s ). k k x k y
10 Ali Sait ALBAYRAK 114 bölünerek standartlaştırılmaktadır. Nihai regresyon katsayıları elde edildiğinde ise, katsayılar orijinal ölçü birimlerine dönüştürülmektedir. LS tekniğiyle regresyon katsayıları ( Bˆ ) aşağıdaki gibi hesaplanmaktadır: ' 1 ' B = ( X X) X Y (8) Değişkenler standartlaştırıldığından ve R bağımsız değişkenler arasındaki korelasyon matrisini gösterdiğinden X X = R dir. Bu tahminlerin beklenen değerleri anakütle değerlerine eşit olacağından bu tahminler yansızdır. Yani; E (B) = B Tahminlerin varyans-kovaryans matrisi ise, (9) 1 V ( B ) = σ R dir ve y ler standartlaştırılmış olduğundan, σ = 1 dir. Buradan; jj 1 (bˆ j ) = r = = VIF eşitliği yazılabilir. 1 R V j R j ; X j değişkeninin bağımlı, analizdeki diğer bağımsız değişkenlerin ise bağımsız değişkenler olarak alınan modelin kareli korelasyon (belirlilik) katsayısını göstermektedir. Böylece bu varyans VIF değerine eşit olmaktadır. Görüldüğü gibi eşitliğin paydasında yer alan R, 1 e yaklaştıkça varyans (ve bu yüzden VIF) değeri büyümektedir. Burada VIF için kritik değer (cut-off value), daha önce belirtildiği gibi, 10 dur. Diğer taraftan R için kritik değer 0,90 olmaktadır. Bu nedenle analizdeki bağımsız değişkenlerden herhangi birisi bağımlı değişken olarak alınıp geriye kalan diğer değişkenler arasındaki R değeri 0,90 veya daha büyük ise, çoklu doğrusal bağlantı sorunu söz konusu olmaktadır. Ridge regresyon analizinde korelasyon matrisinin köşegen değerlerine küçük bir yanlılık sabiti eklenerek, yanlı standartlaştırılmış regresyon katsayıları aşağıdaki gibi hesaplanmaktadır: ~ ~ 1 ' 1 ' B = (X X + kι) X Y veya B = (R + kι) X Y (10)
11 ZKÜ Sosyal Bilimler Dergisi Cilt 1, Sayı 1, Burada k, 1 den küçük pozitif sayısal bir değerdir (genelde k 0,3 tür). Bu tahminin yanlılık büyüklüğü beklenen değeri aşağıdaki gibidir. ~ 1 E ( B B) = [( X X + kι) X X Ι] B (11) ve kovaryans matrisi aşağıdaki eşitlikle elde edilmektedir: ~ 1 1 V( B ) = ( X X + kι) X X( X X + kι) (1) Buradan, belirli bir k değeri için, yanlı tahminlere ait ortalama hata karelerinin beklenen değerinin enküçük kareler tekniğiyle elde edilen tahminlerden daha küçük olduğu gösterilebilmektedir. Fakat optimum k sabiti gerçek regresyon katsayılarının (tahmin edilecek) bilinmesine bağlıdır. Optimum çözümü garanti edebilecek bir yaklaşım henüz bulunamamıştır. Burada k, 0 ile 1 aralığında değerler alabilmektedir. k, 1 e yaklaştıkça tahminlerin yanlılığı artmakta, fakat varyansları azalmaktadır. Optimum k sabitini araştırmak için yanlı standartlaştırılmış regresyon katsayıları ile k arasında hesaplanan ve yanlı regresyon grafiği (Ridge Trace) adı verilen grafiklerden yaralanılmaktadır (Hoerl vd., 1970:69-8). Bu grafiklerde yanlı regresyon katsayıları k nın bir fonksiyonu olarak gösterilmektedir. Optimum k değeri, yanlı standartlaştırılmış regresyon katsayılarının durağanlaştığı bölgeden seçilmektedir. Genelde standartlaştırılmış regresyon katsayıları ilkönce küçük k değerleriyle çok anormal bir biçimde değişmekte ve daha sonra durağanlaşmaktadır. Regresyon katsayılarının durağanlaştığı bu bölgede olası enküçük k değeri optimum k değeri olarak seçilmektedir. Optimum k değerinin seçiminde kullanılan diğer kriterler arasında katsayıların kuramsal beklentilere uygunluğunu, durağanlığını, makul büyüklüğünü, kabul edilebilir hata kareleri toplamını ve minimum VIF leri (bağımsız değişkenler için birlikte 1 e yaklaşan VIF değerlerini) sağlayan k sabiti yaklaşımları sayılabilir (Anderson, 1998). Uygulamada tüm kriterlerin birlikte değerlendirilmesi en sağlıklı yaklaşım olarak kabul edilmektedir..4. Temel Bileşenler Regresyon (PC) Analizi Matris notasyonuyla verilen aşağıdaki regresyon modelini dikkate alalım: Y = XB + e (13)
12 Ali Sait ALBAYRAK 116 Y, bağımlı değişkeni; X bağımsız değişkenleri; B, regresyon katsayılarını ve e, hata terimini göstermektedir. Temel bileşenler (PC) analizinde ilk olarak hem bağımlı hem de bağımsız değişkenler ortalamadan farkları alınıp standart sapmalarına bölünerek standartlaştırılmaktadır (NCSS Inc., 001). Nihai regresyon katsayıları gösterildiğinde ise, değişkenler orijinal ölçeğine dönüştürülmektedir. Daha önce belirtildiği gibi LS tekniğiyle regresyon katsayıları aşağıdaki eşitlikle hesaplanmaktadır: 1 Bˆ = (X X) X Y (14) Değişkenler standartlaştırıldığından X X = R dir. Burada R, bağımsız değişkenler için korelasyon matrisini göstermektedir. PC regresyon analizini gerçekleştirmek için bağımsız değişkenler temel bileşenlere dönüştürülür (NCSS Inc., 001). Bu matematik olarak aşağıdaki gibi yazılmaktadır: X X = PDP = Z Z (15) Eşitlikte PC modelini tanımlayan D, X X özdeğerlerinin köşegen matrisini; P, X X özvektör matrisini ve Z, veri matrisini (X yapısına benzer) göstermektedir. Temel bileşenler (P) ortogonal olduğundan P P = Ι dır. Böylece orijinal değişkenlerin (X) ağırlıklı ortalamalarını ifade eden yeni değişkenler (Z) türetilmektedir. Bu durum, regresyon analizine başlamadan önce değişkenlerin logaritmik veya karekök dönüşümlerinin alınmasından farklı bir şey değildir. Bu yeni değişkenler temel bileşen olduğu için, bu bileşenler arasındaki korelasyonlar sıfırdır. X1, X, X3 gibi değişkenlerle analize başlanmışsa, Z1, Z ve Z3 gibi dönüştürülmüş değişkenler elde edilmektedir. Çok küçük özdeğerler hesaplanması durumunda çok güçlü çoklu doğrusal bağlantı (severe multicolinearity) sorunu söz konusu olmaktadır. Bu sorunun üstesinden gelebilmek için düşük özdeğerlerle özdeşleşen bileşenler analizden çıkartılmaktadır. Genelde göreceli olarak özdeğeri küçük bir veya iki (en çok) temel bileşen elde edilmektedir. Örneğin üç değişkenli bir modelde özdeğeri küçük sadece bir temel bileşen elde edilmişse, Z3 (üçüncü temel bileşen) analizden çıkartılmaktadır (NCSS Inc., 001). Böylece Y değişkeni bağımlı ve Z1 ve Z bileşenleri ise bağımsız değişkenler olarak alınan modelde artık çoklu doğrusal bağlantı söz konusu olmamaktadır. Daha sonra sonuçlar X ölçeğine geri
13 ZKÜ Sosyal Bilimler Dergisi Cilt 1, Sayı 1, dönüştürülerek B nin tahminleri elde edilir. Bu tahminler yanlı olacaktır. Fakat bu yanlılığın büyüklüğü varyansın azaltılmasıyla dengeleneceği umulmaktadır. Diğer bir anlatımla PC tahminlerinin hata kareleri ortalamasının LS tahminlerinden daha küçük olması beklenmektedir. Matematik olarak, asal bileşenlerin özel doğası gereği, regresyon katsayılarının tahmini aşağıdaki gibidir (NCSS Inc., 001): A ˆ 1 = ( Z Z) 1 Z Y = D Z Y (16) Artık bu eşitlik, değişik bağımsız değişken seti üzerine uygulanan LS regresyonudur. Böylece  ve Bˆ gibi iki regresyon katsayıları seti arasındaki ilişkiler ise aşağıdaki gibi yazılmaktadır: Aˆ = P Bˆ ve Bˆ = PAˆ (17) Â' nın ilgili elementi sıfıra eşitlenerek ilgili temel bileşen analizden çıkartılabilir. Böylece PC regresyonu aşağıdaki adımlarla özetlenebilir (NCSS Inc., 001): X matrisi için PC analizi uygulanarak temel bileşenler (Z) elde edilir.  katsayılar matrisinin enküçük kareler tahminlerini elde etmek için Y ile Z arasında LS regresyonu uygulanır. Â' nın en son elementi sıfıra eşitlenir. Son aşamada Bˆ = PAˆ eşitliği kullanılarak hesaplanan katsayılar orijinal ölçeğine dönüştürülmektedir. Son olarak, RR tekniğinde k yanlılık sabitinin seçiminde yaşanan belirsizliğin aksine, PC analizinde elimine edilecek temel bileşenlerin sayısı göreceli olarak daha kesindir. Diğer bir anlatımla çoklu doğrusal bağlantı sorununu çözmek için özdeğeri göreceli olarak küçük olan bileşenlerin analizden çıkartılması gerektiği hususu daha kesindir. 6 Görüldüğü gibi PC tekniğinde, RR tekniğindeki k yanlılık sabitinin seçimi gibi bir belirsizlik söz konusu değildir. 6 Bir korelasyon matrisinin tipik özdeğerinin büyüklüğü 1 olduğundan, özdeğeri 1 den çok küçük olan bileşenler analizden çıkartılmaktadır ve genelde verilecek karar açık ve nettir. Bilindiği gibi standartlaştırılmış değişkenler için bir korelasyon matrisinin özdeğeri bağımsız değişken sayısının toplamına eşittir. Örneğin, üç bağımsız değişkenli bir korelasyon matrisinin özdeğerleri toplamı 3 tür. Korelasyon matrisinin tipik özdeğeri ise bu korelasyon matrisinin özdeğerleri toplamının ortalamasına (yani 3/3=1) eşittir.
14 Ali Sait ALBAYRAK UYGULAMA: BEDEN AĞIRLIĞI VERİLERİ İÇİN LS, RR VE PC TEKNİKLERİYLE ELDE EDİLEN SONUÇLARIN KARŞILAŞTIRILMASI Araştırmada kullanılan veriler, İstanbul Üniversitesi İstanbul Tıp Fakültesi Hastanesine şişmanlık şikayeti ile başvuran hastalar arasından tesadüfi olarak elde edilmiştir. Diğer bir anlatımla araştırmanın anakütlesi İstanbul Tıp Fakültesine şişmanlık şikayeti ile başvuran hastalar, kullanılan örnekleme tekniği basit tesadüfi bir örneklemedir. Araştırmada dört değişken kullanılmaktadır: Beden ağırlığı (kg), deri alanı (cm ), uyluk kemiğinin çevresinin uzunluğu (cm) ve belden yukarı ölçülen kasların çevrelerinin uzunluğu (cm). Araştırmada 0 kişiden elde edilen ölçüm sonuçları (veriler tablosu) Tablo 1 de verilmektedir. Araştırmada 0 kişi üzerinde ölçülen veriler ve LS ve RR teknikleri için yazılan makro komutları Tablo 1 de verilmektedir. LS, RR ve PC teknikleriyle elde edilen sonuçlar ise Tablo de özetlenmektedir. 7 LS analizine göre beden ağırlığı ile açıklayıcı değişkenler arasındaki doğrusal ilişkinin %89,5 olduğu ve beden ağırlığında meydana gelen değişimlerin yaklaşık %80,1 i bağımsız değişkenler tarafından açıklandığı anlaşılmaktadır [Tablo : 1.1]. Ayrıca LS tekniğiyle elde edilen ANOVA tablosu incelendiğinde %5 veya %1 geleneksel anlamlılık düzeylerinde modelin anlamlı (güvenilir) olduğu (F=1,488; p=,000) görülmektedir [Tablo : 1.]. Modelin yüksek belirlilik (R =%80,1) ve korelasyon katsayısının (R=%89,5) aksine katsayılar tablosu incelendiğinde hiçbir değişkenin kısmi t testine göre anlamlı olmadığı görülmektedir [Tablo : 1.3]. Bu durum daha önce belirtildiği gibi, çoklu doğrusal bağlantı probleminin bir göstergesidir. Aynı sonuca çoklu doğrusal bağlantı ile ilgili istatistiklerin incelenmesiyle de varılmaktadır [Tablo : 1.4]. Burada bağımsız değişkenler için hesaplanan korelasyon matrisi, VIF ve TV değerleri, R 1.3, R.13, R 3.1 ile korelasyonların özdeğerleri için hesaplanan CN (koşul sayısı) ve CI (koşul endeksi) değerleri verilmektedir (Tablo : 1.4). Korelasyon matrisi incelendiğinde X1 ve X değişkenleri arasında çok yüksek bir ilişki (%9,4) görülmektedir. X1, X ve X3 bağımsız değişkenleri için hesaplanan VIF ler sırasıyla yaklaşık olarak 755, 601 ve 111 olarak elde edilmiş ve bu değerler kritik VIF değerinin (10) oldukça üstündedir. 7 LS ve RR sonuçları SPSS 11.5 istatistik paket programında makro komutlar yazılarak elde edilmiştir.
15 ZKÜ Sosyal Bilimler Dergisi Cilt 1, Sayı 1, Bağımsız değişkenlerden her biri bağımlı değişken olarak alınıp geriye kalan diğer bağımsız değişkenler arasındaki ilişkiler incelendiğinde bu ilişkilerin 0,90 dan büyük olduğu görülmektedir. Hesaplanan korelasyonlara ait özdeğerlerden yararlanarak elde edilen CN (koşul sayısı = 308,97) ve CI (koşul endeksi = 55,036) değerleri kritik değerlerden (1000 ve 30) büyüktür [Tablo : 1.4]. Bu istatistiklerin tamamı verilerde çok güçlü çoklu doğrusal bağlantı problemi olduğunun bir kanıtıdır. Ridge regresyon analizi sonuçlarının birinci kısmında belirli yanlılık katsayılarına göre R, standartlaştırılmış ridge regresyon katsayıları ile bu katsayılara ait VIF değerlerindeki değişimler verilmektedir [Tablo : 3.1]. Bu verilerden yararlanarak optimum k sabiti standartlaştırılmış ridge regresyon katsayılarının durağanlaşmaya başladığı ve bu katsayılara ait VIF değerlerinin birlikte 1 e yaklaştığı noktada (k=%) seçilir.
ÇOKLU DOĞRUSAL BAĞLANTI HALİNDE ENKÜÇÜK KARELER TEKNİĞİNİN ALTERNATİFİ YANLI TAHMİN TEKNİKLERİ VE BİR UYGULAMA
 ÇOKLU DOĞRUSAL BAĞLANTI HALİNDE ENKÜÇÜK KARELER TEKNİĞİNİN ALTERNATİFİ YANLI TAHMİN TEKNİKLERİ VE BİR UYGULAMA Yrd. Doç. Dr. Ali Sait ALBAYRAK Zonguldak Karaelmas Üniversitesi Çaycuma İktisadi ve İdari
ÇOKLU DOĞRUSAL BAĞLANTI HALİNDE ENKÜÇÜK KARELER TEKNİĞİNİN ALTERNATİFİ YANLI TAHMİN TEKNİKLERİ VE BİR UYGULAMA Yrd. Doç. Dr. Ali Sait ALBAYRAK Zonguldak Karaelmas Üniversitesi Çaycuma İktisadi ve İdari
ÇOKLU DOĞRUSAL BAĞLANTI HALİNDE ENKÜÇÜK KARELER TEKNİĞİNİN ALTERNATİFİ YANLI TAHMİN TEKNİKLERİ VE BİR UYGULAMA
 ZKÜ Sosyal Bilimler Dergisi Cilt 1, Sayı 1, 005, ss. 105-16 ÇOKLU DOĞRUSAL BAĞLANTI HALİNDE ENKÜÇÜK KARELER TEKNİĞİNİN ALTERNATİFİ YANLI TAHMİN TEKNİKLERİ VE BİR UYGULAMA Yrd. Doç. Dr. Ali Sait ALBAYRAK
ZKÜ Sosyal Bilimler Dergisi Cilt 1, Sayı 1, 005, ss. 105-16 ÇOKLU DOĞRUSAL BAĞLANTI HALİNDE ENKÜÇÜK KARELER TEKNİĞİNİN ALTERNATİFİ YANLI TAHMİN TEKNİKLERİ VE BİR UYGULAMA Yrd. Doç. Dr. Ali Sait ALBAYRAK
Examining the Ridge Regression Analysis of the Number of Foreign Tourists Coming to Turkey
 2 nd International Congress of Tourism & Management Researches - 2015 Examining the Ridge Regression Analysis of the Number of Foreign Tourists Coming to Turkey Derya İSPİR a, Barış Ergül b, Arzu Altın
2 nd International Congress of Tourism & Management Researches - 2015 Examining the Ridge Regression Analysis of the Number of Foreign Tourists Coming to Turkey Derya İSPİR a, Barış Ergül b, Arzu Altın
3. TAHMİN En Küçük Kareler (EKK) Yöntemi 1
 3. TAHMİN 3.1. En Küçük Kareler (EKK) Yöntemi 1 En Küçük Kareler (EKK) yöntemi, regresyon çözümlemesinde en yaygın olarak kullanılan, daha sonra ele alınacak bazı varsayımlar altında çok aranan istatistiki
3. TAHMİN 3.1. En Küçük Kareler (EKK) Yöntemi 1 En Küçük Kareler (EKK) yöntemi, regresyon çözümlemesinde en yaygın olarak kullanılan, daha sonra ele alınacak bazı varsayımlar altında çok aranan istatistiki
Ekonometri I VARSAYIMLARI
 Ekonometri I ÇOK DEĞİŞKENLİ REGRESYON MODELİNİN VARSAYIMLARI Hüseyin Taştan Temmuz 23, 2006 İçindekiler 1 Varsayım MLR.1: Parametrelerde Doğrusallık 1 2 Varsayım MLR.2: Rassal Örnekleme 1 3 Varsayım MLR.3:
Ekonometri I ÇOK DEĞİŞKENLİ REGRESYON MODELİNİN VARSAYIMLARI Hüseyin Taştan Temmuz 23, 2006 İçindekiler 1 Varsayım MLR.1: Parametrelerde Doğrusallık 1 2 Varsayım MLR.2: Rassal Örnekleme 1 3 Varsayım MLR.3:
İSTATİSTİKSEL DARALTICI (SHRINKAGE) MODEL VE UYGULAMALARI * A Statistical Shrinkage Model And Its Applications*
 Ç.Ü. Fen Bilimleri Enstitüsü Yıl:010 Cilt:-1 İSTATİSTİKSEL DARALTICI (SHRINKAGE) MODEL VE UYGULAMALARI * A Statistical Shrinkage Model And Its Applications* Işıl FİDANOĞLU İstatistik Anabilim Dalı Fikri
Ç.Ü. Fen Bilimleri Enstitüsü Yıl:010 Cilt:-1 İSTATİSTİKSEL DARALTICI (SHRINKAGE) MODEL VE UYGULAMALARI * A Statistical Shrinkage Model And Its Applications* Işıl FİDANOĞLU İstatistik Anabilim Dalı Fikri
İÇİNDEKİLER 1. GİRİŞ...
 İÇİNDEKİLER 1. GİRİŞ... 1 1.1. Regresyon Analizi... 1 1.2. Uygulama Alanları ve Veri Setleri... 2 1.3. Regresyon Analizinde Adımlar... 3 1.3.1. Problemin İfadesi... 3 1.3.2. Konu ile İlgili Potansiyel
İÇİNDEKİLER 1. GİRİŞ... 1 1.1. Regresyon Analizi... 1 1.2. Uygulama Alanları ve Veri Setleri... 2 1.3. Regresyon Analizinde Adımlar... 3 1.3.1. Problemin İfadesi... 3 1.3.2. Konu ile İlgili Potansiyel
Koşullu Öngörümleme. Bu nedenle koşullu öngörümleme gerçekleştirilmelidir.
 Koşullu Öngörümleme Ex - ante (tasarlanan - umulan) öngörümleme söz konusu iken açıklayıcı değişkenlerin hatasız bir şekilde bilindiği varsayımı gerçekçi olmayan bir varsayımdır. Çünkü bazı açıklayıcı
Koşullu Öngörümleme Ex - ante (tasarlanan - umulan) öngörümleme söz konusu iken açıklayıcı değişkenlerin hatasız bir şekilde bilindiği varsayımı gerçekçi olmayan bir varsayımdır. Çünkü bazı açıklayıcı
1 Araştırma Makalesi. Hayvansal Üretim Verilerinde Çoklu Bağlantı Probleminin Yanlı Regresyon Yöntemi İle Çözümlenmesi
 1 Araştırma Makalesi Hayvansal Üretim Verilerinde Çoklu Bağlantı Probleminin Yanlı Regresyon Yöntemi İle Çözümlenmesi İrfan ÖZTÜRK HÜ, Ziraat Fakültesi, Zootekni Bölümü, Şanlıurfa Geliş (Received): 12.09.2014
1 Araştırma Makalesi Hayvansal Üretim Verilerinde Çoklu Bağlantı Probleminin Yanlı Regresyon Yöntemi İle Çözümlenmesi İrfan ÖZTÜRK HÜ, Ziraat Fakültesi, Zootekni Bölümü, Şanlıurfa Geliş (Received): 12.09.2014
3 KESİKLİ RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI
 ÖNSÖZ İÇİNDEKİLER III Bölüm 1 İSTATİSTİK ve SAYISAL BİLGİ 11 1.1 İstatistik ve Önemi 12 1.2 İstatistikte Temel Kavramlar 14 1.3 İstatistiğin Amacı 15 1.4 Veri Türleri 15 1.5 Veri Ölçüm Düzeyleri 16 1.6
ÖNSÖZ İÇİNDEKİLER III Bölüm 1 İSTATİSTİK ve SAYISAL BİLGİ 11 1.1 İstatistik ve Önemi 12 1.2 İstatistikte Temel Kavramlar 14 1.3 İstatistiğin Amacı 15 1.4 Veri Türleri 15 1.5 Veri Ölçüm Düzeyleri 16 1.6
KORELASYON VE REGRESYON ANALİZİ. Doç. Dr. Bahar TAŞDELEN
 KORELASYON VE REGRESYON ANALİZİ Doç. Dr. Bahar TAŞDELEN Günlük hayattan birkaç örnek Gelişim dönemindeki bir çocuğun boyu ile kilosu arasındaki ilişki Bir ailenin tükettiği günlük ekmek sayısı ile ailenin
KORELASYON VE REGRESYON ANALİZİ Doç. Dr. Bahar TAŞDELEN Günlük hayattan birkaç örnek Gelişim dönemindeki bir çocuğun boyu ile kilosu arasındaki ilişki Bir ailenin tükettiği günlük ekmek sayısı ile ailenin
YABANCI DİL EĞİTİMİ VEREN ÖZEL BİR EĞİTİM KURUMUNDAKİ ÖĞRENCİLERİN BEKLENTİLERİNİN ARAŞTIRILMASI. Sibel SELİM 1 Efe SARIBAY 2
 Dokuz Eylül Üniversitesi Sosyal Bilimler Enstitüsü Dergisi Cilt 5, Sayı:2, 2003 YABANCI DİL EĞİTİMİ VEREN ÖZEL BİR EĞİTİM KURUMUNDAKİ ÖĞRENCİLERİN BEKLENTİLERİNİN ARAŞTIRILMASI Sibel SELİM 1 Efe SARIBAY
Dokuz Eylül Üniversitesi Sosyal Bilimler Enstitüsü Dergisi Cilt 5, Sayı:2, 2003 YABANCI DİL EĞİTİMİ VEREN ÖZEL BİR EĞİTİM KURUMUNDAKİ ÖĞRENCİLERİN BEKLENTİLERİNİN ARAŞTIRILMASI Sibel SELİM 1 Efe SARIBAY
YTÜ İktisat Bölümü EKONOMETRİ I Ders Notları
 Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri I Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. ed., 2002, Thomson Learning. Ch. 5: SEKK (OLS) nin Asimptotik Özellikleri
Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri I Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. ed., 2002, Thomson Learning. Ch. 5: SEKK (OLS) nin Asimptotik Özellikleri
YTÜ İktisat Bölümü EKONOMETRİ I Ders Notları
 Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri I Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. ed., 2002, Thomson Learning. Ch. 5: SEKK (OLS) nin Asimptotik Özellikleri
Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri I Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. ed., 2002, Thomson Learning. Ch. 5: SEKK (OLS) nin Asimptotik Özellikleri
Ch. 5: SEKK (OLS) nin Asimptotik Özellikleri
 Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri I Ders Notları Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. ed., 2002, Thomson Learning. Ch. 5: SEKK (OLS) nin Asimptotik
Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri I Ders Notları Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. ed., 2002, Thomson Learning. Ch. 5: SEKK (OLS) nin Asimptotik
Matris Cebiriyle Çoklu Regresyon Modeli
 Matris Cebiriyle Çoklu Regresyon Modeli Hüseyin Taştan Mart 00 Klasik Regresyon Modeli k açıklayıcı değişkenden oluşan regresyon modelini her gözlem i için aşağıdaki gibi yazabiliriz: y i β + β x i + β
Matris Cebiriyle Çoklu Regresyon Modeli Hüseyin Taştan Mart 00 Klasik Regresyon Modeli k açıklayıcı değişkenden oluşan regresyon modelini her gözlem i için aşağıdaki gibi yazabiliriz: y i β + β x i + β
Örnek. Aşağıdaki veri setlerindeki X ve Y veri çiftlerini kullanarak herbir durumda X=1,5 için Y nin hangi değerleri alacağını hesaplayınız.
 Örnek Aşağıdaki veri setlerindeki X ve Y veri çiftlerini kullanarak herbir durumda X=1,5 için Y nin hangi değerleri alacağını hesaplayınız. i. ii. X 1 2 3 4 1 2 3 4 Y 2 3 4 5 4 3 2 1 Örnek Aşağıdaki veri
Örnek Aşağıdaki veri setlerindeki X ve Y veri çiftlerini kullanarak herbir durumda X=1,5 için Y nin hangi değerleri alacağını hesaplayınız. i. ii. X 1 2 3 4 1 2 3 4 Y 2 3 4 5 4 3 2 1 Örnek Aşağıdaki veri
BKİ farkı Standart Sapması (kg/m 2 ) A B BKİ farkı Ortalaması (kg/m 2 )
 4. SUNUM 1 Gözlem ya da deneme sonucu elde edilmiş sonuçların, rastlantıya bağlı olup olmadığının incelenmesinde kullanılan istatistiksel yöntemlere HİPOTEZ TESTLERİ denir. Sonuçların rastlantıya bağlı
4. SUNUM 1 Gözlem ya da deneme sonucu elde edilmiş sonuçların, rastlantıya bağlı olup olmadığının incelenmesinde kullanılan istatistiksel yöntemlere HİPOTEZ TESTLERİ denir. Sonuçların rastlantıya bağlı
İstatistiksel Kavramların Gözden Geçirilmesi
 İstatistiksel Kavramların Gözden Geçirilmesi İstatistiksel Çıkarsama Ekonometri 1 Konu 3 Sürüm 2,0 (Ekim 2011) UADMK Açık Lisans Bilgisi İşbu belge, Creative Commons Attribution-Non-Commercial ShareAlike
İstatistiksel Kavramların Gözden Geçirilmesi İstatistiksel Çıkarsama Ekonometri 1 Konu 3 Sürüm 2,0 (Ekim 2011) UADMK Açık Lisans Bilgisi İşbu belge, Creative Commons Attribution-Non-Commercial ShareAlike
Korelasyon, Korelasyon Türleri ve Regresyon
 Korelasyon, Korelasyon Türleri ve Regresyon İçerik Korelasyon Korelasyon Türleri Korelasyon Katsayısı Regresyon KORELASYON Korelasyon iki ya da daha fazla değişken arasındaki doğrusal ilişkiyi gösterir.
Korelasyon, Korelasyon Türleri ve Regresyon İçerik Korelasyon Korelasyon Türleri Korelasyon Katsayısı Regresyon KORELASYON Korelasyon iki ya da daha fazla değişken arasındaki doğrusal ilişkiyi gösterir.
İÇİNDEKİLER. BÖLÜM 1 Değişkenler ve Grafikler 1. BÖLÜM 2 Frekans Dağılımları 37
 İÇİNDEKİLER BÖLÜM 1 Değişkenler ve Grafikler 1 İstatistik 1 Yığın ve Örnek; Tümevarımcı ve Betimleyici İstatistik 1 Değişkenler: Kesikli ve Sürekli 1 Verilerin Yuvarlanması Bilimsel Gösterim Anlamlı Rakamlar
İÇİNDEKİLER BÖLÜM 1 Değişkenler ve Grafikler 1 İstatistik 1 Yığın ve Örnek; Tümevarımcı ve Betimleyici İstatistik 1 Değişkenler: Kesikli ve Sürekli 1 Verilerin Yuvarlanması Bilimsel Gösterim Anlamlı Rakamlar
İÇİNDEKİLER ÖN SÖZ...
 İÇİNDEKİLER ÖN SÖZ... v GİRİŞ... 1 1. İSTATİSTİK İN TARİHÇESİ... 1 2. İSTATİSTİK NEDİR?... 3 3. SAYISAL BİLGİDEN ANLAM ÇIKARILMASI... 4 4. BELİRSİZLİĞİN ELE ALINMASI... 4 5. ÖRNEKLEME... 5 6. İLİŞKİLERİN
İÇİNDEKİLER ÖN SÖZ... v GİRİŞ... 1 1. İSTATİSTİK İN TARİHÇESİ... 1 2. İSTATİSTİK NEDİR?... 3 3. SAYISAL BİLGİDEN ANLAM ÇIKARILMASI... 4 4. BELİRSİZLİĞİN ELE ALINMASI... 4 5. ÖRNEKLEME... 5 6. İLİŞKİLERİN
2. BASİT DOĞRUSAL REGRESYON 12
 1. GİRİŞ 1 1.1 Regresyon ve Model Kurma / 1 1.2 Veri Toplama / 5 1.3 Regresyonun Kullanım Alanları / 9 1.4 Bilgisayarın Rolü / 10 2. BASİT DOĞRUSAL REGRESYON 12 2.1 Basit Doğrusal Regresyon Modeli / 12
1. GİRİŞ 1 1.1 Regresyon ve Model Kurma / 1 1.2 Veri Toplama / 5 1.3 Regresyonun Kullanım Alanları / 9 1.4 Bilgisayarın Rolü / 10 2. BASİT DOĞRUSAL REGRESYON 12 2.1 Basit Doğrusal Regresyon Modeli / 12
BÖLÜM 6 MERKEZDEN DAĞILMA ÖLÇÜLERİ
 1 BÖLÜM 6 MERKEZDEN DAĞILMA ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel
1 BÖLÜM 6 MERKEZDEN DAĞILMA ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel
YARI LOGARİTMİK MODELLERDE KUKLA DECİşKENLERİN KA TSA YıLARıNIN YORUMU
 Marmara Üniversitesi U.B.F. Dergisi YIL 2005, CİLT XX, SAyı 1 YARI LOGARİTMİK MODELLERDE KUKLA DECİşKENLERİN KA TSA YıLARıNIN YORUMU Yrd. Doç. Dr. Ebru ÇACLAYAN' Arş. Gör. Burak GÜRİş" Büyüme modelleri,
Marmara Üniversitesi U.B.F. Dergisi YIL 2005, CİLT XX, SAyı 1 YARI LOGARİTMİK MODELLERDE KUKLA DECİşKENLERİN KA TSA YıLARıNIN YORUMU Yrd. Doç. Dr. Ebru ÇACLAYAN' Arş. Gör. Burak GÜRİş" Büyüme modelleri,
Ch. 12: Zaman Serisi Regresyonlarında Ardışık Bağıntı (Serial Correlation) ve Değişen Varyans
 Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri II Ders Notları Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. ed., 2002, Thomson Learning. Ch. 12: Zaman Serisi Regresyonlarında
Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri II Ders Notları Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. ed., 2002, Thomson Learning. Ch. 12: Zaman Serisi Regresyonlarında
ORİJİNAL MAKALE / ORIGINAL ARTICLE. Çoklu Doğrusal Bağıntı Varlığında En Küçük Karelere Alternatif Yaklaşım: Ridge Regresyon
 ORİJİNAL MAKALE / ORIGINAL ARTICLE Düzce Üniversitesi Sağlık Bilimleri Enstitüsü Dergisi / DÜ Sağlık Bil Enst Derg Journal of Duzce University Health Sciences Institute / J DU Health Sci Inst ISSN: 2146-443X
ORİJİNAL MAKALE / ORIGINAL ARTICLE Düzce Üniversitesi Sağlık Bilimleri Enstitüsü Dergisi / DÜ Sağlık Bil Enst Derg Journal of Duzce University Health Sciences Institute / J DU Health Sci Inst ISSN: 2146-443X
İstatistik ve Olasılık
 İstatistik ve Olasılık KORELASYON ve REGRESYON ANALİZİ Doç. Dr. İrfan KAYMAZ Tanım Bir değişkenin değerinin diğer değişkendeki veya değişkenlerdeki değişimlere bağlı olarak nasıl etkilendiğinin istatistiksel
İstatistik ve Olasılık KORELASYON ve REGRESYON ANALİZİ Doç. Dr. İrfan KAYMAZ Tanım Bir değişkenin değerinin diğer değişkendeki veya değişkenlerdeki değişimlere bağlı olarak nasıl etkilendiğinin istatistiksel
YTÜ İktisat Bölümü EKONOMETRİ I Ders Notları
 Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri I Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. edition, Thomson Learning Appendix B: Olasılık ve Dağılım Teorisi
Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri I Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. edition, Thomson Learning Appendix B: Olasılık ve Dağılım Teorisi
YTÜ İktisat Bölümü EKONOMETRİ I Ders Notları
 Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri I Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. edition, Thomson Learning Appendix B: Olasılık ve Dağılım Teorisi
Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri I Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. edition, Thomson Learning Appendix B: Olasılık ve Dağılım Teorisi
Appendix B: Olasılık ve Dağılım Teorisi
 Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri I Ders Notları Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. edition, Thomson Learning Appendix B: Olasılık ve Dağılım
Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri I Ders Notları Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. edition, Thomson Learning Appendix B: Olasılık ve Dağılım
Yrd. Doç. Dr. Mehmet Güçlü
 Dersin Adı DERS ÖĞRETİM PLANI Ekonometri I Dersin Kodu ECO 301 Dersin Türü (Zorunlu, Seçmeli) Dersin Seviyesi (Ön Lisans, Lisans, Yüksek Lisans, Doktora) Dersin AKTS Kredisi 6 Haftalık Ders Saati 4 Haftalık
Dersin Adı DERS ÖĞRETİM PLANI Ekonometri I Dersin Kodu ECO 301 Dersin Türü (Zorunlu, Seçmeli) Dersin Seviyesi (Ön Lisans, Lisans, Yüksek Lisans, Doktora) Dersin AKTS Kredisi 6 Haftalık Ders Saati 4 Haftalık
Doç. Dr. Dilek ALTAŞ İSTATİSTİKSEL ANALİZ
 I Doç. Dr. Dilek ALTAŞ İSTATİSTİKSEL ANALİZ II Yayın No : 2845 Teknik Dizisi : 158 1. Baskı Şubat 2013 İSTANBUL ISBN 978-605 - 377 868-4 Copyright Bu kitabın bu basısı için Türkiye deki yayın hakları BETA
I Doç. Dr. Dilek ALTAŞ İSTATİSTİKSEL ANALİZ II Yayın No : 2845 Teknik Dizisi : 158 1. Baskı Şubat 2013 İSTANBUL ISBN 978-605 - 377 868-4 Copyright Bu kitabın bu basısı için Türkiye deki yayın hakları BETA
Örneklemden elde edilen parametreler üzerinden kitle parametreleri tahmin edilmek istenmektedir.
 ÇIKARSAMALI İSTATİSTİKLER Çıkarsamalı istatistikler, örneklemden elde edilen değerler üzerinde kitleyi tanımlamak için uygulanan istatistiksel yöntemlerdir. Çıkarsamalı istatistikler; Tahmin Hipotez Testleri
ÇIKARSAMALI İSTATİSTİKLER Çıkarsamalı istatistikler, örneklemden elde edilen değerler üzerinde kitleyi tanımlamak için uygulanan istatistiksel yöntemlerdir. Çıkarsamalı istatistikler; Tahmin Hipotez Testleri
BİYOİSTATİSTİK DERSLERİ AMAÇ VE HEDEFLERİ
 BİYOİSTATİSTİK DERSLERİ AMAÇ VE HEDEFLERİ DÖNEM I-I. DERS KURULU Konu: Bilimsel yöntem ve istatistik Amaç: Biyoistatistiğin tıptaki önemini kavrar ve sonraki dersler için gerekli terminolojiye hakim olur.
BİYOİSTATİSTİK DERSLERİ AMAÇ VE HEDEFLERİ DÖNEM I-I. DERS KURULU Konu: Bilimsel yöntem ve istatistik Amaç: Biyoistatistiğin tıptaki önemini kavrar ve sonraki dersler için gerekli terminolojiye hakim olur.
KONULAR. 14 Ekim 2012. Ders Kitabı: Introductory Econometrics: A Modern Approach (2nd ed.) J. Wooldridge. 1 Yıldız Teknik Üniversitesi
 ÇOKLU REGRESYON ANALİZİNDE EK KONULAR Hüseyin Taştan 1 1 Yıldız Teknik Üniversitesi İktisat Bölümü Ders Kitabı: Introductory Econometrics: A Modern Approach (2nd ed.) J. Wooldridge 14 Ekim 2012 Ekonometri
ÇOKLU REGRESYON ANALİZİNDE EK KONULAR Hüseyin Taştan 1 1 Yıldız Teknik Üniversitesi İktisat Bölümü Ders Kitabı: Introductory Econometrics: A Modern Approach (2nd ed.) J. Wooldridge 14 Ekim 2012 Ekonometri
BİRDEN ÇOK BAĞIMLI DEĞİŞKENİ OLAN MODELLER
 BİRDEN ÇOK BAĞIMLI DEĞİŞKENİ OLAN MODELLER Birden çok bağımlı değişkenin yer aldığı modelleri incelemek amacıyla kullanılan modeller Birden Çok Bağımlı Değişkenli Regresyon Modelleri ya da kısaca MRM ler
BİRDEN ÇOK BAĞIMLI DEĞİŞKENİ OLAN MODELLER Birden çok bağımlı değişkenin yer aldığı modelleri incelemek amacıyla kullanılan modeller Birden Çok Bağımlı Değişkenli Regresyon Modelleri ya da kısaca MRM ler
Korelasyon ve Regresyon
 Korelasyon ve Regresyon Korelasyon- (lineer korelasyon) Açıklayıcı (Bağımsız) Değişken x çalışma zamanı ayakkabı numarası İki değişken arasındaki ilişkidir. Günlük sigara sayısı SAT puanı boy Yanıt (Bağımlı)
Korelasyon ve Regresyon Korelasyon- (lineer korelasyon) Açıklayıcı (Bağımsız) Değişken x çalışma zamanı ayakkabı numarası İki değişken arasındaki ilişkidir. Günlük sigara sayısı SAT puanı boy Yanıt (Bağımlı)
1.58 arasındaki her bir değeri alabileceği için sürekli bir
 7.SUNUM Hatırlanacağı gibi, kesikli rassal değişkenler sonlu (örneğin; 0, 1, 2,...,10) veya sayılabilir sonsuzlukta (örneğin; 0, 1, 2,...) değerler alabilmektedir. Fakat birçok uygulamada, rassal değişkenin
7.SUNUM Hatırlanacağı gibi, kesikli rassal değişkenler sonlu (örneğin; 0, 1, 2,...,10) veya sayılabilir sonsuzlukta (örneğin; 0, 1, 2,...) değerler alabilmektedir. Fakat birçok uygulamada, rassal değişkenin
ÖRNEK BULGULAR. Tablo 1: Tanımlayıcı özelliklerin dağılımı
 BULGULAR Çalışma tarihleri arasında Hastanesi Kliniği nde toplam 512 olgu ile gerçekleştirilmiştir. Olguların yaşları 18 ile 28 arasında değişmekte olup ortalama 21,10±1,61 yıldır. Olguların %66,4 ü (n=340)
BULGULAR Çalışma tarihleri arasında Hastanesi Kliniği nde toplam 512 olgu ile gerçekleştirilmiştir. Olguların yaşları 18 ile 28 arasında değişmekte olup ortalama 21,10±1,61 yıldır. Olguların %66,4 ü (n=340)
Çoklu Doğrusal Bağlantı Durumunda Ridge ve Temel Bileşenler Regresyon Analiz Yöntemlerinin Kullanımı
 Atatürk Üniversitesi Ziraat Fakültesi Dergisi, 41 (1), 53-57, 2010 Journal of Agricultural Faculty of Atatürk University, 41 (1), 53-57, 2010 ISSN : 1300-9036 Araştırma Makalesi/Research Article Çoklu
Atatürk Üniversitesi Ziraat Fakültesi Dergisi, 41 (1), 53-57, 2010 Journal of Agricultural Faculty of Atatürk University, 41 (1), 53-57, 2010 ISSN : 1300-9036 Araştırma Makalesi/Research Article Çoklu
14 Ekim Ders Kitabı: Introductory Econometrics: A Modern Approach (2nd ed.) J. Wooldridge. 1 Yıldız Teknik Üniversitesi
 DEĞİŞEN VARYANS Hüseyin Taştan 1 1 Yıldız Teknik Üniversitesi İktisat Bölümü Ders Kitabı: Introductory Econometrics: A Modern Approach (2nd ed.) J. Wooldridge 14 Ekim 2012 Ekonometri I: Değişen Varyans
DEĞİŞEN VARYANS Hüseyin Taştan 1 1 Yıldız Teknik Üniversitesi İktisat Bölümü Ders Kitabı: Introductory Econometrics: A Modern Approach (2nd ed.) J. Wooldridge 14 Ekim 2012 Ekonometri I: Değişen Varyans
17 Ekim Ders Kitabı: Introductory Econometrics: A Modern Approach (2nd ed.) J. Wooldridge. 1 Yıldız Teknik Üniversitesi
 ÇOK DEĞİŞKENLİ REGRESYON ANALİZİ: TAHMİN Hüseyin Taştan 1 1 Yıldız Teknik Üniversitesi İktisat Bölümü Ders Kitabı: Introductory Econometrics: A Modern Approach (2nd ed.) J. Wooldridge 17 Ekim 2012 Ekonometri
ÇOK DEĞİŞKENLİ REGRESYON ANALİZİ: TAHMİN Hüseyin Taştan 1 1 Yıldız Teknik Üniversitesi İktisat Bölümü Ders Kitabı: Introductory Econometrics: A Modern Approach (2nd ed.) J. Wooldridge 17 Ekim 2012 Ekonometri
OLS Yönteminin Asimptotik (Büyük Örneklem) Özellikleri SIRADAN EN KÜÇÜK KARELER (OLS) Asimptotik Özellikler: Tutarlılık. Asimptotik Özellikler
 1 SIRADAN EN KÜÇÜK KARELER (OLS) YÖNTEMİNİN ASİMPTOTİK ÖZELLİKLERİ Hüseyin Taştan 1 1 Yıldız Teknik Üniversitesi İktisat Bölümü Ders Kitabı: Introductory Econometrics: A Modern Approach (2nd ed.) J. Wooldridge
1 SIRADAN EN KÜÇÜK KARELER (OLS) YÖNTEMİNİN ASİMPTOTİK ÖZELLİKLERİ Hüseyin Taştan 1 1 Yıldız Teknik Üniversitesi İktisat Bölümü Ders Kitabı: Introductory Econometrics: A Modern Approach (2nd ed.) J. Wooldridge
2. REGRESYON ANALİZİNİN TEMEL KAVRAMLARI Tanım
 2. REGRESYON ANALİZİNİN TEMEL KAVRAMLARI 2.1. Tanım Regresyon analizi, bir değişkenin başka bir veya daha fazla değişkene olan bağımlılığını inceler. Amaç, bağımlı değişkenin kitle ortalamasını, açıklayıcı
2. REGRESYON ANALİZİNİN TEMEL KAVRAMLARI 2.1. Tanım Regresyon analizi, bir değişkenin başka bir veya daha fazla değişkene olan bağımlılığını inceler. Amaç, bağımlı değişkenin kitle ortalamasını, açıklayıcı
Japon bıldırcınlarında yumurta ak indeksinin ridge regresyon yöntemiyle tahmin edilmesi *
 Akademik Ziraat Dergisi (): -20 (202) ISSN: 247-6403 http://azd.odu.edu.tr Araştırma (Research) Japon bıldırcınlarında yumurta ak indeksinin ridge regresyon yöntemiyle tahmin edilmesi * Fatih ÜÇKARDEŞ,
Akademik Ziraat Dergisi (): -20 (202) ISSN: 247-6403 http://azd.odu.edu.tr Araştırma (Research) Japon bıldırcınlarında yumurta ak indeksinin ridge regresyon yöntemiyle tahmin edilmesi * Fatih ÜÇKARDEŞ,
SIRADAN EN KÜÇÜK KARELER (OLS)
 SIRADAN EN KÜÇÜK KARELER (OLS) YÖNTEMİNİN ASİMPTOTİK ÖZELLİKLERİ Hüseyin Taştan 1 1 Yıldız Teknik Üniversitesi İktisat Bölümü Ders Kitabı: Introductory Econometrics: A Modern Approach (2nd ed.) J. Wooldridge
SIRADAN EN KÜÇÜK KARELER (OLS) YÖNTEMİNİN ASİMPTOTİK ÖZELLİKLERİ Hüseyin Taştan 1 1 Yıldız Teknik Üniversitesi İktisat Bölümü Ders Kitabı: Introductory Econometrics: A Modern Approach (2nd ed.) J. Wooldridge
YTÜ İktisat Bölümü EKONOMETRİ I Ders Notları
 Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri I Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. edition, Thomson Learning Appendix C: İstatistiksel Çıkarsama Doç.
Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri I Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. edition, Thomson Learning Appendix C: İstatistiksel Çıkarsama Doç.
Appendix C: İstatistiksel Çıkarsama
 Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri I Ders Notları Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. edition, Thomson Learning Appendix C: İstatistiksel Çıkarsama
Yıldız Teknik Üniversitesi İktisat Bölümü Ekonometri I Ders Notları Ders Kitabı: J.M. Wooldridge, Introductory Econometrics A Modern Approach, 2nd. edition, Thomson Learning Appendix C: İstatistiksel Çıkarsama
Temel İstatistik. Y.Doç.Dr. İbrahim Turan Mart Tanımlayıcı İstatistik. Dağılımları Tanımlayıcı Ölçüler Dağılış Ölçüleri
 Temel İstatistik Tanımlayıcı İstatistik Dağılımları Tanımlayıcı Ölçüler Dağılış Ölçüleri Y.Doç.Dr. İbrahim Turan Mart 2011 DAĞILIM / YAYGINLIK ÖLÇÜLERİ Verilerin değişkenlik durumu ve dağılışın şeklini
Temel İstatistik Tanımlayıcı İstatistik Dağılımları Tanımlayıcı Ölçüler Dağılış Ölçüleri Y.Doç.Dr. İbrahim Turan Mart 2011 DAĞILIM / YAYGINLIK ÖLÇÜLERİ Verilerin değişkenlik durumu ve dağılışın şeklini
BASİT REGRESYON MODELİ
 BASİT REGRESYON MODELİ Hüseyin Taştan 1 1 Yıldız Teknik Üniversitesi İktisat Bölümü Ders Kitabı: Introductory Econometrics: A Modern Approach (2nd ed.) J. Wooldridge 14 Ekim 2012 Ekonometri I: Basit Regresyon
BASİT REGRESYON MODELİ Hüseyin Taştan 1 1 Yıldız Teknik Üniversitesi İktisat Bölümü Ders Kitabı: Introductory Econometrics: A Modern Approach (2nd ed.) J. Wooldridge 14 Ekim 2012 Ekonometri I: Basit Regresyon
YILLARI ARASINDA GÜNEY CAROLINA DA OKUL İÇİ ŞİDDET İSTATİSKLERİ ANALİZİ (Bir Önceki Projeden Devam Edilecektir)
 1996-1998 YILLARI ARASINDA GÜNEY CAROLINA DA OKUL İÇİ ŞİDDET İSTATİSKLERİ ANALİZİ (Bir Önceki Projeden Devam Edilecektir) Hazırlayan : Süleyman Öğrekçi 1996 ve 1998 yılları arasında Güney Carolina da resmi
1996-1998 YILLARI ARASINDA GÜNEY CAROLINA DA OKUL İÇİ ŞİDDET İSTATİSKLERİ ANALİZİ (Bir Önceki Projeden Devam Edilecektir) Hazırlayan : Süleyman Öğrekçi 1996 ve 1998 yılları arasında Güney Carolina da resmi
İÇİNDEKİLER ÖNSÖZ... Örneklem Genişliğinin Elde edilmesi... 1
 İÇİNDEKİLER ÖNSÖZ... v 1. BÖLÜM Örneklem Genişliğinin Elde edilmesi... 1 1.1. Kitle ve Parametre... 1 1.2. Örneklem ve Tahmin Edici... 2 1.3. Basit Rastgele Örnekleme... 3 1.4. Tabakalı Rastgele Örnekleme...
İÇİNDEKİLER ÖNSÖZ... v 1. BÖLÜM Örneklem Genişliğinin Elde edilmesi... 1 1.1. Kitle ve Parametre... 1 1.2. Örneklem ve Tahmin Edici... 2 1.3. Basit Rastgele Örnekleme... 3 1.4. Tabakalı Rastgele Örnekleme...
H.Ü. Bilgi ve Belge Yönetimi Bölümü BBY 208 Sosyal Bilimlerde Araştırma Yöntemleri II (Bahar 2012) SPSS Ders Notları II (19 Nisan 2012)
 H.Ü. Bilgi ve Belge Yönetimi Bölümü BBY 208 Sosyal Bilimlerde Araştırma Yöntemleri II (Bahar 2012) SPSS Ders Notları II (19 Nisan 2012) Aşağıdaki analizlerde lise öğrencileri veri dosyası kullanılmıştır.
H.Ü. Bilgi ve Belge Yönetimi Bölümü BBY 208 Sosyal Bilimlerde Araştırma Yöntemleri II (Bahar 2012) SPSS Ders Notları II (19 Nisan 2012) Aşağıdaki analizlerde lise öğrencileri veri dosyası kullanılmıştır.
LOJİSTİK REGRESYON ANALİZİ
 LOJİSTİK REGRESYON ANALİZİ Lojistik Regresyon Analizini daha kolay izleyebilmek için bazı terimleri tanımlayalım: 1. Değişken (incelenen özellik): Bireyden bireye farklı değerler alabilen özellik, fenomen
LOJİSTİK REGRESYON ANALİZİ Lojistik Regresyon Analizini daha kolay izleyebilmek için bazı terimleri tanımlayalım: 1. Değişken (incelenen özellik): Bireyden bireye farklı değerler alabilen özellik, fenomen
DEĞİŞEN VARYANS DURUMUNDA EN KÜÇÜK KARELER TEKNİĞİNİN ALTERNATİFİ AĞIRLIKLI REGRESYON ANALİZİ VE BİR UYGULAMA
 DEĞİŞEN VARYANS DURUMUNDA EN KÜÇÜK KARELER TEKNİĞİNİN ALTERNATİFİ AĞIRLIKLI REGRESYON ANALİZİ VE BİR UYGULAMA Yrd.Doç.Dr. Ali Sait ALBAYRAK * ÖZET Bu çalışmanın amacı, en küçük kareler (EKK) tekniğinin
DEĞİŞEN VARYANS DURUMUNDA EN KÜÇÜK KARELER TEKNİĞİNİN ALTERNATİFİ AĞIRLIKLI REGRESYON ANALİZİ VE BİR UYGULAMA Yrd.Doç.Dr. Ali Sait ALBAYRAK * ÖZET Bu çalışmanın amacı, en küçük kareler (EKK) tekniğinin
4. TAHMİN SONUÇLARININ DEĞERLENDİRİLMESİ Katsayıların Yorumu
 4. TAHMİN SONUÇLARININ DEĞERLENDİRİLMESİ 4.1. Katsayıların Yorumu Y i = β 0 + β 1 X 1i + β X i + + β k X ki + u i gibi çok açıklayıcı değişkene sahip bir modelde, anakütle regresyon fonksiyonu, E(Y i X
4. TAHMİN SONUÇLARININ DEĞERLENDİRİLMESİ 4.1. Katsayıların Yorumu Y i = β 0 + β 1 X 1i + β X i + + β k X ki + u i gibi çok açıklayıcı değişkene sahip bir modelde, anakütle regresyon fonksiyonu, E(Y i X
Akdeniz Üniversitesi
 F. Ders Tanıtım Formu Dersin Adı Öğretim Dili EKONOMETRİ I Türkçe Dersin Verildiği Düzey Ön Lisans ( ) Lisans (x ) Yüksek Lisans( ) Doktora( ) Eğitim Öğretim Sistemi Örgün Öğretim (x ) İkinci Örgün Öğretim
F. Ders Tanıtım Formu Dersin Adı Öğretim Dili EKONOMETRİ I Türkçe Dersin Verildiği Düzey Ön Lisans ( ) Lisans (x ) Yüksek Lisans( ) Doktora( ) Eğitim Öğretim Sistemi Örgün Öğretim (x ) İkinci Örgün Öğretim
ÇOKLU REGRESYON ANALİZİNDE VARSAYIMLARDAN SAPMALARIN İNCELENMESİ
 ÇOKLU REGRESYON ANALİZİNDE VARSAYIMLARDAN SAPMALARIN İNCELENMESİ 1. ÇOKLU REGRESYON ANALİZİ VE VARSAYIMALARDAN SAPMALAR 1.1. Çoklu Regresyon modeli Varsayımları 1.2. Tahmincilerin anlamlılığının sınanması
ÇOKLU REGRESYON ANALİZİNDE VARSAYIMLARDAN SAPMALARIN İNCELENMESİ 1. ÇOKLU REGRESYON ANALİZİ VE VARSAYIMALARDAN SAPMALAR 1.1. Çoklu Regresyon modeli Varsayımları 1.2. Tahmincilerin anlamlılığının sınanması
14 Ekim 2012. Ders Kitabı: Introductory Econometrics: A Modern Approach (2nd ed.) J. Wooldridge. 1 Yıldız Teknik Üniversitesi
 ÇOK DEĞİŞKENLİ REGRESYON ANALİZİ: ÇIKARSAMA Hüseyin Taştan 1 1 Yıldız Teknik Üniversitesi İktisat Bölümü Ders Kitabı: Introductory Econometrics: A Modern Approach (2nd ed.) J. Wooldridge 14 Ekim 2012 Ekonometri
ÇOK DEĞİŞKENLİ REGRESYON ANALİZİ: ÇIKARSAMA Hüseyin Taştan 1 1 Yıldız Teknik Üniversitesi İktisat Bölümü Ders Kitabı: Introductory Econometrics: A Modern Approach (2nd ed.) J. Wooldridge 14 Ekim 2012 Ekonometri
ANADOLU ÜNİVERSİTESİ REGRESYON KATSAYILARININ GÜVEN ARALIĞI = + REGRESYON KATSAYILARININ GÜVEN ARALIĞI
 ANADOLU ÜNİVERSİTESİ Deney Tasarımı ve Regresyon Analizi Regresyonda Güven Aralıkları ve Hipotez Testleri Doç. Dr. Nihal ERGİNEL-2015 REGRESYON KATSAYILARININ GÜVEN ARALIĞI + in güven aralığı : i-) n 30
ANADOLU ÜNİVERSİTESİ Deney Tasarımı ve Regresyon Analizi Regresyonda Güven Aralıkları ve Hipotez Testleri Doç. Dr. Nihal ERGİNEL-2015 REGRESYON KATSAYILARININ GÜVEN ARALIĞI + in güven aralığı : i-) n 30
YANLILIK. Yanlılık örneklem istatistiği değerlerinin evren parametre değerinden herhangi bir sistematik sapması olarak tanımlanır.
 AED 310 İSTATİSTİK YANLILIK Yanlılık örneklem istatistiği değerlerinin evren parametre değerinden herhangi bir sistematik sapması olarak tanımlanır. YANLILIK Yanlı bir araştırma tasarımı uygulandığında,
AED 310 İSTATİSTİK YANLILIK Yanlılık örneklem istatistiği değerlerinin evren parametre değerinden herhangi bir sistematik sapması olarak tanımlanır. YANLILIK Yanlı bir araştırma tasarımı uygulandığında,
DOĞRUSAL ZAMAN SERİSİ MODELLERİ. Durağan ARIMA Modelleri: Otoregresiv Modeller AR(p) Süreci
 DOĞRUSAL ZAMAN SERİSİ MODELLERİ Durağan ARIMA Modelleri: Otoregresiv Modeller AR(p) Süreci Tek Değişkenli Zaman Serisi Modelleri Ekonomik verilerin analizi ile ekonomik değişkenlerin gelecekte alabilecekleri
DOĞRUSAL ZAMAN SERİSİ MODELLERİ Durağan ARIMA Modelleri: Otoregresiv Modeller AR(p) Süreci Tek Değişkenli Zaman Serisi Modelleri Ekonomik verilerin analizi ile ekonomik değişkenlerin gelecekte alabilecekleri
DERS BİLGİLERİ Ders Kodu Yarıyıl T+U Saat Kredi AKTS Çok Değişkenli İstatistik EKO428 Bahar Ön Koşul Dersin Dili
 DERS BİLGİLERİ Ders Kodu Yarıyıl T+U Saat Kredi AKTS Çok Değişkenli İstatistik EKO428 Bahar 3+0 3 3 Ön Koşul Yok Dersin Dili Türkçe Dersin Seviyesi Lisans Dersin Türü Seçmeli Dersi Veren Öğretim Elemanı
DERS BİLGİLERİ Ders Kodu Yarıyıl T+U Saat Kredi AKTS Çok Değişkenli İstatistik EKO428 Bahar 3+0 3 3 Ön Koşul Yok Dersin Dili Türkçe Dersin Seviyesi Lisans Dersin Türü Seçmeli Dersi Veren Öğretim Elemanı
BİYOİSTATİSTİK Korelasyon Analizi Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH
 BİYOİSTATİSTİK Korelasyon Analizi Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 Bir değişkenin değerinin,
BİYOİSTATİSTİK Korelasyon Analizi Yrd. Doç. Dr. Aslı SUNER KARAKÜLAH Ege Üniversitesi, Tıp Fakültesi, Biyoistatistik ve Tıbbi Bilişim AD. Web: www.biyoistatistik.med.ege.edu.tr 1 Bir değişkenin değerinin,
PARAMETRİK TESTLER. Tek Örneklem t-testi. 200 öğrencinin matematik dersinden aldıkları notların ortalamasının 70 e eşit olup olmadığını test ediniz.
 PARAMETRİK TESTLER Tek Örneklem t-testi 200 öğrencinin matematik dersinden aldıkları notların ortalamasının 70 e eşit olup olmadığını test ediniz. H0 (boş hipotez): 200 öğrencinin matematik dersinden aldıkları
PARAMETRİK TESTLER Tek Örneklem t-testi 200 öğrencinin matematik dersinden aldıkları notların ortalamasının 70 e eşit olup olmadığını test ediniz. H0 (boş hipotez): 200 öğrencinin matematik dersinden aldıkları
ÜSTEL DÜZLEŞTİRME YÖNTEMİ
 ÜSEL DÜLEŞİRME YÖNEMİ ÜSEL DÜLEŞİRME YÖNEMİ Bu bölüme kadar anlatılan yöntemler zaman içinde değişmeyen parametre varsayımına uygun serilerin tahminlerinde kullanılmaktaydı. Bu tür seriler deterministik
ÜSEL DÜLEŞİRME YÖNEMİ ÜSEL DÜLEŞİRME YÖNEMİ Bu bölüme kadar anlatılan yöntemler zaman içinde değişmeyen parametre varsayımına uygun serilerin tahminlerinde kullanılmaktaydı. Bu tür seriler deterministik
ZAMAN SERİLERİNDE REGRESYON ANALİZİ
 ZAMAN SERİLERİNDE REGRESYON ANALİZİ 1 1. GİRİŞ Trent, serinin genelinde yukarıya ya da aşağıya doğru olan hareketlere denmektedir. Bu hareket bazen düz bir doğru şeklinde olmaktadır. Bu tür harekete sahip
ZAMAN SERİLERİNDE REGRESYON ANALİZİ 1 1. GİRİŞ Trent, serinin genelinde yukarıya ya da aşağıya doğru olan hareketlere denmektedir. Bu hareket bazen düz bir doğru şeklinde olmaktadır. Bu tür harekete sahip
İçindekiler. Ön Söz... xiii
 İçindekiler Ön Söz.................................................... xiii Bölüm 1 İstatistiğe Giriş....................................... 1 1.1 Giriş......................................................1
İçindekiler Ön Söz.................................................... xiii Bölüm 1 İstatistiğe Giriş....................................... 1 1.1 Giriş......................................................1
Regresyon. Regresyon korelasyon ile yakından ilişkilidir
 Regresyon Regresyona Giriş Regresyon korelasyon ile yakından ilişkilidir Regresyon bir bağımlı değişken ile (DV) bir veya daha fazla bağımsız değişken arasındaki doğrusal ilişkiyi inceler. DV için başka
Regresyon Regresyona Giriş Regresyon korelasyon ile yakından ilişkilidir Regresyon bir bağımlı değişken ile (DV) bir veya daha fazla bağımsız değişken arasındaki doğrusal ilişkiyi inceler. DV için başka
DİNAMİK PANEL VERİ MODELLERİ. FYT Panel Veri Ekonometrisi 1
 DİNAMİK PANEL VERİ MODELLERİ FYT Panel Veri Ekonometrisi 1 Dinamik panel veri modeli (tek gecikme için) aşağıdaki gibi gösterilebilir; y it y it 1 x v it ' it i Gecikmeli bağımlı değişkenden başka açıklayıcı
DİNAMİK PANEL VERİ MODELLERİ FYT Panel Veri Ekonometrisi 1 Dinamik panel veri modeli (tek gecikme için) aşağıdaki gibi gösterilebilir; y it y it 1 x v it ' it i Gecikmeli bağımlı değişkenden başka açıklayıcı
BAĞIMLI KUKLA DEĞİŞKENLİ MODELLER A- KADININ İŞGÜCÜNE KATILIM MODELİ NİN DOM İLE E-VIEWS DA ÇÖZÜMÜ
 BAĞIMLI KUKLA DEĞİŞKENLİ MODELLER A- KADININ İŞGÜCÜNE KATILIM MODELİ NİN DOM İLE E-VIEWS DA ÇÖZÜMÜ Modeldeki değişken tanımları aşağıdaki gibidir: IS= 1 i.kadının bir işi varsa (ya da iş arıyorsa) 0 Diğer
BAĞIMLI KUKLA DEĞİŞKENLİ MODELLER A- KADININ İŞGÜCÜNE KATILIM MODELİ NİN DOM İLE E-VIEWS DA ÇÖZÜMÜ Modeldeki değişken tanımları aşağıdaki gibidir: IS= 1 i.kadının bir işi varsa (ya da iş arıyorsa) 0 Diğer
Örnek 4.1: Tablo 2 de verilen ham verilerin aritmetik ortalamasını hesaplayınız.
 .4. Merkezi Eğilim ve Dağılım Ölçüleri Merkezi eğilim ölçüleri kitleye ilişkin bir değişkenin bütün farklı değerlerinin çevresinde toplandığı merkezi bir değeri gösterirler. Dağılım ölçüleri ise değişkenin
.4. Merkezi Eğilim ve Dağılım Ölçüleri Merkezi eğilim ölçüleri kitleye ilişkin bir değişkenin bütün farklı değerlerinin çevresinde toplandığı merkezi bir değeri gösterirler. Dağılım ölçüleri ise değişkenin
ELEKTRONİK MÜHENDİSLİĞİ NDE KİMYA EĞİTİMİNİN GEREKLİLİĞİNİN İKİ DEĞİŞKENLİ KORELASYON YÖNTEMİ İLE İSTATİSTİKSEL OLARAK İNCELENMESİ
 ELEKTRONİK MÜHENDİSLİĞİ NDE KİMYA EĞİTİMİNİN GEREKLİLİĞİNİN İKİ DEĞİŞKENLİ KORELASYON YÖNTEMİ İLE İSTATİSTİKSEL OLARAK İNCELENMESİ Güven SAĞDIÇ Dokuz Eylül Üniversitesi Mühendislik Fakültesi Elektrik-Elektronik
ELEKTRONİK MÜHENDİSLİĞİ NDE KİMYA EĞİTİMİNİN GEREKLİLİĞİNİN İKİ DEĞİŞKENLİ KORELASYON YÖNTEMİ İLE İSTATİSTİKSEL OLARAK İNCELENMESİ Güven SAĞDIÇ Dokuz Eylül Üniversitesi Mühendislik Fakültesi Elektrik-Elektronik
QUANTILE REGRESYON * Quantile Regression
 QUANTILE REGRESYON * Quantile Regression Fikriye KURTOĞLU İstatistik Anabilim Dalı Olcay ARSLAN İstatistik Anabilim Dalı ÖZET Bu çalışmada, Lineer Regresyon analizinde kullanılan en küçük kareler yöntemine
QUANTILE REGRESYON * Quantile Regression Fikriye KURTOĞLU İstatistik Anabilim Dalı Olcay ARSLAN İstatistik Anabilim Dalı ÖZET Bu çalışmada, Lineer Regresyon analizinde kullanılan en küçük kareler yöntemine
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 6- İSTATİSTİK VE REGRESYON ANALİZİ Doç. Dr. Ali Rıza YILDIZ 1 İSTATİSTİK VE REGRESYON ANALİZİ Bütün noktalardan geçen bir denklem bulmak yerine noktaları temsil eden, yani
MAK 210 SAYISAL ANALİZ BÖLÜM 6- İSTATİSTİK VE REGRESYON ANALİZİ Doç. Dr. Ali Rıza YILDIZ 1 İSTATİSTİK VE REGRESYON ANALİZİ Bütün noktalardan geçen bir denklem bulmak yerine noktaları temsil eden, yani
Normal Dağılımlılık. EKK tahmincilerinin ihtimal dağılımları u i nin ihtimal dağılımı hakkında yapılan varsayıma bağlıdır.
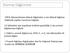 Normal Dağılımlılık EKK tahmincilerinin ihtimal dağılımları u i nin ihtimal dağılımı hakkında yapılan varsayıma bağlıdır. b tahminleri için uygulanan testlerin geçerliliği u i nin normal dağılmasına bağlıdır.
Normal Dağılımlılık EKK tahmincilerinin ihtimal dağılımları u i nin ihtimal dağılımı hakkında yapılan varsayıma bağlıdır. b tahminleri için uygulanan testlerin geçerliliği u i nin normal dağılmasına bağlıdır.
Meslek lisesi ve devlet lisesine giden N tane öğrenci olduğu ve bunların yıllık okul harcamalarına ait verilerin olduğu varsayılsın.
 KUKLA DEĞİŞKENLİ MODELLER Bir kukla değişkenli modeller (Varyans Analiz Modelleri) Kukla değişkenlerin diğer kantitatif değişkenlerle alındığı modeller (Kovaryans Analizi Modeller) Kukla değişkenlerin
KUKLA DEĞİŞKENLİ MODELLER Bir kukla değişkenli modeller (Varyans Analiz Modelleri) Kukla değişkenlerin diğer kantitatif değişkenlerle alındığı modeller (Kovaryans Analizi Modeller) Kukla değişkenlerin
8.Hafta. Değişkenlik Ölçüleri. Öğr.Gör.Muhsin ÇELİK. Uygun değişkenlik ölçüsünü hesaplayıp yorumlayabilecek,
 İSTATİSTİK 8.Hafta Değişkenlik Ölçüleri Hedefler Bu üniteyi çalıştıktan sonra; Uygun değişkenlik ölçüsünü hesaplayıp yorumlayabilecek, Serilerin birbirlerine değişkenliklerini yorumlayabileceksiniz. 2
İSTATİSTİK 8.Hafta Değişkenlik Ölçüleri Hedefler Bu üniteyi çalıştıktan sonra; Uygun değişkenlik ölçüsünü hesaplayıp yorumlayabilecek, Serilerin birbirlerine değişkenliklerini yorumlayabileceksiniz. 2
BÖLÜM 12 STUDENT T DAĞILIMI
 1 BÖLÜM 12 STUDENT T DAĞILIMI 'Student t dağılımı' ya da kısaca 't dağılımı'; normal dağılım ve Z dağılımının da içerisinde bulunduğu 'sürekli olasılık dağılımları' ailesinde yer alan dağılımlardan bir
1 BÖLÜM 12 STUDENT T DAĞILIMI 'Student t dağılımı' ya da kısaca 't dağılımı'; normal dağılım ve Z dağılımının da içerisinde bulunduğu 'sürekli olasılık dağılımları' ailesinde yer alan dağılımlardan bir
Oluşturulan evren listesinden örnekleme birimlerinin seçkisiz olarak çekilmesidir
 Bilimsel Araştırma Yöntemleri Prof. Dr. Şener Büyüköztürk Doç. Dr. Ebru Kılıç Çakmak Yrd. Doç. Dr. Özcan Erkan Akgün Doç. Dr. Şirin Karadeniz Dr. Funda Demirel Örnekleme Yöntemleri Evren Evren, araştırma
Bilimsel Araştırma Yöntemleri Prof. Dr. Şener Büyüköztürk Doç. Dr. Ebru Kılıç Çakmak Yrd. Doç. Dr. Özcan Erkan Akgün Doç. Dr. Şirin Karadeniz Dr. Funda Demirel Örnekleme Yöntemleri Evren Evren, araştırma
Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü
 Mühendislikte İstatistiksel Yöntemler Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü 1 Araştırma sonuçlarının açıklanmasında frekans tablosu
Mühendislikte İstatistiksel Yöntemler Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü 1 Araştırma sonuçlarının açıklanmasında frekans tablosu
Normal Dağılımlılık. EKK tahmincilerinin ihtimal dağılımları u i nin ihtimal dağılımı hakkında yapılan varsayıma bağlıdır.
 Normal Dağılımlılık EKK tahmincilerinin ihtimal dağılımları u i nin ihtimal dağılımı hakkında yapılan varsayıma bağlıdır. β tahminleri için uygulanan testlerin geçerliliği u i nin normal dağılmasına bağlıdır.
Normal Dağılımlılık EKK tahmincilerinin ihtimal dağılımları u i nin ihtimal dağılımı hakkında yapılan varsayıma bağlıdır. β tahminleri için uygulanan testlerin geçerliliği u i nin normal dağılmasına bağlıdır.
EME 3117 SİSTEM SIMÜLASYONU. Girdi Analizi. Özet İstatistikler ve Histogram (Minitab)(1) Örnek: Eczane İçin Servis Süreleri
 EME 3117 1 2 Girdi Analizi SİSTEM SIMÜLASYONU Modellenecek sistemi (prosesi) dokümante et. Veri toplamak için bir plan geliştir. Veri topla. Verilerin grafiksel ve istatistiksel analizini yap. Girdi Analizi-I
EME 3117 1 2 Girdi Analizi SİSTEM SIMÜLASYONU Modellenecek sistemi (prosesi) dokümante et. Veri toplamak için bir plan geliştir. Veri topla. Verilerin grafiksel ve istatistiksel analizini yap. Girdi Analizi-I
ÖNGÖRÜ TEKNĐKLERĐ ÖDEV 5 (KEY)
 ÖNGÖRÜ TEKNĐKLERĐ ÖDEV (KEY) Aşağıda verilen Y zaman sersisi bir ürünle ilgili satışları,aylar itibariyle, gösteren bir seridir. a) Bu serinin garfiğini çizip serinin taşıdığı desenleri (Trend, mevsimsellik
ÖNGÖRÜ TEKNĐKLERĐ ÖDEV (KEY) Aşağıda verilen Y zaman sersisi bir ürünle ilgili satışları,aylar itibariyle, gösteren bir seridir. a) Bu serinin garfiğini çizip serinin taşıdığı desenleri (Trend, mevsimsellik
SÜREKLİ RASSAL DEĞİŞKENLER
 SÜREKLİ RASSAL DEĞİŞKENLER Sürekli Rassal Değişkenler Sürekli Rassal Değişken: Değerleriölçümyadatartımla elde edilen, bir başka anlatımla sayımla elde edilemeyen, değişkene sürekli rassal değişken denir.
SÜREKLİ RASSAL DEĞİŞKENLER Sürekli Rassal Değişkenler Sürekli Rassal Değişken: Değerleriölçümyadatartımla elde edilen, bir başka anlatımla sayımla elde edilemeyen, değişkene sürekli rassal değişken denir.
Kullanılacak İstatistikleri Belirleme Ölçütleri. Değişkenin Ölçek Türü ya da Yapısı
 ARAŞTIRMA MODELLİLERİNDE KULLANILACAK İSTATİSTİKLERİ BELİRLEME ÖLÇÜTLERİ Parametrik mi Parametrik Olmayan mı? Kullanılacak İstatistikleri Belirleme Ölçütleri Değişken Sayısı Tek değişkenli (X) İki değişkenli
ARAŞTIRMA MODELLİLERİNDE KULLANILACAK İSTATİSTİKLERİ BELİRLEME ÖLÇÜTLERİ Parametrik mi Parametrik Olmayan mı? Kullanılacak İstatistikleri Belirleme Ölçütleri Değişken Sayısı Tek değişkenli (X) İki değişkenli
Çoklu Regresyon Korelasyon Analizinde Varsayımdan Sapmalar ve Çimento Sektörü Üzerine Uygulama *
 Çoklu Regresyon Korelasyon Analizinde Varsayımdan Sapmalar ve Çimento Sektörü Üzerine Uygulama * Erkan SEVİNÇ ** Giriş Bu çalışmada İMKB de taş ve toprağa dayalı sanayi altında işlem gören şirketlerin
Çoklu Regresyon Korelasyon Analizinde Varsayımdan Sapmalar ve Çimento Sektörü Üzerine Uygulama * Erkan SEVİNÇ ** Giriş Bu çalışmada İMKB de taş ve toprağa dayalı sanayi altında işlem gören şirketlerin
Sistolik Kan Basıncının Tahmininde Yanlı Regresyon Yöntemlerinin Kullanılması +
 ARAŞTIRMA / RESEARCH REPORT İnönü Üniversitesi Tıp Fakültesi Dergisi 2010;17(4):347-53 Sistolik Kan Basıncının Tahmininde Yanlı Regresyon Yöntemlerinin Kullanılması + Esra Pamukçu*, Cemil Çolak**, Sinan
ARAŞTIRMA / RESEARCH REPORT İnönü Üniversitesi Tıp Fakültesi Dergisi 2010;17(4):347-53 Sistolik Kan Basıncının Tahmininde Yanlı Regresyon Yöntemlerinin Kullanılması + Esra Pamukçu*, Cemil Çolak**, Sinan
Student t Testi. Doç. Dr. Ertuğrul ÇOLAK. Eskişehir Osmangazi Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı
 Student t Testi Doç. Dr. Ertuğrul ÇOLAK Eskişehir Osmangazi Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı Konu Başlıkları Tek örnek t testi SPSS de tek örnek t testi uygulaması Bağımsız iki örnek
Student t Testi Doç. Dr. Ertuğrul ÇOLAK Eskişehir Osmangazi Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı Konu Başlıkları Tek örnek t testi SPSS de tek örnek t testi uygulaması Bağımsız iki örnek
TABLO I: Bağımlı değişken; Tüketim,- bağımsız değişkenler; gelir ve fiyat olmak üzere değişkenlere ait veriler verilmiştir.
 EKONOMETRİ II Uygulama - Otokorelasyon TABLO I: Bağımlı değişken; Tüketim,- bağımsız değişkenler; gelir ve fiyat olmak üzere Tuketim 58 Gelir 3959 Fiyat 312 değişkenlere ait veriler verilmiştir. 56 3858
EKONOMETRİ II Uygulama - Otokorelasyon TABLO I: Bağımlı değişken; Tüketim,- bağımsız değişkenler; gelir ve fiyat olmak üzere Tuketim 58 Gelir 3959 Fiyat 312 değişkenlere ait veriler verilmiştir. 56 3858
ÇOKLU REGRESYON MODELİ. Bir bağımlı değişkene etki eden çok sayıda bağımsız değişkeni analize dahil ederek çoklu regresyon modeli uygulanabilir.
 ÇOKLU REGRESYON MODELİ Bir bağımlı değişkene etki eden çok sayıda bağımsız değişkeni analize dahil ederek çoklu regresyon modeli uygulanabilir. Y=b 1 + b X + b X + u Y=b 1 + b X + b X +...+ b k X k + u
ÇOKLU REGRESYON MODELİ Bir bağımlı değişkene etki eden çok sayıda bağımsız değişkeni analize dahil ederek çoklu regresyon modeli uygulanabilir. Y=b 1 + b X + b X + u Y=b 1 + b X + b X +...+ b k X k + u
SİSTOLİK KAN BASINCINI ETKİLEYEBİLECEK FAKTÖRLERİN RİDGE REGRESYON ANALİZİ İLE İNCELENMESİ VE ÇOKLU BAĞLANTI PROBLEMİ
 T.C. FIRAT ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ SİSTOLİK KAN BASINCINI ETKİLEYEBİLECEK FAKTÖRLERİN RİDGE REGRESYON ANALİZİ İLE İNCELENMESİ VE ÇOKLU BAĞLANTI PROBLEMİ YÜKSEK LİSANS TEZİ Esra PAMUKÇU Anabilim
T.C. FIRAT ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ SİSTOLİK KAN BASINCINI ETKİLEYEBİLECEK FAKTÖRLERİN RİDGE REGRESYON ANALİZİ İLE İNCELENMESİ VE ÇOKLU BAĞLANTI PROBLEMİ YÜKSEK LİSANS TEZİ Esra PAMUKÇU Anabilim
IİSTATIİSTIİK. Mustafa Sezer PEHLI VAN
 IİSTATIİSTIİK Mustafa Sezer PEHLI VAN İstatistik nedir? İstatistik, veri anlamına gelir, İstatistik, sayılarla uğraşan bir bilim dalıdır, İstatistik, eksik bilgiler kullanarak doğru sonuçlara ulaştıran
IİSTATIİSTIİK Mustafa Sezer PEHLI VAN İstatistik nedir? İstatistik, veri anlamına gelir, İstatistik, sayılarla uğraşan bir bilim dalıdır, İstatistik, eksik bilgiler kullanarak doğru sonuçlara ulaştıran
 009 BS 400- İstatistik sonılannın cevaplanmasında gerekli olabilecek tablolar ve formüller bu kitapçığın sonunda verilmiştir. 1. şağıdakilerden hangisi doğal birimdir? l TV alıcısı Bl Trafik kazası CL
009 BS 400- İstatistik sonılannın cevaplanmasında gerekli olabilecek tablolar ve formüller bu kitapçığın sonunda verilmiştir. 1. şağıdakilerden hangisi doğal birimdir? l TV alıcısı Bl Trafik kazası CL
İstatistik ve Olasılık
 İstatistik ve Olasılık Ders 8: Prof. Dr. İrfan KAYMAZ Tanım Tahmin (kestirim veya öngörü): Mevcut bilgi ve deneylere dayanarak olayın bütünü hakkında bir yargıya varmaktır. Bu anlamda, anakütleden çekilen
İstatistik ve Olasılık Ders 8: Prof. Dr. İrfan KAYMAZ Tanım Tahmin (kestirim veya öngörü): Mevcut bilgi ve deneylere dayanarak olayın bütünü hakkında bir yargıya varmaktır. Bu anlamda, anakütleden çekilen
Basit ve Çoklu Doğrusal Regresyon
 Basit ve Çoklu Doğrusal Regresyon Dr. Eren Can Aybek erencan@aybek.net www.olcme.net IBM SPSS Statistics ile Basit Doğrusal Regresyon Bir yordayıcı değişkene ait değerleri bildiğimizde, sürekli bir yordanan
Basit ve Çoklu Doğrusal Regresyon Dr. Eren Can Aybek erencan@aybek.net www.olcme.net IBM SPSS Statistics ile Basit Doğrusal Regresyon Bir yordayıcı değişkene ait değerleri bildiğimizde, sürekli bir yordanan
REGRESYON ANALİZİ VE UYGULAMA. Yrd. Doç. Dr. Hidayet Takcı
 REGRESYON ANALİZİ VE UYGULAMA Yrd. Doç. Dr. Hidayet Takcı htakci@cumhuriyet.edu.tr Sunum içeriği Bu sunumda; Lojistik regresyon konu anlatımı Basit doğrusal regresyon problem çözümleme Excel yardımıyla
REGRESYON ANALİZİ VE UYGULAMA Yrd. Doç. Dr. Hidayet Takcı htakci@cumhuriyet.edu.tr Sunum içeriği Bu sunumda; Lojistik regresyon konu anlatımı Basit doğrusal regresyon problem çözümleme Excel yardımıyla
