CORDIC METODU KULLANILARAK TRİGONOMETRİK HESAP MAKİNESİ SİMÜLASYONU
|
|
|
- Onur Aytaç
- 7 yıl önce
- İzleme sayısı:
Transkript
1 OD METODU KULLANLAAK TİGONOMETİK HESAP MAKİNESİ SİMÜLASYONU Ahmet SETBAŞ 1 Selçuk SEVGEN 2 e-posta: 1 asertbas@istanbul.edu.tr e-posta: 2 sevgens@istanbul.edu.tr 1,2 İstanbul Üniversitesi, Mühendislik Fakültesi, Bilgisayar Mühendisliği Bölümü, 34850, Avcılar, İstanbul Anahtar Kelimeler: Bilgisayar Aritmetiği, OD Algoritması, Trigonometrik Simülatör ÖZ Bu çalışmada, OD algoritmaları kullanılarak trigonometrik fonksiyonların değerleri etkin ve hızlı bir şekilde hesaplanması amaçlanmıştır. Bu amaçla, programlama dilinde trigonometrik bir hesap makinası simülatörü geliştirilmiştir. Sin, cos, tan, cotan, sinh, cosh, tanh, cotanh ve ters fonksiyonlarının simülasyonları elde edilmiştir. 1. GİİŞ OD (Oordinate, otation Dgital omputer) sinüs, cosinüs, üstel fonksiyonlar, logaritma gibi çeşitli gerçek zamanlı yüksek prezisyonlu aritmetik hesaplamalar için geliştirilen zeki ve etkin bir algoritma ailesidir yılında Volder [1] tarafından ortaya konulan gerçekten önemli bu algoritmalar, n iterasyonda n bit doğrulukla sözkonusu fonksiyonları hesaplayabilmekte ve her iterasyonda az sayıda toplama ve öteleme işlemlerini gerektirmektedir. Algoritma, Walther [2] tarafından genişletilerek bölme, çarpma, karakök hesaplama, hiperbolik ve üstel fonksiyon hesaplama gibi diğer aritmetik işlemleri de yapabilecek yeteneğe kavuşturuldu. Son yıllarda, literatürde OD algoritmalarını kullanarak değişik aritmetik hesaplamalar ve farklı gerçekleme metodlarını içeren çalışmaların arttığı görülmektedir [3-5]. Bilindiği gibi, klasik olarak, trigonometrik hesaplamalar için seriye açılım veya polinom yaklaşım metodları kullanılmaktadır. OD algoritmaları kullanılarak trigonometrik fonksiyonların geliştirilmesi, hızlı ve etkin olarak hesaplama gücünün artmasına neden olmaktadır. Bu çalışmada, trigonometrik fonksiyonların değerlerini hızlı bir şekilde hesaplayabilen bir hesap makinası simülatörü gerçekleştirilmiştir. Bu amaçla, trigonometrik fonksiyonların değerlerini hesaplamak için OD algoritmasının nasıl kullanıldığı üzerinde durulmuştur. Makalenin 2. bölümünde, genel OD algoritması tanıtlanması, 3. bölümde geliştirilen OD simülatörünün tüm fonksiyonları, 4. bölümde ise elde edilen sonuçlar verilecektir. 2. GENEL OD ALGOİTMAS Verilen bir θ açısı (-π/2 θ π/2) için, genelleştirilmiş OD denklemleri aşağıdaki gibi verilebilir[6]. x (i+1) = x (i) µd i y (i) 2 -i y (i+1) = y (i) + µd i x (i) 2 -i (1) z (i+1) = z (i) d i e (i) Burada d i katsayıları değeri ± 1 olan ve signum fonksiyonu ile tanımlanan katsayılardır. d i = sgn (z (i) ) = 1 (z (i) 0), -1 (z (i) < 0) (1) denklemlerinden de görüleceği gibi, x (i+1) ve y (i+1) hesaplamaları i bit sağa öteleme ve sadece 1 toplama/çıkarma işlemlerini gerektirmektedir. e (i) önceden hesaplanarak bir tablo halinde saklandığı gözönünde tutulursa, her OD iterasyonu 2 öteleme, 3 toplama/çıkarma ve 1 tablo okuma (lookup table) işlemi ile ilgilidir. Ayrıca, µ parametresi farklı OD hesaplamalarını belirleyen bir sabittir: µ=1 dairesel açı değişimleri e (i) = tan i µ=0 doğrusal değişimler e (i) = 2 -i µ= -1 hiperbolik açı değişimleri e (i) = tanh i Bu çalışmada, özellikle µ=1 seçilerek dairesel OD ve µ= -1 seçilerek hiperbolik OD hesaplamaları yapılmıştır. Böylelikle trigonometrik hesap makinasının sağladığı sinüs (sin), cosinüs (cos), tanjant (tan), cotanjant (cot), sinüs hiperbolik (sinh), cosinüs hiperbolik (cosh), tanjant hiperbolik (tanh) ve cotanjant hiperbolik (coth) fonksiyonları ve ters fonksiyonları OD metoduyla hesaplanmıştır.
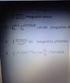
2 Dairesel OD (µ=1) iterasyon sonuclarını karakterize eden denklemler (2) de verilmiştir. Bu denklemler, z (i) açısı sıfıra zorlandığı için rotasyonel mod adı ile anılmaktadır. x (m) = K(x cosz y sinz) y (m) = K(y cosz + x sinz) (2) z (m) = 0 Bu modda, temel kural z i sıfıra götürecek şekilde d i (-1,1) katsayılarını seçmektir. İterasyona başlangıç değeri ; x 0 =1/K= [cos(α (i) )] = [1/(1+tan(α (i) ) 2 )] 1/2, y=0 seçilirse, x (m) =cosz, y (m) =sinz değerlerine yakınsayacaktır (tanz=sinz/cosz, cotanz=1/tanz). Dairesel OD iterasyonlarını kullanmanın ikinci bir yolu, vektörel mod olarak bilinen ve (2) denklemlerinin farklı bir şekilde yazılması ile elde edilen (3) denklemlerini referans almaktır. x (m) = K(x 2 + y 2 ) 1/2 y (m) =0 (3) z (m) = z + tan -1 (y/x) Dairesel vektörel mod olarak da isimlendirilen bu yöntemde temel kural, y i sıfıra götürecek şekilde d i (-1,1) katsayılarını seçmektir. İterasyona başlangıç değeri x 0 =1, z 0 =0 seçilirse, z (m) =tan -1 (y/x) değerine yakınsayacaktır. Algoritmaya giriş koşulu olarak, x 0 =w, y 0 =(1-w 2 ) 1/2 değerleri girilirse, z=cos -1 (w)= tan -1 [(1-w 2 ) 1/2 /w]; x 0 =(1-w 2 ) 1/2, y 0 =w değerleri girilirse, z=sin -1 (w)= tan -1 [w/(1-w 2 ) 1/2 ]; hesaplamaları yaptırılabilir. Diğer taraftan (µ=-1 seçilerek elde edilen) hiperbolik OD iterasyon sonuclarını karakterize eden denklemler (4) de görülmektedir. Yöntemde, Z sıfıra zorlandığı için hiperbolik rotasyonel mod olarak da isimlendirilir. x (m) = K (x coshz + y sinhz) y (m) = K(y coshz + x sinhz) (4) z (m) = 0 Dairesel rotasyonel moda benzer şekilde, iterasyona başlangıç değeri olarak; x 0 =1/K = [cosh(α (i) )] = [1/(1-tan(α (i) ) 2 )] 1/2, y=0 seçilirse, x (m) =coshz, y (m) =sinhz değerlerine yakınsayacaktır (tanhz= sinhz/coshz, cothz=1/tanhz). Ters hiperbolik fonksiyonların hesaplanabilmesi için, hiperbolik vektörel mod kullanılmıştır: x (m) = K(x 2 - y 2 ) 1/2 y (m) =0 (5) z (m) = z + tanh -1 (y/x) Benzer şekilde, iterasyona başlangıç değeri x 0 =1, z 0 =0 seçilirse, z (m) =tanh -1 (y/x) değerine yakınsayacaktır. Algoritmaya giriş koşulu olarak, x 0 =w+1, y 0 =w-1 değerleri için, z=(1/2)ln(w)= tan -1 [(1-w 2 ) 1/2 /w]; x 0 =w+1+(1-w 2 ) 1/2, y 0 =w-1+(1-w 2 ) 1/2 değerleri için, z=cosh -1 (w)= ln(w+(1-w 2 ) 1/2 ); x 0 =w+1+(1+w 2 ) 1/2, y 0 =w-1+(1+w 2 ) 1/2 değerleri için, z=sinh -1 (w)= ln(w+(1+w 2 ) 1/2 ); hesaplamaları yaptırılabilir. Elde edilen tüm OD hesaplamaları toplu olarak Şekil 1 de görülmektedir. 3. TİGONOMETİK SİMÜLATÖ Bu bölümde, sin, cos, tan, cotan, sinh, cosh, tanh, cotanh ve ters fonksiyonlarını hesaplamak için geliştirilen trigonometrik bir hesap makinası simülatörünün tüm fonksiyonları detaylı olarak incelenmiştir. Simülasyon sonuçları, hesaplama iterasyonlarının açık gösterimleri şeklinde verilmiştir. Simülatör, programlama dilinde geliştirilmiştir. Şekil 2 de, simülatörün kullanımı için tasarımlanan kullanıcı arayüzü modeli verilmiştir. (Arcsinh(0.5) hesaplamasının yaptırılması için arayüzün kullanımı görünmektedir / Şekil 2). Tablo 1-4 te, tüm trigonometrik OD hesaplamaları için elde edilen iterasyon adımları verilmiştir. Bu hesaplamalar; 30 0 için temel trigonometrik fonksiyonlar (Tablo1), değeri için trigonometrik ters fonksiyonlar (Tablo 2), 1 değeri için hiberbolik fonksiyonlar (Tablo 3), 0.5 için ters hiberbolik sinüs ve tanjant fonksiyonları vede 3 için ters hiperbolik kotanjant fonksiyonu (Tablo 4) hesaplamalarından oluşmaktadır.
3 Tablo 1. Trigonometrik OD hesaplamaları Tablo3. Hiperbolik OD hesaplamaları Tablo 2. Ters Trigonometrik OD hesaplamaları Tablo 4. Ters Hiperbolik OD hesaplamaları
4 Tablo 1 de, trigonometrik fonksiyonların yakınsaması 32 iterasyonda (8 dijit doğruluk), Tablo 2-4 te verilen hiperbolik fonksiyon ve ters fonksiyonlarının hesaplanması 26 iterasyonda (6 dijit doğruluk) gerçeklenmiştir. Algoritma, hiperbolik sinüs ve cosinüs fonksiyonlarının hesaplanmasında z < 1.13 kısıtı ve ters hiperbolik tanjant hesaplamasında ise y < 0.81 kısıtı ile istenilen doğrulukta yakınsama sağlayabilmektedir. Ters hiperbolik kosinüs fonksiyonu z < 1 için tanımlı olmadığından bu algoritma ile hesaplanması direk olarak yapılamamıştır, ancak ters hiperbolik sinüs fonksiyonu üzerinden hesaplama yaptırılabilir. 4. SONUÇLA Bu çalışmada, trigonometrik fonksiyonların hesaplanmasında klasik yaklaşımlara göre daha etkin ve hızlı hesaplama gücüne sahip bulunan OD Algoritmaları kullanılarak bir trigonometrik hesap makinesi simülatörü gerçekleştirilmiştir. Algoritmanın yakınsama hızının yüksekliği, N iterasyonda sonuçların N-bit doğrulukla elde edilmesini sağlayabilmektedir. OD algoritmaları üstel ve logaritmik fonksiyonların hesaplanmasında da etkin olarak kullanılabilir. Bu nedenle, simülatör diğer fonksiyonları da içerecek şekilde zenginleştirilerek daha yüksek hesaplama yeteneğine kavuşturulmalıdır. 5. KAYNAKLA [1] Volder, J.E., The OD Trigonometric omputing Technique,E Trans. Electronic omputers, Vol.8, September 1959, pp [2] Walther, J.S., A Unified Algorithm for Elementary Functions, Proc.Spring Joint omputer onf., 1971, pp [3] Duprat, J. and J.M. Muller, The OD Algorithm: New esults for Fast VLS mplementation, EEE Trans. omputers, Vol.42, No.2, 1993, pp [4] Mazenc,., X. Merrheim, and J.M. Muller, omputing Functions cos -1 and sin -1 Using OD, EEE Trans. omputers, Vol.42, No.1, 1993, pp [5] Phatak, D.S., Double Step Branching OD: A New Algorithm for Fast Sive and osine Genaration,, EEE Trans. omputers, Vol. 47, May 1998, pp [6] Parhami B., omputer Arithmetic/ Algorithms and Hardware Designs, Oxford University Press, 2000.
5 otasyonel Mod Vektörel Mod İlk koşullar: x 0 =1/K, y=0 İlk koşullar: x 0 =1, z=0x DAİESEL x O K(xcosz-ysinz) x O K(x 2 +y 2 ) 1/2 OD y D K(ycosz+xsinz) y D 0 µ=1 z 0 z z+tan -1 (y/x) x= cosz, y=sinz, tanz=y/x, cotz=x/y cos -1 w=tan -1 [(1-w 2 )/w] 1/2 sin -1 w=tan -1 [w/(1-w 2 )] 1/2 İlk koşullar: x 0 =1/K, y=0 İlk koşullar: x 0 =1, z=0 x O K (xcoshz-ysinhz) x O K (x 2 -y 2 ) 1/2 y D K (ycoshz+xsinhz) y D 0 HİPEBOLİK z 0 z z+tanh -1 (y/x) OD µ=-1 x= coshz, y=sinhz, tanhz=y/x, cothz=x/y ln(w)= 2tan -1 [(1-w 2 ) 1/2 /w]; sinh -1 (w)= ln(w+(1+w 2 ) 1/2 ); cosh -1 (w)= ln(w+(1-w 2 ) 1/2 ); Şekil 1. Trigonometrik OD Hesaplamaları Şekil 2. Trigonometrik Hesap Makinası Kullanıcı Arayüzü
[ 1, 1] alınırsa bu fonksiyon birebir ve örten olur. Bu fonksiyonun tersine arkkosinüs. f 1 (x) = sin 1 (x), 1 x 1
![[ 1, 1] alınırsa bu fonksiyon birebir ve örten olur. Bu fonksiyonun tersine arkkosinüs. f 1 (x) = sin 1 (x), 1 x 1 [ 1, 1] alınırsa bu fonksiyon birebir ve örten olur. Bu fonksiyonun tersine arkkosinüs. f 1 (x) = sin 1 (x), 1 x 1](/thumbs/96/127250868.jpg) ..3 Ters Trigonometrik Fonksionlar Önceki kesimde belirtilen bütün trigonometrik fonksionlar perodik olduklarından görüntü kümesindeki her değeri sonsuz noktada alırlar. Bölece trigonometrik fonksionlar
..3 Ters Trigonometrik Fonksionlar Önceki kesimde belirtilen bütün trigonometrik fonksionlar perodik olduklarından görüntü kümesindeki her değeri sonsuz noktada alırlar. Bölece trigonometrik fonksionlar
ARAZİ ÖLÇMELERİ Z P. O α X P. α = yatay açı. ω = düşey açı. µ =eğim açısı. ω + µ = 100 g
 Trigonometrik Fonksiyonlar Z Z P P ω µ P O α α = yatay açı P P ω = düşey açı µ =eğim açısı ω + µ = 100 g Şekil 9 üç Boyutlu koordinat sisteminde açı tiplerinin tasviri. Trigonometrik kavramlara geçmeden
Trigonometrik Fonksiyonlar Z Z P P ω µ P O α α = yatay açı P P ω = düşey açı µ =eğim açısı ω + µ = 100 g Şekil 9 üç Boyutlu koordinat sisteminde açı tiplerinin tasviri. Trigonometrik kavramlara geçmeden
1. GİRİŞ Örnek: Bir doğru boyunca hareket eden bir cismin başlangıç noktasına göre konumu s (metre), zamanın t (saniye) bir fonksiyonu olarak
 DERS: MATEMATİK I MAT0(09) ÜNİTE: TÜREV ve UYGULAMALARI KONU: A. TÜREV. GİRİŞ Bir doğru boyunca hareket eden bir cismin başlangıç noktasına göre konumu s (metre) zamanın t (saniye) bir fonksiyonu olarak
DERS: MATEMATİK I MAT0(09) ÜNİTE: TÜREV ve UYGULAMALARI KONU: A. TÜREV. GİRİŞ Bir doğru boyunca hareket eden bir cismin başlangıç noktasına göre konumu s (metre) zamanın t (saniye) bir fonksiyonu olarak
ÜNİTE İÇİNDEKİLER HEDEFLER MATEMATİKSEL METOTLAR. NESNE TABANLI PROGRAMLAMA I Okt. Mustafa AKBUĞA. (Math Sınıfı ve Metotları)
 MATEMATİKSEL METOTLAR (Math Sınıfı ve Metotları) İÇİNDEKİLER Matemetiksel Metotlar Üstel Metotlar Logaritmik Metotlar Trigonometrik Metotlar Ters Trigonometrik Metotlar Hiperbolik Metotlar Yuvarlatma Metotları
MATEMATİKSEL METOTLAR (Math Sınıfı ve Metotları) İÇİNDEKİLER Matemetiksel Metotlar Üstel Metotlar Logaritmik Metotlar Trigonometrik Metotlar Ters Trigonometrik Metotlar Hiperbolik Metotlar Yuvarlatma Metotları
MATLAB. Temel işlemler, Vektörler, Matrisler DOÇ. DR. ERSAN KABALCI
 MATLAB Temel işlemler, Vektörler, Matrisler DOÇ. DR. ERSAN KABALCI İçerik Matlab Nedir? Matlab ın Kullanım Alanları Matlab Açılış Ekranı Matlab Programı İle Temel İşlemlerin Gerçekleştirilmesi Vektör İşlemleri
MATLAB Temel işlemler, Vektörler, Matrisler DOÇ. DR. ERSAN KABALCI İçerik Matlab Nedir? Matlab ın Kullanım Alanları Matlab Açılış Ekranı Matlab Programı İle Temel İşlemlerin Gerçekleştirilmesi Vektör İşlemleri
V cn V ca. V bc. V bn. V ab 30. -V bn. V an HATIRLATMALAR. Faz-Faz ve Faz-Nötr Gerilimleri. Yıldız ve Üçgen Bağlı Yüklerde Akım-Gerilim İlişkileri
 HATIRLATMALAR Faz-Faz ve Faz-Nötr Gerilimleri V cn V ca V ab 30 10 V an V bn V bc V ab 30 -V bn cos30 30 V an cos30 3 3 30 Yıldız ve Üçgen Bağlı Yüklerde Akım-Gerilim İlişkileri Üçgen Bağlı Yük: V LN =
HATIRLATMALAR Faz-Faz ve Faz-Nötr Gerilimleri V cn V ca V ab 30 10 V an V bn V bc V ab 30 -V bn cos30 30 V an cos30 3 3 30 Yıldız ve Üçgen Bağlı Yüklerde Akım-Gerilim İlişkileri Üçgen Bağlı Yük: V LN =
11. SINIF MATEMATİK DERSİ İLERİ DÜZEY ÖĞRETİM PROGRAMI
 11. SINIF MATEMATİK DERSİ İLERİ DÜZEY ÖĞRETİM PROGRAMI Programın öğrencilerde geliştirmeyi hedeflediği becerilerle 11. sınıf matematik öğretim programı ilişkisi Modelleme/Problem çözme Matematiksel Süreç
11. SINIF MATEMATİK DERSİ İLERİ DÜZEY ÖĞRETİM PROGRAMI Programın öğrencilerde geliştirmeyi hedeflediği becerilerle 11. sınıf matematik öğretim programı ilişkisi Modelleme/Problem çözme Matematiksel Süreç
Projenin Amacı: Çok kullanılan trigonometrik oranların farklı ve pratik yöntemlerle bulunması
 Projenin Adı: Trigonometrik Oranlar için Pratik Yöntemler Projenin Amacı: Çok kullanılan trigonometrik oranların farklı ve pratik yöntemlerle bulunması GİRİŞ: Matematiksel işlemlerde, lazım olduğunda,
Projenin Adı: Trigonometrik Oranlar için Pratik Yöntemler Projenin Amacı: Çok kullanılan trigonometrik oranların farklı ve pratik yöntemlerle bulunması GİRİŞ: Matematiksel işlemlerde, lazım olduğunda,
KLASİK ÇARPMA ALGORİTMALARININ DONANIMSAL SİMÜLASYONLARI VE PERFORMANS DEĞERLENDİRİMİ
 KLASİK ÇARPMA ALGORİTMALARININ DONANIMSAL SİMÜLASYONLARI VE PERFORMANS DEĞERLENDİRİMİ R. Selami Özbey 1 ve Ahmet Sertbaş 2 1 TUBİTAK/UEKAE (Ulusal Elektronik ve Kriptoloji Araştırma Enstitüsü) 2 İstanbul
KLASİK ÇARPMA ALGORİTMALARININ DONANIMSAL SİMÜLASYONLARI VE PERFORMANS DEĞERLENDİRİMİ R. Selami Özbey 1 ve Ahmet Sertbaş 2 1 TUBİTAK/UEKAE (Ulusal Elektronik ve Kriptoloji Araştırma Enstitüsü) 2 İstanbul
7.2 Fonksiyon ve Fonksiyon Tanımları (I) Fonksiyon ve Fonksiyon Tanımları (II)
 7.2 Fonksiyon ve Fonksiyon Tanımları (I) Tanım kümesindeki her elemanın değer kümesinde bir ve yalnız bir görüntüsü varsa, tanım kümesinden değer kümesine olan bağıntıya fonksiyon denir. Fonksiyonu f ile
7.2 Fonksiyon ve Fonksiyon Tanımları (I) Tanım kümesindeki her elemanın değer kümesinde bir ve yalnız bir görüntüsü varsa, tanım kümesinden değer kümesine olan bağıntıya fonksiyon denir. Fonksiyonu f ile
2.2 Bazıözel fonksiyonlar
 . Bazıözel fonksionlar Kuvvet fonksionu, polinomlar ve rasonel fonksionlar, mutlak değer ve tam değer fonksionları, pratik grafik çizimleri. 1-) Lineer fonksionlar: m ve n sabit saılar olmak üzere f()
. Bazıözel fonksionlar Kuvvet fonksionu, polinomlar ve rasonel fonksionlar, mutlak değer ve tam değer fonksionları, pratik grafik çizimleri. 1-) Lineer fonksionlar: m ve n sabit saılar olmak üzere f()
DERS: MATEMATİK I MAT101(04)
 DERS: MATEMATİK I MAT0(0) ÜNİTE: FONKSİYONLAR KONU:. TRİGONOMETRİK FONKSİYONLAR Öncelikle açı ölçü birimlerine göz atalım: Bilindiği gibi bir tam açının ölçüsü 0 derecedir. Diğer bir açı ölçü birimi de
DERS: MATEMATİK I MAT0(0) ÜNİTE: FONKSİYONLAR KONU:. TRİGONOMETRİK FONKSİYONLAR Öncelikle açı ölçü birimlerine göz atalım: Bilindiği gibi bir tam açının ölçüsü 0 derecedir. Diğer bir açı ölçü birimi de
4. HAFTA BLM323 SAYISAL ANALİZ. Okt. Yasin ORTAKCI.
 4. HAFTA BLM33 SAYISAL ANALİZ Okt. Yasin ORTAKCI yasinortakci@karabuk.edu.tr Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi BLM33 DOĞRUSAL OLMAYAN (NONLINEAR) DENKLEM SİSTEMLERİ Mühendisliğin
4. HAFTA BLM33 SAYISAL ANALİZ Okt. Yasin ORTAKCI yasinortakci@karabuk.edu.tr Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi BLM33 DOĞRUSAL OLMAYAN (NONLINEAR) DENKLEM SİSTEMLERİ Mühendisliğin
θ x Örnek...1 : Örnek...2 : KARMAŞIK SAYILAR 3 Alıştırmalar KARMAŞIK SAYININ KUTUPSAL (TRİGONOMETRİK) GÖSTERİMİ 1) z = 1 + i 2) z = 1 i
 KARMAŞIK SAYININ KUTUPSAL (TRİGONOMETRİK) GÖSTERİMİ z = a + bi y karmaşık sayısının kartezyen bi koordinatları z=(a, b) dir. Ya da görüntüsü A noktasıdır. A Alıştırmalar Karmaş ık sa yıs ın ın kutupsal
KARMAŞIK SAYININ KUTUPSAL (TRİGONOMETRİK) GÖSTERİMİ z = a + bi y karmaşık sayısının kartezyen bi koordinatları z=(a, b) dir. Ya da görüntüsü A noktasıdır. A Alıştırmalar Karmaş ık sa yıs ın ın kutupsal
fonksiyonu için in aralığındaki bütün değerleri için sürekli olsun. in bu aralıktaki olsun. Fonksiyonda meydana gelen artma miktarı
 10.1 Türev Kavramı fonksiyonu için in aralığındaki bütün değerleri için sürekli olsun. in bu aralıktaki bir değerine kadar bir artma verildiğinde varılan x = x 0 + noktasında fonksiyonun değeri olsun.
10.1 Türev Kavramı fonksiyonu için in aralığındaki bütün değerleri için sürekli olsun. in bu aralıktaki bir değerine kadar bir artma verildiğinde varılan x = x 0 + noktasında fonksiyonun değeri olsun.
Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi
 JEODEZİ 6 1 Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi Jeodezik gözlemler, hesaplamalarda kullanılmadan önce, referans elipsoidin yüzeyine indirgenir. Bu işlem, arazide yapılan gözlemler l jeoidin
JEODEZİ 6 1 Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi Jeodezik gözlemler, hesaplamalarda kullanılmadan önce, referans elipsoidin yüzeyine indirgenir. Bu işlem, arazide yapılan gözlemler l jeoidin
ÖZEL ÇORUM ADA ÖZEL ÖĞRETİM KURSU MATEMATİK 3 BİLİM GRUBU ÇERÇEVE PROGRAMI
 ÖZEL ÇORUM ADA ÖZEL ÖĞRETİM KURSU MATEMATİK 3 BİLİM GRUBU ÇERÇEVE PROGRAMI 1.KURUM ADI: Özel Çorum Ada Özel Öğretim Kursu 2. KURUMUN ADRESİ: Yavruturna Mah. Kavukçu Sok. No:46/A ÇORUM/MERKEZ 3. KURUCUNUN
ÖZEL ÇORUM ADA ÖZEL ÖĞRETİM KURSU MATEMATİK 3 BİLİM GRUBU ÇERÇEVE PROGRAMI 1.KURUM ADI: Özel Çorum Ada Özel Öğretim Kursu 2. KURUMUN ADRESİ: Yavruturna Mah. Kavukçu Sok. No:46/A ÇORUM/MERKEZ 3. KURUCUNUN
TRİGONOMETRİK FONKSİYONLARIN GRAFİKLERİ
 TRİGONOMETRİK FONKSİYONLARIN GRAFİKLERİ A. PERİYODİK FONKSİYONLAR A, düna ve güneşin hareketleri, a ve güneş tutulmaları her 7 ılda bir Halle kuruklu ıldızının dünamızı ziareti periodik olarak medana gelen
TRİGONOMETRİK FONKSİYONLARIN GRAFİKLERİ A. PERİYODİK FONKSİYONLAR A, düna ve güneşin hareketleri, a ve güneş tutulmaları her 7 ılda bir Halle kuruklu ıldızının dünamızı ziareti periodik olarak medana gelen
AKSARAY KANUNİ ANADOLU İMAM HATİP LİSESİ 2015-2016 EĞİTİM ÖĞRETİM YILI MATEMATİK DERSİ 11.SINIFLAR ÜNİTELENDİRİLMİŞ YILLIK PLANI TEKNİKLER
 AKSARAY KANUNİ ANADOLU İMAM HATİP LİSESİ 015-01 EĞİTİM ÖĞRETİM YILI MATEMATİK DERSİ 11.SINIFLAR ÜNİTELENDİRİLMİŞ YILLIK PLANI SÜRE: MANTIK(30) ÖNERMELER VE BİLEŞİK ÖNERMELER(18) 1. Önermeyi, önermenin
AKSARAY KANUNİ ANADOLU İMAM HATİP LİSESİ 015-01 EĞİTİM ÖĞRETİM YILI MATEMATİK DERSİ 11.SINIFLAR ÜNİTELENDİRİLMİŞ YILLIK PLANI SÜRE: MANTIK(30) ÖNERMELER VE BİLEŞİK ÖNERMELER(18) 1. Önermeyi, önermenin
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 4- LİNEER OLMAYAN DENKLEMLERİN ÇÖZÜMÜ Doç. Dr. Ali Rıza YILDIZ MAK 210 - Sayısal Analiz 1 LİNEER OLMAYAN DENKLEMLERİN ÇÖZÜMÜ Matematikte veya hidrolik, dinamik, mekanik, elektrik
MAK 210 SAYISAL ANALİZ BÖLÜM 4- LİNEER OLMAYAN DENKLEMLERİN ÇÖZÜMÜ Doç. Dr. Ali Rıza YILDIZ MAK 210 - Sayısal Analiz 1 LİNEER OLMAYAN DENKLEMLERİN ÇÖZÜMÜ Matematikte veya hidrolik, dinamik, mekanik, elektrik
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Bu bölümde eşitsizlik kısıtlarına bağlı bir doğrusal olmayan kısıta sahip problemin belirlenen stasyoner noktaları
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Bu bölümde eşitsizlik kısıtlarına bağlı bir doğrusal olmayan kısıta sahip problemin belirlenen stasyoner noktaları
Tek Değişkenli Optimizasyon OPTİMİZASYON. Gradient Tabanlı Yöntemler. Bisection (İkiye Bölme) Yöntemi
 OPTİMİZASYON Gerçek hayatta, çok değişkenli optimizasyon problemleri karmaşıktır ve nadir olarak problem tek değişkenli olur. Bununla birlikte, tek değişkenli optimizasyon algoritmaları çok değişkenli
OPTİMİZASYON Gerçek hayatta, çok değişkenli optimizasyon problemleri karmaşıktır ve nadir olarak problem tek değişkenli olur. Bununla birlikte, tek değişkenli optimizasyon algoritmaları çok değişkenli
HOMOGEN OLMAYAN DENKLEMLER
 n. mertebeden homogen olmayan lineer bir diferansiyel denklemin y (n) + p 1 (x)y (n 1) + + p n 1 (x)y + p n (x)y = f(x) (1) şeklinde olduğunu ve bununla ilgili olan n. mertebeden lineer homogen denlemin
n. mertebeden homogen olmayan lineer bir diferansiyel denklemin y (n) + p 1 (x)y (n 1) + + p n 1 (x)y + p n (x)y = f(x) (1) şeklinde olduğunu ve bununla ilgili olan n. mertebeden lineer homogen denlemin
İÇİNDEKİLER ÖNSÖZ Bölüm 1 SAYILAR 11 Bölüm 2 KÜMELER 31 Bölüm 3 FONKSİYONLAR
 İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 11 1.1. Sayı Kümeleri 12 1.1.1.Doğal Sayılar Kümesi 12 1.1.2.Tam Sayılar Kümesi 13 1.1.3.Rasyonel Sayılar Kümesi 14 1.1.4. İrrasyonel Sayılar Kümesi 16 1.1.5. Gerçel
İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 11 1.1. Sayı Kümeleri 12 1.1.1.Doğal Sayılar Kümesi 12 1.1.2.Tam Sayılar Kümesi 13 1.1.3.Rasyonel Sayılar Kümesi 14 1.1.4. İrrasyonel Sayılar Kümesi 16 1.1.5. Gerçel
Ç NDEK LER. Bölüm 4: Üslü Say lar...44 Üslü fadeler...44 Al t rmalar...47 Test Sorular...49
 Ç NDEK LER Bölüm1: Say Sistemleri...1 Say Sistemi...2 Desimal (Onluk) Say Sistemi...2 Say Basamaklar ve Taban...4 Binary ( kilik) Say Sistemi...4 Oktal (Sekizlik) Say Sistemi...7 Heksadesimal (Onalt l
Ç NDEK LER Bölüm1: Say Sistemleri...1 Say Sistemi...2 Desimal (Onluk) Say Sistemi...2 Say Basamaklar ve Taban...4 Binary ( kilik) Say Sistemi...4 Oktal (Sekizlik) Say Sistemi...7 Heksadesimal (Onalt l
SAYISAL ÇÖZÜMLEME. Yrd.Doç.Dr.Esra Tunç Görmüş. 1.Hafta
 SAYISAL ÇÖZÜMLEME Yrd.Doç.Dr.Esra Tunç Görmüş 1.Hafta Sayısal çözümleme nümerik analiz nümerik çözümleme, approximate computation mühendislikte sayısal yöntemler Computational mathematics Numerical analysis
SAYISAL ÇÖZÜMLEME Yrd.Doç.Dr.Esra Tunç Görmüş 1.Hafta Sayısal çözümleme nümerik analiz nümerik çözümleme, approximate computation mühendislikte sayısal yöntemler Computational mathematics Numerical analysis
ÇEV 2006 Mühendislik Matematiği (Sayısal Analiz) DEÜ Çevre Mühendisliği Bölümü Doç.Dr. Alper ELÇĐ
 Giriş ÇEV 2006 Mühendislik Matematiği (Sayısal Analiz) DEÜ Çevre Mühendisliği Bölümü Doç.Dr. Alper ELÇĐ Sayısal Analiz Nedir? Mühendislikte ve bilimde, herhangi bir süreci tanımlayan karmaşık denklemlerin
Giriş ÇEV 2006 Mühendislik Matematiği (Sayısal Analiz) DEÜ Çevre Mühendisliği Bölümü Doç.Dr. Alper ELÇĐ Sayısal Analiz Nedir? Mühendislikte ve bilimde, herhangi bir süreci tanımlayan karmaşık denklemlerin
ANADOLU ÜNİVERSİTESİ AÇIKÖĞRETİM FAKÜLTESİ İLKÖĞRETİM ÖĞRETMENLİĞİ LİSANS TAMAMLAMA PROGRAMI. Analiz. Cilt 2. Ünite 8-14
 ANADOLU ÜNİVERSİTESİ AÇIKÖĞRETİM FAKÜLTESİ İLKÖĞRETİM ÖĞRETMENLİĞİ LİSANS TAMAMLAMA PROGRAMI Analiz Cilt 2 Ünite 8-14 T.C. ANADOLU ÜNİVERSİTESİ YAYINLARI NO: 1082 AÇIKÖĞRETİM FAKÜLTESİ YAYINLARI NO: 600
ANADOLU ÜNİVERSİTESİ AÇIKÖĞRETİM FAKÜLTESİ İLKÖĞRETİM ÖĞRETMENLİĞİ LİSANS TAMAMLAMA PROGRAMI Analiz Cilt 2 Ünite 8-14 T.C. ANADOLU ÜNİVERSİTESİ YAYINLARI NO: 1082 AÇIKÖĞRETİM FAKÜLTESİ YAYINLARI NO: 600
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Trigonometrik Fonksiyonlar
 Trigonometrik Fonksiyonlar Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 6 Amaçlar Bu üniteyi çalıştıktan sonra; açı kavramını hatırlayacak, açıların derece ölçümünü radyan ölçümüne ve tersine çevirebilecek, trigonometrik
Trigonometrik Fonksiyonlar Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 6 Amaçlar Bu üniteyi çalıştıktan sonra; açı kavramını hatırlayacak, açıların derece ölçümünü radyan ölçümüne ve tersine çevirebilecek, trigonometrik
TRIGONOMETRI AÇI, YÖNLÜ AÇI, YÖNLÜ YAY
 TRIGONOMETRI AÇI, YÖNLÜ AÇI, YÖNLÜ YAY A. AÇI Başlangıç noktaları aynı olan iki ışının birleşim kümesine açı denir. Bu ışınlara açının kenarları, başlangıç noktasına ise açının köşesi denir. B. YÖNLÜ AÇI
TRIGONOMETRI AÇI, YÖNLÜ AÇI, YÖNLÜ YAY A. AÇI Başlangıç noktaları aynı olan iki ışının birleşim kümesine açı denir. Bu ışınlara açının kenarları, başlangıç noktasına ise açının köşesi denir. B. YÖNLÜ AÇI
BAZI İLLER İÇİN GÜNEŞ IŞINIM ŞİDDETİ, GÜNEŞLENME SÜRESİ VE BERRAKLIK İNDEKSİNİN YENİ ÖLÇÜMLER IŞIĞINDA ANALİZİ
 Güneş Günü Sempozyumu 99-28 Kayseri, 2-27 Haziran 1999 BAZI İLLER İÇİN GÜNEŞ IŞINIM ŞİDDETİ, GÜNEŞLENME SÜRESİ VE BERRAKLIK İNDEKSİNİN YENİ ÖLÇÜMLER IŞIĞINDA ANALİZİ Hüsamettin BULUT Çukurova Üni. Müh.
Güneş Günü Sempozyumu 99-28 Kayseri, 2-27 Haziran 1999 BAZI İLLER İÇİN GÜNEŞ IŞINIM ŞİDDETİ, GÜNEŞLENME SÜRESİ VE BERRAKLIK İNDEKSİNİN YENİ ÖLÇÜMLER IŞIĞINDA ANALİZİ Hüsamettin BULUT Çukurova Üni. Müh.
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 2- HATA VE HATA KAYNAKLARI Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ Bir denklemin veya problemin çözümünde kullanılan sayısal yöntem belli bir giriş verisini işleme tabi tutarak sayısal
MAK 210 SAYISAL ANALİZ BÖLÜM 2- HATA VE HATA KAYNAKLARI Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ Bir denklemin veya problemin çözümünde kullanılan sayısal yöntem belli bir giriş verisini işleme tabi tutarak sayısal
ALTERNATİF AKIMIN VEKTÖRLERLE GÖSTERİLMESİ
 1 ALTERNATİF AKIMIN VEKTÖRLERLE GÖSTERİLMESİ Fazör: Zamanla değişen gerilim ve akımın gösterildiği vektörlerdir. Vektör büyüklüğü maksimum değere eşit alınmayıp en çok kullanılan etkin değere eşit alınır.
1 ALTERNATİF AKIMIN VEKTÖRLERLE GÖSTERİLMESİ Fazör: Zamanla değişen gerilim ve akımın gösterildiği vektörlerdir. Vektör büyüklüğü maksimum değere eşit alınmayıp en çok kullanılan etkin değere eşit alınır.
TRİGONMETRİK FONKSİYONLAR: DİK ÜÇGEN YAKLAŞIMI
 TRİGONMETRİK FONKSİYONLAR: DİK ÜÇGEN YAKLAŞIMI Diyelim ki yeryüzünden güneşe olan mesafeyi bulmak istiyoruz. Şerit metre kullanmak açıkçası pratik değildir. Bu nedenle bu sorunun üstesinden gelmek için
TRİGONMETRİK FONKSİYONLAR: DİK ÜÇGEN YAKLAŞIMI Diyelim ki yeryüzünden güneşe olan mesafeyi bulmak istiyoruz. Şerit metre kullanmak açıkçası pratik değildir. Bu nedenle bu sorunun üstesinden gelmek için
ARASINAV SORULARININ ÇÖZÜMLERİ GÜZ DÖNEMİ A A A A A A A
 AKDENİZ ÜNİVERSİTESİ MATEMATİK BÖLÜMÜ BİTİRME ÖDEVİ I ARASINAV SORULARININ ÇÖZÜMLERİ - 6 GÜZ DÖNEMİ ADI SOYADI :... NO :... A A A A A A A SINAV TARİHİ VE SAATİ : Bu sınav 4 sorudan oluşmaktadır ve sınav
AKDENİZ ÜNİVERSİTESİ MATEMATİK BÖLÜMÜ BİTİRME ÖDEVİ I ARASINAV SORULARININ ÇÖZÜMLERİ - 6 GÜZ DÖNEMİ ADI SOYADI :... NO :... A A A A A A A SINAV TARİHİ VE SAATİ : Bu sınav 4 sorudan oluşmaktadır ve sınav
Zeki Optimizasyon Teknikleri
 Zeki Optimizasyon Teknikleri Ara sınav - 25% Ödev (Haftalık) - 10% Ödev Sunumu (Haftalık) - 5% Final (Proje Sunumu) - 60% - Dönem sonuna kadar bir optimizasyon tekniğiyle uygulama geliştirilecek (Örn:
Zeki Optimizasyon Teknikleri Ara sınav - 25% Ödev (Haftalık) - 10% Ödev Sunumu (Haftalık) - 5% Final (Proje Sunumu) - 60% - Dönem sonuna kadar bir optimizasyon tekniğiyle uygulama geliştirilecek (Örn:
MATEMATİK BİLİM GRUBU III KURS PROGRAMI
 MATEMATİK BİLİM GRUBU III KURS PROGRAMI 1.Kurumun Adı 2.Kurumun adresi 3.Kurucunun Adı 4.Programın Adı : OĞUZHAN ÖZKAYA ÖZEL ÖĞRETİM KURSU : Onur Mahallesi Leylak Sok.No:9 Balçova-İzmir : Oğuzhan Özkaya
MATEMATİK BİLİM GRUBU III KURS PROGRAMI 1.Kurumun Adı 2.Kurumun adresi 3.Kurucunun Adı 4.Programın Adı : OĞUZHAN ÖZKAYA ÖZEL ÖĞRETİM KURSU : Onur Mahallesi Leylak Sok.No:9 Balçova-İzmir : Oğuzhan Özkaya
Ayrık zamanlı sinyaller için de ayrık zamanlı Fourier dönüşümleri kullanılmatadır.
 Bölüm 6 Z-DÖNÜŞÜM Sürekli zamanlı sinyallerin zaman alanından frekans alanına geçişi Fourier ve Laplace dönüşümleri ile mümkün olmaktadır. Laplace, Fourier dönüşümünün daha genel bir şeklidir. Ayrık zamanlı
Bölüm 6 Z-DÖNÜŞÜM Sürekli zamanlı sinyallerin zaman alanından frekans alanına geçişi Fourier ve Laplace dönüşümleri ile mümkün olmaktadır. Laplace, Fourier dönüşümünün daha genel bir şeklidir. Ayrık zamanlı
ALTERNATİF AKIMIN VEKTÖRLERLE GÖSTERİLMESİ
 1 ALTERNATİF AKIMIN VEKTÖRLERLE GÖSTERİLMESİ ALTERNATİF AKIMIN VEKTÖRLERLE GÖSTERİLMESİ Fazör: Zamanla değişen gerilim ve akımın gösterildiği vektörlerdir. Vektör büyüklüğü maksimum değere eşit alınmayıp
1 ALTERNATİF AKIMIN VEKTÖRLERLE GÖSTERİLMESİ ALTERNATİF AKIMIN VEKTÖRLERLE GÖSTERİLMESİ Fazör: Zamanla değişen gerilim ve akımın gösterildiği vektörlerdir. Vektör büyüklüğü maksimum değere eşit alınmayıp
Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre
 Jeodezi 7 1 Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre Elipsoid yüzeyinin küçük parçalarında oluşan küçük üçgenlerin (kenarları 50-60 km den küçük) hesaplanmasında klasik jeodezide
Jeodezi 7 1 Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre Elipsoid yüzeyinin küçük parçalarında oluşan küçük üçgenlerin (kenarları 50-60 km den küçük) hesaplanmasında klasik jeodezide
ZAMAN SERİLERİNDE REGRESYON ANALİZİ
 ZAMAN SERİLERİNDE REGRESYON ANALİZİ 1 1. GİRİŞ Trent, serinin genelinde yukarıya ya da aşağıya doğru olan hareketlere denmektedir. Bu hareket bazen düz bir doğru şeklinde olmaktadır. Bu tür harekete sahip
ZAMAN SERİLERİNDE REGRESYON ANALİZİ 1 1. GİRİŞ Trent, serinin genelinde yukarıya ya da aşağıya doğru olan hareketlere denmektedir. Bu hareket bazen düz bir doğru şeklinde olmaktadır. Bu tür harekete sahip
FEN FAKÜLTESİ MATEMATİK BÖLÜMÜ YAZ OKULU DERS İÇERİGİ. Bölümü Dersin Kodu ve Adı T P K AKTS
 Bir Dönemde Okutulan Ders Saati MAT101 Genel I (Mühendislik Fakültesi Bütün Bölümler, Fen Fakültesi Kimya ve Astronomi Bölümleri) 1 Kümeler, reel sayılar, bir denklem veya eşitsizliğin grafiği 2 Fonksiyonlar,
Bir Dönemde Okutulan Ders Saati MAT101 Genel I (Mühendislik Fakültesi Bütün Bölümler, Fen Fakültesi Kimya ve Astronomi Bölümleri) 1 Kümeler, reel sayılar, bir denklem veya eşitsizliğin grafiği 2 Fonksiyonlar,
12. SINIF. Ağırlık (%) SAYILAR VE CEBİR ÜSTEL VE LOGARİTMİK FONKSİYONLAR Üstel Fonksiyon 1 8 4
 12. SINIF No Konular Kazanım Sayısı Ders Saati Ağırlık (%) 12.1. ÜSTEL VE LOGARİTMİK FONKSİYONLAR 6 36 17 12.1.1. Üstel Fonksiyon 1 8 4 12.1.2. Logaritma Fonksiyonu 3 18 8 12.1.3 Üstel, Logaritmik Denklemler
12. SINIF No Konular Kazanım Sayısı Ders Saati Ağırlık (%) 12.1. ÜSTEL VE LOGARİTMİK FONKSİYONLAR 6 36 17 12.1.1. Üstel Fonksiyon 1 8 4 12.1.2. Logaritma Fonksiyonu 3 18 8 12.1.3 Üstel, Logaritmik Denklemler
Hyperbolik Fonksiyonlar
 2 38 Bölüm 8 Hyperbolik Fonksiyonlar Hiperbolik fonksiyonlar iferensiyel enklemlerin çözümüme önemli rol oynar. Trigonometrik fonksiyonları anıran aları varır. Trigonometrik fonksiyonların alarını sonunu
2 38 Bölüm 8 Hyperbolik Fonksiyonlar Hiperbolik fonksiyonlar iferensiyel enklemlerin çözümüme önemli rol oynar. Trigonometrik fonksiyonları anıran aları varır. Trigonometrik fonksiyonların alarını sonunu
ÖZEL ÖĞRETİM KURSU MATEMATİK-III ÇERÇEVE PROGRAMI. : Kesikkapı Mah. Atatürk Cad. No 79 Fethiye /MUĞLA
 ÖZEL ÖĞRETİM KURSU MATEMATİK-III ÇERÇEVE PROGRAMI 1.KURUMUN ADI 2.KURUMUN ADRESİ 3.KURUCUNUN ADI :Tercih Özel Öğretim Kursu : Kesikkapı Mah. Atatürk Cad. No 79 Fethiye /MUĞLA : ARTI ÖZEL EĞİTİM ÖĞRETİM
ÖZEL ÖĞRETİM KURSU MATEMATİK-III ÇERÇEVE PROGRAMI 1.KURUMUN ADI 2.KURUMUN ADRESİ 3.KURUCUNUN ADI :Tercih Özel Öğretim Kursu : Kesikkapı Mah. Atatürk Cad. No 79 Fethiye /MUĞLA : ARTI ÖZEL EĞİTİM ÖĞRETİM
Yrd. Doç. Dr. A. Burak İNNER
 Yrd. Doç. Dr. A. Burak İNNER Kocaeli Üniversitesi Bilgisayar Mühendisliği Yapay Zeka ve Benzetim Sistemleri Ar-Ge Lab. http://yapbenzet.kocaeli.edu.tr Doğrusal Ara Değer Hesabı Lagrance Polinom İnterpolasyonu
Yrd. Doç. Dr. A. Burak İNNER Kocaeli Üniversitesi Bilgisayar Mühendisliği Yapay Zeka ve Benzetim Sistemleri Ar-Ge Lab. http://yapbenzet.kocaeli.edu.tr Doğrusal Ara Değer Hesabı Lagrance Polinom İnterpolasyonu
DENEY 3: DTMF İŞARETLERİN ÜRETİLMESİ VE ALGILANMASI
 DENEY 3: DTMF İŞARETLERİN ÜRETİLMESİ VE ALGILANMASI AMAÇ: DTMF işaretlerin yapısının, üretim ve algılanmasının incelenmesi. MALZEMELER TP5088 ya da KS58015 M8870-01 ya da M8870-02 (diğer eşdeğer entegreler
DENEY 3: DTMF İŞARETLERİN ÜRETİLMESİ VE ALGILANMASI AMAÇ: DTMF işaretlerin yapısının, üretim ve algılanmasının incelenmesi. MALZEMELER TP5088 ya da KS58015 M8870-01 ya da M8870-02 (diğer eşdeğer entegreler
Geriye Yayılım ve Levenberg Marquardt Algoritmalarının YSA Eğitimlerindeki Başarımlarının Dinamik Sistemler Üzerindeki Başarımı. Mehmet Ali Çavuşlu
 Geriye Yayılım ve Levenberg Marquardt Algoritmalarının YSA Eğitimlerindeki Başarımlarının Dinamik Sistemler Üzerindeki Başarımı Mehmet Ali Çavuşlu Özet Yapay sinir ağlarının eğitiminde genellikle geriye
Geriye Yayılım ve Levenberg Marquardt Algoritmalarının YSA Eğitimlerindeki Başarımlarının Dinamik Sistemler Üzerindeki Başarımı Mehmet Ali Çavuşlu Özet Yapay sinir ağlarının eğitiminde genellikle geriye
3. ARİTMETİK FONKSİYONLAR ~ (~ tamsayı)
 . ARİMEİK FONKSİYONLAR.1. ~ (~ tamsayı) Yalnız bir tam sayının değerini bir arttırarak tersini veren fonksiyondur. amsayı pozitif ise bir arttırır ve negatifini, tamsayı negatif ise bir arttırır ve pozitifini
. ARİMEİK FONKSİYONLAR.1. ~ (~ tamsayı) Yalnız bir tam sayının değerini bir arttırarak tersini veren fonksiyondur. amsayı pozitif ise bir arttırır ve negatifini, tamsayı negatif ise bir arttırır ve pozitifini
ARAZİ ÖLÇMELERİ Z P. O α X P. α = yatay açı. ω = düşey açı. µ =eğim açısı. ω + µ = 100 g
 Trigonometrik Fonksiyonlar ARAZİ ÖLÇMELERİ Z Z P P ω µ P O α α = yatay açı P P ω = düşey açı µ =eğim açısı ω + µ = 100 g Şekil 9 üç Boyutlu koordinat sisteminde açı tiplerinin tasviri. Trigonometrik kavramlara
Trigonometrik Fonksiyonlar ARAZİ ÖLÇMELERİ Z Z P P ω µ P O α α = yatay açı P P ω = düşey açı µ =eğim açısı ω + µ = 100 g Şekil 9 üç Boyutlu koordinat sisteminde açı tiplerinin tasviri. Trigonometrik kavramlara
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik İkiye Bölme / Yarılama Yöntemi Genel olarak f x = 0 gerek şartını sağlamak oldukça doğrusal olmayan ve bu sebeple çözümü
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik İkiye Bölme / Yarılama Yöntemi Genel olarak f x = 0 gerek şartını sağlamak oldukça doğrusal olmayan ve bu sebeple çözümü
TRİGONMETRİK FONKSİYONLAR: DİK ÜÇGEN YAKLAŞIMI
 TRİGONMETRİK FONKSİYONLAR: DİK ÜÇGEN YAKLAŞIMI Diyelim ki yeryüzünden güneşe olan mesafeyi bulmak istiyoruz. Şerit metre kullanmak açıkçası pratik değildir. Bu nedenle bu sorunun üstesinden gelmek için
TRİGONMETRİK FONKSİYONLAR: DİK ÜÇGEN YAKLAŞIMI Diyelim ki yeryüzünden güneşe olan mesafeyi bulmak istiyoruz. Şerit metre kullanmak açıkçası pratik değildir. Bu nedenle bu sorunun üstesinden gelmek için
Okut. Yüksel YURTAY. İletişim : (264) Sayısal Analiz. Giriş.
 Okut. Yüksel YURTAY İletişim : Sayısal Analiz yyurtay@sakarya.edu.tr www.cs.sakarya.edu.tr/yyurtay (264) 295 58 99 Giriş 1 Amaç : Mühendislik problemlerinin bilgisayar ortamında çözümünü mümkün kılacak
Okut. Yüksel YURTAY İletişim : Sayısal Analiz yyurtay@sakarya.edu.tr www.cs.sakarya.edu.tr/yyurtay (264) 295 58 99 Giriş 1 Amaç : Mühendislik problemlerinin bilgisayar ortamında çözümünü mümkün kılacak
TÜREV VE UYGULAMALARI
 TÜREV VE UYGULAMALARI 1-TÜREVİN TANIMI VE GÖSTERİLİŞİ a,b R olmak üzere, f:[a,b] R fonksiyonu verilmiş olsun. x 0 (a,b) için lim x X0 f(x)-f( x 0 ) limiti bir gerçel sayı ise bu limit değerine f fonksiyonunun
TÜREV VE UYGULAMALARI 1-TÜREVİN TANIMI VE GÖSTERİLİŞİ a,b R olmak üzere, f:[a,b] R fonksiyonu verilmiş olsun. x 0 (a,b) için lim x X0 f(x)-f( x 0 ) limiti bir gerçel sayı ise bu limit değerine f fonksiyonunun
Fonksiyonlar (Altprogram)
 Fonksiyonlar (Altprogram) C Programlama Dili fonksiyon olarak adlandırılan alt programların birleştirilmesi kavramına dayanır. Bir C programı bir ya da daha çok fonksiyonun bir araya gelmesi ile oluşur.
Fonksiyonlar (Altprogram) C Programlama Dili fonksiyon olarak adlandırılan alt programların birleştirilmesi kavramına dayanır. Bir C programı bir ya da daha çok fonksiyonun bir araya gelmesi ile oluşur.
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Altın Oran (Golden Section Search) Arama Metodu Tek değişkenli bir f(x) fonksiyonunu ele alalım. [Bazı x ler için f
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Altın Oran (Golden Section Search) Arama Metodu Tek değişkenli bir f(x) fonksiyonunu ele alalım. [Bazı x ler için f
Mühendislikte Sayısal Çözüm Yöntemleri NÜMERİK ANALİZ. Prof. Dr. İbrahim UZUN
 Mühendislikte Sayısal Çözüm Yöntemleri NÜMERİK ANALİZ Prof. Dr. İbrahim UZUN Yayın No : 2415 İşletme-Ekonomi Dizisi : 147 5. Baskı Eylül 2012 - İSTANBUL ISBN 978-605 - 377-438 - 9 Copyright Bu kitabın
Mühendislikte Sayısal Çözüm Yöntemleri NÜMERİK ANALİZ Prof. Dr. İbrahim UZUN Yayın No : 2415 İşletme-Ekonomi Dizisi : 147 5. Baskı Eylül 2012 - İSTANBUL ISBN 978-605 - 377-438 - 9 Copyright Bu kitabın
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 7- SAYISAL TÜREV Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ İntegral işlemi gibi türev işlemi de mühendislikte çok fazla kullanılan bir işlemdir. Basit olarak bir fonksiyonun bir noktadaki
MAK 210 SAYISAL ANALİZ BÖLÜM 7- SAYISAL TÜREV Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ İntegral işlemi gibi türev işlemi de mühendislikte çok fazla kullanılan bir işlemdir. Basit olarak bir fonksiyonun bir noktadaki
V cn V ca. V bc. V bn. V ab. -V bn. V an HATIRLATMALAR. Faz-Faz ve Faz-Nötr Gerilimleri. Yıldız ve Üçgen Bağlı Yüklerde Akım-Gerilim İlişkileri
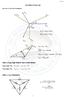 HATIRLATMALAR Faz-Faz ve Faz-Nötr Gerilimleri V cn V ca V ab 30 10 V an V aa = V cc = V bb V aa = V bb = V cc V bn V bc V ab 30 -V bn V aa = V aa V bb V aa = V aa cos(30) 30 V an V aa = V aa cos(30) =
HATIRLATMALAR Faz-Faz ve Faz-Nötr Gerilimleri V cn V ca V ab 30 10 V an V aa = V cc = V bb V aa = V bb = V cc V bn V bc V ab 30 -V bn V aa = V aa V bb V aa = V aa cos(30) 30 V an V aa = V aa cos(30) =
MATEMATİK ÖĞRETMENLİK ALAN BİLGİSİ - DENEME SINAVI DENEME. Diğer sayfaya geçiniz.
 MATEMATİK. DENEME ÖĞRETMENLİK ALAN BİLGİSİ - DENEME SINAVI. f : X tanımlı y = f() fonksiyonu için lim f ( ) = L ise aşağıdaki önermelerden kaç tanesi kesinlikle doğrudur? 0 I. X dir. 0 II. f() fonksiyonu
MATEMATİK. DENEME ÖĞRETMENLİK ALAN BİLGİSİ - DENEME SINAVI. f : X tanımlı y = f() fonksiyonu için lim f ( ) = L ise aşağıdaki önermelerden kaç tanesi kesinlikle doğrudur? 0 I. X dir. 0 II. f() fonksiyonu
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
KISITLI OPTİMİZASYON
 KISITLI OPTİMİZASYON SİMPLEKS YÖNTEMİ Simpleks Yöntemi Simpleks yöntemi iteratif bir prosedürü gerektirir. Bu iterasyonlar ile gerçekçi çözümlerin olduğu bölgenin (S) bir köşesinden başlayarak amaç fonksiyonunun
KISITLI OPTİMİZASYON SİMPLEKS YÖNTEMİ Simpleks Yöntemi Simpleks yöntemi iteratif bir prosedürü gerektirir. Bu iterasyonlar ile gerçekçi çözümlerin olduğu bölgenin (S) bir köşesinden başlayarak amaç fonksiyonunun
MAT 101, MATEMATİK I, FİNAL SINAVI 08 ARALIK (10+10 p.) 2. (15 p.) 3. (7+8 p.) 4. (15+10 p.) 5. (15+10 p.) TOPLAM
 TOBB-ETÜ, MATEMATİK BÖLÜMÜ, GÜZ DÖNEMİ 2014-2015 MAT 101, MATEMATİK I, FİNAL SINAVI 08 ARALIK 2014 Adı Soyadı: No: İMZA: 1. 10+10 p.) 2. 15 p.) 3. 7+8 p.) 4. 15+10 p.) 5. 15+10 p.) TOPLAM 1. a) NOT: Tam
TOBB-ETÜ, MATEMATİK BÖLÜMÜ, GÜZ DÖNEMİ 2014-2015 MAT 101, MATEMATİK I, FİNAL SINAVI 08 ARALIK 2014 Adı Soyadı: No: İMZA: 1. 10+10 p.) 2. 15 p.) 3. 7+8 p.) 4. 15+10 p.) 5. 15+10 p.) TOPLAM 1. a) NOT: Tam
BİLGİSAYAR PROGRAMLAMA MATLAB
 BİLGİSAYAR PROGRAMLAMA MATLAB Arş. Gör. Ahmet ARDAHANLI Kafkas Üniversitesi Mühendislik Fakültesi Bu hafta? 1. Matlab ve Programlama Ortamı 2. Matlab Komut Penceresi 3. Matlab de değişken tanımlama 4.
BİLGİSAYAR PROGRAMLAMA MATLAB Arş. Gör. Ahmet ARDAHANLI Kafkas Üniversitesi Mühendislik Fakültesi Bu hafta? 1. Matlab ve Programlama Ortamı 2. Matlab Komut Penceresi 3. Matlab de değişken tanımlama 4.
EĞİTİM ÖĞRETİM YILI ANADOLU LİSESİ 12.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLIK PLANI 12.SINIF KAZANIM VE SÜRE TABLOSU
 08-09 EĞİTİM ÖĞRETİM YILI ANADOLU LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. ÜSTEL VE LOGARİTMİK FONKSİYONLAR
08-09 EĞİTİM ÖĞRETİM YILI ANADOLU LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. ÜSTEL VE LOGARİTMİK FONKSİYONLAR
Algoritmalar ve Programlama. DERS - 4 Yrd. Doç. Dr. Ahmet SERBES
 Algoritmalar ve Programlama DERS - 4 Yrd. Doç. Dr. Ahmet SERBES Geçen Derste Değişken oluşturma Skaler Diziler, vektörler Matrisler Aritmetik işlemler Bazı fonksiyonların kullanımı Operatörler İlk değer
Algoritmalar ve Programlama DERS - 4 Yrd. Doç. Dr. Ahmet SERBES Geçen Derste Değişken oluşturma Skaler Diziler, vektörler Matrisler Aritmetik işlemler Bazı fonksiyonların kullanımı Operatörler İlk değer
ARŞİV FONKSİYONLARI VE ÖZELLİKLERİ TANIM İSİM VE ARGÜMAN ARGÜMAN/FONK. TİPİ AÇIKLAMA
 FONKSİYONLAR Sayısal bilgiler üzerinde direkt olarak kullanılabilen ve kendilerine özgü işlemleri gerçekleştiren ifadelerdir. Hazır fonksiyonlar Aritmetik deyim fonksiyonu (kullanıcı tarafında tanımlanan
FONKSİYONLAR Sayısal bilgiler üzerinde direkt olarak kullanılabilen ve kendilerine özgü işlemleri gerçekleştiren ifadelerdir. Hazır fonksiyonlar Aritmetik deyim fonksiyonu (kullanıcı tarafında tanımlanan
Algoritmalar. Sıralama Problemi ve Analizi. Bahar 2017 Doç. Dr. Suat Özdemir 1
 Algoritmalar Sıralama Problemi ve Analizi Bahar 2017 Doç. Dr. Suat Özdemir 1 Sıralama Problemi ve Analizi Bu bölümde öncelikle bir diğer böl-ve-yönet yöntemine dayalı algoritma olan Quick Sort algoritması
Algoritmalar Sıralama Problemi ve Analizi Bahar 2017 Doç. Dr. Suat Özdemir 1 Sıralama Problemi ve Analizi Bu bölümde öncelikle bir diğer böl-ve-yönet yöntemine dayalı algoritma olan Quick Sort algoritması
ESKİŞEHİR OSMANGAZİ ÜNİVERSİTESİ
 ESKİŞEHİR OSMANGAZİ ÜNİVERSİTESİ Mühendislik Mimarlık Fakültesi İnşaat Mühendisliği Bölümü E-Posta: ogu.ahmet.topcu@gmail.com Web: http://mmf2.ogu.edu.tr/atopcu Bilgisayar Destekli Nümerik Analiz Ders
ESKİŞEHİR OSMANGAZİ ÜNİVERSİTESİ Mühendislik Mimarlık Fakültesi İnşaat Mühendisliği Bölümü E-Posta: ogu.ahmet.topcu@gmail.com Web: http://mmf2.ogu.edu.tr/atopcu Bilgisayar Destekli Nümerik Analiz Ders
MATEMATĠKSEL ĠġLEMLER
 MATEMATĠKSEL ĠġLEMLER 2. HAFTA MATEMATĠKSEL ĠġLEM KOMUTLARI (FONKSĠYONLARI) Matematiksel (aritmetik) işlemlerin gerçekleştirilmesini sağlayan komutlar (fonksiyonlar) dır. C deki matematiksel fonksiyonlar
MATEMATĠKSEL ĠġLEMLER 2. HAFTA MATEMATĠKSEL ĠġLEM KOMUTLARI (FONKSĠYONLARI) Matematiksel (aritmetik) işlemlerin gerçekleştirilmesini sağlayan komutlar (fonksiyonlar) dır. C deki matematiksel fonksiyonlar
28/04/2014 tarihli LYS-1 Matematik-Geometri Testi konu analizi SORU NO LYS 1 MATEMATİK TESTİ KAZANIM NO KAZANIMLAR 1 / 31
 SORU NO LYS 1 MATEMATİK TESTİ A B KAZANIM NO KAZANIMLAR 1 1 / 31 11 32159 Rasyonel sayı kavramını açıklar. 2 12 32151 İki ya da daha çok doğal sayının en büyük ortak bölenini ve en küçük ortak katını bulur.
SORU NO LYS 1 MATEMATİK TESTİ A B KAZANIM NO KAZANIMLAR 1 1 / 31 11 32159 Rasyonel sayı kavramını açıklar. 2 12 32151 İki ya da daha çok doğal sayının en büyük ortak bölenini ve en küçük ortak katını bulur.
DERS BİLGİ FORMU. Zorunlu Ders X. Haftalık Ders Saati Okul Eğitimi Süresi
 DERSİN ADI MATEMATİK 1 BÖLÜM PROGRAM DÖNEMİ DERSİN DİLİ DERS KATEGORİSİ ÖN ŞARTLAR SÜRE VE DAĞILIMI KREDİ DERSİN AMACI ÖĞRENME ÇIKTILARI VE YETERLİKLER DERSİN İÇERİĞİ VE DAĞILIMI (MODÜLLER VE HAFTALARA
DERSİN ADI MATEMATİK 1 BÖLÜM PROGRAM DÖNEMİ DERSİN DİLİ DERS KATEGORİSİ ÖN ŞARTLAR SÜRE VE DAĞILIMI KREDİ DERSİN AMACI ÖĞRENME ÇIKTILARI VE YETERLİKLER DERSİN İÇERİĞİ VE DAĞILIMI (MODÜLLER VE HAFTALARA
 TMOZ/tmoz@yahoogroups.com Kasım - 2005 Ters trigonometrik fonksiyonlar Eyüp Kamil Yeşilyurt Alaattin Altuntaş Mustafa Yağcı Dikkat edilmeyen veya önemsenmeyen ayrıntılar bir gün sizi de rahatsız edebilir.
TMOZ/tmoz@yahoogroups.com Kasım - 2005 Ters trigonometrik fonksiyonlar Eyüp Kamil Yeşilyurt Alaattin Altuntaş Mustafa Yağcı Dikkat edilmeyen veya önemsenmeyen ayrıntılar bir gün sizi de rahatsız edebilir.
MAT355 Kompleks Fonksiyonlar Teorisi I Hafta 12. 3.3. Trigonometrik ve Hiperbolik Fonksiyonlar ve Tersleri., cosx = eix + e ix 2i
 MAT355 Kompleks Fonksiyonlar Teorisi I Hafta 1 3.3. Trigonometrik ve Hiperbolik Fonksiyonlar ve Tersleri e ix = cosx+isinx ve e ix = cosx isinx denklemlerinden yararlanılarak, her x reel sayısı için, sinx
MAT355 Kompleks Fonksiyonlar Teorisi I Hafta 1 3.3. Trigonometrik ve Hiperbolik Fonksiyonlar ve Tersleri e ix = cosx+isinx ve e ix = cosx isinx denklemlerinden yararlanılarak, her x reel sayısı için, sinx
T.C. DOKUZ EYLÜL ÜNİVERSİTESİ SOSYAL BİLİMLER ENSTİTÜSÜ EKONOMETRİ ANABİLİM DALI EKONOMETRİ DOKTORA PROGRAMI
 T.C. DOKUZ EYLÜL ÜNİVERSİTESİ SOSYAL BİLİMLER ENSTİTÜSÜ EKONOMETRİ ANABİLİM DALI EKONOMETRİ DOKTORA PROGRAMI Genişletilmiş Lagrange Yöntemi Hazırlayan: Nicat GASIM Öğretim Üyesi Prof. Dr. İpek Deveci KARAKOÇ
T.C. DOKUZ EYLÜL ÜNİVERSİTESİ SOSYAL BİLİMLER ENSTİTÜSÜ EKONOMETRİ ANABİLİM DALI EKONOMETRİ DOKTORA PROGRAMI Genişletilmiş Lagrange Yöntemi Hazırlayan: Nicat GASIM Öğretim Üyesi Prof. Dr. İpek Deveci KARAKOÇ
HAFTA 8: FOURIER SERİLERİ ÖZELLİKLERİ. İçindekiler
 HAFA 8: FOURIER SERİLERİ ÖZELLİKLERİ İçindekiler 4.4. Fourier serisinin özellikleri... 2 4.4.1 Doğrusallık özelliği (Linearity property)... 2 4.4.2 Zamanda tersine çevirme özelliği (ime Reversal Property)...
HAFA 8: FOURIER SERİLERİ ÖZELLİKLERİ İçindekiler 4.4. Fourier serisinin özellikleri... 2 4.4.1 Doğrusallık özelliği (Linearity property)... 2 4.4.2 Zamanda tersine çevirme özelliği (ime Reversal Property)...
Excel' de formüller yazılırken iki farklı uygulama kullanılır. Bunlardan;
 7. FORMÜLLER SEKMESİ Excel in en çok kullanılan yönü hesaplama yönüdür. Hesaplamalar Formüller aracılığıyla yapılır. Formüller sekmesi anlatılırken sık kullanılan formüller ve formül yazımı da anlatılacaktır.
7. FORMÜLLER SEKMESİ Excel in en çok kullanılan yönü hesaplama yönüdür. Hesaplamalar Formüller aracılığıyla yapılır. Formüller sekmesi anlatılırken sık kullanılan formüller ve formül yazımı da anlatılacaktır.
7 TAYLOR SER I GÖSTER IMLER I
 7 TAYLOR SER I GÖSTER IMLER I Bir f fonksiyonu analitiklik bölgesi içinde f () X a n ( 0 ) n şeklinde bir kuvvet serisi gösterimine sahiptir. E¼ger a n f (n) ( 0 ) seçilirse bu kuvvet serisi Taylor serisi
7 TAYLOR SER I GÖSTER IMLER I Bir f fonksiyonu analitiklik bölgesi içinde f () X a n ( 0 ) n şeklinde bir kuvvet serisi gösterimine sahiptir. E¼ger a n f (n) ( 0 ) seçilirse bu kuvvet serisi Taylor serisi
CEVAP ANAHTARI. Tempo Testi D 2-B 3-A 4-A 5-C 6-B 7-B 8-C 9-B 10-D 11-C 12-D 13-C 14-C
 01. BÖLÜM: FONKSİYONLARLA İLGİLİ UYGULAMALAR - 1 1-E 2-D 3-C 4-E 5-B 6-C 7-C 8-B 9-C 10-D 11-C - 2 1-D 2-E 3-C 4-D 5-E 6-E 7-C 8-D 9-E 10-B - 3 1-E 2-A 3-B 4-D 5-A 6-E 7-E 8-C 9-C 10-C 11-C 1-A 2-B 3-E
01. BÖLÜM: FONKSİYONLARLA İLGİLİ UYGULAMALAR - 1 1-E 2-D 3-C 4-E 5-B 6-C 7-C 8-B 9-C 10-D 11-C - 2 1-D 2-E 3-C 4-D 5-E 6-E 7-C 8-D 9-E 10-B - 3 1-E 2-A 3-B 4-D 5-A 6-E 7-E 8-C 9-C 10-C 11-C 1-A 2-B 3-E
LYS MATEMATİK DENEME - 1
 LYS MATEMATİK DENEME - BU SORULAR FİNAL EĞİTİM KURUMLARI TARAFINDAN SAĞLANMIŞTIR. İZİNSİZ KOPYALANMASI VE ÇOĞALTILMASI YASAKTIR, YAPILDIĞI TAKDİRDE CEZAİ İŞLEM UYGULANACAKTIR. LYS MATEMATİK TESTİ. Bu testte
LYS MATEMATİK DENEME - BU SORULAR FİNAL EĞİTİM KURUMLARI TARAFINDAN SAĞLANMIŞTIR. İZİNSİZ KOPYALANMASI VE ÇOĞALTILMASI YASAKTIR, YAPILDIĞI TAKDİRDE CEZAİ İŞLEM UYGULANACAKTIR. LYS MATEMATİK TESTİ. Bu testte
Sayfa No. Test No İÇİNDEKİLER TRİGONOMETRİ
 TRİGONOMETRİ İÇİNDEKİLER Sayfa No Test No YÖNLÜ AÇI VE YÖNLÜ YAY KAVRAMI -AÇI ÖLÇÜ BİRİMLERİ...00-00.... BİRİM ÇEMBER...00-00.... BİR AÇININ ESAS ÖLÇÜSÜ...00-00.... BİR AÇININ TRİGONOMETRİK ORANLARININ
TRİGONOMETRİ İÇİNDEKİLER Sayfa No Test No YÖNLÜ AÇI VE YÖNLÜ YAY KAVRAMI -AÇI ÖLÇÜ BİRİMLERİ...00-00.... BİRİM ÇEMBER...00-00.... BİR AÇININ ESAS ÖLÇÜSÜ...00-00.... BİR AÇININ TRİGONOMETRİK ORANLARININ
SBA/ANR 2016 Spor Biyomekaniği ( Bahar) Ders 3: Açısal Kinematik
 SBA/ANR 2016 Spor Biyomekaniği (2016-2017 Bahar) Ders 3: Açısal Kinematik Arif Mithat AMCA amithat@hacettepe.edu.tr 1 Hareket Türleri Doğrusal Hareket Düz bir çizgi ya da eğri üzerinde olan harekettir.
SBA/ANR 2016 Spor Biyomekaniği (2016-2017 Bahar) Ders 3: Açısal Kinematik Arif Mithat AMCA amithat@hacettepe.edu.tr 1 Hareket Türleri Doğrusal Hareket Düz bir çizgi ya da eğri üzerinde olan harekettir.
1203608-SIMÜLASYON DERS SORUMLUSU: DOÇ. DR. SAADETTIN ERHAN KESEN. Ders No:5 Rassal Değişken Üretimi
 1203608-SIMÜLASYON DERS SORUMLUSU: DOÇ. DR. SAADETTIN ERHAN KESEN Ders No:5 RASSAL DEĞIŞKEN ÜRETIMI Bu bölümde oldukça yaygın bir biçimde kullanılan sürekli ve kesikli dağılımlardan örneklem alma prosedürleri
1203608-SIMÜLASYON DERS SORUMLUSU: DOÇ. DR. SAADETTIN ERHAN KESEN Ders No:5 RASSAL DEĞIŞKEN ÜRETIMI Bu bölümde oldukça yaygın bir biçimde kullanılan sürekli ve kesikli dağılımlardan örneklem alma prosedürleri
Bölüm-4. İki Boyutta Hareket
 Bölüm-4 İki Boyutta Hareket Bölüm 4: İki Boyutta Hareket Konu İçeriği 4-1 Yer değiştirme, Hız ve İvme Vektörleri 4-2 Sabit İvmeli İki Boyutlu Hareket 4-3 Eğik Atış Hareketi 4-4 Bağıl Hız ve Bağıl İvme
Bölüm-4 İki Boyutta Hareket Bölüm 4: İki Boyutta Hareket Konu İçeriği 4-1 Yer değiştirme, Hız ve İvme Vektörleri 4-2 Sabit İvmeli İki Boyutlu Hareket 4-3 Eğik Atış Hareketi 4-4 Bağıl Hız ve Bağıl İvme
Diferensiyel Denklemler I Uygulama Notları
 2004 Diferensiyel Denklemler I Uygulama Notları Mustafa Özdemir İçindekiler Temel Bilgiler...................................................................... 2 Tam Diferensiyel Denklemler........................................................4
2004 Diferensiyel Denklemler I Uygulama Notları Mustafa Özdemir İçindekiler Temel Bilgiler...................................................................... 2 Tam Diferensiyel Denklemler........................................................4
Hiperbolik Fonksiyonlar
 Matematik Dünas, 0-III Kapak Konusu: İntegral IV Hiperbolik Fonksionlar sinh olarak a z - lan kosinüs sinüs hiperbolik fonksionlar ndan geçmiflte k saca sö zet mifltik Bu az da bu fonksionlardan biraz
Matematik Dünas, 0-III Kapak Konusu: İntegral IV Hiperbolik Fonksionlar sinh olarak a z - lan kosinüs sinüs hiperbolik fonksionlar ndan geçmiflte k saca sö zet mifltik Bu az da bu fonksionlardan biraz
Yrd. Doç. Dr. A. Burak İNNER
 Yrd. Doç. Dr. A. Burak İNNER Kocaeli Üniversitesi Bilgisayar Mühendisliği Yapay Zeka ve Benzetim Sistemleri Ar-Ge Lab. http://yapbenzet.kocaeli.edu.tr DOĞRUSAL OLMAYAN (NONLINEAR) DENKLEM SİSTEMLERİ Mühendisliğin
Yrd. Doç. Dr. A. Burak İNNER Kocaeli Üniversitesi Bilgisayar Mühendisliği Yapay Zeka ve Benzetim Sistemleri Ar-Ge Lab. http://yapbenzet.kocaeli.edu.tr DOĞRUSAL OLMAYAN (NONLINEAR) DENKLEM SİSTEMLERİ Mühendisliğin
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 8- SAYISAL İNTEGRASYON 1 GİRİŞ Mühendislikte sık karşılaşılan matematiksel işlemlerden biri integral işlemidir. Bilindiği gibi integral bir büyüklüğün toplam değerinin bulunması
MAK 210 SAYISAL ANALİZ BÖLÜM 8- SAYISAL İNTEGRASYON 1 GİRİŞ Mühendislikte sık karşılaşılan matematiksel işlemlerden biri integral işlemidir. Bilindiği gibi integral bir büyüklüğün toplam değerinin bulunması
T.C. MİLLİ EĞİTİM BAKANLIĞI ÖZEL ÇORUM ADA ÖZEL ÖĞRETİM KURSU MATEMATİK V BİLİM GRUBU ÇERÇEVE PROGRAMI
 T.C. MİLLİ EĞİTİM BAKANLIĞI ÖZEL ÇORUM ADA ÖZEL ÖĞRETİM KURSU MATEMATİK V BİLİM GRUBU ÇERÇEVE PROGRAMI 1 1. KURUMUN ADI : Özel Çorum Ada Özel Öğretim Kursu 2. KURUMUN ADRESİ : Yavruturna mah. Kavukçu sok.
T.C. MİLLİ EĞİTİM BAKANLIĞI ÖZEL ÇORUM ADA ÖZEL ÖĞRETİM KURSU MATEMATİK V BİLİM GRUBU ÇERÇEVE PROGRAMI 1 1. KURUMUN ADI : Özel Çorum Ada Özel Öğretim Kursu 2. KURUMUN ADRESİ : Yavruturna mah. Kavukçu sok.
ÖZEL ÖĞRETİM KURSU MATEMATİK-V ÇERÇEVE PROGRAMI. 3. KURUCUNUN ADI :ARTI ÖZEL EĞİTİM ÖĞRETİM Danışmanlık Turizm Hizmetleri Ticaret İth. İhr. Ltd. Şti.
 ÖZEL ÖĞRETİM KURSU MATEMATİK-V ÇERÇEVE PROGRAMI 1. KURUMUN ADI : Tercih Özel Öğretim Kursu 2. KURUMUN ADRESİ : Kesikkapı Mah. Atatürk Cad. No 79 Fethiye /MUĞLA 3. KURUCUNUN ADI :ARTI ÖZEL EĞİTİM ÖĞRETİM
ÖZEL ÖĞRETİM KURSU MATEMATİK-V ÇERÇEVE PROGRAMI 1. KURUMUN ADI : Tercih Özel Öğretim Kursu 2. KURUMUN ADRESİ : Kesikkapı Mah. Atatürk Cad. No 79 Fethiye /MUĞLA 3. KURUCUNUN ADI :ARTI ÖZEL EĞİTİM ÖĞRETİM
Günümüz bilgi toplumunda bilgisayar, her alanda kendine yer edinmiş ve insana, bir çok işlemde yardımcı olarak büyük kolaylık sağlamaktadır.
 I. GİRİŞ Günümüz bilgi toplumunda bilgisayar, her alanda kendine yer edinmiş ve insana, bir çok işlemde yardımcı olarak büyük kolaylık sağlamaktadır. İnsanların elle yaptığı ve yapmakta olduğu bir çok
I. GİRİŞ Günümüz bilgi toplumunda bilgisayar, her alanda kendine yer edinmiş ve insana, bir çok işlemde yardımcı olarak büyük kolaylık sağlamaktadır. İnsanların elle yaptığı ve yapmakta olduğu bir çok
9 B ol um Türevin Uygulamaları
 2 Bölüm 9 Türevin Uygulamaları 64 BÖLÜM 9. TÜREVİN UYGULAMALARI Bölüm 0 Türev Tanım 0. y = f () fonksiyonu (a,b) aralığında tanımlı ve 0 (a,b) olsun. y = f ( 0 ) h 0 f ( 0 + h) f ( 0 ) h iti varsa, bu
2 Bölüm 9 Türevin Uygulamaları 64 BÖLÜM 9. TÜREVİN UYGULAMALARI Bölüm 0 Türev Tanım 0. y = f () fonksiyonu (a,b) aralığında tanımlı ve 0 (a,b) olsun. y = f ( 0 ) h 0 f ( 0 + h) f ( 0 ) h iti varsa, bu
Zeki Optimizasyon Teknikleri
 Zeki Optimizasyon Teknikleri Tabu Arama (Tabu Search) Doç.Dr. M. Ali Akcayol Tabu Arama 1986 yılında Glover tarafından geliştirilmiştir. Lokal minimum u elimine edebilir ve global minimum u bulur. Değerlendirme
Zeki Optimizasyon Teknikleri Tabu Arama (Tabu Search) Doç.Dr. M. Ali Akcayol Tabu Arama 1986 yılında Glover tarafından geliştirilmiştir. Lokal minimum u elimine edebilir ve global minimum u bulur. Değerlendirme
1. KURUMUN ADI : Özel Osmaniye Artı Bilim Temel Lisesi. 3. KURUCUNUN ADI : Sinerji Eğitimcilik San. Tic. Ltd. Şti./Celal DEMİR
 1. KURUMUN ADI : Özel Osmaniye Artı Bilim Temel Lisesi 2. KURUMUN ADRESİ : Cumhuriyet Mah. Akyar Cad. No:87/B 3. KURUCUNUN ADI : Sinerji Eğitimcilik San. Tic. Ltd. Şti./Celal DEMİR 4. PROGRAMIN ADI : MATEMATİK
1. KURUMUN ADI : Özel Osmaniye Artı Bilim Temel Lisesi 2. KURUMUN ADRESİ : Cumhuriyet Mah. Akyar Cad. No:87/B 3. KURUCUNUN ADI : Sinerji Eğitimcilik San. Tic. Ltd. Şti./Celal DEMİR 4. PROGRAMIN ADI : MATEMATİK
3.2. DP Modellerinin Simpleks Yöntem ile Çözümü Primal Simpleks Yöntem
 3.2. DP Modellerinin Simpleks Yöntem ile Çözümü 3.2.1. Primal Simpleks Yöntem Grafik çözüm yönteminde gördüğümüz gibi optimal çözüm noktası, her zaman uygun çözüm alanının bir köşe noktası ya da uç noktası
3.2. DP Modellerinin Simpleks Yöntem ile Çözümü 3.2.1. Primal Simpleks Yöntem Grafik çözüm yönteminde gördüğümüz gibi optimal çözüm noktası, her zaman uygun çözüm alanının bir köşe noktası ya da uç noktası
Ders Adı Kodu Yarıyılı T+U Saati Ulusal Kredisi AKTS. Kompleks Matematik EEE203 3 3+0 3 4
 DERS BİLGİLERİ Ders Adı Kodu Yarıyılı T+U Saati Ulusal Kredisi AKTS Kompleks Matematik EEE203 3 3+0 3 4 Ön Koşul Dersleri Dersin Dili Dersin Seviyesi Dersin Türü İngilizce Lisans Zorunlu / Yüz Yüze Dersin
DERS BİLGİLERİ Ders Adı Kodu Yarıyılı T+U Saati Ulusal Kredisi AKTS Kompleks Matematik EEE203 3 3+0 3 4 Ön Koşul Dersleri Dersin Dili Dersin Seviyesi Dersin Türü İngilizce Lisans Zorunlu / Yüz Yüze Dersin
Şekil 2 Hareketin başladığı an
 Şekil 2 Hareketin başladığı an Bir savaş uçağı şekildeki gibi 1500 km/sa hızla sorti (dalışa geçerek bombardıman gerçekleştirmek) için harekete başlıyor ve eğrilik yarıçapı 300m. olan dairesel yörüngede
Şekil 2 Hareketin başladığı an Bir savaş uçağı şekildeki gibi 1500 km/sa hızla sorti (dalışa geçerek bombardıman gerçekleştirmek) için harekete başlıyor ve eğrilik yarıçapı 300m. olan dairesel yörüngede
Yapı Sistemlerinin Hesabı İçin. Matris Metotları. Prof.Dr. Engin ORAKDÖĞEN Doç.Dr. Ercan YÜKSEL Bahar Yarıyılı
 Yapı Sistemlerinin Hesabı İçin Matris Metotları 05-06 Bahar Yarıyılı Prof.Dr. Engin ORAKDÖĞEN Doç.Dr. Ercan YÜKSEL BÖLÜM VIII HAREKET DENKLEMİ ZORLANMIŞ TİTREŞİMLER SERBEST TİTREŞİMLER Bu bölümün hazırlanmasında
Yapı Sistemlerinin Hesabı İçin Matris Metotları 05-06 Bahar Yarıyılı Prof.Dr. Engin ORAKDÖĞEN Doç.Dr. Ercan YÜKSEL BÖLÜM VIII HAREKET DENKLEMİ ZORLANMIŞ TİTREŞİMLER SERBEST TİTREŞİMLER Bu bölümün hazırlanmasında
