ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ FUZZY METRİK UZAYLARDA ORTAK SABİT NOKTA TEOREMLERİ ÜZERİNE.
|
|
|
- Batur Bayar
- 5 yıl önce
- İzleme sayısı:
Transkript
1 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ FUZZY METRİK UZAYLARDA ORTAK SABİT NOKTA TEOREMLERİ ÜZERİNE Müzeyyen SANGURLU MATEMATİK ANABİLİM DALI ANKARA 2011 Her hakkı saklıdır
2 ÖZET Yüksek Lisans Tezi FUZZY METR IK UZAYLARDA ORTAK SAB IT NOKTA TEOREMLER I ÜZER INE Müzeyyen SANGURLU Ankara Üniversitesi Fen Bilimleri Enstitüsü Matematik Anabilim Dal Dan şman: Doç. Dr. Erdal GÜNER Bu tez dört bölümden oluşmaktad r. Ilk bölüm giriş k sm na ayr lm şt r. Ikinci bölümde, baz temel kavramlara yer verilmiştir. Üçüncü bölümde, fuzzy metrik uzay n tan m, bu uzaylar için örnekler ve fuzzy metrik uzaylar n baz özellikleri verilmiştir. Son bölümde, baz fonksiyonlar n tan mlar verilmiş ve bu fonksiyonlar n aralar ndaki ilişkiler incelenmiştir. Sonra bu fonksiyonlar için ortak sabit nokta teoremleri verilmiş ve baz sonuçlar elde edilmiştir. Haziran 2011, 57 sayfa Anahtar Kelimeler : Fuzzy metrik uzay, sabit nokta, sabit nokta teoremi, ba¼gdaşabilirlik, yar ba¼gdaşabilirlik, R-zay f komutati ik i
3 ABSTRACT Master Thesis ON THEOREMS OF COMMON FIXED POINTS IN FUZZY METRIC SPACES Müzeyyen SANGURLU Ankara University Graduate School of Natural And Applied Sciences Department of Mathematics Supervisor: Assoc. Prof. Dr. Erdal GÜNER This thesis consists of four chapters. The rst chapter is devoted to the introduction. In the second chapter, some basic concepts have been recalled. In the third chapter, de nition of fuzzy metric spaces, examples for fuzzy metric spaces and some properties of fuzzy metric spaces have been given. In the nal chapter, de nitions of some functions have been given and relations between these functions have been considired. Then, theorems of common xed point for these functions have been given and some results have been introduced. June 2011, 57 pages Key Words: Fuzzy metric space, xed point, theorem of xed point, compatiblity, semi compatiblity, R-weakly comutativity ii
4 TEŞEKKÜR Bu çal şma konusunu bana veren, araşt rmalar m n her aşamas nda engin bilgilerini benden hiçbir zaman esirgemeyen ve matematiksel düşünme yetene¼gimi geliştirmeme yard mc olan dan şman hocam Say n Doç. Dr. Erdal GÜNER (Ankara Üniversitesi Fen Fakültesi Matematik Bölümü) e yüksek lisans e¼gitimim süresince bana destek olan arkadaşlar m Emre TAŞ, Tu¼gba YURDAKAD IM, Nuray EVC IN e ve hayat m boyunca yan mda oldu¼gu gibi çal şmalar m süresince de fedakarl klar göstererek beni destekleyen aileme sonsuz teşekkür ederim. Müzeyyen SANGURLU Ankara, Haziran 2011 iii
5 IÇ INDEK ILER ÖZET... i ABSTRACT... ii TEŞEKKÜR... iii S IMGELER D IZ IN I... v 1. G IR IŞ TEMEL KAVRAMLAR FUZZY METR IK UZAYLAR FUZZY METR IK UZAYLARDA BAZI FONKS IYONLAR IÇ IN SAB IT NOKTA TEOREMLER I Fuzzy Metrik Uzaylarda -Tipi Ba¼gdaşabilir Fonksiyonlar Için Sabit Nokta Teoremleri Fuzzy Metrik Uzaylarda -Tipi Ba¼gdaşabilir Fonksiyonlar Için Sabit Nokta Teoremleri Fuzzy Metrik Uzaylarda Yar Ba¼gdaşabilir Fonksiyonlar Için Sabit Nokta Teoremleri Fuzzy Metrik Uzaylarda R- Zay f Komutatif Fonksiyonlar Için Sabit Nokta Teoremleri KAYNAKLAR ÖZGEÇM IŞ iv
6 S IMGELER D IZ IN I I x d (X; d) M (X; M; ) B(x; r; t) B[x; r; t] ^ _ A ^ B A _ B A c A X dan I = [0; 1] ya tan mlanan fonksiyonlar n kümesi Üçgen norm Metrik Metrik Uzay Fuzzy metrik Fuzzy metrik uzay Fuzzy metrik uzaydaki aç k yuvar Fuzzy metrik uzaydaki kapal yuvar Fuzzy kümelerde kesişim Fuzzy kümelerde birleşim A ve B kümelerinin in mumu A ve B kümelerinin supremumu A kümesinin tümleyeni A fuzzy kümesinin üyelik fonksiyonu v
7 1. G IR IŞ Boştan farkl bir küme üzerinde metrik ve iki nokta aras ndaki uzakl k kavram n n nas l tan mlanaca¼g matemati¼gin temel problemlerinden biri olmuştur y l nda Frechet, boştan farkl bir küme üzerindeki metrik yap s üzerinde çal şm ş, kümenin farkl iki eleman aras ndaki uzakl ¼g n pozitif bir reel say olmas gerekti¼gini göstermiştir. Ancak bu süreçte küme tan m yetersiz kalm şt r. Örne¼gin küme tan m na göre k rm z renkteki cisimlerin kümesi oluşturulabilir fakat renk anlay ş kişiden kişiye de¼gişti¼ginden bu kümenin elemanlar tek türlü tan mlanamamaktad r. E¼ger k rm z renklerin tonlar na [0; 1] aral ¼g ndaki say lar karş l k getirilirse, bu küme herkesin kabul edece¼gi ve daha kullan şl halde tan mlanabilir. Zadeh (1965), fuzzy küme tan m n yaparak bilimin bir çok dal nda önemli uygulamalar n bulmuş ve kendisi bir Elektrik-Elektronik Mühendisi oldu¼gu halde böyle bir çal şma yapmakla fuzzy küme kavram n n teknoloji ile gerçekte ne kadar yak ndan ilgili oldu¼gunu göstermiştir. Matemati¼gin birçok dal nda da fuzzy kümeler kavram n kullanarak çok önemli baz sonuçlar elde etmiştir. Böylece fuzzy küme üzerinde de metrik yap s n oluşturmak, fuzzy matemati¼ginin temel problemlerinden biri olmuştur. Bu alandaki ilk çal şmay Kramosil ve Michalek (1975) sonra Erceg (1979) ve Deng (1982) yapm şt r. Fang (1992), Kaleva ve Seikkala (1984), Edelstein (1962) ve Istratescu (1961) n n daha önceden üzerinde çal şt ¼g sabit nokta teoremlerini fuzzy için ispatlam şlard r. Sessa (1982) zay f komutati ik kavram n, Junck (1986) ise ba¼gdaşabilirlik kavram n vermiştir. Daha sonra Junck (1993) metrik uzaylarda -tipi ba¼gdaşabilir dönüşümler konusunu ele alm ş, Cho (1997) ise bu konuyu fuzzy metrik uzaylara genişletmiştir. Pathak (1998) metrik uzaylarda -tipi ba¼gdaşabilirlik konusunu ele alm ş, Cho (1998) ise bu konuyu fuzzy metrik uzaylara taş m şt r. Cho, Sharma ve Sahu (1995) yar ba¼gdaşabilirlik konusu ile ilgili çal şmalar yapm şt r. Vasuki (1999) fuzzy metrik uzaylalarda R-zay f komutatif fonksiyonlar n ortak sabit nokta teoremlerini ele alm şt r. Kütükçü, Türko¼glu ve Y ld z (2006) ise fuzzy metrik uzaylar üzerinde -tipi ba¼gdaşabilir fonksiyonlar n ortak sabit nokta teoremlerini incelemişlerdir. 1
8 2. TEMEL KAVRAMLAR Bu bölümde daha sonraki bölümler için temel oluşturan kavramlar verilecektir. Tan m 2.1 : [0; 1] [0; 1]! [0; 1] bir ikili işlem olsun. E¼ger işlemi 8a; b; c; d 2 [0; 1] için (1) a b = b a (2) a (b c) = (a b) c (3) sürekli (4) a 1 = a (5) a c ve b d iken a b c d şartlar n sa¼gl yorsa a surekli t norm denir (Schweizer ve Sklar 1960). Örnek 2.1 8a; b 2 [0; 1] için ab =minfa; bg, ab =maksf0; a+b şeklinde tan mlanan işlemler sürekli t-normdur. 1g ve ab = a:b Tan m 2.2 X 6=?, I = [0; 1] olmak üzere X kümesinden I ya tan mlanan fonksiyonlar n kümesini I x ile gösterelim. I x in her bir eleman na X in bir fuzzy kümesi denir. X in bir fuzzy alt kümesi, A : X! I üyelik fonksiyonu ile karakterize edilen A = f(x; A (x)) : x 2 Xg X I kümesine denir. A (x), A fuzzy kümesinin üyelik derecesi olarak yorumlanabilir. Örnek 2.2 8x 2 X için X = f(x; 1); x 2 Xg,? = f(x; 0); x 2 Xg kümeleri birer fuzzy kümesidir. Ayr ca her küme fuzzy kümesi olup tersi do¼gru de¼gildir. Not 2.1 X de harhangi iki küme A ve B olsun. (1) A B () A (x) B (x) (2) A = B () A (x) = B (x) (3) A _ B = C () C (x) =maksf A (x); B (x)g (4) A ^ B = D =) D (x) =minf A (x); B (x) (5) A c () c A (x) = 1 A(x) 2
9 (6) A B = A ^ B c () A B (x) =minf A (x); B c(x)g Not 2.2 A \ A c =?; A [ A c = X olmak zorunda de¼gildir. Örnek 2.3 X = fa; b; cg; A = f(a; 0:3); (b; 0:6); (c; 0:5)g; B = f(a; 0:2); (b; 0:7); (c; 0:4)g olsun. A [ B = A _ B = maksf A (x); B (x)g = f(a; 0:3); (b; 0:7); (c; 0:5)g A \ B = A ^ B = minf A (x); B (x) = f(a; 0:2); (b; 0:6); (c; 0:4)g elde edilir. A c = fa; 0:7); (b; 0:4); (c; 0:5)g olup A \ A c = f(a; 0:3); (b; 0:4); (c; 0:5)g 6=? A [ A c = f(a; 0:7); (b; 0:6); (c; 0:5)g 6= X oldu¼gu görülür. Tan m 2.3 X boş olmayan bir küme ve f : X! X herhangi bir dönüşüm olsun. E¼ger f(x 0 ) = x 0 olacak şekilde bir x 0 2 X varsa, bu x 0 noktas na f nin bir sabit noktas d r denir. Yani f(x 0 ) = x 0 fonksiyon denkleminin çözümü, f nin bir sabit noktas d r. Baz dönüşümlerin sabit noktas olmad ¼g halde, baz lar n n birden fazla sabit noktas olabilir. Örnek 2.4 f : R! R; f(x) = x 2 fonksiyonunun 0 ve 1 olmak üzere iki sabit noktas vard r. Örnek 2.5 X 6=? olmak üzere I : X! X birim fonksiyonu için tüm noktalar birer sabit noktad r. Örnek 2.6 f : R! R; f(x) = 0 fonksiyonun sabit noktas sadece 0 d r. 3
10 Teorem 2.1 f : X! X sürekli bir fonksiyon ve X kümesinde sabit nokta özelli¼gi sa¼glans n. E¼ger h : X! Y bir homeomor zm ise Y kümesinde de sabit nokta özelli¼gi sa¼glan r. Ispat: f : X! X sürekli fonksiyon olsun. X sabit nokta özelli¼gini sa¼glad ¼g ndan f(x 0 ) = x 0 şart n sa¼glayan en az bir x 0 2 X say s vard r. h : X! Y bir homeomor zm oldu¼gundan g = h f h 1 fonksiyonu süreklidir. h(x 0 ) = y 0 2 Y eşitli¼ginden x 0 = h 1 (y 0 ) ifadesi yaz labilir. g(y 0 ) = (h f h 1 ) (y0 ) = (h(f(h 1 (y 0 ))) = h(f(x 0 )) = h(x 0 ) = y 0 elde edilir. Bu durumda g(y 0 ) = y 0 oldu¼gundan Y kümesinde de sabit nokta özelli¼ginin sa¼gland ¼g görülür. 4
11 3. FUZZY METR IK UZAYLARIN BAZI ÖZELL IKLER I Bu bölümde fuzzy metrik uzaylar tan mlanarak bu uzaylar n baz özellikleri verilecektir. Tan m 3.1 X boş olmayan herhangi bir küme, işlemi sürekli bir t-norm ve M de X 2 (0; 1) üzerinde bir fuzzy küme olsun. E¼ger M, 8 x; y; z 2 X ve t; s > 0 için (F-1) M(x; y; t) > 0; (F-2) M(x; y; t) = 1, x = y; (F-3) M(x; y; t) = M(y; x; t); (F-4) M(x; y; t) M(y; z; s) M(x; z; t + s); (F-5) M(x; y; ) : (0; 1)! [0; 1] sürekli koşullar n sa¼gl yorsa M ye X üzerinde bir fuzzy metrik ve (X; M; ) üçlüsüne de fuzzy metrik uzay denir. Burada M(x; y; t) nin anlam, t ye göre x ve y aras ndaki yak nl ¼g n derecesi olarak yorumlanabilir (George ve Veeramani 1994). Örnek 3.1 X = R olsun ve a b = a:b olsun. 8 x; y; z 2 X ve t 2 (0; 1) için, M(x; y; t) = exp( jx yj t (X; M; ) bir fuzzy metrik uzayd r (George ve Veeramani 1994). Gerçekten (F-1) jx yj 0 =) jx yj t 0 ) şeklinde tan mlanan =) jx yj t 0 =) exp( jx t yj ) > 0 (F-2) M(x; y; t) = 1 () exp( jx t yj ) = 1 () jx yj t = 0 () jx yj = 0 () x = y 5
12 jx yj jy (F-3) M(x; y; t) = exp( g = exp( t (F-4) jx zj jx yj + jy zj oldu¼gundan t xj g = M(y; x; t) jx zj ( t + s )jx yj + ( t + s )jy zj t s jx zj jx yj jy zj + t + s t s e jx e jx zj t+s e yj t+s e jx yj jy zj t :e s jx yj t :e jy zj s M(x; z; t + s) M(x; y; t) M(y; z; s) elde edilir. (F-5) t 0 > 0 olsun. lim t!t 0 M(x; y; t) = lim t!t0 e jx yj t = e jx yj t 0 = M(x; y; t 0 ) bulunur. Teorem 3.1 (X; d) bir metrik uzay ve a b = a:b olsun. 8k; m; n 2 R + için M d (x; y; t) = kt n kt n + md(x; y) olarak tan mlanan fonksiyon bir fuzzy metriktir (George ve Veeramani 1994). Sonuç 3.1 Teorem 3.1 de k = m = n = 1 al n rsa M d (x; y; t) = t t + d(x; y) elde edilir. M d ye d taraf ndan indirgenen standart fuzzy metrik denir. 6
13 Ispat: (F-1) M d (x; y; t) > 0 (F-2) M d (x; y; t) = 1 () t t + d(x; y) = 1 () d(x; y) = 0 () x = y t (F-3) M d (x; y; t) = t + d(x; y) = t t + d(y; x) = M d(y; x; t) (F-4) d(x; z) d(x; y) + d(y; z) oldu¼gundan d(x; z) t + s t d(x; y) + t + s d(y; z) s d(x; z) t + s d(x; y) t + d(y; z) s d(x; z) t + s sd(x; y) + td(y; z) st t + s + d(x; z) t + s st + sd(x; y) + td(y; z) st t + s + d(x; z) t + s st + sd(x; y) + td(y; z) + d(x; y)d(y; z) st t + s + d(x; z) t + s [t + d(x; y)][s + d(y; z)] st t + s t + s + d(x; z) t t + d(x; y) s s + d(y; z) M(x; y; t + s) M(x; y; t) M(y; z; s) elde edilir. 7
14 (F-5) t 0 0 olsun. t limm d (x; y; t) = lim t!t 0 t!t0 t + d(x; y) = t 0 t 0 + d(x; y) = M(x; y; t 0) elde edilir. Teorem x; y 2 X için M(x; y; ) azalmayan bir fonksiyondur (Grabiec 1988). Ispat: 0 < t < s olsun. Kabul edelim ki M(x; y; t) > M(x; y; s) olsun. O halde M(x; y; t) M(y; y; s t) M(x; y; s) < M(x; y; t) yaz labilir. Di¼ger taraftan oldu¼gundan M(y; y; s t) = 1 M(x; y; t) < M(x; y; t) bulunur ve böylece bir çelişki elde edilir. Yani M(x; y; t) M(x; y; s) eşitsizli¼ginin sa¼glanmas gerekir. Bu durumda M(x; y; ) azalmayan bir fonksiyondur. Not 3.1 (i) (X; M; ) bir fuzzy metrik uzay olsun. 8x; y 2 X, t > 0 ve 0 < r < 1 için M(x; y; kt) > 1 r koşulu sa¼glan yorsa 0 < t 0 < t ve M(x; y; t 0 ) > 1 r olacak şekilde bir t 0 say s vard r. (ii) r 1 ; r 2 ; r 3 ; r 4 ; r 5 2 (0; 1) olmak üzere r 1 > r 2 için r 1 r 3 > r 2 kosulunu sa¼glayan bir r 3 ve herhangi bir r 4 için r 5 r 5 r 4 olacak biçimde bir r 5 bulunabilir (George ve Veeramani 1994). 8
15 Tan m 3.2 (X; M; ) bir fuzzy metrik uzay olsun. x 2 X; 0 < r < 1 ve t > 0 olmak üzere B(x; r; t) = fy 2 X : M(x; y; t) > 1 rg kümesine (X; M; ) fuzzy metrik uzay nda x merkezli r yar çapl aç k yuvar, B[x; r; t] = fy 2 X : M(x; y; t) 1 rg kümesine de (X; M; ) fuzzy metrik uzay nda x merkezli r yar çapl kapal yuvar denir. Tan m 3.3 (X; M; ) bir fuzzy metrik uzay ve A X olsun. E¼ger 8 x 2 A için B(x; r; t) A olacak biçimde t > 0 ve 0 < r < 1 varsa A ya (X; M; ) fuzzy metrik uzay nda bir aç k küme denir. Teorem 3.3 Fuzzy metrik uzaylarda her aç k yuvar aç k bir kümedir. Ispat : 8x 2 X; 0 < r < 1 ve t > 0 olmak üzere herhangi bir B(x; r; t) aç k yuvar göz önüne alal m. E¼ger y 2 B(x; r; t) ise M(x; y; t) > 1 r olaca¼g ndan 0 < t 0 < t ve M(x; y; t 0 ) > 1 r olacak biçimde bir t 0 say s vard r. r 0 = M(x; y; t 0 ) olsun. r 0 > 1 r oldu¼gundan r 0 > 1 s > 1 r olacak biçimde bir 0 < s < 1 bulunabilir. Not 2.1(ii) den r 0 r 1 > 1 s olacak şekilde bir r 1 2 (0; 1) vard r. B(y; 1 r 1 ; t t 0 ) aç k yuvar n alal m. Bu durumda B(y; 1 r 1 ; t t 0 ) B(x; r; t) dir. Gerçekten herhangi bir z 2 B(y; 1 r 1 ; t t 0 ) için M(y; z; t t 0 ) > 1 (1 r 1 ) = r 1 bulunur. Fuzzy metrik uzay n (F-4) şart ndan M(x; z; t) M(x; y; t 0 ) M(y; z; t t 0 ) 9
16 yaz labilir ve dolay s yla M(x; z; t) r 0 r 1 1 s > 1 r elde edilir. Buradan z 2 B(x; r; t) bulunur. Bu da B(x; r; t) aç k yuvar n n aç k küme oldu¼gunu gösterir. Teorem 3.4 Fuzzy metrik uzaylarda her kapal yuvar kapal bir kümedir. Ispat: B[x; r; t] = B[x; r; t] oldu¼gunu gösterelim. (i) B[x; r; t] B[x:r; t] dir. Yani bir kümenin tüm de¼gme noktalar n n kümesine o kümenin kapan ş denir ve bir küme daima de¼gme noktalar n n kümesinin alt kümesi oldu¼gundan B[x; r; t] B[x:r; t] daima sa¼glan r. (ii) B[x; r; t] B[x; r; t] oldu¼gu gösterilmelidir. y 2 B[x; r; t] olsun. X 1:say{labilir oldu¼gundan y n! y olacak şekilde fy n g B[x; r; t] dizisi vard r. fy n g B[x; r; t] =) 8n 2 N için M(x; y n ; t) 1 dir. Ayr ca y n! y oldu¼gundan her 2 (0; 1) için M(y; y n ; t)! 1 dir. Buna göre r M(x; y; t + ) M(x; y n ; t) M(y n ; y; ) eşitsizli¼ginde limit al n rsa M(x; y; t + ) lim n!1 M(x; y n ; t) lim n!1 M(y n ; y; ) (1 r) 1 = 1 r elde edilir. n 2 N için = 1 n al n rsa M(x; y; t + 1 n ) 1 r 10
17 eşitsizli¼gi elde edilir. Bu eşitsizlikte limit al n rsa lim M(x; y; t + 1 ) 1 r =) M(x; y; t) 1 r =) y 2 B[x:r; t] n!1 n elde edilir. Böylece B[x; r; t] B[x; r; t] oldu¼gu gösterilmiş olur. Teorem 3.5 Her fuzzy metrik uzay bir Hausdor uzay d r. Ispat: (X; M; ) bir fuzzy metrik uzay ve x; y 2 X; x 6= y olsun. x 6= y =) 0 < M(x; y; t) < 1 dir. r = M(x; y; t) denilirse her bir r 0 2 (r; 1) için r 1 r 1 r 0 olacak şekilde r 1 2 (0; 1) bulunur. Şimdi B(x; 1 r 1 ; t ) ve B(y; 1 2 r 1; t ) 2 aç k yuvarlar n alal m. Kabul edelim ki, B(x; 1 r 1 ; t 2 ) \ B(y; 1 r 1; t 2 ) 6=? olsun. O halde 9z 2 B(x; 1 r 1 ; t 2 ) \ B(y; 1 r 1; t 2 ) =) M(x; z; t 2 ) > 1 (1 r 1) = r 1 ve M(y; z; t 2 ) > 1 (1 r 1) = r 1 yaz labilir. Buradan r = M(x; y; t) M(x; z; t 2 ) M(y; z; t 2 ) > r 1 r 1 r 0 > r bulunur. Yani r > r elde edilir ki bu da bir çelişkidir. O halde B(x; 1 r 1 ; t 2 ) \ B(y; 1 r 1; t 2 ) =? olup (X; M; ) bir Hausdor uzay d r. 11
18 Teorem 3.6 (X; d) bir metrik uzay ve X üzerinde tan ml bir fuzzy metrik t M(x; y; t) = t + d(x; y) olsun. Bu durumda d taraf ndan elde edilen ( d) topolojisi ile M taraf ndan elde edilen ( M ) topolojisi ayn d r. Ispat: d = M oldu¼gunu gösterelim: (i) d M oldu¼gunu görmek için 8x 2 X, 8r > 0 için 9r 0 2 (0; 1) 3 B M (x; r 0 ; t) B d (x; r) oldu¼gunu gösterelim: r 0 = r t + r olsun. y 2 B M (x; r 0 ; t) =) M(x; y; t) > 1 r 0 =) M(x; y; t) > 1 r t + r =) M(x; y; t) > t t + r =) t t + d(x; y) > t t + r =) t + d(x; y) < t + r =) d(x; y) < r =) y 2 B d (x; r) elde edilir. O halde B M (x; r 0 ; t) B d (x; r) dir. (ii) M d oldu¼gunu göstermek için 8x 2 X, 8r 0 2 (0; 1) için 9r > 0 3 B d (x; r) B M (x; r 0 ; t) oldu¼gunu gösterelim: r = y 2 B d (x; r) tr0 1 r 0 olsun =) d(x; y) < tr0 1 r 0 =) d(x; y) < r0 t 1 r 0 =) d(x; y) 1 + < 1 + r0 t 1 r 0 =) t + d(x; y) < 10 t 1 r 0 =) t t + d(x; y) > 1 r0 =) M(x; y; t) = 1 r 0 =) y 2 B M (x; r 0 ; t) 12
19 elde edilir. O halde B d (x; r) B M (x; r 0 ; t) dir. Tan m 3.4 (X; M; ) bir fuzzy metrik uzay ve X de bir fx n g dizisi olsun. E¼ger 8t > 0 için lim n!1 M(x n ; x; t) = 1 ise fx n g dizisi bir x 2 X noktas na yak nsar denir (Grabiec 1988). Teorem 3.7 (X; M; ) bir fuzzy metrik uzay ve M fuzzy metrik taraf ndan indirgenen bir topoloji olsun. O zaman X deki bir fx n g dizisinin bir x 2 X e yak nsamas için gerekli ve yeterli kosul n! 1 iken M(x n ; x; t)! 1 olmas d r. Ispat: ( =) :) Sabit bir t > 0 ve x n! x olsun. O zaman her bir 0 < r < 1 için 9n 0 2 N vard r 3 8n n 0 için x n 2 B(x; r; t) dir. Buradan M(x n; x; t) > 1 r ve 1 M(x n ; x; t) < r olur. Böylece n! 1 için M(x n ; x; t)! 1 bulunur. ( (= :) Her bir t > 0 için n! 1 iken M(x n ; x; t)! 1 olsun. O zaman verilen her 0 < r < 1 için 9n 0 2 N vard r 3 8n n 0 için 1 M(x n ; x; t) < r dir ve buradan M(x n ; x; t) > 1 r olur. Bu da x 2 B(x n ; r; t) oldu¼gunu gösterir. O halde x n! x dir. Tan m 3.5 fx n g, (X; M; ) fuzzy metrik uzay nda bir dizi olsun. E¼ger her 0 < < 1, t > 0 için 9n 0 2 N 3 8n; m n 0 için M(x n ; x m ; t) > 1 oluyorsa fx n g dizisine fuzzy metrik uzayda bir Cauchy dizisi denir. E¼ger bir fuzzy metrik uzay ndaki her Cauchy dizisi uzaydaki bir noktaya yak nsar ise bu fuzzy metrik uzaya tam fuzzy metrik uzay denir (Grabiec 1988). Fuzzy metrik uzayda bir Cauchy dizisi aşa¼g daki şekilde de tan mlanabilir: Tan m 3.6 (X; M; ) bir fuzzy metrik uzay ve X de bir fx n g dizisi olsun. E¼ger 8t > 0 ve her bir p > 0 için lim n!1 M(x n+p ; x n ; t) = 1 ise fx n g bir Cauchy dizisidir denir (Grabiec 1988). 13
20 Teorem 3.8 Standart (X; M d ; ) fuzzy metrik uzay n n tam olmas için gerekli ve yeterli kosul (X; d) metrik uzay n n tam olmas d r. Ispat: ( =) :) (X; M d ; ) standart fuzzy metrik uzay tam ve fx n g X de bir Cauchy dizisi olsun. O zaman 8 > 0 için 9n 0 2 N 3 8n; m n 0 için d(x n ; x m ) < dur. Standart fuzzy metrik tan m ndan 8n; m n 0 ve 8t > 0 için M d (x n ; x m ; t) = t t + d(x n ; x m ) > oldu¼gundan 0 < r < 1 koşulunu sa¼glayan her r için = t t + rt 1 r al n rsa M d (x n ; x m ; t) > 1 r elde edilir. Yani fx n g dizisi (X; M d ; ) standart fuzzy metrik uzay nda Cauchy dizisi olur. (X; M d ; ) fuzzy metrik uzay tam oldu¼gundan fx n g Cauchy dizisi X de bir x noktas na yak nsar. O halde yaz labilir. Buradan M d (x n ; x; t) = t t + d(x n ; x) = 1 lim M t d(x n ; x; t) = lim n!1 n!1 t + d(x n ; x) = 1 () lim d(x n; x) = 0 n!1 bulunur. Bu ise (X; d) metrik uzay nda n! 1 iken x n! x oldu¼gunu gösterir. O halde (X; d) metrik uzay tamd r. ( (= :) (X; d) metrik uzay tam olsun. (X; M d ; ) standart fuzzy metrik uzay nda bir fx n g X Cauchy dizisi al ns n. O zaman 8 0 < r < 1; t > 0 için 9n 0 2 N vard r 3 8n; m n 0 için M d (x n ; x m ; t) > 1 r dir. 14
21 Standart metrik tan m ndan M d (x n ; x m ; t) = t t + d(x n ; x m ) > 1 =) d(x n ; x m ) < rt 1 r r yaz labilir. = rt 1 r al n rsa, 8 > 0 ve 8n; m n 0 için d(x n ; x m ) < bulunur. Yani fx n g dizisi (X; d) metrik uzay nda Cauchy dizisidir. X tam oldu¼gundan fx n g dizisi X de bir x noktas na yak nsar ve lim n!1 d(x n ; x) = 0 elde edilir. Buradan lim M t d(x n ; x; t) = lim n!1 n!1 t + d(x n ; x) = t t = 1 elde edilir. Yani fx n g dizisi (X; M d ; ) uzay nda x noktas na yak nsar ve dolay s yla (X; M d ; ) standart fuzzy metrik uzay tamd r. Not 3.2 (X; M; ) bir fuzzy metrik uzay olmak üzere 8 x; y 2 X için (F-6) lim n!1 M(x; y; t) = 1 oluyorsa (X; M; ) fuzzy metrik uzay na (F-6) şart n sa¼gl yor denir. Lemma 3.1 (X; M; ); bir fuzzy metrik uzay öyle ki 8 x; y 2 X için t! 1 iken M(x; y; t)! 1 olsun. 8 x; y 2 X ve 8t > 0 için M(x; y; kt) M(x; y; t) ise x = y dir (Mishra 1994). Ispat: E¼ger 8t > 0 ve baz k 2 (0; 1) sabiti için M(x; y; kt) M(x; y; t) ise 8 x; y 2 X ve 8s > 0 için M(x; y; s) M(x; y; s k ) M(x; y; s s ) ::: M(x; y; k2 k ) n yaz labilir. n! 1 için limit al n rsa M(x; y; s) = 1 bulunur. Bu ise x = y demektir. 15
22 Lemma 3.2 (X; M; ); (F-6) şart n sa¼glayan bir fuzzy metrik uzay ve fx n g; X de bir dizi olsun. 8 t > 0 ve n = 1; 2; ::: için M(x n+2 ; x n+1 ; kt) M(x n+1 ; x n ; t) olacak şekilde k 2 (0; 1) sabiti varsa fx n g; X de bir Cauchy dizisidir (Mishra 1994 ve Cho 1997). 16
23 4. FUZZY METR IK UZAYLARDA BAZI FONKS IYONLAR IÇ IN SAB IT NOKTA TEOREMLER I Bu bölümde fuzzy metrik uzaylarda ()-tipi ba¼gdaşabilir, ()-tipi ba¼gdaşabilir, yar ba¼gdaşabilir ve R-zay f komutatif fonksiyonlar tan mlanarak bu fonksiyonlar n sabit nokta teoremleri ele al nacakt r. 4.1 Fuzzy Metrik Uzaylarda () Tipi Ba¼gdaşabilir Fonksiyonlar Için Sabit Nokta Teoremleri Bu k s mda ()-tipi ba¼gdaşabilir fonksiyonun tan m yap larak bu fonksiyonlarla ilgili baz karakterizasyonlar verilecektir. Tan m (X; M; ) tam bir fuzzy metrik uzay ve A; B : X! X iki fonksiyon olsun. Herhangi bir z 2 X için lim Ax n = lim Bx n = z olacak şekilde X de bir n!1 n!1 fx n g dizisi var ve t > 0 için lim M(ABx n; BAx n ; t) = 1 n!1 oluyorsa A ve B ba¼gdaşabilirdir denir (Mishra 1994). Tan m (X; M; ) tam bir fuzzy metrik uzay ve A; B : X! X iki fonksiyon olsun. Herhangi bir z 2 X için lim Ax n = lim Bx n = z olacak şekilde X de bir n!1 n!1 fx n g dizisi var ve t > 0 için lim M(ABx n; BBx n ; t) = 1 ve lim M(BAx n ; AAx n ; t) = 1 n!1 n!1 oluyorsa A ve B; () tipi ba¼gdaşabilirdir denir (Cho 1997). 17
24 Önerme (X; M; ); 8t 2 [0; 1] için t t t ile verilen tam bir fuzzy metrik uzay ve A; B : X! X sürekli iki fonksiyon olsun. A ve B ba¼gdaşabilir () A ve B; () tipi ba¼gdaşabilir (Cho 1997). Önerme (X; M; ); 8t 2 [0; 1] için t t t ile verilen tam bir fuzzy metrik uzay ve A; B : X! X iki fonksiyon olsun. A ve B () tipi ba¼gdaşabilir ve herhangi bir z 2 X için Az = Bz =) ABz = BBz = AAz dir (Cho 1997). Önerme (X; M; ); 8t 2 [0; 1] için t t t ile verilen tam bir fuzzy metrik uzay ve A; B : X! X iki fonksiyon olsun. A ve B ba¼gdaşabilir ve herhangi bir z 2 X için lim Ax n = lim Bx n = z olacak şekilde X de bir fx n g dizisi varsa n!1 n!1 (1) E¼ger A z de sürekli ise lim BAx n = Az n!1 (2) E¼ger A ve B z de sürekli ise ABz = BAz ve Az = Bz koşullar sa¼glan r (Cho 1997). Teorem (X; M; ); (F-6) şartn sa¼glayan ve 8 t 2 [0; 1] için t t t ile verilen tam bir fuzzy metrik uzay olsun. A; B; S; T; P; Q : X! X fonksiyonlar olmak üzere (1) P (X) AB(X); Q(X) ST (X); (2) AB = BA; ST = T S; P B = BP; QS = SQ; QT = T Q; (3) A; B; S ve T sürekli, (4) (P; AB) ve (Q; ST ) ikilileri ()-tipi ba¼gdaşabilir, (5) 8x; y 2 X; 2 (0; 2) ve t > 0 için M(P x; Qy; kt) M(ABx; P x; t) M(ST y; Qy; t) M(ST y; P x; t) M(ABx; Qy; (2 )t) M(ABx; ST y; t) olacak şekilde k 2 (0; 1) varsa bu durumda A; B; S; T; P, Q nun X de ortak tek bir sabit noktas vard r (Sharma 2002). 18
25 Ispat: Teorem 4.1.1(1) den P (X) AB(X) oldu¼gundan P x 0 = ABx 1 olacak şekilde x 1 2 X ve Q(X) ST (X) oldu¼gundan Qx 1 = ST x 2 olacak şekilde x 2 2 X vard r. Bu şekilde devam ederek bir fy n g dizisi y 2n = P x 2n = ABx 2n+1; n = 0; 1; 2; ::: y 2n+1 = Qx 2n+1 = ST x 2n+2; n = 0; 1; 2; ::: şeklinde oluşturulabilir. Teorem 4.1.1(5) den 8 t > 0 ve = 1 q; q 2 (0; 1) için M(y 2n+1 ; y 2n+2 ; kt) = M(P x 2n+1 ; Qx 2n+2 ; kt) M(ABx 2n+1 ; P x 2n+1 ; t) M(ST x 2n+2 ; Qx 2n+2 ; t) M(ST x 2n+2 ; P x 2n+1 ; t) M(ABx 2n+1 ; Qx 2n+2 ; (2 )t) M(ABx 2n+1 ; ST x 2n+2 ; t) = M(y 2n ; y 2n+1 ; t) M(y 2n+1 ; y 2n+2 ; t) M(y 2n+1 ; y 2n+1 ; (1 q)t) M(y 2n ; y 2n+2 ; (1 + q)t) M(y 2n ; y 2n+1 ; t) M(y 2n ; y 2n+1 ; t) M(y 2n+1 ; y 2n+2 ; t) 1 M(y 2n ; y 2n+1 ; t) M(y 2n+1 ; y 2n+2 ; qt) M(y 2n ; y 2n+1 ; t) M(y 2n ; y 2n+1 ; t) M(y 2n+1 ; y 2n+2 ; t) M(y 2n ; y 2n+1 ; qt) oldu¼gundan M(y 2n+1 ; y 2n+2 ; kt) M(y 2n ; y 2n+1 ; t) M(y 2n+1 ; y 2n+2 ; t) M(y 2n ; y 2n+1 ; qt) (4.1.1) elde edilir. 19
26 sürekli t norm ve M(x; y; ) sürekli oldu¼gundan (4.1.1) de q! 1 için limit al n rsa M(y 2n+1 ; y 2n+2 ; kt) M(y 2n ; y 2n+1 ; t) M(y 2n+1 ; y 2n+2 ; t) (4.1.2) elde edilir. Benzer şekilde M(y 2n+2 ; y 2n+3 ; kt) M(y 2n+1 ; y 2n+2 ; t) M(y 2n+2 ; y 2n+3 ; t) (4.1.3) bulunur. (4.1.2) ve (4.1.3) den M(y n+1 ; y n+2 ; kt) M(y n ; y n+1 ; t) M(y n+1 ; y n+2 ; t); n = 1; 2; 3; ::: eşitsizli¼gi elde edilir. Pozitif n ve p say lar için M(y n+1 ; y n+2 ; kt) M(y n ; y n+1 ; t) M(y n+1 ; y n+2 ; yaz labilir. O halde p! 1 için M(y n+1 ; y n+2 ; t k p ) t k p )! 1 olaca¼g ndan M(y n+1 ; y n+2 ; kt) M(y n ; y n+1 ; t) bulunur. Lemma 3.2 den fy n g bir Cauchy dizisidir. X uzay tam oldu¼gundan fy n g bir z 2 X noktas na yak nsar. O halde n! 1 iken P x 2n ; Qx 2n+1 ; ST x 2n+1! z elde edilir. A ve B sürekli fonksiyonlar ve (P; AB) ikilisi ()-tipi ba¼gdaşabilir oldu¼gundan Önerme 4.1.3(1) den n! 1 iken P (AB)x 2n+1! ABz ve (AB) 2 x 2n+1! ABz elde edilir. 20
27 Benzer şekilde S ve T sürekli fonksiyonlar ve (Q; ST ) ikilisi ()-tipi ba¼gdaşabilir oldu¼gundan Önerme 4.1.3(1) den n! 1 iken O(ST )x 2n+2! ST ve(st ) 2 x 2n+2! ST z elde edilir. Teorem 4.1.1(5) de x = (AB)x 2n+1, y = x 2n+2 ve = 1 al n rsa M(P (AB)x 2n+1 ; Qx 2n+2 ; kt) M((AB) 2 x 2n+1 ; P (AB)x 2n+1 ; t) M(ST x 2n+2 ; Qx 2n+2 ; t) M(ST x 2n+2 ; P (AB)x 2n+1 ; t) M((AB) 2 x 2n+1 ; Qx 2n+2 ; t) M((AB) 2 x 2n+1 ; ST x 2n+2 ; t) eşitsizli¼gi elde edilir. n! 1 için limit al n rsa M(ABz; z; kt) 1 1 M(z; ABz; t) M(ABz; z; t) M(ABz; z; t) M(ABz; z; t) bulunur. Lemma 3.1 den ABz = z oldu¼gu görülür. Teorem (5) de x = P x 2n, y = x 2n+1 ve = 1 al n rsa M(P (P x 2n ); Qx 2n+1 ; kt) M(AB(P x 2n ); P (P x 2n ); t) M(ST x 2n+1 ; Qx 2n+1 ; t) M(ST x 2n+1 ; P (P x 2n ); t) M(AB(P (P x 2n ); Qx 2n+1 ; t) M(AB(P x 2n ); ST x 2n+1 ; t) eşitsizli¼gi elde edilir. n! 1 için limit al n rsa M(P z; z; kt) M(z; P z; t) M(z; z; t) M(z; P z; t) M(z; z; t) M(z; z; t) = M(z; P z; t) 1 M(z; P z; t) 1 1 M(P z; z; t) 21
28 eşitsizli¼gi elde edilir. Lemma 3.1 den P z = z dir. O halde ABz = z = P z elde edilir. Şimdi Bz = z oldu¼gunu gösterelim. Teorem 4.1.1(5) de x = Bz, y = x 2n+1 ve = 1 al n rsa ve Teorem 4.1.1(2) den M(P (Bz); Qx 2n+1 ; kt) M(AB(Bz); P (Bz); t) M(ST x 2n+1 ; Qx 2n+1 ; t) M(ST x 2n+1 ; P (Bz); t) M(AB(Bz); Qx 2n+1 ; t) M(AB(Bz); ST x 2n+1 ; t) elde edilir. n! 1 için limit al n rsa M(Bz; z; kt) M(Bz; Bz; t) M(z; z; t) M(z; Bz; t) M(Bz; z; t) M(Bz; z; t) = 1 1 M(z; Bz; t) M(Bz; z; t) M(Bz; z; t) M(Bz; z; t) bulunur. O halde Lemma 3.1 den Bz = z yaz labilir. ABz = z oldu¼gundan Az = z elde edilir. Teorem 4.1.1(5) de x = z, y = ST x 2n+2 ve = 1 al n rsa M(P z; Q(ST )x 2n+2 ; kt) M(ABz; P z; t) M((ST ) 2 x 2n+2 ; Q(ST )x 2n+2 ; t) M((ST ) 2 x 2n+2 ; P z; t) M(ABz; Q(ST )x 2n+2 ; t) M(ABz; (ST ) 2 x 2n+2 ; t) eşitsizli¼gi elde edilir. n! 1 için limit al n rsa M(z; ST z; kt) M(z; z; t) M(ST z; ST z; t) M(ST z; z; t) M(z; ST z; t) M(z; ST z; t) = 1 1 M(ST z; z; t) M(z; ST z; t) M(z; ST z; t) M(z; ST z; t) elde edilir ve Lemma 3.1 den ST z = z oldu¼gu görülür. 22
29 Teorem 4.1.1(5) de x = z, y = Qx 2n+1 ve = 1 a l n rsa ve Teorem (2) den M(P z; Q(Qx 2n+1 ); kt) M(ABz; P z; t) M(ST (Qx 2n+1 ); Q(Qx 2n+1 ); t) M(ST (Qx 2n+1 ); P z; t) M(ABz; Q(Qx 2n+1 ); t) M(ABz; ST (Qx 2n+1 ); t) elde edilir. n! 1 için limit al n rsa M(z; Qz; kt) M(z; z; t) M(z; Qz; t) M(z; z; t) M(z; Qz; t) M(z; z; t) = 1 M(z; Qz; t) 1 M(z; Qz; t) 1 M(z; Qz; t) bulunur. Lemma 3.1 den Qz = z elde edilir ve dolay s yla ST z = z = Qz oldu¼gu görülür. Teorem 4.1.1(5) de x = z, y = T z ve = 1 al n rsa ve Teorem 4.1.1(2) den M(P z; Q(T z); kt) M(ABz; P z; t) M(ST (T z); Q(T z); t) M(ST (T z); P z; t) M(ABz; Q(T z); t) M(ABz; ST (T z); t) = M(z; z; t) M(T z; T z; t) M(T z; z; t) M(z; T z; t) M(z; T z; t) = 1 1 M(T z; z; t) M(z; T z; t) M(z; T z; t) M(T z; z; t) bulunur. Lemma 3.1 den T z = z elde edilir. ST z = z oldu¼gundan Sz = z dir. Bütün bu sonuçlar birleştirilirse Az = Bz = Sz = T z = P z = Qz = z oldu¼gu ve dolay s yla z noktas n n A; B; S; T; P; Q nun ortak sabit noktas oldu¼gu görülür. 23
30 Kabul edelim ki A; B; S; T; P; Q nun baska bir ortak sabit noktas w (w 6= z) olsun. Teorem 4.1.1(5) de = 1 al n rsa M(P z; Qw; kt) M(ABz; P z; t) M(ST w; Qw; t) M(ST w; P z; ) M(ABz; Qw; t) M(ABz; ST w; t) elde edilir. Dolay s yla M(z; w; kt) M(z; z; t) M(w; w; t) M(w; z; t) M(z; w; t) M(z; w; t) = 1 1 M(w; z; t) M(z; w; t) M(z; w; t) = M(z; w; t) bulunur ve Lemma 3.1 den z = w oldu¼gu görülür. Bu da teoremin ispat n tamamlar. Teorem de B = T = I x al n rsa aşa¼g daki sonuç elde edilir: Sonuç (X; M; ); (F-6) şartn sa¼glayan ve 8t 2 [0; 1] için t t t ile verilen tam bir fuzzy metrik uzay olsun. A; S; P; Q : X! X fonksiyonlar olmak üzere (1) P (X) A(X); Q(X) S(X); (2) (P; A) ve (Q; S) ikilileri ()-tipi ba¼gdaşabilir, (3) A ve S ve sürekli, (4) 8x; y 2 X; 2 (0; 2) ve t > 0 için M(P x; Qy; kt) M(Ax; P x; t) M(Sy; Qy; t) M(Sy; P x; t) M(Ax; Qy; (2 )t) M(Ax; Sy; t) olacak şekilde k 2 (0; 1) varsa bu durumda A; S; P ve Q nun X de ortak tek bir sabit noktas vard r. 24
31 Teorem de A = B = S = T = I x al n rsa aşa¼g daki sonuç elde edilir: Sonuç (X; M; ); (F-6) şartn sa¼glayan ve 8t 2 [0; 1] için tt t ile verilen tam bir fuzzy metrik uzay olsun. P, Q : X! X iki fonksiyon olmak üzere 8x; y 2 X; 2 (0; 2) ve t > 0 için M(P x; Qy; kt) M(x; P x; t) M(y; Qy; t) M(y; P x; t) M(x; Qy; (2 )t) M(x; y; t) olacak şekilde k 2 (0; 1) varsa bu durumda P, Q nun X de ortak tek bir sabit noktas vard r. Teorem de P = Q; A = S; ve B = T = I x al n rsa aşa¼g daki sonuç elde edilir: Sonuç (X; M; ); (F-6) şartn sa¼glayan ve 8t 2 [0; 1] için t t t ile verilen tam bir fuzzy metrik uzay olsun. P ve S; X de ()-tipi ba¼gdaşabilir fonksiyonlar olmak üzere P (X) S(X) olsun. E¼ger S sürekli ise 8x; y 2 X; 2 (0; 2) ve t > 0 için M(P x; P y; kt) M(Sx; P x; t) M(Sy; P y; t) M(Sy; P x; t) M(Sx; P y; (2 )t) M(Sx; Sy; t) olacak şekilde k 2 (0; 1) varsa bu durumda P ve S nin X de ortak tek bir sabit noktas vard r. Örnek X = [0; 1] ve a b = a b olsun. d(x; y) = jx yj şeklinde tan mlanan d metri¼gi taraf ndan üretilen standart fuzzy metrik, 8x; y 2 X; t 2 [0; 1] t için M(x; y; t) = ; M(x; y; 0) = 0 olarak tan mlans n. Aç kça görülür ki t + jx yj (X; M; ) bir fuzzy metrik uzayd r. 8x 2 X için A; B; S; T; P ve Q fonksiyonlar Ax = x; Bx = x 2 ; Sx = x 5 ; T x = x 3 ; P x = x 6 ve Qx = 0 olarak tan mlans n. 25
32 O halde P (X) = [0; 1 6 ] [0; 1 2 ] = AB(X) ve Q(X) = f0g [0; 1 ] = ST (X) 5 elde edilir ki Teorem 4.1.1(1) in sa¼gland ¼g görülür. E¼ger k = 1 2 ; t = 1, = 1 al n rsa Teorem 4.1.1(5) de sa¼glan r. Teorem 4.1.1(2) nin ve Teorem 4.1.1(3) ün de sa¼gland ¼g aç kt r. Herhangi bir 0 2 X için lim P x n = lim ABx n = 0 ve lim x n = 0 n!1 n!1 n!1 olacak şekilde X de bir (x n ) dizisi vard r ve lim M(P (AB)x n; (AB) 2 x n ; t) = 1 ve lim M(AB(P )x n ; P 2 x n ; t) = 1 n!1 n!1 sa¼glan r. Dolay s yla (P; AB) ikilisi ()-tipi ba¼gdaşabilirdir. Benzer şekilde (Q; ST ) ikilisi de ()-tipi ba¼gdaşabilirdir. Böylece Teorem 4.1.1(4) de sa¼gland ¼g ndan A; B; S; T; P, Q nun X de ortak tek bir sabit noktas vard r. 4.2 Fuzzy Metrik Uzaylarda () Tipi Ba¼gdaşabilir Fonkiyonlar Için Sabit Nokta Teoremleri Bu k s mda ()-tipi ba¼gdaşabilir fonksiyonun tan m yap larak bu fonksiyonlarla ilgili baz karakterizasyonlar verilecektir. Tan m (X; M; ) bir fuzzy metrik uzay ve A; B : X! X iki fonksiyon olsun. Herhangi bir z 2 X için lim Ax n = lim Bx n = z olacak şekilde X de bir fx n g dizisi n!1 n!1 var ve t > 0 için lim M(AAx n; BBx n ; t) = 1 n!1 oluyorsa A ve B, () tipi ba¼gdaşabilirdir denir (Cho 1998). Önerme (X; M; ) bir fuzzy metrik uzay ve A; B : X! X sürekli iki fonksiyon olsun. A ve B ba¼gdaşabilir () A ve B; () tipi ba¼gdaşabilir (Kütükçü vd. 2006). 26
33 Önerme (X; M; ) bir fuzzy metrik uzay ve A; B : X! X iki fonksiyon olsun. E¼ger A ve B ba¼gdaşabilir ve baz z 2 X için Az = Bz ise ABz = BBz = BAz = AAz dir (Kütükçü vd. 2006). Önerme (X; M; ) bir fuzzy metrik uzay ve A; B : X! X () tipi ba¼gdaşabilir fonksiyonlar olsun. Herhangi bir z 2 X için lim Ax n = lim Bx n = z olacak n!1 n!1 şekilde X de bir fx n g dizisi olsun. O halde aşa¼g daki şartlar sa¼glan r: (1) E¼ger A z de sürekli ise lim BBx n = Az; n!1 (2) E¼ger B z de sürekli ise lim AAx n = Bz; n!1 (3) E¼ger A ve B z de sürekli ise ABz = BAz ve Az = Bz dir (Kütükçü vd. 2006). Örnek X = R ve a b = a b olsun. d(x; y) = jx yj şeklinde tan mlanan d metri¼gi taraf ndan üretilen standart fuzzy metrik 8x; y 2 X; t 2 [0; 1] için t M(x; y; t) = ; M(x; y; 0) = 0 olarak tan mlans n. Aç kça görülür ki t + jx yj sürekli t-normu ile verilen (X; M; ) bir fuzzy metrik uzayd r. A; B : X! X fonksiyonlar ve 8 < 1 ; x 6= 0 Ax = x 3 : 1 ; x = 1 8 < 1 ; x 6= 0 Bx = x 2 : 2 ; x = 1 olarak verilsin. O halde A ve B fonksiyonlar n n ikisi de x = 0 noktas nda sürekli de¼gildir. X deki fx n g dizisinin genel terimi x n = n olsun. O halde lim Ax n = lim Bx n = 0 n!1 n!1 oldu¼gu aç kt r. Di¼ger taraftan lim M(AAx n; BBx n ; t) = 0 ve lim M(ABx n ; BAx n ; t) = 1 n!1 n!1 oldu¼gundan A ve B ba¼gdaşabilir olup () tipi ba¼gdaşabilir de¼gildir. 27
34 Teorem (X; M; ) tam bir fuzzy metrik uzay ve P; S; T, Q : X! X fonksiyonlar olmak üzere (1) P T (X) [ QS(X) ST (X); (2) 8x; y 2 X, t > 0 ve p + q a = 1 koşulunu sa¼glayan 0 < p; q < 1; 0 a < 1 için M 2 (P x; Qy; kt) [M(Sx; P x; kt)m(t y; Qy; kt)] M 2 (T y; Qy; kt) +am(t y; Qy; kt)m(sx; Qy; 2kt) [pm(sx; P x; t) + qm(sx; T y; t)]m(sx; Qy; 2kt) olacak şekilde k 2 (0; 1) sabiti var, (3) S ve T sürekli ve ST = T S; (4) (P; S) ve (Q; T ) ikilileri () tipi ba¼gdaşabilir ise P; S; T, Q nun X içinde ortak tek bir sabit noktas vard r (Kütükçü vd. 2006). Ispat: x 0 ; X in herhangi bir noktas olsun. Teorem 4.2.1(1) den X de bir fx n g dizisi aşa¼g daki gibi inşa edilebilir: P T x 2n = ST x 2n+1 ; QSx 2n+1 = ST x 2n+2 ; n = 0; 1; 2; (4.2.1) Şimdi T x 2n = x; Sx 2n+1 = y olsun. 0 < k < 1 ve 8 t > 0 için, Teorem 4.2.1(2) den M 2 (P T x 2n ; QSx 2n+1 ; kt) [M(ST x 2n ; P T x 2n ; kt)m(t Sx 2n+1 ; QSx 2n+1 ; kt)] M 2 (T Sx 2n+1 ; QSx 2n+1 ; kt) +am(t Sx 2n+1 ; QSx 2n+1 ; kt)m(st x 2n ; QSx 2n+1 ; 2kt) [pm(st x 2n ; P T x 2n ; t) + qm(st x 2n ; T Sx 2n+1 ; t)]m(st x 2n ; QSx 2n+1 ; 2kt) 28
35 elde edilir. (4.2.1) den M 2 (ST x 2n+1 ; ST x 2n+2 ; kt) [M(ST x 2n ; ST x 2n+1 ; kt)m(t Sx 2n+1 ; ST x 2n+2 ; kt)] M 2 (T Sx 2n+1 ; ST x 2n+2 ; kt) +am(t Sx 2n+1 ; ST x 2n+2 ; kt)m(st x 2n ; ST x 2n+2 ; 2kt) [pm(st x 2n ; ST x 2n+1 ; t) + qm(st x 2n ; T Sx 2n+1 ; t)]m(st x 2n ; ST x 2n+2 ; 2kt) bulunur. z n = ST x n olsun. O halde M 2 (z 2n+1 ; z 2n+2 ; kt) [M(z 2n ; z 2n+1 ; kt)m(z 2n+1 ; z 2n+2 ; kt)] M 2 (z 2n+1 ; z 2n+2 ; kt) + am(z 2n+1 ; z 2n+2 ; kt)m(z 2n ; z 2n+2 ; 2kt) [pm(z 2n ; z 2n+1 ; t) + qm(z 2n ; z 2n+1 ; t)]m(z 2n ; z 2n+2 ; 2kt) yaz labilir. Dolay s yla M 2 (z 2n+1 ; z 2n+2 ; kt) [M(z 2n ; z 2n+1 ; kt)m(z 2n+1 ; z 2n+2 ; kt)] +am(z 2n+1 ; z 2n+2 ; 2kt)M(z 2n ; z 2n+2 ; 2kt) [p + q]m(z 2n ; z 2n+1 ; t)m(z 2n ; z 2n+2 ; 2kt) elde edilir ve buradan M(z 2n+1 ; z 2n+2 ; kt)[m(z 2n ; z 2n+1 ; kt) M(z 2n+1 ; z 2n+2 ; kt)] +am(z 2n+1 ; z 2n+2 ; kt)m(z 2n ; z 2n+2 ; 2kt) [p + q]m(z 2n ; z 2n+1 ; t)m(z 2n ; z 2n+2 ; 2kt) bulunur. Daha sonra M(z 2n+1 ; z 2n+2 ; kt)m(z 2n ; z 2n+2 ; kt) +am(z 2n+1 ; z 2n+2 ; kt)m(z 2n ; z 2n+2 ; 2kt) [p + q]m(z 2n ; z 2n+1 ; t)m(z 2n ; z 2n+2 ; 2kt) 29
36 eşitsizli¼gi elde edilir. Buradan (1 + a)m(z 2n+1 ; z 2n+2 ; kt)m(z 2n ; z 2n+2 ; 2kt) [p + q]m(z 2n ; z 2n+1 ; t)m(z 2n ; z 2n+2 ; 2kt) yaz labilir ve M(z 2n+1 ; z 2n+2 ; kt) M(z 2n ; z 2n+1 ; t) eşitsizli¼gi bulunur. Benzer şekilde, 0 < k < 1 ve 8 t > 0 için M(z 2n+2 ; z 2n+3 ; kt) M(z 2n+1 ; z 2n+2 ; t) elde edilir. Genel olarak, 0 < k < 1, 8t > 0; ve m = 1; 2; ::: için M(z m+1 ; z m+2 ; kt) M(z m ; z m+1 ; t) yaz labilir. Dolay s yla Lemma 3.2 den fz n g X de bir Cauchy dizisidir ve (X; M; ) uzay tam oldu¼gundan X de bir z noktas na yak nsar. fp T x 2n g ve fqsx 2n+1 g; fz n g dizisinin altdizileri oldu¼gundan n! 1 iken P T x 2n! z ve QSx 2n+1! z dir. y n = T x n ve w n = Sx n ; n = 1; 2; ::: olsun. O halde n! 1 için P y 2n! z; Sy 2n! z; T w 2n+1! z ve Qw 2n+1! z dir ve M(P P y 2n ; SSy 2n ; t)! 1 ve M(QQw 2n+1 ; T T w 2n+1 ; t)! 1 elde edilir. T nin süreklili¼ginden ve Önerme den n! 1 iken T Qw 2n+1! T z ve QQw 2n+1! T z 30
37 elde edilir. Teorem 4.2.1(2) de x = y 2n ve y = Qw 2n+1 al n rsa M 2 (P y 2n ; QQw 2n+1 ; kt) [M(Sy 2n ; P y 2n ; kt)m(t Qw 2n+1 ; QQw 2n+1 ; kt)] M 2 (T Qw 2n+1; QQw 2n+1 ; kt) +am(t Qw 2n+1; QQw 2n+1 ; kt)m(sy 2n ; QQw 2n+1 ; 2kt) [pm(sy 2n; P y 2n ; t) + qm(sy 2n ; T Qw 2n+1; t)]m(sy 2n ; QQw 2n+1 ; 2kt) elde edilir. Buradan M 2 (z; T z; kt) [M(z; z; kt)m(t z; T z; kt)] M 2 (T z; T z; kt) +am(t z ; T z; kt)m(z; T z; 2kt) [pm(z ; z; t) + qm(z; T z; t)]m(z; T z; 2kt) bulunur. Fuzzy metrik uzay n (F-2) şart kullan l rsa M 2 (z; T z; kt) am(z; T z; 2kt) [p + qm(z; T z; t)]m(z; T z; 2kt) elde edilir. O halde M 2 (z; T z; kt) + am(z; T z; 2kt) [p + qm(z; T z; t)]m(z; T z; 2kt) yaz labilir ve 8x; y 2 X ve t > 0 için, M(x; y; ) azalmayan oldu¼gundan M(z; T z; 2kt)M(z; T z; t) + am(z; T z; 2kt) [p + qm(z; T z; t)]m(z; T z; 2kt) M(z; T z; t) + a p + qm(z; T z; t) M(z; T z; t) p a 1 q = 1 eşitsizli¼gi elde edilir. Fuzzy metrik tan m ndan M(z; T z; t) > 1 olamayaca¼g ndan M(z; T z; t) = 1 dir. Bu ise z = T z demektir. Benzer şekilde z = Sz yaz labilir. 31
38 Teorem 4.2.1(2) de x = y 2n ve y = z al n rsa M 2 (P y 2n ; Qz; kt) [M(Sy 2n ; P y 2n ; kt)m(t z; Qz; kt)] M 2 (T z ; Qz; kt) +am(t z ; Qz; kt)m(sy 2n ; Qz; 2kt) [pm(sy 2n; P y 2n ; t) + qm(sy 2n ; T z ; t)]m(sy 2n ; Qz; 2kt) elde edilir ve dolay s yla M 2 (z; Qz; kt) [M(z; z; kt)m(z; Qz; kt)] M 2 (z ; Qz; kt) +am(z ; Qz; kt)m(z; Qz; 2kt) [pm(z ; z; t) + qm(z; z ; t)]m(z; Qz; 2kt) bulunur. Buradan M 2 (z; Qz; kt) M(z; Qz; kt) M 2 (z ; Qz; kt) +am(z ; Qz; kt)m(z; Qz; 2kt) [p + q]m(z; Qz; 2kt) yaz labilir. Bu ise M(z; Qz; kt)[m(z; Qz; kt) 1] +am(z ; Qz; kt)m(z; Qz; 2kt) [p + q]m(z; Qz; 2kt) demektir. 8x; y 2 X için, M(x; y; ) azalmayan oldu¼gundan M(z; Qz; 2kt)M(z; Qz; kt) + am(z ; Qz; kt)m(z; Qz; 2kt) [p + q]m(z; Qz; 2kt) 32
39 yaz labilir. 0 < k < 1 ve 8t > 0 için M(z; Qz; kt) + am(z ; Qz; kt) p + q M(z; Qz; kt) p + q 1 + a = 1 elde edilir. Bu ise z = Qz demektir. Benzer olarak z = P z elde edilir ve dolay s yla z noktas P; S; Q, T nin ortak tek sabit noktas d r. Kabul edelim ki P; S; Q, T nin başka bir ortak sabit noktas v (v 6= z) olsun. Teorem 4.2.1(2) den M 2 (P z; Qv; kt) [M(Sz; P z; kt)m(t v; Qv; kt)] M 2 (T v ; Qv; kt) +am(t v ; Qv; kt)m(sz; Qv; 2kt) [pm(sz ; P z; t) + qm(sz; T v ; t)]m(sz; Qv; 2kt) yaz labilir. Buradan M 2 (z; v; kt) [M(z; z; kt)m(v; v; kt)] M 2 (v ; v; kt) +am(v ; v; kt)m(z; v; 2kt) [pm(z ; z; t) + qm(z; v ; t)]m(z; v; 2kt) elde edilir. Gerekli işlemler yap l rsa M 2 (z; v; kt) + am(z; v; 2kt) [p + qm(z; v ; t)]m(z; v; 2kt) bulunur. 8x; y 2 X için, M(x; y; ) azalmayan oldu¼gundan M(z; v; t)m(z; v; 2kt) + am(z; v; 2kt) [p + qm(z; v ; t)]m(z; v; 2kt) yaz labilir. 8 t > 0 için M(z; v; t) p a 1 q = 1 elde edilir. Bu ise z = v demektir. O halde P; S; Q, T tek bir ortak noktaya sahiptir. 33
40 E¼ger Teorem de a = 0 al n rsa aşa¼g daki sonuç elde edilir: Sonuç (X; M; ) tam bir fuzzy metrik uzay ve P; S; T, Q : X! X fonksiyonlar olsun. Teorem in (1), (3) ve (4) şartlar ayn kalmak üzere 8x; y 2 X, t > 0 ve p + q = 1 koşulunu sa¼glayan 0 < p; q < 1 için M 2 (P x; Qy; kt) [M(Sx; P x; kt)m(t y; Qy; kt)] M 2 (T y; Qy; kt) [pm(sx; P x; t) + qm(sx; T y; t)]m(sx; Qy; 2kt) olacak şekilde k 2 (0; 1) sabiti varsa bu durumda P; S; T, Q nun X de ortak tek bir sabit noktas vard r. E¼ger Teorem de S = T al n rsa aşa¼g daki sonuç elde edilir: Sonuç (X; M; ) tam bir fuzzy metrik uzay ve P; S; Q : X! X fonksiyonlar olmak üzere (1) P (X) [ Q(X) S(X); (2) 8x; y 2 X, t > 0 ve p + q a = 1 koşulunu sa¼glayan 0 < p; q < 1; 0 a < 1 için M 2 (P x; Qy; kt) [M(Sx; P x; kt)m(sy; Qy; kt)] M 2 (Sy; Qy; kt) +am(sy; Qy; kt)m(sx; Qy; 2kt) [pm(sx; P x; t) + qm(sx; Sy; t)]m(sx; Qy; 2kt) olacak şekilde k 2 (0; 1) sabiti var, (3) S sürekli; (4) (P; S) ve (Q; S) ikilileri () tipi ba¼gdaşabilir ise P; S, Q nun X de ortak tek bir sabit noktas vard r. 34
41 E¼ger Teorem de S = T ve P = Q al n rsa aşa¼g daki sonuç elde edilir: Sonuç (X; M; ) tam bir fuzzy metrik uzay ve P, S : X! X iki fonksiyon olmak üzere (1) P (X) S(X); (2) 8x; y 2 X ve t > 0; 0 < p; q < 1; 0 a < 1 öyle ki p + q a = 1 için M 2 (P x; P y; kt) [M(Sx; P x; kt)m(sy; P y; kt)] M 2 (Sy; P y; kt) +am(sy; P y; kt)m(sx; P y; 2kt) [pm(sx; P x; t) + qm(sx; Sy; t)]m(sx; P y; 2kt) olacak şekilde k 2 (0; 1) sabiti var, (3) S sürekli; (4) (P; S) ikilisi () tipi ba¼gdaşabilir ise P ve S nin X içinde ortak tek bir sabit noktas vard r. E¼ger Teorem de S = T = I x al n rsa aşa¼g daki sonuç elde edilir: Sonuç (X; M; ) tam bir fuzzy metrik uzay ve P, Q : X! X iki fonksiyon olsun. 8x; y 2 X ve t > 0; 0 < p; q < 1; 0 a < 1 öyle ki p + q a = 1 için M 2 (P x; Qy; kt) [M(x; P x; kt)m(y; Qy; kt)] M 2 (y; Qy; kt) +am(y; Qy; kt)m(x; Qy; 2kt) [pm(x; P x; t) + qm(x; y; t)]m(x; Qy; 2kt) olacak şekilde k 2 (0; 1) sabiti varsa bu durumda P ve Q nun X de ortak tek bir sabit noktas vard r. Örnek X = 1 n : n 2 N [ f0g olmak üzere X üzerinde d(x; y) = jx yj şeklinde tan mlanan d metri¼gi verilsin. 8x; y 2 X; t 2 [0; 1] için M(x; y; t) = M(x; y; 0) = 0 şeklinde tan mlans n. t t + jx yj ; 35
42 Aç kça görülür ki a b = a b şeklinde tan mlanan sürekli t-normu ile (X; M; ) bir fuzzy metrik uzayd r. P; S; Q; T : X! X fonksiyonlar, 8x 2 X için P x = x 4 ; Sx = x ; T x = x; Qx = 0 2 olarak verisin. O halde P T (X) [ QS(X) = 1 1 4n : n 2 N [ f0g 2n : n 2 N [ f0g = ST (X) elde edilir ve Teorem 4.2.1(1) sa¼glan r. k = 1, t = 1 al n rsa ST = T S ve S, 2 T fonksiyonlar sürekli oldu¼gundan Teorem 4.2.1(2) ve Teorem 4.2.1(3) sa¼glan r. Herhangi bir 0 2 X için lim P x n = lim Sx n = 0 olacak şekilde X de (x n ) = 1 n!1 n!1 n dizisi vard r ve t > 0 için oldu¼gundan (P; S) ikilisi () lim M(P P x n; SSx n ; t) = 1 n!1 tipi ba¼gdaşabilirdir. Benzer şekilde (Q; T ) ikilisi de () tipi ba¼gdaşabilirdir. O halde Teorem 4.2.1(4) de sa¼glan r ve dolay s yla P; S; Q, T nin ortak tek bir sabit noktaya sahiptir. 4.3 Fuzzy Metrik Uzaylarda Yar Ba¼gdaşabilir Fonksiyonlar Için Sabit Nokta Teoremleri Bu k s mda yar ba¼gdaşabilir fonksiyonun tan m yap larak bu fonksiyonlarla ilgili baz karakterizasyonlar verilecektir. Tan m (X; M; ) tam bir fuzzy metrik uzay ve A, S : X! X iki fonksiyon olsun. E¼ger herhangi bir z 2 X için n! 1 iken Ax n ; Sx n! z olacak şekilde X de bir fx n g dizisi var ve 8 t > 0 için M(ASx n ; Sz; t)! 1 36
43 oluyorsa A ve S, yar ba¼gdaşabilirdir denir (Cho vd. 1995). (A; S) ikilisi yar ba¼gdaşabilir olsun. Ay = Sy olmas şart yla (x n ) = y ve x = Ay = Sy al n rsa ASy = SAy oldu¼gu görülür. Teorem (X; M; ) tam bir fuzzy metrik uzay ve 8a; b 2 X için a b = min(a; b) olsun. S; T, A : X! X fonksiyonlar olsun. S ve T fonksiyonlar sürekli olmak üzere (1) A(X) S(X) \ T (X); (2) (A; S) ve (A; T ) ikilileri yar ba¼gdaşabilir; (3) 8x; y 2 X ve t > 0 için r : [0; 1]! [0; 1] sürekli fonksiyon olmak üzere M(Ax; Ay; t) r minfm(sx; T y; t); M(Sx; Ax; t); M(Sx; Ay; t); M(T y; Ay; t)g (4) Herbir 0 < t < 1 için r(t) > t ve t = 1 için r(t) = 1 ise A; S, T nin X de tek bir ortak sabit noktas vard r (Chauan vd. 2010). Ispat: x 0 2 X herhangi bir sabit nokta olsun. A(X) S(X) oldu¼gundan Ax 0 = Sx 1 olacak şekilde x 1 2 X, yine A(X) T (X) oldu¼gundan Ax 1 = T x 2 olacak şekilde x 2 2 X noktas vard r. Bu şekilde devam edilirse X de bir fy n g dizisi y 2n = Sx 2n+1 = Ax 2n ve y 2n+1 = T x 2n+2 = Ax 2n+1 ; n 2 N [ f0g şeklinde inşa edilebilir. M n = M(Ax n ; Ax n+1 ; t) olsun. O halde M 2n = M(Ax 2n+1 ; Ax 2n ; t) dir. Teorem 4.3.1(3) de x = x 2n+1 ve y = x 2n al n rsa M 2n r minfm(sx 2n+1 ; T x 2n ; t); M(Sx 2n+1 ; Ax 2n+1 ; t); M(Sx 2n+1 ; Ax 2n ; t) ; M(T x 2n ; Ax 2n; t)g = r minfm(ax 2n ; Ax 2n 1 ; t); M(Ax 2n ; Ax 2n+1 ; t); M(Ax 2n ; Ax 2n ; t) ; M(Ax 2n 1 ; Ax 2n; t)g = r minfm 2n 1 ; M 2n ; 1; M 2n 1 g (4.3.1) 37
44 elde edilir. M 2n 1 > M 2n olsun. r nin tan m ndan ve (4.3.1) den M 2n r(m 2n ) > M 2n olur ve böylece bir çelişki elde edilir. Bu yüzden M 2n M 2n 1 (4.3.2) dir. (4.3.1) ve (4.3.2) den M 2n r(m 2n 1 ) > M 2n 1 (4.3.3) elde edilir. O halde fm 2n g dizisi 0 n < 1 için [0; 1] aral ¼g ndaki pozitif say lar n artan bir dizisidir ve bu yüzden bir L 1 limitine yak nsar. Iddia ediyoruz ki L = 1 olsun. E¼ger L < 1 ise (4.3.3) de n! 1 için limit al n rsa L r(l) > L elde edilir ki bu bir çelişkidir. O halde L = 1 dir. Herhangi bir pozitif p için M(Ax n ; Ax n+p ; t) M(Ax n ; Ax n+1 ; t p ) M(Ax n+1; Ax n+2 ; t p ) ::: M(Ax n+p 1; Ax n+p ; t p ) M(Ax n ; Ax n+1 ; t p ) ::: M(Ax n; Ax n+1 ; t p ) elde edilir ve t > 0 için lim n!1 M(Ax n ; Ax n+1 ; t)! 1 oldu¼gundan lim M(Ax n; Ax n+p ; t) 1 1 :::1 = 1 n!1 elde edilir. Yani fax n g dizisi X de bir Cauchy dizisidir. X uzay tam oldu¼gundan fax n g dizisi bir z 2 X noktas na yak nsar. fsx 2n+1 g ve ft x 2n+2 g, fax n g dizisinin altdizileri oldu¼gundan ayn noktaya yak nsarlar. S fonksiyonu sürekli oldu¼gundan SAx n! Sz ve SSx n! Sz elde edilir. 38
45 Ayn zamanda (A; S) yar ba¼gdaşabilir oldu¼gundan ASx n! Sz dir. Teorem 4.3.1(3) de x = Sx n ; y = x n al n rsa M(ASx n ; Ax n ; t) r minfm(ssx n ; T x n ; t); M(SSx n ; ASx n ; t); M(SSx n ; Ax n ; t) ; M(T x n ; Ax n ; t)g elde edilir. n! 1 için limit aln rsa M(Sz; z; t) r minfm(sz; z; t); M(Sz; Sz; t); M(Sz; z; t); M(z; z; t)g rm(sz; z; t) > M(Sz; z; t) eşitsizli¼gi elde edilir. O halde Sz = z dir. Teorem 4.3.1(3) de x = z; y = x n al n rsa Az = z elde edilir. Buradan Sz = z = Az bulunur. T sürekli oldu¼gundan T T x n! T z ve T Ax n! T z olur. Ayn zamanda (A; T ) yar ba¼gdaşabilir oldu¼gundan AT x n! T z dir. Teorem 4.3.1(3) de x = x n ; y = T x n al n rsa M(Ax n ; AT x n ; t) r minfm(sx n ; T T x n ; t); M(Sx n ; Ax n ; t); M(Sx n ; AT x n ; t) ; M(T T x n ; AT x n ; t)g bulunur. n! 1 için limit aln rsa M(z; T z; t) r minfm(z; T z; t); M(z; z; t); M(z; T z; t); M(T z; T z; t)g rm(z; T z; t) > M(z; T z; t) elde edilir. O halde T z = z dir. Böylece Az = Sz = T z = z oldu¼gu görülür. Dolay s yla z noktas A; S ve T nin tek ortak sabit noktas d r. Kabul edelim ki A; S ve T nin başka bir ortak noktas u (u 6= z) olsun. O halde Au = Su = T u = u olur. 39
46 Teorem 4.3.1(3) de x = z; y = u al n rsa M(Az; Au; t) r minfm(sz; T u; t); M(Sz; Az; t); M(Sz; Au; t); M(T u; Au; t)g elde edilir. n! 1 için limit al n rsa M(z; u; t) r minfm(z; u; t); M(z; z; t); M(z; u; t); M(u; u; t)g rm(z; u; t) > M(z; u; t) elde edilir ki bu bir çelişkidir. O halde z = u dur. Dolay s yla A; S ve T nin ortak sabit noktas tek olup z dir. E¼ger Teorem de S = T al n rsa aşa¼g daki sonuç elde edilir: Sonuç (X; M; ) tam bir fuzzy metrik uzay ve 8a; b 2 X için ab = min(a; b) olsun. S, A : X! X iki fonksiyon ve S sürekli olmak üzere (1) A(X) S(X); (2) (A; S) ikilisi yar ba¼gdaşabilir, (3) 8x; y 2 X ve t > 0 için r : [0; 1]! [0; 1] sürekli fonksiyon olmak üzere M(Ax; Sy; t) r minfm(sx; Sy; t); M(Sx; Ax; t); M(Sx; Ay; t); M(Sy; Ay; t)g (4) Her bir 0 < t < 1 için r(t) > t ve t = 1 için r(t) = 1 ise A ve S nin X de tek bir ortak sabit noktas vard r. Teorem 4.3.2: (X; M; ) tam bir fuzzy metrik uzay ve 8a; b 2 X için a b = min(a; b) olsun. S; T; A, B : X! X fonksiyonlar ve S, T sürekli olmak üzere (1) A(X) [ B(X) S(X) \ T (X); (2) (A; T ) ve (B; S) ikilileri yar ba¼gdaşabilir, 40
47 (3) 8x; y 2 X ve t > 0 için ve a; b; c 0 öyle ki q < (a + b + c) < 1 olmak üzere am(t x; Sy; t) + bm(t x; Ax; t) + cm(sy; By; t) + maxfm(ax; Sy; t); M(By; T x; t)g qm(ax; By; t) ise A; B; S, T nin X de tek bir ortak sabit noktas vard r (Chauan vd. 2010). Ispat: x 0 2 X herhangi bir sabit nokta olsun. A(X) S(X) oldu¼gundan Ax 0 = Sx 1 olacak şekilde x 1 2 X, yine A(X) T (X) oldu¼gundan Ax 1 = T x 2 olacak şekilde x 2 2 X noktas vard r. Bu şekilde devam edilirse X de bir fy n g dizisi y 2n = Sx 2n+1 = Ax 2n ve y 2n+1 = T x 2n+2 = Bx 2n+1 ; n 2 N [ f0g şeklinde oluşturulabilir. 8n için M n = M(y n ; y n+1 ; t) < 1 olsun. Teorem 4.3.1(3) de x = x 2n ve y = x 2n+1 al n rsa am(t x 2n ; Sx 2n+1 ; t) + bm(t x 2n ; Ax 2n ; t) + cm(sx 2n+1 ; Bx 2n+1 ; t) + maxfm(ax 2n ; Sx 2n+1 ; t); M(Bx 2n+1 ; T x 2n ; t)g qm(ax 2n ; Bx 2n+1 ; t) elde edilir. Buradan am(y 2n 1 ; y 2n ; t) + bm(y 2n ; y 2n 1 ; t) + cm(y 2n+1 ; y 2n ; t) + maxfm(y 2n ; y 2n ; t); M(y 2n+1 ; y 2n 1 ; t)g qm(y 2n ; y 2n+1 ; t) bulunur. 41
48 Daha sonra (a + b)m 2n 1 + cm 2n + 1 qm 2n elde edilir. Böylece eşitsizli¼gi yaz labilir. p = (q c)m 2n (a + b)m 2n > (a + b)m 2n 1 (a + b) (q c) > 1 için M 2n pm 2n 1 > M 2n 1 (4.3.4) elde edilir. Sonuç olarak fm 2n g dizisi 0 n < 1 için [0; 1] aral ¼g ndaki pozitif say lar n artan bir dizisidir ve bu yüzden bir L 1 limitine yak nsar. Iddia ediyoruz ki L = 1 olsun. E¼ger L < 1 ise (4.3.4) de n! 1 için limit al n rsa L r(l) > L elde edilir ki bu bir çelişkidir. O halde L = 1 dir. Herhangi bir pozitif p için M(y n ; y n+p ; t) M(y n ; y n+1 ; t p ) M(y n+1; y n+2 ; t p ) ::: M(y n+p 1; y n+p ; t p ) M(y n ; y n+1 ; t p ) ::: M(y n; y n+1 ; t p ) eşitsizli¼gi yaz labilir. t > 0 için lim n!1 M(y n ; y n+1 ; t)! 1 oldu¼gundan lim M(y n; y n+p ; t) 1 1 :::1 = 1 n!1 elde edilir. Yani fy n g dizisi X de bir Cauchy dizisidir. X uzay tam oldu¼gundan fy n g dizisi bir z 2 X noktas na yak nsar. Teorem 4.3.1(3) deki eşitsizlik kullan larak a + b q c > 1 için X de bir Cauchy dizisi elde edilir. Dolay s yla fax 2ng; fbx 2n+1 g; fsx 2n+1 g ve ft x 2n+2 g altdizileri de Cauchy dizisi olup ayn z noktas na yak nsar. T sürekli oldu¼gundan T Ax n! T z ve T T x n! T z dir. Ayn zamanda (A; T ) ikilisi yar ba¼gdaşabilir oldu¼gundan AT x n! T z dir. 42
49 Teorem 4.3.1(3) de x = T x n ; y = x n al n rsa am(t T x n ; Sx n ; t) + bm(t x n ; AT x n ; t) + cm(sx n ; Bx n ; t) + maxfm(at x n ; Sx n ; t); M(Bx n ; T T x n ; t)g qm(at x n ; Bx n ; t) elde edilir. n! 1 için limit al n rsa am(t z; z; t) + bm(z; T z; t) + cm(z; z; t) + maxfm(t z; z; t); M(z; T z; t)g qm(t z; z; t) eşitsizli¼gi elde edilir ve buradan am(t z; z; t) + bm(z; T z; t) + c + M(T z; z; t) qm(t z; z; t) c (q a b 1)M(T z; z; t) M(T z; z; t) c q a b 1 > 1 yaz labilir. M(T z; z; t) > 1 olamayaca¼g ndan T z = z dir. Teorem 4.3.1(3) de x = z; y = x n al n rsa am(t z; Sx n ; t) + bm(t z; Az; t) + cm(sx n ; Bx n ; t) + maxfm(az; Sx n ; t); M(Bx n ; T z; t)g qm(az; Bx n ; t) 43
2. Topolojik Uzaylarda Ba¼glant l l k Ba¼glant l Topolojik Uzaylar. Tan m (X; ) topolojik uzay n n her biri boş kümeden farkl olan ayr k
 2. Topolojik Uzaylarda Ba¼glant l l k 2.1. Ba¼glant l Topolojik Uzaylar Tan m 2.1.1. (X; ) topolojik uzay n n her biri boş kümeden farkl olan ayr k iki aç ktan oluşan bir örtüsü yok ise, (X; ) topolojik
2. Topolojik Uzaylarda Ba¼glant l l k 2.1. Ba¼glant l Topolojik Uzaylar Tan m 2.1.1. (X; ) topolojik uzay n n her biri boş kümeden farkl olan ayr k iki aç ktan oluşan bir örtüsü yok ise, (X; ) topolojik
1.3. Normal Uzaylar. Bu bölümde; regülerlikten daha kuvvetli bir ay rma aksiyomu tan mlanarak. baz temel özellikleri incelenecektir.
 1.3. Normal Uzaylar Bu bölümde; regülerlikten daha kuvvetli bir ay rma aksiyomu tan mlanarak baz temel özellikleri incelenecektir. Tan m 1.3.1. (X; ) bir Hausdor uzay olsun. E¼ger, 8F; K 2 F; F \ K = ;
1.3. Normal Uzaylar Bu bölümde; regülerlikten daha kuvvetli bir ay rma aksiyomu tan mlanarak baz temel özellikleri incelenecektir. Tan m 1.3.1. (X; ) bir Hausdor uzay olsun. E¼ger, 8F; K 2 F; F \ K = ;
T.C. PAMUKKALE ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MATEMATİK ANABİLİM DALI
 T.C. PAMUKKALE ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MATEMATİK ANABİLİM DALI LATİSLERDE TÜREVLER YÜKSEK LİSANS TEZİ UTKU PEHLİVAN DENİZLİ, OCAK - 2015 T.C. PAMUKKALE ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
T.C. PAMUKKALE ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MATEMATİK ANABİLİM DALI LATİSLERDE TÜREVLER YÜKSEK LİSANS TEZİ UTKU PEHLİVAN DENİZLİ, OCAK - 2015 T.C. PAMUKKALE ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
fonksiyonu, her x 6= 1 reel say s için tan ml d r. (x 1)(x+1) = = x + 1 yaz labilir. Bu da; f (x) = L
 Limit Bu bölümde, matematik analizde temel bir görevi olan it kavram incelenecektir. Analizdeki bir çok problemin çözümünde it kavram na gereksinim duyulmaktad r. Bunlardan baz lar ; bir noktada bir e¼griye
Limit Bu bölümde, matematik analizde temel bir görevi olan it kavram incelenecektir. Analizdeki bir çok problemin çözümünde it kavram na gereksinim duyulmaktad r. Bunlardan baz lar ; bir noktada bir e¼griye
FONKS IYONEL ANAL IZE G IR IŞ I Aras nav Sorular
 Ad ve Soyad : Numaras : FONKS IYONEL ANAL IZE G IR IŞ I Aras nav Sorular 30.11.2007 1. Aşa¼g daki ifadelerin do¼gru olup olmad klar n nedenlerini aç klayarak yaz n z. (a) (X; kk) bir normlu uzay ve M bunun
Ad ve Soyad : Numaras : FONKS IYONEL ANAL IZE G IR IŞ I Aras nav Sorular 30.11.2007 1. Aşa¼g daki ifadelerin do¼gru olup olmad klar n nedenlerini aç klayarak yaz n z. (a) (X; kk) bir normlu uzay ve M bunun
Fonksiyonel Analize Giriş I Ara S nav Sorular 29 Kas m Bir metrik uzayda her kapal yuvar kapal bir kümedir. Ispatlay n z.
 Fonksiyonel Analize Giriş I Ara S nav Sorular 29 Kas m 2010 1 Bir metrik uzayda her kapal yuvar kapal bir kümedir. Ispatlay n z. 2 (a) d (x; y) = Z 1 0 jx (t) y (t)j 1 + jx (t) y (t)j dt fonksiyonunun
Fonksiyonel Analize Giriş I Ara S nav Sorular 29 Kas m 2010 1 Bir metrik uzayda her kapal yuvar kapal bir kümedir. Ispatlay n z. 2 (a) d (x; y) = Z 1 0 jx (t) y (t)j 1 + jx (t) y (t)j dt fonksiyonunun
A; e A; A kümelerini tan mlay n z. (x) = fb 2 B : x 2 Bg
 Genel Topolojiye Giriş I Ara S nav Sorular 30 Kas m 2010 1 (X; T ) bir topolojik uzay ve A X olsun. 2 (a) Ikinci say labilir topolojik uzay ne demektir? Tan mlay n z. A; e A; A ve @A kümelerini tan mlay
Genel Topolojiye Giriş I Ara S nav Sorular 30 Kas m 2010 1 (X; T ) bir topolojik uzay ve A X olsun. 2 (a) Ikinci say labilir topolojik uzay ne demektir? Tan mlay n z. A; e A; A ve @A kümelerini tan mlay
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ GENELLEŞTİRİLMİŞ TOPOLOJİLERDE BAZI YENİ SONUÇLAR. Sevda SAĞIROĞLU PEKER
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ GENELLEŞTİRİLMİŞ TOPOLOJİLERDE BAZI YENİ SONUÇLAR Sevda SAĞIROĞLU PEKER MATEMATİK ANABİLİM DALI ANKARA 2009 Her hakkı saklıdır ÖZET Doktora Tezi
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ GENELLEŞTİRİLMİŞ TOPOLOJİLERDE BAZI YENİ SONUÇLAR Sevda SAĞIROĞLU PEKER MATEMATİK ANABİLİM DALI ANKARA 2009 Her hakkı saklıdır ÖZET Doktora Tezi
6 Devirli Kodlar. 6.1 Temel Tan mlar
 6 Devirli Kodlar 6.1 Temel Tan mlar Tan m S F n q için e¼ger (a 0 ; a 1 ; : : : ; a n 1 ) 2 S iken (a n 1 ; a 1 ; : : : ; a n 2 ) 2 S oluyorsa S kümesine devirli denir. E¼ger bir C do¼grusal kodu devirli
6 Devirli Kodlar 6.1 Temel Tan mlar Tan m S F n q için e¼ger (a 0 ; a 1 ; : : : ; a n 1 ) 2 S iken (a n 1 ; a 1 ; : : : ; a n 2 ) 2 S oluyorsa S kümesine devirli denir. E¼ger bir C do¼grusal kodu devirli
NÜMER IK ANAL IZ. Nuri ÖZALP. Sabit Nokta ve Fonksiyonel Yineleme. Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP Sabit Nokta ve Fonksiyonel Yineleme Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 3 7! Sabit Nokta ve Fonksiyonel Yineleme 1 / 23 Sabit Nokta
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP Sabit Nokta ve Fonksiyonel Yineleme Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 3 7! Sabit Nokta ve Fonksiyonel Yineleme 1 / 23 Sabit Nokta
(z z 0 ) n. n=1. Z f (z) dz = 2ib 1
 0 RE IDÜ TEOR IS I Tan m. f fonksiyonu z 0 noktas nda ayr k singülerli¼ge sahip olsun. Bu durumda f fonksiyonu 0 < jz z 0 j < " bölgesinde X X f(z) = a n (z z 0 ) n b n + (z z 0 ) n Laurent seri aç l m
0 RE IDÜ TEOR IS I Tan m. f fonksiyonu z 0 noktas nda ayr k singülerli¼ge sahip olsun. Bu durumda f fonksiyonu 0 < jz z 0 j < " bölgesinde X X f(z) = a n (z z 0 ) n b n + (z z 0 ) n Laurent seri aç l m
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ FUZZY HALKALAR VE FUZZY İDEALLER ÜZERİNE. Deniz Pınar DENİZ MATEMATİK ANABİLİM DALI
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ FUZZY HALKALAR VE FUZZY İDEALLER ÜZERİNE Deniz Pınar DENİZ MATEMATİK ANABİLİM DALI ANKARA 2011 Her hakkı saklıdır ÖZET Yüksek Lisans Tezi
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ FUZZY HALKALAR VE FUZZY İDEALLER ÜZERİNE Deniz Pınar DENİZ MATEMATİK ANABİLİM DALI ANKARA 2011 Her hakkı saklıdır ÖZET Yüksek Lisans Tezi
NÜMER IK ANAL IZ. Nuri ÖZALP FONKS IYONLARA YAKLAŞIM. Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP FONKS IYONLARA YAKLAŞIM Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 4 7! FONKS IYONLARA YAKLAŞIM 1 / 21 1 Polinom Interpolasyonu Newton Formu
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP FONKS IYONLARA YAKLAŞIM Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 4 7! FONKS IYONLARA YAKLAŞIM 1 / 21 1 Polinom Interpolasyonu Newton Formu
Bir H Hilbert uzay üzerinde herhangi bir kompakt simetrik T operatörü için,
 Ritz Yöntemi Kullan larak Integral Operatörlerin Özde¼gerlerinin Yaklaş k Hesab Yüksel SOYKAN, Erkan TAŞDEM IR, Melih GÖCEN Zonguldak Karaelmas Üniversitesi, Fen Edebiyat Fakültesi, Matematik Bölümü, 6700
Ritz Yöntemi Kullan larak Integral Operatörlerin Özde¼gerlerinin Yaklaş k Hesab Yüksel SOYKAN, Erkan TAŞDEM IR, Melih GÖCEN Zonguldak Karaelmas Üniversitesi, Fen Edebiyat Fakültesi, Matematik Bölümü, 6700
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ İKİNCİ BASAMAKTAN DİFERENSİYEL DENKLEMLER İÇİN ARALIK SALINIM KRİTERİ.
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ İKİNCİ BASAMAKTAN DİFERENSİYEL DENKLEMLER İÇİN ARALIK SALINIM KRİTERİ Neslihan ÇAVUNT MATEMATİK ANABİLİM DALI ANKARA 202 Her hakkı saklıdır
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ İKİNCİ BASAMAKTAN DİFERENSİYEL DENKLEMLER İÇİN ARALIK SALINIM KRİTERİ Neslihan ÇAVUNT MATEMATİK ANABİLİM DALI ANKARA 202 Her hakkı saklıdır
MAT216 TOPOLOJ IYE G IR IŞ DERS NOTLARI by Mehmet K rdar
 MAT216 TOPOLOJ IYE G IR IŞ DERS NOTLARI by Mehmet K rdar Içindekiler 1. Topolojinin Tan m, Ilk Örnekler, Aç k ve Kapal Kümeler 2. Topolojilerin Karş laşt r lmas ve Alt Uzay 3. Baz ve Alt Baz 4. Metrik
MAT216 TOPOLOJ IYE G IR IŞ DERS NOTLARI by Mehmet K rdar Içindekiler 1. Topolojinin Tan m, Ilk Örnekler, Aç k ve Kapal Kümeler 2. Topolojilerin Karş laşt r lmas ve Alt Uzay 3. Baz ve Alt Baz 4. Metrik
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ SIRA SÜREKLİ OPERATÖRLERİN LİMİTLERİ. Ercan KARADAŞ MATEMATİK ANABİLİM DALI ANKARA 2007
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ SIRA SÜREKLİ OPERATÖRLERİN LİMİTLERİ Ercan KARADAŞ MATEMATİK ANABİLİM DALI ANKARA 2007 Her Hakkı Saklıdır Anne ve Babam a ÖZET Yüksek Lisans
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ SIRA SÜREKLİ OPERATÖRLERİN LİMİTLERİ Ercan KARADAŞ MATEMATİK ANABİLİM DALI ANKARA 2007 Her Hakkı Saklıdır Anne ve Babam a ÖZET Yüksek Lisans
1. Metrik Uzaylar ve Topolojisi
 1. Metrik Uzaylar ve Topolojisi Euclidean R uzayının tabanının B = {(a, b) : a, b R} olduğunu biliyoruz. Demek ki bu uzayda belirleyiçi unsur açık aralıklar. Her açık aralık (a, b) için, olmak üzere, d
1. Metrik Uzaylar ve Topolojisi Euclidean R uzayının tabanının B = {(a, b) : a, b R} olduğunu biliyoruz. Demek ki bu uzayda belirleyiçi unsur açık aralıklar. Her açık aralık (a, b) için, olmak üzere, d
8 LAURENT SER I GÖSTER IMLER I
 8 LAURENT SER I GÖSTER IMLER I Tan m. C n ; n 0; ; ; : : : kompleks sabitler olmak üere serisine Laurent serisi denir. Burada n X C n ( X X X C n ( 0 ) n a n ( 0 ) n b n + ( 0 ) n 0 ) n dir. Teore8.. (Laurent
8 LAURENT SER I GÖSTER IMLER I Tan m. C n ; n 0; ; ; : : : kompleks sabitler olmak üere serisine Laurent serisi denir. Burada n X C n ( X X X C n ( 0 ) n a n ( 0 ) n b n + ( 0 ) n 0 ) n dir. Teore8.. (Laurent
1.4 Tam Metrik Uzay ve Tamlaması
 1.4. Tam Metrik Uzay ve Tamlaması 15 1.4 Tam Metrik Uzay ve Tamlaması Öncelikle şunu not edelim: (X, d) bir metrik uzay, (x n ), X de bir dizi ve x X ise lim n d(x n, x) = 0 = lim n,m d(x n, x m ) = 0
1.4. Tam Metrik Uzay ve Tamlaması 15 1.4 Tam Metrik Uzay ve Tamlaması Öncelikle şunu not edelim: (X, d) bir metrik uzay, (x n ), X de bir dizi ve x X ise lim n d(x n, x) = 0 = lim n,m d(x n, x m ) = 0
GENELLEŞTİRİLMİŞ FUZZY KOMŞULUK SİSTEMİ ÜZERİNE
 ÖZEL EGE LİSESİ GENELLEŞTİRİLMİŞ FUZZY KOMŞULUK SİSTEMİ ÜZERİNE HAZIRLAYAN ÖĞRENCİ: Berk KORKUT DANIŞMAN ÖĞRETMEN: Gizem GÜNEL İZMİR 2013 İÇİNDEKİLER 1. PROJENİN AMACI 3.33 2. GİRİŞ... 3 3. YÖNTEM 3 4.
ÖZEL EGE LİSESİ GENELLEŞTİRİLMİŞ FUZZY KOMŞULUK SİSTEMİ ÜZERİNE HAZIRLAYAN ÖĞRENCİ: Berk KORKUT DANIŞMAN ÖĞRETMEN: Gizem GÜNEL İZMİR 2013 İÇİNDEKİLER 1. PROJENİN AMACI 3.33 2. GİRİŞ... 3 3. YÖNTEM 3 4.
13.Konu Reel sayılar
 13.Konu Reel sayılar 1. Temel dizi 2. Temel dizilerde toplama ve çarpma 3. Reel sayılar kümesi 4. Reel sayılar kümesinde toplama ve çarpma 5. Reel sayılar kümesinde sıralama 6. Reel sayılar kümesinin tamlık
13.Konu Reel sayılar 1. Temel dizi 2. Temel dizilerde toplama ve çarpma 3. Reel sayılar kümesi 4. Reel sayılar kümesinde toplama ve çarpma 5. Reel sayılar kümesinde sıralama 6. Reel sayılar kümesinin tamlık
20. ULUSAL ANTALYA MATEMAT IK OL IMP IYATI SORULARI A A A A A A A
 KDEN IZ ÜN IVERS ITES I 20. ULUSL NTLY MTEMT IK OL IMP IYTI SORULRI DI SOYDI :...CEP TEL :... OKUL...ŞEH IR :... SINIF :...Ö ¼GRETMEN :... eposta :... IMZ :... SINV TR IH I VE ST I : 3 May s 2015 - Pazar
KDEN IZ ÜN IVERS ITES I 20. ULUSL NTLY MTEMT IK OL IMP IYTI SORULRI DI SOYDI :...CEP TEL :... OKUL...ŞEH IR :... SINIF :...Ö ¼GRETMEN :... eposta :... IMZ :... SINV TR IH I VE ST I : 3 May s 2015 - Pazar
Analiz III Ara S nav Sorular 24 Kas m 2010
 Analiz III Ara S nav Sorular 24 Kas m 2010 1 Aşa¼g daki ifadelerin do¼gru olup olmad klar n nedenlerini aç klayarak yaz n z. (a) R n uzay n n aç k olmayan her alt kümesi kapal d r. (b) A = fx 2 [0; 1]
Analiz III Ara S nav Sorular 24 Kas m 2010 1 Aşa¼g daki ifadelerin do¼gru olup olmad klar n nedenlerini aç klayarak yaz n z. (a) R n uzay n n aç k olmayan her alt kümesi kapal d r. (b) A = fx 2 [0; 1]
2010 oldu¼gundan x 2 = 2010 ve
 ) 444400 say s ndaki rakamlar n yerleri de¼giştirilerek 7 basamakl kaç farkl say yaz labilir? Çözüm : Bu rakamlar n bütün farkl 7 li dizilişlerinin say s 7! olacakt r. Bu dizilişlerin 4!! soldan ilk rakam
) 444400 say s ndaki rakamlar n yerleri de¼giştirilerek 7 basamakl kaç farkl say yaz labilir? Çözüm : Bu rakamlar n bütün farkl 7 li dizilişlerinin say s 7! olacakt r. Bu dizilişlerin 4!! soldan ilk rakam
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ. Aylin AYKUT MATEMATİK ANABİLİM DALI ANKARA Her hakkı saklıdır
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ SİNGÜLER POTANSİYELLİ STRUM-LIOUVILLE OPERATÖRLERİ Aylin AYKUT MATEMATİK ANABİLİM DALI ANKARA Her hakkı saklıdır ÖZET Yüksek Lisans Tezi S
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ SİNGÜLER POTANSİYELLİ STRUM-LIOUVILLE OPERATÖRLERİ Aylin AYKUT MATEMATİK ANABİLİM DALI ANKARA Her hakkı saklıdır ÖZET Yüksek Lisans Tezi S
Ad ve Soyad : Numaras : Analiz III Aras nav Sorular
 Analiz III Aras nav Sorular 30. 11. 2006 1. (a) A = fx 2 R : x 2 4x 5 < 0g ise sup A =? (b) A R boş olmayan ve üstten s n rl bir küme olsun. > 0 ise sup(a) = sup A oldu¼gunu gösteriniz. 2. A = f(x; y)
Analiz III Aras nav Sorular 30. 11. 2006 1. (a) A = fx 2 R : x 2 4x 5 < 0g ise sup A =? (b) A R boş olmayan ve üstten s n rl bir küme olsun. > 0 ise sup(a) = sup A oldu¼gunu gösteriniz. 2. A = f(x; y)
AKDEN IZ ÜN IVERS ITES I 21. ULUSAL ANTALYA MATEMAT IK OL IMP IYATI SORULARI
 KDEN IZ ÜN IVERS ITES I 21. ULUSL NTLY MTEMT IK OL IMP IYTI SORULRI DI SOYDI :...CEP TEL :... OKUL...ŞEH IR :... SINIF :...Ö ¼GRETMEN :... eposta :... IMZ :... SINV TR IH I VE ST I : 14 May s 2016 - Cumartesi
KDEN IZ ÜN IVERS ITES I 21. ULUSL NTLY MTEMT IK OL IMP IYTI SORULRI DI SOYDI :...CEP TEL :... OKUL...ŞEH IR :... SINIF :...Ö ¼GRETMEN :... eposta :... IMZ :... SINV TR IH I VE ST I : 14 May s 2016 - Cumartesi
1998 ULUSAL ANTALYA MATEMAT IK OL IMP IYATI B IR INC I AŞAMA SORULARI
 1998 ULUSL NTLY MTEMT IK OL IMP IYTI IR INC I ŞM SORULRI Lise 1- S nav Sorular 1. T = 1! +! + 3! + ::: + 1997! + 1998! toplam n n son iki basama¼g ndaki rakamlar n toplam kaçt r? ) 13 ) 9 C) 6 D) E) Hiçbiri.
1998 ULUSL NTLY MTEMT IK OL IMP IYTI IR INC I ŞM SORULRI Lise 1- S nav Sorular 1. T = 1! +! + 3! + ::: + 1997! + 1998! toplam n n son iki basama¼g ndaki rakamlar n toplam kaçt r? ) 13 ) 9 C) 6 D) E) Hiçbiri.
DÜZCE ÜN IVERS ITES I FEN-EDEB IYAT FAKÜLTES I
 DÜZCE ÜN IVERS ITES I FEN-EDEB IYAT FAKÜLTES I MATEMAT IK BÖLÜMÜ 203-204 BAHAR YARIYILI D IFERANS IYEL DENKLEMLER II ARA SINAV 2 Nisan 204 Süre: 90 dakika CEVAP ANAHTARI. (5p) Belirsiz katsay lar yöntemini
DÜZCE ÜN IVERS ITES I FEN-EDEB IYAT FAKÜLTES I MATEMAT IK BÖLÜMÜ 203-204 BAHAR YARIYILI D IFERANS IYEL DENKLEMLER II ARA SINAV 2 Nisan 204 Süre: 90 dakika CEVAP ANAHTARI. (5p) Belirsiz katsay lar yöntemini
ANAL IZ III Aras nav Sorular
 Ad ve Soyad : Numaras : ANAL IZ III Aras nav Sorular 26.11.27 1. x 1 = p 3 ve x n+1 = p 3 + x n ; n = 1; 2; ::: biçiminde tan mlanan (x n ) dizisinin yak nsak oldu¼gunu gösteriniz ve limitini bulunuz.(2)
Ad ve Soyad : Numaras : ANAL IZ III Aras nav Sorular 26.11.27 1. x 1 = p 3 ve x n+1 = p 3 + x n ; n = 1; 2; ::: biçiminde tan mlanan (x n ) dizisinin yak nsak oldu¼gunu gösteriniz ve limitini bulunuz.(2)
SORULAR. 1. Aşa¼g daki limitleri bulunuz. Cevab n z n aşamalar n belirtiniz. lim. 1 n sin. lim. q 1 x 1+x
 SOULA. Aşa¼g daki limitleri bulunuz. Cevab n z n aşamalar n belirtiniz. lim! lim sin(t )dt sin 4 np n! i= n sin i n. q + arcsin belirli integralini hesalay n z. Cevab n z n aşamalar n belirtiniz. 3. 4
SOULA. Aşa¼g daki limitleri bulunuz. Cevab n z n aşamalar n belirtiniz. lim! lim sin(t )dt sin 4 np n! i= n sin i n. q + arcsin belirli integralini hesalay n z. Cevab n z n aşamalar n belirtiniz. 3. 4
MIT Açık Ders Malzemeleri Kompleks Değişkenli Fonksiyonlar 2008 Güz
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 18.112 Kompleks Değişkenli Fonksiyonlar 2008 Güz Bu materyallerden alıntı yapmak ya Kullanım Şartları hakkında bilgi almak için http://ocw.mit.edu/terms http://tuba.acikders.org.tr
MIT Açık Ders Malzemeleri http://ocw.mit.edu 18.112 Kompleks Değişkenli Fonksiyonlar 2008 Güz Bu materyallerden alıntı yapmak ya Kullanım Şartları hakkında bilgi almak için http://ocw.mit.edu/terms http://tuba.acikders.org.tr
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ TOPLANABİLME METOTLARI VE İTERASYON. Rüya YEĞİN MATEMATİK ANABİLİM DALI ANKARA 2011
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ TOPLANABİLME METOTLARI VE İTERASYON Rüya YEĞİN MATEMATİK ANABİLİM DALI ANKARA 2011 Her hakkı saklıdır ÖZET Yüksek Lisans Tezi TOPLANAB ILME
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ TOPLANABİLME METOTLARI VE İTERASYON Rüya YEĞİN MATEMATİK ANABİLİM DALI ANKARA 2011 Her hakkı saklıdır ÖZET Yüksek Lisans Tezi TOPLANAB ILME
1999 ULUSAL ANTALYA MATEMAT IK OL IMP IYATI B IR INC I AŞAMA SORULARI
 1999 ULUSL NTLY MTMT IK L IMP IYTI IR IN I ŞM SRULRI Lise 1- S nav Sorular 1. f1; ; 3; :::; 1999g kümesinin, eleman say s tek say olan kaç tane alt kümesi vard r? ) 1999 ) 1998 ) 1998-1 ) 999 ) hiçbiri.
1999 ULUSL NTLY MTMT IK L IMP IYTI IR IN I ŞM SRULRI Lise 1- S nav Sorular 1. f1; ; 3; :::; 1999g kümesinin, eleman say s tek say olan kaç tane alt kümesi vard r? ) 1999 ) 1998 ) 1998-1 ) 999 ) hiçbiri.
MATEMAT IK-I (SORULAR)
 Part I MATEMAT IK-I (SORULAR) SAYILAR. irrasyonel midir?. 7 say s n n irrasyonel oldu¼gunu gösteriniz. (Gauss Teoremini kullan n z.) 3. + 3 say s n n irrasyonel oldu¼gunu gösteriniz. (Gauss Teoremini kullan
Part I MATEMAT IK-I (SORULAR) SAYILAR. irrasyonel midir?. 7 say s n n irrasyonel oldu¼gunu gösteriniz. (Gauss Teoremini kullan n z.) 3. + 3 say s n n irrasyonel oldu¼gunu gösteriniz. (Gauss Teoremini kullan
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ SONSUZ JACOBİ MATRİSLERİ İÇİN SPEKTRAL EŞİTSİZLİKLER. Yelda AYGAR
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ SONSUZ JACOBİ MATRİSLERİ İÇİN SPEKTRAL EŞİTSİZLİKLER Yelda AYGAR MATEMATİK ANABİLİM DALI ANKARA 008 Her hakkı saklıdır ÖZET Yüksek Lisans
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ SONSUZ JACOBİ MATRİSLERİ İÇİN SPEKTRAL EŞİTSİZLİKLER Yelda AYGAR MATEMATİK ANABİLİM DALI ANKARA 008 Her hakkı saklıdır ÖZET Yüksek Lisans
17. ULUSAL ANTALYA MATEMAT IK OL IMP IYATLARI B IR INC I AŞAMA SORULARI A A A A A A A
 AKDEN IZ ÜN IVERS ITES I 17. ULUSAL ANTALYA MATEMAT IK OL IMP IYATLARI B IR INC I AŞAMA SORULARI A A A A A A A SINAV TAR IH I VE SAAT I : 24 MART 2012 - Cumartesi 10.00-12.30 Bu s nav 25 sorudan oluşmaktad
AKDEN IZ ÜN IVERS ITES I 17. ULUSAL ANTALYA MATEMAT IK OL IMP IYATLARI B IR INC I AŞAMA SORULARI A A A A A A A SINAV TAR IH I VE SAAT I : 24 MART 2012 - Cumartesi 10.00-12.30 Bu s nav 25 sorudan oluşmaktad
Bu dedi im yaln zca 0,9 say s için de il, 0 la 1 aras ndaki herhangi bir say için geçerlidir:
 Yak nsamak B u yaz da, ilerde s k s k kullanaca m z bir olguyu tan mlayaca z ve matemati in en önemli kavramlar ndan birine (limit kavram na) de inece iz. Asl nda okur anlataca m kavram sezgisel olarak
Yak nsamak B u yaz da, ilerde s k s k kullanaca m z bir olguyu tan mlayaca z ve matemati in en önemli kavramlar ndan birine (limit kavram na) de inece iz. Asl nda okur anlataca m kavram sezgisel olarak
NÜMER IK ANAL IZ. Nuri ÖZALP MATEMAT IKSEL ÖNB ILG ILER. Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP MATEMAT IKSEL ÖNB ILG ILER Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 1 7! MATEMAT IKSEL ÖNB ILG ILER 1 / 15 Kaynaklar Nümerik Analiz-Bilimsel
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP MATEMAT IKSEL ÖNB ILG ILER Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 1 7! MATEMAT IKSEL ÖNB ILG ILER 1 / 15 Kaynaklar Nümerik Analiz-Bilimsel
NÜMER IK ANAL IZ. Nuri ÖZALP L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ 1 / Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ 1 / 1 Denklemlerin Köklerini Bulma Giriş Denklemlerin Köklerini Bulma
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ 1 / 1 Denklemlerin Köklerini Bulma Giriş Denklemlerin Köklerini Bulma
ÜN TE II L M T. Limit Sa dan ve Soldan Limit Özel Fonksiyonlarda Limit Limit Teoremleri Belirsizlik Durumlar Örnekler
 ÜN TE II L M T Limit Sa dan ve Soldan Limit Özel Fonksiyonlarda Limit Limit Teoremleri Belirsizlik Durumlar Örnekler MATEMAT K 5 BU BÖLÜM NELER AMAÇLIYOR? Bu bölümü çal flt n zda (bitirdi inizde), *Bir
ÜN TE II L M T Limit Sa dan ve Soldan Limit Özel Fonksiyonlarda Limit Limit Teoremleri Belirsizlik Durumlar Örnekler MATEMAT K 5 BU BÖLÜM NELER AMAÇLIYOR? Bu bölümü çal flt n zda (bitirdi inizde), *Bir
T.C. SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
 T.C. SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ SOFT TOPOLOJİK UZAYLAR ÜZERİNE Uğur ÇOŞKUN YÜKSEK LİSANS Matematik Anabilim Dalı HAZİRAN-2014 KONYA Her Hakkı Saklıdır TEZ BİLDİRİMİ Bu tezdeki bütün bilgilerin
T.C. SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ SOFT TOPOLOJİK UZAYLAR ÜZERİNE Uğur ÇOŞKUN YÜKSEK LİSANS Matematik Anabilim Dalı HAZİRAN-2014 KONYA Her Hakkı Saklıdır TEZ BİLDİRİMİ Bu tezdeki bütün bilgilerin
1. GRUPLAR. c (Birleşme özelliği) sağlanır. 2) a G için a e e a a olacak şekilde e G (e ye birim eleman denir) vardır.
 1. GRUPLAR Tanım 1.1. G boş olmayan bir küme ve, G de bir ikili işlem olsun. (G yapısına aşağıdaki aksiyomları sağlıyorsa bir grup denir., ) cebirsel 1) a b cg,, için a( bc) ( ab) c (Birleşme özelliği)
1. GRUPLAR Tanım 1.1. G boş olmayan bir küme ve, G de bir ikili işlem olsun. (G yapısına aşağıdaki aksiyomları sağlıyorsa bir grup denir., ) cebirsel 1) a b cg,, için a( bc) ( ab) c (Birleşme özelliği)
Dördüncü K s m: Gerçel Say lar Yap s
 Dördüncü K s m: Gerçel Say lar Yap s 331 13. Gerçel Say lar Kümesi Nihayet gerçel say lar tan mlayaca z. Bir sonraki bölümde gerçel say lar üzerine dört ifllemi ve s ralamay tan mlay p bunlar n özelliklerini
Dördüncü K s m: Gerçel Say lar Yap s 331 13. Gerçel Say lar Kümesi Nihayet gerçel say lar tan mlayaca z. Bir sonraki bölümde gerçel say lar üzerine dört ifllemi ve s ralamay tan mlay p bunlar n özelliklerini
ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
 ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ Nuray GÜL İKİ TOPOLOJİLİ UZAYLARDA BAZI AYIRMA AKSİYOMLARI MATEMATİK ANABİLİM DALI ADANA, 2011 ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ Nuray GÜL İKİ TOPOLOJİLİ UZAYLARDA BAZI AYIRMA AKSİYOMLARI MATEMATİK ANABİLİM DALI ADANA, 2011 ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
Kahramanmaras Sutcu Imam University Journal of Engineering Sciences
 KSU Mühendislik Bilimleri Dergisi, 0(), 017 16 KSU Journal of Engineering Sciences, 0(), 017 Kahramanmaras Sutcu Imam University Journal of Engineering Sciences G-Metrik Uzayda Zayıf Uyumlu Dönüşümler
KSU Mühendislik Bilimleri Dergisi, 0(), 017 16 KSU Journal of Engineering Sciences, 0(), 017 Kahramanmaras Sutcu Imam University Journal of Engineering Sciences G-Metrik Uzayda Zayıf Uyumlu Dönüşümler
Olas l k Hesaplar (II)
 Olas l k Hesaplar (II) B ir önceki yaz daki örneklerde olay say s sonluydu. Örne in, iki zarla 21 olay vard. fiimdi olay say m z sonsuz yapaca z. Kolay bir soruyla bafllayal m: [0, 1] aral nda rastgele
Olas l k Hesaplar (II) B ir önceki yaz daki örneklerde olay say s sonluydu. Örne in, iki zarla 21 olay vard. fiimdi olay say m z sonsuz yapaca z. Kolay bir soruyla bafllayal m: [0, 1] aral nda rastgele
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ ÜSTEL İNTEGRAL FONKSİYONLARIN. Çağla CAN MATEMATİK ANABİLİM DALI ANKARA 2012
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEİ ÜSTEL İNTEGRAL FONKSİYONLARIN DÜGÜN YAKINSAKLIĞI Çağla CAN MATEMATİK ANABİLİM DALI ANKARA 0 Her hakkı saklıdır ÖET Yüksek Lisans Tezi ÜSTEL
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEİ ÜSTEL İNTEGRAL FONKSİYONLARIN DÜGÜN YAKINSAKLIĞI Çağla CAN MATEMATİK ANABİLİM DALI ANKARA 0 Her hakkı saklıdır ÖET Yüksek Lisans Tezi ÜSTEL
NÜMER IK ANAL IZ. Nuri ÖZALP. SAYISAL TÜREV ve INTEGRAL. Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP SAYISAL TÜREV ve INTEGRAL Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 1 / 23 1 Say sal Türev ve Richardson
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP SAYISAL TÜREV ve INTEGRAL Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 1 / 23 1 Say sal Türev ve Richardson
14.Konu Reel sayılarının topolojisi. 1.Tanım:, verilsin. açık aralığına noktasının -komşuluğu denir. { } kümesine nın delinmiş -komşuluğu denir.
 14.Konu Reel sayılarının topolojisi 1.Teorem: cismi tamdır. 1.Tanım:, verilsin. açık aralığına noktasının -komşuluğu denir. { } kümesine nın delinmiş -komşuluğu denir. 2.Tanım: ve verilsin. nın her komşuluğunda
14.Konu Reel sayılarının topolojisi 1.Teorem: cismi tamdır. 1.Tanım:, verilsin. açık aralığına noktasının -komşuluğu denir. { } kümesine nın delinmiş -komşuluğu denir. 2.Tanım: ve verilsin. nın her komşuluğunda
TOPOLOGY TEST A³a dakilerden hangisi bir süzgeç de ildir? 3. A³a dakilerden hangisi a³kn bir süzgeç de ildir?
 1 TOPOLOGY TEST 02 1. S ailesi X kümesi üzerinde bir süzgeç ise, a³a dakilerden hangisi sa lanmaz? (a) / S (b) * S (c) X S (d) A, B S A B S (e) (V S ) (V W ) W S 2. A³a dakilerden hangisi bir süzgeç de
1 TOPOLOGY TEST 02 1. S ailesi X kümesi üzerinde bir süzgeç ise, a³a dakilerden hangisi sa lanmaz? (a) / S (b) * S (c) X S (d) A, B S A B S (e) (V S ) (V W ) W S 2. A³a dakilerden hangisi bir süzgeç de
POL NOMLAR. Polinomlar
 POL NOMLAR ÜN TE 1. ÜN TE 1. ÜN TE 1. ÜN TE 1. ÜN T POL NOMLAR Polinomlar 1. Kazan m: Gerçek kat say l ve tek de i kenli polinom kavram n örneklerle aç klar, polinomun derecesini, ba kat say s n, sabit
POL NOMLAR ÜN TE 1. ÜN TE 1. ÜN TE 1. ÜN TE 1. ÜN T POL NOMLAR Polinomlar 1. Kazan m: Gerçek kat say l ve tek de i kenli polinom kavram n örneklerle aç klar, polinomun derecesini, ba kat say s n, sabit
M IKRO IKT ISAT 2. V IZE SINAVI 19 ARALIK 2009
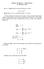 M IKRO IKT ISAT 2. V IZE SINAVI 19 ARALIK 2009 Soru 1: Aşa¼g daki gibi bir üretim fonksiyonu verilsin: = L 1=3 K 2=3 Eme¼gin yat w = ve sermayenin yat r = 1 olsun. a- Firma kadar ç kt üretmek istemektedir.
M IKRO IKT ISAT 2. V IZE SINAVI 19 ARALIK 2009 Soru 1: Aşa¼g daki gibi bir üretim fonksiyonu verilsin: = L 1=3 K 2=3 Eme¼gin yat w = ve sermayenin yat r = 1 olsun. a- Firma kadar ç kt üretmek istemektedir.
Çözümlü Yüksek Matematik Problemleri. Yrd. Doç. Dr. Erhan Pişkin
 Çözümlü Yüksek Matematik Problemleri Yrd. Doç. Dr. Erhan Pişkin 1 Yrd. Doç. Dr. Erhan PİŞKİN ÇÖZÜMLÜ YÜKSEK MATEMATİK PROBLEMLERİ 1 ISBN 978-605-318-249-8 Kitap içeriğinin tüm sorumluluğu yazarına aittir.
Çözümlü Yüksek Matematik Problemleri Yrd. Doç. Dr. Erhan Pişkin 1 Yrd. Doç. Dr. Erhan PİŞKİN ÇÖZÜMLÜ YÜKSEK MATEMATİK PROBLEMLERİ 1 ISBN 978-605-318-249-8 Kitap içeriğinin tüm sorumluluğu yazarına aittir.
7 TAYLOR SER I GÖSTER IMLER I
 7 TAYLOR SER I GÖSTER IMLER I Bir f fonksiyonu analitiklik bölgesi içinde f () X a n ( 0 ) n şeklinde bir kuvvet serisi gösterimine sahiptir. E¼ger a n f (n) ( 0 ) seçilirse bu kuvvet serisi Taylor serisi
7 TAYLOR SER I GÖSTER IMLER I Bir f fonksiyonu analitiklik bölgesi içinde f () X a n ( 0 ) n şeklinde bir kuvvet serisi gösterimine sahiptir. E¼ger a n f (n) ( 0 ) seçilirse bu kuvvet serisi Taylor serisi
PAMUKKALE ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ TOPLANABİLEN VEYA SINIRLI OLAN DİZİ UZAYLARI ARASINDAKİ DÖNÜŞÜMLERİN ÖZELLİKLERİ
 PAMUKKALE ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ TOPLANABİLEN VEYA SINIRLI OLAN DİZİ UZAYLARI ARASINDAKİ DÖNÜŞÜMLERİN ÖZELLİKLERİ YÜKSEK LİSANS TEZİ İnci BİRGİN Anabilim Dalı : Matematik Programı : Matematik
PAMUKKALE ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ TOPLANABİLEN VEYA SINIRLI OLAN DİZİ UZAYLARI ARASINDAKİ DÖNÜŞÜMLERİN ÖZELLİKLERİ YÜKSEK LİSANS TEZİ İnci BİRGİN Anabilim Dalı : Matematik Programı : Matematik
SDÜ Matematik Bölümü Analiz-IV Final S nav
 Dersin Kodu: MAT0 Dönemi: 00-0 Bahar Tarihi: 0.0.0 Saat:. 00 Yer: Am III-IV Süre: 90 Dakika Dersin Sorumlusu Gözetmenler SDÜ Matematik Bölümü Analiz-IV Final S nav : Prof. Dr. Seril PEHL IVAN : Araş. Gör.
Dersin Kodu: MAT0 Dönemi: 00-0 Bahar Tarihi: 0.0.0 Saat:. 00 Yer: Am III-IV Süre: 90 Dakika Dersin Sorumlusu Gözetmenler SDÜ Matematik Bölümü Analiz-IV Final S nav : Prof. Dr. Seril PEHL IVAN : Araş. Gör.
TG 12 ÖABT İLKÖĞRETİM MATEMATİK
 KAMU PERSONEL SEÇME SINAVI ÖĞRETMENLİK ALAN BİLGİSİ TESTİ İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ TG ÖABT İLKÖĞRETİM MATEMATİK Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının
KAMU PERSONEL SEÇME SINAVI ÖĞRETMENLİK ALAN BİLGİSİ TESTİ İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ TG ÖABT İLKÖĞRETİM MATEMATİK Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının
Topolojik Uzaylarda Süreklilik Çeşitleri Üzerine
 S Ü Fen Ed Fak Fen Derg Sayı 26 (2005) 43-50, KONYA Topolojik Uzaylarda Süreklilik Çeşitleri Üzerine Kemal USLU 1, Şaziye YÜKSEL Selçuk Üniversitesi Fen Edebiyat Fakültesi Matematik Bölümü Kampüs-Konya
S Ü Fen Ed Fak Fen Derg Sayı 26 (2005) 43-50, KONYA Topolojik Uzaylarda Süreklilik Çeşitleri Üzerine Kemal USLU 1, Şaziye YÜKSEL Selçuk Üniversitesi Fen Edebiyat Fakültesi Matematik Bölümü Kampüs-Konya
Bu tanım aralığı pozitif tam sayılar olan f(n) fonksiyonunun değişim aralığı n= 1, 2, 3,, n,
 DİZİLER Tamamen belirli bir kurala göre sıralanmış sayılar topluluğuna veya kümeye Dizi denir. Belirli bir kurala göre birbiri ardınca gelen bu sayıların her birine dizinin terimi ve hepsine birden dizinin
DİZİLER Tamamen belirli bir kurala göre sıralanmış sayılar topluluğuna veya kümeye Dizi denir. Belirli bir kurala göre birbiri ardınca gelen bu sayıların her birine dizinin terimi ve hepsine birden dizinin
MIT Açık Ders Malzemeleri Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için
 MIT Açık Ders Malzemeleri http://ocw.mit.edu Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için http://ocw.mit.edu/terms veya http://www.acikders.org.tr adresini ziyaret
MIT Açık Ders Malzemeleri http://ocw.mit.edu Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için http://ocw.mit.edu/terms veya http://www.acikders.org.tr adresini ziyaret
; k = 1; 2; ::: a (k)
 Analiz III Ara S nav 2 Kas m 2 x k = ; 2 ; :::; ; k = ; 2; ::: olmak üzere (x k ) R dizisi veriliyor. ; dizi ise (x k ) dizisi de yak nsak olur. Ispatlay n z. 2 ; :::; 2 A; B R olsun. A B ise A B olur
Analiz III Ara S nav 2 Kas m 2 x k = ; 2 ; :::; ; k = ; 2; ::: olmak üzere (x k ) R dizisi veriliyor. ; dizi ise (x k ) dizisi de yak nsak olur. Ispatlay n z. 2 ; :::; 2 A; B R olsun. A B ise A B olur
Sonlu Lineer Uzayların Doğru Dereceleri Üzerine. Metin Şahin YÜKSEK LİSANS TEZİ. Matematik ve Bilgisayar Bilimleri Anabilim Dalı
 Sonlu Lineer Uzayların Doğru Dereceleri Üzerine Metin Şahin YÜKSEK LİSANS TEZİ Matematik ve Bilgisayar Bilimleri Anabilim Dalı Ağustos 2013 On Line Degrees Of The Finite Linear Spaces Metin Şahin MASTER
Sonlu Lineer Uzayların Doğru Dereceleri Üzerine Metin Şahin YÜKSEK LİSANS TEZİ Matematik ve Bilgisayar Bilimleri Anabilim Dalı Ağustos 2013 On Line Degrees Of The Finite Linear Spaces Metin Şahin MASTER
2014 LYS MATEMATİK. P(x) x 2 x 3 polinomunda. 2b a ifade- x lü terimin. olduğuna göre, katsayısı kaçtır? değeri kaçtır? ifadesinin değeri kaçtır? 4.
 04 LYS MATEMATİK. a b b a ifade- ab olduğuna göre, sinin değeri kaçtır? 5. P() polinomunda katsayısı kaçtır? 4 lü terimin. ifadesinin değeri kaçtır? 4. yy y 4y y olduğuna göre, + y toplamının değeri kaçtır?
04 LYS MATEMATİK. a b b a ifade- ab olduğuna göre, sinin değeri kaçtır? 5. P() polinomunda katsayısı kaçtır? 4 lü terimin. ifadesinin değeri kaçtır? 4. yy y 4y y olduğuna göre, + y toplamının değeri kaçtır?
BİR SAYININ ÖZÜ VE DÖRT İŞLEM
 ÖZEL EGE LİSESİ BİR SAYININ ÖZÜ VE DÖRT İŞLEM HAZIRLAYAN ÖĞRENCİ: Sıla Avar DANIŞMAN ÖĞRETMEN: Gizem Günel İZMİR 2012 İÇİNDEKİLER 1. PROJENİN AMACI.. 3 2. GİRİŞ... 3 3. YÖNTEM. 3 4. ÖN BİLGİLER... 3 5.
ÖZEL EGE LİSESİ BİR SAYININ ÖZÜ VE DÖRT İŞLEM HAZIRLAYAN ÖĞRENCİ: Sıla Avar DANIŞMAN ÖĞRETMEN: Gizem Günel İZMİR 2012 İÇİNDEKİLER 1. PROJENİN AMACI.. 3 2. GİRİŞ... 3 3. YÖNTEM. 3 4. ÖN BİLGİLER... 3 5.
NEUTROSOPHIC TOPOLOJİK UZAYLARDA SÜREKLİLİK GÜLŞAH KAYA
 T.C. ORDU ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ NEUTROSOPHIC TOPOLOJİK UZAYLARDA SÜREKLİLİK GÜLŞAH KAYA YÜKSEK LİSANS TEZİ ORDU 2017 ÖZET NEUTROSOPHIC TOPOLOJİK UZAYLARDA SÜREKLİLİK Gülşah KAYA Ordu Üniversitesi
T.C. ORDU ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ NEUTROSOPHIC TOPOLOJİK UZAYLARDA SÜREKLİLİK GÜLŞAH KAYA YÜKSEK LİSANS TEZİ ORDU 2017 ÖZET NEUTROSOPHIC TOPOLOJİK UZAYLARDA SÜREKLİLİK Gülşah KAYA Ordu Üniversitesi
BÖLÜM 1. Matematiksel ndüksiyon Prensibi
 BÖLÜM 1 Matematiksel ndüksiyon Prensibi Matematiksel indüksiyon prensibini kullanarak a³a daki e³it(siz)liklerin her n N için gerçeklendi ini ispatlaynz. 1. 1 2 + 2 2 + 3 2 + + n 2 = n(n+1)(2n+1) 6 2.
BÖLÜM 1 Matematiksel ndüksiyon Prensibi Matematiksel indüksiyon prensibini kullanarak a³a daki e³it(siz)liklerin her n N için gerçeklendi ini ispatlaynz. 1. 1 2 + 2 2 + 3 2 + + n 2 = n(n+1)(2n+1) 6 2.
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ PARÇALI SÜREKLİ ARGÜMENTLİ DİFERENSİYEL DENKLEMLER. Gizem SEYHAN
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ PARÇALI SÜREKLİ ARGÜMENTLİ DİFERENSİYEL DENKLEMLER Gizem SEYHAN MATEMATİK ANABİLİM DALI ANKARA 28 Her hakkı saklıdır ÖZET Yüksek Lisans Tezi
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ PARÇALI SÜREKLİ ARGÜMENTLİ DİFERENSİYEL DENKLEMLER Gizem SEYHAN MATEMATİK ANABİLİM DALI ANKARA 28 Her hakkı saklıdır ÖZET Yüksek Lisans Tezi
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ LOKAL İNTEGRALLENEBİLİR FONKSİYON UZAYLARINDA KOROVKİN TİPİ YAKLAŞIMLAR.
 ANKARA ÜNİVERSİTESİ FEN İLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEİ LOKAL İNTEGRALLENEİLİR FONKSİYON UAYLARINDA KOROVKİN TİPİ YAKLAŞIMLAR Nilay ŞAHİN MATEMATİK ANAİLİM DALI ANKARA Her hakkı saklıdır ÖET Yüksek
ANKARA ÜNİVERSİTESİ FEN İLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEİ LOKAL İNTEGRALLENEİLİR FONKSİYON UAYLARINDA KOROVKİN TİPİ YAKLAŞIMLAR Nilay ŞAHİN MATEMATİK ANAİLİM DALI ANKARA Her hakkı saklıdır ÖET Yüksek
TOPOLOJ TEST B. (d) Dizinin limiti yoktur; y lma noktas yoktur. 4. Dizisel süreklilik hangi uzaylarda süreklili e denktir?
 1 TOPOLOJ TEST B 1. {( 1) n 1 n : n > 0} dizisi için a³a dakilerden hangisi do rudur? (a) Dizinin limiti 1 ve +1 dir; y lma noktas 1 ve +1 dir. (b) Dizinin limiti 1 ve +1 dir; y lma noktas yoktur. (c)
1 TOPOLOJ TEST B 1. {( 1) n 1 n : n > 0} dizisi için a³a dakilerden hangisi do rudur? (a) Dizinin limiti 1 ve +1 dir; y lma noktas 1 ve +1 dir. (b) Dizinin limiti 1 ve +1 dir; y lma noktas yoktur. (c)
TOPOLOJ TEST A. 1. A³a dakilerden hangisi topoloji tanmlama yöntemi de ildir?
 1 TOPOLOJ TEST A 1. A³a dakilerden hangisi topoloji tanmlama yöntemi de ildir? (a) Açk kümeleri belirleme (b) Kapal kümeleri belirleme (c) Alt-kümeleri belirleme (d) Kaplamlar belirleme (e) çlemleri belirleme
1 TOPOLOJ TEST A 1. A³a dakilerden hangisi topoloji tanmlama yöntemi de ildir? (a) Açk kümeleri belirleme (b) Kapal kümeleri belirleme (c) Alt-kümeleri belirleme (d) Kaplamlar belirleme (e) çlemleri belirleme
ab H bulunur. Şu halde önceki önermenin i) koşulu da sağlanır ve H G bulunur.
 3.ALT GRUPLAR HG, Tanım 3.. (G, ) bir grup ve nin boş olmayan bir alt kümesi olsun. Eğer (H, ) bir grup ise H ye G nin bir alt grubu denir ve H G ile gösterilir. Not 3.. a)(h, ), (G, ) grubunun alt grubu
3.ALT GRUPLAR HG, Tanım 3.. (G, ) bir grup ve nin boş olmayan bir alt kümesi olsun. Eğer (H, ) bir grup ise H ye G nin bir alt grubu denir ve H G ile gösterilir. Not 3.. a)(h, ), (G, ) grubunun alt grubu
Topolojik Uzay. Kapak Konusu: Topoloji
 Kapak Konusu: Topoloji Topolojik Uzay Geçen yaz da nin, ad na aç k dedi imiz baz altkümelerini tan mlad k ve bir fonksiyonun süreklili ini tamamen aç k kümeler yard m yla (hiç ve kullanmadan) ifade ettik.
Kapak Konusu: Topoloji Topolojik Uzay Geçen yaz da nin, ad na aç k dedi imiz baz altkümelerini tan mlad k ve bir fonksiyonun süreklili ini tamamen aç k kümeler yard m yla (hiç ve kullanmadan) ifade ettik.
ZAMAN SKALASINDA LİNEER OLMAYAN İNTEGRAL EŞİTSİZLİKLERİ. YÜKSEK LİSANS TEZİ Hakan TEMİZ. Danışman Doç. Dr. Mustafa Kemal YILDIZ
 ZAMAN SKALASINDA LİNEER OLMAYAN İNTEGRAL EŞİTSİZLİKLERİ YÜKSEK LİSANS TEZİ Hakan TEMİZ Danışman Doç. Dr. Mustafa Kemal YILDIZ MATEMATİK ANABİLİM DALI Haziran, 2014 AFYON KOCATEPE ÜNİVERSİTESİ FEN BİLİMLERİ
ZAMAN SKALASINDA LİNEER OLMAYAN İNTEGRAL EŞİTSİZLİKLERİ YÜKSEK LİSANS TEZİ Hakan TEMİZ Danışman Doç. Dr. Mustafa Kemal YILDIZ MATEMATİK ANABİLİM DALI Haziran, 2014 AFYON KOCATEPE ÜNİVERSİTESİ FEN BİLİMLERİ
MC 311/ANAL Z III ARA SINAV I ÇÖZÜMLER
 MC 311/ANAL Z III ARA SINAV I ÇÖZÜMLER (1) A³a daki her bir önermenin do ru mu yanl³ m oldu unu belirleyiniz. Do ruysa, gerekçe gösteriniz; yanl³sa, bir kar³-örnek veriniz. (a) (a n ) n N dizisi yaknsak
MC 311/ANAL Z III ARA SINAV I ÇÖZÜMLER (1) A³a daki her bir önermenin do ru mu yanl³ m oldu unu belirleyiniz. Do ruysa, gerekçe gösteriniz; yanl³sa, bir kar³-örnek veriniz. (a) (a n ) n N dizisi yaknsak
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ SINIR KOŞULLARINDA SPEKTRAL PARAMETRE BULUNAN NON-SELFADJOİNT FARK OPERATÖRLERİNİN
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ SINIR KOŞULLARINDA SPEKTRAL PARAMETRE BULUNAN NON-SELFADJOİNT FARK OPERATÖRLERİNİN SPEKTRAL ANALİZİ Turhan KÖPRÜBAŞI MATEMATİK ANABİLİM DALI ANKARA
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ SINIR KOŞULLARINDA SPEKTRAL PARAMETRE BULUNAN NON-SELFADJOİNT FARK OPERATÖRLERİNİN SPEKTRAL ANALİZİ Turhan KÖPRÜBAŞI MATEMATİK ANABİLİM DALI ANKARA
NÜMER IK ANAL IZ. Nuri ÖZALP L INEER S ISTEMLER IN ÇÖZÜMÜ. Bilimsel Hesaplama Matemati¼gi, Gazi Kitabevi 2012
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi, Gazi Kitabevi 0 Nuri ÖZALP L INEER S ISTEMLER IN ÇÖZÜMÜ Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 6 7! L INEER S ISTEMLER IN ÇÖZÜMÜ / 9 . LU ve Cholesky
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi, Gazi Kitabevi 0 Nuri ÖZALP L INEER S ISTEMLER IN ÇÖZÜMÜ Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 6 7! L INEER S ISTEMLER IN ÇÖZÜMÜ / 9 . LU ve Cholesky
1.BÖLÜM SORU SORU. (x 1) (x 3) = A + B. x 3 ise, d(p(x)) ve d(q(x)) polinomlar n derecelerini göstermek. A. B çarp m kaçt r?
 1.BÖLÜM MATEMAT K Derginin bu say s nda Polinomlar konusunda çözümlü sorular yer almaktad r. Bu konuda, ÖSS de ç kan sorular n çözümü için gerekli temel bilgileri ve pratik yollar, sorular m z n çözümü
1.BÖLÜM MATEMAT K Derginin bu say s nda Polinomlar konusunda çözümlü sorular yer almaktad r. Bu konuda, ÖSS de ç kan sorular n çözümü için gerekli temel bilgileri ve pratik yollar, sorular m z n çözümü
MIT Açık Ders Malzemeleri Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için
 MIT Açık Ders Malzemeleri http://ocw.mit.edu Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için http://ocw.mit.edu/terms veya http://www.acikders.org.tr adresini ziyaret
MIT Açık Ders Malzemeleri http://ocw.mit.edu Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için http://ocw.mit.edu/terms veya http://www.acikders.org.tr adresini ziyaret
n ; = w! =(w 1 ; :::; w n ) (1.2.2) ; :::; + :::
 1. G IR IŞ 1.1. Ön Bilgiler Laplace denklemi, zik ve mühendisli¼gin pekçok alan nda ortaya ç kt ¼g ndan matematikçilerin, mühendislerin ve bilim adamlar n n büyük bir ilgi alan olmuştur. Potansiyel Teorinin
1. G IR IŞ 1.1. Ön Bilgiler Laplace denklemi, zik ve mühendisli¼gin pekçok alan nda ortaya ç kt ¼g ndan matematikçilerin, mühendislerin ve bilim adamlar n n büyük bir ilgi alan olmuştur. Potansiyel Teorinin
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ SOBOLEV UZAYLARINDA YAKLAŞIM. Sezgin SUCU MATEMATİK ANABİLİM DALI ANKARA 2009
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEİ SOBOLEV UAYLARINDA YAKLAŞIM Sezgin SUCU MATEMATİK ANABİLİM DALI ANKARA 29 Her hakkı saklıdır ÖET Yüksek Lisans Tezi SOBOLEV UAYLARINDA YAKLAŞIM
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEİ SOBOLEV UAYLARINDA YAKLAŞIM Sezgin SUCU MATEMATİK ANABİLİM DALI ANKARA 29 Her hakkı saklıdır ÖET Yüksek Lisans Tezi SOBOLEV UAYLARINDA YAKLAŞIM
MATEMAT K. Doç. Dr. Ergün ERO LU stanbul Üniversitesi letme Fakültesi
 LETME, KT SAT ve SOSYAL B L MLER Ç N MATEMAT K Doç. Dr. Ergün ERO LU stanbul Üniversitesi letme Fakültesi DORA STANBUL 2013 DORA Bas m Yay n Da t m Ltd. ti. letme, ktisat ve Sosyal Bilimler çin Matematik
LETME, KT SAT ve SOSYAL B L MLER Ç N MATEMAT K Doç. Dr. Ergün ERO LU stanbul Üniversitesi letme Fakültesi DORA STANBUL 2013 DORA Bas m Yay n Da t m Ltd. ti. letme, ktisat ve Sosyal Bilimler çin Matematik
İKİNCİ MERTEBEDEN LİNEER DİFERANSİYEL DENKLEMLER İÇİN HAREKETLİ SINIR DEĞER PROBLEMİ
 Yüksek Lisans Tezi Tezi Hazırlaуan Kalima MOLDOKULOVA Matematik Anabilim Dalı 2014 KIRGIZİSTAN-TÜRKİYE MANAS ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MATEMATİK ANABİLİM DALI İKİNCİ MERTEBEDEN LİNEER DİFERANSİYEL
Yüksek Lisans Tezi Tezi Hazırlaуan Kalima MOLDOKULOVA Matematik Anabilim Dalı 2014 KIRGIZİSTAN-TÜRKİYE MANAS ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MATEMATİK ANABİLİM DALI İKİNCİ MERTEBEDEN LİNEER DİFERANSİYEL
OPERATÖRLER BÖLÜM 4. 4.1 Giriş. 4.2. Aritmetik Operatörler
 BÖLÜM 4. OPERATÖRLER 4.1 Giriş Turbo Pascal programlama dilinde de diğer programlama dillerinde olduğu gibi operatörler, yapılan işlem türüne göre aritmetik, mantıksal ve karşılaştırma operatörleri olmak
BÖLÜM 4. OPERATÖRLER 4.1 Giriş Turbo Pascal programlama dilinde de diğer programlama dillerinde olduğu gibi operatörler, yapılan işlem türüne göre aritmetik, mantıksal ve karşılaştırma operatörleri olmak
PROBLEM SET I ARALIK 2009
 PROBLEM SET I - 5 09 ARALIK 009 Soru 1 (Besanko ve Braeutigam (00), sayfa 405): Aşa¼g da tam rekabet piyasas nda faaliyet gösteren bir rman n k sa dönem toplam maliyet fonksiyonu verilmiştir: Piyasa denge
PROBLEM SET I - 5 09 ARALIK 009 Soru 1 (Besanko ve Braeutigam (00), sayfa 405): Aşa¼g da tam rekabet piyasas nda faaliyet gösteren bir rman n k sa dönem toplam maliyet fonksiyonu verilmiştir: Piyasa denge
Çalışma Soruları 1. a) x > 5 b) y < -3 c) xy > 0 d) x 3 < y e) (x-2) 2 + y 2 > 1. ( ) 2x
 Çalışma Soruları. Aşağıdaki denklemleri çözünüz: a) 7x = 4x + b) x 7x = x 4 c) x 4 x + = 0. Aşağıdaki eşitsizliklerin çözüm kümelerini belirleyiniz ve aralıklar cinsinden ifade ediniz: a) 4x > 9 b) x 4
Çalışma Soruları. Aşağıdaki denklemleri çözünüz: a) 7x = 4x + b) x 7x = x 4 c) x 4 x + = 0. Aşağıdaki eşitsizliklerin çözüm kümelerini belirleyiniz ve aralıklar cinsinden ifade ediniz: a) 4x > 9 b) x 4
Önsav 1. Her fley yukardaki gibi olsun. {ƒ 1 (V) g 1 (W) : V X, W Y, V ve W aç k}
 Kapak Konusu: Topoloji Çarp m Topolojisi Bu yaz da topolojik uzaylar n kartezyen çarp m n do al bir topolojik uzay yap s yla donataca z. E er ve topolojik uzaylarsa, üzerine en do al topolojik yap, herhalde,
Kapak Konusu: Topoloji Çarp m Topolojisi Bu yaz da topolojik uzaylar n kartezyen çarp m n do al bir topolojik uzay yap s yla donataca z. E er ve topolojik uzaylarsa, üzerine en do al topolojik yap, herhalde,
1) 6 kişilik bir aile yuvarlak bir masa etraf nda, anne ile baban n yan yana oturmamas koşulu ile kaç farkl biçimde oturabilir?
 ) 6 kişilik bir aile yuvarlak bir masa etraf nda, anne ile baban n yan yana oturmamas koşulu ile kaç farkl biçimde oturabilir? Çözüm: Önce, anne ile baban n yan yana oturma durumunu düşünelim. Anne ile
) 6 kişilik bir aile yuvarlak bir masa etraf nda, anne ile baban n yan yana oturmamas koşulu ile kaç farkl biçimde oturabilir? Çözüm: Önce, anne ile baban n yan yana oturma durumunu düşünelim. Anne ile
0 = ρ(x,x) ρ(x,y)+ρ(y,x) = 2ρ(x,y) 0, x = y δ(x,y) = κ(z 1,z 2 ) = z 1 z 2, (z 1,z 2 C) (17.27)
 230 BÖLÜM 17. METR K UZAYLAR 17.2 METR K METR K UZAY KAVRAMI Normlanm³ bir uzay, her³eyden önce bir vektör uzaydr, yani (X, ) normlanm³ bir uzay ise, X kümesi üzerinde bir vektör uzay yaps vardr. Oysa,
230 BÖLÜM 17. METR K UZAYLAR 17.2 METR K METR K UZAY KAVRAMI Normlanm³ bir uzay, her³eyden önce bir vektör uzaydr, yani (X, ) normlanm³ bir uzay ise, X kümesi üzerinde bir vektör uzay yaps vardr. Oysa,
NÜMER IK ANAL IZ. Nuri ÖZALP L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ 1 / Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ 1 / 27 Çok farkl durumlara uygulanabilen genel bir yöntemdir. Reel de¼gişkenli,
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ 1 / 27 Çok farkl durumlara uygulanabilen genel bir yöntemdir. Reel de¼gişkenli,
Çözümlü Yüksek Matematik Problemleri. Doç. Dr. Erhan Pişkin
 Çözümlü Yüksek Matematik Problemleri Doç. Dr. Erhan Pişkin Doç. Dr. Erhan PİŞKİN ÇÖZÜMLÜ YÜKSEK MATEMATİK PROBLEMLERİ ISBN 978-605-38-45-5 Kitap içeriğinin tüm sorumluluğu yazarına aittir. 06, Pegem Akademi
Çözümlü Yüksek Matematik Problemleri Doç. Dr. Erhan Pişkin Doç. Dr. Erhan PİŞKİN ÇÖZÜMLÜ YÜKSEK MATEMATİK PROBLEMLERİ ISBN 978-605-38-45-5 Kitap içeriğinin tüm sorumluluğu yazarına aittir. 06, Pegem Akademi
f( F) f(f) K = K F f 1 f( F) f 1 (K) = F F f 1 (S ) = [f 1 (S)] f(x) S V
![f( F) f(f) K = K F f 1 f( F) f 1 (K) = F F f 1 (S ) = [f 1 (S)] f(x) S V f( F) f(f) K = K F f 1 f( F) f 1 (K) = F F f 1 (S ) = [f 1 (S)] f(x) S V](/thumbs/59/43279328.jpg) Bölüm 6 SÜREKL FONKS YONLAR 6.1 YEREL SÜREKL L K Tanm 6.1.1. (X, T ) ve (Y, S) topolojik uzaylar ile f : X Y fonksiyonu verilsin. E er f(x 0 ) ö esinin her V kom³ulu una kar³lk f(u) V olacak ³ekilde x
Bölüm 6 SÜREKL FONKS YONLAR 6.1 YEREL SÜREKL L K Tanm 6.1.1. (X, T ) ve (Y, S) topolojik uzaylar ile f : X Y fonksiyonu verilsin. E er f(x 0 ) ö esinin her V kom³ulu una kar³lk f(u) V olacak ³ekilde x
NÜMER IK ANAL IZ. Nuri ÖZALP L INEER S ISTEMLER IN ÇÖZÜMÜ. Bilimsel Hesaplama Matemati¼gi, Gazi Kitabevi 2012
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi, Gazi Kitabevi 0 Nuri ÖZALP L INEER S ISTEMLER IN ÇÖZÜMÜ Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 6! L INEER S ISTEMLER IN ÇÖZÜMÜ / . Pivotlama ve
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi, Gazi Kitabevi 0 Nuri ÖZALP L INEER S ISTEMLER IN ÇÖZÜMÜ Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 6! L INEER S ISTEMLER IN ÇÖZÜMÜ / . Pivotlama ve
ÜNİTE 5 KESİKLİ RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI
 ÜNİTE 5 KESİKLİ RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI 1 Rassal Değişken Bir deney ya da gözlemin şansa bağlı sonucu bir değişkenin aldığı değer olarak düşünülürse, olasılık ve istatistikte böyle bir
ÜNİTE 5 KESİKLİ RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI 1 Rassal Değişken Bir deney ya da gözlemin şansa bağlı sonucu bir değişkenin aldığı değer olarak düşünülürse, olasılık ve istatistikte böyle bir
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ KÜRE ÜZERİNDEKİ KONİKLERE YENİ BİR YAKLAŞIM Esra EMİR MATEMATİK ANABİLİM DALI ANKARA 2010 Her hakkı saklıdır ÖZET Yüksek Lisans Tezi KÜRE
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ KÜRE ÜZERİNDEKİ KONİKLERE YENİ BİR YAKLAŞIM Esra EMİR MATEMATİK ANABİLİM DALI ANKARA 2010 Her hakkı saklıdır ÖZET Yüksek Lisans Tezi KÜRE
MATEMATİK ÖĞRETMENLİK ALAN BİLGİSİ - DENEME SINAVI DENEME. Diğer sayfaya geçiniz.
 MATEMATİK. DENEME ÖĞRETMENLİK ALAN BİLGİSİ - DENEME SINAVI. f : X tanımlı y = f() fonksiyonu için lim f ( ) = L ise aşağıdaki önermelerden kaç tanesi kesinlikle doğrudur? 0 I. X dir. 0 II. f() fonksiyonu
MATEMATİK. DENEME ÖĞRETMENLİK ALAN BİLGİSİ - DENEME SINAVI. f : X tanımlı y = f() fonksiyonu için lim f ( ) = L ise aşağıdaki önermelerden kaç tanesi kesinlikle doğrudur? 0 I. X dir. 0 II. f() fonksiyonu
MIT Açık Ders Malzemeleri Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için
 MIT Açık Ders Malzemeleri http://ocm.mit.edu Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için http://ocm.mit.edu/terms veya http://tuba.açık ders.org.tr adresini ziyaret
MIT Açık Ders Malzemeleri http://ocm.mit.edu Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için http://ocm.mit.edu/terms veya http://tuba.açık ders.org.tr adresini ziyaret
: Bir d do rusu üzerinde; A, B, C ve D noktalar alal m. d. n n uzunlu u denir ve. d d1 d2 F G. E, F d G, H d ve ise. d // d 1 2
 VI. ÖLÜM ÜZLEME VEKTÖRLER YÖNLÜ RU PRÇSI Tan m : üzlemde ve noktalar verilsin. [] n n dan e do ru önlendirildi ini düflünelim. öle do ru parçalar na, önlü do ru parçalar denir. önlü do ru parças, ile gösterilir.
VI. ÖLÜM ÜZLEME VEKTÖRLER YÖNLÜ RU PRÇSI Tan m : üzlemde ve noktalar verilsin. [] n n dan e do ru önlendirildi ini düflünelim. öle do ru parçalar na, önlü do ru parçalar denir. önlü do ru parças, ile gösterilir.
MATM 133 MATEMATİK LOJİK. Dr. Doç. Çarıyar Aşıralıyev
 MATM 133 MATEMATİK LOJİK Dr. Doç. Çarıyar Aşıralıyev 5.KONU Cebiresel yapılar; Grup, Halka 1. Matematik yapı 2. Denk yapılar ve eş yapılar 3. Grup 4. Grubun basit özellikleri 5. Bir elemanın kuvvetleri
MATM 133 MATEMATİK LOJİK Dr. Doç. Çarıyar Aşıralıyev 5.KONU Cebiresel yapılar; Grup, Halka 1. Matematik yapı 2. Denk yapılar ve eş yapılar 3. Grup 4. Grubun basit özellikleri 5. Bir elemanın kuvvetleri
