Yıldız Teknik Üniversitesi Endüstri Mühendisliği Bölümü KARAR TEORİSİ. Oyun Teorisi Yaklaşımı
|
|
|
- Pinar Baybaşin
- 8 yıl önce
- İzleme sayısı:
Transkript
1 Yıldız Teknik Üniversitesi Endüstri Mühendisliği Bölümü KARAR TEORİSİ Oyun Teorisi Yaklaşımı Doç. Dr. İhsan KAYA Oyun Teorisi-Doç. Dr. İhsan KAYA 1 Tanım: Oyun teorisi «Birbiriyle rekabet halinde olan iki ya da daha fazla karar vericinin aynı anda birbirlerinden habersiz olarak birer hareket tarzı seçtiği ve her birinin uyguladığı hareket tarzının diğerinin kazancını doğrudan etkilediği durumları birer oyun olarak modelleyip analiz etmek maksadıyla kullanılan matematiksel bir teoridir». Uygulama Alanları: Askeri faaliyetler, Siyasi faaliyetler, Spor müsabakaları, Reklam ve pazarlama faaliyetleri, Şans oyunları. Oyun Teorisi-Doç. Dr. İhsan KAYA 2 / 412 1
2 Sınıflandırma OYUN TÜRLERİ * Karar Vericilerin Sayısına Göre; İki kişili oyunlar n kişili oyunlar * Sonuçlarına Göre; Sabit toplamlı oyunlar Sabit toplamlı olmayan oyunlar Oyuncuların kazanç ve kayıpları toplamı sıfır ise, sıfır toplamlı oyun denir. Sıfır toplamlı oyunlar, c=0 olan sabit toplamlı oyunlardır. İki kişili, sıfır toplamlı oyunlar matematiksel olarak basit olduklarından, oyun teorisinin ilkelerinin tanıtılmasında en sık kullanılan oyun türüdür. Oyun Teorisi-Doç. Dr. İhsan KAYA 3 İki Kişili Sıfır Toplamlı Oyunlar Temel Özellikleri İki adet oyuncu vardır ve bunlar satır oyuncusu ve sütun oyuncusu olarak adlandırılırlar. Oyunculardan birinin kazancı (karı) diğerinin kaybına (zararına) eşittir. Satır oyuncusu toplam m adet stratejiden birini uygular iken sütun oyuncusu da aynı anda n adet stratejiden birini kullanır. Oyun Teorisi-Doç. Dr. İhsan KAYA 4 2
3 Kabuller: İKİ Kİki Kişili Sıfır Toplamlı Oyunlar İŞİLİ, SIFIR TOPLAMLI OYUNLAR Her iki oyuncu da oldukça mantıklı kişilerdir. Her iki oyuncu da sadece kendi faydalarını artıracak stratejileri seçerler. Oyuncular riske girmeden kendileri için garanti olan en iyi kazancı elde etmeye çalışırlar. Oyunlarda belirsizlik hakimdir, yani oyuncular oyuna başlamadan önce rakibinin hangi stratejiyi kullanacağını bilmezler. Oyun Teorisi-Doç. Dr. İhsan KAYA 5 Kazanç Matrisi * Oyun problemlerinde oyuncuların bütün stratejilerine karşılık gelen kazanç değerleri bir matris şeklinde gösterilir ve bu matrise Kazanç Matrisi adı verilir. İki Kişili Sıfır Toplamlı Bir Oyunun Kazanç Matrisi Sütun Oyuncusunun Stratejisi Strateji 1 Strateji 2... Strateji n Strateji 1 a 11 a a 1n Satır Oyuncusunun Stratejisi Strateji 2 a 21 a a 2n Strateji m a m1 a m2... a mn Oyun Teorisi-Doç. Dr. İhsan KAYA 6 3
4 Örnek * Bu oyunda her iki oyuncu aynı anda ya tek yada çift parmağını gösterir. Oyuna başlamadan önce oyuncular birisi tek diğeri çift olmak üzere aralarında anlaşırlar. Parmak sayılarının toplamı tek sayı olursa, yani oyuncular farklı sayıda parmak gösterirlerse, oyunculardan birisi (örneğin satır oyuncusu) kazanır. Parmak sayılarının toplamı çift sayı olursa yani oyuncular aynı sayıda parmak gösterilirse diğer oyuncu (sütun oyuncusu) kazanır. Kazanan oyuncu kaybedenden 1 birim alır. Tek Çift Oyununun Kazanç Matrisi Satır Oyuncusu (TEK) Sütun Oyuncusu (ÇİFT) Oyun Teorisi-Doç. Dr. İhsan KAYA 7 Örnek: Tek çift gösterme ve tek çift söyleme oyunu * İki kişi arasında oynanan bir oyunda; oyuncular aynı anda hem bir ya da iki parmak göstermekte, hem de tek ya da çift diye bağırarak rakibinin parmak sayısını tahmin etmektedirler. Karşısındakinin parmak sayısını doğru tahmin eden oyuncu her iki oyuncunun parmak sayılarının toplamı kadar puan kazanmakta, yanlış tahminde bulunan oyuncu ise toplam parmak sayısı kadar puan kaybetmektedir. Her iki oyuncu da doğru tahmin etmiş ya da her ikisi de bilememiş ise beraberlik söz konusu olup oyuncular sıfır puan almaktadırlar. Bu oyun iki kişili sıfır toplamlı bir oyun olarak modellenecektir. Oyun Teorisi-Doç. Dr. İhsan KAYA 8 4
5 * Burada her iki oyuncu için kullanabilecek dört strateji vardır: 1nci strateji ; tek parmak gösterip tek söylemek (TT) 2nci strateji ; tek parmak gösterip çift söylemek (TÇ) 3ncü strateji; çift parmak gösterip tek söylemek (ÇT) 4ncü strateji; çift parmak gösterip çift söylemek (ÇÇ) Kazanç Matrisi Sütun Oyuncusu 1 (TT) 2 (TÇ) 3 (ÇT) 4 (ÇÇ) 1 (TT) Satır Oyuncusu 2 (TÇ) (ÇT) (ÇÇ) Oyun Teorisi-Doç. Dr. İhsan KAYA 9 DENGE NOKTASI VE KARARLI OYUNLAR SATIR OYUNCUSU; kendi stratejilerinin her biri için, kazanabileceği minimum kazancı saptar ve bunlar arasından maksimum değerli kazancın bulunduğu stratejiyi seçer, SÜTUN OYUNCUSU ise; her bir stratejisinden kaybedebileceği maksimum değerleri saptar ve bu maksimum kayıplar arasından minimum kaybın bulunduğu stratejiyi seçer. Böylece her oyuncu; rakibi ne seçerse seçsin kendi stratejisi ile belirlediği sonuçtan daha kötüsü ile karşılaşmamayı garanti altına alır. Oyun Teorisi-Doç. Dr. İhsan KAYA 10 5
6 DENGE NOKTASI VE KARARLI OYUNLAR Denge Noktasına Sahip İki Kişili Sıfır Toplamlı Bir Oyunun Satır Oyuncusuna Göre Kazanç Matrisi Sütun Oyuncusunun Stratejisi Strateji 1 Strateji 2 Strateji 3 Satır Minimumu Satır Oyuncusunun Stratejisi Sütun Maksimumu Strateji Strateji Strateji Oyun Teorisi-Doç. Dr. İhsan KAYA 11 Denge Noktası ve Kararlı Oyunlar Sütun Oyuncusunun Stratejisi Strateji 1 Strateji 2 Strateji 3 Satır Minimumu Satır Strateji Oyuncusunun Strateji Stratejisi Strateji Sütun Maksimumu Satır oyuncusu 1nci stratejiyi seçerse; sütun oyuncusu mantıklı hareket ederek kendisine en az kaybı verdirecek olan 1nci ya da 2nci stratejisini kullanır ve 4 birim kaybeder (birinci satırdaki en küçük rakamlar), yani satır oyuncusu 4 birim kazanır, 2nci stratejiyi seçerse; sütün oyuncusu 3ncü stratejiyi seçer ve 1 birim kaybeder, 3ncü stratejiyi seçerse; sütun oyuncusu 2nci stratejiyi seçer ve 5 birim kaybeder. Oyun Teorisi-Doç. Dr. İhsan KAYA 12 6
7 Denge Noktası ve Kararlı Oyunlar Bu durumda satır oyuncusu hangi satırı seçerse seçsin o satırın en küçük değerine eşit bir kazanç elde eder. (satır minimumları) Bu değerler satır oyuncusunun garanti olan kazançlarıdır. O halde satır oyuncusu kendi kazancını maksimum yapmak isteyeceği için, satır minimumları arasından maksimum olan değeri elde etmek ister. maks {4, 1, 5} = 5 satır oyuncusu 3ncü stratejiyi seçer. Oyun Teorisi-Doç. Dr. İhsan KAYA 13 Denge Noktası ve Kararlı Oyunlar Sütun Oyuncusunun Stratejisi Strateji 1 Strateji 2 Strateji 3 Satır Minimumu Satır Strateji Oyuncusunun Strateji Stratejisi Strateji Sütun Maksimumu Sütun oyuncusu 1nci stratejiyi seçerse; satır oyuncusu mantıklı hareket ederek sütun oyuncusuna en fazla kaybı verdirecek olan 3ncü stratejisini kullanır (birinci sütundaki en büyük rakam), yani satır oyuncusu 6 birim kazanır, 2nci stratejiyi seçerse; satır oyuncusu 3ncü stratejiyi seçer ve 5 birim kazanır, 3ncü stratejiyi seçerse; satır oyuncusu 1nci stratejiyi seçer ve 10 birim kazanır. Oyun Teorisi-Doç. Dr. İhsan KAYA 14 7
8 Denge Noktası ve Kararlı Oyunlar Sonuçta sütun oyuncusu hangi sütunu seçerse seçsin o sütunun en büyük değerine eşit bir kaybı olur (sütun maksimumları). Bu değerler sütun oyuncusunun kaybedeceği en büyük değerlerdir (garanti olan kayıplarıdır). Bu durumda sütun oyuncusu kendi kaybını en düşük seviyede tutmaya çalışacak, yani sütun maksimumları arasından minimum olan değeri kaybetmek isteyecektir. min {6, 5, 10} = 5 sütun oyuncusu 2nci stratejiyi seçer. Oyun Teorisi-Doç. Dr. İhsan KAYA 15 Denge Noktası ve Kararlı Oyunlar Denge Noktasının Koşulu: maks (satır minimumları) = min (sütun maksimumları) maksimin = minimaks * Denge noktası öyle bir noktadır ki oyuncular tek taraflı olarak stratejilerini değiştirirler ise durumlarında bir iyileşme söz konusu olmaz (daha da kötüye gidebilirler). * Denge noktasının bir diğer özelliği ise şöyle açıklanabilir: Bu nokta yer aldığı satırdaki en küçük sayı ve yer aldığı sütundaki ise en büyük sayıdır. Bu özellikleri gözlemek suretiyle denge noktasının olup olmadığı incelenebilir. * Denge noktasına sahip olan oyunlar kararlı oyun olarak adlandırılırlar. Oyun Teorisi-Doç. Dr. İhsan KAYA 16 8
9 Denge Noktası ve Kararlı Oyunlar Sütun Oyuncusunun Stratejisi Strateji 1 Strateji 2 Strateji 3 Satır Minimumu Satır Oyuncusunun Stratejisi Sütun Maksimumu Strateji Strateji Strateji maksimin = minimaks = v = 5 * Saf Strateji : İki kişili sıfır toplamlı bir oyun denge noktasına sahip ise oyunun optimal çözümüne göre her oyuncu oyun boyunca yalnızca bir stratejisini kullanır, yani oyun saf stratejiler ile oynanır. Bu stratejiler oyunun denge noktasını oluşturan satır ve sütundur. * Oyun Teorisi-Doç. Dr. İhsan KAYA 17 Denge Noktası ve Kararlı Oyunlar Oyunun Değeri (v): Optimal çözümde satır oyuncusunun kazanacağı ve sütun oyuncusunun kaybedeceği değere oyunun değeri denir ve sıfır toplamlı oyunlarda her iki oyuncu için bu değer aynıdır. Dengeli oyunlarda oyunun değeri denge noktasındaki kazanç değerine eşittir. Oyun Teorisi-Doç. Dr. İhsan KAYA 18 9
10 Üstünlük Stratejisi Bir oyuncunun herhangi bir i stratejisi her zaman (rakibin bütün hareket tarzlarına karşı) en az diğer bir i stratejisinin sağladığı faydayı sağlıyor ve rakibin en az bir stratejisi karşısında da i stratejisinden daha iyi bir fayda sağlıyor ise i stratejisi i stratejisine göre üstündür denir ve i stratejisini alt eder (saf dışı bırakır). Alt edilen strateji kazanç matrisinden çıkarılarak bundan sonraki işlemlerde göz önünde bulundurulmaz. Satır Oyuncusunun Stratejisi Sütun Oyuncusunun Stratejisi Strateji 1 Strateji 2 Strateji 3 Strateji Strateji Strateji Oyun Teorisi-Doç. Dr. İhsan KAYA 19 Örnek Rakip iki otomobil firması kış dönemi satışlarını artırmak amacıyla reklam faaliyetlerine başlamayı planlamaktadır. Reklam kampanyası 2 haftalık olarak planlanmaktadır. Firmalar radyo veya televizyon olmak üzere iki ortam üzerinde yoğunlaşmakta olup reklam ya her birinde birer hafta yayınlanacak, ya da her iki hafta aynı ortamda yayınlanacaktır: Strateji 1: 1 hafta radyoda ve 1 hafta televizyonda reklam yayınlamak Strateji 2: 2 hafta radyoda reklam yayınlamak Strateji 3: 2 hafta televizyonda reklam yayınlamak Reklam anlaşması reklam şirketi ile her firma arasında gizli olarak kalacağından her firma kendi anlaşmasını yapmadan önce rakibinin hareket tarzını bilmeyecektir. Buna göre her firma yöneylem araştırmacılarından, kendilerinin ve rakip firmanın uygulayacağı hareket tarzına göre, bu iki haftanın değerlendirilmesi ile ilgili olarak her kombinasyonda ne kadar müşteri kazanacağını veya kaybedeceğini incelemelerini istemiştir. Oyun Teorisi-Doç. Dr. İhsan KAYA 20 10
11 1 Satır Oyuncusunun Stratejisi Sütun Oyuncusunun Stratejisi Strateji 1 Strateji 2 Strateji 3 Strateji Strateji Strateji * Sütun oyuncusunun üstün bir stratejisi yoktur. * Satır oyuncusunun 1nci stratejisi 3ncü stratejiye göre üstündür * Satır oyuncusunun üstün bir stratejisi yoktur. * Sütun oyuncusunun 1nci ve 2nci stratejileri 3ncü stratejiye göre üstündür. Oyun Teorisi-Doç. Dr. İhsan KAYA (1, 1) noktası bir denge noktasıdır maksimin = minimaks = 1 Oyun Teorisi-Doç. Dr. İhsan KAYA 22 11
12 Kararsız Oyunlar Denge noktası bulunmayan iki kişili sıfır toplamlı oyunlar kararsız oyun olarak adlandırılır. Kararsız oyunlarda oyuncular stratejilerinin olasılık dağılımını (her bir stratejinin kullanılma olasılığını ya da oranını) saptayarak bu olasılıklara göre stratejilerini kullanırlar. Satır oyuncusunun m adet stratejisi ve sütun oyuncusunun n adet stratejisi varsa; x i = satır oyuncusunun i stratejisini kullanma olasılığı (oranı); (i=1, 2,..., m) y j = sütun oyuncusunun j stratejisini kullanma olasılığı (oranı); (j=1, 2,..., n ) x i ve y j olasılık olduğuna göre; 1. 0 x i 1 (i=1, 2,, m); 0 y j 1 ( j=1, 2,, n) 2. m i 1 n x i y j j 1 1 Oyun Teorisi-Doç. Dr. İhsan KAYA 23 Kararsız Oyunlar Sütun Oyuncusu Olasılık y 1 y 2... y n Olasılık Strateji n Satır Oyuncusu x 1 1 a 11 a a 1n x 2 2 a 21 a a 2n x m m a m1 a m2... a mn Satır oyuncusu x 1, x 2,..., x m olasılıklarını, sütun oyuncusu da y 1, y 2,..., y n olasılıklarını belirleyerek oyun planlarını oluştururlar. Bu (x 1, x 2,..., x m ) ve (y 1, y 2,..., y n ) olasılıklarına karma strateji adı verilir ve orijinal stratejilerin her biri ise saf strateji olarak adlandırılır. Oyun Teorisi-Doç. Dr. İhsan KAYA 24 12
13 Kararsız Oyunlar Karma stratejilerle oynanan bir oyunda satır oyuncusunun beklenen kazancı (sütun oyuncusunun beklenen kaybı); her strateji kombinasyonunun sağlayacağı ortalama kazanç değerlerini hesaplayıp bütün kombinasyonlar için bu değerleri toplayarak bulunur. Buna göre; v = a 11 x 1 y 1 + a 12 x 1 y a mn x m y n V m n i 1 j 1 a x y ij i j Oyun Teorisi-Doç. Dr. İhsan KAYA 25 Kararsız Oyunlar Minimaks Maksimin Teoremi: Karma stratejilerin belirlenmesinde de yine minimaks maksimin kriteri kullanılır. Satır oyuncusu maksimin kriterine göre minimum beklenen kazancını maksimum yapan karma stratejiyi; sütun oyuncusu ise minimaks kriterine göre maksimum beklenen kaybını minimum yapan karma stratejiyi seçer. Maksimin değerini V ile ve minimaks değerini V ile gösterelim. Buna göre denge noktası bulunmayan iki kişili sıfır toplamlı bir oyunda optimal stratejiler aşağıdaki teoreme göre bulunur ; V = V = V(oyunun değeri) eşitliğini sağlayan stratejiler optimal karma stratejilerdir. Oyun Teorisi-Doç. Dr. İhsan KAYA 26 13
14 Grafik Çözüm Yaklaşımı Oyunculardan birisinin yalnızca iki stratejisi var ise (2x2, mx2 ve 2xn Boyutlu Oyunlar) o zaman grafik metodunu kullanarak optimal karma stratejiler bulunabilir. Eğer her oyuncunun ikiden fazla stratejisi var ise (alt edilebilecek bütün stratejileri çıkardıktan sonra) bu durumda ileride görüleceği gibi oyun, bir doğrusal programlama modeli olarak yazılıp çözülebilir. Oyun Teorisi-Doç. Dr. İhsan KAYA 27 Grafik Çözüm Yaklaşımı Satır oyuncusunun iki stratejisi var ise karma stratejisi (x 1, x 2 ) olasılıkları ile tanımlanır ve bu durumda x 2 =1 x 1 olacağından tek değişken olan x 1 in optimal değerini bulmak gerekmektedir. Bunun için de öncelikle rakibin (sütun oyuncusu) her bir saf stratejisine karşılık gelen kazancı x 1 in fonksiyonu olarak çizilir ve bu grafikte minimum kazancı maksimum yapan nokta, yani maksimin noktası belirlenir. Sütun oyuncusu için çözüm yapılıyorsa bu sefer maksimum kaybı minimum yapan nokta yani minimaks noktası bulunur. Oyun Teorisi-Doç. Dr. İhsan KAYA 28 14
15 Sütun Oyuncusu Olasılık y 1 y 2 Satır Oyuncusu Olasılık Strateji 1 2 x X 2 =1-X Satır oyuncusunun beklenen kazancı x 1 Maksimin noktası /4 1/2 3/ x 1 2 x 1 * 3 4 Oyun Teorisi-Doç. Dr. İhsan KAYA 29 Sütun Oyuncusu Satır Oyuncusu Sütun oyuncusunun beklenen kaybı Olasılık y 1 y 2 Olasılık Strateji 1 2 x X 2 =1-X Minimaks noktası y 1 1/4 1/2 3/4 1.0 y 1 * y 1 2 Oyun Teorisi-Doç. Dr. İhsan KAYA 30 15
16 Lineer Programlama Yaklaşımı Satır Oyuncusunun Doğrusal Programlama Modeli Maks v a 11 x 1 + a 21 x a m1 x m v a 12 x 1 + a 22 x a m2 x m v a 1n x 1 + a 2n x a mn x m v x 1 + x x m = 1 x i 0 (i=1, 2,, m); v sınırsız Min w Sütun Oyuncusunun Doğrusal Programlama Modeli a 11 y 1 + a 12 y a 1n y n w a 21 y 1 + a 22 y a 2n y n w a m1 y 1 + a m2 y a mn y n w y 1 + y y n = 1 y j 0 ( j=1, 2,, n); w sınırsız Oyun Teorisi-Doç. Dr. İhsan KAYA 31 Örnek 3 stratejinin söz konusu olduğu bir oyun için kazanç matrisi aşağıdaki gibi elde edilmiştir: B1 B2 B3 A A A Bu oyun için doğrusal programlama modellerini elde ediniz? Oyun Teorisi-Doç. Dr. İhsan KAYA 32 /
17 Çözüm B1 B2 B3 Satır Min A A A Sütun Mak Oyun karma stratejili bir oyundur ve oyunun değeri -2 ile 2 arasında değişmektedir. Bu oyun için doğrusal programlama modelleri aşağıdaki gibi elde edilir: Oyun Teorisi-Doç. Dr. İhsan KAYA 33 / Çözüm Satır oyuncusu için doğrusal programlama modeli: Maks z= v 3x 2x 5x v x 4x 6x v x x 2x v x x x x, x, x v sınırlandırılmamış Çözüm: x x x v Oyun Teorisi-Doç. Dr. İhsan KAYA 34 /
18 Çözüm Sütun oyuncusu için doğrusal programlama modeli: Min z= v 3y y 3y v y 4y y v y 6y 2y v y y y y, y, y v sınırlandırılmamış Çözüm: y y y Oyun Teorisi-Doç. Dr. İhsan KAYA 35 / Örnek * İki kişi arasında oynanan bir oyunda oyuncular aynı anda elleri ile taş, kağıt ya da makas işaretini gösterirler. Makas kağıda göre, kağıt taşa göre ve taş ise makasa göre üstün olup, üstün olan işareti gösteren oyuncu diğerinden 1 puan kazanır. Bu problemi iki kişili sıfır toplamlı bir oyun olarak modelleyelim. Satır Oyuncusu Sütun Oyuncusu Strateji Taş Kağıt Makas Taş Kağıt Makas Satır Min Sütun Maks Oyun Teorisi-Doç. Dr. İhsan KAYA 36 18
19 Örnek : İki televizyon kanalı, 20:00 21:00 zaman dilimi süresince 100 milyon kişilik izleyici kitlesini çekmek için rekabet halindedirler. İki kanal, bu zaman diliminde yayınlayacakları programı aynı anda duyurmak zorundadırlar. Her kanalın muhtemel seçenekleri ile her seçenek için 1nci kanalın izleyici sayısı (milyon olarak) tabloda verilmiştir. Birinci Kanal Western Klasik Komedi İkinci Kanal Western Klasik Komedi Örneğin, her iki kanal filmi seçerse, kazanç matrisi 35 milyon seyircinin 1nci kanalı ve =65 milyon seyircinin 2nci kanalı tercih edeceğini göstermektedir. Oyun Teorisi-Doç. Dr. İhsan KAYA 37 Kazanç Matrisi: İkinci Kanal Western Klasik Komedi Satır Min. Birinci Kanal Western Klasik Komedi Sütun Maks Oyun Teorisi-Doç. Dr. İhsan KAYA 38 19
20 İki Kişili Sabit Toplamlı Olmayan Oyunlar Örnek : Firar eden ve bir soyguna karışan iki mahkum yeniden yakalanmış ve yeni suçlarından yargılanmayı beklemektedirler. Suçlu olmalarına rağmen, savcı onları mahkum ettirmek için yeterli delil olmadığını düşünmektedir. Bu yüzden savcı mahkumları suçu itiraf etmeye ve diğeri aleyhinde tanıklık yapmaya zorlamak için, her mahkuma şunu söyler: Eğer sadece biriniz itiraf eder ve arkadaşınız aleyhine tanıklık yaparsanız, inkar eden kesinlikle 20 yıl hapis cezasına mahkum edilirken itiraf eden serbest kalır. Her ikiniz de itiraf ederseniz, 5 er yıl hapse mahkum olursunuz. Hiç biriniz itiraf etmezseniz, her ikiniz de önceki suçun devamı olarak 1 er yıl hapis cezası alırsınız. Mahkumlar mahkeme önüne çıkıncaya kadar kesinlikle birbirleri ile görüşemeyeceklerdir. Buna göre mahkumlar ne yapmalıdır? Oyun Teorisi-Doç. Dr. İhsan KAYA 39 * Çözüm: Burada öncelikle mahkumların birbirleriyle haberleşemediği varsayılmaktadır. Savcının açıklamasına göre tarafların stratejileri ve kazançları Tabloda gösterilmektedir. Hapis istenmeyen bir şey olduğu için değerler matriste negatif olarak belirtilmiştir. Parantez içindeki ilk rakam 1nci mahkumun, ikinci rakam ise 2nci mahkumun kazancını göstermektedir. Birinci Mahkum İtiraf İnkar İkinci Mahkum İtiraf İnkar ( 5, 5) (0, 20) ( 20,0) ( 1, 1) Oyun Teorisi-Doç. Dr. İhsan KAYA 40 20
21 İki Kişili Sabit Toplamlı Olmayan Oyunlar * Örnek : Bir şehirdeki iki rakip lokantanın (A ve B) yıllık satış gelirleri toplamı 240 birimdir. Lokantalar gelecek yıl için reklam bütçelerini planlamaktadırlar. Her iki lokanta da reklam için 6 veya 10 birim para ayırabilecektir. Eğer birisi reklam için diğerinden daha fazla harcarsa, çok harcayan lokanta toplam satış gelirinin 190 birimini elde edecektir. Her ikisi de aynı miktarda harcarsa karı eşit olarak paylaşacaklardır. Her bir birim satış 0.1 birim kar bırakmaktadır. Diyelim ki her iki lokanta da net karını (satış geliri reklam harcamaları) maksimum yapmak istiyor. Bu oyun için denge noktasını bulunuz. Lokanta A 10 6 Lokanta B 10 6 (2, 2) (9, 1) ( 1, 9) (6, 6) Oyun Teorisi-Doç. Dr. İhsan KAYA 41 * Örnek : İki komşu ülke, silahlanma yarışı yüzünden yeni bir silah konusunda iki strateji üzerinde düşünmektedirler: Yeni bir silah geliştirmek veya mevcut durumu korumak. Bu problemin kazanç matrisi Tabloda olup, bu matris silahın sadece bir ülke tarafından geliştirilmesi durumunda herhangi bir silah geliştirmeyip mevcut durumu koruyan ülkenin işgal edilebileceği ve sonuçta silah geliştiren ülke için 20 birimlik bir kazanç ve işgal edilen ülke için ise 100 birimlik bir kayıp oluşacağı varsayımına göre hazırlanmıştır. Ayrıca, yeni bir silah geliştirmenin 10 birimlik bir maliyeti olduğu da diğer bir varsayım olarak değerlendirilmektedir. B Ülkesi A Ülkesi Yeni silah geliştirmek Durumu korumak Yeni silah geliştirmek Durumu korumak ( 10, 10) (10, 100) ( 100, 10) (0, 0) Oyun Teorisi-Doç. Dr. İhsan KAYA 42 21
22 Kaynakça Wayne L. Winston, Operations Research: Applications and Algorithms, Thomson, 2004 Hamdy A. Taha, Operations Research: An Introduction, Prentice Hall, White, D.J., Operational Research, John Wiley &Sons, Yöneylem Araştırması Ders Kitabı, 2012, KHO Yayınları. Oyun Teorisi-Doç. Dr. İhsan KAYA 43 /
Tam ve Karma Stratejili Oyunlar. İki Kişili Oyunlar için
 Tam ve Karma Stratejili Oyunlar İki Kişili Oyunlar için İki kişili-sıfır toplamlı oyunlar Sabit toplamlı oyunların bir türüdür, Sabit olan toplam 0 a eşittir. Temel Özellikleri Oyunculardan birinin kazancı
Tam ve Karma Stratejili Oyunlar İki Kişili Oyunlar için İki kişili-sıfır toplamlı oyunlar Sabit toplamlı oyunların bir türüdür, Sabit olan toplam 0 a eşittir. Temel Özellikleri Oyunculardan birinin kazancı
İki kişili-sıfır toplamlı oyunlar. Tam ve Karma Stratejili Oyunlar. Varsayımlar. Sıfır toplamlı oyunlar
 İki kişili-sıfır toplamlı oyunlar Tam ve Karma Stratejili Oyunlar İki Kişili Oyunlar için Sabit toplamlı oyunların bir türüdür, Sabit olan toplam 0 a eşittir. Temel Özellikleri Oyunculardan birinin kazancı
İki kişili-sıfır toplamlı oyunlar Tam ve Karma Stratejili Oyunlar İki Kişili Oyunlar için Sabit toplamlı oyunların bir türüdür, Sabit olan toplam 0 a eşittir. Temel Özellikleri Oyunculardan birinin kazancı
OYUN TEORİSİ. Özlem AYDIN. Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü
 OYUN TEORİSİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü TANIM ''Oyun Teorisi'', iki yada daha fazla rakibi belirli kurallar altında birleştirerek karşılıklı olarak çelişen olasılıklar
OYUN TEORİSİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü TANIM ''Oyun Teorisi'', iki yada daha fazla rakibi belirli kurallar altında birleştirerek karşılıklı olarak çelişen olasılıklar
Oyun Teorisine (Kuramına) Giriş
 Oyun Teorisi Oyun Teorisine (uramına) Giriş Şimdiye kadar, karar modellerinde bireysel kararlar ve çözüm yöntemleri ele alınmıştı. adece tek karar vericinin olduğu karar modellerinde belirsizlik ve risk
Oyun Teorisi Oyun Teorisine (uramına) Giriş Şimdiye kadar, karar modellerinde bireysel kararlar ve çözüm yöntemleri ele alınmıştı. adece tek karar vericinin olduğu karar modellerinde belirsizlik ve risk
Yöneylem Araştırması III
 Öğr. Gör. Dr. Hakan ÇERÇİOĞLU cercioglu@gazi.edu.tr BÖLÜM I: Hedef Programlama HEDEF PROGRAMLAMAYA GİRİŞ ÖNCELİKSİZ HEDEF PROGRAMLAMA ÖNCELİKLİ HEDEF PROGRAMLAMA HEDEF PROGRAMLAMA MODELLERİNİN ÇÖZÜMÜ Bugüne
Öğr. Gör. Dr. Hakan ÇERÇİOĞLU cercioglu@gazi.edu.tr BÖLÜM I: Hedef Programlama HEDEF PROGRAMLAMAYA GİRİŞ ÖNCELİKSİZ HEDEF PROGRAMLAMA ÖNCELİKLİ HEDEF PROGRAMLAMA HEDEF PROGRAMLAMA MODELLERİNİN ÇÖZÜMÜ Bugüne
KARAR TEORİSİ. Özlem AYDIN. Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü
 KARAR TEORİSİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü Karar Ortamları Karar Analizi, alternatiflerin en iyisini seçmek için akılcı bir sürecin kullanılması ile ilgilenir. Seçilen
KARAR TEORİSİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü Karar Ortamları Karar Analizi, alternatiflerin en iyisini seçmek için akılcı bir sürecin kullanılması ile ilgilenir. Seçilen
DARÜŞŞAFAKA LİSESİ SALİH ZEKİ LİSE ÖĞRENCİLERİ ARASI MATEMATİK PROJELERİ YARIŞMASI
 DARÜŞŞAFAKA LİSESİ SALİH ZEKİ LİSE ÖĞRENCİLERİ ARASI MATEMATİK PROJELERİ YARIŞMASI PROJENİN ADI: OYUN TEORİSİ İLE İSTANBUL TRAFİĞİNİN İNCELENMESİ HAZIRLAYANLAR: ECE TUNÇKOL-BERKE OĞUZ AKIN MEV KOLEJİ ÖZEL
DARÜŞŞAFAKA LİSESİ SALİH ZEKİ LİSE ÖĞRENCİLERİ ARASI MATEMATİK PROJELERİ YARIŞMASI PROJENİN ADI: OYUN TEORİSİ İLE İSTANBUL TRAFİĞİNİN İNCELENMESİ HAZIRLAYANLAR: ECE TUNÇKOL-BERKE OĞUZ AKIN MEV KOLEJİ ÖZEL
Yöneylem Araştırması Dersi OYUN TEORİSİ. Oyuncusu Stratejisi. Stratejileri. Oyuncusu Stratejisi Stratejisi Cı Cı (3 4
 Yöneylem Araştırması Dersi OYUN TEORİSİ ÖRNEK 1- Satır oyuncusunun iki (Tı, T 2 ), sütun oyuncusunun dört (Y 1, Y 2, Y 3, Y 4 ) stratejisinin bulunduğu bir oyunun, satır oyuncusunun kazançlarına göre düzenlenen
Yöneylem Araştırması Dersi OYUN TEORİSİ ÖRNEK 1- Satır oyuncusunun iki (Tı, T 2 ), sütun oyuncusunun dört (Y 1, Y 2, Y 3, Y 4 ) stratejisinin bulunduğu bir oyunun, satır oyuncusunun kazançlarına göre düzenlenen
Oyun Teorisi IENG 456 Karar Vermede Analitik Yaklaşımlar
 Oyun Teorisi IENG 456 Karar Vermede Analitik Yaklaşımlar Bu ders notlarının hazırlanmasında Doç. Dr. İbrahim Çil in ders notlarından faydalanılmıştır. Yrd. Doç. Dr. Hacer GÜNER GÖREN Pamukkale Üniversitesi
Oyun Teorisi IENG 456 Karar Vermede Analitik Yaklaşımlar Bu ders notlarının hazırlanmasında Doç. Dr. İbrahim Çil in ders notlarından faydalanılmıştır. Yrd. Doç. Dr. Hacer GÜNER GÖREN Pamukkale Üniversitesi
Toplam maliyete/gelire göre yer seçimi Faktör ağırlıklandırma Başabaş noktası analizi Oyun kuramı
 Anadolu Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2013-2014 Güz Dönemi Toplam maliyete/gelire göre yer seçimi Faktör ağırlıklandırma Başabaş
Anadolu Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2013-2014 Güz Dönemi Toplam maliyete/gelire göre yer seçimi Faktör ağırlıklandırma Başabaş
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Hessien Matris-Quadratik Form Mutlak ve Bölgesel Maksimum-Minimum Noktalar Giriş Kısıtlı ve kısıtsız fonksiyonlar için
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Hessien Matris-Quadratik Form Mutlak ve Bölgesel Maksimum-Minimum Noktalar Giriş Kısıtlı ve kısıtsız fonksiyonlar için
KARAR TEORİSİ VE ANALİZİ. OYUN TEORİSİ Prof. Dr. İbrahim Çil
 KARAR TEORİSİ VE ANALİZİ OYUN TEORİSİ Prof. Dr. İbrahim Çil Bu derste; Oyun teorisi konusu ele alınacak. Neden oyun teorisine gerek duyulduğu açıklanacak, statik oyunların yapısı ve çözüm yöntemleri üzerinde
KARAR TEORİSİ VE ANALİZİ OYUN TEORİSİ Prof. Dr. İbrahim Çil Bu derste; Oyun teorisi konusu ele alınacak. Neden oyun teorisine gerek duyulduğu açıklanacak, statik oyunların yapısı ve çözüm yöntemleri üzerinde
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Bu bölümde eşitsizlik kısıtlarına bağlı bir doğrusal olmayan kısıta sahip problemin belirlenen stasyoner noktaları
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Bu bölümde eşitsizlik kısıtlarına bağlı bir doğrusal olmayan kısıta sahip problemin belirlenen stasyoner noktaları
Yıldız Teknik Üniversitesi Endüstri Mühendisliği Bölümü KARAR TEORİSİ MARKOV SÜREÇLERİ. Markov Analizi
 Yıldız Teknik Üniversitesi Endüstri Mühendisliği Bölümü KARAR TEORİSİ MARKOV SÜREÇLERİ Doç. Dr. İhsan KAYA Markov Analizi Markov analizi, bugün çalışan bir makinenin ertesi gün arızalanma olasılığının
Yıldız Teknik Üniversitesi Endüstri Mühendisliği Bölümü KARAR TEORİSİ MARKOV SÜREÇLERİ Doç. Dr. İhsan KAYA Markov Analizi Markov analizi, bugün çalışan bir makinenin ertesi gün arızalanma olasılığının
SAĞLIK KURUMLARINDA OPERASYON YÖNETİMİ
 DİKKATİNİZE: BURADA SADECE ÖZETİN İLK ÜNİTESİ SİZE ÖRNEK OLARAK GÖSTERİLMİŞTİR. ÖZETİN TAMAMININ KAÇ SAYFA OLDUĞUNU ÜNİTELERİ İÇİNDEKİLER BÖLÜMÜNDEN GÖREBİLİRSİNİZ. SAĞLIK KURUMLARINDA OPERASYON YÖNETİMİ
DİKKATİNİZE: BURADA SADECE ÖZETİN İLK ÜNİTESİ SİZE ÖRNEK OLARAK GÖSTERİLMİŞTİR. ÖZETİN TAMAMININ KAÇ SAYFA OLDUĞUNU ÜNİTELERİ İÇİNDEKİLER BÖLÜMÜNDEN GÖREBİLİRSİNİZ. SAĞLIK KURUMLARINDA OPERASYON YÖNETİMİ
CEBİRDEN SEÇME KONULAR
 CEBİRDEN SEÇME KONULAR MATRİS OYUNLARI HAZIRLAYANLAR : METEHAN ŞAHİN 080216030 SEDA SAYAR 080216062 AYSU CANSU ÇOĞALAN 080216058 ÖĞRETİM GÖREVLİSİ : PROF.DR. NEŞET AYDIN ARŞ. GRV. AYKUT OR ÇANAKKALE 2012
CEBİRDEN SEÇME KONULAR MATRİS OYUNLARI HAZIRLAYANLAR : METEHAN ŞAHİN 080216030 SEDA SAYAR 080216062 AYSU CANSU ÇOĞALAN 080216058 ÖĞRETİM GÖREVLİSİ : PROF.DR. NEŞET AYDIN ARŞ. GRV. AYKUT OR ÇANAKKALE 2012
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ
 ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTıRMA MODELININ TANıMı Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTıRMA MODELININ TANıMı Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
yöneylem araştırması Nedensellik üzerine diyaloglar I
 yöneylem araştırması Nedensellik üzerine diyaloglar I i Yayın No : 3197 Eğitim Dizisi : 149 1. Baskı Ocak 2015 İSTANBUL ISBN 978-605 - 333-225 1 Copyright Bu kitabın bu basısı için Türkiye deki yayın hakları
yöneylem araştırması Nedensellik üzerine diyaloglar I i Yayın No : 3197 Eğitim Dizisi : 149 1. Baskı Ocak 2015 İSTANBUL ISBN 978-605 - 333-225 1 Copyright Bu kitabın bu basısı için Türkiye deki yayın hakları
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Quadratic Programming Bir karesel programlama modeli aşağıdaki gibi tanımlanır. Amaç fonksiyonu: Maks.(veya Min.) z
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Quadratic Programming Bir karesel programlama modeli aşağıdaki gibi tanımlanır. Amaç fonksiyonu: Maks.(veya Min.) z
END. İKTİSADI VE OYUN TEORİSİ (BİRİNCİ ÖDEV)
 END. İKTİSADI VE OYUN TEORİSİ (BİRİNCİ ÖDEV) AÇIKLAMALAR Ödevlerinizin teslimi, 14 Kasim 2013 günü saat 09:30-12:30 da yapılacaktır. Sorular aynı gün örgün (13:15) ve ikinci öğretim (17:00) dersinde çözüleceği
END. İKTİSADI VE OYUN TEORİSİ (BİRİNCİ ÖDEV) AÇIKLAMALAR Ödevlerinizin teslimi, 14 Kasim 2013 günü saat 09:30-12:30 da yapılacaktır. Sorular aynı gün örgün (13:15) ve ikinci öğretim (17:00) dersinde çözüleceği
HESSİEN MATRİS QUADRATİK FORM MUTLAK ve BÖLGESEL MAKS-MİN NOKTALAR
 HESSİEN MATRİS QUADRATİK FORM MUTLAK ve BÖLGESEL MAKS-MİN NOKTALAR Kısıtlı ve kısıtsız fonksiyonlar için maksimum veya minimum (ekstremum) noktalarının belirlenmesinde diferansiyel hesabı kullanarak çeşitli
HESSİEN MATRİS QUADRATİK FORM MUTLAK ve BÖLGESEL MAKS-MİN NOKTALAR Kısıtlı ve kısıtsız fonksiyonlar için maksimum veya minimum (ekstremum) noktalarının belirlenmesinde diferansiyel hesabı kullanarak çeşitli
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ
 ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTIRMA MODELİNİN TANIMI Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTIRMA MODELİNİN TANIMI Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik (Eşitlik Kısıtlı Türevli Yöntem) Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik (Eşitlik Kısıtlı Türevli Yöntem) Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde
Yöneylem Araştırması III
 Yöneylem Araştırması III Doç. Dr. Hakan ÇERÇİOĞLU cercioglu@gazi.edu.tr Yöneylem Araştırması III 1 BÖLÜM I: Hedef Programlama HEDEF PROGRAMLAMAYA GİRİŞ ÖNCELİKSİZ HEDEF PROGRAMLAMA ÖNCELİKLİ HEDEF PROGRAMLAMA
Yöneylem Araştırması III Doç. Dr. Hakan ÇERÇİOĞLU cercioglu@gazi.edu.tr Yöneylem Araştırması III 1 BÖLÜM I: Hedef Programlama HEDEF PROGRAMLAMAYA GİRİŞ ÖNCELİKSİZ HEDEF PROGRAMLAMA ÖNCELİKLİ HEDEF PROGRAMLAMA
BÖLÜM I: Hedef Programlama. Prof.Dr. Bilal TOKLU. HEDEF PROGRAMLAMAYA GİRİŞ HEDEF PROGRAMLAMA MODELLERİNİN ÇÖZÜMÜ
 Yöneylem Araştırması III Prof.Dr. Bilal TOKLU btoklu@gazi.edu.tr Yöneylem Araştırması III BÖLÜM I: Hedef Programlama HEDEF PROGRAMLAMAYA GİRİŞ ÖNCELİKSİZ HEDEF PROGRAMLAMA ÖNCELİKLİ HEDEF PROGRAMLAMA HEDEF
Yöneylem Araştırması III Prof.Dr. Bilal TOKLU btoklu@gazi.edu.tr Yöneylem Araştırması III BÖLÜM I: Hedef Programlama HEDEF PROGRAMLAMAYA GİRİŞ ÖNCELİKSİZ HEDEF PROGRAMLAMA ÖNCELİKLİ HEDEF PROGRAMLAMA HEDEF
Öğrencilerde Akıllı Telefon Kullanımının Özellikleri Bakımından Oyun Teorisi ile Analiz Edilmesi
 Aksaray Üniversitesi İktisadi ve İdari Bilimler Fakültesi Dergisi. 7(2). 67-76 2015 Aksaray Üniversitesi İktisadi ve İdari Bilimler Fakültesi http://iibfdergi.aksaray.edu.tr Öğrencilerde Akıllı Telefon
Aksaray Üniversitesi İktisadi ve İdari Bilimler Fakültesi Dergisi. 7(2). 67-76 2015 Aksaray Üniversitesi İktisadi ve İdari Bilimler Fakültesi http://iibfdergi.aksaray.edu.tr Öğrencilerde Akıllı Telefon
EM302 Yöneylem Araştırması 2 Doğrusal Olmayan Programlamaya Giriş. Dr. Özgür Kabak
 EM302 Yöneylem Araştırması 2 Doğrusal Olmayan Programlamaya Giriş Dr. Özgür Kabak Doğrusal Olmayan Programlama Eğer bir Matematiksel Programlama modelinin amaç fonksiyonu ve/veya kısıtları doğrusal değil
EM302 Yöneylem Araştırması 2 Doğrusal Olmayan Programlamaya Giriş Dr. Özgür Kabak Doğrusal Olmayan Programlama Eğer bir Matematiksel Programlama modelinin amaç fonksiyonu ve/veya kısıtları doğrusal değil
Karar Vermede Oyun Teorisi Tekniği Ve Bir Uygulama
 97 Karar Vermede Oyun Teorisi Tekniği Ve Bir Uygulama Bahman Alp RENÇBER * Özet Bu çalışmanın amacı, günümüzde rekabet ortamında karar verme durumunda olan sistemlerin araştırılmasıdır. Bu amaçla verileri
97 Karar Vermede Oyun Teorisi Tekniği Ve Bir Uygulama Bahman Alp RENÇBER * Özet Bu çalışmanın amacı, günümüzde rekabet ortamında karar verme durumunda olan sistemlerin araştırılmasıdır. Bu amaçla verileri
28 C j -Z j /2 0
 3.2.6. Dual Problem ve Ekonomik Yorumu Primal Model Z maks. = 4X 1 + 5X 2 (kar, pb/gün) X 1 + 2X 2 10 6X 1 + 6X 2 36 8X 1 + 4X 2 40 (işgücü, saat/gün) (Hammadde1, kg/gün) (Hammadde2, kg/gün) 4 5 0 0 0
3.2.6. Dual Problem ve Ekonomik Yorumu Primal Model Z maks. = 4X 1 + 5X 2 (kar, pb/gün) X 1 + 2X 2 10 6X 1 + 6X 2 36 8X 1 + 4X 2 40 (işgücü, saat/gün) (Hammadde1, kg/gün) (Hammadde2, kg/gün) 4 5 0 0 0
OYUNLAR KURAMI Giriş oyunlar kuramı Oyunlar Kuramındaki Tanımlar oyun oyuncu sıfır toplamlı iki kişilik oyunlar strateji
 OYUNLAR KURAMI Giriş Günlük hayatta karşılaşılan bazı sorunlarda değişkenlerin tümü kontrolümüz altında olmayıp iki ya da daha fazla tarafça da kontrol edilebilir. Yani değikenlerden bir kısmı bizim, diğer
OYUNLAR KURAMI Giriş Günlük hayatta karşılaşılan bazı sorunlarda değişkenlerin tümü kontrolümüz altında olmayıp iki ya da daha fazla tarafça da kontrol edilebilir. Yani değikenlerden bir kısmı bizim, diğer
OYUNLAR TEORİSİNİN MADEN ARAMALARINA UYGULANMASI
 OYUNLAR TEORİSİNİN MADEN ARAMALARINA UYGULANMASI Hüsnü KALE Maden Tetkik ve Arama Enstitüsü, Ankara GİRİŞ İki rakip satranç masası başına oturduğu zaman, her ikisi de kendi kullandıkları taktiklere karşı,
OYUNLAR TEORİSİNİN MADEN ARAMALARINA UYGULANMASI Hüsnü KALE Maden Tetkik ve Arama Enstitüsü, Ankara GİRİŞ İki rakip satranç masası başına oturduğu zaman, her ikisi de kendi kullandıkları taktiklere karşı,
OYUN TEORİSİNE DOĞRU Yard.Doç.Dr.Deniz Giz
 OYUN TEORİSİNE DOĞRU Yard.Doç.Dr.Deniz Giz ÖZET Herhangi bir teori veya bir modelin amacı bir soruna çözüm bulmaktır. Bir oyunun çözümü oyuncuların nasıl karar vereceklerinin öngörülmesine bağlıdır. Oyuncular
OYUN TEORİSİNE DOĞRU Yard.Doç.Dr.Deniz Giz ÖZET Herhangi bir teori veya bir modelin amacı bir soruna çözüm bulmaktır. Bir oyunun çözümü oyuncuların nasıl karar vereceklerinin öngörülmesine bağlıdır. Oyuncular
Yöneylem Araştırması II
 Yöneylem Araştırması II Öğr. Gör. Dr. Hakan ÇERÇİOĞLU cercioglu@gazi.edu.tr BÖLÜM I: Doğrusal Programlama Tekrarı Doğrusal Programlama Tanımı Doğrusal Programlama Varsayımları Grafik Çözüm Metodu Simpleks
Yöneylem Araştırması II Öğr. Gör. Dr. Hakan ÇERÇİOĞLU cercioglu@gazi.edu.tr BÖLÜM I: Doğrusal Programlama Tekrarı Doğrusal Programlama Tanımı Doğrusal Programlama Varsayımları Grafik Çözüm Metodu Simpleks
MARKOV ZİNCİRLERİNDE DURUMLARIN SINIFLANDIRILMASI
 SAKARYA UNIVERSİTESİ ENDUSTRI MUHENDISLIĞI YÖNEYLEM ARAŞTIRMASI II MARKOV ZİNCİRLERİNDE DURUMLARIN SINIFLANDIRILMASI DERS NOTLARI 1 Önceki derslerimizde pek çok geçişten sonra n-adım geçiş olasılıklarının
SAKARYA UNIVERSİTESİ ENDUSTRI MUHENDISLIĞI YÖNEYLEM ARAŞTIRMASI II MARKOV ZİNCİRLERİNDE DURUMLARIN SINIFLANDIRILMASI DERS NOTLARI 1 Önceki derslerimizde pek çok geçişten sonra n-adım geçiş olasılıklarının
DOĞRUSAL OLMAYAN PROGRAMLAMA -I-
 DOĞRUSAL OLMAYAN PROGRAMLAMA -I- Dışbükeylik / İçbükeylik Hazırlayan Doç. Dr. Nil ARAS Anadolu Üniversitesi, Endüstri Mühendisliği Bölümü İST38 Yöneylem Araştırması Dersi 0-0 Öğretim Yılı Doğrusal olmayan
DOĞRUSAL OLMAYAN PROGRAMLAMA -I- Dışbükeylik / İçbükeylik Hazırlayan Doç. Dr. Nil ARAS Anadolu Üniversitesi, Endüstri Mühendisliği Bölümü İST38 Yöneylem Araştırması Dersi 0-0 Öğretim Yılı Doğrusal olmayan
KONU 4: DOĞRUSAL PROGRAMLAMA MODELİ İÇİN ÇÖZÜM YÖNTEMLERİ I
 KONU 4: DOĞRUSAL PROGRAMLAMA MODELİ İÇİN ÇÖZÜM YÖNTEMLERİ I 4.1. Dışbükeylik ve Uç Nokta Bir d.p.p. de model kısıtlarını aynı anda sağlayan X X X karar değişkenleri... n vektörüne çözüm denir. Eğer bu
KONU 4: DOĞRUSAL PROGRAMLAMA MODELİ İÇİN ÇÖZÜM YÖNTEMLERİ I 4.1. Dışbükeylik ve Uç Nokta Bir d.p.p. de model kısıtlarını aynı anda sağlayan X X X karar değişkenleri... n vektörüne çözüm denir. Eğer bu
Saf Stratejilerde Evrimsel Kararlılık Bilgi Notu Ben Polak, Econ 159a/MGT 522a Ekim 9, 2007
 Saf Stratejilerde Evrimsel Kararlılık Ben Polak, Econ 159a/MGT 522a Ekim 9, 2007 Diyelim ki oyunlarda stratejiler ve davranışlar akıl yürüten insanlar tarafından seçilmiyor, ama oyuncuların genleri tarafından
Saf Stratejilerde Evrimsel Kararlılık Ben Polak, Econ 159a/MGT 522a Ekim 9, 2007 Diyelim ki oyunlarda stratejiler ve davranışlar akıl yürüten insanlar tarafından seçilmiyor, ama oyuncuların genleri tarafından
Risk ve Belirsizlik. 1. Karar Analizleri 2. Karar Ağaçları 3. Oyun Teorisi. Karar Verme Aşamasındaki Bileşenler
 Risk ve Belirsizlik Altında Karar Verme KONU 6 1. Karar Analizleri 2. Karar Ağaçları 3. Oyun Teorisi i Karar Verme Aşamasındaki Bileşenler Gelecekte gerçekleşmesi mümkün olan olaylar Olası Durumlar şeklinde
Risk ve Belirsizlik Altında Karar Verme KONU 6 1. Karar Analizleri 2. Karar Ağaçları 3. Oyun Teorisi i Karar Verme Aşamasındaki Bileşenler Gelecekte gerçekleşmesi mümkün olan olaylar Olası Durumlar şeklinde
Simpleks Yöntemde Duyarlılık Analizleri
 3.2.4. Simpleks Yöntemde Duyarlılık Analizleri Duyarlılık analizinde doğrusal programlama modelinin parametrelerindeki değişikliklerinin optimal çözüm üzerindeki etkileri araştırılmaktadır. Herhangi bir
3.2.4. Simpleks Yöntemde Duyarlılık Analizleri Duyarlılık analizinde doğrusal programlama modelinin parametrelerindeki değişikliklerinin optimal çözüm üzerindeki etkileri araştırılmaktadır. Herhangi bir
Temelleri. Doç.Dr.Ali Argun Karacabey
 Doğrusal Programlamanın Temelleri Doç.Dr.Ali Argun Karacabey Doğrusal Programlama Nedir? Bir Doğrusal Programlama Modeli doğrusal kısıtlar altında bir doğrusal ğ fonksiyonun değerini ğ maksimize yada minimize
Doğrusal Programlamanın Temelleri Doç.Dr.Ali Argun Karacabey Doğrusal Programlama Nedir? Bir Doğrusal Programlama Modeli doğrusal kısıtlar altında bir doğrusal ğ fonksiyonun değerini ğ maksimize yada minimize
m=n şeklindeki matrislere kare matris adı verilir. şeklindeki matrislere ise sütun matrisi denir. şeklindeki A matrisi bir kare matristir.
 Matrisler Satır ve sütunlar halinde düzenlenmiş tabloya matris denir. m satırı, n ise sütunu gösterir. a!! a!" a!! a!" a!! a!! a!! a!! a!" m=n şeklindeki matrislere kare matris adı verilir. [2 3 1] şeklinde,
Matrisler Satır ve sütunlar halinde düzenlenmiş tabloya matris denir. m satırı, n ise sütunu gösterir. a!! a!" a!! a!" a!! a!! a!! a!! a!" m=n şeklindeki matrislere kare matris adı verilir. [2 3 1] şeklinde,
Optimizasyon İçin Kök(Generic) Model (Doğrusal-Olmayan Programlama Modeli)
 ISLE 403 YÖNEYLEM ARAŞTIRMASI I DERS 2 NOTLAR Optimizasyon İçin Kök(Generic) Model (Doğrusal-Olmayan Programlama Modeli) X, karar değişkenlerinin bir vektörü olsun. z, g 1, g 2,...,g m fonksiyonlardır.
ISLE 403 YÖNEYLEM ARAŞTIRMASI I DERS 2 NOTLAR Optimizasyon İçin Kök(Generic) Model (Doğrusal-Olmayan Programlama Modeli) X, karar değişkenlerinin bir vektörü olsun. z, g 1, g 2,...,g m fonksiyonlardır.
Anadolu Üniversitesi Endüstri Mühendisliği Bölümü İST328 Yöneylem Araştırması 2 Dersi Bahar Dönemi. Hazırlayan: Doç. Dr.
 Anadolu Üniversitesi Endüstri Mühendisliği Bölümü İST8 Yöneylem Araştırması Dersi 00-0 Bahar Dönemi Hazırlayan: Doç. Dr. Nil ARAS AÇIKLAMA Bu sunu izleyen kaynaklardaki örnek ve bilgilerden faydalanarak
Anadolu Üniversitesi Endüstri Mühendisliği Bölümü İST8 Yöneylem Araştırması Dersi 00-0 Bahar Dönemi Hazırlayan: Doç. Dr. Nil ARAS AÇIKLAMA Bu sunu izleyen kaynaklardaki örnek ve bilgilerden faydalanarak
YÖNEYLEM ARAŞTIRMASI - I
 YÖNEYLEM ARAŞTIRMASI - I 1/71 İçerik n Bulunması Kuzey-Batı Köşe Yöntemi En Küçük Maliyetli Göze Yöntemi Sıra / Sütun En Küçüğü Yöntemi Vogel Yaklaşım Metodu (VAM) Optimum Çözümün Bulunması Atlama Taşı
YÖNEYLEM ARAŞTIRMASI - I 1/71 İçerik n Bulunması Kuzey-Batı Köşe Yöntemi En Küçük Maliyetli Göze Yöntemi Sıra / Sütun En Küçüğü Yöntemi Vogel Yaklaşım Metodu (VAM) Optimum Çözümün Bulunması Atlama Taşı
KISITLI OPTİMİZASYON
 KISITLI OPTİMİZASYON SİMPLEKS YÖNTEMİ Simpleks Yöntemi Simpleks yöntemi iteratif bir prosedürü gerektirir. Bu iterasyonlar ile gerçekçi çözümlerin olduğu bölgenin (S) bir köşesinden başlayarak amaç fonksiyonunun
KISITLI OPTİMİZASYON SİMPLEKS YÖNTEMİ Simpleks Yöntemi Simpleks yöntemi iteratif bir prosedürü gerektirir. Bu iterasyonlar ile gerçekçi çözümlerin olduğu bölgenin (S) bir köşesinden başlayarak amaç fonksiyonunun
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik İkiye Bölme / Yarılama Yöntemi Genel olarak f x = 0 gerek şartını sağlamak oldukça doğrusal olmayan ve bu sebeple çözümü
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik İkiye Bölme / Yarılama Yöntemi Genel olarak f x = 0 gerek şartını sağlamak oldukça doğrusal olmayan ve bu sebeple çözümü
YÖNEYLEM ARAŞTIRMASI - I
 YÖNEYLEM ARAŞTIRMASI - I 1/19 İçerik Yöneylem Araştırmasının Dalları Kullanım Alanları Yöneylem Araştırmasında Bazı Yöntemler Doğrusal (Lineer) Programlama, Oyun Teorisi, Dinamik Programlama, Tam Sayılı
YÖNEYLEM ARAŞTIRMASI - I 1/19 İçerik Yöneylem Araştırmasının Dalları Kullanım Alanları Yöneylem Araştırmasında Bazı Yöntemler Doğrusal (Lineer) Programlama, Oyun Teorisi, Dinamik Programlama, Tam Sayılı
Karar değişkenlere ilişkin fonksiyonların ve bu fonksiyonlara ilişkin sınırlamaların tanımlanması
 İNŞAAT PROJELERİNİN PROGRAMLAMA, TASARIM VE YAPIM SÜRECİNDE OPTİMİZASYON Doğrusal Optimizasyon Optimizasyon Kuramı (Eniyileme Süreci) Doğrusal Olmayan Optimizasyon Optimizasyon en iyi çözümü bulma sürecidir.
İNŞAAT PROJELERİNİN PROGRAMLAMA, TASARIM VE YAPIM SÜRECİNDE OPTİMİZASYON Doğrusal Optimizasyon Optimizasyon Kuramı (Eniyileme Süreci) Doğrusal Olmayan Optimizasyon Optimizasyon en iyi çözümü bulma sürecidir.
18.034 İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
14.12 Oyun Teorisi Ders Notları
 14.1 Oyun Teorisi Ders Notları Muhamet Yıldız Ders 15-18 1 Eksik Bilgili Statik Oyunlar Şu ana kadar, herhangi bir oyuncu tarafından bilinen herhangi bir bilgi parçasının tüm oyuncular tarafından bilindiği
14.1 Oyun Teorisi Ders Notları Muhamet Yıldız Ders 15-18 1 Eksik Bilgili Statik Oyunlar Şu ana kadar, herhangi bir oyuncu tarafından bilinen herhangi bir bilgi parçasının tüm oyuncular tarafından bilindiği
Final Sınavı. Güz 2005
 Econ 159a/MGT 522a Ben Polak Güz 2005 Bu defter kitap kapalı bir sınavdır. Sınav süresi 120 dakikadır (artı 60 dakika okuma süresi) Toplamda 120 puan vardır (artı 5 ekstra kredi). Sınavda 4 soru ve 6 sayfa
Econ 159a/MGT 522a Ben Polak Güz 2005 Bu defter kitap kapalı bir sınavdır. Sınav süresi 120 dakikadır (artı 60 dakika okuma süresi) Toplamda 120 puan vardır (artı 5 ekstra kredi). Sınavda 4 soru ve 6 sayfa
VEKTÖR UZAYLARI 1.GİRİŞ
 1.GİRİŞ Bu bölüm lineer cebirin temelindeki cebirsel yapıya, sonlu boyutlu vektör uzayına giriş yapmaktadır. Bir vektör uzayının tanımı, elemanları skalar olarak adlandırılan herhangi bir cisim içerir.
1.GİRİŞ Bu bölüm lineer cebirin temelindeki cebirsel yapıya, sonlu boyutlu vektör uzayına giriş yapmaktadır. Bir vektör uzayının tanımı, elemanları skalar olarak adlandırılan herhangi bir cisim içerir.
Bir Doğrusal Programlama Modelinin Genel Yapısı
 Bir Doğrusal Programlama Modelinin Genel Yapısı Amaç Fonksiyonu Kısıtlar M i 1 N Z j 1 N j 1 a C j x j ij x j B i Karar Değişkenleri x j Pozitiflik Koşulu x j >= 0 Bu formülde kullanılan matematik notasyonların
Bir Doğrusal Programlama Modelinin Genel Yapısı Amaç Fonksiyonu Kısıtlar M i 1 N Z j 1 N j 1 a C j x j ij x j B i Karar Değişkenleri x j Pozitiflik Koşulu x j >= 0 Bu formülde kullanılan matematik notasyonların
Karar Verme. Karar Verme ve Oyun Teorisi. Kararların Özellikleri. Karar Analizi
 Karar Verme Karar Verme ve Oyun Teorisi Yrd.Doç.Dr. Gökçe BAYSAL TÜRKÖLMEZ Belirli bir amaca ulaşabilmek için, Değişik alternatiflerin belirlenmesi ve Bunlar içinden en etkilisinin seçilmesi işlemidir.
Karar Verme Karar Verme ve Oyun Teorisi Yrd.Doç.Dr. Gökçe BAYSAL TÜRKÖLMEZ Belirli bir amaca ulaşabilmek için, Değişik alternatiflerin belirlenmesi ve Bunlar içinden en etkilisinin seçilmesi işlemidir.
DOKUZ EYLÜL ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ DEKANLIĞI DERS/MODÜL/BLOK TANITIM FORMU. Dersin Kodu: END 3620
 Dersi Veren Birim: Endüstri Mühendisliği Dersin Türkçe Adı: YÖNEYLEM ARAŞTIRMASI II Dersin Orjinal Adı: YÖNEYLEM ARAŞTIRMASI II Dersin Düzeyi:(Ön lisans, Lisans, Yüksek Lisans, Doktora) Lisans Dersin Kodu:
Dersi Veren Birim: Endüstri Mühendisliği Dersin Türkçe Adı: YÖNEYLEM ARAŞTIRMASI II Dersin Orjinal Adı: YÖNEYLEM ARAŞTIRMASI II Dersin Düzeyi:(Ön lisans, Lisans, Yüksek Lisans, Doktora) Lisans Dersin Kodu:
DOĞRUSAL PROGRAMLAMADA DUALİTE (DUALITY)
 DOĞRUSAL PROGRAMLAMADA DUALİTE (DUALITY) 1 DOĞRUSAL PROGRAMLAMADA İKİLİK (DUALİTE-DUALITY) Doğrusal programlama modelleri olarak adlandırılır. Aynı modelin değişik bir düzende oluşturulmasıyla Dual (İkilik)
DOĞRUSAL PROGRAMLAMADA DUALİTE (DUALITY) 1 DOĞRUSAL PROGRAMLAMADA İKİLİK (DUALİTE-DUALITY) Doğrusal programlama modelleri olarak adlandırılır. Aynı modelin değişik bir düzende oluşturulmasıyla Dual (İkilik)
18.034 İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Bu optimal reklam-satış oranının reklam etkinliğini (reklam esnekliği) fiyat esnekliğine bölerek de hesaplarız anlamına gelir.
 Sloan Yönetim Okulu 15.010/ 15.011 Massachusetts Teknoloji Enstitüsü Đş Kararları için Đktisadi Analiz Profesör McAdams, Montero, Stoker ve van den Steen 2000 Final Sınavı Cevapları: Asistanların Notlandırması
Sloan Yönetim Okulu 15.010/ 15.011 Massachusetts Teknoloji Enstitüsü Đş Kararları için Đktisadi Analiz Profesör McAdams, Montero, Stoker ve van den Steen 2000 Final Sınavı Cevapları: Asistanların Notlandırması
Yöneylem Araştırması I (IE 222) Ders Detayları
 Yöneylem Araştırması I (IE 222) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Yöneylem Araştırması I IE 222 Güz 3 2 0 4 5 Ön Koşul Ders(ler)i Math 275 Doğrusal
Yöneylem Araştırması I (IE 222) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Yöneylem Araştırması I IE 222 Güz 3 2 0 4 5 Ön Koşul Ders(ler)i Math 275 Doğrusal
Poisson Dağılımı Özellikleri ve Olasılıkların Hesaplanması
 Özellikleri ve Olasılıkların Hesaplanması Doç. Dr. Ertuğrul ÇOLAK Eskişehir Osmangazi Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı Poisson dağılımı kesikli dağılımlar içinde Binom dağılımından
Özellikleri ve Olasılıkların Hesaplanması Doç. Dr. Ertuğrul ÇOLAK Eskişehir Osmangazi Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı Poisson dağılımı kesikli dağılımlar içinde Binom dağılımından
Matematiksel modellerin elemanları
 Matematiksel modellerin elemanları Op#mizasyon ve Doğrusal Programlama Maksimizasyon ve Minimizasyon örnekleri, Doğrusal programlama modeli kurma uygulamaları 6. DERS 1. Karar değişkenleri: Bir karar verme
Matematiksel modellerin elemanları Op#mizasyon ve Doğrusal Programlama Maksimizasyon ve Minimizasyon örnekleri, Doğrusal programlama modeli kurma uygulamaları 6. DERS 1. Karar değişkenleri: Bir karar verme
GEDİZ ÜNİVERSİTESİ SİSTEM MÜHENDİSLİĞİ YÜKSEK LİSANS PROGRAMI SMY 544 ALGORİTMALAR GÜZ 2015
 GEDİZ ÜNİVERSİTESİ SİSTEM MÜHENDİSLİĞİ YÜKSEK LİSANS PROGRAMI SMY 544 ALGORİTMALAR GÜZ 2015 Algoritmalar Ders 9 Dinamik Programlama SMY 544, ALGORİTMALAR, Güz 2015 Ders#9 2 Dinamik Programlama Böl-ve-fethet
GEDİZ ÜNİVERSİTESİ SİSTEM MÜHENDİSLİĞİ YÜKSEK LİSANS PROGRAMI SMY 544 ALGORİTMALAR GÜZ 2015 Algoritmalar Ders 9 Dinamik Programlama SMY 544, ALGORİTMALAR, Güz 2015 Ders#9 2 Dinamik Programlama Böl-ve-fethet
3.2. DP Modellerinin Simpleks Yöntem ile Çözümü Primal Simpleks Yöntem
 3.2. DP Modellerinin Simpleks Yöntem ile Çözümü 3.2.1. Primal Simpleks Yöntem Grafik çözüm yönteminde gördüğümüz gibi optimal çözüm noktası, her zaman uygun çözüm alanının bir köşe noktası ya da uç noktası
3.2. DP Modellerinin Simpleks Yöntem ile Çözümü 3.2.1. Primal Simpleks Yöntem Grafik çözüm yönteminde gördüğümüz gibi optimal çözüm noktası, her zaman uygun çözüm alanının bir köşe noktası ya da uç noktası
HEDEF PROGRAMLAMA. Hedef programlama yaklaşımında, sistemlerin birden fazla ve genellikle birbiriyle çatışan hedeflerinin olması durumu söz konusudur.
 HEDEF PROGRAMLAMA Doç. Dr. İhsan KAYA YTU Enüstri Mühenisliği Bölümü Heef Programlama Heef programlama yaklaşımına, sistemlerin biren fazla ve genellikle birbiriyle çatışan heeflerinin olması urumu söz
HEDEF PROGRAMLAMA Doç. Dr. İhsan KAYA YTU Enüstri Mühenisliği Bölümü Heef Programlama Heef programlama yaklaşımına, sistemlerin biren fazla ve genellikle birbiriyle çatışan heeflerinin olması urumu söz
4.1. Gölge Fiyat Kavramı
 4. Gölge Fiyat Kavramı 4.1. Gölge Fiyat Kavramı Gölge fiyatlar doğrusal programlama modellerinde kısıtlarla açıklanan kaynakların bizim için ne kadar değerli olduklarını gösterirler. Şimdi bir örnek üzerinde
4. Gölge Fiyat Kavramı 4.1. Gölge Fiyat Kavramı Gölge fiyatlar doğrusal programlama modellerinde kısıtlarla açıklanan kaynakların bizim için ne kadar değerli olduklarını gösterirler. Şimdi bir örnek üzerinde
Ara Sınav Yanıtları Econ 159a/MGT 522a Ben Polak Güz 2007
 Ara Sınav Yanıtları Econ 159a/MGT 522a Ben Polak Güz 2007 Aşağıdaki yanıtlar puanları almak için gerekenden daha fazladır. Genelde daha öz açıklamalar daha iyidir. Soru 1. (15 toplam puan). Kısa yanıtlı
Ara Sınav Yanıtları Econ 159a/MGT 522a Ben Polak Güz 2007 Aşağıdaki yanıtlar puanları almak için gerekenden daha fazladır. Genelde daha öz açıklamalar daha iyidir. Soru 1. (15 toplam puan). Kısa yanıtlı
Bülent Turgay DİZDAROĞLif. 1. P lan lam a ve Risk
 T A R IM S A L İŞ L E T M E P L A N L A M A S IN D A RİSK: BİR O Y U N T E O R İS İ D E N E M E S İ Bülent Turgay DİZDAROĞLif 1. P lan lam a ve Risk İşletme yönetiminin önemli bir unsuru olan planlama,
T A R IM S A L İŞ L E T M E P L A N L A M A S IN D A RİSK: BİR O Y U N T E O R İS İ D E N E M E S İ Bülent Turgay DİZDAROĞLif 1. P lan lam a ve Risk İşletme yönetiminin önemli bir unsuru olan planlama,
Genel Graf Üzerinde Mutlak 1-merkez
 Genel Graf Üzerinde Mutlak 1-merkez Çözüm yöntemine geçmeden önce bazı tanımlara ihtiyaç vardır. Dikkate alınan G grafındaki düğümleri 1 den n e kadar numaralandırın. Uzunluğu a(i, j)>0 olarak verilen
Genel Graf Üzerinde Mutlak 1-merkez Çözüm yöntemine geçmeden önce bazı tanımlara ihtiyaç vardır. Dikkate alınan G grafındaki düğümleri 1 den n e kadar numaralandırın. Uzunluğu a(i, j)>0 olarak verilen
Language: English / Turkish
 Rules of Coerceo by Coerceo Company Erhan Turkish translation by Erhan Çubukcuoğlu Türkçe Language: English / Turkish Copyright (Ticari haklar) Bu döküman Coerceo şirketinin resmi yazılı izni olmaksızın
Rules of Coerceo by Coerceo Company Erhan Turkish translation by Erhan Çubukcuoğlu Türkçe Language: English / Turkish Copyright (Ticari haklar) Bu döküman Coerceo şirketinin resmi yazılı izni olmaksızın
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Altın Oran (Golden Section Search) Arama Metodu Tek değişkenli bir f(x) fonksiyonunu ele alalım. [Bazı x ler için f
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Altın Oran (Golden Section Search) Arama Metodu Tek değişkenli bir f(x) fonksiyonunu ele alalım. [Bazı x ler için f
İKTİSAT BİLİMİ VE İKTİSATTAKİ TEMEL KAVRAMLAR
 İÇİNDEKİLER Önsöz BİRİNCİ BÖLÜM İKTİSAT BİLİMİ VE İKTİSATTAKİ TEMEL KAVRAMLAR 1.1.İktisat Bilimi 1.2.İktisadi Kavramlar 1.2.1.İhtiyaçlar 1.2.2.Mal ve Hizmetler 1.2.3.Üretim 1.2.4.Fayda, Değer ve Fiyat
İÇİNDEKİLER Önsöz BİRİNCİ BÖLÜM İKTİSAT BİLİMİ VE İKTİSATTAKİ TEMEL KAVRAMLAR 1.1.İktisat Bilimi 1.2.İktisadi Kavramlar 1.2.1.İhtiyaçlar 1.2.2.Mal ve Hizmetler 1.2.3.Üretim 1.2.4.Fayda, Değer ve Fiyat
Ders 8 in Özeti YÖNEYLEM ARAŞTIRMASI III. Markov Süreçleri Ders 9. Bir Markov Zincirinin Sınıflandırılması. Örnek: Kumarbazın İflası
 Ders 8 in Özeti YÖEYLEM ARAŞTIRMASI III Markov Süreçleri Ders 9 Durağan Dağılım Koşulsuz olasılık dağılımı (n) P Uzun Dönem Analizi Limit (Kararlı Hal) Dağılımı,,..., Bir Markov Zincirinin Sınıflandırılması
Ders 8 in Özeti YÖEYLEM ARAŞTIRMASI III Markov Süreçleri Ders 9 Durağan Dağılım Koşulsuz olasılık dağılımı (n) P Uzun Dönem Analizi Limit (Kararlı Hal) Dağılımı,,..., Bir Markov Zincirinin Sınıflandırılması
Gürc r an n B ange g r
 Gürcan Banger Hareket Noktası Kendi işini kurmaya karar vermede başlıca etkenler şunlardır: 1. İşini kaybetmek, 2. İşsizlik döneminin uzun sürmesine tepki, 3. Bir iş fırsatının belirlenmesi, 4. Daha çok
Gürcan Banger Hareket Noktası Kendi işini kurmaya karar vermede başlıca etkenler şunlardır: 1. İşini kaybetmek, 2. İşsizlik döneminin uzun sürmesine tepki, 3. Bir iş fırsatının belirlenmesi, 4. Daha çok
x 1,x 2,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu;
 4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ Doğrusal Denklem Sistemi x,x,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu; a x + a x + L + a x = b n n a x + a x + L + a x = b n n a x + a
4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ Doğrusal Denklem Sistemi x,x,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu; a x + a x + L + a x = b n n a x + a x + L + a x = b n n a x + a
Finansal Yatırım ve Portföy Yönetimi. Ders 7 Modern Portföy Teorisi
 Finansal Yatırım ve Portföy Yönetimi Ders 7 Modern Portföy Teorisi Kurucusu Markowitz dir. 1990 yılında bu çalışmasıyla Nobel Ekonomi ödülünü MertonH. Miller ve William F. Sharpe ilepaylaşmıştır. Modern
Finansal Yatırım ve Portföy Yönetimi Ders 7 Modern Portföy Teorisi Kurucusu Markowitz dir. 1990 yılında bu çalışmasıyla Nobel Ekonomi ödülünü MertonH. Miller ve William F. Sharpe ilepaylaşmıştır. Modern
Sonuçlanmamış bir cephede rakibinizin dilediğiniz bir birlik kartını alın ve kendi tarafinıza geçirerek istediğiniz bir cepheye yerleştirin.
 İçerİk: Sonuçlanmamış bir cephede rakibinizin dilediğiniz bir birlik kartını alın ve kendi tarafinıza geçirerek istediğiniz bir cepheye yerleştirin. 60 Birlik Kartı 10 Taktik Kartı 9 ahşap Cephe Piyonu
İçerİk: Sonuçlanmamış bir cephede rakibinizin dilediğiniz bir birlik kartını alın ve kendi tarafinıza geçirerek istediğiniz bir cepheye yerleştirin. 60 Birlik Kartı 10 Taktik Kartı 9 ahşap Cephe Piyonu
TEKELC REKABET VE OLİGOPOL PİYASALAR
 BÖLÜM 12 TEKELC REKABET VE OLİGOPOL PİYASALAR Tekelci rekabet (Monopolistic competition) Piyasya girişin serbest olduğu ve her firmanın kendi markasını (brand) üretip sattığı, ürünün farklılaştırılmış
BÖLÜM 12 TEKELC REKABET VE OLİGOPOL PİYASALAR Tekelci rekabet (Monopolistic competition) Piyasya girişin serbest olduğu ve her firmanın kendi markasını (brand) üretip sattığı, ürünün farklılaştırılmış
14.12 Oyun Teorisi Ders Notları
 14.12 Oyun Teorisi Ders Notları Giriş Muhamet Yıldız (Ders 1) Oyun Teorisi Çok Kişili Karar Teorisi için yanlış bir isimlendirmedir. Oyun Teorisi, birden çok ajanın bulunduǧu ve her ajanın ödülünün diǧer
14.12 Oyun Teorisi Ders Notları Giriş Muhamet Yıldız (Ders 1) Oyun Teorisi Çok Kişili Karar Teorisi için yanlış bir isimlendirmedir. Oyun Teorisi, birden çok ajanın bulunduǧu ve her ajanın ödülünün diǧer
Bu durumu, konum bazında bileşenlerini, yani dalga fonksiyonunu, vererek tanımlıyoruz : ) 1. (ikx x2. (d)
 Ders 10 Metindeki ilgili bölümler 1.7 Gaussiyen durum Burada, 1-d de hareket eden bir parçacığın önemli Gaussiyen durumu örneğini düşünüyoruz. Ele alış biçimimiz kitaptaki ile neredeyse aynı ama bu örnek
Ders 10 Metindeki ilgili bölümler 1.7 Gaussiyen durum Burada, 1-d de hareket eden bir parçacığın önemli Gaussiyen durumu örneğini düşünüyoruz. Ele alış biçimimiz kitaptaki ile neredeyse aynı ama bu örnek
Sequence Oyununun Minimaks Algoritması Kullanılarak Tasarlanması ve Geliştirilmesi
 Sequence Oyununun Minimaks Algoritması Kullanılarak Tasarlanması ve Geliştirilmesi Yavuz Kömeçoğlu Çetin Oktay Nilgün İncereis Levent Yıldız Yrd. Doç. Dr. Aslı Uyar Özkaya XoX Oyunu Puanlama Sistemi Sequence
Sequence Oyununun Minimaks Algoritması Kullanılarak Tasarlanması ve Geliştirilmesi Yavuz Kömeçoğlu Çetin Oktay Nilgün İncereis Levent Yıldız Yrd. Doç. Dr. Aslı Uyar Özkaya XoX Oyunu Puanlama Sistemi Sequence
Sistem Mühendisliği. Prof. Dr. Ferit Kemal Sönmez
 Sistem Mühendisliği Prof. Dr. Ferit Kemal Sönmez Organizasyon Teorileri 20. yüzyılın başından itibaren insan ilişkilerinin her alandaki giderek artan önemi, iki dünya savaşı ve 1960 ların sosyal devrimleri,
Sistem Mühendisliği Prof. Dr. Ferit Kemal Sönmez Organizasyon Teorileri 20. yüzyılın başından itibaren insan ilişkilerinin her alandaki giderek artan önemi, iki dünya savaşı ve 1960 ların sosyal devrimleri,
Veriye Dayalı Karar Verme (Bölüm 2) Can Akkan
 Veriye Dayalı Karar Verme (Bölüm 2) Can Akkan 1 Ders Planı 1. Karar Problemleri i. Karar problemlerinin bileşenleri ii. Değerler, amaçlar, bağlam iii. Etki diagramları 2. Model Girdilerinde Belirsizlik
Veriye Dayalı Karar Verme (Bölüm 2) Can Akkan 1 Ders Planı 1. Karar Problemleri i. Karar problemlerinin bileşenleri ii. Değerler, amaçlar, bağlam iii. Etki diagramları 2. Model Girdilerinde Belirsizlik
Yöneylem Araştırması II (IE 323) Ders Detayları
 Yöneylem Araştırması II (IE 323) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Yöneylem Araştırması II IE 323 Güz 3 2 0 4 5.5 Ön Koşul Ders(ler)i IE 222
Yöneylem Araştırması II (IE 323) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Yöneylem Araştırması II IE 323 Güz 3 2 0 4 5.5 Ön Koşul Ders(ler)i IE 222
Bekleme Hattı Teorisi
 Bekleme Hattı Teorisi Sürekli Parametreli Markov Zincirleri Tanım 1. * +, durum uzayı * +olan sürekli parametreli bir süreç olsun. Aşağıdaki özellik geçerli olduğunda bu sürece sürekli parametreli Markov
Bekleme Hattı Teorisi Sürekli Parametreli Markov Zincirleri Tanım 1. * +, durum uzayı * +olan sürekli parametreli bir süreç olsun. Aşağıdaki özellik geçerli olduğunda bu sürece sürekli parametreli Markov
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
a2 b3 cij: birim başına ulaşım maliyeti xij: taşıma miktarı
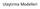 Ulaştırma Modelleri Ulaştırma modeli Ulaştırma modeli doğrusal programlama modellerinin özel bir türüdür. Modelin amacı bir işletmenin belirli kapasitedeki üretim merkezlerinden, belirli talebi olan tüketim
Ulaştırma Modelleri Ulaştırma modeli Ulaştırma modeli doğrusal programlama modellerinin özel bir türüdür. Modelin amacı bir işletmenin belirli kapasitedeki üretim merkezlerinden, belirli talebi olan tüketim
2. Sonsuz uzunluk kabul edilebilmesi için çubuklar ne kadar uzunlukta olmalıdır? Resim 1
 Örnek 3-9*: 5 mm çapında çok uzun bir çubuğun bir ucu T b =100 C sabit sıcaklıkta tutulmaktadır. Çubuğun yüzeyi T =25 C de ve ısı transfer katsayısı (h) 100 W/m 2 K olan çevresindeki hava (air) ile temastadır.
Örnek 3-9*: 5 mm çapında çok uzun bir çubuğun bir ucu T b =100 C sabit sıcaklıkta tutulmaktadır. Çubuğun yüzeyi T =25 C de ve ısı transfer katsayısı (h) 100 W/m 2 K olan çevresindeki hava (air) ile temastadır.
Türk-Alman Üniversitesi. Ders Bilgi Formu
 Türk-Alman Üniversitesi Ders Bilgi Formu Dersin Adı Dersin Kodu Dersin Yarıyılı Yöneylem Araştırması WNG301 5 ECTS Ders Uygulama Laboratuar Kredisi (saat/hafta) (saat/hafta) (saat/hafta) 6 2 2 0 Ön Koşullar
Türk-Alman Üniversitesi Ders Bilgi Formu Dersin Adı Dersin Kodu Dersin Yarıyılı Yöneylem Araştırması WNG301 5 ECTS Ders Uygulama Laboratuar Kredisi (saat/hafta) (saat/hafta) (saat/hafta) 6 2 2 0 Ön Koşullar
ÜÇ ÇUBUK MEKANİZMASI
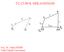 ÜÇ ÇUBUK MEKNİZMSI o l min l, lmaks B l,, B o Doç. Dr. Cihan DEMİR Yıldız Teknik Üniversitesi Dört çubuk mekanizmalarının uygulama alanı çok geniş olmasına rağmen bu uygulamalar üç değişik gurupta toplanabilir.
ÜÇ ÇUBUK MEKNİZMSI o l min l, lmaks B l,, B o Doç. Dr. Cihan DEMİR Yıldız Teknik Üniversitesi Dört çubuk mekanizmalarının uygulama alanı çok geniş olmasına rağmen bu uygulamalar üç değişik gurupta toplanabilir.
ii) S 2LW 2WH 2LW 2WH S 2WH 2LW S 3( x 1) 5( x 2) 5 3x 3 5x x Maliye Bölümü EKON 103 Matematik I / Mart 2018 Proje 2 CEVAPLAR C.1) C.
 C.1) x1 x 1 4 4( x1) x 6 4x 4 x 6 x 46 x Maliye Bölümü EKON 10 Matematik I / Mart 018 Proje CEVAPLAR C.) i) S LW WH LW WH S LW WH S W W W S L H W ii) S LW WH WH LW S WH LW S W W W S H L W C.) ( x1) 5(
C.1) x1 x 1 4 4( x1) x 6 4x 4 x 6 x 46 x Maliye Bölümü EKON 10 Matematik I / Mart 018 Proje CEVAPLAR C.) i) S LW WH LW WH S LW WH S W W W S L H W ii) S LW WH WH LW S WH LW S W W W S H L W C.) ( x1) 5(
ENDÜSTRİ MÜHENDİSLİĞİ BÖLÜM BAŞKANLIĞI DERS TANITIM BİLGİLERİ
 ENDÜSTRİ MÜHENDİSLİĞİ BÖLÜM BAŞKANLIĞI DERS TANITIM BİLGİLERİ Dersin Adı Kodu Sınıf/Y.Y. Ders Saati Kredi AKTS (T+U+L) ŞEBEKE MODELLERİ EN-413 4/I 3+0+0 3 5 Dersin Dili : İngilizce Dersin Seviyesi : Lisans
ENDÜSTRİ MÜHENDİSLİĞİ BÖLÜM BAŞKANLIĞI DERS TANITIM BİLGİLERİ Dersin Adı Kodu Sınıf/Y.Y. Ders Saati Kredi AKTS (T+U+L) ŞEBEKE MODELLERİ EN-413 4/I 3+0+0 3 5 Dersin Dili : İngilizce Dersin Seviyesi : Lisans
DOKUZ EYLÜL ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ DEKANLIĞI DERS/MODÜL/BLOK TANITIM FORMU. Dersin Kodu: END 4910
 Dersi Veren Birim: Endüstri Mühendisliği Dersin Türkçe Adı: MATEMATİKSEL PROGRAMLAMADA SEÇİLMİŞ KONULAR Dersin Orjinal Adı: MATEMATİKSEL PROGRAMLAMADA SEÇİLMİŞ KONULAR Dersin Düzeyi:(Ön lisans, Lisans,
Dersi Veren Birim: Endüstri Mühendisliği Dersin Türkçe Adı: MATEMATİKSEL PROGRAMLAMADA SEÇİLMİŞ KONULAR Dersin Orjinal Adı: MATEMATİKSEL PROGRAMLAMADA SEÇİLMİŞ KONULAR Dersin Düzeyi:(Ön lisans, Lisans,
4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ
 4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ Doğrusal Denklem Sistemi x 1,x 2,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu; a x a x a x b 11 1 12 2 1n n 1 a x a x a x b 21 1 22 2 2n n
4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ Doğrusal Denklem Sistemi x 1,x 2,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu; a x a x a x b 11 1 12 2 1n n 1 a x a x a x b 21 1 22 2 2n n
Tedarik Zinciri Yönetimi
 Tedarik Zinciri Yönetimi -Tedarikçi Seçme Kararları- Yrd. Doç. Dr. Mert TOPOYAN Satın Alma Bir ișletme, dıșarıdan alacağı malzeme ya da hizmetlerle ilgili olarak satın alma (tedarik) fonksiyonunda beș
Tedarik Zinciri Yönetimi -Tedarikçi Seçme Kararları- Yrd. Doç. Dr. Mert TOPOYAN Satın Alma Bir ișletme, dıșarıdan alacağı malzeme ya da hizmetlerle ilgili olarak satın alma (tedarik) fonksiyonunda beș
YILDIZ TEKNİK ÜNİVERSİTESİ BEDEN EĞİTİMİ BÖLÜMÜ REKTÖRLÜK KUPASI FAKÜLTELER ARASI ÖĞRENCİ TURNUVALARI GENEL KURALLARI
 FAKÜLTELER ARASI ÖĞRENCİ TURNUVALARI GENEL KURALLARI. Turnuvanın yürütülmesinden Beden Eğitimi Bölümü sorumludur. Her türlü olay karşısında Beden Eğitimi Bölümü tarafından alınan kararlar uygulanacaktır..
FAKÜLTELER ARASI ÖĞRENCİ TURNUVALARI GENEL KURALLARI. Turnuvanın yürütülmesinden Beden Eğitimi Bölümü sorumludur. Her türlü olay karşısında Beden Eğitimi Bölümü tarafından alınan kararlar uygulanacaktır..
Konu 10 Oyun Teorisi: Oligopol Piyasaların İç Mahiyeti
 .. Konu 10 Oyun si: Oligopol Piyasaların İç Mahiyeti Hadi Yektaş Uluslararası Antalya Üniversitesi İşletme Tezsiz Yüksek Lisans Programı 1 / 82 Hadi Yektaş Oyun si: Oligopol Piyasaların İç Mahiyeti İçerik.1.2.3.4
.. Konu 10 Oyun si: Oligopol Piyasaların İç Mahiyeti Hadi Yektaş Uluslararası Antalya Üniversitesi İşletme Tezsiz Yüksek Lisans Programı 1 / 82 Hadi Yektaş Oyun si: Oligopol Piyasaların İç Mahiyeti İçerik.1.2.3.4
MIT OpenCourseWare http://ocw.mit.edu. 14.30 Ekonomide İstatistiksel Yöntemlere Giriş Bahar 2009
 MIT OpenCourseWare http://ocw.mit.edu 14.30 Ekonomide İstatistiksel Yöntemlere Giriş Bahar 2009 Bu materyale atıfta bulunmak ve kullanım koşulları için http://ocw.mit.edu/terms sayfasını ziyaret ediniz.
MIT OpenCourseWare http://ocw.mit.edu 14.30 Ekonomide İstatistiksel Yöntemlere Giriş Bahar 2009 Bu materyale atıfta bulunmak ve kullanım koşulları için http://ocw.mit.edu/terms sayfasını ziyaret ediniz.
Ekonomi I. Doç.Dr.Tufan BAL. 11.Bölüm: Oligopol Piyasası. Not:Bu sunun hazırlanmasında büyük oranda Prof.Dr.Tümay ERTEK in Temel Ekonomi kitabından
 Ekonomi I 11.Bölüm: Oligopol Piyasası Doç.Dr.Tufan BAL Not:Bu sunun hazırlanmasında büyük oranda Prof.Dr.Tümay ERTEK in Temel Ekonomi kitabından faydalanılmıştır. 2 11.1.Oligopol Piyasasının Özellikleri
Ekonomi I 11.Bölüm: Oligopol Piyasası Doç.Dr.Tufan BAL Not:Bu sunun hazırlanmasında büyük oranda Prof.Dr.Tümay ERTEK in Temel Ekonomi kitabından faydalanılmıştır. 2 11.1.Oligopol Piyasasının Özellikleri
Türk-Alman Üniversitesi İktisadi ve İdari Bilimler Fakültesi İşletme Bölümü Ders Bilgi Formu
 Türk-Alman Üniversitesi İktisadi ve İdari Bilimler Fakültesi İşletme Bölümü Ders Bilgi Formu Dersin Adı Dersin Kodu Dersin Yarıyılı Yöneylem Araştırması BWL315 5 ECTS Ders Uygulama Laboratuar Kredisi (saat/hafta)
Türk-Alman Üniversitesi İktisadi ve İdari Bilimler Fakültesi İşletme Bölümü Ders Bilgi Formu Dersin Adı Dersin Kodu Dersin Yarıyılı Yöneylem Araştırması BWL315 5 ECTS Ders Uygulama Laboratuar Kredisi (saat/hafta)
