ELEKTROMANYETİK DALGALAR DERSİ YAZ DÖNEMİ
|
|
|
- Nazar Tekeli
- 7 yıl önce
- İzleme sayısı:
Transkript
1 DERS İÇERİĞİNE GENEL BAKIŞ ELEKTROMANYETİK DALGALAR DERSİ YAZ DÖNEMİ Yrd. Doç. Dr. Seyit Ahmet Sis MMF 7. kat, ODA No: 3, Dahili:
2 DERS İÇERİĞİNE GENEL BAKIŞ Ders İçeriği : Vektörel işlemlerin hatırlatmasıyla başlanıp, elektrostatik ve magnetostatikin temel teorem ve eşitlikerinden bahsedilecek, daha sonra dersin tamamına yakınında elektrodinamik konuları işlenecektir. Bu bağlamda işlenmesi planlanan konular: Maxwell denklemleri, düzlemsel dalgalar (plane waves), Dalgaların farklı ortamlara arasında yayılımında davranışları (örn. yansıma, kırımla...), Işıma ve antenler (sadece temelleri verilecek, spesifik antenlere girilmeyecek) Ders Kaynakları: 1) Fawwaz Ulaby,Eric Michielssen and Umberto Ravaioli Fundamentals of Applied Electromagnetics 5 th or 6 th edition. 2) Schaum s Elektromanyetik, 2. baskıdan çeviri 3) David Cheng, Fieild and Wave Electromagnetics (Türkçeside mevcuttur) 4) Davif J. Griffiths Introduction to Electrodnamics Vize % 40, Final % 60 2
3 DERS İÇERİĞİNE GENEL BAKIŞ 1. Ders 2. Ders 3. Ders 4. Ders 5. Ders Vektör analizi, elektrostatik temellerinin kabaca tekrarı 6. Ders 7. Ders 8. Ders 9. Ders 10. Ders 11. Ders 12. Ders 13. Ders 3
4 VEKTÖR ANALİZİ Elektrik ve Manyetik alanlar vektörel büyüklüklerdir Bu bağlamda lisans düzeyinde hâli hazırda verilmiş olan vektör analizi üzerinden kısaca geçmenin faydası vardır Vektörün Matematiksel İfadesi Birim Vektör (Unit Vector) 4
5 VEKTÖR ANALİZİ x,y ve z kordinatları, baz vektörü olarak isimlendirilen, birim vektörleriyle gösterilirler Ax, Ay ve Az A vektörünün izdüşümleridir! 5
6 VEKTÖR ANALİZİ VEKTÖRÜN BOYU: BİRİM VEKTÖR: A vektörünün yönünü gösteren boyu 1 birim olan vektör: Dolayısıyla, kartezyen kordinatlarda tanımlanan bu A vektörü kendi birim vektörüyle aşağıdaki gibi de gösterilir. 6
7 VEKTÖR ANALİZİ VEKTÖR TOPLAMA VE ÇIKARMA İŞLEMLERİ 7
8 VEKTÖR ANALİZİ VEKTORLERDE ÇARPMA İŞLEMLERİ BASİT ÇARPMA İŞLEMİ, SKALAR ÇARPMA İŞLEMİ, VEKTÖREL ÇARPMA İŞLEMİ Bir vektörün bir skalarla çarpımıdır: BASİT ÇARPMA İŞLEMİ A k pozitif ve 1 den büyük ka Vektörün boyu k kadar artar, yönü ise k pozitif ise A yönündedir. k negatif ise A yönündedir. 8
9 VEKTÖR ANALİZİ VECTORLERDE ÇARPMA İŞLEMLERİ SKALAR ÇARPMA İŞLEMİ (NOKTA ÇARPIMI) İki vektörün aynı bileşenlerinin genliklerinin çarpılıp toplanmasıdır. Çarpım sonucu bir vektör değil skalar bir büyüklüktür. Bu nedenle 2 tane vektör çarpımı olsada bu işleme skalar çarpım denmektedir Geometrik manada skalar çarpım: vektörlerden birinin genliği ile diğer vektörün bu vektör üzerine iz düşmü büyüklüğünün çarpımıdır. 9
10 VEKTÖR ANALİZİ DOLAYISIYLA VECTORLERDE ÇARPMA İŞLEMLERİ VEKTÖREL ÇARPMA İŞLEMİ (ÇAPRAZ ÇARPIM) Geometrik manada: Çarpımın sonucu, yönü iki çarpan vektörün olduğu düzleme dikolan ve genliğide, bu iki çarpan vektörün oluşturduğü paralel kenarın eşit olan bir vektördür. Yada : NOT: Çarpımın sonucu yine bir vektördür. Bu yüzden buna vektörel çarpım denir Sağ el kuralıyla yönü bulabiliriz! 10
11 ORTAGONAL KORDİNAT SİSTEMLERİ Elektromanyetikte fiziksel nitelikler (örn E, H) zamana ve konuma bağlı büyüklüklerdir. Değişim yönleride birim vektörler vasıtasıyla gösterilir. Uzayda bir konumun yerini, yada bir vektörel büyüklüğün (örn E ve H) yönünü 3 boyutlu kordinat sistemlerini kullanarak tanımlarız. KORDİNAT SİSTEMLERİ Ortagonal Kordinat Sistemleri Bütün kordinatlar birbirine dik EM problemlerin çözümünde sıklıkla kullanılır 3 tür ortagonal kordinat sistemi vardır: Kartezyen kordinat sistemi Silindirik kordinat sistemi Küresel kordinat sistemi Ortagonal Olmayan Kordinat Sistemleri Kordinatların kimisi birbirine dik olmayabilir Çok özel durumlarda kullanılır ve nadiren pratik problemlerin çözümüyle ilgilidir. 11
12 ORTAGONAL KORDİNAT SİSTEMLERİ KARTEZYEN KORDİNAT SİSTEMİ Birim kordinatlar x, y ve z ile gösterilirler. diferansiyel uzunluk diferansiyel alan Diferansiyel hacim 12
13 ORTAGONAL KORDİNAT SİSTEMLERİ SİLİNDİRK KORDİNAT SİSTEMİ Silindirk kordinatlarda bir vektör aşağıdaki gibi gösterilir: yönlerindeki bileşenlerdir Diferansiyel uzunluk, diferansiyel yüzey ve diferansiyel hacim: 13
14 ORTAGONAL KORDİNAT SİSTEMLERİ SİLİNDİRK KORDİNAT SİSTEMİ ÖRN: Aşağıdaki matematiksel ifadeyle belirlenen silindirik yüzeyin alanını bulunuz! CEVAP: Görüldüğü üzere bahsedilen alanı bulmak için aldığımız integral silindirik kordinatlarda alınmıştır. Aynı alanı kartezyen kordinatlarda integralini alarak bulmak oldukça zordur! Dolayısıyla, problemin türüne göre en uygun kordinat sisteminin seçilip işlem yapılması gerekmektedir. 14
15 ORTAGONAL KORDİNAT SİSTEMLERİ SİLİNDİRK KORDİNAT SİSTEMİ ÖRN: Aşağıdaki A vektörünün birim vektörünü bulunuz! 15
16 ORTAGONAL KORDİNAT SİSTEMLERİ KÜRESEL KORDİNAT SİSTEMİ Herhangibir nokta R, θ ve değişkenleriyle gösterilir. Birim vektörler, yada diğer bir deyişle baz vektörler φ ve Aşağıdaki kurala uyarlar: Bir vektör aşağıdaki şekilde ifade edilir: 16
17 ORTAGONAL KORDİNAT SİSTEMLERİ KÜRESEL KORDİNAT SİSTEMİ 17
18 ORTAGONAL KORDİNAT SİSTEMLERİ KÜRESEL KORDİNAT SİSTEMİ ÖRN: Yarıçapı 2 cm olan bir kürenin içindeki yük yoğunluğu dur. Bu kürenin içerisindeki toplam yükü bulunuz. CEVAP: 18
19 ORTAGONAL KORDİNAT SİSTEMLERİ ORTAGONAL KORDİNAT SİSTEMLERİ ÖZETİ 19
20 ORTAGONAL KORDİNAT SİSTEMLERİ DEL OPERATÖRÜ Del operatörü, yada kimi yerde Nabla operatörü olarak da bilinir, bir vektörel kısmi türev operatörüdür. Kendisi bir vektördür Diğer vektörel yada skalar büyüklüklere uygulanır. Sembolü ORTAGONAL KORDİNAT SİSTEMLERİNDE DEL OPERATÖRÜ AŞAĞIDAKİ GİBİDİR Kartezyen Silindirik Küresel 20
21 ORTAGONAL KORDİNAT SİSTEMLERİ GRADYAN (GRADIENT) Del operatörü bir skalar büyüklüğe (fonksiyona) basit çarpım şeklinde uygulanır ve sonucu bir vektörel büyüklüktür. Gradyan, yada DEL operatörü: Bir T (x,y,z) skalar fonksiyonuna uygulandığında: 21
22 ORTAGONAL KORDİNAT SİSTEMLERİ DİVERJANS (DIVERGENCE) Diverjans DEL operatörünün bir vektörle noktasal çarpımıdır. İki vektörün noktasal çarpımı skalar büuükül olduğu için, divejansın sonucu skalardır. ROTASYON (CURL) Rotasyon DEL operatörüyle bir vektörün çapraz çarpımıdır. Sonuç yine vektörel bir büyüklüktür. 22
23 ORTAGONAL KORDİNAT SİSTEMLERİ DEL OPERATÖRÜNÜN İŞLEMLERİ 23
24 ORTAGONAL KORDİNAT SİSTEMLERİ VEKTÖR ANALİZİ, OPERATÖRLER VE KORDİNAT SİSTEMLERİ İLE İLGİLİ BAZI ÖDEVLER 1) Yarı çapı 5 cm olan, ve z= -3 cm den z= 3 cm ye uzana silindirin alanını silindirik kordinatlarda integralini alarak bulunuz! NOT: Silindirin hacim formülünü kullanarak yapmayınız. Silindirik kordinatlarda integrali alarak yapınız! 2) Aşağıda kartezyen, silindirik ve küresel kordinatlarda birim vektörlerin birbirleri ile çapraz çarpımları verilmektedir. Bu çarpımların doğruluğunu önceki slaytlarda gördüğümüz (slayt 10) çapraz çarpımın sonucunun yönünü sağ el kuralıyla tayin edebileceğimizi görmüştük. Aşağıdaki birim vektör çarpımlarının doğruluğunu kağıt üzerine çizerek sağ el kuralını düşünerek gözleyiniz! kartezyen silindirik küresel 3) Aşağıdaki fonksiyonunun gradyenti, diverjansı yada rotasyonundan hangisi alınabilir. Yapılabilen işlemi yapınız! 24
25 ELEKTROSTATİK ELEKTROSTATİK (ZAMANLA DEĞİŞMEYEN ELEKTRİK ALAN) HATIRLATMA! 25
26 ELEKTROSTATİK COULOMB KUVVETİ Aralarında r mesafesi olan q1 ve q2 yüklerinin birbirlerine uyguladıkları kuvvet. Gerçek manada, yani mekaniksel olarak bu yükler birbirlerini iter yada çeker. Elektrostatikte sabit yükler üzerinden hesaplamalar yapılır. Bu yüzde Elektrostatik denmektedir. Haraketli yüklerinde itme çekme kuvveti vardır. Fakat bunların incelemesi elektrostatik içerisinde değil ilerleyen kısımlarda elektromanyetik de açıklanacaktır. (Newton) ELEKTRİK ALAN Bir q yükünün oluşturduğu elektrik alan (E) ise, o q yükünün 1 C luk birim yüke uyguladığı Coulomb kuvvetidir. Yani elektrik alan dediğimiz şey Coulomb kuvvetinin özel hali gibidir. X 1 Bir q yükünden dolayı 1 C luk bir yüke uygulana Coulomb kuvvetidir! 26
27 ELEKTROSTATİK ELEKTRİK ALAN İKİ YÜK TEK YÜK q yükünün oluşturduğu elektrik alan vektörleri gösterilmektedir! 27
28 ELEKTROSTATİK ELEKTRİK ALAN Birden fazla yükün bir noktada oluşturduğu Elektrik Alan (E) En genel halde: 28
29 ELEKTROSTATİK ELEKTRİK ALAN Sürekli dağılımlı yüklerin bir noktada oluşturduğu Elektrik Alan (E) Sürekli dağılımlı en genel haldeki diferansiyel yük yoğunluğunun (dq) bir noktada oluşturduğu diferansiyel elektrik alan (de) Hacimsel yük yoğunluğu ile ilgileniyorsak: Verilen hacimdeki toplam yükün bahsedilen noktada oluşturduğu elektrik alan: 29
30 ELEKTROSTATİK ELEKTRİK ALAN Sürekli dağılımlı yüklerin bir noktada oluşturduğu Elektrik Alan (E) Yüzey yada çizgisel yük yoğunluğu olan yük kaynaklarından bahsediyorsak: Deplasman Vektörü (Displacement Vector, D) 30
31 ELEKTROSTATİK ELEKTRİK ALAN D = εe = ε 0 ε r E Malzemenin özelliği! Gauss Yasası İntegral Formu Kapalı bir hacimin içerisindeki toplam yük Hacimin yüzeyi Toplam Yük= Q C Yük yoğunluğu ise= ρ v C/m 3 (birim hacimdeki yük) Gauss Yasası Diferansiyel Formu 31
32 ELEKTROSTATİK ELEKTRİK ALAN 32
33 ELEKTROSTATİK ELEKTRİK ALAN 33
34 ELEKTROSTATİK Gauss Yasası Diferansiyel Formu Gauss Yasası İntegral Formu 34
ELEKTROMANYETIK ALAN TEORISI
 ELEKTROMANYETIK ALAN TEORISI kaynaklar: 1) Electromagnetic Field Theory Fundamentals Guru&Hiziroglu 2) A Student s Guide to Maxwell s Equations Daniel Fleisch 3) Mühendislik Elektromanyetiğinin Temelleri
ELEKTROMANYETIK ALAN TEORISI kaynaklar: 1) Electromagnetic Field Theory Fundamentals Guru&Hiziroglu 2) A Student s Guide to Maxwell s Equations Daniel Fleisch 3) Mühendislik Elektromanyetiğinin Temelleri
TEMEL İŞLEMLER KAVRAMLAR
 EM 420 Yüksek Gerilim Tekniği TEMEL İŞLEMLER VE KAVRAMLAR YRD.DOÇ. DR. CABBAR VEYSEL BAYSAL ELEKTRIK & ELEKTRONIK YÜK. MÜH. Not: Tüm slaytlar listelenen ders kaynaklarından alıntı yapılarak ve faydalanılarak
EM 420 Yüksek Gerilim Tekniği TEMEL İŞLEMLER VE KAVRAMLAR YRD.DOÇ. DR. CABBAR VEYSEL BAYSAL ELEKTRIK & ELEKTRONIK YÜK. MÜH. Not: Tüm slaytlar listelenen ders kaynaklarından alıntı yapılarak ve faydalanılarak
Bu bölümde Coulomb yasasının bir sonucu olarak ortaya çıkan Gauss yasasının kullanılmasıyla simetrili yük dağılımlarının elektrik alanlarının çok
 Gauss Yasası Bu bölümde Coulomb yasasının bir sonucu olarak ortaya çıkan Gauss yasasının kullanılmasıyla simetrili yük dağılımlarının elektrik alanlarının çok daha kullanışlı bir şekilde nasıl hesaplanabileceği
Gauss Yasası Bu bölümde Coulomb yasasının bir sonucu olarak ortaya çıkan Gauss yasasının kullanılmasıyla simetrili yük dağılımlarının elektrik alanlarının çok daha kullanışlı bir şekilde nasıl hesaplanabileceği
Bölüm 24 Gauss Yasası
 Bölüm 24 Gauss Yasası Elektrik Akısı Gauss Yasası Gauss Yasasının Yüklü Yalıtkanlara Uygulanması Elektrostatik Dengedeki İletkenler Öğr. Gör. Dr. Mehmet Tarakçı http://kisi.deu.edu.tr/mehmet.tarakci/ Elektrik
Bölüm 24 Gauss Yasası Elektrik Akısı Gauss Yasası Gauss Yasasının Yüklü Yalıtkanlara Uygulanması Elektrostatik Dengedeki İletkenler Öğr. Gör. Dr. Mehmet Tarakçı http://kisi.deu.edu.tr/mehmet.tarakci/ Elektrik
ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ ELEKTROMANYETİK DALGA TEORİSİ VİZE SORULARI :.. OKUL NO ADI SOYADI
 ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ ELEKTROMANYETİK DALGA TEORİSİ VİZE SORULARI 18.04.2011 OKUL NO :.. ADI SOYADI :.. S-1 z-ekseni boyunca az yönünde 15A akı taşıya bir akı fila a ı mevcuttur. H yi Kartezyen
ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ ELEKTROMANYETİK DALGA TEORİSİ VİZE SORULARI 18.04.2011 OKUL NO :.. ADI SOYADI :.. S-1 z-ekseni boyunca az yönünde 15A akı taşıya bir akı fila a ı mevcuttur. H yi Kartezyen
III. BÖLÜM ELEKTRİK POTANSİYELİ
 39 III. BÖLÜM ELEKTRİK POTANSİYELİ 3.1 POTANSİYEL ENERJİ VE İŞ Elektrik alanının içinde yüklü bir parçacık hareket ederse elektrik alani parçacık üzerine bir kuvvet uygular ve iş yapar. F =q. E Yapılan
39 III. BÖLÜM ELEKTRİK POTANSİYELİ 3.1 POTANSİYEL ENERJİ VE İŞ Elektrik alanının içinde yüklü bir parçacık hareket ederse elektrik alani parçacık üzerine bir kuvvet uygular ve iş yapar. F =q. E Yapılan
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
2-MANYETIK ALANLAR İÇİN GAUSS YASASI
 2-MANYETIK ALANLAR İÇİN GAUSS YASASI Elektrik yükleri yani pozitif ve negatif yükler birbirlerinden ayrı ve izole halde düşünülebilirler. Bu durum, Kuzey ve güney manyetik kutuplar için de söz konusu olabilir
2-MANYETIK ALANLAR İÇİN GAUSS YASASI Elektrik yükleri yani pozitif ve negatif yükler birbirlerinden ayrı ve izole halde düşünülebilirler. Bu durum, Kuzey ve güney manyetik kutuplar için de söz konusu olabilir
Elektromanyetik Alan Kaynakları (1)
 (4) Elektrostatik Giriş Elektrostatik zamana bağlı olarak değişen elektrik alanlar için temel oluşturur. Pek çok elektronik cihazın çalışması elektrostatik üzerine kuruludur. Bunlara örnek olarak osiloskop,
(4) Elektrostatik Giriş Elektrostatik zamana bağlı olarak değişen elektrik alanlar için temel oluşturur. Pek çok elektronik cihazın çalışması elektrostatik üzerine kuruludur. Bunlara örnek olarak osiloskop,
Elektrostatik Elektrik Alan Elektrik Akı Kondansatör. Kaynak : Serway-Beichner Bölüm 23, 24, 26
 Elektrostatik Elektrik Alan Elektrik Akı Kondansatör Kaynak : Serway-Beichner Bölüm 23, 24, 26 İndüksiyon Nötr Maddenin indüksiyon yoluyla yüklenmesi (Bir yük türünün diğer yük türüne göre daha fazla olması)
Elektrostatik Elektrik Alan Elektrik Akı Kondansatör Kaynak : Serway-Beichner Bölüm 23, 24, 26 İndüksiyon Nötr Maddenin indüksiyon yoluyla yüklenmesi (Bir yük türünün diğer yük türüne göre daha fazla olması)
ELEKTROMANYETİK DALGALAR
 ELEKTROMANYETİK DALGALAR Hareket eden bir yük manyetik alan oluşturur. Yük sabit hızla hareket ederse, sabit bir akım ve sabit bir manyetik alan oluşturur. Yük osilasyon hareketi yaparsa değişken bir manyetik
ELEKTROMANYETİK DALGALAR Hareket eden bir yük manyetik alan oluşturur. Yük sabit hızla hareket ederse, sabit bir akım ve sabit bir manyetik alan oluşturur. Yük osilasyon hareketi yaparsa değişken bir manyetik
ELEKTROMANYETİK ALAN TEORİSİ
 ELEKTROMANYETİK ALAN TEORİSİ Hafta Konu 1 Vektör Analizi 2 Koordinat Sistemleri ve Dönüşümler 3 Elektrik Yükleri ve Alanlar 4 Elektriksel Akı ve Gauss Yasası 5 Diverjansın Fiziksel Anlamı ve Uygulamaları
ELEKTROMANYETİK ALAN TEORİSİ Hafta Konu 1 Vektör Analizi 2 Koordinat Sistemleri ve Dönüşümler 3 Elektrik Yükleri ve Alanlar 4 Elektriksel Akı ve Gauss Yasası 5 Diverjansın Fiziksel Anlamı ve Uygulamaları
A A = A 2 x + A 2 y + A 2 z (1) A A. Üç-boyutlu uzayda, iki tane vektörü kartezyen koordinatlarda dikkate alalım: A = Axˆx + A y ŷ + A z ẑ,
 Vektör Analizi(Özet) Bir vektörün büyüklüğü(boyu) Birim vektör A A = A 2 + A 2 y + A 2 z (1) A â A (2) İki vektörün skaler(nokta) çarpımı Üç-boyutlu uzayda, iki tane vektörü kartezyen koordinatlarda dikkate
Vektör Analizi(Özet) Bir vektörün büyüklüğü(boyu) Birim vektör A A = A 2 + A 2 y + A 2 z (1) A â A (2) İki vektörün skaler(nokta) çarpımı Üç-boyutlu uzayda, iki tane vektörü kartezyen koordinatlarda dikkate
Diverjans teoremi ise bir F vektörüne ait hacim ve yüzey İntegralleri arasındaki ilişkiyi ortaya koyar ve. biçiminde ifade edilir.
 Maxwell denklemlerini intagral bicimlerinin elde edilmesinde Stokes ve Diverjans Teoremlerinden yararlanilir. Stokes Teoremiaşağıdaki gibi ifade edilir, bir F vektörüne ait yüzey integrali ile çizgi integrali
Maxwell denklemlerini intagral bicimlerinin elde edilmesinde Stokes ve Diverjans Teoremlerinden yararlanilir. Stokes Teoremiaşağıdaki gibi ifade edilir, bir F vektörüne ait yüzey integrali ile çizgi integrali
Elektromanyetik Dalga Teorisi
 Elektromanyetik Dalga Teorisi Ders-2 Dalga Denkleminin Çözümü Düzlem Elektromanyetik Dalgalar Enine Elektromanyetik Dalgalar Kayıplı Ortamda Düzlem Dalgalar Düzlem Dalgaların Polarizasyonu Dalga Denkleminin
Elektromanyetik Dalga Teorisi Ders-2 Dalga Denkleminin Çözümü Düzlem Elektromanyetik Dalgalar Enine Elektromanyetik Dalgalar Kayıplı Ortamda Düzlem Dalgalar Düzlem Dalgaların Polarizasyonu Dalga Denkleminin
ELEKTROMANYETİK ALAN TEORİSİ
 ELEKTROMANYETİK ALAN TEORİSİ Hafta Konu 1 Vektör Analizi 2 Koordinat Sistemleri ve Dönüşümler 3 Elektrik Yükleri ve Alanlar 4 Elektriksel Akı ve Gauss Yasası 5 Diverjansın Fiziksel Anlamı ve Uygulamaları
ELEKTROMANYETİK ALAN TEORİSİ Hafta Konu 1 Vektör Analizi 2 Koordinat Sistemleri ve Dönüşümler 3 Elektrik Yükleri ve Alanlar 4 Elektriksel Akı ve Gauss Yasası 5 Diverjansın Fiziksel Anlamı ve Uygulamaları
EMAT ÇALIŞMA SORULARI
 EMAT ÇALIŞMA SORULARI 1) A = 4. ı x 2. ı y ı z ve B = ı x + 4. ı y 4. ı z vektörlerinin dik olduğunu gösteriniz. İki vektörün skaler çarpımlarının sıfır olması gerekir. A. B = 4.1 + ( 2). 4 + ( 1). ( 4)
EMAT ÇALIŞMA SORULARI 1) A = 4. ı x 2. ı y ı z ve B = ı x + 4. ı y 4. ı z vektörlerinin dik olduğunu gösteriniz. İki vektörün skaler çarpımlarının sıfır olması gerekir. A. B = 4.1 + ( 2). 4 + ( 1). ( 4)
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
TEMEL MEKANİK 4. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 TEMEL MEKANİK 4 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
TEMEL MEKANİK 4 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
ELEKTRİKSEL POTANSİYEL
 ELEKTRİKSEL POTANSİYEL Elektriksel Potansiyel Enerji Elektriksel potansiyel enerji kavramına geçmeden önce Fizik-1 dersinizde görmüş olduğunuz iş, potansiyel enerji ve enerjinin korunumu kavramları ile
ELEKTRİKSEL POTANSİYEL Elektriksel Potansiyel Enerji Elektriksel potansiyel enerji kavramına geçmeden önce Fizik-1 dersinizde görmüş olduğunuz iş, potansiyel enerji ve enerjinin korunumu kavramları ile
ELEKTRİK VE MANYETİZMA
 ELEKTRİK VE MANYETİZMA Prof. Dr. İlker DİNÇER Fakültesi, Fizik Mühendisliği Bölümü 1 Ders Hakkında Fizik-II Elektrik ve Manyetizma Dersinin Amacı Bu dersin amacı, fen ve mühendislik öğrencilerine elektrik
ELEKTRİK VE MANYETİZMA Prof. Dr. İlker DİNÇER Fakültesi, Fizik Mühendisliği Bölümü 1 Ders Hakkında Fizik-II Elektrik ve Manyetizma Dersinin Amacı Bu dersin amacı, fen ve mühendislik öğrencilerine elektrik
olduğundan A ve B sabitleri sınır koşullarından
 TEMEL ELEKTROT SİSTEMLERİ Eş Merkezli Küresel Elektrot Sistemi Merkezleri aynı, aralarında dielektrik madde bulunan iki küreden oluşur. Elektrik Alanı ve Potansiyel Yarıçapları ve ve elektrotlarına uygulanan
TEMEL ELEKTROT SİSTEMLERİ Eş Merkezli Küresel Elektrot Sistemi Merkezleri aynı, aralarında dielektrik madde bulunan iki küreden oluşur. Elektrik Alanı ve Potansiyel Yarıçapları ve ve elektrotlarına uygulanan
ELASTİSİTE TEORİSİ I. Yrd. Doç Dr. Eray Arslan
 ELASTİSİTE TEORİSİ I Yrd. Doç Dr. Eray Arslan Mühendislik Tasarımı Genel Senaryo Analitik çözüm Fiziksel Problem Matematiksel model Diferansiyel Denklem Problem ile ilgili sorular:... Deformasyon ne kadar
ELASTİSİTE TEORİSİ I Yrd. Doç Dr. Eray Arslan Mühendislik Tasarımı Genel Senaryo Analitik çözüm Fiziksel Problem Matematiksel model Diferansiyel Denklem Problem ile ilgili sorular:... Deformasyon ne kadar
2 Ders Kodu: FZK Ders Türü: Zorunlu 4 Ders Seviyesi Lisans
 FİZİKSEL MATEMATİK II 1 Ders Adi: FİZİKSEL MATEMATİK II 2 Ders Kodu: FZK2004 3 Ders Türü: Zorunlu 4 Ders Seviyesi Lisans 5 Dersin Verildiği Yıl: 2 6 Dersin Verildiği Yarıyıl 4 7 Dersin AKTS Kredisi: 8.00
FİZİKSEL MATEMATİK II 1 Ders Adi: FİZİKSEL MATEMATİK II 2 Ders Kodu: FZK2004 3 Ders Türü: Zorunlu 4 Ders Seviyesi Lisans 5 Dersin Verildiği Yıl: 2 6 Dersin Verildiği Yarıyıl 4 7 Dersin AKTS Kredisi: 8.00
Üç Boyutlu Uzayda Koordinat sistemi
 Üç Boyutlu Uzayda Koordinat sistemi Uzayda bir noktayı ifade edebilmek için ilk önce O noktasını (başlangıç noktası) ve bu noktadan geçen ve birbirine dik olan üç yönlü doğruyu seçerek sabitlememiz gerekir.
Üç Boyutlu Uzayda Koordinat sistemi Uzayda bir noktayı ifade edebilmek için ilk önce O noktasını (başlangıç noktası) ve bu noktadan geçen ve birbirine dik olan üç yönlü doğruyu seçerek sabitlememiz gerekir.
9.14 Burada u ile u r arasındaki açı ve v ile u θ arasındaki acının θ olduğu dikkate alınarak trigonometrik eşitliklerden; İfadeleri elde edilir.
 9.14 Burada u ile u r arasındaki açı ve v ile u θ arasındaki acının θ olduğu dikkate alınarak trigonometrik eşitliklerden; İfadeleri elde edilir. 9.15 Bu bölümde verilen koordinat dönüşümü uygulanırsa;
9.14 Burada u ile u r arasındaki açı ve v ile u θ arasındaki acının θ olduğu dikkate alınarak trigonometrik eşitliklerden; İfadeleri elde edilir. 9.15 Bu bölümde verilen koordinat dönüşümü uygulanırsa;
7. BÖLÜM İÇ ÇARPIM UZAYLARI İÇ ÇARPIM UZAYLARI İÇ ÇARPIM UZAYLARI İÇ ÇARPIM UZAYLARI .= 1 1 + + Genel: Vektörler bölümünde vektörel iç çarpım;
 İÇ ÇARPIM UZAYLARI 7. BÖLÜM İÇ ÇARPIM UZAYLARI Genel: Vektörler bölümünde vektörel iç çarpım;.= 1 1 + + Açıklanmış ve bu konu uzunluk ve uzaklık kavramlarını açıklamak için kullanılmıştır. Bu bölümde öklit
İÇ ÇARPIM UZAYLARI 7. BÖLÜM İÇ ÇARPIM UZAYLARI Genel: Vektörler bölümünde vektörel iç çarpım;.= 1 1 + + Açıklanmış ve bu konu uzunluk ve uzaklık kavramlarını açıklamak için kullanılmıştır. Bu bölümde öklit
Elektromanyetik Dalga Teorisi
 Elektromanyetik Dalga Teorisi Ders-1 Diferansiyel Formda Maxwell Denklemleri İntegral Formda Maxwell Denklemleri Fazörlerin Kullanımı Zamanda Harmonik Alanlar Malzeme Ortamı Dalga Denklemleri Michael Faraday,
Elektromanyetik Dalga Teorisi Ders-1 Diferansiyel Formda Maxwell Denklemleri İntegral Formda Maxwell Denklemleri Fazörlerin Kullanımı Zamanda Harmonik Alanlar Malzeme Ortamı Dalga Denklemleri Michael Faraday,
YÜKSEK GERİLİM TEKNİĞİNİN UYGULAMA ALANLARI
 YÜKSEK GERİLİM TEKNİĞİNİN UYGULAMA ALANLARI Yüksek gerilim tekniğinin gelişiminde olanak sağlayan en önemli etken, bu sayede büyük miktarda enerjinin bir noktadan diğerine ekonomik bir biçimde taşınabilmesidir.
YÜKSEK GERİLİM TEKNİĞİNİN UYGULAMA ALANLARI Yüksek gerilim tekniğinin gelişiminde olanak sağlayan en önemli etken, bu sayede büyük miktarda enerjinin bir noktadan diğerine ekonomik bir biçimde taşınabilmesidir.
İÇİNDEKİLER ÖNSÖZ Bölüm 1 SAYILAR 11 Bölüm 2 KÜMELER 31 Bölüm 3 FONKSİYONLAR
 İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 11 1.1. Sayı Kümeleri 12 1.1.1.Doğal Sayılar Kümesi 12 1.1.2.Tam Sayılar Kümesi 13 1.1.3.Rasyonel Sayılar Kümesi 14 1.1.4. İrrasyonel Sayılar Kümesi 16 1.1.5. Gerçel
İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 11 1.1. Sayı Kümeleri 12 1.1.1.Doğal Sayılar Kümesi 12 1.1.2.Tam Sayılar Kümesi 13 1.1.3.Rasyonel Sayılar Kümesi 14 1.1.4. İrrasyonel Sayılar Kümesi 16 1.1.5. Gerçel
Fizik II Elektrik ve Manyetizma Akım, Direnç ve Elektromotor Kuvvet
 Ders Hakkında Fizik-II Elektrik ve Manyetizma Dersinin Amacı Bu dersin amacı, fen ve mühendislik öğrencilerine elektrik ve manyetizmanın temel kanunlarını lisans düzeyinde öğretmektir. Dersin İçeriği Hafta
Ders Hakkında Fizik-II Elektrik ve Manyetizma Dersinin Amacı Bu dersin amacı, fen ve mühendislik öğrencilerine elektrik ve manyetizmanın temel kanunlarını lisans düzeyinde öğretmektir. Dersin İçeriği Hafta
DOKUZ EYLÜL ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ YAYINLARI NO: 203
 DOKUZ EYLÜL ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ YAYINLARI NO: 203 ÖNSÖZ Fakültemizin ikinci yarıyılında okutulan Matematik II dersi için hazırlanan bu kitap, Analitik Geometri kitabının devamı niteliğinde
DOKUZ EYLÜL ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ YAYINLARI NO: 203 ÖNSÖZ Fakültemizin ikinci yarıyılında okutulan Matematik II dersi için hazırlanan bu kitap, Analitik Geometri kitabının devamı niteliğinde
Ödev 1. Ödev1: 600N luk kuvveti u ve v eksenlerinde bileşenlerine ayırınız. 600 N
 Ödev 1 Ödev1: 600N luk kuvveti u ve v eksenlerinde bileşenlerine ayırınız. 600 N 1 600 N 600 N 600 N u sin120 600 N sin 30 u 1039N v sin 30 600 N sin 30 v 600N 2 Ödev 2 Ödev2: 2 kuvvetinin şiddetini, yönünü
Ödev 1 Ödev1: 600N luk kuvveti u ve v eksenlerinde bileşenlerine ayırınız. 600 N 1 600 N 600 N 600 N u sin120 600 N sin 30 u 1039N v sin 30 600 N sin 30 v 600N 2 Ödev 2 Ödev2: 2 kuvvetinin şiddetini, yönünü
FİZ217 TİTREŞİMLER VE DALGALAR DERSİNİN 2. ARA SINAV SORU CEVAPLARI
 1) Gerilmiş bir ipte enine titreşimler denklemi ile tanımlıdır. Değişkenlerine ayırma yöntemiyle çözüm yapıldığında için [ ] [ ] ifadesi verilmiştir. 1.a) İpin enine titreşimlerinin n.ci modunu tanımlayan
1) Gerilmiş bir ipte enine titreşimler denklemi ile tanımlıdır. Değişkenlerine ayırma yöntemiyle çözüm yapıldığında için [ ] [ ] ifadesi verilmiştir. 1.a) İpin enine titreşimlerinin n.ci modunu tanımlayan
TEMEL MEKANİK 5. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 TEMEL MEKANİK 5 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
TEMEL MEKANİK 5 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
Jeodezi
 1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
İnce Antenler. Hertz Dipolü
 İnce Antenler Çapları boylarına göre küçük olan antenlere ince antenler denir. Alanların hesabında antenlerin sonsuz ince kabul edilmesi kolaylık sağlar. Ancak anten empedansı bulunmak istendiğinde kalınlığın
İnce Antenler Çapları boylarına göre küçük olan antenlere ince antenler denir. Alanların hesabında antenlerin sonsuz ince kabul edilmesi kolaylık sağlar. Ancak anten empedansı bulunmak istendiğinde kalınlığın
Nokta uzayda bir konumu belirtir. Noktanın 0 boyutlu olduğu kabul edilir. Herhangi bir büyüklüğü yoktur.
 Üç Boyutlu Geometri Nokta (Point,Vertex) Nokta uzayda bir konumu belirtir. Noktanın 0 boyutlu olduğu kabul edilir. Herhangi bir büyüklüğü yoktur. Kartezyen Koordinat Sistemi Uzayda bir noktayı tanımlamak
Üç Boyutlu Geometri Nokta (Point,Vertex) Nokta uzayda bir konumu belirtir. Noktanın 0 boyutlu olduğu kabul edilir. Herhangi bir büyüklüğü yoktur. Kartezyen Koordinat Sistemi Uzayda bir noktayı tanımlamak
BİLGİ TAMAMLAMA VEKTÖRLER
 DİNAMİK BİLGİ TAMAMLAMA VEKTÖRLER Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü VEKTÖRLER Kapsam Büyüklük yanında ayrıca yön
DİNAMİK BİLGİ TAMAMLAMA VEKTÖRLER Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü VEKTÖRLER Kapsam Büyüklük yanında ayrıca yön
Parametrik doğru denklemleri 1
 Parametrik doğru denklemleri 1 A noktasından geçen, doğrultman (doğrultu) vektörü w olan d doğrusunun, k parametresine göre parametrik denklemi: AP k w P A k w P A k w P A k W (P değişken nokta) A w P
Parametrik doğru denklemleri 1 A noktasından geçen, doğrultman (doğrultu) vektörü w olan d doğrusunun, k parametresine göre parametrik denklemi: AP k w P A k w P A k w P A k W (P değişken nokta) A w P
Faraday Yasası. 31. Bölüm
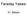 Faraday Yasası 31. Bölüm 1. Faraday İndüksiyon Yasası Faraday ve Henri: Değişen manyetik alanlar da emk (dolayısıyla akım) oluşturur. Şekilde görüldüğü gibi akım ile değişen manyetik alan arasında bir
Faraday Yasası 31. Bölüm 1. Faraday İndüksiyon Yasası Faraday ve Henri: Değişen manyetik alanlar da emk (dolayısıyla akım) oluşturur. Şekilde görüldüğü gibi akım ile değişen manyetik alan arasında bir
MANYETİK ALAN KAYNAKLARI Biot Savart Yasası
 Fiz 1012 Ders 6 MANYETİK ALAN KAYNAKLARI Biot Savart Yasası Hareket Eden Parçacığın Manyetik Alanı Akım Taşıyan İletkenin Manyetik Alanı Ampère Yasası Manyetik Akı Gauss Yasası Yerdeğiştirme Akımı (Ampère
Fiz 1012 Ders 6 MANYETİK ALAN KAYNAKLARI Biot Savart Yasası Hareket Eden Parçacığın Manyetik Alanı Akım Taşıyan İletkenin Manyetik Alanı Ampère Yasası Manyetik Akı Gauss Yasası Yerdeğiştirme Akımı (Ampère
Fizik Dr. Murat Aydemir
 Fizik-1 2017-2018 Dr. Murat Aydemir Ankara University, Physics Engineering, Bsc Durham University, Physics, PhD University of Oxford, Researcher, Post-Doc Ofis No: 35 Merkezi Derslikler Binasi murat.aydemir@erzurum.edu.tr
Fizik-1 2017-2018 Dr. Murat Aydemir Ankara University, Physics Engineering, Bsc Durham University, Physics, PhD University of Oxford, Researcher, Post-Doc Ofis No: 35 Merkezi Derslikler Binasi murat.aydemir@erzurum.edu.tr
FİZ 216 ELEKTRİK ve MANYETİZMA GRADİYENT DİVERJANS ROTASYONEL (KÖRL) HELMHOLTZ TEOREMİ KOORDİNAT SİSTEMLERİ
 FİZ 216 ELEKTRİK ve MANYETİZMA GRADİYENT DİVERJANS ROTASYONEL (KÖRL) HELMHOLTZ TEOREMİ KOORDİNAT SİSTEMLERİ (del) operatörü, Bir f skaler alanına etkirse: f GRADİYENT Bir A vektör alanı ile skaler çarpılırsa:
FİZ 216 ELEKTRİK ve MANYETİZMA GRADİYENT DİVERJANS ROTASYONEL (KÖRL) HELMHOLTZ TEOREMİ KOORDİNAT SİSTEMLERİ (del) operatörü, Bir f skaler alanına etkirse: f GRADİYENT Bir A vektör alanı ile skaler çarpılırsa:
8.Konu Vektör uzayları, Alt Uzaylar
 8.Konu Vektör uzayları, Alt Uzaylar 8.1. Düzlemde vektörler Düzlemdeki her noktası ile reel sayılardan oluşan ikilisini eşleştirebiliriz. Buna P noktanın koordinatları denir. y-ekseni P x y O dan P ye
8.Konu Vektör uzayları, Alt Uzaylar 8.1. Düzlemde vektörler Düzlemdeki her noktası ile reel sayılardan oluşan ikilisini eşleştirebiliriz. Buna P noktanın koordinatları denir. y-ekseni P x y O dan P ye
Fizik 102-Fizik II /II
 1 -Fizik II 2010-2011/II Gauss Yasası Nurdan Demirci Sankır Ofis: 325, Tel: 2924331 Kaynaklar: Giancoli, Physics, Principles With Applications, Prentice Hall Serway, Beichner, Fen ve Mühendislik için Fizik
1 -Fizik II 2010-2011/II Gauss Yasası Nurdan Demirci Sankır Ofis: 325, Tel: 2924331 Kaynaklar: Giancoli, Physics, Principles With Applications, Prentice Hall Serway, Beichner, Fen ve Mühendislik için Fizik
Karabük Üniversitesi, Mühendislik Fakültesi...www.IbrahimCayiroglu.com. STATİK (2. Hafta)
 AĞIRLIK MERKEZİ STATİK (2. Hafta) Ağırlık merkezi: Bir cismi oluşturan herbir parçaya etki eden yerçeki kuvvetlerinin bileşkesinin cismin üzerinden geçtiği noktaya Ağırlık Merkezi denir. Şekil. Ağırlık
AĞIRLIK MERKEZİ STATİK (2. Hafta) Ağırlık merkezi: Bir cismi oluşturan herbir parçaya etki eden yerçeki kuvvetlerinin bileşkesinin cismin üzerinden geçtiği noktaya Ağırlık Merkezi denir. Şekil. Ağırlık
MIT 8.02, Bahar 2002 Ödev # 1 Çözümler
 Adam S. Bolton bolton@mit.edu MIT 8.02, Bahar 2002 Ödev # 1 Çözümler 15 Şubat 2002 Problem 1.1 Kütleçekim ve Elektrostatik kuvvetlerin bağıl şiddetleri. Toz parçacıkları 50 µm çapında ve böylece yarıçapları
Adam S. Bolton bolton@mit.edu MIT 8.02, Bahar 2002 Ödev # 1 Çözümler 15 Şubat 2002 Problem 1.1 Kütleçekim ve Elektrostatik kuvvetlerin bağıl şiddetleri. Toz parçacıkları 50 µm çapında ve böylece yarıçapları
Konik Kesitler ve Formülleri
 Konik Kesitler ve Formülleri Konik Kesitler ve Formülleri B 1 (0, b) P (x, y) A 2 ( a, 0) F 2 ( c, 0) F 1 (c, 0) A 1 (a, 0) B 2 (0, b) Şekil 1: Elips x2 a 2 + y2 b 2 = 1. Konik Kesitler ve Formülleri B
Konik Kesitler ve Formülleri Konik Kesitler ve Formülleri B 1 (0, b) P (x, y) A 2 ( a, 0) F 2 ( c, 0) F 1 (c, 0) A 1 (a, 0) B 2 (0, b) Şekil 1: Elips x2 a 2 + y2 b 2 = 1. Konik Kesitler ve Formülleri B
MEKANİZMA TEKNİĞİ (3. Hafta)
 MEKANİZMALARIN KİNEMATİK ANALİZİ Temel Kavramlar MEKANİZMA TEKNİĞİ (3. Hafta) Bir mekanizmanın Kinematik Analizinden bahsettiğimizde, onun üzerindeki tüm uzuvların yada istenilen herhangi bir noktanın
MEKANİZMALARIN KİNEMATİK ANALİZİ Temel Kavramlar MEKANİZMA TEKNİĞİ (3. Hafta) Bir mekanizmanın Kinematik Analizinden bahsettiğimizde, onun üzerindeki tüm uzuvların yada istenilen herhangi bir noktanın
Noktasal Cismin Dengesi
 Noktasal Cismin Dengesi Bu bölümde; Kuvvetleri bieşenlerine ayırma ve kartezyen vektör şeklinde ifade etme yöntemleri noktasal cismin dengesini içeren problemleri çözmede kullanılacaktır. Bölüm 3 DOÇ.DR.
Noktasal Cismin Dengesi Bu bölümde; Kuvvetleri bieşenlerine ayırma ve kartezyen vektör şeklinde ifade etme yöntemleri noktasal cismin dengesini içeren problemleri çözmede kullanılacaktır. Bölüm 3 DOÇ.DR.
KARABÜK ÜNİVERSİTESİ Öğretim Üyesi: Doç.Dr. Tamila ANUTGAN
 KARABÜK ÜNİVERSİTESİ Öğretim Üyesi: Doç.Dr. Tamila ANUTGAN 1 2 3 4 5 6 7 8 Örnek: Bir disk boyunca elektrik akısı r = 0.10 m A 30 E 3 210 N/C A (0.10 m) E 54 N m 2 2 0.0314 m EA cos (2.010 / C Örnek: Bir
KARABÜK ÜNİVERSİTESİ Öğretim Üyesi: Doç.Dr. Tamila ANUTGAN 1 2 3 4 5 6 7 8 Örnek: Bir disk boyunca elektrik akısı r = 0.10 m A 30 E 3 210 N/C A (0.10 m) E 54 N m 2 2 0.0314 m EA cos (2.010 / C Örnek: Bir
3-1 Koordinat Sistemleri Bir cismin konumunu tanımlamak için bir yönteme gereksinim duyarız. Bu konum tanımlaması koordinat kullanımı ile sağlanır.
 Bölüm 3 VEKTÖRLER Bölüm 3: Vektörler Konu İçeriği Sunuş 3-1 Koordinat Sistemleri 3-2 Vektör ve Skaler nicelikler 3-3 Vektörlerin Bazı Özellikleri 3-4 Bir Vektörün Bileşenleri ve Birim Vektörler Sunuş Fizikte
Bölüm 3 VEKTÖRLER Bölüm 3: Vektörler Konu İçeriği Sunuş 3-1 Koordinat Sistemleri 3-2 Vektör ve Skaler nicelikler 3-3 Vektörlerin Bazı Özellikleri 3-4 Bir Vektörün Bileşenleri ve Birim Vektörler Sunuş Fizikte
Giriş Bir çok mekanik problemi Newton yasaları ile çözülebilir, ancak bu teknik bazı problemlerin çözümünde yetersiz kalabilir yada çok zor bir yaklaş
 Bölüm 7 Enerji Giriş Bir çok mekanik problemi Newton yasaları ile çözülebilir, ancak bu teknik bazı problemlerin çözümünde yetersiz kalabilir yada çok zor bir yaklaşım halide gelebilir. Bu tür problemlerin
Bölüm 7 Enerji Giriş Bir çok mekanik problemi Newton yasaları ile çözülebilir, ancak bu teknik bazı problemlerin çözümünde yetersiz kalabilir yada çok zor bir yaklaşım halide gelebilir. Bu tür problemlerin
Hareket halindeki elektrik yüklerinin oluşturduğu bir sistem düşünelim. Belirli bir bölgede net bir yük akışı olduğunda, akımın mevcut olduğu
 Akım ve Direnç Elektriksel olaylarla ilgili buraya kadar yaptığımız tartışmalar durgun yüklerle veya elektrostatikle sınırlı kalmıştır. Şimdi, elektrik yüklerinin hareket halinde olduğu durumları inceleyeceğiz.
Akım ve Direnç Elektriksel olaylarla ilgili buraya kadar yaptığımız tartışmalar durgun yüklerle veya elektrostatikle sınırlı kalmıştır. Şimdi, elektrik yüklerinin hareket halinde olduğu durumları inceleyeceğiz.
STATIK VE MUKAVEMET 4. Ağırlık Merkezi. Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ
 STATIK VE MUKAVEMET 4. Ağırlık Merkezi Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ AĞIRLIK MERKEZİ Gerçekte yükler yayılı olup, tekil yük problemlerin çözümünü kolaylaştıran bir idealleştirmedir. Statikte çok küçük
STATIK VE MUKAVEMET 4. Ağırlık Merkezi Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ AĞIRLIK MERKEZİ Gerçekte yükler yayılı olup, tekil yük problemlerin çözümünü kolaylaştıran bir idealleştirmedir. Statikte çok küçük
Bölüm 3: Vektörler. Kavrama Soruları. Konu İçeriği. Sunuş. 3-1 Koordinat Sistemleri
 ölüm 3: Vektörler Kavrama Soruları 1- Neden vektörlere ihtiyaç duyarız? - Vektör ve skaler arasındaki fark nedir? 3- Neden vektörel bölme işlemi yapılamaz? 4- π sayısı vektörel mi yoksa skaler bir nicelik
ölüm 3: Vektörler Kavrama Soruları 1- Neden vektörlere ihtiyaç duyarız? - Vektör ve skaler arasındaki fark nedir? 3- Neden vektörel bölme işlemi yapılamaz? 4- π sayısı vektörel mi yoksa skaler bir nicelik
3. V, R 3 ün açık bir altkümesi olmak üzere, c R. p noktasında yüzeye dik olduğunu gösteriniz.(10
 Diferenisyel Geometri 2 Yazokulu 2010 AdıSoyadı: No : 1. ϕ (u, v) = ( u + 2v, v + 2u, u 2 v ) parametrizasyonu ile verilen M kümesinin bir regüler yüzey olduğunu gösteriniz. (15 puan) 3. V, R 3 ün açık
Diferenisyel Geometri 2 Yazokulu 2010 AdıSoyadı: No : 1. ϕ (u, v) = ( u + 2v, v + 2u, u 2 v ) parametrizasyonu ile verilen M kümesinin bir regüler yüzey olduğunu gösteriniz. (15 puan) 3. V, R 3 ün açık
Doç.Dr. Cesim ATAŞ MEKANİK ŞEKİL DEĞİŞTİREN CİSİMLER MEKANİĞİ DİNAMİK
 STATİK (Ders Notları) Kaynak: Engineering Mechanics: Statics, SI Version, 6th Edition, J. L. Meriam, L. G. Kraige, Wiley Yardımcı Kaynak: Mühendislik Mekaniği: Statik, R.C Hibbeler & S.C. Fan, Literatür
STATİK (Ders Notları) Kaynak: Engineering Mechanics: Statics, SI Version, 6th Edition, J. L. Meriam, L. G. Kraige, Wiley Yardımcı Kaynak: Mühendislik Mekaniği: Statik, R.C Hibbeler & S.C. Fan, Literatür
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve Çözümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLE 1. GİİŞ - Skalerler ve ektörler - Newton Kanunları 2. KUET SİSTEMLEİ - İki Boyutlu
Statik Ders Notları Sınav Soru ve Çözümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLE 1. GİİŞ - Skalerler ve ektörler - Newton Kanunları 2. KUET SİSTEMLEİ - İki Boyutlu
DİNAMİK - 1. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 DİNAMİK - 1 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü http://acikders.ankara.edu.tr/course/view.php?id=190 1. HAFTA Kapsam:
DİNAMİK - 1 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü http://acikders.ankara.edu.tr/course/view.php?id=190 1. HAFTA Kapsam:
Mimar Sinan Güzel Sanatlar Üniversitesi, Fizik Bölümü Fizik II Dersi Birinci Ara Sınavı
 Mimar Sinan Güzel Sanatlar Üniversitesi, Fizik Bölümü Fizik II Dersi Birinci Ara Sınavı 27 Mart 2010 Hazırlayan: Yamaç Pehlivan Başlama saati: 11:00 Bitiş Saati: 12:20 Toplam Süre: 80 Dakika Lütfen adınızı
Mimar Sinan Güzel Sanatlar Üniversitesi, Fizik Bölümü Fizik II Dersi Birinci Ara Sınavı 27 Mart 2010 Hazırlayan: Yamaç Pehlivan Başlama saati: 11:00 Bitiş Saati: 12:20 Toplam Süre: 80 Dakika Lütfen adınızı
Üç Boyutlu Uzayda Koordinat sistemi
 Üç Boyutlu Uzayda Koordinat sistemi Uzayda bir noktayı ifade edebilmek için ilk önce O noktasını (başlangıç noktası) ve bu noktadan geçen ve birbirine dik olan üç yönlü doğruyu seçerek sabitlememiz gerekir.
Üç Boyutlu Uzayda Koordinat sistemi Uzayda bir noktayı ifade edebilmek için ilk önce O noktasını (başlangıç noktası) ve bu noktadan geçen ve birbirine dik olan üç yönlü doğruyu seçerek sabitlememiz gerekir.
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ
 BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
Statik Manyetik Alan
 Statik Manyetik Alan Amper Kanunu Manyetik Vektör Potansiyeli Maxwell in diverjans eşitliği Endüktans 1 Amper Kanununun İntegral Formu 2 Amper Kanununun İntegral Formu z- ekseni boyunca uzanan çok uzun
Statik Manyetik Alan Amper Kanunu Manyetik Vektör Potansiyeli Maxwell in diverjans eşitliği Endüktans 1 Amper Kanununun İntegral Formu 2 Amper Kanununun İntegral Formu z- ekseni boyunca uzanan çok uzun
1. STATİĞE GİRİŞ 1.1 TANIMLAR MEKANİK RİJİT CİSİMLER MEKANİĞİ ŞEKİL DEĞİŞTİREN CİSİMLER AKIŞKANLAR MEKANİĞİ DİNAMİK STATİK
 STATİK Ders Notları Kaynaklar: 1.Engineering Mechanics: Statics, 9e, Hibbeler, Prentice Hall 2.Engineering Mechanics: Statics, SI Version, 6th Edition, J. L. Meriam, L. G. Kraige 1. STATİĞE GİRİŞ 1.1 TANIMLAR
STATİK Ders Notları Kaynaklar: 1.Engineering Mechanics: Statics, 9e, Hibbeler, Prentice Hall 2.Engineering Mechanics: Statics, SI Version, 6th Edition, J. L. Meriam, L. G. Kraige 1. STATİĞE GİRİŞ 1.1 TANIMLAR
Manyetik Alan Şiddeti ve Ampere Devre Yasası
 Manyetik Alan Şiddeti ve Ampere Devre Yasası Elektrik alanlar için elektrik akı yoğunluğunu, elektrik alan şiddeti cinsinden tanımlamıştık. Buna benzer şekilde manyetik alan şiddetiyle manyetik akı yoğunluğu
Manyetik Alan Şiddeti ve Ampere Devre Yasası Elektrik alanlar için elektrik akı yoğunluğunu, elektrik alan şiddeti cinsinden tanımlamıştık. Buna benzer şekilde manyetik alan şiddetiyle manyetik akı yoğunluğu
SIĞA VE DİELEKTRİKLER
 SIĞA VE DİELEKTRİKLER Birbirlerinden bir boşluk veya bir yalıtkanla ayrılmış iki eşit büyüklükte fakat zıt işaretli yük taşıyan iletkenlerin oluşturduğu yapıya kondansatör adı verilirken her bir iletken
SIĞA VE DİELEKTRİKLER Birbirlerinden bir boşluk veya bir yalıtkanla ayrılmış iki eşit büyüklükte fakat zıt işaretli yük taşıyan iletkenlerin oluşturduğu yapıya kondansatör adı verilirken her bir iletken
Lineer Dönüşümler ÜNİTE. Amaçlar. İçindekiler. Yazar Öğr. Grv.Dr. Nevin ORHUN
 Lineer Dönüşümler Yazar Öğr. Grv.Dr. Nevin ORHUN ÜNİTE 7 Amaçlar Bu üniteyi çalıştıktan sonra; Vektör uzayları arasında tanımlanan belli fonksiyonları tanıyacak, özelliklerini öğrenecek, Bir dönüşümün,
Lineer Dönüşümler Yazar Öğr. Grv.Dr. Nevin ORHUN ÜNİTE 7 Amaçlar Bu üniteyi çalıştıktan sonra; Vektör uzayları arasında tanımlanan belli fonksiyonları tanıyacak, özelliklerini öğrenecek, Bir dönüşümün,
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 3 Parçacık Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 3 Parçacık Dengesi Bu bölümde,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 3 Parçacık Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 3 Parçacık Dengesi Bu bölümde,
Manyetik Alanlar. Benzer bir durum hareketli yükler içinde geçerli olup bu yüklerin etrafını elektrik alana ek olarak bir manyetik alan sarmaktadır.
 Manyetik Alanlar Manyetik Alanlar Duran ya da hareket eden yüklü parçacığın etrafını bir elektrik alanın sardığı biliyoruz. Hatta elektrik alan konusunda şu sonuç oraya konulmuştur. Durgun bir deneme yükü
Manyetik Alanlar Manyetik Alanlar Duran ya da hareket eden yüklü parçacığın etrafını bir elektrik alanın sardığı biliyoruz. Hatta elektrik alan konusunda şu sonuç oraya konulmuştur. Durgun bir deneme yükü
Kaynaklar Shepley L. Ross, Differential Equations (3rd Edition), 1984.
 Çankırı Karatekin Üniversitesi Matematik Bölümü 2015 Kaynaklar Shepley L. Ross, Differential Equations (3rd Edition), 1984. (Adi ) Bir ya da daha fazla bağımsız değişkenden oluşan bağımlı değişken ve türevlerini
Çankırı Karatekin Üniversitesi Matematik Bölümü 2015 Kaynaklar Shepley L. Ross, Differential Equations (3rd Edition), 1984. (Adi ) Bir ya da daha fazla bağımsız değişkenden oluşan bağımlı değişken ve türevlerini
Tanımlar, Geometrik ve Matemetiksel Temeller. Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ. JDF329 Fotogrametri I Ders Notu
 FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İzdüşüm merkezi(o):
FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İzdüşüm merkezi(o):
ELEKTRİK VE MANYETİZMA
 ELEKTRİK VE MANYETİZMA Prof. Dr. İlker DİNÇER Fakültesi, Fizik Mühendisliği Bölümü 1 Ders Hakkında FizikII Elektrik ve Manyetizma Dersinin Amacı Bu dersin amacı, fen ve mühendislik öğrencilerine elektrik
ELEKTRİK VE MANYETİZMA Prof. Dr. İlker DİNÇER Fakültesi, Fizik Mühendisliği Bölümü 1 Ders Hakkında FizikII Elektrik ve Manyetizma Dersinin Amacı Bu dersin amacı, fen ve mühendislik öğrencilerine elektrik
AKDENİZ ÜNİVERSİTESİ. Anten Parametrelerinin Temelleri. Samet YALÇIN
 AKDENİZ ÜNİVERSİTESİ Anten Parametrelerinin Temelleri Samet YALÇIN Anten Parametrelerinin Temelleri GİRİŞ: Bir antenin parametrelerini tanımlayabilmek için anten parametreleri gereklidir. Anten performansından
AKDENİZ ÜNİVERSİTESİ Anten Parametrelerinin Temelleri Samet YALÇIN Anten Parametrelerinin Temelleri GİRİŞ: Bir antenin parametrelerini tanımlayabilmek için anten parametreleri gereklidir. Anten performansından
Chapter 1 İçindekiler
 Chapter 1 İçindekiler Kendinizi Test Edin iii 10 Birinci Mertebeden Diferansiel Denklemler 565 10.1 Arılabilir Denklemler 566 10. Lineer Denklemler 571 10.3 Matematiksel Modeller 576 10.4 Çözümü Olmaan
Chapter 1 İçindekiler Kendinizi Test Edin iii 10 Birinci Mertebeden Diferansiel Denklemler 565 10.1 Arılabilir Denklemler 566 10. Lineer Denklemler 571 10.3 Matematiksel Modeller 576 10.4 Çözümü Olmaan
Fizik II Elektrik ve Manyetizma Elektriksel Potansiyel
 Ders Hakkında FizikII Elektrik ve Manyetizma Dersinin Amacı Bu dersin amacı, fen ve mühendislik öğrencilerine elektrik ve manyetizmanın temel kanunlarını lisans düzeyinde öğretmektir. Dersin İçeriği Hafta
Ders Hakkında FizikII Elektrik ve Manyetizma Dersinin Amacı Bu dersin amacı, fen ve mühendislik öğrencilerine elektrik ve manyetizmanın temel kanunlarını lisans düzeyinde öğretmektir. Dersin İçeriği Hafta
Gerçekte yükler yayılı olup, tekil yük problemlerin çözümünü kolaylaştıran bir idealleştirmedir.
 STATIK VE MUKAVEMET 4. Ağırlık Merkezi AĞIRLIK MERKEZİ Gerçekte yükler yayılı olup, tekil yük problemlerin çözümünü kolaylaştıran bir idealleştirmedir. Statikte çok küçük bir alana etki eden birbirlerine
STATIK VE MUKAVEMET 4. Ağırlık Merkezi AĞIRLIK MERKEZİ Gerçekte yükler yayılı olup, tekil yük problemlerin çözümünü kolaylaştıran bir idealleştirmedir. Statikte çok küçük bir alana etki eden birbirlerine
Ankara Üniversitesi Fen Fakültesi Matematik Bölümü A-Grubu Bahar Yarıyılı Bölüm-III Özeti Ankara Aysuhan Ozansoy
 FİZ12 FİZİK-II Ankara Üniversitesi Fen Fakültesi Matematik Bölümü A-Grubu 217-218 Bahar Yarıyılı Bölüm-III Özeti 6.3.217 Ankara Aysuhan Ozansoy «When I have clarified and exhausted a subject, then I turn
FİZ12 FİZİK-II Ankara Üniversitesi Fen Fakültesi Matematik Bölümü A-Grubu 217-218 Bahar Yarıyılı Bölüm-III Özeti 6.3.217 Ankara Aysuhan Ozansoy «When I have clarified and exhausted a subject, then I turn
18.034 İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Math 322 Diferensiyel Denklemler Ders Notları 2012
 1 Genel Tanımlar Bir veya birden fazla fonksiyonun türevlerini içeren denklemlere diferensiyel denklem denmektedir. Diferensiyel denklemler Adi (Sıradan) diferensiyel denklemler ve Kısmi diferensiyel denklemler
1 Genel Tanımlar Bir veya birden fazla fonksiyonun türevlerini içeren denklemlere diferensiyel denklem denmektedir. Diferensiyel denklemler Adi (Sıradan) diferensiyel denklemler ve Kısmi diferensiyel denklemler
Bölüm-4. İki Boyutta Hareket
 Bölüm-4 İki Boyutta Hareket Bölüm 4: İki Boyutta Hareket Konu İçeriği 4-1 Yer değiştirme, Hız ve İvme Vektörleri 4-2 Sabit İvmeli İki Boyutlu Hareket 4-3 Eğik Atış Hareketi 4-4 Bağıl Hız ve Bağıl İvme
Bölüm-4 İki Boyutta Hareket Bölüm 4: İki Boyutta Hareket Konu İçeriği 4-1 Yer değiştirme, Hız ve İvme Vektörleri 4-2 Sabit İvmeli İki Boyutlu Hareket 4-3 Eğik Atış Hareketi 4-4 Bağıl Hız ve Bağıl İvme
FİZ 216 ELEKTRİK ve MANYETİZMA GRADİYENT DİVERJANS ROTASYONEL (KÖRL) KOORDİNAT SİSTEMLERİ HELMHOLTZ TEOREMİ
 FİZ 216 ELEKTRİK ve MANYETİZMA GRADİYENT DİVERJANS ROTASYONEL (KÖRL) KOORDİNAT SİSTEMLERİ HELMHOLTZ TEOREMİ GRADİYENT: f(,y,z) her noktada sürekli ve türevlenebilir bir skaler alan olsun. Herhangi bir
FİZ 216 ELEKTRİK ve MANYETİZMA GRADİYENT DİVERJANS ROTASYONEL (KÖRL) KOORDİNAT SİSTEMLERİ HELMHOLTZ TEOREMİ GRADİYENT: f(,y,z) her noktada sürekli ve türevlenebilir bir skaler alan olsun. Herhangi bir
EŞ POTANSİYEL VE ELEKTRİK ALAN ÇİZGİLERİ. 1. Zıt yükle yüklenmiş iki iletkenin oluşturduğu eş potansiyel çizgileri araştırıp bulmak.
 EŞ POTANSİYEL VE ELEKTRİK ALAN ÇİZGİLERİ AMAÇ: 1. Zıt yükle yüklenmiş iki iletkenin oluşturduğu eş potansiyel çizgileri araştırıp bulmak. 2. Bu eş potansiyel çizgileri kullanarak elektrik alan çizgilerinin
EŞ POTANSİYEL VE ELEKTRİK ALAN ÇİZGİLERİ AMAÇ: 1. Zıt yükle yüklenmiş iki iletkenin oluşturduğu eş potansiyel çizgileri araştırıp bulmak. 2. Bu eş potansiyel çizgileri kullanarak elektrik alan çizgilerinin
MIT 8.02, Bahar 2002 Ödev # 2 Çözümler
 Adam S. Bolton bolton@mit.edu MIT 8.02, Bahar 2002 Ödev # 2 Çözümler 22 Şubat 2002 Problem 2.1 İçi boş bir metalik küre içerisindeki bir noktasal yükün elektrik alanı - Gauss Yasası İş Başında Bu problemi
Adam S. Bolton bolton@mit.edu MIT 8.02, Bahar 2002 Ödev # 2 Çözümler 22 Şubat 2002 Problem 2.1 İçi boş bir metalik küre içerisindeki bir noktasal yükün elektrik alanı - Gauss Yasası İş Başında Bu problemi
Matematiksel Analiz III (MATH 235) Ders Detayları
 Matematiksel Analiz III (MATH 235) Ders Detayları Ders Adı Matematiksel Analiz III Ders Kodu MATH 235 Dönemi Ders Uygulama Saati Saati Laboratuar Kredi AKTS Saati Güz 4 2 0 5 8 Ön Koşul Ders(ler)i Math
Matematiksel Analiz III (MATH 235) Ders Detayları Ders Adı Matematiksel Analiz III Ders Kodu MATH 235 Dönemi Ders Uygulama Saati Saati Laboratuar Kredi AKTS Saati Güz 4 2 0 5 8 Ön Koşul Ders(ler)i Math
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
ELEKTROMANYETIK DALGALAR
 ELEKTROMANYETIK DALGALAR EEM 10/1/2018 AG 1 kaynaklar: 1) Muhendislikelektromenyetiginin temelleri, David K. Cheng, Palme Yayincilik 2) Electromagnetic Field Theory Fundamentals, Guru&Hiziroglu 3) A Student
ELEKTROMANYETIK DALGALAR EEM 10/1/2018 AG 1 kaynaklar: 1) Muhendislikelektromenyetiginin temelleri, David K. Cheng, Palme Yayincilik 2) Electromagnetic Field Theory Fundamentals, Guru&Hiziroglu 3) A Student
DENİZ HARP OKULU TEMEL BİLİMLER BÖLÜM BAŞKANLIĞI DERS TANITIM BİLGİLERİ
 DENİZ HARP OKULU TEMEL BİLİMLER BÖLÜM BAŞKANLIĞI DERS TANITIM BİLGİLERİ Dersin Adı Kodu Sınıf/Y.Y. Ders Saati (T+U+L) Kredi AKTS MATEMATİK-II FEB-121 1/ 2. YY 5+0+0 5 5 Dersin Dili Dersin Seviyesi : Türkçe
DENİZ HARP OKULU TEMEL BİLİMLER BÖLÜM BAŞKANLIĞI DERS TANITIM BİLGİLERİ Dersin Adı Kodu Sınıf/Y.Y. Ders Saati (T+U+L) Kredi AKTS MATEMATİK-II FEB-121 1/ 2. YY 5+0+0 5 5 Dersin Dili Dersin Seviyesi : Türkçe
DOKUZ EYLÜL ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ DEKANLIĞI DERS/MODÜL/BLOK TANITIM FORMU MATEMATİK II. Dersin Kodu: MAT 1010
 Dersi Veren Birim: Mühendislik Fakültesi Dersin Adı: MATEMATİK II Dersin Düzeyi:(Ön lisans, Lisans, Yüksek Lisans, Doktora) Lisans Dersin Kodu: MAT 1010 Dersin Öğretim Dili: Türkçe Formun Düzenleme / Yenilenme
Dersi Veren Birim: Mühendislik Fakültesi Dersin Adı: MATEMATİK II Dersin Düzeyi:(Ön lisans, Lisans, Yüksek Lisans, Doktora) Lisans Dersin Kodu: MAT 1010 Dersin Öğretim Dili: Türkçe Formun Düzenleme / Yenilenme
Mühendislik Mekaniği Dinamik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 13 Parçacık Kinetiği: Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 13 Parçacık
Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 13 Parçacık Kinetiği: Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 13 Parçacık
1. Hafta Uygulama Soruları
 . Hafta Uygulama Soruları ) x ekseni, x = doğrusu, y = x ve y = x + eğrileri arasında kalan alan nedir? ) y = x 3 ve y = 4 x 3 parabolleri arasında kalan alan nedir? 3) y = x, x y = 4 eğrileri arasında
. Hafta Uygulama Soruları ) x ekseni, x = doğrusu, y = x ve y = x + eğrileri arasında kalan alan nedir? ) y = x 3 ve y = 4 x 3 parabolleri arasında kalan alan nedir? 3) y = x, x y = 4 eğrileri arasında
Buna göre, eşitliği yazılabilir. sayılara rasyonel sayılar denir ve Q ile gösterilir. , -, 2 2 = 1. sayıdır. 2, 3, 5 birer irrasyonel sayıdır.
 TEMEL KAVRAMLAR RAKAM Bir çokluk belirtmek için kullanılan sembollere rakam denir. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembolleri birer rakamdır. 2. TAMSAYILAR KÜMESİ Z = {..., -3, -2, -1, 0, 1, 2, 3, 4,... }
TEMEL KAVRAMLAR RAKAM Bir çokluk belirtmek için kullanılan sembollere rakam denir. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembolleri birer rakamdır. 2. TAMSAYILAR KÜMESİ Z = {..., -3, -2, -1, 0, 1, 2, 3, 4,... }
İÇİNDEKİLER xiii İÇİNDEKİLER LİSTESİ BÖLÜM 1 ELEKTRİK YÜKÜ 1.1. ELEKTRİK YÜKÜ VE ÖZELLİKLERİ YALITKANLAR VE İLETKENLER...
 İÇİNDEKİLER xiii İÇİNDEKİLER LİSTESİ BÖLÜM 1 ELEKTRİK YÜKÜ 1.1. ELEKTRİK YÜKÜ VE ÖZELLİKLERİ... 2 1.2. YALITKANLAR VE İLETKENLER... 4 1.2.1. İletkenler, Yalıtkanlar ve Yarıiletkenler... 4 1.2.2. Topraklanma...
İÇİNDEKİLER xiii İÇİNDEKİLER LİSTESİ BÖLÜM 1 ELEKTRİK YÜKÜ 1.1. ELEKTRİK YÜKÜ VE ÖZELLİKLERİ... 2 1.2. YALITKANLAR VE İLETKENLER... 4 1.2.1. İletkenler, Yalıtkanlar ve Yarıiletkenler... 4 1.2.2. Topraklanma...
STATİK AĞIRLIK MERKEZİ. 3.1 İki Boyutlu Cisimler 3.2 Düzlem Eğriler 3.3 Bileşik Cisimler. 3.4 Integrasyon ile ağırlık merkezi hesabı
 1 STATİK AĞIRLIK MERKEZİ 3.1 İki Boyutlu Cisimler 3.2 Düzlem Eğriler 3.3 Bileşik Cisimler 3.4 Integrasyon ile ağırlık merkezi hesabı 3.5 Pappus-Guldinus Teoremi 3.6 Yayılı Yüke Eşdeğer Tekil Yük 3.7 Sıvı
1 STATİK AĞIRLIK MERKEZİ 3.1 İki Boyutlu Cisimler 3.2 Düzlem Eğriler 3.3 Bileşik Cisimler 3.4 Integrasyon ile ağırlık merkezi hesabı 3.5 Pappus-Guldinus Teoremi 3.6 Yayılı Yüke Eşdeğer Tekil Yük 3.7 Sıvı
DOKUZ EYLÜL ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ DEKANLIĞI DERS/MODÜL/BLOK TANITIM FORMU. Dersin Kodu: MAT 1010
 Dersi Veren Birim: Mühendislik Fakültesi Dersin Türkçe Adı: MATEMATİK II Dersin Orjinal Adı: MATEMATİK II Dersin Düzeyi:(Ön lisans, Lisans, Yüksek Lisans, Doktora) Lisans Dersin Kodu: MAT 1010 Dersin Öğretim
Dersi Veren Birim: Mühendislik Fakültesi Dersin Türkçe Adı: MATEMATİK II Dersin Orjinal Adı: MATEMATİK II Dersin Düzeyi:(Ön lisans, Lisans, Yüksek Lisans, Doktora) Lisans Dersin Kodu: MAT 1010 Dersin Öğretim
DİNAMİK Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi. Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 DİNAMİK - 11 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü 11. HAFTA Kapsam: İmpuls Momentum yöntemi İmpuls ve momentum ilkesi
DİNAMİK - 11 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü 11. HAFTA Kapsam: İmpuls Momentum yöntemi İmpuls ve momentum ilkesi
EĞİTİM-ÖĞRETİM YILI 12. SINIF İLERİ DÜZEL MATEMATİK DERSİ DESTEKLEME VE YETİŞTİRME KURSU KAZANIMLARI VE TESTLERİ
 KASIM EKİM 2017-2018 EĞİTİM-ÖĞRETİM YILI 12. SINIF İLERİ DÜZEL MATEMATİK DERSİ DESTEKLEME VE YETİŞTİRME KURSU KAZANIMLARI VE TESTLERİ 1 4 TÜREV 12.1.1.1. Bir fonksiyonun bir noktadaki limiti, soldan limiti
KASIM EKİM 2017-2018 EĞİTİM-ÖĞRETİM YILI 12. SINIF İLERİ DÜZEL MATEMATİK DERSİ DESTEKLEME VE YETİŞTİRME KURSU KAZANIMLARI VE TESTLERİ 1 4 TÜREV 12.1.1.1. Bir fonksiyonun bir noktadaki limiti, soldan limiti
