Ayrıca tez çalışmalarım boyunca manevi desteğini benden esirgemeyen aileme de şükranlarımı sunarım.
|
|
|
- Sanaz Ayla Keskin
- 8 yıl önce
- İzleme sayısı:
Transkript
1 ÖNSÖZ Tez çalışmalarım boyunca gösterdiği her türlü destek ve yardımdan dolayı değerli hocalarım Prof.Dr. Aydın AKAN ve Prof.Dr. Tamer DEMİRALP e en içten dileklerimle teşekkür ederim. EEG kayıtlarının alınmasına olanak sağlayan İstanbul Tıp Fakültesi Anesteziyoloji AD üyesi Doç.Dr. Tülay Seyhan ÖZKAN a, Fizyoloji AD çalışanları Dr. Zübeyir BAYRAKTAROĞLU, Dr. Atilla USLU, Dr. Ezgi T. ERDOĞAN ve Psk. Itır KAŞIKÇI ya da teşekkürü borç bilirim. Doktora öğrenciliğimle birlikte başladığım TC Istanbul Kültür Üniversitesi ndeki görevim vesilesi ile beraber çalışma fırsatı bulduğum değerli hocalarıma ve çalışma arkadaşlarıma teşekkür ederim. Ayrıca tez çalışmalarım boyunca manevi desteğini benden esirgemeyen aileme de şükranlarımı sunarım. Aralık, 2010 Güray GÜRKAN i
2 İÇİNDEKİLER ÖNSÖZ... İÇİNDEKİLER... ŞEKİL LİSTESİ... TABLO LİSTESİ... SEMBOL VE KISALTMA LİSTESİ... ÖZET... SUMMARY... i ii iv vi vii ix x 1 GİRİŞ GENEL KISIMLAR ANESTEZİ İLE BEYİNDE OLUŞAN İŞLEVSEL DEĞİŞİMLER KULLANILAN DİĞER ELEKTROFİZYOLOJİK YÖNTEMLER MEVCUT ANESTEZİ DERİNLİĞİ TAKİP CİHAZLARI MALZEME VE YÖNTEM KAYIT PROTOKOLÜ KAYIT SİSTEMİ Kanal Montajı Ön Kuvvetlendirici ve Örnekleme BIS Cihazı Spontan ve İşitsel Kayıt Kontrolü İşaretlemeler ÖNİŞLEME ADIMLARI İZGESEL KÖŞE FREKANSI α VE β ORANLARI İZGESEL ENTROPİ ZAMAN-FREKANS ANALİZİ Kısa Zamanlı Fourier Dönüşümü Stockwell Dönüşümü ve Koherans Analizi İKİZ İZGESEL ANALİZ Hz İŞİTSEL DURAĞAN HAL YANITI ANALİZİ BAĞIMSIZ BİLEŞEN ANALİZİ GRANGER NEDENSELLİĞİ VE BAĞLANTISALLIK ANALİZİ Özbağlanımlı Modelleme Çokdeğişkenli Özbağlanımlı Modelleme Granger Nedenselliği ii
3 Kısmi Yönlü Koherans BULGULAR EEG KAYITLARI VE İYİLEŞTİRME BIS, SEF90 VE DİĞER İZGESEL DEĞİŞİMLER YAPILAN DİĞER ANALİZLER GKYK ANALİZLERİ TARTIŞMA VE SONUÇ KAYNAKLAR ÖZGEÇMİŞ iii
4 ŞEKİL LİSTESİ Şekil 1.1 : Genel anestezi - Fiziksel değişimler... 2 Şekil 2.1 : EEG Frekans Bantları... 4 Şekil 2.2 : Bantlara göre güç değişimleri... 6 Şekil 2.3 : İşitsel Uyarılmış Potansiyel Bileşenleri... 8 Şekil 2.4 : İşitsel Potansiyellere ait tepelerin anestezi derinliği ile değişim i Şekil 2.5 : BIS Monitörü Şekil 2.6 : Entropy Monitörü Şekil 2.7 : Narcotrend Monitörü Şekil 2.8 : CSI Monitörü Şekil 2.9 : Sedline Monitörü Şekil 3.1 : Operasyon Öncesi Şekil 3.2 : Kayıt Protokolü Şekil 3.3 : 15 Kanallı EEG Montajı Şekil 3.4 : BIS cihazının elektrot bağlantıları Şekil 3.5 : BIS ekranı Şekil 3.6 : BIS değerlerinin ve İşitsel Uyaran kodlarının birlikte gösterimi Şekil 3.7 : Kayıt Sistemin Blok Diyagramı Şekil 3.8 : BrainVision Header Dosyası Şekil 3.9 : BrainVision Marker Dosyası Şekil 3.10 : İzgesel Köşe Frekansının gösterimi Şekil 3.11 : SEF-90 Değişimi Şekil 3.12 : İzgesel Dağılım - Entropi İlişkisi Şekil 3.13 : Kümülant ve İkiz izge Simetri Bölgeleri Şekil 3.14 : İkiz izgesel Analizin ayırt ediciliği Şekil 3.15 : Göz açık/kapalı durumdaki ikiz izge Şekil 3.16 : Farklı işitsel uyaran frekansları ve elde edilen işitsel cevap Şekil 3.17 : Saçılım Grafikleri Şekil 3.18 : İki Gauss dağılıma sahip değişkenin birleşik dağılım fonksiyonu Şekil 3.19 : EEG verisi örneği Şekil 3.20 : 15 kanallı gözlem verisinin kovaryans matrisi Şekil 3.21 : Elde edilen U ve D matrisleri Şekil 3.22 : Beyazlaştırılmış yeni gözlem verisinin kovaryans matrisi Şekil 3.23 : Çeşitli dağılım fonksiyonları ve Basıklık değerleri Şekil 3.24 : Matlab ile üretilen gizli kaynaklar Şekil 3.25 : Elde edilen dağılımlar Şekil 3.26 : Döndürme açısı ve Basıklık İlişkisi Şekil 3.27 : 1. test sinyaline ait Zamanla Değişen ÖB Modelleme ve izgesel dağılımlar Şekil test sinyali ve Zamanla Değişen ÖB Modelleme sonucu elde edilen kestirim hataları Şekil 3.29 Gürültü seviyesi ve kestirim hatası ilişkisi (1. test sinyali) iv
5 Şekil 3.30 : 2. test sinyaline ait Zamanla Değişen ÖB Modelleme ve izgesel dağılımlar Şekil test sinyali ve Zamanla Değişen ÖB Modelleme sonucu elde edilen kestirim hataları Şekil 3.32 Gürültü seviyesi ve kestirim hatası ilişkisi (2. test sinyali) Şekil 3.33 : İki değişkenli Granger Nedenselliği Şekil 3.34 : KYK ve YTF yöntemlerini karşılaştırmak için kullanılan model Şekil 3.35 : YTF Değerleri Şekil 3.36 : KYK Değerleri Şekil 3.37 : Üretilen Sinyaller Şekil 3.38 : Yazılan fonksiyonlarla hesaplanan Kısmi Yönlü Koherans Değerleri 59 Şekil 4.1 : Filtrelemenin EEG üzerine etkisi Şekil 4.2 : Anestezi altında EEG nin değişimi Şekil 4.3 : BIS, SEF90, Güç Oranları ve İzgesel Entropi Değişimleri Şekil 4.4 : BIS, SEF90, Güç Oranları ve İzgesel Entropi Değişimleri Şekil 4.5 : Alınan BIS değer dağılımları Şekil 4.6 : Hesaplanan SEF-90 değer dağılımları Şekil 4.7 : Hesaplanan β Oranı değer dağılımları Şekil 4.8 : Hesaplanan İzgesel Entropi değer dağılımları Şekil 4.9 : h16 kodlu hastanın Spontan α Testi Şekil 4.10 : h20 kodlu hastanın Spontan α Testi Şekil 4.11 : Artan anestezi derinliği ile kanallarda yaşanan izgesel değişim Şekil 4.12 : Artan anestezi derinliği ile kanallarda yaşanan izgesel değişim Şekil 4.13 : Artan anestezi derinliği ile kanallarda yaşanan izgesel değişim Şekil 4.14 : Artan anestezi derinliği ile kanallarda yaşanan izgesel değişim Şekil 4.15 : Anestezinin derinleşmesi ile oluşan yeni α aktivitesi Şekil 4.16 : Ayılma süresinde kanallarda oluşan izgesel değişimler Şekil 4.17 : Uyanık ve anestezi altındaki durumlar için izgesel gösterimler Şekil 4.18 : Uyanık ve anestezi altındaki durumlar α merkez frekansları Şekil 4.19 : Uyuma Dönemine ait Stockwell koherans değişimleri Şekil 4.20 : Ayılma dönemine ait Stockwell koherans değişimleri Şekil 4.21 : Uyanık ve anestezi durumunda hesaplanan ikiz izge Şekil 4.22 : BBA sonucu elde edilen bileşenler - hasta Şekil 4.23 : Bağımsız bileşenlere ait izgesel analizler - hasta Şekil 4.24 : Bağımsız bileşenlere ait topografik (uzaysal) dağılımlar - hasta Şekil 4.25 : BBA sonucu elde edilen bileşenler - hasta Şekil 4.26 : Bağımsız bileşenlere ait izgesel analizler - hasta Şekil 4.27 : Bağımsız bileşenlere ait topografik (uzaysal) dağılımlar - hasta Şekil 4.28 : Uyuma dönemindeki GKYK değişimleri - hasta Şekil 4.29 : Uyuma dönemindeki GKYK değişimleri - hasta Şekil 4.30 : Uyuma dönemindeki GKYK değişimleri - hasta Şekil 4.31 : Uyuma dönemindeki GKYK değişimleri - hasta Şekil 4.32 : Uyuma dönemindeki GKYK değişimleri - hasta Şekil 4.33 : Uyuma dönemindeki GKYK değişimleri - hasta Şekil 4.34 : Uyuma dönemindeki GKYK değişimleri - hasta Şekil 4.35 : Uyuma dönemindeki GKYK değişimleri - hasta Şekil 4.36 : Uyuma dönemindeki GKYK değişimleri - hasta Şekil 4.37 : Uyuma dönemindeki GKYK değişimleri - hasta Şekil 5.1 : BIS İzgesel Değişim Tutarlılığı, hasta v
6 Şekil 5.2 : BIS İzgesel Değişim Tutarlılığı, hasta Şekil 5.3 : BIS İzgesel Değişim Tutarlılığı, hasta vi
7 TABLO LİSTESİ Tablo 3.1 : Örnekleme Parametreleri Tablo 3.2 : İşitsel kayıt kontrol işaretlemeleri Tablo 4.1 : Hastalar ve kayıt süreleri vi
8 SEMBOL VE KISALTMA LİSTESİ SEF MAK EEG İBSY UN ESAN BIS SE RE Preop Op r α r β S(f) p(x) H(x) S N (f) X(k) w(τ) δ(τ) f s f norm W(τ, d) w(τ, f) SC(t, f) M x (t) c x n R x (τ) B(f 1, f 2 ) DHY BBA P(x, y) s i (t) a ji s A x İng. Spectral Edge Frequency İzgesel Köşe Frekansı Minimum Alveolar Konsantrasyon Elektroensefalogram İşitsel Beyin Sapı Yanıtı Uygunsuz Negativite Erken Sağ Anterior Negatifliği İng. Bispectral Index, İkiz izge İndeksi İng. State Entropy Durum Entropisi İng. Response Entropy Cevap Entropisi Operasyon Öncesi Dönem Operasyon Dönemi α Oranı β Oranı İzgesel Güç Yoğunluğu Olasılık Yoğunluk Fonksiyonu Shannon Entropisi Normalize İzgesel Güç Yoğunluğu Ayrık Fourier Dönüşüm Katsayıları Pencere Dizisi Birim Darbe Örnekleme Frekansı Normalize Frekans Ayrık Dalgacık Dönüşümü Ana Dalgacık Fonksiyonu Stockwell Koherans Fonksiyonu x(t) Değişkenine Ait Moment Üreten Fonksiyon x(t) Değişkenine Ait n. Derece Moment Özilinti Fonksiyonu İkiz İzge Fonksiyonu Durağan Hal Yanıt Bağımsız Bileşen Analizi x ve y Değişkenlerine Ait Bütünleşik Olasılık Dağılımı i. Bağımsız Bileşen Ağırlık Katsayıları Bağımsız Bileşenler Vektörü Gözlem (Kanal) Vektörü Karıştırıcı Matris vii
9 z D U I w n X(z) TÖ Φ ÖB A k v i (n) Σ YTF YKF KYKF π i j (f) σ i w i (n) GKYKF Beyazlaştırılmış Gözlem Vektörü Özdeğerleri İçeren Köşegen Matris Özvektörleri İçeren Matris Birim Matris BBA Algoritmasına Ait Gözlem Ağırlık Katsayıları x(n) Ayrık Sinyali İçin Tanımlanan z Dönüşümü Tekil Özayrışım Maliyet Fonksiyonu Özbağlanımlı Çok Değişkenli ÖB Modele Ait Kare Katsayı Matrisleri ÖB Model İçin Kullanılan i. Kanala Ait Gözlem Çok Kanallı Beyaz Gürültü Bileşenine Ait Kovaryans Matrisi Yönlü Transfer Fonksiyonu Yönlü Koherans Fonksiyonu Kısmi Yönlü Koherans Fonksiyonu Kanallar Arası Tanımlanan KYKF i. Kanala Ait Kovaryans KYKF Benzetimi İçin Kullanılan Beyaz Gürültü Bileşeni Genelleştirilmiş Kısmi Yönlü Koherans Fonksiyonu viii
10 ÖZET EEG SİNYALLERİNİN ANALİZİ İLE ANESTEZİ DERİNLİĞİ TESPİTİ Bu tez çalışmasında propofol anestezisi altında 15 Kanallı EEG kayıtlaması kullanılarak değişimler incelenmiş ve anestezi derinliği tespiti için kullanılabilecek yeni yöntemler araştırılmıştır. EEG kayıtları jinekolojik operasyon esnasında genel anestezi uygulanan hasta grubundan alınmıştır. Kayıtların çevrimdışı olarak işlenmesi MATLAB ortamında gerçekleştirilmiştir. Öncelikle mevcut anestezi takip cihazları ve kullanılan parametreler genişçe incelenmiş ve hesaplamaları yapılmıştır. Yapılan izgesel analizler sonucunda anestezi durumunda aktif kalan frontal EEG kanalları arasında bağlantısallık analizi önerilmiştir. Çok Kanallı Özbağlanımlı Model kullanılarak Zamanla Değişen Kısmi Yönlü Koherans değerleri ile yapılan bu analizler sonucunda tüm hastalarda derinleşen anestezi derinliği ile birlikte kanallar arası bağlantısallık değişimi gözlenmiştir. ix
11 SUMMARY DETERMINING THE DEPTH OF ANESTHESIA BY THE ANALYSIS OF EEG SIGNALS In this thesis, it was aimed to propose a new parameter for estimation of depth of anaesthesia by using 15 channel EEG. The recordings were taken from 30 subjects undergoing general anaesthesia for gynecological surgery. The offline processing was realized in MATLAB. First part of the thesis involved literature search of analysis methods that are currently used in current commercial depth of anaethesia monitors and simulations were done. As a result of spectral analysis of EEG channels, the application of connectivity was proposed between channels that were also shown to be active under anaesthesia. By using Multivariate Autoregressive Modeling and Timevarying Partial Directed Coherence values were extracted and the evolution of connectivity changes during deepening stage of anaesthesia was revealed in all patients. x
12 1 1 GİRİŞ Anestezi genellikle cerrahi müdahalelerden önce uygulanan, bedenin tümünün ya da belli bir bölümünün ağrıya duyarsız hale gelmesini sağlayan işleme verilen addır. Kelime, Yunanca hissetmek anlamındaki aesthetos köküne, -siz, -sız anlamı veren anekinin eklenmesi ile oluşmuştur. Anestezi, anestezik denilen ve özellikle sinir sistemi hücrelerinin biyolojik fonksiyonlarını yavaşlatan veya durduran ilaçlarla sağlanır. Anestezi vücudun küçük bir bölümüne uygulanabileceği gibi (lokal), hastada bilinç kaybına neden olacak şekilde (genel) de uygulanabilir. Genel anestezide merkezi sinir sisteminin çalışması o derece yavaşlatılır ki hastanın acıya karşı duyarlılığı ve bilinci kaybolur. Anestetiklerden kolay uçucu veya gaz halinde bulunanlar solunum yoluyla, uçucu olmayan sıvı anestetikler ise enjeksiyonla doğrudan damara verilir. Genel anestezi önemli cerrahi operasyonlarda kullanılmaktadır. Hasta derin bir uyku halindedir ve bir çeşit felçli durumdadır. Fakat hastanın operasyon sırasındaki ağrıya olan duyarsızlığı ile uygulanan anestezik miktarı arasında önemli bir denge bulunmaktadır. Cerrahi operasyonlarda, anestezik maddenin kullanımında bir kontrol aracı olarak anestezi derinliğinin güvenilir ve girişimsel olmayan (non-invazif ) bir şekilde görüntülenmesi çok önemlidir. Bu tür bir gereksinim, uygun anestezi derinliğinden olabildiğince emin olmak ve anestezik maddeyi hastaya gereğinden fazla vermeden uyanıklığı önlemek için zorunludur [1, 2]. Anestezinin, çok derin uygulandığı durumda hastanın kardiyovasküler sistemini de etkilediği ve operasyon sonrasında kalıcı olabilen hasarlara neden olduğu bilinmektedir. Diğer taraftan, anestezik ilacın az verilmesi durumunda, hastanın ağrıyı hissettiği, ani fiziksel tepkilerde bulunduğu bildirilmektedir [3, 4, 5]. Bu nedenle hastanın en uygun anestezi seviyesinde tutulabilmesi klinik uygulamada hala çözülememiş bir problemdir. Anestezi derinliğini anlamada kullanılan geleneksel yöntemler kalp atım hızı, kan basıncı, göz bebeği büyüklüğü, nefes sıklığı ve terleme gibi değişikliklere bağlı
13 2 Şekil 1.1: Genel anestezi sırasında yaşanan fiziksel değişimler [1] ölçümleri içerir (Şekil 1.1). Fakat bu fiziksel belirtiler ameliyatın türüne ve hastaya bağlı olarak değişim göstermektedir. Anestetik maddeler beynin korteksini doğrudan etkilediğinden anestezi derinliğini saptamak için son yıllarda geleneksel yöntemlere ek olarak elektroensefalogram (EEG) kayıtlarını kullanarak beyin aktivitesinin izlenmesi de büyük ilgi çekmektedir [1]. Yukarıda belirtilen nedenle, EEG kaydı yoluyla anestezi derinliğinin saptanması konusunda son yıllarda ticari olarak birçok cihaz üretilmiştir. Fakat bu cihazlardan hiçbiri % 100 başarıma sahip değildir [1, 2]. Bu tez çalışmasının genel amacı anestezi takip cihazlarında kullanılabilecek yeni bir parametrenin araştırılmasını oluşturmaktadır. Genel Kısımlar bölümünde EEG sinyalinde anestezi altında meydana gelen değişikler, yapılan diğer çalışmalar eşliğinde sunulmaktadır. Ayrıca bu amaçla üretilmiş ticari cihazlar hakkında da bilgiler verilecektir. Malzeme ve Yöntem bölümünde ise çalışmalar süresince kullanılan EEG kayıtlarının alındığı hasta grubu, kayıt sırasında kullanılan montaj şekli, sinyal yükselteci, bilgisayar vb. bağlantılar hakkında bilgiler verilecektir. Verilerin sabit diske kaydedilmesinden sonra uygulanan metotlar Ön İşleme Adımları alt kısmında anlatılacaktır. Daha sonra tez çalışması süresince incelenen ve anestezi derinliği takip monitörlerinde kullanıldığı öğrenilen SEF, α-β oranları, İzgesel Entropi ve SyncFastSlow parametreleri
14 3 anlatılacaktır. Son olarak da bu tez kapsamında önerilen yöntemler (Zaman-Frekans Analizi, Bağımsız Bileşen Analizi, Stockwell Koheransı, Nedensellik Analizi ve Kısmi Yönlü Koherans Analizleri) sunulacaktır. Bulgular kısmında alınan EEG örnekleri ve elde edilen sonuçları sunulacaktır. Tartışma ve Sonuç bölümünde ise analiz sonuçları kullanılarak daha önce yapılan çalışmalar kıyaslanacak ve anestezinin EEG ye olan etkisinin gösterilmesi ile ilgili öneriler sunulacaktır.
15 4 2 GENEL KISIMLAR 2.1 ANESTEZİ İLE BEYİNDE OLUŞAN İŞLEVSEL DEĞİŞİMLER Anestezikler, merkezi sinir sisteminde bilinci sağlayan bileşenleri bastırarak (ya da inhibe ederek) hissizliğe ve bilinç kaybına yol açar. Dolayısı ile, kortikal bölgedeki bu değişikliklerin, beyindeki sinaptik aktivite sonucu oluşan EEG sinyalleri ile kestirilebileceği gösterilmiştir [6]. Şekil 2.1 de EEG sinyaline ait frekans bantları gösterilmektedir. Şekil 2.1: EEG Frekans Bantları Valdês Sosa ve ark. [7], elektrot sistemi kullanarak çeşitli anestezik maddelerin EEG üzerine etkisini incelemişlerdir. Makalede aynı zamanda literatürde anestezide EEG değişimini çok sayıda elektrot kullanarak inceleyen çalışmaların azlığından da bahsedilmektedir. Enjeksiyon öncesi, sonrası, bilincin kaybolması ve bilincin açılması şeklinde bölünen durumların herbiri için 2.5 saniye uzunluğundaki (bozucu sinyallerden (artifaktan) arındırılmış) belirli sayıda (24 48) segmentin ortalaması alınarak belirtilen durumlarla ilgili çıkarımlar yapılmaktadır. Herbir durum için (0 25 Hz) aralığındaki ve ayrı ayrı δ ( Hz), θ ( Hz), α ( Hz), β ( Hz) bantlarındaki izgesel güçler hesaplanarak durumlar arası değişim incelenmektedir. Ayrıca ön arka ve
16 5 sağ sol beyin yarımküreleri arasındaki koheransın değişimi de incelenmektedir. Bulgularda artan anestezi derinliği ile birlikte 0 25 Hz arasındaki frekans bandında ön tarafta fazla olmak üzere artış bildirilmektedir. Ayrıca hesaplanan yakın kanal koherans değerlerinin düşük frekanslarda arttığı, fakat daha uzak (ön arka, sağ sol) beyin bölgeleri arasında azaldığı da gösterilmektedir. Bu değişimlerin anestezinin hafiflemesi ve hastanın uyanması ile tersinir olarak gözlenmiş olduğu da ifade edilmektedir. Alkire ve ark. [8], propofol ile genel anestezi uygulanmış deneklerin PET görüntüleme yöntemi altında beyninde meydana gelen değişimleri göstermeye çalışmışlardır. Edindikleri bulgulara göre, bilinç kaybı ile birlikte beynin bütününde ortalama serebral metabolik aktivitede kabuk bölgesinde altkabuk bölgesinden daha fazla olmak üzere % 38 lik bir azalma gerçekleşmektedir. Metabolik aktivitenin genel olarak düşüşü belirli bir eşik seviyesinin altına indiğinde bilinç kaybının gözlendiği de ifade edilmektedir. Feshchenko ve ark. [9], propofol ve sevofloran anestezisi altında deneklerde görülen α aktivitesindeki artışa dikkat çekmişlerdir. Propofolü, 0.5, 1, 2 MAK (Minimum Alveolar Konsantrasyon) 1 seviyeleri ile ayrı ayrı uygulayan grup, uyanık deneklerde görülen normal α ritminin, derinleşen anestezi (artan MAK seviyesi) ile yerini frontal bölgede artan ve normal α ritminin tepe frekansından daha düşük olan ikinci bir α ritmine bıraktığını önesürmüşlerdir. Yapılan çalışmalar sonucunda anesteziklerin aşağıdaki genel etkileri özetlenebilir: Hz bandında (Üst Beta ve Gama Bandı) azalma Yavaş dalgalanmalarda artma (Teta ve Delta) Frontal bölge elektrotlarının gücünde büyük miktarda artma EEG eşzamanlılığında belirgin bir artma Frontal ve parietal bölgeler arasındaki frekans kuplajında azalma. 1 Herbir volatil (solunum yolu ile verilen) anestezik için deneysel olarak tanımlanan bu değer, anestezik maddenin uygulandığı hasta grubunun % 50 sinin ağrılı uyaranlara karşı etkisiz kalmasına yetecek olan akciğer buhar yoğunluğudur. Tanımlanan bu seviyeler anestezik maddelerin etki güçlerinin kıyaslanmasını mümkün kılmaktadır.
17 6 Anestetik maddenin kesilmesi ile birlikte hasta belirli bir süre sonunda uyanmaktadır. Derin anesteziden hastanın uyanmasına kadar geçen süre zarfında yukarıda sayılan değişimlerin bir nevi tersi yaşanmaktadır (Şekil 2.2). Şekil 2.2: Uyanma evresinde yaşanan güç değişimleri [1] Anestezinin, çok derin uygulandığı durumda hastanın kardiyovasküler sistemi etkilediği ve operasyon sonrasında kalıcı olabilen hasarlara neden olduğu bilinmektedir. Diğer taraftan, anestetik ilacın az verilmesi durumunda, hastanın ağrıyı hissettiği, ani fiziksel tepkilerde bulunduğu ve operasyon sırasında yaşadıklarını hatırladığı bildirilmektedir [10, 11, 12, 13]. Farkındalık göz önünde bulundurulduğunda, literatürde cevap aranan sorular genel olarak: - Hasta ağrıyı operasyon sırasında hissediyor mu? - Ağrı hissettiğini operasyon sonrası net olarak hatırlıyor mu?
18 7 - Hasta ağrı hissetmese de operasyon esnasında duyduklarını farkında olmadan anımsıyor mu? şeklindedir. Literatürde Priming olarak isimlendirilen farkında olmadan öğrenme hafızaya alma durumunun, özellikle anestezinin yeteri kadar derinleşmediği safhalarında görüldüğü çeşitli çalışmalarda [14, 15, 16] gösterilmiştir. Daha önce de belirtildiği gibi hastanın algı düzeyini kesin olarak ölçebilmek, dolayısı ile hastayı en uygun anestezi seviyesinde tutulabilmek klinik uygulamada hala çözülememiş bir problemdir. 2.2 KULLANILAN DİĞER ELEKTROFİZYOLOJİK YÖNTEMLER Anestezikler EEG yi karakteristik bir biçimde etkilediklerinden dolayı EEG veya uyarılmış potansiyel dalgalarından türeyen anestezi derinliğinin kanıtlarını elde etmek için birçok yöntem bulunmaktadır [17, 18, 20, 21, 22]. Uyarılmış potansiyeller görsel, duysal ya da işitsel yolla elde edilebilmektedir. Bunların arasında işitsel potansiyeller, anestezinin derinleşmesi ile en geç kaybolan potansiyel olması yönünden önem taşımaktadır [23]. İşitsel potansiyeller, beynin işitsel uyarımı sonucu EEG ye yansıyan genel olarak küçük genlikli sinyallerdir. İşitsel potansiyel kayıtlarında protokole bağlı olarak, tekli ya da uzun süren uyaranlar uygulanabilir. İşitsel potansiyel İşitsel Beyin Sapı Yanıtı İBSY (İng. Auditory Brainstem Response, ABR) Orta Süreli (Gecikmeli) İşitsel Uyarılmış Potansiyel OSUİP (İng. Midlatency Auditory Evoked Potential, MLAEP) Uzun Süreli İşitsel Uyarılmış Potansiyel USİUP (İng. Long Latency Auditory Evoked Potential, LLAEP) gibi kısımlardan oluşmaktadır. (Şekil 2.3). İşitsel beyin sapı yanıtı ortaya çıkan ilk ve en hızlı bileşendir. İBSY klinik çalışmalarda beyin sapındaki hasarları teşhis etmek için kullanılmaktadır. Sonrasında oluşan Orta Süreli Uyarılmış Potansiyel daha düşük
19 8 frekans bileşenlerine sahip olmakla birlikte, genlik olarak belirgin tepelere (Pa, Na, Pb, Nb) sahiptir. Şekil 2.3: İşitsel Uyarılmış Potansiyel Bileşenleri [41] İşitsel potansiyellerin beyin sapından kortikal bölgeye, oradan da işitme korteksine uzanan hiyerarşik bir şekilde üretildiği literatürde kabul gören bir kavramdır [24]. İşitsel Olayla İlişkili Beyin Potansiyelleri (İOİBP) (İng. Auditory Event Related Potentials, AERPs) farklı sedasyon 2 düzeyleri veya sedasyon altındaki hastanın tepkisel (ya da kognitif ) durumunu kesin olarak değerlendirmeyi ayırt etmek için bir yol sağlamaktadır [23, 25]. Esas olarak primer işitsel korteksteki aktiviteyi araştıran işitsel uyarılmış potansiyelin aksine, USİUP ler (veya İOİBP ler) işitsel duysal hafıza, müzik ve dil süreci ve garip uyarılara dikkat yönelimi gibi diğer kortikal alanları kapsayabilen üst nöral mekanizmaları yansıtır [26, 27]. USİUP nin dalga formundaki ilk pozitif sapması negatif bir sapma olan N1 ile izlenen P1 tepesidir. P1 işitsel uyarının duysal kodlamasını yansıtmaktadır. Bunun yanı sıra, N1 işitsel ortamın herhangi bir subjektif boyutunun, farklı degişikliklerin bilinçli arayışını yansıttığı varsayılmaktadır [28]. N1 genliği, artan sedasyonla birlikte azalmaktadır. Aksine P1 genliği sadece bilincin kapalı olmasından etkilenmekte fakat derin sedasyonla degişmemektedir [29]. Bilincin kapalı oldugunu 2 Sedasyon, hastanın bilinci kaybolmaksızın sakinleştirilmesinin biraz ötesinde ilaçlarla rahatlatılmasıdır. Hasta işlem sırasında komut alabilir, söylenenleri yapabilir ancak işlem sonrasında neler yapıldğını hatırlamaz.
20 9 gösteren BIS değerleri için P1 ve N1 tepelerinin var olması (her ikisi de farklı nöral topluluklardan destek almasına rağmen her iki bileşenin nöral oluşumunun işitsel kortekste olduğu var sayılmaktadır) yüzeyel anestezi altında işitsel kortekste nöronla aktiviteyi gösteren nörogörüntüleme çalışmalarını desteklemektedir. Sedasyonun etkilerini işitsel süreçlerde araştırmak için kullanılan bir yöntem de Uygunsuz Negativite dir (İng. Mismatch Negativity, MMN) [26, 31]. UN, tekrarlayan standart uyarıların serisi ile oluşan ters ya da hedef bir uyarı ile sağlanır (örneğin: standart tonların tekrarlayan serilerinde, frekanstaki terslikler bir UN oluşturur). UN nin akustik bilgi için dikkat çeken kısa süreli depo vazifesi gören işitsel duysal hafızanın çalışma sürecini yansıttığı düşünülmektedir. Yakın zamanda, işitsel duysal hafızanın doza bağımlı yıkımı UN kayıtlarıyla gösterilmiştir. UN genliği, artan sedasyonla azalmaktadır [25, 29, 30]. Bu, bilinç kapalı iken hafıza sistemindeki bozulmada artan sedasyonla, temporal ve frontal beyin bölgelerinde yerleşen ağ yapının geliştirdiği UN ile, nöronal aktivitede sürekli bir azalma olduğunu göstermektedir. Metodolojik zorluklar dolayısı ile ilaçların konuşma üzerine etkileri henüz İOİUBP ile araştırılamamıştır. Bununla beraber, söz dizimi bilgisinin oluşumu müzikal uyarılar kullanılarak araştırılmıştır. Müzik söz dizimi düzensizlikleri Erken Sağ Anterior Negatifliği (ESAN) (İng. Early Right Anterior Negativity, (ERAN)) sağlamaktadır; bu bileşen, konuşmanın söz dizimi sürecinde de görevli beyin bölgelerinde oluşur. Yeni çalışmalar UN gibi ESAN ında propofolle meydana gelen ağır sedasyonla sürekli azaldığını göstermektedir (Şekil 2.4). ESAN, UN den daha hafif anestezi derinliğinde yok olmaktadır. 2.3 MEVCUT ANESTEZİ DERİNLİĞİ TAKİP CİHAZLARI Günümüzde yaygın olarak kullanılmakta olan cihaz (ve üretilen indeks) isimleri: - BIS indeksi - ASPECT MEDICAL SYSTEMS - ENTROPY indeksi - DATEX OHMEDA - NARCOTREND indeksi - MONITORTECHNIK
21 10 Şekil 2.4: Beyindeki İşitsel Potansiyellere ait ortaya çıkan tepelerin anestezi derinliği ile değişimleri [46] - PSI (Hasta durum indeksi) - SEDLINE - CSI (Serebral durum indeksi) şeklindedir. BIS cihazı (Şekil 2.5), asıl ismini yüksek dereceli izgesel analiz yöntemlerinden biri olan Bispectrum, İkiz izge kelimesinden alır. Aspect Medical Systems firması tarafından üretilen cihaz, ilk anestezi derinliği izleme cihazı olması yönünden önem taşır. Şekil 2.5: BIS Monitörü Halen klinik uygulamalarda en çok ilgi gören ürün olan cihazın ürettiği BIS değeri, alın bölgesindeki 4 elekrottan alınan EEG verisinden oluşturulmaktadır (Şekil 2.5) aralığında üretilen BIS değerlerinin önerilen yorumları ise:
22 arası: Hasta uyanık, farkında, hafıza ve bilinçli hatırlama tam, arası: Artmış sedasyon ve hafızanın bozulduğu durumdur, uyarı ile hasta uyandırılabilir, arası: Cerrahi anestezi. Ameliyat sonrası hatırlama olasılığı düşük, işitsel süreç ve refleks hareketler mevcut, arası: Kortikal nöron baskılanması artmıştır, - 0 değeri:: Tam kortikal elektriksel sessizlik anlamındadır. Entropy indeksini üreten cihaz (Şekil 2.6) ise ismini bilgi kuramındaki entropi kavramından alır. Adından da anlaşılacağı üzere, kullanılan algoritma EEG sinyalindeki bilgi içeriğini, dolayısı ile düzensizliği ve kestirilebilirliği ölçer. İleride de anlatılacağı gibi anestezi altında EEG sinyalinin düzensizliğinin azaldığı görülmüştür. Cihaz, zaman alanından ziyade izgesel alandaki düzensizliği (ya da tersi olarak bilgi zenginliğini) gösteren SE (State Entropy - Durum Entropisi) ve RE (Response Entropy - Cevap Entropisi) denilen 2 indeks üreterek hastanın durumunu kestirmeye çalışır arasındaki değerler BIS cihazına benzer durum bildirirler. Şekil 2.6: Entropy Monitörü Narcotrend (Şekil 2.7) indeksi ise, EEG sinyalinde görsel olarak A ve E arasındaki harflerle sınıflandırılabilen dalga şekillerinden hareketle, anestezi altında elde edilen sinyalleri ileride açıklanacak olan zaman ve frekans yöntemleri ile de destekleyerek sınıflandırmaktadır. CSI (Şekil 2.8) indeksi ise, elde taşınabilen bir cihaz vasıtası ile oluşturulmaktadır. Bu cihaz EEG nin çeşitli frekans bantlarındaki güç oranları ile hastanın durumunu
23 12 Şekil 2.7: Narcotrend Monitörü kestirmeye çalışır. Durum indeksi yine arasında bir sayı olarak gösterilmektedir. Şekil 2.8: CSI Monitörü SEDLine cihazı 4 adet elektrottan alınan EEG sinyalleri ile, bilinç kaybı sonucu frontal ve oksipital bölgeler arasında oluşan güç kaymalarını saptayarak bir kestirim yapmaktadır. Ana olarak 2 ekrana sahip olan SEDLine, bir ekranda ham EEG yi, diğer ekranda ise izgesel güç yoğunluğunu gösterir (Şekil 2.9). Bu çalışmada elde edilen sonuçlara referans olması için BIS anestezi derinliği monitörü kullanılmıştır.
24 13 Şekil 2.9: Sedline Monitörü
25 14 3 MALZEME VE YÖNTEM 3.1 KAYIT PROTOKOLÜ Kayıtlar için İstanbul Tıp Fakültesi, Anesteziyoloji AD bünyesinde gerçekleştirilen jinekolojik operasyonlarla, yaşları 26 ile 72 arasında değişen toplam 28 hastadan kayıt alınmıştır (Hasta yaş ortlaması= 45,4). Alınan kayıtlardan, Propofol alerjisi 3 olduğu saptanan 2 hastanın kayıtları kullanılmamıştır. Şekil 3.1: Operasyon öncesi Ortalama saat kadar süren kayıt işlemi hasta operasyona alınmadan önce başlatılmış- tır. Pre-Op olarak isimlendirilen bu kayıt sürecinde, 300 er saniyelik Gözler Açık, Gözler Kapalı, Göz Açık - Spontan ve 40 Hz İşitsel Uyaranlı kayıt uygulanmasının ardından Pre-Op bölümü tamamlanmıştır. Daha sonra hasta operasyon odasına alınmış, BIS cihazı da bağlandıktan sonra kaydın Op bölümüne geçilmiştir. Bu bölümde ise 3 Bu tür hastalarda anestetik olarak Sevofloran kullanılmıştır.
26 15 Spontan olarak başlayan kayıt, Propofol uygulanması ve anestezinin oturmasının 4 ardından 10 dakika aralıklarla İşitsel ve Spontan kayıtlamalarla devam etmiştir. Anestetik madde kesilip hasta uyanma sürecine girmeden önce başlayan en son Spontan kayıtlamanın ardından tam bir kayıt sonlanmıştır. Op segmentinde en uzun kısımları ilk ve son Spontan kayıt süreçleri oluşturmaktadır (Şekil 3.2). Şekil 3.2: Uygulanan Kayıt Protokolü 3.2 KAYIT SİSTEMİ Operasyon süresince EEG sinyalinin alınması ve daha sonra ameliyat sırasında olanlar hakkında bilgi edinilebilmesi için donanım ve yazılım ağı kullanılmıştır. Kayıt sistemi blok diyagramı Şekil 3.7 de gösterilmektedir Kanal Montajı EEG sinyalleri 10/20 elektrot yerleştirme sistemine uygun bir şekilde 15 kanaldan (Fp1, Fp2, F7, F3, Fz, F4, F8, T7, C3, Cz, C4, T8, P3, Pz, P4) birleşik kulak memelerine referanslı olarak kaydedilmiştir (Şekil 3.3). 4 Anestezinin oturması anestezi uzmanı tarafından BIS değerine bakarak belirlenmektedir.
27 16 Şekil 3.3: 15 Kanallı EEG Montajı Ön Kuvvetlendirici ve Örnekleme Sinyal kuvvetlendirici olarak 32 kanal kapasiteli ve kendi yazılımına sahip Brainamp isimli cihaz kullanılmıştır. Bu cihaz ile birlikte sağlanan BrainVision Recorder (Brain Products, Almanya) yazılımı ile hem kuvvetlendiricinin parametreleri ayarlanabilmekte, hem de EEG verisi gerçek zamanlı olarak bilgisayar ekranında gözlemlenip sabit diske kaydedilebilmektedir. Kayıt öncesi elektrot-deri empedans değerleri de bu program sayesinde düşük seviyelere (<5 K) ayarlanabilmektedir. Kullanılan örnekleme parametreleri Tablo 3.1 de gösterilmiştir. Tablo 3.1: Örnekleme Parametreleri Kuvvetlendirici Kazancı (A V ) : 10 6 Örnekleme Frekansı ( f s ) : 1 khz Örnekleme Çözünürlüğü : 12 bit RC Filtre (DC Filter) : 0.1 Hz Yüksek Geçiren Filtre (Anti-aliasing Filter) : 250 Hz BIS Cihazı Daha önce de belirtildiği gibi, sonuçlara referans alınabilmesi için, şuanda en geniş kullanıcı grubuna sahip olan BIS anestezi derinliği takip cihazı kullanılmıştır. Hastanın alın bölgesine bağlanan ve cihaz üreticisi tarafından sağlanan özel bir elektrot ağı ile EEG verisi cihaza aktrılmaktadır (Şekil 3.4). Sağlanan bu elektrot takımı belirli bir kullanım sürecinden sonra cihaz tarafından kabul edilmemektedir. Cihazın ekranında (Şekil 3.5) ise 5 saniyede bir güncellenen BIS indeksi dışında, o anki sinyal kalitesi (SQI
28 17 - Signal Quality Index), EMG aktivasyonu, belli bir süre içindeki EEG sinyali ve BIS gidişatı gösterilmektedir. Şekil 3.4: BIS cihazının elektrot bağlantıları Şekil 3.5: BIS ekranı: a) anlık BIS indeksi, b) BIS gidişatı,c) Sinyal kalite derecesi, d) EMG aktivasyon derecesi, e) EEG sinyali Spontan ve İşitsel Kayıt Kontrolü Operasyon sırasında uygulanan Spontan ve İşitsel Uyaranlı segmentler MATLAB ortamında yazılan program aracılığı ile kontrol edilmektedir. Buna göre operasyon odası öncesi veya süresince alınan kayda başlanırken, kayıt (Preop veya Op şeklinde) isimlendirilir. Daha sonra uygun bölümler kayıt operatörü tarafından başlatılarak gerekli protokol sağlanır İşaretlemeler Operasyon süresince sayısallaştırılan 15 kanallı EEG verisinin yanısıra, verilen ilaçlar, MATLAB ile kontrol edilen operasyon etapları ve hastada görülen durumlar da kaydedilmiştir. Kayıtlar sırasında
29 18 Spontan durumdaki Göz Açma-Göz Kapama etapları arası geçiş, İlaçların verilmeye başlanması/durdurulması, Belirli operasyon safhalarına geçiş, Hastada gözlenen durumlar (kanama, hareketlilik, uyanma, vb.) gibi operasyon bilgileri, BrainVision programına yorum (comment) olarak işaretlenir. İşitsel Uyaran segmentleri ise, kayıt yapılan bilgisayardan MATLAB ile üretilen işitsel paradigma başlarken ve sonlanırken, paralel port vasıtası ile ana Brainamp ünitesine belirli bir koda sahip Trigger ile gönderilir. Daha sonra tıpkı yorum işaretinde olduğu gibi BrainVision recorder programında ilgili süreye bu kod işaretlenmiş olur. İşitsel kayıt başlangıç ve bitiş kodları Tablo 3.2 de görülebilir. Alınan BIS değerleri ve kodlar da Şekil 3.6 de gösterilmiştir. Tablo 3.2: İşitsel kayıt başlangıç ve bitiş kodları İşitsel Kayıt Başla S 40 İşitsel Kayıt Bitir S 41 Şekil 3.6: Bir hastadan tüm ameliyat boyunca alınan BIS değerlerinin ve İşitsel Uyaran kodlarının birlikte gösterimi
30 19 Şekil 3.7: EEG kayıtları için kullanılan sistemin blok diagramı
31 ÖNİŞLEME ADIMLARI Bütün kayıtlar, hastanın uyanması ile sonlandırılmıştır 5. Kayıt için kullanılan BrainVision programının sabit diske kaydettiği veri, 15 kanallı EEG sinyalini, ameliyat sırasında kayıt operatörü tarafından yazılan yorumları ve BIS değerlerini içermektedir. Kaydedilen dosyalar, hasta0xx_preop.eeg hasta0xx_preop.vhdr hasta0xx_preop.vmrk hasta0xx_op.eeg hasta0xx_op.vhdr hasta0xx_op.vmrk isimli dosyalar olmaktadır. İsimlerinden de anlaşılacağı gibi kaydedilen veriler öncelikle Preop ve Op kısımlarına ayrılır. Herbir kısım için EEG verisinin saklandığı *.eeg dosyası, kuvvetlendirme, montaj, örnekleme ayarları ve diğer tanım dosya isimlerinin saklandığı *.vhdr dosyası (Şekil 3.8) ile, BIS değeri ve işaretlemelerin saklandığı *.vmrk dosyası (Şekil 3.9) bulunmaktadır. Sabitdiske kaydedilen verilerin bundan sonraki tüm sinyal işleme adımları MATLAB ortamında geliştirlen fonksiyonlarla gerçekleştirilmiştir. 3.4 İZGESEL KÖŞE FREKANSI Literatürde anestezi ile ilgili olarak kullanılmakta olan en eski parametredir [1, 2, 34]. İzgesel köşe frekansı, ya da İngilizce adı ile SEF - Spectral Edge Frequency parametresi, mevcut izgedeki güç dağılımı ile ilgili bilgi verir. Anestezi ile ilgili önemli bir parametre olan SEF-90 parametresi, toplam izgesel gücün,% 90 ını kapsayan frekans aralığını 5 Genel olarak hastanın uyanması ile BIS değerinin 90 ve üstüne çıkması gözlenmektedir. Bazı kayıtlarda hastanın uyanmasına rağmen 70 civarında seyreden BIS değerlerine de rastlanmıştır.
32 21 Şekil 3.8: BrainVision Recorder Header dosyası örneği tanımlamaktadır. Benzer bir şekilde SEF-50 parametresi ise izgesel güç dağılımını 2 eşit parçaya ayıran frekansı yani medyan frekansı verir (Şekil 3.10). İlerideki bölümde de gösterileceği gibi SEF-90, uyanık bir hasta için Hz civarında iken, derinleşen anestezi ile birlikte Hz e gerilemektedir (Şekil 3.11). 3.5 α VE β ORANLARI Bu parametre belli uzunluktaki EEG sinyalinin kestirilen izgesinde, tanımlanan bantların güç dağılımı hakkında bilgi vermektedir. Daha önce de değilindiği gibi, anestezinin derinleşme ve uyanma süreçlerinde belirtilen oranlar ciddi biçimde değişim göstermektedir. Literatürde α ve β oranları ve r α = log( S S 6 12 ) (3.1) r β = log( S S ) (3.2) şeklinde tanımlanmaktadır [36].
33 22 Şekil 3.9: BrainVision Recorder, Marker dosyası örneği 3.6 İZGESEL ENTROPİ Literatürde bilgi ölçütü olarak kullanılan ve Shannon tarafından tanımlanan entropi kavramı, p(x) olasılık yoğunluk fonksiyonuna sahip x rastgele değişkeni için H(x) = p(x i ) log p(x i ) (3.3) şeklinde tanımlanır. Entropi bir rastgele değişkenin bilgi içeriği hakkında bilgi vermektedir. Buna göre, gerçekleşme ihtimali yüksek olan olaylarla ilgili edinilen haberin bilgi niceliği, gerçekleşme ihtimali düşük olan olaylarla ilgili edinilen haberin bilgi niceliğinden çok daha küçüktür. Hatta gerçekleşmesi kesin olan bir olayla ilgili haberin bilgi içeriği 0 dır. Yukarıda bahsi geçen x rastgele değişkeni ve p(x) olasılık yoğunluk fonksiyonu arasındaki ilişki, f (frekans) rastgele değişkeni ve izgesel yoğunluk fonksiyonu arasında da kurulabilir. EEG sinyalinden elde edilen S(f) izgesel kestirimleri S N ( f i ) = S ( f i) j S ( f j ) (3.4)
34 23 Şekil 3.10: İzgesel Köşe Frekansının gösterimi şeklinde normalize edilirse, izgesel olasılık yoğunluğu elde edilmiş olur. Dolayısı ile izgesel entropi H( f ) = S N ( f i ) log(s N ( f i )) (3.5) şeklinde tanımlanabilir. i Şekil 3.12, elde edilen iki farklı S(f) kestirimini ve entropilerini karşılaştırmaktadır. Uyanık bir kişinin EEG izgesi hemen hemen bütün frekanslarda bileşen içerirken, ileride de gösterileceği gibi anestezi altında sadece düşük frekanslarda yoğunlaşan tepeleri mevcuttur. Meydana gelen bu değişiklik hesaplanan entropi değerine düşüş olarak yansır [76, 77, 78, 79]. Elde edilen entropi değerleri 0 1 arasında değişim göstermektedir. 3.7 ZAMAN-FREKANS ANALİZİ Şimdiye dek sunulan metotlar, aslında EEG sinyalinden elde edilen izgesel dağılımı belirli bir dönüşüm ile tek bir sayıya indirgemektedir. Tez çalışmasının ilk bölümlerini oluşturan bilinen parametre incelemelerinin ardından, ilk olarak izgesel dağılımın anestezi süresince zamansal ve uzaysal evrimi üzerine incelemeler yapılmıştır.
35 24 Şekil 3.11: SEF-90 parametresinin anestezi sırasında değişimi[35] Şekil 3.12: İzgesel Dağılım - Entropi İlişkisi Kısa Zamanlı Fourier Dönüşümü EEG sinyalinde, daha önce belirtilen parametrelerin de hesaplanmasında ilk başta Kısa Zamanlı Fourier Dönüşümü kullanılmıştır. Ayrık zamanlı hali ile bu dönüşüm X( f ) = N 1 n=0 x(n)e j 2π f fs n (3.6) şeklindedir. N ayrık zamanlı x(n) sinyalinin nokta sayısını, f gerçek frekansı, f s ise örnekleme frekansını belirtmektedir. Bu formülde Nyquist örnekleme teoremine göre hesaplanması anlamlı frekans aralığı 0 < f < f s /2 şeklindedir. Diğer bir değişle hesaplama için kullanılan açısal frekans değişimleri 0 < φ < π olur. Matlab ortamında, Hızlı Fourier Dönüşüm (FFT) fonskiyonu ile hesaplanan ayrık zaman yönteminde ise
36 25 (3.6) formülü X(k) = N 1 n=0 x(n)e j 2πk N n (3.7) şeklini alır. Bu şekilde birim çember etrafında 2π/N aralıklarla N tane frekans noktasında 0 ile 2π arasındaki tüm değerler hesaplanmaktadır. Daha önce incelenen SEF, İzgesel Entropi, vb. parametrelerin hesaplanabilmesi için de Fourier dönüşümü uygulanması gereken ortak yöntemdir. Bahsi geçen parametrelerin zamanla değişimi, genel olarak belirli uzunluktaki kayan pencere yöntemi ile hesaplanan izgesel kestirimler kullanılarak yapılır. Buna göre alınan x(n) EEG sinyali, Nw 2 xseg i = x(n)w(n m.i) w(τ) = δ(τ j) (3.8) biçiminde alt segmentlere ayrılır, daha sonra her alt segment için bir Fourier dönüşümü uygulanır. Kayan pencerenin boyutu (süresi) N w, kayma miktarı m olarak gösterilmiştir. Kısa zamanlı Fourier dönüşümü olarak kullanılan (3.8) eşitliği, tez çalışması genelinde pencere uzunluğu N w =2 saniye, kayma miktarı m =1 saniye olarak seçilmiştir. j= Nw 2 Örnekleme frekansının ( f s ) 1kHz ve pencere boyutunun 2 saniye (2000 örnek) olduğu göz önünde bulundurulursa, Matlab programında bulunan fft.m fonksiyonu ile her bir segmentin 0.5 Hz çözünürlükteki Fourier dönüşümü için birim çember 2000 noktaya bölünür. Daha önce de belirtildiği gibi, 0 ile 999. noktalar, Hz frekans aralığına denk gelir. Klinik uygulamalarda EEG nin kullanılan frekans aralığının 100 Hz altı olduğu düşünülürse, yapılan dönüşüm işleminin çok da verimli olmadığı söylenebilir. Zira bahsi geçen frekans aralığının gösterimi için, yapılan hesaplamadan sadece ilk 200 nokta yeterlidir. Bu amaçla, hem frekans çözünürlüğünü hem de ilgilenilen frekans aralığının belirlenebildiği fftcoef.m fonksiyonu oluşturulmuştur. Buna göre (3.6) eşitliği, X( f norm(i) ) = N 1 n=0 x(n)e j2π f norm(i)n (3.9) biçiminde düşünülür. Burada f norm(i) = f f s. (3.10)
37 26 Bu fonksiyon aynı zamanda alt pencerelere indirgenmiş zaman serisine de uygulanabilmektedir. Frekans çözünürlüğü, fonksiyona girdi olarak verilen normalize frekans dizisi ile seçilebilmektedir. Örneğin fnorm=[0:0.1:50]/1000 şeklinde (1000 Hz lik örnekleme frekansı ile) normalize edilmiş ve 0.1 Hz aralıklarla değişen 0-50 Hz aralığındaki frekans dizisinin bahsi geçen fonksiyona girdi olarak uygulanması ile, normal fft.m noktalı dönüşüm işlemi aynı sonucu verir. Görüldüğü gibi oluşturulan fonksiyon yapılan işlem sayısı bakımından oldukça verimlidir Stockwell Dönüşümü ve Koherans Analizi Kısa zamanlı Fourier dönüşümüne ek olarak uygulanan zaman-frekans analiz metotlarından biri de Stockwell dönüşümüdür. Stockwell Dönüşüm ifadesine temelde dalgacık analiz metodundan yola çıkarak ulaşılabilir. Herhangi x(t) sinyalinin dalgacık dönüşümü W(τ, d) = x(t)w(t τ, d)dt (3.11) ifadesi ile tanımlanmaktadır. Burada, d = 1/ f olmak üzere ana dalgacık w(t, f ) = f 2π e (t τ)2 f 2 2 (3.12) şeklinde seçilmesi ile, Stockwell dönüşümü genel olarak S (t, f ) = e j2π f τ W(t, d) (3.13) olarak yazılabilir. Buradan da asıl hali ile S x (τ, f ) = x(t) f e (t τ)2 f 2 2 e 2π f t dt (3.14) 2π şeklindeki dönüşüm ifadesi tanımlanmaktadır [71]. Bu şekilde herhangi x(t) sinyalinin ayrık şekilde düşünülen f i frekansları için S x (τ, f i ) bileşenleri ayrı ayrı hesaplanabilir. Stockwell dönüşümü ile hesaplanan zaman-frekans dağılımları herhangi iki sinyal arasındaki koherans analizinde kullanılabilir. Buna göre, belirli pencerelerle x(t) ve y(t) rastgele sinyalleri için hesaplanan S x (t, f ) ve S y (t, f ) Stockwell dönüşümleri kullanılarak S P xx (t, f ) = E{S x (t, f )S x(t, f )} S P yy (t, f ) = E{S y (t, f )S y(t, f )} S P xy (t, f ) = E{S x (t, f )S y(t, f )} (3.15)
38 27 güç izge kestirimleri hesaplanır. Dolayısı ile x(t) ve y(t) arasındaki koherans S C xy (t, f ) = S P xy (t, f ) 2 S P xx (t, f )S P yy (t, f ) (3.16) biçiminde tanımlanır [72, 73]. Hesaplamada Stockwell dönüşümü kullanıldığından, bu koherans ifadesi Stockwell Koheransı olarak isimlendirilmektedir. 3.8 İKİZ İZGESEL ANALİZ Yüksek dereceden izgesel analiz sınıfına giren İkiz izgesel Analiz (Bispectrum), frekanslar arası etkileşimi göstermek için kullanılmaktadır. Uyanık bir bireyde bilinç, algı ve düşünme gibi olguların beyinde birçok frekansı içeren kodlamalı bir şekilde yapıldığı bilinmektedir [40,?, 45, 46, 48]. Bilincin kaybolması ile bu bütünleşik frekans bileşenleri arasındaki ilişkinin değiştiği düşünülürse, ikiz izgesel analizinin de değişim göstereceği şüphesizdir. Olasılık teorisinde x(t) değişkenine ait moment üreten fonksiyon M x (t) E{e tx }, t R (3.17) şeklindedir. İfadedeki e tx teriminin e tx = 1 + tx + t2 x 2 seri açılımından, 2! + t3 x 3 3! +..., (3.18) M x (t) = E{e tx } = 1 + tc x 1 + t2 c x 2 (0) 2! yazılabilir. Yukarıdaki eşitlikte + t3 c x 3 (0, 0) +..., (3.19) 3! c x 1 = E{x(t)}, cx 2 (τ 1) = E{x(t)x(t + τ 1 )}, c x 3 (τ 1, τ 2 ) = E{x(t)x(t + τ 1 )x(t + τ 2 )} (3.20) şeklindedir [53, 54, 55]. Dolayısı ile E{x n } = c (n) x (0) = n M x (0). (3.21) tn Eşitlik (3.20),
39 28 µ x = c x 1 σ 2 x = c x 2 (0) (cx 1 )2 şeklindeki artan derecedeki moment ve kümülantları içermektedir. Başka bir deyişle 1.moment ifadesi ortalama değer, 2.moment ifadesi ise özilinti fonksiyonunu ile ilişkilidir. Literatürde kullanılan ifade ile özilinti fonksiyonu R x (τ) = c x 2 (τ) (3.22) Bir sinyalin özilinti fonksiyonu ile izgesel güç yoğunluğu arasında S x ( f ) = R x (τ)e j2π f τ (3.23) şeklinde bir ilişki mevcuttur (Wiener-Khinchin teoremi). Yani özilinti fonksiyonunun Fourier dönüşümü sinyalin izgesel güç yoğunluğuna eşittir. Benzer bir şekilde, aynı sinyalin c x 3 (τ 1, τ 2 ) 3.dereceden kümülant ifadesinin B x ( f 1, f 2 ) = c x 3 (τ 1, τ 2 )e j2π( f 1τ 1 + f 2 τ 2 ) (3.24) şeklinde tanımlanan 2 boyutlu Fourier dönüşümü çift izgenin tanımını oluşturur. Çift izge tek boyutlu frekans analizi ile B x ( f 1, f 2 ) = X( f 1 )X( f 2 )X( f 1 + f 2 ) (3.25) şeklinde de hesaplanmaktadır (X( f ) = F{x(n)}). Normal frekans analizinden farklı olarak, ikiz izge analizi frekanslar arası doğrusal olmayan etkileşimleri açığa çıkarır [53, 54, 55, 56, 57, 58, 59, 60, 61, 62, 63]. Aslında genel olarak yüksek mertebeden istatistiksel analizin kullanılmasında Gauss olmayan sistemleri ayırt edebilmek Minumum faz özelliği olmayan sistemleri ayırt edebilmek ve bu tür sinyalleri üretebilmek Sinyallerin doğrusal olmayan özelliklerini çıkartıp sınıflandırabilmek, ve vb. özellikleri bulunmaktadır.
40 29 İkiz izge fonksiyonunun hesaplanması simetri özellikleri ile basit bir şekilde yapılmaktadır. 3. dereceden kümülant fonksiyonunun simetri özellikleri (Şekil 3.13-a): c x 3 (τ 1, τ 2 ) = c x 3 (τ 2, τ 1 ) = c x 3 ( τ 2, τ 1 τ 2 ) = c x 3 (τ 2 τ 1, τ 1 ) = c x 3 (τ 1 τ 2, τ 2 ) = c x 3 ( τ 1, τ 2 τ 1 ) (3.26) şeklinde sıralanabilir. Bu eşitliklerden görüleceği gibi, Şekil 3.13 de hesaplanacak herhangi bölge ile kümülant fonksiyonunun kalan bütün değerleri de bulunabilir. Örnek olarak τ 1 = 0, τ 1 = τ 2 doğruları ile sınırlandırılan ve τ 2 > 0 olduğu bölgenin (I.bölge) hesaplanması yeterlidir. Bu özellikler ve (3.24) ifadesinden B x ( f 1, f 2 ) = B x ( f 2, f 1 ) = B x( f 2, f 1 ) = B x ( f 1, f 1 f 2 ) = B x ( f 1 f 2, f 1 ) = B x ( f 2, f 1 f 2 ) = B x ( f 1 f 2, f 2 ) (3.27) eşitlikleri yazılabilir. Dolayısı ile kümülant fonksiyonuna benzer bir şekilde, ikiz izge fonksiyonunun hesabı için, örneğin, f 2 > 0, f 1 > f 2 ve f 1 + f 2 < π ile sınırlı üçgensel alanda kalan bölgenin hesaplanması yeterlidir (Şekil 3.13-b). İkiz izge analizinin frekanslar arası etkileşimi ortaya çıkarma özelliğini, aynı frekans bileşenlerine sahip x 1 (n) = cos(2πλ 1 n + ϕ 1 ) + cos(2πλ 2 n + ϕ 2 ) + cos(2πλ 3 n + ϕ 3 ) x 2 (n) = cos(2πλ 1 n + ϕ 1 ) + cos(2πλ 2 n + ϕ 2 ) + cos(2πλ 3 n + (ϕ 1 + ϕ 2 )) (3.28) işaretlerini göz önüne alalım. Burada λ 3 = λ 1 + λ 2 ve ϕ 1, ϕ 2, ϕ 3 [0, 2π] arasında birbiçimli (uniform) dağılıma sahip bağımsız değişkenlerdir. Söz konusu iki işaret, Şekil 3.14-a da gösterildiği gibi benzer izgesel dağılıma sahiptir. Ancak ikiz izgesel analiz uygulandığında, x 2 sinyalindeki λ 1 ve λ 2 frekanslarının faz toplamına eşit olan 3.bileşenden dolayı, B x2 (λ 1, λ 2 ) değeri 0 dan farklı bir değer alır (Şekil 3.14-b).
41 30 Şekil 3.13: Simetri bölgeleri: (a) Kümülant. (b) İkiz izge [53] İkiz izge analizi kişinin farklı durumlarında alınmış EEG kayıtlarına uygulandığında ayırt edici sonuçlar elde edilmiştir [69]. Şekil 3.15, kişiden göz kapalı ve açık durumlar için alınmış EEG sinyaline uygulanan analiz sonuçlarını göstermektedir. Buna göre iki durum arasında gözler kapalı iken elde edilen (10 Hz, 10 Hz) tepesi, gözler açldığında genliğini kaybetmektedir. Ek olarak gözler açıldığında, daha düşük frekansların birbirini etkilediği de şekilden anlaşılmaktadır. Görüldüğü gibi ikiz izge analizi tek frekanslı izgesel analize göre daha geniş bir analiz alanı yaratmaktadır. BIS cihazına da ismini veren ikiz izge analizi, anestezi derinliğinin takibi için de kullanılmaktadır. Cihaz, SFS (Synch-Fast-Slow) şeklinde isimlendirilen, α ve β oranları gibi ikiz izge yüzeyindeki güç dağılım oranını yansıtan parametreyi hesaplamaktadır. Deneysel olarak, S FS = log( 47.0Hz f =0.5Hz B x( f, f ) 47.0Hz f =40.0Hz B x( f, f ) ) (3.29) şeklinde tanımlanan [6] SFS parametresi BIS cihazının anestezi derinliğini kestirmek için kullandığı özgün parametresidir 6. 6 Bu parametre ile ilgili kesin formül bilinmektedir. Rampil e ait makalede [6] geçen formüle daha sonra
42 31 Şekil 3.14: a) x 1 ve x 2 sinyallerinin frekans dağılımları. b) Sinyallerin ikiz izgesel dağılımları. İkiz izgesel analizi uygulamak üzere fastbispectrum.m ana fonksiyonu yazılmıştır. Bu fonksiyon (3.25) eşitliğinde tanımlanan üçlü çarpımı, önce normal izgesel hesap yapılıp daha sonra buradan oluşturulan 2 vektör ve 1 adet matrisin çarpımı ve alınan ortalamalarla hızlı bir şekilde hesaplanmaktadır Hz İŞİTSEL DURAĞAN HAL YANITI ANALİZİ İşitsel potansiyeller daha önce de belirtildiği gibi spontan EEG ye kıyasla oldukça düşük genliklere sahiptir. Bu sinyallerin analiz edilebilmesi için kabul gören bir yol zaman alanında ortalama alma yöntemidir. Buna göre işitsel uyaranlı EEG sinyalleri (darbeli) uyaran frekansına bağlı olarak belirli uzunluktaki alt kümelere bölünmekte ve ortalamaları alınmaktadır. Bu şekilde rastgele dağılmış olan spontan EEG verisi ve gürültü azalırken, belirgin bir kuralla beyinde üretilen işitsel sinyal daha yüksek gürültü sinyal oranıyla elde edilebilmektedir. S. Hagihira nın çalışmasında [52] da değinilmekte, fakat formülün yapılan isteğe rağmen ASPECT Systems tarafından tam olarak açıklanmadığı anlatılmaktadır.
43 32 Şekil 3.15: Göz açık ve kapalı durumda elde edilen ikiz izge [69] Herbir uyaran sonucu üretilen İşitsel Uyarılmış Potansiyel, uyaran frekansının arttırılması ile üst üste binmeye başlar ve uzun zaman sabitine sahip bir RC devresinin yüksek frekansla uyarılması gibi periyodik bir dalga halini alır (Şekil 3.16). Oluşan bu dalga uyaran frekansındaki Durağan Hal Cevabı olarak isimlendirilir. Literatürde 40 Hz olarak geçen İşitsel Durağan Hal uyarım frekansı aslında Hz arasındaki uyaran frekanslarını temsil eder. Bu frekanstaki uyaranların önemi ise üstkortekste bilinç ve farkındalıkla ilgili olduğu öne sürülen γ bandındaki sinyallerin zaman ya da frekans alanlarındaki genlikleri hakkında bilgi verebilmesidir. 40 Hz DHY nin anestezi altında değişimini incelemek amacı ile Matlab ortamında 25 ms aralıklı ve 2 ms uzunluklu darbeler üretilerek kulaklık vasıtası ile hastaya dinletilmiştir BAĞIMSIZ BİLEŞEN ANALİZİ Mühendislik ve klinik çalışmalarda karşılaşılan çok değişkenli sinyaller, çoğu zaman gizli ve kolay gözlenemeyen ya da kaydedilemeyen sinyallerin karışımından oluşan
44 33 Şekil 3.16: Farklı işitsel uyaran frekansları ile elde edilen cevabın zaman ve frekans alanındaki gösterimleri: Düşük uyaran frekansında elde edilen cevap bilinen işitsel potansiyele benzer olurken artan frekansla uyaran frekansında baskın salınıma sahip (Durağan Hal) cevap elde edilmektedir [44]. dolaylı gözlemler olabilmektedir. Örnek olarak, EEG, beynin çeşitli yerlerinde farklı ya da eş-zamanlı oluşan sinyallerin, yine kafatasında farklı yerlere yerleştirilen birden fazla elektrotla (en aza indirgenen fakat engellenmesi mümkün olmayan) gürültülü bir şekilde kaydedilmesi ile elde edilir. İşte faktör analizi, elde edilen bu karmaşık sinyallerin altında yatan asıl (gizli) sinyalleri bulmayı hedefler. Bu çalışmada da yöntemin kullanım amacı, daha sonra gösterileceği gibi anestezinin derinleşmesi ve hafifleşmesi ile EEG de oluşan değişimlerin izgesel ve eşlik eden topografik dağılım olarak ayrıştırılmasıdır. Bağımsız Bileşen Analizi (İng. Independent Component Analysis, ICA) Herault ve Jutten tarafından 1983 yılında ortaya atılmıştır. BBA yöntemi, birbirinden istatistiksel olarak bağımsız olan bileşenleri arar. Herhangi iki x, y değişkenine ait olasılık dağılımları, P(x, y) = P(x).P(y) (3.30) eşitliğini sağlıyorsa, bu değişkenler bağımsız değişkenlerdir. Başka bir deyişle, x değişkeni hakkında bildiğimiz şey, y değişkeni hakkında herhangi bir bilgi vermeyecektir (Şekil 3.17). BBA yönteminde, ulaşılmak istenen n tane s i gizli bileşen ile m tane x j gözlemi arasında, x j = a j1 s 1 + a j2 s a jn s n, j (3.31)
45 34 Şekil 3.17: Saçılım Grafikleri, a) Bağımlı Değişkenler: Bu durumda x veya y değerinin bilinmesi, diğer değer ile ilgili ipucu vermektedir., b) Bağımsız Değişkenler: x veya y değerinden herhangi birinin bilinmesi bir fark yaratmamaktadır. eşitliğine sahip model oluşturulur. Bu model, gizli bileşenlerden gözlemlerin üretilmesine dayandığı için meydana getirici (İng. generative) model olarak isimlendirilir [81]. Modelde herbir değişkenin zamandan bağımsız olarak rastgele bir değişkene ait olduğu varsayımı yapılmaktadır. Dolayısı ile (3.31) Eşitliğinde s i (t) ve x j (t) değerleri zaman indeksi olmadan gösterilmiştir. Eşitliği s = {s 1, s 2,..., s n } ve = {x 1, x 2,..., x m } olacak şekilde x x = As (3.32) matris eşitliği şeklinde yazmak mümkündür. Burada A matrisi, karıştırıcı matris olarak adlandırılır. İleride de kullanılacağı gibi bu eşitlik, a j A matrisinin j. satırını göstermek üzere, n = a i s i (3.33) x i=1 şeklinde de yazılabilir. BBA yönteminde işleme başlanırken, bilinen vektörleri ile birlikte önemli bir varsayım x yapılmaktadır. Bu varsayım, ulaşılmak istenen s i gizli kaynaklarının, aralarında istatistiksel bağımsız olduklarıdır. Dolayısı ile BBA yönteminde algoritma, s j değerlerini aralarında olabildiğince istatistiksel bağımsız yapan A karıştırıcı matrisinin kestirilmesine dayanmaktadır. Yöntemin çalışması için gerekli önemli bir koşul da s i gizli değişkenlerinin ayrıca Gauss olmayan olasılık dağılım fonksiyonlarına sahip
46 35 olmalarıdır. Bunun nedeni ise dağılım fonksiyonları Gaus olan iki rastgele değişkenin birleşik dağılım fonksiyonunun tamamıyle simetrik olmasıdır. Örnek olarak birim varyansa ve 0 ortalamaya sahip birbirinden bağımsız x 1 ve x 2 rastgele değişkenleri için, x2 x2 p(x 1 ) = e 1 2 2π, p(x 2 ) = e 2 2 (x2 +x 2 p(x 1, x 2 ) = e 1 2 ) 2 2π 2π (3.34) olacaktır (Şekil 3.18). Dolayısı ile BBA algoritması hiçbir çözüme yakınsama gösterememektedir [81]. Şekil 3.18: İki Gaus dağılıma sahip değişkenin birleşik dağılım fonksiyonu BBA algoritması hesaplama sayısını azaltmak ve çözümü kolaylaştırmak için gözlem verisi birtakım ön adımlardan geçirilir. Bunlardan ilki gözlem verisini 0 ortalamaya çekmektir. Literatürde centering olarak isimlendirilen bu işlem gözlem değişkenine ait x m = E{x } ortalama vektörünün çıkarılması ile yapılır. Dolayısı ile herbir gözlem artık 0 etrafında dağılımlara sahip olacaktır (Şekil 3.19). Gözlem verisi ortalandıktan sonra 2. adımı bu gözlemlerin beyazlaştırılması alır. Beyazlaş- tırma, gözlem değişkenlerinin aralarında ilintisiz olması ve herbirinin birim varyansa sahip olması demektir. Yani, beyazlaştırılan yeni gözlem değişkeni z olmak üzere, E{zz T } = I (3.35)
47 36 Şekil 3.19: BBA uygulanacak 15 kanallı 0 ortalamalı EEG (gözlem) verisi hedeflenmektedir. Bunu sağlamak için matris dönüşüm yöntemlerinden Tekil Özayrışım (İng. Emprical Value Decomposition) uygulanır. TÖ yöntemi kare matris yapısındaki kovaryans matrisini (Şekil 3.20) E{x x T } = UDU T (3.36) şeklinde U ve D matrislerine ayırır. Bu matrislerden U ortogonal (UU T = I) özvektörler matrisi, D ise diyagonal özdeğerler matrisidir (D = diag{d 1, d 2,..., d m }) (Şekil 3.21). Elde edilen bu matrisler kullanılarak z = D 1/2 U T x (3.37) beyazlaştırılmış z gözlem verisi elde edilir. Sağlama yapılırsa E{zz T } = E{D 1/2 U T x (D 1/2 U T x ) T } = E{D 1/2 U T x x T UD 1/2 } = D 1/2 U T E{x x T }UD 1/2 = D 1/2 U T UDU T UD 1/2 = I (3.38)
48 37 Şekil 3.20: 15 kanallı gözlem verisinin kovaryans matrisi Dolayısı ile elde edilen yeni gözlem verileri (kanalları) birbirleri ile ilintisiz ve birim varyanslı hale getirilmiştir (Şekil 3.22). Daha önceden tanımlanan (3.32) dönüşümü x = As D 1/2 U T x = D 1/2 U T As z = Ãs (3.39) şeklinde yazılırsa, birim varyanslı gizli s i bileşenlerini, yine birim varyanslı yeni gözlem değişkenine dönüştüren yeni bir à karıştırıcı matrisi tanımlanmış olur. Benzer bir şekilde E{zz T } = I = E{Ãs (Ãs ) T } = E{Ãs s T à T } = ÃE{s s T }à T I = Ãà T (3.40) eşitliği ile, kestirilmek istenen karıştırıcı matrisin ortogonal olacağı açıktır. Dolayısı ile aslında beyazlaştırma işlemi sayesinde, normalde n 2 tane elemanı olan A matrisinin, ortogonal olması nedeni ile sadece n(n + 1)/2 tane elemanının kestirilmesi yetecektir. Basitleştirmeden dolayı BBA her zaman beyazlaştırma işlemi ile başlamaktadır
49 38 Şekil 3.21: Elde edilen U ve D matrisleri Şekil 3.22: Beyazlaştırılmış yeni gözlem verisinin kovaryans matrisi [81, 82, 86, 87, 83, 88]. Beyazlaştırma işleminden sonra BBA, Gaus fonksiyonundan olabildiğince farklı olasılık dağılımlarına sahip s i gizli bileşenlerini arar. BBA yönteminde bu amaçla birçok yöntem tanımlanmıştır [80]. Yöntemlerden en yaygın olarak kullanılanı Basıklık ( İng. kurtosis) değerini arttırmaya dayalı FASTICA algoritmasıdır. İstatistik literatüründe x rastgele değişkenine ait basıklık bas{x} = E{x 4 } 3E{x 2 } 2 (3.41) şeklinde tanımlanmaktadır. Gauss dağılımı için, 4.moment 3E{x 2 } 2 değerine eşit olduğundan, Gauss dağılımına sahip bir değişkenin basıklık değeri 0 dır. Rastgele
50 39 değişkenler, 0 ın altında (İng. subgaussian, platykurtic) ya da üstünde (İng. supergaussian, leptokurtic) basıklık değerlerine sahip olabilirler (Şekil 3.23). Dolayısı ile BBA algoritmasının bu kısmında yapıldığı gibi basıklığın mutlak değerinin arttırılması, Gauss dağılımından uzaklaşan bir dağılımın bulunmasına olanak sağlar. Şekil 3.23: Çeşitli dağılım fonksiyonları ve Basıklık değerleri (D: Laplace, S : Hiperbolik Sekant, L: Lojistik, N: Gaus, C= Raised Cosine, W= Wigner, U = Hepsibir dağılımlar). FASTICA algoritmasının işleyişi, 2 gizli bileşenli gözlem ile kolayca gösterilebilir. Matlab altında oluşturulan s 1 ve s 2 birim varyansı rastgele değişkenleri ve yine rastgele oluştu- rulan A karıştırıcı matrisi kullanılarak öncelikle gerçek hayatta gözlem olarak elde edilen 2 kanallı = {x 1, x 2 } gözlem matrisi oluşturulur (Şekil 3.24). Yapılan x beyazlaştırma işleminin öncesi ve sonrasındaki dağılımlar Şekil 3.25 de gösterilmiştir. Şekil 3.25 dan görülebileceği gibi, sadece iki adet gözlem kanalının olması durumunda BBA işlemi basitçe ortak dağılım fonksiyonunun döndürülmesi ile gerçekleştirilebilir. Uygun döndürme açısı, herbir açı için elde edilen yeni z tek kanallı gözlem vektörüne ait kurtosis değişiminin en yüksek olduğu açı olacaktır (Şekil 3.26).
51 40 Şekil 3.24: Matlab ile üretilen s 1 ve s 2 gizli kaynakları Şekil 3.25: Beyazlaştırma işlemi öncesi ve sonrası ortak dağılımlar Tek bir bileşen için z = [ w1 w 2 ] T z = w T z (3.42) şeklinde elde edilen tek kanallı yeni gözlem vektörü, birim varyansın sağlanması adına w = 1 (3.43) sağlanacak şekilde algoritma güncellenmektedir. Daha çok sayıdaki gizli değişkenin kestirilmesinde de benzer bir algoritma kullanılmaktadır. [80, 81]. Sıradan BBA yönteminin kullanıldığı çalışmalarda [82, 83, 84, 85] sinyallerin zamansal yapısıyla ilgilenilmemekte, sadece istatistiksel bağımsız oldukları varsayılmaktadır.
52 41 Şekil 3.26: Dağılıma uygulunan döndürme açısı ve oluşan tek kanallı yeni değişkene ait basıklık değişimi Bununla birlikte litatürde sinyallerin zamansal [88, 89, 90] ve uzaysal [91, 92] yapısına göre tanımlanan BBA yöntemleri de bulunmaktadır GRANGER NEDENSELLİĞİ VE BAĞLANTISALLIK ANALİZİ Bu bölümde anestezi derinliği ve EEG kanalları arasındaki bağlantısallık ilişkisi analizinin teorik kısmı incelenecektir. Bununla ilgili olarak doğrusal Özbağlanımlı (İng. Autoregressive) Modelleme, Granger Nedenselliği ve Kısmi Yönlü Koherans kavramları da anlatılacaktır Özbağlanımlı Modelleme Parametrik sinyal modelleme yöntemlerinden biri olan Özbağlanımlı (ÖB) modelleme, durağan x(n) sinyali için X(z) = H(z)E(z) = b 0 + b 1 z b M z M E(z) (3.44) a 0 + a 1 z a N z N şeklinde ifade edilmektedir. Eşitlikte X(z), H(z) ve E(z) sırasıyla modellenen x(n) sinyalinin, sisteme ait h(n) birim darbe cevabının ve sistemin girişi olan e(n) beyaz gürültü sinyalinin F(z) = N f k=0 f (k)z k (3.45)
53 42 şeklinde tanımlanan z dönüşümlerini temsil etmektedir. (3.44) eşitliği X(z) = b 0 + M k=1 b k z k a 0 + N k=1 a E(z) k kz (3.46) şeklinde kısaltılabilir. Burada sadece b i katsayılarının varlığı (a i = 0, i 0) sistemin sonlu uzunlukta (M tane) darbe cevabına sahip filtreden (F.I.R.) geçirilmesi anlamına gelir. Bu durumda kullanılan parametrik modelleme yöntemi M.dereceden Yürüyen Ortalama (Moving Average) yöntemi adını alır. Diğer durumda ise (b i = 0, i 0), N. dereceden ÖB parametrik modeli elde edilir. Bu durumda beyaz gürültü sinyali e(n) sonsuz uzunlukta darbe cevabına sahip filtreden (I.I.R.) geçirilerek x(n) hedef sinyali elde edilmektedir. 3. farklı durum olarak, her iki katsayı kümesinin de 0 dan farklı olduğu durumda elde edilen model ise Özbağlanımlı Yürüyen Ortalamalı model adını alır (İng. ARMA). Bir sonraki bölümde kullanılacak olan yöntem olduğundan bahsi geçen diğer modelleme yöntemleri anlatılmayacaktır. ÖB modelleme Yukarıda durağan x(n) sinyali için tanımlanan, p. dereceden (zamanla değişmeyen) ÖB model, X(z)(a 0 + x(n) + E(z) X(z) = a 0 + N k=1 a kz k N a k z k ) = E(z) k=1 Inv{z}, a 0 = 1 N a k x(n k) = e(n) k=1 x(n) = N a k x(n k) + e(n) (3.47) k=1 şeklinde ayrık zamanda ifade edilmektedir. Başka bir bakış açısı ile bu model, yine durağan x(n) sinyalinin bilinen n = 0, 1, 2.., N değerleri için p ˆx(n) = a k x(n k) (3.48) k=1 biçimindeki ileri kestirim eşitliği olarak da tanımlanır. Yani x(n) değişkeninin herhangi bir n anındaki değeri, daha önceki p tane değerinin ağırlıklandırılmış toplamı biçiminde ifade edilebilir. Bu durumda e(n), gerçek değer ile kestirilen değer arasındaki e(n) = x(n) ˆx(n) (3.49)
54 43 şeklinde tanımlanan kestirim hatasına dönüşür. Teorik olarak, model katsayıları e(n) hata sinyaline ait gücü minimize edecek şekilde hesaplanır. Diğer bir ifade ile f (n, a 1, a 2,.., a p ) = Σ e(n) 2 (3.50) ile tanımlanan fonksiyon için f (n, a 1, a 2,.., a p ) a k = 0 (3.51) eşitliğini sağlayan a k katsayıları bulunur. İleri kestirim için p. dereceden kullanılarak ÖB Modelde sinyalin gözlemlenen değerleri x(p) = a 1 x(p 1) a p 1 x(1) + a p x(0) x(p + 1) = a 1 x(p) a p 1 x(2) + a p x(1) x(p + 2) = a 1 x(p + 1) a p 1 x(3) + a p x(2)... x(n 1) = a 1 x(n 2) a p 1 x(n p) + a p x(n p 1) (3.52) eşitlik kümesi yazılabilir. Daha sonra bu eşitlikler x(p 1)... x(1) x(0) x(p)... x(2) x(1) X = x(p + 1)... x(3) x(2) x(n 2)... x(n p) x(n p 1) b = x(p) x(p + 1) x(p + 2).. x(n 1), a = a(1) a(2) a(3).. a(p) (3.53) (3.54) tanımlanarak Xa = b (3.55) matris eşitliği biçimine dönüştürülür. Yukarıda bahsi geçen hata minimizasyon problemi asıl olarak Φ = b Xa 2 (3.56)
55 44 ifadesine benzer bir şekilde En Küçük Kareler (EKK) yöntemi ile çözülebilir [93, 94, 95]. Burada maliyet fonksiyonu kestirim hatasının gücünü göstermektedir. Sistemin çözümü istenilen ÖB Model katsayılarının EKK yöntemi ile çözümünü verir. Çalışmalarda bu matris denkleminin çözümü MATLAB programında bulunan lscov.m fonksiyonu ile yapılmıştır. Durağan olmayan sinyallerin de zamanla değişen ÖB model ile temsili önerilmiştir. Yine e(n) gürültü sinyalinden üretilen durağan olmayan x(n) sinyaline ait ÖB model p x(n) = a k (n)x(n k) + e(n) (3.57) k=1 şeklini alır. Eşitlikte, durağan sinyale ait model için yazılan a k katsayılarının da zamanla değiştiği görülmektedir. Literatürde model katsayılarını kestirmek amacı ile katsayıların belirli taban fonksiyonlarla temsili önerilmiştir [112]. Tez çalışmaları sırasında, öncelikle tek bir EEG kanalı için denenen bu modele göre zamanla değişen katsayılar q a k (n) = a km u m (n) (3.58) m=0 şeklindeki q+1 tane (tercihen tanımlı oldukları uzayda birbirine dik) u m (n) fonksiyonunun doğrusal toplamı biçiminde yazılır. Bu şekilde (3.59) eşitliği, p q x(n) = a km u m (n)x(n k) + e(n) (3.59) k=1 m=0 şekline dönüşür. Zamanla değişen katsayıların bu şekildeki yazılımı sayesinde, model katsayılarının kestirimi sadece seçilen taban fonksiyonlarına ait (zamanla değişmeyen) katsayıların bulunması şeklindeki probleme dönüşmektedir [112, 114]. Katsayıların çözümü için literatürde önerilen yönteme göre ilk olarak c k,l (i, j) = u k (n)u l (n)x(n i)x(n j), k, l = {0, 1,..., q} (3.60) i=1 k=0 n biçimindeki genelleştirilmiş korelasyon (ya da kovaryans) fonksiyonu tanımlanır. Bu fonksiyona göre katsayılar p q a ik c kl (i, j) = c 0l (0, j) (3.61)
56 45 eşitlikleri ile tanımlı denklem sistemini sağlar. Eşitliği matris biçiminde yazmak da mümkündür. Bu amaçla öncelikle katsayılar vektörü a = [ a 10 a a p0 a 11 a a p1... a 1q a 2q... a pq ] T (3.62) daha sonra da eşitliğin sağ tarafını oluşturan elemanlar vektörü b = [ c 01 (0, 1) c 01 (0, 2)... c 01 (0, p) c 02 (0, 1) c 02 (0, 2)... c 0q (0, p) ] T (3.63) son olarak da pxp elemanlı c kl (1, 1) c kl (1, 2)... c kl (1, p) c Φ kl = kl (2, 1) c kl (2, 2)... c kl (2, p), k, l = {0, 1,.., q} (3.64) c kl (1, 1) c kl (1, 2)... c kl (1, p) kare matrisleri tanımlanır. Bu şekilde (3.61) eşitliği, Φ 00 Φ Φ 0q Φ 10 Φ Φ 1q a = b (3.65) Φ q0 Φ q1... Φ qq biçimindeki Yule-Walker eşitliklerine benzeyen matris eşitliğine dönüşür. Bu matris eşitliği daha önce de gösterildiği gibi EKK yöntemi ile çözülebilmektedir.hesaplanan a vektörü kullanılarak zamanla değişen ÖB modele ait gerçek model katsayıları, daha önce tanımlanan 3.58 eşitliği kullanılarak elde edilir. Zamanla değişen katsayıları modellemek için kullanılacak olan taban fonksiyonları seçilirken, modellenen sinyale ait izgenin değişim hızı göz önünde bulundurulmaktadır. Buna göre literatürde kullanılan fonksiyonlar Legendre, Fourier ve Ayrık Kosinüs Dönüşüm (İng. Discrete Cosine Transformation, DCT) Taban Fonksiyonları, Walsh, Haar gibi ayrık zaman fonksiyonlarıdır [114, 115, 116, 117]. Tez çalışmaları kapsamında, zamanla değişen ÖB model katsayılarının bulunması için daha önce durağan ÖB model katsayılarının hesabı için kullanılan yöntem uyarlanmıştır. Buna göre (3.48) eşitliğine benzer bir şekilde p q ˆx(n) = a km u m (n)x(n k), n = {p, p + 1,..., N} (3.66) k=1 m=0
57 46 yazılabilir. Gözlemlenen herbir n = {p, p + 1,..., N} değeri için yazılırsa x(p) = a 10 u 0 (p)x(p 1) a p0 u 0 (p)x(0) a pq u q (p)x(0) x(p + 1) = a 10 u 0 (p + 1)x(p) a p0 u 0 (p)x(1) a pq u q (p + 1)x(1) x(p + 2) = a 10 u 0 (p + 2)x(p + 1) a p0 u 0 (p)x(2) a pq u q (p + 2)x(2)... x(n) = a 10 u 0 (N)x(N 1) a p0 u 0 (N)x(N p) a pq u q (N)x(N p) (3.67) şeklindeki eşitlik sistemi elde edilir. Bu eşitlik sistemi dikkatlice incelendiğinde gözlem ve fonksiyonların ardışıl değerlerinin kullanıldığı görülmektedir. Dolayısıyla, x(r) = {x(r), x(r + 1),..., x(n p + r)} T r = {0, 1,.., p} (3.68) şeklindeki p + 1 tane gözlem vektörünü u m = {u m (p), u m (p + 1),..., u m (N)} T m = {0, 1,.., q} (3.69) şeklindeki q + 1 tane fonksiyon vektörünü tanımlayarak eşitlik sistemini x(p) = [ u 0 x(p 1)... u 0 x(0)... u q x(0) ] a (3.70) biçiminde yazmak mümkündür. Burada a = [ a a p0... a pq ] T (3.71) vektörü eşitlik sistemine ait hesaplanacak katsayıları içeren vektördür. Matris denkleminin (EKK yöntemi ile) çözümünün ardından a k (n) model katsayıları daha önce tanımlanan 3.58 eşitliği kullanılarak elde edilir. Yöntemden bağımsız olarak, elde edilen a k (n) katysayılarından, durağan olmayan x(n) sinyalinin zamanla değişen izgesel kestirimini hesaplamak mümkündür. Buna göre daha önce de tanımlandığı gibi birim varyanslı e(n) sinaylinden üretilen durağan x(n) sinyali için S x (w) = X(z) z=e jw = H(z)E(z) z=e jw = p z=e jw (3.72) a k z k k=1
58 47 biçiminde sabit katsayılı ÖB model ile kestirilebilen izgesel dağılım, zamanla değişen katsayılar kullanılarak S x (n, w) = X(n, z) z=e jw = H(n, z)e(z) z=e jw = biçiminde hesaplanabilir p z=e jw (3.73) a k (n)z k k=1 Zamanla değişen tek kanallı ÖB model yaklaşımının genelleştirilmiş korelasyon ve vektör yöntemleri ile çözümleri yazılan fonksiyonlarla gerçeklenmiş ve karşılaştırılmıştır. Ayrık kösinüs ve Legendre taban fonksiyonlarının kullanılabildiği bu fonksiyonlar ayrıca oluşturulan iki tip sinyal için test edilmiştir. Benzetilen sinyallerden ilki x 1 (t) = cos(2πφ(t)t), φ(t) = 3t, 0 < t < 5s 30, 5 < t < 10s (3.74) şeklinde 5 saniyelik doğrusal cıvıltı (İng. Linear Chirp) ve ardından 5 saniyelik sabit ton (30 Hz) içeren sinyaldir. İkinci sinyal ise frekansı zamanla 25 Hz civarında (sinus sinyali şeklinde) değişen x 2 (t) = cos(2πφ(t)t), φ(t) = cos(2π15t) (3.75) sinyalidir. ÖB model derecesi 4 (p = 4) ve kullanılan taban fonksiyon sayısı 3 (q + 1 = 3) seçilerek oluşturulan tvarbasis.m fonksiyonunun çeşitli gürültü seviyelerini de içeren başarımı DCT ve Legendre fonksiyonları için test edilmiştir.
59 48 Şekil 3.27: 1. test sinyali, izgesel dağılımı ve Zamanla Değişen ÖB Modelleme sonucu elde edilen izgesel dağılımlar Çokdeğişkenli Özbağlanımlı Modelleme EEG kanallarının herbiri ayrı bir x(n) sinyalini temsil etmektedir. Dolayısı ile herbir kanal için ayrı ayrı ÖB Model hesaplanabilir. Fakat ÖB Modelleme aynı anda birden fazla gözleme (kanala) sahip sinyaller için hesaplanabilmektedir. Çokdeğişkenli ÖB Modelleme (İng. Multivariate AR Modelling) isimli bu yöntemde yine tek kanallı modelleme yöntemine benzer bir şekilde (n) v = A 1ṽ(n 1) + A 2 ṽ(n 2) A p ṽ(n p) (3.76) eşitliği ile yazılabilir. Burada (n) v = v 1 (n) v 2 (n)... v M (n), A k = a 11 (k) a 12 (k)... a 1M (k) a 21 (k) a 22 (k)... a 2M (k) a MM (k) a M2 (k)... a MM (k) (3.77)
60 49 Şekil 3.28: 1. test sinyali ve Zamanla Değişen ÖB Modelleme sonucu elde edilen kestirim hataları Şekil 3.29: Gürültü seviyesi ve kestirim hatası ilişkisi (1. test sinyali)
61 50 Şekil 3.30: 2. test sinyali, izgesel dağılımı ve Zamanla Değişen ÖB Modelleme sonucu elde edilen izgesel dağılımlar Şekil 3.31: 2. test sinyali ve Zamanla Değişen ÖB Modelleme sonucu elde edilen kestirim hataları
62 51 Şekil 3.32: Gürültü seviyesi ve kestirim hatası ilişkisi (2. test sinyali) sırası ile M boyutlu gözlem vektörü (n = 0, 1,..N 1) ve AR katsayılarını içeren p adet (model derecesi) kare matrislerdir. İlk değişkene göre eşitliklerin açık hali v 1 (n 1) v 1 (n 2) v v 1 (n) = A 1 (1, :) 2 (n 1) v + A... 2 (1, :) 2 (n 2) A... p (1, :) v M (n 1) v M (n 2) v 1 (n p) v 2 (n p)... v M (n p) (3.78) biçimindedir. Eşitlikte A k (1, :) ifadesi A k matrisinin 1. satır vektörünü temsil etmektedir. Eşitlik n = p için v 1 (p) = A 1 (1, :) v 1 (p 1) v 2 (p 1)... v M (p 1) + A 2 (1, :) v 1 (p 2) v 2 (n 2)... v M (p 2) A p (1, :) v 1 (0) v 2 (0)... v M (0) (3.79) şeklini alır. Bu matris eşitliği v 1 (p) = [ A 1 (1, :) A 2 (1, :)... A p (1, :) ] v 1) (p v 2) (p... (0) v buradan da v 1 (p) = [ ṽ T (p 1) ṽ T (p 2)... ṽ T (0) ] A T 1 (1, :) A T 2 (1, :)... A T p(1, :) (3.80)
63 52 biçimine dönüşür. Daha önceden de belirtildiği gibi, yukarıdaki eşitlik gözlem matrisine ait ilk p tane değer kullanılarak yazılmıştır. v 1 (n) değişkenine ait eşitliklerin tümünde A k (1, :) elemanları bulunacağından, (3.80) eşitliği n = p, p+1,..., N değerleri (gözlemleri) için v 1 (p) v T (p 1) ṽ T (p 2)... ṽ T (0) A T v 1 (p + 1) v = T (p) ṽ T (p 1)... ṽ T 1 (1, :) (1) A T 2 (1, :) v 1 (N 1) v T (N 2) ṽt (p 2)... ṽt (N 1 p) A T p(1, :) şeklindeki matris denklemi elde edilir. Bu denklemi v 1 (p) v T (p 1) ṽ T (p 2)... ṽ T (0) b 1 = v 1 (p + 1) v, V = T (p) ṽ T (p 1)... ṽ T (1) v 1 (N 1) v T (N 2) ṽ T (p 2)... ṽ T (N 1 p) dönüşümleri ile A T 1 (1, :) b 1 = V A T 2 (1, :)... A T p(1, :) (3.81) (3.82) (3.83) biçiminde yazmak mümkündür. Bu denklem sisteminin EKK yöntemiyle çözümü, A k kare matrislerinin 1.satır vektör elemanlarını, dolayısı ile ÖB modelin 1.değişkene ait katsayılarını verir. Formül tüm değişkenler için v i (p) b i = v i (p + 1)... v i (N 1) (3.84) şeklindeki dönüşümden A T 1 (i, :) b i = V A T 2 (i, :)... A T p(i, :) (3.85) denklem sistemleri yazılabilir. Bu sistemlerin çözümü, M boyutlu ve N elemanlı v gözleminin MAR(p) şeklinde gösterilen p. dereceden çok değişkenli ÖB model katsayılarını verir. Bahsedilen yöntem EKK yöntemi ile katsayıları kestirmektedir. Literatürde özilinti fonksiyonundan yola çıkarak tanımlanan metotlar da mevcuttur [108].
64 53 Bahsi geçen bu yöntem, yazılan arfit.m Matlab fonksiyonu ile gerçeklenmiştir. Fonksiyona girdi olarak verilen 15 kanallı EEG verisi, model derecesinin azaltılması için 1kHz yerine 100 Hz lik örnekleme frekansına indirilmiş, daha sonra herbir kanal için (3.85) Eşitliği çözülerek model katsayıları bulunmuştur Granger Nedenselliği Britanyalı ekonomist Clive William John Granger (4 Eylül Mayıs 2009) tarafından ortaya atılan ekonomik zaman serisi analiz yöntemi [93], diğer alanlardaki zaman serilerine de başarı ile uygulanmıştır. Granger Nedensellik Analizi (ya da Testi), temelde herhangi iki değişkenin gelecek değerlerinin birbilerine olan bağımlılığını ölçmeyi amaçlar. Granger nedensellik hipotezine göre: Bir X değişkeninin, sadece kendi geçmiş değerleri kullanıldığında elde edilen ileri değerlerinin kestirim hatası, etkilendiği düşünülen diğer Y değişkeninin geçmiş değerleri de kullanıldığında azalıyorsa, Y değişkeni X değişkenine neden oluyor denebilir. Fakat bunun tersinin olması şart değildir. Tersinin varlığı da yine aynı test ile ölçülebilir. Herhangi x 1 ve x 2 değişkenlerinin p. dereceden regresyon modeli kullanılarak, aralarında bulunan doğrusal nedensellik ilişkisi x 1 (n) = p k=1 a 11(k)x 1 (n k) + p k=1 a 12(k)x 2 (n k) + e 1 (n) x 2 (n) = p k=1 a 21(k)x 1 (n k) + p k=1 a 22(k)x 2 (n k) + e 2 (n) (3.86) şeklinde ifade edilebilir. Burada a 12 (k) ve a 21 (k) katsayıları, x 1 ve x 2 değişkenlerinin birbirlerine olan etkisini temsil etmektedir (Şekil 3.33). Eşitlik sonlarına eklenen e 1 ve e 2 vektörleri ise, kestirim hatası(ing. prediction error, residual) olarak modeli tamamlamaktadır. Şekil 3.33: İki değişkenli Granger Nedenselliği
65 54 (n) x = {x 1(n), x 2 (n),.., x N (n)} ve E(n) = {e 1 (n), e 2 (n),..., e N (n)} birbirleri ile ilintisiz, sıfır ortalamalı beyaz gürültü kanalları olmak üzere, (3.86) eşitliği (3.76) eşitliğine benzer bir şekilde (n) x = A 1x (n 1) + A 2 x (n 2) A p x (n p) + E(n) p (n) x = A p x (n p) + E(n) (3.87) k=1 yazılabilir. Bu eşitliği tek bir kanal için yazmak gerekirse x i (n) = p k=1 N a i j (p)x j (n k) + e i (n) (3.88) j=1 olur. Çok kanallı bu modele göre, i. gözlem kanalı, e i (n) beyaz gürültü sinyali ve kendisini de içeren j adet kanalın geçmiş değerlerinin belirli katsayılar ile ağırlıklandırılmasıyla elde edilmektedir. Daha önceki bölümde anlatıldığı gibi, a i j (k) katsayıları (3.85) eşitliğiyle oluşturulan denklem sisteminin çözümü ile hesaplanmaktadır Kısmi Yönlü Koherans Birönceki bölümde tanımlanan (3.87) çok değişkenli model p X(z) = A p X(z)z k + E(z) k=1 p X(z) = I A p z k k=1 1 E(z) X(z) = H(z)E(z) (3.89) şeklinde yazılabilir. Burada H(z), değişkenler (kanallar) arası ilişkiyi yansıtan çok yönlü transfer fonksiyonu oluşturmaktadır. Herhangi iki kanalın birbirlerine olan etkisi (Granger nedenselliği) farklı olabileceginden H(z) transfer fonksiyonu simetrik olmayacaktır. Z dönüşümü yerine izgesel alanda önceki eşitlik X( f ) = H( f )E( f ) şeklinde yazılırsa X( f )X( f ) = S x ( f ) = H( f )E( f )E( f ) H H( f ) H = H( f ) H( f ) H (3.90)
66 55 olur [100]. Eşitlikte, E(n) beyaz gürültü bileşeninin kovaryans matrisidir. Buradan da anlaşılacağı gibi, farzedilen modelde E(n) vektörleri; birbirlerinden bağımsız, birim varyanslı beyaz gürültü kanal örneklerini temsil etmektedir. Hesaplanan modelin doğruluk derecesi de yine bu matrisin diyagonallik derecesi ile ölçülmektedir. Çok değişkenli ÖB model kullanarak EEG kanalları arasındaki bağlantısallık analizi çalışmaları ilk olarak Kaminski ve ark. [96] tarafından yapılmıştır. Tanımlamış oldukları Yönlü Transfer Fonksiyon (YTF)(İng. Directed Transfer Function, DTF) metodunu kullanarak, uyanık ve uyku durumunda kaydedilen EEG için 0-30 Hz arası koherans değişimlerini incelemişlerdir. Buna göre m kanallı gözlem için j. kanaldan i. kanala tanımlı transfer fonksiyon YT F i j ( f ) = H i j ( f ) 2 m k=1 H ik ( f ) 2 (3.91) şeklindedir. Paydada bulunan ve H( f ) transfer fonksiyonunun i. satır elemanlarının kareleri toplamından oluşan terim, j. kanaldan i. kanala tanımlı YTF fonksiyonunun [0 1] arasında tanımlı olmasını sağlamaktadır. Bu metoda sunulduktan sonraki yıllarda birçok çalışmada deyinilmektedir [98, 100, 110]. Bu konu ile ilgili başka bir çalışma ise Baccalâ ve ark. [97] tarafından yapılmıştır. Granger doğrusal modelinden yola çıkarak Yönlü Koherans (İng. Directed Coherence, DC) yöntemini öneren grup, [99] çalışması ile Granger nedenselliği ile birebir uyumlu olan Kısmi Yönlü Koherans (KYK)(İng. Partial Directed Coherence, PDC) metodunu da ortaya atmıştır. İkiden fazla kaynak bağlantısallığı için daha uygun olduğu belirtilen bu yönteme aynı grubun [101] derin kayıt EEG çalışmasında da deyinilmiş ve uygulanmıştır. Aynı yöntem Winterhalder ve ark. [106] tarafından EMG ve EEG sinyalleri arasındaki (kaynak/hedef) bağlantısallık analizine uygulanmıştır. Tanıma göre, yine m kanallı gözlemden j. kanaldan (kaynak) i. kanala (hedef) doğru varolan Kısmi Yönlü Koherans (π i j ), kestirilen (3.89) eşitliğindeki ÖB model katsayı matrislerinin oluşturduğu izgesel matris ifadesi ile π i j ( f ) = Ã i j ( f ) m k=1 Ãk jãh k j (3.92)
67 56 şeklinde tanımlanmaktadır. Burada { 1 Ai à i j ( f ) = j ( f ), i = j A i j ( f ), i j (3.93) Önerilen KYK metodunun bir sonraki ilerlemesi, yine Baccalâ ve ark. [102] tarafından sağlanmıştır. KYK ile ilgili yapılan analizler, koherans analizi için kullanılan ÖB model ile birlikte varolan artanın (gürültü bileşeni), kanallar arası farklı olmasının sonuçları olumsuz etkilediğini ortaya çıkarmıştır. Bunu iyileştirme amacı ile, (3.92) eşitliğine herbir kanalın gürültü varyansı π i j ( f ) = m k=1 à i j ( f )/σ i ) (Ãk j à H k j /σ 2 k (3.94) şeklinde eklenmiştir. Yeni şekliyle bu fonksiyon Genelleştirilmiş Kısmi Yönlü Koherans Fonksiyon (GKYK) (İng. Generalized Partial Directed Coherence, gpdc) olarak isimlendirilmektedir [102, 103]. Taxidis ve ark. [103], bu formülle ilgili olarak bir anlamlılık derecesi hesaplamışlardır. Derin kayıtlama ile alınan Birim Ünite Aktivite (İng. Single Unit Activity, SUA) ve Yerel alan Potansiyellerine (İng. Local Field Potentials, LFPs) uyguladıkları bu yöntem ile anestezi altında kortiko-hipokampal fonksiyonel bağlantısallık değişimini incelemişlerdir. KYK yöntemini öneren Baccalâ ve ark. [99], bu yöntemi daha önce önerilen YTF yöntemi ile karşılaştırmasını yapmışlardır. Buna göre x 1 (n) = x 1 (n 1) x 1 (n 2) + 0.5x 5 (n 2) + w 1 (n) x 2 (n) = 0.5x 1 (n) + w 2 (n) x 3 (n) = 0.4x 2 (n 2) + w 3 (n) x 4 (n) = 0.5x 3 (n 1) x 4 (n 1) x 5 (n 1) + w 4 (n) x 5 (n) = 0.25x 4 (n 1) x 5 (n) + w 5 (n) (3.95) modeli ile tanımlanan (Şekil 3.34) sistemin bağlantısallığı analiz edilmiştir. Eşitlikte x i gözlemleri, w i ise beyaz gürültü kanallarını temsil etmektedir. Görüldüğü gibi x 1 değişkeni, sadece x 5 değişkeni dışındaki diğer değişkenleri (x 2, x 3, x 4 ) doğrudan etkilemektedir. Sadece x 4 ile x 5 arasında karşılıklı bir etkileşim vardır. İlgili makalede sunulan YTF ve KYK değerleri Şekil 3.35 ve 3.36 de gösterilmektedir.
68 57 Şekil 3.34: KYK ve YTF yöntemlerini karşılaştırmak için kullanılan model [99] Şekil 3.35: (3.95) sistemi için YTF dağılımı [99] Tez çalışmaları altında Matlab ortamında yazılan PDC.m, arfit.m fonksiyonlarını test etmek amacı ile (3.95) eşitliğindeki model 2000 örnek için gerçeklenmiştir. İlk olarak beyaz gürültü kanalları w i (n) üretilmiş, daha sonra model yazılarak x i (n) sinyalleri oluşturul- muştur (Şekil 3.37). Hesaplanan KYK değerleri ile Baccalâ ve ark. nın çalışmasında gösterilen sonuçlar oldukça benzerlik göstermektedir (Şekil 3.38). Hesaplanan değerler, Şekil 3.34 ile tanımlanan sistemi oluşturan x i elemanlarının birbirleri üzerine olan etkilerini açıkça göstermektedir. 5 eleman için çıkarılan 5x5 biçimindeki GKYK dağılımlarında, herhangi j. kanaldan, i. kanala olan etki görülmektedir. Dikkat edilirse, köşegeni oluşturan (π i j ( f )) GKYK dağılımları, herbir kanalda 1 e yakın değerdedir. GKYK, bir kanalın geriye kalan herbir kanala olan ayrı
69 58 Şekil 3.36: (3.95) sistemi için KYK dağılımı [99] ayrı etkilerinin (İng. outflows) oranını gösterdiğinden, daha çok kendi üzerine beslenen (dışa etkisi az olan) bir elemana ait π i i ( f ) değeri, ilgilenilen frekans aralığı için 1 civarında değer alır. Şekil 3.38 ile gösterilen GKYK dağılım matrisinde de, diğer kanallara en çok etki gösteren x i elemanına ait (π 1 1 ( f )) fonksiyonu, düşük frekanslar için 1 den küçük değerler almaktadır. Bunun nedeni 1. elemanın, 2., 3. ve 4. elemanları etkilemesinden kaynaklanmaktadır.
Örnek 4.1: Tablo 2 de verilen ham verilerin aritmetik ortalamasını hesaplayınız.
 .4. Merkezi Eğilim ve Dağılım Ölçüleri Merkezi eğilim ölçüleri kitleye ilişkin bir değişkenin bütün farklı değerlerinin çevresinde toplandığı merkezi bir değeri gösterirler. Dağılım ölçüleri ise değişkenin
.4. Merkezi Eğilim ve Dağılım Ölçüleri Merkezi eğilim ölçüleri kitleye ilişkin bir değişkenin bütün farklı değerlerinin çevresinde toplandığı merkezi bir değeri gösterirler. Dağılım ölçüleri ise değişkenin
BAŞKENT ÜNİVERSİTESİ BİYOMEDİKAL MÜHENDİSLİĞİ BÖLÜMÜ
 BAŞKENT ÜNİVERSİTESİ BİYOMEDİKAL MÜHENDİSLİĞİ BÖLÜMÜ BME43 BİYOMEDİKAL İŞARET İŞLEME I LABORATUVAR DERSİ Deneyin Adı: Güç Sektral Yoğunluğu DENEY 7 Deneyin Amacı: Güç Sektral Yoğunluğu Tesiti ve MATLAB
BAŞKENT ÜNİVERSİTESİ BİYOMEDİKAL MÜHENDİSLİĞİ BÖLÜMÜ BME43 BİYOMEDİKAL İŞARET İŞLEME I LABORATUVAR DERSİ Deneyin Adı: Güç Sektral Yoğunluğu DENEY 7 Deneyin Amacı: Güç Sektral Yoğunluğu Tesiti ve MATLAB
Ayrık Fourier Dönüşümü
 Ayrık Fourier Dönüşümü Tanım: 0 n N 1 aralığında tanımlı N uzunluklu bir dizi x[n] nin AYRIK FOURIER DÖNÜŞÜMÜ (DFT), ayrık zaman Fourier dönüşümü (DTFT) X(e jω ) nın0 ω < 2π aralığında ω k = 2πk/N, k =
Ayrık Fourier Dönüşümü Tanım: 0 n N 1 aralığında tanımlı N uzunluklu bir dizi x[n] nin AYRIK FOURIER DÖNÜŞÜMÜ (DFT), ayrık zaman Fourier dönüşümü (DTFT) X(e jω ) nın0 ω < 2π aralığında ω k = 2πk/N, k =
RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI. Yrd. Doç. Dr. Emre ATILGAN
 RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI Yrd. Doç. Dr. Emre ATILGAN 1 RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI Olasılığa ilişkin olayların çoğunluğunda, deneme sonuçlarının bir veya birkaç yönden incelenmesi
RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI Yrd. Doç. Dr. Emre ATILGAN 1 RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI Olasılığa ilişkin olayların çoğunluğunda, deneme sonuçlarının bir veya birkaç yönden incelenmesi
HAFTA 11: ÖRNEKLEME TEOREMİ SAMPLING THEOREM. İçindekiler
 HAFA 11: ÖRNEKLEME EOREMİ SAMPLING HEOREM İçindekiler 6.1 Bant sınırlı sürekli zaman sinyallerinin örneklenmesi... 2 6.2 Düzgün (uniform), periyodik örnekleme... 3 6.3 Bant sınırlı sürekli bir zaman sinyaline
HAFA 11: ÖRNEKLEME EOREMİ SAMPLING HEOREM İçindekiler 6.1 Bant sınırlı sürekli zaman sinyallerinin örneklenmesi... 2 6.2 Düzgün (uniform), periyodik örnekleme... 3 6.3 Bant sınırlı sürekli bir zaman sinyaline
İÇİNDEKİLER ÖN SÖZ...
 İÇİNDEKİLER ÖN SÖZ... v GİRİŞ... 1 1. İSTATİSTİK İN TARİHÇESİ... 1 2. İSTATİSTİK NEDİR?... 3 3. SAYISAL BİLGİDEN ANLAM ÇIKARILMASI... 4 4. BELİRSİZLİĞİN ELE ALINMASI... 4 5. ÖRNEKLEME... 5 6. İLİŞKİLERİN
İÇİNDEKİLER ÖN SÖZ... v GİRİŞ... 1 1. İSTATİSTİK İN TARİHÇESİ... 1 2. İSTATİSTİK NEDİR?... 3 3. SAYISAL BİLGİDEN ANLAM ÇIKARILMASI... 4 4. BELİRSİZLİĞİN ELE ALINMASI... 4 5. ÖRNEKLEME... 5 6. İLİŞKİLERİN
3. TAHMİN En Küçük Kareler (EKK) Yöntemi 1
 3. TAHMİN 3.1. En Küçük Kareler (EKK) Yöntemi 1 En Küçük Kareler (EKK) yöntemi, regresyon çözümlemesinde en yaygın olarak kullanılan, daha sonra ele alınacak bazı varsayımlar altında çok aranan istatistiki
3. TAHMİN 3.1. En Küçük Kareler (EKK) Yöntemi 1 En Küçük Kareler (EKK) yöntemi, regresyon çözümlemesinde en yaygın olarak kullanılan, daha sonra ele alınacak bazı varsayımlar altında çok aranan istatistiki
5. Elektriksel Büyüklüklerin Ölçülebilen Değerleri
 Elektrik devrelerinde ölçülebilen büyüklükler olan; 5. Elektriksel Büyüklüklerin Ölçülebilen Değerleri Akım Gerilim Devrede bulunan kaynakların tiplerine göre değişik şekillerde olabilir. Zamana bağlı
Elektrik devrelerinde ölçülebilen büyüklükler olan; 5. Elektriksel Büyüklüklerin Ölçülebilen Değerleri Akım Gerilim Devrede bulunan kaynakların tiplerine göre değişik şekillerde olabilir. Zamana bağlı
İstatistik ve Olasılık
 İstatistik ve Olasılık KORELASYON ve REGRESYON ANALİZİ Doç. Dr. İrfan KAYMAZ Tanım Bir değişkenin değerinin diğer değişkendeki veya değişkenlerdeki değişimlere bağlı olarak nasıl etkilendiğinin istatistiksel
İstatistik ve Olasılık KORELASYON ve REGRESYON ANALİZİ Doç. Dr. İrfan KAYMAZ Tanım Bir değişkenin değerinin diğer değişkendeki veya değişkenlerdeki değişimlere bağlı olarak nasıl etkilendiğinin istatistiksel
BKİ farkı Standart Sapması (kg/m 2 ) A B BKİ farkı Ortalaması (kg/m 2 )
 4. SUNUM 1 Gözlem ya da deneme sonucu elde edilmiş sonuçların, rastlantıya bağlı olup olmadığının incelenmesinde kullanılan istatistiksel yöntemlere HİPOTEZ TESTLERİ denir. Sonuçların rastlantıya bağlı
4. SUNUM 1 Gözlem ya da deneme sonucu elde edilmiş sonuçların, rastlantıya bağlı olup olmadığının incelenmesinde kullanılan istatistiksel yöntemlere HİPOTEZ TESTLERİ denir. Sonuçların rastlantıya bağlı
Matris Cebiriyle Çoklu Regresyon Modeli
 Matris Cebiriyle Çoklu Regresyon Modeli Hüseyin Taştan Mart 00 Klasik Regresyon Modeli k açıklayıcı değişkenden oluşan regresyon modelini her gözlem i için aşağıdaki gibi yazabiliriz: y i β + β x i + β
Matris Cebiriyle Çoklu Regresyon Modeli Hüseyin Taştan Mart 00 Klasik Regresyon Modeli k açıklayıcı değişkenden oluşan regresyon modelini her gözlem i için aşağıdaki gibi yazabiliriz: y i β + β x i + β
Stokastik Süreçler. Bir stokastik süreç ya da rastgele süreç şöyle tanımlanabilir.
 Bir stokastik süreç ya da rastgele süreç şöyle tanımlanabilir. Zamanla değişen bir rastgele değişkendir. Rastgele değişkenin alacağı değer zamanla değişmektedir. Deney çıktılarına atanan rastgele bir zaman
Bir stokastik süreç ya da rastgele süreç şöyle tanımlanabilir. Zamanla değişen bir rastgele değişkendir. Rastgele değişkenin alacağı değer zamanla değişmektedir. Deney çıktılarına atanan rastgele bir zaman
2. REGRESYON ANALİZİNİN TEMEL KAVRAMLARI Tanım
 2. REGRESYON ANALİZİNİN TEMEL KAVRAMLARI 2.1. Tanım Regresyon analizi, bir değişkenin başka bir veya daha fazla değişkene olan bağımlılığını inceler. Amaç, bağımlı değişkenin kitle ortalamasını, açıklayıcı
2. REGRESYON ANALİZİNİN TEMEL KAVRAMLARI 2.1. Tanım Regresyon analizi, bir değişkenin başka bir veya daha fazla değişkene olan bağımlılığını inceler. Amaç, bağımlı değişkenin kitle ortalamasını, açıklayıcı
İÇİNDEKİLER. BÖLÜM 1 Değişkenler ve Grafikler 1. BÖLÜM 2 Frekans Dağılımları 37
 İÇİNDEKİLER BÖLÜM 1 Değişkenler ve Grafikler 1 İstatistik 1 Yığın ve Örnek; Tümevarımcı ve Betimleyici İstatistik 1 Değişkenler: Kesikli ve Sürekli 1 Verilerin Yuvarlanması Bilimsel Gösterim Anlamlı Rakamlar
İÇİNDEKİLER BÖLÜM 1 Değişkenler ve Grafikler 1 İstatistik 1 Yığın ve Örnek; Tümevarımcı ve Betimleyici İstatistik 1 Değişkenler: Kesikli ve Sürekli 1 Verilerin Yuvarlanması Bilimsel Gösterim Anlamlı Rakamlar
Sayısal Filtre Tasarımı
 Sayısal Filtre Tasarımı Sayısal Filtreler Filtreler ayrık zamanlı sistemlerdir. Filtreler işaretin belirli frekanslarını güçlendirmek veya zayıflatmak, belirli frekanslarını tamamen bastırmak veya belirli
Sayısal Filtre Tasarımı Sayısal Filtreler Filtreler ayrık zamanlı sistemlerdir. Filtreler işaretin belirli frekanslarını güçlendirmek veya zayıflatmak, belirli frekanslarını tamamen bastırmak veya belirli
İŞARET ve SİSTEMLER (SIGNALS and SYSTEMS) Dr. Akif AKGÜL oda no: 303 (T4 / EEM)
 İşaret ve Sistemler İŞARET ve SİSTEMLER (SIGNALS and SYSTEMS) Dr. Akif AKGÜL aakgul@sakarya.edu.tr oda no: 303 (T4 / EEM) Kaynaklar: 1. Signals and Systems, Oppenheim. (Türkçe versiyonu: Akademi Yayıncılık)
İşaret ve Sistemler İŞARET ve SİSTEMLER (SIGNALS and SYSTEMS) Dr. Akif AKGÜL aakgul@sakarya.edu.tr oda no: 303 (T4 / EEM) Kaynaklar: 1. Signals and Systems, Oppenheim. (Türkçe versiyonu: Akademi Yayıncılık)
TANIMLAYICI İSTATİSTİKLER
 TANIMLAYICI İSTATİSTİKLER Tanımlayıcı İstatistikler ve Grafikle Gösterim Grafik ve bir ölçüde tablolar değişkenlerin görsel bir özetini verirler. İdeal olarak burada değişkenlerin merkezi (ortalama) değerlerinin
TANIMLAYICI İSTATİSTİKLER Tanımlayıcı İstatistikler ve Grafikle Gösterim Grafik ve bir ölçüde tablolar değişkenlerin görsel bir özetini verirler. İdeal olarak burada değişkenlerin merkezi (ortalama) değerlerinin
BÖLÜM 6 MERKEZDEN DAĞILMA ÖLÇÜLERİ
 1 BÖLÜM 6 MERKEZDEN DAĞILMA ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel
1 BÖLÜM 6 MERKEZDEN DAĞILMA ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel
BÖLÜM 12 STUDENT T DAĞILIMI
 1 BÖLÜM 12 STUDENT T DAĞILIMI 'Student t dağılımı' ya da kısaca 't dağılımı'; normal dağılım ve Z dağılımının da içerisinde bulunduğu 'sürekli olasılık dağılımları' ailesinde yer alan dağılımlardan bir
1 BÖLÜM 12 STUDENT T DAĞILIMI 'Student t dağılımı' ya da kısaca 't dağılımı'; normal dağılım ve Z dağılımının da içerisinde bulunduğu 'sürekli olasılık dağılımları' ailesinde yer alan dağılımlardan bir
ALTERNATĐF AKIM (AC) I AC NĐN ELDE EDĐLMESĐ; KARE VE ÜÇGEN DALGALAR
 ALTERNATĐF AKIM (AC) I AC NĐN ELDE EDĐLMESĐ; KARE VE ÜÇGEN DALGALAR 1.1 Amaçlar AC nin Elde Edilmesi: Farklı ve değişken DC gerilimlerin anahtar ve potansiyometreler kullanılarak elde edilmesi. Kare dalga
ALTERNATĐF AKIM (AC) I AC NĐN ELDE EDĐLMESĐ; KARE VE ÜÇGEN DALGALAR 1.1 Amaçlar AC nin Elde Edilmesi: Farklı ve değişken DC gerilimlerin anahtar ve potansiyometreler kullanılarak elde edilmesi. Kare dalga
Tanımlayıcı İstatistikler. Yrd. Doç. Dr. Emre ATILGAN
 Tanımlayıcı İstatistikler Yrd. Doç. Dr. Emre ATILGAN 1 Tanımlayıcı İstatistikler Yer Gösteren Ölçüler Yaygınlık Ölçüleri Merkezi Eğilim Ölçüleri Konum Ölçüleri 2 3 Aritmetik Ortalama Aritmetik ortalama,
Tanımlayıcı İstatistikler Yrd. Doç. Dr. Emre ATILGAN 1 Tanımlayıcı İstatistikler Yer Gösteren Ölçüler Yaygınlık Ölçüleri Merkezi Eğilim Ölçüleri Konum Ölçüleri 2 3 Aritmetik Ortalama Aritmetik ortalama,
Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü
 Mühendislikte İstatistiksel Yöntemler Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü 1 Araştırma sonuçlarının açıklanmasında frekans tablosu
Mühendislikte İstatistiksel Yöntemler Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü 1 Araştırma sonuçlarının açıklanmasında frekans tablosu
rasgele değişkeninin olasılık yoğunluk fonksiyonu,
 3.6. Bazı Sürekli Dağılımlar 3.6.1 Normal Dağılım Normal dağılım hem uygulamalı hem de teorik istatistikte kullanılan oldukça önemli bir dağılımdır. Normal dağılımın istatistikte önemli bir yerinin olmasının
3.6. Bazı Sürekli Dağılımlar 3.6.1 Normal Dağılım Normal dağılım hem uygulamalı hem de teorik istatistikte kullanılan oldukça önemli bir dağılımdır. Normal dağılımın istatistikte önemli bir yerinin olmasının
VEKTÖR UZAYLARI 1.GİRİŞ
 1.GİRİŞ Bu bölüm lineer cebirin temelindeki cebirsel yapıya, sonlu boyutlu vektör uzayına giriş yapmaktadır. Bir vektör uzayının tanımı, elemanları skalar olarak adlandırılan herhangi bir cisim içerir.
1.GİRİŞ Bu bölüm lineer cebirin temelindeki cebirsel yapıya, sonlu boyutlu vektör uzayına giriş yapmaktadır. Bir vektör uzayının tanımı, elemanları skalar olarak adlandırılan herhangi bir cisim içerir.
Olaya Ġlişkin Potansiyel Kayıt Yöntemleri Kognitif Paradigmalar
 Olaya Ġlişkin Potansiyel Kayıt Yöntemleri Kognitif Paradigmalar Prof. Dr. Sacit Karamürsel İstanbul Tıp Fakültesi, Fizyoloji Anabilim Dalı sacit@istanbul.edu.tr Elektroansefalogram (EEG), merkezi sinir
Olaya Ġlişkin Potansiyel Kayıt Yöntemleri Kognitif Paradigmalar Prof. Dr. Sacit Karamürsel İstanbul Tıp Fakültesi, Fizyoloji Anabilim Dalı sacit@istanbul.edu.tr Elektroansefalogram (EEG), merkezi sinir
İstatistik ve Olasılık
 İstatistik ve Olasılık Örnekleme Planlar ve Dağılımları Prof. Dr. İrfan KAYMAZ Tanım İncelenen olayın ait olduğu anakütlenin bütünüyle dikkate alınması zaman, para, ekipman ve bunun gibi nedenlerden dolayı
İstatistik ve Olasılık Örnekleme Planlar ve Dağılımları Prof. Dr. İrfan KAYMAZ Tanım İncelenen olayın ait olduğu anakütlenin bütünüyle dikkate alınması zaman, para, ekipman ve bunun gibi nedenlerden dolayı
13. Olasılık Dağılımlar
 13. Olasılık Dağılımlar Mühendislik alanında karşılaşılan fiziksel yada fiziksel olmayan rasgele değişken büyüklüklerin olasılık dağılımları için model alınabilecek çok sayıda sürekli ve kesikli fonksiyon
13. Olasılık Dağılımlar Mühendislik alanında karşılaşılan fiziksel yada fiziksel olmayan rasgele değişken büyüklüklerin olasılık dağılımları için model alınabilecek çok sayıda sürekli ve kesikli fonksiyon
SİNYALLER VE SİSTEMLERİN MATLAB YARDIMIYLA BENZETİMİ
 SİNYALLER VE SİSTEMLERİN MATLAB YARDIMIYLA BENZETİMİ 2.1. Sinyal Üretimi Bu laboratuarda analog sinyaller ve sistemlerin sayısal bir ortamda benzetimini yapacağımız için örneklenmiş sinyaller üzerinde
SİNYALLER VE SİSTEMLERİN MATLAB YARDIMIYLA BENZETİMİ 2.1. Sinyal Üretimi Bu laboratuarda analog sinyaller ve sistemlerin sayısal bir ortamda benzetimini yapacağımız için örneklenmiş sinyaller üzerinde
DENEY 3: DTMF İŞARETLERİN ÜRETİLMESİ VE ALGILANMASI
 DENEY 3: DTMF İŞARETLERİN ÜRETİLMESİ VE ALGILANMASI AMAÇ: DTMF işaretlerin yapısının, üretim ve algılanmasının incelenmesi. MALZEMELER TP5088 ya da KS58015 M8870-01 ya da M8870-02 (diğer eşdeğer entegreler
DENEY 3: DTMF İŞARETLERİN ÜRETİLMESİ VE ALGILANMASI AMAÇ: DTMF işaretlerin yapısının, üretim ve algılanmasının incelenmesi. MALZEMELER TP5088 ya da KS58015 M8870-01 ya da M8870-02 (diğer eşdeğer entegreler
18.034 İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
İstatistik ve Olasılık
 İstatistik ve Olasılık Ders 8: Prof. Dr. İrfan KAYMAZ Tanım Tahmin (kestirim veya öngörü): Mevcut bilgi ve deneylere dayanarak olayın bütünü hakkında bir yargıya varmaktır. Bu anlamda, anakütleden çekilen
İstatistik ve Olasılık Ders 8: Prof. Dr. İrfan KAYMAZ Tanım Tahmin (kestirim veya öngörü): Mevcut bilgi ve deneylere dayanarak olayın bütünü hakkında bir yargıya varmaktır. Bu anlamda, anakütleden çekilen
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 5- SONLU FARKLAR VE İNTERPOLASYON TEKNİKLERİ Doç. Dr. Ali Rıza YILDIZ MAK 210 - Sayısal Analiz 1 İNTERPOLASYON Tablo halinde verilen hassas sayısal değerler veya ayrık noktalardan
MAK 210 SAYISAL ANALİZ BÖLÜM 5- SONLU FARKLAR VE İNTERPOLASYON TEKNİKLERİ Doç. Dr. Ali Rıza YILDIZ MAK 210 - Sayısal Analiz 1 İNTERPOLASYON Tablo halinde verilen hassas sayısal değerler veya ayrık noktalardan
SÜREKLİ ŞANS DEĞİŞKENLERİ. Üstel Dağılım Normal Dağılım
 SÜREKLİ ŞANS DEĞİŞKENLERİ Üstel Dağılım Normal Dağılım 1 Üstel Dağılım Meydana gelen iki olay arasındaki geçen süre veya bir başka ifadeyle ilgilenilen olayın ilk defa ortaya çıkması için geçen sürenin
SÜREKLİ ŞANS DEĞİŞKENLERİ Üstel Dağılım Normal Dağılım 1 Üstel Dağılım Meydana gelen iki olay arasındaki geçen süre veya bir başka ifadeyle ilgilenilen olayın ilk defa ortaya çıkması için geçen sürenin
Analitik Hiyerarşi Prosesi (AHP) Yrd.Doç.Dr. Sabahattin Kerem AYTULUN
 Analitik Hiyerarşi Prosesi (AHP) Yrd.Doç.Dr. Sabahattin Kerem AYTULUN Giriş AHP Thomas L.Saaty tarafından 1970'lerde ortaya atılmıştır. Amaç alternatifler arasından en iyisinin seçilmesidir. Subjektif
Analitik Hiyerarşi Prosesi (AHP) Yrd.Doç.Dr. Sabahattin Kerem AYTULUN Giriş AHP Thomas L.Saaty tarafından 1970'lerde ortaya atılmıştır. Amaç alternatifler arasından en iyisinin seçilmesidir. Subjektif
Şekil 1.1 Genliği kuvantalanmamış sürekli zamanlı işaret. İşaretin genliği sürekli değerler alır. Buna analog işaret de denir.
 İŞARETLER Sayısal işaret işleme, işaretlerin sayısal bilgisayar ya da özel amaçlı donanımda bir sayılar dizisi olarak gösterilmesi ve bu işaret dizisi üzerinde çeşitli işlemler yaparak, istenen bir bilgi
İŞARETLER Sayısal işaret işleme, işaretlerin sayısal bilgisayar ya da özel amaçlı donanımda bir sayılar dizisi olarak gösterilmesi ve bu işaret dizisi üzerinde çeşitli işlemler yaparak, istenen bir bilgi
Örneklemden elde edilen parametreler üzerinden kitle parametreleri tahmin edilmek istenmektedir.
 ÇIKARSAMALI İSTATİSTİKLER Çıkarsamalı istatistikler, örneklemden elde edilen değerler üzerinde kitleyi tanımlamak için uygulanan istatistiksel yöntemlerdir. Çıkarsamalı istatistikler; Tahmin Hipotez Testleri
ÇIKARSAMALI İSTATİSTİKLER Çıkarsamalı istatistikler, örneklemden elde edilen değerler üzerinde kitleyi tanımlamak için uygulanan istatistiksel yöntemlerdir. Çıkarsamalı istatistikler; Tahmin Hipotez Testleri
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 6- İSTATİSTİK VE REGRESYON ANALİZİ Doç. Dr. Ali Rıza YILDIZ 1 İSTATİSTİK VE REGRESYON ANALİZİ Bütün noktalardan geçen bir denklem bulmak yerine noktaları temsil eden, yani
MAK 210 SAYISAL ANALİZ BÖLÜM 6- İSTATİSTİK VE REGRESYON ANALİZİ Doç. Dr. Ali Rıza YILDIZ 1 İSTATİSTİK VE REGRESYON ANALİZİ Bütün noktalardan geçen bir denklem bulmak yerine noktaları temsil eden, yani
Beyin salınımları ve bağlanırlık
 Beyin salınımları ve bağlanırlık FF seminerleri Tolga Esat Özkurt 09/11/12 İnsan beyni YeAşkinler için 1300-1400 gram (~ vücudun 50 de 1 i), enerjinin ise 1/5 ini tükeayor 100 milyar nöron Nöronlar: beynin
Beyin salınımları ve bağlanırlık FF seminerleri Tolga Esat Özkurt 09/11/12 İnsan beyni YeAşkinler için 1300-1400 gram (~ vücudun 50 de 1 i), enerjinin ise 1/5 ini tükeayor 100 milyar nöron Nöronlar: beynin
2. BASİT DOĞRUSAL REGRESYON 12
 1. GİRİŞ 1 1.1 Regresyon ve Model Kurma / 1 1.2 Veri Toplama / 5 1.3 Regresyonun Kullanım Alanları / 9 1.4 Bilgisayarın Rolü / 10 2. BASİT DOĞRUSAL REGRESYON 12 2.1 Basit Doğrusal Regresyon Modeli / 12
1. GİRİŞ 1 1.1 Regresyon ve Model Kurma / 1 1.2 Veri Toplama / 5 1.3 Regresyonun Kullanım Alanları / 9 1.4 Bilgisayarın Rolü / 10 2. BASİT DOĞRUSAL REGRESYON 12 2.1 Basit Doğrusal Regresyon Modeli / 12
SÜREKLĠ OLASILIK DAĞILIMLARI
 SÜREKLĠ OLASILIK DAĞILIMLARI Sayı ekseni üzerindeki tüm noktalarda değer alabilen değişkenler, sürekli değişkenler olarak tanımlanmaktadır. Bu bölümde, sürekli değişkenlere uygun olasılık dağılımları üzerinde
SÜREKLĠ OLASILIK DAĞILIMLARI Sayı ekseni üzerindeki tüm noktalarda değer alabilen değişkenler, sürekli değişkenler olarak tanımlanmaktadır. Bu bölümde, sürekli değişkenlere uygun olasılık dağılımları üzerinde
İçindekiler. Ön Söz... xiii
 İçindekiler Ön Söz.................................................... xiii Bölüm 1 İstatistiğe Giriş....................................... 1 1.1 Giriş......................................................1
İçindekiler Ön Söz.................................................... xiii Bölüm 1 İstatistiğe Giriş....................................... 1 1.1 Giriş......................................................1
LOJİSTİK REGRESYON ANALİZİ
 LOJİSTİK REGRESYON ANALİZİ Lojistik Regresyon Analizini daha kolay izleyebilmek için bazı terimleri tanımlayalım: 1. Değişken (incelenen özellik): Bireyden bireye farklı değerler alabilen özellik, fenomen
LOJİSTİK REGRESYON ANALİZİ Lojistik Regresyon Analizini daha kolay izleyebilmek için bazı terimleri tanımlayalım: 1. Değişken (incelenen özellik): Bireyden bireye farklı değerler alabilen özellik, fenomen
İşaret ve Sistemler. Ders 2: Spektral Analize Giriş
 İşaret ve Sistemler Ders 2: Spektral Analize Giriş Spektral Analiz A 1.Cos (2 f 1 t+ 1 ) ile belirtilen işaret: f 1 Hz frekansında, A 1 genliğinde ve fazı da Cos(2 f 1 t) ye göre 1 olan parametrelere sahiptir.
İşaret ve Sistemler Ders 2: Spektral Analize Giriş Spektral Analiz A 1.Cos (2 f 1 t+ 1 ) ile belirtilen işaret: f 1 Hz frekansında, A 1 genliğinde ve fazı da Cos(2 f 1 t) ye göre 1 olan parametrelere sahiptir.
BÖLÜM I GİRİŞ (1.1) y(t) veya y(x) T veya λ. a t veya x. Şekil 1.1 Dalga. a genlik, T peryod (veya λ dalga boyu)
 BÖLÜM I GİRİŞ 1.1 Sinyal Bir sistemin durum ve davranış bilgilerini taşıyan, bir veya daha fazla değişken ile tanımlanan bir fonksiyon olup veri işlemde dalga olarak adlandırılır. Bir dalga, genliği, dalga
BÖLÜM I GİRİŞ 1.1 Sinyal Bir sistemin durum ve davranış bilgilerini taşıyan, bir veya daha fazla değişken ile tanımlanan bir fonksiyon olup veri işlemde dalga olarak adlandırılır. Bir dalga, genliği, dalga
7. BÖLÜM İÇ ÇARPIM UZAYLARI İÇ ÇARPIM UZAYLARI İÇ ÇARPIM UZAYLARI İÇ ÇARPIM UZAYLARI .= 1 1 + + Genel: Vektörler bölümünde vektörel iç çarpım;
 İÇ ÇARPIM UZAYLARI 7. BÖLÜM İÇ ÇARPIM UZAYLARI Genel: Vektörler bölümünde vektörel iç çarpım;.= 1 1 + + Açıklanmış ve bu konu uzunluk ve uzaklık kavramlarını açıklamak için kullanılmıştır. Bu bölümde öklit
İÇ ÇARPIM UZAYLARI 7. BÖLÜM İÇ ÇARPIM UZAYLARI Genel: Vektörler bölümünde vektörel iç çarpım;.= 1 1 + + Açıklanmış ve bu konu uzunluk ve uzaklık kavramlarını açıklamak için kullanılmıştır. Bu bölümde öklit
Uyku skorlama-2 (Temel EEG grafo elemanlar)
 Uyku skorlama-2 (Temel EEG grafo elemanlar) Dr. Hikmet YILMAZ XVII. Uyku Tıbbı Hekimliği Sertifikasyon Kursu Uyku Tıbbı Teknisyenliği Sertifikasyon Kursu 26 Şubat-2 Mart 2014 Spice Otel, Belek, Antalya
Uyku skorlama-2 (Temel EEG grafo elemanlar) Dr. Hikmet YILMAZ XVII. Uyku Tıbbı Hekimliği Sertifikasyon Kursu Uyku Tıbbı Teknisyenliği Sertifikasyon Kursu 26 Şubat-2 Mart 2014 Spice Otel, Belek, Antalya
Ayrık-Zaman Sistemler
 Ayrık-Zaman Sistemler Bir ayrık-zaman sistemi, bir giriş dizisi x[n] yi işleyerek daha iyi özelliklere sahip bir çıkış dizisi y[n] oluşturur. Çoğu uygulamalarda ayrık-zaman sistemi bir giriş ve bir çıkıştan
Ayrık-Zaman Sistemler Bir ayrık-zaman sistemi, bir giriş dizisi x[n] yi işleyerek daha iyi özelliklere sahip bir çıkış dizisi y[n] oluşturur. Çoğu uygulamalarda ayrık-zaman sistemi bir giriş ve bir çıkıştan
Kontrol Sistemlerinin Analizi
 Sistemlerin analizi Kontrol Sistemlerinin Analizi Otomatik kontrol mühendisinin görevi sisteme uygun kontrolör tasarlamaktır. Bunun için öncelikle sistemin analiz edilmesi gerekir. Bunun için test sinyalleri
Sistemlerin analizi Kontrol Sistemlerinin Analizi Otomatik kontrol mühendisinin görevi sisteme uygun kontrolör tasarlamaktır. Bunun için öncelikle sistemin analiz edilmesi gerekir. Bunun için test sinyalleri
3.5. Devre Parametreleri
 3..3 3.5. Devre Parametreleri 3.5. Devre Parametreleri Mikrodalga mühendisliğinde doğrusal mikrodalga devrelerini karakterize etmek için dört tip devre parametreleri kullanılır: açılma parametreleri (parametreleri)
3..3 3.5. Devre Parametreleri 3.5. Devre Parametreleri Mikrodalga mühendisliğinde doğrusal mikrodalga devrelerini karakterize etmek için dört tip devre parametreleri kullanılır: açılma parametreleri (parametreleri)
Merkezi Eğilim ve Dağılım Ölçüleri
 Merkezi Eğilim ve Dağılım Ölçüleri Soru Öğrencilerin derse katılım düzeylerini ölçmek amacıyla geliştirilen 16 soruluk bir test için öğrencilerin ilk 8 ve son 8 soruluk yarılardan aldıkları puanlar arasındaki
Merkezi Eğilim ve Dağılım Ölçüleri Soru Öğrencilerin derse katılım düzeylerini ölçmek amacıyla geliştirilen 16 soruluk bir test için öğrencilerin ilk 8 ve son 8 soruluk yarılardan aldıkları puanlar arasındaki
ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ İLETİŞİM LABORATUARI SAYISAL FİLTRELER
 SAYISAL FİLTRELER Deney Amacı Sayısal filtre tasarımının ve kullanılmasının öğrenilmesi. Kapsam Ayrık zamanlı bir sistem transfer fonksiyonunun elde edilmesi. Filtren frekans tepkes elde edilmesi. Direct
SAYISAL FİLTRELER Deney Amacı Sayısal filtre tasarımının ve kullanılmasının öğrenilmesi. Kapsam Ayrık zamanlı bir sistem transfer fonksiyonunun elde edilmesi. Filtren frekans tepkes elde edilmesi. Direct
2011 Third International Conference on Intelligent Human-Machine Systems and Cybernetics
 2011 Third International Conference on Intelligent Human-Machine Systems and Cybernetics Özet: Bulanık bir denetleyici tasarlanırken karşılaşılan en önemli sıkıntı, bulanık giriş çıkış üyelik fonksiyonlarının
2011 Third International Conference on Intelligent Human-Machine Systems and Cybernetics Özet: Bulanık bir denetleyici tasarlanırken karşılaşılan en önemli sıkıntı, bulanık giriş çıkış üyelik fonksiyonlarının
RASGELE SÜREÇLER İ.Ü. ELEKTRİK ELEKTRONİK MÜHENDİSLİĞİ İLETİŞİM LABORATUVARI ARALIK, 2007
 RASGELE SÜREÇLER İ.Ü. ELEKTRİK ELEKTRONİK MÜHENDİSLİĞİ İLETİŞİM LABORATUVARI ARALIK, 007 1 Tekdüze Dağılım Bir X rasgele değişkenin, a ve b arasında tekdüze dağılımlı olabilmesi için olasılık yoğunluk
RASGELE SÜREÇLER İ.Ü. ELEKTRİK ELEKTRONİK MÜHENDİSLİĞİ İLETİŞİM LABORATUVARI ARALIK, 007 1 Tekdüze Dağılım Bir X rasgele değişkenin, a ve b arasında tekdüze dağılımlı olabilmesi için olasılık yoğunluk
MAK1010 MAKİNE MÜHENDİSLİĞİ BİLGİSAYAR UYGULAMALARI
 .. MAK MAKİNE MÜHENDİSLİĞİ BİLGİSAYAR UYGULAMALARI Polinom MATLAB p=[8 ] d=[ - ] h=[ -] c=[ - ] POLİNOMUN DEĞERİ >> polyval(p, >> fx=[ -..9 -. -.9.88]; >> polyval(fx,9) ans =. >> x=-.:.:.; >> y=polyval(fx,;
.. MAK MAKİNE MÜHENDİSLİĞİ BİLGİSAYAR UYGULAMALARI Polinom MATLAB p=[8 ] d=[ - ] h=[ -] c=[ - ] POLİNOMUN DEĞERİ >> polyval(p, >> fx=[ -..9 -. -.9.88]; >> polyval(fx,9) ans =. >> x=-.:.:.; >> y=polyval(fx,;
Prof.Dr.İhsan HALİFEOĞLU
 Prof.Dr.İhsan HALİFEOĞLU FREKANS DAĞILIMLARINI TANIMLAYICI ÖLÇÜLER Düzenlenmiş verilerin yorumlanması ve daha ileri düzeydeki işlemler için verilerin bütününe ait tanımlayıcı ve özetleyici ölçülere ihtiyaç
Prof.Dr.İhsan HALİFEOĞLU FREKANS DAĞILIMLARINI TANIMLAYICI ÖLÇÜLER Düzenlenmiş verilerin yorumlanması ve daha ileri düzeydeki işlemler için verilerin bütününe ait tanımlayıcı ve özetleyici ölçülere ihtiyaç
DOĞRUSAL ZAMAN SERİSİ MODELLERİ. Durağan ARIMA Modelleri: Otoregresiv Modeller AR(p) Süreci
 DOĞRUSAL ZAMAN SERİSİ MODELLERİ Durağan ARIMA Modelleri: Otoregresiv Modeller AR(p) Süreci Tek Değişkenli Zaman Serisi Modelleri Ekonomik verilerin analizi ile ekonomik değişkenlerin gelecekte alabilecekleri
DOĞRUSAL ZAMAN SERİSİ MODELLERİ Durağan ARIMA Modelleri: Otoregresiv Modeller AR(p) Süreci Tek Değişkenli Zaman Serisi Modelleri Ekonomik verilerin analizi ile ekonomik değişkenlerin gelecekte alabilecekleri
Güç Spektral Yoğunluk (PSD) Fonksiyonu
 1 Güç Spektral Yoğunluk (PSD) Fonksiyonu Otokorelasyon fonksiyonunun Fourier dönüşümü j f ( ) FR ((τ) ) = R ( (τ ) ) e j π f τ S f R R e d dτ S ( f ) = F j ( f )e j π f ( ) ( ) f τ R S f e df R (τ ) =
1 Güç Spektral Yoğunluk (PSD) Fonksiyonu Otokorelasyon fonksiyonunun Fourier dönüşümü j f ( ) FR ((τ) ) = R ( (τ ) ) e j π f τ S f R R e d dτ S ( f ) = F j ( f )e j π f ( ) ( ) f τ R S f e df R (τ ) =
ELEKTRİK ENERJİ SİSTEMLERİNDE OLUŞAN HARMONİKLERİN FİLTRELENMESİNİN BİLGİSAYAR DESTEKLİ MODELLENMESİ VE SİMÜLASYONU
 T.C. MARMARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ ELEKTRİK ENERJİ SİSTEMLERİNDE OLUŞAN HARMONİKLERİN FİLTRELENMESİNİN BİLGİSAYAR DESTEKLİ MODELLENMESİ VE SİMÜLASYONU Mehmet SUCU (Teknik Öğretmen, BSc.)
T.C. MARMARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ ELEKTRİK ENERJİ SİSTEMLERİNDE OLUŞAN HARMONİKLERİN FİLTRELENMESİNİN BİLGİSAYAR DESTEKLİ MODELLENMESİ VE SİMÜLASYONU Mehmet SUCU (Teknik Öğretmen, BSc.)
Enerji Sistemleri Mühendisliği Bölümü
 YALOVA ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ Enerji Sistemleri Mühendisliği Bölümü ESM 413 Enerji Sistemleri Laboratuvarı-II RL, RC ve RLC DEVRELERİNİN AC ANALİZİ Puanlandırma Sistemi: Hazırlık Soruları:
YALOVA ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ Enerji Sistemleri Mühendisliği Bölümü ESM 413 Enerji Sistemleri Laboratuvarı-II RL, RC ve RLC DEVRELERİNİN AC ANALİZİ Puanlandırma Sistemi: Hazırlık Soruları:
Hatalar Bilgisi ve İstatistik Ders Kodu: Kredi: 3 / ECTS: 5
 Ders Kodu: 0010070021 Kredi: 3 / ECTS: 5 Yrd. Doç. Dr. Serkan DOĞANALP Necmettin Erbakan Üniversitesi Harita Mühendisliği Bölümü Konya 07.01.2015 1 Giriş 2 Giriş Matematiksel istatistiğin konusu yığın
Ders Kodu: 0010070021 Kredi: 3 / ECTS: 5 Yrd. Doç. Dr. Serkan DOĞANALP Necmettin Erbakan Üniversitesi Harita Mühendisliği Bölümü Konya 07.01.2015 1 Giriş 2 Giriş Matematiksel istatistiğin konusu yığın
Zahmetsiz örüntü tanıma: Nokta bulutlarının karşılaştırılması yoluyla veri-tabanlı ve parametresiz istatistiksel öğrenme
 Zahmetsiz örüntü tanıma: Nokta bulutlarının karşılaştırılması yoluyla veri-tabanlı ve parametresiz istatistiksel öğrenme Doç. Dr. Bilge Karaçalı Biyomedikal Veri İşleme Laboratuvarı Elektrik-Elektronik
Zahmetsiz örüntü tanıma: Nokta bulutlarının karşılaştırılması yoluyla veri-tabanlı ve parametresiz istatistiksel öğrenme Doç. Dr. Bilge Karaçalı Biyomedikal Veri İşleme Laboratuvarı Elektrik-Elektronik
Temel İstatistik. Y.Doç.Dr. İbrahim Turan Mart Tanımlayıcı İstatistik. Dağılımları Tanımlayıcı Ölçüler Dağılış Ölçüleri
 Temel İstatistik Tanımlayıcı İstatistik Dağılımları Tanımlayıcı Ölçüler Dağılış Ölçüleri Y.Doç.Dr. İbrahim Turan Mart 2011 DAĞILIM / YAYGINLIK ÖLÇÜLERİ Verilerin değişkenlik durumu ve dağılışın şeklini
Temel İstatistik Tanımlayıcı İstatistik Dağılımları Tanımlayıcı Ölçüler Dağılış Ölçüleri Y.Doç.Dr. İbrahim Turan Mart 2011 DAĞILIM / YAYGINLIK ÖLÇÜLERİ Verilerin değişkenlik durumu ve dağılışın şeklini
BÖLÜM 13 HİPOTEZ TESTİ
 1 BÖLÜM 13 HİPOTEZ TESTİ Bilimsel yöntem aşamalarıyla tanımlanmış sistematik bir bilgi üretme biçimidir. Bilimsel yöntemin aşamaları aşağıdaki gibi sıralanabilmektedir (Karasar, 2012): 1. Bir problemin
1 BÖLÜM 13 HİPOTEZ TESTİ Bilimsel yöntem aşamalarıyla tanımlanmış sistematik bir bilgi üretme biçimidir. Bilimsel yöntemin aşamaları aşağıdaki gibi sıralanabilmektedir (Karasar, 2012): 1. Bir problemin
Sistem Dinamiği. Bölüm 2- Dinamik Cevap ve Laplace Dönüşümü. Doç.Dr. Erhan AKDOĞAN
 Sistem Dinamiği - Dinamik Cevap ve Laplace Dönüşümü Doç. Sunumlarda kullanılan semboller: El notlarına bkz. Yorum Soru MATLAB Bolum No.Alt Başlık No.Denklem Sıra No Denklem numarası Şekil No Şekil numarası
Sistem Dinamiği - Dinamik Cevap ve Laplace Dönüşümü Doç. Sunumlarda kullanılan semboller: El notlarına bkz. Yorum Soru MATLAB Bolum No.Alt Başlık No.Denklem Sıra No Denklem numarası Şekil No Şekil numarası
ANALOG FİLTRELEME DENEYİ
 ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ ANALOG FİLTRELEME DENEYİ Ölçme ve telekomünikasyon tekniğinde sık sık belirli frekans bağımlılıkları olan devreler gereklidir. Genellikle belirli bir frekans bandının
ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ ANALOG FİLTRELEME DENEYİ Ölçme ve telekomünikasyon tekniğinde sık sık belirli frekans bağımlılıkları olan devreler gereklidir. Genellikle belirli bir frekans bandının
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 8- SAYISAL İNTEGRASYON 1 GİRİŞ Mühendislikte sık karşılaşılan matematiksel işlemlerden biri integral işlemidir. Bilindiği gibi integral bir büyüklüğün toplam değerinin bulunması
MAK 210 SAYISAL ANALİZ BÖLÜM 8- SAYISAL İNTEGRASYON 1 GİRİŞ Mühendislikte sık karşılaşılan matematiksel işlemlerden biri integral işlemidir. Bilindiği gibi integral bir büyüklüğün toplam değerinin bulunması
Nicel / Nitel Verilerde Konum ve Değişim Ölçüleri. BBY606 Araştırma Yöntemleri 2013-2014 Bahar Dönemi 13 Mart 2014
 Nicel / Nitel Verilerde Konum ve Değişim Ölçüleri BBY606 Araştırma Yöntemleri 2013-2014 Bahar Dönemi 13 Mart 2014 1 Konum ölçüleri Merkezi eğilim ölçüleri Verilerin ortalamaya göre olan gruplanması nasıl?
Nicel / Nitel Verilerde Konum ve Değişim Ölçüleri BBY606 Araştırma Yöntemleri 2013-2014 Bahar Dönemi 13 Mart 2014 1 Konum ölçüleri Merkezi eğilim ölçüleri Verilerin ortalamaya göre olan gruplanması nasıl?
Görüntü İşleme. Dijital Görüntü Tanımları. Dijital görüntü ise sayısal değerlerden oluşur.
 Görüntü İşleme Görüntü işleme, dijital bir resim haline getirilmiş olan gerçek yaşamdaki görüntülerin bir girdi resim olarak işlenerek, o resmin özelliklerinin ve görüntüsünün değiştirilmesidir. Resimler
Görüntü İşleme Görüntü işleme, dijital bir resim haline getirilmiş olan gerçek yaşamdaki görüntülerin bir girdi resim olarak işlenerek, o resmin özelliklerinin ve görüntüsünün değiştirilmesidir. Resimler
Ders İçerik Bilgisi. Sistem Davranışlarının Analizi. Dr. Hakan TERZİOĞLU. 1. Geçici durum analizi. 2. Kalıcı durum analizi. MATLAB da örnek çözümü
 Dr. Hakan TERZİOĞLU Ders İçerik Bilgisi Sistem Davranışlarının Analizi 1. Geçici durum analizi 2. Kalıcı durum analizi MATLAB da örnek çözümü 2 Dr. Hakan TERZİOĞLU 1 3 Geçici ve Kalıcı Durum Davranışları
Dr. Hakan TERZİOĞLU Ders İçerik Bilgisi Sistem Davranışlarının Analizi 1. Geçici durum analizi 2. Kalıcı durum analizi MATLAB da örnek çözümü 2 Dr. Hakan TERZİOĞLU 1 3 Geçici ve Kalıcı Durum Davranışları
Hipotez Testlerine Giriş. Hipotez Testlerine Giriş
 Hipotez Testlerine Giriş Hipotez Testlerine Giriş Hipotez Testlerine Giriş Gözlem ya da deneme sonucu elde edilmiş sonuçların, raslantıya bağlı olup olmadığının incelenmesinde kullanılan istatistiksel
Hipotez Testlerine Giriş Hipotez Testlerine Giriş Hipotez Testlerine Giriş Gözlem ya da deneme sonucu elde edilmiş sonuçların, raslantıya bağlı olup olmadığının incelenmesinde kullanılan istatistiksel
BM202 SAYISAL ÇÖZÜMLEME
 BM202 SAYISAL ÇÖZÜMLEME DOÇ.DR. CİHAN KARAKUZU DERS-2 1 Ders2-Sayısal Hesaplamalarda Gerek Duyulabilecek Matlab İşlemleri MATLAB, çok paradigmalı (bir şeyin nasıl üretileceği konusunda örnek, model) sayısal
BM202 SAYISAL ÇÖZÜMLEME DOÇ.DR. CİHAN KARAKUZU DERS-2 1 Ders2-Sayısal Hesaplamalarda Gerek Duyulabilecek Matlab İşlemleri MATLAB, çok paradigmalı (bir şeyin nasıl üretileceği konusunda örnek, model) sayısal
İnsan beyni, birbiri ile karmaşık ilişkiler içinde bulunan nöron hücreleri kitlesidir. Tüm aktivitelerimizi kontrol eder, yaradılışın en görkemli ve
 YAPAY SİNİRAĞLARI İnsan beyni, birbiri ile karmaşık ilişkiler içinde bulunan nöron hücreleri kitlesidir. Tüm aktivitelerimizi kontrol eder, yaradılışın en görkemli ve gizemli harikalarından biridir. İnsan
YAPAY SİNİRAĞLARI İnsan beyni, birbiri ile karmaşık ilişkiler içinde bulunan nöron hücreleri kitlesidir. Tüm aktivitelerimizi kontrol eder, yaradılışın en görkemli ve gizemli harikalarından biridir. İnsan
Sayısal İşaret İşleme Dersi Laboratuvarı
 1. Örnekleme Öncelikle boş bir m dosyası oluşturarak aşağıdaki kodları bu boş m dosyasının içine yazılacaktır. Periyodik bir sinyal olan x(t) = Acos ( 2π T 0 t) = 6cos (2000πt) sinyali incelenmek üzere
1. Örnekleme Öncelikle boş bir m dosyası oluşturarak aşağıdaki kodları bu boş m dosyasının içine yazılacaktır. Periyodik bir sinyal olan x(t) = Acos ( 2π T 0 t) = 6cos (2000πt) sinyali incelenmek üzere
Şekil 1. DEÜ Test Asansörü kuyusu.
 DOKUZ EYLÜL ÜNĐVERSĐTESĐ TEST ASANSÖRÜ KUYUSUNUN DEPREM YÜKLERĐ ETKĐSĐ ALTINDAKĐ DĐNAMĐK DAVRANIŞININ ĐNCELENMESĐ Zeki Kıral ve Binnur Gören Kıral Dokuz Eylül Üniversitesi, Mühendislik Fakültesi, Makine
DOKUZ EYLÜL ÜNĐVERSĐTESĐ TEST ASANSÖRÜ KUYUSUNUN DEPREM YÜKLERĐ ETKĐSĐ ALTINDAKĐ DĐNAMĐK DAVRANIŞININ ĐNCELENMESĐ Zeki Kıral ve Binnur Gören Kıral Dokuz Eylül Üniversitesi, Mühendislik Fakültesi, Makine
TIBBİ ENSTRUMANTASYON TASARIM VE UYGULAMALARI SAYISAL FİLTRELER
 TIBBİ ENSTRUMANTASYON TASARIM VE UYGULAMALARI SAYISAL FİLTRELER SUNU PLANI Analog sayısal çevirici FIR Filtreler IIR Filtreler Adaptif Filtreler Pan-Tompkins Algoritması Araş. Gör. Berat Doğan 08/04/2015
TIBBİ ENSTRUMANTASYON TASARIM VE UYGULAMALARI SAYISAL FİLTRELER SUNU PLANI Analog sayısal çevirici FIR Filtreler IIR Filtreler Adaptif Filtreler Pan-Tompkins Algoritması Araş. Gör. Berat Doğan 08/04/2015
MOD419 Görüntü İşleme
 MOD419 Görüntü İşleme Ders Kitabı: Digital Image Processing by Gonzalez and Woods Puanlama: %30 Lab. %20 Vize %10 Quizes %40 Final %60 devam mecburiyeti Görüntü İşleme ye Giriş Görüntü İşleme Nedir? Özellikle
MOD419 Görüntü İşleme Ders Kitabı: Digital Image Processing by Gonzalez and Woods Puanlama: %30 Lab. %20 Vize %10 Quizes %40 Final %60 devam mecburiyeti Görüntü İşleme ye Giriş Görüntü İşleme Nedir? Özellikle
Zaman Serileri-1. If you have to forecast, forecast often. EDGAR R. FIEDLER, American economist. IENG 481 Tahmin Yöntemleri Dr.
 Zaman Serileri-1 If you have to forecast, forecast often. EDGAR R. FIEDLER, American economist IENG 481 Tahmin Yöntemleri Dr. Hacer Güner Gören Zaman Serisi nedir? Kronolojik sırayla elde edilen verilere
Zaman Serileri-1 If you have to forecast, forecast often. EDGAR R. FIEDLER, American economist IENG 481 Tahmin Yöntemleri Dr. Hacer Güner Gören Zaman Serisi nedir? Kronolojik sırayla elde edilen verilere
DENEY 3: DFT-Discrete Fourier Transform. 2 cos Ω d. 2 sin Ω d FOURIER SERİSİ
 DENEY 3: DFT-Discrete Fourier Transform FOURIER SERİSİ Herhangi bir periyodik işaret sonsuz sayıda sinüzoidalin ağırlıklı toplamı olarak ifade edilebilir: 2 cosω sinω 1 Burada Ώ 0 birinci (temel) harmonik
DENEY 3: DFT-Discrete Fourier Transform FOURIER SERİSİ Herhangi bir periyodik işaret sonsuz sayıda sinüzoidalin ağırlıklı toplamı olarak ifade edilebilir: 2 cosω sinω 1 Burada Ώ 0 birinci (temel) harmonik
Elektrofizyolojiye Giriş
 Elektrofizyolojiye Giriş Dr.İbrahim Öztura Dokuz Eylül Üniversitesi Tıp Fakültesi Nöroloji Ana Bilim Dalı Nörofizyoloji Bilim Dalı & DEÜHastanesi Epilepsi ve Uyku Merkezi Hans Berger Elektroensefalografiyi
Elektrofizyolojiye Giriş Dr.İbrahim Öztura Dokuz Eylül Üniversitesi Tıp Fakültesi Nöroloji Ana Bilim Dalı Nörofizyoloji Bilim Dalı & DEÜHastanesi Epilepsi ve Uyku Merkezi Hans Berger Elektroensefalografiyi
BÖLÜM 5 MERKEZİ EĞİLİM ÖLÇÜLERİ
 1 BÖLÜM 5 MERKEZİ EĞİLİM ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel sayma
1 BÖLÜM 5 MERKEZİ EĞİLİM ÖLÇÜLERİ Gözlenen belli bir özelliği, bu özelliğe ilişkin ölçme sonuçlarını yani verileri kullanarak betimleme, istatistiksel işlemlerin bir boyutunu oluşturmaktadır. Temel sayma
İçindekiler vii Yazarların Ön Sözü xiii Çevirenin Ön Sözü xiv Teşekkürler xvi Semboller Listesi xvii. Ölçme, İstatistik ve Araştırma...
 İçindekiler İçindekiler vii Yazarların Ön Sözü xiii Çevirenin Ön Sözü xiv Teşekkürler xvi Semboller Listesi xvii BÖLÜM 1 Ölçme, İstatistik ve Araştırma...1 Ölçme Nedir?... 3 Ölçme Süreci... 3 Değişkenler
İçindekiler İçindekiler vii Yazarların Ön Sözü xiii Çevirenin Ön Sözü xiv Teşekkürler xvi Semboller Listesi xvii BÖLÜM 1 Ölçme, İstatistik ve Araştırma...1 Ölçme Nedir?... 3 Ölçme Süreci... 3 Değişkenler
Lineer Cebir. Doç. Dr. Niyazi ŞAHİN TOBB. İçerik: 1.1. Lineer Denklemlerin Tanımı 1.2. Lineer Denklem Sistemleri 1.3. Matrisler
 Lineer Cebir Doç. Dr. Niyazi ŞAHİN TOBB İçerik: 1.1. Lineer Denklemlerin Tanımı 1.2. Lineer Denklem Sistemleri 1.3. Matrisler Bölüm 1 - Lineer Eşitlikler 1.1. Lineer Eşitliklerin Tanımı x 1, x 2,..., x
Lineer Cebir Doç. Dr. Niyazi ŞAHİN TOBB İçerik: 1.1. Lineer Denklemlerin Tanımı 1.2. Lineer Denklem Sistemleri 1.3. Matrisler Bölüm 1 - Lineer Eşitlikler 1.1. Lineer Eşitliklerin Tanımı x 1, x 2,..., x
8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak ya Kullanım Şartları hakkında bilgi almak için
MIT Açık Ders Malzemeleri http://ocw.mit.edu 8.333 İstatistiksel Mekanik I: Parçacıkların İstatistiksel Mekaniği 2007 Güz Bu materyallerden alıntı yapmak ya Kullanım Şartları hakkında bilgi almak için
UYKU EVRELERİNİN SKORLANMASI. Dr. Selda KORKMAZ
 UYKU EVRELERİNİN SKORLANMASI Dr. Selda KORKMAZ UYKU EVRELERİ: AASM-2007 a. Evre W b. Evre N1 c. Evre N2 d. Evre N3 e. Evre R EPOKLARIN SKORLANMASI Çalışmanın başlangıcından itibaren 30 saniyelik epoklar
UYKU EVRELERİNİN SKORLANMASI Dr. Selda KORKMAZ UYKU EVRELERİ: AASM-2007 a. Evre W b. Evre N1 c. Evre N2 d. Evre N3 e. Evre R EPOKLARIN SKORLANMASI Çalışmanın başlangıcından itibaren 30 saniyelik epoklar
BÖLÜM 1 ÖLÇME VE DEĞERLENDİRMEDE TEMEL KAVRAMLAR
 İÇİNDEKİLER BÖLÜM 1 ÖLÇME VE DEĞERLENDİRMEDE TEMEL KAVRAMLAR I. Öğretimde Ölçme ve Değerlendirmenin Gerekliliği... 2 II. Ölçme Kavramı... 3 1. Tanımı ve Unsurları... 3 2. Aşamaları... 3 2.1. Ölçülecek
İÇİNDEKİLER BÖLÜM 1 ÖLÇME VE DEĞERLENDİRMEDE TEMEL KAVRAMLAR I. Öğretimde Ölçme ve Değerlendirmenin Gerekliliği... 2 II. Ölçme Kavramı... 3 1. Tanımı ve Unsurları... 3 2. Aşamaları... 3 2.1. Ölçülecek
SÜREKLİ RASSAL DEĞİŞKENLER
 SÜREKLİ RASSAL DEĞİŞKENLER Sürekli Rassal Değişkenler Sürekli Rassal Değişken: Değerleriölçümyadatartımla elde edilen, bir başka anlatımla sayımla elde edilemeyen, değişkene sürekli rassal değişken denir.
SÜREKLİ RASSAL DEĞİŞKENLER Sürekli Rassal Değişkenler Sürekli Rassal Değişken: Değerleriölçümyadatartımla elde edilen, bir başka anlatımla sayımla elde edilemeyen, değişkene sürekli rassal değişken denir.
Z = S n E(S n ) V ar(sn ) = S n nµ. S nn. n 1/2 n σ
 YTÜ-İktisat İstatistik II Merkezi Limit Teoremi 1 MERKEZİ LİMİT TEOREMİ CENTRAL LIMIT THEOREM X 1,X 2,...,X n herbirinin ortalaması µ ve varyansı σ 2 olan ve aynı dağılıma uyan n tane bağımsız r.d. olsun.
YTÜ-İktisat İstatistik II Merkezi Limit Teoremi 1 MERKEZİ LİMİT TEOREMİ CENTRAL LIMIT THEOREM X 1,X 2,...,X n herbirinin ortalaması µ ve varyansı σ 2 olan ve aynı dağılıma uyan n tane bağımsız r.d. olsun.
YAPAY SİNİR AĞI KULLANARAK DEPREM EĞİLİMİNİN KESTİRİMİ. Umut FIRAT
 YAPAY SİNİR AĞI KULLANARAK DEPREM EĞİLİMİNİN KESTİRİMİ Umut FIRAT ufirat@yahoo.com Öz: Depremler yeryüzünde en çok yıkıma neden olan doğal afetlerdir. Bu durum, depremlerin önceden tahmin edilmesi fikrini
YAPAY SİNİR AĞI KULLANARAK DEPREM EĞİLİMİNİN KESTİRİMİ Umut FIRAT ufirat@yahoo.com Öz: Depremler yeryüzünde en çok yıkıma neden olan doğal afetlerdir. Bu durum, depremlerin önceden tahmin edilmesi fikrini
BMÜ-421 Benzetim ve Modelleme Kesikli Olay Benzetimi. İlhan AYDIN
 BMÜ-421 Benzetim ve Modelleme Kesikli Olay Benzetimi İlhan AYDIN KESİKLİ-OLAY BENZETİMİ Kesikli olay benzetimi, durum değişkenlerinin zaman içinde belirli noktalarda değiştiği sistemlerin modellenmesi
BMÜ-421 Benzetim ve Modelleme Kesikli Olay Benzetimi İlhan AYDIN KESİKLİ-OLAY BENZETİMİ Kesikli olay benzetimi, durum değişkenlerinin zaman içinde belirli noktalarda değiştiği sistemlerin modellenmesi
İşaret ve Sistemler. Ders 3: Periyodik İşaretlerin Frekans Spektrumu
 İşaret ve Sistemler Ders 3: Periyodik İşaretlerin Frekans Spektrumu Fourier Serileri Periyodik işaretlerin spektral analizini yapabilmek için periyodik işaretler sinüzoidal işaretlerin toplamına dönüştürülür
İşaret ve Sistemler Ders 3: Periyodik İşaretlerin Frekans Spektrumu Fourier Serileri Periyodik işaretlerin spektral analizini yapabilmek için periyodik işaretler sinüzoidal işaretlerin toplamına dönüştürülür
İSTATİSTİKSEL PROSES KONTROLÜ
 İSTATİSTİKSEL PROSES KONTROLÜ ZTM 433 KALİTE KONTROL VE STANDARDİZASYON PROF: DR: AHMET ÇOLAK İstatistiksel işlem kontrolü (İPK), işlemle çeşitli istatistiksel metotların ve analiz sapmalarının kullanımını
İSTATİSTİKSEL PROSES KONTROLÜ ZTM 433 KALİTE KONTROL VE STANDARDİZASYON PROF: DR: AHMET ÇOLAK İstatistiksel işlem kontrolü (İPK), işlemle çeşitli istatistiksel metotların ve analiz sapmalarının kullanımını
 009 BS 400- İstatistik sonılannın cevaplanmasında gerekli olabilecek tablolar ve formüller bu kitapçığın sonunda verilmiştir. 1. şağıdakilerden hangisi doğal birimdir? l TV alıcısı Bl Trafik kazası CL
009 BS 400- İstatistik sonılannın cevaplanmasında gerekli olabilecek tablolar ve formüller bu kitapçığın sonunda verilmiştir. 1. şağıdakilerden hangisi doğal birimdir? l TV alıcısı Bl Trafik kazası CL
İSTATİSTİK EXCEL UYGULAMA
 İSTATİSTİK EXCEL UYGULAMA EXCEL UYGULAMA Bu bölümde Excel ile ilgili temel bilgiler sunulacak ve daha sonra İstatistiksel Uygulamalar hakkında bilgi verilecektir. İşlenecek Konular: Merkezi eğilim Ölçüleri
İSTATİSTİK EXCEL UYGULAMA EXCEL UYGULAMA Bu bölümde Excel ile ilgili temel bilgiler sunulacak ve daha sonra İstatistiksel Uygulamalar hakkında bilgi verilecektir. İşlenecek Konular: Merkezi eğilim Ölçüleri
k ise bir gerçek sayı olsun. Buna göre aşağıdaki işlemler Matlab da yapılabilir.
 MATRİS TRANSPOZU: Bir matrisin satırlarını sütun, sütunlarınıda satır yaparak elde edilen matrise transpoz matris denilir. Diğer bir değişle, eğer A matrisi aşağıdaki gibi tanımlandıysa bu matrisin transpoz
MATRİS TRANSPOZU: Bir matrisin satırlarını sütun, sütunlarınıda satır yaparak elde edilen matrise transpoz matris denilir. Diğer bir değişle, eğer A matrisi aşağıdaki gibi tanımlandıysa bu matrisin transpoz
GENETİK ALGORİTMALARA GİRİŞ (II) BİNARİ KODLANMIŞ GA
 GENETİK ALGORİTMALARA GİRİŞ (II) BİNARİ KODLANMIŞ GA Nedim TUTKUN Düzce Üniversitesi Elektrik Elektronik Mühendisliği Bölümü nedimtutkun@duzce.edu.tr Düzce Üniversitesi Elektrik&Elektronik Mühendisliği
GENETİK ALGORİTMALARA GİRİŞ (II) BİNARİ KODLANMIŞ GA Nedim TUTKUN Düzce Üniversitesi Elektrik Elektronik Mühendisliği Bölümü nedimtutkun@duzce.edu.tr Düzce Üniversitesi Elektrik&Elektronik Mühendisliği
Santral (merkezi) sinir sistemi
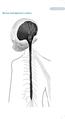 Santral (merkezi) sinir sistemi 1 2 Beyin birçok dokunun kontrollerini üstlenmiştir. Çalışması hakkında hala yeterli veri edinemediğimiz beyin, hafıza ve karar verme organı olarak kabul edilir. Sadece
Santral (merkezi) sinir sistemi 1 2 Beyin birçok dokunun kontrollerini üstlenmiştir. Çalışması hakkında hala yeterli veri edinemediğimiz beyin, hafıza ve karar verme organı olarak kabul edilir. Sadece
Beklenti Anketi ne İlişkin Yöntemsel Açıklama
 Beklenti Anketi ne İlişkin Yöntemsel Açıklama İstatistik Genel Müdürlüğü Reel Sektör Verileri Müdürlüğü İçindekiler I- Amaç... 3 II- Kapsam... 3 III- Yöntem... 3 IV- Tanımlar ve Hesaplamalar... 3 V- Yayımlama...
Beklenti Anketi ne İlişkin Yöntemsel Açıklama İstatistik Genel Müdürlüğü Reel Sektör Verileri Müdürlüğü İçindekiler I- Amaç... 3 II- Kapsam... 3 III- Yöntem... 3 IV- Tanımlar ve Hesaplamalar... 3 V- Yayımlama...
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
EEM HABERLEŞME TEORİSİ NİĞDE ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ
 EEM3006 - HABERLEŞME TEORİSİ NİĞDE ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ EEM3006 - HABERLEŞME TEORİSİ Dersin Öğretim Elemanı: Yrd. Doç. Dr. Yasin KABALCI Ders Görüşme
EEM3006 - HABERLEŞME TEORİSİ NİĞDE ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ EEM3006 - HABERLEŞME TEORİSİ Dersin Öğretim Elemanı: Yrd. Doç. Dr. Yasin KABALCI Ders Görüşme
