Frekans Analiz Yöntemleri I Bode Eğrileri
|
|
|
- Yonca Önder
- 10 yıl önce
- İzleme sayısı:
Transkript
1 Frekan Analiz Yöntemleri I Bode Eğrileri Prof.Dr. Galip Canever 1
2 Frekan cevabı analizi 1930 ve 1940 lı yıllarda Nyquit ve Bode tarafından geliştirilmiştir ve 1948 de Evan tarafından geliştirilen kök yer eğrilerinden öncedir. Frekan metodunun zaman tanım aralığındaki metodalara göre belirgin avantajları vardır: 1 Fizikel datalardan tranfer fonkiyonunun modellenmei Faz ilerletici kompanatör taarlarken kararlı hal hataının ve geçici cevap şartlarının karşılanmaı 3 Lineer olmayan itemlerin kararlılığının bulunmaında 4 Kök yer eğrii çizimindeki belirizliklere karşı
3 HP 35670A Dinamik Sinyal Analizörü fizikel itemden frekan Cevabı bilgilerini toplar.elde edilen bilgi analizde, taarımda veya Sitemin matematikel modelinin elde edilmeinde kullanılabilir. 3
4 Kararlı halde, lineer bir iteme inüoidal bir giriş uygulandığında item aynı frekanta bir inüoidal üretir. Bu çıkış cevabı giriş ile aynı frekanta olmaıyla beraber genlik ve faz açıı ile girişten farklılaşır. Bu farklılıklar frekanın fonkiyonudur. M Co t φ1 M φ İle göterilir. Sitemini inceleyelim 4
5 Sitemin girişi ft inüoidali ie kararlı hal çıkış fonkiyonu aynı frekanta olan xtdir. Giriş Çıkış 5
6 Kararlı hal çıkış inüoidali: M [ ] φ = M M φ φ 0 0 i i Dolayııyla itemin fonkiyonu: M M = 0 M i Sitemin fazı ie: φ = φ φ 0 i 6
7 Giriş Fonkiyonu: r t = ACo t BSint B r t = A B Co t tan 1 A M = A B tan 1 B φ = i i A A jb M i e j φ i 7
8 8 G B A C = Zorlanmış Çözüm ile Doğal Çözümü keirlere ayırma yöntemi ile elde edebiliriz. G j j B A C = 1 j K j K C =
9 9 φ φ φ φ j e M M j e M M c G i G i j G i j G i = Ter Lapla alındığında, G i G i t j t j G i e e M M t c φ φ φ φ = G i G i t Co M M t c φ φ = G G i M i M M φ φ φ = 0 0 G M G j G φ = j G j G =
10 Frekan Cevabının Çizilmei Bir G iteminin frekan yanıtı bir iki şekilde çizilebilir: Örnek: =jw için 1 Genlik ve fazın frekanın bir fonkiyonu cininden ayrı ayrı çizilmei Kutupal olarak genlik ve fazörün aynı eğri üzerinde çizilmei G G j 1 = 1 = j Sitemini analitik olarak ifade ediniz, frekan yanıtını genlik ve faözörü ayrı ayrı eğriler olarak ve aynı eğri olarak çiziniz. j G j = 4 10
11 Bu itemin genliği: G j = M = 1 Gj nın fazı ie: φ = tan 1 Bode eğrilerinde genelde genlik deibeldb cininden ifade edilir. Bir M kazancının deibel değeri 0logM dir. Ayrıca hem kazanç hemde frekan ekenleri logaritmiktir. Dolayııyla Bode eğrimizde genlik ; 0log Açı ie; φ M = = tan 1 0log, 1 log 4, log 4 Eken takımıyla çizilir. 11
12 1
13 Genlik ile açı kutupal olarak çizildiğinde ie M φ 1 = 4 tan 1 13
14 Logaritmik Çizimin Avantajları Elle hızlıca çizmek mümkün Genlik ve frekan için çok geniş ınırlar kolayca göterilebilir Çok karmaşık tranfer fonkiyonları kolayca çizilebilir ve çarpım veya bölüm halinde olan terimler baitçe grafikel toplama ve çıkarma ile daha kolay anlaşılabilir. Rakam katlandıkça db değeri 6dB artar. 14
15 15 Aimptotik Yaklaşımlar: Bode Eğrileri Logaritimik genlik ve faz frekan eğrilerinin logaritmik açıal hıza göre çizimleri düz çizgilerin toplamı yaklaşımı ile baitleştirilebilir n m n p p p z z z K G = Sitemini dikkate alalım. Bu itemin genlik frekan cevabı her bir terim genlik frekan cevaplarının çarpımıdır. j n m n p p p z z z K j G = Eğer herbir kutup ve ıfırın genlik cevabını biliyorak toplam genlik cevabını bulabiliriz.
16 Logaritmik olarak çalışırak toplam genlik ifadeini elde etmemiz kolaylaşır. Zira paydakiıfırlar çarpımlar toplanacak, paydadaki çarpımlar ie çıkartılacak. Deibel olarak yazacak olurak: 0logG j = 0logK 0log z 1 0log z... 0log m 0log p 1... j Eğer her bir terimi biliyorak cebrik toplamları ile onucu kolayca elde edebiliriz. Ayrıca her bir terimin düz çizgi yaklaşımını biliyorak bu düz çizgilerin toplanıp çıkartılmaı ile grafik kolayca çizilebilir. 16
17 G=a nın BodeÇizimi G j = j a = a1 j a G j a olur. Düşük frekanlarda, Deibel cininden genlik: 0log M=0log a M = G j ve abittir. Yükek frekanlarda, >>a G G j = j a = j a a 0 = 90 = a j a
18 Deibel cininden genlik: 0log M=0log a 0 log M = 0log a 0log = 0log a a<< Eğer db veya 0log M yi0log ya göre çizicek olurak, yukarıdaki denklem doğru denklemi olur: Eğrinin eğimi 0 dir. y=0x Her katlayan frekan 0log ve 6db artmaına ebep olur ve eğri 6dB/oktav lık eğim ile artar.burada oktav frekanın katlayanıdır,,4,8,16,
19 Düz eğri yaklaşımına aimptot denir. Düşük frekan yaklaşımına düşük frekan aimptotu, yükek frekan yaklaşımına yükek frekan aimptotu denir. a frekanına da köşe frekanı denir. a nın BodeGenlik Eğrii 19
20 Faz cevabını inceleyecek olurak: G j = j a = a1 j a İfadeine göre köşe frekanında=a açı 45 0 olmalıdır. G j = a aj Düşük frekanlarda G j a İfadeine göre açı O 0 olmalıdır. Yükek frekanlarda G j a a 0 = 90 = 90 0 İfadeine göre açı 9O 0 olmalıdır. 0
21 a nın BodeFaz Eğrii 1
22
23 3
24 G G=1/a nın Bode Çizimi = 1 a = a 1 a Bu tranfer fonkiyonu 0log1/a düşük frekan aimptotuna ahiptir. Bode eğrii köe frekanı, a rad/ ya ulaşıncaya kadar abittir. Yükek frekanlarda: 1 G = a 1 a j = a 1 j a = 1 a a = 90 4
25 db olarak, 1 0 log M = 0 log 0 log = 0 a a G= in Bode Çizimi log G= adece yükek frekan aimptotuna ahiptir. =j, 0log genliğindedir. Böylece Bode eğrii 6dB/oktav0dB/dekad lık eğimli ve =1 de 0dB den geçen bir doğrudur. Fazı ie abit 90 0 dir G=1/ in Bode Çizimi G=1/ Bode eğrii -6dB/oktav0dB/dekad lık eğimli ve =1 de 0dB den geçen bir doğrudur. Fazı ie abit dir 5
26 G= 6
27 G=1/ 7
28 8
29 9
30 Örnek: G = K 3 1 Bode eğriini çiziniz? İlk olarak köşe frekanları:-1, -, -3. Genlik eğrii en küçük köşe frekanından 1 dekad önce başlamalı ve en yükek köşe frekanından 1 dekad onraına kadar devam etmelidir. Öyleye 0.1 rad ile 100 rad araı uygun bir eçimdir. =0.1 değeri bütün a ifadeleri için düşük frekantır=0 böylece 3K G j0.1 = = 15K 0.11 K genlik eğriini yukarı veya aşağı kaydır 30
31 31
32 3
33 Bode eğrii =0.1 değerinde, 0log15=3.5dB değeri ile başlıyor. Paydadaki teriminden dolayı hemen -6dB/oktav lık eğimle düşüşe geçiyor. =1 değerinde, 1terimi bir - 6dB/oktav lık eğim daha ekiliyor ve eğri toplam -1dB/oktav lık eğim ile düşüşüne devam ediyor. Daha onra = değerinde, terimi bir -6dB/oktav lık eğim daha ekiliyor ve eğri toplam -18dB/oktav lık eğime ahip oluyor. =3 değerinde, 3terimi bir 6dB/oktav lık pozitif eğim ekliyor ve eğrinin toplam eğimi - 1dB/oktav oluyor ve bundan onra başka köşe frekanı olmadığı için eğri bu eğimle devam eder. Bode faz eğriide benzer şekilde elde edilebilir, köşe frekanının 1 dekad öncei ve 1 dekad onraında kırılmaların olmaı biraz daha dikkat gerektirir. 33
34 34
35 35
36 G= ζ n n in Bode Çizimi İkinci derece itemlerin Bode eğrilerinin çizimlerini inceleyeceğiz. G = ζ n Birinci derece itemlerin akine ikinci derece itemlerde ζ nin bazı değerleri için gerçek frekan cevabı ile aimptotik yaklaşımdaki frekan cevabı araındaki fark ihmal edilebilecek eviyeden büyük olabilir. Düşük frekanlarda, Düşük frekanlarda genlik ie, n n n G = 0 0log M = 0log G j = 0logn 0 36
37 Yükek frekanlarda, G G j = Yükek frekanlarda genlik ie, 0log M = 0log G j = 0log Eğim 40dB/oktav yada 40dB/dekad = 40log Dikkat edilecek olura = n iken düşük ve yükek frekan aimptotları aynıdır. Dolayııyla n ikinci derece itemin köşe frekanıdır. 37
38 38
39 Faz ı ie düşük frekanlarda 0 derece, yükek frekanlarda ie 180 derecedir. Doğal frekanta açı: G j = ζ = jζ = n için onuç n n n j n j ζ olduğundan doğal frekantaki açı Dolayııyla 0.1 n ile 10 n araında açı 90 0 /dekad ile yükelir. G= n / ζ n n in Bode Çizimi n Genlik eğrii doğal frekanta kırılır ve -1dB/oktav 40dB/dekad lık eğim ile azalır. Faz düşük frekanlarda 0 derecedir ve 0.1 n ile 10 n araında açı /dekad açı ile azalır ve 10 n den onra -180 decede kalır. 39
40 nin değişen ζ değerleri için Bode Genlik Eğrileri 40
41 nin değişen ζ değerleri için Bode Faz Eğrileri 41
42 nin değişen ζ değerleri için Bode Genlik Eğrileri 4
43 nin değişen ζ değerleri için Bode Faz Eğrileri 43
44 Örnek: 3 G = 5 Bode eğriini çiziniz? G nin düşük frekan değeri =0 alınarak 3/50 yada 4.44dB olarak bulunur. Bode eğrii bu değer ile başlar ve ilk köşe frekanı - ye kadar bu değer ile devam eder. deki kutup -0dB/dekad lık bir eğimle bir onraki köşe frekanı -3 e kadar devam eder. -3 deki ıfır, 0dB/dekad lık bir pozitif eğim oluşturur ki net eğim bu noktadan onra 0 olur. 5 rad/ de ie ikinci derece terim devreye girer ve 40dB/dekad lık bir pozitif eğim oluşturarak onuza kadar devam eder. 44
45 45
46 46
47 47
48 48
Ders #9. Otomatik Kontrol. Kararlılık (Stability) Prof.Dr.Galip Cansever. 26 February 2007 Otomatik Kontrol. Prof.Dr.
 Der #9 Otomatik Kontrol Kararlılık (Stability) 1 Kararlılık, geçici rejim cevabı ve ürekli hal hataı gibi kontrol taarımcıının üç temel unurundan en önemli olanıdır. Lineer zamanla değişmeyen itemlerin
Der #9 Otomatik Kontrol Kararlılık (Stability) 1 Kararlılık, geçici rejim cevabı ve ürekli hal hataı gibi kontrol taarımcıının üç temel unurundan en önemli olanıdır. Lineer zamanla değişmeyen itemlerin
Kök Yer Eğrileri. Doç.Dr. Haluk Görgün. Kontrol Sistemleri Tasarımı. Doç.Dr. Haluk Görgün
 Kök Yer Eğrileri Bir kontrol taarımcıı itemin kararlı olup olmadığını ve kararlılık dereceini bilmek, diferaniyel denklem çözmeden bir analiz ile item performaını tahmin etmek iter. Geribelemeli kontrol
Kök Yer Eğrileri Bir kontrol taarımcıı itemin kararlı olup olmadığını ve kararlılık dereceini bilmek, diferaniyel denklem çözmeden bir analiz ile item performaını tahmin etmek iter. Geribelemeli kontrol
ESM406- Elektrik Enerji Sistemlerinin Kontrolü. 2. SİSTEMLERİN MATEMATİKSEL MODELLENMESİ Laplace Dönüşümü
 ESM406- Elektrik Enerji Sitemlerinin Kontrolü. SİSTEMLERİN MATEMATİKSEL MODELLENMESİ Laplace Dönüşümü.. Hedefler Bu bölümün hedefleri:. Komplek değişkenlerin tanıtılmaı.. Laplace Tranformayonun tanıtılmaı..
ESM406- Elektrik Enerji Sitemlerinin Kontrolü. SİSTEMLERİN MATEMATİKSEL MODELLENMESİ Laplace Dönüşümü.. Hedefler Bu bölümün hedefleri:. Komplek değişkenlerin tanıtılmaı.. Laplace Tranformayonun tanıtılmaı..
DİNAMİK DEVRELERİN FREKANS DOMENİNDE İNCELENMESİ, FREKANS KARAKTERİSTİKLERİ VE BODE DİYAGRAMLARI
 DENEY NO: 9 DİNAMİK DEVRELERİN FREKANS DOMENİNDE İNCELENMESİ, FREKANS KARAKTERİSTİKLERİ VE BODE DİYAGRAMLARI Deneyin Amacı: Lineer-zamanla değişmeyen -kapılı devrelerin Genlik-Frekan ve Faz-Frekan karakteritiklerinin
DENEY NO: 9 DİNAMİK DEVRELERİN FREKANS DOMENİNDE İNCELENMESİ, FREKANS KARAKTERİSTİKLERİ VE BODE DİYAGRAMLARI Deneyin Amacı: Lineer-zamanla değişmeyen -kapılı devrelerin Genlik-Frekan ve Faz-Frekan karakteritiklerinin
ÇOKLU ALT SİSTEMLERİN SADELEŞTİRİLMESİ
 73 BÖLÜM 5 ÇOKLU ALT SİSTEMLERİN SADELEŞTİRİLMESİ 5. Blok Diyagramları Blok diyagramları genellikle frekan domenindeki analizlerde kullanılır. Şekil 5. de çoklu alt-itemlerde kullanılan blok diyagramları
73 BÖLÜM 5 ÇOKLU ALT SİSTEMLERİN SADELEŞTİRİLMESİ 5. Blok Diyagramları Blok diyagramları genellikle frekan domenindeki analizlerde kullanılır. Şekil 5. de çoklu alt-itemlerde kullanılan blok diyagramları
Bölüm 7 - Kök- Yer Eğrisi Teknikleri
 Bölüm 7 - Kök- Yer Eğrii Teknikleri Kök yer eğrii tekniği kararlı ve geçici hal cevabı analizinde kullanılmaktadır. Bu grafikel teknik kontrol iteminin performan niteliklerini tanımlamamıza yardımcı olur.
Bölüm 7 - Kök- Yer Eğrii Teknikleri Kök yer eğrii tekniği kararlı ve geçici hal cevabı analizinde kullanılmaktadır. Bu grafikel teknik kontrol iteminin performan niteliklerini tanımlamamıza yardımcı olur.
Otomatik Kontrol. Blok Diyagramlar ve İşaret Akış Diyagramları. Prof.Dr.Galip Cansever. Ders #3. 26 February 2007 Otomatik Kontrol
 Der # Otomatik Kontrol Blok Diyagramlar ve İşaret Akış Diyagramları ProfDralip Canever 6 February 007 Otomatik Kontrol ProfDralip Canever Karmaşık itemler bir çok alt itemin bir araya gelmeiyle oluşmuştur
Der # Otomatik Kontrol Blok Diyagramlar ve İşaret Akış Diyagramları ProfDralip Canever 6 February 007 Otomatik Kontrol ProfDralip Canever Karmaşık itemler bir çok alt itemin bir araya gelmeiyle oluşmuştur
ESM 406 Elektrik Enerji Sistemlerinin Kontrolü 4. TRANSFER FONKSİYONU VE BLOK DİYAGRAM İNDİRGEME
 . TRNSFER FONKSİYONU VE BLOK DİYRM İNDİREME. Hedefler Bu bölümün amacı;. Tranfer fonkiyonu ile blok diyagramları araındaki ilişki incelemek,. Fizikel itemlerin blok diyagramlarını elde etmek, 3. Blok diyagramlarının
. TRNSFER FONKSİYONU VE BLOK DİYRM İNDİREME. Hedefler Bu bölümün amacı;. Tranfer fonkiyonu ile blok diyagramları araındaki ilişki incelemek,. Fizikel itemlerin blok diyagramlarını elde etmek, 3. Blok diyagramlarının
H09 Doğrusal kontrol sistemlerinin kararlılık analizi. Yrd. Doç. Dr. Aytaç Gören
 H09 Doğrual kontrol itemlerinin kararlılık analizi MAK 306 - Der Kapamı H01 İçerik ve Otomatik kontrol kavramı H0 Otomatik kontrol kavramı ve devreler H03 Kontrol devrelerinde geri belemenin önemi H04
H09 Doğrual kontrol itemlerinin kararlılık analizi MAK 306 - Der Kapamı H01 İçerik ve Otomatik kontrol kavramı H0 Otomatik kontrol kavramı ve devreler H03 Kontrol devrelerinde geri belemenin önemi H04
Ders #10. Otomatik Kontrol. Sürekli Hal Hataları. Prof.Dr.Galip Cansever. 26 February 2007 Otomatik Kontrol. Prof.Dr.
 Der #0 Otomatik ontrol Sürekli Hal Hataları Prof.Dr.alip Canever Prof.Dr.alip Canever Denetim Sitemlerinin analiz ve taarımında üç kritere odaklanılır:. eçici Rejim Cevabı. ararlılık 3. Sürekli Hal ararlı
Der #0 Otomatik ontrol Sürekli Hal Hataları Prof.Dr.alip Canever Prof.Dr.alip Canever Denetim Sitemlerinin analiz ve taarımında üç kritere odaklanılır:. eçici Rejim Cevabı. ararlılık 3. Sürekli Hal ararlı
Kontrol Sistemleri. Kontrolcüler. Yrd. Doç. Dr. Aytaç GÖREN
 ontrol Sitemleri ontrolcüler Doğrual Sitemlerin Sınıflandırılmaı: Birinci Mertebeden Gecikmeli BMG Sitemler: x a T 1 x a t x e t Son değer teoremi : x x x adr adr adr lim xa 0 lim 0 T 1 t T t 2T t 3T t
ontrol Sitemleri ontrolcüler Doğrual Sitemlerin Sınıflandırılmaı: Birinci Mertebeden Gecikmeli BMG Sitemler: x a T 1 x a t x e t Son değer teoremi : x x x adr adr adr lim xa 0 lim 0 T 1 t T t 2T t 3T t
Kontrol Sistemleri Tasarımı. Kontrolcü Tasarımı Tanımlar ve İsterler
 ontrol Sitemleri Taarımı ontrolcü Taarımı Tanımlar ve İterler Prof. Dr. Bülent E. Platin ontrolcü Taarımı İterleri Birincil iterler: ararlılık alıcı rejim hataı Dinamik davranış İterlerin işlevel boyutu:
ontrol Sitemleri Taarımı ontrolcü Taarımı Tanımlar ve İterler Prof. Dr. Bülent E. Platin ontrolcü Taarımı İterleri Birincil iterler: ararlılık alıcı rejim hataı Dinamik davranış İterlerin işlevel boyutu:
3. DİNAMİK. bağıntısı ile hesaplanır. Birimi m/s ile ifade edilir.
 3. DİNAMİK Dinamik konuu Kinematik ve Kinetik alt başlıklarında incelenecektir. Kinematik, hareket halindeki bir itemin konum (poziyon), hız ve ivmeini, bunların oluşmaını ağlayan kuvvet ya da moment etkiini
3. DİNAMİK Dinamik konuu Kinematik ve Kinetik alt başlıklarında incelenecektir. Kinematik, hareket halindeki bir itemin konum (poziyon), hız ve ivmeini, bunların oluşmaını ağlayan kuvvet ya da moment etkiini
problem 111) s+1=0 koku nedir s=-1 s+5=0 koku nedir s=-5
 problem ) +=0 koku nedir =- +5=0 koku nedir =-5-5=0 koku nedir =+5 -------------------------- -------------------------- problem ) +=0, ifirdan onuza kadar degiire kok nail degiir. +=0 kokleri 0 0 - -
problem ) +=0 koku nedir =- +5=0 koku nedir =-5-5=0 koku nedir =+5 -------------------------- -------------------------- problem ) +=0, ifirdan onuza kadar degiire kok nail degiir. +=0 kokleri 0 0 - -
Kök Yer Eğrileri ile Tasarım
 Kök Yer Eğrileri ile Taarım Prof.Dr. Galip Canever Kök Yer Eğriinden Kazanç ın Belirlenmei Kök yer eğrii K nın pozitif değerleri için denkleminin muhtemel köklerini göteren eğridir. KG ( ) Taarımın amacı
Kök Yer Eğrileri ile Taarım Prof.Dr. Galip Canever Kök Yer Eğriinden Kazanç ın Belirlenmei Kök yer eğrii K nın pozitif değerleri için denkleminin muhtemel köklerini göteren eğridir. KG ( ) Taarımın amacı
Otomatik Kontrol. Fiziksel Sistemlerin Modellenmesi. Prof.Dr.Galip Cansever. Elektriksel Sistemeler Mekaniksel Sistemler. Ders #4
 Der #4 Otomatik Kontrol Fizikel Sitemlerin Modellenmei Elektrikel Sitemeler Mekanikel Sitemler 6 February 007 Otomatik Kontrol Kontrol itemlerinin analizinde ve taarımında en önemli noktalardan bir tanei
Der #4 Otomatik Kontrol Fizikel Sitemlerin Modellenmei Elektrikel Sitemeler Mekanikel Sitemler 6 February 007 Otomatik Kontrol Kontrol itemlerinin analizinde ve taarımında en önemli noktalardan bir tanei
DENEY 1 Laplace Dönüşümü
 DENEY 1 Laplace Dönüşümü DENEYİN AMACI 1. Laplace dönüşümü uygulamaını anlamak.. Simulink yardımıyla Laplace dönüşüm çiftlerinin benzetimini yapmak. 3. ACS-1000 Analog Kontrol Sitemini kullanarak, Laplace
DENEY 1 Laplace Dönüşümü DENEYİN AMACI 1. Laplace dönüşümü uygulamaını anlamak.. Simulink yardımıyla Laplace dönüşüm çiftlerinin benzetimini yapmak. 3. ACS-1000 Analog Kontrol Sitemini kullanarak, Laplace
Bölüm 7 Sinüsoidal Kalıcı Durum Devre Analizi
 Bölüm 7 Sinüoidal Kalıcı Durum Devre Analizi 7. Sinüoidal kaynaklar 7. Ortalama ve Etkin Değer 7.3 Karmaşık Sayılar 7.4 Sinüoidallerin Fazör Göterimi 7.5 Devrelerin Sinüzoidal Kalıcı Durum Cevabı 7.6 Devrelerin
Bölüm 7 Sinüoidal Kalıcı Durum Devre Analizi 7. Sinüoidal kaynaklar 7. Ortalama ve Etkin Değer 7.3 Karmaşık Sayılar 7.4 Sinüoidallerin Fazör Göterimi 7.5 Devrelerin Sinüzoidal Kalıcı Durum Cevabı 7.6 Devrelerin
Deney-1 Analog Filtreler
 Đleişim Siemleri ab. Noları Arş.Gör.Koray GÜRKAN [email protected] Deney- Analog Filreler Đleişim iemlerinde, örneğin FM bandında 00 MHz de yayın yapacak olan bir radyo vericiinde modülayon onraı oraya
Đleişim Siemleri ab. Noları Arş.Gör.Koray GÜRKAN [email protected] Deney- Analog Filreler Đleişim iemlerinde, örneğin FM bandında 00 MHz de yayın yapacak olan bir radyo vericiinde modülayon onraı oraya
OTOMATİK KONTROL SİSTEMLERİ DOĞRUSAL (LİNEER) GERİ BESLEMELİ SİSTEMLERİN KARARLILIĞI
 OOMAİ ONROL SİSEMLERİ DOĞRUSAL LİNEER GERİ BESLEMELİ SİSEMLERİN ARARLILIĞI ararlılık Denetim Sitemlerinden; ararlılık Hızlı cevap Az veya ıfır hata Minimum aşım gibi kriterleri ağlamaı beklenir. ararlılık;
OOMAİ ONROL SİSEMLERİ DOĞRUSAL LİNEER GERİ BESLEMELİ SİSEMLERİN ARARLILIĞI ararlılık Denetim Sitemlerinden; ararlılık Hızlı cevap Az veya ıfır hata Minimum aşım gibi kriterleri ağlamaı beklenir. ararlılık;
>> pretty(f) s exp(10) 1/ s + 1 1/100 (s + 1) + 1 s
 ELN5 OTOMATİK KONTROL MATLAB ÖRNEKLERİ - LAPLACE VE TERS LAPLACE DÖNÜŞÜMÜ UYGULAMALARI: Symbolic Math Toolbox içinde tanımlı olan laplace ve ilaplace komutları ile Laplace ve Ter Laplace dönüşümlerinin
ELN5 OTOMATİK KONTROL MATLAB ÖRNEKLERİ - LAPLACE VE TERS LAPLACE DÖNÜŞÜMÜ UYGULAMALARI: Symbolic Math Toolbox içinde tanımlı olan laplace ve ilaplace komutları ile Laplace ve Ter Laplace dönüşümlerinin
Sistem Dinamiği. Bölüm 9- Frekans Domeninde Sistem Analizi. Doç.Dr. Erhan AKDOĞAN
 Sistem Dinamiği Bölüm 9- Frekans Domeninde Sistem Analizi Sunumlarda kullanılan semboller: El notlarına bkz. Yorum Bolum No.Alt Başlık No.Denklem Sıra No Denklem numarası Şekil No Şekil numarası Dikkat
Sistem Dinamiği Bölüm 9- Frekans Domeninde Sistem Analizi Sunumlarda kullanılan semboller: El notlarına bkz. Yorum Bolum No.Alt Başlık No.Denklem Sıra No Denklem numarası Şekil No Şekil numarası Dikkat
Kontrol Sistemleri Tasarımı
 Kontrol Sitemleri Taarımı Kök Yer Eğrii ile Kontrolcü Taarımı Prof. Dr. Bülent E. Platin Kontrol Sitemlerinde Taarım İterleri Zaman Yanıtı Özellik Kararlılık Kalıcı Rejim Yanıtı Geçici rejim Yanıtı Kapalı
Kontrol Sitemleri Taarımı Kök Yer Eğrii ile Kontrolcü Taarımı Prof. Dr. Bülent E. Platin Kontrol Sitemlerinde Taarım İterleri Zaman Yanıtı Özellik Kararlılık Kalıcı Rejim Yanıtı Geçici rejim Yanıtı Kapalı
EGE ÜNİVERSİTESİ-MÜHENDİSLİK FAKÜLTESİ-MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ 1 MK371 ISI TRANSFERİ (2+2) DERSİ
 EGE ÜNİVERSİESİ-MÜHENDİSİK FAKÜESİ-MAKİNA MÜHENDİSİĞİ BÖÜMÜ 1 MK371 ISI RANSFERİ (+) DERSİ-ÖZE BİGİER: (8.6) EGE ÜNİVERSİESİ-MÜHENDİSİK FAKÜESİ MAKİNA MÜHENDİSİĞİ BÖÜMÜ MK371 ISI RANSFERİ (+) DERSİ.BÖÜM
EGE ÜNİVERSİESİ-MÜHENDİSİK FAKÜESİ-MAKİNA MÜHENDİSİĞİ BÖÜMÜ 1 MK371 ISI RANSFERİ (+) DERSİ-ÖZE BİGİER: (8.6) EGE ÜNİVERSİESİ-MÜHENDİSİK FAKÜESİ MAKİNA MÜHENDİSİĞİ BÖÜMÜ MK371 ISI RANSFERİ (+) DERSİ.BÖÜM
H03 Kontrol devrelerinde geri beslemenin önemi. Yrd. Doç. Dr. Aytaç Gören
 H03 ontrol devrelerinde geri belemenin önemi Yrd. Doç. Dr. Aytaç ören MA 3026 - Der apamı H0 İçerik ve Otomatik kontrol kavramı H02 Otomatik kontrol kavramı ve devreler H03 ontrol devrelerinde geri belemenin
H03 ontrol devrelerinde geri belemenin önemi Yrd. Doç. Dr. Aytaç ören MA 3026 - Der apamı H0 İçerik ve Otomatik kontrol kavramı H02 Otomatik kontrol kavramı ve devreler H03 ontrol devrelerinde geri belemenin
YÜZÜNCÜ YIL ÜNİVERSİTESİ ELEKTRİK ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ ANALOG ELEKTRONİK DENEY RAPORU
 YÜZÜNCÜ YIL ÜNİVERSİTESİ ELEKTRİK ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ ANALOG ELEKTRONİK DENEY RAPORU DENEY NO : DENEYİN ADI : YAPILIŞ TARİHİ: GRUP ÜYELERİ : 1. 2. 3. DERSİN SORUMLU ÖĞRETİM ÜYESİ: Yrd. Doç.
YÜZÜNCÜ YIL ÜNİVERSİTESİ ELEKTRİK ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ ANALOG ELEKTRONİK DENEY RAPORU DENEY NO : DENEYİN ADI : YAPILIŞ TARİHİ: GRUP ÜYELERİ : 1. 2. 3. DERSİN SORUMLU ÖĞRETİM ÜYESİ: Yrd. Doç.
12.7 Örnekler PROBLEMLER
 2. 2.2 2.3 2.4 Giriş Bir Kuvvetin ve Bir Momentin İşi Virtüel İş İlkei Genelleştirilmiş Koordinatlar Örnekler Potaniyel Enerji 2.5 Sürtünmeli Makinalar ve Mekanik Verim 2.6 Denge 2.7 Örnekler PROBLEMLER
2. 2.2 2.3 2.4 Giriş Bir Kuvvetin ve Bir Momentin İşi Virtüel İş İlkei Genelleştirilmiş Koordinatlar Örnekler Potaniyel Enerji 2.5 Sürtünmeli Makinalar ve Mekanik Verim 2.6 Denge 2.7 Örnekler PROBLEMLER
NEWTON HAREKEET YASALARI
 NEWTON HAREKEET YASALARI ) m= kg kütleli bir cimin belli bir zaman onraki yer değiştirmei x = At / olarak veriliyor. A= 6,0 m/ / dir. Cime etkiyen net kuvveti bulunuz. Kuvvetin zamana bağlı olduğuna dikkat
NEWTON HAREKEET YASALARI ) m= kg kütleli bir cimin belli bir zaman onraki yer değiştirmei x = At / olarak veriliyor. A= 6,0 m/ / dir. Cime etkiyen net kuvveti bulunuz. Kuvvetin zamana bağlı olduğuna dikkat
 Yukarıdaki şekilde, birim geribeslemeli bir kontrol sisteminin ileri yol transfer fonksiyonuna ait, sistemin orijinal çevrim kazancı K = 1 için deneysel olarak elde edilmiş Bode eğrisi verilmiştir. Aşağıdaki
Yukarıdaki şekilde, birim geribeslemeli bir kontrol sisteminin ileri yol transfer fonksiyonuna ait, sistemin orijinal çevrim kazancı K = 1 için deneysel olarak elde edilmiş Bode eğrisi verilmiştir. Aşağıdaki
TRANSİSTÖRLÜ YÜKSELTEÇLERDE GERİBESLEME
 TRANSİSTÖRLÜ YÜKSELTEÇLERDE GERİBESLEME Amaç Elektronikte geniş uygulama alanı bulan geribesleme, sistemin çıkış büyüklüğünden elde edilen ve giriş büyüklüğü ile aynı nitelikte bir işaretin girişe gelmesi
TRANSİSTÖRLÜ YÜKSELTEÇLERDE GERİBESLEME Amaç Elektronikte geniş uygulama alanı bulan geribesleme, sistemin çıkış büyüklüğünden elde edilen ve giriş büyüklüğü ile aynı nitelikte bir işaretin girişe gelmesi
DİELEKTRİK ÖZELLİKLER
 0700 ENEJİ HATLAINDA ÇAPAZLAMA! zun meafeli enerji taşıma hatlarında iletkenler belirli meafelerde (L/) çarazlanarak direğe monte edilirler! Çarazlama yaılmadığı durumlarda: Fazların reaktan ve kaaiteleri
0700 ENEJİ HATLAINDA ÇAPAZLAMA! zun meafeli enerji taşıma hatlarında iletkenler belirli meafelerde (L/) çarazlanarak direğe monte edilirler! Çarazlama yaılmadığı durumlarda: Fazların reaktan ve kaaiteleri
Otomatik Kontrol (Doğrusal sistemlerde Kararlılık Kriterleri) - Ders sorumlusu: Doç.Dr.HilmiKuşçu
 ROOT-LOCUS TEKNİĞİ Lineer kontrol sistemlerinde en önemli kontrollerden biri belirli bir sistem parametresi değişirken karakteristik denklem köklerinin nasıl bir yörünge izlediğinin araştırılmasıdır. Kapalı
ROOT-LOCUS TEKNİĞİ Lineer kontrol sistemlerinde en önemli kontrollerden biri belirli bir sistem parametresi değişirken karakteristik denklem köklerinin nasıl bir yörünge izlediğinin araştırılmasıdır. Kapalı
PASİF ve YARI AKTİF SÜSPANSİYON SİSTEMLERİNİN TİTREŞİM YALITIM PERFORMANSININ İNCELENMESİ
 9. Ululararaı Makina Taarı ve İalat Kongrei 3 5 Eylül 000, ODTÜ, Ankara, Türkiye PASİF ve YARI AKTİF SÜSPANSİYON SİSTEMLERİNİN TİTREŞİM YALITIM PERFORMANSININ İNCELENMESİ Meut ŞENGİRGİN, Uludağ Üniveritei
9. Ululararaı Makina Taarı ve İalat Kongrei 3 5 Eylül 000, ODTÜ, Ankara, Türkiye PASİF ve YARI AKTİF SÜSPANSİYON SİSTEMLERİNİN TİTREŞİM YALITIM PERFORMANSININ İNCELENMESİ Meut ŞENGİRGİN, Uludağ Üniveritei
ITAP Fizik Olimpiyat Okulu
 n 8 Eylül Deneme Sınavı (Prof.Dr.Ventilav Dimitrov) Konu: Karmaşık ekanik Soruları Soru. Yarıçapı R olan iki homojen küre yatay pürüzüz bir çubuğa şekildeki gibi geçirilmiştir. Kütlei m olan hareketiz
n 8 Eylül Deneme Sınavı (Prof.Dr.Ventilav Dimitrov) Konu: Karmaşık ekanik Soruları Soru. Yarıçapı R olan iki homojen küre yatay pürüzüz bir çubuğa şekildeki gibi geçirilmiştir. Kütlei m olan hareketiz
dir. Periyodik bir sinyalin örneklenmesi sırasında, periyot başına alınmak istenen ölçüm sayısı N
 DENEY 7: ÖRNEKLEME, AYRIK SİNYALLERİN SPEKTRUMLARI VE ÖRTÜŞME OLAYI. Deneyin Amacı Bu deneyde, ürekli inyallerin zaman ve rekan uzaylarında örneklenmei, ayrık inyallerin ektrumlarının elde edilmei ve örtüşme
DENEY 7: ÖRNEKLEME, AYRIK SİNYALLERİN SPEKTRUMLARI VE ÖRTÜŞME OLAYI. Deneyin Amacı Bu deneyde, ürekli inyallerin zaman ve rekan uzaylarında örneklenmei, ayrık inyallerin ektrumlarının elde edilmei ve örtüşme
Sistem Modellerinin Zaman Cevabı ve Performans Kriterleri
 Korol Siemleri Taarımı Siem Modellerii Zama Cevabı ve Performa Krierleri Prof.Dr. Galip Caever Korol Siemleri Taarımı Prof.Dr.Galip Caever Kapalı dögü iemi oluşurulmaıda öce iem modelide geçici rejim cevabıı
Korol Siemleri Taarımı Siem Modellerii Zama Cevabı ve Performa Krierleri Prof.Dr. Galip Caever Korol Siemleri Taarımı Prof.Dr.Galip Caever Kapalı dögü iemi oluşurulmaıda öce iem modelide geçici rejim cevabıı
Temel Yasa. Kartezyen koordinatlar (düz duvar) Silindirik koordinatlar (silindirik duvar) Küresel koordinatlar
 Temel Yaa Fourier ıı iletim yaaı İLETİMLE ISI TRANSFERİ Ek bağıntı/açıklamalar k: ıı iletim katayıı A: ıı tranfer yüzey alanı : x yönünde ıcaklık gradyanı Kartezyen koordinatlar (düz duvar Genel ıı iletimi
Temel Yaa Fourier ıı iletim yaaı İLETİMLE ISI TRANSFERİ Ek bağıntı/açıklamalar k: ıı iletim katayıı A: ıı tranfer yüzey alanı : x yönünde ıcaklık gradyanı Kartezyen koordinatlar (düz duvar Genel ıı iletimi
Alçak Geçiren Flitre ve Faz Farkı Kavramı
 EEM 3 - Elektrik - Elektronik Mühendiliğe Giriş Deney ralık 08 lçak Geçiren Flitre ve Faz Farkı Kavramı. İlgili Devre Şemaı ve Teorik Formülayon Şekil. lçak geçiren litre ve girişe uygulanan üoidal. Kirchho
EEM 3 - Elektrik - Elektronik Mühendiliğe Giriş Deney ralık 08 lçak Geçiren Flitre ve Faz Farkı Kavramı. İlgili Devre Şemaı ve Teorik Formülayon Şekil. lçak geçiren litre ve girişe uygulanan üoidal. Kirchho
ELECO '2012 Elektrik - Elektronik ve Bilgisayar Mühendisliği Sempozyumu, 29 Kasım - 01 Aralık 2012, Bursa
 ELECO ' Elektrik - Elektronik ve Bilgiayar Mühendiliği Sempozyumu, 9 Kaım - Aralık, Bura Zaman Gecikmeli Yük Frekan Kontrol Siteminin ekaiu Yöntemi Kullanılarak Kararlılık Analizi Stability Analyi of Time-Delayed
ELECO ' Elektrik - Elektronik ve Bilgiayar Mühendiliği Sempozyumu, 9 Kaım - Aralık, Bura Zaman Gecikmeli Yük Frekan Kontrol Siteminin ekaiu Yöntemi Kullanılarak Kararlılık Analizi Stability Analyi of Time-Delayed
Cebirsel Fonksiyonlar
 Cebirsel Fonksiyonlar Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 4 Amaçlar Bu üniteyi çalıştıktan sonra; polinom, rasyonel ve cebirsel fonksiyonları tanıyacak ve bu türden bazı fonksiyonların grafiklerini öğrenmiş
Cebirsel Fonksiyonlar Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 4 Amaçlar Bu üniteyi çalıştıktan sonra; polinom, rasyonel ve cebirsel fonksiyonları tanıyacak ve bu türden bazı fonksiyonların grafiklerini öğrenmiş
Bir Uçağın Yatış Kontrol Sistem Tasarımında Klasik ve Bulanık Denetleyici Etkileri
 Makine Teknolojileri Elektronik Dergii Cilt: 7, No: 1, 010 (31-4) Electronic Journal of Machine Technologie Vol: 7, No: 1, 010 (31-4) TENOLOJĐ ARAŞTIRMALAR www.teknolojikaratirmalar.com e-issn:1304-4141
Makine Teknolojileri Elektronik Dergii Cilt: 7, No: 1, 010 (31-4) Electronic Journal of Machine Technologie Vol: 7, No: 1, 010 (31-4) TENOLOJĐ ARAŞTIRMALAR www.teknolojikaratirmalar.com e-issn:1304-4141
ELEKTRĐK MOTORLARI SÜRÜCÜLERĐ EELP212 DERS 04
 EELP1 DERS 04 Özer ŞENYURT Nian 10 1 ELEKTRĐK MOTORLARI Özer ŞENYURT Nian 10 ELEKTRĐK MOTORLARI Özer ŞENYURT Nian 10 3 ASENKRON MOTORLAR Endütride en azla kullanılan motorlardır. Doğru akım motorlarına
EELP1 DERS 04 Özer ŞENYURT Nian 10 1 ELEKTRĐK MOTORLARI Özer ŞENYURT Nian 10 ELEKTRĐK MOTORLARI Özer ŞENYURT Nian 10 3 ASENKRON MOTORLAR Endütride en azla kullanılan motorlardır. Doğru akım motorlarına
1.Seviye ITAP 09 Aralık_2011 Sınavı Dinamik III
 .Seviye ITAP 9 Aralık_ Sınavı Dinamik III.Kütlei m=.kg olan bir taş, yükekliği h=5m olan bir kaleden yatay yönde v =5m/ hızı ile atılıyor. Cimin kinetik ve potaniyel enerjiini zamanın fonkiyonu olarak
.Seviye ITAP 9 Aralık_ Sınavı Dinamik III.Kütlei m=.kg olan bir taş, yükekliği h=5m olan bir kaleden yatay yönde v =5m/ hızı ile atılıyor. Cimin kinetik ve potaniyel enerjiini zamanın fonkiyonu olarak
Bölüm 9 KÖK-YER EĞRİLERİ YÖNTEMİ
 Bölüm 9 KÖK-YER EĞRİLERİ YÖNTEMİ Kapalı-döngü denetim sisteminin geçici-durum davranışının temel özellikleri kapalı-döngü kutuplarından belirlenir. Dolayısıyla problemlerin çözümlenmesinde, kapalı-döngü
Bölüm 9 KÖK-YER EĞRİLERİ YÖNTEMİ Kapalı-döngü denetim sisteminin geçici-durum davranışının temel özellikleri kapalı-döngü kutuplarından belirlenir. Dolayısıyla problemlerin çözümlenmesinde, kapalı-döngü
GÜVENİLİR OLMAYAN SİSTEMLER İÇİN ARALIK ÇİZELGELEMESİ PROBLEMİ
 İtanbul Ticaret Üniveritei Fen Bilimleri Dergii Yıl: 6 Sayı:12 Güz 2007/2. 67-79 GÜVENİLİR OLMAYAN SİSTEMLER İÇİN ARALIK ÇİZELGELEMESİ PROBLEMİ Deniz TÜRSEL ELİİYİ, Selma GÜRLER ÖZET Bu çalışmada, her
İtanbul Ticaret Üniveritei Fen Bilimleri Dergii Yıl: 6 Sayı:12 Güz 2007/2. 67-79 GÜVENİLİR OLMAYAN SİSTEMLER İÇİN ARALIK ÇİZELGELEMESİ PROBLEMİ Deniz TÜRSEL ELİİYİ, Selma GÜRLER ÖZET Bu çalışmada, her
Süleyman ŞENYURT **, Zeynep ÖZGÜNER
 Ordu Üniv. il. ek. Derg.,ilt:,Sayı:,1,58-81/Ordu Univ. J. Sci. ech.,vol:,o:,1,58-81 ERRAD EĞRİ ÇİFİİ KÜRESEL GÖSERGELERİİ GEODEZİK EĞRİLİKLERİ VE Aİİ LİFLERİ ÖZE Süleyman ŞEYUR, Zeynep ÖZGÜER Ordu Üniveritei,
Ordu Üniv. il. ek. Derg.,ilt:,Sayı:,1,58-81/Ordu Univ. J. Sci. ech.,vol:,o:,1,58-81 ERRAD EĞRİ ÇİFİİ KÜRESEL GÖSERGELERİİ GEODEZİK EĞRİLİKLERİ VE Aİİ LİFLERİ ÖZE Süleyman ŞEYUR, Zeynep ÖZGÜER Ordu Üniveritei,
25. KARARLILIK KAPALI ÇEVRİM SİSTEMLERİNİN KARARLILIK İNCELENMESİ
 25. KARARLILIK KAPALI ÇEVRİM SİSTEMLERİNİN KARARLILIK İNCELENMESİ a-) Routh Hurwitz Kararlılık Ölçütü b-) Kök Yer Eğrileri Yöntemi c-) Nyquist Yöntemi d-) Bode Yöntemi 1 2 3 4 a) Routh Hurwitz Kararlılık
25. KARARLILIK KAPALI ÇEVRİM SİSTEMLERİNİN KARARLILIK İNCELENMESİ a-) Routh Hurwitz Kararlılık Ölçütü b-) Kök Yer Eğrileri Yöntemi c-) Nyquist Yöntemi d-) Bode Yöntemi 1 2 3 4 a) Routh Hurwitz Kararlılık
Sistemin derecesi, sistemin karakteristik denkleminin en sade halinde (çarpansız) paydadaki s nin en yüksek derecesidir.
 43 BÖLÜM 3 ZAMAN CEVABI Sitemi derecei, itemi karakteritik deklemii e ade halide (çarpaız) paydadaki i e yükek dereceidir. Bir Trafer Fokiyouu Kutupları Trafer fokiyou G() N()/N() şeklide ifade edilire,
43 BÖLÜM 3 ZAMAN CEVABI Sitemi derecei, itemi karakteritik deklemii e ade halide (çarpaız) paydadaki i e yükek dereceidir. Bir Trafer Fokiyouu Kutupları Trafer fokiyou G() N()/N() şeklide ifade edilire,
OTOMATİK KONTROL SİSTEMLERİ İŞARET AKIŞ DİYAGRAMLARI SIGNAL FLOW GRAPH
 OTOMATİK KONTROL SİSTEMLERİ İŞARET AKIŞ DİYAGRAMLARI SIGNAL FLOW GRAPH İŞARET AKIŞ DİYAGRAMLARI İşaret akış diyagramları blok diyagramlara bir alternatiftir. Fonksiyonel bloklar, işaretler, toplama noktaları
OTOMATİK KONTROL SİSTEMLERİ İŞARET AKIŞ DİYAGRAMLARI SIGNAL FLOW GRAPH İŞARET AKIŞ DİYAGRAMLARI İşaret akış diyagramları blok diyagramlara bir alternatiftir. Fonksiyonel bloklar, işaretler, toplama noktaları
4. HAFTA BLM323 SAYISAL ANALİZ. Okt. Yasin ORTAKCI.
 4. HAFTA BLM33 SAYISAL ANALİZ Okt. Yasin ORTAKCI [email protected] Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi BLM33 DOĞRUSAL OLMAYAN (NONLINEAR) DENKLEM SİSTEMLERİ Mühendisliğin
4. HAFTA BLM33 SAYISAL ANALİZ Okt. Yasin ORTAKCI [email protected] Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi BLM33 DOĞRUSAL OLMAYAN (NONLINEAR) DENKLEM SİSTEMLERİ Mühendisliğin
d K d6 m Karışımın özkütlesini bulalım. (1) 6m kütleli sıvının özkütlesini bulalım.
 1.. Karışıın özkütleini bulalı. d K 6 v v v d 9 3v (1) 6 kütleli ıvının özkütleini bulalı. O noktaına göre oent alırak şekildeki T niceliğinin büyüklüğünü bulabiliriz. 7P. = P.1 + T.4 Bu ifade yardııyla
1.. Karışıın özkütleini bulalı. d K 6 v v v d 9 3v (1) 6 kütleli ıvının özkütleini bulalı. O noktaına göre oent alırak şekildeki T niceliğinin büyüklüğünü bulabiliriz. 7P. = P.1 + T.4 Bu ifade yardııyla
Devreler II Ders Notları
 Devreler II Der Noları 3-4 LAPLACE DÖNÜŞÜMÜNÜN DURUM DENKLEMLERİNİN ÇÖZÜMÜNDE KULLANILMAI Doğrual zamanla değişmeyen bir devrenin analizi için oluşan durum denklemi abi kaayılı doğrual diferaniyel denklem
Devreler II Der Noları 3-4 LAPLACE DÖNÜŞÜMÜNÜN DURUM DENKLEMLERİNİN ÇÖZÜMÜNDE KULLANILMAI Doğrual zamanla değişmeyen bir devrenin analizi için oluşan durum denklemi abi kaayılı doğrual diferaniyel denklem
5. MODEL DENEYLERİ İLE GEMİ DİRENCİNİ BELİRLEME YÖNTEMLERİ
 5. MODEL DENEYLEİ İLE GEMİ DİENİNİ BELİLEME YÖNTEMLEİ Gei projeinin değişik erelerinde iteatik odel deneylerine dayalı yaklaşık yöntelerle gei topla direnci e dolayııyla gei ana akine gücü belirlenektedir.
5. MODEL DENEYLEİ İLE GEMİ DİENİNİ BELİLEME YÖNTEMLEİ Gei projeinin değişik erelerinde iteatik odel deneylerine dayalı yaklaşık yöntelerle gei topla direnci e dolayııyla gei ana akine gücü belirlenektedir.
MOSFET BSIM3V3 EŞİK GERİLİMİ VE MOBİLİTE PARAMETRELERİNİN GENETİK ALGORİTMA İLE ÇIKARTILMASI
 MOSFET BSIM3V3 EŞİK GERİLİMİ VE MOBİLİTE PARAMETRELERİNİN GENETİK ALGORİTMA İLE ÇIKARTILMASI M.Emin BAŞAK 1 Ayten KUNTMAN Hakan KUNTMAN 3 1, İtanbul Üniveritei,Mühendilik Fakültei, Elektrik&Elektronik
MOSFET BSIM3V3 EŞİK GERİLİMİ VE MOBİLİTE PARAMETRELERİNİN GENETİK ALGORİTMA İLE ÇIKARTILMASI M.Emin BAŞAK 1 Ayten KUNTMAN Hakan KUNTMAN 3 1, İtanbul Üniveritei,Mühendilik Fakültei, Elektrik&Elektronik
H(s) B(s) V (s) Yer Kök Eğrileri. Şekil13. V s R s = K H s. B s =1için. 1 K H s
 Yer Kök Eğrileri R(s) K H(s) V (s) V s R s = K H s 1 K H s B s =1için B(s) Şekil13 Kapalı çevrim sistemin kutupları 1+KH(s)=0 özyapısal denkleminden elde edilir. b s H s = a s a s K b s =0 a s K b s =0
Yer Kök Eğrileri R(s) K H(s) V (s) V s R s = K H s 1 K H s B s =1için B(s) Şekil13 Kapalı çevrim sistemin kutupları 1+KH(s)=0 özyapısal denkleminden elde edilir. b s H s = a s a s K b s =0 a s K b s =0
2. Bölüm Ses, Ses bileşenleri, İnsan kulağının duyarlılığı, İşitsel-Fizyolojik yeğinlik, Grafik gösterme biçimleri Prof. Dr.
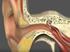 AKUSTİK TEMEL KONULARI SUNUMU 2. Bölüm Ses, Ses bileşenleri, İnsan kulağının duyarlılığı, İşitsel-Fizyolojik yeğinlik, Grafik gösterme biçimleri Prof. Dr. Neşe Yüğrük AKDAĞ BİRDEN FAZLA SES DÜZEYİNİN TOPLAMINI
AKUSTİK TEMEL KONULARI SUNUMU 2. Bölüm Ses, Ses bileşenleri, İnsan kulağının duyarlılığı, İşitsel-Fizyolojik yeğinlik, Grafik gösterme biçimleri Prof. Dr. Neşe Yüğrük AKDAĞ BİRDEN FAZLA SES DÜZEYİNİN TOPLAMINI
BÖLÜM 1 GİRİŞ, TERMODİNAMİK HATIRLATMALAR
 BÖLÜM GİİŞ, EMODİNAMİK HAILAMALA.-ermodinamik hatırlatmalar..- Mükemmel gaz..- İç enerji e antali..3- ermodinamiğin. kanunu..4- Antroi e termodinamiğin. kanunu..5- Antroinin healanmaı..6- İzantroik bağıntılar.-
BÖLÜM GİİŞ, EMODİNAMİK HAILAMALA.-ermodinamik hatırlatmalar..- Mükemmel gaz..- İç enerji e antali..3- ermodinamiğin. kanunu..4- Antroi e termodinamiğin. kanunu..5- Antroinin healanmaı..6- İzantroik bağıntılar.-
ÇĐFT SARKAÇ SĐSTEMĐNĐN KAYAN KĐPLĐ KONTROLÜ
 ÇĐFT SARKAÇ SĐSTEMĐNĐN KAYAN KĐPLĐ KONTROLÜ Yuuf ALTUN Metin DEMĐRTAŞ 2 Elektrik Elektronik Mühendiliği Bölümü Mühendilik Mimarlık Fakültei Balıkeir Üniveritei, 45, Cağış, Balıkeir e-pota: [email protected]
ÇĐFT SARKAÇ SĐSTEMĐNĐN KAYAN KĐPLĐ KONTROLÜ Yuuf ALTUN Metin DEMĐRTAŞ 2 Elektrik Elektronik Mühendiliği Bölümü Mühendilik Mimarlık Fakültei Balıkeir Üniveritei, 45, Cağış, Balıkeir e-pota: [email protected]
FREKANS CEVABI YÖNTEMLERİ FREKANS ALANI CEVABI VEYA SİNUSOİDAL GİRİŞ CEVABI
 FREKANS CEVABI YÖNEMLERİ FREKANS ALANI CEVABI VEYA SİNUSOİDAL GİRİŞ CEVABI G(s (r(t ı Laplace döüşümü; A(s B(s A(s (s p (s p L(s p C(s G(sR(s R(s R s A(s B(s R(s A(s R a C(s L B(s s s j s j s p a b b s
FREKANS CEVABI YÖNEMLERİ FREKANS ALANI CEVABI VEYA SİNUSOİDAL GİRİŞ CEVABI G(s (r(t ı Laplace döüşümü; A(s B(s A(s (s p (s p L(s p C(s G(sR(s R(s R s A(s B(s R(s A(s R a C(s L B(s s s j s j s p a b b s
Bölüm 2: Bir Boyutta Hareket
 Bölüm : Bir Boyua Hareke Kavrama Soruları 1- Harekeli bir cimin yer değişirmei ile aldığı yol aynımıdır? - Hız ile üra araındaki fark nedir? 3- Oralama ve ani hız araındaki fark nedir? 4- Ne zaman oralama
Bölüm : Bir Boyua Hareke Kavrama Soruları 1- Harekeli bir cimin yer değişirmei ile aldığı yol aynımıdır? - Hız ile üra araındaki fark nedir? 3- Oralama ve ani hız araındaki fark nedir? 4- Ne zaman oralama
ÜNİTE MATEMATİK-1 İÇİNDEKİLER HEDEFLER ÜSTEL VE LOGARİTMA FONKSİYONLARI. Prof.Dr.Ahmet KÜÇÜK. Üstel Fonksiyon Logaritma Fonksiyonu
 HEDEFLER İÇİNDEKİLER ÜSTEL VE LOGARİTMA FONKSİYONLARI Üstel Fonksiyon Logaritma Fonksiyonu MATEMATİK-1 Prof.Dr.Ahmet KÜÇÜK Bu ünite çalışıldıktan sonra, Üstel fonksiyonun tanımı öğrenilecek Üstel fonksiyonun
HEDEFLER İÇİNDEKİLER ÜSTEL VE LOGARİTMA FONKSİYONLARI Üstel Fonksiyon Logaritma Fonksiyonu MATEMATİK-1 Prof.Dr.Ahmet KÜÇÜK Bu ünite çalışıldıktan sonra, Üstel fonksiyonun tanımı öğrenilecek Üstel fonksiyonun
DENEY-4. Transistörlü Yükselteçlerin Frekans Analizi
 DENEY-4 Transistörlü Yükselteçlerin Frekans Analizi Deneyin Amacı: BJT yapmak. transistörlerle yapılan yükselteçlerin alçak ve yüksek frekans analizlerini Teorinin Özeti: Şimdiye kadar gördüğümüz transistörlü
DENEY-4 Transistörlü Yükselteçlerin Frekans Analizi Deneyin Amacı: BJT yapmak. transistörlerle yapılan yükselteçlerin alçak ve yüksek frekans analizlerini Teorinin Özeti: Şimdiye kadar gördüğümüz transistörlü
Deney 5 : Ayrık Filtre Tasarımı. Prof. Dr. Aydın Akan Bahattin Karakaya Umut Gündoğdu Yeşim Hekim Tanç
 İ. Ü. Elektrik&Elektronik Müh. Böl. İŞARET İŞLEME ve UYGULAMALARI Deney 5 : Ayrık Filtre Tasarımı Prof. Dr. Aydın Akan Bahattin Karakaya Umut Gündoğdu Yeşim Hekim Tanç Deney 5 : Ayrık Filtre Tasarımı 1.
İ. Ü. Elektrik&Elektronik Müh. Böl. İŞARET İŞLEME ve UYGULAMALARI Deney 5 : Ayrık Filtre Tasarımı Prof. Dr. Aydın Akan Bahattin Karakaya Umut Gündoğdu Yeşim Hekim Tanç Deney 5 : Ayrık Filtre Tasarımı 1.
BİR ISIL SİSTEMİN MODELLENMESİ VE SIEMENS SIMATIC S7 200 PLC İLE KONTROLÜ
 BİR ISIL SİSTEMİN MODELLENMESİ VE SIEMENS SIMATIC S7 200 PLC İLE KONTROLÜ Tanel YÜCELEN 1 Özgür KAYMAKÇI 2 Salman KURTULAN 3. 1,2,3 Elektrik Mühendiliği Bölümü Elektrik-Elektronik Fakültei İtanbul Teknik
BİR ISIL SİSTEMİN MODELLENMESİ VE SIEMENS SIMATIC S7 200 PLC İLE KONTROLÜ Tanel YÜCELEN 1 Özgür KAYMAKÇI 2 Salman KURTULAN 3. 1,2,3 Elektrik Mühendiliği Bölümü Elektrik-Elektronik Fakültei İtanbul Teknik
ÜNİTE. MATEMATİK-1 Yrd.Doç.Dr.Ömer TARAKÇI İÇİNDEKİLER HEDEFLER DOĞRULAR VE PARABOLLER
 HEDEFLER İÇİNDEKİLER DOĞRULAR VE PARABOLLER Birinci Dereceden Polinom Fonksiyonlar ve Doğru Doğru Denklemlerinin Bulunması İkinci Dereceden Polinom Fonksiyonlar ve Parabol MATEMATİK-1 Yrd.Doç.Dr.Ömer TARAKÇI
HEDEFLER İÇİNDEKİLER DOĞRULAR VE PARABOLLER Birinci Dereceden Polinom Fonksiyonlar ve Doğru Doğru Denklemlerinin Bulunması İkinci Dereceden Polinom Fonksiyonlar ve Parabol MATEMATİK-1 Yrd.Doç.Dr.Ömer TARAKÇI
Direnç(330Ω), bobin(1mh), sığa(100nf), fonksiyon generatör, multimetre, breadboard, osiloskop. Teorik Bilgi
 DENEY 8: PASİF FİLTRELER Deneyin Amaçları Pasif filtre devrelerinin çalışma mantığını anlamak. Deney Malzemeleri Direnç(330Ω), bobin(1mh), sığa(100nf), fonksiyon generatör, multimetre, breadboard, osiloskop.
DENEY 8: PASİF FİLTRELER Deneyin Amaçları Pasif filtre devrelerinin çalışma mantığını anlamak. Deney Malzemeleri Direnç(330Ω), bobin(1mh), sığa(100nf), fonksiyon generatör, multimetre, breadboard, osiloskop.
PI KONTROLÖR TASARIMI ÖDEVİ
 PI ONTROLÖR TASARIMI ÖDEVİ ONTROLÖR İLE TASARIM ontrolör Taarım riterleri Taarım riterleri genellile itemine yapmaı geretiğini belirtme ve naıl yaptığını değerlendirme için ullanılır. Bu riterler her bir
PI ONTROLÖR TASARIMI ÖDEVİ ONTROLÖR İLE TASARIM ontrolör Taarım riterleri Taarım riterleri genellile itemine yapmaı geretiğini belirtme ve naıl yaptığını değerlendirme için ullanılır. Bu riterler her bir
Tanım: Kök yer eğrisi sistem parametrelerinin değişimi ile sistemin kapalı döngü köklerinin s düzlemindeki yerini gösteren grafiktir.
 Kök Yer Eğrileri Kök Yer Eğrileri Bir kontrol tasarımcısı sistemin kararlı olup olmadığını ve kararlılık derecesini bilmek, diferansiyel denklem çözmeden bir analiz ile sistem performansını tahmin etmek
Kök Yer Eğrileri Kök Yer Eğrileri Bir kontrol tasarımcısı sistemin kararlı olup olmadığını ve kararlılık derecesini bilmek, diferansiyel denklem çözmeden bir analiz ile sistem performansını tahmin etmek
ELEKTRİK VE ELEKTRİK DEVRELERİ 2
 1 ELEKTİK VE ELEKTİK DEVELEİ ALTENATİF AKIM Enstrümantal Analiz, Doğru Akım Analitik sinyal transduserlerinden çıkan elektrik periyodik bir salınım gösterir. Bu salınımlar akım veya potansiyelin zamana
1 ELEKTİK VE ELEKTİK DEVELEİ ALTENATİF AKIM Enstrümantal Analiz, Doğru Akım Analitik sinyal transduserlerinden çıkan elektrik periyodik bir salınım gösterir. Bu salınımlar akım veya potansiyelin zamana
Otomatik Kontrol I. Laplace Dönüşümü. Vasfi Emre Ömürlü
 Oomaik Konrol I Laplace Dönüşümü Vafi Emre Ömürlü Laplace Dönüşümü: Özellikleri eoremleri Kımî Keirlere Ayırma By Vafi Emre Ömürlü, Ph.D., 7 Laplace ranform I i advanageou o olve By uing, we can conver
Oomaik Konrol I Laplace Dönüşümü Vafi Emre Ömürlü Laplace Dönüşümü: Özellikleri eoremleri Kımî Keirlere Ayırma By Vafi Emre Ömürlü, Ph.D., 7 Laplace ranform I i advanageou o olve By uing, we can conver
Uydu Kentlerin Tasarımı için Bir Karar Destek Sistemi ve Bilişim Sistemi Modeli Önerisi
 Akademik Bilişim 0 - XII. Akademik Bilişim Konferanı Bildirileri 0-2 Şubat 200 Muğla Üniveritei Uydu Kentlerin Taarımı için Bir Karar Detek Sitemi ve Bilişim Sitemi Modeli Önerii TC Beykent Üniveritei
Akademik Bilişim 0 - XII. Akademik Bilişim Konferanı Bildirileri 0-2 Şubat 200 Muğla Üniveritei Uydu Kentlerin Taarımı için Bir Karar Detek Sitemi ve Bilişim Sitemi Modeli Önerii TC Beykent Üniveritei
Programı : Savunma Teknolojileri
 İSTANBUL TEKNİK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ İNSANSIZ HAVA ARAÇLARINDA YEDEKLİ ÇALIŞMA YÜKSEK LİSANS TEZİ Müh. Hüeyin Fatih Lokumcu Programı : Savunma Teknolojileri TEMMUZ 2008 İSTANBUL TEKNİK
İSTANBUL TEKNİK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ İNSANSIZ HAVA ARAÇLARINDA YEDEKLİ ÇALIŞMA YÜKSEK LİSANS TEZİ Müh. Hüeyin Fatih Lokumcu Programı : Savunma Teknolojileri TEMMUZ 2008 İSTANBUL TEKNİK
YAVAŞ DEĞİŞEN ÜNİFORM OLMAYAN AKIM
 YAVAŞ DEĞİŞEN ÜNİFORM OLMAYAN AKIM Yavaş değişen akımların analizinde kullanılacak genel denklem bir kanal kesitindeki toplam enerji yüksekliği: H = V g + h + z x e göre türevi alınırsa: dh d V = dx dx
YAVAŞ DEĞİŞEN ÜNİFORM OLMAYAN AKIM Yavaş değişen akımların analizinde kullanılacak genel denklem bir kanal kesitindeki toplam enerji yüksekliği: H = V g + h + z x e göre türevi alınırsa: dh d V = dx dx
BÖLÜM 7. Sürekli hal hatalarının değerlendirilmesinde kullanılan test dalga şekilleri: Dalga Şekli Giriş Fiziksel karşılığı. Sabit Konum.
 9 BÖLÜM 7 SÜRELİ HAL HATALARI ontrol itmlrinin analizind v dizaynında üç özlliğ odaklanılır, bunlar ; ) İtniln bir gçici hal cvabı ürtmk. ( T, %OS, ζ, ω n, ) ) ararlı olmaı. ıaca kutupların diky knin olunda
9 BÖLÜM 7 SÜRELİ HAL HATALARI ontrol itmlrinin analizind v dizaynında üç özlliğ odaklanılır, bunlar ; ) İtniln bir gçici hal cvabı ürtmk. ( T, %OS, ζ, ω n, ) ) ararlı olmaı. ıaca kutupların diky knin olunda
TOBB Ekonomi ve Teknoloji Üniversitesi Mühendislik Fakültesi Elektrik ve Elektronik Mühendisliği Bölümü ELE 301 Kontrol Sistemleri I.
 TOBB Ekonomi ve Teknoloji Üniversitesi Mühendislik Fakültesi Elektrik ve Elektronik Mühendisliği Bölümü ELE Kontrol Sistemleri I Final Sınavı 9 Ağustos 24 Adı ve Soyadı: Bölüm: No: Sınav süresi 2 dakikadır.
TOBB Ekonomi ve Teknoloji Üniversitesi Mühendislik Fakültesi Elektrik ve Elektronik Mühendisliği Bölümü ELE Kontrol Sistemleri I Final Sınavı 9 Ağustos 24 Adı ve Soyadı: Bölüm: No: Sınav süresi 2 dakikadır.
OTOMATİK KONTROL SİSTEMLERİ BLOK DİYAGRAM İNDİRGEME KURALLARI
 OTOMATİK KONTROL SİSTEMLERİ BLOK DİYAGRAM İNDİRGEME KURALLARI BLOK DİYAGRAM İNDİRGEME KURALLARI Örnek 9: Aşağıdaki açık çevrim blok diyagramının transfer fonksiyonunu bulunuz? 2 BLOK DİYAGRAM İNDİRGEME
OTOMATİK KONTROL SİSTEMLERİ BLOK DİYAGRAM İNDİRGEME KURALLARI BLOK DİYAGRAM İNDİRGEME KURALLARI Örnek 9: Aşağıdaki açık çevrim blok diyagramının transfer fonksiyonunu bulunuz? 2 BLOK DİYAGRAM İNDİRGEME
18.034 İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Sistem Dinamiği. Bölüm 2- Dinamik Cevap ve Laplace Dönüşümü. Doç.Dr. Erhan AKDOĞAN
 Sistem Dinamiği - Dinamik Cevap ve Laplace Dönüşümü Doç. Sunumlarda kullanılan semboller: El notlarına bkz. Yorum Soru MATLAB Bolum No.Alt Başlık No.Denklem Sıra No Denklem numarası Şekil No Şekil numarası
Sistem Dinamiği - Dinamik Cevap ve Laplace Dönüşümü Doç. Sunumlarda kullanılan semboller: El notlarına bkz. Yorum Soru MATLAB Bolum No.Alt Başlık No.Denklem Sıra No Denklem numarası Şekil No Şekil numarası
Dik koordinat sisteminde yatay eksen x ekseni (apsis ekseni), düşey eksen ise y ekseni (ordinat ekseni) dir.
 ANALĐTĐK GEOMETRĐ 1. Analitik Düzlem Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da
ANALĐTĐK GEOMETRĐ 1. Analitik Düzlem Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da
Haberleşme Gecikmeli Hibrid Enerji Üretim Sisteminin Kararlılık Analizi
 EEB 06 Elektrik-Elektronik ve Bilgiayar Sempozyumu, -3 Mayı 06, Tokat TÜRKİYE Haberleşme Gecikmeli Hibrid Enerji Üretim Siteminin Kararlılık Analizi Hakan GÜNDÜZ Şahin SÖNMEZ Saffet AYASUN Niğde Üniveritei,
EEB 06 Elektrik-Elektronik ve Bilgiayar Sempozyumu, -3 Mayı 06, Tokat TÜRKİYE Haberleşme Gecikmeli Hibrid Enerji Üretim Siteminin Kararlılık Analizi Hakan GÜNDÜZ Şahin SÖNMEZ Saffet AYASUN Niğde Üniveritei,
Güven Aralığı Hesaplamaları ÖRNEKLER
 Güven Aralığı Healamaları ÖRNEKLER Standart normal dağılım ile olaılık healamaları Standart normal dağılım ile olaılık healamaları 1 1 2 2 3 3 f ( x) dx P(( 1 ) x ( 1 )) 0.6826 f ( x) dx P(( 2 ) x ( 2
Güven Aralığı Healamaları ÖRNEKLER Standart normal dağılım ile olaılık healamaları Standart normal dağılım ile olaılık healamaları 1 1 2 2 3 3 f ( x) dx P(( 1 ) x ( 1 )) 0.6826 f ( x) dx P(( 2 ) x ( 2
KANATÇIKLI ROTORLARDA TİTREŞİM ANALİZİ. Raşit KIRIŞIK DOKTORA TEZİ MAKİNA MÜHENDİSLİĞİ GAZİ ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ EYLÜL 2010 ANKARA
 KANATÇIKLI ROTORLARDA TİTREŞİM ANALİZİ Raşit KIRIŞIK DOKTORA TEZİ MAKİNA MÜHENDİSLİĞİ GAZİ ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ EYLÜL 010 ANKARA iv KANATÇIKLI ROTORLARDA TİTREŞİM ANALİZİ (Doktora Tezi)
KANATÇIKLI ROTORLARDA TİTREŞİM ANALİZİ Raşit KIRIŞIK DOKTORA TEZİ MAKİNA MÜHENDİSLİĞİ GAZİ ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ EYLÜL 010 ANKARA iv KANATÇIKLI ROTORLARDA TİTREŞİM ANALİZİ (Doktora Tezi)
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Rüzgar Türbininde Kullanılan AC/DC Çeviricilerde Uzay Vektörü Modülasyonu Yöntemi ile Kontrol
 Rüzgar ürbininde Kullanılan AC/DC Çeviricilerde Uzay ektörü Modülayonu Yöntemi ile Kontrol Cenk Cengiz Eyüp Akpınar Dokuz Eylül Üniveritei Elektrik ve Elektronik Mühenliği Bölümü Kaynaklar Yerleşkei, Buca-İzmir
Rüzgar ürbininde Kullanılan AC/DC Çeviricilerde Uzay ektörü Modülayonu Yöntemi ile Kontrol Cenk Cengiz Eyüp Akpınar Dokuz Eylül Üniveritei Elektrik ve Elektronik Mühenliği Bölümü Kaynaklar Yerleşkei, Buca-İzmir
18.034 İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Çevrimsel yüklemeye maruz tabakalı kompozitlerin maksimum yorulma ömrü için optimum tasarımı
 Ululararaı Katılımlı 7. Makina Teorii Sempozyumu, İzmir, -7 Haziran 05 Çevrimel yüklemeye maruz tabakalı kompozitlerin makimum yorulma ömrü için optimum taarımı H. Arda Deveci * H. Seçil Artem İzmir Intitute
Ululararaı Katılımlı 7. Makina Teorii Sempozyumu, İzmir, -7 Haziran 05 Çevrimel yüklemeye maruz tabakalı kompozitlerin makimum yorulma ömrü için optimum taarımı H. Arda Deveci * H. Seçil Artem İzmir Intitute
Yrd. Doç. Dr. A. Burak İNNER
 Yrd. Doç. Dr. A. Burak İNNER Kocaeli Üniversitesi Bilgisayar Mühendisliği Yapay Zeka ve Benzetim Sistemleri Ar-Ge Lab. http://yapbenzet.kocaeli.edu.tr DOĞRUSAL OLMAYAN (NONLINEAR) DENKLEM SİSTEMLERİ Mühendisliğin
Yrd. Doç. Dr. A. Burak İNNER Kocaeli Üniversitesi Bilgisayar Mühendisliği Yapay Zeka ve Benzetim Sistemleri Ar-Ge Lab. http://yapbenzet.kocaeli.edu.tr DOĞRUSAL OLMAYAN (NONLINEAR) DENKLEM SİSTEMLERİ Mühendisliğin
Türev Uygulamaları ÜNİTE. Amaçlar. İçindekiler. Yazar Prof.Dr. Vakıf CAFEROV
 Türev Uygulamaları Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 10 Amaçlar Bu üniteyi çalıştıktan sonra; türev kavramı yardımı ile fonksiyonun monotonluğunu, ekstremum noktalarını, konvekslik ve konkavlığını, büküm
Türev Uygulamaları Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 10 Amaçlar Bu üniteyi çalıştıktan sonra; türev kavramı yardımı ile fonksiyonun monotonluğunu, ekstremum noktalarını, konvekslik ve konkavlığını, büküm
Ders #2. Otomatik Kontrol. Laplas Dönüşümü. Prof.Dr.Galip Cansever
 Ders #2 Otomatik Kontrol Laplas Dönüşümü Prof.Dr.Galip Cansever Pierre-Simon Laplace, 1749-1827 Matematiçi ve Astronomdur. http://www-history.mcs.st-andrews.ac.uk/biographies/laplace.html LAPLAS DÖNÜŞÜMÜ
Ders #2 Otomatik Kontrol Laplas Dönüşümü Prof.Dr.Galip Cansever Pierre-Simon Laplace, 1749-1827 Matematiçi ve Astronomdur. http://www-history.mcs.st-andrews.ac.uk/biographies/laplace.html LAPLAS DÖNÜŞÜMÜ
ZEMİN EPS (GEOFOAM) TEMAS YÜZEYİNİN SONLU ELEMANLARLA MODELLENMESİ
 ZEMİN EPS (GEOFOAM) TEMAS YÜZEYİNİN SONLU ELEMANLARLA MODELLENMESİ Ahmet ŞENOL 1 Mutafa Aytekin 2 1 Yrd.Doç.Dr., Cumhuriyet Üniveritei Mühendilik Fakültei İnşaat Müh. Böl., 58140 Siva Tel: 0346 2191010-2224
ZEMİN EPS (GEOFOAM) TEMAS YÜZEYİNİN SONLU ELEMANLARLA MODELLENMESİ Ahmet ŞENOL 1 Mutafa Aytekin 2 1 Yrd.Doç.Dr., Cumhuriyet Üniveritei Mühendilik Fakültei İnşaat Müh. Böl., 58140 Siva Tel: 0346 2191010-2224
HİDROLİK SİSTEMLERDE ENERJİ KAYIPLARI VE YÜK DUYARLI SİSTEMLERE GEÇİŞ
 17 HİDROLİK SİSTEMLERDE ENERJİ KAYILARI VE YÜK DUYARLI SİSTEMLERE GEÇİŞ İmail OBUT ÖZET Hidrolik itemlerde ea olu itenen; yükü hareket ettirmek için kullanılan gücün, hidrolik omayı tahrik eden elektrik
17 HİDROLİK SİSTEMLERDE ENERJİ KAYILARI VE YÜK DUYARLI SİSTEMLERE GEÇİŞ İmail OBUT ÖZET Hidrolik itemlerde ea olu itenen; yükü hareket ettirmek için kullanılan gücün, hidrolik omayı tahrik eden elektrik
ANALOG FİLTRELEME DENEYİ
 ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ ANALOG FİLTRELEME DENEYİ Ölçme ve telekomünikasyon tekniğinde sık sık belirli frekans bağımlılıkları olan devreler gereklidir. Genellikle belirli bir frekans bandının
ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ ANALOG FİLTRELEME DENEYİ Ölçme ve telekomünikasyon tekniğinde sık sık belirli frekans bağımlılıkları olan devreler gereklidir. Genellikle belirli bir frekans bandının
LPG DEPOLAMA TANKLARININ GAZ VERME KAPASİTELERİNİN İNCELENMESİ
 825 LPG DEPOLAMA TAKLARII GAZ VERME KAPASİTELERİİ İCELEMESİ Fehmi AKGÜ 1. ÖZET Sunulan çalışmada, LPG depolama tanklarının gaz verme kapaitelerinin belirlenmei amacına yönelik zamana bağlı ve ürekli rejim
825 LPG DEPOLAMA TAKLARII GAZ VERME KAPASİTELERİİ İCELEMESİ Fehmi AKGÜ 1. ÖZET Sunulan çalışmada, LPG depolama tanklarının gaz verme kapaitelerinin belirlenmei amacına yönelik zamana bağlı ve ürekli rejim
YAĞLAMA VE KAYMALI YATAKLAR
 YAĞLAMA TĐPLERĐ YAĞLAMA VE KAYMALI YATAKLAR Yağlamanın beş farklı şekli tanımlanabilir. 1) Hidrodinamik ) Hidrotatik 3) Elatohidrodinamik 4) Sınır 5) Katı-film VĐSKOZĐTE τ F du = = A µ dy du U = dy h τ
YAĞLAMA TĐPLERĐ YAĞLAMA VE KAYMALI YATAKLAR Yağlamanın beş farklı şekli tanımlanabilir. 1) Hidrodinamik ) Hidrotatik 3) Elatohidrodinamik 4) Sınır 5) Katı-film VĐSKOZĐTE τ F du = = A µ dy du U = dy h τ
ZENER DİYOTLAR. Hedefler
 ZENER DİYOTLAR Hedefler Bu üniteyi çalıştıktan sonra; Zener diyotları tanıyacak ve çalışma prensiplerini kavrayacaksınız. Örnek devreler üzerinde Zener diyotlu regülasyon devrelerini öğreneceksiniz. 2
ZENER DİYOTLAR Hedefler Bu üniteyi çalıştıktan sonra; Zener diyotları tanıyacak ve çalışma prensiplerini kavrayacaksınız. Örnek devreler üzerinde Zener diyotlu regülasyon devrelerini öğreneceksiniz. 2
U.Ü. Mühendislik Mimarlık Fakültesi Elektronik Mühendisliği Bölümü ELN3102 OTOMATİK KONTROL Bahar Dönemi Yıliçi Sınavı Cevap Anahtarı
 U.Ü. Mühendislik Mimarlık Fakültesi Elektronik Mühendisliği Bölümü ELN30 OTOMATİK KONTROL 00 Bahar Dönemi Yıliçi Sınavı Cevap Anahtarı Sınav Süresi 90 dakikadır. Sınava Giren Öğrencinin AdıSoyadı :. Prof.Dr.
U.Ü. Mühendislik Mimarlık Fakültesi Elektronik Mühendisliği Bölümü ELN30 OTOMATİK KONTROL 00 Bahar Dönemi Yıliçi Sınavı Cevap Anahtarı Sınav Süresi 90 dakikadır. Sınava Giren Öğrencinin AdıSoyadı :. Prof.Dr.
KARAYOLU VE DEMİRYOLU PROJELERİNDE ORTOMETRİK YÜKSEKLİK HESABI: EN KÜÇÜK KARELER İLE KOLLOKASYON
 TMMOB Harita ve Kadatro Mühendileri Odaı 13. Türkiye Harita Bilimel ve Teknik Kurultayı 18 Nian 011, Ankara KARAYOLU VE DEMİRYOLU PROJELERİNDE ORTOMETRİK YÜKSEKLİK HESABI: EN KÜÇÜK KARELER İLE KOLLOKASYON
TMMOB Harita ve Kadatro Mühendileri Odaı 13. Türkiye Harita Bilimel ve Teknik Kurultayı 18 Nian 011, Ankara KARAYOLU VE DEMİRYOLU PROJELERİNDE ORTOMETRİK YÜKSEKLİK HESABI: EN KÜÇÜK KARELER İLE KOLLOKASYON
Ders # Otomatik Kontrol. Kök Yer Eğrileri. Prof.Dr.Galip Cansever. Otomatik Kontrol. Prof.Dr.Galip Cansever
 Ders #-3 Kök Yer Eğrileri Bir kontrol tasarımcısı sistemin kararlı olup olmadığını ve kararlılık derecesini bilmek, diferansiyel denklem çözmeden bir analiz ile sistem performasını tahmin etmek ister.
Ders #-3 Kök Yer Eğrileri Bir kontrol tasarımcısı sistemin kararlı olup olmadığını ve kararlılık derecesini bilmek, diferansiyel denklem çözmeden bir analiz ile sistem performasını tahmin etmek ister.
