YILLAR ÖSS-YGS
|
|
|
- Gülbahar Bahadır
- 8 yıl önce
- İzleme sayısı:
Transkript
1 YILLAR ÖSS-YGS / - 2/ 2/ / LYS OBEB OKEK OBEB: iki veya daha fazla sayıyı birlikte bölebilen en büyük tamsayıya bu sayıların OBEB i denir Sayılar asal çarpanlarına ayrılır Ortak asal çarpanların en küçük üslüleri alınıp çarpılır OKEK: iki veya daha fazla sayıya birlikte bölünebilen en küçük pozitif tamsayıya bu sayıların OKEK i denir Sayılar asal çarpanlarına ayrılır Ortak asal çarpanların en büyük üslüleri alınıp çarpılır (a, b) obeb, OBEB( a, b) a ile b nin obebi (EBOB) ( a, b) okek, OKEK( a, b) a ile b nin okeki(ekok) Her iki sayıyı bölen sayıların çarpımı obeb, ortak olan olmayan tüm bölenlerin çarpımı da okek i verir Bu durumda; OBEB : 25 = OKEK : = 260 ÖRNEK( 2 ) 05 ve 47 nin obeb ve okek i kaçtır? NOT: i) a ve b sayıları için ; OBEB(a,b)OKEK(a,b) = ab dir (bu kural sadece iki sayı için geçerlidir) ii) a<b olmak üzere; OBEB(a,b) a<b OKEK(a,b) dir OBEB : 37 = 2 OKEK: 357²=735 iii) A ve B aralarında asal iki sayı olsun OBEB(A,B) = OKEK(A,B) = AB a c OBEB( a d, b c) iv) OBEB, = b d OKEK( b, d) a c OKEK( a, c) OKEK, = b d OBEB( b, d) ÖRNEK( ) 90 ile 40 ın obeb ve okek i kaçtır? wwwglobalderscom ÖRNEK( 3 ) 20,72 ve 68 in obeb ve okek i kaçtır? OBEB: 22 = 4 OKEK: 2³3²57=520
2 ÖRNEK( 4 ) 26,45 ve 85 in obeb ve okek i kaçtır? OBEB = OKEK = 23²537 =9890 ÖRNEK( 6 ) 5,2 ve 2 ile bölündüğünde daima 2 kalanını veren en küçük sayı kaçtır? Sayımız A olsun A 5 A 2 A 2 x y z A = 5x+2 = 2y+2 = 2z+2 ĐKĐ SAYI ĐÇĐN KISA YOL: iki sayı verilsin biri paya diğeri paydaya yazılıp bir kesir oluşturulur -kesir en sade şekle getirilir 36 3 örneğin; 36ve48 sayıları için = bu orantıda içlerin veya dışların çarpımı OKEK i, payların veya paydaların çarpımı da OBEB i verir ÖRNEK( 5 ) a,b,c Z ve B=3a+=7b+5=c+9 koşulunu sağlayan 3 basamaklı en büyük sayı kaçtır? Her taraftan 2 çıkarılırsa A-2 = 5x = 2y = 2z Demek ki A-2 sayısı 5,2 ve 2 in okek inin bir katıdır A-2 =OKEK(5,2,2)kat A-2 = 420kat En küçük dendiği için kat= seçilir A-2 = 420 A=422 bulunur ÇÖZÜM Her iki tarafa 2 eklenirse B+2=3a+3=7b+7=c+ B+2= 3(a+) = 7(b+) = (c+) B+2 sayısı hem 3, hem7 ve hem de in katıdır Yani B+2 sayısı 3,7, nin okek inin bir katıdır Okek(3,7,) = 23 B+2 =23kat Burada kat a değerler vererek istenen bulunur Kat=4 için B+2 = 234 B+2 = 924 B =922 bulunur ÖRNEK( 7 ) 6,2 ve 5 i tam bölen en büyük sayı kaçtır? Bu sayıları bölen en büyük sayı 6,2 ve 5 in obeb i olur o halde OBEB (6,2,5)=3 bulunur wwwglobalderscom 2
3 ÖRNEK( 8 ) Eni 00 m, boyu 250 m olan bir bahçe eşit büyüklükteki kare parsellere ayrılacak En az kaç parsel elde edilir? (C: 0) x x 250m 00m ÖRNEK( 0 ) Obeb ile Okek leri çarpımı 048 olan iki sayıdan biri 262 ise diğeri kaçtır? Kural: obeb(x,y)okek(x,y)=xy 048 = 262y y=4 bulunur ÖRNEK( ) Boyutları 9,2 ve 5 cm olan dikdörtgenler prizması şeklindeki bir kaşar peyniri farelere verilmek üzere küp şeklinde dilimlere ayrılacak En az kaç dilim elde edilir? x sayısı hem 00, hem de 250 yi bölmelidir Yani x sayısı 00 ve 250 nin obeb idir x=obeb(00,250)=50 m Bahçenin Alanı Parsel sayısı = Parselin Alanı = =0 tane parsel bulunur Elde edilecek küplerin kenarları eşit ve bu kenarların 9,2 ve 5 i bölmesi gerekir 2cm ÖRNEK( 9 ) Eni 00 m, boyu 250 m olan bir bahçe en az kaç kare parsele ayrılır? (C: 4) 9cm x 5cm Bu soruyu önceki sorudan ayıran eşit kelimesidir Bu soruda eşit kelimesi olmadığından obeb-okek ile çözemeyiz Mümkün olan en büyük kare parseller elde edecek şekilde parçalamalar yapılır 50m 00m 00m x = obeb(9,2,5)=3 cm Dilim Sayısı = Prizmanın Hacmi Küp Dilim lerin Hacmi = = 60 adet dilim elde edilir m ÖRNEK( 2 ) 60 kg lık leblebi, 90 kg lık ceviz ve 80 kg lık çekirdek birbirine karıştırılmadan eşit hacimli torbalara doldurulacaktır En az kaç torba gereklidir? o halde cevap 4 kare parsel olacaktır wwwglobalderscom 3
4 Önce torbaların kaç kg lik olmaları gerektiğini bulalım Bu torba 60,90 ve 80 kg lik çerezleri artmayacak şekilde bölmeli Bu da 60,90 ve 80 i bölen bir ağırlık olmalı Bu ağırlığa x dersek X = obeb(60,90,80) = 30 kg Şimdi her çerez torbasından kaç yeni torba çıkar ona bakalım = 2, = 3, = toplam = = torba bulunur ÖRNEK( 3 ) Boyutları 3,6 ve 5 cm olan kutulardan en az kaç tanesiyle bir küp yapılabilir? çözmek demektir Bu yüzden size hangi işlemi yapacağınız hususunda yardımcı olacak bir pratik verelim VERĐLEN ĐSTENEN ĐŞLEM Büyük Küçük OBEB Küçük Büyük OKEK ÖRNEK( 4 ) Boyutları 42 ve 54 m olan dikdörtgen bir bahçe, etrafına eşit aralıklı ve köşelere birer ağaç gelecek şekilde ağaçlandırılacaktır En az kaç ağaç gereklidir? (Büyük verilmiş küçük isteniyor O halde obeb bulacağız) Obeb(42,54) = 6 m bulunan bu değer iki ağaç arası mesafedir Önceki sorulardan farklı olarak bu sefer bütüne ulaşmaya çalışacağız 6cm Bahçenin çevresi = 2(42+ 54) = 92 m Dikilecek ağaç sayısı 92 6 =32 bulunur ÖRNEK( 5 ) Boyutları 42 ve 54 m olan dikdörtgen bir bahçe, etrafına ve içine eşit aralıklı ve köşelere birer ağaç gelecek şekilde ağaçlandırılacaktır En az kaç ağaç gereklidir? 3 cm 5cm X Küpün bir kenarı bu kutuların ebatlarına bölünmesi gerektiğinden bize okek gerekecek Küpün bir kenarına x dersek x = okek(3,6,5) = 30 cm Küpün Hacmi Kutu Sayısı = Kutunun Hacmi = = 00 adet kutu gereklidir NOT: bir soruda obeb mi, okek mi kullanacağımızı anlamak sorunun yarısını wwwglobalderscom 4 (Verilen büyük, isten küçük olduğundan obeb gereklidir) Diğer sorudan farklı olarak bahçenin içine de ağaç dikileceğinden, ilk yapılacak iki ağaç arası mesafenin bulunmasıdır Obeb(42,54) = 6 m iki ağaç arası mesafedir Şimdi bahçede kaç satır ağaç ve her satırda kaç ağaç dilecek, onu bulalım
5 Şekli dikkatli incelediğimizde oluşan satır sayısının 8 ve sütun sayısının da 0 olduğunu görürüz O halde dikilecek ağaç sayısı ; 80 = 80 olur (her soruyu böyle çizerek çözmek zordur Gelin buna bir pratik verelim 42:6=7 eder ama bizim 8 satırımız var 54:6 = 9 eder ama bizim 0 sütunumuz var Demek ki Bir Kenar Uzunluğu + bize satır ve Bulunan obeb sütun sayısını verir Bundan sonra bu yöntemi kullanarak çizimde kaybolan zamanı kazanabiliriz) Đfadenin bilinmeyenli olması fikrimizi bozmasın yapılacak bellidir Verilen büyük, istenen küçük, o halde önce obeb bulacağız 2 a + 7a+ 0 =(a+2)(a+5) 3a+6 = 3(a+2) (a+2)(a+5) 3(a+2) a+2 (a+5) 3 a görüldüğü gibi her iki ifadeyi bölen (a+2) dir o halde Obeb = (a+2) dir ÖRNEK( 6 ) A,x,y,z Z + ve A=5x+2=7y+2=3z+2 ise x+y+z en az kaçtır? A=5x+2=7y+2=3z+2 taraftan 2 çıkarırsak ifadesinde her A-2 = 5x = 7y = 3z elde edilir Bu da A-2 sayısının 5,7 ve 3 ün bir katı olduğunu gösterir A-2 = Okek(5,7,3)kat A-2 = 455kat burada kat= seçilirse A-2=455 bulunur ifadeler tek tek eşitlenirse; Dikdörtgenin Alanı karelerin sayısı = Karenin Alanı (a+ 2)(a+ 5)(3(a+ 2) = (a+ 2)(a+ 2) = 3(a+5) tane kare elde edilir Karelerin er birinin alanı da (a+2)(a+2) = (a+2)² bulunur NOT: bilinmeyenli veya üslü olarak verilen ifadelerin obeb-okek leri alınırken sayılar üslü şekilde gösterilmek kaydıyla; Obeb: ortak olanların üss küçük olanlar Okek: ortak olanların üssü büyük olanlar ile ortak olmayanların hepsi alınır A-2=455=5x=7y=3z x=9, y=65, z=35 bulunur x+y+z =9 bulunur ÖRNEK( 8 ) A= 2³3²5 ve B=2²37 ise Obeb(A,B) ve Okek(A,B) nedir Obeb = 2²3 = 2 Okek = 2³3²57 = 2520 bulunur 2 ÖRNEK( 7 ) Eni ( a + 7a+ 0 ) ve boyu (3a+6) birim olan dikdörtgeni eşit ve en büyük alana sahip kaç kareye ayırabiliriz Ve bu karelerin birinin alanı ne olur? ÖRNEK( 9 ) 360 m lik dairesel bir yarış pistinde hızları sırasıyla 40 m/dk, 60 m/dk ve 90 m/dk olan üç araç yarışıyor Aynı yönde beraber hareket etmelerinden kaç dk sonra yine aynı noktadan beraber geçerler? wwwglobalderscom 5
6 Önce her bir aracın bir turu kaç dk da attığını bulalım; I Araç : 360 =9 dk 40 II Araç : = 6 dk III Araç : =4 dk Şimdi berberce aynı anda başlangıç noktasından geçiş sürelerini bulalım Okek(4,6,9)= 36 dk olur ÖRNEK( 22 ) Farklı iki doğal sayının Obeb i 2, Okek i 72 ise bu iki sayının toplamı a) En az kaçtır? b) En çok kaçtır? Obeb sayıların ortak çarpanı olduğundan bunu ayıralım kalanları sayılara bölüştürürüz ÖRNEK( 20 ) Ahmet ile Hasan aynı cins meyveden farklı kilolarda satın almışlar ve biri bin diğeri bin lira ödemiştir Buna göre bu meyvenin kilogramı en fazla kaç bin lira olabilir? Meyvenin kilosuna x dersek, x in 8750 ve 4000 i bölmesi gerekir Yani ortak bölen olacak Obeb(8750,4000)=750 bulunur ÖRNEK( 2 ) A ve B gibi iki sayı için Obeb=Okek ise bu iki sayının çarpımı kaç olabilir? sayılarımıza a ve b dersek a = 2x ve b = 2y olsun a) x=3 ve y =2 olursa a =23=36 ve b = 22=24 a + b = =60 b) x= ve y =32 olursa a =2=2 ve b = 26=72 a + b = = 84 ÖRNEK( 23 ) Bir markette eşit büyüklükte 320 den fazla kavanoz vardır Bu kavanozlar raflara 6,7,8 er dizildiğinde son dizilen rafta sırasıyla 3,,7 kavanozluk yer eksik kalıyor buna göre bu markette en az kaç kavanoz vardır? A) 5 B) 27 C) 32 D) 64 E) 20 Marketteki kavanoz sayısı A olsun A= 6x-3 = 7y- = 8z-7 Her tarafa 5 eklersek Kural: obebokek=ab Kurala göre gidersek sol taraf bir tamkare oluyor o halde AB bir sayının karesidir Yani cevap D şıkkı olur A+5 = 6x-3+5=7y-+5=8z-7+5 A+5 = 6x+2 = 7y+4 = 8z+8 A+5 = 6(x+2) = 7(y+2) = 8(z+) A+5 sayısı 6,7 ve 8 in bir katıdır wwwglobalderscom 6
7 A+5 = Okek(6,7,8)kat A+5 = 68kat A=68kat-5 > 320 şartını sağlaması için kat a 2 veririz A= > 320 A = > 320 A = 32 >320 O halde markette en az 32 kavanoz vardır ÖRNEK( 24 ) Üç vapur farklı hatlarda seyrediyorlar vapurlar sırasıyla 3/2 sa, ¼ sa, ve 4/5 sa aralıklarla limandan sefer düzenliyorlar Saat 3:00 da beraber limandan ayrılan bu vapurlar saat kaçta yine aynı limandan ayrılırlar? a=23=26 b=35=5 a+b = 4 olduğu görülür O halde a-b = 26-5 = bulunur ÖRNEK( 26 ) a ve b ardışık çift doğal sayılar ve Obeb(a,b) + Okek(a,b)=46 ise (a+2) ve (b+2) nin Okek i kaçtır? Ardışık çift sayılar x ve y ardışık sayı olmak üzere 2x ve 2y şeklindedir Bu yüzden sayılar ; a= 2x ve b=2y olmak üzere Önce aynı anda geçtikleri süreyi bulalım Okek( 3,, )= (3,, 4) okek = 2 (2, 4,5) obeb =2sa Saat 3:00 da ilk geçişlerinden 2 saat sonra tekrar aynı yerden geçerler O halde 3:00+2:00=25:00 bir gün 24 saat olduğundan 25-24= yani gece saat 0:00 da yine aynı limandan geçerler ÖRNEK( 25 ) Aralarında asal a ve b sayılarının Okek i 390 ve a+b=4 ise a b=? (a>b) 2x 2y 2 x y x y y Obeb(a,b) =2 ve Okek(a,b)=2xy 2+2xy =46 2xy = 44 xy = 72 x=8 ve y=9 dur a=28=6 ve b=29=8 dir a+2 = 8 ve b+2=20 dir Okek(8,20)=80 bulunur Đki sayı aralarında asal ise okek leri sayıların çarpımıdır(kural) O halde ab=390 Önce 390 çarpanlarına ayrılır = 2353 bu çarpanlardan toplamları 4 eden iki grup oluşturalım wwwglobalderscom 7 ÖRNEK( 27 ) 3762 sayısına en az kaç eklemeliyiz ki, oluşan sayı3,5,7 ve 9 ile tam bölünsün Sayıya x ekleyelim 3762+x = 3a=5b=7c=9c olur Demek ki 3762 sayısı 3,5,7 ve 9 un bir katıdır 3762+x=Okek(3,5,7,9)kat 3762+x= 35kat
8 kat=2 seçilirse 3762+x= x=3780 x= c=8 bulunur ÖRNEK( 28 ) a,b,c Z + olmak üzere; X=2a+=3b+2=5c+4 ise kaç tane iki basamaklı X sayısı yazılabilir? Her tarafa eklenirse X+=2a+2=3b+3=5c+5 X+=2(a+)=3(b+)=5(c+) Bu durumda X+ sayısı 2,3 ve 5 in bir katı olur X+=Okek(2,3,5)kat X+=30kat X=30kat- Kat= için X=29 Kat=2 için X=59 Kat=3 için X=89 Yani 3 tane X iki basamaklı sayı elde edilir ÖRNEK( 29 ) Farklı iki doğal sayının Okek i 80 ise bu iki sayının toplamı en fazla kaç olur? (C: 270) Sayılar farklı denmese ikisi de 80 alınabilirdi Ancak farklı dediği için birini ;çarpanlardan birtanesini ayırmak sureti ile değiştiririz Ayrılacak sayı çarpanların en küçüğü olmalı ki kalan sayı fazla küçülmesin 80 = 2²3²5 2 en küçükleridir O halde bir sayıyı 80, diğerini de 23²5=90 seçeriz = 270 bulunur ÖRNEK( 30 ) Farklı iki doğal sayının Okek i 20 ise bu iki sayının toplamı en az kaç olur? Toplamları en az olsun isteniyorsa Okek i aralarında asal ve birbirine yakın iki sayı şeklinde parçalarız = görüldüğü gibi aynı olan sayılar birleştirilerek aralarında asal gruplar oluşturuluyor sayı = 8 2 sayı =35=5 sayıların toplamı 8+5 = 23 bulunur ÖRNEK( 3 ) Üçgen şeklindeki bir bahçenin etrafına eşit aralıklarla ağaç dikilecek Boyutları 8,2 ve 6 br olan üçgenin köşelerine birer ağaç dikildiğine göre daha kaç ağaca ihtiyaç vardır? Önce ağaçlar arası eşit mesafe bulunur Obeb(8,2,6)= 4 Üçgenin çevresi =8+2+6=36 Ağaç sayısı 36:4=9 3 tane daha önce dikilmiş 9-3=6 ağaca ihtiyaç vardır ÖRNEK( 32 ) (5,a,75)obeb =5 ve (5,a,75)okek=050 ise a en küçük kaçtır? Okek i oluşturan sayılardan belli olan ikisindeki çarpanlar dikkate alınarak a ya mümkün olan en az çarpan verilir Obeb=5 olduğundan a da 5 olmalıdır wwwglobalderscom 8
9 3 ve 5² zaten 5 ve 75 ten elde ediliyor Geriye bunlardan elde edilemeyen 2 ve 7 kalıyor onları da a ya verirsek A=527=70 bulunur ÖRNEK( 33 ) Mehmet bilyelerini 5 er, 6 şar ve 7 şer sayınca hep bir bilyesi artıyor Buna göre Mehmet in en az kaç bilyesi var? (ÖSS-88) Mehmet in bilye sayısı X olsun X =5a+=6b+=7c+ Her taraftan eksiltirsek X- =5a=6b=7c bu durumda (X-) sayısı 5,6 ve 7 nin bir katı olur ÖRNEK( 35 ) Bir sepetteki güller 5 er demetlenince 2 gül, 7 şer demetlenince 3 gül artmaktadır Buna göre sepette en az kaç gül vardır? (ÖYS-9) A) 7 B) 24 C) 27 D) 37 E) 38 ÇÖZÜM : Gül sayısı X olsun X=5a+2=7b+3 Her tarafa 8 eklersek X+8=5a+2+8=7b+3+8 X+8=5a+20=7b+2 X+8=5(a+4)=7(b+3) X-=Okek(5,6,7)kat X- = 20kat Kat= seçersek X-=20 X=2 bulunur ÖRNEK( 34 ) 7 ve 5 ile bölündüğünde her iki bölümde 2 kalanını veren en küçük pozitif sayının rakamları toplamı kaçtır? (ÖSS-9) Sayımız X olsun X+8=Okek(5,7)kat X+8=35kat Kat= için X+8=35 X=7 bulunur ÇÖZÜM2: Bu soruyu daha pratik olarak şöyle çözebiliriz Şıklardan 5 e bölününce 2, 7 ye bölününce 3 kalanını veren en küçük sayı sorumuzun cevabıdır O halde A şıkkı sorumuzun cevabıdır 7 =53+2 ve 7=72+2 X= 5a+2=7b+2 Her taraftan 2 çıkarırsak X-2=5a=7b Yani (X-2) sayısı 5 ve 7 nin bir katıdır X-2=Okek(5,7)kat X-2=35kat Kat= seçilirse X-2=35 X=37 bulunur buradan 3+7=0 dur wwwglobalderscom 9 ÖRNEK( 36 ) Okek i 30 olan farklı iki sayının toplamı en fazla kaçtır? (ÖSS-96) A) 53 B) 45 C) 83 D) 3 E) 7 Sayılardan birini 30, diğerini 5 seçersek 30+5=45 bulunur cevap B şıkkı (Benzer soruyu daha önce çözmüştük 30=235 olduğundan toplam büyük olsun diye ikinci sayı için çarpanlardan en küçüğü ayrılır, kalan 35=5 ikinci sayı kabul edilir)
10 ÖRNEK( 37 ) Bir kutudaki kalemlerin sayısının en az 87, en çok 30 olduğu bilinmektedir Kutudaki kalemler 3 er, 6 şar ve7 şer sayıldığında her seferinde2 kalem artmaktadır Buna göre kutuda kaç kalem vardır? (ÖSS-96) A) 08 B) 4 C) 7 D) 20 E) 28 Kutudaki kalem sayısı X olsun X= 3a+2=6b+2=7c+2 Her taraftan 2 çıkarırsak X-2=3a=6b=7c Yani (X-2) sayısı 3,6 ve 7 nin bir katıdır X-2=Okek(3,6,7)kat X-2=42kat X=42kat+2 87<42kat+2<30 olacağından en uygun kat değeri 3 tür 423+2=28 eder Cevap E şıkkı ÖRNEK( 39 ) 6,7 ve 8 ile kalansız bölünebilen 4000 den küçük sayıların en büyüğünün onlar basamağındaki rakam kaçtır? (C: 6) (ÖSS 2003) Sayı X olsun X= 6a=7b=8c X=Okek(6,7,8)kat X= 68kat <4000 olacak şekilde bir kat seçelim Kat= 23 seçilirse 6823=3864<4000 şartı sağlar O halde 3864 ün onlar basamağı 6 dır ÖRNEK( 38 ) Toplamları 26 olan a ve b pozitif tamsayılarının en küçük ortak katı 05 tir Buna göre a b =? (ÖSS-2000) YAZAN ĐBRAHĐM HALĐL BABAOĞLU Matematik Öğretmeni wwwglobalderscom a=37=2 ve b=5 seçilirse a+b=2+5=26 olduğundan a-b=2-5=6 bulunur wwwglobalderscom 0
EBOB - EKOK EBOB VE EKOK UN BULUNMASI. 2. Yol: En Büyük Ortak Bölen (Ebob) En Küçük Ortak Kat (Ekok) www.unkapani.com.tr. 1. Yol:
 EBOB - EKOK En Büyük Ortak Bölen (Ebob) İki veya daha fazla pozitif tamsayıyı aynı anda bölen pozitif tamsayıların en büyüğüne bu sayıların en büyük ortak böleni denir ve kısaca Ebob ile gösterilir. Örneğin,
EBOB - EKOK En Büyük Ortak Bölen (Ebob) İki veya daha fazla pozitif tamsayıyı aynı anda bölen pozitif tamsayıların en büyüğüne bu sayıların en büyük ortak böleni denir ve kısaca Ebob ile gösterilir. Örneğin,
Asal Çarpanlara Ayırma / EBOB-EKOK ORTAK DERSLER MATEMATİK. Prof. Dr. Emin KASAP
 3 Asal Çarpanlara Ayırma / EBOB-EKOK ORTAK DERSLER MATEMATİK Prof Dr Emin KASAP 1 Ünite: 5 ASAL ÇARPANLARA AYIRMA / EBOB - EKOK Prof Dr Emin KASAP İçindekiler 51 ASAL ÇARPANLARA AYIRMa 3 511 Asal Sayılar
3 Asal Çarpanlara Ayırma / EBOB-EKOK ORTAK DERSLER MATEMATİK Prof Dr Emin KASAP 1 Ünite: 5 ASAL ÇARPANLARA AYIRMA / EBOB - EKOK Prof Dr Emin KASAP İçindekiler 51 ASAL ÇARPANLARA AYIRMa 3 511 Asal Sayılar
SAYILARIN ASAL ÇARPANLARINA AYRILMASI
 ASAL SAYILAR Asal sayılar, 1 ve kendisinden başka pozitif tam böleni olmayan 1' den büyük tamsayılardır. En küçük asal sayı, 2' dir. 2 asal sayısı dışında çift asal sayı yoktur. Yani, 2 sayısı dışındaki
ASAL SAYILAR Asal sayılar, 1 ve kendisinden başka pozitif tam böleni olmayan 1' den büyük tamsayılardır. En küçük asal sayı, 2' dir. 2 asal sayısı dışında çift asal sayı yoktur. Yani, 2 sayısı dışındaki
8.Sınıf MATEMATİK. Çarpanlar ve Katlar Konu Testi. Test sayısının tek bölenlerinin sayısı aşağıdakilerden
 Çarpanlar ve Katlar Konu Testi MATEMATİK 8.Sınıf Test-01 1. I. 1, her sayının bölenidir. II. 2, asal bir çarpandır. III. Her sayı kendisinin bir çarpanıdır. IV. Bir sayının çarpanları, aynı zamanda o sayının
Çarpanlar ve Katlar Konu Testi MATEMATİK 8.Sınıf Test-01 1. I. 1, her sayının bölenidir. II. 2, asal bir çarpandır. III. Her sayı kendisinin bir çarpanıdır. IV. Bir sayının çarpanları, aynı zamanda o sayının
MATEMATİK ASAL ÇARPANLARA AYIRMA. ÖRNEK 120 sayısını asal çarpanlarına ayırınız. ÖRNEK 150 sayısının asal çarpanları toplamını bulunuz.
 MATEMATİK ASAL ÇARPANLARA AYIRMA A S A L Ç A R P A N L A R A A Y I R M A T a n ı m : Bir tam sayıyı, asal sayıların çarpımı olarak yazmaya, asal çarpanlarına ayırma denir. 0 sayısını asal çarpanlarına
MATEMATİK ASAL ÇARPANLARA AYIRMA A S A L Ç A R P A N L A R A A Y I R M A T a n ı m : Bir tam sayıyı, asal sayıların çarpımı olarak yazmaya, asal çarpanlarına ayırma denir. 0 sayısını asal çarpanlarına
ÇARPANLAR ve KATLAR ASAL SAYILAR. Örnek-2 : 17 ve 27 sayılarının asal sayı olup olmadığını inceleyelim.
 SINIF ÇARPANLAR ve KATLAR www.tayfunolcum.com 8.1.1.1: Verilen pozitif tam sayıların çarpanlarını bulur; pozitif tam sayıları üslü ifade ya da üslü ifadelerin çarpımı seklinde yazar. Çarpan ( bölen ) Her
SINIF ÇARPANLAR ve KATLAR www.tayfunolcum.com 8.1.1.1: Verilen pozitif tam sayıların çarpanlarını bulur; pozitif tam sayıları üslü ifade ya da üslü ifadelerin çarpımı seklinde yazar. Çarpan ( bölen ) Her
Ortak Bölenlerin En Büyüğü & Ortak Katların En Küçüğü
 Sayfa : 1 60 ve 72 nin OBEB VE toplamları kaçtır? A) 30 B) 360 C) 372 D) 420 E) 448 24, 36, 60 sayılarının i OBEB inin kaç katıdır? A) 12 B) 20 C) 30 D) 45 E) 54 Cevaplar: C C Sayfa : 2 54 ve 78 sayılarını
Sayfa : 1 60 ve 72 nin OBEB VE toplamları kaçtır? A) 30 B) 360 C) 372 D) 420 E) 448 24, 36, 60 sayılarının i OBEB inin kaç katıdır? A) 12 B) 20 C) 30 D) 45 E) 54 Cevaplar: C C Sayfa : 2 54 ve 78 sayılarını
OBEB OKEK ÇÖZÜMLÜ SORULAR
 OBEB OKEK ÇÖZÜMLÜ SORULAR 1) 4, 36 ve 48 sayılarının ortak bölenlerinin en büyüğü kaçtır? A) 1 B)16 C) 18 D) 4 E) 7 1) Sayılarınhepsini aynı anda asal çarpanlarına ayıralım; 4 36 48 1 18 4 6 9 1 3 9 6
OBEB OKEK ÇÖZÜMLÜ SORULAR 1) 4, 36 ve 48 sayılarının ortak bölenlerinin en büyüğü kaçtır? A) 1 B)16 C) 18 D) 4 E) 7 1) Sayılarınhepsini aynı anda asal çarpanlarına ayıralım; 4 36 48 1 18 4 6 9 1 3 9 6
MATEMATİK DERSİ UZAKTAN EĞİTİM DERS NOTLARI 3. HAFTA
 MATEMATİK DERSİ UZAKTAN EĞİTİM DERS NOTLARI 3. HAFTA 3. Ondalık Sayılarda İşlemler: Toplama - Çıkarma: Ondalık kesirler toplanırken, virgüller alt alta gelecek şekilde yazılır ve doğal sayılarda toplama-çıkarma
MATEMATİK DERSİ UZAKTAN EĞİTİM DERS NOTLARI 3. HAFTA 3. Ondalık Sayılarda İşlemler: Toplama - Çıkarma: Ondalık kesirler toplanırken, virgüller alt alta gelecek şekilde yazılır ve doğal sayılarda toplama-çıkarma
Ortak Bölenlerin En Büyüğü & Ortak Katların En Küçüğü
 Sayfa : 1 60 ve 72 nin OBEB VE toplamları kaçtır? A) 30 B) 360 C) 372 D) 420 E) 448 24, 36, 60 sayılarının i OBEB inin kaç katıdır? A) 12 B) 20 C) 30 D) 45 E) 54 Cevaplar: C C Sayfa : 2 54 ve 78 sayılarını
Sayfa : 1 60 ve 72 nin OBEB VE toplamları kaçtır? A) 30 B) 360 C) 372 D) 420 E) 448 24, 36, 60 sayılarının i OBEB inin kaç katıdır? A) 12 B) 20 C) 30 D) 45 E) 54 Cevaplar: C C Sayfa : 2 54 ve 78 sayılarını
Asal Çarpan, OBEB - OKEK
 Isınma Hareketleri 1 Uygun eşleştirmeleri yapınız. I. 15 in doğal sayı çarpanları II. 1 nin tam sayı bölenleri a) 1,, 3, 4, 6, 1 1,, 3, 4, 6, 1 b) 1, 3, 5, 15 III. 140 ın asal çarpanlara ayrılışı c) 140
Isınma Hareketleri 1 Uygun eşleştirmeleri yapınız. I. 15 in doğal sayı çarpanları II. 1 nin tam sayı bölenleri a) 1,, 3, 4, 6, 1 1,, 3, 4, 6, 1 b) 1, 3, 5, 15 III. 140 ın asal çarpanlara ayrılışı c) 140
Örnek...1 : Yandaki bölme işlemin de bölüm ile kalanın toplamı kaçtır?
 BÖLME İŞLEMİ VE ÖZELLİKLERİ A, B, C, K doğal sayılar ve B 0 olmak üzere, BÖLÜNEN A B C BÖLEN BÖLÜM Örnek...4 : x sayısının y ile bölümündeki bölüm 2 ve kalan 5 tir. y sayısının z ile bölümündeki bölüm
BÖLME İŞLEMİ VE ÖZELLİKLERİ A, B, C, K doğal sayılar ve B 0 olmak üzere, BÖLÜNEN A B C BÖLEN BÖLÜM Örnek...4 : x sayısının y ile bölümündeki bölüm 2 ve kalan 5 tir. y sayısının z ile bölümündeki bölüm
90 sayısının asal çarpanlarının toplamı kaçtır?
 90 sayısının asal çarpanlarının toplamı kaçtır? 2 a.3 b.5 c =750 olduğuna göre a+b-c kaçtır? 25 ve 41 i böldüğünde 1 kalanını veren en büyük doğal sayı kaçtır? 6 ve 8 e bölünebilen iki basamaklı en büyük
90 sayısının asal çarpanlarının toplamı kaçtır? 2 a.3 b.5 c =750 olduğuna göre a+b-c kaçtır? 25 ve 41 i böldüğünde 1 kalanını veren en büyük doğal sayı kaçtır? 6 ve 8 e bölünebilen iki basamaklı en büyük
Örnek...1 : Yandaki bölme işlemin de bölüm ile kalanın toplamı kaçtır?
 BÖLME İŞLEMİ VE ÖZELLİKLERİ A, B, C, K doğal sayılar ve B 0 olmak üzere, BÖLÜNEN A B C BÖLEN BÖLÜM Örnek...4 : x sayısının y ile bölümündeki bölüm 2 ve kalan 5 tir. y sayısının z ile bölümündeki bölüm
BÖLME İŞLEMİ VE ÖZELLİKLERİ A, B, C, K doğal sayılar ve B 0 olmak üzere, BÖLÜNEN A B C BÖLEN BÖLÜM Örnek...4 : x sayısının y ile bölümündeki bölüm 2 ve kalan 5 tir. y sayısının z ile bölümündeki bölüm
sayısının asal çarpanlarına ayrılmış biçimi aşağıdakilerden. 1. Aşağıdakilerden hangisi 96 sayısının çarpanlarından A) 16 B) 28 C) 32 D) 48
 1. Aşağıdakilerden hangisi 96 sayısının çarpanlarından biri değildir? A) 16 B) 28 C) 32 D) 48 4. 216 sayısının asal çarpanlarına ayrılmış biçimi aşağıdakilerden hangisidir? A) 3 2 2 3 5 B) 2 2 2 3 C) 2
1. Aşağıdakilerden hangisi 96 sayısının çarpanlarından biri değildir? A) 16 B) 28 C) 32 D) 48 4. 216 sayısının asal çarpanlarına ayrılmış biçimi aşağıdakilerden hangisidir? A) 3 2 2 3 5 B) 2 2 2 3 C) 2
egitim ögretim yili matematik AÇIK UÇLU SORULAR
 2017-2018 egitim ögretim yili matematik AÇIK UÇLU SORULAR 8 ADI SOYADI: 1- NO: Altuğ un aklından tuttuğu sayının asal çarpanlarının en küçüğü 5, en büyüğü 11 dir. Buna göre Altuğ un aklından tuttuğu sayının
2017-2018 egitim ögretim yili matematik AÇIK UÇLU SORULAR 8 ADI SOYADI: 1- NO: Altuğ un aklından tuttuğu sayının asal çarpanlarının en küçüğü 5, en büyüğü 11 dir. Buna göre Altuğ un aklından tuttuğu sayının
TEMEL MATEMATİĞE GİRİŞ - Matematik Kültürü - 5
 1 14 ve 1 sayılarına tam bölünebilen üç basamaklı kaç farklı doğal sayı vardır? x = 14.a = 1b x= ekok(14, 1 ).k, (k pozitif tamsayı) x = 4.k x in üç basamaklı değerleri istendiğinden k =, 4, 5, 6, 7,,
1 14 ve 1 sayılarına tam bölünebilen üç basamaklı kaç farklı doğal sayı vardır? x = 14.a = 1b x= ekok(14, 1 ).k, (k pozitif tamsayı) x = 4.k x in üç basamaklı değerleri istendiğinden k =, 4, 5, 6, 7,,
KC00-SS.08YT05. Kolay Temel Matematik. Üniversite Haz rl k 1. 8 ( 3 + 2) 6. 3! 3 ( 3 3)": ( 3) x = 3 ve y = 2 3. ( 5) + ( 7) (+2) + 4
 Üniversite Haz rl k Sözcükte Do al ve Say lar Söz Öbeklerinde ve Tam Say lar Anlam - I - I Kolay Temel Matematik. 8 ( + ) A) 7 B) 8 C) 9 D) 0 E) 6.! ( )": ( ) A) B) 0 C) D) E). 7. + 5 A) 6 B) 7 C) 8 D)
Üniversite Haz rl k Sözcükte Do al ve Say lar Söz Öbeklerinde ve Tam Say lar Anlam - I - I Kolay Temel Matematik. 8 ( + ) A) 7 B) 8 C) 9 D) 0 E) 6.! ( )": ( ) A) B) 0 C) D) E). 7. + 5 A) 6 B) 7 C) 8 D)
MATEMATİK. Denemenin çözümlerine "www.zekakupuyayinlari.com.tr / portal" adresinden cevap anahtarlarına tıklayarak ulaşabilirsiniz.
 MATEMATİK Denemenin çözümlerine "www.zekakupuyayinlari.com.tr / portal" adresinden cevap anahtarlarına tıklayarak ulaşabilirsiniz. 1. DÖNEM DENEME 1 1. 4. 28 ve 35 sayılarının EKOK ve EBOB u kaçtır? EKOK
MATEMATİK Denemenin çözümlerine "www.zekakupuyayinlari.com.tr / portal" adresinden cevap anahtarlarına tıklayarak ulaşabilirsiniz. 1. DÖNEM DENEME 1 1. 4. 28 ve 35 sayılarının EKOK ve EBOB u kaçtır? EKOK
MATEMATİK. Temel Kavramlar I. Test a ve b doğal sayılardır. 5. Ardışık 5 tek sayının toplamı 115 tir. 6. x ve y tamsayılardır.
 MATEMATİK Test 0 Temel Kavramlar I. a ve b doğal sayılardır. a + b = 7 olduğuna göre, a.b çarpımının alabileceği en büyük değer kaçtır?. Ardışık tek sayının toplamı tir. Buna göre, bu sayıların en büyüğü
MATEMATİK Test 0 Temel Kavramlar I. a ve b doğal sayılardır. a + b = 7 olduğuna göre, a.b çarpımının alabileceği en büyük değer kaçtır?. Ardışık tek sayının toplamı tir. Buna göre, bu sayıların en büyüğü
ÜNİVERSİTEYE GİRİŞ SINAV SORULARI
 ÜNİVERSİTEYE GİRİŞ SINAV SORULARI 1. 1999 ÖSS a, b, c pozitif gerçel (reel) sayılar olmak üzere a+ b ifadesindeki her sayı 3 ile çarpılırsa aşağıdakilerden hangisi elde c edilir? 3 a+ b A) B) c a+ 3b C)
ÜNİVERSİTEYE GİRİŞ SINAV SORULARI 1. 1999 ÖSS a, b, c pozitif gerçel (reel) sayılar olmak üzere a+ b ifadesindeki her sayı 3 ile çarpılırsa aşağıdakilerden hangisi elde c edilir? 3 a+ b A) B) c a+ 3b C)
6. Rakamları farklı, iki basamaklı farklı beş doğal sayının. 7. A = 7 + 11 + 15 + 19 + + 99 veriliyor.
 Bölüm: Doğal Sayılar ve Tamsayılar Test: Temel Kavramlar. abc ve cba üç basamaklı doğal sayılardır. abc cba = 97 olduğuna göre, abc biçiminde yazılabilecek en küçük doğal sayının rakamları toplamı A) B)
Bölüm: Doğal Sayılar ve Tamsayılar Test: Temel Kavramlar. abc ve cba üç basamaklı doğal sayılardır. abc cba = 97 olduğuna göre, abc biçiminde yazılabilecek en küçük doğal sayının rakamları toplamı A) B)
1. ÜNİTE 2. ÜNİTE 3. ÜNİTE. Bölüm 1 : Üslü Sayılar... 8. Bölüm 2 : Doğal Sayılar... 18. Bölüm 3 : Doğal Sayı Problemleri... 30
 İçindekiler 1. ÜNİTE Bölüm 1 : Üslü Sayılar... 8 Bölüm 2 : Doğal Sayılar... 18 Bölüm 3 : Doğal Sayı Problemleri... 30 Bölüm 4 :- Çarpanlar ve Katlar, Bölünebilme... 40 Bölüm 5 : Asal Sayılar, Ortak Bölenler,
İçindekiler 1. ÜNİTE Bölüm 1 : Üslü Sayılar... 8 Bölüm 2 : Doğal Sayılar... 18 Bölüm 3 : Doğal Sayı Problemleri... 30 Bölüm 4 :- Çarpanlar ve Katlar, Bölünebilme... 40 Bölüm 5 : Asal Sayılar, Ortak Bölenler,
M a t e m a t i k. 8. Sınıf & Ders Notları
 ÇARPANLAR VE KATLAR Hatırlatma: Asal Sayı: 1 ve kendisinden başka bir sayıya bölünemeyen, 1 den büyük doğal sayılara asal sayı denir. Buna göre asal sayılar : 2, 3, 5, 7, 11, 13, 17, 19, 23, 29,.. Örnek
ÇARPANLAR VE KATLAR Hatırlatma: Asal Sayı: 1 ve kendisinden başka bir sayıya bölünemeyen, 1 den büyük doğal sayılara asal sayı denir. Buna göre asal sayılar : 2, 3, 5, 7, 11, 13, 17, 19, 23, 29,.. Örnek
Çözüm : * ebob = = * ekok = = * ve 36 sayılarının ebob ve ekok u kaçtır?
 1) 24 ve 36 sayılarının ebob ve ekok u kaçtır? 24 36 2 * ebob = 2.2.3 =12 12 18 2 * ekok = 2.2.2.3.3 = 72 6 9 2 3 9 3 * 1 3 3 1 Ebob ( 24, 36 ) = 12 ( * lı olanların çarpımı) Ekok ( 24, 36 ) = 72 ( Hepsinin
1) 24 ve 36 sayılarının ebob ve ekok u kaçtır? 24 36 2 * ebob = 2.2.3 =12 12 18 2 * ekok = 2.2.2.3.3 = 72 6 9 2 3 9 3 * 1 3 3 1 Ebob ( 24, 36 ) = 12 ( * lı olanların çarpımı) Ekok ( 24, 36 ) = 72 ( Hepsinin
TEMEL MATEMATİK. 1. Bu testte 40 soru vardır. 2. Cevaplarınızı, cevap kâğıdının Temel Matematik Testi için ayrılan kısmına işaretleyiniz.
 TEMEL MTEMTİK. u testte 0 soru vardır.. evaplarınızı, cevap kâğıdının Temel Matematik Testi için ayrılan kısmına işaretleyiniz.. ir satranç tahtasındaki 6 kareye den 6 e kadar olan doğal sayılar yazılıyor.
TEMEL MTEMTİK. u testte 0 soru vardır.. evaplarınızı, cevap kâğıdının Temel Matematik Testi için ayrılan kısmına işaretleyiniz.. ir satranç tahtasındaki 6 kareye den 6 e kadar olan doğal sayılar yazılıyor.
Ýþlem Yeteneði Temel Kavramlar Sayý Basamaklarý Taban Aritmetiði Bölme ve Bölünebilme Ebob-Ekok
 Ödev Tarihi :... Ödev Kontrol Tarihi :... Kontrol Eden :... LYS MATEMATİK - I Ödev Kitapçığı (MF-TM) Ýþlem Yeteneði Temel Kavramlar Sayý Basamaklarý Taban Aritmetiði Bölme ve Bölünebilme Ebob-Ekok Adý
Ödev Tarihi :... Ödev Kontrol Tarihi :... Kontrol Eden :... LYS MATEMATİK - I Ödev Kitapçığı (MF-TM) Ýþlem Yeteneði Temel Kavramlar Sayý Basamaklarý Taban Aritmetiði Bölme ve Bölünebilme Ebob-Ekok Adý
BÖLÜNEBĐLME KURALLARI
 YILLAR 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 ÖSS-YGS - 2 2-2 1 1-1 1 kalanı bulmak için sağdan ve + ile başlamak gerekir BÖLÜNEBĐLME KURALLARI 2 Đle Bölünebilme: tüm çift sayılar, yani birler
YILLAR 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 ÖSS-YGS - 2 2-2 1 1-1 1 kalanı bulmak için sağdan ve + ile başlamak gerekir BÖLÜNEBĐLME KURALLARI 2 Đle Bölünebilme: tüm çift sayılar, yani birler
EN BÜYÜK ORTAK BÖLEN EBOB
 EN BÜYÜK ORTAK BÖLEN 1 ve 18 in bölenlerini bulalım ve ortak olanlarını inceleyelim. 1 nin bölenleri: 1,,,4,6,1 18 in bölenleri: 1,,,6,9,18 Aşağıdaki sayı ikililerinin en büyük ortak bölenini ebob bulunuz.
EN BÜYÜK ORTAK BÖLEN 1 ve 18 in bölenlerini bulalım ve ortak olanlarını inceleyelim. 1 nin bölenleri: 1,,,4,6,1 18 in bölenleri: 1,,,6,9,18 Aşağıdaki sayı ikililerinin en büyük ortak bölenini ebob bulunuz.
2012 YGS MATEMATİK SORU VE ÇÖZÜMLERİ. b 27 18. 3. a 12 8 A) 4 2 B) 3 3 C) 4 D) 5 E) 6. Çözüm : Cevap : E. 4. x ve y birer gerçel sayı olmak üzere,
 01 YGS MATEMATİK SORU VE ÇÖZÜMLERİ 1. 10, 5,1 0,5 0, işleminin sonucu kaçtır? A) 5 B) 5,5 C) 6 D) 6,5 E) 7. a 1 8 b 7 18 olduğuna göre a b çarpımı kaçtır? A) 4 B) C) 4 D) 5 E) 6 10, 5,1 105 1 41 1 5 0,
01 YGS MATEMATİK SORU VE ÇÖZÜMLERİ 1. 10, 5,1 0,5 0, işleminin sonucu kaçtır? A) 5 B) 5,5 C) 6 D) 6,5 E) 7. a 1 8 b 7 18 olduğuna göre a b çarpımı kaçtır? A) 4 B) C) 4 D) 5 E) 6 10, 5,1 105 1 41 1 5 0,
Tek Doğal Sayılar; Çift Doğal Sayılar
 Bölüm BÖLÜNEBİLME VE ÇARPANLARA AYIRMA. Bölünebilme Kuralları Bir a doğal sayısı bir b sayma sayısına bölündüğünde bölüm bir doğal sayı ve kalan sıfır ise, a doğal sayısı b sayma sayısına bölünebilir.
Bölüm BÖLÜNEBİLME VE ÇARPANLARA AYIRMA. Bölünebilme Kuralları Bir a doğal sayısı bir b sayma sayısına bölündüğünde bölüm bir doğal sayı ve kalan sıfır ise, a doğal sayısı b sayma sayısına bölünebilir.
YGS MATEMATİK SORU BANKASI
 YGS MATEMATİK SORU BANKASI Sebahattin ÖLMEZ www.limityayinlari.com Sınavlara Hazırlık Serisi YGS Matematik Soru Bankası ISBN: 978-60-48--9 Copyright Lmt Limit Yayınları Bu kitabın tüm hakları Lmt Limit
YGS MATEMATİK SORU BANKASI Sebahattin ÖLMEZ www.limityayinlari.com Sınavlara Hazırlık Serisi YGS Matematik Soru Bankası ISBN: 978-60-48--9 Copyright Lmt Limit Yayınları Bu kitabın tüm hakları Lmt Limit
OBEB - OKEK Test -1. 6. OKEK( 14, 20) kaçtır? 1. OBEB(16, 20, 48) kaçtır? 7. OBEB, 2. OBEB(56, 140, 280) kaçtır? 3. OKEK(10, 15, 25) kaçtır?
 OE - OKEK Test -1 1. OE(16, 0, 8) kaçtır? A) ) ) ) 6 E) 8 6. OKEK( 1, 0) kaçtır? A) 10 ) 160 ) 180 ) 10 E) 0. OE(56, 10, 80) kaçtır? 7. OE, 15 5 kaçtır? A) 1 ) 0 ) ) 8 E) A) 75 ) 75 ) 5 ) 5 E) 5. OKEK(10,
OE - OKEK Test -1 1. OE(16, 0, 8) kaçtır? A) ) ) ) 6 E) 8 6. OKEK( 1, 0) kaçtır? A) 10 ) 160 ) 180 ) 10 E) 0. OE(56, 10, 80) kaçtır? 7. OE, 15 5 kaçtır? A) 1 ) 0 ) ) 8 E) A) 75 ) 75 ) 5 ) 5 E) 5. OKEK(10,
MERKEZİ ORTAK SINAV KAZANDIRAN MATEMATİK FÖYÜ
 MERKEZİ ORTAK SINAV KAZANDIRAN MATEMATİK FÖYÜ ÖRNEK: 18 sayısının pozitif çarpanları nelerdir? Çarpımları 18 olan sayılar arayalım. 18 = 1. 18 18 =. 9 18 =. 6 Her doğal sayı iki doğal sayının çarpımı şeklinde
MERKEZİ ORTAK SINAV KAZANDIRAN MATEMATİK FÖYÜ ÖRNEK: 18 sayısının pozitif çarpanları nelerdir? Çarpımları 18 olan sayılar arayalım. 18 = 1. 18 18 =. 9 18 =. 6 Her doğal sayı iki doğal sayının çarpımı şeklinde
++ :8. SINIF. ÜNİTE Çarpanlar ve Katlar UYGULAMA BÖLÜMÜ. Anla-Uygula
 ÜNİTE 1 8.1.1 Çarpanlar ve Katlar Anla-Uygula 1 A B ++ :8. SINIF C D UYGULAMA BÖLÜMÜ 8.1.1.2 İki doğal sayının en büyük ortak bölenini (EBOB) ve en küçük ortak katını (EKOK) hesaplar; ilgili problemleri
ÜNİTE 1 8.1.1 Çarpanlar ve Katlar Anla-Uygula 1 A B ++ :8. SINIF C D UYGULAMA BÖLÜMÜ 8.1.1.2 İki doğal sayının en büyük ortak bölenini (EBOB) ve en küçük ortak katını (EKOK) hesaplar; ilgili problemleri
SAYI VE KESĐR PROBLEMLERĐ
 YILLAR 1996 1997 1998 1999 000 001 00 003 004 005 ÖSS 3 3 4 ÖYS SAYI VE KESĐR PROBLEMLERĐ Bir sayının 5 eksiği = x-5 Bir sayının 10 fazlası _x+10 Bir sayının katı :x Bir sayının /3 ün = 3 Bir sayının 4/5
YILLAR 1996 1997 1998 1999 000 001 00 003 004 005 ÖSS 3 3 4 ÖYS SAYI VE KESĐR PROBLEMLERĐ Bir sayının 5 eksiği = x-5 Bir sayının 10 fazlası _x+10 Bir sayının katı :x Bir sayının /3 ün = 3 Bir sayının 4/5
Atatürk Anadolu. Bölme, Bölünebilme, Asal Sayılar, Obeb, Okek, Rasyonel Sayılar, Basit Eşitsizlikler ve Mutlak Değer Üzerine Kısa Çalışmalar
 Atatürk Anadolu Lisesi M A T E M A T İ K Bölme, Bölünebilme, Asal Sayılar, Obeb, Okek, Rasyonel Sayılar, Basit Eşitsizlikler ve Mutlak Değer Üzerine Kısa Çalışmalar KONYA \ SELÇUKLU 07 Bölme, Bölünebilme,
Atatürk Anadolu Lisesi M A T E M A T İ K Bölme, Bölünebilme, Asal Sayılar, Obeb, Okek, Rasyonel Sayılar, Basit Eşitsizlikler ve Mutlak Değer Üzerine Kısa Çalışmalar KONYA \ SELÇUKLU 07 Bölme, Bölünebilme,
EN BÜYÜK ORTAK BÖLEN (EBOB) NOT: 12 ve 6 sayılarının En Büyük Ortak Böleni EBOB (12,18)=6 veya (12,18) EBOB =6 şeklinde ifade edilir.
 8.1.8 EN BÜYÜK ORTAK BÖLEN (EBOB) İki veya daha fazla sayma sayısının ortak bölenlerinden en büyük olanına, bu sayıların En Büyük Ortak Böleni EBOB u denir. NOT: 12 ve 6 sayılarının En Büyük Ortak Böleni
8.1.8 EN BÜYÜK ORTAK BÖLEN (EBOB) İki veya daha fazla sayma sayısının ortak bölenlerinden en büyük olanına, bu sayıların En Büyük Ortak Böleni EBOB u denir. NOT: 12 ve 6 sayılarının En Büyük Ortak Böleni
5. Üç basamaklı ABC doğal sayısı 2 ile, 5 ile ve 9 ile tam. 6. Dört basamaklı AB24 sayısının 36 ile bölümünden kalan iki
 Bölme ve Bölünebilme BÖLÜM 03 Test 01 1 Üç basamaklı 5AB sayısı iki basamaklı AB sayısına bölündüğünde, bölüm 13 ve kalan 8 olmaktadır Buna göre, A + B toplamı A) 5 B) 6 C) 7 D) 8 E) 9 5AB = 13 AB + 8
Bölme ve Bölünebilme BÖLÜM 03 Test 01 1 Üç basamaklı 5AB sayısı iki basamaklı AB sayısına bölündüğünde, bölüm 13 ve kalan 8 olmaktadır Buna göre, A + B toplamı A) 5 B) 6 C) 7 D) 8 E) 9 5AB = 13 AB + 8
BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ DENKLEMLER
 YILLAR 00 00 00 00 00 00 007 008 009 00 ÖSS-YGS - - - - - - - - BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ DENKLEMLER a,b R ve a 0 olmak üzere ab=0 şeklindeki denklemlere Birinci dereceden bir bilinmeyenli denklemler
YILLAR 00 00 00 00 00 00 007 008 009 00 ÖSS-YGS - - - - - - - - BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ DENKLEMLER a,b R ve a 0 olmak üzere ab=0 şeklindeki denklemlere Birinci dereceden bir bilinmeyenli denklemler
1. ÜNİTE:SAYILAR VE İŞLEMLER
 1. ÜNİTE:SAYILAR VE İŞLEMLER 2 DERS SAATİ:Verilen iki doğal sayının aralarında asal olup olmadığını belirler. ASAL SAYILAR 1 ve kendisinden başka hiçbir sayma sayısı ile bölünemeyen 1 den büyük doğal sayılara
1. ÜNİTE:SAYILAR VE İŞLEMLER 2 DERS SAATİ:Verilen iki doğal sayının aralarında asal olup olmadığını belirler. ASAL SAYILAR 1 ve kendisinden başka hiçbir sayma sayısı ile bölünemeyen 1 den büyük doğal sayılara
KARTEZYEN ÇARPIM VE BAĞINTI
 KRTEZYEN ÇRPIM VE BĞINTI 3. Bölüm TEST -2 1. β={(x,y):2x+y=8,x,y N} şeklinde tanımlı β bağıntısı kaç elemanlıdır? ) 4 B) 5 C) 6 D) 7 E) 8 6. R'de bağıntısı yansıyan ise a.b kaçtır? ) 18 B) 9 C) 2 D) 18
KRTEZYEN ÇRPIM VE BĞINTI 3. Bölüm TEST -2 1. β={(x,y):2x+y=8,x,y N} şeklinde tanımlı β bağıntısı kaç elemanlıdır? ) 4 B) 5 C) 6 D) 7 E) 8 6. R'de bağıntısı yansıyan ise a.b kaçtır? ) 18 B) 9 C) 2 D) 18
YGS ÖNCESİ. 1) 1! + 3! + 5! ! Toplamının birler basamağındaki rakam kaçtır?
 1) 1! + 3! + 5! +. + 1453! Toplamının birler basamağındaki rakam kaçtır? 6) Rakamları sıfırdan farklı iki basamaklı bir AB doğal sayının rakamları yer değiştiğinde sayının değeri 63 artıyor. Buna göre,
1) 1! + 3! + 5! +. + 1453! Toplamının birler basamağındaki rakam kaçtır? 6) Rakamları sıfırdan farklı iki basamaklı bir AB doğal sayının rakamları yer değiştiğinde sayının değeri 63 artıyor. Buna göre,
MATEMATİK Fasikül 1 KONU ANLATIMLI FASİKÜL SET ÖLÇEN SIRA SENDE UYGULAMALARI ÇÖZÜMLÜ ÖRNEK SORULAR
 ATU MATEMATİK Fasikül 1 KONU ANLATIMLI FASİKÜL SET ZENGİN İÇERİKLİ ÖZGÜN KONU ANLATIMI ÖLÇEN SIRA SENDE UYGULAMALARI ÇÖZÜMLÜ ÖRNEK SORULAR BİLGİ KONTROLÜ ODAKLI KARMA SORULAR PEKİŞTİREN BÖLÜMLERİ AKILLI
ATU MATEMATİK Fasikül 1 KONU ANLATIMLI FASİKÜL SET ZENGİN İÇERİKLİ ÖZGÜN KONU ANLATIMI ÖLÇEN SIRA SENDE UYGULAMALARI ÇÖZÜMLÜ ÖRNEK SORULAR BİLGİ KONTROLÜ ODAKLI KARMA SORULAR PEKİŞTİREN BÖLÜMLERİ AKILLI
Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı. ALES / Sonbahar / Sayısal II / 19 Aralık 2010. Matematik Soruları ve Çözümleri
 Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı ALES / Sonbahar / Sayısal II / 19 Aralık 010 Matematik Soruları ve Çözümleri 1. a, b ve c sıfırdan farklı gerçel sayılar olmak üzere aşağıdaki ifadelerden
Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı ALES / Sonbahar / Sayısal II / 19 Aralık 010 Matematik Soruları ve Çözümleri 1. a, b ve c sıfırdan farklı gerçel sayılar olmak üzere aşağıdaki ifadelerden
2017 MÜKEMMEL YGS MATEMATİK
 2017 MÜKEMMEL YGS MATEMATİK 1. 2,31 0,33 0,65 0,13 + 3,6 0,6 işleminin sonucu kaçtır? A)0,5 B) 0,8 C)0,9 D)5 E)8 4. Üç basamaklı ABB doğal sayısı 4 e ve 9 a kalansız bölünmektedir. Buna göre, A+B toplamının
2017 MÜKEMMEL YGS MATEMATİK 1. 2,31 0,33 0,65 0,13 + 3,6 0,6 işleminin sonucu kaçtır? A)0,5 B) 0,8 C)0,9 D)5 E)8 4. Üç basamaklı ABB doğal sayısı 4 e ve 9 a kalansız bölünmektedir. Buna göre, A+B toplamının
Özel AKEV İlköğretim Okulu Fen ve Matematik Olimpiyatı
 Özel KEV İlköğretim Okulu Fen ve Matematik Olimpiyatı DİKKT! CEVP KĞIDININ TEST -- BÖLÜMÜNE MTEMTİK SORULRI İŞRETLENECEKTİR. ) 3 basamaklı 4 tane sayının aritmetik ortalaması 400 dür. Bu dört sayının birler
Özel KEV İlköğretim Okulu Fen ve Matematik Olimpiyatı DİKKT! CEVP KĞIDININ TEST -- BÖLÜMÜNE MTEMTİK SORULRI İŞRETLENECEKTİR. ) 3 basamaklı 4 tane sayının aritmetik ortalaması 400 dür. Bu dört sayının birler
1. BÖLÜM Mantık BÖLÜM Sayılar BÖLÜM Rasyonel Sayılar BÖLÜM I. Dereceden Denklemler ve Eşitsizlikler
 ORGANİZASYON ŞEMASI 1. BÖLÜM Mantık... 7. BÖLÜM Sayılar... 13 3. BÖLÜM Rasyonel Sayılar... 93 4. BÖLÜM I. Dereceden Denklemler ve Eşitsizlikler... 103 5. BÖLÜM Mutlak Değer... 113 6. BÖLÜM Çarpanlara Ayırma...
ORGANİZASYON ŞEMASI 1. BÖLÜM Mantık... 7. BÖLÜM Sayılar... 13 3. BÖLÜM Rasyonel Sayılar... 93 4. BÖLÜM I. Dereceden Denklemler ve Eşitsizlikler... 103 5. BÖLÜM Mutlak Değer... 113 6. BÖLÜM Çarpanlara Ayırma...
ORAN-ORANTI TEST 1. 1) Asağıdaki şekillerde mavi bölgelerin kırmızı bölgelere oranını bulunuz. a) b) c)
 7BÖLÜM ORAN - ORANTI ORAN-ORANTI TEST 1 1) Asağıdaki şekillerde mavi bölgelerin kırmızı bölgelere oranını bulunuz. a) b) c) ) Aşağıda okunuşları verilen oranları yazınız. a) 16 nın 14 e oranı b) 6 nın
7BÖLÜM ORAN - ORANTI ORAN-ORANTI TEST 1 1) Asağıdaki şekillerde mavi bölgelerin kırmızı bölgelere oranını bulunuz. a) b) c) ) Aşağıda okunuşları verilen oranları yazınız. a) 16 nın 14 e oranı b) 6 nın
TEMEL KAVRAMLAR MATEMAT K. 6. a ve b birer do al say r. a 2 b 2 = 19 oldu una göre, a + 2b toplam kaçt r? (YANIT: 28)
 TEMEL KAVRAMLAR 6. a ve b birer do al say r. a b = 19 oldu una göre, a + b toplam (YANIT: 8) 1. ( 4) ( 1) 6 1 i leminin sonucu (YANIT: ). ( 6) ( 3) ( 4) ( 17) ( 5) :( 11) leminin sonucu (YANIT: 38) 7.
TEMEL KAVRAMLAR 6. a ve b birer do al say r. a b = 19 oldu una göre, a + b toplam (YANIT: 8) 1. ( 4) ( 1) 6 1 i leminin sonucu (YANIT: ). ( 6) ( 3) ( 4) ( 17) ( 5) :( 11) leminin sonucu (YANIT: 38) 7.
140. 2< a< 1 ise kesrinin değeri aşağıdakilerden hangisi olamaz? (3,7) a 1,9 2,4 2,7 3,2 3,7. a a c b ve c a a b c
 138. a ve b gerçel sayılardır. a < a, 6a b 5= 0 b ne olabilir? (11) 4 5 8 11 1 139. < 0 olmak üzere, 4 3. =? ( 3 ) a 1 140. < a< 1 ise kesrinin değeri aşağıdakilerden hangisi olamaz? (3,7) a 1,9,4,7 3,
138. a ve b gerçel sayılardır. a < a, 6a b 5= 0 b ne olabilir? (11) 4 5 8 11 1 139. < 0 olmak üzere, 4 3. =? ( 3 ) a 1 140. < a< 1 ise kesrinin değeri aşağıdakilerden hangisi olamaz? (3,7) a 1,9,4,7 3,
YILLAR 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 ÖSS-YGS
 YILLAR 6 7 8 ÖSS-YGS - - / /LYS ONDALIK SAYILAR Paydası ve un pozitif kuvveti şeklinde olan veya u şekle dönüştürüleilen kesirlere ondalık kesir(ondalık sayı) denir 7,,,,,7 6 (,6)gii 8 8 NOT: ondalık sayıların
YILLAR 6 7 8 ÖSS-YGS - - / /LYS ONDALIK SAYILAR Paydası ve un pozitif kuvveti şeklinde olan veya u şekle dönüştürüleilen kesirlere ondalık kesir(ondalık sayı) denir 7,,,,,7 6 (,6)gii 8 8 NOT: ondalık sayıların
Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı. ALES / Sonbahar / Sayısal I / 16 Kasım Matematik Soruları ve Çözümleri 24 E) <
 Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı ALES / Sonbahar / Sayısal I / 6 Kasım 008 Matematik Soruları ve Çözümleri. Aşağıdaki kesirlerin en büyüğü hangisidir? 0 A) B) C) 3 D) 4 E) 5 Çözüm 0
Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı ALES / Sonbahar / Sayısal I / 6 Kasım 008 Matematik Soruları ve Çözümleri. Aşağıdaki kesirlerin en büyüğü hangisidir? 0 A) B) C) 3 D) 4 E) 5 Çözüm 0
ÇARPANLAR VE KATLAR I sayısının asal çarpanlarına ayrılmış hâli aşağıdakilerden A) B) C) D)
 8. Sınıf MATEMATİK ÇARPANLAR VE KATLAR I. Aşağıdakilerden hangisi 6 nın çarpanlarından biridir? A) 3 B) 6 C) 8 D) TEST. 360 sayısının asal çarpanlarına ayrılmış hâli aşağıdakilerden hangisidir? A) 3. 3.
8. Sınıf MATEMATİK ÇARPANLAR VE KATLAR I. Aşağıdakilerden hangisi 6 nın çarpanlarından biridir? A) 3 B) 6 C) 8 D) TEST. 360 sayısının asal çarpanlarına ayrılmış hâli aşağıdakilerden hangisidir? A) 3. 3.
İLKMATZUM 8. SINIF MATEMATİK 2016 DENEME-2
 A KİTAPÇIK TÜRÜ İLKMATZUM 8. SINIF MATEMATİK 2016 DENEME-2 Bu deneme de emeği geçen bütün İlkMatZum öğretmenlerine teşekkürü borç biliriz. WWW.OGRETMENFORUMU.COM Adı ve Soyadı Sınıfı Öğrenci Numarası.../.../2016
A KİTAPÇIK TÜRÜ İLKMATZUM 8. SINIF MATEMATİK 2016 DENEME-2 Bu deneme de emeği geçen bütün İlkMatZum öğretmenlerine teşekkürü borç biliriz. WWW.OGRETMENFORUMU.COM Adı ve Soyadı Sınıfı Öğrenci Numarası.../.../2016
5. a ve b birer pozitif tam sayıdır. A) 1 B) 2 C) 3 D) 14 E) a ve b birer doğal sayıdır. 7. a ve b birer pozitif tam sayıdır.
 Üniversite Haz rl k Sözcükte Do al ve Say lar Söz Öbeklerinde ve Tam Say lar Anlam - I - I YGS Temel Matematik. 8 + 4. + 8 : 4 işleminin sonucu A) 8 B) 9 C) D) 5 E) 8 5. a ve b birer pozitif tam sayıdır.
Üniversite Haz rl k Sözcükte Do al ve Say lar Söz Öbeklerinde ve Tam Say lar Anlam - I - I YGS Temel Matematik. 8 + 4. + 8 : 4 işleminin sonucu A) 8 B) 9 C) D) 5 E) 8 5. a ve b birer pozitif tam sayıdır.
Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı. ALES / Sonbahar / Sayısal II / 15 Kasım Matematik Soruları ve Çözümleri = 5 = ( 5 ) 2
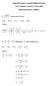 Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı ALES / Sonbahar / Sayısal II / 15 Kasım 2009 Matematik Soruları ve Çözümleri 1. 0,04 25 1 2 işleminin sonucu kaçtır? A) 10 B) 20 C) 25 D) 40 E) 60 Çözüm
Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı ALES / Sonbahar / Sayısal II / 15 Kasım 2009 Matematik Soruları ve Çözümleri 1. 0,04 25 1 2 işleminin sonucu kaçtır? A) 10 B) 20 C) 25 D) 40 E) 60 Çözüm
C) p = 7 için, 2p + 1 = 2.7 + 1 = 15 asal olmadığından, Sophie Germen asal sayısı değildir.
 Meslek Yüksekokulları Đle Açık Öğretim Ön Lisans Programları Mezunlarının Lisans Öğrenimine Dikey Geçiş Sınavı Dikey Geçiş Sınavı / DGS / 4 Temmuz 010 Matematik Soruları ve Çözümleri 1. 0, nin 5 katı olan
Meslek Yüksekokulları Đle Açık Öğretim Ön Lisans Programları Mezunlarının Lisans Öğrenimine Dikey Geçiş Sınavı Dikey Geçiş Sınavı / DGS / 4 Temmuz 010 Matematik Soruları ve Çözümleri 1. 0, nin 5 katı olan
ÇALIŞMA KAĞIDI Kazanım: Çarpanlar ve Katlar
 ÇALIŞMA KAĞIDI Kazanım: Çarpanlar ve Katlar 8 basamaklı en büyük asal sayının kaç tane çarpanı vardır? 30 sayısının çarpanlarını yazınız Asal çarpanlarına ayrılış halı 2 3.5 3 olan sayıyı 96 sayısının
ÇALIŞMA KAĞIDI Kazanım: Çarpanlar ve Katlar 8 basamaklı en büyük asal sayının kaç tane çarpanı vardır? 30 sayısının çarpanlarını yazınız Asal çarpanlarına ayrılış halı 2 3.5 3 olan sayıyı 96 sayısının
ÇARPANLAR VE KATLAR ÖRNEK. 8 Sayılar ve İşlemler. 2 x x 2 x 6. 2 x 2 x 2 x 9
 ÇARPANLAR VE KATLAR POZİTİF TAM SAYILARIN ÇARPANLARI Her pozitif tam sayı, iki doğal sayının çarpımı olarak yazılabilir. Bu iki doğal sayıdan her birine o sayının çarpanı denir. Bir sayının çarpanı aynı
ÇARPANLAR VE KATLAR POZİTİF TAM SAYILARIN ÇARPANLARI Her pozitif tam sayı, iki doğal sayının çarpımı olarak yazılabilir. Bu iki doğal sayıdan her birine o sayının çarpanı denir. Bir sayının çarpanı aynı
ASAL SAYILAR ASAL SAYILAR
 Kazanım : Asal sayıları özellikleriyle belirler. Doğal sayıların asal çarpanlarını belirler. ASAL SAYILAR 1 ve kendisinden başka hiçbir sayma sayısına tam bölünemeyen 1 den büyük doğal sayılara asal sayılar
Kazanım : Asal sayıları özellikleriyle belirler. Doğal sayıların asal çarpanlarını belirler. ASAL SAYILAR 1 ve kendisinden başka hiçbir sayma sayısına tam bölünemeyen 1 den büyük doğal sayılara asal sayılar
TEMEL KAVRAMLAR Test -1
 TEMEL KAVRAMLAR Test -1 1. 6 ( ) 4 A) B) 3 C) 4 D) 5 E) 6 5. 4 [1 ( 3). ( 8)] A) 4 B) C) 0 D) E) 4. 48: 8 5 A) 1 B) 6 C) 8 D) 1 E) 16 6. 4 7 36:9 18 : 3 A) 1 B) 8 C) D) 4 E) 8 3. (4: 3 + 1):4 A) 3 B) 5
TEMEL KAVRAMLAR Test -1 1. 6 ( ) 4 A) B) 3 C) 4 D) 5 E) 6 5. 4 [1 ( 3). ( 8)] A) 4 B) C) 0 D) E) 4. 48: 8 5 A) 1 B) 6 C) 8 D) 1 E) 16 6. 4 7 36:9 18 : 3 A) 1 B) 8 C) D) 4 E) 8 3. (4: 3 + 1):4 A) 3 B) 5
YGS - LYS SAYILAR KONU ÖZETLİ ÇÖZÜMLÜ SORU BANKASI
 YGS - LYS SAYILAR KONU ÖZETLİ LÜ SORU BANKASI ANKARA ÖN SÖZ Sevgili Öğrenciler, ÖSYM nin son yıllarda yaptığı sınavlardaki matematik sorularının eski sınav sorularından çok farklı olduğu herkes tarafından
YGS - LYS SAYILAR KONU ÖZETLİ LÜ SORU BANKASI ANKARA ÖN SÖZ Sevgili Öğrenciler, ÖSYM nin son yıllarda yaptığı sınavlardaki matematik sorularının eski sınav sorularından çok farklı olduğu herkes tarafından
TEST-8. Yandaki at resminin bir bölümü silinmiştir. Aşağıdaki şekillerden hangisi bu resmi tamamlar? A) B) C) D)
 TEST-8 Matematik Yarışmalarına Hazırlık 1 Yandaki at resminin bir bölümü silinmiştir. Aşağıdaki şekillerden hangisi bu resmi tamamlar? A) B) C) D) 2 Yandaki kareden çizgiler boyunca kesilerek çeşitli şekiller
TEST-8 Matematik Yarışmalarına Hazırlık 1 Yandaki at resminin bir bölümü silinmiştir. Aşağıdaki şekillerden hangisi bu resmi tamamlar? A) B) C) D) 2 Yandaki kareden çizgiler boyunca kesilerek çeşitli şekiller
MATEMATİK DERS PLÂNI. : Doğal Sayılar (Asal Sayılar Bölünebilme O.B.E.B ve O.K.E.K)
 MATEMATİK DERS PLÂNI Başlangıç Tarihi :.. Dersin adı Sınıf Öğrenme Alanı Alt Öğrenme Alanı Planlanan Süre : Matematik : 9. Sınıf : Sayılar : Doğal Sayılar (Asal Sayılar Bölünebilme O.B.E.B ve O.K.E.K)
MATEMATİK DERS PLÂNI Başlangıç Tarihi :.. Dersin adı Sınıf Öğrenme Alanı Alt Öğrenme Alanı Planlanan Süre : Matematik : 9. Sınıf : Sayılar : Doğal Sayılar (Asal Sayılar Bölünebilme O.B.E.B ve O.K.E.K)
ÖZEL EGE LİSESİ 11. MATEMATİK YARIŞMASI 7. SINIF ELEME SINAVI TEST SORULARI
 . a,b,c negatif tam sayılardır. (a + 3).b b< c< a ve; = 6 olduğuna c göre, a+b+c toplamının en büyük değeri 4. 50 kişinin çalıştığı bir şirkette 25 kişi İngilizce, 6 kişi Fransızca biliyor. En çok bir
. a,b,c negatif tam sayılardır. (a + 3).b b< c< a ve; = 6 olduğuna c göre, a+b+c toplamının en büyük değeri 4. 50 kişinin çalıştığı bir şirkette 25 kişi İngilizce, 6 kişi Fransızca biliyor. En çok bir
Örnek...6 : Yandaki bölme işleminde A ve n birer doğal sayıdır. A nın alabileceği en küçük ve en bü yük değerleri bulunu z.
 MODÜLER ARİTMETİK ( BÖLME BÖLÜNEBİLME KURALLARI ÖKLİT ALGORİTMASI DEĞERLENDİRME ) BÖLME İŞLEMİ VE ÖZELLİKLERİ A, B, C, K doğal sayılar ve B olmak üzere, BÖLÜNEN A B C BÖLEN BÖLÜM Örnek...5 : A, B, C birbirinden
MODÜLER ARİTMETİK ( BÖLME BÖLÜNEBİLME KURALLARI ÖKLİT ALGORİTMASI DEĞERLENDİRME ) BÖLME İŞLEMİ VE ÖZELLİKLERİ A, B, C, K doğal sayılar ve B olmak üzere, BÖLÜNEN A B C BÖLEN BÖLÜM Örnek...5 : A, B, C birbirinden
Temel Matematik Testi - 5
 Test kodunu sitemizde kullanarak sonucunuzu öğrenebilir, soruların video çözümlerini izleyebilirsiniz. Test Kodu: 005. u testte 40 soru vardır.. Tavsiye edilen süre 40 dakikadır. Temel Matematik Testi
Test kodunu sitemizde kullanarak sonucunuzu öğrenebilir, soruların video çözümlerini izleyebilirsiniz. Test Kodu: 005. u testte 40 soru vardır.. Tavsiye edilen süre 40 dakikadır. Temel Matematik Testi
DENEME II 15.12.2013. 1. Bir havuzun tamamını A musluğu 12 saatte doldururken havuzun 1 3
 DENEME II 5..03. Bir havuzun tamamını A musluğu saatte doldururken havuzun 3 ünde bulunan bir B musluğu 0 saatte boşaltıyor. Havuz boş iken iki musluk aynı anda açılırsa havuz kaç saatte dolar? A) 30 B)
DENEME II 5..03. Bir havuzun tamamını A musluğu saatte doldururken havuzun 3 ünde bulunan bir B musluğu 0 saatte boşaltıyor. Havuz boş iken iki musluk aynı anda açılırsa havuz kaç saatte dolar? A) 30 B)
12-A. Sayılar - 1 TEST
 -A TEST Sayılar -. Birbirinden farklı beş pozitif tam sayının toplamı 0 dur. Bu sayılardan sadece ikisi den büyüktür. Bu sayılardan üç tanesi çift sayıdır. Buna göre bu sayılardan en büyüğü en çok kaç
-A TEST Sayılar -. Birbirinden farklı beş pozitif tam sayının toplamı 0 dur. Bu sayılardan sadece ikisi den büyüktür. Bu sayılardan üç tanesi çift sayıdır. Buna göre bu sayılardan en büyüğü en çok kaç
d) x TABAN ARĐTMETĐĞĐ
 YILLAR 00 00 00 00 00 007 008 009 010 011 ÖSS-YGS - 1 1 - - - - - - - TABAN ARĐTMETĐĞĐ Genel olarak 10 luk sayı sistemini kullanırız fakat başka sayı sistemlerine de ihtiyaç duyarız Örneğin bilgisayarın
YILLAR 00 00 00 00 00 007 008 009 010 011 ÖSS-YGS - 1 1 - - - - - - - TABAN ARĐTMETĐĞĐ Genel olarak 10 luk sayı sistemini kullanırız fakat başka sayı sistemlerine de ihtiyaç duyarız Örneğin bilgisayarın
ÇARPANLAR VE KATLAR. Başarı Başaracağım Diye Başlayanındır. 1
 ÇARPANLAR VE KATLAR Başarı Başaracağım Diye Başlayanındır. 1 ÖRNEK 1 48 sayısının çarpanlarını bulalım. 1.Gökkuşağı yöntemi 48 sayısının çarpanlarını küçükten büyüğe sıralayarak eşleştiriniz. 48 çarpanlarını
ÇARPANLAR VE KATLAR Başarı Başaracağım Diye Başlayanındır. 1 ÖRNEK 1 48 sayısının çarpanlarını bulalım. 1.Gökkuşağı yöntemi 48 sayısının çarpanlarını küçükten büyüğe sıralayarak eşleştiriniz. 48 çarpanlarını
DOĞAL SAYILARDA TOPLAMA VE ÇARPMA
 YILLAR 00 00 004 00 006 007 008 009 010 011 ÖSS-YGS DOĞAL SAYILARDA TOPLAMA VE ÇARPMA Örnek( 1 ) - - - - (I) yandaki işleme x 1 (II) göre (I) çarpan - - - - kaçtır? 40 + - - - - - - - - - - (ÖSS-8) 40
YILLAR 00 00 004 00 006 007 008 009 010 011 ÖSS-YGS DOĞAL SAYILARDA TOPLAMA VE ÇARPMA Örnek( 1 ) - - - - (I) yandaki işleme x 1 (II) göre (I) çarpan - - - - kaçtır? 40 + - - - - - - - - - - (ÖSS-8) 40
Temel Kavramlar 1 Doğal sayılar: N = {0, 1, 2, 3,.,n, n+1,..} kümesinin her bir elamanına doğal sayı denir ve N ile gösterilir.
 Temel Kavramlar 1 Doğal sayılar: N = {0, 1, 2, 3,.,n, n+1,..} kümesinin her bir elamanına doğal sayı denir ve N ile gösterilir. a) Pozitif doğal sayılar: Sıfır olmayan doğal sayılar kümesine Pozitif Doğal
Temel Kavramlar 1 Doğal sayılar: N = {0, 1, 2, 3,.,n, n+1,..} kümesinin her bir elamanına doğal sayı denir ve N ile gösterilir. a) Pozitif doğal sayılar: Sıfır olmayan doğal sayılar kümesine Pozitif Doğal
4 3 ü ile sinin farkı 9 olan sayıyı bulalım.
 KESİR PROBLEMLERİ Bir sayısının ü : tir. ü ile sinin farkı 9 olan sayıyı bulalım. İstenen sayı olsun. Bir sayısının ü : tür. Bir sayısının yarısının fazlası : tür. 9.. 9 9 ( ) () 9 ( 9).( ) bulunur. Bir
KESİR PROBLEMLERİ Bir sayısının ü : tir. ü ile sinin farkı 9 olan sayıyı bulalım. İstenen sayı olsun. Bir sayısının ü : tür. Bir sayısının yarısının fazlası : tür. 9.. 9 9 ( ) () 9 ( 9).( ) bulunur. Bir
ÖZEL EGE LİSESİ EGE BÖLGESİ OKULLAR ARASI 16.MATEMATİK YARIŞMASI 6. SINIF FİNAL SORULARI
 6. SINIF FİNAL SORULARI 1. a b ve a,b N olmak üzere, altı basamaklı (aaabbb) sayısının 4 ile bölümünden kalan 1 dir. Üç basamaklı (bba) sayısı 9 ile kalansız bölünebildiğine göre, iki basamaklı (aa) sayısının
6. SINIF FİNAL SORULARI 1. a b ve a,b N olmak üzere, altı basamaklı (aaabbb) sayısının 4 ile bölümünden kalan 1 dir. Üç basamaklı (bba) sayısı 9 ile kalansız bölünebildiğine göre, iki basamaklı (aa) sayısının
Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı. ALES / Sonbahar / Sayısal I / 15 Kasım 2009. Matematik Soruları ve Çözümleri
 Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı ALES / Sonbahar / Sayısal I / 5 Kasım 2009 Matematik Soruları ve Çözümleri. + işleminin sonucu kaçtır? A) 2 B) C) 4 D) 2 E) Çözüm + = + = 4 2 = 4. 2
Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı ALES / Sonbahar / Sayısal I / 5 Kasım 2009 Matematik Soruları ve Çözümleri. + işleminin sonucu kaçtır? A) 2 B) C) 4 D) 2 E) Çözüm + = + = 4 2 = 4. 2
6BÖLÜM ONDALIK SAYILAR
 6BÖLÜM ONDALIK SAYILAR ONDALIK SAYILAR TEST ) Aşağıdaki kesirleri ondalık sayıya çeviriniz. a) 3 b) 2 c) 9 d) 4 5 25 20 2) Aşağıdaki ondalık sayıların basamaklarındaki rakamların sayı ve basamak değerlerini
6BÖLÜM ONDALIK SAYILAR ONDALIK SAYILAR TEST ) Aşağıdaki kesirleri ondalık sayıya çeviriniz. a) 3 b) 2 c) 9 d) 4 5 25 20 2) Aşağıdaki ondalık sayıların basamaklarındaki rakamların sayı ve basamak değerlerini
TEOG HAZIRLIK. Musa BOR
 TEOG HAZIRLIK sınıf. Musa BOR AFG Matbaa Yayıncılık Kağ. İnş. Ltd. Şti. Buca OSB, BEGOS 2. Bölge 3/20 Sk. No: 17 Buca-İZMİR Tel: 0.232.442 01 01-442 03 03 Faks: 442 06 60 Bu kitabın tüm hakları AFG Matbaa
TEOG HAZIRLIK sınıf. Musa BOR AFG Matbaa Yayıncılık Kağ. İnş. Ltd. Şti. Buca OSB, BEGOS 2. Bölge 3/20 Sk. No: 17 Buca-İZMİR Tel: 0.232.442 01 01-442 03 03 Faks: 442 06 60 Bu kitabın tüm hakları AFG Matbaa
KILAVUZ SORU ÇÖZÜMLERİ Matematik
 9. Çarpanlar ve Katlar b Dikdörtgenin alanı 4 cm olduğuna göre, kısa ve uzun kenarının çarpımı 4 cm 'dir. a. b = 4 a 6. Asal Çarpanlar A B C D E Yukarıda verilen asal çarpanlara ayırma işleminin son satırında
9. Çarpanlar ve Katlar b Dikdörtgenin alanı 4 cm olduğuna göre, kısa ve uzun kenarının çarpımı 4 cm 'dir. a. b = 4 a 6. Asal Çarpanlar A B C D E Yukarıda verilen asal çarpanlara ayırma işleminin son satırında
KARIŞIM PROBLEMLERĐ. Karışım Problemleri YILLAR 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 MATEMATĐK ĐM 8 8+ .100 =.
 YILLAR 02 03 04 0 06 07 08 09 11 ÖSS-YGS - 1 - - - - - - - - KARIŞIM PROBLEMLERĐ ve y maddelerinden oluşan bir da sırasıyla ve y miktar madde varsa bu daki maddesinin yüzdesi Saf madde dir + y Toplam kesrimizi
YILLAR 02 03 04 0 06 07 08 09 11 ÖSS-YGS - 1 - - - - - - - - KARIŞIM PROBLEMLERĐ ve y maddelerinden oluşan bir da sırasıyla ve y miktar madde varsa bu daki maddesinin yüzdesi Saf madde dir + y Toplam kesrimizi
Çarpanlar ve Katlar Föyü KAZANIMLAR
 1 Çarpanlar ve Katlar Föyü KAZANIMLAR Verilen pozitif sayıların pozitif tam sayı çarpanlarını bulur, pozitif tam sayıların pozitif tam sayı çarpanlarını üslü ifadelerin çarpımı şeklinde yazar. İki doğal
1 Çarpanlar ve Katlar Föyü KAZANIMLAR Verilen pozitif sayıların pozitif tam sayı çarpanlarını bulur, pozitif tam sayıların pozitif tam sayı çarpanlarını üslü ifadelerin çarpımı şeklinde yazar. İki doğal
4BÖLÜM. ASAL SAYILAR, BÖLÜNEBİLME ve ÇARPANLARA AYIRMA
 4BÖLÜM ASAL SAYILAR, BÖLÜNEBİLME ve ÇARPANLARA AYIRMA ASAL SAYILAR, BÖLÜNEBİLME ve ÇARPANLARA AYIRMA TEST 1 1) Aşağıdaki sayılardan kaç tanesi 80 sayısının çarpanıdır? 1,2,3,4,5,6,7,8,9,10,12,15,18,20,25,30,40,45,80
4BÖLÜM ASAL SAYILAR, BÖLÜNEBİLME ve ÇARPANLARA AYIRMA ASAL SAYILAR, BÖLÜNEBİLME ve ÇARPANLARA AYIRMA TEST 1 1) Aşağıdaki sayılardan kaç tanesi 80 sayısının çarpanıdır? 1,2,3,4,5,6,7,8,9,10,12,15,18,20,25,30,40,45,80
Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı. ALES / Sonbahar / Sayısal I / 16 Kasım Matematik Soruları ve Çözümleri 24 E) <
 Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı ALES / Sonbahar / Sayısal I / 6 Kasım 2008 Matematik Soruları ve Çözümleri. Aşağıdaki kesirlerin en büyüğü hangisidir? 0 A) B) 2 2 C) 3 2 D) 22 24 E)
Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı ALES / Sonbahar / Sayısal I / 6 Kasım 2008 Matematik Soruları ve Çözümleri. Aşağıdaki kesirlerin en büyüğü hangisidir? 0 A) B) 2 2 C) 3 2 D) 22 24 E)
AKADEMİK PERSONEL VE LİSANSÜSTÜ EĞİTİMİ GİRİŞ SINAVI (ALES)
 00000000001 AKADEMİK PERSONEL VE LİSANSÜSTÜ EĞİTİMİ GİRİŞ SINAVI (ALES) plam cevaplama süresi 150 akikadır. (,5 saat) SAYISAL BÖLÜM SAYISAL - 1 TESTİ Sınavın bu bölümünden alacağınız standart puan, Sayısal
00000000001 AKADEMİK PERSONEL VE LİSANSÜSTÜ EĞİTİMİ GİRİŞ SINAVI (ALES) plam cevaplama süresi 150 akikadır. (,5 saat) SAYISAL BÖLÜM SAYISAL - 1 TESTİ Sınavın bu bölümünden alacağınız standart puan, Sayısal
ÇARPANLAR VE KATLAR BİR DOĞAL SAYININ ÇARPANLARINI BULMA. 3. Aşağıda verilen sayıların çarpanlarından asal olanları belirleyelim.
 ÇARPANLAR VE KATLAR 8.1.1.1. Verilen pozitif tam sayıların çarpanlarını bulur; pozitif tam sayıları üslü ifade yada üslü ifadelerin çarpımı şeklinde yazar. BİR DOĞAL SAYININ ÇARPANLARINI BULMA Her doğal
ÇARPANLAR VE KATLAR 8.1.1.1. Verilen pozitif tam sayıların çarpanlarını bulur; pozitif tam sayıları üslü ifade yada üslü ifadelerin çarpımı şeklinde yazar. BİR DOĞAL SAYININ ÇARPANLARINI BULMA Her doğal
3. a 12 8 A) 4 2 B) 3 3 C) 4 D) 5 E) 6
 10,25 3,1 1. 0,5 0,2 işleminin sonuu kaçtır? ) 5 B) 5,5 C) 6 D) 6,5 E) 7 3. a 12 8 b 27 18 olduğuna göre, a b çarpımı kaçtır? ) 4 2 B) 3 3 C) 4 D) 5 E) 6 2. 2 3 6 4.6 2 3 3 2.3 işleminin sonuu kaçtır?
10,25 3,1 1. 0,5 0,2 işleminin sonuu kaçtır? ) 5 B) 5,5 C) 6 D) 6,5 E) 7 3. a 12 8 b 27 18 olduğuna göre, a b çarpımı kaçtır? ) 4 2 B) 3 3 C) 4 D) 5 E) 6 2. 2 3 6 4.6 2 3 3 2.3 işleminin sonuu kaçtır?
Bölünebilme Kuralları. Birler basamağındaki rakamı : {0, 2, 4, 6, 8} rakamlarından herhangi biri olan her sayı 2 ile tam bölünür.
 2 İLE BÖLÜNEBİLME: Birler basamağındaki rakamı : {0, 2, 4, 6, 8} rakamlarından herhangi biri olan her sayı 2 ile tam bölünür. Tek sayıların 2 ile bölümünden kalan 1 dir Dört basamaklı 729x sayısı 2 ile
2 İLE BÖLÜNEBİLME: Birler basamağındaki rakamı : {0, 2, 4, 6, 8} rakamlarından herhangi biri olan her sayı 2 ile tam bölünür. Tek sayıların 2 ile bölümünden kalan 1 dir Dört basamaklı 729x sayısı 2 ile
ÖZEL EGE LİSESİ 15. OKULLAR ARASI MATEMATİK YARIŞMASI 7. SINIF ELEME SINAVI SORULARI
 . a ve b pozitif tam sayılar olmak üzere a 2b+2 2 b+4 yukarıdaki bölme işleminde, a nın alabileceği en küçük değer kaçtır?. 25 soruluk bir sınavda her doğru cevaba 5 puan verilirken, her yanlış cevaptan
. a ve b pozitif tam sayılar olmak üzere a 2b+2 2 b+4 yukarıdaki bölme işleminde, a nın alabileceği en küçük değer kaçtır?. 25 soruluk bir sınavda her doğru cevaba 5 puan verilirken, her yanlış cevaptan
Kazanım: Doğal sayıların kendisiyle tekrarlı çarpımlarını üslü nicelik olarak yazar. 5) 6.(2+3)-7= işleminin sonucu kaçtır? A) 22 B) 37 C) 8 D) 23
 Kazanım: Doğal sayıların kendisiyle tekrarlı çarpımlarını üslü nicelik olarak yazar. 1) Aşağıda verilen üslü ifadelerin açılımlarını yazınız? 5) 6.(2+3)-7= işleminin sonucu kaçtır? A) 22 B) 37 C) 8 D)
Kazanım: Doğal sayıların kendisiyle tekrarlı çarpımlarını üslü nicelik olarak yazar. 1) Aşağıda verilen üslü ifadelerin açılımlarını yazınız? 5) 6.(2+3)-7= işleminin sonucu kaçtır? A) 22 B) 37 C) 8 D)
1. BÖLÜM. 2. Aþaðýdaki þekillerden hangisinin d doðrusuna göre simetriði çizildiðinde, bir düzgün çokgen elde edilir? DD
 6. SINIF COÞMAYA SORULARI 1. BÖLÜM 3. DÝKKAT! Bu bölümde 1 den 10 a kadar puan deðeri 1,25 olan sorular vardýr. 1. 1 birim 1 birim Van Gölü nün haritasý yukarýda verilmiþtir. Haritada 1 birim uzunluk 19
6. SINIF COÞMAYA SORULARI 1. BÖLÜM 3. DÝKKAT! Bu bölümde 1 den 10 a kadar puan deðeri 1,25 olan sorular vardýr. 1. 1 birim 1 birim Van Gölü nün haritasý yukarýda verilmiþtir. Haritada 1 birim uzunluk 19
EN KÜÇÜK ORTAK KAT (EKOK) EKOK UYGULAMA SORULARI : 1) Aşağıda verilen sayıların EKOK'unu bulunuz.
 8.1.7 EN KÜÇÜK ORTAK KAT (EKOK) İki veya daha fazla sayma sayısının ortak katlarından en küçük olanına, bu sayıların En Küçük Ortak Katı olan EKOK u denir. 8.1.7 EKOK UYGULAMA SORULARI : 1) Aşağıda verilen
8.1.7 EN KÜÇÜK ORTAK KAT (EKOK) İki veya daha fazla sayma sayısının ortak katlarından en küçük olanına, bu sayıların En Küçük Ortak Katı olan EKOK u denir. 8.1.7 EKOK UYGULAMA SORULARI : 1) Aşağıda verilen
Konu Anlatımı Açık Uçlu Sorular Çoktan Seçmeli Sorular Doğru Yanlış Soruları Boşluk Doldurmalı Sorular Çıkmış Sorular
 Maths@bi 8 3.BÖLÜM Kareköklü Sayılar Konu Anlatımı Açık Uçlu Sorular Çoktan Seçmeli Sorular Doğru Yanlış Soruları Boşluk Doldurmalı Sorular Çıkmış Sorular Kerime ASKER-Abdullah ASKER Matematik Öğretmeni
Maths@bi 8 3.BÖLÜM Kareköklü Sayılar Konu Anlatımı Açık Uçlu Sorular Çoktan Seçmeli Sorular Doğru Yanlış Soruları Boşluk Doldurmalı Sorular Çıkmış Sorular Kerime ASKER-Abdullah ASKER Matematik Öğretmeni
Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı. ALES / Sonbahar / Sayısal II / 16 Kasım Matematik Soruları ve Çözümleri
 Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı ALES / Sonbahar / Sayısal II / 6 Kasım 008 Matematik Soruları ve Çözümleri. a 3 < 5 7 eşitsizliğini sağlayan en küçük a doğal sayısı kaçtır? A) 4 B)
Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı ALES / Sonbahar / Sayısal II / 6 Kasım 008 Matematik Soruları ve Çözümleri. a 3 < 5 7 eşitsizliğini sağlayan en küçük a doğal sayısı kaçtır? A) 4 B)
( ) FAKTÖRĐYEL YILLAR /LYS. Örnek( 4.)
 YILLAR 00 003 004 005 006 007 008 009 00 0 ÖSS-YGS - - - - 0/ - / /LYS FAKTÖRĐYEL Örnek( 4) 3)!! ) )! 4 )!? den n e kadar olan sayıların çarpımına n! denir n! 34(n-)n 0!!! 3! 3 6 4! 34 4 5!3450 Örnek(
YILLAR 00 003 004 005 006 007 008 009 00 0 ÖSS-YGS - - - - 0/ - / /LYS FAKTÖRĐYEL Örnek( 4) 3)!! ) )! 4 )!? den n e kadar olan sayıların çarpımına n! denir n! 34(n-)n 0!!! 3! 3 6 4! 34 4 5!3450 Örnek(
Problemler A 2-B 3-E 4-C 5-E 6-A 7-E 8-C
 Problemler 1 1. 5. 6. 2. 7. 3. 4. 8. 1-A 2-B 3-E 4-C 5-E 6-A 7-E 8-C Problemler 1 9. 12. - 13. soruları as ağıdaki bilgilere göre birbirinden 10. - 11. soruları as ağıdaki bilgilere göre birbirinden 12.
Problemler 1 1. 5. 6. 2. 7. 3. 4. 8. 1-A 2-B 3-E 4-C 5-E 6-A 7-E 8-C Problemler 1 9. 12. - 13. soruları as ağıdaki bilgilere göre birbirinden 10. - 11. soruları as ağıdaki bilgilere göre birbirinden 12.
EŞĐTSĐZLĐKLER MATEMATĐK ĐM. Eşitsizlikler YILLAR /LYS. 14) Özel olarak. x >x ÖZELLĐKLER.
 YILLAR 00 00 00 00 006 007 008 009 00 0 ÖSS-YGS - - - - - / - /LYS EŞĐTSĐZLĐKLER =y,,, y,,, < y y,,, > y,,, y (tarif et ) ÖZELLĐKLER ) > veya < 0
YILLAR 00 00 00 00 006 007 008 009 00 0 ÖSS-YGS - - - - - / - /LYS EŞĐTSĐZLĐKLER =y,,, y,,, < y y,,, > y,,, y (tarif et ) ÖZELLĐKLER ) > veya < 0
İSTANBUL İLİ İLKÖĞRETİM OKULLARI 4, 5, 6. SINIFLAR ARASI MATEMATİK OLİMPİYATI SORU KİTAPÇIĞI 13 NİSAN 2013 T.C İSTANBUL VALİLİĞİ ÖZEL AKASYA KOLEJİ
 İSTANBUL İLİ İLKÖĞRETİM OKULLARI 4, 5, 6. SINIFLAR ARASI MATEMATİK OLİMPİYATI SORU KİTAPÇIĞI 13 NİSAN 2013 T.C İSTANBUL VALİLİĞİ ÖZEL AKASYA KOLEJİ DİKKAT: 1. Soru kitapçıklarını kontrol ederek, baskı
İSTANBUL İLİ İLKÖĞRETİM OKULLARI 4, 5, 6. SINIFLAR ARASI MATEMATİK OLİMPİYATI SORU KİTAPÇIĞI 13 NİSAN 2013 T.C İSTANBUL VALİLİĞİ ÖZEL AKASYA KOLEJİ DİKKAT: 1. Soru kitapçıklarını kontrol ederek, baskı
İSTANBUL İLİ İLKÖĞRETİM OKULLARI 4, 5, 6. SINIFLAR ARASI MATEMATİK OLİMPİYATI SORU KİTAPÇIĞI 13 NİSAN 2013 T.C İSTANBUL VALİLİĞİ ÖZEL AKASYA KOLEJİ
 İSTANBUL İLİ İLKÖĞRETİM OKULLARI 4, 5, 6. SINIFLAR ARASI MATEMATİK OLİMPİYATI SORU KİTAPÇIĞI 13 NİSAN 2013 T.C İSTANBUL VALİLİĞİ ÖZEL AKASYA KOLEJİ DİKKAT: 1. Soru kitapçıklarını kontrol ederek, baskı
İSTANBUL İLİ İLKÖĞRETİM OKULLARI 4, 5, 6. SINIFLAR ARASI MATEMATİK OLİMPİYATI SORU KİTAPÇIĞI 13 NİSAN 2013 T.C İSTANBUL VALİLİĞİ ÖZEL AKASYA KOLEJİ DİKKAT: 1. Soru kitapçıklarını kontrol ederek, baskı
