KILAVUZ SORU ÇÖZÜMLERİ Matematik
|
|
|
- Yeter Akbaş
- 5 yıl önce
- İzleme sayısı:
Transkript
1 9. Çarpanlar ve Katlar b Dikdörtgenin alanı 4 cm olduğuna göre, kısa ve uzun kenarının çarpımı 4 cm 'dir. a. b = 4 a 6. Asal Çarpanlar A B C D E Yukarıda verilen asal çarpanlara ayırma işleminin son satırında E sayısı 7'ye bölünerek sonuç bulunmuştur. Bu nedenle E sayısının değeri 7'dir. 7 E= 7 a ve b'nin tam sayı olduğu sorunun içerisinde belirtilmiş 4'ün çarpanları 4 a. b = şeklindedir. Dikdörtgenin çevresinin en fazla olmasını istiyorsak a ve b 'ye birbirine en uzak olan değerler olan ve 4 değerlerini veririz. D sayısı 'e bölünerek E sayısı yani 7 bulunmuştur. Bu nedenle D sayısı; D= 7. = D= bulunur. C sayısı 'e bölünerek D sayısı yani bulunmuş. Bu nedenle C sayısı; C=. = 0 C= 0 bulunur. cm B sayısı 'ye bölünerek C sayısı yani 0 bulunmuş. Bu nedenle B sayısı; B= 0. = 0 B= 0 bulunur. 4 cm Çevre =. (a + b) =.( + 4) = 0 cm Doğru yanıt A seçeneğidir. A sayısı 'ye bölünerek B sayısı yani 0 bulunmuş. Bu nedenle A sayısı; A= 0. = 40 A= 40 bulunur. A + B + C + D + E = = 777
2 Bir Sayıyı Üslü Biçimde İfade Etme Ebob sayısının asal çarpanlarına ayrılmış hâli EBOB (0, 40) EBOB (0, 40) = 4. = şeklindedir. 70 sayısının asal çarpanlarına ayrılmış hâli.. 7 şeklindedir sayısının asal çarpanlarına ayrılmış hâli I. öncül doğrudur. EBOB(0, 90) EBOB(0, 90) =.. = 0 II. öncül doğrudur. EBOB (80, 40) şeklindedir. 9 sayısının asal çarpanlarına ayrılmış hâli. şeklindedir sayısı dışında tüm sayıların üslü ifadelerin çarpımı şeklinde yazılışı verilmiştir. EBOB (80, 40) =.. = 60 III. öncül doğrudur. EBOB (70,80) EBOB (70, 80) =.. = 90 IV. öncül yanlıştır.
3 Ekok 4. I numaralı kutuya yazılacak sayı 4 ve 60 sayısının EKOK'una eşittir IV numaralı kutuya yazılacak sayı 90 ve 80'in EKOK'una eşittir EKOK (90,80) = 4.. EKOK (4, 60) =.. A seçeneği doğrudur. = = 80 D seçeneği doğrudur. = = 70 II numaralı kutuya yazılacak. Sayı 4 ve 80 sayısının EKOK'una eşittir EBOB - EKOK KARMA EKOK (4,80) = 4.. B seçeneği doğrudur. = = 70 III numaralı kutuya yazılacak sayı 90 ve 60 sayılarının EKOK'una eşittir EBOB (00, 6) =. = 6 A seçeneği doğrudur. 7 EKOK (00, 6) =... 7 = 600 B seçeneği doğrudur. EKOK (90, 60) =.. = 80 C seçeneği yanlıştır. 4 sayısı 00 sayısının bölenidir. Ancak 6 sayısının böleni değildir. C seçeneği yanlıştır. Sayıların EBOB'u. olduğuna göre ortak asal bölenleri ve 'tür.
4 ?. EBOB Problemleri Bahçe 4 m EKOK Problemleri A seçeneğinde kartonun etrafına çizilecek çizgilerin arasındaki mesafenin eşit ve en fazla olabilmesi için 0 ve 4 sayılarının EBOB'u bulunur. 0 cm Bahçenin etrafına dikilecek ağaçların arasındaki mesafenin en fazla olması istenmektedir. Bu nedenle dikilecek ağaçlar arasındaki mesafenin her iki sayıyı birlikte bölebilen en büyük sayı yani iki sayının EBOB'u olmalıdır B seçeneğinde bahsedilen kare şeklindeki odanın, fayansların kenar uzunluğu olan 0 cm ve 4 cm'nin ortak katı olmalıdır. Odanın kenar uzunluğunun en az olması istendiğinden en küçük ortak kat yani EKOK bulunmalıdır. C seçeneğinde Ahmet bilyelerini onarlı ve on beşerli gruplara ayırabildiğine göre, Ahmet'in bilyelerinin sayısı 0 ve 'in katıdır. Bilyelerin en az kaç tane olduğu sorulduğundan 0 ve 'in en küçük ortak katı yani EKOK'u bulunur. 0 L ve 4 L meyve suyunu dolduracağımız en büyük hacimli şişeler 0 ve 4'in EBOB'U kadar olmalıdır. EBOB(0, 4) =. = 6 Ağaçlar arasındaki mesafe 6 cm olmalıdır. toplamda 8 ağaç gereklidir. 6 cm 6 cm Bahçe 6 cm 6 cm 6 cm 6 cm 6 cm 6 cm 6 cm 4 cm Aralarında Asal Sayılar Asal sayılar bir ve kendisinden başka böleni olmayan sayılardır. Aralarında asal sayılar ise 'den başka ortak böleni olmayan sayılardır. İki farklı asal sayı aynı zamanda aralarında asaldır. Örneğin ile 7 veya ile 7 gibi bu nedenle I. öncül doğrudur. Aralarında asal sayıların 'den başka böleni yoktur. Bu nedenle II. öncül doğrudur. III. öncül doğrudur çünkü ve sayıları aralarında asaldır. Bu sayıların birisi tek diğeri ise çift sayıdır. IV. öncül yanlıştır. Sayıların ikiside çift olursa sayılar ortak olarak 'ye bölünebilir.
5 Aralarında Asal Sayıların Ebob ve Ekokları A seçeneğinde x yerine, y yerine sayısı yazıldığında ifade yanlış olur. B seçeneğindeki ifade tamamen yanlıştır. Aralarında asal sayıların EBOB'u 'dir. Dolayısıyla aralarında asal sayıların çarpımları ekoklarına eşit olur. Bu nedenle C seçeneği doğrudur. D seçeneğinde x yerine, y yerine sayısı yazıldığında ifade yanlış olur. Pozitif Üs = eşitliğinden a = olur ve a= 'dir. 4 = 7 eşitliğinden 7 b = 7 olur ve b= 'tür. b a ifadesi = 9 olur. Doğru yanıt A seçeneğidir. Pozitif Sayıların Negatif Kuvvetleri 8. Sayının üssü negatif ise sayı ters çevrilerek üssü pozitif yapılır. I. sayısı ( ) şeklinde yazılabilir negatif kuvvette tabandaki sayı ters çevrilerek üssü pozitif yapılabilir. Yani ( ) = ( ) şeklinde yazılabilir. Üslü Sayılar Üslü Biçimde İfade Etme = 8 4 olduğu için x = 8 ve y= 4.. = olduğu için a= ve b= A) x a = 8 olur. x a = doğrudur. B) y a = 4 olur. y a = doğrudur. C) b x = 8 olur. b x = doğrudur. D) y a = 4 olur. y a = yanlış olur. 8 tane ( ) =.. = 7 I. öncül doğrudur. II. 4 sayısında ( 4 ) = ( 4 ) olur. ( 4 ) = 4. 4 = olduğundan, II. öncülün 6 4 = yanlış olduğu görülür. 8 III. Farklı bir tarzda çözümlemek gerekirse a = a veya b = b olduğundan 6 = = III. öncül yanlıştır IV. 9 = = olduğundan IV. öncülde 9 8 doğrudur.
6 Negatif Sayıların Kuvvetleri Çözümleme. 60,0 sayısını çözümlersek 6. Negatif bir sayının çift kuvvetleri pozitif, tek kuvvetlerinin negatif olduğunu hatırlayalım. ( ) çift = + ve ( ) tek = Fakat; ( ) = + 9 iken = 9 olduğunu unutmayalım incelemek gerekirse ( ) = ( ).( ); kuvvetimiz parantezin üstünde olduğundan parantezli bir şekilde ( )'ü almalıyız. =. için ise kuvvetimiz sadece sayının 'ün üstünde olduğundan, işaretimiz işlemin başında kalır sayımız ise kendisiyle tekrarlı kuvveti kadar çarpılır. 60,0 = 6 x 00 + x x + 0 x 0, + x 0, 0 = 6 x 0 + x 0 + x 0 olduğu görülür. 60,0 = (6.0 x ) + (.0 y ) + (.0 z ) x=, y= ve z= yerlerine koyarsak A= ifadesini çözümleyebiliriz. Düzenlediğimizde; A= elde edilir. Buradan; A= ,0 = 0,0 0,0 ifadesini elde ederiz. A) ( 8) = ( 8). ( 8) = + 64 görüldüğü gibi kuvvetimiz çift olduğundan sonuç pozitif çıktı. A seçeneği yanlıştır. B) ( ) kuvvetimiz tek sayı olduğundan sonucun negatif olması gerekir. ( ) B seçeneği yanlıştır. C) ( 4) kuvvetimiz tek olduğundan sonuç negatiftir.şimdi inceleyelim. ( 4) = ( 4).( 4).( 4)= 64 C seçeneği doğrudur. D) ( ) kuvvetimiz tek sonuç negatif olmalı fakat incelediğimiz ( ) = ( ) negatif kuvvet özelliği uygulanır. D seçeneği yanlış olduğu anlaşılır. Üslü İfadelerle İlgili Temel Kurallar Çarpma 0. Bir örnek ile incelersek. = (.. ). (. ) 'nin kere tekrarlı çarpımını görürüz.. = (üslerin toplandığını anlayabiliriz.) Burada bir kaç örnek ile. = + = 4. 4 = 4 +( ) = 4 olur. a x. a y = a x+y denilebilir. Şimdi verilen seçenekleri incelersek A). = +( ) = doğrudur. B) 4. = ( 4)+( ) = 6 doğrudur. C) 4. = 4+ = 6 olduğundan C seçeneği yanlıştır. D) ( ) 4.( ) = ( ) 4+ =( ) 6 doğrudur.
7 Çarpma 0. a x.b x = (a. b) x bir örnek ile inceleyelim.. =... =. = olduğundan. =(.) = diyebiliriz. Tabanları farklı üsleri aynı sayılar çarpılırken tabanlar çarpılır, ortak üs ise çarpıma üs olarak yazılır. a x.b x = (a.b) x olur Şimdi öncüllerimizi inceleyelim. I. x. x = (.) x = x doğrudur. Bölme 9. I. öncülümüzü incelersek; 9 : = 9 = = 7 olur. Tabanları aynı üslü sayıları bölerken payın üssünden paydanın üssü çıkarılır, bulunan sonuç tabana üs olarak yazılır. a x a = y ax y I. öncülümüzü incelerkende gördüğümüz gibi 9 = 9 = 7 doğrudur. II. 7 k. k = (7.) k = k olduğundan II. öncülümüz yanlıştır. II. = ( ) ( ) = + = olması gerekir. III. a. a = (.) a = 6 a doğrudur. IV. 4 y = (.) y = y. y 4 y = (.8) y = y. 8 y veya 4 y =(4.6) y = 4 y.6 y olabilir. Bu yüzden 4 y = 4 y.8 y IV. öncülümüz yanlıştır. V. b = (.6) b = b.6 b veya b = (.4) b = b.4 b verilen öncülümüzün doğru olduğunu görürüz. : = yanlıştır. III. 6 = 6 = 4 olması gerekir. 6 : = 4 yanlıştır. IV. = 4 ( ) ( 4) = +4 = doğrudur. II. ve IV öncüller yanlıştır.
8 9. 6 x = 8 eşitliğinde içler dışlar çarpımı yaparsak Negatif Üs 6 x. 6 6 = 8. 8 eşitliğini elde ederiz. Tabanlar aynı ise Üsler aynı ise üsler toplanır. tabanlar çarpılır. (a x.a y = a x+y ) (a x.b x = (a.b) x ) 6 x+6 = (.) 8 6 x+6 = 6 8 eşitliğinde üsler aynı olmak zorundadır. x + 6 = 8 x= olur. 0. Tabanlarımız; ve kuvvet (üs)'lerimiz; 4, ve olacağından I. öncülümüz II. öncülümüz III. öncülümüz 4 IV. öncülümüz B) seçeneği yanlıştır. Bir bilgimizi daha hatırlayarak seçenekleri inceleyelim. Tabanları farklı, üsleri aynı olan sayıları bölerken tabanlar bölünür, ortak üs bölümün üssü olarak yazılır. a x b = ( a x b )x ; (a 0, b 0) 6 x A) = ( 6 x )x = X ; ( x=, bulunmuştur) x = = 4 doğrudur. x B) 4 = ( x 4 )x = X ; x = = 9 B seçeneği yanlıştır. C) x = ( x )x = X ; x = = 9 doğrudur. D) 9 x 6 x = ( 9 6 )x = ( )x ; ( )x = ( ) = 9 4 doğrudur. Negatif üs mantığını anlamaya çalışalım. =.. =. = = Her adımda sonucun 'e 0 = = =. = = bölündüğüni görebiliyoruz. Her adımda 'e bölmeye devam ediyoruz.
9 Üslü İfadenin Üssü O. Kuvvet 9. I. öncül için 6. 6 = Bir örnek ile inceleyelim. ( ) = ( ). ( ). ( ) (En dıştaki kuvvetimiz 'ü kullandık.) = ++ (Tabanlar aynı ise üsler toplanır.) a x.a y = a x+y ) = 6 ( ) = 6 olduğunu gördük. Bir üslü sayının üssü alınırken üsler çarpılır. (a x ) y =a x.y Üslü sayılar çarpılırken tabanlar aynı ise üsler toplanır. I adım doğrudur. II. öncül için 68 8 = 8 üslü sayılar bölünürken üsler aynı ise tabanları bölünür. II adım doğrudur. III. öncül için 8. 6 = I. öncülde olduğu gibi doğru yapılmıştır. IV. öncül için ( ) 0 = 4 0 = olması gerekirken yanlış sonuç bulunmuştur. B) işleminin sonucunu yanlış bulmuştur. DİKKAT!!! Negatif bir sayının çift kuvveti pozitif ( ) çift = + Negatif bir sayının tek kuvveti negatif ( ) tek = olur. ( ) 4 = parantezin dışındaki çift kuvvet sonucu (+) pozitif hâle getirdi. ( 4 ) = parantezin dışındaki tek kuvvet () sonucu negatif olarak bıraktı. Öncüllerimizi incelersek; ( x ) y = xy = x.y = olması ( a ) b = a.b = 4 a.b = 4 olması gerekir. I. x= ve y=4 ; x.y= olabilir. II. III. IV. D) I,II ve IV olur. a= 8 ve b=; a.b= 4 olabilir. x= ve y=8 ; x.y= 6 olamaz. a= 6 ve y= 4; a için 4'ün çarpanlarında 6, y için 'nin çarpanlarında 4 olduğundan a=6 ve y=4 olabilir. 8. Seçeneği bu soru için doğru cevaptır. 0'un Kuvvetleri A) 6,.0 8 = ( 6, 0 ).(08 x0) = 6,.0 9 doğru sonuca ulaşırız. B),8.0 6 = (,8 x0).( ) = 8,.0 7 doğru sonuca ulaşırız. C), = (,6 x00). ( ) = 6,.0 8 doğru sonuca ulaşırız. D),6.0 6 = (,6 x 0). ( ) =,6.0 doğru sonuca ulaşırız. Çözümlerinde anlaşılabileceği gibi a,bcd x 0 4 = ab, cd x 0 = abc,d x 0 Virgül bir basamak sola kaydırılında 0'un kuvvetinin arttığını, virgül bir basamak sağa kaydırılınca 0'un kuvvetinin azalacığını fark ettiniz mi?
10 Çok Küçük Sayılar 0. 0, virgül sağa kaydırılacağından 0'un kuvveti azalacak. 0, = 0, olacağından a= 6 bulunur. Çok Büyük Sayılar = 400 x 0 7 = 4 x 0 9 olacağından x= 7 ve y=4 olur. y x = 4 7 = 6 bulunur. Doğru yanıt A seçeneğidir. 0, = 96.0 olacağından b=96 bulunur. a+b= =90 Doğru yanıt A seçeneğidir. Çok Büyük Sayıların Bilimsel Gösterimi 9. a.0n, a < 0 ve n Z ifadesinin bilimsel gösterim olduğunu biliyoruz km =, x 0 8 km olarak bilimsel gösterimi D seçeneğinde doğru verilmiştir. 9. K, L, M ve N sayılarını karşılaştırabilmek için 0'un kuvvetlerini eşitlemeliyiz. L ve M'nin üslerini 6 yapabiliriz. L=,7 x 0 = 7 x 0 6 M= 0,6 x 0 =,6 x 0 6 Buradan 0,8.0 6,.0 6, N K M L Çok Büyük ve Çok Küçük Sayıları Karşılaştırma 0. 6,4 milyon = , = olacağından 6,4 milyon = 6, ,00004 = 4 x 0 6 olacağından 4 x 0 6 > 4, x = ,8 milyar = olacağından >,8 milyar Doğru yanıt A seçeneğidir.
11 Kareköklü Sayılar Tam Kare Doğal Sayılar. Bir doğal sayının karesi olan sayılar, tam kare sayılardır. Bu tanıma göre;,4,9,6,... gibi sayılar tam kare sayılardır. 4, 6, 4, 6, 4, 6. Karesel Bölgenin Alanı ile Kenarı 6 cm 6 cm 8 cm 'den küçük birler basamağında 6 rakamı bulunan tam kare sayı buluruz. Bu sorumuzda öncelikle telin uzunluğunu bulmamız gerekir. Karesel bölgelerin alanları ile bu karesel bölgelerin birer kenarı arasında ilişki; alanlarının karekökleri bir kenar uzunluğuna eşittir. 6 cm olan karenin, bir kenar uzunluğu; ò6 = 4 cm, 6 cm olan karenin, bir kenar uzunluğu; ò6 = 6 cm, 8 cm olan karenin, bir kenar uzunluğu; ò8 = 9 cm olacağından, Telin uzunluğu; karelerin çevre uzunlukları toplamına; = 76 cm'dir. 9 9 Ç= 79 cm 9 9 Telimiz ile oluşturabilceğimiz en büyük karenin çevresi 76 cm ve bir kenarının uzunluğu 9 cm olur. Alanını hesaplamımız gerekirse; A= 9 =6 cm 'dir.
12 Cebir Karoları ve Birim Kareler 6. Alanı br olan cebir karosu; br br br şekildeki gibidir. Elimizde bulunan 0 adet cebir karosu'na A) adet cebir karosu eklenirse, br alana sahip, kenar uzunluğu br olan bir kare oluşturulabilir. B) 4 adet cebir karosu çıkarılırsa; 6 br alana sahip, kenar uzunluğu 4 br olan bir kare oluşturulabilir. C) 6 adet cebir karosu eklenirse; 6 br alana sahip, kenar uzunluğu 6 br olan bir kare oluşturulabilir. 4. Tam Kare Doğal Sayıların Karekökleri A) ( 6) = ( 6). ( 6) = 6 6 = 6 x 6 = 6 6 ve 6 karesi 6'dır. B) ó96 = 4 ifadesi doğrudur. C) Hiç bir tam sayının karesi negatif bir sayı olamaz. Negatif bir sayının da karekökü alınamaz. ó 44 sayısının karekökü alınamaz. D) 8 adet cebir karosu çıkarılırsa; br alana sahip cebir karolar ile kenar uzunluğu 6 br olan bir kare oluşturulamaz. D) ( 0) = ( 0). ( 0) = 00 0 = 0 x 0 = 00 doğrudur. 0. Alanları 8 br, 49 br ve br olan karelerin kenarlarının uzunlukları; ò8 = 9 br Tam Kare Olmayan Sayıların Kareköklerini Tahmin Etme. Şekilde 0 ile 'in yerlerine ò49 = 7 br ó00 ó ò = br, olarak bulunur. Şekilleri incelediğimizde; D seçeneğinde verilen karelerin kenar uzunluklarının doğru olduğu görülür. ó00 ile ó 'i kullanırsak ; " " ifadesinin ó00 'den büyük ve ó'den küçük olduğu anlaşılır. Bu durumda A, C ve D seçenekleri elenir.
13 Rasyonel ve İrrasyonel Sayılar 4. Şekilde de görüldüğü gibi; sayma sayılar kümesi doğal sayıların, doğal sayılar kümesi tam sayıların, tam sayılar kümesi rasyonel sayıların ve rasyonel sayılarda gerçek sayıların alt kümesidir. Kareköklü Bir Sayıyı añb Şeklinde Yazma 6. A ve B doğal sayılarını seçeneklerde verilenlere göre inceleyelim. A) ó00 ifadesinin kat sayısı görünmeyen "" olabilir. AñB = ó00; 6. Devirli Ondalık Gösterimler A),4 = B),0 = = = 8 90 olacağından hatalı ifade B seçeneğinde verilmiştir. 9 C),9 = = 7 ifadesi doğrudur. 9 9 D) 0,4 = 4 9 ifadesi doğrudur. Kareköklü Sayılarda Çarpma ve Bölme İşlemi "A en küçük 'dir." ifadesi doğrudur. B) B'nin en küçük değerinin 0 olabilmesini incelersek ó00 = 0.0 olması gerekir. 0, tam kare bir sayı olmadığından kare kökün dışına çıkamaz. "B 'nin en küçük değeri 0'dur" ifadesi yanlıştır. C) A'nın en büyük değeri 0 olabilmesini incelersek; 00 = 00. ifadesini kullanarak ó00 = 00. = 0ñ elde ederiz. " A'nın en büyük değeri 0 'dur." İfadesi doğrudur. D) AñB = ó00 eşitliğinde; "B'nin en büyük değeri 00'dür." İfadesi doğrudur. 7. Kareköklü sayılarda çarpma ve bölme işlemi yapılırken karekök içerisinde bulunan sayılar kendi aralarında, kat sayılarında kendi aralarında çarpılıp bölüneceğini hatırlayalım. añx añx. bñy = a.b óx.y ve bñy = a b x y añb Şeklindeki İfadede Katsayıyı Kök içine Alma A) ñ (ñ ) = ñ.ñ ñ. = 6 ñ doğrudur. 6ò8 B) ñ6 = 6. 8 = ñ doğrudur. 6 C) ñ.ñ =. = 6 olması gerekir. Hatalı sonuç verilmiştir. D) 6ò ñ7 = 6 7 = ñ doğrudur. 9. ò =. = 4. = ó 9ñ = 9. = 8. = ó40 ò8 =.8 = 9.8 = ó4 7ñ6 = 7.6 = 49.6 = ó94 olacağından D seçeneği ó7 sayısı boş kutulara gelemez.
14 Kareköklü Sayılarda Sıralama 7. Kareköklü sayıları sıralarken kök dışındaki sayıları kök içine almalıyız. ñ = ò ve 4ñ = ò48 ò7 < ò < ò8 < ò48 şeklinde sıralayabiliriz. 8. Ondalık Kesirlerin Kareköklerini Belirleme A b ò7 < ñ < ò8 < 4ñ seçeneği doğrudur. A= a. b olduğundan a Köklü Sayıyı Doğal Sayı Yapma,6 = ó,69. b eşitliğini kullanmalıyız. 4. ò40. a = 4.0. a = ò0. a ò0. a ifadesi tam sayı olması için, a=ò0'dur. ò7. b =..b = ñ.b ñ.b ifadesi tam sayı olması için, b=ñ'dür. a ve b'nin en küçük değerleri bulunduğuna göre a. b = ò0. ñ = ò0 olur. Kareköklü Sayılarla Toplama ve Çıkarma 6 00 = = 0. b 6 00 b 0 00.b = 60 b=,. b C seçeneğinde verilen kareköklü ifade incelenecek olursa, = ó,44 = = =, olduğu görülür. 0. AB uzunluğu, alanı 8 cm olan karenin bir kenarıdır. IABI= ò8 = 9. = ñ olur. BC ve CD uzunluğu, alanı 0 cm olan karenin birer kenarlarıdır. IBCI = ICDI = ò0 =. = ñ olur. DE ve EF uzunluğu, alanı 00cm olan karenin birer kenarıdır. IDEI = IEFI = ó00 = 00. = 0ñ olur. Toplam yürünen yol; IABI + IBCI + ICDI + IDEI + IEFI olacağından ñ + ñ + ñ + 0ñ +0ñ = ñ olur.
12-A. Sayılar - 1 TEST
 -A TEST Sayılar -. Birbirinden farklı beş pozitif tam sayının toplamı 0 dur. Bu sayılardan sadece ikisi den büyüktür. Bu sayılardan üç tanesi çift sayıdır. Buna göre bu sayılardan en büyüğü en çok kaç
-A TEST Sayılar -. Birbirinden farklı beş pozitif tam sayının toplamı 0 dur. Bu sayılardan sadece ikisi den büyüktür. Bu sayılardan üç tanesi çift sayıdır. Buna göre bu sayılardan en büyüğü en çok kaç
ÇARPANLAR VE KATLAR I sayısının asal çarpanlarına ayrılmış hâli aşağıdakilerden A) B) C) D)
 8. Sınıf MATEMATİK ÇARPANLAR VE KATLAR I. Aşağıdakilerden hangisi 6 nın çarpanlarından biridir? A) 3 B) 6 C) 8 D) TEST. 360 sayısının asal çarpanlarına ayrılmış hâli aşağıdakilerden hangisidir? A) 3. 3.
8. Sınıf MATEMATİK ÇARPANLAR VE KATLAR I. Aşağıdakilerden hangisi 6 nın çarpanlarından biridir? A) 3 B) 6 C) 8 D) TEST. 360 sayısının asal çarpanlarına ayrılmış hâli aşağıdakilerden hangisidir? A) 3. 3.
MATEMATİK DERSİ UZAKTAN EĞİTİM DERS NOTLARI 3. HAFTA
 MATEMATİK DERSİ UZAKTAN EĞİTİM DERS NOTLARI 3. HAFTA 3. Ondalık Sayılarda İşlemler: Toplama - Çıkarma: Ondalık kesirler toplanırken, virgüller alt alta gelecek şekilde yazılır ve doğal sayılarda toplama-çıkarma
MATEMATİK DERSİ UZAKTAN EĞİTİM DERS NOTLARI 3. HAFTA 3. Ondalık Sayılarda İşlemler: Toplama - Çıkarma: Ondalık kesirler toplanırken, virgüller alt alta gelecek şekilde yazılır ve doğal sayılarda toplama-çıkarma
ÇARPANLAR VE KATLAR. Başarı Başaracağım Diye Başlayanındır. 1
 ÇARPANLAR VE KATLAR Başarı Başaracağım Diye Başlayanındır. 1 ÖRNEK 1 48 sayısının çarpanlarını bulalım. 1.Gökkuşağı yöntemi 48 sayısının çarpanlarını küçükten büyüğe sıralayarak eşleştiriniz. 48 çarpanlarını
ÇARPANLAR VE KATLAR Başarı Başaracağım Diye Başlayanındır. 1 ÖRNEK 1 48 sayısının çarpanlarını bulalım. 1.Gökkuşağı yöntemi 48 sayısının çarpanlarını küçükten büyüğe sıralayarak eşleştiriniz. 48 çarpanlarını
Mustafa Sezer PEHLİVAN. Yüksek İhtisas Üniversitesi Beslenme ve Diyetetik Bölümü
 * Yüksek İhtisas Üniversitesi Beslenme ve Diyetetik Bölümü SAYILAR Doğal Sayılar, Tam Sayılar, Rasyonel Sayılar, N={0,1,2,3,,n, } Z={,-3,-2,-1,0,1,2,3, } Q={p/q: p,q Z ve q 0} İrrasyonel Sayılar, I= {p/q
* Yüksek İhtisas Üniversitesi Beslenme ve Diyetetik Bölümü SAYILAR Doğal Sayılar, Tam Sayılar, Rasyonel Sayılar, N={0,1,2,3,,n, } Z={,-3,-2,-1,0,1,2,3, } Q={p/q: p,q Z ve q 0} İrrasyonel Sayılar, I= {p/q
8. SINIF MATEMATiK KAREKÖKLÜ SAYILAR
 0 8. SINIF MATEMATiK KAREKÖKLÜ SAYILAR KAREKÖKLÜ SAYI KAVRAMI Karekök ile gösterilir. karekökünün içi negatif bir sayıya eşit olamaz. ÖR: Aşağıda verilen eşitliklere göre x lerin alabileceği değerleri
0 8. SINIF MATEMATiK KAREKÖKLÜ SAYILAR KAREKÖKLÜ SAYI KAVRAMI Karekök ile gösterilir. karekökünün içi negatif bir sayıya eşit olamaz. ÖR: Aşağıda verilen eşitliklere göre x lerin alabileceği değerleri
EBOB - EKOK EBOB VE EKOK UN BULUNMASI. 2. Yol: En Büyük Ortak Bölen (Ebob) En Küçük Ortak Kat (Ekok) www.unkapani.com.tr. 1. Yol:
 EBOB - EKOK En Büyük Ortak Bölen (Ebob) İki veya daha fazla pozitif tamsayıyı aynı anda bölen pozitif tamsayıların en büyüğüne bu sayıların en büyük ortak böleni denir ve kısaca Ebob ile gösterilir. Örneğin,
EBOB - EKOK En Büyük Ortak Bölen (Ebob) İki veya daha fazla pozitif tamsayıyı aynı anda bölen pozitif tamsayıların en büyüğüne bu sayıların en büyük ortak böleni denir ve kısaca Ebob ile gösterilir. Örneğin,
1. BÖLÜM Mantık BÖLÜM Sayılar BÖLÜM Rasyonel Sayılar BÖLÜM I. Dereceden Denklemler ve Eşitsizlikler
 ORGANİZASYON ŞEMASI 1. BÖLÜM Mantık... 7. BÖLÜM Sayılar... 13 3. BÖLÜM Rasyonel Sayılar... 93 4. BÖLÜM I. Dereceden Denklemler ve Eşitsizlikler... 103 5. BÖLÜM Mutlak Değer... 113 6. BÖLÜM Çarpanlara Ayırma...
ORGANİZASYON ŞEMASI 1. BÖLÜM Mantık... 7. BÖLÜM Sayılar... 13 3. BÖLÜM Rasyonel Sayılar... 93 4. BÖLÜM I. Dereceden Denklemler ve Eşitsizlikler... 103 5. BÖLÜM Mutlak Değer... 113 6. BÖLÜM Çarpanlara Ayırma...
8.Sınıf MATEMATİK. Çarpanlar ve Katlar Konu Testi. Test sayısının tek bölenlerinin sayısı aşağıdakilerden
 Çarpanlar ve Katlar Konu Testi MATEMATİK 8.Sınıf Test-01 1. I. 1, her sayının bölenidir. II. 2, asal bir çarpandır. III. Her sayı kendisinin bir çarpanıdır. IV. Bir sayının çarpanları, aynı zamanda o sayının
Çarpanlar ve Katlar Konu Testi MATEMATİK 8.Sınıf Test-01 1. I. 1, her sayının bölenidir. II. 2, asal bir çarpandır. III. Her sayı kendisinin bir çarpanıdır. IV. Bir sayının çarpanları, aynı zamanda o sayının
Konu Anlatımı Açık Uçlu Sorular Çoktan Seçmeli Sorular Doğru Yanlış Soruları Boşluk Doldurmalı Sorular Çıkmış Sorular
 Maths@bi 8 3.BÖLÜM Kareköklü Sayılar Konu Anlatımı Açık Uçlu Sorular Çoktan Seçmeli Sorular Doğru Yanlış Soruları Boşluk Doldurmalı Sorular Çıkmış Sorular Kerime ASKER-Abdullah ASKER Matematik Öğretmeni
Maths@bi 8 3.BÖLÜM Kareköklü Sayılar Konu Anlatımı Açık Uçlu Sorular Çoktan Seçmeli Sorular Doğru Yanlış Soruları Boşluk Doldurmalı Sorular Çıkmış Sorular Kerime ASKER-Abdullah ASKER Matematik Öğretmeni
KC00-SS.08YT05. Kolay Temel Matematik. Üniversite Haz rl k 1. 8 ( 3 + 2) 6. 3! 3 ( 3 3)": ( 3) x = 3 ve y = 2 3. ( 5) + ( 7) (+2) + 4
 Üniversite Haz rl k Sözcükte Do al ve Say lar Söz Öbeklerinde ve Tam Say lar Anlam - I - I Kolay Temel Matematik. 8 ( + ) A) 7 B) 8 C) 9 D) 0 E) 6.! ( )": ( ) A) B) 0 C) D) E). 7. + 5 A) 6 B) 7 C) 8 D)
Üniversite Haz rl k Sözcükte Do al ve Say lar Söz Öbeklerinde ve Tam Say lar Anlam - I - I Kolay Temel Matematik. 8 ( + ) A) 7 B) 8 C) 9 D) 0 E) 6.! ( )": ( ) A) B) 0 C) D) E). 7. + 5 A) 6 B) 7 C) 8 D)
MATEMATİK ÜSLÜ SAYILAR. Tam Sayıların Tam Sayı Kuvveti. Üslü sayı, bir sayının kendisi ile tekrarlı çarpımıdır.
 Kazanım Tam sayıların tam sayı kuvvetlerini belirler. MATEMATİK KAZANIM FÖYÜ- Tam Sayıların Tam Sayı Kuvveti.Adım..Adım...Adım Yanda verilen örüntünüyü 6.Adıma kadar ilerletiniz. HATIRLA Üslü sayı, bir
Kazanım Tam sayıların tam sayı kuvvetlerini belirler. MATEMATİK KAZANIM FÖYÜ- Tam Sayıların Tam Sayı Kuvveti.Adım..Adım...Adım Yanda verilen örüntünüyü 6.Adıma kadar ilerletiniz. HATIRLA Üslü sayı, bir
Atatürk Anadolu. Temel Kavramlar Üzerine Kısa Çalışmalar
 Atatürk Anadolu Lisesi M A T E M A T İ K Temel Kavramlar Üzerine Kısa Çalışmalar KONYA \ SELÇUKLU 01 MATEMATİK 1. TEMEL KAVRAMLAR 1.1. RAKAM Sayıların yazılmasında kullanılan sembollere rakam denir. Onluk
Atatürk Anadolu Lisesi M A T E M A T İ K Temel Kavramlar Üzerine Kısa Çalışmalar KONYA \ SELÇUKLU 01 MATEMATİK 1. TEMEL KAVRAMLAR 1.1. RAKAM Sayıların yazılmasında kullanılan sembollere rakam denir. Onluk
SAYILAR SAYI KÜMELERİ
 SAYILAR SAYI KÜMELERİ 1.Sayma Sayıları Kümesi: S=N =1,2,3,... 2. Doğal Sayılar Kümesi : N=0,1,2,... 3. Tamsayılar Kümesi : Z=..., 2, 1,0,1,2,... Sıfırın sağında bulunan 1,2,3,. tamsayılarına pozitif tamsayılar
SAYILAR SAYI KÜMELERİ 1.Sayma Sayıları Kümesi: S=N =1,2,3,... 2. Doğal Sayılar Kümesi : N=0,1,2,... 3. Tamsayılar Kümesi : Z=..., 2, 1,0,1,2,... Sıfırın sağında bulunan 1,2,3,. tamsayılarına pozitif tamsayılar
ÜSLÜ SAYILAR. AMAÇ 1: 6 ve 7. Sınıflarda görmüş olduğumuz üslü ifadelerdeki temel kavramları hatırlama
 AMAÇ 1: 6 ve 7. Sınıflarda görmüş olduğumuz üslü ifadelerdeki temel kavramları hatırlama KURAL: Bir sayının belli bir sayıda yan yana çarpımının kolay yoldan gösterimine üslü sayılar denir. Örneğin 5 sayısının
AMAÇ 1: 6 ve 7. Sınıflarda görmüş olduğumuz üslü ifadelerdeki temel kavramları hatırlama KURAL: Bir sayının belli bir sayıda yan yana çarpımının kolay yoldan gösterimine üslü sayılar denir. Örneğin 5 sayısının
SAYILAR SAYI KÜMELERİ
 1 SAYILAR SAYI KÜMELERİ 1.Sayma Sayıları Kümesi: S=N =1,2,3,... 2. Doğal Sayılar Kümesi : N=0,1,2,... 3. Tamsayılar Kümesi : Z=..., 2, 1,0,1,2,... Sıfırın sağında bulunan 1,2,3,. tamsayılarına pozitif
1 SAYILAR SAYI KÜMELERİ 1.Sayma Sayıları Kümesi: S=N =1,2,3,... 2. Doğal Sayılar Kümesi : N=0,1,2,... 3. Tamsayılar Kümesi : Z=..., 2, 1,0,1,2,... Sıfırın sağında bulunan 1,2,3,. tamsayılarına pozitif
TAMSAYILAR. 9www.unkapani.com.tr. Z = {.., -3, -2, -1, 0, 1, 2, 3, } kümesinin her bir elemanına. a, b, c birer tamsayı olmak üzere, Burada,
 TAMSAYILAR Z = {.., -, -, -, 0,,,, } kümesinin her bir elemanına tamsayı denir. Burada, + Z = {,,,...} kümesine, pozitif tamsayılar kümesi denir. Z = {...,,,,} kümesine, negatif tamsayılar kümesi denir.
TAMSAYILAR Z = {.., -, -, -, 0,,,, } kümesinin her bir elemanına tamsayı denir. Burada, + Z = {,,,...} kümesine, pozitif tamsayılar kümesi denir. Z = {...,,,,} kümesine, negatif tamsayılar kümesi denir.
Buna göre, eşitliği yazılabilir. sayılara rasyonel sayılar denir ve Q ile gösterilir. , -, 2 2 = 1. sayıdır. 2, 3, 5 birer irrasyonel sayıdır.
 TEMEL KAVRAMLAR RAKAM Bir çokluk belirtmek için kullanılan sembollere rakam denir. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembolleri birer rakamdır. 2. TAMSAYILAR KÜMESİ Z = {..., -3, -2, -1, 0, 1, 2, 3, 4,... }
TEMEL KAVRAMLAR RAKAM Bir çokluk belirtmek için kullanılan sembollere rakam denir. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembolleri birer rakamdır. 2. TAMSAYILAR KÜMESİ Z = {..., -3, -2, -1, 0, 1, 2, 3, 4,... }
CK MTP21 AYRINTILAR. 5. Sınıf Matematik. Konu Tarama No
 5. Sınıf 01 Milyonlar 02 Örüntüler Adı 03 Doğal Sayılarla Toplama ve Çıkarma İşlemleri 04 Doğal Sayılarla Çarpma ve Bölme İşlemleri 05 Zihinden İşlemler, Bölme İşleminde Kalanı Yorumlama, Çarpma ve Bölme
5. Sınıf 01 Milyonlar 02 Örüntüler Adı 03 Doğal Sayılarla Toplama ve Çıkarma İşlemleri 04 Doğal Sayılarla Çarpma ve Bölme İşlemleri 05 Zihinden İşlemler, Bölme İşleminde Kalanı Yorumlama, Çarpma ve Bölme
MATEMATİK. Denemenin çözümlerine "www.zekakupuyayinlari.com.tr / portal" adresinden cevap anahtarlarına tıklayarak ulaşabilirsiniz.
 MATEMATİK Denemenin çözümlerine "www.zekakupuyayinlari.com.tr / portal" adresinden cevap anahtarlarına tıklayarak ulaşabilirsiniz. 1. DÖNEM DENEME 1 1. 4. 28 ve 35 sayılarının EKOK ve EBOB u kaçtır? EKOK
MATEMATİK Denemenin çözümlerine "www.zekakupuyayinlari.com.tr / portal" adresinden cevap anahtarlarına tıklayarak ulaşabilirsiniz. 1. DÖNEM DENEME 1 1. 4. 28 ve 35 sayılarının EKOK ve EBOB u kaçtır? EKOK
SINIF TEST. Üslü Sayılar A) 4 B) 5 C) 6 D) 7 A) - 5 B) - 4 C) 5 D) 7. sayısı aşağıdakilerden hangisine eşittir?
 8. SINIF. Üslü Sayılar - = T olduğuna göre T kaçtır? A) - B) - C) D) 7 TEST.. 0 - işleminin sonucu kaç basamaklı bir sayıdır? A) B) C) 6 D) 7. n =- 7 için n ifadesinin değeri kaçtır? A) - 8 B) - C) 8 D)
8. SINIF. Üslü Sayılar - = T olduğuna göre T kaçtır? A) - B) - C) D) 7 TEST.. 0 - işleminin sonucu kaç basamaklı bir sayıdır? A) B) C) 6 D) 7. n =- 7 için n ifadesinin değeri kaçtır? A) - 8 B) - C) 8 D)
ÇARPANLAR ve KATLAR ASAL SAYILAR. Örnek-2 : 17 ve 27 sayılarının asal sayı olup olmadığını inceleyelim.
 SINIF ÇARPANLAR ve KATLAR www.tayfunolcum.com 8.1.1.1: Verilen pozitif tam sayıların çarpanlarını bulur; pozitif tam sayıları üslü ifade ya da üslü ifadelerin çarpımı seklinde yazar. Çarpan ( bölen ) Her
SINIF ÇARPANLAR ve KATLAR www.tayfunolcum.com 8.1.1.1: Verilen pozitif tam sayıların çarpanlarını bulur; pozitif tam sayıları üslü ifade ya da üslü ifadelerin çarpımı seklinde yazar. Çarpan ( bölen ) Her
90 sayısının asal çarpanlarının toplamı kaçtır?
 90 sayısının asal çarpanlarının toplamı kaçtır? 2 a.3 b.5 c =750 olduğuna göre a+b-c kaçtır? 25 ve 41 i böldüğünde 1 kalanını veren en büyük doğal sayı kaçtır? 6 ve 8 e bölünebilen iki basamaklı en büyük
90 sayısının asal çarpanlarının toplamı kaçtır? 2 a.3 b.5 c =750 olduğuna göre a+b-c kaçtır? 25 ve 41 i böldüğünde 1 kalanını veren en büyük doğal sayı kaçtır? 6 ve 8 e bölünebilen iki basamaklı en büyük
ÜSLÜ SAYILAR SİBEL BAŞ AKDENİZ ÜNİVERSİTESİ EĞİTİM FAK. İLKÖĞRT. MAT. ÖĞRT. 2. SINIF
 ÜSLÜ SAYILAR SİBEL BAŞ 20120907010 AKDENİZ ÜNİVERSİTESİ EĞİTİM FAK. İLKÖĞRT. MAT. ÖĞRT. 2. SINIF 1 ANLATIMI ÜSLÜ SAYILAR KONU Üslü sayılar konu anlatımı içeriği; Üslü sayıların gösterimi, Negatif üslü
ÜSLÜ SAYILAR SİBEL BAŞ 20120907010 AKDENİZ ÜNİVERSİTESİ EĞİTİM FAK. İLKÖĞRT. MAT. ÖĞRT. 2. SINIF 1 ANLATIMI ÜSLÜ SAYILAR KONU Üslü sayılar konu anlatımı içeriği; Üslü sayıların gösterimi, Negatif üslü
2. ÜNİTE RASYONEL,ÜSLÜ VE KÖKLÜ SAYILAR
 2. ÜNİTE RASYONEL,ÜSLÜ VE KÖKLÜ SAYILAR KONULAR 1. RASYONEL SAYILAR 2. Kesir Çeşitleri 3. Kesirlerin Sadeleştirilmesi 4. Rasyonel Sayılarda Sıralama 5. Rasyonel Sayılarda İşlemler 6. ÜSLÜ İFADE 7. Üssün
2. ÜNİTE RASYONEL,ÜSLÜ VE KÖKLÜ SAYILAR KONULAR 1. RASYONEL SAYILAR 2. Kesir Çeşitleri 3. Kesirlerin Sadeleştirilmesi 4. Rasyonel Sayılarda Sıralama 5. Rasyonel Sayılarda İşlemler 6. ÜSLÜ İFADE 7. Üssün
ÜNİVERSİTEYE GİRİŞ SINAV SORULARI
 ÜNİVERSİTEYE GİRİŞ SINAV SORULARI 1. 1999 ÖSS a, b, c pozitif gerçel (reel) sayılar olmak üzere a+ b ifadesindeki her sayı 3 ile çarpılırsa aşağıdakilerden hangisi elde c edilir? 3 a+ b A) B) c a+ 3b C)
ÜNİVERSİTEYE GİRİŞ SINAV SORULARI 1. 1999 ÖSS a, b, c pozitif gerçel (reel) sayılar olmak üzere a+ b ifadesindeki her sayı 3 ile çarpılırsa aşağıdakilerden hangisi elde c edilir? 3 a+ b A) B) c a+ 3b C)
a = b ifadesine kareköklü ifade denir.
 KAREKÖKLÜ SAYILAR Rasyonel sayılar kümesi sayı ekseninde sık olmasına rağmen sayı eksenini tam dolduramamaktadır;çünkü sayı doğrusu üzerinde görüntüsü olduğu halde rasyonel olmayan sayılar da vardır. Karesi
KAREKÖKLÜ SAYILAR Rasyonel sayılar kümesi sayı ekseninde sık olmasına rağmen sayı eksenini tam dolduramamaktadır;çünkü sayı doğrusu üzerinde görüntüsü olduğu halde rasyonel olmayan sayılar da vardır. Karesi
Atatürk Anadolu. Bölme, Bölünebilme, Asal Sayılar, Obeb, Okek, Rasyonel Sayılar, Basit Eşitsizlikler ve Mutlak Değer Üzerine Kısa Çalışmalar
 Atatürk Anadolu Lisesi M A T E M A T İ K Bölme, Bölünebilme, Asal Sayılar, Obeb, Okek, Rasyonel Sayılar, Basit Eşitsizlikler ve Mutlak Değer Üzerine Kısa Çalışmalar KONYA \ SELÇUKLU 07 Bölme, Bölünebilme,
Atatürk Anadolu Lisesi M A T E M A T İ K Bölme, Bölünebilme, Asal Sayılar, Obeb, Okek, Rasyonel Sayılar, Basit Eşitsizlikler ve Mutlak Değer Üzerine Kısa Çalışmalar KONYA \ SELÇUKLU 07 Bölme, Bölünebilme,
Viyana İmam Hatip Lisesi Öğrenci Seçme Sınavı - Matematik
 Viyana İmam Hatip Lisesi Öğrenci Seçme Sınavı - Matematik 1. Ünite: Geometriden Olasılığa 1. Bölüm: Yansıyan ve Dönen Şekiller, Fraktallar Yansıma, Öteleme, Dönme Fraktallar 2. Bölüm: Üslü Sayılar Tam
Viyana İmam Hatip Lisesi Öğrenci Seçme Sınavı - Matematik 1. Ünite: Geometriden Olasılığa 1. Bölüm: Yansıyan ve Dönen Şekiller, Fraktallar Yansıma, Öteleme, Dönme Fraktallar 2. Bölüm: Üslü Sayılar Tam
3 7 üs(kuvvet) 5 2 ( 4 3 ( 7 5 (
 Bu konuda üslü sayılarla ilgili kazanımları maddeler halide işleyeceğiz Normalde 8 sınıf matematik kazanımları üslü sayılar konusunda negatif üs kavramı ile başlamasına rağmen bu çalışma kağıdında 6sınıf
Bu konuda üslü sayılarla ilgili kazanımları maddeler halide işleyeceğiz Normalde 8 sınıf matematik kazanımları üslü sayılar konusunda negatif üs kavramı ile başlamasına rağmen bu çalışma kağıdında 6sınıf
SAYILAR DOĞAL VE TAM SAYILAR
 1 SAYILAR DOĞAL VE TAM SAYILAR RAKAM: Sayıları ifade etmek için kullandığımız 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembollerinden her birine rakam denir. Soru: a ve b farklı rakamlar olmak üzere a + b nin alabileceği
1 SAYILAR DOĞAL VE TAM SAYILAR RAKAM: Sayıları ifade etmek için kullandığımız 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembollerinden her birine rakam denir. Soru: a ve b farklı rakamlar olmak üzere a + b nin alabileceği
MATEMATİK KÖKLÜ SAYILAR
 MATEMATİK Kazanım= Tam kare pozitif tam sayılarla bu sayıların karekökleri arasındaki ilişkiyi belirler. KAZANIM FÖYÜ-1 ÖRNEK= Aşağıda verilen tablodaki boşluklara uygun doğal sayılar gelecek şekilde doldurunuz.
MATEMATİK Kazanım= Tam kare pozitif tam sayılarla bu sayıların karekökleri arasındaki ilişkiyi belirler. KAZANIM FÖYÜ-1 ÖRNEK= Aşağıda verilen tablodaki boşluklara uygun doğal sayılar gelecek şekilde doldurunuz.
Çözüm : * ebob = = * ekok = = * ve 36 sayılarının ebob ve ekok u kaçtır?
 1) 24 ve 36 sayılarının ebob ve ekok u kaçtır? 24 36 2 * ebob = 2.2.3 =12 12 18 2 * ekok = 2.2.2.3.3 = 72 6 9 2 3 9 3 * 1 3 3 1 Ebob ( 24, 36 ) = 12 ( * lı olanların çarpımı) Ekok ( 24, 36 ) = 72 ( Hepsinin
1) 24 ve 36 sayılarının ebob ve ekok u kaçtır? 24 36 2 * ebob = 2.2.3 =12 12 18 2 * ekok = 2.2.2.3.3 = 72 6 9 2 3 9 3 * 1 3 3 1 Ebob ( 24, 36 ) = 12 ( * lı olanların çarpımı) Ekok ( 24, 36 ) = 72 ( Hepsinin
KPSS MATEMATİK KONU ANLATIMLI SORU BANKASI ANKARA
 KPSS MATEMATİK KONU ANLATIMLI SORU BANKASI ANKARA İÇİNDEKİLER Matematiğe Giriş... Temel Kavramlar... Bölme - Bölünebilme Kuralları... 85 EBOB - EKOK... Rasyonel Sayılar... Basit Eşitsizlikler... 65 Mutlak
KPSS MATEMATİK KONU ANLATIMLI SORU BANKASI ANKARA İÇİNDEKİLER Matematiğe Giriş... Temel Kavramlar... Bölme - Bölünebilme Kuralları... 85 EBOB - EKOK... Rasyonel Sayılar... Basit Eşitsizlikler... 65 Mutlak
OBEB OKEK ÇÖZÜMLÜ SORULAR
 OBEB OKEK ÇÖZÜMLÜ SORULAR 1) 4, 36 ve 48 sayılarının ortak bölenlerinin en büyüğü kaçtır? A) 1 B)16 C) 18 D) 4 E) 7 1) Sayılarınhepsini aynı anda asal çarpanlarına ayıralım; 4 36 48 1 18 4 6 9 1 3 9 6
OBEB OKEK ÇÖZÜMLÜ SORULAR 1) 4, 36 ve 48 sayılarının ortak bölenlerinin en büyüğü kaçtır? A) 1 B)16 C) 18 D) 4 E) 7 1) Sayılarınhepsini aynı anda asal çarpanlarına ayıralım; 4 36 48 1 18 4 6 9 1 3 9 6
Asal Çarpanlara Ayırma / EBOB-EKOK ORTAK DERSLER MATEMATİK. Prof. Dr. Emin KASAP
 3 Asal Çarpanlara Ayırma / EBOB-EKOK ORTAK DERSLER MATEMATİK Prof Dr Emin KASAP 1 Ünite: 5 ASAL ÇARPANLARA AYIRMA / EBOB - EKOK Prof Dr Emin KASAP İçindekiler 51 ASAL ÇARPANLARA AYIRMa 3 511 Asal Sayılar
3 Asal Çarpanlara Ayırma / EBOB-EKOK ORTAK DERSLER MATEMATİK Prof Dr Emin KASAP 1 Ünite: 5 ASAL ÇARPANLARA AYIRMA / EBOB - EKOK Prof Dr Emin KASAP İçindekiler 51 ASAL ÇARPANLARA AYIRMa 3 511 Asal Sayılar
ÇARPANLAR VE KATLAR. Başarı Başaracağım Diye Başlayanındır. 2
 ÇARPANLAR VE KATLAR Başarı Başaracağım Diye Başlayanındır. 2 Bir Sayının Çarpanları 12 birim kare ile dikdörtgensel bölgeler oluşturalım. Çarpanlarını ve bölenlerini bulalım.? br? br? br? br? br *br 12
ÇARPANLAR VE KATLAR Başarı Başaracağım Diye Başlayanındır. 2 Bir Sayının Çarpanları 12 birim kare ile dikdörtgensel bölgeler oluşturalım. Çarpanlarını ve bölenlerini bulalım.? br? br? br? br? br *br 12
ÜSLÜ SAYILARLA İLGİLİ TEMEL KURALLAR. (2 ) demek 2 tane 2 3 'ün çarpımı demektir. (2 ) = 2.2 = 2 eder.
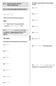 8.. ÜSLÜ SAYILARLA İLGİLİ TEMEL KURALLAR 8...A ÜSLÜ SAYILARIN KUVVETİNİ ALMA ) Aşağıda verilen eşitlikte bilinmeyen harfleri bulunuz. 6 a. 6 ( ) 8 b b) 7 Üslü bir sayının üssü alınırken, üsler çarpılır.
8.. ÜSLÜ SAYILARLA İLGİLİ TEMEL KURALLAR 8...A ÜSLÜ SAYILARIN KUVVETİNİ ALMA ) Aşağıda verilen eşitlikte bilinmeyen harfleri bulunuz. 6 a. 6 ( ) 8 b b) 7 Üslü bir sayının üssü alınırken, üsler çarpılır.
1-)BİLİNMESİ GEREKEN ÜSLÜ İFADELER VE DEĞERLERİ
 1-)BİLİNMESİ GEREKEN ÜSLÜ İFADELER VE DEĞERLERİ * 2 0 = * 3 0 = * 4 0 = * 5 0 = * 2 1 = * 3 1 = * 4 1 = * 5 1 = * 2 2 = * 3 2 = * 4 2 = * 5 2 = * 2 3 = * 3 3 = * 4 3 = * 5 3 = * 2 4 = * 3 4 = * 4 4 = *
1-)BİLİNMESİ GEREKEN ÜSLÜ İFADELER VE DEĞERLERİ * 2 0 = * 3 0 = * 4 0 = * 5 0 = * 2 1 = * 3 1 = * 4 1 = * 5 1 = * 2 2 = * 3 2 = * 4 2 = * 5 2 = * 2 3 = * 3 3 = * 4 3 = * 5 3 = * 2 4 = * 3 4 = * 4 4 = *
7) Üç basamaklı en büyük hangi sayının karekökü bir doğal sayıdır? yazılamaz? 9) işleminin sonucu kaçtır?
 Kareköklü Sayılar Konu Tekrar Testi - 1 1) Aşağıdakilerden hangisi tam kare bir sayı değildir? A)144 B) 56 C) 61 D) 89 7) Üç basamaklı en büyük hangi sayının karekökü bir doğal sayıdır? A)999 B) 961 C)
Kareköklü Sayılar Konu Tekrar Testi - 1 1) Aşağıdakilerden hangisi tam kare bir sayı değildir? A)144 B) 56 C) 61 D) 89 7) Üç basamaklı en büyük hangi sayının karekökü bir doğal sayıdır? A)999 B) 961 C)
MATEMATİK ASAL ÇARPANLARA AYIRMA. ÖRNEK 120 sayısını asal çarpanlarına ayırınız. ÖRNEK 150 sayısının asal çarpanları toplamını bulunuz.
 MATEMATİK ASAL ÇARPANLARA AYIRMA A S A L Ç A R P A N L A R A A Y I R M A T a n ı m : Bir tam sayıyı, asal sayıların çarpımı olarak yazmaya, asal çarpanlarına ayırma denir. 0 sayısını asal çarpanlarına
MATEMATİK ASAL ÇARPANLARA AYIRMA A S A L Ç A R P A N L A R A A Y I R M A T a n ı m : Bir tam sayıyı, asal sayıların çarpımı olarak yazmaya, asal çarpanlarına ayırma denir. 0 sayısını asal çarpanlarına
SINIF CEVAP ANAHTARI
 8. SINIF CEVAP ANAHTARI 1. ÜNİTE: ÇARPANLAR, KATLAR, ÜSLÜ SAYILAR, KAREKÖKLÜ İFADELER ÇARPANLAR VE KATLAR (ASAL ÇARPANLAR) 1-B 2-D 3-A 4-D 5-D 6-C 7-C 8-A 9-B 10-A 11-A 12-D ÇARPANLAR VE KATLAR (EBOB -
8. SINIF CEVAP ANAHTARI 1. ÜNİTE: ÇARPANLAR, KATLAR, ÜSLÜ SAYILAR, KAREKÖKLÜ İFADELER ÇARPANLAR VE KATLAR (ASAL ÇARPANLAR) 1-B 2-D 3-A 4-D 5-D 6-C 7-C 8-A 9-B 10-A 11-A 12-D ÇARPANLAR VE KATLAR (EBOB -
A) 5 1, 5 2 B) 5 0, 5 3 C) 5-2, 5 3 D) 5 4, 5-1 A) 20 = 2 5 B) 24 = 2 6 C) 27 = 3 3 D) 35 = 3 5
 1. 3. Yukarıdaki asal çarpan ağacına göre, aşağıdaki ifadelerden hangisi yanlıştır? A) Asal çarpanları 2 ve 3 tür. B) 6 adet pozitif tamsayı böleni vardır. C) Tüm bölenlerinin toplamı 28 dir. D) 2 2.3
1. 3. Yukarıdaki asal çarpan ağacına göre, aşağıdaki ifadelerden hangisi yanlıştır? A) Asal çarpanları 2 ve 3 tür. B) 6 adet pozitif tamsayı böleni vardır. C) Tüm bölenlerinin toplamı 28 dir. D) 2 2.3
4BÖLÜM. ASAL SAYILAR, BÖLÜNEBİLME ve ÇARPANLARA AYIRMA
 4BÖLÜM ASAL SAYILAR, BÖLÜNEBİLME ve ÇARPANLARA AYIRMA ASAL SAYILAR, BÖLÜNEBİLME ve ÇARPANLARA AYIRMA TEST 1 1) Aşağıdaki sayılardan kaç tanesi 80 sayısının çarpanıdır? 1,2,3,4,5,6,7,8,9,10,12,15,18,20,25,30,40,45,80
4BÖLÜM ASAL SAYILAR, BÖLÜNEBİLME ve ÇARPANLARA AYIRMA ASAL SAYILAR, BÖLÜNEBİLME ve ÇARPANLARA AYIRMA TEST 1 1) Aşağıdaki sayılardan kaç tanesi 80 sayısının çarpanıdır? 1,2,3,4,5,6,7,8,9,10,12,15,18,20,25,30,40,45,80
TEMEL KAVRAMLAR MATEMAT K. 6. a ve b birer do al say r. a 2 b 2 = 19 oldu una göre, a + 2b toplam kaçt r? (YANIT: 28)
 TEMEL KAVRAMLAR 6. a ve b birer do al say r. a b = 19 oldu una göre, a + b toplam (YANIT: 8) 1. ( 4) ( 1) 6 1 i leminin sonucu (YANIT: ). ( 6) ( 3) ( 4) ( 17) ( 5) :( 11) leminin sonucu (YANIT: 38) 7.
TEMEL KAVRAMLAR 6. a ve b birer do al say r. a b = 19 oldu una göre, a + b toplam (YANIT: 8) 1. ( 4) ( 1) 6 1 i leminin sonucu (YANIT: ). ( 6) ( 3) ( 4) ( 17) ( 5) :( 11) leminin sonucu (YANIT: 38) 7.
ISBN NUMARASI: ISBN NUMARASI: ISBN NUMARASI: ISBN NUMARASI:
 Bu formun ç kt s n al p ço altarak ö rencilerinizin ücretsiz Morpa Kampüs yarıyıl tatili üyeli inden yararlanmalar n sa layabilirsiniz.! ISBN NUMARASI: 65482465 ISBN NUMARASI: 65482465! ISBN NUMARASI:
Bu formun ç kt s n al p ço altarak ö rencilerinizin ücretsiz Morpa Kampüs yarıyıl tatili üyeli inden yararlanmalar n sa layabilirsiniz.! ISBN NUMARASI: 65482465 ISBN NUMARASI: 65482465! ISBN NUMARASI:
EN BÜYÜK ORTAK BÖLEN EBOB
 EN BÜYÜK ORTAK BÖLEN 1 ve 18 in bölenlerini bulalım ve ortak olanlarını inceleyelim. 1 nin bölenleri: 1,,,4,6,1 18 in bölenleri: 1,,,6,9,18 Aşağıdaki sayı ikililerinin en büyük ortak bölenini ebob bulunuz.
EN BÜYÜK ORTAK BÖLEN 1 ve 18 in bölenlerini bulalım ve ortak olanlarını inceleyelim. 1 nin bölenleri: 1,,,4,6,1 18 in bölenleri: 1,,,6,9,18 Aşağıdaki sayı ikililerinin en büyük ortak bölenini ebob bulunuz.
8.Sınıf MATEMATİK KONU ANLATIMI. Testler. Konu Anlatımı. Uygulama
 8.Sınıf MATEMATİK Konu Anlatımı Alt başlıklara ayrılmış, detaylandırılmış konu anlatımı ve bunlarla ilgili çözümlü örnek sorular konuyu kavramınızı sağlayacaktır. Uygulama Testler Konu anlatımın sonlarında
8.Sınıf MATEMATİK Konu Anlatımı Alt başlıklara ayrılmış, detaylandırılmış konu anlatımı ve bunlarla ilgili çözümlü örnek sorular konuyu kavramınızı sağlayacaktır. Uygulama Testler Konu anlatımın sonlarında
ÜNİTE: RASYONEL SAYILAR KONU: Rasyonel Sayılar Kümesinde Çıkarma İşlemi
 ÜNTE: RASYONEL SAYILAR ONU: Rasyonel Sayılar ümesinde Çıkarma şlemi ÖRNE SORULAR VE ÇÖZÜMLER. işleminin sonucu B) D) ki rasyonel sayının farkını bulmak için çıkan terimin toplama işlemine göre tersi alınarak
ÜNTE: RASYONEL SAYILAR ONU: Rasyonel Sayılar ümesinde Çıkarma şlemi ÖRNE SORULAR VE ÇÖZÜMLER. işleminin sonucu B) D) ki rasyonel sayının farkını bulmak için çıkan terimin toplama işlemine göre tersi alınarak
AKADEMİK PERSONEL VE LİSANSÜSTÜ EĞİTİMİ GİRİŞ SINAVI (ALES)
 00000000001 AKADEMİK PERSONEL VE LİSANSÜSTÜ EĞİTİMİ GİRİŞ SINAVI (ALES) plam cevaplama süresi 150 akikadır. (,5 saat) SAYISAL BÖLÜM SAYISAL - 1 TESTİ Sınavın bu bölümünden alacağınız standart puan, Sayısal
00000000001 AKADEMİK PERSONEL VE LİSANSÜSTÜ EĞİTİMİ GİRİŞ SINAVI (ALES) plam cevaplama süresi 150 akikadır. (,5 saat) SAYISAL BÖLÜM SAYISAL - 1 TESTİ Sınavın bu bölümünden alacağınız standart puan, Sayısal
d) x TABAN ARĐTMETĐĞĐ
 YILLAR 00 00 00 00 00 007 008 009 010 011 ÖSS-YGS - 1 1 - - - - - - - TABAN ARĐTMETĐĞĐ Genel olarak 10 luk sayı sistemini kullanırız fakat başka sayı sistemlerine de ihtiyaç duyarız Örneğin bilgisayarın
YILLAR 00 00 00 00 00 007 008 009 010 011 ÖSS-YGS - 1 1 - - - - - - - TABAN ARĐTMETĐĞĐ Genel olarak 10 luk sayı sistemini kullanırız fakat başka sayı sistemlerine de ihtiyaç duyarız Örneğin bilgisayarın
Örnek...1 : Yandaki bölme işlemin de bölüm ile kalanın toplamı kaçtır?
 BÖLME İŞLEMİ VE ÖZELLİKLERİ A, B, C, K doğal sayılar ve B 0 olmak üzere, BÖLÜNEN A B C BÖLEN BÖLÜM Örnek...4 : x sayısının y ile bölümündeki bölüm 2 ve kalan 5 tir. y sayısının z ile bölümündeki bölüm
BÖLME İŞLEMİ VE ÖZELLİKLERİ A, B, C, K doğal sayılar ve B 0 olmak üzere, BÖLÜNEN A B C BÖLEN BÖLÜM Örnek...4 : x sayısının y ile bölümündeki bölüm 2 ve kalan 5 tir. y sayısının z ile bölümündeki bölüm
TEOG. Matematik ÇÖZÜM KİTAPÇIĞI
 TEOG ÇÖZÜM KİTAPÇIĞI Deneme. (Çarpanlar ve Katlar) EKOK (0,60) 0 Bu araçlar ilk defa 0 saniye dakika sonra yan yana gelirler.. (Üslü İfadeler) ^0, h c m c m 0 0. 6 6 0 olduğundan geriye 0 0 00 km yol.
TEOG ÇÖZÜM KİTAPÇIĞI Deneme. (Çarpanlar ve Katlar) EKOK (0,60) 0 Bu araçlar ilk defa 0 saniye dakika sonra yan yana gelirler.. (Üslü İfadeler) ^0, h c m c m 0 0. 6 6 0 olduğundan geriye 0 0 00 km yol.
MERKEZİ ORTAK SINAV KAZANDIRAN MATEMATİK FÖYÜ
 MERKEZİ ORTAK SINAV KAZANDIRAN MATEMATİK FÖYÜ ÖRNEK: 18 sayısının pozitif çarpanları nelerdir? Çarpımları 18 olan sayılar arayalım. 18 = 1. 18 18 =. 9 18 =. 6 Her doğal sayı iki doğal sayının çarpımı şeklinde
MERKEZİ ORTAK SINAV KAZANDIRAN MATEMATİK FÖYÜ ÖRNEK: 18 sayısının pozitif çarpanları nelerdir? Çarpımları 18 olan sayılar arayalım. 18 = 1. 18 18 =. 9 18 =. 6 Her doğal sayı iki doğal sayının çarpımı şeklinde
Çarpan Kavramı ve Asal Çarpanlara Ayırma 5. A B C A) 25 B) 60 C) 75 D) A) 78 B) 138 C) 246 D) 576 MATEMATİK 8
 8 MTEMTİK Çarpan Kavramı ve sal Çarpanlara yırma Test. 8 sayısının asal çarpanlarına ayrılmış hâli aşağıdakilerden hangisidir? ). ) 8.7 C). D)..7. C D Yanda verilen bölen listesi yöntemine göre, ) ) 6
8 MTEMTİK Çarpan Kavramı ve sal Çarpanlara yırma Test. 8 sayısının asal çarpanlarına ayrılmış hâli aşağıdakilerden hangisidir? ). ) 8.7 C). D)..7. C D Yanda verilen bölen listesi yöntemine göre, ) ) 6
Ahmet SAĞDIÇ - Sinan SARITAŞ. Matematik. TEOG Soru Yapısına %100 Uygun. Gelebilecek Soru Kalıpları. Kazanım ve Konulara Göre Sınıflandırma
 Ahmet SAĞDIÇ - Sinan SARITAŞ Matematik TEOG Soru Yapısına %100 Uygun Gelebilecek Soru Kalıpları Kazanım ve Konulara Göre Sınıflandırma Copyright Bu soruların her hakkı ÇANTA Yayıncılık A.Ş. ye aittir.
Ahmet SAĞDIÇ - Sinan SARITAŞ Matematik TEOG Soru Yapısına %100 Uygun Gelebilecek Soru Kalıpları Kazanım ve Konulara Göre Sınıflandırma Copyright Bu soruların her hakkı ÇANTA Yayıncılık A.Ş. ye aittir.
Örnek...1 : Yandaki bölme işlemin de bölüm ile kalanın toplamı kaçtır?
 BÖLME İŞLEMİ VE ÖZELLİKLERİ A, B, C, K doğal sayılar ve B 0 olmak üzere, BÖLÜNEN A B C BÖLEN BÖLÜM Örnek...4 : x sayısının y ile bölümündeki bölüm 2 ve kalan 5 tir. y sayısının z ile bölümündeki bölüm
BÖLME İŞLEMİ VE ÖZELLİKLERİ A, B, C, K doğal sayılar ve B 0 olmak üzere, BÖLÜNEN A B C BÖLEN BÖLÜM Örnek...4 : x sayısının y ile bölümündeki bölüm 2 ve kalan 5 tir. y sayısının z ile bölümündeki bölüm
2) Aşağıda verilen işlemleri yazınız. g) ( ) 3) Aşağıda verilen işlemleri yazınız. 4) Aşağıda verilen işlemleri yazınız.
 8.2. ÜSLÜ SAYILARDA İŞLEM 8.2..A ÜSLÜ SAYILARDA TOPLAMA VE ÇIKARMA İŞLEMİ 2) Aşağıda verilen işlemleri yazınız. 2 ( + 2) + ( ) 3 ( 2) + ( 2) Üslü sayılarda toplama veya çıkarma işleminde her üslü niceliğin
8.2. ÜSLÜ SAYILARDA İŞLEM 8.2..A ÜSLÜ SAYILARDA TOPLAMA VE ÇIKARMA İŞLEMİ 2) Aşağıda verilen işlemleri yazınız. 2 ( + 2) + ( ) 3 ( 2) + ( 2) Üslü sayılarda toplama veya çıkarma işleminde her üslü niceliğin
Bir bütünün eş parçalarının bütüne olan oranı kesir olarak adlandırılır. b Payda
 Matematik6 Bir Bakışta Matematik Kazanım Defteri Özet bilgi alanları... Kesirlerle İşlemler KESİR ve KESİRLERDE SIRALAMA Bir bütünün eş parçalarının bütüne olan oranı kesir olarak adlandırılır. Bir kesirde
Matematik6 Bir Bakışta Matematik Kazanım Defteri Özet bilgi alanları... Kesirlerle İşlemler KESİR ve KESİRLERDE SIRALAMA Bir bütünün eş parçalarının bütüne olan oranı kesir olarak adlandırılır. Bir kesirde
ÜNİTE: TAM SAYILAR KONU: Tam Sayılar Kümesinde Çıkarma İşlemi
 ÜNE: AM AYIAR N: am ayılar ümesinde Çıkarma şlemi ÖRNE RAR VE ÇÖZÜMER 1. [(+17) (+25)] + [( 12) (+21)] işleminin sonucu A) 41 B) 25 C) 25 D) 41 Çıkarma işlemi yapılırken çıkanın işareti değişir ve eksilen
ÜNE: AM AYIAR N: am ayılar ümesinde Çıkarma şlemi ÖRNE RAR VE ÇÖZÜMER 1. [(+17) (+25)] + [( 12) (+21)] işleminin sonucu A) 41 B) 25 C) 25 D) 41 Çıkarma işlemi yapılırken çıkanın işareti değişir ve eksilen
8. SINIF MATEMATİK ÜSLÜ İFADELER
 . SINIF MATEMATİK ÜSLÜ İFADELER... Tam sayıların, tam sayı kuvvetlerini hesaplar, üslü ifade şeklinde yazar....... a.a.a.a...a a n HATIRLATMA KÖŞESİ- n HATIRLATMA KÖŞESİ- Her sayının sıfırıncı kuvveti
. SINIF MATEMATİK ÜSLÜ İFADELER... Tam sayıların, tam sayı kuvvetlerini hesaplar, üslü ifade şeklinde yazar....... a.a.a.a...a a n HATIRLATMA KÖŞESİ- n HATIRLATMA KÖŞESİ- Her sayının sıfırıncı kuvveti
EN BÜYÜK ORTAK BÖLEN (EBOB) NOT: 12 ve 6 sayılarının En Büyük Ortak Böleni EBOB (12,18)=6 veya (12,18) EBOB =6 şeklinde ifade edilir.
 8.1.8 EN BÜYÜK ORTAK BÖLEN (EBOB) İki veya daha fazla sayma sayısının ortak bölenlerinden en büyük olanına, bu sayıların En Büyük Ortak Böleni EBOB u denir. NOT: 12 ve 6 sayılarının En Büyük Ortak Böleni
8.1.8 EN BÜYÜK ORTAK BÖLEN (EBOB) İki veya daha fazla sayma sayısının ortak bölenlerinden en büyük olanına, bu sayıların En Büyük Ortak Böleni EBOB u denir. NOT: 12 ve 6 sayılarının En Büyük Ortak Böleni
ÇARPANLAR VE KATLAR ÖRNEK. 8 Sayılar ve İşlemler. 2 x x 2 x 6. 2 x 2 x 2 x 9
 ÇARPANLAR VE KATLAR POZİTİF TAM SAYILARIN ÇARPANLARI Her pozitif tam sayı, iki doğal sayının çarpımı olarak yazılabilir. Bu iki doğal sayıdan her birine o sayının çarpanı denir. Bir sayının çarpanı aynı
ÇARPANLAR VE KATLAR POZİTİF TAM SAYILARIN ÇARPANLARI Her pozitif tam sayı, iki doğal sayının çarpımı olarak yazılabilir. Bu iki doğal sayıdan her birine o sayının çarpanı denir. Bir sayının çarpanı aynı
Tek Doğal Sayılar; Çift Doğal Sayılar
 Bölüm BÖLÜNEBİLME VE ÇARPANLARA AYIRMA. Bölünebilme Kuralları Bir a doğal sayısı bir b sayma sayısına bölündüğünde bölüm bir doğal sayı ve kalan sıfır ise, a doğal sayısı b sayma sayısına bölünebilir.
Bölüm BÖLÜNEBİLME VE ÇARPANLARA AYIRMA. Bölünebilme Kuralları Bir a doğal sayısı bir b sayma sayısına bölündüğünde bölüm bir doğal sayı ve kalan sıfır ise, a doğal sayısı b sayma sayısına bölünebilir.
FAKTÖRİYEL. TANIM Pozitif ilk n tam sayının çarpımı n = n! biçiminde gösterilir. n Faktöriyel okunur.
 FAKTÖRİYEL TANIM Pozitif ilk n tam sayının çarpımı 1.2.3 n = n! biçiminde gösterilir. n Faktöriyel okunur. 1!=1 2!=1.2=2 3!=1.2.3=6 4!=1.2.3.4=24 5!=1.2.3.4.5=120 gibi. Özel olarak; 0! = 1 olarak tanımlanmıştır.
FAKTÖRİYEL TANIM Pozitif ilk n tam sayının çarpımı 1.2.3 n = n! biçiminde gösterilir. n Faktöriyel okunur. 1!=1 2!=1.2=2 3!=1.2.3=6 4!=1.2.3.4=24 5!=1.2.3.4.5=120 gibi. Özel olarak; 0! = 1 olarak tanımlanmıştır.
MATEMATİK. Temel Kavramlar I. Test a ve b doğal sayılardır. 5. Ardışık 5 tek sayının toplamı 115 tir. 6. x ve y tamsayılardır.
 MATEMATİK Test 0 Temel Kavramlar I. a ve b doğal sayılardır. a + b = 7 olduğuna göre, a.b çarpımının alabileceği en büyük değer kaçtır?. Ardışık tek sayının toplamı tir. Buna göre, bu sayıların en büyüğü
MATEMATİK Test 0 Temel Kavramlar I. a ve b doğal sayılardır. a + b = 7 olduğuna göre, a.b çarpımının alabileceği en büyük değer kaçtır?. Ardışık tek sayının toplamı tir. Buna göre, bu sayıların en büyüğü
5. Üç basamaklı ABC doğal sayısı 2 ile, 5 ile ve 9 ile tam. 6. Dört basamaklı AB24 sayısının 36 ile bölümünden kalan iki
 Bölme ve Bölünebilme BÖLÜM 03 Test 01 1 Üç basamaklı 5AB sayısı iki basamaklı AB sayısına bölündüğünde, bölüm 13 ve kalan 8 olmaktadır Buna göre, A + B toplamı A) 5 B) 6 C) 7 D) 8 E) 9 5AB = 13 AB + 8
Bölme ve Bölünebilme BÖLÜM 03 Test 01 1 Üç basamaklı 5AB sayısı iki basamaklı AB sayısına bölündüğünde, bölüm 13 ve kalan 8 olmaktadır Buna göre, A + B toplamı A) 5 B) 6 C) 7 D) 8 E) 9 5AB = 13 AB + 8
Çarpanlar ve Katlar Föyü KAZANIMLAR
 1 Çarpanlar ve Katlar Föyü KAZANIMLAR Verilen pozitif sayıların pozitif tam sayı çarpanlarını bulur, pozitif tam sayıların pozitif tam sayı çarpanlarını üslü ifadelerin çarpımı şeklinde yazar. İki doğal
1 Çarpanlar ve Katlar Föyü KAZANIMLAR Verilen pozitif sayıların pozitif tam sayı çarpanlarını bulur, pozitif tam sayıların pozitif tam sayı çarpanlarını üslü ifadelerin çarpımı şeklinde yazar. İki doğal
KAREKÖKLÜ SAYILAR. a) 15 h) 18 b) 32 ı) 49 c) 81 i) 72 d) 27 j) 36 e) 9 k) 121 f) 45 l) 256 g) 25 m) 152
 KAREKÖKLÜ SAYILAR kök sembolü kök derecesi dir 8. sınıfta kök derecesi olan kökleri öğreneceğiz. Bir kökün en küçük derecesi dir. En genel kullanılan ve en küçük kök olduğu için derecesi yazılmaz. Fakat
KAREKÖKLÜ SAYILAR kök sembolü kök derecesi dir 8. sınıfta kök derecesi olan kökleri öğreneceğiz. Bir kökün en küçük derecesi dir. En genel kullanılan ve en küçük kök olduğu için derecesi yazılmaz. Fakat
1. ÜNİTE:SAYILAR VE İŞLEMLER
 1. ÜNİTE:SAYILAR VE İŞLEMLER 2 DERS SAATİ:Verilen iki doğal sayının aralarında asal olup olmadığını belirler. ASAL SAYILAR 1 ve kendisinden başka hiçbir sayma sayısı ile bölünemeyen 1 den büyük doğal sayılara
1. ÜNİTE:SAYILAR VE İŞLEMLER 2 DERS SAATİ:Verilen iki doğal sayının aralarında asal olup olmadığını belirler. ASAL SAYILAR 1 ve kendisinden başka hiçbir sayma sayısı ile bölünemeyen 1 den büyük doğal sayılara
ÜNİTE 1: TEMEL KAVRAMLAR
 MATEMATİK ÜNİTE : TEMEL KAVRAMLAR Temel Kavramlar ADF 0 RAKAM Sayı oluşturmak için kullanılan sembollere... denir. 0 luk sayma düzenindeki rakamlar 0,,,... 8 ve 9 olup 0 tanedir. örnek a, b, c sıfırdan
MATEMATİK ÜNİTE : TEMEL KAVRAMLAR Temel Kavramlar ADF 0 RAKAM Sayı oluşturmak için kullanılan sembollere... denir. 0 luk sayma düzenindeki rakamlar 0,,,... 8 ve 9 olup 0 tanedir. örnek a, b, c sıfırdan
TEST. Çarpanlar ve Katlar. 1. Asal çarpanların çarpımı olan sayı kaçtır? sayısının kaç tane birbirinden farklı asal çarpanı vardır?
 Çarpanlar ve Katlar 8. Sınıf Matematik Soru Bankası TEST. Asal çarpanların çarpımı..5 olan sayı kaçtır? A) 40 B) 480 C) 60 D) 70 4. 60 sayısının kaç tane birbirinden farklı asal çarpanı vardır? A) B) C)
Çarpanlar ve Katlar 8. Sınıf Matematik Soru Bankası TEST. Asal çarpanların çarpımı..5 olan sayı kaçtır? A) 40 B) 480 C) 60 D) 70 4. 60 sayısının kaç tane birbirinden farklı asal çarpanı vardır? A) B) C)
MATEMATİK SORU BANKASI. ezberbozan serisi GEOMETRİ 30. KPSS tamamı çözümlü. eğitimde
 ezberbozan serisi MATEMATİK GEOMETRİ KPSS 2017 SORU BANKASI eğitimde tamamı çözümlü 30. Kerem Köker Kenan Osmanoğlu Levent Şahin Uğur Özçelik Ahmet Tümer Yılmaz Ceylan KOMİSYON KPSS EZBERBOZAN MATEMATİK
ezberbozan serisi MATEMATİK GEOMETRİ KPSS 2017 SORU BANKASI eğitimde tamamı çözümlü 30. Kerem Köker Kenan Osmanoğlu Levent Şahin Uğur Özçelik Ahmet Tümer Yılmaz Ceylan KOMİSYON KPSS EZBERBOZAN MATEMATİK
5. SINIF MATEMATİK YILLIK PLANI
 5. SINIF MATEMATİK YILLIK PLANI 2018-2019 DOĞAL SAYILAR VE İŞLEMLER 1.hafta 17-23 Eylül Milyonlar 5.1.1.1 5.1.1.2 6 01 1-2 2.hafta 24-30 Eylül Örüntüler 5.1.1.3 11 02 3-4 3.hafta 01-07 Ekim Doğal Sayılarda
5. SINIF MATEMATİK YILLIK PLANI 2018-2019 DOĞAL SAYILAR VE İŞLEMLER 1.hafta 17-23 Eylül Milyonlar 5.1.1.1 5.1.1.2 6 01 1-2 2.hafta 24-30 Eylül Örüntüler 5.1.1.3 11 02 3-4 3.hafta 01-07 Ekim Doğal Sayılarda
İÇİNDEKİLER BASİT EŞİTSİZLİKLER. HARFLİ İFADELER Harfli İfadeler ve Elemanları Eşitsizlik Sembolleri ve İşaretin Eşitsizlik İfadesi...
 İÇİNDEKİLER HARFLİ İFADELER Harfli İfadeler ve Elemanları... 1 Benzer Terim... Harfli İfadenin Terimlerini Toplayıp Çıkarma... Harfli İfadelerin Terimlerini Çarpma... Harfli İfadelerde Parantez Açma...
İÇİNDEKİLER HARFLİ İFADELER Harfli İfadeler ve Elemanları... 1 Benzer Terim... Harfli İfadenin Terimlerini Toplayıp Çıkarma... Harfli İfadelerin Terimlerini Çarpma... Harfli İfadelerde Parantez Açma...
ÇARPANLAR VE KATLAR ÖĞRENİYORUM
 ÖĞRENİYORUM Bir pozitif tam sayıyı birden fazla pozitif tam sayının çarpımı şeklinde yazarken kullandığımız her bir sayıya o sayının çarpanı denir. Örnek: nin çarpanları,, 3, 4, 6 ve dir. UYGULUYORUM Verilmeyen
ÖĞRENİYORUM Bir pozitif tam sayıyı birden fazla pozitif tam sayının çarpımı şeklinde yazarken kullandığımız her bir sayıya o sayının çarpanı denir. Örnek: nin çarpanları,, 3, 4, 6 ve dir. UYGULUYORUM Verilmeyen
1 ÜNİTE SAYILAR VE İŞLEMLER
 1 ÜNİTE SAYILAR VE İŞLEMLER TAM SAYILARLA ÇARPMA VE BÖLME İŞLEMLERİ 7.1.1.1. Tam sayılarla çarpma ve bölme işlemlerini yapar. 7.1.1.2. Tam sayılarla işlemler yapmayı gerektiren problemleri çözer. 7.1.1.3.
1 ÜNİTE SAYILAR VE İŞLEMLER TAM SAYILARLA ÇARPMA VE BÖLME İŞLEMLERİ 7.1.1.1. Tam sayılarla çarpma ve bölme işlemlerini yapar. 7.1.1.2. Tam sayılarla işlemler yapmayı gerektiren problemleri çözer. 7.1.1.3.
MATEMATİK Fasikül 1 KONU ANLATIMLI FASİKÜL SET ÖLÇEN SIRA SENDE UYGULAMALARI ÇÖZÜMLÜ ÖRNEK SORULAR
 ATU MATEMATİK Fasikül 1 KONU ANLATIMLI FASİKÜL SET ZENGİN İÇERİKLİ ÖZGÜN KONU ANLATIMI ÖLÇEN SIRA SENDE UYGULAMALARI ÇÖZÜMLÜ ÖRNEK SORULAR BİLGİ KONTROLÜ ODAKLI KARMA SORULAR PEKİŞTİREN BÖLÜMLERİ AKILLI
ATU MATEMATİK Fasikül 1 KONU ANLATIMLI FASİKÜL SET ZENGİN İÇERİKLİ ÖZGÜN KONU ANLATIMI ÖLÇEN SIRA SENDE UYGULAMALARI ÇÖZÜMLÜ ÖRNEK SORULAR BİLGİ KONTROLÜ ODAKLI KARMA SORULAR PEKİŞTİREN BÖLÜMLERİ AKILLI
KONU: ÇARPANLAR VE KATLAR
 8. SINIF KONU DEĞERLENDİRE SINAVI- KONU: ÇARPANLAR VE KATLAR. Ahmet 80 metre uzunluğundaki bir ipi eşit şekilde kesmek istiyor. Buna göre Ahmet ipi aşağıda verilen aralıklardan hangisi ile keserse, eşit
8. SINIF KONU DEĞERLENDİRE SINAVI- KONU: ÇARPANLAR VE KATLAR. Ahmet 80 metre uzunluğundaki bir ipi eşit şekilde kesmek istiyor. Buna göre Ahmet ipi aşağıda verilen aralıklardan hangisi ile keserse, eşit
Önce parantez içindeki işlemler yapılır. 150:(6+3.8)-5 = 150:(6+24)-5 = 150:30-5 = 5-5 = 0 ( A ) :5-3 = = 11 ( C )
 Önce ÇARPMA ve Bölme, sonra Toplama ve Çıkarma. 3.4+10:5-3 = 12+2-3 = 11 ( C ) Önce parantez içindeki işlemler yapılır. 150:(6+3.8)-5 = 150:(6+24)-5 = 150:30-5 = 5-5 = 0 ( A ) 72:24+64:16 = 3+4 = 7 ( B
Önce ÇARPMA ve Bölme, sonra Toplama ve Çıkarma. 3.4+10:5-3 = 12+2-3 = 11 ( C ) Önce parantez içindeki işlemler yapılır. 150:(6+3.8)-5 = 150:(6+24)-5 = 150:30-5 = 5-5 = 0 ( A ) 72:24+64:16 = 3+4 = 7 ( B
TEOG. Sayma Sayıları ve Doğal Sayılar ÇÖZÜM ÖRNEK ÇÖZÜM ÖRNEK SAYI BASAMAKLARI VE SAYILARIN ÇÖZÜMLENMESİ 1. DOĞAL SAYILAR.
 TEOG Sayma Sayıları ve Doğal Sayılar 1. DOĞAL SAYILAR 0 dan başlayıp artı sonsuza kadar giden sayılara doğal sayılar denir ve N ile gösterilir. N={0, 1, 2, 3,...,n, n+1,...} a ve b doğal sayılar olmak
TEOG Sayma Sayıları ve Doğal Sayılar 1. DOĞAL SAYILAR 0 dan başlayıp artı sonsuza kadar giden sayılara doğal sayılar denir ve N ile gösterilir. N={0, 1, 2, 3,...,n, n+1,...} a ve b doğal sayılar olmak
SAYILARIN ASAL ÇARPANLARINA AYRILMASI
 ASAL SAYILAR Asal sayılar, 1 ve kendisinden başka pozitif tam böleni olmayan 1' den büyük tamsayılardır. En küçük asal sayı, 2' dir. 2 asal sayısı dışında çift asal sayı yoktur. Yani, 2 sayısı dışındaki
ASAL SAYILAR Asal sayılar, 1 ve kendisinden başka pozitif tam böleni olmayan 1' den büyük tamsayılardır. En küçük asal sayı, 2' dir. 2 asal sayısı dışında çift asal sayı yoktur. Yani, 2 sayısı dışındaki
TABAN ARĠTMETĠĞĠ. ÇÖZÜM (324) 5 = = = = 89 bulunur. Doğru Seçenek C dir.
 TABAN ARĠTMETĠĞĠ Kullandığımız 10 luk sayma sisteminde sayılar {0,1,2,3,4,5,6,7,8,9} kümesinin elemanları (Rakam) kullanılarak yazılır. En büyük elemanı 9 olan, 10 elemanlı bir kümedir. Onluk sistemde;
TABAN ARĠTMETĠĞĠ Kullandığımız 10 luk sayma sisteminde sayılar {0,1,2,3,4,5,6,7,8,9} kümesinin elemanları (Rakam) kullanılarak yazılır. En büyük elemanı 9 olan, 10 elemanlı bir kümedir. Onluk sistemde;
MATEMATİK Fasikül 1 KONU ANLATIMLI FASİKÜL SET ÖLÇEN SIRA SENDE UYGULAMALARI ÇÖZÜMLÜ ÖRNEK SORULAR
 ATU MATEMATİK Fasikül KONU ANLATIMLI FASİKÜL SET ZENGİN İÇERİKLİ ÖZGÜN KONU ANLATIMI ÖLÇEN SIRA SENDE UYGULAMALARI ÇÖZÜMLÜ ÖRNEK SORULAR BİLGİ KONTROLÜ ODAKLI KARMA SORULAR PEKİŞTİREN BİRLİKTE ÇÖZELİM
ATU MATEMATİK Fasikül KONU ANLATIMLI FASİKÜL SET ZENGİN İÇERİKLİ ÖZGÜN KONU ANLATIMI ÖLÇEN SIRA SENDE UYGULAMALARI ÇÖZÜMLÜ ÖRNEK SORULAR BİLGİ KONTROLÜ ODAKLI KARMA SORULAR PEKİŞTİREN BİRLİKTE ÇÖZELİM
ÖSYM nin Sorduğu Tüm Sorular DGS. Tamamı Çözümlü ÇIKMIŞ SORULAR. Temmuz Dahil
 ÖSYM nin Sorduğu Tüm Sorular DGS Tamamı Çözümlü ÇIKMIŞ SORULAR 00 00 005 006 007 008 009 00 0 Temmuz Dahil Komisyon DGS TAMAMI ÇÖZÜMLÜ ÇIKMIŞ SORULAR ISBN 978-975-879-06- Kitapta yer alan bölümlerin tüm
ÖSYM nin Sorduğu Tüm Sorular DGS Tamamı Çözümlü ÇIKMIŞ SORULAR 00 00 005 006 007 008 009 00 0 Temmuz Dahil Komisyon DGS TAMAMI ÇÖZÜMLÜ ÇIKMIŞ SORULAR ISBN 978-975-879-06- Kitapta yer alan bölümlerin tüm
140. 2< a< 1 ise kesrinin değeri aşağıdakilerden hangisi olamaz? (3,7) a 1,9 2,4 2,7 3,2 3,7. a a c b ve c a a b c
 138. a ve b gerçel sayılardır. a < a, 6a b 5= 0 b ne olabilir? (11) 4 5 8 11 1 139. < 0 olmak üzere, 4 3. =? ( 3 ) a 1 140. < a< 1 ise kesrinin değeri aşağıdakilerden hangisi olamaz? (3,7) a 1,9,4,7 3,
138. a ve b gerçel sayılardır. a < a, 6a b 5= 0 b ne olabilir? (11) 4 5 8 11 1 139. < 0 olmak üzere, 4 3. =? ( 3 ) a 1 140. < a< 1 ise kesrinin değeri aşağıdakilerden hangisi olamaz? (3,7) a 1,9,4,7 3,
EĞİTİM ÖĞRETİM YILI LİDER ŞİŞLİ İLKOKULU/ORTAOKULU
 4. SINIF MATEMATİK KAZANIMLARI 4, 5 ve 6 basamaklı doğal sayıları okur ve yazar. 10 000 e kadar (10 000 dahil) yüzer ve biner sayar. 10 000 e kadar (10 000 dahil) yüzer ve biner sayar. 4, 5 ve 6 basamaklı
4. SINIF MATEMATİK KAZANIMLARI 4, 5 ve 6 basamaklı doğal sayıları okur ve yazar. 10 000 e kadar (10 000 dahil) yüzer ve biner sayar. 10 000 e kadar (10 000 dahil) yüzer ve biner sayar. 4, 5 ve 6 basamaklı
Çarpanlar ve Katlar
 8.1.1. Çarpanlar ve Katlar 8.1.2. Üslü İfadeler 8.1.3. Kareköklü İfadeler 8.2.1. Cebirsel İfadeler ve Özdeşlikler 8.1.1.1 Verilen pozitif tam sayıların çarpanlarını bulur; pozitif tam sayıları üslü ifade
8.1.1. Çarpanlar ve Katlar 8.1.2. Üslü İfadeler 8.1.3. Kareköklü İfadeler 8.2.1. Cebirsel İfadeler ve Özdeşlikler 8.1.1.1 Verilen pozitif tam sayıların çarpanlarını bulur; pozitif tam sayıları üslü ifade
5. a ve b birer pozitif tam sayıdır. A) 1 B) 2 C) 3 D) 14 E) a ve b birer doğal sayıdır. 7. a ve b birer pozitif tam sayıdır.
 Üniversite Haz rl k Sözcükte Do al ve Say lar Söz Öbeklerinde ve Tam Say lar Anlam - I - I YGS Temel Matematik. 8 + 4. + 8 : 4 işleminin sonucu A) 8 B) 9 C) D) 5 E) 8 5. a ve b birer pozitif tam sayıdır.
Üniversite Haz rl k Sözcükte Do al ve Say lar Söz Öbeklerinde ve Tam Say lar Anlam - I - I YGS Temel Matematik. 8 + 4. + 8 : 4 işleminin sonucu A) 8 B) 9 C) D) 5 E) 8 5. a ve b birer pozitif tam sayıdır.
AKILLI. sınıf. Musa BOR
 AKILLI sınıf. Musa BOR AFG Matbaa Yayıncılık Kağ. İnş. Ltd. Şti. Buca OSB, BEGOS 2. Bölge 3/20 Sk. No: 17 Buca-İZMİR Tel: 0.232.442 01 01-442 03 03 Faks: 442 06 60 Bu kitabın tüm hakları AFG Matbaa Yay.
AKILLI sınıf. Musa BOR AFG Matbaa Yayıncılık Kağ. İnş. Ltd. Şti. Buca OSB, BEGOS 2. Bölge 3/20 Sk. No: 17 Buca-İZMİR Tel: 0.232.442 01 01-442 03 03 Faks: 442 06 60 Bu kitabın tüm hakları AFG Matbaa Yay.
sayısının asal çarpanlarına ayrılmış biçimi aşağıdakilerden. 1. Aşağıdakilerden hangisi 96 sayısının çarpanlarından A) 16 B) 28 C) 32 D) 48
 1. Aşağıdakilerden hangisi 96 sayısının çarpanlarından biri değildir? A) 16 B) 28 C) 32 D) 48 4. 216 sayısının asal çarpanlarına ayrılmış biçimi aşağıdakilerden hangisidir? A) 3 2 2 3 5 B) 2 2 2 3 C) 2
1. Aşağıdakilerden hangisi 96 sayısının çarpanlarından biri değildir? A) 16 B) 28 C) 32 D) 48 4. 216 sayısının asal çarpanlarına ayrılmış biçimi aşağıdakilerden hangisidir? A) 3 2 2 3 5 B) 2 2 2 3 C) 2
ÇARPANLAR ve KATLAR. Uygulama-1. Asal Sayılar. Pozitif Bir Tam Sayının Çarpanlarını Bulma. Aşağıdaki sayıların çarpanlarını (bölenlerini) bulunuz.
 Asal Sayılar Sadece kendisine ve sayısına bölünebilen 'den büyük tam sayılara asal sayı denir. En küçük asal sayı 2'dir ÇARPANLAR ve KATLAR Uygulama- Aşağıdaki sayıların çarpanlarını (bölenlerini) 36=
Asal Sayılar Sadece kendisine ve sayısına bölünebilen 'den büyük tam sayılara asal sayı denir. En küçük asal sayı 2'dir ÇARPANLAR ve KATLAR Uygulama- Aşağıdaki sayıların çarpanlarını (bölenlerini) 36=
T. C. Manisa Celal Bayar Üniversitesi Kırkağaç Meslek Yüksekokulu Öğretim Yılı Güz Yarıyılı MATEMATİK Dersi Final Sınavı Çalışma Soruları
 T. C. Manisa Celal Bayar Üniversitesi Kırkağaç Meslek Yüksekokulu 016-017 Öğretim Yılı Güz Yarıyılı MATEMATİK Dersi Final Sınavı Çalışma Soruları 1) 3. [15 3(8: )] 9 =? a) 16 b) 14 c) 0 d) 14 e) 16 6)
T. C. Manisa Celal Bayar Üniversitesi Kırkağaç Meslek Yüksekokulu 016-017 Öğretim Yılı Güz Yarıyılı MATEMATİK Dersi Final Sınavı Çalışma Soruları 1) 3. [15 3(8: )] 9 =? a) 16 b) 14 c) 0 d) 14 e) 16 6)
Dikkat: Bir eleman, her iki kümede de olsa bile sadece bir kez yazılır.
 KÜMELER Kümelerin birleşimi (A B ): Kümelerin bütün elemanlarından oluşur. Kümelerin kesişimi (A B): Kümelerin ortak elemanlarından oluşur. Kümelerin Farkı (A \ B ) veya (A - B ): Birinci kümede olup ikinci
KÜMELER Kümelerin birleşimi (A B ): Kümelerin bütün elemanlarından oluşur. Kümelerin kesişimi (A B): Kümelerin ortak elemanlarından oluşur. Kümelerin Farkı (A \ B ) veya (A - B ): Birinci kümede olup ikinci
ales dört bin soru tarzına en yakın EŞİT AĞIRLIK ve SAYISAL ADAYLARA ALES SORU BANKASI Kenan Osmanoğlu - Kerem Köker - Savaş Doğan
 ales 2015 tarzına en yakın dört bin soru EŞİT AĞIRLIK ve SAYISAL ADAYLARA ALES SORU BANKASI Kenan Osmanoğlu - Kerem Köker - Savaş Doğan Kenan Osmanoğlu - Kerem Köker - Savaş Doğan ALES Eşit Ağırlık ve
ales 2015 tarzına en yakın dört bin soru EŞİT AĞIRLIK ve SAYISAL ADAYLARA ALES SORU BANKASI Kenan Osmanoğlu - Kerem Köker - Savaş Doğan Kenan Osmanoğlu - Kerem Köker - Savaş Doğan ALES Eşit Ağırlık ve
Bu ürünün bütün hakları. ÇÖZÜM DERGİSİ YAYINCILIK SAN. TİC. LTD. ŞTİ. ne aittir. Tamamının ya da bir kısmının ürünü yayımlayan şirketin
 Bu ürünün bütün hakları ÇÖZÜM DERGİSİ YAYINCILIK SAN. TİC. LTD. ŞTİ. ne aittir. Tamamının ya da bir kısmının ürünü yayımlayan şirketin önceden izni olmaksızın fotokopi ya da elektronik, mekanik herhangi
Bu ürünün bütün hakları ÇÖZÜM DERGİSİ YAYINCILIK SAN. TİC. LTD. ŞTİ. ne aittir. Tamamının ya da bir kısmının ürünü yayımlayan şirketin önceden izni olmaksızın fotokopi ya da elektronik, mekanik herhangi
KPSS soruda SORU GENEL YETENEK - GENEL KÜLTÜR MATEMATİK GEOMETRİ TAMAMI ÇÖZÜMLÜ SORU BANKASI
 KPSS 019 10 soruda 86 SORU GENEL YETENEK - GENEL KÜLTÜR MATEMATİK GEOMETRİ TAMAMI ÇÖZÜMLÜ SORU BANKASI Komisyon KPSS LİSANS MATEMATİK - GEOMETRİ SORU BANKASI ISBN 978-605-41-77-0 Kitapta yer alan bölümlerin
KPSS 019 10 soruda 86 SORU GENEL YETENEK - GENEL KÜLTÜR MATEMATİK GEOMETRİ TAMAMI ÇÖZÜMLÜ SORU BANKASI Komisyon KPSS LİSANS MATEMATİK - GEOMETRİ SORU BANKASI ISBN 978-605-41-77-0 Kitapta yer alan bölümlerin
Ortak Bölenlerin En Büyüğü & Ortak Katların En Küçüğü
 Sayfa : 1 60 ve 72 nin OBEB VE toplamları kaçtır? A) 30 B) 360 C) 372 D) 420 E) 448 24, 36, 60 sayılarının i OBEB inin kaç katıdır? A) 12 B) 20 C) 30 D) 45 E) 54 Cevaplar: C C Sayfa : 2 54 ve 78 sayılarını
Sayfa : 1 60 ve 72 nin OBEB VE toplamları kaçtır? A) 30 B) 360 C) 372 D) 420 E) 448 24, 36, 60 sayılarının i OBEB inin kaç katıdır? A) 12 B) 20 C) 30 D) 45 E) 54 Cevaplar: C C Sayfa : 2 54 ve 78 sayılarını
ASAL SAYILAR - TAM BÖLENLER - FAKTÖRİYEL Test -1
 ASAL SAYILAR - TAM BÖLENLER - FAKTÖRİYEL Test -1 1. ve y aralarında asal iki doğal sayıdır. 7 y 11 olduğuna göre, y farkı 5. 364 sayısının en büyük asal böleni A) 3 B) 7 C) 11 D) 13 E) 17 A) B) 3 C) 4
ASAL SAYILAR - TAM BÖLENLER - FAKTÖRİYEL Test -1 1. ve y aralarında asal iki doğal sayıdır. 7 y 11 olduğuna göre, y farkı 5. 364 sayısının en büyük asal böleni A) 3 B) 7 C) 11 D) 13 E) 17 A) B) 3 C) 4
