HÜCRESEL ÜRETİMDE TEZGAH YERLEŞİMİ. A Attila İŞLİER 1 Osmangazi Üniversitesi, Endüstri Mühendisliği Bölümü 1
|
|
|
- Umut Erbakan
- 8 yıl önce
- İzleme sayısı:
Transkript
1 iletişim HÜCRESEL ÜRETİMDE TEZGAH YERLEŞİMİ A Attila İŞLİER 1 Osmangazi Üniversitesi, Endüstri Mühendisliği Bölümü 1 TESİS VE TESİS YERLEŞİMİ Yerleşim sorunu, birbirlerine hizmet veren tesisler için bir kaynak tahsisi problemidir. Burada tahsis edilecek kaynak, problemin boyut sayısına bağlı olarak alan veya hacim, genel olarak da; yerdir [Brandeau ve Chiu, 1989]. Tesis terimi, akla gelebilecek her çeşit üretim aracının genel adıdır. Her işlem başka bir araç gerektirdiğinden, üretim tesisleri büyük bir çeşitlilik gösterir. Tüm tesislerin ortak özelliği, hepsinin belli bir yer kaplamasıdır. Tesislerin yerleştirilmesinde, tesisin yer aldığı konuma bağlı olan bir amaç eniyilenmeye çalışılır. Bu amaç, ortalama taşıma süresinin, toplam taşıma yükünün veya tesisler arası en büyük uzaklığın enküçüklenmesi olabilir. Problem çoğu kez tek bir amaca, malzeme aktarma maliyetlerinin enküçüklenmesine dayandırılır. Bu maliyetler de üretim hacmi, ürün karışımı ve uzaklıkların bir fonksiyonudur. Diğer yandan, hacim ve ürün karışımı talebe, uzaklıklar da tesislerin konumlarına bağlıdır. Talebin yapısını değiştirmek güç olduğundan, tesis tasarımcıları öncelikle tesislerin konumları ile oynayarak uzaklıkları, dolayısıyla da malzeme aktarma maliyetlerini düşürmeye çalışırlar [Kochhar ve Heragu, 1998]. Malzeme taşıma maliyetlerinin yanında, yakınlık ilişkileri gibi diğer amaçların da eniyilenmesi istendiğinde, bu amaçlar ağırhklandırılarak, bunların ağırlıklı toplamından oluşan bir fayda fonksiyonu tanımlanır ve bu fonksiyonu eniyileyecek yerleşim düzenlemesinin belirlenmesine çalışılır. Amaçlara verilen ağırlıklar nesnel yöntemlerle belirlenemediğinden, değişik kişilerce farklı durum ve zamanlarda verilecek ağırlıkların, problemin çözümüne farklı sonuçlar getireceği düşünülebilir. Ancak, Dweiri ve Meier (1996), bulanık karar ortamında yapılan ve ikili karşılaştırmalarla denetlenen ağırlıklandırmanın çözüme dinamizmin yanında tutarlılık da getirdiğini belirtmektedir. Meiler ve Gau (1996), farklı ağırlıklandırma durumlannda bile amaç fonksiyonunu eniyileyecek tek bir çözümün bulunabileceğini göstermiştir. Bir başka deyişle, çözümün ağırlıklara duyarlılığı yeterince düşük olabilmektedir. Bu nedenle, gerçekte çok amaçlı bir yapıda olan yerleşim düzenlemesi problemi, genelde tek amaçlı bir probleme indirgenip çözülmektedir. BÖLÜMLER VE BLOK GÖSTERİMİ Geleneksel yerleşim düzenlemesi yöntemlerinden biri olan sistematik tesis planlaması [Muther,1973], genelden özele giden bir yapıya sahiptir. Bu yöntemde bölümler, yeri, şekli ve ölçüleri belirlenen oturma alanı içinde, birbirine göre konumlandırılır. Sonra bölümlerin iç yerleşimi yapılıp, uygulama planları hazırlanır. Burada bölüm, farklı özellik ve yapılarda olan birçok tezgah ve diğer donanımın yer aldığı bir üretim birimi anlamındadır. Bir fabrikada bulunabilecek yüzlerce tezgahı ve bunlar arasındaki tüm ikili ilişkileri bir arada ele almak olanaksızdır. Bu nedenle fabrikayı bloklarla gösterilen bölümlere ayırmak, problemin çözülebilmesini sağlamaktadır. Bu bloklar, söz konusu bölümlerde bulunan tezgahların kapladığı alanlar, bunlar arasındaki boşluklar ve diğer kullanım alanlannın toplamına eşit bir alana sahip olan 18
2 dikdörtgenlerdir. Bu dikdörtgenler, içindeki aynntılara yer vermeksizin, bölümün tamamını temsil eder. Blok yerleşimi, bu dikdörtgenlerin fabrika için ayrılmış oturma alanında konumlandırılması demektir. Konumlandırma sırasında, dikdörtgenlerin basıklıktan (en/boy oranlan) ve gerekirse alanlan değiştirilir. Tüm bloklar, -kendisi de genelde bir dikdörtgen olanfabrika oturma alanı içine sığdırılır. Konumlandırmada, aralarında yakın ilişki olan bölümlerin yan yana getirilmesine çalışılır. Sistematik tesis planlaması, aynı yöntemi daha sonra da bölümlerin iç yerleşimine uygulamakta, tezgah düzeyinde yerleştirme yapmak için değişik bir yol önermemektedir. Blok kavramının kullanımı, sistematik tesis planlamasıyla sınırlı değildir. Diğer birçok geleneksel yöntem ve bilgisayar destekli çözüm paketleri de bu yaklaşımın, problemi bölerek çözme özelliğinden yararlanmaktadırlar. Ancak, grup teknolojisi (GT), robotik, hücresel üretim (HÜ) ve esnek üretim sistemleri (EÜS) gibi yeni imalat teknolojileri ve felsefeleri için, blok yerleşimine dayanan çözümler yetersiz kalmaktadır. Yüzlerce tezgahtan oluşan bölümler yerine, daha küçük tezgah gruplarının oluşjurduğuhücrelerin kullanımına dayanan bu üretim sistemlerinde, yerleşim planları daha teknik ayrıntılar gerektirmektedir. Diğer yandan bu birimlerdeki tezgah sayılannın azlığı, bu aynntı düzeyindeki yöntem ve gösterimleri de olurlu kılmaktadır. HÜCRELERDE TEZGAH YERLEŞİMİ GT ve EÜS gibi yeni üretim teknoloji ve felsefelerinin sağladıkları yararlar, üretim hücrelerinin yaygınlaşmasına neden olmaktadır. Geleneksel yerleşim düzenlemesi tekniklerinin, üretim hücrelerinin yerleşim düzenlemesinde yetersiz kaldığından söz eden Rajasekharan vd. [1998], özellikle hücre eksenleri, hücreler arası yerleşim ve alma-bırnkma noktalan üzerinde durmaktadır. Tam ve Chan [ 199S], blok yerleşiminin gerçek hayatta önemi olan birçok geometrik kısıb göz ardı ettiği için, geleneksel yerleşim algoritmaları ile elde edilen çözümlerin uygulanmasında büyük zorluklar yaşandığını belirtmektedir. Yerleşim düzenlemesi yöntemlerinin çoğunun blok gösterimine dayandığını söyleyen Mata ve Tubaileh [1998], malzeme aktarma donanımı, giriş-çıkış istasyonla«ve tesis yönü gibi yapıyı ve işletimi etkileyen birçok özelliğin bu tür gösterimde yer almadığına dikkati çekmektedir. Tezgahlar arası boşluklar üzerinde duran Gen vd. [1994], bu problem için bulanık mantık ve genetik algoritmalara dayanan bir çözüm yolu önermektedir. Tezgah yerleşim tiplerini, doğrusal (tek sıralı), çok sıralı, yarım çember, U-şeklinde ve halka şeklinde olmak üzere beş gruba ayıran Hassan [1994], tezgah yerleşiminin özelliklerini şu şekilde sıralamaktadır: Aynı hücredeki tezgahlar arasında önemli şekil ve ölçü farklılıkları yoktur, bu nedenle duyarlılığı kaybetmeksizin, tezgah büyüklükleri ve tezgahlar arası uzaklıklar eşit olarak alınıp yerleşim, Şekil l'deki gibi şematik olarak gösterilebilir. Blok yerleşiminin dayandığı nitel ilişkilere karşılık, tezgah yerleşimi daha çok nicel ilişkilere dayandırılabilmektedir. Blok yerleşiminde gösterilemeyen kapasite kullanım oranı, kuyruk süresi-boyu, geri dönme atlama, akış yönü, alma-bırakma noktası ve tezgah-adam atama gibi birçok özel kunu i ı yerleşiminde ele alınabilir. Şekil 1. Tezgah Yerleşim Tipleri 19
3 Ayrıntı düzeyi yüksek olduğu için, daha özenli bir analiz ve daha çok veri gerektirir. Tezgahlann bir hat boyunca dizilmesi ile doğrusal bir yerleşim elde edilmektedir. Şekil l'deki diğer yerleşim tiplerinin de doğrusal yerleşimden türetildiği düşünülebilir. Malzeme aktarma aracı olarak robot kullanılması halinde, tezgahların bir doğru parçası yerine, merkezinde robotun yer aldığı bir yay üzerine dizilmesi ile, robotun dönme eksenine uygun bir yerleşim elde edilir. Hattın uzun, hata ayrılan yerin kısa olması halinde, hatun yansını geriye döndürerek, U şeklinde bir yerleşim elde edilir. Halka şeklindeki yerleşim de, U'nun iki ucunun birleştirilmesiyle ortaya çıkmaktadır. Çok sıralı yerleşim ise, birkaç hattın paralel olarak yerleştirilmesiyle oluşur. Ancak, bu hatlar arasında kurulan diğer bağlantılar, çok sıralı yerleşimdeki malzeme akışını karmaşıklaştırmaktadır. Bir başka açıdan bakıldığında, doğrusal yerleşimin ürüne göre yerleşime, çok sıralı yerleşimin de, sürece göre yerleşime karşı geldiği söylenebilir. HALKA TİPİ YERLEŞİM VE GEZİ ÇİZELGESİ Chase ve Aquilano [1989], U şeklindeki yerleşimin, uzun hatları dar yere sığdırmanın yanında, almabırakma noktalarını birleştirmek, işçilerin birbirini desteklemesini ve takım ruhunun oluşmasını sağlamak gibi diğer yararları üzerinde de durmaktadır. Aynı yararlar, halka tipi yerleşim için de söz konusudur. Bu yerleşim tipinde, elle veya götürücü (konveyör) ile yapılan taşıma, robot, AGV, vb. ile yapılacak taşımaya göre daha ekonomik olmaktadır. Götürücüler malzeme iletiminden başka, bir çeşit stoklama işlevi de görebilmekte, bazen üzerinde işlemlerin yürütüldüğü platformları da oluşturabilmektedir. Groover [1987] taşırken stoklama, stoklarken üretme, üretirken taşıma, bir başka deyişle üretim-stok-taşıma bütünleşmesi yönündeki eğilimleri önemle vurgulamaktadır. Halka yerleşimini destekleyen götürücüler, bu bütünleşmede önemli bir yer almalarının yanında, akışın düzenliliği ve sürekliliğinin sağlanmasında da yararlı olmaktadırlar. Götürücüleri teknik olarak iki yönlü çalıştırmak mümkünse de, halka şeklindeki bir düzenlemede iyi bir akış için tek yönlü hareket daha elverişlidir. Sadece saat yönünde veya bu yönün tersinde hareket ile yön değiştirmekten kaynaklanacak karışıklıklar önlenebilecektir. Şekil l'de doğrusal yerleşim için gösterilmiş olan atlama ve geri dönme durumlarıyla halka tipi yerleşimde de karşılaşılabilir. Bir hücrede işlenecek tüm parçalann rotalan genelde aynı olamayacağı için, belli bir parçanın işlem sırası için yapılan bir yerleşim düzenlemesi, diğer parçalar için uygun olmayabilir. Bunun sonucunda, bazı parçalar bazı işlemleri görmeyecek (atlama), bazen de ters yönde taşımalar (geri dönme) gerekecektir. Göreceği işlem sayısı n olan bir parça için hazırlanacak nxn ölçüsündeki bir G matrisi taşıma yükü verilerini tutmakta kullanılabilir. Şekil 2 a'da, rotası ACABA olan bir parçanın ABCD doğrusal yerleşimindeki taşıma sayıları görülmektedir (yerleşim sırasının değişmesi, elemanların değeri değişmeksizin satır ve sütunların yer değiştirmesine neden olacaktır). Bu gösterimde i den j ye taşıma varsa, matrisin karşı gelen elemanı 1 arttırılmakta, taşıma yoksa değiştirilmemektedir (başlangıçta tüm elemanlar 0 ). Bu durumda ilerleme yönündeki taşımalar ana köşegenin üstünde, ters yöndeki taşımalar da altında yer alacaktır. Aynı yerleşimde üretilecek BABA rotalı bir başka parçanın yükünü gösteren matris, Şekil 2 b'de verilmiştir (B'den A'ya iki taşıma var). İlk parçadan bir dönemde (örneğin bir ayda) 4000 adet, ikinci parçadan da 3000 adet yapılacaksa, bu yerleşimin gezi çizelgesi, Şekil 2 c'deki gibi olur (Parçanın gezi çizelgesi ile yerleşim düzeninin gezi çizelgesi farklı kavramlardır). Doğrusal yerleşimde, ana köşegene çizilen paraleller (Şekil 2 c), tesislerin birbirine olan uzaklıklarını gösterecektir. Örneğin AB, BC ve CD üstteki ilk paralelde (çaprazda) yer aldıkları için birbirlerinden birer birim, AC vebd ise ikinci çaprazda olduktan için ikişer birim uzaktadırlar (tezgahlar arası uzaklıklar eşit alınmaktadır). Aynı şeyler alttaki çaprazlar için de söylenebilir. Farklı sıralamalarla -satır ve sütunların yerleri değişeceğinden- uzaktaki elemanlar, ana köşegene yaklaştırılıp, taşıma yükü Şekil 2. Gezi Çizelgeleri 20
4 . azaltılabilir. Moment uygulamalı gezi çizelgesi olarak tanınan bir geleneksel yöntemde, özellikle köşegenin altındaki elemanları azaltıp, ters yönde taşımaların kötü etkisi giderilmeye çalışılır [Koçer, 1974]. HALKA YERLEŞİMİNDE SIRALAMA İdeal bir akışta, parça hattaki tüm tezgahlara sırasıyla uğramalıdır. Ancak tezgah sıralamasıyla farklı parça rotaları arasındaki uyumsuzluk nedeniyle, atlama ve geri dönmeler kaçınılmaz olmaktadır. Götürücü, tezgahların üzerinden değil de önünden geçer (Şekil 3). Bu nedenle bazı tezgahlara uğranılmaması yolu uzatırsa da, atlanan tezgahların çalışmasına engel olmaz. Ancak geri dönüşler, malzeme akışını olumsuz yönde etkilediklerinden, bunlardan kaçınmaya çalışılır. Bu nedenle örneğin, sekiz tezgahlı bir hatta bir geri gitmektense, yedi ileri gitmek tercih edilebilir (doğrusu bu en aşırı durumdur). Şekil 3. Halka Tipi Yerleşim ve Malzeme Akışı Askin ve Standrige [1993], hücresel üretimde grup büyüklüğünün "ortak hedefe yönelme olanağı verecek kadar küçük; bu hedefe ulaşmak için gerekli kaynaklan içerecek kadar da büyük" tutulması gerektiğini; bunun için de; 6 ila 12 arası tezgah sayısının uygun, 7 tezgahın ise ideal olduğunu belirtmektedir. Farklı n adet nesne bir çember üzenndep n =(n-l)! farklı şekilde dizilebilir. Bu durumda ideal büyüklükte bir halka için (7-1)1=720 çözüm söz konusudur (simetri dolayısıyla bu sayı da yarıya inecektir). Bu büyüklükte bir problem, sayımlama yöntemi ile (tüm uygun çözümleri tek tek kontrol ederek) rahatlıkla çözülebilir. Halka yerleşimi bir çeşit sıralamaya dayandığı için, daha büyük problemler de genetik algoritmalar (GA) ile çözülmeye elverişlidir. Ürün çeşitleri, bunların rotalan ve üretim hacimleri, hücrenin gezi çizelgesini belirlemektedir. Bu çizelgenin satır ve sütunlarını paralel olarak değiştirmekle, aynı çizelgenin farklı gösterimleri elde edilir. Şekil 4 a'daki 1. ve 3. sütunlann, buna paralel olarak da, 1. ve 3. satırların Şekil 4 b' deki gibi değiştirilmesiyle a'daki ABCD yerine CBAD sıralamasının gezi çizelgesi elde edilmiştir. Düzenlenebilecek diğer gösterimlerden biri olan c'deki sıralama, en iyi çözümü göstermektedir. Çünkü, matrisin sıfır olmayan elemanlannın tümünün ana köşegenden uzaklığı, bir birimdir. Bir başka deyişle, i. işlemi izleyen j. işlem, bir sonraki tezgahta yapılmaktadır. Bu durum, atlama ve geri dönmelerin olmadığını ve ideal akışın sağlandığını göstermektedir. Şekil 4 d'de, ana köşegene paralel olan çaprazlar gösterilmektedir. Üst üçgendeki ikinci çapraz üzerindeki elemanlar bir tezgah atlama, üçüncü çapraz üzerindeki elemanlar da iki tezgah atlama durumlarını göstermektedirler. Doğrusal yerleşimde, alttaki çaprazlar üzerindeki elemanlar, geri dönüş anlamına gelmekte, ana köşegenden uzaklaştıkça da geriye doğru atlanan tezgah sayısı artmaktadır. Tek yönlü halka yerleşiminde ise, Kristof Kolomb'un batıya giderek doğudaki Hindistan'a ulaşmak istemesi gibi, gerideki tezgahlara ileriye giderek erişilmekte, böylelikle de akışın sürekliliğini bozmaktan kaçınılmaktadır. Alttaki ilk çaprazda bulunan elemanlar bir önceki tezgaha, k. çaprazdakiler de, geriye doğru k. tezgaha dönüşleri göstermektedir. Genelde i. tezgah ile;', tezgah arasındaki uzaklık i- ; dir (herhangi iki tezgah arasındaki uzaklık bir birim). Alt üçgendeki elemanlar (i>j), geri dönmeleri gösterir. Halkadaki tezgah sayısı n iken, alt üçgende i. tezgah ile;, tezgah arasındaki uzaklık, d=n+j-i olur. Şekil 4. Halkada Farklı Sıralama ve Uzaklıklar 21
5 PROBLEMİN MODELLENMESI VE ÇÖZÜMÜ Bir hücrede üretilebilecek tüm parçaların rotaları aynı olamayacağından, malzeme aktanmında atlama ve geriye dönmeler kaçınılmaz olmaktadır. Tek yönlü hareket kısıü ile, geriye doğru olan hareketler, atlamaya dönüştürülerek bunların akışa zararlı etkileri azaltdabilmektedir. Gezi çizelgesinin üst üçgenindeki elemanlar (i<j), doğal at/amaların sayısını, alt üçgenindeki elemanlar da (/<0 zorlanmış ctf/amalann sayısını vermekte, geri dönme artık söz konusu olmamaktadır. Belli bir yerleşim şekli için toplam faşıma yükü y, i için g u =0 ve d u =0 olmak üzere aşağıdaki eşitlikle hesaplanabilir: (1) Her sıralama, farklı sayıda doğal ve zorlanmış atlamalar getirecek, bunun sonucunda da, her sıralamanın yükü farklı olacaktır. Bu sıralamalardan en iyisini (en küçük toplam taşıma yükünü veren çözümü) araştıran problem şu şekilde modellenebilir: (2) (3) (4) (5) k.a. Problemin yapısı, sayımlama ile çözümün yetersiz kalacağı büyük problemlerde genetik algoritma (GA) kullanımına elverişli ise de, burada kullanılacak GA'nın tasarımında aşağıdaki güçlüklerin aşılması gerekmektedir: i) Çözüm seçeneklerinin kromozom yapısında modellenmesi, ü) Her tezgahın her kromozomda bir kez yer alması (genetik işlemler, bu şarta uymayan kromozomların ortaya çıkmasına neden olur), iii) Çözüme hızla yaklaşmayı sağlayacak parametrelerin bulunması. 22 Şekil 3'deki yerleşim, YABCDEFG kromozomu ile gösterilebilir. Burada, yükleme boşaltma istasyonundan başlayıp saat yönünde ilerleyerek tüm tezgahlar kaydedilerek eldeki yerleşim bir kromozomla gösterilmiş ve tasanmın ilk zorluğu aşılmıştan Ancak, kromozomlara uygulanacak çaprazlama işlemleri sonunda ortaya çıkacak kromozomlar bazı tezgahları içermezken, diğer bazı tezgahlan tekrarlı olarak içerir duruma düşecektir. Bu hatayı düzletmek için, her çaprazlamayı bir tamir yordamının izlemesi ve bu şekilde ikinci zorluğun da yenilmesi gerekmektedir. Üreme hızı, populasyon büyüklüğü, mutasyon hızı gibi parametrelerin en iyi değerleri, probleme bağımlı olduğundan, son zorluğun yenilmesi ancak zaman içerisindeki uygulama ve deneylerle sağlanabilecektir. Bu bölümde verilen modelin amaç fonksiyonu olan 5 numaralı eşittik, aynı zamanda GA'nın dauyum /onksîyonudur. Başlangıçta rassal olarak türetilen belli sayıdaki çözümün en iyilerine çaprazlama işleminin uygulanmasıyla, kaliteli 1 kısmi sıralamalar (shemata) kromozomlann yapısı içinde yoğunlaşacak ve yeni çözümler (kuşaklar) önceki çözümlerden (eski kuşaklardan) daha iyi niteliklere sahip olacaklardır. Genetik algoritmalann temel teoremi, algoritmanın yakınsadığını ve kuşaklar ilerledikçe daha iyi çözümlere ulaşılacağını belirtmektedir. Algoritmanın alt eniyi noktalara takılmaması, bütünsel en iyiyi bulma şansını kaybetmemesi için populasyon (belli, bir anda elde tutulan kromozom kümesi) çeşitliliğinin yüksek tutulması, bir başka deyişle zaman içinde tüm kromozomların birbirine benzemeye başlamasının engellenmesi gerekir. Bu amaçla zaman zaman iç çaprazlama (bir kromozomda rassal olarak iki tezgahın yerini değiştirme) işlemi.uygulanabilir. İç çaprazlama kromozomlar arasında tezgah alış-verişine neden olmayacağı için, bu işlemden sonra tamir gerekmez. Ortaya çıkan iyi çözümlerin genetik işlemler sonucunda kaybolmaması için bir seçkindi strateji uygulanması yararlı olur (Her kuşaktaki en iyi bir kaç çözümü, o kuşaktaki en kötü çözümler üzerine kopyalamakla eldeki en iyi çözümde gerileme olması engellenecektir). GA'nın uyum gücü yüksek (daha düşük taşıma yükü yeren) çözümleri türetmek ve bunların varlıklannı sürdürmek yolundaki katkılanyla, kuşaklar ilerledikçe giderek daha iyi çözümler elde edilecektir. Genetik işlemlerin yeterli sayıda tekrarı ile tatmin edici (bazen de en iyi) çözüme ulaşılır ve
6 algoritmanın çalışması durdurulur. Aşağıdaki algoritma, genetik işlemlerin halka tasarımında kullanımını toplu olarak göstermektedir: Procedure GA; Begin t:=0; türet; end; while t<tekrar_sayısı then begin end; t:=t+l; değerlendir; al; seç; çaprazla; tamir_et; rassal; if rassal<eşik then iç_çaprazla; ekle; Bu algoritmadaki türet yordamı, rassal olarak başlangıç populasyonunu türetecek, değerlendir yordamı t. populasyondaki tüm kromozomlann uyum fonksiyonlarını hesaplayacak, seç yordamı da, uyum gücü yüksek kromozomlara daha yüksek şans tanıyarak kromozomlar arasından rassal bir seçim yapacaktır. Seç yordamının seçtiği kromozomlar, yine bu yordamın rassal olarak belirlediği kırılma noktalarından, çaprazla yordamı ile çaprazlanacakbr. Çaprazlama sonunda ortaya çıkacak kromozomlarda bazı tezgahlar hiç yer almazken, bazı tezgahlar birden fazla tekrarlanacaklardır. Bu istenmeyen durum tamir_et yordamı ile düzeltilir. Rassal yordamının türettiği rassal sayı, bir eşik değerinden küçük ise, iç_çaprazla yordamıyla kromozoma bir çeşit mutasyon işlemi uygulanıp, çeşitliliğin azalması engellenir. Eldeki en iyi çözümün genetik işlemlerle bozulmasını engelleyen seçkinci strateji ise, al ve ekle yordamları aracılığıyla uygulanmaktadır. Genetik işlemlere başlamadan al yordamı ile en iyi çözümlerin kopyaları çıkarılır, sonra bu çözümler ekle yordamı ile populasyonun en kötü çözümlerinin yerine koyulur. Tüm bu işlemlerin tekrar_sayısı kez yinelenmesiyle, halka tasarımının dayandırılacağı iylbir çözüm elde edilir. SONUÇ VE ÖNERİLER Odaklanmış fabrika, HÜ, EÜS, JIT ve yerinde üretim gibi eğilimler, tezgahlann daha küçük üretim birimleri oluşturacak şekilde düzenlenmelerine yol açmaktadır. Bu birimlerde tek sıralı (akış) ve çok sıralı (süreç) yerleşimler yanında, U ve halka şeklindeki yerleşimler de pratik ve kuramsal önemleri dolayısıyla araşürmacılann dikkatini çekmektedir. Özellikle halka şeklindeki yerleşim, çevrime uygun yapısıyla geri dönüşleri engellemek; götürücü kullanımı sayesinde detaşıma-stoklama bütünleşmesi sağlamak olanağını sunmaktadır. Tezgahlann halka şeklinde düzenlenmesiyle geri dönüşler önlenmekte; temel işlevi malzeme aktarma olan götürücüler, geçici stoklama yetenekleriyle de tampon stok problemini hafifletmekte; böylelikle de daha düzgün bir akış sağlayıp sistemin verimliliğini arttırmaktadır. Tezgah sıralamasına dayanan bu yerleşim düzenlemesi için geliştirilip altıncı bölümde verilen model, geri dönüşleri azaltarak toplam taşıma yüklerini en küçüklemektedir. Ürün rotalan ve üretim hacmine bağlı olan gezi çizelgesi matrisinin elemanları, tezgah sıralamasının değişmesiyle değer değiştirmemekle birlikte, yer değiştirirler. Bu da uzaklıklann, buna bağlı olarak da toplam taşıma yüklerinin değişmesi demektir. Her tezgahı bir kez içeren her sıralama, bir uygun çözümdür. Bu olurlu çözümlerden biri en küçük taşıma yükünü verecektir. Bu en iyi çözüm, az sayıda tezgah içeren problemlerde sayımlama yöntemiyle bulunabilir. Problemin kombinatorik yapısı, daha büyük problemlerde sayımlama ile çözümü olanaksız kılmaktadır. Bu durumda, rassal olarak türetilen çok sayıda sıralamanın yükünü hesaplayıp, bunlar arasından en düşük yükü veren çözüm benimsenebilir. Biraz daha karmaşık, ancak son derece etkin bir başka çözüm yolu da GA'dan yararlanmaktır. GA, çözüm uzayının çék küçük bir kısmını sistemli bir şekilde tarayarak, en iyi çözüme büyük hızla yaklaşır. Bölüm 6'da ana hatlarıyla verilen algoritma, daha büyük ölçekli halka yerleşimi problemlerine çözüm bulmak amacıyla tasarlanmıştır. İzleyeri çalışmalarda, halka yerleşimini en basit şekliyle ele alan bu algoritmanın iki yönde geliştirilmesi planlanmaktadır: Zaman boyutunu da hesaba katarak, işlem süreleri, tezgah yükleri, paralel tezgahlar, kapasite kullanım O/f anları, ara stok miktarları ve götürücü kapasitelerinin de incelenebilmesi ve çizelgeleme için bir destek sağlanması, Halka için geliştirilmiş modeli çok sıralı yerleşime uyarlayarak daha genel çözüm yollarının araştırılması. Burada gerçekleştirilen ve planlanan çalışmalarda, tezgahların eşit büyüklükte olduklan, komşu iki tezgah arası uzaklıkların da birbirine eşit bulunduğu varsayılmıştır. Daha gerçekçi çözümler için, farklı 23
7 iletişim tezgah boyutları, değişik alma-bırakma noktaları, halka için birden fazla giriş-çıkış istasyonu gibi özel durumlar modele katılabilir. Bulanık mantık yardımıyla tezgahlar arası boşluklar, tezgah şekilleri ve oval olmayan halka yapıları da ele alınabilir. KAYNAKÇA 1. Askin, R. G. ve Standrige C. R. [1993], Modeling and Analysis of Manufacturing Systems, John Wiley and Sons Inc. 2. Brandeau, M. L. ve Chiu, S. S. [1989], "An overview of Representative Problems in Location Research", Management Science, V. 35, N. 6, Chase, R. B. ve Aquilano, N. J. [1989], Production and Operation Management: A life Cycle Approach, Richard D. Irwin, Inc. 4. Dweiri, E ve Meier, F. A. [1996], "Application of Fuzzy Decision Making in Facilities Layout Planning", InternaöonalJournal of Production Research, V. 34, N. 11, Gen, M., Ida, K., Cheng, C. [1995], "Multirow Machine Layout Problem in Fuzzy Environment Using Genetic Algorithms", Computers and Industrial Engineering, V29, N.l-4, Groover, M. R [1987], Automation, Production Systems and Computer Integrated Manufacturing, Prentice Hall International Inc. 7. Hassan, M. M. D. [1994], "Machine Layout Problem in Manufacturing Facilities", International Journal of Production Research, V. 32, N. 11, Kochhar, J. S. ve Heragu, S. S. [1998], "Multi-Hope: A Tool for Multiple Floor Layout Problems", International Journal of Production Research, V. 36, N. 12, Koçer, M. [1974], Fabrika Organizasyonu ve Dizaynı, Güven Kitabevi, Ankara. 10. Mata, V ve Tubaileh, A. [1998], "The Machine Layout Problem in Robot Cells", International Journal of Production Research, V. 36, N. 5, Meiler, R. D. ve Gau, K. Y. [1996], "Facility Layout Objective Functions and Robust Layout", International Journal of Production Research, V. 34, N. 10, Muther; R. [1973], Systematic Layout Planning, Cahners Books, Boston. 13. Rajasekharan, M., Peters, B. A., Yang, T. [1998], "A Genetic Algorithm for Facility Layout Design in Flexible Manufacturing Systems", International Journal of Production Research, V. 36, N. 1, Tarn, K. Y ve Chan, S. K. [1998], "Solving Facility Layout Problems with Geometric Constraints Using Parallel Genetic Algorithms: Experimentation and Findings", International Journal of Production Research, V. 36, N.12, III. ULUSAL EMDÜSTRİ-İŞL TM MÜHENDİSLİĞİ KURULTAYl "ENDÜSTRİ-İŞLETME MÜHENDİSLİeİ'NİN DÖNÜ, BU6ÜNÜ, YARINI" EKİM 2001 KOCAELİ ÜNİVERSİTESİ TURİZM ve OTELCİLİK YÜKSEK OKULU UYGULAMA OTELİ DERBENT/KOCAELİ İletişim: MMO Kocaeli Şube Ömerağa Mah. Alemdar Cad. Soydan İş Mrkz. No:34 Kat:3 Daire:! 00 - İzmit Tel: Faks: E-posta: kocaeli@kocaeli.mmo.org.tr 24
IENG 227 Modern Üretim Yaklaşımları
 IENG 227 Modern Üretim Yaklaşımları Pamukkale Üniversitesi Endüstri Mühendisliği Bölümü IENG 227 Modern Üretim Yaklaşımları Dr. Hacer Güner Gören Esnek Üretim Sistemleri Esnek Üretim Sistemleri Bir esnek
IENG 227 Modern Üretim Yaklaşımları Pamukkale Üniversitesi Endüstri Mühendisliği Bölümü IENG 227 Modern Üretim Yaklaşımları Dr. Hacer Güner Gören Esnek Üretim Sistemleri Esnek Üretim Sistemleri Bir esnek
YZM 5257 YAPAY ZEKA VE UZMAN SİSTEMLER DERS#6: GENETİK ALGORİTMALAR
 YZM 5257 YAPAY ZEKA VE UZMAN SİSTEMLER DERS#6: GENETİK ALGORİTMALAR Sınıflandırma Yöntemleri: Karar Ağaçları (Decision Trees) Örnek Tabanlı Yöntemler (Instance Based Methods): k en yakın komşu (k nearest
YZM 5257 YAPAY ZEKA VE UZMAN SİSTEMLER DERS#6: GENETİK ALGORİTMALAR Sınıflandırma Yöntemleri: Karar Ağaçları (Decision Trees) Örnek Tabanlı Yöntemler (Instance Based Methods): k en yakın komşu (k nearest
Kaynak: A. İŞLİER, TESİS PLANLAMASI, 1997
 Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2016-2017 Güz Dönemi Kaynak: A. İŞLİER, TESİS PLANLAMASI, 1997 2 Tesis Yer Seçimi Problemi (TYSP) TEK AMAÇLI
Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2016-2017 Güz Dönemi Kaynak: A. İŞLİER, TESİS PLANLAMASI, 1997 2 Tesis Yer Seçimi Problemi (TYSP) TEK AMAÇLI
Temel yerleşim tipleri. Sistematik tesis planlaması. Mühendislik Fakültesi Endüstri Mühendisliği Bölümü
 Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Temel yerleşim tipleri Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2016-2017 Güz Dönemi Sistematik tesis planlaması 2 YER SEÇİMİ X YERLEŞİM DÜZENLEMESİ
Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Temel yerleşim tipleri Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2016-2017 Güz Dönemi Sistematik tesis planlaması 2 YER SEÇİMİ X YERLEŞİM DÜZENLEMESİ
GENETİK ALGORİTMA ÖZNUR CENGİZ HİLAL KOCA
 GENETİK ALGORİTMA ÖZNUR CENGİZ 201410306014 HİLAL KOCA 150306024 GENETİK ALGORİTMA Genetik Algoritma yaklaşımının ortaya çıkışı 1970 lerin başında olmuştur. 1975 te John Holland ın makine öğrenmesi üzerine
GENETİK ALGORİTMA ÖZNUR CENGİZ 201410306014 HİLAL KOCA 150306024 GENETİK ALGORİTMA Genetik Algoritma yaklaşımının ortaya çıkışı 1970 lerin başında olmuştur. 1975 te John Holland ın makine öğrenmesi üzerine
GENETİK ALGORİTMALAR. Araş. Gör. Nesibe YALÇIN BİLECİK ÜNİVERSİTESİ
 GENETİK ALGORİTMALAR Araş. Gör. Nesibe YALÇIN BİLECİK ÜNİVERSİTESİ GENETİK ALGORİTMALAR Genetik algoritmalar, Darwin in doğal seçim ve evrim teorisi ilkelerine dayanan bir arama ve optimizasyon yöntemidir.
GENETİK ALGORİTMALAR Araş. Gör. Nesibe YALÇIN BİLECİK ÜNİVERSİTESİ GENETİK ALGORİTMALAR Genetik algoritmalar, Darwin in doğal seçim ve evrim teorisi ilkelerine dayanan bir arama ve optimizasyon yöntemidir.
1 ÜRETİM VE ÜRETİM YÖNETİMİ
 İÇİNDEKİLER ÖNSÖZ III Bölüm 1 ÜRETİM VE ÜRETİM YÖNETİMİ 13 1.1. Üretim, Üretim Yönetimi Kavramları ve Önemi 14 1.2. Üretim Yönetiminin Tarihisel Gelişimi 18 1.3. Üretim Yönetiminin Amaçları ve Fonksiyonları
İÇİNDEKİLER ÖNSÖZ III Bölüm 1 ÜRETİM VE ÜRETİM YÖNETİMİ 13 1.1. Üretim, Üretim Yönetimi Kavramları ve Önemi 14 1.2. Üretim Yönetiminin Tarihisel Gelişimi 18 1.3. Üretim Yönetiminin Amaçları ve Fonksiyonları
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ
 ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTIRMA MODELİNİN TANIMI Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTIRMA MODELİNİN TANIMI Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü. Doç. Dr. Nil ARAS ENM411 Tesis Planlaması Güz Dönemi
 Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2018-2019 Güz Dönemi Tesis Planlama Süreci (imalat ve montaj tesisleri için) 2
Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2018-2019 Güz Dönemi Tesis Planlama Süreci (imalat ve montaj tesisleri için) 2
Zeki Optimizasyon Teknikleri
 Zeki Optimizasyon Teknikleri Genetik Algoritma (Genetic Algorithm) Doç.Dr. M. Ali Akcayol Genetik Algoritma 1970 li yıllarda John Holland tarafından geliştirilmiştir. 1989 yılında David E. Goldberg Genetik
Zeki Optimizasyon Teknikleri Genetik Algoritma (Genetic Algorithm) Doç.Dr. M. Ali Akcayol Genetik Algoritma 1970 li yıllarda John Holland tarafından geliştirilmiştir. 1989 yılında David E. Goldberg Genetik
Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü. Doç. Dr. Nil ARAS ENM411 Tesis Planlaması Güz Dönemi
 Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2018-2019 Güz Dönemi 2 Tesis ihtiyaçlarının belirlenmesinde 3 önemli faktör Akış
Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2018-2019 Güz Dönemi 2 Tesis ihtiyaçlarının belirlenmesinde 3 önemli faktör Akış
Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü. Doç. Dr. Nil ARAS ENM411 Tesis Planlaması Güz Dönemi
 Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2018-2019 Güz Dönemi 2 F : Vardiya başına gereken makina sayısı S : Standart süre
Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2018-2019 Güz Dönemi 2 F : Vardiya başına gereken makina sayısı S : Standart süre
Gezgin Satıcı Probleminin İkili Kodlanmış Genetik Algoritmalarla Çözümünde Yeni Bir Yaklaşım. Mehmet Ali Aytekin Tahir Emre Kalaycı
 Gezgin Satıcı Probleminin İkili Kodlanmış Genetik Algoritmalarla Çözümünde Yeni Bir Yaklaşım Mehmet Ali Aytekin Tahir Emre Kalaycı Gündem Gezgin Satıcı Problemi GSP'yi Çözen Algoritmalar Genetik Algoritmalar
Gezgin Satıcı Probleminin İkili Kodlanmış Genetik Algoritmalarla Çözümünde Yeni Bir Yaklaşım Mehmet Ali Aytekin Tahir Emre Kalaycı Gündem Gezgin Satıcı Problemi GSP'yi Çözen Algoritmalar Genetik Algoritmalar
AKIŞ SİSTEMLERİ, FAALİYET İLİŞKİLERİ ve ALAN GEREKSİNİMLERİ
 Anadolu Üniversitesi Mühendislik Mimarlık Fakültesi Endüstri Mühendisliği Bölümü AKIŞ SİSTEMLERİ, FAALİYET İLİŞKİLERİ ve ALAN GEREKSİNİMLERİ Hazırlayan: Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2010-2011
Anadolu Üniversitesi Mühendislik Mimarlık Fakültesi Endüstri Mühendisliği Bölümü AKIŞ SİSTEMLERİ, FAALİYET İLİŞKİLERİ ve ALAN GEREKSİNİMLERİ Hazırlayan: Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2010-2011
m=n şeklindeki matrislere kare matris adı verilir. şeklindeki matrislere ise sütun matrisi denir. şeklindeki A matrisi bir kare matristir.
 Matrisler Satır ve sütunlar halinde düzenlenmiş tabloya matris denir. m satırı, n ise sütunu gösterir. a!! a!" a!! a!" a!! a!! a!! a!! a!" m=n şeklindeki matrislere kare matris adı verilir. [2 3 1] şeklinde,
Matrisler Satır ve sütunlar halinde düzenlenmiş tabloya matris denir. m satırı, n ise sütunu gösterir. a!! a!" a!! a!" a!! a!! a!! a!! a!" m=n şeklindeki matrislere kare matris adı verilir. [2 3 1] şeklinde,
GRUP TEKNOLOJİSİ. Yrd. Doç. Dr. Tijen Över Özçelik
 Yrd. Doç. Dr. Tijen Över Özçelik tover@sakarya.edu.tr Grup Teknolojisinde Performans Değerlendirme Ölçütleri Hücresel İmalat sistemlerinin tasarımında önemli olan konulardan biri oluşturulan hücrelerin
Yrd. Doç. Dr. Tijen Över Özçelik tover@sakarya.edu.tr Grup Teknolojisinde Performans Değerlendirme Ölçütleri Hücresel İmalat sistemlerinin tasarımında önemli olan konulardan biri oluşturulan hücrelerin
ÜRETİM SİSTEMLERİ ve ÖZELLİKLERİ
 ÜRETİM SİSTEMLERİ ve ÖZELLİKLERİ Üretim sistemleri hammaddelerin bitmiş ürüne dönüştürüldükleri sistemlerdir. Bu sistemler için oluşturulacak simülasyon modelleri tamamen üretim sisteminin tipine ve verilecek
ÜRETİM SİSTEMLERİ ve ÖZELLİKLERİ Üretim sistemleri hammaddelerin bitmiş ürüne dönüştürüldükleri sistemlerdir. Bu sistemler için oluşturulacak simülasyon modelleri tamamen üretim sisteminin tipine ve verilecek
GRUP TEKNOLOJİSİ VE HÜCRESEL ÜRETİM
 GRUP TEKNOLOJİSİ VE HÜCRESEL ÜRETİM GRUP TEKNOLOJİSİ VE HÜCRESEL ÜRETİM Grup Teknolojisi Ve Hücresel Üretim Kavramları Grup teknolojisi oldukça geniş bir kavramdır. Üretim ve endüstri mühendisliği alanlarında
GRUP TEKNOLOJİSİ VE HÜCRESEL ÜRETİM GRUP TEKNOLOJİSİ VE HÜCRESEL ÜRETİM Grup Teknolojisi Ve Hücresel Üretim Kavramları Grup teknolojisi oldukça geniş bir kavramdır. Üretim ve endüstri mühendisliği alanlarında
Tedarik Zinciri Yönetimi
 Tedarik Zinciri Yönetimi -Tedarik Zinciri Ağı Tasarımı- Yrd. Doç. Dr. Mert TOPOYAN Ağ tasarımı, tedarik zinciri açısından üç karar düzeyini de ilgilendiren ve bu düzeylerde etkisi olan bir konudur. Zincirin
Tedarik Zinciri Yönetimi -Tedarik Zinciri Ağı Tasarımı- Yrd. Doç. Dr. Mert TOPOYAN Ağ tasarımı, tedarik zinciri açısından üç karar düzeyini de ilgilendiren ve bu düzeylerde etkisi olan bir konudur. Zincirin
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ
 ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTıRMA MODELININ TANıMı Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTıRMA MODELININ TANıMı Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
Zeki Optimizasyon Teknikleri
 Zeki Optimizasyon Teknikleri Tabu Arama (Tabu Search) Doç.Dr. M. Ali Akcayol Tabu Arama 1986 yılında Glover tarafından geliştirilmiştir. Lokal minimum u elimine edebilir ve global minimum u bulur. Değerlendirme
Zeki Optimizasyon Teknikleri Tabu Arama (Tabu Search) Doç.Dr. M. Ali Akcayol Tabu Arama 1986 yılında Glover tarafından geliştirilmiştir. Lokal minimum u elimine edebilir ve global minimum u bulur. Değerlendirme
T.C. Ölçme, Seçme ve Yerleştirme Merkezi
 T.C. Ölçme, Seçme ve Yerleştirme Merkezi LİSANS YERLEŞTİRME SINAVI-1 MATEMATİK TESTİ 11 HAZİRAN 2017 PAZAR Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının veya bir kısmının
T.C. Ölçme, Seçme ve Yerleştirme Merkezi LİSANS YERLEŞTİRME SINAVI-1 MATEMATİK TESTİ 11 HAZİRAN 2017 PAZAR Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının veya bir kısmının
T.C. Ölçme, Seçme ve Yerleştirme Merkezi
 T.C. Ölçme, Seçme ve Yerleştirme Merkezi LİSANS YERLEŞTİRME SINAVI-1 MATEMATİK TESTİ 11 HAZİRAN 2017 PAZAR Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının veya bir kısmının
T.C. Ölçme, Seçme ve Yerleştirme Merkezi LİSANS YERLEŞTİRME SINAVI-1 MATEMATİK TESTİ 11 HAZİRAN 2017 PAZAR Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının veya bir kısmının
Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü. Doç. Dr. Nil ARAS ENM411 Tesis Planlaması Güz Dönemi
 Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2018-2019 Güz Dönemi 2 3 Öğrenme çıktıları Tesis planlaması ile ürün, süreç ve
Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2018-2019 Güz Dönemi 2 3 Öğrenme çıktıları Tesis planlaması ile ürün, süreç ve
DOKUZ EYLÜL ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ DEKANLIĞI DERS/MODÜL/BLOK TANITIM FORMU
 Dersi Veren Birim: Endüstri Mühendisliği Dersin Türkçe Adı: TESİS TASARIMI VE MALZEME AKTARMA SİSTEMLERİ Dersin Orjinal Adı: TESİS TASARIMI VE MALZEME AKTARMA SİSTEMLERİ Dersin Düzeyi:(Ön lisans, Lisans,
Dersi Veren Birim: Endüstri Mühendisliği Dersin Türkçe Adı: TESİS TASARIMI VE MALZEME AKTARMA SİSTEMLERİ Dersin Orjinal Adı: TESİS TASARIMI VE MALZEME AKTARMA SİSTEMLERİ Dersin Düzeyi:(Ön lisans, Lisans,
SOBA BORUSU AÇINIM LEVHALARININ KESİLMESİNDE MALİYETLERİN ENKÜÇÜKLENMESİ
 SOBA BORUSU AÇINIM LEVHALARININ KESİLMESİNDE MALİYETLERİN ENKÜÇÜKLENMESİ Doğan EROL Anadolu Üniversitesi Endüstri Mühendisliği Bölümü 1. PROBLEMİN TANIMLANMASI Şekil - 1'de 5 değişik soba borusu için açınım
SOBA BORUSU AÇINIM LEVHALARININ KESİLMESİNDE MALİYETLERİN ENKÜÇÜKLENMESİ Doğan EROL Anadolu Üniversitesi Endüstri Mühendisliği Bölümü 1. PROBLEMİN TANIMLANMASI Şekil - 1'de 5 değişik soba borusu için açınım
Lineer Cebir. Doç. Dr. Niyazi ŞAHİN TOBB. İçerik: 1.1. Lineer Denklemlerin Tanımı 1.2. Lineer Denklem Sistemleri 1.3. Matrisler
 Lineer Cebir Doç. Dr. Niyazi ŞAHİN TOBB İçerik: 1.1. Lineer Denklemlerin Tanımı 1.2. Lineer Denklem Sistemleri 1.3. Matrisler Bölüm 1 - Lineer Eşitlikler 1.1. Lineer Eşitliklerin Tanımı x 1, x 2,..., x
Lineer Cebir Doç. Dr. Niyazi ŞAHİN TOBB İçerik: 1.1. Lineer Denklemlerin Tanımı 1.2. Lineer Denklem Sistemleri 1.3. Matrisler Bölüm 1 - Lineer Eşitlikler 1.1. Lineer Eşitliklerin Tanımı x 1, x 2,..., x
ISK116 - Bölüm 1. Grup Teknolojisi
 ISK - Bölüm Grup Teknolojisi Grup Teknolojisi (GT) Grup teknolojisi benzerliklerden faydalanarak büyük ve karmaşık bir üretim sisteminin, küçük ve kolay kontrol edilebilir sistemlere dönüştürülmesi hedeflenmektedir.
ISK - Bölüm Grup Teknolojisi Grup Teknolojisi (GT) Grup teknolojisi benzerliklerden faydalanarak büyük ve karmaşık bir üretim sisteminin, küçük ve kolay kontrol edilebilir sistemlere dönüştürülmesi hedeflenmektedir.
GENETİK ALGORİTMALAR BÜŞRA GÜRACAR
 GENETİK ALGORİTMALAR BÜŞRA GÜRACAR 201420404036 İÇERİK Genetik Algoritmanın, Amacı Kullanım Alanları Kavramları Uygulama Adımları Parametreler Genetik Algoritma Kodlama Türleri Genetik Algoritma Genetik
GENETİK ALGORİTMALAR BÜŞRA GÜRACAR 201420404036 İÇERİK Genetik Algoritmanın, Amacı Kullanım Alanları Kavramları Uygulama Adımları Parametreler Genetik Algoritma Kodlama Türleri Genetik Algoritma Genetik
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 5- SONLU FARKLAR VE İNTERPOLASYON TEKNİKLERİ Doç. Dr. Ali Rıza YILDIZ MAK 210 - Sayısal Analiz 1 İNTERPOLASYON Tablo halinde verilen hassas sayısal değerler veya ayrık noktalardan
MAK 210 SAYISAL ANALİZ BÖLÜM 5- SONLU FARKLAR VE İNTERPOLASYON TEKNİKLERİ Doç. Dr. Ali Rıza YILDIZ MAK 210 - Sayısal Analiz 1 İNTERPOLASYON Tablo halinde verilen hassas sayısal değerler veya ayrık noktalardan
1989 ÖYS. olduğuna göre a-b kaçtır? A) 2 B) 2 C) 2 2 D) 2 2 E) 4
 989 ÖYS. a a a b 8 olduğuna göre a-b kaçtır? C). a ile b nin aritmetik ortalaması 5 tir. a ile geometrik ortalaması 0, b ile geometrik ortalaması 0 olan sayı nedir? 0 C) 8 ise a+b+d toplamı ne-. a+b+c=d
989 ÖYS. a a a b 8 olduğuna göre a-b kaçtır? C). a ile b nin aritmetik ortalaması 5 tir. a ile geometrik ortalaması 0, b ile geometrik ortalaması 0 olan sayı nedir? 0 C) 8 ise a+b+d toplamı ne-. a+b+c=d
Çizelgeleme Nedir? Bir ürünün üretilmesi/hizmetin sunumu için
 Üretim Çizelgeleme Çizelgeleme Nedir? Bir ürünün üretilmesi/hizmetin sunumu için işgörenin nerede, ne zaman gerekli olduğunun, gerekli faaliyetlerin zamanlamasının, üretime başlama ve üretimi tamamlama
Üretim Çizelgeleme Çizelgeleme Nedir? Bir ürünün üretilmesi/hizmetin sunumu için işgörenin nerede, ne zaman gerekli olduğunun, gerekli faaliyetlerin zamanlamasının, üretime başlama ve üretimi tamamlama
SİMPLEKS ALGORİTMASI Yapay değişken kullanımı
 Fen Bilimleri Enstitüsü Endüstri Mühendisliği Anabilim Dalı ENM53 Doğrusal Programlamada İleri Teknikler SİMPLEKS ALGORİTMASI Yapay değişken kullanımı Hazırlayan: Doç. Dr. Nil ARAS, 6 AÇIKLAMA Bu sununun
Fen Bilimleri Enstitüsü Endüstri Mühendisliği Anabilim Dalı ENM53 Doğrusal Programlamada İleri Teknikler SİMPLEKS ALGORİTMASI Yapay değişken kullanımı Hazırlayan: Doç. Dr. Nil ARAS, 6 AÇIKLAMA Bu sununun
Üretim/İşlemler Yönetimi 2. Yrd. Doç. Dr. Mert TOPOYAN
 Üretim/İşlemler Yönetimi 2 Sistem Kavramı Belirli bir ortak amacı elde etmek için birlikte çalışan bileşenlerden oluşan bütündür. Büyük sistemler kendilerini oluşturan alt sistemlerden oluşur. Açık sistem:
Üretim/İşlemler Yönetimi 2 Sistem Kavramı Belirli bir ortak amacı elde etmek için birlikte çalışan bileşenlerden oluşan bütündür. Büyük sistemler kendilerini oluşturan alt sistemlerden oluşur. Açık sistem:
OTOMATİK KONTROL SİSTEMLERİ TEMEL KAVRAMLAR VE TANIMLAR
 OTOMATİK KONTROL SİSTEMLERİ TEMEL KAVRAMLAR VE TANIMLAR KONTROL SİSTEMLERİ GİRİŞ Son yıllarda kontrol sistemleri, insanlığın ve uygarlığın gelişme ve ilerlemesinde çok önemli rol oynayan bir bilim dalı
OTOMATİK KONTROL SİSTEMLERİ TEMEL KAVRAMLAR VE TANIMLAR KONTROL SİSTEMLERİ GİRİŞ Son yıllarda kontrol sistemleri, insanlığın ve uygarlığın gelişme ve ilerlemesinde çok önemli rol oynayan bir bilim dalı
COĞRAFİ BİLGİ SİSTEMLERİ VE ANALİTİK HİYERARŞİ YÖNTEMİ İLE DÜZENLİ DEPONİ YER SEÇİMİ: İSTANBUL İLİ ÖRNEĞİ. Doğuş Güler Prof. Dr. Tahsin Yomralıoğlu
 COĞRAFİ BİLGİ SİSTEMLERİ VE ANALİTİK HİYERARŞİ YÖNTEMİ İLE DÜZENLİ DEPONİ YER SEÇİMİ: İSTANBUL İLİ ÖRNEĞİ Doğuş Güler Prof. Dr. Tahsin Yomralıoğlu İTÜ, Geomatik Mühendisliği Bölümü, 34469 Maslak İstanbul,
COĞRAFİ BİLGİ SİSTEMLERİ VE ANALİTİK HİYERARŞİ YÖNTEMİ İLE DÜZENLİ DEPONİ YER SEÇİMİ: İSTANBUL İLİ ÖRNEĞİ Doğuş Güler Prof. Dr. Tahsin Yomralıoğlu İTÜ, Geomatik Mühendisliği Bölümü, 34469 Maslak İstanbul,
TAM ZAMANINDA ÜRETİM (JUST IN TIME MANUFACTURING)
 TAM ZAMANINDA ÜRETİM (JUST IN TIME MANUFACTURING) TAM ZAMANINDA ÜRETİM (JUST IN TIME MANUFACTURING) İstenilen zamanda İstenilen miktarda Her türlü kaynak israfını önleyecek şekilde yapılan üretim Tam Zamanında
TAM ZAMANINDA ÜRETİM (JUST IN TIME MANUFACTURING) TAM ZAMANINDA ÜRETİM (JUST IN TIME MANUFACTURING) İstenilen zamanda İstenilen miktarda Her türlü kaynak israfını önleyecek şekilde yapılan üretim Tam Zamanında
9. SINIF Geometri TEMEL GEOMETRİK KAVRAMLAR
 TEMEL GEOMETRİK KAVRAMLAR 9. SINIF Geometri Amaç-1: Nokta, Doğru, Düzlem, Işın ve Uzayı Kavrayabilme. 1. Nokta, doğru, düzlem ve uzay kavramlarım açıklama. 2. Farklı iki noktadan geçen doğru sayışım söyleme
TEMEL GEOMETRİK KAVRAMLAR 9. SINIF Geometri Amaç-1: Nokta, Doğru, Düzlem, Işın ve Uzayı Kavrayabilme. 1. Nokta, doğru, düzlem ve uzay kavramlarım açıklama. 2. Farklı iki noktadan geçen doğru sayışım söyleme
İŞ AKIŞI ve YERLEŞTİRME TİPLERİ
 İŞ AKIŞI ve YERLEŞTİRME TİPLERİ İş akışı tipleri önce, fabrika binasının tek veya çok katlı olmasına göre, yatay ve düşey olmak üzere iki grupta toplanabilir. Yatay iş akışı tiplerinden bazı örneklerde
İŞ AKIŞI ve YERLEŞTİRME TİPLERİ İş akışı tipleri önce, fabrika binasının tek veya çok katlı olmasına göre, yatay ve düşey olmak üzere iki grupta toplanabilir. Yatay iş akışı tiplerinden bazı örneklerde
Tedarik Zinciri Yönetimi
 Tedarik Zinciri Yönetimi -Tedarikçi Seçme Kararları- Yrd. Doç. Dr. Mert TOPOYAN Satın Alma Bir ișletme, dıșarıdan alacağı malzeme ya da hizmetlerle ilgili olarak satın alma (tedarik) fonksiyonunda beș
Tedarik Zinciri Yönetimi -Tedarikçi Seçme Kararları- Yrd. Doç. Dr. Mert TOPOYAN Satın Alma Bir ișletme, dıșarıdan alacağı malzeme ya da hizmetlerle ilgili olarak satın alma (tedarik) fonksiyonunda beș
Tesisler ve Donanımlar. Kapasite Planlaması. Tahmin
 Ürün ve hizmet üretme sistemine ve nasıl organize olacağına karar verilmesi Yeni ürün ve hizmet planlamasının bir aşamasıdır Kapasite planlamasını, ekipman seçimini ve yerleşke tasarımını etkiler. Süreç
Ürün ve hizmet üretme sistemine ve nasıl organize olacağına karar verilmesi Yeni ürün ve hizmet planlamasının bir aşamasıdır Kapasite planlamasını, ekipman seçimini ve yerleşke tasarımını etkiler. Süreç
Montaj Hatti Tasarımı ve Analizi - 5
 Balıkesir Universitesi, Endustri Muhendisligi Bolumu 2017-2018 Bahar Yariyili Montaj Hatti Tasarımı ve Analizi - 5 Yrd. Doç. Dr. Ibrahim Kucukkoc http://ikucukkoc.baun.edu.tr 2 En Erken ve En Gec Istasyon
Balıkesir Universitesi, Endustri Muhendisligi Bolumu 2017-2018 Bahar Yariyili Montaj Hatti Tasarımı ve Analizi - 5 Yrd. Doç. Dr. Ibrahim Kucukkoc http://ikucukkoc.baun.edu.tr 2 En Erken ve En Gec Istasyon
İÇİNDEKİLER. Bölüm 2 CEBİR 43
 İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 13 1.1 Doğal Sayılar 15 1.1.1. Tek ve Çift Sayılar 15 1.1.2. Asal Sayılar 15 1.1.3 Doğal Sayıların Özellikleri 15 1.1.4 Doğal Sayılarda Özel Toplamlar 16 1.1.5. Faktöriyel
İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 13 1.1 Doğal Sayılar 15 1.1.1. Tek ve Çift Sayılar 15 1.1.2. Asal Sayılar 15 1.1.3 Doğal Sayıların Özellikleri 15 1.1.4 Doğal Sayılarda Özel Toplamlar 16 1.1.5. Faktöriyel
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 3 Laminanın Mikromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 3 Laminanın Mikromekanik
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 3 Laminanın Mikromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 3 Laminanın Mikromekanik
DİZGE TABANLI BİLEŞEN DENEMELERİNİN TASARIMINDA BEKLENEN DİZGE YAŞAM SÜRESİNİN MODELLENMESİ 1
 DİZGE TABANLI BİLEŞEN DENEMELERİNİN TASARIMINDA BEKLENEN DİZGE YAŞAM SÜRESİNİN MODELLENMESİ 1 Emre YAMANGİL Orhan FEYZİOĞLU Süleyman ÖZEKİCİ Galatasaray Üniversitesi Galatasaray Üniversitesi Koç Üniversitesi
DİZGE TABANLI BİLEŞEN DENEMELERİNİN TASARIMINDA BEKLENEN DİZGE YAŞAM SÜRESİNİN MODELLENMESİ 1 Emre YAMANGİL Orhan FEYZİOĞLU Süleyman ÖZEKİCİ Galatasaray Üniversitesi Galatasaray Üniversitesi Koç Üniversitesi
Genetik Algoritmalar (GA) Genetik Algoritmalar Đçerik Nesin Matematik Köyü E rim Ç lı l ş ı ta t yı Nisan, 2012 Mustafa Suphi Erden
 Genetik Algoritmalar Nesin Matematik Köyü Evrim Çalıştayı 20-23 Nisan, 202 Genetik Algoritmalar (GA Đçerik Biyolojiden esinlenme GA nın özellikleri GA nın unsurları uygulama Algoritma Şema teoremi Mustafa
Genetik Algoritmalar Nesin Matematik Köyü Evrim Çalıştayı 20-23 Nisan, 202 Genetik Algoritmalar (GA Đçerik Biyolojiden esinlenme GA nın özellikleri GA nın unsurları uygulama Algoritma Şema teoremi Mustafa
Fabrika Tasarımı (MFGE 478) Ders Detayları
 Fabrika Tasarımı (MFGE 478) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Fabrika Tasarımı MFGE 478 Güz 3 0 0 3 5 Ön Koşul Ders(ler)i Dersin Dili Dersin
Fabrika Tasarımı (MFGE 478) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Fabrika Tasarımı MFGE 478 Güz 3 0 0 3 5 Ön Koşul Ders(ler)i Dersin Dili Dersin
Tedarik Zinciri Yönetiminde Yapay Zeka Teknikler
 Tedarik Zinciri Yönetiminde Yapay Zeka Teknikler Doç.Dr.Mehmet Hakan Satman mhsatman@istanbul.edu.tr İstanbul Üniversitesi 2014.10.22 Doç.Dr.Mehmet Hakan Satmanmhsatman@istanbul.edu.tr Tedarik Zinciri
Tedarik Zinciri Yönetiminde Yapay Zeka Teknikler Doç.Dr.Mehmet Hakan Satman mhsatman@istanbul.edu.tr İstanbul Üniversitesi 2014.10.22 Doç.Dr.Mehmet Hakan Satmanmhsatman@istanbul.edu.tr Tedarik Zinciri
Yerleşim Tasarımı Algoritmaları
 Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2018-2019 Güz Dönemi Yerleşim Tasarımı Algoritmaları 2 TP ye özel paketleri /
Eskişehir Teknik Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2018-2019 Güz Dönemi Yerleşim Tasarımı Algoritmaları 2 TP ye özel paketleri /
Endüstri Mühendisliğine Giriş
 NOT: MRP ve TAM ZAMANINDA ÜRETİM ARASINDAKİ FARKLAR ile ilgili notlar sizlere çalışmanız için derste işlenmemiştir Endüstri Mühendisliğine Giriş 26 Aralık 2012, Şişli-Ayazağa, İstanbul, Türkiye. Yard.
NOT: MRP ve TAM ZAMANINDA ÜRETİM ARASINDAKİ FARKLAR ile ilgili notlar sizlere çalışmanız için derste işlenmemiştir Endüstri Mühendisliğine Giriş 26 Aralık 2012, Şişli-Ayazağa, İstanbul, Türkiye. Yard.
BAŞABAŞ NOKTASI ANALİZİ
 BAŞABAŞ NOKTASI ANALİZİ Herhangi bir işe girişirken, genellikle o iş için harcanacak çaba ve kaynaklarla, o işten sağlanacak fayda karşılaştırılır. Bu karşılaştırmada amaç, kaynaklara (üretim faktörlerine)
BAŞABAŞ NOKTASI ANALİZİ Herhangi bir işe girişirken, genellikle o iş için harcanacak çaba ve kaynaklarla, o işten sağlanacak fayda karşılaştırılır. Bu karşılaştırmada amaç, kaynaklara (üretim faktörlerine)
(Computer Integrated Manufacturing)
 1 (Computer Integrated Manufacturing) 2 1 Bilgisayarlı Sayısal Kontrol; ekipman mekanizmaların hareketlerinin doğru ve hassas biçimde gerçekleştirilmesinde bilgisayarların kullanılması, programlama ile
1 (Computer Integrated Manufacturing) 2 1 Bilgisayarlı Sayısal Kontrol; ekipman mekanizmaların hareketlerinin doğru ve hassas biçimde gerçekleştirilmesinde bilgisayarların kullanılması, programlama ile
Algoritmalar ve Karmaşıklık
 Algoritmalar ve Karmaşıklık Ders 11 Algoritma Ayrık matematikte karşılaşılan bir çok problem sınıfı mevcuttur. Örneğin, verilen tamsayı grubu içindeki en büyük olanının bulunması, verilen bir kümenin bütün
Algoritmalar ve Karmaşıklık Ders 11 Algoritma Ayrık matematikte karşılaşılan bir çok problem sınıfı mevcuttur. Örneğin, verilen tamsayı grubu içindeki en büyük olanının bulunması, verilen bir kümenin bütün
Karabük Üniversitesi, Mühendislik Fakültesi...www.IbrahimCayiroglu.com. STATİK (2. Hafta)
 AĞIRLIK MERKEZİ STATİK (2. Hafta) Ağırlık merkezi: Bir cismi oluşturan herbir parçaya etki eden yerçeki kuvvetlerinin bileşkesinin cismin üzerinden geçtiği noktaya Ağırlık Merkezi denir. Şekil. Ağırlık
AĞIRLIK MERKEZİ STATİK (2. Hafta) Ağırlık merkezi: Bir cismi oluşturan herbir parçaya etki eden yerçeki kuvvetlerinin bileşkesinin cismin üzerinden geçtiği noktaya Ağırlık Merkezi denir. Şekil. Ağırlık
KABLOSUZ İLETİŞİM
 KABLOSUZ İLETİŞİM 805540 HÜCRE KAVRAMI GİRİŞİM VE KAPASİTE İçerik 3 Hücre Kavramı Girişim ve Sistem Kapasitesi Eski Sistemler 4 Başlangıçta çok güçlü tek bir verici Çok geniş kapsama alanı Aynı frekansların
KABLOSUZ İLETİŞİM 805540 HÜCRE KAVRAMI GİRİŞİM VE KAPASİTE İçerik 3 Hücre Kavramı Girişim ve Sistem Kapasitesi Eski Sistemler 4 Başlangıçta çok güçlü tek bir verici Çok geniş kapsama alanı Aynı frekansların
Temel ve Uygulamalı Araştırmalar için Araştırma Süreci
 BÖLÜM 8 ÖRNEKLEME Temel ve Uygulamalı Araştırmalar için Araştırma Süreci 1.Gözlem Genel araştırma alanı 3.Sorunun Belirlenmesi Sorun taslağının hazırlanması 4.Kuramsal Çatı Değişkenlerin açıkça saptanması
BÖLÜM 8 ÖRNEKLEME Temel ve Uygulamalı Araştırmalar için Araştırma Süreci 1.Gözlem Genel araştırma alanı 3.Sorunun Belirlenmesi Sorun taslağının hazırlanması 4.Kuramsal Çatı Değişkenlerin açıkça saptanması
ÜRETİM SİSTEMLERİ GELENEKSEL
 İmalat nin Sınıflandırılması ÜRETİM SİSTEMLERİ GELENEKSEL ATÖLYE TİPİ AKIŞ TİPİ DERS II GELENEKSEL İMALAT SİSTEMLERİ ÜRETİM SİSTEMLERİ MODERN HÜCRESEL ESNEK TAM ZAMANINDA Kesikli üretim, talebin üretim
İmalat nin Sınıflandırılması ÜRETİM SİSTEMLERİ GELENEKSEL ATÖLYE TİPİ AKIŞ TİPİ DERS II GELENEKSEL İMALAT SİSTEMLERİ ÜRETİM SİSTEMLERİ MODERN HÜCRESEL ESNEK TAM ZAMANINDA Kesikli üretim, talebin üretim
Karar Verme ve Oyun Teorisi
 Karar Problemlerinin Modellenmesinde Kullanılan raçlar Karar Verme ve Oyun Teorisi Karar Problemlerinin Modellenmesinde Kullanılan raçlar Karmaşık karar problemlerinin anlaşılmasını kolaylaştırmak amacıyla,
Karar Problemlerinin Modellenmesinde Kullanılan raçlar Karar Verme ve Oyun Teorisi Karar Problemlerinin Modellenmesinde Kullanılan raçlar Karmaşık karar problemlerinin anlaşılmasını kolaylaştırmak amacıyla,
Bilgisayar Mühendisliği. Bilgisayar Mühendisliğine Giriş 1
 Bilgisayar Mühendisliği Bilgisayar Mühendisliğine Giriş 1 Mühendislik Nedir? Mühendislik, bilim ve matematiğin yararlı cihaz ve sistemlerin üretimine uygulanmasıdır. Örn: Elektrik mühendisleri, elektronik
Bilgisayar Mühendisliği Bilgisayar Mühendisliğine Giriş 1 Mühendislik Nedir? Mühendislik, bilim ve matematiğin yararlı cihaz ve sistemlerin üretimine uygulanmasıdır. Örn: Elektrik mühendisleri, elektronik
Tesis Planlama (IE 407) Ders Detayları
 Tesis Planlama (IE 407) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Tesis Planlama IE 407 Bahar 3 0 0 3 3.5 Ön Koşul Ders(ler)i Dersin Dili Dersin Türü
Tesis Planlama (IE 407) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Tesis Planlama IE 407 Bahar 3 0 0 3 3.5 Ön Koşul Ders(ler)i Dersin Dili Dersin Türü
Fonksiyon Optimizasyonunda Genetik Algoritmalar
 01-12-06 Ümit Akıncı Fonksiyon Optimizasyonunda Genetik Algoritmalar 1 Fonksiyon Optimizasyonu Fonksiyon optimizasyonu fizikte karşımıza sık çıkan bir problemdir. Örneğin incelenen sistemin kararlı durumu
01-12-06 Ümit Akıncı Fonksiyon Optimizasyonunda Genetik Algoritmalar 1 Fonksiyon Optimizasyonu Fonksiyon optimizasyonu fizikte karşımıza sık çıkan bir problemdir. Örneğin incelenen sistemin kararlı durumu
ÖZDEĞERLER- ÖZVEKTÖRLER
 ÖZDEĞERLER- ÖZVEKTÖRLER GİRİŞ Özdeğerler, bir matrisin orijinal yapısını görmek için kullanılan alternatif bir yoldur. Özdeğer kavramını açıklamak için öncelikle özvektör kavramı ele alınsın. Bazı vektörler
ÖZDEĞERLER- ÖZVEKTÖRLER GİRİŞ Özdeğerler, bir matrisin orijinal yapısını görmek için kullanılan alternatif bir yoldur. Özdeğer kavramını açıklamak için öncelikle özvektör kavramı ele alınsın. Bazı vektörler
İŞLETME VE ORGANİZASYON STAJI UYGULAMA ESASLARI
 İŞLETME VE ORGANİZASYON STAJI UYGULAMA ESASLARI ENDÜSTRİ MÜHENDİSLİĞİ BÖLÜMÜ İŞLETME VE ORGANİZASYON STAJI UYGULAMA ESASLARI 2014 İŞLETME VE ORGANİZASYON STAJI UYGULAMA ESASLARI Açıklama Staj yapılan işletmelerde
İŞLETME VE ORGANİZASYON STAJI UYGULAMA ESASLARI ENDÜSTRİ MÜHENDİSLİĞİ BÖLÜMÜ İŞLETME VE ORGANİZASYON STAJI UYGULAMA ESASLARI 2014 İŞLETME VE ORGANİZASYON STAJI UYGULAMA ESASLARI Açıklama Staj yapılan işletmelerde
Öğrenci Seçme Sınavı (Öss) / 15 Nisan Matematik Soruları ve Çözümleri
 Öğrenci Seçme Sınavı (Öss) / 5 Nisan 990 Matematik Soruları ve Çözümleri. 0,0703.(0,3 0,) işleminin sonucu kaçtır? A) 0,00703 B) 0,0703 C) 0,703 D) 0,0703 E) 0,00703 Çözüm 0,0703.(0,3 0,) 0,0703.0, 0,00703.
Öğrenci Seçme Sınavı (Öss) / 5 Nisan 990 Matematik Soruları ve Çözümleri. 0,0703.(0,3 0,) işleminin sonucu kaçtır? A) 0,00703 B) 0,0703 C) 0,703 D) 0,0703 E) 0,00703 Çözüm 0,0703.(0,3 0,) 0,0703.0, 0,00703.
KAPASİTE KAVRAMI ve KAPASİTE ÇEŞİTLERİ
 KAPASİTE KAVRAMI ve KAPASİTE ÇEŞİTLERİ Bir işletme için kapasite değerlemesinin önemi büyüktür. Daha başlangıçta kurulacak işletmenin üretim kapasitesinin çok iyi hesaplanması gerekir ve elde edilen verilere
KAPASİTE KAVRAMI ve KAPASİTE ÇEŞİTLERİ Bir işletme için kapasite değerlemesinin önemi büyüktür. Daha başlangıçta kurulacak işletmenin üretim kapasitesinin çok iyi hesaplanması gerekir ve elde edilen verilere
Endüstri Mühendisliği - 1. yarıyıl. Academic and Social Orientation. 441000000001101 Fizik I Physics I 3 0 1 4 4 6 TR
 - - - - - Bölüm Seçin - - - - - Gönder Endüstri Mühendisliği - 1. yarıyıl 141000000001101 Akademik ve Sosyal Oryantasyon Academic and Social Orientation 1 0 0 1 0 1 TR 441000000001101 Fizik I Physics I
- - - - - Bölüm Seçin - - - - - Gönder Endüstri Mühendisliği - 1. yarıyıl 141000000001101 Akademik ve Sosyal Oryantasyon Academic and Social Orientation 1 0 0 1 0 1 TR 441000000001101 Fizik I Physics I
a2 b3 cij: birim başına ulaşım maliyeti xij: taşıma miktarı
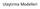 Ulaştırma Modelleri Ulaştırma modeli Ulaştırma modeli doğrusal programlama modellerinin özel bir türüdür. Modelin amacı bir işletmenin belirli kapasitedeki üretim merkezlerinden, belirli talebi olan tüketim
Ulaştırma Modelleri Ulaştırma modeli Ulaştırma modeli doğrusal programlama modellerinin özel bir türüdür. Modelin amacı bir işletmenin belirli kapasitedeki üretim merkezlerinden, belirli talebi olan tüketim
FMS=Flexible Manufacturing Systems
 1 FMS=Flexible Manufacturing Systems 2 3 4 Eğeryukarıdaki tüm sorularıncevabı evet ise imalatsistemi esnek olarak tanımlanabilir. Burada en çok önem verilmesi gereken testler 1 ve 2 numaralı testlerdir.
1 FMS=Flexible Manufacturing Systems 2 3 4 Eğeryukarıdaki tüm sorularıncevabı evet ise imalatsistemi esnek olarak tanımlanabilir. Burada en çok önem verilmesi gereken testler 1 ve 2 numaralı testlerdir.
OTOMATİK KONTROL SİSTEMLERİ TEMEL KAVRAMLAR VE TANIMLAR
 OTOMATİK KONTROL SİSTEMLERİ TEMEL KAVRAMLAR VE TANIMLAR KONTROL SİSTEMLERİ GİRİŞ Son yıllarda kontrol sistemleri, insanlığın ve uygarlığın gelişme ve ilerlemesinde çok önemli rol oynayan bir bilim dalı
OTOMATİK KONTROL SİSTEMLERİ TEMEL KAVRAMLAR VE TANIMLAR KONTROL SİSTEMLERİ GİRİŞ Son yıllarda kontrol sistemleri, insanlığın ve uygarlığın gelişme ve ilerlemesinde çok önemli rol oynayan bir bilim dalı
Matrisler ve matris işlemleri
 2.Konu Matrisler ve matris işlemleri Kaynaklar: 1.Uygulamalı lineer cebir. 7.baskıdan çeviri.bernhard Kollman, David R.Hill/çev.Ed. Ömer Akın, Palma Yayıncılık, 2002 2.Lineer Cebir. Feyzi Başar.Surat Universite
2.Konu Matrisler ve matris işlemleri Kaynaklar: 1.Uygulamalı lineer cebir. 7.baskıdan çeviri.bernhard Kollman, David R.Hill/çev.Ed. Ömer Akın, Palma Yayıncılık, 2002 2.Lineer Cebir. Feyzi Başar.Surat Universite
Neden Endüstri Mühendisliği Bölümünde Yapmalısınız?
 Lisansüstü Eğitiminizi Neden Endüstri Mühendisliği Bölümünde Yapmalısınız? Uludağ Üniversitesi Mühendislik-Mimarlık Fakültesi Endüstri Mühendisliği Bölümü, 1990 yılında kurulmuş ve ilk mezunlarını 1994
Lisansüstü Eğitiminizi Neden Endüstri Mühendisliği Bölümünde Yapmalısınız? Uludağ Üniversitesi Mühendislik-Mimarlık Fakültesi Endüstri Mühendisliği Bölümü, 1990 yılında kurulmuş ve ilk mezunlarını 1994
 LYS Y OĞRU MTMTİK TSTİ LYS-. u testte Matematik ile ilgili soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için ayrılan kısmına işaretleyiniz.. u testteki süreniz 7 dakikadır.. a ve b asal
LYS Y OĞRU MTMTİK TSTİ LYS-. u testte Matematik ile ilgili soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için ayrılan kısmına işaretleyiniz.. u testteki süreniz 7 dakikadır.. a ve b asal
Tanımlayıcı İstatistikler. Yrd. Doç. Dr. Emre ATILGAN
 Tanımlayıcı İstatistikler Yrd. Doç. Dr. Emre ATILGAN 1 Tanımlayıcı İstatistikler Yer Gösteren Ölçüler Yaygınlık Ölçüleri Merkezi Eğilim Ölçüleri Konum Ölçüleri 2 3 Aritmetik Ortalama Aritmetik ortalama,
Tanımlayıcı İstatistikler Yrd. Doç. Dr. Emre ATILGAN 1 Tanımlayıcı İstatistikler Yer Gösteren Ölçüler Yaygınlık Ölçüleri Merkezi Eğilim Ölçüleri Konum Ölçüleri 2 3 Aritmetik Ortalama Aritmetik ortalama,
Algoritmalar. Arama Problemi ve Analizi. Bahar 2016 Doç. Dr. Suat Özdemir 1
 Algoritmalar Arama Problemi ve Analizi Bahar 2016 Doç. Dr. Suat Özdemir 1 Arama Problemi Sıralama algoritmaları gibi arama algoritmaları da gerçek hayat bilgisayar mühendisliği problemlerinin çözümünde
Algoritmalar Arama Problemi ve Analizi Bahar 2016 Doç. Dr. Suat Özdemir 1 Arama Problemi Sıralama algoritmaları gibi arama algoritmaları da gerçek hayat bilgisayar mühendisliği problemlerinin çözümünde
Üretim Sistemleri Analizi
 Üretim Sistemleri Analizi Ekonomistlerin "fayda yaratmak", mühendislerin ise "fiziksel bir varlık üzerinde onun değerini artıracak bir değişiklik yapmak, hammadde veya yarı mamulleri kullanılabilir bir
Üretim Sistemleri Analizi Ekonomistlerin "fayda yaratmak", mühendislerin ise "fiziksel bir varlık üzerinde onun değerini artıracak bir değişiklik yapmak, hammadde veya yarı mamulleri kullanılabilir bir
T I M U R K A R A Ç AY - H AY D A R E Ş C A L C U L U S S E Ç K I N YAY I N C I L I K A N K A R A
 T I M U R K A R A Ç AY - H AY D A R E Ş C A L C U L U S S E Ç K I N YAY I N C I L I K A N K A R A Contents Bibliography 11 CONTENTS 5 0.1 Kartezyen Çarpım 0.2 Sıralı İkililer Şimdiye kadar sıra ya da
T I M U R K A R A Ç AY - H AY D A R E Ş C A L C U L U S S E Ç K I N YAY I N C I L I K A N K A R A Contents Bibliography 11 CONTENTS 5 0.1 Kartezyen Çarpım 0.2 Sıralı İkililer Şimdiye kadar sıra ya da
Algoritma ve Akış Diyagramları
 Algoritma ve Akış Diyagramları Bir problemin çözümüne ulaşabilmek için izlenecek ardışık mantık ve işlem dizisine ALGORİTMA, algoritmanın çizimsel gösterimine ise AKIŞ DİYAGRAMI adı verilir 1 Akış diyagramları
Algoritma ve Akış Diyagramları Bir problemin çözümüne ulaşabilmek için izlenecek ardışık mantık ve işlem dizisine ALGORİTMA, algoritmanın çizimsel gösterimine ise AKIŞ DİYAGRAMI adı verilir 1 Akış diyagramları
BİR MONTAJ HATTI ÜRETİM SİSTEMİNDE OPTİMAL İŞGÜCÜ DAĞILIMININ ARENA PROCESS ANALYZER (PAN) VE OPTQUEST KULLANILARAK BELİRLENMESİ
 BİR MONTAJ HATTI ÜRETİM SİSTEMİNDE OPTİMAL İŞGÜCÜ DAĞILIMININ ARENA PROCESS ANALYZER (PAN) VE OPTQUEST KULLANILARAK BELİRLENMESİ Özgür ARMANERİ Dokuz Eylül Üniversitesi Özet Bu çalışmada, bir montaj hattı
BİR MONTAJ HATTI ÜRETİM SİSTEMİNDE OPTİMAL İŞGÜCÜ DAĞILIMININ ARENA PROCESS ANALYZER (PAN) VE OPTQUEST KULLANILARAK BELİRLENMESİ Özgür ARMANERİ Dokuz Eylül Üniversitesi Özet Bu çalışmada, bir montaj hattı
KAPASİTE PLANLAMASI ve ÖLÇME KRİTERLERİ
 KAPASİTE PLANLAMASI ve ÖLÇME KRİTERLERİ Kuruluş yeri belirlenen bir üretim biriminin üretim miktarı açısından hangi büyüklükte veya kapasitede olması gerektiği işletme literatüründe kapasite planlaması
KAPASİTE PLANLAMASI ve ÖLÇME KRİTERLERİ Kuruluş yeri belirlenen bir üretim biriminin üretim miktarı açısından hangi büyüklükte veya kapasitede olması gerektiği işletme literatüründe kapasite planlaması
Anadolu Üniversitesi Endüstri Mühendisliği Bölümü İST328 Yöneylem Araştırması 2 Dersi Bahar Dönemi. Hazırlayan: Doç. Dr.
 Anadolu Üniversitesi Endüstri Mühendisliği Bölümü İST8 Yöneylem Araştırması Dersi 00-0 Bahar Dönemi Hazırlayan: Doç. Dr. Nil ARAS AÇIKLAMA Bu sunu izleyen kaynaklardaki örnek ve bilgilerden faydalanarak
Anadolu Üniversitesi Endüstri Mühendisliği Bölümü İST8 Yöneylem Araştırması Dersi 00-0 Bahar Dönemi Hazırlayan: Doç. Dr. Nil ARAS AÇIKLAMA Bu sunu izleyen kaynaklardaki örnek ve bilgilerden faydalanarak
Yazılım Mühendisliği 1
 Yazılım Mühendisliği 1 HEDEFLER Yazılım, program ve algoritma kavramları anlar. Yazılım ve donanım maliyetlerinin zamansal değişimlerini ve nedenleri hakkında yorum yapar. Yazılım mühendisliği ile Bilgisayar
Yazılım Mühendisliği 1 HEDEFLER Yazılım, program ve algoritma kavramları anlar. Yazılım ve donanım maliyetlerinin zamansal değişimlerini ve nedenleri hakkında yorum yapar. Yazılım mühendisliği ile Bilgisayar
Mühendislik Fakültesi Endüstri Mühendisliği Bölümü. Yerleşim Tasarımı. Algoritmaları. Doç. Dr. Nil ARAS ENM411 Tesis Planlaması Güz Dönemi
 Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Yerleşim Tasarımı Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2016-2017 Güz Dönemi Algoritmaları 2 TP ye özel paketleri / modülleri kullanmak Genel amaçlı
Mühendislik Fakültesi Endüstri Mühendisliği Bölümü Yerleşim Tasarımı Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2016-2017 Güz Dönemi Algoritmaları 2 TP ye özel paketleri / modülleri kullanmak Genel amaçlı
NRM Makina Teknolojisiyle Endüstriye Değer Katıyor. Kalitemizin Temelinde Ar-Ge Var
 NRM Makina Teknolojisiyle Endüstriye Değer Katıyor NRM Makina, imalat sektöründe faaliyet gösteren tüm firmalar için robotik otomasyon sistemleri üreten bir teknoloji şirketidir. Türkiye deki ve dünyadaki
NRM Makina Teknolojisiyle Endüstriye Değer Katıyor NRM Makina, imalat sektöründe faaliyet gösteren tüm firmalar için robotik otomasyon sistemleri üreten bir teknoloji şirketidir. Türkiye deki ve dünyadaki
Algoritmalar. Sıralama Problemi ve Analizi. Bahar 2017 Doç. Dr. Suat Özdemir 1
 Algoritmalar Sıralama Problemi ve Analizi Bahar 2017 Doç. Dr. Suat Özdemir 1 Sıralama Problemi ve Analizi Bu bölümde öncelikle bir diğer böl-ve-yönet yöntemine dayalı algoritma olan Quick Sort algoritması
Algoritmalar Sıralama Problemi ve Analizi Bahar 2017 Doç. Dr. Suat Özdemir 1 Sıralama Problemi ve Analizi Bu bölümde öncelikle bir diğer böl-ve-yönet yöntemine dayalı algoritma olan Quick Sort algoritması
YÖK TEZLERİ PROJE KELİME TARAMASI
 YÖK TEZLERİ PROJE KELİME TARAMASI YÖK Tezleri Proje Kelimesi Taraması Sonuçları Toplam Çalışma Sayısı 1833 İncelenen 1673 İlgisiz 372 Toplam İncelenen 1301 X Projesi 720 Proje Yönetimi 123 Yatırım Projeleri
YÖK TEZLERİ PROJE KELİME TARAMASI YÖK Tezleri Proje Kelimesi Taraması Sonuçları Toplam Çalışma Sayısı 1833 İncelenen 1673 İlgisiz 372 Toplam İncelenen 1301 X Projesi 720 Proje Yönetimi 123 Yatırım Projeleri
ii) S 2LW 2WH 2LW 2WH S 2WH 2LW S 3( x 1) 5( x 2) 5 3x 3 5x x Maliye Bölümü EKON 103 Matematik I / Mart 2018 Proje 2 CEVAPLAR C.1) C.
 C.1) x1 x 1 4 4( x1) x 6 4x 4 x 6 x 46 x Maliye Bölümü EKON 10 Matematik I / Mart 018 Proje CEVAPLAR C.) i) S LW WH LW WH S LW WH S W W W S L H W ii) S LW WH WH LW S WH LW S W W W S H L W C.) ( x1) 5(
C.1) x1 x 1 4 4( x1) x 6 4x 4 x 6 x 46 x Maliye Bölümü EKON 10 Matematik I / Mart 018 Proje CEVAPLAR C.) i) S LW WH LW WH S LW WH S W W W S L H W ii) S LW WH WH LW S WH LW S W W W S H L W C.) ( x1) 5(
Kablo Üretim Çizelgeleme Paketi. dinamo Kablo GANT. dinamo KABLO Kablo Üretim Planlama/Çizelgeleme Paketi Bilgi Dosyası
 dinamo Kablo GANT dinamo KABLO Kablo Üretim Planlama/Çizelgeleme Paketi Bilgi Dosyası KABLO Üretim Planlama ve Maliyetlendirme Yazılımı dinamo Kablo GANT Kimin İçin? dinamo Kablo GANT, kablo üretimi yapan,
dinamo Kablo GANT dinamo KABLO Kablo Üretim Planlama/Çizelgeleme Paketi Bilgi Dosyası KABLO Üretim Planlama ve Maliyetlendirme Yazılımı dinamo Kablo GANT Kimin İçin? dinamo Kablo GANT, kablo üretimi yapan,
7. BÖLÜM İÇ ÇARPIM UZAYLARI İÇ ÇARPIM UZAYLARI İÇ ÇARPIM UZAYLARI İÇ ÇARPIM UZAYLARI .= 1 1 + + Genel: Vektörler bölümünde vektörel iç çarpım;
 İÇ ÇARPIM UZAYLARI 7. BÖLÜM İÇ ÇARPIM UZAYLARI Genel: Vektörler bölümünde vektörel iç çarpım;.= 1 1 + + Açıklanmış ve bu konu uzunluk ve uzaklık kavramlarını açıklamak için kullanılmıştır. Bu bölümde öklit
İÇ ÇARPIM UZAYLARI 7. BÖLÜM İÇ ÇARPIM UZAYLARI Genel: Vektörler bölümünde vektörel iç çarpım;.= 1 1 + + Açıklanmış ve bu konu uzunluk ve uzaklık kavramlarını açıklamak için kullanılmıştır. Bu bölümde öklit
VEKTÖR UZAYLARI 1.GİRİŞ
 1.GİRİŞ Bu bölüm lineer cebirin temelindeki cebirsel yapıya, sonlu boyutlu vektör uzayına giriş yapmaktadır. Bir vektör uzayının tanımı, elemanları skalar olarak adlandırılan herhangi bir cisim içerir.
1.GİRİŞ Bu bölüm lineer cebirin temelindeki cebirsel yapıya, sonlu boyutlu vektör uzayına giriş yapmaktadır. Bir vektör uzayının tanımı, elemanları skalar olarak adlandırılan herhangi bir cisim içerir.
İÇİNDEKİLER. Birinci Bölüm Üretim Yönetiminde Temel Kavramlar
 İÇİNDEKİLER Birinci Bölüm Üretim Yönetiminde Temel Kavramlar 1.1. Giriş... 2 1.2. Üretim Faktörleri ve Üretim... 3 1.3. Üretim ve İşlemler Yönetimi... 6 1.4. Üretim ve İşlemler Yönetiminin Kapsamı... 7
İÇİNDEKİLER Birinci Bölüm Üretim Yönetiminde Temel Kavramlar 1.1. Giriş... 2 1.2. Üretim Faktörleri ve Üretim... 3 1.3. Üretim ve İşlemler Yönetimi... 6 1.4. Üretim ve İşlemler Yönetiminin Kapsamı... 7
Üretim Yönetimi Nedir?
 Üretim Yönetimi Üretim Yönetimi Nedir? Üretim süreçlerini ilgilendiren tüm kararların alınması ile ilgili disiplindir. Üretilen malların istenilen nicelikte ve zamanda en az giderle oluşmasını amaçlar
Üretim Yönetimi Üretim Yönetimi Nedir? Üretim süreçlerini ilgilendiren tüm kararların alınması ile ilgili disiplindir. Üretilen malların istenilen nicelikte ve zamanda en az giderle oluşmasını amaçlar
PAU ENDÜSTRİ MÜHENDİSLİĞİ. IENG 328 - Üretim Planlama ve Kontrolü 2
 PAU ENDÜSTRİ MÜHENDİSLİĞİ IENG 328 - Üretim Planlama ve Kontrolü 2 1 Dersin amacı Endüstri mühendisliğinin temel konularından biri olan üretim planlaması ve kontrolü ile ilgili temel kavram ve tekniklerin
PAU ENDÜSTRİ MÜHENDİSLİĞİ IENG 328 - Üretim Planlama ve Kontrolü 2 1 Dersin amacı Endüstri mühendisliğinin temel konularından biri olan üretim planlaması ve kontrolü ile ilgili temel kavram ve tekniklerin
Genel Graf Üzerinde Mutlak 1-merkez
 Genel Graf Üzerinde Mutlak 1-merkez Çözüm yöntemine geçmeden önce bazı tanımlara ihtiyaç vardır. Dikkate alınan G grafındaki düğümleri 1 den n e kadar numaralandırın. Uzunluğu a(i, j)>0 olarak verilen
Genel Graf Üzerinde Mutlak 1-merkez Çözüm yöntemine geçmeden önce bazı tanımlara ihtiyaç vardır. Dikkate alınan G grafındaki düğümleri 1 den n e kadar numaralandırın. Uzunluğu a(i, j)>0 olarak verilen
BÖLÜM 9 ÇÖZÜLMESİ ÖNERİLEN ÖRNEK VE PROBLEMLER
 BÖLÜM 9 ÇÖZÜLMESİ ÖNERİLEN ÖRNEK VE PROBLEMLER b) İkinci süreç eğik atış hareketine karşılık geliyor. Orada örendiğin problem çözüm adımlarını kullanarak topun sopadan ayrıldığı andaki hızını bağıntı olarak
BÖLÜM 9 ÇÖZÜLMESİ ÖNERİLEN ÖRNEK VE PROBLEMLER b) İkinci süreç eğik atış hareketine karşılık geliyor. Orada örendiğin problem çözüm adımlarını kullanarak topun sopadan ayrıldığı andaki hızını bağıntı olarak
Bölüm 9 KÖK-YER EĞRİLERİ YÖNTEMİ
 Bölüm 9 KÖK-YER EĞRİLERİ YÖNTEMİ Kapalı-döngü denetim sisteminin geçici-durum davranışının temel özellikleri kapalı-döngü kutuplarından belirlenir. Dolayısıyla problemlerin çözümlenmesinde, kapalı-döngü
Bölüm 9 KÖK-YER EĞRİLERİ YÖNTEMİ Kapalı-döngü denetim sisteminin geçici-durum davranışının temel özellikleri kapalı-döngü kutuplarından belirlenir. Dolayısıyla problemlerin çözümlenmesinde, kapalı-döngü
Endüstri Mühendisliğine Giriş
 Endüstri Mühendisliğine Giriş 5 ve 19 Aralık 2012, Şişli-Ayazağa, İstanbul, Türkiye. Yard. Doç. Dr. Kamil Erkan Kabak Endüstri Mühendisliği Bölümü,, Şişli-Ayazağa, İstanbul, Türkiye erkankabak@beykent.edu.tr
Endüstri Mühendisliğine Giriş 5 ve 19 Aralık 2012, Şişli-Ayazağa, İstanbul, Türkiye. Yard. Doç. Dr. Kamil Erkan Kabak Endüstri Mühendisliği Bölümü,, Şişli-Ayazağa, İstanbul, Türkiye erkankabak@beykent.edu.tr
ÇOK KRİTERLİ KARAR VERME TEKNİKLERİ. Dersin Amacı Çok Kriterli Karar Verme Yaklaşımının Genel Yapısı. Dr.Öğr.Üyesi Gökçe BAYSAL TÜRKÖLMEZ
 ÇOK KRİTERLİ KARAR VERME TEKNİKLERİ Dr.Öğr.Üyesi Gökçe BAYSAL TÜRKÖLMEZ Zeleny (1982) multiple criteria decision making kitabına aşağıdaki cümle ile başlar: ıt has become more and more difficult to see
ÇOK KRİTERLİ KARAR VERME TEKNİKLERİ Dr.Öğr.Üyesi Gökçe BAYSAL TÜRKÖLMEZ Zeleny (1982) multiple criteria decision making kitabına aşağıdaki cümle ile başlar: ıt has become more and more difficult to see
DOĞRUSAL OLMAYAN PROGRAMLAMA -I-
 DOĞRUSAL OLMAYAN PROGRAMLAMA -I- Dışbükeylik / İçbükeylik Hazırlayan Doç. Dr. Nil ARAS Anadolu Üniversitesi, Endüstri Mühendisliği Bölümü İST38 Yöneylem Araştırması Dersi 0-0 Öğretim Yılı Doğrusal olmayan
DOĞRUSAL OLMAYAN PROGRAMLAMA -I- Dışbükeylik / İçbükeylik Hazırlayan Doç. Dr. Nil ARAS Anadolu Üniversitesi, Endüstri Mühendisliği Bölümü İST38 Yöneylem Araştırması Dersi 0-0 Öğretim Yılı Doğrusal olmayan
Genetik Algoritmalar. Bölüm 1. Optimizasyon. Yrd. Doç. Dr. Adem Tuncer E-posta:
 Genetik Algoritmalar Bölüm 1 Optimizasyon Yrd. Doç. Dr. Adem Tuncer E-posta: adem.tuncer@yalova.edu.tr Optimizasyon? Optimizasyon Nedir? Eldeki kısıtlı kaynakları en iyi biçimde kullanmak olarak tanımlanabilir.
Genetik Algoritmalar Bölüm 1 Optimizasyon Yrd. Doç. Dr. Adem Tuncer E-posta: adem.tuncer@yalova.edu.tr Optimizasyon? Optimizasyon Nedir? Eldeki kısıtlı kaynakları en iyi biçimde kullanmak olarak tanımlanabilir.
