1. MATEMATİKSEL MODELLEME
|
|
|
- Volkan Uygun
- 9 yıl önce
- İzleme sayısı:
Transkript
1 . MATEMATİKSEL MODELLEME İşletmeler çabuk ve iabetli kararlar alabilmeleri büyük ölçüde itematik yaklaşıma gerekinim duyarlar. İter ayıal analizler, iter yöneylem araştırmaı adı altında olun uygulanmakta veya geliştirilmekte olan ve matematik model kullanan bütün yöntemler, eaında işletme orunlarının matematik olarak programlanmaı ve çözümünden başka bir şey değildir. İşletme problemlerinin matematik modellerinden yararlanarak çözümü üreci, bulunan onuçların gerçeğe uygunluk derecelerinin araştırılmaı, gerekli kontrollerin yapılmaı ve trateilerin aptanmaı ile tamamlanır. İşte matematik modellerin kuruluşu, çözümü, kontrolü ve uygulamaı trateilerinin aptanmaından oluşan bu üreç matematik programlamayı oluşturmaktadır. Karar Problemi Problem Tanımı Matematikel Modelleme Problem Tanımı Alternatiflerin Araştırılmaı Değerlendirme Seçim Gözlem Model Geliştirme Çözüm Tet Sonuçların Analizi Varayımlar ve ınırların belirlenmei Karar değişkenleri Matematikel ilişkiler Kııtlar En iyi alternatifin eçimi Uygulama Bilimel karar alma üreci modellere dayanır. Karar almada kullanılabilecek çok çeşitli modeller ve teknikler geliştirilmiştir. Bunlar; doğrual programlama, ulaştırma modelleri, Leontief modeli, şebeke analizi, tok modelleri, oyun kuramı, bekleme hattı modelleri, dinamik programlama, tam ayılı programlama, Markov analizi, doğrual olmayan programlama vb.dir.
2 YÖNEYLEM ARAŞTIRMASI DETERMİNİSTİK MODELLER STOKASTİK MODELLER Doğrual Programlama Markov Zincirleri Tam Sayılı Doğrual Programlama Kuyruk Teorii Doğrual Olmayan Programlama Dinamik Programlama Ulaştırma Problemleri Buluşal Yaklaşımlar Çok Amaçlı Karar Verme. DOĞRUSAL PROGRAMLAMA İşletme problemlerinin, ayıal verilerle en bait şekilde anlatımı doğrual programlama ile olanaklıdır. Günümüzde, işletme, ekonomi ve muhaebe dallarını yakından ilgilendiren konulardan biri olan doğrual programlama, aynı zamanda yöneylem araştırmaı için de en önemli konulardan biridir. Doğrual Programlama, optimizayon problemlerinin çözümünde kullanılan bir yöntemdir. 947 'de, George Dantzig doğrual programlama problemlerinin çözümünde kullanılan etkin bir yol olan Simplek Algoritma ' yı buldu ve bu buluşla birlikte doğrual Programlama, ıklıkla ve hemen her ektörde kullanılmaya başlandı. Doğrual programlama, belli doğrual eşitliklerin veya eşitizliklerin kııtlayıcı koşulları altında doğrual bir amaç fonkiyonunu optimum hale getirmek biçiminde tanımlanabilir. Optimum hale getirmek, belli bir amaca en az marafla ulaşmak ya da belli kaynaklarla en çok ürünü ağlamak anlamına gelir. (Ein,998:4) Doğrual programlama ürecinde, önce gerekli bilgiler toplanır, probleme ait bir model kurulur ve daha onra bu modelin çözümleri bilgiayar detekli yazılım paketleri ile bulunur. Bu çözümlerin gerçek yaşam problemlerine uygulanabilirliği tet edildikten onra yöneticilere unulur.
3 .. DOĞRUSAL PROGRAMLAMANIN MATEMATİKSEL YAPISI Doğrual programlamanın üç önemli bileşeni vardır: Amaç fonkiyonu, kııtlayıcı fonkiyonlar ve pozitif kııtlama (Bealey, 3). Amaç Fonkiyonu: Doğrual programlama modelinde doğrual biçimde ifade edilen bir amaç fonkiyonu vardır. Amaç fonkiyonu, kâr makimizayonu ya da maliyet minimizayonu şeklinde olur. Amaç fonkiyonu Z, kontrol edilebilir değişkenler (=,,,n) ve abit katayılar (birim başına kâr ya da birim başına maliyet katayıları) c (=,,,n) olmak üzere n c. =,,..., = biçiminde ifade edilebilir. Bu amaç fonkiyonun açık yazılımı ie şöyledir: Z = c + c cnn Kııtlayıcı Fonkiyonlar: İşletmeler, faaliyetlerini bir takım kııtlayıcı koşullar altında ürdürürler. Makinelerin kapaite kullanımları, iş gücü, finanman, zaman ınırlılığı vb. gibi koşullar bu kııtlayıcılara örnek olarak verilebilir. Kııtlayıcılar, teknoloi matrii a i, ihtiyaç vektörü b i olmak üzere tandart makimizayon probleminde; n n = a b, i =,,..., m i i Standart minimizayon probleminde ie; n = a b, i =,,..., m i i Biçiminde ifade edilirler. Standart doğrual programlama problemlerinde ya da yanı ıra = işareti hem makimizayonda hem de minimizayon problemlerinde kullanılabilir. Örneğin makinelerin tam kapaite ile çalışmaları durumunda = lik kullanılır. Standart olmayan doğrual programlama problemlerinde kııtlayıcıların ağındaki işaretler, ya da = işaretleri karışık olarak da kullanılabilmektedir (Hacıalihoğlu, 99:38).
4 Pozitif Kııtlama: İşletme faaliyetleri koordinat düzleminin birinci bölgeinde meydana gelir. Yani, negatif üretim ya da negatif maliyet olmayacağından karar değişkenleri lerin negatif olmaı düşünülemez. Bu, matematikel olarak, =,,..., n biçiminde ifade edilir. Yukarıdaki açıklamalar doğrultuunda bir doğrual programlama probleminin genel yapıı;. Kâr makimizayonunda; Amaç fonkiyonu; Z = c, =,,,..., n ma n = Kııtlayıcılar; n ai bi, i =,,..., m, =,,..., n = Pozitif kııtlama;.maliyet minimizayonu; Amaç fonkiyonu;, =,,..., n i Z = c, =,,,..., n min n = Kııtlayıcılar; n ai bi, i =,,..., m, =,,..., n =
5 Pozitif kııtlama; biçiminde verilir., =,,..., n i Yukarıda genel matematikel modeli verilen doğrual programlama modeli daha açık biçimde aşağıdaki gibi yazılabilir. Amaç fonkiyonu; Kııtlayıcılar: Zma = c + c cnn a + a a nn b a + a a n n b a a a b m m + m m mn mn m Pozitif Kııtlama:,,, n Kâr makimizayonu olan bu modelde kııtlayıcı eşitizliklerin ağ tarafındaki işareti yerine işareti yazılıra maliyet minimizayonunun matematikel modeli elde edilmiş olur. Bu model, matri göterimi ile de aşağıdaki gibi yazılabilir. a i katayılarından oluşan teknoloik matri; A = a a a a a a a a a n n m m mn
6 İhtiyaç vektörü; b b B = b n fiyat (ya da maliyet) katayılarından oluşan vektörü de şeklinde verilire, Amaç fonkiyonu; X = n ZM in/ M a = ( cc cn ) n Kııtlayıcılar; a a a a a a a a n n m mn n = b b b n Pozitif kııtlama;, =,,..., n i şeklinde olur.
7 Doğrual programlama yönteminin kullanılışlığı, bilgiayar yazılımlarındaki gelişmeler ile daha da artmıştır (Taha,:). Doğrual programlama problemlerinin bilgiayar ortamında çözümü için LINDO, QSB, DEAP, TORA gibi çeşitli programlar geliştirilmiştir. Bu programların yanı ıra herkeçe rahatlıkla elde edilebilecek ve kullanımı kolay olan Ecel ile de bu problemleri çözmek olanaklıdır. Window un çok yaygınlaşmış olmaı, ofi uygulama programlarının hemen herkeçe kullanılabilmei, bu problemlerin Ecel de çözümünü önemli kılmaktadır... DOĞRUSAL PROGRAMLAMANIN VARSAYIMLARI Doğrual programlamanın varayımları aşağıdaki gibidir:.belirlilik (Certainty).Doğruallık (Linearity) 3.Bölünebilirlik (Diviibility) 4.Toplanabilirlik (Additivity) 5.Orantıallık (Proportionality). Belirlilik Varayımı: Bir doğrual programlama modelinde yer alan parametrelerin bilindiği ve değişmediği kabul edilir. Yani, birim başına kar ya da maliyetlerin ( c ), her faaliyet için gerekli olan kaynak miktarlarının ( a i) ve mevcut kaynak miktarlarının ( b i ) kein olarak bilindiği varayılır. Bu varayımın kabul edilmeiyle doğrual programlama problemlerinin çözümü kolaylaşmaktadır. Ancak, uygulamada bu parametrelerin ık ık değişme eğiliminde olmaı, doğrual programlamada duyarlılık analizi çalışmalarının yürütülmeini gerektirmektedir. Problemin optimum çözümü elde edildikten onra duyarlılık analizi başlığı altında parametrelerdeki değişmelerin optimal çözüm üzerindeki etkileri incelenebilir.. Bölünebilirlik Varayımı: Bölünebilirlik varayımı ile karar değişkenlerinin optimal çözüm değerlerinin keirli değerler alabileceği kabul edilir. Örneğin herhangi bir doğrual programlama modelinin optimal çözümünde 4.6 adet araba üretileceği gibi bir üretim çıktıı onucuna ulaşılabilir. Keirli optimal çözüm değerleri Tam Sayı Programlama algoritmalarıyla tamayılaştırılır. 3. Doğruallık Varayımı: Bir doğrual programlama modelinin amaç fonkiyonu ve kııt denklemleri doğrual olmalıdır. Bir başka deyişle ler birinci dereceden değişkenler olmalıdır. Bir işletmenin girdiler ile çıktıları araında doğrual bir ilişki olduğu varayılır 4. Toplanabilirlik Varayımı: Herhangi bir değişkenin amaç fonkiyonuna katkıı, diğer karar değişkenlerinin değerlerinden bağımızdır. Örnek olarak Zma = 3 + şeklinde bir amaç fonkiyonu olun. nin değeri ne olura olun, birim ünite üretimiyle amaç fonkiyonuna amaç fonkiyonuna her zaman 3 pb. katkı yapacaktır.
8 Bir değişkenin her bir kııt denkleminin ol tarafına yaptığı katkı diğer değişkenlerin değerlerinden bağımızdır. + 6 (Kııt ) (Kııt ) şeklinde adet kııt denklemi olun. in değeri ne olura olun birim ünite üretimi birim kaynak ve 3 birim kaynak 3 kullanımı gerektirir. 5.Orantıallık Varayımı: Her bir karar değişkeninin amaç fonkiyonuna ve kııt denklemlerinin ol tarafına yapacağı katkı karar değişkeninin değeri ile orantılıdır. Örnek olarak bir adet A tipi oyuncağın amaç fonkiyonu katkıı.8 TL ie dört adet A tipi oyuncağın amaç fonkiyonuna toplam katkıı bunun dört katı olan 3. TL (4.8) olacaktır. Bir adet A tipi oyuncak platik departmanında 4 dakikada işleniyora, 5 adet A tipi oyuncak bunun beş katı olan dakikada (45=) işlenecektir..3. DOĞRUSAL PROGRAMLAMANIN BAZI UYGULAMA ALANLARI Çok ayıda değişkenli ve kııt denklemli doğrual programlama problemleri bilgiayar programları yardımıyla hızlıca çözümlenebildiği için birçok alanda önemli uygulamalardan öz edilebilir. Doğrual programlamanın bazı uygulama alanları aşağıda verilmiştir:. Üretim planlama ve envanter kontrolü. Ulaştırma ve loitik problemleri 3. Atama problemleri 4. Peronel çizelgeleme 5. Pazarlama Problemleri 6. Sermaye bütçeleme problemleri 7. Portföy eçimi problemleri 8. Yatırım problemleri 9. Karışım problemleri.4. DOĞRUSAL PROGRAMLAMADA ÇÖZÜM KAVRAMLARI Doğrual programlama probleminin çözümünde kullanılan tanımları şöyle ıralanabilir: a) Çözüm Bir doğrual programlama probleminin kııtlayıcı fonkiyonlarının hepini birden ağlayan karar değişkenlerinin (,,..., n ) oluşturduğu kümeye çözüm denir.
9 b) Uygun Çözüm Doğrual programlama probleminin tüm kııtlarını doyuran çözüm. c) Optimal Çözüm Tüm uygun çözümler araında amaç fonkiyonunu iyi karşılayanı optimal çözümdür. d) Deenere (bozulan) Çözüm Çözümün bir veya birkaç temel değişkeninin değeri ıfıra, bozulan çözüm adı verilir..5. EXCEL VE ÇÖZÜCÜ Ecel, Microoft firmaı tarafından geliştirilmiş bir heap tablou programıdır. Window ve Macintoh ortamları için hazırlanmıştır ve şu anda dünyada en çok kullanılan programlardan biriidir. Ecel mühendilere, mimarlara, muhaebecilere ve bütün meleklerdeki inanların heaplama gerekinimlerini gidermek için kullanılabilir. Bu gerekinimler bait toplama işlemleri olabileceği gibi yükek matematik problemlerinin hızlı bir biçimde çözülmeine ya da mimarlık heaplarının yapılmaı da olabilir. Çözücü, verilen kııtlar altında bir amaç işlevin belirli değişkenler için çözümünü ağlar (Yavuz, 999:54). Çözücü ile n. dereceden bir bilinmeyenli denklem çözülebileceği gibi n bilinmeyenli m adet denklem itemini de çözmek olanaklıdır. Çözücünün Etkinleştirilmei ve Örnek Uygulama Bir doğrual programlama probleminin ya da bir denklem iteminin çözümü için öncelikle Ecel in araçlar menüünde çözücü işlevinin olup olmadığı kontrol edilmelidir. Eğer çözücü yok ie izleyen şekilde görüldüğü gibi Araçlar menüünden Eklentilere gelinerek çözücü eklentii onaylanmalıdır.
10 Eğer Araçlar menüünde çözücü işlevi var ie doğrual programlama problemlerini ya da denklem itemlerini çözmek olanaklı olacaktır. İzleyen örneklerde bir makimizayon, bir de minimizayon probleminin Ecel de çözüm üreci adım adım açıklanmıştır. Amaç Fonkiyonu : Zma = Kııtlayıcılar: Pozitif Kııtlama:, Öncelikle Ecel çalışma ayfaındaki A ve B adrelerine X ve X girilmeli ve A ve B adrelerine (ıfır) değeri yazılmalıdır (Şekil.). Sonraki adımda uygun bir hücreye gelinerek (Örnekte D hücrei) bu hücreye amaç fonkiyonu izleyen biçimde yazılır: = 5*A+8*B Amaç fonkiyonundan onra da kııtlayıcılar benzer şekilde yan hücrelere girilir. Örnek uygulama için kııtlayıcı fonkiyonların yazılışı ve hücre adreleri izleyen biçimdeki gibi girilmiştir: E Hücreine =4*A+6*B-4 F Hücreine =*A+B-8 G Hücreine =3*A+9*B-36 H Hücreine =A Bu denklemlerin girilmeinden onra, çözüm öncei hücrelerde oluşan durum izleyen şekildeki gibidir: Bu aşamadan onra aktif hücre olarak amaç fonkiyonun bulunduğu D hücrei eçilmeli ve araçlar menüünden çözücü işlevi çalıştırılmalıdır. Çözümün ve gerekli parametrelerin tanımlanacağı çözücü parametreleri pencerei açılacaktır.
11 Bu penceredeki Hedef Hücre, amaç fonkiyonun bulunduğu hücredir. Çünkü elde edilen çözüm onucunda en yükek kâr ya da en düşük maliyet (optimum onuç) bu hücrede gerçekleşecektir. Eşittir: parametreinde ie eğer kâr makimizayonu problemi çözüleceke En Büyük, maliyet minimizayonu çözüleceke En Küçük alternatifi onaylanmalıdır. Eğer yalnızca denklem itemi çözüleceke bu durumda Eşittir= parametrei eçilmelidir. Değişen hücreler kımı ie makimizayon ya da minimizayon probleminin çözümü onucunda elde edilecek X ve X değerleridir. Kııtlamalar bölümü ie kııtlayıcı fonkiyonların tanımlandığı bölümdür. Ekle düğmei tıklanarak kııtlayıcı fonkiyonlar ıraıyla eçilmelidir. Benzer şekilde diğer kııtlayıcılarda tek tek girilmelidir. Burada Tamam düğmei onaylanarak ya da tekrar Ekle düğmei eçilerek daha onraki kııtlayıcıların girilmei ağlanabilir. Bütün kııtlayıcıların girilmeiyle elde edilen çözücü parametreleri pencerei elde edilecektir.
12 Bu aşama ile bütün çözücü parametrelerin girilmei tamamlanmış olur. Çöz düğmeinin tıklanmaı ile doğrual programlama problemi çözülür. Denklemin çözücü işlevi ile çözümünden elde edilen Ecel çalışma ayfaı izleyen biçimdeki gibidir. Çalışma ayfaında da görüldüğü gibi X=, =4 ve amaç fonkiyon Zma=3 olarak bulunmuştur. İzleyen D.P. Probleminde ie minimizayon örneğinin Ecel çözücüü ile çözümü verilmiştir. Amaç Fonkiyonu: Zmin = Kııtlayıcılar: Pozitif Kııtlama: ,, 3 Ecel çalışma ayfaındaki A, B ve C adrelerine X,X ve X3 girilmeli ve A, B ve C adrelerine (ıfır) değeri yazılmalıdır. Sonraki adımda uygun bir hücreye gelinerek (Örnekte E hücrei) bu hücreye amaç fonkiyonu izleyen biçimde yazılmalıdır: =4*A+8*B+36*C Amaç fonkiyonundan onra da kııtlayıcılar benzer şekilde yan hücrelere girilmelidir. Kııtlayıcı fonkiyonların yazılışı ve hücre adreleri izleyen biçimdeki gibi girilmiştir:
13 F Hücreine =4*A+*B+3*C-5 G Hücreine =6*A+B+9*C-8 H Hücreine =A I Hücreine =B J Hücreine =C Bu denklemlerin girilmeinden onra hücrelerde oluşan durum izleyen şekildeki gibidir. Bu aşamadan onra aktif hücre olarak amaç fonkiyonun bulunduğu D hücrei eçilmeli ve araçlar menüünden çözücü işlevi çalıştırılmalıdır. Çözücü parametreleri örnek probleme uygun olarak izleyen biçimde tanımlanmıştır. Bu parametrelerin tanımlanmaından onra Çöz düğmei tıklanır ve optimum çözüm elde edilmiş olur. Çöz düğmeinin tıklanmaından onra elde edilen Ecel çalışma ayfaı izleyen biçimde elde edilmiştir Çalışma ayfaında da görüldüğü gibi X=,66667, =, 3=, ve amaç fonkiyonu Zmin=3 olarak bulunmuştur.
14 .6. SİMPLEKS YÖNTEMİ Simplek yöntemi, amaç fonkiyonunu en büyük (makimum) veya en küçük (minimum) yapacak en iyi çözüme adım adım yaklaşan bir (heaplama yöntemi) algoritmadır. Bu nedenle, problemin çözümüne bir uç noktaından başlayarak optimum noktaya daha yakın bir ikinciine, oradan bir üçüncüüne atlayarak en iyi çözümü veren kenar noktaına ulaşmamızı ağlar. Simplek yöntemi ilk kez 947 yılında G.B.Dantzig tarafından kullanılmıştır. Uygulamada problemin değişkenleri çok fazla olduğunda doğrual programlama problemlerinin çözümü implek yöntemi ile ağlanır. Simplek yöntemi cebirel tekrarlama işlemine dayanır. Yöntemde önce başlangıç implek tablou düzenlenir. Sonra tekrarlayıcı işlemler ile belirli bir heap yöntemi içinde gelişen çözümlere doğru ilerleyerek optimal çözüme ulaşıncaya kadar işlemler ürdürülür. Gelişen çözüm tablolarında amaç fonkiyonunun ve karar değişkenlerinin değişen değerleri gözlenebilir. Simplek yöntemine başlamadan önce problemlerin doğru biçimde ifade edilmei gerekir. Doğrual Programlama Makimizayon Problemlerini Çözmek için Gerekli Aşamalar. Doğrual programlama modeli kurulur.. Model tandart formda yazılır. Doğrual programlama problemlerinin tandart formda olmaı için bütün kııtlar eşitlik, bütün değişkenler pozitif olmalıdır. Eğer i. kııtın tipi küçük eşit ( ) şeklindeye i gölge değişkeni eklenerek eşitlik elde edilir. Gölge değişken i. kııt tarafından kullanılmayan kaynak miktarıdır. Eğer i. kııtın tipi büyük eşit ( ) şeklindeye ei atıl değişkeni eklenerek eşitlik elde edilir. Atıl değişken, i. kııtın aşım miktarıdır. 3. Başlangıç implek tablo oluşturulur. Z ve c Z değerleri heaplanır. 4. Optimal çözüm elde edilene kadar aşağıdaki aşamalar tekrarlanır. a) Çözüme okmak için en yükek pozitif değere ahip c Z ütunu eçilir (Pivot Sütun). b) Çözümden çıkacak değişken ağ taraf oran teti ile belirlenir (Pivot atır). c) Pivot atır için yeni değerler heaplanır. d) Elde edilen tablo için Z ve c Z değerleri bulunur. Eğer ıfırdan büyük bir c Z değeri elde edilire.aşamaya dönülür. Aki durumda optimal çözüme ulaşılmıştır.
15 Örnek Bir mobilya firmaı ıra, maa ve andalye üretimi yapmaktadır. Her bir mobilyanın üretimi için tahta yanııra boya ve marangozluk atölyelerinin aşağıdaki tabloda verilen ürelerde kullanılmaı gerekmektedir. Kaynak Sıra Maa Sandalye Tahta( m ) 8 6 Boya Atölyei (aat) 4.5 Marangozluk At.(a.).5.5 Firmanın elinde 48 mtahta, aat boya ve 8 aat marangozluk atölyei işgücü vardır. Bir ıranın atış fiyatı 6 TL, bir maanın atış fiyatı 3 TL ve bir andalyenin atış fiyatı TL dir. Sıra ve andalyeler için talep ınırız olmaına rağmen, en fazla 5 adet maa atılabilmektedir. Bu mobilya firmaı mevcut kaynakları kullanarak kaçar adet mobilya üretmelidir? Firmanın elde edebileceği makimum kazanç nedir? Doğrual Programlama Modelinin Kurulmaı Karar Değişkenleri = Üretilen ıra miktarı = Üretilen maa miktarı = Üretilen andalye miktarı 3 Amaç Fonkiyonu Toplam gelirin makimizayonu Z ma = Model Z ma = (Tahta kııtı) (Boya kııtı) (Marangozluk kııtı) 3
16 5 (Talep kııtı),, (Pozitiflik Kııtı) 3 Problemin tandart formu aşağıdaki gibidir: Z = ma = = = = 5 4,,,,,, c () Temel ÇS Değişkenler c z z 6 3 Pivot Sütun Pivot ayı: Pivot ütun ve atırın keişimindeki ayıya pivot ayı denir. Pivot atırdaki her ayının yeni değeri, ayının pivot ayıya bölünmei ile elde edilir. /.5/.75.5/.5 / / /.5 / 8/ 4 Diğer atırlardaki ayılar aşağıdaki formüle göre elde edilir:
17 Yeni değer = Eki Değer- [(pivot ayının ütündeki veya altındaki ayı) (yeni pivot atırda karşılık gelen değer)] Eki atırı (8*yeni temel değişken atırı) Yeni atırı Eki atırı (4*yeni temel değişken atırı) Yeni atırı Eki 4 atırı (yeni temel değişken atırı) Yeni 4 atırı 5 6 c 6 c z z
18 Optimal Tablo 6 c 6 c z z
Matematiksel modellerin elemanları
 Matematiksel modellerin elemanları Op#mizasyon ve Doğrusal Programlama Maksimizasyon ve Minimizasyon örnekleri, Doğrusal programlama modeli kurma uygulamaları 6. DERS 1. Karar değişkenleri: Bir karar verme
Matematiksel modellerin elemanları Op#mizasyon ve Doğrusal Programlama Maksimizasyon ve Minimizasyon örnekleri, Doğrusal programlama modeli kurma uygulamaları 6. DERS 1. Karar değişkenleri: Bir karar verme
Simpleks Yönteminde Kullanılan İlave Değişkenler (Eşitliğin yönüne göre):
 DP SİMPLEKS ÇÖZÜM Simpleks Yöntemi, amaç fonksiyonunu en büyük (maksimum) veya en küçük (minimum) yapacak en iyi çözüme adım adım yaklaşan bir algoritma (hesaplama yöntemi) dir. Bu nedenle, probleme bir
DP SİMPLEKS ÇÖZÜM Simpleks Yöntemi, amaç fonksiyonunu en büyük (maksimum) veya en küçük (minimum) yapacak en iyi çözüme adım adım yaklaşan bir algoritma (hesaplama yöntemi) dir. Bu nedenle, probleme bir
Ders #9. Otomatik Kontrol. Kararlılık (Stability) Prof.Dr.Galip Cansever. 26 February 2007 Otomatik Kontrol. Prof.Dr.
 Der #9 Otomatik Kontrol Kararlılık (Stability) 1 Kararlılık, geçici rejim cevabı ve ürekli hal hataı gibi kontrol taarımcıının üç temel unurundan en önemli olanıdır. Lineer zamanla değişmeyen itemlerin
Der #9 Otomatik Kontrol Kararlılık (Stability) 1 Kararlılık, geçici rejim cevabı ve ürekli hal hataı gibi kontrol taarımcıının üç temel unurundan en önemli olanıdır. Lineer zamanla değişmeyen itemlerin
Yöneylem Araştırması II
 Yöneylem Araştırması II Öğr. Gör. Dr. Hakan ÇERÇİOĞLU [email protected] BÖLÜM I: Doğrusal Programlama Tekrarı Doğrusal Programlama Tanımı Doğrusal Programlama Varsayımları Grafik Çözüm Metodu Simpleks
Yöneylem Araştırması II Öğr. Gör. Dr. Hakan ÇERÇİOĞLU [email protected] BÖLÜM I: Doğrusal Programlama Tekrarı Doğrusal Programlama Tanımı Doğrusal Programlama Varsayımları Grafik Çözüm Metodu Simpleks
ESM406- Elektrik Enerji Sistemlerinin Kontrolü. 2. SİSTEMLERİN MATEMATİKSEL MODELLENMESİ Laplace Dönüşümü
 ESM406- Elektrik Enerji Sitemlerinin Kontrolü. SİSTEMLERİN MATEMATİKSEL MODELLENMESİ Laplace Dönüşümü.. Hedefler Bu bölümün hedefleri:. Komplek değişkenlerin tanıtılmaı.. Laplace Tranformayonun tanıtılmaı..
ESM406- Elektrik Enerji Sitemlerinin Kontrolü. SİSTEMLERİN MATEMATİKSEL MODELLENMESİ Laplace Dönüşümü.. Hedefler Bu bölümün hedefleri:. Komplek değişkenlerin tanıtılmaı.. Laplace Tranformayonun tanıtılmaı..
Temelleri. Doç.Dr.Ali Argun Karacabey
 Doğrusal Programlamanın Temelleri Doç.Dr.Ali Argun Karacabey Doğrusal Programlama Nedir? Bir Doğrusal Programlama Modeli doğrusal kısıtlar altında bir doğrusal ğ fonksiyonun değerini ğ maksimize yada minimize
Doğrusal Programlamanın Temelleri Doç.Dr.Ali Argun Karacabey Doğrusal Programlama Nedir? Bir Doğrusal Programlama Modeli doğrusal kısıtlar altında bir doğrusal ğ fonksiyonun değerini ğ maksimize yada minimize
doğrusal programlama DOĞRUSAL PROGRAMLAMA (GENEL)
 DOĞRUSAL PROGRAMLAMA (GENEL) Belirli bir amacın gerçekleşmesini etkileyen bazı kısıtlayıcı koşulların ve bu kısıtlayıcı koşulların doğrusal eşitlik ya da eşitsizlik biçiminde verilmesi durumunda amaca
DOĞRUSAL PROGRAMLAMA (GENEL) Belirli bir amacın gerçekleşmesini etkileyen bazı kısıtlayıcı koşulların ve bu kısıtlayıcı koşulların doğrusal eşitlik ya da eşitsizlik biçiminde verilmesi durumunda amaca
Doğrusal Programlama. Prof. Dr. Ferit Kemal Sönmez
 Doğrusal Programlama Prof. Dr. Ferit Kemal Sönmez Doğrusal Programlama Belirli bir amacın gerçekleşmesini etkileyen bazı kısıtlayıcı koşulların ve bu kısıtlayıcı koşulların doğrusal eşitlik ya da eşitsizlik
Doğrusal Programlama Prof. Dr. Ferit Kemal Sönmez Doğrusal Programlama Belirli bir amacın gerçekleşmesini etkileyen bazı kısıtlayıcı koşulların ve bu kısıtlayıcı koşulların doğrusal eşitlik ya da eşitsizlik
YÖNEYLEM ARAŞTIRMASI - I
 YÖNEYLEM ARAŞTIRMASI - I /0 İçerik Matematiksel Modelin Kurulması Grafik Çözüm DP Terminolojisi DP Modelinin Standart Formu DP Varsayımları 2/0 Grafik Çözüm İki değişkenli (X, X2) modellerde kullanılabilir,
YÖNEYLEM ARAŞTIRMASI - I /0 İçerik Matematiksel Modelin Kurulması Grafik Çözüm DP Terminolojisi DP Modelinin Standart Formu DP Varsayımları 2/0 Grafik Çözüm İki değişkenli (X, X2) modellerde kullanılabilir,
Frekans Analiz Yöntemleri I Bode Eğrileri
 Frekan Analiz Yöntemleri I Bode Eğrileri Prof.Dr. Galip Canever 1 Frekan cevabı analizi 1930 ve 1940 lı yıllarda Nyquit ve Bode tarafından geliştirilmiştir ve 1948 de Evan tarafından geliştirilen kök yer
Frekan Analiz Yöntemleri I Bode Eğrileri Prof.Dr. Galip Canever 1 Frekan cevabı analizi 1930 ve 1940 lı yıllarda Nyquit ve Bode tarafından geliştirilmiştir ve 1948 de Evan tarafından geliştirilen kök yer
ESM 406 Elektrik Enerji Sistemlerinin Kontrolü 4. TRANSFER FONKSİYONU VE BLOK DİYAGRAM İNDİRGEME
 . TRNSFER FONKSİYONU VE BLOK DİYRM İNDİREME. Hedefler Bu bölümün amacı;. Tranfer fonkiyonu ile blok diyagramları araındaki ilişki incelemek,. Fizikel itemlerin blok diyagramlarını elde etmek, 3. Blok diyagramlarının
. TRNSFER FONKSİYONU VE BLOK DİYRM İNDİREME. Hedefler Bu bölümün amacı;. Tranfer fonkiyonu ile blok diyagramları araındaki ilişki incelemek,. Fizikel itemlerin blok diyagramlarını elde etmek, 3. Blok diyagramlarının
YÖNEYLEM ARAŞTIRMASI - I
 YÖNEYLEM ARAŞTIRMASI - I 1/19 İçerik Yöneylem Araştırmasının Dalları Kullanım Alanları Yöneylem Araştırmasında Bazı Yöntemler Doğrusal (Lineer) Programlama, Oyun Teorisi, Dinamik Programlama, Tam Sayılı
YÖNEYLEM ARAŞTIRMASI - I 1/19 İçerik Yöneylem Araştırmasının Dalları Kullanım Alanları Yöneylem Araştırmasında Bazı Yöntemler Doğrusal (Lineer) Programlama, Oyun Teorisi, Dinamik Programlama, Tam Sayılı
H09 Doğrusal kontrol sistemlerinin kararlılık analizi. Yrd. Doç. Dr. Aytaç Gören
 H09 Doğrual kontrol itemlerinin kararlılık analizi MAK 306 - Der Kapamı H01 İçerik ve Otomatik kontrol kavramı H0 Otomatik kontrol kavramı ve devreler H03 Kontrol devrelerinde geri belemenin önemi H04
H09 Doğrual kontrol itemlerinin kararlılık analizi MAK 306 - Der Kapamı H01 İçerik ve Otomatik kontrol kavramı H0 Otomatik kontrol kavramı ve devreler H03 Kontrol devrelerinde geri belemenin önemi H04
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ
 ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTIRMA MODELİNİN TANIMI Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTIRMA MODELİNİN TANIMI Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
3. DİNAMİK. bağıntısı ile hesaplanır. Birimi m/s ile ifade edilir.
 3. DİNAMİK Dinamik konuu Kinematik ve Kinetik alt başlıklarında incelenecektir. Kinematik, hareket halindeki bir itemin konum (poziyon), hız ve ivmeini, bunların oluşmaını ağlayan kuvvet ya da moment etkiini
3. DİNAMİK Dinamik konuu Kinematik ve Kinetik alt başlıklarında incelenecektir. Kinematik, hareket halindeki bir itemin konum (poziyon), hız ve ivmeini, bunların oluşmaını ağlayan kuvvet ya da moment etkiini
Uydu Kentlerin Tasarımı için Bir Karar Destek Sistemi ve Bilişim Sistemi Modeli Önerisi
 Akademik Bilişim 0 - XII. Akademik Bilişim Konferanı Bildirileri 0-2 Şubat 200 Muğla Üniveritei Uydu Kentlerin Taarımı için Bir Karar Detek Sitemi ve Bilişim Sitemi Modeli Önerii TC Beykent Üniveritei
Akademik Bilişim 0 - XII. Akademik Bilişim Konferanı Bildirileri 0-2 Şubat 200 Muğla Üniveritei Uydu Kentlerin Taarımı için Bir Karar Detek Sitemi ve Bilişim Sitemi Modeli Önerii TC Beykent Üniveritei
GÜVENİLİR OLMAYAN SİSTEMLER İÇİN ARALIK ÇİZELGELEMESİ PROBLEMİ
 İtanbul Ticaret Üniveritei Fen Bilimleri Dergii Yıl: 6 Sayı:12 Güz 2007/2. 67-79 GÜVENİLİR OLMAYAN SİSTEMLER İÇİN ARALIK ÇİZELGELEMESİ PROBLEMİ Deniz TÜRSEL ELİİYİ, Selma GÜRLER ÖZET Bu çalışmada, her
İtanbul Ticaret Üniveritei Fen Bilimleri Dergii Yıl: 6 Sayı:12 Güz 2007/2. 67-79 GÜVENİLİR OLMAYAN SİSTEMLER İÇİN ARALIK ÇİZELGELEMESİ PROBLEMİ Deniz TÜRSEL ELİİYİ, Selma GÜRLER ÖZET Bu çalışmada, her
ÇOKLU ALT SİSTEMLERİN SADELEŞTİRİLMESİ
 73 BÖLÜM 5 ÇOKLU ALT SİSTEMLERİN SADELEŞTİRİLMESİ 5. Blok Diyagramları Blok diyagramları genellikle frekan domenindeki analizlerde kullanılır. Şekil 5. de çoklu alt-itemlerde kullanılan blok diyagramları
73 BÖLÜM 5 ÇOKLU ALT SİSTEMLERİN SADELEŞTİRİLMESİ 5. Blok Diyagramları Blok diyagramları genellikle frekan domenindeki analizlerde kullanılır. Şekil 5. de çoklu alt-itemlerde kullanılan blok diyagramları
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ
 ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTıRMA MODELININ TANıMı Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTıRMA MODELININ TANıMı Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
12.7 Örnekler PROBLEMLER
 2. 2.2 2.3 2.4 Giriş Bir Kuvvetin ve Bir Momentin İşi Virtüel İş İlkei Genelleştirilmiş Koordinatlar Örnekler Potaniyel Enerji 2.5 Sürtünmeli Makinalar ve Mekanik Verim 2.6 Denge 2.7 Örnekler PROBLEMLER
2. 2.2 2.3 2.4 Giriş Bir Kuvvetin ve Bir Momentin İşi Virtüel İş İlkei Genelleştirilmiş Koordinatlar Örnekler Potaniyel Enerji 2.5 Sürtünmeli Makinalar ve Mekanik Verim 2.6 Denge 2.7 Örnekler PROBLEMLER
Bölüm 7 - Kök- Yer Eğrisi Teknikleri
 Bölüm 7 - Kök- Yer Eğrii Teknikleri Kök yer eğrii tekniği kararlı ve geçici hal cevabı analizinde kullanılmaktadır. Bu grafikel teknik kontrol iteminin performan niteliklerini tanımlamamıza yardımcı olur.
Bölüm 7 - Kök- Yer Eğrii Teknikleri Kök yer eğrii tekniği kararlı ve geçici hal cevabı analizinde kullanılmaktadır. Bu grafikel teknik kontrol iteminin performan niteliklerini tanımlamamıza yardımcı olur.
Kontrol Sistemleri. Kontrolcüler. Yrd. Doç. Dr. Aytaç GÖREN
 ontrol Sitemleri ontrolcüler Doğrual Sitemlerin Sınıflandırılmaı: Birinci Mertebeden Gecikmeli BMG Sitemler: x a T 1 x a t x e t Son değer teoremi : x x x adr adr adr lim xa 0 lim 0 T 1 t T t 2T t 3T t
ontrol Sitemleri ontrolcüler Doğrual Sitemlerin Sınıflandırılmaı: Birinci Mertebeden Gecikmeli BMG Sitemler: x a T 1 x a t x e t Son değer teoremi : x x x adr adr adr lim xa 0 lim 0 T 1 t T t 2T t 3T t
YÖNEYLEM ARAŞTIRMASI - I
 YÖNEYLEM ARAŞTIRMASI - I 1/71 İçerik n Bulunması Kuzey-Batı Köşe Yöntemi En Küçük Maliyetli Göze Yöntemi Sıra / Sütun En Küçüğü Yöntemi Vogel Yaklaşım Metodu (VAM) Optimum Çözümün Bulunması Atlama Taşı
YÖNEYLEM ARAŞTIRMASI - I 1/71 İçerik n Bulunması Kuzey-Batı Köşe Yöntemi En Küçük Maliyetli Göze Yöntemi Sıra / Sütun En Küçüğü Yöntemi Vogel Yaklaşım Metodu (VAM) Optimum Çözümün Bulunması Atlama Taşı
EM302 Yöneylem Araştırması 2 Doğrusal Olmayan Programlamaya Giriş. Dr. Özgür Kabak
 EM302 Yöneylem Araştırması 2 Doğrusal Olmayan Programlamaya Giriş Dr. Özgür Kabak Doğrusal Olmayan Programlama Eğer bir Matematiksel Programlama modelinin amaç fonksiyonu ve/veya kısıtları doğrusal değil
EM302 Yöneylem Araştırması 2 Doğrusal Olmayan Programlamaya Giriş Dr. Özgür Kabak Doğrusal Olmayan Programlama Eğer bir Matematiksel Programlama modelinin amaç fonksiyonu ve/veya kısıtları doğrusal değil
Bir Doğrusal Programlama Modelinin Genel Yapısı
 Bir Doğrusal Programlama Modelinin Genel Yapısı Amaç Fonksiyonu Kısıtlar M i 1 N Z j 1 N j 1 a C j x j ij x j B i Karar Değişkenleri x j Pozitiflik Koşulu x j >= 0 Bu formülde kullanılan matematik notasyonların
Bir Doğrusal Programlama Modelinin Genel Yapısı Amaç Fonksiyonu Kısıtlar M i 1 N Z j 1 N j 1 a C j x j ij x j B i Karar Değişkenleri x j Pozitiflik Koşulu x j >= 0 Bu formülde kullanılan matematik notasyonların
Kök Yer Eğrileri. Doç.Dr. Haluk Görgün. Kontrol Sistemleri Tasarımı. Doç.Dr. Haluk Görgün
 Kök Yer Eğrileri Bir kontrol taarımcıı itemin kararlı olup olmadığını ve kararlılık dereceini bilmek, diferaniyel denklem çözmeden bir analiz ile item performaını tahmin etmek iter. Geribelemeli kontrol
Kök Yer Eğrileri Bir kontrol taarımcıı itemin kararlı olup olmadığını ve kararlılık dereceini bilmek, diferaniyel denklem çözmeden bir analiz ile item performaını tahmin etmek iter. Geribelemeli kontrol
Otomatik Kontrol. Blok Diyagramlar ve İşaret Akış Diyagramları. Prof.Dr.Galip Cansever. Ders #3. 26 February 2007 Otomatik Kontrol
 Der # Otomatik Kontrol Blok Diyagramlar ve İşaret Akış Diyagramları ProfDralip Canever 6 February 007 Otomatik Kontrol ProfDralip Canever Karmaşık itemler bir çok alt itemin bir araya gelmeiyle oluşmuştur
Der # Otomatik Kontrol Blok Diyagramlar ve İşaret Akış Diyagramları ProfDralip Canever 6 February 007 Otomatik Kontrol ProfDralip Canever Karmaşık itemler bir çok alt itemin bir araya gelmeiyle oluşmuştur
İkinci dersin notlarında yer alan Gepetto Marangozhanesi örneğini hatırlayınız.
 ISLE 403 YÖNEYLEM ARAŞTIRMASI DERS 3 NOTLAR DP Modellerinin Standart Biçimde Gösterimi: İkinci dersin notlarında yer alan Gepetto Marangozhanesi örneğini hatırlayınız. Gepetto Marangozhanesi için DP modeli
ISLE 403 YÖNEYLEM ARAŞTIRMASI DERS 3 NOTLAR DP Modellerinin Standart Biçimde Gösterimi: İkinci dersin notlarında yer alan Gepetto Marangozhanesi örneğini hatırlayınız. Gepetto Marangozhanesi için DP modeli
OYUN TEORİSİ. Özlem AYDIN. Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü
 OYUN TEORİSİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü TANIM ''Oyun Teorisi'', iki yada daha fazla rakibi belirli kurallar altında birleştirerek karşılıklı olarak çelişen olasılıklar
OYUN TEORİSİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü TANIM ''Oyun Teorisi'', iki yada daha fazla rakibi belirli kurallar altında birleştirerek karşılıklı olarak çelişen olasılıklar
Optimizasyon İçin Kök(Generic) Model (Doğrusal-Olmayan Programlama Modeli)
 ISLE 403 YÖNEYLEM ARAŞTIRMASI I DERS 2 NOTLAR Optimizasyon İçin Kök(Generic) Model (Doğrusal-Olmayan Programlama Modeli) X, karar değişkenlerinin bir vektörü olsun. z, g 1, g 2,...,g m fonksiyonlardır.
ISLE 403 YÖNEYLEM ARAŞTIRMASI I DERS 2 NOTLAR Optimizasyon İçin Kök(Generic) Model (Doğrusal-Olmayan Programlama Modeli) X, karar değişkenlerinin bir vektörü olsun. z, g 1, g 2,...,g m fonksiyonlardır.
KARAYOLU VE DEMİRYOLU PROJELERİNDE ORTOMETRİK YÜKSEKLİK HESABI: EN KÜÇÜK KARELER İLE KOLLOKASYON
 TMMOB Harita ve Kadatro Mühendileri Odaı 13. Türkiye Harita Bilimel ve Teknik Kurultayı 18 Nian 011, Ankara KARAYOLU VE DEMİRYOLU PROJELERİNDE ORTOMETRİK YÜKSEKLİK HESABI: EN KÜÇÜK KARELER İLE KOLLOKASYON
TMMOB Harita ve Kadatro Mühendileri Odaı 13. Türkiye Harita Bilimel ve Teknik Kurultayı 18 Nian 011, Ankara KARAYOLU VE DEMİRYOLU PROJELERİNDE ORTOMETRİK YÜKSEKLİK HESABI: EN KÜÇÜK KARELER İLE KOLLOKASYON
EGE ÜNİVERSİTESİ-MÜHENDİSLİK FAKÜLTESİ-MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ 1 MK371 ISI TRANSFERİ (2+2) DERSİ
 EGE ÜNİVERSİESİ-MÜHENDİSİK FAKÜESİ-MAKİNA MÜHENDİSİĞİ BÖÜMÜ 1 MK371 ISI RANSFERİ (+) DERSİ-ÖZE BİGİER: (8.6) EGE ÜNİVERSİESİ-MÜHENDİSİK FAKÜESİ MAKİNA MÜHENDİSİĞİ BÖÜMÜ MK371 ISI RANSFERİ (+) DERSİ.BÖÜM
EGE ÜNİVERSİESİ-MÜHENDİSİK FAKÜESİ-MAKİNA MÜHENDİSİĞİ BÖÜMÜ 1 MK371 ISI RANSFERİ (+) DERSİ-ÖZE BİGİER: (8.6) EGE ÜNİVERSİESİ-MÜHENDİSİK FAKÜESİ MAKİNA MÜHENDİSİĞİ BÖÜMÜ MK371 ISI RANSFERİ (+) DERSİ.BÖÜM
İÇİNDEKİLER. Bölüm 1 YÖNEYLEM ARAŞTIRMASINA GİRİŞ 11. 1.1. Temel Kavramlar 14 1.2. Modeller 17 1.3. Diğer Kavramlar 17 Değerlendirme Soruları 19
 İÇİNDEKİLER ÖNSÖZ III Bölüm 1 YÖNEYLEM ARAŞTIRMASINA GİRİŞ 11 1.1. Temel Kavramlar 14 1.2. Modeller 17 1.3. Diğer Kavramlar 17 Değerlendirme Soruları 19 Bölüm 2 DOĞRUSAL PROGRAMLAMA 21 2.1 Doğrusal Programlamanın
İÇİNDEKİLER ÖNSÖZ III Bölüm 1 YÖNEYLEM ARAŞTIRMASINA GİRİŞ 11 1.1. Temel Kavramlar 14 1.2. Modeller 17 1.3. Diğer Kavramlar 17 Değerlendirme Soruları 19 Bölüm 2 DOĞRUSAL PROGRAMLAMA 21 2.1 Doğrusal Programlamanın
KISITLI OPTİMİZASYON
 KISITLI OPTİMİZASYON SİMPLEKS YÖNTEMİ Simpleks Yöntemi Simpleks yöntemi iteratif bir prosedürü gerektirir. Bu iterasyonlar ile gerçekçi çözümlerin olduğu bölgenin (S) bir köşesinden başlayarak amaç fonksiyonunun
KISITLI OPTİMİZASYON SİMPLEKS YÖNTEMİ Simpleks Yöntemi Simpleks yöntemi iteratif bir prosedürü gerektirir. Bu iterasyonlar ile gerçekçi çözümlerin olduğu bölgenin (S) bir köşesinden başlayarak amaç fonksiyonunun
TAMSAYILI PROGRAMLAMA
 TAMSAYILI PROGRAMLAMA Doğrusal programlama problemlerinde sık sık çözümün tamsayı olması gereken durumlar ile karşılaşılır. Örneğin ele alınan problem masa, sandalye, otomobil vb. üretimlerinin optimum
TAMSAYILI PROGRAMLAMA Doğrusal programlama problemlerinde sık sık çözümün tamsayı olması gereken durumlar ile karşılaşılır. Örneğin ele alınan problem masa, sandalye, otomobil vb. üretimlerinin optimum
Ders #10. Otomatik Kontrol. Sürekli Hal Hataları. Prof.Dr.Galip Cansever. 26 February 2007 Otomatik Kontrol. Prof.Dr.
 Der #0 Otomatik ontrol Sürekli Hal Hataları Prof.Dr.alip Canever Prof.Dr.alip Canever Denetim Sitemlerinin analiz ve taarımında üç kritere odaklanılır:. eçici Rejim Cevabı. ararlılık 3. Sürekli Hal ararlı
Der #0 Otomatik ontrol Sürekli Hal Hataları Prof.Dr.alip Canever Prof.Dr.alip Canever Denetim Sitemlerinin analiz ve taarımında üç kritere odaklanılır:. eçici Rejim Cevabı. ararlılık 3. Sürekli Hal ararlı
ÖZLEM AYDIN TRAKYA ÜNİVERSİTESİ BİLGİSAYAR MÜHENDİSLİĞİ BÖLÜMÜ
 YÖNEYLEM ARAŞTIRMASI (OPERATIONAL RESEARCH) ÖZLEM AYDIN TRAKYA ÜNİVERSİTESİ BİLGİSAYAR MÜHENDİSLİĞİ BÖLÜMÜ SUNUM PLANI Yöneylem araştırmasının Tanımı Tarihçesi Özellikleri Aşamaları Uygulama alanları Yöneylem
YÖNEYLEM ARAŞTIRMASI (OPERATIONAL RESEARCH) ÖZLEM AYDIN TRAKYA ÜNİVERSİTESİ BİLGİSAYAR MÜHENDİSLİĞİ BÖLÜMÜ SUNUM PLANI Yöneylem araştırmasının Tanımı Tarihçesi Özellikleri Aşamaları Uygulama alanları Yöneylem
Önsöz... XIII Önsöz (Hava Harp Okulu Basımı)...XV BÖLÜM 1 1. YÖNEYLEM ARAŞTIRMASINA GİRİŞ... 1
 İÇİNDEKİLER Önsöz... XIII Önsöz (Hava Harp Okulu Basımı)...XV BÖLÜM 1 1. YÖNEYLEM ARAŞTIRMASINA GİRİŞ... 1 1.1. Yöneticilik / Komutanlık İşlevi ve Gerektirdiği Nitelikler... 2 1.1.1. Yöneticilik / Komutanlık
İÇİNDEKİLER Önsöz... XIII Önsöz (Hava Harp Okulu Basımı)...XV BÖLÜM 1 1. YÖNEYLEM ARAŞTIRMASINA GİRİŞ... 1 1.1. Yöneticilik / Komutanlık İşlevi ve Gerektirdiği Nitelikler... 2 1.1.1. Yöneticilik / Komutanlık
MOSFET BSIM3V3 EŞİK GERİLİMİ VE MOBİLİTE PARAMETRELERİNİN GENETİK ALGORİTMA İLE ÇIKARTILMASI
 MOSFET BSIM3V3 EŞİK GERİLİMİ VE MOBİLİTE PARAMETRELERİNİN GENETİK ALGORİTMA İLE ÇIKARTILMASI M.Emin BAŞAK 1 Ayten KUNTMAN Hakan KUNTMAN 3 1, İtanbul Üniveritei,Mühendilik Fakültei, Elektrik&Elektronik
MOSFET BSIM3V3 EŞİK GERİLİMİ VE MOBİLİTE PARAMETRELERİNİN GENETİK ALGORİTMA İLE ÇIKARTILMASI M.Emin BAŞAK 1 Ayten KUNTMAN Hakan KUNTMAN 3 1, İtanbul Üniveritei,Mühendilik Fakültei, Elektrik&Elektronik
ENM 557 ÇOK ÖLÇÜTLÜ KARAR VERME
 GAZİ ÜNİVERSİTESİ MÜHENDİSLİK-MİMARLIK FAKÜLTESİ FEN BİLİMLERİ ENSTİTÜSÜ ENM 557 ÇOK ÖLÇÜTLÜ KARAR VERME GALATASARAY SK nın 2009-2010 Sezonu 2 Dönemi için Forvet Seçim Problemi DERSİN SORUMLUSU: Yrd Doç
GAZİ ÜNİVERSİTESİ MÜHENDİSLİK-MİMARLIK FAKÜLTESİ FEN BİLİMLERİ ENSTİTÜSÜ ENM 557 ÇOK ÖLÇÜTLÜ KARAR VERME GALATASARAY SK nın 2009-2010 Sezonu 2 Dönemi için Forvet Seçim Problemi DERSİN SORUMLUSU: Yrd Doç
Çözümlemeleri" adlı yüksek lisans tezini başarıyla tamamlayarak 2001'de mezun oldu.
 Dersi Veren Öğretim Üyesi: Doç. Dr. Mehmet KORKMAZ Özgeçmişi Mehmet KORKMAZ, 1975 yılında Malatya da doğdu. İlkokul, ortaokul ve liseyi memleketi olan Isparta da tamamladı. 1996 yılında İ.Ü. Orman Fakültesi,
Dersi Veren Öğretim Üyesi: Doç. Dr. Mehmet KORKMAZ Özgeçmişi Mehmet KORKMAZ, 1975 yılında Malatya da doğdu. İlkokul, ortaokul ve liseyi memleketi olan Isparta da tamamladı. 1996 yılında İ.Ü. Orman Fakültesi,
TOPRAKLAMA AĞLARININ ÜÇ BOYUTLU TASARIMI
 TOPRAKLAMA AĞLARININ ÜÇ BOYUTLU TASARIMI Fikri Barış UZUNLAR [email protected] Özcan KALENDERLİ [email protected] İtanbul Teknik Üniveritei, Elektrik-Elektronik Fakültei Elektrik
TOPRAKLAMA AĞLARININ ÜÇ BOYUTLU TASARIMI Fikri Barış UZUNLAR [email protected] Özcan KALENDERLİ [email protected] İtanbul Teknik Üniveritei, Elektrik-Elektronik Fakültei Elektrik
Otomatik Kontrol. Fiziksel Sistemlerin Modellenmesi. Prof.Dr.Galip Cansever. Elektriksel Sistemeler Mekaniksel Sistemler. Ders #4
 Der #4 Otomatik Kontrol Fizikel Sitemlerin Modellenmei Elektrikel Sitemeler Mekanikel Sitemler 6 February 007 Otomatik Kontrol Kontrol itemlerinin analizinde ve taarımında en önemli noktalardan bir tanei
Der #4 Otomatik Kontrol Fizikel Sitemlerin Modellenmei Elektrikel Sitemeler Mekanikel Sitemler 6 February 007 Otomatik Kontrol Kontrol itemlerinin analizinde ve taarımında en önemli noktalardan bir tanei
3.2. DP Modellerinin Simpleks Yöntem ile Çözümü Primal Simpleks Yöntem
 3.2. DP Modellerinin Simpleks Yöntem ile Çözümü 3.2.1. Primal Simpleks Yöntem Grafik çözüm yönteminde gördüğümüz gibi optimal çözüm noktası, her zaman uygun çözüm alanının bir köşe noktası ya da uç noktası
3.2. DP Modellerinin Simpleks Yöntem ile Çözümü 3.2.1. Primal Simpleks Yöntem Grafik çözüm yönteminde gördüğümüz gibi optimal çözüm noktası, her zaman uygun çözüm alanının bir köşe noktası ya da uç noktası
İbrahim Küçükkoç Arş. Gör.
 Doğrusal Programlamada Karışım Problemleri İbrahim Küçükkoç Arş. Gör. Balikesir Üniversitesi Endüstri Mühendisliği Bölümü Mühendislik-Mimarlık Fakültesi Çağış Kampüsü 10145 / Balıkesir 0 (266) 6121194
Doğrusal Programlamada Karışım Problemleri İbrahim Küçükkoç Arş. Gör. Balikesir Üniversitesi Endüstri Mühendisliği Bölümü Mühendislik-Mimarlık Fakültesi Çağış Kampüsü 10145 / Balıkesir 0 (266) 6121194
KONU 4: DOĞRUSAL PROGRAMLAMA MODELİ İÇİN ÇÖZÜM YÖNTEMLERİ I
 KONU 4: DOĞRUSAL PROGRAMLAMA MODELİ İÇİN ÇÖZÜM YÖNTEMLERİ I 4.1. Dışbükeylik ve Uç Nokta Bir d.p.p. de model kısıtlarını aynı anda sağlayan X X X karar değişkenleri... n vektörüne çözüm denir. Eğer bu
KONU 4: DOĞRUSAL PROGRAMLAMA MODELİ İÇİN ÇÖZÜM YÖNTEMLERİ I 4.1. Dışbükeylik ve Uç Nokta Bir d.p.p. de model kısıtlarını aynı anda sağlayan X X X karar değişkenleri... n vektörüne çözüm denir. Eğer bu
Duyarlılık Analizi, modelde veri olarak kabul edilmiş parametrelerde meydana gelen değişimlerin optimum çözüme etkisinin incelenmesidir.
 ISLE 403 YÖNEYLEM ARAŞTIRMASI I DERS IV NOTLAR Bağlayıcı Kısıtlar ve Bağlayıcı Olmayan Kısıtlar: Bağlayıcı Kısıtlar, denklemleri optimum çözüm noktasında kesişen kısıtlardır. Bağlayıcı-Olmayan Kısıtlar,
ISLE 403 YÖNEYLEM ARAŞTIRMASI I DERS IV NOTLAR Bağlayıcı Kısıtlar ve Bağlayıcı Olmayan Kısıtlar: Bağlayıcı Kısıtlar, denklemleri optimum çözüm noktasında kesişen kısıtlardır. Bağlayıcı-Olmayan Kısıtlar,
Kontrol Sistemleri Tasarımı
 Kontrol Sitemleri Taarımı Kök Yer Eğrii ile Kontrolcü Taarımı Prof. Dr. Bülent E. Platin Kontrol Sitemlerinde Taarım İterleri Zaman Yanıtı Özellik Kararlılık Kalıcı Rejim Yanıtı Geçici rejim Yanıtı Kapalı
Kontrol Sitemleri Taarımı Kök Yer Eğrii ile Kontrolcü Taarımı Prof. Dr. Bülent E. Platin Kontrol Sitemlerinde Taarım İterleri Zaman Yanıtı Özellik Kararlılık Kalıcı Rejim Yanıtı Geçici rejim Yanıtı Kapalı
GRID INDUCTANCE IN SUBSTATION GROUNDING GRID DESIGN BASED ON GENETIC ALGORITHMS
 5. Ululararaı İleri Teknolojiler Sempozyumu (IATS 9), 3-5 Mayı 29, Karabük, Türkiye GENETİK ALGORİTMALARA DAYALI İLETİM MERKEZİ TOPRAKLAMA AĞI TASARIMINDA AĞ İNDÜKTANSI GRID INDUCTANCE IN SUBSTATION GROUNDING
5. Ululararaı İleri Teknolojiler Sempozyumu (IATS 9), 3-5 Mayı 29, Karabük, Türkiye GENETİK ALGORİTMALARA DAYALI İLETİM MERKEZİ TOPRAKLAMA AĞI TASARIMINDA AĞ İNDÜKTANSI GRID INDUCTANCE IN SUBSTATION GROUNDING
ELECO '2012 Elektrik - Elektronik ve Bilgisayar Mühendisliği Sempozyumu, 29 Kasım - 01 Aralık 2012, Bursa
 ELECO ' Elektrik - Elektronik ve Bilgiayar Mühendiliği Sempozyumu, 9 Kaım - Aralık, Bura Zaman Gecikmeli Yük Frekan Kontrol Siteminin ekaiu Yöntemi Kullanılarak Kararlılık Analizi Stability Analyi of Time-Delayed
ELECO ' Elektrik - Elektronik ve Bilgiayar Mühendiliği Sempozyumu, 9 Kaım - Aralık, Bura Zaman Gecikmeli Yük Frekan Kontrol Siteminin ekaiu Yöntemi Kullanılarak Kararlılık Analizi Stability Analyi of Time-Delayed
SÜREKLİ RASSAL DEĞİŞKENLER
 SÜREKLİ RASSAL DEĞİŞKENLER Sürekli Rassal Değişkenler Sürekli Rassal Değişken: Değerleriölçümyadatartımla elde edilen, bir başka anlatımla sayımla elde edilemeyen, değişkene sürekli rassal değişken denir.
SÜREKLİ RASSAL DEĞİŞKENLER Sürekli Rassal Değişkenler Sürekli Rassal Değişken: Değerleriölçümyadatartımla elde edilen, bir başka anlatımla sayımla elde edilemeyen, değişkene sürekli rassal değişken denir.
DOĞRUSAL PROGRAMLAMANIN ÖZEL TÜRLERİ
 DOĞRUSAL PROGRAMLAMANIN ÖZEL TÜRLERİ TRANSPORTASYON (TAŞIMA, ULAŞTIRMA) TRANSİT TAŞIMA (TRANSSHIPMENT) ATAMA (TAHSİS) TRANSPORTASYON (TAŞIMA) (ULAŞTIRMA) TRANSPORTASYON Malların birden fazla üretim (kaynak,
DOĞRUSAL PROGRAMLAMANIN ÖZEL TÜRLERİ TRANSPORTASYON (TAŞIMA, ULAŞTIRMA) TRANSİT TAŞIMA (TRANSSHIPMENT) ATAMA (TAHSİS) TRANSPORTASYON (TAŞIMA) (ULAŞTIRMA) TRANSPORTASYON Malların birden fazla üretim (kaynak,
Yöneylem Araştırması I Dersi 2. Çalışma Soruları ve Cevapları/
 Yöneylem Araştırması I Dersi 2. Çalışma Soruları ve Cevapları/25.12.2016 1. Bir deri firması standart tasarımda el yapımı çanta ve bavul üretmektedir. Firma üretmekte olduğu her çanta başına 400TL, her
Yöneylem Araştırması I Dersi 2. Çalışma Soruları ve Cevapları/25.12.2016 1. Bir deri firması standart tasarımda el yapımı çanta ve bavul üretmektedir. Firma üretmekte olduğu her çanta başına 400TL, her
YAĞLAMA VE KAYMALI YATAKLAR
 YAĞLAMA TĐPLERĐ YAĞLAMA VE KAYMALI YATAKLAR Yağlamanın beş farklı şekli tanımlanabilir. 1) Hidrodinamik ) Hidrotatik 3) Elatohidrodinamik 4) Sınır 5) Katı-film VĐSKOZĐTE τ F du = = A µ dy du U = dy h τ
YAĞLAMA TĐPLERĐ YAĞLAMA VE KAYMALI YATAKLAR Yağlamanın beş farklı şekli tanımlanabilir. 1) Hidrodinamik ) Hidrotatik 3) Elatohidrodinamik 4) Sınır 5) Katı-film VĐSKOZĐTE τ F du = = A µ dy du U = dy h τ
X-X DOĞRULTUSUNDA KESİT DONATI HESABI
 1 KİRİŞ DONATI HESABI Kiriş yükleri heaplandıktan onra keitler alınarak tatik heap yapılır. Keitler alınırken her kirişin bir keit içinde kalmaı ağlanır. BİRO yöntemi uygulanarak her kirişin menet ve açıklık
1 KİRİŞ DONATI HESABI Kiriş yükleri heaplandıktan onra keitler alınarak tatik heap yapılır. Keitler alınırken her kirişin bir keit içinde kalmaı ağlanır. BİRO yöntemi uygulanarak her kirişin menet ve açıklık
yöneylem araştırması Nedensellik üzerine diyaloglar I
 yöneylem araştırması Nedensellik üzerine diyaloglar I i Yayın No : 3197 Eğitim Dizisi : 149 1. Baskı Ocak 2015 İSTANBUL ISBN 978-605 - 333-225 1 Copyright Bu kitabın bu basısı için Türkiye deki yayın hakları
yöneylem araştırması Nedensellik üzerine diyaloglar I i Yayın No : 3197 Eğitim Dizisi : 149 1. Baskı Ocak 2015 İSTANBUL ISBN 978-605 - 333-225 1 Copyright Bu kitabın bu basısı için Türkiye deki yayın hakları
EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER
 EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER LAGRANGE YÖNTEMİ Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde değişkenler ve kısıtlar genel olarak şeklinde gösterilir. fonksiyonlarının
EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER LAGRANGE YÖNTEMİ Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde değişkenler ve kısıtlar genel olarak şeklinde gösterilir. fonksiyonlarının
Yöneylem Araştırması III
 Yöneylem Araştırması III Doç. Dr. Hakan ÇERÇİOĞLU [email protected] Yöneylem Araştırması III 1 BÖLÜM I: Hedef Programlama HEDEF PROGRAMLAMAYA GİRİŞ ÖNCELİKSİZ HEDEF PROGRAMLAMA ÖNCELİKLİ HEDEF PROGRAMLAMA
Yöneylem Araştırması III Doç. Dr. Hakan ÇERÇİOĞLU [email protected] Yöneylem Araştırması III 1 BÖLÜM I: Hedef Programlama HEDEF PROGRAMLAMAYA GİRİŞ ÖNCELİKSİZ HEDEF PROGRAMLAMA ÖNCELİKLİ HEDEF PROGRAMLAMA
BÖLÜM I: Hedef Programlama. Prof.Dr. Bilal TOKLU. HEDEF PROGRAMLAMAYA GİRİŞ HEDEF PROGRAMLAMA MODELLERİNİN ÇÖZÜMÜ
 Yöneylem Araştırması III Prof.Dr. Bilal TOKLU [email protected] Yöneylem Araştırması III BÖLÜM I: Hedef Programlama HEDEF PROGRAMLAMAYA GİRİŞ ÖNCELİKSİZ HEDEF PROGRAMLAMA ÖNCELİKLİ HEDEF PROGRAMLAMA HEDEF
Yöneylem Araştırması III Prof.Dr. Bilal TOKLU [email protected] Yöneylem Araştırması III BÖLÜM I: Hedef Programlama HEDEF PROGRAMLAMAYA GİRİŞ ÖNCELİKSİZ HEDEF PROGRAMLAMA ÖNCELİKLİ HEDEF PROGRAMLAMA HEDEF
Kontrol Sistemleri Tasarımı. Kontrolcü Tasarımı Tanımlar ve İsterler
 ontrol Sitemleri Taarımı ontrolcü Taarımı Tanımlar ve İterler Prof. Dr. Bülent E. Platin ontrolcü Taarımı İterleri Birincil iterler: ararlılık alıcı rejim hataı Dinamik davranış İterlerin işlevel boyutu:
ontrol Sitemleri Taarımı ontrolcü Taarımı Tanımlar ve İterler Prof. Dr. Bülent E. Platin ontrolcü Taarımı İterleri Birincil iterler: ararlılık alıcı rejim hataı Dinamik davranış İterlerin işlevel boyutu:
ÖRNEKLER-VEKTÖR UZAYLARI 1. Çözüm: w=k 1 u+k 2 v olmalıdır.
 ÖRNEKLER-VEKTÖR UZAYLARI. vektör uzayında yer alan w=(9 7) vektörünün, u=( -), v=(6 ) vektörlerinin doğrusal bir kombinasyonu olduğunu ve z=( - 8) vektörünün ise bu vektörlerin doğrusal bir kombinasyonu
ÖRNEKLER-VEKTÖR UZAYLARI. vektör uzayında yer alan w=(9 7) vektörünün, u=( -), v=(6 ) vektörlerinin doğrusal bir kombinasyonu olduğunu ve z=( - 8) vektörünün ise bu vektörlerin doğrusal bir kombinasyonu
ULUSLARARASI ANTALYA ÜNİVERSİTESİ ENDÜSTRİ MÜHENDİSLİĞİ BÖLÜMÜ DERS KATALOĞU
 ULUSLARARASI ANTALYA ÜNİVERSİTESİ ENDÜSTRİ MÜHENDİSLİĞİ BÖLÜMÜ DERS KATALOĞU ZORUNLU DERSLER IE 201 - Operasyon Modelleme Karar vermedeki belirsizlik rolü de dahil olmak üzere işletme kararlarının matematiksel
ULUSLARARASI ANTALYA ÜNİVERSİTESİ ENDÜSTRİ MÜHENDİSLİĞİ BÖLÜMÜ DERS KATALOĞU ZORUNLU DERSLER IE 201 - Operasyon Modelleme Karar vermedeki belirsizlik rolü de dahil olmak üzere işletme kararlarının matematiksel
DENEY 1 Laplace Dönüşümü
 DENEY 1 Laplace Dönüşümü DENEYİN AMACI 1. Laplace dönüşümü uygulamaını anlamak.. Simulink yardımıyla Laplace dönüşüm çiftlerinin benzetimini yapmak. 3. ACS-1000 Analog Kontrol Sitemini kullanarak, Laplace
DENEY 1 Laplace Dönüşümü DENEYİN AMACI 1. Laplace dönüşümü uygulamaını anlamak.. Simulink yardımıyla Laplace dönüşüm çiftlerinin benzetimini yapmak. 3. ACS-1000 Analog Kontrol Sitemini kullanarak, Laplace
YÖNEYLEM ARAŞTIRMASI - II
 YÖNEYLEM ARAŞTIRMASI - II Araş. Gör. Murat SARI 1/35 I Giriş Biri diğerini izleyen ve karşılıklı etkileri olan bir dizi kararın bütünüyle ele alındığı problemler için geliştirilen karar modelleri ve bunların
YÖNEYLEM ARAŞTIRMASI - II Araş. Gör. Murat SARI 1/35 I Giriş Biri diğerini izleyen ve karşılıklı etkileri olan bir dizi kararın bütünüyle ele alındığı problemler için geliştirilen karar modelleri ve bunların
Genetik Algoritma ile Kuru bir Trafonun Maliyet Optimizasyonu
 enetik Algoritma ile Kuru bir Trafonun Maliyet Optimizayonu Mehmed Çelebi 1 1 El-Elektronik Mühendiliği Bölümü Celal Bayar Üniveritei [email protected] Özet Bu çalışmada daha önce analitik yöntemle
enetik Algoritma ile Kuru bir Trafonun Maliyet Optimizayonu Mehmed Çelebi 1 1 El-Elektronik Mühendiliği Bölümü Celal Bayar Üniveritei [email protected] Özet Bu çalışmada daha önce analitik yöntemle
Devreler II Ders Notları
 Devreler II Der Noları 3-4 LAPLACE DÖNÜŞÜMÜNÜN DURUM DENKLEMLERİNİN ÇÖZÜMÜNDE KULLANILMAI Doğrual zamanla değişmeyen bir devrenin analizi için oluşan durum denklemi abi kaayılı doğrual diferaniyel denklem
Devreler II Der Noları 3-4 LAPLACE DÖNÜŞÜMÜNÜN DURUM DENKLEMLERİNİN ÇÖZÜMÜNDE KULLANILMAI Doğrual zamanla değişmeyen bir devrenin analizi için oluşan durum denklemi abi kaayılı doğrual diferaniyel denklem
Genetik Algoritma ile Kuru bir Trafonun Maliyet Optimizasyonu
 Genetik Algoritma ile Kuru bir Trafonun Maliyet Optimizayonu Mehmed Çelebi 1 1 El-Elektronik Mühendiliği Bölümü Celal Bayar Üniveritei [email protected] Özet Bu çalışmada daha önce analitik yöntemle
Genetik Algoritma ile Kuru bir Trafonun Maliyet Optimizayonu Mehmed Çelebi 1 1 El-Elektronik Mühendiliği Bölümü Celal Bayar Üniveritei [email protected] Özet Bu çalışmada daha önce analitik yöntemle
SĐGORTA ŞĐRKETLERĐNĐN SATIŞ PERFORMANSLARININ VERĐ ZARFLAMA ANALĐZĐ YÖNTEMĐYLE BELĐRLENMESĐ ÖZET
 Muğla Üniveritei Soyal Bilimler Entitüü Dergii (ĐLKE) Güz 2005 Sayı 15 SĐGORTA ŞĐRKETLERĐNĐN SATIŞ PERFORMANSLARININ VERĐ ZARFLAMA ANALĐZĐ YÖNTEMĐYLE BELĐRLENMESĐ ÖZET Zehra BAŞKAYA * Cüneyt AKAR ** Bu
Muğla Üniveritei Soyal Bilimler Entitüü Dergii (ĐLKE) Güz 2005 Sayı 15 SĐGORTA ŞĐRKETLERĐNĐN SATIŞ PERFORMANSLARININ VERĐ ZARFLAMA ANALĐZĐ YÖNTEMĐYLE BELĐRLENMESĐ ÖZET Zehra BAŞKAYA * Cüneyt AKAR ** Bu
( ) BSIM MOSFET Model Parametrelerinin Ölçüm Yoluyla Belirlenmesine Yönelik Algoritmalar. Şuayb YENER 1 Hakan KUNTMAN 2. Özetçe. 2 BSIM MOSFET Modeli
 BSIM MOSFE Model lerinin Ölçüm Yoluyla Belirlenmeine Yönelik Algoritmalar Şuayb YENER 1 Hakan UNMAN 1 Elektrik ve Elektronik Mühendiliği Bölümü, Sakarya Üniveritei, 545, Eentepe, Sakarya Elektronik ve
BSIM MOSFE Model lerinin Ölçüm Yoluyla Belirlenmeine Yönelik Algoritmalar Şuayb YENER 1 Hakan UNMAN 1 Elektrik ve Elektronik Mühendiliği Bölümü, Sakarya Üniveritei, 545, Eentepe, Sakarya Elektronik ve
Z c 0 ise, problem için en iyilik koşulları (dual. X b 0 oluyorsa, aynı zamanda primal
 KONU 12: DUAL SİMPLEKS YÖNTEM P: min Z cx AX b X (121) biçiminde tanımlı bir dpp de, B herhangi bir temel olsun Bu temel için, simpleks tabloda tüm temel dışı değişkenlere ilişkin tüm Z c ise, problem
KONU 12: DUAL SİMPLEKS YÖNTEM P: min Z cx AX b X (121) biçiminde tanımlı bir dpp de, B herhangi bir temel olsun Bu temel için, simpleks tabloda tüm temel dışı değişkenlere ilişkin tüm Z c ise, problem
ÇĐFT SARKAÇ SĐSTEMĐNĐN KAYAN KĐPLĐ KONTROLÜ
 ÇĐFT SARKAÇ SĐSTEMĐNĐN KAYAN KĐPLĐ KONTROLÜ Yuuf ALTUN Metin DEMĐRTAŞ 2 Elektrik Elektronik Mühendiliği Bölümü Mühendilik Mimarlık Fakültei Balıkeir Üniveritei, 45, Cağış, Balıkeir e-pota: [email protected]
ÇĐFT SARKAÇ SĐSTEMĐNĐN KAYAN KĐPLĐ KONTROLÜ Yuuf ALTUN Metin DEMĐRTAŞ 2 Elektrik Elektronik Mühendiliği Bölümü Mühendilik Mimarlık Fakültei Balıkeir Üniveritei, 45, Cağış, Balıkeir e-pota: [email protected]
DOKUZ EYLÜL ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ DEKANLIĞI DERS/MODÜL/BLOK TANITIM FORMU. Dersin Kodu: IND 3907
 Dersi Veren Birim: Endüstri Mühendisliği Dersin Türkçe Adı: MATEMATİKSEL MODELLEME ve UYGULAMALARI Dersin Orjinal Adı: MATHEMATICAL MODELING AND APPLICATIONS Dersin Düzeyi:(Ön lisans, Lisans, Yüksek Lisans,
Dersi Veren Birim: Endüstri Mühendisliği Dersin Türkçe Adı: MATEMATİKSEL MODELLEME ve UYGULAMALARI Dersin Orjinal Adı: MATHEMATICAL MODELING AND APPLICATIONS Dersin Düzeyi:(Ön lisans, Lisans, Yüksek Lisans,
DENKLEM SİSTEMLERİ. ifadesinde a sayısı bilinmeyenin katsayısı ve b ise sabit sayıdır.
 DENKLEM SİSTEMLERİ 1) BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ DENKLEMLER: a,bϵ R ve olmak üzere; şeklindeki denklemlere birinci dereceden bir bilinmeyenli denklem denir. Bu tür denklemlerde sadece bir bilinmeyen
DENKLEM SİSTEMLERİ 1) BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ DENKLEMLER: a,bϵ R ve olmak üzere; şeklindeki denklemlere birinci dereceden bir bilinmeyenli denklem denir. Bu tür denklemlerde sadece bir bilinmeyen
KARAR TEORİSİ. Özlem AYDIN. Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü
 KARAR TEORİSİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü Karar Ortamları Karar Analizi, alternatiflerin en iyisini seçmek için akılcı bir sürecin kullanılması ile ilgilenir. Seçilen
KARAR TEORİSİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü Karar Ortamları Karar Analizi, alternatiflerin en iyisini seçmek için akılcı bir sürecin kullanılması ile ilgilenir. Seçilen
KONU 3: DOĞRUSAL PROGRAMLAMA PROBLEMLERİ İLE İLGİLİ ÖRNEKLER
 KONU 3: DOĞRUSAL PROGRAMLAMA PROBLEMLERİ İLE İLGİLİ ÖRNEKLER Örnek 1: Bir boya fabrikası hem iç hem dış boya üretiyor. Boya üretiminde A ve B olmak üzere iki tip hammadde kullanılıyor. Bir günde A hammaddesinden
KONU 3: DOĞRUSAL PROGRAMLAMA PROBLEMLERİ İLE İLGİLİ ÖRNEKLER Örnek 1: Bir boya fabrikası hem iç hem dış boya üretiyor. Boya üretiminde A ve B olmak üzere iki tip hammadde kullanılıyor. Bir günde A hammaddesinden
Sistem Mühendisliği. Prof. Dr. Ferit Kemal Sönmez
 Sistem Mühendisliği Prof. Dr. Ferit Kemal Sönmez Organizasyon Teorileri 20. yüzyılın başından itibaren insan ilişkilerinin her alandaki giderek artan önemi, iki dünya savaşı ve 1960 ların sosyal devrimleri,
Sistem Mühendisliği Prof. Dr. Ferit Kemal Sönmez Organizasyon Teorileri 20. yüzyılın başından itibaren insan ilişkilerinin her alandaki giderek artan önemi, iki dünya savaşı ve 1960 ların sosyal devrimleri,
LPG DEPOLAMA TANKLARININ GAZ VERME KAPASİTELERİNİN İNCELENMESİ
 825 LPG DEPOLAMA TAKLARII GAZ VERME KAPASİTELERİİ İCELEMESİ Fehmi AKGÜ 1. ÖZET Sunulan çalışmada, LPG depolama tanklarının gaz verme kapaitelerinin belirlenmei amacına yönelik zamana bağlı ve ürekli rejim
825 LPG DEPOLAMA TAKLARII GAZ VERME KAPASİTELERİİ İCELEMESİ Fehmi AKGÜ 1. ÖZET Sunulan çalışmada, LPG depolama tanklarının gaz verme kapaitelerinin belirlenmei amacına yönelik zamana bağlı ve ürekli rejim
Bekleme Hattı Teorisi
 Bekleme Hattı Teorisi Sürekli Parametreli Markov Zincirleri Tanım 1. * +, durum uzayı * +olan sürekli parametreli bir süreç olsun. Aşağıdaki özellik geçerli olduğunda bu sürece sürekli parametreli Markov
Bekleme Hattı Teorisi Sürekli Parametreli Markov Zincirleri Tanım 1. * +, durum uzayı * +olan sürekli parametreli bir süreç olsun. Aşağıdaki özellik geçerli olduğunda bu sürece sürekli parametreli Markov
a2 b3 cij: birim başına ulaşım maliyeti xij: taşıma miktarı
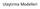 Ulaştırma Modelleri Ulaştırma modeli Ulaştırma modeli doğrusal programlama modellerinin özel bir türüdür. Modelin amacı bir işletmenin belirli kapasitedeki üretim merkezlerinden, belirli talebi olan tüketim
Ulaştırma Modelleri Ulaştırma modeli Ulaştırma modeli doğrusal programlama modellerinin özel bir türüdür. Modelin amacı bir işletmenin belirli kapasitedeki üretim merkezlerinden, belirli talebi olan tüketim
BİR ISIL SİSTEMİN MODELLENMESİ VE SIEMENS SIMATIC S7 200 PLC İLE KONTROLÜ
 BİR ISIL SİSTEMİN MODELLENMESİ VE SIEMENS SIMATIC S7 200 PLC İLE KONTROLÜ Tanel YÜCELEN 1 Özgür KAYMAKÇI 2 Salman KURTULAN 3. 1,2,3 Elektrik Mühendiliği Bölümü Elektrik-Elektronik Fakültei İtanbul Teknik
BİR ISIL SİSTEMİN MODELLENMESİ VE SIEMENS SIMATIC S7 200 PLC İLE KONTROLÜ Tanel YÜCELEN 1 Özgür KAYMAKÇI 2 Salman KURTULAN 3. 1,2,3 Elektrik Mühendiliği Bölümü Elektrik-Elektronik Fakültei İtanbul Teknik
İstatistik ve Olasılık
 İstatistik ve Olasılık KORELASYON ve REGRESYON ANALİZİ Doç. Dr. İrfan KAYMAZ Tanım Bir değişkenin değerinin diğer değişkendeki veya değişkenlerdeki değişimlere bağlı olarak nasıl etkilendiğinin istatistiksel
İstatistik ve Olasılık KORELASYON ve REGRESYON ANALİZİ Doç. Dr. İrfan KAYMAZ Tanım Bir değişkenin değerinin diğer değişkendeki veya değişkenlerdeki değişimlere bağlı olarak nasıl etkilendiğinin istatistiksel
Standart modellerde öncelikle kısıt denklemleri eşitlik haline çevrilmelidir. Öncelikle ilk kısıta bakalım.
 3. Simpleks Yöntem Doğrusal programlama modelleri grafik yöntem dışında simpleks yöntem adı altında özel bir yöntemle çözülebilir. Bu yöntem Simple Matrix kelimlerinin kısaltmasıdır ve bir çeşit matris
3. Simpleks Yöntem Doğrusal programlama modelleri grafik yöntem dışında simpleks yöntem adı altında özel bir yöntemle çözülebilir. Bu yöntem Simple Matrix kelimlerinin kısaltmasıdır ve bir çeşit matris
YÖNEYLEM ARAŞTIRMASI-I
 YÖNEYLEM ARAŞTIRMASI-I İST205U KISA ÖZET DİKKAT Burada ilk 4 sahife gösterilmektedir. Özetin tamamı için sipariş veriniz www.kolayaof.com 1 1.ÜNİTE Yöneylem Araştırmasına Giriş GİRİŞ Yöneylem Araştırması
YÖNEYLEM ARAŞTIRMASI-I İST205U KISA ÖZET DİKKAT Burada ilk 4 sahife gösterilmektedir. Özetin tamamı için sipariş veriniz www.kolayaof.com 1 1.ÜNİTE Yöneylem Araştırmasına Giriş GİRİŞ Yöneylem Araştırması
dir. Periyodik bir sinyalin örneklenmesi sırasında, periyot başına alınmak istenen ölçüm sayısı N
 DENEY 7: ÖRNEKLEME, AYRIK SİNYALLERİN SPEKTRUMLARI VE ÖRTÜŞME OLAYI. Deneyin Amacı Bu deneyde, ürekli inyallerin zaman ve rekan uzaylarında örneklenmei, ayrık inyallerin ektrumlarının elde edilmei ve örtüşme
DENEY 7: ÖRNEKLEME, AYRIK SİNYALLERİN SPEKTRUMLARI VE ÖRTÜŞME OLAYI. Deneyin Amacı Bu deneyde, ürekli inyallerin zaman ve rekan uzaylarında örneklenmei, ayrık inyallerin ektrumlarının elde edilmei ve örtüşme
Tarımda Mühendislik Düşünce Sistemi. Prof. Dr. Ferit Kemal SÖNMEZ
 Tarımda Mühendislik Düşünce Sistemi Prof. Dr. Ferit Kemal SÖNMEZ Sistem Aralarında ilişki veya bağımlılık bulunan elemanlardan oluşan bir yapı veya organik bütündür. Bir sistem alt sistemlerden oluşmuştur.
Tarımda Mühendislik Düşünce Sistemi Prof. Dr. Ferit Kemal SÖNMEZ Sistem Aralarında ilişki veya bağımlılık bulunan elemanlardan oluşan bir yapı veya organik bütündür. Bir sistem alt sistemlerden oluşmuştur.
Kök Yer Eğrileri ile Tasarım
 Kök Yer Eğrileri ile Taarım Prof.Dr. Galip Canever Kök Yer Eğriinden Kazanç ın Belirlenmei Kök yer eğrii K nın pozitif değerleri için denkleminin muhtemel köklerini göteren eğridir. KG ( ) Taarımın amacı
Kök Yer Eğrileri ile Taarım Prof.Dr. Galip Canever Kök Yer Eğriinden Kazanç ın Belirlenmei Kök yer eğrii K nın pozitif değerleri için denkleminin muhtemel köklerini göteren eğridir. KG ( ) Taarımın amacı
Gerçek uygulamalarda, standart normal olmayan sürekli bir rassal. değişken, sıfırdan farklı bir ortalama ve birden farklı standart sapma
 2 13.1 Normal Dağılımın Standartlaştırılması Gerçek uygulamalarda, standart normal olmayan sürekli bir rassal değişken, sıfırdan farklı bir ortalama ve birden farklı standart sapma değerleriyle normal
2 13.1 Normal Dağılımın Standartlaştırılması Gerçek uygulamalarda, standart normal olmayan sürekli bir rassal değişken, sıfırdan farklı bir ortalama ve birden farklı standart sapma değerleriyle normal
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Endüstri Mühendisliği Tezli Yüksek Lisans Dersler Tablosu
 Endüstri Mühendisliği Tezli Yüksek Lisans Dersler Tablosu Zorunlu Dersler Ders Kodu Ders Adı Teorik Uygulama Toplam AKTS IENG540 Optimizasyon Modelleri ve Algoritmalar 3 0 3 8 IENG560 Olasılıksal Analiz
Endüstri Mühendisliği Tezli Yüksek Lisans Dersler Tablosu Zorunlu Dersler Ders Kodu Ders Adı Teorik Uygulama Toplam AKTS IENG540 Optimizasyon Modelleri ve Algoritmalar 3 0 3 8 IENG560 Olasılıksal Analiz
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Bu bölümde eşitsizlik kısıtlarına bağlı bir doğrusal olmayan kısıta sahip problemin belirlenen stasyoner noktaları
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Bu bölümde eşitsizlik kısıtlarına bağlı bir doğrusal olmayan kısıta sahip problemin belirlenen stasyoner noktaları
YÖNEYLEM ARAŞTIRMALARI 1
 YÖNEYLEM ARAŞTIRMALARI 1 1.HAFTA Amacı:Karar vericiler işletmelerde sahip oldukları kaynakları; insan gücü makine ve techizat sermaye kullanarak belirli kararlar almak ister. Örneğin; en iyi üretim miktarı
YÖNEYLEM ARAŞTIRMALARI 1 1.HAFTA Amacı:Karar vericiler işletmelerde sahip oldukları kaynakları; insan gücü makine ve techizat sermaye kullanarak belirli kararlar almak ister. Örneğin; en iyi üretim miktarı
Rüzgar Türbininde Kullanılan AC/DC Çeviricilerde Uzay Vektörü Modülasyonu Yöntemi ile Kontrol
 Rüzgar ürbininde Kullanılan AC/DC Çeviricilerde Uzay ektörü Modülayonu Yöntemi ile Kontrol Cenk Cengiz Eyüp Akpınar Dokuz Eylül Üniveritei Elektrik ve Elektronik Mühenliği Bölümü Kaynaklar Yerleşkei, Buca-İzmir
Rüzgar ürbininde Kullanılan AC/DC Çeviricilerde Uzay ektörü Modülayonu Yöntemi ile Kontrol Cenk Cengiz Eyüp Akpınar Dokuz Eylül Üniveritei Elektrik ve Elektronik Mühenliği Bölümü Kaynaklar Yerleşkei, Buca-İzmir
ÜNYE MESLEK YÜKSEKOKULU İNSAN KAYNAKLARI YÖNETİMİ PROGRAMI
 ÜNYE MELEK YÜKEKOKULU İNAN KAYNAKLARI YÖNETİMİ PROGRAMI DERİN KODU VE ADI Z/ T P B ACT DERİN KODU VE ADI Z/ T P B ACT İKY 101 Genel İşletme Z 4-4 5 İKY 102 Bilgisayara Giriş-II Z 2-2 2 İKY 103 İktisada
ÜNYE MELEK YÜKEKOKULU İNAN KAYNAKLARI YÖNETİMİ PROGRAMI DERİN KODU VE ADI Z/ T P B ACT DERİN KODU VE ADI Z/ T P B ACT İKY 101 Genel İşletme Z 4-4 5 İKY 102 Bilgisayara Giriş-II Z 2-2 2 İKY 103 İktisada
BÖLÜM SEÇMELİ DERS LİSTESİ
 Endüstri Mühendisliği Bölümü eçmeli Ders Uygulama Esasları; 1. Bölüm seçmeli ders (ENDD 411): Bölüm seçmeli ders listesinden seçilmelidir. 2. Fakülte seçmeli ders (MFD 421): Fakülte seçmeli ders listesinden
Endüstri Mühendisliği Bölümü eçmeli Ders Uygulama Esasları; 1. Bölüm seçmeli ders (ENDD 411): Bölüm seçmeli ders listesinden seçilmelidir. 2. Fakülte seçmeli ders (MFD 421): Fakülte seçmeli ders listesinden
KUADRATİK FORM. Tanım: Kuadratik Form. Bir q(x 1,x 2,,x n ) fonksiyonu
 KUADRATİK FORMLAR KUADRATİK FORM Tanım: Kuadratik Form Bir q(x,x,,x n ) fonksiyonu q x : n şeklinde tanımlı ve x i x j bileşenlerinin doğrusal kombinasyonu olan bir fonksiyon ise bir kuadratik formdur.
KUADRATİK FORMLAR KUADRATİK FORM Tanım: Kuadratik Form Bir q(x,x,,x n ) fonksiyonu q x : n şeklinde tanımlı ve x i x j bileşenlerinin doğrusal kombinasyonu olan bir fonksiyon ise bir kuadratik formdur.
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Quadratic Programming Bir karesel programlama modeli aşağıdaki gibi tanımlanır. Amaç fonksiyonu: Maks.(veya Min.) z
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Quadratic Programming Bir karesel programlama modeli aşağıdaki gibi tanımlanır. Amaç fonksiyonu: Maks.(veya Min.) z
Kalıtım. Mendel in Çalışmaları
 Canlı vücudunu oluşturan karakterleri üremeyle neilden neile aktarılmaını inceleyen kalıtım birimine genetik denir. Anne ve babadan gelen eşey hücreleri zigotu oluşturur. Bu hücrelerle birlikte gelen kromozomlar
Canlı vücudunu oluşturan karakterleri üremeyle neilden neile aktarılmaını inceleyen kalıtım birimine genetik denir. Anne ve babadan gelen eşey hücreleri zigotu oluşturur. Bu hücrelerle birlikte gelen kromozomlar
İÇİNDEKİLER ÖNSÖZ Bölüm 1 SAYILAR 11 Bölüm 2 KÜMELER 31 Bölüm 3 FONKSİYONLAR
 İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 11 1.1. Sayı Kümeleri 12 1.1.1.Doğal Sayılar Kümesi 12 1.1.2.Tam Sayılar Kümesi 13 1.1.3.Rasyonel Sayılar Kümesi 14 1.1.4. İrrasyonel Sayılar Kümesi 16 1.1.5. Gerçel
İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 11 1.1. Sayı Kümeleri 12 1.1.1.Doğal Sayılar Kümesi 12 1.1.2.Tam Sayılar Kümesi 13 1.1.3.Rasyonel Sayılar Kümesi 14 1.1.4. İrrasyonel Sayılar Kümesi 16 1.1.5. Gerçel
