STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
|
|
|
- İbrahi̇m Metin
- 7 yıl önce
- İzleme sayısı:
Transkript
1 Statik ers Notları Sınav Soru ve Çözümleri ĞHN MÜHENİSİK MEKNİĞİ STTİK
2 MÜHENİSİK MEKNİĞİ STTİK İÇİNEKİER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMERİ - İki Boutlu Kuvvet Sistemleri - Üç Boutlu Kuvvet Sistemleri 3. ENGE - üzlemde enge - Üç Boutta enge 4. YPIR - üzlem Kafes Sistemler - Çerçeveler ve Makinalar 5. SÜRTÜNME 6. KÜTE MERKEZERİ ve GEOMETRİK MERKEZER
3 STTİK 4 YPIR
4 STTİK 4.1 üzlem Kafes Sistemler
5 Statik Yapılar 4.1. üzlem Kafes Sistemler 1 Kafes sistemler, "alnızca iki kuvvet taşıan elemanlar"ın birbirine bağlanması ile ortaa çıkan apılardır. Bu elemanların, serbestçe dönen ve moment iletmediği farzedilen pimlerle birbirine bağlandığı düşünülür. Eğer elemanların tamamı anı düzlemde er alıorsa o zaman düzlem kafes sistemlerden bahsedilir. Elemanlar, elde edilen apının rijit olabilmesi için, üçgenler oluşturacak şekilde birleştirilirler. Rijit, çökmez. Yük taşıabilir. Rijit değil, çöker. Yük taşıamaz. İki üçgene bölünürse ük taşıabilecek hale gelir. ğır ükleri taşımakta kullanılan apıların kendi ağırlıklarının mümkün olduğu kadar hafif olması istenir. Bu amaçla krenler, köprüler, çatılar vb. apılar kafes sistem tekniği ile tasarlanır. Elemanların bağlantı noktalarından geçen doğru, taşıdığı kuvvetlerin ortak tesir çizgisidir ve bu kuvvetler çekme vea basma önünde olabilirler. Bir eleman herhangi bir erinden haali olarak kesilirse o kesitte elemanın ucundaki kuvveti dengeleecek şekilde bir kuvvet olduğu görülür.
6 Statik Yapılar 4.1. üzlem Kafes Sistemler 2 Kafes sistemlerin taşıdığı ükler, eğer aılı ük ise elemanları bağlaan pimlere ugulanan tekil üklere indirgenirler. Tekil ükler elemanların uç noktalarının dışında arada bir ere ugulanmaz. Kafes sistemlerin kendi ağırlıkları taşıdıkları üke nazaran, çoğunlukla, ihmal edilir. İhmal edilmediği zaman bir elemanın ağırlığı ikie bölünerek uç noktalarındaki pimlere ugulanır. üğüm Yöntemi Kafes sistemlerin tasarımı apılırken elemanların taşıdığı kuvvetler bulunmalıdır. Bu kuvvetleri bulmak amacı ile takip edilen iki temel aklaşım vardır: - üğüm öntemi, - Kesim öntemi. Kafes sistemin parçalarının birbirine birleştirildiği erlere düğüm denir. Bu düğümlerde elemanların birbirine bir pim vasıtası ile bağlandığı farzedilir. üğüm önteminde bu pimlerin dengesi incelenerek bilinmeenler bulunur. B F B C B G E ΣF = 0 ΣF = 0 pimi B G G G enge kategorisi bir noktada kesişen kuvvetler kategorisi olduğundan Bir düğümün dengesinden en fazla 2 bilinmeen bulunabilir.
7 Statik Yapılar 4.1. üzlem Kafes Sistemler 3 Kafes sistemin tamamının dengesinden de ilave denklemler elde edilebilir. Mesnet tepkileri bulunabilir.! Bir üçgeni oluşturan çubuklardaki kuvvetlerin kendi aralarında dengede olduğu sölenemez. F F F B G E C B G E C CE = 0 C E Özel düğümler F 3 = 0 F 3 = 0 F 2 = 0 F 1 F 2 F 1 F 2 F 1 P ΣF = 0 F 1 = F 2 ΣF = 0 F 3 = 0 ΣF = 0 F 1 = F 2 ΣF = 0 F 3 = 0 ΣF = 0 F 1 = P ΣF = 0 F 2 = 0
8 Statik Yapılar 4.1. üzlem Kafes Sistemler 4 F 1 F 2 F 1 F 2 F 3 F 3 P F 1 F 2 F 2 F1 F 2 F1 ΣF = 0 F 1 = F 2 F 3 F 1 = F 2 = F 3 P F 1 = F 2 = P F 4 F 1 = 0 F 1 F 2 ' F 2 = 0 EF = 0 F 3 ' ΣF ' = 0 F 1 = F 2 ΣF = 0 F 3 = F 4 ΣF = 0 ΣF ' = 0 F 1 = 0 F 2 = 0 İki sabit mesnet arasındaki çubuk kuvvet taşımaz. EF = 0
9 Statik Yapılar 4.1. üzlem Kafes Sistemler 5 Kafes sistemler tasarlanırken bazen ukarıdaki gibi iki tane kablo çapraz olarak takılabilir. Bu durumda kablolardan sadece birisi ük taşır. Eğer hangisinin ük taşıdığı kestirilemiorsa o zaman herhangi birisi ük taşıan eleman olarak alınır. iğerinin ük taşımadığı kabul edilir. Yapılan hesaplamanın sonucunda ük taşıdığı düşünülen kabloda çekme kuvveti bulunursa demekki apılan kabul doğrudur. Basma kuvveti bulunursa, bir kablo basma kuvveti taşıamaacağı için apılan kabulün tersi doğrudur. B B B B B B Bir düğümde çekme olan çubuk kuvveti diğer düğümde de çekmedir. B kuvveti düğümünde çekme ise B düğümünde de çekmedir. B B B B B B Bir düğümde basma olan çubuk kuvveti diğer düğümde de basmadır. B kuvveti düğümünde basma ise B düğümünde de basmadır.
10 Statik Yapılar 4.1. üzlem Kafes Sistemler 6 Behcet Örnek Problem ĞHN 4/1 Şekildeki gibi mesnetlenmiş ve üklenmiş olan kafes sistemin her bir çubuğunun taşıdığı kuvveti bulunuz. Bütün üçgenler eşkenardır. Verilenler: 1 = 4 kn Çözüm 2 = 8 kn 3 = 2 kn o C Tekerlekli mesnette ortaa çıkan tepki kuvveti daima daanma üzeine diktir. 2 C düğümü: C C İstenenler: B =? Çubukların bounu 2 birim alalım. E =? BC =? ΣM = 0 B =? BE =? 4 (1) 8 (2) 2 (3) + C sin30 o (4) = 0 C =? C = 13 kn E =? ' 30 o C BC 30 o C = 13 kn C ΣF = 0 C sin30 o C sin = 0 ΣF ' = 0 C BC cos30 o = 0 30 o BC C = BC cos30 o C = BC cos C = 7.51 kn BC = kn
11 Statik Yapılar 4.1. üzlem Kafes Sistemler 7 Behcet Örnek Problem ĞHN 4/1 Şekildeki gibi mesnetlenmiş ve üklenmiş olan kafes sistemin her bir çubuğunun taşıdığı kuvveti bulunuz. Bütün üçgenler eşkenardır. Verilenler: 1 = 4 kn 2 = 8 kn 3 = 2 kn düğümü: B E Çözüm (devamı) Bir çubuğun bir düğümünde çekme olan çubuk kuvveti, diğer düğümünde de çekmedir. C kuvveti C düğümünde çekme olarak bulunduğu için C = 7.51 kn düğümünde de çekmedir. E düğümü: ΣF = 0 2 kn C sin B sin 2 = 0 E E BE E = 6.35 kn B düğümü: 8 kn İstenenler: B = 5.2 kn B =? ΣF = 0 E =? C cos + B cos E = 0 BC =? E = 6.35 kn B =? BE =? C =? E =? ΣF = 0 E + BE cos E cos = 0 ΣF = 0 E = 8.66 kn 4 kn BE sin + E sin 4 = 0 BE = 4.04 kn Yön belirtir. Seçilen önde değil, ters öndedir. B B BC = kn BE = 4.04 kn B = 5.2 kn ΣF = 0 B + BE cos B cos BC = 0 B = kn
12 Statik Yapılar 4.1. üzlem Kafes Sistemler 8 Behcet Örnek Problem ĞHN 4/2 Şekildeki gibi mesnetlenmiş ve üklenmiş olan kafes sistemin B ve BE çubuklarının taşıdığı kuvvetleri bulunuz. Bütün iç açılar a vea 120 o dir. Verilenler: FG G düğümü: 120 o 120 o G EG Çözüm E düğümü: BE E BE E EG = E EG EG = sin120 o sin120 o BE = EG = BE = EG = FG İstenenler: B =? EG BE =? B düğümü: B B BE B B B BE = B = BE = B = Bu kafes sistemin tamamı üçgenlerden medana gelmemiştir. Fakat rijit bir apı ortaa çıkmıştır, ük taşıabilmektedir.
13 Statik Yapılar 4.1. üzlem Kafes Sistemler 9 Behcet Örnek Problem ĞHN 4/3 Şekildeki gibi mesnetlenmiş olan kafes sistemin her bir çubuğunun kütlesi 40 kg olduğuna göre her bir çubuğa gelen ortalama kuvveti hesaplaınız. Verilenler: Çözüm W = mg m = 40 kg = 8 m g = 9.81 m/s 2 İstenenler: B =? E =? BC =? B =? BE =? C =? E =? C Kafes sistem ükleme açısından ve anı zamanda geometrik olarak simetrik olduğu için: E = C B = BC BE = B E düğümü: E = 1133 N W T = C = W T / 2 = 1373 N 1.5W E 30 o 30 o E BE ΣF = 0 W T = 40 (7) (9.81) = 2747 N Kafes sistemin tamamının ağırlığı düğümü: E ve B çubuklarının ağırlıklarının arısını düğümüne etki ettiririz. E cos30 o 1.5 W BE cos30 o = 0 BE = 454 N ΣF = 0 E sin30 o + BE sin30 o E = 0 E = 794 N Çubukların ağırlıklarını, ihmal etmediğimiz zaman, uç noktalarındaki pimlere etki eden iki kuvvete böleriz. Bir çubuğun ağırlığına W dielim. W E B = 1373 N ΣF = 0 W = 392 N W E sin = 0 ΣF = 0 E = 1133 N B E cos = 0 B = 566 N
14 Statik Yapılar 4.1. üzlem Kafes Sistemler 10 Behcet Örnek Problem ĞHN 4/4 Şekildeki gibi mesnetlenmiş ve üklenmiş olan kafes sistem, dış taraftaki çubuklardan ve içerideki iki çapraz kablodan oluşmuştur. C ve B kabloları basma taşıamaan elemanlardır. ükü (a) B düğümüne, (b) C düğümüne ugulandığı zaman elemanlarda ortaa çıkan kuvvetleri bulunuz. Verilenler: Çözüm İki tane kablo çapraz olarak takıldığı zaman kablolardan sadece birisi ük taşır. Eğer hangisinin ük taşıdığı kestirilemiorsa o zaman herhangi birisi ük taşıan eleman olarak alınır. iğerinin ük taşımadığı kabul edilir. C nin çekme taşıdığını ve B nin ük taşımadığını kabul edelim. B = 0 (a) ükü B den ugulanıor: B düğümü: C düğümü: düğümü: C BC = B B İstenenler: BC B =? C =? ΣF = 0 B = 0 =? BC =? ΣF = 0 BC = B =? C =? BC = C C C C C = 4 / 3 C = 5 / 3 C ΣF = 0 = 0 C kuvveti pozitif çıktı. emekki apılan seçim doğrudur. C kablosu ük taşır. B kablosu taşımaz. B = 0
15 Statik Yapılar 4.1. üzlem Kafes Sistemler 11 Behcet Örnek Problem ĞHN 4/4 Şekildeki gibi mesnetlenmiş ve üklenmiş olan kafes sistem, dış taraftaki çubuklardan ve içerideki iki çapraz kablodan oluşmuştur. C ve B kabloları basma taşıamaan elemanlardır. ükü (a) B düğümüne, (b) C düğümüne ugulandığı zaman elemanlarda ortaa çıkan kuvvetleri bulunuz. Verilenler: Çözüm (devamı) İki tane kablo çapraz olarak takıldığı zaman kablolardan sadece birisi ük taşır. Eğer hangisinin ük taşıdığı kestirilemiorsa o zaman herhangi birisi ük taşıan eleman olarak alınır. iğerinin ük taşımadığı kabul edilir. C nin çekme taşıdığını ve B nin ük taşımadığını kabul edelim. B = 0 (b) ükü C den ugulanıor: B düğümü: C düğümü: düğümü: B B İstenenler: BC B =? C =? ΣF = 0 B = 0 =? BC =? ΣF = 0 BC = 0 B =? C =? 3 C 5 4 C C C C = 4 / 3 C = 5 / 3 C C ΣF = 0 = 0 C kuvveti pozitif çıktı. emekki apılan seçim doğrudur. C kablosu ük taşır. B kablosu taşımaz. B = 0
16 Statik Yapılar 4.1. üzlem Kafes Sistemler 12 Kesim Yöntemi Elemanların taşıdığı kuvvetleri bulmak amacı ile aşağıdaki gibi kesim apılarak sadece kafes sistemin bir kısmının dengesi incelenebilir. engesi incelenen kısmın denge kategorisi genel kategori ise üç tane bağımsız denklem vardır. F G B C E F G B GE BE BC ΣF = 0 ΣF = 0 ΣM = 0 Yandaki denklemler erine alternatif denge denklemleri de kullanılabilir. Bilinmeenlerden iki tanesinin tesir çizgisinin kesiştiği bir noktaa göre moment alınarak bir denklemden bir bilinmeen direk olarak bulunabilir. Kesim öntemi ile en fazla 3 bilinmeen bulunabilir. olaısı ile, mecbur kalmadıkça, bir kesimde 3 ten fazla eleman kesmemee dikkat edilir. Eğer bilinmeen saısı 3 ten fazla ise birden fazla kesim apılabilir. F Belirsiz durum ortaa çıkmaması için Kesim çizgisi düğümlerden geçmemelidir.! Mesnet tepkileri kafes sistemin tamamının dengesinden de bulunabilir. Kafes sistemlerin çözümünde sadece düğüm öntemini vea sadece kesim öntemini kullanmak erine iki öntem birlikte de kullanılabilir.
17 Statik Yapılar 4.1. üzlem Kafes Sistemler 13 Behcet Örnek Problem ĞHN 4/5 Şekildeki gibi mesnetlenmiş ve üklenmiş olan kafes sistemin BC, BE ve BF elemanlarındaki kuvvetleri bulunuz. Üçgenler eşkenardır. Verilenler: Çözüm BC BE 1 sin EF 1 B ΣM E = 0 ΣM = 0 BF EF BC (sin ) (1) = 0 BC (sin ) BE sin (1) = 0 ΣF = 0 İstenenler: BC = /sin BC = BE = /sin BF sin = 0 BC =? BE =? BF =? BF = /sin
18 Statik Yapılar 4.1. üzlem Kafes Sistemler 14 Behcet Örnek Problem ĞHN 4/6 Şekildeki gibi mesnetlenmiş ve üklenmiş olan kafes sistemin GM elemanındaki kuvveti bulunuz. Verilenler: Çözüm 12 m 1 3 GH GM 9 m 6 m 8 3 m 5 MN 3 α K S ΣM S = 0 İstenenler: K = 4 Kafes sistemin tamamının dengesinden bulunur. GM sinα (12) + (12) + (9) + (/2) (6) K (6) = 0 GM = 0 GM =? GM çubuğundaki kuvveti, düğüm öntemi ile bulmamız istensedi altı tane pimin dengesini incelememiz gerekecekti. Burada bir tek denge denklemi ile sonuca gidilmiştir.
19 Statik Yapılar 4.1. üzlem Kafes Sistemler 15 Behcet Örnek Problem ĞHN 4/7 Şekildeki gibi mesnetlenmiş ve üklenmiş olan kafes sistemin IJ elemanındaki kuvveti bulunuz. Verilenler: Çözüm 7 Boutlar metre cinsindendir. IJ İstenenler: = 150 kn Kafes sistemin tamamının dengesinden bulunur. ΣM = 0 IJ (7) + 75 (10) + 25 (16) (20) = 0 IJ = kn IJ =? IJ çubuğundaki kuvveti, düğüm öntemi ile bulmamız istensedi beş tane pimin dengesini incelememiz gerekecekti. Burada bir tek denge denklemi ile sonuca gidilmiştir.
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve leri DĞHN MÜHENDİSLİK MEKNİĞİ STTİK MÜHENDİSLİK MEKNİĞİ STTİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki Boyutlu Kuvvet
Statik Ders Notları Sınav Soru ve leri DĞHN MÜHENDİSLİK MEKNİĞİ STTİK MÜHENDİSLİK MEKNİĞİ STTİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki Boyutlu Kuvvet
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve Çöümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki Boutlu
Statik Ders Notları Sınav Soru ve Çöümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki Boutlu
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve Çözümleri DĞHN MÜHENDİSLİK MEKNİĞİ STTİK MÜHENDİSLİK MEKNİĞİ STTİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki outlu Kuvvet
Statik Ders Notları Sınav Soru ve Çözümleri DĞHN MÜHENDİSLİK MEKNİĞİ STTİK MÜHENDİSLİK MEKNİĞİ STTİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki outlu Kuvvet
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve Çözümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları. KUVVET SİSTEMLERİ - İki Boutlu
Statik Ders Notları Sınav Soru ve Çözümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları. KUVVET SİSTEMLERİ - İki Boutlu
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve Çöümleri DĞHN MÜHENDİSLİK MEKNİĞİ STTİK MÜHENDİSLİK MEKNİĞİ STTİK İÇİNDEKİLE 1. GİİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLEİ - İki Boutlu Kuvvet
Statik Ders Notları Sınav Soru ve Çöümleri DĞHN MÜHENDİSLİK MEKNİĞİ STTİK MÜHENDİSLİK MEKNİĞİ STTİK İÇİNDEKİLE 1. GİİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLEİ - İki Boutlu Kuvvet
BÖLÜM 4 YAPISAL ANALİZ (KAFESLER-ÇERÇEVELER-MAKİNALAR)
 BÖLÜM 4 YAPISAL ANALİZ (KAESLER-ÇERÇEVELER-MAKİNALAR) 4.1 Kafesler: Basit Kafes: İnce çubukların uçlarından birleştirilerek luşturulan apıdır. Bileştirme genelde 1. Barak levhalarına pimler ve kanak vasıtası
BÖLÜM 4 YAPISAL ANALİZ (KAESLER-ÇERÇEVELER-MAKİNALAR) 4.1 Kafesler: Basit Kafes: İnce çubukların uçlarından birleştirilerek luşturulan apıdır. Bileştirme genelde 1. Barak levhalarına pimler ve kanak vasıtası
KOÜ. Mühendislik Fakültesi Makine Mühendisliği ( 1. ve 2. Öğretim ) Bölümleri MÜH 110 Statik Dersi - 1. Çalışma Soruları 03 Mart 2017
 KÜ. Mühendislik Fakültesi Makine Mühendisliği ( 1. ve 2. Öğretim ) ölümleri SRU-1) Mühendislik apılarında kullanılan elemanlar için KSN (Tarafsız eksen) kavramını tanımlaınız ve bir kroki şekil çizerek
KÜ. Mühendislik Fakültesi Makine Mühendisliği ( 1. ve 2. Öğretim ) ölümleri SRU-1) Mühendislik apılarında kullanılan elemanlar için KSN (Tarafsız eksen) kavramını tanımlaınız ve bir kroki şekil çizerek
STATİK-MUKAVEMET 1. YIL İÇİ SINAVI m m. 4.5 m
 dı /Soadı : No : İmza: STTİK-MUKVEMET 1. YI İÇİ SINVI 06-11-2013 Örnek Öğrenci No 010030403 abcd DF deki çekme kuvveti 15(a+c)kN olduğuna göre E noktasındaki bağ kuvvetlerini 20 kn 20 kn 20 kn 20 kn h
dı /Soadı : No : İmza: STTİK-MUKVEMET 1. YI İÇİ SINVI 06-11-2013 Örnek Öğrenci No 010030403 abcd DF deki çekme kuvveti 15(a+c)kN olduğuna göre E noktasındaki bağ kuvvetlerini 20 kn 20 kn 20 kn 20 kn h
TEST SORULARI Adı /Soyadı : No : İmza: xaxxbxcde STATİK-MUKAVEMET 1.YILİÇİ SINAVI
 dı /Soadı : No : İmza: STTİK-MUKVEMET 1.YIİÇİ SINVI 21-03-2011 Örnek Öğrenci No 010030403 ---------------------abcde R= 5(a +b) cm Şekildeki taşııcı sistemin bağ kuvvetlerini bulunuz =2(a+e) N =(a) m =2(a
dı /Soadı : No : İmza: STTİK-MUKVEMET 1.YIİÇİ SINVI 21-03-2011 Örnek Öğrenci No 010030403 ---------------------abcde R= 5(a +b) cm Şekildeki taşııcı sistemin bağ kuvvetlerini bulunuz =2(a+e) N =(a) m =2(a
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve Çözümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLE 1. GİİŞ - Skalerler ve ektörler - Newton Kanunları 2. KUET SİSTEMLEİ - İki Boyutlu
Statik Ders Notları Sınav Soru ve Çözümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLE 1. GİİŞ - Skalerler ve ektörler - Newton Kanunları 2. KUET SİSTEMLEİ - İki Boyutlu
İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz Sıfır-Kuvvet Elemanları Kesme Metodu ile Analiz
 Yapıların Analizi Konu Çıktıları İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz Sıfır-Kuvvet Elemanları Kesme Metodu ile Analiz Kafesleri oluşturan elemenlara etki eden
Yapıların Analizi Konu Çıktıları İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz Sıfır-Kuvvet Elemanları Kesme Metodu ile Analiz Kafesleri oluşturan elemenlara etki eden
İ.T.Ü. Makina Fakültesi Mekanik Ana Bilim Dalı Bölüm 4 BÖLÜM IV. Düzlem Kafesler. En çok kullanılan köprü kafesleri. En çok kullanılan çatı kafesleri
 İ.T.Ü. Makina akültesi ÖLÜM IV üzlem Kafesler En çok kullanılan köprü kafesleri En çok kullanılan çatı kafesleri İ.T.Ü. Makina akültesi Mühendislik olalarında genel olarak birden çok katı cisim birbirine
İ.T.Ü. Makina akültesi ÖLÜM IV üzlem Kafesler En çok kullanılan köprü kafesleri En çok kullanılan çatı kafesleri İ.T.Ü. Makina akültesi Mühendislik olalarında genel olarak birden çok katı cisim birbirine
δ / = P L A E = [+35 kn](0.75 m)(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir.
(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir. δ / = P L A E = [+35 kn](0.75 m)(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir.](/thumbs/68/59308868.jpg) A-36 malzemeden çelik çubuk, şekil a gösterildiği iki kademeli olarak üretilmiştir. AB ve BC kesitleri sırasıyla A = 600 mm ve A = 1200 mm dir. A serbest ucunun ve B nin C ye göre yer değiştirmesini belirleyiniz.
A-36 malzemeden çelik çubuk, şekil a gösterildiği iki kademeli olarak üretilmiştir. AB ve BC kesitleri sırasıyla A = 600 mm ve A = 1200 mm dir. A serbest ucunun ve B nin C ye göre yer değiştirmesini belirleyiniz.
KUVVETLER VEKTÖRDÜR BU YÜZDEN CEBİRSEL VEKTÖR TEKNİKLERİ KULLANMALIYIZ
 Rijit Cisim Dengesi KUVVETLER VEKTÖRDÜR BU YÜZDEN CEBİRSEL VEKTÖR TEKNİKLERİ KULLANMALIYIZ KUVVET SİSTEMİ 2 B KUVVET SİSTEMLERİ Detaylar 1- KO-LİNEER 2- BİR NOKTADA BULUŞAN (KONKÜRENT) 3- PARALEL 4- GENEL
Rijit Cisim Dengesi KUVVETLER VEKTÖRDÜR BU YÜZDEN CEBİRSEL VEKTÖR TEKNİKLERİ KULLANMALIYIZ KUVVET SİSTEMİ 2 B KUVVET SİSTEMLERİ Detaylar 1- KO-LİNEER 2- BİR NOKTADA BULUŞAN (KONKÜRENT) 3- PARALEL 4- GENEL
Hedefler. Kafeslerde oluşan kuvvetlerin hesaplanması: düğüm noktaları metodu kesme metodu
 Yapıların Analizi Hedefler Kafeslerde oluşan kuvvetlerin hesaplanması: düğüm noktaları metodu kesme metodu Konu Çıktıları İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz
Yapıların Analizi Hedefler Kafeslerde oluşan kuvvetlerin hesaplanması: düğüm noktaları metodu kesme metodu Konu Çıktıları İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz
Ödev 1. Ödev1: 600N luk kuvveti u ve v eksenlerinde bileşenlerine ayırınız. 600 N
 Ödev 1 Ödev1: 600N luk kuvveti u ve v eksenlerinde bileşenlerine ayırınız. 600 N 1 600 N 600 N 600 N u sin120 600 N sin 30 u 1039N v sin 30 600 N sin 30 v 600N 2 Ödev 2 Ödev2: 2 kuvvetinin şiddetini, yönünü
Ödev 1 Ödev1: 600N luk kuvveti u ve v eksenlerinde bileşenlerine ayırınız. 600 N 1 600 N 600 N 600 N u sin120 600 N sin 30 u 1039N v sin 30 600 N sin 30 v 600N 2 Ödev 2 Ödev2: 2 kuvvetinin şiddetini, yönünü
V. KAFES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir.
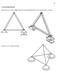 78 V. KES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir. Uzayda ise en az 6 çubuk gereklidir. 79 İhtiyaçlara göre yeni çubukların ilavesiyle
78 V. KES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir. Uzayda ise en az 6 çubuk gereklidir. 79 İhtiyaçlara göre yeni çubukların ilavesiyle
YAPISAL ANALİZ DOÇ.DR. KAMİLE TOSUN FELEKOĞLU
 YAPISAL ANALİZ DOÇ.DR. KAMİLE TOSUN FELEKOĞLU 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla
YAPISAL ANALİZ DOÇ.DR. KAMİLE TOSUN FELEKOĞLU 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla
Karabük Üniversitesi, Mühendislik Fakültesi...www.IbrahimCayiroglu.com. STATİK (4. Hafta)
 KAFES SİSTEMLER STATİK (4. Hafta) Düz eksenden oluşan çubukların birbiriyle birleştirilmesiyle elde edilen sistemlere kafes sistemler denir. Çubukların birleştiği noktalara düğüm noktaları adı verilir.
KAFES SİSTEMLER STATİK (4. Hafta) Düz eksenden oluşan çubukların birbiriyle birleştirilmesiyle elde edilen sistemlere kafes sistemler denir. Çubukların birleştiği noktalara düğüm noktaları adı verilir.
STATİK. Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -8-
 1 STATİK Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -8- Giriş 2 Denge denklemlerini, mafsala bağlı elemanlarda oluşan yapıları analiz etmek için kullanacağız. Bu analiz, dengede olan bir yapının
1 STATİK Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -8- Giriş 2 Denge denklemlerini, mafsala bağlı elemanlarda oluşan yapıları analiz etmek için kullanacağız. Bu analiz, dengede olan bir yapının
VEKTÖRLER KT YRD.DOÇ.DR. KAMİLE TOSUN FELEKOĞLU
 VEKTÖRLER KT YRD.DOÇ.DR. KMİLE TOSUN ELEKOĞLU 1 Mekanik olaları ölçmekte a da değerlendirmekte kullanılan matematiksel büüklükler: Skaler büüklük: sadece bir saısal değeri tanımlamakta kullanılır, pozitif
VEKTÖRLER KT YRD.DOÇ.DR. KMİLE TOSUN ELEKOĞLU 1 Mekanik olaları ölçmekte a da değerlendirmekte kullanılan matematiksel büüklükler: Skaler büüklük: sadece bir saısal değeri tanımlamakta kullanılır, pozitif
STATİK. Ders_6. Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü. Ders notları için: GÜZ
 STATİK Ders_6 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2017-2018 GÜZ BASİT KAFESLER, DÜĞÜM NOKTALARI METODU VE SIFIR KUVVET ELEMANLARI
STATİK Ders_6 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2017-2018 GÜZ BASİT KAFESLER, DÜĞÜM NOKTALARI METODU VE SIFIR KUVVET ELEMANLARI
Kafes Sistemler. Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir.
 Kafes Sistemler Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir. Kafes Sistemler Birçok uygulama alanları vardır. Çatı sistemlerinde, Köprülerde, Kulelerde, Ve benzeri
Kafes Sistemler Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir. Kafes Sistemler Birçok uygulama alanları vardır. Çatı sistemlerinde, Köprülerde, Kulelerde, Ve benzeri
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve Çözümleri DĞHN MÜHENDİSLİK MEKNİĞİ STTİK MÜHENDİSLİK MEKNİĞİ STTİK İÇİNDEKİLE 1. GİİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLEİ - İki Boyutlu Kuvvet
Statik Ders Notları Sınav Soru ve Çözümleri DĞHN MÜHENDİSLİK MEKNİĞİ STTİK MÜHENDİSLİK MEKNİĞİ STTİK İÇİNDEKİLE 1. GİİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLEİ - İki Boyutlu Kuvvet
6.12 Örnekler PROBLEMLER
 6.1 6. 6.3 6.4 6.5 6.6 6.7 Çok Parçalı Taşıyıcı Sistemler Kafes Sistemler Kafes Köprüler Kafes Çatılar Tam, Eksik ve Fazla Bağlı Kafes Sistemler Kafes Sistemler İçin Çözüm Yöntemleri Kafes Sistemlerde
6.1 6. 6.3 6.4 6.5 6.6 6.7 Çok Parçalı Taşıyıcı Sistemler Kafes Sistemler Kafes Köprüler Kafes Çatılar Tam, Eksik ve Fazla Bağlı Kafes Sistemler Kafes Sistemler İçin Çözüm Yöntemleri Kafes Sistemlerde
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ
 İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
ÇATI MAKASINA GELEN YÜKLER
 ÇATI MAKASINA GELEN YÜKLER Bir yapıyı dış etkilere karşı koruyan taşıyıcı sisteme çatı denir. Belirli aralıklarla yerleştirilen çatı makaslarının, yatay taşıyıcı eleman olan aşıklarla birleştirilmesi ile
ÇATI MAKASINA GELEN YÜKLER Bir yapıyı dış etkilere karşı koruyan taşıyıcı sisteme çatı denir. Belirli aralıklarla yerleştirilen çatı makaslarının, yatay taşıyıcı eleman olan aşıklarla birleştirilmesi ile
PROF.DR. MURAT DEMİR AYDIN. ***Bu ders notları bir sonraki slaytta verilen kaynak kitaplardan alıntılar yapılarak hazırlanmıştır.
 PO.D. MUAT DEMİ AYDIN ***Bu ders notları bir sonraki slatta verilen kanak kitaplardan alıntılar apılarak hazırlanmıştır. Mühendisler için Vektör Mekaniği: STATİK.P. Beer, E.. Johnston Çeviri Editörü: Ömer
PO.D. MUAT DEMİ AYDIN ***Bu ders notları bir sonraki slatta verilen kanak kitaplardan alıntılar apılarak hazırlanmıştır. Mühendisler için Vektör Mekaniği: STATİK.P. Beer, E.. Johnston Çeviri Editörü: Ömer
YAPI STATİĞİ II (Hiperstatik Sistemler) Yrd. Doç. Dr. Selçuk KAÇIN
 YAPI STATİĞİ II (Hiperstatik Sistemler) Yrd. Doç. Dr. Selçuk KAÇIN Yapı Sistemleri: İzostatik (Statikçe Belirli) Sistemler : Bir sistemin tüm kesit tesirlerini (iç kuvvetlerini) ve mesnet reaksiyonlarını
YAPI STATİĞİ II (Hiperstatik Sistemler) Yrd. Doç. Dr. Selçuk KAÇIN Yapı Sistemleri: İzostatik (Statikçe Belirli) Sistemler : Bir sistemin tüm kesit tesirlerini (iç kuvvetlerini) ve mesnet reaksiyonlarını
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
KARADENİZ TEKNİK ÜNİVERSİTESİ
 KARADENİZ TEKNİK ÜNİVERSİTESİ Mühendislik Fakültesi Makine Mühendisliği Bölümü MM 1000 STATİK ÖDEV II Son teslim tarihi: 13 Mayıs Cuma 10:00 (I, II. Öğretim Grupları) Soru Çözümü: 13 Mayıs Cuma 14:00,
KARADENİZ TEKNİK ÜNİVERSİTESİ Mühendislik Fakültesi Makine Mühendisliği Bölümü MM 1000 STATİK ÖDEV II Son teslim tarihi: 13 Mayıs Cuma 10:00 (I, II. Öğretim Grupları) Soru Çözümü: 13 Mayıs Cuma 14:00,
KUVVET, MOMENT ve DENGE
 2.1. Kuvvet 2.1.1. Kuvvet ve cisimlere etkileri Kuvvetler vektörel büyüklüklerdir. Kuvvet vektörünün; uygulama noktası, kuvvetin cisme etkidiği nokta; doğrultu ve yönü, kuvvetin doğrultu ve yönü; modülüyse
2.1. Kuvvet 2.1.1. Kuvvet ve cisimlere etkileri Kuvvetler vektörel büyüklüklerdir. Kuvvet vektörünün; uygulama noktası, kuvvetin cisme etkidiği nokta; doğrultu ve yönü, kuvvetin doğrultu ve yönü; modülüyse
MÜHENDİSLİK MEKANİĞİ (STATİK)
 MÜHENDİSLİK MEKANİĞİ (STATİK) Prof. Dr. Metin OLGUN Ankara Üniversitesi Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü HAFTA KONU 1 Giriş, temel kavramlar, statiğin temel ilkeleri 2-3 Düzlem kuvvetler
MÜHENDİSLİK MEKANİĞİ (STATİK) Prof. Dr. Metin OLGUN Ankara Üniversitesi Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü HAFTA KONU 1 Giriş, temel kavramlar, statiğin temel ilkeleri 2-3 Düzlem kuvvetler
Nlαlüminyum 5. αlüminyum
 Soru 1. Bileşik bir çubuk iki rijit mesnet arasına erleştirilmiştir. Çubuğun sol kısmı bakır olup kesit alanı 60 cm, sağ kısmı da alüminum olup kesit alanı 40 cm dir. Sistem 7 C de gerilmesidir. Alüminum
Soru 1. Bileşik bir çubuk iki rijit mesnet arasına erleştirilmiştir. Çubuğun sol kısmı bakır olup kesit alanı 60 cm, sağ kısmı da alüminum olup kesit alanı 40 cm dir. Sistem 7 C de gerilmesidir. Alüminum
VECTOR MECHANICS FOR ENGINEERS: STATICS
 Seventh E 4 Equilibrium CHAPTER VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. of Rigid Bodies Lecture Notes: J. Walt Oler Texas Tech University Seventh E CHAPTER VECTOR
Seventh E 4 Equilibrium CHAPTER VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. of Rigid Bodies Lecture Notes: J. Walt Oler Texas Tech University Seventh E CHAPTER VECTOR
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 7 İç Kuvvetler Kaynak: Mühendislik Mekaniği: Statik, R. C. Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 7. İç Kuvvetler Bu bölümde, bir
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 7 İç Kuvvetler Kaynak: Mühendislik Mekaniği: Statik, R. C. Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 7. İç Kuvvetler Bu bölümde, bir
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
KONU 3. STATİK DENGE
 KONU 3. STATİK DENGE 3.1 Giriş Bir cisme etki eden dış kuvvet ve momentlerin toplamı 0 ise cisim statik dengededir denir. Kuvvet ve moment toplamlarının 0 olması sırasıyla; ötelenme ve dönme denge şartlarıdır.
KONU 3. STATİK DENGE 3.1 Giriş Bir cisme etki eden dış kuvvet ve momentlerin toplamı 0 ise cisim statik dengededir denir. Kuvvet ve moment toplamlarının 0 olması sırasıyla; ötelenme ve dönme denge şartlarıdır.
STATIK MUKAVEMET. Doç. Dr. NURHAYAT DEĞİRMENCİ
 STATIK MUKAVEMET Doç. Dr. NURHAYAT DEĞİRMENCİ STATİK DENGE KOŞULLARI Yapı elemanlarının tasarımında bu elemanlarda oluşan iç kuvvetlerin dağılımının bilinmesi gerekir. Dış ve iç kuvvetlerin belirlenmesinde
STATIK MUKAVEMET Doç. Dr. NURHAYAT DEĞİRMENCİ STATİK DENGE KOŞULLARI Yapı elemanlarının tasarımında bu elemanlarda oluşan iç kuvvetlerin dağılımının bilinmesi gerekir. Dış ve iç kuvvetlerin belirlenmesinde
Gerçekte yükler yayılı olup, tekil yük problemlerin çözümünü kolaylaştıran bir idealleştirmedir.
 STATIK VE MUKAVEMET 4. Ağırlık Merkezi AĞIRLIK MERKEZİ Gerçekte yükler yayılı olup, tekil yük problemlerin çözümünü kolaylaştıran bir idealleştirmedir. Statikte çok küçük bir alana etki eden birbirlerine
STATIK VE MUKAVEMET 4. Ağırlık Merkezi AĞIRLIK MERKEZİ Gerçekte yükler yayılı olup, tekil yük problemlerin çözümünü kolaylaştıran bir idealleştirmedir. Statikte çok küçük bir alana etki eden birbirlerine
Saf Eğilme (Pure Bending)
 Saf Eğilme (Pure Bending) Bu bölümde, doğrusal, prizmatik, homojen bir elemanın eğilme etkisi altındaki deformasonları incelenecek. Burada çıkarılacak formüller, en kesiti an az bir eksene göre simetrik
Saf Eğilme (Pure Bending) Bu bölümde, doğrusal, prizmatik, homojen bir elemanın eğilme etkisi altındaki deformasonları incelenecek. Burada çıkarılacak formüller, en kesiti an az bir eksene göre simetrik
STATİK. Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -3-
 1 STATİK Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -3- Moment KUVVET SİSTEMLERİ 2 Moment, bir kuvvetin bir nokta veya bir eksen etrafında oluşturduğu döndürme etkisinin ölçüsüdür. Momentin büyüklüğü
1 STATİK Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -3- Moment KUVVET SİSTEMLERİ 2 Moment, bir kuvvetin bir nokta veya bir eksen etrafında oluşturduğu döndürme etkisinin ölçüsüdür. Momentin büyüklüğü
MADDESEL NOKTALARIN DİNAMİĞİ
 MÜHENDİSLİK MEKNİĞİ DİNMİK MDDESEL NOKTLRIN DİNMİĞİ DİNMİK MDDESEL NOKTLRIN DİNMİĞİ İÇİNDEKİLER 1. GİRİŞ - Konum, Hız ve İvme - Newton Kanunları 2. MDDESEL NOKTLRIN KİNEMTİĞİ - Doğrusal Hareket - Düzlemde
MÜHENDİSLİK MEKNİĞİ DİNMİK MDDESEL NOKTLRIN DİNMİĞİ DİNMİK MDDESEL NOKTLRIN DİNMİĞİ İÇİNDEKİLER 1. GİRİŞ - Konum, Hız ve İvme - Newton Kanunları 2. MDDESEL NOKTLRIN KİNEMTİĞİ - Doğrusal Hareket - Düzlemde
STATİK KUVVET ANALİZİ (2.HAFTA)
 STATİK KUVVET ANALİZİ (2.HAFTA) Mekanik sistemler üzerindeki kuvvetler denge halindeyse sistem hareket etmeyecektir. Sistemin denge hali için gerekli kuvvetlerin hesaplanması statik hesaplamalarla yapılır.
STATİK KUVVET ANALİZİ (2.HAFTA) Mekanik sistemler üzerindeki kuvvetler denge halindeyse sistem hareket etmeyecektir. Sistemin denge hali için gerekli kuvvetlerin hesaplanması statik hesaplamalarla yapılır.
z z Genel yükleme durumunda, bir Q noktasını üç boyutlu olarak temsil eden kübik gerilme elemanı üzerinde 6 bileşeni
 GERİLME VE ŞEKİL DEĞİŞTİRME DÖNÜŞÜM BAĞINTILARI Q z Genel ükleme durumunda, bir Q noktasını üç boutlu olarak temsil eden kübik gerilme elemanı üzerinde 6 bileşeni gösterilebilir: σ, σ, σ z, τ, τ z, τ z.
GERİLME VE ŞEKİL DEĞİŞTİRME DÖNÜŞÜM BAĞINTILARI Q z Genel ükleme durumunda, bir Q noktasını üç boutlu olarak temsil eden kübik gerilme elemanı üzerinde 6 bileşeni gösterilebilir: σ, σ, σ z, τ, τ z, τ z.
Vektörler. Skaler büyüklükler. Vektörlerin 2 ve 3 boyutta gösterimi. Vektörel büyüklükler. 1. Şekil I de A vektörü gösterilmiştir.
 1 Vektörler Skaler büüklükler 1. de A vektörü gösterilmiştir. Özellikler: Sadece büüklüğü (şiddeti) vardır. Negatif olabilir. Skaler fiziksel büüklüklerin birimi vardır. Örnekler: Zaman Kütle Hacim Özkütle
1 Vektörler Skaler büüklükler 1. de A vektörü gösterilmiştir. Özellikler: Sadece büüklüğü (şiddeti) vardır. Negatif olabilir. Skaler fiziksel büüklüklerin birimi vardır. Örnekler: Zaman Kütle Hacim Özkütle
VECTOR MECHANICS FOR ENGINEERS: STATICS
 Seventh Edition VECTOR ECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi Tel: 85 31 46 / 116 E-mail: acarh@itu.edu.tr Web: http://atlas.cc.itu.edu.tr/~acarh
Seventh Edition VECTOR ECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi Tel: 85 31 46 / 116 E-mail: acarh@itu.edu.tr Web: http://atlas.cc.itu.edu.tr/~acarh
VECTOR MECHANICS FOR ENGINEERS: STATICS
 Seventh Edition VECTOR MECHANICS OR ENGINEERS: STATICS erdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi Tel: 285 31 46 / 116 E-mail: acarh@itu.edu.tr Web: http://atlas.cc.itu.edu.tr/~acarh
Seventh Edition VECTOR MECHANICS OR ENGINEERS: STATICS erdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi Tel: 285 31 46 / 116 E-mail: acarh@itu.edu.tr Web: http://atlas.cc.itu.edu.tr/~acarh
Noktasal Cismin Dengesi
 Noktasal Cismin Dengesi Bu bölümde; Kuvvetleri bieşenlerine ayırma ve kartezyen vektör şeklinde ifade etme yöntemleri noktasal cismin dengesini içeren problemleri çözmede kullanılacaktır. Bölüm 3 DOÇ.DR.
Noktasal Cismin Dengesi Bu bölümde; Kuvvetleri bieşenlerine ayırma ve kartezyen vektör şeklinde ifade etme yöntemleri noktasal cismin dengesini içeren problemleri çözmede kullanılacaktır. Bölüm 3 DOÇ.DR.
STATIK VE MUKAVEMET 4. Ağırlık Merkezi. Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ
 STATIK VE MUKAVEMET 4. Ağırlık Merkezi Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ AĞIRLIK MERKEZİ Gerçekte yükler yayılı olup, tekil yük problemlerin çözümünü kolaylaştıran bir idealleştirmedir. Statikte çok küçük
STATIK VE MUKAVEMET 4. Ağırlık Merkezi Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ AĞIRLIK MERKEZİ Gerçekte yükler yayılı olup, tekil yük problemlerin çözümünü kolaylaştıran bir idealleştirmedir. Statikte çok küçük
TAŞIMA GÜCÜ. n = 17 kn/m3 YASD
 TAŞIMA GÜCÜ PROBLEM 1: Diğer bilgilerin şekilde verildiği durumda, a) Genişliği 1.9 m, uzunluğu 15 m şerit temel; b) Bir kenarı 1.9 m olan kare tekil temel; c) Çapı 1.9 m olan dairesel tekil temel; d)
TAŞIMA GÜCÜ PROBLEM 1: Diğer bilgilerin şekilde verildiği durumda, a) Genişliği 1.9 m, uzunluğu 15 m şerit temel; b) Bir kenarı 1.9 m olan kare tekil temel; c) Çapı 1.9 m olan dairesel tekil temel; d)
MÜHENDİSLER İÇİN VEKTÖR MEKANİĞİ: STATİK. Bölüm 1 Temel Kavramlar ve İlkeler
 MÜHENDİSLER İÇİN VEKTÖR MEKANİĞİ: STATİK Bölüm 1 Temel Kavramlar ve İlkeler Mekanik Mekanik Rijit-Cisim Mekaniği Şekil değiştiren Cismin Mekaniği Statik Dinamik Dengedeki Cisimler Hareketsiz veya durgun
MÜHENDİSLER İÇİN VEKTÖR MEKANİĞİ: STATİK Bölüm 1 Temel Kavramlar ve İlkeler Mekanik Mekanik Rijit-Cisim Mekaniği Şekil değiştiren Cismin Mekaniği Statik Dinamik Dengedeki Cisimler Hareketsiz veya durgun
Elemanlardaki İç Kuvvetler
 Elemanlardaki İç Kuvvetler Bölüm Öğrenme Çıktıları Yapı elemanlarında oluşan iç kuvvetler. Eksenel kuvvet, Kesme kuvvet ve Eğilme Momenti Denklemleri ve Diyagramları. Bölüm Öğrenme Çıktıları Elemanlarda
Elemanlardaki İç Kuvvetler Bölüm Öğrenme Çıktıları Yapı elemanlarında oluşan iç kuvvetler. Eksenel kuvvet, Kesme kuvvet ve Eğilme Momenti Denklemleri ve Diyagramları. Bölüm Öğrenme Çıktıları Elemanlarda
KOCAELİ ÜNİVERSİTESİ Mühendislik Fakültesi Makina Mühendisliği Bölümü Mukavemet I Final Sınavı
 KOCEİ ÜNİVERSİTESİ Mühendislik akültesi Makina Mühendisliği ölümü Mukavemet I inal Sınavı dı Soadı : 9 Ocak 0 Sınıfı : h No : SORU : Şekildeki ucundan ankastre, ucundan serbest olan kirişinin uzunluğu
KOCEİ ÜNİVERSİTESİ Mühendislik akültesi Makina Mühendisliği ölümü Mukavemet I inal Sınavı dı Soadı : 9 Ocak 0 Sınıfı : h No : SORU : Şekildeki ucundan ankastre, ucundan serbest olan kirişinin uzunluğu
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 5 Rijit Cisim Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 5. Rijit Cisim Dengesi Denge,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 5 Rijit Cisim Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 5. Rijit Cisim Dengesi Denge,
TAŞIMA GÜCÜ. γn = 18 kn/m m YASD. G s = 3 c= 10 kn/m 2 φ= 32 o γd = 20 kn/m3. γn = 17 kn/m3. 1 m N k. 0.5 m. 0.5 m. W t YASD. φ= 28 o. G s = 2.
 TAŞIMA GÜCÜ PROBLEM 1:Diğer bilgilerin şekilde verildiği durumda, a) Genişliği 1.9 m, uzunluğu 15 m şerit temel; b) Bir kenarı 1.9 m olan kare tekil temel; c) Çapı 1.9 m olan dairesel tekil temel; d) 1.9
TAŞIMA GÜCÜ PROBLEM 1:Diğer bilgilerin şekilde verildiği durumda, a) Genişliği 1.9 m, uzunluğu 15 m şerit temel; b) Bir kenarı 1.9 m olan kare tekil temel; c) Çapı 1.9 m olan dairesel tekil temel; d) 1.9
Prof. Dr. Ayşe Daloğlu Karadeniz Teknik Üniversitesi İnşaat Mühendisliği Bölümü. INSA 473 Çelik Tasarım Esasları Basınç Çubukları
 Prof. Dr. şe Daloğlu INS 473 Çelik Tasarım Esasları asınç Çubukları asınç Çubukları Çerçeve Çubuklarının urkulma oları kolonunun burkulma bou: ve belirlenir kolon temele bağlısa (ankastre) =1.0 (mafsallı)
Prof. Dr. şe Daloğlu INS 473 Çelik Tasarım Esasları asınç Çubukları asınç Çubukları Çerçeve Çubuklarının urkulma oları kolonunun burkulma bou: ve belirlenir kolon temele bağlısa (ankastre) =1.0 (mafsallı)
Girdi kuvvetleri ile makinaya değişik biçimlerde uygulanan dış kuvvetler kastedilmektedir (input forces). Çıktı kuvvetleri ise elde edilen kuvvetleri
 ÇERÇEVELER Çerçeveler kafesler gibi genellikle sabit duran taşıyıcı sistemlerdir. Bir çerçeveyi kafesten ayıran en belirgin özellik, en az bir elemanının çok kuvvet elemanı (multi force member) oluşudur.
ÇERÇEVELER Çerçeveler kafesler gibi genellikle sabit duran taşıyıcı sistemlerdir. Bir çerçeveyi kafesten ayıran en belirgin özellik, en az bir elemanının çok kuvvet elemanı (multi force member) oluşudur.
Rijit Cisimlerin Dengesi
 Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
YAPI STATİĞİ MESNETLER
 YAPI STATİĞİ MESNETLER Öğr.Gör. Gültekin BÜYÜKŞENGÜR STATİK Kirişler Yük Ve Mesnet Çeşitleri Mesnetler Ve Mesnet Reaksiyonları 1. Kayıcı Mesnetler 2. Sabit Mesnetler 3. Ankastre (Konsol) Mesnetler 4. Üç
YAPI STATİĞİ MESNETLER Öğr.Gör. Gültekin BÜYÜKŞENGÜR STATİK Kirişler Yük Ve Mesnet Çeşitleri Mesnetler Ve Mesnet Reaksiyonları 1. Kayıcı Mesnetler 2. Sabit Mesnetler 3. Ankastre (Konsol) Mesnetler 4. Üç
STATIK VE MUKAVEMET. 6.Düzlem ve Uzay kafes Sistemler. Doç. Dr. NURHAYAT DEĞİRMENCİ
 STATIK VE MUKAVEMET 6.Düzlem ve Uzay kafes Sistemler Doç. Dr. NURHAYAT DEĞİRMENCİ Birbirlerine bağlı birden fazla parçadan yapılmış sistemlerin dengesi için dıs kuvvetlere ilaveten iç kuvvetler de düşünülmelidir.
STATIK VE MUKAVEMET 6.Düzlem ve Uzay kafes Sistemler Doç. Dr. NURHAYAT DEĞİRMENCİ Birbirlerine bağlı birden fazla parçadan yapılmış sistemlerin dengesi için dıs kuvvetlere ilaveten iç kuvvetler de düşünülmelidir.
MATERIALS. Basit Eğilme. Third Edition. Ferdinand P. Beer E. Russell Johnston, Jr. John T. DeWolf. Lecture Notes: J. Walt Oler Texas Tech University
 CHAPTER BÖLÜM MECHANICS MUKAVEMET OF I MATERIALS Ferdinand P. Beer E. Russell Johnston, Jr. John T. DeWolf Basit Eğilme Lecture Notes: J. Walt Oler Teas Tech Universit Düzenleen: Era Arslan 2002 The McGraw-Hill
CHAPTER BÖLÜM MECHANICS MUKAVEMET OF I MATERIALS Ferdinand P. Beer E. Russell Johnston, Jr. John T. DeWolf Basit Eğilme Lecture Notes: J. Walt Oler Teas Tech Universit Düzenleen: Era Arslan 2002 The McGraw-Hill
MÜHENDİSLİK MEKANİĞİ (STATİK)
 MÜHENDİSLİK MEKANİĞİ (STATİK) Prof. Dr. Metin OLGUN Ankara Üniversitesi Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü HAFTA KONU 1 Giriş, temel kavramlar, statiğin temel ilkeleri 2-3 Düzlem kuvvetler
MÜHENDİSLİK MEKANİĞİ (STATİK) Prof. Dr. Metin OLGUN Ankara Üniversitesi Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü HAFTA KONU 1 Giriş, temel kavramlar, statiğin temel ilkeleri 2-3 Düzlem kuvvetler
Rijit Cisimlerin Dengesi
 Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering
 SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering İNM 212 YAPI STATİĞİ I STABİLİTE STATİKÇE BELİRSİZLİK KİNEMATİK BELİRSİZLİK Y.DOÇ.DR. MUSTAFA KUTANİS kutanis@sakarya.edu.tr
SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering İNM 212 YAPI STATİĞİ I STABİLİTE STATİKÇE BELİRSİZLİK KİNEMATİK BELİRSİZLİK Y.DOÇ.DR. MUSTAFA KUTANİS kutanis@sakarya.edu.tr
MÜHENDİSLİK YAPILARI ÇERÇEVELER VE MAKİNALAR
 MÜHENDİSLİK YAPILARI ÇERÇEVELER VE MAKİNALAR ÇERÇEVELER Çerçeveler kafesler gibi genellikle sabit duran taşıyıcı sistemlerdir. Bir çerçeveyi kafesten ayıran en belirgin özellik, en az bir elemanının çok
MÜHENDİSLİK YAPILARI ÇERÇEVELER VE MAKİNALAR ÇERÇEVELER Çerçeveler kafesler gibi genellikle sabit duran taşıyıcı sistemlerdir. Bir çerçeveyi kafesten ayıran en belirgin özellik, en az bir elemanının çok
BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER. Yatay bir düzlem yüzeye gelen hidrostatik kuvvetin büyüklüğünü ve etkime noktasını bulmak istiyoruz.
 BTMIŞ YÜZEYLERE ELEN HİDROSTTİK KUVVETLER DÜZLEM YÜZEYLER Yata Yüeler Sıvı üei Yata bir dülem üee gelen idrostatik kuvvetin büüklüğünü ve etkime noktasını bulmak istioru. d d Kuvvetin Büüklüğü :Şekil deki
BTMIŞ YÜZEYLERE ELEN HİDROSTTİK KUVVETLER DÜZLEM YÜZEYLER Yata Yüeler Sıvı üei Yata bir dülem üee gelen idrostatik kuvvetin büüklüğünü ve etkime noktasını bulmak istioru. d d Kuvvetin Büüklüğü :Şekil deki
MÜHENDİSLER İÇİN VEKTÖR MEKANİĞİ: STATİK. Bölüm 1 Temel Kavramlar ve İlkeler
 MÜHENDİSLER İÇİN VEKTÖR MEKANİĞİ: STATİK Bölüm 1 Temel Kavramlar ve İlkeler Niye Statik? Statik, fizik ve matematik derslerlerinde edindiğiniz bilgilerin üzerine bilgi katmayı amaçlayan bir derstir. Bu
MÜHENDİSLER İÇİN VEKTÖR MEKANİĞİ: STATİK Bölüm 1 Temel Kavramlar ve İlkeler Niye Statik? Statik, fizik ve matematik derslerlerinde edindiğiniz bilgilerin üzerine bilgi katmayı amaçlayan bir derstir. Bu
Mühendislik Mekaniği Dinamik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 17 Rijit Cismin Düzlemsel Kinetiği; Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok.
Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 17 Rijit Cismin Düzlemsel Kinetiği; Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok.
ÇALIŞMA SORULARI. Şekilde gösterildiği gibi yüklenmiş ankastre mesnetli kirişteki mesnet tepkilerini bulunuz.
 ÇALIŞMA SORULARI Üniform yoğunluğa sahip plaka 270 N ağırlığındadır ve A noktasından küresel mafsal ile duvara bağlanmıştır. Ayrıca duvara C ve D noktasından bağlanmış halatlarla desteklenmektedir. Serbest
ÇALIŞMA SORULARI Üniform yoğunluğa sahip plaka 270 N ağırlığındadır ve A noktasından küresel mafsal ile duvara bağlanmıştır. Ayrıca duvara C ve D noktasından bağlanmış halatlarla desteklenmektedir. Serbest
TEKNOLOJİNİN BİLİMSEL İLKELERİ. Öğr. Gör. Adem ÇALIŞKAN
 TEKNOLOJİNİN BİLİMSEL İLKELERİ 5 Ağırlık merkezi STATİK Bir cisim moleküllerden meydana gelir. Bu moleküllerin her birine yer çekimi kuvveti etki eder. Bu yer çekimi kuvvetlerinin cismi meydana getiren
TEKNOLOJİNİN BİLİMSEL İLKELERİ 5 Ağırlık merkezi STATİK Bir cisim moleküllerden meydana gelir. Bu moleküllerin her birine yer çekimi kuvveti etki eder. Bu yer çekimi kuvvetlerinin cismi meydana getiren
Varsayımlar ve Tanımlar Tekil Yükleri Aktaran Kablolar Örnekler Yayılı Yük Aktaran Kablolar. 7.3 Yatayda Yayılı Yük Aktaran Kablolar
 7.1 7.2 Varsayımlar ve Tanımlar Tekil Yükleri Aktaran Kablolar Örnekler Yayılı Yük Aktaran Kablolar 7.3 Yatayda Yayılı Yük Aktaran Kablolar 7.4 Örnekler Kendi Ağırlığını Taşıyan Kablolar (Zincir Eğrisi)
7.1 7.2 Varsayımlar ve Tanımlar Tekil Yükleri Aktaran Kablolar Örnekler Yayılı Yük Aktaran Kablolar 7.3 Yatayda Yayılı Yük Aktaran Kablolar 7.4 Örnekler Kendi Ağırlığını Taşıyan Kablolar (Zincir Eğrisi)
2. Basınç ve Akışkanların Statiği
 2. Basınç ve Akışkanların Statiği 1 Basınç, bir akışkan tarafından birim alana uygulanan normal kuvvet olarak tanımlanır. Basıncın birimi pascal (Pa) adı verilen metrekare başına newton (N/m 2 ) birimine
2. Basınç ve Akışkanların Statiği 1 Basınç, bir akışkan tarafından birim alana uygulanan normal kuvvet olarak tanımlanır. Basıncın birimi pascal (Pa) adı verilen metrekare başına newton (N/m 2 ) birimine
İNŞ 1012 STATİK. Ders notları
 İNŞ 1012 STATİK Ders notları Doç.Dr. Burak Felekoğlu İnşaat Müh. Bölümü, Yapı Malzemesi Laboratuvarı 2.kat Tel: 0 232301 7041 Ders Saatleri - ÖÖ: Çarşamba 8:30-9:15 9:30-11:15 İÖ: Perşembe: 18:50-19:35
İNŞ 1012 STATİK Ders notları Doç.Dr. Burak Felekoğlu İnşaat Müh. Bölümü, Yapı Malzemesi Laboratuvarı 2.kat Tel: 0 232301 7041 Ders Saatleri - ÖÖ: Çarşamba 8:30-9:15 9:30-11:15 İÖ: Perşembe: 18:50-19:35
Doç.Dr. Cesim ATAŞ MEKANİK ŞEKİL DEĞİŞTİREN CİSİMLER MEKANİĞİ DİNAMİK
 STATİK (Ders Notları) Kaynak: Engineering Mechanics: Statics, SI Version, 6th Edition, J. L. Meriam, L. G. Kraige, Wiley Yardımcı Kaynak: Mühendislik Mekaniği: Statik, R.C Hibbeler & S.C. Fan, Literatür
STATİK (Ders Notları) Kaynak: Engineering Mechanics: Statics, SI Version, 6th Edition, J. L. Meriam, L. G. Kraige, Wiley Yardımcı Kaynak: Mühendislik Mekaniği: Statik, R.C Hibbeler & S.C. Fan, Literatür
Kafes Sistemler. Doğru eksenli çubukların birbirlerine mafsallı olarak birleşmesinden meydana gelen taşıyıcı sistemlere Kafes Sistemler denir.
 KAFES SİSTEMLER Doğru eksenli çubukların birbirlerine mafsallı olarak birleşmesinden meydana gelen taşıyıcı sistemlere Kafes Sistemler denir. Özellikle büyük açıklıklı dolu gövdeli sistemler öz ağırlıklarının
KAFES SİSTEMLER Doğru eksenli çubukların birbirlerine mafsallı olarak birleşmesinden meydana gelen taşıyıcı sistemlere Kafes Sistemler denir. Özellikle büyük açıklıklı dolu gövdeli sistemler öz ağırlıklarının
Aşağıdaki Web sitesinden dersle ilgili bilgi alınabilir. Ders, uygulama ve ödevlerle ilgili bilgiler yeri geldiğinde yayınlanacaktır.
 MK 04: MUKVEMET Öğr.Gör.Dr. hmet Taşkesen MUKVEMET GİRİŞ DERS STLERİ Öğr.Gör.Dr. hmet Taşkesen, Makina Bölümü, Tel: 1680/1844, e-posta: taskesen@gazi.edu.tr Teorik Ders (3 saat) + Ödevler + Quizler Uygulama
MK 04: MUKVEMET Öğr.Gör.Dr. hmet Taşkesen MUKVEMET GİRİŞ DERS STLERİ Öğr.Gör.Dr. hmet Taşkesen, Makina Bölümü, Tel: 1680/1844, e-posta: taskesen@gazi.edu.tr Teorik Ders (3 saat) + Ödevler + Quizler Uygulama
MECHANICS OF MATERIALS
 00 The McGraw-Hill Companies, Inc. All rights reserved. T E CHAPTER 7 Gerilme MECHANICS OF MATERIALS Ferdinand P. Beer E. Russell Johnston, Jr. John T. DeWolf Dönüşümleri Fatih Alibeoğlu 00 The McGraw-Hill
00 The McGraw-Hill Companies, Inc. All rights reserved. T E CHAPTER 7 Gerilme MECHANICS OF MATERIALS Ferdinand P. Beer E. Russell Johnston, Jr. John T. DeWolf Dönüşümleri Fatih Alibeoğlu 00 The McGraw-Hill
BURKULMA DENEYİ DENEY FÖYÜ
 T.C. ONDOKUZ MYIS ÜNİVERSİTESİ MÜHENDİSLİK FKÜLTESİ MKİN MÜHENDİSLİĞİ BÖLÜMÜ BURKULM DENEYİ DENEY FÖYÜ HZIRLYNLR Prof.Dr. Erdem KOÇ Yrd.Doç.Dr. İbrahim KELEŞ EKİM 1 SMSUN BURKULM DENEYİ 1. DENEYİN MCI
T.C. ONDOKUZ MYIS ÜNİVERSİTESİ MÜHENDİSLİK FKÜLTESİ MKİN MÜHENDİSLİĞİ BÖLÜMÜ BURKULM DENEYİ DENEY FÖYÜ HZIRLYNLR Prof.Dr. Erdem KOÇ Yrd.Doç.Dr. İbrahim KELEŞ EKİM 1 SMSUN BURKULM DENEYİ 1. DENEYİN MCI
11. SINIF KONU ANLATIMLI. 1. ÜNİTE: KUVVET VE HAREKET 8. Konu TORK VE DENGE ETKİNLİK VE TEST ÇÖZÜMLERİ
 11. SINI NU ANAIMI 1. ÜNİE: UVVE VE HAREE 8. onu R VE DENGE EİNİ VE ES ÇÖZÜMERİ 8 ork ve Denge 1. Ünite 8. onu (ork ve Denge) A nın Çözümleri 1. Çubuk dengede olduğuna göre noktasına göre toplam tork sıfırdır.
11. SINI NU ANAIMI 1. ÜNİE: UVVE VE HAREE 8. onu R VE DENGE EİNİ VE ES ÇÖZÜMERİ 8 ork ve Denge 1. Ünite 8. onu (ork ve Denge) A nın Çözümleri 1. Çubuk dengede olduğuna göre noktasına göre toplam tork sıfırdır.
STATIK VE MUKAVEMET 3. Rijit cisimlerin dengesi, Denge denklemleri, Serbest cisim diyagramı. Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ
 STATIK VE MUKAVEMET 3. Rijit cisimlerin dengesi, Denge denklemleri, Serbest cisim diyagramı Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları
STATIK VE MUKAVEMET 3. Rijit cisimlerin dengesi, Denge denklemleri, Serbest cisim diyagramı Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları
DÜZLEM KAFES SİSTEMLER. Copyright 2010 Pearson Education South Asia Pte Ltd
 Copyright 2010 Pearson Education South Asia Pte Ltd Aynı düzlem içinde birbirlerine uç noktalarından bağlanarak bir rijid yapı oluşturan çubuklar topluluğuna düzlem kafes sistemi denir. Bir kafes sistemi,
Copyright 2010 Pearson Education South Asia Pte Ltd Aynı düzlem içinde birbirlerine uç noktalarından bağlanarak bir rijid yapı oluşturan çubuklar topluluğuna düzlem kafes sistemi denir. Bir kafes sistemi,
MEKANİZMA TEKNİĞİ (3. HAFTA)
 MEKANİZMA TEKNİĞİ (3. HAFTA) STATİĞİN TEMEL İLKELERİ VE VEKTÖR MATEMATİĞİ Mekanik sistemler üzerindeki kuvvetler denge halindeyse sistem hareket etmeyecektir. Sistemin denge hali için gerekli kuvvetlerin
MEKANİZMA TEKNİĞİ (3. HAFTA) STATİĞİN TEMEL İLKELERİ VE VEKTÖR MATEMATİĞİ Mekanik sistemler üzerindeki kuvvetler denge halindeyse sistem hareket etmeyecektir. Sistemin denge hali için gerekli kuvvetlerin
2. KUVVET SİSTEMLERİ 2.1 Giriş
 2. KUVVET SİSTEMLERİ 2.1 Giriş Kuvvet: Şiddet (P), doğrultu (θ) ve uygulama noktası (A) ile karakterize edilen ve bir cismin diğerine uyguladığı itme veya çekme olarak tanımlanabilir. Bu parametrelerden
2. KUVVET SİSTEMLERİ 2.1 Giriş Kuvvet: Şiddet (P), doğrultu (θ) ve uygulama noktası (A) ile karakterize edilen ve bir cismin diğerine uyguladığı itme veya çekme olarak tanımlanabilir. Bu parametrelerden
Hiperstatik sistemlerin çözümünde, yer değiştirmelerin küçük olduğu ve gerilme - şekil değiştirme bağıntılarının lineer olduğu kabul edilmektedir.
 1. HİPERSTATİK SİSTEMLER 1.1. Giriş Bir sistemin hesabının amacı, dış etkilerden meydana gelen kesit tesirlerini, şekil değiştirmelerini ve yer değiştirmelerini belirlemektir. İzostatik sistemlerde, yalnız
1. HİPERSTATİK SİSTEMLER 1.1. Giriş Bir sistemin hesabının amacı, dış etkilerden meydana gelen kesit tesirlerini, şekil değiştirmelerini ve yer değiştirmelerini belirlemektir. İzostatik sistemlerde, yalnız
MKM 308 Makina Dinamiği. Eşdeğer Noktasal Kütleler Teorisi
 MKM 308 Eşdeğer Noktasal Kütleler Teorisi Eşdeğer Noktasal Kütleler Teorisi Maddesel Nokta (Noktasal Kütleler) : Mekanikte her cisim zihnen maddesel noktalara ayrılabilir yani noktasal kütlelerden meydana
MKM 308 Eşdeğer Noktasal Kütleler Teorisi Eşdeğer Noktasal Kütleler Teorisi Maddesel Nokta (Noktasal Kütleler) : Mekanikte her cisim zihnen maddesel noktalara ayrılabilir yani noktasal kütlelerden meydana
STATİK DOÇ.DR. KAMİLE TOSUN FELEKOĞLU. Ders notları için: GÜZ JEOLOJİ MÜH.
 STATİK STATİK DOÇ.DR. KAMİLE TOSUN FELEKOĞLU Ders notları için: http://kisi.deu.edu.tr/kamile.tosun/ 2014-2015 GÜZ JEOLOJİ MÜH. ÖÖ/İÖ 54-58 2 Değerlendirme 1. Ara sınav (%25) 2. Ara sınav (%25) Final (%50)
STATİK STATİK DOÇ.DR. KAMİLE TOSUN FELEKOĞLU Ders notları için: http://kisi.deu.edu.tr/kamile.tosun/ 2014-2015 GÜZ JEOLOJİ MÜH. ÖÖ/İÖ 54-58 2 Değerlendirme 1. Ara sınav (%25) 2. Ara sınav (%25) Final (%50)
YARIYIL İÇİ ÇALIŞMALARI SIRA KATKI YÜZDESİ Ara Sınav 1 60 Kısa Sınav 2 30 Ödev 1 10 Toplam 100 Finalin Başarıya Oranı 50 Yıliçinin Başarıya Oranı 50
 YARIYIL İÇİ ÇALIŞMALARI SIRA KATKI YÜZDESİ Ara Sınav 1 60 Kısa Sınav 2 30 Ödev 1 10 Toplam 100 Finalin Başarıya Oranı 50 Yıliçinin Başarıya Oranı 50 Toplam 100 1 Mukavemet ve Statiğin Önemi 2 Statiğin
YARIYIL İÇİ ÇALIŞMALARI SIRA KATKI YÜZDESİ Ara Sınav 1 60 Kısa Sınav 2 30 Ödev 1 10 Toplam 100 Finalin Başarıya Oranı 50 Yıliçinin Başarıya Oranı 50 Toplam 100 1 Mukavemet ve Statiğin Önemi 2 Statiğin
Gerilme Dönüşümü. Bölüm Hedefleri
 Gerilme Dönüşümü Bölüm Hedefleri Bu bölümde, belirli bir koordinat sisteminde tanımlı gerilme bileşenlerinin, farklı eğimlere sahip koordinat sistemlerine nasıl dönüştürüleceği üzerinde durulacaktır. Gerekli
Gerilme Dönüşümü Bölüm Hedefleri Bu bölümde, belirli bir koordinat sisteminde tanımlı gerilme bileşenlerinin, farklı eğimlere sahip koordinat sistemlerine nasıl dönüştürüleceği üzerinde durulacaktır. Gerekli
Kesit Tesirleri Tekil Kuvvetler
 Statik ve Mukavemet Kesit Tesirleri Tekil Kuvvetler B ÖĞR.GÖR.GÜLTEKİN BÜYÜKŞENGÜR Çevre Mühendisliği Mukavemet Şekil Değiştirebilen Cisimler Mekaniği Kesit Tesiri ve İşaret Kabulleri Kesit Tesiri Diyagramları
Statik ve Mukavemet Kesit Tesirleri Tekil Kuvvetler B ÖĞR.GÖR.GÜLTEKİN BÜYÜKŞENGÜR Çevre Mühendisliği Mukavemet Şekil Değiştirebilen Cisimler Mekaniği Kesit Tesiri ve İşaret Kabulleri Kesit Tesiri Diyagramları
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 5 Rijit Cisim Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 5. Rijit Cisim Dengesi Denge,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 5 Rijit Cisim Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 5. Rijit Cisim Dengesi Denge,
MOMENT VARIGNON
 STATİK- MUKAVEMET - Dülem ve Ua Kuvvetler KUVVET.1 Kuvvet vektörü ve kuvvein Tanımı. Vektörün Şieti ve Vektörlerin Toplamı.3 Üç Boutlu Uaa Kuvvet Bileşenleri.4 Üç boutlu uaa kuvvetlerin toplamı ve enge
STATİK- MUKAVEMET - Dülem ve Ua Kuvvetler KUVVET.1 Kuvvet vektörü ve kuvvein Tanımı. Vektörün Şieti ve Vektörlerin Toplamı.3 Üç Boutlu Uaa Kuvvet Bileşenleri.4 Üç boutlu uaa kuvvetlerin toplamı ve enge
Mekanik, Statik Denge
 Mekanik, Statik Denge Mardin Artuklu Üniversitesi 2. Hafta-01.03.2012 İdris Bedirhanoğlu url : www.dicle.edu.tr/a/idrisb e-mail : idrisbed@gmail.com 0532 657 14 31 Statik **Statik; uzayda kuvvetler etkisi
Mekanik, Statik Denge Mardin Artuklu Üniversitesi 2. Hafta-01.03.2012 İdris Bedirhanoğlu url : www.dicle.edu.tr/a/idrisb e-mail : idrisbed@gmail.com 0532 657 14 31 Statik **Statik; uzayda kuvvetler etkisi
7. STABİLİTE HESAPLARI
 7. STABİLİTE HESAPLARI Çatı sistemlerinde; Kafes kirişlerin (makasların) montaj aşamasında ve kafes düzlemine dik rüzgar ve deprem etkileri altında, mesnetlerini birleştiren eksen etrafında dönerek devrilmelerini
7. STABİLİTE HESAPLARI Çatı sistemlerinde; Kafes kirişlerin (makasların) montaj aşamasında ve kafes düzlemine dik rüzgar ve deprem etkileri altında, mesnetlerini birleştiren eksen etrafında dönerek devrilmelerini
Basit Kafes Sistemler
 YAPISAL ANALİZ 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla kullanılan ahşap gergi elemanları
YAPISAL ANALİZ 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla kullanılan ahşap gergi elemanları
1. STATİĞE GİRİŞ 1.1 TANIMLAR MEKANİK RİJİT CİSİMLER MEKANİĞİ ŞEKİL DEĞİŞTİREN CİSİMLER AKIŞKANLAR MEKANİĞİ DİNAMİK STATİK
 STATİK Ders Notları Kaynaklar: 1.Engineering Mechanics: Statics, 9e, Hibbeler, Prentice Hall 2.Engineering Mechanics: Statics, SI Version, 6th Edition, J. L. Meriam, L. G. Kraige 1. STATİĞE GİRİŞ 1.1 TANIMLAR
STATİK Ders Notları Kaynaklar: 1.Engineering Mechanics: Statics, 9e, Hibbeler, Prentice Hall 2.Engineering Mechanics: Statics, SI Version, 6th Edition, J. L. Meriam, L. G. Kraige 1. STATİĞE GİRİŞ 1.1 TANIMLAR
TEMEL MEKANİK 14. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 TEMEL MEKANİK 14 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
TEMEL MEKANİK 14 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
ÖZEL EGE LİSESİ OKULLAR ARASI 14.MATEMATİK YARIŞMASI 8. SINIFLAR FİNAL SORULARI
 8 SINIFLAR FİNAL SORULARI 1 3+ 1 denkleminin çözüm kümesini bulunuz ( R ) Aritmetik bir dizinin ilk 0 teriminin toplamı 400 ve dördüncü terimi olduğuna göre, birinci terimini bulunuz 3 4 öğrencinin katıldığı
8 SINIFLAR FİNAL SORULARI 1 3+ 1 denkleminin çözüm kümesini bulunuz ( R ) Aritmetik bir dizinin ilk 0 teriminin toplamı 400 ve dördüncü terimi olduğuna göre, birinci terimini bulunuz 3 4 öğrencinin katıldığı
TEKNOLOJİNİN BİLİMSEL İLKELERİ
 TEKNOLOJİNİN BİLİMSEL İLKELERİ Öğr. Gör. Fatih KURTULUŞ 4.BÖLÜM: STATİK MOMENT - MOMENT (TORK) Moment (Tork): Kuvvetin döndürücü etkisidir. F 3 M ile gösterilir. Vektörel büyüklüktür. F 4 F 3. O. O F 4
TEKNOLOJİNİN BİLİMSEL İLKELERİ Öğr. Gör. Fatih KURTULUŞ 4.BÖLÜM: STATİK MOMENT - MOMENT (TORK) Moment (Tork): Kuvvetin döndürücü etkisidir. F 3 M ile gösterilir. Vektörel büyüklüktür. F 4 F 3. O. O F 4
DEFORMASYON VE STRAİN ANALİZİ
 DEFORMASYON VE STRAİN ANALİZİ Tek Eksenli Gerilme Koşullarında Deformason ve Strain Cisimler gerilmelerin etkisi altında kaldıkları aman şekillerinde bir değişiklik medana gelir. Bu değişiklik gerilmenin
DEFORMASYON VE STRAİN ANALİZİ Tek Eksenli Gerilme Koşullarında Deformason ve Strain Cisimler gerilmelerin etkisi altında kaldıkları aman şekillerinde bir değişiklik medana gelir. Bu değişiklik gerilmenin
