Doç. Dr. Mustafa KÖKSAL
|
|
|
- Mehmed Karadere
- 7 yıl önce
- İzleme sayısı:
Transkript
1 TA EV) SAYILI DOĞRUSAL PROGRAMLAMA MODELİ ÇÖZÜM YÖNTEMLERİ VE BİR DEĞERLEME Doç. Dr. Mustafa KÖKSAL 1.1 GİRlIŞ Matematik programlama denilince akla hemen Doğrusal Programlama ve simpleks çözüm tekniği gelmektedir. Gerçekten, Doğrusal Programlama modeli ve çözüm tekniği simpleks, biraz sonra değineceğimiz Tamsayılı Programlama problemlerinin çözüm algoritmaları içinde de kullanılmakta, böylece optimizasyon çalışmalarının temel taşını oluşturmaktadır. Bir Doğrusal Programlara (DP) modelinin genel formülasyonu şu şekilde ifade edilir: Amaç Fonksiyonu n Optimize Z = 2 CjXj Kısıtlayıcı Koşullar S a,jxj (<, =)bi, i = 1,2,,m.için xj> 0 j = 1,2,,n için Buna göre bir DP modelinin varsayımları şöyle özetlenebilir: a) Oeterministik bir modeldir. Modeldeki herbir katsayı sabit.ve kesinlikle biliniyor olmalıdır.
2 b} Amaç fonksiyonu ve her kısıtlayıcı denklem üneer olmalıdır. c) Karar değişkenleri bölünebilir olmalıdır (1) Simpleks Çözüm Yöntemi Bir DP probleminin simpleks yöntemi ile çözümlenebilmesi için standart forma getirilmesi gerekir: Tüm kısıtların (^) olması halinde standart form; optimize Z =* 2 CJXJ kısıtlayıcı koşullar 2 âijxj + S, = b { I = 1,,m ve Xj > 0, İ = 1,,n Si > 0, i - 1,.,m fi. kısıtın gevşek değişkeni) olarak ifade edilir. Bu şartlar altında başlangıç simpleks tablosu düzenlenerek simpleks algoritması problemi aşağıdaki gibi çözer (2): Simpleks Yöntemin Adımları: 1. Problemi bir gaye fonksiyonu ve bir dizi kısıplayıcı koşül denklemleri Üe formüle et. (Standart Forma getir), (1) Dantzing, Georgo B.: «Linear Programming and Extonsİons», Prlnceton Unfverslty Press, 1963, s. 6. (2) Thierauf, R. J. - Grosse, R. A.: «Decislon Making Through Operaiions Research» John Wi ey and Sons, Inc., New York, 1970, s. 250.
3 2. Başlangıç tablosunu gevşek değişkenlerle düzenle ve Z J( Cj - Zj satırlarını hesapla, 3. Çözüme hangi değişkenin gireceğini belirle (en büyük Cj - Zj değeri), 4. 'Hangi değişkeni (çözümden) temelden çkkaracağına karar ver (Miktar (sabitler) kolonunun optimum veya anahtar sütunundaki karşılığı katsayı değerlerine bölünmesinden ortaya çıkan oranların en küçüğü), 5. Giren değişken için yeni satır değerlerini hesapla ve bu değerleri yeni tabloya yerleştir. 6. Diğer satır değerlerini de hesapla ve yeni tabloya koy. Yeni Zj ve Cj - Zj satırlarını hesapla. Şayet Cj - Zj satırında pozitif değer kalmadı ise çözüm optimumdur. Pozitif değer varsa (Cj - Zj de) 3, 4, 5 ve 6. adımları tekrarla. Minimizasyon Problemlerinde Cj - Zj satırlarında en büyük negatif değerli değişken i!k defa çözüme sokulur. Karar Değişkenleri Gevşek Değişkenler C fi Temel Değişkenler 0 s E û S: c, c, C,. c n u x, x, «n x n s, s } s m a.. am ajı a» a am a 5 n 0 u 1 ÇÖ2ÜIB seti b tu w c ; ıcr> c; b û) X. <"ı t:,. <u 2.1. TAMSA YILI DOĞRUSAL PROGRAMLARI MODBLİ (TDP) Tamsayılı Doğrusal Programlara matematiksel programlama tekniklerinden birisidir. Gerçekte Doğrusal Programlamanın
4 özel bir durumudur. Tüm değişkenlerin tamsayı olması durumunda 'salt' (pure) tamsayıfı programlama, sadece seçilen bazı değişkenlerin tamsayı olması durumunda 'karma' (mixed) tamsayılı programlama söz konusudur. Model formüle edilirse; Amaç Fonksiyonu: optimize Z = 2 CjXj J=1 kısıtlayıcı koşullar S a ;j Xj b İ5 i 1, 2,...m için Xj> 0 j = 1, 2,,n için Xj tamsayılı j = 1,2,,p (<n) şeklindedir. Notasyoniaria ifade edecek olursak dördüncü koşulda p = n olması halinde salt, aksi durumda karma tamsayılı programlama modeli karşımıza çıkar. Ayrıca amaç fonksiyonu uygulamaya bağlı olarak maksimum veya minimum olabileceği gibi, kısıtlayıcı koşullarda (>) eşitsizlikleri veya (=) eşitliklerini içerebilir. ' Tamsayı değişkenlerin sadece sıfır veya bir olması durumunda TOP nin özel bir hali olan sıftr-bir (0-1) programlama problemi ortaya çıkar (3). Ulaştırma (Transport) modeli arz (sj) ve talep (dj) değerlerinin tamsayı olması koşulu ile bir salt TOP problemi olarak nitelenebileceği gibi, atama (yükleme) modeli de Ö - 1 programfarna problemine bir örnek teşkil eder. (3) Budnick, F. S. - Mojena, R. - Volîmann, T. E.: «Princlpfeş of Operatİohs Research for Management» Richard D. lrwin Inc., Homewood Illinois, 1977, s. 275.
5 Bilindiği gibi lineer programlama modelinde değişkenlerin bölünebilir olma varsayımı yapılmaktadır. Simpleks yaklaşımın sonunda elde edilen karar değişkenleri de uygulamanın niteliklerine göre; örneğin, mamul karışımı probleminde kesirli miktarlar, yatırım bütçeiemesinde bir projenin bir bölümü veya işlere tahsis edilen işçilerin kesirli birimler olması gibi sonuçlar verecektir. Kesirli sonuçların yuvarlatılarak tamsayıya çevrilmesi ise çözümün mümkün olmayan veya 'optimal olmayan' bir niteliğe bürünmesine yol açabilir. Bazı durumlarda sayıların yuvarlatılması işlemi devamlı surette 'mümkün olmayan' sonuçlar verir (4).. ' TOP problemlerinin DP problemlerinin özel bir hali olduğunu belirttikten sonra, optimal tamsayılı olmayan bir TDB problemi çözümünün optimal tamsayılı <bir çözümden daima iyi veya ona eşit olacağını burada belirtelim. Başka bir deyişle 4 koşulunun sınırlayıcı özelliği bir TOP probleminde amaç fonksiyonun maksimum değerinin bir DP problemi için karşılığı olan çözüm değerinden daha küçüktür. Grafik üzerinde gösterecek olursak, basit bir hava kargo taşımacılık problemi aşağıdaki gibi formüle edilmişse; z max = 20xı 4-10x z kısıtlayıcı koşullar: 5x, + 4x 3 < 23 (Hacim) 2x,, + 5x ^13 (Ağırlık) x,, x 2 negatif olmayan tamsayılar olmak üzere Şekil 1.1 elde edilir. Optimal OP çözümü sadece 4.8 konteynıriık Xı ürününün sevkjyatını önermektedir. Gerçekte bir konteynırın 0.8 inin gön- (4) Glover; F. - Samme-r, D. C: «Pitfalls of Rounding in Discrete Management Decision Problems», Decision Cciences, Vol. 6., No. 2, April 1975, s
6 derilmesi mümkün olmadığından problem TOP Özelliğini taşımaktadır. Tamsayı olmayan 4.8 çözüm değerini en yakın tamsayı 5 değerine çıkarttığımızda, şekilden de görüleceği gi'bi ilk kısıt çiğnenmektedir. (+) ile gösterilen diğer tamsayı çözüm noktalarından (x, = 4ı, x 2 = 0). seti için 2 = 80 elde edilmektedir. Bu sonuç mümkün ve tamsayılı olmasına rağmen optimal değildir. Grafikten de görüleceği gibi optimal sonuç (xı = 4ı, X 2 1) seti için (2 = 90) olmaktadır. Literatürde tamsayılı olmayan ve tamsayılı olan optimal Z değerleri arasındaki farka genellikle «bölünmezlik maliyeti» adı verilmektedir (5). Bölünmezlik maliyeti bu spesifik örnek için (96 90=6) olarak, hesaplanabilir. Şekiî: 1 - Kargo Problemi Grafik Gösterimi, (5) Budnİk - Nojena - Vollmân; a.g.e., s \
7 2.2. TAMSAYI LI PROGRAM LAMA MODELİ ÇÖZÜM YÖNTEMLERİ Görüldüğü gibi birçok işletme problemi TDP problemi gibi formüle edebilmektedir. TDP problemlerini çözmek için genel ve özel nitelikli çeşith algoritmalar mevcuttur. Bundan sonraki bölümlerde genelden özele doğru TDP probleminin çözüm yöntemleri tartışılacaktır Dal Sınır Algoritması Dai-Sınır Algoritması salt ve karma TDP problemleri yanışım 0-1 problemleri için uygundur. Başlangıçta orijinal problemin simpleks yöntemine göre optimal çözümü bulunur. Eğer bu çözüm tamsayılı olma koşulunu gereekleştirmiyorsa, orijinal problem daha fazla kısıtlı alt problemlere ayrıştırılır. Alt problemler tekrar simplekse göre çözülerek sonuçlara bakılır, tamsayılı sonuçlar elde edilene kadar bu özel arama rutininde devam edilir. Her düğümde simlpeks uygulandığı için dal sınır algoritması daha fazla sınır koşulu altında bir dizi doğrusal programlama probleminin çözümü diye tanımlamak mümkündür (6). Dal-sınır algoritmasının yapısını anlamak için belki en kolay yol bir örnek üzerinde açıklamaktır. örnek Problem; z max = 40xı + 90x 2 kısıtlayıcı koşullar: 9x, + 7x 2 < 56 7x, + 20x 2 < 70 xı, x 2 pozitif tamsayı Şekil: 2 den görüldüğü gibi simpleks çözümü b noktasında elde edilmektedir (xı.= 4,809, x ve Z, = ).. (6) Plano, D. - McMillan, C. Jr., «Dİ3rete Optimization - Integer Programming and NelVvork Analysis for Management Decisfons», Prantice - Half, Inc., Englewood Cliffs, New Jersey, 1971, s. 75.
8 Şekil; 2 Örnek Problemin Grafik Gösterimi. Her iki değişken de tamsayı değildir. O halde dal-sınır yöntemine başvurulabilir. Dal-sıntr yönteminde tamsayı olmayan karar değişkenlerinden herhangi biri, seçilerek dallanma başlatılır. xı değişkeni seçildiği takdirde x T < 4 ve xı > 5 koşullarına göre (xı - 4 ve xt = 5 değerleri arasındaki alanın çözüm alanı olarak alınmadığı kabul edilir). Orjinal problem iki yavru probleme ayrıştırılır, Bkz. : Şekil 3. Yeni formüle edilen problemler süreklilik varsayımına göre simpleks yöntemi ile çözümlendiğinde aşağıdaki sonuçlar elde edilir: 12
9 Problem (2) Problem (3) Z = = x, = x, = x 2 = 2=100 x 2 = Şokil: 3 Ana Problemden Ayrıştırılmış Yavru Problemlerin Grafik Gösterimi Yine xı dışında kalan değişkenlerin tamsayı olmadığı görülmektedir. Sonuçları yorumlarsak; x, in dört veya daha az değerleri için Z nin 349 dan daha büyük değerler alması beklenemez. Aynı şekilde xı in beş veya daha büyük değerleri içinde Z nin 341,390 i aşması söz konusu değildir. Mümkün çözüm aramaya devam ederken dal-smır algoritması, elde edilen sonuçlardan üstün olan düğümden (veya yavru problem) dallanmayı sürdürme prensibini uygular. Analiz sonuçları 2. problemden dallanmanın daha umut verici olduğunu göstermektedir. x 2 < 2 ve x 2 > 3 yeni kısıtlayıcı koşullarına göre 4. ve 5. problemler çözümlenirse şekil 4 deki özet sonuçlar elde edilir. 4. problemin amaç fonksiyonu 340 ve değişkenleri tam sayılıdır. 5. problemin sonuçları ise tamsayılı değildir. Ayrıca dallanmaya 13
10 devam edilirse Z değerinden daha büyük bir değer elde edilemeyeceğinden arama işlemi bu seviyede kesilir. Böylece optimal sonuç x^ = 4.0 ve x 2 + 2, Z = diyebilmemiz için problem 3 sonuçları ile problem 4 sonuçlarının da kıyaslanması gerekmektedir. Z = değeri 3. problemin x 2 < 1 ve x 2 >\ ek kısıtlarına göre 6. ve 7. problemler şeklinde tekrar çözülmesini böylece 4. problemden daha İyi bir sohucun bu bölgelerde olup olmadığını aramayı öngörmektedir. Bu özelliğinden dolayı dal-sınır algoritmasına «Geri İzleme» yöntemi diyenler de vardır (7). Ancak şekil 4. de de özetlendiği üzere daha iyi sonuçlar elde edilemediğinden optimal çözümün x, - x 2 = 2 ve Z 340 olduğu anlaşılmaktadır. H s 35$ %İ0 K. - V tüt* *, = -l.tıî. z = '% 2 İD V * ı : 5.0DO i *. = İAZ$ y± - 3.D» i _ 3ÛÎ. ^ DO Şekil 4 Örnek Problemin Dal-Sınır örnekte ele alınan dal-sınır algoritması şekil 5'de verilen akış diyagramına göre çözülmüştür. Bir başka deyişle bir dalsınır algoritmasının akışı şekil 5'dekİ diyagram gibi özetlenebilir (8), (7) VVagner, Harvey M.: «Principles of Management Science», Prontice- Hall. 1970, s. 300., / (8) Land, A. H. - Doig, A.: «An Automatic Method of Solvİng Discrete Programming Problems», Econometrica, 28, 1960, s /
11 Daha önce de belirtildiği gibî hem salt hem de karma TDP problemlere uygulanan bu teknik, örnek problemde sadece x t in tamsayı olması koşuluna göre ilk dallanmada optimal sonucu verecekti. (Xi = 4.0, x 2 = 2.1 ve Z = 349.0). O halde karma tamsayılı problemler için dal-şınır tekniği daha cazip bir yaklaşım olarak nitelenebilir (9) Kesen Düzlem Algoritması Gerek salt, gerekse karma tamsayılı programlama modellerinin çözümünde kullanılan diğer bir teknik de Gomory'nin kesen düzlem algoritmasıdır (10). Dll-sınır yönteminde olduğu gibi bu teknik de problemin süreklilik halindeki optimal çözümü ile işe başlar. Bayet optimal çözüm tamsayı koşullarını sağlamıyorsa, yeni kısıtlar formüle edilerek probleme eklenir. Bu kısıtlar iki-boyutlu problemlerde düzlemleri, n-boyutlu problemlerde ise hiperdüzlemleri temsil etmektedirler. Kesen düzlemler hiçbir tamsayılı çözüm noktasını dışarıda bırakmayacak veya elimine etmeyecek biçimde mümkün çözüm alanını veya uzayını sınırlar. Doğrusal programlama problemlerinden hatırlanacak olursa, optimal çözümlerden en az birisi çözüm alanının köşelerinden birisinde ortaya çıkmaktadır. Simpleks algoritması da bu nedenle, optimal sonucu buluna dek köşe noktalarını sistematik bir tarama işlemine tabi tutmaktadır. DP modelinde tüm köşe noktalarının tamsayı olması gerekmediğinden, kesen düzlem yöntemi tamsayılı köşe noktalarını içerecek şekilde mümkün çözüm alanını yeniden belirlemektedir. Bunu başardığı anda, simpleks uygulanırsa optimal tamsayılı bir çözüm elde edilebilmektedir. Oal-sınır yönteminde örnek iki değişkenli mekanizasyon problemi için kesen düzlem yaklaşımı Şekil 6'da grafik olarak temsil edilmektedir. Optimum sonuç yine x, = 4, x 2 = 2 olan c noktasında elde edilmektedir. (9) Plane, D, - McMİllan, C: a.g.e., s. 82. (10) Goriıory, R. E.: «An Algorithm for Integer Solutions to Linear Prograrns» Recent Advancas in Methematİcal Programming, Graves and VVolfe (editors) McGraw-Hill Bok Company, 1963.
12 _ 1- - Orjinal problemin ' tamsayılı olmayan şeklini çöz. Bunu geçici olarak A problemi diye *çağır. A problemi çözümünden tamsayı olmayan bir xj değişkenini seç. Kj değeri bj ise A problemine sıra i l e aşağıdaki kısıtları ekleyerek i k i yavru problen: düzenle; a. xj bj nin tamsayı kısmı b. Xj b: cen büyük bir sonraki tamsayı İki alt problemi simplekse göre çöz.! Mevcut durumda yavrusu olmayan tüm mümkün problemlerden gaye fonksiyonunda en i y i değerlisini belirle, bu problemi tekrar A diye isimlendir. Şekil: 5 Dai-Sınır Algoritması Akış Diyagramı.
13 Şekil 6 Kesen Düzlem Algoritması örnek probleminin grafik gösterimi Grup Teorik Yaklaşımı Bu metot bir TDP problemini sırt çantası (knapsack) problemine dönüştürerek çözüm arar. Bu çözüm tekniğinin ayrıntıları yazının boyutlarını çok genişleteceğinden şimdilik kapsam dışı bırakılmıştır Sezgisel Yaklaşımlar Sezgisel ( = Heuristic) karşılığı kullanılan bir nevi el yordamı ile çözüm arama yöntemidir. Sezgisel yöntemler Maier, Pazer ve Nawell'e (11) göre; karşılıklı bağdaşmaz olması gerekmeyen üç alt setten oluşmaktadır. Bunlar sıra ile; a) Sezgisel problem çözme, b) Yapay akıt, (11) Meier, R. C. - Newell, W. T. - Pazer, H.L: «Simulatİon in Business and Ecönomics» Prentice-Hall, Inc., 1969, s
14 c) İnsan düşüncesinin simuiasyonudur. Bizim burada sözünü edeceğimiz bu altsetlerdeh ilki olup, amaç bir problemin özelliği dikkate alınarak çözüm uzayını tarama çabalarının azaltılmasıdır. Sezgisel yöntemler özel amaçlı ve genel amaçlı olarak da ayırdediiebilir. özel amaçlı sezgisele örnek; satrançta kullanılan kurallardır. Genel amaçlı sezgisellerin başında ise ilk Giren İlk Çıkar (FIFO) kuralı gelmektedir. FIFO kuralı envanter değerleme ve kuyruk sistemlerine oldukça geniş uygulama olanağı bulmuştur. Diğer bir sezgisel metot problemi DP kodu İle çözmek ve çözüm vektöründeki sonuçları, mümkün bir çözüm elde edene kadar tamsayıya çevirmek olabilirdi. Fakat bu çözümün optimalden çok uzak olabileceği daha önce belirtilmişti. Sezgisel yöntemler birçok problemde kullanılmakla beraber bilhassa, enumerasyon (sayılama) ile optimal çözümün arandığı büyük kombinatorik problemler veya TDP problemlerinin çözümünde, çözüm uzayının sınırlı bir taramasını yaparak mümkün çözümü bulabilmektedir TAMSAYILI PROGRAMLAMA MODELİ ÇÖZÜM YÖNTEMLERİNİN DEĞ E RLENOİ RİMESİ; Tamsayılı programlama problemlerinde ana sorun, formülasyondan ziyade problemin etkin biçimde çözümüdür. Her metodun kendine özgü avantaj ve dezavantajları vardır. Bir problem için çok iyi sonuç veren bir yöntem, benzer bir başka problemde başarısızlığa uğrayabilmektedir. En iyi çözüm algoritmasının seçimi araştırmacının bilgisi ve tecrübesi yanısıra sezgisine de dayandığı için bir sanat olarak nitelendirilebilir. Aşağıdaki satırlarda TDP çözüm algoritmalarının bir değerlendirilmesi yapılmaktadır; Kesen Düzlem Algoritması Gomory'nin kesen düzlem algoritması kolaylıkla bilgisayarda kodlanabilecek özelliktedir. Belirli sayıda iterasyondan son-
15 ra optimal çözüme kavuşulacağı varsayılmakla birlikte, genellikle bu sayı bilgisayarla çalışılmasına rağmen çok büyük olabilmektedir. Bu yöntemde diğer bir problem yuvarlatma (round-off) hatalarına karşı hassas oluşudur. Kesirli değerlerle çalışıldığı için bilgisayarda ondalık aritmetik kullanılması zorunluluğu vardır.-birçok bilgisayar kodunda çift duyarlı (double precision) aritmetik özellik mevcut olmakla beraber, problem her İterasyonda büyüyen sayıda kesen düzlemlerle çözümlenmeye çalışıldığı İçin bazen bu da yetersiz kalabilmektedir (12). Kesen düzlem algoritmasının diğer bir özelliği, amaç fonk-. siyonu bir platoya ulaştığında, İterasyondan iterasyona önemli bir ilerlemenin kaydedilememesidir. Birçok kesen düzlem eklenmesine rağmen amaç fonksiyonunun değerinde oldukça küçük değişiklikler elde edilebilir. Büyük boyutlu problemlerde olduğu kadar, küçük problemlerde de bu pahalı özellik veya dez-. avantajla sık sık karşılaşılabilmektedir. Bu sakıncayı gidermek için uzmanların geliştirilmiş, bu bölgeden (platodan), kurtulma hilelerine çözüm algoritması içinde başvurulmuştur. Bu algoritmanın diğer bir sakıncası da ajî ve bi değerleri olan problemlerde zorlanmasıdır. Son olarak, kesen düzlem yöntemi bir (duai-simpleks) dual metot olduğu için eleştirilmektedir. Bu teknik, mümkün olmayan bir çözümle İterasyonlara başlamakta ve optimal çözüm elde edene kadar bulduğu sonuçlar mümkün olmayan özellik taşımaktadır. Şayet metot optımale yakınsaklaşmaz ise veya yakınsaklaşmayı tamamlamasına izin vermek çok pahalıya mal olacak ise, kullanıcı bilgisayarda, programı kestiği noktada ne bir 'optimale yakın' ne de iyi bir 'mümkün çözüm' elde edebilmiş olmaktadır. (12) Geoffrion, A. M.: Marsten R. E., «Integer Programming Algorİthms: A Frameıvork and State of the Art Survey», Management Selence, 18, 7 (March 1972)ı
16 özetle, kesen düzlemin başarısı problemin şekline bağlıdır. Optimal çözüme ulaşmak için, bazen sadece kısıtların sırasını değiştirmek, gerekli kesen düzlemlerin sayısını önemli ölçüde etkileyebilmektedir Kısmi Sayılama (Enumerasyon) Yöntemleri a) Dal-sınır Algoritması;, Bu yöntem küçük boyutlu problemlerin çözümünde oldukça etkin olmakla beraber, problem 50. değişken ve 25 kısıttan fazla olan büyük problemlerde veya ilk simpleks. çözüm, optimal tamsayılı çözümden bir hayli uzakta ise, gerekli iterasyon- İarın sayısı aşırı derecede büyüyebilmededir. Sadece problemin boyutu çözüm karmaşıklığı için neden değildir. Belirli bazı problemler büyük dalların dudanmasına müsaade ederken, diğer bazıları en uç noktaya kadar taramayı gerektirebilir. Fakat, kesen düzlemle mukayese edildiğinde, dal-sınır yönteminin optimuma yakınsaklaşması zaman (maliyet) açısından durdurulsa dahi, değeri olan bir mümkün çözümü kullanıcıya sunması açısından ter* cih edilmelidir. Daha önce de belirtildiği gibi bilhassa karma tamsayılı programlama da iyi bir yöntemdir. I b) Gizli Sayılama Algoritması: Gizli sayılamanın en önemli avantajı tamsayılı aritmetik kullanmasıdır. Böylece kodlamada sabit nokta aritmetik özellikten yararlanarak, yuvarlatma problemleri ortadan kalkar, üstelik hafıza gereksinimi, bu yöntemde simpleksle ilgili diğerlerinden daha azdır. Fakat genel bir TDP probleminin 0-1 eşdeğerine dönüştürülerek çözülmesi de birçok değişkenin eklenmesine sebeb olur. Böyle durumlarda hafıza kapasitesi ve zamanı çok kritik olabilir. 20
Başlangıç Temel Programının Bilinmemesi Durumu
 aşlangıç Temel Programının ilinmemesi Durumu İlgili kısıtlarda şartlar ( ) ise bunlara gevşek (slack) değişkenler eklenerek eşitliklere dönüştürülmektedir. Ancak sınırlayıcı şartlar ( ) veya ( = ) olduğu
aşlangıç Temel Programının ilinmemesi Durumu İlgili kısıtlarda şartlar ( ) ise bunlara gevşek (slack) değişkenler eklenerek eşitliklere dönüştürülmektedir. Ancak sınırlayıcı şartlar ( ) veya ( = ) olduğu
Yöneylem Araştırması II
 Yöneylem Araştırması II Öğr. Gör. Dr. Hakan ÇERÇİOĞLU [email protected] BÖLÜM I: Doğrusal Programlama Tekrarı Doğrusal Programlama Tanımı Doğrusal Programlama Varsayımları Grafik Çözüm Metodu Simpleks
Yöneylem Araştırması II Öğr. Gör. Dr. Hakan ÇERÇİOĞLU [email protected] BÖLÜM I: Doğrusal Programlama Tekrarı Doğrusal Programlama Tanımı Doğrusal Programlama Varsayımları Grafik Çözüm Metodu Simpleks
TAMSAYILI PROGRAMLAMA
 TAMSAYILI PROGRAMLAMA Doğrusal programlama problemlerinde sık sık çözümün tamsayı olması gereken durumlar ile karşılaşılır. Örneğin ele alınan problem masa, sandalye, otomobil vb. üretimlerinin optimum
TAMSAYILI PROGRAMLAMA Doğrusal programlama problemlerinde sık sık çözümün tamsayı olması gereken durumlar ile karşılaşılır. Örneğin ele alınan problem masa, sandalye, otomobil vb. üretimlerinin optimum
Doğrusal Programlamada Grafik Çözüm
 Doğrusal Programlamada Grafik Çözüm doğrusal programlama PROBLEMİN ÇÖZÜLMESİ (OPTİMUM ÇÖZÜM) Farklı yöntemlerle çözülebilir Grafik çözüm (değişken sayısı 2 veya 3 olabilir) Simpleks çözüm Bilgisayar yazılımlarıyla
Doğrusal Programlamada Grafik Çözüm doğrusal programlama PROBLEMİN ÇÖZÜLMESİ (OPTİMUM ÇÖZÜM) Farklı yöntemlerle çözülebilir Grafik çözüm (değişken sayısı 2 veya 3 olabilir) Simpleks çözüm Bilgisayar yazılımlarıyla
28 C j -Z j /2 0
 3.2.6. Dual Problem ve Ekonomik Yorumu Primal Model Z maks. = 4X 1 + 5X 2 (kar, pb/gün) X 1 + 2X 2 10 6X 1 + 6X 2 36 8X 1 + 4X 2 40 (işgücü, saat/gün) (Hammadde1, kg/gün) (Hammadde2, kg/gün) 4 5 0 0 0
3.2.6. Dual Problem ve Ekonomik Yorumu Primal Model Z maks. = 4X 1 + 5X 2 (kar, pb/gün) X 1 + 2X 2 10 6X 1 + 6X 2 36 8X 1 + 4X 2 40 (işgücü, saat/gün) (Hammadde1, kg/gün) (Hammadde2, kg/gün) 4 5 0 0 0
KISITLI OPTİMİZASYON
 KISITLI OPTİMİZASYON SİMPLEKS YÖNTEMİ Simpleks Yöntemi Simpleks yöntemi iteratif bir prosedürü gerektirir. Bu iterasyonlar ile gerçekçi çözümlerin olduğu bölgenin (S) bir köşesinden başlayarak amaç fonksiyonunun
KISITLI OPTİMİZASYON SİMPLEKS YÖNTEMİ Simpleks Yöntemi Simpleks yöntemi iteratif bir prosedürü gerektirir. Bu iterasyonlar ile gerçekçi çözümlerin olduğu bölgenin (S) bir köşesinden başlayarak amaç fonksiyonunun
EM302 Yöneylem Araştırması 2. Dr. Özgür Kabak
 EM302 Yöneylem Araştırması 2 Dr. Özgür Kabak TP Çözümü TP problemlerinin çözümü için başlıca iki yaklaşım vardır kesme düzlemleri (cutting planes) dal sınır (branch and bound) tüm yaklaşımlar tekrarlı
EM302 Yöneylem Araştırması 2 Dr. Özgür Kabak TP Çözümü TP problemlerinin çözümü için başlıca iki yaklaşım vardır kesme düzlemleri (cutting planes) dal sınır (branch and bound) tüm yaklaşımlar tekrarlı
Simpleks Yönteminde Kullanılan İlave Değişkenler (Eşitliğin yönüne göre):
 DP SİMPLEKS ÇÖZÜM Simpleks Yöntemi, amaç fonksiyonunu en büyük (maksimum) veya en küçük (minimum) yapacak en iyi çözüme adım adım yaklaşan bir algoritma (hesaplama yöntemi) dir. Bu nedenle, probleme bir
DP SİMPLEKS ÇÖZÜM Simpleks Yöntemi, amaç fonksiyonunu en büyük (maksimum) veya en küçük (minimum) yapacak en iyi çözüme adım adım yaklaşan bir algoritma (hesaplama yöntemi) dir. Bu nedenle, probleme bir
doğrusal programlama DOĞRUSAL PROGRAMLAMA (GENEL)
 DOĞRUSAL PROGRAMLAMA (GENEL) Belirli bir amacın gerçekleşmesini etkileyen bazı kısıtlayıcı koşulların ve bu kısıtlayıcı koşulların doğrusal eşitlik ya da eşitsizlik biçiminde verilmesi durumunda amaca
DOĞRUSAL PROGRAMLAMA (GENEL) Belirli bir amacın gerçekleşmesini etkileyen bazı kısıtlayıcı koşulların ve bu kısıtlayıcı koşulların doğrusal eşitlik ya da eşitsizlik biçiminde verilmesi durumunda amaca
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ
 ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTIRMA MODELİNİN TANIMI Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTIRMA MODELİNİN TANIMI Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
Doğrusal Programlama. Prof. Dr. Ferit Kemal Sönmez
 Doğrusal Programlama Prof. Dr. Ferit Kemal Sönmez Doğrusal Programlama Belirli bir amacın gerçekleşmesini etkileyen bazı kısıtlayıcı koşulların ve bu kısıtlayıcı koşulların doğrusal eşitlik ya da eşitsizlik
Doğrusal Programlama Prof. Dr. Ferit Kemal Sönmez Doğrusal Programlama Belirli bir amacın gerçekleşmesini etkileyen bazı kısıtlayıcı koşulların ve bu kısıtlayıcı koşulların doğrusal eşitlik ya da eşitsizlik
DOĞRUSAL PROGRAMLAMADA DUALİTE (DUALITY)
 DOĞRUSAL PROGRAMLAMADA DUALİTE (DUALITY) 1 DOĞRUSAL PROGRAMLAMADA İKİLİK (DUALİTE-DUALITY) Doğrusal programlama modelleri olarak adlandırılır. Aynı modelin değişik bir düzende oluşturulmasıyla Dual (İkilik)
DOĞRUSAL PROGRAMLAMADA DUALİTE (DUALITY) 1 DOĞRUSAL PROGRAMLAMADA İKİLİK (DUALİTE-DUALITY) Doğrusal programlama modelleri olarak adlandırılır. Aynı modelin değişik bir düzende oluşturulmasıyla Dual (İkilik)
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ
 ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTıRMA MODELININ TANıMı Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
ULAŞTIRMA MODELİ VE ÇEŞİTLİ ULAŞTIRMA MODELLERİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü ULAŞTıRMA MODELININ TANıMı Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir.
YÖNEYLEM ARAŞTIRMASI - I
 YÖNEYLEM ARAŞTIRMASI - I /0 İçerik Matematiksel Modelin Kurulması Grafik Çözüm DP Terminolojisi DP Modelinin Standart Formu DP Varsayımları 2/0 Grafik Çözüm İki değişkenli (X, X2) modellerde kullanılabilir,
YÖNEYLEM ARAŞTIRMASI - I /0 İçerik Matematiksel Modelin Kurulması Grafik Çözüm DP Terminolojisi DP Modelinin Standart Formu DP Varsayımları 2/0 Grafik Çözüm İki değişkenli (X, X2) modellerde kullanılabilir,
KONU 4: DOĞRUSAL PROGRAMLAMA MODELİ İÇİN ÇÖZÜM YÖNTEMLERİ I
 KONU 4: DOĞRUSAL PROGRAMLAMA MODELİ İÇİN ÇÖZÜM YÖNTEMLERİ I 4.1. Dışbükeylik ve Uç Nokta Bir d.p.p. de model kısıtlarını aynı anda sağlayan X X X karar değişkenleri... n vektörüne çözüm denir. Eğer bu
KONU 4: DOĞRUSAL PROGRAMLAMA MODELİ İÇİN ÇÖZÜM YÖNTEMLERİ I 4.1. Dışbükeylik ve Uç Nokta Bir d.p.p. de model kısıtlarını aynı anda sağlayan X X X karar değişkenleri... n vektörüne çözüm denir. Eğer bu
TP SORUNLARININ ÇÖZÜMLERİ
 TP SORUNLARININ ÇÖZÜMLERİ (Bu notlar Doç.Dr. Şule Önsel tarafıdan hazırlanmıştır) TP problemlerinin çözümü için başlıca iki yaklaşım vardır. İlk geliştirilen yöntem kesme düzlemleri (cutting planes) olarak
TP SORUNLARININ ÇÖZÜMLERİ (Bu notlar Doç.Dr. Şule Önsel tarafıdan hazırlanmıştır) TP problemlerinin çözümü için başlıca iki yaklaşım vardır. İlk geliştirilen yöntem kesme düzlemleri (cutting planes) olarak
3.2. DP Modellerinin Simpleks Yöntem ile Çözümü Primal Simpleks Yöntem
 3.2. DP Modellerinin Simpleks Yöntem ile Çözümü 3.2.1. Primal Simpleks Yöntem Grafik çözüm yönteminde gördüğümüz gibi optimal çözüm noktası, her zaman uygun çözüm alanının bir köşe noktası ya da uç noktası
3.2. DP Modellerinin Simpleks Yöntem ile Çözümü 3.2.1. Primal Simpleks Yöntem Grafik çözüm yönteminde gördüğümüz gibi optimal çözüm noktası, her zaman uygun çözüm alanının bir köşe noktası ya da uç noktası
Maksimizasyon s.t. İşçilik, saat) (Kil, kg)
 Simplex ile Çözüm Yöntemi Doç. Dr. Fazıl GÖKGÖZ 1 Doğrusal Programlama Modeli Maksimizasyon s.t. İşçilik, saat) (Kil, kg) 2 Doç. Dr. Fazıl GÖKGÖZ Yrd.Doç. Dr. Fazıl GÖKGÖZ 1 Modelin Standard Hali Maksimizasyon
Simplex ile Çözüm Yöntemi Doç. Dr. Fazıl GÖKGÖZ 1 Doğrusal Programlama Modeli Maksimizasyon s.t. İşçilik, saat) (Kil, kg) 2 Doç. Dr. Fazıl GÖKGÖZ Yrd.Doç. Dr. Fazıl GÖKGÖZ 1 Modelin Standard Hali Maksimizasyon
Zeki Optimizasyon Teknikleri
 Zeki Optimizasyon Teknikleri Ara sınav - 25% Ödev (Haftalık) - 10% Ödev Sunumu (Haftalık) - 5% Final (Proje Sunumu) - 60% - Dönem sonuna kadar bir optimizasyon tekniğiyle uygulama geliştirilecek (Örn:
Zeki Optimizasyon Teknikleri Ara sınav - 25% Ödev (Haftalık) - 10% Ödev Sunumu (Haftalık) - 5% Final (Proje Sunumu) - 60% - Dönem sonuna kadar bir optimizasyon tekniğiyle uygulama geliştirilecek (Örn:
SİMPLEKS ALGORİTMASI Yapay değişken kullanımı
 Fen Bilimleri Enstitüsü Endüstri Mühendisliği Anabilim Dalı ENM53 Doğrusal Programlamada İleri Teknikler SİMPLEKS ALGORİTMASI Yapay değişken kullanımı Hazırlayan: Doç. Dr. Nil ARAS, 6 AÇIKLAMA Bu sununun
Fen Bilimleri Enstitüsü Endüstri Mühendisliği Anabilim Dalı ENM53 Doğrusal Programlamada İleri Teknikler SİMPLEKS ALGORİTMASI Yapay değişken kullanımı Hazırlayan: Doç. Dr. Nil ARAS, 6 AÇIKLAMA Bu sununun
İkinci dersin notlarında yer alan Gepetto Marangozhanesi örneğini hatırlayınız.
 ISLE 403 YÖNEYLEM ARAŞTIRMASI DERS 3 NOTLAR DP Modellerinin Standart Biçimde Gösterimi: İkinci dersin notlarında yer alan Gepetto Marangozhanesi örneğini hatırlayınız. Gepetto Marangozhanesi için DP modeli
ISLE 403 YÖNEYLEM ARAŞTIRMASI DERS 3 NOTLAR DP Modellerinin Standart Biçimde Gösterimi: İkinci dersin notlarında yer alan Gepetto Marangozhanesi örneğini hatırlayınız. Gepetto Marangozhanesi için DP modeli
Bir Doğrusal Programlama Modelinin Genel Yapısı
 Bir Doğrusal Programlama Modelinin Genel Yapısı Amaç Fonksiyonu Kısıtlar M i 1 N Z j 1 N j 1 a C j x j ij x j B i Karar Değişkenleri x j Pozitiflik Koşulu x j >= 0 Bu formülde kullanılan matematik notasyonların
Bir Doğrusal Programlama Modelinin Genel Yapısı Amaç Fonksiyonu Kısıtlar M i 1 N Z j 1 N j 1 a C j x j ij x j B i Karar Değişkenleri x j Pozitiflik Koşulu x j >= 0 Bu formülde kullanılan matematik notasyonların
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Bu bölümde eşitsizlik kısıtlarına bağlı bir doğrusal olmayan kısıta sahip problemin belirlenen stasyoner noktaları
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Bu bölümde eşitsizlik kısıtlarına bağlı bir doğrusal olmayan kısıta sahip problemin belirlenen stasyoner noktaları
Optimizasyon İçin Kök(Generic) Model (Doğrusal-Olmayan Programlama Modeli)
 ISLE 403 YÖNEYLEM ARAŞTIRMASI I DERS 2 NOTLAR Optimizasyon İçin Kök(Generic) Model (Doğrusal-Olmayan Programlama Modeli) X, karar değişkenlerinin bir vektörü olsun. z, g 1, g 2,...,g m fonksiyonlardır.
ISLE 403 YÖNEYLEM ARAŞTIRMASI I DERS 2 NOTLAR Optimizasyon İçin Kök(Generic) Model (Doğrusal-Olmayan Programlama Modeli) X, karar değişkenlerinin bir vektörü olsun. z, g 1, g 2,...,g m fonksiyonlardır.
Kısıtsız Optimizasyon OPTİMİZASYON Kısıtsız Optimizasyon
 OPTİMİZASYON Bu bölümde çok değişkenli kısıtsız optimizasyon problemlerinin çözüm yöntemleri incelenecektir. Bu bölümde anlatılacak yöntemler, kısıtlı optimizasyon problemlerini de çözebilmektedir. Bunun
OPTİMİZASYON Bu bölümde çok değişkenli kısıtsız optimizasyon problemlerinin çözüm yöntemleri incelenecektir. Bu bölümde anlatılacak yöntemler, kısıtlı optimizasyon problemlerini de çözebilmektedir. Bunun
Lineer Programlama. Doğrusal terimi, hem amaç hem de kısıtları temsil eden matematiksel fonksiyonların doğrusal olduğunu gösterir.
 LİNEER PROGRAMLAMA Giriş Uygulamada karşılaşılan birçok optimizasyon problemi kısıtlar içerir. Yani optimizasyon probleminde amaç fonksiyonuna ilave olarak çözümü kısıtlayıcı ek denklemler mevcuttur. Bu
LİNEER PROGRAMLAMA Giriş Uygulamada karşılaşılan birçok optimizasyon problemi kısıtlar içerir. Yani optimizasyon probleminde amaç fonksiyonuna ilave olarak çözümü kısıtlayıcı ek denklemler mevcuttur. Bu
İÇİNDEKİLER ÖNSÖZ Bölüm 1 SAYILAR 11 Bölüm 2 KÜMELER 31 Bölüm 3 FONKSİYONLAR
 İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 11 1.1. Sayı Kümeleri 12 1.1.1.Doğal Sayılar Kümesi 12 1.1.2.Tam Sayılar Kümesi 13 1.1.3.Rasyonel Sayılar Kümesi 14 1.1.4. İrrasyonel Sayılar Kümesi 16 1.1.5. Gerçel
İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 11 1.1. Sayı Kümeleri 12 1.1.1.Doğal Sayılar Kümesi 12 1.1.2.Tam Sayılar Kümesi 13 1.1.3.Rasyonel Sayılar Kümesi 14 1.1.4. İrrasyonel Sayılar Kümesi 16 1.1.5. Gerçel
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Altın Oran (Golden Section Search) Arama Metodu Tek değişkenli bir f(x) fonksiyonunu ele alalım. [Bazı x ler için f
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Altın Oran (Golden Section Search) Arama Metodu Tek değişkenli bir f(x) fonksiyonunu ele alalım. [Bazı x ler için f
Zeki Optimizasyon Teknikleri
 Zeki Optimizasyon Teknikleri Tabu Arama (Tabu Search) Doç.Dr. M. Ali Akcayol Tabu Arama 1986 yılında Glover tarafından geliştirilmiştir. Lokal minimum u elimine edebilir ve global minimum u bulur. Değerlendirme
Zeki Optimizasyon Teknikleri Tabu Arama (Tabu Search) Doç.Dr. M. Ali Akcayol Tabu Arama 1986 yılında Glover tarafından geliştirilmiştir. Lokal minimum u elimine edebilir ve global minimum u bulur. Değerlendirme
İÇİNDEKİLER. Bölüm 1 YÖNEYLEM ARAŞTIRMASINA GİRİŞ 11. 1.1. Temel Kavramlar 14 1.2. Modeller 17 1.3. Diğer Kavramlar 17 Değerlendirme Soruları 19
 İÇİNDEKİLER ÖNSÖZ III Bölüm 1 YÖNEYLEM ARAŞTIRMASINA GİRİŞ 11 1.1. Temel Kavramlar 14 1.2. Modeller 17 1.3. Diğer Kavramlar 17 Değerlendirme Soruları 19 Bölüm 2 DOĞRUSAL PROGRAMLAMA 21 2.1 Doğrusal Programlamanın
İÇİNDEKİLER ÖNSÖZ III Bölüm 1 YÖNEYLEM ARAŞTIRMASINA GİRİŞ 11 1.1. Temel Kavramlar 14 1.2. Modeller 17 1.3. Diğer Kavramlar 17 Değerlendirme Soruları 19 Bölüm 2 DOĞRUSAL PROGRAMLAMA 21 2.1 Doğrusal Programlamanın
İleri Yöneylem Araştırması Uygulamaları Tam Sayılı Programlama
 İleri Yöneylem Araştırması Uygulamaları Tam Sayılı Programlama Dr. Özgür Kabak 2016-2017 Güz } Gerçek hayattaki bir çok problem } tam sayılı değişkenlerin ve } doğrusal kısıt ve amaç fonksiyonları ile
İleri Yöneylem Araştırması Uygulamaları Tam Sayılı Programlama Dr. Özgür Kabak 2016-2017 Güz } Gerçek hayattaki bir çok problem } tam sayılı değişkenlerin ve } doğrusal kısıt ve amaç fonksiyonları ile
Matematiksel modellerin elemanları
 Matematiksel modellerin elemanları Op#mizasyon ve Doğrusal Programlama Maksimizasyon ve Minimizasyon örnekleri, Doğrusal programlama modeli kurma uygulamaları 6. DERS 1. Karar değişkenleri: Bir karar verme
Matematiksel modellerin elemanları Op#mizasyon ve Doğrusal Programlama Maksimizasyon ve Minimizasyon örnekleri, Doğrusal programlama modeli kurma uygulamaları 6. DERS 1. Karar değişkenleri: Bir karar verme
MATRİSEL ÇÖZÜM TABLOLARIYLA DUYARLILIK ANALİZİ
 SİMPLEKS TABLONUN YORUMU MATRİSEL ÇÖZÜM TABLOLARIYLA DUYARLILIK ANALİZİ Şu ana kadar verilen bir DP probleminin çözümünü ve çözüm şartlarını inceledik. Eğer orijinal modelin parametrelerinde bazı değişiklikler
SİMPLEKS TABLONUN YORUMU MATRİSEL ÇÖZÜM TABLOLARIYLA DUYARLILIK ANALİZİ Şu ana kadar verilen bir DP probleminin çözümünü ve çözüm şartlarını inceledik. Eğer orijinal modelin parametrelerinde bazı değişiklikler
Genetik Algoritmalar. Bölüm 1. Optimizasyon. Yrd. Doç. Dr. Adem Tuncer E-posta:
 Genetik Algoritmalar Bölüm 1 Optimizasyon Yrd. Doç. Dr. Adem Tuncer E-posta: [email protected] Optimizasyon? Optimizasyon Nedir? Eldeki kısıtlı kaynakları en iyi biçimde kullanmak olarak tanımlanabilir.
Genetik Algoritmalar Bölüm 1 Optimizasyon Yrd. Doç. Dr. Adem Tuncer E-posta: [email protected] Optimizasyon? Optimizasyon Nedir? Eldeki kısıtlı kaynakları en iyi biçimde kullanmak olarak tanımlanabilir.
Tek Değişkenli Optimizasyon OPTİMİZASYON. Gradient Tabanlı Yöntemler. Bisection (İkiye Bölme) Yöntemi
 OPTİMİZASYON Gerçek hayatta, çok değişkenli optimizasyon problemleri karmaşıktır ve nadir olarak problem tek değişkenli olur. Bununla birlikte, tek değişkenli optimizasyon algoritmaları çok değişkenli
OPTİMİZASYON Gerçek hayatta, çok değişkenli optimizasyon problemleri karmaşıktır ve nadir olarak problem tek değişkenli olur. Bununla birlikte, tek değişkenli optimizasyon algoritmaları çok değişkenli
İbrahim Küçükkoç Arş. Gör.
 Doğrusal Programlamada Karışım Problemleri İbrahim Küçükkoç Arş. Gör. Balikesir Üniversitesi Endüstri Mühendisliği Bölümü Mühendislik-Mimarlık Fakültesi Çağış Kampüsü 10145 / Balıkesir 0 (266) 6121194
Doğrusal Programlamada Karışım Problemleri İbrahim Küçükkoç Arş. Gör. Balikesir Üniversitesi Endüstri Mühendisliği Bölümü Mühendislik-Mimarlık Fakültesi Çağış Kampüsü 10145 / Balıkesir 0 (266) 6121194
DOĞRUSAL PROGRAMLAMANIN ÖZEL TÜRLERİ
 DOĞRUSAL PROGRAMLAMANIN ÖZEL TÜRLERİ TRANSPORTASYON (TAŞIMA, ULAŞTIRMA) TRANSİT TAŞIMA (TRANSSHIPMENT) ATAMA (TAHSİS) TRANSPORTASYON (TAŞIMA) (ULAŞTIRMA) TRANSPORTASYON Malların birden fazla üretim (kaynak,
DOĞRUSAL PROGRAMLAMANIN ÖZEL TÜRLERİ TRANSPORTASYON (TAŞIMA, ULAŞTIRMA) TRANSİT TAŞIMA (TRANSSHIPMENT) ATAMA (TAHSİS) TRANSPORTASYON (TAŞIMA) (ULAŞTIRMA) TRANSPORTASYON Malların birden fazla üretim (kaynak,
Tarımda Mühendislik Düşünce Sistemi. Prof. Dr. Ferit Kemal SÖNMEZ
 Tarımda Mühendislik Düşünce Sistemi Prof. Dr. Ferit Kemal SÖNMEZ Sistem Aralarında ilişki veya bağımlılık bulunan elemanlardan oluşan bir yapı veya organik bütündür. Bir sistem alt sistemlerden oluşmuştur.
Tarımda Mühendislik Düşünce Sistemi Prof. Dr. Ferit Kemal SÖNMEZ Sistem Aralarında ilişki veya bağımlılık bulunan elemanlardan oluşan bir yapı veya organik bütündür. Bir sistem alt sistemlerden oluşmuştur.
Duyarlılık analizi, bir doğrusal programlama probleminde belirlenen katsayı değerlerinin
 DUYARLILIK ANALİZİ Duyarlılık analizi, bir doğrusal programlama probleminde belirlenen katsayı değerlerinin değişmesinin problemin optimal çözümü üzerine etkisini incelemektedir. Oluşturulan modeldeki
DUYARLILIK ANALİZİ Duyarlılık analizi, bir doğrusal programlama probleminde belirlenen katsayı değerlerinin değişmesinin problemin optimal çözümü üzerine etkisini incelemektedir. Oluşturulan modeldeki
BİR MONTAJ HATTI ÜRETİM SİSTEMİNDE OPTİMAL İŞGÜCÜ DAĞILIMININ ARENA PROCESS ANALYZER (PAN) VE OPTQUEST KULLANILARAK BELİRLENMESİ
 BİR MONTAJ HATTI ÜRETİM SİSTEMİNDE OPTİMAL İŞGÜCÜ DAĞILIMININ ARENA PROCESS ANALYZER (PAN) VE OPTQUEST KULLANILARAK BELİRLENMESİ Özgür ARMANERİ Dokuz Eylül Üniversitesi Özet Bu çalışmada, bir montaj hattı
BİR MONTAJ HATTI ÜRETİM SİSTEMİNDE OPTİMAL İŞGÜCÜ DAĞILIMININ ARENA PROCESS ANALYZER (PAN) VE OPTQUEST KULLANILARAK BELİRLENMESİ Özgür ARMANERİ Dokuz Eylül Üniversitesi Özet Bu çalışmada, bir montaj hattı
Üçüncü adımda ifade edilen özel kısıtları oluģturabilmek için iki genel yöntem geliģtirilmiģtir:
 TAMSAYILI DOGRUSAL PROGRAMLAMA ALGORİTMALARI TDP Algoritmaları, doğrusal programlamanın baģarılı sonuçlar ve yöntemlerinden yararlanma üzerine inģa edilmiģtir. Bu algoritmalardaki stratejiler üç adım içermektedir:
TAMSAYILI DOGRUSAL PROGRAMLAMA ALGORİTMALARI TDP Algoritmaları, doğrusal programlamanın baģarılı sonuçlar ve yöntemlerinden yararlanma üzerine inģa edilmiģtir. Bu algoritmalardaki stratejiler üç adım içermektedir:
T.C. DOKUZ EYLÜL ÜNİVERSİTESİ SOSYAL BİLİMLER ENSTİTÜSÜ EKONOMETRİ ANABİLİM DALI EKONOMETRİ DOKTORA PROGRAMI
 T.C. DOKUZ EYLÜL ÜNİVERSİTESİ SOSYAL BİLİMLER ENSTİTÜSÜ EKONOMETRİ ANABİLİM DALI EKONOMETRİ DOKTORA PROGRAMI Genişletilmiş Lagrange Yöntemi Hazırlayan: Nicat GASIM Öğretim Üyesi Prof. Dr. İpek Deveci KARAKOÇ
T.C. DOKUZ EYLÜL ÜNİVERSİTESİ SOSYAL BİLİMLER ENSTİTÜSÜ EKONOMETRİ ANABİLİM DALI EKONOMETRİ DOKTORA PROGRAMI Genişletilmiş Lagrange Yöntemi Hazırlayan: Nicat GASIM Öğretim Üyesi Prof. Dr. İpek Deveci KARAKOÇ
YÖNEYLEM ARAŞTIRMASI - II
 YÖNEYLEM ARAŞTIRMASI - II Araş. Gör. Murat SARI 1/35 I Giriş Biri diğerini izleyen ve karşılıklı etkileri olan bir dizi kararın bütünüyle ele alındığı problemler için geliştirilen karar modelleri ve bunların
YÖNEYLEM ARAŞTIRMASI - II Araş. Gör. Murat SARI 1/35 I Giriş Biri diğerini izleyen ve karşılıklı etkileri olan bir dizi kararın bütünüyle ele alındığı problemler için geliştirilen karar modelleri ve bunların
4.1. Gölge Fiyat Kavramı
 4. Gölge Fiyat Kavramı 4.1. Gölge Fiyat Kavramı Gölge fiyatlar doğrusal programlama modellerinde kısıtlarla açıklanan kaynakların bizim için ne kadar değerli olduklarını gösterirler. Şimdi bir örnek üzerinde
4. Gölge Fiyat Kavramı 4.1. Gölge Fiyat Kavramı Gölge fiyatlar doğrusal programlama modellerinde kısıtlarla açıklanan kaynakların bizim için ne kadar değerli olduklarını gösterirler. Şimdi bir örnek üzerinde
METASEZGİSEL YÖNTEMLER
 METASEZGİSEL YÖNTEMLER Ara sınav - 30% Ödev (Haftalık) - 20% Final (Proje Sunumu) - 50% - Dönem sonuna kadar bir optimizasyon tekniğiyle uygulama geliştirilecek (Örn: Zaman çizelgeleme, en kısa yol bulunması,
METASEZGİSEL YÖNTEMLER Ara sınav - 30% Ödev (Haftalık) - 20% Final (Proje Sunumu) - 50% - Dönem sonuna kadar bir optimizasyon tekniğiyle uygulama geliştirilecek (Örn: Zaman çizelgeleme, en kısa yol bulunması,
OYUN TEORİSİ. Özlem AYDIN. Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü
 OYUN TEORİSİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü TANIM ''Oyun Teorisi'', iki yada daha fazla rakibi belirli kurallar altında birleştirerek karşılıklı olarak çelişen olasılıklar
OYUN TEORİSİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü TANIM ''Oyun Teorisi'', iki yada daha fazla rakibi belirli kurallar altında birleştirerek karşılıklı olarak çelişen olasılıklar
EM302 Yöneylem Araştırması 2 Doğrusal Olmayan Programlamaya Giriş. Dr. Özgür Kabak
 EM302 Yöneylem Araştırması 2 Doğrusal Olmayan Programlamaya Giriş Dr. Özgür Kabak Doğrusal Olmayan Programlama Eğer bir Matematiksel Programlama modelinin amaç fonksiyonu ve/veya kısıtları doğrusal değil
EM302 Yöneylem Araştırması 2 Doğrusal Olmayan Programlamaya Giriş Dr. Özgür Kabak Doğrusal Olmayan Programlama Eğer bir Matematiksel Programlama modelinin amaç fonksiyonu ve/veya kısıtları doğrusal değil
SAYISAL ÇÖZÜMLEME. Sayısal Çözümleme
 SAYISAL ÇÖZÜMLEME 1 SAYISAL ÇÖZÜMLEME 4. Hafta DENKLEM ÇÖZÜMLERİ 2 İÇİNDEKİLER Denklem Çözümleri Doğrusal Olmayan Denklem Çözümleri Grafik Yöntemleri Kapalı Yöntemler İkiye Bölme (Bisection) Yöntemi Adım
SAYISAL ÇÖZÜMLEME 1 SAYISAL ÇÖZÜMLEME 4. Hafta DENKLEM ÇÖZÜMLERİ 2 İÇİNDEKİLER Denklem Çözümleri Doğrusal Olmayan Denklem Çözümleri Grafik Yöntemleri Kapalı Yöntemler İkiye Bölme (Bisection) Yöntemi Adım
Okut. Yüksel YURTAY. İletişim : (264) Sayısal Analiz. Giriş.
 Okut. Yüksel YURTAY İletişim : Sayısal Analiz [email protected] www.cs.sakarya.edu.tr/yyurtay (264) 295 58 99 Giriş 1 Amaç : Mühendislik problemlerinin bilgisayar ortamında çözümünü mümkün kılacak
Okut. Yüksel YURTAY İletişim : Sayısal Analiz [email protected] www.cs.sakarya.edu.tr/yyurtay (264) 295 58 99 Giriş 1 Amaç : Mühendislik problemlerinin bilgisayar ortamında çözümünü mümkün kılacak
Örnek. Aşağıdaki veri setlerindeki X ve Y veri çiftlerini kullanarak herbir durumda X=1,5 için Y nin hangi değerleri alacağını hesaplayınız.
 Örnek Aşağıdaki veri setlerindeki X ve Y veri çiftlerini kullanarak herbir durumda X=1,5 için Y nin hangi değerleri alacağını hesaplayınız. i. ii. X 1 2 3 4 1 2 3 4 Y 2 3 4 5 4 3 2 1 Örnek Aşağıdaki veri
Örnek Aşağıdaki veri setlerindeki X ve Y veri çiftlerini kullanarak herbir durumda X=1,5 için Y nin hangi değerleri alacağını hesaplayınız. i. ii. X 1 2 3 4 1 2 3 4 Y 2 3 4 5 4 3 2 1 Örnek Aşağıdaki veri
ENDÜSTRİ MÜHENDİSLİĞİ BÖLÜMÜ YÖNEYLEM ARAŞTIRMASI DERSİ LINDO
 ÜRİ MÜHİSLİĞİ BÖLÜMÜ YÖNEYLEM ARAŞTIRMASI DERSİ LINDO Hazırlayanlar Prof. Dr. Bilal TOKLU Arş. Gör. Talip KELLEGÖZ KASIM 2004 1. Giriş 1 LINDO (Linear, INteractive, and Discrete Optimizer) doğrusal ve
ÜRİ MÜHİSLİĞİ BÖLÜMÜ YÖNEYLEM ARAŞTIRMASI DERSİ LINDO Hazırlayanlar Prof. Dr. Bilal TOKLU Arş. Gör. Talip KELLEGÖZ KASIM 2004 1. Giriş 1 LINDO (Linear, INteractive, and Discrete Optimizer) doğrusal ve
Genel Graf Üzerinde Mutlak 1-merkez
 Genel Graf Üzerinde Mutlak 1-merkez Çözüm yöntemine geçmeden önce bazı tanımlara ihtiyaç vardır. Dikkate alınan G grafındaki düğümleri 1 den n e kadar numaralandırın. Uzunluğu a(i, j)>0 olarak verilen
Genel Graf Üzerinde Mutlak 1-merkez Çözüm yöntemine geçmeden önce bazı tanımlara ihtiyaç vardır. Dikkate alınan G grafındaki düğümleri 1 den n e kadar numaralandırın. Uzunluğu a(i, j)>0 olarak verilen
Simpleks Yöntemde Duyarlılık Analizleri
 3.2.4. Simpleks Yöntemde Duyarlılık Analizleri Duyarlılık analizinde doğrusal programlama modelinin parametrelerindeki değişikliklerinin optimal çözüm üzerindeki etkileri araştırılmaktadır. Herhangi bir
3.2.4. Simpleks Yöntemde Duyarlılık Analizleri Duyarlılık analizinde doğrusal programlama modelinin parametrelerindeki değişikliklerinin optimal çözüm üzerindeki etkileri araştırılmaktadır. Herhangi bir
KOMBİNATORYAL OPTİMİZASYON
 KOMBİNATORYAL OPTİMİZASYON İnsanların, daha iyi nasıl olabilir ya da nasıl elde edilebilir?, sorusuna cevap aramaları, teknolojinin gelişmesini sağlayan en önemli etken olmuştur. Gerçek hayatı daha kolay
KOMBİNATORYAL OPTİMİZASYON İnsanların, daha iyi nasıl olabilir ya da nasıl elde edilebilir?, sorusuna cevap aramaları, teknolojinin gelişmesini sağlayan en önemli etken olmuştur. Gerçek hayatı daha kolay
Türk-Alman Üniversitesi. Ders Bilgi Formu
 Türk-Alman Üniversitesi Ders Bilgi Formu Dersin Adı Dersin Kodu Dersin Yarıyılı Yöneylem Araştırması WNG301 5 ECTS Ders Uygulama Laboratuar Kredisi (saat/hafta) (saat/hafta) (saat/hafta) 6 2 2 0 Ön Koşullar
Türk-Alman Üniversitesi Ders Bilgi Formu Dersin Adı Dersin Kodu Dersin Yarıyılı Yöneylem Araştırması WNG301 5 ECTS Ders Uygulama Laboratuar Kredisi (saat/hafta) (saat/hafta) (saat/hafta) 6 2 2 0 Ön Koşullar
ALTIN ORAN ARAMA (GOLDEN SECTION SEARCH) METODU
 ALTIN ORAN ARAMA (GOLDEN SECTION SEARCH) METODU Tek değişkenli bir f(x) fonksiyonunu ele alalım. [Bazı x ler için f (x) bulunamayabilir.] Aşağıdaki DOP modelini çözmek istediğimizi var sayalım. Max f(x)
ALTIN ORAN ARAMA (GOLDEN SECTION SEARCH) METODU Tek değişkenli bir f(x) fonksiyonunu ele alalım. [Bazı x ler için f (x) bulunamayabilir.] Aşağıdaki DOP modelini çözmek istediğimizi var sayalım. Max f(x)
YÖNEYLEM ARAŞTIRMASI - I
 YÖNEYLEM ARAŞTIRMASI - I 1/19 İçerik Yöneylem Araştırmasının Dalları Kullanım Alanları Yöneylem Araştırmasında Bazı Yöntemler Doğrusal (Lineer) Programlama, Oyun Teorisi, Dinamik Programlama, Tam Sayılı
YÖNEYLEM ARAŞTIRMASI - I 1/19 İçerik Yöneylem Araştırmasının Dalları Kullanım Alanları Yöneylem Araştırmasında Bazı Yöntemler Doğrusal (Lineer) Programlama, Oyun Teorisi, Dinamik Programlama, Tam Sayılı
BLM-431 YAPAY ZEKA. Ders-5 Bilgili Arama Yöntemleri. Yrd. Doç. Dr. Ümit ATİLA
 BLM-431 YAPAY ZEKA Ders-5 Bilgili Arama Yöntemleri Yrd. Doç. Dr. Ümit ATİLA [email protected] http://web.karabuk.edu.tr/umitatilla/ Arama Grafları Eğer arama uzayı ağaç yapısından değil de graf
BLM-431 YAPAY ZEKA Ders-5 Bilgili Arama Yöntemleri Yrd. Doç. Dr. Ümit ATİLA [email protected] http://web.karabuk.edu.tr/umitatilla/ Arama Grafları Eğer arama uzayı ağaç yapısından değil de graf
Yöneylem Araştırması I (IE 222) Ders Detayları
 Yöneylem Araştırması I (IE 222) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Yöneylem Araştırması I IE 222 Güz 3 2 0 4 5 Ön Koşul Ders(ler)i Math 275 Doğrusal
Yöneylem Araştırması I (IE 222) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Yöneylem Araştırması I IE 222 Güz 3 2 0 4 5 Ön Koşul Ders(ler)i Math 275 Doğrusal
Kesikli Programlama (IE 506) Ders Detayları
 Kesikli Programlama (IE 506) Ders Detayları Ders Adı Ders Dönemi Ders Uygulama Laboratuar Kredi AKTS Kodu Saati Saati Saati Kesikli Programlama IE 506 Güz 3 0 0 3 7.5 Ön Koşul Ders(ler)i Dersin Dili Dersin
Kesikli Programlama (IE 506) Ders Detayları Ders Adı Ders Dönemi Ders Uygulama Laboratuar Kredi AKTS Kodu Saati Saati Saati Kesikli Programlama IE 506 Güz 3 0 0 3 7.5 Ön Koşul Ders(ler)i Dersin Dili Dersin
yöneylem araştırması Nedensellik üzerine diyaloglar I
 yöneylem araştırması Nedensellik üzerine diyaloglar I i Yayın No : 3197 Eğitim Dizisi : 149 1. Baskı Ocak 2015 İSTANBUL ISBN 978-605 - 333-225 1 Copyright Bu kitabın bu basısı için Türkiye deki yayın hakları
yöneylem araştırması Nedensellik üzerine diyaloglar I i Yayın No : 3197 Eğitim Dizisi : 149 1. Baskı Ocak 2015 İSTANBUL ISBN 978-605 - 333-225 1 Copyright Bu kitabın bu basısı için Türkiye deki yayın hakları
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Quadratic Programming Bir karesel programlama modeli aşağıdaki gibi tanımlanır. Amaç fonksiyonu: Maks.(veya Min.) z
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Quadratic Programming Bir karesel programlama modeli aşağıdaki gibi tanımlanır. Amaç fonksiyonu: Maks.(veya Min.) z
OPTİMİZASYON TEKNİKLERİ-2. Hafta
 GİRİŞ OPTİMİZASYON TEKNİKLERİ-2. Hafta Mühendislik açısından bir işin tasarlanıp, gerçekleştirilmesi yeterli değildir. İşin en iyi çözüm yöntemiyle en verimli bir şekilde yapılması bir anlam ifade eder.
GİRİŞ OPTİMİZASYON TEKNİKLERİ-2. Hafta Mühendislik açısından bir işin tasarlanıp, gerçekleştirilmesi yeterli değildir. İşin en iyi çözüm yöntemiyle en verimli bir şekilde yapılması bir anlam ifade eder.
Türk-Alman Üniversitesi İktisadi ve İdari Bilimler Fakültesi İşletme Bölümü Ders Bilgi Formu
 Türk-Alman Üniversitesi İktisadi ve İdari Bilimler Fakültesi İşletme Bölümü Ders Bilgi Formu Dersin Adı Dersin Kodu Dersin Yarıyılı Yöneylem Araştırması BWL315 5 ECTS Ders Uygulama Laboratuar Kredisi (saat/hafta)
Türk-Alman Üniversitesi İktisadi ve İdari Bilimler Fakültesi İşletme Bölümü Ders Bilgi Formu Dersin Adı Dersin Kodu Dersin Yarıyılı Yöneylem Araştırması BWL315 5 ECTS Ders Uygulama Laboratuar Kredisi (saat/hafta)
KISALTILMIŞ SİMPLEKS YÖNTEMİ
 KISALTILMIŞ SİMPLEKS YÖNTEMİ Öğr. Görv. Dr. Orhan İDİL (İ.Ü. İşletme Fakültesi) İstatistik Demografi ve İktisadi Analizler Kürsüsü l.l. Doğrusal Programlama Problemleri : Doğrusal programlama problemlerinde
KISALTILMIŞ SİMPLEKS YÖNTEMİ Öğr. Görv. Dr. Orhan İDİL (İ.Ü. İşletme Fakültesi) İstatistik Demografi ve İktisadi Analizler Kürsüsü l.l. Doğrusal Programlama Problemleri : Doğrusal programlama problemlerinde
OPTİMİZASYON TEKNİKLERİ. Kısıtsız Optimizasyon
 OPTİMİZASYON TEKNİKLERİ Kısıtsız Optimizasyon Giriş Klasik optimizasyon yöntemleri minimum veya maksimum değerlerini bulmak için türev gerektiren ve gerektirmeyen teknikler olarak bilinirler. Bu yöntemler
OPTİMİZASYON TEKNİKLERİ Kısıtsız Optimizasyon Giriş Klasik optimizasyon yöntemleri minimum veya maksimum değerlerini bulmak için türev gerektiren ve gerektirmeyen teknikler olarak bilinirler. Bu yöntemler
Temelleri. Doç.Dr.Ali Argun Karacabey
 Doğrusal Programlamanın Temelleri Doç.Dr.Ali Argun Karacabey Doğrusal Programlama Nedir? Bir Doğrusal Programlama Modeli doğrusal kısıtlar altında bir doğrusal ğ fonksiyonun değerini ğ maksimize yada minimize
Doğrusal Programlamanın Temelleri Doç.Dr.Ali Argun Karacabey Doğrusal Programlama Nedir? Bir Doğrusal Programlama Modeli doğrusal kısıtlar altında bir doğrusal ğ fonksiyonun değerini ğ maksimize yada minimize
Doğrusal Programlama (IE 502) Ders Detayları
 Doğrusal Programlama (IE 502) Ders Detayları Ders Adı Ders Dönemi Ders Uygulama Laboratuar Kredi AKTS Kodu Saati Saati Saati Doğrusal Programlama IE 502 Güz 3 0 0 3 7.5 Ön Koşul Ders(ler)i Dersin Dili
Doğrusal Programlama (IE 502) Ders Detayları Ders Adı Ders Dönemi Ders Uygulama Laboratuar Kredi AKTS Kodu Saati Saati Saati Doğrusal Programlama IE 502 Güz 3 0 0 3 7.5 Ön Koşul Ders(ler)i Dersin Dili
DOKUZ EYLÜL ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ DEKANLIĞI DERS/MODÜL/BLOK TANITIM FORMU. Dersin Kodu: END 3519
 Dersi Veren Birim: Endüstri Mühendisliği Dersin Türkçe Adı: YÖNEYLEM ARAŞTIRMASI I Dersin Orjinal Adı: YÖNEYLEM ARAŞTIRMASI I Dersin Düzeyi:(Ön lisans, Lisans, Yüksek Lisans, Doktora) Lisans Dersin Kodu:
Dersi Veren Birim: Endüstri Mühendisliği Dersin Türkçe Adı: YÖNEYLEM ARAŞTIRMASI I Dersin Orjinal Adı: YÖNEYLEM ARAŞTIRMASI I Dersin Düzeyi:(Ön lisans, Lisans, Yüksek Lisans, Doktora) Lisans Dersin Kodu:
EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER
 EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER LAGRANGE YÖNTEMİ Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde değişkenler ve kısıtlar genel olarak şeklinde gösterilir. fonksiyonlarının
EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER LAGRANGE YÖNTEMİ Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde değişkenler ve kısıtlar genel olarak şeklinde gösterilir. fonksiyonlarının
TRAKYA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MAKİNA MÜHENDİSLİĞİ ANABİLİM DALI DOKTORA PROGRAMI ŞEKİL TANIMA ÖDEV 2 KONU : DESTEK VEKTÖR MAKİNELERİ
 TRAKYA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MAKİNA MÜHENDİSLİĞİ ANABİLİM DALI DOKTORA PROGRAMI ŞEKİL TANIMA ÖDEV 2 KONU : DESTEK VEKTÖR MAKİNELERİ Kenan KILIÇASLAN Okul No:1098107203 1. DESTEK VEKTÖR MAKİNELER
TRAKYA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MAKİNA MÜHENDİSLİĞİ ANABİLİM DALI DOKTORA PROGRAMI ŞEKİL TANIMA ÖDEV 2 KONU : DESTEK VEKTÖR MAKİNELERİ Kenan KILIÇASLAN Okul No:1098107203 1. DESTEK VEKTÖR MAKİNELER
ĐST 349 Doğrusal Programlama ARA SINAV I 15 Kasım 2006
 ĐST 49 Doğrusal Programlama ARA SINAV I 15 Kasım 006 Adı Soyadı:KEY No: 1. Aşağıdaki problemi grafik yöntemle çözünüz. Đkinci kısıt için marjinal değeri belirleyiniz. Maximize Z X 1 + 4 X subject to: X
ĐST 49 Doğrusal Programlama ARA SINAV I 15 Kasım 006 Adı Soyadı:KEY No: 1. Aşağıdaki problemi grafik yöntemle çözünüz. Đkinci kısıt için marjinal değeri belirleyiniz. Maximize Z X 1 + 4 X subject to: X
Yöneylem Araştırması II (IE 323) Ders Detayları
 Yöneylem Araştırması II (IE 323) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Yöneylem Araştırması II IE 323 Güz 3 2 0 4 5.5 Ön Koşul Ders(ler)i IE 222
Yöneylem Araştırması II (IE 323) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Yöneylem Araştırması II IE 323 Güz 3 2 0 4 5.5 Ön Koşul Ders(ler)i IE 222
YÖNEYLEM ARAŞTIRMASI-I
 YÖNEYLEM ARAŞTIRMASI-I İST205U KISA ÖZET DİKKAT Burada ilk 4 sahife gösterilmektedir. Özetin tamamı için sipariş veriniz www.kolayaof.com 1 1.ÜNİTE Yöneylem Araştırmasına Giriş GİRİŞ Yöneylem Araştırması
YÖNEYLEM ARAŞTIRMASI-I İST205U KISA ÖZET DİKKAT Burada ilk 4 sahife gösterilmektedir. Özetin tamamı için sipariş veriniz www.kolayaof.com 1 1.ÜNİTE Yöneylem Araştırmasına Giriş GİRİŞ Yöneylem Araştırması
KONU 13: GENEL UYGULAMA
 KONU : GENEL UYGULAMA Kahve üretimi apan bir şirket anı zamanda cezve ve fincan üretmektedir. Üretilen cezveler ve fincanlar boama kısmında işlem görmekte ve arıca fincanlar kaplanmaktadır. Bir cezve apımı
KONU : GENEL UYGULAMA Kahve üretimi apan bir şirket anı zamanda cezve ve fincan üretmektedir. Üretilen cezveler ve fincanlar boama kısmında işlem görmekte ve arıca fincanlar kaplanmaktadır. Bir cezve apımı
KİNETİK MODEL PARAMETRELERİNİN BELİRLENMESİNDE KULLANILAN OPTİMİZASYON TEKNİKLERİNİN KIYASLANMASI
 KİNETİK MODEL PARAMETRELERİNİN BELİRLENMESİNDE KULLANILAN OPTİMİZASYON TEKNİKLERİNİN KIYASLANMASI Hatice YANIKOĞLU a, Ezgi ÖZKARA a, Mehmet YÜCEER a* İnönü Üniversitesi Mühendislik Fakültesi Kimya Mühendisliği
KİNETİK MODEL PARAMETRELERİNİN BELİRLENMESİNDE KULLANILAN OPTİMİZASYON TEKNİKLERİNİN KIYASLANMASI Hatice YANIKOĞLU a, Ezgi ÖZKARA a, Mehmet YÜCEER a* İnönü Üniversitesi Mühendislik Fakültesi Kimya Mühendisliği
Üretim Sistemleri (IE 509) Ders Detayları
 Üretim Sistemleri (IE 509) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Üretim Sistemleri IE 509 Seçmeli 3 0 0 3 7.5 Ön Koşul Ders(ler)i Dersin Dili Dersin
Üretim Sistemleri (IE 509) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Saati Uygulama Saati Laboratuar Saati Kredi AKTS Üretim Sistemleri IE 509 Seçmeli 3 0 0 3 7.5 Ön Koşul Ders(ler)i Dersin Dili Dersin
HESSİEN MATRİS QUADRATİK FORM MUTLAK ve BÖLGESEL MAKS-MİN NOKTALAR
 HESSİEN MATRİS QUADRATİK FORM MUTLAK ve BÖLGESEL MAKS-MİN NOKTALAR Kısıtlı ve kısıtsız fonksiyonlar için maksimum veya minimum (ekstremum) noktalarının belirlenmesinde diferansiyel hesabı kullanarak çeşitli
HESSİEN MATRİS QUADRATİK FORM MUTLAK ve BÖLGESEL MAKS-MİN NOKTALAR Kısıtlı ve kısıtsız fonksiyonlar için maksimum veya minimum (ekstremum) noktalarının belirlenmesinde diferansiyel hesabı kullanarak çeşitli
ENDÜSTRİ MÜHENDİSLİĞİ BÖLÜM BAŞKANLIĞI DERS TANITIM BİLGİLERİ
 ENDÜSTRİ MÜHENDİSLİĞİ BÖLÜM BAŞKANLIĞI DERS TANITIM BİLGİLERİ Dersin Adı Kodu Sınıf/Y.Y. Ders Saati Kredi AKTS (T+U+L) ŞEBEKE MODELLERİ EN-413 4/I 3+0+0 3 5 Dersin Dili : İngilizce Dersin Seviyesi : Lisans
ENDÜSTRİ MÜHENDİSLİĞİ BÖLÜM BAŞKANLIĞI DERS TANITIM BİLGİLERİ Dersin Adı Kodu Sınıf/Y.Y. Ders Saati Kredi AKTS (T+U+L) ŞEBEKE MODELLERİ EN-413 4/I 3+0+0 3 5 Dersin Dili : İngilizce Dersin Seviyesi : Lisans
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Yönetim için Sayısal Yöntemler (AVM306) Ders Detayları
 Yönetim için Sayısal Yöntemler (AVM306) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Uygulama Laboratuar Kredi AKTS Saati Saati Saati Yönetim için Sayısal Yöntemler AVM306 Bahar 3 0 0 3 6 Ön Koşul Ders(ler)i
Yönetim için Sayısal Yöntemler (AVM306) Ders Detayları Ders Adı Ders Kodu Dönemi Ders Uygulama Laboratuar Kredi AKTS Saati Saati Saati Yönetim için Sayısal Yöntemler AVM306 Bahar 3 0 0 3 6 Ön Koşul Ders(ler)i
18.034 İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 2- HATA VE HATA KAYNAKLARI Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ Bir denklemin veya problemin çözümünde kullanılan sayısal yöntem belli bir giriş verisini işleme tabi tutarak sayısal
MAK 210 SAYISAL ANALİZ BÖLÜM 2- HATA VE HATA KAYNAKLARI Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ Bir denklemin veya problemin çözümünde kullanılan sayısal yöntem belli bir giriş verisini işleme tabi tutarak sayısal
Ders Kodu Dersin Adı Yarıyıl Teori Uygulama Lab Kredisi AKTS IND 621 Stokastik Süreçler
 İçerik Ders Kodu Dersin Adı Yarıyıl Teori Uygulama Lab Kredisi AKTS IND 621 Stokastik Süreçler 1 3 0 0 3 8 Ön Koşul Derse Kabul Koşulları Dersin Dili Türü Dersin Düzeyi Dersin Amacı İngilizce Zorunlu Doktora
İçerik Ders Kodu Dersin Adı Yarıyıl Teori Uygulama Lab Kredisi AKTS IND 621 Stokastik Süreçler 1 3 0 0 3 8 Ön Koşul Derse Kabul Koşulları Dersin Dili Türü Dersin Düzeyi Dersin Amacı İngilizce Zorunlu Doktora
YÖNEYLEM ARAŞTIRMASI - III
 YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Hessien Matris-Quadratik Form Mutlak ve Bölgesel Maksimum-Minimum Noktalar Giriş Kısıtlı ve kısıtsız fonksiyonlar için
YÖNEYLEM ARAŞTIRMASI - III Prof. Dr. Cemalettin KUBAT Yrd. Doç. Dr. Özer UYGUN İçerik Hessien Matris-Quadratik Form Mutlak ve Bölgesel Maksimum-Minimum Noktalar Giriş Kısıtlı ve kısıtsız fonksiyonlar için
a2 b3 cij: birim başına ulaşım maliyeti xij: taşıma miktarı
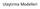 Ulaştırma Modelleri Ulaştırma modeli Ulaştırma modeli doğrusal programlama modellerinin özel bir türüdür. Modelin amacı bir işletmenin belirli kapasitedeki üretim merkezlerinden, belirli talebi olan tüketim
Ulaştırma Modelleri Ulaştırma modeli Ulaştırma modeli doğrusal programlama modellerinin özel bir türüdür. Modelin amacı bir işletmenin belirli kapasitedeki üretim merkezlerinden, belirli talebi olan tüketim
4. HAFTA BLM323 SAYISAL ANALİZ. Okt. Yasin ORTAKCI.
 4. HAFTA BLM33 SAYISAL ANALİZ Okt. Yasin ORTAKCI [email protected] Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi BLM33 DOĞRUSAL OLMAYAN (NONLINEAR) DENKLEM SİSTEMLERİ Mühendisliğin
4. HAFTA BLM33 SAYISAL ANALİZ Okt. Yasin ORTAKCI [email protected] Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi BLM33 DOĞRUSAL OLMAYAN (NONLINEAR) DENKLEM SİSTEMLERİ Mühendisliğin
GEOMETRİK PROGRAMLAMADA GEOMETRİK-HARMONİK ORTALAMA EŞİTSİZLİGİNİN ROLÜ VE FONKSİYONEL
 M.Ü.İ.İ.B.F. Dergisi Prof.Dr.Kenan ERKURAL'a Armağan Yıl:J998, Cilt: XIV, Say. ı:2, s.53-59. GEOMETRİK PROGRAMLAMADA GEOMETRİK-HARMONİK ORTALAMA EŞİTSİZLİGİNİN ROLÜ VE FONKSİYONEL 1-GİRİŞ DÖNÜŞÜMLER Tuncay
M.Ü.İ.İ.B.F. Dergisi Prof.Dr.Kenan ERKURAL'a Armağan Yıl:J998, Cilt: XIV, Say. ı:2, s.53-59. GEOMETRİK PROGRAMLAMADA GEOMETRİK-HARMONİK ORTALAMA EŞİTSİZLİGİNİN ROLÜ VE FONKSİYONEL 1-GİRİŞ DÖNÜŞÜMLER Tuncay
DERS BİLGİLERİ. Ders Kodu Yarıyıl T+U Saat Kredi AKTS KOMBİNATORİK ENİYİLEME ESYE
 DERS BİLGİLERİ Ders Kodu Yarıyıl T+U Saat Kredi AKTS KOMBİNATORİK ENİYİLEME ESYE621 3+0 3 7 Ön Koşul Dersleri ISE222 veya eşdeğer bir optimizasyona giriş dersi Dersin Dili Dersin Seviyesi Dersin Türü İngilizce
DERS BİLGİLERİ Ders Kodu Yarıyıl T+U Saat Kredi AKTS KOMBİNATORİK ENİYİLEME ESYE621 3+0 3 7 Ön Koşul Dersleri ISE222 veya eşdeğer bir optimizasyona giriş dersi Dersin Dili Dersin Seviyesi Dersin Türü İngilizce
DİĞER ANALİZ TEKNİKLERİ
 DİĞER ANALİZ TEKNİKLERİ İÇERİK EŞDEĞERLİK DOĞRUSALLIK KAYNAK DÖNÜŞÜMÜ SUPERPOZİSYONUN UYGULANMASI THEVENIN VE NORTON TEOREMLERİ ENFAZLA GÜÇ AKTARIMI EE-201, Ö.F.BAY 1 DİĞER ANALİZ TEKNİKLERİ ÖĞRENME HEDEFLERİ
DİĞER ANALİZ TEKNİKLERİ İÇERİK EŞDEĞERLİK DOĞRUSALLIK KAYNAK DÖNÜŞÜMÜ SUPERPOZİSYONUN UYGULANMASI THEVENIN VE NORTON TEOREMLERİ ENFAZLA GÜÇ AKTARIMI EE-201, Ö.F.BAY 1 DİĞER ANALİZ TEKNİKLERİ ÖĞRENME HEDEFLERİ
Önsöz... XIII Önsöz (Hava Harp Okulu Basımı)...XV BÖLÜM 1 1. YÖNEYLEM ARAŞTIRMASINA GİRİŞ... 1
 İÇİNDEKİLER Önsöz... XIII Önsöz (Hava Harp Okulu Basımı)...XV BÖLÜM 1 1. YÖNEYLEM ARAŞTIRMASINA GİRİŞ... 1 1.1. Yöneticilik / Komutanlık İşlevi ve Gerektirdiği Nitelikler... 2 1.1.1. Yöneticilik / Komutanlık
İÇİNDEKİLER Önsöz... XIII Önsöz (Hava Harp Okulu Basımı)...XV BÖLÜM 1 1. YÖNEYLEM ARAŞTIRMASINA GİRİŞ... 1 1.1. Yöneticilik / Komutanlık İşlevi ve Gerektirdiği Nitelikler... 2 1.1.1. Yöneticilik / Komutanlık
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
DEÜ MÜHENDİSLİK FAKÜLTESİ MÜHENDİSLİK BİLİMLERİ DERGİSİ Cilt: 13 Sayı:1 sh.1-8 Ocak 2011
 DEÜ MÜHENDİSLİK FAKÜLTESİ MÜHENDİSLİK BİLİMLERİ DERGİSİ Cilt: 13 Sayı:1 sh.1-8 Ocak 011 BİR KAMPÜS AĞINDA ACİL TELEFON MERKEZLERİ YERLEŞTİRİLMESİ PROBLEMİNİN MATEMATİKSEL MODELLEMESİ (MATHEMATICAL MODELLING
DEÜ MÜHENDİSLİK FAKÜLTESİ MÜHENDİSLİK BİLİMLERİ DERGİSİ Cilt: 13 Sayı:1 sh.1-8 Ocak 011 BİR KAMPÜS AĞINDA ACİL TELEFON MERKEZLERİ YERLEŞTİRİLMESİ PROBLEMİNİN MATEMATİKSEL MODELLEMESİ (MATHEMATICAL MODELLING
Altın Oran Arama Metodu(Golden Search)
 Altın Oran Arama Metodu(Golden Search) Bir f(x) (tek değişkenli) fonksiyonunu ele alalım. [Bazı x ler için f (x) bulunamayabilir.] Aşağıdaki DOP modelini çözmek istediğimizi var sayalım. Max f(x) a x b
Altın Oran Arama Metodu(Golden Search) Bir f(x) (tek değişkenli) fonksiyonunu ele alalım. [Bazı x ler için f (x) bulunamayabilir.] Aşağıdaki DOP modelini çözmek istediğimizi var sayalım. Max f(x) a x b
Ulaştırma ve Atama. Konu 2. Ulaştırma Modeli. Doç. Dr. Fazıl GÖKGÖZ
 Ulaştırma ve Atama Modelleri Konu 2 Ulaştırma Modeli 1. Farklı kaynaklardan temin edilen bir ürün, mümkün olan minimum maliyetle farklı istikametlere taşınmaktadır. 2. Her kaynak noktası sabit sayıda ürün
Ulaştırma ve Atama Modelleri Konu 2 Ulaştırma Modeli 1. Farklı kaynaklardan temin edilen bir ürün, mümkün olan minimum maliyetle farklı istikametlere taşınmaktadır. 2. Her kaynak noktası sabit sayıda ürün
DOKUZ EYLÜL ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ DEKANLIĞI DERS/MODÜL/BLOK TANITIM FORMU. Dersin Kodu: MAT 1009
 Dersi Veren Birim: Mühendislik Fakültesi Dersin Türkçe Adı: MATEMATİK I Dersin Orjinal Adı: MATEMATİK I Dersin Düzeyi:(Ön lisans, Lisans, Yüksek Lisans, Doktora) Lisans Dersin Kodu: MAT 1009 Dersin Öğretim
Dersi Veren Birim: Mühendislik Fakültesi Dersin Türkçe Adı: MATEMATİK I Dersin Orjinal Adı: MATEMATİK I Dersin Düzeyi:(Ön lisans, Lisans, Yüksek Lisans, Doktora) Lisans Dersin Kodu: MAT 1009 Dersin Öğretim
Ulaştırma Problemleri
 Ulaştırma Problemleri Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir. Bu modelde, malların kaynaklardan (fabrika gibi )hedeflere (depo gibi) taşınmasıyla ilgilenir. Buradaki amaç
Ulaştırma Problemleri Ulaştırma modeli, doğrusal programlama probleminin özel bir şeklidir. Bu modelde, malların kaynaklardan (fabrika gibi )hedeflere (depo gibi) taşınmasıyla ilgilenir. Buradaki amaç
