YAPI STATİĞİ II. Hasan KAPLAN. Denizli (İlk Baskı 1999-Gözden Geçirilmekte olan Taslak Kitap)
|
|
|
- Umut Derviş
- 6 yıl önce
- İzleme sayısı:
Transkript
1 YAPI STATİĞİ II Hasan KAPLAN Denizli-3 (İlk Baskı 999-Gözden Geçirilmekte olan Taslak Kitap) Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli
2 ÖNSÖZ Bu kitapta, deplasman yöntemi ile çubuklardan oluģan taģıyıcı sistemlerin analizi yer almaktadır. Çubuklardan oluģan taģıyıcı sistem modellerinin sonlu elemanlar yönteminin çubuk sistemler içi özel uygulaması olan rijitlik matrisi yöntemi ile çözümü hedeflenmiģtir. Rijitlik matrisi yöntemi, bir taģıyıcı sistemin tanımlanmıģ düğümlerde birleģen elemanlar ile modellenmesi ve sisteme etkiyen yükler ile sistemin özellikleri arasında yazılacak iliģki ile düğümlerdeki ötelenme ve dönemlerin hesaplanmasına dayanmaktadır. Sistemin bilinmeyen deplasmanları ile bilinen yükleri arasında iliģki kuran matrisin oluģturulması ile çözüm yapılmaktadır. Kitabın lisans düzeyinde okutulmakta olan YAPI STATĠĞĠ II derslerinde kaynak alınması beklenmektedir. Bunun yanında Yüksek Lisans düzeyinde de verilen Ġleri Yapı Analizi konularında da yararlı olabilecektir. Birinci bölümde, çubuk taģıyıcı sistemler ve hiperstatiklik dereceleri, ikinci bölümde, çubuklardan oluģan taģıyıcı sistemlerin ve çubukların serbestlik dereceleri yer almaktadır. Üçüncü bölümde, rijitlik kavramı verilmekte ve çubuklar için rijitlik etki katsayılarının nasıl elde edildiği verilmektedir. Dördüncü bölümde koordinat dönüģümü yer almıģtır. Altıncı bölümde rijitlik matrisi yöntemi, yedinci bölümde ise çubuklardan oluģan çeģitli taģıyıcı sistem modellerinin rijitlik matrisi ile çözümü verilmektedir. Sekizinci ve dokuzuncu bölümlerde kısaca Açı ve Cross yöntemleri ele alınmıģtır. Ek de yapı analizi için bilinmesi Ģart olan matrisler ve matrislerle iģlemler yer almaktadır. Ek de ise çok kullanılan bazı tablolar verilmiģtir. Yapıların taģıyıcı sistemlerinin analizinde deplasman yöntemine dayalı yazılımlar kullanılmaktadır. Hiperstatik sistemlerin çözümünün Kuvvet, Cross ve Açı yöntemleri kullanılabilmektedir. Kuvvet yöntemi, her taģıyıcı sistem için sistematik olmadığından programlamaya elveriģli değildir. Bir takım basitleģtirici kabuller içeren Cross ve Açı (ikisi aynı) yöntemleri ise kesin sonuçlardan oldukça uzaklaģmaktadırlar. Bilgisayarlar ile yapılan çözümlerde kullanılan sonlu elemanlar yöntemi ile en uyumlu olanı Rijitlik matrisi yöntemidir. Açı ve Cross yöntemleri için kullanılan denklemler rijitlik matrisi yöntemi ile ilgili denklemlerden kolayca elde edilebilmektedir. Bu kitapta uygulanmakta olan YAPI STATĠĞĠ II dersi kapsamında yer alan konular verilmeye çalıģılmıģtır. Rijitlik matrisi ile ilgili kavramların anlaģılması ile kolayca öğrenilebilecek olan Açı ve Cross (Moment Dağıtma) yöntemi ile ilgili kısımlar kısa tutulmuģtur. Mekanik ve Yapı statiği I dersi kapsamındaki konuların (özellikle kuvvet yöntemi) biliniyor olması, anlama kolaylığı sağlayacaktır. Kitabın geliģtirilmesi için interaktif yazılımlar kullanılması ile mümkündür. Ele alınana örneklerin yük-deplasman iliģkilerinin yazılımlar ile görsel olarak ifade edilmesi ve okuyucuya sunulması mümkündür. Yapı statiği I Müfredatı içinde yer alan, Kuvvet Metodu ve Tesir çizgileri de kitap kapsamı içine alınabilir. Perdeli yapıların hesabı için bir bölüm ayrılabilir. DavranıĢa yönelik daha fazla görseller içeren örnekler ve çözümlerdeki kabullerin dayandığı bazı temel prensipler de kitaba ilave edilebilir. Faydalı olması ümidi ile Hasan KAPLAN, 3 Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli
3 . Hiperstatik Sistemlerin Tanımı GİRİŞ Yapılan Kabuller Statikçe Hiperstatiklik Hiperstatiklik Derecesinin Hesaplanması.... SERBESTLİK DERECELERİ GİRİŞ Çubuklar ve Serbestlik Dereceleri Sistem Serbestlik Derecesi Düzlem Kafes sistemin Serbestlik Derecesi Uzay Kafes Sistemin Serbestlik Derecesi Düzlem Çerçevenin Serbestlik Derecesi Uzay Çerçevenin Serbestlik Derecesi Düzlem Izgara Sistemin Serbestlik Derecesi Rijitlik ve Rijitlik Etki Katsayıları Giriş Rijitlik kavramı ve rijitlik denklemi Çubuk rijitlik denklemleri Düzlem kafes çubuğu rijitlik denklemi Düzlem Çerçeve Çubuğu Rijitlik Denklemi Düzlem Çerçeve Çubuğu rijitlik etki katsayıları Izgara Sistem Çubuğu Rijitlik Denklemi Uzay Çerçeve Çubuğunun Rijitlik Katsayıları KOORDİNAT DÖNÜŞÜMÜ Düzlem sistemler için koordinat dönüşümü Düzlem Kafes Sistemde koordinat dönüşümü Düzlem Çerçeve Çubuğunda Koordinat Dönüşümü Uzay sistemler için koordinat dönüşümü Uzay çerçeve Çubuğu Transformasyon Matrisi Sistem Koordinatlarında Eleman Rijitlik Denklemi ANKASTRELİK UÇ KUVVETLERİ RİJİTLİK MATRİSİ YÖNTEMİ Giriş Rijitlik Matrisi Yönteminde İşlem Sırası Kotlama Tekniği RİJİTLİK MATRİSİ YÖNTEMİ -ÇÖZÜMLÜÖRNEKLER GİRİŞ AÇI METODU GİRİŞ Rijitlik Matrisi Yöntemi ile ilişki Düğüm noktası sabit sistemlerin Açı yöntemi ile çözümü Düğüm noktası sabit sistemlerin Açı yöntemi ile çözümü İçin Takip edilecek adımlar Düğüm noktası Hareketli sistemler CROSS YÖNTEMİ GİRİŞ Düğüm noktaları Sabit Sistemler Moment Dağıtma ve geçiş katsayıları Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 3
4 9.. Düğüm Noktası sabit sistemlerin Çözümünde İşlem Sırası BİLGİSAYAR İLE MODELLENEREK ÇÖZÜMÜ YAPILAN ÇEŞİTLİ TAŞIYICI SİSTEMLER SAP9 İLE İLGİLİ BİLGİLER BAZI PROBLEMLER İÇİN SAP9 DATA DOSYALARI Bilgisayar ile çözümü yapılan bazı taģıyıcı sistemlerin modelleri verilmiģtir. Çözümde SAP 9 veya SAP kullanılmıģtır SAP İLE YAPI ANALİZİ... 5 Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 4
5 . GİRİŞ B Ö L Ü M I. H i p e r s t a t i k S i s t e m l e r i n Ta n ı m ı Gerçekte taģıyıcı sistemi oluģturan elemanlar üç boyutludur. Ancak bir çok taģıyıcı sistem elemanının sadece uzunlukları kullanılarak taģıyıcı sistem Ģeması elde edilir. Bu tür elemanlara çubuk, oluģturulan sisteme de çubuk sistemler denilmektedir. Lisans düzeyindeki yapı analizi derslerinde de bu sistemlerin kesit tesirlerinin belirlenmesi hedeflenir. Bu kitabın önemli bir bölümü, çubuklardan oluģan taģıyıcı sistemlerin analizine ayrılmıģtır. Ele alınan tipik çubuk sistemler; sürekli kiriģ, düzlem kafes, düzlem çerçeve, uzay çerçeve, ızgara sistem ve uzay kafes sistemler olarak sınıflandırılabilir (ġekil.). a) Sürekli kiriş b) Düzlem kafes kiriş c) Düzlem çerçeve d) Tek katlı uzay çerçeve e) Izgara Sistem f) Uzay kafes ġekil. Çubuklardan oluģan taģıyıcı sistemler Bilgi ve iletiģim çağının en vazgeçilmez aracı bilgisayarlar olmaktadır. Her alanda kullanılmaya baģlayan bilgisayarlar yapı analizinde de kullanılmaktadır. Bilgisayar kullanımının yaygınlaģması ile klasik yöntemler yerini modern yöntemlere terk etmektedir. Bilgisayar gerektirmeyen yöntemlerle çözümler yapılarak sistemlerin davranıģlarının öğrenilmesi de önem arz etmektedir. Yapısal analiz yapacak olan mühendis adayları, yaklaģık yöntemlerle ancak davranıģ bilgisi ve kesit tesirleri hakkında bilgi edinebilmektedir. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 5
6 Uygulamaya atıldığında, tüm çözümlerin bilgisayar ile yapıldığı bir ortamla karģılaģılmakta, teori ve uygulama arasında geçiģ sağlayamamaktadır. Bunun için Lisans düzeyinde verilen Yapı Statiği derslerinde sadece el ile çözüme dayalı yöntemlerin öğretilmesinin yanında, bilgisayar destekli modern yöntemlerin de verilmesi gerekmektedir. Bir köprü (kiriş) Bir sanayii yapısında düzlem kafes sistem kullanılması Hasar görmüģ bir taģıyıcı sistem ġekil. Çubuklarla teģkil edilen çeģitli yapılar Bu kitapta bir takım basitleģtirici kabullere dayalı olarak geliģtirilen klasik yöntemler ile daha kesin çözümler sunan modern yöntemlerin bir karģılaģtırılması da yapılmaktadır. El ile çözüme dayalı klasik yöntemlerin lisans düzeyindeki eğitimde kullanılması ancak gerçek Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 6
7 sistemlerin çözümünde mutlaka bilgisayarlar kullanılarak daha gerçekçi çözümlerin yapılması gerektiği hususu da açık bir Ģekilde ortaya konmaktadır... Yapılan Kabuller Bu kitapta verilen çözümlerde Ģu kabuller yapılmaktadır; Ele alınan sistemler statik yükler için çözülmektedir Sistemler için yük-deplasman iliģkisinin lineer olduğu kabul edilmiģtir. Böylece ele alınan sistemlerin malzemesinin Hooke yasasına uyduğu kabul edilmiģtir. Deplasmanların sistemin geometrisine nazaran çok küçük olduğu dolayısıyla yapının geometrisinde bozulma olmadığı kabul edilmektedir. Süperpozisyon prensibi geçerlidir. Bu durumda, farklı yüklemeler için elde edilen kesit tesirleri ve deplasmanlar süperpozisyon prensibi ile toplanarak, yüklerin tamamının birlikte etkimesi halindeki kesit tesirleri ve deplasmanlar elde edilebilecektir. Gerçekte, betonarmeden teģkil edilen taģıyıcı sistemlerde malzemenin yük-deplasman iliģkisi lineer olmamaktadır. Ancak uygulamada, yapıların büyük bir bölümü küçük miktarda deplasman yapacak Ģekilde dizayn edilmektedirler. Deplasman değerlerinin, elemanın geometrisi yanında çok küçük olması halinde sistemlerin lineer davrandığı kabul edilebilir. Daha hassas çözüm gerektiren yapılar için lineer olmayan elosto-plastik davranıģ dikkate alınarak analizler yapılmalıdır... Statikçe Hiperstatiklik XYZ Uzayında, dıģ yüklerin etkisinde olan bir taģıyıcı sistemi ele alalım. Sistemin dengede olması için x,y ve z eksenlerine göre yazılacak denge denklemlerinin sağlanması gerekir. Yani her eksen için, eksen doğrultusunda etkiyen doğrusal kuvvetlerin toplamı ve eksen etrafında etkiyen momentlerin toplamı sıfıra eģit olmalıdır. (.) Denge denklemindeki yük ifadesi içine mesnet reaksiyonları da dahil edilmektedir. DıĢ yükler elemanlar tarafından mesnetlere aktarılmakta ve aktarılan bu kuvvetlere karģı mesnetlerde reaksiyonlar oluģmaktadır. Sistemin dengede olabilmesi için, mesnetlerde oluģan reaksiyonların da dikkate alınması ile yazılacak olan. denge denklemlerinin sağlanması gerekir. düzlem veya uzay sistemler için denge denklemi sayısı farklıdır. Uzay sistem için her eksen yönünde kuvvetler ve her eksen etrafında momentler olmak üzere toplam altı adet denge denklemi yazılabilir. Düzlem taģıyıcı sistemlerde denge denklemi sayısı üçe inecektir. Bu durumda denge için. de ifadesi ile verilen Ģartların sağlanması gerekir. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 7
8 (.) Bir taģıyıcı sistemin analizi, yüklerden dolayı oluģan; mesnet reaksiyonlarının, deformasyonların ve sistemi meydana getiren elemanların iç kuvvetlerinin hesaplanmasını kapsar. Eleman iç kuvvetli olan Eksenel kuvvet, kesme kuvveti ve eğilme momentinin elemanların uzunlukları boyunca nasıl değiģtiğinin grafik olarak gösterilmesi ve maksimum değerlerinin ortaya konulması da analizin amacıdır. Ġç kuvvetlere kesit tesirleri, çizilen grafiklere de kesit tesirleri diyagramı da denilmektedir. İzostatik Sistem: Bir taģıyıcı sistemde, mesnet reaksiyonları ve herhangi bir kesitteki kesit tesirleri denge denklemleri ile hesaplanabiliyorsa, bu tür sistemlere izostatik sistemler denilir. Hiperstatik Sistem: Bir taģıyıcı sistemde denge denklemlerinden fazla bilinmeyen varsa bu tür sistemlere statikçe hiperstatik sistemler denilir. TaĢıyıcı sistem içten veya dıģtan hiperstatik olabilir. Bazı sistemler hem içten hem de dıģtan hiperstatiktir. Dıştan hiperstatik sistemler; Bir sistemin mesnet reaksiyonlarının sayısı denge denklemlerinden fazla ise sistem dıģtan hiperstatik olur. Bir uzay taģıyıcı sistemin mesnet reaksiyonu sayısı 6 dan fazla ise sistem dıģtan hiperstatik olur. Düzlem sistemde ise mesnet reaksiyonu sayısı 3 ten fazla ise sistem dıģtan hiperstatik olur. ġekil. de verilen sistemler dıģtan hiperstatik sistemler için örnek olarak verilebilir. ġekil.3 Hiperstatik düzlem sistemler ġekil.3 de verilen düzlem sistemlerin mesnet reaksiyonları sayısı 6 dır. Düzlem sistemler için üç adet denge denklemi vardır. Bu sistemlerde hiperstatiklik derecesi 6-3=3 Ģeklindedir. Her iki sistem de 3. dereceden dıģtan hiperstatiktir. Bu sistemlerin çözümü için mesnet reaksiyonlarının hesaplanması yeterli olacaktır. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 8
9 ġekil.4 Mafsal bulunan sistemlerde hiperstatiklik derecesi TaĢıyıcı sistemin herhangi bir kesitinde bazı kesit tesirlerinin sıfır olması söz konusu olabilir. Örneğin ara mafsal bulunan bir kesitte eğilme momenti sıfır olacaktır. Bu durum, ilgili kesitte, sistem için ilave bir denklemin yazılabilmesini sağlamaktadır. Sistemin hiperstatiklik derecesi belirlenirken ara mafsal olup olmadığına da bakılmalıdır. ġekil.4 de verilen sistemlerde birer ara mafsal bulunduğundan hiperstatiklik derecesi her iki sistem için de dir. İçten hiperstatik sistemler; Bir sistemin mesnet reaksiyonlarının hesabı için denge denklemleri yeterli ancak tüm sistemdeki kesit tesirlerinin belirlenmesi için denge denklemleri yetersiz kalıyorsa, sistem içten hiperstatik olur (ġekil.5) ġekil.5 Ġçten hiperstatik taģıyıcı sistemler ġekil.5 de verilen çerçeve ve kafes sistemi ele alalım. Her iki sistemin de bilinmeyen mesnet reaksiyonları sayısı 3 tür. Mesnet reaksiyonları denge denklemleri ile Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 9
10 belirlenebilecektir. Ancak, kesim yapılarak taģıyıcı sistemin dengesi yazılacak olursa, kesit tesirleri sayısının denge denklenmelerinden fazla olduğu görülecektir. Bu yüzden çubukların kesit tesirlerinin hesabı için denge denklemleri yeterli olamayacaktır. ġekil.5a daki çerçeve sistem üçüncü dereceden içten hiperstatiktir. ġekil.5c deki gibi çerçevenin bir çubuğu kesilerek sistem izostatik hale gelecektir. ġekil.5b deki kafes sistemin izostatik hale gelmesi için ise diyagonal çubuklardan birinin kesilmesi gerekmektedir(ġekil.5d). ġu halde, Ģekil.5b de görülen kafes sistem. dereceden içten hiperstatik olmaktadır. İçten ve dıştan hiperstatik sistem:taģıyıcı sistemler hem içten hem de dıģtan hiperstatik olabilirler. Ġçten ve dıģtan hiperstatik sistemler için, Ģekil.5 de verilen sistemlerin kayıcı olan mesnetlerinin sabit hale getirilerek elde edildiği ve Ģekil.6 da verilen sistemleri örnek olarak verebiliriz. ġekil.6 DıĢtan ve içten Hiperstatik taģıyıcı sistemler ġekil.6 da verilen her iki sistemde de bilinmeyen mesnet reaksiyonlarının sayısı 4 tür. Düzlem sistemler için denge denklemi sayısı 3 olduğuna göre sistemler. dereceden dıģtan hiperstatiktir. Aynı zamanda Ģekil.6a daki sistemde bir kapalı çerçeve meydana gelmiģ olduğundan çubuklardan birisinin kesilmesi halinde üç adet bilinmeyen kesit tesiri de ortaya çıkacaktır. Dolayısıyla bu sistem 3. dereceden içten de hiperstatiktir. Böylece, çerçeve 4. dereceden hiperstatiktir. ġekil.6b deki sistem ise. dereceden içten hiperstatik olmaktadır. ġekil.6b de verilen kafes sistem toplam. dereceden hiperstatik olmaktadır. ġimdi de ġekil.7 de verilen uzay çerçeveyi inceleyelim. Dört adet ankastre mesnedi olan uzay çerçevenin mesnetlerinden birisi üzerinde reaksiyonlar gösterilmiģtir. Doğrusal kuvvetler R ile eksenler etrafındaki dönmeler ise M ile gösterilmiģtir. ġekil.7 deki çift oklar, ilgili eksen etrafındaki momentleri göstermektedir. Her düğümde 6 adet mesnet reaksiyonu olduğundan, iki yönde de tek açıklı ve tek katlı uzay çerçevede toplam bilinmeyen mesnet reaksiyonu sayısı 4 adettir. Uzay sistem için 6 adet denge denklemi söz konusu olduğuna göre, sistem 4-6=8 dereceden dıģtan hiperstatiktir. Mesnet reaksiyonları belirlendikten sonra 4 adet kolonun kesit tesirleri hesaplanabilir ancak kiriģler kapalı çerçeve oluģturduğundan bir kesim yapılması gerekir. Uzay sistemde, bir kesitte, iki kesme kuvveti, bir eksenel kuvvet, iki eğilme momenti ve bir burulma momenti olmak üzere toplam altı adet kesit tesiri olduğundan bir kesim ile 6 adet bilinmeyen ortaya çıkacaktır. Buna göre sistemimiz 6. Dereceden içten de hiperstatiktir. Sistemin toplam hiperstatiklik derecesi 8+6=4 tür. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli
11 ġekil.7 Ankastre mesnetli uzay çerçeve Düğümleri rijit bağlanmıģ olan Ģekil.8 deki ızgara sistemin hiperstatiklik derecesini belirleyelim. Bu ızgara sistemini oluģturan çubuklar; eğilme momenti, burulma momenti ve kesme kuvvetine maruzdurlar. Bu tür sistemlere düzlemine dik yüklü çerçevelerde denilebilir. Kaset döģemeler ve iki yönde sürekli temeller (ızgara temeller) bu sistemlere örnek olarak verilebilir. ġekil.8 Izgara sistem Izgara sisteme etki eden dıģ yükler sadece düģeyde olduğu kabul edilirse, her düğümde adet moment ve bir doğrusal kuvvet olmak üzere 3 bilinmeyen mesnet reaksiyonu oluģacaktır. Bir düğümdeki mesnet reaksiyonları Ģekil üzerinde gösterilmiģtir. Izgara sistem için yazılabilecek denklem sayısı 3 üçtür. Ele alınan sistemin her düğümünde 3 bilinmeyen olduğuna göre toplam bilinmeyen sayısı 3x8=4 tanedir. Sistemin dıģtan hiperstatiklik derecesi 4-3= dir. Mesnet reaksiyonları belirlendikten sonra, ABCD kapalı alanını oluģturan kiriģler hariç diğer kiriģlerin kesit tesirleri hesaplanabilir. ABCD kapalı çerçevesini oluģturan kiriģlerin kesit tesirlerinin hesabı için bir adet kesim yapmak gerekir. Izgara sistem çubuğunda bir kesitte, bilinmeyen kesit tesirleri sayısı 3 olduğundan, sistem 3. dereceden içten hiperstatik olmaktadır. Sistemin toplam hiperstatiklik derecesi +3=4 olur...3 Hiperstatiklik Derecesi (HSD) nin Belirlenmesi İçin Formüller Yukarıdaki paragrafta çeģitli sistemlerin hiperstatiklik dereceleri, denge denklemleri ve sistemdeki bilinmeyenlere bağlı olarak hesaplanmıģtı. Gerçek yapılarda bir çok eleman ve düğümler olacağından bu Ģekli ile hiperstatiklik derecesinin belirlenmesinde zorluklar olacaktır. Bunun yerine bir matematiksel ifadenin kullanılması gerekmektedir. Bu bölümde Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli
12 her taģıyıcı sistemi ele alarak hiperstatiklik derecesi için matematiksel ifadeler elde edilecektir...3. Düzlem Kafes Sistem m elemanlı ve j düğümlü bir düzlem kafes ele alalım. Tüm sistem için bilinmeyen sayısı r reaksiyon kuvveti sayısı, m çubuk kuvvetleri sayısı olmak üzere m+r kadar olacaktır. Diğer taraftan her düğümde denge denklemi; F x =, F y = (.3) Ģeklindedir. Böylece tüm sistem için yazılabilecek denklem sayısı j dir. Kafes sistemin hiperstatiklik derecesini belirleyen ifade; HSD=(m+r)-j (.4) Ģeklinde olur. ġekil.9 Hiperstatik düzlem kafes sistem ġekil.9 daki kafes sistemde bilinmeyen mesnet reaksiyonları sayısı r=4, düğüm sayısı j= ve çubuk sayısı m=8 dir. Sistemin hiperstatiklik derecesi; HSD=(8+4)-x= olur. Sistemin mesnet reaksiyonları sayısı 4 olduğuna göre sistem. dereceden dıģtan hiperstatik olmaktadır (4-3=)...3. Uzay Kafes Sistem Uzay kafes sistemde her düğüm için 3 denge denklemi; F x =, F y =, F Z =, (.4) Ģeklindedir. Böylece tüm sistem için yazılabilecek denklem sayısı 3j dir. Yine bilinmeyen sayısı çubuk kuvvetleri ve mesnet reaksiyonları m+r kadar olacaktır. Buna göre uzay kafes sistemin hiperstatiklik derecesini belirleyen ifade; HSD=(m+r)-3j (.5) Ģeklinde olur. ġekil.a daki uzay kafes sistemde düğüm sayısı j=4, reaksiyon sayısı r=9 ve çubuk sayısı m=3 tür. Bu sistem için, HSD=(3+9)-3x4= tür. Dolayısıyla bu sistem izostatiktir. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli
13 ġekil.b deki sistemde ise düğüm sayısı j=8, mesnet reaksiyonu sayısı r= ve çubuk sayısı ise m=3 dür. Buna göre sistemin hiperstatiklik derecesi HSD=(3+)-3x8=. Sistem birinci dereceden hiperstatiktir. 6-7 çubuğunun kaldırılması ile sistem izostatik hale gelir Düzlem Çerçeve ġekil. Ġzostatik ve hiperstatik uzay kafes sistemler Düzlem çerçeve çubuğunda, keme kuvveti, normal kuvvet ve eğilme momentinden oluģan üç adet bilinmeyen kesit tesiri vardır. Buna göre m elemanlı bir düzlem çerçevede bilinmeyen sayısı 3m+r kadar olacaktır. Diğer taraftan her düğüm için 3 denge denklemi yazılabilir. Buna göre düzlem çerçevenin hiperstatiklik derecesi; HSD=(3m+r)-3j (.6) Ģeklinde hesaplanır. Burada m eleman sayısını, r mesnet reaksiyonları sayısını j ise çerçevedeki düğüm sayısını (mesnetler dahil) göstermektedir. Örnek olarak Ģekil. de verilen düzlem çerçevelerin hiperstatiklik derecelerini belirleyelim. ġekil.a daki sistem de çubuk sayısı m=3, düğüm sayısı j=4 ve mesnet reaksiyonları sayısı r=6 olduğuna göre; hiperstatiklik derecesi HSD=(6+3.3)-3.4=3 olur. ġekil.b deki katlı düzlem çerçeve sistem de çubuk sayısı m=6, düğüm sayısı j=6 ve mesnet reaksiyonları sayısı r=6 olduğuna göre; hiperstatiklik derecesi ; HSD=(6+3.6)-3.6=6 olur. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 3
14 ġekil. Hiperstatik düzlem çerçeveler..3.4 Uzay Çerçeve Yapılar gerçekte üç boyutlu elemanlardan oluģmaktadır. Bir yapının analizi için oluģturulan üç boyutlu taģıyıcı sistem modeli Ģekil. de verilmiģtir. ġekil. Bir yapının taģıyıcı sisteminin üç boyutlu olarak modellenmesi Uzay çerçeve çubuğunda, her kesitte 6 adet bilinmeyen kesit tesiri (P x, P y, P z, M x, M y, M z ) vardır. Her düğüm için 6 denge denklemi yazılabilir. Buna göre düzlem çerçevenin hiperstatiklik derecesi; HSD=(6m+r)-6j (.7) Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 4
15 Ģeklinde hesaplanır. Burada m eleman sayısını, r mesnet reaksiyonları sayısını j ise çerçevedeki düğüm sayısını (mesnetler dahil) göstermektedir. Örnek olarak Ģekil.3 de verilen uzay çerçevelerin hiperstatiklik derecelerini belirleyelim. ġekil.3 Hiperstatik uzay çerçeve sistemler ġekil.a da verilen tek katlı uzay çerçevede eleman sayısı m=8, düğüm sayısı j=8, 4 adet mesnetteki mesnet reaksiyonu sayısı ise r=4*6=4 tür. Buna göre çerçevenin hiperstatiklik derecesi; HSD=(6*8+4)-6*8=4 tür. ġekil b de verilen iki katlı uzay çerçevede ise eleman sayısı m=6, düğüm sayısı j= ve 4 adet mesnetteki toplam reaksiyonu sayısı r=4*6=4 tür. Çerçevenin hiperstatiklik derecesi; dir. HSD=(6*6+4)-6*= Izgara sistem Bir ızgara sistem çubuğunda 3 adet bilinmeyen kesit tesiri vardır. Bunlar eğilme momenti, burulma momenti ve kesme kuvvetidir. Izgara sistemin her düğümü için de 3 denge denklemi yazılabilir. Buna göre ızgara sistemin hiperstatiklik derecesi; HSD=(3m+r)-3j (.8) Ģeklinde hesaplanır. Örnek olarak Ģekil.4 de verilen ızgara sistemin hiperstatiklik derecesini hesaplayalım. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 5
16 ġekil.4 Hiperstatik Izgara Sistem ġekil.3 de verilen iki yönde de iki açıklıklı ve ankastre mesnetli ızgara sistemde eleman sayısı m=, düğüm sayısı j=, 8 mesnetteki mesnet reaksiyonu sayısı ise r=8*3=4 tür. ızgaranın hiperstatiklik derecesi; HSD=(*3+4)-*3=4 tür Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 6
17 . GİRİŞ B Ö L Ü M I I. S E R B E S T L İ K D E R E C E L E R İ Yapı analizi ile uğraģan mühendisin görevi, yapıların taģıyıcı sistemlerini, güvenli, ekonomik, estetik ve fonksiyonel olacak Ģekilde projelendirmek ve inģa etmektir. Yapı analizi yapan inģaat mühendisi, projelerinde ve uygulamalarında geliģen teknolojiden yaralanmak zorundadır. 98 li yıllarda defter büyüklüğündeki bir bilgisayar ile boyutu on binlere varan bir denklem sisteminin çözülebileceği hayal edilemezken, artık bu gerçekleģmiģ ve basit kabuller içeren klasik yöntemler yerini daha gerçekçi çözümler sunan modern yöntemlere bırakmıģtır. Ülkemiz topraklarının %8 inden fazlası deprem kuģağında yer almaktadır. Orta Ģiddette bile olsa her deprem afeti sonrasında büyük can ve mal kayıpları ortaya çıkmakta, ülke maddi ve manevi olarak zarar görmektedir. Son yıllarda olan ve kent merkezlerinde betonarme yapıların depreme dayanıksız olduğunu ortaya koyan depremlerden alınması gereken önemli dersler vardır. Günümüzde depremlerde oluģan hasarların nedenleri bilinmektedir. Bu hasarların nasıl önleneceği de her mühendis tarafından bilinmesi gereken esaslardandır. Depreme dayanıklı yapı tasarımının en önemli aģaması; taģıyıcı sistemin gerçek davranıģının bilinmesi ve buna göre analizinin yapılarak projelendirilmesidir. GeliĢen bilgi teknolojilerine bağlı olarak yaygınlaģan ve vazgeçilmez hale gelen modelleme ve analiz yazılımlar da kullanılarak; daha gerçekçi çözümler sunan yöntemlerin tercih edilmesi gerekmektedir. Son zamanlarda her tür taģıyıcı sistem yazılım geliģtirmeye en uygun Deplasman Yöntemi kullanılarak hızlı ve ekonomik bir Ģekilde analiz edilebilmektedir. Deplasman yönetiminde; taģıyıcı sistemin düğümlerindeki yer değiģtirme ve dönmeler Deplasman olarak isimlendirilmektedir. Sisteme etkiyen yükler ve bu deplasmanlar arasında, sistemi meydana getiren elemanların geometrisi ve malzeme özelliklerine bağlı bir iliģki vardır. Yük ve deformasyonların iliģkilerinin matematiksel olarak modellenmesi ve bilinen sistem özellikleri ve yükler altında bilinmeyen olarak ele alınan deplasmanların hesabına, sonra da bu deplasmandan dolayı oluģan iç kuvvetlerin belirlenmesine deplasman yöntemi denilmektedir. TaĢıyıcı sistemler, elemanların düğümlerde birleģtirilmesi ile teģkil edilirler. TaĢıyıcı sistemi meydana getiren eleman üzerinde gerçekte sonsuz tane düğüm vardır. Aynı zamanda iki düğüm arasında tanımlanabilecek sonsuz sayıda eleman da olacaktır. Sonsuz sayıdaki elamanlar yerine, belirli düğümlere bağlanan sonlu sayıdaki elemanın kesit tesirleri ve deformasyonlarının belirlenmesi yeterli olacaktır. Bazı taģıyıcı sistemlerde eleman boyutları küçüldükçe, elde edilen sonuçlar gerçek davranıģa daha fazla yakınsamaktadır. Deplasman yönetiminin genel adı olan Sonlu Elemanlar Yöntemi de bu modelleme yaklaģımından adını almıģtır. Çubuklardan oluģan taģıyıcı sistemlerde de esasında sonsuz sayıda düğüm ve bu düğümlere bağlanmıģ olan eleman kabul edilebilir. Yeterli doğrulukta çözüm elde etmek için; taģıyıcı sitemin baģka bir sisteme bağlandığı, eksenlerin ve yüklerin değiģtiği noktalar düğüm olarak kabul edilerek sonsuz sayıdaki düğüm sonlu sayıya indirilir. Bir çerçeve sistemde kiriģ ile kolonun birleģim noktası ve kolonların temele bağlandığı noktalar düğüm olarak ele alınır. BelirlenmiĢ düğümlerdeki tutulmamıģ deplasmanların toplam sayısına serbestlik derecesi denilmektedir. Sistemi meydana getiren her eleman, birleģtiği düğümlerde meydana gelen deplasmanlar ile zorlanır ve buna bağlı olarak uçlarında kuvvetler oluģur. Bu kuvvetlerin Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 7
18 dengede olması ile sistem yük taģımaya devam edecektir. Bir sistemin dengede olması için, düğümlerde denge ve süreklilik (uygunluk) denklemlerinin sağlanması gerekir. Düğümlere bağlanan elemanların uç kuvvetleri ve düğüme etkiyen direk yükler arasında yazılacak olan denge denklemleri sağlanmalıdır. Düğümlerde denge: Düğümde birleģen çubukların uç kuvvetleri (düğüme aktardıkları kuvvetler) ile düğüme etkiyen dıģ yükler dengede olmalıdır. Süreklilik (uygunluk şartı): Aynı düğümde birleģen çubukların, düğümdeki uçları, aynı ötelenme ve dönmeleri yapacaktır. Yani bir düğümdeki dönme ve ötelenmeler biliniyorsa, o düğüme bağlı olan çubukların uçlarındaki dönme ve ötelenmeler de biliniyor olacaktır. Çünkü ilgili düğümdeki tüm çubuklar aynı ötelenme ve dönmelere maruz kalacaktır. Bu duruma süreklilik Ģartı denilmektedir. Dönme ve ötelenmelerin hepsine birden deplasman denilecek ve sistem deplasmanları D i ile eleman uç deplasmanları ise d i ile gösterilecektir. Çubuk uçlarındaki kesit tesirleri ise uç kuvvetleri olarak adlandırılacak ve p i ile gösterilecektir. Uç kuvvetleri ve deplasmanlardaki i indisi deplasman-uç kuvvet numarasını gösterecektir. Düğüm serbestlik derecesi: Düğümlerde birbirinden bağımsız deplasmanların sayısına düğüm serbestlik derecesi denilmektedir. Sistem serbestlik derecesi: Sistemin düğümlerindeki bağımsız deplasmanların toplam sayısına Sistem serbestlik derecesi denilir. Çubuk (eleman) serbestlik derecesi: Ġki düğüm arasında uzanan bir elemanın (çubuğun) serbestlik derecesi, düğüm serbestlik derecesinin katına eģittir. Eleman uçlarındaki bağımsız deplasmanların toplam sayısına eleman serbestlik derecesi denilir. Birinci bölümde hiperstatik sistemler tanımlanarak, taģıyıcı sistem türüne göre hiperstatiklik derecelerinin nasıl hesaplanacağına dair formülasyon verilmiģti. Bu bölümde, sistemin düğümlerindeki deplasman sayılarına bağlı olarak hesap edilen sistem serbestlik derecelerinin belirlenmesi yapılacaktır.. Çubuklar ve Serbestlik Dereceleri Çerçeve, kiriģ ve kafes sistem taģıyıcı sistemleri temsil etmek üzere modellenen Çubuk TaĢıyıcı Sistemler ; düğümlerde birleģen çubuk elemanlar ile modellenirler. Elemanlar ile ilgili büyüklükler, denklemler ifade edilirken bağlandıkları düğümlerin ötelenme ve dönme durumları dikkate alınır. Çubukların i ve j uçlarındaki uç kuvveti veya uç deplasmanı sayısına çubuk serbestlik derecesi denir. Diğer bir tanımı ile, çubuk serbestlik derecesi; sistemin düğüm serbestlik derecesinin iki katıdır denilebilir. ÇeĢitli taģıyıcı sistem için çubuk serbestlik dereceleri Tablo. de verilmiģtir. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 8
19 Tablo. Taşıyıcı sistem ve çubuk serbestlik dereceleri TaĢıyıcı Sistem Çubuk Serbestlik Derecesi ve uç deplasmanları Düzlem Kafes: Düzlem kafes çubuğu, yerel koordinatlarda serbestlik derecesine sahiptir. Ancak düzlem kafes sistemde her düğümde Serbestlik derecesi vardır. ĠĢlem kolaylığı bakımından, iki uçtaki bir serbestlik derecesi dik bileģenlere ayrılarak düzlem kafes çubuğu için toplam 4 serbestlik derecesi elde edilebilir. d d y i x e j A,E,L Yerel koordinatlarda y ' e i x d d 4 j d 3 A,E,L SD=4 d Sistem koordinatlarında Uzay kafes: Uzay kafes çubuğu, yerel koordinatlarda serbestlik derecesine sahiptir. Ancak uzay kafes çubuğu uzayda herhangi bir konumda olabileceğinden, her düğümdeki bir serbestlik derecesini xyz eksen takımlarına göre ayrı ayrı yazmak mümkündür. Uzay kafes sistemde her düğümde 3 Serbestlik derecesi vardır. Uzay kafes sitemde çubuk serbestlik derecesi 6 dır. d d d x y i x e j A,E,L Yerel koordinatlarında z i d d 6 j d 5 e A,E,L y d4 d 3 Sistem koordinatlarında SD=6 Düzlem Çerçeve: xy düzleminde bulunan çerçeve çubuğunun her düğümünde ötelenme ve bir dönme olmak üzere üç serbestlik derecesi vardır. Düzlem çerçeve çubuğunun serbestlik derecesi altıdır. d d y d 3 i e A,E,I,L j d 5 d 4 d 6 x SD=6 Uzay Çerçeve: XYZ Uzayında herhangi bir konumda bulunan uzay çerçeve çubuğunun her uçunda sırası ile x, y, z doğrultusunda üç ötelenme, yine sırası ile x, y, z etrafında 3 dönme olmak üzere toplam 6 serbestlik derecesi vardır. Uzay çerçeve çubuğu için serbestlik derecesi dir. d 5 d d z x d 3 d 5 i y e A,E,G,I x,i z, J,L d 4 d 6 d d7 j d 9 d d 8 d SD= Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 9
20 Düzlem Izgara: Düzlem ızgaralar, düzlemine dik yüklü çerçevelerdir. Yatay düzlemde birbirine rijit bağlı çubuklardan oluģan ızgara sistemin her düğümünde, dönme ve bir de düģeyde ötelenme vardır. Düzlem ızgara çubuğunun serbestlik derecesi 6 dır. d y z d d i e d 4 3 j A,E,I x,l,g,j d x d 5 5 d 6 SD=6 Çubuk uçlarında her serbestlik derecesine karģılık bir de uç kuvveti vardır. En genel halde bir çubukta, bir düğümdeki uç kuvvetleri; eksenel kuvvet, kesme kuvveti ve 3 adet momentten oluģur (Uzay çerçeve). Momentlerden si eğilme biri ise burulma momentidir. TaĢıyıcı sistemin türüne göre bu uç kuvvetlerinden bazıları elimine olacaktır (ortadan kalkacaktır). Çubuk sistemlerinin teģkil edildiği çubuklar ve bir düğümünde meydan gelen kesit tesirleri (j düğümündeki uç kuvvetleri) Tablo. de verilmiģtir. Tablo. Çubuklar ve uç kuvvetleri Uzay Çerçeve Çubuğu: Uzay çerçeve çubuğu xyz eksen takımında, herhangi bir konumda olabilir. Çubuğun her ucunda, eksen doğrultularında kuvvetler ve eksen etrafında momentler olmak üzere toplam 6 adet uç kuvveti vardır. Kuvvet ve momentleri pozitif yönleri sağ el kuralına göre belirlenmektedir. Düzlem Çerçeve Çubuğu: Düzlem çerçeve çubuğu xy düzlemindedir ve yükler bu düzlemde etki eder. Çubuk uçlarında x ve y yönünde doğrusal kuvvetler, okuyucuya doğru yönelmiģ olan z ekseni etrafında ise eğilme momenti vardır. Düzlem Izgara Çubuğu: Çubuklar birbirine rijit olarak bağlanmıģtır. TaĢıyıcı sistem yatay xy düzlemindedir. Yükler bu düzlem içinde etkimektedir. Düzlem ızgara çubuğunun her ucunda bir kesme kuvveti, iki de moment Ģeklinde olmak üzere toplam üç kuvvet vardır. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli
21 Kafes Sistem Çubuğu: Düzlem kafes sitemde, yükler yz düzleminde etkimektedir. Her düğümdeki yük genel koordinatlara indirgenirken bileģene ayrılır. Uzay kafes sistemde ise yük herhangi bir doğrultuda olabilir. Çubuk uç kuvveti de üç eksen doğrultusunda bileģene ayrılabilir. Tablo. de uç deplasmanları verilirken dönmeler çift ok ile gösterilmiģti. Her deplasmana karģılık bir uç kuvveti meydana geleceğinden, bir düğümdeki uç deplasmanları da Tablo. deki gibi gösterilebilir. Burada momentler yerine dönmeler, kuvvetler yerine de ötelenmeler yazılacaktır..3 Sistem Serbestlik Derecesi Çubukların düğümlerde birleģmesi ile oluģan sisteme bir dıģ yük etkidiği zaman, sistemin düğümleri bu dıģ yükler altında ötelenme ve dönmeler Ģeklinde yer değiģtirir. Deplasman yöntemi ile çözümünde, bilinmeyenler düğüm deplasmanlarıdır. Deplasmanlar hesaplandıktan sonra bu deplasmanların sebep olacağı kesit tesirleri kolayca hesaplanabilir. Bir sistemde önce düğüm deplasmanlarının belirlenmesi ve sonra da bu deplasmanlar sonucu ortaya çıkan iç kuvvetlerin belirlenmesine dayalı yöntemlere deplasman yöntemi denilir. Sistem Serbestlik derecesi: TaĢıyıcı sistemin düğümlerindeki bağımsız deplasmanlarının toplam sayısına sistem serbestlik derecesi denir. TaĢıyıcı sistemin mesnetlerinde bazı deplasmanları önlenmiģtir. Bu sistemin mesnet Ģartlarına bağlıdır. Bir düzlem çerçeve taģıyıcı sistemin ankastre mesnedinde tüm deplasmanlar önlenmiģtir. Basit mesnette ise sadece dönme söz konusu olup ötelenme önlenmiģtir. Ancak düzlem çerçevenin bir ara düğüm için iki doğrultuda ötelenme ve birde dönme söz konusudur..3. Düzlem Kafes Sistemin Serbestlik Derecesi Düzlem kafes sitemde her düğümde serbestlik derecesi vardır. Düzlem kafes sistemdeki mesnetler dahil düğüm sayısının katından mesnet reaksiyonları sayısı çıkartılarak sistemin serbestlik derecesi hesaplanır. Düzlem kafes sistem için serbestlik derecesi ifadesi; SD = j - r. dir. Burada; SD: serbestlik derecesi, j: düğüm sayısı (mesnetler dahil), r: mesnet reaksiyonları sayısı olmaktadır. ġekil. de verilen düzlem kafes sistemde toplam düğüm vardır., 3 ve 5 numaralı düğümleri mesnettir.. ve 3. düğümlerde x yönünde kayıcı mesnet olduğundan, bu doğrultudaki deplasmanlar tutulmamıģtır. 5. düğümde ise sabit mesnet olduğundan her iki yöndeki deplasmanlar da tutulmuģtur. Sistemin serbestlik derecesi; SD=* -4=6 dır. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli
22 . ġekil. Düzlem kafes sistemde serbestlik derecesi.3. Uzay Kafes Sistemin Serbestlik Derecesi Uzay kafes sistemin her düğümünde x, y ve z doğrultularına birer ötelenme vardır. Mesnetlerde ötelenmelerin tamamı veya bazıları. Uzay kafes sistemin serbestlik derecesi; SD = 3j - r.. Ģeklindedir. ġekil.a daki sistem için; düğüm sayısı j=3, reaksiyon sayısı r=3*3 olduğuna göre sistemin serbestlik derecesi; SD=4*3-3*3=3 olacaktır. Sekiz düğümü olan Şekil..b deki sistem için ise SD=8*3-4*3= dir. ġekil. Uzay kafes sistemlerde serbestlik derecesi.3.3 Düzlem Çerçevenin Serbestlik Derecesi Düzlem çerçeve taģıyıcı sistemin her düğümünde bir dönme ve iki ötelenme vardır. Düzlem çerçevenin serbestlik derecesi; SD = 3j - r (.3) Ģeklinde hesaplanır. Burada r mesnet reaksiyonları sayısını j ise çerçevedeki düğüm sayısını (mesnetler dahil) göstermektedir. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli
23 ġekil.3 Düzlem çerçevelerde serbestlik derecesi Örnek olarak Şekil.3 de verilen düzlem çerçevelerin serbestlik dereceleri belirlenmiģtir. Her iki mesnedi de ankastre olan Şekil.3a daki düzlem çerçevenin serbestlik derecesi; SD=4x3-x3=6 dır. Çerçevenin bir düğümündeki ötelenmeler ve dönme Ģekil üzerinde gösterilmiģtir. ġekil.3b deki iki katlı çerçevede bir mesnet ankastre bir mesnet de sabittir. Mesnet reaksiyonları sayısı 5 tir. Çerçevenin serbestlik derecesi; SD=6x3-5= dir..3.4 Uzay Çerçevenin Serbestlik Derecesi Bir uzay çerçeve taģıyıcı sistemin düğümünde 6 adet bilinmeyen deplasman vardır. Mesnetlerinde bazı deplasmanlar önlenmiģ olabilir. Uzay çerçeve taģıyıcı sistem için serbestlik derecesi; SD = 6j - r (.4.) ġekil.4 Uzay çerçevelerde serbestlik derecesi Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 3
24 Ģeklindedir. ġekil.4 te verilen uzay çerçevelerin serbestlik derecelerini belirleyelim. ġekil.4a da verilen tek katlı uzay çerçevenin 7. düğümündeki deplasmanlar Ģekil üzerinde gösterilmiģtir. Bu deplasmanlardan; D : x yönündeki ötelenmeyi, D : y yönündeki ötelenmeyi, D 3 : z yönündeki ötelenmeyi, D 4 : x ekseni etrafındaki dönmeyi, D 5 : y ekseni etrafındaki dönmeyi, D 6 : z ekseni etrafındaki dönmeyi, göstermektedir. Kabul edilen eksen takımı da Ģekilde görülmektedir. Tek katlı çerçevenin düğüm sayısı j=8, mesnet reaksiyonları sayısı r=4x6=4 tür. Buna göre, bu çerçevenin serbestlik derecesi; SD=8x6-4=4 tür. ġekil.4b de verilen iki katlı uzay çerçevede ise düğüm sayısı j=, 4 adet mesnetteki toplam reaksiyonu sayısı r=4x6=4 tür. Çerçevenin serbestlik derecesi; SD=x6-4=48 dir..3.5 Düzlem Izgara Sistemin Serbestlik Derecesi Yatay düzlemde bulunan ve düğümlerinde birbirine rijit olarak bağlanmıģ olan bir düzlem ızgara sistemin her düğümünde, dönme ve bir de düģeyde ötelenme olmak üzere toplam 3 adet bilinmeyen deplasman vardır. Mesnet Ģartlarına göre bu deplasmanlardan bazıları mesnetlerde önlenmiģ olabilir. Buna göre ızgara sistemin serbestlik derecesi; SD = 3j-r (.5) Ģeklinde hesaplanır. ġimdi de ġekil.5 te verilen ızgara sistemin serbestlik derecesini hesaplayalım. ġekil.5 Izgara sistemin serbestlik derecesi Izgara sistemin 5 numaralı düğümündeki deplasmanlar Ģekil üzerinde gösterilmiģtir. Bu düğümdeki deplasmanlardan; D : z yönündeki ötelenmeyi, D : x ekseni etrafındaki dönmeyi, D 3 : y ekseni etrafındaki dönmeyi, ifade etmektedir. Ġki yönde iki açıklığı bulunan ve mesnetleri ankastre olan ızgara sistemde düğüm sayısı j=, 8 mesnetteki mesnet reaksiyonu sayısı ise r=8x3=4 tür. Izgaranın serbestlik derecesi; SD = x3-4 = 36 dır. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 4
25 B ö l ü m I I I 3. R i j i t l i k v e R i j i t l i k E t k i K a t s a y ı l a r ı 3. Giriş Bilgisayar ile yapı analizine en uygun yöntem deplasman yöntemidir. Programlama çok kolay ve yöntem her taģıyıcı sistem için genel olduğundan, birçok yerli ve yabancı bilgisayar programları deplasman yöntemi kullanılarak yazılmıģtır. Lisans düzeyinde yapı sistemlerinin analizi anlatılırken, temel davranıģ olan rijitlik, yük ve deplasman iliģkisinin de kavranması deplasman yöntemi ile daha kolay olmaktadır. Kainattaki her malzemenin deformasyona zorlanması durumunda bir direnç gösterdiği, fizik, malzeme ve mekanik derslerinden bilinmektedir. Malzemenin yük altındaki idealleģtirilmiģ davranıģını, o malzemeden teģkil edilen sistemler için genelleģtirerek kullanabiliriz. Bilgisayar kullanımına paralel olarak yaygınlaģan matris metotları her sahada olduğu gibi yapı analizinde de kullanılmaktadır. Her bilinmeyen denklemde birtakım katsayılar vardır. Bu katsayıların matris ifadesini elde ederek yapılan çözümlere matris metotları ile çözüm denilmektedir. Malzeme özelliklerine ve sistemin geometrisine bağlı katsayılar matrisi, sistemin ya da elemanın yük-deplasman iliģkisinin belirlenmesinde kullanılmaktadır. Klasik yöntemlerde kullanılan birim deplasman sabitleri, genel anlamda rijitlik katsayıları olarak da bilinmektedir. Çubukların serbestlik derecelerine bağlı olarak, bu rijitlik katsayılarından oluģan kare, mutlak pozitif ve simetrik olan bir katsayılar matrisi vardır. Bu katsayılar matrisine rijitlik matrisi denilir. TaĢıyıcı sistemin rijitliği; sistemi meydana getiren çubukların rijitliklerinin uygun Ģekilde birleģtirilmesinden elde edilir. Elde edilen sistem rijitliği de sistem denkleminin katsayılar matrisi olarak ifade edilebilir. Sistem rijitlik matrisi; sistemin deformasyonları ile yükleri arasında iliģki kuran kare, mutlak pozitif ve simetrik bir matristir. Rijitlik Matrisi yönteminde, sistemi meydana getiren her çubuğun rijitlik matrislerinin ve sistemin rijitlik matrisinin bilinmesi gerekir. Çubuk rijitlik matrisi, çubuk serbestlik derecesine bağlı olarak rijitlik katsayılarından oluģacaktır. DeğiĢik taģıyıcı sistem elemanları için rijitlik matrislerinin elde edilmesi için bir çok yöntem mevcuttur. Bu kitapta enerji (kuvvet) yöntemi ile rijitlik katsayıları elde edilecektir. 3. Rijitlik kavramı ve rijitlik denklem i Rijitlik, bir cismin yük altında Ģekil değiģtirmeye karģı gösterdiği direnme gücü olarak tanımlanabilir. Yapı analizinde geliģtirilen denge denklemleri ve bunların dayandığı matematiksel yaklaģımlar, yük ve deformasyon iliģkisinin belirlenmesini hedeflemektedir. ġekil 3. deki cismi, tanımlanmıģ bir doğrultuda D ötelenmesine zorlayan Q kuvveti ile D ötelenmesi arasında bir iliģki vardır. Lineer elastik olan ve Hooke yasasına uyan bir cisim için bu iliģki de lineer olacaktır. ġekil 3. de lineer elastik cisim için yük deplasman iliģkisi verilmiģtir. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 5
26 Q, yük Deformasyondan önce D Q Deformasyondan sonra D, deplasman ġekil 3. Yük altında deformasyon yapan bir cisim ġekil 3. Lineer elastik bir cisim için Yük-Deplasman iliģkisi ġekil 3.'de verilen yük- deplasman eğrisinin eğiminden; Q tan α= dir. Bu katsayıyı K ile tarif edersek; K = Q, D D K.D=Q (3.) yazılabilir. Denklem 3. e rijitlik denklemi denilmektedir. Burada K rijitlik, D deplasman ve Q yük olmaktadır. Cisim sonsuz rijit ise deplasman sıfır olacağından K sonsuza gidecektir. Cismin rijitliği sıfır ise deplasmana karģı hirç bir direnç olmayacağından; D sonsuza gidecektir. Gerçekte her cismin ya da sistemin belirli bir düzeyde rijitliği söz konusudur. ġekil 3.3 te verilen eksenel çekmeye maruz prizmatik bir çubuğu ele alalım. E,A P L d P, Eksenel Kuvvet Diyagramı ġekil 3.3 Eksenel çekmeye maruz bir prizmatik çubuk Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 6
27 E elastisite modülü olmak üzere, A en kesitine sahip L uzunluğundaki çubuğun, eksenel P yükü etkisindeki eksenel doğrultudaki boy değiģimini enerji yöntemi ile elde edebiliriz. DıĢ kuvvetin iģinin iç kuvvetin yaptığı Ģekil değiģtirme enerjisine eģit olacağından; Pxd = L ò P.P dx = P.P.L yazılabilir. Buradan eksenel yöndeki uzama (deplasman) E.A EA δ = PL EA (3.) Ģeklinde olacaktır. Buradaki E, çubuk malzemesinin eksenel yöndeki elastisite modülüdür. Elastisite modülü, her malzemenin gerilme-ģekil değiģtirme bağıntılarından bilinen sabit bir değeridir. Örneğin çelik için. 6 kg/cm dir. L ve A çubuk kesit özellikleri olduğuna göre yük ve deplasman arasındaki iliģki; veya (3.3) Ģeklinde ifade edilebilir. Görüldüğü gibi, çubuk rijitliği yük ile deplasman arasında bir iliģki kurmaktadır. Birden fazla deplasman ve yük olması halinde, deplasmanlar deplasman vektörü, yükler yük vektörü ve Kij den oluģan katsayılar matrisi ise rijitlik matrisi olarak adlandırılır. Çubuk rijitlik matrislerindeki kij terimlerine rijitlik etki katsayıları denilmektedir. Rijitlik etki katsayısı (birim deplasman sabiti): Yapı statiğinde rijitlik etki katsayısı, geniģ anlamı ile belirli bir doğrultuda birim deplasman temin edebilmek için taģıyıcı sisteme uygulanması gereken kuvvet olarak tarif edilebilir. Bu tanıma göre birim deplasman temin etmek için P değerinin EA/L kadar olacağı görülmektedir. Bu terim, prizmatik çubuğun eksenel rijitlik katsayısı ya da eksenel yöndeki birim deplasman sabiti olmaktadır. 3.3 Çubuk rijitlik denklemler i Çubuk rijitlik denklemleri, enerji yöntemi kullanılarak elde edilebilir. Burada denklemin nasıl elde edileceği ele alınmadan, 3. denkleminden faydalanılacaktır. Bir çubuğun uçlarında, serbestlik dereceleri doğrultusunda deplasman yaptırılacak olursa, bu deplasmanlara karģılık çubuk uç kuvvetleri meydana gelir. Bazı çubuklarda ara yükler de olabilir. Bu durumda ara yüklerin, eģ değer düğüm yükleri olarak düğümlere indirgenmesi ve uç kuvvetlerin hesabında dikkate alınması gerekmektedir. Bu bölümde, düzlem kafes çubuğu, düzlem çerçeve çubuğu ve uzay çerçeve çubuğu için çubuk rijitlik denklemleri verilecektir. İşaret Kabulü: Ötelenme ve dönmelere, ayrı ayrı isimlendirmedikçe deplasman denilecek ve pozitif yönleri eksen doğrultusunda olacaktır. Yine doğrusal kuvvet ve momentlere, ayrıca belirtilmemiģse ortak olarak kuvvet tabiri kullanılacaktır. Kuvvetler için de pozitif yön eksen doğrultusu olacaktır. Moment ve dönmelerin pozitif yönleri belirlenirken, sağ el vida kuralı geçerli olacaktır. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 7
28 3.3. Düzlem kafes çubuğu rijitlik denklemi Kuvvetin tatbik edildiği yerdeki okun numarasını (i) ile ve birim deplasmanın bulunduğu yerdeki okun numarasını da (j) ile gösterirsek, bir taģıyıcı elemanın k ij rijitlik katsayısını Ģu Ģekilde tarif edebiliriz. k ij : TaĢıyıcı elemanın tarif edilmiģ bütün serbestlik dereceleri doğrultusundaki deplasmanlar sıfır iken, yalnız " j " oku doğrultusunda birim bir deplasman meydana getirebilmek için " i " doğrultusunda elemana dıģtan uygulanması gereken kuvvet. k ii : TaĢıyıcı elemanın tarif edilmiģ bütün serbestlik dereceleri doğrultusundaki deplasmanlar sıfır iken, yalnız i oku doğrultusunda birim bir deplasman meydana getirebilmek için gene i doğrultusunda elemana dıģtan uygulanması gereken kuvvet Düzlem kafes çubuğu rijitlik denklemi iki Ģekilde ifade edilebilir; a) Yerel koordinatlarda b) Genel koordinatlarda P,d y i x e j p,d a) Yerel koordinatlarda P 4, d 4 P, d y y ' i A,E,L e j x P 3, d 3 P, d x b) Sistem koordinatlarında(x y :sistem koord.) ġekil 3.4 Kafes sistem çubuğu uç deplasmanları ve uç kuvvetleri ġekil 3.4a da ele alınan düzlem kafes çubuğunun uç kuvvetleri p, p ile ve uç deplasmanları da d, d ile gösterilmiģtir. Buna göre çubuk serbestlik derecesi olacaktır. Çubuk için rijitlik denklemi; p = k d + k d ( 3.4) p = k d + k d Ģeklinde yazılabilir. Burada k ij terimleri rijitlik katsayıları olmaktadır. Bu değerlerin nasıl elde edileceği daha sonra ele alınacaktır. Bu denklem matris formunda; Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 8
29 (3.5) Ģeklinde ifade edebiliriz. Aynı ifadeyi kapalı formda, {p} = [k] {d} (3.6 ) Ģeklinde yazabiliriz ki bu denkleme kafes çubuğunun rijitlik denklemi denir. Bu denklemde; {p}: uç kuvvetleri vektörü, {d}: deplasman vektörü, [k] : rijitlik matrisidir. Görüldüğü gibi, rijitlik matrisi çubuğun uç deplasmanlarını, aynı doğrultulardaki uç kuvvetlerine bağlayan bir katsayılar matrisidir. Bir rijitlik denkleminden bahsederken, aynı zamanda o denklemin bağlı olduğu eksen takımını da tarif etmek gerekir. Çünkü her değiģik eksen takımına yeni bir rijitlik matrisi karģılık gelir. TaĢıyıcı sistemin çözümünde, eleman denklemleri aynı eksen takımında yazılarak birleģtirilmektedir. Kafes çubuğun sistem koordinatlarındaki denklemi 4x4 boyutunda olacaktır. ġekil 3.4b de verilen kafes sistem çubuğunun sistem koordinatlarındaki denklemi; p = k d + k d +k 3 d 3 + k 4 d 4 p = k d + k d + k 3 d 3 + k 4 d 4 p 3 = k 3 d + k 3 d +k 33 d 3 + k 34 d 4 (3.7) p 4 = k 4 d + k 4 d + k 33 d 3 + k 44 d 4 Ģeklinde yazılabilir. Bu denklem matris formunda; (3.8 ) TaĢıyıcı elemanın geometrisi ve elastik parametreleri ile bu k ij değerlerine, birim deplasmanlarla ilgili olmalarından dolayı rijitlik katsayıları denmektedir. Bu katsayılar tamamen bağımsız değildirler. Aralarında statik denge denklemlerini sağladıkları gibi, Betti- Maxwell`in karģıtlık prensibi gereğince de k ij =k ji dir. Yani eleman rijitlik matrisi köģegene göre simetriktir. ġekil 3.5 de kafes çubuğu için birim deplasman durumları ve rijitlik katsayıları gösterilmiģtir. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 9
30 d = d = y y k i x e k j k i x e j k A,E,L a) A,E,L b) ġekil 3.5 Düzlem kafes çubuğu için birim deplasmanlar 3.3 ifadesinden yararlanarak, ġekil 3.5a da d = Ģartını sağlayan; değerlerinin olduğu yazılabilir. Benzer Ģekilde, ġekil 3.5b de d = Ģartını sağlayan; değerleridir. Böylece kafes çubuğu için yerel koordinatlardaki rijitlik matrisi; veya, (3.9) Ģeklinde elde edilir. Bu ifadelerin elde edilmesi için çok çeģitli yöntemler kullanılmaktadır. En yaygın olarak enerji yöntemleri, Ģekil fonksiyonları, esneklik matrisi gibi yöntemler kullanılabilir. ġekil 3.4a'da verilen kafes çubuğu için elde edilen rijitlik matrisi eleman koordinatlarındadır. Bunun sistem koordinatlarına dönüģtürülmesi için (ġekil 3.4b), i ve j düğümlerindeki tek ifadelerin iki bileģene ayrılması gerekmektedir. Eleman koordinatlarında elde edilen 3.9 ifadesinde verilen eleman rijitlik matrisi, koordinat dönüģümü ile sistem koordinatlarına dönüģtürülerek; [k]' = EA L é ë c cs c cs cs s cs s c cs c cs cs s cs s ù û (3.) Ģeklinde elde edilebilir. Burada; c=coss=sin olmaktadır. açısı, çubuk x ekseni ile sistem x' ekseni arasındaki açıdır. Bu açı saat ibresinin tersi yönünde ölçülecektir (ġekil 3.4b). Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 3
31 3.3. Düzlem Çerçeve Çubuğu Rijitlik Denklemi Düzlem çerçeve çubuğunun her düğümünde iki ötelenme ve bir dönme olmak üzere toplam altı serbestlik derecesi bulunmaktadır. Her serbestlik derecesine karģılık bir de uç kuvveti bulunmaktadır. Çubuk üzerinde ara yük bulunuyorsa, bu ara yüklere karģılık düğümlerde ankastrelik uç kuvvetleri denilen reaksiyon kuvvetleri de meydana gelecektir. Çubuk ankastrelik uç kuvvetleri, çubuğun her iki ucu ankastre iken, ara yüklerden dolayı meydana gelen ankastre mesnet reaksiyonları olmaktadır. Düğümlerde hesaplanan Bu ankastrelik uç kuvvetlerinin ters iģaretlileri aynı zamanda düğümlere indirgenmiģ eģdeğer yükleri de vermektedir. Düzlem çerçeve çubuğu 6 serbestlik dereceli olduğundan; çubuk uç deplasmanları ile uç kuvvetleri arasındaki iliģki 6x6 lık bir katsayılar matrisi ile kurulmaktadır. Bu matrise, çerçeve çubuğu rijitlik matrisi denilecektir. y i e j 4 x 3 A,E,I,L 5 6 ġekil 3.6 Düzlem Çerçeve çubuğunda iģaret kabulü y f i e j f 4 x f f 3 A,E,I,L f 5 f 6 ġekil 3.7 Düzlem Çerçeve çubuğunda ankastrelik uç kuvvetleri y p i e j p 4 x p p 3 A,E,I,L p 5 p 6 ġekil 3.8 Düzlem Çerçeve çubuğunda uç kuvvetleri y d d 3 d i e j A,E,I,L ġekil 3.9 Düzlem Çerçeve çubuğunda uç deplasmanları Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 3 p 5 d 4 d 6 x
32 d = y k i e j k 4 x k k 3 A,E,I,L k 5 k 6 ġekil 3. Düzlem Çerçeve çubuğunda d = durumu ve ilgili rijitlik katsayıları d = y k i e j k 4 x k k 3 A,E,I,L k 5 k 6 ġekil 3. Düzlem Çerçeve çubuğunda d = durumu ve ilgili rijitlik katsayıları d 3 = y k 3 i e j k 43 x k 3 k 33 A,E,I,L k 53 k 63 ġekil 3. Düzlem Çerçeve çubuğunda d 3 = durumu ve ilgili rijitlik katsayıları Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 3
33 d 4 = y k 4 i e j k 44 x k 4 k 34 A,E,I,L k 54 k 64 ġekil 3.3 Düzlem Çerçeve çubuğunda d 4 = durumu ve ilgili rijitlik katsayıları d 5 = y k 5 k 35 k 5 i e j A,E,I,L k 55 k 65 ġekil 3.4 Düzlem Çerçeve çubuğunda d 5 = durumu ve ilgili rijitlik katsayıları k 45 x y d 6 = k 6 i e j k 46 x k 6 k 36 A,E,I,L k 56 k 66 ġekil 3.5 Düzlem Çerçeve çubuğunda d 6 = durumu ve ilgili rijitlik katsayıları Gerçekte çubukta birim uç deplasmanı yerine gerçek d,...d 6 deplasmanları bulunmaktadır. Çubuktaki bu uç deplasmanları ve uç kuvvetleri arasındaki iliģki; (3.) Ģeklinde olacaktır. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 33
34 Düzlem çerçeve çubuğu için eleman denklemini, kapalı formda; [k]{d}+{f}={p} (3.) Ģeklinde ifade edebiliriz Burada; [k]: eleman koordinatlarında eleman rijitlik matrisi {d}: eleman uç deplasmanları vektörü {f}: eleman ankastrelik uç kuvvetleri vektörü {p}: eleman uç kuvvetleri vektörü olmaktadır. Yapı sisteminin çözümünde genellikle düğüm deplasmanları önce hesaplandığından, her elemanın düğüm deplasmanları dolayısıyla uç deplasmanları bilinmektedir. Ġstenen; bu deplasman durumunda eleman uç kuvvetlerinin ne olacağıdır. Uç kuvvetleri ve ara yüklerin değiģimi biliniyorsa, belirlenen düğüm deplasmanları altında; elemanın herhangi bir kesitindeki kesit tesirleri hesaplanabilir Düzlem Çerçeve Çubuğu rijitlik etki katsayıları Her düğümünde iki ötelenme ve bir dönme serbestlik derecesi olmak üzere toplam 6 serbestlik derecesi olan düzlem çerçeve çubuğunun rijitlik etki katsayıları 6 =36 tanedir. Rijitlik katsayılarından oluģan rijitlik matrisi 6x6 boyutunda bir kare matristir. Matrisin fiziksel anlamı gereği ve karģıtlık teoremi gereği, rijitlik matrisi simetrik, mutlak pozitif tanımlı bir matristir. Rijitlik katsayıları (birim deplasman sabitleri) çeģitli yöntemler ile hesaplanabilir. Bunlar; Enerji yöntemi, enerjinin minimizasyonu Elastik eğrinin denklemi ile ilgili diferansiyel denklem Birim deplasman verilmesi Birim yükleme (Esneklik matrisi) ile şeklindedir Esneklik Matrisi Yöntemi ile Rijitlik etki katsayılarının hesabı Denklem 3. de verilen çubuk rijitlik denklemini i ve j düğümleri için alt matrisler kullanarak; ì {p} ü é i í ý = [k] ii [k] ù ì ij {p} î j þ [k] ji [k] ë jj. {d} ü i ì { f } ü i í ý+ í ý (3.3) {d} û î j { f } þ î j þ Ģeklinde yazmak mümkündür. eleman rijitlik denklemini i ve j düğümleri için yazarsak; {p} i =[k] ii.{d} i +[k] ij.{d} j +{ f } i {p} j =[k] ii.{d} i +[k] ij.{d} j +{ f } i elde edilir. Burada; (3.4a) (3.4b) Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 34
35 (3.5) Eleman üzerindeki ara yükler ve j düğümündeki deplasmanlar sıfır ise, {p} i =[k] ii.{d} i (3.6) ifadesi kalır. Bu denklemden i düğümü deplasmanları hesaplanacak olursa; (3.7) elde edilir. Burada [f] ii matrisine esneklik (fleksibilite) matrisi denilmektedir. Açık formda; (3.8) Ģeklinde ifade edilebilir. f ij : esneklik (fleksibilite) katsayısı, j doğrultusundaki birim yükten dolayı i düğümündeki deplasman olarak tarif edilmektedir. i düğümüne sıra ile birim yüklemeler yapılarak fleksibilite katsayıları hesaplanabilir P =, (P =, P 3 =) yüklemesi y P = f i e j x f f 3 A,E,I,L N Yalnız P = iken çubuğun kesit tesirleri diyagramları çizilmiģtir. ġekilden de görüldüğü gibi yükleme eksenel yönde olduğundan, çubukta kesit tesiri olarak sadece eksenel kuvvet oluģmaktadır. Bilindiği gibi, bir sistemde, sistem dengede ve kararlı ise dıģ kuvvetlerin yaptığı iģ iç kuvvetlerin yaptığı iģe eģit olacaktır. Buna göre; xf = L L N.N ò dx = ò. dx = L EA EA EA Eksenel yükün kesme ve eğile üzerinde etkisi olmadığından; ve 3 dogrultularında da yükler bulunmadığından; P = yüklemesi durumunda f =, f 3 =, elde edilir. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 35
36 P = (P =, P 3 =) yüklemesi y f i e j x f f 3 A, E, I, L P = + V (Kesme kuvvet diyagramı) + L M (Moment diyagramı) ĠĢ ifadelerinin eģitliğinden; f = (Normal kuvvet sıfır) ve L L M xf =.M dx+ V.V kdx EI GA f = L3 3EI + kl GA L 3 kl elde edilir. Burada terimi eğilme deformasyonundan dolayı yapılan iģi, terimi ise 3EI GA kayma deformasyonlarından dolayı yapılan iģi temsil etmektedir. Ġkinci terimde yer alan k, kesit faktörü olmaktadır. Dikdörtgen kesitler için. alınmaktadır. Kayma deformasyonlarının katkıları ihmal edilecekse, ikinci terim hesaba katılmayacaktır. P 3 = yüklemesi y f 3 i e j x P 3 = f 33 f 3 A, E, I, L - M 3 f 3 = f 3 = (Normal ve kesme yönünde kuvvet etkimemektedir). ĠĢ ilkesi ile; L L M xf 33 = 3.M 3 (-).(-) dx = dx; EI EI f 33 = L EI L L M f 3 = f 3 = 3.M (-).(x) L dx = dx = EI EI EI i ucu için esneklik matrisi yazılacak olursa; Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 36
37 é [ f ] ii = ë L EA L 3 3EI + kl GA L EI L EI L EI ù û (3.9) (3.) a = EIk L GA (3.) olup kayma deformasyonlarının katkısını göstermektedir. Eğer kayma deformasyonları ihmal edilecek ise, = alınmalıdır. i ucundaki rijitlik kat sayıları esneklik katsayılarından yararlanılarak hesaplanmıģ oldu. Rijitlik katsayıları arasında denge denklemleri sağlanmalıdır. ġimdi de her üç durum için de denge denklemleri yolu ile, i ucundaki birim deplasmanlardan dolayı j ucunda meydana gelen reaksiyonlardan (rijitlik katsayılarını) oluģan [k] ji alt matrisinin terimlerini elde edelim. d =, d = d 3 =d 4 = d 5 =d 6 = durumu d = y k i e j k 4 x k k 3 A,E,I,L k 5 k 6 F X =;k +k 4 =, k 4 = - k =- F y =;k +k 5 =, k 5 = - k = M i =;k 5.L+k 6 +k 3 =, k 6 = d =, d = d 3 =d 4 = d 5 =d 6 = durumu Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 37
38 d = y k i e j k 4 x k k 3 A,E,I,L k 5 k 6 F X =;k +k 4 =, k 4 = - k = F y =;k +k 5 =, k 5 = - k = - M i =;k 5.L+k 6 +k 3 =, k 6 = d 3 =, d = d =d 4 = d 5 =d 6 = durumu d 3 = y k 3 i e j k 43 x k 3 k 33 A,E,I,L k 53 k 63 F X =;k 3 +k 43 =, k 43 = - k 3 = F y =;k 3 +k 53 =, k 53 = - k 3 =- M i =;k 53.L+k 63 +k 33 =, k 63 = Hesaplanan terimleri matris olarak gösterelim; (3.) Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 38
39 Bu seferde j düğümüne birim yüklemeler yaparak [k] jj ve [k] ij alt matrislerini benzer Ģekilde hesaplayabiliriz. Yine Eleman üzerindeki ara yükler ve i düğümündeki deplasmanlar sıfır ise, ifadesi kalır. Bu denklemden j düğümü deplasmanları hesaplanacak olursa; açık formda; (3.3) Ģeklinde ifade edilebilir. j düğümüne sıra ile birim yüklemeler yapılarak fleksibilite katsayıları hesaplanabilir. P 4 = (P 5 =,P 6 =) yüklemesi y i e f 44 P 4 = x A,E,I,L j f 54 f 64 N 4 + Virtüel iģ prensibini uygulayarak; f 54 =, f 64 =, elde edilir. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 39
40 P 5 = (P 4 =, P 6 =) yüklemesi y i e f 45 x A, E, I, L j f 65 P 5 = f 55 - V 5 L + M 5 Ġç ve dıģ kuvvetlerin yaptığı iģin eģitliğini kullanarak; f 45 = ve elde edilir. P 6 = (P 4 =, P 5 =) yüklemesi y P 6 = f 56 i x e A, E, I, L j f 66 f 46 + M 6 f 46 = Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 4
41 (3.4) (3.5) Denge durumundan faydalanarak [k] ij alt matrisini hesaplayabiliriz. d 4 =, d =d = d 3 = d 5 =d 6 = durumu d 4 = y k 4 i e j k 44 x k 4 k 34 A,E,I,L k 54 k 64 F X =;k 4 +k 44 =, k 4 = -k 44 =- F y =;k 4 +k 54 =, k 54 = - k 4 = M i =;k 54.L+k 64 +k 34 =, k 34 = d 5 =, d = d = d 3 =d 4 =d 6 = durumu Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 4
42 d 5 = y k 5 i e j k 45 x k 5 k 35 A,E,I,L k 55 k 65 F X =;k 5 +k 45 =, k 5 = - k 45 = F y =;k 5 +k 55 =, k 5 = - k 55 = - M i =;k 55.L+k 65 +k 35 =, k 35 = - d 6 =, d = d = d 3 = d 4 = d 5 = durumu d 6 = y k 6 i e j k 46 x k 6 k 36 A,E,I,L k 56 k 66 F X =;k 6 +k 46 =, k 6 = - k 46 = F y =;k 6 +k 56 =, k 6 = - k 56 = M i =; k 56.L+k 66 +k 36 =, k 36 = Elde edilenleri matris formunda yazarak [k] ij alt matrisini; (3.6) olarak elde ederiz. Alt matrisleri birleģtirerek çerçeve eleman için rijitlik matrisi; Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 4
43 (3.7) Ģeklinde elde edilir. Bu matrise, eleman koordinatlarına eleman rijitlik matrisi denilecektir. Bu matrisin sistem koordinatlarına transferi için dönüģüm matrisinden faydalanılacaktır Izgara Sistem Çubuğu Rijitlik Denklemi ġekil 3.7 Izgara Sistem ve eleman serbestlik derecesi xy düzlemi içinde yer alan, yükleri düzlemine dik olarak etkiyen ve çubukları bir birine rijit olarak bağlanan ızgara sistemde, her düğümde iki dönme ve bir doğrusal olmak üzere 3 serbestlik derecesi vardır. Bu durumda her elemanın uçunda bir kesme iki de moment olmak üzere toplam üç kesit tesiri meydana gelir (ġekil 3.7). Bu kesit tesirlerine karģılık, her düğümde iki adet dönme ve bir de düģey ötelenme söz konusudur. Dönmelerden birisi eğilme diğeri ise burulma nedeni ile meydana gelmektedir. Eğilme ve ötelenme ile ilgili rijitlik katsayıları, düzlem çerçeve çubuğunda, ilgili serbestlik dereceleri için hesaplananlar ile aynı olacaktır. Burada yalnız burulma ile ilgili rijitlik katsayısının hesabı yeterli olacaktır. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 43
44 4 5 j 6 z y i 3 x ġekil 3.8 Düzlem ızgara çubuğunda serbestlik dereceleri ve numaralama Uçlarında sadece burulma serbestlik derecesi olan bir çubuk ele alalım; p, d G,J,L j p, d i x ġekil 3.9 Yalnız burulma serbestlik derecesi olan çubuk ġekil 3. Burulma serbestlikleri için birim deplasmanlar ve ilgili rijitlik katsayıları Mukavemetten, burulma ve dönme arasındaki iliģki; (3.8) olarak bilinmektedir. Çubuğun j düğümü ankastre olursa (deplasman önlenirse) ve i düğümüne birim dönme yaptırılırsa, i düğümünde d = yapan, kuvvet; = M bl GJ Þ, M b = k = GJ L olur. Buna karģılık j düğümünde reaksiyon kuvveti olarak; Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 44
45 oluģacaktır. Benzer Ģekilde i düğümü tutulur ve j düğümünde birim deplasman yaptırılırsa k = k = GJ L k = k = - GJ L olarak elde edilir. Uçlarında yalnız burulma olan bir çubuğun rijitlik denklemi; ì í î P P ü ý þ = é k k ùì d ü í ý ëk k ûîd þ = GJ é -ùì d ü í ý L ë- ûî þ d (3.9) olur. Düzlem çerçeve rijitlik matrisi ve (3.9) denklemi kullanılarak, ġekil 3.8 de verilen 6 serbestlik derecesi için eleman rijitlik matrisi, é [k] = ë EI (+α)l 3 GJ L 6EI (+α)l - EI (+a)l 3 - GJ L - 6EI (+a)l 6EI - EI - 6EI (+α)l (+α)l 3 (+α)l - GJ L (4+α)EI 6EI (+a)l (+α)l 6EI (+a)l ( -a)ei (+a)l ( -a)ei (+a)l EI - 6EI (+a)l 3 (+a)l GJ L - 6EI (+a)l (4 +a)ei (+a)l ù û (3.3) Uzay Çerçeve Çubuğunun Rijitlik Katsayıları Uzay çerçeve çubuğu xyz eksen takımında, herhangi bir konumda olabilir. Çubuğun her ucunda, eksen doğrultularında kuvvetler ve eksen etrafında momentler olmak üzere toplam 6 adet uç kuvveti vardır. Kuvvet ve momentlerin pozitif yönleri sağ el vida kuralına göre belirlenmektedir. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 45
46 Z m Z y p y Uzay çerçeve çubuğu M y M x x M z p z p x z ġekil 3. Uzay çerçeve çubuğunda bir kesitteki uç kuvvetleri Uzay çerçeve çubuğunun rijitlik katsayıları, düzlem çerçeve çubuğuna benzer Ģekilde elde edilebilir. Bilindiği gibi, k ij terimini elde etmek için, diğer serbestlik dereceleri doğrultusundaki tüm deplasmanlar tutulmuģ iken, j doğrultusunda birim bir deplasman meydan gelmesi halinde, elastik eğrinin Ģeklini muhafaza etmek için gereken kuvvetler olarak tanımlanmaktadır. Yani, tarif edilmiģ bütün deplasman doğrultuları teker teker ele alınmalı ve her seferinde bunlara birim deplasman vererek uç kuvvetleri hesaplanmalıdır. bütün bu iģlemler uzay çerçeve çubuğu için yapılmıģ ve Ģekil 3. 'de gösterilmiģtir. ġekil 3. de, uçlarında birim deformasyonlar bulunan bir uzay çerçeve çubuğunun uç kuvvetleri, her birim deplasman için ayrı ayrı gösterilmiģtir. Aslında bir çubuk, taģıyıcı sistemin yüklenmesinden sonra, birim deplasmanlara değil, d,d,d 3,d 4,d 5,...,d gibi sıfır olmayan sonlu uç deplasmanlarına maruz kalır. Bütün bu deplasmanların hepsinin aynı anda etkilerini içine alan p, p, p 3, p 4, p 5,...,p kuvvetlerini bulmak için, süperpozisyon kuralına baģvurmak ve her deplasman hali için oluģan kuvvetleri toplamak gerekir. Herhangi bir doğrultudaki kuvveti bulmak için bu yöntem, bütün deplasmanlara tatbik edilir ve aynı doğrultudaki kuvvetlerin bileģenleri süperpoze edilirse, uzay çerçeve sistemin çubuk kuvvetleri için rijitlik denklemi p = k d + k d + k 3 d k d + f... (3.3) p = k d + k d + k 3 d k d + f Ģeklinde elde edilir. Görüldüğü gibi rijitlik katsayıları, çubuğun uç deplasmanlarını, uçlardaki kesit tesirlerine bağlayan, malzemenin geometrisi ve elastik özellikleri ile ilgili katsayılardır.(3.3) de verilen rijitlik denklemi matris formunda; ( 3.3) Ģeklinde yazılabilir. Kapalı formda {p} x =[k] x {d} x +{f} x (3.33) Burada {P}=uç kuvvetleri vektörü, {d}= uç deplasmanları vektörü, {f}=ankastrelik uç kuvvetleri vektörü, [k]= çubuk rijitlik matrisidir. Y m Y m 46 Yapı EA/L Statiği, Ders d Notları- = Prof. Dr. Hasan -EA/L KAPLAN, Pamukkale GIx/L Üniversitesi ĠnĢaat d 4 Mühendisliği = Bölümü-Denizli GIx/L X m X m
47 Y m Y m -EA/L d 7 = EA/L X m -GIx/L d = GIx/L X m Z m Z m Y m EIz / L 3 Y m -EIz/L 3-6EIz/L d 8 = - 6EIz/L X m EIy/L d = 4EIy/L -6EIy/L 6EIy/L X m Z m Z m Y m Y m 6EIz/L -6EIz/L 6EIy/L 6EIy/L d 9 = X m -EIy / L 3 EIy / L 3 Z m Z m EIz/L d = ġekil 3. Uzay çerçeve çubuğu için rijitlik katsayıları. 4EIz/L X m Sisteme etki eden dıģ yükler (düğüm yükleri haricinde) biliniyor ise, bu tesirlerin düğümlere olan etkileri uygun formüllerle hesaplanarak, {f} ankastrelik uç kuvvetleri vektörü hesaplanır. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 47
48 Bunun yanında, uç deplasmanları {d} bilinince, [k] rijitlik matrisi ile {d} vektörünün çarpımından, aranan {p} uç kuvvetleri vektörü hesaplanır. Çubuk uç kuvvetlerinin tam değerinin hesabı için elde edilen bu çarpıma {f} vektörü ilave edilmelidir. é [ k] = ë EA L EI Z L 3 6EI Z L EI Y L 3-6EI Y L GI X L - 6EI Y L - EA L 4EI Y L 6EI Z L 4EI Z L - EI Z - 6EI Z L 3 L - EI Y L 3 - GI X L - 6EI Y L 6EI Y L EI Y L 6EI Z L EI Z L - EA L - EI Z L 3 6EI Z L - EI Y L 3-6EI Y L - GI X L - 6EI Y L EI Y L - 6EI Z L EA L EI Z L EI Z - 6EI Z L 3 L EI Y L 3 GI X L 6EI Y L 6EI Y L 4EI Y L - 6EI Z L 4EI Z L ù û Denklem (3.34) Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 48
49 B Ö L Ü M 4 4. K O O R D İ N AT D Ö N Ü Ş Ü M Ü 4. Düzlem sistemler için koordinat dönüşümü Mühendislik mekaniğinde, büyüklükler ifade edilirken hangi eksen takımına ait olduğunun da belirlenmesi gerekir. Örneğin bir kesitin atalet momenti, her eksen takımına göre farklı değerler alabilecektir. Benzer Ģekilde bir elemana ait rijitlik denklemi de bağlı olduğu eksen takımına göre değiģir. Eleman rijitlik denklemleri, eleman koordinatları ve sistem koordinatlarında olmak üzere iki Ģekilde yazılabilir. Sistem, düğümlerde birleģen ve düğümlerde aynı ortak deplasmanı yapan birden fazla çubuktan meydana gelebilmektedir. Sistem için bir koordinat takımı, olmasına karģın her elemanın kendi koordinat takımı bulunmaktadır. Eleman koordinatları: xy, düzlemi içinde yer alan bir elemanın x ekseni eleman boyunca uzanmaktadır. y ekseni ise, x ekseninin saat ibresi tersi yönünde 9 dönülerek elde edilmektedir. z ekseni ise okuyucuya doğru yönelmiģtir ġekil 4. Eleman ve sistem koordinatları Sistem koordinatları: Sistemi meydana getiren tüm elemanlar için ortak kabul edilebilecek bir koordinat sistemi (x y ) Sistemi meydana getiren elemanların denklemleri, ortak bir koordinat takımı olan sistem koordinatlarında ifade edilirse, iģlemler daha kolay olacaktır. BaĢlangıçta eleman koordinatlarında elde edilen eleman rijitlik matrisi ve ankastrelik uç kuvvetleri vektörü, dönüģüm matrisleri kullanılarak sistem koordinatlarına dönüģtürülür. Eleman koordinatlarında uç deplasmanları veya kuvvetleri istenmesi halinde de yine dönüģüm ifadesinden faydalanılır. P kuvveti hem x y eksen takımında hem de kadar döndürülmüģ olan xy eksen takımlarında bileģenlerine ayrılabilir. Ayrıca x y eksen takımında verilen bileģenlerden, xy eksen takımındaki değerleri elde etmek de mümkündür. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 49
50 ġekil 4. Koordinat dönüģümü ġekil 4. de P x ve P y kuvvetlerinin x ve y doğrultularındaki bileģenleri gösterilmiģtir. x ve y yönündeki kuvvetlerin dengesinden; P x = P x cos + P y sinp y = P x cos - P y sin yazılabilir. z yönünde eksende kayma olmadığından; P z = P z olacaktır. Matris formunda; (4.a) olur. Kapalı formda; {p}=[t].{p} (4.b) Ģeklinde ifade edilebilir. Burada [t] : transformasyon alt matrisi olup (4.) Ģeklinde verilmektedir. {p}: Eleman k oordinatlarındaki bileģenler, {p} : Sistem koordinatlarındaki bileģenler olmaktadır. {p} biliniyor ise; {p} =[t] -.{p} Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 5
51 ile hesaplanabilir. DönüĢüm alt matrisinin tersi aynı zamanda transpozuna eģit olmaktadır; [t] - =[t] t (4.3) dir. Böylece bir düğüme ait eleman koordinatlarındaki büyüklüklerin sistem koordinatlarına dönüģümleri; {p} =[t] t.{p} (4.4) {f} =[t] t.{f} (4.5) {d} =[t] t.{d} (4.6) Ģeklinde ifade edilir. 4.. Düzlem Kafes Sistemde koordinat dönüşümü Düzlem kafes sistemde, çubuğun düğümlerinde yalnız kuvvetler söz konusu olduğundan, transformasyon alt matrisi; (4.7) Ģeklindedir. y P,d i e j p,d x Eleman koordinatları P 4, d 4 P, d y y ' i A,E,L e j x P 3, d 3 P, d x Sistem koordinatlarında(x y :sistem koord.) (4.8) Benzer Ģekilde deplasmanlar için de dönüģüm yapılabilir. Eleman rijitlik matrisinin ifadesi daha önce verilmiģti. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 5
52 4.. Düzlem Çerçeve Çubuğunda Koordinat Dönüşümü y j d 4 d d i d 3 y e A,E,I,L Sistem koordinatları e d 5 x j d 6 d 6 d 4 x i A,E,I,L d 5 d d 3 Eleman koordinatları d ġekil 4.3 Düzlem çerçeve çubuğunda transformasyon 6 serbestlik derecesi olan düzlem çerçeve çubuğunda; olmak üzere dönüģüm matrisi; (4.9) dir. Uç deplasmanları, uç kuvvetleri ve ankastrelik uç kuvvetleri için 4.4.,4.5 ve 4.6 ifadeleri kullanılır. 4. Uzay sistemler için koordinat dönüşümü Eleman koordinatları: Lokal Eksen Takımı Çubuğun kendi ekseni ile bu eksene dik en kesitteki asal atalet momenti eksenlerinden oluģan ve sağ el vida kuralına uyan x m, y m, z m koordinat takımına çubuk lokal eksen takımı denir. Çubuğu en kesitteki ağırlık merkezlerini birleģtiren boyuna eksen x m, büyük ve küçük atalet eksenleri de y m ve z m ile gösterilir, ( ġekil 4.4 ). Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 5
53 Y z m j x m i y m X Z ġekil 4.4 Uzay çerçeve çubuğu eksen takımları. Uzay bir çerçeve çubuğunda hangi atalet ekseninin y m veya z m olarak seçileceğine dair bir kural yoktur. Fakat seçim yapıldıktan sonra, doğal olarak hesaplarda seçilen atalet eksenine karģılık gelen atalet değerleri kullanılmalıdır. Çubuk lokal eksenleri çubuğun ötelenmesi ile ötelenir ve çubuğun dönmesi ile dönerler. Sistemi oluģturan bir çubuğun eksen takımı ile diğer bir çubuğun eksen takımı arasında hiç bir beraberlik yoktur. Çubuklar sistem içinde farklı farklı konumlarda bulunabilirler. Sistem koordinatları: Global Eksen Takımı TaĢıyıcı sistemin denge denklemlerini yazabilmek ve bir düğüm noktasında birleģen çubukların uç kuvvet ve deplasmanlarını tek bir koordinat eksenine döndürebilmek için bütün sisteme ait olmak üzere, sağ el vida kaidesine uygun olarak seçilen, karģılıklı birbirine dik X, Y ve Z eksenlerine global eksen takımı ya da sistem koordinatları denir. Global eksenlerin doğrultuları tamamen çubuk eksenlerinden bağımsızdır ve çubuğun konumu ile ilgileri yoktur. Bu eksenler analizi yapılan taģıyıcı sitemin üzerine çizilmiģ gibidir. Bir çubuğun asal atalet eksenleri olan y m ve z m eksenlerinin en kesit düzlemi içindeki yerini belirleyebilmek için, en kesit içinde, dönmeden sabit duran yeni bir eksen takımına ihtiyaç vardır. Çünkü y m ve z m eksenleri en kesit düzlemi içinde, çubuk boy ekseni olan x m etrafında 36 o dönerek herhangi bir konumu iģgal edebilirler. Bu özel konumu gösteren eksenler x mo, y mo ve z mo ile ġekil 4.5 'de gösterilmiģtir. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 53
54 Y z m z mo j ( X j, Y j, Z j ) ( X i, Y i, Z i ) i y m x m = x mo y mo X Z ġekil 4.5 Uzay çerçeve çubuğu eksen takımları ( Özel konum ) Hangi eksen takımında çalıģılırsa çalıģılsın, koordinat eksenlerinin pozitif yönlerinde elde edilmiģ olan uç kuvvetleri ve uç ötelenmeleri pozitif olur. Momentlerin ve dönmelerin iģaretleri sağ el vida kuralına göre belirlenir. 4.. Uzay çerçeve Çubuğu Transformasyon Matrisi Uzay çerçeve çubuğunun her bir düğüm noktasında üç ötelenme ve üç dönme olmak üzere toplam altı serbestlik derecesi vardır. Dönme vektörleri ile ötelenme vektörleri birbirleri ile ilgili değildir. Aynı Ģekilde kuvvet vektörleri de moment vektörlerinden bağımsızdır. Kuvvet vektörlerinin transformasyonu için; (4.) ve momentlerin transformasyonu; (4.) Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 54
55 Ģeklinde yapılır. Bu iki transformasyon iģlemi tek bir denklem takımı halinde yazılmak istenirse, köģegen dıģı bloklar sıfır olmak üzere; (4.) ifadesi elde edilir. Bir uzay çerçeve çubuğunun uçlarındaki on iki adet hareket serbestisinin hepsinin birden, toplu halde transformasyonunu sağlayabilmek için (4.3) ifadesi kullanılır. Burada [T] ` ye çubuk transformasyon matrisi denir. Transformasyon matrisi, köģegen boyunca, [t] dönüģüm alt matrislerini (doğrultu kosinüsleri matrislerini) içerir. Uzay çerçeve çubuğu için transformasyon matrisi [T]; (4.4) Ģeklindedir. [t] dönüģüm alt matrisinin genel ifadesi, Ģekil 4.5 'de gösterilen ve x m etrafında oluģan dönmesini de içerecek Ģekilde denklem 4.5 de verilmektedir. (4.5) Burada L uzay çerçeve çubuğunun boyu olmak üzere, Cx, Cy ve Cz ifadeleri; (4.6) Ģeklindedir. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 55
56 4.3 Sistem Koordinatlarında Eleman Rijitlik De nklemi Bir düğüm noktasında birleģen çubukların rijitlik terimlerini toplayabilmek için, o çubukların rijitlik matrislerinin ortak bir eksen takımına göre yazılmıģ olması gerekir. Yani, çubuk rijitliklerini süperpoze edebilmek için, bütün rijitlik matrisleri hep aynı doğrultulardaki serbestlik derecelerine karģılık gelmelidir. Çubuk uçlarında farklı doğrultularda oluģan deplasman ve kuvvet vektörlerini ortak bir eksen takımında ifade etmek gerekir. Lokal çubuk eksen takımına göre yazılan eleman denkleminin, bu ortak eksen takımına aktarılması sağlanmalıdır. Bilindiği gibi, bir çubuğun uç kuvvetlerinin karģılık gelen deplasmanlar üzerinde yaptıkları iģin toplamı sabit olup eksen takımı ne olursa olsun değeri değiģmez. Yani, global eksenlerde verilen çubuk kuvvetlerinin, kendi doğrultularındaki deplasmanları üzerinde yaptığı iģ, çubuk eksenlerine göre verilmiģ eģdeğer kuvvet takımının karģılık gelen deplasmanlar üzerinde yaptığı iģe eģittir. Kuvvet ve deplasmanların her iki eksen takımına göre de dönüģüm ifadeleri daha önce elde edilmiģti. Bu temel prensipten hareket edilerek eleman koordinatlarında verilen sistem denklemi, sistem koordinatlarına dönüģtürülebilir. Eleman koordinatlarında eleman rijitlik denklemi; [k]{d}+{f}={p} (4.7) idi. {p}=[t].{p} {f}= [T].{f} (4.8) {d}=[t].{d} ifadeleri 4.6 da yerine yazılırsa; [k] [T]{d} +[T]{f} =[T]{p} (4.9) elde edilir. 4.8 in her iki tarafı da soldan [T] T ile çarpılırsa; [T] T [k] [T]{d} +[T] T [T]{f} =[T] T [T]{p} (4. [T] T [T]=[I] olduğundan; sistem koordinatlarında eleman rijitlik denklemi; [k] {d} +{f} ={p} (4.) olarak elde edilir. Burada, sistem koordinatlarında eleman rijitlik matrisi; [k] =[T] T [k] [T] (4.) dir. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 56
57 Önce eleman koordinatlarında eleman denklemi elde edilir. Elemanlar için dönüģüm matrisleri hesaplanarak, eleman denklemi sistem koordinatlarında elde edilir. Sistem denklemi eleman denklemlerinin uygun Ģekilde birleģiminden elde edilir. Sistem denkleminden elde edilen sistem düğüm deplasmanlarından uygun olanlar alınarak, i her elemanın sistem koordinatlarındaki düğüm deplasmanları belirlenmiģ olur. Bundan sonra istenilirse tekrar transformasyon yapılarak, uç deplasmanları eleman koordinatlarında elde edilir ve eleman uç kuvvetleri, eleman koordinatlarındaki eleman rijitlik denkleminden hesaplanır. Bunun yerine, eleman uç kuvvetleri, sistem koordinatlarına elde edildikten sonra eleman koordinatlarına da dönüģtürülebilir. Görüldüğü gibi, bir elemanın sistem içinde hangi pozisyonda bulunduğu önem arz etmektedir. Bunun, elemanın tanımlanması esnasında belirlenmesi gerekmektedir. Yapı Statiği, Ders Notları- Prof. Dr. Hasan KAPLAN, Pamukkale Üniversitesi ĠnĢaat Mühendisliği Bölümü-Denizli 57
58 B Ö L Ü M 5 5. A N K A S T R E L Ġ K U Ç K U V V E T L E R Ġ Ankastrelik uç kuvvetleri; bir çubuğun her iki ucunun ankastre mesnetli olması halinde üzerindeki ara yüklerden dolayı mesnetlerde meydana gelen reaksiyonlarını ifade eder. Ara yüklerin iki ucu eģdeğer düğüm yükü olarak indirgenmesinde önce ankastrelik uç kuvvetleri belirlenir, sonra bu kuvvetlerin ters iģaretlileri çubuk uçlarına eskitilirse ara yükler düğümlere indirgenebilir. Üzerinde ara yük bulunan ve iki ucundan ankastre olarak mesnetlenen çubuğun, ankastre mesnetlerindeki mesnet reaksiyonlarını içeren vektöre; çubuk ankastrelik uç kuvvetleri vektörü denilmektedir. Düzlem çerçeve çubuğunun her düğümünde iki ötelenme ve bir dönme olmak üzere toplam altı serbestlik derecesi bulunmaktadır. Her serbestlik derecesine karģılık bir de ankastrelik uç kuvveti bulunmaktadır. ġekil 5. de verilen iģaret kabulüne göre xy düzleminde etkiyen yükler için ankastrelik uç kuvvetleri Ģekil 5. de gösterilmiģtir. Düzlem çerçeve için verilen ankastrelik uç kuvvetleri vektörü, ilgili elemanları sıfır yapılarak uzay çerçeve çubuğu içinde geçerlidir. Yüklerin eleman koordinatlarında etkimesi durumu için elde edilen ankastrelik uç kuvvetleri vektörü, koordinat dönüģümü ile sistem koordinatlarına dönüģtürülebilir. y 3 i e A,E,I,L j x ġekil 5. Düzlem Çerçeve çubuğunda iģaret kabulü y f i e j f 4 x f f 3 A,E,I,L f 5 f 6 ġekil 5. Düzlem Çerçeve çubuğunda ankastrelik uç kuvvetleri Ģekil 5. de verilen ankastrelik uç kuvvetleri vektör Ģeklinde, dir. Çubuk x eksenine dik yönde ve düģeyde etkidiği kabul edilen çeģitli yükleme Ģekilleri için çubukların ankastrelik uç kuvvetleri vektörleri ġekil 5.3 de verilmiģtir. 58
59 59
60 ġekil 5.3 Çerçeve çubukları için yükleme Ģekilleri ve ankastrelik uç kuvvetleri vektörleri 6
61
62 B Ö L Ü M 6 6. R İ J İ T L İ K M AT R İ S İ Y Ö N T E M İ 6. Giriş Bu bölümde adımları anlatılacak olan rijitlik matrisi yöntemi için daha önceki bölümlerde verilen kavramların bilinmesi gerekmektedir. Rijitlik matrisi yöntemi, sisteme etki eden dıģ yükler ve sistemin düğümlerindeki deplasmanlar arasında yazılacak olan denklemlerin çözümüne dayanmaktadır. Her sistem dıģ yükler altında rijitliği oranında direnç gösterir. Aynı dıģ etki altında rijitliği yüksek olan taģıyıcı sistem daha az miktarda deplasman yaparken, rijitliği az olan sistem daha fazla deplasman yapacaktır. Bilgisayar teknolojisindeki geliģmelere paralel olarak, taģıyıcı sistemin daha gerçekçi çözümünü yapan deplasman yöntemi yaygın olarak kullanılır hale gelmiģtir. Deplasman yönteminin, çubuk, kabuk ve levha gibi. Elemanlardan oluģan her tür taģıyıcı sistemin analizinde geniģ kapsamlı olarak kullanılabilen Ģekli genel olarak Sonlu Elemanlar Yöntemi olarak bilinmektedir. Bugün bilgisayar programlarının hemen hemen tamamı deplasman yöntemi ile çözüm yapmaktadır. Programlamaya elveriģli, her tür taģıyıcı sistem ve yükleme için genel ve sistematik olan rijitlik matrisi yöntemi, yapı analizinde önemli bir yer tutmaktadır. 6. Rijitlik Matrisi Yönteminde İşlem Sırası Her taģıyıcı sistem düğümlerde birleģen elemanlardan meydana gelmektedir. Sistemin düğüm bilgileri ve eleman bilgileri uygun Ģekilde tanımlanarak, düğümlerde ve elemanlarda oluģan etkiler (deplasman, kesit tesiri) rijitlik matrisi yöntemi ile kolayca hesaplanabilir. AĢağıda rijitlik matrisi ile çözümde takip edilecek olan iģlem sırası maddeler halinde verilmiģtir. Bu adımlar izlenerek ele alınan örneklerin çözümü 7. Bölümde yer almaktadır. Düğümlere sıra ile numara verilir. Elemanlar numaralanır. Düğüm serbestlik dereceleri ve mesnet Ģartları dikkate alınarak sistemin serbestlik derecesi belirlenir. Bunun için her deplasmana sıra ile bir numara verilir. TutulmuĢ olan doğrultulara sıfır yazılır. Elemanların hangi düğüme bağlandıkları ve sistem içinde hangi deplasmanları yapmakta olduğu belirlenir. Eleman rijitlik matrisleri [k], eleman koordinatlarında elde edilir. [k] =[T] T [k] [T] dönüģümü yapılarak eleman rijitlik matrisleri sistem koordinatlarında elde edilir. 6
63 Üzerinde ara yük bulunan elemanlar için {f} ankastrelik uç kuvvetleri vektörleri eleman koordinatlarında elde edilir. {f} =[T] T {f} dönüģümü yapılarak, eleman ankastrelik uç kuvvetlerinin sistem koordinatlarındaki karģılığı elde edilir. Sitem rijitlik matrisi [K], eleman rijitlik matrislerinin birleģtirilmesi ile elde edilir. Bunun için düğümlerde uygunluk ve süreklilik Ģartlarına dayalı ifadeler kullanılabilir. En yaygın olarak kodlama tekniği kullanılmaktadır. Eleman ankastrelik uç kuvvetlerinin ters iģaretlileri ilgili düğümlere etkitilerek, doğrudan düğüme etkiyen direk yükler de dikkate alınarak sistem yük vektörü {Q} hesaplanır. Sistemde, sıcaklık değiģimi ve mesnet çökmeleri söz konusu ise, bu etkilerden dolayı oluģan ankastrelik uç kuvvetleri hesaplanarak eģ değer düğüm yükleri elde edilebilir. Sistem denklemi [K]{D}={Q} çözülerek bilinmeyen düğüm deplasmanları elde edilir. Bu lineer denklem sisteminin çözümünde, gauss eliminasyon yöntemi kullanılabilir. Hesaplanan düğüm deplasmanlarından ilgili bileģenler alınarak, her eleman için sistem koordinatlarındaki düğüm deplasmanlarını içeren {d} vektörleri belirlenir. Eleman denklemi [k] {d} +{f} ={p} çözülerek, sistem koordinatlarında eleman uç kuvvetleri hesaplanır. {p}=[t]{p} ifadesi ile, eleman koordinatlarında eleman uç kuvvetleri hesaplanır. Ara yükler de dikkate alınarak elemanlar için kesit tesirleri diyagramları çizilir. 6.3 Kodlama Tekniği Kodlama tekniği programlamaya elveriģli ve anlaģılması kolay bir yöntemdir. Eleman denklemlerinden sistem denkleminin elde edilmesi ve sistem düğüm deplasmanlarından eleman deplasman vektörlerinin belirlenmesinde kullanılmaktadır. Programlamaya oldukça elveriģli olan bu yöntem, herhangi bir düğüm noktasında birleģen çubukların rijitliklerinin toplanması iģlemini son derece kolaylaģtırır. Bir çubuğun baģ ve son düğüm noktalarının numaraları, o çubuğun taģıyıcı sistem içinde iģgal ettiği yeri belirtir. Buna çubuğun tarifi de denilmektedir. TaĢıyıcı sistemi meydana getiren çubuklar, sistemin düğüm serbestlik derecesinin iki katı kadar serbestlik derecesine sahiptir. Deplasman yönteminde, problemin bilinmeyenleri düğüm deplasmanlarıdır. Düğüm deplasmanlarının hangilerinin eleman uç deplasmanları olduğunu belirleyebilmek için, sistem deplasmanlarına sıra ile birer numara verilmektedir (ġekil 6.). Numaralama iģlemi aynı zamanda sistem denklemindeki matrislerin boyutunu da belirlemektedir. 6
64 ġekil 6. Bir uzay çerçevede, eleman numaraları, düğüm numaraları ve düğüm deplasmanlarının kodlanmıģ hali ġekil 6. de bir uzay çerçeve için düğümlerin, elemanların ve düğüm serbestlik derecelerinin numaralanmıģ hali görülmektedir. Düğüm deplasmanları numaralanırken, önce ötelenmeler sonra da dönmelerin numaralandığı ve eksenlerde alfabetik sıraya uyulduğu kabul edilir. TutulmuĢ olan bir serbestlik derecesi ile numaralanır. Deplasmanları sıra ile numaralanmıģ bir taģıyıcı sistemde, herhangi bir çubuğun baģ ve sonuna isabet eden düğüm noktalarındaki deplasman numaralarının, yan yana yazılması ile elde edilen rakama, o çubuğun kod numarası denir. Çubuk elemanlarda, kod numarasındaki deplasman numaralarının adedi, sistemin tipik bir düğüm noktasındaki serbestlik derecesinin iki katıdır. Çünkü bir çubukta iki uç vardır ve her deplasman numarasının bir hane iģgal ettiği kabul edilirse, bir uzay çerçeve çubuğunun kod numarasında hane vardır. Her bir hanede, o haneye tekabül eden deplasman numarası yazılıdır. Eğer bir düğüm noktasında mesnet varsa veya herhangi bir doğrultuda deplasman sıfır ise, o haneye sıfır yazılır. (ġekil 6.) ġekil 6. 'de verilen taģıyıcı sistemin kotlama tablosu da tablo 6. de verilmiģtir.,, 3 ve 4 numaralı düğümler ankastre olduğu için hareket oluģmamaktadır. Dolayısıyla kotlama tablosunda karģılık gelen değerleri sıfırdır. Tablo 6.. TaĢıyıcı sistemin kotlama tablosu Çubuk Tarifi Kod Numaraları No i-j
65 TaĢıyıcı sistemin herhangi bir düğüm noktasında birleģen bütün çubukların o düğüm noktasında, herhangi bir deplasman doğrultusuna karģılık gelen rijitlik terimlerinin toplamı, taģıyıcı sistemin o deplasman doğrultusundaki rijitlik terimini verir. Ancak böyle bir toplama yapabilmek için, global sistem eksenlerine transforme edilmiģ çubuk matrislerini kullanmak gerekir. ġekil 6. 'de gösterilen uzay çerçeve örneğini ele alalım. Görüldüğü gibi bu sistemde, hepsi beģinci düğümde olmak üzere toplam altı adet hareket serbestisi vardır. Diğer düğümler ankastre olduğu için hareket serbestisi oluģmamaktadır. Yani karģılık gelen kod numaraları sıfırdır. Bu problemin çözümünde yapılması gereken ilk adım, sistemi oluģturan bütün elemanlar için lokal eksenlere ait eleman rijitlik matrislerini hesaplamaktır. Bundan sonraki adım transformasyon matrisini kullanarak, bütün elemanlar için global sistem eksenlerine ait eleman rijitlik matrislerini hesaplamaktır. Örnek olarak seçilen yapı sisteminde toplam altı adet hareket serbestisi bulunduğundan, sistemi temsil eden rijitlik matrisi 6x6 boyutunda olacaktır. Yapılması gereken iģlem, bütün elemanlar için tek tek hesaplanan global eksenlerdeki rijitlik matrislerini ve bu elemanlara ait kod numaralarını kullanarak sistem rijitlik matrisini hesaplamaktır. Bu iģlem sonucunda tablo 6. de verilen sistem rijitlik matrisi elde edilir. Kod numarasındaki hane numaralarının yan yana getirilmesinden ortaya çıkan rakam çifti, global eksenlerdeki çubuk rijitlik matrisinden alınacak terimin satır ve sütün numarasını, bu hanelere karşılık gelen deplasman numaralarının yan yana getirilmesinden ortaya çıkan rakam çifti ise, çubuk rijitlik matrisinden alınan terimin, sistem rijitlik matrisinde yerleştirileceği yerin satır ve sütun numarasını verir. Sonuçta elde edilecek sistem rijitlik matrisi aģağıdaki Ģekilde oluģacaktır. k ij terimlerinde i ilgili elemana ait matristeki satır numarasını, j sütun numarasını, üst indis ise hangi elemana ait olduğunu göstermektedir. Simetrik matris olduğundan üst üçgen ayrıca gösterilmemiģtir. Tablo 6. Sistem Rijitlik Matrisi (k 77 ) +(k 77 ) + (k 77 ) 3 +(k 77 ) 4 (k ) +(k ) + (k 87 ) +(k 87 ) + (k 87 ) 3 +(k 87 ) (k 88 ) 3 +(k 88 ) 4 3 (k 97 ) +(k 97 ) + (k 97 ) 3 +(k 97 ) 4 (k 98 ) +(k 98 ) + (k 98 ) 3 +(k 98 ) 4 (k 99 ) +(k 99 ) + (k 99 ) 3 +(k 99 ) 4 4 (k 7 ) +(k 7 ) + (k 7 ) 3 +(k 7 ) 4 (k 8 ) +(k 8 ) + (k 8 ) 3 +(k 8 ) 4 (k 9 ) +(k 9 ) + (k 9 ) 3 +(k 9 ) 4 (k ) +(k ) + (k ) +(k ) 4 5 (k 7 ) +(k 7 ) + (k 8 ) +(k 8 ) + (k 9 ) +(k 9 ) + (k ) +(k (k ) +(k ) + (k 7 ) 3 +(k 7 ) 4 (k 8 ) 3 +(k 8 ) 4 (k 9 ) 3 +(k 9 ) 4 ) + (k ) (k ) 3 +(k ) 4 3 +(k ) 4 6 (k 7 ) +(k 7 ) + (k 8 ) +(k 8 ) + (k 9 ) +(k 9 ) + (k ) +(k (k ) +(k ) + (k ) +(k ) + (k 7 ) 3 +(k 7 ) 4 (k 8 ) 3 +(k 8 ) 4 (k 9 ) 3 +(k 9 ) 4 ) + (k ) (k ) 3 +(k ) 4 (k ) 3 +(k ) 4 3 +(k ) 4 Bilinmeyen sistem deplasmanlarının elde edilmesi için hesaplanması gereken bir diğer vektör de sistem yük vektörüdür. Bir taģıyıcı sistemin üzerine tesir eden dıģ yükler tesir ettikleri yer bakımından iki gurupta toplanabilirler. Birinci gurup yükler doğrudan doğruya sistemin düğüm noktalarına etki ederler ve sistem yük vektörüne direk olarak yerleģtirilirler. Ġkinci gurup yükler ise elemanı oluģturan düğüm noktaları arasına, yani açıklıklara (lokal veya global eksenler doğrultusunda olabilirler ) etki ederler. Bu ikinci tip yüklerin düğümler 64
66 üzerindeki etkilerinin hesaplanması için, taģıyıcı sistemin bütün çubukları uçlarından ankastre kabul edilir ve çubuklar üzerindeki yüklerin ankastre uçlarda meydana getirdikleri ankastre reaksiyonları, bilinen formülasyonlarla hesaplanır. Hesaplanan bu reaksiyonların ters iģaretlileri düğüm noktalarına doğrudan etki eden birinci gurup yükler ile toplanır. Transformasyon kuralı burada da aynen geçerlidir. Eleman lokal eksenlerinde yapılan yüklemeler ve hesaplanan reaksiyonlar varsa, bu tesirler önceden hesaplanan transformasyon matrisleri yardımı ile global sistem eksenlerine transforme edilmelidir. Sonuçta taģıyıcı sisteme ait rijitlik denklemi; (6.) Ģeklinde elde edilmiģ olur. Sistem rijitlik matrisi ve sistem yük vektörü bilindiği için, {D} sistem deplasman vektörü, bilinen lineer denklem sistemi çözüm yöntemlerinden herhangi birisi ile hesaplanabilir. Sonuçta kotlama tablosundaki numaralara karģılık gelen hareket serbestileri yönünde, etkiyen yüklemeler altında sistemin yapmıģ olduğu deplasmanlar elde edilmiģ olur. 65
67 matris tersi alınırken, matrisin boyutunun önemi olunmaksızın determinant alınarak işlem yapılır. Aramak istediğinizi buraya yazınız. ARA Matrisin tersinin alınması (Mantrix Inverse) Home / Bilgisayar Matematiği C/C++ Kod Örnekleri / Matrisin tersinin alınması (... Yazarın Yeni Çıkan Kitabı Rapid Miner ile Veri Madenciliği Kasım 9, 8 Şadi Evren ŞEKER Bilgisayar Matematiği/ C/C++/ Kod Örnekleri 95 Comments Yazan : Şadi Evren ŞEKER Bir matrisin tersini almak çarpma işlemine göre tersini almak anlamındadır. Örneğin A ve B matrislerinin çarpımından C matrisi çıkıyorsa; C matrisi ile A matrisinin tersi B matrisini vermelidir. Bunu bir nevi bölme olarak düşünmek de mümkündür. boyutlu bir matrisin tersini bulmak içn öncelike determinantı hesaplanır ardından aşağıda gösterildiği üzere elemanları yer değiştirilir: Weka ile Veri Madenciliği: Yukarda, ilk satırda verilen A matrisinin determinantı hesaplanmış ( A ) ve gösterilen yerdeğiştirmiş matris ile skalar (scalar) çarpım yapılmıştır. Sonuçta elde edilen matris, orjinal A matrisinin tersidir. Matris 3 3 boyutlarında olsaydı bu hesaplama aşağıdaki şekilde yapılmalıydı: *Kitabı ücretsiz edinmek isteyen öğrenciler lütfen öğrenci maillerinden bana mail atsınlar. BilgisayarKavramlari YouTube 3K Bilgisayar Kavramları Youtube da Görüldüğü üzere matrisin boyutunun değişmesi halinde ters alma işlemi de değişmektedir. Yukarıdaki mantık ile örneğin 4 4 lük bir matris in tersi alınırken önce 3 3 alt matrislerinin yazılması ardından her bir alt matrisin determinantının yukarıdakine benzer şekilde yerleştirilmesi gerekir. 4 4 lük matrisin tersinin alınması (Utku Bey in isteği üzerine yazıyorum) C ile Programlamaya Giriş. Ders: Temeller Bilgisayar Kavramları Kanal Tanıtımı Veri Yapılarına Giriş ve Bağlı Listeler (Linked List) -VY SQL - (Veri Tabanı Eğitim Serisi 3)
68 Örneğin matris boyutu nxn ise bu matriste (n-)x(n-) boyutlarındaki alt matrislerin determinantlarının yer değiştirmiş halleri hesaplanır ve / A değeri ile skalar çarpım yapılır. Örneğin matrisimiz aşağıdaki şekilde 4 4 boyutlarında bir matris olsun Bilgisayar Mühendisliği Zevkli mi? Zorlukları Neler? Acı Gerçekler ve Bilgisayar Mühendisliği (Soru Cevap 3 Temmuz 6) Yukarıdaki bu matrisin tersini almak için öncelikle determinantını hesaplayalım: Veri Tabanı Yönetim Sistemleri - (DBMS Giriş) (DBMS Eğitim Serisi ) Java Giriş /6 Sonraki» YouTube Kanalını ziyaret edin» Bilgisayar 7,3 Bin beğenme Sayfayı Beğen Arkadaşların arasında bunu ilk beğenen sen ol Ters alma işlemi için determinant sıfırdan farklı olmalıdır. Ardından matrisin tersini alalım: Kategoriler algoritma analizi (teory of algorithms Automata (otomatlar, özdevinirler bilgisayar felsefesi Bilgisayar Grafiği (Computer Graphics Buradaki kapalı şekilde yazılan b değerleri ters alma işleminden sonra yapılan yer değiştirmeyi göstermektedir. Yani örneğin b değeri,. satır ve. sütundaki değerleri kapanmış halde matrisin determinantının alınması ile bulunur. Benzer şekilde b3 değeri için, orjinal matriste bulunan. satır ve 3. sütundaki sayılar dışında kalan sayılardan (ki bu sayılar 3 3 boyutlarında bir matris oluşturur) elde edilen determinant değeridir. Buradaki b değerleri, matrisin verilen satır ve sütun için kofaktörüdür (cofactor). Bu değerleri açık şekilde yazacak olursak: Bilgisayar Kavramları Bilgisayar Matematiği Bilgisayar Standartları C/C++ Derleyiciler Doğal Dil İşleme (NLP Donanım ( Hardware Dosya Organizasyonu (File Organisation graf teorisi (graph theory, çizge kuramı işletim sistemleri JAVA Kod Örnekleri Scheme (Lisp Kuantum Hesaplama Mantık Devreleri (Logic Circuits MIS (Yönetim Bilişim Sistemleri Nesne Yönelimli Programlama Network(Ağ Web Teknolojileri
69 Programlama Dilleri Resim İşleme (Image Processing Scheme (lisp Sınavlar Sistem Programlama (System Programming şeklinde sayıları sıralayabiliriz. Yukarıdaki ters alma işlemi kısaca olay iki parçadan oluşuyor, birinci aşamada determinant almanız gerekiyor (nxn boyutundaki bir matris determinantı bilgisayar kullanarak en kolay leibniz yöntemi ile alınır) ikinci adımda b terimlerini hesaplamanız gerekiyor. Bu terimlerin hesabı için hangi koordinat hesaplanacaksa, o koordinatın satır ve sütunu kapatılıp geri kalan elemanlar bir sarmal şeklinde çarpılır. Bu durumu linkteki örnekten açıkça görebilirsiniz. Örneğin b için. satır ve. sütun kapatılıp kalan elemanlar bir sarmal şeklinde çarpılıp toplanmıştır. Burada mod işlemi ile sarmallık sağlanabilir. Gauss Jordan Yöntemi Gelen bir soru üzerine, Gauss Jordan yöntemini adım adım anlatan yeni bir bölüm ekliyorum. Öncelikle yukarıdaki kodda, Gauss Jordan metodunu kullanıyoruz. Bu metotta amaç bir matrisin tersini almak için tersi olan matris ile çarpımını, birim matrise dönüştürmektir. Son Kullanıcı Temel Bilimler Uncategorized Veri Güvenliği(Cryptography Veri Madenciliği (Data Mining Metin Madenciliği (Text Mining Veri Madenciliği (Data Mining Veri Sıkıştırma (Data Compression Veri Tabanı (Database veri yapıları yapay zeka (artificial intelligence Yapay Sinir Ağları (Artificial Neural Networks Yazılım Mühendisliği (Software Engineering A x A - = I işlemine göre şayet A matrisinin tersi isteniyorsa A x B = I, şeklinde yazdığımız B matrisi, A matrisinin tersidir ve I = A x B, şeklinde yazılabilir. Buradaki B matrisini elde ederken aslında birim matris üzerinde işlem yapılarak A matrisinin tersi alınmış olur. Örneğin aşağıdaki matrisi ele alalım: Son Eklenenler Rapid Miner ile K-NN Uygulaması Kemmi Normalleştirme (Quantile Normalization) Ters Parça Algoritması (Reverse Factor Algorithm) Genetik Programlama (Genetic Programming) JAVA dilinde WEKA ile kod geliştirilmesi Eş-Eğitim (Co-Training) Bu matrisin tersini alırken öncelikle yanına bir çizgi çekip birim matrisi yazıyoruz: Metin Madenciliği (Text Mining) BT'nin İşletmelere Etkisi Ana Üretim Planlaması (Master Manufacturing Planning) BOM (Bill of Materials) Ürün Reçetesi Meta Buradaki amacımız sol ve sağ tarafta aynı işlemleri yaparak sol tarafta birim matrisi elde etmektir. Böylelikle sağ tarafta matrisin tersi oluşacaktır. Bu satırlar üzerinde yapılan işlemlerre yalın satır işlemleri (elementary row operations) ismi verilir. Bu işlemler aşağıdaki şekilde sıralanabilir: Giriş Yazılar RSS Yorumlar RSS WordPress.org bir satırın bir sabit ile çarpılması Bir satırın diğer bir satır ile yer değiştirmesi Bir satırın diğer bir satırdan çıkarılması
70 Elbette yukarıdaki bu işlemler, çizginin iki tarafına da uygulanacaktır. Buradaki işlemler aslında bir matriste bir denklemin tutulması durumunda denklemler üzerine yapılan işlemlere benzetilebilir. Örneğin 3 bilinmeyenli 3 denklem ele alınırsa bir denklemin diğer denklemin çözümünde kullanılırken yapılan işlemler gibidir. Şimdi matrisin tersini alma işlemi ile devam edelim. Amacımız ilk sütunu birim matrise benzetmek. İlk sütunda 3. satırda bulunan tek farklı sayıdır. Dolayısıyla 3. satırın ilk terimini yapabilmek için ilk satırı, 3. satırdan çıkarabiliriz. - yukarıdaki işlem sonucunda görüldüğü üzere çizginin solundaki ilk satır 3. satırdan ve çizginin sağındaki ilk satır yine çizginin sağındaki 3. satırdan çıkarılmıştır. çizginin solunda elde edilen 3. satır aslında birim matrisin ikinci satırıdır. O halde 3. satır ile. satırı yer değiştirirsek matrisin sol tarafından birim matrise daha çok yaklaşılmış olunur. - Yine 3. satırı birim matrise benzetmek için bu sefer. satırın mislini, 3. satırdan çıkarmak yeterlidir. - - Yukarıda görüldüğü üzere çizginin iki yanında da ikinci satır ile çarpılmış ve 3. satırdan çıkarılmıştır. Sırada ilk satırı birim matrise benzetmek var. Bu işlem için ilk satırdan 3. satırı çıkarmak yeterlidir: Görüldüğü üzere çizginin sol tarafından birim matri elde edildi. Bu durumda matrisin sağ tarafında elde ettiğimiz matris, ilk matrisin tersidir sonucunu bulmuş oluruz. Programlama Matrisin tersinin alınması işleminin bilgisayarlar marifetiyle yapılması için algoritmik bir yaklaşıma ihtiyaç vardır. Bu bağlamda matrisin boyu ve içeriğinden bağımsız olarka matrisin
71 Utku Deniz Bir başka WordPress sitesi Anasayfa İletişim Yeni Başlayanlar için Matlab Gauss Eliminasyon ve Gauss Jordan Yöntemleri Utku Deniz tarafından 9 Kasım 3 tarihinde gönderildi Bu yazımızda Lineer(Doğrusal) denklem sistemlerinin çözümünde kullanılan Gauss Eliminasyon(Gauss Yok Etme) ve Gauss Jordan yöntemlerini anlatacağız. Bu yöntemler özellikle büyük denklem sistemlerinin çözümünde kolaylık sağlamaktadır. 3 3 lük bir matrisi çözerken çok pratik gözükmemesine rağmen bu yöntemler lik bir matrisin çözümünde büyük fayda sağlamaktadır. Özellikle bilgisayar uygulaması haline getirildiğinde pratik bir şekilde çözüme ulaşılabilmesini sağlayan yöntemlerdir. Şimdi lafı fazla uzatmadan yöntemlerin nasıl uygulandığına bakalım. Gauss Eliminasyon (Gauss Yok Etme) Metodu Şekil de görülen denklem sistemini Gauss Eliminasyon yöntemiyle çözmek için öncelikle Şekil de görülen matris formunda yazmalıyız. Ara Son Yazılar Gauss Eliminasyon ve Gauss Jordan Yöntemleri Yeni Başlayanlar için Matlab Merhaba dünya! Arşivler Kasım 3 Ekim 3 Kategoriler Genel Matlab Sayısal Analiz Meta Giriş Yazılar RSS Yorumlar RSS WordPress.org Şekil Şekil de görülen x, y ve z değerlerinin kat sayılarıyla oluşturulan matris Şekil de görülmektedir. Şekil de görülen matrise çeşitli satır işlemleri uygulayarak Şekil 3 de görülen forma dönüşmeye çalışacağız. Şekil Şekil 3 Şekil de görülen matrisin ilk satırının ilk sütunu zaten olduğu için ilk satıra bu aşamada bir işlem yapmamıza gerek yok dolayısıyla. satırın ilk elemanını yaparak başlayacağız. İkinci satırın ilk elemanı Şekil 4 3 tür. İlk satırımızı kullanarak bu 3 değerini yapmalıyız. Bu nedenle Şekil 4 de görüldüğü gibi. satırın tamamını 3 ile çarparak. satırdan çıkartıyoruz. Burada kesinlikle unutulmaması gereken şey uygulanacak işlemlerin bütün satıra yansıtılmasıdır. Şekil 5 İkinci satırın ilk elemanını yaptığımıza göre şimdi köşegen üzerinde yer alan. satırın. sütun elemanı olan -4 ü yapmalıyız. Bunun için Şekil 5 de görüldüğü gibi. satırın tamamını -4 e bölüyoruz. İkici satır Şekil 3 de görülen forma girdiği için şimdi sıra 3. satırda.
72 Şimdi 3. satırın ilk elemanını yapmak için. satırımızı kullanıyoruz. 3. satırın ilk elemanı ve. satırın ilk elemanı olduğu için. satırın tamamını Şekil 6 da görüldüğü gibi ile çarparak 3. satırdan çıkartıyoruz. Şekil 6 Şekil 7 Matrisimizi Şekil 3 de görülen forma dönüştürmek için Şekil 6 da görülen 3. satırın. elemanı olan -5 i haline getirmeliyiz. Bu yüzden Şekil 7 de görüldüğü gibi. satırı 5 ile çarpıp 3. satıra ekliyoruz. Şimdi de matrisimizi Şekil 3 de görülen matrise benzetmek için gereken son matris işlemi olan 3. satırın son elemanını yapmalıyız. Şekil 8 de görüldüğü gibi 3. satırı 4/3 ile çarpmak bu işlem için yeterli. Şekil 8 Şekil 9 Şekil 8 de görülen matris Şekil 3 de görülen matrise benziyor dolayısıyla artık satır işlemlerimiz bitti buradan sonra tekrar matris formundan denklem formuna geçiyoruz Şekil 8 de görülen matrisi denklemler şeklinde yazarsak Şekil 9 da ki denklem sistemini elde ederiz. Şekil 9 da z nin değerinin 3 olduğu görülmektedir. Şimdi aşağıdan yukarı doğru bu denklemleri adım adım çözeceğiz. Şekil Şekil 9 da görülen. denklemde z gördüğümüz yere 3 yazıp y nin değerini hesapladığımızda olduğunu görürüz yine benzer şekilde, y ve z nin değerlerini bildiğimize göre Şekil 9 da görülen ilk denklemde yerlerine yazarak Şekil de görüldüğü gibi x değerini hesaplayabiliriz. Şekil de görülen denkleme hesaplanan x, y ve z Şekil değerlerini yazarak denklemi sağlayıp sağlamadıklarına bakarak işlemleri doğru yapıp yapmadığımızı kontrol edebiliriz. Böylece x, y ve z değerlerini Gauss Eliminasyon (Gauss Yok Etme) yöntemiyle hesaplamış olduk. x, y ve z değerleri sırasıyla, ve 3 olarak bulunmuştur. Gauss Jordan Yöntemi Gauss Eliminasyon ve Gauss Jordan yöntemleri arasında aslında pek farklılık yoktur. Bu yöntemde de verilen denklem sistemi matris biçiminde yazılır ve çeşitli satır işlemleri yapılarak doğrusal(lineer) denklem sistemlerinin çözüm kümeleri hesaplanır. Asıl farklılık çözüm kümesi hesaplanırken denklem sistemini matris olarak yazma, matris satır işlemleri ve tekrar denklem sistemi formuna dönüp aritmetik işlem yapma basamakları yerine denklem sistemi matris formunda yazılır ve matris satır işlemleri kullanılarak çözüme ulaşılır. Gauss Eliminasyon yönteminde çözülen örnek üzerinden devam edersek; Şekil de verilen denklem sistemi Şekil de verilen matris formuna dönüştürülmüştü ardından Şekil 3 de gösterilen matris formuna dönüşümün sağlanması için Şekil 4 8 arasındaki işlem basamakları takip edilmişti. Bu
73 Şekil Şekil 3 de gösterilen matris formuna dönüştürmek istememiz. süreç Şekil de kısaca gösterilmiştir. Gauss Jordan yöntemindeki temel fark ise elimizdeki başlangıç matrisini Şekil 3 de gösterilen matris formuna değil de Şekil 3 de görülen matris incelendiğinde Şekil 3 de görülen matris ile olan benzerliği hemen dikkat çekmektedir. Şekil 3 de verilen matrisin köşegeni değerlerinden köşegen altında kalan matris elemanları ise değerlerinden oluşmaktadır. Şekil 3 de görülen matrisin ise köşegenin üstünde kalan matris elemanları da değerlerinden oluşmaktadır. Bu sebeple Şekil de görülen son matris üzerinden Gauss Jordan yöntemine devam ediyoruz. Şekil 3 Şekil 4 Şekil 4 de görüldüğü gibi. satırın 3. elemanını yapmak için 3. satırı 7/4 ile çarpıp. satırdan çıkartıyoruz.. satırda Şekil 3 de görülen. satıra benzediğine göre artık. satırı Şekil 3 deki. satıra benzetebiliriz. 3. satırı ile çarpıp. satırdan çıkardığımızda. satırın 3. elemanının olduğu Şekil 5 de görülmektedir. benzer şekilde. satırı ile çarpıp. satırdan çıkardığımızda. satırın. elemanının da olduğu Şekil 6 da görülmektedir. Şekil 5 Şekil 6 Şekil 4, 5 ve 6 da görülen işlemler aracılığıyla Şekil 3 de görülen matris formuna ulaşmış olduk. Şekil 6 da da görüldüğü gibi x, y ve z değerleri sırasıyla, ve 3 tür. Değerleri Şekil de yerine yazarak sistemin çözümü olup olmadığını kontrol edebiliriz. Görüşmek üzere. Bu yazı Sayısal Analiz kategorisine gönderilmiş ve analiz, çözümü, denklem, eliminasyon, gauss, gauss eliminasyon, gauss eliminasyon örnek soru çözümü, gauss jordan, gauss jordan örnek soru çözümü, jordan, lineer, metod, örnek, Sayısal, sayısal analiz, sistemi, soru, yok etme yöntemi, yöntem ile etiketlenmiş. Kalıcı bağlantıyı yer imlerinize ekleyin. Yeni Başlayanlar için Matlab Gauss Eliminasyon ve Gauss Jordan Yöntemleri için 5 cevap Ömer der ki: 3 Kasım 4 tarihinde, saat 6:33 Eline sağlık, çok açıklayıcı anlatmışsın. Cevapla Cihad der ki: 3 Kasım 4 tarihinde, saat 4: Çok teşekkürler harika bir anlatım bu yoğun tempomda teşekkür etmeden geçmeye içim el vermedi Cevapla
74 B Ö L Ü M V I I 7. R Ġ J Ġ T L Ġ K M AT R Ġ S Ġ Y Ö N T E M Ġ - Ç Ö Z Ü M L Ü Ö R N E K L E R 7. GİRİŞ Programlamaya elveriģli, her tür taģıyıcı sistem ve yükleme için genel ve sistematik olan rijitlik matrisi yöntemi, yapı analizinde önemli bir yer tutmaktadır. Bu bölümde önceki bölümlerde verilen, eleman rijitlik denklemleri, koordinat dönüģümleri, eleman ankastrelik uç kuvvetleri bilgileri ve rijitlik matrisi yöntemi iģlem sırası kullanılarak örnek özümler yapılmıģtır. Eleman denklemlerinden sistem denkleminin elde edilmesi ve sistem düğüm deplasmanlarından eleman deplasman vektörlerinin belirlenmesinde kotlama tekniği kullanılmaktadır. Bu nedenle, çözümlerde her problem için kotlama tablosu hazırlanmıģtır. Eleman denklemlerinden sistem denklemleri elde edilirken, eleman kod numaraları vektörlerinden faydalanılmıģtır. Örneğin, bir elemanın sitem rijitlik matrisine katkısının belirlenmesinde, eleman kod numaraları matrisin üzerine satır olarak, sağ tarafına ise sütun olarak yazılmıģtır. Böylece eleman rijitlik matrislerinden hangi terimlerin, sistem rijitlik matrisinin hangi satır ve sütununa katkıda bulunacağı tespit edilmiģ olmaktadır. Sitem denklemindeki sistem yük vektörü, taģıyıcı sistemin üzerine tesir eden dıģ yüklerden hesaplanmaktadır. DıĢ yükler sistem üzerine iki Ģekilde tesir etmektedir. Yükler doğrudan doğruya sistemin düğüm noktalarına etkiyorsa, bu yükler sistem yük vektörüne direk olarak yerleģtirilirler. Eğer yükler elemanı oluģturan düğüm noktaları arasında, yani açıklıklarda etki ediyorlarsa, bu yüklerin düğümlere indirgenmesi gerekmektedir. Bunun için, eleman ankastrelik uç kuvvetlerinin sistem koordinatlarında elde edilerek düğümlere ters iģaretli olarak etki ettirilirler. Bu bölümde verilen çözümlerde kolaylık olması bakımında elastisite modülü E, en kesit alanı A ve atalet momenti I yerine alınmıģtır. Gerçek düğüm deplasmanları gerçek EI ve EA değerlerine bölünerek elde edilebilir. elde edilen kesit uç kuvvetlerinde (kesit tesirlerinde) bir değiģiklik olmayacaktır. Çözümlü örneklerde, yükleme Ģekli, düğüm ve eleman tanımları ile düğüm deplasmanlarını gösteren kotlama tablosu verilmiģtir. Her çözüm için ayrıca kesit tesirleri diyagramları da Ģekiller halinde verilmiģtir. Uç kuvvetlerinden kesit tesirleri diyagramlarına geçiģte, mukavemetten bilinen pozitif eğilme yönü ve pozitif kesme yönü esas alınmıģtır. 66
75 Örnek P = kn I P = kn 3 L = 5 m Kodlama Tablosu Eleman No Tarifi Kod Numarası - 3 Eleman Rijitlik Matrisleri é EA EA - L L EI 6EI EI 6EI - L 3 L L 3 L 6EI 4EI 6EI EI - L L L L [ k] = EA EA - L L EI 6EI EI 6EI L 3 L L 3 L 6EI EI 6EI 4EI - ë L L L L E=, A=, I=,L=5 ù û [ ] = k é ë ù û 3 Sistem koordinatlarındaki eleman rijitlik matrisleri sistem koordinatlarındaki rijitlik matrisi, [T] koordinat dönüşüm matrisi olmak üzere; idi. Burada nolu elemanın sistem rijitlik matrisi ile eleman rijitlik matrisi birbirine eşittir. Buna bağlı olarak olduğu için [ k ] = k [ ] ' = é ë ù û 3 Sistem Rijitlik Matrisi nolu elemanın sistem koordinatlarındaki rijitlik matrisi elde edilmiş ve elemanın kod numaraları matris üzerine satır, sağ tarafına ise sütun olarak yazılmıştır. Buna göre kodlama satırı ve sütunundaki rakamlardan faydalanılarak sistem rijitlik matrisi; 67
76 é [ K] = ë ù û 3 şeklinde elde edilmiştir. Sistemimizde iki düğüm vardı. Bir tanesi ankastre olduğundan tüm deplasmanlar önlenmiştir.. Düğüm ise serbest olduğundan iki yönde ötelenme ve bir dönmeden oluşan 3 serbestlik derecesine sahiptir. Böylece sistemimiz 3 serbestlik derecele olmaktadır. Sistem rijitlik matrisi de 3x3 boyutundadır. Görüldüğü gibi sistem rijitlik matrisi simetrik ve mutlak pozitif bir matristir. Eleman ankastrelik uç kuvvetleri nolu elemanın üzerinde açıklık ortasından tekil yük etkimektedir. Bunun için Şekil 5.3 de verilen ankastrelik uç kuvvetleri; ì f = í î P PL 8 P PL 8 ü ì ý = í þ î şeklinde olacaktır. 5 5 Sistem Yük vektörü ü ý þ 3 Sistem yük vektörü, sistem koordinatlarındaki ankastrelik uç kuvvetlerinin ters işaretlileri (- ile çarpılarak) toplanıp, varsa düğüm yükleri direkt olarak matrise ilave edilmesi ile bulunur. Eleman ankastrelik uç kuvvetlerinden hangilerinin sistem yük vektöründe nerede yer alacağına, yine eleman kod numaraları vektörü ile karar verilmektedir. Bunun için numaralı elemanın ankastrelik uç kuvvetleri vektörünün sağ tarafına kod numaraları da yazılmıştır. Buna göre, ve 3 nolu serbestlik dereceleri doğrultusunda etkimekte olan eş değer düğüm yükleri alınarak sistem yük vektörü; Q 5 3 şeklinde hesaplanmıştır. 68
77 Sistem Denklemi çözümü Lineer denklem sistemi olan sistem denklemi çözülerek bilinmeyen düğüm deplasmanları hesaplanabilir. Denklemin çözümünde Gaus eliminasyon yöntemi kullanılabilir. Veya rijitlik matrisinin tersi alınarak yük vektörü ile çarpılmak sureti ile bilinmeyenler bulunabilir. Sistem denklemi şeklinde idi. İfadeler yerine konulur ve denklem çözülürse; {D} D.4 * D.8 D 3 5 olarak elde edilir. Eleman Deplasman vektörleri Sistemde iki düğüm arasında yer alan elemanın uç deplasmanlarının hangileri olduğu, eleman kod numaralından belirlenir. Her hangi bir kod numarası sistemdeki bir deplasman numarasına karşılık gelmektedir. Bu şekilde belirlenen eleman uç kuvvetleri vektörleri sistem koordinatlarında olacaktır. Gerekirse bunlar transformasyon ile eleman koordinatlarına da dönüştürülebilir. Burada nolu elemanın sistem koordinatlarındaki deplasman matrisi ile eleman koordinatlarındaki deplasman matrisi, olduğu için birbirinin aynıdır. d d D D D Çubuk Uç Kuvvetlerinin Hesabı Çubuk uç kuvvetleri eleman denklemi kullanılarak hesaplanır. Uç kuvvetleri sistem koordinatlarında veya eleman koordinatlarında elde edilebilir. Burada dikkat edilecek husus, değerlerin hepsinin aynı koordinatlarda olmasıdır. nolu elemanın çubuk uç kuvvetleri 69
78 Kesit Tesirleri Hesaplanan çubuk uç kuvvetleri, iģaret kabulü de dikkate alınarak çubuk uçlarında gösterilir. Çubuk uç kuvvetlerinin ters iģaretlileri de çubukların bağlı oldukları düğümlere etki ettirilir Kesit Tesirleri Diyagramları Kabul edilen pozitif eğilme ve kayma yönleri de dikkate alınarak kesit tesirleri diyagramları çizilir. Pozitif eğilme ve kesme yönleri Örnek Üniform yayılı yüklü konsol kiriģ, rijitlik matrisi yöntemi ile çözülmüģtür. Adımlarla ilgili detaylı açıklama. Örnekte yapılmıģtı. 7
79 Kodlama Tablosu Eleman No Tarifi Kod Numarası - 3 Eleman Rijitlik Matrisleri.5 k E= A= I= L ise elemanın boyu alınacaktır. Sistem koordinatlarındaki eleman rijitlik matrisleri [T] koordinat dönüģüm matrisi ve sistem koordinatlarındaki rijitlik matrisi olmak üzere; idi. Burada nolu elemanın sistem rijitlik matrisi ile eleman rijitlik matrisi olduğu için birbirine eģittir. Buna bağlı olarak k k ' Sistem Rijitlik Matrisi 7
80 K Eleman Ankastrelik uç kuvvetleri Sistem Yük vektörü Sistem yük vektörü, sistem koordinatlarındaki ankastrelik uç kuvvetlerinin ters iģaretlileri toplanıp, varsa düğüm yükleri direkt olarak matrise ilave edilmesi ile bulunur. Sistem Denklemi çözümü sistem denklemi {D} vektörü bulunur. Ģeklinde idi. Ġfadeler yerine konulur ve denklem çözülürse; Eleman Deplasman vektörleri Burada nolu elemanın sistem koordinatlarındaki deplasman matrisi ile eleman koordinatlarındaki deplasman matrisi olduğu için birbirinin aynıdır. 7
81 Çubuk Uç Kuvvetlerinin Hesabı Kesit Tesirleri Sistem Kesit Tesirleri Diyagramları 73
82 Örnek 3 ġekilde verilen sürekli kiriģi rijitlik matrisi metodu ile çözelim. KiriĢin yükleme durumu ve düğüm serbestlik dereceleri aģağıda verilmiģtir. q = kn/m E, I,A E, I, A 4 m 3 m 3 3 Kodlama Tablosu Eleman No Tarifi Kod Numarası Eleman Rijitlik Matrisleri KiriĢte E= A= I= L ise elemanın boyu alınacaktır. Sistem koordinatlarındaki eleman rijitlik matrisleri [T] koordinat dönüģüm matrisi ve sistem koordinatlarındaki rijitlik matrisi olmak üzere; 74
83 idi. Burada nolu elemanın sistem rijitlik matrisi ile eleman rijitlik matrisi olduğu için birbirine eģittir. Buna bağlı olarak Sistem Rijitlik Matrisi Eleman Ankastrelik uç kuvvetleri vektörleri (Ġkinci eleman üzerinde yük bulunmamaktadır) Sistem Yük vektörü Sistem yük vektörü, sistem koordinatlarındaki ankastrelik uç kuvvetlerinin ters iģaretlileri toplanıp, varsa düğüm yükleri direkt olarak matrise ilave edilmesi ile bulunur. Sistem Denklemi çözümü Sistemin düğüm deplasmanları vektörü Eleman Deplasman vektörleri Burada nolu eleman ve nolu elemanın sistem koordinatlarındaki deplasman matrisi ile eleman koordinatlarındaki deplasman matrisi olduğu için birbirinin aynıdır. 75
84 Çubuk Uç Kuvvetlerinin Hesabı nolu elemanın çubuk uç kuvvetleri nolu elemanın çubuk uç kuvvetleri için; Kesit Tesirleri 76
85 Kesit Tesirleri Diyagramları T (kn) M (knm) 77
86 Örnek 4 Bir düģey bir de yatay elemandan oluģan düzlem çerçevenin rijitlik matrisi yöntemi ile çözümü P = kn I P = kn 3 I h = 4 m 3 L = 5 m a) b) Kodlama Tablosu Eleman No Tarifi Kod Numarası Eleman Rijitlik Matrisleri E= A= I= L ise elemanın boyu alınacaktır. Sistem koordinatlarındaki eleman rijitlik matrisleri [T] koordinat dönüģüm matrisi ve sistem koordinatlarındaki rijitlik matrisi olmak üzere; 78
87 79 idi. Burada nolu elemanın sistem rijitlik matrisi ile eleman rijitlik matrisi olduğu için birbirine eģittir. nolu eleman için dönüģüm matrisi; Ģeklindedir. Bu elemanın tarifi -3 olduğundan, saat ibresi yönünde 7 dönülmektedir. Sistem Rijitlik Matrisi Eleman Ankastrelik uç kuvvetleri vektörleri } { } { f PL P PL P f
88 Sistem Yük vektörü Sistem yük vektörü, sistem koordinatlarındaki ankastrelik uç kuvvetlerinin ters iģaretlilerinin direkt düğüm yükleri ile toplanmasından elde edilir. Sistem Denklemi çözümü Sistem denklemi çözülürse; düğüm deplasmanları; Ģeklinde bulunur. Eleman Deplasman vektörleri olduğu için nolu elemanın sistem koordinatlarındaki deplasman matrisi ile eleman koordinatlarındaki deplasman matrisi birbirin aynıdır. Çubuk Uç Kuvvetlerinin Hesabı nolu elemanın çubuk uç kuvvetleri 8
89 nolu elemanın çubuk uç kuvvetleri için; Kesit Tesirleri P = kn.38 knm kn kn.3 knm P = kn kn 5.49 kn.65 knm 5.8 kn kn Normal kuvvet deðerleri italik olarak gösterilmiþtir. 5.8 kn kn 8.68 knm Kesit Tesirleri Diyagramları 8
90 Örnek 5 Örnek 4 de verilen çerçeveyi, kiriģin üniform yayılı yükle yüklenmesi durumu için çözelim. E,A,I q = kn/m 3 E, A, I h = 3 m 3 L = 4 m Kodlama Tablosu Eleman No Tarifi Kod Numarası Eleman Rijitlik Matrisleri.5 k
91 k Sistem koordinatlarındaki eleman rijitlik matrisleri Sistem Rijitlik Matrisi Eleman Ankastrelik uç kuvvetleri Sistem Yük vektörü 83
92 Sistem Denklemi çözümü Eleman Deplasman vektörleri Çubuk Uç Kuvvetlerinin Hesabı nolu elemanın çubuk uç kuvvetleri nolu elemanın çubuk uç kuvvetleri için; Kesit Tesirleri 84
93 9.945 kn q = kn kn knm knm 9.37 kn kn knm 9.85 kn kn Normal kuvvet deðerleri italik olarak gösterilmiþtir kn kn.3 knm 85
94 Örnek 6 Bir karģılaģtırma yapılması maksadı ile Örnek 5 de verilen çerçeve sistemi eksenel deformasyonlar ihmal edilerek yeniden çözülmüģtür. Örnek 5 de verilen çerçevede eksenel deformasyonlar ihmal edecek olursak, nolu düğümde tek serbestlik derecesi kalır. Bu durumdaki çözüm, yaklaģık yöntemler (Crosss ve Açı) ile aynı sonucu verecektir. E,A,I q = kn E, A, I h = 3 m 3 L = 4 m Kodlama Tablosu Eleman No Tarifi Kod Numarası Eleman Rijitlik Matrisleri k k Sistem koordinatlarındaki eleman rijitlik matrisleri k Sistem Rijitlik Matrisi 86
95 Eleman Ankastrelik uç kuvvetleri Sistem Yük vektörü Sistem Denklemi çözümü Eleman Deplasman vektörleri Çubuk Uç Kuvvetlerinin Hesabı nolu elemanın çubuk uç kuvvetleri nolu elemanın çubuk uç kuvvetleri için; 87
96 Kesit Tesirleri q = kn kn kn knm 73.3 knm kn 7.7 kn 53.3 knm 6.66 kn kn Normal kuvvet deðerleri italik olarak gösterilmiþtir kn kn 6.66 knm Kesit Tesirleri Diyagramları N (kn) T (kn)
97 Örnek 7 ġekilde verilen tek katlı düzlem çerçevenin kesit tesirleri diyagramları belirlenecektir. düğümü serbest olan çerçeve taģıyıcı sistemin sistem serbestlik derecesi 6 dır. E,A,I q =5 kn/m E, A, I E, A, I h = 5 m L = 8 m Kodlama Tablosu Eleman No Tarifi Kod Numarası Eleman Rijitlik Matrisleri E= A= I= L ise elemanın boyu alınacaktır. ve nolu elemanlar aynı özellikte olduğundan matrisleri aynı olacaktır. Kodlama için her iki matris ile yapılacak olan iģlemler bir arada gösterilmiģtir 89
98 .5 k Sistem koordinatlarındaki eleman rijitlik matrisleri ve. Elemanların rijitlik matrisleri sistem koordinatlarında elde edilmiģtir. Sistem Rijitlik Matrisi Eleman Ankastrelik uç kuvvetleri vektörleri.. ve. Elemanlar yüksüzdür. Sadece 3. Elemanda ara yük vardır 9
99 Sistem Yük vektörü Sistem yük vektörü, sistem koordinatlarındaki ankastrelik uç kuvvetlerinin ters iģaretlileri toplanıp, varsa düğüm yükleri direkt olarak matrise ilave edilmesi ile bulunur. Sistem Denklemi çözümü, Eleman Deplasman vektörleri 9
100 Çubuk Uç Kuvvetlerinin Hesabı nolu elemanın çubuk uç kuvvetleri, nolu elemanın çubuk uç kuvvetleri için;, 3 nolu elemanın çubuk uç kuvvetleri için; Kesit Tesirleri q =5 kn/m knm.386 kn.386 kn knm 6 kn 6 kn knm knm 6 kn.386 kn 6 kn 6 kn.386 kn Normal kuvvet değerleri italik olarak gösterilmiştir. 6 kn.386 kn.386 kn knm knm 9
101 Kesit Tesirleri Diyagramları Örnek 8 Örnek 7 de ele alınan çerçevede eksenel deformasyonlar ihmal edilerek çözüm yapılmıģtır. Bu durumda kolonlardaki boy değiģimi ihmal edildiği için düģeydeki serbestlik dereceleri sıfır olacaktır. E,A,I q =5 kn/m E, A, I E, A, I h = 5 m L = 8 m Kodlama Tablosu Eleman No Tarifi Kod Numarası
102 Eleman Rijitlik Matrisleri E= A= I= L ise elemanın boyu alınacaktır..5 k Sistem koordinatlarındaki eleman rijitlik matrisleri Sistem Rijitlik Matrisi Eleman Ankastrelik uç kuvvetleri Sistem Yük vektörü 94
103 Sistem Denklemi çözümü Eleman Deplasman vektörleri Çubuk Uç Kuvvetlerinin Hesabı nolu elemanın çubuk uç kuvvetleri 95
104 nolu elemanın çubuk uç kuvvetleri için; 3 nolu elemanın çubuk uç kuvvetleri için; Kesit Tesirleri q =5 kn knm.386 kn.386 kn knm 6 kn 6 kn knm knm kn.386 kn kn kn.386 kn Normal kuvvet değerleri italik olarak gösterilmiştir. kn.386 kn.386 kn knm knm 96
105 Kesit Tesirleri Diyagramları Örnek 9 Düğümlerde sadece dönme serbestlik derecelerini dikkate alarak aynı çerçevenin kesit tesirleri diyagramlarını çizelim. Bu durumda sistemimiz düğüm noktaları sabit sistem olacaktır. E,A,I q =5 kn/m E, A, I E, A, I h = 5 m L = 8 m Kodlama Tablosu Eleman No Tarifi Kod Numarası Eleman Rijitlik Matrisleri E= A= I= L ise elemanın boyu alınacaktır. 97
106 k k Sistem koordinatlarındaki eleman rijitlik matrisleri Sistem Rijitlik Matrisi Eleman Ankastrelik uç kuvvetleri vektörleri Sistem Yük vektörü Sistem Denklemi çözümü, 98
107 Eleman Deplasman vektörleri Çubuk Uç Kuvvetlerinin Hesabı nolu elemanın çubuk uç kuvvetleri nolu elemanın çubuk uç kuvvetleri için; 3 nolu elemanın çubuk uç kuvvetleri için; 99
108 Kesit Tesirleri q =5 kn/m knm kn kn knm 6 kn 6 kn knm knm kn kn kn kn kn Normal kuvvet değerleri italik olarak gösterilmiştir. kn kn kn knm knm Kesit Tesirleri Diyagramları M (knm)
109 Örnek ġekilde verilen iki katlı çerçeveyi rijitlik matrisi yöntemi ile çözelim E, A, I q = kn/m E,A,I E, A, I q =5 kn/m E,A,I h = 3 m E, A, I E, A, I h = 5 m L = 8 m Kodlama Tablosu Eleman Rijitlik Matrisleri Eleman No Tarifi Kod Numarası E=, A=, I=ve L elemanın boyu alınacaktır. 94
110 Sistem koordinatlarındaki eleman rijitlik matrisleri (5 ve 6. Elemanlar sistem koordinatlarında olduklarından eleman koordinatlarındaki matrisleri aynı zamanda sistem koordinatlarındakine eģittir) Sistem Rijitlik Matrisi Sistem serbestlik derecelidir. é [ K] = ë ù û
111 Eleman Ankastrelik uç kuvvetleri vektörleri ì {f } = { f } = { f } 3 = { f } 4 =, {f } 5 = í î ql ql ql - ql ü ì ý = í î þ ü ý þ ì {f } 6 = í î ql ql ql - ql ü ì ý = í î þ ü ý þ Sistem Yük vektörü Sistem yük vektörü, sistem koordinatlarındaki ankastrelik uç kuvvetlerinin ters iģaretlileri toplanıp, varsa düğüm yükleri direkt olarak matrise ilave edilmesi ile bulunur. ì ü { Q} = í ý î þ Sistem Denklemi çözümü Sistem denklemi vektörü bulunur. Ģeklinde idi. Ġfadeler yerine konulur ve denklem çözülürse; {D} 96
112 ì { D} = í î D D D 3 D 4 D 5 D 6 D 7 D 8 D 9 D D D ü ì ý = í î þ ü ý þ Eleman Deplasman vektörleri Çubuk Uç Kuvvetlerinin Hesabı nolu elemanın çubuk uç kuvvetleri 97
113 nolu elemanın çubuk uç kuvvetleri 3 nolu elemanın çubuk uç kuvvetleri için; 4 nolu elemanın çubuk uç kuvvetleri için; 5 nolu elemanın çubuk uç kuvvetleri için; 98
114 6 nolu elemanın çubuk uç kuvvetleri için;, Kesit Tesirleri q = kn 9.8 knm kn kn 9.8 knm 6 kn 6 kn 9.79 knm 9.79 knm 4 kn 74.4 kn 4 kn Normal kuvvet değerleri italik olarak gösterilmiştir kn 4 kn 74.4 kn 4 kn 74.4 kn knm knm q =5 kn knm kn kn knm 6 kn 6 kn 37. knm 37. knm kn 6.86 kn kn 6.86 kn kn 6.86 kn kn 6.86 kn 3.7 knm 3.7 knm 99
115 Kesit Tesirleri Diyagramları N (kn) - T (kn) M (knm)
116 Örnek Örnek da verilen problemi kolonlardaki eksenel deformasyonları ihmal ederek rijitlik matrisi yöntemi ile çözelim. Bu durumda her düğümde bir dönme birde yatay doğrultuda olmak üzere iki serbestlik derecesi olacaktır. Sistemin toplam serbestlik derecesi 8 dir. E, A, I E,A,I q =5 kn/m E,A,I q = kn/m E, A, I h = 3 m E, A, I E, A, I h = 5 m L = 8 m Kodlama Tablosu Eleman No Tarifi Kod Numarası Eleman Rijitlik Matrisleri E= A= I= L ise elemanın boyu alınacaktır.
117 Sistem koordinatlarındaki eleman rijitlik matrisleri 5 ve 6 numaralı elemanlar sistem koordinatlarında yer almaktadır. Eleman koordinatlarındaki matrisleri aynı zamanda sistem koordinatlarındaki olmaktadır. Sadece kolonlar için transpoz iģlemleri yapılacaktır. Sistem Rijitlik Matrisi
118 Eleman Yük vektörleri Sistem Yük vektörü Sistem yük vektörü, sistem koordinatlarındaki ankastrelik uç kuvvetlerinin ters iģaretlileri toplanıp, varsa düğüm yükleri direkt olarak matrise ilave edilmesi ile bulunur. Sistem Denklemi çözümü Eleman Deplasman vektörleri 3
119 Çubuk Uç Kuvvetlerinin Hesabı nolu elemanın çubuk uç kuvvetleri nolu elemanın çubuk uç kuvvetleri 3 nolu elemanın çubuk uç kuvvetleri için; é { p} 3 = ë ù ì * í û î ü ý+ þ ì { p} 3 = í î ü ý þ 4 nolu elemanın çubuk uç kuvvetleri için; é { p} 4 = ë ù ì * í û î ü ì ý + { p} 4 = í þ î ü ý þ 4
120 5 nolu elemanın çubuk uç kuvvetleri için; é { p} 5 = ë ù ì * í û î ü ì ý + í þ î ü ý þ ì { p} 5 = í î ü ý þ 6 nolu elemanın çubuk uç kuvvetleri için; é { p} 6 = ë ù ì * í û î ü ì ý+ í þ î ü ý þ ì { p} 6 = í î ü ý þ 5
121 Kesit Tesirleri q = kn 9.8 knm kn kn 9.8 knm 6 kn 6 kn 9.79 knm 9.79 knm kn 74.4 kn kn Normal kuvvet değerleri italik olarak gösterilmiştir kn kn 74.4 kn kn 74.4 kn knm knm q =5 kn knm kn kn knm 6 kn 6 kn 37. knm 37. knm kn 6.86 kn kn 6.86 kn kn 6.86 kn kn 6.86 kn 3.7 knm 3.7 knm 6
122 Kesit Tesirleri Diyagramları N (kn) - - T (kn) M (knm)
123 Örnek Örnek - de verilen iki katlı çerçevenin düğüm noktaları sabit sistem olarak çözümü. Bu durumda her düğümde sadece dönmeler meydana gelecektir. Düğümlerdeki yatay yer değiģtirmeler ve kolonlardaki eksenel deformasyonlar terk edilmiģtir. Bu durumdaki çözüm Cross ve Açı yöntemi ile aynı çözümü verecektir. E, A, I q = kn/m E,A,I E, A, I q =5 kn/m E,A,I h = 3 m E, A, I E, A, I h = 5 m L = 8 m Kodlama Tablosu Eleman No Tarifi Kod Numarası Eleman Rijitlik Matrisleri E=, A=, I= L ise elemanın boyu alınacaktır. [ k ] = k [ ] = é ë ù û 8
124 [ k 3 ] = k 4 [ ] = é ë ù û 3 4 [ k 5 ] = k 6 [ ] = é ë ù û 3 4 = [ k 5 ]' = [ k 6 ]' Sistem koordinatlarındaki eleman rijitlik matrisleri [ k ] ' = k [ ] ' = é ë ù û 4 3 [ k 3 ] ' = k 4 [ ] ' = é ë ù û 3 4 9
125 Sistem Rijitlik Matrisi é [ K] = ë ù û 3 4 Eleman Ankastrelik uç kuvvetleri vektörleri ì { f } 5 = í î ü ý þ ì {f } 6 = í î ü ý þ 3 4 Sistem Yük vektörü ì { Q} = í î ü ý þ 3 4 Sistem Denklemi çözümü Eleman Deplasman vektörleri
126 Çubuk Uç Kuvvetlerinin Hesabı nolu elemanın çubuk uç kuvvetleri nolu elemanın çubuk uç kuvvetleri 3 nolu elemanın çubuk uç kuvvetleri için; 4 nolu elemanın çubuk uç kuvvetleri için;
127 5 nolu elemanın çubuk uç kuvvetleri için; 6 nolu elemanın çubuk uç kuvvetleri için;
128 Kesit Tesirleri q = kn/m knm kn kn knm 4 kn 4 kn knm knm kn kn kn kn kn Normal kuvvet değerleri italik olarak gösterilmiştir. kn kn kn knm knm knm kn q =5 kn kn knm 6 kn 6 kn.788 knm.788 knm kn kn kn 6.86 kn kn kn kn kn.394 knm.394 knm 3
129 Kesit Tesirleri Diyagramları M (knm)
130 Örnek 3 Kafes sistemlerin rijitlik matrisi ile çözümüne ait bir örnek ele alınmıģtır. Bilindiği gibi düzlem kafes sitemin her düğümünde x ve y yönünde ötelenme olmak üzere iki serbestlik derecesi vardır. Bu serbestlik derecelerinden bazıları mesnet olan düğümlerde tutulmuģ olabilir. P = kn m P = kn m 5 m Kodlama Tablosu Eleman Rijitlik Matrisleri Eleman No Tarifi Kod Numarası E= A= L ise elemanın boyu alınacaktır. Sistem koordinatlarındaki eleman rijitlik matrisleri [T] koordinat dönüģüm matrisi ve sistem koordinatlarındaki rijitlik matrisi olmak üzere; idi. yukarıdaki iģlemler yapılırsa sistem koordinatlarında eleman rijitlik matrisi; 3
131 olarak bulunur. Kafes sistem çubuğunda ara yük olmadığı için eleman rijitlik denklemleri doğrudan sistem koordinatlarında kullanılabilir. Sistem Rijitlik Matrisi Sistem Yük vektörü Sistem yük vektörü, sistem koordinatlarında etki eden düğüm yüklerinden elde edilmektedir. 4
132 5 Eleman Deplasman vektörleri 5 75 } { } { 75 } { } { d D D D d d D D d Çubuk Uç Kuvvetlerinin Hesabı Kafes sistemlerde çubuk uç kuvvetleri; ile hesaplanmaktadır. nolu elemanın çubuk uç kuvvetleri nolu elemanın çubuk uç kuvvetleri; Sistem Denklemi çözümü
133 3 nolu elemanın çubuk uç kuvvetleri; 4 nolu elemanın çubuk uç kuvvetleri; 5 nolu elemanın çubuk uç kuvvetleri; Kesit Tesirleri(Uç kuvvetlerinin şekil üzerinde gösteriliş) P = kn 7.7 kn.64 kn kn kn kn.64 kn 5 kn 5 kn 5 kn 5 kn P = kn 6
134 Örnek 4 Gerçekte sistemler üç boyutlu uzayda yer almaktadır. uzay çerçeve için rijitlik matrisi formülasyonu kullanılarak her taģıyıcı sistemin çözümü yapılabilir. Ancak uzay çerçevede bilinmeyen sayısı daha fazla olduğundan, çözümlerin el ile yapılması zor olmaktadır. Örnek olarak tek katlı simetrik bir uzay çerçeve rijitlik matrisi yöntemi ile çözülmüģtür. q = kn/m h = 3 m b = m a = m Uzay çerçeve TaĢıyıcı sistem z 4 3 y x Uzay çerçeve TaĢıyıcı sistemin düğümlerindeki deplasmanların numaralanması 7
135 Kodlama Tablosu Eleman No Tarifi Kod Numarası E=, A=, I x =, I y = J= ve L ise elemanın boyu alınacaktır. Sistemin çözümü için yapılan ara iģlemler uzun olduğundan burada sadece sonuçlar verilmiģtir. Düğümlerin deplasman ve dönmeleri Düğüm no U (x) U (y) U (z) R (x) R (y) R (z) D D -3 D D 7 D 8-3 D D D 5 D 6 D D D 7 D 3 - D 4-3 D D D 7 D D 9 - D -3 D D D 3 D 4 Eleman Uç Kuvvetleri Eleman No Düğü m no i-j Normal Kuvvet - Düzleminde -3 Düzleminde Kesme Kuvveti Moment Kesme Kuvveti Moment i j Burulma 8
136 i j i j i j i j i j i j i j Kesit Tesirleri Elemanların kesit tesirleri uç kuvvetleri tablosundan okunabilir. Burada bir kolon ve bir de kiriģ için uç kuvvetleri Ģekil üzerinde gösterilmiģtir. ġekilde taralı yüzeyler bakıģ yönünü göstermektedir. Uzay çerçeve çubuğunda eksen kuvvet, iki yönde kesme kuvveti, burulma momenti ve iki yönde eğilme momenti olmak üzere toplam 6 adet kesit tesiri bulunmaktadır. Momentler çift okla gösterilmiģtir. Ayrıca sistemin deforme olmuģ Ģeklide abartılı bir Ģekilde verilmiģtir. 9
137
138 Örnek 5 Düzlemine dik yüklü sistemler (ızgara temel, kaset döģeme) içinde bir örnek rijitlik matrisi yöntemi ile çözülmüģtür. Ara iģlemlerin tamamı yerine sonuçlar verilmiģtir. q = kn/m m m m z y x m m m Düzlemine dik yüklü taģıyıcı sistem z 3 y x Düzlemine dik yüklü taģıyıcı sistemde düğüm serbestlik derecelir ve kod numaralrı 5 4
139 Kodlama Tablosu Eleman No Tarifi Kod Numarası E=, A=, I x =, I y =, J = ve L ise elemanın boyu alınmıģtır. Eleman Uç Kuvvetleri Izgara sistemde bir elemanda her düğümde kesme, eğilme ve burulma olmak üzere üç adet uç kuvveti vardır. Izgara sistem çözülerek elde edilen uç kuvvetleri aģağıda verilmiģtir. Eleman No Düğü m no i-j Normal Kuvvet - Düzleminde -3 Düzleminde Kesme Kuvveti Moment Kesme Kuvveti Moment Burul ma i j i j i j i 5.36 j i j i 5.36 j i 5.36 j i j i 5.36 j i j i j i j
140 Düğümlerin deplasman ve dönmeleri Elemanları birbirine rijit olarak bağlanmıģ olan ve yüklerin xy düzlemine dik olarak z yönünde etkidiği ızgara sistemde her düğümde z yönünde ötelenme, x etrafında dönme ve y etrafında dönme olmak üzere 3 serbestlik derecesi vardır. Bu serbestlik dereceli doğrultusunda da kesme, eğilme ve moment olmak üzere üç adet uç kuvveti bulunacaktır. Ele alınan örnek taģıyıcı sistem için hesaplanan düğüm deplasmanları aģağıda verilmiģtir. Düğüm no U (z) R (x) R (y) D D D D D D D D D D 9.84 D 9.84 D 3
141 Kesit Tesirleri Izgara sistemin iki çubuğu için kesit tesirleri Ģekil üzerinde gösterilmiģtir. Taralı yüzler bakıģ yönünü göstermektedir. Izgara sistemin yük altındaki davranıģı 4
142 BÖLÜM VIII 8. G İRİŞ 8. A Ç I M E T O D U Rijitlik matrisi yöntemi, açı yöntemi diye bilinen ve deformasyonları bilinmeyen olarak ele alan klasik bir yöntemin genelleģtirilmiģ halidir. Açı yöntemi deplasman yönteminin özel bir uygulamasıdır. Düzlem çerçevelerin ve sürekli kiriģlerin yaklaģık çözümünde kullanılmaktadır. Özellikle çubuklardaki boy değiģimleri ihmal edilerek çözüm yapıldığından yazılan denge denklemlerinin sayısı az olmaktadır. Ancak elde edilen çözüm yaklaģık olmaktadır. Kesit tesirlerinin kavranması ve davranıģ bilgisin geliģtirilmesine yönelik olarak kullanılmaktadır. Çoğu zaman bilgisayar gerektirmeden çözüm yapabilme imkanı sunmaktadır. Günümüzde her sahada kullanılan bilgisayarların yapı analizi derslerinde de kullanılması kaçınılmazdır. Bu kitabın esas içeriği, rijitlik matrisi yöntemi ile yapı analizinin yapılabilmesi üzerine bina edilmiģtir. Ancak rijitlik matrisi yönteminin özel hali olan açı yöntemi de bir bölümde ele alınmamıģtır. Açı yöntemi ile yapılan çözümlerin gerçek çözümlerden ne kadar uzaklaģtığı ayrıca irdelenecektir. 8. Rijitlik Matrisi Yöntemi ile ilişki 3 i y e E, A, I, L ġekil 8.. Bir düzlem çerçeve çubuğunda genel halde serbestlik dereceleri ġekil 8. de verilen iģaret kabulüne göre, bir düzlem çerçeve çubuğunun uç kuvvetleri ve uç deplasmanları arasında denge denklemi ve çubuk birim deplasman sabitleri daha önce elde edilmiģti Ara yük de bulunan bir düzlem çerçeve çubuğunun rijitlik denklemi (çubuk denge denklemi); 6 j 5 4 x é ë EA L EA L EI L 3 6EI L EI L 3 6EI L 4EI L 6EI L 6EI L EI L EA L EI L 3 6EI L EA L EI L 3 6EI L 6EI L EI L 6EI L 4EI L ù. û ì í î d d d 3 d 4 d 5 d 6 ü ì ý+ í þ î f f f 3 f 4 f 5 f 6 ü ì ý = í þ î p p p 3 p 4 p 5 p 6 ü ý(8.) þ idi. Eksenel deformasyonlar ihmal edilirse çubuk denge denklemi;
143 (8.) olur. 8. ifadesini açık formda; (8.3) Ģeklinde yazabiliriz. d 4, j d, i d 3, j i d, j i A,E,I,L j a) Eksenel deplasmanlar ihmal, b)sadece dönme serbestlik derecesi olması hali ġekil 8.. Düzlem çerçeve çubuğunun deformasyondan sonraki durumu Denklem 8.3 de i uçundaki uç momenti p, j ucundaki uç momenti ise p 4 olmaktadır. i ve j uçlarındaki dönmeler de sıra ile d ve d 4 deplasmanları olmaktadır. i ucundaki uç momenti M ij, dönme i, ve j ucundaki uç momenti M ij, dönme j olmak üzere; (8.4) elde edilir. Uçlardaki relatif ötelenme d=d -d 3 olmak üzere 8.4 ifadesi; 3
144 (8.5) olur. Bu denklem çubuk için yazılmıģ olan uç momentleri denge denklemi olmaktadır. Açı yöntemi ile sistemler incelenirken iki kısma ayrılmaktadır; a) Düğüm noktası sabit sistemler b) Düğüm noktası hareketli sistemler Denklem 8.5 düğüm noktası hareketli sistemler için denge denklemleri olmaktadır. 8.3 Düğüm noktası sabit sistemlerin Açı yöntemi ile çözümü Düğüm noktaları sabit sistemler, düğüm noktalarındaki ötelenmelerin sıfır, fakat dönmelerin serbest olduğu sistemlerdir. Bu sistemlerde eksenel kuvvet ve kesme kuvvetlerinden dolayı meydana gelen deformasyonlar, eğilme momentinden dolayı meydana gelenlere göre ihmal edilmektedir. Bu gru ptaki sistemler iki Ģekilde oluģabilir. a) Sistemin Ģekli nedeni ile bütün yüklemeler için düğümlerdeki lineer deplasmanların sıfıra eģit olduğu sistemler q = kn/m E, I,A 4 m E, I, A 3 m 3 ġekil 8.3. Düğüm noktaları sabit kabul edilebilen sürekli kiriģ 4
145 E,A,I q = kn/m E, A, I h = 3 m 3 L = 4 m ġekil 8.4. Düğüm noktaları sabit kabul edilebilen düzlem çerçeve b) Sistemin ve yüklemenin özellikleri nedeni ile düğümlerdeki ötelenmelerin sıfır olduğu taģıyıcı sistemler q =5 kn/m E,A,I E, A, I E, A, I h = 5 m L = 8 m ġekil 8.5. Simetrik sistem ve yüklemeden dolayı düğüm noktaları sabit kabul edilebilen düzlem çerçeve Ancak bu sistemlerdeki elemanların eksenel deplasmanlarının sıfır olduğu kabul edilmektedir. ġu unutulmamalıdır ki, sonuçlar açısından gerçek çözüm olan rijitlik matrisi yöntemi ile açı yöntemi arasında farklılıklar olacaktır. Denklem 8. ile verilen eleman denklemlerinde d ve d deplasmanlarının sıfır olduğu kabul edilirse; (8.6) ifadesi elde edilir. Burada uç dönmeleri, uç momentleri ise M ile gösterilmiģtir. Denklem (8.6) aynı zamanda uçlarında sadece dönme serbestlik derecesi bulunan çubukların rijitlik denklemi olmaktadır. Açık formda; 5
146 (8.7) olur. Bir düzlem çerçeve taģıyıcı sistemin her düğümü için kuvvet ve moment denge denklemi olmak üzere üç denge denklemi yazılabilir. Düğümlerdeki lineer deplasmanlar sıfır kabul edilirse bu denge denklemlerinde yalnızca moment denge denklemi yeterli olacaktır. Bir i düğümünde 4 durum için moment oluģur;. Bütün dönmeler sıfır iken düğüme gelen dıģ yükler, direk momentler M i ankastrelik uç kuvvetleri; Ma ij +M i. i ve diğer bütün dönmeler ve dıģ kuvvetler sıfır durumu; i.k ii 3. j ve diğer bütün dönmeler ve dıģ kuvvetler sıfır durumu; j. k ij 4. i ve j den baģka lar ; ( Bu durumda i düğümünde, diğer düğümlerdeki dönmelerden dolayı moment oluģmaz) j i M i j j ġekil 8.6. Düzlem çerçeveni i düğümü Dört durumun birlikte düģünülmesi (süperpozisyon) düğüm denge denklemi; Ģeklinde elde edilecektir. Burada ; (8.8) Ma ij : i-j çubuğunun i düğümündeki ankastrelik uç momenti M i ; i düğümüne etki eden direk dıģ moment i : i düğümündeki dönme j : j düğümündeki dönme k ii : i-j düğümü arasında uzanan herhangi bir çubuğun, diğer bütün deplasmanları sıfır iken i düğümünde birim deplasman meydana gelmesi için i düğümüne etkimesi gereken moment. (birim deplasman sabiti) k ji : i-j düğümü arasında uzanan herhangi bir çubuğun, diğer bütün deplasmanları sıfır iken i düğümünde birim deplasman meydana gelirken j düğümünden etkimesi gereken moment (birim deplasman sabiti) 6
147 8.3. Düğüm noktası sabit sistemlerin Açı yöntemi ile çözümü İçin Takip edilecek adımlar Düğüm noktaları sabit sistemleri açı yöntemi ile çözümünde iģlem sırası aģağıda verilmiģtir.. TaĢıyıcı sistemin düğümleri numaralanır. Düğümlerde tutulmuģ olan dönmeler ve bilinmeyen düğüm dönmeleri iģaretlenir 3. Eleman birim deplasman sabitleri hesaplanır 4. Eleman ankastrelik uç momentleri hesaplanır. Bölüm 6 da verilen tablo kullanılabilir 5. Bilinmeyen dönme bulunan her düğüm için düğüm denge denklemi yazılır 6. Düğümlerde yazılan denge denklemlerinden oluģan denklem sistemi çözülerek bilinmeyen düğüm dönmeleri hesaplanır 7. Eleman denklemleri kullanılarak, eleman uç momentleri hesaplanır 8. Eleman uç kesme kuvvetleri, denge denklemi ile hesaplanır 9. Sistemin taģıma Ģeması çizilerek uç kuvvetleri Ģekil üzerinde gösterilir. Bu arada düğümlerde denge Ģartı da dikkate alınarak çubuk eksenel kuvvetleri belirlenir (düğümlerin incelenmesi). Diyagramlar çizilir 7
148 Örnek Yedinci bölümde rijitlik matrisi yöntemi ile çözülmüģ olan çerçeve, yukarıda verilmiģ olan iģlem sırası kullanılarak açı yöntemi ile de çözülecektir. E,A,I q = kn/m E, A, I h = 3 m 3 3 L = 4 m Sistemin ve 3 numaralı düğümleri ankastre olduğundan dönmeler tutulmuģtur. Yalnız numaralı düğümde dönmesi sistemin bilinmeyenidir. Eleman birim deplasman katsayıları Birinci eleman için Ġkinci eleman için Eleman Ankastrelik uç kuvvetleri Yalnız birinci elemanda yük vardır Düğüm denge denklemleri Sistemin bilinmeyen tek dönmesi numaralı düğümdeki dir. Bunun için düğümde denge denkleminin yazılması yeterli olacaktır. Düğüm denge denklemi ve dönmesi; 8
149 M M a aij M.[( k k (EI i. i ii ) ( k k ij ) ].( k.333ei. j ).( k 3 ) ) EI rad EI Ģeklinde hesap edilir. Eleman Uç Momentleri Eleman uç momentleri için ifade; Ģeklinde idi Her eleman için bu denklemi uygulayarak iki adet uç momenti elde edebiliriz. numaralı eleman (- arasında) numaralı eleman (-3 arasında) EI EI M 3 (. 3 ) M a3 ( ) 6. 66kNm L EI 3 Eleman Uç kesme Kuvvetleri Eleman uç kesme kuvvetleri için denklem; idi elemanın uç kuvvetleri 9
150 elemanın uç kuvvetleri Kesit Tesirleri q = kn/m kn kn knm 73.3 knm kn 7.7 kn 53.3 knm knm 6.66 kn kn 53.3 knm kn 7.7 kn 6.66 knm Kesit Tesirleri Diyagramları 3
151 Örnek ġekilde verilen sürekli kiriģi açı yöntemi ile çözelim. KiriĢin yükleme durumu ve düğüm serbestlik dereceleri aģağıda verilmiģtir. q = kn E, I,A 4 m E, I, A 3 m 3 3 Sistemin düğümü olduğundan dönmesi tutulmuģtur. ve 3 numaralı düğümlerindeki ve 3 dönmeleri sistemin bilinmeyenidir. Eleman birim deplasman katsayıları Birinci eleman için Ġkinci eleman için 3
152 Eleman Ankastrelik uç kuvvetleri Yalnız birinci elemanda yük vardır Düğüm denge denklemleri ve 3 numaralı düğümlerde bilinmeyen adet dönme olduğundan bu düğümlerde denge denklemleri yazılacaktır. Düğümünde denge denklemi 3 Düğümünde denge denklemi Ģeklinde hesap edilir. Deplasmanların Hesabı ve numaralı denklemler birlikte çözülerek; düğüm dönmeleri hesaplanabilir. Eleman Uç Momentleri Her eleman için moment denge denklemi uygulayarak iki adet uç momenti elde edebiliriz. numaralı eleman (- arasında) 3
153 numaralı eleman (-3 arasında) Eleman Uç Kesme Kuvvetleri Eleman uç kesme kuvvetleri için denklem; idi elemanın uç kuvvetleri elemanın uç kuvvetleri Kesit Tesirleri knm kn q = kn/m kn 44.4 knm 44.4 knm kn kn knm kn kn 4.87 kn 4.87 kn 33
154 Kesit Tesirleri Diyagramları 34
155 8.4 Düğüm noktası Hareketli sistemler Açı yöntemi ile çözümde, düğüm noktası hareketli sistemler için yapılan formülasyon sonuçta rijitlik matrisi yöntemindeki algoritmaya ulaģmaktadır. Her düğüm noktası için iki kuvvet bir de moment olmak üzere üç denge denklemi yazılabilmektedir. Bilindiği gibi, rijitlik matrisi yönteminde de her düğüm için 3 serbestlik derecesi mevcuttur. Eksenel deplasmanlar ihmal edilecek olursa, biri ötelenme ve diğeri dönme olmak üzere her düğümde iki serbestlik derecesi oluģur. d, i d 4, j d, d 3, j i i A,E,I,L j ġekil 8.7. Düzlem çerçeve çubuğunun deformasyondan sonraki durumu Bazen, tüm bina kolonlarının düģey olması dolayısıyla, yatay yükler için çözümde, aynı kattaki düğümlerin aynı yatay ötelenme yaptıkları kabul edilebilir. ġekil 8.7b de verilen sistemde çubuklardaki eksenel deformasyonlar ihmal edilirse, sistemin serbestlik derecesi 3 olacaktır. p = kn E,A,I E, A, I E, A, I h = 5 m L = 8 m ġekil 8.7b.Düğüm noktası hareketli sistem Sistemin çözümü için; 4 ve 3 düğümünde moment denge denklemleri ve yatayda kesme kuvveti dengesi yazılmalıdır. Diğer taraftan her eleman için eleman uç deplasmanları, birim deplasman sabitleri, ankastrelik uç kuvvetleri ve uç kuvvetleri için de; 35
156 Ģeklindeki denge denklemleri yazılabilir (). Düğümlerde denge ve uygunluk Ģartları da dikkate alınarak bilinmeyen deplasmanlar bulunabilir. Düğüm noktası hareketli sistemlerin açı yöntemi ile formülasyonunun sonunda elde edilen denklemler, rijitlik matrisi ile aynı olacaktır. Bu nedenle bu sistemlerin çözümünün daha sistematik ve anlaģılması kolay olan rijitlik matrisi yöntemi ile yapılması tavsiye edilmektedir. 36
157 BÖLÜM IX 9. GİRİŞ 9. C R O S S Y Ö N T E M İ Cross metodu, esas bakımından, açı metodundaki denklem takımının ardıģık iģlemlerle çözülmesinden ibarettir. Fakat Cross metodunda denklem yazılmadan adım adım denge durumuna yaklaģılmaktadır. Bu metotta bilinmeyen olarak çubuk uçlarındaki kuvvetler seçilmektedir. Cross yönteminde de taģıyıcı sistemler iki Ģekilde ele alınmaktadır; a) Düğüm noktası sabit sistemler b) Düğüm noktası hareketli sistemler Düğüm noktası sabit sistemlerde, düğümlerdeki lineer ötelenmeler ihmal edilmektedir. Dolayısıyla, çözümler yaklaģık olacaktır. Düğüm noktaları hareketli sistemlerde ise çözüm için yapılan formülasyon sonunda rijitlik matrisi ile yapılan ile aynı olmaktadır. Bu nedenle düğüm noktası hareketli sistemler ele alınmayacaktır. 9. Düğüm Noktaları Sabit Sistemler Bir sistem kendine etkiyen yükler altında deformasyon yapar ve denge durumuna gelir. Bu durumda düğüm noktaları kadar dönmüģtür. Düğüm noktaları sabit olduğundan lineer deplasmanlar sıfırdır. Çubuklar, düğüm noktalarına uç momentleri uygulayacaklardır. Her düğüm noktası, bu uç momentleri ve varsa dıģ momentler altında dengededir. Düğüm noktaları sabit sistemlerde düğümlerin dengesi için yalnız moment denge denklemi yazılır. Kuvvetler dengesi, momentler belirlendikten sonra kesme ve eksenel kuvvetlerin belirlenmesinde kullanılır. BaĢlangıçta sistemin bütün düğüm noktalarının dönmeye karģı kilitlendiği varsayılır. Bu durumda düğümlerde birleģen çubukların uçlarında yalnız ankastrelik uç momentleri olacaktır. DıĢ kuvvetler ve kilitlere uygulanan momentler ile, sistem deformasyon yapacak ve denge durumuna gelecektir. Ancak bu denge durumu gerçek denge durumu değildir. Düğüm noktalarından birisindeki kilit açılarak serbest bırakılırsa, bu düğüm bir miktar dönecek ve denge konumuna ulaģacaktır. Bu dönmeden dolayı düğümde birleģen çubukların uçlarında momentler oluģacak ve bu momentlerden bir kısmı da komģu düğümlere bağlı olan çubukların diğer uçlarına geçecektir. Geçen bu momentler, kilit momentlerine ilave edilecektir. Kilidi kaldırılarak kilitsiz olarak dengede duran bu düğüme tekrar kilit takalım. Aynı Ģekilde mesnetler hariç tüm düğümlerde sıra ile kilit kaldırma iģlemi yapılsın. Ġlk düğüme tekrar gelindiğinde, kilitsiz iken dengede olan ve kilitlenen düğüme yeni kilit momentleri gelmiģ olacaktır. Ġlk düğüm ikinci kere serbest bırakılınca bir miktar döner ve denge konumuna ulaģır. Bu seferki dönme daha az olacaktır. BaĢlangıçtaki gibi, bu dönme dolayısıyla yine çubukların uçlarında momentler meydana gelir. Bu uç momentlerinin bir miktarı komģu düğümlere kilit momenti olarak aktarılır. Bu iģlemlere kilit momentleri sıfıra yaklaģana kadar devam edilir. 35
158 ġekil Moment Dağıtma ve geçiş katsayıları ġekil 9.'de verilen sistemde numaralı düğüm dengesini yazalım; (9.) elde edilir. Uç momentleri formülleri; (9.) şeklinde idi. 9. ifadelerinde i = ve j = yazılırsa M ij momentleri için; (9.3) ifadeleri elde edilir. yerine 9. deki ifadesi yazılırsa; (9.4) 36
159 Benzer Ģekilde M ji momentleri; (9.5) ifadeleri elde edilir. yerine 9. deki ifadesi yazılırsa; (9.6) elde edilir. Burada; :GeçiĢ sayısı :Dağıtma katsayısı olmaktadır. GeçiĢ, ancak ankastre kenar mesnette veya ara mesnette söz konusudur. Moment taģımayan basit mesnetlere moment geçiģi olmaz. Bu mesnetlerde dıģ moment var ise, komģu ara düğüme geçiģ olacaktır. Bu geçiģ katsayıları çubukları birim deplasman sabitleri ile ilgili olduğu için sabittir ve.5'dir. EI kii 4 L i = k EI ji L i EI kii 3 L i = ġekil 9. Birim deplasman sabiti j i j ġekil 9.3 Bir ucu basit mesnet olan çubukta birim deplasman sabiti 9.. Düğüm Noktası Sabit Sistemlerin Çözümünde İşlem Sırası Cross yöntemi ile çözümde Ģu aģamalar takip edilir;. Sistemin düğümleri ve elemanları numaralanır.. Çubukların ara yüklerinden dolayı oluģan ankastrelik mesnet momentleri hesaplanır. 3. Çubuk rijitlikleri hesaplanır. 37
160 4. Moment dağıtılacak olan (kilit vurulacak olan) ara düğümler için dağıtma katsayıları r ij değerleri hesaplanır. 5. Kenarlarda basit mesnette konsol momenti var ise ilgili yüze yazılır. Dağıtma katsayısı alınarak dengeleme kenarlarda yapılır. 6. Düğümlerde moment farkı sıfıra yaklaģana kadar dengeleme iģlemine devam edilir. 7. TaĢıyıcı sistem taģıma Ģeması çizilerek uç kuvvetleri belirlenir. 8. Kesit tesiri diyagramları çizilir. / / / 4 / ġekil 9.4. GeçiĢ katsayıları Örnek ġekilde verilen sistemin kesit tesiri diyagramlarını cross yöntemi ile çizelim. P = kn P = kn A I B I h = 4 m C L = 5 m Çubuk Ankastrelik Uç Momentleri M aab =-M aba =(PL/8)=5 knm Çubuk Rijitlikleri 38
161 Dağıtma Katsayıları Dağıtma sadece B düğümünde yapılacaktır. Moment Dengelemesi / / Taşıma Şeması ve Diyagramlar 5.75 kn kn
162 NOT: Cross Yöntemi ile düğüm noktaları hareketli sistemin çözümü yerine, rijitlik matrisi yönteminin tercih edilmesi tavsiye edilmektedir. 4
163 BÖLÜM X. B İ L G İ S AYA R İ L E M O D E L L E N E R E K Ç Ö Z Ü M Ü YA P I L A N Ç E Ş İ T L İ T A Ş I Y I C I S İ S T E M L E R. SAP9 İLE İLGİLİ BİLGİLER Bilgisayar ile yapı analizi yapılması için Ģüphesiz bir çok paket program bulunmaktadır. Bu sahada yaygın olarak referans alınabilecek olan yazılımlar, orjini ABD nin Kaliforniya eyaletindeki Berkeley Üniversitesi ĠnĢaat Mühendisliği bölümünde geliģtirilen ve halen ComputersStructures ve ComputersEngineering Firmalarınca geliģtirilerek pazarlanmakta olan SAP (Structural Analysis Programs) serisi programların eğitimde kullanılması tercih edilmiģtir. Bu programların en son SAP serisi lisanslı olarak bölümümüzde mevcuttur. Ayrıca eğitim versiyonu da ögrencilere verilmiģtir. Yapı analizinde sonlu elemanlar yöntemi yaygın olarak kullanılmaktadır. Bu kısımda, sonlu elemanlar yöntemi ile çözüm yapan SAP 9 programında data hazırlama ile ilgili kısaca bilgi verilmiģtir. SAP9 ile yapı sistemlerinin çözümü için, sistemin bilgisayara tanıtılması gerekmektedir. Bunun için gerekli olan DATA dosyası ASCII text olarak herhangi bir editör programında yazılabilir. SAP9 ile her tür yükleme altında çubuklar, kabuklar, plaklar ve üç boyutlu eleman kullanılarak modellenen katı cisimler çözülebilmektedir. DATA dosyasında, bilgiler ayıraç denilen ana baģlıklar altında yazılmaktadır. Problemin türüne göre bu ayıraçlardan gerekli olanlar kullanılmaktadır. En genel Ģekilde SAP 9 için yazılabilecek ayıraçlar (baģlıklar) aģağıda verilmiģtir. PROBLEMĠN BAġLIĞI (Çıktı sayfasının en üstüne yazılması istenen açıklama) SYSTEM JOINTS RESTRAINTS SPRINGS MASSES POTENTIAL CONSTRAINTS FRAME SHELL ASOLID SOLID LOADS DISPLACEMENTS PRESTRESS SPEC TIMEH COMBO SELECT 4
164 Yapı Statiği II dersi kapsamında çubuklardan oluģan taģıyıcı sistemlerin statik yükler altında çözümü yer almaktadır. Bu nedenle çubuklardan oluģan taģıyıcı sistemlerin çözümü için gerekli olan baģlıklar ve açıklamalar aģağıda kısaca ele alınacaktır. Daha detaylı bilgi için program kullanım klavuzuna bakılabilir. PROBLEMĠN BAġLIĞI (Çıktı sayfanın en üstüne yazılması istenen açıklama) SYSTEM L= yükleme sayısı JOINTS Düğüm koordinatları bilgisayar tanımlanmaktadır. Her düğümün koordinatı; J x=... y= z= ġeklinde girilebileceği gibi, J x=... y= z= G= Q= A= F= L= S= Gibi genelleģtirme ifadeleri ile de düğümler otomatik türetilebilir. : Düğüm koordinatlarının tanımlanması ile ilgili örnek kn q= kn/m y 3 A=.8 m, I=. m 4 x A=.8 m, I=. m 4 6 m E=3,, kn/m 4 3 A=.6 m I=.663 m 4 6 m 6 m ġekil. sistem koordinatlarının baģlangıç noktası olarak düğümü alınır ve çerçevenin xy düzleminde yer aldığı kabul edilirse, yukarıdaki sistemin düğüm koordinatları aģağıdaki Ģekillerde tarif edilebilir x= y= x=6 y= 3 x= y= 4 x=6 y=-6 veya x= y= 3 x= y= G=,3, 4 x=6 y=-6 RESTRAINTS Düğümlerin serbestlik dereceleri bu satırda tanımlanmaktadır. D R= X, Y, Z, X, Y, Z veya 4
165 D,D,ARTIM R= X, Y, Z, X, Y, Z Ģeklinde tanımlanabilir. X Y Z X Y Z X ekseni doğrultusundaki ötelenme Y ekseni doğrultusundaki ötelenme Z ekseni doğrultusundaki ötelenme X ekseni etrafındaki dönme Y ekseni etrafındaki dönme Z ekseni etrafındaki dönme olmaktadır. Herhangi bir serbestlik derecesi doğrultusundaki deplasmanın önlenip önlenmediğinin bilgisayara tarif edilmesi için ve rakamları kullanılmaktadır. ġekil. de verilen sistemin düğüm serbestlik derecelerini tanımlayalım;,3, R=,,,,, 4 R=,,,,, 4. düğüm, mafsal olduğundan z ekseni etrafındaki dönme serbesttir. SPRINGS Belirli serbestlik dereceleri doğrultusundaki yay katsayıları bu baģlık altında tanımlanmaktadır. Elastik mesnetler yay katsayıları ile modellenebilir. D veya K=K X, K Y, K Z, K X, K Y, K Z D,D,ARTIM K=K X, K Y, K Z, K X, K Y, K Z Ģeklinde tanımlanabilir. K X K Y K Z K X K Y K Z X ekseni doğrultusundaki ötelenmeye karģı koyan yay katsayısı Y ekseni doğrultusundaki ötelenmeye karģı koyan yay katsayısı Z ekseni doğrultusundaki ötelenmeye karģı koyan yay katsayısı X ekseni etrafındaki dönmeye karģı koyan yay katsayısı Y ekseni etrafındaki dönmeye karģı koyan yay katsayısı Z ekseni etrafındaki dönmeye karģı koyan yay katsayısı olmaktadır. Herhangi bir doğrultuda yay katsayısı yok ise o doğrultuda sıfır yazılacaktır. Bu yay katsayıları, sistem rijitlik matrisinde ilgili serbestlik derecesinin bulunduğu satırda köģegen üzerindeki terime ilave edilmektedir. CONSTRAINTS 43
166 Bazı serbestlik derecelerinin birbirine eģitlenmesi bu baģlık altında yapılmaktadır. Rijit diyafram kabulünde bir kattaki tüm yatay ötelenmelerin aynı olması, çubuklardaki eksenel deformasyonların ihmal edilmesi gibi hususlar bu baģlık altında tanımlanır. D, D, Ġ C=c, c, c 3, c 4, c 5, c 6 I=i, i, i 3, i 4, i 5, i 6 c nolu düğümün birinci deformasyonunu D nolu düğümün birinci deformasyonuna eģitle. Bu eģitleme iģlemini c, c 3, c 4, c 5, c 6 için de yap. FRAME Çubukların kesit özellikleri, ara yükler ve çubukların sistem içinde hangi düğümler arasında yer aldıkları bu baģlık altında verilmektedir. Genel formu; NM=...NL= X=s, s,... s nld, Y=s, s,... s nld Z=s, s,... s nld P= s, s,... s nld NSEC= Ģeklindedir. Kullanılan indislerin açıklamaları tabloda yapılmıģtır. NM NL X Y Z P NSEC si Farklı kesit özelliği olan tipik çubuk sayısı Tipik açıklık yükü sayısı s, s,... s nld yüklemelerde zati ağırlığın X yönü çarpanı s, s,... s nld yüklemelerde zati ağırlığın Y yönü çarpanı s, s,... s nld yüklemelerde zati ağırlığın Z yönü çarpanı s, s,... s nld yüklemelerde öngerme kuvvet çarpanı Çubukta sonuç istenen ara nokta sayısı Yükleme numarası Yukarıda belirtilen NM kadar kesit özellikleri ayrı ayrı tanımlanmalıdır. i A= J= I=I,I 3 AS=A,A 3 E= G= W= M= TC= kullanılan indislerin açıklamaları tabloda verilmiģtir. i Tipik çubuk kesit numarasu A En kesit alanı J Burulma atalet momentı I Atalet momentleri AS Kayma en kesit alanı E Elastisite modülü G Kayma modülü W Birim boydaki zati ağırlık M Birim boydaki kütle TC Isıl genleģme katsayısı Ġstenilirse en kesit özellikleri bilgisayara da hesaplattırılabilir. Bunun için A,J,I ve AS yerine SH=... T=... Ģeklinde iki terim ilave edilebilir. 44
167 ÇeĢitli tip kesitler için SH ve T nin tarifi tabloda verilmiģtir. Kesit ġekli YazılıĢı Kesit ġekli YazılıĢı SH=R T= t 3, t SH=P T=t 3, t w 3 t 3 t w 3 t 3 t t t SH=I T=t 3, t t,t ft,t w,t b,t fb t f SH=C T= t 3, t,t f,t w 3 t ft t 3 t w 3 t 3 t f t w t fb t t b t SH=T T=t 3, t,t f,t w t w SH=L T= t 3, t,t f,t w t f 3 t 3 3 t 3 t w t t f t w 3 t f t w t 3 SH=B T= t 3, t,t f,t w t f t ekseni çubuk boyunca uzanmaktadır Çubuklarda uç kuvvetleri ve bakıģ yönü ile ilgili pozitif değerler aģağıda verilmiģtir. Pozitif Eksenel kuvvet ve burulma momenti 45
168 - düzleminde Pozitif moment ve kesme kuvveti -3 Düzleminde pozitif moment ve pozitif kesme kuvveti Kesit özelikleri tanımlandıktan sonra, tipik açıklık yükleri NL kadar alt alta tanımlanır. i WL=q, q, q 3 T=T, T, T 3 PLD=(d,P -, P 3-3 ), (...) Yayılı yükler sistem koordinatlarında girilecekse, WL=q, q, q 3 yerine WG=q x, q y, q z Ģeklinde yazılmalıdır. Kesit ve ara yük çeģitleri tanımlandıktan sonra, her elemanın hangi tipik en kesite sahip olduğu, sistemin hangi düğümleri arasında hangi bakıģ yönünde yer aldığı ve varsa üzerine hangi tür ara yükün etkidiği tarif edilmelidir. e,i,j M=tip,tip,v LP=j,j NSL=tip,tip,...tipnld G=n,noartım,iartım,jartım Burada e eleman numarası, i; elemanın ilk ucu, j; elemanın son ucundaki düğüm numaraları olmaktadır. M ile elemanın hangi malzeme grubunda yer aldığı, NSL ile de elemanın üzerinde hangi tür tipik yükün bulunduğu tarif edilmektedir. G ile benzer elemanlar türetilmektedir. LP:j ve j düğümleri arasında bir vektör tarif etmektedir. Bu vektör ekseni ve 3 eksenlerinin pozitif yönleri ile tarifli çeyrek dilimin içinde herhangi bir yönü belirlemelidir. Eğer 3 ekseni global eksenlerden biri ile çakıģık ise, yardımcı vektör tarif etme yerine aģağıdaki seçeneklerden birisi kullanılır. 3 EKSENĠ J,J 3 EKSENĠ J,J Z ye paralel ise, -Z ye paralel ise -, Y ye paralel ise, -Y ye paralel ise -, X e paralel ise 3, -X e paralel ise -3, 46
169 LOADS Düğümlere etkiyen direkt yükler bu baģlık altında verilir. d,d,artım L=yükleme no F=Px,Py,Pz,Mx,My,Mz Ģeklinde direkt düğüm yükleri tanımlanır DISPLACEMENTS Sistemin bazı serbestlik derecesi doğrultusundaki deplasmanları biliniyorsa, bu deplasmanlar nedeni ile oluģacak kesit tesirlerinin de hesabı mümkündür. Bir nevi, bu bilinen deplasmanlar da taģıyıcı sisteme dıģ yük olarak etki etmektedir. Bu duruma mesnet çökmeleri Ģeklinde rastlamak mümkündür. Düğümlerde bilinen deplasmanlar aģağıdaki Ģekilde tarif edilebilmektedir D veya D= X, Y, Z, X, Y, Z D,D,ARTIM D= X, Y, Z, X, Y, Z Burada, X, Y, Z, X, Y, Z, altı serbestlik derecesi doğrultusunda bilinen deplasmanların nümerik değerleri olmaktadır. COMBO Birden fazla yüklemelerin katsayılar ile çarpılarak topanması iģlemi bu baģlık altında yapılır. i C= s, s,... s nld Ģeklinde her kombinasyon için bir satır yazılabilir. Burada s i, i. yüklemenin süperpozisyon çarpanı olmaktadır. Bu kısımda, yapı statiği II dersi kapsamında anlatılan proplemlerin SAP9 ile çözümünde bazı bilgiler kısaca ele alınmıģtır. ġüphesiz ilgili programın kullanım klavuzunda ve/veya çeģitli kiģilerce düzenlenen kurslarda anlatılan kurs notlarında daha detaylı bilgiler yer almaktadır. Okuyucuların bu kaynaklardan da yararlanmaları tavsiye edilmektedir. Ancak bazı problemler için hazırlanan data dosyaları ve çözümlerinden elde edilen Ģekiller aģağıda verilmektedir. Bu DATA dosyaları da yukarıda verilen kısa bilgilerin ıģığı altında incelenirse, konu daha iyi anlaģılacaktır.. BAZI PROPLEMLER İÇİN SAP9 DATA DOSYALARI YAPI STATIGI II SINAV95 SYSTEM L= RESTRAINTS,3,, R=,,,,, R=,,,,, JOINTS X= Y= 47
170 X= Y=5 3 X=6 Y=5 : FRAME NM= NSL= A=5 I= E= A=5 I=8 E= WL=,-5,, M= LP=,,3 M= LP= NL= : LOADS F=,-,,,,- L= SORU A:CERCEVE SYSTEM L= RESTRAINTS,3, R=,,,,, : JOINTS X= Y= X= Y=4 3 X= Y=4 : FRAME NM= NSL= A= E= I= A= E= I= WL=,-,, NM= LP=,,,3 NM= LP=, NL= : LOADS F=, Y Y X X 3 SINAV96 SINAV96 FRAME LOADS UNDEFORMED SHAPE LOAD MINIMA w -.E+ P.E+ MAXIMA w -.E+ P.E+ OPTIONS JOINT IDS ALL JOINTS ELEMENT IDS WIRE FRAME Yükleme SAP9 Eleman ve Düğüm numaraları: SAP9 48
171 Y X Y X SINAV95 FRAME OUTPUT M33 LOAD SINAV95 DEFORMED SHAPE LOAD ENVELOPES MIN < > -.43E+ AT 6. MAX < >.3E+ AT.5 MINIMA X.E+ Y E- Z.E+ MAXIMA X.669E- Y.E+ Z.E+ Moment Diyagramı SAP9 Deforme olmuģ Ģekli SAP9 YAPI SATTIGI II SYSTEM L= RESTRAINTS,3, R=,,,,, 4,9, R=,,,,, JOINTS X= Y= 3 X=8 Y= G=,3, 7 X= Y=6 G=,7,3 8 X=4 Y=6 G=,8,3 9 X=8 Y=6 G=3,9,3 : FRAME NM= NSL= A= I= E= A= I= E= WG=,- WG=,-,,4 M= G=,3,3,3,,5 M= G=,3,3,3 3,3,6 M= G=,3,3,3 7,4,5 M= NL= G=,,, 9,7,8 M= NL= G=,,, : : LOADS : 4,7,3 F=5 49
172 5 Bilgisayar ile çözümü yapılan bazı taşıyıcı sistemlerin modelleri verilmiştir. Çözümde SAP 9 veya SAP kullanılmıştır. SAP9 X Y Z sun UNDEFORMED SHAPE OPTIONS WIRE FRAME SAP9 X Y Z UNDEFORMED SHAPE OPTIONS ELEMENT IDS WIRE FRAME
173 Y Z X osma UNDEFORMED SHAPE OPTIONS WIRE FRAME SAP9 GeniĢ açıklıklı bir sanayi veya sanat yapısı modeli Üç boyutlu bir çelik bina çerçevesi modeli 5
174 Uzay Kafes sistemin SAP de çözümü.3 SAP İLE YAPI ANALİZİ Bugün itibarı ile, SAP serisinin en geliģmiģ versiyonu SAP dir. Eğitim versiyonunda sınırlı büyüklükteki taģıyıcı sistemin analizi yapılmaktadır. Pamukkale Üniversitesi Mühendislik Fakültesi ĠnĢaat Mühendisliği Bölümü Yapı Ana Bilim Dalında, SAP lisanslı olarak kullanılmaktadır. Sonlu elemanlar yöntemi ile her tür yapının, her tür yükleme altında analiz ve boyutlamasını yapan program Windows altında çalıģmaktadır. Veri giriģi ve sonuçların izlenmesi grafik ekrandan kolayca yapılabilmektedir. Programın kullanımı ile ilgili bilgiler kullanım klavuzlarında geniģ bir Ģekilde yer almaktadır. SAP 9 ile çözüm yapmayı bilenler için bir hatırlatma yapılmak istenmiģtir. Yapı analizinde bilgisayar kullanımı zorunlu hale gelmiģtir. Yapı statiği II dersi kapsamında da temel davranıģ ve kavramlar verildikten sonra, öğrencinin bir program yardımı ile her tür yapı sistemini analiz edecek bilgiye ulaģması hedeflenmeketedir. Bunun için uygulamaların ve öğrencilerin ders dıģındaki çalıģmaların büyük faydası olacaktır. 5
175 a SAP de taģıyıcı sistemler kolayca tanımlanabilmektedir. 53
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ
 İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
YAPI STATİĞİ II (Hiperstatik Sistemler) Yrd. Doç. Dr. Selçuk KAÇIN
 YAPI STATİĞİ II (Hiperstatik Sistemler) Yrd. Doç. Dr. Selçuk KAÇIN Yapı Sistemleri: İzostatik (Statikçe Belirli) Sistemler : Bir sistemin tüm kesit tesirlerini (iç kuvvetlerini) ve mesnet reaksiyonlarını
YAPI STATİĞİ II (Hiperstatik Sistemler) Yrd. Doç. Dr. Selçuk KAÇIN Yapı Sistemleri: İzostatik (Statikçe Belirli) Sistemler : Bir sistemin tüm kesit tesirlerini (iç kuvvetlerini) ve mesnet reaksiyonlarını
Doç. Dr. Bilge DORAN
 Doç. Dr. Bilge DORAN Bilgisayar teknolojisinin ilerlemesi doğal olarak Yapı Mühendisliğinin bir bölümü olarak tanımlanabilecek sistem analizi (hesabı) kısmına yansımıştır. Mühendislik biliminde bilindiği
Doç. Dr. Bilge DORAN Bilgisayar teknolojisinin ilerlemesi doğal olarak Yapı Mühendisliğinin bir bölümü olarak tanımlanabilecek sistem analizi (hesabı) kısmına yansımıştır. Mühendislik biliminde bilindiği
Hiperstatik sistemlerin çözümünde, yer değiştirmelerin küçük olduğu ve gerilme - şekil değiştirme bağıntılarının lineer olduğu kabul edilmektedir.
 1. HİPERSTATİK SİSTEMLER 1.1. Giriş Bir sistemin hesabının amacı, dış etkilerden meydana gelen kesit tesirlerini, şekil değiştirmelerini ve yer değiştirmelerini belirlemektir. İzostatik sistemlerde, yalnız
1. HİPERSTATİK SİSTEMLER 1.1. Giriş Bir sistemin hesabının amacı, dış etkilerden meydana gelen kesit tesirlerini, şekil değiştirmelerini ve yer değiştirmelerini belirlemektir. İzostatik sistemlerde, yalnız
Yapı Sistemlerinde Elverişsiz Yüklemeler:
 Yapı Sistemlerinde Elverişsiz Yüklemeler: Yapılara etkiyen yükler ile ilgili çeşitli sınıflama tipleri vardır. Bu sınıflamalarda biri de yapı yükleri ve ilave yükler olarak yapılan sınıflamadır. Bu sınıflama;
Yapı Sistemlerinde Elverişsiz Yüklemeler: Yapılara etkiyen yükler ile ilgili çeşitli sınıflama tipleri vardır. Bu sınıflamalarda biri de yapı yükleri ve ilave yükler olarak yapılan sınıflamadır. Bu sınıflama;
ELASTİSİTE TEORİSİ I. Yrd. Doç Dr. Eray Arslan
 ELASTİSİTE TEORİSİ I Yrd. Doç Dr. Eray Arslan Mühendislik Tasarımı Genel Senaryo Analitik çözüm Fiziksel Problem Matematiksel model Diferansiyel Denklem Problem ile ilgili sorular:... Deformasyon ne kadar
ELASTİSİTE TEORİSİ I Yrd. Doç Dr. Eray Arslan Mühendislik Tasarımı Genel Senaryo Analitik çözüm Fiziksel Problem Matematiksel model Diferansiyel Denklem Problem ile ilgili sorular:... Deformasyon ne kadar
YAPI STATİĞİ MESNETLER
 YAPI STATİĞİ MESNETLER Öğr.Gör. Gültekin BÜYÜKŞENGÜR STATİK Kirişler Yük Ve Mesnet Çeşitleri Mesnetler Ve Mesnet Reaksiyonları 1. Kayıcı Mesnetler 2. Sabit Mesnetler 3. Ankastre (Konsol) Mesnetler 4. Üç
YAPI STATİĞİ MESNETLER Öğr.Gör. Gültekin BÜYÜKŞENGÜR STATİK Kirişler Yük Ve Mesnet Çeşitleri Mesnetler Ve Mesnet Reaksiyonları 1. Kayıcı Mesnetler 2. Sabit Mesnetler 3. Ankastre (Konsol) Mesnetler 4. Üç
Tanım: Boyuna doğrultuda eksenel basınç kuvveti taşıyan elemanlara Basınç Çubuğu denir.
 BASINÇ ÇUBUKLARI Tanım: Boyuna doğrultuda eksenel basınç kuvveti taşıyan elemanlara Basınç Çubuğu denir. Basınç çubukları, sadece eksenel basınç kuvvetine maruz kalırlar. Bu çubuklar üzerinde Eğilme ve
BASINÇ ÇUBUKLARI Tanım: Boyuna doğrultuda eksenel basınç kuvveti taşıyan elemanlara Basınç Çubuğu denir. Basınç çubukları, sadece eksenel basınç kuvvetine maruz kalırlar. Bu çubuklar üzerinde Eğilme ve
PERDELĠ BETONARME YAPILAR ĠÇĠN DOĞRUSAL OLMAYAN ANALĠZ METOTLARI
 PERDELĠ BETONARME YAPILAR ĠÇĠN DOĞRUSAL OLMAYAN ANALĠZ METOTLARI Nonlinear Analysis Methods For Reinforced Concrete Buildings With Shearwalls Yasin M. FAHJAN, KürĢat BAġAK Gebze Yüksek Teknoloji Enstitüsü,
PERDELĠ BETONARME YAPILAR ĠÇĠN DOĞRUSAL OLMAYAN ANALĠZ METOTLARI Nonlinear Analysis Methods For Reinforced Concrete Buildings With Shearwalls Yasin M. FAHJAN, KürĢat BAġAK Gebze Yüksek Teknoloji Enstitüsü,
Yapısal Analiz Programı SAP2000 Bilgi Aktarımı ve Kullanımı. Doç.Dr. Bilge Doran
 Yapısal Analiz Programı SAP2000 Bilgi Aktarımı ve Kullanımı Dersin Adı : Yapı Mühendisliğinde Bilgisayar Uygulamaları Koordinatörü : Doç.Dr.Bilge DORAN Öğretim Üyeleri/Elemanları: Dr. Sema NOYAN ALACALI,
Yapısal Analiz Programı SAP2000 Bilgi Aktarımı ve Kullanımı Dersin Adı : Yapı Mühendisliğinde Bilgisayar Uygulamaları Koordinatörü : Doç.Dr.Bilge DORAN Öğretim Üyeleri/Elemanları: Dr. Sema NOYAN ALACALI,
V. KAFES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir.
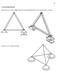 78 V. KES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir. Uzayda ise en az 6 çubuk gereklidir. 79 İhtiyaçlara göre yeni çubukların ilavesiyle
78 V. KES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir. Uzayda ise en az 6 çubuk gereklidir. 79 İhtiyaçlara göre yeni çubukların ilavesiyle
Betonarme Yapılarda Perde Duvar Kullanımının Önemi
 Betonarme Yapılarda Perde Duvar Kullanımının Önemi ĠnĢaat Yüksek Mühendisi MART 2013 Mustafa Berker ALICIOĞLU Manisa Çevre ve ġehircilik Müdürlüğü, Yapı Denetim ġube Müdürlüğü Özet: Manisa ve ilçelerinde
Betonarme Yapılarda Perde Duvar Kullanımının Önemi ĠnĢaat Yüksek Mühendisi MART 2013 Mustafa Berker ALICIOĞLU Manisa Çevre ve ġehircilik Müdürlüğü, Yapı Denetim ġube Müdürlüğü Özet: Manisa ve ilçelerinde
MUKAVEMET Öğr. Gör. Fatih KURTULUŞ
 www.sakarya.edu.tr MUKAVEMET Öğr. Gör. Fatih KURTULUŞ www.sakarya.edu.tr 1. DÜŞEY YÜKLÜ KİRİŞLER Cisimlerin mukavemeti konusunun esas problemi, herhangi bir yapıya uygulanan bir kuvvetin oluşturacağı gerilme
www.sakarya.edu.tr MUKAVEMET Öğr. Gör. Fatih KURTULUŞ www.sakarya.edu.tr 1. DÜŞEY YÜKLÜ KİRİŞLER Cisimlerin mukavemeti konusunun esas problemi, herhangi bir yapıya uygulanan bir kuvvetin oluşturacağı gerilme
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
MÜHENDİSLİK MEKANİĞİ (STATİK)
 MÜHENDİSLİK MEKANİĞİ (STATİK) Prof. Dr. Metin OLGUN Ankara Üniversitesi Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü HAFTA KONU 1 Giriş, temel kavramlar, statiğin temel ilkeleri 2-3 Düzlem kuvvetler
MÜHENDİSLİK MEKANİĞİ (STATİK) Prof. Dr. Metin OLGUN Ankara Üniversitesi Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü HAFTA KONU 1 Giriş, temel kavramlar, statiğin temel ilkeleri 2-3 Düzlem kuvvetler
Açı Yöntemi. 1 ql 8. Açı yöntemi olarak adlandırılan denklemlerin oluşturulmasında aşağıda gösterilen işaret kabulü yapılmaktadır.
 çı Yöntemi Kuvvet ve -oment yöntemlerinde, ilave denklemleri zorlamaların sistem üzerinde oluşturduğu deformasyonların sistemde oluşturulan suni serbestliklerden dolayı oluşan deformasyonlardan ne kadar
çı Yöntemi Kuvvet ve -oment yöntemlerinde, ilave denklemleri zorlamaların sistem üzerinde oluşturduğu deformasyonların sistemde oluşturulan suni serbestliklerden dolayı oluşan deformasyonlardan ne kadar
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 5 Rijit Cisim Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 5. Rijit Cisim Dengesi Denge,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 5 Rijit Cisim Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 5. Rijit Cisim Dengesi Denge,
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Doç. Dr. Muhammet Cerit Öğretim Üyesi Makine Mühendisliği Bölümü (Mekanik Ana Bilim Dalı) Elektronik posta ( ):
 Tanışma ve İletişim... Doç. Dr. Muhammet Cerit Öğretim Üyesi Makine Mühendisliği Bölümü (Mekanik Ana Bilim Dalı) Elektronik posta (e-mail): mcerit@sakarya.edu.tr Öğrenci Başarısı Değerlendirme... Öğrencinin
Tanışma ve İletişim... Doç. Dr. Muhammet Cerit Öğretim Üyesi Makine Mühendisliği Bölümü (Mekanik Ana Bilim Dalı) Elektronik posta (e-mail): mcerit@sakarya.edu.tr Öğrenci Başarısı Değerlendirme... Öğrencinin
KAYMA GERİLMESİ (ENİNE KESME)
 KAYMA GERİLMESİ (ENİNE KESME) Demir yolu traversleri çok büyük kesme yüklerini taşıyan kiriş olarak davranır. Bu durumda, eğer traversler ahşap malzemedense kesme kuvvetinin en büyük olduğu uçlarından
KAYMA GERİLMESİ (ENİNE KESME) Demir yolu traversleri çok büyük kesme yüklerini taşıyan kiriş olarak davranır. Bu durumda, eğer traversler ahşap malzemedense kesme kuvvetinin en büyük olduğu uçlarından
SONLU ELEMANLAR YÖNTEMİ
 SONLU ELEMANLAR YÖNTEMİ Kurs Kapsamı SONLU ELEMANLAR KAVRAMI SONLU ELEMANLAR FORMULASYONU UYGULAMALARI Sonlu Elemanlar Çözümleri Rijitlik Metodu Esneklik Metodu Karışık Kullanımlar Rijitlik Metodu Kullanılarak
SONLU ELEMANLAR YÖNTEMİ Kurs Kapsamı SONLU ELEMANLAR KAVRAMI SONLU ELEMANLAR FORMULASYONU UYGULAMALARI Sonlu Elemanlar Çözümleri Rijitlik Metodu Esneklik Metodu Karışık Kullanımlar Rijitlik Metodu Kullanılarak
İZOSTATİK (STATİKÇE BELİRLİ) SİSTEMLER
 İZOSTATİK (STATİKÇE BELİRLİ) SİSTEMLER Yapı Elemanları İnşaat Mühendisliği ile ilgili yapı sistemleri üç ayrı tipteki yapı elemanlarının birleşiminden oluşur. 1)Çubuk Elemanlar: İki boyutu üçüncü boyutuna
İZOSTATİK (STATİKÇE BELİRLİ) SİSTEMLER Yapı Elemanları İnşaat Mühendisliği ile ilgili yapı sistemleri üç ayrı tipteki yapı elemanlarının birleşiminden oluşur. 1)Çubuk Elemanlar: İki boyutu üçüncü boyutuna
EKSENEL YÜKLERDEN OLUŞAN GERILME VE ŞEKİL DEĞİŞİMİ Eksenel yüklü elemanlarda meydana gelen normal gerilmelerin nasıl hesaplanacağı daha önce ele
 EKSENEL YÜKLERDEN OLUŞAN GERILME VE ŞEKİL DEĞİŞİMİ Eksenel yüklü elemanlarda meydana gelen normal gerilmelerin nasıl hesaplanacağı daha önce ele alınmıştı. Bu bölümde ise, eksenel yüklü elemanların şekil
EKSENEL YÜKLERDEN OLUŞAN GERILME VE ŞEKİL DEĞİŞİMİ Eksenel yüklü elemanlarda meydana gelen normal gerilmelerin nasıl hesaplanacağı daha önce ele alınmıştı. Bu bölümde ise, eksenel yüklü elemanların şekil
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 7 İç Kuvvetler Kaynak: Mühendislik Mekaniği: Statik, R. C. Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 7. İç Kuvvetler Bu bölümde, bir
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 7 İç Kuvvetler Kaynak: Mühendislik Mekaniği: Statik, R. C. Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 7. İç Kuvvetler Bu bölümde, bir
Karabük Üniversitesi, Mühendislik Fakültesi...www.IbrahimCayiroglu.com. STATİK (4. Hafta)
 KAFES SİSTEMLER STATİK (4. Hafta) Düz eksenden oluşan çubukların birbiriyle birleştirilmesiyle elde edilen sistemlere kafes sistemler denir. Çubukların birleştiği noktalara düğüm noktaları adı verilir.
KAFES SİSTEMLER STATİK (4. Hafta) Düz eksenden oluşan çubukların birbiriyle birleştirilmesiyle elde edilen sistemlere kafes sistemler denir. Çubukların birleştiği noktalara düğüm noktaları adı verilir.
Burulma (Torsion) Amaçlar
 (Torsion) Amaçlar Bu bölümde şaftlara etkiyen burulma kuvvetlerinin etkisi incelenecek. Analiz dairesel kesitli şaftlar için yapılacak. Eleman en kesitinde oluşan gerilme dağılımı ve elemanda oluşan burulma
(Torsion) Amaçlar Bu bölümde şaftlara etkiyen burulma kuvvetlerinin etkisi incelenecek. Analiz dairesel kesitli şaftlar için yapılacak. Eleman en kesitinde oluşan gerilme dağılımı ve elemanda oluşan burulma
AÇI YÖNTEMİ Slope-deflection Method
 SAKARYA ÜNİVERSİTESİ İNŞAAT ÜHENDİSLİĞİ BÖLÜÜ Department of Civil Engineering İN 303 YAPI STATIĞI II AÇI YÖNTEİ Slope-deflection ethod Y.DOÇ.DR. USTAA KUTANİS kutanis@sakarya.edu.tr Sakarya Üniversitesi,
SAKARYA ÜNİVERSİTESİ İNŞAAT ÜHENDİSLİĞİ BÖLÜÜ Department of Civil Engineering İN 303 YAPI STATIĞI II AÇI YÖNTEİ Slope-deflection ethod Y.DOÇ.DR. USTAA KUTANİS kutanis@sakarya.edu.tr Sakarya Üniversitesi,
Rijit Cisimlerin Dengesi
 Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
29. Düzlem çerçeve örnek çözümleri
 9. Düzlem çerçeve örnek çözümleri 9. Düzlem çerçeve örnek çözümleri Örnek 9.: NPI00 profili ile imal edilecek olan sağdaki düzlem çerçeveni normal, kesme ve moment diyagramları çizilecektir. Yapı çeliği
9. Düzlem çerçeve örnek çözümleri 9. Düzlem çerçeve örnek çözümleri Örnek 9.: NPI00 profili ile imal edilecek olan sağdaki düzlem çerçeveni normal, kesme ve moment diyagramları çizilecektir. Yapı çeliği
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 2 Laminanın Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 2 Laminanın Makromekanik
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 2 Laminanın Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 2 Laminanın Makromekanik
23. Sistem denge denklemlerinin direkt kurulması
 . Sistem denge denklemlerinin direkt kurulması. Sistem denge denklemlerinin direkt kurulması Sonlu elemanlar metodu el hesapları için değil, bilgisayarda yazılımlar ile kullanılması için geliştirilmiştir.
. Sistem denge denklemlerinin direkt kurulması. Sistem denge denklemlerinin direkt kurulması Sonlu elemanlar metodu el hesapları için değil, bilgisayarda yazılımlar ile kullanılması için geliştirilmiştir.
Kirişlerde Kesme (Transverse Shear)
 Kirişlerde Kesme (Transverse Shear) Bu bölümde, doğrusal, prizmatik, homojen ve lineer elastik davranan bir elemanın eksenine dik doğrultuda yüklerin etkimesi durumunda en kesitinde oluşan kesme gerilmeleri
Kirişlerde Kesme (Transverse Shear) Bu bölümde, doğrusal, prizmatik, homojen ve lineer elastik davranan bir elemanın eksenine dik doğrultuda yüklerin etkimesi durumunda en kesitinde oluşan kesme gerilmeleri
Kafes Sistemler. Doğru eksenli çubukların birbirlerine mafsallı olarak birleşmesinden meydana gelen taşıyıcı sistemlere Kafes Sistemler denir.
 KAFES SİSTEMLER Doğru eksenli çubukların birbirlerine mafsallı olarak birleşmesinden meydana gelen taşıyıcı sistemlere Kafes Sistemler denir. Özellikle büyük açıklıklı dolu gövdeli sistemler öz ağırlıklarının
KAFES SİSTEMLER Doğru eksenli çubukların birbirlerine mafsallı olarak birleşmesinden meydana gelen taşıyıcı sistemlere Kafes Sistemler denir. Özellikle büyük açıklıklı dolu gövdeli sistemler öz ağırlıklarının
28. Sürekli kiriş örnek çözümleri
 28. Sürekli kiriş örnek çözümleri SEM2015 programında sürekli kiriş için tanımlanmış özel bir eleman yoktur. Düzlem çerçeve eleman kullanılarak sürekli kirişler çözülebilir. Ancak kiriş mutlaka X-Y düzleminde
28. Sürekli kiriş örnek çözümleri SEM2015 programında sürekli kiriş için tanımlanmış özel bir eleman yoktur. Düzlem çerçeve eleman kullanılarak sürekli kirişler çözülebilir. Ancak kiriş mutlaka X-Y düzleminde
Proje Genel Bilgileri
 Proje Genel Bilgileri Çatı Kaplaması : Betonarme Döşeme Deprem Bölgesi : 1 Yerel Zemin Sınıfı : Z2 Çerçeve Aralığı : 5,0 m Çerçeve Sayısı : 7 aks Malzeme : BS25, BÇIII Temel Taban Kotu : 1,0 m Zemin Emniyet
Proje Genel Bilgileri Çatı Kaplaması : Betonarme Döşeme Deprem Bölgesi : 1 Yerel Zemin Sınıfı : Z2 Çerçeve Aralığı : 5,0 m Çerçeve Sayısı : 7 aks Malzeme : BS25, BÇIII Temel Taban Kotu : 1,0 m Zemin Emniyet
STATIK MUKAVEMET. Doç. Dr. NURHAYAT DEĞİRMENCİ
 STATIK MUKAVEMET Doç. Dr. NURHAYAT DEĞİRMENCİ STATİK DENGE KOŞULLARI Yapı elemanlarının tasarımında bu elemanlarda oluşan iç kuvvetlerin dağılımının bilinmesi gerekir. Dış ve iç kuvvetlerin belirlenmesinde
STATIK MUKAVEMET Doç. Dr. NURHAYAT DEĞİRMENCİ STATİK DENGE KOŞULLARI Yapı elemanlarının tasarımında bu elemanlarda oluşan iç kuvvetlerin dağılımının bilinmesi gerekir. Dış ve iç kuvvetlerin belirlenmesinde
STATIK VE MUKAVEMET 3. Rijit cisimlerin dengesi, Denge denklemleri, Serbest cisim diyagramı. Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ
 STATIK VE MUKAVEMET 3. Rijit cisimlerin dengesi, Denge denklemleri, Serbest cisim diyagramı Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları
STATIK VE MUKAVEMET 3. Rijit cisimlerin dengesi, Denge denklemleri, Serbest cisim diyagramı Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları
İNM 208 DERS TANITIM
 SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering İNM 208 YAPI STATIĞI II İNM 208 DERS TANITIM Y.Doç.Dr. Mustafa KUTANİS DR.MUSTAFA KUTANİS SLIDE 1 ADRES INM 208 YAPI STATİĞİ
SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering İNM 208 YAPI STATIĞI II İNM 208 DERS TANITIM Y.Doç.Dr. Mustafa KUTANİS DR.MUSTAFA KUTANİS SLIDE 1 ADRES INM 208 YAPI STATİĞİ
EĞİLME. Köprünün tabyası onun eğilme gerilmesine karşı koyma dayanımı esas alınarak boyutlandırılır.
 EĞİLME Köprünün tabyası onun eğilme gerilmesine karşı koyma dayanımı esas alınarak boyutlandırılır. EĞİLME Mühendislikte en önemli yapı ve makine elemanları mil ve kirişlerdir. Bu bölümde, mil ve kirişlerde
EĞİLME Köprünün tabyası onun eğilme gerilmesine karşı koyma dayanımı esas alınarak boyutlandırılır. EĞİLME Mühendislikte en önemli yapı ve makine elemanları mil ve kirişlerdir. Bu bölümde, mil ve kirişlerde
Karabük Üniversitesi, Mühendislik Fakültesi...www.IbrahimCayiroglu.com. STATİK (3. Hafta)
 TAŞIYICI SİSTEMLER VE MESNET TEPKİLERİ STATİK (3. Hafta) Taşıyıcı Sistemler Bir yapıya etki eden çeşitli kuvvetleri güvenlik sınırları içinde taşıyan ve bu kuvvetleri zemine aktaran sistemlere taşıyıcı
TAŞIYICI SİSTEMLER VE MESNET TEPKİLERİ STATİK (3. Hafta) Taşıyıcı Sistemler Bir yapıya etki eden çeşitli kuvvetleri güvenlik sınırları içinde taşıyan ve bu kuvvetleri zemine aktaran sistemlere taşıyıcı
Kesit Tesirleri Tekil Kuvvetler
 Statik ve Mukavemet Kesit Tesirleri Tekil Kuvvetler B ÖĞR.GÖR.GÜLTEKİN BÜYÜKŞENGÜR Çevre Mühendisliği Mukavemet Şekil Değiştirebilen Cisimler Mekaniği Kesit Tesiri ve İşaret Kabulleri Kesit Tesiri Diyagramları
Statik ve Mukavemet Kesit Tesirleri Tekil Kuvvetler B ÖĞR.GÖR.GÜLTEKİN BÜYÜKŞENGÜR Çevre Mühendisliği Mukavemet Şekil Değiştirebilen Cisimler Mekaniği Kesit Tesiri ve İşaret Kabulleri Kesit Tesiri Diyagramları
 5. 5. 5.3 5.4 5.5 5.6 5.7 5.8 Rijit Cisimde Denge Düzlem Kuvvetlerde Denge Hali Düzlemde Serbestlik Derecesi Bağ Çeşitleri Pandül Ayak Düzlem Taşıyıcı Sistemler Düzlem Taşıyıcı Sistemlerde Yükleme Durumları
5. 5. 5.3 5.4 5.5 5.6 5.7 5.8 Rijit Cisimde Denge Düzlem Kuvvetlerde Denge Hali Düzlemde Serbestlik Derecesi Bağ Çeşitleri Pandül Ayak Düzlem Taşıyıcı Sistemler Düzlem Taşıyıcı Sistemlerde Yükleme Durumları
Saf Eğilme(Pure Bending)
 Saf Eğilme(Pure Bending) Saf Eğilme (Pure Bending) Bu bölümde doğrusal, prizmatik, homojen bir elemanın eğilme etkisi altındaki şekil değiştirmesini/ deformasyonları incelenecek. Burada çıkarılacak formüller
Saf Eğilme(Pure Bending) Saf Eğilme (Pure Bending) Bu bölümde doğrusal, prizmatik, homojen bir elemanın eğilme etkisi altındaki şekil değiştirmesini/ deformasyonları incelenecek. Burada çıkarılacak formüller
Rijit Cisimlerin Dengesi
 Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Eksenel Yükleme Amaçlar
 Eksenel Yükleme Amaçlar Geçtiğimiz bölümlerde eksenel yüklü elemanlarda oluşan normal gerilme ve normal şekil değiştirme konularını gördük, Bu bölümde ise deformasyonların bulunması ile ilgili bir metot
Eksenel Yükleme Amaçlar Geçtiğimiz bölümlerde eksenel yüklü elemanlarda oluşan normal gerilme ve normal şekil değiştirme konularını gördük, Bu bölümde ise deformasyonların bulunması ile ilgili bir metot
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Tablo 1 Deney esnasında kullanacağımız numunelere ait elastisite modülleri tablosu
 BASİT MESNETLİ KİRİŞTE SEHİM DENEYİ Deneyin Amacı Farklı malzeme ve kalınlığa sahip kirişlerin uygulanan yükün kirişin eğilme miktarına oranı olan rijitlik değerin değişik olduğunun gösterilmesi. Kiriş
BASİT MESNETLİ KİRİŞTE SEHİM DENEYİ Deneyin Amacı Farklı malzeme ve kalınlığa sahip kirişlerin uygulanan yükün kirişin eğilme miktarına oranı olan rijitlik değerin değişik olduğunun gösterilmesi. Kiriş
BETONARME-II ONUR ONAT HAFTA-1 VE HAFTA-II
 BETONARME-II ONUR ONAT HAFTA-1 VE HAFTA-II GENEL BİLGİLER Yapısal sistemler düşey yüklerin haricinde aşağıda sayılan yatay yüklerin etkisine maruz kalmaktadırlar. 1. Deprem 2. Rüzgar 3. Toprak itkisi 4.
BETONARME-II ONUR ONAT HAFTA-1 VE HAFTA-II GENEL BİLGİLER Yapısal sistemler düşey yüklerin haricinde aşağıda sayılan yatay yüklerin etkisine maruz kalmaktadırlar. 1. Deprem 2. Rüzgar 3. Toprak itkisi 4.
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 2 Laminanın Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 2 Laminanın Makromekanik
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 2 Laminanın Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 2 Laminanın Makromekanik
İNŞAAT MÜHENDİSLİĞİNE GİRİŞ
 İNŞAAT MÜHENDİSLİĞİNE GİRİŞ Yrd. Doç. Dr. Merve Sağıroğlu MEKANİK ANABİLİM DALI Kaynaklar: Yrd. Doç. Dr. Banu YAĞCI İnşaat Mühendisliğine Giriş Ders notları KTÜ 2011-2012 Güz dönemi İnşaat Mühendisliğine
İNŞAAT MÜHENDİSLİĞİNE GİRİŞ Yrd. Doç. Dr. Merve Sağıroğlu MEKANİK ANABİLİM DALI Kaynaklar: Yrd. Doç. Dr. Banu YAĞCI İnşaat Mühendisliğine Giriş Ders notları KTÜ 2011-2012 Güz dönemi İnşaat Mühendisliğine
REZA SHIRZAD REZAEI 1
 REZA SHIRZAD REZAEI 1 Tezin Amacı Köprü analiz ve modellemesine yönelik çalışma Akberabad kemer köprüsünün analizi ve modellenmesi Tüm gerçek detayların kullanılması Kalibrasyon 2 KEMER KÖPRÜLER Uzun açıklıklar
REZA SHIRZAD REZAEI 1 Tezin Amacı Köprü analiz ve modellemesine yönelik çalışma Akberabad kemer köprüsünün analizi ve modellenmesi Tüm gerçek detayların kullanılması Kalibrasyon 2 KEMER KÖPRÜLER Uzun açıklıklar
Mukavemet-II PROF. DR. MURAT DEMİR AYDIN
 Mukavemet-II PROF. DR. MURAT DEMİR AYDIN KAYNAK KİTAPLAR Cisimlerin Mukavemeti F.P. BEER, E.R. JOHNSTON Mukavemet-2 Prof.Dr. Onur SAYMAN, Prof.Dr. Ramazan Karakuzu Mukavemet Mehmet H. OMURTAG 1 SİMETRİK
Mukavemet-II PROF. DR. MURAT DEMİR AYDIN KAYNAK KİTAPLAR Cisimlerin Mukavemeti F.P. BEER, E.R. JOHNSTON Mukavemet-2 Prof.Dr. Onur SAYMAN, Prof.Dr. Ramazan Karakuzu Mukavemet Mehmet H. OMURTAG 1 SİMETRİK
İki Boyutlu Yapılar için Doğrudan Rijitlik Metodu (Direct Stiffness Method) (İleri Yapı Statiği II. Kısım)
 İki Boyutlu Yapılar için Doğrudan Rijitlik Metodu (Direct Stiffness Method) (İleri Yapı Statiği II. Kısım) Doç. Dr. Özgür Özçelik Dokuz Eylül Üniversitesi, Müh. Fak., İnşaat Müh. Böl. Genel Genel Genel
İki Boyutlu Yapılar için Doğrudan Rijitlik Metodu (Direct Stiffness Method) (İleri Yapı Statiği II. Kısım) Doç. Dr. Özgür Özçelik Dokuz Eylül Üniversitesi, Müh. Fak., İnşaat Müh. Böl. Genel Genel Genel
R d N 1 N 2 N 3 N 4 /2 /2
 . SÜREKLİ TEELLER. Giriş Kolon yüklerinin büyük ve iki kolonun birbirine yakın olmasından dolayı yapılacak tekil temellerin çakışması halinde veya arsa sınırındaki kolon için eksantrik yüklü tekil temel
. SÜREKLİ TEELLER. Giriş Kolon yüklerinin büyük ve iki kolonun birbirine yakın olmasından dolayı yapılacak tekil temellerin çakışması halinde veya arsa sınırındaki kolon için eksantrik yüklü tekil temel
DÜZLEMDE GERİLME DÖNÜŞÜMLERİ
 3 DÜZLEMDE GERİLME DÖNÜŞÜMLERİ Gerilme Kavramı Dış kuvvetlerin etkisi altında dengedeki elastik bir cismi matematiksel bir yüzeyle rasgele bir noktadan hayali bir yüzeyle ikiye ayıracak olursak, F 3 F
3 DÜZLEMDE GERİLME DÖNÜŞÜMLERİ Gerilme Kavramı Dış kuvvetlerin etkisi altında dengedeki elastik bir cismi matematiksel bir yüzeyle rasgele bir noktadan hayali bir yüzeyle ikiye ayıracak olursak, F 3 F
Yapisal Analiz Programi SAP2000 Bilgi Aktarimi ve Kullanimi
 Yapisal Analiz Programi SAP2000 Bilgi Aktarimi ve Kullanimi Dr. Bilge DORAN Dr. Sema NOYAN ALACALI ÖNSÖZ Günümüzde bilgisayar teknolojisinin hizla ilerlemesinin dogal bir sonucu olarak insaat mühendisligi
Yapisal Analiz Programi SAP2000 Bilgi Aktarimi ve Kullanimi Dr. Bilge DORAN Dr. Sema NOYAN ALACALI ÖNSÖZ Günümüzde bilgisayar teknolojisinin hizla ilerlemesinin dogal bir sonucu olarak insaat mühendisligi
Rijit Cisimlerin Dengesi
 Rijit Cisimlerin Dengesi 1 Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Rijit Cisimlerin Dengesi 1 Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
DEPREM HESABI. Doç. Dr. Mustafa ZORBOZAN
 BETONARME YAPI TASARIMI DEPREM HESABI Doç. Dr. Mustafa ZORBOZAN Mart 2009 GENEL BİLGİ 18 Mart 2007 ve 18 Mart 2008 tarihleri arasında ülkemizde kaydedilen deprem etkinlikleri Kaynak: http://www.koeri.boun.edu.tr/sismo/map/tr/oneyear.html
BETONARME YAPI TASARIMI DEPREM HESABI Doç. Dr. Mustafa ZORBOZAN Mart 2009 GENEL BİLGİ 18 Mart 2007 ve 18 Mart 2008 tarihleri arasında ülkemizde kaydedilen deprem etkinlikleri Kaynak: http://www.koeri.boun.edu.tr/sismo/map/tr/oneyear.html
ÇELİK YAPILAR EKSENEL BASINÇ KUVVETİ ETKİSİ. Hazırlayan: Yard.Doç.Dr.Kıvanç TAŞKIN
 ÇELİK YAPILAR EKSENEL BASINÇ KUVVETİ ETKİSİ Hazırlayan: Yard.Doç.Dr.Kıvanç TAŞKIN TANIM Eksenel basınç kuvveti etkisindeki yapısal elemanlar basınç elemanları olarak isimlendirilir. Basınç elemanlarının
ÇELİK YAPILAR EKSENEL BASINÇ KUVVETİ ETKİSİ Hazırlayan: Yard.Doç.Dr.Kıvanç TAŞKIN TANIM Eksenel basınç kuvveti etkisindeki yapısal elemanlar basınç elemanları olarak isimlendirilir. Basınç elemanlarının
İÇİNDEKİLER. ÖNSÖZ... iii İÇİNDEKİLER... v
 İÇİNDEKİLER ÖNSÖZ... iii İÇİNDEKİLER... v BÖLÜM 1.... 1 1.1. GİRİŞ VE TEMEL KAVRAMLAR... 1 1.2. LİNEER ELASTİSİTE TEORİSİNDE YAPILAN KABULLER... 3 1.3. GERİLME VE GENLEME... 4 1.3.1. Kartezyen Koordinatlarda
İÇİNDEKİLER ÖNSÖZ... iii İÇİNDEKİLER... v BÖLÜM 1.... 1 1.1. GİRİŞ VE TEMEL KAVRAMLAR... 1 1.2. LİNEER ELASTİSİTE TEORİSİNDE YAPILAN KABULLER... 3 1.3. GERİLME VE GENLEME... 4 1.3.1. Kartezyen Koordinatlarda
Elastisite Teorisi Hooke Yasası Normal Gerilme-Şekil değiştirme
 Elastisite Teorisi Hooke Yasası Normal Gerilme-Şekil değiştirme Gerilme ve Şekil değiştirme bileşenlerinin lineer ilişkileri Hooke Yasası olarak bilinir. Elastisite Modülü (Young Modülü) Tek boyutlu Hooke
Elastisite Teorisi Hooke Yasası Normal Gerilme-Şekil değiştirme Gerilme ve Şekil değiştirme bileşenlerinin lineer ilişkileri Hooke Yasası olarak bilinir. Elastisite Modülü (Young Modülü) Tek boyutlu Hooke
MUKAVEMET DERSİ. (Temel Kavramlar) Prof. Dr. Berna KENDİRLİ
 MUKAVEMET DERSİ (Temel Kavramlar) Prof. Dr. Berna KENDİRLİ Ders Planı HAFTA KONU 1 Giriş, Mukavemetin tanımı ve genel ilkeleri 2 Mukavemetin temel kavramları 3-4 Normal kuvvet 5-6 Gerilme analizi 7 Şekil
MUKAVEMET DERSİ (Temel Kavramlar) Prof. Dr. Berna KENDİRLİ Ders Planı HAFTA KONU 1 Giriş, Mukavemetin tanımı ve genel ilkeleri 2 Mukavemetin temel kavramları 3-4 Normal kuvvet 5-6 Gerilme analizi 7 Şekil
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 5 Rijit Cisim Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 5. Rijit Cisim Dengesi Denge,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 5 Rijit Cisim Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 5. Rijit Cisim Dengesi Denge,
Mukavemet-I. Yrd.Doç.Dr. Akın Ataş
 Mukavemet-I Yrd.Doç.Dr. Akın Ataş Bölüm 5 Eğilmede Kirişlerin Analizi ve Tasarımı Kaynak: Cisimlerin Mukavemeti, F.P. Beer, E.R. Johnston, J.T. DeWolf, D.F. Mazurek, Çevirenler: A. Soyuçok, Ö. Soyuçok.
Mukavemet-I Yrd.Doç.Dr. Akın Ataş Bölüm 5 Eğilmede Kirişlerin Analizi ve Tasarımı Kaynak: Cisimlerin Mukavemeti, F.P. Beer, E.R. Johnston, J.T. DeWolf, D.F. Mazurek, Çevirenler: A. Soyuçok, Ö. Soyuçok.
(, ) = + + yönünde yer değiştirme fonksiyonu
 . Üçgen levha eleman, düzlem gerilme durumu. Üçgen levha eleman, düzlem gerilme durumu Çok katlı yapılardaki deprem perdeleri ve yüksek kirişler düzlem levha gibi davranır. Sağdaki şekilde bir levha sistem
. Üçgen levha eleman, düzlem gerilme durumu. Üçgen levha eleman, düzlem gerilme durumu Çok katlı yapılardaki deprem perdeleri ve yüksek kirişler düzlem levha gibi davranır. Sağdaki şekilde bir levha sistem
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
MOMENT DAĞITMA HARDY CROSS YÖNTEMİ
 SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSİĞİ BÖÜMÜ Department of Civil Engineering İNM 208 YAPI STATIĞI II MOMENT DAĞITMA HARDY CROSS YÖNTEMİ Y.DOÇ.DR. MUSTAFA KUTANİS kutanis@sakarya.edu.tr Sakarya Üniversitesi,
SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSİĞİ BÖÜMÜ Department of Civil Engineering İNM 208 YAPI STATIĞI II MOMENT DAĞITMA HARDY CROSS YÖNTEMİ Y.DOÇ.DR. MUSTAFA KUTANİS kutanis@sakarya.edu.tr Sakarya Üniversitesi,
INSA 473 Çelik Tasarım Esasları Basınç Çubukları
 INS 473 Çelik Tasarım Esasları asınç Çubukları Çubuk ekseni doğrultusunda basınç kuvveti aktaran çubuklara basınç çubuğu denir. Çubuk ekseni doğrultusunda basınç kuvveti aktaran çubuklara basınç çubuğu
INS 473 Çelik Tasarım Esasları asınç Çubukları Çubuk ekseni doğrultusunda basınç kuvveti aktaran çubuklara basınç çubuğu denir. Çubuk ekseni doğrultusunda basınç kuvveti aktaran çubuklara basınç çubuğu
Bina Türü Yapı Sistemlerinin Analizi Üzerine Rijit Döşeme ve Sınır Şartları ile İlgili Varsayımların Etkisi
 Bina Türü Yapı Sistemlerinin Analizi Üzerine Rijit Döşeme ve Sınır Şartları ile İlgili Varsayımların Etkisi Rasim Temür İstanbul Üniversitesi İnşaat Mühendisliği Anabilim Dalı Sunum Planı Giriş Rijit Döşeme
Bina Türü Yapı Sistemlerinin Analizi Üzerine Rijit Döşeme ve Sınır Şartları ile İlgili Varsayımların Etkisi Rasim Temür İstanbul Üniversitesi İnşaat Mühendisliği Anabilim Dalı Sunum Planı Giriş Rijit Döşeme
GERİLME ANALİZİ VE MOHR ÇEMBERİ MUKAVEMET
 GERİLME ANALİZİ VE MOHR ÇEMBERİ MUKAVEMET Yrd. Doç. Dr. Emine AYDIN Yrd. Doç. Dr. Elif BORU 1 GENEL YÜKLEME DURUMUNDA GERİLME ANALİZİ Daha önce incelenen gerilme örnekleri eksenel yüklü yapı elemanları
GERİLME ANALİZİ VE MOHR ÇEMBERİ MUKAVEMET Yrd. Doç. Dr. Emine AYDIN Yrd. Doç. Dr. Elif BORU 1 GENEL YÜKLEME DURUMUNDA GERİLME ANALİZİ Daha önce incelenen gerilme örnekleri eksenel yüklü yapı elemanları
7. Kafes sistem sayısal örnekleri
 7. Kafes sistem sayısal örnekleri 7. Düzlem kafes sistem sayısal örneği Şekil 7. deki kafes sistem elastisite modülü.. 5 N/mm olan çelik borulardan imal edilmiştir. a noktasındaki kuvvetlerinden oluşan:
7. Kafes sistem sayısal örnekleri 7. Düzlem kafes sistem sayısal örneği Şekil 7. deki kafes sistem elastisite modülü.. 5 N/mm olan çelik borulardan imal edilmiştir. a noktasındaki kuvvetlerinden oluşan:
SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering
 SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering İNM 212 YAPI STATİĞİ I STABİLİTE STATİKÇE BELİRSİZLİK KİNEMATİK BELİRSİZLİK Y.DOÇ.DR. MUSTAFA KUTANİS kutanis@sakarya.edu.tr
SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering İNM 212 YAPI STATİĞİ I STABİLİTE STATİKÇE BELİRSİZLİK KİNEMATİK BELİRSİZLİK Y.DOÇ.DR. MUSTAFA KUTANİS kutanis@sakarya.edu.tr
JFM 301 SİSMOLOJİ ELASTİSİTE TEORİSİ Elastisite teorisi yer içinde dalga yayılımını incelerken çok yararlı olmuştur.
 JFM 301 SİSMOLOJİ ELASTİSİTE TEORİSİ Elastisite teorisi yer içinde dalga yayılımını incelerken çok yararlı olmuştur. Prof. Dr. Gündüz Horasan Deprem dalgalarını incelerken, yeryuvarının esnek, homojen
JFM 301 SİSMOLOJİ ELASTİSİTE TEORİSİ Elastisite teorisi yer içinde dalga yayılımını incelerken çok yararlı olmuştur. Prof. Dr. Gündüz Horasan Deprem dalgalarını incelerken, yeryuvarının esnek, homojen
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 6 Yapısal Analiz Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 6. Yapısal Analiz Şekilde görüldüğü
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 6 Yapısal Analiz Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 6. Yapısal Analiz Şekilde görüldüğü
STATİK KUVVET ANALİZİ (2.HAFTA)
 STATİK KUVVET ANALİZİ (2.HAFTA) Mekanik sistemler üzerindeki kuvvetler denge halindeyse sistem hareket etmeyecektir. Sistemin denge hali için gerekli kuvvetlerin hesaplanması statik hesaplamalarla yapılır.
STATİK KUVVET ANALİZİ (2.HAFTA) Mekanik sistemler üzerindeki kuvvetler denge halindeyse sistem hareket etmeyecektir. Sistemin denge hali için gerekli kuvvetlerin hesaplanması statik hesaplamalarla yapılır.
Gerilme Dönüşümleri (Stress Transformation)
 Gerilme Dönüşümleri (Stress Transformation) Bu bölümde, bir noktaya etkiyen ve bir koordinat ekseni ile ilişkili gerilme bileşenlerini, başka bir koordinat sistemi ile ilişkili gerilme bileşenlerine dönüştürmek
Gerilme Dönüşümleri (Stress Transformation) Bu bölümde, bir noktaya etkiyen ve bir koordinat ekseni ile ilişkili gerilme bileşenlerini, başka bir koordinat sistemi ile ilişkili gerilme bileşenlerine dönüştürmek
BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM
 BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM 4.1. Giriş Bir önceki bölümde, hareket denklemi F = ma nın, maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini
BÖLÜM 4: MADDESEL NOKTANIN KİNETİĞİ: İMPULS ve MOMENTUM 4.1. Giriş Bir önceki bölümde, hareket denklemi F = ma nın, maddesel noktanın yer değiştirmesine göre integrasyonu ile elde edilen iş ve enerji denklemlerini
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 4 Kuvvet Sistemi Bileşkeleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 4. Kuvvet Sitemi Bileşkeleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 4 Kuvvet Sistemi Bileşkeleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 4. Kuvvet Sitemi Bileşkeleri
Rijit cisim mekaniği, diyagramdan da görüldüğü üzere statik ve dinamik olarak ikiye ayrılır. Statik dengede bulunan cisimlerle, dinamik hareketteki
 Rijit cisim mekaniği, diyagramdan da görüldüğü üzere statik ve dinamik olarak ikiye ayrılır. Statik dengede bulunan cisimlerle, dinamik hareketteki cisimlerle uğraşır. Statik, kuvvet etkisi altında cisimlerin
Rijit cisim mekaniği, diyagramdan da görüldüğü üzere statik ve dinamik olarak ikiye ayrılır. Statik dengede bulunan cisimlerle, dinamik hareketteki cisimlerle uğraşır. Statik, kuvvet etkisi altında cisimlerin
ÖZHENDEKCİ BASINÇ ÇUBUKLARI
 BASINÇ ÇUBUKLARI Kesit zoru olarak yalnızca eksenel doğrultuda basınca maruz kalan elemanlara basınç çubukları denir. Bu tip çubuklara örnek olarak pandül kolonları, kafes sistemlerin basınca çalışan dikme
BASINÇ ÇUBUKLARI Kesit zoru olarak yalnızca eksenel doğrultuda basınca maruz kalan elemanlara basınç çubukları denir. Bu tip çubuklara örnek olarak pandül kolonları, kafes sistemlerin basınca çalışan dikme
UYGULAMALI ELASTİSİTE TEORİSİ
 KOCAELİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ UYGULAMALI ELASTİSİTE TEORİSİ Prof.Dr. Paşa YAYLA 2010 ÖNSÖZ Bu kitabın amacı öğrencilere elastisite teorisi ile ilgili teori ve formülasyonu
KOCAELİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNA MÜHENDİSLİĞİ BÖLÜMÜ UYGULAMALI ELASTİSİTE TEORİSİ Prof.Dr. Paşa YAYLA 2010 ÖNSÖZ Bu kitabın amacı öğrencilere elastisite teorisi ile ilgili teori ve formülasyonu
Elastisite Teorisi Düzlem Problemleri için Sonuç 1
 Elastisite Teorisi Düzlem Problemleri için Sonuç 1 Düzlem Gerilme durumu için: Bilinmeyenler: Düzlem Şekil değiştirme durumu için: Bilinmeyenler: 3 gerilme bileşeni : 3 gerilme bileşeni : 3 şekil değiştirme
Elastisite Teorisi Düzlem Problemleri için Sonuç 1 Düzlem Gerilme durumu için: Bilinmeyenler: Düzlem Şekil değiştirme durumu için: Bilinmeyenler: 3 gerilme bileşeni : 3 gerilme bileşeni : 3 şekil değiştirme
BURULMA (TORSİON) Dairesel Kesitli Çubukların (Millerin) Burulması MUKAVEMET - Ders Notları - Prof.Dr. Mehmet Zor
 3 BURULMA (TORSİON) Dairesel Kesitli Çubukların (Millerin) Burulması 1.1.018 MUKAVEMET - Ders Notları - Prof.Dr. Mehmet Zor 1 3. Burulma Genel Bilgiler Burulma (Torsion): Dairesel Kesitli Millerde Gerilme
3 BURULMA (TORSİON) Dairesel Kesitli Çubukların (Millerin) Burulması 1.1.018 MUKAVEMET - Ders Notları - Prof.Dr. Mehmet Zor 1 3. Burulma Genel Bilgiler Burulma (Torsion): Dairesel Kesitli Millerde Gerilme
6. Sistemin toplam potansiyeli, rijitlik matrisi ve kurulması
 6 Sistemin toplam potansiyeli, rijitlik matrisi ve kurulması 6 Sistemin noktalarında süreklilik koşulu : Her elemanın düğüm noktası aynı zamanda sistemin de düğüm noktası olduğundan, sistemin noktaları
6 Sistemin toplam potansiyeli, rijitlik matrisi ve kurulması 6 Sistemin noktalarında süreklilik koşulu : Her elemanın düğüm noktası aynı zamanda sistemin de düğüm noktası olduğundan, sistemin noktaları
δ / = P L A E = [+35 kn](0.75 m)(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir.
(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir. δ / = P L A E = [+35 kn](0.75 m)(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir.](/thumbs/68/59308868.jpg) A-36 malzemeden çelik çubuk, şekil a gösterildiği iki kademeli olarak üretilmiştir. AB ve BC kesitleri sırasıyla A = 600 mm ve A = 1200 mm dir. A serbest ucunun ve B nin C ye göre yer değiştirmesini belirleyiniz.
A-36 malzemeden çelik çubuk, şekil a gösterildiği iki kademeli olarak üretilmiştir. AB ve BC kesitleri sırasıyla A = 600 mm ve A = 1200 mm dir. A serbest ucunun ve B nin C ye göre yer değiştirmesini belirleyiniz.
Elemanlardaki İç Kuvvetler
 Elemanlardaki İç Kuvvetler Bölüm Öğrenme Çıktıları Yapı elemanlarında oluşan iç kuvvetler. Eksenel kuvvet, Kesme kuvvet ve Eğilme Momenti Denklemleri ve Diyagramları. Bölüm Öğrenme Çıktıları Elemanlarda
Elemanlardaki İç Kuvvetler Bölüm Öğrenme Çıktıları Yapı elemanlarında oluşan iç kuvvetler. Eksenel kuvvet, Kesme kuvvet ve Eğilme Momenti Denklemleri ve Diyagramları. Bölüm Öğrenme Çıktıları Elemanlarda
6.12 Örnekler PROBLEMLER
 6.1 6. 6.3 6.4 6.5 6.6 6.7 Çok Parçalı Taşıyıcı Sistemler Kafes Sistemler Kafes Köprüler Kafes Çatılar Tam, Eksik ve Fazla Bağlı Kafes Sistemler Kafes Sistemler İçin Çözüm Yöntemleri Kafes Sistemlerde
6.1 6. 6.3 6.4 6.5 6.6 6.7 Çok Parçalı Taşıyıcı Sistemler Kafes Sistemler Kafes Köprüler Kafes Çatılar Tam, Eksik ve Fazla Bağlı Kafes Sistemler Kafes Sistemler İçin Çözüm Yöntemleri Kafes Sistemlerde
Mühendislik Mekaniği Dinamik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 17 Rijit Cismin Düzlemsel Kinetiği; Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok.
Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 17 Rijit Cismin Düzlemsel Kinetiği; Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok.
5. RITZ metodunun elemana uygulanması, elemanın rijitlik matrisi
 5. RITZ metodunun elemana uygulanması, elemanın rijitlik matrisi u bölümde RITZ metodu eleman bazında uygulanacak, elemanın yer değiştirme fonksiyonu, şekil değiştirme, gerilme bağıntıları, toplam potansiyeli,
5. RITZ metodunun elemana uygulanması, elemanın rijitlik matrisi u bölümde RITZ metodu eleman bazında uygulanacak, elemanın yer değiştirme fonksiyonu, şekil değiştirme, gerilme bağıntıları, toplam potansiyeli,
MECHANICS OF MATERIALS
 T E CHAPTER 2 Eksenel MECHANICS OF MATERIALS Ferdinand P. Beer E. Russell Johnston, Jr. John T. DeWolf Yükleme Fatih Alibeyoğlu Eksenel Yükleme Bir önceki bölümde, uygulanan yükler neticesinde ortaya çıkan
T E CHAPTER 2 Eksenel MECHANICS OF MATERIALS Ferdinand P. Beer E. Russell Johnston, Jr. John T. DeWolf Yükleme Fatih Alibeyoğlu Eksenel Yükleme Bir önceki bölümde, uygulanan yükler neticesinde ortaya çıkan
KATI CİSİMLERİN BAĞIL İVME ANALİZİ:
 KATI CİSİMLERİN BAĞIL İVME ANALİZİ: Genel düzlemsel hareket yapmakta olan katı cisim üzerinde bulunan iki noktanın ivmeleri aralarındaki ilişki, bağıl hız v A = v B + v B A ifadesinin zamana göre türevi
KATI CİSİMLERİN BAĞIL İVME ANALİZİ: Genel düzlemsel hareket yapmakta olan katı cisim üzerinde bulunan iki noktanın ivmeleri aralarındaki ilişki, bağıl hız v A = v B + v B A ifadesinin zamana göre türevi
Transformasyonlar (İleri Yapı Statiği)
 (İleri Yapı Statiği) Doç. Dr. Özgür Özçelik Dokuz Eylül Üniversitesi, Müh. Fak., İnşaat Müh. Böl. Sunum Ana Hattı Transformasyonlar Rijit uç bölgesi transformasyonu Global Lokal eksen transformasyonu Temel
(İleri Yapı Statiği) Doç. Dr. Özgür Özçelik Dokuz Eylül Üniversitesi, Müh. Fak., İnşaat Müh. Böl. Sunum Ana Hattı Transformasyonlar Rijit uç bölgesi transformasyonu Global Lokal eksen transformasyonu Temel
GERİLME Cismin kesilmiş alanı üzerinde O
 GERİLME Cismin kesilmiş alanı üzerinde O ile tanımlı noktasına etki eden kuvvet ve momentin kesit alana etki eden gerçek yayılı yüklerin bileşke etkisini temsil ettiği ifade edilmişti. Cisimlerin mukavemeti
GERİLME Cismin kesilmiş alanı üzerinde O ile tanımlı noktasına etki eden kuvvet ve momentin kesit alana etki eden gerçek yayılı yüklerin bileşke etkisini temsil ettiği ifade edilmişti. Cisimlerin mukavemeti
İNŞ 320- Betonarme 2 Ders Notları / Prof Dr. Cengiz DÜNDAR Arş. Gör. Duygu BAŞLI
 a) Denge Burulması: Yapı sistemi veya elemanında dengeyi sağlayabilmek için burulma momentine gereksinme varsa, burulma denge burulmasıdır. Sözü edilen gereksinme, elastik aşamada değil taşıma gücü aşamasındaki
a) Denge Burulması: Yapı sistemi veya elemanında dengeyi sağlayabilmek için burulma momentine gereksinme varsa, burulma denge burulmasıdır. Sözü edilen gereksinme, elastik aşamada değil taşıma gücü aşamasındaki
Noktasal Cismin Dengesi
 Noktasal Cismin Dengesi Bu bölümde; Kuvvetleri bieşenlerine ayırma ve kartezyen vektör şeklinde ifade etme yöntemleri noktasal cismin dengesini içeren problemleri çözmede kullanılacaktır. Bölüm 3 DOÇ.DR.
Noktasal Cismin Dengesi Bu bölümde; Kuvvetleri bieşenlerine ayırma ve kartezyen vektör şeklinde ifade etme yöntemleri noktasal cismin dengesini içeren problemleri çözmede kullanılacaktır. Bölüm 3 DOÇ.DR.
ELASTİK ZEMİNE OTURAN SÜREKLİ TEMELLERİN KUVVET YÖNTEMİ İLE ANALİZİ VE SAYISAL HESABI İÇİN GELİŞTİRİLEN BİLGİSAYAR PROGRAMI
 DEÜ MÜHENDİSLİK FAKÜLTESİ FEN ve MÜHENDİSLİK DERGİSİ Cilt: 3 Sayı: 3 sh. 33-50 Ekim 2001 ELASTİK ZEMİNE OTURAN SÜREKLİ TEMELLERİN KUVVET YÖNTEMİ İLE ANALİZİ VE SAYISAL HESABI İÇİN GELİŞTİRİLEN BİLGİSAYAR
DEÜ MÜHENDİSLİK FAKÜLTESİ FEN ve MÜHENDİSLİK DERGİSİ Cilt: 3 Sayı: 3 sh. 33-50 Ekim 2001 ELASTİK ZEMİNE OTURAN SÜREKLİ TEMELLERİN KUVVET YÖNTEMİ İLE ANALİZİ VE SAYISAL HESABI İÇİN GELİŞTİRİLEN BİLGİSAYAR
T.C. BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ MIM331 MÜHENDİSLİKTE DENEYSEL METODLAR DERSİ
 T.C. BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ MIM331 MÜHENDİSLİKTE DENEYSEL METODLAR DERSİ 3 NOKTA EĞME DENEY FÖYÜ ÖĞRETİM ÜYESİ YRD.DOÇ.DR.ÖMER KADİR
T.C. BİLECİK ŞEYH EDEBALİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ MAKİNE VE İMALAT MÜHENDİSLİĞİ BÖLÜMÜ MIM331 MÜHENDİSLİKTE DENEYSEL METODLAR DERSİ 3 NOKTA EĞME DENEY FÖYÜ ÖĞRETİM ÜYESİ YRD.DOÇ.DR.ÖMER KADİR
KUVVET, MOMENT ve DENGE
 2.1. Kuvvet 2.1.1. Kuvvet ve cisimlere etkileri Kuvvetler vektörel büyüklüklerdir. Kuvvet vektörünün; uygulama noktası, kuvvetin cisme etkidiği nokta; doğrultu ve yönü, kuvvetin doğrultu ve yönü; modülüyse
2.1. Kuvvet 2.1.1. Kuvvet ve cisimlere etkileri Kuvvetler vektörel büyüklüklerdir. Kuvvet vektörünün; uygulama noktası, kuvvetin cisme etkidiği nokta; doğrultu ve yönü, kuvvetin doğrultu ve yönü; modülüyse
SONLU FARKLAR GENEL DENKLEMLER
 SONLU FARKLAR GENEL DENKLEMLER Bir elastik ortamın gerilme probleminin Airy gerilme fonksiyonu ile formüle edilebilen halini göz önüne alalım. Problem matematiksel olarak bölgede biharmonik denklemi sağlayan
SONLU FARKLAR GENEL DENKLEMLER Bir elastik ortamın gerilme probleminin Airy gerilme fonksiyonu ile formüle edilebilen halini göz önüne alalım. Problem matematiksel olarak bölgede biharmonik denklemi sağlayan
YAPI ve DEPREM MÜHENDİSLİĞİNDE MATRİS YÖNTEMLER. Prof. Dr. Hikmet Hüseyin ÇATAL. Prof. Dr. Hikmet Hüseyin ÇATAL. (III. Baskı)
 DOKUZ EYLÜL ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ YAYINLARI NO:294 YAPI ve DEPREM MÜHENDİSLİĞİNDE MATRİS YÖNTEMLER YAPI ve DEPREM MÜHENDİSLİĞİNDE MATRİS YÖNTEMLER (III. Baskı) Prof. Dr. Hikmet Hüseyin ÇATAL
DOKUZ EYLÜL ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ YAYINLARI NO:294 YAPI ve DEPREM MÜHENDİSLİĞİNDE MATRİS YÖNTEMLER YAPI ve DEPREM MÜHENDİSLİĞİNDE MATRİS YÖNTEMLER (III. Baskı) Prof. Dr. Hikmet Hüseyin ÇATAL
