6. Sistemin toplam potansiyeli, rijitlik matrisi ve kurulması
|
|
|
- Engin Suvari
- 7 yıl önce
- İzleme sayısı:
Transkript
1 6 Sistemin toplam potansiyeli, rijitlik matrisi ve kurulması 6 Sistemin noktalarında süreklilik koşulu : Her elemanın düğüm noktası aynı zamanda sistemin de düğüm noktası olduğundan, sistemin noktaları dış yükler altında yer değiştirince, aynı noktaya bağlı eleman noktası da aynı yer değiştirmeyi yapmak zorundadır Bu eşitliğin matematik ifadesini aşağıdaki örnek ile kurmaya çalışalım Şekil 6 de düzlem kafes sistemin genel yer değiştirmeleri, şekil 6a da ise aynı sistemin elemanlarının genel yer değiştirmeleri görülmektedir Bunlar arasında x U 4 xˆ U Sistem düğümü Eleman düğümü U 6 U 5 m U U Şekil 6: Sistem yer değiştirmeleri x xˆ ˆx ˆx nolu elemanda: nolu elemanda: eşitlikleri olmak zorundadır Matris notasyonunda aşağıdaki gibi düzenleyebiliriz: elemanın genel yer değiştirmeleri elemanın genel yer değiştirmeleri Eleman düğüm no Tüm elemanların genel yer değiştirmelerinin vektörü Bağlantı matrisi Sistem düğüm no Sistemin yer değiştirme vektörü Görüldüğü gibi a matrisi ve sayıları içerir Düğümlerde elemanların genel yer değiştirmelerini sistem yer değiştirmelerine eşit olmaya zorlamaktadır Bunun anlamı, elemanları sistem düğümlerine bağladığı, elemanları birleştirerek tekrar sistemi oluşturduğudur Bu nedenle bağlantı matrisi de denir Bağlantı matrisi sistemin düğüm serbestlik derecesi boyutlu kare alt matrislere bölünebilir Alt matrisler sıfır veya birim matristir bağlantı matrisi tüm elemanların genel yer değiştirmelerini sistemin yer değiştirmelerine eşitler (6) Genel olarak a çok büyük bir matristir Teorik açıdan, sistemin toplam potansiyelinin hesabında, önemli olmakla birlikte ne el hesaplarında ne de yazılımlarda oluşturulur Sadece sıfır ve birim alt matrislerden oluştuğu için hesapları, a yı kullanmadan, aynı anlama gelen, basit bir yolla yürütmek mümkündür Bu durum ilerleyen konularda açıklık kazanacaktır Compatibility condition at system nodes Ahmet TOPÇU, Sonlu Elemanlar Metodu, Eskişehir Osmangazi Üniversitesi, 5, Sayfa 56
2 Sistem yükleri ile eleman genel kuvvetleri arasındaki bağıntı: Şekil 45 de görülen sistem kuvvetleri 46 da görülen sistem yer değiştirmeleri ile iş yaparlar: " Şekil 47 de görülen eleman genel yer değiştirmeleri 48 de görülen eleman genel kuvvetleri ile iş yaparlar: ( ) % +( ) % Bu bağıntıyı şöyle yazabiliriz: ( ) ( ) 5 Tüm elemanların genel yer değiştirmeleri vektörünün transpozu % % B % Bu iki iş birbirine eşittir: " % 6 bağıntısından yerine yazılarak bulunan " % % bağıntısında her iki tarafın aynı sayı(iş) olduğu düşünülürse " % (6) olması gerektiği anlaşılır Bu bağıntı sistemin toplam potansiyelinin hesabında gerekli olacaktır + Tüm elemanların genel kuvvetleri vektörü bağlantı matrisinin transpozu tüm elemanların genel uç kuvvetlerini sistemin düğüm kuvvetlerine bağlar Sistem düğümlerinde kuvvet dengesi olmalı anlamındadır 6 Sistemin toplam potansiyeli ve rijitlik matrisi Sistemin toplam potansiyeli elemanların toplam potansiyellerinin toplamıdır Sistemin s eleman ile modellendiğini varsayalım 55 den ( + *,( * + - ( * ) * * ( * ) % * *, ( ( ) ( ) % + ( ) ( ) % + ( ) ( ) % + ( + ) + + ( + ) % + ( % ( ) ( ) ( ) ( + ) 5 ( ) ( ) ( ) ( + ) 5 % % + 8 : ( % olduğu yukarıdaki bağıntıların incelenmesinden anlaşılır 6 ve 6 yerine yazılarak ( % ; < < ( > " Sistemin toplam potansiyeli " (6) sistemin toplam potansiyeli bulunur Tüm elemanların genel rijitlik matrislerini içeren köşegen matris > " (64) matrisine sistemin rijitlik matrisi denir Boyutu sistemin serbestlik derecesi kadar ve simetriktir Terimleri sabit sayılardan oluşur Tüm elemanların genel yer değiştirmelerini içeren vektör % Tüm elemanların genel uç kuvvetlerini içeren vektör System stiffness matrix Ahmet TOPÇU, Sonlu Elemanlar Metodu, Eskişehir Osmangazi Üniversitesi, 5, Sayfa 57
3 6 Sistemin denge koşulu 6 Sistemin toplam potansiyeli, rijitlik matrisi ve kurulması 6 toplam potansiyelinde düğüm yer değiştirme vektörü parametredir(terimlerinin sayısal değerleri henüz bilinmeyen vektör) Sistemin denge konumunda 6 toplam potansiyeli minimum olur: CD C CE CE F > " " G > " " > " " Sistemin denge koşulu (65) sistemin denge koşulu olarak bulunur > ", 64 den görüldüğü gibi, elemanların rijitlik matrislerinden ve 6 de tanımlanan bağlantı matrisinden hesaplanan sabit terimlidir " sistem düğüm yüklerinin vektörüdür, bilinmektedir 65 denklem sisteminde sadece sistem düğümlerinin yer değiştirme vektörü bilinmemektedir Ancak, bu denklem sisteminden hesaplanamaz, çünkü > " tekildir(det > " ve > " I tanımsız) Bunun nedeni sistemin sınır(mesnet) koşullarının henüz dikkate alınmamış olmasıdır Mesnetsiz sistem şekil değiştirmez fakat yer değiştirir(rijit yer değiştirme) Sistemin mesnet koşullarından ne anlıyoruz: mesnetlerde bazı yer değiştirmelerin sınırlandırılması, yani sistemin uzayda bir yere sabitlenmesi gereğini anlıyoruz Bu da vektörünün bazı terimlerinin verilmiş olması gerektiği anlamındadır Mesnet koşulu sayısı, sistem rijit yer değiştirmeyecek kadar olmalıdır 64 Sistemin sınır(mesnet) koşullarının 4 işlenmesi: Sistemin sınır koşullarının 65 denklem sistemine nasıl işleneceğini şekil 6 deki basit sistem ile açıklamaya çalışalım Sistemin koordinat sistemi, numaralanması, yük ve yer değiştirme modeli 6a ve 6b deki gibi olsun x x m P 4 P " m U 4 U P 6 P 5 m P P x U 6 U 5 m U U x Şekil 6a: Sistem düğüm yükleri Şekil 6b: Sistem düğüm yer değiştirmeleri Şekil 6a ya göre " 5 ve Şekil 6b ye göre yer değiştirme vektörü " 5 ve sistemin serbestlik derecesi 6 dır 65 denklem sistemindeki > " rijitlik matrisi 6x6 boyutlu ve sabit sayılardan oluşan bir matris olacaktır > " ın sabit sayılarını k ij ile gösterelim: Equilibrium condition of the system Örnek: düzlem bir çerçevenin bir ankastre mesnetinde yatay, düşey hareket ve dönme sıfır olmalıdır, yani mesnetteki yer değiştirmelerin değeri bilinmektedir Örnek: Basit kirişte en az bir sabit ve bir hareketli mesnet olmalı Konsol kirişte bir uç ankastre olmalı Aksi halde kiriş veya konsol rijit yer değiştirir Rijit yer değiştiren sistemlere "Labil" (Labile kararsız, stabil olmayan) sistem denir, çözümü yoktur 4 System boundry conditions, restrains Ahmet TOPÇU, Sonlu Elemanlar Metodu, Eskişehir Osmangazi Üniversitesi, 5, Sayfa 58
4 > " Sistemin düğüm numaraları Sistem rijitlik matrisi ; < ın özellikleri: Boyutu sistemin serbestlik derecesi kadardır(örneğimizdeki düzlem kafes sistemde serbestlik derecesi6, dolayısıyla > " 6x6 boyutundadır) Simetriktir(örneğin, dir) *P terimleri sabit sayılardır Tekildir(LMN > ", > " I tanımsız) Alt matrislerden oluşur Her alt matrisin boyutu sistem düğüm serbestlik derecesi kadardır(örneğimizde: x) Band matristir 65 denklem sisteminin açık yazılmış şekli: ; < < düğümde x ve x yönü denge denklemleri düğümde x ve x yönü denge denklemleri düğümde x ve x yönü denge denklemleri (66) Bu bağıntıda > " ın tüm terimleri 64 ten bilinmektedir Ayrıca " ve vektörlerinin de bazı terimleri bilinmektedir Hesaplarda kuvvet birimi olarak kn kullanıldığını varsayalım 6 ye göre noktasında, dür, ve noktasındaki,,, bilinmemektedir(reaksiyonlar) Yük vektörü " 5 olur 66 denklem sisteminde yerine yazarsak: ; < < düğümde x ve x yönü denge denklemleri düğümde x ve x yönü denge denklemleri düğümde x ve x yönü denge denklemleri Reaksiyonlar (67) Sistemin sınır şartlarına gelince: ve noktaları mesnettir, buradaki yer değiştirmelerin değerleri sıfır olarak bilinmektedir, şekil 6b den Buradaki sayıları, 69 un köşegeninde görülen sayılarının nereden geldiğini açıklamak için yazılmıştır,,, (68) olması gerektiği anlaşılır > " ın, 4, 5, ve 6 kolonları sıfır ile çarpılınca > " ın bu kolonlarındaki sayılar sıfır olur Simetriden dolayı aynı nolu satırların da sıfır olması gerekir Sıfırlanan satırlara 68 denklemlerini yazarız Buna göre sınır koşullarını 67 ye aşağıdaki gibi işleyelim: ; GENEL: * koşulunu işlemek için: i satır ve (simetri nedeniyle) i kolondaki sayılar sıfırlanır i satır-kolona, karşı tarafa yazılır Böylece * denklemi denklem sistemine eklenmiş olur (69) > (6) 69 denklemleri 68 mesnet koşullarını aynen içermektedir > matrisi artık tekil değildir, çünkü sistem ve noktalarında tutuludur, uzayda gezemez, yani rijit yer değiştiremez LMN >, > I tanımlıdır Denklem sistemi çözülerek yer değiştirme vektörü bulunur Çözüm sonucunda,,, olarak bulunacaktır, bu da 68 koşullarının aynısıdır Aslında çözüm ile sadece, çözüm öncesi değerleri bilinmeyen,, yer değiştirmeleri belirlenmektedir Diğerlerinin değerleri zaten bilinmektedir Ahmet TOPÇU, Sonlu Elemanlar Metodu, Eskişehir Osmangazi Üniversitesi, 5, Sayfa 59
5 Bu küçük örnekte 6 denklemin 4 ü mesnet koşuludur Büyük sistemlerde durum bunun tam tersidir: Denklem sayısı çok, mesnet koşulu sayısı azdır Örneğin düğümlü bir kafes sistemin bir sabit bir de basit kayıcı mesneti olsun Her düğümde serbestlik derecesi olduğundan sistemin serbestlik derecesi x, yani denklemli bir sistem olacaktır Sınır koşulu sayısı ise sadece tür 69 denklem sistemi genel olarak çok büyüktür, çok küçük sistemler dışında elle çözümü mümkün değildir GAUSS indirgeme metodu veya CHOLESKY metodu kullanılabilir > matrisi simetrik olduğu için yazılımlarda genellikle CHOLESKY tercih edilir 65 Reaksiyonların hesabı Şekil 6a nın ve noktalarındaki,,, düğüm kuvvetleri mesnet reaksiyonlarıdır Sınır koşulları işlenmeden önceki 67 denklem sisteminin son 4 denklemi bu noktalardaki denge denklemleridir Sınır koşulları işlenince bu denklemler, 69 da görüldüğü gibi, kaybolmaktadır Reaksiyonların hesaplanabilmesi için, sınır koşulları işlenmeden önce, bu denklemlerin kopyalanarak saklanması(bir kâğıda yazılması, hard diske depolanması) gerekir: Q R Q R Mesnet noktalarında denge denklemleri (6) E 69 ün çözümünden bulunan vektörü 6 de yerine yazılır,,,, reaksiyon kuvvetleri bulunur Sınır koşulunun mesnet çökmesi içermesi durumu: Mesnet çökmesi problemi yapı statiği derslerinden bilinir Örneğin, bir sürekli kirişin bir mesnedinin S kadar çökmesi durumunda iç kuvvetleri hesaplayınız diye sorulur Aslında mesnedin çökmemesi, yer değiştirmemesi gerekir Ama, öngörülemeyen bir nedenle, çökerse sistemde büyük iç kuvvetler oluşur "Çökme" kelimesi SEMde çok daha genel yorumlanmalıdır Bir mesnetin herhangi bir serbestlik yönünde bir nedenle yer değiştirmesi olarak anlaşılmalıdır, yani sadece düşey yer değiştirme değildir Mesnet çökmesi olan bir sistemde ilgili yer değiştirme sıfır değil çökme kadardır, çökme doğrultusundaki yer değiştirmenin değeri biliniyor anlamındadır Bu değer ile sistem rijitlik matrisinin ilgili kolonu çarpılarak denklem sisteminin karşı tarafına atılır Diğer tüm işlemler yukarıda açıklandığı gibidir Bir örnekle açıklayalım: Şekil 6 deki sistemin mesnetleri verilen yük altında şekildeki kadar yer değiştirirse sınır koşulları ne olur? m mm Mesnet yer değiştirmesi Sistemin numaralandırılması ve koordinat eksenleri 6a ve 6b deki gibi olduğu, hesaplarda kn ve mm birimlerinin kullanıldığı varsayımıyla sınır koşulları,,, (6) olacaktır Sınır koşulları işlenmiş denklem sistemi mm m Mesnet yer değiştirmesi Şekil 6: Çözülmesi istenen düzlem kafes sistem kn ; U V WX:YXZ çö8[x:\y]xy ^_şy ]üğü[ 8``XZ_Xa\ (6) olacaktır Dikkat edilirse, sıfırdan farklı olan U 4- ve U 5- mesnet çökmeleri rijitlik matrisinin 4 ve 5 kolonları ile çarpılarak denklem sisteminin karşı tarafına atıldıktan sonra 6 sınır koşulları işlenmiştir 6 denklem sisteminden hesaplandığında 6 koşulları sağlanır vektörü 6 de yerine yazılarak mesnet reaksiyonları bulunur Denklem sistemi çözüm yöntemleri için bak: bölüm,4,5,6 ve 7 Reactions, support forces, boundry forces Ahmet TOPÇU, Sonlu Elemanlar Metodu, Eskişehir Osmangazi Üniversitesi, 5, Sayfa 6
6 66 Sistem rijitlik matrisinin direkt kurulması 64 bağıntısına göre sistem rijitlik matrisi > " dır Ancak hem hem de çok büyük olduğundan bu çarpım hem el hesaplarında hem de programlarda yapılmaz ve matrisleri, boyutu düğüm serbestlik derecesi olan alt matrislerden oluşur 6 de verilen matrisinin alt matrisleri sıfır veya birim matristir Bu nedenle 64 çarpımı daki eleman rijitlik matrislerinin alt matrislerinin > " ın ilgili bloklarına eklenmesinden başka bir işlevi yoktur Çarpımı yapmak yerine > " aşağıda açıklanan yolla tek bir çarpma dahi yapmadan kurulur İşlemler şekil 64 deki düzlem kafes sistem örneği üzerinde açıklanacaktır x xˆ ˆx xˆ ˆx m x Şekil 64: Düzlem kafes sistem ) Sistem genel ve yerel koordinat sistemi seçilir, Düğüm ve elemanlar numaralanır, Şekil 64 ) Düğüm serbestlik derecesi belirlenir, örnekte dir ) Sistemin serbestlik derecesi belirlenir, örnekte 6 dır 4) Sistemin serbestlik derecesi boyutlu boş bir > " matrisi hazırlanır, örnekte 6x6 boyutlu 6x6 boyutlu boş > " matrisi 5) > " matrisi boyutu sistemin düğüm serbestlik derecesi olan alt matrislere bölünür, örnekte x Alt matrislerin üstüne sistemin düğüm numaraları sırayla yazılır Örnekte -- Aynı numaralar alt matrislerin soluna (veya sağına) da yazılır Alt matrisler düğüm numaraları ile adlandırılır - alt matrisi düğüm ile düğümdeki alt matris anlamındadır x boyutlu alt matrislere bölünmüş > " matrisi x boyutlu - alt matrisi Sistemin düğüm numaraları x boyutlu - alt matrisi Ahmet TOPÇU, Sonlu Elemanlar Metodu, Eskişehir Osmangazi Üniversitesi, 5, Sayfa 6
7 6) Birinci elemanın genel rijitlik matrisi kurulur, aynı boyutlu alt matrislere bölünür, elemanın düğüm numaraları alt matrislerin üstüne ve soluna yazılır Elemanın düğüm numaraları, yerel orijinin bulunduğu düğümden başlanarak, sırayla yazılır Örneğimizde elemanın orijini noktasında olduğundan bloklar üstüne ve soluna - yazılmalı(- değil) Elemanın düğüm numaraları düğüm, ikinci düğüm elemanın genel rijitlik matrisi x boyutlu alt matrislere bölünmüştür Bloklar - olarak numaralanmış, çünkü yerel orijin noktasındadır *P terimi elemanın i satır ve j kolonundaki sayı anlamındadır Elemanın düğüm numaraları düğüm, ikinci düğüm k k k k 4 k k k k 4 x boyutlu - alt matrisi k k k k 4 k 4 k 4 k 4 k 44 x boyutlu - alt matrisi Elemanın i-j düğümündeki alt matrisi sistem rijitlik matrisinin aynı i-j alt matrisideki sayılarla toplanır: Elemanın - alt matrisi sistemin - alt matrisine, - alt matrisi sistemin - alt matrisine, - alt matrisi sistemin - alt matrisine, - alt matrisi sistemin - alt matrisine eklenir elemanın genel rijitlik matrisi Sistem rijitlik matrisi > " k k k k 4 k k k k 4 k k 4 k 4 k 44 k k k 4 k 4 k k k k 4 k 4 k 4 k 4 k 44 k k 4 k k 4 k k k k 7) İkinci elemanın genel rijitlik matrisi kurulur, alt matrislere bölünür, elemanın düğüm numaraları alt matrislerin üstüne ve soluna yazılır Elemanın düğüm numaraları, yerel orijinin bulunduğu düğümden başlanarak, sırayla yazılır Örneğimizde elemanın orijini noktasında olduğundan bloklar üstüne ve soluna - yazılmalı(- değil) Elemanın i-j alt matrisleri sistem rijitlik matrisinin i-j bloklarına eklenir elemanın genel rijitlik matrisi Sistem rijitlik matrisi > " k k k k 4 k k k k 4 k +k k 4+k 4 k 4+k 4 k 44+k 44 k k k 4 k 4 k k k 4 k 4 k k k k 4 k 4 k 4 k 4 k 44 k k 4 k k 4 k k k k k k 4 k k 4 k k k k 8) Üçüncü elemanın genel rijitlik matrisi kurulur, alt matrisleri sistem rijitlik matrisine taşınır Örneğimizde eleman yoktur 9) Ahmet TOPÇU, Sonlu Elemanlar Metodu, Eskişehir Osmangazi Üniversitesi, 5, Sayfa 6
23. Sistem denge denklemlerinin direkt kurulması
 . Sistem denge denklemlerinin direkt kurulması. Sistem denge denklemlerinin direkt kurulması Sonlu elemanlar metodu el hesapları için değil, bilgisayarda yazılımlar ile kullanılması için geliştirilmiştir.
. Sistem denge denklemlerinin direkt kurulması. Sistem denge denklemlerinin direkt kurulması Sonlu elemanlar metodu el hesapları için değil, bilgisayarda yazılımlar ile kullanılması için geliştirilmiştir.
7. Kafes sistem sayısal örnekleri
 7. Kafes sistem sayısal örnekleri 7. Düzlem kafes sistem sayısal örneği Şekil 7. deki kafes sistem elastisite modülü.. 5 N/mm olan çelik borulardan imal edilmiştir. a noktasındaki kuvvetlerinden oluşan:
7. Kafes sistem sayısal örnekleri 7. Düzlem kafes sistem sayısal örneği Şekil 7. deki kafes sistem elastisite modülü.. 5 N/mm olan çelik borulardan imal edilmiştir. a noktasındaki kuvvetlerinden oluşan:
5. RITZ metodunun elemana uygulanması, elemanın rijitlik matrisi
 5. RITZ metodunun elemana uygulanması, elemanın rijitlik matrisi u bölümde RITZ metodu eleman bazında uygulanacak, elemanın yer değiştirme fonksiyonu, şekil değiştirme, gerilme bağıntıları, toplam potansiyeli,
5. RITZ metodunun elemana uygulanması, elemanın rijitlik matrisi u bölümde RITZ metodu eleman bazında uygulanacak, elemanın yer değiştirme fonksiyonu, şekil değiştirme, gerilme bağıntıları, toplam potansiyeli,
(, ) = + + yönünde yer değiştirme fonksiyonu
 . Üçgen levha eleman, düzlem gerilme durumu. Üçgen levha eleman, düzlem gerilme durumu Çok katlı yapılardaki deprem perdeleri ve yüksek kirişler düzlem levha gibi davranır. Sağdaki şekilde bir levha sistem
. Üçgen levha eleman, düzlem gerilme durumu. Üçgen levha eleman, düzlem gerilme durumu Çok katlı yapılardaki deprem perdeleri ve yüksek kirişler düzlem levha gibi davranır. Sağdaki şekilde bir levha sistem
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ
 İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
p 2 p Üçgen levha eleman, düzlem şekil değiştirme durumu
 Üçgen levha eleman düzlem şekil değiştirme durumu Üçgen levha eleman düzlem şekil değiştirme durumu İstinat duvarı basınçlı uzun boru tünel ağırlık barajı gibi yapılar düzlem levha gibi davranırlar Uzun
Üçgen levha eleman düzlem şekil değiştirme durumu Üçgen levha eleman düzlem şekil değiştirme durumu İstinat duvarı basınçlı uzun boru tünel ağırlık barajı gibi yapılar düzlem levha gibi davranırlar Uzun
4. Sonlu elemanlar yer değiştirme metodu, modelleme, tanımlar
 4. Sonlu Elemanlar Yer Değiştirme Metodu modelleme tanımlar 4. Sonlu elemanlar yer değiştirme metodu modelleme tanımlar. bölümde örneklerle açıklanan RITZ metodu.5. ve.5 bağıntıları yerine kullanılabilen
4. Sonlu Elemanlar Yer Değiştirme Metodu modelleme tanımlar 4. Sonlu elemanlar yer değiştirme metodu modelleme tanımlar. bölümde örneklerle açıklanan RITZ metodu.5. ve.5 bağıntıları yerine kullanılabilen
33. Üçgen levha-düzlem gerilme örnek çözümleri
 33. Üçgen levha-düzlem gerilme örnek çözümleri Örnek 33.1: Şekil 33.1 deki, kalınlığı 20 cm olan betonarme perdenin malzemesi C25/30 betonudur. Tepe noktasında 1000 kn yatay yük etkimektedir. a) 1 noktasındaki
33. Üçgen levha-düzlem gerilme örnek çözümleri Örnek 33.1: Şekil 33.1 deki, kalınlığı 20 cm olan betonarme perdenin malzemesi C25/30 betonudur. Tepe noktasında 1000 kn yatay yük etkimektedir. a) 1 noktasındaki
36. Basit kuvvet metodu
 36. Basit kuvvet metodu Basit kuvvet metodu hakkında çok kısa bilgi verilecektir. Basit kuvvet metodunda hiperstatik bilinmeyenlerinin hesaplanmasına, dolayısıyla buna ait denklem sisteminin kurulmasına
36. Basit kuvvet metodu Basit kuvvet metodu hakkında çok kısa bilgi verilecektir. Basit kuvvet metodunda hiperstatik bilinmeyenlerinin hesaplanmasına, dolayısıyla buna ait denklem sisteminin kurulmasına
İki Boyutlu Yapılar için Doğrudan Rijitlik Metodu (Direct Stiffness Method) (İleri Yapı Statiği II. Kısım)
 İki Boyutlu Yapılar için Doğrudan Rijitlik Metodu (Direct Stiffness Method) (İleri Yapı Statiği II. Kısım) Doç. Dr. Özgür Özçelik Dokuz Eylül Üniversitesi, Müh. Fak., İnşaat Müh. Böl. Genel Genel Genel
İki Boyutlu Yapılar için Doğrudan Rijitlik Metodu (Direct Stiffness Method) (İleri Yapı Statiği II. Kısım) Doç. Dr. Özgür Özçelik Dokuz Eylül Üniversitesi, Müh. Fak., İnşaat Müh. Böl. Genel Genel Genel
R 1Y kn R 1X R 1Z R 4Y R 3Y 4 R 4X R 3Z R 3X R 4Z. -90 kn. 80 kn 80 kn R 1Y =10 R 1X =-10 R 4Y =10 R 1Z =0 R 3Y =70 4 R 3X =-70 R 4X =0
 27. Uzay kafes örnek çözümleri Örnek 27.: Şekil 27. de verilen uzay kafes sistem çelik borulardan imal edilecektir. a noktasındaki dış yüklerden oluşan eleman kuvvetleri, reaksiyonlar, gerilmeler ve düğüm
27. Uzay kafes örnek çözümleri Örnek 27.: Şekil 27. de verilen uzay kafes sistem çelik borulardan imal edilecektir. a noktasındaki dış yüklerden oluşan eleman kuvvetleri, reaksiyonlar, gerilmeler ve düğüm
34. Dörtgen plak örnek çözümleri
 34. Dörtgen plak örnek çözümleri Örnek 34.1: Teorik çözümü Timoshenko 1 tarafından verilen dört tarafından ankastre ve merkezinde P=100 kn tekil yükü olan kare plağın(şekil 34.1) çözümü 4 farklı model
34. Dörtgen plak örnek çözümleri Örnek 34.1: Teorik çözümü Timoshenko 1 tarafından verilen dört tarafından ankastre ve merkezinde P=100 kn tekil yükü olan kare plağın(şekil 34.1) çözümü 4 farklı model
29. Düzlem çerçeve örnek çözümleri
 9. Düzlem çerçeve örnek çözümleri 9. Düzlem çerçeve örnek çözümleri Örnek 9.: NPI00 profili ile imal edilecek olan sağdaki düzlem çerçeveni normal, kesme ve moment diyagramları çizilecektir. Yapı çeliği
9. Düzlem çerçeve örnek çözümleri 9. Düzlem çerçeve örnek çözümleri Örnek 9.: NPI00 profili ile imal edilecek olan sağdaki düzlem çerçeveni normal, kesme ve moment diyagramları çizilecektir. Yapı çeliği
SEM2015 programı kullanımı
 SEM2015 programı kullanımı Basit Kuvvet metodu kullanılarak yazılmış, öğretim amaçlı, basit bir sonlu elemanlar statik analiz programdır. Çözebileceği sistemler: Düzlem/uzay kafes: Evet Düzlem/uzay çerçeve:
SEM2015 programı kullanımı Basit Kuvvet metodu kullanılarak yazılmış, öğretim amaçlı, basit bir sonlu elemanlar statik analiz programdır. Çözebileceği sistemler: Düzlem/uzay kafes: Evet Düzlem/uzay çerçeve:
28. Sürekli kiriş örnek çözümleri
 28. Sürekli kiriş örnek çözümleri SEM2015 programında sürekli kiriş için tanımlanmış özel bir eleman yoktur. Düzlem çerçeve eleman kullanılarak sürekli kirişler çözülebilir. Ancak kiriş mutlaka X-Y düzleminde
28. Sürekli kiriş örnek çözümleri SEM2015 programında sürekli kiriş için tanımlanmış özel bir eleman yoktur. Düzlem çerçeve eleman kullanılarak sürekli kirişler çözülebilir. Ancak kiriş mutlaka X-Y düzleminde
Lineer Cebir. Doç. Dr. Niyazi ŞAHİN TOBB. İçerik: 1.1. Lineer Denklemlerin Tanımı 1.2. Lineer Denklem Sistemleri 1.3. Matrisler
 Lineer Cebir Doç. Dr. Niyazi ŞAHİN TOBB İçerik: 1.1. Lineer Denklemlerin Tanımı 1.2. Lineer Denklem Sistemleri 1.3. Matrisler Bölüm 1 - Lineer Eşitlikler 1.1. Lineer Eşitliklerin Tanımı x 1, x 2,..., x
Lineer Cebir Doç. Dr. Niyazi ŞAHİN TOBB İçerik: 1.1. Lineer Denklemlerin Tanımı 1.2. Lineer Denklem Sistemleri 1.3. Matrisler Bölüm 1 - Lineer Eşitlikler 1.1. Lineer Eşitliklerin Tanımı x 1, x 2,..., x
25. SEM2015 programı kullanımı
 25. SEM2015 programı kullanımı Basit Kuvvet metodu kullanılarak yazılmış, öğretim amaçlı, basit bir sonlu elemanlar statik analiz programdır. Program kısaca tanıtılacak, sonraki bölümlerde bu program ile
25. SEM2015 programı kullanımı Basit Kuvvet metodu kullanılarak yazılmış, öğretim amaçlı, basit bir sonlu elemanlar statik analiz programdır. Program kısaca tanıtılacak, sonraki bölümlerde bu program ile
Karabük Üniversitesi, Mühendislik Fakültesi...www.IbrahimCayiroglu.com. STATİK (4. Hafta)
 KAFES SİSTEMLER STATİK (4. Hafta) Düz eksenden oluşan çubukların birbiriyle birleştirilmesiyle elde edilen sistemlere kafes sistemler denir. Çubukların birleştiği noktalara düğüm noktaları adı verilir.
KAFES SİSTEMLER STATİK (4. Hafta) Düz eksenden oluşan çubukların birbiriyle birleştirilmesiyle elde edilen sistemlere kafes sistemler denir. Çubukların birleştiği noktalara düğüm noktaları adı verilir.
ÖZDEĞERLER- ÖZVEKTÖRLER
 ÖZDEĞERLER- ÖZVEKTÖRLER GİRİŞ Özdeğerler, bir matrisin orijinal yapısını görmek için kullanılan alternatif bir yoldur. Özdeğer kavramını açıklamak için öncelikle özvektör kavramı ele alınsın. Bazı vektörler
ÖZDEĞERLER- ÖZVEKTÖRLER GİRİŞ Özdeğerler, bir matrisin orijinal yapısını görmek için kullanılan alternatif bir yoldur. Özdeğer kavramını açıklamak için öncelikle özvektör kavramı ele alınsın. Bazı vektörler
Transformasyonlar (İleri Yapı Statiği)
 (İleri Yapı Statiği) Doç. Dr. Özgür Özçelik Dokuz Eylül Üniversitesi, Müh. Fak., İnşaat Müh. Böl. Sunum Ana Hattı Transformasyonlar Rijit uç bölgesi transformasyonu Global Lokal eksen transformasyonu Temel
(İleri Yapı Statiği) Doç. Dr. Özgür Özçelik Dokuz Eylül Üniversitesi, Müh. Fak., İnşaat Müh. Böl. Sunum Ana Hattı Transformasyonlar Rijit uç bölgesi transformasyonu Global Lokal eksen transformasyonu Temel
Hedefler. Kafeslerde oluşan kuvvetlerin hesaplanması: düğüm noktaları metodu kesme metodu
 Yapıların Analizi Hedefler Kafeslerde oluşan kuvvetlerin hesaplanması: düğüm noktaları metodu kesme metodu Konu Çıktıları İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz
Yapıların Analizi Hedefler Kafeslerde oluşan kuvvetlerin hesaplanması: düğüm noktaları metodu kesme metodu Konu Çıktıları İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz
YAPI STATİĞİ II (Hiperstatik Sistemler) Yrd. Doç. Dr. Selçuk KAÇIN
 YAPI STATİĞİ II (Hiperstatik Sistemler) Yrd. Doç. Dr. Selçuk KAÇIN Yapı Sistemleri: İzostatik (Statikçe Belirli) Sistemler : Bir sistemin tüm kesit tesirlerini (iç kuvvetlerini) ve mesnet reaksiyonlarını
YAPI STATİĞİ II (Hiperstatik Sistemler) Yrd. Doç. Dr. Selçuk KAÇIN Yapı Sistemleri: İzostatik (Statikçe Belirli) Sistemler : Bir sistemin tüm kesit tesirlerini (iç kuvvetlerini) ve mesnet reaksiyonlarını
 5. 5. 5.3 5.4 5.5 5.6 5.7 5.8 Rijit Cisimde Denge Düzlem Kuvvetlerde Denge Hali Düzlemde Serbestlik Derecesi Bağ Çeşitleri Pandül Ayak Düzlem Taşıyıcı Sistemler Düzlem Taşıyıcı Sistemlerde Yükleme Durumları
5. 5. 5.3 5.4 5.5 5.6 5.7 5.8 Rijit Cisimde Denge Düzlem Kuvvetlerde Denge Hali Düzlemde Serbestlik Derecesi Bağ Çeşitleri Pandül Ayak Düzlem Taşıyıcı Sistemler Düzlem Taşıyıcı Sistemlerde Yükleme Durumları
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 5 Rijit Cisim Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 5. Rijit Cisim Dengesi Denge,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 5 Rijit Cisim Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 5. Rijit Cisim Dengesi Denge,
Hiperstatik sistemlerin çözümünde, yer değiştirmelerin küçük olduğu ve gerilme - şekil değiştirme bağıntılarının lineer olduğu kabul edilmektedir.
 1. HİPERSTATİK SİSTEMLER 1.1. Giriş Bir sistemin hesabının amacı, dış etkilerden meydana gelen kesit tesirlerini, şekil değiştirmelerini ve yer değiştirmelerini belirlemektir. İzostatik sistemlerde, yalnız
1. HİPERSTATİK SİSTEMLER 1.1. Giriş Bir sistemin hesabının amacı, dış etkilerden meydana gelen kesit tesirlerini, şekil değiştirmelerini ve yer değiştirmelerini belirlemektir. İzostatik sistemlerde, yalnız
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
YAPI STATİĞİ MESNETLER
 YAPI STATİĞİ MESNETLER Öğr.Gör. Gültekin BÜYÜKŞENGÜR STATİK Kirişler Yük Ve Mesnet Çeşitleri Mesnetler Ve Mesnet Reaksiyonları 1. Kayıcı Mesnetler 2. Sabit Mesnetler 3. Ankastre (Konsol) Mesnetler 4. Üç
YAPI STATİĞİ MESNETLER Öğr.Gör. Gültekin BÜYÜKŞENGÜR STATİK Kirişler Yük Ve Mesnet Çeşitleri Mesnetler Ve Mesnet Reaksiyonları 1. Kayıcı Mesnetler 2. Sabit Mesnetler 3. Ankastre (Konsol) Mesnetler 4. Üç
VEKTÖR UZAYLARI 1.GİRİŞ
 1.GİRİŞ Bu bölüm lineer cebirin temelindeki cebirsel yapıya, sonlu boyutlu vektör uzayına giriş yapmaktadır. Bir vektör uzayının tanımı, elemanları skalar olarak adlandırılan herhangi bir cisim içerir.
1.GİRİŞ Bu bölüm lineer cebirin temelindeki cebirsel yapıya, sonlu boyutlu vektör uzayına giriş yapmaktadır. Bir vektör uzayının tanımı, elemanları skalar olarak adlandırılan herhangi bir cisim içerir.
TEKNOLOJİNİN BİLİMSEL İLKELERİ. Öğr. Gör. Adem ÇALIŞKAN
 TEKNOLOJİNİN BİLİMSEL İLKELERİ 5 Ağırlık merkezi STATİK Bir cisim moleküllerden meydana gelir. Bu moleküllerin her birine yer çekimi kuvveti etki eder. Bu yer çekimi kuvvetlerinin cismi meydana getiren
TEKNOLOJİNİN BİLİMSEL İLKELERİ 5 Ağırlık merkezi STATİK Bir cisim moleküllerden meydana gelir. Bu moleküllerin her birine yer çekimi kuvveti etki eder. Bu yer çekimi kuvvetlerinin cismi meydana getiren
8. HAFTA BLM323 SAYISAL ANALİZ. Okt. Yasin ORTAKCI.
 8. HAFTA BLM323 SAYISAL ANALİZ Okt. Yasin ORTAKCI yasinortakci@karabuk.edu.tr Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 2 MATRİSLER Matris veya dizey, dikdörtgen bir sayılar tablosu
8. HAFTA BLM323 SAYISAL ANALİZ Okt. Yasin ORTAKCI yasinortakci@karabuk.edu.tr Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi 2 MATRİSLER Matris veya dizey, dikdörtgen bir sayılar tablosu
m=n şeklindeki matrislere kare matris adı verilir. şeklindeki matrislere ise sütun matrisi denir. şeklindeki A matrisi bir kare matristir.
 Matrisler Satır ve sütunlar halinde düzenlenmiş tabloya matris denir. m satırı, n ise sütunu gösterir. a!! a!" a!! a!" a!! a!! a!! a!! a!" m=n şeklindeki matrislere kare matris adı verilir. [2 3 1] şeklinde,
Matrisler Satır ve sütunlar halinde düzenlenmiş tabloya matris denir. m satırı, n ise sütunu gösterir. a!! a!" a!! a!" a!! a!! a!! a!! a!" m=n şeklindeki matrislere kare matris adı verilir. [2 3 1] şeklinde,
Doç. Dr. Bilge DORAN
 Doç. Dr. Bilge DORAN Bilgisayar teknolojisinin ilerlemesi doğal olarak Yapı Mühendisliğinin bir bölümü olarak tanımlanabilecek sistem analizi (hesabı) kısmına yansımıştır. Mühendislik biliminde bilindiği
Doç. Dr. Bilge DORAN Bilgisayar teknolojisinin ilerlemesi doğal olarak Yapı Mühendisliğinin bir bölümü olarak tanımlanabilecek sistem analizi (hesabı) kısmına yansımıştır. Mühendislik biliminde bilindiği
DENKLEM DÜZENEKLERI 1
 DENKLEM DÜZENEKLERI 1 Dizey kuramının önemli bir kullanım alanı doğrusal denklem düzeneklerinin çözümüdür. 2.1. Doğrusal düzenekler Doğrusal denklem düzeneği (n denklem n bilinmeyen) a 11 x 1 + a 12 x
DENKLEM DÜZENEKLERI 1 Dizey kuramının önemli bir kullanım alanı doğrusal denklem düzeneklerinin çözümüdür. 2.1. Doğrusal düzenekler Doğrusal denklem düzeneği (n denklem n bilinmeyen) a 11 x 1 + a 12 x
Doç. Dr. Muhammet Cerit Öğretim Üyesi Makine Mühendisliği Bölümü (Mekanik Ana Bilim Dalı) Elektronik posta ( ):
 Tanışma ve İletişim... Doç. Dr. Muhammet Cerit Öğretim Üyesi Makine Mühendisliği Bölümü (Mekanik Ana Bilim Dalı) Elektronik posta (e-mail): mcerit@sakarya.edu.tr Öğrenci Başarısı Değerlendirme... Öğrencinin
Tanışma ve İletişim... Doç. Dr. Muhammet Cerit Öğretim Üyesi Makine Mühendisliği Bölümü (Mekanik Ana Bilim Dalı) Elektronik posta (e-mail): mcerit@sakarya.edu.tr Öğrenci Başarısı Değerlendirme... Öğrencinin
25. SEM2015 programı ve kullanımı
 25. SEM2015 programı ve kullanımı Kuvvet metodu kullanılarak yazılmış, öğretim amaçlı, basit bir sonlu elemanlar statik analiz programdır. Program kısaca tanıtılacak, sonraki bölümlerde bu program ile
25. SEM2015 programı ve kullanımı Kuvvet metodu kullanılarak yazılmış, öğretim amaçlı, basit bir sonlu elemanlar statik analiz programdır. Program kısaca tanıtılacak, sonraki bölümlerde bu program ile
Açı Yöntemi. 1 ql 8. Açı yöntemi olarak adlandırılan denklemlerin oluşturulmasında aşağıda gösterilen işaret kabulü yapılmaktadır.
 çı Yöntemi Kuvvet ve -oment yöntemlerinde, ilave denklemleri zorlamaların sistem üzerinde oluşturduğu deformasyonların sistemde oluşturulan suni serbestliklerden dolayı oluşan deformasyonlardan ne kadar
çı Yöntemi Kuvvet ve -oment yöntemlerinde, ilave denklemleri zorlamaların sistem üzerinde oluşturduğu deformasyonların sistemde oluşturulan suni serbestliklerden dolayı oluşan deformasyonlardan ne kadar
SONLU FARKLAR GENEL DENKLEMLER
 SONLU FARKLAR GENEL DENKLEMLER Bir elastik ortamın gerilme probleminin Airy gerilme fonksiyonu ile formüle edilebilen halini göz önüne alalım. Problem matematiksel olarak bölgede biharmonik denklemi sağlayan
SONLU FARKLAR GENEL DENKLEMLER Bir elastik ortamın gerilme probleminin Airy gerilme fonksiyonu ile formüle edilebilen halini göz önüne alalım. Problem matematiksel olarak bölgede biharmonik denklemi sağlayan
AÇI YÖNTEMİ Slope-deflection Method
 SAKARYA ÜNİVERSİTESİ İNŞAAT ÜHENDİSLİĞİ BÖLÜÜ Department of Civil Engineering İN 303 YAPI STATIĞI II AÇI YÖNTEİ Slope-deflection ethod Y.DOÇ.DR. USTAA KUTANİS kutanis@sakarya.edu.tr Sakarya Üniversitesi,
SAKARYA ÜNİVERSİTESİ İNŞAAT ÜHENDİSLİĞİ BÖLÜÜ Department of Civil Engineering İN 303 YAPI STATIĞI II AÇI YÖNTEİ Slope-deflection ethod Y.DOÇ.DR. USTAA KUTANİS kutanis@sakarya.edu.tr Sakarya Üniversitesi,
GEO182 Lineer Cebir. Matrisler. Matrisler. Dersi Veren: Dr. İlke Deniz Derse Devam: %70. Vize Sayısı: 1
 GEO182 Lineer Cebir Dersi Veren: Dr. İlke Deniz 2018 GEO182 Lineer Cebir Derse Devam: %70 Vize Sayısı: 1 Başarı Notu: Yıl içi Başarı Notu %40 + Final Sınavı Notu %60 GEO182 Lineer Cebir GEO182 Lineer Cebir
GEO182 Lineer Cebir Dersi Veren: Dr. İlke Deniz 2018 GEO182 Lineer Cebir Derse Devam: %70 Vize Sayısı: 1 Başarı Notu: Yıl içi Başarı Notu %40 + Final Sınavı Notu %60 GEO182 Lineer Cebir GEO182 Lineer Cebir
Yapı Sistemlerinde Elverişsiz Yüklemeler:
 Yapı Sistemlerinde Elverişsiz Yüklemeler: Yapılara etkiyen yükler ile ilgili çeşitli sınıflama tipleri vardır. Bu sınıflamalarda biri de yapı yükleri ve ilave yükler olarak yapılan sınıflamadır. Bu sınıflama;
Yapı Sistemlerinde Elverişsiz Yüklemeler: Yapılara etkiyen yükler ile ilgili çeşitli sınıflama tipleri vardır. Bu sınıflamalarda biri de yapı yükleri ve ilave yükler olarak yapılan sınıflamadır. Bu sınıflama;
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
30. Uzay çerçeve örnek çözümleri
 . Ua çerçeve örnek çöümleri. Ua çerçeve örnek çöümleri Ua çerçeve eleman sonlu elemanlar metodunun en karmaşık elemanıdır. Bunun nedenleri: ) Her eleman için erel eksen takımı seçilmesi gerekir. Elemanın
. Ua çerçeve örnek çöümleri. Ua çerçeve örnek çöümleri Ua çerçeve eleman sonlu elemanlar metodunun en karmaşık elemanıdır. Bunun nedenleri: ) Her eleman için erel eksen takımı seçilmesi gerekir. Elemanın
Rijit cisim mekaniği, diyagramdan da görüldüğü üzere statik ve dinamik olarak ikiye ayrılır. Statik dengede bulunan cisimlerle, dinamik hareketteki
 Rijit cisim mekaniği, diyagramdan da görüldüğü üzere statik ve dinamik olarak ikiye ayrılır. Statik dengede bulunan cisimlerle, dinamik hareketteki cisimlerle uğraşır. Statik, kuvvet etkisi altında cisimlerin
Rijit cisim mekaniği, diyagramdan da görüldüğü üzere statik ve dinamik olarak ikiye ayrılır. Statik dengede bulunan cisimlerle, dinamik hareketteki cisimlerle uğraşır. Statik, kuvvet etkisi altında cisimlerin
35. Karma sistem örnek çözümleri
 35. Karma sistem örnek çözümleri SEM2025 de düzlem kafes ve düzlem çerçeve karma sistem çözülebilir. Bunun dışında, örneğin, aynı sistemde plak, levha veya çerçeve eleman içeren karma sistem çözümü programda
35. Karma sistem örnek çözümleri SEM2025 de düzlem kafes ve düzlem çerçeve karma sistem çözülebilir. Bunun dışında, örneğin, aynı sistemde plak, levha veya çerçeve eleman içeren karma sistem çözümü programda
Özdeğer ve Özvektörler
 Özdeğer ve Özvektörler Yazar Öğr.Grv.Dr.Nevin ORHUN ÜNİTE 9 Amaçlar Bu üniteyi çalıştıktan sonra; bir lineer dönüşümün ve bir matrisin özdeğer ve özvektör kavramlarını anlayacak, bir dönüşüm matrisinin
Özdeğer ve Özvektörler Yazar Öğr.Grv.Dr.Nevin ORHUN ÜNİTE 9 Amaçlar Bu üniteyi çalıştıktan sonra; bir lineer dönüşümün ve bir matrisin özdeğer ve özvektör kavramlarını anlayacak, bir dönüşüm matrisinin
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 3- LİNEER DENKLEM SİSTEMLERİNİN ÇÖZÜMÜ Doç. Dr. Ali Rıza YILDIZ 1 LİNEER DENKLEM SİSTEMLERİ Bilimsel ve teknolojik çalışmalarda karşılaşılan matematikle ilgili belli başlı
MAK 210 SAYISAL ANALİZ BÖLÜM 3- LİNEER DENKLEM SİSTEMLERİNİN ÇÖZÜMÜ Doç. Dr. Ali Rıza YILDIZ 1 LİNEER DENKLEM SİSTEMLERİ Bilimsel ve teknolojik çalışmalarda karşılaşılan matematikle ilgili belli başlı
Kafes Sistemler. Doğru eksenli çubukların birbirlerine mafsallı olarak birleşmesinden meydana gelen taşıyıcı sistemlere Kafes Sistemler denir.
 KAFES SİSTEMLER Doğru eksenli çubukların birbirlerine mafsallı olarak birleşmesinden meydana gelen taşıyıcı sistemlere Kafes Sistemler denir. Özellikle büyük açıklıklı dolu gövdeli sistemler öz ağırlıklarının
KAFES SİSTEMLER Doğru eksenli çubukların birbirlerine mafsallı olarak birleşmesinden meydana gelen taşıyıcı sistemlere Kafes Sistemler denir. Özellikle büyük açıklıklı dolu gövdeli sistemler öz ağırlıklarının
Kafes Sistemler. Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir.
 Kafes Sistemler Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir. Kafes Sistemler Birçok uygulama alanları vardır. Çatı sistemlerinde, Köprülerde, Kulelerde, Ve benzeri
Kafes Sistemler Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir. Kafes Sistemler Birçok uygulama alanları vardır. Çatı sistemlerinde, Köprülerde, Kulelerde, Ve benzeri
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
6.12 Örnekler PROBLEMLER
 6.1 6. 6.3 6.4 6.5 6.6 6.7 Çok Parçalı Taşıyıcı Sistemler Kafes Sistemler Kafes Köprüler Kafes Çatılar Tam, Eksik ve Fazla Bağlı Kafes Sistemler Kafes Sistemler İçin Çözüm Yöntemleri Kafes Sistemlerde
6.1 6. 6.3 6.4 6.5 6.6 6.7 Çok Parçalı Taşıyıcı Sistemler Kafes Sistemler Kafes Köprüler Kafes Çatılar Tam, Eksik ve Fazla Bağlı Kafes Sistemler Kafes Sistemler İçin Çözüm Yöntemleri Kafes Sistemlerde
TUNCELİ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ LİNEER CEBİR DERSİ 2012 GÜZ DÖNEMİ ÇIKMIŞ VİZE,FİNAL VE BÜTÜNLEME SORULARI ÖĞR.GÖR.
 UNCELİ ÜNİVERSİESİ MÜHENDİSLİK FAKÜLESİ LİNEER CEBİR DERSİ 0 GÜZ DÖNEMİ ÇIKMIŞ VİZE,FİNAL VE BÜÜNLEME SORULARI ÖĞR.GÖR.İNAN ÜNAL www.inanunal.com UNCELİ ÜNİVERSİESİ MÜHENDİSLİK FAKÜLESİ MAKİNE MÜHENDİSLİĞİ
UNCELİ ÜNİVERSİESİ MÜHENDİSLİK FAKÜLESİ LİNEER CEBİR DERSİ 0 GÜZ DÖNEMİ ÇIKMIŞ VİZE,FİNAL VE BÜÜNLEME SORULARI ÖĞR.GÖR.İNAN ÜNAL www.inanunal.com UNCELİ ÜNİVERSİESİ MÜHENDİSLİK FAKÜLESİ MAKİNE MÜHENDİSLİĞİ
ii) S 2LW 2WH 2LW 2WH S 2WH 2LW S 3( x 1) 5( x 2) 5 3x 3 5x x Maliye Bölümü EKON 103 Matematik I / Mart 2018 Proje 2 CEVAPLAR C.1) C.
 C.1) x1 x 1 4 4( x1) x 6 4x 4 x 6 x 46 x Maliye Bölümü EKON 10 Matematik I / Mart 018 Proje CEVAPLAR C.) i) S LW WH LW WH S LW WH S W W W S L H W ii) S LW WH WH LW S WH LW S W W W S H L W C.) ( x1) 5(
C.1) x1 x 1 4 4( x1) x 6 4x 4 x 6 x 46 x Maliye Bölümü EKON 10 Matematik I / Mart 018 Proje CEVAPLAR C.) i) S LW WH LW WH S LW WH S W W W S L H W ii) S LW WH WH LW S WH LW S W W W S H L W C.) ( x1) 5(
SONLU ELEMANLAR YÖNTEMİ
 SONLU ELEMANLAR YÖNTEMİ Kurs Kapsamı SONLU ELEMANLAR KAVRAMI SONLU ELEMANLAR FORMULASYONU UYGULAMALARI Sonlu Elemanlar Çözümleri Rijitlik Metodu Esneklik Metodu Karışık Kullanımlar Rijitlik Metodu Kullanılarak
SONLU ELEMANLAR YÖNTEMİ Kurs Kapsamı SONLU ELEMANLAR KAVRAMI SONLU ELEMANLAR FORMULASYONU UYGULAMALARI Sonlu Elemanlar Çözümleri Rijitlik Metodu Esneklik Metodu Karışık Kullanımlar Rijitlik Metodu Kullanılarak
BİL 810 İnşaat Mühendisliğinde Bilgisayar Uygulamaları
 BİL 810 İnşaat Mühendisliğinde Bilgisayar Uygulamaları Excel ile grafik kullanımı (Yüzey Grafiği) Siyah-Beyaz çıktı için işaretleyici şeklinin değiştirilmesi Excel ile Çizilmiş Grafiğin Word e ile kullanılması
BİL 810 İnşaat Mühendisliğinde Bilgisayar Uygulamaları Excel ile grafik kullanımı (Yüzey Grafiği) Siyah-Beyaz çıktı için işaretleyici şeklinin değiştirilmesi Excel ile Çizilmiş Grafiğin Word e ile kullanılması
Tablo 1 Deney esnasında kullanacağımız numunelere ait elastisite modülleri tablosu
 BASİT MESNETLİ KİRİŞTE SEHİM DENEYİ Deneyin Amacı Farklı malzeme ve kalınlığa sahip kirişlerin uygulanan yükün kirişin eğilme miktarına oranı olan rijitlik değerin değişik olduğunun gösterilmesi. Kiriş
BASİT MESNETLİ KİRİŞTE SEHİM DENEYİ Deneyin Amacı Farklı malzeme ve kalınlığa sahip kirişlerin uygulanan yükün kirişin eğilme miktarına oranı olan rijitlik değerin değişik olduğunun gösterilmesi. Kiriş
SAP 2000 İLE BETONARME HESAPLAMA. Hazırlayan: Dr. Onur TUNABOYU Eskişehir Teknik Üniversitesi Müh. Fak. İnşaat Müh. Bölümü
 SAP 2000 İLE BETONARME HESAPLAMA Hazırlayan: Dr. Onur TUNABOYU Eskişehir Teknik Üniversitesi Müh. Fak. İnşaat Müh. Bölümü SİSTEMİN MODELLENMESİ 1- Birim seçilir. 2- File New Model Grid Only IZGARA (GRID)
SAP 2000 İLE BETONARME HESAPLAMA Hazırlayan: Dr. Onur TUNABOYU Eskişehir Teknik Üniversitesi Müh. Fak. İnşaat Müh. Bölümü SİSTEMİN MODELLENMESİ 1- Birim seçilir. 2- File New Model Grid Only IZGARA (GRID)
Şayet bir lineer sistemin en az bir çözümü varsa tutarlı denir.
 GAZI UNIVERSITY ENGINEERING FACULTY INDUSTRIAL ENGINEERING DEPARTMENT ENM 205 LINEAR ALGEBRA COURSE ENGLISH-TURKISH GLOSSARY Linear equation: a 1, a 2, a 3,.,a n ; b sabitler ve x 1, x 2,...x n ler değişkenler
GAZI UNIVERSITY ENGINEERING FACULTY INDUSTRIAL ENGINEERING DEPARTMENT ENM 205 LINEAR ALGEBRA COURSE ENGLISH-TURKISH GLOSSARY Linear equation: a 1, a 2, a 3,.,a n ; b sabitler ve x 1, x 2,...x n ler değişkenler
Rijit Cisimlerin Dengesi
 Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ
 4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ Doğrusal Denklem Sistemi x 1,x 2,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu; a x a x a x b 11 1 12 2 1n n 1 a x a x a x b 21 1 22 2 2n n
4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ Doğrusal Denklem Sistemi x 1,x 2,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu; a x a x a x b 11 1 12 2 1n n 1 a x a x a x b 21 1 22 2 2n n
Yapısal Analiz Programı SAP2000 Bilgi Aktarımı ve Kullanımı. Doç.Dr. Bilge Doran
 Yapısal Analiz Programı SAP2000 Bilgi Aktarımı ve Kullanımı Dersin Adı : Yapı Mühendisliğinde Bilgisayar Uygulamaları Koordinatörü : Doç.Dr.Bilge DORAN Öğretim Üyeleri/Elemanları: Dr. Sema NOYAN ALACALI,
Yapısal Analiz Programı SAP2000 Bilgi Aktarımı ve Kullanımı Dersin Adı : Yapı Mühendisliğinde Bilgisayar Uygulamaları Koordinatörü : Doç.Dr.Bilge DORAN Öğretim Üyeleri/Elemanları: Dr. Sema NOYAN ALACALI,
STATİK. Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -8-
 1 STATİK Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -8- Giriş 2 Denge denklemlerini, mafsala bağlı elemanlarda oluşan yapıları analiz etmek için kullanacağız. Bu analiz, dengede olan bir yapının
1 STATİK Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -8- Giriş 2 Denge denklemlerini, mafsala bağlı elemanlarda oluşan yapıları analiz etmek için kullanacağız. Bu analiz, dengede olan bir yapının
Matematikte karşılaştığınız güçlükler için endişe etmeyin. Emin olun benim karşılaştıklarım sizinkilerden daha büyüktür.
 - 1 - ÖĞRENME ALANI CEBİR BÖLÜM KARMAŞIK SAYILAR ALT ÖĞRENME ALANLARI 1) Karmaşık Sayılar Karmaşık Sayıların Kutupsal Biçimi KARMAŞIK SAYILAR Kazanım 1 : Gerçek sayılar kümesini genişletme gereğini örneklerle
- 1 - ÖĞRENME ALANI CEBİR BÖLÜM KARMAŞIK SAYILAR ALT ÖĞRENME ALANLARI 1) Karmaşık Sayılar Karmaşık Sayıların Kutupsal Biçimi KARMAŞIK SAYILAR Kazanım 1 : Gerçek sayılar kümesini genişletme gereğini örneklerle
Çerçeve ve Makineler
 Çerçeve ve Makineler Hedefler Mafsal (pim) ile tutturulmuş çerçeve ve makine elemanlarına etki eden kuvvetlerin analizi. Çerçeve ve Makineler Çok kuvvet elemanı içeren mafsal ile tutturulmuş yapılardır.
Çerçeve ve Makineler Hedefler Mafsal (pim) ile tutturulmuş çerçeve ve makine elemanlarına etki eden kuvvetlerin analizi. Çerçeve ve Makineler Çok kuvvet elemanı içeren mafsal ile tutturulmuş yapılardır.
Lineer Denklem Sistemleri Kısa Bilgiler ve Alıştırmalar
 Lineer Denklem Sistemleri Kısa Bilgiler ve Alıştırmalar Bir Matrisin Rankı A m n matrisinin determinantı sıfırdan farklı olan alt kare matrislerinin boyutlarının en büyüğüne A matrisinin rankı denir. rank(a)
Lineer Denklem Sistemleri Kısa Bilgiler ve Alıştırmalar Bir Matrisin Rankı A m n matrisinin determinantı sıfırdan farklı olan alt kare matrislerinin boyutlarının en büyüğüne A matrisinin rankı denir. rank(a)
Rijit Cisimlerin Dengesi
 Rijit Cisimlerin Dengesi 1 Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Rijit Cisimlerin Dengesi 1 Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
DÜZLEMDE GERİLME DÖNÜŞÜMLERİ
 3 DÜZLEMDE GERİLME DÖNÜŞÜMLERİ Gerilme Kavramı Dış kuvvetlerin etkisi altında dengedeki elastik bir cismi matematiksel bir yüzeyle rasgele bir noktadan hayali bir yüzeyle ikiye ayıracak olursak, F 3 F
3 DÜZLEMDE GERİLME DÖNÜŞÜMLERİ Gerilme Kavramı Dış kuvvetlerin etkisi altında dengedeki elastik bir cismi matematiksel bir yüzeyle rasgele bir noktadan hayali bir yüzeyle ikiye ayıracak olursak, F 3 F
STATİK KUVVET ANALİZİ (2.HAFTA)
 STATİK KUVVET ANALİZİ (2.HAFTA) Mekanik sistemler üzerindeki kuvvetler denge halindeyse sistem hareket etmeyecektir. Sistemin denge hali için gerekli kuvvetlerin hesaplanması statik hesaplamalarla yapılır.
STATİK KUVVET ANALİZİ (2.HAFTA) Mekanik sistemler üzerindeki kuvvetler denge halindeyse sistem hareket etmeyecektir. Sistemin denge hali için gerekli kuvvetlerin hesaplanması statik hesaplamalarla yapılır.
δ / = P L A E = [+35 kn](0.75 m)(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir.
(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir. δ / = P L A E = [+35 kn](0.75 m)(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir.](/thumbs/68/59308868.jpg) A-36 malzemeden çelik çubuk, şekil a gösterildiği iki kademeli olarak üretilmiştir. AB ve BC kesitleri sırasıyla A = 600 mm ve A = 1200 mm dir. A serbest ucunun ve B nin C ye göre yer değiştirmesini belirleyiniz.
A-36 malzemeden çelik çubuk, şekil a gösterildiği iki kademeli olarak üretilmiştir. AB ve BC kesitleri sırasıyla A = 600 mm ve A = 1200 mm dir. A serbest ucunun ve B nin C ye göre yer değiştirmesini belirleyiniz.
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 5 Rijit Cisim Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 5. Rijit Cisim Dengesi Denge,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 5 Rijit Cisim Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 5. Rijit Cisim Dengesi Denge,
.:: BÖLÜM I ::. MATRİS ve DETERMİNANT
 SAKARYA ÜNİVERSİTESİ İŞLETME FAKÜLTESİ İŞLETME BÖLÜMÜ.:: BÖLÜM I ::. MATRİS ve DETERMİNANT Halil İbrahim CEBECİ BÖLÜM I 1. Matris Cebirine Giriş MATRİS VE DETERMİNANT Sayıların, değişkenlerin veya parametrelerin
SAKARYA ÜNİVERSİTESİ İŞLETME FAKÜLTESİ İŞLETME BÖLÜMÜ.:: BÖLÜM I ::. MATRİS ve DETERMİNANT Halil İbrahim CEBECİ BÖLÜM I 1. Matris Cebirine Giriş MATRİS VE DETERMİNANT Sayıların, değişkenlerin veya parametrelerin
Elemanlardaki İç Kuvvetler
 Elemanlardaki İç Kuvvetler Bölüm Öğrenme Çıktıları Yapı elemanlarında oluşan iç kuvvetler. Eksenel kuvvet, Kesme kuvvet ve Eğilme Momenti Denklemleri ve Diyagramları. Bölüm Öğrenme Çıktıları Elemanlarda
Elemanlardaki İç Kuvvetler Bölüm Öğrenme Çıktıları Yapı elemanlarında oluşan iç kuvvetler. Eksenel kuvvet, Kesme kuvvet ve Eğilme Momenti Denklemleri ve Diyagramları. Bölüm Öğrenme Çıktıları Elemanlarda
Matris Cebiriyle Çoklu Regresyon Modeli
 Matris Cebiriyle Çoklu Regresyon Modeli Hüseyin Taştan Mart 00 Klasik Regresyon Modeli k açıklayıcı değişkenden oluşan regresyon modelini her gözlem i için aşağıdaki gibi yazabiliriz: y i β + β x i + β
Matris Cebiriyle Çoklu Regresyon Modeli Hüseyin Taştan Mart 00 Klasik Regresyon Modeli k açıklayıcı değişkenden oluşan regresyon modelini her gözlem i için aşağıdaki gibi yazabiliriz: y i β + β x i + β
STATIK VE MUKAVEMET 3. Rijit cisimlerin dengesi, Denge denklemleri, Serbest cisim diyagramı. Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ
 STATIK VE MUKAVEMET 3. Rijit cisimlerin dengesi, Denge denklemleri, Serbest cisim diyagramı Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları
STATIK VE MUKAVEMET 3. Rijit cisimlerin dengesi, Denge denklemleri, Serbest cisim diyagramı Yrd. Doç. Dr. NURHAYAT DEĞİRMENCİ Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları
TEKNOLOJİNİN BİLİMSEL İLKELERİ. Öğr. Gör. Adem ÇALIŞKAN
 TEKNOLOJİNİN BİLİMSEL İLKELERİ 4 Skaler: Fiziki büyüklükler SKALER BÜYÜKLÜK SEMBOLÜ BİRİMİ Kütle m Kilogram Hacim V m 3 Zaman t Saniye Sıcaklık T Kelvin Sadece sayısal değer ve birim verilerek ifade edilen
TEKNOLOJİNİN BİLİMSEL İLKELERİ 4 Skaler: Fiziki büyüklükler SKALER BÜYÜKLÜK SEMBOLÜ BİRİMİ Kütle m Kilogram Hacim V m 3 Zaman t Saniye Sıcaklık T Kelvin Sadece sayısal değer ve birim verilerek ifade edilen
DENEY-4 WHEATSTONE KÖPRÜSÜ VE DÜĞÜM GERİLİMLERİ YÖNTEMİ
 DENEY- WHEATSTONE KÖPÜSÜ VE DÜĞÜM GEİLİMLEİ YÖNTEMİ Deneyin Amacı: Wheatson köprüsünün anlaşılması, düğüm gerilimi ile dal gerilimi arasındaki ilişkinin incelenmesi. Kullanılan Alet-Malzemeler: a) DC güç
DENEY- WHEATSTONE KÖPÜSÜ VE DÜĞÜM GEİLİMLEİ YÖNTEMİ Deneyin Amacı: Wheatson köprüsünün anlaşılması, düğüm gerilimi ile dal gerilimi arasındaki ilişkinin incelenmesi. Kullanılan Alet-Malzemeler: a) DC güç
Rijit Cisimlerin Dengesi
 Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
KONU 3. STATİK DENGE
 KONU 3. STATİK DENGE 3.1 Giriş Bir cisme etki eden dış kuvvet ve momentlerin toplamı 0 ise cisim statik dengededir denir. Kuvvet ve moment toplamlarının 0 olması sırasıyla; ötelenme ve dönme denge şartlarıdır.
KONU 3. STATİK DENGE 3.1 Giriş Bir cisme etki eden dış kuvvet ve momentlerin toplamı 0 ise cisim statik dengededir denir. Kuvvet ve moment toplamlarının 0 olması sırasıyla; ötelenme ve dönme denge şartlarıdır.
V. KAFES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir.
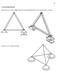 78 V. KES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir. Uzayda ise en az 6 çubuk gereklidir. 79 İhtiyaçlara göre yeni çubukların ilavesiyle
78 V. KES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir. Uzayda ise en az 6 çubuk gereklidir. 79 İhtiyaçlara göre yeni çubukların ilavesiyle
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Mukavemet-II PROF. DR. MURAT DEMİR AYDIN
 Mukavemet-II PROF. DR. MURAT DEMİR AYDIN KAYNAK KİTAPLAR Cisimlerin Mukavemeti F.P. BEER, E.R. JOHNSTON Mukavemet-2 Prof.Dr. Onur SAYMAN, Prof.Dr. Ramazan Karakuzu Mukavemet Mehmet H. OMURTAG 1 SİMETRİK
Mukavemet-II PROF. DR. MURAT DEMİR AYDIN KAYNAK KİTAPLAR Cisimlerin Mukavemeti F.P. BEER, E.R. JOHNSTON Mukavemet-2 Prof.Dr. Onur SAYMAN, Prof.Dr. Ramazan Karakuzu Mukavemet Mehmet H. OMURTAG 1 SİMETRİK
İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz Sıfır-Kuvvet Elemanları Kesme Metodu ile Analiz
 Yapıların Analizi Konu Çıktıları İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz Sıfır-Kuvvet Elemanları Kesme Metodu ile Analiz Kafesleri oluşturan elemenlara etki eden
Yapıların Analizi Konu Çıktıları İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz Sıfır-Kuvvet Elemanları Kesme Metodu ile Analiz Kafesleri oluşturan elemenlara etki eden
Örnek...3 : Aşağıdaki ifadelerden hangileri bir dizinin genel terim i olabilir? Örnek...4 : Genel terimi w n. Örnek...1 : Örnek...5 : Genel terimi r n
 DİZİLER Tanım kümesi pozitif tam sayılar kümesi olan her fonksiyona dizi denir. Örneğin f : Z + R, f (n )=n 2 ifadesi bir dizi belirtir. Diziler değer kümelerine göre adlandırılırlar. Dizinin değer kümesi
DİZİLER Tanım kümesi pozitif tam sayılar kümesi olan her fonksiyona dizi denir. Örneğin f : Z + R, f (n )=n 2 ifadesi bir dizi belirtir. Diziler değer kümelerine göre adlandırılırlar. Dizinin değer kümesi
YAZILI SINAV SORU ÖRNEKLERİ MATEMATİK
 YAZILI SINAV SORU ÖRNEKLERİ MATEMATİK SORU 1: Aşağıdaki grafik, bir okuldaki spor yarışmasına katılan öğrencilerin yaşa göre dağılışını göstermektedir. Öğrenci sayısı 5 3 9 10 1 14 Yaş 1.1: Yukarıdaki
YAZILI SINAV SORU ÖRNEKLERİ MATEMATİK SORU 1: Aşağıdaki grafik, bir okuldaki spor yarışmasına katılan öğrencilerin yaşa göre dağılışını göstermektedir. Öğrenci sayısı 5 3 9 10 1 14 Yaş 1.1: Yukarıdaki
MUTO YÖNTEMİ. Çerçeve Sistemlerin Yatay Yüklere Göre Çözümlenmesi. 2. Katta V 2 = F 2 1. Katta V 1 = F 1 + F 2 1/31
 Çerçeve Sistemlerin Yatay Yüklere Göre Çözümlenmesi MUTO Yöntemi (D katsayıları yöntemi) Hesap adımları: 1) Taşıyıcı sistem her kat kolonlarından kesilerek üste kalan yatay kuvvetlerin toplamlarından her
Çerçeve Sistemlerin Yatay Yüklere Göre Çözümlenmesi MUTO Yöntemi (D katsayıları yöntemi) Hesap adımları: 1) Taşıyıcı sistem her kat kolonlarından kesilerek üste kalan yatay kuvvetlerin toplamlarından her
MKM 308 Makina Dinamiği. Eşdeğer Noktasal Kütleler Teorisi
 MKM 308 Eşdeğer Noktasal Kütleler Teorisi Eşdeğer Noktasal Kütleler Teorisi Maddesel Nokta (Noktasal Kütleler) : Mekanikte her cisim zihnen maddesel noktalara ayrılabilir yani noktasal kütlelerden meydana
MKM 308 Eşdeğer Noktasal Kütleler Teorisi Eşdeğer Noktasal Kütleler Teorisi Maddesel Nokta (Noktasal Kütleler) : Mekanikte her cisim zihnen maddesel noktalara ayrılabilir yani noktasal kütlelerden meydana
8.Konu Vektör uzayları, Alt Uzaylar
 8.Konu Vektör uzayları, Alt Uzaylar 8.1. Düzlemde vektörler Düzlemdeki her noktası ile reel sayılardan oluşan ikilisini eşleştirebiliriz. Buna P noktanın koordinatları denir. y-ekseni P x y O dan P ye
8.Konu Vektör uzayları, Alt Uzaylar 8.1. Düzlemde vektörler Düzlemdeki her noktası ile reel sayılardan oluşan ikilisini eşleştirebiliriz. Buna P noktanın koordinatları denir. y-ekseni P x y O dan P ye
MEKANİZMA TEKNİĞİ (3. HAFTA)
 MEKANİZMA TEKNİĞİ (3. HAFTA) STATİĞİN TEMEL İLKELERİ VE VEKTÖR MATEMATİĞİ Mekanik sistemler üzerindeki kuvvetler denge halindeyse sistem hareket etmeyecektir. Sistemin denge hali için gerekli kuvvetlerin
MEKANİZMA TEKNİĞİ (3. HAFTA) STATİĞİN TEMEL İLKELERİ VE VEKTÖR MATEMATİĞİ Mekanik sistemler üzerindeki kuvvetler denge halindeyse sistem hareket etmeyecektir. Sistemin denge hali için gerekli kuvvetlerin
x 1,x 2,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu;
 4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ Doğrusal Denklem Sistemi x,x,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu; a x + a x + L + a x = b n n a x + a x + L + a x = b n n a x + a
4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ Doğrusal Denklem Sistemi x,x,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu; a x + a x + L + a x = b n n a x + a x + L + a x = b n n a x + a
TEMEL MEKANİK 10. Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü
 TEMEL MEKANİK 10 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
TEMEL MEKANİK 10 Yrd. Doç. Dr. Mehmet Ali Dayıoğlu Ankara Üniversitesi Ziraat Fakültesi Tarım Makinaları ve Teknolojileri Mühendisliği Bölümü Ders Kitapları: Mühendisler İçin Vektör Mekaniği, Statik, Yazarlar:
ÇATI MAKASINA GELEN YÜKLER
 ÇATI MAKASINA GELEN YÜKLER Bir yapıyı dış etkilere karşı koruyan taşıyıcı sisteme çatı denir. Belirli aralıklarla yerleştirilen çatı makaslarının, yatay taşıyıcı eleman olan aşıklarla birleştirilmesi ile
ÇATI MAKASINA GELEN YÜKLER Bir yapıyı dış etkilere karşı koruyan taşıyıcı sisteme çatı denir. Belirli aralıklarla yerleştirilen çatı makaslarının, yatay taşıyıcı eleman olan aşıklarla birleştirilmesi ile
Matrisler ve matris işlemleri
 2.Konu Matrisler ve matris işlemleri Kaynaklar: 1.Uygulamalı lineer cebir. 7.baskıdan çeviri.bernhard Kollman, David R.Hill/çev.Ed. Ömer Akın, Palma Yayıncılık, 2002 2.Lineer Cebir. Feyzi Başar.Surat Universite
2.Konu Matrisler ve matris işlemleri Kaynaklar: 1.Uygulamalı lineer cebir. 7.baskıdan çeviri.bernhard Kollman, David R.Hill/çev.Ed. Ömer Akın, Palma Yayıncılık, 2002 2.Lineer Cebir. Feyzi Başar.Surat Universite
VECTOR MECHANICS FOR ENGINEERS: STATICS
 Seventh E 4 Equilibrium CHAPTER VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. of Rigid Bodies Lecture Notes: J. Walt Oler Texas Tech University Seventh E CHAPTER VECTOR
Seventh E 4 Equilibrium CHAPTER VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. of Rigid Bodies Lecture Notes: J. Walt Oler Texas Tech University Seventh E CHAPTER VECTOR
VEKTÖRLER. 1. Skaler Büyüklükler
 VEKTÖRLER Fizikte bazı büyüklükler sayılarla ifade edilebildiği halde, bazılarının ifade edilebilmesinde sayılar yeterli olmamaktadır. Sayılarla birlikte yönün de belirtilmesi gerekir. Bu nedenle fizikte
VEKTÖRLER Fizikte bazı büyüklükler sayılarla ifade edilebildiği halde, bazılarının ifade edilebilmesinde sayılar yeterli olmamaktadır. Sayılarla birlikte yönün de belirtilmesi gerekir. Bu nedenle fizikte
Yapı Sistemlerinin Hesabı İçin. Matris Metotları. Prof.Dr. Engin ORAKDÖĞEN Doç.Dr. Ercan YÜKSEL Bahar Yarıyılı
 Yapı Sistemlerinin Hesabı İçin Matris Metotları 05-06 Bahar Yarıyılı Prof.Dr. Engin ORAKDÖĞEN Doç.Dr. Ercan YÜKSEL BÖLÜM VIII HAREKET DENKLEMİ ZORLANMIŞ TİTREŞİMLER SERBEST TİTREŞİMLER Bu bölümün hazırlanmasında
Yapı Sistemlerinin Hesabı İçin Matris Metotları 05-06 Bahar Yarıyılı Prof.Dr. Engin ORAKDÖĞEN Doç.Dr. Ercan YÜKSEL BÖLÜM VIII HAREKET DENKLEMİ ZORLANMIŞ TİTREŞİMLER SERBEST TİTREŞİMLER Bu bölümün hazırlanmasında
Örnek...3 : Aşağıdaki ifadelerden hangileri bir dizinin genel terim i olabilir?
 DİZİLER Tanım kümesi pozitif tam sayılar kümesi olan her fonksiyona dizi denir. Örneğin f : Z + R, f (n )=n 2 ifadesi bir dizi belirtir. Diziler, değer kümelerine göre adlandırı - lırlar. Dizinin değer
DİZİLER Tanım kümesi pozitif tam sayılar kümesi olan her fonksiyona dizi denir. Örneğin f : Z + R, f (n )=n 2 ifadesi bir dizi belirtir. Diziler, değer kümelerine göre adlandırı - lırlar. Dizinin değer
Karabük Üniversitesi, Mühendislik Fakültesi...www.IbrahimCayiroglu.com. STATİK (3. Hafta)
 TAŞIYICI SİSTEMLER VE MESNET TEPKİLERİ STATİK (3. Hafta) Taşıyıcı Sistemler Bir yapıya etki eden çeşitli kuvvetleri güvenlik sınırları içinde taşıyan ve bu kuvvetleri zemine aktaran sistemlere taşıyıcı
TAŞIYICI SİSTEMLER VE MESNET TEPKİLERİ STATİK (3. Hafta) Taşıyıcı Sistemler Bir yapıya etki eden çeşitli kuvvetleri güvenlik sınırları içinde taşıyan ve bu kuvvetleri zemine aktaran sistemlere taşıyıcı
KATI CİSİMLERİN BAĞIL İVME ANALİZİ:
 KATI CİSİMLERİN BAĞIL İVME ANALİZİ: Genel düzlemsel hareket yapmakta olan katı cisim üzerinde bulunan iki noktanın ivmeleri aralarındaki ilişki, bağıl hız v A = v B + v B A ifadesinin zamana göre türevi
KATI CİSİMLERİN BAĞIL İVME ANALİZİ: Genel düzlemsel hareket yapmakta olan katı cisim üzerinde bulunan iki noktanın ivmeleri aralarındaki ilişki, bağıl hız v A = v B + v B A ifadesinin zamana göre türevi
3. BÖLÜM MATRİSLER 1
 3. BÖLÜM MATRİSLER 1 2 11 21 1 m1 a a a v 12 22 2 m2 a a a v 1 2 n n n mn a a a v gibi n tane vektörün oluşturduğu, şeklindeki sıralanışına matris denir. 1 2 n A v v v Matris A a a a a a a a a a 11 12
3. BÖLÜM MATRİSLER 1 2 11 21 1 m1 a a a v 12 22 2 m2 a a a v 1 2 n n n mn a a a v gibi n tane vektörün oluşturduğu, şeklindeki sıralanışına matris denir. 1 2 n A v v v Matris A a a a a a a a a a 11 12
KOÜ. Mühendislik Fakültesi Makine Mühendisliği Bölümü (1. ve 2.Öğretim / B Şubesi) MMK208 Mukavemet II Dersi - 1. Çalışma Soruları 23 Şubat 2019
 SORU-1) Aynı anda hem basit eğilme hem de burulma etkisi altında bulunan yarıçapı R veya çapı D = 2R olan dairesel kesitli millerde, oluşan (meydana gelen) en büyük normal gerilmenin ( ), eğilme momenti
SORU-1) Aynı anda hem basit eğilme hem de burulma etkisi altında bulunan yarıçapı R veya çapı D = 2R olan dairesel kesitli millerde, oluşan (meydana gelen) en büyük normal gerilmenin ( ), eğilme momenti
