4UZAYDA SÜSLEMELER, DÖNME
|
|
|
- Melek Elmas
- 8 yıl önce
- İzleme sayısı:
Transkript
1 4UZYD SÜSLEMELER, DÖNME VE PERSPEKTİF ÇİZİMLER Safa No 1. KTI CİSİMLERLE, TEK VE ÇOK YÜZEYLİLERLE YPILR OLUŞTURM ÇOK YÜZLÜLERLE OLUŞTURULMUŞ UZYSL KPLMLR ÇOK YÜZLÜLERİN YÜZEYLERİNİ SÜSLEME VERİLEN YPILR DÖNME HREKETİ UYGULM VERİLEN YPILRIN BİR VE İKİ NOKT PERSPEKTİF ÇİZİMLERİ
2 KVRMSL DIM ETK NL K KTI CİSİMLERLE, TEK VE ÇOK YÜZEYLİLERLE YPILR OLUŞTURM şağıdaki tasarımlar çoküelilerle oluşturulmuştur. Bu apıların hangi çok üelilerle oluşturulduğunu inceleini. ÇOK YÜZLÜLERLE OLUŞTURULMUŞ UZYSL KPLMLR Ua küplerle kaplanmıştır. Ua dügün altıgen primalarla kaplanmıştır. Dügün sekiülünün köşelerinden piramitler kesilerek çokülü oluşturulmuştur. Bu çokülünün karesel bölge üeleri birleştirilerek ua kaplanmıştır. Küp, köşelerinden dügün sekiülünün boutlarında kesilerek kesik küp oluşturulur. Kesik küp ile dügün sekiülünün üçgensel bölge üleri birleştirilerek ve kalan boşluklara dügün sekiülü erleştirilerek ua kaplanmıştır. 201
3 KVRMSL DIM HTIRLTMLR Örüntü a da moaik döşeme Herhangi bir üei hiçbir boşluk bırakmadan a da üst üste gelmeden kaplaan bir vea daha fala şeklin bir araa gelerek oluşturduğu birleşime örüntü denir. Bu kareler örüntü olufltururlar. Birçok örüntü türü olmasına karşın dügün çokgenlerle oluşturulan sadece iki tür örüntü bulunmaktadır. Dügün örüntü ve arı dügün örüntü. Dügün örüntü Bu çemberler örüntü oluflturmalar. Tek çeşit dügün çokgenden oluşan örüntüe dügün örüntü denir. SİMETRİ Tam olarak iki eş parçaa arılabilen vea çeşitli şekillerde döndürüldüğünde orijinal halini alan bir şeklin simetrisi vardır. Bir dülem vea katı cisim simetrik değilse asimetrik olarak adlandırılır. İki tür simetri vardır: Yansıma ve dönme. Eşkenar üçgen, kare ve dügün altıgen, dügün örüntü oluşturan üç farklı dügün çokgendir. Yarı dügün örüntü Birden fala çeşit dügün çokgen tarafından oluşturulan örüntüe arı dügün örüntü denir. Çokgenlerin bulunduğu tüm köşe noktalardaki şablon anıdır. Yansıma simetrisi a da doğru simetrisi Bir şekil, bir doğru vea dülemle bölündüğünde oluşan parçaların birbirinin ana görüntüsü olduğu simetrie ansıma simetrisi denir. Seki tane arı dügün örüntü vardır. Bu örüntüler eşkenar üçgenlerin, karelerin, altıgenlerin, sekigenlerin ve onikigenlerin birleşmesile oluşurlar. Her iki arım diğerinin ana görüntüsü olduğu için bu kelebek ansıma simetrisine sahiptir. Her iki arım diğerinin ana görüntüsü olduğu için bu tabak ansıma simetrisine sahiptir. 202
4 KVRMSL DIM Simetri doğrusu a da ana doğrusu Bir dülemi, birbirinin ana görüntüsü olacak şekilde bölen doğrua simetri doğrusu denir. Bir dülemin birden fala simetri doğrusu olabilir. fiekildeki ok, bir tane simetri do rusuna sahiptir. Simetri dülemi fiekildeki ld, dört tane simetri do rusuna sahiptir. Bir katı cismi birbirinin ana görüntüsü olacak şekilde bölen düleme simetri dülemi denir. Bir katı cismin birden fala simetri dülemi olabilir. Dönme simetrisi katı Bir şekil bir tam devir (360 ) aparken şeklin orijinal halini aldığı durum saısına dönme simetrisi katı denir. Bu dört köfleli ld n dört tane dönme simetrisi kat vard r. fiekil bir tam devir aparken dört defa orijinal hali gibi göükmüfltür. Dönme simetrisi merkei Bir dülemin, etrafında döndüğünde kendi orijinal şeklini aldığı noktaa dönme simetresi merkei denir. Bu dikdörtgenler primas n n üç tane simetri dülemi vard r. fiekildeki nokta, seki köfleli ld n dönme simetrisi merkeidir. Dönme simetrisi Bir şeklin sabit bir nokta * vea çigi üerinde döndürüldüğünde orijinal şeklini almasına dönme simetresi denir. Dönme simetri ekseni Bir katı cismin, etrafında döndüğünde kendi orijinal şeklini aldığı doğrua dönme simetrisi ekseni denir. Bu dikdörtgen dönme simetrisine sahiptir. Dönme simetrisi ekseni fiekildeki dikdörtgenler primas, bu eksene göre dört katl dönme simetrisine sahiptir. 203
5 KVRMSL DIM TŞIM Geometride, bir doğrunun, dülemin vea katı cismin eri, boutu vea şekli taşıma işlemile değişebilir. Taşıma işlemi apılan doğru, dülem vea katı cisme nesne, sonuca ise görüntü denir. Taşıma işleminin gerçekleştirilmesi, nesnenin kendi görüntüsüne gönderimi olarak adlandırılır. Gönderilen görüntüler; üerindeki işaretile tanımlanır. Örneğin B doğrusu B olarak gönderilir. Öteleme Bir nesnenin döndürülmeden vea ansıtılmadan eni bir ere taşınmasına öteleme denir. Ötelenmiş görüntü, nesne ile anı boutlara ve şekle sahiptir. Verilen bir noktadan belirlenen bir önde apılan konum değişimine er değiştirme denir. Öteleme sırasında, her nokta eşit miktarda er değiştirir ve bu değişim vektör olarak tanımlanabilir: Yansıma ekseni B Görüntü C 1 B Nesne C ekseni 3 1 vektörü bu üçgenin eni erine götürülürken gerçekleflen er de ifltirmesini tanımlar. Her nokta 3 birim sa a ve 1 birim ukarı hareket etmifltir. Her bir noktanın simetri doğrusuna eşit uaklıkta er alan ve doğrula aralarında dik açı (90 ) bulunan başka bir noktaa gönderilerek taşınmasına ansıma denir. Eğer ansıtılacak nesne dülemse simetri doğrusu bir doğrudur. Eğer nesne bir katı cisimse simetri doğrusu bir dülemdir. Yansıan görüntünün bout ve açıları orijinal nesneninki ile anıdır, ancak algılanışı farklıdır. Yani, görüntünün önü arkasına gelmiştir. Dönme Bir nesnenin üerindeki bütün noktaların (nesnenin katı cisim vea dülem olmasına bağlı olarak), sabit bir noktaa (dönme merkei) vea doğrua (dönme ekseni) olan uaklığı anı kalcak şekilde çevrilerek taşınmasına dönme denir. Oluşan görüntünün açı ve boutları nesneninki ile anıdır ancak görüntünün kendisi farklı bir açıda ve erdedir. Nesne Dönme ekseni Görüntü Bu apı taflı, dönme ekseni üerinde döndürülerek eni konumunu almıfltır. Dönme merkei nesnenin içinde, kenarında vea dışında olabilir. Dönme merkeini bulmak için nesnenin üerindeki herhangi iki nokta görüntü üerindeki eş noktalarıla birleştirilir ve her doğrunun dik açıortaı çiilir. Dik açıortaların kesişim noktası dönme merkeini verir. Nesne B C P Bir nesnenin döndürüldüğü açıa dönme açısı denir. Eğer dönme açısı saat önünün tersine doğrusa açıa poitif denir. Eğer saat önündese negatif denir. C Görüntü B P noktası, dik açıortaların kesiflim eri ve dönme merkeidir. Nesne C Görüntü C Saat önünün tersinde vea poitif dönme Saat önünde vea negatif dönme Yansıan görüntü nesne ile anı flekle ve bouta sahiptir ama nesnenin tam tersidir., ve uaklıkları ana do rusunun her iki tarafında da anıdır. B Ötelemeli ansıma Bir nesnenin öteleme aptıktan sonra ötelemee paralel bir ana ( simetri ) doğrusu üerinde ansıma apması olula taşınmasına ötelemeli ansıma denir. Görüntünün boutları ve açıları nesneninkilerle anıdır ancak görüntü ters dönmüş ve er değiştirmiştir. 204
6 KVRMSL DIM Görüntü 3. Çokülülerin Yüelerini Süsleme Çok ülülerin üeleri kaplanırken; çok ülülerin açınımlarına dülemsel kaplama teknikleri ugulanır. çınımlar kapatıldığında apılan desenlerin üst üste gelmemesi ve üede boşluk kalmaması görekir. Süslemeler, boşluk kalmaacak ve motifler çakışmaacak biçimde üelerin örtülmesile oluşturalan kaplamaları ve üelerde apılan desen, motif vb. çalışmaları da içerecek biçimde ek alınır. ETK NL K Yanda dügün sekiülünün açınımı verilmiştir. Her bir üdeki eşkenar üçgensel bölgede dülemsel kaplama tekniklerile motif oluşturunu. Bu motifle dügün sekiülünün üei süslenmiş olacaktır. Periodik Kaplama Nesne Bu model, ötelemeli ansımaa u ramıfltır. Yüelerin güel görünmeleri için geometrik şekillerle süslenmesi a da karolarla kaplanması, günümüde ve geçmişte oldukça sık tercih edilen bir öntemdir. Her gün üerinde ürüdüğümü parke taşlarıla döşenmiş ol ve kaldırımlar, geometrik şekillere sahip karolarla süslemee en güel örneklerdir. Sadece çokgensel bölgelerden (paralelkenarsal, dikdörtgensel, eşkenar dörtgensel, karesel ve dügün altıgensel bölgelerden) birbirile alnı öteleme dönüşümü kullanılarak dülemde boşluk kalmaacak ve çakışmaacak biçimde dülemin örtülmesine periodik kaplama denir. Öteleme dönüşümü kullanılmadan dülemde boşluk kalmaacak ve çakışmaacak biçimde çokgensel bölgele örtülmesine periodik olmaan kaplama denir. Periodik kaplamada iki önde kendini tekrar eden kısımlar, içlerindeki küçük kaplamalar anı olan paralel kenarlarla gösterilebilir. Pentapleks Kaplamalar Roger Penrose, genel görelilik teorisi üerine aptığı çalışmalarıla bilinen ünlü bir fiikçidir. Penrose periodik olmadan dülemi kaplaabilen karo kümeleri üerine 1973 ılında çalışmaa başlaıp biri altılı, diğer ikisi ikili olmak üere toplam üç farklı pentapleks karo kümesi oluşturmuştur. Penrose den önce dülemi periodik olarak kaplamaan karo kümeleri üerinde çalışan Wang, Berger ve Robinson kare karolar kullanılmıştır. Penrose bu konuda herhangi bir şekle sahip çokgenler kullanabilir. dior. Zaten karolarla beşli dönel simetrie sahip kaplama apılması da mümkün değildir. Periodik kaplaması mümkün olmaıp beşli dönel simetrie sahip kaplama apılabilen karo kümeleri pentapleks karo kümeleri olarak, pentapleks karo kümelerinden apılan kaplamalara da petapleks kaplamalar denir. Penrose un ilk keşfettiği pentapleks karo kümesi altı karodan oluşur ve P1 olarak tanımlanmıştır. P1 karo kümesi dülemi, dügün beşgenler ve en a saıda ilave geometrik şekil kullanarak periodik olmadan kaplamaa çalışmaktan çıkarılmış bir sonuçtur. Yol ve kaldırım kaplamasında kullanılan parke tafllarına örnekler. 205
7 KVRMSL DIM Bir dügün beşgenin etrafına, kenarları tam olarak birbirine apışacak şekilde beş dügün beşgen koarak işe başlaıp, kaplama beşli dönel simetrie sahip olacak şekilde ilerletilmiştir. İlk pentapleks karo kümesi olan Penrose nun altılı karo kümesi (P1) bir dügün beşgen etrafına erleştirilen beşgen ve üç farklı karodan apılmış beşli dönel simetrie sahip kaplamadan çıkarılmış sonuçtur. Osmanlı kapılarındaki karolardan oluşturulan pentapleks karo kümeleri Osmanlı imparatorluğu döneminde kapılarda kullanılan süsleme tekniğindeki kaplamaların içinde kısa bir süre ilerleen, merkeinde bir dügün beşgenin olduğu ve beşli dönme simetrisine sahip üç adet sonlu kaplamanın olması ilginçtir. Platon un şekilleri (Platonik Cisimler) rşimet in şekilleri Osmanlı kapılarının içinde rastladığımı, merkeinde dügün beşgenlerin olduğu beşli dönel simetrie sahip üç nokta sonlu kaplama. Sadece Osmanlı kapılarında kullanılan karolardan eni pentapleks karo kümelerinin oluşturulması için tanımlanan pentapleks harita karolarının kenarları. Platon un şekilleri olarak bilinen beş adet üç boutlu dügün geometrik şekilden ve rşimet in şekilleri olarak bilinen on üç adet arı dügün geometrik şekilden sadece Platon un şekillerinden (dügün beşgenlerden oluşan) on ikiülü köşelerindeki standart şekil boulmadan kaplanabilir. Tüm üleri Osmanlı kapılarındaki karolarla kaplanmış on iki ülü, dügün beşgen prima ve dügün ongen prima. Şekillerin her üünün kaplaması anı kaplama olmakla birlikte, tüm kenarlar kaplamaı bomadan birleşmektedir. 206
8 KVRMSL DIM 4. Verilen Yapılara Dönme Hareketi Ugulama X, Y, Z eksenleri etrafında 90, 180 ve 270 lik dönme hareketlerini inceleelim. Önce bir küpün her üüne dönme hareketi ugulandığında hareketin rahatlıkla anlaşılabileceği farklı şekil, harf vb. semboller aılır. Örnek: Kalp sembolünün bulunduğu ü ukarı gelecek şekilde bir küp andaki gibi sabitlensin. Eksenlere göre 90, 180 ve 270 lik dönme hareketinin görüntülerini çielim. Z ekseni etrafında 90 lik dönme hareketi ekseni etrafında 180 lik dönme hareketi Z ekseni etrafında 180 lik bir dönme hareketi ekseni etrafında 90 lik dönme hareketi Z ekseni etrafında 270 lik dönme hareketi ekseni etrafında 270 lik dönme hareketi 207
9 KVRMSL DIM Örnek: Kalp sembolünün bulunduğu ü ukarı gelecek şekilde bir küp andaki gibi sabitlenior. eksenine göre saat önünün tersine 90, 180 ve 270 derecelik dönme hareketinin görüntülerini çielim. eksenine göre saat önünün tersine 90 lik dönme hareketi Perspektif Çeşitleri KSONOMETR K PERSPEKT F 30 PRLEL PERSPEKT F E K PERSPEKT F PERSPEKT F KVL YER KB NE M L TER ZOMETR K D METR K TR METR K KON K (Merkei) PERSPEKT F eksenine göre saat önünün tersine 180 lik dönme hareketi B R NOKTLI K NOKTLI K1 K1 K2 K1 ÜÇ NOKTLI eksenine göre saat önünün tersine 270 lik dönme hareketi K2 K Merkei (konik) perspektif, daha çok mimari çiimlerde kullanılmaktadır. Bir apı vea apı topluluğunun emin ve çevresile ilişkisini daha çiim halindeken değerlendirebilmek amacıla perspektif önemli bir ere sahiptir. Bu kesimde merkei (konik) perspektiften bir noktalı ve iki noktalı perspektif çiimler ele alınacaktır. 208
10 KVRMSL DIM 5. Verilen Yapıların Bir ve İki Nokta Perspektif Çiimleri 1. Nokta Perspektifi Prima modelinin ön üü, resmin (çiimin) dülemine paralel olarak apılıorsa bu perspektif çiim tipine bir nokta perspektif denir. Bir Nokta Perspektif Çiimi Perspektif idüşüm: Cisimlerin görünüşünü iki boutlu dülem üerinde, insan üünün gördüğü gibi üç boutlu olarak çiebilme olanağı sağlaan idüşüm öntemlerine perspektif idüşümü adı verilir. İdüşüm: Bir nesnenin bir dülem üerine düşürülen görüntüsüne idüşüm denir. Örneğin bir cisme bir ışık kanağından ışınlar gönderildiğinde o cismin arkasındaki bir dülem üerine gölgesi düşer bu gölge o cismin idüşümüdür. Bakış noktası: Perspektifi çiilecek nesnee gönderilecek bakış ışınlarının kanaklandığı sabit noktaa (gölemcinin göünün bulunduğu nokta) bakış noktası denir. Bakış Uaklığı: Bakış noktasının perspektifi çiilecek nesnee olan uaklığına bakış uaklığı denir. Bakış Yüksekliği: a) Ön ve Üst Yüü Görünen Cisimlerin Çiimi Perspektif çiimi apılacak cisme ön üü ile üst tabanı görünecek şekilde erleştirilir. Kutunun ön üü olarak şekilde kağıt dülemine bir dikdörtgen çiilir. Dikdörtgenin üst tarafına dikdörtgene paralel olacak şekilde bir doğru çiilir. Dikdörtgen tabanının orta noktası hiasında olacak şekilde, doğru üerinde bir nokta belirlenir. Belirlenen bu noktaa dikdörtgenin köşelerinden noktalı doğru parçaları çiilir. Bakış noktasının, er düleminden olan üksekliğine bakış üksekliği denir. Bakış üksekliği ufuk üksekliği olup gölemcinin bouna bağlı olarak ukarı, aşağı hareket eder. İdüşüm (Resim) Dülemi: Üerinde perspektif idüşüm görüntüsünün resmedileceği düşe düleme idüşüm dülemi denir. Ufuk Çigisi: Ufuk çigisinin görünmediği mekânlarda nesnee bakan kişinin gölerinden geçtiği far edilen ata dülemle, düşe idüşüm düleminin kesişme çigisine ufuk çigisi denir. Kabolan Nokta (Kaçan Nokta vea Kaçış Noktası): Bakış noktasından (göden) uaklaşarak sonsua doğru giden ve gerçekte birbirine paralel oldukları halde resim dülemine paralel olmadıkları için birbirine aklaşarak birleşiormuş gibi görünen doğruların kesişme noktasına kabolan nokta denir. Yer Dülemi (Yer Çigisi): İdüşüm düleminin er ile medana getirdiği arakesite er dülemi denir. Noktalı doğru parçaları arasında kalacak ve ata doğrua paralel olacak şekilde doğru parçası çiilerek kutunun üst arıtları oluşturulur. rkadaki diğer dike ve ata doğru parçaları noktalı olarak çiilir. Fala çiimler silinerek çiim tamamlanmış olur. 209
11 KVRMSL DIM b) Ön, Üst ve Sol Yüleri Görünen Cisimlerin Çiimi Perspektif çiimi apılacak cisim ön üü, üst tabanı ve sol üü görünecek şekilde erleştirilir. Kutunun ön üü olacak şekilde kağıt dülemine bir dikdörtgen çiilir. Dikdörtgenin üst tarafına dikdörtgene paralel olacak şekilde bir doğru çiilir. Dikdörtgenin sol etrafında olacak şekilde doğru üerinde kefi bir nokta işaretlenir. Belirlenen noktaa dikdörtgenin köşelerinden noktalı doğru parçaları çiilir. Noktalı doğru parçaları arasında kalacak ve ata doğrua paralel olacak biçimde doğru parçası çiilerek kutunun üst arıtları oluşturulur. Belirlenen noktaa dikdörtgenin köşelerinden noktalı doğru parçaları çiilir. Noktalı doğru parçaları arasında kalacak ve ata doğrua paralel olacak biçimde doğru parçası çiilerek kutunun alt arıtları oluşturulur. rkadaki diğer ata ve dike doğru parçaları noktalı olarak çiilir. Fala çiimler silinerek çiim tamamlanır. Çiim apılırken arka planda kalan doğru parçaları noktalı olarak çiilir. Fala çiimler silinerek çiim tamamlanır. ETK NL K şağıdaki çiimde küpün bir nokta perspektif çiimi apılmıştır. Çiimi inceleini ve nasıl apıldığını açıklaını. c) Ön, lt ve Sol Yüeleri Görünen Cisimlerin Çiimi Perspektif çiimi apılacak cisim, ön üü, alt tabanı ve sol üü görünecek şekilde erleştirilir. Kutunun ön üü olacak şekilde kağıt dülemine bir dikdörtgen çiilir. Dikdörtgenin sol tarafında kalacak şekilde doğru üerinde kefi bir nokta işaretlenir. Cismin üksekli i K düflüm dülemi Bakıfl noktası Kabolan nokta Ufuk çigisi Bak fl üksekli i Yer dülemi İdüşüm dülemine paralel ve arkasında olan üst ve ön görünüşleri verilmiş olan cismin bir nokta perspektif çiim aşamaları aşağıdaki şekillerde verilmiştir. İnceleini. 210
12 KVRMSL DIM Cisim üksekli i Cisim üksekli i Üstten görünüm Önden görünüm Üstten görünüm Önden görünüm E Bak fl noktas Ufuk çigisi E düflüm dülemi Bak fl üksekli i Yer dülemi düflüm dülemi Bak fl noktas Ufuk çigisi Bak fl üksekli i Yer dülemi Yandaki şekilde önden görünümü verilen dikdörtgenler primasının verilen noktaa göre perspektifini çielim. ÇÖZÜM ÖRNEK Üstten görünüm E düflüm dülemi Bak fl noktas Cisim üksekli i Önden görünüm Ufuk çigisi Bak fl üksekli i Yer dülemi Üstten görünüm E düflüm dülemi Bak fl noktas Cisim üksekli i Önden görünüm Ufuk çigisi Bak fl üksekli i Yer dülemi 211
13 KVRMSL DIM ÖRNEK Yandaki şekilde verilen 1 nokta perspektifinde kabolan nokta aşağıdakilerden hangisidir? ) K B) P C) L D) M E) N ÇÖZÜM Yukarıdaki çiimde an arıtlar K L M N P noktalı doğrularla uatıldığında bu doğruların M noktasında kesiştiği görülür. O halde kabolan nokta M dir. Yanıt: D ÖRNEK Yandaki üçgen primanın verilen kabolan noktaa göre perspektifi aşağıdaklierden hangisidir? ) B) 2. İki Nokta Perspektifi Prima modelinin ön üü (sağ ve sol ülerin kesiştiği dike arıt) resmin (çiimin) dülemine parelel değilse bu perspektif çiiminde iki kabolan nokta vardır. Bu çiim tekniğine iki nokta perspektifi denir. a. lt ve Yan Yüleri Görünen Cisimlerin Çiimi Perspektif çiimi apılacak cisim anı köşede kesişen üç üünden alt üü ile sağ ve sol tarafı görünecek şekilde erleştirilir. Kutunun kağıt dülemine paralel olmaan ön üündeki arıt için dike bir doğru parçası çiilir. Dike doğru parçasının alt tarafına ata bir doğru çiilir ve doğru üerine iki kabolan nokta işaretlenir. Dike doğru parçasının uçları noktalı doğrularla doğru üerindeki iki noktaa birleştirilir. C) D) Cismin uunluğu ve genişliği için noktalı doğrular arasına dike doğrular çiilir. E) Cismin arkasında kalan arıtları çiilir. ÇÖZÜM Üçgen primanın üst tabanının üç köşesi kabolan noktaa noktalı doğrularla birleştirilir. Yan ülerin oluşması için noktalı doğruların arasında kalacak şekilde üçgen primanın üst tabanına paralel olan doğru parçaları çiildiğinde bir nokta perspektif çiimi tamamlanır. Yanıt: B lt tabanı ve görünmeen üleri oluşturulur. Fala çiimler silinerek çiim tamamlanır. 212
14 KVRMSL DIM b. Üst Yüü ve Yan Yüleri Görünen Cisimlerin Çiimi Perspektif çiimi apılacak cisim anı köşede kesişen üç üünden üst üü ile sağ ve sol anı görünecek şekilde erleştirilir. Kutunun kağıt dülemine paralel olmaan ön üündeki arıt için dike bir doğru parçası çiilir. Dike doğru parçasının üst tarafına ata bir doğru çiilir. Yata doğrunun sağ ve sol tarafında kefi birer nokta işaretlenir. Dike doğru parçasının uçları noktalı doğrularla doğru üerindeki noktalara birleştirilir. Yukarıdaki şekilde verilen perspektif çiimindeki kabolan nokta(lar) aşağıdakilerden hangisidir? ) X Y B) X Z C) Y L D) X L E) X Z L ÇÖZÜM ÖRNEK X Y Z K L X Y Z K L Şekilde sol ve sağ ülerin alt ve üst tabanlarını oluşturan doğrular üerinde kabolan noktalar verilen doğrua noktalarla çiilen doğrular aşağıdaki şekildeki gibi X ve L noktasında kesişirler. Yanıt: D ETK NL K Cismin uunluğu ve genişliği için noktalı doğrular arasına dike doğrular çiilir. şağıdaki çiimde bir küpün iki nokta perspektif çiimi apılmıştır. Çiimin nasıl apıldığını açıklaını. K 1 K 2 düflüm dülemi Cismin arkasında kalan arıtları çiilir. Üst tabanı ve görünmeen üleri oluşturulur. Bak fl noktas Kabolan nokta Kabolan nokta Ufuk çigisi Fala çiimler silinerek çiim tamamlanır. Cisim üksekli i Bak fl üksekli i Yer dülemi 213
15 KVRMSL DIM Dügün Sekiülü Oluşturma Süsleme adet pipet alınır. Seki pipete eşit uaklıklarda 15 delik açılır. 2. Delik açılmış 2 pipet ve bir tane delik açılmamış pipet alınıp içlerinden ip geçirilerek aşağıdaki gibi eşkenar üçgen oluşturulur. Bener biçimde üç eşkenar üçgen daha oluşturulur. 3. Eşkenar üçgenlerden iki tanesi aşağıdaki gibi iple birleştirilir. Bener biçimde diğer iki eşkenar üçgen de iple birleştirilir. 4. ETK NL K 3. adımda oluşturulan eşkenar üçgenler bir deliksi ve iki delikli pipet eşkenar üçgen oluşturulacak biçimde içlerinden aşağıda belirtildiği gibi ip geçirilerek birleştirilir. 7. Oluşturulan dügün sekiülü iskeletindeki pipetlerdeki deliklerden ipler geçirilerek aşağıdaki gibi vea bener apı oluşturulur. 8. Oluşturulan apıdaki doğru parçaları arasındaki ilişkiler açıklanır. 1. ÇOKYÜZLÜLER VE ÇINIMLRI PLTONİK (PLTONIC) Bitifl Bafllangıç adımda oluşturulan dügün sekiülü iskeletindeki pipetlerden aşağıda belirtildiği gibi ip geçirilerek birleştirilir. Bitifl Bafllangıç adımda pipetlerin içlerinden geçirilen ip çekilip düğümlenerek dügün sekiülü iskeleti oluşturulur. 214
16 3. KVRMSL DIM 1. RŞİMED (RCHIMEDES)
17 4. KVRMSL DIM
18 KVRMSL DIM KEPLER
19 1. F B E K C D Yukarıdaki bir nokta perspektif çiimleri harflerle adlandırılmıştır. Buna göre görünüm bakımından apılan eşleştirmelerden hangisi anlıştır? ) D K B) G L C) M C D) H F E) E N Çöüm: ) D ve K cisimleri ufuk çigisinin altında olup kabolan noktaların solundadırlar. B) G ve L cisimleri ufuk çigisinin önünde olup kabalon noktanın sağındadırlar. C) M ve C cisimleri ufuk çigisinin üstünde olup kabalon noktanın solundadırlar. D) H ve F cisimleri ufuk çigisinin altında fakat H kabolan noktanın solunda, F ise sağında olduğundan bu eşleştirme anlıştır. E) E ile N cisimleri ufuk çigisinin altında ve kabolan noktanın ne sağında ne solunda olup sadece ön üleri görünmektedir. L G N + M UYGULM DIMI H 3. Çöüm: I. Kabolan noktanın solunda ve ufuk çigisinin altında olup üst üü görünmektedir. II. III. IV. Kabolan noktanın solunda ve ufuk çigisinin altında olup üst üü görünmektedir. Kabolan noktanın solunda fakat ufuk çigisinin önünde olduğundan üstü görünmemektedir. Kabolan noktanın solunda ve ufuk çigisinin altında olup üst üü görünmektedir. V. Ufuk çigisinin altında kaldığından üst üü görünmekte fakat kabolan noktanın sağında olduğundan sağ üü görünmektedir. Bu durumda cevap 3 tane olacaktır. sol sol üst sol üst üst sa üst sol 2. I. II. III. IV. V. Yukarıdaki bir nokta perspektif çiimlerinden kaç tanesi sol üst görünümlüdür? Şekildeki bir nokta perspektif çiimler için aşağıdakilerden hangisi anlıştır? ) lttan görünümlü beş prima vardır. B) Üstten görünümlü dört prima vardır. C) Sağdan görünümlü beş prima vardır. D) Soldan görünümlü dört prima vardır. E) Sağ ve üstten görünümlü iki prima vardır. 218
20 Çöüm: lt sa lt üst lt sa sa sa üst sa ) Ufuk çigisinin üstünde beş prima olup altları görünmektedir. B) Ufuk çigisinin altında dört prima olup üstleri görünmektedir. C) Kabolan noktanın sağında beş prima olup an üleri göründüğünden beş prima sağdan görünümlüdür. D) Kabolan noktanın solunda dört prima olmasına karşın an üleri görünen üç prima olduğundan bu seçenek anlıştır. E) Ufuk çigisinin altında kalarak sağ üü görünen iki prima vardır. lt sol sol lt üst sol üst UYGULM DIMI 5. Yanda verilen iki nokta perspektif çiimlerinde C ufuk çigisine göre apılan B eşleştirmelerden hangisi doğrudur? ) D I. B) B D F E C) C E D D) B E E) F II. Çöüm: Şekilde ile K cisimleri ufuk çigisinin altında, B ile D, ufuk çigisinin önünde, E cismi ufuk çigisinin arkasında (vea hiasında) olup C ile F ise ufuk çigisinin üstündedirler dolaısıla B şıkkı doğru eşleştirme olup diğerleri anlıştır Yukarıdaki çiimlerden kaç tanesi iki nokta perspektif çiimidir? ) 1 B) 2 C) 3 D) 4 E) 5 B C D E F G Çöüm: B C D Yukarıdaki çiimde kabolan nokta vea noktalar aşağıdaki şıklardan hangisinde doğru olarak verilmiştir? ) Yalnı B) Yalnı B C) B ve C D) B ve E E) ile D E F H I K Çöüm: ufuk KN çigisi B C D E F G Kabolan noktaların bulunabilmesi için kabolan doğruların çiilmesi gerekir. Çiimler ufuk çigisine devam ettirildiklerinde solda B, sağda ise E noktalarına ulaşıldığından bu iki nokta perspektif çiim olup anlı D şıkkı olacaktır. D Çiimler ufuk çigisine erleştirildiklerinde sahip oldukları kabolan noktalar ve saıları görünmektedir. Buna göre, iki kabolan noktaa sahip üç tane çiim vardır. Yanıt: C 219
21 1. SINM DIMI 3. 1 I. II. Yukarıdaki bir nokta perspektif çiimleri için aşağıdakilerden hangisi anlıştır? ) Üstten görünümlü doku tane cisim vardır. B) Karşıdan görünümlü iki tane cisim vardır. C) Soldan görünümlü beş tane cisim vardır. D) Sağ üstten görünümlü üç tane cisim vardır. E) Sağ alttan görünümlü alnı bir tane cisim vardır. III. Yukarıdaki çiimlerden hangisi vea hangileri kabolan doğrulara model olabilir? IV. ) I ve II B) I ve III C) II ve IV D) I, III ve IV E) Hepsi 2. I. II. III. 4. B C D E F G IV. V. Yukarıdaki verilen çiimde kabolan nokta vea noktalar aşağıdakilerden hangisidir? Yukarıdaki numaralı çiimlerden hangisi vea hangileri bir nokta perspektif çiimidir? ) ve G B) ve F C) B ve F D) Yalnı D E) Yalnı B ) Yalnı I B) I ve III C) I ve IV D) II ve V E) IV ve V 220 1) C 2) B 3) B 4) C
22 5. I. II. III. C.. B. SINM DIMI Yukarıdaki iki nokta perspektif çiimler ufuk çigilerine göre eşleştirildiğinde doğru eşleştirme aşağıdakilerden hangisidir? 1 7. Yandaki çiim hangi teknik kullanılarak çiilmiştir? ) Kare primaa alttan bakıldığı durumdaki iki nokta perspektifi B) Kare primaa alttan bakıldığı durumdaki iki nokta perspektifi C) Kare primaa üstten bakıldığı durumdaki bir nokta perspektifi D) Kare primaa alttan bakıldığı durumdaki bir nokta perspektifi E) Bu bir perspektif çiim değildir. 8. şağıdakilerden hangisi perspektif çiim değildir? ) B) D) E) C) I II II ) B C B) C B C) B C D) C B E) C B 9. şağıdaki iki nokta perspektif çiimlerden hangisi görünüş bakımından diğerlerinden farklıdır? 6. ) B) C) D) E) Yukarıdaki çiimlerden kaç tanesi iki nokta perspektif çiiminin üstten görünümüdür? ) 1 B) 2 C) 3 D) 4 E) 5 5) 6) C 7) E 8) D 9) C 221
23 SINM DIMI 1. Ufuk çigisinin çiimin altında ve kabolan noktanın solunda olduğu dikdörtgenler primasının perspektif çiimi aşağıdakilerden hangisidir? ) B) C) D) E) B C D E F Yukarıda perspektif çiimi verilen primanın kabolan nokta vea noktaları aşağıdakilerden hangisidir? ) D B) E C) F D) E ve F E) D, E ve F 2. Yukarıdaki çiimin perspektif görünümü aşağıdakilerden hangisidir? ) Bir nokta perspektifi soldan ve üstten görünüm B) Bir nokta perspektifi sağdan ve üstten görünüm C) Bir nokta perspektifi sağdan ve alltan görünüm D) İki nokta perspektifi üstten görünüm E) İki nokta perspektifi alttan görünüm 5. B C D E Yukarıdaki çiim için aşağıdakilerden hangisi anlıştır? ) Ufuk çigisinin altında üç cisim vardır. B) Kaçış noktasının solunda olduğu iki cisim vardır. C) Sadece ön ve üst üü görünen cisim iki nokta perspektif çiimdir. D) Sol üstten görünüme sahip tek cisim vardır. E) lttan görünümü verilen iki cisim vardır. Yukarıda perspektif çiimi verilen primanın kabolan nokta vea noktaları aşağıdakilerden hangisidir? ) Yalnı B) Yalnı C C) ve E D), C ve E E) B ve D 222 1) C 2) C 3) B 4) 5) C
24 SINM DIMI 6. şağıdakilerden hangisi dikdörtgenler primasına sağ üstten bakıldığında perspektif çiimidir? 8. 2 ) B) C) D) E) Yukarıdaki çiim için aşağıdakilerden hangisi doğrudur? ) İki nokta perspektifi andan ve üstten görünüm B) İki nokta perspektifi andan ve alttan görünüm C) İki nokta perspektifi andan görünüm D) Bir nokta perspektifi soldan görünüm E) Bir nokta perspektifi sağdan görünüm Yukarıdaki şekil için aşağıdakilerden hangisi anlıştır? ) İki nokta perspektif çiimdir. B) Üstten bakılmaktadır. C) Ufuk çigisi üsttedir. D) Piramidin çiimidir. E) Üç üü görülebilmektedir. Yukarıdaki çiimlerden kaç tanesi iki nokta perspektif çiimdir? ) 1 B) 2 C) 3 D) 4 E) 5 6) B 7) D 8) C 9) C 223
12. SINIF. Uzayda Vektörler-1 TEST. 1. Uzaydaki doğru parçaları için aşağıdaki önermelerden hangisi yanlıştır?
 1. SINIF Uada Vektörler-1 1. Uadaki doğru parçaları için aşağıdaki önermelerden hangisi anlıştır? Akırı doğru parçaları farklı dülemlerdedir. Akırı doğru parçaları farklı doğrultudadır. İki doğru parçasının
1. SINIF Uada Vektörler-1 1. Uadaki doğru parçaları için aşağıdaki önermelerden hangisi anlıştır? Akırı doğru parçaları farklı dülemlerdedir. Akırı doğru parçaları farklı doğrultudadır. İki doğru parçasının
ÖRNEK ÖRNEK ÖRNEK ÖRNEK
 Öteleme ve yansımanın birlikte kullanıldığı dönüşümlere ötelemeli yansıma denir. Düzlemde yansıma ve ötelemeli yansıma dönüşümlerinde uzaklıklar korunurken açıların yönleri değişir. Ötelemeli yansıma dönüşümünde
Öteleme ve yansımanın birlikte kullanıldığı dönüşümlere ötelemeli yansıma denir. Düzlemde yansıma ve ötelemeli yansıma dönüşümlerinde uzaklıklar korunurken açıların yönleri değişir. Ötelemeli yansıma dönüşümünde
Page 1. b) Görünüşlerdeki boşluklar prizma üzerinde sırasıyla oluşturulur. Fazla çizgiler silinir, koyulaştırma yapılarak perspektif tamamlanır.
 TEKNİK BİLİMLER MESLEK YÜKSEKOKULU Teknik Resim İzometrik Perspektifler Küpün iz düşüm düzlemi üzerindeki döndürülme açısı eşit ise kenar uzunluklarındaki kısalma miktarı da aynı olur. Bu iz düşüme, izometrik
TEKNİK BİLİMLER MESLEK YÜKSEKOKULU Teknik Resim İzometrik Perspektifler Küpün iz düşüm düzlemi üzerindeki döndürülme açısı eşit ise kenar uzunluklarındaki kısalma miktarı da aynı olur. Bu iz düşüme, izometrik
Geometrik Örüntüler. Geometride Temel Kavramlar Uzamsal İlişkiler
 Geometrik Cisimler ve Şekiller Geometrik Örüntüler Geometride Temel Kavramlar Uzamsal İlişkiler Geometrik Cisimlerin Yüzeyleri Geometrik Cisimler Prizmaların Benzer ve Farklı Yönleri Geometrik Şekiller
Geometrik Cisimler ve Şekiller Geometrik Örüntüler Geometride Temel Kavramlar Uzamsal İlişkiler Geometrik Cisimlerin Yüzeyleri Geometrik Cisimler Prizmaların Benzer ve Farklı Yönleri Geometrik Şekiller
TEK ve ÇOK YÜZEYLİ KAPALI YÜZEYLER ve KATI CİSİMLER 1 TEST
 ve Ç ÜLİ PLI ÜLR ve S I İSİMLR.. P(a,, ) ukarıdaki dik koordinat sisteminde (,, ) olduğuna göre, dikdörtgenler prizmasının hacmi kaç br tür? nalitik uzayda yukarıdaki dikdörtgenler prizmasının yüzey alanı
ve Ç ÜLİ PLI ÜLR ve S I İSİMLR.. P(a,, ) ukarıdaki dik koordinat sisteminde (,, ) olduğuna göre, dikdörtgenler prizmasının hacmi kaç br tür? nalitik uzayda yukarıdaki dikdörtgenler prizmasının yüzey alanı
TEST. Dönüşüm Geometrisi. 1. y 5. 4
 Dönüşüm Geometrisi 8. Sınıf Matematik Soru ankası TEST 33 1. 4. (0, 4) (5,4) (3, 0) Koordinat düzlemi üzerinde verilen ve noktaları arasındaki uzaklık kaç birimdir? ) 5 ) 3 2 4 2 5 2 Koordinat düzlemi
Dönüşüm Geometrisi 8. Sınıf Matematik Soru ankası TEST 33 1. 4. (0, 4) (5,4) (3, 0) Koordinat düzlemi üzerinde verilen ve noktaları arasındaki uzaklık kaç birimdir? ) 5 ) 3 2 4 2 5 2 Koordinat düzlemi
PİRAMİT, KONİ VE KÜRENİN ALANLARI
 PİRAMİT, KNİ VE KÜRENİN ALANLARI KAZANIMLAR Piramit kavramı Piramitin yüzey alanı Kesik piramitin yüzey alanı Düzgün dörtyüzlü kavramı Piramitin dönme simetri açısı Koni kavramı Koninin yüzey alanı Kesik
PİRAMİT, KNİ VE KÜRENİN ALANLARI KAZANIMLAR Piramit kavramı Piramitin yüzey alanı Kesik piramitin yüzey alanı Düzgün dörtyüzlü kavramı Piramitin dönme simetri açısı Koni kavramı Koninin yüzey alanı Kesik
Geometrik Örüntüler. Geometrik Cisimlerin Yüzeyleri Geometrik Cisimler Prizmaların Benzer ve Farklı Yönleri Geometrik Şekiller. Geometrik Örüntüler
 Geometrik Cisimler ve Şekiller Geometrik Örüntüler Geometride Temel Kavramlar Uzamsal İlişkiler Geometrik Cisimlerin Yüzeyleri Geometrik Cisimler Prizmaların Benzer ve Farklı Yönleri Geometrik Şekiller
Geometrik Cisimler ve Şekiller Geometrik Örüntüler Geometride Temel Kavramlar Uzamsal İlişkiler Geometrik Cisimlerin Yüzeyleri Geometrik Cisimler Prizmaların Benzer ve Farklı Yönleri Geometrik Şekiller
Teknik Resim 4. HAFTA
 Teknik Resim 4. HAFTA PERSPEKTİF NEDİR? Perspektif, iz düşüm kurallarına göre kâğıt düzlemi üzerine çizilmiş, üç boyutu da görülen (en, derinlik ve yükseklik) bir cismin iz düşümünden ibarettir. PERSPEKTİF
Teknik Resim 4. HAFTA PERSPEKTİF NEDİR? Perspektif, iz düşüm kurallarına göre kâğıt düzlemi üzerine çizilmiş, üç boyutu da görülen (en, derinlik ve yükseklik) bir cismin iz düşümünden ibarettir. PERSPEKTİF
ÖRNEK: Öteleme ile oluşturulmuş bir süsleme. ÖRNEK: 2)GEOMETRİK HAREKETLER
 ÖTELEME: Bir şeklin duruşunun, biçiminin, boyutlarının bozulmadan yer değiştirmesine o şekli öteleme denir. Ötelemede biçim, boyut, yön değişmez. Yer değişir. Bir şekil ötelendiği zaman şekil üzerindeki
ÖTELEME: Bir şeklin duruşunun, biçiminin, boyutlarının bozulmadan yer değiştirmesine o şekli öteleme denir. Ötelemede biçim, boyut, yön değişmez. Yer değişir. Bir şekil ötelendiği zaman şekil üzerindeki
DERS 5. Çok Değişkenli Fonksiyonlar, Kısmi Türevler
 DERS 5 Çok Değişkenli Fonksionlar Kısmi Türevler 5.1. Çok Değişkenli Fonksionlar. Reel saılar kümesi R ile gösterilmek üere ve her n için olarak tanımlanır. R R 3 {( ): R} = {( ) : R} = {( L ): L R} n
DERS 5 Çok Değişkenli Fonksionlar Kısmi Türevler 5.1. Çok Değişkenli Fonksionlar. Reel saılar kümesi R ile gösterilmek üere ve her n için olarak tanımlanır. R R 3 {( ): R} = {( ) : R} = {( L ): L R} n
Perspektif: Bir cismin bir bakışta, genel olarak üç yüzünün birden görünecek şekilde çizilen resimlerine denir. PERSPEKTİF. Kavaliyer Kabinet Militer
 Perspektif Perspektifler Perspektif: Bir cismin bir bakışta, genel olarak üç yüzünün birden görünecek şekilde çizilen resimlerine denir. PERSPEKTİF ksonometrik perspektif Paralel perspektif Eğik perspektif
Perspektif Perspektifler Perspektif: Bir cismin bir bakışta, genel olarak üç yüzünün birden görünecek şekilde çizilen resimlerine denir. PERSPEKTİF ksonometrik perspektif Paralel perspektif Eğik perspektif
İNS1101 MÜHENDİSLİK ÇİZİMİ. Bingöl Üniversitesi İnşaat Mühendisliği Bölümü 2018
 İNS1101 MÜHENDİSLİK ÇİZİMİ Bingöl Üniversitesi İnşaat Mühendisliği Bölümü 2018 TEKNİK RESİM Teknik resim, teknik elemanların üretim yapabilmeleri için anlatmak istedikleri teknik özelliklerin biçim ve
İNS1101 MÜHENDİSLİK ÇİZİMİ Bingöl Üniversitesi İnşaat Mühendisliği Bölümü 2018 TEKNİK RESİM Teknik resim, teknik elemanların üretim yapabilmeleri için anlatmak istedikleri teknik özelliklerin biçim ve
YGS GEOMETRİ DENEME 1
 YGS GTİ 1 G 1) G ) şağıdaki adımlar takip edilerek geometrik çizim yapıl- bir üçgen mak isteniyor = = m() = 7 o = 9 cm, = 1 cm, m() = 90 olacak şekilde dik üçgeni çiziliyor = eşitliğini sağlayan Î [] noktası
YGS GTİ 1 G 1) G ) şağıdaki adımlar takip edilerek geometrik çizim yapıl- bir üçgen mak isteniyor = = m() = 7 o = 9 cm, = 1 cm, m() = 90 olacak şekilde dik üçgeni çiziliyor = eşitliğini sağlayan Î [] noktası
TEKNİK RESİM DERSİ ÖĞR. GÖR. BERIVAN POLAT
 TEKNİK RESİM DERSİ ÖĞR. GÖR. BERIVAN POLAT DERS 6 Perspektif Cismin üç yüzünü gösteren, tek görünüşlü resimlerdir. Cisimlerin, gözümüzün gördüğü şekle benzer özelliklerdeki üç boyutlu (hacimsel) anlatımını
TEKNİK RESİM DERSİ ÖĞR. GÖR. BERIVAN POLAT DERS 6 Perspektif Cismin üç yüzünü gösteren, tek görünüşlü resimlerdir. Cisimlerin, gözümüzün gördüğü şekle benzer özelliklerdeki üç boyutlu (hacimsel) anlatımını
Kuadratik Yüzeyler Uzayda İkinci Dereceden Yüzeyler
 İÇİNDEKİLER Kuadratik Yüeler Uada İkinci Dereceden Yüeler 1 0.1. Elipsoid 2 0.2. Hiperboloid 4 0.2.1. Tek Kanatlı Hiperboloid 4 0.2.2. Çift Kanatlı Hiperboloid 4 0.3. Paraboloid 5 0.3.1. Eliptik Paraboloid
İÇİNDEKİLER Kuadratik Yüeler Uada İkinci Dereceden Yüeler 1 0.1. Elipsoid 2 0.2. Hiperboloid 4 0.2.1. Tek Kanatlı Hiperboloid 4 0.2.2. Çift Kanatlı Hiperboloid 4 0.3. Paraboloid 5 0.3.1. Eliptik Paraboloid
Eğer piramidin tabanı düzgün çokgense bu tip piramitlere düzgün piramit denir.
 PİRAMİTLER Bir düzlemde kapalı bir bölge ile bu düzlemin dışında bir T noktası alalım. Kapalı bölgenin tüm noktalarının T noktası ile birleştirilmesi sonucunda oluşan cisme piramit denir. T noktası piramidin
PİRAMİTLER Bir düzlemde kapalı bir bölge ile bu düzlemin dışında bir T noktası alalım. Kapalı bölgenin tüm noktalarının T noktası ile birleştirilmesi sonucunda oluşan cisme piramit denir. T noktası piramidin
TEKNİK RESİM. Ders Notları: Mehmet Çevik Dokuz Eylül Üniversitesi. Perspektifler-2
 TEKNİK RESİM 2010 Ders Notları: Mehmet Çevik Dokuz Eylül Üniversitesi Perspektifler-2 2/25 Perspektifler-2 Perspektifler-2 Perspektif Çeşitleri Dimetrik Perspektif Trimetrik Perspektif Eğik Perspektif
TEKNİK RESİM 2010 Ders Notları: Mehmet Çevik Dokuz Eylül Üniversitesi Perspektifler-2 2/25 Perspektifler-2 Perspektifler-2 Perspektif Çeşitleri Dimetrik Perspektif Trimetrik Perspektif Eğik Perspektif
Page 1. İz Düşüm Çeşitleri ve Metotları
 4. İz Düşümler TEKNİK BİLİMLER MESLEK YÜKSEKOKULU Teknik Resim Genel Bilgi Kullandığımız bir çok eşya ve makineyi veya bunlara ait parçaların imal edilebilmesi için şekillerini ifade eden resimlerinin
4. İz Düşümler TEKNİK BİLİMLER MESLEK YÜKSEKOKULU Teknik Resim Genel Bilgi Kullandığımız bir çok eşya ve makineyi veya bunlara ait parçaların imal edilebilmesi için şekillerini ifade eden resimlerinin
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve Çöümleri DĞHN MÜHENDİSLİK MEKNİĞİ STTİK MÜHENDİSLİK MEKNİĞİ STTİK İÇİNDEKİLE 1. GİİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLEİ - İki Boutlu Kuvvet
Statik Ders Notları Sınav Soru ve Çöümleri DĞHN MÜHENDİSLİK MEKNİĞİ STTİK MÜHENDİSLİK MEKNİĞİ STTİK İÇİNDEKİLE 1. GİİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLEİ - İki Boutlu Kuvvet
2. Afla daki çokgenlerden hangisi düzgün. 1. Afla dakilerden hangisi çokgen de ildir? çokgen de ildir? A) B) A) B) C) D) C) D)
 Ad : Soyad : S n f : Nu. : Okulu : Çokgenler Dörtgenler MATEMAT K TEST 15 1. Afla dakilerden hangisi çokgen de ildir? 4. Afla daki çokgenlerden hangisi düzgün çokgen de ildir? 2. Afla daki çokgenlerden
Ad : Soyad : S n f : Nu. : Okulu : Çokgenler Dörtgenler MATEMAT K TEST 15 1. Afla dakilerden hangisi çokgen de ildir? 4. Afla daki çokgenlerden hangisi düzgün çokgen de ildir? 2. Afla daki çokgenlerden
DUVAR KAĞIDI GRUPLARI
 DUVAR KAĞIDI GRUPLARI Fulya Taştan Bir düzlemi (odanın zeminini, voleybol sahasını) bir çeşit karoyla kaplayabilmek için birbirinden bağımsız en azından iki yönde karoları ötelemek gerekir elbette. Bunu
DUVAR KAĞIDI GRUPLARI Fulya Taştan Bir düzlemi (odanın zeminini, voleybol sahasını) bir çeşit karoyla kaplayabilmek için birbirinden bağımsız en azından iki yönde karoları ötelemek gerekir elbette. Bunu
Batuhan zeka oyunu olan satrancın kurallarını öğrendikten sonra, yandaki satranç tahtasında
 6.ÜNİTE İLFEN YYINILIK atuhan zeka oyunu olan satrancın kurallarını öğrendikten sonra, yandaki satranç tahtasında bulunan taşları (at, kale, piyon) kurallar doğrultusunda hareket ettiriyor. Hangi taşın
6.ÜNİTE İLFEN YYINILIK atuhan zeka oyunu olan satrancın kurallarını öğrendikten sonra, yandaki satranç tahtasında bulunan taşları (at, kale, piyon) kurallar doğrultusunda hareket ettiriyor. Hangi taşın
NLİTİK EMETRİ lan ve ğırlık Merkezi 5. ölüm Örnek 0 nalitik düzlemde üçgen [] açıorta [] // [] (6 0 (6 (6 (6 0 [H] [] [K] [] H = K = br K ile H üçgenl
![NLİTİK EMETRİ lan ve ğırlık Merkezi 5. ölüm Örnek 0 nalitik düzlemde üçgen [] açıorta [] // [] (6 0 (6 (6 (6 0 [H] [] [K] [] H = K = br K ile H üçgenl NLİTİK EMETRİ lan ve ğırlık Merkezi 5. ölüm Örnek 0 nalitik düzlemde üçgen [] açıorta [] // [] (6 0 (6 (6 (6 0 [H] [] [K] [] H = K = br K ile H üçgenl](/thumbs/70/62427826.jpg) NLİTİK EMETRİ lan ve ğırlık Merkezi 5. ölüm lan Örnek 0 nalitik düzlemde ( 0 c h b h a h c b ( 0 ( 0 a a h b h a b c h lan( = = = c Yukarıdaki verilenlere göre lan( kaç birimkaredir? 6 8 9 E c b Taban:
NLİTİK EMETRİ lan ve ğırlık Merkezi 5. ölüm lan Örnek 0 nalitik düzlemde ( 0 c h b h a h c b ( 0 ( 0 a a h b h a b c h lan( = = = c Yukarıdaki verilenlere göre lan( kaç birimkaredir? 6 8 9 E c b Taban:
UZAY KAVRAMI VE UZAYDA DOĞRULAR
 UZAY KAVRAMI VE UZAYDA DOĞRULAR Cisimlerin kapladığı yer ve içinde bulundukları mekan uzaydır. Doğruda sadece uzunluk, düzlemde uzunluk ve genişlik söz konusudur. Uzayda ise uzunluk ve genişliğin yanında
UZAY KAVRAMI VE UZAYDA DOĞRULAR Cisimlerin kapladığı yer ve içinde bulundukları mekan uzaydır. Doğruda sadece uzunluk, düzlemde uzunluk ve genişlik söz konusudur. Uzayda ise uzunluk ve genişliğin yanında
Ek 6: 6-8 Sınıflar Matematik Öğrenme Alanları ve Alt Öğrenme Alanları
 Ek 6: 6-8 Sınıflar Matematik Öğrenme Alanları ve Alt Öğrenme Alanları SINIFLAR 6. SINIF 7. SINIF 8. SINIF ö ğ r e n m e a l a n l a r ı sayılar geometri ölçme Olasılık ve istatistik a l t ö ğ r e n m e
Ek 6: 6-8 Sınıflar Matematik Öğrenme Alanları ve Alt Öğrenme Alanları SINIFLAR 6. SINIF 7. SINIF 8. SINIF ö ğ r e n m e a l a n l a r ı sayılar geometri ölçme Olasılık ve istatistik a l t ö ğ r e n m e
OPTİK Işık Nedir? Işık Kaynakları Işık Nasıl Yayılır? Tam Gölge - Yarı Gölge güneş tutulması
 OPTİK Işık Nedir? Işığı yaptığı davranışlarla tanırız. Işık saydam ortamlarda yayılır. Işık foton denilen taneciklerden oluşur. Fotonların belirli bir dalga boyu vardır. Bazı fiziksel olaylarda tanecik,
OPTİK Işık Nedir? Işığı yaptığı davranışlarla tanırız. Işık saydam ortamlarda yayılır. Işık foton denilen taneciklerden oluşur. Fotonların belirli bir dalga boyu vardır. Bazı fiziksel olaylarda tanecik,
OPTİK. Işık Nedir? Işık Kaynakları
 OPTİK Işık Nedir? Işığı yaptığı davranışlarla tanırız. Işık saydam ortamlarda yayılır. Işık foton denilen taneciklerden oluşur. Fotonların belirli bir dalga boyu vardır. Bazı fiziksel olaylarda tanecik,
OPTİK Işık Nedir? Işığı yaptığı davranışlarla tanırız. Işık saydam ortamlarda yayılır. Işık foton denilen taneciklerden oluşur. Fotonların belirli bir dalga boyu vardır. Bazı fiziksel olaylarda tanecik,
Saat Yönünde 90 Derecelik Dönme Hareketi. Saatin Tersi Yönünde 90 Derecelik Dönme Hareketi
 Saat Yönünde 9 Derecelik Dönme Hareketi Saatin Tersi Yönünde 9 Derecelik Dönme Hareketi çizilmiş olan üçgenin orjin etrafında saat yönünde 9 lik dönme hareketine ait görüntüsünü çizip bu üçgenin köşe koordinatlarını
Saat Yönünde 9 Derecelik Dönme Hareketi Saatin Tersi Yönünde 9 Derecelik Dönme Hareketi çizilmiş olan üçgenin orjin etrafında saat yönünde 9 lik dönme hareketine ait görüntüsünü çizip bu üçgenin köşe koordinatlarını
4. Çok büyük ve çok küçük pozitif sayıları bilimsel gösterimle ifade eder.
 LENDİRME ŞEMASI ÜNİTE Üslü 1. Bir tam sayının negatif kuvvetini belirler ve rasyonel sayı olarak ifade eder.. Ondalık kesirlerin veya rasyonel sayıların kendileriyle tekrarlı çarpımını üslü sayı olarak
LENDİRME ŞEMASI ÜNİTE Üslü 1. Bir tam sayının negatif kuvvetini belirler ve rasyonel sayı olarak ifade eder.. Ondalık kesirlerin veya rasyonel sayıların kendileriyle tekrarlı çarpımını üslü sayı olarak
5. ÜNİTE İZDÜŞÜMÜ VE GÖRÜNÜŞ ÇIKARMA
 5. ÜNİTE İZDÜŞÜMÜ VE GÖRÜNÜŞ ÇIKARMA KONULAR 1. İzdüşüm Metodları 2. Temel İzdüşüm Düzlemleri 3. Cisimlerin İzdüşümleri 4. Görünüş Çıkarma BU ÜNİTEYE NEDEN ÇALIŞMALIYIZ? İz düşümü yöntemlerini, Görünüş
5. ÜNİTE İZDÜŞÜMÜ VE GÖRÜNÜŞ ÇIKARMA KONULAR 1. İzdüşüm Metodları 2. Temel İzdüşüm Düzlemleri 3. Cisimlerin İzdüşümleri 4. Görünüş Çıkarma BU ÜNİTEYE NEDEN ÇALIŞMALIYIZ? İz düşümü yöntemlerini, Görünüş
1 (c) herhangi iki kompleks sayı olmak üzere
 KOMPLEKS FONKSİYONLAR TEORİSİ UYGULAMA SORULARI- Problem. Aşağıdaki (a) ve (b) de olmak üere (a) olduklarını gösterini. (b) (c) Imi Re Çöüm (a) i olsun. i i (b) i olsun. i i i i i i i i i i Im i Re i (c)
KOMPLEKS FONKSİYONLAR TEORİSİ UYGULAMA SORULARI- Problem. Aşağıdaki (a) ve (b) de olmak üere (a) olduklarını gösterini. (b) (c) Imi Re Çöüm (a) i olsun. i i (b) i olsun. i i i i i i i i i i Im i Re i (c)
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve Çözümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları. KUVVET SİSTEMLERİ - İki Boutlu
Statik Ders Notları Sınav Soru ve Çözümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları. KUVVET SİSTEMLERİ - İki Boutlu
BATMIŞ YÜZEYLERE GELEN HİDROSTATİK KUVVETLER. Yatay bir düzlem yüzeye gelen hidrostatik kuvvetin büyüklüğünü ve etkime noktasını bulmak istiyoruz.
 BTMIŞ YÜZEYLERE ELEN HİDROSTTİK KUVVETLER DÜZLEM YÜZEYLER Yata Yüeler Sıvı üei Yata bir dülem üee gelen idrostatik kuvvetin büüklüğünü ve etkime noktasını bulmak istioru. d d Kuvvetin Büüklüğü :Şekil deki
BTMIŞ YÜZEYLERE ELEN HİDROSTTİK KUVVETLER DÜZLEM YÜZEYLER Yata Yüeler Sıvı üei Yata bir dülem üee gelen idrostatik kuvvetin büüklüğünü ve etkime noktasını bulmak istioru. d d Kuvvetin Büüklüğü :Şekil deki
TEST. Düzgün Çokgenler. 4. Bir iç açısı 140 olan düzgün çokgenin iç açılar 5. A B. 2. Bir dış açısı Çevresi. toplamı kaç derecedir?
 üzgün Çokgenler 7. Sınıf Matematik Soru ankası S 49 1. 4. ir iç açısı 140 olan düzgün çokgenin iç açılar toplamı kaç derecedir? ) 70 ) 900 ) 1080 ) 160 Şekilde verilen düzgün çokgenine göre, I., köşesine
üzgün Çokgenler 7. Sınıf Matematik Soru ankası S 49 1. 4. ir iç açısı 140 olan düzgün çokgenin iç açılar toplamı kaç derecedir? ) 70 ) 900 ) 1080 ) 160 Şekilde verilen düzgün çokgenine göre, I., köşesine
2013 2014 EĞİTİM ÖĞRETİM YILI 8. SINIF MATEMATİK DERSİ KONULARININ ÇALIŞMA TAKVİMİNE GÖRE DAĞILIM ÇİZELGESİ ALT ÖĞRENME. Örüntü ve Süslemeler
 2013 2014 EĞİTİM ÖĞRETİM YILI 8. SINIF MATEMATİK DERSİ KONULARININ ÇALIŞMA TAKVİMİNE GÖRE DAĞILIM ÇİZELGESİ SÜRE ÖĞRENME Ay Hafta D.Saati ALANI EYLÜL 2 Geometri 2 3 Geometri 2 Geometri 2 Olasılıkve ALT
2013 2014 EĞİTİM ÖĞRETİM YILI 8. SINIF MATEMATİK DERSİ KONULARININ ÇALIŞMA TAKVİMİNE GÖRE DAĞILIM ÇİZELGESİ SÜRE ÖĞRENME Ay Hafta D.Saati ALANI EYLÜL 2 Geometri 2 3 Geometri 2 Geometri 2 Olasılıkve ALT
PARABOL. çözüm. kavrama sorusu. çözüm. kavrama sorusu
 PARABL Bu bölümde birinci dereceden fonksion =f()=a+b ve ikinci dereceden fonksion =f()=a +b+c grafiklerini üzesel olarak inceleeceğiz. f()=a +b+c ikinci dereceden bir bilinmeenli polinom fonksionun grafiği
PARABL Bu bölümde birinci dereceden fonksion =f()=a+b ve ikinci dereceden fonksion =f()=a +b+c grafiklerini üzesel olarak inceleeceğiz. f()=a +b+c ikinci dereceden bir bilinmeenli polinom fonksionun grafiği
Geometrik Cisimler ve Şekiller. Uzamsal İlişkiler Geometrik Örüntüler. Geometrik Şekiller Geometrik Cisimler. Uzamsal İlişkiler Geometrik Örüntüler
 Onluklar ve Birlikler Geometrik Cisimler ve Şekiller Uzamsal İlişkiler Geometrik Örüntüler Geometrik Şekiller Geometrik Cisimler Uzamsal İlişkiler Geometrik Örüntüler SınıfMatematik Matematik 2. 2.Sınıf
Onluklar ve Birlikler Geometrik Cisimler ve Şekiller Uzamsal İlişkiler Geometrik Örüntüler Geometrik Şekiller Geometrik Cisimler Uzamsal İlişkiler Geometrik Örüntüler SınıfMatematik Matematik 2. 2.Sınıf
1. Yukar daki çubuk makarna afla dakilerden hangisinin modelidir? Yukar daki rakamlardan kaç tanesinde dikey do ru modeli vard r?
 Ad : Soyad : S n f : Nu. : Okulu : 1. Yukar daki çubuk makarna afla dakilerden hangisinin modelidir? Do ru Düzlem Nokta 5. MATEMAT K TEST 19 Ifl n Do ru Do ru parças 2. Afla daki hangi do runun çizgi modeli
Ad : Soyad : S n f : Nu. : Okulu : 1. Yukar daki çubuk makarna afla dakilerden hangisinin modelidir? Do ru Düzlem Nokta 5. MATEMAT K TEST 19 Ifl n Do ru Do ru parças 2. Afla daki hangi do runun çizgi modeli
DEFORMASYON VE STRAİN ANALİZİ
 DEFORMASYON VE STRAİN ANALİZİ Tek Eksenli Gerilme Koşullarında Deformason ve Strain Cisimler gerilmelerin etkisi altında kaldıkları aman şekillerinde bir değişiklik medana gelir. Bu değişiklik gerilmenin
DEFORMASYON VE STRAİN ANALİZİ Tek Eksenli Gerilme Koşullarında Deformason ve Strain Cisimler gerilmelerin etkisi altında kaldıkları aman şekillerinde bir değişiklik medana gelir. Bu değişiklik gerilmenin
30. Uzay çerçeve örnek çözümleri
 . Ua çerçeve örnek çöümleri. Ua çerçeve örnek çöümleri Ua çerçeve eleman sonlu elemanlar metodunun en karmaşık elemanıdır. Bunun nedenleri: ) Her eleman için erel eksen takımı seçilmesi gerekir. Elemanın
. Ua çerçeve örnek çöümleri. Ua çerçeve örnek çöümleri Ua çerçeve eleman sonlu elemanlar metodunun en karmaşık elemanıdır. Bunun nedenleri: ) Her eleman için erel eksen takımı seçilmesi gerekir. Elemanın
2013 2014 EĞİTİM ÖĞRETİM YILI 8. SINIF MATEMATİK DERSİ KAZANIMLARININ ÇALIŞMA TAKVİMİNE GÖRE DAĞILIM ÇİZELGESİ KAZANIMLAR
 KASIM EKİM EYLÜL Ay Hafta D.Saat i 0 04 EĞİTİM ÖĞRETİM YILI 8. SINIF MATEMATİK DERSİ KAZANIMLARININ ÇALIŞMA TAKVİMİNE GÖRE SÜRE ÖĞRENME ALANI ALT ÖĞRENME ALANI Örüntü Süslemeler si KAZANIMLAR.Doğru, çokgen
KASIM EKİM EYLÜL Ay Hafta D.Saat i 0 04 EĞİTİM ÖĞRETİM YILI 8. SINIF MATEMATİK DERSİ KAZANIMLARININ ÇALIŞMA TAKVİMİNE GÖRE SÜRE ÖĞRENME ALANI ALT ÖĞRENME ALANI Örüntü Süslemeler si KAZANIMLAR.Doğru, çokgen
MHN 113 Teknik Resim ve Tasarı Geometri 2
 6. ÖLÜM İZDÜŞÜM MHN 113 Teknik Resim ve Tasarı Geometri 2 6. İZDÜŞÜM 6.1. GENEL İLGİLER Uzaydaki bir cisim, bir düzlem önünde tutulup bu cisme karşıdan bakılacak olursa, cismin düzlem üzerine bir görüntüsü
6. ÖLÜM İZDÜŞÜM MHN 113 Teknik Resim ve Tasarı Geometri 2 6. İZDÜŞÜM 6.1. GENEL İLGİLER Uzaydaki bir cisim, bir düzlem önünde tutulup bu cisme karşıdan bakılacak olursa, cismin düzlem üzerine bir görüntüsü
1- AYNALI STEREOSKOP UYGULAMASI. X (Uçuş Doğrultusu) H1 H1. 1. resim (sol) 2. resim (sağ) KARTON ÜZERİNDEKİ İŞLEMLER D 1 D 2
 - YNLI STEREOSKO UYGULMSI KRTON ÜZERİNDEKİ İŞLEMLER D D 70 cm 6 cm X (Uçuş Doğrultusu) 00 cm Yukardaki bilgiler karton üzerine çizilir. Kartonun sağ alt köşesine çalışan kişilerin no-adı soadı, resim numaraları,
- YNLI STEREOSKO UYGULMSI KRTON ÜZERİNDEKİ İŞLEMLER D D 70 cm 6 cm X (Uçuş Doğrultusu) 00 cm Yukardaki bilgiler karton üzerine çizilir. Kartonun sağ alt köşesine çalışan kişilerin no-adı soadı, resim numaraları,
9. SINIF Geometri TEMEL GEOMETRİK KAVRAMLAR
 TEMEL GEOMETRİK KAVRAMLAR 9. SINIF Geometri Amaç-1: Nokta, Doğru, Düzlem, Işın ve Uzayı Kavrayabilme. 1. Nokta, doğru, düzlem ve uzay kavramlarım açıklama. 2. Farklı iki noktadan geçen doğru sayışım söyleme
TEMEL GEOMETRİK KAVRAMLAR 9. SINIF Geometri Amaç-1: Nokta, Doğru, Düzlem, Işın ve Uzayı Kavrayabilme. 1. Nokta, doğru, düzlem ve uzay kavramlarım açıklama. 2. Farklı iki noktadan geçen doğru sayışım söyleme
4. BÖLÜM GEOMETRİK ÇİZİMLER
 4. ÖLÜM GEOMETRİK ÇİZİMLER MHN 113 Teknik Resim ve Tasarı Geometri 2 4. GEOMETRİK ÇİZİMLER 4.1. ir doğruyu istenilen sayıda eşit parçalara bölmek 1. - doğrusunun bir ucundan herhangi bir açıda yardımcı
4. ÖLÜM GEOMETRİK ÇİZİMLER MHN 113 Teknik Resim ve Tasarı Geometri 2 4. GEOMETRİK ÇİZİMLER 4.1. ir doğruyu istenilen sayıda eşit parçalara bölmek 1. - doğrusunun bir ucundan herhangi bir açıda yardımcı
Genel Bilgi. İz Düşüm Düzlemleri ve Bölgeler. Yrd. Doç. Dr. Garip GENÇ Şekil: İz düşüm düzlemlerine bakış doğrultuları. Page 1.
 TEKNİK BİLİMLER MESLEK YÜKSEKOKULU Teknik Resim Genel Bilgi Uzaydaki cisimlerin eksiksiz bir anlatımı için, ana boyutlarıyla birlikte parçanın bitmiş hallerinden ve üzerindeki işlemlerle birlikte diğer
TEKNİK BİLİMLER MESLEK YÜKSEKOKULU Teknik Resim Genel Bilgi Uzaydaki cisimlerin eksiksiz bir anlatımı için, ana boyutlarıyla birlikte parçanın bitmiş hallerinden ve üzerindeki işlemlerle birlikte diğer
İlkokulu - 3/ Sınıfı *** Matematik *** Geometrik şekiller - 3
 İlkokulu - 3/ Sınıfı *** Matematik *** Geometrik şekiller - 3 Adım Soyadım : Okul Numaram:. S ü l e y m a n O C A K S ü l e y m a n O C A K S O ü l C e y A m a K n İlkokulu - 3/ Sınıfı *** Matematik ***
İlkokulu - 3/ Sınıfı *** Matematik *** Geometrik şekiller - 3 Adım Soyadım : Okul Numaram:. S ü l e y m a n O C A K S ü l e y m a n O C A K S O ü l C e y A m a K n İlkokulu - 3/ Sınıfı *** Matematik ***
MEB Ölçme, Değerlendirme ve Sınav Hizmetleri Genel Müdürlüğü MATEMATİK TESTİ ,4 işleminin sonucu kaçtır?
 Ölçme, eğerlendirme ve Sınav Hizmetleri Genel Müdürlüğü MTEMTİ TESTİ. 2 5 20 + 25 işleminin sonucu kaçtır? ) 5 ) 6 5 ) 2 5 ) 27 5. 5 5, işleminin sonucu kaçtır? 9 ) ) 8 ) 6 ) 5 2. 2 Şekilde, verilen modeller
Ölçme, eğerlendirme ve Sınav Hizmetleri Genel Müdürlüğü MTEMTİ TESTİ. 2 5 20 + 25 işleminin sonucu kaçtır? ) 5 ) 6 5 ) 2 5 ) 27 5. 5 5, işleminin sonucu kaçtır? 9 ) ) 8 ) 6 ) 5 2. 2 Şekilde, verilen modeller
Üçgende Açı ABC bir ikizkenar. A üçgen 30
 1. 4. bir ikizkenar üçgen 0 = m () = 0 m () = 70 70 Kıble : Müslümanların namaz kılarken yönelmeleri gereken, Mekke kentinde bulunan Kabe'yi gösteren yön. arklı iki ülkede bulunan ve noktalarındaki iki
1. 4. bir ikizkenar üçgen 0 = m () = 0 m () = 70 70 Kıble : Müslümanların namaz kılarken yönelmeleri gereken, Mekke kentinde bulunan Kabe'yi gösteren yön. arklı iki ülkede bulunan ve noktalarındaki iki
TEMEL BAZI KAVRAMLAR. Uzay: İçinde yaşadığımız sonsuz boşluktur. Uzay, bir noktalar kümesidir. Uzay, bütün varlıkları içine alır.
 1 TEMEL ZI KVRMLR Nokta: Kalemin kâğıda, tebeşirin tahtaya bıraktığı ize nokta denir. Nokta boyutsuzdur. Yani; noktanın eni, boyu ve yüksekliği yoktur. ütün geometrik şekiller noktalardan oluşur. Noktalar
1 TEMEL ZI KVRMLR Nokta: Kalemin kâğıda, tebeşirin tahtaya bıraktığı ize nokta denir. Nokta boyutsuzdur. Yani; noktanın eni, boyu ve yüksekliği yoktur. ütün geometrik şekiller noktalardan oluşur. Noktalar
2014 LYS GEOMETRİ 3. A. parabolü ile. x 1 y a 9 çemberinin üç noktada kesişmesi için a kaç olmalıdır?
 014 LYS GOMTRİ 1. y 1 1 y a 9 çemberinin üç noktada kesişmesi için a kaç olmalıdır? parabolü ile. O merkezli çeyrek çemberde O deltoid olduğuna göre, taralı alan kaç birim karedir? O. d:y a b doğrusu -ekseni
014 LYS GOMTRİ 1. y 1 1 y a 9 çemberinin üç noktada kesişmesi için a kaç olmalıdır? parabolü ile. O merkezli çeyrek çemberde O deltoid olduğuna göre, taralı alan kaç birim karedir? O. d:y a b doğrusu -ekseni
Teknik Resim TEKNİK BİLİMLER MESLEK YÜKSEKOKULU. 3. Geometrik Çizimler. Yrd. Doç. Dr. Garip GENÇ
 TEKNİK BİLİMLER MESLEK YÜKSEKOKULU Teknik Resim Genel Bilgi Teknik resimde bir şekli çizmek için çizim takımlarından faydalanılır. Çizilecek şekil üzerinde eşit bölüntüler, paralel doğrular, teğet birleşmeler,
TEKNİK BİLİMLER MESLEK YÜKSEKOKULU Teknik Resim Genel Bilgi Teknik resimde bir şekli çizmek için çizim takımlarından faydalanılır. Çizilecek şekil üzerinde eşit bölüntüler, paralel doğrular, teğet birleşmeler,
Demek ki ölçmeye çalıştığımız açı dar açıdır. üçgen. gönye. dar açı
 Dar Açı Gönyemizin dik kısmını herhangi bir şeklin köşesine yerleştirdiğimizde, şeklin köşesindeki açı gönyeden küçük olursa o köşedeki açıya dar açı denir. gönye Demek ki ölçmeye çalıştığımız açı dar
Dar Açı Gönyemizin dik kısmını herhangi bir şeklin köşesine yerleştirdiğimizde, şeklin köşesindeki açı gönyeden küçük olursa o köşedeki açıya dar açı denir. gönye Demek ki ölçmeye çalıştığımız açı dar
MATEMATİK TESTİ LYS YE DOĞRU. 1. Bu testte Matematik ile ilgili 50 soru vardır.
 MTMTİK TSTİ LYS-. u testte Matematik ile ilgili 0 soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için ayrılan kısmına işaretleyiniz.. u testteki süreniz 7 dakikadır.. a, b, c birer reel sayı
MTMTİK TSTİ LYS-. u testte Matematik ile ilgili 0 soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için ayrılan kısmına işaretleyiniz.. u testteki süreniz 7 dakikadır.. a, b, c birer reel sayı
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve Çöümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki Boutlu
Statik Ders Notları Sınav Soru ve Çöümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki Boutlu
Örnek...1 : f (x)=2x 2 5x+6 parabolü K(2,p) noktasından geçiyorsa p kaçtır? Örnek...2 : Aşağıda çeşitli parabol grafikleri verilmiştir incele yi niz.
 a, b,c R,a 0 olmak koşulula f ()=a 2 +b+c fonksionuna ikinci dereceden bir değişkenli fonksion ve bu fonksionun belirttiği eğrie de parabol denir. Uarı ir parabolün grafiği başkatsaı olan a saısına bağlı
a, b,c R,a 0 olmak koşulula f ()=a 2 +b+c fonksionuna ikinci dereceden bir değişkenli fonksion ve bu fonksionun belirttiği eğrie de parabol denir. Uarı ir parabolün grafiği başkatsaı olan a saısına bağlı
KATI CİSİMLER DİK PRİZMALARIN ALAN VE HACİMLERİ 1. DİKDÖRTGENLER PRİZMASI. Uyarı PRİZMA. Üst taban. Ana doğru. Yanal. Yanal Alan. yüz. Yanal.
 TI İSİM İZM İZM irbirine paralel iki düzlem içinde yer alan iki eş çokgensel bölgenin tüm noktalarının karşılıklı olarak birleştirilmesiyle elde edilen cisme İZM denir. İ İZMIN N V HİMİ Tüm dik rizmalarda
TI İSİM İZM İZM irbirine paralel iki düzlem içinde yer alan iki eş çokgensel bölgenin tüm noktalarının karşılıklı olarak birleştirilmesiyle elde edilen cisme İZM denir. İ İZMIN N V HİMİ Tüm dik rizmalarda
Uzaysal Görüntü İyileştirme/Filtreleme. Doç. Dr. Fevzi Karslı fkarsli@ktu.edu.tr
 Uasal Görüntü İileştirme/Filtreleme Doç. Dr. Fevi Karslı karsli@ktu.edu.tr İileştirme Herhangi bir ugulama için, görüntüü orijinalden daha ugun hale getirmek Ugunluğu her bir ugulama için sağlamak. Bir
Uasal Görüntü İileştirme/Filtreleme Doç. Dr. Fevi Karslı karsli@ktu.edu.tr İileştirme Herhangi bir ugulama için, görüntüü orijinalden daha ugun hale getirmek Ugunluğu her bir ugulama için sağlamak. Bir
MATEMATİK MATEMATİK-GEOMETRİ SINAVI LİSANS YERLEŞTİRME SINAVI-1 TESTİ SORU KİTAPÇIĞI 08
 LİSNS YRLŞTİRM SINVI- MTMTİK-GMTRİ SINVI MTMTİK TSTİ SRU KİTPÇIĞI 08 U SRU KİTPÇIĞI LYS- MTMTİK TSTİ SRULRINI İÇRMKTİR. . u testte 0 soru vardýr. MTMTİK TSTİ. evaplarýnýzý, cevap kâðýdýnın Matematik Testi
LİSNS YRLŞTİRM SINVI- MTMTİK-GMTRİ SINVI MTMTİK TSTİ SRU KİTPÇIĞI 08 U SRU KİTPÇIĞI LYS- MTMTİK TSTİ SRULRINI İÇRMKTİR. . u testte 0 soru vardýr. MTMTİK TSTİ. evaplarýnýzý, cevap kâðýdýnın Matematik Testi
ÜÇ BOYUTLU HALDE GERİLME VE DEFORMASYON
 III- BÖLÜM III 7. Üçgen gerilme hali: ÜÇ BOYUTLU HLD GRİLM V DFORMSYON Sürekli bir ortam içindeki herhangi bir noktadan boutları.. olsun çok küçük bir primatik eleman çıkartalım. Bu elemanın üelerine gelen
III- BÖLÜM III 7. Üçgen gerilme hali: ÜÇ BOYUTLU HLD GRİLM V DFORMSYON Sürekli bir ortam içindeki herhangi bir noktadan boutları.. olsun çok küçük bir primatik eleman çıkartalım. Bu elemanın üelerine gelen
Geometrik şekillerin çizimi
 Geometrik şekillerin çizimi ir doğruya dışındaki P noktasından P geçen paralel doğru çizmek 1. P noktası merkez kabul edilir. yayı kadar açılan pergelle doğrusu kesiştirilerek noktası elde edilir. 3. Pergel
Geometrik şekillerin çizimi ir doğruya dışındaki P noktasından P geçen paralel doğru çizmek 1. P noktası merkez kabul edilir. yayı kadar açılan pergelle doğrusu kesiştirilerek noktası elde edilir. 3. Pergel
12. SINIF GEOMETRİ KONU ÖZETİ
 2012 12. SINIF GEOMETRİ KONU ÖZETİ TOLGA YAVAN Matematik Öğretmeni ÜNİTE 1: UZAYDA VEKTÖRLER Hepsi birden aynı düzlemde olmayan tüm noktaların kümesine uzay denir. Uzayda farklı iki noktadan bir ve yalnız
2012 12. SINIF GEOMETRİ KONU ÖZETİ TOLGA YAVAN Matematik Öğretmeni ÜNİTE 1: UZAYDA VEKTÖRLER Hepsi birden aynı düzlemde olmayan tüm noktaların kümesine uzay denir. Uzayda farklı iki noktadan bir ve yalnız
1. TEMEL ÇİZİMLER. Pergel Yardımıyla Dik Doğru Çizmek. 1. Doğru üzerindeki P noktası merkez olmak üzere çizilen yaylarla D ve G noktaları işaretlenir.
 1. TEMEL ÇİZİMLER Pergel Yardımıyla ik oğru Çizmek 1. oğru üzerindeki P noktası merkez olmak üzere çizilen yaylarla ve G noktaları işaretlenir. 2. ve G merkez olmak üzere doğru dışında kesişecek şekilde
1. TEMEL ÇİZİMLER Pergel Yardımıyla ik oğru Çizmek 1. oğru üzerindeki P noktası merkez olmak üzere çizilen yaylarla ve G noktaları işaretlenir. 2. ve G merkez olmak üzere doğru dışında kesişecek şekilde
8. SINIF MATEMATİK A. 4. Bir basketbol sahasında orta yuvarlak denilen 2 olan dairesel bölgenin
 . (- 3) -2 saısı aşağıdaki saılardan hangisi ile çarpılırsa sonuç 3 olur? 3 3 B) 3 C) 3 2 D) ( ) - 3-3 4. Bir basketbol sahasında orta uvarlak denilen ve alanı 9, 72 m 2 olan dairesel bölgenin çapı kaç
. (- 3) -2 saısı aşağıdaki saılardan hangisi ile çarpılırsa sonuç 3 olur? 3 3 B) 3 C) 3 2 D) ( ) - 3-3 4. Bir basketbol sahasında orta uvarlak denilen ve alanı 9, 72 m 2 olan dairesel bölgenin çapı kaç
NOKTANIN ANALİTİK İNCELEMESİ NOKTANIN ANALİTİK İNCELEMESİ
 NKTANIN ANALİTİK İNCELEMESİ NKTANIN ANALİTİK İNCELEMESİ Başlangıç noktasında birbirine dik olan iki saı doğrusunun oluşturduğu sisteme "Dik Koordinat Sistemi" denir. Dik Koordinat Sisteminin belirttiği
NKTANIN ANALİTİK İNCELEMESİ NKTANIN ANALİTİK İNCELEMESİ Başlangıç noktasında birbirine dik olan iki saı doğrusunun oluşturduğu sisteme "Dik Koordinat Sistemi" denir. Dik Koordinat Sisteminin belirttiği
6. ABCD dikdörtgeninde
 Çokgenler ve örtgenler Test uharrem Şahin. enar sayısı ile köşegen sayısı toplamı olan düzgün çokgenin bir dış açısı kaç derecedir? ) ) 0 ) ) 0 ). Şekilde dikdörtgeninin içindeki P noktasının üç köşeye
Çokgenler ve örtgenler Test uharrem Şahin. enar sayısı ile köşegen sayısı toplamı olan düzgün çokgenin bir dış açısı kaç derecedir? ) ) 0 ) ) 0 ). Şekilde dikdörtgeninin içindeki P noktasının üç köşeye
Çokgenler. Dörtgenler. Çember. Simetri. Örüntü ve Süslemeler. Düzlem. Geometrik Cisimler
 MTEMT K Çokgenler örtgenler Çember Simetri Örüntü ve Süslemeler üzlem Geometrik isimler Temel Kaynak 5 Çokgenler ÇOKGENLER E F En az üç do ru parças n n, birer uçlar ortak olacak flekilde ard fl k olarak
MTEMT K Çokgenler örtgenler Çember Simetri Örüntü ve Süslemeler üzlem Geometrik isimler Temel Kaynak 5 Çokgenler ÇOKGENLER E F En az üç do ru parças n n, birer uçlar ortak olacak flekilde ard fl k olarak
TASARI GEOMETRİ SINAV SORULARI
 TASARI GEOMETRİ SINAV SORULARI 1. Alın iz düşümüne parelel veya çakışık olan doğrular profilde hangi ı verir? 9. Doğrunun düzlemi deldiği noktayı düzlem geçirme metodu ile bulunuz. A) Profil ve alınla
TASARI GEOMETRİ SINAV SORULARI 1. Alın iz düşümüne parelel veya çakışık olan doğrular profilde hangi ı verir? 9. Doğrunun düzlemi deldiği noktayı düzlem geçirme metodu ile bulunuz. A) Profil ve alınla
Açıların Özellikleri ve Ölçü Birimleri
 çıların Özellikleri ve Ölçü irimleri 1. ÜNİT ÇIRIN ÖZİRİ V ÖÇÜ İRİRİ çı; aynı başlangıç noktasından çıkan iki ışının oluşturduğu geometrik şekildir. [O ve [O ışınlarına açının kenarları denir. O noktası
çıların Özellikleri ve Ölçü irimleri 1. ÜNİT ÇIRIN ÖZİRİ V ÖÇÜ İRİRİ çı; aynı başlangıç noktasından çıkan iki ışının oluşturduğu geometrik şekildir. [O ve [O ışınlarına açının kenarları denir. O noktası
VEKTÖRLER KT YRD.DOÇ.DR. KAMİLE TOSUN FELEKOĞLU
 VEKTÖRLER KT YRD.DOÇ.DR. KMİLE TOSUN ELEKOĞLU 1 Mekanik olaları ölçmekte a da değerlendirmekte kullanılan matematiksel büüklükler: Skaler büüklük: sadece bir saısal değeri tanımlamakta kullanılır, pozitif
VEKTÖRLER KT YRD.DOÇ.DR. KMİLE TOSUN ELEKOĞLU 1 Mekanik olaları ölçmekte a da değerlendirmekte kullanılan matematiksel büüklükler: Skaler büüklük: sadece bir saısal değeri tanımlamakta kullanılır, pozitif
İZDÜŞÜM PRENSİPLERİ 8X M A 0.14 M A C M 0.06 A X 45. M42 X 1.5-6g 0.1 M B M
 0.08 M A 8X 7.9-8.1 0.1 M B M M42 X 1.5-6g 0.06 A 6.6 6.1 9.6 9.4 C 8X 45 0.14 M A C M 86 20.00-20.13 İZDÜŞÜM C A 0.14 B PRENSİPLERİ 44.60 44.45 B 31.8 31.6 0.1 9.6 9.4 25.5 25.4 36 Prof. Dr. 34 Selim
0.08 M A 8X 7.9-8.1 0.1 M B M M42 X 1.5-6g 0.06 A 6.6 6.1 9.6 9.4 C 8X 45 0.14 M A C M 86 20.00-20.13 İZDÜŞÜM C A 0.14 B PRENSİPLERİ 44.60 44.45 B 31.8 31.6 0.1 9.6 9.4 25.5 25.4 36 Prof. Dr. 34 Selim
3. Ünsal Tülbentçi Matematik Yarışması Mayıs 2014 8.Sınıf Sayfa 1
 . Alanı 36 5 olan bir ABC ikizkenar üçgeninde ==2 ise bu üçgende B den AC ye inilen dikmenin ayağının C noktasına olan uzaklığı nedir? ) 2,8) 3) 3,2 ) 3,7 ) 4, 2. Ayrıt uzunlukları 4, 0 ve 4 5 olan dikdörtgenler
. Alanı 36 5 olan bir ABC ikizkenar üçgeninde ==2 ise bu üçgende B den AC ye inilen dikmenin ayağının C noktasına olan uzaklığı nedir? ) 2,8) 3) 3,2 ) 3,7 ) 4, 2. Ayrıt uzunlukları 4, 0 ve 4 5 olan dikdörtgenler
ÜNİTELENDİRME ŞEMASI
 LENDİRME ŞEMASI ÜNİTE DOĞRULAR VE AÇILAR. Aynı düzlemde olan üç doğrunun birbirine göre durumlarını belirler ve inşa eder.. Paralel iki doğrunun bir kesenle yaptığı açıların eş olanlarını ve bütünler olanlarını
LENDİRME ŞEMASI ÜNİTE DOĞRULAR VE AÇILAR. Aynı düzlemde olan üç doğrunun birbirine göre durumlarını belirler ve inşa eder.. Paralel iki doğrunun bir kesenle yaptığı açıların eş olanlarını ve bütünler olanlarını
Fonksiyonlar ve Grafikleri
 Fonksionlar ve Grafikleri Isınma Hareketleri Aşağıda verilenleri inceleiniz. A f f(a) 7 f: Çocukları annelerine götürüor. Fonksion olma şartı: Her çocuğun annesi olmalı ve bir tane olmalı. ( çocuk annenin
Fonksionlar ve Grafikleri Isınma Hareketleri Aşağıda verilenleri inceleiniz. A f f(a) 7 f: Çocukları annelerine götürüor. Fonksion olma şartı: Her çocuğun annesi olmalı ve bir tane olmalı. ( çocuk annenin
Görünüş çıkarmak için, cisimlerin özelliğine göre belirli kurallar uygulanır.
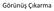 Görünüş Çıkarma Görünüş çıkarma? Parçanın bitmiş halini gösteren eşlenik dik iz düşüm kurallarına göre belirli yerlerde, konumlarda ve yeterli sayıda çizilmiş iz düşümlere GÖRÜNÜŞ denir. Görünüş çıkarmak
Görünüş Çıkarma Görünüş çıkarma? Parçanın bitmiş halini gösteren eşlenik dik iz düşüm kurallarına göre belirli yerlerde, konumlarda ve yeterli sayıda çizilmiş iz düşümlere GÖRÜNÜŞ denir. Görünüş çıkarmak
TEST. Doğrusal Denklemler kg domates ile 2 kg salça yapılmaktadır. 2. Aşağıda verilen, 5. Cebinde 50 si bulunan Nehir babasından her
 Doğrusal Denklemler 7. Sınıf Matematik Soru Bankası TEST. t Zaman (sn) 0 0 0 0 Yol (m) 0 00 0 00 Yukarıdaki tabloda bir koşucunun metre cinsinden aldığı ol ile sanie cinsinden harcadığı zaman verilmiştir.
Doğrusal Denklemler 7. Sınıf Matematik Soru Bankası TEST. t Zaman (sn) 0 0 0 0 Yol (m) 0 00 0 00 Yukarıdaki tabloda bir koşucunun metre cinsinden aldığı ol ile sanie cinsinden harcadığı zaman verilmiştir.
10. SINIF. Sayma TEST. 1. Bir otobüse binen 3 yolcu yan yana duran 4 boş koltuğa kaç farklı şekilde oturabilirler?
 SINI Sama. ir otobüse binen olcu an ana duran boş koltuğa kaç farklı şekilde oturabilirler? ) ) ) 8 ) 6 ) 8 KZNI KVR. = #,,,,, - kümesinin elemanları kullanılarak basamaklı rakamları birbirinden farklı
SINI Sama. ir otobüse binen olcu an ana duran boş koltuğa kaç farklı şekilde oturabilirler? ) ) ) 8 ) 6 ) 8 KZNI KVR. = #,,,,, - kümesinin elemanları kullanılarak basamaklı rakamları birbirinden farklı
LYS GENEL KATILIMLI TÜRKİYE GENELİ ONLİNE DENEME SINAVI
 LYS GNL KTILIMLI TÜRKİY GNLİ NLİN NM SINVI GMTRİ (M-TM) 1. u testte Geometri ile ilgili 30 soru vardır.. evaplarınızı, cevap kâğıdının Geometri Testi için arılan kısmına işaretleiniz. 3. u test için süreniz
LYS GNL KTILIMLI TÜRKİY GNLİ NLİN NM SINVI GMTRİ (M-TM) 1. u testte Geometri ile ilgili 30 soru vardır.. evaplarınızı, cevap kâğıdının Geometri Testi için arılan kısmına işaretleiniz. 3. u test için süreniz
İÇİNDEKİLER UZAY AKSİYOMLARI... 001-006... 01-03 UZAYDA DOGRU VE DÜZLEMLER... 007-010... 04-05 DİK İZDÜŞÜM... 011-014... 06-07
 UZY GEMETRİ İÇİNDEKİLER Safa No Test No UZY KSİYMLRI... 001-00... 01-0 UZYD DGRU VE DÜZLEMLER... 007-010... 0-05 DİK İZDÜŞÜM... 011-01... 0-07 PRİZMLR... 015-0... 08-1 KÜP... 05-00... 1-15 SİLİNDİR...
UZY GEMETRİ İÇİNDEKİLER Safa No Test No UZY KSİYMLRI... 001-00... 01-0 UZYD DGRU VE DÜZLEMLER... 007-010... 0-05 DİK İZDÜŞÜM... 011-01... 0-07 PRİZMLR... 015-0... 08-1 KÜP... 05-00... 1-15 SİLİNDİR...
10. ÜNİTE HACİM VE SIVI ÖLÇÜLERİ, KATI CİSİMLERİN ALAN VE HACİMLERİ MESLEKİ UYGULAMALARI
 10. ÜNİTE HACİM VE SIVI ÖLÇÜLERİ, KATI CİSİMLERİN ALAN VE HACİMLERİ MESLEKİ UYGULAMALARI KONULAR HACİM VE HACİM ÖLÇÜLERİ KAVRAMI HACİM ÖLÇÜLERİ BİRİMLERİ 1. Metreküpün Katları As Katları 2. Birimlerin
10. ÜNİTE HACİM VE SIVI ÖLÇÜLERİ, KATI CİSİMLERİN ALAN VE HACİMLERİ MESLEKİ UYGULAMALARI KONULAR HACİM VE HACİM ÖLÇÜLERİ KAVRAMI HACİM ÖLÇÜLERİ BİRİMLERİ 1. Metreküpün Katları As Katları 2. Birimlerin
Geometrik Cisimler ve Şekiller. Uzamsal İlişkiler Geometrik Örüntüler. Geometrik Şekiller Geometrik Cisimler. Uzamsal İlişkiler Geometrik Örüntüler
 ? Geometrik Cisimler ve Şekiller Uzamsal İlişkiler Geometrik Örüntüler Geometrik Şekiller Geometrik Cisimler Uzamsal İlişkiler Geometrik Örüntüler SınıfMatematik Matematik 2. 2.Sınıf 11 Geometrik Şekiller
? Geometrik Cisimler ve Şekiller Uzamsal İlişkiler Geometrik Örüntüler Geometrik Şekiller Geometrik Cisimler Uzamsal İlişkiler Geometrik Örüntüler SınıfMatematik Matematik 2. 2.Sınıf 11 Geometrik Şekiller
ÖZEL EGE LİSESİ OKULLAR ARASI 12.MATEMATİK YARIŞMASI 8. SINIF FİNAL SORULARI Dikkat: Yanıtlarınızı size verilen yanıt kağıtlarına yazınız.
 OKULLAR ARASI 1.MATEMATİK YARIŞMASI 8. SINIF FİNAL SORULARI Dikkat: Yanıtlarınızı size verilen anıt kağıtlarına azınız. 1) Yukarıdaki şekilde AH BC BE DE m (BÂH) = m(aĉb) AH = BE BD = DC ve m (CBE) = dir.
OKULLAR ARASI 1.MATEMATİK YARIŞMASI 8. SINIF FİNAL SORULARI Dikkat: Yanıtlarınızı size verilen anıt kağıtlarına azınız. 1) Yukarıdaki şekilde AH BC BE DE m (BÂH) = m(aĉb) AH = BE BD = DC ve m (CBE) = dir.
- 2-1 0 1 2 + 4a a 0 a 4a
 İKİNCİ DERECEDEN FNKSİYNLARIN GRAFİKLERİ a,b,c,z R ve a 0 olmak üzere, F : R R f() = a + b + c şeklinde tanımlanan fonksionlara ikinci dereceden bir değişkenli fonksionlar denir. Bu tür fonksionların grafikleri
İKİNCİ DERECEDEN FNKSİYNLARIN GRAFİKLERİ a,b,c,z R ve a 0 olmak üzere, F : R R f() = a + b + c şeklinde tanımlanan fonksionlara ikinci dereceden bir değişkenli fonksionlar denir. Bu tür fonksionların grafikleri
PİRAMİTLER ENFORMATİK BİLGİSAYAR DERSİ
 2011 PİRAMİTLER ENFORMATİK BİLGİSAYAR DERSİ 15.12.2011 ĠÇĠNDEKĠLER ÜNİTE HAKKINDA GENEL BİLGİ... 3 KONULAR... 4 PİRAMİTLER... 4 KARE PİRAMİT... 5 EŞKENAR ÜÇGEN PİRAMİT... 6 DÜZGÜN DÖRTYÜZLÜ... 6 DÜZGÜN
2011 PİRAMİTLER ENFORMATİK BİLGİSAYAR DERSİ 15.12.2011 ĠÇĠNDEKĠLER ÜNİTE HAKKINDA GENEL BİLGİ... 3 KONULAR... 4 PİRAMİTLER... 4 KARE PİRAMİT... 5 EŞKENAR ÜÇGEN PİRAMİT... 6 DÜZGÜN DÖRTYÜZLÜ... 6 DÜZGÜN
Mustafa YAĞCI, yagcimustafa@yahoo.com Parabol Denkleminin Yazılması
 www.mustafaagci.com.tr, 11 Cebir Notları Mustafa YAĞCI, agcimustafa@ahoo.com Parabol Denkleminin Yazılması B ir doğru kaç noktasıla bellidi? İki, değil mi Çünkü tek bir noktadan geçen istediğimiz kadar
www.mustafaagci.com.tr, 11 Cebir Notları Mustafa YAĞCI, agcimustafa@ahoo.com Parabol Denkleminin Yazılması B ir doğru kaç noktasıla bellidi? İki, değil mi Çünkü tek bir noktadan geçen istediğimiz kadar
MATEMATİK 2+2 UYGULAMALI ÖĞRENME SETİ. Her Haftaya Bir Bölüm ÇEK KOPAR SINIF
 MATEMATİK 2 SINIF UYGULAMALI ÖĞRENME SETİ ÇEK KOPAR 10 9 11 12 1 2 3 2+2 Her Haftaya Bir Bölüm 8 4 Copyright Şifre Yayıncılık ve Eğitim Gereçleri Tic. A.Ş. Bu kitabın her hakkı Şifre Yayıncılık ve Eğitim
MATEMATİK 2 SINIF UYGULAMALI ÖĞRENME SETİ ÇEK KOPAR 10 9 11 12 1 2 3 2+2 Her Haftaya Bir Bölüm 8 4 Copyright Şifre Yayıncılık ve Eğitim Gereçleri Tic. A.Ş. Bu kitabın her hakkı Şifre Yayıncılık ve Eğitim
GAZİ ÜNİVERSİTESİ TEKNİK EĞİTİM FAKÜLTESİ ÖĞRENCİNİN
 GAZİ ÜNİVERSİTESİ TEKNİK EĞİTİM FAKÜLTESİ ÖĞRENCİNİN ADI SOYADI : YILMAZ YILMAZTÜRK NO : 041227063 ÖĞRETİM YILI : 2007 2008 BÖLÜMÜ : MAKĠNE EĞĠTĠMĠ PROGRAMI : MAKĠNE RESĠM ve KONST. ÖĞRETMENLĠĞĠ YÖNETİCİ
GAZİ ÜNİVERSİTESİ TEKNİK EĞİTİM FAKÜLTESİ ÖĞRENCİNİN ADI SOYADI : YILMAZ YILMAZTÜRK NO : 041227063 ÖĞRETİM YILI : 2007 2008 BÖLÜMÜ : MAKĠNE EĞĠTĠMĠ PROGRAMI : MAKĠNE RESĠM ve KONST. ÖĞRETMENLĠĞĠ YÖNETİCİ
STATICS. Equivalent Systems of Forces VECTOR MECHANICS FOR ENGINEERS: Seventh Edition CHAPTER. Ferdinand P. Beer E. Russell Johnston, Jr.
 Seventh E 3 Rigid CHAPTER VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Lecture Notes: J. Walt Oler Teas Tech Universit Bodies: Equivalent Sstems of Forces Seventh
Seventh E 3 Rigid CHAPTER VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Lecture Notes: J. Walt Oler Teas Tech Universit Bodies: Equivalent Sstems of Forces Seventh
Karabük Üniversitesi, Mühendislik Fakültesi...www.IbrahimCayiroglu.com. STATİK (2. Hafta)
 AĞIRLIK MERKEZİ STATİK (2. Hafta) Ağırlık merkezi: Bir cismi oluşturan herbir parçaya etki eden yerçeki kuvvetlerinin bileşkesinin cismin üzerinden geçtiği noktaya Ağırlık Merkezi denir. Şekil. Ağırlık
AĞIRLIK MERKEZİ STATİK (2. Hafta) Ağırlık merkezi: Bir cismi oluşturan herbir parçaya etki eden yerçeki kuvvetlerinin bileşkesinin cismin üzerinden geçtiği noktaya Ağırlık Merkezi denir. Şekil. Ağırlık
8. SINIF YARIYIL ÇALIŞMA TESTİ TEST 1 ( ) TEKRAR EDEN YANSIYAN ve DÖNEN ŞEKİLLER HİSTOGRAM STANDART SAPMA
 8. SINIF YARIYIL ÇALIŞMA TESTİ TEKRAR EDEN YANSIYAN ve DÖNEN ŞEKİLLER HİSTOGRAM STANDART SAPMA TEST 1 (11-1) 1. I. Geometrik fraktal kendini giderek küçülen veya büyüyen boyutta yineler. II. Fraktalın
8. SINIF YARIYIL ÇALIŞMA TESTİ TEKRAR EDEN YANSIYAN ve DÖNEN ŞEKİLLER HİSTOGRAM STANDART SAPMA TEST 1 (11-1) 1. I. Geometrik fraktal kendini giderek küçülen veya büyüyen boyutta yineler. II. Fraktalın
Yukar daki kare ve dikdörtgene göre eflitlikleri tan mlay n z. AB =... =... =... =...
 Üçgen, Kare ve ikdörtgen MTEMT K KRE VE KÖRTGEN Kare ve ikdörtgenin Özellikleri F E Kare ve dikdörtgenin her kenar uzunlu u birer do ru parças d r. Kare ve dikdörtgenin kenar, köfle ve aç say lar eflittir.
Üçgen, Kare ve ikdörtgen MTEMT K KRE VE KÖRTGEN Kare ve ikdörtgenin Özellikleri F E Kare ve dikdörtgenin her kenar uzunlu u birer do ru parças d r. Kare ve dikdörtgenin kenar, köfle ve aç say lar eflittir.
Fonksiyonlar ve Grafikleri
 Fonksionlar ve Grafikleri Isınma Hareketleri Aşağıda verilenleri inceleiniz. A f f(a) 7 çocuk baan f: Çocukları annelerine götürüor. Fonksion olma şartı: Her çocuğun annesi olmalı ve bir tane olmalı. (
Fonksionlar ve Grafikleri Isınma Hareketleri Aşağıda verilenleri inceleiniz. A f f(a) 7 çocuk baan f: Çocukları annelerine götürüor. Fonksion olma şartı: Her çocuğun annesi olmalı ve bir tane olmalı. (
2012 YGS MATEMATİK Soruları
 01 YGS MATEMATİK Soruları 1. 10, 1, 0, 0, işleminin sonucu kaçtır? A) B), C) 6 D) 6, E) 7. + ABC 4 x 864 Yukarıda verilenlere göre, çarpma işleminin sonucu kaçtır? A) 8974 B) 907 C) 9164 D) 94 E) 98. 6
01 YGS MATEMATİK Soruları 1. 10, 1, 0, 0, işleminin sonucu kaçtır? A) B), C) 6 D) 6, E) 7. + ABC 4 x 864 Yukarıda verilenlere göre, çarpma işleminin sonucu kaçtır? A) 8974 B) 907 C) 9164 D) 94 E) 98. 6
Dik İzdüşüm Teorisi. Prof. Dr. Muammer Nalbant. Muammer Nalbant
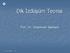 Dik İzdüşüm Teorisi Prof. Dr. Muammer Nalbant Muammer Nalbant 2017 1 Dik İzdüşüm Terminolojisi Bakış Noktası- 3 boyutlu uzayda bakılan nesneden sonsuz uzaktaki herhangi bir yer. Bakış Hattı- gözlemcinin
Dik İzdüşüm Teorisi Prof. Dr. Muammer Nalbant Muammer Nalbant 2017 1 Dik İzdüşüm Terminolojisi Bakış Noktası- 3 boyutlu uzayda bakılan nesneden sonsuz uzaktaki herhangi bir yer. Bakış Hattı- gözlemcinin
T.C. Ölçme, Seçme ve Yerleştirme Merkezi
 T.C. Ölçme, Seçme ve Yerleştirme Merkezi LİSANS YERLEŞTİRME SINAVI-1 GEOMETRİ TESTİ 19 HAZİRAN 2016 PAZAR Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının veya bir kısmının
T.C. Ölçme, Seçme ve Yerleştirme Merkezi LİSANS YERLEŞTİRME SINAVI-1 GEOMETRİ TESTİ 19 HAZİRAN 2016 PAZAR Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının veya bir kısmının
Y ll k Plan MATEMAT K 8. SINIF Ö RETMEN KILAVUZ K TABI
 ÜNİTELENDİRİLMİŞ YILLIK PLAN MATEMAT K 8. SINIF Ö RETMEN KILAVUZ K TABI 9 SINIF : 8 LEND R LM fi Y I L L I K P L A N ÖRÜNTÜ VE SÜSLEMELER. Do ru, çokgen ve çember modellerinden örüntüler infla eder, çizer
ÜNİTELENDİRİLMİŞ YILLIK PLAN MATEMAT K 8. SINIF Ö RETMEN KILAVUZ K TABI 9 SINIF : 8 LEND R LM fi Y I L L I K P L A N ÖRÜNTÜ VE SÜSLEMELER. Do ru, çokgen ve çember modellerinden örüntüler infla eder, çizer
TEST: 6. Verilenlere göre EF =? A) 1 B) 2 C) 3 D) 4 E) 5 A) 7 B) 8 C) 10 D) 11 E) 12. x eksenini 5 te, y eksenini 7 de kesen doğrunun denklemi
 TEST: 6 5. 1. Verilenlere göre EF =? A) 1 B) 2 C) 3 D) 4 E) 5 A) 7 B) 8 C) 10 D) 11 E) 12 2. 6. x eksenini 5 te, y eksenini 7 de kesen doğrunun denklemi aşağıdakilerden hangisidir? A) 7x+5y=35 B) 7x-5y=35
TEST: 6 5. 1. Verilenlere göre EF =? A) 1 B) 2 C) 3 D) 4 E) 5 A) 7 B) 8 C) 10 D) 11 E) 12 2. 6. x eksenini 5 te, y eksenini 7 de kesen doğrunun denklemi aşağıdakilerden hangisidir? A) 7x+5y=35 B) 7x-5y=35
I 5. SINIF ÖĞRENME ALANI ALT ÖĞRENME ALANI KAZANIM I- 01 I- 02 II- 01 II- 02 II- 03
 I 5. SINIF MATEMATİK VE İŞLEMLER 1.1. En çok dokuz basamaklı doğal sayıları okur ve yazar. 1.2. En çok dokuz basamaklı doğal sayıların bölüklerini, basamaklarını ve rakamların basamak değerlerini belirtir.
I 5. SINIF MATEMATİK VE İŞLEMLER 1.1. En çok dokuz basamaklı doğal sayıları okur ve yazar. 1.2. En çok dokuz basamaklı doğal sayıların bölüklerini, basamaklarını ve rakamların basamak değerlerini belirtir.
1997 ÖSS Soruları. 5. Rakamları birbirinden farklı olan üç basamaklı en büyük doğal sayı aşağıdakilerden hangisi ile kalansız bölünebilir?
 997 ÖSS Soruları. ( ) + ( ).( ) işleminin sonucu kaçtır? ) ) ) ) 8 6 ) 6. Rakamları birbirinden farklı olan üç basamaklı en büük doğal saı aşağıdakilerden hangisi ile kalansız bölünebilir? ) ) 9 ) 6 )
997 ÖSS Soruları. ( ) + ( ).( ) işleminin sonucu kaçtır? ) ) ) ) 8 6 ) 6. Rakamları birbirinden farklı olan üç basamaklı en büük doğal saı aşağıdakilerden hangisi ile kalansız bölünebilir? ) ) 9 ) 6 )
