Otomatik Kontrol. Fiziksel Sistemlerin Modellenmesi. Prof.Dr.Galip Cansever. Dişli Takımları Elektromekaniksel Sistemler. Ders #5
|
|
|
- Asli Coşkun
- 6 yıl önce
- İzleme sayısı:
Transkript
1 Dr #5 Ooik onrol Fizikl Silrin Modllni Dişli Tkılrı Elkroknikl Silr Prof.Dr.Glip Cnvr 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr
2 Mknikl Silrin Trnfr Fonkiyonlrı Dişli Tkılrı Vili biikllri düşünli. Yokuş çıkrkn dh fzl ork vrn v dh yvş gidcğiiz vi gçirilir. Düz yold i dh z ork v dh hzl hız ypılbiln vi gçirilir. ıc, dişli kılrı biikl v yolu hız v orkn birini rcih dilrk şlşirir. Hr bir dişli çvrind lınn yol şi olduğundn: r θ r θ 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr
3 θ θ r r İki dişlinin çıl yr dğişirlri diş yılrı il r ornılıdır. Torklr rındki ilişki nıl? Eğr dişlilrin nrjiyi borb diğini v dpoldığını vryck olurk:. dişliy vriln nrji,. dişlidn lınn nrjiy şiir. Eğr dişlilrin nrjiyi borb diğini v dpoldığını vryck olurk:. dişliy vriln nrji,. dişlidn lınn nrjiy şiir. T θ T θ 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr 3
4 T T θ θ 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr 4
5 Dişlilrin knikl pdnlrı üri duruund: θ dki dişli kıız şdğr dvr: 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr 5
6 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr 6 Hrk dnkli: T D θ θ yi şdğr θ cinindn yzck olurk: T D θ Düznldiğiizd: T D θ
7 Dirl knikl pdnlr yukrıdki şkildki gibi dişli ornlrının kriy ornılı olrk diğr rf indirgnbilir. Aynı rnforörlrdki pdnlrın indirgni gibi. 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr 7
8 Örnk: Siin, θ /T rnfr fonkiyonunu yzınız. Hr bir l için ırıyl çözüli grkn iki difrniyl dnkl ollı gibi görün d, l lnlrı dişli kındn dolyı linr birbirindn bğıız hrk dzlr. Bu bpl iin rblik drci birdir v bir n hrk dnkli vrdır. 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr 8
9 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr 9, D v T i dişlinin diğr rfın indirgyck olurk T D θ D T G θ
10 Dişli rni olı duruund: 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr 0
11 Örnk: Siin, θ /T rnfr fonkiyonunu yzınız. 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr
12 Sidki dişli rninin dişlilri kyıpız dişlilr dğil. Hr birinin l v vizkoz ürüni vr. Trnfr fonkiyonunu ld k için büün pdnlrı giriş şf ın indirgyli. Dikk dilck olur büün pdnlr için dişli ornı ynı dğildir. Örnğin; D, / il indirgnirkn İl indirgnckir. Tü şdğr i: 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr
13 G θ T 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr D θ T D 3
14 Elkroknikl Silrin Trnfr Fonkiyonlrı ASA uçuş iülörü, robo kolun kullnıldığı bir lkro knik i 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr 4
15 Moorlr lkroknik ilr n güzl örnkir. Grili girişi çıkış döny bir yr dğişiry bbiy vrir. Sbi ıknılı bir DC oor v rnfr fonkiyonu 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr 5
16 DC kinnın nyik lnı bi ıknılr rındn ürilkdir. Dönn, hrkli pç ndüvi il dlndırılır v içindn i kıı kr. Mnyik ln içind bulunn v içindn kı kn ndüvi FBl i kuvvin ruz klır v dönr. Mnyik ln içind bulunn v dönn ndüvi uçlrınd Blv Grilii ndüklnir, bu grili r lkrooor kuvvi dı vrilir. v b dθ d Lpl dönüşüü ypığıızd: V θ Endüvi dvr dnkli i: b R I LI V E Moorun üriği ork : T I 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr 6
17 I T Trnfr fonkiyonunu ld k üzr kı v grilii yrin yzlı; R L T bθ E Giriş v çıkış rındki rnfr fonkiyonu, θ /E, bulbilk için T yi θ cinindn yzlıyız. X Biri yükü döndürn oorun ipik şdğri ndüvidki şdğr l, dh onr bu ş dğr lin yük linid içrdiğini görcğiz. D ndüvidki şdğr önü lnı, dh onr bu ş dğr önü lnının yük önü lnını d içrdiğini görcğiz. 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr 7
18 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr 8 D T θ E D L R b θ θ X İfdini d yrin yzck olurk; Endüvi ndüknı, L yı, ndüvi dirnci, R, y gör küçük olduğunu vryrk; E D R b θ b R D R E θ α θ E Dh biç;
19 Eşdğr lnlr, v D yi inclyli; Sırıyl,D oorun L,D L yükün l v önü lnlrı v bu dğrlri bildiğiizi vrylı. Dişli kıını göz önünd bulundurrk ndüviy indirgnn şdğr l v önü lnı; L D D D L 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr 9
20 Mknikl bilri incldik şidi rnfr fonkiyonundki lkrikl bilri nıl ld dcğiizi inclyli: Elkril bilr, çoğu zn dinor i il ld dilirlr. Dinoor ind i grili lınd oorun ork v hızı ölçülür. Bu i nly çlışlı: R L T bθ E olrk ld dilişi, ndüvi ndüknı, L yı, ndüvi dirnci, R, y gör küçük olduğunu vryrk; R θ T bω ω d rrlı hld bi dc grilid; R T ω b 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr 0
21 b T ω R R ω 0 i; T 0 i; ω T ll bo R b Elkrikl kyılr: R T ll b ω bo 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr
22 Örnk: Yukrd vriln dc oorun ork-hız krkriiği yndki gibidir. Bu oorun θ L /E rnfr fonkiyonunu ld diniz. 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr
23 L R T ll D D D L b ω bo θ E / /0 olduğundn, θ L E Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr 3
DENEY 10 PM DC Servo Motor Karakteristikleri
 DNY 0 PM DC Srvo Moor rkrklr DNYİN AMACI. PM DC rvo oorlrın krkrk prrlrn nlk.. PM DC rvo oorlrın krkrk prrlrn ölçk. GİİŞ Dc rvo oor, konrol lr çlışlrınd, konrol orn uygun olrk konrol yönlr glşrk çn, konrol
DNY 0 PM DC Srvo Moor rkrklr DNYİN AMACI. PM DC rvo oorlrın krkrk prrlrn nlk.. PM DC rvo oorlrın krkrk prrlrn ölçk. GİİŞ Dc rvo oor, konrol lr çlışlrınd, konrol orn uygun olrk konrol yönlr glşrk çn, konrol
formundadır. Burada verilen bir f fonksiyonu F fonksiyonuna dönüşür ve F fonksiyonuna f in fonksiyon dönüşümü denir. K(s,t) ye çekirdek denir.
 LPLCE DÖNÜŞÜMÜ Lpl dönüşümü yrdımı il ğ rflı difrniyl dnklmin ğ rfınd bulunn fonkiyonun ürkliliği bozul bil(bmk,impul fonkiyonu) difrniyl dnklmlr çözülbilkir. Bu ip dnklmlrl lkrik imlrini çözrkn krşılşılır.
LPLCE DÖNÜŞÜMÜ Lpl dönüşümü yrdımı il ğ rflı difrniyl dnklmin ğ rfınd bulunn fonkiyonun ürkliliği bozul bil(bmk,impul fonkiyonu) difrniyl dnklmlr çözülbilkir. Bu ip dnklmlrl lkrik imlrini çözrkn krşılşılır.
LOGARİTMA. Örnek: çizelim. Çözüm: f (x) a biçiminde tanımlanan fonksiyona üstel. aşağıda verilmiştir.
 LOGARİTMA I. Üstl Fonksiyonlr v Logritmik Fonksiyonlr şitliğini sğlyn dğrini bulmk için ypıln işlm üs lm işlmi dnir. ( =... = 8) y şitliğini sğlyn y dğrini bulmk için ypıln işlm üslü dnklmi çözm dnir.
LOGARİTMA I. Üstl Fonksiyonlr v Logritmik Fonksiyonlr şitliğini sğlyn dğrini bulmk için ypıln işlm üs lm işlmi dnir. ( =... = 8) y şitliğini sğlyn y dğrini bulmk için ypıln işlm üslü dnklmi çözm dnir.
Critical Firing Angle Determining for DC Motor Drive Fed by Controlled Rectifier by Using Neural Networks
 Dnili Doğruluu il Blnn DA Moor İçin Kriik Tikl Açıının Ypy Sinir Ağı Kullnılrk Blirlni Criil Firing Angl Drining for DC Moor Driv Fd y Conrolld ifir y Uing Nurl Nwork M. Zki BİGİN Aluğ NGİN Mühndilik Fküli,
Dnili Doğruluu il Blnn DA Moor İçin Kriik Tikl Açıının Ypy Sinir Ağı Kullnılrk Blirlni Criil Firing Angl Drining for DC Moor Driv Fd y Conrolld ifir y Uing Nurl Nwork M. Zki BİGİN Aluğ NGİN Mühndilik Fküli,
2005 ÖSS BASIN KOPYASI SAYISAL BÖLÜM BU BÖLÜMDE CEVAPLAYACAĞINIZ TOPLAM SORU SAYISI 90 DIR. Matematiksel İlişkilerden Yararlanma Gücü,
 005 ÖSS SIN KPYSI SYISL ÖLÜM İKKT! U ÖLÜME EVPLYĞINIZ TPLM SRU SYISI 90 IR. İlk 45 Soru Son 45 Soru Mtemtiksel İlişkilerden Yrrlnm Gücü, Fen ilimlerindeki Temel Kvrm ve İlkelerle üşünme Gücü ile ilgilidir.
005 ÖSS SIN KPYSI SYISL ÖLÜM İKKT! U ÖLÜME EVPLYĞINIZ TPLM SRU SYISI 90 IR. İlk 45 Soru Son 45 Soru Mtemtiksel İlişkilerden Yrrlnm Gücü, Fen ilimlerindeki Temel Kvrm ve İlkelerle üşünme Gücü ile ilgilidir.
2.3 Ötelemeli Mekanik Sistemlerin Transfer Fonksiyonları
 Bölü : Frekn-doeninde Modellee yf 4. Öteleeli Meknik Sitelerin rnfer Fonkiyonlrı Meknik itelerin dvrnışlrı kütle, yy ve vikoz ürtüne ile odelleneilir. ütle ve yy, elektrik devrelerindeki kondntör ve endüktör
Bölü : Frekn-doeninde Modellee yf 4. Öteleeli Meknik Sitelerin rnfer Fonkiyonlrı Meknik itelerin dvrnışlrı kütle, yy ve vikoz ürtüne ile odelleneilir. ütle ve yy, elektrik devrelerindeki kondntör ve endüktör
Magnetic Materials. 4. Ders: Paramanyetizma-2. Numan Akdoğan.
 Mgntic Mtrils 4. Drs: Prmnytizm-2 Numn Akdoğn kdogn@gyt.du.tr Gbz Institut of Tchnology Dprtmnt of Physics Nnomgntism nd Spintronic Rsrch Cntr (NASAM) Kuntum mkniği klsik torinin özlliklrini dğiştirmdn,
Mgntic Mtrils 4. Drs: Prmnytizm-2 Numn Akdoğn kdogn@gyt.du.tr Gbz Institut of Tchnology Dprtmnt of Physics Nnomgntism nd Spintronic Rsrch Cntr (NASAM) Kuntum mkniği klsik torinin özlliklrini dğiştirmdn,
BÖLÜM 7. Sürekli hal hatalarının değerlendirilmesinde kullanılan test dalga şekilleri: Dalga Şekli Giriş Fiziksel karşılığı. Sabit Konum.
 9 BÖLÜM 7 SÜRELİ HAL HATALARI ontrol itmlrinin analizind v dizaynında üç özlliğ odaklanılır, bunlar ; ) İtniln bir gçici hal cvabı ürtmk. ( T, %OS, ζ, ω n, ) ) ararlı olmaı. ıaca kutupların diky knin olunda
9 BÖLÜM 7 SÜRELİ HAL HATALARI ontrol itmlrinin analizind v dizaynında üç özlliğ odaklanılır, bunlar ; ) İtniln bir gçici hal cvabı ürtmk. ( T, %OS, ζ, ω n, ) ) ararlı olmaı. ıaca kutupların diky knin olunda
UFUK ÖZERMAN- 2012-2013 Page 1
 - GÜZ P,Q,R fokiolrı poliom olmk üzr d d P Q R d d v P d d Q d P d R P p q dklmi içi P şrıı ğl = okı di ok dir, çözümlri di okıı civrıd şklid rrız. =+-+- +... = = okı; p=q/ P, q= R/ P fokiolrı okıd liik
- GÜZ P,Q,R fokiolrı poliom olmk üzr d d P Q R d d v P d d Q d P d R P p q dklmi içi P şrıı ğl = okı di ok dir, çözümlri di okıı civrıd şklid rrız. =+-+- +... = = okı; p=q/ P, q= R/ P fokiolrı okıd liik
Sistem Dinamiği ve Modellemesi. Doğrusal Sistemlerin Sınıflandırılması Doğrusal Sistemlerin Zaman Davranışı
 Sim Dinmiği v Modllmi Doğrul Simlrin Sınıflndırılmı Doğrul Simlrin Zmn Dvrnışı Giriş: Sim dinmiği çözümlmind, frklı fizikl özlliklr şıyn doğrul imlrin krkriiklrini blirlyn ml bğınılr rınd bnzrlik noloji
Sim Dinmiği v Modllmi Doğrul Simlrin Sınıflndırılmı Doğrul Simlrin Zmn Dvrnışı Giriş: Sim dinmiği çözümlmind, frklı fizikl özlliklr şıyn doğrul imlrin krkriiklrini blirlyn ml bğınılr rınd bnzrlik noloji
e sayısı. x için e. x x e tabanında üstel fonksiyona doğal üstel fonksiyon (natural exponential function) denir. (0,0)
 DERS 4 Üstl v Logaritik Fonksionlar 4.. Üstl Fonksionlar(Eponntial Functions). > 0, olak üzr f ( ) = dnkli il tanılanan fonksiona taanında üstl fonksion (ponntial function with as ) dnir. Üstl fonksionun
DERS 4 Üstl v Logaritik Fonksionlar 4.. Üstl Fonksionlar(Eponntial Functions). > 0, olak üzr f ( ) = dnkli il tanılanan fonksiona taanında üstl fonksion (ponntial function with as ) dnir. Üstl fonksionun
BÖLÜM 4 LİNEER DİFERANSİYEL DENKLEM SİSTEMLERİ
 BÖLÜM LİNEER DİFERANSİYEL DENKLEM SİSTEMLERİ GİRİŞ Dnklm sismlrin linr cbir drsindn şin olmlısınız Anck bu ür dnklmlrd hrhngi bir difrnsiyl büyüklük vy ürv bulunmz Bşk bir dyişl cbirsl dnklm sismi, y (
BÖLÜM LİNEER DİFERANSİYEL DENKLEM SİSTEMLERİ GİRİŞ Dnklm sismlrin linr cbir drsindn şin olmlısınız Anck bu ür dnklmlrd hrhngi bir difrnsiyl büyüklük vy ürv bulunmz Bşk bir dyişl cbirsl dnklm sismi, y (
İletkende seri olarak tel direnci ve magnetik alandan doğan reaktans ile şönt olarak elektrik alandan doğan toprak kapasitesi mevcuttur.
 9 ÖÜM 4 İETİM HT 4.. İltim hatlarının yapısı üksk grilim iltim hatlarında malzm olarak çlik özlü alüminyum iltknlr kullanılır. ( luminium onductor tl inforcd) Kanada standardı olarak tüm dünyada kuş isimlri
9 ÖÜM 4 İETİM HT 4.. İltim hatlarının yapısı üksk grilim iltim hatlarında malzm olarak çlik özlü alüminyum iltknlr kullanılır. ( luminium onductor tl inforcd) Kanada standardı olarak tüm dünyada kuş isimlri
İletkende seri olarak tel direnci ve magnetik alandan doğan reaktans ile şönt olarak elektrik alandan doğan toprak kapasitesi mevcuttur.
 9 ÖÜM 4 İETİM HT 4.. İltim hatlarının yapısı üksk grilim iltim hatlarında malzm olarak çlik özlü alüminyum iltknlr kullanılır. ( luminium onductor tl inforcd) Kanada standardı olarak tüm dünyada kuş isimlri
9 ÖÜM 4 İETİM HT 4.. İltim hatlarının yapısı üksk grilim iltim hatlarında malzm olarak çlik özlü alüminyum iltknlr kullanılır. ( luminium onductor tl inforcd) Kanada standardı olarak tüm dünyada kuş isimlri
YÜKSEK GERİLİMLERİN ÜRETİLMESİ DARBE GERİLİMLERİ
 7.05.0 YÜKSEK GEİLİMLEİN Ø Ø Ø Çşili yalıkan malzmlrin lkrikl açıdan dayanımını blirlybilmk için yükk grilimlr ihiyaç vardır. Yükk grilimlr gnl olarak 3 ınıfa ayrılırlar. Yükk alrnaif (HVA) grilimlr Yükk
7.05.0 YÜKSEK GEİLİMLEİN Ø Ø Ø Çşili yalıkan malzmlrin lkrikl açıdan dayanımını blirlybilmk için yükk grilimlr ihiyaç vardır. Yükk grilimlr gnl olarak 3 ınıfa ayrılırlar. Yükk alrnaif (HVA) grilimlr Yükk
TEST 1 ÇÖZÜMLER NEWTON IN HAREKET YASALARI
 TEST 1 ÇÖZÜMER NEWTON IN HAREET ASAARI 1 P P 3 3 1 (/s) Şekil-I Şekil-II Şekil-III Or sürünesiz olduğundn kuvve ile ive doğru ornılıdır Bu durud, 3 3 P olur Bun göre, > P olur CEAP B ESEN AINARI 6 - grfiğinin
TEST 1 ÇÖZÜMER NEWTON IN HAREET ASAARI 1 P P 3 3 1 (/s) Şekil-I Şekil-II Şekil-III Or sürünesiz olduğundn kuvve ile ive doğru ornılıdır Bu durud, 3 3 P olur Bun göre, > P olur CEAP B ESEN AINARI 6 - grfiğinin
DENEY 2: AM MODÜLASYON / DEMODÜLASYON
 DENEY 2: AM MODÜLASYON / DEMODÜLASYON AMAÇ: Genlik odülyonu ve deodülyonun ilişkin teorik heplrın ypılı, odültör ve deodültör devrelerinin gerçeklenerek teel kvrlrın inelenei. MALZEMELER Oilokop, güç kyngı
DENEY 2: AM MODÜLASYON / DEMODÜLASYON AMAÇ: Genlik odülyonu ve deodülyonun ilişkin teorik heplrın ypılı, odültör ve deodültör devrelerinin gerçeklenerek teel kvrlrın inelenei. MALZEMELER Oilokop, güç kyngı
DERS 9. Grafik Çizimi, Maksimum Minimum Problemleri
 DERS 9 Grafik Çizimi, Maksimum Minimum Problmlri Bundan öncki drst bir fonksiyonun grafiğini çizmk için izlnbilck yol v yapılabilck işlmlr l alındı. Bu drst, grafik çizim stratjisini yani grafik çizimind
DERS 9 Grafik Çizimi, Maksimum Minimum Problmlri Bundan öncki drst bir fonksiyonun grafiğini çizmk için izlnbilck yol v yapılabilck işlmlr l alındı. Bu drst, grafik çizim stratjisini yani grafik çizimind
3. Bir integral bantlı fren resmi çizerek fren kuvveti ve fren açma işinin nasıl bulunduğunu adım adım gösteriniz (15p).
 Ü L E Y M A N D E M Ġ R E L Ü N Ġ V E R Ġ T E Ġ M Ü H E N D Ġ L Ġ K F A K Ü L T E Ġ M A K Ġ N A M Ü H E N D Ġ L Ġ Ğ Ġ B Ö L Ü M Ü I. öğrtim II. öğrtim MAK-43 MT-Trnsport Tkniği ÖĞRENCĠ ADI OYADI NUMARA
Ü L E Y M A N D E M Ġ R E L Ü N Ġ V E R Ġ T E Ġ M Ü H E N D Ġ L Ġ K F A K Ü L T E Ġ M A K Ġ N A M Ü H E N D Ġ L Ġ Ğ Ġ B Ö L Ü M Ü I. öğrtim II. öğrtim MAK-43 MT-Trnsport Tkniği ÖĞRENCĠ ADI OYADI NUMARA
Örnek...3 : Örnek...1 : ABCD yamuk [AC] köşegen E [AC] [AB] // [CD] AB = AE. Örnek...2 : ABCD yamuk [AB] // [CD] BC = CE AE = BE. Örnek...
![Örnek...3 : Örnek...1 : ABCD yamuk [AC] köşegen E [AC] [AB] // [CD] AB = AE. Örnek...2 : ABCD yamuk [AB] // [CD] BC = CE AE = BE. Örnek... Örnek...3 : Örnek...1 : ABCD yamuk [AC] köşegen E [AC] [AB] // [CD] AB = AE. Örnek...2 : ABCD yamuk [AB] // [CD] BC = CE AE = BE. Örnek...](/thumbs/84/89541332.jpg) YU ( YU TNII ORT TN YU NI İİZNR YU İ YU ) YU TNII Ylnız iki kenrı birbirine prlel oln dörtgene YU denir. [] // [] ise ymuktur. rlel oln kenrlr ymuğun tbnlrıdır. [] ve [] tbn. iğer iki kenr yn kenrlrdır.
YU ( YU TNII ORT TN YU NI İİZNR YU İ YU ) YU TNII Ylnız iki kenrı birbirine prlel oln dörtgene YU denir. [] // [] ise ymuktur. rlel oln kenrlr ymuğun tbnlrıdır. [] ve [] tbn. iğer iki kenr yn kenrlrdır.
DERS 9. Grafik Çizimi, Maksimum-Minimum Problemleri. 9.1. Grafik çiziminde izlenecek adımlar. y = f(x) in grafiğini çizmek için
 DERS 9 Grafik Çizimi, Maksimum-Minimum Problmlri 9.. Grafik çizimind izlnck adımlar. y f() in grafiğini çizmk için Adım. f() i analiz diniz. (f nin tanım kümsi, f() in tanımlı olduğu tüm rl sayıların oluşturduğu
DERS 9 Grafik Çizimi, Maksimum-Minimum Problmlri 9.. Grafik çizimind izlnck adımlar. y f() in grafiğini çizmk için Adım. f() i analiz diniz. (f nin tanım kümsi, f() in tanımlı olduğu tüm rl sayıların oluşturduğu
GEMO DS217A. Genel Özellikler: İLERİ / GERİ SAYICI
 İLERİ / GERİ SAYICI DS7A Gnl Özlliklr: x6 n, çift tli, çift kontklı, ilri/gri yıcı Fz frklı giriş il ilri/gri ym Şifr korumlı Sçilbilir ym frknı 0.0000 il 9.99999 rınd çilbiln klibryon çrpnı. il 5. bmk
İLERİ / GERİ SAYICI DS7A Gnl Özlliklr: x6 n, çift tli, çift kontklı, ilri/gri yıcı Fz frklı giriş il ilri/gri ym Şifr korumlı Sçilbilir ym frknı 0.0000 il 9.99999 rınd çilbiln klibryon çrpnı. il 5. bmk
300 = Ders notlarındaki ilgili çizelgeye göre; kömür için üst kaplama kalınlığı 4 mm, alt kaplama kalınlığı 2 mm olarak seçilmiştir.
 Soru-) Eğii, uzunluğu 50 olan dsandr y bant konvyör kurularak bununla saatt 300 ton tüvönan taş köürü taşınacaktır. Bant konvyörü boyutlandırınız. Kabullr: Bant hızı :,5 /s Köür yoğunluğu : 0,9 ton/ 3
Soru-) Eğii, uzunluğu 50 olan dsandr y bant konvyör kurularak bununla saatt 300 ton tüvönan taş köürü taşınacaktır. Bant konvyörü boyutlandırınız. Kabullr: Bant hızı :,5 /s Köür yoğunluğu : 0,9 ton/ 3
ÇOKGENLER Çokgenler çokgen Dışbükey (Konveks) ve İçbükey (Konkav) Çokgenler dış- bükey (konveks) çokgen içbükey (konkav) çokgen
 ÇONLR Çokgenler rdışık en z üç noktsı doğrusl olmyn, düzlemsel şekillere çokgen denir. Çokgenler kenr syılrın göre isimlendirilirler. Üçgen, dörtgen, beşgen gibi. ışbükey (onveks) ve İçbükey (onkv) Çokgenler
ÇONLR Çokgenler rdışık en z üç noktsı doğrusl olmyn, düzlemsel şekillere çokgen denir. Çokgenler kenr syılrın göre isimlendirilirler. Üçgen, dörtgen, beşgen gibi. ışbükey (onveks) ve İçbükey (onkv) Çokgenler
7.SINIF: ÇOKGENLER ÇOKGENDE AÇILAR. Doğrusal olmayan üç veya daha fazla noktanın birleşmesiyle oluşan kapalı geometrik şekillere çokgen denir.
 7.SINIF: ÇOKGNLR oğrusl olmyn üç vey dh fzl noktnın birleşmesiyle oluşn kplı geometrik şekillere çokgen denir. n kenrlı bir çokgenin bir dış çısının ölçüsü 360/n dir. n kenrlı bir çokgenin bir iç çısının
7.SINIF: ÇOKGNLR oğrusl olmyn üç vey dh fzl noktnın birleşmesiyle oluşn kplı geometrik şekillere çokgen denir. n kenrlı bir çokgenin bir dış çısının ölçüsü 360/n dir. n kenrlı bir çokgenin bir iç çısının
11. BÖLÜM. Paralelkenar ve Eşkenar Dörtgen A. PARALELKENAR B. PARALELKENARIN ÖZEL LİKLERİ ÇÖZÜM ÖRNEK ÇÖZÜM ÖRNEK
 G O M T R İ www.kdemivizyon.com.tr. ÖÜM Prlelkenr ve şkenr örtgen. PRNR rşılıklı kenrlrı prlel oln dörtgenlere prlelkenr denir. [] // [] [] // [] = =. PRNRIN ÖZ İRİ. rşılıklı çılr eş ve rdışık çılr ütünlerdir.
G O M T R İ www.kdemivizyon.com.tr. ÖÜM Prlelkenr ve şkenr örtgen. PRNR rşılıklı kenrlrı prlel oln dörtgenlere prlelkenr denir. [] // [] [] // [] = =. PRNRIN ÖZ İRİ. rşılıklı çılr eş ve rdışık çılr ütünlerdir.
Atomlardan Kuarklara. Test 1
 4 Atomlardan Kuarklara Tst. Nötronlar, tkilşim parçacıkları dğil, madd parçacıklarıdır. Bu ndnl yanlış olan E sçnğidir. 5. Elktriksl olarak yüklü lptonlar zayıf çkirdk kuvvtlri aracılığıyla tkilşim girrlr.
4 Atomlardan Kuarklara Tst. Nötronlar, tkilşim parçacıkları dğil, madd parçacıklarıdır. Bu ndnl yanlış olan E sçnğidir. 5. Elktriksl olarak yüklü lptonlar zayıf çkirdk kuvvtlri aracılığıyla tkilşim girrlr.
Çevre ve Alan. İlköğretim 6. Sınıf
 Çevre ve Aln İlköğretim 6. Sınıf Çevre Merhb,ilk olrk seninle birlikte evin çevresini bulmy çlışlım Kırmızı çizgiler evin çevre uzunluğunu verir. Çevre Şimdi sır futbol shsınd Çevre Şimdi,Keloğlnın Pmuk
Çevre ve Aln İlköğretim 6. Sınıf Çevre Merhb,ilk olrk seninle birlikte evin çevresini bulmy çlışlım Kırmızı çizgiler evin çevre uzunluğunu verir. Çevre Şimdi sır futbol shsınd Çevre Şimdi,Keloğlnın Pmuk
x ise x kaçtır?{ C : }
 İZMİR FEN LİSESİ LOGARİTMA ÇALIŞMA SORULARI LOGARİTMA FONKSİYONU. ( ) ( ) f m m m R C : fonksionunun m { ( 0,) } dim tnımlı olmsı için?.. f ( ) ( ) fonksionunun tnım kümsind kç tn tm sı vrdır?{ C : }.
İZMİR FEN LİSESİ LOGARİTMA ÇALIŞMA SORULARI LOGARİTMA FONKSİYONU. ( ) ( ) f m m m R C : fonksionunun m { ( 0,) } dim tnımlı olmsı için?.. f ( ) ( ) fonksionunun tnım kümsind kç tn tm sı vrdır?{ C : }.
6 ise. = b = c = d. olsun. x 3 = 0. x = 3 için Q(3 + 2) = 6. ve sayılarının sayısına uzaklığı sayısı kadar ise c a = d. Q(5) = 6 dır.
 TYT / MTEMTİ eneme - 9. 7 + + + = + 9 = + = + = = bulunur. 0 evp : ^ + h. ^+ h = ^+ h $ ^+ h & ^+ h = & ^+ h = $ ^+ h = ^ h $ ^+ h & ^+ h = 6 ^+ h@ = ^ + h urdn = bulunur. evp :. 0,, ^ h + 0, $ ^0, h,,
TYT / MTEMTİ eneme - 9. 7 + + + = + 9 = + = + = = bulunur. 0 evp : ^ + h. ^+ h = ^+ h $ ^+ h & ^+ h = & ^+ h = $ ^+ h = ^ h $ ^+ h & ^+ h = 6 ^+ h@ = ^ + h urdn = bulunur. evp :. 0,, ^ h + 0, $ ^0, h,,
DS-72A. Genel Özellikler: ĠLERĠ / GERĠ SAYICI
 DS-7A ĠLERĠ / GERĠ SAYICI Gnl Özlliklr: x6 n, çift tli, çift kontklı, ilri/gri yıcı Fz frklı giriş il ilri/gri ym Şifr korumlı Sçilbilir ym frknı 0.0000 il 9.99999 rınd çilbiln klibryon çrpnı. il 5. bmk
DS-7A ĠLERĠ / GERĠ SAYICI Gnl Özlliklr: x6 n, çift tli, çift kontklı, ilri/gri yıcı Fz frklı giriş il ilri/gri ym Şifr korumlı Sçilbilir ym frknı 0.0000 il 9.99999 rınd çilbiln klibryon çrpnı. il 5. bmk
ÜÇGENDE ALAN. Alan(ABC)= 1 2. (taban x yükseklik)
 ÜÇGN LN Üçgende ln Şekilde verilen üçgeninde,, üçgenin köşeleri, [], [], [] üçgenin kenrlrıdır. c b üçgeninin kenrlrı dlndırılırken, her kenr krşısınd bulunn köşenin hrfi ile isimlendirilir. üçgeninin
ÜÇGN LN Üçgende ln Şekilde verilen üçgeninde,, üçgenin köşeleri, [], [], [] üçgenin kenrlrıdır. c b üçgeninin kenrlrı dlndırılırken, her kenr krşısınd bulunn köşenin hrfi ile isimlendirilir. üçgeninin
LYS 1 / MATEMATİK DENEME ÇÖZÜMLERİ
 LYS / MATEMATİK DENEME ÇÖZÜMLERİ Dnm. ^ h ^ h ^h ^^h h ^^h h. ^ h ^ h ^ h Cvp C m. ^ h ^ h Cvp C 9 9 9, ulunur.. Cvp A Cvp B. İfdlri trf trf topllım.. n n n _ n n,,,,, için ifd tmsı olur. 9 ulunur. ^ h
LYS / MATEMATİK DENEME ÇÖZÜMLERİ Dnm. ^ h ^ h ^h ^^h h ^^h h. ^ h ^ h ^ h Cvp C m. ^ h ^ h Cvp C 9 9 9, ulunur.. Cvp A Cvp B. İfdlri trf trf topllım.. n n n _ n n,,,,, için ifd tmsı olur. 9 ulunur. ^ h
3N MOBİL HABERLEŞME HİZMETLERİNDE HİZMET KALİTESİ ÖLÇÜTLERİNİN ELDE EDİLMESİNE İLİŞKİN TEBLİĞ
 3N MOBİL HABERLEŞME HİZMETLERİNDE HİZMET KALİTESİ ÖLÇÜTLERİNİN ELDE EDİLMESİNE İLİŞKİN TEBLİĞ BİRİNCİ BÖLÜM Aç, Kps, Dynk, Tnılr ve Kısltlr Aç MADDE 1 (1) Bu Tebliğin cı, IMT 2000/UMTS Altypılrının Kurulsı
3N MOBİL HABERLEŞME HİZMETLERİNDE HİZMET KALİTESİ ÖLÇÜTLERİNİN ELDE EDİLMESİNE İLİŞKİN TEBLİĞ BİRİNCİ BÖLÜM Aç, Kps, Dynk, Tnılr ve Kısltlr Aç MADDE 1 (1) Bu Tebliğin cı, IMT 2000/UMTS Altypılrının Kurulsı
İ.T.Ü. Makina Fakültesi Mekanik Ana Bilim Dalı Bölüm 7. Seviye Düzlemi
 İTÜ Makina Fakültsi Ağırlığın Potansiyl Enrjisi W=, δh kadar yukarıya doğru yr dğiştirsin, Virtül iş, δu = Wδh= δh NOT: Eğr cisi aşağıya doğru δh yr dğişii yapıyorsa v +h aşağıya doğru is δu = Wδh= δh
İTÜ Makina Fakültsi Ağırlığın Potansiyl Enrjisi W=, δh kadar yukarıya doğru yr dğiştirsin, Virtül iş, δu = Wδh= δh NOT: Eğr cisi aşağıya doğru δh yr dğişii yapıyorsa v +h aşağıya doğru is δu = Wδh= δh
1982 ÖSS =3p olduğuna göre p kaçtır? A) 79 B) 119 C) 237 E) A) 60 B) 90 C) 120 D) 150 E) 160
 8 ÖSS. Bir çiftlikte 800 koun 00 inek ve 600 mnd vrdır. Bu hvnlrın tümü bir dire grfikle gösterilirse ineklerle ilgili dilimin merkez çısı kç derece olur? A) 60 B) 0 C) 0 D) 0 E) 60 6. 0 - =p olduğun göre
8 ÖSS. Bir çiftlikte 800 koun 00 inek ve 600 mnd vrdır. Bu hvnlrın tümü bir dire grfikle gösterilirse ineklerle ilgili dilimin merkez çısı kç derece olur? A) 60 B) 0 C) 0 D) 0 E) 60 6. 0 - =p olduğun göre
S1:10, S2:30, S3:20, S4:40 Puan Süre: 100 dakika 17 Nisan 2008
 Mikroişlmi Sistmlr Viz Sınvı S1:10, S2:30, S3:20, S4:40 Pun Sür: 100 kik 17 Nisn 2008 1) 18-45 işlmini ikili tn rçklyiniz. 18 00010010 45 00101101-45 için 2 y tümlyn lınır; 1 tümlm 11010010, sonr un 1
Mikroişlmi Sistmlr Viz Sınvı S1:10, S2:30, S3:20, S4:40 Pun Sür: 100 kik 17 Nisn 2008 1) 18-45 işlmini ikili tn rçklyiniz. 18 00010010 45 00101101-45 için 2 y tümlyn lınır; 1 tümlm 11010010, sonr un 1
FIRAT ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ EMÜ-419 OTOMATİK KONTROL LABORATUARI DENEY 5
 FIRT ÜNİVERSİTESİ MÜHENDİSLİK FKÜLTESİ ELEKTRİKELEKTRONİK MÜHENDİSLİĞİ ÖLÜMÜ EMÜ419 OTOMTİK KONTROL LORTURI DENEY 5 PID KONTROLÖR KRKTERİSTİKLERİNİN İNELENMESİ VE NLOG OLRK POZİSYON KONTROL SİSTEMLERİNDE
FIRT ÜNİVERSİTESİ MÜHENDİSLİK FKÜLTESİ ELEKTRİKELEKTRONİK MÜHENDİSLİĞİ ÖLÜMÜ EMÜ419 OTOMTİK KONTROL LORTURI DENEY 5 PID KONTROLÖR KRKTERİSTİKLERİNİN İNELENMESİ VE NLOG OLRK POZİSYON KONTROL SİSTEMLERİNDE
VEKTÖRLER ÜNİTE 5. ÜNİTE 5. ÜNİTE 5. ÜNİTE 5. ÜNİT
 VKTÖRLR ÜNİT 5. ÜNİT 5. ÜNİT 5. ÜNİT 5. ÜNİT VKTÖRLR 1. Kznım : Vektör kvrmını çıklr.. Kznım : İki vektörün toplmını ve vektörün ir gerçek syıyl çrpımını ceirsel ve geometrik olrk gösterir. VKTÖRLR 1.
VKTÖRLR ÜNİT 5. ÜNİT 5. ÜNİT 5. ÜNİT 5. ÜNİT VKTÖRLR 1. Kznım : Vektör kvrmını çıklr.. Kznım : İki vektörün toplmını ve vektörün ir gerçek syıyl çrpımını ceirsel ve geometrik olrk gösterir. VKTÖRLR 1.
DÜZCE ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ EET305 OTOMATİK KONTROL I Dr. Uğur HASIRCI
 DÜZCE ÜNİVERSİTESİ TENOLOJİ FAÜLTESİ ELETRİ-ELETRONİ MÜHENDİSLİĞİ BÖLÜMÜ EET305 OTOMATİ ONTROL I ALICI DURUM HATASI ontrol sistmlrinin tasarımında üç tml kritr göz önünd bulundurulur: Gçici Durum Cvabı
DÜZCE ÜNİVERSİTESİ TENOLOJİ FAÜLTESİ ELETRİ-ELETRONİ MÜHENDİSLİĞİ BÖLÜMÜ EET305 OTOMATİ ONTROL I ALICI DURUM HATASI ontrol sistmlrinin tasarımında üç tml kritr göz önünd bulundurulur: Gçici Durum Cvabı
BELÝRLÝ (SINIRLI) ÝNTEGRAL
 Blirli Ýntgrl BELÝRLÝ (SINIRLI) ÝNTEGRAL f, fonksiyonu [, ] rlðnd intgrllniln ir fonksiyon, (, ) olsun, ifdsin f() fonksiyonun (, ) rlðndki lirli intgrli vy = v = doðrulr il snrl f() ðrisi il o ksni rsndki
Blirli Ýntgrl BELÝRLÝ (SINIRLI) ÝNTEGRAL f, fonksiyonu [, ] rlðnd intgrllniln ir fonksiyon, (, ) olsun, ifdsin f() fonksiyonun (, ) rlðndki lirli intgrli vy = v = doðrulr il snrl f() ðrisi il o ksni rsndki
7.SINIF: PARALELKENARIN ve ÜÇGENİN ALANI
 7.SINIF: PRLLKNRIN ve ÜÇGNİN LNI ikdörtgen şeklindeki ir krtonu şekildeki gii işretlenen yerden kesip diğer trf eklediğimizde krtonun eksilmediğini,sdece görüntüsünün değiştiğini görürüz. Prlelkenrd Yükseklik
7.SINIF: PRLLKNRIN ve ÜÇGNİN LNI ikdörtgen şeklindeki ir krtonu şekildeki gii işretlenen yerden kesip diğer trf eklediğimizde krtonun eksilmediğini,sdece görüntüsünün değiştiğini görürüz. Prlelkenrd Yükseklik
Devre Teorisi Ders Notu Dr. Nurettin ACIR ve Dr. Engin Cemal MENGÜÇ BÖLÜM VI. DENGELENMİŞ ÜÇ FAZLI DEVRELER ( 3f )
 Dr. urettin ACIR ve Dr. Engin Cel MEGÜÇ BÖÜM VI DEGEEMİŞ ÜÇ FAZI DEVREER ( 3 ) Elektriğin üreti, iletii ve dğıtıı genelde 3 devrelerde gerçekleştirilir. Detylı nlizi güç siste uznlrının konusu olkl irlikte,
Dr. urettin ACIR ve Dr. Engin Cel MEGÜÇ BÖÜM VI DEGEEMİŞ ÜÇ FAZI DEVREER ( 3 ) Elektriğin üreti, iletii ve dğıtıı genelde 3 devrelerde gerçekleştirilir. Detylı nlizi güç siste uznlrının konusu olkl irlikte,
DİNAMİK BÖLÜM 7 MODEL SORU 1 DEK SORULARIN ÇÖZÜMLER. Hız-zaman grafiğinin eğimi ivmeyi verir. L cisminin ivmesi, al = = 3a
 DİNAİ BÖÜ 7 ODE SORU 1 DE SORUARIN ÇÖZÜER h z 1 h z V V V θ V V 0 t t t, ve cisilerinin iveleri; V V V t 0 t V 0 V t 0 t zn 0 θ t zn Hız-zn rğinin eğii iveyi verir V V V cisinin ivesi, t t V cisinin ivesi,
DİNAİ BÖÜ 7 ODE SORU 1 DE SORUARIN ÇÖZÜER h z 1 h z V V V θ V V 0 t t t, ve cisilerinin iveleri; V V V t 0 t V 0 V t 0 t zn 0 θ t zn Hız-zn rğinin eğii iveyi verir V V V cisinin ivesi, t t V cisinin ivesi,
VİNÇTE ÇELİK KONSTRÜKSİYON
 0 Haziran www.guvn-kua.h VİNÇTE ÇEİ ONSTRÜSİON ÖZET _09 M. Güvn UT Smbollr v anaklar için "_00_ClikonsruksionaGiris.do" a bakınız. oordina ksnlri "GENE GİRİŞ" d blirildiği gibi DIN 8800 T gör alınmışır.
0 Haziran www.guvn-kua.h VİNÇTE ÇEİ ONSTRÜSİON ÖZET _09 M. Güvn UT Smbollr v anaklar için "_00_ClikonsruksionaGiris.do" a bakınız. oordina ksnlri "GENE GİRİŞ" d blirildiği gibi DIN 8800 T gör alınmışır.
PARK VE BAHÇELER MÜDÜRLÜĞÜ
 PRK V BÇLR MÜDÜRLÜĞÜ LKTRİK V SU RIZLRI İŞ KIŞ ŞMSI PRKLRDN VY BLDİY BİRİMLRİNDN SU İL İLGİLİ RIZ BİLGİSİ GLMSİ PRKLRDN LKTRİK RIZSI BİLGİSİ GLMSİ SU RIZ KİBİN BİLGİ VRİLMSİ SU İŞLRİ MÜDÜRLÜĞÜ LKTRİK BİRİMİ
PRK V BÇLR MÜDÜRLÜĞÜ LKTRİK V SU RIZLRI İŞ KIŞ ŞMSI PRKLRDN VY BLDİY BİRİMLRİNDN SU İL İLGİLİ RIZ BİLGİSİ GLMSİ PRKLRDN LKTRİK RIZSI BİLGİSİ GLMSİ SU RIZ KİBİN BİLGİ VRİLMSİ SU İŞLRİ MÜDÜRLÜĞÜ LKTRİK BİRİMİ
YÜZDE VE FAĐZ PROBLEMLERĐ
 YILLAR 00 003 00 00 006 007 008 009 010 011 ÖSS-YGS 3 1 1 1 3 YÜZDE VE FAĐZ PROBLEMLERĐ YÜZDE: Bir syının yüzde sı= dır ÖRNEK(1) % i 0 oln syıyı bullım syımız olsun 1 = 0 = 0 ÖRNEK() 800 ün % ini bullım
YILLAR 00 003 00 00 006 007 008 009 010 011 ÖSS-YGS 3 1 1 1 3 YÜZDE VE FAĐZ PROBLEMLERĐ YÜZDE: Bir syının yüzde sı= dır ÖRNEK(1) % i 0 oln syıyı bullım syımız olsun 1 = 0 = 0 ÖRNEK() 800 ün % ini bullım
Eğitim-Öğretim Güz Yarıyılı Diferansiyel Denklemler Dersi Çalışma Soruları
 - Eğiim-Öğrim Güz rıılı Difril Dklmlr Dri Çlışm Sorlrı 6 // Aşğıd vril kvv rilrii kıklık rıçplrıı lirliiz. = = di ok civrıd kvv rii rdımıl vril difril dklmlri çözüüz. - -= - + -= - + += dklmii kil oklrıı
- Eğiim-Öğrim Güz rıılı Difril Dklmlr Dri Çlışm Sorlrı 6 // Aşğıd vril kvv rilrii kıklık rıçplrıı lirliiz. = = di ok civrıd kvv rii rdımıl vril difril dklmlri çözüüz. - -= - + -= - + += dklmii kil oklrıı
Üslü İfadelerde İşlemler (Temel Kurallar) - Çalışma Kağıdı Ortaokul Matematik Kafası $ = k) 81 $ 243 = Kerim Hoca. p) 125 $ 625 = w) 3
 .Sınıf Mtemtik ÜSLÜ İFADELER Yyın No : / Kznım :... + Üssün Üssü ve Sırlm Bir üslü ifdenin üssü lındığınd üsler çrpılır.. Alıştırmlr Aşğıdki işlemlerin sonuçlrını üslü biçimde yzınız. y ^ h y ) ^ h b)
.Sınıf Mtemtik ÜSLÜ İFADELER Yyın No : / Kznım :... + Üssün Üssü ve Sırlm Bir üslü ifdenin üssü lındığınd üsler çrpılır.. Alıştırmlr Aşğıdki işlemlerin sonuçlrını üslü biçimde yzınız. y ^ h y ) ^ h b)
ELM207 Analog Elektronik
 ELM7 Alog Elkroik Giriş Bir Fourir srisi priyodik bir ) oksiyouu, kosiüs v siüslri sosuz oplmı biçimid bir çılımdır. ) cos b si ) Bşk dyişl, hrhgi bir priyodik oksiyo sbi bir dğr, kosiüs v siüs oksiyolrıı
ELM7 Alog Elkroik Giriş Bir Fourir srisi priyodik bir ) oksiyouu, kosiüs v siüslri sosuz oplmı biçimid bir çılımdır. ) cos b si ) Bşk dyişl, hrhgi bir priyodik oksiyo sbi bir dğr, kosiüs v siüs oksiyolrıı
ÇÖZÜMLER HAREKET. 4. hız. t(s) zaman
 TEST ÇÖZÜMER HAREET. rlığınd rç durmkdır. (m) o rlığınd rcın ı sbiir. o o o II. yrgı ynlışır. o nınd bşlngıç noksın oln uzklığı: o o o III. yrgı ynlışır.. nın d cis min konum ko nu mu ir. I. yr gı doğ
TEST ÇÖZÜMER HAREET. rlığınd rç durmkdır. (m) o rlığınd rcın ı sbiir. o o o II. yrgı ynlışır. o nınd bşlngıç noksın oln uzklığı: o o o III. yrgı ynlışır.. nın d cis min konum ko nu mu ir. I. yr gı doğ
THÉVENİN, NORTON, MAKSİMUM GÜÇ TEOREMİ ve DEVRE PARAMETRELERİ
 DENEY NO: 4 THÉENİN, NORTON, MAKSİMUM GÜÇ TEOREMİ ve DERE PARAMETRELERİ Mlzeme ve Cihz Litei:. 330 direnç det. k direnç 3 det 3.. k direnç det 4. 3.3 k direnç det 5. 5.6 k direnç det 6. 0 k direnç det
DENEY NO: 4 THÉENİN, NORTON, MAKSİMUM GÜÇ TEOREMİ ve DERE PARAMETRELERİ Mlzeme ve Cihz Litei:. 330 direnç det. k direnç 3 det 3.. k direnç det 4. 3.3 k direnç det 5. 5.6 k direnç det 6. 0 k direnç det
Anadolu Üniversitesi Mühendislik Fakültesi Endüstri Mühendisliği Bölümü. Doç. Dr. Nil ARAS ENM411 Tesis Planlaması 2015-2016 Güz Dönemi
 Andolu Üniversitesi Mühendislik Fkültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Plnlmsı 2015-2016 Güz Dönemi 2 Tesis (fcility) Tesis : Belli bir iş için kurulmuş ypı Tesis etmek :
Andolu Üniversitesi Mühendislik Fkültesi Endüstri Mühendisliği Bölümü Doç. Dr. Nil ARAS ENM411 Tesis Plnlmsı 2015-2016 Güz Dönemi 2 Tesis (fcility) Tesis : Belli bir iş için kurulmuş ypı Tesis etmek :
İntegral ile Alan Hesabı Konu Anlatım Testi
 Testin Çözümü İntegrl ile ln Hesı Konu nltım Testi Sf : f() f() g() g() = න f g d Soru : = f = + + 4 = g = + Soru : = g = Yukrıdki şekilde doğru ve prol rsınd kln ln kç r dir? = f = 4 Yukrıdki şekilde
Testin Çözümü İntegrl ile ln Hesı Konu nltım Testi Sf : f() f() g() g() = න f g d Soru : = f = + + 4 = g = + Soru : = g = Yukrıdki şekilde doğru ve prol rsınd kln ln kç r dir? = f = 4 Yukrıdki şekilde
[BC] // [AD] [AC] ve [BD] AD =6 br BC =10 br. olduğuna göre, EF MN k a ç birimdir? Ayr ı c a. [AC] ve [BD] EF =6 br BC =8 br.
![[BC] // [AD] [AC] ve [BD] AD =6 br BC =10 br. olduğuna göre, EF MN k a ç birimdir? Ayr ı c a. [AC] ve [BD] EF =6 br BC =8 br. [BC] // [AD] [AC] ve [BD] AD =6 br BC =10 br. olduğuna göre, EF MN k a ç birimdir? Ayr ı c a. [AC] ve [BD] EF =6 br BC =8 br.](/thumbs/65/52892858.jpg) YU ( YU TII ORT T YU LI İİZR YU İ YU ) YU TII ORT T Y l n ı z ik i k e n r ı b i r b i r i n e p r l e l l n d ö r t g e n e Y U d e n i r. [ ] / / [ ] i s e y m u k t u r. y m u ğ u n d, ve L kenr rt
YU ( YU TII ORT T YU LI İİZR YU İ YU ) YU TII ORT T Y l n ı z ik i k e n r ı b i r b i r i n e p r l e l l n d ö r t g e n e Y U d e n i r. [ ] / / [ ] i s e y m u k t u r. y m u ğ u n d, ve L kenr rt
ÖZEL EGE LİSESİ OKULLAR ARASI 18. MATEMATİK YARIŞMASI 8. SINIF TEST SORULARI
 ., ÖZEL EGE LİSESİ OKULLR RSI 8. MTEMTİK YRIŞMSI 8. SINI TEST SORULRI 5. 0,0008.0 b 0,0000.0 ise; b.0 kç bsmklı bir sıdır? olduğun göre, ifdesinin değeri şğıdkilerden hngisine eşittir? ) 80 ) 8 ) 8 ) 8
., ÖZEL EGE LİSESİ OKULLR RSI 8. MTEMTİK YRIŞMSI 8. SINI TEST SORULRI 5. 0,0008.0 b 0,0000.0 ise; b.0 kç bsmklı bir sıdır? olduğun göre, ifdesinin değeri şğıdkilerden hngisine eşittir? ) 80 ) 8 ) 8 ) 8
6 DC Motorlar. Harici Uyartımlı DC Motor. E a - I V / R K K. i a =i L R a. i f. R f. f f f. a a ind. a a a a a. Tind. ind
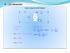 6 DC Motorlr Hrici Uyrtımlı DC Motor i + i =i L R V R E V - V / R K (1) E K E V R (2) K E V R K K K V R (4) K K 2 ( 3) E 1 6 DC Motorlr Hrici Uyrtımlı DC Motor Eğer endüvide üklenen gerilim (E ) ormülünde
6 DC Motorlr Hrici Uyrtımlı DC Motor i + i =i L R V R E V - V / R K (1) E K E V R (2) K E V R K K K V R (4) K K 2 ( 3) E 1 6 DC Motorlr Hrici Uyrtımlı DC Motor Eğer endüvide üklenen gerilim (E ) ormülünde
11. SINIF KONU ANLATIMLI. 1. ÜNİTE: KUVVET VE HAREKET 3. Konu NEWTON UN HAREKET YASALARI ETKİNLİK VE TEST ÇÖZÜMLERİ
 11. SINIF KONU ANLAIMLI 1. ÜNİE: KUVVE VE HAREKE. Konu NEWON UN HAREKE YASALARI EKİNLİK VE ES ÇÖZÜMLERİ Newton un Hreket Ylrı 1. Ünite. Konu (Vektörler) 5. tepki kuvveti A nın Çözüleri 1. I II III etki
11. SINIF KONU ANLAIMLI 1. ÜNİE: KUVVE VE HAREKE. Konu NEWON UN HAREKE YASALARI EKİNLİK VE ES ÇÖZÜMLERİ Newton un Hreket Ylrı 1. Ünite. Konu (Vektörler) 5. tepki kuvveti A nın Çözüleri 1. I II III etki
DRC üst taban, 6 alt taban olmak üzere 12 mavi kare vardır. 4. Sekiz basamaklı herhangi bir özel sayı x = abcdefgh olsun. Deneme - 2 / Mat.
 Deneme - / Mt MATEMATİK DENEMESİ. 6 üst tn, 6 lt tn olmk üzere mvi kre vrdır. Ypının tüm yüzeyi kreden oluştuğun göre, 6 7. 0,.., f -, 0, p. 0,. c- m.,,. ^- h.. 7. ^- h 7 - ulunur. +. c m olur. ( ) 9 c
Deneme - / Mt MATEMATİK DENEMESİ. 6 üst tn, 6 lt tn olmk üzere mvi kre vrdır. Ypının tüm yüzeyi kreden oluştuğun göre, 6 7. 0,.., f -, 0, p. 0,. c- m.,,. ^- h.. 7. ^- h 7 - ulunur. +. c m olur. ( ) 9 c
Işığın Yansıması ve Düzlem Ayna Çözümleri
 2 şığın Ynsımsı ve Düzlem Ayn Çözümleri 1 Test 1 1. 38 38 52 52 Ynsıyn ışının yüzeyin normli ile yptığı çıy ynsım çısı denir. Bu durumd ynsım çısı şekilde gösterildiği gibi 38 dir. 4. şıklı cisminin ve
2 şığın Ynsımsı ve Düzlem Ayn Çözümleri 1 Test 1 1. 38 38 52 52 Ynsıyn ışının yüzeyin normli ile yptığı çıy ynsım çısı denir. Bu durumd ynsım çısı şekilde gösterildiği gibi 38 dir. 4. şıklı cisminin ve
KIVIRMA İŞLEMİNİN ŞEKİL ve BOYUTLARI
 2011 Şut KIVIRMA İŞEMİNİN ŞEKİ ve BOYUTARI Hzırlyn: Adnn YIMAZ AÇINIM DEĞERERİ 50-21 DİKKAT: İyi niyet, ütün dikkt ve çm krşın ynlışlr olilir. Bu nedenle onucu orumluluk verecek ynlışlıklr için, hiçir
2011 Şut KIVIRMA İŞEMİNİN ŞEKİ ve BOYUTARI Hzırlyn: Adnn YIMAZ AÇINIM DEĞERERİ 50-21 DİKKAT: İyi niyet, ütün dikkt ve çm krşın ynlışlr olilir. Bu nedenle onucu orumluluk verecek ynlışlıklr için, hiçir
Yarım Toplayıcı (Half Adder): İki adet birer bitlik sayıyı toplayan bir devredir. a: Birinci Sayı a b c s. a b. s c.
 Syıl Devreler (Lojik Devreleri) Tümleştirilmiş Kominezonl Devre Elemnlrı Syıl itemlerin gerçekleştirilmeinde çokç kullnıln lojik devreler, klik ğlçlrın ir ry getirilmeiyle tümleştirilmiş devre olrk üretilirler
Syıl Devreler (Lojik Devreleri) Tümleştirilmiş Kominezonl Devre Elemnlrı Syıl itemlerin gerçekleştirilmeinde çokç kullnıln lojik devreler, klik ğlçlrın ir ry getirilmeiyle tümleştirilmiş devre olrk üretilirler
1990 ÖYS 1. 7 A) 91 B) 84 C) 72 D) 60 E) 52 A) 52 B) 54 C) 55 D) 56 E) 57
 99 ÖYS. si oln si kçtır? A) 9 B) 8 C) D) 6 E) 5 6. Bir nın yşı, iki çocuğunun yşlrı toplmındn üyüktür. yıl sonr nın yşı, çocuklrının yşlrı toplmının ktı olcğın göre ugün kç yşınddır? A) 5 B) 5 C) 55 D)
99 ÖYS. si oln si kçtır? A) 9 B) 8 C) D) 6 E) 5 6. Bir nın yşı, iki çocuğunun yşlrı toplmındn üyüktür. yıl sonr nın yşı, çocuklrının yşlrı toplmının ktı olcğın göre ugün kç yşınddır? A) 5 B) 5 C) 55 D)
Üstel Dağılım SÜREKLİ ŞANS DEĞİŞKENLERİNİN OLASILIK YOĞUNLUK FONKSİYONLARI
 ..3 SÜREKLİ ŞNS DEĞİŞKENLERİNİN OLSILIK YOĞUNLUK FONKSİYONLRI Üstl Dağılım Sürkli Üniform Dağılım Normal Dağılım Üstl Dağılım Mydana gln iki olay arasındaki gçn sür vya ir aşka ifadyl ilgilniln olayın
..3 SÜREKLİ ŞNS DEĞİŞKENLERİNİN OLSILIK YOĞUNLUK FONKSİYONLRI Üstl Dağılım Sürkli Üniform Dağılım Normal Dağılım Üstl Dağılım Mydana gln iki olay arasındaki gçn sür vya ir aşka ifadyl ilgilniln olayın
DESTEK DOKÜMANI. Mali tablo tanımları menüsüne Muhasebe/Mali tablo tanımları altından ulaşılmaktadır.
 Mali Tablolar Mali tablo tanımları mnüsün Muhasb/Mali tablo tanımları altından ulaşılmatadır. Mali tablolarla ilgili yapılabilc işlmlr ii gruba ayrılır. Mali Tablo Tanımları Bu bölümd firmanın ullanacağı
Mali Tablolar Mali tablo tanımları mnüsün Muhasb/Mali tablo tanımları altından ulaşılmatadır. Mali tablolarla ilgili yapılabilc işlmlr ii gruba ayrılır. Mali Tablo Tanımları Bu bölümd firmanın ullanacağı
1 a) TEVENİN (THEVENIN) TEOREMİNİN DENEYSEL OLARAK DOĞRULANMASI. Amaç: Tevenin teoremini doğrulamak ve yük direnci üzerinden akan akımı bulmak.
 1 ) TEVENİN (THEVENIN) TEOREMİNİN DENEYSEL OLARAK DOĞRULANMASI Amç: Tevenin teoremini doğrulmk ve yük direnci üzerinden kn kımı ulmk. Gerekli Ekipmnlr: DA Güç Kynğı, Ampermetre, Voltmetre, Dirençler, Dizilim
1 ) TEVENİN (THEVENIN) TEOREMİNİN DENEYSEL OLARAK DOĞRULANMASI Amç: Tevenin teoremini doğrulmk ve yük direnci üzerinden kn kımı ulmk. Gerekli Ekipmnlr: DA Güç Kynğı, Ampermetre, Voltmetre, Dirençler, Dizilim
ÜÇGENDE BENZERLİK. Benzerlik. Benzerlik Oranı. Uyarı
 ÜÇN NZRLİK enzerlik eometride benzerlik kvrmı görsel olrk birbiri ile ynı oln şekiller için kullnılır. enzer iki şeklin krşılıklı kenrlrı rsınd sbit bir orn vrdır. iz bu bölümde sdece üçgenler rsındki
ÜÇN NZRLİK enzerlik eometride benzerlik kvrmı görsel olrk birbiri ile ynı oln şekiller için kullnılır. enzer iki şeklin krşılıklı kenrlrı rsınd sbit bir orn vrdır. iz bu bölümde sdece üçgenler rsındki
LYS Matemat k Deneme Sınavı
 LYS Mtemtk Deneme Sınvı. İki bsmklı bir sının rkmlrı toplmı dir. Rkmlrı er değiştirdiğinde elde edilen sı, ilk sının sinden fzldır.. Birbirinden frklı tne pozitif tmsının OKEK i olduğun göre, en çok kçtır?
LYS Mtemtk Deneme Sınvı. İki bsmklı bir sının rkmlrı toplmı dir. Rkmlrı er değiştirdiğinde elde edilen sı, ilk sının sinden fzldır.. Birbirinden frklı tne pozitif tmsının OKEK i olduğun göre, en çok kçtır?
ÜSTEL DAĞILIM. üstel dağılımın parametresidir. Birikimli üstel dağılım fonksiyonu da, olarak bulunur. olduğu açık olarak görülmektedir.
 ÜSTL DAĞILIM Tanım : X > olma üzr sürli bir rasgl dğişn olsun. ğr a > için X rassal dğişni aşağıdai gibi bir dağılıma sahip olursa X rasgl dğişnin üsl dağılmış rassal dğişn v onsiyonuna da üsl dağılım
ÜSTL DAĞILIM Tanım : X > olma üzr sürli bir rasgl dğişn olsun. ğr a > için X rassal dğişni aşağıdai gibi bir dağılıma sahip olursa X rasgl dğişnin üsl dağılmış rassal dğişn v onsiyonuna da üsl dağılım
TEST 16-1 KONU DÜZLEM AYNA. Çözümlerİ ÇÖZÜMLERİ
 OU 6 Ü Çözümler. TST 6-,7 ÇÖÜR,6 5. Bir cismin görüntüsünün nerede görüneceğini bkn kişinin bulunduğu yer belirlemez. nin görüntüsü nolu noktd olduğu için her iki gözlemci ynı yerde görür. V 3,5 6. 7 kez
OU 6 Ü Çözümler. TST 6-,7 ÇÖÜR,6 5. Bir cismin görüntüsünün nerede görüneceğini bkn kişinin bulunduğu yer belirlemez. nin görüntüsü nolu noktd olduğu için her iki gözlemci ynı yerde görür. V 3,5 6. 7 kez
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
 BÖÜ DİNAİ ODE SORU - 1 DEİ SORUARIN ÇÖZÜERİ 1 ( ) (+) 0N 6/s 6/s 60 10N N 10N 0N 1N cis i uy gu l nn net kuv vet cis i ön ce (+) yön de y vş l tır Ci si dur duk tn son r ( ) yön de hız l nır Cis in iv
BÖÜ DİNAİ ODE SORU - 1 DEİ SORUARIN ÇÖZÜERİ 1 ( ) (+) 0N 6/s 6/s 60 10N N 10N 0N 1N cis i uy gu l nn net kuv vet cis i ön ce (+) yön de y vş l tır Ci si dur duk tn son r ( ) yön de hız l nır Cis in iv
Bilgi Tabanı (Uzman) Karar Verme Kontrol Kural Tabanı. Bulanık. veya. Süreç. Şekil 1 Bulanık Denetleyici Blok Şeması
 Bulanık Dntlyicilr Bilgi Tabanı (Uzman) Anlık (Kskin) Girişlr Bulandırma Birimi Bulanık µ( ) Karar Vrm Kontrol Kural Tabanı Bulanık µ( u ) Durulama Birimi Anlık(Kskin) Çıkış Ölçklm (Normali zasyon) Sistm
Bulanık Dntlyicilr Bilgi Tabanı (Uzman) Anlık (Kskin) Girişlr Bulandırma Birimi Bulanık µ( ) Karar Vrm Kontrol Kural Tabanı Bulanık µ( u ) Durulama Birimi Anlık(Kskin) Çıkış Ölçklm (Normali zasyon) Sistm
UYGULAMALI DİFERANSİYEL DENKLEMLER
 UYGULAMALI DİFERANSİYEL DENKLEMLER Homojn Hal Gtirilbiln Diransil Dnklmlr a b cd a' b' c' d 0 Şklindki diransil dnklm homojn olmamasına rağmn basit bir dğişkn dönüşümü il homojn hal dönüştürülbilir. a
UYGULAMALI DİFERANSİYEL DENKLEMLER Homojn Hal Gtirilbiln Diransil Dnklmlr a b cd a' b' c' d 0 Şklindki diransil dnklm homojn olmamasına rağmn basit bir dğişkn dönüşümü il homojn hal dönüştürülbilir. a
ÇÖZÜMLER. 3. I. Ortam sürtünmesiz ise, a) Di na mi ğin te mel pren si bi sis te me uy gu lan dığın 30 T 1 T 1. II. Ortamın sürtünme katsayısı 0,1 ise,
 BÖÜM DİNAMİ AIŞIRMAAR ÇÖZÜMER DİNAMİ 1 4kg 0N yty M düzle rsınd : rsınd cisin ivesi /s olduğundn cise uygulnn kuvvet, 1 4 0 N olur M rsınd : M rsınd cisin ivesi /s olduğundn cise etki eden sürtüne kuvveti,
BÖÜM DİNAMİ AIŞIRMAAR ÇÖZÜMER DİNAMİ 1 4kg 0N yty M düzle rsınd : rsınd cisin ivesi /s olduğundn cise uygulnn kuvvet, 1 4 0 N olur M rsınd : M rsınd cisin ivesi /s olduğundn cise etki eden sürtüne kuvveti,
ETİL ASETAT ÜRETİMİNİN YAPILDIĞI TEPKİMELİ DAMITMA KOLONUNUN AYIRIMLI ( DECOUPLING ) PID KONTROLÜ
 Onuncu Ulual Kimya Mühndiliği Kongri, 3-6 Eylül 2012, Koç Ünivriti, İtanbul ETİL ASETAT ÜRETİMİNİN YAPILDIĞI TEPKİMELİ DAMITMA KOLONUNUN AYIRIMLI ( DECOUPLING ) PID KONTROLÜ Abdulwahab GIWA, Sülyman KARACAN
Onuncu Ulual Kimya Mühndiliği Kongri, 3-6 Eylül 2012, Koç Ünivriti, İtanbul ETİL ASETAT ÜRETİMİNİN YAPILDIĞI TEPKİMELİ DAMITMA KOLONUNUN AYIRIMLI ( DECOUPLING ) PID KONTROLÜ Abdulwahab GIWA, Sülyman KARACAN
Örnek...4 : Örnek...5 : Örnek...6 : Örnek...7 : ( 3x2 + x 3) dx=? Örnek...1 : Örnek...2 : Örnek...8 : ln2 (e 2x +e x )dx=? ln1. Örnek...
 KURALLARI. f ( )= f ( ). f ( )= Örnk... : ( + 7+ )=? 7. k. f ( ) =k. f ( ) Örnk... : sin =?. (f ( )±g ( ))= f ( )± g( ). c f ( )= f ( )+f ( ), c c< 6. (-).min(f())< f ( )=
KURALLARI. f ( )= f ( ). f ( )= Örnk... : ( + 7+ )=? 7. k. f ( ) =k. f ( ) Örnk... : sin =?. (f ( )±g ( ))= f ( )± g( ). c f ( )= f ( )+f ( ), c c< 6. (-).min(f())< f ( )=
ASİT-BAZ TEORİSİ. (TİTRASYON) Prof. Dr. Mustafa DEMİR. M.DEMİR(ADU) ASİT-BAZ TEORİSİ (titrasyon) 1
 ASİT-BAZ TEORİSİ (TİTRASYON) Prof. Dr. Mustf DEMİR M.DEMİR(ADU) 009-05-ASİT-BAZ TEORİSİ (titrsyon) 1 Arhenius (su teorisi) 1990 Asit: Sud iyonlştığınd iyonu veren, bz ise O - iyonu veren mddelerdir. Cl,NO,
ASİT-BAZ TEORİSİ (TİTRASYON) Prof. Dr. Mustf DEMİR M.DEMİR(ADU) 009-05-ASİT-BAZ TEORİSİ (titrsyon) 1 Arhenius (su teorisi) 1990 Asit: Sud iyonlştığınd iyonu veren, bz ise O - iyonu veren mddelerdir. Cl,NO,
{ } { } Ters Dönüşüm Yöntemi
 KESĐKLĐ DAĞILIMLARDAN RASGELE SAYI ÜRETME Trs Dönüşüm Yöntmi F dağılım fonksiyonuna sahip bir X rasgl dğişknin dağılımından sayı ürtmk için n çok kullanılan yöntmlrdn biri, F dağılım fonksiyonunun gnllştirilmiş
KESĐKLĐ DAĞILIMLARDAN RASGELE SAYI ÜRETME Trs Dönüşüm Yöntmi F dağılım fonksiyonuna sahip bir X rasgl dğişknin dağılımından sayı ürtmk için n çok kullanılan yöntmlrdn biri, F dağılım fonksiyonunun gnllştirilmiş
Asenkron Makinanın Alan Yönlendirme Kontrolünde FPGA Kullanımı ALAN İ., AKIN Ö.
 Asnkron Makinanın Alan Yönlndirm Kontrolünd FPGA Kullanımı ALAN İ., AKIN Ö. ABSTRACT In this study, th fasibility of usag of fild programmabl gat arrays (FPGA) in th fild orintd control (FOC) of induction
Asnkron Makinanın Alan Yönlndirm Kontrolünd FPGA Kullanımı ALAN İ., AKIN Ö. ABSTRACT In this study, th fasibility of usag of fild programmabl gat arrays (FPGA) in th fild orintd control (FOC) of induction
çizilen doğru boyunca birim vektörü göstermektedir. q kaynak yükünün konum vektörü r ve Q deneme E( r) = 1 q
 Elektrosttik(Özet) Coulomb Yssı Noktsl bir q yükünün kendisinden r kdr uzktki bir Q yüküne uyguldığı kuvvet, şğıdki Coulomb yssı ile ifde edilir: F = 1 qq ˆr (1) r2 burd boşluğun elektriksel geçirgenlik
Elektrosttik(Özet) Coulomb Yssı Noktsl bir q yükünün kendisinden r kdr uzktki bir Q yüküne uyguldığı kuvvet, şğıdki Coulomb yssı ile ifde edilir: F = 1 qq ˆr (1) r2 burd boşluğun elektriksel geçirgenlik
ÜSLÜ İFADELER VE ÜSTEL FONKSİYONLAR LOGARİTMA FONKSİYONU, ÜSTEL, LOGARİTMİK DENKLEM VE EŞİTSİZLİKLER
 BÖÜ ÜÜ İFD V Ü FOİO Üslü İfdlrd İşlmlr...7 Üslü Dnklmlr... Üstl Fonksiyon...7 ygulm stlri...5 BÖÜ OGİ FOİO, Ü, OGİİ D V ŞİİZİ ogritm Fonksiyonu...7 ogritm Fonksiyonunun Özlliklri...9 bn Dğiştirm...55 Üstl
BÖÜ ÜÜ İFD V Ü FOİO Üslü İfdlrd İşlmlr...7 Üslü Dnklmlr... Üstl Fonksiyon...7 ygulm stlri...5 BÖÜ OGİ FOİO, Ü, OGİİ D V ŞİİZİ ogritm Fonksiyonu...7 ogritm Fonksiyonunun Özlliklri...9 bn Dğiştirm...55 Üstl
(, ) ( ) [ ] [ ] ve [ ] [ ] ( ) ( ) ÜÇGENLERDE TRİGONOMETRİK ÖZELLİKLER. A. Kosinüs Teoremi: Herhangi bir ABC
![(, ) ( ) [ ] [ ] ve [ ] [ ] ( ) ( ) ÜÇGENLERDE TRİGONOMETRİK ÖZELLİKLER. A. Kosinüs Teoremi: Herhangi bir ABC (, ) ( ) [ ] [ ] ve [ ] [ ] ( ) ( ) ÜÇGENLERDE TRİGONOMETRİK ÖZELLİKLER. A. Kosinüs Teoremi: Herhangi bir ABC](/thumbs/67/57138703.jpg) ÜÇGNLR TRİGONOMTRİK ÖZLLİKLR. Kosinüs Teoremi: Herhngi ir üçgeninin, kenr uzunluklrı,, ise; = +... os = +... os = +... os İspt: Şekilde görüldüğü üçgeni, köşesi ile orijin, kenrı ile ekseni ile çkışk şekilde
ÜÇGNLR TRİGONOMTRİK ÖZLLİKLR. Kosinüs Teoremi: Herhngi ir üçgeninin, kenr uzunluklrı,, ise; = +... os = +... os = +... os İspt: Şekilde görüldüğü üçgeni, köşesi ile orijin, kenrı ile ekseni ile çkışk şekilde
Kesir Örnek Çözüm. 1. Yandaki şekilde bir TEST - 1. 1. Taralı alanı gösteren. bütün 8 eş parçaya bölünmüş ve bu parçalardan 3 tanesi
 Kesir.. Trlı lnı gösteren kesri bulunuz. kesrini ile genişlettiğimizde elde edilecek kesri bulunuz.. Yndki şekilde bir bütün 8 eş prçy bölünmüş ve bu prçlrdn tnesi trnmıştır. Trlı lnı gösteren kesir syısı
Kesir.. Trlı lnı gösteren kesri bulunuz. kesrini ile genişlettiğimizde elde edilecek kesri bulunuz.. Yndki şekilde bir bütün 8 eş prçy bölünmüş ve bu prçlrdn tnesi trnmıştır. Trlı lnı gösteren kesir syısı
Basınç Elemanları Elastik ve inelastik burkulma Etkili Boy. Bölüm 4. Yrd. Doç. Dr. Muharrem Aktaş 2009-Bahar
 Bsınç Elemnlrı Elstik ve inelstik burkulm Etkili Boy Bölüm 4 Yrd. Doç. Dr. Muhrrem Aktş 009-Bhr Yısl çelik elemnlrının, eğilme momenti olmksızın sdece eksenel bsınç kuvveti ltınd olduğu durumlr vrdır.
Bsınç Elemnlrı Elstik ve inelstik burkulm Etkili Boy Bölüm 4 Yrd. Doç. Dr. Muhrrem Aktş 009-Bhr Yısl çelik elemnlrının, eğilme momenti olmksızın sdece eksenel bsınç kuvveti ltınd olduğu durumlr vrdır.
( ) ( ) Be. β - -bozunumu : +β - + ν + Q - Atomik kütleler cinsinden : (1) β + - bozunumu : nötral atom negatif iyon leptonlar
 6.. BETA BOZUUU Çkirdğin pozitif vya ngatif lktron yayması vya atomdan bir lktron yakalaması yolu il atom numarası ± 1 kadar dğişir. β - -bozunumu : ( B 4 4 ( B 4 nötral atom Atomik kütllr insindn : (
6.. BETA BOZUUU Çkirdğin pozitif vya ngatif lktron yayması vya atomdan bir lktron yakalaması yolu il atom numarası ± 1 kadar dğişir. β - -bozunumu : ( B 4 4 ( B 4 nötral atom Atomik kütllr insindn : (
11. SINIF GEOMETRİ. A, B ve C noktaları O merkezli çember üzerinde. Buna göre, BE uzunluğu kaç cm dir? B) 7 3 C) 8 3 A) 5 2 E) 9 5 D) 7 5 (2008 - ÖSS)
 ÇMR ÖSS SRULRI 1., ve noktlrı merkezli çember üzerinde m( ) = m( ) =. ir dik üçgeni için, = cm ve = 4 cm olrk veriliyor. Merkezi, yrıçpı [] oln bir çember, üçgenin kenrını ve noktlrınd kesiyor. un göre,
ÇMR ÖSS SRULRI 1., ve noktlrı merkezli çember üzerinde m( ) = m( ) =. ir dik üçgeni için, = cm ve = 4 cm olrk veriliyor. Merkezi, yrıçpı [] oln bir çember, üçgenin kenrını ve noktlrınd kesiyor. un göre,
TEST 12-1 KONU ELEKTRİK AKIMI. Çözümlerİ ÇÖZÜMLERİ
 OU 1 T Çözümlr TST 1-1 ÇÖÜ 5. 6 4 1. irncin boyuna bağlı olup olmadığını araştırdığı için ksitlri aynı, boyları farklı tllr kullanılmalıdır. Tllr aynı cins olmalı. u durumda v nolu tllr olmalıdır. 1. -
OU 1 T Çözümlr TST 1-1 ÇÖÜ 5. 6 4 1. irncin boyuna bağlı olup olmadığını araştırdığı için ksitlri aynı, boyları farklı tllr kullanılmalıdır. Tllr aynı cins olmalı. u durumda v nolu tllr olmalıdır. 1. -
12. a = log 5 7, b = log 3 2 ve c = log 2 13 sayıları arasındaki. 13. log 3 75 sayısı aşağıdaki aralıkların hangisinde bulunur?
 www.mtemtikclub.cm, 00 MC Cebir Ntlrı Gökhn DEMĐR, gdemir@h.cm.tr Lgritm. lg TEST I lg + lg 9 işleminin snucu C) 4. lg + = ise kçtır? 9 C) 4 9. lg 7! = ise lg 8! C) + 0. lg = ve lg = b ise lg 9 0 nin ve
www.mtemtikclub.cm, 00 MC Cebir Ntlrı Gökhn DEMĐR, gdemir@h.cm.tr Lgritm. lg TEST I lg + lg 9 işleminin snucu C) 4. lg + = ise kçtır? 9 C) 4 9. lg 7! = ise lg 8! C) + 0. lg = ve lg = b ise lg 9 0 nin ve
DOĞUŞ ÜNİVERSİTESİ MATEMATİK KLÜBÜ FEN LİSELERİ TAKIM YARIŞMASI 2007 SORULARI
 DOĞUŞ ÜNİVERSİTESİ MATEMATİK KLÜBÜ FEN LİSELERİ TAKIM YARIŞMASI 007 SORULARI Doğuş Ünivrsitsi Matmatik Kulübü tarafından düznlnn matmatik olimpiyatları, fn lislri takım yarışması sorularından bazıları
DOĞUŞ ÜNİVERSİTESİ MATEMATİK KLÜBÜ FEN LİSELERİ TAKIM YARIŞMASI 007 SORULARI Doğuş Ünivrsitsi Matmatik Kulübü tarafından düznlnn matmatik olimpiyatları, fn lislri takım yarışması sorularından bazıları
KAYNAKLI BAĞLANTILAR (Örnekler)
 KAYNAKLI AĞLANTILAR (Örneler) ÖRNEK 1: 50 N lu bir ü, şeilde görüldüğü gibi, 00 li çeli nl nlnış bğlntı prçsı rcılığı ile trıltdır. Kn üzerinde oluşn siu gerilei esplınız. [ ] A 0.707 5 190 180 irincil
KAYNAKLI AĞLANTILAR (Örneler) ÖRNEK 1: 50 N lu bir ü, şeilde görüldüğü gibi, 00 li çeli nl nlnış bğlntı prçsı rcılığı ile trıltdır. Kn üzerinde oluşn siu gerilei esplınız. [ ] A 0.707 5 190 180 irincil
TEST. Rasyonel Sayılar. 1. Aşağıdaki bilgilerden hangisi yanlıştır? 2. Aşağıda verilen, 3. Aşağıdaki sayılardan hangisi hem tam sayı,
 Rsyonel Syılr. Sınıf Mtemtik Soru Bnksı TEST. Aşğıdki bilgilerden hngisi ynlıştır? A) Rsyonel syılr Q sembolü ile gösterilir. B) Her tm syı bir rsyonel syıdır. şeklinde yzıln bütün syılr rsyoneldir. b
Rsyonel Syılr. Sınıf Mtemtik Soru Bnksı TEST. Aşğıdki bilgilerden hngisi ynlıştır? A) Rsyonel syılr Q sembolü ile gösterilir. B) Her tm syı bir rsyonel syıdır. şeklinde yzıln bütün syılr rsyoneldir. b
Sistem Dinamiği ve Modellemesi
 8..0 Sit Diiği v Modlli Doğrul Sitlri Z Dvrışı II. Mrtbd Gili Sitlr Giriş: Sit diiği çözülid, frlı fizil özllilr tşıy doğrul itlri rtritilrii blirly tl bğıtılr rıd bzrli (oloji) urulbili ouud itlri blirli
8..0 Sit Diiği v Modlli Doğrul Sitlri Z Dvrışı II. Mrtbd Gili Sitlr Giriş: Sit diiği çözülid, frlı fizil özllilr tşıy doğrul itlri rtritilrii blirly tl bğıtılr rıd bzrli (oloji) urulbili ouud itlri blirli
ÇAPRAZ AKIŞLI ISI DEĞİŞTİRİCİ
 ÇAPRAZ AKIŞLI ISI DEĞİŞTİRİCİ MAK-LAB012 1. DENEY DÜZENEĞİNİN TANITILMASI Düznk sas olarak dikdörtgn ksitli bir kanaldan ibarttir. 1 hp gücündki lktrik motorunun çalıştırdığı bir vantilatör il kanal içind
ÇAPRAZ AKIŞLI ISI DEĞİŞTİRİCİ MAK-LAB012 1. DENEY DÜZENEĞİNİN TANITILMASI Düznk sas olarak dikdörtgn ksitli bir kanaldan ibarttir. 1 hp gücündki lktrik motorunun çalıştırdığı bir vantilatör il kanal içind
Öğrenci Seçme Sınavı (Öss) / 17 Haziran Matematik I Soruları ve Çözümleri
 Öğrenci Seçme Sınvı (Öss) / 7 Hzirn 007 Mtemtik I Sorulrı ve Çözümleri.. 7 işleminin sonucu kçtır? A) B) 9 C) D) E) Çözüm. 7..9.. + işleminin sonucu kçtır? 4 8 A) 8 B) 8 C) 8 D) 4 E) 4 Çözüm + 4 8 8 4+
Öğrenci Seçme Sınvı (Öss) / 7 Hzirn 007 Mtemtik I Sorulrı ve Çözümleri.. 7 işleminin sonucu kçtır? A) B) 9 C) D) E) Çözüm. 7..9.. + işleminin sonucu kçtır? 4 8 A) 8 B) 8 C) 8 D) 4 E) 4 Çözüm + 4 8 8 4+
Vektör - Kuvvet. Test 1 in Çözümleri 5. A) B) C) I. grubun oyunu kazanabilmesi için F 1. kuvvetinin F 2
 7 Vektör - uvvet 1 Test 1 in Çözümleri 5. A) B) C) 1. 1 2 I. grubun oyunu kznbilmesi için 1 kuvvetinin 2 den büyük olmsı gerekir. A seçeneğinde her iki grubun uyguldığı kuvvetler eşittir. + + + D) E) 2.
7 Vektör - uvvet 1 Test 1 in Çözümleri 5. A) B) C) 1. 1 2 I. grubun oyunu kznbilmesi için 1 kuvvetinin 2 den büyük olmsı gerekir. A seçeneğinde her iki grubun uyguldığı kuvvetler eşittir. + + + D) E) 2.
IKTI 102 25 Mayıs, 2010 Gazi Üniversitesi-İktisat Bölümü
 DERS NOTU 10 (Rviz Edildi, kısaltıldı!) ENFLASYON İŞSİZLİK PHILLIPS EĞRİSİ TOPLAM ARZ (AS) EĞRİSİ TEORİLERİ Bugünki drsin içriği: 1. TOPLAM ARZ, TOPLAM TALEP VE DENGE... 1 1.1 TOPLAM ARZ EĞRİSİNDE (AS)
DERS NOTU 10 (Rviz Edildi, kısaltıldı!) ENFLASYON İŞSİZLİK PHILLIPS EĞRİSİ TOPLAM ARZ (AS) EĞRİSİ TEORİLERİ Bugünki drsin içriği: 1. TOPLAM ARZ, TOPLAM TALEP VE DENGE... 1 1.1 TOPLAM ARZ EĞRİSİNDE (AS)
Sunum ve Sistematik. Bu başlıklar altında uygulamalar yaparak öğrenciye yorum, analiz, sentez yetisinin geliştirilmesi hedeflenmiştir.
 Sunum ve Sistemtik ÖLÜM: ÖRTNLR LIŞTIRMLR u bşlık ltınd her bölüm kznımlr yrılmış, kznımlr tek tek çözümlü temel lıştırmlr ve sorulr ile trnmıştır. Özellikle bu kısmın sınıf içinde öğrencilerle işlenmesi
Sunum ve Sistemtik ÖLÜM: ÖRTNLR LIŞTIRMLR u bşlık ltınd her bölüm kznımlr yrılmış, kznımlr tek tek çözümlü temel lıştırmlr ve sorulr ile trnmıştır. Özellikle bu kısmın sınıf içinde öğrencilerle işlenmesi
KÜRESEL AYNALAR. 1. Çukur aynanın odağı F, merkezi M (2F) dir. Aşağıdaki ışınlar çukur aynada yansıdıktan sonra şekillerdeki gibi yol izler.
 . BÖLÜ ÜRESEL AYNALAR ALŞRALAR ÇÖZÜLER ÜRESEL AYNALAR. Çukur ynnın odğı, merkez () dr. Aşğıdk ışınlr çukur ynd ynsıdıktn sonr şekllerdek b yol zler. / / 7 / / / / / 8 / / / / / 9 / / / / N 0 OPİ . Çukur
. BÖLÜ ÜRESEL AYNALAR ALŞRALAR ÇÖZÜLER ÜRESEL AYNALAR. Çukur ynnın odğı, merkez () dr. Aşğıdk ışınlr çukur ynd ynsıdıktn sonr şekllerdek b yol zler. / / 7 / / / / / 8 / / / / / 9 / / / / N 0 OPİ . Çukur
Pontiklerin altında hacim koruma
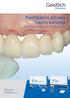 Pontilrin ltınd hcim orum Gitlich Biomtril ürünlri il - Sırt Korum çözümlri Dh fzl bilgi için www.gitlich-biomtril.com Sırt Korum - Bitç Sırt orum diş çimi onrı lvolr ırtın ontürünü orum için uygulnn bir
Pontilrin ltınd hcim orum Gitlich Biomtril ürünlri il - Sırt Korum çözümlri Dh fzl bilgi için www.gitlich-biomtril.com Sırt Korum - Bitç Sırt orum diş çimi onrı lvolr ırtın ontürünü orum için uygulnn bir
HAREKET. Bölüm -1. r r. KONUM: (X) Bir yerin seçilen bir noktaya göre yönlü uzaklığıdır. Vektörel bir büyüklüktür.
 Bölüm -1 : Bir cismin durn y d hreke eden bşk bir cisme göre zmnl yerdeğişirmesidir. ONU: () Bir yerin seçilen bir noky göre yönlü uzklığıdır. Vekörel bir büyüklükür. Uşk ilinin konumu nedir? Bir çocuk,
Bölüm -1 : Bir cismin durn y d hreke eden bşk bir cisme göre zmnl yerdeğişirmesidir. ONU: () Bir yerin seçilen bir noky göre yönlü uzklığıdır. Vekörel bir büyüklükür. Uşk ilinin konumu nedir? Bir çocuk,
