JEODEZİK AĞLARIN ŞEKİL YÖNÜNDEN OPTİMİZASYONUNDA ARDIŞIK DENGELEME YÖNTEMİNİN KULLANILMASI
|
|
|
- Berkant Şirin
- 5 yıl önce
- İzleme sayısı:
Transkript
1 PMUKKLE ÜNİVERSİESİ MÜHENDİSLİK FKÜLESİ PMUKKLE UNIVERSIY ENGINEERING COLLEGE MÜHENDİ SLİ K B İ L İ MLERİ DERGİ S İ JOURNL OF ENGINEERING SCIENCES YIL CİL SYI SYF : 998 : 4 : - : 63-6 JEODEZİK ĞLRIN ŞEKİL YÖNÜNDEN OPİMİZSYONUND RDIŞIK DENGELEME YÖNEMİNİN KULLNILMSI Yasemin UZUN, slan DİLVER, Haluk KONK Karadeniz eknik Üniversitesi, Mühendislik Fakültesi, Jeodezi ve Fotogrametri Mühendisliği Bölümü, rabzon ÖZE Gelişen teknolojiye paralel olarak ölçme alet ve yöntemlerinde ve jeodezik ağ oluşturma kavramında büyük değişiklikler olmuştur. Her ne kadar ölçme işlemleri kolaylaşmışsa da artık çalışmalarda işgücü ve zamanın da en uygun biçimde kullanılması arzulanmaktadır. Bu nedenle jeodezik ağların oluşturulmasında istenilen amaca göre en uygun ölçme planı, en uygun ağırlık dağılımı ve en uygun değerlendirme modelinin kullanılması büyük önem taşımaktadır. Bu işlemlere Jeodezik ğların Optimizasyonu denir ve bu işlem ağın tasarımı aşamasında gerçekleştirilebilir. Özellikle, ölçme planının bir kısmının önceden belli olduğu ve öngörülen amaç fonksiyonunun yeterince sağlanamadığı ağların en uygunlaştırılması işleminde; yalnızca eklenen ya da çıkarılan ölçülerin amaç fonksiyonuna katkılarının doğrudan hesaplandığı ardışık dengeleme yönteminden yararlanılabilir. nahtar Kelimeler : Jeodezik ağ, Ölçme planı, rdışık dengeleme, Optimizasyon USING SEQUENIL DJUSMEN MEHOD IN OPIMIZION OF HE CONFIGURION OF GEODEIC NEWORKS BSRC In the field of surveying, surveying techniques and instruments are advancing with the support of ever evolving technology. Establishing a geodetic network is one of the areas witnessing big changes from this respect. lthough measurements have become easier to perform, an optimum use of time and resources is still very important. herefore, determining observation plan, weights, surveying and computation techniques which best serve the need carry a great importance in setting up a geodetic network. he work involved is known as the Optimization of Geodetic Networks and its parameters could be estimated during the design of the network. Specifially, in optimization the networks where observation plan is partially known beforehand and postulated objective function is not well provided, the sequential adjustment method in which contributions of added or deleted observations are directly computed can be used. Key Words : Geodetic network, Observation plan, Sequential adjustment, Optimization. GİRİŞ Yeryüzünde noktaların konumlarının belirlenmesi ve daha sonra yapılacak çalışmalarda kullanılabilmeleri için; her şeyden önce tüm sorunlara cevap verebilecek nitelikte, her türlü ölçü hatalarına karşı duyarlı, presizyonu fazla ve güvenilir jeodezik ağlar oluşturulur. Bu amaçla oluşturulan jeodezik ağlardan elde edilen nokta konumlarının (koordinatlarının) anlamlılığı, yapılacak her çalışmanın aynı duyarlıkta referans sistemine sahip olması ile mümkün olur. Günümüzde yapılan tüm haritacılık çalışmaları 63
2 jeodezik ağlarla konumları belirlenmiş noktalara dayandırılmaktadır. Bu nedenle yapılacak çalışmanın arzulanan doğruluğa ve duyarlığa ulaşması, nokta konumlarının doğruluğuna ve dolayısı ile jeodezik ağların duyarlığına bağlıdır. Son yıllarda ölçme alet ve tekniklerindeki gelişmelere rağmen, çalışmaların dayandırıldığı noktaların beklenen duyarlığı göstermemesi, yeni çalışmaların duyarlığını etkilemektedir. Jeodezik ağların tasarımı, geliştirilmesi ya da iyileştirilmesi sırasında; bir amaç fonksiyonu seçilerek ağın datumunun, geometrik şeklinin ya da noktaların konumlarının en uygun biçimde belirlenmesi işlemine jeodezik ağların optimizasyonu denir. Kurulan jeodezik ağların kurulma amaçlarına göre istenen bazı duyarlıkları sağlamaları gerekir. Bu duyarlık isteklerinin sağlanıp sağlanmadığı duyarlık ölçütleri ile denetlenir. Duyarlık ölçütleri, geçerli bir dengeleme modeli için gerçekçi bilgiler taşırlar. Dengeleme modelinin geçerli olup olmadığı veya değerlendirme aşamasında bir model hatasının oluşup oluşmadığı güven ölçütleri ile denetlenir. Dengeleme sonuçlarına ve onların duyarlıklarına ilişkin yorumlar güven ölçütlerinin sağlanması durumunda gerçekçi olurlar. Günümüzün teknolojik olanaklarını da göz önüne alırsak; ele alınan jeodezik ağın tasarımı aşamasında hangi tür ölçülerin yapılmasının doğruluk, duyarlık ve güvenilirlik isteklerine en olumlu katkıyı sağlayacağını, bu amaca uygun ve etkin çözüm algoritmaları geliştirerek belirleyebiliriz. Bu amaçla oldukça kullanışlı olan çözüm tekniklerinden birisi de ardışık dengeleme tekniğidir. Bu çalışmada jeodezik ağların optimizasyonu konusu özetlenmiş, jeodezik ağların şekil yönünden optimizasyonu ve III. derece optimizasyon işlemlerinde oldukça kullanışlı olan söz konusu ardışık dengeleme yöntemi anlatılmıştır. Sayısal uygulama için örnek bir test ağı seçilmiş ve ulaşılan sonuçlar sergilenmiştir.. JEODEZİK ĞLRIN OPİMİZSYONU Günümüzde jeodezik ağlar mühendislik hizmetlerine temel oluşturacak sabit noktalar ve bölgesel haritalar elde etmek amacı için kurulmaktadırlar. yrıca yapılan büyük mühendislik çalışmalarında zamanla oluşabilecek deformasyonların belirlenmesi ve yer hareketlerinin izlenmesi amacı ile de jeodezik ağlar kurulmaktadır. Optimizasyon işlemi seçilen amaç fonksiyonlarına ya da tasarım parametrelerine göre sınıflandırılabilir... maç Fonksiyonlarına Göre Optimizasyon Optimizasyon işlemi jeodezik ağların seçilen bir amaç fonksiyonuna göre tasarlanması, geliştirilmesi ve iyileştirilmesi işlemlerini içerir. Seçilen amaç fonksiyonu duyarlık isteklerini içeriyorsa duyarlık optimizasyonu, güven isteklerini içeriyorsa güven optimizasyonu, para, emek ve zaman gibi parametreleri içeriyorsa matematiksel optimizasyon söz konusu olur... Duyarlık Optimizasyonu Duyarlık, bir ağın kalitesinin göstergesidir. Duyarlık yönünden uygun bir ağ, her noktada aynı duyarlığa sahip olmalıdır. Jeodezik ağlardan beklenen duyarlık isteklerinin gerçekleşmesi için; amaç fonksiyonu olarak noktalara göre tanımlanan duyarlık ölçütleri (koordinat bilinmeyenlerinin ortalama hataları, Helmert ortalama hata elipslerinin yarı eksenleri) ya da global duyarlık ölçütleri (hacim ölçütü, güven hiper elipsoidinin yarı eksenleri) kullanılabilir. Bu ölçütlerden optimizasyon işleminde en kullanışlı olanları global duyarlık ölçütleridir. Skaler amaçlı duyarlık istekleri yerine kurulması planlanan bir ağın duyarlık yönünden homojen ve izotrop olması öngörülebilir. Bu durumda söz konusu istekleri karşılayan ve ağın koordinatlarından türetilen homojen ve izotrop özellikli ölçüt matrisleri kullanılır. Bir jeodezik ağın duyarlık yönünden en uygun duruma getirilmesi istendiğinde şu aşamalar izlenir. Ölçme planı taslağı düzenlenir. Noktaların yaklaşık koordinatları ve birim ölçünün karesel ortalama hatasının öncül değeri ile oluşturulan varyans - kovaryans matrisi K XX yardımı ile ağın duyarlık yönünden zayıf olduğu noktalar ve bu zayıflıkların doğrultuları belirlenir. Gereğinde ağa yeni noktalar eklenerek duyarlık yönünden yetersiz bulunan noktalar için ek ölçme planı düzenlenir. Geliştirilen ölçme planına göre tekrar ağın duyarlık yönünden incelemesi yapılır ve tüm noktalar duyarlık yönünden yeterli duruma getirilir. ğda istenilen ve beklenen duyarlık isteklerini içeren yapay ölçüt matrisi C XX oluşturulur ve bu Mühendislik Bilimleri Dergisi (-) Journal of Engineering Sciences (-) 63-6
3 matristen yararlanılarak uygulanacak bir ağırlık optimizasyonu ile ölçülerin ağırlıkları belirlenir. Ölçüt matrisinin geliştirilmiş ölçme planı ve en uygun duruma getirilmiş ağırlıklarla hesaplanan varyans - kovaryans matrisi K XX ile eşdeğer olup olmadıkları test edilir. Duyarlık isteklerini içeren yapay ölçüt matrisi C XX ile ağda gerçekleşen duyarlıkları gösteren K XX eşdeğer bulunurlarsa ağın duyarlık yönünden en uygun durumda olduğuna karar verilir (Konak,995).. 3. Güven Optimizasyonu Jeodezik ağların güvenirliği, ağın geometrik yapısının model hatalarına karşı duyarlığıdır. Model hatalarının ortaya çıkarılmasına uygun yapıdaki ağlar güvenilir ağlar olarak adlandırılır. Buradan model hatalarının ortaya çıkarılmasının ağın geometrik yapısına bağlı olduğu anlaşılır (Öztürk, 98). Bir jeodezik ağda duyarlık ölçütleri, ancak dengelemenin matematik modelinin doğru kurulduğu durumda gerçekçi sonuç verirler. Eğer dengeleme işleminde kurulan fonksiyonel model, ölçülerle bilinmeyenler arasındaki geometrik ve fiziksel özelliklere uygun değilse, stokastik model ölçülerin duyarlıklarını ve korelasyonlarını tam olarak yansıtmıyorsa jeodezik ağda model hataları ortaya çıkar. Dengeleme işleminde model hataları güven ölçütleri ile denetlenir. Güven ölçütleri olarak model hipotezinin testi, redundanz payı, iç güven ölçütü ve dış güven ölçütü örnek olarak verilebilir. Bir jeodezik ağın güven yönünden en uygun duruma getirilmesi istendiğinde şu aşamalar izlenir. ğda oluşabilecek model hatalarının denetlenmesi amacı ile her bir ölçünün fazla ölçü sayısındaki payı (redundanz payı) r i ve ortalama fazla ölçü sayısı r = - (u/n) hesaplanır. Fazla ölçü sayısındaki payları r i, ortalama fazla ölçü sayısı r dan küçük olan ölçülerin diğer ölçüler yardımı ile yeterince denetlenemediklerine karar verilir. Söz konusu ölçülere dik yönde yeni ölçüler planlanır. İç güven ölçütleri ve dış güven ölçütleri hesaplanır. ğa ilişkin ölçüler gözden geçirilir. İç güven ölçütleri ve dış güven ölçütleri yönünden iyi denetlenemediklerine karar verilen ölçülere dik yönde yeni ölçüler planlanır. Gereğinde ağın masraf, zaman ve emek yönünden en uygun duruma getirilmesi için çok iyi denetlendiklerine karar verilen ölçüler ölçme planından çıkarılır. Geliştirilen ölçme planı gözden geçirilir ve tasarım kesinleştirilir (Kurt,996).. 4. Matematik Optimizasyon Bilimsel, teknik ya da ekonomik yatırımlarda; eldeki hammadde, işgücü, donanım ile en az birim zamanda en uygun kazanımlar amaçlanmaktadır. Yatırımların gerektirdiği önemli kısıtlayıcılar (olanaklar) herhangi bir parametre ile, amaç da ilgili parametrelerin belirli bir fonksiyonu olarak tanımlanabiliyorsa bir matematiksel optimizasyon söz konusu olur (Konak, 995). Bu problemde ağın datumu, geometrik şekli ve noktaların konumları belli olarak varsayılmakta, yalnızca ölçü ağırlıklarının belirlenmesi istenmektedir (yan, 98).. 5. asarım Parametrelerine Göre Optimizasyon Jeodezik ağların optimizasyonu problemi, bir amaç fonksiyonu seçilerek belirlenmesi gereken tasarım parametrelerine göre dört gruba ayrılabilir Derece Optimizasyon Kurulan jeodezik ağ noktalarının ya da bunların fonksiyonlarının karesel ortalama hatalarının en küçük olması öngörülen duyarlık optimizasyonu probleminde amaç fonksiyonunun gerçekleşmesi için ağın datumunun en uygun şekilde belirlenmesi işlemine. derece optimizasyon denir. Bu optimizasyon işleminde noktaların yaklaşık konumlarının, ağın geometrik yapısının ve ölçü duyarlıklarının bilindikleri varsayılmakta, problem içinde bu veriler değiştirilmemektedir. ğdan beklenen duyarlık istekleri ağın datum parametrelerinin (konum, ölçek ve yöneltme) seçimine bağlıdır. ğ noktalarının bir kaçının sabit alındığı ağlarda bağıl duyarlık ölçütlerinden, noktaların tümünün koordinatlarının bilinmeyen olarak seçildiği serbest ağlarda iç duyarlık ölçütlerinden söz edilir. Başka bir deyişle; bir datum optimizasyonu işlemi aynı zamanda katsayılar matrisinin rank bozukluğunun giderilmesi anlamına da gelmektedir. Bir datum optimizasyonu probleminde katsayılar matrisi ve P ağırlık matrisi bellidir ve bu durumda en uygun ters ağırlıklar matrisi Q XX in belirlenmesi amaçlanmaktadır.. 7. I. Derece Optimizasyon Mühendislik Bilimleri Dergisi (-) Journal of Engineering Sciences (-) 63-6
4 ğın datumunun, ölçü duyarlıklarının ve gözlem planının bilindiği varsayılarak en uygun yaklaşık koordinatların belirlenmesi işlemine. derece optimizasyon denir. ynı zamanda, bir ağda noktaların yaklaşık koordinatları ağın geometrik yapısını yansıtan katsayılar matrisini de belirlemektedir. Bu sebeple optimizasyon işleminde P ve Q XX matrislerinin bilindiği varsayılmakta, matrisinin en uygun şekilde belirlenmesi amaçlanmaktadır. En uygun yaklaşık koordinatların belirlenmesi işlemi yapıldığından bu optimizasyona konum optimizasyonu da denilmektedir. Bu optimizasyon işleminde ağın datumu belirlidir, yeni noktaların yaklaşık koordinatları da ağın kurulacağı bölgenin elimizde olan bir haritası yardımı ile belirlenir. Bölgenin topoğrafik ve meteorolojik yapısı incelenerek ve eldeki ölçme aletleri göz önünde bulundurularak ölçü duyarlığı tahmin edilebilir. Düşünsel (amaçlanan duyarlık isteklerini içeren) ters ağırlık matrisi Q oluşturulur. Q matrisi oluşturulurken, ğ noktalarının güven elipslerinin homojen ve izotop yapıda olmalarına, Bağıl güven elipslerinin d yarıçaplı daireler olmalarına, Varyans-kovaryans matrisinin aylor-karman yapısında olmasına dikkat edilir (Öztürk ve Şerbetçi, 99). ğın iç noktalarından başlayarak noktalar ele alınır ve iterasyon yapılarak en uygun nokta konumları belirlenir. Belirlenen nokta konumlarına göre katsayılar matrisi kurulur. Bu matrisle Q = ( P) + invers matrisi hesaplanır ve düşünsel olarak kurulan Q invers matrisi ile karşılaştırılır. d = vek (D) = Q i i - Q fark vektörü hesaplanır. (d d) min = min (d d) olduğu durumda noktaların en uygun yerleri belirlenmiş olur.. 8. II. Derece Optimizasyon Jeodezik ağlarda ağın datumunun, geometrik şeklinin ve ağdaki ölçülerin ölçü duyarlıklarının bilindiği durumda en uygun ölçme planının belirlenmesi ya da ölçülerin ağırlıklarının en uygun şekilde belirlenmesi işlemine II. derece optimizasyon denir. Bu optimizasyon işleminde Q XX ve matrislerinin bilindiği durumlarda en uygun P matrisi belirlenmesi amaçlanmaktadır. Gerçekleştirilecek bir ağırlık optimizasyonu işlemi sonunda hesaplanan değişken yapılı ağırlık matrisi P yardımıyla d = vek(d) = Q XX -( P) + fark vektörü hesaplanır. (d d) min = min (d d) olduğu durumda en uygun ağırlıklar belirlenmiş olur.. 9. III. Derece Optimizasyon İstenilen amaca uygun olmayan jeodezik ağların amaç fonksiyonunu sağlayacak şekilde geliştirilmesi ve iyileştirilmesi işlemine III. derece optimizasyon denir. Böyle bir optimizasyon probleminde en uygun duruma getirilmesi istenilen parametrelerin, örneğin katsayılar matrisi ve P ağırlık matrisinin bir bölümü önceden bilinmektedir. Mevcut bir jeodezik ağın geometrik şeklinin iyileştirilmesi ve geliştirilmesi işlemlerinde, ğa yeni ölçüler eklenebilir, ğa yeni noktalar eklenebilir, ğa hem yeni ölçüler hem de yeni noktalar eklenebilir, ğ yeni ölçüler ve yeni noktalar eklenerek yeni ölçülerin en uygun ağırlıkları belirlenebilir. Jeodezik ağın geometrik şeklinin geliştirilmesi ve iyileştirilmesi işlemlerinde yapay veriler kullanılarak simülasyon yöntemi ile sonuç elde edilmeye çalışılır. Simülasyon yöntemlerinde amaç fonksiyonuna uygun bir ağ oluşana kadar işlem tekrar edilir. Örneğin ağın tüm ölçüleri ile dengeleme işlemine başlanıp her tekrarlamada amaç fonksiyonuna en az etkiyi yapan ölçü, ölçme planından çıkarılabileceği gibi çözüm için yeterli sayıda bilgi ile dengeleme işlemine başlayıp her tekrarlamada amaç fonksiyonuna en çok etkiyi yapan ölçü ölçme planına eklenerek de çözüm bulunabilir. Bu yöntemde yapılan her değişiklik için dengeleme işlemi tekrarlandığı için kullanılan zaman fazla olur. Bu nedenle çok noktalı ağlar için bu yöntem tercih edilmez (Mikhail, 98). Jeodezik ağın geometrik şeklinin geliştirilmesi ve iyileştirilmesi işlemlerinde kullanılabilen bu amaca yönelik çözüm yöntemlerinden biri de ardışık dengeleme yöntemidir. 3. RDIŞIK DENGELEME YÖNEMİ Daha önceden kurulmuş fakat istenilen amaca uygun olmayan nirengi ağlarının bir amaç fonksiyonuna göre geliştirilmesi ve iyileştirilmesi işleminde III. derece optimizasyon veya yeni planlanan ağların amaç fonksiyonuna uygun olacak şekilde ölçme planının belirlenmesi işlemine I. derecede optimizasyon denilmektedir. Bu şekilde yapılacak çözümde belirlenmek istenen bilinmeyenlerin bir kısmı önceden bilinebilir. maç fonksiyonuna uygun olmayan bir ağ için ölçme planı belirleniyorsa, ilk ölçme planından elde edilmiş Mühendislik Bilimleri Dergisi (-) Journal of Engineering Sciences (-) 63-6
5 katsayılar matrisi, yeni oluşturulan ölçme planından elde edilen yeni katsayılar matrisinin bir alt matrisi olacaktır. rdışık dengeleme yöntemi; iyileştirilmesi istenen veya yeni tasarlanan ağlarda öngörülen amaca uygun ölçü planının belirlenmesi amacıyla eklenmesi ya da çıkarılması düşünülen ölçülerden elde edilen ek katsayılar matrisi ve gözlem vektörünün, eski dengeleme sonuçlarına katkılarının hesaplanması işlemidir. Bu yöntemin matematik modeli en genel şekliyle, F (, l) = F (, l ) = () eşitlikleriyle verilebilir. Burada F ilk l gözlemleriyle, F ise eklenen veya çıkarılan I gözlemleriyle bilinmeyenlerini hesaplamak için kurulan matematik modellerdir. l ve gözlemleri P ve P ağırlıklı ve korelasyonsuz, bilinmeyenleri de P ağırlıklı olarak düşünülür. () eşitliği yaklaşık değerleri ile aylor serisine açılarak doğrusallaştırma yapılırsa, + Bv + w = + Bv + w = eşitlikleri elde edilir. Bu eşitliklerde kullanılan, F F F F =, =, B =, B = l l () katsayı matrislerini, v ve v ; l ve l gözlemlerine dengeleme sonucunda getirilecek düzeltme vektörlerini, w, w ise sabit terimleri (kapanma artık hataları) göstermektedir. Bu durumda parametrelerin tek anlamlı değerlerini elde edebilmek amacıyla En Küçük Kareler ilkesine göre yazılan koşulların gerçekleşmesi için Langrange korelatları ile genişletilmiş Lagrange fonksiyonu, P v Ω= [ v v ] P v + P [ ] + + k k B v w B v w (3) olarak yazılabilir. Bu eşitliğin minimum olması için parametrelere göre alınan kısmı türevler sıfıra eşitlenerek kurulan normal denklemler, P B P B B B P X v v k + w = k w (4) şeklinde elde edilir. Buradan parametrelerinin çözümünü elde edebilmek için v, v, k, k bilinmeyenleri cebirsel olarak yok edilir. Bu işlem için Gauss algoritması kullanılabileceği gibi bunun bir benzeri olan 969 da hompson tarafından geliştirilen teknikte kullanılabilir. Bu teknik aşağıdaki gibi açıklanabilir. B Z U C D Y + V = ( D C B) Y ( V C U) eşitliğinde Z bilinmeyeni = (5) şeklinde yok edilir (Nickerson, 979). Bu şekilde v, v, k, k bilinmeyenleri sırası ile yok edilirlerse, B P - B = M, B P - B = M kısaltmaları ile e bağlı bir denklem [ M + P + M ] M w + M w = [ M + P ] + M w X = + (6) olarak elde edilir. Bu eşitlikte F modelinin olmadığı düşünülürse eşitliğin bilinmeyeni için En Küçük Kareler ilkesine geri dönüleceği görülür. Yazılan (6) eşitliğinden yeni F modelinin eklenmesiyle ortaya çıkan sonuçların normal denklemlere eklenerek normal denklem matrisinin güncelleştirilebileceği görülmektedir. Eğer F modeli eklenen değil de çıkarılan gözlemleri içerseydi F modelinden oluşan sonuçlar normal denklemlerden çıkarılacaktı. (6) ifadesi, - N = M + P, U = M w - kısaltmaları ile bilinmeyenleri için çözülürse, - - ( ) ( ) = N ± M U ± M w (7) Mühendislik Bilimleri Dergisi (-) Journal of Engineering Sciences (-) 63-6
6 eşitliği elde edilir. Bu eşitliğin çözümü için ilgili işlemlerin yapılmasından sonra, - = ( ± ) ( ± ) X N M U - - N M M w m (8) eşitliği bulunur. Bu son iki eşitlikte üstteki işaretler modelde eklenen gözlemlerin olduğu durumu, alttaki işaretler modelde çıkarılan gözlemler olduğu durumu göstermektedir. (8) eşitliğindeki terimlerin katsayılarını daha kullanışlı hale getirebilmek için matris cebrinde verilen - - ( ± ) m ( ± ) ( S ± R ) R S ( R± S ) S R S S R S S (9) özdeşliklerden faydalanılır. Bu özdeşlikler (8) eşitliğine uygulanırsa, ( ) ( ± ) X= N U ± N M ± N N U m - - N M N w - - eşitliği elde edilir. Bu eşitlikteki N U ifadesi F modelindeki koordinat bilinmeyenlerinin çözümüdür. Böylece son ifade, ( ) - = N ± M ± N ( + w ) () şekline dönüşmüş olur. Bu eşitliklerden yalnızca l gözlemlerinden oluşan düzeltme denklemlerinin ilk sonuçlara eklenmesiyle kesin sonucun elde edilebileceği görülmektedir. l gözlemlerinden oluşan matrisler daha küçük boyutlu olacağından () eşitliği, (7) eşitliğinden daha az hesap gerektirir. Böylece hem zaman hem de bellek kaybı sorunu ortadan kalkmış olur. Eski ve yeni gözlemlere getirilecek düzeltmeler, ( ) ( ) v = P B ( B P B ) + w v = P B ( B P B ) + w () bağıntısından hesaplanabilir. yrıca koordinat bilinmeyenlerinin ters ağırlık matrisi () eşitliğinden; ters ağırlık katsayılarının yayılma kuralına göre, ( ) Q = N = N ± M () olarak bulunur. Bu eşitliğe (9) özdeşliği uygulanırsa daha sade, istenen amaca yönelik bir ifade olarak, ( ) Q = N N ( ± M + N N ) (3) eşitliği elde edilir. Bu eşitlik sabit sayılı noktadan kurulması tasarlanan nirengi ağlar için ana matematik model olarak alınabilir. Değişken nokta sayılı nirengi ağlarının tasarımı ve iyileştirilmesinde, istenilen duyarlığa cevap verecek optimum tasarım için ölçme planına nokta eklenebilir ve çıkarılabilir. Bu durumda çözüm koordinat bilinmeyenlerinin eklenmesi ve çıkarılmasıdır. Bunun için genel matematik model, F F (,l) = (,,l ) = (4) şeklinde tanımlanabilir. Bu eşitlikler yaklaşık değerler yardımıyla doğrusallaştırılırsa, neticede () deki doğrusallaştırma işlemine ait katsayılara ilave olarak, F =, F = katsayıları elde edilir. Buradan düzeltme koşul denklemleri () ye benzer şekilde, B + B v w + v w = (5) olarak yazılabilir. Bir önceki bölümde anlatıldığı şekilde En Küçük Kareler ilkesine göre çözüm için normal denklem sistemi kurulursa, eşitliklerinden hesaplandıktan sonra birim ağırlıklı ölçünün ortalama hatası; m =± [ v P v ] + [ v P v ] n + n u Mühendislik Bilimleri Dergisi (-) Journal of Engineering Sciences (-) 63-6
7 P B P B B B P X P X v v k k w + = w Q = (N N N N ) (9) - Q = (N N N N ) - () eşitlikleri bulunur. Burada () eşitliğine (9) özdeşliklerinin ilki uygulanırsa Q için, denklem sistemi elde edilir. Burada yine l ve l gözlemleri korelasyonsuz ve, bilinmeyenleri P, P ağırlıklarında olduğu kabul edilir. Bu denklem sisteminde, yukarıda anlatılan şekilde v, v, k, k bilinmeyenleri yok edilirse ve sonuçla ilgili eşitliklerde, M = BP B, M = BP B N = ( M + P ), U = ( M w ) N = N+ ( M ) N = ( M ), N = ( M + P ) U = U + ( M w ), U = ( M w ) (6) kısaltmaları kullanılırsa, koordinat bilinmeyenleri için, N N = N N U U (7) eşitliği yazılabilir. Bu eşitlikteki katsayılar matrisinin tersi için, N N N N Q Q = Q Q gösterimi kullanılarak, bir kare matrisin tersi ile soldan veya sağdan çarpımının birim matris olacağı kuralından hareketle, N N N N Q Q Q Q E = E eşitliği yazılabilir. Bu matris eşitliğinde ilgili çarpım işlemlerinin yapılması sonucu elde edilen matris denklemlerinin çözümünden ters ağırlık matrisinin elemanları için, Q = N N Q (8) - Q = N + N N ( N N N N ) N N ve (9) eşitliği bu eşitlikte yerine yazılırsa Q = N + N N Q N N () eşitliği elde edilir. Yine (6) eşitliğine (9) özdeşliklerinin ilki uygulanırsa N için - N = N N (M + N ) N () eşitliği bulunur. rtık (7) eşitliği için tüm ifadeler bulunmuştur. Fakat bu problemde bilinmeyenlerin eklenmesi ve çıkarılması gibi iki farklı durum söz konusu olur. Bilinmeyenlerin eklenmesi durumunda vektörlerin ve matrislerin boyutları artacak, bilinmeyenlerin çıkarılması durumunda ise azalacaktır. Bu sorun +/- işaretleri ile çözülemeyecek kadar karmaşıktır. Bu nedenle bu iki durum ayrı olarak ele alınabilir. 3.. Yeni Noktaların (Bilinmeyenlerin) Eklenmesi: Bu durumda yukarıda geliştirilen mevcut eşitlikler kullanılır.,, B matrislerinden N i bulmak ilk adımdır. (8), (9), () ve () eşitliklerinden Q, Q, Q bulunur. Böylece normal denklemlerin ters matrisi bulunmuş olur. Sabit vektör U (6) eşitliğinden bulunur ve l, bilinmeyenlerinin çözümü (I7) eşitliğiyle elde edilebilir. Bu metot fazla sayıda bilinmeyen içeren çözümde yeni bilinmeyenlerin eklenmesi durumunda çok faydalanılır. Böylece bu yöntemle çok az hesap yaparak arzulanan sonuca varılır. 3.. Yeni Noktaların (Bilinmeyenlerin) Çıkarılması Bu durum eklenen bilinmeyenlerin iptali olarak düşünülebilir. N yeni normal denklemlerin tersi ve sabit vektör U bilinmektedir. İstenen eski N ve Mühendislik Bilimleri Dergisi (-) Journal of Engineering Sciences (-) 63-6
8 sabit vektör U in bulunmasıdır. (6) eşitliklerinden - N için ifade N = N- M şeklindedir. Bu eşitliğe (9) eşitliklerinin ilki uygulanırsa N =N +N (M N ) N (3) eşitliği elde edilir. () eşitliğinin tersi alınarak N için ifade - N = Q + N N N şeklinde bulunur. Bu ifadeye de (9) özdeşliklerinin ilki uygulanırsa, - N =Q Q N (N + N Q N ) N Q (4) eşitliği elde edilir. Bu eşitlik (3) de yerine yazılarak N ve (6) eşitliğinden U hesaplanır. bilinmeyenleri ise = N U ile bulunur. 4. SYISL UYGULM Bu sayısal uygulamada ölçme planına eklenebilecek tüm ölçülerin sırası ile amaç fonksiyonuna etkisinin irdelenmesi ve amaç fonksiyonunu minimum yapan ölçülerin ölçme planına alınması en uygun yaklaşım biçimidir. ncak uygulamada; bir şekil optimizasyonu işleminde, ardışık dengeleme yönteminin oldukça etkin ve kullanışlı bir yöntem olduğunun sayısal olarak da vurgulanması amaçlanmıştır. Uygulama modeli olarak bir test ağı tasarlanmış ve ardışık dengeleme yöntemi ile çözüm için Basic programlama dilinde yazılan bir programdan yararlanılmıştır (Uzun, 995). Jeodezik ağın geometrik şeklinin (ölçme planının) irdelenmesi için bir amaç fonksiyonu seçilmelidir. Bu çalışmada amaç fonksiyonu olarak noktalara göre tanımlanan duyarlık ölçütlerinden biri olan ağ noktalarına ilişkin hata elipsleri ele alınmıştır. Hata elipslerinin büyük yarı eksenleri hi ile küçük yarı eksenleri B hi arasında hi - B hi <. cm. kadar fark olması amaç fonksiyonu olarak seçilmiştir. Uygulama için seçilen jeodezik ağın ölçüleri şöyledir. ablo. Sabit Noktaların Koordinat Değerleri Nokta No Y(m) X(m) ablo. Noktaların Yaklaşık Koordinat Değerleri Nokta No Y(m) X(m) ablo 3. Doğrultu Ölçü Değerleri DN BN Doğrultu DN BN Doğrultu ablo 4. Ölçülen Kenarlar DN BN Kenar (m) ablo 5. Ölçme Planına Eklenen Doğrultu Ölçüsü DN BN Doğrultu (g) ablo 6. Ölçme Planına Eklenen Kenar Ölçüsü DN BN Kenar (m) Bu ölçülerle yapılan dengeleme sonucunda elde edilen geometrik şekil Şekil de verilmektedir. Mühendislik Bilimleri Dergisi (-) Journal of Engineering Sciences (-) 63-6
9 Şekil. İlk ölçülerle elde edilen geometrik şekil Bu şekil incelenirse 4 ve 39 numaralı noktaların duyarlıklarının arzulanan amaç fonksiyonuna uygun olmadığı görülür. Bu ölçme planına 4-4 doğrultusu eklenerek verilen bağıntılarla çözüm yeniden yapılırsa Şekil elde edilir. Şekil. Ölçme planına doğrultu ölçüsü eklenerek elde edilen geometrik şekil Bu şeklin incelenmesinden sadece 38 noktasının duyarlığının amaç fonksiyonuna uygun olmadığı görülmektedir. Bu ölçünün de dahil olduğu ölçme planına 39-4 kenarı eklenerek yapılan çözümden Şekil 3 elde edilmiştir. Şekil 3. Ölçme planına kenar ölçüsü eklenerek elde edilen geometrik şekil Sonuçta bu şekilde tüm noktaların istenilen duyarlığı sağladıkları görülmüştür. 5. SONUÇ Gerek alt yapı ve gerekse özel mühendislik hizmetlerine yönelik jeodezik araştırmalar; bu amaca uygun kalite ve doğrulukta jeodezik ağlar gerektirmektedir. ynı zamanda bu ağların ortak bir referans sistemine sahip olmaları istenir ve böyle bir referans sistemi de koordinatları önceden bilinen ve arzulanan doğrulukta birbirleriyle uyuşumlu oldukları kabul edilen noktalara dayandırılarak elde edilebilir. Günümüzde istenilen amaca uygun jeodezik ağlar oluşturulabilmektedir. Fakat yeni oluşturulan jeodezik ağlar eski ağlarla aynı koordinat sistemine sahip olurlarsa anlamlı olurlar. Her ne kadar yeni oluşturulan ağlar istenilen duyarlığa uygun yapıda olsalar da ağın duyarlığı, sabit noktaların duyarlığından doğrudan etkilenir. Bu nedenle hem ön görülen duyarlıkları sağlayan yeni jeodezik ağlar oluşturması, hem de eski jeodezik ağların söz konusu duyarlıkları sağlamaları istenir. Bu istekler jeodezik ağların optimizasyon işlemi ile gerçekleştirilebilir. Bu çalışmada jeodezik ağların şekil yönünden optimizasyonunda kullanılabilen yöntemlerden biri olan ardışık dengeleme yöntemi için bir inceleme yapılmıştır. Bilgisayar hem zaman, hem de işgücü yönünden hesap işlerinde büyük avantajlar sağlamasına rağmen, hesaplamada kullanılan bellek ve zaman çok önemlidir. rdışık dengeleme yöntemi ile; ilk ölçme planından elde edilen sonuçlara sadece eklenen veya çıkarılan ölçülerle oluşturulan yeni ölçme planının katkıları hesaplanmaktadır. Mühendislik Bilimleri Dergisi (-) Journal of Engineering Sciences (-) 63-6
10 Bu durumda hesap için kullanılan zamanda ve bellekte çok büyük kazanımlar sağlanabilmektedir. Ölçme planındaki ölçülerin seçilen amaç fonksiyonuna etkileri bu yöntemle araştırılabilmekte ve en uygun ölçme planı belirlenebilmektedir. Jeodezik ağın tasarımı aşamasında, bölgenin haritası ve ölçme koşulları göz önünde bulundurularak yapılabilecek ölçüler belirlenebilir. Bu ölçüler ardışık dengeleme yöntemi ile değerlendirilerek amaç fonksiyonuna katkıları belirlenebilir ve böylece hızlı ve kolay bir biçimde şekil optimizasyonu sonuçlarına ulaşılabilir. 6. KYNKLR eknik Üniversitesi Yer Bilimleri Fakültesi Yayın No: 39, Karadeniz eknik Üniversitesi Basımevi, rabzon. Öztürk, E. ve Şerbetçi, M. 99. Dengeleme Hesabı Cilt IIl, Karadeniz eknik Üniversitesi Mühendislik Mimarlık Fakültesi Yayın No : 4, Karadeniz eknik Üniversitesi Basımevi, rabzon. Uzun, Y Yersel Yöntemlerle Kurulan Nirengi ğlarında En Uygun Geometrik Şeklin asarımı Üzerine Bir İnceleme, Yüksek Lisans ezi, Karadeniz eknik Üniversitesi Fen Bilimleri Enstitüsü, rabzon. yan,. 98. Jeodezik ğların Optimizasyonu, Doçentlik ezi, İstanbul eknik Üniversitesi İnşaat Fakültesi, İstanbul. Konak, H Yüzey ğlarının Optimizasyonu, Doktora ezi, Karadeniz eknik Üniversitesi Fen Bilimleri Enstitüsü, rabzon. Kurt, O GPS Ölçülerinin Değerlendirildiği Yermerkezli Üç Boyutlu Jeodezik ğlarda Duyarlık ve Güven Optimizasyonu, Yüksek Lisans ezi, Karadeniz eknik Üniversitesi Fen Bilimleri Enstitüsü, rabzon. Mikhail, E. M. 98. Obsevations and Least Squares, Purdue University, U. S.. Nickerson, B. G Interactive Network Design, University of New Brunswick, Department of Surveying Engineering, ecnical Raport No:6O, Canada. Öztürk, E. 98. Jeodezik ğlarda Güven Ölçütleri ve Ölçme Planının En Uygunlaştırılması, Karadeniz Mühendislik Bilimleri Dergisi (-) Journal of Engineering Sciences (-) 63-6
JEODEZİK AĞLARIN OPTİMİZASYONU
 JEODEZİK AĞLARIN OPTİMİZASYONU Jeodezik Ağların Tasarımı 10.HAFTA Dr.Emine Tanır Kayıkçı,2017 OPTİMİZASYON Herhangi bir yatırımın gerçekleştirilmesi sırasında elde bulunan, araç, hammadde, para, işgücü
JEODEZİK AĞLARIN OPTİMİZASYONU Jeodezik Ağların Tasarımı 10.HAFTA Dr.Emine Tanır Kayıkçı,2017 OPTİMİZASYON Herhangi bir yatırımın gerçekleştirilmesi sırasında elde bulunan, araç, hammadde, para, işgücü
KADASTRO HARİTALARININ SAYISALLAŞTIRILMASINDA KALİTE KONTROL ANALİZİ
 KADASTRO HARİTALARININ SAYISALLAŞTIRILMASINDA KALİTE KONTROL ANALİZİ Yasemin ŞİŞMAN, Ülkü KIRICI Sunum Akış Şeması 1. GİRİŞ 2. MATERYAL VE METHOD 3. AFİN KOORDİNAT DÖNÜŞÜMÜ 4. KALİTE KONTROL 5. İRDELEME
KADASTRO HARİTALARININ SAYISALLAŞTIRILMASINDA KALİTE KONTROL ANALİZİ Yasemin ŞİŞMAN, Ülkü KIRICI Sunum Akış Şeması 1. GİRİŞ 2. MATERYAL VE METHOD 3. AFİN KOORDİNAT DÖNÜŞÜMÜ 4. KALİTE KONTROL 5. İRDELEME
Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi
 JEODEZİ 6 1 Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi Jeodezik gözlemler, hesaplamalarda kullanılmadan önce, referans elipsoidin yüzeyine indirgenir. Bu işlem, arazide yapılan gözlemler l jeoidin
JEODEZİ 6 1 Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi Jeodezik gözlemler, hesaplamalarda kullanılmadan önce, referans elipsoidin yüzeyine indirgenir. Bu işlem, arazide yapılan gözlemler l jeoidin
İKİ BOYUTLU AĞLARDA AĞIRLIK SEÇİMİNİN DENGELEME SONUÇLARINA ETKİSİ VE GPS KOORDİNATLARI İLE KARŞILAŞTIRILMASI
 SELÇUK TEKNİK ONLİNE DERGİSİ / ISSN 1302 6178 Volume 1, Number: 3 2001 İKİ BOYUTLU AĞLARDA AĞIRLIK SEÇİMİNİN DENGELEME SONUÇLARINA ETKİSİ VE GPS KOORDİNATLARI İLE KARŞILAŞTIRILMASI Doç Dr. Cevat İNAL S.Ü.
SELÇUK TEKNİK ONLİNE DERGİSİ / ISSN 1302 6178 Volume 1, Number: 3 2001 İKİ BOYUTLU AĞLARDA AĞIRLIK SEÇİMİNİN DENGELEME SONUÇLARINA ETKİSİ VE GPS KOORDİNATLARI İLE KARŞILAŞTIRILMASI Doç Dr. Cevat İNAL S.Ü.
B = 2 f ρ. a 2. x A' σ =
 TÜRKİYE ULUSAL JEODEZİ KOMİSYONU (TUJK) 004 YILI BİLİMSEL TOPLANTISI MÜHENDİSLİK ÖLÇMELERİNDE JEODEZİK AĞLAR ÇALIŞTAYI JEODEZİK GPS AĞLARININ TASARIMINDA BİLGİSAYAR DESTEKLİ SİMÜLASYON YÖNTEMİNİN KULLANIMI
TÜRKİYE ULUSAL JEODEZİ KOMİSYONU (TUJK) 004 YILI BİLİMSEL TOPLANTISI MÜHENDİSLİK ÖLÇMELERİNDE JEODEZİK AĞLAR ÇALIŞTAYI JEODEZİK GPS AĞLARININ TASARIMINDA BİLGİSAYAR DESTEKLİ SİMÜLASYON YÖNTEMİNİN KULLANIMI
Âna nirengi doğrultuları için p = 1 m 2 o Ara nirengi doğrultuları için p a =------------ m\
 4. ÖLÇÜLERİN AĞIRLIKLARININ SAPTANMASI Ana, ara ve tamamlayıcı nirengi doğrultularının herbiri gruplar halinde ele alınarak bunların ortalama hatalarının öncül (a priori) değerleri, üçgen kapanmalarından
4. ÖLÇÜLERİN AĞIRLIKLARININ SAPTANMASI Ana, ara ve tamamlayıcı nirengi doğrultularının herbiri gruplar halinde ele alınarak bunların ortalama hatalarının öncül (a priori) değerleri, üçgen kapanmalarından
DENGELEME HESABI-I DERS NOTLARI
 DENGELEME HESABI-I DERS NOTLARI Dengeleme Hesabı Adımları, En Küçük Kareler İlkesine Giriş, Korelasyon Prof. Dr. Mualla YALÇINKAYA Yrd. Doç. Dr. Emine TANIR KAYIKÇI Karadeniz Teknik Üniversitesi, Harita
DENGELEME HESABI-I DERS NOTLARI Dengeleme Hesabı Adımları, En Küçük Kareler İlkesine Giriş, Korelasyon Prof. Dr. Mualla YALÇINKAYA Yrd. Doç. Dr. Emine TANIR KAYIKÇI Karadeniz Teknik Üniversitesi, Harita
Jeodezide Yaklaşım Yöntemleri: Enterpolasyon ve Kollokasyon
 Jeodezide Yöntemleri: ve Lisansüstü Ders Notları Yrd. Doç. Dr. Aydın ÜSTÜN Selçuk Üniversitesi Fen Bilimleri Enstitüsü e-posta: austun@selcuk.edu.tr Konya, 2007 A. Üstün yöntemleri 1 / 28 Bir soruyu ya
Jeodezide Yöntemleri: ve Lisansüstü Ders Notları Yrd. Doç. Dr. Aydın ÜSTÜN Selçuk Üniversitesi Fen Bilimleri Enstitüsü e-posta: austun@selcuk.edu.tr Konya, 2007 A. Üstün yöntemleri 1 / 28 Bir soruyu ya
GPS AĞLARININ DUYARLIK ve GÜVENĐRLĐĞĐNĐN BAZ OPTĐMĐZASYONU ĐLE ĐRDELENMESĐ
 GPS AĞLARININ DUYARLIK ve GÜVENĐRLĐĞĐNĐN BAZ OPTĐMĐZASYONU ĐLE ĐRDELENMESĐ Orhan KURT okurt@kocaeli.edu.tr 30 Nisan 2009 KOCAELĐ ÜNĐVERSĐTESĐ Jeodezi ve Fotogrametri Mühendisliği Bölümü Bölüm Đçi Seminer
GPS AĞLARININ DUYARLIK ve GÜVENĐRLĐĞĐNĐN BAZ OPTĐMĐZASYONU ĐLE ĐRDELENMESĐ Orhan KURT okurt@kocaeli.edu.tr 30 Nisan 2009 KOCAELĐ ÜNĐVERSĐTESĐ Jeodezi ve Fotogrametri Mühendisliği Bölümü Bölüm Đçi Seminer
Lineer Denklem Sistemleri Kısa Bilgiler ve Alıştırmalar
 Lineer Denklem Sistemleri Kısa Bilgiler ve Alıştırmalar Bir Matrisin Rankı A m n matrisinin determinantı sıfırdan farklı olan alt kare matrislerinin boyutlarının en büyüğüne A matrisinin rankı denir. rank(a)
Lineer Denklem Sistemleri Kısa Bilgiler ve Alıştırmalar Bir Matrisin Rankı A m n matrisinin determinantı sıfırdan farklı olan alt kare matrislerinin boyutlarının en büyüğüne A matrisinin rankı denir. rank(a)
Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre
 Jeodezi 7 1 Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre Elipsoid yüzeyinin küçük parçalarında oluşan küçük üçgenlerin (kenarları 50-60 km den küçük) hesaplanmasında klasik jeodezide
Jeodezi 7 1 Elipsoid Üçgenlerinin Hesaplanması Yedek Hesap Yüzeyi olarak Küre Elipsoid yüzeyinin küçük parçalarında oluşan küçük üçgenlerin (kenarları 50-60 km den küçük) hesaplanmasında klasik jeodezide
JEODEZİK GPS AĞLARINDA DUYARLIK ve
 I. ULUSAL MÜHENDİSLİK ÖLÇMELERİ SEMPOZYUMU JEODEZİK GPS AĞLARINDA DUYARLIK ve GÜVEN ANALİZİ Mualla YALÇINKAYA Kamil TEKE Temel BAYRAK mualla@ktu.edu.tr k_teke@ktu.edu.tr temelbayrak@hotmail.com ÇALIŞMANIN
I. ULUSAL MÜHENDİSLİK ÖLÇMELERİ SEMPOZYUMU JEODEZİK GPS AĞLARINDA DUYARLIK ve GÜVEN ANALİZİ Mualla YALÇINKAYA Kamil TEKE Temel BAYRAK mualla@ktu.edu.tr k_teke@ktu.edu.tr temelbayrak@hotmail.com ÇALIŞMANIN
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
ARAZİ ÖLÇMELERİ. Temel Ödev I: Koordinatları belirli iki nokta arasında ki yatay mesafenin
 Temel ödevler Temel ödevler, konum değerlerinin bulunması ve aplikasyon işlemlerine dair matematiksel ve geometrik hesaplamaları içeren yöntemlerdir. öntemlerin isimleri genelde temel ödev olarak isimlendirilir.
Temel ödevler Temel ödevler, konum değerlerinin bulunması ve aplikasyon işlemlerine dair matematiksel ve geometrik hesaplamaları içeren yöntemlerdir. öntemlerin isimleri genelde temel ödev olarak isimlendirilir.
GPS ile Ölçülen Jeodezik Ağlarda Duyarlık ve Güven Optimizasyonu
 GPS ile Ölçülen Jeodezik Ağlarda Duyarlık ve Güven Optimizasyonu Mualla Yalçınkaya, Kamil eke, emel Bayrak Karadeniz eknik Üniversitesi Mühendislik Mimarlık Fakültesi Jeodezi ve Fotogrametri Müh. 618 rabzon,
GPS ile Ölçülen Jeodezik Ağlarda Duyarlık ve Güven Optimizasyonu Mualla Yalçınkaya, Kamil eke, emel Bayrak Karadeniz eknik Üniversitesi Mühendislik Mimarlık Fakültesi Jeodezi ve Fotogrametri Müh. 618 rabzon,
Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu
 JEODEZİ9 1 Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu u ve v Gauss parametrelerine bağlı olarak r r ( u, v) yer vektörü ile verilmiş bir Ω yüzeyinin, u*, v* Gauss parametreleri ile verilmiş
JEODEZİ9 1 Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu u ve v Gauss parametrelerine bağlı olarak r r ( u, v) yer vektörü ile verilmiş bir Ω yüzeyinin, u*, v* Gauss parametreleri ile verilmiş
I. Ulusal Mühendislik Ölçmeleri Sempozyumu. Analyzing Precision and Reliability of Geodetic GPS Networks
 I. Ulusal Mühendislik Ölçmeleri Sempozyumu M. YALÇINKAYA 1, K. EKE 1,. BAYRAK 1 Karadeniz eknik Üniversitesi, Mühendislik-Mimarlık Fakültesi, Jeodezi ve Fotogrametri Müh. Bölümü, 618, rabzon, ürkiye, mualla@ktu.edu.tr,
I. Ulusal Mühendislik Ölçmeleri Sempozyumu M. YALÇINKAYA 1, K. EKE 1,. BAYRAK 1 Karadeniz eknik Üniversitesi, Mühendislik-Mimarlık Fakültesi, Jeodezi ve Fotogrametri Müh. Bölümü, 618, rabzon, ürkiye, mualla@ktu.edu.tr,
Bölüm 2: Kuvvet Vektörleri. Mühendislik Mekaniği: Statik
 Bölüm 2: Kuvvet Vektörleri Mühendislik Mekaniği: Statik Hedefler Kuvvetleri toplama, bileşenlerini ve bileşke kuvvetlerini Paralelogram Kuralı kullanarak belirleme. Diktörtgen (Cartesian) koordinat sistemi
Bölüm 2: Kuvvet Vektörleri Mühendislik Mekaniği: Statik Hedefler Kuvvetleri toplama, bileşenlerini ve bileşke kuvvetlerini Paralelogram Kuralı kullanarak belirleme. Diktörtgen (Cartesian) koordinat sistemi
olmak üzere 4 ayrı kütükte toplanan günlük GPS ölçüleri, baz vektörlerinin hesabı için bilgisayara aktarılmıştır (Ersoy.97).
 1-) GPS Ölçülerinin Yapılması Ölçülerin yapılacağı tarihlerde kısa bir süre gözlem yapılarak uydu efemerisi güncelleştirilmiştir. Bunun sonunda ölçü yapılacak bölgenin yaklaşık koordinatlarına göre, bir
1-) GPS Ölçülerinin Yapılması Ölçülerin yapılacağı tarihlerde kısa bir süre gözlem yapılarak uydu efemerisi güncelleştirilmiştir. Bunun sonunda ölçü yapılacak bölgenin yaklaşık koordinatlarına göre, bir
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 7- SAYISAL TÜREV Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ İntegral işlemi gibi türev işlemi de mühendislikte çok fazla kullanılan bir işlemdir. Basit olarak bir fonksiyonun bir noktadaki
MAK 210 SAYISAL ANALİZ BÖLÜM 7- SAYISAL TÜREV Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ İntegral işlemi gibi türev işlemi de mühendislikte çok fazla kullanılan bir işlemdir. Basit olarak bir fonksiyonun bir noktadaki
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 5- SONLU FARKLAR VE İNTERPOLASYON TEKNİKLERİ Doç. Dr. Ali Rıza YILDIZ MAK 210 - Sayısal Analiz 1 İNTERPOLASYON Tablo halinde verilen hassas sayısal değerler veya ayrık noktalardan
MAK 210 SAYISAL ANALİZ BÖLÜM 5- SONLU FARKLAR VE İNTERPOLASYON TEKNİKLERİ Doç. Dr. Ali Rıza YILDIZ MAK 210 - Sayısal Analiz 1 İNTERPOLASYON Tablo halinde verilen hassas sayısal değerler veya ayrık noktalardan
DENGELEME HESABI-I DERS NOTLARI
 DENGELEME HESABI-I DERS NOTLARI Ağırlıkları Eşit Dolaysız (Direkt) Ölçüler Dengelemesi Prof. Dr. Mualla YALÇINKAYA Yrd. Doç. Dr. Emine TANIR KAYIKÇI Karadeniz Teknik Üniversitesi, Harita Mühendisliği Bölümü
DENGELEME HESABI-I DERS NOTLARI Ağırlıkları Eşit Dolaysız (Direkt) Ölçüler Dengelemesi Prof. Dr. Mualla YALÇINKAYA Yrd. Doç. Dr. Emine TANIR KAYIKÇI Karadeniz Teknik Üniversitesi, Harita Mühendisliği Bölümü
MÜHENDİSLİK ÖLÇMELERİ UYGULAMASI (HRT4362) 8. Yarıyıl
 İnşaat Fakültesi Harita Mühendisliği Bölümü Ölçme Tekniği Anabilim Dalı MÜHENDİSLİK ÖLÇMELERİ UYGULAMASI (HRT4362) 8. Yarıyıl D U L K Kredi 2 0 2 3 ECTS 2 0 2 3 UYGULAMA-1 ELEKTRONİK ALETLERİN KALİBRASYONU
İnşaat Fakültesi Harita Mühendisliği Bölümü Ölçme Tekniği Anabilim Dalı MÜHENDİSLİK ÖLÇMELERİ UYGULAMASI (HRT4362) 8. Yarıyıl D U L K Kredi 2 0 2 3 ECTS 2 0 2 3 UYGULAMA-1 ELEKTRONİK ALETLERİN KALİBRASYONU
GÜZ DÖNEMİ ARASINAV SORULARI. 1. Sayısal çözümleme ve fonksiyonu tanımlayarak kullanıldığı alanları kısaca açıklayınız?
 MAK 05 SAYISAL ÇÖZÜMLEME S Ü L E Y M A N D E M Ġ R E L Ü N Ġ V E R S Ġ T E S Ġ M Ü H E N D Ġ S L Ġ K F A K Ü L T E S Ġ M A K Ġ N A M Ü H E N D Ġ S L Ġ Ğ Ġ B Ö L Ü M Ü I. öğretim II. öğretim A şubesi B
MAK 05 SAYISAL ÇÖZÜMLEME S Ü L E Y M A N D E M Ġ R E L Ü N Ġ V E R S Ġ T E S Ġ M Ü H E N D Ġ S L Ġ K F A K Ü L T E S Ġ M A K Ġ N A M Ü H E N D Ġ S L Ġ Ğ Ġ B Ö L Ü M Ü I. öğretim II. öğretim A şubesi B
Jeodezi
 1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
YERSEL YÖNTEMLERLE ÖLÇÜLEN JEODEZİK AĞLARIN ÜÇ BOYUTLU DENGELENMESİ
 23 YERSEL YÖNTEMLERLE ÖLÇÜLEN JEODEZİK AĞLARIN ÜÇ BOYUTLU DENGELENMESİ Veysel ATASOY İ, GİRİŞ Jeodezinin günümüzdeki tanımı, üç boyutlu ve zaman değişkenli bir uzayda yerin çekim alanını da kapsamak koşuluyla
23 YERSEL YÖNTEMLERLE ÖLÇÜLEN JEODEZİK AĞLARIN ÜÇ BOYUTLU DENGELENMESİ Veysel ATASOY İ, GİRİŞ Jeodezinin günümüzdeki tanımı, üç boyutlu ve zaman değişkenli bir uzayda yerin çekim alanını da kapsamak koşuluyla
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Matris Cebiriyle Çoklu Regresyon Modeli
 Matris Cebiriyle Çoklu Regresyon Modeli Hüseyin Taştan Mart 00 Klasik Regresyon Modeli k açıklayıcı değişkenden oluşan regresyon modelini her gözlem i için aşağıdaki gibi yazabiliriz: y i β + β x i + β
Matris Cebiriyle Çoklu Regresyon Modeli Hüseyin Taştan Mart 00 Klasik Regresyon Modeli k açıklayıcı değişkenden oluşan regresyon modelini her gözlem i için aşağıdaki gibi yazabiliriz: y i β + β x i + β
DENGELEME HESABI-I DERS NOTLARI
 DENGELEME HESABI-I DERS NOTLARI Ağırlık ve Ters Ağırlık (Kofaktör) Prof. Dr. Mualla YALÇINKAYA Yrd. Doç. Dr. Emine TANIR KAYIKÇI Karadeniz Teknik Üniversitesi, Harita Mühendisliği Bölümü Trabzon, 016 AĞIRLIK
DENGELEME HESABI-I DERS NOTLARI Ağırlık ve Ters Ağırlık (Kofaktör) Prof. Dr. Mualla YALÇINKAYA Yrd. Doç. Dr. Emine TANIR KAYIKÇI Karadeniz Teknik Üniversitesi, Harita Mühendisliği Bölümü Trabzon, 016 AĞIRLIK
Yrd. Doç. Dr. Kurtuluş Sedar GÖRMÜŞ
 Yrd. Doç. Dr. Kurtuluş Sedar GÖRMÜŞ Giriş ve Amaç Hata Teorisi, Hata Türleri Ölçü ve Hata Hata Türleri Doğruluk Ölçütleri Kovaryans ve Korelasyon Hata Yayılma Kuralı Ölçülerin Dengelenmesi Dolaysız Ölçüler
Yrd. Doç. Dr. Kurtuluş Sedar GÖRMÜŞ Giriş ve Amaç Hata Teorisi, Hata Türleri Ölçü ve Hata Hata Türleri Doğruluk Ölçütleri Kovaryans ve Korelasyon Hata Yayılma Kuralı Ölçülerin Dengelenmesi Dolaysız Ölçüler
JEOİD ve JEOİD BELİRLEME
 JEOİD ve JEOİD BELİRLEME İÇİNDEKİLER GİRİŞ JEODEZİDE YÜKSEKLİK SİSTEMLERİ Jeopotansiyel Yükseklikler (C) Dinamik Yükseklikler (H D ) Normal Yükseklik (H N ) Elipsoidal Yükseklik Ortometrik Yükseklik Atmosferik
JEOİD ve JEOİD BELİRLEME İÇİNDEKİLER GİRİŞ JEODEZİDE YÜKSEKLİK SİSTEMLERİ Jeopotansiyel Yükseklikler (C) Dinamik Yükseklikler (H D ) Normal Yükseklik (H N ) Elipsoidal Yükseklik Ortometrik Yükseklik Atmosferik
SAYISAL ÇÖZÜMLEME. Yrd.Doç.Dr.Esra Tunç Görmüş. 1.Hafta
 SAYISAL ÇÖZÜMLEME Yrd.Doç.Dr.Esra Tunç Görmüş 1.Hafta Sayısal çözümleme nümerik analiz nümerik çözümleme, approximate computation mühendislikte sayısal yöntemler Computational mathematics Numerical analysis
SAYISAL ÇÖZÜMLEME Yrd.Doç.Dr.Esra Tunç Görmüş 1.Hafta Sayısal çözümleme nümerik analiz nümerik çözümleme, approximate computation mühendislikte sayısal yöntemler Computational mathematics Numerical analysis
GPS İle Ölçülen Jeodezik Ağlarda Duyarlık ve Güven Optimizasyonu
 GPS İle Ölçülen Jeodezik Ağlarda Duyarlık ve Güven Optimizasyonu Y. Mualla 1,. Kamil, B. emel 3 1 Karadeniz eknik Üniversitesi Mühendislik Mimarlık Fakültesi Jeodezi ve Fotogrametri Müh. 618 rabzon, mualla@ktu.edu.tr
GPS İle Ölçülen Jeodezik Ağlarda Duyarlık ve Güven Optimizasyonu Y. Mualla 1,. Kamil, B. emel 3 1 Karadeniz eknik Üniversitesi Mühendislik Mimarlık Fakültesi Jeodezi ve Fotogrametri Müh. 618 rabzon, mualla@ktu.edu.tr
GERİLME ANALİZİ VE MOHR ÇEMBERİ MUKAVEMET
 GERİLME ANALİZİ VE MOHR ÇEMBERİ MUKAVEMET Yrd. Doç. Dr. Emine AYDIN Yrd. Doç. Dr. Elif BORU 1 GENEL YÜKLEME DURUMUNDA GERİLME ANALİZİ Daha önce incelenen gerilme örnekleri eksenel yüklü yapı elemanları
GERİLME ANALİZİ VE MOHR ÇEMBERİ MUKAVEMET Yrd. Doç. Dr. Emine AYDIN Yrd. Doç. Dr. Elif BORU 1 GENEL YÜKLEME DURUMUNDA GERİLME ANALİZİ Daha önce incelenen gerilme örnekleri eksenel yüklü yapı elemanları
MADDESEL NOKTANIN EĞRİSEL HAREKETİ
 Silindirik Koordinatlar: Bazı mühendislik problemlerinde, parçacığın hareketinin yörüngesi silindirik koordinatlarda r, θ ve z tanımlanması uygun olacaktır. Eğer parçacığın hareketi iki eksende oluşmaktaysa
Silindirik Koordinatlar: Bazı mühendislik problemlerinde, parçacığın hareketinin yörüngesi silindirik koordinatlarda r, θ ve z tanımlanması uygun olacaktır. Eğer parçacığın hareketi iki eksende oluşmaktaysa
TRABZON İLİ İÇİN JEOİD ONDÜLASYONLARI BELİRLEME AMACIYLA ENTERPOLASYON YÖNTEMLERİNİN UYGULANMASI
 TMMOB Harita ve Kadastro Mühendisleri Odası, 15. Türkiye Harita Bilimsel ve Teknik Kurultayı, 25 28 Mart 2015, Ankara. TRABZON İLİ İÇİN JEOİD ONDÜLASYONLARI BELİRLEME AMACIYLA ENTERPOLASYON YÖNTEMLERİNİN
TMMOB Harita ve Kadastro Mühendisleri Odası, 15. Türkiye Harita Bilimsel ve Teknik Kurultayı, 25 28 Mart 2015, Ankara. TRABZON İLİ İÇİN JEOİD ONDÜLASYONLARI BELİRLEME AMACIYLA ENTERPOLASYON YÖNTEMLERİNİN
SONLU FARKLAR GENEL DENKLEMLER
 SONLU FARKLAR GENEL DENKLEMLER Bir elastik ortamın gerilme probleminin Airy gerilme fonksiyonu ile formüle edilebilen halini göz önüne alalım. Problem matematiksel olarak bölgede biharmonik denklemi sağlayan
SONLU FARKLAR GENEL DENKLEMLER Bir elastik ortamın gerilme probleminin Airy gerilme fonksiyonu ile formüle edilebilen halini göz önüne alalım. Problem matematiksel olarak bölgede biharmonik denklemi sağlayan
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Okut. Yüksel YURTAY. İletişim : (264) Sayısal Analiz. Giriş.
 Okut. Yüksel YURTAY İletişim : Sayısal Analiz yyurtay@sakarya.edu.tr www.cs.sakarya.edu.tr/yyurtay (264) 295 58 99 Giriş 1 Amaç : Mühendislik problemlerinin bilgisayar ortamında çözümünü mümkün kılacak
Okut. Yüksel YURTAY İletişim : Sayısal Analiz yyurtay@sakarya.edu.tr www.cs.sakarya.edu.tr/yyurtay (264) 295 58 99 Giriş 1 Amaç : Mühendislik problemlerinin bilgisayar ortamında çözümünü mümkün kılacak
İstatistik ve Olasılık
 İstatistik ve Olasılık KORELASYON ve REGRESYON ANALİZİ Doç. Dr. İrfan KAYMAZ Tanım Bir değişkenin değerinin diğer değişkendeki veya değişkenlerdeki değişimlere bağlı olarak nasıl etkilendiğinin istatistiksel
İstatistik ve Olasılık KORELASYON ve REGRESYON ANALİZİ Doç. Dr. İrfan KAYMAZ Tanım Bir değişkenin değerinin diğer değişkendeki veya değişkenlerdeki değişimlere bağlı olarak nasıl etkilendiğinin istatistiksel
Özdeğer ve Özvektörler
 Özdeğer ve Özvektörler Yazar Öğr.Grv.Dr.Nevin ORHUN ÜNİTE 9 Amaçlar Bu üniteyi çalıştıktan sonra; bir lineer dönüşümün ve bir matrisin özdeğer ve özvektör kavramlarını anlayacak, bir dönüşüm matrisinin
Özdeğer ve Özvektörler Yazar Öğr.Grv.Dr.Nevin ORHUN ÜNİTE 9 Amaçlar Bu üniteyi çalıştıktan sonra; bir lineer dönüşümün ve bir matrisin özdeğer ve özvektör kavramlarını anlayacak, bir dönüşüm matrisinin
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 2- HATA VE HATA KAYNAKLARI Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ Bir denklemin veya problemin çözümünde kullanılan sayısal yöntem belli bir giriş verisini işleme tabi tutarak sayısal
MAK 210 SAYISAL ANALİZ BÖLÜM 2- HATA VE HATA KAYNAKLARI Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ Bir denklemin veya problemin çözümünde kullanılan sayısal yöntem belli bir giriş verisini işleme tabi tutarak sayısal
3.2. DP Modellerinin Simpleks Yöntem ile Çözümü Primal Simpleks Yöntem
 3.2. DP Modellerinin Simpleks Yöntem ile Çözümü 3.2.1. Primal Simpleks Yöntem Grafik çözüm yönteminde gördüğümüz gibi optimal çözüm noktası, her zaman uygun çözüm alanının bir köşe noktası ya da uç noktası
3.2. DP Modellerinin Simpleks Yöntem ile Çözümü 3.2.1. Primal Simpleks Yöntem Grafik çözüm yönteminde gördüğümüz gibi optimal çözüm noktası, her zaman uygun çözüm alanının bir köşe noktası ya da uç noktası
DENKLEM DÜZENEKLERI 1
 DENKLEM DÜZENEKLERI 1 Dizey kuramının önemli bir kullanım alanı doğrusal denklem düzeneklerinin çözümüdür. 2.1. Doğrusal düzenekler Doğrusal denklem düzeneği (n denklem n bilinmeyen) a 11 x 1 + a 12 x
DENKLEM DÜZENEKLERI 1 Dizey kuramının önemli bir kullanım alanı doğrusal denklem düzeneklerinin çözümüdür. 2.1. Doğrusal düzenekler Doğrusal denklem düzeneği (n denklem n bilinmeyen) a 11 x 1 + a 12 x
JEODEZİK VERİLERİN İSTATİSTİK ANALİZİ. Prof. Dr. Mualla YALÇINKAYA
 JEODEZİK VERİLERİN İSTATİSTİK ANALİZİ Prof. Dr. Mualla YALÇINKAYA Karadeniz Teknik Üniversitesi, Harita Mühendisliği Bölümü Trabzon, 2018 DOĞRULUK ve DUYARLIK (Hassasiyet) DOĞRULUK ve DUYARLIK Doğruluk,
JEODEZİK VERİLERİN İSTATİSTİK ANALİZİ Prof. Dr. Mualla YALÇINKAYA Karadeniz Teknik Üniversitesi, Harita Mühendisliği Bölümü Trabzon, 2018 DOĞRULUK ve DUYARLIK (Hassasiyet) DOĞRULUK ve DUYARLIK Doğruluk,
AEAZÎ DÜZENLEMELERİ KONUSUNDA MATEMATİKSEL BÎR YAKLAŞIM
 3 DERGİDEN MEKTUP Sayın üyemiz, amacımız üyelerimize mesleki sorunlara cevap veren, güncel bilgileri aktarmaktır. Ancak, bütün çabalarımıza rağmen, dergimizde zaman zaman dizgi hatalan olmakta bütün titizliğimize
3 DERGİDEN MEKTUP Sayın üyemiz, amacımız üyelerimize mesleki sorunlara cevap veren, güncel bilgileri aktarmaktır. Ancak, bütün çabalarımıza rağmen, dergimizde zaman zaman dizgi hatalan olmakta bütün titizliğimize
GPS AĞLARINDA EN UYGUN GÖZLEM ZAMANLARININ PLANLANMASI
 TMMOB Harita ve Kadastro Mühendisleri Odası 1. Türkiye Harita Bilimsel ve Teknik Kurultayı 8 Mart - 1 Nisan 5, Ankara GPS AĞLARINDA EN UYGUN GÖZLEM ZAMANLARININ PLANLANMASI O. Kurt 1, H. Konak, E. Öztürk
TMMOB Harita ve Kadastro Mühendisleri Odası 1. Türkiye Harita Bilimsel ve Teknik Kurultayı 8 Mart - 1 Nisan 5, Ankara GPS AĞLARINDA EN UYGUN GÖZLEM ZAMANLARININ PLANLANMASI O. Kurt 1, H. Konak, E. Öztürk
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 3- LİNEER DENKLEM SİSTEMLERİNİN ÇÖZÜMÜ Doç. Dr. Ali Rıza YILDIZ 1 LİNEER DENKLEM SİSTEMLERİ Bilimsel ve teknolojik çalışmalarda karşılaşılan matematikle ilgili belli başlı
MAK 210 SAYISAL ANALİZ BÖLÜM 3- LİNEER DENKLEM SİSTEMLERİNİN ÇÖZÜMÜ Doç. Dr. Ali Rıza YILDIZ 1 LİNEER DENKLEM SİSTEMLERİ Bilimsel ve teknolojik çalışmalarda karşılaşılan matematikle ilgili belli başlı
Lineer Cebir. Doç. Dr. Niyazi ŞAHİN TOBB. İçerik: 1.1. Lineer Denklemlerin Tanımı 1.2. Lineer Denklem Sistemleri 1.3. Matrisler
 Lineer Cebir Doç. Dr. Niyazi ŞAHİN TOBB İçerik: 1.1. Lineer Denklemlerin Tanımı 1.2. Lineer Denklem Sistemleri 1.3. Matrisler Bölüm 1 - Lineer Eşitlikler 1.1. Lineer Eşitliklerin Tanımı x 1, x 2,..., x
Lineer Cebir Doç. Dr. Niyazi ŞAHİN TOBB İçerik: 1.1. Lineer Denklemlerin Tanımı 1.2. Lineer Denklem Sistemleri 1.3. Matrisler Bölüm 1 - Lineer Eşitlikler 1.1. Lineer Eşitliklerin Tanımı x 1, x 2,..., x
Uzay Geriden Kestirme
 Uzay Geriden Kestirme (Eğik Uzunluklarla veya Düşey Açılarla Üçboyutlu Konum Belirleme ) Sebahattin BEKTAŞ* GİRİŞ Konum belirleme problemi günümüzde de jeodezinin en önemli problemi olmaya devam etmektedir.
Uzay Geriden Kestirme (Eğik Uzunluklarla veya Düşey Açılarla Üçboyutlu Konum Belirleme ) Sebahattin BEKTAŞ* GİRİŞ Konum belirleme problemi günümüzde de jeodezinin en önemli problemi olmaya devam etmektedir.
4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ
 4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ Doğrusal Denklem Sistemi x 1,x 2,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu; a x a x a x b 11 1 12 2 1n n 1 a x a x a x b 21 1 22 2 2n n
4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ Doğrusal Denklem Sistemi x 1,x 2,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu; a x a x a x b 11 1 12 2 1n n 1 a x a x a x b 21 1 22 2 2n n
GPS ağlarının dengelenmesinden önce ağın iç güvenirliğini artırmak ve hataları elimine etmek için aşağıda sıralanan analizler yapılır.
 13. GPS AĞLARININ DENGELENMESİ 13.1 GPS ÖLÇMELERİ GPS ( Global Positioning System ) alıcıları kullanılarak yer istasyonu ile uydu arasındaki uzunluklar ölçülür ve noktaların konumları belirlenir. GPS ile
13. GPS AĞLARININ DENGELENMESİ 13.1 GPS ÖLÇMELERİ GPS ( Global Positioning System ) alıcıları kullanılarak yer istasyonu ile uydu arasındaki uzunluklar ölçülür ve noktaların konumları belirlenir. GPS ile
Bu bölümde Coulomb yasasının bir sonucu olarak ortaya çıkan Gauss yasasının kullanılmasıyla simetrili yük dağılımlarının elektrik alanlarının çok
 Gauss Yasası Bu bölümde Coulomb yasasının bir sonucu olarak ortaya çıkan Gauss yasasının kullanılmasıyla simetrili yük dağılımlarının elektrik alanlarının çok daha kullanışlı bir şekilde nasıl hesaplanabileceği
Gauss Yasası Bu bölümde Coulomb yasasının bir sonucu olarak ortaya çıkan Gauss yasasının kullanılmasıyla simetrili yük dağılımlarının elektrik alanlarının çok daha kullanışlı bir şekilde nasıl hesaplanabileceği
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ
 İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 6- İSTATİSTİK VE REGRESYON ANALİZİ Doç. Dr. Ali Rıza YILDIZ 1 İSTATİSTİK VE REGRESYON ANALİZİ Bütün noktalardan geçen bir denklem bulmak yerine noktaları temsil eden, yani
MAK 210 SAYISAL ANALİZ BÖLÜM 6- İSTATİSTİK VE REGRESYON ANALİZİ Doç. Dr. Ali Rıza YILDIZ 1 İSTATİSTİK VE REGRESYON ANALİZİ Bütün noktalardan geçen bir denklem bulmak yerine noktaları temsil eden, yani
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER
 EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER LAGRANGE YÖNTEMİ Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde değişkenler ve kısıtlar genel olarak şeklinde gösterilir. fonksiyonlarının
EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER LAGRANGE YÖNTEMİ Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde değişkenler ve kısıtlar genel olarak şeklinde gösterilir. fonksiyonlarının
Zeki Optimizasyon Teknikleri
 Zeki Optimizasyon Teknikleri Ara sınav - 25% Ödev (Haftalık) - 10% Ödev Sunumu (Haftalık) - 5% Final (Proje Sunumu) - 60% - Dönem sonuna kadar bir optimizasyon tekniğiyle uygulama geliştirilecek (Örn:
Zeki Optimizasyon Teknikleri Ara sınav - 25% Ödev (Haftalık) - 10% Ödev Sunumu (Haftalık) - 5% Final (Proje Sunumu) - 60% - Dönem sonuna kadar bir optimizasyon tekniğiyle uygulama geliştirilecek (Örn:
Harita Projeksiyonları
 Harita Projeksiyonları Bölüm Prof.Dr. İ. Öztuğ BİLDİRİCİ Amaç ve Kapsam Harita projeksiyonlarının amacı, yeryüzü için tanımlanmış bir referans yüzeyi üzerinde belli bir koordinat sistemine göre tanımlı
Harita Projeksiyonları Bölüm Prof.Dr. İ. Öztuğ BİLDİRİCİ Amaç ve Kapsam Harita projeksiyonlarının amacı, yeryüzü için tanımlanmış bir referans yüzeyi üzerinde belli bir koordinat sistemine göre tanımlı
Uygulamada Gauss-Kruger Projeksiyonu
 JEODEZİ12 1 Uygulamada Gauss-Kruger Projeksiyonu Gauss-Kruger Projeksiyonunda uzunluk deformasyonu, noktanın X ekseni olarak alınan ve uzunluğu unluğu koruyan koordinat başlangıç meridyenine uzaklığının
JEODEZİ12 1 Uygulamada Gauss-Kruger Projeksiyonu Gauss-Kruger Projeksiyonunda uzunluk deformasyonu, noktanın X ekseni olarak alınan ve uzunluğu unluğu koruyan koordinat başlangıç meridyenine uzaklığının
DERS 3 ÖLÇÜ HATALARI Kaynak: İ.ASRİ
 Ölçme Bilgisi DERS 3 ÖLÇÜ HATALARI Kaynak: İ.ASRİ Çizim Hassasiyeti Haritaların çiziminde veya haritadan bilgi almada ne kadar itina gösterilirse gösterilsin kaçınılmayacak bir hata vardır. Buna çizim
Ölçme Bilgisi DERS 3 ÖLÇÜ HATALARI Kaynak: İ.ASRİ Çizim Hassasiyeti Haritaların çiziminde veya haritadan bilgi almada ne kadar itina gösterilirse gösterilsin kaçınılmayacak bir hata vardır. Buna çizim
GPS AĞLARININ İNTERAKTİF TASARIMI
 TUJK 00 Çalıştayı, Zonguldak GPS AĞLARININ İNTERAKTİF TASARIMI Mustafa ACAR, M. Onur KAPLAN, Tevfik AYAN İ.T.Ü. İnşaat Fakültesi Jeodezi ve Fotogrametri Mühendisliği Bölümü, Maslak/İstanbul acarmusta@itu.edu.tr,
TUJK 00 Çalıştayı, Zonguldak GPS AĞLARININ İNTERAKTİF TASARIMI Mustafa ACAR, M. Onur KAPLAN, Tevfik AYAN İ.T.Ü. İnşaat Fakültesi Jeodezi ve Fotogrametri Mühendisliği Bölümü, Maslak/İstanbul acarmusta@itu.edu.tr,
23. Sistem denge denklemlerinin direkt kurulması
 . Sistem denge denklemlerinin direkt kurulması. Sistem denge denklemlerinin direkt kurulması Sonlu elemanlar metodu el hesapları için değil, bilgisayarda yazılımlar ile kullanılması için geliştirilmiştir.
. Sistem denge denklemlerinin direkt kurulması. Sistem denge denklemlerinin direkt kurulması Sonlu elemanlar metodu el hesapları için değil, bilgisayarda yazılımlar ile kullanılması için geliştirilmiştir.
DEFORMASYON İZLEME AĞLARINDA KALİTE KONTROL
 DEFORMASYO İZLEME AĞLARIDA KALİTE KOTROL E. Yavuz,, S. Demirkaya Yıldız Teknik Üniversitesi, Meslek Yüksek Okulu, İstanbul, yavuze@yildiz.edu.tr, demirkay@yi ldiz.edu.tr ÖZET Deformasyonları izleme amacıyla
DEFORMASYO İZLEME AĞLARIDA KALİTE KOTROL E. Yavuz,, S. Demirkaya Yıldız Teknik Üniversitesi, Meslek Yüksek Okulu, İstanbul, yavuze@yildiz.edu.tr, demirkay@yi ldiz.edu.tr ÖZET Deformasyonları izleme amacıyla
JEODEZİK GPS AĞLARININ ÖLÇÜT MATRİSLERİ İLE ÖLÇÜ PLANI OPTİMİZASYONU
 MMOB Harita ve Kadastro Mühendisleri Odası 10. ürkiye Harita Bilimsel ve eknik Kurultayı 8 Mart - 1 Nisan 005, nkara JEODEİK GPS ĞLRININ ÖLÇÜ MRİSLERİ İLE ÖLÇÜ PLNI OPİMİSONU K. eke 1, M. alçınkaya 1 1
MMOB Harita ve Kadastro Mühendisleri Odası 10. ürkiye Harita Bilimsel ve eknik Kurultayı 8 Mart - 1 Nisan 005, nkara JEODEİK GPS ĞLRININ ÖLÇÜ MRİSLERİ İLE ÖLÇÜ PLNI OPİMİSONU K. eke 1, M. alçınkaya 1 1
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Yrd. Doç. Dr. Aycan M. MARANGOZ. BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI
 FOTOGRAMETRİ II FOTOGRAMETRİK DEĞERLENDİRME - TEK RESİM DEĞERLENDİRMESİ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
FOTOGRAMETRİ II FOTOGRAMETRİK DEĞERLENDİRME - TEK RESİM DEĞERLENDİRMESİ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
T.C. MİLLİ SAVUNMA BAKANLIĞI HARİTA GENEL KOMUTANLIĞI HARİTA YÜKSEK TEKNİK OKULU KOMUTANLIĞI ANKARA
 T.C. MİLLİ SAVUNMA BAKANLIĞI HARİTA GENEL KOMUTANLIĞI HARİTA YÜKSEK TEKNİK OKULU KOMUTANLIĞI ANKARA ÇİFT STANDART DAİRELİ KONFORM LAMBERT PROJEKSİYONUNDA TÜRKİYE HARİTASININ YAPILMASI Hrt. Tğm. Soner ÖZDEMİR
T.C. MİLLİ SAVUNMA BAKANLIĞI HARİTA GENEL KOMUTANLIĞI HARİTA YÜKSEK TEKNİK OKULU KOMUTANLIĞI ANKARA ÇİFT STANDART DAİRELİ KONFORM LAMBERT PROJEKSİYONUNDA TÜRKİYE HARİTASININ YAPILMASI Hrt. Tğm. Soner ÖZDEMİR
Eski Yunanca'dan batı dillerine giren Fotogrametri sözcüğü 3 kök sözcükten oluşur. Photos(ışık) + Grama(çizim) + Metron(ölçme)
 FOTOGRAMETRİ FOTOGRAMETRİ Eski Yunanca'dan batı dillerine giren Fotogrametri sözcüğü 3 kök sözcükten oluşur. Photos(ışık) + Grama(çizim) + Metron(ölçme) Buna göre ışık yardımı ile ölçme (çizim yapabilme)
FOTOGRAMETRİ FOTOGRAMETRİ Eski Yunanca'dan batı dillerine giren Fotogrametri sözcüğü 3 kök sözcükten oluşur. Photos(ışık) + Grama(çizim) + Metron(ölçme) Buna göre ışık yardımı ile ölçme (çizim yapabilme)
10. TÜRKİYE HARİTA BİLİMSEL VE TEKNİK KURULTAYI (M.YALÇINKAYA & K.TEKE )
 1. ÜRKİYE HARİA BİLİMEL VE EKNİK KURULAYI JEODEZİK GP AĞLARININ ÖLÇÜ MARİLERİ İLE ÖLÇÜ PLANI OPİMİZAYONU Mualla YALÇINKAYA & Kamil EKE 1. ÜRKİYE HARİA BİLİMEL VE EKNİK KURULAYI (M.YALÇINKAYA & K.EKE )
1. ÜRKİYE HARİA BİLİMEL VE EKNİK KURULAYI JEODEZİK GP AĞLARININ ÖLÇÜ MARİLERİ İLE ÖLÇÜ PLANI OPİMİZAYONU Mualla YALÇINKAYA & Kamil EKE 1. ÜRKİYE HARİA BİLİMEL VE EKNİK KURULAYI (M.YALÇINKAYA & K.EKE )
DENEY-4 WHEATSTONE KÖPRÜSÜ VE DÜĞÜM GERİLİMLERİ YÖNTEMİ
 DENEY- WHEATSTONE KÖPÜSÜ VE DÜĞÜM GEİLİMLEİ YÖNTEMİ Deneyin Amacı: Wheatson köprüsünün anlaşılması, düğüm gerilimi ile dal gerilimi arasındaki ilişkinin incelenmesi. Kullanılan Alet-Malzemeler: a) DC güç
DENEY- WHEATSTONE KÖPÜSÜ VE DÜĞÜM GEİLİMLEİ YÖNTEMİ Deneyin Amacı: Wheatson köprüsünün anlaşılması, düğüm gerilimi ile dal gerilimi arasındaki ilişkinin incelenmesi. Kullanılan Alet-Malzemeler: a) DC güç
TOPOĞRAFYA Temel Ödevler / Poligonasyon
 TOPOĞRAFYA Temel Ödevler / Poligonasyon Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Temel Ödevler / Poligonasyon Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ
 KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ Doç. Dr. İsmail Hakkı GÜNEŞ İstanbul Teknik Üniversitesi ÖZET Küresel ve Elipsoidal koordinatların.karşılaştırılması amacı ile bir noktasında astronomik
KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ Doç. Dr. İsmail Hakkı GÜNEŞ İstanbul Teknik Üniversitesi ÖZET Küresel ve Elipsoidal koordinatların.karşılaştırılması amacı ile bir noktasında astronomik
Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü
 Mühendislikte İstatistiksel Yöntemler Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü 1 Araştırma sonuçlarının açıklanmasında frekans tablosu
Mühendislikte İstatistiksel Yöntemler Yrd. Doç. Dr. Fatih TOSUNOĞLU Erzurum Teknik Üniversitesi Mühendislik Fakültesi İnşaat Mühendisliği Bölümü 1 Araştırma sonuçlarının açıklanmasında frekans tablosu
ELEKTRO-OPTİK UZUNLUK ÖLÇMELERİNDE DÜZELTMELER VE İNDİRGEMELER
 ELEKTRO-OPTİK UZUNLUK ÖLÇMELERİNDE DÜZELTMELER VE İNDİRGEMELER *ErdalKOÇAK Summary Medium and short range distances are generally measured hy electro-opîical method insurvey sîudies. The aîmospheric correctioııs
ELEKTRO-OPTİK UZUNLUK ÖLÇMELERİNDE DÜZELTMELER VE İNDİRGEMELER *ErdalKOÇAK Summary Medium and short range distances are generally measured hy electro-opîical method insurvey sîudies. The aîmospheric correctioııs
JDF 116 / 120 ÖLÇME TEKNİĞİ / BİLGİSİ II POLİGONASYON
 JDF 116 / 120 ÖLÇME TEKNİĞİ / BİLGİSİ II POLİGONASYON Yrd. Doç. Dr. HÜSEYİN KEMALDERE Jeodezik Noktaların Sınıflandırması (BÖHHBÜY-Md:8) Noktaların sınıflandırılması aşağıdaki şekildedir: a) Uzay ve uydu
JDF 116 / 120 ÖLÇME TEKNİĞİ / BİLGİSİ II POLİGONASYON Yrd. Doç. Dr. HÜSEYİN KEMALDERE Jeodezik Noktaların Sınıflandırması (BÖHHBÜY-Md:8) Noktaların sınıflandırılması aşağıdaki şekildedir: a) Uzay ve uydu
TOPOĞRAFYA. Ölçme Bilgisinin Konusu
 TOPOĞRAFYA Topoğrafya, bir arazi yüzeyinin tabii veya suni ayrıntılarının meydana getirdiği şekil. Bu şeklin kâğıt üzerinde harita ve tablo şeklinde gösterilmesiyle ilgili ölçme, hesap ve çizim işlerinin
TOPOĞRAFYA Topoğrafya, bir arazi yüzeyinin tabii veya suni ayrıntılarının meydana getirdiği şekil. Bu şeklin kâğıt üzerinde harita ve tablo şeklinde gösterilmesiyle ilgili ölçme, hesap ve çizim işlerinin
x 1,x 2,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu;
 4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ Doğrusal Denklem Sistemi x,x,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu; a x + a x + L + a x = b n n a x + a x + L + a x = b n n a x + a
4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ Doğrusal Denklem Sistemi x,x,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu; a x + a x + L + a x = b n n a x + a x + L + a x = b n n a x + a
HARMONİK DENKLEM. Burada göz önüne alınacak problem Dirichlet problemidir; yani fonksiyonun sınırda kendisinin verilmesi halidir. 2 2 (15.
 HARMONİK DENKLEM Harmonik denklemin sağ tarafının sıfır olması haline Laplace, sağ tarafının sıfır olmaması haline de Possion denklemi adı verilir. Possion ve Laplace denklemi, kısaca harmonik denklem
HARMONİK DENKLEM Harmonik denklemin sağ tarafının sıfır olması haline Laplace, sağ tarafının sıfır olmaması haline de Possion denklemi adı verilir. Possion ve Laplace denklemi, kısaca harmonik denklem
Motivasyon Matrislerde Satır İşlemleri Eşelon Matris ve Uygulaması Satırca İndirgenmiş Eşelon Matris ve Uygulaması Matris Tersi ve Uygulaması Gauss
 Motivasyon Matrislerde Satır İşlemleri Eşelon Matris ve Uygulaması Satırca İndirgenmiş Eşelon Matris ve Uygulaması Matris Tersi ve Uygulaması Gauss Jordan Yöntemi ve Uygulaması Performans Ölçümü 2 Bu çalışmada,
Motivasyon Matrislerde Satır İşlemleri Eşelon Matris ve Uygulaması Satırca İndirgenmiş Eşelon Matris ve Uygulaması Matris Tersi ve Uygulaması Gauss Jordan Yöntemi ve Uygulaması Performans Ölçümü 2 Bu çalışmada,
Yrd. Doç. Dr. Aycan M. MARANGOZ. BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI
 FOTOGRAMETRİ II FOTOGRAMETRİK NİRENGİ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/ İÇERİK Giriş Yer Kontrol Noktaları
FOTOGRAMETRİ II FOTOGRAMETRİK NİRENGİ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/ İÇERİK Giriş Yer Kontrol Noktaları
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 8- SAYISAL İNTEGRASYON 1 GİRİŞ Mühendislikte sık karşılaşılan matematiksel işlemlerden biri integral işlemidir. Bilindiği gibi integral bir büyüklüğün toplam değerinin bulunması
MAK 210 SAYISAL ANALİZ BÖLÜM 8- SAYISAL İNTEGRASYON 1 GİRİŞ Mühendislikte sık karşılaşılan matematiksel işlemlerden biri integral işlemidir. Bilindiği gibi integral bir büyüklüğün toplam değerinin bulunması
Başlangıç Temel Programının Bilinmemesi Durumu
 aşlangıç Temel Programının ilinmemesi Durumu İlgili kısıtlarda şartlar ( ) ise bunlara gevşek (slack) değişkenler eklenerek eşitliklere dönüştürülmektedir. Ancak sınırlayıcı şartlar ( ) veya ( = ) olduğu
aşlangıç Temel Programının ilinmemesi Durumu İlgili kısıtlarda şartlar ( ) ise bunlara gevşek (slack) değişkenler eklenerek eşitliklere dönüştürülmektedir. Ancak sınırlayıcı şartlar ( ) veya ( = ) olduğu
VERİ MADENCİLİĞİ (Kümeleme) Yrd.Doç.Dr. Kadriye ERGÜN
 VERİ MADENCİLİĞİ (Kümeleme) Yrd.Doç.Dr. Kadriye ERGÜN kergun@balikesir.edu.tr İçerik Kümeleme İşlemleri Kümeleme Tanımı Kümeleme Uygulamaları Kümeleme Yöntemleri Kümeleme (Clustering) Kümeleme birbirine
VERİ MADENCİLİĞİ (Kümeleme) Yrd.Doç.Dr. Kadriye ERGÜN kergun@balikesir.edu.tr İçerik Kümeleme İşlemleri Kümeleme Tanımı Kümeleme Uygulamaları Kümeleme Yöntemleri Kümeleme (Clustering) Kümeleme birbirine
Ölçme Bilgisi Jeofizik Mühendisliği Bölümü
 Ölçme Bilgisi Jeofizik Mühendisliği Bölümü Yrd. Doç. Dr. H. Ebru ÇOLAK ecolak@ktu.edu.tr Karadeniz Teknik Üniversitesi, GISLab Trabzon www.gislab.ktu.edu.tr/kadro/ecolak DÜŞEY MESAFELERİN YÜKSEKLİKLERİN
Ölçme Bilgisi Jeofizik Mühendisliği Bölümü Yrd. Doç. Dr. H. Ebru ÇOLAK ecolak@ktu.edu.tr Karadeniz Teknik Üniversitesi, GISLab Trabzon www.gislab.ktu.edu.tr/kadro/ecolak DÜŞEY MESAFELERİN YÜKSEKLİKLERİN
fonksiyonu için in aralığındaki bütün değerleri için sürekli olsun. in bu aralıktaki olsun. Fonksiyonda meydana gelen artma miktarı
 10.1 Türev Kavramı fonksiyonu için in aralığındaki bütün değerleri için sürekli olsun. in bu aralıktaki bir değerine kadar bir artma verildiğinde varılan x = x 0 + noktasında fonksiyonun değeri olsun.
10.1 Türev Kavramı fonksiyonu için in aralığındaki bütün değerleri için sürekli olsun. in bu aralıktaki bir değerine kadar bir artma verildiğinde varılan x = x 0 + noktasında fonksiyonun değeri olsun.
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü TOPOGRAFYA (HRT3351) Yrd. Doç. Dr. Ercenk ATA
 Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü 4. HAFTA KOORDİNAT SİSTEMLERİ VE HARİTA PROJEKSİYONLARI Coğrafi Koordinat Sistemi Yeryüzü üzerindeki bir noktanın konumunun enlem
Yıldız Teknik Üniversitesi İnşaat Fakültesi Harita Mühendisliği Bölümü 4. HAFTA KOORDİNAT SİSTEMLERİ VE HARİTA PROJEKSİYONLARI Coğrafi Koordinat Sistemi Yeryüzü üzerindeki bir noktanın konumunun enlem
ELEKTRONİK VE HABERLEŞME MÜHENDİSLİĞİ ÖLÇME VE DEVRE LABORATUVARI DENEY 2
 ELEKTRONİK VE HABERLEŞME MÜHENDİSLİĞİ ÖLÇME VE DEVRE LABORATUVARI DENEY 2 2.1. ÇEVRE AKIMLAR YÖNTEMİ Elektrik devrelerinin çözümünde kullanılan en basit ve en kolay yöntemlerden biri çevre akımları yöntemidir.
ELEKTRONİK VE HABERLEŞME MÜHENDİSLİĞİ ÖLÇME VE DEVRE LABORATUVARI DENEY 2 2.1. ÇEVRE AKIMLAR YÖNTEMİ Elektrik devrelerinin çözümünde kullanılan en basit ve en kolay yöntemlerden biri çevre akımları yöntemidir.
a) x +3 = 8 b) x -4 = -2 c) x -7 = 4 d) x +5 = 6 e) x +8 = 2 f) x -1= -8 x +3 = 5 denkleminin çözümünü bulunuz.
 Denklemler bilinmeyen - cebirsel ifade - 7 denklem Bir cebirsel ifade bir sonuca eşit oluyorsa buna denklem denir. Bazı denklemlerin çözümü yoktur, bazı denklemlerin sonsuz, bazı denklemlerin bir, iki,
Denklemler bilinmeyen - cebirsel ifade - 7 denklem Bir cebirsel ifade bir sonuca eşit oluyorsa buna denklem denir. Bazı denklemlerin çözümü yoktur, bazı denklemlerin sonsuz, bazı denklemlerin bir, iki,
KALİTE FONKSİYON DAĞILIMI QUALITY FUNCTION DEPLOYMENT (QFD)
 KALİTE FONKSİYON DAĞILIMI QUALITY FUNCTION DEPLOYMENT (QFD) Yaşar ERAYMAN YÜKSEL FEN BİLİMLERİ ENSTİTÜSÜ TEKSTİL MÜHENDİSLİĞİ ANABİLİM DALI SEMİNER MAYIS 2017 Giriş Kalite Fonksiyon Dağılımı (QFD), ürün
KALİTE FONKSİYON DAĞILIMI QUALITY FUNCTION DEPLOYMENT (QFD) Yaşar ERAYMAN YÜKSEL FEN BİLİMLERİ ENSTİTÜSÜ TEKSTİL MÜHENDİSLİĞİ ANABİLİM DALI SEMİNER MAYIS 2017 Giriş Kalite Fonksiyon Dağılımı (QFD), ürün
OYUN TEORİSİ. Özlem AYDIN. Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü
 OYUN TEORİSİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü TANIM ''Oyun Teorisi'', iki yada daha fazla rakibi belirli kurallar altında birleştirerek karşılıklı olarak çelişen olasılıklar
OYUN TEORİSİ Özlem AYDIN Trakya Üniversitesi Bilgisayar Mühendisliği Bölümü TANIM ''Oyun Teorisi'', iki yada daha fazla rakibi belirli kurallar altında birleştirerek karşılıklı olarak çelişen olasılıklar
DENGELEME HESABI-I DERS NOTLARI
 DENGELEME HESABI-I DERS NOTLARI Giriş, Hata ve Düzeltme Prof. Dr. Mualla YALÇINKAYA Yrd. Doç. Dr. Emine TANIR KAYIKÇI Karadeniz Teknik Üniversitesi, Harita Mühendisliği Bölümü Trabzon, 2016 HAFTALIK DERS
DENGELEME HESABI-I DERS NOTLARI Giriş, Hata ve Düzeltme Prof. Dr. Mualla YALÇINKAYA Yrd. Doç. Dr. Emine TANIR KAYIKÇI Karadeniz Teknik Üniversitesi, Harita Mühendisliği Bölümü Trabzon, 2016 HAFTALIK DERS
Yöneylem Araştırması II
 Yöneylem Araştırması II Öğr. Gör. Dr. Hakan ÇERÇİOĞLU cercioglu@gazi.edu.tr BÖLÜM I: Doğrusal Programlama Tekrarı Doğrusal Programlama Tanımı Doğrusal Programlama Varsayımları Grafik Çözüm Metodu Simpleks
Yöneylem Araştırması II Öğr. Gör. Dr. Hakan ÇERÇİOĞLU cercioglu@gazi.edu.tr BÖLÜM I: Doğrusal Programlama Tekrarı Doğrusal Programlama Tanımı Doğrusal Programlama Varsayımları Grafik Çözüm Metodu Simpleks
Hatalar Bilgisi ve İstatistik Ders Kodu: Kredi: 3 / ECTS: 5
 Ders Kodu: 0010070021 Kredi: 3 / ECTS: 5 Yrd. Doç. Dr. Serkan DOĞANALP Necmettin Erbakan Üniversitesi Harita Mühendisliği Bölümü Konya 07.01.2015 1 Giriş 2 Giriş Matematiksel istatistiğin konusu yığın
Ders Kodu: 0010070021 Kredi: 3 / ECTS: 5 Yrd. Doç. Dr. Serkan DOĞANALP Necmettin Erbakan Üniversitesi Harita Mühendisliği Bölümü Konya 07.01.2015 1 Giriş 2 Giriş Matematiksel istatistiğin konusu yığın
İÇİNDEKİLER BASİT EŞİTSİZLİKLER. HARFLİ İFADELER Harfli İfadeler ve Elemanları Eşitsizlik Sembolleri ve İşaretin Eşitsizlik İfadesi...
 İÇİNDEKİLER HARFLİ İFADELER Harfli İfadeler ve Elemanları... 1 Benzer Terim... Harfli İfadenin Terimlerini Toplayıp Çıkarma... Harfli İfadelerin Terimlerini Çarpma... Harfli İfadelerde Parantez Açma...
İÇİNDEKİLER HARFLİ İFADELER Harfli İfadeler ve Elemanları... 1 Benzer Terim... Harfli İfadenin Terimlerini Toplayıp Çıkarma... Harfli İfadelerin Terimlerini Çarpma... Harfli İfadelerde Parantez Açma...
EĞİTİM-ÖĞRETİM YILI 8. SINIF MATEMATİK DERSİ KAZANIMLARININ ÇALIŞMA TAKVİMİNE GÖRE DAĞILIM ÇİZELGESİ SÜRE
 Ay 2016 2017 EĞİTİM-ÖĞRETİM YILI 8. SINIF MATEMATİK DERSİ KAZANIMLARININ ÇALIŞMA TAKVİMİNE GÖRE DAĞILIM ÇİZELGESİ SÜRE Hafta ÖĞRENME ALANI ALT ÖĞRENME ALANI KAZANIMLAR EYLÜL 3 4 Sayılar ve İşlemler Çarpanlar
Ay 2016 2017 EĞİTİM-ÖĞRETİM YILI 8. SINIF MATEMATİK DERSİ KAZANIMLARININ ÇALIŞMA TAKVİMİNE GÖRE DAĞILIM ÇİZELGESİ SÜRE Hafta ÖĞRENME ALANI ALT ÖĞRENME ALANI KAZANIMLAR EYLÜL 3 4 Sayılar ve İşlemler Çarpanlar
G( q ) yer çekimi matrisi;
 RPR (DÖNEL PRİZATİK DÖNEL) EKLE YAPISINA SAHİP BİR ROBOTUN DİNAİK DENKLELERİNİN VEKTÖR-ATRİS FORDA TÜRETİLESİ Aytaç ALTAN Osmancık Ömer Derindere eslek Yüksekokulu Hitit Üniversitesi aytacaltan@hitit.edu.tr
RPR (DÖNEL PRİZATİK DÖNEL) EKLE YAPISINA SAHİP BİR ROBOTUN DİNAİK DENKLELERİNİN VEKTÖR-ATRİS FORDA TÜRETİLESİ Aytaç ALTAN Osmancık Ömer Derindere eslek Yüksekokulu Hitit Üniversitesi aytacaltan@hitit.edu.tr
Fotogrametride işlem adımları
 Fotogrametride işlem adımları Uçuş planının hazırlanması Arazide yer kontrol noktalarının tesisi Resim çekimi Değerlendirme Analitik değerlendirme Dijital değerlendirme Değerlendirme Analog değerlendirme
Fotogrametride işlem adımları Uçuş planının hazırlanması Arazide yer kontrol noktalarının tesisi Resim çekimi Değerlendirme Analitik değerlendirme Dijital değerlendirme Değerlendirme Analog değerlendirme
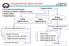
Şekil 7.1 Bir tankta sıvı birikimi
 6 7. DİFERENSİYEL DENKLEMLERİN SAYISAL ÇÖZÜMLERİ Diferensiyel denklemlerin sayısal integrasyonunda kullanılabilecek bir çok yöntem vardır. Tecrübeler dördüncü mertebe (Runge-Kutta) yönteminin hemen hemen
6 7. DİFERENSİYEL DENKLEMLERİN SAYISAL ÇÖZÜMLERİ Diferensiyel denklemlerin sayısal integrasyonunda kullanılabilecek bir çok yöntem vardır. Tecrübeler dördüncü mertebe (Runge-Kutta) yönteminin hemen hemen
