Euler Yöntemleri ve Hata Analizi
|
|
|
- Si̇mge Ecevit
- 5 yıl önce
- İzleme sayısı:
Transkript
1 Bölüm 2 Euler Yöntemleri ve Hata Analizi Bu bölümde başlangıç değer problemleri için İleri ve geri Euler yöntemlerini inceleyerek, Hata analizi için gerekli olan yerel kesme hatası, yerel hata, kümülatif hata ve kararlılık gibi kavramları tanıtıyor ve Euler yöntemlerindeki karşılıklarınıbelirliyoruz. Ayrıca Geri Euler yönteminin nonlineer problemlere nasıl uygulanabileceğini inceliyor ve Komşu çözüm eğrilerinin davranışının bir sayısal yöntemin performansınınasıl etkilediğini inceliyoruz. 2.1 İleri Euler yöntemi y = f(t, y), t (a, b) (2.1) y(a) = y 0 başlangıç değer problemini göz önüne alalım.[a, b] aralığını h uzunluklu n adet alt aralığa bölelim ve elde edilen aralıkların uç noktalarını t 1 = a, t 2 = a + h,..., t n+1 = a + nh = a + n(b a)/n = b
2 2 Euler Yöntemleri ve Hata Analizi ile gösterelim. (2.1) başlangıç değer probleminin t i, i = 2,..., (n + 1) noktalarındaki gerçek çözümünü y(t i ) ile gösterelim. İleri Euler yöntemi üç farklı yöntemle türetilebilir: 1. (2.1) denklemindeki y (t i ) türevi için O(h) hatası ile ileri fark yaklaşımınıkullanarak y (t i ) = (y(t i+1 ) y(t i ))/h + O(h) = f(t i, y(t i )), h 0 (2.2) elde ederiz. Bu bağıntıdan yeterince küçük h adım uzunluğu için O(h) terimini ihmal ederek Y i = y(ti ) yaklaşımlarıiçin (Y i+1 Y i )/h = f(t i, Y i ), i = 1,..., n (2.3) Y 1 = y(a) ile tanımlanan ileri Euler fark denklemini elde ederiz. (2.3) biçiminde ifade edilen sayısal yönteme standart biçimde yazılmış yöntem adı verilmektedir. Standart biçimde yazılan bir sayısal yaklaşımda, yaklaşımın sol ve sağ tarafındaki terimler, sırasıyla ilgili diferensiyel denklemin sol ve sağ tarafında yer alan terimleri temsil ederler. (2.3) yaklaşımında (Y i+1 Y i )/h terimi diferensiyel denklemin solundaki y (t i ) için bir yaklaşım iken, f(t i, Y i ) ise f(t i, y(t i )) için bir yaklaşımdır. (2.3) ile tanımlanan Euler yaklaşımları, hesaplamalar için daha uygun olan formatında yazılabilir. Y i+1 = Y i + hf(t i, Y i ), i = 1, 2,... (2.4) Y 1 = y(a) (2.4) ile tanımlanan ileri Euler yaklaşımlarınıgeometrik olarak inceleyelim: Şekil 2.1 de t 1 noktasındaki eğimle ulaşılan Y 2 yaklaşımının, bu noktadan itibaren eğri boyunca değişen f(t, y) eğimiyle ulaşılan y(t 2 ) noktasından doğal olarak farklıolduğu görülmektedir. Öte yandan t 1 ilk nokta olduğu için bu nokta hesaplanan eğim olan f(t 1, Y 1 ) gerçek eğimdir. Diğer t i, i = 1, 2, 3,, n noktalarında hata oluşumuna neden olan iki faktör ise sırasıyla, çözüm eğrisinin
3 2.1 İleri Euler yöntemi 3 Şekil 2.1: Y 2 = Y 1 + hf(t 1, Y 1 ) yaklaşımının Y 1 değerinden elde edilişi (t i, y(t i )) noktasında hesaplanmasıgereken y (t i ) = f(t i, y(t i ) gerçek eğimi yerine, (t i, Y i ) noktasından geçen komşu çözüm eğrisine ait f(t i, Y i ) eğimine sahip olduğunun kabul edilmesi ve ayrıca çözüm eğrisinin [t i, t i+1 ] aralığıboyunca f(t i, Y i ) yaklaşık eğimi ile doğrusal olarak hareket ettiğini kabul edilmesidir. 2. Yukarıda türev terimi için uygun bir yaklaşımla elde edilen ileri Euler yöntemi, integral için uygun yaklaşım yardımıyla da türetilebilir: Bunun için (2.1) in her iki yanının [t i, t i+1 ] aralığında integralini alarak ti+1 t i y (t)dt = y(t i+1 ) y(t i ) = ti+1 t i f(t, y(t))dt (2.5) elde ederiz. (2.5) in sağ tarafındaki integrale sol dikdörtgen kuralıile yaklaşarak, y(t i+1 ) y(t i ) = hf(t i, y(t i )) veya Y i = y(ti ) için Y i+1 = Y i + hf(t i, Y i ), i = 1, 2,... ileri Euler yaklaşımlarınıelde ederiz.
4 4 Euler Yöntemleri ve Hata Analizi 3. Son olarak ileri Euler yöntemi Taylor teoremi yardımıyla da elde edilebilir: y(t i+1 ) = y(t i ) + hy (t i ) + O(h 2 ), h 0 açılımında, (2.1) den y (t i ) = f(t i, y(t i )) yazarak y(t i+1 ) = y(t i ) + hf(t i, y(t i )) + O(h 2 ), h 0 = y(ti ) + hf(t i, y(t i )) veya Y i = y(ti ), f(t i, y(t i )) = f(t i, Y i ) için yukarıdaki ilk iki yöntemle de elde edilen ve (2.4) ile verilen ileri Euler yaklaşımlarınıelde ederiz. Gözlem 2.1. Adım uzunluğunun yeterince küçük seçilmemesi ve komşu çözüm eğrilerinin benzer davranışlar göstermemeleri durumunda ileri Euler yöntemi ile kabul edilemeyecek büyüklükte hatalar beklenmelidir. Çünkü adım uzunluğunun yeterince küçük seçilmemesi durumunda (2.2) de türev için ileri fark ve benzer biçimde (2.5) deki integral için sol dikdörtgen yaklaşımı iyi sonuç vermez. Komşu çözüm eğrilerinin benzer davranış göstermemesi durumunda ise f(t i, y(t i )) = f(t i, Y i ) yaklaşımıiyi bir yaklaşım olarak değerlendirilemez(bakınız Gözlem 2.3). Bu konu özellikle bir sonraki bölümde inceleyeceğimiz ve hassas(stiff ) problem olarak adlandırılan ve komşu çözüm eğrilerinin birbirinden farklı davranış gösterdĭgi problemlerde daha çok göze çarpar. ÖRNEK 2.1. başlangıç değer problemi verilsin. y = 2t 3y y(0) = 0.5 Problemin gerçek çözümünü belirleyiniz. h = 1/5 adım uzunluğu ile [0, 1] aralĭgındaki yaklaşık çözümleri ileri Euler yöntemi ile belirleyiniz.
5 2.1 İleri Euler yöntemi 5 Her noktada yaklaşık çözüm, gerçek çözüm ve hata değerlerinden oluşan yaklaşım tablosunu belirleyiniz. Gerçek çözüm ile ileri Euler yaklaşımlarınıyön alanlarıiçerisinde grafiksel olarak göstererek, yaklaşımların komşu çözüm eğrilerini nasıl takip ettiğini gözlemleyiniz. İleri Euler yöntemi yaklaşım tablosu uygun MATLAB/Octave programıyardımıyla da elde ediniz. Çözüm. Verilen lineer denklemin keyfi y(0) = y 0 başlangıç değeri için gerçek çözümünü diferensiyel denklem derslerinden y = 2/3t 2/9 + e 3t (y 0 2/9) (2.6) olarak elde ederiz. y(0) = 1/2 için ise verilen problemin çözümünü olarak elde ederiz. y = 2/3t 2/9 + 13/18e 3t Hatırlatma 2.1. Örnek 2.1 de verilen lineer diferensiyel denklem gibi birçok denklemin analitik çözümü sembolik cebir programlarıyardımıyla elde edilebilir. Maxima ücretsiz bir sembolik cebir programıdır. Matematiksel özelliklerinin tanıtımı [?] de yer almaktadır. Yukarıda verilen problemin Maxima ortamında analitik çözümü aşağıda yer almaktadır: h = 1/5 için elde edilen alt aralıkların uç noktalarıaşağıda verilmektedir: t 1 = 0, t 2 = t 1 + h = 1/5 = 0.2, t 3 = t 2 + h = 2/5 = 0.4, t 4 = 3/5 = 0.6, t 5 = 4/5 = 0.8, t 6 = 1. Bu noktalarındaki yaklaşık çözümler ise sırasıyla, olmak üzere Y 1 = y(t 1 ) = y(0) = 0.5 Y 2 = Y 1 + hf(t 1, Y 1 ) = ( ) = 0.2
6 6 Euler Yöntemleri ve Hata Analizi Y 3 = Y 2 + hf(t 2, Y 2 ) = ( ) = 0.16 ve benzer biçimde olarak elde edilir. Y 4 = , Y 5 = ve Y 6 = Yukarıda elde edilen yaklaşımlar ile belirtilen t i noktalarındaki gerçek çözüm ve aşağıda kümülatif hata olarak tanımlayacağımız E i = y(t i ) Y i hata değerleri Tablo 2.1 de verilmektedir. h = 0.2 adım uzunluğu için Euler yaklaşımları ve gerçek çözümün grafiği ile [0, 1] [0, 1] bölgesindeki eğim alanları Şekil 2.2 de verilmektedir. Örnek 2.1 verileri ile İleri Euler Yöntemi uygulamasıprogram 2.1(indisli versiyon) ve Program 2.2(indis kullanmayan versiyon) ile verilmektedir. Daha sonraki uygulamalarımızda indis kullanmayacağız.
7 2.1 İleri Euler yöntemi 7 t i Y i y(t i ) E i Tablo 2.1: Örnek 2.1 için Euler yaklaşımları, gerçek değerler ve kümülatif hata Şekil 2.2: h = 0.2 adım uzunluğu ile Euler yaklaşımları(o), gerçek çözüm(çizgi) ve yön alanları Örnek 2.1 için OCTAVE quiver komutu yardımıyla elde edillen yön alanlarıile bazıçözüm eğrileri ve ileri Euler yaklaşımlarışekil 2.3 de sunulmaktadır. Gözlem 2.2. Örnek 2.1 için farklıy(0) = y 0 değerleri ile elde edilen y = 2/3t 2/9 + e 3t (y 0 2/9) çözüm ailesini inceledĭgimizde, herbirinin t için y 0 = 2/9 özel başlangıç değeri için elde edilen y = 2/3t 2/9 doğrusuna asimtot oldukları, yani t için y 2/3 ortak eğimiyle birlikte hareket ettikleri görülmektedir. Bu durumda komşu çözüm eğrileri üzerinden hesaplanan f(t i, Y i ) eğimiyle hareket eden ileri Euler yöntemi iyi sonuç vermektedir.
8 8 Euler Yöntemleri ve Hata Analizi % function euler(a,b,n,y1) % Örnek 2.1 verileri ile ileri Euler Yöntemi(indisli versiyon) h=(b-a)/n; %h: adı m uzunlugu T=a:h:b;Y(1)=y1; for i=1:n Y(i+1)=Y(i)+h*f(T(i),Y(i)); end plot(t,y, *-k, linewidth,2); hold on; Yg=gc(T,y1); plot(t,yg, linewidth,2); function yp=f(t,y) yp=2*t-3*y; function yg=gc(t,y1) yg=exp(-3*t)*(y1+2/9)+(2*t)/3-2/9; % Program 2.1: ileri Euler Yöntemi Uygulaması(indis kullanan versiyon) ÖRNEK 2.2. başlangıç değer problemi verilsin. y = 2t + 3y y(0) = 0.5 Problemin gerçek çözümünü belirleyiniz. h = 1/5 adım uzunluğu ile [0, 1] aralĭgındaki yaklaşık çözümleri ileri Euler yöntemi ile belirleyiniz. Her noktada yaklaşık çözüm, gerçek çözüm ve hata değerlerinden oluşan yaklaşım tablosunu belirleyiniz. h = 3/40 adım uzunluklarıiçin Euler yaklaşımlarıve Çözüm. y(0) = 0.2, 0, 1/9, 1.7/9, 2/9, 2.1/9 için gerçek çözüm grafiklerini aynıeksende grafiksel olarak göstererek, ileri Euler yaklaşımlarının komşu çözüm eğrilerini nasıl takip ettiklerini gözlemleyiniz.
9 2.1 İleri Euler yöntemi 9 % function euler(a,b,n,y1) % Örnek 2.1 verileri ile ileri Euler Yöntemi(indis kullanmayan versiyon) h=(b-a)/n; %h: adı m uzunlugu t=a;y=y1; T=t1;Y=y1; for i=1:n y=y+h*f(t,y); % ileri Euler adı mı t=t+h; % Güncel zaman degeri T=[T;t];Y=[Y;y]; %T ve Y zincirleri için yeni halka ilavesi end plot(t,y, *-k, linewidth,2); hold on; Yg=gc(T,y1); plot(t,yg, linewidth,2); function yp=f(t,y) yp=2*t-3*y; function yg=gc(t,y1) yg=exp(-3*t)*(y1+2/9)+(2*t)/3-2/9; % Program 2.2: ileri Euler Yöntemi Uygulaması(indis kullanmayan versiyon) Problemin analitik çözümü olarak elde edilir. y = e 3t (y(0) 2/9) + (2t)/3 + 2/9 h = 1/5 için elde edilen yaklaşım tablosu Tablo 2.2 de verilmektedir. t i Y i y(t i ) E i Tablo 2.2: Örnek 2.2 için yaklaşım tablosu Artan t i değerleri için Örnek 2.1 in tersine bu defa E i = Y i y(t i ) hatalarının arttığına dikkat ediniz.
10 10 Euler Yöntemleri ve Hata Analizi Şekil 2.3: Örnek 2.1 için yön alanları ile bazı çözüm eğrileri(çizgi) ve ileri Euler yaklaşımları(o). h = 3/40 adım uzunluklarıiçin Euler yaklaşımlarıve y = e 3t (y(0) 2/9) + (2t)/3 + 2/9 olarak elde edilen gerçek çözümün grafiği y(0) = 0.2, 0, 1/9, 1.7/9, 2/9, 2.1/9 başlangıç değerleri için Şekil 2.4 de verilmektedir. Gözlem 2.3. Örnek 2.2 için farklıy(0) = y 0 değerleri ile elde edilen y = 2/3t 2/9 + e 3t (y 0 2/9) çözüm ailesini inceledĭgimizde, herbirinin t için y 0 = 2/9 özel başlangıç değeri için elde edilen y = 2/3t 2/9 doğrusundan uzaklaştıkları, yani t için farklı y eğimiyle birlikte hareket ettikleri görülmektedir. Bu durumda komşu çözüm eğrileri üzerinden hesaplanan f(t i, Y i ) eğimiyle hareket eden ileri Euler yöntemi iyi sonuç vermemektedir. 2.2 Bir yöntemin hata analizi Bir sayısal yöntemin verilen bir diferensiyel denklem için uygun bir yöntem olup olmadığınıbelirlerken yerel kesme hatasıadıverilen bir hata ölçütü kullanılmaktadır. Benzer biçimde uygun olarak seçilen bir sayısal yöntem ile elde
11 2.2 Bir yöntemin hata analizi Şekil 2.4: Örnek 2.2 için yön alanları, çözüm eğrileri(-) ve ileri Euler yaklaşımları edilen yaklaşımların problemin gerçek çözüme yaklaşım düzeyini ölçerken de yerel hata ve kümülatif hata gibi birbiri ile ilgili hata ölçütleri kullanılmaktadır. Şimdi bu kavramlarıinceleyerek Örnek 9.1 de verilen başlangıç değer problemi için hesaplamaya çalışalım. Öncelikle yerel kesme hatasını inceleyim: TANIM 2.1. (Yerel kesme hatası) (2.1) ile verilen başlangıç değer probleminin h > 0 adım uzunluğu ile, t i (a, b) noktasında oluşan yerel kesme hatası, problemin y = y(t) gerçek çözümünün standart biçimde ifade edilen sonlu fark yaklaşımınısağlamadĭgımiktar olarak tanımlanır ve E k (t i ; h) ile gösterilir. ÖRNEK 2.3. (2.1) ile tanımlanan başlangıç değer probleminin çözümünün [a, b] aralĭgında ikinci basamaktan türevi mevcut ve sürekli olduğunu kabul edelim. Bu durumda ileri Euler yönteminin yerel kesme hatasının E k (t i ; h) = O(h), h 0 olduğunu gösteriniz. İleri Euler yönteminin (2.3) ile verilen standardart biçiminde, y(t) çözümünü yerine yazarak E k (t i ; h) = ((y(t i + h) y(t i )))/h f(t i, y(t i )) (2.7) yerel kesme hatasınıelde ederiz. t i (a, b), h > 0 için Taylor teoreminden y(t i + h) = y(t i ) + hy (t i ) + h 2 /2y (c), c (t i, t i+1 ) (2.8)
12 12 Euler Yöntemleri ve Hata Analizi elde ederiz. (2.8) i (2.7) de yerine yazarak elde ederiz. E k (t i ; h) = ((y(t i + h) y(t i )))/h f(t i, y(t i )) = (2.9) = h/2y (c) = O(h), h 0 (2.10) Gözlem 2.4. (2.1) başlangıç değer probleminin çözümünün varlĭgı için f(t, y) fonksiyonunun başlangıç noktasını içeren bir dikdörtgende sürekli olmasıyeterli iken, (2.9) ile verilen hata tahmininde y(t) nin ikinci basamaktan sürekli türeve sahip olmasıgerektĭgine dikkat ediniz. TANIM 2.2. (Diferensiyel denklemle uyumlu yöntem) Adım uzunluğu sıfıra yaklaşırken, yerel kesme hatası da sıfıra yaklaşan sayısal yönteme diferensiyel denklemle uyumlu yöntem adıverilmektedir. (2.9) ile verilen yerel kesme hatasıgereğince, İleri Euler yöntemi uyumlu bir yöntemdir. Yerel kesme hatası ile yakından ilişkili olan bir diğer hata kavramı ise yerel hatadır. TANIM 2.3. (Yerel Hata) t i noktasında gerçek y(t i ) değerinin kullanıldĭgıkabul edilerek, t i+1 = t i + h noktasındaki değer hesaplanırken oluşan hataya(gerçek çözüm ve ilgili yaklaşım arasındaki farka) sayısal yöntemin t i noktasındaki yerel hatasıadıverilir ve E yerel (t i, h) ile gösterilir. Bu tanımda yerel sözcüğü, sadece tek bir adımda oluşan hata kavramını vurgulamaktadır. ÖRNEK 2.4. İleri Euler yöntemi için E yerel (t i, h) = O(h 2 ), h 0 olduğunu gösteriniz. Yukarıda verilen yerel hata tanım ve İleri Euler yönteminden E yerel (t i, h) = y(t i+1 ) [y(t i ) + hf(t i, y(t i )] (2.11) elde ederiz. y(t i+1 ) in t i noktasındaki Taylor açılımını, yani,
13 2.2 Bir yöntemin hata analizi 13 y(t i+1 ) = y(t i ) + hy (t i ) + h 2 /2y (c i ), c i (t i, t i+1 ) ifadesini (2.11) de yerine yazarak elde ederiz. E yerel (t i, h) = y(t i+1 ) [y(t i ) + hf(t i, y(t i )] = h 2 /2y (c i ) = O(h 2 ), h 0 (2.12) Uyarı. (2.12) ifadesinde köşeli parantez içerisinde Euler yönteminde kullanılan Y i yaklaşımı yerine y(t i ) gerçek değerinin kullanıldĭgına dikkat edelim. Dolayısıyla yerel hata hesaplanırken, t i noktasına kadar hata yapılmadĭgı kabul edilerek sadece t i noktasından t i+1 noktasına geçişte tek adımda oluşan hata dikkate alınmaktadır. Örnek 2.1 deki başlangıç değer problemi için h = 1/10 ile [0, 1] aralığındaki sonlu sayıda noktada oluşan ve (2.12) ile tanımlanan yerel hata Tablo 2.1 in dördüncü sütununda gösterilmektedir. Uyarı. E yerel (t i, h) = he k (t i ; h) olduğuna dikkat edelim. Bir diğer hata ölçüm kavramıise kümülatif hatadır: TANIM 2.4. (Kümülatif hata) t i noktasındaki kümülatif hata, t 2 noktasından başlayarak t i noktasına kadar yapılan yerel hataların toplamıolarak tanımlanır ve E(t i ; h) = Y i y(t i ) ile gösterilir. ÖRNEK 2.5. (2.1) başlangıç değer probleminin y = y(t) çözümünün [a, b] aralĭgında ikinci basamaktan türevi mevcut ve sürekli olduğunu kabul edelim, t i (a, b), h > 0 olmak üzere İleri Euler yöntemi için E(t i ; h) = O(h), h 0 olduğunu gösteriniz. İleri Euler yöntemi için t i noktasında oluşan kümülatif hatayıhesaplayalım. [t 1, t i ] aralığınıh = (t i t 1 )/(i 1) uzunluklu (i 1) adet alt aralığa
14 14 Euler Yöntemleri ve Hata Analizi bölelim. Kümülatif hata tanımıgereğince E(t i ; h) = Y i y(t i ) i = E yerel (y, t j, h) j=2 = h 2 /2y (c 2 ) + h 2 /2y (c 3 ) h 2 /2y (c i ) i = h/2(t i t 1 )(1/(i 1)) y (c i ), c i (t i 1, t i ) j=2 = h/2(t i t 1 )y (c) = O(h), h 0, c (a, b) elde ederiz. Yukarıdaki son eşitlikte sürekli fonksiyonlar için ara değer teoreminden i y (c) = (1/(i 1)) y (c i ), c (a, b) sağlanacak biçimde en az bir c (a, b) noktasının var olduğu gerçeğini kullandık. TANIM 2.5. (Bir yöntemin basamağı) Kümülatif hatasıo(h m ) ile verilen yönteme m inci basamaktan yöntem adıverilir. Gözlem 2.5. İleri Euler yöntemi birinci basamaktan bir yöntemdir. j=2 ÖRNEK 2.6. Örnek 2.1 için [0, 1] aralĭgında h = 1/10 adım uzunluğu ve y(0) = 0.5 başlangıç değeri ile İleri Euler Yaklaşım Tablosunu(Sayısal yaklaşımlar, Yerel hata ve Kümülatif hata değerleri) hesaplayınız. Çözüm. Program 2.3 ile elde edilen yaklaşımlar Tablo 2.3 de verilmiştir. Gözlem 2.6. İleri Euler yöntemi için yerel hata ve kümülatif hata terimlerinin her birinin gerçek çözümün ikinci türevi ile, yani y ile orantılıolduğu görülmektedir. Örnek 2.1 için y (t) = 9y(0)e 3t
15 2.2 Bir yöntemin hata analizi 15 % % Örnek 2.1 verileri ile ileri Euler % yöntemi hata analizi % function sonuc=eulerh(h,t) y=0.5; t=0; yg=gc(t); yerelh=abs(yg-y); kumh=yerelh; sonuc=[t y yg yerelh kumh ]; while t<t y=y+h*f(t,y); yerelh=gc(t+h)-(gc(t)+h*f(t,gc(t))); kumh=gc(t+h)-y; t=t+h; sonuc=[sonuc;t y gc(t) yerelh kumh ]; end function yp=f(t,y) yp=2*t-3*y; function yp=gc(t) yp=2/3*t-2/9+13/18*exp(-3*t); % Program 2.3: ileri Euler ile hata Analizi olup bu fonksiyon t nin artan değerleri için üstel olarak sıfıra yaklaşmaktadır. Bu nedenle Tablo 2.3 de belirtilen hata değerleri de benzer kalitatif davranışı göstermektedir. Ancak Örnek 2.2 için y (t) = 9y(0)e 3t olup, bu fonksiyon t nin artan değerleri için mutlak değerce artmaktadır. Bu durumda oluşan yaklaşım hata değerlerinin de mutlak değerce artması beklenmektedir. ÖRNEK 2.7. Örnek 2.1 için [0, 2] aralĭgında h = 0.1 adım uzunluğu ile başlayarak her defasında bir önceki adım uzunluğunun yarısınıalmak suretiyle ileri Euler yöntemi ile elde edilen yaklaşımların T = 2 noktasındaki kümülatif hata tablosunu yedi farklı h değeri için elde ediniz. Elde ettĭginiz sonuçlar kümülatif hatanın O(h), h 0 olduğunu doğruluyor mu? Çözüm.
16 16 Euler Yöntemleri ve Hata Analizi T Y(Euler) Y(Gerçek) Yerel H. KümH Tablo 2.3: Örnek 2.1 e ait yaklaşımlar ve oluşan hatalar Kümülatif hata değerleri Tablo 2.4 de verilmektedir. Adım Uzunluğu Kümülatif Hata O(h) Tablo 2.4: Adım uzunluğuna göre Kümülatif Hata Kümülatif hatalar adım uzunluğuna bağlıolarak, bir önceki adım uzunluğuna karşılık gelen hatanın yaklaşık olarak yarısına eşit olduğu görülmektedir. Bu sonuç, sayısal verilerin de teorik olarak elde edilen O(h) kümülatif hatasıile uyumlu olduğunu göstermektedir. ÖRNEK 2.8. y = f(t, y) = 100y, y(0) = 1 başlangıç değer problemi verilsin. Problemin gerçek çözümünün y(t) = e 100t
17 2.2 Bir yöntemin hata analizi 17 ile verildĭgine ve t için y(t) 0 olduğuna dikkat ediniz. Herhangi h > 0 adım uzunluğu ve ileri Euler yöntemi ile elde edilen {Y i } dizisinin de gerçek çözümle uyumlu bir benzer davranış göstermesi, Y i 0,i özellĭginin sağlanabilmesi için h adım uzunluğu üzerindeki kısıtlamayıbelirleyiniz. Çözüm. Verilen problem için İleri Euler yaklaşımlarını Y i+1 = Y i + h( 100Y i ) = (1 100h)Y i, i = 1, 2,... olarak tanımlayalım. Bu yaklaşımlardan Y i+1 = (1 100h)Y i = (1 100h) 2 Y i 1 =... = (1 100h) i Y 1 elde ederiz. i için Y i 0(ve dolayısıyla Y i+1 0) için olmalıdır. Bu son eşitsizlikten ise veya 1 100h < 1 1 < 1 100h < 1 2 < 100h < 0 ve h > 0 olduğundan, h < 1/50 kısıtlamasının sağlanmasıgerektiğini görürüz. Genelde y = ay, a < 0 problemi için yukarıdaki işlemleri tekrar ederek ah ( 2, 0) elde ederiz. ( 2, 0) aralığına ileri Euler yönteminin mutlak kararlılık bölgesi adıverilir. Mutlak kararlılık bölgesi i iken sayısal yöntemle sınırlıçözümler elde edilebilmesi için adım uzunluğunun sağlaması gereken kriteri belirler. Farklıyöntemlerin mutlak kararlılık bölgeleri Bölüm 10 da incelenecektir. Yukarıdaki örnekte ileri Euler yöntemi için elde edilen kısıtlama, uzun zaman aralıklarında pratik bazı problemlerin çözümünde aşırı hesaplama yüküne neden olmaktadır. Bu durumda daha büyük adım uzunlukları ile gerçek çözümle benzer davranış gösteren sayısal yaklaşım yöntemlerinin kulanılması zorunlu olmaktadır. Bu bağlamda akla gelen ilk yöntem aşağıda incelenen Geri Euler yöntemidir.
18 18 Euler Yöntemleri ve Hata Analizi 2.3 Geri Euler yöntemi İleri Euler yöntemine benzer olarak (2.1) denklemindeki y türevi için t i+1 noktasında O(h) hatasıile bu defa geri fark yaklaşımıkullanılmak suretiyle veya y (t i+1 ) = (y(t i+1 ) y(t i ))/h + O(h) = (Y i+1 Y i )/h = f(t i+1, Y i+1 ) (Y i+1 Y i )/h = f(t i+1, Y i+1 ), i = 1,..., n (2.13) Y 1 = y(a) ile tanımlanan geri Euler fark denklemi veya iterasyonu elde edilir iterasyonu Y i+1 = Y i + hf(t i+1, Y i+1 ), i = 1,..., n (2.14) Y 1 = y(a) olarak da ifade edilebilir. Ancak ileri Euler yönteminden farklıolarak, (2.14) ile tanımlanan iterasyon ile genelde Y i+1 değerini i inci adımdaki (t i, Y i ) verileri ile elde etmek mümkün değildir. Bu tür yöntemlere kapalıyöntemler adıverilmektedir. ÖRNEK 2.9. Örnek 2.1 e ait başlangıç değer problemi için Y 0 = 0.5 başlangıç değeri ve h = 1/5 adım uzunluğu ile [0, 1] aralĭgındaki geri Euler yaklaşımlarını belirleyiniz. Çözüm. y = 2t 3y y(0) = 0.5 Başlangıç değer problemine geri Euler yöntemi uygulanırsa, Y i+1 = Y i + hf(t i+1, Y i+1 ) = Y i + h(2t i+1 3Y i+1 ) veya Y i+1 = (Y i + 2ht i+1 )/(1 + 3h), i = 1, 2,... Y 1 = 0.5
19 2.3 Geri Euler yöntemi 19 elde edilir. olup, t 1 = 0, t 2 = 1/5, t 3 = 0.4, t 4 = 0.6, t 5 = 0.8, t 6 = 1 Y 2 = (Y 1 + 2ht 2 )/(1 + 3h) = ( /5 1/5)/(1 + 3/5) = elde edilir. Benzer biçimde yaklaşımlarıelde edilir. Y 3 = , Y 4 = , Y 5 = , Y 6 = ÖRNEK Örnek (2.8) de verilen problemin geri Euler yöntemi ile elde edilen {Y i } yaklaşımlar dizisinin analitik çözümle uyumlu, yani Y i 0, i, olmasıiçin h > 0 adım uzunluğu üzerinde bir kısıtlama olmadĭgını gösteriniz. Verilen problem için geri Euler yaklaşımlarını Y i+1 = Y i + h( 100Y i+1 ), i = 1, 2,... olarak tanımlayalım. Bu yaklaşımlardan Y i Y i+1 = h Y i 1 = ( h) 2 =... Y 1 = ( h) i elde ederiz. h > 0 adım uzunluğu üzerinde hiç bir kısıtlama olmaksızın i için Y i+1 0(ve dolayısıyla Y i 0) elde ederiz Nonlineer Problemler için sabit nokta iterasyonuyla Geri Euler yöntemi Verilen problemin nonlineer olmasıdurumunda (2.14) denklemi Y i+1 e göre çözülemez. Bu durumda Y i+1 in belirlenme problemi g(y) = Y i + hf(t i+1, y)
20 20 Euler Yöntemleri ve Hata Analizi fonksiyonunun sabit noktasınıbelirleme problemi olarak düşünülebilir ve her i için y n+1 = g(y n ) = Y i + hf(t i+1, y n ), n = 0, 1, 2 (2.15) iterasyonunun uygun y 0 (örneğin y 0 = Y i ) ile yakınsadığınokta Y i+1 olarak elde edilebilir. Geri Euler yöntemi de ileri Euler ile aynıbasamaktandır, yani kümülatif hatasıo(h) dır. Ancak avantajı, gerçek çözüm ile benzer davranışlarıgösteren çözümler için adım uzunluğunun ileri Euler yöntemine göre çok küçük seçilme zorunluluğunun olmamasıdır. Bu konu bölüm 9.4 te incelenmektedir. Her adımda sabit nokta iterasyonu ile Y i+1 noktasınıprogram 2.4 ile elde edilmiştir. % % Sabit Nokta iterasyonu ile Geri Euler % yöntemi uygulaması % Örnek: y =1+y^2,y(0)=1,[0,1/2] % function geuler(n) a=0;b=1/2;y(1)=1;epsilon=0.001; h=(b-a)/n; t=a:h:b; for i=1:n fark=1;y1=y(i); while fark>epsilon y2=y(i)+h*f(t(i)+h,y1); fark=abs(y2-y1); y1=y2; end y(i+1)=y2; end yg=tan(t+pi/4); sonuc=[t y yg abs(y-yg) ]; plot(t,y, -o, linewidth,2);hold on; plot(t,yg,.-r, linewidth,2);hold on; function yp=f(t,y) yp=1+y^2; % Program 2.4: Geri Euler Yöntemi Uygulaması(Sabit Nokta)
21 2.3 Geri Euler yöntemi 21 ÖRNEK y = 1 + y 2, y(0) = 1 başlangıç değer probleminin çözümü y(t) = tan(t + π/4) olarak elde edilir. Problemin h = 0.1, 0.05, 0.025, , adım uzunlukları ile t = 0.5 noktasındaki yaklaşımlarını sabit nokta iterasyonlu Geri Euler yöntemi yardımıyla belirleyiniz. t = 0.5 noktasında farklı h adım uzunluklarıile kümülatif hatalarıhesaplayarak, yöntemin kümülatif hatasının basamağınıtahmin etmeye çalışınız. Çözüm. Verilen başlangıç değer probleminin t = 0 başlangıç noktasıyla çözümü [0, π/4) aralığında tanımlıdır. h = 0.1 için elde edilen yaklaşımlar aşağıdaki tabloda verilmektedir. Tablodan görüleceği üzere t = 0.5 noktasında analitik t y yg hata inf inf Tablo 2.5: Örnek 2.11 e ait yaklaşım tablosu çözüm mevcut olmasına rağmen sayısal çözüm hesaplanamamıştır. Bunun nedeni t = 0.4 noktasında Y 4 = başlangıç değeri ile oluşturulan (2.15) iterasyonunun t = pi/4 noktası komşuluğundaki çok büyük eğimli komşu çözüm eğrileri dolayısıyla ıraksamış olmasıdır. Öte yandan diğer h değerleri için ise t = 0.5 noktasında sırasıyla Tablo 2.6 de verilen yaklaşık çözüm ve hata değerlerini elde ederiz. Bu tablodan da h adım uzunluğunun ikiye bölünmesiyle kümülatif hatanın da yaklaşık olarak iki kat küçüldüğünü görüyoruz. Bu sonuç ise geri Euler yönteminin kümülatif hatasının da pratik olarak O(h) olduğunu ifade eder. Öteyandan y = 1 + y 2, y(0) = y 0
22 22 Euler Yöntemleri ve Hata Analizi h y yg hata hata oranları / = / = / = Tablo 2.6: Farklıadım uzunluklarıile t = 0.5 noktasındaki yaklaşımlar başlangıç değer probleminin çözümü dır. h = 0.05 adım uzunluğu ve y = tan(t + a tan(y 0 )) y 0 = 0.2, 0.4, 0.6, 0.8, 1 başlangıç değerleri için [0, 0.5] aralığında elde edilen geri Euler çözümleri ve gerçek çözüm eğrileriyle yön alanlarışekil 2.5 te verilmektedir Şekil 2.5: Geri Euler çözümleri, gerçek çözüm eğrileri ve yön alanları Tablo 2.7 da y 0 = 0.2 ve y 0 = 0.8 için y (t) nin belirtilen t noktalarındaki değerleri verilmektedir. Tablo 2.7 değerleri ve Şekil 2.5 incelendiğinde y (t i ) değerlerinin büyük olduğu noktalarda kümülatif hataların da büyük olduğu gözlemlenmektedir. Bu sonuç ise pratik olarak ta kümülatif hatanın y (t) ile orantılıolduğunu ifade eder.
23 2.4 Uyumluluk, Kararlılık ve Yakınsaklık 23 t i y (t i ), (y0 = 0.2) y (t i ), (y0 = 0.8) Tablo 2.7: Örnek 2.11 için farklıbaşlangıç değerleri ile yaklaşım tablosu Nonlineer problemler için Newton iterasyonuyla Geri Euler yöntemi Alternatif olarak (2.14) problemi F (t i+1, y; Y i ) = y Y i hf(t i+1, y) (2.16) fonksiyonunun sıfıryerini belirleme problemi olarak düşünülerek, her i için y n+1 = y n F (t i+1, y n ; Y i )/F y (t i+1, y n ; Y i ), n = 0, 1, 2,... (2.17) ile tanımlanan Newton iterasyonu uygulanabilir. Bu şekilde tanımlanan iterasyon için y 0 = Y i uygun bir seçenek olarak düşünülebilir. Örnek 2.11 için Newton yöntemi ile Geri Euler uygulamasıprogram 2.5 ile gerçekleştirilmektedir. Program 2.5 ile Geri Euler yönteminin Newton yöntemi ile birlikte gerçekleştirilen uygulamasınıörnek 2.11 için gerçekleştiriniz(alıştırma 14). 2.4 Uyumluluk, Kararlılık ve Yakınsaklık Önceki bölümde incelediğimiz hata kavramları, sonlu fark yaklaşımının ilgili diferensiyel denklemi hangi düzeyde temsil edebileceğinin birer ölçüsü idiler. Basamağı yüksek olan bir sonlu fark yaklaşımı, ilgili diferensiyel denklem için bu anlamda tercih sebebidir. Ancak hesaplamaların bilgisayar sayısistemi üzerinde gerçekleştirilmiş olması, her aritmetik işlem sonucunda oluşmasıbeklenen ve kesme hatasıkaynaklıhataya ilaveten yuvarlama hatasıadı verilen hataya neden olmaktadır(bknz Bölüm 2). Sonlu fark yöntemlerinin bir kısmıher adımda oluşmasımuhtemel yuvarlama hatalarınıçözüm bölgesi
24 24 Euler Yöntemleri ve Hata Analizi üzerinde kontrollü olarak biriktirirken, diğer bir kısmında söz konusu birikim ancak adım uzunluğunun belirli bir değerden küçük seçilmesi durumunda sağlanabilmektedir. En kötü ihtimalle, adım uzunluğu ne olursa olsun, yuvarlama hatalarının kontrolsüz olarak artmasına engel olunamayan ve pratik olarak kullanılamayan fark yöntemleri de mevcuttur. Bu yöntemler sırasıyla şartsız olarak sayısal kararlı, şartlı sayısal kararlı ve sayısal kararsız olarak adlandırılmaktadırlar. Bu amaçla teknik olarak aşağıda verilen tanımıyla yöntemin sayısal olarak kararlıolmasıyani yuvarlama hatalarınıkontrollü olarak biriktirebilmesi gerekmektedir. TANIM 2.6. (Bir yöntemin sayısal kararlılĭgı) Tanım kümesinde keyfi olarak seçilen bir t n = nh = sabit noktasındaki yerel kesme hatası, h 0(dolayısıyla n ) için sıfıra yaklaşırken aynınoktadaki kümülatif hata da sıfıra yaklaşıyorsa, ilgili yönteme sayısal kararlıyöntem adıverilmektedir. Yukarıdaki tanıma göre, seçilen sabit noktada fark denklemi diferensiyel denklemi daha iyi temsil ederken sayısal çözümle elde edilen yaklaşımların da problemin gerçek çözümüne yakınsamasıarzu edilmektedir. Diğer deyimle, diferensiyel denklemle uyumlu olan yöntem sayısal olarak ta kararlı olması durumunda iyi sonuçlar üretebilmektedir. Aşağıdaki Teorem ile İleri Euler yönteminin sayısal olarak kararlıolduğu ifade edilmektedir. TEOREM 2.1. (İleri Euler yönteminin sayısal kararlılık kriteri)(2.1) ile tanımlanan başlangıç değer probleminde f fonksiyonu ve f/ y kısmi türevinin (t 1, y 1 ) başlangıç noktasınıiçeren bir D = [a, b] [c, d] dikdörtgeninde sürekli olduğunu ve ayrıca M = max { f/ y, (t, y) D} olduğunu kabul edelim. İleri Euler yöntemi (2.1) problemi için sayısal kararlıdır. İspat. h adım uzunluğu ve D dikdörtgeni içerisinde kalan t i, i = 1, 2,, n noktalarıile (2.1) problemi için D bölgesi içerisinde kalan ve Y i+1 = Y i + hf(t i, Y i ), i = 1, 2,, n (2.18)
25 2.4 Uyumluluk, Kararlılık ve Yakınsaklık 25 ile tanımlanan Euler yaklaşımlarınıgöz önüne alalım. y(t) gerçek çözümünün her t i noktasında E k (t i, h) ile gösterilen kesme hatasıile y(t i+1 ) = y(t i ) + hf(t i, y(t i )) + he k (t i, h) (2.19) bağıntısınısağladığınıbiliyoruz. t i noktasındaki kümülatif hatayıise kısaca e i = y(t i ) Y i notasyonu ile gösterelim. (2.18) yı(2.19) den taraf tarafa çıkararak, e i+1 = e i + h(f(t i, y(t i )) f(t i, Y i )) + he k (t i, h) (2.20) bağıntısını elde ederiz. f fonksiyonu y değişkenine göre türevlenebilir ve türevi sürekli olduğundan türevler için Ortalama Değer Teoremine göre f(t i, Y i ) f(t i, y(t i )) = f/ y(c i )e i (2.21) sağlanacak biçimde Y i ve y(t i ) noktalarıarasında bir c i noktasımevcuttur. (2.21) bağıntısını(2.20) da yazarak e i+1 = (1 + h f/ y(t i, c i ))e i + he k (t i, h) elde ederiz. İleri Euler yöntemi için yerel kesme hatasıtanımıgereği E k = max i(i=1,2,...,n) E k (t i, h) = max i(i=1,2,...,n) h 2 y (c i ) Bh eşitsizliğini sağlayan B > 0 sabiti mevcuttur. Buradan e i+1 (1 + hm)e i + Bh 2, i = 1, 2,..., n eşitsizliği sağlanır. e 1 = 0 olduğundan(ilk adımda Y 1 = y(t 1 )) e 2 = he k (t 1, h) h E k Bh 2
26 26 Euler Yöntemleri ve Hata Analizi e 3 (1 + Mh) e 2 + Bh 2 (1 + Mh)Bh 2 + Bh 2 = (1 + (1 + Mh))Bh 2. e n+1 (1 + (1 + Mh) + (1 + Mh) (1 + Mh) (n 1) )Bh 2 = ((1 + Mh) n 1)/((1 + Mh) 1)Bh 2 = [((1 + Mh) n 1)/M]Bh B M (emhn 1)h = 1 M (em(t n+1 t 1 ) 1)Bh = 1 M (em(b a) 1)Bh Son eşitsizlik n + 1 inci adımdaki kümülatif hatanın, kesme hatasının üst sınırı ile sınırlandığı göstermektedir. Yukarıda son satırda 1 + Mh e Mh eşitsizliğini kullandık. Bu durumda sabit t n = nh noktasında h 0(ve dolayısıyla n ) için kesme hatasısıfıra yaklaşırken, kümülatif hata da sıfıra yaklaşır. O halde yöntem kararlıdır. ÖRNEK y = ay, a > 0, y(0) = 1 probleminin [0, 1] aralĭgında h > 0 adım uzunluğu ile elde edilen ileri Euler yaklaşımlarıile sağ uç noktada oluşan kümülatif hatanın ɛ > 0 değerinden küçük olması için seçilebilecek en büyük h adım uzunluğu ne olmalıdır? Çözüm. [0, 1] aralĭgınıh = 1/n uzunluklu alt aralıklara bölelim.t 1 = 0, t 2 = h,..., t n+1 = 1 olmak üzere yukarıdaki teoreme göre t n+1 = 1 noktasında oluşan hata, e n+1 1 M (em(b a) 1)Bh < ɛ için h < Mɛ (e M 1)B elde ederiz. Örneğimiz için gerçek çözüm y = e at, y (t) = a 2 e at ve M = a, B = max 0 c 1 ( y (c)/2 ) = a 2 e a
27 2.4 Uyumluluk, Kararlılık ve Yakınsaklık 27 olup, h < aɛ a 2 e a (e a 1) sağlanmalıdır. a = 1 için h < ɛ, a = 2 için h < ɛ elde ederiz. Buradan a nın artan değerleri için daha küçük adım uzunluklarıkullanmamız gerektiği sonucunu elde ederiz. TANIM 2.7. (Bir yöntemin Yakınsaklĭgı) Sabit bir t i = ih [a, b] noktasında i (ve dolayısıyla t i noktasını sabit kılacak biçimde h 0) için e i = (y(t i ) Y i ) 0 ise sayısal yönteme t i noktasında yakınsak yöntem adıverilir. Eğer yöntem t i [a, b] noktasında yakınsak ise bu taktirde yönteme belirtilen aralıkta yakınsak yöntem adıverilir. TEOREM 2.2. (Lax Denklik Teoremi) Sabit katsayılı bir başlangıç değer problemi için uyumluluk ve kararlılık, yakınsaklĭga denktir. Çünkü uyumlu bir yöntemde adım uzunluğu sıfıra yaklaşırken kesme hatasının da sıfıra yaklaştığınıbiliyoruz. Kararlıyöntemde ise kesme hatasının sıfıra yaklaşmasıhatanın sıfıra yaklaşmasınısağlamaktadır. O halde uyumlu ve kararlıbir yöntemde adım uzunluğu sıfıra yaklaşırken hata da sıfıra yaklaşmalıdır. Dolayısıyla yöntem yakınsak olmalıdır. Bu sonucun tersi de doğrudur. Sonuç 2.1. Euler yöntemi, Teorem 2.1 den kararlı bir yöntemdir. Ayrıca yöntemin uyumlu olduğunu biliyoruz. O halde yöntem yakınsaktır. Sonuç 2.2. Geri Euler yönteminin kararlılĭgı Teorem 2.1 e benzer biçimde gösterilebilir(alıştırma 15). Ayrıca yöntem uyumlu bir yöntemdir(alıştırma 10). O halde, Lax denklik teoremi gereğince Geri Euler yöntemi de yakınsak bir yöntemdir. Alıştırmalar y = t + 3y, y(0) = 1 başlangıç değer problemi verilmiş olsun. (a) Problemin gerçek çözümünün ile verildiğini kontrol ediniz. y(t) = 10e3t 9 t 3 1 9
28 28 Euler Yöntemleri ve Hata Analizi (b) Y 1 = y(0) = 1 ve h = 1/4 adım uzunluğu ile [0, 1] aralĭgındaki ileri Euler yaklaşımlarınıhesaplayınız. (c) t i = ih, i = 1, 2,..., 5 noktalarında y(t i ) gerçek çözüm değerlerini hesaplayınız. (d) e i = y(t i ) Y i, i = 1, 2,..., 5 kümülatif hatalarınıbelirleyiniz. (e) Elde ettiğiniz sonuçları, sütunlarında sırasıyla (t i,y i,y(t i ),e i ) değerleri yer alan bir yaklaşım tablosuyla ifade ediniz. 2. Soru 1 (b-d) şıklarınıgeri Euler yöntemi için gerçekleştiriniz. 3. Soru 1 i y = t 3y, y(0) = 1 başlangıç değer problemi için ve ileri Euler yöntemi ile tekrarlayınız.(gerçek çözümün y(t) = 10e 3t 9 + t olarak verildiğini kontrol ediniz) 4. Soru 1 i y = t 3y, y(0) = 1 başlangıç değer problemi için ve Geri Euler yöntemi ile tekrarlayınız. 5. Soru 1 ve Soru 3 için ileri Euler yöntemi ile elde ettiğiniz kümülatif hataları karşılaştırınız. Artan t değerleri için kümülatif hatalar nasıl değişiyor? 6. Soru 2 ve Soru 4 için geri Euler yöntemi ile elde ettiğiniz kümülatif hataları karşılaştırınız. Artan t değerleri için kümülatif hatalar nasıl değişiyor? 7. Soru 1 ve Soru 3 te tanımlanan denklemlere ait komşu çözüm eğrileri ve yön alanlarıaşağıda verilmektedir. Öncelikle hangi şeklin hangi denkleme ait olduğunu belirleyerek, Soru 5 te elde ettiğiniz sonuçları, ilgili şekle ait komşu çözüm eğrileri cinsinden yorumlayınız.
29 2.4 Uyumluluk, Kararlılık ve Yakınsaklık İleri Euler yöntemi için verilen programıaşağıdaki başlangıç değer problemlerinin belirtilen aralıklarda, belirtilen adım uzunluklarıile çalıştırarak, her bir problem için yöntem yaklaşım tablosunu(tablo 9.2) elde ediniz. = ln(5)/4 nok- (a) y = y(4 y), y(0) = 1, [0, 10], h = 0.1 (b) y = y(4 y), y(0) = 5, [0, 10], h = 0.1 (c) y = y(4 y), y(0) = 1, [0, 2/5], h = 0.01 (d) c) şıkkında verilen başlangıç değer probleminin t tasında sınırlıolmadĭgınıgösteriniz. 9. (Adım uzunluğuna göre kümülatif hata) Soru 1 deki başlangıç değer problemini h = 0.1, h = 0.05, h = adım uzunlukları ile ve ileri Euler yöntemiyle [0, 2] aralĭgında çözerek, t = 2 noktasındaki kümülatif hatalarınıkarşılaştıralım. Kümülatif hatalar nasıl değişmektedir. Elde ettiğiniz sonuçlar teorik olarak elde edilen O(h) hatasınıdoğruluyor mu? 10. Soru 9 u Geri Euler yöntemi için tekrar ediniz. Geri Euler yönteminin kümülatif hatasıhakkında ne düşünüyorsunuz? 11. y = ay, y(0) = y 1, a > 0, başlangıç değer problemi için (h < 1/ a ) için ileri Euler iterasyonlarının y = 0 denge noktasına monoton yakınsak, (1/ a < h < 2/ a ) için ise salınımlı yakınsak, yani ardışık yaklaşımların denge noktasının sağında ve solunda yer aldĭgınıgösteriniz.(not:p, g(t) nin bir sabit noktasıve t 1 başlangıç noktasıp ye yeterince yakın olmak üzere, t i+1 = g(t i ), i = 1, 2,... iterasyonu verilmiş olsun. Eğer 0 < g (p) < 1 ise iterasyon monoton yakınsak, 1 < g (p) < 0 ise iterasyon salınımlıolarak yakınsaktır.)
30 30 Euler Yöntemleri ve Hata Analizi 12. y = t + y, y(0) = 1 başlangıç değer problemi verilmiş olsun ve ileri Euler yöntemiyle elde edilecek olan yaklaşımlar için adım uzunluğunun h > 0 olduğunu kabul edelim. (a) Problemin y(t) çözümünü belirleyiniz. (b) t 1 = 0, t 2 = h, t 3 = 2h, olmak üzere t 2 noktasında oluşan E k (t 2, h) = y(t 3) y(t 2 ) h f(t 2, y(t 2 )) kesme hatasının h > 0 parametresine bağlıolarak E k (t 2, h) = he t 2 = O(h), h 0 biçiminde ifade edilebileceğini gösteriniz. (c) t 2 noktasında oluşan yerel hatanın olduğunu gösteriniz. E yerel (t 2, h) = he k (t 2, h) = O(h 2 ), h 0 (d) Y 2, Y 3 yaklaşımlarınıh cinsinden belirleyiniz. 13. Soru 12 yi geri Euler yöntemi için tekrar ediniz. 14. Geri Euler Yönteminin yerel Kesme hatası, Yerel Hata ve Kümülatif hatalarınıbelirleyerek, ileri Euler yöntemine ait sonuçlarla karşılaştırınız. 15. İleri Euler yönteminin kararlılık analizini takip ederek, Geri Euler yönteminin de kararlıolduğunu ispatlayınız. 16. Sabit nokta iterasyonunu kullanan Geri Euler yöntemi yardımıyla Soru 8-a da verilen problemin yaklaşık çözümlerini elde ediniz. 17. Newton yöntemini kullanan Geri Euler yöntemi yardımıyla soru 8-a da verilen problemin yaklaşık çözümlerini elde ediniz. 18. Newton yöntemini kullanan Geri Euler yöntemi yardımıyla, Örnek2.11 için h = 0.1,h = h/2 = 0.05,h = h/4 = alarak t = 1 anında oluşan kümülatif hataların nasıl değiştiğini gözlemleyiniz. Elde ettiğiniz sonuçların yöntemin tahmini kümülatif hatasıile uyumlu mudur?
31 2.4 Uyumluluk, Kararlılık ve Yakınsaklık Canlınüfus modeli(verhulst, 1838) olarak bilinen dn/dt = rn(1 N/K), N(0) = N 0 başlangıç değer problemini gözönüne alalım. Bu modelde N(t), t anındaki canlı nüfusunu, r nüfus artış oranını, K ortamın barındırabileceği maksimum nüfusu ve N 0 ise başlangıç anı olarak kabul edilen t = 0 anındaki nüfusu temsil etmektedir. Bu model için aşağıdaki analitik ve sayısal irdelemeyi gerçekleştirelim: (a) Problemin analitik çözümünün N(t) = (N 0 Ke rt )/((K + N 0 (e rt 1))) olduğunu gösteriniz.(not: Denklemin değişkenlerine ayrılabilen bir denklem olduğuna dikkat ediniz.) (b) lim t N(t) = K olduğunu gösteriniz. (c) İleri Euler yöntemi ile problemin (b) de belirtilen özelliği sağlayan çözümü için problem parametreleri cinsinden adım uzunluğu en fazla ne olabilir?(ipucu: N = K asimtotik kararlıdenge noktasıkomşuluğunda verilen diferensiyel denkleme karşılık gelen lineer denklemi belirleyerek, Soru 11 deki analizinden faydalanınız). (d) N 0 = 400, 800, 2000 başlangıç değerleri ve r = 0.5, K = 1500 için [0, 10] aralĭgındaki çözüm eğrilerini uygun adım uzunluğu ve ileri Euler yöntemi ile elde ediniz. (e) N = K denge noktasının asimtotik kararlıbir denge noktasıolduğunu gösteriniz.(not: Komşu çözüm eğrileri artan zaman değerleri için N = K denge noktasına yakınsıyorlarsa, denge noktasına asimtotik kararlı denge noktası adı verilmektedir. N 0 > K için dn/dt < 0, N 0 < K için dn/dt > 0 olduğunu gösteriniz.) (f) Elde ettiğiniz Euler yaklaşımları ile gerçek çözümün grafiklerini aynı eksende çizerek, çözümleri karşılaştırınız. Elde ettiğiniz çözüm eğrileri N = K denge noktasının kararlıolmasıyla uyumlu mudur? 20. Proje (Sınırsız çözümleri ayıklayacak ve kümülatif hata kontrolü gerçekleştirecek biçimde Euler yöntemini geliştirelim). Soru 7-c de karşılaşılan ve sonlu t anında analitik çözümün sınırsız olması durumu başlangıç değer problemlerinde karşılaşılan tipik bir durumdur. Bu
32 32 Euler Yöntemleri ve Hata Analizi durumda önceden belirtilen ve sınırsız çözüme ulaşılan t noktasınıiçeren bir aralıkta sayısal çözüm belirlemeye çalışmak anlamlı değildir. O halde kullanılabilecek en küçük adım uzunluğu ile de mutlak değerce belirli bir değerden büyük bir yaklaşıma ulaşıldĭgında yönteme ait iterasyonlar durmalıdır. İkinci önemli bir nokta ise, genelde gerçek çözümü bilemeyeceğimiz için belirtilen aralıkta elde edilen sayısal yaklaşımın gerçek çözümü hangi düzeyde temsil edebildiğidir. Bu durumda elde edilen yaklaşımın iyi bir yaklaşım olup olmadĭgını kontrol eden bir mekanizma da geliştirilmelidir. Aşağıdaki adımlar yukarıda belirtilen hususları dikkate alarak ileri Euler yönteminin daha esnek bir versiyonunu geliştirmek için ipuçlarıolarak kabul edilebilir. Bu ipuçları doğrultusunda uygun bir algoritma ve algoritmaya ait program geliştiriniz. Geliştirdiğiniz program ile Soru 8 c yi çözmeye çalışınız. (a) Tahmini olarak seçilen bir başlangıç h adım uzunluğu ile elde ettiğiniz değerler mutlak değerce belirtilen Y max (örneğin 1x10 4 ) değerinden küçük kaldĭgı sürece yöntemi aralık sağ uç noktasına ulaşana kadar uygulayınız. (b) Eğer sağ uç noktaya ulaşmadan değerleriniz mutlak değerce Y max a ulaşmış ise, h adım uzunluğunu küçülterek(örneğin h yerine h/2 alarak) iterasyon işlemini tekrar ediniz. Bu işlemi sağ uç noktaya kadar tekrar ediniz. Eğer önceden belirlediğiniz en küçük h(örneğin 1x10 4 ) değeri ile de sağ uç noktaya kadar ulaşamadıysanız, sınırlı çözüm olarak elde ettiğiniz yaklaşımları grafiksel olarak kullanıcıya sununuz. (c) Sağ uç noktaya ulaşmanız durumunda, önceki adımla sağ uç nokta için elde ettiğiniz yaklaşım değeri ile yeni adım uzunluğu ile elde ettiğiniz yaklaşım değeri arasındaki fark mutlak değerce uygun bir biçimde belirleyeceğiniz fark(örneğin 1x10 4 ) sabiti nden küçük kalıyorsa işlemi doğru adım uzunluğu ile gerçekleştirilmiştir. Tanım kümesinde farklı adım uzunluklarıile elde ettiğiniz sonuçlarıgrafiksel olarak kullanıcıya sununuz. (d) Değilse adım uzunluğunu tekrar küçülterek gerekirse kabul edilebilir en küçük h adım uzunluğu ile de işleme devam ediniz.
33 2.4 Uyumluluk, Kararlılık ve Yakınsaklık 33 % % Newton iterasyonu ile Geri Euler Uygulaması % Örnek: y =1+y^2,y(0)=y0 % function sonuc=geulernewt(n)...(baslangic degerler ve sabitler) for i=1:n test=1;y1=y(i);sayac=0; while test y2=y1-f(t+h,y1,y(i))/fy(t+h,y1,y(i)); fark=abs(y2-y1); y1=y2; sayac=sayac+1; test=(fark>tol)&(sayac<max_sayac); if sayac==max_sayac error( iraksak iterasyon ); end end y(i+1)=y2;t(i+1)=t(i)+h; end...(gerçek çözüm, hata ve grafik çizimleri) function yp=f(t,y) yp=1+y^2; function yp=fy(t,y) yp=2*y; function yp=f(t,y,yi) yp=y-yi-h*f(t+h,y); function yp=fy(t,y,yi) yp=1-h*fy(t+h,y); % Program 2.5: Geri Euler Yöntemi Uygulaması(Newton)
Euler Yöntemleri ve Hata Analizi
 Bölüm 2 Euler Yöntemleri ve Hata Analizi Bu bölümde başlangıç değer problemleri için İleri ve geri Euler yöntemlerini inceleyerek, Hata analizi için gerekli olan yerel kesme hatası, yerel hata, kümülatif
Bölüm 2 Euler Yöntemleri ve Hata Analizi Bu bölümde başlangıç değer problemleri için İleri ve geri Euler yöntemlerini inceleyerek, Hata analizi için gerekli olan yerel kesme hatası, yerel hata, kümülatif
Yüksek basamaktan tek adım Sonlu Fark Yöntemleri
 Bölüm Yüksek basamaktan tek adım Sonlu Fark Yöntemleri Bu bölümde, birinci basamaktan başlangıç değer problemleri için Tek adım (Yamuk, Düzeltilmiş Euler(Heun), Runge-Kutta yöntemlerinin nasıl elde edildikleri,
Bölüm Yüksek basamaktan tek adım Sonlu Fark Yöntemleri Bu bölümde, birinci basamaktan başlangıç değer problemleri için Tek adım (Yamuk, Düzeltilmiş Euler(Heun), Runge-Kutta yöntemlerinin nasıl elde edildikleri,
Elemanter fonksiyonlarla yaklaşım ve hata
 Elemanter fonksiyonlarla yaklaşım ve hata Prof. Dr. Erhan Coşkun Karadeniz Teknik Üniversitesi, Fen Fakültesi Matematik Bölümü Kasım, 2018 e 5 Kasım, 2018 1 / 48 Elemanter fonksiyonlarla yaklaşım ve hata
Elemanter fonksiyonlarla yaklaşım ve hata Prof. Dr. Erhan Coşkun Karadeniz Teknik Üniversitesi, Fen Fakültesi Matematik Bölümü Kasım, 2018 e 5 Kasım, 2018 1 / 48 Elemanter fonksiyonlarla yaklaşım ve hata
Sayısal Analiz. Prof. Dr. Erhan Coşkun. Karadeniz Teknik Üniversitesi, Fen Fakültesi, Ekim, 2018
 Sayısal Analiz Prof. Dr. Erhan Coşkun Karadeniz Teknik Üniversitesi, Fen Fakültesi, Matematik Bölümü E-posta:erhan@ktu.edu.tr Ekim, 2018 E. Coşkun (KTÜ) Bölüm 1 Ekim, 2018 1 / 40 Matematiksel Analiz Analitik
Sayısal Analiz Prof. Dr. Erhan Coşkun Karadeniz Teknik Üniversitesi, Fen Fakültesi, Matematik Bölümü E-posta:erhan@ktu.edu.tr Ekim, 2018 E. Coşkun (KTÜ) Bölüm 1 Ekim, 2018 1 / 40 Matematiksel Analiz Analitik
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Hatalar ve Bilgisayar Aritmetiği
 Hatalar ve Bilgisayar Aritmetiği Analitik yollardan çözemediğimiz birçok matematiksel problemi sayısal yöntemlerle bilgisayarlar aracılığı ile çözmeye çalışırız. Bu şekilde Sayısal yöntemler kullanarak
Hatalar ve Bilgisayar Aritmetiği Analitik yollardan çözemediğimiz birçok matematiksel problemi sayısal yöntemlerle bilgisayarlar aracılığı ile çözmeye çalışırız. Bu şekilde Sayısal yöntemler kullanarak
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 7- SAYISAL TÜREV Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ İntegral işlemi gibi türev işlemi de mühendislikte çok fazla kullanılan bir işlemdir. Basit olarak bir fonksiyonun bir noktadaki
MAK 210 SAYISAL ANALİZ BÖLÜM 7- SAYISAL TÜREV Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ İntegral işlemi gibi türev işlemi de mühendislikte çok fazla kullanılan bir işlemdir. Basit olarak bir fonksiyonun bir noktadaki
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 2- HATA VE HATA KAYNAKLARI Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ Bir denklemin veya problemin çözümünde kullanılan sayısal yöntem belli bir giriş verisini işleme tabi tutarak sayısal
MAK 210 SAYISAL ANALİZ BÖLÜM 2- HATA VE HATA KAYNAKLARI Doç. Dr. Ali Rıza YILDIZ 1 GİRİŞ Bir denklemin veya problemin çözümünde kullanılan sayısal yöntem belli bir giriş verisini işleme tabi tutarak sayısal
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 5- SONLU FARKLAR VE İNTERPOLASYON TEKNİKLERİ Doç. Dr. Ali Rıza YILDIZ MAK 210 - Sayısal Analiz 1 İNTERPOLASYON Tablo halinde verilen hassas sayısal değerler veya ayrık noktalardan
MAK 210 SAYISAL ANALİZ BÖLÜM 5- SONLU FARKLAR VE İNTERPOLASYON TEKNİKLERİ Doç. Dr. Ali Rıza YILDIZ MAK 210 - Sayısal Analiz 1 İNTERPOLASYON Tablo halinde verilen hassas sayısal değerler veya ayrık noktalardan
Ankara Üniversitesi Kütüphane ve Dokümantasyon Daire Başkanlığı Açık Ders Malzemeleri. Ders izlence Formu
 Ankara Üniversitesi Kütüphane ve Dokümantasyon Daire Başkanlığı Açık Ders Malzemeleri Ders izlence Formu Dersin Kodu ve İsmi Dersin Sorumlusu Dersin Düzeyi MAT407 REEL ANALİZ Prof. Dr. Ertan İBİKLİ ve
Ankara Üniversitesi Kütüphane ve Dokümantasyon Daire Başkanlığı Açık Ders Malzemeleri Ders izlence Formu Dersin Kodu ve İsmi Dersin Sorumlusu Dersin Düzeyi MAT407 REEL ANALİZ Prof. Dr. Ertan İBİKLİ ve
Şekil 7.1 Bir tankta sıvı birikimi
 6 7. DİFERENSİYEL DENKLEMLERİN SAYISAL ÇÖZÜMLERİ Diferensiyel denklemlerin sayısal integrasyonunda kullanılabilecek bir çok yöntem vardır. Tecrübeler dördüncü mertebe (Runge-Kutta) yönteminin hemen hemen
6 7. DİFERENSİYEL DENKLEMLERİN SAYISAL ÇÖZÜMLERİ Diferensiyel denklemlerin sayısal integrasyonunda kullanılabilecek bir çok yöntem vardır. Tecrübeler dördüncü mertebe (Runge-Kutta) yönteminin hemen hemen
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Türev Uygulamaları. 9.1 Ortalama Değer teoremi
 1 2 Bölüm 9 Türev Uygulamaları 9.1 Ortalama Değer teoremi Türevin çok farklı uygulamaları vardır. Bunlar arasında çok önemli olan bazılarını ele alacağız. Ortalama Değer Teoremi ni daha önce görmüştük.
1 2 Bölüm 9 Türev Uygulamaları 9.1 Ortalama Değer teoremi Türevin çok farklı uygulamaları vardır. Bunlar arasında çok önemli olan bazılarını ele alacağız. Ortalama Değer Teoremi ni daha önce görmüştük.
4. HAFTA BLM323 SAYISAL ANALİZ. Okt. Yasin ORTAKCI.
 4. HAFTA BLM33 SAYISAL ANALİZ Okt. Yasin ORTAKCI yasinortakci@karabuk.edu.tr Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi BLM33 DOĞRUSAL OLMAYAN (NONLINEAR) DENKLEM SİSTEMLERİ Mühendisliğin
4. HAFTA BLM33 SAYISAL ANALİZ Okt. Yasin ORTAKCI yasinortakci@karabuk.edu.tr Karabük Üniversitesi Uzaktan Eğitim Uygulama ve Araştırma Merkezi BLM33 DOĞRUSAL OLMAYAN (NONLINEAR) DENKLEM SİSTEMLERİ Mühendisliğin
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 8- SAYISAL İNTEGRASYON 1 GİRİŞ Mühendislikte sık karşılaşılan matematiksel işlemlerden biri integral işlemidir. Bilindiği gibi integral bir büyüklüğün toplam değerinin bulunması
MAK 210 SAYISAL ANALİZ BÖLÜM 8- SAYISAL İNTEGRASYON 1 GİRİŞ Mühendislikte sık karşılaşılan matematiksel işlemlerden biri integral işlemidir. Bilindiği gibi integral bir büyüklüğün toplam değerinin bulunması
1. Hafta Uygulama Soruları
 . Hafta Uygulama Soruları ) x ekseni, x = doğrusu, y = x ve y = x + eğrileri arasında kalan alan nedir? ) y = x 3 ve y = 4 x 3 parabolleri arasında kalan alan nedir? 3) y = x, x y = 4 eğrileri arasında
. Hafta Uygulama Soruları ) x ekseni, x = doğrusu, y = x ve y = x + eğrileri arasında kalan alan nedir? ) y = x 3 ve y = 4 x 3 parabolleri arasında kalan alan nedir? 3) y = x, x y = 4 eğrileri arasında
BÖLÜNMÜŞ FARKLAR (DİVİDED DİFFERENCES)
 BÖLÜNMÜŞ FARKLAR (DİVİDED DİFFERENCES) Lagrange ve Neville yöntemlerinin bazı olumsuz yanları vardır: İşlem sayısı çok fazladır (bazı başka yöntemlere kıyasla) Data setinde bir nokta ilavesi veya çıkartılması
BÖLÜNMÜŞ FARKLAR (DİVİDED DİFFERENCES) Lagrange ve Neville yöntemlerinin bazı olumsuz yanları vardır: İşlem sayısı çok fazladır (bazı başka yöntemlere kıyasla) Data setinde bir nokta ilavesi veya çıkartılması
ÇEV 2006 Mühendislik Matematiği (Sayısal Analiz) DEÜ Çevre Mühendisliği Bölümü Doç.Dr. Alper ELÇĐ
 Giriş ÇEV 2006 Mühendislik Matematiği (Sayısal Analiz) DEÜ Çevre Mühendisliği Bölümü Doç.Dr. Alper ELÇĐ Sayısal Analiz Nedir? Mühendislikte ve bilimde, herhangi bir süreci tanımlayan karmaşık denklemlerin
Giriş ÇEV 2006 Mühendislik Matematiği (Sayısal Analiz) DEÜ Çevre Mühendisliği Bölümü Doç.Dr. Alper ELÇĐ Sayısal Analiz Nedir? Mühendislikte ve bilimde, herhangi bir süreci tanımlayan karmaşık denklemlerin
x e göre türev y sabit kabul edilir. y ye göre türev x sabit kabul edilir.
 TÜREV y= f(x) fonksiyonu [a,b] aralığında tanımlı olsun. Bu aralıktaki bağımsız x değişkenini h kadar arttırdığımızda fonksiyon değeri de buna bağlı olarak değişecektir. Fonksiyondaki artma miktarını değişkendeki
TÜREV y= f(x) fonksiyonu [a,b] aralığında tanımlı olsun. Bu aralıktaki bağımsız x değişkenini h kadar arttırdığımızda fonksiyon değeri de buna bağlı olarak değişecektir. Fonksiyondaki artma miktarını değişkendeki
2 1 fonksiyonu veriliyor. olacak şekilde ortalama değer teoremini sağlayacak bir c sayısının var olup olmadığını araştırınız. Eğer var ise bulunuz.
 ANALİZ 1.) a) sgn. sgn( 1) = 1 denkleminin çözüm kümesini b) f ( ) 3 1 fonksiyonu veriliyor. olacak şekilde ortalama değer teoremini sağlayacak bir c sayısının var olup olmadığını araştırınız. Eğer var
ANALİZ 1.) a) sgn. sgn( 1) = 1 denkleminin çözüm kümesini b) f ( ) 3 1 fonksiyonu veriliyor. olacak şekilde ortalama değer teoremini sağlayacak bir c sayısının var olup olmadığını araştırınız. Eğer var
SORU 1: Herbir A R kümesi için A G ve λ (A) = λ (G) olacak şekilde. ÇÖZÜM 1: B sayılabilir bir küme olsun. Bu durumda λ (B) = 0 gerçeklenir.
 2.4 Lebesgue Dış Ölçüsü ve Lebesgue Ölçüsü SORU : Herbir A R kümesi için A G ve λ (A) = λ (G) olacak şekilde G R kümesinin varlığınıgösteriniz? ÇÖZÜM : B sayılabilir bir küme olsun. Bu durumda λ (B) =
2.4 Lebesgue Dış Ölçüsü ve Lebesgue Ölçüsü SORU : Herbir A R kümesi için A G ve λ (A) = λ (G) olacak şekilde G R kümesinin varlığınıgösteriniz? ÇÖZÜM : B sayılabilir bir küme olsun. Bu durumda λ (B) =
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
18.034 İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Matematik Ders Notları. Doç. Dr. Murat Donduran
 Matematik Ders Notları Doç. Dr. Murat Donduran Mart 18, 28 2 İçindekiler 1 Tanımlı Integral Uygulamaları 5 1.1 Olasılık.............................. 5 3 4 İÇINDEKILER Bölüm 1 Tanımlı Integral Uygulamaları
Matematik Ders Notları Doç. Dr. Murat Donduran Mart 18, 28 2 İçindekiler 1 Tanımlı Integral Uygulamaları 5 1.1 Olasılık.............................. 5 3 4 İÇINDEKILER Bölüm 1 Tanımlı Integral Uygulamaları
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
18.034 İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
TÜREV VE UYGULAMALARI
 TÜREV VE UYGULAMALARI A R, a A ve f de A da tanımlı bir fonksiyon olsun. Eğer f(x) f(a) lim x a x a limiti veya x=a+h koymakla elde edilen f(a+h) f(a) lim h 0 h Bu türev f (a), df dx limiti varsa f fonksiyonu
TÜREV VE UYGULAMALARI A R, a A ve f de A da tanımlı bir fonksiyon olsun. Eğer f(x) f(a) lim x a x a limiti veya x=a+h koymakla elde edilen f(a+h) f(a) lim h 0 h Bu türev f (a), df dx limiti varsa f fonksiyonu
Okut. Yüksel YURTAY. İletişim : (264) Sayısal Analiz. Giriş.
 Okut. Yüksel YURTAY İletişim : Sayısal Analiz yyurtay@sakarya.edu.tr www.cs.sakarya.edu.tr/yyurtay (264) 295 58 99 Giriş 1 Amaç : Mühendislik problemlerinin bilgisayar ortamında çözümünü mümkün kılacak
Okut. Yüksel YURTAY İletişim : Sayısal Analiz yyurtay@sakarya.edu.tr www.cs.sakarya.edu.tr/yyurtay (264) 295 58 99 Giriş 1 Amaç : Mühendislik problemlerinin bilgisayar ortamında çözümünü mümkün kılacak
13.Konu Reel sayılar
 13.Konu Reel sayılar 1. Temel dizi 2. Temel dizilerde toplama ve çarpma 3. Reel sayılar kümesi 4. Reel sayılar kümesinde toplama ve çarpma 5. Reel sayılar kümesinde sıralama 6. Reel sayılar kümesinin tamlık
13.Konu Reel sayılar 1. Temel dizi 2. Temel dizilerde toplama ve çarpma 3. Reel sayılar kümesi 4. Reel sayılar kümesinde toplama ve çarpma 5. Reel sayılar kümesinde sıralama 6. Reel sayılar kümesinin tamlık
Sayısal Analiz(Prof. Dr. Erhan Coşkun, KTU,
 Bölüm 1 Sayısal Analiz(Prof. Dr. Erhan Coşkun, KTU, erhan@ktu.edu.tr) Bu bölümde matematiksel analiz türleri olarak bilinen analitik, sayısal, kalitatif ve sembolik analiz yöntemlerini kısaca tanıtarak,
Bölüm 1 Sayısal Analiz(Prof. Dr. Erhan Coşkun, KTU, erhan@ktu.edu.tr) Bu bölümde matematiksel analiz türleri olarak bilinen analitik, sayısal, kalitatif ve sembolik analiz yöntemlerini kısaca tanıtarak,
Bu tanım aralığı pozitif tam sayılar olan f(n) fonksiyonunun değişim aralığı n= 1, 2, 3,, n,
 DİZİLER Tamamen belirli bir kurala göre sıralanmış sayılar topluluğuna veya kümeye Dizi denir. Belirli bir kurala göre birbiri ardınca gelen bu sayıların her birine dizinin terimi ve hepsine birden dizinin
DİZİLER Tamamen belirli bir kurala göre sıralanmış sayılar topluluğuna veya kümeye Dizi denir. Belirli bir kurala göre birbiri ardınca gelen bu sayıların her birine dizinin terimi ve hepsine birden dizinin
Runge-Kutta Metodu. Runge-Kutta metodu
 Runge-Kutta metodu Runge-Kutta Metodu dy dx = f(x, y), y(0) = y 0 (1) bicimindeki birinci dereceden adi diferansiyel denklemleri numerik olarak cozmekte kullanilan bir metottur. Runge-Kutta metodunu kullanabilmek
Runge-Kutta metodu Runge-Kutta Metodu dy dx = f(x, y), y(0) = y 0 (1) bicimindeki birinci dereceden adi diferansiyel denklemleri numerik olarak cozmekte kullanilan bir metottur. Runge-Kutta metodunu kullanabilmek
Diferansiyel denklemler uygulama soruları
 . Aşağıdaki diferansiyel denklemleri sınıflandırınız. a) d y d d + y = 0 b) 5 d dt + 4d + 9 = cos 3t dt Diferansiyel denklemler uygulama soruları 0.0.3 c) u + u [ ) ] d) y + = c d. y + 3 = 0 denkleminin,
. Aşağıdaki diferansiyel denklemleri sınıflandırınız. a) d y d d + y = 0 b) 5 d dt + 4d + 9 = cos 3t dt Diferansiyel denklemler uygulama soruları 0.0.3 c) u + u [ ) ] d) y + = c d. y + 3 = 0 denkleminin,
Elemanter Fonksiyonlarla Yaklaşım ve Hata
 Bölüm 5 Elemanter Fonksiyonlarla Yaklaşım ve Hata Bu bölümde önelikle verilen bir ayrık veri kümesi için standart ve ağırlıklıen küçük kareler yöntemi ile en uygun yaklaşım polinomunun nasıl belirleneeğini
Bölüm 5 Elemanter Fonksiyonlarla Yaklaşım ve Hata Bu bölümde önelikle verilen bir ayrık veri kümesi için standart ve ağırlıklıen küçük kareler yöntemi ile en uygun yaklaşım polinomunun nasıl belirleneeğini
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
İÇİNDEKİLER ÖNSÖZ Bölüm 1 SAYILAR 11 Bölüm 2 KÜMELER 31 Bölüm 3 FONKSİYONLAR
 İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 11 1.1. Sayı Kümeleri 12 1.1.1.Doğal Sayılar Kümesi 12 1.1.2.Tam Sayılar Kümesi 13 1.1.3.Rasyonel Sayılar Kümesi 14 1.1.4. İrrasyonel Sayılar Kümesi 16 1.1.5. Gerçel
İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 11 1.1. Sayı Kümeleri 12 1.1.1.Doğal Sayılar Kümesi 12 1.1.2.Tam Sayılar Kümesi 13 1.1.3.Rasyonel Sayılar Kümesi 14 1.1.4. İrrasyonel Sayılar Kümesi 16 1.1.5. Gerçel
SAYISAL ÇÖZÜMLEME. Yrd.Doç.Dr.Esra Tunç Görmüş. 1.Hafta
 SAYISAL ÇÖZÜMLEME Yrd.Doç.Dr.Esra Tunç Görmüş 1.Hafta Sayısal çözümleme nümerik analiz nümerik çözümleme, approximate computation mühendislikte sayısal yöntemler Computational mathematics Numerical analysis
SAYISAL ÇÖZÜMLEME Yrd.Doç.Dr.Esra Tunç Görmüş 1.Hafta Sayısal çözümleme nümerik analiz nümerik çözümleme, approximate computation mühendislikte sayısal yöntemler Computational mathematics Numerical analysis
Bilgisayar sayısistemi, aritmetiği ve hata
 Bölüm 2 Bilgisayar sayısistemi, aritmetiği ve hata Sayısal yöntemler için gerekli en temel araçlar bilgisayarlardır, fakat sayısal yöntemler analitik analiz yöntemlerinden alışık olduğumuz reel veya kompleks
Bölüm 2 Bilgisayar sayısistemi, aritmetiği ve hata Sayısal yöntemler için gerekli en temel araçlar bilgisayarlardır, fakat sayısal yöntemler analitik analiz yöntemlerinden alışık olduğumuz reel veya kompleks
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ
 BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
BÖLÜM 1: MADDESEL NOKTANIN KİNEMATİĞİ 1.1. Giriş Kinematik, daha öncede vurgulandığı üzere, harekete sebep olan veya hareketin bir sonucu olarak ortaya çıkan kuvvetleri dikkate almadan cisimlerin hareketini
1. GRUPLAR. c (Birleşme özelliği) sağlanır. 2) a G için a e e a a olacak şekilde e G (e ye birim eleman denir) vardır.
 1. GRUPLAR Tanım 1.1. G boş olmayan bir küme ve, G de bir ikili işlem olsun. (G yapısına aşağıdaki aksiyomları sağlıyorsa bir grup denir., ) cebirsel 1) a b cg,, için a( bc) ( ab) c (Birleşme özelliği)
1. GRUPLAR Tanım 1.1. G boş olmayan bir küme ve, G de bir ikili işlem olsun. (G yapısına aşağıdaki aksiyomları sağlıyorsa bir grup denir., ) cebirsel 1) a b cg,, için a( bc) ( ab) c (Birleşme özelliği)
18.034 İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MAK 210 SAYISAL ANALİZ
 MAK 210 SAYISAL ANALİZ BÖLÜM 6- İSTATİSTİK VE REGRESYON ANALİZİ Doç. Dr. Ali Rıza YILDIZ 1 İSTATİSTİK VE REGRESYON ANALİZİ Bütün noktalardan geçen bir denklem bulmak yerine noktaları temsil eden, yani
MAK 210 SAYISAL ANALİZ BÖLÜM 6- İSTATİSTİK VE REGRESYON ANALİZİ Doç. Dr. Ali Rıza YILDIZ 1 İSTATİSTİK VE REGRESYON ANALİZİ Bütün noktalardan geçen bir denklem bulmak yerine noktaları temsil eden, yani
HOMOGEN OLMAYAN DENKLEMLER
 n. mertebeden homogen olmayan lineer bir diferansiyel denklemin y (n) + p 1 (x)y (n 1) + + p n 1 (x)y + p n (x)y = f(x) (1) şeklinde olduğunu ve bununla ilgili olan n. mertebeden lineer homogen denlemin
n. mertebeden homogen olmayan lineer bir diferansiyel denklemin y (n) + p 1 (x)y (n 1) + + p n 1 (x)y + p n (x)y = f(x) (1) şeklinde olduğunu ve bununla ilgili olan n. mertebeden lineer homogen denlemin
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
FEN FAKÜLTESİ MATEMATİK BÖLÜMÜ YAZ OKULU DERS İÇERİGİ. Bölümü Dersin Kodu ve Adı T P K AKTS
 Bir Dönemde Okutulan Ders Saati MAT101 Genel I (Mühendislik Fakültesi Bütün Bölümler, Fen Fakültesi Kimya ve Astronomi Bölümleri) 1 Kümeler, reel sayılar, bir denklem veya eşitsizliğin grafiği 2 Fonksiyonlar,
Bir Dönemde Okutulan Ders Saati MAT101 Genel I (Mühendislik Fakültesi Bütün Bölümler, Fen Fakültesi Kimya ve Astronomi Bölümleri) 1 Kümeler, reel sayılar, bir denklem veya eşitsizliğin grafiği 2 Fonksiyonlar,
KISITLI OPTİMİZASYON
 KISITLI OPTİMİZASYON SİMPLEKS YÖNTEMİ Simpleks Yöntemi Simpleks yöntemi iteratif bir prosedürü gerektirir. Bu iterasyonlar ile gerçekçi çözümlerin olduğu bölgenin (S) bir köşesinden başlayarak amaç fonksiyonunun
KISITLI OPTİMİZASYON SİMPLEKS YÖNTEMİ Simpleks Yöntemi Simpleks yöntemi iteratif bir prosedürü gerektirir. Bu iterasyonlar ile gerçekçi çözümlerin olduğu bölgenin (S) bir köşesinden başlayarak amaç fonksiyonunun
TÜREV VE UYGULAMALARI
 TÜREV VE UYGULAMALARI 1-TÜREVİN TANIMI VE GÖSTERİLİŞİ a,b R olmak üzere, f:[a,b] R fonksiyonu verilmiş olsun. x 0 (a,b) için lim x X0 f(x)-f( x 0 ) limiti bir gerçel sayı ise bu limit değerine f fonksiyonunun
TÜREV VE UYGULAMALARI 1-TÜREVİN TANIMI VE GÖSTERİLİŞİ a,b R olmak üzere, f:[a,b] R fonksiyonu verilmiş olsun. x 0 (a,b) için lim x X0 f(x)-f( x 0 ) limiti bir gerçel sayı ise bu limit değerine f fonksiyonunun
Şimdi de [ ] vektörünün ile gösterilen boyu veya büyüklüğü Pisagor. teoreminini iki kere kullanarak
![Şimdi de [ ] vektörünün ile gösterilen boyu veya büyüklüğü Pisagor. teoreminini iki kere kullanarak Şimdi de [ ] vektörünün ile gösterilen boyu veya büyüklüğü Pisagor. teoreminini iki kere kullanarak](/thumbs/17/146647.jpg) 10.Konu İç çarpım uzayları ve özellikleri 10.1. ve üzerinde uzunluk de [ ] vektörünün ile gösterilen boyu veya büyüklüğü Pisagor teoreminden dir. 1.Ö.: [ ] ise ( ) ( ) ve ( ) noktaları gözönüne alalım.
10.Konu İç çarpım uzayları ve özellikleri 10.1. ve üzerinde uzunluk de [ ] vektörünün ile gösterilen boyu veya büyüklüğü Pisagor teoreminden dir. 1.Ö.: [ ] ise ( ) ( ) ve ( ) noktaları gözönüne alalım.
ALTIN ORAN ARAMA (GOLDEN SECTION SEARCH) METODU
 ALTIN ORAN ARAMA (GOLDEN SECTION SEARCH) METODU Tek değişkenli bir f(x) fonksiyonunu ele alalım. [Bazı x ler için f (x) bulunamayabilir.] Aşağıdaki DOP modelini çözmek istediğimizi var sayalım. Max f(x)
ALTIN ORAN ARAMA (GOLDEN SECTION SEARCH) METODU Tek değişkenli bir f(x) fonksiyonunu ele alalım. [Bazı x ler için f (x) bulunamayabilir.] Aşağıdaki DOP modelini çözmek istediğimizi var sayalım. Max f(x)
EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER
 EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER LAGRANGE YÖNTEMİ Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde değişkenler ve kısıtlar genel olarak şeklinde gösterilir. fonksiyonlarının
EŞİTLİK KISITLI TÜREVLİ YÖNTEMLER LAGRANGE YÖNTEMİ Bu metodu incelemek için Amaç fonksiyonu Min.z= f(x) Kısıtı g(x)=0 olan problemde değişkenler ve kısıtlar genel olarak şeklinde gösterilir. fonksiyonlarının
Yrd. Doç. Dr. A. Burak İNNER
 Yrd. Doç. Dr. A. Burak İNNER Kocaeli Üniversitesi Bilgisayar Mühendisliği Yapay Zeka ve Benzetim Sistemleri Ar-Ge Lab. http://yapbenzet.kocaeli.edu.tr DOĞRUSAL OLMAYAN (NONLINEAR) DENKLEM SİSTEMLERİ Mühendisliğin
Yrd. Doç. Dr. A. Burak İNNER Kocaeli Üniversitesi Bilgisayar Mühendisliği Yapay Zeka ve Benzetim Sistemleri Ar-Ge Lab. http://yapbenzet.kocaeli.edu.tr DOĞRUSAL OLMAYAN (NONLINEAR) DENKLEM SİSTEMLERİ Mühendisliğin
Şekil 6.1 Basit sarkaç
 Deney No : M5 Deney Adı : BASİT SARKAÇ Deneyin Amacı yer çekimi ivmesinin belirlenmesi Teorik Bilgi : Sabit bir noktadan iple sarkıtılan bir cisim basit sarkaç olarak isimlendirilir. : Basit sarkaçta uzunluk
Deney No : M5 Deney Adı : BASİT SARKAÇ Deneyin Amacı yer çekimi ivmesinin belirlenmesi Teorik Bilgi : Sabit bir noktadan iple sarkıtılan bir cisim basit sarkaç olarak isimlendirilir. : Basit sarkaçta uzunluk
BÖLÜM 9 ÇÖZÜLMESİ ÖNERİLEN ÖRNEK VE PROBLEMLER
 BÖLÜM 9 ÇÖZÜLMESİ ÖNERİLEN ÖRNEK VE PROBLEMLER b) İkinci süreç eğik atış hareketine karşılık geliyor. Orada örendiğin problem çözüm adımlarını kullanarak topun sopadan ayrıldığı andaki hızını bağıntı olarak
BÖLÜM 9 ÇÖZÜLMESİ ÖNERİLEN ÖRNEK VE PROBLEMLER b) İkinci süreç eğik atış hareketine karşılık geliyor. Orada örendiğin problem çözüm adımlarını kullanarak topun sopadan ayrıldığı andaki hızını bağıntı olarak
Kaynaklar Shepley L. Ross, Differential Equations (3rd Edition), 1984.
 Çankırı Karatekin Üniversitesi Matematik Bölümü 2015 Kaynaklar Shepley L. Ross, Differential Equations (3rd Edition), 1984. (Adi ) Bir ya da daha fazla bağımsız değişkenden oluşan bağımlı değişken ve türevlerini
Çankırı Karatekin Üniversitesi Matematik Bölümü 2015 Kaynaklar Shepley L. Ross, Differential Equations (3rd Edition), 1984. (Adi ) Bir ya da daha fazla bağımsız değişkenden oluşan bağımlı değişken ve türevlerini
4.3. Türev ile İlgili Teoremler
 4.. Türev ile İlgili Teoremler Bu kesimde ortalama değer teoremini vereceğiz. Ortalama değer teoremini ispatlarken kullanılacak olan Fermat teoremini ve diğer bazı teoremleri ispat edeceğiz. 4...Teorem
4.. Türev ile İlgili Teoremler Bu kesimde ortalama değer teoremini vereceğiz. Ortalama değer teoremini ispatlarken kullanılacak olan Fermat teoremini ve diğer bazı teoremleri ispat edeceğiz. 4...Teorem
Genel Graf Üzerinde Mutlak 1-merkez
 Genel Graf Üzerinde Mutlak 1-merkez Çözüm yöntemine geçmeden önce bazı tanımlara ihtiyaç vardır. Dikkate alınan G grafındaki düğümleri 1 den n e kadar numaralandırın. Uzunluğu a(i, j)>0 olarak verilen
Genel Graf Üzerinde Mutlak 1-merkez Çözüm yöntemine geçmeden önce bazı tanımlara ihtiyaç vardır. Dikkate alınan G grafındaki düğümleri 1 den n e kadar numaralandırın. Uzunluğu a(i, j)>0 olarak verilen
Proje Adı: Sonlu Bir Aritmetik Dizinin Terimlerinin Kuvvetleri Toplamının İndirgeme Bağıntısıyla Bulunması.
 Proje Adı: Sonlu Bir Aritmetik Dizinin Terimlerinin Kuvvetleri Toplamının İndirgeme Bağıntısıyla Bulunması. Projenin Amacı: Aritmetik bir dizinin ilk n-teriminin belirli tam sayı kuvvetleri toplamının
Proje Adı: Sonlu Bir Aritmetik Dizinin Terimlerinin Kuvvetleri Toplamının İndirgeme Bağıntısıyla Bulunması. Projenin Amacı: Aritmetik bir dizinin ilk n-teriminin belirli tam sayı kuvvetleri toplamının
Yrd. Doç. Dr. A. Burak İNNER
 Yrd. Doç. Dr. A. Burak İNNER Kocaeli Üniversitesi Bilgisayar Mühendisliği Yapay Zeka ve Benzetim Sistemleri Ar-Ge Lab. http://yapbenzet.kocaeli.edu.tr Doğrusal Ara Değer Hesabı Lagrance Polinom İnterpolasyonu
Yrd. Doç. Dr. A. Burak İNNER Kocaeli Üniversitesi Bilgisayar Mühendisliği Yapay Zeka ve Benzetim Sistemleri Ar-Ge Lab. http://yapbenzet.kocaeli.edu.tr Doğrusal Ara Değer Hesabı Lagrance Polinom İnterpolasyonu
11.Konu Tam sayılarda bölünebilme, modüler aritmetik, Diofant denklemler
 11.Konu Tam sayılarda bölünebilme, modüler aritmetik, Diofant denklemler 1. Asal sayılar 2. Bir tam sayının bölenleri 3. Modüler aritmetik 4. Bölünebilme kuralları 5. Lineer modüler aritmetik 6. Euler
11.Konu Tam sayılarda bölünebilme, modüler aritmetik, Diofant denklemler 1. Asal sayılar 2. Bir tam sayının bölenleri 3. Modüler aritmetik 4. Bölünebilme kuralları 5. Lineer modüler aritmetik 6. Euler
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 10 Eylemsizlik Momentleri Kaynak: Mühendislik Mekaniği: Statik, R. C.Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 10. Eylemsizlik Momentleri
Diferensiyel denklemler sürekli sistemlerin hareketlerinin ifade edilmesinde kullanılan denklemlerdir.
 .. Diferensiyel Denklemler y f (x) de F ( x, y, y, y,...) 0 veya y f ( x, y, y,...) x ve y değişkenlerinin kendileri ve türevlerini içinde bulunduran denklemlerdir. (Türevler; "Bağımlı değişkenin değişiminin
.. Diferensiyel Denklemler y f (x) de F ( x, y, y, y,...) 0 veya y f ( x, y, y,...) x ve y değişkenlerinin kendileri ve türevlerini içinde bulunduran denklemlerdir. (Türevler; "Bağımlı değişkenin değişiminin
ÖĞRENME ALANI TEMEL MATEMATİK BÖLÜM TÜREV. ALT ÖĞRENME ALANLARI 1) Türev 2) Türev Uygulamaları TÜREV
 - 1 - ÖĞRENME ALANI TEMEL MATEMATİK BÖLÜM TÜREV ALT ÖĞRENME ALANLARI 1) Türev 2) Türev Uygulamaları TÜREV Kazanım 1 : Türev Kavramını fiziksel ve geometrik uygulamalar yardımıyla açıklar, türevin tanımını
- 1 - ÖĞRENME ALANI TEMEL MATEMATİK BÖLÜM TÜREV ALT ÖĞRENME ALANLARI 1) Türev 2) Türev Uygulamaları TÜREV Kazanım 1 : Türev Kavramını fiziksel ve geometrik uygulamalar yardımıyla açıklar, türevin tanımını
ÜNİTE. MATEMATİK-1 Prof.Dr.Ahmet KÜÇÜK İÇİNDEKİLER HEDEFLER TÜREV VE TÜREV ALMA KURALLARI. Türev Türev Alma Kuralları
 HEDEFLER İÇİNDEKİLER TÜREV VE TÜREV ALMA KURALLARI Türev Türev Alma Kuralları MATEMATİK-1 Prof.Dr.Ahmet KÜÇÜK Bu üniteyi çalıştıktan sonra Burada türevin tanımı verilecek, Geometride bir eğrinin bir noktadaki
HEDEFLER İÇİNDEKİLER TÜREV VE TÜREV ALMA KURALLARI Türev Türev Alma Kuralları MATEMATİK-1 Prof.Dr.Ahmet KÜÇÜK Bu üniteyi çalıştıktan sonra Burada türevin tanımı verilecek, Geometride bir eğrinin bir noktadaki
Ayrık-Zaman Sistemler
 Ayrık-Zaman Sistemler Bir ayrık-zaman sistemi, bir giriş dizisi x[n] yi işleyerek daha iyi özelliklere sahip bir çıkış dizisi y[n] oluşturur. Çoğu uygulamalarda ayrık-zaman sistemi bir giriş ve bir çıkıştan
Ayrık-Zaman Sistemler Bir ayrık-zaman sistemi, bir giriş dizisi x[n] yi işleyerek daha iyi özelliklere sahip bir çıkış dizisi y[n] oluşturur. Çoğu uygulamalarda ayrık-zaman sistemi bir giriş ve bir çıkıştan
9 B ol um Türevin Uygulamaları
 2 Bölüm 9 Türevin Uygulamaları 64 BÖLÜM 9. TÜREVİN UYGULAMALARI Bölüm 0 Türev Tanım 0. y = f () fonksiyonu (a,b) aralığında tanımlı ve 0 (a,b) olsun. y = f ( 0 ) h 0 f ( 0 + h) f ( 0 ) h iti varsa, bu
2 Bölüm 9 Türevin Uygulamaları 64 BÖLÜM 9. TÜREVİN UYGULAMALARI Bölüm 0 Türev Tanım 0. y = f () fonksiyonu (a,b) aralığında tanımlı ve 0 (a,b) olsun. y = f ( 0 ) h 0 f ( 0 + h) f ( 0 ) h iti varsa, bu
SONLU FARKLAR GENEL DENKLEMLER
 SONLU FARKLAR GENEL DENKLEMLER Bir elastik ortamın gerilme probleminin Airy gerilme fonksiyonu ile formüle edilebilen halini göz önüne alalım. Problem matematiksel olarak bölgede biharmonik denklemi sağlayan
SONLU FARKLAR GENEL DENKLEMLER Bir elastik ortamın gerilme probleminin Airy gerilme fonksiyonu ile formüle edilebilen halini göz önüne alalım. Problem matematiksel olarak bölgede biharmonik denklemi sağlayan
Mühendislikte Sayısal Çözüm Yöntemleri NÜMERİK ANALİZ. Prof. Dr. İbrahim UZUN
 Mühendislikte Sayısal Çözüm Yöntemleri NÜMERİK ANALİZ Prof. Dr. İbrahim UZUN Yayın No : 2415 İşletme-Ekonomi Dizisi : 147 5. Baskı Eylül 2012 - İSTANBUL ISBN 978-605 - 377-438 - 9 Copyright Bu kitabın
Mühendislikte Sayısal Çözüm Yöntemleri NÜMERİK ANALİZ Prof. Dr. İbrahim UZUN Yayın No : 2415 İşletme-Ekonomi Dizisi : 147 5. Baskı Eylül 2012 - İSTANBUL ISBN 978-605 - 377-438 - 9 Copyright Bu kitabın
Ayrık Fourier Dönüşümü
 Ayrık Fourier Dönüşümü Tanım: 0 n N 1 aralığında tanımlı N uzunluklu bir dizi x[n] nin AYRIK FOURIER DÖNÜŞÜMÜ (DFT), ayrık zaman Fourier dönüşümü (DTFT) X(e jω ) nın0 ω < 2π aralığında ω k = 2πk/N, k =
Ayrık Fourier Dönüşümü Tanım: 0 n N 1 aralığında tanımlı N uzunluklu bir dizi x[n] nin AYRIK FOURIER DÖNÜŞÜMÜ (DFT), ayrık zaman Fourier dönüşümü (DTFT) X(e jω ) nın0 ω < 2π aralığında ω k = 2πk/N, k =
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MATLAB DA SAYISAL ANALİZ DOÇ. DR. ERSAN KABALCI
 MATLAB DA SAYISAL ANALİZ DOÇ. DR. ERSAN KABALCI Konu Başlıkları Lineer Denklem Sistemlerinin Çözümü İntegral ve Türev İntegral (Alan) Türev (Sayısal Fark ) Diferansiyel Denklem çözümleri Denetim Sistemlerinin
MATLAB DA SAYISAL ANALİZ DOÇ. DR. ERSAN KABALCI Konu Başlıkları Lineer Denklem Sistemlerinin Çözümü İntegral ve Türev İntegral (Alan) Türev (Sayısal Fark ) Diferansiyel Denklem çözümleri Denetim Sistemlerinin
Math 322 Diferensiyel Denklemler Ders Notları 2012
 1 Genel Tanımlar Bir veya birden fazla fonksiyonun türevlerini içeren denklemlere diferensiyel denklem denmektedir. Diferensiyel denklemler Adi (Sıradan) diferensiyel denklemler ve Kısmi diferensiyel denklemler
1 Genel Tanımlar Bir veya birden fazla fonksiyonun türevlerini içeren denklemlere diferensiyel denklem denmektedir. Diferensiyel denklemler Adi (Sıradan) diferensiyel denklemler ve Kısmi diferensiyel denklemler
HESSİEN MATRİS QUADRATİK FORM MUTLAK ve BÖLGESEL MAKS-MİN NOKTALAR
 HESSİEN MATRİS QUADRATİK FORM MUTLAK ve BÖLGESEL MAKS-MİN NOKTALAR Kısıtlı ve kısıtsız fonksiyonlar için maksimum veya minimum (ekstremum) noktalarının belirlenmesinde diferansiyel hesabı kullanarak çeşitli
HESSİEN MATRİS QUADRATİK FORM MUTLAK ve BÖLGESEL MAKS-MİN NOKTALAR Kısıtlı ve kısıtsız fonksiyonlar için maksimum veya minimum (ekstremum) noktalarının belirlenmesinde diferansiyel hesabı kullanarak çeşitli
Altın Oran Arama Metodu(Golden Search)
 Altın Oran Arama Metodu(Golden Search) Bir f(x) (tek değişkenli) fonksiyonunu ele alalım. [Bazı x ler için f (x) bulunamayabilir.] Aşağıdaki DOP modelini çözmek istediğimizi var sayalım. Max f(x) a x b
Altın Oran Arama Metodu(Golden Search) Bir f(x) (tek değişkenli) fonksiyonunu ele alalım. [Bazı x ler için f (x) bulunamayabilir.] Aşağıdaki DOP modelini çözmek istediğimizi var sayalım. Max f(x) a x b
fonksiyonu için in aralığındaki bütün değerleri için sürekli olsun. in bu aralıktaki olsun. Fonksiyonda meydana gelen artma miktarı
 10.1 Türev Kavramı fonksiyonu için in aralığındaki bütün değerleri için sürekli olsun. in bu aralıktaki bir değerine kadar bir artma verildiğinde varılan x = x 0 + noktasında fonksiyonun değeri olsun.
10.1 Türev Kavramı fonksiyonu için in aralığındaki bütün değerleri için sürekli olsun. in bu aralıktaki bir değerine kadar bir artma verildiğinde varılan x = x 0 + noktasında fonksiyonun değeri olsun.
İstatistik ve Olasılık
 İstatistik ve Olasılık Rastgele Değişkenlerin Dağılımları I Prof. Dr. İrfan KAYMAZ Ders konusu Bu derste; Rastgele değişkenlerin tanımı ve sınıflandırılması Olasılık kütle fonksiyonu Olasılık yoğunluk
İstatistik ve Olasılık Rastgele Değişkenlerin Dağılımları I Prof. Dr. İrfan KAYMAZ Ders konusu Bu derste; Rastgele değişkenlerin tanımı ve sınıflandırılması Olasılık kütle fonksiyonu Olasılık yoğunluk
MATEMATİK BİLİM GRUBU III KURS PROGRAMI
 MATEMATİK BİLİM GRUBU III KURS PROGRAMI 1.Kurumun Adı 2.Kurumun adresi 3.Kurucunun Adı 4.Programın Adı : OĞUZHAN ÖZKAYA ÖZEL ÖĞRETİM KURSU : Onur Mahallesi Leylak Sok.No:9 Balçova-İzmir : Oğuzhan Özkaya
MATEMATİK BİLİM GRUBU III KURS PROGRAMI 1.Kurumun Adı 2.Kurumun adresi 3.Kurucunun Adı 4.Programın Adı : OĞUZHAN ÖZKAYA ÖZEL ÖĞRETİM KURSU : Onur Mahallesi Leylak Sok.No:9 Balçova-İzmir : Oğuzhan Özkaya
Şekil 6.2 Çizgisel interpolasyon
 45 Yukarıdaki şekil düzensiz bir X,Y ilişkisini göstermektedir. bu fonksiyon eğri üzerindeki bir dizi noktayı birleştiren bir seri düzgün çizgi halindeki bölümlerle açıklanabilir. Noktaların sayısı ne
45 Yukarıdaki şekil düzensiz bir X,Y ilişkisini göstermektedir. bu fonksiyon eğri üzerindeki bir dizi noktayı birleştiren bir seri düzgün çizgi halindeki bölümlerle açıklanabilir. Noktaların sayısı ne
MAK 210 SAYISAL ANALİZ
 MAK 10 SAYISAL ANALİZ BÖLÜM 9-DİFERANSİYEL DENKLEMLERİN SAYISAL ÇÖZÜMÜ 1 GİRİŞ Diferansiyel denklemler, mühendislikte fiziksel olayların modellenmesinde sık karşılaşılan denklemlerdendir. Dolayısıyla bu
MAK 10 SAYISAL ANALİZ BÖLÜM 9-DİFERANSİYEL DENKLEMLERİN SAYISAL ÇÖZÜMÜ 1 GİRİŞ Diferansiyel denklemler, mühendislikte fiziksel olayların modellenmesinde sık karşılaşılan denklemlerdendir. Dolayısıyla bu
Bir değişkenin bir sabite mümkün olduğu kadar çok yaklaşması durumu ancak onun limitiyle ifade edilebilir.
 LİMİT VE SÜREKLİLİK A- LİMİTLER Bir top 10 metre yükseklikten bırakılmaktadır. Top yere vurduktan sonra ilk yüksekliğin 2/5 i kadar sıçramakta ve bunu her yükseliş için devam ettirmektedir. Topun sıçrayacağı
LİMİT VE SÜREKLİLİK A- LİMİTLER Bir top 10 metre yükseklikten bırakılmaktadır. Top yere vurduktan sonra ilk yüksekliğin 2/5 i kadar sıçramakta ve bunu her yükseliş için devam ettirmektedir. Topun sıçrayacağı
Sonsuz Diziler ve Seriler
 Sonsuz Diziler ve Seriler İki veya birden çok sonlu sayıdaki sayının nasıl toplanacağını herkes bilir. Peki sonsuz tane sayıyı nasıl toplarız? Bu sorunun cevabını bu bölümde vermeye çalışacağız. Diziler
Sonsuz Diziler ve Seriler İki veya birden çok sonlu sayıdaki sayının nasıl toplanacağını herkes bilir. Peki sonsuz tane sayıyı nasıl toplarız? Bu sorunun cevabını bu bölümde vermeye çalışacağız. Diziler
MB5002 NÜMERİK ANALİZ
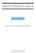 MB500 NÜMERİK ANALİZ Ders Notları Yrd. Doç. Dr. Emel YAVUZ DUMAN İstanbul Kültür Üniversitesi Matematik-Bilgisayar Bölümü c 01, Emel Yavuz Duman Tüm hakkı saklıdır. Bu notlar Örgün Öğretimde Uzaktan Öğretim
MB500 NÜMERİK ANALİZ Ders Notları Yrd. Doç. Dr. Emel YAVUZ DUMAN İstanbul Kültür Üniversitesi Matematik-Bilgisayar Bölümü c 01, Emel Yavuz Duman Tüm hakkı saklıdır. Bu notlar Örgün Öğretimde Uzaktan Öğretim
Fonksiyonlarda limiti öğrenirken değişkenlerin limitini ve sağdan-soldan limit kavramlarını öğreneceksiniz.
 8.2. Fonksiyonlarda Limit Fonksiyonlarda limiti öğrenirken değişkenlerin limitini ve sağdan-soldan limit kavramlarını öğreneceksiniz. 8.2.1. Değişkenin Limiti Sonsuz sayıda değer alabilen bir x değişkeninin
8.2. Fonksiyonlarda Limit Fonksiyonlarda limiti öğrenirken değişkenlerin limitini ve sağdan-soldan limit kavramlarını öğreneceksiniz. 8.2.1. Değişkenin Limiti Sonsuz sayıda değer alabilen bir x değişkeninin
Bu kısımda işlem adı verilen özel bir fonksiyon çeşidini ve işlemlerin önemli özelliklerini inceleyeceğiz.
 Bölüm 3 Gruplar Bu bölümde ilk olarak bir küme üzerinde tanımlı işlem kavramını ele alıp işlemlerin bazı özelliklerini inceleyeceğiz. Daha sonra kümeler ve üzerinde tanımlı işlemlerden oluşan cebirsel
Bölüm 3 Gruplar Bu bölümde ilk olarak bir küme üzerinde tanımlı işlem kavramını ele alıp işlemlerin bazı özelliklerini inceleyeceğiz. Daha sonra kümeler ve üzerinde tanımlı işlemlerden oluşan cebirsel
AKSARAY KANUNİ ANADOLU İMAM HATİP LİSESİ 2015-2016 EĞİTİM ÖĞRETİM YILI MATEMATİK DERSİ 11.SINIFLAR ÜNİTELENDİRİLMİŞ YILLIK PLANI TEKNİKLER
 AKSARAY KANUNİ ANADOLU İMAM HATİP LİSESİ 015-01 EĞİTİM ÖĞRETİM YILI MATEMATİK DERSİ 11.SINIFLAR ÜNİTELENDİRİLMİŞ YILLIK PLANI SÜRE: MANTIK(30) ÖNERMELER VE BİLEŞİK ÖNERMELER(18) 1. Önermeyi, önermenin
AKSARAY KANUNİ ANADOLU İMAM HATİP LİSESİ 015-01 EĞİTİM ÖĞRETİM YILI MATEMATİK DERSİ 11.SINIFLAR ÜNİTELENDİRİLMİŞ YILLIK PLANI SÜRE: MANTIK(30) ÖNERMELER VE BİLEŞİK ÖNERMELER(18) 1. Önermeyi, önermenin
T I M U R K A R A Ç AY, H AY D A R E Ş, O R H A N Ö Z E R K A L K U L Ü S N O B E L
 T I M U R K A R A Ç AY, H AY D A R E Ş, O R H A N Ö Z E R K A L K U L Ü S N O B E L 1 Denklemler 1.1 Doğru deklemleri İki noktası bilinen ya da bir noktası ile eğimi bilinen doğruların denklemlerini yazabiliriz.
T I M U R K A R A Ç AY, H AY D A R E Ş, O R H A N Ö Z E R K A L K U L Ü S N O B E L 1 Denklemler 1.1 Doğru deklemleri İki noktası bilinen ya da bir noktası ile eğimi bilinen doğruların denklemlerini yazabiliriz.
MAT MATEMATİK I DERSİ
 MATEMATİK BÖLÜMÜ MAT 0 - MATEMATİK I DERSİ ÇALIŞMA SORULARI Bölüm : Fonksiyonlar. Tanım Kümesi ) f() = ln fonksiyonu verilsin. Tanım kümesini bulunuz. ((0, )\{}) Bölüm : Limit ve Süreklilik.. Limit L Hospital
MATEMATİK BÖLÜMÜ MAT 0 - MATEMATİK I DERSİ ÇALIŞMA SORULARI Bölüm : Fonksiyonlar. Tanım Kümesi ) f() = ln fonksiyonu verilsin. Tanım kümesini bulunuz. ((0, )\{}) Bölüm : Limit ve Süreklilik.. Limit L Hospital
İÇİNDEKİLER. Bölüm 2 CEBİR 43
 İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 13 1.1 Doğal Sayılar 15 1.1.1. Tek ve Çift Sayılar 15 1.1.2. Asal Sayılar 15 1.1.3 Doğal Sayıların Özellikleri 15 1.1.4 Doğal Sayılarda Özel Toplamlar 16 1.1.5. Faktöriyel
İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 13 1.1 Doğal Sayılar 15 1.1.1. Tek ve Çift Sayılar 15 1.1.2. Asal Sayılar 15 1.1.3 Doğal Sayıların Özellikleri 15 1.1.4 Doğal Sayılarda Özel Toplamlar 16 1.1.5. Faktöriyel
Artan-Azalan Fonksiyonlar Ekstremumlar. Yard. Doç. Dr. Mustafa Akkol
 Artan-Azalan Fonksiyonlar Ekstremumlar Yard. Doç. Dr. Mustaa Akkol Artan ve Azalan Fonksiyonlar Tanım: a,b aralığında tanımlı bir onksiyonu verilsin., a,b ve için, ise onksiyonu a,b aralığında artan, ise
Artan-Azalan Fonksiyonlar Ekstremumlar Yard. Doç. Dr. Mustaa Akkol Artan ve Azalan Fonksiyonlar Tanım: a,b aralığında tanımlı bir onksiyonu verilsin., a,b ve için, ise onksiyonu a,b aralığında artan, ise
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
18.034 İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
T I M U R K A R A Ç AY - H AY D A R E Ş C A L C U L U S S E Ç K I N YAY I N C I L I K A N K A R A
 T I M U R K A R A Ç AY - H AY D A R E Ş C A L C U L U S S E Ç K I N YAY I N C I L I K A N K A R A Contents Rasyonel Fonksiyonlar 5 Bibliography 35 Inde 39 Rasyonel Fonksiyonlar Polinomlar Yetmez! Bölme
T I M U R K A R A Ç AY - H AY D A R E Ş C A L C U L U S S E Ç K I N YAY I N C I L I K A N K A R A Contents Rasyonel Fonksiyonlar 5 Bibliography 35 Inde 39 Rasyonel Fonksiyonlar Polinomlar Yetmez! Bölme
Erciyes Üniversitesi, Mühendislik Fakültesi, İnşaat Mühendisliği Bölümü İNŞ-201 Nümerik Analiz Dersi Final Sınavı
 Erciyes Üniversitesi, Mühendislik Fakültesi, İnşaat Mühendisliği Bölümü İNŞ-201 Nümerik Analiz Dersi Final Sınavı (30)1.a) İki reel sayının mantissa ları (gövde kısımları) eşit ve mantissa1 = mantissa2
Erciyes Üniversitesi, Mühendislik Fakültesi, İnşaat Mühendisliği Bölümü İNŞ-201 Nümerik Analiz Dersi Final Sınavı (30)1.a) İki reel sayının mantissa ları (gövde kısımları) eşit ve mantissa1 = mantissa2
Otomatik Kontrol. Kapalı Çevrim Kontrol Sistemin Genel Gereklilikleri
 Otomatik Kontrol Kapalı Çevrim Kontrol Sistemin Genel Gereklilikleri H a z ı r l aya n : D r. N u r d a n B i l g i n Kapalı Çevrim Kontrol Kapalı Çevrim Kontrol Sistemin Genel Gereklilikleri Bir önceki
Otomatik Kontrol Kapalı Çevrim Kontrol Sistemin Genel Gereklilikleri H a z ı r l aya n : D r. N u r d a n B i l g i n Kapalı Çevrim Kontrol Kapalı Çevrim Kontrol Sistemin Genel Gereklilikleri Bir önceki
