ÜNİTE: RASYONEL SAYILAR KONU: Rasyonel Sayılar Kümesinde Çıkarma İşlemi
|
|
|
- Elmas Kaner
- 6 yıl önce
- İzleme sayısı:
Transkript
1 ÜNTE: RASYONEL SAYILAR ONU: Rasyonel Sayılar ümesinde Çıkarma şlemi ÖRNE SORULAR VE ÇÖZÜMLER. işleminin sonucu B) D) ki rasyonel sayının farkını bulmak için çıkan terimin toplama işlemine göre tersi alınarak eksilenle toplanır. işleminde eksilen, çıkandır. ün toplama işlemine göre tersi + () + + () 8 tür II. YOL: Parantez önündeki işaretler dağıtılır ve parantezler kaldırılır (Mutlak değerce büyük sayıdan küçük sayı çıkarılır büyük () sayının işareti alınır.) (). işleminin sonucu B) D) Bir tam sayıdan bir rasyonel sayıyı çıkarmak için önce payda eşitlenir. Sonra çıkanın toplama işlemine göre tersi alınır ve eksilen ile toplanır. () () + + LÖĞRETM 8 MATEMAT
2 . 0 Yukarıdaki sayı doğrusu üzerinde gösterilen işlem + ( ) + B) + ( + ) ( ) + D) + ( + ) + 0 Ardışık iki tam sayının arası iki eş parçaya bölündüğü için payda olur. Önce birim sağa sonra birim sola gidilerek sonuca ulaşılmıştır. O halde sayı doğrusu üzerinde gösterilen işlem; ( + ) dır.. Aşağıdaki ifadelerden kaç tanesi doğrudur? l. + ll. lll. 0 0 IV B) D) l. + eşitliği yanlıştır çünkü + + tür. ll. lll. 0 eşitliği doğrudur. 0 eşitliği yanlıştır çünkü tir. IV eşitliği yanlıştır çünkü çıkarma işleminin değişme özelliği yoktur tür tür. l., lll., IV. ifadeler yanlış, ll. ifade doğrudur. MATEMAT LÖĞRETM
3 B) 0 0 işleminin sonucu nedir? D) (Payda eşitlenir, Ekok (,, 0) 0) 0 () () () () 8 (şaretler aynı olduğu için sayılar toplanır ve işaret aynen yazılır.) (Tam sayılı kesre çevrilir.) Aşağıdaki ifadelerden hangisi ya da hangileri doğrudur? l. ll. lll. + + Yalnız l B) l ve ll l ve lll D) l, ll ve lll l. ll. lll. + eşitliği doğrudur. + + () () + eşitliği yanlıştır çünkü eşitliği doğrudur. l. ve lll. ifadeler doğru, ll. ifade yanlıştır. (Tam sayılı kesri bileşik kesre çevirelim.),, () + () () () 8 + LÖĞRETM 0 MATEMAT
4 . 0 + a ve + 0 b ise a + b toplamının sonucu B) D) 0 + a a 0 + (Sıfır, toplama işlemine göre etkisiz elemandır.) a b + 0 b + a + b + + () () eşitliğine göre a kaçtır? a 0 8 B) 0 D)..... (Parantez içindeki işlemler yapılır.) a 0 a..... (Sadeleştirmeler yapılır.) a 0 a 0 a 0 dir. MATEMAT LÖĞRETM
5 . l. ki rasyonel sayının farkı yine bir rasyonel sayıdır. ll. Rasyonel sayılarda çıkarma işleminin değişme özelliği yoktur. lll. sayısının çıkarma işlemine göre tersi tür. Yukarıdaki ifadelerden hangisi ya da hangileri doğrudur? l B) l ve ll ll D) l, ll ve lll + işleminin sonucu. ( ) B) D) O U. işleminin sonucu kaçtır? B) D). + işleminin sonucu B) D). - 0 L S T. + işleminin sonucu 0 B) 0 0 D) 0 Yukarıdaki sayı doğrusu üzerinde gösterilen işlem aşağıdakilerden hangisidir? B) + D) 8. işleminin sonucu B) D).. + işleminin sonucu kaçtır? - B) - - D) -.. işleminin sonucu B) - D) - LÖĞRETM MATEMAT
6 0.. + Δ. + Δ. eşitliğini sağlayan Δ sayısı B) D). işleminin sonucu için aşağıdakilerden hangisi doğrudur? En küçük pozitif tam sayıdır. B) ten büyüktür. Tam kısmı tür. D) Negatif rasyonel sayıdır.. rasyonel sayısının çarpma işlemine göre tersi a, toplama işlemine göre tersi b ise a b ifadesinin sonucu B) işleminin sonucu nedir? B) 8 8 D) D) O U L eşitsizliğini sağlayan en küçük a tam sayısı kaçtır?. ( ) < a. işleminin sonucu B) 8 D) S T - B) 0 D). + + işleminin sonucu B) D). Bir miktar ceviz çocuğa paylaştırılıyor. Birinci çocuğa cevizlerin i, ikinci çocuğa i ve üçüncü çocuğa i veriliyor. 8 Dördüncü çocuğa verilen cevizlerin kesir değeri nedir? 8 B) D) işleminin sonucu B) 8 D) MATEMAT LÖĞRETM
7 . 0 + işleminin çözümü aşağıda verilmiştir. l. adım: ll. adım: lll. adım: + + IV. adım: +. a eşitliğinde a sayısı B) D) şlemin çözümü yapılırken kaçıncı adımdan itibaren hata yapılmıştır? l. B) ll. lll. D) IV.. Bir memur maaşının ünü ev kirasına, kalanın ünü mutfak masrafına ayırıyor. Geriye 0 YTL si kaldığına göre memurun maaşının tamamı kaç YTL dir? O 0 B) 00 0 D) Δ 0 eşitliğinde Δ yerine 00 aşağıdaki rasyonel sayılardan hangisi yazılmalıdır? 00 B) 00 0 D) U L S T işleminin sonucu aşağıdakilerden hangisidir? 0 B) 0 D). m eşitliğinde m sayısı B). a b, a. b - ise işleminin sonucu aşağıdakilerden b a hangisidir? D) - B) 0 D) LÖĞRETM MATEMAT
8 ÜNTE: RASYONEL SAYILAR ONU: Rasyonel Sayılar ümesinde Bölme şlemi ve Özellikleri ÖRNE SORULAR VE ÇÖZÜMLER. 8 : işleminin sonucu B) D) Bir rasyonel sayıyı sıfırdan farklı bir rasyonel sayıya bölmek için bölünen rasyonel sayı, bölen rasyonel sayının çarpma işlemine göre tersi ile çarpılır. Yani birinci kesir aynen yazılır, ikinci kesir ters çevrilir, çarpılır. a c Q, Q ve c 0 koşulu ile b d a c a d axd : x dir. b d b c bxc 8 : 8 x (sadeleştirme yapılır.) işleminin sonucu. : ( + ) B) D) 0 Aynı işaretli iki rasyonel sayının bölümü pozitif, ters işaretli iki rasyonel sayının bölümü negatif rasyonel sayıdır. (+) : (+) (+) (+) : (-) (-) (-) : (-) (+) (-) : (+) (-) Bir rasyonel sayı bir tam sayıya veya bir tam sayı bir rasyonel sayıya bölünürken tam sayının paydası alınır. : ( + ) x + 0 MATEMAT LÖĞRETM
9 . : işleminin sonucu kaçtır? - B) - D) Bölme işlemi yaparken önce tam sayılı kesirler bileşik kesre çevrilir. 8 : : (kinci kesir ters çevrilip, çarpma işlemi yapılır.) 8 x x + (Sadeleştirme yapılır.) ((-) ile (-) nin çarpımı (+) dır.). : a ve : b ise a.b işleminin sonucu B) D) Bir rasyonel sayının + e bölümü, o rasyonel sayının kendisine eşittir. a : a x a + sayısının sıfırdan farklı bir rasyonel sayıya bölümü, bölen rasyonel sayının çarpma işlemine göre tersine eşittir. b : b x b a.b x LÖĞRETM MATEMAT
10 . Aşağıdaki işlemlerden hangisi ya da hangileri doğrudur? l. : ( ) + ll. ( ) : + lll. : 0 0 IV. 0 : + 0 l ve ll B) l ve lll ll ve lll D) l ve IV l. : ( ) + eşitliği doğrudur çünkü : ( ) + ll. ( ) : eşitliği yanlıştır çünkü ( ) x + dir. : + ( )x + dir. lll. : 0 0 eşitliği yanlıştır çünkü bir bölme işleminde bölen sıfır olamaz. Bölen sıfır ise o bölme işlemi a tanımsızdır. b 0 olmak üzere a : b c dir. tanımsızdır. 0 IV. 0 : + 0 eşitliği doğrudur çünkü bir bölme işleminde bölünen sıfır ise bölüm sıfırdır. 0 b 0 olmak üzere 0 dır. b Δ. + : Yukarıdaki eşitlikte Δ yerine gelebilecek uygun sayı B) D) alansız bir bölme işleminde; Bölünen bölen x bölüm Bölünen : bölen bölüm Δ + : bölünen : bölen bölüm Δ + x bölünen bölen x bölüm Δ + + Δ tür. MATEMAT LÖĞRETM
11 . Aşağıdaki ifadelerden hangisi yanlıştır? Rasyonel sayılar kümesi sıfır hariç bölme işlemine göre kapalıdır. B) Rasyonel sayılar kümesinde bölme işleminin değişme özelliği yoktur. Rasyonel sayılar kümesinde bölme işleminin birleşme özelliği yoktur. D) Rasyonel sayılar kümesinde bölme işleminin birim elemanı + dir. apalılık özelliği vardır. Örnek: Q, Q Değişme özelliği yoktur. 0 Örnek: : x : x 0 Birleşme özelliği yoktur. Örnek: : : : x : : x : 0 : : 0 x x Rasyonel sayılar kümesinde bölme işleminin birim elemanı + dir. ifadesi yanlıştır çünkü rasyonel sayılar kümesinde bölme işleminin birim elemanı yoktur : + işleminin sonucu 0 B) 0 D) : + (Önce bölme işlemi yapılır.) + + x + (Sadeleştirme yapılır.) + + (şaretler parantez içine dağıtılır ve parantezler kaldırılır.) + (Payda eşitlenir.) (0) 0 0 () () LÖĞRETM 8 MATEMAT
12 + : işleminin sonucu nedir? - B) - - D). ( ). : işleminin sonucu 0 B) D). Aşağıdaki ifadelerden hangisi tanımsızdır? : ( ) + : B) ( ) 0 : + D) : 0 O U.. : işleminin sonucu 8 B) D) L S T. : + işleminin sonucu B). + : işleminin sonucu 8 B) D) D) 8. : : işleminin sonucu nedir? 8.. : işleminin sonucu B) D) 0 B) 0 D) MATEMAT LÖĞRETM
13 . : m eşitliğine göre aşağıdakilerden hangisi yazılabilir? : m B) x m : m D) m :. (-) : (-). işleminin sonucu - B) - D). : a + eşitliğini sağlayan a değeri 0. : +. işleminin 8 sonucu O B) D) B) D) U L S. :. : işleminin sonucu T [ ].. ( ) : ( + ) işleminin sonucu - B) - D) 0 0 B) D). : : : işleminin sonucu 0 B) D). : ise Δ yerine gelebilecek Δ uygun sayı - B) - D) LÖĞRETM 80 MATEMAT
14 . + : Δ : + eşitliğinde Δ - B). + : işleminin sonucu sayısının kaç katıdır? - B) - D) D) a 8. + x eşitliğinde a yerine gelebilecek uygun sayı aşağıdakilerden hangisidir? 8 B) D) 0. inin i 8 olan sayı kaçtır? 8 80 B) 0 0 D) 00. işleminin sonucu O U L S 0 B) D) T. 00 metre uzunluğundaki bir top kumaşın 8 ünün i kaç metredir? 0 B) 0 D) 0 0. a : ve : b ise a.b 0 çarpımı B) - D) -. : + + sayısının katı - B) 0 D). Bir turist grubunun i bayandır. Gruptaki bayanların sayısı 0 olduğuna göre turist grubunda kaç kişi vardır? B) D) MATEMAT 8 LÖĞRETM
15 ÜNTE: RASYONEL SAYILAR ONU: Çok Büyük Sayılar (0 un Pozitif uvvetleri) ve Çok üçük Sayılar (0 un Negatif uvvetleri) ve Bu Sayılarla Yapılan şlemler ÖRNE SORULAR VE ÇÖZÜMLER sayısı aşağıdakilerden hangisine eşittir? x 0 8 B) 0 x 0, x 0 8 D), x 0 0, 00, 000. şeklindeki sayıları 0 un kuvveti olarak yazmak için den sonraki sıfırların sayısı 0 a üs olarak yazılır. Örnek: x x 0 dir. x 0 sayısı seçeneklerde bulunmadığı için sayı düzenlenir. sayısı 0 ile bölünür ve, elde edilir. O halde 0 sayısının üssü artar. x 0, x 0 8 dir. Çok büyük sayılar düzenlenirken katsayı 0 un kuvvetleriyle çarpılır, 0 un üssü azalır. (0,x0 0 x 0 ) 0 un kuvvetlerine bölünürken 0 un üssü artar. (, x 0 0, x 0 ) sayısının bilimsel gösterimi 0, x 0 B), x 0 8 x 0 D) x 0 a x 0 m sayısında a çarpanı ile 0 arasında ( dahil) ve m tam sayı ise bu gösterime bilimsel gösterim denir. O halde bilimsel gösterim; m pozitif tam sayı, a gerçek sayı ve a < 0 ise a x 0 m dir x 0 ( sayısı ile 0 arasında değildir.), x 0 8 (, < 0 ve 8 Z) işleminin sonucu B) 0 00 D) 000 LÖĞRETM 8 MATEMAT
16 0 un tam kuvveti olan iki sayı çarpılırken; üsler toplanır ve toplamın sonucu 0 un üssü olarak yazılır.(üslü sayılarda çarpma işlemi yapılırken tabanlar aynı ise üsler toplanır.) 0 a x 0 b 0 a+b Örneğin; 0 x dir. 0 un tam kuvveti olan iki sayı bölünürken bölünen sayının üssünden bölen sayının üssü çıkarılır ve fark 0 un üssü olarak yazılır. (Üslü sayılarda bölme işlemi yaparken tabanlar aynı ise üsler çıkarılır.) a 0 ab 0 ve 0 a : 0 b 0 a b b Örneğin; 0 0 tir ,8 x 0 m ise m sayısı B) D) ,8 x 0 m x 0 (Sayının sonundaki sıfırların sayısı 0 un kuvvetidir.),8 sayısını elde etmek için 8 sayısı 00 e bölünür. Yani basamak sola gidilir, o halde üs sayı büyür, 0 iken 0 olur. 8 x 0,8 x 0,8 x 0,8 x 0 m ise m dır.. ( x 0 ) + ( x 0 ) + 0 işleminin sonucu x 0 B), x 0, x 0 D) 0 0 un tam kuvveti olan sayılar toplanırken, önce kuvvetler (üsler) eşit değilse, eşitlenir sonra katsayılar toplanır ve bulunan toplam, 0 un kuvveti olan sayıya çarpan olarak yazılır. ( x 0 ) + ( x 0 ) + 0 ( x 0 ) + ( x 0 ) + ( x 0 ) 0 x ( + + ) (0 ortak paranteze alınır, katsayılar toplanır.) x 0, x 0 x 0 seçeneklerde olmadığı için sayısını 0 a böldük ve 0 in üssü arttı, 0 oldu. x 0, x 0 dır. MATEMAT 8 LÖĞRETM
17 . (0, x 0 8 ) (, x 0 ) işleminin sonucu x 0 8 B) x 0 x 0 D) x 0 0 un kuvvetlerini bulunduran (a x 0 m ) şeklindeki sayılar çıkarılırken; önce kuvvetler (üsler) eşit değilse, eşitlenir sonra katsayılar çıkarılır ve bulunan fark 0 un kuvveti olan sayıya çarpan olarak yazılır. 0, x 0 8 x 0 0 x 0 (Virgül sağa kaydıkça yani sayı 0 un kuvvetleri ile çarpıldıkça kuvvet azalır.), x 0 x 0 (Bir basamak sağa kaydı, üs azaldı.) (0, x 0 8 ) (, x 0 ) (0 x 0 ) ( x 0 ) 0 x (0 ) (0 ortak paranteze alınır, katsayılar çıkarılır.) x 0. 0,x0 0,x0 xx0 xx0 işleminin sonucu 0 B) D) un kuvvetlerini bulunduran sayılar çarpılırken; katsayıların çarpımı katsayı olarak 0 un kuvvetlerinin toplamı da 0 a üs olarak yazılır. 0, x 0 x x 0 (0, x ) x (0 x 0 ) x 0 + x 0 0, x 0 x x 0 (0, x ) x (0 x 0 ) 0, x 0 + 0, x 0 0 x 0 0,x0 xx0 x0 0 (Bölünenin üssünden bölenin üssü çıkarılır.) 0,x0 xx0 x ,0 x 0-0, x 0 -m ise m sayısı B) 8 D) 0 (a x 0 m ) sayısında a sayısı 0 un kuvvetleri ile çarpılırken 0 un üssü olan m sayısı azalır. 0,0 sayısı 0 ile çarpılırsa 0, sayısı elde edilir. O halde 0 un üssü azalır. 0 -, 0-8 olur. 0,0 x 0-0, x 0-8 dir. 0, x 0-8 0, x 0 -m ise m 8 dir.. Hidrojen gazının yoğunluğu 0,0000 g/cm tür. Buna göre hidrojen gazının yoğunluğunun bilimsel gösterimi.0 B) 0,.0 0,.0 - D).0 - ÖĞRETM 8 MATEMAT
18 Çok küçük sayılarda bilimsel gösterim: m pozitif tam sayı, a gerçek sayı ve a < 0 olmak üzere a x 0 -m dir. 0,0000 x 0 - a x 0 -m ise a, m tir. 0. x 0 - +, x 0 - işleminin sonucu x 0 - B) x 0-8 x 0 - D) x 0 - Çok küçük sayılarda toplama veya çıkarma işlemi yapmak için önce 0 un kuvvetleri eşitlenir sonra katsayılar arasındaki işlem yapılır ve katsayı olarak yazılır. Sayıları 0 un kuvveti biçiminde düzenlerken; katsayı 0 un kuvvetleriyle çarpılırsa 0 un üssü azalır, katsayı 0 un kuvvetleriyle bölünürse 0 un üssü artar. Örnek;, x 0 - x 0 - (0 ile çarpıldı üs azaldı.) 00 x 0 - x 0 - (0 ile bölündü üs arttı.) x 0 - +, x 0 - x x 0 - ( + ) x 0-00 x 0 - x 0 - (,x0 )x(x0 ). ax0 0 0,x0 ise a sayısı x 0 - B) x 0 - x 0 D) x 0 Çok küçük sayılar çarpılırken; kat sayıların çarpımı katsayı olarak, 0 un kuvvetlerinin toplamı da 0 a üs olarak yazılır. (Çarpma işleminde tabanlar aynı ise üsler toplanır.) 0 - x 0-0 (-) + (-) 0-8 dir. Bölme işleminde ise 0 un kuvvetlerinin farkı 0 a üs olarak yazılır. (Bölme işleminde bölünenin üssünden bölenin üssü çıkarılır.) 8 0 ( 8) ( ) tir. 0 (,x0 )x(x0 ) (x0 )x(x0 ) (x)x(0 x0 ) 0x0 ( ) ( ) + x0 x0 0 0,x0 x0 x0 x0 x0.,.0 0,.0 + 0, işleminin sonucu 0, B) 0 D) 00 Önce 0 un kuvvetleri eşitlenir, sonra toplama ve daha sonra bölme işlemi yapılır.,.0 + 0, ( + ) , ( + ).0.0 (Bölme işleminde üsler çıkartılır.) 0.0 ( ) ( ) MATEMAT 8 LÖĞRETM
19 . Aşağıdaki eşitliklerden hangisi yanlıştır? 0 000, x 0 B), x 0-0,0, x 0 - D) 0 0, x 0 -., x 0 8 0, x 0 m eşitliğinde m yerine hangi sayı gelmelidir? B) 8 0 D). Aşağıdakilerden hangisi bilimsel gösterimdir?.0 - B) 0.0-0,.0 - D).0 -., x 0 -, x 0 n eşitliğinde n yerine hangi sayı gelmelidir? - B) - - D) sayısının bilimsel gösterimi x 0 B) 0, x 0, x 0 8 D), x 0-8 O U L S T 8., işleminin sonucu 0 B) 0 0 D) , işleminin sonucu 0,.0 B),.0.0 D).0. 0,000 x 0 -, x 0 a ise a - B) - - D) -8., a.0 8 ise a sayısı 0,0 B) 0,, D) sayısı kaç basamaklıdır? B) 0 D) LÖĞRETM 8 MATEMAT
20 . a x 0 b 0,0000 ise aşağıdakilerden hangisi doğrudur? a ise b - dır. B) a ise b + dır. a 0, ise b - dır. D) a 0, ise b + dır.. 0,0 x x 0-8 0,00 x 0 - işleminin sonucu aşağıdakilerden hangisidir?, x 0 - B), x 0 - x 0 - D) x işleminin sonucu nedir?.0 B).0 0 D) 0. 8x0 0,x0 işleminin sonucu x0 0 B) 0 00 D) 00 O U L S T A ise A için 0 aşağıdakilerden hangisi doğrudur? işleminin sonucu basamaklı bir sayıdır. B) basamaklı bir sayıdır. ye bölümünden kalan dir. D) e tam bölünür. 0 B) 0 - D) 0 -.,.0-0,.0 - işleminin sonucu.0-0 B) D).0-8. x0 + 0,0x0 işleminin sonucu 0,x0 B) 0 D) 0 MATEMAT 8 LÖĞRETM
21 : işleminin sonucu ,0x0 0, n tam sayısı kaçtır? n x0 eşitliğini sağlayan 0,0 B) 0, 0 D) 00 - B) - D) işleminin sonucu.0. 0,x0,x0 işleminin sonucu 0,x0 + x0 0 B) 0 D) 8 B) D) O U L S T , işleminin.0 sonucu 0 x 0 - B) x ,00 a x 0 - ve 0,0000 x 0 b ise a : b işleminin sonucu aşağıdakilerden hangisidir? -8 B) - D) 8 x 0 - D) x , işleminin sonucu 0,.0 B) 0 D) LÖĞRETM 88 MATEMAT
ÜNİTE: TAM SAYILAR KONU: Tam Sayılar Kümesinde Çıkarma İşlemi
 ÜNE: AM AYIAR N: am ayılar ümesinde Çıkarma şlemi ÖRNE RAR VE ÇÖZÜMER 1. [(+17) (+25)] + [( 12) (+21)] işleminin sonucu A) 41 B) 25 C) 25 D) 41 Çıkarma işlemi yapılırken çıkanın işareti değişir ve eksilen
ÜNE: AM AYIAR N: am ayılar ümesinde Çıkarma şlemi ÖRNE RAR VE ÇÖZÜMER 1. [(+17) (+25)] + [( 12) (+21)] işleminin sonucu A) 41 B) 25 C) 25 D) 41 Çıkarma işlemi yapılırken çıkanın işareti değişir ve eksilen
SAYILAR SAYI KÜMELERİ
 SAYILAR SAYI KÜMELERİ 1.Sayma Sayıları Kümesi: S=N =1,2,3,... 2. Doğal Sayılar Kümesi : N=0,1,2,... 3. Tamsayılar Kümesi : Z=..., 2, 1,0,1,2,... Sıfırın sağında bulunan 1,2,3,. tamsayılarına pozitif tamsayılar
SAYILAR SAYI KÜMELERİ 1.Sayma Sayıları Kümesi: S=N =1,2,3,... 2. Doğal Sayılar Kümesi : N=0,1,2,... 3. Tamsayılar Kümesi : Z=..., 2, 1,0,1,2,... Sıfırın sağında bulunan 1,2,3,. tamsayılarına pozitif tamsayılar
SAYILAR SAYI KÜMELERİ
 1 SAYILAR SAYI KÜMELERİ 1.Sayma Sayıları Kümesi: S=N =1,2,3,... 2. Doğal Sayılar Kümesi : N=0,1,2,... 3. Tamsayılar Kümesi : Z=..., 2, 1,0,1,2,... Sıfırın sağında bulunan 1,2,3,. tamsayılarına pozitif
1 SAYILAR SAYI KÜMELERİ 1.Sayma Sayıları Kümesi: S=N =1,2,3,... 2. Doğal Sayılar Kümesi : N=0,1,2,... 3. Tamsayılar Kümesi : Z=..., 2, 1,0,1,2,... Sıfırın sağında bulunan 1,2,3,. tamsayılarına pozitif
TAMSAYILAR. 9www.unkapani.com.tr. Z = {.., -3, -2, -1, 0, 1, 2, 3, } kümesinin her bir elemanına. a, b, c birer tamsayı olmak üzere, Burada,
 TAMSAYILAR Z = {.., -, -, -, 0,,,, } kümesinin her bir elemanına tamsayı denir. Burada, + Z = {,,,...} kümesine, pozitif tamsayılar kümesi denir. Z = {...,,,,} kümesine, negatif tamsayılar kümesi denir.
TAMSAYILAR Z = {.., -, -, -, 0,,,, } kümesinin her bir elemanına tamsayı denir. Burada, + Z = {,,,...} kümesine, pozitif tamsayılar kümesi denir. Z = {...,,,,} kümesine, negatif tamsayılar kümesi denir.
SAYILAR DOĞAL VE TAM SAYILAR
 1 SAYILAR DOĞAL VE TAM SAYILAR RAKAM: Sayıları ifade etmek için kullandığımız 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembollerinden her birine rakam denir. Soru: a ve b farklı rakamlar olmak üzere a + b nin alabileceği
1 SAYILAR DOĞAL VE TAM SAYILAR RAKAM: Sayıları ifade etmek için kullandığımız 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembollerinden her birine rakam denir. Soru: a ve b farklı rakamlar olmak üzere a + b nin alabileceği
ÜSLÜ SAYILAR. AMAÇ 1: 6 ve 7. Sınıflarda görmüş olduğumuz üslü ifadelerdeki temel kavramları hatırlama
 AMAÇ 1: 6 ve 7. Sınıflarda görmüş olduğumuz üslü ifadelerdeki temel kavramları hatırlama KURAL: Bir sayının belli bir sayıda yan yana çarpımının kolay yoldan gösterimine üslü sayılar denir. Örneğin 5 sayısının
AMAÇ 1: 6 ve 7. Sınıflarda görmüş olduğumuz üslü ifadelerdeki temel kavramları hatırlama KURAL: Bir sayının belli bir sayıda yan yana çarpımının kolay yoldan gösterimine üslü sayılar denir. Örneğin 5 sayısının
ÜSLÜ SAYILAR SİBEL BAŞ AKDENİZ ÜNİVERSİTESİ EĞİTİM FAK. İLKÖĞRT. MAT. ÖĞRT. 2. SINIF
 ÜSLÜ SAYILAR SİBEL BAŞ 20120907010 AKDENİZ ÜNİVERSİTESİ EĞİTİM FAK. İLKÖĞRT. MAT. ÖĞRT. 2. SINIF 1 ANLATIMI ÜSLÜ SAYILAR KONU Üslü sayılar konu anlatımı içeriği; Üslü sayıların gösterimi, Negatif üslü
ÜSLÜ SAYILAR SİBEL BAŞ 20120907010 AKDENİZ ÜNİVERSİTESİ EĞİTİM FAK. İLKÖĞRT. MAT. ÖĞRT. 2. SINIF 1 ANLATIMI ÜSLÜ SAYILAR KONU Üslü sayılar konu anlatımı içeriği; Üslü sayıların gösterimi, Negatif üslü
İÇİNDEKİLER BASİT EŞİTSİZLİKLER. HARFLİ İFADELER Harfli İfadeler ve Elemanları Eşitsizlik Sembolleri ve İşaretin Eşitsizlik İfadesi...
 İÇİNDEKİLER HARFLİ İFADELER Harfli İfadeler ve Elemanları... 1 Benzer Terim... Harfli İfadenin Terimlerini Toplayıp Çıkarma... Harfli İfadelerin Terimlerini Çarpma... Harfli İfadelerde Parantez Açma...
İÇİNDEKİLER HARFLİ İFADELER Harfli İfadeler ve Elemanları... 1 Benzer Terim... Harfli İfadenin Terimlerini Toplayıp Çıkarma... Harfli İfadelerin Terimlerini Çarpma... Harfli İfadelerde Parantez Açma...
Atatürk Anadolu. Bölme, Bölünebilme, Asal Sayılar, Obeb, Okek, Rasyonel Sayılar, Basit Eşitsizlikler ve Mutlak Değer Üzerine Kısa Çalışmalar
 Atatürk Anadolu Lisesi M A T E M A T İ K Bölme, Bölünebilme, Asal Sayılar, Obeb, Okek, Rasyonel Sayılar, Basit Eşitsizlikler ve Mutlak Değer Üzerine Kısa Çalışmalar KONYA \ SELÇUKLU 07 Bölme, Bölünebilme,
Atatürk Anadolu Lisesi M A T E M A T İ K Bölme, Bölünebilme, Asal Sayılar, Obeb, Okek, Rasyonel Sayılar, Basit Eşitsizlikler ve Mutlak Değer Üzerine Kısa Çalışmalar KONYA \ SELÇUKLU 07 Bölme, Bölünebilme,
TEOG. Sayma Sayıları ve Doğal Sayılar ÇÖZÜM ÖRNEK ÇÖZÜM ÖRNEK SAYI BASAMAKLARI VE SAYILARIN ÇÖZÜMLENMESİ 1. DOĞAL SAYILAR.
 TEOG Sayma Sayıları ve Doğal Sayılar 1. DOĞAL SAYILAR 0 dan başlayıp artı sonsuza kadar giden sayılara doğal sayılar denir ve N ile gösterilir. N={0, 1, 2, 3,...,n, n+1,...} a ve b doğal sayılar olmak
TEOG Sayma Sayıları ve Doğal Sayılar 1. DOĞAL SAYILAR 0 dan başlayıp artı sonsuza kadar giden sayılara doğal sayılar denir ve N ile gösterilir. N={0, 1, 2, 3,...,n, n+1,...} a ve b doğal sayılar olmak
2. ÜNİTE RASYONEL,ÜSLÜ VE KÖKLÜ SAYILAR
 2. ÜNİTE RASYONEL,ÜSLÜ VE KÖKLÜ SAYILAR KONULAR 1. RASYONEL SAYILAR 2. Kesir Çeşitleri 3. Kesirlerin Sadeleştirilmesi 4. Rasyonel Sayılarda Sıralama 5. Rasyonel Sayılarda İşlemler 6. ÜSLÜ İFADE 7. Üssün
2. ÜNİTE RASYONEL,ÜSLÜ VE KÖKLÜ SAYILAR KONULAR 1. RASYONEL SAYILAR 2. Kesir Çeşitleri 3. Kesirlerin Sadeleştirilmesi 4. Rasyonel Sayılarda Sıralama 5. Rasyonel Sayılarda İşlemler 6. ÜSLÜ İFADE 7. Üssün
ÜNİTE 1: TEMEL KAVRAMLAR
 MATEMATİK ÜNİTE : TEMEL KAVRAMLAR Temel Kavramlar ADF 0 RAKAM Sayı oluşturmak için kullanılan sembollere... denir. 0 luk sayma düzenindeki rakamlar 0,,,... 8 ve 9 olup 0 tanedir. örnek a, b, c sıfırdan
MATEMATİK ÜNİTE : TEMEL KAVRAMLAR Temel Kavramlar ADF 0 RAKAM Sayı oluşturmak için kullanılan sembollere... denir. 0 luk sayma düzenindeki rakamlar 0,,,... 8 ve 9 olup 0 tanedir. örnek a, b, c sıfırdan
KC00-SS.08YT05. Kolay Temel Matematik. Üniversite Haz rl k 1. 8 ( 3 + 2) 6. 3! 3 ( 3 3)": ( 3) x = 3 ve y = 2 3. ( 5) + ( 7) (+2) + 4
 Üniversite Haz rl k Sözcükte Do al ve Say lar Söz Öbeklerinde ve Tam Say lar Anlam - I - I Kolay Temel Matematik. 8 ( + ) A) 7 B) 8 C) 9 D) 0 E) 6.! ( )": ( ) A) B) 0 C) D) E). 7. + 5 A) 6 B) 7 C) 8 D)
Üniversite Haz rl k Sözcükte Do al ve Say lar Söz Öbeklerinde ve Tam Say lar Anlam - I - I Kolay Temel Matematik. 8 ( + ) A) 7 B) 8 C) 9 D) 0 E) 6.! ( )": ( ) A) B) 0 C) D) E). 7. + 5 A) 6 B) 7 C) 8 D)
Atatürk Anadolu. Temel Kavramlar Üzerine Kısa Çalışmalar
 Atatürk Anadolu Lisesi M A T E M A T İ K Temel Kavramlar Üzerine Kısa Çalışmalar KONYA \ SELÇUKLU 01 MATEMATİK 1. TEMEL KAVRAMLAR 1.1. RAKAM Sayıların yazılmasında kullanılan sembollere rakam denir. Onluk
Atatürk Anadolu Lisesi M A T E M A T İ K Temel Kavramlar Üzerine Kısa Çalışmalar KONYA \ SELÇUKLU 01 MATEMATİK 1. TEMEL KAVRAMLAR 1.1. RAKAM Sayıların yazılmasında kullanılan sembollere rakam denir. Onluk
Buna göre, eşitliği yazılabilir. sayılara rasyonel sayılar denir ve Q ile gösterilir. , -, 2 2 = 1. sayıdır. 2, 3, 5 birer irrasyonel sayıdır.
 TEMEL KAVRAMLAR RAKAM Bir çokluk belirtmek için kullanılan sembollere rakam denir. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembolleri birer rakamdır. 2. TAMSAYILAR KÜMESİ Z = {..., -3, -2, -1, 0, 1, 2, 3, 4,... }
TEMEL KAVRAMLAR RAKAM Bir çokluk belirtmek için kullanılan sembollere rakam denir. 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembolleri birer rakamdır. 2. TAMSAYILAR KÜMESİ Z = {..., -3, -2, -1, 0, 1, 2, 3, 4,... }
2) Aşağıda verilen işlemleri yazınız. g) ( ) 3) Aşağıda verilen işlemleri yazınız. 4) Aşağıda verilen işlemleri yazınız.
 8.2. ÜSLÜ SAYILARDA İŞLEM 8.2..A ÜSLÜ SAYILARDA TOPLAMA VE ÇIKARMA İŞLEMİ 2) Aşağıda verilen işlemleri yazınız. 2 ( + 2) + ( ) 3 ( 2) + ( 2) Üslü sayılarda toplama veya çıkarma işleminde her üslü niceliğin
8.2. ÜSLÜ SAYILARDA İŞLEM 8.2..A ÜSLÜ SAYILARDA TOPLAMA VE ÇIKARMA İŞLEMİ 2) Aşağıda verilen işlemleri yazınız. 2 ( + 2) + ( ) 3 ( 2) + ( 2) Üslü sayılarda toplama veya çıkarma işleminde her üslü niceliğin
SINIF TEST. Üslü Sayılar A) 4 B) 5 C) 6 D) 7 A) - 5 B) - 4 C) 5 D) 7. sayısı aşağıdakilerden hangisine eşittir?
 8. SINIF. Üslü Sayılar - = T olduğuna göre T kaçtır? A) - B) - C) D) 7 TEST.. 0 - işleminin sonucu kaç basamaklı bir sayıdır? A) B) C) 6 D) 7. n =- 7 için n ifadesinin değeri kaçtır? A) - 8 B) - C) 8 D)
8. SINIF. Üslü Sayılar - = T olduğuna göre T kaçtır? A) - B) - C) D) 7 TEST.. 0 - işleminin sonucu kaç basamaklı bir sayıdır? A) B) C) 6 D) 7. n =- 7 için n ifadesinin değeri kaçtır? A) - 8 B) - C) 8 D)
TAM SAYILARLA TOPLAMA ÇIKARMA
 7. Kazanım Tam sayılarla toplama çıkarma işlemlerini yapar. SINIF MATEMATİK tam SAYILAR TAM SAYILARLA TOPLAMA ÇIKARMA ( + 6) + ( + ) ( + 8) ( ) + ( ) ( 9) 8 Aynı işaretli sayılarda toplama yapılırken,
7. Kazanım Tam sayılarla toplama çıkarma işlemlerini yapar. SINIF MATEMATİK tam SAYILAR TAM SAYILARLA TOPLAMA ÇIKARMA ( + 6) + ( + ) ( + 8) ( ) + ( ) ( 9) 8 Aynı işaretli sayılarda toplama yapılırken,
UYGUN MATEMATİK 5 SORU BANKASI. HAZIRLAYANLAR Fatih KOCAMAN Meryem ER. : Sad k Uygun E itim Yay nlar. : Yaz n Matbaas / stanbul
 UYGUN MATEMATİK SORU BANKASI HAZIRLAYANLAR Fatih KOCAMAN Meryem ER AR-GE Editör : Ş. Yunus MUSLULAR : Dr. Özgür AYDIN Prg. Gel. Uzm. : Özden TAŞAR Pedagog Dan şman Dizgi Bask : Hilâl GENÇAY : Psikiyatr
UYGUN MATEMATİK SORU BANKASI HAZIRLAYANLAR Fatih KOCAMAN Meryem ER AR-GE Editör : Ş. Yunus MUSLULAR : Dr. Özgür AYDIN Prg. Gel. Uzm. : Özden TAŞAR Pedagog Dan şman Dizgi Bask : Hilâl GENÇAY : Psikiyatr
12-A. Sayılar - 1 TEST
 -A TEST Sayılar -. Birbirinden farklı beş pozitif tam sayının toplamı 0 dur. Bu sayılardan sadece ikisi den büyüktür. Bu sayılardan üç tanesi çift sayıdır. Buna göre bu sayılardan en büyüğü en çok kaç
-A TEST Sayılar -. Birbirinden farklı beş pozitif tam sayının toplamı 0 dur. Bu sayılardan sadece ikisi den büyüktür. Bu sayılardan üç tanesi çift sayıdır. Buna göre bu sayılardan en büyüğü en çok kaç
Rakam : Sayıları yazmaya yarayan sembollere rakam denir.
 A. SAYILAR Rakam : Sayıları yazmaya yarayan sembollere rakam denir. Sayı : Rakamların çokluk belirten ifadesine sayı denir.abc sayısı a, b, c rakamlarından oluşmuştur.! Her rakam bir sayıdır. Fakat bazı
A. SAYILAR Rakam : Sayıları yazmaya yarayan sembollere rakam denir. Sayı : Rakamların çokluk belirten ifadesine sayı denir.abc sayısı a, b, c rakamlarından oluşmuştur.! Her rakam bir sayıdır. Fakat bazı
Mustafa Sezer PEHLİVAN. Yüksek İhtisas Üniversitesi Beslenme ve Diyetetik Bölümü
 * Yüksek İhtisas Üniversitesi Beslenme ve Diyetetik Bölümü SAYILAR Doğal Sayılar, Tam Sayılar, Rasyonel Sayılar, N={0,1,2,3,,n, } Z={,-3,-2,-1,0,1,2,3, } Q={p/q: p,q Z ve q 0} İrrasyonel Sayılar, I= {p/q
* Yüksek İhtisas Üniversitesi Beslenme ve Diyetetik Bölümü SAYILAR Doğal Sayılar, Tam Sayılar, Rasyonel Sayılar, N={0,1,2,3,,n, } Z={,-3,-2,-1,0,1,2,3, } Q={p/q: p,q Z ve q 0} İrrasyonel Sayılar, I= {p/q
biçimindeki ifadelere iki değişkenli polinomlar denir. Bu polinomda aynı terimdeki değişkenlerin üsleri toplamından en büyük olanına polinomun dereces
 TANIM n bir doğal sayı ve a 0, a 1, a 2,..., a n 1, a n birer gerçel sayı olmak üzere, P(x) = a 0 + a 1 x + a 2 x 2 +... + a n 1 x n 1 +a n x n biçimindeki ifadelere x değişkenine bağlı, gerçel (reel)
TANIM n bir doğal sayı ve a 0, a 1, a 2,..., a n 1, a n birer gerçel sayı olmak üzere, P(x) = a 0 + a 1 x + a 2 x 2 +... + a n 1 x n 1 +a n x n biçimindeki ifadelere x değişkenine bağlı, gerçel (reel)
7 2 işleminin sonucu kaçtır? A) 7 B) 6 C) 5 D) 4 E) 3. Not : a buluruz. Doğru Cevap : E şıkkı
 ) 3 4 5 3 0 A) B) 6 C) 5 D) 4 E) 3 0 Not : a 0 3 4 5 3 4 5 3 3 3.3.3... ÜSLÜ SAYILAR QUİZİ VE CEVAPLARI 6 4 4 3 buluruz. Doğru Cevap : E şıkkı 0 ) n bir doğal saı olmak üzere, ( ) ( ) n ( ) n n n A) 4
) 3 4 5 3 0 A) B) 6 C) 5 D) 4 E) 3 0 Not : a 0 3 4 5 3 4 5 3 3 3.3.3... ÜSLÜ SAYILAR QUİZİ VE CEVAPLARI 6 4 4 3 buluruz. Doğru Cevap : E şıkkı 0 ) n bir doğal saı olmak üzere, ( ) ( ) n ( ) n n n A) 4
1-)BİLİNMESİ GEREKEN ÜSLÜ İFADELER VE DEĞERLERİ
 1-)BİLİNMESİ GEREKEN ÜSLÜ İFADELER VE DEĞERLERİ * 2 0 = * 3 0 = * 4 0 = * 5 0 = * 2 1 = * 3 1 = * 4 1 = * 5 1 = * 2 2 = * 3 2 = * 4 2 = * 5 2 = * 2 3 = * 3 3 = * 4 3 = * 5 3 = * 2 4 = * 3 4 = * 4 4 = *
1-)BİLİNMESİ GEREKEN ÜSLÜ İFADELER VE DEĞERLERİ * 2 0 = * 3 0 = * 4 0 = * 5 0 = * 2 1 = * 3 1 = * 4 1 = * 5 1 = * 2 2 = * 3 2 = * 4 2 = * 5 2 = * 2 3 = * 3 3 = * 4 3 = * 5 3 = * 2 4 = * 3 4 = * 4 4 = *
1. BÖLÜM. Sayılarda Temel Kavramlar. Bölme - Bölünebilme - Faktöriyel EBOB - EKOK. Kontrol Noktası 1
 1. BÖLÜM Sayılarda Temel Kavramlar Bölme - Bölünebilme - Faktöriyel EBOB - EKOK Kontrol Noktası 1 Isınma Hareketleri 1 Uygun eşleştirmeleri yapınız. I. {0, 1, 2,..., 9} II. {1, 2, 3,...} III. {0, 1, 2,
1. BÖLÜM Sayılarda Temel Kavramlar Bölme - Bölünebilme - Faktöriyel EBOB - EKOK Kontrol Noktası 1 Isınma Hareketleri 1 Uygun eşleştirmeleri yapınız. I. {0, 1, 2,..., 9} II. {1, 2, 3,...} III. {0, 1, 2,
Viyana İmam Hatip Lisesi Öğrenci Seçme Sınavı - Matematik
 Viyana İmam Hatip Lisesi Öğrenci Seçme Sınavı - Matematik 1. Ünite: Geometriden Olasılığa 1. Bölüm: Yansıyan ve Dönen Şekiller, Fraktallar Yansıma, Öteleme, Dönme Fraktallar 2. Bölüm: Üslü Sayılar Tam
Viyana İmam Hatip Lisesi Öğrenci Seçme Sınavı - Matematik 1. Ünite: Geometriden Olasılığa 1. Bölüm: Yansıyan ve Dönen Şekiller, Fraktallar Yansıma, Öteleme, Dönme Fraktallar 2. Bölüm: Üslü Sayılar Tam
1. BÖLÜM Mantık BÖLÜM Sayılar BÖLÜM Rasyonel Sayılar BÖLÜM I. Dereceden Denklemler ve Eşitsizlikler
 ORGANİZASYON ŞEMASI 1. BÖLÜM Mantık... 7. BÖLÜM Sayılar... 13 3. BÖLÜM Rasyonel Sayılar... 93 4. BÖLÜM I. Dereceden Denklemler ve Eşitsizlikler... 103 5. BÖLÜM Mutlak Değer... 113 6. BÖLÜM Çarpanlara Ayırma...
ORGANİZASYON ŞEMASI 1. BÖLÜM Mantık... 7. BÖLÜM Sayılar... 13 3. BÖLÜM Rasyonel Sayılar... 93 4. BÖLÜM I. Dereceden Denklemler ve Eşitsizlikler... 103 5. BÖLÜM Mutlak Değer... 113 6. BÖLÜM Çarpanlara Ayırma...
MATEMATİK Kazanım =Rasyonel sayıları tanır ve sayı doğrusunda gösterir. RASYONEL SAYILAR VE SAYI DOĞRUSUNDA GÖSTERME
 .SINIF MATEMATİK Kazanım Rasyonel sayıları tanır ve sayı doğrusunda gösterir. RASYONEL SAYILAR VE SAYI DOĞRUSUNDA GÖSTERME RASYONEL SAYILAR 0,,,,... gibi a şeklinde yazılabilen sayılara rasyonel sayılar
.SINIF MATEMATİK Kazanım Rasyonel sayıları tanır ve sayı doğrusunda gösterir. RASYONEL SAYILAR VE SAYI DOĞRUSUNDA GÖSTERME RASYONEL SAYILAR 0,,,,... gibi a şeklinde yazılabilen sayılara rasyonel sayılar
140. 2< a< 1 ise kesrinin değeri aşağıdakilerden hangisi olamaz? (3,7) a 1,9 2,4 2,7 3,2 3,7. a a c b ve c a a b c
 138. a ve b gerçel sayılardır. a < a, 6a b 5= 0 b ne olabilir? (11) 4 5 8 11 1 139. < 0 olmak üzere, 4 3. =? ( 3 ) a 1 140. < a< 1 ise kesrinin değeri aşağıdakilerden hangisi olamaz? (3,7) a 1,9,4,7 3,
138. a ve b gerçel sayılardır. a < a, 6a b 5= 0 b ne olabilir? (11) 4 5 8 11 1 139. < 0 olmak üzere, 4 3. =? ( 3 ) a 1 140. < a< 1 ise kesrinin değeri aşağıdakilerden hangisi olamaz? (3,7) a 1,9,4,7 3,
Örnek...4 : P(x) = 3x + 2 ve Q(x)= x 2 +4x -3 polinomları için a) P(x). Q(x) b)x.p(x) 2.Q(x) işlem lerini ya pınız.
 POLİNOMLARDA Polinomlarda To plama ve Çıkarma P(x) ve Q(x) iki polinom olsun. P(x) + Q(x) veya P(x) Q(x) işlemi yapılırken eşit dereceli terimlerin katsayıları işlemine göre toplanır veya çıkarılır. Örnek...1
POLİNOMLARDA Polinomlarda To plama ve Çıkarma P(x) ve Q(x) iki polinom olsun. P(x) + Q(x) veya P(x) Q(x) işlemi yapılırken eşit dereceli terimlerin katsayıları işlemine göre toplanır veya çıkarılır. Örnek...1
Örnek...3 : Aşağıdaki ifadelerden hangileri bir dizinin genel terim i olabilir?
 DİZİLER Tanım kümesi pozitif tam sayılar kümesi olan her fonksiyona dizi denir. Örneğin f : Z + R, f (n )=n 2 ifadesi bir dizi belirtir. Diziler, değer kümelerine göre adlandırı - lırlar. Dizinin değer
DİZİLER Tanım kümesi pozitif tam sayılar kümesi olan her fonksiyona dizi denir. Örneğin f : Z + R, f (n )=n 2 ifadesi bir dizi belirtir. Diziler, değer kümelerine göre adlandırı - lırlar. Dizinin değer
sayısının binler bölüğündeki 5 rakamının basamak değeri kaçtır? Yukarıdaki toplama işlemine göre verilmeyen toplanan kaçtır?
 5.SNF MTEMTİK UYG. 1.DÖNEM 1.YZ SOU 1. 398 531 793 sayısının binler bölüğündeki 5 rakamının basamak değeri kaçtır? ) 500 ) 5000 C) 50000 D) 500000 6. 3 6 4 8 2 1 0 9 9 5 7 1 Yukarıdaki toplama işlemine
5.SNF MTEMTİK UYG. 1.DÖNEM 1.YZ SOU 1. 398 531 793 sayısının binler bölüğündeki 5 rakamının basamak değeri kaçtır? ) 500 ) 5000 C) 50000 D) 500000 6. 3 6 4 8 2 1 0 9 9 5 7 1 Yukarıdaki toplama işlemine
MATEMATİK ÜSLÜ SAYILAR. Tam Sayıların Tam Sayı Kuvveti. Üslü sayı, bir sayının kendisi ile tekrarlı çarpımıdır.
 Kazanım Tam sayıların tam sayı kuvvetlerini belirler. MATEMATİK KAZANIM FÖYÜ- Tam Sayıların Tam Sayı Kuvveti.Adım..Adım...Adım Yanda verilen örüntünüyü 6.Adıma kadar ilerletiniz. HATIRLA Üslü sayı, bir
Kazanım Tam sayıların tam sayı kuvvetlerini belirler. MATEMATİK KAZANIM FÖYÜ- Tam Sayıların Tam Sayı Kuvveti.Adım..Adım...Adım Yanda verilen örüntünüyü 6.Adıma kadar ilerletiniz. HATIRLA Üslü sayı, bir
MATEMATİK SORU BANKASI. ezberbozan serisi GEOMETRİ 30. KPSS tamamı çözümlü. eğitimde
 ezberbozan serisi MATEMATİK GEOMETRİ KPSS 2017 SORU BANKASI eğitimde tamamı çözümlü 30. Kerem Köker Kenan Osmanoğlu Levent Şahin Uğur Özçelik Ahmet Tümer Yılmaz Ceylan KOMİSYON KPSS EZBERBOZAN MATEMATİK
ezberbozan serisi MATEMATİK GEOMETRİ KPSS 2017 SORU BANKASI eğitimde tamamı çözümlü 30. Kerem Köker Kenan Osmanoğlu Levent Şahin Uğur Özçelik Ahmet Tümer Yılmaz Ceylan KOMİSYON KPSS EZBERBOZAN MATEMATİK
TAM SAYILARLA TOPLAMA İŞLEMİ
 . Sınıf Matematik AD SOYAD C E V A P L A R I M NUMARAM A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D TAM SAYILARLA TOPLAMA İŞLEMİ.
. Sınıf Matematik AD SOYAD C E V A P L A R I M NUMARAM A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D TAM SAYILARLA TOPLAMA İŞLEMİ.
MATEMATİK. Doç Dr Murat ODUNCUOĞLU
 MATEMATİK Doç Dr Murat ODUNCUOĞLU Mesleki Matematik 1 TEMEL KAVRAMLAR RAKAM Sayıları yazmak için kullandığımız işaretlere rakam denir. Sayıları ifade etmeye yarayan sembollere rakam denir. Rakamlar 0,1,2,3,4,5,6,7,8,9
MATEMATİK Doç Dr Murat ODUNCUOĞLU Mesleki Matematik 1 TEMEL KAVRAMLAR RAKAM Sayıları yazmak için kullandığımız işaretlere rakam denir. Sayıları ifade etmeye yarayan sembollere rakam denir. Rakamlar 0,1,2,3,4,5,6,7,8,9
1. BÖLÜM Polinomlar BÖLÜM II. Dereceden Denklemler BÖLÜM II. Dereceden Eşitsizlikler BÖLÜM Parabol
 ORGANİZASYON ŞEMASI . BÖLÜM Polinomlar... 7. BÖLÜM II. Dereceden Denklemler.... BÖLÜM II. Dereceden Eşitsizlikler... 9. BÖLÜM Parabol... 5 5. BÖLÜM Trigonometri... 69 6. BÖLÜM Karmaşık Sayılar... 09 7.
ORGANİZASYON ŞEMASI . BÖLÜM Polinomlar... 7. BÖLÜM II. Dereceden Denklemler.... BÖLÜM II. Dereceden Eşitsizlikler... 9. BÖLÜM Parabol... 5 5. BÖLÜM Trigonometri... 69 6. BÖLÜM Karmaşık Sayılar... 09 7.
ECEM ERDURU GAMZE SERİN ZEHRA SABUR EMİNE ÖLMEZ. o TAMSAYILAR KONUSU ANLATILMAKTADIR
 ECEM ERDURU GAMZE SERİN ZEHRA SABUR EMİNE ÖLMEZ o TAMSAYILAR KONUSU ANLATILMAKTADIR Sıfırın sağındaki sayılar pozitif tam sayılar, sıfırın solundaki sayılar negatif tam sayılardır. Pozitif tam sayılar,
ECEM ERDURU GAMZE SERİN ZEHRA SABUR EMİNE ÖLMEZ o TAMSAYILAR KONUSU ANLATILMAKTADIR Sıfırın sağındaki sayılar pozitif tam sayılar, sıfırın solundaki sayılar negatif tam sayılardır. Pozitif tam sayılar,
KESİRLER BİRİM KESİRLERİ SIRALAMA. Birim kesirlerde paydası büyük olan kesir daha küçüktür.
 BİRİM KESİRLERİ SIRALAMA Bir bütünün eş parçalarından her birine kesir denir. Payı olan kesirlere birim kesir denir. Birim kesirlerde paydası büyük olan kesir daha küçüktür.,, 8 kesirlerini sıralayınız.
BİRİM KESİRLERİ SIRALAMA Bir bütünün eş parçalarından her birine kesir denir. Payı olan kesirlere birim kesir denir. Birim kesirlerde paydası büyük olan kesir daha küçüktür.,, 8 kesirlerini sıralayınız.
Örnek...3 : Aşağıdaki ifadelerden hangileri bir dizinin genel terim i olabilir? Örnek...4 : Genel terimi w n. Örnek...1 : Örnek...5 : Genel terimi r n
 DİZİLER Tanım kümesi pozitif tam sayılar kümesi olan her fonksiyona dizi denir. Örneğin f : Z + R, f (n )=n 2 ifadesi bir dizi belirtir. Diziler değer kümelerine göre adlandırılırlar. Dizinin değer kümesi
DİZİLER Tanım kümesi pozitif tam sayılar kümesi olan her fonksiyona dizi denir. Örneğin f : Z + R, f (n )=n 2 ifadesi bir dizi belirtir. Diziler değer kümelerine göre adlandırılırlar. Dizinin değer kümesi
3 7 üs(kuvvet) 5 2 ( 4 3 ( 7 5 (
 Bu konuda üslü sayılarla ilgili kazanımları maddeler halide işleyeceğiz Normalde 8 sınıf matematik kazanımları üslü sayılar konusunda negatif üs kavramı ile başlamasına rağmen bu çalışma kağıdında 6sınıf
Bu konuda üslü sayılarla ilgili kazanımları maddeler halide işleyeceğiz Normalde 8 sınıf matematik kazanımları üslü sayılar konusunda negatif üs kavramı ile başlamasına rağmen bu çalışma kağıdında 6sınıf
MATEMATİK DERSİ UZAKTAN EĞİTİM DERS NOTLARI 3. HAFTA
 MATEMATİK DERSİ UZAKTAN EĞİTİM DERS NOTLARI 3. HAFTA 3. Ondalık Sayılarda İşlemler: Toplama - Çıkarma: Ondalık kesirler toplanırken, virgüller alt alta gelecek şekilde yazılır ve doğal sayılarda toplama-çıkarma
MATEMATİK DERSİ UZAKTAN EĞİTİM DERS NOTLARI 3. HAFTA 3. Ondalık Sayılarda İşlemler: Toplama - Çıkarma: Ondalık kesirler toplanırken, virgüller alt alta gelecek şekilde yazılır ve doğal sayılarda toplama-çıkarma
Örnek...1 : Yandaki bölme işlemin de bölüm ile kalanın toplamı kaçtır?
 BÖLME İŞLEMİ VE ÖZELLİKLERİ A, B, C, K doğal sayılar ve B 0 olmak üzere, BÖLÜNEN A B C BÖLEN BÖLÜM Örnek...4 : x sayısının y ile bölümündeki bölüm 2 ve kalan 5 tir. y sayısının z ile bölümündeki bölüm
BÖLME İŞLEMİ VE ÖZELLİKLERİ A, B, C, K doğal sayılar ve B 0 olmak üzere, BÖLÜNEN A B C BÖLEN BÖLÜM Örnek...4 : x sayısının y ile bölümündeki bölüm 2 ve kalan 5 tir. y sayısının z ile bölümündeki bölüm
ÜSLÜ SAYILARLA İLGİLİ TEMEL KURALLAR. (2 ) demek 2 tane 2 3 'ün çarpımı demektir. (2 ) = 2.2 = 2 eder.
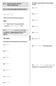 8.. ÜSLÜ SAYILARLA İLGİLİ TEMEL KURALLAR 8...A ÜSLÜ SAYILARIN KUVVETİNİ ALMA ) Aşağıda verilen eşitlikte bilinmeyen harfleri bulunuz. 6 a. 6 ( ) 8 b b) 7 Üslü bir sayının üssü alınırken, üsler çarpılır.
8.. ÜSLÜ SAYILARLA İLGİLİ TEMEL KURALLAR 8...A ÜSLÜ SAYILARIN KUVVETİNİ ALMA ) Aşağıda verilen eşitlikte bilinmeyen harfleri bulunuz. 6 a. 6 ( ) 8 b b) 7 Üslü bir sayının üssü alınırken, üsler çarpılır.
YGS - LYS SAYILAR KONU ÖZETLİ ÇÖZÜMLÜ SORU BANKASI
 YGS - LYS SAYILAR KONU ÖZETLİ LÜ SORU BANKASI ANKARA ÖN SÖZ Sevgili Öğrenciler, ÖSYM nin son yıllarda yaptığı sınavlardaki matematik sorularının eski sınav sorularından çok farklı olduğu herkes tarafından
YGS - LYS SAYILAR KONU ÖZETLİ LÜ SORU BANKASI ANKARA ÖN SÖZ Sevgili Öğrenciler, ÖSYM nin son yıllarda yaptığı sınavlardaki matematik sorularının eski sınav sorularından çok farklı olduğu herkes tarafından
MODÜLER ARİTMETİK. Örnek:
 MODÜLER ARİTMETİK Bir doğal sayının ile bölünmesinden elde edilen kalanlar kümesi { 0,, } dir. ile bölünmesinden elde edilen kalanlar kümesi { 0,,, } tür. Tam sayılar kümesi üzerinde tanımlanan {( x, y)
MODÜLER ARİTMETİK Bir doğal sayının ile bölünmesinden elde edilen kalanlar kümesi { 0,, } dir. ile bölünmesinden elde edilen kalanlar kümesi { 0,,, } tür. Tam sayılar kümesi üzerinde tanımlanan {( x, y)
Örnek...1 : Yandaki bölme işlemin de bölüm ile kalanın toplamı kaçtır?
 BÖLME İŞLEMİ VE ÖZELLİKLERİ A, B, C, K doğal sayılar ve B 0 olmak üzere, BÖLÜNEN A B C BÖLEN BÖLÜM Örnek...4 : x sayısının y ile bölümündeki bölüm 2 ve kalan 5 tir. y sayısının z ile bölümündeki bölüm
BÖLME İŞLEMİ VE ÖZELLİKLERİ A, B, C, K doğal sayılar ve B 0 olmak üzere, BÖLÜNEN A B C BÖLEN BÖLÜM Örnek...4 : x sayısının y ile bölümündeki bölüm 2 ve kalan 5 tir. y sayısının z ile bölümündeki bölüm
MATEMATİK ASAL ÇARPANLARA AYIRMA. ÖRNEK 120 sayısını asal çarpanlarına ayırınız. ÖRNEK 150 sayısının asal çarpanları toplamını bulunuz.
 MATEMATİK ASAL ÇARPANLARA AYIRMA A S A L Ç A R P A N L A R A A Y I R M A T a n ı m : Bir tam sayıyı, asal sayıların çarpımı olarak yazmaya, asal çarpanlarına ayırma denir. 0 sayısını asal çarpanlarına
MATEMATİK ASAL ÇARPANLARA AYIRMA A S A L Ç A R P A N L A R A A Y I R M A T a n ı m : Bir tam sayıyı, asal sayıların çarpımı olarak yazmaya, asal çarpanlarına ayırma denir. 0 sayısını asal çarpanlarına
KILAVUZ SORU ÇÖZÜMLERİ Matematik
 9. Çarpanlar ve Katlar b Dikdörtgenin alanı 4 cm olduğuna göre, kısa ve uzun kenarının çarpımı 4 cm 'dir. a. b = 4 a 6. Asal Çarpanlar A B C D E Yukarıda verilen asal çarpanlara ayırma işleminin son satırında
9. Çarpanlar ve Katlar b Dikdörtgenin alanı 4 cm olduğuna göre, kısa ve uzun kenarının çarpımı 4 cm 'dir. a. b = 4 a 6. Asal Çarpanlar A B C D E Yukarıda verilen asal çarpanlara ayırma işleminin son satırında
ASAL SAYILAR - TAM BÖLENLER - FAKTÖRİYEL Test -1
 ASAL SAYILAR - TAM BÖLENLER - FAKTÖRİYEL Test -1 1. ve y aralarında asal iki doğal sayıdır. 7 y 11 olduğuna göre, y farkı 5. 364 sayısının en büyük asal böleni A) 3 B) 7 C) 11 D) 13 E) 17 A) B) 3 C) 4
ASAL SAYILAR - TAM BÖLENLER - FAKTÖRİYEL Test -1 1. ve y aralarında asal iki doğal sayıdır. 7 y 11 olduğuna göre, y farkı 5. 364 sayısının en büyük asal böleni A) 3 B) 7 C) 11 D) 13 E) 17 A) B) 3 C) 4
TAM SAYILAR. Tam Sayılarda Dört İşlem
 TAM SAYILAR Tam Sayılarda Dört İşlem Pozitif ve negatif tam sayılar konu anlatımı ve örnekler içermektedir. Tam sayılarda dört işlem ve bu konuyla ilgili örnek soru çözümleri bulunmaktadır. Grup_09 29.11.2011
TAM SAYILAR Tam Sayılarda Dört İşlem Pozitif ve negatif tam sayılar konu anlatımı ve örnekler içermektedir. Tam sayılarda dört işlem ve bu konuyla ilgili örnek soru çözümleri bulunmaktadır. Grup_09 29.11.2011
p sayısının pozitif bölenlerinin sayısı 14 olacak şekilde kaç p asal sayısı bulunur?
 07.10.2006 1. Kaç p asal sayısı için, x 3 x + 2 (x r) 2 (x s) (mod p) denkliğinin tüm x tam sayıları tarafından gerçeklenmesini sağlayan r, s tamsayıları bulunabilir? 2. Aşağıdaki ifadelerin hangisinin
07.10.2006 1. Kaç p asal sayısı için, x 3 x + 2 (x r) 2 (x s) (mod p) denkliğinin tüm x tam sayıları tarafından gerçeklenmesini sağlayan r, s tamsayıları bulunabilir? 2. Aşağıdaki ifadelerin hangisinin
AKADEMİK PERSONEL VE LİSANSÜSTÜ EĞİTİMİ GİRİŞ SINAVI (ALES)
 00000000001 AKADEMİK PERSONEL VE LİSANSÜSTÜ EĞİTİMİ GİRİŞ SINAVI (ALES) plam cevaplama süresi 150 akikadır. (,5 saat) SAYISAL BÖLÜM SAYISAL - 1 TESTİ Sınavın bu bölümünden alacağınız standart puan, Sayısal
00000000001 AKADEMİK PERSONEL VE LİSANSÜSTÜ EĞİTİMİ GİRİŞ SINAVI (ALES) plam cevaplama süresi 150 akikadır. (,5 saat) SAYISAL BÖLÜM SAYISAL - 1 TESTİ Sınavın bu bölümünden alacağınız standart puan, Sayısal
ÇARPANLAR VE KATLAR I sayısının asal çarpanlarına ayrılmış hâli aşağıdakilerden A) B) C) D)
 8. Sınıf MATEMATİK ÇARPANLAR VE KATLAR I. Aşağıdakilerden hangisi 6 nın çarpanlarından biridir? A) 3 B) 6 C) 8 D) TEST. 360 sayısının asal çarpanlarına ayrılmış hâli aşağıdakilerden hangisidir? A) 3. 3.
8. Sınıf MATEMATİK ÇARPANLAR VE KATLAR I. Aşağıdakilerden hangisi 6 nın çarpanlarından biridir? A) 3 B) 6 C) 8 D) TEST. 360 sayısının asal çarpanlarına ayrılmış hâli aşağıdakilerden hangisidir? A) 3. 3.
TEMEL KAVRAMLAR. SAYI KÜMELERİ 1. Doğal Sayılar
 TEMEL KAVRAMLAR Rakam: Sayıları ifade etmeye yarayan sembollere rakam denir. Bu semboller {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} kümesinin elemanlarıdır., b ve c birer rakamdır. 15 b = c olduğuna göre, + b + c
TEMEL KAVRAMLAR Rakam: Sayıları ifade etmeye yarayan sembollere rakam denir. Bu semboller {0, 1, 2, 3, 4, 5, 6, 7, 8, 9} kümesinin elemanlarıdır., b ve c birer rakamdır. 15 b = c olduğuna göre, + b + c
 TEMEL KAVRAMLAR A: SAYI Sayıları ifade etmeye yarayan sembollere rakam denir. Ör: 0,1,2,3,4,5,6 Rakamların çokluk belirtecek şekilde bir araya getirilmesiyle oluşturulan ifadeler ifadesine sayı denir.
TEMEL KAVRAMLAR A: SAYI Sayıları ifade etmeye yarayan sembollere rakam denir. Ör: 0,1,2,3,4,5,6 Rakamların çokluk belirtecek şekilde bir araya getirilmesiyle oluşturulan ifadeler ifadesine sayı denir.
www.derssunumlari.com
 . BÖLÜM: KESİRLER HER YERDE Kesirleri Karşılaştıralım, Toplayalım ve Çıkaralım 7 7 7 ile kesirlerini karşılaştırınız ve bu 8 8 kesirleri sayı doğrusunda gösteriniz. 8 Pay üï Payda : Bir bütünün kaç parçaya
. BÖLÜM: KESİRLER HER YERDE Kesirleri Karşılaştıralım, Toplayalım ve Çıkaralım 7 7 7 ile kesirlerini karşılaştırınız ve bu 8 8 kesirleri sayı doğrusunda gösteriniz. 8 Pay üï Payda : Bir bütünün kaç parçaya
Bir bütünün eş parçalarının bütüne olan oranı kesir olarak adlandırılır. b Payda
 Matematik6 Bir Bakışta Matematik Kazanım Defteri Özet bilgi alanları... Kesirlerle İşlemler KESİR ve KESİRLERDE SIRALAMA Bir bütünün eş parçalarının bütüne olan oranı kesir olarak adlandırılır. Bir kesirde
Matematik6 Bir Bakışta Matematik Kazanım Defteri Özet bilgi alanları... Kesirlerle İşlemler KESİR ve KESİRLERDE SIRALAMA Bir bütünün eş parçalarının bütüne olan oranı kesir olarak adlandırılır. Bir kesirde
8. SINIF MATEMATiK KAREKÖKLÜ SAYILAR
 0 8. SINIF MATEMATiK KAREKÖKLÜ SAYILAR KAREKÖKLÜ SAYI KAVRAMI Karekök ile gösterilir. karekökünün içi negatif bir sayıya eşit olamaz. ÖR: Aşağıda verilen eşitliklere göre x lerin alabileceği değerleri
0 8. SINIF MATEMATiK KAREKÖKLÜ SAYILAR KAREKÖKLÜ SAYI KAVRAMI Karekök ile gösterilir. karekökünün içi negatif bir sayıya eşit olamaz. ÖR: Aşağıda verilen eşitliklere göre x lerin alabileceği değerleri
Rasyonel Sayılarla İşlemler. takip edilir.
 Matematik Bir Bakışta Matematik Kazanım Defteri Rasyonel Sayılarla İşlemler Özet bilgi alanları... RASYONEL SAYILARLA ÇOK ADIMLI İŞLEMLER Çok adımlı işlemlerde şu sıra takip edilir : Parantez içindeki
Matematik Bir Bakışta Matematik Kazanım Defteri Rasyonel Sayılarla İşlemler Özet bilgi alanları... RASYONEL SAYILARLA ÇOK ADIMLI İŞLEMLER Çok adımlı işlemlerde şu sıra takip edilir : Parantez içindeki
5. a ve b birer pozitif tam sayıdır. A) 1 B) 2 C) 3 D) 14 E) a ve b birer doğal sayıdır. 7. a ve b birer pozitif tam sayıdır.
 Üniversite Haz rl k Sözcükte Do al ve Say lar Söz Öbeklerinde ve Tam Say lar Anlam - I - I YGS Temel Matematik. 8 + 4. + 8 : 4 işleminin sonucu A) 8 B) 9 C) D) 5 E) 8 5. a ve b birer pozitif tam sayıdır.
Üniversite Haz rl k Sözcükte Do al ve Say lar Söz Öbeklerinde ve Tam Say lar Anlam - I - I YGS Temel Matematik. 8 + 4. + 8 : 4 işleminin sonucu A) 8 B) 9 C) D) 5 E) 8 5. a ve b birer pozitif tam sayıdır.
Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı. ALES / Đlkbahar / Sayısal II / 10 Mayıs Matematik Soruları ve Çözümleri
 Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı ALES / Đlkbahar / Sayısal II / 0 Mayıs 009 Matematik Soruları ve Çözümleri. ( ) 4 işleminin sonucu kaçtır? A) B) C) 4 D) E) 6 Çözüm ( ) 4 ( ) 4 4 6.
Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı ALES / Đlkbahar / Sayısal II / 0 Mayıs 009 Matematik Soruları ve Çözümleri. ( ) 4 işleminin sonucu kaçtır? A) B) C) 4 D) E) 6 Çözüm ( ) 4 ( ) 4 4 6.
{ x,y x y + 19 = 0, x, y R} = 3 tir. = sonlu kümesinin 32 tane alt kümesinde
 1. Aşağıdaki kümelerden hangisi sonsuz küme belirtir? A) A = { x 4 < x < 36,x N} B) B = { x 19 < x,x asal sayı} C) C = { x x = 5k,0 < x < 100,k Z} D) D = { x x = 5, x Z} E) E = { x x < 19,x N}. A, B ve
1. Aşağıdaki kümelerden hangisi sonsuz küme belirtir? A) A = { x 4 < x < 36,x N} B) B = { x 19 < x,x asal sayı} C) C = { x x = 5k,0 < x < 100,k Z} D) D = { x x = 5, x Z} E) E = { x x < 19,x N}. A, B ve
Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı. ALES / Đlkbahar / Sayısal II / 10 Mayıs Matematik Soruları ve Çözümleri
 Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı ALES / Đlkbahar / Sayısal II / 0 Mayıs 009 Matematik Soruları ve Çözümleri. ( ) 4 işleminin sonucu kaçtır? A) B) C) 4 D) E) 6 Çözüm ( ) 4 ( ) 4 4 6.
Akademik Personel ve Lisansüstü Eğitimi Giriş Sınavı ALES / Đlkbahar / Sayısal II / 0 Mayıs 009 Matematik Soruları ve Çözümleri. ( ) 4 işleminin sonucu kaçtır? A) B) C) 4 D) E) 6 Çözüm ( ) 4 ( ) 4 4 6.
a = b ifadesine kareköklü ifade denir.
 KAREKÖKLÜ SAYILAR Rasyonel sayılar kümesi sayı ekseninde sık olmasına rağmen sayı eksenini tam dolduramamaktadır;çünkü sayı doğrusu üzerinde görüntüsü olduğu halde rasyonel olmayan sayılar da vardır. Karesi
KAREKÖKLÜ SAYILAR Rasyonel sayılar kümesi sayı ekseninde sık olmasına rağmen sayı eksenini tam dolduramamaktadır;çünkü sayı doğrusu üzerinde görüntüsü olduğu halde rasyonel olmayan sayılar da vardır. Karesi
ÜNİVERSİTEYE GİRİŞ SINAV SORULARI
 ÜNİVERSİTEYE GİRİŞ SINAV SORULARI 1. 1999 ÖSS a, b, c pozitif gerçel (reel) sayılar olmak üzere a+ b ifadesindeki her sayı 3 ile çarpılırsa aşağıdakilerden hangisi elde c edilir? 3 a+ b A) B) c a+ 3b C)
ÜNİVERSİTEYE GİRİŞ SINAV SORULARI 1. 1999 ÖSS a, b, c pozitif gerçel (reel) sayılar olmak üzere a+ b ifadesindeki her sayı 3 ile çarpılırsa aşağıdakilerden hangisi elde c edilir? 3 a+ b A) B) c a+ 3b C)
MERKEZİ ORTAK SINAV KAZANDIRAN MATEMATİK FÖYÜ
 MERKEZİ ORTAK SINAV KAZANDIRAN MATEMATİK FÖYÜ ÖRNEK: 18 sayısının pozitif çarpanları nelerdir? Çarpımları 18 olan sayılar arayalım. 18 = 1. 18 18 =. 9 18 =. 6 Her doğal sayı iki doğal sayının çarpımı şeklinde
MERKEZİ ORTAK SINAV KAZANDIRAN MATEMATİK FÖYÜ ÖRNEK: 18 sayısının pozitif çarpanları nelerdir? Çarpımları 18 olan sayılar arayalım. 18 = 1. 18 18 =. 9 18 =. 6 Her doğal sayı iki doğal sayının çarpımı şeklinde
1.1 Üslü İfadeler: Üslü ifadelerle ilgili aşağıdaki kuralların hatırlanması faydalıdır.
 FİNANSAL MATEMATİK ALTYAPI. Üslü İfadeler: Üslü ifadelerle ilgili aşağıdaki kuralların hatırlanması faydalıdır. i-) Toplama: Eşit üslü benzer ifadelerin katsayıları toplanır. 3a 5 +,5a 5 =,5a 5 a 3-7a
FİNANSAL MATEMATİK ALTYAPI. Üslü İfadeler: Üslü ifadelerle ilgili aşağıdaki kuralların hatırlanması faydalıdır. i-) Toplama: Eşit üslü benzer ifadelerin katsayıları toplanır. 3a 5 +,5a 5 =,5a 5 a 3-7a
SAYILAR MATEMATİK KAF03 BASAMAK KAVRAMI TEMEL KAVRAM 01. İki basamaklı en küçük sayı : İki basamaklı en büyük negatif sayı :.
 SAYILAR BASAMAK KAVRAMI İki basamaklı en küçük sayı : İki basamaklı en büyük negatif sayı :. Üç basamaklı rakamları farklı en küçük sayı :. SORU 5 MATEMATİK KAF03 TEMEL KAVRAM 01 Üç basamaklı birbirinden
SAYILAR BASAMAK KAVRAMI İki basamaklı en küçük sayı : İki basamaklı en büyük negatif sayı :. Üç basamaklı rakamları farklı en küçük sayı :. SORU 5 MATEMATİK KAF03 TEMEL KAVRAM 01 Üç basamaklı birbirinden
EĞİTİM ÖĞRETİM YILI LİDER ŞİŞLİ İLKOKULU/ORTAOKULU
 4. SINIF MATEMATİK KAZANIMLARI 4, 5 ve 6 basamaklı doğal sayıları okur ve yazar. 10 000 e kadar (10 000 dahil) yüzer ve biner sayar. 10 000 e kadar (10 000 dahil) yüzer ve biner sayar. 4, 5 ve 6 basamaklı
4. SINIF MATEMATİK KAZANIMLARI 4, 5 ve 6 basamaklı doğal sayıları okur ve yazar. 10 000 e kadar (10 000 dahil) yüzer ve biner sayar. 10 000 e kadar (10 000 dahil) yüzer ve biner sayar. 4, 5 ve 6 basamaklı
TABAN ARĠTMETĠĞĠ. ÇÖZÜM (324) 5 = = = = 89 bulunur. Doğru Seçenek C dir.
 TABAN ARĠTMETĠĞĠ Kullandığımız 10 luk sayma sisteminde sayılar {0,1,2,3,4,5,6,7,8,9} kümesinin elemanları (Rakam) kullanılarak yazılır. En büyük elemanı 9 olan, 10 elemanlı bir kümedir. Onluk sistemde;
TABAN ARĠTMETĠĞĠ Kullandığımız 10 luk sayma sisteminde sayılar {0,1,2,3,4,5,6,7,8,9} kümesinin elemanları (Rakam) kullanılarak yazılır. En büyük elemanı 9 olan, 10 elemanlı bir kümedir. Onluk sistemde;
2. Matematiksel kavramları organize bir şekilde sunarak, bu kavramları içselleştirmenizi sağlayacak pedagojik bir alt yapı ile yazılmıştır.
 Sevgili Öğrenciler, Matematik ilköğretimden üniversiteye kadar çoğu öğrencinin korkulu rüyası olmuştur. Buna karşılık, istediğiniz üniversitede okuyabilmeniz büyük ölçüde YGS ve LYS'de matematik testinde
Sevgili Öğrenciler, Matematik ilköğretimden üniversiteye kadar çoğu öğrencinin korkulu rüyası olmuştur. Buna karşılık, istediğiniz üniversitede okuyabilmeniz büyük ölçüde YGS ve LYS'de matematik testinde
KPSS MATEMATİK KONU ANLATIMLI SORU BANKASI ANKARA
 KPSS MATEMATİK KONU ANLATIMLI SORU BANKASI ANKARA İÇİNDEKİLER Matematiğe Giriş... Temel Kavramlar... Bölme - Bölünebilme Kuralları... 85 EBOB - EKOK... Rasyonel Sayılar... Basit Eşitsizlikler... 65 Mutlak
KPSS MATEMATİK KONU ANLATIMLI SORU BANKASI ANKARA İÇİNDEKİLER Matematiğe Giriş... Temel Kavramlar... Bölme - Bölünebilme Kuralları... 85 EBOB - EKOK... Rasyonel Sayılar... Basit Eşitsizlikler... 65 Mutlak
a) x +3 = 8 b) x -4 = -2 c) x -7 = 4 d) x +5 = 6 e) x +8 = 2 f) x -1= -8 x +3 = 5 denkleminin çözümünü bulunuz.
 Denklemler bilinmeyen - cebirsel ifade - 7 denklem Bir cebirsel ifade bir sonuca eşit oluyorsa buna denklem denir. Bazı denklemlerin çözümü yoktur, bazı denklemlerin sonsuz, bazı denklemlerin bir, iki,
Denklemler bilinmeyen - cebirsel ifade - 7 denklem Bir cebirsel ifade bir sonuca eşit oluyorsa buna denklem denir. Bazı denklemlerin çözümü yoktur, bazı denklemlerin sonsuz, bazı denklemlerin bir, iki,
İl temsilcimiz sizinle irtibata geçecektir.
 Biz, Sizin İçin Farklı Düşünüyor Farklı Üretiyor Farklı Uyguluyoruz Biz, Sizin İçin Farklıyız Sizi de Farklı Görmek İstiyoruz Soru Bankası matematik konularını yeni öğrenen öğrenciler için TMOZ öğretmenlerince
Biz, Sizin İçin Farklı Düşünüyor Farklı Üretiyor Farklı Uyguluyoruz Biz, Sizin İçin Farklıyız Sizi de Farklı Görmek İstiyoruz Soru Bankası matematik konularını yeni öğrenen öğrenciler için TMOZ öğretmenlerince
matematik kpss soru yeni konularla yeni sorularla yeni sınav sistemine göre hazırlanmıştır sayısal akıl yürütme mantıksal akıl yürütme
 kpss 04 akıcı ayrıntılı güncel konu anlatımları örnekler yorumlar uyarılar pratik bilgiler ösym tarzında özgün sorular ve açıklamaları matematik sayısal akıl yürütme mantıksal akıl yürütme 0 kpss de 85
kpss 04 akıcı ayrıntılı güncel konu anlatımları örnekler yorumlar uyarılar pratik bilgiler ösym tarzında özgün sorular ve açıklamaları matematik sayısal akıl yürütme mantıksal akıl yürütme 0 kpss de 85
EBOB - EKOK EBOB VE EKOK UN BULUNMASI. 2. Yol: En Büyük Ortak Bölen (Ebob) En Küçük Ortak Kat (Ekok) www.unkapani.com.tr. 1. Yol:
 EBOB - EKOK En Büyük Ortak Bölen (Ebob) İki veya daha fazla pozitif tamsayıyı aynı anda bölen pozitif tamsayıların en büyüğüne bu sayıların en büyük ortak böleni denir ve kısaca Ebob ile gösterilir. Örneğin,
EBOB - EKOK En Büyük Ortak Bölen (Ebob) İki veya daha fazla pozitif tamsayıyı aynı anda bölen pozitif tamsayıların en büyüğüne bu sayıların en büyük ortak böleni denir ve kısaca Ebob ile gösterilir. Örneğin,
KPSS soruda SORU GENEL YETENEK - GENEL KÜLTÜR MATEMATİK GEOMETRİ TAMAMI ÇÖZÜMLÜ SORU BANKASI
 KPSS 019 10 soruda 86 SORU GENEL YETENEK - GENEL KÜLTÜR MATEMATİK GEOMETRİ TAMAMI ÇÖZÜMLÜ SORU BANKASI Komisyon KPSS LİSANS MATEMATİK - GEOMETRİ SORU BANKASI ISBN 978-605-41-77-0 Kitapta yer alan bölümlerin
KPSS 019 10 soruda 86 SORU GENEL YETENEK - GENEL KÜLTÜR MATEMATİK GEOMETRİ TAMAMI ÇÖZÜMLÜ SORU BANKASI Komisyon KPSS LİSANS MATEMATİK - GEOMETRİ SORU BANKASI ISBN 978-605-41-77-0 Kitapta yer alan bölümlerin
MATEMATİK. Temel Kavramlar I. Test a ve b doğal sayılardır. 5. Ardışık 5 tek sayının toplamı 115 tir. 6. x ve y tamsayılardır.
 MATEMATİK Test 0 Temel Kavramlar I. a ve b doğal sayılardır. a + b = 7 olduğuna göre, a.b çarpımının alabileceği en büyük değer kaçtır?. Ardışık tek sayının toplamı tir. Buna göre, bu sayıların en büyüğü
MATEMATİK Test 0 Temel Kavramlar I. a ve b doğal sayılardır. a + b = 7 olduğuna göre, a.b çarpımının alabileceği en büyük değer kaçtır?. Ardışık tek sayının toplamı tir. Buna göre, bu sayıların en büyüğü
7.Sınıf MATEMATİK KONU ANLATIMI. Testler. Konu Anlatımı. Uygulama
 7.Sınıf MATEMATİK Konu Anlatımı Alt başlıklara ayrılmış, detaylandırılmış konu anlatımı ve bunlarla ilgili çözümlü örnek sorular konuyu kavramınızı sağlayacaktır. Uygulama Testler Konu anlatımın sonlarında
7.Sınıf MATEMATİK Konu Anlatımı Alt başlıklara ayrılmış, detaylandırılmış konu anlatımı ve bunlarla ilgili çözümlü örnek sorular konuyu kavramınızı sağlayacaktır. Uygulama Testler Konu anlatımın sonlarında
10.Konu Tam sayıların inşası
 10.Konu Tam sayıların inşası 1. Tam sayılar kümesi 2. Tam sayılar kümesinde toplama ve çarpma 3. Pozitif ve negatif tam sayılar 4. Tam sayılar kümesinde çıkarma 5. Tam sayılar kümesinde sıralama 6. Bir
10.Konu Tam sayıların inşası 1. Tam sayılar kümesi 2. Tam sayılar kümesinde toplama ve çarpma 3. Pozitif ve negatif tam sayılar 4. Tam sayılar kümesinde çıkarma 5. Tam sayılar kümesinde sıralama 6. Bir
2BÖLÜM DOĞAL SAYILAR ve DÖRT İŞLEM
 2BÖLÜM DOĞAL SAYILAR ve DÖRT İŞLEM DOĞAL SAYILAR ve DÖRT İŞLEM TEST 1 1) Güzelyurt ta oturan bir aile piknik için arabayla Karpaz a gidip, geri dönüyor. Bu yolculuk sonunda arabanın km göstergesini kontrol
2BÖLÜM DOĞAL SAYILAR ve DÖRT İŞLEM DOĞAL SAYILAR ve DÖRT İŞLEM TEST 1 1) Güzelyurt ta oturan bir aile piknik için arabayla Karpaz a gidip, geri dönüyor. Bu yolculuk sonunda arabanın km göstergesini kontrol
qwertyuiopasdfghjklzxcvbnmq wertyuiopasdfghjklzxcvbnmqw ertyuiopasdfghjklzxcvbnmqwer tyuiopasdfghjklzxcvbnmqwerty uiopasdfghjklzxcvbnmqwertyui
 qwertyuiopasdfghjklzxcvbnmq wertyuiopasdfghjklzxcvbnmqw ertyuiopasdfghjklzxcvbnmqwer FİZİK İÇİN MATEMATİK tyuiopasdfghjklzxcvbnmqwerty --------------------------------------- uiopasdfghjklzxcvbnmqwertyui
qwertyuiopasdfghjklzxcvbnmq wertyuiopasdfghjklzxcvbnmqw ertyuiopasdfghjklzxcvbnmqwer FİZİK İÇİN MATEMATİK tyuiopasdfghjklzxcvbnmqwerty --------------------------------------- uiopasdfghjklzxcvbnmqwertyui
MATEMATİK Fasikül 1 KONU ANLATIMLI FASİKÜL SET ÖLÇEN SIRA SENDE UYGULAMALARI ÇÖZÜMLÜ ÖRNEK SORULAR
 ATU MATEMATİK Fasikül KONU ANLATIMLI FASİKÜL SET ZENGİN İÇERİKLİ ÖZGÜN KONU ANLATIMI ÖLÇEN SIRA SENDE UYGULAMALARI ÇÖZÜMLÜ ÖRNEK SORULAR BİLGİ KONTROLÜ ODAKLI KARMA SORULAR PEKİŞTİREN BÖLÜMLERİ AKILLI
ATU MATEMATİK Fasikül KONU ANLATIMLI FASİKÜL SET ZENGİN İÇERİKLİ ÖZGÜN KONU ANLATIMI ÖLÇEN SIRA SENDE UYGULAMALARI ÇÖZÜMLÜ ÖRNEK SORULAR BİLGİ KONTROLÜ ODAKLI KARMA SORULAR PEKİŞTİREN BÖLÜMLERİ AKILLI
TEMEL KAVRAMLAR. a Q a ve b b. a b c 4. a b c 40. 7a 4b 3c. a b c olmak üzere a,b ve pozitif. 2x 3y 5z 84
 N 0,1,,... Sayı kümesine doğal sayı kümesi denir...., 3,, 1,0,1,,3,... sayı kümesine tamsayılar kümesi denir. 1,,3,... saı kümesine sayma sayıları denir.pozitif tamsayılar kümesidir. 15 y z x 3 5 Eşitliğinde
N 0,1,,... Sayı kümesine doğal sayı kümesi denir...., 3,, 1,0,1,,3,... sayı kümesine tamsayılar kümesi denir. 1,,3,... saı kümesine sayma sayıları denir.pozitif tamsayılar kümesidir. 15 y z x 3 5 Eşitliğinde
(m+2) +5<0. 7/m+3 + EŞİTSİZLİKLER A. TANIM
 EŞİTSİZLİKLER A. TANIM f(x)>0, f(x) - eşitsizliğinin
EŞİTSİZLİKLER A. TANIM f(x)>0, f(x) - eşitsizliğinin
DÖRDÜNCÜ BÖLÜM. 4.1. Aritmetik işlemler
 DÖRDÜNCÜ BÖLÜM 4.1. Aritmetik işlemler Bu bölümde öğrencilerin lisede bildikleri aritmetik işlemleri hatırlatacağız. Bütün öğrencilerin en azından tamsayıların toplama, çıkarma, çarpma ve bölme işlemlerini
DÖRDÜNCÜ BÖLÜM 4.1. Aritmetik işlemler Bu bölümde öğrencilerin lisede bildikleri aritmetik işlemleri hatırlatacağız. Bütün öğrencilerin en azından tamsayıların toplama, çıkarma, çarpma ve bölme işlemlerini
T. C. Manisa Celal Bayar Üniversitesi Kırkağaç Meslek Yüksekokulu Öğretim Yılı Güz Yarıyılı MATEMATİK Dersi Final Sınavı Çalışma Soruları
 T. C. Manisa Celal Bayar Üniversitesi Kırkağaç Meslek Yüksekokulu 016-017 Öğretim Yılı Güz Yarıyılı MATEMATİK Dersi Final Sınavı Çalışma Soruları 1) 3. [15 3(8: )] 9 =? a) 16 b) 14 c) 0 d) 14 e) 16 6)
T. C. Manisa Celal Bayar Üniversitesi Kırkağaç Meslek Yüksekokulu 016-017 Öğretim Yılı Güz Yarıyılı MATEMATİK Dersi Final Sınavı Çalışma Soruları 1) 3. [15 3(8: )] 9 =? a) 16 b) 14 c) 0 d) 14 e) 16 6)
ünite12 POLİNOMLAR Polinomlar
 ünite1 POOM = 1 Polinomlar 0 1 1. şağıdakilerden hangileri bir polinom değildir?. x 4 + 3. x 3 3x 5 +. x 6 1 V. x 4 1 + V. 5x 1 8 POOM POOM 5. P(x) = (a )x + (b + 3)x + ab 1 polinomu sabit bir polinom
ünite1 POOM = 1 Polinomlar 0 1 1. şağıdakilerden hangileri bir polinom değildir?. x 4 + 3. x 3 3x 5 +. x 6 1 V. x 4 1 + V. 5x 1 8 POOM POOM 5. P(x) = (a )x + (b + 3)x + ab 1 polinomu sabit bir polinom
T I M U R K A R A Ç AY - H AY D A R E Ş C A L C U L U S S E Ç K I N YAY I N C I L I K A N K A R A
 T I M U R K A R A Ç AY - H AY D A R E Ş C A L C U L U S S E Ç K I N YAY I N C I L I K A N K A R A Contents Rasyonel Fonksiyonlar 5 Bibliography 35 Inde 39 Rasyonel Fonksiyonlar Polinomlar Yetmez! Bölme
T I M U R K A R A Ç AY - H AY D A R E Ş C A L C U L U S S E Ç K I N YAY I N C I L I K A N K A R A Contents Rasyonel Fonksiyonlar 5 Bibliography 35 Inde 39 Rasyonel Fonksiyonlar Polinomlar Yetmez! Bölme
her biri 3 1 biçiminde de gösterilebilir. 5 dir.
 Bölüm KESİRLER. Kesir ve Kesir Çeşitleri Kesir Kavramı Şekildeki bütün dört eş parçaya bölünmüş bun- lardan biri taranmıştır. Taralı kısım bu dört eş paydan biridir. Bu büyüklüğü sayılarla biçiminde gösterir;
Bölüm KESİRLER. Kesir ve Kesir Çeşitleri Kesir Kavramı Şekildeki bütün dört eş parçaya bölünmüş bun- lardan biri taranmıştır. Taralı kısım bu dört eş paydan biridir. Bu büyüklüğü sayılarla biçiminde gösterir;
ARDIŞIK SAYILAR. lab2_pc32 BERRIN_ESMA_OZGE
 2011 ARDIŞIK SAYILAR lab2_pc32 BERRIN_ESMA_OZGE 29.11.2011 İçindekiler bu konu 4. Sınıf müfredatında yer almaktadır... 2 ardisik sayılarda dört işlem... Hata! Yer işareti tanımlanmamış. ardisik sayilarda
2011 ARDIŞIK SAYILAR lab2_pc32 BERRIN_ESMA_OZGE 29.11.2011 İçindekiler bu konu 4. Sınıf müfredatında yer almaktadır... 2 ardisik sayılarda dört işlem... Hata! Yer işareti tanımlanmamış. ardisik sayilarda
8. SINIF MATEMATİK ÜSLÜ İFADELER
 . SINIF MATEMATİK ÜSLÜ İFADELER... Tam sayıların, tam sayı kuvvetlerini hesaplar, üslü ifade şeklinde yazar....... a.a.a.a...a a n HATIRLATMA KÖŞESİ- n HATIRLATMA KÖŞESİ- Her sayının sıfırıncı kuvveti
. SINIF MATEMATİK ÜSLÜ İFADELER... Tam sayıların, tam sayı kuvvetlerini hesaplar, üslü ifade şeklinde yazar....... a.a.a.a...a a n HATIRLATMA KÖŞESİ- n HATIRLATMA KÖŞESİ- Her sayının sıfırıncı kuvveti
Çözüm : * ebob = = * ekok = = * ve 36 sayılarının ebob ve ekok u kaçtır?
 1) 24 ve 36 sayılarının ebob ve ekok u kaçtır? 24 36 2 * ebob = 2.2.3 =12 12 18 2 * ekok = 2.2.2.3.3 = 72 6 9 2 3 9 3 * 1 3 3 1 Ebob ( 24, 36 ) = 12 ( * lı olanların çarpımı) Ekok ( 24, 36 ) = 72 ( Hepsinin
1) 24 ve 36 sayılarının ebob ve ekok u kaçtır? 24 36 2 * ebob = 2.2.3 =12 12 18 2 * ekok = 2.2.2.3.3 = 72 6 9 2 3 9 3 * 1 3 3 1 Ebob ( 24, 36 ) = 12 ( * lı olanların çarpımı) Ekok ( 24, 36 ) = 72 ( Hepsinin
Konu Anlatımı Açık Uçlu Sorular Çoktan Seçmeli Sorular Doğru Yanlış Soruları Boşluk Doldurmalı Sorular Çıkmış Sorular
 Maths@bi 8 3.BÖLÜM Kareköklü Sayılar Konu Anlatımı Açık Uçlu Sorular Çoktan Seçmeli Sorular Doğru Yanlış Soruları Boşluk Doldurmalı Sorular Çıkmış Sorular Kerime ASKER-Abdullah ASKER Matematik Öğretmeni
Maths@bi 8 3.BÖLÜM Kareköklü Sayılar Konu Anlatımı Açık Uçlu Sorular Çoktan Seçmeli Sorular Doğru Yanlış Soruları Boşluk Doldurmalı Sorular Çıkmış Sorular Kerime ASKER-Abdullah ASKER Matematik Öğretmeni
TAM SAYILARDA ÇARPMA BÖLME İŞLEMLERİ ESRA ÇAKIR
 Kazanım: Tam sayılarla çarpma ve bölme işlemleri yapar. Tam sayılarla işlemler yapmayı gerektiren problemleri çözer. HATIRLATMA :TAM SAYILARDA TOPLAMA İŞLEMİ Aynı işaretli tam sayılar toplanırken işaretleri
Kazanım: Tam sayılarla çarpma ve bölme işlemleri yapar. Tam sayılarla işlemler yapmayı gerektiren problemleri çözer. HATIRLATMA :TAM SAYILARDA TOPLAMA İŞLEMİ Aynı işaretli tam sayılar toplanırken işaretleri
Yeşilköy Anadolu Lisesi
 Yeşilköy Anadolu Lisesi TANIM (KONUYA GİRİŞ) a, b, c gerçel sayı ve a ¹ 0 olmak üzere, ax 2 + bx + c = 0 biçimindeki her açık önermeye ikinci dereceden bir bilinmeyenli denklem denir. Bu açık önermeyi
Yeşilköy Anadolu Lisesi TANIM (KONUYA GİRİŞ) a, b, c gerçel sayı ve a ¹ 0 olmak üzere, ax 2 + bx + c = 0 biçimindeki her açık önermeye ikinci dereceden bir bilinmeyenli denklem denir. Bu açık önermeyi
1 ÜNİTE SAYILAR VE İŞLEMLER
 1 ÜNİTE SAYILAR VE İŞLEMLER TAM SAYILARLA ÇARPMA VE BÖLME İŞLEMLERİ 7.1.1.1. Tam sayılarla çarpma ve bölme işlemlerini yapar. 7.1.1.2. Tam sayılarla işlemler yapmayı gerektiren problemleri çözer. 7.1.1.3.
1 ÜNİTE SAYILAR VE İŞLEMLER TAM SAYILARLA ÇARPMA VE BÖLME İŞLEMLERİ 7.1.1.1. Tam sayılarla çarpma ve bölme işlemlerini yapar. 7.1.1.2. Tam sayılarla işlemler yapmayı gerektiren problemleri çözer. 7.1.1.3.
ÇARPANLAR VE KATLAR. Başarı Başaracağım Diye Başlayanındır. 1
 ÇARPANLAR VE KATLAR Başarı Başaracağım Diye Başlayanındır. 1 ÖRNEK 1 48 sayısının çarpanlarını bulalım. 1.Gökkuşağı yöntemi 48 sayısının çarpanlarını küçükten büyüğe sıralayarak eşleştiriniz. 48 çarpanlarını
ÇARPANLAR VE KATLAR Başarı Başaracağım Diye Başlayanındır. 1 ÖRNEK 1 48 sayısının çarpanlarını bulalım. 1.Gökkuşağı yöntemi 48 sayısının çarpanlarını küçükten büyüğe sıralayarak eşleştiriniz. 48 çarpanlarını
