Kafes Sistemler Turesses
|
|
|
- Ayşe Cumali
- 7 yıl önce
- İzleme sayısı:
Transkript
1 Kafes Sistemler Turesses Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir. Turesses are a carrier system formed by the bar elements. Each bar element connects to others at its end (joints).
2 Kafes Sistemler Birçok uygulama alanları vardır. Application areas of the Turesses Çatı sistemlerinde,(roof systems) Köprülerde, (Bridges) Kulelerde, (Towers) Ve benzeri bir çok yapılarda kullanılır.
3 Kafes Sistemler Başlıca Özellikler ve Kabuller: Main properties and assumptions for turesses Bağlantı noktalarında (düğümlerde) sadece tekil kuvvetler oluşur. Bağlantılardaki moment tepkisi ihmal edilir. (The single forces occur on the joint and reaction moments at the joint are neglected. ) Herbir çubuğa ekseni doğrultusunda kuvvet düşer. Yani tüm çubuklar çift kuvvet elemanıdır. (Each bar force is through the bar axis; i.e each bar is the twoforce member.) Çözümlerde çubuk ağırlıkları ihmal edilir. (The weight of the bars are neglected) Sisteme sadece bağlantı (düğüm) noktalarından dış kuvvetler etki eder. (The extarnal forces act on the joints only) Herbir bağlantı noktasına «düğüm noktası» ismi verilir.
4 Kafes Sistemler Tipleri: (Types of the Trusse) 1- Uzay Kafes Sistemleri: 3 Boyutlu sistemlerdir. 3 dimensions Trusses Systems 2- Düzlem Kafes Sistemleri: 2 boyutlu sistemlerdir. Plane Systems of Trusses (3 boyutlu olmasına rağmen, geometri, yükleme ve dış bağlantıların simetrikliliği söz konusu ise 2 boyutta incelenebilen sistemler de olabilir.) Ders kapsamında amacımız: Dış kuvvetler belli iken, herbir çubuğa veya belirli çubuklara düşen kuvvetleri hesaplamaktır. Ders kapsamında sadece düzlem kafes sistemler incelenecektir. Our Aims in this chapter are Calculating the bar forces, when the extarnal forces are known. We will examine the plane trusses systems only.
5 Kafes Sistemler Çubuk veya Düğümlere Düşen Kuvvetler ve Hesaplama Yöntemleri : Calculation Methods of Bar and joint forces: Kafes sistemlerde herbir düğüm noktasına ve çubuklara düşün kuvvetleri daha net görebilmek için yandaki örneği inceleyelim. Examine this example for understanding the forces at bars and joints 30kN Dikkat edilirse herbir düğüme, bağlı olduğu çubukların herbirinden bir kuvvet gelir. Çubuklara ise eşit şiddette-zıt yönde bağlı olduğu herbir düğümden bir tepki kuvveti gelir (etki-tepki). Tüm düğüm ve çubuk kuvvetleri sistemin iç kuvvetleri olarak isimlendirilir ve toplamları sıfırdır.. Bir çubuk kuvvetinin( örn: AC ) doğrultusu mutlaka çubuğa paraleldir. Püf noktası 5.1: Çubuk kuvvetinin yönü nasıl seçilmeli? Bu sorunun cevabı ise: İlk kez bu kuvvet yerleştirilirken çubukğa paralel olmak kaydıyla keyfi bir yönde (sağa-sola, yukarı aşağı) seçilir. Ancak aynı kuvvetin yönü 2., 3., yerleştirmede keyfi seçilemez. İlk yerleştirmeye bağlı olarak seçilir. Örneğin AC kuvveti ilk kez yerleştirilirken keyfi olarak A düğümüne sola doğru etki ettirlimiş. AC çubuğunun A ucuna mecburen sağa olmalıdır (etki-tepki). AC çubuğunun C ucuna sola doğru olmaldır ki çubuk dengede olsun. C düğümüne ise sağa olmalıdır (etki-tepki). Hesaplar sonucu kuvvetin işareti «-» çıkarsa seçtiğimiz yönün tersine yönde olduğunu gösterir. Ancak bu durumda kuvvetin yönü çevrilmez, hesaplarda «-» işareti ile birlikte kullanılır. Çevrilirse işareti de değiştirilmelidir.
6 Çubuk veya Düğümlere Düşen Kuvvetleri Hesaplama Yöntemleri: Calculation Methods of Bar and joint forces: Aynı örneğe devam edersek, Öncelikle bağlantı noktalarındaki kuvvetler tüm sistemin dengesinde hesaplanır: irstly, the reaction and external forces are calculated by the equilibrium of the whole system. x =0 E x + T. cos 30 o = 0 y =0 E y + T. sin 30 o = 0 M E =0 T = 0 T= 80kN E x = 69.28kN E y =10 kn bulunur. Püf noktası 5.2: Bazı problemlerde mesnet tepkilerini hesaplamaya gerek kalmadan, istenen çubuk kuvvetleri bulunabilir. Bu durumu görebilmek ve alışmak için bol soru çözülmesinde fayda vardır. Kesim yönteminde, mesnetlerin tümü kesimin bir tarafında kalıyorsa mesnet tepkilerini bulmaya gerek kalmaz.kesimin diğer tarafı incelenir ve çubuk kuvvetleri bulunabilir.
7 Çubuk veya Düğümlere Düşen Kuvvetleri Hesaplama Yöntemleri : Calculation Methods of Bar and joint forces: Şimdi iç kuvvet ismi verdiğimiz çubuk ve düğümlere düşen kuvvetleri hesaplayacağız. Now, we are going to calculate the forces at the bars and joints (i.e; internal forces by using two different methods) Bunun için 2 yöntem vardır: 1. Yöntem : Düğüm Yöntemi (The method of Joint) Çözüm: A düğümünden başlanabilir. Çünkü 2 bilinmeyen kuvvet vardır. We can start at the joint A. Because there are two unknown force. Bu yöntemde herbir düğümün dengesi yazılır ve x =0 AC + AB cos 60 o =0 kuvvetler hesaplanır. In this method, the forces can be calculated by the equlibrium of each joint Herbir düğüm için x =0, y =0 olmak üzere 2 denklem yazılabilir. Tüm kuvvetler aynı noktadan geçtiği için moment denklemi yazılamaz. Bu nedenle bir düğümde 2 bilinmeyen olması gerekir. Çözüm aşamasında düğüm sırası önemlidir. Örnekten bu durum daha iyi anlaşılacaktır. Totaly 2 different independent equations ( x =0, y =0 ) can be writen for each joints. The order of the joint calculation is important. y =0-30+ AB sin 60 o =0 AC = 17.32kN, AB = 34.64kN Şimdi B düğümüne geçilebilir. Çünkü B düğümünde 2 bilinmeyen kaldı x =0 BC cos 60 o + BD cos 60 o =0 y =0 BC. sin 60 o sin 60 o =0 BC = 34.64kN, BD = 34.64kN x =0 BC cos 60 o + AC CE CD cos 60 o =0 y =0 BC. sin 60 o + CD sin 60 o -20 = 0 CD = 57.74kN, CE = 63.51kN Benzer şekilde E veya D düğümlerinin dengesinden DE = 11.55kN bulunur.
8 2. Yöntem : Kesim Yönetimi (the method of section) II Bu yöntem mekaniğin önemli bir prensibi olan ayırma prensibine dayanır. This method rely on the separation principle. Ayrıma prensibi: dış kuvvetlerin etkisindeki bir sistem dengede ise, hayâli bazda ayırdığımız bir parçası da iç ve dış kuvvetlerin etkisiyle ayrı ayrı dengededir. İncelediğimiz örnekteki kafes sistem dış kuvvetlerin etkisi ile dengededir. O halde hayali olarak yaptığımız I-I kesiminden sonra sol veya sağ parçası da dengededir. Bu parçalara, kesilen bölgeden çubuk kuvvetleri dış kuvvet gibi etki ettirilir. Ve 3 denge denklemi ( x =0, y =0, M E =0 ) yardımıyla bu çubuk kuvvetleri bulunur. I - I kesiminde sağ tarafın SCD si ve dengesi II I - I kesiminde sol tarafın SCD si ve dengesi x =0 BC cos 60 o BD + AC =0 y =0 BC. sin 60 o -30 = 0 M C =0 BD. 5. sin60 o -30x5= 0 BC = BD = 34.64kN, işaretinin negatif «-» çıkması seçtiğimiz yönün tersine olduğunu gösterir. x =0 BC cos 60 o + BD AC cos 30 o = 0 y =0 BC. sin 60 o sin 30 o = 0 BC = BD = 34.64kN, M E =0 BD. 5. sin60 o + T BC. sin 60 o = 0 Kuvvet yönleri ilk defa keyfi seçilir. 3 denklemden 3 bilinmeyen bulanabileceği için genelde ilk kesimde 3 çubuk kesilir.. Diğer çubuk kuvvetlerini bulmak için II-II kesimi yapılabilir
9 Örnek Problem: Verilen kafes sistemindeki çubuk kuvvetlerini düğüm metodunu kullanarak bulunuz. (Calculate all bar forces at this system) S AB S AD.sin θ = S AB S AD. 3 5 S AD.cos θ 20 = S AD S DE S AD.sin θ + S DB Sin θ = S DE S 3 5 DB S AD.Cos θ +S DB Cos θ = S DB 4 5 5
10 Örnek: Şekildeki kafes sistemde GE, GC ve BC çubuklarındaki kuvvetleri bulunuz. ind the forces at the bars GE, GC and BC Çözüm: a a BC M 0 G 300(4) 400(3) (3) N (T) BC GE GE M 0 C 300(8) (3) 0 GE 800 N 800 N (C) GC 0 y GC N (T)
11 Örnek: C çubuğundaki kuvveti bulunuz. ind the force at the bar C Çözüm: Mesnet tepkileri bulunur. a a-a kesimi O o C sin 45 12m 3kN 8 m 4.75kN 4m 0 C M kN C a
12 Örnek: EB çubuğundaki kuvveti bulunuz. ind the orce at the Bar EB b b a a-a kesimi a b-b kesimi ED ED M 0 ED B 1000(4) 3000(2) 4000(4) sin 30 (4) 0 o 3000 N 3000 N (C) E E EB 0 E x y E o cos cos N 3000 N (C) 0 o sin sin N (T) o o EB
13 Alttaki Kafes Sistemlerde Soru işareti olan çubuklardaki kuvvetleri hesaplayınız. (Cevapları soruların yanında verilmiştir. Yöntem Serbesttir.) BC = P/
Kafes Sistemler. Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir.
 Kafes Sistemler Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir. Kafes Sistemler Birçok uygulama alanları vardır. Çatı sistemlerinde, Köprülerde, Kulelerde, Ve benzeri
Kafes Sistemler Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir. Kafes Sistemler Birçok uygulama alanları vardır. Çatı sistemlerinde, Köprülerde, Kulelerde, Ve benzeri
Ödev 1. Ödev1: 600N luk kuvveti u ve v eksenlerinde bileşenlerine ayırınız. 600 N
 Ödev 1 Ödev1: 600N luk kuvveti u ve v eksenlerinde bileşenlerine ayırınız. 600 N 1 600 N 600 N 600 N u sin120 600 N sin 30 u 1039N v sin 30 600 N sin 30 v 600N 2 Ödev 2 Ödev2: 2 kuvvetinin şiddetini, yönünü
Ödev 1 Ödev1: 600N luk kuvveti u ve v eksenlerinde bileşenlerine ayırınız. 600 N 1 600 N 600 N 600 N u sin120 600 N sin 30 u 1039N v sin 30 600 N sin 30 v 600N 2 Ödev 2 Ödev2: 2 kuvvetinin şiddetini, yönünü
STATİK DENGE VE KUVVET ANALİZİ Static Equilibrium and Force Analysis
 STATİK DENGE VE KUVVET ANALİZİ Static Equilibrium and Force Analysis Bu bölümde durağan halde dengede olan rijit sistemlere etki eden kuvvetlerin hesaplanması görülecektir. In this chapter we learn the
STATİK DENGE VE KUVVET ANALİZİ Static Equilibrium and Force Analysis Bu bölümde durağan halde dengede olan rijit sistemlere etki eden kuvvetlerin hesaplanması görülecektir. In this chapter we learn the
Çerçeveler ve Basit Makinalar
 Çerçeveler ve Basit Makinalar Çeşitli elemanların birbirlerine bağlanması ile oluşan sistemlerdir. Kafes sistemlerden farklı olarak, elemanlar birbirlerine 2 den fazla noktadan bağlanabilir ve dış kuvvetler
Çerçeveler ve Basit Makinalar Çeşitli elemanların birbirlerine bağlanması ile oluşan sistemlerdir. Kafes sistemlerden farklı olarak, elemanlar birbirlerine 2 den fazla noktadan bağlanabilir ve dış kuvvetler
STATİK. Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -8-
 1 STATİK Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -8- Giriş 2 Denge denklemlerini, mafsala bağlı elemanlarda oluşan yapıları analiz etmek için kullanacağız. Bu analiz, dengede olan bir yapının
1 STATİK Prof. Dr. Akgün ALSARAN - Öğr. Gör. Fatih ALİBEYOĞLU -8- Giriş 2 Denge denklemlerini, mafsala bağlı elemanlarda oluşan yapıları analiz etmek için kullanacağız. Bu analiz, dengede olan bir yapının
STATİK. Ders_6. Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü. Ders notları için: GÜZ
 STATİK Ders_6 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2017-2018 GÜZ BASİT KAFESLER, DÜĞÜM NOKTALARI METODU VE SIFIR KUVVET ELEMANLARI
STATİK Ders_6 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2017-2018 GÜZ BASİT KAFESLER, DÜĞÜM NOKTALARI METODU VE SIFIR KUVVET ELEMANLARI
KONU 3. STATİK DENGE
 KONU 3. STATİK DENGE 3.1 Giriş Bir cisme etki eden dış kuvvet ve momentlerin toplamı 0 ise cisim statik dengededir denir. Kuvvet ve moment toplamlarının 0 olması sırasıyla; ötelenme ve dönme denge şartlarıdır.
KONU 3. STATİK DENGE 3.1 Giriş Bir cisme etki eden dış kuvvet ve momentlerin toplamı 0 ise cisim statik dengededir denir. Kuvvet ve moment toplamlarının 0 olması sırasıyla; ötelenme ve dönme denge şartlarıdır.
İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz Sıfır-Kuvvet Elemanları Kesme Metodu ile Analiz
 Yapıların Analizi Konu Çıktıları İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz Sıfır-Kuvvet Elemanları Kesme Metodu ile Analiz Kafesleri oluşturan elemenlara etki eden
Yapıların Analizi Konu Çıktıları İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz Sıfır-Kuvvet Elemanları Kesme Metodu ile Analiz Kafesleri oluşturan elemenlara etki eden
V. KAFES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir.
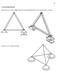 78 V. KES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir. Uzayda ise en az 6 çubuk gereklidir. 79 İhtiyaçlara göre yeni çubukların ilavesiyle
78 V. KES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir. Uzayda ise en az 6 çubuk gereklidir. 79 İhtiyaçlara göre yeni çubukların ilavesiyle
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve leri DĞHN MÜHENDİSLİK MEKNİĞİ STTİK MÜHENDİSLİK MEKNİĞİ STTİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki Boyutlu Kuvvet
Statik Ders Notları Sınav Soru ve leri DĞHN MÜHENDİSLİK MEKNİĞİ STTİK MÜHENDİSLİK MEKNİĞİ STTİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki Boyutlu Kuvvet
Engineering Mechanics: Statics in SI Units, 12e. Equilibrium of a Particle
 Engineering Mechanics: Statics in SI Units, 12e 3 Equilibrium of a Particle Bölüm Hedefleri Parçacık serbest cisim diyagramı Denge denklemleri kullanılarak parçacık denge problemleri çözümü Bölüm Özeti
Engineering Mechanics: Statics in SI Units, 12e 3 Equilibrium of a Particle Bölüm Hedefleri Parçacık serbest cisim diyagramı Denge denklemleri kullanılarak parçacık denge problemleri çözümü Bölüm Özeti
YAPI STATİĞİ MESNETLER
 YAPI STATİĞİ MESNETLER Öğr.Gör. Gültekin BÜYÜKŞENGÜR STATİK Kirişler Yük Ve Mesnet Çeşitleri Mesnetler Ve Mesnet Reaksiyonları 1. Kayıcı Mesnetler 2. Sabit Mesnetler 3. Ankastre (Konsol) Mesnetler 4. Üç
YAPI STATİĞİ MESNETLER Öğr.Gör. Gültekin BÜYÜKŞENGÜR STATİK Kirişler Yük Ve Mesnet Çeşitleri Mesnetler Ve Mesnet Reaksiyonları 1. Kayıcı Mesnetler 2. Sabit Mesnetler 3. Ankastre (Konsol) Mesnetler 4. Üç
Karabük Üniversitesi, Mühendislik Fakültesi...www.IbrahimCayiroglu.com. STATİK (4. Hafta)
 KAFES SİSTEMLER STATİK (4. Hafta) Düz eksenden oluşan çubukların birbiriyle birleştirilmesiyle elde edilen sistemlere kafes sistemler denir. Çubukların birleştiği noktalara düğüm noktaları adı verilir.
KAFES SİSTEMLER STATİK (4. Hafta) Düz eksenden oluşan çubukların birbiriyle birleştirilmesiyle elde edilen sistemlere kafes sistemler denir. Çubukların birleştiği noktalara düğüm noktaları adı verilir.
VECTOR MECHANICS FOR ENGINEERS: STATICS
 Seventh Edition VECTOR ECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi Tel: 85 31 46 / 116 E-mail: acarh@itu.edu.tr Web: http://atlas.cc.itu.edu.tr/~acarh
Seventh Edition VECTOR ECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi Tel: 85 31 46 / 116 E-mail: acarh@itu.edu.tr Web: http://atlas.cc.itu.edu.tr/~acarh
VECTOR MECHANICS FOR ENGINEERS: STATICS
 Seventh Edition VECTOR MECHANICS OR ENGINEERS: STATICS erdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi Tel: 285 31 46 / 116 E-mail: acarh@itu.edu.tr Web: http://atlas.cc.itu.edu.tr/~acarh
Seventh Edition VECTOR MECHANICS OR ENGINEERS: STATICS erdinand P. Beer E. Russell Johnston, Jr. Ders Notu: Hayri ACAR İstanbul Teknik Üniveristesi Tel: 285 31 46 / 116 E-mail: acarh@itu.edu.tr Web: http://atlas.cc.itu.edu.tr/~acarh
YAPISAL ANALİZ DOÇ.DR. KAMİLE TOSUN FELEKOĞLU
 YAPISAL ANALİZ DOÇ.DR. KAMİLE TOSUN FELEKOĞLU 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla
YAPISAL ANALİZ DOÇ.DR. KAMİLE TOSUN FELEKOĞLU 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla
BURULMA (TORSİON) Dairesel Kesitli Çubukların (Millerin) Burulması MUKAVEMET - Ders Notları - Prof.Dr. Mehmet Zor
 3 BURULMA (TORSİON) Dairesel Kesitli Çubukların (Millerin) Burulması 1.1.018 MUKAVEMET - Ders Notları - Prof.Dr. Mehmet Zor 1 3. Burulma Genel Bilgiler Burulma (Torsion): Dairesel Kesitli Millerde Gerilme
3 BURULMA (TORSİON) Dairesel Kesitli Çubukların (Millerin) Burulması 1.1.018 MUKAVEMET - Ders Notları - Prof.Dr. Mehmet Zor 1 3. Burulma Genel Bilgiler Burulma (Torsion): Dairesel Kesitli Millerde Gerilme
6.12 Örnekler PROBLEMLER
 6.1 6. 6.3 6.4 6.5 6.6 6.7 Çok Parçalı Taşıyıcı Sistemler Kafes Sistemler Kafes Köprüler Kafes Çatılar Tam, Eksik ve Fazla Bağlı Kafes Sistemler Kafes Sistemler İçin Çözüm Yöntemleri Kafes Sistemlerde
6.1 6. 6.3 6.4 6.5 6.6 6.7 Çok Parçalı Taşıyıcı Sistemler Kafes Sistemler Kafes Köprüler Kafes Çatılar Tam, Eksik ve Fazla Bağlı Kafes Sistemler Kafes Sistemler İçin Çözüm Yöntemleri Kafes Sistemlerde
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 6 Yapısal Analiz Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 6. Yapısal Analiz Şekilde görüldüğü
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 6 Yapısal Analiz Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 6. Yapısal Analiz Şekilde görüldüğü
 5. 5. 5.3 5.4 5.5 5.6 5.7 5.8 Rijit Cisimde Denge Düzlem Kuvvetlerde Denge Hali Düzlemde Serbestlik Derecesi Bağ Çeşitleri Pandül Ayak Düzlem Taşıyıcı Sistemler Düzlem Taşıyıcı Sistemlerde Yükleme Durumları
5. 5. 5.3 5.4 5.5 5.6 5.7 5.8 Rijit Cisimde Denge Düzlem Kuvvetlerde Denge Hali Düzlemde Serbestlik Derecesi Bağ Çeşitleri Pandül Ayak Düzlem Taşıyıcı Sistemler Düzlem Taşıyıcı Sistemlerde Yükleme Durumları
BÖLÜM 4 YAPISAL ANALİZ (KAFESLER-ÇERÇEVELER-MAKİNALAR)
 BÖLÜM 4 YAPISAL ANALİZ (KAESLER-ÇERÇEVELER-MAKİNALAR) 4.1 Kafesler: Basit Kafes: İnce çubukların uçlarından birleştirilerek luşturulan apıdır. Bileştirme genelde 1. Barak levhalarına pimler ve kanak vasıtası
BÖLÜM 4 YAPISAL ANALİZ (KAESLER-ÇERÇEVELER-MAKİNALAR) 4.1 Kafesler: Basit Kafes: İnce çubukların uçlarından birleştirilerek luşturulan apıdır. Bileştirme genelde 1. Barak levhalarına pimler ve kanak vasıtası
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ
 İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
Noktasal Cismin Dengesi
 Noktasal Cismin Dengesi Bu bölümde; Kuvvetleri bieşenlerine ayırma ve kartezyen vektör şeklinde ifade etme yöntemleri noktasal cismin dengesini içeren problemleri çözmede kullanılacaktır. Bölüm 3 DOÇ.DR.
Noktasal Cismin Dengesi Bu bölümde; Kuvvetleri bieşenlerine ayırma ve kartezyen vektör şeklinde ifade etme yöntemleri noktasal cismin dengesini içeren problemleri çözmede kullanılacaktır. Bölüm 3 DOÇ.DR.
Hedefler. Kafeslerde oluşan kuvvetlerin hesaplanması: düğüm noktaları metodu kesme metodu
 Yapıların Analizi Hedefler Kafeslerde oluşan kuvvetlerin hesaplanması: düğüm noktaları metodu kesme metodu Konu Çıktıları İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz
Yapıların Analizi Hedefler Kafeslerde oluşan kuvvetlerin hesaplanması: düğüm noktaları metodu kesme metodu Konu Çıktıları İki-Kuvvet Elemanları Basit (2 Boyutlu) Kafesler Düğüm Noktaları Metodu ile Analiz
ÇATI MAKASINA GELEN YÜKLER
 ÇATI MAKASINA GELEN YÜKLER Bir yapıyı dış etkilere karşı koruyan taşıyıcı sisteme çatı denir. Belirli aralıklarla yerleştirilen çatı makaslarının, yatay taşıyıcı eleman olan aşıklarla birleştirilmesi ile
ÇATI MAKASINA GELEN YÜKLER Bir yapıyı dış etkilere karşı koruyan taşıyıcı sisteme çatı denir. Belirli aralıklarla yerleştirilen çatı makaslarının, yatay taşıyıcı eleman olan aşıklarla birleştirilmesi ile
VECTOR MECHANICS FOR ENGINEERS: STATICS
 Seventh E 4 Equilibrium CHAPTER VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. of Rigid Bodies Lecture Notes: J. Walt Oler Texas Tech University Seventh E CHAPTER VECTOR
Seventh E 4 Equilibrium CHAPTER VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. of Rigid Bodies Lecture Notes: J. Walt Oler Texas Tech University Seventh E CHAPTER VECTOR
STATICS. Equivalent Systems of Forces VECTOR MECHANICS FOR ENGINEERS: Seventh Edition CHAPTER. Ferdinand P. Beer E. Russell Johnston, Jr.
 Seventh E 3 Rigid CHAPTER VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Lecture Notes: J. Walt Oler Teas Tech Universit Bodies: Equivalent Sstems of Forces Seventh
Seventh E 3 Rigid CHAPTER VECTOR MECHANICS FOR ENGINEERS: STATICS Ferdinand P. Beer E. Russell Johnston, Jr. Lecture Notes: J. Walt Oler Teas Tech Universit Bodies: Equivalent Sstems of Forces Seventh
Kesit Tesirleri Tekil Kuvvetler
 Statik ve Mukavemet Kesit Tesirleri Tekil Kuvvetler B ÖĞR.GÖR.GÜLTEKİN BÜYÜKŞENGÜR Çevre Mühendisliği Mukavemet Şekil Değiştirebilen Cisimler Mekaniği Kesit Tesiri ve İşaret Kabulleri Kesit Tesiri Diyagramları
Statik ve Mukavemet Kesit Tesirleri Tekil Kuvvetler B ÖĞR.GÖR.GÜLTEKİN BÜYÜKŞENGÜR Çevre Mühendisliği Mukavemet Şekil Değiştirebilen Cisimler Mekaniği Kesit Tesiri ve İşaret Kabulleri Kesit Tesiri Diyagramları
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 7 İç Kuvvetler Kaynak: Mühendislik Mekaniği: Statik, R. C. Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 7. İç Kuvvetler Bu bölümde, bir
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 7 İç Kuvvetler Kaynak: Mühendislik Mekaniği: Statik, R. C. Hibbeler, S. C. Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 7. İç Kuvvetler Bu bölümde, bir
Varsayımlar ve Tanımlar Tekil Yükleri Aktaran Kablolar Örnekler Yayılı Yük Aktaran Kablolar. 7.3 Yatayda Yayılı Yük Aktaran Kablolar
 7.1 7.2 Varsayımlar ve Tanımlar Tekil Yükleri Aktaran Kablolar Örnekler Yayılı Yük Aktaran Kablolar 7.3 Yatayda Yayılı Yük Aktaran Kablolar 7.4 Örnekler Kendi Ağırlığını Taşıyan Kablolar (Zincir Eğrisi)
7.1 7.2 Varsayımlar ve Tanımlar Tekil Yükleri Aktaran Kablolar Örnekler Yayılı Yük Aktaran Kablolar 7.3 Yatayda Yayılı Yük Aktaran Kablolar 7.4 Örnekler Kendi Ağırlığını Taşıyan Kablolar (Zincir Eğrisi)
Rijit Cisimlerin Dengesi
 Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Çerçeve ve Makineler
 Çerçeve ve Makineler Hedefler Mafsal (pim) ile tutturulmuş çerçeve ve makine elemanlarına etki eden kuvvetlerin analizi. Çerçeve ve Makineler Çok kuvvet elemanı içeren mafsal ile tutturulmuş yapılardır.
Çerçeve ve Makineler Hedefler Mafsal (pim) ile tutturulmuş çerçeve ve makine elemanlarına etki eden kuvvetlerin analizi. Çerçeve ve Makineler Çok kuvvet elemanı içeren mafsal ile tutturulmuş yapılardır.
İÇ KUVVETLER. Amaçlar: Bir elemanda kesit yöntemiyle iç kuvvetlerin bulunması Kesme kuvveti ve moment diyagramlarının çizilmesi
 İÇ KUVVELER maçlar: ir elemanda kesit yöntemiyle iç kuvvetlerin bulunması Kesme kuvveti ve moment diyagramlarının çizilmesi Yapısal elemanlarda oluşan iç kuvvetler ir yapısal veya mekanik elemanın tasarımı,
İÇ KUVVELER maçlar: ir elemanda kesit yöntemiyle iç kuvvetlerin bulunması Kesme kuvveti ve moment diyagramlarının çizilmesi Yapısal elemanlarda oluşan iç kuvvetler ir yapısal veya mekanik elemanın tasarımı,
İÇ KUVVETLER. Amaçlar: Bir elemanda kesit yöntemiyle iç kuvvetlerin bulunması Kesme kuvveti ve moment diyagramlarının çizilmesi
 İÇ KUVVETLER maçlar: ir elemanda kesit yöntemiyle iç kuvvetlerin bulunması Kesme kuvveti ve moment diyagramlarının çizilmesi Yapısal elemanlarda oluşan iç kuvvetler ir yapısal veya mekanik elemanın tasarımı,
İÇ KUVVETLER maçlar: ir elemanda kesit yöntemiyle iç kuvvetlerin bulunması Kesme kuvveti ve moment diyagramlarının çizilmesi Yapısal elemanlarda oluşan iç kuvvetler ir yapısal veya mekanik elemanın tasarımı,
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik ers Notları Sınav Soru ve Çözümleri ĞHN MÜHENİSİK MEKNİĞİ STTİK MÜHENİSİK MEKNİĞİ STTİK İÇİNEKİER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMERİ - İki Boutlu Kuvvet Sistemleri
Statik ers Notları Sınav Soru ve Çözümleri ĞHN MÜHENİSİK MEKNİĞİ STTİK MÜHENİSİK MEKNİĞİ STTİK İÇİNEKİER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMERİ - İki Boutlu Kuvvet Sistemleri
FLUID MECHANICS PRESSURE AND MOMENTUM FORCES A-PRESSURE FORCES. Example
 A-PRESSURE FORCES FLUID MECHANICS PRESSURE AND MOMENTUM FORCES Consider a duct as shown in figure. First identify the control volume on which to conduct a force balance. The inner passage is filled with
A-PRESSURE FORCES FLUID MECHANICS PRESSURE AND MOMENTUM FORCES Consider a duct as shown in figure. First identify the control volume on which to conduct a force balance. The inner passage is filled with
KUVVETLER VEKTÖRDÜR BU YÜZDEN CEBİRSEL VEKTÖR TEKNİKLERİ KULLANMALIYIZ
 Rijit Cisim Dengesi KUVVETLER VEKTÖRDÜR BU YÜZDEN CEBİRSEL VEKTÖR TEKNİKLERİ KULLANMALIYIZ KUVVET SİSTEMİ 2 B KUVVET SİSTEMLERİ Detaylar 1- KO-LİNEER 2- BİR NOKTADA BULUŞAN (KONKÜRENT) 3- PARALEL 4- GENEL
Rijit Cisim Dengesi KUVVETLER VEKTÖRDÜR BU YÜZDEN CEBİRSEL VEKTÖR TEKNİKLERİ KULLANMALIYIZ KUVVET SİSTEMİ 2 B KUVVET SİSTEMLERİ Detaylar 1- KO-LİNEER 2- BİR NOKTADA BULUŞAN (KONKÜRENT) 3- PARALEL 4- GENEL
KATI CİSİMLERİN BAĞIL İVME ANALİZİ:
 KATI CİSİMLERİN BAĞIL İVME ANALİZİ: Genel düzlemsel hareket yapmakta olan katı cisim üzerinde bulunan iki noktanın ivmeleri aralarındaki ilişki, bağıl hız v A = v B + v B A ifadesinin zamana göre türevi
KATI CİSİMLERİN BAĞIL İVME ANALİZİ: Genel düzlemsel hareket yapmakta olan katı cisim üzerinde bulunan iki noktanın ivmeleri aralarındaki ilişki, bağıl hız v A = v B + v B A ifadesinin zamana göre türevi
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 3 Parçacık Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 3 Parçacık Dengesi Bu bölümde,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 3 Parçacık Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 3 Parçacık Dengesi Bu bölümde,
Uzay Çatı Sistemlerinin ANSYS Paket Programı Kullanılarak Statik Analizi
 Fırat Üniv. Fen ve Müh. Bil. Der. Science and Eng. J of Fırat Univ. 18 (1), 105-112, 2006 18 (1), 105-112, 2006 Uzay Çatı Sistemlerinin ANSYS Paket Programı Kullanılarak Statik Analizi M. Yavuz SOLMAZ
Fırat Üniv. Fen ve Müh. Bil. Der. Science and Eng. J of Fırat Univ. 18 (1), 105-112, 2006 18 (1), 105-112, 2006 Uzay Çatı Sistemlerinin ANSYS Paket Programı Kullanılarak Statik Analizi M. Yavuz SOLMAZ
YAPI STATİĞİ II (Hiperstatik Sistemler) Yrd. Doç. Dr. Selçuk KAÇIN
 YAPI STATİĞİ II (Hiperstatik Sistemler) Yrd. Doç. Dr. Selçuk KAÇIN Yapı Sistemleri: İzostatik (Statikçe Belirli) Sistemler : Bir sistemin tüm kesit tesirlerini (iç kuvvetlerini) ve mesnet reaksiyonlarını
YAPI STATİĞİ II (Hiperstatik Sistemler) Yrd. Doç. Dr. Selçuk KAÇIN Yapı Sistemleri: İzostatik (Statikçe Belirli) Sistemler : Bir sistemin tüm kesit tesirlerini (iç kuvvetlerini) ve mesnet reaksiyonlarını
STATİK KUVVET ANALİZİ (2.HAFTA)
 STATİK KUVVET ANALİZİ (2.HAFTA) Mekanik sistemler üzerindeki kuvvetler denge halindeyse sistem hareket etmeyecektir. Sistemin denge hali için gerekli kuvvetlerin hesaplanması statik hesaplamalarla yapılır.
STATİK KUVVET ANALİZİ (2.HAFTA) Mekanik sistemler üzerindeki kuvvetler denge halindeyse sistem hareket etmeyecektir. Sistemin denge hali için gerekli kuvvetlerin hesaplanması statik hesaplamalarla yapılır.
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
Karabük Üniversitesi, Mühendislik Fakültesi...www.IbrahimCayiroglu.com. STATİK (3. Hafta)
 TAŞIYICI SİSTEMLER VE MESNET TEPKİLERİ STATİK (3. Hafta) Taşıyıcı Sistemler Bir yapıya etki eden çeşitli kuvvetleri güvenlik sınırları içinde taşıyan ve bu kuvvetleri zemine aktaran sistemlere taşıyıcı
TAŞIYICI SİSTEMLER VE MESNET TEPKİLERİ STATİK (3. Hafta) Taşıyıcı Sistemler Bir yapıya etki eden çeşitli kuvvetleri güvenlik sınırları içinde taşıyan ve bu kuvvetleri zemine aktaran sistemlere taşıyıcı
KUVVET, MOMENT ve DENGE
 2.1. Kuvvet 2.1.1. Kuvvet ve cisimlere etkileri Kuvvetler vektörel büyüklüklerdir. Kuvvet vektörünün; uygulama noktası, kuvvetin cisme etkidiği nokta; doğrultu ve yönü, kuvvetin doğrultu ve yönü; modülüyse
2.1. Kuvvet 2.1.1. Kuvvet ve cisimlere etkileri Kuvvetler vektörel büyüklüklerdir. Kuvvet vektörünün; uygulama noktası, kuvvetin cisme etkidiği nokta; doğrultu ve yönü, kuvvetin doğrultu ve yönü; modülüyse
Rijit Cisimlerin Dengesi
 Rijit Cisimlerin Dengesi 1 Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Rijit Cisimlerin Dengesi 1 Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Gerilme Dönüşümleri (Stress Transformation)
 Gerilme Dönüşümleri (Stress Transformation) Bu bölümde, bir noktaya etkiyen ve bir koordinat ekseni ile ilişkili gerilme bileşenlerini, başka bir koordinat sistemi ile ilişkili gerilme bileşenlerine dönüştürmek
Gerilme Dönüşümleri (Stress Transformation) Bu bölümde, bir noktaya etkiyen ve bir koordinat ekseni ile ilişkili gerilme bileşenlerini, başka bir koordinat sistemi ile ilişkili gerilme bileşenlerine dönüştürmek
MKM 308 Makina Dinamiği. Eşdeğer Noktasal Kütleler Teorisi
 MKM 308 Eşdeğer Noktasal Kütleler Teorisi Eşdeğer Noktasal Kütleler Teorisi Maddesel Nokta (Noktasal Kütleler) : Mekanikte her cisim zihnen maddesel noktalara ayrılabilir yani noktasal kütlelerden meydana
MKM 308 Eşdeğer Noktasal Kütleler Teorisi Eşdeğer Noktasal Kütleler Teorisi Maddesel Nokta (Noktasal Kütleler) : Mekanikte her cisim zihnen maddesel noktalara ayrılabilir yani noktasal kütlelerden meydana
FIRAT ÜNĐ. MÜHENDĐSLĐK FAK. ĐNŞAAT MÜH. BÖLÜMÜ 2009-2010 Güz ĐMÜ-413 Bilgisayar Destekli Boyutlandırma Arasınav (13 Kasım 2009) No: Adı Soyadı: Đmza:
 FIRAT ÜNĐ. MÜHENDĐSLĐK FAK. ĐNŞAAT MÜH. BÖLÜMÜ 29-21 Güz ĐMÜ-413 Bilgisayar Destekli Boyutlandırma Arasınav (13 Kasım 29) No: Adı Soyadı: Đmza: Şekilde verilmiş olan düzlem kafes sistemin, a. (5 p.) Serbestlik
FIRAT ÜNĐ. MÜHENDĐSLĐK FAK. ĐNŞAAT MÜH. BÖLÜMÜ 29-21 Güz ĐMÜ-413 Bilgisayar Destekli Boyutlandırma Arasınav (13 Kasım 29) No: Adı Soyadı: Đmza: Şekilde verilmiş olan düzlem kafes sistemin, a. (5 p.) Serbestlik
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ
 RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
RİJİT CİSİMLERİN DÜZLEMSEL KİNEMATİĞİ MUTLAK GENEL DÜZLEMSEL HAREKET: Genel düzlemsel hareket yapan bir karı cisim öteleme ve dönme hareketini eşzamanlı yapar. Eğer cisim ince bir levha olarak gösterilirse,
Rijit Cisimlerin Dengesi
 Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Rijit Cisimlerin Dengesi Rijit Cisimlerin Dengesi Bu bölümde, rijit cisim dengesinin temel kavramları ele alınacaktır: Rijit cisimler için denge denklemlerinin oluşturulması Rijit cisimler için serbest
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 5 Rijit Cisim Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 5. Rijit Cisim Dengesi Denge,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 5 Rijit Cisim Dengesi Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 5. Rijit Cisim Dengesi Denge,
Hiperstatik sistemlerin çözümünde, yer değiştirmelerin küçük olduğu ve gerilme - şekil değiştirme bağıntılarının lineer olduğu kabul edilmektedir.
 1. HİPERSTATİK SİSTEMLER 1.1. Giriş Bir sistemin hesabının amacı, dış etkilerden meydana gelen kesit tesirlerini, şekil değiştirmelerini ve yer değiştirmelerini belirlemektir. İzostatik sistemlerde, yalnız
1. HİPERSTATİK SİSTEMLER 1.1. Giriş Bir sistemin hesabının amacı, dış etkilerden meydana gelen kesit tesirlerini, şekil değiştirmelerini ve yer değiştirmelerini belirlemektir. İzostatik sistemlerde, yalnız
Gerilme Dönüşümleri (Stress Transformation)
 Gerilme Dönüşümleri (Stress Transformation) Bubölümdebirnoktayaetkiyen vebelli bir koordinat ekseni/düzlemi ile ilişkili gerilme bileşenlerini, başka bir koordinat sistemi/başka bir düzlem ile ilişkili
Gerilme Dönüşümleri (Stress Transformation) Bubölümdebirnoktayaetkiyen vebelli bir koordinat ekseni/düzlemi ile ilişkili gerilme bileşenlerini, başka bir koordinat sistemi/başka bir düzlem ile ilişkili
YAPISAL ANALİZ YRD.DOÇ.DR. KAMİLE TOSUN FELEKOĞLU
 YAPISAL ANALİZ YRD.DOÇ.DR. KAMİLE TOSUN FELEKOĞLU 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla
YAPISAL ANALİZ YRD.DOÇ.DR. KAMİLE TOSUN FELEKOĞLU 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 2 Kuvvet Vektörleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö.Soyuçok. 2 Kuvvet Vektörleri Bu bölümde,
STATIK VE MUKAVEMET. 6.Düzlem ve Uzay kafes Sistemler. Doç. Dr. NURHAYAT DEĞİRMENCİ
 STATIK VE MUKAVEMET 6.Düzlem ve Uzay kafes Sistemler Doç. Dr. NURHAYAT DEĞİRMENCİ Birbirlerine bağlı birden fazla parçadan yapılmış sistemlerin dengesi için dıs kuvvetlere ilaveten iç kuvvetler de düşünülmelidir.
STATIK VE MUKAVEMET 6.Düzlem ve Uzay kafes Sistemler Doç. Dr. NURHAYAT DEĞİRMENCİ Birbirlerine bağlı birden fazla parçadan yapılmış sistemlerin dengesi için dıs kuvvetlere ilaveten iç kuvvetler de düşünülmelidir.
DENEY-4 WHEATSTONE KÖPRÜSÜ VE DÜĞÜM GERİLİMLERİ YÖNTEMİ
 DENEY- WHEATSTONE KÖPÜSÜ VE DÜĞÜM GEİLİMLEİ YÖNTEMİ Deneyin Amacı: Wheatson köprüsünün anlaşılması, düğüm gerilimi ile dal gerilimi arasındaki ilişkinin incelenmesi. Kullanılan Alet-Malzemeler: a) DC güç
DENEY- WHEATSTONE KÖPÜSÜ VE DÜĞÜM GEİLİMLEİ YÖNTEMİ Deneyin Amacı: Wheatson köprüsünün anlaşılması, düğüm gerilimi ile dal gerilimi arasındaki ilişkinin incelenmesi. Kullanılan Alet-Malzemeler: a) DC güç
q = 48 kn/m q = 54 kn/m 4 m 5 m 3 m 3 m
 Soru 1) (50 Puan) şağıda verilen sistemin üzerine etkiyen yükler ve konumları şekil üzerinde belirtilmiştir. una ek olarak mesneti cm aşağı yönlü oturmuştur. Tüm kolon ve kirişlerin atalet momenti, elastik
Soru 1) (50 Puan) şağıda verilen sistemin üzerine etkiyen yükler ve konumları şekil üzerinde belirtilmiştir. una ek olarak mesneti cm aşağı yönlü oturmuştur. Tüm kolon ve kirişlerin atalet momenti, elastik
Mukavemet. Betonarme Yapılar. İç Kuvvet Diyagramları. Dr. Haluk Sesigür İ.T.Ü. Mimarlık Fakültesi Yapı ve Deprem Mühendisliği
 Betonarme Yapılar Dr. Haluk Sesigür İ.T.Ü. Mimarlık Fakültesi Yapı ve Deprem Mühendisliği KİRİŞ MESNETLENME TİPLERİ VE YÜKLER KİRİŞ MESNETLENME TİPLERİ VE YÜKLER (a) Basit kiriş (b) Sürekli kiriş (c) Konsol
Betonarme Yapılar Dr. Haluk Sesigür İ.T.Ü. Mimarlık Fakültesi Yapı ve Deprem Mühendisliği KİRİŞ MESNETLENME TİPLERİ VE YÜKLER KİRİŞ MESNETLENME TİPLERİ VE YÜKLER (a) Basit kiriş (b) Sürekli kiriş (c) Konsol
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve Çöümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki Boutlu
Statik Ders Notları Sınav Soru ve Çöümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLER 1. GİRİŞ - Skalerler ve Vektörler - Newton Kanunları 2. KUVVET SİSTEMLERİ - İki Boutlu
4. Sonlu elemanlar yer değiştirme metodu, modelleme, tanımlar
 4. Sonlu Elemanlar Yer Değiştirme Metodu modelleme tanımlar 4. Sonlu elemanlar yer değiştirme metodu modelleme tanımlar. bölümde örneklerle açıklanan RITZ metodu.5. ve.5 bağıntıları yerine kullanılabilen
4. Sonlu Elemanlar Yer Değiştirme Metodu modelleme tanımlar 4. Sonlu elemanlar yer değiştirme metodu modelleme tanımlar. bölümde örneklerle açıklanan RITZ metodu.5. ve.5 bağıntıları yerine kullanılabilen
ihmal edilmeyecektir.
 q h q q h h q q q y z L 2 x L 1 L 1 L 2 Kolon Perde y x L 1 L 1 L 1 = 6.0 m L 2 = 4.0 m h= 3.0 m q= 50 kn (deprem) tüm kirişler üzerinde 8 kn/m lik düzgün yayılı yük (ölü), tüm döşemeler üzerinde 3 kn/m
q h q q h h q q q y z L 2 x L 1 L 1 L 2 Kolon Perde y x L 1 L 1 L 1 = 6.0 m L 2 = 4.0 m h= 3.0 m q= 50 kn (deprem) tüm kirişler üzerinde 8 kn/m lik düzgün yayılı yük (ölü), tüm döşemeler üzerinde 3 kn/m
2. KUVVET SİSTEMLERİ 2.1 Giriş
 2. KUVVET SİSTEMLERİ 2.1 Giriş Kuvvet: Şiddet (P), doğrultu (θ) ve uygulama noktası (A) ile karakterize edilen ve bir cismin diğerine uyguladığı itme veya çekme olarak tanımlanabilir. Bu parametrelerden
2. KUVVET SİSTEMLERİ 2.1 Giriş Kuvvet: Şiddet (P), doğrultu (θ) ve uygulama noktası (A) ile karakterize edilen ve bir cismin diğerine uyguladığı itme veya çekme olarak tanımlanabilir. Bu parametrelerden
Elemanlardaki İç Kuvvetler
 Elemanlardaki İç Kuvvetler Bölüm Öğrenme Çıktıları Yapı elemanlarında oluşan iç kuvvetler. Eksenel kuvvet, Kesme kuvvet ve Eğilme Momenti Denklemleri ve Diyagramları. Bölüm Öğrenme Çıktıları Elemanlarda
Elemanlardaki İç Kuvvetler Bölüm Öğrenme Çıktıları Yapı elemanlarında oluşan iç kuvvetler. Eksenel kuvvet, Kesme kuvvet ve Eğilme Momenti Denklemleri ve Diyagramları. Bölüm Öğrenme Çıktıları Elemanlarda
3B Kuvvet Momenti. Üç Boyutlu Kuvvet Sistemi
 3B Kuvvet Momenti Üç Boyutlu Kuvvet Sistemi M = r (vektör) X F (vektör) Her F kuvvetinin uzunluk r vektörünü bul Eğer verilmemişse, F kuvvetini de vektörel ifade et. Uzunluk vektörünü r bulmak için: Uzunlık
3B Kuvvet Momenti Üç Boyutlu Kuvvet Sistemi M = r (vektör) X F (vektör) Her F kuvvetinin uzunluk r vektörünü bul Eğer verilmemişse, F kuvvetini de vektörel ifade et. Uzunluk vektörünü r bulmak için: Uzunlık
DÜZLEMDE GERİLME DÖNÜŞÜMLERİ
 3 DÜZLEMDE GERİLME DÖNÜŞÜMLERİ Gerilme Kavramı Dış kuvvetlerin etkisi altında dengedeki elastik bir cismi matematiksel bir yüzeyle rasgele bir noktadan hayali bir yüzeyle ikiye ayıracak olursak, F 3 F
3 DÜZLEMDE GERİLME DÖNÜŞÜMLERİ Gerilme Kavramı Dış kuvvetlerin etkisi altında dengedeki elastik bir cismi matematiksel bir yüzeyle rasgele bir noktadan hayali bir yüzeyle ikiye ayıracak olursak, F 3 F
VECTOR MECHANICS FOR ENGINEERS: STATICS
 Seventh Edition VECTOR MECHANICS FOR ENGINEERS: STATICS Fedinand P. Bee E. Russell Johnston, J. Des Notu: Hayi ACAR İstanbul Teknik Üniveistesi Tel: 285 31 46 / 116 E-mail: acah@itu.edu.t Web: http://atlas.cc.itu.edu.t/~acah
Seventh Edition VECTOR MECHANICS FOR ENGINEERS: STATICS Fedinand P. Bee E. Russell Johnston, J. Des Notu: Hayi ACAR İstanbul Teknik Üniveistesi Tel: 285 31 46 / 116 E-mail: acah@itu.edu.t Web: http://atlas.cc.itu.edu.t/~acah
GERİLME Cismin kesilmiş alanı üzerinde O
 GERİLME Cismin kesilmiş alanı üzerinde O ile tanımlı noktasına etki eden kuvvet ve momentin kesit alana etki eden gerçek yayılı yüklerin bileşke etkisini temsil ettiği ifade edilmişti. Cisimlerin mukavemeti
GERİLME Cismin kesilmiş alanı üzerinde O ile tanımlı noktasına etki eden kuvvet ve momentin kesit alana etki eden gerçek yayılı yüklerin bileşke etkisini temsil ettiği ifade edilmişti. Cisimlerin mukavemeti
Denk Kuvvet Sistemleri
 Denk Kuvvet Sistemleri TEK KUVVETİN DENK KUVVET SİSTEMİ Hareket eden bir kuvvetin etkisi. 1. KUVVETİN KENDİ ETKİ ÇİZGİSİ ÜZERİNDE AKTARILMASI. 2. KUVVETİN KENDİ ETKİ ÇİZGİSİ DIŞINA AKTARILMASI. Denk Kuvvet
Denk Kuvvet Sistemleri TEK KUVVETİN DENK KUVVET SİSTEMİ Hareket eden bir kuvvetin etkisi. 1. KUVVETİN KENDİ ETKİ ÇİZGİSİ ÜZERİNDE AKTARILMASI. 2. KUVVETİN KENDİ ETKİ ÇİZGİSİ DIŞINA AKTARILMASI. Denk Kuvvet
Doç. Dr. Muhammet Cerit Öğretim Üyesi Makine Mühendisliği Bölümü (Mekanik Ana Bilim Dalı) Elektronik posta ( ):
 Tanışma ve İletişim... Doç. Dr. Muhammet Cerit Öğretim Üyesi Makine Mühendisliği Bölümü (Mekanik Ana Bilim Dalı) Elektronik posta (e-mail): mcerit@sakarya.edu.tr Öğrenci Başarısı Değerlendirme... Öğrencinin
Tanışma ve İletişim... Doç. Dr. Muhammet Cerit Öğretim Üyesi Makine Mühendisliği Bölümü (Mekanik Ana Bilim Dalı) Elektronik posta (e-mail): mcerit@sakarya.edu.tr Öğrenci Başarısı Değerlendirme... Öğrencinin
Örnek 1 (Virtüel iş çözümü için; Bakınız : Ders Notu Sayfa 23 - Örnek 4)
 Örnek 1 (Virtüel iş çözümü için; Bakınız : Ders Notu Sayfa 23 - Örnek 4) Şekil 1.1. İzostatik sistem EA GA 0, EI = 2.10 4 knm 2, E = 2.10 8, t =10-5 1/, h =60cm (taşıyıcı eleman yüksekliği, her yerde)
Örnek 1 (Virtüel iş çözümü için; Bakınız : Ders Notu Sayfa 23 - Örnek 4) Şekil 1.1. İzostatik sistem EA GA 0, EI = 2.10 4 knm 2, E = 2.10 8, t =10-5 1/, h =60cm (taşıyıcı eleman yüksekliği, her yerde)
STATİK MÜHENDİSLİK MEKANİĞİ. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN. Behcet DAĞHAN
 Statik Ders Notları Sınav Soru ve Çözümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLE 1. GİİŞ - Skalerler ve ektörler - Newton Kanunları 2. KUET SİSTEMLEİ - İki Boyutlu
Statik Ders Notları Sınav Soru ve Çözümleri DAĞHAN MÜHENDİSLİK MEKANİĞİ STATİK MÜHENDİSLİK MEKANİĞİ STATİK İÇİNDEKİLE 1. GİİŞ - Skalerler ve ektörler - Newton Kanunları 2. KUET SİSTEMLEİ - İki Boyutlu
Mesnetler A, B ve C noktalarõ şekildeki gibi Z doğrultusunda mesnetlenmiş (sabitlenmiş) tir.
 Problem M X-Y Düzleminde A Noktasında Dönebilen Düz Plak Beton E =3600 ksi, Poisson Oranõ= 0.2 Mevcut Serbestlikler UZ, RX, RY Mesnetler A, B ve C noktalarõ şekildeki gibi Z doğrultusunda mesnetlenmiş
Problem M X-Y Düzleminde A Noktasında Dönebilen Düz Plak Beton E =3600 ksi, Poisson Oranõ= 0.2 Mevcut Serbestlikler UZ, RX, RY Mesnetler A, B ve C noktalarõ şekildeki gibi Z doğrultusunda mesnetlenmiş
Mukavemet. Betonarme Yapılar. İç Kuvvet Diyagramları. Dr. Haluk Sesigür İ.T.Ü. Mimarlık Fakültesi Yapı ve Deprem Mühendisliği
 Betonarme Yapılar Dr. Haluk Sesigür İ.T.Ü. Mimarlık Fakültesi Yapı ve Deprem Mühendisliği KİRİŞ MESNETLENME TİPLERİ VE YÜKLER KİRİŞ MESNETLENME TİPLERİ VE YÜKLER (a) Basit kiriş (b) Sürekli kiriş (c) Konsol
Betonarme Yapılar Dr. Haluk Sesigür İ.T.Ü. Mimarlık Fakültesi Yapı ve Deprem Mühendisliği KİRİŞ MESNETLENME TİPLERİ VE YÜKLER KİRİŞ MESNETLENME TİPLERİ VE YÜKLER (a) Basit kiriş (b) Sürekli kiriş (c) Konsol
6. Sistemin toplam potansiyeli, rijitlik matrisi ve kurulması
 6 Sistemin toplam potansiyeli, rijitlik matrisi ve kurulması 6 Sistemin noktalarında süreklilik koşulu : Her elemanın düğüm noktası aynı zamanda sistemin de düğüm noktası olduğundan, sistemin noktaları
6 Sistemin toplam potansiyeli, rijitlik matrisi ve kurulması 6 Sistemin noktalarında süreklilik koşulu : Her elemanın düğüm noktası aynı zamanda sistemin de düğüm noktası olduğundan, sistemin noktaları
Basit Kafes Sistemler
 YAPISAL ANALİZ 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla kullanılan ahşap gergi elemanları
YAPISAL ANALİZ 1 Basit Kafes Sistemler Kafes sistemler uç noktalarından birleştirilmiş narin elemanlardan oluşan yapılardır. Bu narin elemanlar, yapısal sistemlerde sıklıkla kullanılan ahşap gergi elemanları
Saf Eğilme(Pure Bending)
 Saf Eğilme(Pure Bending) Saf Eğilme (Pure Bending) Bu bölümde doğrusal, prizmatik, homojen bir elemanın eğilme etkisi altındaki şekil değiştirmesini/ deformasyonları incelenecek. Burada çıkarılacak formüller
Saf Eğilme(Pure Bending) Saf Eğilme (Pure Bending) Bu bölümde doğrusal, prizmatik, homojen bir elemanın eğilme etkisi altındaki şekil değiştirmesini/ deformasyonları incelenecek. Burada çıkarılacak formüller
δ / = P L A E = [+35 kn](0.75 m)(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir.
(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir. δ / = P L A E = [+35 kn](0.75 m)(10 ) = mm Sonuç pozitif olduğundan çubuk uzayacak ve A noktası yukarı doğru yer değiştirecektir.](/thumbs/68/59308868.jpg) A-36 malzemeden çelik çubuk, şekil a gösterildiği iki kademeli olarak üretilmiştir. AB ve BC kesitleri sırasıyla A = 600 mm ve A = 1200 mm dir. A serbest ucunun ve B nin C ye göre yer değiştirmesini belirleyiniz.
A-36 malzemeden çelik çubuk, şekil a gösterildiği iki kademeli olarak üretilmiştir. AB ve BC kesitleri sırasıyla A = 600 mm ve A = 1200 mm dir. A serbest ucunun ve B nin C ye göre yer değiştirmesini belirleyiniz.
MUKAVEMET I ÇÖZÜMLÜ ÖRNEKLER
 MUKAEMET I ÇÖZÜMÜ ÖRNEKER ders notu Yard. Doç. Dr. Erdem DAMCI Şubat 15 Mukavemet I - Çözümlü Örnekler / 7 Örnek 1. Üzerinde yalnızca yayılı yük bulunan ve açıklığı olan bir basit kirişe ait eğilme momenti
MUKAEMET I ÇÖZÜMÜ ÖRNEKER ders notu Yard. Doç. Dr. Erdem DAMCI Şubat 15 Mukavemet I - Çözümlü Örnekler / 7 Örnek 1. Üzerinde yalnızca yayılı yük bulunan ve açıklığı olan bir basit kirişe ait eğilme momenti
YAPI MÜHENDİSLİĞİ BİLGİSAYAR UYGULAMALARI
 YÜZÜNCÜ YIL ÜNİVERSİTESİ MÜHENDİSLİK MİMARLIK FAKÜLTESİ İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ YAPI MÜHENDİSLİĞİ BİLGİSAYAR UYGULAMALARI Yrd. Doç. Dr. Barış Erdil YAPI MÜHENDİSLİĞİ NEDİR? STRUCTURAL ENGINEERING IS
YÜZÜNCÜ YIL ÜNİVERSİTESİ MÜHENDİSLİK MİMARLIK FAKÜLTESİ İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ YAPI MÜHENDİSLİĞİ BİLGİSAYAR UYGULAMALARI Yrd. Doç. Dr. Barış Erdil YAPI MÜHENDİSLİĞİ NEDİR? STRUCTURAL ENGINEERING IS
Kirişlerde İç Kuvvetler
 Kirişlerde İç Kuvvetler B noktasındaki iç kuvvetlerin bulunması B noktasındaki iç kuvvetler sol ve sağ parça İki boyutlu problemlerde eleman kesitinde üç farklı iç kuvvet oluşur! 2D 3D Pozitif normal/eksenel
Kirişlerde İç Kuvvetler B noktasındaki iç kuvvetlerin bulunması B noktasındaki iç kuvvetler sol ve sağ parça İki boyutlu problemlerde eleman kesitinde üç farklı iç kuvvet oluşur! 2D 3D Pozitif normal/eksenel
BURSA TEKNİK ÜNİVERSİTESİ DOĞA BİLİMLERİ, MİMARLIK VE MÜHENDİSLİK FAKÜLTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ 3 NOKTA EĞME DENEYİ FÖYÜ
 BURSA TEKNİK ÜNİVERSİTESİ DOĞA BİLİMLERİ, MİMARLIK VE MÜHENDİSLİK FAKÜLTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ 3 NOKTA EĞME DENEYİ FÖYÜ BURSA - 2016 1. GİRİŞ Eğilme deneyi malzemenin mukavemeti hakkında tasarım
BURSA TEKNİK ÜNİVERSİTESİ DOĞA BİLİMLERİ, MİMARLIK VE MÜHENDİSLİK FAKÜLTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ 3 NOKTA EĞME DENEYİ FÖYÜ BURSA - 2016 1. GİRİŞ Eğilme deneyi malzemenin mukavemeti hakkında tasarım
Mühendislik Mekaniği Statik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 4 Kuvvet Sistemi Bileşkeleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 4. Kuvvet Sitemi Bileşkeleri
Mühendislik Mekaniği Statik Yrd.Doç.Dr. Akın Ataş Bölüm 4 Kuvvet Sistemi Bileşkeleri Kaynak: Mühendislik Mekaniği: Statik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok. 4. Kuvvet Sitemi Bileşkeleri
MÜHENDİSLİK MEKANİĞİ (STATİK)
 MÜHENDİSLİK MEKANİĞİ (STATİK) Prof. Dr. Metin OLGUN Ankara Üniversitesi Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü HAFTA KONU 1 Giriş, temel kavramlar, statiğin temel ilkeleri 2-3 Düzlem kuvvetler
MÜHENDİSLİK MEKANİĞİ (STATİK) Prof. Dr. Metin OLGUN Ankara Üniversitesi Ziraat Fakültesi Tarımsal Yapılar ve Sulama Bölümü HAFTA KONU 1 Giriş, temel kavramlar, statiğin temel ilkeleri 2-3 Düzlem kuvvetler
Örnek 1 (Kuvvet yöntemi çözümü için Bakınız: Ders Notu Sayfa 52 - Örnek 4)
 Örnek 1 (Kuvvet yöntemi çözümü için Bakınız: Ders Notu Sayfa 52 - Örnek 4) 0.4 cm 0.6 cm 0.2 cm 1/1000 Şekil 1.1. Hiperstatik sistem EA GA 0, EI = 3.10 4 knm 2, E =4.25.10 8, t =10-5 1/, h =50cm (taşıyıcı
Örnek 1 (Kuvvet yöntemi çözümü için Bakınız: Ders Notu Sayfa 52 - Örnek 4) 0.4 cm 0.6 cm 0.2 cm 1/1000 Şekil 1.1. Hiperstatik sistem EA GA 0, EI = 3.10 4 knm 2, E =4.25.10 8, t =10-5 1/, h =50cm (taşıyıcı
MAK 308 MAKİNA DİNAMİĞİ Bahar Dr. Nurdan Bilgin
 MAK 308 MAKİNA DİNAMİĞİ 2017-2018 Bahar Dr. Nurdan Bilgin MAKİNALARDA KUVVET ANALİZİ Mekanizmalar, sadece kinematik özellikleri karşılamak üzere tasarlandıklarında, bir makinenin parçası olarak kullanıldığında
MAK 308 MAKİNA DİNAMİĞİ 2017-2018 Bahar Dr. Nurdan Bilgin MAKİNALARDA KUVVET ANALİZİ Mekanizmalar, sadece kinematik özellikleri karşılamak üzere tasarlandıklarında, bir makinenin parçası olarak kullanıldığında
25. SEM2015 programı ve kullanımı
 25. SEM2015 programı ve kullanımı Kuvvet metodu kullanılarak yazılmış, öğretim amaçlı, basit bir sonlu elemanlar statik analiz programdır. Program kısaca tanıtılacak, sonraki bölümlerde bu program ile
25. SEM2015 programı ve kullanımı Kuvvet metodu kullanılarak yazılmış, öğretim amaçlı, basit bir sonlu elemanlar statik analiz programdır. Program kısaca tanıtılacak, sonraki bölümlerde bu program ile
ÇALIŞMA SORULARI. Şekilde gösterildiği gibi yüklenmiş ankastre mesnetli kirişteki mesnet tepkilerini bulunuz.
 ÇALIŞMA SORULARI Üniform yoğunluğa sahip plaka 270 N ağırlığındadır ve A noktasından küresel mafsal ile duvara bağlanmıştır. Ayrıca duvara C ve D noktasından bağlanmış halatlarla desteklenmektedir. Serbest
ÇALIŞMA SORULARI Üniform yoğunluğa sahip plaka 270 N ağırlığındadır ve A noktasından küresel mafsal ile duvara bağlanmıştır. Ayrıca duvara C ve D noktasından bağlanmış halatlarla desteklenmektedir. Serbest
Burulma (Torsion): Dairesel Kesitli Millerde Gerilme ve Şekil Değiştirmeler
 Burulma (orsion): Dairesel Kesitli Millerde Gerilme ve Şekil Değiştirmeler Endüstiryel uygulamalarda en çok rastlanan yükleme tiplerinden birisi dairsel kesitli millere gelen burulma momentleridir. Burulma
Burulma (orsion): Dairesel Kesitli Millerde Gerilme ve Şekil Değiştirmeler Endüstiryel uygulamalarda en çok rastlanan yükleme tiplerinden birisi dairsel kesitli millere gelen burulma momentleridir. Burulma
MEKANİZMA TEKNİĞİ (3. HAFTA)
 MEKANİZMA TEKNİĞİ (3. HAFTA) STATİĞİN TEMEL İLKELERİ VE VEKTÖR MATEMATİĞİ Mekanik sistemler üzerindeki kuvvetler denge halindeyse sistem hareket etmeyecektir. Sistemin denge hali için gerekli kuvvetlerin
MEKANİZMA TEKNİĞİ (3. HAFTA) STATİĞİN TEMEL İLKELERİ VE VEKTÖR MATEMATİĞİ Mekanik sistemler üzerindeki kuvvetler denge halindeyse sistem hareket etmeyecektir. Sistemin denge hali için gerekli kuvvetlerin
23. Sistem denge denklemlerinin direkt kurulması
 . Sistem denge denklemlerinin direkt kurulması. Sistem denge denklemlerinin direkt kurulması Sonlu elemanlar metodu el hesapları için değil, bilgisayarda yazılımlar ile kullanılması için geliştirilmiştir.
. Sistem denge denklemlerinin direkt kurulması. Sistem denge denklemlerinin direkt kurulması Sonlu elemanlar metodu el hesapları için değil, bilgisayarda yazılımlar ile kullanılması için geliştirilmiştir.
STATİK. Ders_5. Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü. Ders notları için: GÜZ
 STATİK Ders_5 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2017-2018 GÜZ RİJİT CİSMİN DENGESİ VE SERBEST CİSİM DİYAGRAMI Bugünün Hedefleri:
STATİK Ders_5 Doç.Dr. İbrahim Serkan MISIR DEÜ İnşaat Mühendisliği Bölümü Ders notları için: http://kisi.deu.edu.tr/serkan.misir/ 2017-2018 GÜZ RİJİT CİSMİN DENGESİ VE SERBEST CİSİM DİYAGRAMI Bugünün Hedefleri:
Mühendislik Mekaniği Dinamik. Yrd.Doç.Dr. Akın Ataş
 Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 17 Rijit Cismin Düzlemsel Kinetiği; Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok.
Mühendislik Mekaniği Dinamik Yrd.Doç.Dr. Akın Ataş Bölüm 17 Rijit Cismin Düzlemsel Kinetiği; Kuvvet ve İvme Kaynak: Mühendislik Mekaniği: Dinamik, R.C.Hibbeler, S.C.Fan, Çevirenler: A. Soyuçok, Ö. Soyuçok.
EĞİLME. Köprünün tabyası onun eğilme gerilmesine karşı koyma dayanımı esas alınarak boyutlandırılır.
 EĞİLME Köprünün tabyası onun eğilme gerilmesine karşı koyma dayanımı esas alınarak boyutlandırılır. EĞİLME Mühendislikte en önemli yapı ve makine elemanları mil ve kirişlerdir. Bu bölümde, mil ve kirişlerde
EĞİLME Köprünün tabyası onun eğilme gerilmesine karşı koyma dayanımı esas alınarak boyutlandırılır. EĞİLME Mühendislikte en önemli yapı ve makine elemanları mil ve kirişlerdir. Bu bölümde, mil ve kirişlerde
SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering
 SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering İNM 212 YAPI STATİĞİ I STABİLİTE STATİKÇE BELİRSİZLİK KİNEMATİK BELİRSİZLİK Y.DOÇ.DR. MUSTAFA KUTANİS kutanis@sakarya.edu.tr
SAKARYA ÜNİVERSİTESİ MF İNŞAAT MÜHENDİSLİĞİ BÖLÜMÜ Department of Civil Engineering İNM 212 YAPI STATİĞİ I STABİLİTE STATİKÇE BELİRSİZLİK KİNEMATİK BELİRSİZLİK Y.DOÇ.DR. MUSTAFA KUTANİS kutanis@sakarya.edu.tr
Girdi kuvvetleri ile makinaya değişik biçimlerde uygulanan dış kuvvetler kastedilmektedir (input forces). Çıktı kuvvetleri ise elde edilen kuvvetleri
 ÇERÇEVELER Çerçeveler kafesler gibi genellikle sabit duran taşıyıcı sistemlerdir. Bir çerçeveyi kafesten ayıran en belirgin özellik, en az bir elemanının çok kuvvet elemanı (multi force member) oluşudur.
ÇERÇEVELER Çerçeveler kafesler gibi genellikle sabit duran taşıyıcı sistemlerdir. Bir çerçeveyi kafesten ayıran en belirgin özellik, en az bir elemanının çok kuvvet elemanı (multi force member) oluşudur.
STATIK MUKAVEMET. Doç. Dr. NURHAYAT DEĞİRMENCİ
 STATIK MUKAVEMET Doç. Dr. NURHAYAT DEĞİRMENCİ STATİK DENGE KOŞULLARI Yapı elemanlarının tasarımında bu elemanlarda oluşan iç kuvvetlerin dağılımının bilinmesi gerekir. Dış ve iç kuvvetlerin belirlenmesinde
STATIK MUKAVEMET Doç. Dr. NURHAYAT DEĞİRMENCİ STATİK DENGE KOŞULLARI Yapı elemanlarının tasarımında bu elemanlarda oluşan iç kuvvetlerin dağılımının bilinmesi gerekir. Dış ve iç kuvvetlerin belirlenmesinde
EEM211 ELEKTRİK DEVRELERİ-I
 EEM211 ELEKTRİK DEVRELERİ-I Prof. Dr. Selçuk YILDIRIM Siirt Üniversitesi Elektrik-Elektronik Mühendisliği Kaynak (Ders Kitabı): Fundamentals of Electric Circuits Charles K. Alexander Matthew N.O. Sadiku
EEM211 ELEKTRİK DEVRELERİ-I Prof. Dr. Selçuk YILDIRIM Siirt Üniversitesi Elektrik-Elektronik Mühendisliği Kaynak (Ders Kitabı): Fundamentals of Electric Circuits Charles K. Alexander Matthew N.O. Sadiku
MÜHENDİSLİK YAPILARI ÇERÇEVELER VE MAKİNALAR
 MÜHENDİSLİK YAPILARI ÇERÇEVELER VE MAKİNALAR ÇERÇEVELER Çerçeveler kafesler gibi genellikle sabit duran taşıyıcı sistemlerdir. Bir çerçeveyi kafesten ayıran en belirgin özellik, en az bir elemanının çok
MÜHENDİSLİK YAPILARI ÇERÇEVELER VE MAKİNALAR ÇERÇEVELER Çerçeveler kafesler gibi genellikle sabit duran taşıyıcı sistemlerdir. Bir çerçeveyi kafesten ayıran en belirgin özellik, en az bir elemanının çok
