İ Ç İ NDEKİ LER. Jeodezik Problemlerin Çözümünde Hesap.Makinelerinden Faydalanma Y. Müh. Nazmf YILDIZ
|
|
|
- Onur Çağrı
- 7 yıl önce
- İzleme sayısı:
Transkript
1 İ Ç İ NDEKİ LER Transformasyonlar ve uygulanması ~ Y. Müh. Burhan TANSÜĞ Sayfa 3 Kadastronun Yenilenmesi Müh. Şevket ARISOY 15 Jeodezik Problemlerin Çözümünde Hesap.Makinelerinden Faydalanma Y. Müh. Nazmf YILDIZ 3 Ölçülmüş Kabul Edilen Açılarla Şartlı Dengelemeye Dair Y. Müh. Muzaffer ŞERBETÇİ 5 4 Haberler
2 HURİM VE KADASTRO MÜHENDİSLİĞİ TMMOB Harita ve Kadastro Mühendisleri Odası tarafından dört ayda bir Ocak, Mayıs, Eylül aylarında yayınlanır. Sahibi : Harita ve Kadastro Mühendisleri Odası adma ' Başkan' M. Emin ERTÜRK -.», Çorumlu Müdür : Kadir PALA *, Yayın Kurulu. : Erkanli HÜSEYİN Erdoğan ÖRÜKLÜ Haldun ÖZEN Kadir PALA Ahmet YAŞAYAN yönetim ve Mü racaat yeri : Demirtepe - Sümer Sok. No : 12/2 Yenişehir - ANKARA Tel İ Piatı : 5 TL. Yıllık abonesi t 15 TL. Dizildiği ve Basıldığı yer : Güzel İstanbul Matbaası Ankara tlân tarifesi : Arka dış* kapak' 600 TL. On iç kapak = 500 TL... Arka iç kapak =450 TL. IS sahifeler = 400 TL. '. Yaran sahifeler = 250 TL., * 1/4 samfe ' 150 TL. Devamlı ilân verenlere % 20 indirim yapılır. H Yayınlanan bütün yazılara telif ve tercüme hakkı ödenir. % Gönderilen yazılar yayınlansın yayınlanmasın geri verilmez 0 Yazı ve ilânlardaki fikirler yazarlarına aittir. Odayı ve Dergiyi sorumlu kılmaz. 0 Çevirilerden doğacak hertürlü sorumluluk çevirene aittir. % Dergide yayınlanmak üzere gönderilen yazıların daktilo ile aeyrek satır olarak yazılması, şekillerin aydıngere çini mürekkeple çizilmesi, şekil yerlerinin belir tilmesi ve yazıların imzalanmış olarak iki nüsha gönderilmesi lâzımdır. Kısa yazılar tercih edilir..
3 Transformasyonlar ve Uygulanması Yazan : Y. Müh. Burhan TANSUĞ İ.Y.T.O. Öğretim Üyesi I Transformasyonun Genel Tarifi İ Transformasyon, koordinat değerlerinin belirli bir koordinat sisteminden diğer bir sisteme dönüşümüdür. Burada söz konusu edilen sistemler dik koordinat sistemleridir. Transformasyon, ı I Düzlem transformasyon II Uzay transformasyon olmak üzere iki şekilde ele alınabilir ve çözülebilir. Düzlem transformasyon, iki boyutlu sistemlerin; uzay transformasyon ise isminden de anlaşılacağı gibi üç boyutlu (x, y, z) sistemlerin dönüşümünde kullanılan bir metotdur. Düzlem transformasyon çözüm şekline göre; a)benzer veya Helmert transformasyonu b)afin transformasyonu c)konform transformasyon diye üçe ayrılır. Transformasyonların uygulanmasına değişik şekillerde rastlanmaktadır. Örneğin, ayni bir bölgede tesis edilmiş iki bağımsız nirengi ağının başlangıç değerlerinin ve semtlerinin farklı olması halinde sistemler arasında bir transformasyonla bütün sabit noktaların veya sınır noktalarının koordinatları ayni bir sisteme dönüştürülebilir. Bu sistemlerden biri memleket koordinat sisteminde (sağa, yukarı) olabilir. Daha sık rastlanan bir uygulama şekli de fotogrametridedir. Bilindiği gibi fotogrametride kullanılan koordinat sistemleri resim koordinatları, makina veya model koordinatları ve kolon koordinatlarıdır. Havadan alınmış bir resim çifti birinci sınıf bir kıymetlendirme aletine yerleştirilir. Ölçü markası işaretlenmiş (veya işaretlenmemiş) sınır noktalarına dikkatle oturtulur. Makina koordinatları okunur veya bir informasyon taşıyıcısına geçirilir. Elektronik bir hesap makinası yardımıyla bu değerler memleket koordinat sistemine dönüştürülür* Sonuç olarak bütün noktaların memleket koordinat değerleri elde edil-. a
4 miş olur. Kadastroda çok kullanılan ve nümerik kadastro ismi verilen bu çalışma metodu kıymetli arazilerde uygulanmakta ve ölçü hassasiyetini oldukça arttırmaktadır. Diğer bir uygulama şekli de bir stereokomparator aracılığı ile resim koordinatlarının okunması (1-2 p, m hassasiyetinde) ve bir uzay transformasyonla kolon koordinatlarına ve burdan ikinci bir uzay transformasyonla memleket koordinatlarına geçilmesidir. Pratikte değişik aşamalardan sonra ancak iterasyonlarla gerçekleştirilen ve oldukça uzun olan bu işleme analitik kıymetlendirme ismi verilmektedir. Bu yazıda uzay ve konform dönüşüm ele alınmayacak yalnız Helmert ve Afin transformasyon metotlarının çözümüne değinmekle yetinilecektir. 2 Transformasyonun matematik temelleri : > ; ıf Benzer Transformasyonlar: 1 Verilen iki koordinat sistemi x, y (örneğin makina koordinatlav ' n ) ve X/ Y (memleket koordinatları) eksenleriyle belirtelim. Sistem* ler evvelâ aynı yönlü olsunlar. (Şekil : 1) 4 Burada, C,, C 2 sistemlerin başlangıç farkları m sistemler arasındaki ölçek kat sayısı a sistemlerin dönüklüğü (semt farkı) ne tekabül etsin. Şekil 1 den faydalanarak aşağıdaki bağıntılar kolayca yazılabilir. X = d -j- m x cos a -f- m y sin a Y = C 2 -f-m y cosa m x sin«... (1)
5 m ve a bir dönüşüm için sabit kalacaklarından alınarak m cosa = a m sin«= b X = C! + ax + by Y= C 2 + ay bx... (2) yazılır. Eğer sistemler ters yönlü olsalardı, yani şekil 2 de görüldüğü gibi x ve i eksenlerinin yönleri birbirine karşıt olmasaydı (2) eşitliğinde x ve y yer değiştireceğinden, değişik kombinasyonlar için :, X = Cı + ay+bx Y = C 2 + ax^by...,... ( 3 ) * x = c ı + a y b x» * Y = C 2 + ax + by... (4) X = Q + ax by Y= C 2 + ay + bx... (5) eşitlikleri yazılabilir. (2) eşitliğinde C l7 C 2, a ve b olmak üzere dört bilinmeyen vardır. Bu demektir ki en az iki noktanın her iki sistemde de koordinatlarıyla verilmesi halinde bu iki bilinmeyenli iki denklem çözülebilir ve bilinmeyenler elde edilebilir. Fotogrametride olduğu gibi ikiden fazla koordinatlarıyla bilinen sabit noktaların mevcut olması halinde değişik sonuçlar elde edilir ki, bu bize bîr dengeleme imkânı sağlar. İlk hamlede Q ve C 2 den kurtulmak için ağırlık merkezlerine indirgenmiş koordinatlara geçelim. Ağırlık merkezine indirgenmiş koordinatları x'/ Y' ve x', y'; ağırlık merkezlerinin koordinatlarını ise x m 'Y m ve x rt 'ym '' e gösterirsek [Y] [,Xİ Y m = Xm C= n n [y] ' [x] n n yazabiliriz. Burada «n» koordinatlarıyla verilmiş sabit nokta sayısıdır. Ağırlık merkezine indirgenmiş koordinatlar, Y ', ' Y, Y Y' 2 = Y 2 Y m v ', v, v x ' 2==X2 Xm ı n = ' n»m X n : X" X"i ' ' 5
6 y'l = Yi '/m *'l = Xv-----X m y'a = ya y m x' 2 = x 2 x m.. Y n - Yn-----ym X n = X n X m hesaplanır ve teşkil edilen (2) eşitliğinde C u C 2 kaybolur ve X' = ax' + by f Y' = ay' bx'... (6) denklemleri bulunur. Hata denklemlerine geçilerek v xl =ax',+ by',-x', v y ı=.ay',-bx', Y', ' v xs = ax' 2 + by' 2 -x' 2 v y2 = a y' 2 b x' 2 Y' 2 ' * A xn = a x' n + b y'n x'n v yn = a y' n - b x' n Y' n 1 elde edilir... [v x v x ] + [v y v y ] nin minumum olabilmesi için bu ifadenin değişkenmiş gibi kabul edilen f a ve b ye göre türevlerinin sıfır olması gerekir. ' ' S S = o s s = 0 Jb cîb türevleri alındığında 2vxix', + 2vijx'j v yl y' 1 + 2v y2 y' =0 2v Jt ı/, + 2vx2y' v y1 xv 2 v y2 x' 2... =0.. (8) (7) yardımıyla (8) eşitlikleri teşkil edilir. [x' x'] a + [x' y'] b - [x' X'] + [y /] a [x' y] b - [/ Y'] = 0 [x' /] a + [y /] b [y X'] [x' y'] a + [x' x']-b + [x' Y'] =0 v e. _ E>c'X'] + [y'y'] _. [x'x'] + [/y'] ~ III [y'x'] [x'y'i II...(9) b = = - [x'x.'] + [y'y'] bulunur. ; 6 III
7 Eğer sistemler ters yönlü olsaydı _ [x' r] + [y x'] Cx'x'] + [//] [X' X'] - [y Y'] b = : [x x'] + [y y'] bulunacaktı. Son olarak...no) m = y a 2 + b 2... (11) ve '. ' " * b m sin a tga = = ,.(12), ' a m cos a * formülüyle ölçek kat sayısı ve dönüklük açısı hesaplanır-. Cı ve C 2 yi bulmak için (2) den faydalanılır. Cı = X m a x m b y m * * C 2 = Y m ay m + bx m... (13) Bu şekilde elde edilen bilinmeyenler ve (2) formülleri ile dönüştürme yapılır. Dönüştürülen yeni koordinat değerlerine X", Y" denerek, v x =X X", Vy = Y Y". hataları bulunur. En sonunda [V 2 y].+ [V 2 X ] " m 2 = : (14) 2(n 2) hakkında bilgi edi- formülüyle ortalama hata ve transformasyon sıhhati nilmiş olur. Fotdgrametrî pratiğinde çalışılan aletin makina koordinatları için kabul edilen pozitif yönlere göre kullanılacak formülleri seçmek mümkündür Afin Transformasyonu: izdüşüm geometrisinde afin izdüşüm paralel bir projeksiyonda izdüşüm düzlemlerinin paralel olmaması halidir. Ayni şekilde dönüşümü düşünülen sistemlerin bulundukları düzlemler afin iseler artık bir benzer transformasyon söz konusu olamaz. Bir üçgen ağının daha üst dereceff bir ağa bağlanması için en uygun dönüştürme afin transformasyonudur. '. 7
8 Afin transformasyonda kullanılan genel formül X = C, + a, x + b, y Y= C 2 + b2x + a 2 y...(15) dîr. Fakat biz ilerideki formül çıkarmalarında şekil benzerliği bakımından (15) yerine (5) e benzeyen bir eşitliği alacağız. X = C, + a ı x b,y Y= C 2 + b2x + a 2 y...(16) (15) ve (16) eşitliklerinde, afin durumdan dolayı a! ve a 2, bı ve b^ katsayıları farklıdırlar. Problemin çözülebilmesi ve izdüşümün tersinir olabilmesi için kolayca görüleceği gibi ** ~~J ^ 0 veya a, b 2 + a 2 b, 0 a 2 D 2» olması gerekir. (16) eşitliklerinde bilinmeyen sayısı altı tanedir. O halde çözüm için en az altı tane denkleme ihtiyaç vardır. Bu ise bir doğru üzerinde olmayan üç noktanın koordihatlarıyla verilmesi gerekir anlamına gelir. (Üçer noktası ile bilinen düzlemler) < Afin transformasyonda ölçek herbir doğrultu için ayrıdır. Doğrultunun yönü değiştikçe ölçek de değişir. Açı koruyan (konform) değildir. Açıların deformasyonu, açı kenarlarının doğrultusuna bağlıdır. Tepe noktasının konumuna bağlı değildir. Diğer taraftan afin transformasyonda, 1 Bir doğrunun izdüşümü gene bir doğrudur, 2 Paralel doğruların izdüşümleri gene paraleldir 3 Orijinal üçgenle izdüşürülen üçgenin yüzölçümleri arasındaki oran transformasyon detarmînantına eşittir 4 Armonik ve anormonîk bölüm aynen kalır Basit çözüm : Bilinmeyenlerin çözülmesi için evvela yalnız üç noktanın koordînatlanyla verildiğini varsayalım. (16) eşitliğinden faydalanarak, Xj = C, + a, x, b, y, X 2 = Q + aı x 2 b, y 2 X 3 ±= C, + a,x 3 b,y 3....;...(17) Y, = Q + b 2 x, + a 2 Yi Y 2 = Cj + b 2 x 2 -f a 2 y 2 Y 3 = C 2 + b 2 Xa + a 2 y 3 yazılır. Buradan da, 3 : '
9 $
10 10
11 ve ortalama hata için bulunur. y V X VX + VyVy (27) 2(n 3) Örnek: İ.Y.T.O. Fotogrametri Laboratuarında A 5 kıymetlendirme aletinde ayni resim çiftinde bilinen koordinat değerleri aşağıda verilen sabit noktalar yardımıyla Helmert ve Afin transformasyon hesapları ayrı ekipler tarafından yapılmış ve örnekleri ekli hesaplar sonucunda aşağıdaki ortalama hatalar elde edilmiştir. Not : Fotogrametride alınan bu örnek herhangibir keyfi sistem veya şehir sisteminin memleket nirengisine dönüşümü için düşünülebilir.), ' Verilen değerler: Resim boyutları 18x18 cm * Kamera sabitesi f = 114,06 Uçuş yüksekliği h = 2530 m Resim ölçeği 1/17000 Model ölçeği 1/5000 Resimler, oldukça düz bir arazi bahis konusu olduğundan Haliert / metoduyla cihetlendirilmiş ve resim koordinatları iki devirde ikişer defa yapılan okumaların ortalamasından alınmıştır. Transformasyon bilinmeyenlerinin hesabı dengelemeli olarak 4 nokta yardımıyla yapılmıştır. Beşinci noktası ve yeni alınan bir A, noktasının 8 koordinatları Helmert ve Afin formülleriyle, hesaplanarak kıyaslama yapılmıştır. Sabit noktaların koordinat değerleri : Nokta No. Y X h , ,25 413, , ,98 413, , ,84 412, , ,00 414, , ,86 415,41 Alette.okunan model koordinatları (Ortalama) Nokta No.. y f x^ h , ,51 414, , ,19 413, , ,37 413, , ,42 412, , ,13 414,60 A 5152, ,73 413,
12 Cetvel 1 de Helmert transformasyon (cetve! A 5 için hazırlanmıştır) işlemi yürütülmüş ve Helmert transformasyonu için ortalama hata m H rumuzuyla belirtilerek
13 _ J 4117 mn V = İ/T029 =+0,33 m bulunmuştur. 8 4 Cetvel 2 de Afin transformasyon bilinmeyenleri hesaplanmış ve ortalama, hata ITIA için Nokta Y X * A XA v y V* , , , , , , , , , , , , , , , , , , , , ~Â , ,18 nia V = ^/98 =+0,10 m bulunmuştur. 13
14 1942 numaralı noktanın koordinatlarında bulunan f y = 0,38 ve f x = 0,24 m lik fark sabit nokta tayinindeki tecviz sınırlarının içinde kalmaktadır, (1/5000 ölçekli kadastral - topoğrafik memleket haritaları standartları 2 Mart-17 Nisan 1962). İkinci bir ekip' tarafından ayni noktalar ve ayni modelde yapılan yeni bir ölçü ve hesapla m H = zt 0/^5 m m A = + 0,33 m bulunmuştur. %. L İ TERATÜR, İ Claus,. Z.f.V s/579 " 2 Merkel, Blass,. A.V.N JLehmaım,. Z.f.V s/ Lehmann, Z.f.V Szangoîies, K. Dre Arbeit mitdem Coordımeter. 6 Wolf, H. Ausglerehimg navh der Meth. der kleinsten Quadrate. s/442. DUYURU Odamız çalınma merkezi, satırı ahnan yeni daireye taşvnrm ttr. Her türlü yazışmaların bu adrese yapılması rica olunur. Yönetim Kurulu Yeni adresimiz :. TMM.0.B. ' Harita ve Kadastro Mühendisleri Odası Demirtepe - Sümer Sök'. No : 12/2 Tel: Yenişehir - Ankara U
BİLİNMEYENLİ ŞART DENKLEMLERİ VE EKSİK ÖLÇÜLÜ NİRENÇİ AÖLARI
 BİLİNMEYENLİ ŞART DENKLEMLERİ VE EKSİK ÖLÇÜLÜ NİRENÇİ AÖLARI Prof. Ekrem ULSOY».----İçlerinde bilinmeyenlerin bulunduğu şart denklemleri, dengeleme li- ^: terâtüründe dengelemenin.en genel şeklî olarak
BİLİNMEYENLİ ŞART DENKLEMLERİ VE EKSİK ÖLÇÜLÜ NİRENÇİ AÖLARI Prof. Ekrem ULSOY».----İçlerinde bilinmeyenlerin bulunduğu şart denklemleri, dengeleme li- ^: terâtüründe dengelemenin.en genel şeklî olarak
Fotogrametride işlem adımları
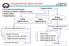 Fotogrametride işlem adımları Uçuş planının hazırlanması Arazide yer kontrol noktalarının tesisi Resim çekimi Değerlendirme Analitik değerlendirme Dijital değerlendirme Değerlendirme Analog değerlendirme
Fotogrametride işlem adımları Uçuş planının hazırlanması Arazide yer kontrol noktalarının tesisi Resim çekimi Değerlendirme Analitik değerlendirme Dijital değerlendirme Değerlendirme Analog değerlendirme
ÎÇÎNDEKÎLER. 1 : 500 Ölçekli Topografik Plânların Sıhhati... 3. Çevirem : Erdoğan ÖRÜKLÜ
 ÎÇÎNDEKÎLER Sayfa 1 : 500 Ölçekli Topografik Plânların Sıhhati... 3 Çevirem : Erdoğan ÖRÜKLÜ Münih Olimpiyat Tesislerinin Çatılarının Açınımlarının Çıkarılması... 16 Çeviren : Âlaellin MİMSİN Deformasyon
ÎÇÎNDEKÎLER Sayfa 1 : 500 Ölçekli Topografik Plânların Sıhhati... 3 Çevirem : Erdoğan ÖRÜKLÜ Münih Olimpiyat Tesislerinin Çatılarının Açınımlarının Çıkarılması... 16 Çeviren : Âlaellin MİMSİN Deformasyon
HARİTA VE KADASTRO MÜHENDİSLİĞİ
 HARİTA VE KADASTRO MÜHENDİSLİĞİ TMMOB Harita ve Kadastro Mühendisleri Odası tarafından üç ayda bir Ocak, Mayıs, Eylül aylarında yayınlanır. Sahibi : Harita ve Kadastro Mühendisleri Odası Adına Başkan M.
HARİTA VE KADASTRO MÜHENDİSLİĞİ TMMOB Harita ve Kadastro Mühendisleri Odası tarafından üç ayda bir Ocak, Mayıs, Eylül aylarında yayınlanır. Sahibi : Harita ve Kadastro Mühendisleri Odası Adına Başkan M.
Fotogrametrinin Optik ve Matematik Temelleri
 Fotogrametrinin Optik ve Matematik Temelleri Resim düzlemi O : İzdüşüm (projeksiyon ) merkezi P : Arazi noktası H : Asal nokta N : Nadir noktası c : Asal uzaklık H OH : Asal eksen (Alım ekseni) P OP :
Fotogrametrinin Optik ve Matematik Temelleri Resim düzlemi O : İzdüşüm (projeksiyon ) merkezi P : Arazi noktası H : Asal nokta N : Nadir noktası c : Asal uzaklık H OH : Asal eksen (Alım ekseni) P OP :
Fotogrametride Koordinat Sistemleri
 Fotogrametride Koordinat Sistemleri Komparator koordinat sistemi, Resim koordinat sistemi / piksel koordinat sistemi, Model veya çekim koordinat sistemi, Jeodezik koordinat sistemi 08 Ocak 2014 Çarşamba
Fotogrametride Koordinat Sistemleri Komparator koordinat sistemi, Resim koordinat sistemi / piksel koordinat sistemi, Model veya çekim koordinat sistemi, Jeodezik koordinat sistemi 08 Ocak 2014 Çarşamba
Fotogrametrinin Optik ve Matematik Temelleri
 Fotogrametrinin Optik ve Matematik Temelleri Resim düzlemi O : İzdüşüm (projeksiyon ) merkezi P : Arazi noktası H : Asal nokta N : Nadir noktası c : Asal uzaklık H OH : Asal eksen (Alım ekseni) P OP :
Fotogrametrinin Optik ve Matematik Temelleri Resim düzlemi O : İzdüşüm (projeksiyon ) merkezi P : Arazi noktası H : Asal nokta N : Nadir noktası c : Asal uzaklık H OH : Asal eksen (Alım ekseni) P OP :
Tanımlar, Geometrik ve Matemetiksel Temeller. Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ. JDF329 Fotogrametri I Ders Notu
 FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İzdüşüm merkezi(o):
FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İzdüşüm merkezi(o):
Yrd. Doç. Dr. Aycan M. MARANGOZ. BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF329 FOTOGRAMETRİ I DERSi NOTLARI
 FOTOGRAMETRİ I GEOMETRİK ve MATEMATİK TEMELLER Yrd. Doç. Dr. Aycan M. MARANGOZ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF329 FOTOGRAMETRİ I DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
FOTOGRAMETRİ I GEOMETRİK ve MATEMATİK TEMELLER Yrd. Doç. Dr. Aycan M. MARANGOZ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF329 FOTOGRAMETRİ I DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
Yrd. Doç. Dr. Aycan M. MARANGOZ. BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF329 FOTOGRAMETRİ I DERSi NOTLARI
 FOTOGRAMETRİ I GEOMETRİK ve MATEMATİK TEMELLER Yrd. Doç. Dr. Aycan M. MARANGOZ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF329 FOTOGRAMETRİ I DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
FOTOGRAMETRİ I GEOMETRİK ve MATEMATİK TEMELLER Yrd. Doç. Dr. Aycan M. MARANGOZ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF329 FOTOGRAMETRİ I DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
JEODEZİDE KULLANILAN KOORDİNATLAR, BUNLARIN BİRBİRLERİNE DÖNÜŞÜMLERİ ve PROJEKSİYON
 JEODEZİDE KULLANILAN KOORDİNATLAR, BUNLARIN BİRBİRLERİNE DÖNÜŞÜMLERİ ve PROJEKSİYON Ekrem ULSOY (İstanbul) I KOORDİNATLAR. Jeodezide koordinatlar, yer yüzündeki noktaların belirlenmesinde kullanılır. Bu
JEODEZİDE KULLANILAN KOORDİNATLAR, BUNLARIN BİRBİRLERİNE DÖNÜŞÜMLERİ ve PROJEKSİYON Ekrem ULSOY (İstanbul) I KOORDİNATLAR. Jeodezide koordinatlar, yer yüzündeki noktaların belirlenmesinde kullanılır. Bu
KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ
 KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ Doç. Dr. İsmail Hakkı GÜNEŞ İstanbul Teknik Üniversitesi ÖZET Küresel ve Elipsoidal koordinatların.karşılaştırılması amacı ile bir noktasında astronomik
KÜRESEL VE ELİPSOİDAL KOORDİNATLARIN KARŞİLAŞTİRİLMASİ Doç. Dr. İsmail Hakkı GÜNEŞ İstanbul Teknik Üniversitesi ÖZET Küresel ve Elipsoidal koordinatların.karşılaştırılması amacı ile bir noktasında astronomik
TOPOĞRAFYA Temel Ödevler / Poligonasyon
 TOPOĞRAFYA Temel Ödevler / Poligonasyon Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
TOPOĞRAFYA Temel Ödevler / Poligonasyon Yrd. Doç. Dr. Aycan M. MARANGOZ ÇEVRE MÜHENDİSLİĞİ BÖLÜMÜ JDF 264/270 TOPOĞRAFYA DERSİ NOTLARI http://geomatik.beun.edu.tr/marangoz http://jeodezi.karaelmas.edu.tr/linkler/akademik/marangoz/marangoz.htm
Projeksiyon Kavramı. Meridyenler ve paraleller eşitliklere göre düzleme aktarılır. 1) m : harita üzerinde paralelleri çizen yarıçap
 Projeksiyon Kavramı Meridyenler ve paraleller eşitliklere göre düzleme aktarılır. 1) m : harita üzerinde paralelleri çizen yarıçap ) α: harita üzerinde meridyenler arasındaki açıyı ifade eder. m = α =
Projeksiyon Kavramı Meridyenler ve paraleller eşitliklere göre düzleme aktarılır. 1) m : harita üzerinde paralelleri çizen yarıçap ) α: harita üzerinde meridyenler arasındaki açıyı ifade eder. m = α =
Bölüm-4. İki Boyutta Hareket
 Bölüm-4 İki Boyutta Hareket Bölüm 4: İki Boyutta Hareket Konu İçeriği 4-1 Yer değiştirme, Hız ve İvme Vektörleri 4-2 Sabit İvmeli İki Boyutlu Hareket 4-3 Eğik Atış Hareketi 4-4 Bağıl Hız ve Bağıl İvme
Bölüm-4 İki Boyutta Hareket Bölüm 4: İki Boyutta Hareket Konu İçeriği 4-1 Yer değiştirme, Hız ve İvme Vektörleri 4-2 Sabit İvmeli İki Boyutlu Hareket 4-3 Eğik Atış Hareketi 4-4 Bağıl Hız ve Bağıl İvme
JDF 242 JEODEZİK ÖLÇMELER 2. HAFTA DERS SUNUSU. Yrd. Doç. Dr. Hüseyin KEMALDERE
 JDF 242 JEODEZİK ÖLÇMELER 2. HAFTA DERS SUNUSU Yrd. Doç. Dr. Hüseyin KEMALDERE 3 boyutlu uzayda Jeoit Z Y X Dünyaya en uygun elipsoid modeli ve yer merkezli dik koordinat sistemi Ülkemizde 2005
JDF 242 JEODEZİK ÖLÇMELER 2. HAFTA DERS SUNUSU Yrd. Doç. Dr. Hüseyin KEMALDERE 3 boyutlu uzayda Jeoit Z Y X Dünyaya en uygun elipsoid modeli ve yer merkezli dik koordinat sistemi Ülkemizde 2005
NÎRENÇİ NOKTALARININ ARANMASI
 NÎRENÇİ NOKTALARININ ARANMASI Yazan ; -.. İsmail Hakkı GÜNEŞ 1, '. ' ' (Ankara) Haritaları yapılmış meskun ve meskun olmayan alanlarda bulunamıyan ve taşları kaybolan nirengilerin yeraltındaki sigorta
NÎRENÇİ NOKTALARININ ARANMASI Yazan ; -.. İsmail Hakkı GÜNEŞ 1, '. ' ' (Ankara) Haritaları yapılmış meskun ve meskun olmayan alanlarda bulunamıyan ve taşları kaybolan nirengilerin yeraltındaki sigorta
Nokta uzayda bir konumu belirtir. Noktanın 0 boyutlu olduğu kabul edilir. Herhangi bir büyüklüğü yoktur.
 Üç Boyutlu Geometri Nokta (Point,Vertex) Nokta uzayda bir konumu belirtir. Noktanın 0 boyutlu olduğu kabul edilir. Herhangi bir büyüklüğü yoktur. Kartezyen Koordinat Sistemi Uzayda bir noktayı tanımlamak
Üç Boyutlu Geometri Nokta (Point,Vertex) Nokta uzayda bir konumu belirtir. Noktanın 0 boyutlu olduğu kabul edilir. Herhangi bir büyüklüğü yoktur. Kartezyen Koordinat Sistemi Uzayda bir noktayı tanımlamak
ARAZİ ÖLÇMELERİ. İki Boyutlu Koordinat sistemleri Arası Dönüşüm
 İki Boyutlu Koordinat sistemleri Arası Dönüşüm Amaç, bir koordinat sistemine göre elde edilmiş olan koordinatların, diğer bir koordinat sistemindeki koordinat değerlerini elde etmektir. İki haritanın koordinat
İki Boyutlu Koordinat sistemleri Arası Dönüşüm Amaç, bir koordinat sistemine göre elde edilmiş olan koordinatların, diğer bir koordinat sistemindeki koordinat değerlerini elde etmektir. İki haritanın koordinat
Dik koordinat sisteminde yatay eksen x ekseni (apsis ekseni), düşey eksen ise y ekseni (ordinat ekseni) dir.
 ANALĐTĐK GEOMETRĐ 1. Analitik Düzlem Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da
ANALĐTĐK GEOMETRĐ 1. Analitik Düzlem Bir düzlemde dik kesişen iki sayı doğrusunun oluşturduğu sisteme analitik düzlem denir. Analitik düzlem, dik koordinat sistemi veya dik koordinat düzlemi olarak da
İSTANBUL DA FARKLI TARİHLERDE YAPILMIŞ DOĞALGAZ ALT YAPI HARİTALARININ DOĞRULUK YÖNÜNDEN BİR KARŞILAŞTIRMASI
 İSTANBUL DA FARKLI TARİHLERDE YAPILMIŞ DOĞALGAZ ALT YAPI HARİTALARININ DOĞRULUK YÖNÜNDEN BİR KARŞILAŞTIRMASI H. KURŞUN 1, Y. KALKAN 2 1 İstanbul Gaz Dağıtım Anonim Şirketi, Etüd Proje harita Müdürlüğü,İstanbul.
İSTANBUL DA FARKLI TARİHLERDE YAPILMIŞ DOĞALGAZ ALT YAPI HARİTALARININ DOĞRULUK YÖNÜNDEN BİR KARŞILAŞTIRMASI H. KURŞUN 1, Y. KALKAN 2 1 İstanbul Gaz Dağıtım Anonim Şirketi, Etüd Proje harita Müdürlüğü,İstanbul.
Math 322 Diferensiyel Denklemler Ders Notları 2012
 1 Genel Tanımlar Bir veya birden fazla fonksiyonun türevlerini içeren denklemlere diferensiyel denklem denmektedir. Diferensiyel denklemler Adi (Sıradan) diferensiyel denklemler ve Kısmi diferensiyel denklemler
1 Genel Tanımlar Bir veya birden fazla fonksiyonun türevlerini içeren denklemlere diferensiyel denklem denmektedir. Diferensiyel denklemler Adi (Sıradan) diferensiyel denklemler ve Kısmi diferensiyel denklemler
(m+2) +5<0. 7/m+3 + EŞİTSİZLİKLER A. TANIM
 EŞİTSİZLİKLER A. TANIM f(x)>0, f(x) - eşitsizliğinin
EŞİTSİZLİKLER A. TANIM f(x)>0, f(x) - eşitsizliğinin
KADASTRO HARİTALARININ SAYISALLAŞTIRILMASINDA KALİTE KONTROL ANALİZİ
 KADASTRO HARİTALARININ SAYISALLAŞTIRILMASINDA KALİTE KONTROL ANALİZİ Yasemin ŞİŞMAN, Ülkü KIRICI Sunum Akış Şeması 1. GİRİŞ 2. MATERYAL VE METHOD 3. AFİN KOORDİNAT DÖNÜŞÜMÜ 4. KALİTE KONTROL 5. İRDELEME
KADASTRO HARİTALARININ SAYISALLAŞTIRILMASINDA KALİTE KONTROL ANALİZİ Yasemin ŞİŞMAN, Ülkü KIRICI Sunum Akış Şeması 1. GİRİŞ 2. MATERYAL VE METHOD 3. AFİN KOORDİNAT DÖNÜŞÜMÜ 4. KALİTE KONTROL 5. İRDELEME
HARİTA VE KADASTRO MÜHENDİSLİĞİ
 HARİTA VE KADASTRO MÜHENDİSLİĞİ TMMOB Harita ve Kadastro Mühendisleri Odası tarafından her yılın İlkbahar, yaz, sonbahar, kış dönemlerinde yayınlanır. Sahibi : Harita ve Kadastro Mühendisleri Odası Adına
HARİTA VE KADASTRO MÜHENDİSLİĞİ TMMOB Harita ve Kadastro Mühendisleri Odası tarafından her yılın İlkbahar, yaz, sonbahar, kış dönemlerinde yayınlanır. Sahibi : Harita ve Kadastro Mühendisleri Odası Adına
Kenar Ağlarının Dengelenmesi 4 '*" E. ULSOY ~TM;.".;'_...; Dünyanın Şekli ve Yükseklikler Hakkında 8 ".''"_... Dr.; A. AIÎŞOY' ' " '/ \ "...
 r^'-v : -' i ç-1»m> E-k-î : -L~E-R -... - ; - : - : - - Sayfa Kenar Ağlarının Dengelenmesi 4 '*" E. ULSOY ~TM;.".;'_...; Dünyanın Şekli ve Yükseklikler Hakkında 8 ".''"_.... Dr.; A. AIÎŞOY' ' " '/ \ "...
r^'-v : -' i ç-1»m> E-k-î : -L~E-R -... - ; - : - : - - Sayfa Kenar Ağlarının Dengelenmesi 4 '*" E. ULSOY ~TM;.".;'_...; Dünyanın Şekli ve Yükseklikler Hakkında 8 ".''"_.... Dr.; A. AIÎŞOY' ' " '/ \ "...
Âna nirengi doğrultuları için p = 1 m 2 o Ara nirengi doğrultuları için p a =------------ m\
 4. ÖLÇÜLERİN AĞIRLIKLARININ SAPTANMASI Ana, ara ve tamamlayıcı nirengi doğrultularının herbiri gruplar halinde ele alınarak bunların ortalama hatalarının öncül (a priori) değerleri, üçgen kapanmalarından
4. ÖLÇÜLERİN AĞIRLIKLARININ SAPTANMASI Ana, ara ve tamamlayıcı nirengi doğrultularının herbiri gruplar halinde ele alınarak bunların ortalama hatalarının öncül (a priori) değerleri, üçgen kapanmalarından
Lineer Denklem Sistemleri Kısa Bilgiler ve Alıştırmalar
 Lineer Denklem Sistemleri Kısa Bilgiler ve Alıştırmalar Bir Matrisin Rankı A m n matrisinin determinantı sıfırdan farklı olan alt kare matrislerinin boyutlarının en büyüğüne A matrisinin rankı denir. rank(a)
Lineer Denklem Sistemleri Kısa Bilgiler ve Alıştırmalar Bir Matrisin Rankı A m n matrisinin determinantı sıfırdan farklı olan alt kare matrislerinin boyutlarının en büyüğüne A matrisinin rankı denir. rank(a)
KORELASYONLU ÖLÇÜLER DENÇELEMESİNE AİT BİR ÖRNEK
 KORELASYONLU ÖLÇÜLER DENÇELEMESİNE AİT BİR ÖRNEK Ekrem ULSOY Korelasyonlu ölçüler; müstakil olmayan, birbiri ile ilgili ölçülerdir. «Korelasyon derecesi» dengeleme hesabındaki ağırlık katsayıları ile tarif
KORELASYONLU ÖLÇÜLER DENÇELEMESİNE AİT BİR ÖRNEK Ekrem ULSOY Korelasyonlu ölçüler; müstakil olmayan, birbiri ile ilgili ölçülerdir. «Korelasyon derecesi» dengeleme hesabındaki ağırlık katsayıları ile tarif
Değişken içeren ve değişkenlerin belli değerleri için doğru olan cebirsel eşitliklere denklem denir.
 1 DENKLEMLER: Değişken içeren ve değişkenlerin belli değerleri için doğru olan cebirsel eşitliklere denklem denir. Bir denklemde eşitliği sağlayan(doğrulayan) değerlere; verilen denklemin kökleri veya
1 DENKLEMLER: Değişken içeren ve değişkenlerin belli değerleri için doğru olan cebirsel eşitliklere denklem denir. Bir denklemde eşitliği sağlayan(doğrulayan) değerlere; verilen denklemin kökleri veya
BEÜ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ
 BEÜ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ KOORDİNAT DÖNÜŞÜMÜ, DATUM TRANSFORMASYONU Prof.Dr.RASİM DENİZ MAYS 2014 ZONGULDAK KOORDİNAT DÖNÜŞÜMÜ,DATUM TRANSFORMASYONU 1-Genel Bilgiler Aynı datumdaki koordinatların
BEÜ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ KOORDİNAT DÖNÜŞÜMÜ, DATUM TRANSFORMASYONU Prof.Dr.RASİM DENİZ MAYS 2014 ZONGULDAK KOORDİNAT DÖNÜŞÜMÜ,DATUM TRANSFORMASYONU 1-Genel Bilgiler Aynı datumdaki koordinatların
Harita Projeksiyonları
 Özellikler Harita Projeksiyonları Bölüm 3: Silindirik Projeksiyonlar İzdüşüm yüzeyi, küreyi saran ya da kesen bir silindir seçilir. Silindirik projeksiyonlar genellikle normal konumda ekvator bölgesinde
Özellikler Harita Projeksiyonları Bölüm 3: Silindirik Projeksiyonlar İzdüşüm yüzeyi, küreyi saran ya da kesen bir silindir seçilir. Silindirik projeksiyonlar genellikle normal konumda ekvator bölgesinde
Parametrik doğru denklemleri 1
 Parametrik doğru denklemleri 1 A noktasından geçen, doğrultman (doğrultu) vektörü w olan d doğrusunun, k parametresine göre parametrik denklemi: AP k w P A k w P A k w P A k W (P değişken nokta) A w P
Parametrik doğru denklemleri 1 A noktasından geçen, doğrultman (doğrultu) vektörü w olan d doğrusunun, k parametresine göre parametrik denklemi: AP k w P A k w P A k w P A k W (P değişken nokta) A w P
Bağımsız Model Blok Dengeleme için Model Oluşturma ve Ön Sayısal Bilgi İşlemleri
 Bağımsız Model Blok Dengeleme için Model Oluşturma ve Ön Sayısal Bilgi İşlemleri Eminnur AYHAN* 1. Giriş Fotogrametrik nirengi çeşitli ölçütlere göre sınıflandırılabilir. Bu ölçütler dengelemede kullanılan
Bağımsız Model Blok Dengeleme için Model Oluşturma ve Ön Sayısal Bilgi İşlemleri Eminnur AYHAN* 1. Giriş Fotogrametrik nirengi çeşitli ölçütlere göre sınıflandırılabilir. Bu ölçütler dengelemede kullanılan
ÖLÇME BİLGİSİ. Sunu 1- Yatay Ölçme. Yrd. Doç. Dr. Muhittin İNAN & Arş. Gör. Hüseyin YURTSEVEN
 ÖÇME BİGİİ unu - atay Ölçme rd. Doç. Dr. Muhittin İNAN & Arş. Gör. Hüseyin URTEVEN COĞRAFİ BİGİ İTEMİNİ OUŞTURABİMEK İÇİN BİGİ TOPAMA ÖNTEMERİ ATA ÖÇMEER (,) ATA AÇIAR VE MEAFEERİN ÖÇÜMEİ ERE ÖÇMEER DÜŞE
ÖÇME BİGİİ unu - atay Ölçme rd. Doç. Dr. Muhittin İNAN & Arş. Gör. Hüseyin URTEVEN COĞRAFİ BİGİ İTEMİNİ OUŞTURABİMEK İÇİN BİGİ TOPAMA ÖNTEMERİ ATA ÖÇMEER (,) ATA AÇIAR VE MEAFEERİN ÖÇÜMEİ ERE ÖÇMEER DÜŞE
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ
 İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
İKİ BOYUTLU ÇUBUK SİSTEMLER İÇİN YAPI ANALİZ PROGRAM YAZMA SİSTEMATİĞİ Yapı Statiği nde incelenen sistemler çerçeve sistemlerdir. Buna ek olarak incelenen kafes ve karma sistemler de aslında çerçeve sistemlerin
FOTO'.GRAMERİ - KARTOGRAFYA
 FOTO'.GRAMERİ - KARTOGRAFYA ILLINOIS ÜNİVERSİTESİNDE STEREOMEÎRIK KAMERALARLA YAPILAN ÇALIŞMALAR ' VE SONUÇLARI Yazan : H. M. KARARA Illinois Üniversitesi Urbana - ABD ÖZ: «Stereometrik kameralar ile çekilen
FOTO'.GRAMERİ - KARTOGRAFYA ILLINOIS ÜNİVERSİTESİNDE STEREOMEÎRIK KAMERALARLA YAPILAN ÇALIŞMALAR ' VE SONUÇLARI Yazan : H. M. KARARA Illinois Üniversitesi Urbana - ABD ÖZ: «Stereometrik kameralar ile çekilen
DOĞRUNUN ANALİTİK İNCELEMESİ
 Koordinatlar DOĞRUNUN ANALİTİK İNCELEMESİ Bilindiği gibi, düzlemdeki her bir noktaya bir (a,b) sıralı ikilisi, her bir (a,b) sıralı ikilisine bir nokta karşılık gelir. Eğer bir A noktasına karşılık gelen
Koordinatlar DOĞRUNUN ANALİTİK İNCELEMESİ Bilindiği gibi, düzlemdeki her bir noktaya bir (a,b) sıralı ikilisi, her bir (a,b) sıralı ikilisine bir nokta karşılık gelir. Eğer bir A noktasına karşılık gelen
İKİ BOYUTLU AĞLARDA AĞIRLIK SEÇİMİNİN DENGELEME SONUÇLARINA ETKİSİ VE GPS KOORDİNATLARI İLE KARŞILAŞTIRILMASI
 SELÇUK TEKNİK ONLİNE DERGİSİ / ISSN 1302 6178 Volume 1, Number: 3 2001 İKİ BOYUTLU AĞLARDA AĞIRLIK SEÇİMİNİN DENGELEME SONUÇLARINA ETKİSİ VE GPS KOORDİNATLARI İLE KARŞILAŞTIRILMASI Doç Dr. Cevat İNAL S.Ü.
SELÇUK TEKNİK ONLİNE DERGİSİ / ISSN 1302 6178 Volume 1, Number: 3 2001 İKİ BOYUTLU AĞLARDA AĞIRLIK SEÇİMİNİN DENGELEME SONUÇLARINA ETKİSİ VE GPS KOORDİNATLARI İLE KARŞILAŞTIRILMASI Doç Dr. Cevat İNAL S.Ü.
ARAZİ ÖLÇMELERİ. Koordinat sistemleri. Kartezyen koordinat sistemi
 Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
deniyle - birden çok aletin aynı anda bir tek derleme bilgisayarmca denetlenmesi bazı aksakıklara neden olmaktadır.
 deniyle - birden çok aletin aynı anda bir tek derleme bilgisayarmca denetlenmesi bazı aksakıklara neden olmaktadır. 7) Fotogrametrik modellerden harita üretim amacına yönelik olarak derlenen veriler, mikrobilgisayarların
deniyle - birden çok aletin aynı anda bir tek derleme bilgisayarmca denetlenmesi bazı aksakıklara neden olmaktadır. 7) Fotogrametrik modellerden harita üretim amacına yönelik olarak derlenen veriler, mikrobilgisayarların
İKİNCİ DERECEDEN DENKLEMLER
 İKİNCİ DERECEDEN DENKLEMLER İkinci Dereceden Denklemler a, b ve c reel sayı, a ¹ 0 olmak üzere ax + bx + c = 0 şeklinde yazılan denklemlere ikinci dereceden bir bilinmeyenli denklem denir. Aşağıdaki denklemlerden
İKİNCİ DERECEDEN DENKLEMLER İkinci Dereceden Denklemler a, b ve c reel sayı, a ¹ 0 olmak üzere ax + bx + c = 0 şeklinde yazılan denklemlere ikinci dereceden bir bilinmeyenli denklem denir. Aşağıdaki denklemlerden
ARAZİ ÖLÇMELERİ. Koordinat sistemleri. Kartezyen koordinat sistemi
 Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
Koordinat sistemleri Coğrafik objelerin haritaya aktarılması, objelerin detaylarına ait koordinatların düzleme aktarılması ile oluşur. Koordinat sistemleri kendi içlerinde kartezyen koordinat sistemi,
lerin tesirinden hesaplanacak şakul sapması Ölçülen şakul sapmasından çıkartılır :
 lerin tesirinden hesaplanacak şakul sapması Ölçülen şakul sapmasından çıkartılır : 3 (8) formülüne göre elde edilen indirgenmiş A% şakul sapması Md bölümden oluşur : Formülde kıyas düzleminin altındaki
lerin tesirinden hesaplanacak şakul sapması Ölçülen şakul sapmasından çıkartılır : 3 (8) formülüne göre elde edilen indirgenmiş A% şakul sapması Md bölümden oluşur : Formülde kıyas düzleminin altındaki
T] = (a- A) cotgş (6) şeklindedir. (1) ve (6) formüllerinin bir araya getirilmesi ile (a A) = (X L) sincp (7) Laplace denklemi elde edilir.
![T] = (a- A) cotgş (6) şeklindedir. (1) ve (6) formüllerinin bir araya getirilmesi ile (a A) = (X L) sincp (7) Laplace denklemi elde edilir. T] = (a- A) cotgş (6) şeklindedir. (1) ve (6) formüllerinin bir araya getirilmesi ile (a A) = (X L) sincp (7) Laplace denklemi elde edilir.](/thumbs/55/35591809.jpg) * = 2 + rf (3) \ cos AQ, r\ % sin A o (4) \ cos A o + IQ sin A o = % (5) bağıntılarıda yazılabilir. (1) eşitliğine göre elde edilen r\ doğu-batı bileşeni astronomik ve leşenleri elde edilmiş oldu. MZ A
* = 2 + rf (3) \ cos AQ, r\ % sin A o (4) \ cos A o + IQ sin A o = % (5) bağıntılarıda yazılabilir. (1) eşitliğine göre elde edilen r\ doğu-batı bileşeni astronomik ve leşenleri elde edilmiş oldu. MZ A
Kafes Sistemler. Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir.
 Kafes Sistemler Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir. Kafes Sistemler Birçok uygulama alanları vardır. Çatı sistemlerinde, Köprülerde, Kulelerde, Ve benzeri
Kafes Sistemler Birbirlerine uç noktalarından bağlanmış çubuk elemanların oluşturduğu sistemlerdir. Kafes Sistemler Birçok uygulama alanları vardır. Çatı sistemlerinde, Köprülerde, Kulelerde, Ve benzeri
Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu
 JEODEZİ9 1 Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu u ve v Gauss parametrelerine bağlı olarak r r ( u, v) yer vektörü ile verilmiş bir Ω yüzeyinin, u*, v* Gauss parametreleri ile verilmiş
JEODEZİ9 1 Genel Olarak Bir Yüzeyin Diğer Bir Yüzeye Projeksiyonu u ve v Gauss parametrelerine bağlı olarak r r ( u, v) yer vektörü ile verilmiş bir Ω yüzeyinin, u*, v* Gauss parametreleri ile verilmiş
Lineer Cebir. Doç. Dr. Niyazi ŞAHİN TOBB. İçerik: 1.1. Lineer Denklemlerin Tanımı 1.2. Lineer Denklem Sistemleri 1.3. Matrisler
 Lineer Cebir Doç. Dr. Niyazi ŞAHİN TOBB İçerik: 1.1. Lineer Denklemlerin Tanımı 1.2. Lineer Denklem Sistemleri 1.3. Matrisler Bölüm 1 - Lineer Eşitlikler 1.1. Lineer Eşitliklerin Tanımı x 1, x 2,..., x
Lineer Cebir Doç. Dr. Niyazi ŞAHİN TOBB İçerik: 1.1. Lineer Denklemlerin Tanımı 1.2. Lineer Denklem Sistemleri 1.3. Matrisler Bölüm 1 - Lineer Eşitlikler 1.1. Lineer Eşitliklerin Tanımı x 1, x 2,..., x
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
GERİLME ANALİZİ VE MOHR ÇEMBERİ MUKAVEMET
 GERİLME ANALİZİ VE MOHR ÇEMBERİ MUKAVEMET Yrd. Doç. Dr. Emine AYDIN Yrd. Doç. Dr. Elif BORU 1 GENEL YÜKLEME DURUMUNDA GERİLME ANALİZİ Daha önce incelenen gerilme örnekleri eksenel yüklü yapı elemanları
GERİLME ANALİZİ VE MOHR ÇEMBERİ MUKAVEMET Yrd. Doç. Dr. Emine AYDIN Yrd. Doç. Dr. Elif BORU 1 GENEL YÜKLEME DURUMUNDA GERİLME ANALİZİ Daha önce incelenen gerilme örnekleri eksenel yüklü yapı elemanları
9. SINIF Geometri TEMEL GEOMETRİK KAVRAMLAR
 TEMEL GEOMETRİK KAVRAMLAR 9. SINIF Geometri Amaç-1: Nokta, Doğru, Düzlem, Işın ve Uzayı Kavrayabilme. 1. Nokta, doğru, düzlem ve uzay kavramlarım açıklama. 2. Farklı iki noktadan geçen doğru sayışım söyleme
TEMEL GEOMETRİK KAVRAMLAR 9. SINIF Geometri Amaç-1: Nokta, Doğru, Düzlem, Işın ve Uzayı Kavrayabilme. 1. Nokta, doğru, düzlem ve uzay kavramlarım açıklama. 2. Farklı iki noktadan geçen doğru sayışım söyleme
GPS/INS Destekli Havai Nirengi
 GPS/INS Destekli Havai Nirengi GPS/INS (IMU) destekli hava nirengide izdüşüm merkezi koordinatları (WGS84) ve dönüklükler direk ölçülür. İzdüşüm merkezi koordinatları kinematik GPS ile ölçülür. GPS ile
GPS/INS Destekli Havai Nirengi GPS/INS (IMU) destekli hava nirengide izdüşüm merkezi koordinatları (WGS84) ve dönüklükler direk ölçülür. İzdüşüm merkezi koordinatları kinematik GPS ile ölçülür. GPS ile
1. O(0,0) merkezli, 3 birim yarıçaplı. 2. x 2 +y 2 =16 denklemi ile verilen. 3. O(0,0) merkezli ve A(3,4)
 HAZİNE-1 Düzlemde sabit M(a,b) noktasından eşit uzaklıkta bulunan noktaların geometrik yeri, M merkezli R yarıçaplı çemberdir. HAZİNE-2 O(0,0) merkezli, R yarıçaplı çemberin denklemi; x 2 +y 2 =R 2 dir.
HAZİNE-1 Düzlemde sabit M(a,b) noktasından eşit uzaklıkta bulunan noktaların geometrik yeri, M merkezli R yarıçaplı çemberdir. HAZİNE-2 O(0,0) merkezli, R yarıçaplı çemberin denklemi; x 2 +y 2 =R 2 dir.
dir. Fonksiyonun (a,b) aralığında integrali ise, her aralıkta alınan integral değerlerini toplanarak, aşağıda verilen şekilde elde edilir.
 SAYISAL İNTEGRASYON TEK KATLI İNTEGRASYON Sayısal integrasyon çok geniş bir konudur. Burada problemli olmayan (genelde integrantın tekilliği olmayan, fazla salınım yapmayan, yaklaşım problemi bulunmayan)
SAYISAL İNTEGRASYON TEK KATLI İNTEGRASYON Sayısal integrasyon çok geniş bir konudur. Burada problemli olmayan (genelde integrantın tekilliği olmayan, fazla salınım yapmayan, yaklaşım problemi bulunmayan)
Polinomlar, Temel Kavramlar, Polinomlar Kümesinde Toplama, Çıkarma, Çarpma TEST D 9. E 10. C 11. B 14. D 16. D 12. C 12. A 13. B 14.
 1. Ünite: Polinomlar Polinomlar, Temel Kavramlar, Polinomlar Kümesinde Toplama, Çıkarma, Çarpma 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 Polinomlarda Bölme, Bölüm ve Kalan Bulma 1 1 1 1 1 1 1 1 1
1. Ünite: Polinomlar Polinomlar, Temel Kavramlar, Polinomlar Kümesinde Toplama, Çıkarma, Çarpma 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 Polinomlarda Bölme, Bölüm ve Kalan Bulma 1 1 1 1 1 1 1 1 1
DENGELEME HESABI-I DERS NOTLARI
 DENGELEME HESABI-I DERS NOTLARI Dengeleme Hesabı Adımları, En Küçük Kareler İlkesine Giriş, Korelasyon Prof. Dr. Mualla YALÇINKAYA Yrd. Doç. Dr. Emine TANIR KAYIKÇI Karadeniz Teknik Üniversitesi, Harita
DENGELEME HESABI-I DERS NOTLARI Dengeleme Hesabı Adımları, En Küçük Kareler İlkesine Giriş, Korelasyon Prof. Dr. Mualla YALÇINKAYA Yrd. Doç. Dr. Emine TANIR KAYIKÇI Karadeniz Teknik Üniversitesi, Harita
SONLU FARKLAR GENEL DENKLEMLER
 SONLU FARKLAR GENEL DENKLEMLER Bir elastik ortamın gerilme probleminin Airy gerilme fonksiyonu ile formüle edilebilen halini göz önüne alalım. Problem matematiksel olarak bölgede biharmonik denklemi sağlayan
SONLU FARKLAR GENEL DENKLEMLER Bir elastik ortamın gerilme probleminin Airy gerilme fonksiyonu ile formüle edilebilen halini göz önüne alalım. Problem matematiksel olarak bölgede biharmonik denklemi sağlayan
V. KAFES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir.
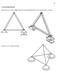 78 V. KES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir. Uzayda ise en az 6 çubuk gereklidir. 79 İhtiyaçlara göre yeni çubukların ilavesiyle
78 V. KES SİSTEMLER: Düzlemde en az üç adet çubuğun birbirlerine mafsala birleştirilmesiyle elde edilmiş taşıyıcı sistemdir. Uzayda ise en az 6 çubuk gereklidir. 79 İhtiyaçlara göre yeni çubukların ilavesiyle
8. SINIF 2 BiLiNMEYENLi DENKLEM SiSTEMLERi
 14 8. SINIF 2 BiLiNMEYENLi DENKLEM SiSTEMLERi İçerisinde 2 tane bilinmeyen bulunan ve bilinmeyenlerin derecesi en fazla 1 olan eşitliklere birinci dereceden iki bilinmeyenli denklem sistemleri denir. Çözüm
14 8. SINIF 2 BiLiNMEYENLi DENKLEM SiSTEMLERi İçerisinde 2 tane bilinmeyen bulunan ve bilinmeyenlerin derecesi en fazla 1 olan eşitliklere birinci dereceden iki bilinmeyenli denklem sistemleri denir. Çözüm
Gerilme Dönüşümleri (Stress Transformation)
 Gerilme Dönüşümleri (Stress Transformation) Bubölümdebirnoktayaetkiyen vebelli bir koordinat ekseni/düzlemi ile ilişkili gerilme bileşenlerini, başka bir koordinat sistemi/başka bir düzlem ile ilişkili
Gerilme Dönüşümleri (Stress Transformation) Bubölümdebirnoktayaetkiyen vebelli bir koordinat ekseni/düzlemi ile ilişkili gerilme bileşenlerini, başka bir koordinat sistemi/başka bir düzlem ile ilişkili
DİK KOORDİNAT SİSTEMİ VE
 Ölçme Bilgisi DERS 6 DİK KOORDİNAT SİSTEMİ VE TEMEL ÖDEVLER Kaynak: İ.ASRİ (Gümüşhane Ü) M. Zeki COŞKUN ( İTÜ ) TEODOLİT Teodolitler, yatay ve düşey açıları yeteri incelikte ölçmeye yarayan optik aletlerdir.
Ölçme Bilgisi DERS 6 DİK KOORDİNAT SİSTEMİ VE TEMEL ÖDEVLER Kaynak: İ.ASRİ (Gümüşhane Ü) M. Zeki COŞKUN ( İTÜ ) TEODOLİT Teodolitler, yatay ve düşey açıları yeteri incelikte ölçmeye yarayan optik aletlerdir.
Üç Boyutlu Uzayda Koordinat sistemi
 Üç Boyutlu Uzayda Koordinat sistemi Uzayda bir noktayı ifade edebilmek için ilk önce O noktasını (başlangıç noktası) ve bu noktadan geçen ve birbirine dik olan üç yönlü doğruyu seçerek sabitlememiz gerekir.
Üç Boyutlu Uzayda Koordinat sistemi Uzayda bir noktayı ifade edebilmek için ilk önce O noktasını (başlangıç noktası) ve bu noktadan geçen ve birbirine dik olan üç yönlü doğruyu seçerek sabitlememiz gerekir.
1. BÖLÜM uzayda Bir doğrunun vektörel ve parametrik denklemi... 71. 2. BÖLÜM uzayda düzlem denklemleri... 77
 UZAYDA DOĞRU VE DÜZLEM Sayfa No. BÖLÜM uzayda Bir doğrunun vektörel ve parametrik denklemi.............. 7. BÖLÜM uzayda düzlem denklemleri.......................................... 77. BÖLÜM uzayda Bir
UZAYDA DOĞRU VE DÜZLEM Sayfa No. BÖLÜM uzayda Bir doğrunun vektörel ve parametrik denklemi.............. 7. BÖLÜM uzayda düzlem denklemleri.......................................... 77. BÖLÜM uzayda Bir
DENKLEM SİSTEMLERİ. ifadesinde a sayısı bilinmeyenin katsayısı ve b ise sabit sayıdır.
 DENKLEM SİSTEMLERİ 1) BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ DENKLEMLER: a,bϵ R ve olmak üzere; şeklindeki denklemlere birinci dereceden bir bilinmeyenli denklem denir. Bu tür denklemlerde sadece bir bilinmeyen
DENKLEM SİSTEMLERİ 1) BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ DENKLEMLER: a,bϵ R ve olmak üzere; şeklindeki denklemlere birinci dereceden bir bilinmeyenli denklem denir. Bu tür denklemlerde sadece bir bilinmeyen
Gerilme Dönüşümleri (Stress Transformation)
 Gerilme Dönüşümleri (Stress Transformation) Bu bölümde, bir noktaya etkiyen ve bir koordinat ekseni ile ilişkili gerilme bileşenlerini, başka bir koordinat sistemi ile ilişkili gerilme bileşenlerine dönüştürmek
Gerilme Dönüşümleri (Stress Transformation) Bu bölümde, bir noktaya etkiyen ve bir koordinat ekseni ile ilişkili gerilme bileşenlerini, başka bir koordinat sistemi ile ilişkili gerilme bileşenlerine dönüştürmek
1. Analitik düzlemde P(-4,3) noktasının eksenlerden ve O başlangıç noktasından uzaklığı kaç birimdir?
 HAZİNE- HAZİNE-2 O başlangıç noktasında dik kesişen iki sayı ekseninin oluşturduğu sisteme koordinat sistemi denir. Bir noktanın x-eksenindeki dik izdüşümüne karşılık gelen x sayısına noktanın apsis i
HAZİNE- HAZİNE-2 O başlangıç noktasında dik kesişen iki sayı ekseninin oluşturduğu sisteme koordinat sistemi denir. Bir noktanın x-eksenindeki dik izdüşümüne karşılık gelen x sayısına noktanın apsis i
 5. 5. 5.3 5.4 5.5 5.6 5.7 5.8 Rijit Cisimde Denge Düzlem Kuvvetlerde Denge Hali Düzlemde Serbestlik Derecesi Bağ Çeşitleri Pandül Ayak Düzlem Taşıyıcı Sistemler Düzlem Taşıyıcı Sistemlerde Yükleme Durumları
5. 5. 5.3 5.4 5.5 5.6 5.7 5.8 Rijit Cisimde Denge Düzlem Kuvvetlerde Denge Hali Düzlemde Serbestlik Derecesi Bağ Çeşitleri Pandül Ayak Düzlem Taşıyıcı Sistemler Düzlem Taşıyıcı Sistemlerde Yükleme Durumları
MOTORLAR VE TRAKTÖRLER Dersi 10
 MOTORLAR VE TRAKTÖRLER Dersi 10 Traktör Mekaniği Traktörlerde ağırlık merkezi yerinin tayini Hareketsiz durumdaki traktörde kuvvetler Arka dingili muharrik traktörlerde kuvvetler Çeki Kancası ve Çeki Demirine
MOTORLAR VE TRAKTÖRLER Dersi 10 Traktör Mekaniği Traktörlerde ağırlık merkezi yerinin tayini Hareketsiz durumdaki traktörde kuvvetler Arka dingili muharrik traktörlerde kuvvetler Çeki Kancası ve Çeki Demirine
Uzayda Simetri. A(x, y, z) noktasının O(a, b, c) noktasına göre simetriği B(x, y, z ) ise O noktası [AB] nın orta noktasıdır.
![Uzayda Simetri. A(x, y, z) noktasının O(a, b, c) noktasına göre simetriği B(x, y, z ) ise O noktası [AB] nın orta noktasıdır. Uzayda Simetri. A(x, y, z) noktasının O(a, b, c) noktasına göre simetriği B(x, y, z ) ise O noktası [AB] nın orta noktasıdır.](/thumbs/55/36610671.jpg) Uzayda Simetri Hazırlayan Halit Çelik Matematik Öğretmeni Noktaya Göre Simetri: A(x, y, z) noktasının O(a, b, c) noktasına göre simetriği B(x, y, z ) ise O noktası [AB] nın orta noktasıdır. Buna göre şeklinde
Uzayda Simetri Hazırlayan Halit Çelik Matematik Öğretmeni Noktaya Göre Simetri: A(x, y, z) noktasının O(a, b, c) noktasına göre simetriği B(x, y, z ) ise O noktası [AB] nın orta noktasıdır. Buna göre şeklinde
Elipsoid Yüzünde Jeodezik Dik Koordinatlar (Soldner Koordinatları) ve Temel Ödev Hesapları
 JEODEZİ8 1 Elipsoid Yüzünde Jeodezik Dik Koordinatlar (Soldner Koordinatları) ve Temel Ödev Hesapları Jeodezik dik koordinatları tanımlamak için önce bir meridyen x ekseni olarak alınır. Bunun üzerinde
JEODEZİ8 1 Elipsoid Yüzünde Jeodezik Dik Koordinatlar (Soldner Koordinatları) ve Temel Ödev Hesapları Jeodezik dik koordinatları tanımlamak için önce bir meridyen x ekseni olarak alınır. Bunun üzerinde
BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ DENKLEMLER
 YILLAR 00 00 00 00 00 00 007 008 009 00 ÖSS-YGS - - - - - - - - BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ DENKLEMLER a,b R ve a 0 olmak üzere ab=0 şeklindeki denklemlere Birinci dereceden bir bilinmeyenli denklemler
YILLAR 00 00 00 00 00 00 007 008 009 00 ÖSS-YGS - - - - - - - - BİRİNCİ DERECEDEN BİR BİLİNMEYENLİ DENKLEMLER a,b R ve a 0 olmak üzere ab=0 şeklindeki denklemlere Birinci dereceden bir bilinmeyenli denklemler
Harita Projeksiyonları
 Harita Projeksiyonları Bölüm Prof.Dr. İ. Öztuğ BİLDİRİCİ Amaç ve Kapsam Harita projeksiyonlarının amacı, yeryüzü için tanımlanmış bir referans yüzeyi üzerinde belli bir koordinat sistemine göre tanımlı
Harita Projeksiyonları Bölüm Prof.Dr. İ. Öztuğ BİLDİRİCİ Amaç ve Kapsam Harita projeksiyonlarının amacı, yeryüzü için tanımlanmış bir referans yüzeyi üzerinde belli bir koordinat sistemine göre tanımlı
HOMOGEN OLMAYAN DENKLEMLER
 n. mertebeden homogen olmayan lineer bir diferansiyel denklemin y (n) + p 1 (x)y (n 1) + + p n 1 (x)y + p n (x)y = f(x) (1) şeklinde olduğunu ve bununla ilgili olan n. mertebeden lineer homogen denlemin
n. mertebeden homogen olmayan lineer bir diferansiyel denklemin y (n) + p 1 (x)y (n 1) + + p n 1 (x)y + p n (x)y = f(x) (1) şeklinde olduğunu ve bununla ilgili olan n. mertebeden lineer homogen denlemin
Kompozit Malzemeler ve Mekaniği. Yrd.Doç.Dr. Akın Ataş
 Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Kompozit Malzemeler ve Mekaniği Yrd.Doç.Dr. Akın Ataş Bölüm 4 Laminatların Makromekanik Analizi Kaynak: Kompozit Malzeme Mekaniği, Autar K. Kaw, Çevirenler: B. Okutan Baba, R. Karakuzu. 4 Laminatların
Yrd. Doç. Dr. Aycan M. MARANGOZ. BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI
 FOTOGRAMETRİ II FOTOGRAMETRİK DEĞERLENDİRME - TEK RESİM DEĞERLENDİRMESİ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
FOTOGRAMETRİ II FOTOGRAMETRİK DEĞERLENDİRME - TEK RESİM DEĞERLENDİRMESİ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/
Diferensiyel denklemler sürekli sistemlerin hareketlerinin ifade edilmesinde kullanılan denklemlerdir.
 .. Diferensiyel Denklemler y f (x) de F ( x, y, y, y,...) 0 veya y f ( x, y, y,...) x ve y değişkenlerinin kendileri ve türevlerini içinde bulunduran denklemlerdir. (Türevler; "Bağımlı değişkenin değişiminin
.. Diferensiyel Denklemler y f (x) de F ( x, y, y, y,...) 0 veya y f ( x, y, y,...) x ve y değişkenlerinin kendileri ve türevlerini içinde bulunduran denklemlerdir. (Türevler; "Bağımlı değişkenin değişiminin
BÜYÜK ÖLÇEKLİ HARİTA YAPIMINDA STEREOGRAFİK ÇİFT PROJEKSİYONUN UYGULANIŞI
 36 İNCELEME - ARAŞTIRMA BÜYÜK ÖLÇEKLİ HARİTA YAPIMINDA STEREOGRAFİK ÇİFT PROJEKSİYONUN UYGULANIŞI Erdal KOÇAIC*^ ÖZET Büyük ölçekli harita yapımında G İ R İŞ uygulanabilen "Stereografik çift Stereografik
36 İNCELEME - ARAŞTIRMA BÜYÜK ÖLÇEKLİ HARİTA YAPIMINDA STEREOGRAFİK ÇİFT PROJEKSİYONUN UYGULANIŞI Erdal KOÇAIC*^ ÖZET Büyük ölçekli harita yapımında G İ R İŞ uygulanabilen "Stereografik çift Stereografik
Kontrol noktaları (X,Y,Z) Şekil 1- Stereodeğerlendirme ve tek resim değerlendirmesi için kontrol noktaları gereksinimi.
 FOTOGRAMETRİK NİRENGİ 1.GEREKÇE VE TANIM Stereodeğerlendirme yapabilmek için, stereo model alanında, en az üç, olabilirse köşelere gelecek şekilde dört kontrol noktasına gerek vardır. Tek resim değerlendirmesi
FOTOGRAMETRİK NİRENGİ 1.GEREKÇE VE TANIM Stereodeğerlendirme yapabilmek için, stereo model alanında, en az üç, olabilirse köşelere gelecek şekilde dört kontrol noktasına gerek vardır. Tek resim değerlendirmesi
Özel Kasımoğlu Coşkun Fen Lisesi
 4.04.0 tarihinde Okan Üniversitesi Matematik Bölümü tarafından düzenlenen Liselerarası Matematik Yarışması na aşağıda listelenen on iki lise katıldı. Özel Kasımoğlu Coşkun Fen Lisesi Habire Yahşi Anadolu
4.04.0 tarihinde Okan Üniversitesi Matematik Bölümü tarafından düzenlenen Liselerarası Matematik Yarışması na aşağıda listelenen on iki lise katıldı. Özel Kasımoğlu Coşkun Fen Lisesi Habire Yahşi Anadolu
Jeodezi
 1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
1 Jeodezi 5 2 Jeodezik Eğri Elipsoid Üstünde Düşey Kesitler Elipsoid yüzünde P 1 noktasındaki normalle P 2 noktasından geçen düşey düzlem, P 2 deki yüzey normalini içermez ve aynı şekilde P 2 de yüzey
Alan Hesapları. Şekil 14. Üç kenarı belli üçgen alanı
 lan Hesapları lan hesabının doğruluğu alım şekline ve istenile hassasiyet derecesine göre değişir. lan hesapları üç kısma ayrılmıştır. Ölçü değerlerine göre alan hesabı Ölçü ve plan değerlerine göre alan
lan Hesapları lan hesabının doğruluğu alım şekline ve istenile hassasiyet derecesine göre değişir. lan hesapları üç kısma ayrılmıştır. Ölçü değerlerine göre alan hesabı Ölçü ve plan değerlerine göre alan
Elastisite Teorisi Düzlem Problemleri için Sonuç 1
 Elastisite Teorisi Düzlem Problemleri için Sonuç 1 Düzlem Gerilme durumu için: Bilinmeyenler: Düzlem Şekil değiştirme durumu için: Bilinmeyenler: 3 gerilme bileşeni : 3 gerilme bileşeni : 3 şekil değiştirme
Elastisite Teorisi Düzlem Problemleri için Sonuç 1 Düzlem Gerilme durumu için: Bilinmeyenler: Düzlem Şekil değiştirme durumu için: Bilinmeyenler: 3 gerilme bileşeni : 3 gerilme bileşeni : 3 şekil değiştirme
4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ
 4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ Doğrusal Denklem Sistemi x 1,x 2,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu; a x a x a x b 11 1 12 2 1n n 1 a x a x a x b 21 1 22 2 2n n
4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ Doğrusal Denklem Sistemi x 1,x 2,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu; a x a x a x b 11 1 12 2 1n n 1 a x a x a x b 21 1 22 2 2n n
Özdeğer ve Özvektörler
 Özdeğer ve Özvektörler Yazar Öğr.Grv.Dr.Nevin ORHUN ÜNİTE 9 Amaçlar Bu üniteyi çalıştıktan sonra; bir lineer dönüşümün ve bir matrisin özdeğer ve özvektör kavramlarını anlayacak, bir dönüşüm matrisinin
Özdeğer ve Özvektörler Yazar Öğr.Grv.Dr.Nevin ORHUN ÜNİTE 9 Amaçlar Bu üniteyi çalıştıktan sonra; bir lineer dönüşümün ve bir matrisin özdeğer ve özvektör kavramlarını anlayacak, bir dönüşüm matrisinin
Bilgisayar Grafikleri
 Bilgisayar Grafikleri Konular: Cismin Tanımlanması Bilindiği gibi iki boyutta noktalar x ve y olmak üzere iki boyutun koordinatları şeklinde ifade edilirler. Üç boyutta da üçüncü boyut olan z ekseni üçücü
Bilgisayar Grafikleri Konular: Cismin Tanımlanması Bilindiği gibi iki boyutta noktalar x ve y olmak üzere iki boyutun koordinatları şeklinde ifade edilirler. Üç boyutta da üçüncü boyut olan z ekseni üçücü
EĞİTİM ÖĞRETİM YILI. FEN LİSESİ 11.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI 11.SINIF KAZANIM VE SÜRE TABLOSU
 08-09 EĞİTİM ÖĞRETİM YILI. FEN LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. TRİGONOMETRİ 8 6 6.. Yönlü Açılar
08-09 EĞİTİM ÖĞRETİM YILI. FEN LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. TRİGONOMETRİ 8 6 6.. Yönlü Açılar
BELĐRLĐ BĐR SIKMA KUVVETĐ ETKĐSĐNDE BĐSĐKLET FREN KOLU KUVVET ANALĐZĐNĐN YAPILMASI
 tasarım BELĐRLĐ BĐR SIKMA KUVVETĐ ETKĐSĐNDE BĐSĐKLET FREN KOLU KUVVET ANALĐZĐNĐN YAPILMASI Nihat GEMALMAYAN, Hüseyin ĐNCEÇAM Gazi Üniversitesi, Makina Mühendisliği Bölümü GĐRĐŞ Đlk bisikletlerde fren sistemi
tasarım BELĐRLĐ BĐR SIKMA KUVVETĐ ETKĐSĐNDE BĐSĐKLET FREN KOLU KUVVET ANALĐZĐNĐN YAPILMASI Nihat GEMALMAYAN, Hüseyin ĐNCEÇAM Gazi Üniversitesi, Makina Mühendisliği Bölümü GĐRĐŞ Đlk bisikletlerde fren sistemi
EĞİTİM-ÖĞRETİM YILI 8. SINIF MATEMATİK DERSİ KAZANIMLARININ ÇALIŞMA TAKVİMİNE GÖRE DAĞILIM ÇİZELGESİ SÜRE
 Ay 2016 2017 EĞİTİM-ÖĞRETİM YILI 8. SINIF MATEMATİK DERSİ KAZANIMLARININ ÇALIŞMA TAKVİMİNE GÖRE DAĞILIM ÇİZELGESİ SÜRE Hafta ÖĞRENME ALANI ALT ÖĞRENME ALANI KAZANIMLAR EYLÜL 3 4 Sayılar ve İşlemler Çarpanlar
Ay 2016 2017 EĞİTİM-ÖĞRETİM YILI 8. SINIF MATEMATİK DERSİ KAZANIMLARININ ÇALIŞMA TAKVİMİNE GÖRE DAĞILIM ÇİZELGESİ SÜRE Hafta ÖĞRENME ALANI ALT ÖĞRENME ALANI KAZANIMLAR EYLÜL 3 4 Sayılar ve İşlemler Çarpanlar
Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi
 JEODEZİ 6 1 Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi Jeodezik gözlemler, hesaplamalarda kullanılmadan önce, referans elipsoidin yüzeyine indirgenir. Bu işlem, arazide yapılan gözlemler l jeoidin
JEODEZİ 6 1 Gözlemlerin Referans Elipsoid Yüzüne İndirgenmesi Jeodezik gözlemler, hesaplamalarda kullanılmadan önce, referans elipsoidin yüzeyine indirgenir. Bu işlem, arazide yapılan gözlemler l jeoidin
11. SINIF. No Konular Kazanım Sayısı GEOMETRİ TRİGONOMETRİ Yönlü Açılar Trigonometrik Fonksiyonlar
 11. SINIF No Konular Kazanım Sayısı GEOMETRİ Ders Saati Ağırlık (%) 11.1. TRİGONOMETRİ 7 56 26 11.1.1. Yönlü Açılar 2 10 5 11.1.2. Trigonometrik Fonksiyonlar 5 46 21 11.2. ANALİTİK GEOMETRİ 4 24 11 11.2.1.
11. SINIF No Konular Kazanım Sayısı GEOMETRİ Ders Saati Ağırlık (%) 11.1. TRİGONOMETRİ 7 56 26 11.1.1. Yönlü Açılar 2 10 5 11.1.2. Trigonometrik Fonksiyonlar 5 46 21 11.2. ANALİTİK GEOMETRİ 4 24 11 11.2.1.
ARAZİ ÖLÇMELERİ. Coğrafik Objenin Alan Bilgisinin Bulunması
 Coğrafik Objenin Alan Bilgisinin Bulunması Bina, kadastro / İmar parseli, göl gibi kapalı alan obje tipinde ki coğrafik objelere ait en önemli bilgi alandır. Coğrafik objelerin alan bilgileri farklı yollarla
Coğrafik Objenin Alan Bilgisinin Bulunması Bina, kadastro / İmar parseli, göl gibi kapalı alan obje tipinde ki coğrafik objelere ait en önemli bilgi alandır. Coğrafik objelerin alan bilgileri farklı yollarla
Eski Yunanca'dan batı dillerine giren Fotogrametri sözcüğü 3 kök sözcükten oluşur. Photos(ışık) + Grama(çizim) + Metron(ölçme)
 FOTOGRAMETRİ FOTOGRAMETRİ Eski Yunanca'dan batı dillerine giren Fotogrametri sözcüğü 3 kök sözcükten oluşur. Photos(ışık) + Grama(çizim) + Metron(ölçme) Buna göre ışık yardımı ile ölçme (çizim yapabilme)
FOTOGRAMETRİ FOTOGRAMETRİ Eski Yunanca'dan batı dillerine giren Fotogrametri sözcüğü 3 kök sözcükten oluşur. Photos(ışık) + Grama(çizim) + Metron(ölçme) Buna göre ışık yardımı ile ölçme (çizim yapabilme)
1. HAFTA. Statik, uzayda kuvvetler etkisi altındaki cisimlerin denge koşullarını inceler.
 1. HAFTA Statik, uzayda kuvvetler etkisi altındaki cisimlerin denge koşullarını inceler. Statikte üç temel büyüklük vardır. Uzay: Fiziksel olayların meydana geldiği geometrik bir bölgedir. İncelenen problemin
1. HAFTA Statik, uzayda kuvvetler etkisi altındaki cisimlerin denge koşullarını inceler. Statikte üç temel büyüklük vardır. Uzay: Fiziksel olayların meydana geldiği geometrik bir bölgedir. İncelenen problemin
AEAZÎ DÜZENLEMELERİ KONUSUNDA MATEMATİKSEL BÎR YAKLAŞIM
 3 DERGİDEN MEKTUP Sayın üyemiz, amacımız üyelerimize mesleki sorunlara cevap veren, güncel bilgileri aktarmaktır. Ancak, bütün çabalarımıza rağmen, dergimizde zaman zaman dizgi hatalan olmakta bütün titizliğimize
3 DERGİDEN MEKTUP Sayın üyemiz, amacımız üyelerimize mesleki sorunlara cevap veren, güncel bilgileri aktarmaktır. Ancak, bütün çabalarımıza rağmen, dergimizde zaman zaman dizgi hatalan olmakta bütün titizliğimize
Yrd. Doç. Dr. Aycan M. MARANGOZ. BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI
 FOTOGRAMETRİ II FOTOGRAMETRİK NİRENGİ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/ İÇERİK Giriş Yer Kontrol Noktaları
FOTOGRAMETRİ II FOTOGRAMETRİK NİRENGİ BEÜ MÜHENDİSLİK FAKÜLTESİ GEOMATİK MÜHENDİSLİĞİ BÖLÜMÜ JDF336 FOTOGRAMETRİ II DERSi NOTLARI http://geomatik.beun.edu.tr/marangoz/ İÇERİK Giriş Yer Kontrol Noktaları
EĞİTİM ÖĞRETİM YILI. ANADOLU LİSESİ 11.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI 11.SINIF KAZANIM VE SÜRE TABLOSU
 08-09 EĞİTİM ÖĞRETİM YILI. ANADOLU LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. TRİGONOMETRİ 7 6 6.. Yönlü
08-09 EĞİTİM ÖĞRETİM YILI. ANADOLU LİSESİ.SINIF MATEMATİK DERSİ ÜNİTELENDİRİLMİŞ YILLLIK PLANI.SINIF KAZANIM VE SÜRE TABLOSU No Konular Kazanım sayısı Ders Saati Ağırlık (%).. TRİGONOMETRİ 7 6 6.. Yönlü
Tanımlar, Geometrik ve Matemetiksel Temeller. Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ. JDF329 Fotogrametri I Ders Notu
 FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İçerik Tanımlar
FOTOGRAMETRİ I Tanımlar, Geometrik ve Matemetiksel Temeller Yrd. Doç. Dr. Saygın ABDİKAN Yrd. Doç. Dr. Aycan M. MARANGOZ JDF329 Fotogrametri I Ders Notu 2015-2016 Öğretim Yılı Güz Dönemi İçerik Tanımlar
PAFTA BÖLÜMLENDİRİLMESİ
 PAFTA BÖLÜMLENDİRİLMESİ Türkiye kadastrosunda yukarıda değinilen ada sistemi pafta bölümleme ve adlandırma sistemi dışında çeşitli pafta bölümleme ve adlandırma sistemleri kullanılmıştır ve Yapım Yönetmeliği
PAFTA BÖLÜMLENDİRİLMESİ Türkiye kadastrosunda yukarıda değinilen ada sistemi pafta bölümleme ve adlandırma sistemi dışında çeşitli pafta bölümleme ve adlandırma sistemleri kullanılmıştır ve Yapım Yönetmeliği
Uzay Geriden Kestirme
 Uzay Geriden Kestirme (Eğik Uzunluklarla veya Düşey Açılarla Üçboyutlu Konum Belirleme ) Sebahattin BEKTAŞ* GİRİŞ Konum belirleme problemi günümüzde de jeodezinin en önemli problemi olmaya devam etmektedir.
Uzay Geriden Kestirme (Eğik Uzunluklarla veya Düşey Açılarla Üçboyutlu Konum Belirleme ) Sebahattin BEKTAŞ* GİRİŞ Konum belirleme problemi günümüzde de jeodezinin en önemli problemi olmaya devam etmektedir.
x 1,x 2,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu;
 4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ Doğrusal Denklem Sistemi x,x,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu; a x + a x + L + a x = b n n a x + a x + L + a x = b n n a x + a
4. BÖLÜM DOĞRUSAL DENKLEM SİSTEMLERİ Doğrusal Denklem Sistemi x,x,,x n ler bilinmeyenler olmak üzere, doğrusal denklemlerin oluşturduğu; a x + a x + L + a x = b n n a x + a x + L + a x = b n n a x + a
