ANKARA ÜN IVERS ITES I FEN B IL IMLER I ENST ITÜSÜ YÜKSEK L ISANS TEZ I YILDIZIL VE KONVEKS FONKS IYONLAR IÇ IN BAZI KR ITERLER
|
|
|
- Ceren Karadag
- 5 yıl önce
- İzleme sayısı:
Transkript
1 ANKARA ÜN IVERS ITES I FEN B IL IMLER I ENST ITÜSÜ YÜKSEK L ISANS TEZ I YILDIZIL VE KONVEKS FONKS IYONLAR IÇ IN BAZI KR ITERLER Mü t ŞAN MATEMAT IK ANAB IL IM DALI ANKARA 2 Her hakk sakl d r
2 TEZ ONAYI Mü t ŞAN taraf ndan haz rlanan Y ld z l ve konveks fonksiyonlar için baz kriterler adl tez çal şmas 23/2/2 tarihinde aşa¼g daki jüri taraf ndan oy birli¼gi ile Ankara Üniversitesi Fen Bilimleri Enstitüsü Matematik Anabilim Dal nda YÜKSEK L ISANS TEZ I olarak kabul edilmiştir. Dan şman : Prof. Dr. Ayhan ŞERBETÇ I Jüri Üyeleri : Başkan : Prof. Dr. Ayhan ŞERBETÇ I Üye : Doç. Dr. Erdal GÜNER Üye : Yrd. Doç. Dr. Hüseyin IRMAK Yukar daki sonucu onaylar m Prof. Dr. Orhan ATAKOL Enstitü Müdürü
3 ÖZET Yüksek Lisans Tezi YILDIZIL VE KONVEKS FONKS IYONLAR IÇ IN BAZI KR ITERLER Mü t ŞAN Ankara Üniversitesi Fen Bilimleri Enstitüsü Matematik Anabilim Dal Dan şman : Prof. Dr. Ayhan Şerbetçi Bu çal şmada, birim dairede analitik ve univalent ya da analitik ve p-de¼gerli olan fonksiyonlar ile delinmiş birim dairede analitik ve univalent ya da analitik ve p- de¼gerli olan fonksiyonlar n y ld z ll k ve konvekslik özellikleri ile bu fonksiyonlar n y ld z l ve konveks olmas için gerek ve yeter koşullar incelenmiştir. Tez dört bölümden oluşmaktad r. Birinci bölüm giriş k sm d r. Ikinci bölümde temel tan m, teoremler ve lemmalar yer alm şt r. Üçüncü bölümde, s ras yla birim dairede univalent, p-de¼gerli, meromorf univalent ve p-de¼gerli meromorf fonksiyonlar n y ld z ll ¼g ve konveksli¼gini karekterize eden çeşitli eşitsizlikler ile y ld z ll k ve konvekslik kavramlar aras nda ba¼g nt lar yer alm şt r. Son bölüm olan dördüncü bölüm ise tezin orjinal k sm d r. Burada, p-de¼gerli meromorf ve meromorf y ld z l ve konveks fonksiyonlarla ilgili özellikleri de içeren çok say da teorem verilmiş ve ispatlanm şt r. Ayr ca, ilgili teoremlerin baz önemli sonuçlar da vurgulanm şt r. Aral k 2, 6 sayfa Anahtar Kelimeler : Birim daire, delinmiş birim daire, analitik fonksiyon, univalent fonksiyon, y ld z l fonksiyon, konveks fonksiyon, p-de¼gerli analitik fonksiyon, meromorf fonksiyon, esas de¼ger, kompleks rasyonel fonksiyon. i
4 ABSTRACT Master Thesis CERTAIN CRITERIA ON STARLIKE AND CONVEX FUNCTIONS Mü t ŞAN Ankara University Graduate Scholl of Natural and Applied Science Department of Mathematics Supervisor: Prof. Dr. Ayhan Şerbetçi In this study, the starlikeness and convexity of analytic and univalent or analytic and p-valent functions in unit disk and analytic and univalent or analytic and p-valent functions in punctured unit disk, and the necessary and su cient conditions to be starlike or convex of this functions are investigated. This Thesis consists of four chapters. The rst chapter is devoted to introduction. In the second chapter, basic de nitions, theorems and lemmas take place. In the three chapter, some inequalities characterize the starlikeness and convexity of, respectively, univalent, p-valent, meromorphic univalent and p-valent meromorphic functions in unit disk and the relations between the concepts of starlikeness and convexity are given. The fourth chapter is the last chapter that is the original part of the thesis. In this chapter, a great number of theorems are given and proved that they include the properties concerning meromorphic univalent and p-valent meromorphic functions in unit disk. Also some important results of related theorems are emphasized. December 2, 6 pages Key Words : Unit disc, punctured unit disc, analytic function, univalent function, starlike function, convex function, p-valent analytic function, meromorphic function, principal value, complex rational function. ii
5 TEŞEKKÜR Bana bu konuda çal şma olana¼g veren ve yard mlar n esirgemeyen tez dan şman m say n Prof. Dr. Ayhan ŞERBETÇ I ye (Ankara Üniversitesi Fen Fakültesi Matematik Bölümü), bu konuda ilerleme imkan veren ve verdi¼gi önemli bilgiler ile bana destek olan say n Yrd. Doç. Dr. Hüseyin IRMAK a (Çank r Karatekin Üniversitesi Matematik Bölümü), tezin yaz m aşamas nda bana yard m eden Nuray YELKEN e ve her türlü deste¼gi ve yard m esirgemeyen aileme sayg ve teşekkürlerimi sunar m. Mü t ŞAN Ankara, Aral k 2 iii
6 IÇ INDEK ILER ÖZET i ABSTRACT ii TEŞEKKÜR iii S IMGELER D IZ IN I iv. G IR IŞ TEMEL KAVRAMLAR YILDIZIL VE KONVEKS FONKS IYONLARLA ILG IL I TEMEL B ILG ILER Bir E¼gri Üzerinde Y ld z ll k ve Konvekslik Univalent Fonksiyonlar n Y ld z ll ¼g ve Konveksli¼gi p-de¼gerli Fonksiyonlar n Y ld z ll ¼g ve Konveksli¼gi Meromorf Fonksiyonlar n Y ld z ll ¼g ve Konveksli¼gi p-e¼gerli Meromorf Fonksiyonlar n Y ld z ll ¼g ve Konveksli¼gi p-de ¼GERL I MEROMORF YILDIZIL VE KONVEKS FONKS IYON- LAR IÇ IN BAZI KR ITERLER KAYNAKLAR ÖZGEÇM IŞ
7 S IMGELER D IZ IN I C Z N R S S C M MS MC A (p) S (p) C (p) M(p) MS(p) MC(p) f (q) (z) Kompleks say lar kümesi Tamsay lar kümesi Do¼gal say lar kümesi el say lar kümesi fz 2 C : jzj < g U kümesinin s n r Normalize edilmiş univalent fonksiyonlar n s n f Normalize edilmiş univalent y ld z l fonksiyonlar n s n f Normalize edilmiş univalent konveks fonksiyonlar n s n f U da meromorf univalent fonksiyonlar n s n f U da meromorf univalent y ld z l fonksiyonlar n s n f U da meromorf univalent konveks fonksiyonlar n s n f U da p-de¼gerli analitik fonksiyonlar n s n f U da p-de¼gerli analitik y ld z l fonksiyonlar n s n f U da p-de¼gerli analitik y ld z l fonksiyonlar n s n f U da meromorf p-de¼gerli fonksiyonlar n s n f U da meromorf p-de¼gerli y ld z l fonksiyonlar n s n f U da meromorf p-de¼gerli konveks fonksiyonlar n s n f Bir f(z) fonksiyonunun q: mertebeden adi türevi v
8 . G IR IŞ Univalent y ld z l fonksiyon kavram ilk olarak Alexander (95) taraf ndan tan t lm şt r. Nevanlinna (92) da bu konu üzerinde detayl araşt rmalar yapm şt r. Daha sonra ise univalent y ld z l ve konveks fonksiyonlar Marx (932), Strohhacker (933) ; Jack (97); McGregor (975), Wilken (98) ve daha bir çok araşt rmac taraf ndan çal ş lm şt r. Y ld z l ve konveks fonksiyon kavram n n birim dairede p-de¼gerli analitik fonksiyonlara genelleştirmesini Robertson (937; 94; 945; 953) ve Goodman (95) taraf ndan yap lm şt r. Daha sonra Blakley (962) ; Sakaguchi (962) ; Hummel (966), Ozaki (94) ; Nunokawa (987) ve birçok araşt rmac p-de¼gerli analitik fonksiyonlar n y ld z ll ¼g ve konveksli¼gi üzerine araşt rmalar yapm şt r. Birim dairede meromorf y ld z l ve konveks fonksiyonlar hakk nda Pommerenke (963), Miller (97), Clunie (959), Nunokawa ve Ahuja (2) ve birçok araşt rmac çal şm şt r. Birim dairede p-de¼gerli meromorf y ld z l ve konveks fonksiyonlar ilgili ba¼g nt lar ilk olarak Royster (963) taraf ndan verilmiştir. Daha sonra ise Aouf ve Hossen (993), Liu ve Owa (998) ve çok say da araşt rmac bu konu üzerinde çal şm şt r. Tezin amac y ld z l k ve konvekslik kavramlar n, aralar ndaki ba¼g nt lar ve adi türev operatörü yard m yla birim dairede meromorf bir fonksiyonun türevlerinin y ld zl l ¼g ve konveksli¼gi ile ilgili genel ba¼g nt lar n vermek ve yine bu fonksiyonun y ld z ll ¼g ve konveksli¼gi üzerine baz ba¼g nt lar bulmaya çal şmakt r. Bunun için ilk önce birim dairede univalent fonksiyonlar n y ld z ll ¼g ve konveksli¼gi ile ilgili kavramlar tan t l p daha sonra bir univalent fonksiyonun hangi şartlar alt nda y ld z l ve konveks oldu¼gu ve y ld z ll k ile konvekslik aras nda ne çeşit ba¼g nt lar oldu¼gu üzerine çal şmalar yap lm şt r. Bu çal şmalar n ayn lar s ras yla birim dairede p-de¼gerli analitik fonksiyonlar, meromorf univalent fonksiyonlar ile meromorf p-de¼gerli fonksiyonlar için yap lm şt r. Bu tez dört bölümden oluşmaktad r. Ikinci bölüm di¼ger bölümler için gerekli olan temel tan m ve teoremleri içermektedir. Üçüncü bölüm birim dairede univalent, p-de¼gerli, meromorf ve p-de¼gerli meromorf olan fonksiyonlar n y ld z ll ¼g ve konveksli¼gi üzerine yap lan çal şmalar yer almaktad r. Son bölüm olan dördüncü bölüm tezin orjinal k sm olup bu bölümde adi türev operatörü tan t lm ş ve adi türev operatörünün p-de¼gerli meromorf fonksiyonlara uygulanmas yla y ld z ll k ve konvekslik ile ilgili ba¼g nt lar ve sonuçlar elde edilmiştir.
9 2. TEMEL KAVRAMLAR Tan m 2. Bir f : C! C fonksiyonu ve bir z 2 C noktas verilsin. E¼ger z n en az bir komşulu¼gundaki her noktada f (z) fonksiyonu diferensiyellenebilir ise bu durumda f (z) ye z da analitiktir denir. Tan m 2.2 Bir B C bölgesinde sonlu say daki kutup noktas d ş nda analitik olan fonksiyonlara meromorf fonksiyon ad verilir. Tan m 2.3 u; v 2 B için Bir f(z) fonksiyonu bir B C bölgesinde bire-bir ise yani; her bir f(u) = f(v) ) u = v oluyor ise f(z) fonksiyonuna, B de univalent (yal nkat, birebir) fonksiyon denir. Tan m 2.4 Kompleks düzlemde bir B bölgesinde al nan w ve w 2 gibi her iki nokta çiftini birbirine ba¼glayan do¼gru parças n n tamam bu bölgenin içinde kal yorsa B bölgesine konvekstir denir. Yani, z 2 B ve z 2 2 B olmak üzere her ( ) için ( )z + z 2 2 B oluyorsa, B bölgesine konveks bölge denir. Tan m 2.5 Kompleks düzlemde w 2 B başlang ç noktal her ş n n B bölgesi ile kesişimi olan noktalar kümesi bir do¼gru parças veya ş n ise B ye w a göre y ld z ld r denir. Tan m 2.6 [a; b] R olmak üzere sürekli bir : [a; b]! C fonksiyonuna C düzleminde bir e¼gridir denir Tan m 2.7 Bir e¼grisi verildi¼ginde (a) = (b) ise, ya kapal e¼gridir denir. Tan m 2.8 Bir e¼grisi sadece t = t 2 için (t ) = (t 2 ) oluyorsa ya basit e¼gridir denir. Bazen basit e¼grilere Jordan e¼grisi de denir. basit bir e¼gri ve (a) = (b) ise ya basit kapal e¼gridir (kapal Jordan e¼grisi) denir. Tan m 2.9 Bir e¼grisi verildi¼ginde türevi var ve sürekli ise ya diferensiyellenebilir e¼gri denir. 2
10 Tan m 2. diferensiyellenebilir e¼gri olsun. E¼ger her t 2 [a; b] için (t) 6= ise ya düzgün e¼gri denir. Tan m 2. Sonlu say da j ; j = ; 2; :::; n düzgün e¼grileri verilmiş olsun. E¼ger bütün j = ; 2; :::; n de¼gerleri için j nin bitim noktas j+ in başlang ç noktas ile çak ş yorsa, bu j e¼grilerinin birleşimi olan e¼grisine çevre(parçal düzgün e¼gri) denir. Özel olarak nin başlang ç noktas n nin bitim noktas ile çak ş yor ise e¼grisine kapal çevre denir. E¼ger bu e¼gri kendini kesmiyorsa bu e¼grisine basit çevre, e¼ger buna ilaveten bu kapal ise bu e¼griye basit kapal çevre denir. Önerme 2. Denklemi z (t) ; a t b olan bir e¼grisi bir B bölgesinde bulunsun ve f : B! C sürekli bir fonksiyon olsun. Bu durumda, (i) w (t) = f (z (t)) de bir e¼gri olur ve buna n n resmi denir. w (t) = f ( (t)) olarak da gösterilir. (ii) z (t) diferensiyellenebilir bir e¼gri ve f analitik ise w (t) = f (z (t)) diferensiyellenebilirdir ve w (t) = f (z (t)) z (t) dir. (iii) z (t) düzgün bir e¼gri, f analitik ve f (z (t)) 6= ise w (t) = f (z (t)) de düzgün e¼gridir. Tan m 2.2 B; C düzleminde bir bölge ve, : [; ]! B, 2 : [; ]! B kapal iki e¼gri olsunlar. E¼ger aşa¼g daki iki koşulu gerçekleyen sürekli bir H : [; ] [; ]! B fonksiyonu var ise ve 2 e¼grileri birbirine homotop e¼grilerdir denir. () Her s 2 [; ] için t! H (t; s) kapal bir e¼gridir. (2) H (t; ) = (t) ; H (t; ) = 2 (t) t 3
11 Tan m 2.3 (Koebe Fonksiyonu) k (z) = z ( z) 2 = z + 2z2 + :::: + nz 2 + ::: = olarak tan ml fonksiyona Koebe Fonksiyonu ad verilir. k (z) Koebe fonksiyonunu şeklinde yazal m. Burada k (z) = z ( z) 2 = 4 T (z) = + z z " 2 + z # z (z 2 U) X nz n dönüşümü U = fz 2 C : jzj < g birim dairesini sa¼g yar düzleme dönüştürdü¼gü için bir konveks fonksiyon olup n= ise U birim dairesini D = C k (z) = z ( z) 2 (z 2 U) w = u + iv : v = ; u < 4 bölgesine dönüştürür. Bu bölge w = a göre y ld z l oldu¼gundan k (z) y ld z l bir fonksiyon olur. Ayr ca D bölgesi her w > 4 de¼geri için y ld z ld r. Tan m 2.4, C de kapal bir e¼gri ve z ; C de bir nokta olsun. z a göre n n indeksi I (; z ) = Z 2i dz z z olarak tan mlan r ve n n z a göre dolan m say s olarak da adland r l r. Bilindi¼gi üzere e¼grisi, z n çevresini I (; z ) defa sarar. Önerme 2.2 (i) r > ve t 2 [; 2n] olmak üzere (t) = z + re it çemberi z a göre n dolan m say s na sahip ise - (t) = z + re it çemberi n dolan m say s na sahiptir. (ii) z ; ve e¼grilerinin üzerinde olmas n. ve e¼grileri Cn fz g da homotopik ise, bu durumda ; I (; z ) = I z 4
12 olur. Teorem 2. (Cauchy Türev Formülü) f(z) fonksiyonu bir B bölgesinde analitik olsun. Bu durumda B de f(z) nin her mertebeden türevi mevcuttur. Ayr ca B de bir z noktas ve z dan geçmeyen ve B bölgesinde bir noktaya homotopik bir kapal çevresi için f (n) (z ) I (; z ) = n! Z 2i f(z) n+ dz n = ; 2; ::: (z z ) dir. (Marsden vd. 999) Teorem 2.2 f(z) foksiyonu D = fz 2 C : jz z j < Rg dairesinde analitik olsun. Bu durumda f(z) fonksiyonu D de z merkezli bir kuvvet seri aç l m na sahiptir ve ; z içine alacak şekilde D de pozitif yönlü, kapal bir çevre olmak üzere f(z) = X a n (z z ) n ve a n = Z 2i n= f (z) (z z ) n+ dz şeklindedir. Teorem 2.3 f(z) fonksiyonu b ; :::; b m kutup noktalar d ş nda B bölgesinde analitik ve a ; :::; a n katl l klar yla birlikte f in s f rlar olsun. Bir kapal çevresi, B bölgesinde bir noktaya homotopik ve a j ile b l noktalar ndan geçmesin. Bu durumda Z " nx dz = 2i I (; a j ) f (z) j= # mx I (; b l ) l= d r. Bu formül meromorf fonksiyonlar için de geçerlidir. (Marsden vd. 999) Sonuç 2.2, C de basit kapal bir çevre olsun. (i) f (z) fonksiyonu y içeren aç k bir kümede sonlu say daki kutup noktalar n n d ş nda analitik ve f (z) nin sonlu say daki kutup noktalar n n ve s f rlar n n hiçbiri üzerinde bulunmas n. Bu durumda katl l klar da hesaba kat larak Z f, f (z) fonksiyonun içindeki s f rlar n n ve P f ise kutup noktalar n n say s olmak üzere Z f (z) dz = 2i [Z f P f ] 5
13 olur. (ii) f (z) fonksiyonu y içeren aç k bir kümede ve içinde analitik olsun. E¼ger f (z) ; üzerinde w ye eşit de¼gil ise Z f (z) w dz = 2iN w dir. N w ; katl l klar ile birlikte f (z) w = denkleminin s f rlar n n say s d r. (Marsden vd. 999) Teorem 2.4 Argüment Ilkesi kapal çevresi ve bu çevre üzerinde bulunmayan bir z noktas üzerinde ilerlerken z z n argümentindeki de¼gişim 2I (; z ) kadard r. Bu ise arg (z z ) = 2I (; z ) olarak ifade edilir. Şimdi arg f ile z, çevresi üzerinde ilerlerken arg f deki de¼gişimi tan mlayal m. Bunun anlam aç k olup e¼ger : [a; b]! C ise t; a dan b ye de¼gişirken arg f ( (t)) yi hesaplayarak arg f ( (b)) arg f ( (a)) fark n bulmakt r. arg f ( (t)) nin t ye göre sürekli de¼gişebilmesi için argüment için bir dal seçilmelidir. Eşde¼ger olarak de¼gişkenleri de¼giştirerek, yani e = f yaz p e arg (z) yi hesaplayarak da bulanabilir. Tan m 2.5 f (z) ; B bölgesinde analitik ve, B bölgesinde bir noktaya homotopik ve f (z) nin herhangi bir s f r ndan geçmeyen kapal bir çevre olsun. Bu durumda arg f = 2I (f ; ) olarak tan mlan r. Burada w = al nmas n n nedeni (f ) (z) 6= olmas d r. Teorem 2.5 f (z) fonksiyonu b ; :::; b m kutup noktalar d ş nda B bölgesinde analitik ve a ; :::; a n katl l klar yla birlikte f (z) nin s f rlar olsun. Ayr ca, ; B bölgesinde bir noktaya homotopik bir e¼gri olup a j veya b l noktalar ndan geçmesin. Bu durumda " nx arg f = 2 I (; a j ) j= # mx I (; b l ) l şeklindedir. 6
14 Önerme 2.3 f(z) fonksiyonu z da analitik, f (z ) 6= olsun. z dan geçen bir düzgün e¼grisinin z daki te¼geti x-ekseni ile aç s yap yorsa, n n f(z) fonksiyonu alt ndaki görüntüsü olan e düzgün e¼grisinin de w = f(z ) da te¼geti vard r ve te¼getinin u-ekseni ile yapt ¼g aç = + arg f (z ) d r Teorem 2.6 f(z); z da analitik ve f (z ) 6= ise, z n bir komşu¼gunda f(z) fonksiyonu univalenttir. Teorem 2.7 B C bir bölge olsun. f : B! C fonksiyonu analitik ve univalent ise her z 2 B için 6= d r. Teorem 2.8 B bir bölge, f fonksiyonu B de analitik ve ; B içinde bir noktaya homotopik olan kapal bir e¼gri olsun. Varsayal m ki I (; z) nin de¼geri ya da ve A = fz 2 B : I (; z) 6= g olsun. E¼ger f(a) n n her bir noktas n n, e = f e¼grisine göre indeksi ise, f (z) fonksiyonu B bölgesinde univalenttir (Başkan 999). Teorem 2.9 C basit kapal bir çevre ve D = iç(c) olsun. Farzedelim ki f (z) fonksiyonu D de analitik ve C de sürekli olsun. z, C nin üzerinde pozitif yönde bir kez dönerken w = f(z) noktas da C = f(c) yi pozitif yönde bir kez tan mlar. Bu durumda C pozitif yönlüdür ve f (z) fonksiyonu univalent olup D yi bire-bir olarak D = iç(c ) ye konform olarak dönüştürür (Marsden 999): Teorem 2. f(z) fonksiyonu bir z noktas ndan analitik ve bu noktada f(z) f(z ) n k:mertebeden (k 2) s f r varsa, z dan geçen ve aralar nda aç s yapan iki düzgün e¼grinin resimleri w da k aç s yaparlar. Dolay s yla da z n bir komşulu¼gu w n bir komşuşu¼gunu k defa örter (Başkan 999). Bu teoreme ilişkin aşa¼g daki örnekleri verebiliriz (Başkan 999). Örnek 2. f(z) = z p fonksiyonu birim çemberini yine birim çembere dönüştürür. Fakat, I (; ) = iken I (f ; ) = p dir. Gerçekten Z 2iI (f ; ) = f (z) dz 7
15 oldu¼gundan, 2iI (f ; ) = Z Z = p = 2pi pz p z p dz z dz bulunur. Ve buradan I (f ; ) = p olur. Bu ise f(z) nin n bir komşulu¼gunu p defa örttü¼günü gösterir. Ayr ca Z 2 d d arg f re i d = Z 2 z f (z) B d Z f (z) i oldu¼gundan arg f nin toplam art ş 2p kadard r. jzj=r f (z) dz C A = 2p Örnek 2.2 f (z) = z + a 2 z 2 + a 3 z 3 + :::: şeklinde seri aç l m na sahip birim çember üzerinde ve içinde tan ml bir fonksiyon olsun. Her z 2 fz 2 C : < jzj r < g için f (z) 6= olsun. O zaman Z 2 d d arg f re i d = Z 2 z B d Z f (z) i jzj=r = 2 = arg f = 2I (f ; ) f (z) dz C A olup buradan I (f ; ) = oldu¼gu aç kt r. Bu arg f nin toplam art ş n verecektir. Şu söylenebilir ki f e¼grisi n bir komşulu¼gunu tam defa döner. Sonuç 2.3 Bir B bölgesinin bütün noktalar nda f (z ) 6= ise, B nin f(b) yi bir defa örtmesi gerekmez. Teorem 2. f(z) fonksiyonu bir z noktas ndan analitik ve bu noktada f (z ) 6= ise, z n bir komşulu¼gu w n bir komşulu¼gunu tam bir defa örter. Teorem 2.2 f(z) fonksiyonu bir z noktas ndan analitik ve bu noktada f (z ) 6= ise, w = f (z ) noktas n n bir komşulu¼gunda tan ml, analitik bir f ters fonksiyonu vard r ve 8
16 d dw f (w) = df (z) =dz dir. Ayr ca f (w ) 6= d r. Teorem 2.3 (Maksimum Modül Teoremi) Varsayal m ki B C s n rl bir bölge olsun. u : B! R fonksiyonu B de sürekli ve harmonik, ayr ca M say s u üzerindeki maksimumu olsun. Bu durumda, (i) Her (x; y) 2 B için u (x; y) M dir. (ii) Baz (x; y) 2 B noktalar için u (x; y) = M ise u fonksiyonu sabittir. Teorem 2.4 (Minimum Modül Teoremi) Varsayal m ki B C s n rl bir bölge olsun. u : B! R fonksiyonu B de sürekli ve harmonik, ayr ca m say s u üzerindeki minumumu olsun. Bu durumda, (i) Her (x; y) 2 B için u (x; y) m dir. (ii) Baz (x; y) 2 B noktalar için u (x; y) = m ise u fonksiyonu sabittir. Tan m 2.6 f(z) ve g(z) fonksiyonlar U birim dairesinde analitik olsun. E¼ger bir l(z) fonksiyonu varsa öyle ki (i) l(z) U da analitik (ii) l() = (iii) z 2 U için jl(z)j < ve f(z) = g(l(z)) ba¼g nt s gerçeklenirse, o zaman f(z) fonksiyonu, g(z) fonksiyonuna "subordine" dir denir ve f(z) g(z) ile gösterilir. Lemma 2. f : U! C analitik, z 2 U noktalar için jf(z)j ve f() = olsun. Bu durumda z 2 U noktalar için jf(z)j jzj ve jf ()j dir. Üstelik z 2 D (z 6= ) için jf(z )j jz j ise c, jcj = özelli¼ginde bir sabit olmak üzere, f(z) = cz biçimindedir. Bu lemma Schwarz lemmas olarak bilinir. (Szegö ve Polya 954) Teorem 2.5 f(z) g(z) olsun. Bu durumda f(u) g(u) ve f() = g() d r. Teorem 2.6 f(z) g(z) olsun. Bu durumda ff(z) : jzj < rg fg(z) : jzj < rg ( < r < ) 9
17 dir. Lemma 2.2 w(z); w() = koşulunu gerçekleyen U da analitik bir fonksiyon ve r 2 R, < r < olsun. E¼ger jw(z)j ; maksimum de¼gerine jzj = r üzerindeki bir z noktas nda ulaş yorsa z w (z ) = cw(z ) (c ) eşitli¼gini sa¼glayacak bir c vard r. 97). Bu lemma, Jack s Lemma olarak bilinir (Jack Bu lemman n genellemesi aşa¼g da verilmiştir. Lemma 2.3 w(z) fonksiyonu w(z) = c n z n + c n+ z n+ + c c+2 z c+2 + (n 2 N) (:3) ile verilmiş olup w(z) 6 (z 2 U) olacak şekilde U da analitik olsun. E¼ger bir z = re i (r 2 R; < r < ) için jw(z )j = max jzjjz jjw(z)j; eşitli¼gi sa¼glan yorsa c 2 R ve c n olmak üzere z w (z ) = cw(z ) d r. (Mocanu 2) Lemma 2.4 N(z) ve D(z), U da analitik, N() = D() = ; D(z); U birim dairesini orjine göre y ld z l olan çok katl bir bölgeye dönüştürsün ve ayr ca U da (N (z)=d (z)) > olsun. Bu durumda U da (N(z)=D(z)) > eşitsizli¼gi sa¼glan r.(libera 965)
18 3. YILDIZIL VE KONVEKS FONKS IYONLARLA ILG IL I TEMEL B ILG ILER 3. Bir E¼gri Üzerinde Y ld z ll k ve Konvekslik Bu kesimde bir z e¼grisinin, bu e¼gri üzerinde analitik olan bir f (z) fonksiyonu alt ndaki görüntüsünün y ld z l ya da konveks olup olmad ¼g üzerinde çal şaca¼g z. bir çember, bir do¼gru parças ya da di¼ger baz temel e¼griler olabilir. Varsayal m ki z e¼grisi düzgün bir e¼gri ve z z : z (t) = x (t) + iy (t) parametrik denklemiyle verilmiş olsun. Burada x (t) ile y (t) ; t ye ba¼g ml reel de¼gerli fonksiyonlar ve t 2 [a; b] dir. z e¼grisi düzgün oldu¼gundan her t 2 [a; b] için z (t) = x (t) + iy (t) 6= d r. Şimdi bir düzgün e¼grinin bir analitik fonksiyon alt ndaki görüntüsünün y ld z l olmas tan m n verelim. Tan m 3.. f (z) ; z : z (t) = x (t) + iy (t) düzgün e¼grisi üzerinde analitik, w; z e¼grisinin f (z) fonksiyonu alt ndaki görüntüsü ve w, w üzerinde bulunmayan bir nokta olsun. E¼ger arg (w w ) azalmayan bir fonksiyon, yani her t 2 [a; b] için ise w e¼grisi w a göre y ld z ld r denir. d dt [arg (w w )] Şimdi tan mdan hareketle ispat kolay olan bir lemma verelim. Lemma 3.. Bir z düzgün e¼grisinin bir analitik f (z) fonksiyonu alt ndaki görüntüsünün y ld z l olmas için gerek ve yeter koşul her t 2 [a; b] için olmas d r. Im z (t) f (z) w Ispat.
19 ln fonksiyonunun tan m ndan, her z 2 C arg z = Im fln zg olarak yaz labilir. Buradan hareketle, fg için ln z = ln jzj + i arg z oldu¼gundan d dt [arg (w w )] = d dt [Im [ln (w w )]] d = Im dt [ln (w w )] d = Im [ln ( f (z) dz w )] dz dt d = Im [ln ( f (z) dz w )] dz dt dz = Im f (z) w dt = Im z (t) f (z) w olur. Böylece istenen ispat tamamlan r. Tan m 3..2 w e¼grisinin te¼getinin argümenti t ye göre azalmayan bir fonksiyon ise w e¼grisine konvekstir denir. Bu durumda, w e¼grisinin konveks olmas için gerek ve yeter koşul her t 2 [a; b] için olmas d r. d dt = d dt [arg (z (t) f (t))] Lemma 3..2 z : z = z (t) düzgün e¼grisi üzerinde 6= oldu¼gunu varsayal m. z nin f (z) analitik fonksiyonu alt ndaki görüntüsü konvekstir ancak ve ancak d r. z (t) Im z (t) + f (z) z (t) Ispat. Lemma 3.. in ispat na benzer şekilde, z nin f (z) alt ndaki görüntüsünün konveks oldu¼gunu kabul edelim. Her z 2 C fg olmak üzere ln z = ln jzj + i arg z ) Im [ln z] = arg z 2
20 olup buradan bulunur. d dt [arg (z (t) :)] = d dt [Im [ln (z (t) )]] d = Im dt ln z (t) + d dz [ln ] dz dt z (t) = Im z (t) + f (z) z (t) 3.2 Univalent Fonksiyonlar n Y ld z ll ¼g ve Konveksli¼gi Verilen herhangi bir fonksiyonun Laurin seri aç l m analitik olmas durumunda bu fonksiyonun Mac g(z) = a + a z + a 2 z 2 + = X a k z k k= şeklindedir. E¼ger g(z) fonksiyonu U da univalent ise g(z) + C dönüşümü U da univalenttir. Her z 2 U için g(z) 6= olmas durumunda a 6= olup f(z) = a (g(z) a ) dönüşümü de U da univalenttir ve X f(z) = z + b z + b 2 z 2 + = z + b k z k ; k= b n = a n a (3.2.) şeklindedir. Tan m 3.2. (3:2:) şeklindeki fonksiyonlara normalize edilmiş fonksiyon denir. Bu fonksiyonlar n oluşturdu¼gu s n f S ile gösterilir. Dikkat edilirse birim dairede analitik ve univalent bir fonksiyonun normalize edilmiş olmas için f() = f () = olmas gerekir. Uyar 3.2. U birim dairesinin f(z) fonksiyonunun alt ndaki görüntüsü g(z) fonksiyonu alt ndaki görüntüsüden sadece dönme, öteleme, uzama ya da k salma kadar farkl olaca¼g ndan yukar da seri aç l m verilen g(z) fonksiyonu yerine normalize edilmiş f(z) fonksiyonu ile işlemler yap larak bulunan sonuçlar g(z) fonksiyonuna genişletilir. 3
21 Tan m E¼ger f (z) 2 S fonksiyonu, U birim dairesini konveks bir bölgeye dönüştürüyorsa f (z) ye konveks fonksiyon denir. s n f C ile gösterilir. Tan m E¼ger Bu fonksiyonlar n oluşturdu¼gu f (z) 2 S fonksiyonu, U birim dairesini w a göre y ld z l bir bölgeye dönüştürüyorsa f (z) ye w a göre y ld z l fonksiyon denir. Özel olarak w = al n rsa f (z) fonksiyonuna y ld z l fonksiyon denir. Bu fonksiyonlar n oluşturdu¼gu s n f S ile gösterilir. Uyar f (z), U da univalent ve analitik olsun. E¼ger f (z), C R : jzj = R çemberini basit kapal bir konveks e¼griye dönüştürüyorsa bu e¼gri konveks bir bölgeyi s n rlar veya konveks bir bölgenin s n r d r. Aksine, E¼ger f (z), C R ; R < ; dairesini konveks bir bölgeye dönüştürüyorsa bu bölgenin s n r basit kapal konveks bir e¼gridir. Benzer ifadeler y ld z l e¼griler için de kullanabilir. Teorem 3.2. (i) f (z), U R = fz : jzj Rg kapal dairesinde analitik ve univalent olsun. Bu durumda f (z) nin; U R n konveks bir bölge üzerine dönüştürmesi için gerek ve yeter koşul her z 2 C R : jzj = R için olmas d r. + zf (z) (3.2.2) (ii) f () = olsun. Bu durumda f (z) nin; U R yi w = a göre y ld z l olan bir bölge üzerine dönüştürmesi için gerek ve yeter koşul her z 2 C R için olmas d r. z (3.2.3) f (z) Ispat. (i) Lemma 3..2 deki z e¼grisi C R çemberi olsun. f (z), U R kapal dairesinde univalent oldu¼gundan bu daire üzerinde - dir ve bu durumda her z 2 U R için 6= d r. O halde Lemma 3..2 den her z 2 C R için z (t) Im z (t) + f (z) z (t) (3.2.4) 4
22 yazabilir. Ayr ca z : z = z (t) e¼grisi C R : jzj = R oldu¼gundan z = it ; t 2 olur. Buradan z (t) = i it = iz ve z (t) = i it = z olarak bulunur. Bu (3:2:4) te yerine koyulursa z (t) Im z (t) + f (z) z (t) bulunur. Böylece ispat tamamlan r. (ii) Benzer olarak = Im iz z iz + f (z) = Im i + f (z) iz = Im i( + zf (z) ) = + zf (z) z e¼grisini C R : jzj = R olarak alal m. f (z) ; U R yi w = a göre y ld z l olan bir bir bölge üzerine dönüştürsün. Bu durumda Lemma 3.. den her z 2 C R için Im z (t) f (z) w (3.2.5) yaz labilir: C R : jzj = R oldu¼gundan z = it ; t 2 dir. Buradan z (t) = i it = iz ve f () = = w al nd ¼g ndan bunlar (3:2:5) te yerine koyulursa elde edilir. Böylece ispat tamamlan r. Im i zf (z) z = (3.2.6) f (z) f (z) Lemma 3.2. f (z) 2 S; = f(u), U R = fz : jzj R < g olmak üzere R = f(u R ) olsun. E¼ger orjine göre y ld z l ise bu durumda R da orjine göre y ld z ld r. Tersine R orjine göre y ld z l ise da orjine göre y ld z ld r. Ispat. orjine göre y ld z l olsun. E¼ger z 2 U ise f(z) 2 ve orjine göre y ld z l oldu¼gundan t olmak üzere tf(z) 2 olur. g (z) = f (tf(z)) şeklinde tan mlanan fonksiyon U da analitiktir ve g () =, jzj < için jg (z)j < d r. Schwarz lemmas ndan jzj < için jg (z)j < jzj elde edilir. 5
23 Varsayal m ki z 2 U R olsun. Bu durumda R = f(u R ) oldu¼gundan f(z ) 2 R ve jg (z )j = f (tf(z )) jz j < R olur. E¼ger z 2 = f (tf(z )) denilirse, jz 2 j R ve f(z 2 ) =tf(z ) 2 R d r. Böylelikle f(z ) 2 R iken tf(z ) 2 R d r, yani R orjine göre y ld z ld r. Aksine R orjine göre y ld z l olsun. n n herhangi bir w noktas baz R < de¼gerleri için R dad r. w n ters görüntüsü olan z = f (w ) noktas R = jz j olacak şekilde U R dad r. Lemma < jzj < halka bölgesindeki her z noktas nda z > f (z) olmas için gerek ve yeter koşul f (z) 2 S fonksiyonunun U birim dairesinde y ld z l olmas d r. Ispat. Teorem 3.2. in (ii) ş kk ndan her z 2 U R ; R < ; için z f (z) oldu¼gu biliniyor. Lemma 3.2., f (z) nin U R da y ld z l olmas durmunda U da da y ld z l oldu¼gunu gösterir. Maksimum modül teoremden dolay ve bu teoremin i harmonik fonksiyonuna uygulanmas yla jzj = R < için h z f(z) elde edilir. z > f (z) Aksine yukar daki eşitsizlik sa¼glan yorsa arg f (z), = arg z ye göre kesin monoton artan olup f (z) fonksiyonu U da y ld z ld r. Lemma Bir : U! C fonksiyonu verilsin. E¼ger 6
24 (i) (z), U da analitik (ii) () = (iii) U da ( (z)) > ve X (iv) (z) = b n z n n= oluyorsa, bu durumda olur. n için jb n j 2 ve jzj r < için j (z)j + r r Ispat. C : z = re i ; 2 olsun. Bu durumda Teorem 2.2 den b n = 2i = 2i Z 2 Z 2 (z) z n+ dz re i (re i ) n+ irei d = 2r n Z 2 re i e ni d veya b n r n = Z 2 2 elde edilir. Di¼ger yandan z n (z) analitik oldu¼gundan re i e in d, n = ; ; 2; ::: (3.2.7) = Z 2 2 re i e in d; n = ; ; 2; ::: d r. re i = U re i + iv re i olmak üzere = Z 2 2 = 2 Z 2 re i e in d = Z 2 2 U re i + iv (U cos n V sin n) + i (V cos n + U sin n) d re i (cos n + i sin n) d 7
25 oldu¼gundan ve Z 2 2 = 2 Z 2 b n r n = Z 2 2 = 2 (re i ) e in d (U cos n V sin n) d i 2 Z 2 re i e in d Z 2 (U cos n + V sin n) d + i 2 elde edilir. Elde edilen bu iki eşitlik toplan rsa (V cos n + U sin n) d Z 2 (V cos n U sin n) d b n r n = Z 2 2 = Z 2 re i e in d + Z 2 2 U re i e in d re i e in d ve buradan bulunur. r! jb n j r n = Z 2 U re i e in d Z 2 U re i d = b + b = 2 iken n 2 için jb n j 2 elde edilir. Di¼ger yandan, X j (z)j = b n z n n= X X jb n j r n = + 2 n= bulunur. Böylece ispat tamamlanm ş olur. Teorem f(z) = z + n= r n = + r r X a n z n 2 S olsun. Bu durumda her n için ja n j n dir. n=2 8
26 Ispat. (z) = zf (z) f (z) = + X b n z n (3.2.8) şeklinde olsun. Lemma ün hipotezleri sa¼gland ¼g ndan her n için jb n j 2 dir. E¼ger (3:2:8) nin her iki yan ilk önce f (z) ile çarp l rsa! X z = f (z) + b n z X oldu¼gunu görülür. Bu ifadeden f (z) = z + a n z n ç kar l rsa, z + 2a 2 z 2 + ::: + na n z n + ::: = z + (a 2 + b ) z 2 + ::: + (a n + a n b + ::: + b n ) z n + ::: n=2 n= n= eşitli¼gi elde edilir. Bu eşitlikten, a 2 = b 2a 3 = a 2 b + b 2.. (n ) a n = a n b + ::: + b n sistemi elde edilir. ja 2 j = jb j 2 olup k = 2; 3; :::; n varsayal m. Bu durumda için ja k j k oldu¼gunu (n ) n (n ) ja n j = ja n b + ::: + b n j 2 ((n ) + (n 2) + ::: + ) = 2 2 ) ja n j n bulunur. Bu da ispat tamamlar. Teorem f (z) = a z + a 2 z 2 + ::: U da analitik ve a 6= olsun. E¼ger U da ise bu durumda f (z) ; U da univalenttir. z > f (z) Ispat. Teoremin hipotezleri göz önüne al nd ¼g nda f (z) fonksiyonun z = da basit s f r n n var oldu¼gu aç kt r. E¼ger < jz j < olacak şekildeki z noktas için f (z ) = 9
27 olmas durumunda z =f (z) fonksiyonunun z noktas nda basit bir kutbu olup z n civar nda key küçüklükte negatif de¼gerler al r, fakat bu (z =f (z)) > oluşu ile çelişir. Lemma 3.2. e göre her R < için U R = fz : jzj R < g da f (z) fonksiyonunun univalent oldu¼gu göstermek yeterli olacakt r. C R : z = R e it ; t 2; R < R < olsun. f (z), U R de bir s f r olup hiç kutup noktas olmad ¼g ndan argüment prensibine göre CR arg f (z) = 2 olup Teorem 2.9 dan f (z) fonksiyonu U R U R olmak üzere U R de univalenttir. Bu da bulunmak istenen şey olup ispat tamamlan r. Lemma f (z) 2 S olsun. f (U) nun konveks olmas için gerek ve yeter koşul her R 2 (; ) için f (U R ) nin konveks olmas d r. Ispat. Lemma 3.2. in ispat nda oldu¼gu gibi = f(u), U R = fz : jzj < R < g olacak şekilde R = f(u R ) olsun. n n konveks oldu¼gunu kabul edelim. Gösterilmesi gereken şey; w ve w 2 ; R de herhangi farkl iki nokta ise t 2 (; ) olmak üzere tw + ( t) w 2 do¼gru parças n n R de oldu¼gudur. z = f (w ) ve z 2 = f (w 2 ) olsun. Aç kt r ki z ; z 2 2 R dir ve varsayal m ki jz j < jz 2 j olsun. konveks oldu¼gundan dolay, U nun (z) = tf z z 2 z + ( t) f (z) t alt ndaki görüntüsü n n alt kümesidir. Bu durumda g (z) = f ( (z)) fonksiyonu U da analitiktir ve Schwarz lemmas ndaki jg (z)j < ve g () = şartlar n sa¼glar. Dolay s yla, jzj < için jg (z)j jzj ve böylece jg (z 2 )j = f (tw + ( t) w 2 ) jz2 j < R (3.2.9) elde edilir. R oldu¼gundan her t 2 (; ) için öyle bir z t 2 U R vard r ki f (z t ) = tw + ( t) w 2 2
28 dir. Fakat (3:2:9) dan j f (f (z t ))j = jz t j < R veya z t 2 U R d r. Böylelikle her tw + ( t) w 2 noktas R dedir. Tersine her R 2 (; ) için R konveks olsun. Bu durumda da konveks olur. Gerçekten, w ve w 2 ; da herhangi farkl iki nokta olsun. R yi R nin z = f (w ) ve z 2 = f (w 2 ) yi içerecek şekilde alal m. Bu durumda R = f (U R ) ; w ve w 2 noktalar n n her ikisini birden içerir. Böylece tw + ( t) w 2 do¼gru parças üzerindeki her nokta R de kal r. R oldu¼gundan bu do¼gru parças dad r. Bu da n n konveks oldu¼gunu gösterir. Lemma Bir f (z) 2 S fonksiyonunun konveks olabilmesi için gerek ve yeter koşul z fonksiyonunun y ld z l olmas d r. (Alexander 95) Ispat. Bir f(z) 2 S fonksiyonu için, z(z) z olup g(z) = z denilirse = z[ + zf (z)] z = + zf (z) z(z) zg (z) = = + zf (z) > z g(z) elde edilir. X Teorem Varsayal m ki f (z) = z + a n z n 2 S Bu durumda her n 2 N için ja n j dir. X Ispat. f (z) = z + a n z n oldu¼gundan n=2 n=2 fonksiyonu konveks olsun. X z = z + na n z n elde edilir. Lemma göz önüne al n rsa, f (z) fonksiyonu U da konveks oldu¼gundan z fonksiyonu U da y ld z l olup Teorem den n=2 n ja n j n veya ja n j bulunur. Bu da ispat tamamlar. 2
29 Tan m f (z) 2 S olsun. E¼ger U da z > f(z) eşitsizli¼gi sa¼glan yor ise, f (z) fonksiyonuna ( < ) mertebeden y ld z l fonksiyon denir. Bu fonksiyonlar n oluşturdu¼gu s n f S () ile gösterilir. Tan m f (z) 2 S olsun. E¼ger U da + zf (z) > eşitsizli¼gi sa¼glan yor ise, f (z) fonksiyonuna ( < ) mertebeden konveks fonksiyon denir. Bu fonksiyonlar n oluşturdu¼gu s n f ise C () ile gösterilir. Uyar S S () ve C C () d r. Lemma f (z) 2 C () olmas için gerek ve yeter koşul z 2 S () olmas d r. Lemma Bütün f (z) 2 C fonksiyonlar için U da z a f (z) a 2 sa¼glans n. Bu durumda U da eşitsizli¼gi sa¼glan r. z f (z) 4 ( a) a 2 Teorem f (z) 2 C () ise f (z) 2 S 2 dir. (Marx 932) Ispat. a = ; a 2 = dizisini oluştural m. Dizinin n.terimi, n 4 ( a ) = 4 ; a 3 = a n = :terimi ve 4 ( a n ) 22 4 ( a 2 ) = 3 ;...
30 rekürans formülünün yard m yla bulunabilir. Lemma ye göre e¼ger U da (I) a n 2 ve (II) z a n f (z) koşullar sa¼glan yor ise bu durumda z a n f (z) eşitsizli¼gi sa¼glan r. n = 2 için a n = a = ve Lemma tenn f (z) 2 C () ise z 2 S () oldu¼gundan yukar daki I ve II eşitsizlikleri sa¼glan r. Şimdi n = 2; 3; ::: için a n 2 ve lim n! a n = 2 oldu¼gunu gösterece¼giz. Di¼ger yandan a k = k 2k (3.2.) oldu¼gu gösterilirse bu iki varsay m ispatlanm ş olur. k = için a = olup do¼grudur. k = n için a n = n 2n a n = 4( a n ) do¼gru olsun. rekürans formülünden a n+ = = n 4 2n (n + ) 2 (n + ) olur ki bu da (3:2:) nun do¼gru oldu¼gunu gösterir. O halde ispat tamamlanm ş olur. Teorem deki sonucun daha geneli aşa¼g daki teoremle verilmiştir. Teorem f (z) 2 C () ( < ) ise () = 2 + p olmak üzere f (z) 2 S ( ()) d r. (Jack 97) Ispat. Bu teoremin ispat için teoremi şu şekilde ifade edilmesi daha uygun olacakt r: 23
31 E¼ger f (z) fonksiyonu ( 2 + 3) =2 ( + ) mertebeden konveks ise bu durumda f (z) fonksiyonu ( + ) =2 mertebeden y ld z ld r. h (z) = z f (z) = w (z) w (z) (3.2.) olarak al ns n. E¼ger U da jw (z)j < oldu¼gunu gösterilirse, bu durumda h (z), birim daireyi w = ( + ) do¼grusunun sa¼g ndaki yar düzleme dönüştüren 2 fonksiyonuna subordinedir. (3:2:) den z z h (z) f (z) = z (3.2.2) elde edilir. (3:2:2) nin her iki yan n n logaritmik türevi al n rsa, h (z) f (z) + h (z) = + zf (z) eşitli¼gi, buradan ise oldu¼gu bulunur. h (z) f (z) + h (z) = + zf (z) jzj = r çemberinin üzerindeki bir noktada jw (z)j maksimum de¼gerini al yorsa Lemma 2.2 kullan labilir, öyle ki bu noktada k olmak üzere + zf (z) = w (z) w (z) kw (z) kw (z) + w (z) w (z) (3.2.3) olur. Şimdi varsayal m ki M(r; w), w (z) nin jzj = r çemberi üzerindeki maksimum de¼geri olmak üzere, baz r < de¼gerleri için M(r; w) = olsun. Bunun gerçekleşti¼gi w (z) noktas nda jwj = dir. (Aç kt r ki w 6= dir.) Bu durumda w (z) = ( + ) ; w (z) 2 kw (z) = w (z) 2 k; 24
32 kw (z) w (z) = 2 k + + w (z) 2 k w (z) 2 k + 2 k + olarak bulunur. Böylece (3:2:3) den + zf (z) w (z) = w (z) 2 ( + ) + 2 k 2 k + = 2 ( + ) 2 k ( + ) kw (z) kw (z) + w (z) w (z) 2 k eşitsizli¼gi elde edilir. Fakat bu f (z) fonksiyonunun ( 2 + 3) =2 ( + ) mertebeden konveks olmas ile çelişir. O halde M(r; w) = olamaz. Bu her r < için do¼gru ve M(; w) = oldu¼gundan M(r; w) = olmal d r. O halde U da jw (z)j < dir. Bu da ispat tamamlar. Teorem daki sonuç için Jack, C () S ( ()) olacak şekilde en büyük () = reel say s n n ne olaca¼g problemini ortaya atm ş ve bu problemin çözümünü McGregor aşa¼g daki teorem ile vermiştir. Teorem f (z) 2 C () ( < ) ise 8 >< () = >: olmak üzere f (z) 2 S ( ()) dir [ 2 2 ] ; 6= 2 2 log 2 ; = 2 9 >= >; 3.3 p-de¼gerli Fonksiyonlar n Y ld z ll ¼g ve Konveksli¼gi Tan m 3.3. f(z) fonksiyonu birim dairede analitik olsun. w = f(z) eşitli¼ginin en fazla p tane kökü varsa f(z) fonksiyonuna p-de¼gerlidir denir. Daha önce normalize edilmiş univalent analitik fonksiyonlar için verdi¼gimiz y ld z ll k ve konvekslik tan mlar n p-de¼gerli analitik fonksiyonlar için genelleştirece¼giz 25
33 p katl bölgelelerde konveks küme kavram n aşa¼g daki yolla genelleştirilir. w b, bir p-katl R bölgesinin bir s n r noktas ve w b (r), w b ile ayn katta bulunan R nin w noktalar n n kümesi olsun ve jw her w b s n r noktas için w b (r) konveks olacak şekilde bir konveks bölge denir. w b j < r eşitsizli¼gi sa¼glans n. E¼ger R bölgesinin r > varsa, R ye lokal f(z), U da analitik ve f (re i ) 6= ise, bu durumda f (z) fonksiyonu jzj < r < dairesini, s n r sürekli dönen te¼gete sahip analitik bir f(re i ) e¼grisi olan bir R (r) bölgesine dönüştürür. bu te¼getle reel eksenin kesişimi ile oluşan aç olsun., n n bir fonksiyonu olarak tek olarak belirlenemez, fakat = iken nin muhtemel de¼gerlerinden birini seçerek bu durum sa¼glanabilir ve nin süreklili¼ginden yararlan l rsa 2 için () belirlenebilir. Bu durumda () eşitsizli¼ginin sa¼glanmas için gerek ve yeter koşul R (r) nin lokal konveks bölge olmas d r. Bu ise bilinen eşitli¼gidir. () = + zf (z) Tan m p pozitif bir tamsay olmak üzere, e¼ger f(z) fonksiyonu U da analitik, f() = ve her r için < r < aral ¼g nda olacak şekilde bir < var ve G (r; ) = + re i f (re i ) > ; 2 (3.3.) f (re i ) Z 2 G(r; )d = 2p (3.3.2) eşitli¼gi sa¼glan yor ise f(z) fonksiyonu C(p) nin eleman d r. E¼ger f(z) 2 C(p) ise f(z) fonksiyonu jzj < r < kümesini lokal olarak konveks bir bölgeye dönüştürür. Bundan başka ; jzj < r çemberinde tam olarak p tane kökü vard r, çok katl köklerin say s na tek noktadaki katl l k da say l r. E¼ger v bu köklerin say s ise 2p = Z 2 G(r; )d = = 2 i = 2 + 2v Z 2 Z 2 + re i f (re i ) d (3.3.3) f (re i ) f (z) dz A 26
34 dir. Sonuç olarak f(z) fonksiyonu U da en fazla p-de¼gerlidir. f(z) c nin köklerinin say s n veren çevre integrali, çevre boyunca arg(f(z) c) nin de¼gişimin 2 ile bölümünü verir. Fakat C(p) s n f n n bir fonksiyonu için R(r) yi s n rlayan e¼gri ; dan 2 ye giderken sürekli bir dönüşe sahip bir e¼gridir ve tüm dönüşlerin toplam say s tam olarak p keredir. Bu yüzden arg(f(z) c) nin de¼gişim 2p yi geçmez. Düzlemdeki bir bölgenin bir noktaya göre y ld z ll ¼g n uygun p-katl bölgelere genelleştirmek için bir w b s n r noktas n verilen noktaya birleştiren do¼gru göz önüne al ns n. w b ; p-katl R bölgesinin s n r olarak tan mlan rsa do¼gru, saat yönünün tersine sürekli bir dönüşe sahiptir. Bu durumda R verilen noktaya göre y ld z ld r denir. Şimdi F (z), U da analitik ve < r < için F (re i ) 6= olsun. E¼ger = arg F (re i ) ise, ; n n bir fonksiyonu olup tek olarak belirlenemez. Fakat = iken nin muhtemel de¼gerlerinden biri seçilerek bu durum sa¼glanabilir ve nin süreklili¼ginden yararlan l rsa 2 için () belirlenebilir. Bu durumda () olmas için gerek ve yeter koşul R (r) nin orjine göre y ld z l olmas d r. Bu ise bilinen eşitli¼gini gerektirir. () = z f (z) Tan m p pozitif bir tamsay olmak üzere, e¼ger F (z) fonksiyonu U da analitik, F () = ve her r için < r < aral ¼g nda olacak şekilde bir < var ve H(r; ) = re i F (re i ) > ( 2) (3.3.4) F (re i ) Z 2 H(r; )d = 2p (3.3.5) eşitli¼gi sa¼glan yor ise F (z) fonksiyonu S(p) nin eleman d r. (3:3:2), nin U da p tane kökü oldu¼gunu gösterirken (3:3:5) ise F (z) fonksiyonunun U da p tane kökü oldu¼gunu gösterir. F (z) fonksiyonunun U da p tane kökü oldu¼gunu görmek için ; dan 2 ye de¼gişirken, de¼gişimi ifade etmek üzere () = arg F (re i ) c ifadesini göz önüne alal m. c sabit olmak üzere, ; dan e de¼gişir. () = 2p oldu¼gu aç kt r. Ayr ca () ; her zaman 27 2 nin tam kat olup c nin jzj < r nin
35 görüntüsünün s n r noktas olan w b ye olan eşitli¼gini(yani; c = w b ) sa¼glayan c de¼geri d ş nda süreklidir. Bu noktalarda () de¼geri 2 s çrar. (3.3.4) ve (3.3.5) ten her c için p tane bunun gibi s n r noktas oldu¼gu ç kar labilir. Sonuç olarak jcj nin yeterince büyük de¼gerleri için () = olur ki () de¼gerindeki s çramalar 2 olmal d r ve her ve c için () 2p dir: p = için S(p) ve C(p) bilinen, s ras yla birebir konveks ve y ld z l fonksiyonlard r ve S() C() dir. p 2 için S(p)! C(p) oldu¼guna dikkat edilmelidir. Lemma 3.3. c 6= bir key sabit olsun. E¼ger f (z) 2 C(p) ise bu durumda F (z) = cz 2 S(p); tersine F (z) 2 S(p) ise f (z) 2 C(p) olup şeklindedir. Z z f (z) = c F (t) dt t Ispat. Belirtilen f (z) ve F (z) fonksiyonlar için zf (z) F (z) = z c + czf (z) cz = + zf (z) olur ve (3:3:5), (3:3:2) yi (3:3:4) ; (3:3:) i gerektirir. Tersi de sa¼gland ¼g ndan istenen gerçekleşir. Şimdi birim dairede analitik olan A (p) s n f n n tan m n verelim. Tan m A (p) ; U birim dairesinde analitik ve X f (z) = a n z n, a p 6= ; p 2 N (3.3.6) n=p şeklindeki seri aç l m na sahip fonksiyonlar n s n f d r. Tan m koşul f 2 A (p) fonksiyonunun p-de¼gerli y ld z l olmas için gerek ve yeter z > f (z) olmas d r. gösterilir. U da p-de¼gerli y ld z l f (z) 2 A (p) fonksiyonlar n n s n f AS (p) ile 28
36 Tan m f 2 A (p) fonksiyonunun p-de¼gerli konveks olmas için gerek ve yeter koşul + zf (z) > olmas d r. gösterilir. U da p-de¼gerli konveks f (z) 2 A (p) fonksiyonlar n n s n f AC (p) ile Lemma f (z) 2 A (p) ve K reel s n rl sabit olmak üzere olsun. Bu durumda < jzj < halkas nda z > K (3.3.7) f (z) f (z) 6= d r. Ispat. < jj < olacak şekilde bir noktas nda f(z); n.(n )mertebeden s f ra sahip olsun. Bu durumda f(z) fonksiyonu g () 6= olmak üzere f(z) = (z ) n g (z) şeklinde yaz labilir. Buradan z f (z) = z n (z ) n g (z) + (z ) n g (z) (z ) n g (z) nz = (z ) + zg (z) g (z) elde edilir. K sa bir hesaplamayla lim (z z! ) z f (z) = lim (z ) z! = lim z! nz + (z nz (z ) + zg (z) g (z) ) zg (z) g (z) bulunur. Bu ise z fonksiyonun z = da basit kutbu oldu¼gunu gösterir ki bu f(z) (3:3:7) ile çelişir. Çünkü (3:3:7) ; z fonksiyonun < jzj < halkas nda kutup f(z) noktas olmad ¼g n gösterir. O halde < jzj < halkas nda f (z) 6= d r. 29 6=
37 Lemma f (z) 2 A (p) ve K reel s n rl sabit olmak üzere olsun. Bu durumda < jzj < halkas nda + zf (z) > K (3.3.8) 6= d r Ispat. Lemma nin ispat na benzer olarak yap l r. Lemma f (z) 2 AS (p) olsun: Bu durumda Z z F (z) = c f (t) dt 2 AS (p + ) veya eşde¼ger olarak d r. zf (z) > (z 2 U) F (z) Ispat. D(z) = zf (z) = zf(z) ve N(z) = F (z) olsun. z = için f(z) = oldu¼gundan N() = D() = ve D(z); orjine göre p + de¼gerli y ld z l bir fonksiyondur, çünkü f (z) 2 AS (p) olmak üzere d r. zd (z) z [zf(z)] z = = + > D (z) zf(z) f(z) Di¼ger yandan basit bir işlem ile bulunur. Buradan D (z) N (z) [zf(z)] f(z) + z = = F (z) f (z) z = + > f(z) N (z) > D (z) 3
38 elde edilir. Lemma 2.4 ün koşullar sa¼gland ¼g na göre N (z) > D (z) olur ki bu da zf (z) > (z 2 U) F (z) olu¼gunu, yani F (z) 2 AS (p + ) olmas n gerektirir. Böylece ispat tamamlan r. Lemma f (z) 2 AS (p) ise bu durumda f (z), U da p-de¼gerlidir. n o Ispat. f (z) 2 AS (p) oldu¼gundan z > olup Lemma göz önüne f(z) al n rsa < jzj < halkas nda f (z) 6= d r. Bu ise f (z) nin sadece z = da p.mertebeden s f r oldu¼gunu gösterir. O halde key bir r; < r < say s için Z 2 re i f (re i ) d = 2p f(re i ) olur. Tan m ten f (z) nin, U da p-de¼gerli oldu¼gunu gösterir. Lemma f (z) 2 AC (p) ise bu durumda f (z), jzj < de p-de¼gerlidir. n o Ispat. f (z) 2 AC (p) oldu¼gundan + zf (z) > olup Lemma e göre < jzj < halkas nda 6= d r. Bu ise nin sadece z = da p.mertebeden s f r oldu¼gunu gösterir. O halde key bir r; < r < say s için Z 2 + re i f (re i ) d = 2p f (re i ) olur. Tan m ten f (z) nin, U da p-de¼gerli oldu¼gunu ç kar labilir. Tan m gerek ve yeter koşul f 2 A (p) fonksiyonunun p-de¼gerli -mertebeden y ld z l olmas için z > f (z) olmas d r. U da p-de¼gerli y ld z l f (z) 2 A (p) fonksiyonlar n n s n f AS (p; ) ile gösterilir. 3
39 Tan m f 2 A (p) fonksiyonunun p-de¼gerli -mertebeden konveks olmas için gerek ve yeter koşul + zf (z) > olmas d r. U da p-de¼gerli konveks f (z) 2 A (p) fonksiyonlar n n s n f AC (p; ) ile gösterilir. Uyar 3.5. Aç kt r ki = için MS (p; ) = MS (p) ve MC (p; ) = MC (p) d r. Ve MS (p; ) MS (p) ve MC (p; ) MC (p) dir.ayr ca p = için MS (; ) = MS () ve MC (; ) = MC () d r. Tan m (3:3:5) de a p = olmas durumunda elde edilen A (p) s n f n n n p- de¼gerli alts n f n e A (p) ile gösterelim. Aç kt r ki yukar daki tüm tan mlamalar ve lemmalar bu s n f için de geçerlidir. Teorem 3.3. f(z) 2 e A (p) ; < p, p 2 N ve z 2 U olsun. O zaman d r. z f(z) p p zf ) (z) > f(z) Teorem f(z) 2 e A (p) ; < p, p 2 N ve z 2 U olsun. O zaman d r. + zf (z) p p ) + zf (z) > Teorem f(z) 2 e A (p) ; < p, p 2 N ve z 2 U olsun. O zaman d r. p f z p p ) (z) > z p 3.4 Meromorf Fonksiyonlar n Y ld z ll ¼g ve Konveksli¼gi z = noktas nda kutup noktas bulunan ve D := fz 2 C : < jzj < g delinmiş birim dairesinde analitik ve univalent olan fonksiyonlar n y ld z ll k ve konvekslik tan mlar aşa¼g daki gibi verilmiştir. 32
40 Tan m 3.4. E¼ger U birim dairedesinde meromorf bir f (z) fonksiyonu ve Z 2 z < f(z) z d = 2 z = re i ; < r < f(z) özelliklerini sa¼gl yor ise f (z) fonksiyonuna U da univalent meromorf y ld z l fonksiyon denir. Tan m E¼ger U birim dairedesinde meromorf bir f fonksiyonu ve Z 2 + zf (z) < + zf (z) d = 2 z = re i ; < r < özelliklerini sa¼gl yor ise f (z) fonksiyonuna U da univalent meromorf konveks fonksiyon denir. Şimdi literatürde s kça araşt r lan univalent meromorf fonksiyonlar n M s n f n n tan m n, bu s n f n y ld z l ve konveks olan alts n ar n n tan m n ve birbirleriyle olan ilişkilerini ifade eden lemma ve teoremleri verelim. Tan m D bölgesinde analitik ve univalent olan f(z) = z + a n+z n+ + a n+2 z n+2 + = z + X k=n+ a k z k (n 2 N) şeklindeki seri aç l ml fonksiyonlar n s n f M(n) ile gösterilir ve bu tür fonksiyonlar meromorf fonksiyondur. Bu tür foksiyonlar z = noktas nda singüler noktaya sahip olup ve e¼ger, ilgili seri aç l m ndaki bütün a k katsay lar negatif ise ilgili seri aç l m na sahip olan fonksiyonlara negatif katsay l meromorf fonksiyonlar, pozitif ise pozitif katsay l meromorf fonksiyonlar ve kompleks ise ilgili fonksiyonlara kompleks katsay l meromorf fonksiyonlar ad verilir. n = al n rsa M = M s n f n elde edilir. Bu s n f ile ilgili tan m ve teoremler aşa¼g da verilmiştir. 33
41 Tan m E¼ger bir f (z) 2 M fonksiyonu birebir ve f(d) nin tümleyeni orjine göre y ld z l ise f (z) fonksiyonuna y ld z ld r denir.(miller vd. 2) Tan m E¼ger D de f (z) 6= ve z > (z 2 D) f(z) eşitsizli¼gi sa¼glan yor ise, bu durumda f (z) 2 M fonksiyonuna D de orjine göre y ld z ld r denir. Meromorf y ld z l fonksiyonlar n s n f MS* ile gösterilir. Tan m E¼ger bir f (z) 2 M fonksiyonu birebir ve f(d) nin tümleyeni orjine göre konveks ise f (z) fonksiyonuna konvekstir denir. Tan m E¼ger D de 6= ve + zf (z) > (z 2 D) eşitsizli¼gi sa¼glan yor ise, f (z) fonksiyonuna D de konvekstir denir. Meromorf konveks fonksiyonlar n s n f MC ile gösterilir. Tan m E¼ger D de f (z) 6= ve z > (z 2 D) f(z) eşitsizli¼gi sa¼glan yor ise, f (z) fonksiyonuna ( < ) mertebeden meromorf y ld z l fonksiyon denir. Bu fonksiyonlar n oluşturdu¼gu s n f MS*() ile gösterilir. Tan m E¼ger D de 6= ve + zf (z) > (z 2 D) eşitsizli¼gi sa¼glan yor ise, f (z) fonksiyonuna ( < ) mertebeden meromorf konveks fonksiyon denir. Bu fonksiyonlar n oluşturdu¼gu s n f ise MC () ile gösterilir. Aç kt r ki = için MS*() = MS ve MC () = MC d r. MS*() MS ve MC () MC dir. Di¼ger yandan 34
42 Lemma 3.4. f (z) 2 MC () ancak ve ancak z 2 MS*() d r. Lemma p(z), U da analitik, p() = ve < olmak üzere p(z) zp (z) > p(z) (3 2) 2 ( ) ; z 2 U oldu¼gunu varsayal m. Bu durumda U da fp(z)g > olur. Ispat. w(z), U da analitik ve w() = olmak üzere p(z) = ( ) + w(z) w(z) + (3.4.) olsun. Her z 2 U için jw(z)j < oldu¼gunu göstermek yeterlidir. E¼ger jzj < jz j eşitsizli¼gini sa¼glayan z ler için jw(z)j < ve jw(z )j = olacak şekilde bir z 2 U varsa bu durumda Lemma 2.2 den z w (z ) = kw(z ); k elde edilir. w(z ) = e i yaz l rsa, (3.4.) den z p (z ) p(z ) = = = = = 2( )z w (z ) ( w(z )) 2 ( ) +w(z) w(z) + 2( )ke i ( e ii ) 2 ( ) +ei e i + 2( )k 2( cos ) 2i sin ( ) + 2( cos ) ( )k ( cos ) + i( ) sin ( )k ( ( cos ) i( ) sin ) 2 ( cos ) 2 + ( ) 2 sin 2 bulunur. Buradan z p (z ) = p(z ) ( )k ( cos ) 2 ( cos ) 2 + ( ) 2 sin 2 (3.4.2) oldu¼gu elde edilir. cos = t denirse t 2 olur ve g (t) = t 2 t 2 + ( ) 2 (2t t 2 ) 35
43 şeklinde yaz l rsa, (3.4.2) şu şekilde ifade edilebilir; z p (z ) = ( )kg (t) p(z ) dir. Basit bir işlem ile g (t) fonksiyonunun minimum de¼gerini t = noktas nda ald ¼g gösterilebilir ve olur. Böylelikle ve p(z ) lim g (t) = t! z p (z ) p(z ) 2 ( ) 2 2 ( ) z p (z ) + p(z ) 2 ( ) = (3 2) 2 ( ) elde edilir. Bu ise varsay mla çelişece¼ginden her z 2 U p(z) nin tan m ndan için jw(z)j < elde edilir. p(z) = ( ) + w(z) w(z) + + w(z) p(z) ) = > w(z) ) (p(z)) > bulunur. Böylece ispat tamamlanm ş olur. Lemma nin uygulanmas ile aşa¼g daki sonuca ulaş l r. Teorem 3.4. < olmak üzere f (z) 2 MC Ispat. p(z) = z f(z) olsun. p() = oldu¼gu aç kt r. Buradan p(z) zp (z) p(z) = bulunur. Lemma göz önüne al n rsa elde edilir. Teorem 3.4.de = (3 2) ise f (z) 2 MS () d r. 2( ) + zf (z) (3 2) 2( ) al n rsa aşa¼g daki sonuca ulaş l r: z >, yani f (z) 2 MS () f(z) 36
44 Sonuç 3.4. f (z) 2 M, D de f (z) 6= ve < olmak üzere her z 2 U için + zf (z) > olsun. Bu durumda her z 2 U için z > f (z) 4 q elde edilir. Sonuç 3.4. de e¼ger! al n r ise şu sonuç elde edilir: Sonuç f (z) 2 MC () ise bu durumda f (z) 2 MS () olur. Uyar 3.4. f (z) = z olsun. D de f (z) 6= oldu¼gu görülür. Di¼ger yandan ( z) 2 z f (z) = + z z ve bulunur. + zf (z) = + z2 z 2 Uyar Sonuç 2 den, e¼ger f fonksiyonu mertebeden meromorf konveks fonksiyon ise bu durumda en az mertebeden meromorf y ld z l bir fonksiyondur. 3.5 p-de¼gerli Meromorf Fonksiyonlar n Y ld z ll ¼g ve Konveksli¼gi Tan m 3.5. E¼ger U birim dairesinde meromorf bir f (z) fonksiyonu olsun. E¼ger f (z) ; jzj = r; < r < çemberlerini orjine göre y ld z l bir e¼griye dönüştürüyorsa ve bu e¼gri üzerindeki bir noktay orjine birleştiren vektör 2p aç l k bir sürekli dönüş yapacak şekilde bir < < say s var ise bu f (z) fonksiyonuna p-de¼gerli y ld z l bir fonksiyondur denir. Analitik olarak ise f fonksiyonunun şu özellikleri sa¼glamas gerekmektedir: ve z < f(z) 37
(z z 0 ) n. n=1. Z f (z) dz = 2ib 1
 0 RE IDÜ TEOR IS I Tan m. f fonksiyonu z 0 noktas nda ayr k singülerli¼ge sahip olsun. Bu durumda f fonksiyonu 0 < jz z 0 j < " bölgesinde X X f(z) = a n (z z 0 ) n b n + (z z 0 ) n Laurent seri aç l m
0 RE IDÜ TEOR IS I Tan m. f fonksiyonu z 0 noktas nda ayr k singülerli¼ge sahip olsun. Bu durumda f fonksiyonu 0 < jz z 0 j < " bölgesinde X X f(z) = a n (z z 0 ) n b n + (z z 0 ) n Laurent seri aç l m
fonksiyonu, her x 6= 1 reel say s için tan ml d r. (x 1)(x+1) = = x + 1 yaz labilir. Bu da; f (x) = L
 Limit Bu bölümde, matematik analizde temel bir görevi olan it kavram incelenecektir. Analizdeki bir çok problemin çözümünde it kavram na gereksinim duyulmaktad r. Bunlardan baz lar ; bir noktada bir e¼griye
Limit Bu bölümde, matematik analizde temel bir görevi olan it kavram incelenecektir. Analizdeki bir çok problemin çözümünde it kavram na gereksinim duyulmaktad r. Bunlardan baz lar ; bir noktada bir e¼griye
SORULAR. 1. Aşa¼g daki limitleri bulunuz. Cevab n z n aşamalar n belirtiniz. lim. 1 n sin. lim. q 1 x 1+x
 SOULA. Aşa¼g daki limitleri bulunuz. Cevab n z n aşamalar n belirtiniz. lim! lim sin(t )dt sin 4 np n! i= n sin i n. q + arcsin belirli integralini hesalay n z. Cevab n z n aşamalar n belirtiniz. 3. 4
SOULA. Aşa¼g daki limitleri bulunuz. Cevab n z n aşamalar n belirtiniz. lim! lim sin(t )dt sin 4 np n! i= n sin i n. q + arcsin belirli integralini hesalay n z. Cevab n z n aşamalar n belirtiniz. 3. 4
MIT Açık Ders Malzemeleri Kompleks Değişkenli Fonksiyonlar 2008 Güz
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 18.112 Kompleks Değişkenli Fonksiyonlar 2008 Güz Bu materyallerden alıntı yapmak ya Kullanım Şartları hakkında bilgi almak için http://ocw.mit.edu/terms http://tuba.acikders.org.tr
MIT Açık Ders Malzemeleri http://ocw.mit.edu 18.112 Kompleks Değişkenli Fonksiyonlar 2008 Güz Bu materyallerden alıntı yapmak ya Kullanım Şartları hakkında bilgi almak için http://ocw.mit.edu/terms http://tuba.acikders.org.tr
Bir H Hilbert uzay üzerinde herhangi bir kompakt simetrik T operatörü için,
 Ritz Yöntemi Kullan larak Integral Operatörlerin Özde¼gerlerinin Yaklaş k Hesab Yüksel SOYKAN, Erkan TAŞDEM IR, Melih GÖCEN Zonguldak Karaelmas Üniversitesi, Fen Edebiyat Fakültesi, Matematik Bölümü, 6700
Ritz Yöntemi Kullan larak Integral Operatörlerin Özde¼gerlerinin Yaklaş k Hesab Yüksel SOYKAN, Erkan TAŞDEM IR, Melih GÖCEN Zonguldak Karaelmas Üniversitesi, Fen Edebiyat Fakültesi, Matematik Bölümü, 6700
8 LAURENT SER I GÖSTER IMLER I
 8 LAURENT SER I GÖSTER IMLER I Tan m. C n ; n 0; ; ; : : : kompleks sabitler olmak üere serisine Laurent serisi denir. Burada n X C n ( X X X C n ( 0 ) n a n ( 0 ) n b n + ( 0 ) n 0 ) n dir. Teore8.. (Laurent
8 LAURENT SER I GÖSTER IMLER I Tan m. C n ; n 0; ; ; : : : kompleks sabitler olmak üere serisine Laurent serisi denir. Burada n X C n ( X X X C n ( 0 ) n a n ( 0 ) n b n + ( 0 ) n 0 ) n dir. Teore8.. (Laurent
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ. Aylin AYKUT MATEMATİK ANABİLİM DALI ANKARA Her hakkı saklıdır
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ SİNGÜLER POTANSİYELLİ STRUM-LIOUVILLE OPERATÖRLERİ Aylin AYKUT MATEMATİK ANABİLİM DALI ANKARA Her hakkı saklıdır ÖZET Yüksek Lisans Tezi S
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ SİNGÜLER POTANSİYELLİ STRUM-LIOUVILLE OPERATÖRLERİ Aylin AYKUT MATEMATİK ANABİLİM DALI ANKARA Her hakkı saklıdır ÖZET Yüksek Lisans Tezi S
NÜMER IK ANAL IZ. Nuri ÖZALP. Sabit Nokta ve Fonksiyonel Yineleme. Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP Sabit Nokta ve Fonksiyonel Yineleme Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 3 7! Sabit Nokta ve Fonksiyonel Yineleme 1 / 23 Sabit Nokta
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP Sabit Nokta ve Fonksiyonel Yineleme Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 3 7! Sabit Nokta ve Fonksiyonel Yineleme 1 / 23 Sabit Nokta
1.3. Normal Uzaylar. Bu bölümde; regülerlikten daha kuvvetli bir ay rma aksiyomu tan mlanarak. baz temel özellikleri incelenecektir.
 1.3. Normal Uzaylar Bu bölümde; regülerlikten daha kuvvetli bir ay rma aksiyomu tan mlanarak baz temel özellikleri incelenecektir. Tan m 1.3.1. (X; ) bir Hausdor uzay olsun. E¼ger, 8F; K 2 F; F \ K = ;
1.3. Normal Uzaylar Bu bölümde; regülerlikten daha kuvvetli bir ay rma aksiyomu tan mlanarak baz temel özellikleri incelenecektir. Tan m 1.3.1. (X; ) bir Hausdor uzay olsun. E¼ger, 8F; K 2 F; F \ K = ;
NÜMER IK ANAL IZ. Nuri ÖZALP FONKS IYONLARA YAKLAŞIM. Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP FONKS IYONLARA YAKLAŞIM Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 4 7! FONKS IYONLARA YAKLAŞIM 1 / 21 1 Polinom Interpolasyonu Newton Formu
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP FONKS IYONLARA YAKLAŞIM Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 4 7! FONKS IYONLARA YAKLAŞIM 1 / 21 1 Polinom Interpolasyonu Newton Formu
T.C. PAMUKKALE ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MATEMATİK ANABİLİM DALI
 T.C. PAMUKKALE ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MATEMATİK ANABİLİM DALI LATİSLERDE TÜREVLER YÜKSEK LİSANS TEZİ UTKU PEHLİVAN DENİZLİ, OCAK - 2015 T.C. PAMUKKALE ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
T.C. PAMUKKALE ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MATEMATİK ANABİLİM DALI LATİSLERDE TÜREVLER YÜKSEK LİSANS TEZİ UTKU PEHLİVAN DENİZLİ, OCAK - 2015 T.C. PAMUKKALE ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
7 TAYLOR SER I GÖSTER IMLER I
 7 TAYLOR SER I GÖSTER IMLER I Bir f fonksiyonu analitiklik bölgesi içinde f () X a n ( 0 ) n şeklinde bir kuvvet serisi gösterimine sahiptir. E¼ger a n f (n) ( 0 ) seçilirse bu kuvvet serisi Taylor serisi
7 TAYLOR SER I GÖSTER IMLER I Bir f fonksiyonu analitiklik bölgesi içinde f () X a n ( 0 ) n şeklinde bir kuvvet serisi gösterimine sahiptir. E¼ger a n f (n) ( 0 ) seçilirse bu kuvvet serisi Taylor serisi
2. Topolojik Uzaylarda Ba¼glant l l k Ba¼glant l Topolojik Uzaylar. Tan m (X; ) topolojik uzay n n her biri boş kümeden farkl olan ayr k
 2. Topolojik Uzaylarda Ba¼glant l l k 2.1. Ba¼glant l Topolojik Uzaylar Tan m 2.1.1. (X; ) topolojik uzay n n her biri boş kümeden farkl olan ayr k iki aç ktan oluşan bir örtüsü yok ise, (X; ) topolojik
2. Topolojik Uzaylarda Ba¼glant l l k 2.1. Ba¼glant l Topolojik Uzaylar Tan m 2.1.1. (X; ) topolojik uzay n n her biri boş kümeden farkl olan ayr k iki aç ktan oluşan bir örtüsü yok ise, (X; ) topolojik
MATEMAT IK-I (SORULAR)
 Part I MATEMAT IK-I (SORULAR) SAYILAR. irrasyonel midir?. 7 say s n n irrasyonel oldu¼gunu gösteriniz. (Gauss Teoremini kullan n z.) 3. + 3 say s n n irrasyonel oldu¼gunu gösteriniz. (Gauss Teoremini kullan
Part I MATEMAT IK-I (SORULAR) SAYILAR. irrasyonel midir?. 7 say s n n irrasyonel oldu¼gunu gösteriniz. (Gauss Teoremini kullan n z.) 3. + 3 say s n n irrasyonel oldu¼gunu gösteriniz. (Gauss Teoremini kullan
6 Devirli Kodlar. 6.1 Temel Tan mlar
 6 Devirli Kodlar 6.1 Temel Tan mlar Tan m S F n q için e¼ger (a 0 ; a 1 ; : : : ; a n 1 ) 2 S iken (a n 1 ; a 1 ; : : : ; a n 2 ) 2 S oluyorsa S kümesine devirli denir. E¼ger bir C do¼grusal kodu devirli
6 Devirli Kodlar 6.1 Temel Tan mlar Tan m S F n q için e¼ger (a 0 ; a 1 ; : : : ; a n 1 ) 2 S iken (a n 1 ; a 1 ; : : : ; a n 2 ) 2 S oluyorsa S kümesine devirli denir. E¼ger bir C do¼grusal kodu devirli
1998 ULUSAL ANTALYA MATEMAT IK OL IMP IYATI B IR INC I AŞAMA SORULARI
 1998 ULUSL NTLY MTEMT IK OL IMP IYTI IR INC I ŞM SORULRI Lise 1- S nav Sorular 1. T = 1! +! + 3! + ::: + 1997! + 1998! toplam n n son iki basama¼g ndaki rakamlar n toplam kaçt r? ) 13 ) 9 C) 6 D) E) Hiçbiri.
1998 ULUSL NTLY MTEMT IK OL IMP IYTI IR INC I ŞM SORULRI Lise 1- S nav Sorular 1. T = 1! +! + 3! + ::: + 1997! + 1998! toplam n n son iki basama¼g ndaki rakamlar n toplam kaçt r? ) 13 ) 9 C) 6 D) E) Hiçbiri.
Fonksiyonel Analize Giriş I Ara S nav Sorular 29 Kas m Bir metrik uzayda her kapal yuvar kapal bir kümedir. Ispatlay n z.
 Fonksiyonel Analize Giriş I Ara S nav Sorular 29 Kas m 2010 1 Bir metrik uzayda her kapal yuvar kapal bir kümedir. Ispatlay n z. 2 (a) d (x; y) = Z 1 0 jx (t) y (t)j 1 + jx (t) y (t)j dt fonksiyonunun
Fonksiyonel Analize Giriş I Ara S nav Sorular 29 Kas m 2010 1 Bir metrik uzayda her kapal yuvar kapal bir kümedir. Ispatlay n z. 2 (a) d (x; y) = Z 1 0 jx (t) y (t)j 1 + jx (t) y (t)j dt fonksiyonunun
NÜMER IK ANAL IZ. Nuri ÖZALP MATEMAT IKSEL ÖNB ILG ILER. Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP MATEMAT IKSEL ÖNB ILG ILER Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 1 7! MATEMAT IKSEL ÖNB ILG ILER 1 / 15 Kaynaklar Nümerik Analiz-Bilimsel
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP MATEMAT IKSEL ÖNB ILG ILER Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 1 7! MATEMAT IKSEL ÖNB ILG ILER 1 / 15 Kaynaklar Nümerik Analiz-Bilimsel
1) 6 kişilik bir aile yuvarlak bir masa etraf nda, anne ile baban n yan yana oturmamas koşulu ile kaç farkl biçimde oturabilir?
 ) 6 kişilik bir aile yuvarlak bir masa etraf nda, anne ile baban n yan yana oturmamas koşulu ile kaç farkl biçimde oturabilir? Çözüm: Önce, anne ile baban n yan yana oturma durumunu düşünelim. Anne ile
) 6 kişilik bir aile yuvarlak bir masa etraf nda, anne ile baban n yan yana oturmamas koşulu ile kaç farkl biçimde oturabilir? Çözüm: Önce, anne ile baban n yan yana oturma durumunu düşünelim. Anne ile
AKDEN IZ ÜN IVERS ITES I 21. ULUSAL ANTALYA MATEMAT IK OL IMP IYATI SORULARI
 KDEN IZ ÜN IVERS ITES I 21. ULUSL NTLY MTEMT IK OL IMP IYTI SORULRI DI SOYDI :...CEP TEL :... OKUL...ŞEH IR :... SINIF :...Ö ¼GRETMEN :... eposta :... IMZ :... SINV TR IH I VE ST I : 14 May s 2016 - Cumartesi
KDEN IZ ÜN IVERS ITES I 21. ULUSL NTLY MTEMT IK OL IMP IYTI SORULRI DI SOYDI :...CEP TEL :... OKUL...ŞEH IR :... SINIF :...Ö ¼GRETMEN :... eposta :... IMZ :... SINV TR IH I VE ST I : 14 May s 2016 - Cumartesi
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ SONSUZ JACOBİ MATRİSLERİ İÇİN SPEKTRAL EŞİTSİZLİKLER. Yelda AYGAR
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ SONSUZ JACOBİ MATRİSLERİ İÇİN SPEKTRAL EŞİTSİZLİKLER Yelda AYGAR MATEMATİK ANABİLİM DALI ANKARA 008 Her hakkı saklıdır ÖZET Yüksek Lisans
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ SONSUZ JACOBİ MATRİSLERİ İÇİN SPEKTRAL EŞİTSİZLİKLER Yelda AYGAR MATEMATİK ANABİLİM DALI ANKARA 008 Her hakkı saklıdır ÖZET Yüksek Lisans
NÜMER IK ANAL IZ. Nuri ÖZALP L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ 1 / Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ 1 / 27 Çok farkl durumlara uygulanabilen genel bir yöntemdir. Reel de¼gişkenli,
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ 1 / 27 Çok farkl durumlara uygulanabilen genel bir yöntemdir. Reel de¼gişkenli,
NÜMER IK ANAL IZ. Nuri ÖZALP L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ 1 / Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ 1 / 1 Denklemlerin Köklerini Bulma Giriş Denklemlerin Köklerini Bulma
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ L INEER OLMAYAN DENKLEMLER IN ÇÖZÜMÜ 1 / 1 Denklemlerin Köklerini Bulma Giriş Denklemlerin Köklerini Bulma
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ İKİNCİ BASAMAKTAN DİFERENSİYEL DENKLEMLER İÇİN ARALIK SALINIM KRİTERİ.
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ İKİNCİ BASAMAKTAN DİFERENSİYEL DENKLEMLER İÇİN ARALIK SALINIM KRİTERİ Neslihan ÇAVUNT MATEMATİK ANABİLİM DALI ANKARA 202 Her hakkı saklıdır
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ İKİNCİ BASAMAKTAN DİFERENSİYEL DENKLEMLER İÇİN ARALIK SALINIM KRİTERİ Neslihan ÇAVUNT MATEMATİK ANABİLİM DALI ANKARA 202 Her hakkı saklıdır
FONKS IYONEL ANAL IZE G IR IŞ I Aras nav Sorular
 Ad ve Soyad : Numaras : FONKS IYONEL ANAL IZE G IR IŞ I Aras nav Sorular 30.11.2007 1. Aşa¼g daki ifadelerin do¼gru olup olmad klar n nedenlerini aç klayarak yaz n z. (a) (X; kk) bir normlu uzay ve M bunun
Ad ve Soyad : Numaras : FONKS IYONEL ANAL IZE G IR IŞ I Aras nav Sorular 30.11.2007 1. Aşa¼g daki ifadelerin do¼gru olup olmad klar n nedenlerini aç klayarak yaz n z. (a) (X; kk) bir normlu uzay ve M bunun
PROBLEM SET I ARALIK 2009
 PROBLEM SET I - 5 09 ARALIK 009 Soru 1 (Besanko ve Braeutigam (00), sayfa 405): Aşa¼g da tam rekabet piyasas nda faaliyet gösteren bir rman n k sa dönem toplam maliyet fonksiyonu verilmiştir: Piyasa denge
PROBLEM SET I - 5 09 ARALIK 009 Soru 1 (Besanko ve Braeutigam (00), sayfa 405): Aşa¼g da tam rekabet piyasas nda faaliyet gösteren bir rman n k sa dönem toplam maliyet fonksiyonu verilmiştir: Piyasa denge
NÜMER IK ANAL IZ. Nuri ÖZALP. SAYISAL TÜREV ve INTEGRAL. Bilimsel Hesaplama Matemati¼gi
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP SAYISAL TÜREV ve INTEGRAL Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 1 / 23 1 Say sal Türev ve Richardson
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi Nuri ÖZALP SAYISAL TÜREV ve INTEGRAL Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 5 7! SAYISAL TÜREV ve INTEGRAL 1 / 23 1 Say sal Türev ve Richardson
17. ULUSAL ANTALYA MATEMAT IK OL IMP IYATLARI B IR INC I AŞAMA SORULARI A A A A A A A
 AKDEN IZ ÜN IVERS ITES I 17. ULUSAL ANTALYA MATEMAT IK OL IMP IYATLARI B IR INC I AŞAMA SORULARI A A A A A A A SINAV TAR IH I VE SAAT I : 24 MART 2012 - Cumartesi 10.00-12.30 Bu s nav 25 sorudan oluşmaktad
AKDEN IZ ÜN IVERS ITES I 17. ULUSAL ANTALYA MATEMAT IK OL IMP IYATLARI B IR INC I AŞAMA SORULARI A A A A A A A SINAV TAR IH I VE SAAT I : 24 MART 2012 - Cumartesi 10.00-12.30 Bu s nav 25 sorudan oluşmaktad
20. ULUSAL ANTALYA MATEMAT IK OL IMP IYATI SORULARI A A A A A A A
 KDEN IZ ÜN IVERS ITES I 20. ULUSL NTLY MTEMT IK OL IMP IYTI SORULRI DI SOYDI :...CEP TEL :... OKUL...ŞEH IR :... SINIF :...Ö ¼GRETMEN :... eposta :... IMZ :... SINV TR IH I VE ST I : 3 May s 2015 - Pazar
KDEN IZ ÜN IVERS ITES I 20. ULUSL NTLY MTEMT IK OL IMP IYTI SORULRI DI SOYDI :...CEP TEL :... OKUL...ŞEH IR :... SINIF :...Ö ¼GRETMEN :... eposta :... IMZ :... SINV TR IH I VE ST I : 3 May s 2015 - Pazar
1999 ULUSAL ANTALYA MATEMAT IK OL IMP IYATI B IR INC I AŞAMA SORULARI
 1999 ULUSL NTLY MTMT IK L IMP IYTI IR IN I ŞM SRULRI Lise 1- S nav Sorular 1. f1; ; 3; :::; 1999g kümesinin, eleman say s tek say olan kaç tane alt kümesi vard r? ) 1999 ) 1998 ) 1998-1 ) 999 ) hiçbiri.
1999 ULUSL NTLY MTMT IK L IMP IYTI IR IN I ŞM SRULRI Lise 1- S nav Sorular 1. f1; ; 3; :::; 1999g kümesinin, eleman say s tek say olan kaç tane alt kümesi vard r? ) 1999 ) 1998 ) 1998-1 ) 999 ) hiçbiri.
ÜN TE II L M T. Limit Sa dan ve Soldan Limit Özel Fonksiyonlarda Limit Limit Teoremleri Belirsizlik Durumlar Örnekler
 ÜN TE II L M T Limit Sa dan ve Soldan Limit Özel Fonksiyonlarda Limit Limit Teoremleri Belirsizlik Durumlar Örnekler MATEMAT K 5 BU BÖLÜM NELER AMAÇLIYOR? Bu bölümü çal flt n zda (bitirdi inizde), *Bir
ÜN TE II L M T Limit Sa dan ve Soldan Limit Özel Fonksiyonlarda Limit Limit Teoremleri Belirsizlik Durumlar Örnekler MATEMAT K 5 BU BÖLÜM NELER AMAÇLIYOR? Bu bölümü çal flt n zda (bitirdi inizde), *Bir
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ PARÇALI SÜREKLİ ARGÜMENTLİ DİFERENSİYEL DENKLEMLER. Gizem SEYHAN
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ PARÇALI SÜREKLİ ARGÜMENTLİ DİFERENSİYEL DENKLEMLER Gizem SEYHAN MATEMATİK ANABİLİM DALI ANKARA 28 Her hakkı saklıdır ÖZET Yüksek Lisans Tezi
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ PARÇALI SÜREKLİ ARGÜMENTLİ DİFERENSİYEL DENKLEMLER Gizem SEYHAN MATEMATİK ANABİLİM DALI ANKARA 28 Her hakkı saklıdır ÖZET Yüksek Lisans Tezi
ANAL IZ III Aras nav Sorular
 Ad ve Soyad : Numaras : ANAL IZ III Aras nav Sorular 26.11.27 1. x 1 = p 3 ve x n+1 = p 3 + x n ; n = 1; 2; ::: biçiminde tan mlanan (x n ) dizisinin yak nsak oldu¼gunu gösteriniz ve limitini bulunuz.(2)
Ad ve Soyad : Numaras : ANAL IZ III Aras nav Sorular 26.11.27 1. x 1 = p 3 ve x n+1 = p 3 + x n ; n = 1; 2; ::: biçiminde tan mlanan (x n ) dizisinin yak nsak oldu¼gunu gösteriniz ve limitini bulunuz.(2)
2010 oldu¼gundan x 2 = 2010 ve
 ) 444400 say s ndaki rakamlar n yerleri de¼giştirilerek 7 basamakl kaç farkl say yaz labilir? Çözüm : Bu rakamlar n bütün farkl 7 li dizilişlerinin say s 7! olacakt r. Bu dizilişlerin 4!! soldan ilk rakam
) 444400 say s ndaki rakamlar n yerleri de¼giştirilerek 7 basamakl kaç farkl say yaz labilir? Çözüm : Bu rakamlar n bütün farkl 7 li dizilişlerinin say s 7! olacakt r. Bu dizilişlerin 4!! soldan ilk rakam
Ç NDEK LER. Bölüm 4: Üslü Say lar...44 Üslü fadeler...44 Al t rmalar...47 Test Sorular...49
 Ç NDEK LER Bölüm1: Say Sistemleri...1 Say Sistemi...2 Desimal (Onluk) Say Sistemi...2 Say Basamaklar ve Taban...4 Binary ( kilik) Say Sistemi...4 Oktal (Sekizlik) Say Sistemi...7 Heksadesimal (Onalt l
Ç NDEK LER Bölüm1: Say Sistemleri...1 Say Sistemi...2 Desimal (Onluk) Say Sistemi...2 Say Basamaklar ve Taban...4 Binary ( kilik) Say Sistemi...4 Oktal (Sekizlik) Say Sistemi...7 Heksadesimal (Onalt l
13.Konu Reel sayılar
 13.Konu Reel sayılar 1. Temel dizi 2. Temel dizilerde toplama ve çarpma 3. Reel sayılar kümesi 4. Reel sayılar kümesinde toplama ve çarpma 5. Reel sayılar kümesinde sıralama 6. Reel sayılar kümesinin tamlık
13.Konu Reel sayılar 1. Temel dizi 2. Temel dizilerde toplama ve çarpma 3. Reel sayılar kümesi 4. Reel sayılar kümesinde toplama ve çarpma 5. Reel sayılar kümesinde sıralama 6. Reel sayılar kümesinin tamlık
Analiz III Ara S nav Sorular 24 Kas m 2010
 Analiz III Ara S nav Sorular 24 Kas m 2010 1 Aşa¼g daki ifadelerin do¼gru olup olmad klar n nedenlerini aç klayarak yaz n z. (a) R n uzay n n aç k olmayan her alt kümesi kapal d r. (b) A = fx 2 [0; 1]
Analiz III Ara S nav Sorular 24 Kas m 2010 1 Aşa¼g daki ifadelerin do¼gru olup olmad klar n nedenlerini aç klayarak yaz n z. (a) R n uzay n n aç k olmayan her alt kümesi kapal d r. (b) A = fx 2 [0; 1]
DÜZCE ÜN IVERS ITES I FEN-EDEB IYAT FAKÜLTES I
 DÜZCE ÜN IVERS ITES I FEN-EDEB IYAT FAKÜLTES I MATEMAT IK BÖLÜMÜ 203-204 BAHAR YARIYILI D IFERANS IYEL DENKLEMLER II ARA SINAV 2 Nisan 204 Süre: 90 dakika CEVAP ANAHTARI. (5p) Belirsiz katsay lar yöntemini
DÜZCE ÜN IVERS ITES I FEN-EDEB IYAT FAKÜLTES I MATEMAT IK BÖLÜMÜ 203-204 BAHAR YARIYILI D IFERANS IYEL DENKLEMLER II ARA SINAV 2 Nisan 204 Süre: 90 dakika CEVAP ANAHTARI. (5p) Belirsiz katsay lar yöntemini
mat 103. Çal şma Sorular 1
 mat 0. Çal şma Sorular. FONKS IYONLA. Aşa¼g daki kurallarla verilen fonksiyonlar n gra klerini çiziniz. (a) f() 4 jj (b) f() jj (c) f() 4 jj (ç) f() j j (d) f() j j (e) f() j j (f) f() j j. Aşa¼g daki
mat 0. Çal şma Sorular. FONKS IYONLA. Aşa¼g daki kurallarla verilen fonksiyonlar n gra klerini çiziniz. (a) f() 4 jj (b) f() jj (c) f() 4 jj (ç) f() j j (d) f() j j (e) f() j j (f) f() j j. Aşa¼g daki
NÜMER IK ANAL IZ. Nuri ÖZALP L INEER S ISTEMLER IN ÇÖZÜMÜ. Bilimsel Hesaplama Matemati¼gi, Gazi Kitabevi 2012
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi, Gazi Kitabevi 0 Nuri ÖZALP L INEER S ISTEMLER IN ÇÖZÜMÜ Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 6 7! L INEER S ISTEMLER IN ÇÖZÜMÜ / 9 . LU ve Cholesky
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi, Gazi Kitabevi 0 Nuri ÖZALP L INEER S ISTEMLER IN ÇÖZÜMÜ Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 6 7! L INEER S ISTEMLER IN ÇÖZÜMÜ / 9 . LU ve Cholesky
2014 LYS MATEMATİK. P(x) x 2 x 3 polinomunda. 2b a ifade- x lü terimin. olduğuna göre, katsayısı kaçtır? değeri kaçtır? ifadesinin değeri kaçtır? 4.
 04 LYS MATEMATİK. a b b a ifade- ab olduğuna göre, sinin değeri kaçtır? 5. P() polinomunda katsayısı kaçtır? 4 lü terimin. ifadesinin değeri kaçtır? 4. yy y 4y y olduğuna göre, + y toplamının değeri kaçtır?
04 LYS MATEMATİK. a b b a ifade- ab olduğuna göre, sinin değeri kaçtır? 5. P() polinomunda katsayısı kaçtır? 4 lü terimin. ifadesinin değeri kaçtır? 4. yy y 4y y olduğuna göre, + y toplamının değeri kaçtır?
BİR SAYININ ÖZÜ VE DÖRT İŞLEM
 ÖZEL EGE LİSESİ BİR SAYININ ÖZÜ VE DÖRT İŞLEM HAZIRLAYAN ÖĞRENCİ: Sıla Avar DANIŞMAN ÖĞRETMEN: Gizem Günel İZMİR 2012 İÇİNDEKİLER 1. PROJENİN AMACI.. 3 2. GİRİŞ... 3 3. YÖNTEM. 3 4. ÖN BİLGİLER... 3 5.
ÖZEL EGE LİSESİ BİR SAYININ ÖZÜ VE DÖRT İŞLEM HAZIRLAYAN ÖĞRENCİ: Sıla Avar DANIŞMAN ÖĞRETMEN: Gizem Günel İZMİR 2012 İÇİNDEKİLER 1. PROJENİN AMACI.. 3 2. GİRİŞ... 3 3. YÖNTEM. 3 4. ÖN BİLGİLER... 3 5.
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ SINIR KOŞULLARINDA SPEKTRAL PARAMETRE BULUNAN NON-SELFADJOİNT FARK OPERATÖRLERİNİN
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ SINIR KOŞULLARINDA SPEKTRAL PARAMETRE BULUNAN NON-SELFADJOİNT FARK OPERATÖRLERİNİN SPEKTRAL ANALİZİ Turhan KÖPRÜBAŞI MATEMATİK ANABİLİM DALI ANKARA
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ SINIR KOŞULLARINDA SPEKTRAL PARAMETRE BULUNAN NON-SELFADJOİNT FARK OPERATÖRLERİNİN SPEKTRAL ANALİZİ Turhan KÖPRÜBAŞI MATEMATİK ANABİLİM DALI ANKARA
Do ufl Üniversitesi Matematik Kulübü Matematik Bireysel Yar flmas 2004 Soru ve Yan tlar
 o ufl Üniversitesi Matematik Kulübü Matematik ireysel Yar flmas 2004 Soru ve Yan tlar Soru. S f rdan farkl bir a say s için sonsuz ondal klarla oluflan ifadesinin de eri nedir? ise, Soru 2. 0 < < 0 olmak
o ufl Üniversitesi Matematik Kulübü Matematik ireysel Yar flmas 2004 Soru ve Yan tlar Soru. S f rdan farkl bir a say s için sonsuz ondal klarla oluflan ifadesinin de eri nedir? ise, Soru 2. 0 < < 0 olmak
TÜREV VE UYGULAMALARI
 TÜREV VE UYGULAMALARI A R, a A ve f de A da tanımlı bir fonksiyon olsun. Eğer f(x) f(a) lim x a x a limiti veya x=a+h koymakla elde edilen f(a+h) f(a) lim h 0 h Bu türev f (a), df dx limiti varsa f fonksiyonu
TÜREV VE UYGULAMALARI A R, a A ve f de A da tanımlı bir fonksiyon olsun. Eğer f(x) f(a) lim x a x a limiti veya x=a+h koymakla elde edilen f(a+h) f(a) lim h 0 h Bu türev f (a), df dx limiti varsa f fonksiyonu
Çözümlü Yüksek Matematik Problemleri. Doç. Dr. Erhan Pişkin
 Çözümlü Yüksek Matematik Problemleri Doç. Dr. Erhan Pişkin Doç. Dr. Erhan PİŞKİN ÇÖZÜMLÜ YÜKSEK MATEMATİK PROBLEMLERİ ISBN 978-605-38-45-5 Kitap içeriğinin tüm sorumluluğu yazarına aittir. 06, Pegem Akademi
Çözümlü Yüksek Matematik Problemleri Doç. Dr. Erhan Pişkin Doç. Dr. Erhan PİŞKİN ÇÖZÜMLÜ YÜKSEK MATEMATİK PROBLEMLERİ ISBN 978-605-38-45-5 Kitap içeriğinin tüm sorumluluğu yazarına aittir. 06, Pegem Akademi
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ ÇOK DEĞİŞKENLİ HİPERGEOMETRİK FONKSİYONLAR. Recep ŞAHİN MATEMATİK ANABİLİM DALI ANKARA 2011
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ ÇOK DEĞİŞKENLİ HİPERGEOMETRİK FONKSİYONLAR Recep ŞAHİN MATEMATİK ANABİLİM DALI ANKARA 2 Her hakkı saklıdır TEZ ONAYI Recep ŞAH IN taraf ndan haz
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ ÇOK DEĞİŞKENLİ HİPERGEOMETRİK FONKSİYONLAR Recep ŞAHİN MATEMATİK ANABİLİM DALI ANKARA 2 Her hakkı saklıdır TEZ ONAYI Recep ŞAH IN taraf ndan haz
ab H bulunur. Şu halde önceki önermenin i) koşulu da sağlanır ve H G bulunur.
 3.ALT GRUPLAR HG, Tanım 3.. (G, ) bir grup ve nin boş olmayan bir alt kümesi olsun. Eğer (H, ) bir grup ise H ye G nin bir alt grubu denir ve H G ile gösterilir. Not 3.. a)(h, ), (G, ) grubunun alt grubu
3.ALT GRUPLAR HG, Tanım 3.. (G, ) bir grup ve nin boş olmayan bir alt kümesi olsun. Eğer (H, ) bir grup ise H ye G nin bir alt grubu denir ve H G ile gösterilir. Not 3.. a)(h, ), (G, ) grubunun alt grubu
yaz labilir. Bu yaz l m da x reel say s na z nin reel k sm ; y reel say s na da z nin sanal k sm denir ve
 Komplex say lar reel say lar n (x; y) s ral ikilileri şeklinde düşünülebilirler. x reel say s s n reel eksen üerindeki (x; 0) noktas şeklinde düşünürsek kompleks say lar kümesinin reel say lar kümesini
Komplex say lar reel say lar n (x; y) s ral ikilileri şeklinde düşünülebilirler. x reel say s s n reel eksen üerindeki (x; 0) noktas şeklinde düşünürsek kompleks say lar kümesinin reel say lar kümesini
İKİNCİ MERTEBEDEN LİNEER DİFERANSİYEL DENKLEMLER İÇİN HAREKETLİ SINIR DEĞER PROBLEMİ
 Yüksek Lisans Tezi Tezi Hazırlaуan Kalima MOLDOKULOVA Matematik Anabilim Dalı 2014 KIRGIZİSTAN-TÜRKİYE MANAS ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MATEMATİK ANABİLİM DALI İKİNCİ MERTEBEDEN LİNEER DİFERANSİYEL
Yüksek Lisans Tezi Tezi Hazırlaуan Kalima MOLDOKULOVA Matematik Anabilim Dalı 2014 KIRGIZİSTAN-TÜRKİYE MANAS ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ MATEMATİK ANABİLİM DALI İKİNCİ MERTEBEDEN LİNEER DİFERANSİYEL
Ad ve Soyad : Numaras : Analiz III Aras nav Sorular
 Analiz III Aras nav Sorular 30. 11. 2006 1. (a) A = fx 2 R : x 2 4x 5 < 0g ise sup A =? (b) A R boş olmayan ve üstten s n rl bir küme olsun. > 0 ise sup(a) = sup A oldu¼gunu gösteriniz. 2. A = f(x; y)
Analiz III Aras nav Sorular 30. 11. 2006 1. (a) A = fx 2 R : x 2 4x 5 < 0g ise sup A =? (b) A R boş olmayan ve üstten s n rl bir küme olsun. > 0 ise sup(a) = sup A oldu¼gunu gösteriniz. 2. A = f(x; y)
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ GENELLEŞTİRİLMİŞ TOPOLOJİLERDE BAZI YENİ SONUÇLAR. Sevda SAĞIROĞLU PEKER
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ GENELLEŞTİRİLMİŞ TOPOLOJİLERDE BAZI YENİ SONUÇLAR Sevda SAĞIROĞLU PEKER MATEMATİK ANABİLİM DALI ANKARA 2009 Her hakkı saklıdır ÖZET Doktora Tezi
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ GENELLEŞTİRİLMİŞ TOPOLOJİLERDE BAZI YENİ SONUÇLAR Sevda SAĞIROĞLU PEKER MATEMATİK ANABİLİM DALI ANKARA 2009 Her hakkı saklıdır ÖZET Doktora Tezi
n ; = w! =(w 1 ; :::; w n ) (1.2.2) ; :::; + :::
 1. G IR IŞ 1.1. Ön Bilgiler Laplace denklemi, zik ve mühendisli¼gin pekçok alan nda ortaya ç kt ¼g ndan matematikçilerin, mühendislerin ve bilim adamlar n n büyük bir ilgi alan olmuştur. Potansiyel Teorinin
1. G IR IŞ 1.1. Ön Bilgiler Laplace denklemi, zik ve mühendisli¼gin pekçok alan nda ortaya ç kt ¼g ndan matematikçilerin, mühendislerin ve bilim adamlar n n büyük bir ilgi alan olmuştur. Potansiyel Teorinin
BÖLÜM 1 1- KOMPLEKS (KARMAŞIK) SAYILAR 1-1 KARMAŞIK SAYILAR VE ÖZELLİKLERİ
 BÖLÜM - KOMPLEKS (KARMAŞIK) SAYILAR - KARMAŞIK SAYILAR VE ÖELLİKLERİ ax + bx +c ikinci derece denkleminin < iken reel köklerinin olmadığını biliyoruz. Örneğin x + denkleminin reel sayılar kümesinde çözümü
BÖLÜM - KOMPLEKS (KARMAŞIK) SAYILAR - KARMAŞIK SAYILAR VE ÖELLİKLERİ ax + bx +c ikinci derece denkleminin < iken reel köklerinin olmadığını biliyoruz. Örneğin x + denkleminin reel sayılar kümesinde çözümü
İşaret ve Sistemler. Ders 11: Laplace Dönüşümleri
 İşaret ve Sistemler Ders 11: Laplace Dönüşümleri Laplace Dönüşüm Tanımı Bir f(t) fonksiyonunun Laplace alındığında oluşan fonksiyon F(s) yada L[f(t)] olarak gösterilir. Burada tanımlanan s: İşaret ve Sistemler
İşaret ve Sistemler Ders 11: Laplace Dönüşümleri Laplace Dönüşüm Tanımı Bir f(t) fonksiyonunun Laplace alındığında oluşan fonksiyon F(s) yada L[f(t)] olarak gösterilir. Burada tanımlanan s: İşaret ve Sistemler
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ FUZZY HALKALAR VE FUZZY İDEALLER ÜZERİNE. Deniz Pınar DENİZ MATEMATİK ANABİLİM DALI
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ FUZZY HALKALAR VE FUZZY İDEALLER ÜZERİNE Deniz Pınar DENİZ MATEMATİK ANABİLİM DALI ANKARA 2011 Her hakkı saklıdır ÖZET Yüksek Lisans Tezi
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ FUZZY HALKALAR VE FUZZY İDEALLER ÜZERİNE Deniz Pınar DENİZ MATEMATİK ANABİLİM DALI ANKARA 2011 Her hakkı saklıdır ÖZET Yüksek Lisans Tezi
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ ÜSTEL İNTEGRAL FONKSİYONLARIN. Çağla CAN MATEMATİK ANABİLİM DALI ANKARA 2012
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEİ ÜSTEL İNTEGRAL FONKSİYONLARIN DÜGÜN YAKINSAKLIĞI Çağla CAN MATEMATİK ANABİLİM DALI ANKARA 0 Her hakkı saklıdır ÖET Yüksek Lisans Tezi ÜSTEL
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEİ ÜSTEL İNTEGRAL FONKSİYONLARIN DÜGÜN YAKINSAKLIĞI Çağla CAN MATEMATİK ANABİLİM DALI ANKARA 0 Her hakkı saklıdır ÖET Yüksek Lisans Tezi ÜSTEL
Düzce Üniversitesi Bilim ve Teknoloji Dergisi
 Düzce Üniversitesi Bilim ve Teknoloji Dergisi, 2 (2014) 154 168 Düzce Üniversitesi Bilim ve Teknoloji Dergisi Derleme Makalesi Ünivalent Fonksiyonlar Teorisinde Geometrik Fonksiyonların Sağladığı Bazı
Düzce Üniversitesi Bilim ve Teknoloji Dergisi, 2 (2014) 154 168 Düzce Üniversitesi Bilim ve Teknoloji Dergisi Derleme Makalesi Ünivalent Fonksiyonlar Teorisinde Geometrik Fonksiyonların Sağladığı Bazı
A; e A; A kümelerini tan mlay n z. (x) = fb 2 B : x 2 Bg
 Genel Topolojiye Giriş I Ara S nav Sorular 30 Kas m 2010 1 (X; T ) bir topolojik uzay ve A X olsun. 2 (a) Ikinci say labilir topolojik uzay ne demektir? Tan mlay n z. A; e A; A ve @A kümelerini tan mlay
Genel Topolojiye Giriş I Ara S nav Sorular 30 Kas m 2010 1 (X; T ) bir topolojik uzay ve A X olsun. 2 (a) Ikinci say labilir topolojik uzay ne demektir? Tan mlay n z. A; e A; A ve @A kümelerini tan mlay
NÜMER IK ANAL IZ. Nuri ÖZALP L INEER S ISTEMLER IN ÇÖZÜMÜ. Bilimsel Hesaplama Matemati¼gi, Gazi Kitabevi 2012
 NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi, Gazi Kitabevi 0 Nuri ÖZALP L INEER S ISTEMLER IN ÇÖZÜMÜ Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 6! L INEER S ISTEMLER IN ÇÖZÜMÜ / . Pivotlama ve
NÜMER IK ANAL IZ Bilimsel Hesaplama Matemati¼gi, Gazi Kitabevi 0 Nuri ÖZALP L INEER S ISTEMLER IN ÇÖZÜMÜ Nuri ÖZALP (Ankara Üni.) NÜMER IK ANAL IZ BÖLÜM 6! L INEER S ISTEMLER IN ÇÖZÜMÜ / . Pivotlama ve
ASAL YAKIN HALKALAR ÜZER NE ON PRIME NEAR-RINGS
 Asal Yak n Halkalar Üzerine C.B.Ü. Fen Bilimleri Dergisi ISSN 135-1385 C.B.U. Journal of Siene 2.2 (26) 135 139 2.2 (26) 135 139 ASAL YAKIN HALKALAR ÜZER NE Ak n Osman ATAGÜN* Eriyes Üniversitesi, Yozgat
Asal Yak n Halkalar Üzerine C.B.Ü. Fen Bilimleri Dergisi ISSN 135-1385 C.B.U. Journal of Siene 2.2 (26) 135 139 2.2 (26) 135 139 ASAL YAKIN HALKALAR ÜZER NE Ak n Osman ATAGÜN* Eriyes Üniversitesi, Yozgat
İSTANBUL TİCARET ÜNİVERSİTESİ BİLGİSAYAR MÜHENDİSLİĞİ BÖLÜMÜ BİLGİSAYAR SİSTEMLERİ LABORATUARI YÜZEY DOLDURMA TEKNİKLERİ
 İSTANBUL TİCARET ÜNİVERSİTESİ BİLGİSAYAR MÜHENDİSLİĞİ BÖLÜMÜ BİLGİSAYAR SİSTEMLERİ LABORATUARI YÜZEY DOLDURMA TEKNİKLERİ Deneyde dolu alan tarama dönüşümünün nasıl yapıldığı anlatılacaktır. Dolu alan tarama
İSTANBUL TİCARET ÜNİVERSİTESİ BİLGİSAYAR MÜHENDİSLİĞİ BÖLÜMÜ BİLGİSAYAR SİSTEMLERİ LABORATUARI YÜZEY DOLDURMA TEKNİKLERİ Deneyde dolu alan tarama dönüşümünün nasıl yapıldığı anlatılacaktır. Dolu alan tarama
Afla da yedi matematiksel olgu bulacaks n z. Bu olgular n
 Seçim Beliti Afla da yedi matematiksel olgu bulacaks n z. Bu olgular n herbiri bir teoremdir, kan tlanm fllard r. Ancak bu olgular, matematikte çok özel bir yeri olan Seçme Beliti kullan larak kan tlanm
Seçim Beliti Afla da yedi matematiksel olgu bulacaks n z. Bu olgular n herbiri bir teoremdir, kan tlanm fllard r. Ancak bu olgular, matematikte çok özel bir yeri olan Seçme Beliti kullan larak kan tlanm
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ ÇOK DEĞİŞKENLİ ORTOGONAL POLİNOMLARIN ÖZELLİKLERİNDE BAZI GENİŞLETMELER.
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ ÇOK DEĞİŞKENLİ ORTOGONAL POLİNOMLARIN ÖZELLİKLERİNDE BAZI GENİŞLETMELER Rabia AKTAŞ MATEMATİK ANABİLİM DALI ANKARA 0 Her hakkı saklıdır TEZ ONAYI
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ DOKTORA TEZİ ÇOK DEĞİŞKENLİ ORTOGONAL POLİNOMLARIN ÖZELLİKLERİNDE BAZI GENİŞLETMELER Rabia AKTAŞ MATEMATİK ANABİLİM DALI ANKARA 0 Her hakkı saklıdır TEZ ONAYI
SDÜ Matematik Bölümü Analiz-IV Final S nav
 Dersin Kodu: MAT0 Dönemi: 00-0 Bahar Tarihi: 0.0.0 Saat:. 00 Yer: Am III-IV Süre: 90 Dakika Dersin Sorumlusu Gözetmenler SDÜ Matematik Bölümü Analiz-IV Final S nav : Prof. Dr. Seril PEHL IVAN : Araş. Gör.
Dersin Kodu: MAT0 Dönemi: 00-0 Bahar Tarihi: 0.0.0 Saat:. 00 Yer: Am III-IV Süre: 90 Dakika Dersin Sorumlusu Gözetmenler SDÜ Matematik Bölümü Analiz-IV Final S nav : Prof. Dr. Seril PEHL IVAN : Araş. Gör.
OPERATÖRLER BÖLÜM 4. 4.1 Giriş. 4.2. Aritmetik Operatörler
 BÖLÜM 4. OPERATÖRLER 4.1 Giriş Turbo Pascal programlama dilinde de diğer programlama dillerinde olduğu gibi operatörler, yapılan işlem türüne göre aritmetik, mantıksal ve karşılaştırma operatörleri olmak
BÖLÜM 4. OPERATÖRLER 4.1 Giriş Turbo Pascal programlama dilinde de diğer programlama dillerinde olduğu gibi operatörler, yapılan işlem türüne göre aritmetik, mantıksal ve karşılaştırma operatörleri olmak
Bu dedi im yaln zca 0,9 say s için de il, 0 la 1 aras ndaki herhangi bir say için geçerlidir:
 Yak nsamak B u yaz da, ilerde s k s k kullanaca m z bir olguyu tan mlayaca z ve matemati in en önemli kavramlar ndan birine (limit kavram na) de inece iz. Asl nda okur anlataca m kavram sezgisel olarak
Yak nsamak B u yaz da, ilerde s k s k kullanaca m z bir olguyu tan mlayaca z ve matemati in en önemli kavramlar ndan birine (limit kavram na) de inece iz. Asl nda okur anlataca m kavram sezgisel olarak
Baki Karl ¼ga. Gazi Üniversitesi Fen Edebiyat Fakültesi Matematik Bölümü Ankara/Türkiye
 H IPERBOL IK VE KÜRESEL ÜÇGENLERIN KENAR UZUNLUKLARINA BA ¼GLI ALAN FORMÜLLER I Baki Karl ¼ga karliaga@gazi.edu.tr Murat Savaş msavas@gazi.edu.tr Gazi Üniversitesi Fen Edebiyat Fakültesi Matematik Bölümü
H IPERBOL IK VE KÜRESEL ÜÇGENLERIN KENAR UZUNLUKLARINA BA ¼GLI ALAN FORMÜLLER I Baki Karl ¼ga karliaga@gazi.edu.tr Murat Savaş msavas@gazi.edu.tr Gazi Üniversitesi Fen Edebiyat Fakültesi Matematik Bölümü
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
: Bir d do rusu üzerinde; A, B, C ve D noktalar alal m. d. n n uzunlu u denir ve. d d1 d2 F G. E, F d G, H d ve ise. d // d 1 2
 VI. ÖLÜM ÜZLEME VEKTÖRLER YÖNLÜ RU PRÇSI Tan m : üzlemde ve noktalar verilsin. [] n n dan e do ru önlendirildi ini düflünelim. öle do ru parçalar na, önlü do ru parçalar denir. önlü do ru parças, ile gösterilir.
VI. ÖLÜM ÜZLEME VEKTÖRLER YÖNLÜ RU PRÇSI Tan m : üzlemde ve noktalar verilsin. [] n n dan e do ru önlendirildi ini düflünelim. öle do ru parçalar na, önlü do ru parçalar denir. önlü do ru parças, ile gösterilir.
MATEMATİK TESTİ LYS YE DOĞRU. 1. Bu testte Matematik ile ilgili 50 soru vardır.
 MTMTİK TSTİ LYS-. u testte Matematik ile ilgili 0 soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için ayrılan kısmına işaretleyiniz.. u testteki süreniz 7 dakikadır.. a, b, c birer reel sayı
MTMTİK TSTİ LYS-. u testte Matematik ile ilgili 0 soru vardır.. evaplarınızı, cevap kâğıdının Matematik Testi için ayrılan kısmına işaretleyiniz.. u testteki süreniz 7 dakikadır.. a, b, c birer reel sayı
POL NOMLAR. Polinomlar
 POL NOMLAR ÜN TE 1. ÜN TE 1. ÜN TE 1. ÜN TE 1. ÜN T POL NOMLAR Polinomlar 1. Kazan m: Gerçek kat say l ve tek de i kenli polinom kavram n örneklerle aç klar, polinomun derecesini, ba kat say s n, sabit
POL NOMLAR ÜN TE 1. ÜN TE 1. ÜN TE 1. ÜN TE 1. ÜN T POL NOMLAR Polinomlar 1. Kazan m: Gerçek kat say l ve tek de i kenli polinom kavram n örneklerle aç klar, polinomun derecesini, ba kat say s n, sabit
EK III POTANSİYELİN TANIMLANMASI
 EK III POTANSİYELİN TANIMLANMASI İki vektörün basamaklı (kademeli) çarpımı: Büyüklükte A ve B olan iki vektörünü ele alalım Bunların T= A.B cosθ çarpımı, tanımlama gereğince basamaklıdır. Bu vektörlerden
EK III POTANSİYELİN TANIMLANMASI İki vektörün basamaklı (kademeli) çarpımı: Büyüklükte A ve B olan iki vektörünü ele alalım Bunların T= A.B cosθ çarpımı, tanımlama gereğince basamaklıdır. Bu vektörlerden
1. GRUPLAR. c (Birleşme özelliği) sağlanır. 2) a G için a e e a a olacak şekilde e G (e ye birim eleman denir) vardır.
 1. GRUPLAR Tanım 1.1. G boş olmayan bir küme ve, G de bir ikili işlem olsun. (G yapısına aşağıdaki aksiyomları sağlıyorsa bir grup denir., ) cebirsel 1) a b cg,, için a( bc) ( ab) c (Birleşme özelliği)
1. GRUPLAR Tanım 1.1. G boş olmayan bir küme ve, G de bir ikili işlem olsun. (G yapısına aşağıdaki aksiyomları sağlıyorsa bir grup denir., ) cebirsel 1) a b cg,, için a( bc) ( ab) c (Birleşme özelliği)
Matematikte karşılaştığınız güçlükler için endişe etmeyin. Emin olun benim karşılaştıklarım sizinkilerden daha büyüktür.
 - 1 - ÖĞRENME ALANI CEBİR BÖLÜM KARMAŞIK SAYILAR ALT ÖĞRENME ALANLARI 1) Karmaşık Sayılar Karmaşık Sayıların Kutupsal Biçimi KARMAŞIK SAYILAR Kazanım 1 : Gerçek sayılar kümesini genişletme gereğini örneklerle
- 1 - ÖĞRENME ALANI CEBİR BÖLÜM KARMAŞIK SAYILAR ALT ÖĞRENME ALANLARI 1) Karmaşık Sayılar Karmaşık Sayıların Kutupsal Biçimi KARMAŞIK SAYILAR Kazanım 1 : Gerçek sayılar kümesini genişletme gereğini örneklerle
10. DİREKT ÇARPIMLAR
 10. DİREKT ÇARPIMLAR Teorem 10.1. H 1,H 2,, H n bir G grubunun alt gruplarının bir ailesi ve H = H 1 H 2 H n olsun. Aşağıdaki ifadeler denktir. a ) dönüşümü altında dır. b) ve olmak üzere her yi tek türlü
10. DİREKT ÇARPIMLAR Teorem 10.1. H 1,H 2,, H n bir G grubunun alt gruplarının bir ailesi ve H = H 1 H 2 H n olsun. Aşağıdaki ifadeler denktir. a ) dönüşümü altında dır. b) ve olmak üzere her yi tek türlü
M IKRO IKT ISAT 2. V IZE SINAVI 19 ARALIK 2009
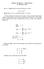 M IKRO IKT ISAT 2. V IZE SINAVI 19 ARALIK 2009 Soru 1: Aşa¼g daki gibi bir üretim fonksiyonu verilsin: = L 1=3 K 2=3 Eme¼gin yat w = ve sermayenin yat r = 1 olsun. a- Firma kadar ç kt üretmek istemektedir.
M IKRO IKT ISAT 2. V IZE SINAVI 19 ARALIK 2009 Soru 1: Aşa¼g daki gibi bir üretim fonksiyonu verilsin: = L 1=3 K 2=3 Eme¼gin yat w = ve sermayenin yat r = 1 olsun. a- Firma kadar ç kt üretmek istemektedir.
ÜNİTE 5 KESİKLİ RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI
 ÜNİTE 5 KESİKLİ RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI 1 Rassal Değişken Bir deney ya da gözlemin şansa bağlı sonucu bir değişkenin aldığı değer olarak düşünülürse, olasılık ve istatistikte böyle bir
ÜNİTE 5 KESİKLİ RASSAL DEĞİŞKENLER VE OLASILIK DAĞILIMLARI 1 Rassal Değişken Bir deney ya da gözlemin şansa bağlı sonucu bir değişkenin aldığı değer olarak düşünülürse, olasılık ve istatistikte böyle bir
Sonlu Lineer Uzayların Doğru Dereceleri Üzerine. Metin Şahin YÜKSEK LİSANS TEZİ. Matematik ve Bilgisayar Bilimleri Anabilim Dalı
 Sonlu Lineer Uzayların Doğru Dereceleri Üzerine Metin Şahin YÜKSEK LİSANS TEZİ Matematik ve Bilgisayar Bilimleri Anabilim Dalı Ağustos 2013 On Line Degrees Of The Finite Linear Spaces Metin Şahin MASTER
Sonlu Lineer Uzayların Doğru Dereceleri Üzerine Metin Şahin YÜKSEK LİSANS TEZİ Matematik ve Bilgisayar Bilimleri Anabilim Dalı Ağustos 2013 On Line Degrees Of The Finite Linear Spaces Metin Şahin MASTER
MATEMAT K TEST. 3. a ve b reel say lar olmak üzere, 3 a = 4 ve 3 2a b 3 = 8 oldu una göre,
 MTMT K TST KKT! + u testte 80 soru vard r. + u test için ar lan cevaplama süresi 5 dakikad r. + evaplar n z, cevap ka d n n Matematik Testi için ar lan k sma iflaretleiniz.. a, b, c pozitif reel sa lard
MTMT K TST KKT! + u testte 80 soru vard r. + u test için ar lan cevaplama süresi 5 dakikad r. + evaplar n z, cevap ka d n n Matematik Testi için ar lan k sma iflaretleiniz.. a, b, c pozitif reel sa lard
FEN FAKÜLTESİ MATEMATİK BÖLÜMÜ YAZ OKULU DERS İÇERİGİ. Bölümü Dersin Kodu ve Adı T P K AKTS
 Bir Dönemde Okutulan Ders Saati MAT101 Genel I (Mühendislik Fakültesi Bütün Bölümler, Fen Fakültesi Kimya ve Astronomi Bölümleri) 1 Kümeler, reel sayılar, bir denklem veya eşitsizliğin grafiği 2 Fonksiyonlar,
Bir Dönemde Okutulan Ders Saati MAT101 Genel I (Mühendislik Fakültesi Bütün Bölümler, Fen Fakültesi Kimya ve Astronomi Bölümleri) 1 Kümeler, reel sayılar, bir denklem veya eşitsizliğin grafiği 2 Fonksiyonlar,
Belirsiz Integraller. 1.1 Ilkel Fonksiyon ve Belirsiz Integral. 1.1.1 Temel Tan mlar ve Sonuc. lar
 Ic. indekiler Belirsiz Integraller 3. Ilkel Fonksiyon ve Belirsiz Integral................ 3.. Temel Tan mlar ve Sonuc.lar............... 3. Temel Integral Alma Yöntemleri................ 0.. De giṣken
Ic. indekiler Belirsiz Integraller 3. Ilkel Fonksiyon ve Belirsiz Integral................ 3.. Temel Tan mlar ve Sonuc.lar............... 3. Temel Integral Alma Yöntemleri................ 0.. De giṣken
Çözümlü Yüksek Matematik Problemleri. Yrd. Doç. Dr. Erhan Pişkin
 Çözümlü Yüksek Matematik Problemleri Yrd. Doç. Dr. Erhan Pişkin 1 Yrd. Doç. Dr. Erhan PİŞKİN ÇÖZÜMLÜ YÜKSEK MATEMATİK PROBLEMLERİ 1 ISBN 978-605-318-249-8 Kitap içeriğinin tüm sorumluluğu yazarına aittir.
Çözümlü Yüksek Matematik Problemleri Yrd. Doç. Dr. Erhan Pişkin 1 Yrd. Doç. Dr. Erhan PİŞKİN ÇÖZÜMLÜ YÜKSEK MATEMATİK PROBLEMLERİ 1 ISBN 978-605-318-249-8 Kitap içeriğinin tüm sorumluluğu yazarına aittir.
2012 LYS MATEMATİK SORU VE ÇÖZÜMLERİ Niyazi Kurtoğlu
 .SORU 8 sayı tabanında verilen (5) 8 sayısının sayı tabanında yazılışı nedir?.soru 6 3 3 3 3 4 6 8? 3.SORU 3 ise 5? 5 4.SORU 4 5 olduğuna göre, ( )? 5.SORU (y z) z(y ) y z yz bulunuz. ifadesinin en sade
.SORU 8 sayı tabanında verilen (5) 8 sayısının sayı tabanında yazılışı nedir?.soru 6 3 3 3 3 4 6 8? 3.SORU 3 ise 5? 5 4.SORU 4 5 olduğuna göre, ( )? 5.SORU (y z) z(y ) y z yz bulunuz. ifadesinin en sade
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
Tanım 2.1. X boş olmayan bir küme olmak üzere X den X üzerine bire-bir fonksiyona permütasyon denir.
 2. SİMETRİK GRUPLAR Tanım 2.1. X boş olmayan bir küme olmak üzere X den X üzerine bire-bir fonksiyona permütasyon denir. Tanım 2.2. boş olmayan bir küme olsun. ile den üzerine bire-bir fonksiyonlar kümesini
2. SİMETRİK GRUPLAR Tanım 2.1. X boş olmayan bir küme olmak üzere X den X üzerine bire-bir fonksiyona permütasyon denir. Tanım 2.2. boş olmayan bir küme olsun. ile den üzerine bire-bir fonksiyonlar kümesini
1.4. KISMİ SIRALAMA VE DENKLİK BAĞINTILARI
 Reel sayılar kümesinin "küçük ya da eşit", bağıntısı ile sıralanmış olduğunu biliyoruz. Bu bağıntı herhangi bir X kümesine aşağıdaki şekilde genelleştirilebilir. Bir X kümesi üzerinde aşağıdaki yansıma,
Reel sayılar kümesinin "küçük ya da eşit", bağıntısı ile sıralanmış olduğunu biliyoruz. Bu bağıntı herhangi bir X kümesine aşağıdaki şekilde genelleştirilebilir. Bir X kümesi üzerinde aşağıdaki yansıma,
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
8. HOMOMORFİZMALAR VE İZOMORFİZMALAR
 8. HOMOMORFİZMALAR VE İZOMORFİZMALAR Şimdiye kadar bir gruptan diğer bir gruba tanımlı olan fonksiyonlarla ilgilenmedik. Bu bölüme aşağıdaki tanımla başlayalım. Tanım 8.1: ve iki grup ve f : G H bir fonksiyon
8. HOMOMORFİZMALAR VE İZOMORFİZMALAR Şimdiye kadar bir gruptan diğer bir gruba tanımlı olan fonksiyonlarla ilgilenmedik. Bu bölüme aşağıdaki tanımla başlayalım. Tanım 8.1: ve iki grup ve f : G H bir fonksiyon
MONOPOL VE MONOPSON. 1.1 Tekelde Toplam Has lat, Ortalama Has lat ve Marjinal Has lat
 CHATER MONOOL VE MONOSON MONOOL Tek sat c ve sonsuz say da al c n n oldu¼gu piyasalard r.. Tekelde Toplam Has lat, Ortalama Has lat ve Marjinal Has lat Önce talep fonksiyonunu elde edelim. Daha sonra toplam
CHATER MONOOL VE MONOSON MONOOL Tek sat c ve sonsuz say da al c n n oldu¼gu piyasalard r.. Tekelde Toplam Has lat, Ortalama Has lat ve Marjinal Has lat Önce talep fonksiyonunu elde edelim. Daha sonra toplam
Cebir Notları. Karmaşık sayılar TEST I. Gökhan DEMĐR, 2006
 MC Karmaşık saılar www.matematikclub.cm, 006 Cebir Ntları Gökhan DEMĐR, gdemir@ah.cm.tr TEST I. i 897 + i 975 + i 997 i 995 tplamının snucu i B) i C) i D) i E) 5i 8. Z = i nin kutupsal biçimi (cs0 + isin0)
MC Karmaşık saılar www.matematikclub.cm, 006 Cebir Ntları Gökhan DEMĐR, gdemir@ah.cm.tr TEST I. i 897 + i 975 + i 997 i 995 tplamının snucu i B) i C) i D) i E) 5i 8. Z = i nin kutupsal biçimi (cs0 + isin0)
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ KÜRE ÜZERİNDEKİ KONİKLERE YENİ BİR YAKLAŞIM Esra EMİR MATEMATİK ANABİLİM DALI ANKARA 2010 Her hakkı saklıdır ÖZET Yüksek Lisans Tezi KÜRE
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ KÜRE ÜZERİNDEKİ KONİKLERE YENİ BİR YAKLAŞIM Esra EMİR MATEMATİK ANABİLİM DALI ANKARA 2010 Her hakkı saklıdır ÖZET Yüksek Lisans Tezi KÜRE
TRIGONOMETRI AÇI, YÖNLÜ AÇI, YÖNLÜ YAY
 TRIGONOMETRI AÇI, YÖNLÜ AÇI, YÖNLÜ YAY A. AÇI Başlangıç noktaları aynı olan iki ışının birleşim kümesine açı denir. Bu ışınlara açının kenarları, başlangıç noktasına ise açının köşesi denir. B. YÖNLÜ AÇI
TRIGONOMETRI AÇI, YÖNLÜ AÇI, YÖNLÜ YAY A. AÇI Başlangıç noktaları aynı olan iki ışının birleşim kümesine açı denir. Bu ışınlara açının kenarları, başlangıç noktasına ise açının köşesi denir. B. YÖNLÜ AÇI
12. SINIF. Fonksiyonlar - 1 TEST. 1. kx + 6 fonksiyonu sabit fonksiyon olduğuna göre aşağıdakilerden hangisidir? k. = 1 olduğuna göre k. kaçtır?
 . SINIF M Fonksionlar. f ( + a ) + vef( ) 7 olduğuna göre a kaçtır? E) TEST. f ( ) k + 6 fonksionu sabit fonksion olduğuna f ( ) göre aşağıdakilerden k E). f( ) 6 k ve f ( ) olduğuna göre k kaçtır? E)
. SINIF M Fonksionlar. f ( + a ) + vef( ) 7 olduğuna göre a kaçtır? E) TEST. f ( ) k + 6 fonksionu sabit fonksion olduğuna f ( ) göre aşağıdakilerden k E). f( ) 6 k ve f ( ) olduğuna göre k kaçtır? E)
Bu tanım aralığı pozitif tam sayılar olan f(n) fonksiyonunun değişim aralığı n= 1, 2, 3,, n,
 DİZİLER Tamamen belirli bir kurala göre sıralanmış sayılar topluluğuna veya kümeye Dizi denir. Belirli bir kurala göre birbiri ardınca gelen bu sayıların her birine dizinin terimi ve hepsine birden dizinin
DİZİLER Tamamen belirli bir kurala göre sıralanmış sayılar topluluğuna veya kümeye Dizi denir. Belirli bir kurala göre birbiri ardınca gelen bu sayıların her birine dizinin terimi ve hepsine birden dizinin
BÖLÜM 1. stanbul Kültür Üniversitesi. Fonksiyonlar - Özellikleri ve Limit Kavram. ³eklinde tanmlanan fonksiyona Dirichlet fonksiyonu ad verilir.
 BÖLÜM 1 0, Q 1. f() = 1, R/Q, Fonksiyonlar - Özellikleri ve Limit Kavram ³eklinde tanmlanan fonksiyona Dirichlet fonksiyonu ad verilir. Buna göre a³a da verilen tanm bölgeleri altnda görüntü cümlelerini
BÖLÜM 1 0, Q 1. f() = 1, R/Q, Fonksiyonlar - Özellikleri ve Limit Kavram ³eklinde tanmlanan fonksiyona Dirichlet fonksiyonu ad verilir. Buna göre a³a da verilen tanm bölgeleri altnda görüntü cümlelerini
SÜREKLİLİK. 9.1 Süreklilik ve Süreksizlik Kavramları
 SÜREKLİLİK Bu bölümde süreklilik kavramı, süreksizlik, sürekli fonksiyonların özellikleri ile buna ilişkin teoremler örnekler ve grafiklerle açıklanmaktadır. 9.1 Süreklilik ve Süreksizlik Kavramları Tanım
SÜREKLİLİK Bu bölümde süreklilik kavramı, süreksizlik, sürekli fonksiyonların özellikleri ile buna ilişkin teoremler örnekler ve grafiklerle açıklanmaktadır. 9.1 Süreklilik ve Süreksizlik Kavramları Tanım
İÇİNDEKİLER ÖNSÖZ Bölüm 1 SAYILAR 11 Bölüm 2 KÜMELER 31 Bölüm 3 FONKSİYONLAR
 İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 11 1.1. Sayı Kümeleri 12 1.1.1.Doğal Sayılar Kümesi 12 1.1.2.Tam Sayılar Kümesi 13 1.1.3.Rasyonel Sayılar Kümesi 14 1.1.4. İrrasyonel Sayılar Kümesi 16 1.1.5. Gerçel
İÇİNDEKİLER ÖNSÖZ III Bölüm 1 SAYILAR 11 1.1. Sayı Kümeleri 12 1.1.1.Doğal Sayılar Kümesi 12 1.1.2.Tam Sayılar Kümesi 13 1.1.3.Rasyonel Sayılar Kümesi 14 1.1.4. İrrasyonel Sayılar Kümesi 16 1.1.5. Gerçel
1. G IR IŞ. x n+1 x n +px n k =0; n=0;1;2;::: (1.1)
 . G IR IŞ Fark denklemleri ile zamana ba¼gl çeşitli do¼ga olaylar n n incelenmesinin do¼gal bir ifadesi olarak karş laş lmaktad r. Zamana ba¼gl de¼gişkenlerin kullan ld ¼g olaylar n pek ço¼gu ayr k (kesikli)
. G IR IŞ Fark denklemleri ile zamana ba¼gl çeşitli do¼ga olaylar n n incelenmesinin do¼gal bir ifadesi olarak karş laş lmaktad r. Zamana ba¼gl de¼gişkenlerin kullan ld ¼g olaylar n pek ço¼gu ayr k (kesikli)
