12.Konu Rasyonel sayılar
|
|
|
- Çağatay Turk
- 8 yıl önce
- İzleme sayısı:
Transkript
1 12.Konu Rasyonel sayılar 1. Rasyonel sayılar 2. Rasyonel sayılar kümesinde toplama ve çarpma 3. Rasyonel sayılar kümesinde çıkarma ve bölme 4. Tam rayonel sayılar 5. Rasyonel sayılar kümesinde sıralama 6. Rasyonel sayıların kuvvetleri 7. Alıştırmalar 1. Rasyonel sayılar 1.Tanım: ( ) olduğuna göre K nin her bir elemanına bir kesir denir ve a ya, ( ) kesrinin payı, b ye ( ) kesrinin paydası, adı verilir. 2.Tanım: ( ) ve ( ) iki kesir Eğer ise ( ) kesri, ( ) kesrine denktir, denir. ( ) ( ) 1.Örnek: ( ) ( ) doğrudur. 1.6=2.3 1.Teorem: Kesirler kümesinde ( ) ( ) için ( ) ( ) biçiminde tanımlanan bağıntısı bir denklik bağıntısıdır. K kümesinde tanımlanan denklik bağıntısı K kümesini denklik sınıflarına ayırır. ( ) denklik sınıfı ( ) ile gösterilebilir. ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 2.Tanım: Kesirlerin K kümesinde tanımlanan denklik bağıntısının K dan ayırdığı her bir denklik sınıfına bir rasyonel sayı denir. Rasyonel sayılar kümesi ile gösterilir. Örnek: ( ), ( ), ( ) denklik sınıflarının her biri rasyonel sayılardır. 1
2 ( ) ( ) ( ) ( ) 2.Teorem: ( ) İspat: ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) 1.Sonuç: olduğuna göre ( =( ) ) ( =( ) ) 2. Rasyonel sayılar kümesinde toplama ve çarpma 1.Tanım: Rasyonel sayılar kümesinde tanımlanan, (( ) ( ) ) ( ) işlemine toplama denir. ( ) rasyonel sayısına ( ) ( ) rasyonel sayılarının toplamı denir. ( ) ( ) biçiminde gösterilir. Yani, ( ) ( ) ( ) Tanıma göre, ( ) ( ) ( ) 2.Tanım: Rasyonel sayılar kümesinde tanımlanan, (( ) ( ) ) ( ) işlemine çarpma denir. ( ) rasyonel sayısına ( ) ( ) rasyonel sayılarının çarpımı denir. ( ) ( ) biçiminde gösterilir. Yani, ( ) ( ) ( ) 1.Teorem: ( ) matematik yapısı bir cisimdir. Ispat: 1.Rasyonel sayılar kümesinde toplama dan ya bir fonksiyon olduğundan kümesi toplama işlemine göre kapalıdır. 2. ( ) ( ) = ( = ) ( ) ( ) ( ) olduğundan toplama işleminin değişme özelliği vardır. 3. (( ) ( ) ) ( ) = ( +( ) ) ( ) ) ( ) ( ) ( ) (( ) ( ) ) olduğundan toplama işleminin birleşme özelliği vardır. 4. için ( ). Öte yandan, ( ) ( ) ( =( ) ) olduğundan nun toplama işlemine göre etkisiz elemanı vardır - ( ) 5. ( + ) ( ) ( ) ( ) ( ) olduğundan her ( ) elemanın toplama işlemine göre tersi vardır ve (. ) 2
3 6. Rasyonel sayılar kümesinde çarpma dan ya bir fonksiyon olduğundan kümesi çarpma işlemine göre kapalıdır. 7. ( ) ( ) = ( = ) ( ) ( ) ( ) olduğundan çarpma işleminin değişme özelliği vardır. 8. (( ) ( ) ) ( ) = ( ) ( ) ( ) ( ) ( ) ( ) (( ) ( ) ) olduğundan çarpma işleminin birleşme özelliği vardır. 9. (( ) (( ) ) ( ) )= ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) olduğundan çarpma işleminin toplama işlemi üzerine dağılma özelliği vardır. Şağdan dadağılma benzer biçimde gösterilir. 10. ( ) ( ) ( ) ( ) olduğundan nun çarpma işlemine göre etkisiz elemanı vardır - ( ) 11. ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) veya ( ) ( ) ( ) ( ) veya ( ) ( ) olduğundan kümesinde sıfırın bölenleri yoktur ( ) ( ) = ( = ) ( ) olduğundan nun toplama işleminin etkisiz elemanından farklı her ( ) elemanının çarpma işlemine göre ters elemanı vardır - ( ) Böylece cisimdir. cisim oduğundan onun elemanlarının katları ve kuvvetleri tanımlıdır. 2.Teorem: ( ) cisminde toplama işleminin sadeleştirme özelliği vardır. Çarpma işleminin, cismin sıfırdan farklı elemanları ile sadeleştirme özelliği vardır. 3. Rasyonel sayılar kümesinde çıkarma ve bölme 3.Tanım: ( ) ( ) ( ) [ ( ] ) rasyonel sayısına ( ) ( ) nin farkı denir. ( ) ( ) ( ) [( ] ) rasyonel sayısına ( ) ( ) nin bölümü denir. ( ) ( ) ( ) ( ) ( ) [ ( ] ) ( ) ( ) ( ) ( ) ( ) ( ) [( ] ) ( ) ( =( ) ) Örnek: ( ) ( ) =( ) ( ) ( ) ( ) =( ) ( ) 3
4 4.Tam rasyonel sayılar 3.Teorem: {( ) } olduğuna göre, ( ) matematik yapısı, ( ) matematik yapısına izomorftur. Ispat: ( ) matematik yapısı halkadır. ( ) fonkiyonuna bakalım. ( ) ( ) için [( ) ( ] ) ( ) (( ) ) (( ) ) ve [( ) ( ] ) ( ) (( ) ) (( ) ) olduğundan bir homomorfizmdir. Bu fonksiyon birebir ve örtendir. Buna göre, fonksiyonu ( ) matematik yapısından ( ) matematik yapısına bir izomorfmizmdir. 4.Tanım: olduğuna göre, ( ) rasyonel sayısına tam rasyonel sayı denir. Kısaca biçimde gösterilir. Bu tamıma göre. herhangi bir ( ) elemanını biçiminde gösterelim. 4.Teorem: ve ise dır. Ispat: ( ) ( ) ( ) ( ) ( ) 5.Tanım: ve 5.Teorem: ve ve a) b) c) d) ise 6.Teorem: a nın b ye bölünmesinden elde edilen bölümün q, kalanın r olması için, ve r<b olması gerekir ve yeter. Örnek: 25= Rasyonel sayılar kümesinde sıralama 4
5 7. Teorem: ( ) =( ) ise cd>0. Ispat: ( ) =( ) ( )( ) ( )( ) ( ) =(ab)(cd) 6.Tanım: :, ( ) ise ve yalnız böyle ise sayısına pozitif rayonel sayı denir ve biçimde yazylyr. Pozitif rasyonel sayılar kümesi: ise ve yalnız böyle ise sayısına negatif rayonel sayı denir ve biçimde yazylyr. Negatif rasyonel sayılar kümesi: 7.Tanım: { biçiminde tanımlanan sayısına x in mutlak değeri denir. 8.Tanım: : olacak biçimde pozitif rasyonel sayı varsa rasyonel sayısı b den küçük denir ve yazılır. yerine bazen yazılır. veya ifadesi biçimde yazılır. 8.Teorem: 9.Teorem: ve 10.Teorem: a) b) ( ), ( ) c) d) ( ) e) f), g) ( ) h) ( ) i) ve 9.Tanım: : veya ise rasyonel sayısı ile z nin arasındadır, denir. 11.Teorem: en az bir rasyonel sayı vardır. 5
6 12.Teorem (Arşimed özelliği): olacak biçimde bir tam sayı vardır. 6. Rasyonel sayıların kuvvetleri 10.Tanım: a) dir. b) dir. c) dir. d) ( ) ye x in n inci kuvveti denir ve x üssü n diye okunur. x e taban n ye üs denir. 13.Teorem: a) ( ) b) ( ) c) d) ve ise e) ( ) 14.Teorem: ise veya. 15.Teorem: n çift tam sayı ise olacak biçimde bir rasyonel sayı yoktur. 11.Tanım: a) tek sayı olmak üzere, olacak biçimde bir sayı varsa bu sayıya a nın n. kuvvetten kökü denir. b) çift sayı ve olmak üzere, olacak biçimde bir pozitif sayı varsa bu sayıya a nın n. kuvvetten pozitif kökü denir. c) çift sayı ve olmak üzere, olacak biçimde bir negatif sayı varsa bu sayıya a nın n. kuvvetten negatif kökü denir. = 12.Tanım: [ ] 16.Teorem: a) ( ) b) c) ( ) d) e) ( ) 6
7 7.Alıştırmalar 1. ( ) kesrine denk olan öyle bir (x,y) kesri bulunuz ki x+y=21 2. Aşağıdaki açık önermelerin daki doğruluk kümesini bulunuz. 3. a) ( ) ( ) b) ( ) ( ) c) ( ) ( ) d) ( ) ( ) rasyonel sayısını en sade biçimde yazınız. 4. ispatlayınız. 5. ispatlayınız. 6. Aşağıdakileri hesaplayınız. a) 3( ) b) ( )( ) c) 0( ) d) [( ] ) e) [( ] ) f) [( ] ) ( )( ) ( ) önermeyi ( )( ) önermeyi 7. olduğuna göre, olduğunu gösteriniz. 8. olduğuna göre, olduğunu gösteriniz. 9. ve olduğuna göre olduğunu gösteriniz. 10. ve ( ) ( ) ( ) olduğunu gösteriniz. 11. ve ( ) ( ) olduğunu gösteriniz. 7
13.Konu Reel sayılar
 13.Konu Reel sayılar 1. Temel dizi 2. Temel dizilerde toplama ve çarpma 3. Reel sayılar kümesi 4. Reel sayılar kümesinde toplama ve çarpma 5. Reel sayılar kümesinde sıralama 6. Reel sayılar kümesinin tamlık
13.Konu Reel sayılar 1. Temel dizi 2. Temel dizilerde toplama ve çarpma 3. Reel sayılar kümesi 4. Reel sayılar kümesinde toplama ve çarpma 5. Reel sayılar kümesinde sıralama 6. Reel sayılar kümesinin tamlık
10.Konu Tam sayıların inşası
 10.Konu Tam sayıların inşası 1. Tam sayılar kümesi 2. Tam sayılar kümesinde toplama ve çarpma 3. Pozitif ve negatif tam sayılar 4. Tam sayılar kümesinde çıkarma 5. Tam sayılar kümesinde sıralama 6. Bir
10.Konu Tam sayıların inşası 1. Tam sayılar kümesi 2. Tam sayılar kümesinde toplama ve çarpma 3. Pozitif ve negatif tam sayılar 4. Tam sayılar kümesinde çıkarma 5. Tam sayılar kümesinde sıralama 6. Bir
8.Konu Sonlu ve sonsuz kümeler, Doğal sayılar
 8.Konu Sonlu ve sonsuz kümeler, Doğal sayılar 1. Eşit güçlü kümeler 2. Sonlu ve sonsuz kümeler 3. Doğal sayılar kümesi 4. Sayılabilir kümeler 5. Doğal sayılar kümesinde toplama 6. Doğal sayılar kümesinde
8.Konu Sonlu ve sonsuz kümeler, Doğal sayılar 1. Eşit güçlü kümeler 2. Sonlu ve sonsuz kümeler 3. Doğal sayılar kümesi 4. Sayılabilir kümeler 5. Doğal sayılar kümesinde toplama 6. Doğal sayılar kümesinde
MATM 133 MATEMATİK LOJİK. Dr. Doç. Çarıyar Aşıralıyev
 MATM 133 MATEMATİK LOJİK Dr. Doç. Çarıyar Aşıralıyev 5.KONU Cebiresel yapılar; Grup, Halka 1. Matematik yapı 2. Denk yapılar ve eş yapılar 3. Grup 4. Grubun basit özellikleri 5. Bir elemanın kuvvetleri
MATM 133 MATEMATİK LOJİK Dr. Doç. Çarıyar Aşıralıyev 5.KONU Cebiresel yapılar; Grup, Halka 1. Matematik yapı 2. Denk yapılar ve eş yapılar 3. Grup 4. Grubun basit özellikleri 5. Bir elemanın kuvvetleri
Cebir Notları. Gökhan DEMĐR, ÖRNEK : A ve A x A nın bir alt kümesinden A ya her fonksiyona
 , 2006 MC Cebir Notları Gökhan DEMĐR, gdemir23@yahoo.com.tr Đşlem ĐŞLEM A ve A x A nın bir alt kümesinden A ya her fonksiyona ikili işlem denir. Örneğin toplama, çıkarma, çarpma birer işlemdir. Đşlemler
, 2006 MC Cebir Notları Gökhan DEMĐR, gdemir23@yahoo.com.tr Đşlem ĐŞLEM A ve A x A nın bir alt kümesinden A ya her fonksiyona ikili işlem denir. Örneğin toplama, çıkarma, çarpma birer işlemdir. Đşlemler
SOYUT CEBİR Tanım 1: Uzunluğu 2 olan dairesel permütasyona transpozisyon denir.
 SOYUT CEBİR Tanım 1: Uzunluğu 2 olan dairesel permütasyona transpozisyon Tanım 2: Bir grubun kendi üzerine izomorfizmine otomorfizm, grubun kendi üzerine homomorfizmine endomorfizm Sadece birebir olan
SOYUT CEBİR Tanım 1: Uzunluğu 2 olan dairesel permütasyona transpozisyon Tanım 2: Bir grubun kendi üzerine izomorfizmine otomorfizm, grubun kendi üzerine homomorfizmine endomorfizm Sadece birebir olan
MODÜLER ARİTMETİK A)1 B)3 C)8 D)11 E)13. TANIM Z tam sayılar kümesinde tanımlı
 MODÜLER ARİTMETİK A)1 B)3 C)8 D)11 E)13 TANIM Z tam sayılar kümesinde tanımlı ={(x,y): x ile y nin farkı n ile tam bölünür} = {(x,y): n x-y, n N + } bağıntısı bir denklik bağıntısıdır. (x,y) ise x y (mod
MODÜLER ARİTMETİK A)1 B)3 C)8 D)11 E)13 TANIM Z tam sayılar kümesinde tanımlı ={(x,y): x ile y nin farkı n ile tam bölünür} = {(x,y): n x-y, n N + } bağıntısı bir denklik bağıntısıdır. (x,y) ise x y (mod
sayıların kümesi N 1 = { 2i-1: i N } ve tüm çift doğal sayıların kümesi N 2 = { 2i: i N } şeklinde gösterilebilecektir. Hiç elemanı olmayan kümeye
 KÜME AİLELERİ GİRİŞ Bu bölümde, bir çoğu daha önceden bilinen incelememiz için gerekli olan bilgileri vereceğiz. İlerde konular işlenirken karşımıza çıkacak kavram ve bilgileri bize yetecek kadarı ile
KÜME AİLELERİ GİRİŞ Bu bölümde, bir çoğu daha önceden bilinen incelememiz için gerekli olan bilgileri vereceğiz. İlerde konular işlenirken karşımıza çıkacak kavram ve bilgileri bize yetecek kadarı ile
1 BAĞINTILAR VE FONKSİYONLAR
 1 BAĞINTILAR VE FONKSİYONLAR Bu bölümde ilk olarak Matematikte çok önemli bir yere sahip olan Bağıntı kavramnı verip daha sonra ise Fonksiyon tanımı verip genel özelliklerini inceleyeceğiz. Tanım 1 A B
1 BAĞINTILAR VE FONKSİYONLAR Bu bölümde ilk olarak Matematikte çok önemli bir yere sahip olan Bağıntı kavramnı verip daha sonra ise Fonksiyon tanımı verip genel özelliklerini inceleyeceğiz. Tanım 1 A B
SAYILAR DOĞAL VE TAM SAYILAR
 1 SAYILAR DOĞAL VE TAM SAYILAR RAKAM: Sayıları ifade etmek için kullandığımız 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembollerinden her birine rakam denir. Soru: a ve b farklı rakamlar olmak üzere a + b nin alabileceği
1 SAYILAR DOĞAL VE TAM SAYILAR RAKAM: Sayıları ifade etmek için kullandığımız 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 sembollerinden her birine rakam denir. Soru: a ve b farklı rakamlar olmak üzere a + b nin alabileceği
T I M U R K A R A Ç AY - H AY D A R E Ş C A L C U L U S S E Ç K I N YAY I N C I L I K A N K A R A
 T I M U R K A R A Ç AY - H AY D A R E Ş C A L C U L U S S E Ç K I N YAY I N C I L I K A N K A R A Contents Rasyonel Fonksiyonlar 5 Bibliography 35 Inde 39 Rasyonel Fonksiyonlar Polinomlar Yetmez! Bölme
T I M U R K A R A Ç AY - H AY D A R E Ş C A L C U L U S S E Ç K I N YAY I N C I L I K A N K A R A Contents Rasyonel Fonksiyonlar 5 Bibliography 35 Inde 39 Rasyonel Fonksiyonlar Polinomlar Yetmez! Bölme
8. HOMOMORFİZMALAR VE İZOMORFİZMALAR
 8. HOMOMORFİZMALAR VE İZOMORFİZMALAR Şimdiye kadar bir gruptan diğer bir gruba tanımlı olan fonksiyonlarla ilgilenmedik. Bu bölüme aşağıdaki tanımla başlayalım. Tanım 8.1: G, ve H, iki grup ve f : G H
8. HOMOMORFİZMALAR VE İZOMORFİZMALAR Şimdiye kadar bir gruptan diğer bir gruba tanımlı olan fonksiyonlarla ilgilenmedik. Bu bölüme aşağıdaki tanımla başlayalım. Tanım 8.1: G, ve H, iki grup ve f : G H
ANADOLU ÜNİVERSİTESİ AÇIKÖĞRETİM FAKÜLTESİ İLKÖĞRETİM ÖĞRETMENLİĞİ LİSANS TAMAMLAMA PROGRAMI. Analiz. Cilt 2. Ünite 8-14
 ANADOLU ÜNİVERSİTESİ AÇIKÖĞRETİM FAKÜLTESİ İLKÖĞRETİM ÖĞRETMENLİĞİ LİSANS TAMAMLAMA PROGRAMI Analiz Cilt 2 Ünite 8-14 T.C. ANADOLU ÜNİVERSİTESİ YAYINLARI NO: 1082 AÇIKÖĞRETİM FAKÜLTESİ YAYINLARI NO: 600
ANADOLU ÜNİVERSİTESİ AÇIKÖĞRETİM FAKÜLTESİ İLKÖĞRETİM ÖĞRETMENLİĞİ LİSANS TAMAMLAMA PROGRAMI Analiz Cilt 2 Ünite 8-14 T.C. ANADOLU ÜNİVERSİTESİ YAYINLARI NO: 1082 AÇIKÖĞRETİM FAKÜLTESİ YAYINLARI NO: 600
Örnek...3 : Aşağıdaki ifadelerden hangileri bir dizinin genel terim i olabilir?
 DİZİLER Tanım kümesi pozitif tam sayılar kümesi olan her fonksiyona dizi denir. Örneğin f : Z + R, f (n )=n 2 ifadesi bir dizi belirtir. Diziler, değer kümelerine göre adlandırı - lırlar. Dizinin değer
DİZİLER Tanım kümesi pozitif tam sayılar kümesi olan her fonksiyona dizi denir. Örneğin f : Z + R, f (n )=n 2 ifadesi bir dizi belirtir. Diziler, değer kümelerine göre adlandırı - lırlar. Dizinin değer
Temel Kavramlar. (r) Sıfırdan farklı kompleks sayılar kümesi: C. (i) Rasyonel sayılar kümesi: Q = { a b
 Bölüm 1 Temel Kavramlar Bu bölümde bağıntı ve fonksiyon gibi bazı temel kavramlar üzerinde durulacak, tamsayıların bazı özellikleri ele alınacaktır. Bu çalışma boyunca kullanılacak bazı kümelerin gösterimleri
Bölüm 1 Temel Kavramlar Bu bölümde bağıntı ve fonksiyon gibi bazı temel kavramlar üzerinde durulacak, tamsayıların bazı özellikleri ele alınacaktır. Bu çalışma boyunca kullanılacak bazı kümelerin gösterimleri
ÜNİTE 1: TEMEL KAVRAMLAR
 MATEMATİK ÜNİTE : TEMEL KAVRAMLAR Temel Kavramlar ADF 0 RAKAM Sayı oluşturmak için kullanılan sembollere... denir. 0 luk sayma düzenindeki rakamlar 0,,,... 8 ve 9 olup 0 tanedir. örnek a, b, c sıfırdan
MATEMATİK ÜNİTE : TEMEL KAVRAMLAR Temel Kavramlar ADF 0 RAKAM Sayı oluşturmak için kullanılan sembollere... denir. 0 luk sayma düzenindeki rakamlar 0,,,... 8 ve 9 olup 0 tanedir. örnek a, b, c sıfırdan
1. ÜNİTE 2. ÜNİTE 3. ÜNİTE. Bölüm 1 : Üslü Sayılar... 8. Bölüm 2 : Doğal Sayılar... 18. Bölüm 3 : Doğal Sayı Problemleri... 30
 İçindekiler 1. ÜNİTE Bölüm 1 : Üslü Sayılar... 8 Bölüm 2 : Doğal Sayılar... 18 Bölüm 3 : Doğal Sayı Problemleri... 30 Bölüm 4 :- Çarpanlar ve Katlar, Bölünebilme... 40 Bölüm 5 : Asal Sayılar, Ortak Bölenler,
İçindekiler 1. ÜNİTE Bölüm 1 : Üslü Sayılar... 8 Bölüm 2 : Doğal Sayılar... 18 Bölüm 3 : Doğal Sayı Problemleri... 30 Bölüm 4 :- Çarpanlar ve Katlar, Bölünebilme... 40 Bölüm 5 : Asal Sayılar, Ortak Bölenler,
ÜNİTE MATEMATİK-1 İÇİNDEKİLER HEDEFLER ÜSTEL VE LOGARİTMA FONKSİYONLARI. Prof.Dr.Ahmet KÜÇÜK. Üstel Fonksiyon Logaritma Fonksiyonu
 HEDEFLER İÇİNDEKİLER ÜSTEL VE LOGARİTMA FONKSİYONLARI Üstel Fonksiyon Logaritma Fonksiyonu MATEMATİK-1 Prof.Dr.Ahmet KÜÇÜK Bu ünite çalışıldıktan sonra, Üstel fonksiyonun tanımı öğrenilecek Üstel fonksiyonun
HEDEFLER İÇİNDEKİLER ÜSTEL VE LOGARİTMA FONKSİYONLARI Üstel Fonksiyon Logaritma Fonksiyonu MATEMATİK-1 Prof.Dr.Ahmet KÜÇÜK Bu ünite çalışıldıktan sonra, Üstel fonksiyonun tanımı öğrenilecek Üstel fonksiyonun
1.4. KISMİ SIRALAMA VE DENKLİK BAĞINTILARI
 Reel sayılar kümesinin "küçük ya da eşit", bağıntısı ile sıralanmış olduğunu biliyoruz. Bu bağıntı herhangi bir X kümesine aşağıdaki şekilde genelleştirilebilir. Bir X kümesi üzerinde aşağıdaki yansıma,
Reel sayılar kümesinin "küçük ya da eşit", bağıntısı ile sıralanmış olduğunu biliyoruz. Bu bağıntı herhangi bir X kümesine aşağıdaki şekilde genelleştirilebilir. Bir X kümesi üzerinde aşağıdaki yansıma,
İÇİNDEKİLER. Mantık Kurallarının Elektrik Devrelerine Uygulanması... 14
 İÇİNDEKİLER 1. BÖLÜM MANTIK Giriş... 1 Genel Olarak Mantık... 1 Mantığın Tarihçesi ve Modern Mantığın Doğuşu... 1 Mantık Öğretimin Önemi ve Amacı... 2 Önerme... 3 VE İşlemi (Birlikte Evetleme, Mantıksal
İÇİNDEKİLER 1. BÖLÜM MANTIK Giriş... 1 Genel Olarak Mantık... 1 Mantığın Tarihçesi ve Modern Mantığın Doğuşu... 1 Mantık Öğretimin Önemi ve Amacı... 2 Önerme... 3 VE İşlemi (Birlikte Evetleme, Mantıksal
SAYILAR SAYI KÜMELERİ
 SAYILAR SAYI KÜMELERİ 1.Sayma Sayıları Kümesi: S=N =1,2,3,... 2. Doğal Sayılar Kümesi : N=0,1,2,... 3. Tamsayılar Kümesi : Z=..., 2, 1,0,1,2,... Sıfırın sağında bulunan 1,2,3,. tamsayılarına pozitif tamsayılar
SAYILAR SAYI KÜMELERİ 1.Sayma Sayıları Kümesi: S=N =1,2,3,... 2. Doğal Sayılar Kümesi : N=0,1,2,... 3. Tamsayılar Kümesi : Z=..., 2, 1,0,1,2,... Sıfırın sağında bulunan 1,2,3,. tamsayılarına pozitif tamsayılar
RASYONEL SAYILAR ELİF ÇAĞLAYAN GAMZE NUR AYDIN HUMAYLA ÖNDER GÜLFER YÜKSEKDAĞ 2011-2012
 RASYONEL SAYILAR ELİF ÇAĞLAYAN GAMZE NUR AYDIN HUMAYLA ÖNDER GÜLFER YÜKSEKDAĞ 2011-2012 İçindekiler RASYONEL SAYILARIN SAYI DOĞRUSUNDA GÖSTERİLMESİ... 5 RASYONEL SAYILARDA SIRALAMA... 8 RASYONEL SAYILARDA
RASYONEL SAYILAR ELİF ÇAĞLAYAN GAMZE NUR AYDIN HUMAYLA ÖNDER GÜLFER YÜKSEKDAĞ 2011-2012 İçindekiler RASYONEL SAYILARIN SAYI DOĞRUSUNDA GÖSTERİLMESİ... 5 RASYONEL SAYILARDA SIRALAMA... 8 RASYONEL SAYILARDA
SAYILAR SAYI KÜMELERİ
 1 SAYILAR SAYI KÜMELERİ 1.Sayma Sayıları Kümesi: S=N =1,2,3,... 2. Doğal Sayılar Kümesi : N=0,1,2,... 3. Tamsayılar Kümesi : Z=..., 2, 1,0,1,2,... Sıfırın sağında bulunan 1,2,3,. tamsayılarına pozitif
1 SAYILAR SAYI KÜMELERİ 1.Sayma Sayıları Kümesi: S=N =1,2,3,... 2. Doğal Sayılar Kümesi : N=0,1,2,... 3. Tamsayılar Kümesi : Z=..., 2, 1,0,1,2,... Sıfırın sağında bulunan 1,2,3,. tamsayılarına pozitif
BÖLÜM I MATEMATİK NEDİR? 13 1.1. Matematik Nedir? 14
 İÇİNDEKİLER Önsöz. V BÖLÜM I MATEMATİK NEDİR? 13 1.1. Matematik Nedir? 14 BÖLÜM II KÜMELER 17 2.1.Küme Tanımı ve Özellikleri 18 2.2 Kümelerin Gösterimi 19 2.2.1 Venn Şeması Yöntemi 19 2.2.2 Liste Yöntemi
İÇİNDEKİLER Önsöz. V BÖLÜM I MATEMATİK NEDİR? 13 1.1. Matematik Nedir? 14 BÖLÜM II KÜMELER 17 2.1.Küme Tanımı ve Özellikleri 18 2.2 Kümelerin Gösterimi 19 2.2.1 Venn Şeması Yöntemi 19 2.2.2 Liste Yöntemi
ıfırdan büyük olan rasyonel sayılara pozitif rasyonel sayılar, sıfırdan küçük rasyonel sayılar da negatif rasyonel sayılar denir.
 1-RASYONEL SAYILAR VE ÖZELLĐKLERĐ A)Rasyonel Sayılar:Birbirine denk olan kesirlerin meydana getirdiği her kümeye rasyonel sayı denir.rasyonel sayıların meydana getirdiği kümelere rasyonel sayılar kümesi
1-RASYONEL SAYILAR VE ÖZELLĐKLERĐ A)Rasyonel Sayılar:Birbirine denk olan kesirlerin meydana getirdiği her kümeye rasyonel sayı denir.rasyonel sayıların meydana getirdiği kümelere rasyonel sayılar kümesi
1.GRUPLAR. c (Birleşme özelliği) sağlanır. 2) a G için a e e a a olacak şekilde e G. vardır. 3) a G için denir) vardır.
 1.GRUPLAR Tanım 1.1. G boş olmayan bir küme ve, G de bir ikili işlem olsun. (G, ) cebirsel yapısına aşağıdaki aksiyomları sağlıyorsa bir grup denir. 1) a, b, c G için a ( b c) ( a b) c (Birleşme özelliği)
1.GRUPLAR Tanım 1.1. G boş olmayan bir küme ve, G de bir ikili işlem olsun. (G, ) cebirsel yapısına aşağıdaki aksiyomları sağlıyorsa bir grup denir. 1) a, b, c G için a ( b c) ( a b) c (Birleşme özelliği)
BÜTÜN : Parçalanmamış eksiksiz olan her şeye bütün denir.
 BÜTÜN : Parçalanmamış eksiksiz olan her şeye bütün denir. KESİR : Bütünün eş parçalarından her birine kesir denir. KESİR SAYISI: Eş parçalara bölünmüş bir bütünün bir veya birkaç parçasına bu bütünün kesri,
BÜTÜN : Parçalanmamış eksiksiz olan her şeye bütün denir. KESİR : Bütünün eş parçalarından her birine kesir denir. KESİR SAYISI: Eş parçalara bölünmüş bir bütünün bir veya birkaç parçasına bu bütünün kesri,
8. HOMOMORFİZMALAR VE İZOMORFİZMALAR
 8. HOMOMORFİZMALAR VE İZOMORFİZMALAR Şimdiye kadar bir gruptan diğer bir gruba tanımlı olan fonksiyonlarla ilgilenmedik. Bu bölüme aşağıdaki tanımla başlayalım. Tanım 8.1: ve iki grup ve f : G H bir fonksiyon
8. HOMOMORFİZMALAR VE İZOMORFİZMALAR Şimdiye kadar bir gruptan diğer bir gruba tanımlı olan fonksiyonlarla ilgilenmedik. Bu bölüme aşağıdaki tanımla başlayalım. Tanım 8.1: ve iki grup ve f : G H bir fonksiyon
Sunum ve Sistematik 1. BÖLÜM: ÖNERMELER
 Sunum ve Sistematik. ÜNİTE: MANTIK KONU ÖZETİ Bu başlık altında, ünitenin en can alıcı bilgileri, kazanım sırasına göre en alt başlıklara ayrılarak hap bilgi niteliğinde konu özeti olarak sunulmuştur..
Sunum ve Sistematik. ÜNİTE: MANTIK KONU ÖZETİ Bu başlık altında, ünitenin en can alıcı bilgileri, kazanım sırasına göre en alt başlıklara ayrılarak hap bilgi niteliğinde konu özeti olarak sunulmuştur..
Bu kısımda işlem adı verilen özel bir fonksiyon çeşidini ve işlemlerin önemli özelliklerini inceleyeceğiz.
 Bölüm 3 Gruplar Bu bölümde ilk olarak bir küme üzerinde tanımlı işlem kavramını ele alıp işlemlerin bazı özelliklerini inceleyeceğiz. Daha sonra kümeler ve üzerinde tanımlı işlemlerden oluşan cebirsel
Bölüm 3 Gruplar Bu bölümde ilk olarak bir küme üzerinde tanımlı işlem kavramını ele alıp işlemlerin bazı özelliklerini inceleyeceğiz. Daha sonra kümeler ve üzerinde tanımlı işlemlerden oluşan cebirsel
(a,b) şeklindeki ifadelere sıralı ikili denir. Burada a'ya 1. bileşen b'ye 2. bileşen denir.
 BĞANTI - FONKSİYON 1. Sıralı İkili : (a,b) şeklindeki ifadelere sıralı ikili denir. Burada a'ya 1. bileşen b'ye 2. bileşen denir.! (x 1,x 2, x 3,x 4,...x n ) : sıralı n li denir. Örnek, (a,b,c) : sıralı
BĞANTI - FONKSİYON 1. Sıralı İkili : (a,b) şeklindeki ifadelere sıralı ikili denir. Burada a'ya 1. bileşen b'ye 2. bileşen denir.! (x 1,x 2, x 3,x 4,...x n ) : sıralı n li denir. Örnek, (a,b,c) : sıralı
3. işleminin birim elemanı vardır, yani her x A için x e = e x = x olacak şekilde e A vardır.
 0.1 GRUPLAR Tanım 1 A kümesi boştan farklıolmak üzere işlemine göre aşağıdaki koşulları gerçekliyorsa (A, ) ikilisine bir Grup denir. 1. kapalılık özelliğine sahiptir, yani her x, y A için x y A olur.
0.1 GRUPLAR Tanım 1 A kümesi boştan farklıolmak üzere işlemine göre aşağıdaki koşulları gerçekliyorsa (A, ) ikilisine bir Grup denir. 1. kapalılık özelliğine sahiptir, yani her x, y A için x y A olur.
Kafes Yapıları. Hatırlatma
 Kafes Yapıları Ders 7 8-1 Hatırlatma Daha önce anlatılan sıra bağıntısını hatırlayalım. A kümesinde bir R bağıntsı verilmiş olsun. R bağıntısı; a. Yansıma (Tüm a A için, sadece ve sadece ara ise yansıyandır(reflexive)).
Kafes Yapıları Ders 7 8-1 Hatırlatma Daha önce anlatılan sıra bağıntısını hatırlayalım. A kümesinde bir R bağıntsı verilmiş olsun. R bağıntısı; a. Yansıma (Tüm a A için, sadece ve sadece ara ise yansıyandır(reflexive)).
Örnek...3 : Aşağıdaki ifadelerden hangileri bir dizinin genel terim i olabilir? Örnek...4 : Genel terimi w n. Örnek...1 : Örnek...5 : Genel terimi r n
 DİZİLER Tanım kümesi pozitif tam sayılar kümesi olan her fonksiyona dizi denir. Örneğin f : Z + R, f (n )=n 2 ifadesi bir dizi belirtir. Diziler değer kümelerine göre adlandırılırlar. Dizinin değer kümesi
DİZİLER Tanım kümesi pozitif tam sayılar kümesi olan her fonksiyona dizi denir. Örneğin f : Z + R, f (n )=n 2 ifadesi bir dizi belirtir. Diziler değer kümelerine göre adlandırılırlar. Dizinin değer kümesi
MAT 302 SOYUT CEBİR II SORULAR. (b) = ise =
 MAT 302 SOYUT CEBİR II SORULAR 1. : bir dönüşüm, olsunlar. a) ( ) = ( ) ( ) b) ( ) ( ) ( ) olduğunu c) ( ) nin eşitliğinin sağlanması için gerekli ve yeterli bir koşulun nin 1 1 olması ile mümkün olduğunu
MAT 302 SOYUT CEBİR II SORULAR 1. : bir dönüşüm, olsunlar. a) ( ) = ( ) ( ) b) ( ) ( ) ( ) olduğunu c) ( ) nin eşitliğinin sağlanması için gerekli ve yeterli bir koşulun nin 1 1 olması ile mümkün olduğunu
ÇANAKKALE ONSEKİZ MART ÜNİVERSİTESİ FEN EDEBİYAT FAKÜLTESİ MATEMATİK BÖLÜMÜ MODÜLER ARİTMETİK
 ÇANAKKALE ONSEKİZ MART ÜNİVERSİTESİ FEN EDEBİYAT FAKÜLTESİ MATEMATİK BÖLÜMÜ MODÜLER ARİTMETİK ÇANAKKALE 2012 ÖNSÖZ Bu kitap Çanakkale Onsekiz Mart Üniversitesi Matematik Bölümünde lisans dersi olarak Cebirden
ÇANAKKALE ONSEKİZ MART ÜNİVERSİTESİ FEN EDEBİYAT FAKÜLTESİ MATEMATİK BÖLÜMÜ MODÜLER ARİTMETİK ÇANAKKALE 2012 ÖNSÖZ Bu kitap Çanakkale Onsekiz Mart Üniversitesi Matematik Bölümünde lisans dersi olarak Cebirden
İÇİNDEKİLER. Önsöz...2. Önermeler ve İspat Yöntemleri...3. Küme Teorisi Bağıntı Fonksiyon İşlem...48
 İÇİNDEKİLER Önsöz...2 Önermeler ve İspat Yöntemleri...3 Küme Teorisi...16 Bağıntı...26 Fonksiyon...38 İşlem...48 Sayılabilir - Sonlu ve Sonsuz Kümeler...56 Genel Tarama Sınavı...58 Önermeler ve İspat Yöntemleri
İÇİNDEKİLER Önsöz...2 Önermeler ve İspat Yöntemleri...3 Küme Teorisi...16 Bağıntı...26 Fonksiyon...38 İşlem...48 Sayılabilir - Sonlu ve Sonsuz Kümeler...56 Genel Tarama Sınavı...58 Önermeler ve İspat Yöntemleri
ÜNİTE: RASYONEL SAYILAR KONU: Rasyonel Sayılar Kümesinde Çıkarma İşlemi
 ÜNTE: RASYONEL SAYILAR ONU: Rasyonel Sayılar ümesinde Çıkarma şlemi ÖRNE SORULAR VE ÇÖZÜMLER. işleminin sonucu B) D) ki rasyonel sayının farkını bulmak için çıkan terimin toplama işlemine göre tersi alınarak
ÜNTE: RASYONEL SAYILAR ONU: Rasyonel Sayılar ümesinde Çıkarma şlemi ÖRNE SORULAR VE ÇÖZÜMLER. işleminin sonucu B) D) ki rasyonel sayının farkını bulmak için çıkan terimin toplama işlemine göre tersi alınarak
KPSS MATEMATÝK. SOYUT CEBÝR ( Genel Tekrar Testi-1) N tam sayılar kümesinde i N için, A = 1 i,i 1
 SOYUT CEBÝR ( Genel Tekrar Testi-1) 1. A = { k k Z, < k 4 } 4. N tam sayılar kümesinde i N için, k 1 B = { k Z, 1 k < 1 } k 1 A = 1 i,i 1 i ( ] kümeleri verildiğine göre, aşağıdakilerden hangisi doğrudur?
SOYUT CEBÝR ( Genel Tekrar Testi-1) 1. A = { k k Z, < k 4 } 4. N tam sayılar kümesinde i N için, k 1 B = { k Z, 1 k < 1 } k 1 A = 1 i,i 1 i ( ] kümeleri verildiğine göre, aşağıdakilerden hangisi doğrudur?
MATM 133 MATEMATİK LOJİK. Dr. Doç. Çarıyar Aşıralıyev
 MATM 133 MATEMATİK LOJİK Dr. Doç. Çarıyar Aşıralıyev 3.KONU Kümeler Teorisi; Küme işlemleri, İkili işlemler 1. Altküme 2. Evrensel Küme 3. Kümelerin Birleşimi 4. Kümelerin Kesişimi 5. Bir Kümenin Tümleyeni
MATM 133 MATEMATİK LOJİK Dr. Doç. Çarıyar Aşıralıyev 3.KONU Kümeler Teorisi; Küme işlemleri, İkili işlemler 1. Altküme 2. Evrensel Küme 3. Kümelerin Birleşimi 4. Kümelerin Kesişimi 5. Bir Kümenin Tümleyeni
SAYILAR. Sayıları yazmak için kullanılan 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 şeklindeki işaretlere rakam denir.
 SAYILAR 1. Rakamlar (Numbers) Sayıları yazmak için kullanılan 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 şeklindeki işaretlere rakam denir. 2. Sayma Sayıları 1 den başlayıp artarak devam eden doğal sayılara sayma sayıları
SAYILAR 1. Rakamlar (Numbers) Sayıları yazmak için kullanılan 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 şeklindeki işaretlere rakam denir. 2. Sayma Sayıları 1 den başlayıp artarak devam eden doğal sayılara sayma sayıları
BMT 206 Ayrık Matematik. Yük. Müh. Köksal GÜNDOĞDU 1
 BMT 206 Ayrık Matematik Yük. Müh. Köksal GÜNDOĞDU 1 Kümeler Yük. Müh. Köksal GÜNDOĞDU 2 Kümeler Kümeler Ayrık Matematiğin en temel konularından biridir Sayma problemleri için önemli Programlama dillerinin
BMT 206 Ayrık Matematik Yük. Müh. Köksal GÜNDOĞDU 1 Kümeler Yük. Müh. Köksal GÜNDOĞDU 2 Kümeler Kümeler Ayrık Matematiğin en temel konularından biridir Sayma problemleri için önemli Programlama dillerinin
ONDALIK GÖSTERİMLER ONDALIK GÖSTERİM. ÖRNEK: Aşağıda verilen kesirlerin ondalık gösterimlerini yazınız.
 ONDALIK GÖSTERİM Paydası 10, 100, 1000 olan kesirlerin virgül kullanarak yazılışına ondalık gösterim denir. Ondalık gösterimlerde virgül tam kısım ile kesir kısmı ayırmak için kullanılır. ÖRNEK: Aşağıda
ONDALIK GÖSTERİM Paydası 10, 100, 1000 olan kesirlerin virgül kullanarak yazılışına ondalık gösterim denir. Ondalık gösterimlerde virgül tam kısım ile kesir kısmı ayırmak için kullanılır. ÖRNEK: Aşağıda
için doğrudur. olmak üzere tüm r mertebeli gruplar için lemma nın doğru olduğunu kabul edelim. G grubunun mertebesi n olsun. ve olsun.
 11. Cauchy Teoremi ve p-gruplar Bu bölümde Lagrange teoreminin tersinin doğru olduğu bir özel durumu inceleyeceğiz. Bu teorem Cauchy tarafından ispatlanmıştır. İlk olarak bu teoremi sonlu değişmeli gruplar
11. Cauchy Teoremi ve p-gruplar Bu bölümde Lagrange teoreminin tersinin doğru olduğu bir özel durumu inceleyeceğiz. Bu teorem Cauchy tarafından ispatlanmıştır. İlk olarak bu teoremi sonlu değişmeli gruplar
MODÜLER ARİTMETİK. Örnek:
 MODÜLER ARİTMETİK Bir doğal sayının ile bölünmesinden elde edilen kalanlar kümesi { 0,, } dir. ile bölünmesinden elde edilen kalanlar kümesi { 0,,, } tür. Tam sayılar kümesi üzerinde tanımlanan {( x, y)
MODÜLER ARİTMETİK Bir doğal sayının ile bölünmesinden elde edilen kalanlar kümesi { 0,, } dir. ile bölünmesinden elde edilen kalanlar kümesi { 0,,, } tür. Tam sayılar kümesi üzerinde tanımlanan {( x, y)
YÜZDE HESAPLARI. X sayısı, herhangi bir reel sayı olmak üzere, bu X sayısını 100
 YÜZDE HESAPLARI Ticari hayatta yapılan ticari işlemler aynı türden bazı çoklukların birbiri ile bölme yoluyla karşılaştırılmasını ve böylece belli bir oranın bulunmasını gerektirir. Örneğin, maliyet fiyati
YÜZDE HESAPLARI Ticari hayatta yapılan ticari işlemler aynı türden bazı çoklukların birbiri ile bölme yoluyla karşılaştırılmasını ve böylece belli bir oranın bulunmasını gerektirir. Örneğin, maliyet fiyati
Leyla Bugay Doktora Nisan, 2011
 ltanguler@cu.edu.tr Çukurova Üniversitesi, Matematik Bölümü Doktora 2010913070 Nisan, 2011 Yarıgrup Teorisi Nedir? Yarıgrup teorisi cebirin en temel dallarından biridir. Yarıgrup terimi ilk olarak 1904
ltanguler@cu.edu.tr Çukurova Üniversitesi, Matematik Bölümü Doktora 2010913070 Nisan, 2011 Yarıgrup Teorisi Nedir? Yarıgrup teorisi cebirin en temel dallarından biridir. Yarıgrup terimi ilk olarak 1904
Tanım Bir X kümesi üzerinde bir karakter dizgisi (string) X kümesindeki. boş karakter dizgisi (null string) denir ve l ile gösterilir.
 BÖLÜM 3 Karakter Dizgileriil i Tanım 3.1.1 Bir X kümesi üzerinde bir karakter dizgisi (string) X kümesindeki öğelerden oluşan bir sonlu dizidir. Hiç bir öğesi olmayan bir karakter dizgisine boş karakter
BÖLÜM 3 Karakter Dizgileriil i Tanım 3.1.1 Bir X kümesi üzerinde bir karakter dizgisi (string) X kümesindeki öğelerden oluşan bir sonlu dizidir. Hiç bir öğesi olmayan bir karakter dizgisine boş karakter
Bu bölümde cebirsel yapıların temelini oluşturan Grup ve özelliklerini inceleyeceğiz.
 1 BİR İŞLEMLİ SİSTEMLER Bu bölümde cebirsel yapıların temelini oluşturan Grup ve özelliklerini inceleyeceğiz. 1.1 İŞLEMLER Bir kümeden kendisine tanımlı olan her fonksiyona birli işlem denir. Örneğin Z
1 BİR İŞLEMLİ SİSTEMLER Bu bölümde cebirsel yapıların temelini oluşturan Grup ve özelliklerini inceleyeceğiz. 1.1 İŞLEMLER Bir kümeden kendisine tanımlı olan her fonksiyona birli işlem denir. Örneğin Z
2 şeklindeki bütün sayılar. 2 irrasyonel sayısı. 2 irrasyonel sayısından elde etmekteyiz. Benzer şekilde 3 irrasyonel sayısı
 1.8.Reel Sayılar Kümesinin Tamlık Özelliği Rasyonel sayılar kümesi ile rasyonel olmayan sayıların kümesi olan irrasyonel sayılar kümesinin birleşimine reel sayılar kümesi denir ve IR ile gösterilir. Buna
1.8.Reel Sayılar Kümesinin Tamlık Özelliği Rasyonel sayılar kümesi ile rasyonel olmayan sayıların kümesi olan irrasyonel sayılar kümesinin birleşimine reel sayılar kümesi denir ve IR ile gösterilir. Buna
KESİRLER BİRİM KESİRLERİ SIRALAMA. Birim kesirlerde paydası büyük olan kesir daha küçüktür.
 BİRİM KESİRLERİ SIRALAMA Bir bütünün eş parçalarından her birine kesir denir. Payı olan kesirlere birim kesir denir. Birim kesirlerde paydası büyük olan kesir daha küçüktür.,, 8 kesirlerini sıralayınız.
BİRİM KESİRLERİ SIRALAMA Bir bütünün eş parçalarından her birine kesir denir. Payı olan kesirlere birim kesir denir. Birim kesirlerde paydası büyük olan kesir daha küçüktür.,, 8 kesirlerini sıralayınız.
SOYUT CEBİR ÇALIŞMA SORULARI HALKALAR I. Soru 1 Standart toplama ve : a b = 0 olarak tanımlanan işlemler altında (Z, +, ) nin
 1 SOYUT CEBİR ÇALIŞMA SORULARI HALKALAR I Soru 1 Standart toplama ve : a b = 0 olarak tanımlanan işlemler altında (Z, +, ) nin bir halka yapısıoluşturup oluşturmadĭgınıinceleyiniz. Soru 2 a, b Z, b tek
1 SOYUT CEBİR ÇALIŞMA SORULARI HALKALAR I Soru 1 Standart toplama ve : a b = 0 olarak tanımlanan işlemler altında (Z, +, ) nin bir halka yapısıoluşturup oluşturmadĭgınıinceleyiniz. Soru 2 a, b Z, b tek
2. ÜNİTE RASYONEL,ÜSLÜ VE KÖKLÜ SAYILAR
 2. ÜNİTE RASYONEL,ÜSLÜ VE KÖKLÜ SAYILAR KONULAR 1. RASYONEL SAYILAR 2. Kesir Çeşitleri 3. Kesirlerin Sadeleştirilmesi 4. Rasyonel Sayılarda Sıralama 5. Rasyonel Sayılarda İşlemler 6. ÜSLÜ İFADE 7. Üssün
2. ÜNİTE RASYONEL,ÜSLÜ VE KÖKLÜ SAYILAR KONULAR 1. RASYONEL SAYILAR 2. Kesir Çeşitleri 3. Kesirlerin Sadeleştirilmesi 4. Rasyonel Sayılarda Sıralama 5. Rasyonel Sayılarda İşlemler 6. ÜSLÜ İFADE 7. Üssün
1. GRUPLAR. c (Birleşme özelliği) sağlanır. 2) a G için a e e a a olacak şekilde e G (e ye birim eleman denir) vardır.
 1. GRUPLAR Tanım 1.1. G boş olmayan bir küme ve, G de bir ikili işlem olsun. (G yapısına aşağıdaki aksiyomları sağlıyorsa bir grup denir., ) cebirsel 1) a b cg,, için a( bc) ( ab) c (Birleşme özelliği)
1. GRUPLAR Tanım 1.1. G boş olmayan bir küme ve, G de bir ikili işlem olsun. (G yapısına aşağıdaki aksiyomları sağlıyorsa bir grup denir., ) cebirsel 1) a b cg,, için a( bc) ( ab) c (Birleşme özelliği)
olsun. Bu halde g g1 g1 g e ve g g2 g2 g e eşitlikleri olur. b G için a b b a değişme özelliği sağlanıyorsa
 1.GRUPLAR Tanım 1.1. G boş olmayan bir küme ve, G de bir ikili işlem olsun. (G, ) cebirsel yapısına aşağıdaki aksiyomları sağlıyorsa bir grup denir. 1), G de bir ikili işlemdir. 2) a, b, c G için a( bc)
1.GRUPLAR Tanım 1.1. G boş olmayan bir küme ve, G de bir ikili işlem olsun. (G, ) cebirsel yapısına aşağıdaki aksiyomları sağlıyorsa bir grup denir. 1), G de bir ikili işlemdir. 2) a, b, c G için a( bc)
Fatih University- Faculty of Engineering- Electric and Electronic Dept.
 Dijital Devre Tasarımı EEE122 A Ref. Morris MANO & Michael D. CILETTI DIGITAL DESIGN 4 th edition Fatih University- Faculty of Engineering- Electric and Electronic Dept. 2. BÖLÜM Boole Cebri ve Mantık
Dijital Devre Tasarımı EEE122 A Ref. Morris MANO & Michael D. CILETTI DIGITAL DESIGN 4 th edition Fatih University- Faculty of Engineering- Electric and Electronic Dept. 2. BÖLÜM Boole Cebri ve Mantık
KARAKTER DİZGİLERİ, BAĞINTILAR, FONKSİYONLAR KESİKLİ MATEMATİKSEL YAPILAR
 KARAKTER DİZGİLERİ, BAĞINTILAR, FONKSİYONLAR KESİKLİ MATEMATİKSEL YAPILAR 2012-2013 Karakter Dizgisi Karakter Dizgisi Üzerine İşlemler Altdizgi Tanım 3.1.1: Bir X kümesi üzerinde bir karakter dizgisi (string)
KARAKTER DİZGİLERİ, BAĞINTILAR, FONKSİYONLAR KESİKLİ MATEMATİKSEL YAPILAR 2012-2013 Karakter Dizgisi Karakter Dizgisi Üzerine İşlemler Altdizgi Tanım 3.1.1: Bir X kümesi üzerinde bir karakter dizgisi (string)
MATEMATİK Kazanım =Rasyonel sayıları tanır ve sayı doğrusunda gösterir. RASYONEL SAYILAR VE SAYI DOĞRUSUNDA GÖSTERME
 .SINIF MATEMATİK Kazanım Rasyonel sayıları tanır ve sayı doğrusunda gösterir. RASYONEL SAYILAR VE SAYI DOĞRUSUNDA GÖSTERME RASYONEL SAYILAR 0,,,,... gibi a şeklinde yazılabilen sayılara rasyonel sayılar
.SINIF MATEMATİK Kazanım Rasyonel sayıları tanır ve sayı doğrusunda gösterir. RASYONEL SAYILAR VE SAYI DOĞRUSUNDA GÖSTERME RASYONEL SAYILAR 0,,,,... gibi a şeklinde yazılabilen sayılara rasyonel sayılar
Mustafa Sezer PEHLİVAN. Yüksek İhtisas Üniversitesi Beslenme ve Diyetetik Bölümü
 * Yüksek İhtisas Üniversitesi Beslenme ve Diyetetik Bölümü SAYILAR Doğal Sayılar, Tam Sayılar, Rasyonel Sayılar, N={0,1,2,3,,n, } Z={,-3,-2,-1,0,1,2,3, } Q={p/q: p,q Z ve q 0} İrrasyonel Sayılar, I= {p/q
* Yüksek İhtisas Üniversitesi Beslenme ve Diyetetik Bölümü SAYILAR Doğal Sayılar, Tam Sayılar, Rasyonel Sayılar, N={0,1,2,3,,n, } Z={,-3,-2,-1,0,1,2,3, } Q={p/q: p,q Z ve q 0} İrrasyonel Sayılar, I= {p/q
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
VEKTÖR UZAYLARI 1.GİRİŞ
 1.GİRİŞ Bu bölüm lineer cebirin temelindeki cebirsel yapıya, sonlu boyutlu vektör uzayına giriş yapmaktadır. Bir vektör uzayının tanımı, elemanları skalar olarak adlandırılan herhangi bir cisim içerir.
1.GİRİŞ Bu bölüm lineer cebirin temelindeki cebirsel yapıya, sonlu boyutlu vektör uzayına giriş yapmaktadır. Bir vektör uzayının tanımı, elemanları skalar olarak adlandırılan herhangi bir cisim içerir.
Örnek 1: 2 x = 3 x = log 2 3. Örnek 2: 3 2x 1 = 2 2x 1 = log 3 2. Örnek 3: 4 x 1 = 7 x 1 = log 4 7. Örnek 4: 2 x = 3 2 x 2 = 3
 Soru : f(x) = log x 4 5 fonksiyonunun tanım aralığını bulunuz? a x = b eşitliğinde a ve b belli iken x i bulmaya logaritma işlemi denir. Üstel fonksiyon bire bir ve örten olduğundan ters fonksiyonu vardır.
Soru : f(x) = log x 4 5 fonksiyonunun tanım aralığını bulunuz? a x = b eşitliğinde a ve b belli iken x i bulmaya logaritma işlemi denir. Üstel fonksiyon bire bir ve örten olduğundan ters fonksiyonu vardır.
1 Vektör Uzayları 2. Lineer Cebir. David Pierce. Matematik Bölümü, MSGSÜ mat.msgsu.edu.tr/~dpierce/
 Vektör Uzayları Lineer Cebir David Pierce 5 Mayıs 2017 Matematik Bölümü, MSGSÜ dpierce@msgsu.edu.tr mat.msgsu.edu.tr/~dpierce/ Bu notlarda, alıştırma olarak her teorem, sonuç, ve örnek kanıtlanabilir;
Vektör Uzayları Lineer Cebir David Pierce 5 Mayıs 2017 Matematik Bölümü, MSGSÜ dpierce@msgsu.edu.tr mat.msgsu.edu.tr/~dpierce/ Bu notlarda, alıştırma olarak her teorem, sonuç, ve örnek kanıtlanabilir;
11. RASYONEL SAYILARIN SIRALANMASI
 11. RASYONEL SAYILARIN SIRALANMASI SIRALAMA SEMBOLLERİ Sıralama sembolleri, sayıların sıralanma şeklini gösterirler. Yani, sıralama sembolleri sayıların küçükten büyüğe veya büyükten küçüğe doğru sıralanmasını
11. RASYONEL SAYILARIN SIRALANMASI SIRALAMA SEMBOLLERİ Sıralama sembolleri, sayıların sıralanma şeklini gösterirler. Yani, sıralama sembolleri sayıların küçükten büyüğe veya büyükten küçüğe doğru sıralanmasını
1. BÖLÜM Mantık BÖLÜM Sayılar BÖLÜM Rasyonel Sayılar BÖLÜM I. Dereceden Denklemler ve Eşitsizlikler
 ORGANİZASYON ŞEMASI 1. BÖLÜM Mantık... 7. BÖLÜM Sayılar... 13 3. BÖLÜM Rasyonel Sayılar... 93 4. BÖLÜM I. Dereceden Denklemler ve Eşitsizlikler... 103 5. BÖLÜM Mutlak Değer... 113 6. BÖLÜM Çarpanlara Ayırma...
ORGANİZASYON ŞEMASI 1. BÖLÜM Mantık... 7. BÖLÜM Sayılar... 13 3. BÖLÜM Rasyonel Sayılar... 93 4. BÖLÜM I. Dereceden Denklemler ve Eşitsizlikler... 103 5. BÖLÜM Mutlak Değer... 113 6. BÖLÜM Çarpanlara Ayırma...
MATM 133 MATEMATİK LOJİK. Dr. Doç. Çarıyar Aşıralıyev
 MATM 133 MATEMATİK LOJİK Dr. Doç. Çarıyar Aşıralıyev 1.KONU Sembolik Mantık; Önermeler, Niceyiciler, Olumsuzluk, İspat yöntemleri KAYNAKLAR 1. Akkaş, S., Hacısalihoğlu, H.H., Özel, Z., Sabuncuoğlu, A.,
MATM 133 MATEMATİK LOJİK Dr. Doç. Çarıyar Aşıralıyev 1.KONU Sembolik Mantık; Önermeler, Niceyiciler, Olumsuzluk, İspat yöntemleri KAYNAKLAR 1. Akkaş, S., Hacısalihoğlu, H.H., Özel, Z., Sabuncuoğlu, A.,
AYRIK YAPILAR ARŞ. GÖR. SONGÜL KARAKUŞ- FIRAT ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ YAZILIM MÜHENDİSLİĞİ BÖLÜMÜ, ELAZIĞ
 AYRIK YAPILAR P r o f. D r. Ö m e r A k ı n v e Y r d. D o ç. D r. M u r a t Ö z b a y o ğ l u n u n Ç e v i r i E d i t ö r l ü ğ ü n ü ü s t l e n d i ğ i «A y r ı k M a t e m a t i k v e U y g u l a
AYRIK YAPILAR P r o f. D r. Ö m e r A k ı n v e Y r d. D o ç. D r. M u r a t Ö z b a y o ğ l u n u n Ç e v i r i E d i t ö r l ü ğ ü n ü ü s t l e n d i ğ i «A y r ı k M a t e m a t i k v e U y g u l a
ÜNİTE. MATEMATİK-1 Prof.Dr.Ahmet KÜÇÜK İÇİNDEKİLER HEDEFLER TÜREV VE TÜREV ALMA KURALLARI. Türev Türev Alma Kuralları
 HEDEFLER İÇİNDEKİLER TÜREV VE TÜREV ALMA KURALLARI Türev Türev Alma Kuralları MATEMATİK-1 Prof.Dr.Ahmet KÜÇÜK Bu üniteyi çalıştıktan sonra Burada türevin tanımı verilecek, Geometride bir eğrinin bir noktadaki
HEDEFLER İÇİNDEKİLER TÜREV VE TÜREV ALMA KURALLARI Türev Türev Alma Kuralları MATEMATİK-1 Prof.Dr.Ahmet KÜÇÜK Bu üniteyi çalıştıktan sonra Burada türevin tanımı verilecek, Geometride bir eğrinin bir noktadaki
Bir bütünün eş parçalarının bütüne olan oranı kesir olarak adlandırılır. b Payda
 Matematik6 Bir Bakışta Matematik Kazanım Defteri Özet bilgi alanları... Kesirlerle İşlemler KESİR ve KESİRLERDE SIRALAMA Bir bütünün eş parçalarının bütüne olan oranı kesir olarak adlandırılır. Bir kesirde
Matematik6 Bir Bakışta Matematik Kazanım Defteri Özet bilgi alanları... Kesirlerle İşlemler KESİR ve KESİRLERDE SIRALAMA Bir bütünün eş parçalarının bütüne olan oranı kesir olarak adlandırılır. Bir kesirde
Örnek...2 : Örnek...3 : Örnek...1 : MANTIK 1. p: Bir yıl 265 gün 6 saattir. w w w. m a t b a z. c o m ÖNERMELER- BİLEŞİK ÖNERMELER
 Terim: Bir bilim dalı içerisinde konuşma dilinden farklı anlamı olan sözcüklerden her birine o bilim dalının bir terimi denir. Önermeler belirtilirler. p,q,r,s gibi harflerle Örneğin açı bir geometri terimi,
Terim: Bir bilim dalı içerisinde konuşma dilinden farklı anlamı olan sözcüklerden her birine o bilim dalının bir terimi denir. Önermeler belirtilirler. p,q,r,s gibi harflerle Örneğin açı bir geometri terimi,
MATM 133 MATEMATİK LOJİK. Dr. Doç. Çarıyar Aşıralıyev
 MATM 133 MATEMATİK LOJİK Dr. Doç. Çarıyar Aşıralıyev 4.KONU Latisler, Boole Cebri 1. Kısmi sıralı kümeler 2. Hasse Diyagramı 3. Infimum, Supremum 4. Latis (Kafes Lattice) 5. Latis (Kafes) Yapıları ve Özellikleri
MATM 133 MATEMATİK LOJİK Dr. Doç. Çarıyar Aşıralıyev 4.KONU Latisler, Boole Cebri 1. Kısmi sıralı kümeler 2. Hasse Diyagramı 3. Infimum, Supremum 4. Latis (Kafes Lattice) 5. Latis (Kafes) Yapıları ve Özellikleri
Grup Homomorfizmaları ve
 Bölüm 7 Grup Homomorfizmaları ve İzomorfizmalar Bu bölümde verilen gruplar arasında grup işlemlerini koruyan fonksiyonları ele alacağız. Bu fonksiyonlar yardımıyla verilen grupların cebirsel yapılarının
Bölüm 7 Grup Homomorfizmaları ve İzomorfizmalar Bu bölümde verilen gruplar arasında grup işlemlerini koruyan fonksiyonları ele alacağız. Bu fonksiyonlar yardımıyla verilen grupların cebirsel yapılarının
3. Ders. Mahir Bilen Can. Mayıs 11, Önceki Dersteki Sorular ile İlgili Açıklamalar
 3. Ders Mahir Bilen Can Mayıs 11, 2016 1 Önceki Dersteki Sorular ile İlgili Açıklamalar Lie nin üçüncü teoremi oarak bilinen ve Cartan tarafından asağıdaki gibi güçlendirilmiş bir teorem ile başlayalım:
3. Ders Mahir Bilen Can Mayıs 11, 2016 1 Önceki Dersteki Sorular ile İlgili Açıklamalar Lie nin üçüncü teoremi oarak bilinen ve Cartan tarafından asağıdaki gibi güçlendirilmiş bir teorem ile başlayalım:
1.1 Üslü İfadeler: Üslü ifadelerle ilgili aşağıdaki kuralların hatırlanması faydalıdır.
 FİNANSAL MATEMATİK ALTYAPI. Üslü İfadeler: Üslü ifadelerle ilgili aşağıdaki kuralların hatırlanması faydalıdır. i-) Toplama: Eşit üslü benzer ifadelerin katsayıları toplanır. 3a 5 +,5a 5 =,5a 5 a 3-7a
FİNANSAL MATEMATİK ALTYAPI. Üslü İfadeler: Üslü ifadelerle ilgili aşağıdaki kuralların hatırlanması faydalıdır. i-) Toplama: Eşit üslü benzer ifadelerin katsayıları toplanır. 3a 5 +,5a 5 =,5a 5 a 3-7a
ÜSLÜ SAYILARLA İLGİLİ TEMEL KURALLAR. (2 ) demek 2 tane 2 3 'ün çarpımı demektir. (2 ) = 2.2 = 2 eder.
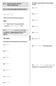 8.. ÜSLÜ SAYILARLA İLGİLİ TEMEL KURALLAR 8...A ÜSLÜ SAYILARIN KUVVETİNİ ALMA ) Aşağıda verilen eşitlikte bilinmeyen harfleri bulunuz. 6 a. 6 ( ) 8 b b) 7 Üslü bir sayının üssü alınırken, üsler çarpılır.
8.. ÜSLÜ SAYILARLA İLGİLİ TEMEL KURALLAR 8...A ÜSLÜ SAYILARIN KUVVETİNİ ALMA ) Aşağıda verilen eşitlikte bilinmeyen harfleri bulunuz. 6 a. 6 ( ) 8 b b) 7 Üslü bir sayının üssü alınırken, üsler çarpılır.
DERS: CEBİRDEN SEÇME KONULAR KONU: ENDOMORFİZMA HALKALARI
 T.C ÇANAKKALE ONSEKİZ MART ÜNİVERSİTESİ FEN EDEBİYAT FAKÜLTESİ MATEMATİK BÖLÜMÜ DERS: CEBİRDEN SEÇME KONULAR KONU: ENDOMORFİZMA HALKALARI ÖĞRETİM ÜYELERİ: PROF.DR. NEŞET AYDIN AR.GÖR. DİDEM YEŞİL HAZIRLAYANLAR:
T.C ÇANAKKALE ONSEKİZ MART ÜNİVERSİTESİ FEN EDEBİYAT FAKÜLTESİ MATEMATİK BÖLÜMÜ DERS: CEBİRDEN SEÇME KONULAR KONU: ENDOMORFİZMA HALKALARI ÖĞRETİM ÜYELERİ: PROF.DR. NEŞET AYDIN AR.GÖR. DİDEM YEŞİL HAZIRLAYANLAR:
MUTLAK DEĞER. Örnek...6 : 1 x > 1 y > 1 z. Örnek...7 : x=1 5, y= 5 2, ise x+y y x x =? Örnek...1 : =? Örnek...8 : Örnek...2 : =?
 TANIM MUTLAK DEĞER Örnek...6 : 1 x > 1 y > 1 z ise x y x z z y =? Bir x reel sayısına karşılık gelen noktanın sayı doğrusunda 0 (sıf ır) a olan uzaklığına x sayısının mutlak değeri denir ve x şeklinde
TANIM MUTLAK DEĞER Örnek...6 : 1 x > 1 y > 1 z ise x y x z z y =? Bir x reel sayısına karşılık gelen noktanın sayı doğrusunda 0 (sıf ır) a olan uzaklığına x sayısının mutlak değeri denir ve x şeklinde
Tanım 2.1. X boş olmayan bir küme olmak üzere X den X üzerine bire-bir fonksiyona permütasyon denir.
 2. SİMETRİK GRUPLAR Tanım 2.1. X boş olmayan bir küme olmak üzere X den X üzerine bire-bir fonksiyona permütasyon denir. Tanım 2.2. boş olmayan bir küme olsun. ile den üzerine bire-bir fonksiyonlar kümesini
2. SİMETRİK GRUPLAR Tanım 2.1. X boş olmayan bir küme olmak üzere X den X üzerine bire-bir fonksiyona permütasyon denir. Tanım 2.2. boş olmayan bir küme olsun. ile den üzerine bire-bir fonksiyonlar kümesini
Modül Teori. Modüller. Prof. Dr. Neşet AYDIN. [01/07] Mart Prof. Dr. Neşet AYDIN (ÇOMÜ - Matematik Bölümü) Modül Teori [01/07] Mart / 50
![Modül Teori. Modüller. Prof. Dr. Neşet AYDIN. [01/07] Mart Prof. Dr. Neşet AYDIN (ÇOMÜ - Matematik Bölümü) Modül Teori [01/07] Mart / 50 Modül Teori. Modüller. Prof. Dr. Neşet AYDIN. [01/07] Mart Prof. Dr. Neşet AYDIN (ÇOMÜ - Matematik Bölümü) Modül Teori [01/07] Mart / 50](/thumbs/62/48180402.jpg) Modül Teori Modüller Prof. Dr. Neşet AYDIN ÇOMÜ - Matematik Bölümü [01/07] Mart 2012 Prof. Dr. Neşet AYDIN (ÇOMÜ - Matematik Bölümü) Modül Teori [01/07] Mart 2012 1 / 50 Giriş M bir toplamsal değişmeli
Modül Teori Modüller Prof. Dr. Neşet AYDIN ÇOMÜ - Matematik Bölümü [01/07] Mart 2012 Prof. Dr. Neşet AYDIN (ÇOMÜ - Matematik Bölümü) Modül Teori [01/07] Mart 2012 1 / 50 Giriş M bir toplamsal değişmeli
Şimdi de [ ] vektörünün ile gösterilen boyu veya büyüklüğü Pisagor. teoreminini iki kere kullanarak
![Şimdi de [ ] vektörünün ile gösterilen boyu veya büyüklüğü Pisagor. teoreminini iki kere kullanarak Şimdi de [ ] vektörünün ile gösterilen boyu veya büyüklüğü Pisagor. teoreminini iki kere kullanarak](/thumbs/17/146647.jpg) 10.Konu İç çarpım uzayları ve özellikleri 10.1. ve üzerinde uzunluk de [ ] vektörünün ile gösterilen boyu veya büyüklüğü Pisagor teoreminden dir. 1.Ö.: [ ] ise ( ) ( ) ve ( ) noktaları gözönüne alalım.
10.Konu İç çarpım uzayları ve özellikleri 10.1. ve üzerinde uzunluk de [ ] vektörünün ile gösterilen boyu veya büyüklüğü Pisagor teoreminden dir. 1.Ö.: [ ] ise ( ) ( ) ve ( ) noktaları gözönüne alalım.
Kesirler. Kesirlere neden ihtiyaç duyulur?
 Kesirler Kesirler Kesirlere neden ihtiyaç duyulur? Kesirler Doğal sayılar günlük yaşantımızda bazı problemlerin çözümünde yetersiz kalır. Kesirler Örneğin, 3 elmayı 2 arkadaşınıza paylaştırdığınızda her
Kesirler Kesirler Kesirlere neden ihtiyaç duyulur? Kesirler Doğal sayılar günlük yaşantımızda bazı problemlerin çözümünde yetersiz kalır. Kesirler Örneğin, 3 elmayı 2 arkadaşınıza paylaştırdığınızda her
1. ÜNİTE: MANTIK. Bölüm 1.1. Önermeler ve Bileşik Önermeler
 . ÜNİTE: MANTIK . ÜNİTE: MANTIK... Önerme Tanım (Önerme) BÖLÜM.. - Doğru ya da yanlış kesin bir hüküm bildiren ifadelere önerme adı veriler. Örneğin Bir hafta 7 gündür. (Doğru) Eskişehir Türkiye'nin başkentidir.
. ÜNİTE: MANTIK . ÜNİTE: MANTIK... Önerme Tanım (Önerme) BÖLÜM.. - Doğru ya da yanlış kesin bir hüküm bildiren ifadelere önerme adı veriler. Örneğin Bir hafta 7 gündür. (Doğru) Eskişehir Türkiye'nin başkentidir.
TAM SAYILARLA TOPLAMA İŞLEMİ
 . Sınıf Matematik AD SOYAD C E V A P L A R I M NUMARAM A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D TAM SAYILARLA TOPLAMA İŞLEMİ.
. Sınıf Matematik AD SOYAD C E V A P L A R I M NUMARAM A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D A B C D TAM SAYILARLA TOPLAMA İŞLEMİ.
Matematik Ders Föyü. Uygulayalım. Terim. Önerme. Doğruluk Değeri. Ortaöğretim Alanı MF - 01 NOT NOT. 1. Aşağıdaki tabloyu tanımlı veya tanımsız
 Ortaöğretim Alanı MF - 01 Matematik Ders Föyü Terim Bir sözcüğün bilim, spor, sanat, meslek vb. içerisinde kazandığı özel anlama terim denir. NOT Küp Matematik Ova Coğrafya Asit Kimya Mercek Fizik Sol
Ortaöğretim Alanı MF - 01 Matematik Ders Föyü Terim Bir sözcüğün bilim, spor, sanat, meslek vb. içerisinde kazandığı özel anlama terim denir. NOT Küp Matematik Ova Coğrafya Asit Kimya Mercek Fizik Sol
Rakam : Sayıları yazmaya yarayan sembollere rakam denir.
 A. SAYILAR Rakam : Sayıları yazmaya yarayan sembollere rakam denir. Sayı : Rakamların çokluk belirten ifadesine sayı denir.abc sayısı a, b, c rakamlarından oluşmuştur.! Her rakam bir sayıdır. Fakat bazı
A. SAYILAR Rakam : Sayıları yazmaya yarayan sembollere rakam denir. Sayı : Rakamların çokluk belirten ifadesine sayı denir.abc sayısı a, b, c rakamlarından oluşmuştur.! Her rakam bir sayıdır. Fakat bazı
Salim. Yüce LİNEER CEBİR
 Prof. Dr. Salim Yüce LİNEER CEBİR Prof. Dr. Salim Yüce LİNEER CEBİR ISBN 978-605-318-030-2 Kitapta yer alan bölümlerin tüm sorumluluğu yazarına aittir. 2015, Pegem Akademi Bu kitabın basım, yayın ve satış
Prof. Dr. Salim Yüce LİNEER CEBİR Prof. Dr. Salim Yüce LİNEER CEBİR ISBN 978-605-318-030-2 Kitapta yer alan bölümlerin tüm sorumluluğu yazarına aittir. 2015, Pegem Akademi Bu kitabın basım, yayın ve satış
İNJEKTİF MODÜLLERE. Ali Pancar Burcu Nişancı Türkmen
 İNJEKTİF MODÜLLERE GİRİŞ Ali Pancar Burcu Nişancı Türkmen Ali PANCAR Burcu NİŞANCI TÜRKMEN İNJEKTİF MODÜLLERE GİRİŞ ISBN 978-605-364-896-3 Kitap içeriğinin tüm sorumluluğu yazarlarına aittir. 2014, Pegem
İNJEKTİF MODÜLLERE GİRİŞ Ali Pancar Burcu Nişancı Türkmen Ali PANCAR Burcu NİŞANCI TÜRKMEN İNJEKTİF MODÜLLERE GİRİŞ ISBN 978-605-364-896-3 Kitap içeriğinin tüm sorumluluğu yazarlarına aittir. 2014, Pegem
Atatürk Anadolu. Bölme, Bölünebilme, Asal Sayılar, Obeb, Okek, Rasyonel Sayılar, Basit Eşitsizlikler ve Mutlak Değer Üzerine Kısa Çalışmalar
 Atatürk Anadolu Lisesi M A T E M A T İ K Bölme, Bölünebilme, Asal Sayılar, Obeb, Okek, Rasyonel Sayılar, Basit Eşitsizlikler ve Mutlak Değer Üzerine Kısa Çalışmalar KONYA \ SELÇUKLU 07 Bölme, Bölünebilme,
Atatürk Anadolu Lisesi M A T E M A T İ K Bölme, Bölünebilme, Asal Sayılar, Obeb, Okek, Rasyonel Sayılar, Basit Eşitsizlikler ve Mutlak Değer Üzerine Kısa Çalışmalar KONYA \ SELÇUKLU 07 Bölme, Bölünebilme,
için Örnek 7.1. simetri grubunu göz önüne alalım. Şu halde dür. Şimdi kalan sınıflarını göz önüne alalım. Eğer ve olarak alırsak işlemini kullanarak
 7. Bölüm Grupları olmak üzere grubunu nasıl inşa ettiğimizi hatırlayalım. grubunun alt grubu grubu tüm olacak şekilde tüm sınıflardan oluşmuştur. Sınıfların toplamını ile, yani ile tanımlamıştık. Şimdi
7. Bölüm Grupları olmak üzere grubunu nasıl inşa ettiğimizi hatırlayalım. grubunun alt grubu grubu tüm olacak şekilde tüm sınıflardan oluşmuştur. Sınıfların toplamını ile, yani ile tanımlamıştık. Şimdi
SÜREKLİLİK. 9.1 Süreklilik ve Süreksizlik Kavramları
 SÜREKLİLİK Bu bölümde süreklilik kavramı, süreksizlik, sürekli fonksiyonların özellikleri ile buna ilişkin teoremler örnekler ve grafiklerle açıklanmaktadır. 9.1 Süreklilik ve Süreksizlik Kavramları Tanım
SÜREKLİLİK Bu bölümde süreklilik kavramı, süreksizlik, sürekli fonksiyonların özellikleri ile buna ilişkin teoremler örnekler ve grafiklerle açıklanmaktadır. 9.1 Süreklilik ve Süreksizlik Kavramları Tanım
Sayılar Kuramına Giriş Özet
 Eğer bir b noktası bir a noktasının sağındaysa, o zaman a, b den küçük ve b, a dan büyük olarak sayılır, ve Sayılar Kuramına Giriş Özet David Pierce a < b, b > a yazılır. Tanıma göre a a, a < b a b, a
Eğer bir b noktası bir a noktasının sağındaysa, o zaman a, b den küçük ve b, a dan büyük olarak sayılır, ve Sayılar Kuramına Giriş Özet David Pierce a < b, b > a yazılır. Tanıma göre a a, a < b a b, a
YILLAR 2002 2003 2004 2005 2006 2007 2008 2009 2010 2011 ÖSS-YGS
 YILLAR 6 7 8 ÖSS-YGS - - / /LYS ONDALIK SAYILAR Paydası ve un pozitif kuvveti şeklinde olan veya u şekle dönüştürüleilen kesirlere ondalık kesir(ondalık sayı) denir 7,,,,,7 6 (,6)gii 8 8 NOT: ondalık sayıların
YILLAR 6 7 8 ÖSS-YGS - - / /LYS ONDALIK SAYILAR Paydası ve un pozitif kuvveti şeklinde olan veya u şekle dönüştürüleilen kesirlere ondalık kesir(ondalık sayı) denir 7,,,,,7 6 (,6)gii 8 8 NOT: ondalık sayıların
ÜSLÜ SAYILAR. AMAÇ 1: 6 ve 7. Sınıflarda görmüş olduğumuz üslü ifadelerdeki temel kavramları hatırlama
 AMAÇ 1: 6 ve 7. Sınıflarda görmüş olduğumuz üslü ifadelerdeki temel kavramları hatırlama KURAL: Bir sayının belli bir sayıda yan yana çarpımının kolay yoldan gösterimine üslü sayılar denir. Örneğin 5 sayısının
AMAÇ 1: 6 ve 7. Sınıflarda görmüş olduğumuz üslü ifadelerdeki temel kavramları hatırlama KURAL: Bir sayının belli bir sayıda yan yana çarpımının kolay yoldan gösterimine üslü sayılar denir. Örneğin 5 sayısının
SORU BANKASI GEOMETRİ KPSS KPSS. Genel Yetenek Genel Kültür. Sayısal ve Mantıksal Akıl Yürütme. Eğitimde. Lise ve Ön Lisans Adayları İçin MATEMATİK
 KPSS Genel Yetenek Genel Kültür Lise ve Ön Lisans Adayları İçin MATEMATİK Sayısal ve Mantıksal Akıl Yürütme KPSS 2016 Pegem Akademi Sınav Komisyonu; 2014 KPSS ye Pegem Yayınları ile hazırlanan adayların,
KPSS Genel Yetenek Genel Kültür Lise ve Ön Lisans Adayları İçin MATEMATİK Sayısal ve Mantıksal Akıl Yürütme KPSS 2016 Pegem Akademi Sınav Komisyonu; 2014 KPSS ye Pegem Yayınları ile hazırlanan adayların,
Çözüm: Z 3 = 27 = 27CiS( +2k ) Z k =3CiS ( ) 3 3 k = 0 için z 0 = 2 k=1 için z 1 = 3
 p ve q iki önerme olsun p q q p dir. p: = 3 ve q: y< 8 alınırsa I ve III ün denk olduğu görülür. Yanıt B Z 3 = 7 = 7CiS( +k ) k Z k =3CiS ( ) 3 3 k = 0 için z 0 = k=1 için z 1 = 3 k = için z = Yanıt A
p ve q iki önerme olsun p q q p dir. p: = 3 ve q: y< 8 alınırsa I ve III ün denk olduğu görülür. Yanıt B Z 3 = 7 = 7CiS( +k ) k Z k =3CiS ( ) 3 3 k = 0 için z 0 = k=1 için z 1 = 3 k = için z = Yanıt A
11.Konu Tam sayılarda bölünebilme, modüler aritmetik, Diofant denklemler
 11.Konu Tam sayılarda bölünebilme, modüler aritmetik, Diofant denklemler 1. Asal sayılar 2. Bir tam sayının bölenleri 3. Modüler aritmetik 4. Bölünebilme kuralları 5. Lineer modüler aritmetik 6. Euler
11.Konu Tam sayılarda bölünebilme, modüler aritmetik, Diofant denklemler 1. Asal sayılar 2. Bir tam sayının bölenleri 3. Modüler aritmetik 4. Bölünebilme kuralları 5. Lineer modüler aritmetik 6. Euler
KÜMELER. Küme nesneler topluluğudur. Bu bölümde kümelerle kurulan matematiksel yapıyı tanıtacağız.
 KÜMELER Küme nesneler topluluğudur. u bölümde kümelerle kurulan matematiksel yapıyı tanıtacağız. Küme kavramı matematiğe girmeden önce matematik denilince akla sayılar ve şekiller gelirdi. Kümeler kuramının
KÜMELER Küme nesneler topluluğudur. u bölümde kümelerle kurulan matematiksel yapıyı tanıtacağız. Küme kavramı matematiğe girmeden önce matematik denilince akla sayılar ve şekiller gelirdi. Kümeler kuramının
T.C. ÇANAKKALE ONSEKİZ MART ÜNİVERSİTESİ
 T.C. ÇANAKKALE ONSEKİZ MART ÜNİVERSİTESİ DERS: CEBİRDEN SEÇME KONULAR KONU: KARDİNAL SAYILAR ÖĞRETİM GÖREVLİLERİ: PROF.DR. NEŞET AYDIN AR.GÖR. DİDEM YEŞİL HAZIRLAYANLAR: DİRENCAN DAĞDEVİREN ELFİYE ESEN
T.C. ÇANAKKALE ONSEKİZ MART ÜNİVERSİTESİ DERS: CEBİRDEN SEÇME KONULAR KONU: KARDİNAL SAYILAR ÖĞRETİM GÖREVLİLERİ: PROF.DR. NEŞET AYDIN AR.GÖR. DİDEM YEŞİL HAZIRLAYANLAR: DİRENCAN DAĞDEVİREN ELFİYE ESEN
8.SINIF MATEMATİK DERSİ PROJE ÖDEVİ
 PROJE ÖDEVİ KONUSU:cisimler/Sizden düzgün geometrik cisimlerin(prizmalar,piramitler, küre ) kapalı maketlerinin hazırlanması istenmektedir. 2)Düzgün prizma ve pramitlerin özelliklerini öğreniniz. 3)Açık
PROJE ÖDEVİ KONUSU:cisimler/Sizden düzgün geometrik cisimlerin(prizmalar,piramitler, küre ) kapalı maketlerinin hazırlanması istenmektedir. 2)Düzgün prizma ve pramitlerin özelliklerini öğreniniz. 3)Açık
Ders 8: Konikler - Doğrularla kesişim
 Ders 8: Konikler - Doğrularla kesişim Geçen ders RP 2 de tekil olmayan her koniğin bir dönüşümün ardından tek bir koniğe dönüştüğü sonucuna vardık; o da {[x : y : z x 2 + y 2 z 2 = 0]} idi. Bu derste bu
Ders 8: Konikler - Doğrularla kesişim Geçen ders RP 2 de tekil olmayan her koniğin bir dönüşümün ardından tek bir koniğe dönüştüğü sonucuna vardık; o da {[x : y : z x 2 + y 2 z 2 = 0]} idi. Bu derste bu
