Bu malzemelere atıfta bulunmak veya kullanım şartlarını öğrenmek için sitesini ziyaret ediniz
|
|
|
- Ekin Poçan
- 8 yıl önce
- İzleme sayısı:
Transkript
1 MIT OpnoursWar Thrmodnamk v Kntk Bahar 8 Bu malzmlr atıfta bulunmak vya kullanım şartlarını öğrnmk çn stsn zyart dnz MODEL SİSTEMLER Molkülr gçş, dönm v rşm çn olan QM nrj svylr l başlamak surtyl bu srbst drclr çn v Q tüm trmodnamk çn çözüm lablr.eld dln sonuçlar molkülr statstğn tmln tşkl dr. Burada klask modl çn QM rşmlrn uyan br çözüm yapacağız v ld ttğmz sonuçları ötlnm v dönm çn olanlarla(türtlmş olanlar dğl vrlnlr) karşılaştıracağız Çft-örgülü polmr modl Br örgüd olan monomr dğr örgüdk ln tklşr. Hr monomr çft ççn olan tklşm nrjs - Bu örgülr br ucundan koparak uç molküllrn tklşmn koparır.daha sonra br sonrakn v daha sonra br sonrak uca da aynısını yapar. Hr koparılmış tklşm, nrjy kadar artırır.en düşük üç nrj svys dğr nrj svylr aşağıda göstrlmştr
2 Djnr olmayan v brbrndn nrjs l ayrılmış olan djnr olmayan şt aralıklı svylr : =n (n=br tamsayı) Çok uzun br polmr çn çok sayıda svy vardır. çnd bulunan hallr çn toplamı sonsuza kadar taşıyablrz çünkü n yüksk nrjlr zatn kt dn çok daha büyüktür (yan toplamdak lgl trmlr hmal dlblr) n n n n... x x x burada x x son drc bast kapalı br şkl alır v hr şy bunu takp dr
3 Q S V kt kt lnq d dt T v V T,V dln dt T ktln kln kt ktln ' gör drclnd rlrs, kt kt kt kln k ktln dğrlr yüksk v düşük sıcaklık sınırlarında özllkl önmldr. Hr ksd gör drclndrlbldğndn molkül başına olan dğrlr bulunablr. Düşük sıcaklık sınırında = v V = dır. Daha öncdn gördüğümüz gb düşük sıcaklık dğrlrnd tüm molküllr tml hald olup sıcaklıktak ufak br dğşm onların konumlarını dğştrmz. Dolayısıyla sstmn nrjs artmaz. / Yüksk T sıınır: lm T /kt kt,lm T V k kt nrj aralığını br kr aştımı T d olan k br artış daha yüksk nrj svylrnn doldurulmasına sbp olur ancak T l olan nrj artışı daha fazla olmaz: T olduğundan yüksk sıcaklık sınırında V T dn bağımsız olur Entrop v olasılık dağılımları Düşük sıcaklık sınırında sadc tml svy doldurulmuş olduğundan S lm T S kln kln /kt kln /kt kln /kt k ln /kt /kt /kt
4 ncak yüksk sıcaklık sınırlarında v Q çn lm T lm T Q lm T kt, lm T Q kt molkülün kaç tan hal trmal olarak grm hakkı olduğunu göstrn br ölçüttür kt çn bu dğr kısaca kt / şklnddr Eğr kt= s molküllr trmal olarak yaklaşık svyy grblrlr Boltzman dağılımı P hr hal çn olan olasılığı vrr En olası nrj svys sıfırdır(djnr olmayan svylr çn) Çok sayıda molkülr svylr doldurulablr Ortalama molkülr nrj <> >> Sstm nrjs =<> >> Enrj svylr tk başlarına büyük farklılıklar göstrblr ancak sstm nrjs dğl Pk nasıl? Q sstmn hallr, E /kt E Sstmn nrjlr,e E /kt yrıca P E E P E E E E E E Q olduğunu hatırlayalım
5 Makroskopk sstm nrjsnn ölçülms dama bu sstm nrjs çn P(E) sonucunu vrmktdr! Sstm nrjs E arttıkça sstmn djnrlğ (E ) kskn br artış göstrr.örnğn ()=; ( )=; ( )=(-)/ / şklnddr Buda daha yüksk nrjl sstmlrn olasılığını artırıcı rol oynar. Sstmn nrjs arttıkça Boltzman faktörü küçülür Bu da düşük nrjl sstmlrn olasılığını artırır Bu ks arasındak dng br ortalamadır. Olasılık kskn br tp vrr! Sstmn nrj n kadar np çıkar? Molkülr ortama nrj=< >, molkülr standart sapma < > Sstm nrjs = molkülr ortalama nrj = < > Sstm standart sapması= ε Bağıl sstm nrj dğşm= 4 ε Makroskopk br sstm çn np çıkmalar olağanüstü küçüktür! Sabt br T sıcaklığında sstm ntrops S k p ln p ncak ntropy S kln şklnd alablrz k burada (E) n olası svynn djnrlğdr. Bu br sakınca yoktur çünkü sstm nrjlrnn aralığı çok ufaktır Ttrşm bölünm fonksyonları v trmodnamk Burada kullanılan çft sarmallı polmr modl molkül v matryallrn kuantum mkanksl rşm şkllr çn aynı nrjlr vrr Klask rşm çn E mv kx KE PE burada m kütly, v hızı, k da kuvvt sabtn göstrmktdr( sadc bu bölümd bu dğr Boltzmann sabt olarak alınacaktır)
6 Doğal rsonans frkansı k m Ttrşm gnlğ v nrjs hr dğr alablr v sürkldr. QM rşm svylr djnr olmayıp şt aralıklarla ayrılmıştır.bu aralık h h k m şklnd olup h plank sabtn göstrmktdr Bu problm daha önc yaptık! Sıfır rşsl nrj olarak n düşük rşm svylr alırsak aynı sonuçları ld drz n n n n... x x x burada x x Q S V kt lnq kt d dt T T,V dln dt T ktln kln t kt ktln ' gör drclnd rlrs, kt kt k kt k ln ktln / Bu sonuçlar molküllrd v malzmlrdk rşmlr açısından önmldr
7 Ttrşm nrjs v ısı kapasts sonuçları v sınır dğrlr Düşük sıcaklık sınırında : = (= (/ )), V = Yüksk sıcaklık sınırında: lm T kt,lm T V k Molkülr rşm frkansları - cm -. K d kt cm - oda sıcaklığında molküllrn çoğu tml halddr (düşük T sınırı) Krstal örgü sının akustk rşm frkansı cm - br çok krstal yüksk T sınırındadır.msla tan molkül çn tan rşm şkl vardır dolayısıyla oda sıcaklığında V =k=nr. Bu molkülr ağırlıkların tayn dlmsnd kullanıldı Enstn 95 d nrjnn sürkl dğl kuantlı olduğunu dda dn dk kms ndn V olduğunu kms açıklayamıyordu çünkü bu durumda kt lk uyarılmış hal nrjsndn çok daha düşük olur(nrjnn sürkl olması durumunda mümkün dğldr) Molkülr ötlnm v dönm v nrjnn klask ş paylaşımı Buradak sonuçlar 5.6 statstk mkank kursunda çıkarılmıştı(tab szn notlarınızda da).br tan tml sonuç:hr srbstlk drcsnd( tan
8 ötlnm, vya tan dönm) yüksk sıcaklık sınırında nrj kt v ısı kapasts V k olur Buna gör ötlnm dönm rşt kt kt kt kt dogrusal vya kt hr rsmskl çn kt kt(dogrusal d ğğ Bu nrjnn kask ş paylaşımıdır. Hr srbstlk drcs klask olarak ½ mv şklnd vrln br kntk nrjy sahptr ( bu nrj dönn csmlrd ½ I olup açısal hızı, I da nrtlk momntn göstrmktdr) Ttrşmsl srbstlk drclrnd kntk nrj ½ mv v potansyl nrj d ½ kx şklnddr. Tüm bu karsl nrj trmlr ay şklnd yazılablr Bu srbstlk drclrndn hrhang br çn olan ortalama nrj /kt / /kt şklnd vrlr. ma ğr svylr brbrn çok yakınsa bu toplama trmlrn ntgrallr çvrblrz. Enrjy klask olarak nclrsk ay ay ay dy dy kt x x x x ay /kt Payı kısımlara ayırarak ntgraln alırsak x x x x x x x u,x dv,v x x x x / x
9 kt Burada ½ kt yüksk sıcaklık sınırında kntk v potansyl nrj srbsts başına olan nrjdr.
İSTATİSTİK TERMODİNAMİK
 MIT OpnCoursWar http://ocw.mt.du 5.60 Thrmodnamk v Kntk Bahar 2008 Bu malzmlr atıfta bulunmak vya kullanım şartlarını öğrnmk çn http://ocw.mt.du/trms stsn zyart dnz İSTATİSTİK TERMODİAMİK İstatstk mkanğn
MIT OpnCoursWar http://ocw.mt.du 5.60 Thrmodnamk v Kntk Bahar 2008 Bu malzmlr atıfta bulunmak vya kullanım şartlarını öğrnmk çn http://ocw.mt.du/trms stsn zyart dnz İSTATİSTİK TERMODİAMİK İstatstk mkanğn
İSTATİSTİK TERMODİNAMİK
 MI OpnCoursWar http://ocw.mt.du 5.60 hrmodnamk v Kntk ahar 008 u malzmlr atıfta bulunmak vya kullanım şartlarını öğrnmk çn http://ocw.mt.du/trms stsn zyart dnz İSİSİK ERMODİMİK Makroskopk trmodnamk sonuçların
MI OpnCoursWar http://ocw.mt.du 5.60 hrmodnamk v Kntk ahar 008 u malzmlr atıfta bulunmak vya kullanım şartlarını öğrnmk çn http://ocw.mt.du/trms stsn zyart dnz İSİSİK ERMODİMİK Makroskopk trmodnamk sonuçların
BURSA TEKNİK ÜNİVERSİTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAKİNE LABORATUVAR DERSİ. İçten Yanmalı Motorlarda Performans ve Enerji Dağılımı Deneyi
 BURSA TEKNİK ÜNİVERSİTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAKİNE LABORATUVAR DERSİ İçtn Yanmalı Motorlarda rformans v Enrj Dağılımı Dny Laboratuvar Tarh: Laboratuvarı Yöntn: Laboratuvar Yr: Laboratuvar Adı:
BURSA TEKNİK ÜNİVERSİTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAKİNE LABORATUVAR DERSİ İçtn Yanmalı Motorlarda rformans v Enrj Dağılımı Dny Laboratuvar Tarh: Laboratuvarı Yöntn: Laboratuvar Yr: Laboratuvar Adı:
Çok Parçalı Basınç Çubukları
 Çok Parçalı Basınç Çubukları Çok parçalı basınç çubukları gnl olarak k gruba arılır. Bunlar; a) Sürkl brlşk parçalardan oluşan çok parçalı basınç çubukları b) Parçaları arasında aralık bulunan çok parçalı
Çok Parçalı Basınç Çubukları Çok parçalı basınç çubukları gnl olarak k gruba arılır. Bunlar; a) Sürkl brlşk parçalardan oluşan çok parçalı basınç çubukları b) Parçaları arasında aralık bulunan çok parçalı
YAPI MEKANİĞİNDE ÖZEL PROBLEMLER ENERJİ YÖNTEMLERİ
 YIDIZ TEKNİK ÜNİVERSİTESİ İNŞAAT MÜHENDİSİĞİ BÖÜMÜ MEKANİK ANABİİM DAI YAPI MEKANİĞİNDE ÖZE PROBEMER ENERJİ YÖNTEMERİ PRO. DR. TRGT KOCATÜRK Hazırlayan : İnş. Müh. ŞERE DOĞŞCAN AKBAŞ -ENERJİ YÖNTEMERİ-.
YIDIZ TEKNİK ÜNİVERSİTESİ İNŞAAT MÜHENDİSİĞİ BÖÜMÜ MEKANİK ANABİİM DAI YAPI MEKANİĞİNDE ÖZE PROBEMER ENERJİ YÖNTEMERİ PRO. DR. TRGT KOCATÜRK Hazırlayan : İnş. Müh. ŞERE DOĞŞCAN AKBAŞ -ENERJİ YÖNTEMERİ-.
DOĞUŞ ÜNİVERSİTESİ MATEMATİK KLÜBÜ FEN LİSELERİ TAKIM YARIŞMASI 2007 SORULARI
 DOĞUŞ ÜNİVERSİTESİ MATEMATİK KLÜBÜ FEN LİSELERİ TAKIM YARIŞMASI 007 SORULARI Doğuş Ünivrsitsi Matmatik Kulübü tarafından düznlnn matmatik olimpiyatları, fn lislri takım yarışması sorularından bazıları
DOĞUŞ ÜNİVERSİTESİ MATEMATİK KLÜBÜ FEN LİSELERİ TAKIM YARIŞMASI 007 SORULARI Doğuş Ünivrsitsi Matmatik Kulübü tarafından düznlnn matmatik olimpiyatları, fn lislri takım yarışması sorularından bazıları
MAK TERMODİNAMİK (CRN: 22594, 22599, 22603, ) BAHAR YARIYILI ARA SINAV-1
 MK - ERMODİNMİK.0.00 CRN: 594, 599, 60, 608 ) 009-00 BHR YRIYILI R SIN- Soru -) Br pston-slndr düznğnd, başlangıçta 75 kpa basınçta doyuş sııbuhar karışıı, 5 kg su bulunaktadır. Suyun.09 kg lık bölüü sıı
MK - ERMODİNMİK.0.00 CRN: 594, 599, 60, 608 ) 009-00 BHR YRIYILI R SIN- Soru -) Br pston-slndr düznğnd, başlangıçta 75 kpa basınçta doyuş sııbuhar karışıı, 5 kg su bulunaktadır. Suyun.09 kg lık bölüü sıı
Termodinamiğin Yasaları:
 NTR0PĐ trop kavramı, makroskopk görüş açısıda (klask trmodamk), mkroskopk görüş açısıda (statstksl trmodamk) v formasyo görüş açısıda (formasyo tors) olmak üzr, üç şkld l alıablr. trop statstksl taımlaması
NTR0PĐ trop kavramı, makroskopk görüş açısıda (klask trmodamk), mkroskopk görüş açısıda (statstksl trmodamk) v formasyo görüş açısıda (formasyo tors) olmak üzr, üç şkld l alıablr. trop statstksl taımlaması
Sakarya Ticaret Borsası. Üye Memnuniyet ve Beklenti Anketi. Raporu
 Tcar sı My v Bkln k Ocak 2016, SAKARYA Tcar sı My v Bklnlrnn Eld Edlms İçn Yapılan k İlşkn r Tcar sı hm ISO 9001 Toplam Kal Yönm Ssm, hm d TOBB Oda/ Akrdasyon Ssmnn grğ olarak My v Bkln k çalışması grçklşrmşr.
Tcar sı My v Bkln k Ocak 2016, SAKARYA Tcar sı My v Bklnlrnn Eld Edlms İçn Yapılan k İlşkn r Tcar sı hm ISO 9001 Toplam Kal Yönm Ssm, hm d TOBB Oda/ Akrdasyon Ssmnn grğ olarak My v Bkln k çalışması grçklşrmşr.
GAZ TÜRBİNLİ BİR ISIL-GÜÇ (KOJENERASYON) ÇEVRİM SANTRALİNİN ENERJİ VE EKSERJİ ANALİZİ: ANKARA ŞARTLARINDA UYGULAMA
 Yıl: 213, Clt: 6, Sayı: 2, Sayfa:19-27 TÜBAV BİLİM DERGİSİ GAZ TÜRBİNLİ BİR ISIL-GÜÇ (KOJENERASYON) ÇEVRİM SANTRALİNİN ENERJİ VE EKSERJİ ANALİZİ: ANKARA ŞARTLARINDA UYGULAMA Murad A. RAHİM 1 *, Duygu GÜNDÜZ
Yıl: 213, Clt: 6, Sayı: 2, Sayfa:19-27 TÜBAV BİLİM DERGİSİ GAZ TÜRBİNLİ BİR ISIL-GÜÇ (KOJENERASYON) ÇEVRİM SANTRALİNİN ENERJİ VE EKSERJİ ANALİZİ: ANKARA ŞARTLARINDA UYGULAMA Murad A. RAHİM 1 *, Duygu GÜNDÜZ
Sosyoekonomi / 2006-1 / 060103. M. Emin İnal & Derviş Topuz & Okyay Uçan. Sosyo Ekonomi. Doğrusal Olasılık ve Logit Modelleri ile Parametre Tahmini
 Sosyokonom / 2006- / 06003. M. Emn İnal & Drvş Topuz & Okyay Uçan Sosyo Ekonom Ocak-Hazran 2006- Doğrusal Olasılık v Logt Modllr l Paramtr Tahmn M. Emn İnal Drvş Topuz Okyay Uçan nal@ngd.du.tr drvs_topuz@ngd.du.tr
Sosyokonom / 2006- / 06003. M. Emn İnal & Drvş Topuz & Okyay Uçan Sosyo Ekonom Ocak-Hazran 2006- Doğrusal Olasılık v Logt Modllr l Paramtr Tahmn M. Emn İnal Drvş Topuz Okyay Uçan nal@ngd.du.tr drvs_topuz@ngd.du.tr
DERS 9. Grafik Çizimi, Maksimum-Minimum Problemleri. 9.1. Grafik çiziminde izlenecek adımlar. y = f(x) in grafiğini çizmek için
 DERS 9 Grafik Çizimi, Maksimum-Minimum Problmlri 9.. Grafik çizimind izlnck adımlar. y f() in grafiğini çizmk için Adım. f() i analiz diniz. (f nin tanım kümsi, f() in tanımlı olduğu tüm rl sayıların oluşturduğu
DERS 9 Grafik Çizimi, Maksimum-Minimum Problmlri 9.. Grafik çizimind izlnck adımlar. y f() in grafiğini çizmk için Adım. f() i analiz diniz. (f nin tanım kümsi, f() in tanımlı olduğu tüm rl sayıların oluşturduğu
AYRIK VE SÜREKLİ ZAMANLI BİRİNCİ DERECEDEN SİGMA-DELTA MODÜLATÖRÜNÜN PRATİK OLARAK GERÇEKLEŞTİRİLMESİ
 AYRIK VE SÜREKLİ ZAMANLI BİRİNCİ DERECEDEN SİGMADELTA MODÜLATÖRÜNÜN PRATİK OLARAK GERÇEKLEŞTİRİLMESİ D. Hanba * v A. Uçar ** *Fırat Ünvrsts Elktronk Blgsaar Eğtm dhanba@frat.du.tr ** Fırat Ünvrsts Elktrk
AYRIK VE SÜREKLİ ZAMANLI BİRİNCİ DERECEDEN SİGMADELTA MODÜLATÖRÜNÜN PRATİK OLARAK GERÇEKLEŞTİRİLMESİ D. Hanba * v A. Uçar ** *Fırat Ünvrsts Elktronk Blgsaar Eğtm dhanba@frat.du.tr ** Fırat Ünvrsts Elktrk
DERS 9. Grafik Çizimi, Maksimum Minimum Problemleri
 DERS 9 Grafik Çizimi, Maksimum Minimum Problmlri Bundan öncki drst bir fonksiyonun grafiğini çizmk için izlnbilck yol v yapılabilck işlmlr l alındı. Bu drst, grafik çizim stratjisini yani grafik çizimind
DERS 9 Grafik Çizimi, Maksimum Minimum Problmlri Bundan öncki drst bir fonksiyonun grafiğini çizmk için izlnbilck yol v yapılabilck işlmlr l alındı. Bu drst, grafik çizim stratjisini yani grafik çizimind
Sakarya Ticaret Bozrsası. Üye Memnuniyet ve Beklenti Anketi. Raporu
 Tcar zsı My v Bkln k Mar 2015, SAKARYA Tcar sı 2014 Yılı My v Bklnlrnn Eld Edlms İçn Yapılan k İlşkn r Tcar sı hm ISO 9001 Toplam Kal Yönm Ssm, hm d TOBB Oda/ Akrdasyon Ssmnn grğ olarak gnş çaplı br My
Tcar zsı My v Bkln k Mar 2015, SAKARYA Tcar sı 2014 Yılı My v Bklnlrnn Eld Edlms İçn Yapılan k İlşkn r Tcar sı hm ISO 9001 Toplam Kal Yönm Ssm, hm d TOBB Oda/ Akrdasyon Ssmnn grğ olarak gnş çaplı br My
ĐKĐ BOYUTLU SINIR TABAKALAR ĐÇĐN ĐNTEGRAL YÖNTEMLERĐ
 ĐKĐ BOYTL SINI TABAKALA ĐÇĐN ĐNTGAL YÖNTMLĐ Kanat prol v bnzr csmlr traınak lamnr sınır tabakaların hsaplanmasına kullanılan sayısal tknklrn br grubu ntgral yöntmlr olarak blnr. Bu yöntmlr gnl olarak sınır
ĐKĐ BOYTL SINI TABAKALA ĐÇĐN ĐNTGAL YÖNTMLĐ Kanat prol v bnzr csmlr traınak lamnr sınır tabakaların hsaplanmasına kullanılan sayısal tknklrn br grubu ntgral yöntmlr olarak blnr. Bu yöntmlr gnl olarak sınır
Elastik Zemine Oturan Kalın Plaklar İçin Kayma Kilitlenmesiz Bir Sonlu Eleman Modeli *
 İMO Tn Drg, 534-5358, Yazı 346 Elast Zmn Oturan Kalın Plalar İçn Kama Kltlnmsz r Sonlu Elman Modl * Korhan ÖZGA* Aş T. DALOĞLU** ÖZ u çalışmada, alınlı doğrultusunda ama şl dğştrmlrn dat alan 4 düğüm notalı
İMO Tn Drg, 534-5358, Yazı 346 Elast Zmn Oturan Kalın Plalar İçn Kama Kltlnmsz r Sonlu Elman Modl * Korhan ÖZGA* Aş T. DALOĞLU** ÖZ u çalışmada, alınlı doğrultusunda ama şl dğştrmlrn dat alan 4 düğüm notalı
HAYVAN BARINAKLARINDA DOĞAL HAVALANDIRMA VERDİSİNİN BELİRLENMESİ İÇİN BİR BİLGİSAYAR PROGRAMI GELİŞTİRİLMESİ
 OMÜ Zr. Fak. Drgs, 005,0(1):30-36 J. f Fac. f Agrc., OMU, 005,0(1):30-36 HAYVAN BARINAKLARINDA DOĞAL HAVALANDIRMA VERDİSİNİN BELİRLENMESİ İÇİN BİR BİLGİSAYAR PROGRAMI GELİŞTİRİLMESİ Gürkan A. K. GÜRDİL
OMÜ Zr. Fak. Drgs, 005,0(1):30-36 J. f Fac. f Agrc., OMU, 005,0(1):30-36 HAYVAN BARINAKLARINDA DOĞAL HAVALANDIRMA VERDİSİNİN BELİRLENMESİ İÇİN BİR BİLGİSAYAR PROGRAMI GELİŞTİRİLMESİ Gürkan A. K. GÜRDİL
4. BİR BOYUTLU ZAMANA BAĞLI ISI İLETİMİ
 üm yayın hakları Prof. Dr. Büln Yşlaa ya ar. İznsz çoğalılamaz. 4. BİR BOYUU ZAMANA BAĞI ISI İEİMİ Zamana bağlı ısı gçş roblmlr gnllkl ssmn sınır koşulları dğşğnd oraya çıkar. Zamana bağlı ısı roblmlrn
üm yayın hakları Prof. Dr. Büln Yşlaa ya ar. İznsz çoğalılamaz. 4. BİR BOYUU ZAMANA BAĞI ISI İEİMİ Zamana bağlı ısı gçş roblmlr gnllkl ssmn sınır koşulları dğşğnd oraya çıkar. Zamana bağlı ısı roblmlrn
DAĞILIMLI GECİKMELİ BİR AV-AVCI SİSTEMİNDE HOPF ÇATALLANMA VE KARARLILIK ANALİZİ
 T.C BAHÇEŞEHİR ÜİVERSİTESİ DAĞILIMLI GECİKMELİ BİR AVAVCI SİSTEMİDE HOPF ÇATALLAMA VE KARARLILIK AALİZİ YÜKSEK LİSAS TEZİ EMİE DEĞİRMECİ İstanbul, 11 T.C BAHÇEŞEHİR ÜİVERSİTESİ Fn Blmlr Ensttüsü Uygulamalı
T.C BAHÇEŞEHİR ÜİVERSİTESİ DAĞILIMLI GECİKMELİ BİR AVAVCI SİSTEMİDE HOPF ÇATALLAMA VE KARARLILIK AALİZİ YÜKSEK LİSAS TEZİ EMİE DEĞİRMECİ İstanbul, 11 T.C BAHÇEŞEHİR ÜİVERSİTESİ Fn Blmlr Ensttüsü Uygulamalı
Bir Kompleks Sayının n inci Kökü.
 Prof.Dr.Hüsy ÇAKALLI Br Komplks Sayıı c Kökü. hrhag br sab doğal sayı olmak ür, br komplks sayıı c kökü, c kuvv bu sayıya ş ola komplks sayıdır. ( r(cos s olsu v (cos s dylm. Bu akdrd ( [ (cos s] dr v
Prof.Dr.Hüsy ÇAKALLI Br Komplks Sayıı c Kökü. hrhag br sab doğal sayı olmak ür, br komplks sayıı c kökü, c kuvv bu sayıya ş ola komplks sayıdır. ( r(cos s olsu v (cos s dylm. Bu akdrd ( [ (cos s] dr v
MONOSİMETRİK VE AÇIK KESİTLİ BİR EULER-BERNOULLI KİRİŞİNİN İKİ FARKLI METOTLA SERBEST TİTREŞİM ANALİZİ
 P A U K K A E Ü Nİ V E İ E İ Ü H E N Dİ İK F A K Ü E İ P A U K K A E U N I V E I Y E N G I N E E I N G F A C U Y Ü H E N Dİ İK Bİİ E İ D E Gİİ J O U N A O F E N G I N E E I N G C I E N C E YI Cİ AYI AYFA
P A U K K A E Ü Nİ V E İ E İ Ü H E N Dİ İK F A K Ü E İ P A U K K A E U N I V E I Y E N G I N E E I N G F A C U Y Ü H E N Dİ İK Bİİ E İ D E Gİİ J O U N A O F E N G I N E E I N G C I E N C E YI Cİ AYI AYFA
Sabit kur sisteminde ise faiz denge sistemi çalışamamaktadır. Çünkü kur sabittir. Yurt içi faiz oranının yurt dışı faize oranına eşit olmalıdır.
 B..A. Dövz Kuru Rjmlr Srbs Kur ssmnd hüküm yrl para brmnn dğr şu şkld dürülblr: gnşlc para polkaları aracılığı l pyasaya para sürrk faz oranlarının düşmsn, faz oranlarının düşms l sıcak para yrl paradan
B..A. Dövz Kuru Rjmlr Srbs Kur ssmnd hüküm yrl para brmnn dğr şu şkld dürülblr: gnşlc para polkaları aracılığı l pyasaya para sürrk faz oranlarının düşmsn, faz oranlarının düşms l sıcak para yrl paradan
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
 6 BÖÜM ATENATİF AKIM MODE SOU - DEKİ SOUAIN ÇÖÜMEİ (t) 30snπt s grlmn maksmum dğr, m 30 volt tkn dğr d, m 30 5 Akımın zamanla dğşm dnklmndn, (t) max sn~t (t) 0 sn00rt Maksmum akım, max 0 A CEAP D İltknn
6 BÖÜM ATENATİF AKIM MODE SOU - DEKİ SOUAIN ÇÖÜMEİ (t) 30snπt s grlmn maksmum dğr, m 30 volt tkn dğr d, m 30 5 Akımın zamanla dğşm dnklmndn, (t) max sn~t (t) 0 sn00rt Maksmum akım, max 0 A CEAP D İltknn
BÖLÜM 5 İKİ VEYA DAHA YÜKSEK BOYUTLU RASGELE DEĞİŞKENLER İki Boyutlu Rasgele Değişkenler
 BÖLÜM 5 İKİ VEYA DAHA YÜKSEK BOYUTLU RASGELE DEĞİŞKENLER 5.. İk Boyutlu Rasgele Değşkenler Br deney yapıldığında, aynı deneyle lgl brçok rasgele değşkenn aynı andak durumunu düşünmek gerekeblr. Böyle durumlarda
BÖLÜM 5 İKİ VEYA DAHA YÜKSEK BOYUTLU RASGELE DEĞİŞKENLER 5.. İk Boyutlu Rasgele Değşkenler Br deney yapıldığında, aynı deneyle lgl brçok rasgele değşkenn aynı andak durumunu düşünmek gerekeblr. Böyle durumlarda
MIT Açık Ders Malzemeleri http://ocw.mit.edu. 5.62 Fizikokimya II 2008 Bahar
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 5.62 Fizikokimya II 2008 Bahar Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak in http://ocw.mit.edu/terms ve http://tuba.acikders.org.tr
MIT Açık Ders Malzemeleri http://ocw.mit.edu 5.62 Fizikokimya II 2008 Bahar Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak in http://ocw.mit.edu/terms ve http://tuba.acikders.org.tr
İki veri setinin yapısının karşılaştırılması
 İk ver set yapısıı karşılaştırılması Dağılım: 6,6,6 Ortalama: 6 Medya: 6 Mod: 6 td. apma: 0 Dağılım: 0,6,1 Ortalama: 6 Medya: 6 Mod: çoklu mod td: apma: 6 Amaç: Görüe Ötese Bakablmek Verler değşkelk durumuu
İk ver set yapısıı karşılaştırılması Dağılım: 6,6,6 Ortalama: 6 Medya: 6 Mod: 6 td. apma: 0 Dağılım: 0,6,1 Ortalama: 6 Medya: 6 Mod: çoklu mod td: apma: 6 Amaç: Görüe Ötese Bakablmek Verler değşkelk durumuu
Üstel Dağılım SÜREKLİ ŞANS DEĞİŞKENLERİNİN OLASILIK YOĞUNLUK FONKSİYONLARI
 ..3 SÜREKLİ ŞNS DEĞİŞKENLERİNİN OLSILIK YOĞUNLUK FONKSİYONLRI Üstl Dağılım Sürkli Üniform Dağılım Normal Dağılım Üstl Dağılım Mydana gln iki olay arasındaki gçn sür vya ir aşka ifadyl ilgilniln olayın
..3 SÜREKLİ ŞNS DEĞİŞKENLERİNİN OLSILIK YOĞUNLUK FONKSİYONLRI Üstl Dağılım Sürkli Üniform Dağılım Normal Dağılım Üstl Dağılım Mydana gln iki olay arasındaki gçn sür vya ir aşka ifadyl ilgilniln olayın
ASTRONOTİK DERS NOTLARI Verim =
 ASTRONOTİK DERS NOTLARI 04 TANIMLAR Katı v sıvı yakıtların n büyük sorunu VERİMLİLİK tr. En y otorlarda bl nrjnn ancak %40 dan yararlanılır. Bu açıdan bakıldığında kyasal yakıtlı otorlar pyc vrszdrlr.
ASTRONOTİK DERS NOTLARI 04 TANIMLAR Katı v sıvı yakıtların n büyük sorunu VERİMLİLİK tr. En y otorlarda bl nrjnn ancak %40 dan yararlanılır. Bu açıdan bakıldığında kyasal yakıtlı otorlar pyc vrszdrlr.
OLASILIK ve ÝSTATÝSTÝK ( Genel Tekrar Testi-1) KPSS MATEMATÝK. Bir anahtarlıktaki 5 anahtardan 2 si kapıyı açmak - tadır.
 OLASILIK v ÝSTATÝSTÝK ( Gnl Tkrar Tsti-1) 1. Bir anahtarlıktaki 5 anahtardan si kapıyı açmak - tadır. Açmayan anahtar bir daha dnnmdiğin gör, bu kapının n çok üçüncü dnmd açılma olasılığı kaçtır? 5 6 7
OLASILIK v ÝSTATÝSTÝK ( Gnl Tkrar Tsti-1) 1. Bir anahtarlıktaki 5 anahtardan si kapıyı açmak - tadır. Açmayan anahtar bir daha dnnmdiğin gör, bu kapının n çok üçüncü dnmd açılma olasılığı kaçtır? 5 6 7
MIT Açık Ders Malzemeleri http://ocw.mit.edu. 5.62 Fizikokimya II 2008 Bahar
 MIT Açık Ders Malzemeleri http://ocw.mit.edu 5.62 Fizikokimya II 2008 Bahar Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için http://ocw.mit.edu/terms ve http://tuba.acikders.org.tr
MIT Açık Ders Malzemeleri http://ocw.mit.edu 5.62 Fizikokimya II 2008 Bahar Bu materyallerden alıntı yapmak veya Kullanım Şartları hakkında bilgi almak için http://ocw.mit.edu/terms ve http://tuba.acikders.org.tr
İLETKEN ve YARIİLETKENLERDE HALL OLAYI
 İLETKEN v YARIİLETKENLERDE HALL OLAYI 1. HALL OLAYI Mtallrdk ltknlk, srst haldk lktronların uygulanan lktrk alan doğrultusundak harktlr ntcsnd ld dlr. Yarıltknlrd s, lktronların harcnd oşluklarda lktrksl
İLETKEN v YARIİLETKENLERDE HALL OLAYI 1. HALL OLAYI Mtallrdk ltknlk, srst haldk lktronların uygulanan lktrk alan doğrultusundak harktlr ntcsnd ld dlr. Yarıltknlrd s, lktronların harcnd oşluklarda lktrksl
ÜSTEL DAĞILIM. üstel dağılımın parametresidir. Birikimli üstel dağılım fonksiyonu da, olarak bulunur. olduğu açık olarak görülmektedir.
 ÜSTL DAĞILIM Tanım : X > olma üzr sürli bir rasgl dğişn olsun. ğr a > için X rassal dğişni aşağıdai gibi bir dağılıma sahip olursa X rasgl dğişnin üsl dağılmış rassal dğişn v onsiyonuna da üsl dağılım
ÜSTL DAĞILIM Tanım : X > olma üzr sürli bir rasgl dğişn olsun. ğr a > için X rassal dğişni aşağıdai gibi bir dağılıma sahip olursa X rasgl dğişnin üsl dağılmış rassal dğişn v onsiyonuna da üsl dağılım
Makine Öğrenmesi 4. hafta
 ain Öğrnmsi 4. hafta Olasılı v Koşullu Olasılı ays Tormi Naïv ays Sınıflayıcı Olasılı Olasılı ifadsinin birço ullanım şli vardır. Rasgl bir A olayının hrhangi bir olaydan bağımsız olara grçlşm ihtimalini
ain Öğrnmsi 4. hafta Olasılı v Koşullu Olasılı ays Tormi Naïv ays Sınıflayıcı Olasılı Olasılı ifadsinin birço ullanım şli vardır. Rasgl bir A olayının hrhangi bir olaydan bağımsız olara grçlşm ihtimalini
NADİR TOPRAK ELEMENTLERİ OKSİTLERİNİN ELEKTRONİK VE OPTİK ÖZELLİKLERİNİN İNCELENMESİ: AB İNİTİO YÖNTEMİ *
 Ç.Ü. Fn v Mühndslk Blmlr Drgs Yıl:016 Clt:34-6 ADİR TOPRAK ELEMETLERİ OKSİTLERİİ ELEKTROİK VE OPTİK ÖZELLİKLERİİ İCELEMESİ: AB İİTİO YÖTEMİ * Invstıgatıonof ElctronıcandOptıcalProprtıs of RarEarthsOxıds:
Ç.Ü. Fn v Mühndslk Blmlr Drgs Yıl:016 Clt:34-6 ADİR TOPRAK ELEMETLERİ OKSİTLERİİ ELEKTROİK VE OPTİK ÖZELLİKLERİİ İCELEMESİ: AB İİTİO YÖTEMİ * Invstıgatıonof ElctronıcandOptıcalProprtıs of RarEarthsOxıds:
İYONİK KANAL AKTİVASYON VE İNAKTİVASYON KAPILARININ DİNAMİK DAVRANIŞI İÇİN ALTERNATİF DENKLEMLER
 PAMUKKALE ÜNİ VERSİ TESİ MÜHENDİ SLİ K FAKÜLTESİ PAMUKKALE UNIVERSITY ENGINEERING COLLEGE MÜHENDİ SLİ K BİLİMLERİ DERGİ S İ JOURNAL OF ENGINEERING SCIENCES YIL CİLT SAYI SAYFA : 003 : 9 : 3 : 349-356 İYONİK
PAMUKKALE ÜNİ VERSİ TESİ MÜHENDİ SLİ K FAKÜLTESİ PAMUKKALE UNIVERSITY ENGINEERING COLLEGE MÜHENDİ SLİ K BİLİMLERİ DERGİ S İ JOURNAL OF ENGINEERING SCIENCES YIL CİLT SAYI SAYFA : 003 : 9 : 3 : 349-356 İYONİK
1. GAZLARIN DAVRANI I
 . GZLRIN DRNI I İdeal Gazlar ç: lm 0 RT İdeal gazlar ç: RT Hacm() basıçla() değşk sıcaklıklarda değşm ekl.. de gösterlmştr. T >T 8 T T T 3 asıç T 4 T T 5 T 7 T 8 Molar Hacm ekl.. Gerçek br gazı değşk sıcaklıklardak
. GZLRIN DRNI I İdeal Gazlar ç: lm 0 RT İdeal gazlar ç: RT Hacm() basıçla() değşk sıcaklıklarda değşm ekl.. de gösterlmştr. T >T 8 T T T 3 asıç T 4 T T 5 T 7 T 8 Molar Hacm ekl.. Gerçek br gazı değşk sıcaklıklardak
USB AJANDA - USB DIARY
 202 USB AJANDA - USB DIARY 70635 12x18 USB TARİHSİZ AJANDA 12x18 USB NOTEBOOK DIARY Ambalaj / Package : Özel Kutu / Gift Box Koli Ebatı / Ctn Size : 53x40,5x21,5 cm Koli Ağırlığı / Ctn Weight : 14 kg 80
202 USB AJANDA - USB DIARY 70635 12x18 USB TARİHSİZ AJANDA 12x18 USB NOTEBOOK DIARY Ambalaj / Package : Özel Kutu / Gift Box Koli Ebatı / Ctn Size : 53x40,5x21,5 cm Koli Ağırlığı / Ctn Weight : 14 kg 80
ELM201 ELEKTRONİK-I DERSİ LABORATUAR FÖYÜ
 T SKY ÜNİESİTESİ TEKNOOJİ FKÜTESİ EEKTİKEEKTONİK MÜHENDİSİĞİ EM01 EEKTONİKI DESİ BOTU FÖYÜ DENEYİ YPTIN: DENEYİN DI: DENEY NO: DENEYİ YPNIN DI v SOYDI: SINIFI: OKU NO: DENEY GUP NO: DENEY TİHİ PO TESİM
T SKY ÜNİESİTESİ TEKNOOJİ FKÜTESİ EEKTİKEEKTONİK MÜHENDİSİĞİ EM01 EEKTONİKI DESİ BOTU FÖYÜ DENEYİ YPTIN: DENEYİN DI: DENEY NO: DENEYİ YPNIN DI v SOYDI: SINIFI: OKU NO: DENEY GUP NO: DENEY TİHİ PO TESİM
KOLON EKSENLERİNİN SEÇİMİNİN KESİT TESİRLERİNE ETKİSİ
 PAMUKKAE ÜNİ VEİ TEİ MÜHENDİ İ K FAKÜTEİ PAMUKKAE UNIVEITY ENGINEEING COEGE MÜHENDİ İ K B İ İ MEİ DEGİ İ JOUNA OF ENGINEEING CIENCE YI CİT AYI AYFA : 6 : 1 : 1 : 65-7 KOON EKENEİNİN EÇİMİNİN KEİT TEİEİNE
PAMUKKAE ÜNİ VEİ TEİ MÜHENDİ İ K FAKÜTEİ PAMUKKAE UNIVEITY ENGINEEING COEGE MÜHENDİ İ K B İ İ MEİ DEGİ İ JOUNA OF ENGINEEING CIENCE YI CİT AYI AYFA : 6 : 1 : 1 : 65-7 KOON EKENEİNİN EÇİMİNİN KEİT TEİEİNE
DÜZCE ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ EET305 OTOMATİK KONTROL I Dr. Uğur HASIRCI
 DÜZCE ÜNİVERSİTESİ TENOLOJİ FAÜLTESİ ELETRİ-ELETRONİ MÜHENDİSLİĞİ BÖLÜMÜ EET305 OTOMATİ ONTROL I ALICI DURUM HATASI ontrol sistmlrinin tasarımında üç tml kritr göz önünd bulundurulur: Gçici Durum Cvabı
DÜZCE ÜNİVERSİTESİ TENOLOJİ FAÜLTESİ ELETRİ-ELETRONİ MÜHENDİSLİĞİ BÖLÜMÜ EET305 OTOMATİ ONTROL I ALICI DURUM HATASI ontrol sistmlrinin tasarımında üç tml kritr göz önünd bulundurulur: Gçici Durum Cvabı
Mühendisler İçin DİFERANSİYEL DENKLEMLER
 Mühndislr İçin DİFERANSİYEL DENKLEMLER Doç. Dr. Tahsin Engin Prof. Dr. Yunus A. Çngl Sakara Ünivrsitsi Makina Mühndisliği Bölümü Elül 8 SAKARYA - - Mühndislr İçin Difransil Dnklmlr İÇİNDEKİLER BÖLÜM BİRİNCİ
Mühndislr İçin DİFERANSİYEL DENKLEMLER Doç. Dr. Tahsin Engin Prof. Dr. Yunus A. Çngl Sakara Ünivrsitsi Makina Mühndisliği Bölümü Elül 8 SAKARYA - - Mühndislr İçin Difransil Dnklmlr İÇİNDEKİLER BÖLÜM BİRİNCİ
Ki- Kare Testi ANADOLU ÜNİVERSİTESİ. ENM 317 MÜHENDİSLİK İSTATİSTİĞİ İYİ UYUM TESTİ Prof.Dr. Nihal ERGİNEL
 ANADOLU ÜNİVERSİTESİ ENM 317 MÜHENDİSLİK İSTATİSTİĞİ İYİ UYUM TESTİ Prof.Dr. Nihal ERGİNEL İYİ UYUM TESTİ Rassal değişkenin olasılık yoğunluk fonksiyonunun ve parametresinin bilinmediği, ancak belirli
ANADOLU ÜNİVERSİTESİ ENM 317 MÜHENDİSLİK İSTATİSTİĞİ İYİ UYUM TESTİ Prof.Dr. Nihal ERGİNEL İYİ UYUM TESTİ Rassal değişkenin olasılık yoğunluk fonksiyonunun ve parametresinin bilinmediği, ancak belirli
dir. Bir başka deyişle bir olayın olasılığı, uygun sonuçların sayısının örnek uzaydaki tüm sonuçların sayısına oranıdır.
 BÖLÜM 3 OLASILIK HESABI 3.. Br Olayın Olasılığı Tanım 3... Br olayın brbrnden ayrık ve ortaya çıkma şansı eşt n mümkün sonucundan m tanes br A olayına uygun se, A olayının P(A) le gösterlen olasılığı P(A)
BÖLÜM 3 OLASILIK HESABI 3.. Br Olayın Olasılığı Tanım 3... Br olayın brbrnden ayrık ve ortaya çıkma şansı eşt n mümkün sonucundan m tanes br A olayına uygun se, A olayının P(A) le gösterlen olasılığı P(A)
Araştırma Makalesi / Research Article. Kayma Mod ile Asenkron Motorun Algılayıcısız Hız Kontrolü
 BEÜ Fn Blml Dg BEU Jounal of Scnc (2), 92-6, 22 (2), 92-6, 22 Aaştıma Makal / Rach Atcl Kayma Mod l Ankon Motoun Algılayıcıız Hız Kontolü Kohan KAYŞL *, Hanf GÜLDEMİR 2 Btl En Ünvt Mühndlk-Mmalık Fakült
BEÜ Fn Blml Dg BEU Jounal of Scnc (2), 92-6, 22 (2), 92-6, 22 Aaştıma Makal / Rach Atcl Kayma Mod l Ankon Motoun Algılayıcıız Hız Kontolü Kohan KAYŞL *, Hanf GÜLDEMİR 2 Btl En Ünvt Mühndlk-Mmalık Fakült
Deney No: 2. Sıvı Seviye Kontrol Deneyi. SAKARYA ÜNİVERSİTESİ Dijital Kontrol Laboratuvar Deney Föyü Deneyin Amacı
 SRY ÜNİVERSİESİ Djtal ontrol Laboratuvar Deney Föyü Deney No: 2 Sıvı Sevye ontrol Deney 2.. Deneyn macı Bu deneyn amacı, doğrusal olmayan sıvı sevye sstemnn belrlenen br çalışma noktası cvarında doğrusallaştırılmış
SRY ÜNİVERSİESİ Djtal ontrol Laboratuvar Deney Föyü Deney No: 2 Sıvı Sevye ontrol Deney 2.. Deneyn macı Bu deneyn amacı, doğrusal olmayan sıvı sevye sstemnn belrlenen br çalışma noktası cvarında doğrusallaştırılmış
Ders 4: Rastgele Değişkenler ve Dağılımları
 Ders 4: Rastgele Değişkenler ve Dağılımları Rastgele değişken kavramı Kesikli ve sürekli rastgele değişkenler İki boyutlu rastgele değişkenler Beklenen değer Varyans Örnek uzaydaki her elemanı bir sayıyla
Ders 4: Rastgele Değişkenler ve Dağılımları Rastgele değişken kavramı Kesikli ve sürekli rastgele değişkenler İki boyutlu rastgele değişkenler Beklenen değer Varyans Örnek uzaydaki her elemanı bir sayıyla
1981 ÜYS Soruları. 1. Bir top kumaşın önce i, sonra da kalanın ü. satılıyor. Geriye 26 m kumaş kaldığına göre, kumaşın tümü kaç metredir?
 98 ÜYS Sorulrı. r top kumşın önce, sonr d klnın ü 5 stılıor. Gere 6 m kumş kldığın göre, kumşın tümü kç metredr? ) 7 ) 65 ) 6 ) 55 ) 5 4. r şekln, u brm uzunluğun göre ln ölçüsü, v brm uzunluğun göre ln
98 ÜYS Sorulrı. r top kumşın önce, sonr d klnın ü 5 stılıor. Gere 6 m kumş kldığın göre, kumşın tümü kç metredr? ) 7 ) 65 ) 6 ) 55 ) 5 4. r şekln, u brm uzunluğun göre ln ölçüsü, v brm uzunluğun göre ln
İSTATİSTİK ÖRNEK SORULARI
 1. Aşağıda gruplandırılmış seri verilmiştir. (n) 0-10 den az 5 10-20 den az 6 20-30 den az 9 30-40 den az 11 40-50 den az 4 50-60 den az 3 TOPLAM 38 İSTATİSTİK ÖRNEK SORULARI a) Mod değerini bulunuz? (15
1. Aşağıda gruplandırılmış seri verilmiştir. (n) 0-10 den az 5 10-20 den az 6 20-30 den az 9 30-40 den az 11 40-50 den az 4 50-60 den az 3 TOPLAM 38 İSTATİSTİK ÖRNEK SORULARI a) Mod değerini bulunuz? (15
Fizik 101: Ders 12 Ajanda. Problemler İş & Enerji Potansiyel Enerji, Kuvvet, Denge Güç
 Fizik 101: Ders 1 Ajanda Probleler İş & Enerji Potansiyel Enerji, Kuvvet, Denge Güç Proble: Yaylı Sapan Yay sabiti k olan iki yaydan bir sapan yapılıştır. Her iki yayın başlangıç uzunluğu x 0. Kütlesi
Fizik 101: Ders 1 Ajanda Probleler İş & Enerji Potansiyel Enerji, Kuvvet, Denge Güç Proble: Yaylı Sapan Yay sabiti k olan iki yaydan bir sapan yapılıştır. Her iki yayın başlangıç uzunluğu x 0. Kütlesi
ÇOKLU REGRESYON MODELİ, ANOVA TABLOSU, MATRİSLERLE REGRESYON ÇÖZÜMLEMESİ,REGRES-YON KATSAYILARININ YORUMU
 6.07.0 ÇOKLU REGRESON MODELİ, ANOVA TABLOSU, MATRİSLERLE REGRESON ÇÖZÜMLEMESİ,REGRES-ON KATSAILARININ ORUMU ÇOKLU REGRESON MODELİ Ekonom ve şletmeclk alanlarında herhang br bağımlı değşken tek br bağımsız
6.07.0 ÇOKLU REGRESON MODELİ, ANOVA TABLOSU, MATRİSLERLE REGRESON ÇÖZÜMLEMESİ,REGRES-ON KATSAILARININ ORUMU ÇOKLU REGRESON MODELİ Ekonom ve şletmeclk alanlarında herhang br bağımlı değşken tek br bağımsız
Ünite 4. Doç. Dr. Hasan TATLI NEM
 Ünit 4 Doç. Dr. Haan TATLI NEM 104 DOYMUŞ BUHAR BASINCI Buhar Baıncı: Hava bir gaz karışımı olduğundan, hr bir gazın toplam baınca olan katkıına kımi baıncı dnir. Su buharı da bir gaz olduğundan, onun
Ünit 4 Doç. Dr. Haan TATLI NEM 104 DOYMUŞ BUHAR BASINCI Buhar Baıncı: Hava bir gaz karışımı olduğundan, hr bir gazın toplam baınca olan katkıına kımi baıncı dnir. Su buharı da bir gaz olduğundan, onun
Fizik 101: Ders 15 Ajanda
 zk 101: Ders 15 Ajanda İk boyutta elastk çarpışma Örnekler (nükleer saçılma, blardo) Impulse ve ortalama kuvvet İk boyutta csmn elastk çarpışması Önces Sonrası m 1 v 1, m 1 v 1, KM KM V KM V KM m v, m
zk 101: Ders 15 Ajanda İk boyutta elastk çarpışma Örnekler (nükleer saçılma, blardo) Impulse ve ortalama kuvvet İk boyutta csmn elastk çarpışması Önces Sonrası m 1 v 1, m 1 v 1, KM KM V KM V KM m v, m
MIT Açık Ders Malzemeleri Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında bilgi almak için
 MIT Açık Ders Malzemeler http://ocm.mt.edu Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında blg almak çn http://ocm.mt.edu/terms veya http://tuba.açık ders.org.tr adresn zyaret ednz. 18.102
MIT Açık Ders Malzemeler http://ocm.mt.edu Bu materyallerden alıntı yapmak veya Kullanım Koşulları hakkında blg almak çn http://ocm.mt.edu/terms veya http://tuba.açık ders.org.tr adresn zyaret ednz. 18.102
ile Saklayın, Koruyun, Sevk Edin...
 HIZLI TÜKETİM ÜRÜNLERİ PAZARLAMA SAN. VE TİC. LTD. ŞTİ. ile Saklayın, Koruyun, Sevk Edin... Ürünü dış etkenlerden korumak ve rahat taşınmasını sağlamak için gerekli tüm ambalaj ve paketleme malzemelerini
HIZLI TÜKETİM ÜRÜNLERİ PAZARLAMA SAN. VE TİC. LTD. ŞTİ. ile Saklayın, Koruyun, Sevk Edin... Ürünü dış etkenlerden korumak ve rahat taşınmasını sağlamak için gerekli tüm ambalaj ve paketleme malzemelerini
kadar ( i. kaynağın gölge fiyatı kadar) olmalıdır.
 KONU : DUAL MODELİN EKONOMİK YORUMU Br prmal-dual model lşks P : max Z cx D: mn Z bv AX b AV c X 0 V 0 bçmnde tanımlı olsun. Prmal modeln en y temel B ve buna lşkn fyat vektörü c B olsun. Z B B BB c X
KONU : DUAL MODELİN EKONOMİK YORUMU Br prmal-dual model lşks P : max Z cx D: mn Z bv AX b AV c X 0 V 0 bçmnde tanımlı olsun. Prmal modeln en y temel B ve buna lşkn fyat vektörü c B olsun. Z B B BB c X
TOPRAK KİRLİLİĞİNİN KONTROLÜ VE NOKTASAL KAYNAKLI KİRLENMİŞ SAHALARA DAİR YÖNETMELİK
 Toprak Krllğnn Kontrolü V Noktasal Kaynaklı Krlnmş Saalara Dar Yöntmlk DOĞA Çvr Yöntm v Altrnat Enrj Tknolojlr Mündslk Danışmanlık Eğtm Hzmtlr San. Tc. Ltd. Şt. TOPRAK KİRLİLİĞİNİN KONTROLÜ VE NOKTASAL
Toprak Krllğnn Kontrolü V Noktasal Kaynaklı Krlnmş Saalara Dar Yöntmlk DOĞA Çvr Yöntm v Altrnat Enrj Tknolojlr Mündslk Danışmanlık Eğtm Hzmtlr San. Tc. Ltd. Şt. TOPRAK KİRLİLİĞİNİN KONTROLÜ VE NOKTASAL
Bölüm 3. Maddenin Isıl Özellikleri ve TERMODİNAMİK. Prof. Dr. Bahadır BOYACIOĞLU
 Bölüm 3 Maddenin Isıl Özellikleri ve TERMODİNAMİK Prof. Dr. Bahadır BOYACIOĞLU Termodinamik Yasaları Termodinamiğin 0. Yasası Termodinamiğin I. Yasası Termodinamiğin II. Yasası Termodinamiğin III. Yasası
Bölüm 3 Maddenin Isıl Özellikleri ve TERMODİNAMİK Prof. Dr. Bahadır BOYACIOĞLU Termodinamik Yasaları Termodinamiğin 0. Yasası Termodinamiğin I. Yasası Termodinamiğin II. Yasası Termodinamiğin III. Yasası
TEMEL KAVRAMLAR Test -1
 TEMEL KAVRAMLAR Test -1 1. 6 ( ) 4 A) B) 3 C) 4 D) 5 E) 6 5. 4 [1 ( 3). ( 8)] A) 4 B) C) 0 D) E) 4. 48: 8 5 A) 1 B) 6 C) 8 D) 1 E) 16 6. 4 7 36:9 18 : 3 A) 1 B) 8 C) D) 4 E) 8 3. (4: 3 + 1):4 A) 3 B) 5
TEMEL KAVRAMLAR Test -1 1. 6 ( ) 4 A) B) 3 C) 4 D) 5 E) 6 5. 4 [1 ( 3). ( 8)] A) 4 B) C) 0 D) E) 4. 48: 8 5 A) 1 B) 6 C) 8 D) 1 E) 16 6. 4 7 36:9 18 : 3 A) 1 B) 8 C) D) 4 E) 8 3. (4: 3 + 1):4 A) 3 B) 5
İ.T.Ü. Makina Fakültesi Mekanik Ana Bilim Dalı Bölüm 7. Seviye Düzlemi
 İTÜ Makina Fakültsi Ağırlığın Potansiyl Enrjisi W=, δh kadar yukarıya doğru yr dğiştirsin, Virtül iş, δu = Wδh= δh NOT: Eğr cisi aşağıya doğru δh yr dğişii yapıyorsa v +h aşağıya doğru is δu = Wδh= δh
İTÜ Makina Fakültsi Ağırlığın Potansiyl Enrjisi W=, δh kadar yukarıya doğru yr dğiştirsin, Virtül iş, δu = Wδh= δh NOT: Eğr cisi aşağıya doğru δh yr dğişii yapıyorsa v +h aşağıya doğru is δu = Wδh= δh
Gazların sıcaklık,basınç ve enerji gibi makro özelliklerini molekül kütlesi, hızı ve sayısı gibi mikroskopik özelliklerine bağlar.
 KİNETİK GAZ KURAMI Gazların sıcaklık,basınç ve enerji gibi makro özelliklerini molekül kütlesi, hızı ve sayısı gibi mikroskopik özelliklerine bağlar. Varsayımları * Gazlar bulundukları kaba göre ve aralarındaki
KİNETİK GAZ KURAMI Gazların sıcaklık,basınç ve enerji gibi makro özelliklerini molekül kütlesi, hızı ve sayısı gibi mikroskopik özelliklerine bağlar. Varsayımları * Gazlar bulundukları kaba göre ve aralarındaki
Anlık ve Ortalama Güç
 ALTERNATİF AK-Dere Analz Bölü-4 AC Güç Anlık Güç Oralaa güç Güç fakörü Akf, reakf güç Kpleks güç Reakf güç düzele (Kpanzasyn aksu akf güç ransfer Anlık Güç, p( (herhang br ank güç p Anlık e Oralaa Güç
ALTERNATİF AK-Dere Analz Bölü-4 AC Güç Anlık Güç Oralaa güç Güç fakörü Akf, reakf güç Kpleks güç Reakf güç düzele (Kpanzasyn aksu akf güç ransfer Anlık Güç, p( (herhang br ank güç p Anlık e Oralaa Güç
ÖZEL EGE LİSESİ EGE BÖLGESİ OKULLAR ARASI 16.MATEMATİK YARIŞMASI 10. SINIF FİNAL SORULARI
 10. SINIF FİNAL SORULARI 1. a,b,c,d sıfırdan farklı reel sayılar olmak üzere, + c + d = 0 denkleminin kökleri a ve b, + a + b = 0 denkleminin kökleri c ve d ise b + d değerini bulunuz.. sin + cos cos +
10. SINIF FİNAL SORULARI 1. a,b,c,d sıfırdan farklı reel sayılar olmak üzere, + c + d = 0 denkleminin kökleri a ve b, + a + b = 0 denkleminin kökleri c ve d ise b + d değerini bulunuz.. sin + cos cos +
300 = Ders notlarındaki ilgili çizelgeye göre; kömür için üst kaplama kalınlığı 4 mm, alt kaplama kalınlığı 2 mm olarak seçilmiştir.
 Soru-) Eğii, uzunluğu 50 olan dsandr y bant konvyör kurularak bununla saatt 300 ton tüvönan taş köürü taşınacaktır. Bant konvyörü boyutlandırınız. Kabullr: Bant hızı :,5 /s Köür yoğunluğu : 0,9 ton/ 3
Soru-) Eğii, uzunluğu 50 olan dsandr y bant konvyör kurularak bununla saatt 300 ton tüvönan taş köürü taşınacaktır. Bant konvyörü boyutlandırınız. Kabullr: Bant hızı :,5 /s Köür yoğunluğu : 0,9 ton/ 3
Bağıl hız ve bağıl ivme..
 Bağıl hız ve bağıl ivme.. Bağıl hareket, farklı referans sistemlerindeki farklı gözlemciler tarafından hareketlerin nasıl gözlemlendiğini ifade eder. Aynı hızla giden iki otomobilden birisinde bulunan
Bağıl hız ve bağıl ivme.. Bağıl hareket, farklı referans sistemlerindeki farklı gözlemciler tarafından hareketlerin nasıl gözlemlendiğini ifade eder. Aynı hızla giden iki otomobilden birisinde bulunan
BAŞKENT ÜNİVERSİTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAK MAKİNE MÜHENDİSLİĞİ LABORATUVARI DENEY - 8
 BAŞKENT ÜNİVERSİTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAK - 402 MAKİNE MÜHENDİSLİĞİ LABORATUVARI DENEY - 8 FARKLI YÜZEY ÖZELLİKLERİNE SAHİP PLAKALARIN ISIL IŞINIM YAYMA ORANLARININ HESAPLANMASI BAŞKENT ÜNİVERSİTESİ
BAŞKENT ÜNİVERSİTESİ MAKİNE MÜHENDİSLİĞİ BÖLÜMÜ MAK - 402 MAKİNE MÜHENDİSLİĞİ LABORATUVARI DENEY - 8 FARKLI YÜZEY ÖZELLİKLERİNE SAHİP PLAKALARIN ISIL IŞINIM YAYMA ORANLARININ HESAPLANMASI BAŞKENT ÜNİVERSİTESİ
PARÇALI DOĞRUSAL REGRESYON
 HAFTA 4 PARÇALI DOĞRUSAL REGRESYO Gölge değşkenn br başka kullanımını açıklamak çn varsayımsal br şrketn satış temslclerne nasıl ödeme yaptığı ele alınsın. Satış prmleryle satış hacm Arasındak varsayımsal
HAFTA 4 PARÇALI DOĞRUSAL REGRESYO Gölge değşkenn br başka kullanımını açıklamak çn varsayımsal br şrketn satış temslclerne nasıl ödeme yaptığı ele alınsın. Satış prmleryle satış hacm Arasındak varsayımsal
5.3. Tekne Yüzeylerinin Matematiksel Temsili
 5.3. Tekne Yüzeylernn atematksel Temsl atematksel yüzey temslnde lk öneml çalışmalar Coons (53) tarafından gerçekleştrlmştr. Ferguson yüzeylernn gelştrlmş hal olan Coons yüzeylernde tüm sınır eğrler çn
5.3. Tekne Yüzeylernn atematksel Temsl atematksel yüzey temslnde lk öneml çalışmalar Coons (53) tarafından gerçekleştrlmştr. Ferguson yüzeylernn gelştrlmş hal olan Coons yüzeylernde tüm sınır eğrler çn
BÖLÜM 1: TEMEL KAVRAMLAR
 BÖLÜM 1: TEMEL KAVRAMLAR İdeal Gaz Yasaları Gazlarla yapılan deneyler, 17. yüzyılda başlamış olup fizikokimya dalında yürütülen ilk bilimsel nitelikteki araştırmalardır. Gazlar için basınç (p), hacim (v),
BÖLÜM 1: TEMEL KAVRAMLAR İdeal Gaz Yasaları Gazlarla yapılan deneyler, 17. yüzyılda başlamış olup fizikokimya dalında yürütülen ilk bilimsel nitelikteki araştırmalardır. Gazlar için basınç (p), hacim (v),
KESİKLİ SEÇİM MODELLERİ
 do:.34/rg...36.56 DERS NOTLARI KESİKLİ SEÇİM MODELLERİ Doç. Dr. /İstanbul Aydın Ünvrsts Ekono v Fnans Bölüü Ergnbay Uğurlu E. Ugurlu, p.-9. Drs Notları Şubat Ktapçık 3 do:.34/rg...36.56 KESİKLİ SEÇİM MODELLERİ
do:.34/rg...36.56 DERS NOTLARI KESİKLİ SEÇİM MODELLERİ Doç. Dr. /İstanbul Aydın Ünvrsts Ekono v Fnans Bölüü Ergnbay Uğurlu E. Ugurlu, p.-9. Drs Notları Şubat Ktapçık 3 do:.34/rg...36.56 KESİKLİ SEÇİM MODELLERİ
YER ÖLÇÜLERİ. Yer ölçüleri, verilerin merkezini veya yığılma noktasını belirleyen istatistiklerdir.
 YER ÖLÇÜLERİ Yer ölçüler, verler merkez veya yığılma oktasıı belrleye statstklerdr. Grafkler bze verler yığılma oktaları hakkıda ö blg vermede yardımcı olurlar. Acak bu değerler gerçek değerler değldr,
YER ÖLÇÜLERİ Yer ölçüler, verler merkez veya yığılma oktasıı belrleye statstklerdr. Grafkler bze verler yığılma oktaları hakkıda ö blg vermede yardımcı olurlar. Acak bu değerler gerçek değerler değldr,
5) Özellikle ithal ürünlerde stok durumu öğrenildikten sonra sipariş verilmesi esastır.
 Fiyat Listesi GENEL SATIŞ SÖZLEŞMESİ 1) Bu fiyat listesi 30.11.2015 tarihine kadar geçerlidir, ancak piyasa şartları gerektirir ise 30.11.2015 tarihinden önce de fiyatları değiştirme hakkımız mahfuzdur.
Fiyat Listesi GENEL SATIŞ SÖZLEŞMESİ 1) Bu fiyat listesi 30.11.2015 tarihine kadar geçerlidir, ancak piyasa şartları gerektirir ise 30.11.2015 tarihinden önce de fiyatları değiştirme hakkımız mahfuzdur.
TG 12 ÖABT İLKÖĞRETİM MATEMATİK
 KAMU PERSONEL SEÇME SINAVI ÖĞRETMENLİK ALAN BİLGİSİ TESTİ İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ TG ÖABT İLKÖĞRETİM MATEMATİK Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının
KAMU PERSONEL SEÇME SINAVI ÖĞRETMENLİK ALAN BİLGİSİ TESTİ İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ TG ÖABT İLKÖĞRETİM MATEMATİK Bu testlerin her hakkı saklıdır. Hangi amaçla olursa olsun, testlerin tamamının
01.04.2010. Tambur dişlisinin tambura montajı
 01.04.0 TAMBURLAR Kaldırma makinalarında kullanılan tamburların yapısı aşağıdaki şkild görülmktdir. 1 4 Tambur dişlisinin tambura montajı 5 6 1 01.04.0 Tamburların yataklanma v tahrik skillri aşağıdaki
01.04.0 TAMBURLAR Kaldırma makinalarında kullanılan tamburların yapısı aşağıdaki şkild görülmktdir. 1 4 Tambur dişlisinin tambura montajı 5 6 1 01.04.0 Tamburların yataklanma v tahrik skillri aşağıdaki
ANADOLU ÜNİVERSİTESİ. ENM 317 Prof. Dr. Nihal ERGİNEL
 ANADOLU ÜNİVERSİTESİ ENM 317 Prof. Dr. Nihal ERGİNEL 2 ÖRNEKLEME Anakütleden n birimlik örnek alınması ve anakütle parametrelerinin örnekten tahmin edilmesidir. 3 ÖRNEKLEME ALMANIN NEDENLERİ Anakütleye
ANADOLU ÜNİVERSİTESİ ENM 317 Prof. Dr. Nihal ERGİNEL 2 ÖRNEKLEME Anakütleden n birimlik örnek alınması ve anakütle parametrelerinin örnekten tahmin edilmesidir. 3 ÖRNEKLEME ALMANIN NEDENLERİ Anakütleye
Kayıplı Dielektrik Cisimlerin Mikrodalga ile Isıtılması ve Uç Etkileri
 Kayıplı Dilktrik Cisimlrin Mikrodalga il Isıtılması v Uç Etkilri Orhan Orhan* Sdf Knt** E. Fuad Knt*** *Univrsity of Padrborn, Hinz ixdorf Institut, Fürstnall, 3302 Padrborn, Almanya orhan@hni.upb.d **Istanbul
Kayıplı Dilktrik Cisimlrin Mikrodalga il Isıtılması v Uç Etkilri Orhan Orhan* Sdf Knt** E. Fuad Knt*** *Univrsity of Padrborn, Hinz ixdorf Institut, Fürstnall, 3302 Padrborn, Almanya orhan@hni.upb.d **Istanbul
ege yayıncılık Oran Orant Özellikleri TEST : 91 a + 3b a b = 5 2 0,44 0,5 = 0,22 oldu una göre, a + b en az kaçt r? A) 3 B) 11 C) 14 D) 15 E) 16
 Orn Ornt Özellikleri TEST : 91 1. 0,44 0,5 = 0,22 5. + 3 = 5 2 2. 3. 4. oldu un göre, kçt r? A) 0,2 B) 0,25 C) 0,5 D) 0,6 E) 0,75 y = 3 4 + y oldu un göre, y orn kçt r? A) 7 B) 1 C) 1 D) 7 E) 10 oldu un
Orn Ornt Özellikleri TEST : 91 1. 0,44 0,5 = 0,22 5. + 3 = 5 2 2. 3. 4. oldu un göre, kçt r? A) 0,2 B) 0,25 C) 0,5 D) 0,6 E) 0,75 y = 3 4 + y oldu un göre, y orn kçt r? A) 7 B) 1 C) 1 D) 7 E) 10 oldu un
DERS 7. Türev Hesabı ve Bazı Uygulamalar II
 DERS 7 Türv Hsabı v Bazı Uygulamalar II Bu rst bilşk fonksiyonlarının türvi il ilgili zincir kuralını, üstl v logaritmik fonksiyonların türvlrini, ortalama v marjinal ortalama ğrlri; rsin sonuna oğru,
DERS 7 Türv Hsabı v Bazı Uygulamalar II Bu rst bilşk fonksiyonlarının türvi il ilgili zincir kuralını, üstl v logaritmik fonksiyonların türvlrini, ortalama v marjinal ortalama ğrlri; rsin sonuna oğru,
İleri Diferansiyel Denklemler
 MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
MIT AçıkDersSistemi http://ocw.mit.edu 18.034 İleri Diferansiyel Denklemler 2009 Bahar Bu bilgilere atıfta bulunmak veya kullanım koşulları hakkında bilgi için http://ocw.mit.edu/terms web sitesini ziyaret
GENETİK ALGORİTMA KULLANILARAK GÜÇ SİSTEMLERİNDE OPTİMAL ÇALIŞMA ŞARTLARININ BELİRLENMESİ
 Gaz Ünv Müh Mm Fak Dr J Fac Eng Arch Gaz Unv Clt 4, No 3, 539-548, 009 ol 4, No 3, 539-548, 009 GENETİK ALGORİTMA KULLANILARAK GÜÇ SİSTEMLERİNDE OPTİMAL ÇALIŞMA ŞARTLARININ BELİRLENMESİ Al ÖZTÜRK v Srhat
Gaz Ünv Müh Mm Fak Dr J Fac Eng Arch Gaz Unv Clt 4, No 3, 539-548, 009 ol 4, No 3, 539-548, 009 GENETİK ALGORİTMA KULLANILARAK GÜÇ SİSTEMLERİNDE OPTİMAL ÇALIŞMA ŞARTLARININ BELİRLENMESİ Al ÖZTÜRK v Srhat
MIT OpenCourseWare http://ocw.mit.edu. 14.30 Ekonomide İstatistiksel Yöntemlere Giriş Bahar 2009
 MIT OpenCourseWare http://ocw.mit.edu 14.30 Ekonomide İstatistiksel Yöntemlere Giriş Bahar 2009 Bu materyale atıfta bulunmak ve kullanım koşulları için http://ocw.mit.edu/terms sayfasını ziyaret ediniz.
MIT OpenCourseWare http://ocw.mit.edu 14.30 Ekonomide İstatistiksel Yöntemlere Giriş Bahar 2009 Bu materyale atıfta bulunmak ve kullanım koşulları için http://ocw.mit.edu/terms sayfasını ziyaret ediniz.
Sürekli Olasılık Dağılım (Birikimli- Kümülatif)Fonksiyonu. Yrd. Doç. Dr. Tijen ÖVER ÖZÇELİK
 Sürekl Olasılık Dağılım Brkml- KümülatFonksyonu Yrd. Doç. Dr. Tjen ÖVER ÖZÇELİK tover@sakarya.edu.tr Sürekl olasılık onksyonları X değşken - ;+ aralığında tanımlanmış br sürekl rassal değşken olsun. Aşağıdak
Sürekl Olasılık Dağılım Brkml- KümülatFonksyonu Yrd. Doç. Dr. Tjen ÖVER ÖZÇELİK tover@sakarya.edu.tr Sürekl olasılık onksyonları X değşken - ;+ aralığında tanımlanmış br sürekl rassal değşken olsun. Aşağıdak
İyon Kaynakları ve Uygulamaları
 İyon Kaynakları v Uygulamaları E. RECEPOĞLU TAEK-Sarayköy Nüklr Araştırma v Eğitim Mrkzi rdal.rcpoglu rcpoglu@tak.gov.tr HPFBU-2012 2012-KARS KONULAR İyon kaynakları hakkında gnl bilgi İyon kaynaklarının
İyon Kaynakları v Uygulamaları E. RECEPOĞLU TAEK-Sarayköy Nüklr Araştırma v Eğitim Mrkzi rdal.rcpoglu rcpoglu@tak.gov.tr HPFBU-2012 2012-KARS KONULAR İyon kaynakları hakkında gnl bilgi İyon kaynaklarının
YÖNETMELİK TOPRAK KİRLİLİĞİNİN KONTROLÜ VE NOKTASAL KAYNAKLI KİRLENMİŞ SAHALARA DAİR YÖNETMELİK
 8 Hazran 2010 SALI Rsmî Gazt Sayı : 27605 Çvr v Orman Bakanlığından: YÖNETMELİK TOPRAK KİRLİLİĞİNİN KONTROLÜ VE NOKTASAL KAYNAKLI KİRLENMİŞ SAHALARA DAİR YÖNETMELİK BİRİNCİ BÖLÜM Amaç, Kapsam, Dayanak
8 Hazran 2010 SALI Rsmî Gazt Sayı : 27605 Çvr v Orman Bakanlığından: YÖNETMELİK TOPRAK KİRLİLİĞİNİN KONTROLÜ VE NOKTASAL KAYNAKLI KİRLENMİŞ SAHALARA DAİR YÖNETMELİK BİRİNCİ BÖLÜM Amaç, Kapsam, Dayanak
BÖLÜM 12-15 HARMONİK OSİLATÖR
 BÖLÜM 12-15 HARMONİK OSİLATÖR Hemen hemen her sistem, dengeye yaklaşırken bir harmonik osilatör gibi davranabilir. Kuantum mekaniğinde sadece sayılı bir kaç problem kesin olarak çözülebilmektedir. Örnekler
BÖLÜM 12-15 HARMONİK OSİLATÖR Hemen hemen her sistem, dengeye yaklaşırken bir harmonik osilatör gibi davranabilir. Kuantum mekaniğinde sadece sayılı bir kaç problem kesin olarak çözülebilmektedir. Örnekler
ENM 316 BENZETİM ÖDEV SETİ
 ENM 16 BENZETİM ÖDEV SETİ Ödev 1. Bir depo ve N adet müşteriden oluşan bir taşımacılık sisteminde araç depodan başlayıp bütün müşterileri teker teker ziyaret ederek depoya geri dönmektedir. Sistemdeki
ENM 16 BENZETİM ÖDEV SETİ Ödev 1. Bir depo ve N adet müşteriden oluşan bir taşımacılık sisteminde araç depodan başlayıp bütün müşterileri teker teker ziyaret ederek depoya geri dönmektedir. Sistemdeki
A A A A A TEMEL MATEMAT K TEST. + Bu bölümdeki cevaplar n z cevap ka d ndaki "TEMEL MATEMAT K TEST " bölümüne iflaretleyiniz. 4.
 TEMEL MTEMT K TEST KKT! + u bölümde cevplyc n z soru sy s 40 t r + u bölümdeki cevplr n z cevp k d ndki "TEMEL MTEMT K TEST " bölümüne iflretleyiniz.. ( + )y + = 0 (b ) + 4y 6 = 0 denklem sisteminin çözüm
TEMEL MTEMT K TEST KKT! + u bölümde cevplyc n z soru sy s 40 t r + u bölümdeki cevplr n z cevp k d ndki "TEMEL MTEMT K TEST " bölümüne iflretleyiniz.. ( + )y + = 0 (b ) + 4y 6 = 0 denklem sisteminin çözüm
Güvenlik Stokları. Tedarik Zincirlerinde Belirsizlik Yönetimi: Güvenlik Stokları. Güvenlik Stokları Belirlenirken Sorulması gereken sorular
 Güvenl Stoları Tedar Zncrlernde Belrszl Yönetm: Güvenl Stoları Güvenl Stoğu: Herhang br dönemde, talebn tahmn edlen mtarın üzernde gerçeleşen mtarını arşılama çn elde bulundurulan sto mtarıdır Q Çevrm
Güvenl Stoları Tedar Zncrlernde Belrszl Yönetm: Güvenl Stoları Güvenl Stoğu: Herhang br dönemde, talebn tahmn edlen mtarın üzernde gerçeleşen mtarını arşılama çn elde bulundurulan sto mtarıdır Q Çevrm
Kobra 3 ile Ohm Yasası
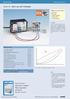 Kobra 3 ile Ohm Yasası LEP İlgili konular Ohm yasası, Özdirenz, Kontakt Direnç, İletkenlik, Güç ve İş Prensip Voltaj ile akım arasındaki ilişki farklı rezistörler için ölçülür. Direnç akımla ilglili olan
Kobra 3 ile Ohm Yasası LEP İlgili konular Ohm yasası, Özdirenz, Kontakt Direnç, İletkenlik, Güç ve İş Prensip Voltaj ile akım arasındaki ilişki farklı rezistörler için ölçülür. Direnç akımla ilglili olan
12. Ders Yarıiletkenlerin Elektronik Özellikleri
 12. Ders Yarıiletkenlerin lektronik Özellikleri T > 0 o K c d v 1 Bu bölümü bitirdiğinizde, Yalıtkan, yarıiletken, iletken, Doğrudan (direk) ve dolaylı (indirek) bant aralığı, tkin kütle, devingenlik,
12. Ders Yarıiletkenlerin lektronik Özellikleri T > 0 o K c d v 1 Bu bölümü bitirdiğinizde, Yalıtkan, yarıiletken, iletken, Doğrudan (direk) ve dolaylı (indirek) bant aralığı, tkin kütle, devingenlik,
TESADÜFİ DEĞİŞKENLERLE İLGİLİ BAZI YAKINSAKLIK ÇEŞİTLERİNİN KARŞILAŞTIRILMASI
 ISSN:1306-3111 e-journal of New Worl Scences Acaemy 2008, Volume: 3, Number: 4 Artcle Number: A0108 NATURAL AND APPLIED SCIENCES MATHEMATICS APPLIED MATHEMATICS Receve: March 2008 Accepte: September 2008
ISSN:1306-3111 e-journal of New Worl Scences Acaemy 2008, Volume: 3, Number: 4 Artcle Number: A0108 NATURAL AND APPLIED SCIENCES MATHEMATICS APPLIED MATHEMATICS Receve: March 2008 Accepte: September 2008
Fizik II Elektrik ve Manyetizma Akım, Direnç ve Elektromotor Kuvvet
 Ders Hakkında Fizik-II Elektrik ve Manyetizma Dersinin Amacı Bu dersin amacı, fen ve mühendislik öğrencilerine elektrik ve manyetizmanın temel kanunlarını lisans düzeyinde öğretmektir. Dersin İçeriği Hafta
Ders Hakkında Fizik-II Elektrik ve Manyetizma Dersinin Amacı Bu dersin amacı, fen ve mühendislik öğrencilerine elektrik ve manyetizmanın temel kanunlarını lisans düzeyinde öğretmektir. Dersin İçeriği Hafta
AN IMPROVED PROGRAMME FOR QUASI STATIC AND KINEMATICS DEFORMATION ANALYSIS IN LEVELLING NETWORK
 ÜKSEKLİK ĞLRND USİ SİK VE KİNEMİK DEFORMSON NLİZİ İÇİN GELİŞİRİLEN PROGRM S. DOĞNLP C. Ö. İĞİ C. İNL B. URGU Slçuk Ünrss Mündslk Mmarlık Faküls Jodz Foogramr Mündslğ Bölümü Jodz nablm Dalı Konya sdoganalp@slcuk.du.r
ÜKSEKLİK ĞLRND USİ SİK VE KİNEMİK DEFORMSON NLİZİ İÇİN GELİŞİRİLEN PROGRM S. DOĞNLP C. Ö. İĞİ C. İNL B. URGU Slçuk Ünrss Mündslk Mmarlık Faküls Jodz Foogramr Mündslğ Bölümü Jodz nablm Dalı Konya sdoganalp@slcuk.du.r
S1:10, S2:30, S3:20, S4:40 Puan Süre: 100 dakika 17 Nisan 2008
 Mikroişlmi Sistmlr Viz Sınvı S1:10, S2:30, S3:20, S4:40 Pun Sür: 100 kik 17 Nisn 2008 1) 18-45 işlmini ikili tn rçklyiniz. 18 00010010 45 00101101-45 için 2 y tümlyn lınır; 1 tümlm 11010010, sonr un 1
Mikroişlmi Sistmlr Viz Sınvı S1:10, S2:30, S3:20, S4:40 Pun Sür: 100 kik 17 Nisn 2008 1) 18-45 işlmini ikili tn rçklyiniz. 18 00010010 45 00101101-45 için 2 y tümlyn lınır; 1 tümlm 11010010, sonr un 1
2
 1 2 3 4 5 6 7 . Fuga JOINT GAMP FG-01 FG-02 FG-03 8 . Fuga JOINT GAMP FG-04 FG-05 FG-06 9 . Fuga JOINT GAMP FG-07 FG-08 FG-09 10 . Fuga JOINT GAMP FG-10 FG-11 FG-12 11 . Fuga JOINT GAMP FG-13 FG-14 FG-15
1 2 3 4 5 6 7 . Fuga JOINT GAMP FG-01 FG-02 FG-03 8 . Fuga JOINT GAMP FG-04 FG-05 FG-06 9 . Fuga JOINT GAMP FG-07 FG-08 FG-09 10 . Fuga JOINT GAMP FG-10 FG-11 FG-12 11 . Fuga JOINT GAMP FG-13 FG-14 FG-15
Türev Uygulamaları ÜNİTE. Amaçlar. İçindekiler. Yazar Prof.Dr. Vakıf CAFEROV
 Türev Uygulamaları Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 10 Amaçlar Bu üniteyi çalıştıktan sonra; türev kavramı yardımı ile fonksiyonun monotonluğunu, ekstremum noktalarını, konvekslik ve konkavlığını, büküm
Türev Uygulamaları Yazar Prof.Dr. Vakıf CAFEROV ÜNİTE 10 Amaçlar Bu üniteyi çalıştıktan sonra; türev kavramı yardımı ile fonksiyonun monotonluğunu, ekstremum noktalarını, konvekslik ve konkavlığını, büküm
1. KEYNESÇİ PARA TALEBİ TEORİSİ
 DERS NOTU 07 KEYNESÇİ PARA TALEBİ TEORİSİ, LM EĞRİSİ VE PARA TALEBİ FAİZ ESNEKLİĞİ Bugünk dersn çerğ: 1. KEYNESÇİ PARA TALEBİ TEORİSİ... 1 1.1 İŞLEMLER (MUAMELELER) TALEBİ... 2 1.2 ÖNLEM (İHTİYAT) TALEBİ...
DERS NOTU 07 KEYNESÇİ PARA TALEBİ TEORİSİ, LM EĞRİSİ VE PARA TALEBİ FAİZ ESNEKLİĞİ Bugünk dersn çerğ: 1. KEYNESÇİ PARA TALEBİ TEORİSİ... 1 1.1 İŞLEMLER (MUAMELELER) TALEBİ... 2 1.2 ÖNLEM (İHTİYAT) TALEBİ...
Kİ KARE ANALİZİ. Doç. Dr. Mehmet AKSARAYLI Ki-Kare Analizleri
 Kİ KAR ANALİZİ 1 Doç. Dr. Mehmet AKSARAYLI www.mehmetaksarayl K-Kare Analzler OLAY 1: Genelde br statstk sınıfında, öğrenclern %60 ının devamlı, %30 unun bazen, %10 unun se çok az derse geldkler düşünülmektedr.
Kİ KAR ANALİZİ 1 Doç. Dr. Mehmet AKSARAYLI www.mehmetaksarayl K-Kare Analzler OLAY 1: Genelde br statstk sınıfında, öğrenclern %60 ının devamlı, %30 unun bazen, %10 unun se çok az derse geldkler düşünülmektedr.
GAUSS IŞINLARININ SAÇILMASININ SINIR KIRINIM DALGASI TEORİSİ İLE İNCELENMESİ
 ludağ Ünvrsts Mühndslk-Mmarlık Fakülts Drgs, Clt 5, Sayı, GASS IŞINLAININ SAÇILMASININ SINI KIINIM DALGASI TEOİSİ İLE İNCELENMESİ ğur YALÇIN * Özt: u çalışmada, Gauss ışınlarının yutucu yarım br düzlmdn
ludağ Ünvrsts Mühndslk-Mmarlık Fakülts Drgs, Clt 5, Sayı, GASS IŞINLAININ SAÇILMASININ SINI KIINIM DALGASI TEOİSİ İLE İNCELENMESİ ğur YALÇIN * Özt: u çalışmada, Gauss ışınlarının yutucu yarım br düzlmdn
Bilgi Tabanı (Uzman) Karar Verme Kontrol Kural Tabanı. Bulanık. veya. Süreç. Şekil 1 Bulanık Denetleyici Blok Şeması
 Bulanık Dntlyicilr Bilgi Tabanı (Uzman) Anlık (Kskin) Girişlr Bulandırma Birimi Bulanık µ( ) Karar Vrm Kontrol Kural Tabanı Bulanık µ( u ) Durulama Birimi Anlık(Kskin) Çıkış Ölçklm (Normali zasyon) Sistm
Bulanık Dntlyicilr Bilgi Tabanı (Uzman) Anlık (Kskin) Girişlr Bulandırma Birimi Bulanık µ( ) Karar Vrm Kontrol Kural Tabanı Bulanık µ( u ) Durulama Birimi Anlık(Kskin) Çıkış Ölçklm (Normali zasyon) Sistm
