ORTOTROP KALIN PLAKLARIN STATİK VE DİNAMİK ANALİZİ YÜKSEK LİSANS TEZİ. : İnşaat Mühendisliği

Transkript

1 İSTANBUL TKNİK ÜNİVRSİTSİ FN BİLİLRİ NSTİTÜSÜ ORTOTROP KALIN PLAKLARIN STATİK V DİNAİK ANALİZİ YÜKSK LİSANS TZİ İnş. ü. Halim ÇALIŞKAN Anabilim Dalı Programı : İnşaat üendisliği : Yapı üendisliği OCAK 7

2 İSTANBUL TKNİK ÜNİVRSİTSİ FN BİLİLRİ NSTİTÜSÜ ORTOTROP KALIN PLAKLARIN STATİK V DİNAİK ANALİZİ YÜKSK LİSANS TZİ İnş. ü. Halim ÇALIŞKAN (55) Tezin nstitüe Verildiği Tari : Aralık 6 Tezin Savunulduğu Tari : 9 Ocak 7 Tez Danışmanı : Doç. Dr. Nial RATLI Diğer Jüri Üeleri : Prof. Dr. Yalçın AKÖZ (altepe Ü.) Yar. Doç. Dr. Feti KADIOĞLU OCAK 7

3 i

4 ÖNSÖZ Bu çalışmada öncelikle izotrop ve ortotrop plaklarda sonlu eleman formülasonu kullanılarak elde edilen fonksionel ardımıla statik ve dinamik analizlere er verilmiştir. lde edilen fonksionel kullanılarak fortran dilinde düzenlenen program ile değişik sınır koşulları altında izotrop ve ortotrop kalın plaklar incelenip farklı problemler çözülmüştür. Yüksek Lisans eğitimimin bounca değerli zamanını ve bilgisini benden esirgemeen er konuda bana destek olup önlendiren sevgili danışmanım Sn. Doç. Dr. Nial RATLI a üzerimde emeği bulunan tüm değerli İnşaat Fakültesi öğretim üelerine sagılarımı sunarım. Arıca profesonel iş aatımda Yüksek Lisansımı tamamlamam için benden desteklerini esirgemeen sevgili meslektaşım Sn. Fati SAYIN A teşekkürlerimi sunarım. Okul aatım bounca bana er konuda destek olan sevgili annem babam kardeşim ve aatımı birleştireceğim nişanlım Aslı TÜRK e en derin sevgilerimi sunarım. ARALIK 6 Halim ÇALIŞKAN ii

5 İÇİNDKİLR TABLO LİSTSİ ŞKİL LİSTSİ SBOL LİSTSİ ÖZT SUARY vi i i ii iii. GİRİŞ. Giriş ve Çalışmanın Amacı. ORTOTROP KALIN PLAK DNKLLRİNİN V FONKSİYONLİN LD DİLSİ 4.. Ortotrop Kalın Plak Denklemlerinin lde dilmesi 4... Yapılan kabuller 4... Denge denklemleri 7... Bileşke gerilme ve şekil değiştirme büüklükleri arasındaki bağıntılar 7.. Fonksionelin lde dilmesi. LAN ATRİSİNİN SONLU LAN FORÜLASYONU KULLANILARAK LD DİLSİ 6.. Dikdörtgen Sonlu leman Tanımı 6.. Ortotrop Kalın Plak İçin leman atrisinin lde dilmesi 4. STATİK ANALİZ 4.. Yaklaşım Testi 4... İzotrop kalın plaklar 4... Basit mesnetli üniform üke maruz izotrop kalın plaklar 4... Ankastre mesnetli üniform üke maruz izotrop kalın plaklar Ortotrop kalın plaklar 9 iii

6 4... Basit mesnetli üniform üke maruz ortotrop kalın plaklar 4... Ankastre mesnetli üniform üke maruz ortotrop kalın plaklar 4.. Kalınlık Değişiminin Sonuçlara tkisi İzotrop kalın plaklar Basit mesnetli üniform üke maruz izotrop kalın plaklar Ankastre mesnetli üniform üke maruz izotrop kalın plaklar Ortotrop kalın plaklar Basit mesnetli d üniform üke maruz ortotrop kalın plaklar Ankastre mesnetli üniform üke maruz ortotrop kalın plaklar Kalınlık değişiminin izotrop-ortotrop plaklar üzerindeki etkisinin değerlendirilmesi Farklı Kalınlık ve Oranları İçin Ortotrop Kalın Plakların Çözümü Basit mesnetli üniform üke maruz kalın ortotrop plaklar Ankastre mesnetli üniform üke maruz kalın ortotrop plaklar Farklı Sınır Koşullarına Saip Üniform Yaılı Yüke aruz Ortotrop Kalın Plakların Çözümü Karşılıklı iki kenarı ankastre diğer kenarları basit oturan üniform düzgün aılı üke maruz ortotrop kalın plakların çözümü Karşılıklı iki kenarı boşta diğer kenarları basit oturan üniform düzgün aılı üke maruz ortotrop kalın plakların çözümü 5 5. DİNAİK ANALİZ İzotrop Kalın Plaklar Basit mesnetli izotrop kalın plaklar Ankastre mesnetli izotrop kalın plaklar Karşılıklı iki kenarı ankastre diğer kenarları basit oturan izotrop kalın plaklar Ortotrop Kalın Plaklar Basit mesnetli ortotrop kalın plaklar Ankastre mesnetli ortotrop kalın plaklar 6 6. PROGRA 6 iv

7 7. SONUÇLAR V TARTIŞA 64 KAYNAKLAR 66 ÖZGÇİŞ 68 v

8 TABLO LİSTSİ Safa No Tablo 4.. : Kenarlarından basit mesnetli üniform aılı üke maruz İzotrop kalın plakta eleman saına göre çökme ve moment değerleri...4 Tablo 4.. : Kenarlarından ankastre mesnetli üniform aılı üke maruz izotrop kalın plakta eleman saına göre çökme ve moment değerleri...7 Tablo 4.. : Kenarlarından basit mesnetli üniform aılı üke maruz ortotrop kalın plakta eleman saına göre çökme ve moment değerleri... Tablo 4.4. : Kenarlarından ankastre mesnetli üniform aılı üke maruz ortotrop plakta eleman saına göre çökme ve moment değerleri... Tablo 4.5: Tablo 4.6. Tablo 4.7. : Kenarlarından basit mesnetli üniform aılı üke maruz izotrop kalın plakta a oranlarına gore çökme ve moment değerleri...7 : Kenarlarından ankastre mesnetli üniform aılı üke maruz izotrop kalın plakta a oranlarına göre çökme ve moment değerleri..8 : Kenarlarından basit mesnetli üniform aılı üke maruz ortotrop kalın plakta çökme ve moment değerleri....9 Tablo 4.8. : Kenarlarından basit mesnetli üniform aılı üke maruz ortotrop kalın plakta a oranlarına göre çökme moment ve kesme kuvveti değerleri Tablo 4.9. Tablo 4.. : Kenarlarından ankastre mesnetli üniform aılı üke maruz ortotrop kalın plakta a oranlarına göre çökme ve moment değerleri.. 4 : Kenarlarından basit mesnetli üniform aılı üke maruz ortotrop kalın plakta Y eğilme momenti için aklaşım testi..4 Tablo 4.. : Kenarlarından basit mesnetli üniform aılı üke maruz izotrop ortotrop plaklarda çökme değerleri karşılaştırılması vi

9 Tablo 4.. : Kenarlarından basit mesnetli üniform aılı üke maruz ortotrop kalın plakta a ve oranlarına göre çökme ve moment değerleri....4 Tablo 4.. : Kenarlarından basit mesnetli üniform aılı üke maruz ortotrop kalın plakta a ve oranlarına göre çökme ve moment değerleri Tablo 4.4. : Kenarlarından ankastre mesnetli üniform aılı üke maruz ortotrop kalın plakta a ve oranlarına göre çökme ve moment değerleri Tablo 4.5. : Karşılıklı iki kenarı ankastre diğer kenarları basit oturan üniform düzgün aılı üke maruz ortotrop plakta a oranlarına gore çökme moment ve kesme kuvveti değerleri Tablo 4.6. : Karşılıklı iki kenarı ankastre diğer kenarları basit oturan üniform düzgün aılı üke maruz ortotrop plakta a ve oranlarına göre çökme moment değerleri...49 Tablo 4.7. : Karşılıklı iki kenarı ankastre diğer kenarları basit oturan üniform düzgün aılı üke maruz ortotrop plakta a ve oranlarına kesme kuvveti değerleri...5 Tablo 4.8. : Karşılıklı iki kenarı boşta diğer kenarları basit oturan üniform düzgün aılı üke maruz ortotrop plakta a oranlarına göre çökme moment ve kesme kuvveti değerleri Tablo 4.9. : Karşılıklı iki kenarı ankastre diğer kenarları basit oturan üniform düzgün aılı üke maruz ortotrop plakta oranlarına göre çökme moment ve kesme kuvveti değerleri....5 Tablo 5.. : Kenarlarından basit mesnetli izotrop kalın plakta a oranlarına göre ϖ Tablo 5.. : Kenarlarından basit mesnetli izotrop kalın plakta ϖ ϖ ϖ ve ϖ vii

10 Tablo 5.. : Kenarlarından ankastre mesnetli üniform izotrop kalın plakta a oranlarına göre ϖ Tablo 5.4. : Kenarlarından ankastre mesnetli izotrop kalın plakta ϖ ϖ ϖ ve ϖ Tablo 5.5. Tablo 5.6. Tablo 5.7. : İki kenarı ankastre diğer kenarları basit oturan izotrop kalın plakların a oranlarına gore ϖ : Kenarlarından ankastre mesnetli üniform aılı üke maruz izotrop kalın plakta ϖ ϖ ϖ ve ϖ : Kenarlarından basit mesnetli ortotrop kalın plakta eleman saısına göre frekans değerleri Tablo 5.8. : Kenarlarından basit mesnetli ortotrop kalın plakta ϖ ϖ ϖ ve ϖ Tablo 5.9. : Kenarlarından basit mesnetli ortotrop kalın plakta a oranlarına göre ϖ ϖ boutsuz doğal frekansları Tablo 5.. : Kenarlarından ankastre mesnetli ortotrop kalın plakta ( Σ n ) eleman saısına göre ϖ Tablo 5.. : Kenarlarından basit mesnetli ortotrop kalın plakta a oranlarına göre ϖ viii

11 ŞKİL LİSTSİ Safa No Şekil.. : Gerilme bileşenleri Şekil.. : Kesit tesirleri Şekil.. : w w in şekil üzerinde gösterilmesi..... Şekil.. Şekil 4.. Şekil 4.. : Global ve doğal koordinat sisteminde dikdörtgen eleman... 7 : İzotrop kenarlarından basit mesnetli dikdörtgen plak.. : İzotrop kenarlarından basit mesnetli üniform üke maruz kalın plakta çökme için aklaşım testi Şekil 4.. : İzotrop kenarlarından basit mesnetli üniform üke maruz kalın plakta eğilme momenti için aklaşım testi Şekil 4.4. Şekil 4.5. : Kenarlarından ankastre mesnetli dikdörtgen plak...6 : İzotrop kenarlarından ankastre mesnetli üniform üke maruz kalın plakta w çökme için aklaşım testi...8 Şekil 4.6. Şekil 4.7. Şekil 4.8. : İzotrop kenarlarından ankastre mesnetli üniform üke maruz kalın plakta eğilme momenti için aklaşım testi....8 : İzotrop kenarlarından ankastre mesnetli üniform üke maruz kalın plakta ankastrelik momenti için aklaşım testi....9 : Ortotrop kenarlarından basit mesnetli üniform üke maruz kalın plakta w çökme için aklaşım testi... Şekil 4.9. Şekil 4.. Şekil 4.. : Ortotrop kenarlarından basit mesnetli üniform üke maruz kalın plakta Y eğilme momenti için aklaşım testi... : Ortotrop kenarlarından basit mesnetli üniform üke maruz kalın plakta Y eğilme momenti için aklaşım testi : Ortotrop kenarlarından ankastre mesnetli üniform üke maruz plakta kalın w çökme için aklaşım testi...4 Şekil 4.. : Ortotrop kenarlarından ankastre mesnetli üniform üke maruz kalın plakta eğilme momenti için aklaşım testi....4 i

12 Şekil 4.. Şekil 4.4. Şekil 4.5. Şekil 4.6. : Ortotrop kenarlarından ankastre mesnetli üniform üke maruz kalın plakta eğilme momenti için aklaşım testi....5 : Ortotrop kenarlarından ankastre mesnetli üniform üke maruz kalın plakta ankastrelik momenti için aklaşım testi....5 : Ortotrop kenarlarından ankastre mesnetli üniform üke maruz kalın plakta ankastrelik momenti için aklaşım testi....6 : Kenarlarından basit mesnetli üniform aılı üke maruz ortotrop kalın plakta kalınlık - w çökme değişimi Şekil 4.7. Şekil 4.8. Şekil 4.9. : Kenarlarından basit mesnetli üniform aılı üke maruz ortotrop kalın plakta kalınlık eğilme momenti değişimi.. 44 : Kenarlarından basit mesnetli üniform aılı üke maruz ortotrop kalın plakta kalınlık eğilme momenti değişimi.. 45 : İki kenarlarından ankastre diğer kenarlarından basit mesnetli dikdörtgen plak Şekil 4.. : İki kenarlarından serbest diğer kenarlarından basit mesnetli dikdörtgen plak Şekil 5.. : Ortotrop kalın plakta ϖ ϖ ϖ ve ϖ e ait mod şekilleri...59 Şekil 6.. : Programa ait akış diagramı 6

13 SBOL LİSTSİ ε ε : Şekil değiştirme alinin ve bileşenleri σ σ σ : z doğrultularındaki normal gerilmeler z : lastisite modülleri µ µ µ z : Poisson oranı γ γ γ : Açı değişimleri z z z τ τ τ : Kama gerilmeleri z : ğilme ve burulma momentleri : Plak kalınlığı Q Q : Kesme kuvvetleri w q : Düşe er değiştirme : Düşe ük : Şekil değiştirme büüklükleri G G z G z : Kama modülleri D Q D : ğilme rijitliği : Operatör [ ; ] : İç çarpım Ψ i : Yaklaşım fonksionları ξ η ξ i η i : Doğal koordinat takımı : i. Düğüm noktasının doğal koordinatları a b : Dikdörtgen sonlu eleman boutları G G : Dikdörtgen elemanın ağırlık merkezi koordinatları [ K ] ϖ : Dikdörtgen elemanın rijitlik matrisi : Frekans parametreleri [ e] : Kütle matrisi ρ : Yoğunluk i

14 ÖZT Bu çalışmada öncelikle Reissner plak teorisi kullanılarak ortotrop kalın plakların statik ve dinamik analizi apılmıştır. Birinci bölümde kalın ve ince plak tanımları üzerinde durulmuş kalın plak teorilerinden Reissner ve indlin teorilerinin karşılaştırılması apılmıştır. Arıca izotrop ve ortotrop kalın plaklarla ilgili literatürde er alan çalışmalara er verilmiştir. İkinci bölümde ortotrop plak denklemleri ortaa konarak Gâteau türevine daalı eni bir fonksionel elde edilmiştir. Gâteau türevile elde edilirken geometrik ve dinamik sınır koşulları kullanılmıştır. Üçüncü bölümde elde edilen fonksionel kullanılarak karışık sonlu eleman öntemi ile eleman matrisi elde edilmiştir. Dördüncü ve beşinci bölümde değişik sınır koşullarına saip üniform aılı üke maruz izotrop ve ortotrop kalın plakların statik ve dinamik analizi apılmıştır. lde edilen sonuçların literatürdeki sonuçlarla karşılaştırılması apılmış ve sonuçların birbirine akın olduğu gözlenmiştir. Altıncı bölümde eleman matrisindeki bilgilerin sınır koşulları göz önünde bulundurularak kodlama ile sistem matrisine aktarılması oluşturulan matrisin çözümü için geliştirilen fortran dilinde azırlanmış program akkında genel bilgiler verilmiştir. Program plakların statik ve dinamik analizine ugundur. Yedinci bölümde elde edilen sonuçlar özetlenmiş orumlara er verilmiştir. SUARY ii

15 In tis stud at first te static and dnamic analsis of tick isotrop and ortotrop plates is made b using Reisner plate teor. First capter is basicl about te definitions of tick and tin plates and ere Reissner and indlin plates teories are compared and contrasted. oreover studies about te tick izotrop and ortotrop plates in te literature are mentioned. In te second capter troug displaing ortotrop plate equations a new function tat is based on Gâteau derivative is obtained. Te functionals ave been obtained b using Gâteau derivative for plates element wit is used geometris and dnamic boundar conditions. In te tird capter troug making use of tat function mied finite element formulation and element matri ave been obtained. In te fourt and five capter static and dnamic analsis of tick izotrop and ortotrop plates tat are subject to uniforml distrubuted load is completed and obtained solutions ave been compared wit in tose avaible te literature. In te sit capter taking te limit conditions of te information in te element matri into consideration its transfer into sstem matri troug codification and some general information about te programme tat is designed for te solution of te matri and tat is prepared in te Fortran language are provided. Te computer program is appropriate for te static and dnamic analsis of te plates. In te sevent capter consequences tat are obtained are summarized and some comments are mentioned. iii

16 .GİRİŞ.. Giriş ve Çalışmanın Amacı Plaklar bir boutu ( plağın kalınlığı ) diğer iki boutunun ( dikdörtgen plak için plağın eni ve bou dairesel plak için çap ) anında küçük olan ve müendislikte çok kullanılan apı elemanlarından biridir. Plaklar ince ve kalın olmak üzere iki grupta toplanabilir. Klasik plak teorisinin ( vea Kircoff plak teorisi ) geçerli olduğu ince plaklarda plak açıklığının kalınlığa oranı ( a ) dan büüktür. İnce plaklarda kama gerilmeleri ( τ z ve τ z ) ve normal gerilme ( σ z ) imal edilir. Kalın plaklarda ise plak açıklığının kalınlığa oranı ( a ) dan küçük olarak tanımlanmıştır ( a ) []. Kalın plakların ince plaklardan farkı plağın kama deformasonunun göz önünde bulundurulmasıdır. Kama deformasonunu dikkate alan plak teorilerinin en agın olarak kullanılanları da Reissner [] ve indlin [4] teorileridir. Literatürdeki bazı çalışmalarda bu teorilerin birbirinin benzeri olduğu görüşü agın olarak benimsenmiş atta iki teori birlikte Reissner-indlin plak teorisi olarak kullanılmıştır. Gerçekte ise bu iki teori arasında bazı farklılıklar vardır. [5] nolu çalışmada bu iki teori arasındaki ana farklılığın Reissner plak teorisinin plak kalınlığı bounca gerilmenin lineer ve kama gerilmesinin parabolik değiştiğini kabul eden tamamlaıcı enerji ifadesinden elde edildiği şeklinde açıklanmıştır. indlin teorisinde ise plak kalınlığı bounca er değiştirmenin lineer olduğu kabul edilmiştir. Böle bir kabule Reissner plak teorisinde gerek duulmaz bu nedenle de Reissner plak teorisinin birinci mertebe kama deformason teorisi olarak tanımlanması doğru değildir. Arıca indlin teorisinde Reissner plak teorisinden

17 farklı olarak σ z normal gerilmesi imal edilmektedir. Bu farklılıklar saısal çözüm apılarak [5] nolu çalışmada detalı olarak incelenmiş ve ortaa konulmuştur. Kalın plak teorileri ince plakların çözümünde de kullanılabileceğine göre klasik plak teorisinin etersiz kaldığı durumlar ortadan kaldırılmıştır. Reissner ve indlin teorilerine daalı farklı çözüm öntemlerinin kullanıldığı çok saıda çalışma literatürde mevcuttur. Bu çalışmalar izotrop ve ortotropik plakların statik dinamik ve stabilitesini kapsamaktadır. [6] nolu çalışmada izotrop ve ortotrop plakların statik çözümü arıklaştırma öntemi ile Kircoff Reissner-indlin üksek mertebeden teorileri esas alınarak apılmıştır. [7] nolu çalışmada IF ( etod of Initial Functions ) metodu kullanılarak ortotrop kalın plakların statik analizi apılmış Ambartsuman ve Reissner teorilerine daalı olarak elde edilen sonuçlarla karşılaştırma apılmıştır. [8] nolu çalışmada sonlu fark metodu kullanılarak ince izotrop ve ortotrop plakların statik analizi apılmıştır. [9] nolu çalışmada karışık sonlu eleman metodu kullanılarak ankastre mesnetli ortotrop plakların statik analizi apılmıştır. [] nolu çalışmada Gâteau türevine daalı karışık sonlu eleman metodu ile ortotropik plakların statik analizi apılmıştır. [] nolu çalışmada ortotropik basit mesnetli plakların statik titreşim ve burkulma esabına er verilmiştir Bu çalışmada Reissner teorisini kullanan Gâteau türevine daalı bir formülason geliştirilmiş ve ortotrop kalın plakların statik ve dinamik analizinde kullanılmıştır. Çözüm için Gâteau türevine daalı bir fonksionel geometrik ve dinamik sınır koşulları ile birlikte elde edilmiştir. Bu fonksionel saısal öntemler için ugundur

18 ve fonksionelde tanımlı büüklükler erangi bir ana işleme gerek duulmaksızın doğrudan bulunabilmektedir. Saısal öntem olarak sonlu eleman öntemi kullanılmıştır. Sonlu eleman öntemi plak problemlerini kolalıkla çözebilen kapsamlı ve sistematik bir öntem olduğu için agın olarak kullanılmaktadır. Bu anlamda farklı sonlu eleman formülasonları gelişmiştir. Bu formülasonlar üç grupta toplanabilir. - Yer değiştirme modeli; Yer değiştirmeler serbest değişken olarak seçilir ve minimum potansiel enerji ilkesi kullanılır. - Kuvvet modeli; İç kuvvetler vea gerilmeler serbest değişken olarak seçilir ve tamamlaıcı enerji ilkesi kullanılır. - Karışık model; Yer değiştirme ve iç kuvvetler serbest değişken olarak seçilmiştir. Hellinder Reissner ve Hu-Wasizu ilkeleri kullanılabilir. Karışık sonlu eleman formülasonunun kullanıldığı mevcut çalışmada kenarlarından basit ankastre mesnetli ve farklı sınır koşulları için üniform aılı üke maruz plakların statik ve dinamik analizi apılmıştır. lde edilen sonuçların karşılaştırılması literatürdeki mevcut çalışmalarla apılmış ve sonuçların uumlu olduğu gözlenmiştir.

19 .ORTOTROP KALIN PLAK DNKLLRİNİN V FONKSİYONLİN LD DİLSİ.. Ortotrop Kalın Plak Denklemlerinin lde dilmesi... Yapılan Kabuller alzeme lineer elastiktir. Altı bileşeni ile verilen bir gerilme alinin medana getirdiği şekil değiştirme alinin bileşenleri esaplanmak istendiğinde önce uzamaların sadece normal gerilmelerden dolaı medana geldiği düşünülerek Denklem. ε u [ σ µ σ µ σ ] z z (..a) ε v [ σ µ σ µ σ ] z z (..b) daa sonra da kama gerilmelerinin sadece açı değişikliği apacağı esasına daanılarak Denklem. elde edilir. [] γ u v + ( + µ ) τ (..a) 4

20 γ γ z z u w + z v w + z ( + µ ) z z ( + µ ) z z τ τ z z (..b) (..c) d d ve dz boutlarına saip bir plak elemanına etki eden gerilme bileşenleri Şekil. de bunların bileşkeleri olan ve kesitin birim bouna isabet eden kesit tesirleri Şekil. de gösterilmiştir. Klasik plak teorisinden farklı olarak lateral gerilmeler ( σ z τ z τ z ) alınmıştır. σ z z dz σ τ z τ τ τ z σ d d Şekil.. : Gerilme Bileşenleri q z Q Q d d Şekil.: Kesit Tesirleri 5

21 Denge denklemlerinde acim kuvvetleri imal edilmektedir. Bernoulli-Navier dik kesitin düzlemliliğini ve dikliğini koruması ipotezi geçerlidir. Klasik plak teorisine göre gerilme-şekil değiştirme bağıntılarından Denklem. elde edilir []. σ z σ z τ z (.) Diğer gerilme bileşenleri ise Şekil. den azılan denge denklemleri ve z±/ de kama gerilmelerinin sıfır olması koşulundan Denklem.4 deki gibi elde edilir. z τ Q z z τ Q (.4) z Şekil. deki gerilme alinin z doğrultusundaki dengesinden de denklem.5 elde edilir. σ z z τ z τ z (.5) z + de σ z de σ q sınır koşullarının kullanılmasıla; z z q z z σ z + (.6) 4 elde edilir. 6

22 ... Denge denklemleri Gerilme bileşenleri ile kesit tesirleri arasındaki bağıntılar Denklem.7 deki gibidir. σ zdz σ zdz τ zdz (.7.a) τ zdz Q τ dz Q τ dz (.7.b) z z Şekil. de verilen dd plak elemanına etki eden q lateral ük ve iç kuvvetler cinsinden denge denklemleri azılacak olursa + Q (.8.a) + Q (.8.b) Q Q + + q (.8.c) elde edilir.... Bileşke Gerilme ve Şekil Değiştirme Büüklükleri Arasındaki Bağıntılar ve w ile tanımlanan bileşke şekil değiştirme büüklükleri gerilme ve er değiştirme bileşenleri olarak iç kuvvetlerle anı işi aparlar. Dolaısıla; 7

23 σ udz vdz σ (.9.a) τ udz τ vdz (.9.b) τ z w dz Q w τ w dz Q w (.9.c) z azılabilir. w w ) değişkenleri cinsinden düşe er değiştirmei ( z tanımlamak üzere Denklem. Denklem.9.a Denklem.9.b ve Denklem.9.c kullanılarak Denklem..a ve Denklem..b elde edilir. uzdz vzdz (..a) z w w dz (..b) Denklem..a daki ifadelerin sırasıla e ve e göre türevleri alınır ve Denklem. Denklem. ve Denklem.6 daki ifadeler kullanılarak Denklem. ve Denklem. elde edilir. µ zq (.) µ µ µ zq (.) 8

24 ve ine Denklem..a ifadelerinin sırasıla e ve e göre türevleri alınır ve Denklem.. Denklem. ve Denklem.7 ifadeleri kullanılarak Denklem. elde edilir. + G (.) Kamanın aptığı iş azılacak olursa; z w γ zτ zdz z dz + G τ (.4) z ifadesi elde edilir. Benzer şekilde; z w γ zτ zdz z dz + G τ (.5) z elde edilir. Denklem.4 de τ z değeri azılacak olursa; z ( + µ ) 9 z ( + µ ) z Q z 4 γ τ zdz dz z z 6 5 Q (.6) ve Denklem.4 ile Denklem.6 dan da; w 6 + Q 5 G z (.7) 9

25 eşitliği elde edilmiş olur. Anı aklaşımla Denklem.8 elde edilir; w G z Q (.8).. Fonksionelin lde dilmesi Denklem.8.a.8.b.8.c....7 ve.8 de elde edilen Ortotrop kalın plak denklemleri toplu olarak tekrar azılacak olursa + Q + Q Q Q + + q µ µ zq µ q µ z (.9) + G w 6 + Q 5 G z w 6 + Q 5 G z elde edilir.

26 Dinamik sınır koşulları ˆ (.) Q Q ˆ Geometrik sınır koşulları ˆ (.) w wˆ şeklinde ifade edilir. Kamadan ve eğilmeden dolaı kesitte medana gelen toplam açı değişikliği de Şekil. de gösterilmiştir. w z Şekil.. w w w w in şekil üzerinde gösterilmesi. lde edilen denklemler kullanılarak Lf diferansiel denklemi QL-f operatörü şeklinde azılabilir. Bu ifadeden fonksionele geçebilmek için Q operatörünün

27 potansiel olduğu gösterilmelidir. Q operatörü lineer denklem takımı alinde azılacak olursa w Q A A q Q w Q Q w P P P P P P P P P P P P P P P P P P P ˆ ˆ ˆ ˆ (.) Denklem. de er alan P katsaıları Denklem. da verilmiştir. P 7 P 8 P 4 P 6 P 5 P 6 P 4 44 P P µ 45 P 5 P µ P P 6 P 6 66 G P P 7 G P z P 8 G P z q A z µ q A z µ (.)

28 Q operatörünün potansiel olabilmesi için Denklem.4 deki koşulun sağlanması gerekir. ( ) ( ) > >< < dq dq ; ; (.4) Buradaki tırnak parantez içindeki ifadelerin iç çarpımını göstermekte olup ve vektörleri nin içinde bulunduğu uzaın elemanlarıdır. ( ) dq ; ve ( ) ; dq ise Q operatörünün ve doğrultusundaki Gâteau türevlerini göstermektedir. Operatörün Gâteau türevleri de şu şekilde tanımlanmaktadır [4]. ( ) ( ) ; + τ τ τu Q u u u dq (.5) Bu tanım kullanılarak Denklem.4 deki iç çarpımlar açık şekli azılacak olursa; ( ) [ ] [ ] [ ] [ ] [ ] ; w Q w Q dq + + [ ] [ ] [ ] [ ] Q [ ] [ ] [ ] [ ] Q w Q G [ ] µ µ [ ] 5 6 z Q Q Q G + µ µ [ ] [ ] [ ] [ ] σ σ ε ε 5 6 w Q Q w Q Q G z + + (.6) benzer işlemler apılarak Denklem.7

29 4 ( ) [ ] [ ] [ ] [ ] [ ] w Q w Q dq + + ; [ ] [ ] [ ] [ ] Q [ ] [ ] [ ] [ ] Q w Q G [ ] µ µ [ ] z Q Q Q G µ µ [ ] [ ] [ ] [ ] σ σ ε ε w Q Q w Q Q G z (.7) eşitlikleri elde edilir. Buradaki köşeli parantezler bölgedeki iç çarpımı göstermektedir. ( ) f f ve ( ) g g bölgede tanımlı iki fonksion olarak kabul edilirse bunların iç çarpımları aşağıdaki gibi tanımlanabilir; [ ] dz fg g f L (.8) [ ] g f g f. Dinamik ve geometrik sınır koşullarının verildiği noktalarda geçerli [ ] g f g f. σ Dinamik sınır koşullarının verildiği noktalarda geçerli [ ] g f g f. ε Geometrik sınır koşullarının verildiği noktalarda geçerli

30 Denklem.6 ve Denklem.7 ifadeleri Denklem.4 de karşılaştırıldığında µ µ (.9) Denklem.9 bağıntısı da göz önünde bulundurularak Q operatörünün potansiel olduğu görülür ve sınır koşulları da; [ Q w] [( Q n + Q n ) w] [ ] [( n + n ) ] + [( n + n ) ] (.) şeklinde elde edilmiş olur. Buradan da fonksionel; I l ( ) < Q( s ) > ds (.) şeklinde elde edilir. Burada s skaler bir büüklüktür.[4] İşlemler apılırsa fonksionel ( ) [ ] + [ ] + [ ] + [ ] I + olarak elde edilir. [ Q ] + [ Q ] + [ Q w ] + [ Q w ] [ q w] µ z 5 µ [ ] µ [ ] + [ ] z 6 [ q ] + [ q ] [ ] µ µ µ [ Q Q ] [ Q Q ] [ ] σ [ Q w] σ (.) 5G 5G z z µ G 5

31 . LAN ATRİSİNİN SONLU LAN FORÜLASYONU KULLANILARAK LD DİLSİ Sonlu eleman formülasonu apılırken değişik sonlu eleman tiplemeleri apılabilir. İki boutlu sonlu eleman dikdörtgen vea üçgen olarak seçilebildiği gibi bu tipler için lineeri quadratik ve kübik düzende nokta tanımlaması apılabilir. Bunun için sonlu eleman fonksionelinin içinde bulunan en büük türev derecesine bakılır ve buna göre şekil fonksionu belirlenir. Bu çalışmada dikdörtgen sonlu eleman tanımı kullanılarak çözümler apılmıştır... Dikdörtgen Sonlu leman Tanımı İkinci bölümde elde edilen fonksionelde bir değişkene göre iki vea daa üksek mertebeden türev bulunmadığı için tamlık ve süreklilik açısından bilineer biçim fonksionu eterli görülerek bu çalışmada sonlu eleman için kenarlar bounca ara noktaları olmaan Dikdörtgen Sonlu leman formülasonu kullanılmıştır. [5] Sonlu elemanda elemanın erangi bir erindeki bilinmeenlerle düğüm noktalarındaki bilinmeenler arasında ilişki biçim fonksionları kullanılarak elde edilir. Bölelikle eleman matrisleri kolalıkla elde edilmektedir. Sonlu eleman tanımında eleman koordinatları ve eleman bilinmeenlerini doğal koordinat sistemi kullanılarak ifade etmek mümkündür. Genel olarak koordinat aklaşımı 6

32 q i q ˆ i i Ψ i i i Ψ q ˆ ; ˆ Ψi (.) i şeklindedir. Burada erangi bir düğüm noktasının elemandaki erel koordinatları ve i i de elemanın q i düğüm noktalarının koordinatlarıdır. Yaklaşım fonksionları Ψˆ i ler de elemanın doğal koordinat sisteminde er biri ± aralığında değişen ξ η değişkenleri cinsinden tanımlanmıştır. Bu Ψˆ i lerin ana özelliği doğal koordinat sisteminde i düğüm noktasında birim olurken diğer düğüm noktalarında sıfır olmalarıdır. η 4 b b G a a ξ Şekil.. Global ve doğal koordinat sisteminde dikdörtgen eleman şekil fonksionları; Ψi ( ξ η) ( + ξξ i )( + ηηi ) (.) 4 biçimindedir. Burada G dikdörtgen ağırlık merkezidir ve 7

33 G ξ a η b G G G (.) ξ ξ η η ξ ξ η η 4 4 olur ve Denklem. er düğüm noktası için azılırsa; Ψ 4 ( ξ η) ( ξ )( η) Ψ ( ξ η) ( ξ )( + η) (.4) 4 Ψ 4 ( ξ η) ( + ξ )( η) Ψ4 4 ( ξ η) ( + ξ )( + η) elde edilir. İkinci bölümde elde edilen fonksionel incelendiğinde dikdörtgen eleman kullanılarak eleman matrisinin elde edilmesinde Denklem.4 deki ifadelerin ve kısmi türevlerine itiaç duulduğu görülür. Bu kısmi türevler zincir kuralına göre Ψˆ i Ψˆ i ξ ξ Ψˆ i Ψˆ i η η (.5) şeklinde esaplanabilir. Burada ξ a a G η b b G (.6) 8

34 olduğuna göre Denklem.5 ψˆ i ψˆ i a ψ ψˆ i ψˆ i b η (.7) şeklini alır. Bu türev işlemleri i 4 e kadar apılacak olursa ˆ Ψ 4a ( +η) ˆ Ψ 4b ( + ξ ) ˆ Ψ 4a ( η) ˆ Ψ 4b ( ξ ) (.8) ˆ Ψ ˆ 4 Ψ 4a 4a ( η) ( +η) ˆ Ψ 4b ( ξ ) ˆ 4 Ψ 4b ( + ξ ) ifadeleri elde edilir. Şekil fonksionu ifadeleri ile bunların kısmi türevlerinin dikdörtgen eleman üzerinde alan integrasonu eleman matrisinin esaplanmasında gerekmektedir. Hesaplamalar apıldığında i...4 j... 4 olmak üzere [ k ] 4ab / 9 4ab /8 4ab /8 4ab / 6 Ψ ˆ Ψ ˆ 4ab /8 4ab / 9 4ab / 6 4ab /8 i jda (.9.a) 4ab /8 4ab / 6 4ab / 9 4ab /8 A 4ab / 6 4ab /8 4ab /8 4ab / 9 9

35 [ k ] A b / Ψˆ Ψˆ b / 6 i jda b / b / 6 b / 6 b / b / 6 b / b / b / 6 b / b / 6 b / 6 b / b / 6 b / (.9.b) [ k ] A a / Ψˆ Ψˆ a / i jda a / 6 a / 6 a / a / a / 6 a / 6 a / 6 a / 6 a / a / a / 6 a / 6 a / a / (.9.c) elde edilir... Ortotrop Kalın Plak İçin leman atrisinin lde dilmesi leman matrisinin esaplanmasında gerekli olan integral ifadeleri üçüncü bölümdeki Denklem.9.a Denklem.9.b ve Denklem.9.c de elde edilmişti bu ifadeler kullanılarak dikdörtgen eleman matrisi genel olarak elde edilmiştir. Denklem.9 ifadelerinde i satırlara j sütunlara karşı gelen indislerdir. Bunlara göre eleman matrisi 6 µ γ 6µ γ γ µ 6 γ 4 G γ 5 5G z γ 6 5G z γ 7 6µ z 5 6µ µ z γ 8 (4.) 5µ olmak üzere

36 Q Q w [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] [ ] T T T T T T T T T T T T k k k k k k k k k k k k k k k k k k k k k k k K γ γ γ γ γ γ γ (4.) 4. ifadesi ve ük vektörü de; [ ] [ ] [ ] q k q k q k 8 7 γ γ (4.) şeklinde elde edilir.

37 4. STATİK ANALİZ. Bölümde sonlu eleman formuna ugun olarak elde edilen eleman matrisi kullanılarak değişik sınır koşullarına saip ortotrop kalın plakların statik analizini apmak mümkündür. Bu analizin apılabilmesi için Fortran dilinde bir program geliştirilmiştir. Program kodlama ile eleman matrisindeki bilgileri sistem matrisine aktarmaktadır. Oluşturulan sistem matrisi kullanılarak da ortotrop kalın plakların statik analizi apılabilir. 4.. Yaklaşım Testi Literatürde çeşitli sınır koşullarına saip plakların kesin ve aklaşık çözümlerini veren çok saıda aın bulmak mümkündür. Sonlu eleman formuna ugun olarak 4. ve 4. ifadelerinden ararlanılarak sistem matrisi elde edilmiş tüm kenarlarından basit ve ankastre mesnetlenmiş plaklara ugulanmıştır. Simetri koşulları kullanılarak dörtte bir plak için elde edilen sonuçlarda eleman saısı arttırılarak bazı büüklükler için kesin çözümlere aklaşım incelenmiş ve aklaşımın alt ve üst limitleri olduğu gözlenmiştir. Benzer aklaşım [6] çalışmasında da elde edilmiştir. Ortotrop plaklar için elde edilen eleman matrisinin ve geliştirilen programın geçerliliğini görebilmek için öncelikle G G G G ve z z µ µ z µ z µ kabul edilerek izotrop plağın statik analizi apılmış ve literatürdeki çalışmalarla karşılaştırılmıştır. lde edilen sonuçların uumluluğu gözlendikten sonra da ortotrop kalın plaklar için çözüm apılmıştır.

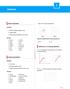
38 4... İzotrop Kalın Plaklar İzotrop kalın plakların çözümü dört tarafından basit ve ankastre mesnetli plaklar için apılmış ve literatürdeki çalışmalarla karşılaştırılmıştır Kenarlarından Basit esnetli Üniform Yüke aruz İzotrop Kalın Plaklar Basit mesnetli izotrop kalın plakların çözümü için Denklem (4.) deki eleman matrisi w t sınır koşulları kullanılarak kodlama ile sistem n matrisi elde edilmiştir. Sistem matrisi farklı eleman saıları için elde edilmiş ve formülasonun stabilitesini göstermek üzere sonuçlar Tablo 4. de farklı eleman saıları için w çökme ve momenti için boutsuz olarak verilmiştir ve literatürdeki mevcut çalışmalarla karşılaştırılmıştır. Tabloda er alan boutsuz büüklükler için tek ve çift saılı elemanlara göre aklaşım Şekil 4. ve Şekil 4. de grafik olarak gösterilmiştir. Yaklaşımın tek ve çift saılı elemanlara göre alt ve üst limitleri olduğu gözlenmiştir. Benzer gözlem daa önce [6] çalışmasında da vurgulanmıştır. Basit mesnet a a Basit mesnet (a) (aa) (a) Basit mesnet Basit mesnet a a Şekil 4.. : Kenarlarından Basit esnetli Dikdörtgen Plak

39 Tablo 4.. : Kenarlarından basit mesnetli üniform aılı üke maruz izotrop kalın plakta eleman saına göre çökme ve moment değerleri (. µ. a 5 ) N ( a a) w 4 ( w qa ) ma ( a a) ( qa ) ma [] K [6] R- [6] H [6] Kama Deformasonu teorisi Klasik plak teorisi Reissner-indlin teorisi Yüksek mertebe teorisi (N leman saısı) 4

40 ÇÖK w(aa) ÇÖK TK SAYILI LANLAR ÇİFT SAYILI LANLAR LAN SAYISI Şekil 4.. : İzotrop kenarlarından basit mesnetli üniform üke maruz kalın plakta çökme için aklaşım testi ĞİL ONTİ ONT (aa) TK SAYILI LANLAR ÇİFT SAYILI LANLAR LAN SAYISI Şekil 4.. : İzotrop kenarlarından basit mesnetli üniform üke maruz kalın plakta eğilme momenti için aklaşım testi 5

41 4... Kenarlarından Ankastre esnetli Üniform Yüke aruz İzotrop Kalın Plaklar Ankastre mesnetli izotrop kalın plakların çözümü için ine Denklem (4) deki eleman matrisi w sınır koşulları ile birlikte kullanılarak kodlama ile sistem matrisi elde edilmiştir. Farklı eleman ağı için çözüm apıldığında tek ve çift eleman saıları için basit mesnetli kalın plaklar için elde edilen sonuçlarla benzer karakterde olduğu gözlenmiştir. Sonuçlar boutsuz olarak Tablo (4.) ve Şekil (4.5) Şekil (4.6) ve Şekil (4.7) de çökme eğilme ve ankastrelik momentler için verilmiştir. Ankastre mesnet a a Ankastre mesnet (a) (aa) (a) Ankastre mesnet Ankastre mesnet a a Şekil 4.4. : Kenarlarından ankastre mesnetli dikdörtgen plak 6

42 Tablo 4.. : Kenarlarından Ankastre esnetli Üniform Yaılı Yüke aruz İzotrop kalın plakta eleman saına göre çökme ve moment değerleri ( µ. a 5 ) ( Dörtte bir plak ) N w w ( a a) w 4 ( qa ) ( a) qa ( a a) ( a a) qa

43 .. ĞİL ONTİ (aa) ÇÖK w(aa) ONT ÇÖK LAN SAYISI Şekil 4.5. : İzotrop kenarlarından ankastre mesnetli üniform üke maruz kalın plakta w çökme için aklaşım testi TK SAYILI LANLAR ÇİFT SAYILI LANLAR TK SAYILI LANLAR. ÇİFT SAYILI LANLAR LAN SAYISI Şekil 4.6. : İzotrop kenarlarından ankastre mesnetli üniform üke maruz kalın plakta eğilme momenti için aklaşım testi 8

44 .45.4 ANKASTRLİK ONTİ (a) ONT.5..5 TK SAYILI LANLAR. ÇİFT SAYILI LANLAR LAN SAYISI Şekil 4.7. : İzotrop kenarlarından ankastre mesnetli üniform üke maruz kalın plakta ankastrelik momenti için aklaşım testi 4... Ortotrop Kalın Plaklar İzotrop plakların çözümü ile kullanılan programın doğruluğu test edilmiş ve ortotrop kalın plakların çözümüne geçilmiştir. Kullanılan öntemin ortotrop plaklar için de stabilitesini göstermek için değişik eleman ağları için basit ve ankastre mesnetli ortotrop kalın plaklar çözülmüş ve sonuçlar literatürdeki çalışmalarla karşılaştırılmıştır. Karşılaştırma apılan problemlerde 5 ; µ µ z µ z.5 ; G Gz. 5 ; Gz. ; a 5 olarak w w qa moment için de 4 alınmıştır. Çökme için boutsuz büüklük ( ) 4 qa şeklinde kullanılmıştır ve tablolar boutsuz büüklüklere göre oluşturulmuştur. 9

45 4... Kenarlarından Basit esnetli Üniform Yüke aruz Ortotrop Kalın Plaklar Basit mesnetli ortotrop kalın plakların çözümü için Denklem (4.) deki eleman matrisi w t sınır koşulları ile birlikte kullanılarak kodlama ile n sistem matrisi elde edilmiştir. Sistem matrisi farklı eleman saıları için çözülmüş ve sonuçlar boutsuz olarak Tablo 4. de verilmiştir. Tek ve çift saılar için Şekil 4.8 Şekil 4.9 Şekil 4. daki grafikler incelendiğinde aklaşımın karakter olarak izotrop kalın plaklarda elde edilen sonuçlara benzediği gözlenmiştir. Tablo 4.. : Kenarlarından basit mesnetli üniform aılı üke maruz ortotrop kalın plakta eleman saına göre çökme ve moment değerleri ( a a) w ( a a) ( a a) N w w 4 ( qa ) ( a a) qa ( a a) qa Ç Redd [] Ç Redd [] Ç Redd [] Ç evcut çalışma

46 . ĞİL ONT ONTİ (aa) ÇÖK w(aa) ÇÖK LAN SAYISI Şekil 4.8. : Ortotrop kenarlarından basit mesnetli üniform üke maruz kalın plakta w çökme için aklaşım testi TK SAYILI LANLAR ÇİFT SAYILI LANLAR.6 TK SAYILI LANLAR ÇİFT SAYILI LANLAR LAN SAYISI Şekil 4.9. : Ortotrop kenarlarından basit mesnetli üniform üke maruz kalın plakta eğilme momenti için aklaşım testi

47 .. ĞİL ONTİ (aa) ONT...9 TK SAYILI LANLAR ÇİFT SAYILI LANLAR LAN SAYISI Şekil 4.. : Ortotrop kenarlarından basit mesnetli üniform üke maruz kalın plakta Y eğilme momenti için aklaşım testi 4... Kenarlarından Ankastre esnetli Üniform Yüke aruz Ortotrop Kalın Plaklar Ankastre mesnetli ortotrop kalın plakların çözümü için ine Denklem (4.) deki eleman matrisi w n t sınır koşulları ile birlikte kullanılarak kodlama ile sistem matrisi elde edilmiştir. Farklı eleman ağları için çözüm apılmış ve sonuçlar Tablo 4.4 de verilmiştir. Sonuçlar Şekil 4. Şekil 4. Şekil 4. Şekil 4.4 ve Şekil 4.5 te çökme eğilme ve ankastrelik moment değerleri için verilmiştir.

48 Tablo 4.4. : Kenarlarından ankastre mesnetli üniform aılı üke maruz ortotrop plakta eleman saına göre çökme ve moment değerleri N w w ( a a) w 4 ( qa ) ( a a) ( a a) qa ( a a) ( a a) qa ( a) ( a ) qa ( a) ( a ) qa

49 .6. ÇÖK ÇÖK w(aa).8 TK SAYILI LANLAR.4 ÇİFT SAYILI LANLAR LAN SAYISI Şekil 4.. : Ortotrop kenarlarından ankastre mesnetli üniform üke maruz kalın plakta w çökme için aklaşım testi 7. ĞİL ONTİ ONT (aa) TK SAYILI LANLAR ÇİFT SAYILI LANLAR LAN SAYISI Şekil 4.. : Ortotrop kenarlarından ankastre mesnetli üniform üke maruz kalın plakta eğilme momenti için aklaşım testi 4

50 .4. ĞİL ONTİ (aa) ONT..8.6 TK SAYILI LANLAR.4 ÇİFT SAYILI LANLAR LAN SAYISI Şekil 4.. : Ortotrop kenarlarından ankastre mesnetli üniform üke maruz kalın plakta eğilme momenti için aklaşım testi ANKASTRLİK ONTİ (a) ONT TK SAYILI LANLAR ÇİFT SAYILI LANLAR LAN SAYISI Şekil 4.4. : Ortotrop kenarlarından ankastre mesnetli üniform üke maruz kalın plakta ankastrelik momenti için aklaşım testi 5

51 . ANKASTRLİK ONTİ ONT (a).6. TK SAYILI LANLAR ÇİFT SAYILI LANLAR LAN SAYISI Şekil 4.5. : Ortotrop kenarlarından ankastret mesnetli üniform üke maruz kalın plakta ankastrelik momenti için aklaşım testi 4.. Kalınlık Değişiminin Sonuçlara tkisi Plak kalınlığındaki değişimin sonuçlar üzerindeki etkisi incelenmiş ve plak kalınlığı azaldıkça kama kilitlenmesi olarak bilinen önemli bir problemin söz konusu olmadığı gözlemlenmiştir. Bu durumu daa açık bir şekilde ortaa koabilmek için değişik kalınlıklı izotrop ve ortotrop kalın plak problemleri incelenmiştir İzotrop Kalın Plaklar Değişik kalınlıklara saip izotrop dört tarafından basit ve ankaste mesnetlenmiş üniform aılı üke maruz plak için çözülmüş ve sonuçlar literatürdeki çalışmalarla karşılaştırılmıştır. Karşılaştırma [] ve [5] nolu çalışma ile apılmış literatürde mevcut diğer çalışmalarla da uumlu olduğu gözlemlenmiştir. 6

52 4... Kenarlarından Basit esnetli Üniform Yüke aruz İzotrop Kalın Plaklar Dört tarafından basit mesnetli plakta farklı plak kalınlıkları için çözüm apılmış ve sonuçlar boutsuz parametrelerle Tablo 4.5 de verilmiştir. Tabloda [5] nolu çalışmada detalı olarak incelenen Reissner ve indlin teorilerinin saısal karşılaştırılmasını da görmek mümkündür. Tablo 4.5. : Kenarlarından basit mesnetli üniform aılı üke maruz izotrop kalın plakta a oranlarına göre çökme ve moment değerleri ( Poisson oranı µ. ) a Lee ve arkadaşları [5] Ç w ( a a) w w D 4 qa Salerno& Goldberg [5] Wang ve arkadaşları [5] [] Lee ve arkadaşları [5] ( a a) qa Wang ve arkadaşları [5] Ç indlin Plak Teorisi Reissner plak Teorisi Kama Deformason Teorisi. Bu çalışmada elde edilen sonuçların [5] de Reisner teorisine göre elde edilen sonuçlarla uumlu olduğu açıkça görülmektedir. indlin ile Reissner teorilerine göre karşılaştırılma apıldığında ise sonuçların birebir anı olmadığı açıktır. Bu durum da [5] de vurgulandığı gibi Reissner-indlin plak teorisi ifadesinin kullanımının doğru olmadığını sölemek mümkündür. 7

53 4... : Kenarlarından Ankastre esnetli Üniform Yüke aruz İzotrop Kalın Plaklar Dört tarafından ankastre mesnetli plakta farklı plak kalınlık oranları için elde edilen maksimum çökme eğilme ve ankastrelik moment değerleri boutsuz olarak Tablo 4.6 da boutsuz olarak verilmiştir. Literatürdeki çalışmalarla uumlu olduğu görülmektedir. Tablo 4.6. : Kenarlarından ankastre mesnetli üniform aılı üke maruz izotrop kalın plakta a oranlarına göre çökme ve moment değerleri ( µ. ) a ÇÖZÜLR w ma ( a a) w D qa 4 ( a a) ( a) qa ( a a) qa a ( ) Ç CFS. [7] LT [7] F [7] Ç CFS. [7] LT [7] F [7] Ç CFS. [7] LT [7].. - F [7] İnce Plak [7] Ç CFS LT F Karışık sonlu eleman metodu Kapalı çözüm Lagrange çarpanı metodu Sonlu elemanlar metodu 8

54 4... Ortotrop Kalın Plaklar Ortotrop plaklar farklı mesnet koşulları ve kalınlıklar için incelenmiş ve literatürdeki sonuçlarla karşılaştırılmıştır. Çözüm G Gz. 5 Gz. µ µ. değerlerine göre apılmıştır. z µ z 4... Kenarlarından Basit esnetli Üniform Yüke aruz Ortotrop Kalın Plaklar Dört kenarından basit mesnetli ortotrop plaklar farklı kalınlıklar için çözülmüş ve elde edilen sonuçlar boutsuz parametrelerle Tablo (4.7) ve Tablo (4.8) de verilmiştir. Literatürdeki mevcut diğer çalışmalarla uumlu olduğu da Tablo (4.7) ve Tablo (4.8) daki değerlerle gösterilmiştir. Tablo 4.7. : Kenarlarından basit mesnetli üniform aılı üke maruz ortotrop kalın plakta çökme ve moment değerleri ( b a a ) ÇÖZÜLR ( a a) w ( wd / qa 4 ) ( a a) ( / qa ) ( a a) ( / qa ) Ç F [8] Redd [8] Redd [] PLTOR4 [] PLTOR9 [] Karışık Sonlu leman etodu PLTOR4 4 PLTOR9 9 Düğüm noktalı sonlu eleman Düğüm noktalı sonlu eleman 9

55 Tablo 4.8. : Kenarlarından basit mesnetli üniform aılı üke maruz ortotrop kalın plakta a oranlarına göre çökme moment ve kesme kuvveti değerleri ( 96 dörtte bir eleman ) 4 Boutsuz çökme ve moment ifadeleri; w w( qa ) qa a Ç ( a a) w wd 4 qa R- [6] Ç ( a a) qa R- [6] Ç ( a a) qa R [6] a Ç Q ( a) Q qa R- [6] Ç ( a) Q Y Q qa R [6] Reissner teorisi Reissner-indlin teorisi. 4

56 4... Kenarlarından Ankastre esnetli Üniform Yüke aruz Ortotrop Kalın Plaklar Dört kenarından ankastre mesnetli ortotrop plaklar farklı kalınlıklar için çözülmüş ve elde edilen sonuçlar boutsuz parametrelerle Tablo (4.9) da verilmiştir. Literatürdeki mevcut diğer çalışmalarla da uumlu olduğu gözlenmiştir bu karşılaştırma da Tablo (4.) de verilmiştir. Tablo 4.9. : Kenarlarından ankastre mesnetli üniform aılı üke maruz ortotrop kalın plakta a oranlarına göre çökme ve moment değerleri 4 ( w w( qa ) qa ) a ( a a) w ( a a) ( a a) ( a) ( a) Tablo 4.. : Kenarlarından ankastre mesnetli üniform aılı üke maruz ortotrop kalın plakta çökme ve moment değerleri ( a ) ÇÖZÜLR ( a a) w ( wd / qa 4 ) ( a a) ( / qa ) ( a) ( / qa ) Ç F [8] Redd [8] Redd [] Plteor4 [] Plteor9 [] Karışık Sonlu leman etodu PLTOR4 PLTOR9 4 düğüm noktalı sonlu eleman 9 düğüm noktalı sonlu eleman 4

57 4... Kalınlık Değişiminin İzotrop-Ortotrop Plaklar Üzerindeki tkisinin Değerlendirilmesi Basit mesnetli izotrop ve ortotrop plaklar için a ve a oranlarına 4 göre elde edilen maksimum boutsuz çökme ( w w( qa ) ) değerleri karşılaştırılmış ve izotrop plaklarda kalınlığın etkisi %4.5 iken ortotrop plaklarda bu etkinin %47.9 mertebesine ulaştığı gözlenmiştir. Bu da kalınlığın etkisinin ortotrop plaklarda izotrop plaklara göre daa fazla olduğunu göstermektedir. Basit mesnetli izotrop-ortotrop plaklar için elde edilen sonuçlar boutsuz olarak Tablo 4. de verilmiştir. Benzer sonuç [] de de elde edilmiştir. Tablo 4.. : Kenarlarından basit mesnetli üniform aılı üke maruz izotroportotrop plaklarda çökme değerleri karşılaştırılması a 5 5 ( a a) w İzotrop Ortotrop Farklı Kalınlık ve Oranları İçin Ortotrop Kalın Plakların Çözümü Literatürdeki mevcut çalışmalarda ortotrop plak çözümlerinde farklı kalınlık ve oranlarının sonuçlara etkisi incelenmiştir. Benzer çalışma a 5 5 ve ;.5 ; ; ; 5 ; 4 için dört tarafından basit ve ankastre mesnetli plaklar için apılmıştır. Çözümlerde G G 5 G z. z. µ µ. alınmıştır. z µ z 4

58 4... Dört Kenarından Basit esnetli Üniform Yüke aruz Kalın Ortotrop Plak Yukarıda belirtilen oranlar için kenarlarından basit mesnetli düzgün aılı üke maruz plak çözümü dörtte bir plak için apılmış ve elde edilen boutsuz olarak 4 ( w w( qa ) qa birlikte Tablo 4. ve Tablo 4. te verilmiştir. qa ) ve diğer çalışmalarla Tablo 4.. : Kenarlarından basit mesnetli üniform aılı üke maruz ortotrop kalın plakta a ve oranlarına göre çökme ve moment değerleri a w. 5 Y w Y w Y a w 5 4 Y w Y w Y Tablo 4. de elde edilen sonuçlara bakıldığında oranı arttığında büürken eğilme momenti küçülmektedir. Bu durum plağın tek doğrultuda çalışmaa başladığını göstermektedir. 4

59 .6 ÇÖK w(aa) ÇÖK ( a/ ) Şekil 4.6. : Kenarlarından basit mesnetli üniform aılı üke maruz ortotrop kalın plakta kalınlık - w çökme değişimi ĞİL ONTİ ONT (aa) ( a/ ) Şekil 4.7. : Kenarlarından basit mesnetli üniform aılı üke maruz ortotrop kalın plakta kalınlık eğilme momenti değişimi 44

60 .5 ĞİL ONTİ BURULA ONTI (aa) ( a/ ) Şekil 4.8. : Kenarlarından basit mesnetli üniform aılı üke maruz ortotrop kalın plakta kalınlık eğilme momenti değişimi Tablo 4.. : Kenarlarından basit mesnetli üniform aılı üke maruz ortotrop kalın plakta a ve oranlarına göre çökme değerleri ( G Gz. 6 G. 5 ) z a IF [7] w Ambartsuman's teor [7] ma q Reissner's Teor [7] Ç Reissner teorisi 45

61 4... Dört Kenarından Ankastre esnetli Üniform Yüke aruz Kalın Ortotrop Plak Yukarıda belirtilen oranlar için kenarlarından ankastre mesnetli düzgün aılı üke maruz plak çözümü dörtte bir plak için apılmış ve elde edilen boutsuz değerler 4 ( w w( qa ) qa w ) şeklinde Tablo 4.4 te verilmiştir. Tablo 4.4. : Kenarlarından ankastre mesnetli üniform aılı üke maruz ortotrop Kalın plakta a ve oranlarına göre çökme ve moment değerleri a. 5 w ( a a) ( a a) ( a) w ( a a) ( a) w ( a a) ( a a) ( a) a 5 4 w ( a a) ( a a) ( a) w ( a a) ( a a) ( a) w ( a a) ( a a) ( a)

62 4.4. Farklı Sınır Koşullarına Saip Üniform Yaılı Yüke aruz Ortotrop Kalın Plakların Çözümü Bölüm 4. te dört kenarından ankastre vea basit mesnetli sınır koşullar göz önünde bulunduruldu ve elde edilen sonuçların literatürle uumlu olduğu gösterildi.bu bölümde karışık sınır koşulları olması durumunda da çözümlerin geçerli olduğunun gösterebilmesi için karşılıklı iki kenarı ankastre diğer kenarları basit ve karşılıklı kenarı boşta diğer kenarları basit oturan ortotrop plak problemleri incelenmiştir Karşılıklı İki Kenarı Ankastre Diğer Kenarları Basit esnetli Üniform Düzgün Yaılı Yüke aruz Ortotrop Kalın Plakların Çözümü Karşılıklı iki kenarı ankastre diğer kenarları basit mesnetli üniform aılı üke maruz ortotrop plaklar için apılan çözümde öncelikle izotrop al incelenmiş ve sonuçlar farklı a değerleri için Tablo 4.5 da verilmiştir. Sonuçların uumluluğu gözlendikten sonra Ortotrop plak çözümüne geçilmiş ve a 5 5 ve ;.5 ; ; ; 5 ; 4 µ µ. z z Y z µ z G G G. 5 Gz. değerleri için çözüm apılmış ve sonuçlar Tablo 4.6. da verilmiştir. Basit a a Ankastre (a) Basit (aa) (a) Ankastre a a Şekil 4.9. : İki kenarlarından ankastre diğer kenarlarından basit mesnetli dikdörtgen plak 47

63 Tablo 4.5. : Karşılıklı iki kenarı ankastre diğer kenarları basit oturan üniform düzgün aılı üke maruz izotrop plakta a oranlarına göre çökme moment ve kesme kuvveti değerleri ( µ ) D ( 96 dörtte bir eleman ) ( a a) w ( a a) ( a a) ( a) a wd Ç 4 qa R- [6] Ç qa R- [6] Ç qa R- [6] Ç qa R [6] Q ( a) Q ( a) a Ç Q qa R- [6] Ç Q qa R [6] Reissner-indlin teorisi Reissner teorisi 48

64 Tablo 4.6. : Karşılıklı iki kenarı ankastre diğer kenarları basit oturan üniform düzgün aılı üke maruz ortotrop plakta a ve oranlarına göre çökme moment değerleri D ( µ µ ) ( a a) w ( a a) ( a a) ( a) a 5 wd Ç 4 qa R- [6] ( a a ) Ç qa R- [6] Ç ( a a ) qa R- [6] ( a ) Ç qa R [6] Reissner-indlin teorisi Reissner teorisi 49

65 Tablo 4.7. : Karşılıklı iki kenarı ankastre diğer kenarları basit oturan üniform düzgün aılı üke maruz ortotrop plakta kuvveti değerleri a ve oranlarına göre kesme a Q ( a) Q qa Q ( a) Q qa Ç R- [6] Ç R- [6] Reissner-indlin teor Karşılıklı İki Kenarı Boşta Diğer Kenarları Basit esnetli Üniform Düzgün Yaılı Yüke aruz Ortotrop Kalın Plakların Çözümü Karşılıklı iki kenarı boşta diğer kenarları basit mesnetli düzgün aılı üke maruz ortotrop plak için apılan çözümde öncelikle izotrop al incelenmiş ve sonuçlar farklı a lar için Tablo 4.8 de verilmiştir. 5

66 Sonuçların uumluluğu gözlendikten sonra ortotrop plak çözümüne geçilmiş ve a 5 5 ve ;.5 ; ; ; 5 ; 4 µ µ. G G G. 5 z z Y Gz. Tablo 9 da verilmiştir. z µ z değerleri için çözüm apılmış ve sonuçlar Basit a a Serbest (a) Basit (aa) (a) Serbest a a Şekil 4.. : İki kenarlarından serbest diğer kenarlarından basit mesnetli dikdörtgen plak Tablo 4.8. : Karşılıklı iki kenarı boşta diğer kenarları basit oturan üniform düzgün aılı üke maruz izotrop plakta a oranlarına göre çökme moment ve kesme kuvveti değerleri( 96 dörttebir eleman ) D ( µ ) a w ( a a) w ma Ç D qa 4 R- [6] w a w ( a) D qa ( ) Ç 4 R- [6] ( a a) ( a a ) Ç qa R- [6] ( a) a qa Ç ( ) R- [6] Q ( a) Q Ç ( a ) qa R Reissner-indlin teor. [6] 5