İKİ SAFHALI ÖRNEKLEME YÖNTEMİNDE ORTALAMA TAHMİN EDİCİLERİ MEAN ESTIMATORS IN TWO PHASE SAMPLING
|
|
|
- Gülbahar Yeşil
- 7 yıl önce
- İzleme sayısı:
Transkript
1 İİ SAFHALI ÖRNELEME ÖNTEMİNDE ORTALAMA TAHMİN EDİİLERİ MEAN ESTIMATORS IN TWO PHASE SAMPLING NİLGÜN ÖGÜL Hacttp Ünivrsitsi Lisansüstü Eğitim-Öğrtim v Sınav öntmliğinin İSTATİSTİ Anabilim Dalı İçin Öngördüğü ÜSE LİSANS TEİ olarak haırlanmıştır. 7
2 Fn Bilimlri Enstitüsü Müdürlüğü'n, Bu çalışma jürimi taraından İSTATİSTİ ANABİLİM DALI 'nda ÜSE LİSANS TEİ olarak kabul dilmiştir. Başkan :... rd. Doç. Dr. aprak Aru ÖDEMİR Ü (Danışman) :.... Pro. Dr. Hüla ÇINGI Ü :... Doç. Dr. m ADILAR ONA Bu t.../.../... tarihind Enstitü öntim urulunca kabul dilmiştir. Pro.Dr. Erdm AGAN FEN BİLİMLERİ ENSTİTÜSÜ MÜDÜRÜ
3 İİ SAFHALI ÖRNELEME ÖNTEMİNDE ORTALAMA TAHMİN EDİİLERİ Nilgün Ögül Ö Bu çalışmada, iki sahalı örnklm öntmi tanıtılmış v bu örnklm öntmind kitl ortalaması tahmini için önriln çşitli oransal v rgrson tahmin dicilr inclnmiştir. Anı amanda bu tahmin dicilrin an v hata karlr ortalamaları ld dilmiştir. Önriln tahmin dicilr birbirlril karşılaştırılmış v hangi koşullar altında hangi tahmin dicilrin tkin oldukları araştırılmıştır. Saısal örnkt, Milli Eğitim Bakanlığı vrilri kullanılmıştır. 6 ılında ÖSS gör rlşn öğrnci saısı ilgilniln dğişkn (), ortaöğrtimdki okul saısı ilk ardımcı dğişkn (), ÖSS haırlık drsan saısı ikinci ardımcı dğişkn () olarak alınmıştır. Önriln tahmin dicilr için an v hata karlr ortalaması hsaplanmıştır. Çalışmanın son bölümünd is, saısal örnklrd ld diln sonuçlara bağlı olarak tahmin dicilrin tkinliklri il ilgili tartışma v orumlar apılmıştır. ANAHTAR ELİMELER: İki sahalı örnklm öntmi, ortalama, oransal tahmin dici, rgrson tahmin dicisi, ardımcı bilgi, tkinlik, an, hata karlr ortalaması. Danışman: Pro.Dr.Hüla Çıngı, Hacttp Ünivrsitsi, İstatistik Bölümü. i
4 MEAN ESTIMATORS IN TWO PHASE SAMPLING Nilgün Ögül ABSTRAT In this stud, two phas sampling is introducd and various man stimators ar studid. Also bias and man squar rror o ths stimators ar obtaind. Estimators ar compard with ach othr and th icint conditions ar invstigatd or ths stimators. In numrical ampl, th data, which ar takn rom Ministr o National Education, ar usd. stud variabl is th numbr o studnts who achivd to ntr th univrsit b OSS am in 6, auiliar variabl is th numbr o high schools and auiliar variabl is th numbr o prparation courss or OSS am. Bias and man squar rror ar calculatd or ths stimators. In th last sction o th stud, discussions and intrprtations ar givn rlatd to man squar rror and icincis o th stimators basd on th rsults o th numrical ampl. E WORDS: Two phas sampling, man, ratio stimator, rgrssion stimator, auiliar inormation, icinc, bias, man squar rror. Advisor: Pro. Dr. Hula ıngı, Hacttp Univrsit, Dpartmnt o Statistics ii
5 TEŞEÜR T çalışmam sürsinc bilgisini, dstğini, hoşgörüsünü bndn sirgmn v bana tin hr aşamasında görüşlril v lştirilril ol göstrn dğrli danışmanım Saın Pro. Dr. Hüla ÇINGI a, katkılarından dolaı Saın Doç. Dr. m ADILAR a, şkati v dstğil hr an anımda olan Saın Öğr. Gr. Dr. Srpil ATAŞ a, ardımlarını sirgmn Uman mal BİRİNİ, manvi dstğini sirgmn çalışma arkadaşlarıma, hr aman anımda olarak bana dstk olan AİLEM içtnlikl tşkkür drim. iii
6 İÇİNDEİLER DİİNİ Saa Ö i ABSTRAT...ii TEŞEÜR.. iii İÇİNDEİLER DİİNİ.iv ÇİELGELER DİİNİ...i SİMGELER VE ISALTMALAR DİİNİ... BİRİNİ BÖLÜM.GİRİŞ. İİNİ BÖLÜM.GENEL BİLGİLER..... öntmin Tanımı..... Bir Örnklmdn Çşitli Tahmin Edicilr.7...Basit tahmin oransal tahmin Doğrusal rgrson tahmini Tahmin Edicinin İstnn Ölliklri Tanım ansılık Etkinlik...4 ÜÇÜNÜ BÖLÜM. İİ SAFHALI ÖRNELEME ÖNTEMİNDE ORANSALTAHMİNEDİİLER lasik Oransal Tahmin Edici iv
7 .. Basit Oransal Tahmin Edici...6. Srivastava Tahmin Edicisi hand Tahmin Edicilri hand tahmin dicisi hand tahmin dicisi-...5.irgra Oransal Tahmin Edicisi Upadhaa tahmin dicisi Singh v Upadhaa Tahmin Edicilri Singh v Upadhaa tahmin dicisi Singh v Upadhaa tahmin dicisi Singh v Upadhaa Tahmin Edicisi Singh v Upadhaa tahmin dicisi Singh Gnllştirilmiş Tahmin Edicisi Prasad, Singh v Singh Tahmin Edicilri Prasad, Singh v Singh tahmin dicisi Prasad, Singh v Singh tahmin dicisi Prasad, Singh v Singh tahmin dicisi Singh v Espjo Tahmin Edicisi DÖRDÜNÜ BÖLÜM 4. İNİRLEME ÖRNELEME ÖNTEMİNDE REGRESON TAHMİN EDİİLERİ lasik Rgrson Tahmin Edici Mohant Tahmin Edicilri v
8 4... Mohant tahmin dicisi Mohant tahmin dicisi irgra Rgrson Tahmin Edicilri irgra rgrson tahmin dicisi irgra rgrson tahmin dicisi Ro Tahmin Edicisi....9 BEŞİNİ BÖLÜM 5. İİ SAFHALI ÖRNELEME ÖNTEMİNDE TAHMİN EDİİ AİLELERİ Singh, Singh v Shukla Tahmin Edici Ailsi Singh, Upadhaa v handra Tahmin Edici Ailsi 95 ALTINI BÖLÜM 6.TAHMİN EDİİLERİN ARŞILAŞTIRILMASI Oransal Tahmin Edicilrinin arşılaştırılması Basit oransal tahmin dici il Srivastava tahmin dicisinin karşılaştırılması Basit oransal tahmin dici il hand tahmin dicisi- in karşılaştırılması Basit oransal tahmin dici il irgra oransal tahmin dicisinin karşılaştırılması hand tahmin dicisi- il irgra oransal tahmin dicisinin karşılaştırılması Upadhaa tahmin dicisi il irgra oransal tahmin dicisinin karşılaştırılması Singh v Upadhaa tahmin dicisi- il Singh v Upadhaa-tahmin dicisi- ün karşılaştırılması..8 vi
9 6..7. Singh v Upadhaa tahmin dicisi- il Singh v Upadhaa tahmin dicisi-4 ün karşılaştırılması Singh v Upadhaa tahmin dicisi- il Singh v Upadhaa tahmin dicisi-4 ün arşılaştırılması Singh v Upadhaa tahmin dicisi- il Singh gnllştirilmiş tahmin dicisi- in karşılaştırılması Singh v Upadhaa tahmin dicisi- il Singh gnllştirilmiş tahmin dicisi- ün karşılaştırılması Singh gnllştirilmiş tahmin dicisi- il Singh gnllştirilmiş tahmin dicisi- nin karşılaştırılması 6... Singh gnllştirilmiş tahmin dicisi- il Singh gnllştirilmiş tahmin dicisi- ün karşılaştırılması Singh gnllştirilmiş tahmin dicisi- il Singh gnllştirilmiş tahmin dicisi- ün karşılaştırılması irgra oransal tahmin dicisi il Prasad, Singh v Singh tahmin dicisi- in karşılaştırılması hand tahmin dicisi- il Prasad, Singh v Singh tahmin dicisi- in karşılaştırılması Upadhaa tahmin dicisi il Prasad, Singh v Singh tahmin dicisi- in karşılaştırılması Upadhaa tahmin dicisi il Prasad, Singh v Singh tahmin dicisi - nin karşılaştırılması Prasad, Singh v Singh tahmin dicisi- il Prasad, Singh v Singh tahmindicisi- nin karşılaştırılması Prasad, Singh v Singh tahmin dicisi- il Prasad, Singh v Singh tahmin dicisi- ün karşılaştırılması Rgrson Tahmin Edicilrinin arşılaştırılması...6 vii
10 6... İki sahalı klasik rgrson tahmin dicisi il Mohant tahmin dicisi- in karşılaştırılması Mohant tahmin dicisi- il irgra rgrson tahmin dicisi- in karşılaştırılması irgra rgrson tahmin dicisi- il irgra rgrson tahmin dicisi- nin karşılaştırılması EDİNİ BÖLÜM 7.SAISAL ÖRNE Torik arşılaştırmaların Ugulamadaki Sonuçları...4 SEİİNİ BÖLÜM 8. SONUÇ VE TARTIŞMA.... ANALAR...6 viii
11 ÇİELGELER DİİNİ Saa Çilg.5.. Tahmin Edici Ailsind Eld Ediln Baı Tahmin Edicilr. Çilg (7.) 6 ılında ÖSS Gör rlşn Öğrnci Saısı, Ortaöğrtimdki Okul Saısı X, ÖSS Haırlık Drsan Saısı Dğişknlrin Ait itl Bilgilri..... Çilg (7.) 6 ılında ÖSS Gör rlşn Öğrnci Saısı, Ortaöğrtimdki Okul Saısı X, ÖSS Haırlık Drsan Saısı Dğişknlrin Ait Örnklm Bilgilri { ( n 765),(n447) } Çilg (7.) Tahmin Edicilrin Tahmin, an v Hata arlr Ortalaması Dğrlri v HO Sıralaması { ( n 765),(n447) }... Çilg(7.4) Ön v Alt Örnklm Büüklüklri... Çilg (7.5) Farklı Ön v Alt Örnklm Büüklüklri İçin Tahmin Edicilrin HO Dğrlri... i
12 SİMGELER VE ISALTMALAR DİİNİ B HO TE Xˆ O Ç itl Rgrson atsaısı Hata arlr Ortalaması Tahmin Edici X Dğişkni için itl Ortalaması Tahmini Oransal Tahmin Edici Çarpımsal Tahmin Edici SO İki Sahalı Oransal Tahmin Edici SÇ İki Sahalı Çarpımsal Tahmin Edici BO Basit Oransal Tahmin Edici s Srivastava Tahmini Edicisi hand Tahmin Edicisi- hand Tahmin Edicisi- U irgra Oransal Tahmin Edicisi Upadhaa Tahmin Edicisi SD Sisodia v Dwivdi Tahmin Edicisi * Sarl Tahmin Edicisi us Upadhaa v Singh Tahmin Edicisi- us Upadhaa v Singh Tahmin Edicisi- su Singh v Upadhaa Tahmin Edicisi- su Singh v Upadhaa Tahmin Edicisi- su Singh v Upadhaa Tahmin Edicisi- su4 Singh v Upadhaa Tahmin Edicisi-4 () sg Singh Gnllştirilmiş Tahmin Edicisi- ( ) sg Singh Gnllştirilmiş Tahmin Edicisi- ( ) sg Singh Gnllştirilmiş Tahmin Edicisi- sg Singh GnllştirilmişTahmin Edicisi Prasad, Singh v Singh Tahmin Edicisi-
13 (,β ) Prasad, Singh v Singh Tahmin Edicisi- (,β,γ ) Prasad, Singh v Singh Tahmin Edicisi- oç Singh v Espjo Tahmin Edicisi SR İki Sahalı lasik Rgrson Tahmin Edicisi M Mohant Tahmin Edicisi- M Mohant Tahmin Edicisi- irgra Rgrson Tahmin Edicisi- irgra Rgrson Tahmin Edicisi- R Ro Tahmin Edicisi SSS Singh, Singh v Shukla Tahmin Edici Ailsi t t t Singh, Upadhaa v handra Tahmin Edici Ailsi- Singh, Upadhaa v handra Tahmin Edici Ailsi- Singh, Upadhaa v handra Tahmin Edici Ailsi- i
14 BİRİNİ BÖLÜM. GİRİŞ İnsanların mantıkları ardımıla bir karar vrmk amacıla kullandıkları öntmlrdn biri örnklm öntmidir. Günümüd, iik, kima, bioloji gibi n dallarında, çşitli mühndislik dallarında, tıp, ca, diş gibi sağlık bilimlri v sosal bilimlrd apılan pk çok araştırmada; kamuou oklamalarında v paarlama araştırmalarında, örnklm öntmindn ararlanılır (Çıngı, 994). Araştırma sonuçlarının gçrli, güvnilir v kullanılabilir olması için vrilrin toplandığı kitlnin ölliği çok önmlidir. En doğru sonuç, aranan bilginin ld dilcği kitlnin tümündn ld diln sonuçtur. Ancak hr aman bu olanaklı dğildir. Öllikl kitl çok büük olduğunda bunu apmak son drc ordur. Bunun için araştırmacılar kitlnin tümünü inclmk rin blirli bir örnklm ürind çalışmak orundadırlar. Ancak baı örnklmlr kitli tümül tmsil drkn baı örnklmlrd bu tmsil oktur. Örnğin bir damla kan vücuttaki bütün kanı tmsil dbilir, ancak bir okuldan sçiln öğrnci tüm okulu tmsil tmbilir. Bu ndnl kişilrin nasıl sçildiği çok önmlidir. Örnklm sürci, örnklm çkimi v tahmin olmak ür iki ksim arılmıştır. Araştırmalarda amaç, ii bir örnklm il ansı, tutarlı v duarlı tahminlr apabilmktir. İi bir örnklm, kitl n ugun örnklm öntminin blirlnmsindn sonra bu öntm gör örnklm büüklüğünün saptanmasıla ld dilbilir. Ugun örnklm öntminin blirlnmsi paramtr ilişkin örnklm varansının n küçük apılmasıla mümkündür. Bu ndnl ugun örnklm öntminin sçimi istatistikt önmli bir r tutar (Çıngı, 994).
15 Bu t çalışmasında amaç, iki sahalı örnklm öntmind apılan çşitli ortalama tahmin dicilrini tanıtmak, bu tahmin dicilrin anlarını v hata karlr ortalamalarını (HO) inclmk, bu tahmin dicilri birbirlril karşılaştırmak v arıca saısal örnklr vrrk konunun daha ii anlaşılmasını sağlamaktır.
16 İİNİ BÖLÜM. GENEL BİLGİLER.. öntmin Tanımı N birimdn oluşan sonlu bir kitld kitl ortalaması tahmin dilmk istnsin. itl ortalaması birçok tahmin öntmil tahmin dilbilir. Basit tahmin bilinn n klasik tahmin öntmidir. İlgilniln dğişkn il üksk ilişkili olan bir ardımcı dğişknin kullanılmasıla tahminlr daha duarlı olmaktadır. ardımcı dğişkn bilgisi oransal, rgrson v çarpımsal tahmin dicilrd kullanılır. Ancak baı araştırmalarda, ardımcı dğişkn ait kitl bilgisin ulaşılamaabilir. Bu durumda iki sahalı örnklm öntmi kullanılır. Bu öntm, ardımcı dğişkn ait kitl bilgilrinin ld dilmsind, hm ugulama bakımdan hm d düşük malitli olması bakımından trcih diln bir örnklm öntmidir. Bu örnklm öntmind amaç, ilk örnklm ardımıla X ardımcı dğişknin ait kitl bilgilrinin n tkin şkild tahminini sağlamak v ikinci sahada sçiln alt örnklmd n tkin tahminini ld tmktir. Bu bakımdan örnklmlrin sçim öntmi çok önmli rol onamaktadır. Bu örnklm öntmi iki sahada grçklşir. İlk sahada X dğişknin ait bilgilrin tahmini için bir örnklm sçilir. Birinci sahada sçiln örnklm ön örnklm (primar-sampl) dnir v s il iad dilir. Ön örnklm, N büüklüğündki kitldn ugun bir örnklm öntmil rin konularak a da konulmadan sçilir v n ( n < N) birimdn oluşur. s örnklmi tamamn X dğişkninin bilgilrinin tahminind kullanılan örnklmdir. X dğişkninin bilgilrinin tahminind ikinci bir ardımcı dğişkn () kullanılabilir. Ön örnklmd X v dğişknlri gölnir. Ön örnklm n kadar büük olursa tahminlrin duarlılığı v doğruluğu o kadar çok artmaktadır. Bu üdn sçim aşamasında ön örnklm büük tutulmaa çalışılır.
17 X dğişknin ait grkli bilgilrin tahmin dilmsindn sonra ikinci sahaa gçilir. İkinci sahada, dğişkninin kitl ortalaması, birinci sahada ld diln X ardımcı dğişkninin bilgilri ardımıla tahmin dilir. İkinci sahada dğişkninin tahmini için bir örnklm sçilir. İkinci sahada sçiln örnklm alt örnklm (sub-sampl) dnir v s il iad dilir. Alt örnklm, ön örnklmdn ugun bir örnklm öntmil rin konularak a da konulmadan sçilir v n ( n n ) < birimdn oluşur. Bu durumda iki örnklm birbirin bağımlı olarak sçilmiş olur. Alt örnklmin büüklüğü d tahminlrin duarlılığı v doğruluğu bakımından çok önmlidir. Örnklm sçimlrind dikkat dilmsi grkn n önmli nokta örnklm büüklüklridir. Hr iki örnklmin büüklüğünün n kadar olması grktiği kararı tahminlrin duarlılıklarında önmli bir tki aratacaktır. Alt örnklm büüklüğü ön örnklm büüklüğündn ala olmamalıdır. Ön örnklm n kadar büük olursa tahminlrin duarlılığı da o kadar ala olacaktır. Bu üdn grk ön örnklmin grks alt örnklmin sçilmsind örnklmlrin büüklüğü, örnklmlrin hangi örnklm öntmil sçilcği v hangi tahmin dicilrin kullanılacağı, tahminlrin duarlılığı v doğruluğu açısından çok önmli olmaktadır. Bu çalışmada ön v alt örnklmlr rin konmadan basit rasgl örnklm il sçilcktir. İki sahalı örnklm öntmind ön v alt örnklm sçimi Şkil.. d göstrildiği gibi olmaktadır. 4
18 N n n X v dğişknlri gölnir. X, v dğişknlri gölnir Şkil.. : İki Sahalı Örnklm öntmind Örnklm Sçimi İki sahalı örnklm öntmind, alt örnklmin ön örnklmdn bağımsı olarak sçildiği durum da sö konusudur. Bu durumda, ön örnklm v alt örnklm kitldn ugun bir örnklm öntmil rin konularak a da rin konulmadan sçilir. Dolaısıla hr iki örnklm d bağımsı olarak sçilir (Diana v Tommasi, 4). Ancak bu durum çok agın olmaan bir durum v ilk duruma gör ugulaması daha or v daha masralıdır. Bu üdn iki sahalı örnklm öntmind, alt örnklmin kitldn sçildiği durumda önriln tahmin dicilr sınırlıdır. İki sahalı örnklm öntmi ilk k 98 ılında Nman taraından ugulanmıştır (Singh, ). Mohant(967), oransal v rgrson tahminlrini iç iç kullanarak incirlm rgrson tahmin dicilri önrmiştir. hand(975), oransal v çarpımsal tahmin dicilri iç iç kullanarak çşitli incirlm oransal tahmin dicilr önrmiştir. 5
19 irgra (98, 984),hand ın önrmiş olduğu tahmin dicilri gliştirrk iç iç oransal-rgrson v rgrson-rgrson incirlm tahmin dicilr önrmiştir. Singh, Singh v Shukla (994), iki sahalı örnklm öntmind kitl ortalaması için bir tahmin dici ailsi önrmişlrdir. Bu tahmin dici ailsind iki ardım dğişkn kullanılmıştır. Singh v Upadhaa (995; ), çşitli incirlm oransal tahmin dicilr önrmişlrdir. Sarl (964), Sisodia v Dwivdi (98), Singh v ahran (99), Upadhaa v Singh (999) tahmin dicilrini gliştirrk iki sahalı örnklm öntmind çşitli oransal tahmin dicilr önrmişlrdir. Singh (), Singh v Upadhaa (995, ) tahmin dicilrind dğişim katsaısı rin standart sapma bilgisini kullanarak ni tahmin dicilr önrmişlrdir Prasad, Singh v Singh (), Srivnkataramana v Trac (98, 98) nin önrdiği dönüşümü kullanarak altrnati bir incirlm oransal tahmin dici önrmişlrdir. Anı amanda, Walsh (97) v Rdd (974) nin önrdiklri tahmin dicilri gliştirrk ni bir incirlm tahmin dici daha önrmişlrdir Ro (), iki ardımcı dğişkn kullanarak ansı bir incirlm rgrson tahmin dicisi önrmiştir. Singh, Upadhaa v.handra (4), iki sahalı örnklm öntmind kitl ortalaması için üç tan tahmin dici ailsi önrmişlrdir. Singh v Espjo(7), Singh v Espjo () oransal-çarpımsal tahmin dicisini gliştirrk ni bir tahmin dici önrmişlrdir. Hartl v Ross (954), Srivastava, Srivastava v har (989), Srivnkataramana v Trac (989), Sahoo v Sahoo (99), Ahmd (998), Upadhaa v Srivastava 6
20 (), handra v Singh (), Diana v Tommasi (, 4) iki sahalı örnklm öntmind tahmin dicilr önrn diğr araştırmacılardır. Td, iki sahalı örnklm öntmind, kitl ortalamasının tahminind kullanılan tahmin dicilr tanıtılmış, bu tahmin dicilrin anı v hata karlr ortalamaları hsaplanmıştır. Arıca, tahmin dicilr, ugun tahmin dicilrl karşılaştırılmış v hangi koşullar altında bu tahmin dicilrin daha tkin oldukları bulunmuştur. Bu çalışmada iki sahalı örnklm öntmind, ön v alt örnklmin şit olasılıklı, rin konmadan basit rasgl örnklm il sçilmsi durumunda, kitl ortalaması için gliştirilmiş tahmin dicilr inclncktir v bu tahmin dicilr tkinlik önündn karşılaştırılacaktır. Arıca ugun bir vri kümsi sçilrk, bu tahmin dicilrl ilgili saısal bir örnk apılacaktır. Saısal örnkt tahmin dicilr, tkinlik açısından inclncktir... Bir Örnklmdn Çşitli Tahmin Edicilr... Basit tahmin Sonlu büüklüktki kitldn n büüklüğünd hrhangi öntml bir örnklm sçilsin. N birimdn oluşan sonlu bir kitldki kitl ortalaması tahmin dilmk istnsin. kitl ortalaması için bilinn n klasik tahmin basit tahmin öntmidir. Basit tahmin, tahmin dilmk istnn dğişknin örnklm ortalaması şklind vrilmktdir. kitl ortalaması için basit tahmin, n i i n (.) şklinddir. 7
21 ... Oransal tahmin Sonlu büüklüktki kitldn n büüklüğünd hrhangi öntml bir örnklm sçilsin. Örnklm birimlrinin iki ölçümü i v i il göstrilbilir. Eğr i i oranı örnklm birimindn örnklm birimin ala dğişknlik göstrmiorsa, bunların örnklm toplamları oranı da örnklm uaının hr bir noktasından diğr noktasına ala bir dğişknlik göstrm. İki dğişkn arasındaki ilişki başlangıç noktasından gçn bir doğru dnklmil göstrilbilir is, bu durumda bu dğişknlrdn biri ardımıla diğri tahmin dilbilir. Böl bir tahmin oransal tahmin adını alır. Burada, ortalaması tahmin dilck dğişkn, ardımcı dğişkn X olsun. Oransal tahminin apılabilmsi için ardımcı dğişkn ait kitl ortalamasının bilinmsi grkir. Eğr bilinmior is, kitl ortalaması iki sahalı örnklm il tahmin dilbilir. Oransal tahmin iki dğişkn arasındaki ilişkinin poiti olduğu durumda kullanılan bir tahmindir. Eğr iki dğişkn arasındaki ilişki ngati is çarpımsal tahmin kullanılır (Çıngı,994). ardımcı dğişkn kitl ortalamasının bilindiği durumda, iki dğişkn arasındaki ilişkinin poiti v ngati olduğu durumlarda oransal v çarpımsal tahminlr sırasıla, X O, (.) Ç (.) X şklinddir. ardımcı dğişkn kitl ortalamasının bilinmdiği, iki dğişkn arasındaki ilişkinin poiti v ngati olduğu durumlarda oransal v çarpımsal tahminlr sırasıla, 8
22 Xˆ SO (.4) SÇ (.5) Xˆ şklinddir. Burada, n i dğişkninin örnklm ortalaması, (.6) n i n i X ardımcı dğişkninin örnklm ortalaması, (.7) n i N X i X ardımcı dğişkninin kitl ortalaması, (.8) N i Xˆ n n i i X ardımcı dğişkninin kitl ortalamasının tahminidir. (.9) Xˆ tahmini, çşitli tahmin dicilr v çşitli örnklm öntmlri kullanılarak n tkin şkild ld dilm çalışılır. Bu ndnl bu tahminin ld dilcği ön örnklmin sçim öntmi v kullanılan tahmin dici çok önmlidir. Ön örnklmin sçimi basit rastgl örnklm, gnişliğ orantılı olasılıklarla küm örnklmsi gibi çşitli örnklm öntmlri kullanılarak grçklştirilbilir. Xˆ tahmini, oransal, çarpımsal, v aşağıdaki bölümd anlatılacak olan rgrson tahmin dicilrl v bu tahmin dicilrin iç iç kullanıldığı tahmin dicilrl ld dilbilir. 9
23 Xˆ tahmini iln bölümlrd daha arıntılı şkild vrilcktir.... Doğrusal rgrson tahmini Rgrson tahmin, i v i arasındaki ilişki hrhangi bir doğru dnklmil göstrilbilir is, duarlılığı artırabilmk için başvurulan bir öntmdir. alnıca iki dğişknin ilişkisindn ararlanılarak bir tahmin apılırsa, bu tahmin doğrusal rgrson tahmin; ikidn ala dğişknin ilişkisindn ararlanılarak apılan tahmin d çoklu rgrson tahmin dnilir. N büüklüğünd bir kitldn n büüklüğündki bir örnklm basit rastgl örnklm il sçilsin. i v i il göstriln iki dğişkn arasındaki ilişki, dülm ürind bir doğru il tmsil dilbilior is, i-inci örnklm birimin gör bu doğrunun ğimi, b i (.) i olur. Burada, i bağımlı, i bağımsı dğişkn olarak alınmaktadır. Buna gör doğrunun dnklmi, i ( ) b (.) i şklind ld dilir. Bnr şkild i nin kitl ortalaması nin doğrusal rgrson tahmini, dr ( X ) b (.) apılabilir. Bu şitlikt b, örnklmdn n küçük karlr öntmil tahmin diln rgrson katsaısı olup,
24 ( i ) i b n (.) ( i )( i ) i n şklinddir (Çıngı, 994)... Tahmin Edicinin İstnn Ölliklri.. Tanım N birimli bir kitldn n birimli k saıda örnklm sçilsin. Sçiln örnklm il tahmin dilck kitl paramtrsi θ olsun; kullanılacak tahmin dici θˆ is, sçilck örnklm bağlı olarak k adt arklı tahmin apılabilcktir. Örnk No Tahmin θˆ θˆ θˆ.... k θˆ k
25 θˆ ların bklnn dğri kitl paramtrsi θ nın dğrin şit olacaktır. E ( θˆ ) θ (.4) θˆ ların varansı, Var () θˆ E[ θˆ E() θˆ ] (.5) şklinddir. itl paramtrsi θ il θˆ ların bklnn dğri birbirin şit olmaabilir. Bu durumda aradaki ark an (bias) olarak adlandırılır. an E( θˆ ) θ (.6) şklinddir. Örnklm hatası is andan arklı bir kavramdır v tahmin dici il kitl paramtrsinin grçk dğri arasındaki arktır. Örnklm Hatası θˆ θ (.7) şklinddir. Farklı örnklmlrdn tahmin dilbilck θˆ lar bir dağılım oluştururlar. Bu dağılım için varansa bnr bir ölçü kullanılmaktadır. Hata karlr ortalaması olarak adlandırılan bu ölçü, θˆ lar il θ arasındaki arkların karlrinin bklnn dğridir. Bu tanıma gör hata karlr ortalaması,
26 HO () θˆ E( θˆ θ) (.8) olarak iad dilir. Eşitlik (.8) dki iad ± E( θˆ ) klnrk açılırsa, [ E() θˆ ] [ E() θˆ θ] HO E θˆ (.9) bulunur. Eşitlik (.9) un sağ taraındaki ilk iad θˆ nın varansına, ikinci iad is anın karsin şittir. ( θˆ ) (an) HO Var (.) Varans aritmtik ortalama traındaki dağılımın, hata karlr ortalaması is, kitl paramtrsinin grçk dğri traındaki dağılımının ölçüsüdür. Ancak anın sıır olması durumunda, ( θˆ ) HO( θˆ ) Var olacaktır. itl paramtrsi θ nın tahmini için sçilck n birimli örnklmdn arklı tahmin dicilr kullanılarak arklı tahminlr apılabilir. Burada önmli olan n ii sonucu vrck tahmin dicinin kullanılmasıdır. En ii tahmini sağlaacak tahmin dicinin baı ölliklri taşıması grkmktdir. Bu ölliklr şunlardır.
27 ... ansılık (Unbias ) an θˆ nın bklnn dğri il θ arasındaki ark olarak tanımlanmıştı. Buna gör θˆ nın θ nın ansı tahmin dicisi olabilmsi için E ( θˆ ) il θ arasındaki ark sıır olmalıdır. Diğr bir iad il E ( θˆ ) θ olmalıdır.... Etkinlik ( Eicinc ) itl paramtrsinin tahmini için birdn ala ansı tahmin dici blirlnbilir. Bu durumda, bu tahmin dicilrdn hangisinin kullanılması il daha ii tahmin apılabilcğini blirlmk için tahmin dicilrin varansları blirlnir. Etkinlik, ansı tahmin dicilrin varansları il ilgili bir kavramdır. Bilindiği gibi, birdn ala srinin ortalamaları birbirin akın va şits dağılımların birbirindn arkını ortaa komak için baı ölçülr hsaplanır. Bu ölçülrdn n çok kullanılanı varanstır. Varansı küçük olan srid aritmtik ortalama traında daha oğun bir dağılım olduğu anlaşılır. Burada, konu kitl paramtrsinin grçk dğrin daha akın tahminlr ld tmk olduğuna gör, tkinliğin ölçüsü hata karlr ortalamasıdır. Birdn ala ansı tahmin sökonusu olduğunda, bunlardan hata karlr ortalaması küçük olan tahmin dici kitl paramtrsinin grçk dğri traında daha oğun bir dağılım göstrdiğindn, bu tahmin dicinin trcih dilmsini grktirmktdir. Hata karlr ortalamasının varans il anın karsi toplamına şit olduğu hatırlanırsa, ansı tahmin dicilr sö konusu olduğundan hata karlr ortalaması varansa şit olacaktır. Bu ndnl varansı küçük olan tahmin dicinin trcih dilmsi il hata karlr ortalaması küçük olan tahmin dici trcih dilmiş olur. 4
28 apılan bu açıklamalar tkinlik için iki şart aranması grktiğini ortaa komaktadır. ) θˆ, θ nın ansı tahmin dicisi is, ) ( θˆ ) Var( θ) Var is θˆ, θ nın tkin tahmin dicisidir. Burada θ, kitl paramtrsi θ nın θˆ tn arklı diğr ansı tahmin dicilrini iad tmktdir. Etkinlik il ilgili olarak buraa kadar apılan açıklamalar, tkinliğin görli bir kavram olduğunu ortaa komaktadır. Ancak birdn ala tahmin dici olması durumunda tkinliktn sö dilbilir v varansı küçük olan tahmin dicinin daha tkin olduğu sölnbilir (Turanlı v Güriş, ). 5
29 ÜÇÜNÜ BÖLÜM. İİ SAFHALI ÖRNELEME ÖNTEMİNDE ORANSAL TAHMİN EDİİLER.. İki Sahalı lasik Oransal Tahmin Edici N birimli sonlu bir kitldn rin konmadan basit rastgl örnklm il n birimli bir ön örnklm sçilsin. Bu ön örnklmd dğişkninin kitl ortalaması tahmin dilsin ( Xˆ ). Ön örnklmd dğişkninin kitl ortalamasının tahminind X dğişkni il ilişkili olan ikinci bir ardımcı dğişkni kullanılabilir. X il dğişkni arasındaki korlason katsaısı, X il dğişkni arasındaki korlason katsaısından küçük olacak şkild ikinci ardımcı dğişkninin sçilmsi grkir. Daha sonra dğişknin kitl ortalamasının tahmini için ön örnklmdn n birimli bir alt örnklm daha sçilsin. Bu alt örnklmd, X v dğişknlri tahmin dilrk oransal tahmin apılabilir. Buna gör kitl ortalaması tahmini için iki sahalı klasik oransal tahmin dicisi şu şkild vrilir: Xˆ SO (. ) Xˆ tahmini ön örnklmdn Bölüm (.) d anlatılan ollarla tahmin dilrk çşitli incirlm oransal tahminlr ld dilbilir... Basit Oransal Tahmin Edici Ön örnklmd X dğişkninin kitl ortalaması basit olla tahmin dilrk ( Xˆ ) Eşitlik (.) rin konulur. Bu tahmin dici basit oransal tahmin dici adı vrilir v BO olarak göstrilir. kitl ortalaması tahmini için basit oransal tahmin dici, BO (.) 6
30 olarak vrilir (Ro, ). Burada,, X ardımcı dğişkninin ön örnklm ortalaması, (.) n n i i v sırasıla v dğişkni için alt örnklm ortalamalarıdır. BO tahmin dicisinin anını v hata karlr ortalamasını ld tmk için ark öntmindn ararlanılır. Fark öntmi Fark öntmi, doğrusal olmaan tahmin dicilrin an v hata karlrini bulmada kullanılan bir öntmdir. Bu öntmd tahmin dici, örnklm dğri il paramtr dğrlri arasındaki arklardan ararlanarak nidn oluşturulur. lasik basit oransal tahmini için ark öntmind, ( ), X X X( ) ; X X X( ) (.4) şklind dğrlr tanımlanır. Tahmin dicidki dğişkn saısı kadar ark trimlri tanımlanır. Bu dğişknlrin bklnn dğrlri { ( )} v kovaransları { ( )} E, karlrinin bklnn dğrlri { E ( i )} i E i j aşağıdaki şkilddir: ( ) E( ) E( ) E (.5) 7
31 8 ( ) S E E ( ) S X X X E E ( ) S X X X E E (.6) ( ) S X X X E E ( ) S X X X E E ( ) S XX X X X X E E. (.7) N n : alt örnklm için örnklm oranı N n : ön örnklm için örnklm oranı (.8) ( )( ) ( ) ( ) N i N i i i N i i i X X :X il arasındaki kitl korlason katsaısı (.9) X S : X il arasındaki kitl dğişim katsaısı S : dğişkni için dğişim katsaısı,
32 S : X dğişkni için dğişim katsaısı, (.) X BO tahmin dicisi Eşitlik (.4) tki li trimlr cinsindn aılarak nidn iad dilirs, BO ( ) ( ) ( ) X X BO ( )( )( ) (.) şklind ld dilir (Çıngı, 4 Drs Notları). ( ) İadsi binom srisi açılımından bulunur. < koşulu altında binom srisi n ni i n ( ) n i i ( n i) n i n! n n!i! n n n n ( )( n )...{ n ( i ) } i! n... n n n n n (.) (.) olarak ld dilir (İnal v Güna, 978 ). Eşitlik (.4) t rin, rin, n rin - aılırsa ( ) koşulu altında aşağıdaki gibi açılır : trimi, < ( ) i i i ( )... (.4) Bu şitlikt.drcdn sonraki li trimlr ihmal dilirs, 9
33 ( ) (.5) olarak ld dilir. Eşitlik (.5), Eşitlik (.) t rin konulup çarpımlar apılırsa, ( )( )( ) BO [ ] BO (.6) olarak bulunur. Eşitlik (.6) da.drcdn sonraki li trimlr ihmal dilirs, [ ] BO (.7) olarak ld dilir. BO tahmin dicisinin anı, ( ) ( ) E an BO BO ( ) [ ] BO E E (.8) olarak bulunur. Eşitlik (.8) d; Eşitlik (.5), Eşitlik (.6), Eşitlik (.7) rin konulursa, BO tahmin dicisinin anı, ( ) [ ] BO an ( ) ( ) [ ( ) ] BO an
34 ( ) [ ] an BO an an ( ) BO ( ) ( ) BO (.9) olarak ld dilir. Burada, ( ), dir. BO tahmin dicisinin hata karlr ortalaması, HO ( ) E( ) BO BO ( ) E[ ] HO (.) BO şklinddir. Bklnn dğrd kar alınıp,.drcdn sonraki li trimlr ihmal dilirs hata karlr ortalaması, ( ) E[ ( )] HO (.) BO olarak ld dilir. Eşitlik (.) d; Eşitlik (.6) v Eşitlik (.7) rin konulursa, BO tahmin dicisinin hata karlr ortalaması, HO HO ( ) [ ( )] BO ( ) [ ( ) ( ) ] BO
35 HO HO ( ) BO ( ) [ ( )] BO (.) olarak ld dilir... Srivastava Tahmin Edicisi Srivastava (97), klasik basit oransal tahmin dicii gliştirrk ni bir tahmin dici önrmiştir. kitl ortalaması için önriln tahmin dici: s (.) şklinddir. Burada, sabit bir katsaıdır. s tahmin dicisi Eşitlik (.4) tki li trimlr cinsindn aılarak nidn iad dilirs, s ( ) X X ( ) ( ) s ( )( )( ) (.4) şklind ld dilir. Bu şitliktki iadlr Eşitlik (.) dn ararlanarak açılırsa, ( ) ( )... (.5) ( ) ( )... (.6)
36 olarak bulunur. Eşitlik (.5) v Eşitlik (.6) da.drcdn sonraki li trimlr ihmal dilirs ( ) ( ) (.7) ( ) ( ) (.8) olarak ld dilir. Eşitlik (.7) v Eşitlik (.8), Eşitlik (.4) d rin konulup çarpımlar apılırsa v.drcdn li trimlr ihmal dilirs, s s ( ) [ ( ) ( ) ( ) ( ) (.9) olarak ld dilir. s tahmin dicisinin anı, an ( ) E( ) s s ( ) [ E s ( ) ( ) E (.) olarak bulunur.
37 4 Eşitlik (.) da; Eşitlik (.5), Eşitlik (.6), Eşitlik (.7) rin konulursa, s tahmin dicisinin anı, ( ) [ ( ) ( ) s an ( ) ( ) [ ( ) ( ) s an ( ) ( ) s an ( ) ( ) s an (.) olarak ld dilir. s tahmin dicisinin hata karlr ortalaması, ( ) ( ) s s E HO ( ) [ ( ) ( ) s E HO (.) şklinddir. Bklnn dğrd kar alınıp,.drcdn sonraki li trimlr ihmal dilirs hata karlr ortalaması, ( ) [ ( )] s E HO (.)
38 olarak ld dilir. Eşitlik (.) d; Eşitlik (.6) v Eşitlik (.7) rin konulursa, hata karlr ortalaması, s tahmin dicisinin HO HO ( ) [ ( )] s ( ) [ ( ) ( ) ] s HO ( ) s HO ( ) [ ( )] s (.4) olarak ld dilir. Önriln tahmin dicid, dğrinin optimum dğrinin bulunmasıla hata karlr ortalamasının minimum dğri bulunabilir. Bu minimum dğr, HO sının optimum dğri bulunmak istnn dğr gör türvinin alınıp sııra şitlnmsil bulunur. [ { }] [ HO( )] ( ) s [ ( )] HO s (.5) Eşitlik (.5) dn, (.6) 5
39 olarak bulunur. dğri, Eşitlik (.) d rin konulursa s tahmin dicisinin anı, an ( ) [ ( ) ( ) ] (.7) min s olarak bulunur. dğri, Eşitlik (.4) t rin konulursa ortalaması, s tahmin dicisinin hata karlr HO min ( ) [ ] s (.8) olarak ld dilir..4 hand Tahmin Edicilri hand (975), iki sahalı örnklm öntmind iki tahmin dici önrmiştir. Bunlardan biri incirlm oransal tahmin dici v diğri incirlm çarpımsal tahmin dicidir.4. hand tahmin dicisi- hand (975), iki ardımcı dğişkn kullanarak incirlm oransal tahmin dici önrmiştir. kitl ortalaması için önriln tahmin dici, (.9) şklinddir. Önrdiği tahmin dicid kitl ortalaması X ön örnklmdn ikinci bir dğişkn ardımıla oransal olla tahmin dilmiştir. v ön örnklm ortalamaları; v 6
40 7 alt örnklm ortalamalarıdır., ikinci ardımcı dğişknin ait kitl ortalaması bilinmktdir. tahmin dicisind ikinci bir ardımcı dğişkn kullanıldığı için ark öntmindn ararlanılarak dğişkni için ni bir dğr tanımlanır : ( ) (.4) ( ) E (.4) ( ) S E E (.4) ( ) S E E ( ) ( ) S X X X E E E (.4) ( )( ) ( ) ( ) N i N i i i N i i i : il arasındaki kitl korlason katsaısı ( )( ) ( ) ( ) N i N i i i N i i i X X :X il arasındaki kitl korlason katsaısı (.44) X S : X il arasındaki kitl dğişim katsaısı S : dğişkni için dğişim katsaısı, (.45)
41 8 tahmin dicisi, Eşitlik (.4) v Eşitlik (.4) daki li trimlr cinsindn aılarak nidn iad dilirs, ( ) ( ) ( ) ( ) X X ( )( ) ( )( ) (.46) şklind ld dilir. Bu şitliktki iadlr Eşitlik (.4) tn ararlanarak açılırsa, ( )... (.47) olarak bulunur. Eşitlik (.47) d.drcdn sonraki li trimlr ihmal dilirs, ( ). (.48) olarak ld dilir. Eşitlik (.5) v Eşitlik (.48), Eşitlik (.46) da rin konulup çarpımlar apılırsa v.drcdn li trimlr ihmal dilirs, ( )( )( )( ) [ ] (.49) olarak ld dilir. tahmin dicisinin anı,
42 9 ( ) ( ) E an ( ) [ ] E E (.5) olarak bulunur. Eşitlik (.5) d; Eşitlik (.5), Eşitlik (.6), Eşitlik (.7), Eşitlik (.4), Eşitlik (.4), Eşitlik (.4) rin konulursa, tahmin dicisinin anı, ( ) [ ] an ( ) ( )( ) [ ( )] an ( ) an ( ) ( ) ( ) [ ] an (.5) olarak ld dilir. Burada, dir. tahmin dicisinin hata karlr ortalaması, ( ) ( ) E HO ( ) [ ] E HO (.5) şklinddir. Bklnn dğrd kar alınıp,.drcdn sonraki li trimlr ihmal dilirs hata karlr ortalaması,
43 HO ( ) [ E ] (.5) olarak ld dilir. Eşitlik (.5) t; Eşitlik (.6), Eşitlik (.7), Eşitlik (.4), Eşitlik (.4) rin konulursa, tahmin dicisinin hata karlr ortalaması, HO ( ) [ ] HO ( ) [ ( )( ) ( )] HO HO ( ) ( ) [ ( ) ( )] (.54) olarak ld dilir. HO HO ( ) [ ( )] BO olduğuna gör, ( ) HO( ) [ ( )] BO (.55) olarak da iad dilbilir..4. hand tahmin dicisi- hand (975), iki ardımcı dğişkn kullanarak incirlm çarpımsal tahmin dici önrmiştir. kitl ortalaması için önriln tahmin dici, (.56)
44 şklinddir. Önrdiği tahmin dicid X kitl ortalaması ön örnklmdn ikinci bir dğişkn ardımıla çarpımsal olla tahmin dilmiştir. v ön örnklm ortalamaları; v alt örnklm ortalamalarıdır. ikinci ardımcı dğişknin ait kitl ortalaması bilinmktdir. tahmin dicisi, Eşitlik (.4) v Eşitlik (.4) daki li trimlr cinsindn aılarak nidn iad dilirs, ( ) X ( ) ( ) X( ) ( )( )( ) ( ) (.57) şklind ld dilir. Bu şitliktki ( ) iadsi şitlik (.4) tn ararlanarak açılırsa, ( )... (.58) olarak bulunur. Eşitlik (.58) d.drcdn sonraki li trimlr ihmal dilirs ( ) (.59) olarak ld dilir. Eşitlik (,59), Eşitlik (.57) d rin konulup çarpımlar apılırsa v.drcdn li trimlr ihmal dilirs, ( )( )( )( ) [ ] (.6)
45 olarak ld dilir. tahmin dicisinin anı, ( ) E( ) an ( ) E[ ] an (.6) olarak bulunur. Eşitlik (.6) d; Eşitlik (.5), Eşitlik (.6), Eşitlik (.7), Eşitlik (.4), Eşitlik (.4), Eşitlik (.4) rin konulursa, tahmin dicisinin anı, ( ) [ ] an an ( ) an ( ) (.6) olarak ld dilir. Burada, dir. tahmin dicisinin hata karlr ortalaması, HO ( ) E( ) ( ) E[ ] HO (.6) şklinddir. Bklnn dğrd kar alınıp,.drcdn sonraki li trimlr ihmal dilirs hata karlr ortalaması,
46 HO ( ) [ E ] (.64) olarak ld dilir. Eşitlik (.64) t; Eşitlik (.6), Eşitlik (.7), Eşitlik (.4), Eşitlik (.4) rin konulursa, tahmin dicisinin hata karlr ortalaması, HO ( ) [ ] ( ) [ ( )( ) ( )] HO HO ( ) ( ) [ ( ) ( )] HO (.65) olarak ld dilir..5. irgra Oransal Tahmin Edicisi irgra (98), iki ardımcı dğişkn kullanarak incirlm oransal tahmin dici önrmiştir. kitl ortalaması için önriln irgra tahmin dicisi, [ b ( )] (.66) şklinddir. Önrdiği bu tahmin dicid kitl ortalaması, Xˆ kitl ortalaması tahmini rin konularak oransal olla tahmin dilmiştir. X kitl ortalaması ön örnklmdn ikinci bir dğişkn ardımıla rgrson olla tahmin dilmiştir.
47 v,ön örnklm ortalamaları; v alt örnklm ortalamalarıdır. b, X il arasındaki örnklm rgrson katsaısıdır ikinci ardımcı dğişknin ait kitl ortalaması bilinmktdir. Tahmin dicinin an v hata karlr ortalaması hsaplanırkn örnklm rgrson katsaısı b, kitl rgrson katsaısı β olarak alınır. N ( i X)( i ) β, X il arasındaki kitl rgrson katsaısı (.67) i N ( i ) i tahmin dicisi, Eşitlik (.4) v Eşitlik (.4) daki li trimlr cinsindn aılarak nidn iad dilirs, ( ) ( ) [ X( ) β { ( )}] (.68) X şklind ld dilir. β tahmin dicid cinsindn aılmak istnirs: S β, S S S S S β S S S β (.69) S şklinddir. Burada; β, cinsindn aılırsa, X β (.7) şklind ld dilir. 4
48 5 β, Eşitlik (.68) d rin konulursa, ( )( ) X Eşitlik (.5), Eşitlik (.68) d rin konulup çarpımlar apılırsa v.drcdn li trimlr ihmal dilirs, [ ] (.7) olarak ld dilir. tahmin dicisinin anı, ( ) ( ) E an ( ) [ ] E an (.7) olarak bulunur. Eşitlik (.7) d; Eşitlik (.5), Eşitlik (.6), Eşitlik (.7), Eşitlik (.4), Eşitlik (.4) v Eşitlik (.4) rin konulursa, tahmin dicisinin anı, ( ) [ ] an ( ) ( )( ) an ( ) an
49 an [ ( ) ( ) ( )] (.7) olarak ld dilir. Burada,,, dir. tahmin dicisinin hata karlr ortalaması, HO ( ) E( ) HO ( ) [ E ] (.74) şklinddir. Bklnn dğrd kar alınıp,.drcdn sonraki li trimlr ihmal dilirs hata karlr ortalaması, HO ( ) [ E ( )] (.75) olarak bulunur. Eşitlik (.75) t; Eşitlik (.6), Eşitlik (.7), Eşitlik (.4), Eşitlik (.4) rin konulursa, tahmin dicisinin hata karlr ortalaması, HO HO ( ) [ ] [ ( ) ( )( ) ( )] HO ( ) 6
50 HO ( ) [ ( ) ( )] (.76) olarak ld dilir. HO HO ( ) [ ( )] BO olduğuna gör, ( ) HO( ) ( ) BO (.77) olarak da iad dilbilir..6. Upadhaa tahmin dicisi Upadhaa (99), iki ardımcı dğişkn kullanarak incirlm oransal tahmin dici önrmiştir. kitl ortalaması için önriln Upadhaa tahmin dicisi, [ b ( )] U (.78) b ( ) şklinddir. Önrdiği tahmin dicid, X kitl ortalaması ön örnklmdn ikinci bir dğişkn ardımıla rgrson olula tahmin dilmiştir. ikinci ardımcı dğişknin ait kitl ortalaması bilinmktdir. b v b örnklm rgrson katsaılarıdır. Tahmin dicinin an v hata karlr ortalamasını hsaplarkn örnklm rgrson katsaısı b v b, sırasıla kitl rgrson katsaısı β v β olarak alınır. U tahmin dicisi, Eşitlik (.4) v Eşitlik (.4) daki li trimlr cinsindn aılarak nidn iad dilirs, U ( ) X [ X( ) β ] X ( ) ( ) ( β X ) ( ) 7
51 8 X β, X β olmak ür, ( ) ( ) ( ) ( ) ( ) ( ) U X X X X X X ( ) ( ) ( )( ) ( ) [ ] U X X ( )( ) ( )( ) ( ) [ ] U ( )( ) ( )( ) ( ) [ ] U (.79) şklind ld dilir. Eşitlik (.79) daki köşli parantdki iad, Eşitlik (.4) tn ararlanarak açılırsa v.drcdn sonraki li trimlr ihmal dilirs, ( )( ) ( ) [ ] ( [ ) ( )] (.8) olarak ld dilir. Eşitlik (.79) da Eşitlik (.8) konulup çarpımlar apılırsa v.drcdn li trimlr ihmal dilirs, ( )( ){ ( [ ) ( )}] U
52 U [ ( ) ( ) ( )] (.8) olarak ld dilir. U tahmin dicisinin anı, an ( ) E( ) U U an [ ( ) E ( ) U ( ) ( )] (.8) olarak bulunur. Eşitlik (.8) d; Eşitlik (.5), Eşitlik (.6), Eşitlik (.7), Eşitlik (.4), Eşitlik (.4), Eşitlik (.4) rin konulursa, U tahmin dicisinin anı, an an ( ) [ ( ) ( )] U ( ) [ ( ) ( )] U (.8) olarak bulunur. U tahmin dicisinin hata karlr ortalaması, HO ( ) E( ) U U HO [ ( ) E ( ) U ( ) ( )] (.84) 9
53 şklinddir. Bklnn dğrd kar alınıp,.drcdn sonraki li trimlr ihmal dilirs hata karlr ortalaması, HO [ ( ) ( U ) E ( ) ( ) ( )] (.85) olarak ld dilir. Eşitlik (.85) t; Eşitlik (.6), Eşitlik (.7), Eşitlik (.8), Eşitlik (.4), Eşitlik (.4) rin konulursa, U tahmin dicisinin hata karlr ortalaması, HO ( U ) [ ( ) ( ) ( ) ) ( ] HO HO HO ( ) ( ) ( ) U ( ) [ ( )] U ( ) [ ( )] U (.86) olarak ld dilir..7. Singh v Upadhaa Tahmin Edicilri Singh v Upadhaa (995, ), çşitli incirlm oransal tahmin dicilr önrmişlrdir. Sarl(964), Sisodia v Dwivdi(98), Singh v ahran(99), Upadhaa v Singh (999) tahmin dicilrini gliştirrk incirlm örnklm öntmind çşitli oransal tahmin dicilr önrmişlrdir (Singh, ). 4
54 .7.. Singh v Upadhaa tahmin dicisi- Singh v Upadhaa (995), Sisodia v Dwivdi(98) tahmin dicisini gliştirrk ni bir tahmin dici önrmişlrdir. Sisodia v Dwivdi (98) tahmin dicisi, X SD (.87) şklinddir kitl ortalaması için önriln tahmin dici, su (.88) şklinddir. Önrdiklri bu tahmin dicid, Xˆ kitl ortalaması, ardımcı dğişkni ardımıla Eşitlik (.87) kullanılarak tahmin dilmiştir. kitl ortalaması kitl ortalaması tahmini Xˆ rin konularak oransal olla tahmin dilmiştir. ikinci ardımcı dğişknin ait kitl ortalaması bilinmktdir. katsaısıdır., dğişkninin dğişim su tahmin dicisi, Eşitlik (.4) v Eşitlik (.4) daki li trimlr cinsindn aılarak nidn iad dilirs, su ( ) ( ) X X( ) ( ) su ( )( )( ) 4
55 4 ( )( )( ) su ( )( )( ) su şklind ld dilir. θ olmak ür, ( )( )( ) ( ) us θ (.89) olarak bulunur. Bu şitliktki ( ) θ iadsi, şitlik (.4) tn ararlanarak açılırsa v.drcdn sonraki li trimlr ihmal dilirs, ( ) θ θ θ (.9) olarak bulunur. Eşitlik (.89) da, Eşitlik (.5) v Eşitlik (.9) rin konulup çarpımlar apılırsa v.drcdn li trimlr ihmal dilirs, ( )( )( )( ) su θ θ [ ( )] su θ (.9) olarak ld dilir. su tahmin dicisinin anı,
56 ( ) E( ) an su su an ( ) [ su E θ ( )] (.9) olarak bulunur. Eşitlik (.9) d; Eşitlik (.5), Eşitlik (.6), Eşitlik (.7), Eşitlik (.4), Eşitlik (.4), Eşitlik (.4) rin konulursa, su tahmin dicisinin anı, an ( ) [ su θ ( )] ( ) [ ( )( ) θ ( )] an su an ( ) su θ ( ) [ ( ) θ ( )] an (.9) su olarak ld dilir. su tahmin dicisinin hata karlr ortalaması, HO ( ) E( ) su su HO ( ) [ su E θ ( )] (.94) 4
57 44 şklinddir. Bklnn dğrd kar alınıp,.drcdn sonraki li trimlr ihmal dilirs hata karlr ortalaması, ( ) [ ( ) { ( )] su θ θ E HO (.95) olarak bulunur. Eşitlik (.95) t; Eşitlik (.6), Eşitlik (.7), Eşitlik (.8), Eşitlik (.4), Eşitlik (.4) rin konulursa, su tahmin dicisinin hata karlr ortalaması, ( ) [ ( ) { ( )] su θ θ HO ( ) ( ) ( ) su θ θ HO ( ) ( ) ( ) [ ] su θ θ HO (.96) olarak ld dilir..7.. Singh v Upadhaa tahmin dicisi- Singh v Upadhaa (), Sarl (964) ün öntmini kullanarak ni bir incirlm oransal tahmin dici önrmiştir. Sarl(964) Tahmin Edicisi, k * (.97) şklinddir. Burada, ( ) k dir
58 kitl ortalaması için önriln tahmin dici, su * us (.98) şklinddir Önrdiklri bu tahmin dicid, Xˆ kitl ortalaması, Eşitlik(.97) kullanılarak tahmin dilmiştir. kitl ortalaması, kitl ortalaması tahmini Xˆ rin konularak oransal olla tahmin dilmiştir., X dğişkninin dğişim katsaısıdır. su tahmin dicisi, Eşitlik (.4) v Eşitlik (.4) daki li trimlr cinsindn aılarak nidn iad dilirs, su ( )( ) ( ) k (.99) şklind olur. Eşitlik (.99) da, Eşitlik (.5) rin konulup çarpımlar apılırsa v.drcdn li trimlr ihmal dilirs, su ( ) k k (.) olarak ld dilir. us tahmin dicisinin anı, ( ) E( ) an su su an ( ) E[ k( ) ( k ) ] su (.) 45
59 olarak bulunur. Eşitlik (.) d; Eşitlik (.5), Eşitlik (.6), Eşitlik (.7), Eşitlik (.4), Eşitlik (.4), Eşitlik (.4) rin konulursa, su tahmin dicisinin anı, an an [ ] ( ) ( k ) su ( ) [ k ( ) ( k ) ] su an an ( ) k ( k ) su ( ) [ k ( ) ( k ) ] su (.) olarak ld dilir. su tahmin dicisinin hata karlr ortalaması, HO HO ( ) E( ) su su ( ) [ k( ) ( k )] (.) su şklinddir. Bklnn dğrd kar alınıp,.drcdn sonraki li trimlr ihmal dilirs hata karlr ortalaması, HO [ ( su ) E k ( ) ( k ) k( k )( )] (.4) olarak bulunur. Eşitlik (.4) t; Eşitlik (.6), Eşitlik (.7), Eşitlik (.8), Eşitlik (.4), Eşitlik (.4) rin konulursa, su tahmin dicisinin hata karlr ortalaması, 46
60 47 ( ) ( ) [ ( ) ( )( )] su k k k k HO ( ) ( )( ) { } ( ) [ ( )( )( )] su k k k k HO ( ) ( ) ( ) su k k k k HO ( ) ( ) { } ( ) ( ) ( ) [ ] su k k k k HO (.5) olarak ld dilir..7.. Singh v Upadhaa tahmin dicisi- Singh v Upadhaa (), kndi önrdiklri tahmin dicilri gliştirrk ni bir karışık incirlm oransal tahmin dici önrmişlrdir. Upadhaa v Singh (999) tahmin dicisi, ( ) ( ) us β X β (.6) şklinddir kitl ortalaması için önriln tahmin dici, ( ) ( ) su β β (.7) şklinddir.
61 Önrdiklri bu tahmin dicid, Xˆ kitl ortalaması, ardımcı dğişkni ardımıla Eşitlik (.6) kullanılarak tahmin dilmiştir. ikinci ardımcı dğişknin ait kitl ortalaması bilinmktdir. kitl ortalaması Xˆ kitl ortalaması tahmini rin konularak oransal olla tahmin dilmiştir., ğişkninin dğişim katsaısıdır, β ( ) dğişkninin basıklık katsaısıdır. su tahmin dicisi, Eşitlik (.4) v Eşitlik (.4) daki li trimlr cinsindn aılarak nidn iad dilirs, su ( ) ( ) X ( ) X β β ( ) ( ) ( ) su ( )( ) ( ) β ( ) ( ) β ( ) su ( )( ) ( ) β β ( ) ( ) β β ( ) ( ) su ( )( ) ( ) β β ( ) ( ) şklind bulunur. β β ( ) ( ) θ olmak ür, su ( )( ) ( )( θ ) (.8) olarak ld dilir. Bu şitliktki ( ) θ iadsi, Eşitlik (.4) tn ararlanarak açılırsa v.drcdn sonraki li trimlr ihmal dilirs, 48
62 49 ( ) θ θ θ (.9) olarak bulunur. Eşitlik (.8) d, Eşitlik (.5), Eşitlik (.9) rin konulup çarpımlar apılırsa v.drcdn li trimlr ihmal dilirs, ( )( )( )( ) su θ θ [ ] su θ θ θ θ (.) olarak ld dilir. su tahmin dicisinin anı, ( ) ( ) E an su su ( ) [ ] su θ θ θ θ E an (.) olarak bulunur. Eşitlik (.) d; Eşitlik (.5), Eşitlik (.6), Eşitlik (.7), Eşitlik (.4), Eşitlik (.4) rin konulursa, su tahmin dicisinin anı, ( ) [ ] su θ θ θ E an ( ) ( ) su θ E an ( ) ( ) [ ] su θ an (.)
63 5 olarak ld dilir. us tahmin dicisinin hata karlr ortalaması, ( ) ( ) su su E HO ( ) [ ] su θ θ θ θ HO (.) şklinddir. Bklnn dğrd kar alınıp,.drcdn sonraki li trimlr ihmal dilirs hata karlr ortalaması, ( ) [ ] su θ θ θ θ E HO (.4) olarak bulunur. Eşitlik (.4) t; Eşitlik (.6), Eşitlik (.7), Eşitlik (.8), Eşitlik (.4), Eşitlik (.4) rin konulursa, su tahmin dicisinin hata karlr ortalaması, ( ) [ ] su θ θ θ θ HO ( ) ( ) su θ θ HO ( ) ( ) ( ) [ ] su θ θ HO (.5) olarak ld dilir.
64 .7.4. Singh v Upadhaa tahmin dicisi-4 Upadhaa v Singh (999) diğr tahmin dicisi, ( ) ( ) X β us (.6) β şklinddir. kitl ortalaması için önriln tahmin dici, ( ) ( ) β su 4 (.7) β şklinddir Önrdiklri bu tahmin dicid, Xˆ kitl ortalaması, ardımcı dğişkni ardımıla Eşitlik (.6) kullanılarak tahmin dilmiştir. kitl ortalaması, Xˆ kitl ortalaması tahmini rin konularak oransal olla tahmin dilmiştir. ikinci ardımcı dğişknin ait kitl ortalaması bilinmktdir. katsaısıdır, β ( ) dğişkninin basıklık katsaısıdır., dğişkninin dğişim su4 tahmin dicisi, Eşitlik (.4) v Eşitlik (.4) daki li trimlr cinsindn aılarak nidn iad dilirs, su 4 ( ) ( ) X ( ) X ( ) ( ) ( ) β β su4 ( )( ) ( ) ( ) β ( ) β ( ) su4 ( )( ) ( ) β β ( ) ( ) β ( ) 5
65 5 ( )( ) ( ) ( ) su4 β (.8) şklind bulunur. ( ) θ β olmak ür, ( )( ) ( )( ) 4 su θ (.9) olarak bulunur. Bu şitliktki ( ) θ iadsi, şitlik (.4) tn ararlanarak açılırsa v.drcdn sonraki li trimlr ihmal dilirs, ( ) θ θ θ (.) olarak bulunur. Eşitlik (.9) da, Eşitlik(.5), Eşitlik(.) rin konulup çarpımlar apılırsa v.drcdn li trimlr ihmal dilirs, ( )( )( )( ) 4 su θ θ [ ] su4 θ θ θ θ (.) olarak iad dilir. Buradan sadc i θ dğrlrin bağlı olarak 4 su tahmin dicisinin an v hata karlr ortalaması anı şkild ld dilir. ( ) ( ) [ ] 4 su θ an (.)
66 HO ( ) [ ( ) θ ( θ )] su4 (.).8. Singh Gnllştirilmiş Tahmin Edicisi Singh (); Singh v Upadhaa(995, ) tahmin dicilrin bnr başka incirlm oransal tahmin dicilr önrmişlrdir. Önrdiklri ni tahmin dicilrd dğişim katsaısı rin kitl ortalaması v dğişim katsaısı biliniorsa, bilinior olacaktır. σ kullanılmışlardır. Eğr ikinci ardımcı dğişknin σ standart sapması da atn Tahmin dicilr bir v ik dğrinin tanımlanmasıla gnllştirilmiş şkild iad dilbilir. v σ ( i,, v k,,,n ) (.4) ik i k i i σ ( n örnklmdki ik v v nın örnklm ortalaması ) (.5) V σ ( itl Ortalaması ) (.6) i i i,, için, β( ), β ( ) olarak iad dilir. için önriln tahmin dici: () σ V, i, σ v için, (.7) sg ( ) β için önriln tahmin dici: ( ) β( ) σ sg V, i, β( ) β ( ) σ v ( ) β için önriln tahmin dici: için, (.8) 5
67 54 ( ) ( ) ( ) sg V v σ β σ β, i, ( ) β için vrilir. (.9) Bu önriln tahmin dici gnllştirilrk aşağıdaki şkild iad dilir: i i i i sg V v σ σ, (i,,) (.) sg tahmin dicisi, Eşitlik (.4) v Eşitlik (.4) daki li trimlr cinsindn aılarak nidn iad dilirs, ( ) ( ) ( ) i i i sg σ σ X X ( )( ) ( ) i i i sg σ σ ( )( ) ( ) i i i i sg σ σ σ ( )( ) ( ) i i sg σ (.) şklind bulunur. i i i σ φ olmak ür, ( )( ) ( )( ) i sg φ (.) olarak bulunur.
68 Bu şitliktki ( ) φ i iadsi, Eşitlik (.4) tn ararlanarak açılırsa v.drcdn sonraki li trimlr ihmal dilirs, ( φ ) φ φ i i i (.) olarak bulunur. Eşitlik (.) d, Eşitlik (.5), Eşitlik (.) rin konulup çarpımlar apılırsa v.drcdn li trimlr ihmal dilirs, sg [ i φ i φ φ i φ ] i (.4) olarak iad dilir. Buradan sadc φ i dğrlrin bağlı olarak usg tahmin dicisinin an v hata karlr ortalaması anı şkild ld dilir. an HO ( ) [ ( ) φ ] sg (.5) ( ) [ ( ) φ ( φ )] sg i (.6) i i Burada i,, için; φ, σ φ β( ) ( ) σ, β φ ( ) dir. β β σ ( ).9. Prasad, Singh v Singh Tahmin Edicilri Prasad, Singh v Singh (), çşitli incirlm örnklm tahmin dicilri önrmişlrdir. Bu tahmin dicilr sırasıla aşağıda inclncktir 55
69 .9.. Prasad, Singh v Singh tahmin dicisi- Prasad (), Singh v Singh, Srivnkataramana v Trac (98,98) nin önrdiği dönüşümü kullanarak altrnati bir incirlm oransal tahmin dici önrmişlrdir Srivnkataramana v Trac (98,98) dönüşümü şu şkilddir: U A, i,,,n (.7) i i Burada, A: sabit bir saıı göstrmktdir. kitl ortalaması için önriln tahmin dici, ( Xˆ ) O u Xˆ U u (.8) U olarak vrilir. Burada, u A (.9) E ( u ) U A (.4) şklinddir. Eşitlik (.9) v Eşitlik (.4), Eşitlik (.8) d rin konulursa önriln tahmin dici, A (.4) A olarak vrilir. 56
70 57 tahmin dicisi, Eşitlik (.4) v Eşitlik (.4) daki li trimlr cinsindn aılarak nidn iad dilirs, A A ( ) ( ) ( ) ( ) A A X X ( )( ) ( ) A A ( )( ) ( ) A (.4) olarak bulunur. Burada, θ A olarak iad dilirs v Eşitlik (.5), Eşitlik (.4) d rin konulup çarpımlar apılırsa v.drcdn sonraki li trimlr ihmal dilirs, ( )( )( )( ) θ [ ( ) ] θ θ (.4) olarak ld dilir. PPS tahmin dicisinin anı, ( ) ( ) E an PPS PPS
71 an ( ) [ PPS E θ ( ) ] θ (.44) olarak bulunur. Eşitlik (.44) t; Eşitlik (.5), Eşitlik (.6), Eşitlik (.7), Eşitlik (.4), Eşitlik (.4) rin konulursa, PPS tahmin dicisinin anı, an an an ( PPS ) [ θ( ) ] ( ) [ θ ] PPS ( ) [ ( ) θ ] PPS (.45) olarak ld dilir. PPS tahmin dicisinin hata karlr ortalaması, HO ( ) E( ) PPS PPS HO ( ) [ PPS E θ ( ) ] θ (.46) şklinddir. Bklnn dğrd kar alınıp,.drcdn sonraki li trimlr ihmal dilirs hata karlr ortalaması, HO ( ) [ PPS E θ θ θ ] θ (.47) Eşitlik (.47) d; Eşitlik (.6), Eşitlik (.7), Eşitlik (.4), Eşitlik (.4) rin konulursa, PPS tahmin dicisinin hata karlr ortalaması, 58
72 HO HO HO HO ( ) [ PPS θ θ θ ( )] ( ) [ θ ( θ )] ( ) [ ( ) θ ( θ )] ( ) HO( ) θ ( θ ) BO (.48) olarak ld dilir. Önriln tahmin dicid tanımlanan θ dğrinin optimum dğrinin bulunmasıla hata karlr ortalamasının minimum dğri bulunabilir. Bu minimum dğr, HO sının optimumu bulunmak istnn dğr gör türvinin alınıp sııra şitlnmsil bulunur. HO ( ) [ { ( ) θ ( θ )} ] θ θ HO θ ( ) [ ( θ )] (.49) Eşitlik (.49) dan θ θ olarak bulunur. Tahmin dicidki A sabit katsaısının dğri bulunarak tahmin dicid rin konulursa, θ A A 59
73 A A olarak bulunur. A dğri, Eşitlik(.4) d rin konulduğunda PPS tahmin dicisi, A A ( ) [ ( )] (.5) olarak bulunur. θ dğri, Eşitlik (.45) t rin konulursa PPS tahmin dicisinin anı, an ( ) [ ( ) ] PPS (.5) θ dğri, Eşitlik (.488) d rin konulursa PPS tahmin dicisinin hata karlr ortalaması, HO min ( ) [ ( ) ] (.5) olarak bulunur. 6
74 .9.. Prasad, Singh v Singh tahmin dicisi- Prasad, Singh v Singh (), Walsh(97) v Rdd(974) nin önrdiklri tahmin dicilri gliştirrk ni bir incirlm tahmin dici daha önrmişlrdir. kitl ortalaması için önriln tahmin dici, (, β ) (.5) [ ] [ ( ) ] β ( β) şklinddir Önrdiklri tahmin dicid, v ön örnklm ortalamaları;,, alt örnklm ortalamalarıdır. ikinci ardımcı dğişknin ait kitl ortalaması bilinmktdir.,β : sabit katsaıları göstrmktdir. v β sabitlrinin aldığı dğr gör tahmin dicilr dğişmktdir. (,β) (, ) için, (,β) (, ) için O, (,β) (, ) için ld dilir. (,β ) tahmin dicisi, Eşitlik (.4) v Eşitlik (.4) daki li trimlr cinsindn aılarak nidn iad dilirs, (,β ) ( ) X( ) ( ) ( ) X( ) [ X ][ β( ) ( β) ] (,β ) ( ) ( ) [ ( )]( β ) (,β ) ( )( )[ ( )] ( β ) (.54) 6
75 olarak bulunur. Bu şitliktki, [ ( )] v ( ) β iadlri şitlik (.4) tn ararlanarak açılırsa v.drcdn sonraki trimlr ihmal dilirs, [ [ ( ) ] ( ) ( ) ( ) ] ( β ) ( β β ) (.55) (.56) olarak ld dilir. Eşitlik (.55) v Eşitlik (.56), Eşitlik (.54) t rin konulup çarpımlar apılırsa v.drcdn li trimlr ihmal dilirs, (,β ) [ ( ) ( β β ) β( β )] (.57) olarak ld dilir. (,β ) tahmin dicisinin anı, an ( ) (,β ) (,β ) ( ) E an [ (,β ) ( ) E ( ) ( β β ) β( β )] (.58) olarak bulunur. Eşitlik (.58) d; Eşitlik (.5), Eşitlik (.6), Eşitlik (.7), Eşitlik (.4), Eşitlik (.4),,β Eşitlik (.4) rin konulursa, tahmin dicisinin anı, ( ) 6
76 an (,β ) ( ) [ ( β ( ) β( β )] an [ ] (,β ) ( ) ( ) β( β ) (.59) olarak ld dilir. (,β ) tahmin dicisinin hata karlr ortalaması, HO ( ) (,β ) (,β ) ( ) E HO [ (,β ) ( ) E ( ) ( β β ) β( β )] (.6) şklinddir. Bklnn dğrd kar alınıp,.drcdn sonraki li trimlr ihmal dilirs hata karlr ortalaması, HO (,β ) ( ) [ β β β β ] (.6) olarak bulunur. Eşitlik (.6) d; Eşitlik (.6), Eşitlik (.7), Eşitlik (.8), Eşitlik (.4), Eşitlik (.4) rin konulursa, HO HO (,β ) tahmin dicisinin hata karlr ortalaması, (,β ) ( ) [ β (,β ) ( ) ( ) β β [ β( β )] ( )] (.6) olarak ld dilir. 6
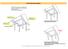
BASİT RASGELE ÖRNEKLEME YÖNTEMİNDE MEDYAN TAHMİN EDİCİLERİ AR. GÖR. SİBEL AL PROF. DR. HÜLYA ÇINGI HACETTEPE ÜNİVERSİTESİ İSTATİSTİK BÖLÜMÜ
 BASİT RASGELE ÖRNEKLEE ÖNTEİNDE EDAN TAHİN EDİCİLERİ AR. GÖR. SİBEL AL PROF. DR. HÜLA ÇINGI HACETTEPE ÜNİVERSİTESİ İSTATİSTİK BÖLÜÜ Kapsam Gnl bilgilr BRÖ yöntmind mdyan tahmin dicilri Tahmin dicilrin
BASİT RASGELE ÖRNEKLEE ÖNTEİNDE EDAN TAHİN EDİCİLERİ AR. GÖR. SİBEL AL PROF. DR. HÜLA ÇINGI HACETTEPE ÜNİVERSİTESİ İSTATİSTİK BÖLÜÜ Kapsam Gnl bilgilr BRÖ yöntmind mdyan tahmin dicilri Tahmin dicilrin
Üstel Dağılım SÜREKLİ ŞANS DEĞİŞKENLERİNİN OLASILIK YOĞUNLUK FONKSİYONLARI
 ..3 SÜREKLİ ŞNS DEĞİŞKENLERİNİN OLSILIK YOĞUNLUK FONKSİYONLRI Üstl Dağılım Sürkli Üniform Dağılım Normal Dağılım Üstl Dağılım Mydana gln iki olay arasındaki gçn sür vya ir aşka ifadyl ilgilniln olayın
..3 SÜREKLİ ŞNS DEĞİŞKENLERİNİN OLSILIK YOĞUNLUK FONKSİYONLRI Üstl Dağılım Sürkli Üniform Dağılım Normal Dağılım Üstl Dağılım Mydana gln iki olay arasındaki gçn sür vya ir aşka ifadyl ilgilniln olayın
LYS Matemat k Deneme Sınavı
 LYS Matmatk Dnm Sınavı. Bir saıı,6 il çarpmak, bu saıı kaça bölmktir? 6. a, b, c saıları sırasıla,, saıları il trs orantılı a b oranı kaçtır? a c 7. v pozitif tamsaılardır.! ifadsi bir asal saıa şittir.
LYS Matmatk Dnm Sınavı. Bir saıı,6 il çarpmak, bu saıı kaça bölmktir? 6. a, b, c saıları sırasıla,, saıları il trs orantılı a b oranı kaçtır? a c 7. v pozitif tamsaılardır.! ifadsi bir asal saıa şittir.
{ } { } Ters Dönüşüm Yöntemi
 KESĐKLĐ DAĞILIMLARDAN RASGELE SAYI ÜRETME Trs Dönüşüm Yöntmi F dağılım fonksiyonuna sahip bir X rasgl dğişknin dağılımından sayı ürtmk için n çok kullanılan yöntmlrdn biri, F dağılım fonksiyonunun gnllştirilmiş
KESĐKLĐ DAĞILIMLARDAN RASGELE SAYI ÜRETME Trs Dönüşüm Yöntmi F dağılım fonksiyonuna sahip bir X rasgl dğişknin dağılımından sayı ürtmk için n çok kullanılan yöntmlrdn biri, F dağılım fonksiyonunun gnllştirilmiş
Mühendisler İçin DİFERANSİYEL DENKLEMLER
 Mühndislr İçin DİFERANSİYEL DENKLEMLER Doç. Dr. Tahsin Engin Prof. Dr. Yunus A. Çngl Sakara Ünivrsitsi Makina Mühndisliği Bölümü Elül 8 SAKARYA - - Mühndislr İçin Difransil Dnklmlr İÇİNDEKİLER BÖLÜM BİRİNCİ
Mühndislr İçin DİFERANSİYEL DENKLEMLER Doç. Dr. Tahsin Engin Prof. Dr. Yunus A. Çngl Sakara Ünivrsitsi Makina Mühndisliği Bölümü Elül 8 SAKARYA - - Mühndislr İçin Difransil Dnklmlr İÇİNDEKİLER BÖLÜM BİRİNCİ
BASİT RASGELE ÖRNEKLEME YÖNTEMİNDE ORANSAL TAHMİN EDİCİLER. Ülkü Hilal Karakülah Hacettepe Üniversitesi, İstatistik Bölümü, İstatistik Anabilim Dalı
 BASİT RASGELE ÖRNEKLEME YÖNTEMİNDE ORANSAL TAHMİN EDİCİLER Ülkü Hilal Karakülah Hacettepe Üniversitesi, İstatistik Bölümü, İstatistik Anabilim Dalı ÖZ Bu çalışmada, basit rasgele örnekleme önteminde, kitle
BASİT RASGELE ÖRNEKLEME YÖNTEMİNDE ORANSAL TAHMİN EDİCİLER Ülkü Hilal Karakülah Hacettepe Üniversitesi, İstatistik Bölümü, İstatistik Anabilim Dalı ÖZ Bu çalışmada, basit rasgele örnekleme önteminde, kitle
VOLEYBOLCULARIN FARKLI MAÇ PERFORMANSLARI İÇİN TEKRARLANAN ÖLÇÜMLER YÖNTEMİNİN KULLANILMASI
 96 OLEBOLCULAIN FAKLI MAÇ PEFOMANSLAI İÇİN TEKALANAN ÖLÇÜMLE ÖNTEMİNİN KULLANILMASI ÖET Gürol IHLIOĞLU Süha KAACA Farklı yr, zaman v matryallr üzrind tkrarlanan dnylr il bir vya birdn fazla faktörün tkisi
96 OLEBOLCULAIN FAKLI MAÇ PEFOMANSLAI İÇİN TEKALANAN ÖLÇÜMLE ÖNTEMİNİN KULLANILMASI ÖET Gürol IHLIOĞLU Süha KAACA Farklı yr, zaman v matryallr üzrind tkrarlanan dnylr il bir vya birdn fazla faktörün tkisi
DÜZCE ÜNİVERSİTESİ TEKNOLOJİ FAKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ EET305 OTOMATİK KONTROL I Dr. Uğur HASIRCI
 DÜZCE ÜNİVERSİTESİ TENOLOJİ FAÜLTESİ ELETRİ-ELETRONİ MÜHENDİSLİĞİ BÖLÜMÜ EET305 OTOMATİ ONTROL I ALICI DURUM HATASI ontrol sistmlrinin tasarımında üç tml kritr göz önünd bulundurulur: Gçici Durum Cvabı
DÜZCE ÜNİVERSİTESİ TENOLOJİ FAÜLTESİ ELETRİ-ELETRONİ MÜHENDİSLİĞİ BÖLÜMÜ EET305 OTOMATİ ONTROL I ALICI DURUM HATASI ontrol sistmlrinin tasarımında üç tml kritr göz önünd bulundurulur: Gçici Durum Cvabı
Bilgi Tabanı (Uzman) Karar Verme Kontrol Kural Tabanı. Bulanık. veya. Süreç. Şekil 1 Bulanık Denetleyici Blok Şeması
 Bulanık Dntlyicilr Bilgi Tabanı (Uzman) Anlık (Kskin) Girişlr Bulandırma Birimi Bulanık µ( ) Karar Vrm Kontrol Kural Tabanı Bulanık µ( u ) Durulama Birimi Anlık(Kskin) Çıkış Ölçklm (Normali zasyon) Sistm
Bulanık Dntlyicilr Bilgi Tabanı (Uzman) Anlık (Kskin) Girişlr Bulandırma Birimi Bulanık µ( ) Karar Vrm Kontrol Kural Tabanı Bulanık µ( u ) Durulama Birimi Anlık(Kskin) Çıkış Ölçklm (Normali zasyon) Sistm
FARKLI SICAKLIKLARDAKİ GÖZENEKLİ İKİ LEVHA ARASINDA AKAN AKIŞKANIN İKİNCİ KANUN ANALİZİ
 FARKLI ICAKLIKLARDAKİ GÖZEEKLİ İKİ LEVHA ARAIDA AKA AKIŞKAI İKİCİ KAU AALİZİ Fthi KAMIŞLI Fırat Ünivrsit Mühndislik Fakültsi Kimya Mühndisliği Bölümü, 39 ELAZIĞ, fkamisli@firat.du.tr Özt Farklı sıcaklıklara
FARKLI ICAKLIKLARDAKİ GÖZEEKLİ İKİ LEVHA ARAIDA AKA AKIŞKAI İKİCİ KAU AALİZİ Fthi KAMIŞLI Fırat Ünivrsit Mühndislik Fakültsi Kimya Mühndisliği Bölümü, 39 ELAZIĞ, fkamisli@firat.du.tr Özt Farklı sıcaklıklara
BÖLÜM 7 TÜRBÜLANSLI SINIR TABAKALAR
 BÖLÜM 7 TÜRBÜLANSLI SINIR TABAKALAR sabit-oğnlkl, sabit-özllikli, harici, türbülanslı sınır tabaka akımları ZB 386 Sınır Tabaka Drs notları - M. TÜRBÜLANSLI SINIR TABAKALAR Türbülans analizindki grksinimlr
BÖLÜM 7 TÜRBÜLANSLI SINIR TABAKALAR sabit-oğnlkl, sabit-özllikli, harici, türbülanslı sınır tabaka akımları ZB 386 Sınır Tabaka Drs notları - M. TÜRBÜLANSLI SINIR TABAKALAR Türbülans analizindki grksinimlr
DESTEK DOKÜMANI. Mali tablo tanımları menüsüne Muhasebe/Mali tablo tanımları altından ulaşılmaktadır.
 Mali Tablolar Mali tablo tanımları mnüsün Muhasb/Mali tablo tanımları altından ulaşılmatadır. Mali tablolarla ilgili yapılabilc işlmlr ii gruba ayrılır. Mali Tablo Tanımları Bu bölümd firmanın ullanacağı
Mali Tablolar Mali tablo tanımları mnüsün Muhasb/Mali tablo tanımları altından ulaşılmatadır. Mali tablolarla ilgili yapılabilc işlmlr ii gruba ayrılır. Mali Tablo Tanımları Bu bölümd firmanın ullanacağı
Makine Öğrenmesi 4. hafta
 ain Öğrnmsi 4. hafta Olasılı v Koşullu Olasılı ays Tormi Naïv ays Sınıflayıcı Olasılı Olasılı ifadsinin birço ullanım şli vardır. Rasgl bir A olayının hrhangi bir olaydan bağımsız olara grçlşm ihtimalini
ain Öğrnmsi 4. hafta Olasılı v Koşullu Olasılı ays Tormi Naïv ays Sınıflayıcı Olasılı Olasılı ifadsinin birço ullanım şli vardır. Rasgl bir A olayının hrhangi bir olaydan bağımsız olara grçlşm ihtimalini
VİNÇTE ÇELİK KONSTRÜKSİYON
 0 Haziran www.guvn-kua.h VİNÇTE ÇEİ ONSTRÜSİON ÖZET _09 M. Güvn UT Smbollr v anaklar için "_00_ClikonsruksionaGiris.do" a bakınız. oordina ksnlri "GENE GİRİŞ" d blirildiği gibi DIN 8800 T gör alınmışır.
0 Haziran www.guvn-kua.h VİNÇTE ÇEİ ONSTRÜSİON ÖZET _09 M. Güvn UT Smbollr v anaklar için "_00_ClikonsruksionaGiris.do" a bakınız. oordina ksnlri "GENE GİRİŞ" d blirildiği gibi DIN 8800 T gör alınmışır.
DERS 9. Grafik Çizimi, Maksimum Minimum Problemleri
 DERS 9 Grafik Çizimi, Maksimum Minimum Problmlri Bundan öncki drst bir fonksiyonun grafiğini çizmk için izlnbilck yol v yapılabilck işlmlr l alındı. Bu drst, grafik çizim stratjisini yani grafik çizimind
DERS 9 Grafik Çizimi, Maksimum Minimum Problmlri Bundan öncki drst bir fonksiyonun grafiğini çizmk için izlnbilck yol v yapılabilck işlmlr l alındı. Bu drst, grafik çizim stratjisini yani grafik çizimind
BÖLÜM 5 SIKIŞTIRILABİLİR LAMİNER SINIR TABAKALAR
 BÖLÜM 5 SIKIŞIRILABİLİR LAMİNER SINIR ABAKALAR 5.1- Giriş 5.- Adabatik dar sıaklığı 5.3- Rfrans sıak öntmi 5.4-1 özl ali 5.5- Birdn farklı andtl saıları için grikazanım faktörü 5.6- Sıkıştırılabilm dönüşümlri:
BÖLÜM 5 SIKIŞIRILABİLİR LAMİNER SINIR ABAKALAR 5.1- Giriş 5.- Adabatik dar sıaklığı 5.3- Rfrans sıak öntmi 5.4-1 özl ali 5.5- Birdn farklı andtl saıları için grikazanım faktörü 5.6- Sıkıştırılabilm dönüşümlri:
Anaparaya Dönüş (Kapitalizasyon) Oranı
 Anaparaya Dönüş (Kapitalizasyon) Oranı Glir gtirn taşınmazlar gnl olarak yatırım aracı olarak görülürlr. Alıcı, taşınmazı satın almak için kullandığı paranın karşılığında bir gtiri bklr. Bundan ötürü,
Anaparaya Dönüş (Kapitalizasyon) Oranı Glir gtirn taşınmazlar gnl olarak yatırım aracı olarak görülürlr. Alıcı, taşınmazı satın almak için kullandığı paranın karşılığında bir gtiri bklr. Bundan ötürü,
DOĞUŞ ÜNİVERSİTESİ MATEMATİK KLÜBÜ FEN LİSELERİ TAKIM YARIŞMASI 2007 SORULARI
 DOĞUŞ ÜNİVERSİTESİ MATEMATİK KLÜBÜ FEN LİSELERİ TAKIM YARIŞMASI 007 SORULARI Doğuş Ünivrsitsi Matmatik Kulübü tarafından düznlnn matmatik olimpiyatları, fn lislri takım yarışması sorularından bazıları
DOĞUŞ ÜNİVERSİTESİ MATEMATİK KLÜBÜ FEN LİSELERİ TAKIM YARIŞMASI 007 SORULARI Doğuş Ünivrsitsi Matmatik Kulübü tarafından düznlnn matmatik olimpiyatları, fn lislri takım yarışması sorularından bazıları
BÖLÜM 3 LAMİNER SINIR TABAKANIN DİFERANSİYEL DENKLEMLERİ VE TAM ÇÖZÜMLERİ
 BÖLÜM 3 LAMİNER SINIR TABAKANIN DİFERANSİYEL DENKLEMLERİ VE TAM ÇÖZÜMLERİ - Nair Stos dnlmlri - Nair Stos dnlmlrinin tam çözümlri - Daimi, ii-botl, laminr sınır tabaa dnlmlri - Daimi, ii-botl, laminr sınır
BÖLÜM 3 LAMİNER SINIR TABAKANIN DİFERANSİYEL DENKLEMLERİ VE TAM ÇÖZÜMLERİ - Nair Stos dnlmlri - Nair Stos dnlmlrinin tam çözümlri - Daimi, ii-botl, laminr sınır tabaa dnlmlri - Daimi, ii-botl, laminr sınır
BÖLÜM 2- HATA VE HATA KAYNAKLARI SORULAR ÇÖZÜMLER & MATLAB PROGRAMLAMA
 Dpartmnt o Mchanical Enginring MAK 0 MÜHENDİSLİKTE SAYISAL YÖNTEMLER BÖLÜM - HATA VE HATA KAYNAKLARI SORULAR ÇÖZÜMLER & MATLAB PROGRAMLAMA Doç. Dr. Ali Rıza YILDIZ Arş. Gör. Emr DEMİRCİ 7.0.0 7.0.0 MAK
Dpartmnt o Mchanical Enginring MAK 0 MÜHENDİSLİKTE SAYISAL YÖNTEMLER BÖLÜM - HATA VE HATA KAYNAKLARI SORULAR ÇÖZÜMLER & MATLAB PROGRAMLAMA Doç. Dr. Ali Rıza YILDIZ Arş. Gör. Emr DEMİRCİ 7.0.0 7.0.0 MAK
( ) ( ) Be. β - -bozunumu : +β - + ν + Q - Atomik kütleler cinsinden : (1) β + - bozunumu : nötral atom negatif iyon leptonlar
 6.. BETA BOZUUU Çkirdğin pozitif vya ngatif lktron yayması vya atomdan bir lktron yakalaması yolu il atom numarası ± 1 kadar dğişir. β - -bozunumu : ( B 4 4 ( B 4 nötral atom Atomik kütllr insindn : (
6.. BETA BOZUUU Çkirdğin pozitif vya ngatif lktron yayması vya atomdan bir lktron yakalaması yolu il atom numarası ± 1 kadar dğişir. β - -bozunumu : ( B 4 4 ( B 4 nötral atom Atomik kütllr insindn : (
IŞINIM VE DOĞAL TAŞINIM DENEYİ
 IŞINIM VE DOĞAL TAŞINIM DENEYİ MAK-LAB005 1. DENEY DÜZENEĞİNİN TANITILMASI Dny düznği, şkild görüldüğü gibi çlik bir basınç kabının içind yatay olarak asılı duran silindirik bir lman ihtiva dr. Elman bakırdan
IŞINIM VE DOĞAL TAŞINIM DENEYİ MAK-LAB005 1. DENEY DÜZENEĞİNİN TANITILMASI Dny düznği, şkild görüldüğü gibi çlik bir basınç kabının içind yatay olarak asılı duran silindirik bir lman ihtiva dr. Elman bakırdan
Ruppert Hız Mekanizmalarında Optimum Dişli Çark Boyutlandırılması İçin Yapay Sinir Ağları Kullanımı
 Makin Tknolojilri Elktronik Drgisi Cilt: 6, No: 2, 2009 (-8) Elctronic Journal of Machin Tchnologis Vol: 6, No: 2, 2009 (-8) TEKNOLOJİK ARAŞTIRMALAR www.tknolojikarastirmalar.com -ISSN:304-44 Makal (Articl)
Makin Tknolojilri Elktronik Drgisi Cilt: 6, No: 2, 2009 (-8) Elctronic Journal of Machin Tchnologis Vol: 6, No: 2, 2009 (-8) TEKNOLOJİK ARAŞTIRMALAR www.tknolojikarastirmalar.com -ISSN:304-44 Makal (Articl)
IKTI 102 25 Mayıs, 2010 Gazi Üniversitesi-İktisat Bölümü
 DERS NOTU 10 (Rviz Edildi, kısaltıldı!) ENFLASYON İŞSİZLİK PHILLIPS EĞRİSİ TOPLAM ARZ (AS) EĞRİSİ TEORİLERİ Bugünki drsin içriği: 1. TOPLAM ARZ, TOPLAM TALEP VE DENGE... 1 1.1 TOPLAM ARZ EĞRİSİNDE (AS)
DERS NOTU 10 (Rviz Edildi, kısaltıldı!) ENFLASYON İŞSİZLİK PHILLIPS EĞRİSİ TOPLAM ARZ (AS) EĞRİSİ TEORİLERİ Bugünki drsin içriği: 1. TOPLAM ARZ, TOPLAM TALEP VE DENGE... 1 1.1 TOPLAM ARZ EĞRİSİNDE (AS)
DRC ile tam bölünebilmesi için bir tane 2 yi ayırıyoruz. 3 ile ) x 2 2x < (
 nm - / YT / MT MTMTİK NMSİ. il tam bölünbilmsi için bir tan i aırıoruz. il bölünmmsi için bütün lri atıoruz... 7 saısının pozitif tam böln saısı ( + ). ( + ). ( + ) bulunur. vap. 0 + + 0 + ) < ( 0 + +
nm - / YT / MT MTMTİK NMSİ. il tam bölünbilmsi için bir tan i aırıoruz. il bölünmmsi için bütün lri atıoruz... 7 saısının pozitif tam böln saısı ( + ). ( + ). ( + ) bulunur. vap. 0 + + 0 + ) < ( 0 + +
TG 12 ÖABT İLKÖĞRETİM MATEMATİK
 KAMU PERSONEL SEÇME SINAVI ÖĞREMENLİK ALAN İLGİSİ ESİ İLKÖĞREİM MAEMAİK ÖĞREMENLİĞİ G ÖA İLKÖĞREİM MAEMAİK u tstlrin hr hakkı saklıdır. Hangi amaçla olursa olsun, tstlrin tamamının va bir kısmının İhtiaç
KAMU PERSONEL SEÇME SINAVI ÖĞREMENLİK ALAN İLGİSİ ESİ İLKÖĞREİM MAEMAİK ÖĞREMENLİĞİ G ÖA İLKÖĞREİM MAEMAİK u tstlrin hr hakkı saklıdır. Hangi amaçla olursa olsun, tstlrin tamamının va bir kısmının İhtiaç
NÜMERİK ANALİZ. Sayısal Yöntemlerin Konusu. Sayısal Yöntemler Neden Kullanılır?!! Denklem Çözümleri
 Saısal Yöntemler Neden Kullanılır?!! NÜMERİK ANALİZ Saısal Yöntemlere Giriş Yrd. Doç. Dr. Hatice ÇITAKOĞLU 2016 Günümüzde ortaa konan problemlerin bazılarının analitik çözümleri apılamamaktadır. Analitik
Saısal Yöntemler Neden Kullanılır?!! NÜMERİK ANALİZ Saısal Yöntemlere Giriş Yrd. Doç. Dr. Hatice ÇITAKOĞLU 2016 Günümüzde ortaa konan problemlerin bazılarının analitik çözümleri apılamamaktadır. Analitik
UYGULAMALI DİFERANSİYEL DENKLEMLER
 UYGULAMALI DİFERANSİYEL DENKLEMLER Homojn Hal Gtirilbiln Diransil Dnklmlr a b cd a' b' c' d 0 Şklindki diransil dnklm homojn olmamasına rağmn basit bir dğişkn dönüşümü il homojn hal dönüştürülbilir. a
UYGULAMALI DİFERANSİYEL DENKLEMLER Homojn Hal Gtirilbiln Diransil Dnklmlr a b cd a' b' c' d 0 Şklindki diransil dnklm homojn olmamasına rağmn basit bir dğişkn dönüşümü il homojn hal dönüştürülbilir. a
TG 13 ÖABT İLKÖĞRETİM MATEMATİK
 KAMU PERSONEL SEÇME SINAVI ÖĞRETMENLİK ALAN İLGİSİ TESTİ İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ TG ÖAT İLKÖĞRETİM MATEMATİK u tstlrin hr hakkı saklıdır. Hangi amaçla olursa olsun, tstlrin tamamının va bir kısmının
KAMU PERSONEL SEÇME SINAVI ÖĞRETMENLİK ALAN İLGİSİ TESTİ İLKÖĞRETİM MATEMATİK ÖĞRETMENLİĞİ TG ÖAT İLKÖĞRETİM MATEMATİK u tstlrin hr hakkı saklıdır. Hangi amaçla olursa olsun, tstlrin tamamının va bir kısmının
) ) (Cai, 2001). Jeodezik ağlar için elde edilen n boyutlu gözlemler vektörünün. (3) birinci derecede momentleri;
 Doğrusal Hipotz stlri il Grinim Analizi Pakiz KÜREÇ * Haluk KONAK Kocali Ünivrsitsi Harita Mühndisliği Bölümü Kocali Özt Sürkli olarak izlnmkt olan Jodzik ağların kalitlri doğruluk v duarlık istklrinin
Doğrusal Hipotz stlri il Grinim Analizi Pakiz KÜREÇ * Haluk KONAK Kocali Ünivrsitsi Harita Mühndisliği Bölümü Kocali Özt Sürkli olarak izlnmkt olan Jodzik ağların kalitlri doğruluk v duarlık istklrinin
Enerji Dönüşüm Temelleri. Bölüm 3 Bir Fazlı Transformatörler
 Enrji Dönüşüm Tmllri Bölüm 3 Bir Fazlı Transformatörlr Birfazlı Transformatorlar GİRİŞ Transformatörlrin grçk özllik v davranışlarını daha kolay anlamak için ilk aşamada idal transformatör üzrind durulacaktır.
Enrji Dönüşüm Tmllri Bölüm 3 Bir Fazlı Transformatörlr Birfazlı Transformatorlar GİRİŞ Transformatörlrin grçk özllik v davranışlarını daha kolay anlamak için ilk aşamada idal transformatör üzrind durulacaktır.
LOGARİTMA. Örnek: çizelim. Çözüm: f (x) a biçiminde tanımlanan fonksiyona üstel. aşağıda verilmiştir.
 LOGARİTMA I. Üstl Fonksiyonlr v Logritmik Fonksiyonlr şitliğini sğlyn dğrini bulmk için ypıln işlm üs lm işlmi dnir. ( =... = 8) y şitliğini sğlyn y dğrini bulmk için ypıln işlm üslü dnklmi çözm dnir.
LOGARİTMA I. Üstl Fonksiyonlr v Logritmik Fonksiyonlr şitliğini sğlyn dğrini bulmk için ypıln işlm üs lm işlmi dnir. ( =... = 8) y şitliğini sğlyn y dğrini bulmk için ypıln işlm üslü dnklmi çözm dnir.
ANADOLU ÜNivERSiTESi BiliM VE TEKNOLOJi DERGiSi ANADOLU UNIVERSITY JOURNAL OF SCIENCE AND TECHNOLOGY CiltNol.:1 - Sayı/No: 1 : (2000)
 ANADOLU ÜNivERSiTESi BiliM VE TEKNOLOJi DERGiSi ANADOLU UNIVERSITY JOURNAL OF SCIENCE AND TECHNOLOGY CiltNol.:1 - Sayı/No: 1 : 105-113 (2000) ARAŞTIRMA MAKALESiIRESEARCH ARTICLE DENG~Li iki-seviye.li ŞANS~
ANADOLU ÜNivERSiTESi BiliM VE TEKNOLOJi DERGiSi ANADOLU UNIVERSITY JOURNAL OF SCIENCE AND TECHNOLOGY CiltNol.:1 - Sayı/No: 1 : 105-113 (2000) ARAŞTIRMA MAKALESiIRESEARCH ARTICLE DENG~Li iki-seviye.li ŞANS~
Kirişli döşemeler (plaklar)
 Kirişli döşmlr (plaklar) Dört tarafından kirişlr oturan döşmlr Knarlarının bazıları boşta olan döşmlr Boşluklu döşmlr Düznsiz gomtrili döşmlr Üç tarafı kirişli bir tarafı boşta döşm Bir tarafı kirişli
Kirişli döşmlr (plaklar) Dört tarafından kirişlr oturan döşmlr Knarlarının bazıları boşta olan döşmlr Boşluklu döşmlr Düznsiz gomtrili döşmlr Üç tarafı kirişli bir tarafı boşta döşm Bir tarafı kirişli
e sayısı. x için e. x x e tabanında üstel fonksiyona doğal üstel fonksiyon (natural exponential function) denir. (0,0)
 DERS 4 Üstl v Logaritik Fonksionlar 4.. Üstl Fonksionlar(Eponntial Functions). > 0, olak üzr f ( ) = dnkli il tanılanan fonksiona taanında üstl fonksion (ponntial function with as ) dnir. Üstl fonksionun
DERS 4 Üstl v Logaritik Fonksionlar 4.. Üstl Fonksionlar(Eponntial Functions). > 0, olak üzr f ( ) = dnkli il tanılanan fonksiona taanında üstl fonksion (ponntial function with as ) dnir. Üstl fonksionun
Biyomedikal Mühendisliği Bölümü TBM 203 Diferansiyel Denklemler* Güz Yarıyılı
 Biomdikal Mühndiliği Bölümü TBM 0 Diranil Dnklmlr* 07-08 Güz Yarıılı Pro. Dr. Yn Emr ERDEMLİ n@kocali.d.tr *B dr notları Yrd. Doç. Dr. Adnan SONDAŞ ın katkılarıla hazırlanmıştır. Diranil Dnklmlr Kanaklar
Biomdikal Mühndiliği Bölümü TBM 0 Diranil Dnklmlr* 07-08 Güz Yarıılı Pro. Dr. Yn Emr ERDEMLİ n@kocali.d.tr *B dr notları Yrd. Doç. Dr. Adnan SONDAŞ ın katkılarıla hazırlanmıştır. Diranil Dnklmlr Kanaklar
Çay Atıklarından Aktif Karbon Üretimi ve Adsorpsiyon Proseslerinde Kullanımı
 ÖZET Çay Atıklarından Aktif Karbon Ürtimi v Adsorpsiyon Prosslrind Kullanımı Mrym OZMAK a, Işıl Gürtn b, Emin YAĞMUR b, Zki AKTAŞ b a DSİ Gn.Md. TAKK Dairsi Başkanlığı, Ankara, 61 b Ankara Ünivrsitsi Mühndislik
ÖZET Çay Atıklarından Aktif Karbon Ürtimi v Adsorpsiyon Prosslrind Kullanımı Mrym OZMAK a, Işıl Gürtn b, Emin YAĞMUR b, Zki AKTAŞ b a DSİ Gn.Md. TAKK Dairsi Başkanlığı, Ankara, 61 b Ankara Ünivrsitsi Mühndislik
BÖLÜM 7. Sürekli hal hatalarının değerlendirilmesinde kullanılan test dalga şekilleri: Dalga Şekli Giriş Fiziksel karşılığı. Sabit Konum.
 9 BÖLÜM 7 SÜRELİ HAL HATALARI ontrol itmlrinin analizind v dizaynında üç özlliğ odaklanılır, bunlar ; ) İtniln bir gçici hal cvabı ürtmk. ( T, %OS, ζ, ω n, ) ) ararlı olmaı. ıaca kutupların diky knin olunda
9 BÖLÜM 7 SÜRELİ HAL HATALARI ontrol itmlrinin analizind v dizaynında üç özlliğ odaklanılır, bunlar ; ) İtniln bir gçici hal cvabı ürtmk. ( T, %OS, ζ, ω n, ) ) ararlı olmaı. ıaca kutupların diky knin olunda
Mehmet Zile Mersin Üniversitesi, Mersin
 ÜÇ FAZLI ASENKRON MAKĐNENĐN BULANIK MANTIK ĐLE VEKTÖR KONTROLÜ Mhmt Zil Mrsin Ünivrsitsi, Mrsin -posta:mhmtzil@yahoo.com.tr ÖZET Birçok lisans programında gnllikl nrji dönüşümü vya lktrik makinlri drsinin
ÜÇ FAZLI ASENKRON MAKĐNENĐN BULANIK MANTIK ĐLE VEKTÖR KONTROLÜ Mhmt Zil Mrsin Ünivrsitsi, Mrsin -posta:mhmtzil@yahoo.com.tr ÖZET Birçok lisans programında gnllikl nrji dönüşümü vya lktrik makinlri drsinin
KANUN TOHUMCULUK KANUNU. Kanun No. 5553 Kabul Tarihi : 31/10/2006 BİRİNCİ BÖLÜM. Amaç, Kapsam ve Tanımlar
 8 Kasım 2006 ÇARŞAMBA Rsmî Gazt Sayı : 26340 KANUN TOHUMCULUK KANUNU Kanun No. 5553 Kabul Tarihi : 31/10/2006 Amaç BİRİNCİ BÖLÜM Amaç, Kapsam v Tanımlar MADDE 1 Bu Kanunun amacı; bitkisl ürtimd vrim v
8 Kasım 2006 ÇARŞAMBA Rsmî Gazt Sayı : 26340 KANUN TOHUMCULUK KANUNU Kanun No. 5553 Kabul Tarihi : 31/10/2006 Amaç BİRİNCİ BÖLÜM Amaç, Kapsam v Tanımlar MADDE 1 Bu Kanunun amacı; bitkisl ürtimd vrim v
MATEMATİK ÖĞRETMENLİĞİ
 T.C. ANADOLU ÜNİVERSİTESİ YAYINLARI NO: 77 AÇIKÖĞRETİM FAKÜLTESİ YAYINLARI NO: 597 MATEMATİK ÖĞRETMENLİĞİ Analitik Gomtri Yazar: Doç.Dr. Hüsin AZCAN Editör: Doç.Dr. Hüsin AZCAN Bu kitabın basım, aım v
T.C. ANADOLU ÜNİVERSİTESİ YAYINLARI NO: 77 AÇIKÖĞRETİM FAKÜLTESİ YAYINLARI NO: 597 MATEMATİK ÖĞRETMENLİĞİ Analitik Gomtri Yazar: Doç.Dr. Hüsin AZCAN Editör: Doç.Dr. Hüsin AZCAN Bu kitabın basım, aım v
Çelik. Her şey hesapladığınız gibi!
 Çlik Hr şy hsapladığınız gibi! idyapi Bilgisayar Dstkli Tasarım Mühndislik Danışmanlık Taahhüt A.Ş. Piyalpaşa Bulvarı Famas Plaza B-Blok No: 10 Kat: 5 Okmydanı Şişli 34384 İstanbul Tl : (0212) 220 55 00
Çlik Hr şy hsapladığınız gibi! idyapi Bilgisayar Dstkli Tasarım Mühndislik Danışmanlık Taahhüt A.Ş. Piyalpaşa Bulvarı Famas Plaza B-Blok No: 10 Kat: 5 Okmydanı Şişli 34384 İstanbul Tl : (0212) 220 55 00
MUKAVEMET I SUNU DERS NOTLARI 2011. EskiĢehir Osmangazi Üniversitesi Mühendislik Mimarlık Fakültesi ĠnĢaat Mühendisliği Bölümü.
 skiģhir Osmangai Ünivrsitsi Mühndislik Mimarlık Fakültsi ĠnĢaat Mühndisliği Bölümü MUKVMT I SUNU DRS NOTLRI 0 Hakan ROL H. Slim ġngl Yunus ÖZÇLĠKÖRS MUKVMT I TML ĠLKLR KSĠT ZORLMLRI GRĠLM ġkġl DĞĠġTĠRM
skiģhir Osmangai Ünivrsitsi Mühndislik Mimarlık Fakültsi ĠnĢaat Mühndisliği Bölümü MUKVMT I SUNU DRS NOTLRI 0 Hakan ROL H. Slim ġngl Yunus ÖZÇLĠKÖRS MUKVMT I TML ĠLKLR KSĠT ZORLMLRI GRĠLM ġkġl DĞĠġTĠRM
YÜK KANCALARI VİDALI BAĞLANTILARINDA KULLANILAN FARKLI VİDA DİŞ PROFİLLERİNİN BİLGİSAYAR DESTEKLİ GERİLME ANALİZİ
 . Ulusal Tasarım İmalat v Analiz Kongrsi 11-1 Kasım 010- Balıksir YÜK KANCALARI VİDALI BAĞLANTILARINDA KULLANILAN FARKLI VİDA DİŞ PROFİLLERİNİN BİLGİSAYAR DESTEKLİ GERİLME ANALİZİ Aydın DEMİRCAN*, M. Ndim
. Ulusal Tasarım İmalat v Analiz Kongrsi 11-1 Kasım 010- Balıksir YÜK KANCALARI VİDALI BAĞLANTILARINDA KULLANILAN FARKLI VİDA DİŞ PROFİLLERİNİN BİLGİSAYAR DESTEKLİ GERİLME ANALİZİ Aydın DEMİRCAN*, M. Ndim
MENKUL KIYMET DEĞERLEMESİ
 MENKUL KIYMET EĞERLEMESİ.. Hiss Sdii Tk ömlik Gtirisii Hsaplaması Bir mkul kıymti gtirisi, bkl akit akımlarıı, şimdiki piyasa fiyatıa şitly iskoto oraıdır. Mkul kıymti özlliği gör bu akit akımları faiz
MENKUL KIYMET EĞERLEMESİ.. Hiss Sdii Tk ömlik Gtirisii Hsaplaması Bir mkul kıymti gtirisi, bkl akit akımlarıı, şimdiki piyasa fiyatıa şitly iskoto oraıdır. Mkul kıymti özlliği gör bu akit akımları faiz
SAĞLIK İLE BÜYÜME GİRİŞ ÖZET ABSTRACT. Yrd. Doç. Dr. İ. Hakan YETKİNER İzmir Ekonomi Üniversitesi
 SAĞLIK İLE BÜYÜME Yrd. Doç. Dr. İ. Hakan YETKİER İzmir Ekonomi Ünivrsitsi hakan.ytkinr@iu.du.tr ÖZET Bu çalışma sağlığın konomik büyüm üzrindki tkilrini inclmktdir. Emğin ürtim katılma tkinliğini blirlyn
SAĞLIK İLE BÜYÜME Yrd. Doç. Dr. İ. Hakan YETKİER İzmir Ekonomi Ünivrsitsi hakan.ytkinr@iu.du.tr ÖZET Bu çalışma sağlığın konomik büyüm üzrindki tkilrini inclmktdir. Emğin ürtim katılma tkinliğini blirlyn
BÖLÜM II A. YE Đ BETO ARME BĐ ALARI TASARIM ÖR EKLERĐ ÖR EK 2
 BÖLÜ II A. YE Đ BETO ARE BĐ ALARI TASARI ÖR EKLERĐ ÖR EK SÜ EKLĐK DÜZEYĐ YÜKSEK 6 KATLI BETO ARE PERDELĐ / ÇERÇEELĐ BĐ A SĐSTEĐ Đ EŞDEĞER DEPRE YÜKÜ YÖ TEĐ ĐLE A ALĐZĐ E TASARII.1. GENEL BĐNA BĐLGĐLERĐ...II./..
BÖLÜ II A. YE Đ BETO ARE BĐ ALARI TASARI ÖR EKLERĐ ÖR EK SÜ EKLĐK DÜZEYĐ YÜKSEK 6 KATLI BETO ARE PERDELĐ / ÇERÇEELĐ BĐ A SĐSTEĐ Đ EŞDEĞER DEPRE YÜKÜ YÖ TEĐ ĐLE A ALĐZĐ E TASARII.1. GENEL BĐNA BĐLGĐLERĐ...II./..
ORTAM SICAKLIĞININ SOĞUTMA ÇEVRİMİNE ETKİSİNİN SAYISAL OLARAK MODELLENMESİ
 ORTAM SICAKLIĞININ SOĞUTMA ÇEVRİMİNE ETKİSİNİN SAYISAL OLARAK MODELLENMESİ Srkan SUNU - Srhan KÜÇÜKA Dokuz Eylül Ünivrsitsi Makina Mühndisliği Bölümü -posta: srhan.kuuka@du.du.tr Özt: Bu çalışmada, komprsör,
ORTAM SICAKLIĞININ SOĞUTMA ÇEVRİMİNE ETKİSİNİN SAYISAL OLARAK MODELLENMESİ Srkan SUNU - Srhan KÜÇÜKA Dokuz Eylül Ünivrsitsi Makina Mühndisliği Bölümü -posta: srhan.kuuka@du.du.tr Özt: Bu çalışmada, komprsör,
SONLU ELEMANLAR YÖNTEMİ İLE TEK FAZLI TRANSFORMATÖRÜN ÇALIŞMA NOKTASININ BELİRLENMESİ. Ali İhsan ÇANAKOĞLU
 Sonlu Elmanlar Yöntmi İl Tk Falı Transformatörün 7. Sayı Aralık 008 Çalışma Noktasının Blirlnmsi SONLU ELEMANLAR YÖNTEMİ İLE TEK FAZLI TRANSFORMATÖRÜN ÇALIŞMA NOKTASININ BELİRLENMESİ Ali İhsan ÇANAKOĞLU
Sonlu Elmanlar Yöntmi İl Tk Falı Transformatörün 7. Sayı Aralık 008 Çalışma Noktasının Blirlnmsi SONLU ELEMANLAR YÖNTEMİ İLE TEK FAZLI TRANSFORMATÖRÜN ÇALIŞMA NOKTASININ BELİRLENMESİ Ali İhsan ÇANAKOĞLU
Asenkron Makinanın Alan Yönlendirme Kontrolünde FPGA Kullanımı ALAN İ., AKIN Ö.
 Asnkron Makinanın Alan Yönlndirm Kontrolünd FPGA Kullanımı ALAN İ., AKIN Ö. ABSTRACT In this study, th fasibility of usag of fild programmabl gat arrays (FPGA) in th fild orintd control (FOC) of induction
Asnkron Makinanın Alan Yönlndirm Kontrolünd FPGA Kullanımı ALAN İ., AKIN Ö. ABSTRACT In this study, th fasibility of usag of fild programmabl gat arrays (FPGA) in th fild orintd control (FOC) of induction
MANYEZİT ARTIĞI KULLANILARAK SULU ÇÖZELTİLERDEN Co(II) İYONLARININ GİDERİMİ
 Onuncu Ulusal Kimya Mühndisliği Kongrsi, 3-6 Eylül 1, Koç Ünivrsitsi, İstanbul MANYEZİT ARTIĞI KULLANILARAK SULU ÇÖZELTİLERDEN Co(II) İYONLARININ GİDERİMİ İlkr KIPÇAK, Turgut Giray ISIYEL Eskişhir Osmangazi
Onuncu Ulusal Kimya Mühndisliği Kongrsi, 3-6 Eylül 1, Koç Ünivrsitsi, İstanbul MANYEZİT ARTIĞI KULLANILARAK SULU ÇÖZELTİLERDEN Co(II) İYONLARININ GİDERİMİ İlkr KIPÇAK, Turgut Giray ISIYEL Eskişhir Osmangazi
SÜLFÜRİK ASİTLE DEHİDRATE EDİLEN BUĞDAY KEPEĞİ İLE Cu(II) İYONLARININ ADSORPSİYONU
 SÜLFÜRİK ASİTLE DEHİDRATE EDİLEN BUĞDAY KEPEĞİ İLE Cu(II) İYONLARININ ADSORPSİYONU A. ÖZER, D.ÖZER Fırat Ünivrsitsi, Mühndislik Fakültsi, Kimya Mühndisliği Bölümü. 23279-ELAZIĞ ÖZET Bu çalışmada, sülfürik
SÜLFÜRİK ASİTLE DEHİDRATE EDİLEN BUĞDAY KEPEĞİ İLE Cu(II) İYONLARININ ADSORPSİYONU A. ÖZER, D.ÖZER Fırat Ünivrsitsi, Mühndislik Fakültsi, Kimya Mühndisliği Bölümü. 23279-ELAZIĞ ÖZET Bu çalışmada, sülfürik
ÜSTEL DAĞILIM. üstel dağılımın parametresidir. Birikimli üstel dağılım fonksiyonu da, olarak bulunur. olduğu açık olarak görülmektedir.
 ÜSTL DAĞILIM Tanım : X > olma üzr sürli bir rasgl dğişn olsun. ğr a > için X rassal dğişni aşağıdai gibi bir dağılıma sahip olursa X rasgl dğişnin üsl dağılmış rassal dğişn v onsiyonuna da üsl dağılım
ÜSTL DAĞILIM Tanım : X > olma üzr sürli bir rasgl dğişn olsun. ğr a > için X rassal dğişni aşağıdai gibi bir dağılıma sahip olursa X rasgl dğişnin üsl dağılmış rassal dğişn v onsiyonuna da üsl dağılım
Bilginin Görselleştirilmesi
 Bilginin Görselleştirilmesi Bundan önceki konularımızda serbest halde azılmış metinlerde gerek duduğumuz bilginin varlığının işlenmee, karşılaştırmaa ve değerlendirmee atkın olmadığını, bu nedenle bilginin
Bilginin Görselleştirilmesi Bundan önceki konularımızda serbest halde azılmış metinlerde gerek duduğumuz bilginin varlığının işlenmee, karşılaştırmaa ve değerlendirmee atkın olmadığını, bu nedenle bilginin
ELM202 ELEKTRONİK-II DERSİ LABORATUAR FÖYÜ
 T SKRY ÜNİERSİTESİ TEKNOLOJİ FKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ ELM202 ELEKTRONİK-II DERSİ LBORTUR FÖYÜ DENEYİ YPTIRN: DENEYİN DI: DENEY NO: DENEYİ YPNIN DI v SOYDI: SINIFI: OKUL NO: DENEY GRUP
T SKRY ÜNİERSİTESİ TEKNOLOJİ FKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ ELM202 ELEKTRONİK-II DERSİ LBORTUR FÖYÜ DENEYİ YPTIRN: DENEYİN DI: DENEY NO: DENEYİ YPNIN DI v SOYDI: SINIFI: OKUL NO: DENEY GRUP
DERS 9. Grafik Çizimi, Maksimum-Minimum Problemleri. 9.1. Grafik çiziminde izlenecek adımlar. y = f(x) in grafiğini çizmek için
 DERS 9 Grafik Çizimi, Maksimum-Minimum Problmlri 9.. Grafik çizimind izlnck adımlar. y f() in grafiğini çizmk için Adım. f() i analiz diniz. (f nin tanım kümsi, f() in tanımlı olduğu tüm rl sayıların oluşturduğu
DERS 9 Grafik Çizimi, Maksimum-Minimum Problmlri 9.. Grafik çizimind izlnck adımlar. y f() in grafiğini çizmk için Adım. f() i analiz diniz. (f nin tanım kümsi, f() in tanımlı olduğu tüm rl sayıların oluşturduğu
Yuvarlakada Kavşakların Kapasiteleri Üzerine Bir Tartışma *
 İMO Tknik Drgi, 21 4935-4958, Yazı 323 Yuvarlakada Kavşakların Kapasitlri Üzrin Bir Tartışma * Srhan TANYEL* Nadir YAYLA** ÖZ Çalışmada, İzmir d bulunan dört kavşağa ait gözlmlrdn yararlanılarak, çok şritli
İMO Tknik Drgi, 21 4935-4958, Yazı 323 Yuvarlakada Kavşakların Kapasitlri Üzrin Bir Tartışma * Srhan TANYEL* Nadir YAYLA** ÖZ Çalışmada, İzmir d bulunan dört kavşağa ait gözlmlrdn yararlanılarak, çok şritli
FIRAT ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ELEKTRİK-ELEKTRONİK MÜHENDİSLİĞİ BÖLÜMÜ EMÜ-419 OTOMATİK KONTROL LABORATUARI DENEY 5
 FIRT ÜNİVERSİTESİ MÜHENDİSLİK FKÜLTESİ ELEKTRİKELEKTRONİK MÜHENDİSLİĞİ ÖLÜMÜ EMÜ419 OTOMTİK KONTROL LORTURI DENEY 5 PID KONTROLÖR KRKTERİSTİKLERİNİN İNELENMESİ VE NLOG OLRK POZİSYON KONTROL SİSTEMLERİNDE
FIRT ÜNİVERSİTESİ MÜHENDİSLİK FKÜLTESİ ELEKTRİKELEKTRONİK MÜHENDİSLİĞİ ÖLÜMÜ EMÜ419 OTOMTİK KONTROL LORTURI DENEY 5 PID KONTROLÖR KRKTERİSTİKLERİNİN İNELENMESİ VE NLOG OLRK POZİSYON KONTROL SİSTEMLERİNDE
Hizmet Kalitesinin Servqual Metodu İle Ölçümü ve Sonuçların Yapısal Eşitlik Modelleri İle Analizi: Öğretmen Evi Uygulaması
 19 Hizmt Kalitsinin Srvqual Mtodu İl Ölçümü v Sonuçların Yapısal Eşitlik Modllri İl Analizi: Öğrtmn Evi Uygulaması Sülyman Ersöz, Mhmt Pınarbaşı, A.Kürşad TÜRKER, Mustafa YÜZÜKIRMIZI Endüstri Mühndisliği
19 Hizmt Kalitsinin Srvqual Mtodu İl Ölçümü v Sonuçların Yapısal Eşitlik Modllri İl Analizi: Öğrtmn Evi Uygulaması Sülyman Ersöz, Mhmt Pınarbaşı, A.Kürşad TÜRKER, Mustafa YÜZÜKIRMIZI Endüstri Mühndisliği
İSTANBUL TEKNİK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ BULANIK PID KONTROLÖRLERİ İÇİN ÇEVRİM İÇİ KURAL AĞIRLIKLANDIRMA YÖNTEMLERİ DOKTORA TEZİ
 İSTANBUL TEKNİK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ BULANIK PID KONTROLÖRLERİ İÇİN ÇEVRİM İÇİ KURAL AĞIRLIKLANDIRMA YÖNTEMLERİ DOKTORA TEZİ Onur KARASAKAL Elktrik Mühndisliği Anabilim Dalı Kontrol v Otomasyon
İSTANBUL TEKNİK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ BULANIK PID KONTROLÖRLERİ İÇİN ÇEVRİM İÇİ KURAL AĞIRLIKLANDIRMA YÖNTEMLERİ DOKTORA TEZİ Onur KARASAKAL Elktrik Mühndisliği Anabilim Dalı Kontrol v Otomasyon
w0= γb0 6.1 B(t)=2B1Cosw1t Şekil 6.1: Sabit B0 ve değişken B(t) alanlarının etkisinde bir dipol momenti.
 DENEY NO : 6 DENEYİN ADI : ELEKTRON SPİN REZONANS (ESR) DENEYİN AMACI : ESR nin tml fiiksl ölliklrinin öğrnilmsi v DPPH örnği için g faktörünün hsaplanması. TEORİK İLGİ : Ronans Kavramı v Manytik Ronans
DENEY NO : 6 DENEYİN ADI : ELEKTRON SPİN REZONANS (ESR) DENEYİN AMACI : ESR nin tml fiiksl ölliklrinin öğrnilmsi v DPPH örnği için g faktörünün hsaplanması. TEORİK İLGİ : Ronans Kavramı v Manytik Ronans
DERS 7. Türev Hesabı ve Bazı Uygulamalar II
 DERS 7 Türv Hsabı v Bazı Uygulamalar II Bu rst bilşk fonksiyonlarının türvi il ilgili zincir kuralını, üstl v logaritmik fonksiyonların türvlrini, ortalama v marjinal ortalama ğrlri; rsin sonuna oğru,
DERS 7 Türv Hsabı v Bazı Uygulamalar II Bu rst bilşk fonksiyonlarının türvi il ilgili zincir kuralını, üstl v logaritmik fonksiyonların türvlrini, ortalama v marjinal ortalama ğrlri; rsin sonuna oğru,
Uzaysal Görüntü İyileştirme/Filtreleme. Doç. Dr. Fevzi Karslı fkarsli@ktu.edu.tr
 Uasal Görüntü İileştirme/Filtreleme Doç. Dr. Fevi Karslı karsli@ktu.edu.tr İileştirme Herhangi bir ugulama için, görüntüü orijinalden daha ugun hale getirmek Ugunluğu her bir ugulama için sağlamak. Bir
Uasal Görüntü İileştirme/Filtreleme Doç. Dr. Fevi Karslı karsli@ktu.edu.tr İileştirme Herhangi bir ugulama için, görüntüü orijinalden daha ugun hale getirmek Ugunluğu her bir ugulama için sağlamak. Bir
YENİLENEBİLİR ENERJİ KAYNAKLARI AÇISINDAN RÜZGAR ENERJİSİNİN TÜRKİYE DEKİ KAPASİTESİ ÖZET
 YENİLENEBİLİR ENERJİ KAYNAKLARI AÇISINDAN RÜZGAR ENERJİSİNİN TÜRKİYE DEKİ KAPASİTESİ LEVENT YILMAZ Istanbul Tknik Ünivrsitsi, İnşaat Fakültsi, Hidrolik v Su Yapıları Kürsüsü, 8626, Maslak, Istanbul. ÖZET
YENİLENEBİLİR ENERJİ KAYNAKLARI AÇISINDAN RÜZGAR ENERJİSİNİN TÜRKİYE DEKİ KAPASİTESİ LEVENT YILMAZ Istanbul Tknik Ünivrsitsi, İnşaat Fakültsi, Hidrolik v Su Yapıları Kürsüsü, 8626, Maslak, Istanbul. ÖZET
Cevap: B. x + y = 5 ve y + z = x = 3z y. x + y = 5 z + y = 3 x t = 2 bulunur. 7x 9y = y 3x 10x = 8y. 3/ 3y = x + z 15k = 4k + z + Cevap: B
 6 LYS/MAT MATEMATİK ÇÖZÜMLERİ DENEME. ( ab) ( ab) 6( ab) 6. 6 y z ( ab) ( ab) 6( ab) 6 6 6y y z 6y ( ab) 6 6( y) ( y z) ab.. olur. y v y z. 7 z y / y z k k z y z y t bulunur. 7 9y y 8y k, y k zk A) y 8,
6 LYS/MAT MATEMATİK ÇÖZÜMLERİ DENEME. ( ab) ( ab) 6( ab) 6. 6 y z ( ab) ( ab) 6( ab) 6 6 6y y z 6y ( ab) 6 6( y) ( y z) ab.. olur. y v y z. 7 z y / y z k k z y z y t bulunur. 7 9y y 8y k, y k zk A) y 8,
Negatif Binom Dağılımı
 Ngatif Binom Dağılımı Brnoulli dnyinin tüm varsayımları ngatif binom dağılımı içind gçrlidir. Binom dağılımında n dnmd adt başarı olasılığı l ğ il ilgilnilirkn, ili ngatif binom dağılımındağ d is şans
Ngatif Binom Dağılımı Brnoulli dnyinin tüm varsayımları ngatif binom dağılımı içind gçrlidir. Binom dağılımında n dnmd adt başarı olasılığı l ğ il ilgilnilirkn, ili ngatif binom dağılımındağ d is şans
y xy = x şeklinde bir özel çözümünü belirleyerek genel
 Difransil Dnklmlr I / 94 A Aşağıdaki difransil dnklmlrin çözümlrini bulunuz d d -( + ) 7 + n( ) +, () + n ( + ) 4 + - + 5 6 - ( - ) + 8 9 - - + + - ( -) d- ( + ) d + Not: Çözüm mtodu olarak: Tam difdnk
Difransil Dnklmlr I / 94 A Aşağıdaki difransil dnklmlrin çözümlrini bulunuz d d -( + ) 7 + n( ) +, () + n ( + ) 4 + - + 5 6 - ( - ) + 8 9 - - + + - ( -) d- ( + ) d + Not: Çözüm mtodu olarak: Tam difdnk
Beta ( ) bozunumu Beta Bozunumu 1
 Bta () bozunumu 05.07.008 Bta Bozunumu 1 Bta bozunumu () 1918 yıllında Çkirdklrin ( - ) lktron yayınlanması bilinn bir olaydı. Fakat çkirdğin bir - yakalaması 1938 yıllında bulunmuştur. Boşalan - yrin
Bta () bozunumu 05.07.008 Bta Bozunumu 1 Bta bozunumu () 1918 yıllında Çkirdklrin ( - ) lktron yayınlanması bilinn bir olaydı. Fakat çkirdğin bir - yakalaması 1938 yıllında bulunmuştur. Boşalan - yrin
ÇAPRAZ AKIŞLI ISI DEĞİŞTİRİCİ
 ÇAPRAZ AKIŞLI ISI DEĞİŞTİRİCİ MAK-LAB012 1. DENEY DÜZENEĞİNİN TANITILMASI Düznk sas olarak dikdörtgn ksitli bir kanaldan ibarttir. 1 hp gücündki lktrik motorunun çalıştırdığı bir vantilatör il kanal içind
ÇAPRAZ AKIŞLI ISI DEĞİŞTİRİCİ MAK-LAB012 1. DENEY DÜZENEĞİNİN TANITILMASI Düznk sas olarak dikdörtgn ksitli bir kanaldan ibarttir. 1 hp gücündki lktrik motorunun çalıştırdığı bir vantilatör il kanal içind
İyon Kaynakları ve Uygulamaları
 İyon Kaynakları v Uygulamaları E. RECEPOĞLU TAEK-Sarayköy Nüklr Araştırma v Eğitim Mrkzi rdal.rcpoglu rcpoglu@tak.gov.tr HPFBU-2012 2012-KARS KONULAR İyon kaynakları hakkında gnl bilgi İyon kaynaklarının
İyon Kaynakları v Uygulamaları E. RECEPOĞLU TAEK-Sarayköy Nüklr Araştırma v Eğitim Mrkzi rdal.rcpoglu rcpoglu@tak.gov.tr HPFBU-2012 2012-KARS KONULAR İyon kaynakları hakkında gnl bilgi İyon kaynaklarının
DENEY 5 İkinci Dereceden Sistem
 DENEY 5 İkici Drcd Sitm DENEYİN AMACI. İkici drcd itmi karaktritiklrii alamak.. Söüm oraı ζ i, ikici drcd itm üzridki tkiii gözlmlmk. 3. Doğal frka i, ikici drcd itm üzridki tkiii gözlmlmk. GENEL BİLGİLER
DENEY 5 İkici Drcd Sitm DENEYİN AMACI. İkici drcd itmi karaktritiklrii alamak.. Söüm oraı ζ i, ikici drcd itm üzridki tkiii gözlmlmk. 3. Doğal frka i, ikici drcd itm üzridki tkiii gözlmlmk. GENEL BİLGİLER
1/1000 ÖLÇEKLİ KADASTRO PAFTALARININ KARTOGRAFİK YÖNTEMLERLE SAYISAL HALE DÖNÜŞTÜRÜLMESİ VE DOĞRULUK ANALİZİ
 1/1000 ÖLÇEKLİ KADASTRO PAFTALARININ KARTOGRAFİK YÖNTEMLERLE SAYISAL HALE DÖNÜŞTÜRÜLMESİ VE DOĞRULUK ANALİZİ ÖZET A. Celan 1, Ö. Mutluoğlu 2, R. Günaslan 3 1 S. Ü. Müh. Mim. Fak., Jeodezi ve Fot. Müh.
1/1000 ÖLÇEKLİ KADASTRO PAFTALARININ KARTOGRAFİK YÖNTEMLERLE SAYISAL HALE DÖNÜŞTÜRÜLMESİ VE DOĞRULUK ANALİZİ ÖZET A. Celan 1, Ö. Mutluoğlu 2, R. Günaslan 3 1 S. Ü. Müh. Mim. Fak., Jeodezi ve Fot. Müh.
TANITIM ve KULLANIM KILAVUZU. Modeller UBA4234-R. Versiyon : KK_UBA_V3.0210
 SAT-IF / CATV Ultra Gniş Bantlı Dağıtım Yükslticilri (UBA-Srisi) TANITIM v KULLANIM KILAVUZU Modllr UBA4234-R Vrsiyon : KK_UBA_V3.0210 1.Gnl Tanıtım UBA Srisi Dağıtım Yükslticilri, uydu (950-2150MHz) v
SAT-IF / CATV Ultra Gniş Bantlı Dağıtım Yükslticilri (UBA-Srisi) TANITIM v KULLANIM KILAVUZU Modllr UBA4234-R Vrsiyon : KK_UBA_V3.0210 1.Gnl Tanıtım UBA Srisi Dağıtım Yükslticilri, uydu (950-2150MHz) v
Atomlardan Kuarklara. Test 1
 4 Atomlardan Kuarklara Tst. Nötronlar, tkilşim parçacıkları dğil, madd parçacıklarıdır. Bu ndnl yanlış olan E sçnğidir. 5. Elktriksl olarak yüklü lptonlar zayıf çkirdk kuvvtlri aracılığıyla tkilşim girrlr.
4 Atomlardan Kuarklara Tst. Nötronlar, tkilşim parçacıkları dğil, madd parçacıklarıdır. Bu ndnl yanlış olan E sçnğidir. 5. Elktriksl olarak yüklü lptonlar zayıf çkirdk kuvvtlri aracılığıyla tkilşim girrlr.
Günlük Bülten. 27 Aralık 2012. Merkez Bankası Baş Ekonomisti Hakan Kara 2012 yılının %6 civarında enflasyonla tamamlanacağını düşündüklerini söyledi
 27 Aralık 2012 Prşmb Günlük Bültn İMKB vrilri İMKB 100 77,991.1 Piyasa Dğri-TÜM ($m) 304,387.4 Halka Açık Piyasa Dğri-TÜM ($m) 87,677.3 Günlük İşlm Hami-TÜM ($m) 1,243.42 Yurtdışı piyasalar Borsalar Kapanış
27 Aralık 2012 Prşmb Günlük Bültn İMKB vrilri İMKB 100 77,991.1 Piyasa Dğri-TÜM ($m) 304,387.4 Halka Açık Piyasa Dğri-TÜM ($m) 87,677.3 Günlük İşlm Hami-TÜM ($m) 1,243.42 Yurtdışı piyasalar Borsalar Kapanış
Lisans Yerleştirme Sınavı 1 (Lys 1) / 18 Haziran Matematik Soruları ve Çözümleri
 Lisans Yrlşirm Sınavı (Lys ) 8 Haziran Mamaik Soruları v Çözümlri. (,5) işlminin sonucu kaçır?, A) 5 B) C) 5 D) E) Çözüm (,5), 5 ( ) ( ) 5 ( ) ( ).( ) 5 ( ) 5 5 6 . < < olduğuna gör, aşağıdakilrdn hangisi
Lisans Yrlşirm Sınavı (Lys ) 8 Haziran Mamaik Soruları v Çözümlri. (,5) işlminin sonucu kaçır?, A) 5 B) C) 5 D) E) Çözüm (,5), 5 ( ) ( ) 5 ( ) ( ).( ) 5 ( ) 5 5 6 . < < olduğuna gör, aşağıdakilrdn hangisi
Magnetic Materials. 4. Ders: Paramanyetizma-2. Numan Akdoğan.
 Mgntic Mtrils 4. Drs: Prmnytizm-2 Numn Akdoğn kdogn@gyt.du.tr Gbz Institut of Tchnology Dprtmnt of Physics Nnomgntism nd Spintronic Rsrch Cntr (NASAM) Kuntum mkniği klsik torinin özlliklrini dğiştirmdn,
Mgntic Mtrils 4. Drs: Prmnytizm-2 Numn Akdoğn kdogn@gyt.du.tr Gbz Institut of Tchnology Dprtmnt of Physics Nnomgntism nd Spintronic Rsrch Cntr (NASAM) Kuntum mkniği klsik torinin özlliklrini dğiştirmdn,
Tahvilin Fiyatı ve Bugünkü Değeri Bir yıl sonra 100 dolar vermeyi taahhüt eden bir tahvilin bugünkü değeri :
 B.E.A. Finansal Piyasalar v Bklnilr Mrkzi hükümin büç açığının karşılanması için piyasaya sunduğu borçlanma aracı ahvillrin iki ml özlliği vardır: a) Tanımlanmış Risk: bu risk anımı vad sonunda ahvili
B.E.A. Finansal Piyasalar v Bklnilr Mrkzi hükümin büç açığının karşılanması için piyasaya sunduğu borçlanma aracı ahvillrin iki ml özlliği vardır: a) Tanımlanmış Risk: bu risk anımı vad sonunda ahvili
1 (c) herhangi iki kompleks sayı olmak üzere
 KOMPLEKS FONKSİYONLAR TEORİSİ UYGULAMA SORULARI- Problem. Aşağıdaki (a) ve (b) de olmak üere (a) olduklarını gösterini. (b) (c) Imi Re Çöüm (a) i olsun. i i (b) i olsun. i i i i i i i i i i Im i Re i (c)
KOMPLEKS FONKSİYONLAR TEORİSİ UYGULAMA SORULARI- Problem. Aşağıdaki (a) ve (b) de olmak üere (a) olduklarını gösterini. (b) (c) Imi Re Çöüm (a) i olsun. i i (b) i olsun. i i i i i i i i i i Im i Re i (c)
AMONYAK/ SU AKIŞKAN ÇİFTİ İLE ÇALIŞAN KAPALI DEVRE SOĞURMALI ISI TRANSFORMATÖRÜNÜN TERMODİNAMİK ANALİZİ
 EKNOLOJİ, (001), Sayı 1-, 9-7 EKNOLOJİ AMONYAK/ SU AKIŞKAN ÇİFİ İLE ÇALIŞAN KAPALI DEVRE SOĞURMALI ISI RANSFORMAÖRÜNÜN ERMODİNAMİK ANALİZİ Musa Galip ÖZKAYA G.Ü. knik Eğitim Fakültsi, Makin Eğitimi Bölümü,
EKNOLOJİ, (001), Sayı 1-, 9-7 EKNOLOJİ AMONYAK/ SU AKIŞKAN ÇİFİ İLE ÇALIŞAN KAPALI DEVRE SOĞURMALI ISI RANSFORMAÖRÜNÜN ERMODİNAMİK ANALİZİ Musa Galip ÖZKAYA G.Ü. knik Eğitim Fakültsi, Makin Eğitimi Bölümü,
DERS 1. Doğrusal Denklem Sistemleri ve Matrisler
 DERS Doğrusal Denklem Sistemleri ve Matrisler Sosal ve Beşeri Bilimlerde Matematik I kitabımıda doğrusal denklemleri tanımlamıştık (safa 85). Arıca, matematiksel modeli doğrusal denklemler içeren problem
DERS Doğrusal Denklem Sistemleri ve Matrisler Sosal ve Beşeri Bilimlerde Matematik I kitabımıda doğrusal denklemleri tanımlamıştık (safa 85). Arıca, matematiksel modeli doğrusal denklemler içeren problem
GÜVEN ARALIKLARI ve İSTATİSTİKSEL ANLAMLILIK. Ankara Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı
 GÜVEN ARALIKLARI ve İSTATİSTİKSEL ANLAMLILIK Ankara Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı Kestirim Pratikte kitle parametrelerinin doğrudan hesaplamak olanaklı değildir. Bunun yerine
GÜVEN ARALIKLARI ve İSTATİSTİKSEL ANLAMLILIK Ankara Üniversitesi Tıp Fakültesi Biyoistatistik Anabilim Dalı Kestirim Pratikte kitle parametrelerinin doğrudan hesaplamak olanaklı değildir. Bunun yerine
DEĞERLEME RAPORU EKİZ KİMYA SANAYİ VE TİCARET A.Ş. 4 ADET PARSEL
 DEĞERLEME RAPORU EKİZ KİMYA SANAYİ VE TİCARET A.Ş. İZMİR MENEMEN - SÜZBEYLİ 4 ADET PARSEL Bu taşınmaz dğrlm raporu, Ekiz Kimya Sanayi v Ticart A.Ş. nin istmi üzrin hazırlanmıştır. İlgilisi v hazırlanış
DEĞERLEME RAPORU EKİZ KİMYA SANAYİ VE TİCARET A.Ş. İZMİR MENEMEN - SÜZBEYLİ 4 ADET PARSEL Bu taşınmaz dğrlm raporu, Ekiz Kimya Sanayi v Ticart A.Ş. nin istmi üzrin hazırlanmıştır. İlgilisi v hazırlanış
Düzce Üniversitesi Bilim ve Teknoloji Dergisi
 Düzc Ünivrsitsi Bilim v Tknoloji Drgisi, 2 (214) 191 198 Düzc Ünivrsitsi Bilim v Tknoloji Drgisi Araştırma Makalsi Dprm Yüklri Altında Kalıcı Şv Dplasmanlarının Tahmini Dniz ÜLGENa,*, H. Kürşat ENGİNb
Düzc Ünivrsitsi Bilim v Tknoloji Drgisi, 2 (214) 191 198 Düzc Ünivrsitsi Bilim v Tknoloji Drgisi Araştırma Makalsi Dprm Yüklri Altında Kalıcı Şv Dplasmanlarının Tahmini Dniz ÜLGENa,*, H. Kürşat ENGİNb
OLASILIK ve ÝSTATÝSTÝK ( Genel Tekrar Testi-1) KPSS MATEMATÝK. Bir anahtarlıktaki 5 anahtardan 2 si kapıyı açmak - tadır.
 OLASILIK v ÝSTATÝSTÝK ( Gnl Tkrar Tsti-1) 1. Bir anahtarlıktaki 5 anahtardan si kapıyı açmak - tadır. Açmayan anahtar bir daha dnnmdiğin gör, bu kapının n çok üçüncü dnmd açılma olasılığı kaçtır? 5 6 7
OLASILIK v ÝSTATÝSTÝK ( Gnl Tkrar Tsti-1) 1. Bir anahtarlıktaki 5 anahtardan si kapıyı açmak - tadır. Açmayan anahtar bir daha dnnmdiğin gör, bu kapının n çok üçüncü dnmd açılma olasılığı kaçtır? 5 6 7
TEST 12-1 KONU ELEKTRİK AKIMI. Çözümlerİ ÇÖZÜMLERİ
 OU 1 T Çözümlr TST 1-1 ÇÖÜ 5. 6 4 1. irncin boyuna bağlı olup olmadığını araştırdığı için ksitlri aynı, boyları farklı tllr kullanılmalıdır. Tllr aynı cins olmalı. u durumda v nolu tllr olmalıdır. 1. -
OU 1 T Çözümlr TST 1-1 ÇÖÜ 5. 6 4 1. irncin boyuna bağlı olup olmadığını araştırdığı için ksitlri aynı, boyları farklı tllr kullanılmalıdır. Tllr aynı cins olmalı. u durumda v nolu tllr olmalıdır. 1. -
Günlük Bülten. 27 Şubat 2013. TCMB, Şubat ayı PPK toplantısı özetini yayınladı
 27 Şuat 2013 Çarşama Günlük Bültn İMKB vrilri İMKB 100 77,514.3 Piyasa Dğri-TÜM ($m) 302,886.2 Halka Açık Piyasa Dğri-TÜM ($m) 86,403.0 Günlük İşlm Hacmi-TÜM ($m) 1,629.94 Yurtdışı piyasalar Borsalar Kapanış
27 Şuat 2013 Çarşama Günlük Bültn İMKB vrilri İMKB 100 77,514.3 Piyasa Dğri-TÜM ($m) 302,886.2 Halka Açık Piyasa Dğri-TÜM ($m) 86,403.0 Günlük İşlm Hacmi-TÜM ($m) 1,629.94 Yurtdışı piyasalar Borsalar Kapanış
Ekonometri I VARSAYIMLARI
 Ekonometri I ÇOK DEĞİŞKENLİ REGRESYON MODELİNİN VARSAYIMLARI Hüseyin Taştan Temmuz 23, 2006 İçindekiler 1 Varsayım MLR.1: Parametrelerde Doğrusallık 1 2 Varsayım MLR.2: Rassal Örnekleme 1 3 Varsayım MLR.3:
Ekonometri I ÇOK DEĞİŞKENLİ REGRESYON MODELİNİN VARSAYIMLARI Hüseyin Taştan Temmuz 23, 2006 İçindekiler 1 Varsayım MLR.1: Parametrelerde Doğrusallık 1 2 Varsayım MLR.2: Rassal Örnekleme 1 3 Varsayım MLR.3:
İstatistik ve Olasılık
 İstatistik ve Olasılık -II Prof. Dr. İrfan KAYMAZ İki Ortalama Farkının Güven Aralığı Anakütle Varyansı Biliniyorsa İki ortalama arasındaki farkın dağılımına ilişkin Z değişkeni: Güven aralığı ifadesinde
İstatistik ve Olasılık -II Prof. Dr. İrfan KAYMAZ İki Ortalama Farkının Güven Aralığı Anakütle Varyansı Biliniyorsa İki ortalama arasındaki farkın dağılımına ilişkin Z değişkeni: Güven aralığı ifadesinde
İletkende seri olarak tel direnci ve magnetik alandan doğan reaktans ile şönt olarak elektrik alandan doğan toprak kapasitesi mevcuttur.
 9 ÖÜM 4 İETİM HT 4.. İltim hatlarının yapısı üksk grilim iltim hatlarında malzm olarak çlik özlü alüminyum iltknlr kullanılır. ( luminium onductor tl inforcd) Kanada standardı olarak tüm dünyada kuş isimlri
9 ÖÜM 4 İETİM HT 4.. İltim hatlarının yapısı üksk grilim iltim hatlarında malzm olarak çlik özlü alüminyum iltknlr kullanılır. ( luminium onductor tl inforcd) Kanada standardı olarak tüm dünyada kuş isimlri
NOKTASAL KAYNAKLI TOPRAK KİRLİLİĞİNİN KONTROLÜ YÖNETMELİĞİ. BİRİNCİ BÖLÜM Amaç, Kapsam, Dayanak ve Tanımlar
 NOKTASAL KAYNAKLI TOPRAK KİRLİLİĞİNİN KONTROLÜ YÖNETMELİĞİ Amaç BİRİNCİ BÖLÜM Amaç, Kapsam, Dayanak v Tanımlar MADDE 1 Bu Yöntmliğin amacı; alıcı ortam olarak toprağın kirliliktn korunması, noktasal kaynaklı
NOKTASAL KAYNAKLI TOPRAK KİRLİLİĞİNİN KONTROLÜ YÖNETMELİĞİ Amaç BİRİNCİ BÖLÜM Amaç, Kapsam, Dayanak v Tanımlar MADDE 1 Bu Yöntmliğin amacı; alıcı ortam olarak toprağın kirliliktn korunması, noktasal kaynaklı
Farklı Kural Tabanları Kullanarak PI-Bulanık Mantık Denetleyici ile Doğru Akım Motorunun Hız Denetim Performansının İncelenmesi
 Ahmt GANİ/APJES II-I (24) 6-23 Farklı Kural Tabanları Kullanarak PI-Bulanık Mantık Dntlyici il Doğru Akım Motorunun Hız Dntim Prformansının İnclnmsi * Ahmt Gani, 2 Hasan Rıza Özçalık, 3 Hakan Açıkgöz,
Ahmt GANİ/APJES II-I (24) 6-23 Farklı Kural Tabanları Kullanarak PI-Bulanık Mantık Dntlyici il Doğru Akım Motorunun Hız Dntim Prformansının İnclnmsi * Ahmt Gani, 2 Hasan Rıza Özçalık, 3 Hakan Açıkgöz,
AR. GÖR. SİBEL AL PROF. DR. HÜLYA ÇINGI HACETTPE ÜNİVERSİTESİ İSTATİSTİK BÖLÜMÜ
 AR. GÖR. SİBEL AL PROF. DR. HÜLYA ÇINGI HACETTPE ÜNİVERSİTESİ İSTATİSTİK BÖLÜMÜ Genel bilgiler Yöntemin tanımı İki safhalı örnekleme yönteminde medyan tahmin edicileri Tahmin edicilerin etkinlikleri Sayısal
AR. GÖR. SİBEL AL PROF. DR. HÜLYA ÇINGI HACETTPE ÜNİVERSİTESİ İSTATİSTİK BÖLÜMÜ Genel bilgiler Yöntemin tanımı İki safhalı örnekleme yönteminde medyan tahmin edicileri Tahmin edicilerin etkinlikleri Sayısal
- BANT TAŞIYICILAR -
 - BANT TAŞIYICILAR - - YAPISAL ÖZELLİKLER Bir bant taşıyıcının nl örünümü aşağıdaki şkild vrilmiştir. Bant taşıyıcıya ismini vrn bant (4) hm taşınacak malzmyi için alan bir kap örvi örn, hm d harkt için
- BANT TAŞIYICILAR - - YAPISAL ÖZELLİKLER Bir bant taşıyıcının nl örünümü aşağıdaki şkild vrilmiştir. Bant taşıyıcıya ismini vrn bant (4) hm taşınacak malzmyi için alan bir kap örvi örn, hm d harkt için
TÜRK EKONOMİSİNDE PARA İKAMESİNİN BELİRLEYİCİLERİNİN SINIR TESTİ YAKLAŞIMI İLE EŞ-BÜTÜNLEŞME ANALİZİ
 TÜRK EKONOMİSİNDE PARA İKAMESİNİN BELİRLEYİCİLERİNİN SINIR TESTİ YAKLAŞIMI İLE EŞ-BÜTÜNLEŞME ANALİZİ Cünyt DUMRUL * ÖZ Bu çalışma ticarî dışa açıklık, bklnn döviz kuru, bklnn nflasyon oranı v Türkiy il
TÜRK EKONOMİSİNDE PARA İKAMESİNİN BELİRLEYİCİLERİNİN SINIR TESTİ YAKLAŞIMI İLE EŞ-BÜTÜNLEŞME ANALİZİ Cünyt DUMRUL * ÖZ Bu çalışma ticarî dışa açıklık, bklnn döviz kuru, bklnn nflasyon oranı v Türkiy il
DEĞERLEME RAPORU REYSAŞ GAYRİMENKUL YATIRIM ORTAKLIĞI A.Ş. KASTAMONU MERKEZ KUZEYKENT 1299 ADA 8 PARSEL ARSA
 DEĞERLEME RAPORU REYSAŞ GAYRİMENKUL YATIRIM ORTAKLIĞI A.Ş. KASTAMONU MERKEZ KUZEYKENT 1299 ADA 8 PARSEL ARSA Bu dğrlm raporu, Rysaş Gayrimnkul Yatırım Ortaklığı A.Ş. nin istmi üzrin hazırlanmıştır. İlgilisi
DEĞERLEME RAPORU REYSAŞ GAYRİMENKUL YATIRIM ORTAKLIĞI A.Ş. KASTAMONU MERKEZ KUZEYKENT 1299 ADA 8 PARSEL ARSA Bu dğrlm raporu, Rysaş Gayrimnkul Yatırım Ortaklığı A.Ş. nin istmi üzrin hazırlanmıştır. İlgilisi
GİRİŞİMCİ WEB SAYFALARININ DEĞERLENDİRİLMESİNDE BULANIK BİLİŞSEL HARİTALAMA YÖNTEMİNİN KULLANIMI
 EKEV AKADEİ DERGİSİ Yıl: 14 Sayı: 44 (Yaz 2010) 335 GİRİŞİCİ WEB SAYFALARININ DEĞERLENDİRİLESİNDE BULANIK BİLİŞSEL HARİTALAA YÖNTEİNİN KULLANII. Dursun KAYA (*) A. Samt HAŞILOĞLU (**) Slçuk Burak HAŞILOĞLU
EKEV AKADEİ DERGİSİ Yıl: 14 Sayı: 44 (Yaz 2010) 335 GİRİŞİCİ WEB SAYFALARININ DEĞERLENDİRİLESİNDE BULANIK BİLİŞSEL HARİTALAA YÖNTEİNİN KULLANII. Dursun KAYA (*) A. Samt HAŞILOĞLU (**) Slçuk Burak HAŞILOĞLU
T.C. SELÇUK ÜNĐVERSĐTESĐ FEN BĐLĐMLERĐ ENSTĐTÜSÜ
 T.C. SELÇUK ÜNĐVERSĐTESĐ FEN BĐLĐMLERĐ ENSTĐTÜSÜ GEROTOR PROFĐLLERĐNĐN OPTĐMĐZASYONU Bkir KARAGÜL YÜKSEK LĐSANS TEZĐ MAKĐNA ANABĐLĐM DALI KONYA 2010 ÖZET Yüksk Lisans Tzi GEROTOR PROFĐLLERĐNĐN OPTĐMĐZASYONU
T.C. SELÇUK ÜNĐVERSĐTESĐ FEN BĐLĐMLERĐ ENSTĐTÜSÜ GEROTOR PROFĐLLERĐNĐN OPTĐMĐZASYONU Bkir KARAGÜL YÜKSEK LĐSANS TEZĐ MAKĐNA ANABĐLĐM DALI KONYA 2010 ÖZET Yüksk Lisans Tzi GEROTOR PROFĐLLERĐNĐN OPTĐMĐZASYONU
SÜLFÜRİK ASİTLE MUAMELE EDİLEN FISTIK KABUKLARI İLE Cr(VI) İYONLARININ ADSORPSİYONU
 SÜLFÜRİK ASİTLE MUAMELE EDİLEN FISTIK KABUKLARI İLE Cr(VI) İYONLARININ ADSORPSİYONU Vyis SELEN, Ali YARAŞ 2, Cansu YILMAZ 3, M. Şaban TANYILDIZI 4, Dursun ÖZER 5 Fırat Ünivrsitsi Mühndislik Fakültsi Kimya
SÜLFÜRİK ASİTLE MUAMELE EDİLEN FISTIK KABUKLARI İLE Cr(VI) İYONLARININ ADSORPSİYONU Vyis SELEN, Ali YARAŞ 2, Cansu YILMAZ 3, M. Şaban TANYILDIZI 4, Dursun ÖZER 5 Fırat Ünivrsitsi Mühndislik Fakültsi Kimya
İçindekiler. Ön Söz... xiii
 İçindekiler Ön Söz.................................................... xiii Bölüm 1 İstatistiğe Giriş....................................... 1 1.1 Giriş......................................................1
İçindekiler Ön Söz.................................................... xiii Bölüm 1 İstatistiğe Giriş....................................... 1 1.1 Giriş......................................................1
