FARKLI VERİ YAPILARINDA KULLANILABİLECEK REGRESYON YÖNTEMLERİ
|
|
|
- Nesrin Kaner
- 8 yıl önce
- İzleme sayısı:
Transkript
1 Anadolu Tarım Blm. Derg., 203,28(3):68-74 Anadolu J Agr Sc, 203,28(3):68-74 do: 0.76/anaas URL: htt://dx.do.org/0.76/anaas Derleme Revew FARKLI VERİ YAPILARINDA KULLANILABİLECEK REGRESYON YÖNTEMLERİ Arzu ARI Hasan ÖNDER* Ondokuz Mayıs Ünverstes, Zraat Fakültes, Zootekn Bölümü, Samsun * honder@omu.edu.tr Gelş Tarh : Kabul Tarh : ÖZET: Regresyon, üzernde durulan yanıt değşken le lşkl olableceğ düşünülen açıklayıcı değşkenlern br fonksyonu olarak fade edlmektedr. Değşkenler arasındak lşknn fonksyonel şekl regresyon modeller le ncelenmektedr. Kullanılması gereken regresyon model vernn yaısına göre farklılık göstermekte ve yanlış model kullanılması hatalı sonuçların elde edlmesne neden olablmektedr. Bu derlemede regresyon modellernden; doğrusal regresyon, lostk regresyon, negatf bnom regresyon, osson regresyon, temel bleşenler regresyonu, robt regresyon, rdge regresyon, Cox regresyon modellernn hang durumlarda kullanılableceğ ncelenmştr. Anahtar kelmeler: Regresyon, Doğrusal regresyon, Doğrusal olmayan regresyonlar REGRESSION MODELS USED FOR DIFFERENT DATA STRUCTURES ABSTRACT: Regresson can be exressed as a functon between nterested resonse varable and exlanatory varables thought to be related on resonse. Functonal form of the relatonsh between the exlanatory varables and resonse varable descrbed as regresson model. The regresson model must be chosen accordng to the data structure. If the chosen model s wrong, t leads to erroneous results. In ths revew, regresson methods were examned to determne whch regresson models such as; lnear regresson, logstc regresson, negatve bnomal regresson, osson regresson, rncal comonents regresson, robt regresson, rdge regresson and Cox regresson, s sutable for dfferent data structure. Key Words: Regresson, Lnear regresson, Nonlnear regressons. GİRİŞ Byolo, tı, ekonom, fzk, kmya ve sosyal blmler gb brçok alanda yaygın olarak kullanılmakta olan regresyon analz, aralarında sebe - sonuç lşks bulunan k veya daha fazla değşken arasındak lşky nceleyen ve bu lşky modellemek çn kullanılan statstksel br analz yöntemdr (Vural, 2007 ). Uygun olmayan regresyon yöntemlernn kullanılması hatalı ve yanıltıcı sonuçların elde edlmesne neden olablmektedr. Regresyon analznde ncelenen değşkenler sürekl ya da keskl yaıda olablmektedr ve bu ver yaısına bağlı olarak farklı regresyon modeller kullanılablmektedr (Özarıcı, 996). Bu çalışma, regresyon yöntemlernden; Doğrusal regresyon, Lostk regresyon, Negatf bnom regresyon, Posson regresyon, Temel bleşenler regresyonu, Probt regresyon, Rdge regresyon, Cox regresyon yöntemlernn hang durumlarda kullanılableceğ konusunda araştırmacılara yol göstermek amacıyla yaılmıştır. 2. REGRESYON YÖNTEMLERİ 2.. Doğrusal regresyon Doğrusal regresyon analz bast doğrusal regresyon ve çoklu doğrusal regresyon olarak k başlık altında ncelenmektedr. Bast regresyon analz, yanıt değşken le tek br açıklayıcı değşken arasındak doğrusal lşky açıklar. Eğer tek br yanıt değşken ve brden fazla açıklayıcı değşken arasındak doğrusal veya eğrsel br lşk tanımlanmak stenrse, lşk çoklu doğrusal regresyon analz le ncelenr (Okur, 2009; Wesberg, 2005). Bast doğrusal regresyonda, Y yanıt değşken, açıklayıcı değşken, β 0 ve β bu değşkenn blnmeyen arametrelern ve ε şansa bağlı hata termlern fade etmek üzere bast doğrusal regresyon model; Y = β 0 + β + ε =,2,...,n olarak yazılablmektedr (Kutner ve ark., 2005). Çoklu doğrusal regresyon model, adet açıklayıcı değşken ve n adet gözlem çn; Y = β 0 + β + β β + ε =, 2,, n şeklnde yazılablmektedr (Kutner ve ark., 2005; Wesberg, 2005). Gerek bast gerekse çoklu doğrusal regresyon analz sonucunda elde edlecek olan regresyon modelne at arametre kestrmlernn güvenlr olablmes çn modelle lgl bazı varsayımların sağlanablmes gerekldr.
2 A. Arı, H. Önder Bast doğrusal regresyon analznde elde edlen regresyon denklemnn tahmn amaçlı kullanılablmes çn; hata termlernn (Є = Y ) şansa bağlı normal dağılım göstermes, hataların beklenen değernn ortalamasının 0 ve varyansının homoen olu σ 2 ye eşt olması, hataların bağımsız olması [Cov (Є, Є ) ] = 0, hata termler le açıklayıcı değşken(ler) arasında korelasyon bulunamaması gb bazı varsayımların sağlanması gerekmektedr (Alma ve Vua, 2008). Çoklu doğrusal regresyonda, bast doğrusal regresyondak varsayımlara laveten açıklayıcı değşkenlern brbrnden bağımsız olması varsayımının da sağlanması gerekmektedr (Vural, 2007). Açıklayıcı değşkenler arasındak bast doğrusal korelasyon katsayılarının sıfır veya sıfıra çok yakın olması şartı seklnde de açıklanablen bu varsayım, statstkte Çoklu doğrusal bağlantı bulunmaması olarak fade edlmektedr (Orhunblge, 2002). Çoklu bağlantı durumda En Küçük Kareler (EKK) kestrm yöntem şlevn ytrmektedr (Vural, 2007). Bu nedenle açıklayıcı değşkenler seçlrken, bu değşkenlern yanıt değşken le bast doğrusal korelasyon katsayılarının yüksek ( e yakın), brbrler arasındak bast doğrusal korelasyon katsayılarının düşük (0 a yakın) olmasına dkkat edlmes önerlmektedr (Damodar, 200). Bu varsayımların sağlanamadığı durumlarda arametre kestrm yöntemlernn değştrlmes önerlmektedr Posson regresyon Araştırmadan elde edlen verlern ölçeğnn sürekl yaıda olmadığı, dğer br fade le kategork verye sah olunduğunda doğrusal regresyon modeller kullanılarak yaılacak analzler etksz, tutarsız ve güvenlmez sonuçlar vereblr. Özellkle, sayma ölçeğnde elde edlen verler çn kullanılablecek en etkn modellerden br Posson regresyon modeldr (Denz, 2005). Posson regresyon model; log e ( Y ) = β 0 + β + β 2 2 K, olu, β0 β β2 2 Y = ( e )( e )( e )K, olarak da tanımlanablmektedr (Demars, 2004). Modelden anlaşılacağı üzere Posson regresyon model tahmn edclern doğrusal fonksyonunun logartmk dönüşümü olarak fade edleblmektedr (URL ). İstatstk lteratüründe bu model log-doğrusal model olarak blnmektedr. x β nın ex( x β ) olarak alınması, beklenen sayma değernn oztf olmasını gerektrr. Bu durum Posson dağılımı çn zorunludur. Posson dağılımında ortalama ve varyansın eştlğ söz konusu olu; μ = E y x ) = V ( y x ), ( olarak gösterleblr. Ortalama ve varyansın eştlğ eşt yayılım olarak fade edlmektedr. Uygulamada sayılarak elde edlen değşkenler genellkle ortalamadan daha büyük varyansa sahtrler. Bu durum aşırı yayılım (overdserson) olarak adlandırılmaktadır. Aşırı yayılım durumunda Posson Regresyon Modelnden elde edlen tahmnler tutarlı fakat etkn değldr (Selm, 2003; Demars, 2004) Negatf Bnom Regresyonu Negatf bnom regresyonunun uygulandığı ver kümesnde değerlern çoğunun sıfır olmasından dolayı dağılış sağa çarıktır. Bu durum, doğrusal regresyon kullanımında kuramsal olarak hatalı olan negatf arametre tahmnlern berabernde getrmektedr (Frome ve ark., 973; Cox, 983; SAS, 2005). Negatf bnom regresyon model çn olasılık yoğunluk fonksyonu; y ( y + d )! α Pr( Y = y; α, d) = ; y = 0,,2K y + d y!( d )! ( α) olarak verleblmektedr. Burada, α br olgunun ortaya çıkma olasılığı [P(Y=)] ve d ndeks veya yayılım arametres olarak adlandırılmaktadır. Negatf bnom regresyonu çözümlemesnde arametre kestrmler Newton-Rahson algortması yardımıyla En Çok Olablrlk yöntem kullanılarak elde edlr. Negatf Bnom regresyonun model eştlğ; E( Y ) = β + β + β + L+ β dr. 0 2 Negatf Bnom regresyonu, Posson regresyonun özel br durumudur. Bu k model arasındak seçm kararı, kestrm elde edlen d katsayısının statstksel anlamlılığı yönünden belrlenr. Eğer d (yayılım arametres), sıfırdan öneml derecede farklı değlse (statstksel olarak öneml değlse), Negatf Bnom regresyonu Posson regresyonuna dönüşür. Bununla beraber, d öneml derecede sıfırdan farklı se, Negatf Bnom regresyonu terch edlmeldr (Hadayegh, 2002; Aktaş ve Saraçbaşı, 2005) Lostk Regresyon Lostk regresyon, statstkte kullanılan br model oluşturma teknğ olu k ya da daha fazla sınıfta fade edleblen keskl verlerde yanıt değşken (Y) çn br model oluşturma teknğdr. Yanıt değşkennn keskl olduğu durumlarda Lostk ya da Probt regresyon yöntemler kullanılmaktadır (Freese and Long, 2006). Modeln amacı, yanıt değşken k değerl veya sınıflandırılmış olduğunda yanıt değşken le açıklayıcı değşken veya değşkenler arasındak lşk açıklayan br model oluşturmaktır (Önder ve Cebec, 2002). Lostk regresyon le doğrusal regresyon yöntem arasında üç öneml fark vardır (Brcan, 2004), bu farklılıklar; 2 69
3 Farklı ver yaılarında kullanılablecek regresyon yöntemler. Doğrusal regresyon analznde tahmn edlecek olan yanıt değşken sürekl ken, Lostk Regresyon Analznde yanıt değşken keskl br değer almaktadır. 2.Doğrusal regresyon analznde yanıt değşkenn değer, Lostk Regresyon Analznde se yanıt değşkenn alableceğ değerlerden brnn gerçekleşme olasılığı tahmn edlr. 3. Doğrusal regresyon analznde açıklayıcı değşkenn çoklu normal dağılım göstermes şartı aranırken, Lostk Regresyon Analznde böyle br şart yoktur. Lostk regresyon analznde, yanıt değşken doğrudan modellenememektedr. Daha doğru br yaklaşımla, lostk regresyon analz, Y yanıt değşkennn değernn brleştrlmş olasılığı üzerne kurulmuştur. Uygulamada çok yaygın olarak yanıt değşkenn başarılı veya oztf çıktı çn 0 ve başarısız veya negatf çıktı çn değern aldığı farz edlr. Yanıt değşken olduğunda olasılık; P( Y olarak gösterleblr. α + β = e =... ) = α + β = + e Lostk regresyon modellerndek çoklu ç lşk, açıklayıcı değşkenler arasındak güçlü korelasyondan kaynaklanır. Lostk regresyondak çoklu ç lşk regresyon katsayılarının kestrmlernn büyüklüğünün ve şaretnn yanlış olarak bulunmasını sağlayablr ve netcede yanıt ve açıklayıcı değşkenler arasındak lşkler hakkında yanlış sonuçlara ulaşılmasına yol açablr (Ürük, 2007; Önder ve Cebec, 2002; Klenbaum ve ark., 998) Probt Regresyon Probt analz lostk regresyona alternatf olarak br veya daha fazla açıklayıcı değşkenn kategork br yanıt değşken (sağ, ölü; çalışıyor, çalışmıyor, ürün satıldı veya satılmadı vb) üzerndek etksn bulmak çn kullanılan br modeldr. Hem lostk hem de Probt regresyon analz brbrlerne oldukça benzer ve elde edlen olasılık tahmnler brbrlerne yakın değerdedr. Lostk regresyon analznde log-odds (olablrlk oranları) kullanılırken, Probtte kümülatf normal dağılım kullanılmaktadır, Temel olarak Probt brkml standart normal dağılışın tersdr (Tocu, 2008, Bek, 2009). Probt modeln altında yatan varsayım, yanıt fonksyonunun Y = α + β + U formunda olmasıdır. Burada gözlemleneblen fakat Y gözlemlenemeyen değşkendr. Y > 0 se Y =, fakat Y < 0 se Y =0 olur (Y değşkennn sonucu atanırken, eşk değer olarak kullanılan c değer genellkle 0 olarak alınmakta olu, sıfır yerne başka sayı değer de kullanılablmektedr (Demars, 2004)). Eğer normal standart değşken Z, çn, Ф (z) kümülatf normal dağılım fonksyonu Ф (z) = P (Z z) olarak tanımlanırsa; α β P( Y = ) = P( u > α β ) = Φ σ α β P ( Y = 0) = P( u α β ) = Φ σ olarak fade edleblr. Probt modelnde brden fazla açıklayıcı değşken olduğu zaman, Pr( Y = / ) = Φ( β ) şeklnde tanımlanır. Burada Φ standart normal olasılık dağılımıdır. β Probt skoru ya da ndeks olarak adlandırılır ve normal dağılıma sahtr. Probt katsayısı β, tahmndek br brmlk artışın Probt skorunda yaacağı β standart samalık yükselmey fade eder. Probt katsayısı bağımsız değşkenn bağımlı değşkene at standart z-değernde yaacağı etky ölçer. Bu katsayıların sayısal büyüklüklernn br önem ve özel br yorumu yoktur, sadece lşknn yönü ve derecesn belrler (Tocu, 2008; Kulendran ve Wong, 20; MacKnnon ve ark., 2007). Şekl. Logt ve Probt brkml dağılımlar Probt ve Logt modeller genellkle yanıt değşkennn k düzeyl olduğu durumlarda uygulanmaktadır. Hesalama zorluğu ve özel tablolara htyaç duyulmaması bakımından Logt modeln Probt modelne göre kolaylığına rağmen, normal olasılık yoğunluk fonksyonunun gerek teorde gerekse uygulamada daha çok kullanılan model olması byolok verlern bazı özellklerne lşkn dağılımlarının normal olasılık yoğunluk fonksyonuna uyum göstermes, hesalamada normal kümülatf dağılım fonksyonunu kullanan Probt modeln uygulama çalışmasında kullanılmasını özendrmektedr (Özarıcı, 996) Temel bleşenler regresyonu Her br bağımsız değşkenn dğer bağımsız değşkenlerle arasındak korelasyon katsayılarının kares olan değer e yakınsa, yüksek derecede çoklu bağlantı olduğu anlaşılablr (Yıldırım, 200). Açıklayıcı değşkenler arasında br ya da daha fazla doğrusal bağıntı olduğunda çoklu bağlantı sorunu ortaya çıkmaktadır (Polat, 2009). Çoklu doğrusal bağlantı roblem, yaılan analzler sonucunda elde 70
4 A. Arı, H. Önder edlen en küçük kareler kestrclernn varyans değerlernn büyük olmasına ve tahmnlern gerçek değerlernden uzaklaşmasına neden olmaktadır (Bulut ve Alın, 2009) ve çoklu bağlantı roblemnn ortaya çıkması durumunda doğrusal regresyon analz etknlğn ytrmektedr. Bu durumda temel bleşenler regresyonu ya da rdge regreson yöntem kullanılablr. Temel bleşenler regresyonu her doğrusal regresyon modelnn br dk açıklayıcı değşkenler kümesne dayanarak yenden açıklanması temel üzerne yaılandırılmış olu, açıklayıcı değşkenler arasında çoklu bağlantı olduğu durumlarda uygulanmaktadır (Özkan, 2009). Çoklu bağlantı durumunda, EKK yerne yanlı kestrm teknklernn kullanılmasının en uygun yaklaşım olduğu blnmektedr (Albayrak, 2006). Yanlı kestrmler veren yöntemlern başında, gerçek değşkenler yerne bunların dk dönüşümlernn kullanıldığı Temel Bleşenler Regresyonu (PCR/Prncal Comonent Regresson) ve korelasyon matrsnn köşegen elemanlarına küçük br oztf sayı eklenerek kestrm varyanslarının küçültüldüğü Rdge Regresyon (RR) yöntem gelmektedr (Polat, 2009). Çoklu doğrusal regresyon modelnde açıklayıcı değşken katsayıları matrs notasyonunda; ˆβ = ( ) y olarak tahmn edleblr ve burada, açıklayıcı değşkenler matrsn ve Y se yanıt değşken vektörünü göstermektedr., bu katsayılar temel bleşenler regresyonunda; ˆβ PC = DΛ D y ye at olarak tahmn edlmektedr. Burada, D, lk adet öz vektör matrs; Λ, ye at lk adet öz vektör çn köşegen matrs göstermektedr (Al-Hassan ve Al-Kassab, 2009). PCR sonucunda elde edlen tahmnler yanlı olur. Ancak varyansın azaltılmasıyla, yanlılıktak büyüklük dengelenr. RR teknğnde k yanlılık sabtnn seçmnde yaşanan belrszlğn aksne, PCR analznde modelden çıkarılacak PC lern sayısı görecel olarak daha tutarlıdır (Albayrak, 20; Aswan ve ark., 20; Al-Hassan ve Al-Kassab, 2009) Rgde regresyon Çoklu doğrusal bağlantı olduğunda yanlı tahmn yöntemlernden Rdge Tahmn Yöntem gerekl olan tüm değşkenlern modele alınmasını sağlar. Bu yöntem çoklu doğrusal bağlantı olduğunda EKK kestrmlernden daha küçük varyanslı arametre kestrmlernn elde edlmesn ve modelden gereksz değşkenlern çıkarılmasını amaçlamaktadır (Karadavut ve ark., 2005). Rdge regresyon yöntem genellkle modeldek k ya da daha fazla açıklayıcı değşken arasında yüksek dereceden lşk olması durumunda kullanılır. Bu yöntemde uygulanırken lk adım olarak açıklayıcı değşkenler standartlaştırılır (Karadavut ve ark., 2005). Standartlaştırılmamış ornal değşkenlern bulunduğu model; y = β 0 + β + K+ β + ε =, 2,, n şeklnde gösterleblmektedr. Bu modeldek açıklayıcı değşkenler standartlaştırılarak, y = μ + γ Z + K+ γ Z + ε model elde edlr (Karadavut ve ark., 2005). Rdge regresyonun yanlı regresyon yöntem olmasına karşın EKK yöntemne göre k öneml katkısı vardır. Bunlar; açıklayıcı değşkenlerde çoklu bağlantıyı elemne etmek ve regresyonda yanlılık karesyle varyansı değştrerek Hata Kareler Ortalamasını azaltmaktır (İek, 20). Rdge regresyon modelnde açıklayıcı değşken katsayıları matrs notasyonunda; ˆβ = ( + ki y, ( k ) ) olarak tahmn edleblmektedr. Burada; k, yanlılık ya da Rgde arametres olarak blnmektedr ve ver kümesnden tahmn edlmeldr (Al-Hassan ve Al- Kassab, 2009). Çoklu regresyon modelnde açıklayıcı değşkenler brbrler le bağlantılı olduklarında EKK β kestrcsnden daha küçük varyanslı β kestrclernden elde edlmesnde, güçlü çoklu bağlantı etks le regresyon katsayılarında oluşan kararsızlıkların grafk üzernde gösterlmesnde ve modeldek gereksz değşkenlern çıkarılması amacıyla Rdge regresyon yöntem kullanılablmektedr (Yıldırım, 200; Pamukçu ve ark., 200) Cox regresyon 20. yüzyılda başlayan yaşam çözümlemes çalışmaları, bu yüzyılın knc yarısı boyunca büyük lerlemeler göstermştr. Bu alandak en etkl gelşmelerden br; yaşam sures üzernde açıklayıcı değşkenlern etklern ölçeblmek çn kullanılan Cox Regresyon Model dr. Parametrk modellern gerektrdğ varsayımların (normallk, bağımsızlık vb.) sağlanmadığı durumlarda Cox regresyon analz, arametrk analzlerden daha etkldr. Cox regresyon modelnn temel varsayımları şu şeklde açıklanablr: bağımsız değşkenlern rsk (hazard) fonksyonu üzerndek etkler loglneerdr ve bağımsız değşkenlern loglneer fonksyonu le rsk fonksyonu arasındak lşk çarımsaldır (Özdamar, 7
5 Farklı ver yaılarında kullanılablecek regresyon yöntemler 200; Laubender ve Bender, 200; Chen ve ark., 2009; Lu ve ark., 200). Bu k varsayıma ek olarak gözlemlern brbrnden bağımsız olmaları ve rsk oranının zamana göre değşmemes, yan sabt olması gerekmektedr (Yay ve ark., 2007). Cox regresyon modelnde yaşam zamanı T nn şartlı dağılımı, Z ve hazard fonksyonu λ (. Z, ) tarafından tanımlanmaktadır ve hazard; λ ( t Z, ) = λ0 ( t)ex( γz + β ), olarak tanımlanablmektedr. Burada; γ, Z ye at regresyon katsayılarını, β se e at regresyon katsayıları vektörünü göstermektedr. λ0 (.) se Z=0 ve =0 olan br denek çn temel alınan hazard fonksyonunu göstermektedr (Laubender ve Bender, 200). Cox regresyon modelnn temel varsayımı olan orantılı hazard varsayımı, hazard oranının zamana karsı sabt olması ya da br breyn hazard fonksyonun dğer breyn hazard fonksyonuna orantılı olması anlamına gelmektedr. Klnk denemelerde özellkle uzun sürel verler söz konusu olduğun da orantısız hazardlar açığa çıkmaktadır. Hazardların orantılı olmaması durumunda se Cox regresyon model yaşam vers çn uygun olmamaktadır (Ata ve ark., 2007; Chen ve ark., 2009). 3. MODEL SEÇİMİ Yukarıda yaılan model tanımlarının ardından, model seçmnde uygulamaya yönelk karar mekanzması verye at hstogram grafğnn yaısına göre aşağıda örnek br çalışma le brlkte Çzelge de verlmştr. 4. SONUÇ Br araştırmada elde edlen verlere hang statstklern uygulanablr olduğunu belrlemek çn bazı ölçütler söz konusudur. Uygun statstk yöntemlerle araştırmayı çözümlemek, araştırmanın güvenrlğn artırmakla brlkte sonuçların tutarlı br şeklde yorumlanmasını da sağlamaktadır. Bu nedenle değşken yaıları, ölçme ölçekler, varsayımların tutarlılığı statstksel çalışmalarda öncelkl olarak dkkate alınması gereken öneml br durumdur. Çözümlemedek adımsal yaklaşımı dkkate almadıklarından araştırmacılar yanıltıcı ve güvenlr olmayan raorlar yayınlayablmektedr. Değşken yaıları seçlecek olan statstksel yöntem belrlemektedr. Elde edlen vernn yaısına uygun modeln seçlmes araştırmadan elde edlen sonuçların güvenrlğn ve tahmn gücünü yükseltecektr. 5. KAYNAKLAR Aktaş, A., Saraçbaşı,O., Negatf Bnom Regresyon Model, VIII. Ulusal Byostatstk Kongres, Eylül 2005, Bursa, Albayrak, A. S Uygulamalı Çok Değşkenl İstatstk Teknkler, Asl Yayın Dağıtım Ltd. Şt. Albayrak, A.S. 20. Çoklu Doğrusal Bağlantı Halnde Enküçük Kareler Teknğnn Alternatf Yanlı Tahmn Teknkler Ve Br Uygulama. sbd.karaelmas.edu.tr/makaleler/ / df. Erşm Tarh: Al-Hassan, Y.M., Al-Kassab, M. M., A Monte Carlo Comarson between Rdge and Prncal Comonents Regresson Methods. Aled Mathematcal Scences, 3(42), Alma, G.Ö., Vua, Ö., Regresyon Analznde Kullanılan En Küçük Kareler Ve En Küçük Medyan Kareler Yöntemlernn Karşılaştırılması. SDÜ Fen Edebyat Fakültes Fen Dergs (E-Derg). 2008, 3(2) Aswan, A., Bckel, P., Tomln, C., 20. Regresson on Manfolds: Estmaton of the Exteror Dervatve. Ann. Statst. 39(), Ata, N., Karasoy, D., Sözer, M.T Orantısız Hazardlar İçn Tabakalandırılmış Cox Regresyon Model ve Meme Kanser Hastaları Üzerne Br Uygulama. Türkye Klnkler J Med Sc, s. 28. Bek, Y., R Programında Doz-Yanıt Uygulamaları Çalıştayı Dnleyc Notları Mayıs 2009, Samsun. Brcan, H Lostk Regresyon Analz: Tı Verler Üzerne Br Uygulama. Kocael Ünverstes Sosyal Blmler Ensttüsü Dergs, 2004 / 2 : Bulut, E., Alın, A., Kısm En Küçük Kareler Regresyon Yöntem Algortmalarından Nals ve PLS - Kernel Algortmalarının Karşılaştırılması ve Br Uygulama. Dokuz Eylül Ünverstes İktsad ve İdar Blmler Fakültes Dergs, 24(2), Chen, M., Ibrahm, J.G., Shao, Q., Maxmum Lkelhood İnference for the Cox Regresson Model wth Alcatons to Mssng Covarates. Journal of Multvarate Analyss 00, Cox, R., 983. Some Remarks on Overdserson. Bometrka,70: Denz, Ö Poısson Regresyon Analz. İstanbul Tcaret Ünverstes Fen Blmler Dergs Yıl:4 Sayı:7 Bahar 2005/ S Damodar, N Temel Ekonometr, 2. Basım, İstanbul: Lteratür Yayıncılık, s.92. Demars, A., Regresson wth Socal Data : Modelng Contnuous and Lmted Resonse Varables. John Wley & Sons, Inc. Hoboken, New Jersey. Freese, J. and Long, J.S., Regresson Models for Categorcal Deendent Varables Usng. Stata. College Staton: Stata Pres. Frome, E.D., Kutner, M.H., Beaucham, J.J., 973. Regresson Analyss of Posson- Dstrbuted Data. Journal of Amercan Statstcal Assocaton, 68(344): Hadayegh, A., Accdent Predcton Models for Safety Evaluaton of Urban Safety Transortaton, Yüksek Lsans Tez, Toronto Ünverstes İnşaat Mühendslğ Bölümü, Kanada. İek, O. 20. Rıdge Regresyon Üzerne Br Çalışma. dar.cu.edu.tr/semozyum/bl28.htm Erşm Tarh:
6 A. Arı, H. Önder Çzelge. Model seçm çn karar mekanzması Yöntem Hstogram grafğ Doğrusal regresyon Ölçme ölçeğnde ve EKK yöntemnn varsayımları sağlanablyor se kullanılmalıdır. Doğrusal regresyonun kullanılableceğ ver kümesne örnek olarak, yanıt değşken ve açıklayıcı değşkenlern tamamının ölçülerek elde edldğ br kasalık canlı ağırlık (yanıt) üzerne doğum ağırlığı ve sütten kesm ağırlığının (açıklayıcı) etks verleblr (URL 2 ) Sayma ölçeğnde ve d arametres sıfırdan statstksel olarak farklı değl se kullanılmalıdır. Posson Posson regresyonun kullanılableceğ ver kümesne örnek olarak, klnk mastts düzeynn (skor) yanıt değşken olduğu ve açıklayıcı değşkenn somatk hücre sayısı olduğu br deneme gösterleblr (URL 3 ) Negatf bnom Sayma ölçeğnde ve d arametres sıfırdan statstksel olarak farklı se kullanılmalıdır. Negatf Bnom regresyonun kullanılableceğ ver kümesne örnek olarak, böcek sayısı (yanıt) üzerne btk çeşd (ndeks) ve btkde yarak sayısının (açıklayıcı) etksnn ncelendğ br araştırma verleblr (URL 4 ) Lostk ve Probt Temel Bleşenler ve Rdge İk veya daha fazla sınıfta grulanan verlerde, brkml artış fadelernde Probt kullanılmalı, olablrlk tahmn çn se Lostk kullanılmalıdır. Lostk regresyonun kullanılableceğ ver kümesne örnek olarak, hayvan sağlığı (sağlıklı, hasta) yanıt değşken üzerne yaş (keskl), süt verm (sürekl), arazt (var, yok) ve barınak durumunun (skor) açıklayıcı değşkenlernn etksnn ncelendğ br çalışma gösterleblr. Probt regresyonun kullanılableceğ ver kümesne örnek olarak, orman yangını (var, yok) yanıt değşken üzerne nem (sürekl), organk madde tabakasının kalınlığı (sürekl), organk madde tabakasının çeşd (ndeks), sıcaklık (sürekl) açıklayıcı değşkenlernn etksnn ncelendğ br çalışma verleblr (URL 5 ). Doğrusal regresyonda çoklu bağlantı olması durumunda, lgsz değşkenlern modelden çıkarılması çn Rdge kullanılmalı, tüm değşkenler modelde tutulmak stenyor se Temel Bleşenler kullanılmalıdır. Temel bleşenler ve Rdge regresyonun kullanılableceğ ver kümesne örnek olarak, çoklu bağlantı olması durumunda, canlı ağırlık (sürekl) yanıt değşken üzerne vücut ölçülernn (sürekl) etksnn ncelendğ br çalışma gösterleblr. Cox Uzun sürel yaşam verlernn modellenmesnde kullanılmalıdır. Cox regresyonun kullanılableceğ ver kümesne örnek olarak, sığırlarda subklnk endometrts rsk üzerne lk tohumlamada gebelk oranı (yüzde), gebelk başına servs sayısı (oran), arty (doğum sırası; keskl), vücut kondsyon skoru (skor) açıklayıcı değşkenlernn etksnn ncelendğ br çalışma gösterleblr (Demars, 2004 ) 73
7 Farklı ver yaılarında kullanılablecek regresyon yöntemler Karadavut, U., Genç, A., Tozluca, A., Kınacı, İ., Aksoyak, Ş., Palta, Ç., Pekgör, A Nohut (Ccer Aretnum L.) Btksnde Verme Etk Eden Bazı Karakterlern Alternatf Regresyon Yöntemleryle Karşılaştırılması. Tarım Blmler Dergs 2005, (3) Klenbaum, D. G., Kuer, L. L., Muller, K. E., Nzam, A., 998, Aled Regresson Analyss and Other Multvarable Methods, 798, Duxbury Press, 5 Forest Lodge Road Pacfc Grove, CA USA. Kulendran, N., Wong, K.K.F., 20. Determnants versus Comoste Leadng Indcators n Predctng Turnng Ponts n Growth Cycle. Journal of Travel Research, 50(4), Kutner, M. H., Nachtshem, C. J., Neter, J. ve L, W., Aled Lnear Statstcal Models. McGraw-Hll Irwn Comanes nc. New York. Laubender, R.P., Bender, R., 200. Estmatng Adusted Rsk Dfference (RD) and Number Needed to Treat (NNT) Measures n the Cox Regresson Model. Statst. Med. 29, Lu, M., Lu, W., Shore, R.E., Zelenuch-Jacuotte, A., 200. Cox Regresson Model wth Tme-Varyng Coeffcents n Nested Case Control Studes. Bostatstcs, (4), MacKnnon, D.P., Lockwood, C.M., Brown, C.H., Wang, W., Hoffman, J.M., The Intermedate Endont Effect n Logstc and Probt Regresson. Clncal Trals, 4, Okur, S Parametrk Ve Parametrk Olmayan Doğrusal Regresyon Analz Yöntemlernn Karşılaştırmalı Olarak İncelenmes. Çukurova Ünverstes Fen Blmler Ensttüsü, Yüksek Lsans Tez, Adana. Orhunblge, N Uygulamalı Regresyon Ve Korelasyon Analz, İ.Ü. İşletme Fakültes Yayınları, İstanbul. Önder, H., Cebec, Z., Lostk Regresyonlarda Değşken Seçm. Çukurova Ünv. Zraat Fakültes Dergs, 7(2),05 4. Özarıcı, Ö Farklı Not Sstemlernde Öğrencnn Başarılı Olma Olasılığının Probt Regresyon Analzyle Değerlendrlmes, Osmangaz Ünverstes Fen Blmler Ensttüsü, Yüksek Lsans Tez. Özdamar, K. 200.SPSS le Byostatstk, Kaan Ktabev, Eskşehr. Özkan, K Torağın Tarla Kaastes Değşmnn Torak Türüne Göre Temel Bleşenler Regresyon Analz İle Modellenmes Süleyman Demrel Ünverstes Orman Fakültes Dergs Ser: A, Sayı: 2, Issn: , Sayfa: -9. Pamukçu, E., Çolak, C., Çalık, S., Kuzu, Z., 200. Sstolk Kan Basıncının Tahmnnde Yanlı Regresyon Yöntemlernn Kullanılması. Journal of Inonu Unversty Medcal Faculty, 7(4), Polat, E Kısm En Küçük Kareler Regresyonu. Hacettee Ünverstes, Fen blmler Ensttüsü, Yüksek Lsans Tez. SAS, SAS/STAT Software:Hangen and Enhanced. SAS, Inst. Inc., USA. Selm, S Sayma Ver Modeller İle Çocuk Sayısı Belrleycler: Türkye dek Seçlmş İller İçn Sosyoekonomk Analzler. D.E.Ü.İ.İ.B.F.Dergs Clt:8 Sayı:2, Ss:3-3. Tocu, Y Çftçlern Tarımsal Destekleme Poltkalarından Faydalanma İstekllğnde Etkl Faktörlern Analz: Erzurum İl Örneğ. Akdenz Ünverstes Zraat Fakültes Dergs, 2(2), URL : htt:// e/ma_cha3.df. Posson Regresson Analyss (Erşm Tarh: ). URL 2 : htt://theclmatescetcsarty.blogsot.com/20/08/nzc lmate-truth-newsletter-no-273.html (Erşm Tarh: ). URL 3 : htt:// (Erşm Tarh: ). URL 4 : htt:// nc0.html (Erşm Tarh: ). URL 5 : htt://archmede.bbl.ulaval.ca/archmede/fchers/23662 /ch07.html (Erşm Tarh: ). Ürük, E., İstatstksel Uygulamalarda Lostk Regresyon Analz. Marmara Vural, A Aykırı Değerlern Regresyon Modellerne Etkler ve Sağlam Kestrcler. Marmara Ünverstes Sosyal Blmler Ensttüsü, Yüksek Lsans Tez, İstanbul. Vural, A Aykırı Değerlern Regresyon Modellerne Etkler ve Sağlam Kestrcler. Marmara Ünverstes Sosyal Blmler Ensttüsü, Yüksek Lsans Tez, İstanbul. Wesberg, S., Aled Lnear Regresson. John Wley & Sons, Inc. Hoboken, New Jersey. Yay, M., Çöker, E., Uysal, Ö Yaflam Analznde Cox Regresyon Model ve Artıkların İncelenmes. Cerrahaşa Tı Dergs, 38:39-45, ISSN: Yıldırım, N., 200. En Küçük Kareler, Rdge Regresyon Ve Robust Regresyon Yöntemlernde Analz Sonuçlarına Aykırı Değerlern Etklernn Belrlenmes. Çukurova Ünverstes Fen Blmler Ensttüsü, Yüksek Lsans Tez, Adana. 74
ÇOKLU REGRESYON MODELİ, ANOVA TABLOSU, MATRİSLERLE REGRESYON ÇÖZÜMLEMESİ,REGRES-YON KATSAYILARININ YORUMU
 6.07.0 ÇOKLU REGRESON MODELİ, ANOVA TABLOSU, MATRİSLERLE REGRESON ÇÖZÜMLEMESİ,REGRES-ON KATSAILARININ ORUMU ÇOKLU REGRESON MODELİ Ekonom ve şletmeclk alanlarında herhang br bağımlı değşken tek br bağımsız
6.07.0 ÇOKLU REGRESON MODELİ, ANOVA TABLOSU, MATRİSLERLE REGRESON ÇÖZÜMLEMESİ,REGRES-ON KATSAILARININ ORUMU ÇOKLU REGRESON MODELİ Ekonom ve şletmeclk alanlarında herhang br bağımlı değşken tek br bağımsız
PARÇALI DOĞRUSAL REGRESYON
 HAFTA 4 PARÇALI DOĞRUSAL REGRESYO Gölge değşkenn br başka kullanımını açıklamak çn varsayımsal br şrketn satış temslclerne nasıl ödeme yaptığı ele alınsın. Satış prmleryle satış hacm Arasındak varsayımsal
HAFTA 4 PARÇALI DOĞRUSAL REGRESYO Gölge değşkenn br başka kullanımını açıklamak çn varsayımsal br şrketn satış temslclerne nasıl ödeme yaptığı ele alınsın. Satış prmleryle satış hacm Arasındak varsayımsal
Korelasyon ve Regresyon
 Korelasyon ve Regresyon 1 Korelasyon Analz İk değşken arasında lşk olup olmadığını belrlemek çn yapılan analze korelasyon analz denr. Korelasyon; doğrusal yada doğrusal olmayan dye kye ayrılır. Korelasyon
Korelasyon ve Regresyon 1 Korelasyon Analz İk değşken arasında lşk olup olmadığını belrlemek çn yapılan analze korelasyon analz denr. Korelasyon; doğrusal yada doğrusal olmayan dye kye ayrılır. Korelasyon
HAFTA 13. kadın profesörlerin ortalama maaşı E( Y D 1) erkek profesörlerin ortalama maaşı. Kestirim denklemi D : t :
 HAFTA 13 GÖLGE EĞİŞKENLERLE REGRESYON (UMMY VARIABLES) Gölge veya kukla (dummy) değşkenler denen ntel değşkenler, cnsyet, dn, ten reng gb hemen sayısallaştırılamayan ama açıklanan değşkenn davranışını
HAFTA 13 GÖLGE EĞİŞKENLERLE REGRESYON (UMMY VARIABLES) Gölge veya kukla (dummy) değşkenler denen ntel değşkenler, cnsyet, dn, ten reng gb hemen sayısallaştırılamayan ama açıklanan değşkenn davranışını
NİTEL TERCİH MODELLERİ
 NİTEL TERCİH MODELLERİ 2300 gözlem sayısı le verlen değşkenler aşağıdak gbdr: calsma: çocuk çalışıyorsa 1, çalışmıyorsa 0 (bağımlı değşken) Anne_egts: Anne eğtm sevyes Baba_egts: Baba eğtm sevyes Kent:
NİTEL TERCİH MODELLERİ 2300 gözlem sayısı le verlen değşkenler aşağıdak gbdr: calsma: çocuk çalışıyorsa 1, çalışmıyorsa 0 (bağımlı değşken) Anne_egts: Anne eğtm sevyes Baba_egts: Baba eğtm sevyes Kent:
Hasar sıklıkları için sıfır yığılmalı kesikli modeller
 www.statstkcler.org İstatstkçler Dergs 5 (01) 3-31 İstatstkçler Dergs Hasar sıklıkları çn sıfır yığılmalı keskl modeller Sema Tüzel Hacettepe Ünverstes Aktüerya Blmler Bölümü 06800-Beytepe, Ankara, Türkye
www.statstkcler.org İstatstkçler Dergs 5 (01) 3-31 İstatstkçler Dergs Hasar sıklıkları çn sıfır yığılmalı keskl modeller Sema Tüzel Hacettepe Ünverstes Aktüerya Blmler Bölümü 06800-Beytepe, Ankara, Türkye
FAKTÖR A ALĐZ SKORLARI KULLA ILARAK KARAYAKA KUZULARI DA CA LI AĞIRLIK TAHMĐ Đ
 Anadolu Tarım Blm. Derg., 2009,24(2):98-102 Anadolu J. Agrc. Sc., 2009,24(2):98-102 Araştırma Research FAKTÖR A ALĐZ SKORLARI KULLA ILARAK KARAYAKA KUZULARI DA CA LI AĞIRLIK TAHMĐ Đ Soner ÇA KAYA* Aydın
Anadolu Tarım Blm. Derg., 2009,24(2):98-102 Anadolu J. Agrc. Sc., 2009,24(2):98-102 Araştırma Research FAKTÖR A ALĐZ SKORLARI KULLA ILARAK KARAYAKA KUZULARI DA CA LI AĞIRLIK TAHMĐ Đ Soner ÇA KAYA* Aydın
Doğrusal Korelasyon ve Regresyon
 Doğrusal Korelasyon ve Regresyon En az k değşken arasındak lşknn ncelenmesne korelasyon denr. Kşlern boyları le ağırlıkları, gelr le gder, öğrenclern çalıştıkları süre le aldıkları not, tarlaya atılan
Doğrusal Korelasyon ve Regresyon En az k değşken arasındak lşknn ncelenmesne korelasyon denr. Kşlern boyları le ağırlıkları, gelr le gder, öğrenclern çalıştıkları süre le aldıkları not, tarlaya atılan
ALGILANAN HİZMET KALİTESİ VE LOJİSTİK REGRESYON ANALİZİ İLE HİZMET TERCİHİNE ETKİSİNİN BELİRLENMESİ. Özet
 Dokuz Eylül Ünverstes Sosyal Blmler Ensttüsü Dergs Yayın Gelş Tarh: 18.02.2011 Clt: 13, Sayı: 1, Yıl: 2011, Sayfa: 21-37 Yayına Kabul Tarh: 17.03.2011 ISSN: 1302-3284 ALGILANAN HİZMET KALİTESİ VE LOJİSTİK
Dokuz Eylül Ünverstes Sosyal Blmler Ensttüsü Dergs Yayın Gelş Tarh: 18.02.2011 Clt: 13, Sayı: 1, Yıl: 2011, Sayfa: 21-37 Yayına Kabul Tarh: 17.03.2011 ISSN: 1302-3284 ALGILANAN HİZMET KALİTESİ VE LOJİSTİK
ENDÜSTRİNİN DEĞİŞİK İŞ KOLLARINDA İHTİYAÇ DUYULAN ELEMANLARIN YÜKSEK TEKNİK EĞİTİM MEZUNLARINDAN SAĞLANMASINDAKİ BEKLENTİLERİN SINANMASI
 V. Ulusal Üretm Araştırmaları Sempozyumu, İstanbul Tcaret Ünverstes, 5-7 Kasım 5 ENDÜSTRİNİN DEĞİŞİK İŞ KOLLARINDA İHTİYAÇ DUYULAN ELEMANLARIN YÜKSEK TEKNİK EĞİTİM MEZUNLARINDAN SAĞLANMASINDAKİ BEKLENTİLERİN
V. Ulusal Üretm Araştırmaları Sempozyumu, İstanbul Tcaret Ünverstes, 5-7 Kasım 5 ENDÜSTRİNİN DEĞİŞİK İŞ KOLLARINDA İHTİYAÇ DUYULAN ELEMANLARIN YÜKSEK TEKNİK EĞİTİM MEZUNLARINDAN SAĞLANMASINDAKİ BEKLENTİLERİN
SEK Yönteminin Güvenilirliği Sayısal Bir Örnek. Ekonometri 1 Konu 11 Sürüm 2,0 (Ekim 2011)
 İk Değşkenl Bağlanım Model SEK Yöntemnn Güvenlrlğ Ekonometr 1 Konu 11 Sürüm,0 (Ekm 011) UADMK Açık Lsans Blgs İşbu belge, Creatve Commons Attrbuton-Non-Commercal ShareAlke 3.0 Unported (CC BY-NC-SA 3.0)
İk Değşkenl Bağlanım Model SEK Yöntemnn Güvenlrlğ Ekonometr 1 Konu 11 Sürüm,0 (Ekm 011) UADMK Açık Lsans Blgs İşbu belge, Creatve Commons Attrbuton-Non-Commercal ShareAlke 3.0 Unported (CC BY-NC-SA 3.0)
KIRMIZI, TAVUK VE BEYAZ ET TALEBİNİN TAM TALEP SİSTEMİ YAKLAŞIMIYLA ANALİZİ
 Süleyman Demrel Ünverstes Sosyal Blmler Ensttüsü Dergs Yıl: 2007/2, Sayı: 6 Journal of Suleyman Demrel Unversty Insttue of Socal Scences Year: 2007/2, Number: 6 KIRMIZI, TAVUK VE BEYAZ ET TALEBİNİN TAM
Süleyman Demrel Ünverstes Sosyal Blmler Ensttüsü Dergs Yıl: 2007/2, Sayı: 6 Journal of Suleyman Demrel Unversty Insttue of Socal Scences Year: 2007/2, Number: 6 KIRMIZI, TAVUK VE BEYAZ ET TALEBİNİN TAM
UYGULAMA 2. Bağımlı Kukla Değişkenli Modeller
 UYGULAMA 2 Bağımlı Kukla Değşkenl Modeller Br araştırmacı Amerka da yüksek lsans ve doktora programlarını kabul ednlmey etkleyen faktörler ncelemek stemektedr. Bu doğrultuda aşağıdak değşkenler ele almaktadır.
UYGULAMA 2 Bağımlı Kukla Değşkenl Modeller Br araştırmacı Amerka da yüksek lsans ve doktora programlarını kabul ednlmey etkleyen faktörler ncelemek stemektedr. Bu doğrultuda aşağıdak değşkenler ele almaktadır.
Sıklık Tabloları ve Tek Değişkenli Grafikler
 Sıklık Tabloları ve Tek Değşkenl Grafkler Sıklık Tablosu Ver dzsnde yer alan değerlern tekrarlama sayılarını çeren tabloya sıklık tablosu denr. Sıklık Tabloları tek değşken çn marjnal tablo olarak adlandırılır.
Sıklık Tabloları ve Tek Değşkenl Grafkler Sıklık Tablosu Ver dzsnde yer alan değerlern tekrarlama sayılarını çeren tabloya sıklık tablosu denr. Sıklık Tabloları tek değşken çn marjnal tablo olarak adlandırılır.
BÖLÜM 5 İKİ VEYA DAHA YÜKSEK BOYUTLU RASGELE DEĞİŞKENLER İki Boyutlu Rasgele Değişkenler
 BÖLÜM 5 İKİ VEYA DAHA YÜKSEK BOYUTLU RASGELE DEĞİŞKENLER 5.. İk Boyutlu Rasgele Değşkenler Br deney yapıldığında, aynı deneyle lgl brçok rasgele değşkenn aynı andak durumunu düşünmek gerekeblr. Böyle durumlarda
BÖLÜM 5 İKİ VEYA DAHA YÜKSEK BOYUTLU RASGELE DEĞİŞKENLER 5.. İk Boyutlu Rasgele Değşkenler Br deney yapıldığında, aynı deneyle lgl brçok rasgele değşkenn aynı andak durumunu düşünmek gerekeblr. Böyle durumlarda
Lojistik Regresyonlarda Değişken Seçimi
 Çukurova Ünverstes Zraat Fakültes Dergs, 7 (2):05-4 Lostk Regresyonlarda Değşken Seçm Hasan ÖNDER () Zeynel CEBECİ (2) Özet Bu çalışmada, lostk regresyonlarda değşken seçm yöntemlernden ler doğru seçm,
Çukurova Ünverstes Zraat Fakültes Dergs, 7 (2):05-4 Lostk Regresyonlarda Değşken Seçm Hasan ÖNDER () Zeynel CEBECİ (2) Özet Bu çalışmada, lostk regresyonlarda değşken seçm yöntemlernden ler doğru seçm,
Sürekli Olasılık Dağılım (Birikimli- Kümülatif)Fonksiyonu. Yrd. Doç. Dr. Tijen ÖVER ÖZÇELİK
 Sürekl Olasılık Dağılım Brkml- KümülatFonksyonu Yrd. Doç. Dr. Tjen ÖVER ÖZÇELİK tover@sakarya.edu.tr Sürekl olasılık onksyonları X değşken - ;+ aralığında tanımlanmış br sürekl rassal değşken olsun. Aşağıdak
Sürekl Olasılık Dağılım Brkml- KümülatFonksyonu Yrd. Doç. Dr. Tjen ÖVER ÖZÇELİK tover@sakarya.edu.tr Sürekl olasılık onksyonları X değşken - ;+ aralığında tanımlanmış br sürekl rassal değşken olsun. Aşağıdak
YARIPARAMETRİK KISMİ DOĞRUSAL PANEL VERİ MODELLERİYLE ULUSLAR ARASI GÖÇ
 Özet YARIPARAMETRİK KISMİ DOĞRUSAL PANEL VERİ MODELLERİYLE ULUSLAR ARASI GÖÇ Atıf EVREN *1 Elf TUNA ** Yarı parametrk panel ver modeller parametrk ve parametrk olmayan modeller br araya getren; br kısmı
Özet YARIPARAMETRİK KISMİ DOĞRUSAL PANEL VERİ MODELLERİYLE ULUSLAR ARASI GÖÇ Atıf EVREN *1 Elf TUNA ** Yarı parametrk panel ver modeller parametrk ve parametrk olmayan modeller br araya getren; br kısmı
Muhasebe ve Finansman Dergisi
 Muhasebe ve Fnansman Dergs Ocak/2012 Farklı Muhasebe Düzenlemelerne Göre Hazırlanan Mal Tablolardan Elde Edlen Fnansal Oranlar İle Şrketlern Hsse Sened Getrler Ve Pyasa Değerler Arasındak İlşk Ahmet BÜYÜKŞALVARCI
Muhasebe ve Fnansman Dergs Ocak/2012 Farklı Muhasebe Düzenlemelerne Göre Hazırlanan Mal Tablolardan Elde Edlen Fnansal Oranlar İle Şrketlern Hsse Sened Getrler Ve Pyasa Değerler Arasındak İlşk Ahmet BÜYÜKŞALVARCI
Tek Yönlü Varyans Analizi
 Tek Yönlü Varyan Analz Nedr ve hang durumlarda kullanılır? den fazla grupların karşılaştırılmaı öz konuu e, çok ayıda t-tet nn kullanılmaı, Tp I hatanın artmaına yol açar; Örneğn, eğer 5 grubu kşerl olarak
Tek Yönlü Varyan Analz Nedr ve hang durumlarda kullanılır? den fazla grupların karşılaştırılmaı öz konuu e, çok ayıda t-tet nn kullanılmaı, Tp I hatanın artmaına yol açar; Örneğn, eğer 5 grubu kşerl olarak
X, R, p, np, c, u ve diğer kontrol diyagramları istatistiksel kalite kontrol diyagramlarının
 1 DİĞER ÖZEL İSTATİSTİKSEL KALİTE KONTROL DİYAGRAMLARI X, R, p, np, c, u ve dğer kontrol dyagramları statstksel kalte kontrol dyagramlarının temel teknkler olup en çok kullanılanlarıdır. Bu teknkler ell
1 DİĞER ÖZEL İSTATİSTİKSEL KALİTE KONTROL DİYAGRAMLARI X, R, p, np, c, u ve dğer kontrol dyagramları statstksel kalte kontrol dyagramlarının temel teknkler olup en çok kullanılanlarıdır. Bu teknkler ell
Sıfır Ağırlıklı Sayma ile Elde Edilen Veriler İçin Çok Seviyeli ZIP Regresyon * Multilevel ZIP Regression for Zero-Inflated Count Data
 Yüzüncü Yıl Ünverstes Fen Blmler Ensttüsü Dergs/ Journal of The Insttute of Natural & Appled Scences 18 (1-):01-08, 013 Araştırma Makales/Research Artcle Sıfır Ağırlıklı Sayma le Elde Edlen Verler İçn
Yüzüncü Yıl Ünverstes Fen Blmler Ensttüsü Dergs/ Journal of The Insttute of Natural & Appled Scences 18 (1-):01-08, 013 Araştırma Makales/Research Artcle Sıfır Ağırlıklı Sayma le Elde Edlen Verler İçn
Farklı Varyans. Var(u i X i ) = Var(u i ) = E(u i2 ) = σ i2. Eşit Varyans. Hata. Zaman
 Farklı Varyans Var(u X ) = Var(u ) = E(u ) = σ Eşt Varyans Y X Farklı Varyans Hata Var(u X ) = Var(u ) = E(u ) = σ Farklı Varyans Zaman Farklı Varyans le Karşılaşılan Durumlar Kest Verlernde. Kar dağıtım
Farklı Varyans Var(u X ) = Var(u ) = E(u ) = σ Eşt Varyans Y X Farklı Varyans Hata Var(u X ) = Var(u ) = E(u ) = σ Farklı Varyans Zaman Farklı Varyans le Karşılaşılan Durumlar Kest Verlernde. Kar dağıtım
FARKLI REGRESYON YÖNTEMLERİ İLE BETA KATSAYISI ANALİZİ
 FARKLI REGRESYON YÖNTEMLERİ İLE BETA KATSAYISI ANALİZİ M.Ensar YEŞİLYURT (*) Flz YEŞİLYURT (**) Özet: Özellkle uzak verlere sahp ver setlernn analz edlmesnde en küçük kareler tahmnclernn kullanılması sapmalı
FARKLI REGRESYON YÖNTEMLERİ İLE BETA KATSAYISI ANALİZİ M.Ensar YEŞİLYURT (*) Flz YEŞİLYURT (**) Özet: Özellkle uzak verlere sahp ver setlernn analz edlmesnde en küçük kareler tahmnclernn kullanılması sapmalı
LOJİSTİK REGRESYON ANALİZİ İLE ESKİŞEHİR İN SİS
 İstanbul Tcaret Ünverstes Fen Blmler Dergs Yıl: 8 Sayı: 16 Güz 2009/2 s. 47-59 LOJİSTİK REGRESYON ANALİZİ İLE ESKİŞEHİR İN SİS KESTİRİMİNİN İNCELENMESİ Cengz AKTAŞ *, Orkun ERKUŞ ** Gelş: 12.10.2009 Kabul:
İstanbul Tcaret Ünverstes Fen Blmler Dergs Yıl: 8 Sayı: 16 Güz 2009/2 s. 47-59 LOJİSTİK REGRESYON ANALİZİ İLE ESKİŞEHİR İN SİS KESTİRİMİNİN İNCELENMESİ Cengz AKTAŞ *, Orkun ERKUŞ ** Gelş: 12.10.2009 Kabul:
YAŞAM ÇÖZÜMLEMESİNDE AYKIRI DEĞERLER OUTLIERS IN SURVIVAL ANALYSIS
 YAŞAM ÇÖZÜMLEMESİNDE AYKIRI DEĞERLER OUTLIERS IN SURVIVAL ANALYSIS NURAY TUNCER PROF. DR. DURDU KARASOY Tez Danışmanı Hacettepe Ünverstes Lsansüstü Eğtm-Öğretm Yönetmelğnn İstatstk Anablm Dalı İçn Öngördüğü
YAŞAM ÇÖZÜMLEMESİNDE AYKIRI DEĞERLER OUTLIERS IN SURVIVAL ANALYSIS NURAY TUNCER PROF. DR. DURDU KARASOY Tez Danışmanı Hacettepe Ünverstes Lsansüstü Eğtm-Öğretm Yönetmelğnn İstatstk Anablm Dalı İçn Öngördüğü
Genel Doğrusal Karışık Modellerde Farklı Kovaryans Yapıları ve Tahmin Yöntemlerinin Performanslarının Karşılaştırılması 1
 Hayvansal Üretm 54(): 8-3, 03 Araştırma Makales Genel Doğrusal Karışık Modellerde Farklı Kovaryans Yapıları ve Tahmn Yöntemlernn Performanslarının Karşılaştırılması Gazel Ser *, Barış Kak, Abdullah Yeşlova,
Hayvansal Üretm 54(): 8-3, 03 Araştırma Makales Genel Doğrusal Karışık Modellerde Farklı Kovaryans Yapıları ve Tahmn Yöntemlernn Performanslarının Karşılaştırılması Gazel Ser *, Barış Kak, Abdullah Yeşlova,
SEK Tahmincilerinin Arzulanan Özellikleri. SEK Tahmincilerinin Arzulanan Özellikleri. Ekonometri 1 Konu 9 Sürüm 2,0 (Ekim 2011)
 SEK Tahmnclernn Arzulanan Özellkler İk Değşkenl Bağlanım Model SEK Tahmnclernn Arzulanan Özellkler Ekonometr 1 Konu 9 Sürüm 2,0 (Ekm 2011) http://www.ackders.org.tr SEK Tahmnclernn Arzulanan Özellkler
SEK Tahmnclernn Arzulanan Özellkler İk Değşkenl Bağlanım Model SEK Tahmnclernn Arzulanan Özellkler Ekonometr 1 Konu 9 Sürüm 2,0 (Ekm 2011) http://www.ackders.org.tr SEK Tahmnclernn Arzulanan Özellkler
EKONOMETRİYE GİRİŞ II ÖDEV 4 ÇÖZÜM
 EKONOMETRİYE GİRİŞ II ÖDEV 4 ÇÖZÜM (Örgün e İknc Öğretm çn) 1. 754 hanehalkına at DOMerset sml Excel dosyasında yer alan erler kullanarak tahmnlenen DOM sonuçları: Dependent Varable: CALISANKADIN Sample:
EKONOMETRİYE GİRİŞ II ÖDEV 4 ÇÖZÜM (Örgün e İknc Öğretm çn) 1. 754 hanehalkına at DOMerset sml Excel dosyasında yer alan erler kullanarak tahmnlenen DOM sonuçları: Dependent Varable: CALISANKADIN Sample:
dir. Bir başka deyişle bir olayın olasılığı, uygun sonuçların sayısının örnek uzaydaki tüm sonuçların sayısına oranıdır.
 BÖLÜM 3 OLASILIK HESABI 3.. Br Olayın Olasılığı Tanım 3... Br olayın brbrnden ayrık ve ortaya çıkma şansı eşt n mümkün sonucundan m tanes br A olayına uygun se, A olayının P(A) le gösterlen olasılığı P(A)
BÖLÜM 3 OLASILIK HESABI 3.. Br Olayın Olasılığı Tanım 3... Br olayın brbrnden ayrık ve ortaya çıkma şansı eşt n mümkün sonucundan m tanes br A olayına uygun se, A olayının P(A) le gösterlen olasılığı P(A)
İyi Tarım Uygulamaları Ve Tüketici Davranışları (Logit Regresyon Analizi)(*)
 Gazosmanpaşa Ünverstes Zraat Fakültes Dergs Journal of Agrcultural Faculty of Gazosmanpasa Unversty http://zraatderg.gop.edu.tr/ Araştırma Makales/Research Artcle JAFAG ISSN: 1300-2910 E-ISSN: 2147-8848
Gazosmanpaşa Ünverstes Zraat Fakültes Dergs Journal of Agrcultural Faculty of Gazosmanpasa Unversty http://zraatderg.gop.edu.tr/ Araştırma Makales/Research Artcle JAFAG ISSN: 1300-2910 E-ISSN: 2147-8848
BANKACILIKTA ETKİNLİK VE SERMAYE YAPISININ BANKALARIN ETKİNLİĞİNE ETKİSİ
 BANKACILIKTA ETKİNLİK VE SERMAYE YAPISININ BANKALARIN ETKİNLİĞİNE ETKİSİ Yrd. Doç. Dr. Murat ATAN - Araş. Gör. Gaye KARPAT ÇATALBAŞ 2 ÖZET Bu çalışma, Türk bankacılık sstem çnde faalyet gösteren tcar bankaların
BANKACILIKTA ETKİNLİK VE SERMAYE YAPISININ BANKALARIN ETKİNLİĞİNE ETKİSİ Yrd. Doç. Dr. Murat ATAN - Araş. Gör. Gaye KARPAT ÇATALBAŞ 2 ÖZET Bu çalışma, Türk bankacılık sstem çnde faalyet gösteren tcar bankaların
ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
 ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS EN KÜÇÜK KARELER, RİDGE REGRESYON VE ROBUST REGRESYON YÖNTEMLERİNDE ANALİZ SONUÇLARINA AYKIRI DEĞERLERİN ETKİLERİNİN BELİRLENMESİ ZOOTEKNİ ANABİLİM
ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS EN KÜÇÜK KARELER, RİDGE REGRESYON VE ROBUST REGRESYON YÖNTEMLERİNDE ANALİZ SONUÇLARINA AYKIRI DEĞERLERİN ETKİLERİNİN BELİRLENMESİ ZOOTEKNİ ANABİLİM
BÖLÜM 1 1.GİRİŞ: İSTATİSTİKSEL DOĞRUSAL MODELLER
 BÖLÜM 1 1.GİRİŞ: İSTATİSTİKSEL DOĞRUSAL MODELLER Blmn amaçlarından br yaşanılan doğa olaylarını tanımlamak ve olayları önceden tahmnlemektr. Bu amacı başarmanın yollarından br olaylar üzernde etkl olduğu
BÖLÜM 1 1.GİRİŞ: İSTATİSTİKSEL DOĞRUSAL MODELLER Blmn amaçlarından br yaşanılan doğa olaylarını tanımlamak ve olayları önceden tahmnlemektr. Bu amacı başarmanın yollarından br olaylar üzernde etkl olduğu
Merkezi Eğilim (Yer) Ölçüleri
 Merkez Eğlm (Yer) Ölçüler Ver setn tanımlamak üzere kullanılan ve genellkle tüm elemanları dkkate alarak ver setn özetlemek çn kullanılan ölçülerdr. Ver setndek tüm elemanları temsl edeblecek merkez noktasına
Merkez Eğlm (Yer) Ölçüler Ver setn tanımlamak üzere kullanılan ve genellkle tüm elemanları dkkate alarak ver setn özetlemek çn kullanılan ölçülerdr. Ver setndek tüm elemanları temsl edeblecek merkez noktasına
Farklı Varyans. Var(u i X i ) = Var(u i ) = E(u i2 ) = s 2 Eşit Varyans
 Farklı Varyans Var(u X ) = Var(u ) = E(u ) = s Eşt Varyans Y X 1 Farklı Varyans Hata Var(u X ) = Var(u ) = E(u ) = s Farklı Varyans Zaman EKKY nn varsayımlarından br anakütle regresyon fonksyonu u lern
Farklı Varyans Var(u X ) = Var(u ) = E(u ) = s Eşt Varyans Y X 1 Farklı Varyans Hata Var(u X ) = Var(u ) = E(u ) = s Farklı Varyans Zaman EKKY nn varsayımlarından br anakütle regresyon fonksyonu u lern
YÖNETİM VE EKONOMİ Yıl:2006 Cilt:13 Sayı:1 Celal Bayar Üniversitesi İ.İ.B.F. MANİSA
 YÖNETİM VE EKONOMİ Yıl:2006 Clt:3 Sayı: Celal Bayar Ünverstes İ.İ.B.F. MANİSA Bulanık Araç Rotalama Problemlerne Br Model Öners ve Br Uygulama Doç. Dr. İbrahm GÜNGÖR Süleyman Demrel Ünverstes, İ.İ.B.F.,
YÖNETİM VE EKONOMİ Yıl:2006 Clt:3 Sayı: Celal Bayar Ünverstes İ.İ.B.F. MANİSA Bulanık Araç Rotalama Problemlerne Br Model Öners ve Br Uygulama Doç. Dr. İbrahm GÜNGÖR Süleyman Demrel Ünverstes, İ.İ.B.F.,
TÜKETĠCĠLERĠN FĠYAT BĠLĠNCĠ ÜZERĠNDE ETKĠLĠ OLAN FAKTÖRLERE ĠLĠġKĠN BĠR ĠNCELEME
 Ġstanbul Ünverstes Ġktsat Fakültes Malye AraĢtırma Merkez Konferansları 46. Ser / Yıl 2004 Prof. Dr. Salh Turhan'a Armağan TÜKETĠCĠLERĠN FĠYAT BĠLĠNCĠ ÜZERĠNDE ETKĠLĠ OLAN FAKTÖRLERE ĠLĠġKĠN BĠR ĠNCELEME
Ġstanbul Ünverstes Ġktsat Fakültes Malye AraĢtırma Merkez Konferansları 46. Ser / Yıl 2004 Prof. Dr. Salh Turhan'a Armağan TÜKETĠCĠLERĠN FĠYAT BĠLĠNCĠ ÜZERĠNDE ETKĠLĠ OLAN FAKTÖRLERE ĠLĠġKĠN BĠR ĠNCELEME
Sabit Varyans. Var(u i X i ) = Var(u i ) = E(u i2 ) = s 2
 X Sabt Varyans Y Var(u X ) = Var(u ) = E(u ) = s Eşt Varyans EKKY nn varsayımlarından br anakütle regresyon fonksyonu u lern eşt varyanslı olmasıdır Her hata term varyansı bağımsız değşkenlern verlen değerlerne
X Sabt Varyans Y Var(u X ) = Var(u ) = E(u ) = s Eşt Varyans EKKY nn varsayımlarından br anakütle regresyon fonksyonu u lern eşt varyanslı olmasıdır Her hata term varyansı bağımsız değşkenlern verlen değerlerne
2005 Gazi Üniversitesi Endüstriyel Sanatlar Eğitim Fakültesi Dergisi Sayı:16, s31-46
 2005 Gaz Ünverstes Endüstryel Sanatlar Eğtm Fakültes Dergs Sayı:16, s31-46 ÖZET BANKALARDA MALİ BAŞARISIZLIĞIN ÖNGÖRÜLMESİ LOJİSTİK REGRESYON VE YAPAY SİNİR AĞI KARŞILAŞTIRMASI 31 Yasemn KESKİN BENLİ 1
2005 Gaz Ünverstes Endüstryel Sanatlar Eğtm Fakültes Dergs Sayı:16, s31-46 ÖZET BANKALARDA MALİ BAŞARISIZLIĞIN ÖNGÖRÜLMESİ LOJİSTİK REGRESYON VE YAPAY SİNİR AĞI KARŞILAŞTIRMASI 31 Yasemn KESKİN BENLİ 1
T.C. SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
 T.C. SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ QUANTILE REGRESYON ve BİR UYGULAMA İlkay ALTINDAĞ YÜKSEK LİSANS TEZİ İSTATİSTİK ANABİLİM DALI Ağustos-1 KONYA Her Hakkı Saklıdır ÖZET YÜKSEK LİSANS TEZİ
T.C. SELÇUK ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ QUANTILE REGRESYON ve BİR UYGULAMA İlkay ALTINDAĞ YÜKSEK LİSANS TEZİ İSTATİSTİK ANABİLİM DALI Ağustos-1 KONYA Her Hakkı Saklıdır ÖZET YÜKSEK LİSANS TEZİ
Makine Öğrenmesi 10. hafta
 Makne Öğrenmes 0. hafta Lagrange Optmzasonu Destek Vektör Maknes (SVM) Karesel (Quadratc) Programlama Optmzason Blmsel term olarak dlmze geçmş olsa da bazen en leme termle karşılık bulur. Matematktek en
Makne Öğrenmes 0. hafta Lagrange Optmzasonu Destek Vektör Maknes (SVM) Karesel (Quadratc) Programlama Optmzason Blmsel term olarak dlmze geçmş olsa da bazen en leme termle karşılık bulur. Matematktek en
AKADEMİK YAKLAŞIMLAR DERGİSİ JOURNAL OF ACADEMIC APPROACHES
 Konut Sahplğnn Belrleycler: Hanehalkı Resler Üzerne Br Uygulama Halm TATLI 1 Özet İnsanların barınma htyacını sağlayan konut, temel htyaçlar arasında yer almaktadır. Konut sahb olmayan ve krada oturan
Konut Sahplğnn Belrleycler: Hanehalkı Resler Üzerne Br Uygulama Halm TATLI 1 Özet İnsanların barınma htyacını sağlayan konut, temel htyaçlar arasında yer almaktadır. Konut sahb olmayan ve krada oturan
Mut Orman İşletmesinde Karaçam, Sedir ve Kızılçam Ağaç Türleri İçin Dip Çap Göğüs Çapı İlişkileri
 Süleyman Demrel Ünverstes, Fen Blmler Ensttüsü, 9-3,(5)- Mut Orman İşletmesnde Karaçam, Sedr ve Kızılçam Ağaç Türler İçn Dp Çap Göğüs Çapı İlşkler R.ÖZÇELİK 1 Süleyman Demrel Ünverstes Orman Fakültes Orman
Süleyman Demrel Ünverstes, Fen Blmler Ensttüsü, 9-3,(5)- Mut Orman İşletmesnde Karaçam, Sedr ve Kızılçam Ağaç Türler İçn Dp Çap Göğüs Çapı İlşkler R.ÖZÇELİK 1 Süleyman Demrel Ünverstes Orman Fakültes Orman
Kİ-KARE TESTLERİ. şeklinde karesi alındığında, Z i. değerlerinin dağılımı ki-kare dağılımına dönüşür.
 Kİ-KARE TESTLERİ A) Kİ-KARE DAĞILIMI VE ÖZELLİKLERİ Örnekleme yoluyla elde edlen rakamların, anakütle rakamlarına uygun olup olmadığı; br başka fadeyle gözlenen değerlern teork( beklenen) değerlere uygunluk
Kİ-KARE TESTLERİ A) Kİ-KARE DAĞILIMI VE ÖZELLİKLERİ Örnekleme yoluyla elde edlen rakamların, anakütle rakamlarına uygun olup olmadığı; br başka fadeyle gözlenen değerlern teork( beklenen) değerlere uygunluk
SUÇ VERİ TABANININ LOJİSTİK REGRESYON ANALİZİ İLE TAHMİNİ: BURSA ÖRNEĞİ Estimating of Crime Database with Logistic Regression Analysis: Bursa Case
 SUÇ VERİ TABANININ LOJİSTİK REGRESYON ANALİZİ İLE TAHMİNİ: BURSA ÖRNEĞİ Estmatng of Crme Database wth Logstc Regresson Analyss: Bursa Case Mehmet NARGELEÇEKENLER * B Özet u çalışmada, Bursa Emnyet Müdürlüğünden
SUÇ VERİ TABANININ LOJİSTİK REGRESYON ANALİZİ İLE TAHMİNİ: BURSA ÖRNEĞİ Estmatng of Crme Database wth Logstc Regresson Analyss: Bursa Case Mehmet NARGELEÇEKENLER * B Özet u çalışmada, Bursa Emnyet Müdürlüğünden
Bitkisel Ürün Sigortası Yaptırma İsteğinin Belirlenmesi: Tokat İli Örneği
 Atatürk Ünv. Zraat Fak. Derg., 42 (2): 153-157, 2011 J. of Agrcultural Faculty of Atatürk Unv., 42 (2): 153-157, 2011 ISSN : 1300-9036 Araştırma Makales/Research Artcle Btksel Ürün Sgortası Yaptırma İsteğnn
Atatürk Ünv. Zraat Fak. Derg., 42 (2): 153-157, 2011 J. of Agrcultural Faculty of Atatürk Unv., 42 (2): 153-157, 2011 ISSN : 1300-9036 Araştırma Makales/Research Artcle Btksel Ürün Sgortası Yaptırma İsteğnn
ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ ÇOKLU İÇ İLİŞKİ VE EKOLOJİK REGRESYON İSTATİSTİK ANABİLİM DALI
 ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ Berrn GÜLTAY YÜKSEK LİSANS TEZİ ÇOKLU İÇ İLİŞKİ VE EKOLOJİK REGRESYON İSTATİSTİK ANABİLİM DALI ADANA, 9 ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ ÇOKLU
ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ Berrn GÜLTAY YÜKSEK LİSANS TEZİ ÇOKLU İÇ İLİŞKİ VE EKOLOJİK REGRESYON İSTATİSTİK ANABİLİM DALI ADANA, 9 ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ ÇOKLU
YAYILI YÜK İLE YÜKLENMİŞ YAPI KİRİŞLERİNDE GÖÇME YÜKÜ HESABI. Perihan (Karakulak) EFE
 BAÜ Fen Bl. Enst. Dergs (6).8. YAYII YÜK İE YÜKENİŞ YAPI KİRİŞERİNDE GÖÇE YÜKÜ HESABI Perhan (Karakulak) EFE Balıkesr Ünverstes ühendslk marlık Fakültes İnşaat üh. Bölümü Balıkesr, TÜRKİYE ÖZET Yapılar
BAÜ Fen Bl. Enst. Dergs (6).8. YAYII YÜK İE YÜKENİŞ YAPI KİRİŞERİNDE GÖÇE YÜKÜ HESABI Perhan (Karakulak) EFE Balıkesr Ünverstes ühendslk marlık Fakültes İnşaat üh. Bölümü Balıkesr, TÜRKİYE ÖZET Yapılar
Rasgele Değişken Üretme Teknikleri
 Rasgele Değşken Üretme Teknkler Amaç Smülasyon modelnn grdlern oluşturacak örneklern üretlmes Yaygın olarak kullanılan ayrık veya sürekl dağılımların örneklenmes sürecn anlamak Yaygın olarak kullanılan
Rasgele Değşken Üretme Teknkler Amaç Smülasyon modelnn grdlern oluşturacak örneklern üretlmes Yaygın olarak kullanılan ayrık veya sürekl dağılımların örneklenmes sürecn anlamak Yaygın olarak kullanılan
Kİ-KARE TESTLERİ A) Kİ-KARE DAĞILIMI VE ÖZELLİKLERİ
 Kİ-KAR TSTLRİ A) Kİ-KAR DAĞILIMI V ÖZLLİKLRİ Örnekleme yoluyla elde edlen rakamların, anakütle rakamlarına uygun olup olmadığı; br başka fadeyle gözlenen değerlern teork( beklenen) değerlere uygunluk gösterp
Kİ-KAR TSTLRİ A) Kİ-KAR DAĞILIMI V ÖZLLİKLRİ Örnekleme yoluyla elde edlen rakamların, anakütle rakamlarına uygun olup olmadığı; br başka fadeyle gözlenen değerlern teork( beklenen) değerlere uygunluk gösterp
REGRESYONDA ETKİLİ GÖZLEMLERİ BELİRLEME YÖNTEMLERİ VE KARŞILAŞTIRMALARI. Can DARICA YÜKSEK LİSANS TEZİ İSTATİSTİK
 REGRESYONDA ETKİLİ GÖZLEMLERİ BELİRLEME YÖNTEMLERİ VE KARŞILAŞTIRMALARI Can DARICA YÜKSEK LİSANS TEZİ İSTATİSTİK GAZİ ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ ŞUBAT 014 ANKARA Can DARICA tarafından hazırlanan
REGRESYONDA ETKİLİ GÖZLEMLERİ BELİRLEME YÖNTEMLERİ VE KARŞILAŞTIRMALARI Can DARICA YÜKSEK LİSANS TEZİ İSTATİSTİK GAZİ ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ ŞUBAT 014 ANKARA Can DARICA tarafından hazırlanan
Antalya Đlinde Serada Domates Üretiminin Kâr Etkinliği Analizi
 Tarım Blmler Dergs Tar. Bl. Der. Derg web sayfası: www.agr.ankara.edu.tr/derg Journal of Agrcultural Scences Journal homepage: www.agr.ankara.edu.tr/journal TARIM BİLİMLERİ DERGİSİ JOURNAL OF AGRICULTURAL
Tarım Blmler Dergs Tar. Bl. Der. Derg web sayfası: www.agr.ankara.edu.tr/derg Journal of Agrcultural Scences Journal homepage: www.agr.ankara.edu.tr/journal TARIM BİLİMLERİ DERGİSİ JOURNAL OF AGRICULTURAL
Obtaining Classical Reliability Terms from Item Response Theory in Multiple Choice Tests
 Ankara Unversty, Journal of Faculty of Educatonal Scences, year: 26, vol: 39, no: 2, 27-44 Obtanng Classcal Relablty Terms from Item Response Theory n Multple Choce Tests Hall Yurdugül * ABSTRACT: The
Ankara Unversty, Journal of Faculty of Educatonal Scences, year: 26, vol: 39, no: 2, 27-44 Obtanng Classcal Relablty Terms from Item Response Theory n Multple Choce Tests Hall Yurdugül * ABSTRACT: The
Kİ KARE ANALİZİ. Doç. Dr. Mehmet AKSARAYLI Ki-Kare Analizleri
 Kİ KAR ANALİZİ 1 Doç. Dr. Mehmet AKSARAYLI www.mehmetaksarayl K-Kare Analzler OLAY 1: Genelde br statstk sınıfında, öğrenclern %60 ının devamlı, %30 unun bazen, %10 unun se çok az derse geldkler düşünülmektedr.
Kİ KAR ANALİZİ 1 Doç. Dr. Mehmet AKSARAYLI www.mehmetaksarayl K-Kare Analzler OLAY 1: Genelde br statstk sınıfında, öğrenclern %60 ının devamlı, %30 unun bazen, %10 unun se çok az derse geldkler düşünülmektedr.
ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ
 ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ Savaş OKUR PARAMETRİK VE PARAMETRİK OLMAYAN BASİT DOĞRUSAL REGRESYON ANALİZ YÖNTEMLERİNİN KARŞILAŞTIRMALI OLARAK İNCELENMESİ ZOOTEKNİ ANABİLİM
ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ Savaş OKUR PARAMETRİK VE PARAMETRİK OLMAYAN BASİT DOĞRUSAL REGRESYON ANALİZ YÖNTEMLERİNİN KARŞILAŞTIRMALI OLARAK İNCELENMESİ ZOOTEKNİ ANABİLİM
LOJ ST K REGRESYON ANAL Z : Ö RENC LER N S GARA ÇME ALI KANLI I ÜZER NE B R UYGULAMA
 LOJ ST K REGRESYON ANAL Z : Ö RENC LER N S GARA ÇME ALI KANLI I ÜZER NE B R UYGULAMA Yrd. Doç. Dr. Cengz AKTA Esk ehr Osmangaz Ünv. Fen-Ed.Fak. statstk Böl. caktas@ogu.edu.tr Öz Sgara, tüm dünyada korunulablr
LOJ ST K REGRESYON ANAL Z : Ö RENC LER N S GARA ÇME ALI KANLI I ÜZER NE B R UYGULAMA Yrd. Doç. Dr. Cengz AKTA Esk ehr Osmangaz Ünv. Fen-Ed.Fak. statstk Böl. caktas@ogu.edu.tr Öz Sgara, tüm dünyada korunulablr
Akıllı Telefon Seçiminin Belirleyicileri: Üniversite Öğrencileri Üzerine Bir Uygulama
 The PDF verson of an unedted manuscrpt has been peer revewed and accepted for publcaton. Based upon the publcaton rules of the journal, the manuscrpt has been formatted, but not fnalzed yet. Before fnal
The PDF verson of an unedted manuscrpt has been peer revewed and accepted for publcaton. Based upon the publcaton rules of the journal, the manuscrpt has been formatted, but not fnalzed yet. Before fnal
Regresyon ve Korelasyon Analizi. Regresyon Analizi
 Regresyo ve Korelasyo Aalz Regresyo Aalz Regresyo Aalz Regresyo aalz, aralarıda sebep-souç lşks bulua k veya daha fazla değşke arasıdak lşky belrlemek ve bu lşky kullaarak o kou le lgl tahmler (estmato)
Regresyo ve Korelasyo Aalz Regresyo Aalz Regresyo Aalz Regresyo aalz, aralarıda sebep-souç lşks bulua k veya daha fazla değşke arasıdak lşky belrlemek ve bu lşky kullaarak o kou le lgl tahmler (estmato)
ATATÜRK ÜNİVERSİTESİ SOSYAL BİLİMLER ENSTİTÜSÜ İŞLETME ANA BİLİM DALI. Serhat BURMAOĞLU
 ATATÜRK ÜNİVERSİTESİ SOSYAL BİLİMLER ENSTİTÜSÜ İŞLETME ANA BİLİM DALI Serhat BURMAOĞLU BİRLEŞMİŞ MİLLETLER KALKINMA PROGRAMI BEŞERİ KALKINMA ENDEKSİ VERİLERİNİ KULLANARAK DİSKRİMİNANT ANALİZİ, LOJİSTİK
ATATÜRK ÜNİVERSİTESİ SOSYAL BİLİMLER ENSTİTÜSÜ İŞLETME ANA BİLİM DALI Serhat BURMAOĞLU BİRLEŞMİŞ MİLLETLER KALKINMA PROGRAMI BEŞERİ KALKINMA ENDEKSİ VERİLERİNİ KULLANARAK DİSKRİMİNANT ANALİZİ, LOJİSTİK
PARAMETRİK OLMAYAN HİPOTEZ TESTLERİ Kİ-KARE TESTLERİ
 PARAMETRİK OLMAYAN HİPOTEZ TESTLERİ Kİ-KARE TESTLERİ 1 Populasyonun nceledğmz br özellğnn dağılışı blenen dağılışlardan brsne, Normal Dağılış, t Dağılışı, F Dağılışı, gb br dağılışa uygun olduğu durumlarda
PARAMETRİK OLMAYAN HİPOTEZ TESTLERİ Kİ-KARE TESTLERİ 1 Populasyonun nceledğmz br özellğnn dağılışı blenen dağılışlardan brsne, Normal Dağılış, t Dağılışı, F Dağılışı, gb br dağılışa uygun olduğu durumlarda
Atatürk Üniversitesi İktisadi ve İdari Bilimler Dergisi, Cilt: 25, Sayı: 1, 2011 225
 Atatürk Ünverstes İktsad ve İdar Blmler Dergs, Clt: 25, Sayı:, 20 225 FİNANSAL ANALİZDE KULLANILAN ORANLAR VE HİSSE SENEDİ GETİRİLERİ ARASINDAKİ İLİŞKİ: EKONOMİK KRİZ DÖNEMLERİ İÇİN İMKB İMALAT SANAYİ
Atatürk Ünverstes İktsad ve İdar Blmler Dergs, Clt: 25, Sayı:, 20 225 FİNANSAL ANALİZDE KULLANILAN ORANLAR VE HİSSE SENEDİ GETİRİLERİ ARASINDAKİ İLİŞKİ: EKONOMİK KRİZ DÖNEMLERİ İÇİN İMKB İMALAT SANAYİ
İSTATİSTİK DERS NOTLARI
 Balıkesr Ünverstes İnşaat Mühendslğ Bölüü uutokkan@balkesr.edu.tr İSTATİSTİK DERS OTLARI Yrd. Doç. Dr. Uut OKKA Hdrolk Anabl Dalı Balıkesr Ünverstes Balıkesr Ünverstes İnşaat Mühendslğ Bölüü İnşaat Mühendslğ
Balıkesr Ünverstes İnşaat Mühendslğ Bölüü uutokkan@balkesr.edu.tr İSTATİSTİK DERS OTLARI Yrd. Doç. Dr. Uut OKKA Hdrolk Anabl Dalı Balıkesr Ünverstes Balıkesr Ünverstes İnşaat Mühendslğ Bölüü İnşaat Mühendslğ
LOJİSTİK REGRESYON VE CART ANALİZİ TEKNİKLERİYLE SOSYAL GÜVENLİK KURUMU İLAÇ PROVİZYON SİSTEMİ VERİLERİ ÜZERİNDE BİR UYGULAMA. Zeynep Burcu KIRAN
 LOJİSTİK REGRESYON VE CART ANALİZİ TEKNİKLERİYLE SOSYAL GÜVENLİK KURUMU İLAÇ PROVİZYON SİSTEMİ VERİLERİ ÜZERİNDE BİR UYGULAMA Zeynep Burcu KIRAN YÜKSEK LİSANS TEZİ İSTATİSTİK GAZİ ÜNİVERSİTESİ FEN BİLİMLERİ
LOJİSTİK REGRESYON VE CART ANALİZİ TEKNİKLERİYLE SOSYAL GÜVENLİK KURUMU İLAÇ PROVİZYON SİSTEMİ VERİLERİ ÜZERİNDE BİR UYGULAMA Zeynep Burcu KIRAN YÜKSEK LİSANS TEZİ İSTATİSTİK GAZİ ÜNİVERSİTESİ FEN BİLİMLERİ
Sansürlenmiş ve Kesikli Regresyon Modelleri
 TOBİT MODEL 1 Sansürlenmş ve Keskl Regresyon Modeller Sınırlı bağımlı değşkenler: sansürlenmş (censored) ve keskl (truncated) regresyon modeller şeklnde k gruba ayrılır. 2 Sansürlenmş ve Keskl Regresyon
TOBİT MODEL 1 Sansürlenmş ve Keskl Regresyon Modeller Sınırlı bağımlı değşkenler: sansürlenmş (censored) ve keskl (truncated) regresyon modeller şeklnde k gruba ayrılır. 2 Sansürlenmş ve Keskl Regresyon
A İSTATİSTİK. 4. X kesikli rasgele (random) değişkenin moment çıkaran. C) 4 9 Buna göre, X in beklenen değeri kaçtır?
 . Br torbada 6 syah, 4 beyaz top vardır. Bu torbadan yerne koyarak top seçlyor. A İSTATİSTİK KPSS/-AB-PÖ/006. Normal dağılıma sahp br rasgele (random) değşkenn varyansı 00 dür. Seçlen topların ksnn de
. Br torbada 6 syah, 4 beyaz top vardır. Bu torbadan yerne koyarak top seçlyor. A İSTATİSTİK KPSS/-AB-PÖ/006. Normal dağılıma sahp br rasgele (random) değşkenn varyansı 00 dür. Seçlen topların ksnn de
kadar ( i. kaynağın gölge fiyatı kadar) olmalıdır.
 KONU : DUAL MODELİN EKONOMİK YORUMU Br prmal-dual model lşks P : max Z cx D: mn Z bv AX b AV c X 0 V 0 bçmnde tanımlı olsun. Prmal modeln en y temel B ve buna lşkn fyat vektörü c B olsun. Z B B BB c X
KONU : DUAL MODELİN EKONOMİK YORUMU Br prmal-dual model lşks P : max Z cx D: mn Z bv AX b AV c X 0 V 0 bçmnde tanımlı olsun. Prmal modeln en y temel B ve buna lşkn fyat vektörü c B olsun. Z B B BB c X
Süleyman Demirel Üniversitesi İktisadi ve İdari Bilimler Fakültesi Y.2008, C.13, S.1 s.111-131.
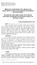 Süleyman Demrel Ünverstes İktsad ve İdar Blmler Fakültes Y.008, C.3, S. s.-3. BİREYSEL EMEKLİLİK FONLARINDA FON YAPILARININ KARMA DENEMELER YÖNTEMİ İLE İNCELENMESİ EXAMINING THE STRUCTURE OF FUNDS BY MIXTURE
Süleyman Demrel Ünverstes İktsad ve İdar Blmler Fakültes Y.008, C.3, S. s.-3. BİREYSEL EMEKLİLİK FONLARINDA FON YAPILARININ KARMA DENEMELER YÖNTEMİ İLE İNCELENMESİ EXAMINING THE STRUCTURE OF FUNDS BY MIXTURE
HİSSE SENETLERİNİN BEKLENEN GETİRİ VE RİSKLERİNİN TAHMİNİNDE ALTERNATİF MODELLER
 İstanbul Ünverstes İktsat Fakültes Malye Araştırma Merkez Konferansları 47. Ser / Yıl 005 Prof. Dr. Türkan Öncel e Armağan HİSSE SENETLERİNİN BEKLENEN GETİRİ VE RİSKLERİNİN TAHMİNİNDE ALTERNATİF MODELLER
İstanbul Ünverstes İktsat Fakültes Malye Araştırma Merkez Konferansları 47. Ser / Yıl 005 Prof. Dr. Türkan Öncel e Armağan HİSSE SENETLERİNİN BEKLENEN GETİRİ VE RİSKLERİNİN TAHMİNİNDE ALTERNATİF MODELLER
Bulanık Mantık ile Hesaplanan Geoid Yüksekliğine Nokta Yüksekliklerinin Etkisi
 Harta Teknolojler Elektronk Dergs Clt: 5, No: 1, 2013 (61-67) Electronc Journal of Map Technologes Vol: 5, No: 1, 2013 (61-67) TEKNOLOJİK ARAŞTIRMALAR www.teknolojkarastrmalar.com e-issn: 1309-3983 Makale
Harta Teknolojler Elektronk Dergs Clt: 5, No: 1, 2013 (61-67) Electronc Journal of Map Technologes Vol: 5, No: 1, 2013 (61-67) TEKNOLOJİK ARAŞTIRMALAR www.teknolojkarastrmalar.com e-issn: 1309-3983 Makale
Kİ-KARE VE KOLMOGOROV SMİRNOV UYGUNLUK TESTLERİNİN SİMULASYON İLE ELDE EDİLEN VERİLER ÜZERİNDE KARŞILAŞTIRILMASI
 C.Ü. İktsad ve İdar Blmler Dergs, Clt 4, Sayı 1, 3 6 Kİ-KARE VE KOLMOGOROV SMİRNOV UYGUNLUK TESTLERİNİN SİMULASYON İLE ELDE EDİLEN VERİLER ÜZERİNDE KARŞILAŞTIRILMASI H. BİRCAN, Y. KARAGÖZ ve Y. KASAPOĞLU
C.Ü. İktsad ve İdar Blmler Dergs, Clt 4, Sayı 1, 3 6 Kİ-KARE VE KOLMOGOROV SMİRNOV UYGUNLUK TESTLERİNİN SİMULASYON İLE ELDE EDİLEN VERİLER ÜZERİNDE KARŞILAŞTIRILMASI H. BİRCAN, Y. KARAGÖZ ve Y. KASAPOĞLU
PROJE SEÇİMİ VE KAYNAK PLANLAMASI İÇİN BİR ALGORİTMA AN ALGORITHM FOR PROJECT SELECTION AND RESOURCE PLANNING
 Dokuz Eylül Ünverstes Sosyal Blmler Ensttüsü Dergs Clt 3, Sayı:2, 2001 PROJE SEÇİMİ VE KAYAK PLALAMASI İÇİ BİR ALGORİTMA lgün MORALI 1 C. Cengz ÇELİKOĞLU 2 ÖZ Kaynak tahss problemler koşullara bağlı olarak
Dokuz Eylül Ünverstes Sosyal Blmler Ensttüsü Dergs Clt 3, Sayı:2, 2001 PROJE SEÇİMİ VE KAYAK PLALAMASI İÇİ BİR ALGORİTMA lgün MORALI 1 C. Cengz ÇELİKOĞLU 2 ÖZ Kaynak tahss problemler koşullara bağlı olarak
TESADÜFİ DEĞİŞKENLERLE İLGİLİ BAZI YAKINSAKLIK ÇEŞİTLERİNİN KARŞILAŞTIRILMASI
 ISSN:1306-3111 e-journal of New Worl Scences Acaemy 2008, Volume: 3, Number: 4 Artcle Number: A0108 NATURAL AND APPLIED SCIENCES MATHEMATICS APPLIED MATHEMATICS Receve: March 2008 Accepte: September 2008
ISSN:1306-3111 e-journal of New Worl Scences Acaemy 2008, Volume: 3, Number: 4 Artcle Number: A0108 NATURAL AND APPLIED SCIENCES MATHEMATICS APPLIED MATHEMATICS Receve: March 2008 Accepte: September 2008
ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ
 ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ Gülesen ÜSTÜNDAĞ BAZI PARAMETRİK OLMAYAN İSTATİSTİKSEL YÖNTEMLERİN İNCELENMESİ İSTATİSTİK ANABİLİM DALI ADANA, 005 ÇUKUROVA ÜNİVERSİTESİ
ÇUKUROVA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ Gülesen ÜSTÜNDAĞ BAZI PARAMETRİK OLMAYAN İSTATİSTİKSEL YÖNTEMLERİN İNCELENMESİ İSTATİSTİK ANABİLİM DALI ADANA, 005 ÇUKUROVA ÜNİVERSİTESİ
Pamukkale Üniversitesi Mühendislik Bilimleri Dergisi Pamukkale University Journal of Engineering Sciences
 Pamukkale Ünverstes Mühendslk Blmler Dergs, Clt 0, Sayı 3, 04, Sayfalar 85-9 Pamukkale Ünverstes Mühendslk Blmler Dergs Pamukkale Unversty Journal of Engneerng Scences PREFABRİK ENDÜSTRİ YAPIARININ ARMONİ
Pamukkale Ünverstes Mühendslk Blmler Dergs, Clt 0, Sayı 3, 04, Sayfalar 85-9 Pamukkale Ünverstes Mühendslk Blmler Dergs Pamukkale Unversty Journal of Engneerng Scences PREFABRİK ENDÜSTRİ YAPIARININ ARMONİ
TEKNOLOJĐK ARAŞTIRMALAR
 www.teknolojkarastrmalar.com ISSN:134-4141 Makne Teknolojler Elektronk Dergs 28 (1) 61-68 TEKNOLOJĐK ARAŞTIRMALAR Kısa Makale Tabakalı Br Dskn Termal Gerlme Analz Hasan ÇALLIOĞLU 1, Şükrü KARAKAYA 2 1
www.teknolojkarastrmalar.com ISSN:134-4141 Makne Teknolojler Elektronk Dergs 28 (1) 61-68 TEKNOLOJĐK ARAŞTIRMALAR Kısa Makale Tabakalı Br Dskn Termal Gerlme Analz Hasan ÇALLIOĞLU 1, Şükrü KARAKAYA 2 1
Tek Yönlü Varyans Analizi (ANOVA)
 VARYANS ANALİZİ İ örne ortalaması arasında farın önem ontrolü, örne büyülüğüne göre z veya testlernden bryle yapılır. Bu testlerle, den fazla örne ortalamasını brlte test etme ve aralarında farın önem
VARYANS ANALİZİ İ örne ortalaması arasında farın önem ontrolü, örne büyülüğüne göre z veya testlernden bryle yapılır. Bu testlerle, den fazla örne ortalamasını brlte test etme ve aralarında farın önem
ARAŞTIRMA MAKALESİ/RESEARCH ARTICLE TEK ÇARPIMSAL SİNİR HÜCRELİ YAPAY SİNİR AĞI MODELİNİN EĞİTİMİ İÇİN ABC VE BP YÖNTEMLERİNİN KARŞILAŞTIRILMASI ÖZ
 ANADOLU ÜNİVERSİTESİ Blm ve Teknoloj Dergs A-Uygulamalı Blmler ve Mühendslk Clt: 14 Sayı: 3 013 Sayfa: 315-38 ARAŞTIRMA MAKALESİ/RESEARCH ARTICLE Faruk ALPASLAN 1, Erol EĞRİOĞLU 1, Çağdaş Hakan ALADAĞ,
ANADOLU ÜNİVERSİTESİ Blm ve Teknoloj Dergs A-Uygulamalı Blmler ve Mühendslk Clt: 14 Sayı: 3 013 Sayfa: 315-38 ARAŞTIRMA MAKALESİ/RESEARCH ARTICLE Faruk ALPASLAN 1, Erol EĞRİOĞLU 1, Çağdaş Hakan ALADAĞ,
KENTSEL ALANDA ET TALEP ANALİZİ: BATI AKDENİZ BÖLGESİ ÖRNEĞİ. Dr. Ali Rıza AKTAŞ 1 Dr. Selim Adem HATIRLI 2
 Journal of Yasar Unversty 2010 3294-3319 KENTSEL ALANDA ET TALEP ANALİZİ: BATI AKDENİZ BÖLGESİ ÖRNEĞİ Dr. Al Rıza AKTAŞ 1 Dr. Selm Adem HATIRLI 2 ÖZET Bu çalışmada, Batı Akdenz Bölges kent merkezlernde
Journal of Yasar Unversty 2010 3294-3319 KENTSEL ALANDA ET TALEP ANALİZİ: BATI AKDENİZ BÖLGESİ ÖRNEĞİ Dr. Al Rıza AKTAŞ 1 Dr. Selm Adem HATIRLI 2 ÖZET Bu çalışmada, Batı Akdenz Bölges kent merkezlernde
Finansal Riskten Korunma Muhasebesinde Etkinliğin Ölçülmesi
 Fnansal Rskten Korunma Muhasebesnde Etknlğn Ölçülmes Dr. Fahreddn OKUDAN * Fath Ünverstes, İİBF. Özet Bu makalenn amacı, etknlk test yöntemlernn ncelenmesdr. TMS 39, rskten korunma muhasebes uygulanablmes
Fnansal Rskten Korunma Muhasebesnde Etknlğn Ölçülmes Dr. Fahreddn OKUDAN * Fath Ünverstes, İİBF. Özet Bu makalenn amacı, etknlk test yöntemlernn ncelenmesdr. TMS 39, rskten korunma muhasebes uygulanablmes
UYUM ĐYĐLĐĞĐ TESTĐ. 2 -n olup. nin dağılımı χ dir ve sd = (k-1-p) dir. Burada k = sınıf sayısı, p = tahmin edilen parametre sayısıdır.
 UYUM ĐYĐLĐĞĐ TESTĐ Posson: H o: Ver Posson dağılıma sahp br ktleden gelmektedr. H a : Ver Posson dağılıma sahp br ktleden gelmemektedr. Böyle br hpotez test edeblmek çn, önce Posson dağılım parametres
UYUM ĐYĐLĐĞĐ TESTĐ Posson: H o: Ver Posson dağılıma sahp br ktleden gelmektedr. H a : Ver Posson dağılıma sahp br ktleden gelmemektedr. Böyle br hpotez test edeblmek çn, önce Posson dağılım parametres
AVRUPA BİRLİĞİ NE ÜYELİK SÜRECİNDE ETKİLİ FAKTÖRLERİN KOŞULLU LOJİSTİK REGRESYON MODELLERİ İLE DEĞERLENDİRİLMESİ
 Ekonometr ve İstatstk Sayı:14 2011 62 83 İSTANBUL ÜNİVERSİTESİ İKTİSAT FAKÜLTESİ EKONOMETRİ VE İSTATİSTİK DERGİSİ AVRUPA BİRLİĞİ NE ÜYELİK SÜRECİNDE ETKİLİ FAKTÖRLERİN KOŞULLU LOJİSTİK REGRESYON MODELLERİ
Ekonometr ve İstatstk Sayı:14 2011 62 83 İSTANBUL ÜNİVERSİTESİ İKTİSAT FAKÜLTESİ EKONOMETRİ VE İSTATİSTİK DERGİSİ AVRUPA BİRLİĞİ NE ÜYELİK SÜRECİNDE ETKİLİ FAKTÖRLERİN KOŞULLU LOJİSTİK REGRESYON MODELLERİ
EMG İşaretlerinin K-Ortalama Algoritması Kullanılarak Öbekleştirilmesi. EMG Signal Analysis Using K-Means Clustering
 KSÜ Mühendslk Blmler Dergs, (), 9 5 KSU Journal of Engneerng Scences, (), 9 EMG İşaretlernn K-Ortalama Algortması Kullanılarak Öbekleştrlmes Mücahd Günay, Ahmet ALKA, KSÜ Mühendslk-Mmarlık Fakültes Elektrk-Elektronk
KSÜ Mühendslk Blmler Dergs, (), 9 5 KSU Journal of Engneerng Scences, (), 9 EMG İşaretlernn K-Ortalama Algortması Kullanılarak Öbekleştrlmes Mücahd Günay, Ahmet ALKA, KSÜ Mühendslk-Mmarlık Fakültes Elektrk-Elektronk
4.5. SOĞUTMA KULELERİNİN BOYUTLANDIRILMASI İÇİN BİR ANALIZ
 Ünsal M.; Varol, A.: Soğutma Kulelernn Boyutlandırılması İçn Br Kuramsal 8 Mayıs 990, S: 8-85, Adana 4.5. SOĞUTMA KULELERİNİN BOYUTLANDIRILMASI İÇİN BİR ANALIZ Asaf Varol Fırat Ünverstes, Teknk Eğtm Fakültes,
Ünsal M.; Varol, A.: Soğutma Kulelernn Boyutlandırılması İçn Br Kuramsal 8 Mayıs 990, S: 8-85, Adana 4.5. SOĞUTMA KULELERİNİN BOYUTLANDIRILMASI İÇİN BİR ANALIZ Asaf Varol Fırat Ünverstes, Teknk Eğtm Fakültes,
Baml deikenin simetrik bulank say olmas durumunda parametre tahmini
 www.statstkcler.org statstkçler Dergs 3 (00) 54-6 statstkçler Dergs Baml dekenn smetrk bulank say olmas durumunda arametre tahmn Kamle anl Kula Ah Evran Ünverstes, Matematk Bölümü, 4000, Krehr, ürkye sanl004@hotmal.com
www.statstkcler.org statstkçler Dergs 3 (00) 54-6 statstkçler Dergs Baml dekenn smetrk bulank say olmas durumunda arametre tahmn Kamle anl Kula Ah Evran Ünverstes, Matematk Bölümü, 4000, Krehr, ürkye sanl004@hotmal.com
İKİ DEĞİŞKENLİ BASİT DOĞRUSAL REGRESYON MODELİ
 İKİ DEĞİŞKENLİ BASİT DOĞRUSAL REGRESON MODELİ Regresyon le ( ler) arasındak ortalama lşknn matematk fonksyonla fadesdr. f ( ) b b Bu lşk eğrselde olablr. Ortalama lşk aşağıdak gb fade edlr: E( ) f ( )
İKİ DEĞİŞKENLİ BASİT DOĞRUSAL REGRESON MODELİ Regresyon le ( ler) arasındak ortalama lşknn matematk fonksyonla fadesdr. f ( ) b b Bu lşk eğrselde olablr. Ortalama lşk aşağıdak gb fade edlr: E( ) f ( )
REGRESYON ANALİZİ BÖLÜM 5-6
 REGRESYON ANALİZİ BÖLÜM 5-6 Yayın Tarh: 03-11-2007 Revzyon No:0 1 5. E.K.K. REGRESYONUNDA KARŞILAŞILAN PROBLEMLER VE BAZI KONU BAŞLIKLARI 2 1 EN KÜÇÜK KARELERDE KARŞILAŞILAN PROBLEMLER EKK da karşılaşılan
REGRESYON ANALİZİ BÖLÜM 5-6 Yayın Tarh: 03-11-2007 Revzyon No:0 1 5. E.K.K. REGRESYONUNDA KARŞILAŞILAN PROBLEMLER VE BAZI KONU BAŞLIKLARI 2 1 EN KÜÇÜK KARELERDE KARŞILAŞILAN PROBLEMLER EKK da karşılaşılan
ASAL BİLEŞENLER ANALİZİNE BOOTSTRAP YAKLAŞIMI
 Ekonometr ve İstatstk Sayı: 2005 5-05 İSTANBUL ÜNİVERSİTESİ İKTİSAT FAKÜLTESİ EKONOMETRİ VE İSTATİSTİK DERGİSİ ASAL BİLEŞENLER ANALİZİNE BOOTSTRAP YAKLAŞIMI Dr. Ayln Aktükün Bu makale 5.2.2004 tarhnde
Ekonometr ve İstatstk Sayı: 2005 5-05 İSTANBUL ÜNİVERSİTESİ İKTİSAT FAKÜLTESİ EKONOMETRİ VE İSTATİSTİK DERGİSİ ASAL BİLEŞENLER ANALİZİNE BOOTSTRAP YAKLAŞIMI Dr. Ayln Aktükün Bu makale 5.2.2004 tarhnde
Üç Boyutlu Yapı-Zemin Etkileşimi Problemlerinin Kuadratik Sonlu Elemanlar ve Sonsuz Elemanlar Kullanılarak Çözümü
 ECAS Uluslararası Yapı ve Deprem Mühendslğ Sempozyumu, Ekm, Orta Doğu Teknk Ünverstes, Ankara, Türkye Üç Boyutlu Yapı-Zemn Etkleşm Problemlernn Kuadratk Sonlu Elemanlar ve Sonsuz Elemanlar Kullanılarak
ECAS Uluslararası Yapı ve Deprem Mühendslğ Sempozyumu, Ekm, Orta Doğu Teknk Ünverstes, Ankara, Türkye Üç Boyutlu Yapı-Zemn Etkleşm Problemlernn Kuadratk Sonlu Elemanlar ve Sonsuz Elemanlar Kullanılarak
DEĞİŞKEN DÖVİZ KURLARI ORTAMINDA GLOBAL BİR ŞİRKETTEKİ ESNEKLİĞİN DEĞERİ VE OPTİMUM KULLANIMI
 DEĞİŞKEN DÖVİZ KURLARI ORTAMINDA GLOBAL BİR ŞİRKETTEKİ ESNEKLİĞİN DEĞERİ VE OPTİMUM KULLANIMI Mehmet Aktan Atatürk Ünverstes, Endüstr Mühendslğ Bölümü, 25240, Erzurum. Özet: Dövz kurlarındak değşmler,
DEĞİŞKEN DÖVİZ KURLARI ORTAMINDA GLOBAL BİR ŞİRKETTEKİ ESNEKLİĞİN DEĞERİ VE OPTİMUM KULLANIMI Mehmet Aktan Atatürk Ünverstes, Endüstr Mühendslğ Bölümü, 25240, Erzurum. Özet: Dövz kurlarındak değşmler,
Devalüasyon, Para, Reel Gelir Değişkenlerinin Dış Ticaret Üzerine Etkisinin Panel Data Yöntemiyle Türkiye İçin İncelenmesi
 Dokuz Eylül Ünverstes Sosyal Blmler Ensttüsü Dergs Clt 6, Sayı:4, 2004 Devalüasyon, Para, Reel Gelr Değşkenlernn Dış Tcaret Üzerne Etksnn Panel Data Yöntemyle Türkye İçn İncelenmes Yrd.Doç.Dr.Ercan BALDEMİR*
Dokuz Eylül Ünverstes Sosyal Blmler Ensttüsü Dergs Clt 6, Sayı:4, 2004 Devalüasyon, Para, Reel Gelr Değşkenlernn Dış Tcaret Üzerne Etksnn Panel Data Yöntemyle Türkye İçn İncelenmes Yrd.Doç.Dr.Ercan BALDEMİR*
Türkiye deki Đşsizlik Oranının Bulanık Doğrusal Regresyon Analiziyle Tahmini
 İstatstkçler Dergs: İstatstk & Aktüerya Journal of Statstcans: Statstcs and Actuaral Scences IDIA 8, 5, -6 Gelş/Receved:6.4.5, Kabul/Accepted: 3.6.5 www.statstkcler.org Türkye dek Đşszlk Oranının Bulanık
İstatstkçler Dergs: İstatstk & Aktüerya Journal of Statstcans: Statstcs and Actuaral Scences IDIA 8, 5, -6 Gelş/Receved:6.4.5, Kabul/Accepted: 3.6.5 www.statstkcler.org Türkye dek Đşszlk Oranının Bulanık
META ANALİZ VE TARIMSAL UYGULAMALAR
 T.C. KAHRAMANMARAŞ SÜTÇÜ İMAM ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ ZOOTEKNİ ANABİLİM DALI META ANALİZ VE TARIMSAL UYGULAMALAR HANDE KÜÇÜKÖNDER YÜKSEK LİSANS TEZİ KAHRAMANMARAŞ Ocak -2007 T.C. KAHRAMANMARAŞ
T.C. KAHRAMANMARAŞ SÜTÇÜ İMAM ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ ZOOTEKNİ ANABİLİM DALI META ANALİZ VE TARIMSAL UYGULAMALAR HANDE KÜÇÜKÖNDER YÜKSEK LİSANS TEZİ KAHRAMANMARAŞ Ocak -2007 T.C. KAHRAMANMARAŞ
Samsun Bölgesindeki Hava Kirliliğinin Neden Olduğu Hastalıkların İstatistiksel Modellenmesi
 KFBD Karadenz Fen Blmler Dergs / The Black Sea Journal of Scences 3(8):27-36, 2013 ISSN: 1309-4726 http://kfbd.gresun.edu.tr Samsun Bölgesndek Hava Krllğnn Neden Olduğu Hastalıkların İstatstksel Modellenmes
KFBD Karadenz Fen Blmler Dergs / The Black Sea Journal of Scences 3(8):27-36, 2013 ISSN: 1309-4726 http://kfbd.gresun.edu.tr Samsun Bölgesndek Hava Krllğnn Neden Olduğu Hastalıkların İstatstksel Modellenmes
Kısa Vadeli Sermaye Girişi Modellemesi: Türkiye Örneği
 Dokuz Eylül Ünverstes İktsad ve İdar Blmler Fakültes Dergs, Clt:24, Sayı:1, Yıl:2009, ss.105-122. Kısa Vadel Sermaye Grş Modellemes: Türkye Örneğ Mehmet AKSARAYLI 1 Özhan TUNCAY 2 Alınma Tarh: 04-2008,
Dokuz Eylül Ünverstes İktsad ve İdar Blmler Fakültes Dergs, Clt:24, Sayı:1, Yıl:2009, ss.105-122. Kısa Vadel Sermaye Grş Modellemes: Türkye Örneğ Mehmet AKSARAYLI 1 Özhan TUNCAY 2 Alınma Tarh: 04-2008,
Sorunun varlığı durumunda hata terimi varyans-kovaryans matrisi Var, Cov(u) = E(uu') = σ 2 I n şeklinde yazılamıyor fakat
 8. DEĞİŞEN VARYANS SORUNU (HETEROSCEDASTICITY) 8.. Değşen Varyans Sorunu Nedr? Matrslerle yan Y = β u Y = β β β 3 3 β k k u, = n genel doğrusal modeln ele alalım. Hata term çn yapılan varsayımlardan brs
8. DEĞİŞEN VARYANS SORUNU (HETEROSCEDASTICITY) 8.. Değşen Varyans Sorunu Nedr? Matrslerle yan Y = β u Y = β β β 3 3 β k k u, = n genel doğrusal modeln ele alalım. Hata term çn yapılan varsayımlardan brs
Erzurum Đlinde Buğday, Arpa ve Çavdarda Girdi Talebi Araştırması
 Tarım Blmler Dergs Tar. Bl. Der. Derg web sayfası: www.agr.ankara.edu.tr/derg Journal of Agrcultural Scences Journal homepage: www.agr.ankara.edu.tr/ournal TARIM BİLİMLERİ DERGİSİ JOURNAL OF AGRICULTURAL
Tarım Blmler Dergs Tar. Bl. Der. Derg web sayfası: www.agr.ankara.edu.tr/derg Journal of Agrcultural Scences Journal homepage: www.agr.ankara.edu.tr/ournal TARIM BİLİMLERİ DERGİSİ JOURNAL OF AGRICULTURAL
Türkiyede ki ĠĢ Kazalarının Yapay Sinir Ağları ile 2025 Yılına Kadar Tahmini
 Türkyede k ĠĢ Kazalarının Yapay Snr Ağları le 2025 Yılına Kadar Tahmn Hüseyn Ceylan ve Murat Avan Kırıkkale Meslek Yüksekokulu, Kırıkkale Ünverstes, Kırıkkale, 71450 Türkye. Kaman Meslek Yüksekokulu, Ah
Türkyede k ĠĢ Kazalarının Yapay Snr Ağları le 2025 Yılına Kadar Tahmn Hüseyn Ceylan ve Murat Avan Kırıkkale Meslek Yüksekokulu, Kırıkkale Ünverstes, Kırıkkale, 71450 Türkye. Kaman Meslek Yüksekokulu, Ah
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ BULANIK HEDONİK REGRESYON. Gökalp Kadri YENTÜR İSTATİSTİK ANABİLİM DALI ANKARA 2011
 ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ BULANIK HEDONİK REGRESYON Gökalp Kadr YENTÜR İSTATİSTİK ANABİLİM DALI ANKARA 011 Her hakkı saklıdır ÖZET Yüksek Lsans Tez BULANIK HEDONİK
ANKARA ÜNİVERSİTESİ FEN BİLİMLERİ ENSTİTÜSÜ YÜKSEK LİSANS TEZİ BULANIK HEDONİK REGRESYON Gökalp Kadr YENTÜR İSTATİSTİK ANABİLİM DALI ANKARA 011 Her hakkı saklıdır ÖZET Yüksek Lsans Tez BULANIK HEDONİK
