Hafta 5: Periyodik İşaretlerin Fourier Serisi Gösterilimi
|
|
|
- Nuray Kaymak
- 5 yıl önce
- İzleme sayısı:
Transkript
1 Hf 5: Priyodi İşrlrin Fourir Srii Görilimi
2 El Alınc An Konulr LI imlrin rmşı ül işrlr ynıı Sürli-zmn priyodi işrlrin Fourir rii görilimi Fourir riinin yınlığı Sürli-zmn Fourir riinin özllilri
3 LI Simlrin Krmşı Ül İşrlr Ynıı LI imlrin nlizind fydlı bir ylşım, işrlri şğıdi ii özlliği ğlyn ml işrlrin doğrul ombinyonu şlind mil mir:. ml işrlr, gniş v fydlı bir işr ümini oluşurbilmlidir.. Bir LI imin ml bir işr ynıı bi olmlıdır. Böylc, LI imin bir giriş ynıı, bi ynılrın doğrul ombinyonu olcır. Bu ii özlliği, hm ürli hm d yrı durumd rmşı ül işrlr ğlmdır. LI bir imin çıışı, girişin rmşı bir bil çrpımın şi giriş SİSEMİN ÖZFONKSİYONU, rmşı bi SİSEMİN ÖZDEĞERİ dnilir. v z rmşı yılr olm üzr, şğıd görildiği gibi ürli-zmnd, yrı-zmnd z n LI imlrin özfoniyonudur.
4 İmpul ynıı h oln bir ürli-zmn LI imin girişin uygulndığınd imin çıışı onvolüyon ingrlindn hplnbilir: Eşiliğin ğındi ingrlin yındığını vrylım. İngrlin dğri bğlıdır vrmşı biryıdır. İngrlin onucunu H il görlim: O hld, y =H çıış, girişin rmşı biryı il çrpımın şiir. Böylc, rmşı ül işrinin ürli-zmn LI imlrin özfoniyonu olduğu görilmiş olur. LI Simlrin Krmşı Ül İşrlr Ynıı d h d h d x h y d h H
5 LI Simlrin Krmşı Ül İşrlr Ynıı Bnzr işlmlr yrı-zmnd ypılbilir. İmpul ynıı h[n] oln bir yrı-zmn LI imin z n girişin oln ynıı onvolüyon oplmındn hplnır: y[ n] n z h[ ] x[ n ] h[ ] z Eşiliğin ğındi oplmnın yındığını vrylım. oplmnın dğri z y bğlıdır vrmşı biryıdır. oplmnın onucunu Hz il görlim: O hld, y[n] =Hzz n çıış, girişin rmşı biryı il çrpımın şiir. Yni, rmşı ülz n işrinin yrı-zmn LI imlrin özfoniyonu olduğunu görmiş oldu. H z h[ ] z h[ ] z n
6 LI Simlrin Krmşı Ül İşrlr Ynıı İmpul ynıı h oln bir ürli-zmn LI im üç d rmşı ül işrin oplmın şi oln bir giriş uygulylım. Özfoniyon özlliğindn, imin rmşı ülişrlr ynıı şöyldir: Sim doğrul olduğundn, rmşı üç ül işrin oplmındn oluşn giriş oln ynıı ül işrlr oln ynılrının oplmın şiir: x 3 3 H H H H H H y 3 3 3
7 LI Simlrin Krmşı Ül İşrlr Ynıı Yurıdi onucu gnllşirbiliriz. Bir ürli-zmn LI imin girişi x, rmşı ülişrlrin ğırlılı oplmı doğrul ombinyonu olun: Doğrullı v özfoniyon özllilrindn, imin çıışı şğıdi gibi olur: Bnzr şild, bir yrı-zmn LI imin girişi x[n], yrı-zmn rmşı ül işrlrin doğrul ombinyonu olun: Simin çıışı şğıdi gibi olur: x y H x [ n] z y [ n] H z z n n
8 LI Simlrin Krmşı Ül İşrlr Ynıı GÖZLEM: Bir LI imin girişi rmşı ül işrlrin doğrul ombinyonu i, çıışı d ynı ül işrlrin doğrul bir ombinyonudur. Çıış işrinin görilimindi yılr, giriş işrinin görilimindi yılr il rmşı ül işrlr rşılı gln im özdğrlrinin çrpımın şiir. x y H Bu gözlm, Fourir v ndiindn onr glnlrin hrhngi bir işrin rmşı ülişrlrin doğrul ombinyonu şlind nıl yzılbilcği hınd rşırm ypmlrın ön y olmuşur. Bu v önümüzdi hflr, oruyu ırıyl ürli v yrı-zmn priyodi işrlr için ynılyc, dh onri hfd priyodi olmyn işrlr durumunu l lcğız. v z hrhngi bir rmşı yı olbilir. Anc, Fourir nlizind v z ırıyl = v z = vryılcır. Lplc v z-dönüşümü onulrınd v z hrhngi bir rmşı yıy gnllşirilcir.
9 LI Simlrin Krmşı Ül İşrlr Ynıı ÖRNEK: Bir ürli-zmn LI imin girişi il çıışı rındi ilişi y=x-3 v im uygulnn giriş x = olun. Simin çıışı şöyldir: y 3 6 Uygulnn giriş bir özfoniyon olduğundn bu onucu lınd bliyordu. Giriş rşılı gln özdğri hplylım. Simin impul ynıının h =-3 olduğu çıır. O hld, Örnğimizd = olduğundn, giriş rşılı gln özdğr H = -6 olr ld dilir. Görüldüğügibiçıış, giriş il giriş rşılı gln ödğrin çrpımın şiir.. H h d 3 d 3
10 Sürli-zmn Priyodi İşrlrin Fourir Srii Görilimi Hrmoni ilişili rmşı ül işrlrin doğrul ombinyonu şlind yzıln bir ürli-zmn işri l llım: x / Hrmoni ilişili ül işrlrin hrbirinin il priyodi olduğunu görmüşü. O hld, x d il priyodiir. = için, oplmdi ül işr biir. = için ül işrlrin ml frnı dır v bu rimlr EMEL vy BİRİNCİ HARMONİK bilşnlr dnir. = içinülişrlrin ml frnı dır v bu rimlr iinci hrmoni bilşnlr dnir. Gnl olr, = N için oplmdi rmşı ül işrlr N. HARMONİK bilşnlr dnir. Priyodi bir işrin yurıdi gibi oplm şlind ifd dilmin FOURİER SERİSİ görilimi dnir.
11 Sürli-zmn Priyodi İşrlrin Fourir Srii Görilimi ÖRNEK: ml frnı oln bir ürli-zmn priyodi işrin Fourir rii görilimi şğıd vrilmişir: Kyılr oplmd yrin onulr işrin nlii ifdi ld dilbilir: Eulr ilişii ullnılr, işr rigonomri foniyonlr cinindn d yzılbilir:. 3,, 4, x x co6 3 co4 co x
12 Hrmoni bilşnlrin işri nıl oluşurduğu şğıd görilmişir.
13 Sürli-zmn Priyodi İşrlrin Fourir Srii Görilimi Sürli-zmn grçl priyodi işrlr için Fourir riinin diğr bir görilimi vrdır. Grçl bir işr için x =x* olduğundn * * * x Son ifd, Fourir rii görilimi il rşılşırılır = * - vy şdğr olr * = - onucu çır. Bu onuçn yrrlnılr Fourir rii şğıdi gibi yzılbilir: x R *
14 Sürli-zmn Priyodi İşrlrin Fourir Srii Görilimi Son ifdd uupl oordinlrd A şlind yzılır şğıd vriln şdğr rigonomri görilim ld dilir: rzyn oordinlrd B + C şlind yzılır şğıd vriln diğr bir rigonomri görilim ld dilir: co R A A x in co R C B C B x
15 Sürli-zmn Priyodi İşrlrin Fourir Srii Görilimi Şimdi d, priyodi bir işr için Fourir rii yılrının hplnbilcğini rışcğız. nıl Fourir rii görilimind, şiliğin hr ii rfı -n il çrpıldın onr çrpımın [,]rlığınd ingrli lınır şğıdi ifd ld dilir: n x d Köşli prnz içindi ifd Eulr formülü ullnılr ynidn düznlnbilir: [ n [ n] d d] [ n] d n d co[ ] in[ n ] d
16 Sürli-zmn Priyodi İşrlrin Fourir Srii Görilimi n için co[-n ] v in[-n ] işrlri / -n ml priyodu il priyodiir. İngrlın lındığı rlı uzunluğund olup ml priyodun -n ıdır. Sinü v oinü işrlrinin bir priyodund, işrlrin ıfırın üünd v lınd ln ıımlrı ynı ln hip olup bu işrlrin bir priyod v dolyııyl d bir priyodun myı ı uzunluğundi bir rlıi ingrli ıfır şiir. n için hr ii ingrl ıfır şiir. = n için, ingrl olup ingrlin onucu y şiir. Özl, [ n] d,, n n O hld, ri görilimindi yılr şöyl hplnır: n n x d
17 Sürli-zmn Priyodi İşrlrin Fourir Srii Görilimi Yurıd bulunn onucun, uzunlulu hrhngi bir rlı için gçrli olduğun di diniz. uzunlulu hrhngi bir rlı boyunc ingrl noyonu il görilm üzr, ürli-zmn priyodi işrin Fourir riin çılımı v çılımdi yılrın hbı şğıdi şililrd vrilmişir: x x d x / / d İşrin ri şlind görilimin SENEZ, yılrın nıl hplncğını vrn şiliğ i ANALİZ dnlmi dnilir. yıı, işri bi vy DC bilşn olup işrin bir priyod boyunc orlm dğridir: x d
18 Sürli-zmn Priyodi İşrlrin Fourir Srii Görilimi ÖRNEK: ml priyodu v ml frnı =/ oln priyodi r dlgnın Fourir rii görilimini ld diniz. ÇÖZÜM: İşrin bir priyodunun mmil ifdi şöyldir:, x, / Fourir rii yılrını bulm için uzunlulu hrhngi bir rlı çilbilir. İşr, = rfınd imri olduğundn rlı olr / / çilmi mnılıdır.
19 Sürli-zmn Priyodi İşrlrin Fourir Srii Görilimi İl önc ı blirlylim. Diğr yılr, bnzr şild hplnır: yılrı bi bir v dğişi dğrlri için şğıd çizilmişir. Bu örn için yılr grçl çıığındn yılr için bir grfi gnli grfiği yrli olmuşur. Kyılrın rmşı yı olmı hlind ii grfiğin gnli v fz grli olcğın di diniz. d d d x / / d d x in in / /
20 Sürli-zmn Priyodi İşrlrin Fourir Srii Görilimi
21 Sürli-zmn Priyodi İşrlrin Fourir Srii Görilimi ÖRNEK: Sinüzoidl işrlr için Fourir rii doğrudn hplnbilir. Aşğıd vriln işrin Fourir rii görilimini ld dlim. Çözüm: Eulr ilişiidn işr rmşı ülişrlrin oplmı şlind yzılbilir: Ohldx nin Fourir rii yılrı ifdy bılr doğrudn yzılbilir 4 co co in x x 4 / 4 / 4 / 4 / 3., 4, 4,, 4 / 4 /
22 Sürli-zmn Priyodi İşrlrin Fourir Srii Görilimi Kyılrın gnliği vfzı, y bğlı olr şğıd çizilmişir
23 Sürli-zmn Priyodi İşrlrin Fourir Srii Görilimi ÖRNEK: Örnlm bhind ullnılc priyodi impul diziinin Fourir rii yılrını bullım. x ÇÖZÜM: İşr, nliz dnlmind yrin onulr yılr hplnbilir. İşr imri olduğundn ingrl rlığı olr / / lm uygundur. / x d / x d / / rlığınd x = olduğundn, / / d No: Yurıdi onucu bulurn şu özlliği ullndı: / / f d f
24 Sürli-zmn Fourir Sriinin Yınlığı Kr dlgd ürizlilr vrdır. Hlbui ri görilimindi hrmoni ilişili rmşı ül işrlrin hpi ürlidir. Süriz bir işrin ürli işrlrl mil dilbilcğin şüphyl bılmışır. Fourir in pilri dönmin u mmiçii Lgrng rfındn vo dilmişir. H, dönmin diğr mmiçilri Lcroix, Mong v Lplc ın Fourir dği bil rşırmlrın yyınlnmı için yrli olmmışır. Fourir in rşırmlrı vfındn onr yyınlnbilmişir. Fourir riinin gçrliliğini görm için, bir ürli-zmn priyodi işrin onlu yıd hrmoni ilişili rmşı ülişrl milini l llım: N ylşılı hını görin: N N x N x x x N N N N
25 Sürli-zmn Fourir Sriinin Yınlığı Frlı ylşılılrı birbiriyl rşılşırbilm için, ylşılı hının boyuunu vrn bir ölçü ullnmmız grlidir. Ölçü olr, bir priyo boyunc hnın nriini ullncğız. Hnın nriini minimum ypn yılrın E N olduğu görilbilir ödvlrin birind bu onuç iplncır!. Yni, hyı minimum ypn yılr Fourir rii yılrın şiir. O hld, x nin Fourir rii görilimi vr, N büyüdüç h zlır v N limi durumund E N ıfır şi olur. Şimdi d priyodi bir işrin hngi oşullr lınd Fourir rii görilimin hip olcğını blirlmy çlışlım. N d x d
26 Sürli-zmn Fourir Sriinin Yınlığı İi duruml rşılşm mümündür: i yılrın hplnmın imn vrn ingrl yınmybilir bzı yılr onuz olbilir, ii yılrın hpi onlu ol bil,bu yılr nz dnlmind yrin onulduğund ld diln ri oriinl işri vrmybilir. Priyodi bir işr, bir priyod boyunc onlu nriy hip, yni x d i, Fourir rii yılrının onluolcğı görilbilir. Bu durumd, işr il Fourir rii görilimi rındi hnın nrii bir priyo boyunc ıfır olcır. x Bu onuç, Fourir rii göriliminin işr şi olduğu nlmın glmdiğini, nc iii rındi fr nri olmdığını blirmdir. Fizil imlr, işrin nriin ynı vrdiğindn, bu nlmd işr il Fourir rii görilimi şdğrdir. İlgilndiğimiz çoğu priyodi işrin nrii onluolupbuişrlr için Fourir rii görilimi mvcuur. d
27 Sürli-zmn Fourir Sriinin Yınlığı Dirichl, priyodi bir işr il Fourir rii göriliminin, işrin üriz olduğu nolr hriç şi olbilmi için oşullrı blirlmişir. Sürizli nolrınd ri, işrin ürizli noınd oldn v ğdn limilrinin orlmın şi olur. Dirichl oşullrı şğıd vrilmişir. Koşul : İşr bir priyod boyunc mul ingrllnbilir olmlıdır: x d Koşul : Bir priyo boyunc, işrin onlu yıd minimum v mimumu olmlıdır. Koşul 3: Sonlu bir rlı, işr onlu yıd ürizli olmlı v ürizli nolrınd işrin dğri d onlu olmlıdır. yrıc Dirichl oşullrını ihll dn işrlr örnlr şğıd vrilmişir.
28 Koşul i ihll dn bir işr Koşul yi ihll dn bir işr Koşul 3 ü ihll dn bir işr
29 Sürli-zmn Fourir Sriinin Yınlığı Dirichl oşullrını ğlmyn işrlrin fizil imlrd rşımız çım olılığının olduç z olduğu örnlrdn görülmdir. 898 yılınd, Amrin fiziçi Albr Michlon, onlu Fourir riini N = 8 dr hplyn bir ygı modrn dıyl hrmoni nlizör glişirmişir. Michlon, ygıını p ço priyodi işr için mişir. Michlon, r dlg için ummdığı onuçlr ld dinc glişirdiği ygıın hlı olbilcğini düşünmüş v onuyu mmil fiziçi Joih Gibb il pylşmışır. Gibb, problmi drinlmin inclmiş v düşünclrini 899 yılınd Michlon il pylşmışır. Priyodi r dlg, Dirichl oşullrını ğldığındn, onlu ridi rim yıı onuz gidrn ürizli nolrınd rinin limii ürizli dğrinin orlmın şi olmlıdır. Diğr nolrd, ri işr yınmlıdır. Çşili N dğrlri için ylşı işr v r dlg şğıd çizilmişir.
30
31 Sürli-zmn Fourir Sriinin Yınlığı Michlon un Gözlmi: Sonlu ri, ürizli nolrınd dlglnmlr vrmdir. Dlglnmlrın p gnliği N dn bğımızdır v N rıç zlmmdır. Gibb in Açılmı: İşrin üriz olmdığı bir noı ürizli noın ylşıç hnın üçü olmı için N büyü olmlıdır. Bu ndnl, N rıç dlglnmlr ürizli noı rfınd yoğunlşır nc dlglnmnın mimum gnliği bi lır. Bu gözlm GIBBS OLAYI dnir. Yni, üriz bir işrin onlu rimli Fourir rii ylşılığı yü frnlı dlglnmlr içrir v ürizli noınd işrn dh yü dğr lır. Sonlu rimli Fourir rii ullnılc, dlglnmlrdi oplm nri ihml dilbilc dr üçü olc şild yrinc büyü N dğri çilmlidir. Limi durumund, hının nrii ıfır olur v Fourir rii yınr.
32 Sürli-zmn Fourir Sriinin Özllilri ml priyodu v ml frnı ω =π/ oln priyodi bir işrin Fourir rii yılrının olduğunu blirm için noyonunu ullncğız. FS x Sürli-zmn Fourir riinin şğıd vriln özllilri rcılığıyl, Fourir rii yılrı bilinn işrlr yrdımıyl çoğu işrin Fourir rii çılımını ld m olylşmdır. Fourir dönüşümü onuund d görcğimiz gibi, çoğu özlli Fourir dönüşümünün özllilrindn ld dilbilir. Bu ndnl, dc n önmli özllilri ırlyc v yorumlycğız.
33 Sürli-zmn Fourir Sriinin Özllilri Özlli Zmnd ölm: FS x i, FS x / İp: Priyodi bir işr, zmnd ölnir priyodiliği orunur v priyodu dğişmz. Ölnmiş y =x- işrinin Fourir rii yılrı b olun: İngrld, τ = - dğişn dönüşümü yplım., uzunluğu oln bir rlı dğişiyor τ d uzunluğu oln bir rlı dğişcir. O hld, b / Yorum: olduğundn, b. b y d x x / Priyodi bir işr ölndiğind Fourir rii yılrının gnliği dğişmz! d d x d
34 Sürli-zmn Fourir Sriinin Özllilri Özlli Zmnd rin çvirm: FS i, FS x x İp: Priyodi bir işr, zmnd rin çvrilir priyodiliği orunur v priyodu dğişmz. Fourir rii çılımındn x- işri x / şlind yzılbilir. oplmd, =-m dğişn dönüşümü ypılır x m / m m Son şili, x- işrinin Fourir rii çılımı olup çılımdi yılr - dır. Yorum: Bir ürli-zmn priyodi işr zmnd rin çvrilir, rşılı gln Fourir rii yılrı d rin çvrilir. O hld, çif işrlrin x=x- Fourir rii yılrı çif = -, işrlrini i =- - olcır.
35 Sürli-zmn Fourir Sriinin Özllilri Özlli 3 Zmnd ölçlm: FS i, FS x x İp: Priyodi bir işr, ölçlndiğind priyodu dğişir. x nin ml priyodu v ml frnı ω =π/ i, xα nin ml priyodu /α v ml frnı αω dır. x nin Fourir rii çılımınd yrin α yzılır x Son şili, ml frnı αω oln işrin Fourir rii görilimi olup çılımdi yılr dır. Yorum: Bir ürli-zmn priyodi işri zmnd ölçlm Fourir rii yılrını dğişirmz.
36 Sürli-zmn Fourir Sriinin Özllilri Özlli 4 Zmnd ürv lm: FS dx FS x i, d İp: Priyodi bir işrin ürvi lınır yin priyodi olur v priyodu dğişmz. x nin Fourir rii çılımınd, şiliğin hr ii rfının y gör ürvi lınır dx d d d d d Son şili, ml frnı ω =π/ oln işrin Fourir rii görilimi olup çılımdi yılr ω =π/ olr görülmdir. Yorum: Bir ürli-zmn priyodi işrin ürvini lm, Fourir rii yılrının hm gnliğini hm d fzını dğişirmdir.
37 Sürli-zmn Fourir Sriinin Özllilri Özlli 5 Prvl ilişii: İp: İngrld, yzıp, x vx * için Fourir rii görilimlrini ullnır Köşli prnz içindi ingrli dh önc hplmışı: O hld, on şili onuz n ingrl olmın rğmn ingrllrin onucu dc l = için, diğr l dğrlrind şiir. Sonuç olr, ii oplm bir oplmy indirgnir v l = olur: d x * x x x l l l l l l d d d x x d x * * * l l l d,, d x *
38 Sürli-zmn Fourir Sriinin Özllilri Prvl İlişiinin Yorumu: Bir işri dğişi şillrd mil m lınd ilv bir bilgi vrmmdir. Bir bış çıınd gizli oln bir bilgi, diğr bir bış çıınd ory çıbilir. İşrin nrii ullnıln görilimdn bğımızdır. Diğr bir dyişl, işrin nriini zmn vy frn uzyınd hplm ynı onucu vrmlidir. Diğr Özllilr: Sürli-zmn Fourir riinin ipını vrmdiğimiz bş özllilri d vrdır. Diğr özllilrin ipı bnzr şild ypılbilir. blod lilnmişir. Özllilrin ümü şğıdi
39 Sürli-zmn Fourir Sriinin Özllilri Özlli Priyodi İşr Fourir Srii Kyılrı Doğrullı Zmnd ölm Frn ölm Eşlni lm Zmnd rin çvirm Zmnd ölçlm Priyodi onvolüyon Zmnd çrpm x / y ml frnı ml priyodu il priyodi Ax By A Bb x / M M / x x α> /α il priyodi v b M x * * x x x y d b x y l l b l
40 Özlli Priyodi İşr Fourir Srii Kyılrı Zmnd ürv lm Zmnd ingrl lm Grçl işrlr için şlni imrili Grçl v çif işrlr Grçl v işrlr Grçl işrlrin çif- yrışırmı Sürli-zmn Fourir Sriinin Özllilri dx d x d x grçl x grçl v çif x grçl v çif / x Ev{ x } [ x grçl] { } xo Od{ x } [ x grçl] m{ } Priyodi İşrlr için Prvl İlişii x d * { } { } m{ } m{ } grçl v çif f rmşı v çif
41 Sürli-zmn Fourir Sriinin Özllilri ÖRNEK: Sürli-zmn Fourir riinin özllilrindn yrrlnr şğıd vriln g işrinin = 4 il priyodi Fourir rii yılrını bullım. ÇÖZÜM: g işrini nliz dnlmind yrin oyr, Fourir rii yılrını blirlybiliriz. Anc, g işrini dh önc Fourir riini hpldığımız priyodi imri r dlg cinindn ifd dip onucu bulcğız. Kr dlg v Fourir rii yılrı, hırlm mcıyl şğıd vrilmişir: in,
42 Priyodi r dlg işrind =4v =llım. Şillrdn, g ilx rındi ilişinin g =x- / olduğu görülmdir.
43 x- işrinin Fourir rii yılrı b olun. Ölm özlliğindn, / DC rimin -/ Fourir rii yılrı c olun. DC işrin ıfırdn frlı bir Fourir rii yıı vrdır:, c /, g işrinin Fourir rii yılrı d olun. Doğrullı özlliğindn b Son ifdd yrin onulur d b c /, /, d in / /,,
44 Sürli-zmn Fourir Sriinin Özllilri ÖRNEK: Sürli-zmn Fourir riinin özllilrindn yrrlnr şğıd vriln x işrinin = 4 il priyodi Fourir rii yılrını bullım. ÇÖZÜM: Bu işrin ürvi, önci örn l lınn g işrin şiir. g v x işrlrinin Fourir rii yılrını ırıyl d v il görlim. ürv özlliğindn, d d / 4 in / / İfd, için gçrlidir. d şiliyrin onulur,, bir priyo boyunc x nin lındi ln priyod bölünr ld dilbilir: x d x d 4
Ele Alınacak Ana Konular. Hafta 5: Periyodik İşaretlerin Fourier Serisi Gösterilimi. LTI Sistemlerin Karmaşık Üstel İşaretlere Yanıtı
 ..5 El Alınc An Konulr LI sismlrin rmşı üsl işrlr ynıı Sürli-zmn priyodi işrlrin Fourir srisi gösrilimi Hf 5: Priyodi İşrlrin Fourir Srisi Gösrilimi Fourir srisinin yınslığı Sürli-zmn Fourir srisinin özllilri
..5 El Alınc An Konulr LI sismlrin rmşı üsl işrlr ynıı Sürli-zmn priyodi işrlrin Fourir srisi gösrilimi Hf 5: Priyodi İşrlrin Fourir Srisi Gösrilimi Fourir srisinin yınslığı Sürli-zmn Fourir srisinin özllilri
Hafta 7: Sürekli-zaman Fourier Dönüşümü
 Hf 7: Sürli-zmn ourir Dönüşümü El Alınc An Konulr Sürli-zmn ourir dönüşümü Sürli-zmn priyodi işrlr için ourir dönüşümü Sürli-zmn ourir dönüşümünün özllilri Doğrusl, sbi syılı difrnsiyl dnlmlrl nımlnn sismlr
Hf 7: Sürli-zmn ourir Dönüşümü El Alınc An Konulr Sürli-zmn ourir dönüşümü Sürli-zmn priyodi işrlr için ourir dönüşümü Sürli-zmn ourir dönüşümünün özllilri Doğrusl, sbi syılı difrnsiyl dnlmlrl nımlnn sismlr
LOGARİTMA. Örnek: çizelim. Çözüm: f (x) a biçiminde tanımlanan fonksiyona üstel. aşağıda verilmiştir.
 LOGARİTMA I. Üstl Fonksiyonlr v Logritmik Fonksiyonlr şitliğini sğlyn dğrini bulmk için ypıln işlm üs lm işlmi dnir. ( =... = 8) y şitliğini sğlyn y dğrini bulmk için ypıln işlm üslü dnklmi çözm dnir.
LOGARİTMA I. Üstl Fonksiyonlr v Logritmik Fonksiyonlr şitliğini sğlyn dğrini bulmk için ypıln işlm üs lm işlmi dnir. ( =... = 8) y şitliğini sğlyn y dğrini bulmk için ypıln işlm üslü dnklmi çözm dnir.
ELM207 Analog Elektronik
 ELM7 Alog Elkroik Giriş Bir Fourir srisi priyodik bir ) oksiyouu, kosiüs v siüslri sosuz oplmı biçimid bir çılımdır. ) cos b si ) Bşk dyişl, hrhgi bir priyodik oksiyo sbi bir dğr, kosiüs v siüs oksiyolrıı
ELM7 Alog Elkroik Giriş Bir Fourir srisi priyodik bir ) oksiyouu, kosiüs v siüslri sosuz oplmı biçimid bir çılımdır. ) cos b si ) Bşk dyişl, hrhgi bir priyodik oksiyo sbi bir dğr, kosiüs v siüs oksiyolrıı
Sistem Dinamiği ve Modellemesi. Doğrusal Sistemlerin Sınıflandırılması Doğrusal Sistemlerin Zaman Davranışı
 Sim Dinmiği v Modllmi Doğrul Simlrin Sınıflndırılmı Doğrul Simlrin Zmn Dvrnışı Giriş: Sim dinmiği çözümlmind, frklı fizikl özlliklr şıyn doğrul imlrin krkriiklrini blirlyn ml bğınılr rınd bnzrlik noloji
Sim Dinmiği v Modllmi Doğrul Simlrin Sınıflndırılmı Doğrul Simlrin Zmn Dvrnışı Giriş: Sim dinmiği çözümlmind, frklı fizikl özlliklr şıyn doğrul imlrin krkriiklrini blirlyn ml bğınılr rınd bnzrlik noloji
Pontiklerin altında hacim koruma
 Pontilrin ltınd hcim orum Gitlich Biomtril ürünlri il - Sırt Korum çözümlri Dh fzl bilgi için www.gitlich-biomtril.com Sırt Korum - Bitç Sırt orum diş çimi onrı lvolr ırtın ontürünü orum için uygulnn bir
Pontilrin ltınd hcim orum Gitlich Biomtril ürünlri il - Sırt Korum çözümlri Dh fzl bilgi için www.gitlich-biomtril.com Sırt Korum - Bitç Sırt orum diş çimi onrı lvolr ırtın ontürünü orum için uygulnn bir
UFUK ÖZERMAN- 2012-2013 Page 1
 - GÜZ P,Q,R fokiolrı poliom olmk üzr d d P Q R d d v P d d Q d P d R P p q dklmi içi P şrıı ğl = okı di ok dir, çözümlri di okıı civrıd şklid rrız. =+-+- +... = = okı; p=q/ P, q= R/ P fokiolrı okıd liik
- GÜZ P,Q,R fokiolrı poliom olmk üzr d d P Q R d d v P d d Q d P d R P p q dklmi içi P şrıı ğl = okı di ok dir, çözümlri di okıı civrıd şklid rrız. =+-+- +... = = okı; p=q/ P, q= R/ P fokiolrı okıd liik
İstatistik I Bazı Matematik Kavramlarının Gözden
 İsttistik I Bzı Mtemtik Kvrmlrının Gözden Geçirilmesi Hüseyin Tştn Ağustos 13, 2006 İçindekiler 1 Toplm İşlemcisi 2 2 Çrpım İşlemcisi 6 3 Türev 7 3.1 Türev Kurllrı.......................... 8 3.1.1 Sbit
İsttistik I Bzı Mtemtik Kvrmlrının Gözden Geçirilmesi Hüseyin Tştn Ağustos 13, 2006 İçindekiler 1 Toplm İşlemcisi 2 2 Çrpım İşlemcisi 6 3 Türev 7 3.1 Türev Kurllrı.......................... 8 3.1.1 Sbit
BÖLÜM 4 LİNEER DİFERANSİYEL DENKLEM SİSTEMLERİ
 BÖLÜM LİNEER DİFERANSİYEL DENKLEM SİSTEMLERİ GİRİŞ Dnklm sismlrin linr cbir drsindn şin olmlısınız Anck bu ür dnklmlrd hrhngi bir difrnsiyl büyüklük vy ürv bulunmz Bşk bir dyişl cbirsl dnklm sismi, y (
BÖLÜM LİNEER DİFERANSİYEL DENKLEM SİSTEMLERİ GİRİŞ Dnklm sismlrin linr cbir drsindn şin olmlısınız Anck bu ür dnklmlrd hrhngi bir difrnsiyl büyüklük vy ürv bulunmz Bşk bir dyişl cbirsl dnklm sismi, y (
formundadır. Burada verilen bir f fonksiyonu F fonksiyonuna dönüşür ve F fonksiyonuna f in fonksiyon dönüşümü denir. K(s,t) ye çekirdek denir.
 LPLCE DÖNÜŞÜMÜ Lpl dönüşümü yrdımı il ğ rflı difrniyl dnklmin ğ rfınd bulunn fonkiyonun ürkliliği bozul bil(bmk,impul fonkiyonu) difrniyl dnklmlr çözülbilkir. Bu ip dnklmlrl lkrik imlrini çözrkn krşılşılır.
LPLCE DÖNÜŞÜMÜ Lpl dönüşümü yrdımı il ğ rflı difrniyl dnklmin ğ rfınd bulunn fonkiyonun ürkliliği bozul bil(bmk,impul fonkiyonu) difrniyl dnklmlr çözülbilkir. Bu ip dnklmlrl lkrik imlrini çözrkn krşılşılır.
Magnetic Materials. 4. Ders: Paramanyetizma-2. Numan Akdoğan.
 Mgntic Mtrils 4. Drs: Prmnytizm-2 Numn Akdoğn kdogn@gyt.du.tr Gbz Institut of Tchnology Dprtmnt of Physics Nnomgntism nd Spintronic Rsrch Cntr (NASAM) Kuntum mkniği klsik torinin özlliklrini dğiştirmdn,
Mgntic Mtrils 4. Drs: Prmnytizm-2 Numn Akdoğn kdogn@gyt.du.tr Gbz Institut of Tchnology Dprtmnt of Physics Nnomgntism nd Spintronic Rsrch Cntr (NASAM) Kuntum mkniği klsik torinin özlliklrini dğiştirmdn,
Hafta 8: Ayrık-zaman Fourier Dönüşümü
 Hafta 8: Ayrı-zama ourir Döüşümü El Alıaca Aa Koular Ayrı-zama ourir döüşümü Ayrı-zama priyodi işartlr içi ourir döüşümü Ayrı-zama ourir döüşümüü özllilri Doğrusal, sabit atsayılı far dlmlriyl taımlaa
Hafta 8: Ayrı-zama ourir Döüşümü El Alıaca Aa Koular Ayrı-zama ourir döüşümü Ayrı-zama priyodi işartlr içi ourir döüşümü Ayrı-zama ourir döüşümüü özllilri Doğrusal, sabit atsayılı far dlmlriyl taımlaa
ÇEKME ÇUBUKLARI VE ÇEKME ÇUBUKLARI EKLERİ
 ÇEKME ÇUBUKARI VE ÇEKME ÇUBUKARI EKERİ Çeme çubulrı; Kfes Çubu Elemnlrı olr Çeli öprülerde, yol plformunun sıldığı hllrd, Büyü çılılı,özellile snyi ypılrınd, çerçevelerde ullnıln gergiler Şelinde yygın
ÇEKME ÇUBUKARI VE ÇEKME ÇUBUKARI EKERİ Çeme çubulrı; Kfes Çubu Elemnlrı olr Çeli öprülerde, yol plformunun sıldığı hllrd, Büyü çılılı,özellile snyi ypılrınd, çerçevelerde ullnıln gergiler Şelinde yygın
Sistem Dinamiği ve Modellemesi
 8..0 Sit Diiği v Modlli Doğrul Sitlri Z Dvrışı II. Mrtbd Gili Sitlr Giriş: Sit diiği çözülid, frlı fizil özllilr tşıy doğrul itlri rtritilrii blirly tl bğıtılr rıd bzrli (oloji) urulbili ouud itlri blirli
8..0 Sit Diiği v Modlli Doğrul Sitlri Z Dvrışı II. Mrtbd Gili Sitlr Giriş: Sit diiği çözülid, frlı fizil özllilr tşıy doğrul itlri rtritilrii blirly tl bğıtılr rıd bzrli (oloji) urulbili ouud itlri blirli
LYS 1 / MATEMATİK DENEME ÇÖZÜMLERİ
 LYS / MATEMATİK DENEME ÇÖZÜMLERİ Dnm. ^ h ^ h ^h ^^h h ^^h h. ^ h ^ h ^ h Cvp C m. ^ h ^ h Cvp C 9 9 9, ulunur.. Cvp A Cvp B. İfdlri trf trf topllım.. n n n _ n n,,,,, için ifd tmsı olur. 9 ulunur. ^ h
LYS / MATEMATİK DENEME ÇÖZÜMLERİ Dnm. ^ h ^ h ^h ^^h h ^^h h. ^ h ^ h ^ h Cvp C m. ^ h ^ h Cvp C 9 9 9, ulunur.. Cvp A Cvp B. İfdlri trf trf topllım.. n n n _ n n,,,,, için ifd tmsı olur. 9 ulunur. ^ h
ÜSTEL DAĞILIM. üstel dağılımın parametresidir. Birikimli üstel dağılım fonksiyonu da, olarak bulunur. olduğu açık olarak görülmektedir.
 ÜSTL DAĞILIM Tanım : X > olma üzr sürli bir rasgl dğişn olsun. ğr a > için X rassal dğişni aşağıdai gibi bir dağılıma sahip olursa X rasgl dğişnin üsl dağılmış rassal dğişn v onsiyonuna da üsl dağılım
ÜSTL DAĞILIM Tanım : X > olma üzr sürli bir rasgl dğişn olsun. ğr a > için X rassal dğişni aşağıdai gibi bir dağılıma sahip olursa X rasgl dğişnin üsl dağılmış rassal dğişn v onsiyonuna da üsl dağılım
Otomatik Kontrol. Fiziksel Sistemlerin Modellenmesi. Prof.Dr.Galip Cansever. Dişli Takımları Elektromekaniksel Sistemler. Ders #5
 Dr #5 Ooik onrol Fizikl Silrin Modllni Dişli Tkılrı Elkroknikl Silr Prof.Dr.Glip Cnvr 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr Mknikl Silrin Trnfr Fonkiyonlrı Dişli Tkılrı Vili biikllri düşünli. Yokuş
Dr #5 Ooik onrol Fizikl Silrin Modllni Dişli Tkılrı Elkroknikl Silr Prof.Dr.Glip Cnvr 6 Fbrury 007 Ooik onrol Prof.Dr.Glip Cnvr Mknikl Silrin Trnfr Fonkiyonlrı Dişli Tkılrı Vili biikllri düşünli. Yokuş
SAYILARIN ÇÖZÜMLENMESĐ ve BASAMAK KAVRAMI
 YILLAR 00 00 004 00 006 007 008 009 010 011 ÖSS-YGS - 1 - - 1-1 1 SAYILARIN ÇÖZÜMLENMESĐ ve BASAMAK KAVRAMI,b,c,d birer rkm olmk üzere ( 0) b = 10 + b bc = 100+10+b bc = 100+10b+c bcd =1000+100b+10c+d
YILLAR 00 00 004 00 006 007 008 009 010 011 ÖSS-YGS - 1 - - 1-1 1 SAYILARIN ÇÖZÜMLENMESĐ ve BASAMAK KAVRAMI,b,c,d birer rkm olmk üzere ( 0) b = 10 + b bc = 100+10+b bc = 100+10b+c bcd =1000+100b+10c+d
THÉVENİN, NORTON, MAKSİMUM GÜÇ TEOREMİ ve DEVRE PARAMETRELERİ
 DENEY NO: 4 THÉENİN, NORTON, MAKSİMUM GÜÇ TEOREMİ ve DERE PARAMETRELERİ Mlzeme ve Cihz Litei:. 330 direnç det. k direnç 3 det 3.. k direnç det 4. 3.3 k direnç det 5. 5.6 k direnç det 6. 0 k direnç det
DENEY NO: 4 THÉENİN, NORTON, MAKSİMUM GÜÇ TEOREMİ ve DERE PARAMETRELERİ Mlzeme ve Cihz Litei:. 330 direnç det. k direnç 3 det 3.. k direnç det 4. 3.3 k direnç det 5. 5.6 k direnç det 6. 0 k direnç det
BÖLÜM 3 : RASLANTI DEĞİŞKENLERİ
 BÖLÜM : RASLANTI DEĞİŞKENLERİ (Rndom Vribles Giriş: Bölüm de olsılık fonksionu, denein örneklem uzını oluşurn sonuçlrın erimleri ile belirleniordu. Örneğin; iki zr ıldığınd, P gelen 6 olsı sırlı ikilinin
BÖLÜM : RASLANTI DEĞİŞKENLERİ (Rndom Vribles Giriş: Bölüm de olsılık fonksionu, denein örneklem uzını oluşurn sonuçlrın erimleri ile belirleniordu. Örneğin; iki zr ıldığınd, P gelen 6 olsı sırlı ikilinin
İntegral Uygulamaları
 İntegrl Uygulmlrı Yzr Prof.Dr. Vkıf CAFEROV ÜNİTE Amçlr Bu üniteyi çlıştıktn sonr; düzlemsel ln ve dönel cisimlerin cimlerinin elirli integrl yrdımı ile esplnileceğini, küre, koni ve kesik koninin cim
İntegrl Uygulmlrı Yzr Prof.Dr. Vkıf CAFEROV ÜNİTE Amçlr Bu üniteyi çlıştıktn sonr; düzlemsel ln ve dönel cisimlerin cimlerinin elirli integrl yrdımı ile esplnileceğini, küre, koni ve kesik koninin cim
ÜNİTE - 7 POLİNOMLAR
 ÜNİTE - 7 BÖLÜM Polinomlr (Temel Kvrmlr) -. p() = 3 + n 6 ifdesi bir polinom belirttiğine göre n en z 5. p( + ) = + 4 + Test - olduğun göre, p() polinomunun ktsyılr toplmı p() polinomund terimlerin kuvvetleri
ÜNİTE - 7 BÖLÜM Polinomlr (Temel Kvrmlr) -. p() = 3 + n 6 ifdesi bir polinom belirttiğine göre n en z 5. p( + ) = + 4 + Test - olduğun göre, p() polinomunun ktsyılr toplmı p() polinomund terimlerin kuvvetleri
Eğitim-Öğretim Güz Yarıyılı Diferansiyel Denklemler Dersi Çalışma Soruları
 - Eğiim-Öğrim Güz rıılı Difril Dklmlr Dri Çlışm Sorlrı 6 // Aşğıd vril kvv rilrii kıklık rıçplrıı lirliiz. = = di ok civrıd kvv rii rdımıl vril difril dklmlri çözüüz. - -= - + -= - + += dklmii kil oklrıı
- Eğiim-Öğrim Güz rıılı Difril Dklmlr Dri Çlışm Sorlrı 6 // Aşğıd vril kvv rilrii kıklık rıçplrıı lirliiz. = = di ok civrıd kvv rii rdımıl vril difril dklmlri çözüüz. - -= - + -= - + += dklmii kil oklrıı
KATSAYILARI LEBESGUE İNTEGRALLENEBİLİR FONKSİYONLAR OLAN ADİ DİFERANSİYEL OPERATÖRLERİN ÖZDEĞERLERİ ÜZERİNE. Alp Arslan Kıraç
 Afyon Koa Ünivrsisi 8 Afyon Koa Univrsiy FEN BİLİMLERİ DERGİSİ JOURNAL OF SCIENCE KATSAYILARI LEBESGUE İNTEGRALLENEBİLİR FONKSİYONLAR OLAN ADİ DİFERANSİYEL OPERATÖRLERİN ÖZDEĞERLERİ ÜZERİNE ÖZET Al Arslan
Afyon Koa Ünivrsisi 8 Afyon Koa Univrsiy FEN BİLİMLERİ DERGİSİ JOURNAL OF SCIENCE KATSAYILARI LEBESGUE İNTEGRALLENEBİLİR FONKSİYONLAR OLAN ADİ DİFERANSİYEL OPERATÖRLERİN ÖZDEĞERLERİ ÜZERİNE ÖZET Al Arslan
1. Değişkenler ve Eğriler: Matematiksel Hatırlatma
 DERS NOTU 01 Son Hli Değildir, tslktır: Ekleme ve Düzenlemeler Ypılck BİR SOSYAL BİLİM OLARAK İKTİSAT VE TEMEL KAVRAMLAR 1 Bugünki dersin işleniş plnı: 1. Değişkenler ve Eğriler: Mtemtiksel Htırltm...
DERS NOTU 01 Son Hli Değildir, tslktır: Ekleme ve Düzenlemeler Ypılck BİR SOSYAL BİLİM OLARAK İKTİSAT VE TEMEL KAVRAMLAR 1 Bugünki dersin işleniş plnı: 1. Değişkenler ve Eğriler: Mtemtiksel Htırltm...
Sistem Dinamiği ve Modellemesi
 5.0.03 Sit Diiği v Modlli Doğrul Sitlri Z Dvrışı II. Mrtbd Gcili Sitlr Giriş: Sit diiği çözülid, frlı fizil özllilr tşıy doğrul itlri rtritilrii blirly tl bğıtılr rıd bzrli (oloji) urulbili oucud itlri
5.0.03 Sit Diiği v Modlli Doğrul Sitlri Z Dvrışı II. Mrtbd Gcili Sitlr Giriş: Sit diiği çözülid, frlı fizil özllilr tşıy doğrul itlri rtritilrii blirly tl bğıtılr rıd bzrli (oloji) urulbili oucud itlri
DESTEK DOKÜMANI. Mali tablo tanımları menüsüne Muhasebe/Mali tablo tanımları altından ulaşılmaktadır.
 Mali Tablolar Mali tablo tanımları mnüsün Muhasb/Mali tablo tanımları altından ulaşılmatadır. Mali tablolarla ilgili yapılabilc işlmlr ii gruba ayrılır. Mali Tablo Tanımları Bu bölümd firmanın ullanacağı
Mali Tablolar Mali tablo tanımları mnüsün Muhasb/Mali tablo tanımları altından ulaşılmatadır. Mali tablolarla ilgili yapılabilc işlmlr ii gruba ayrılır. Mali Tablo Tanımları Bu bölümd firmanın ullanacağı
x ise x kaçtır?{ C : }
 İZMİR FEN LİSESİ LOGARİTMA ÇALIŞMA SORULARI LOGARİTMA FONKSİYONU. ( ) ( ) f m m m R C : fonksionunun m { ( 0,) } dim tnımlı olmsı için?.. f ( ) ( ) fonksionunun tnım kümsind kç tn tm sı vrdır?{ C : }.
İZMİR FEN LİSESİ LOGARİTMA ÇALIŞMA SORULARI LOGARİTMA FONKSİYONU. ( ) ( ) f m m m R C : fonksionunun m { ( 0,) } dim tnımlı olmsı için?.. f ( ) ( ) fonksionunun tnım kümsind kç tn tm sı vrdır?{ C : }.
TYT / MATEMATİK Deneme - 2
 TYT / MTMTİK eneme -. 7 ^7h ^h $ bulunur. evp : 6. b b c 6 c 6, b ve c nin ritmetik ortlmsı O b c 6 bulunur.. y z y z ^ h $ bulunur. evp : 7. y çift ne olurs olsun çift syı olduğundn in yd çift olduğundn
TYT / MTMTİK eneme -. 7 ^7h ^h $ bulunur. evp : 6. b b c 6 c 6, b ve c nin ritmetik ortlmsı O b c 6 bulunur.. y z y z ^ h $ bulunur. evp : 7. y çift ne olurs olsun çift syı olduğundn in yd çift olduğundn
DERS 11. Belirsiz İntegral
 DERS Blirsiz İnral.. Blirsiz İnral. B rs ürvi bilinn bir onksiyonn ynin inşasını l alacağız. Türvi bilinn bir onksiyonn ynin inşası işlmin rs ürv işlmi aniirniaion nir. v F onksiyonlar, F is, F y nin rs
DERS Blirsiz İnral.. Blirsiz İnral. B rs ürvi bilinn bir onksiyonn ynin inşasını l alacağız. Türvi bilinn bir onksiyonn ynin inşası işlmin rs ürv işlmi aniirniaion nir. v F onksiyonlar, F is, F y nin rs
Ç A L I Ş M A N O T L A R I. Sinyaller & Sistemler Fourier Serisi. Sinyallerin Zaman Frekans Analizleri : FOURIER TEORİSİ
 Siyllr & Sismlr Fourir Srisi Siyllri Zm Frks Alizlri : FOURIER EORİSİ Bu bölümd iibr işr işlm sigl procssig kvrm v yömlri ğilrk işrlri liz my çlışcğız. Özllikl bir işri rks bğlı dğişimii gösr lizi çok
Siyllr & Sismlr Fourir Srisi Siyllri Zm Frks Alizlri : FOURIER EORİSİ Bu bölümd iibr işr işlm sigl procssig kvrm v yömlri ğilrk işrlri liz my çlışcğız. Özllikl bir işri rks bğlı dğişimii gösr lizi çok
Üslü İfadelerde İşlemler (Temel Kurallar) - Çalışma Kağıdı Ortaokul Matematik Kafası $ = k) 81 $ 243 = Kerim Hoca. p) 125 $ 625 = w) 3
 .Sınıf Mtemtik ÜSLÜ İFADELER Yyın No : / Kznım :... + Üssün Üssü ve Sırlm Bir üslü ifdenin üssü lındığınd üsler çrpılır.. Alıştırmlr Aşğıdki işlemlerin sonuçlrını üslü biçimde yzınız. y ^ h y ) ^ h b)
.Sınıf Mtemtik ÜSLÜ İFADELER Yyın No : / Kznım :... + Üssün Üssü ve Sırlm Bir üslü ifdenin üssü lındığınd üsler çrpılır.. Alıştırmlr Aşğıdki işlemlerin sonuçlrını üslü biçimde yzınız. y ^ h y ) ^ h b)
S1:10, S2:30, S3:20, S4:40 Puan Süre: 100 dakika 17 Nisan 2008
 Mikroişlmi Sistmlr Viz Sınvı S1:10, S2:30, S3:20, S4:40 Pun Sür: 100 kik 17 Nisn 2008 1) 18-45 işlmini ikili tn rçklyiniz. 18 00010010 45 00101101-45 için 2 y tümlyn lınır; 1 tümlm 11010010, sonr un 1
Mikroişlmi Sistmlr Viz Sınvı S1:10, S2:30, S3:20, S4:40 Pun Sür: 100 kik 17 Nisn 2008 1) 18-45 işlmini ikili tn rçklyiniz. 18 00010010 45 00101101-45 için 2 y tümlyn lınır; 1 tümlm 11010010, sonr un 1
İÇİNDEKİLER. Ön Söz...2. Matris Cebiri...3. Elementer İşlemler Determinantlar Lineer Denklem Sistemleri Vektör Uzayları...
 İÇİNDEKİLER Ön Söz... Mtris Cebiri... Elementer İşlemler... Determinntlr...7 Lineer Denklem Sistemleri...8 Vektör Uzylrı...6 Lineer Dönüşümler...48 Özdeğerler - Özvektörler ve Köşegenleştirme...55 Genel
İÇİNDEKİLER Ön Söz... Mtris Cebiri... Elementer İşlemler... Determinntlr...7 Lineer Denklem Sistemleri...8 Vektör Uzylrı...6 Lineer Dönüşümler...48 Özdeğerler - Özvektörler ve Köşegenleştirme...55 Genel
DENEY 10 PM DC Servo Motor Karakteristikleri
 DNY 0 PM DC Srvo Moor rkrklr DNYİN AMACI. PM DC rvo oorlrın krkrk prrlrn nlk.. PM DC rvo oorlrın krkrk prrlrn ölçk. GİİŞ Dc rvo oor, konrol lr çlışlrınd, konrol orn uygun olrk konrol yönlr glşrk çn, konrol
DNY 0 PM DC Srvo Moor rkrklr DNYİN AMACI. PM DC rvo oorlrın krkrk prrlrn nlk.. PM DC rvo oorlrın krkrk prrlrn ölçk. GİİŞ Dc rvo oor, konrol lr çlışlrınd, konrol orn uygun olrk konrol yönlr glşrk çn, konrol
Tanım : Merkezi orijin ve yarıçapı 1 birim olan çembere trigonometrik çember veya birim çember denir. y B(0,1) C(1,0)
 BÖLÜM TRİGONOMETRİ.. TRİGONOMETRİK BAĞINTILAR... BİRİM ÇEMBER Tnım : Merkezi orijin ve yrıçpı birim oln çembere trigonometrik çember vey birim çember denir. Trigonometrik çemberin denklemi + y dir.yni
BÖLÜM TRİGONOMETRİ.. TRİGONOMETRİK BAĞINTILAR... BİRİM ÇEMBER Tnım : Merkezi orijin ve yrıçpı birim oln çembere trigonometrik çember vey birim çember denir. Trigonometrik çemberin denklemi + y dir.yni
Örnek...1 : a, b ve c birbirlerinden farklı birer rakamdır. a.b+9.b c en çok kaçtır?
 RAKAM Syılrı ifde etmek için kullndığımız 0,,2,3,4,5,6,7,8,9 sembollerine rkm denir. Örnek... :, b ve c birbirlerinden frklı birer rkmdır..b+9.b c en çok kçtır? DOĞAL SAYILAR N={0,,2,3...,n,...} kümesine
RAKAM Syılrı ifde etmek için kullndığımız 0,,2,3,4,5,6,7,8,9 sembollerine rkm denir. Örnek... :, b ve c birbirlerinden frklı birer rkmdır..b+9.b c en çok kçtır? DOĞAL SAYILAR N={0,,2,3...,n,...} kümesine
2009 Soruları. c
 Hırvt ıstn Ulusl Mtemt ık Ol ımp ıytı Tkım Seçme Sınvı Geometr ı 2009 Sorulrı c www.sbelin.wordpress.com sbelinwordpress@gmil.com Hırvtistn d ypıln 2009 yılı TST yni Tkım Seçme Sınvın it geometri sorulrı
Hırvt ıstn Ulusl Mtemt ık Ol ımp ıytı Tkım Seçme Sınvı Geometr ı 2009 Sorulrı c www.sbelin.wordpress.com sbelinwordpress@gmil.com Hırvtistn d ypıln 2009 yılı TST yni Tkım Seçme Sınvın it geometri sorulrı
POLİNOMLAR. Örnek: 4, 2, 7 polinomun katsayılarıdırlar. 5x, derecesi en büyük olan terim olduğundan. ifadelerine polinomun. der tür.
 OLİNOMLAR o,,,... n, n birer reel syı, n bir doğl syı ve belirsiz bir elemn olmk üzere, o.. n n... n. n. biçimindeki ifdelere e göre düzenlenmiş reel ktsyılı ve bir belirsizli polinom denir. in bir polinomu,,r,t,k
OLİNOMLAR o,,,... n, n birer reel syı, n bir doğl syı ve belirsiz bir elemn olmk üzere, o.. n n... n. n. biçimindeki ifdelere e göre düzenlenmiş reel ktsyılı ve bir belirsizli polinom denir. in bir polinomu,,r,t,k
DENKLEM ve EŞİTSİZLİKLER ÜNİTE 2. ÜNİTE 2. ÜNİTE 2. ÜNİTE 2. ÜNİT
 DENKLEM ve EŞİTSİZLİKLER ÜNİTE. ÜNİTE. ÜNİTE. ÜNİTE. ÜNİT BİRİNCİ DERECEDEN DENKLEM ve EŞİTSİZLİKLER. Kznım : Gerçek syılr kümesinde birinci dereceden eşitsizliğin özelliklerini belirtir.. Kznım : Gerçek
DENKLEM ve EŞİTSİZLİKLER ÜNİTE. ÜNİTE. ÜNİTE. ÜNİTE. ÜNİT BİRİNCİ DERECEDEN DENKLEM ve EŞİTSİZLİKLER. Kznım : Gerçek syılr kümesinde birinci dereceden eşitsizliğin özelliklerini belirtir.. Kznım : Gerçek
Sınav Süresi 80 dakikadır. Başarılar
 BAÜ. NECATİBEY EĞİTİM FAKÜLTESİ KİMYA ÖĞRETMENLİĞİ FİZİKSEL KİMYA III ARA SINAVI 7..2009 NO : AD SOYAD :. Aşğıd özelileri verilen ir A4 ğıdı n içeriinde tmmen ynıyr. Kğıdın %80 rnınd C n H 2n O n frmülüne
BAÜ. NECATİBEY EĞİTİM FAKÜLTESİ KİMYA ÖĞRETMENLİĞİ FİZİKSEL KİMYA III ARA SINAVI 7..2009 NO : AD SOYAD :. Aşğıd özelileri verilen ir A4 ğıdı n içeriinde tmmen ynıyr. Kğıdın %80 rnınd C n H 2n O n frmülüne
ÇÖZÜMLER HAREKET. 4. hız. t(s) zaman
 TEST ÇÖZÜMER HAREET. rlığınd rç durmkdır. (m) o rlığınd rcın ı sbiir. o o o II. yrgı ynlışır. o nınd bşlngıç noksın oln uzklığı: o o o III. yrgı ynlışır.. nın d cis min konum ko nu mu ir. I. yr gı doğ
TEST ÇÖZÜMER HAREET. rlığınd rç durmkdır. (m) o rlığınd rcın ı sbiir. o o o II. yrgı ynlışır. o nınd bşlngıç noksın oln uzklığı: o o o III. yrgı ynlışır.. nın d cis min konum ko nu mu ir. I. yr gı doğ
ÜSLÜ İFADELER VE ÜSTEL FONKSİYONLAR LOGARİTMA FONKSİYONU, ÜSTEL, LOGARİTMİK DENKLEM VE EŞİTSİZLİKLER
 BÖÜ ÜÜ İFD V Ü FOİO Üslü İfdlrd İşlmlr...7 Üslü Dnklmlr... Üstl Fonksiyon...7 ygulm stlri...5 BÖÜ OGİ FOİO, Ü, OGİİ D V ŞİİZİ ogritm Fonksiyonu...7 ogritm Fonksiyonunun Özlliklri...9 bn Dğiştirm...55 Üstl
BÖÜ ÜÜ İFD V Ü FOİO Üslü İfdlrd İşlmlr...7 Üslü Dnklmlr... Üstl Fonksiyon...7 ygulm stlri...5 BÖÜ OGİ FOİO, Ü, OGİİ D V ŞİİZİ ogritm Fonksiyonu...7 ogritm Fonksiyonunun Özlliklri...9 bn Dğiştirm...55 Üstl
BÖLÜM 7. Sürekli hal hatalarının değerlendirilmesinde kullanılan test dalga şekilleri: Dalga Şekli Giriş Fiziksel karşılığı. Sabit Konum.
 9 BÖLÜM 7 SÜRELİ HAL HATALARI ontrol itmlrinin analizind v dizaynında üç özlliğ odaklanılır, bunlar ; ) İtniln bir gçici hal cvabı ürtmk. ( T, %OS, ζ, ω n, ) ) ararlı olmaı. ıaca kutupların diky knin olunda
9 BÖLÜM 7 SÜRELİ HAL HATALARI ontrol itmlrinin analizind v dizaynında üç özlliğ odaklanılır, bunlar ; ) İtniln bir gçici hal cvabı ürtmk. ( T, %OS, ζ, ω n, ) ) ararlı olmaı. ıaca kutupların diky knin olunda
Sınav süresi 80 dakika. 1. (a) 20 puan 2 dy. Solution: 2 dy. y = 2t denklemi lineer diferansiyel denklemdir. Denklemin integrasyon çarpanını bulalım.
 May 7, 7 3:-4:3 MATH6 Final Exam / MAT6 Final Sınavı Pag of 7 Your Nam / İsim Soyisim Your Signaur / İmza Sudn ID # / Öğrnci Numarası Profssor s Nam / Öğrim Üysi Kopya çkn vya kopya çkm girişimind bulunan
May 7, 7 3:-4:3 MATH6 Final Exam / MAT6 Final Sınavı Pag of 7 Your Nam / İsim Soyisim Your Signaur / İmza Sudn ID # / Öğrnci Numarası Profssor s Nam / Öğrim Üysi Kopya çkn vya kopya çkm girişimind bulunan
LYS LİMİT. x in 2 ye soldan yaklaşması hangisi ile ifade edilir? şeklinde gösterilir. lim. şeklinde gösterilir. f(x) lim f(x) ise lim f(x) yoktur.
 Mtemtik SAĞDAN VE SOLDAN YAKLAŞMA Yndki tblod bir değişkeninin 4 sısın sğdn ve soldn klşımı ifde edilmiştir. u durumu genellemek gerekirse; değişkeni re el s ı sın, dn kü çük de ğer ler le k l şı or s,
Mtemtik SAĞDAN VE SOLDAN YAKLAŞMA Yndki tblod bir değişkeninin 4 sısın sğdn ve soldn klşımı ifde edilmiştir. u durumu genellemek gerekirse; değişkeni re el s ı sın, dn kü çük de ğer ler le k l şı or s,
BÖLÜM X DEVRE ANALİZİNDE LAPLACE DÖNÜŞÜMÜ
 Devre Terii Der Nu Dr. Nurein AC ve Dr. Engin Ceml MENGÜÇ BÖÜM X DEE ANAİZİNDE APACE DÖNÜŞÜMÜ Devre nlizinde plce; lineer i kyılı diferniyel denklemleri, lineer plinm denklemlerine dönüşürür. Aynı zmnd
Devre Terii Der Nu Dr. Nurein AC ve Dr. Engin Ceml MENGÜÇ BÖÜM X DEE ANAİZİNDE APACE DÖNÜŞÜMÜ Devre nlizinde plce; lineer i kyılı diferniyel denklemleri, lineer plinm denklemlerine dönüşürür. Aynı zmnd
MATRİSLER. r r r A = v v v 3. BÖLÜM. a a L a. v r. a = M a. Matris L L L L. elemanları a ( i = 1,2,..., m ; j = 1,2,... n) cinsinden kısaca A = [ ]
![MATRİSLER. r r r A = v v v 3. BÖLÜM. a a L a. v r. a = M a. Matris L L L L. elemanları a ( i = 1,2,..., m ; j = 1,2,... n) cinsinden kısaca A = [ ] MATRİSLER. r r r A = v v v 3. BÖLÜM. a a L a. v r. a = M a. Matris L L L L. elemanları a ( i = 1,2,..., m ; j = 1,2,... n) cinsinden kısaca A = [ ]](/thumbs/57/40722092.jpg) 3. BÖLÜM 2 v r = M m v r 2 2 = 22 M m2 v r n n 2n = M mn MTRİSLER gibi n tne vektörün oluşturduğu, r r r = v v v [ L ] 2 n şeklindeki sırlnışın mtris denir. 2 nlitik Geometriden Biliyoruz ki : Mtris 2
3. BÖLÜM 2 v r = M m v r 2 2 = 22 M m2 v r n n 2n = M mn MTRİSLER gibi n tne vektörün oluşturduğu, r r r = v v v [ L ] 2 n şeklindeki sırlnışın mtris denir. 2 nlitik Geometriden Biliyoruz ki : Mtris 2
DRC. 4. Sekiz basamaklı herhangi bir özel sayı x = abcdefgh olsun. Deneme - 2 / Mat. c m. m m. y Cevap A. Cevap D 21, 25, = = =. 21.
 Deneme - / Mt MATMATİK DNMSİ. - + -. 0,.., f -, 0, p. 0,. c- m.,,. ^- h.. 7. ^- h 7 - ulunur. +. c m olur.. + + ulunur. ( ) c m + c m. cc m m. c m.. ulunur. evp evp. Sekiz smklı herhngi ir özel syı cdefgh
Deneme - / Mt MATMATİK DNMSİ. - + -. 0,.., f -, 0, p. 0,. c- m.,,. ^- h.. 7. ^- h 7 - ulunur. +. c m olur.. + + ulunur. ( ) c m + c m. cc m m. c m.. ulunur. evp evp. Sekiz smklı herhngi ir özel syı cdefgh
basit cebirsel denkleminin geçerli olduğunu varsayalım. denklemine ait İAD. çıkış düğümüne olan ve kazancı a
 İşret Aış Drmlrı: İşret Aış Drmlrı (İAD), blo drmlrın bstleştrlmş hl olr örüleblr. Ft, İAD fzsel örünüş ve mtemtsel urllr bğlılı ısındn zım urllrı dh serbest oln blo drmlrındn frlıdır. Blo drmlrı, rmşı
İşret Aış Drmlrı: İşret Aış Drmlrı (İAD), blo drmlrın bstleştrlmş hl olr örüleblr. Ft, İAD fzsel örünüş ve mtemtsel urllr bğlılı ısındn zım urllrı dh serbest oln blo drmlrındn frlıdır. Blo drmlrı, rmşı
ÇOKGENLER Çokgenler çokgen Dışbükey (Konveks) ve İçbükey (Konkav) Çokgenler dış- bükey (konveks) çokgen içbükey (konkav) çokgen
 ÇONLR Çokgenler rdışık en z üç noktsı doğrusl olmyn, düzlemsel şekillere çokgen denir. Çokgenler kenr syılrın göre isimlendirilirler. Üçgen, dörtgen, beşgen gibi. ışbükey (onveks) ve İçbükey (onkv) Çokgenler
ÇONLR Çokgenler rdışık en z üç noktsı doğrusl olmyn, düzlemsel şekillere çokgen denir. Çokgenler kenr syılrın göre isimlendirilirler. Üçgen, dörtgen, beşgen gibi. ışbükey (onveks) ve İçbükey (onkv) Çokgenler
kirişli döşeme Dört tarafından kirişlere oturan döşemeler Kenarlarının bazıları boşta olan döşemeler Boşluklu döşemeler Düzensiz geometrili döşemeler
 Kirişli döşmlr Dört tarafından irişlr oturan döşmlr Knarlarının bazıları boşta olan döşmlr Boşlulu döşmlr Düznsiz gomtrili döşmlr bir tarafı irişli üç tarafı boşta döşm (Konsol döşm) Đi tarafı irişli ii
Kirişli döşmlr Dört tarafından irişlr oturan döşmlr Knarlarının bazıları boşta olan döşmlr Boşlulu döşmlr Düznsiz gomtrili döşmlr bir tarafı irişli üç tarafı boşta döşm (Konsol döşm) Đi tarafı irişli ii
RASYONEL SAYILAR KESİR ÇEŞİTLERİ. www.unkapani.com.tr. 1. Basit Kesir. olduğuna göre, a, b tamsayı ve b 0 olmak üzere, a şeklindeki ifadelere
 RASYONEL SAYILAR, tmsyı ve 0 olmk üzere, şeklindeki ifdelere kesir denir. y kesrin pyı, ye kesrin pydsı denir. Örneğin,,,, kesirdir. kesrinde, py kesir çizgisi pyd, 0, 0 ise 0 0 dır.,, 0, syılrı irer 0
RASYONEL SAYILAR, tmsyı ve 0 olmk üzere, şeklindeki ifdelere kesir denir. y kesrin pyı, ye kesrin pydsı denir. Örneğin,,,, kesirdir. kesrinde, py kesir çizgisi pyd, 0, 0 ise 0 0 dır.,, 0, syılrı irer 0
e gibi Laplace dönüşümü olmayan fonksiyonlar kaynak olarak
 Dvr Torii Dr Nou Dr. Nuri ACIR v Dr. Egi Cml MENGÜÇ BÖLÜM IX LAPLACE DÖNÜŞÜMÜ Lplc kiği lir, opluprmrli dvrlrd kullıl güçlü bir liz kiğidir. Lplc döüşümü, bird fzl düğümvolj vy gözkım difriyl dklmlrii
Dvr Torii Dr Nou Dr. Nuri ACIR v Dr. Egi Cml MENGÜÇ BÖLÜM IX LAPLACE DÖNÜŞÜMÜ Lplc kiği lir, opluprmrli dvrlrd kullıl güçlü bir liz kiğidir. Lplc döüşümü, bird fzl düğümvolj vy gözkım difriyl dklmlrii
DRC üst taban, 6 alt taban olmak üzere 12 mavi kare vardır. 4. Sekiz basamaklı herhangi bir özel sayı x = abcdefgh olsun. Deneme - 2 / Mat.
 Deneme - / Mt MATEMATİK DENEMESİ. 6 üst tn, 6 lt tn olmk üzere mvi kre vrdır. Ypının tüm yüzeyi kreden oluştuğun göre, 6 7. 0,.., f -, 0, p. 0,. c- m.,,. ^- h.. 7. ^- h 7 - ulunur. +. c m olur. ( ) 9 c
Deneme - / Mt MATEMATİK DENEMESİ. 6 üst tn, 6 lt tn olmk üzere mvi kre vrdır. Ypının tüm yüzeyi kreden oluştuğun göre, 6 7. 0,.., f -, 0, p. 0,. c- m.,,. ^- h.. 7. ^- h 7 - ulunur. +. c m olur. ( ) 9 c
KIVIRMA İŞLEMİNİN ŞEKİL ve BOYUTLARI
 2011 Şut KIVIRMA İŞEMİNİN ŞEKİ ve BOYUTARI Hzırlyn: Adnn YIMAZ AÇINIM DEĞERERİ 50-21 DİKKAT: İyi niyet, ütün dikkt ve çm krşın ynlışlr olilir. Bu nedenle onucu orumluluk verecek ynlışlıklr için, hiçir
2011 Şut KIVIRMA İŞEMİNİN ŞEKİ ve BOYUTARI Hzırlyn: Adnn YIMAZ AÇINIM DEĞERERİ 50-21 DİKKAT: İyi niyet, ütün dikkt ve çm krşın ynlışlr olilir. Bu nedenle onucu orumluluk verecek ynlışlıklr için, hiçir
DERS 9. Grafik Çizimi, Maksimum Minimum Problemleri
 DERS 9 Grafik Çizimi, Maksimum Minimum Problmlri Bundan öncki drst bir fonksiyonun grafiğini çizmk için izlnbilck yol v yapılabilck işlmlr l alındı. Bu drst, grafik çizim stratjisini yani grafik çizimind
DERS 9 Grafik Çizimi, Maksimum Minimum Problmlri Bundan öncki drst bir fonksiyonun grafiğini çizmk için izlnbilck yol v yapılabilck işlmlr l alındı. Bu drst, grafik çizim stratjisini yani grafik çizimind
6 DC Motorlar. Harici Uyartımlı DC Motor. E a - I V / R K K. i a =i L R a. i f. R f. f f f. a a ind. a a a a a. Tind. ind
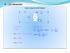 6 DC Motorlr Hrici Uyrtımlı DC Motor i + i =i L R V R E V - V / R K (1) E K E V R (2) K E V R K K K V R (4) K K 2 ( 3) E 1 6 DC Motorlr Hrici Uyrtımlı DC Motor Eğer endüvide üklenen gerilim (E ) ormülünde
6 DC Motorlr Hrici Uyrtımlı DC Motor i + i =i L R V R E V - V / R K (1) E K E V R (2) K E V R K K K V R (4) K K 2 ( 3) E 1 6 DC Motorlr Hrici Uyrtımlı DC Motor Eğer endüvide üklenen gerilim (E ) ormülünde
Lisans Yerleştirme Sınavı 1 (Lys 1) / 18 Haziran Matematik Soruları ve Çözümleri
 Lisans Yrlşirm Sınavı (Lys ) 8 Haziran Mamaik Soruları v Çözümlri. (,5) işlminin sonucu kaçır?, A) 5 B) C) 5 D) E) Çözüm (,5), 5 ( ) ( ) 5 ( ) ( ).( ) 5 ( ) 5 5 6 . < < olduğuna gör, aşağıdakilrdn hangisi
Lisans Yrlşirm Sınavı (Lys ) 8 Haziran Mamaik Soruları v Çözümlri. (,5) işlminin sonucu kaçır?, A) 5 B) C) 5 D) E) Çözüm (,5), 5 ( ) ( ) 5 ( ) ( ).( ) 5 ( ) 5 5 6 . < < olduğuna gör, aşağıdakilrdn hangisi
Cebir Notları Mustafa YAĞCI, Eşitsizlikler
 www.mustfygci.com.tr, 4 Cebir Notlrı Mustf YAĞCI, ygcimustf@yhoo.com Eşitsizlikler S yılr dersinin sonund bu dersin bşını görmüştük. O zmnlr dın sdece birinci dereceden denklemleri içeren mnsınd Bsit Eşitsizlikler
www.mustfygci.com.tr, 4 Cebir Notlrı Mustf YAĞCI, ygcimustf@yhoo.com Eşitsizlikler S yılr dersinin sonund bu dersin bşını görmüştük. O zmnlr dın sdece birinci dereceden denklemleri içeren mnsınd Bsit Eşitsizlikler
YÜZDE VE FAĐZ PROBLEMLERĐ
 YILLAR 00 003 00 00 006 007 008 009 010 011 ÖSS-YGS 3 1 1 1 3 YÜZDE VE FAĐZ PROBLEMLERĐ YÜZDE: Bir syının yüzde sı= dır ÖRNEK(1) % i 0 oln syıyı bullım syımız olsun 1 = 0 = 0 ÖRNEK() 800 ün % ini bullım
YILLAR 00 003 00 00 006 007 008 009 010 011 ÖSS-YGS 3 1 1 1 3 YÜZDE VE FAĐZ PROBLEMLERĐ YÜZDE: Bir syının yüzde sı= dır ÖRNEK(1) % i 0 oln syıyı bullım syımız olsun 1 = 0 = 0 ÖRNEK() 800 ün % ini bullım
B - GERĐLĐM TRAFOLARI:
 ve Seg.Korum_Hldun üyükdor onrım süresinin dh uzun olmsı yrıc rnın izole edilmesini gerektirmesi; rızlnmsı hlinde r tdiltını d gerektireilmesi, v. nedenlerle, özel durumlr dışınd tercih edilmezler. - GERĐLĐM
ve Seg.Korum_Hldun üyükdor onrım süresinin dh uzun olmsı yrıc rnın izole edilmesini gerektirmesi; rızlnmsı hlinde r tdiltını d gerektireilmesi, v. nedenlerle, özel durumlr dışınd tercih edilmezler. - GERĐLĐM
BELÝRLÝ (SINIRLI) ÝNTEGRAL
 Blirli Ýntgrl BELÝRLÝ (SINIRLI) ÝNTEGRAL f, fonksiyonu [, ] rlðnd intgrllniln ir fonksiyon, (, ) olsun, ifdsin f() fonksiyonun (, ) rlðndki lirli intgrli vy = v = doðrulr il snrl f() ðrisi il o ksni rsndki
Blirli Ýntgrl BELÝRLÝ (SINIRLI) ÝNTEGRAL f, fonksiyonu [, ] rlðnd intgrllniln ir fonksiyon, (, ) olsun, ifdsin f() fonksiyonun (, ) rlðndki lirli intgrli vy = v = doðrulr il snrl f() ðrisi il o ksni rsndki
ÜÇGENDE ALAN. Alan(ABC)= 1 2. (taban x yükseklik)
 ÜÇGN LN Üçgende ln Şekilde verilen üçgeninde,, üçgenin köşeleri, [], [], [] üçgenin kenrlrıdır. c b üçgeninin kenrlrı dlndırılırken, her kenr krşısınd bulunn köşenin hrfi ile isimlendirilir. üçgeninin
ÜÇGN LN Üçgende ln Şekilde verilen üçgeninde,, üçgenin köşeleri, [], [], [] üçgenin kenrlrıdır. c b üçgeninin kenrlrı dlndırılırken, her kenr krşısınd bulunn köşenin hrfi ile isimlendirilir. üçgeninin
TG 1 ÖABT İLKÖĞRETİM MATEMATİK
 KAMU PESONEL SEÇME SINAI ÖĞETMENLİK ALAN BİLGİSİ TESTİ İLKÖĞETİM MATEMATİK ÖĞETMENLİĞİ TG ÖABT İLKÖĞETİM MATEMATİK Bu testlerin her hı slıdır. Hngi mçl olurs olsun, testlerin tmmının vey bir ısmının İhtiyç
KAMU PESONEL SEÇME SINAI ÖĞETMENLİK ALAN BİLGİSİ TESTİ İLKÖĞETİM MATEMATİK ÖĞETMENLİĞİ TG ÖABT İLKÖĞETİM MATEMATİK Bu testlerin her hı slıdır. Hngi mçl olurs olsun, testlerin tmmının vey bir ısmının İhtiyç
Basınç Elemanları Elastik ve inelastik burkulma Etkili Boy. Bölüm 4. Yrd. Doç. Dr. Muharrem Aktaş 2009-Bahar
 Bsınç Elemnlrı Elstik ve inelstik burkulm Etkili Boy Bölüm 4 Yrd. Doç. Dr. Muhrrem Aktş 009-Bhr Yısl çelik elemnlrının, eğilme momenti olmksızın sdece eksenel bsınç kuvveti ltınd olduğu durumlr vrdır.
Bsınç Elemnlrı Elstik ve inelstik burkulm Etkili Boy Bölüm 4 Yrd. Doç. Dr. Muhrrem Aktş 009-Bhr Yısl çelik elemnlrının, eğilme momenti olmksızın sdece eksenel bsınç kuvveti ltınd olduğu durumlr vrdır.
Mustafa YAĞCI, yagcimustafa@yahoo.com Parabolün Tepe Noktası
 Mustf YĞCI www.mustfgci.com.tr, 11 Ceir Notlrı Mustf YĞCI, gcimustf@hoo.com Prolün Tepe Noktsı Ö nce ir prolün tepe noktsı neresidir, onu htırltlım. Kc, prolün rtmktn zlm ve zlmktn rtm geçtiği nokt dieiliriz.
Mustf YĞCI www.mustfgci.com.tr, 11 Ceir Notlrı Mustf YĞCI, gcimustf@hoo.com Prolün Tepe Noktsı Ö nce ir prolün tepe noktsı neresidir, onu htırltlım. Kc, prolün rtmktn zlm ve zlmktn rtm geçtiği nokt dieiliriz.
V ort CEVAP: B CEVAP: E CEVAP: B CEVAP: A 3V CEVAP: D. 10. I- Doğru: 2t anında ikiside 4x konumundalar. Y A Y I N D E N İ Z İ CEVAP: C.
 OU 7 OĞRUS HRT Çözümler TST 7-1 ÇÖÜMR 1. meleri ynıır ikisi e poziifir. er eğişirmeler nin +X nin X olup frklıır. X Orlm sür ir. 7. V or = yer eğişirme oplm zmn. 1 = = 1 & & 3 = 1. = = 3. - leri yöne.
OU 7 OĞRUS HRT Çözümler TST 7-1 ÇÖÜMR 1. meleri ynıır ikisi e poziifir. er eğişirmeler nin +X nin X olup frklıır. X Orlm sür ir. 7. V or = yer eğişirme oplm zmn. 1 = = 1 & & 3 = 1. = = 3. - leri yöne.
Ele Alınacak Ana Konular. Hafta 2 İşaretler ve Sistemler. Ayrık-zaman impuls ve birim basamak dizileri
 08.0.05 Ele Alıc A Koulr Süreli-zm ve rı-zm işreler Bğımsız değişei döüşürülmesi Hf İşreler ve Sisemler Üsel ve siüzoidl işreler İmpuls ve birim bsm fosiolrı Süreli-zm ve rı-zm sisemler Sisemleri emel
08.0.05 Ele Alıc A Koulr Süreli-zm ve rı-zm işreler Bğımsız değişei döüşürülmesi Hf İşreler ve Sisemler Üsel ve siüzoidl işreler İmpuls ve birim bsm fosiolrı Süreli-zm ve rı-zm sisemler Sisemleri emel
1997 ÖYS A) 30 B) 35 C) 40 D) 45 E) 50. olduğuna göre, k kaçtır? A) 1 B) 2 C) 3 D) 4 E) 5
 7 ÖYS. 0,00 0,00 k 0,00 olduğun göre, k kçtır? 6. Bir ust günde çift ykkbı, bir klf ise günde çift ykkbı ypmktdır. İkisi birlikte, 8 çift ykkbıyı kç günde yprlr? 0 C) 0 D) 0 C) D). (0 ) ( 0) işleminin
7 ÖYS. 0,00 0,00 k 0,00 olduğun göre, k kçtır? 6. Bir ust günde çift ykkbı, bir klf ise günde çift ykkbı ypmktdır. İkisi birlikte, 8 çift ykkbıyı kç günde yprlr? 0 C) 0 D) 0 C) D). (0 ) ( 0) işleminin
KONUM, HIZ, İVME. Parçacığın herhangi bir t anındaki konum vektörü, sabit Kartezyen koordinatların orijini olan O noktasından P noktasına kadar
 KONUM, HIZ, İVME Prçcık, yörüngeinin eğrilik yrıçpı ile krşılşırıldığınd fizikel boyulrı çok küçük oln ciimdir. Şekil, uzyd genel eğriel bir yörünge boyunc hreke eden e belirli bir nd P nokınd bulunn bir
KONUM, HIZ, İVME Prçcık, yörüngeinin eğrilik yrıçpı ile krşılşırıldığınd fizikel boyulrı çok küçük oln ciimdir. Şekil, uzyd genel eğriel bir yörünge boyunc hreke eden e belirli bir nd P nokınd bulunn bir
3.4 İşlem. 3.4.1 İşlem Kavramı. Etkinlik 3.53. Etkinlik 3.52
 . İşlm.. İşlm Kvrmı Etkinlik.5 A,,, B,, v C,,5, kümlri vriliyor.. AxB kümsini yzınız.. AxB n C y f ğıntısı f x, y x il y n, küçük olmynı içimin tnımlnıyor. AxB f C f ğıntısını ynki gii ir Vnn şmsı il göstriniz.
. İşlm.. İşlm Kvrmı Etkinlik.5 A,,, B,, v C,,5, kümlri vriliyor.. AxB kümsini yzınız.. AxB n C y f ğıntısı f x, y x il y n, küçük olmynı içimin tnımlnıyor. AxB f C f ğıntısını ynki gii ir Vnn şmsı il göstriniz.
SAYISAL ÇÖZÜMLEME. Sayısal Çözümleme
 SYISL ÇÖZÜMLEME Syısl Çözümleme SYISL ÇÖZÜMLEME Hft SYISL ÇÖZÜMLEMEDE HT KVRMI Syısl Çözümleme GİRİŞ Syısl nliz, mtemtik problemlerinin bilgisyr yrdımı ile çözümlenme tekniğidir Genellikle nlitik olrk
SYISL ÇÖZÜMLEME Syısl Çözümleme SYISL ÇÖZÜMLEME Hft SYISL ÇÖZÜMLEMEDE HT KVRMI Syısl Çözümleme GİRİŞ Syısl nliz, mtemtik problemlerinin bilgisyr yrdımı ile çözümlenme tekniğidir Genellikle nlitik olrk
BAĞIMSIZ UYARILMIŞ DC MOTOR DENEY 325-06
 İNÖNÜ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ELEKTRİKELEKTRONİK MÜH. BÖL. 35 ELEKTRİK MAKİNALARI LABORATUVARI I BAĞIMSIZ UYARILMIŞ DC MOTOR DENEY 3506. AMAÇ: Bğımsız uyrılmış DC motorun moment/hız ve verim
İNÖNÜ ÜNİVERSİTESİ MÜHENDİSLİK FAKÜLTESİ ELEKTRİKELEKTRONİK MÜH. BÖL. 35 ELEKTRİK MAKİNALARI LABORATUVARI I BAĞIMSIZ UYARILMIŞ DC MOTOR DENEY 3506. AMAÇ: Bğımsız uyrılmış DC motorun moment/hız ve verim
MUTLAK DEĞER. a ε R olmak üzere; Mutlak Değer MATEMATĐK ĐM YILLAR 2002 203 2004 2005 2006 2007 2008 2009 2010 2011 14) GENEL ÖRNEKLER.
 Mutlk Değer YILLAR 4 6 8 9 1 11 ÖSS-YGS - - - 1 - - 1 - - 1/1 MUTLAK DEĞER ε R olmk üzere;, -, ise < ise ve b reel syı olmk üzere; 1) dır Eğer ise dır ) 14) + n n Z olmk üzere dır 1) f ( ) > g( ) f ( )
Mutlk Değer YILLAR 4 6 8 9 1 11 ÖSS-YGS - - - 1 - - 1 - - 1/1 MUTLAK DEĞER ε R olmk üzere;, -, ise < ise ve b reel syı olmk üzere; 1) dır Eğer ise dır ) 14) + n n Z olmk üzere dır 1) f ( ) > g( ) f ( )
TEST 1 ÇÖZÜMLER NEWTON IN HAREKET YASALARI
 TEST 1 ÇÖZÜMER NEWTON IN HAREET ASAARI 1 P P 3 3 1 (/s) Şekil-I Şekil-II Şekil-III Or sürünesiz olduğundn kuvve ile ive doğru ornılıdır Bu durud, 3 3 P olur Bun göre, > P olur CEAP B ESEN AINARI 6 - grfiğinin
TEST 1 ÇÖZÜMER NEWTON IN HAREET ASAARI 1 P P 3 3 1 (/s) Şekil-I Şekil-II Şekil-III Or sürünesiz olduğundn kuvve ile ive doğru ornılıdır Bu durud, 3 3 P olur Bun göre, > P olur CEAP B ESEN AINARI 6 - grfiğinin
Ankara Üniversitesi Mühendislik Fakültesi, Fizik Mühendisliği Bölümü FZM207. Temel Elektronik-I. Doç. Dr. Hüseyin Sarı
 Ankr Üniversitesi Mühendislik Fkültesi, Fizik Mühendisliği Bölümü FZM207 Temel ElektronikI Doç. Dr. Hüseyin Srı 2. Bölüm: Dirençli Devreler İçerik Temel Yslrın Doğrudn Uygulnışı Kynk Gösterimi ve Dönüşümü
Ankr Üniversitesi Mühendislik Fkültesi, Fizik Mühendisliği Bölümü FZM207 Temel ElektronikI Doç. Dr. Hüseyin Srı 2. Bölüm: Dirençli Devreler İçerik Temel Yslrın Doğrudn Uygulnışı Kynk Gösterimi ve Dönüşümü
İntegralin Uygulamaları
 Bölüm İntegrlin Uygulmlrı. Aln f ve g, [, b] rlığındki her x için f(x) g(x) eşitsizliğini sğlyn sürekli fonksiyonlr olmk üzere y = f(x), y = g(x) eğrileri, x = ve x = b düşey doğrulrı rsındki S bölgesini
Bölüm İntegrlin Uygulmlrı. Aln f ve g, [, b] rlığındki her x için f(x) g(x) eşitsizliğini sğlyn sürekli fonksiyonlr olmk üzere y = f(x), y = g(x) eğrileri, x = ve x = b düşey doğrulrı rsındki S bölgesini
ORAN ORANTI. Örnek...1 : Örnek...4 : Örnek...2 : Örnek...5 : a 1 2 =2b+1 3 =3c 4. Örnek...6 : Bir karışımda bulunan a, b ve c maddeleri arasında
 ORAN ORANTI syısının 0 dn frklı oln b syısın ornı :b vey olrk gösterilir. b İki vey dh fzl ornın eşitlenmesiyle oluşn ifdeye orntı denir. b =c d ifdesine ikili orntı denir. Bir orntı orntı sbitine eşitlenerek
ORAN ORANTI syısının 0 dn frklı oln b syısın ornı :b vey olrk gösterilir. b İki vey dh fzl ornın eşitlenmesiyle oluşn ifdeye orntı denir. b =c d ifdesine ikili orntı denir. Bir orntı orntı sbitine eşitlenerek
LYS 2016 MATEMATİK ÇÖZÜMLERİ
 LYS 06 MATEMATİK ÇÖZÜMLERİ 6.. 5. 5. ( ) 8 6 65 buluruz. 5. 5 5 Doğru Cevp: C Şıkkı 8 7 ()... 9 buluruz. Doğru Cevp : D Şıkkı 9 8 8 9 8 9 8 9 9 9 9 9 8 buluruz. 8 8 8 8 8 Doğru Cevp : A Şıkkı (n )! (n
LYS 06 MATEMATİK ÇÖZÜMLERİ 6.. 5. 5. ( ) 8 6 65 buluruz. 5. 5 5 Doğru Cevp: C Şıkkı 8 7 ()... 9 buluruz. Doğru Cevp : D Şıkkı 9 8 8 9 8 9 8 9 9 9 9 9 8 buluruz. 8 8 8 8 8 Doğru Cevp : A Şıkkı (n )! (n
ELEKTRİK DAĞITIM ȘİRKETLERİNİN SORUMLULUĞUNDAKİ YOL AYDINLATMASINA İLİȘKİN KURALLARIN İRDELENMESİ
 ELEKTRİK DAĞITIM ȘİRKETLERİNİN SORUMLULUĞUNDAKİ YOL AYDINLATMASINA İLİȘKİN KURALLARIN İRDELENMESİ M. Akif ȘENOL 1 Ercüment ÖZDEMİRCİ 2 M. Cengiz TAPLAMACIOĞLU 3 1 Enerji ve Tbii Kynklr Bknlığı, Ankr, 2
ELEKTRİK DAĞITIM ȘİRKETLERİNİN SORUMLULUĞUNDAKİ YOL AYDINLATMASINA İLİȘKİN KURALLARIN İRDELENMESİ M. Akif ȘENOL 1 Ercüment ÖZDEMİRCİ 2 M. Cengiz TAPLAMACIOĞLU 3 1 Enerji ve Tbii Kynklr Bknlığı, Ankr, 2
b göz önünde tutularak, a,
 3.ALT GRUPLAR Tnım 3.. bir grup ve G, nin boş olmyn bir lt kümesi olsun. Eğer ( ise ye G nin bir lt grubu denir ve G ile gösterilir. ) bir grup Not 3.. ) grubunun lt grubu olsun. nin birimi ve nin birimi
3.ALT GRUPLAR Tnım 3.. bir grup ve G, nin boş olmyn bir lt kümesi olsun. Eğer ( ise ye G nin bir lt grubu denir ve G ile gösterilir. ) bir grup Not 3.. ) grubunun lt grubu olsun. nin birimi ve nin birimi
BÖLÜM 5: RADYOAKTİF BOZUNMA
 BÖLÜM 5: RADYOAKTİF BOZUMA Urnyum ve ıryum içeren doğl minerllerin rdyokif ozunumlrı, nükleer fizik çlışmlrının şlmsınd üyük rol oynmışlrdır. Dh kıs yrı-ömürlü çekirdekler ozunrk yok olduklrındn ugün sdece
BÖLÜM 5: RADYOAKTİF BOZUMA Urnyum ve ıryum içeren doğl minerllerin rdyokif ozunumlrı, nükleer fizik çlışmlrının şlmsınd üyük rol oynmışlrdır. Dh kıs yrı-ömürlü çekirdekler ozunrk yok olduklrındn ugün sdece
ELEKTRĐK MOTORLARI ve SÜRÜCÜLERĐ DERS 03
 ELEĐ MOOLA ve SÜÜCÜLEĐ DES 03 Özer ŞENYU Mrt 0 ELEĐ MOOLA ve SÜÜCÜLEĐ DA MOOLANN ELEĐ DEE MODELLEĐ E AAEĐSĐLEĐ ENDÜĐ DEESĐ MODELĐ Endüviye uygulnn gerilim (), zıt emk (E), endüvi srgı direni () ile temsil
ELEĐ MOOLA ve SÜÜCÜLEĐ DES 03 Özer ŞENYU Mrt 0 ELEĐ MOOLA ve SÜÜCÜLEĐ DA MOOLANN ELEĐ DEE MODELLEĐ E AAEĐSĐLEĐ ENDÜĐ DEESĐ MODELĐ Endüviye uygulnn gerilim (), zıt emk (E), endüvi srgı direni () ile temsil
FARKLI SICAKLIKLARDAKİ GÖZENEKLİ İKİ LEVHA ARASINDA AKAN AKIŞKANIN İKİNCİ KANUN ANALİZİ
 FARKLI ICAKLIKLARDAKİ GÖZEEKLİ İKİ LEVHA ARAIDA AKA AKIŞKAI İKİCİ KAU AALİZİ Fthi KAMIŞLI Fırat Ünivrsit Mühndislik Fakültsi Kimya Mühndisliği Bölümü, 39 ELAZIĞ, fkamisli@firat.du.tr Özt Farklı sıcaklıklara
FARKLI ICAKLIKLARDAKİ GÖZEEKLİ İKİ LEVHA ARAIDA AKA AKIŞKAI İKİCİ KAU AALİZİ Fthi KAMIŞLI Fırat Ünivrsit Mühndislik Fakültsi Kimya Mühndisliği Bölümü, 39 ELAZIĞ, fkamisli@firat.du.tr Özt Farklı sıcaklıklara
DOĞUŞ ÜNİVERSİTESİ MATEMATİK KLÜBÜ FEN LİSELERİ TAKIM YARIŞMASI 2007 SORULARI
 DOĞUŞ ÜNİVERSİTESİ MATEMATİK KLÜBÜ FEN LİSELERİ TAKIM YARIŞMASI 007 SORULARI Doğuş Ünivrsitsi Matmatik Kulübü tarafından düznlnn matmatik olimpiyatları, fn lislri takım yarışması sorularından bazıları
DOĞUŞ ÜNİVERSİTESİ MATEMATİK KLÜBÜ FEN LİSELERİ TAKIM YARIŞMASI 007 SORULARI Doğuş Ünivrsitsi Matmatik Kulübü tarafından düznlnn matmatik olimpiyatları, fn lislri takım yarışması sorularından bazıları
π βk F -F 0.4 0.3 0.2 0.1 0 0.01 0.02 0.03 0.04 kayma 1 2 F + F 1 2 Döndüren kasnak Döndürülen kasnak
 TİMAK-Taarım İmalat Analiz Kongri 6-8 Nian 006 - BALIKESİ KAYIŞ KASNAK MEKANİZMALAINDA KAYMA OLAYINI ETKİLEYEN AKTÖLEİN ANALİZİ M. Ndim GEGE Maina Mühndiliği Bölümü Mühndili aülti -Balıir/Türi Özt Kaış
TİMAK-Taarım İmalat Analiz Kongri 6-8 Nian 006 - BALIKESİ KAYIŞ KASNAK MEKANİZMALAINDA KAYMA OLAYINI ETKİLEYEN AKTÖLEİN ANALİZİ M. Ndim GEGE Maina Mühndiliği Bölümü Mühndili aülti -Balıir/Türi Özt Kaış
GELECEĞİ DÜŞÜNEN ÇEVREYE SAYGILI % 70. tasarruf. Sokak, Park ve Bahçelerinizi Daha Az Ödeyerek Daha İyi Aydınlatmak Mümkün
 www.urlsolar.com S L D-S K -6 0 W ile 1 5 0 W St an d art S o kak L a m ba sı F iya t K arşılaşt ırm a sı kw h Ü c reti Yıllık Tü ke tim Ü cre ti Y ıllık T ü ketim Fa rkı kw Sa at G ü n A y Stan d art
www.urlsolar.com S L D-S K -6 0 W ile 1 5 0 W St an d art S o kak L a m ba sı F iya t K arşılaşt ırm a sı kw h Ü c reti Yıllık Tü ke tim Ü cre ti Y ıllık T ü ketim Fa rkı kw Sa at G ü n A y Stan d art
BÖLÜM 3 LAMİNER SINIR TABAKANIN DİFERANSİYEL DENKLEMLERİ VE TAM ÇÖZÜMLERİ
 BÖLÜM 3 LAMİNER SINIR TABAKANIN DİFERANSİYEL DENKLEMLERİ VE TAM ÇÖZÜMLERİ - Nair Stos dnlmlri - Nair Stos dnlmlrinin tam çözümlri - Daimi, ii-botl, laminr sınır tabaa dnlmlri - Daimi, ii-botl, laminr sınır
BÖLÜM 3 LAMİNER SINIR TABAKANIN DİFERANSİYEL DENKLEMLERİ VE TAM ÇÖZÜMLERİ - Nair Stos dnlmlri - Nair Stos dnlmlrinin tam çözümlri - Daimi, ii-botl, laminr sınır tabaa dnlmlri - Daimi, ii-botl, laminr sınır
VEKTÖRLER ÜNİTE 5. ÜNİTE 5. ÜNİTE 5. ÜNİTE 5. ÜNİT
 VKTÖRLR ÜNİT 5. ÜNİT 5. ÜNİT 5. ÜNİT 5. ÜNİT VKTÖRLR 1. Kznım : Vektör kvrmını çıklr.. Kznım : İki vektörün toplmını ve vektörün ir gerçek syıyl çrpımını ceirsel ve geometrik olrk gösterir. VKTÖRLR 1.
VKTÖRLR ÜNİT 5. ÜNİT 5. ÜNİT 5. ÜNİT 5. ÜNİT VKTÖRLR 1. Kznım : Vektör kvrmını çıklr.. Kznım : İki vektörün toplmını ve vektörün ir gerçek syıyl çrpımını ceirsel ve geometrik olrk gösterir. VKTÖRLR 1.
Anaparaya Dönüş (Kapitalizasyon) Oranı
 Anaparaya Dönüş (Kapitalizasyon) Oranı Glir gtirn taşınmazlar gnl olarak yatırım aracı olarak görülürlr. Alıcı, taşınmazı satın almak için kullandığı paranın karşılığında bir gtiri bklr. Bundan ötürü,
Anaparaya Dönüş (Kapitalizasyon) Oranı Glir gtirn taşınmazlar gnl olarak yatırım aracı olarak görülürlr. Alıcı, taşınmazı satın almak için kullandığı paranın karşılığında bir gtiri bklr. Bundan ötürü,
İKİNCİ DERECEDEN DENKLEMLER
 İKİNCİ DERECEDEN DENKLEMLER İKİNCİ DERECEDEN BİR BİLİNMEYENLİ DENKLEMLER TANIMLAR :, b, R ve 0 olmk üzere denklem denir. b = 0 denklemine, ikini dereeden bir bilinmeyenli Bu denklemde, b, gerçel syılrın
İKİNCİ DERECEDEN DENKLEMLER İKİNCİ DERECEDEN BİR BİLİNMEYENLİ DENKLEMLER TANIMLAR :, b, R ve 0 olmk üzere denklem denir. b = 0 denklemine, ikini dereeden bir bilinmeyenli Bu denklemde, b, gerçel syılrın
TEST. Rasyonel Sayılar. 1. Aşağıdaki bilgilerden hangisi yanlıştır? 2. Aşağıda verilen, 3. Aşağıdaki sayılardan hangisi hem tam sayı,
 Rsyonel Syılr. Sınıf Mtemtik Soru Bnksı TEST. Aşğıdki bilgilerden hngisi ynlıştır? A) Rsyonel syılr Q sembolü ile gösterilir. B) Her tm syı bir rsyonel syıdır. şeklinde yzıln bütün syılr rsyoneldir. b
Rsyonel Syılr. Sınıf Mtemtik Soru Bnksı TEST. Aşğıdki bilgilerden hngisi ynlıştır? A) Rsyonel syılr Q sembolü ile gösterilir. B) Her tm syı bir rsyonel syıdır. şeklinde yzıln bütün syılr rsyoneldir. b
EKLEMELİ DC KOMPOUND MOTOR DENEY AMAÇ: Eklemeli kompund bağlanmış DC motorun moment/hız ve verim karakteristiklerini incelemek.
 ĐNÖNÜ ÜNĐVRSĐTSĐ MÜHNDĐSLĐK FAKÜLTSĐ LKTRĐK-LKTRONĐK MÜH. BÖL. KLMLİ DC KOMPOUND MOTOR DNY 324-03. AMAÇ: klemeli kompund bğlnmış DC motorun moment/hız ve verim krkteritiklerini incelemek. 2. UYGULAMALAR:.
ĐNÖNÜ ÜNĐVRSĐTSĐ MÜHNDĐSLĐK FAKÜLTSĐ LKTRĐK-LKTRONĐK MÜH. BÖL. KLMLİ DC KOMPOUND MOTOR DNY 324-03. AMAÇ: klemeli kompund bğlnmış DC motorun moment/hız ve verim krkteritiklerini incelemek. 2. UYGULAMALAR:.
MODEL SORU - 1 DEKİ SORULARIN ÇÖZÜMLERİ
 BÖÜ DİNAİ ODE SORU - 1 DEİ SORUARIN ÇÖZÜERİ 1 ( ) (+) 0N 6/s 6/s 60 10N N 10N 0N 1N cis i uy gu l nn net kuv vet cis i ön ce (+) yön de y vş l tır Ci si dur duk tn son r ( ) yön de hız l nır Cis in iv
BÖÜ DİNAİ ODE SORU - 1 DEİ SORUARIN ÇÖZÜERİ 1 ( ) (+) 0N 6/s 6/s 60 10N N 10N 0N 1N cis i uy gu l nn net kuv vet cis i ön ce (+) yön de y vş l tır Ci si dur duk tn son r ( ) yön de hız l nır Cis in iv
UYGULAMALI DİFERANSİYEL DENKLEMLER
 UYGULAMALI DİFERANSİYEL DENKLEMLER Homojn Hal Gtirilbiln Diransil Dnklmlr a b cd a' b' c' d 0 Şklindki diransil dnklm homojn olmamasına rağmn basit bir dğişkn dönüşümü il homojn hal dönüştürülbilir. a
UYGULAMALI DİFERANSİYEL DENKLEMLER Homojn Hal Gtirilbiln Diransil Dnklmlr a b cd a' b' c' d 0 Şklindki diransil dnklm homojn olmamasına rağmn basit bir dğişkn dönüşümü il homojn hal dönüştürülbilir. a
DENEY 3 Kararlı-Durum Hatası
 DENEY 3 Krrlı-Durum Htsı DENEYİN AMACI 1. Çıkış tpksinin krrlı-durum htsını inclmk. 2. Frklı sistm tiplri için, frklı tst girişlrin vriln tpkdn krrlı-durum htsını ölçmk. GENEL BİLGİLER Bir kontrol sistmi
DENEY 3 Krrlı-Durum Htsı DENEYİN AMACI 1. Çıkış tpksinin krrlı-durum htsını inclmk. 2. Frklı sistm tiplri için, frklı tst girişlrin vriln tpkdn krrlı-durum htsını ölçmk. GENEL BİLGİLER Bir kontrol sistmi
LYS LİMİT VE SÜREKLİLİK KONU ÖZETLİ ÇÖZÜMLÜ SORU BANKASI
 LYS LİMİT VE SÜREKLİLİK KONU ÖETLİ ÇÖÜMLÜ SORU BANKASI ANKARA İÇİNDEKİLER Limit Kvrmı ve Grfik Sorulrı... Limitle İlgili Bzı Özellikler...7 Genişletilmiş Reel Sılrd Limit... Bileşke Fonksionun Limiti...
LYS LİMİT VE SÜREKLİLİK KONU ÖETLİ ÇÖÜMLÜ SORU BANKASI ANKARA İÇİNDEKİLER Limit Kvrmı ve Grfik Sorulrı... Limitle İlgili Bzı Özellikler...7 Genişletilmiş Reel Sılrd Limit... Bileşke Fonksionun Limiti...
Motorlarda Gaz Değişimi
 Motorlrd Gz Dğişii v Aşırı Doldur Motorlrd Gz Dğişii Dört strolu otorlrd v gzost, ii strolu otorlrd süür işllrinin cı, güç strou sonund silindirdi ynış gzlrı dışrı t v bir sonri çvri için tz hv/dolgu il
Motorlrd Gz Dğişii v Aşırı Doldur Motorlrd Gz Dğişii Dört strolu otorlrd v gzost, ii strolu otorlrd süür işllrinin cı, güç strou sonund silindirdi ynış gzlrı dışrı t v bir sonri çvri için tz hv/dolgu il
Makine Öğrenmesi 4. hafta
 ain Öğrnmsi 4. hafta Olasılı v Koşullu Olasılı ays Tormi Naïv ays Sınıflayıcı Olasılı Olasılı ifadsinin birço ullanım şli vardır. Rasgl bir A olayının hrhangi bir olaydan bağımsız olara grçlşm ihtimalini
ain Öğrnmsi 4. hafta Olasılı v Koşullu Olasılı ays Tormi Naïv ays Sınıflayıcı Olasılı Olasılı ifadsinin birço ullanım şli vardır. Rasgl bir A olayının hrhangi bir olaydan bağımsız olara grçlşm ihtimalini
